Analysis of a Stagnation Point Flow with Hybrid Nanoparticles over a Porous Medium

Nomenclature

Highlights

•   This work investigates the unsteady stagnation point flow and mass transfer with chemical reaction.

•   The system of partial differential equations is converted into system of ordinary differential equations via similarity transformations.

•   The concentration profile is obtained for cases such as constant wall concentration, uniform mass flux, general power law wall concentration and general power law mass flux.

•   The axial velocity decreases as the shrinking sheet parameter increases.

1  Introduction

The mass transfer and momentum boundary layer flow have practical interest in the field of polymer process and electrochemistry. Also, the hybrid nanofluid (HNF) flow is a significant field in industry and become an interest field for researchers due to its wide applications. There are many significances of heat transfer over stretching sheet, due to its advantages mentioned by many researchers [1,2]. Aly et al. [3,4] made a comparison between the significances of HNF over NF for the magneto-hydrodynamic (MHD) flow and heat transfer by considering the effect of partial slip. Turkyilmazoglu [5] found the multiple solutions for MHD slip flow of viscoelastic fluid and Anusha et al. [6,7] investigated the unsteady inclined MHD flow for Casson fluid with hybrid nanoparticles in a porous media. Also, Mahabaleshwar et al. [8] investigated the MHD flow behaviour and mass transfer due to porous media. Fang et al. [9] examined the unsteady stagnation point flow and heat transfer to obtain the closed form solutions for prescribed wall temperature and wall heat flux. Mahabaleshwar et al. [10,11] made a research on the MHD flow with carbon nanotubes by considering the effect of mass transpiration and radiation on it. Suresh et al. [12,13] investigated the effect of hybrid nanofluid on heat transfer characteristics and observed that a hybrid nanofluid of (Al2O3-Cu/H2O) had significant heat transfer. Momin [14] investigated the laminar flow in an elevated funnel using mixed convection with a (Al2O3-Cu/H2O) hybrid nanofluid. Recently, the mixed convective flow with radiation is studied by Patil et al. [15] considering the couple stress fluid flow for first order chemical reaction. Furthermore, Mahabaleshwar et al. [16] examined the MHD non-Newtonian fluid flow and heat transfer due to porous surface with heat source/sink by different solution methods. Mahabaleshwar et al. [17] investigated the steady flow with HNF with mass suction, mathematically, and found the solution in algebraic decaying form. Nakhchi et al. [18,19] studied the effect of CuO-water nanofluid on the improvement of entropy production for a double pipe heat exchanger and a double V-cut twisted tapes, respectively. Recently many works are done on HNF flow by researchers such as Zainal et al. [20] on MHD flow due to quadratic stretching/shrinking sheet, Umair et al. [21] on radiative mixed convective flow, more recent developments and applications of HNF are investigated by Sarkar et al. [22], Vishalakshi et al. [23] studied the effect of slips and mass transpiration on the flow over porous sheet and Sneha et al. [24] on dusty HNF. The effect of nanoparticles on the flow is also investigated by Jalali et al. [25] and Bhandari [26].

Motivated by these investigations, the current work investigates the unsteady stagnation point flow of Cu‐Al2O3/H2O HNF over stretching/shrinking sheet embedded in porous media considering mass transpiration and mass transfer with chemical reaction. The present work has many applications related to heating and cooling processes at high temperature ranges. So, HNF has wide applications in heating and cooling systems, refrigeration, space, machining, manufacturing, and etc. Also, the porous media is used to achieve the applications in thermal energy storage, geothermal recovery, grain storage, electrochemical process, flow through filtering device and chemical catalytic reactors. So, the momentum and mass transfer problems were solved analytically to find a solution of velocity and concentration profiles in exponential and hypergeometric forms, respectively. The concentration profile is obtained for four different cases such as constant wall concentration, uniform mass flux, general power law wall concentration and general power law mass flux. These solutions give a rare case of closed form solutions which can be adapted to some other standard problems. The results have well agreement with the work of Fang et al. [9]. The effects of different physical parameters like Darcy number, mass transpiration parameter, stretching/shrinking parameter, and chemical reaction parameter, Schmidt number on velocity and concentration profiles are examined under different situations.

2  Physical Model

The incompressible unsteady stagnation point flow over stretching/shrinking sheet is embedded in porous media with mass transpiration and mass transfer with chemical reaction as shown in Fig. 1. The Cu‐Al2O3/H2O HNF is used as the main fluid flow. The wall and free stream are moving along x-axis with velocity Uw=dax(1−γt)−1 and U∞=ax(1−γt)−1 , respectively and y-axis is perpendicular to it. At the wall; the concentration is maintained constant at Cw with a uniform mass flux mw(1−γt)−1/122 and the concentration of free stream is kept constant at C∞ . The governing 2D continuity, momentum and mass equations are as follows (see Anusha et al. [7], Mahabaleshwar et al. [8]).

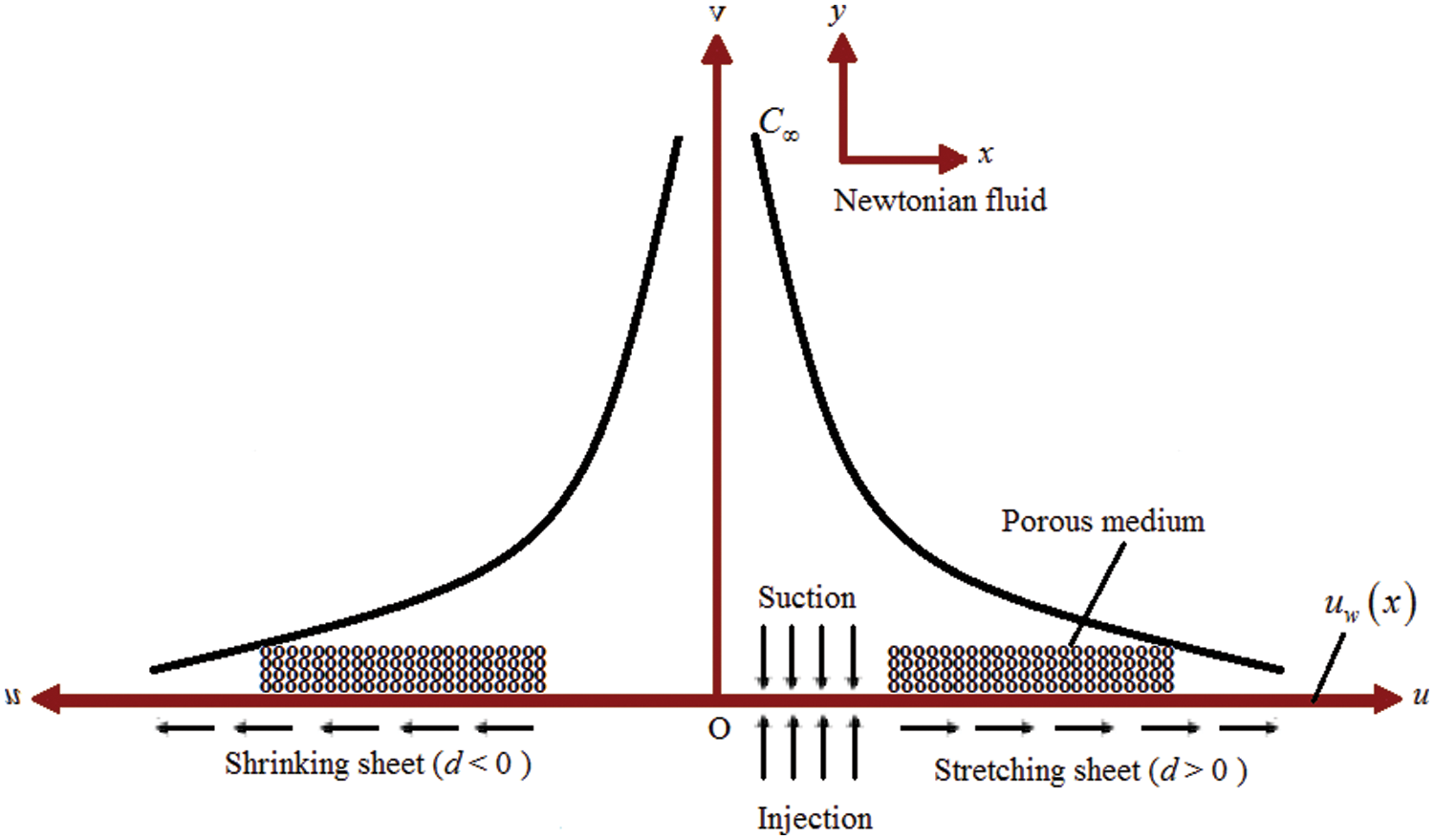
Figure 1: Schematic diagram of the problem

∂u∂x+∂v∂y=0, (1)

∂u∂t+u∂u∂x+v∂u∂y=−1ρhnf∂P∂x+νhnf(∂2u∂x2+∂2u∂y2)+νhnfK(U∞−u), (2)

∂v∂t+u∂v∂x+v∂v∂y=−1ρhnf∂P∂y+νhnf(∂2v∂x2+∂2v∂y2), (3)

∂C∂t+u∂C∂x+v∂C∂y=DB∂2C∂y2−kC(C−C∞), (4)

and the boundary conditions (B.Cs) are,

u(x,0,t)=uw=dax(1−γt),v(x,0,t)=Vw(x,t),C(x,0,t)=Cw(x,t), (5)

u(x,∞,t)=u∞=ax(1−γt),C(x,∞,t)=C∞. (6)

The following similarity transformation is introduced (see Fang et al. [9]) to transform the system of PDEs (1) to (4) into system of ODEs in order to find out the analytical solution,

ψ(x,y,t)=axνf(1−γt)f(η),  ϕ(η)=C−C∞Cw−C∞, where η=yνf(1−γt). (7)

And therefore the velocities along x- and y-axes are obtained as,

u=ax(1−γt)fη(η),v=−aνf(1−γt)f(η), (8)

and wall mass transpiration velocity is,

Vw(x,t)=Vw(t)=−aνf(1−γt)f(0). (9)

On applying x-momentum with u=u∞ to Eq. (2) we can obtain,

−1ρhnf∂P∂x=ax(1−γt)2(γ+a), (10)

Use Eqs. (7), (8) and (10) in Eqs. (2) and (4) to get,

δfηηη+(af+ηγ2)fηη−(γ+afη)fη+γ+a−aδDa−1(1−fη)=0, (11)

ϕηη+Sc(af−γη2)ϕη+aScβϕ=0, (12)

The B.Cs associated with this Eqs. (5) and (6) also reduced as

f(0)=VC,fη(0)=d,fη(∞)=1. (13)

ϕ(0)=1,ϕ(∞)=0, (14)

here, VC=−Vw(x,t)aνf/(1−γt) is the mass transpiration parameter, where it is depend on sign of the constant a , i.e., if a>0 , then a positive VC indicates mass suction and negative VC indicates mass injection, and reversely if a<0 , positive VC indicates mass injection and negative VC indicates mass suction. d=uwu∞ is the wall moving parameter, here also if a>0 , positive d indicates the stretching wall and the negative d indicates shrinking wall and if a<0 , positive d indicates the shrinking wall and the negative d indicates stretching wall.

Also, Sc=νfDB is Schmidt number, β=kCa(1−γt) is chemical reaction parameter, and the quantity δ=δ2δ1 . Further the values and relations are as mentioned in the Table 1.

2.1 Solution of Pressure Term

Since v=v(y,t) Eq. (3) will give,

−1δ1ρf∂P∂y=∂v∂t+v∂v∂y−δ2δ1νf∂2v∂y2, (15)

and

∂P∂y=g(t,y)  will give,

P=∫g(t,y)+h(t,x), (16)

where, h(t,x) is the constant function of the integration respect to y.

On differentiate Eq. (16) w.r.t x to obtain equation as ∂P∂x=∂h(t,x)∂x , this is free from y. From Eq. (10), ∂P∂x can be rewrite as,

−1δ1ρf∂P∂x=ax(1−γt)2(γ+a), (17)

The pressure P can be obtained from Eqs. (15) and (17),

1ρf(P0−P)=δ1ax22(1−γt)2(γ+a), (18)

where, P0 is constant of integration. Integrate Eq. (15) to get,

1ρf(P0−P)=δ1∫0y∂v∂tdy+δ1v22−δ2νf∂v∂y, (19)

From Eqs. (18) and (19),

1ρf(P0−P)=δ1ax22(1−γt)2(γ+a)+δ1∫0y∂v∂tdy+δ1v22−δ2νf∂v∂y, (20)

2.2 Solution for Velocity

Consider a special case with a=−1/2,γ=−1 , then Eq. (11) will give the following form,

δfηηη−12(f−η)fηη+(1+fη)fη−32+δ12Da−1(1−fη)=0, (21)

Defining a new transformation F(η)=f(η)−η , and using this in Eq. (21) will give,

δFηηη−12FFηη+2Fη+12Fη2+12δDa−1Fη=0, (22)

And the associated B.Cs will reduces as,

F(0)=VC,Fη(0)=d−1,Fη(∞)=0. (23)

Assume the solution of Eq. (22) is in the form,

F(η)=c1+c2Exp(−αη). (24)

On applying B.Cs defined in Eq. (23),

c1=VC+1−dα,c2=1−dα, (25)

And on using Eqs. (24) and (25) in Eq. (22) will give,

2δα2+(VC+Da−1)α+d+3=0, (26)

Its roots will obtained as,

α=−(VC+Da−1)+(VC+Da−1)2−8δ(d+3)4δ, (27)

here, to obtain physically feasible solution Eq. (27) must satisfy (VC+Da−1)2−8δ(d+3)≥0 . And Eq. (26) will give,

VC=−2δα−Da−1−(d+3)α=0, (28)

The solution will become,

f(η)=η+VC−1−dα(1−Exp[−αη]), (29)

And axial velocity is given by

fη(η)=1−(1−d)Exp[−αη], (30)

2.3 Solution for Concentration

For the special case a=−1/2,γ=−1 , the Eq. (12) got the form,

ϕηη−12Sc(f−η)ϕη−12Scβϕ=0, (31a)

Use Eq. (29) in above,

ϕηη−Sc2[VC−1−dα+1−dαExp(−αη)]ϕη−12Scβϕ=0, (31b)

Then use Eq. (28) in above,

ϕηη+Sc[δα+Da−12+2α+d−12αExp(−αη)]ϕη−12Scβϕ=0, (32)

On introducing the new variable ε=(1−d)Sc2α2Exp(−αη) in the Eq. (32) will yield,

ε∂2ϕ∂ε2+[1−Sc(δ+Da−12α+2α2)+ε]∂ϕ∂ε−Sc2α2εβϕ=0, (33)

And the B.Cs in terms of new variable are,

ϕ(Sc(1−d)2α2)=1,ϕ(0)=0. (34)

Then the general solution of Eq. (33) in terms of ε is obtained as,

ϕ(ε)=C11εC1H[C1,D+1,−ε], (35)

And Eq. (35) in terms of η will be in the form,

ϕ(η)=C11(1−d)C1(Sc2α2)C1Exp(−C1αη)H[C1,D+1,(d−1)Sc2α2Exp(−αη)], (36)

To obtain value of constant C11 , the B.C in Eq. (14) is used in Eq. (36), the general solution will be,

ϕ(η)=Exp(−C1αη)H[C1,D+1,(d−1)Sc2α2Exp(−αη)]H[C1,D+1,(d−1)Sc2α2], (37)

where, C1=A+D2,D=A2+4B , and here

A=Sc(δ+Da−12α+2α2),B=Scβ2α2 (38)

then wall mass flux is given by,

−ϕη(0)=Sc(1−d)2αC1D+1H[C1+1,D+2,(d−1)Sc2α2]H[C1,D+1,(d−1)Sc2α2], (39)

2.4 Uniform Mass Flux Case

Define the transformation for Eq. (4) as, h(η)=C−C∞mwDν , with following B.Cs,

aty=0,−D∂C∂y=mw(1−γt)asy→∞,C→C∞, (40)

Use Eq. (40) in Eq. (4) for γ=−1 will give,

hηη−Sc2[VC−1−dα+1−dαExp(−αη)]hη−12Scβh=0, (41)

With B.Cs,

hη(0)=−1,h(∞)=0, (42)

The Eq. (41) is similar to Eq. (31b) upto their general solution,

h(η)=C11(1−d)C1(Sc2α2)C1Exp(−C1αη)H[C1,D+1,(d−1)Sc2α2Exp(−αη)], (43)

On using B.Cs as in Eq. (42), Eq. (43) will imply.

h(η)=Exp(−C1αη)H[C1,D+1,(d−1)Sc2α2Exp(−αη)]αC1{H[C1,D+1,(d−1)Sc2α2]+1−dD+1Sc2α2H[C1+1,D+2,(d−1)Sc2α2]}, (44)

2.5 General Power Law Wall Concentration

In the current section we examined the general condition by assuming the wall concentration with a power law dependence on both time and distance as Cw=C∞+Crefxn(1−γt)m , where n,m∈R . Now define the dimensionless concentration as follows:

C=C∞+(Cw−C∞)xn(1−γt)mΦ(η),  and  Φ(η)=C−C∞Cw−C∞, (45)

by applying this new definition in Eq. (4) to obtain the following ODE for γ=−1 ,

Φηη+Sc(af+12η)Φη−Sc(anfη+m−aβ)Φ=0, (46)

With the following B.Cs,

Φ(0)=1,Φ(∞)=0. (47)

For a=−1/2 and using Eqs. (28)–(30), Eq. (46) will reduce to,

Φηη+Sc(δα+12Da−1+2α+(d−1)2αExp[−αη])Φη+Sc(n2[1+(d−1)Exp[−αη]]−m−β2)Φ=0, (48)

By introducing new variable ξ=(d−1)Sc2α2Exp(−αη) in Eq. (48) to obtain,

ξ∂2Φ∂ξ2+(1−A1−ξ)∂Φ∂ξ+(A2ξ+n)Φ=0, (49)

where, A1=Sc(δ+2α2+Da−12α),A2=1α2Sc(n2−m−β2) .

And the B.Cs will reduce to,

Φ(Sc(α−1)2α2)=1,Φ(0)=0. (50)

Now define Φ(ξ)=ξkψ(ξ) in Eq. (49) to convert it into following expression,

ξ∂2ψ∂ξ2+(Γ1−ξ)∂ψ∂ξ−(k−n)ψ=0, (51)

Here Γ=1+2k−A1 , and expression for k is given by,

k=A1±A12−4A22,  with  Sc4α2(2δα2+4+αDa−1)2≥2n−4m−2Γ, (52)

Eq. (51) is the standard form of hypergeometric differential equation and its solution will be in the form of,

ψ(ξ)=C1M(k−n,Γ,ξ), (53)

It gives the solution of Eq. (49) in the form, ϕ(ξ)=C1ξkM(k−n,Γ,ξ) , therefore the solution of Eq. (48) with B.Cs as in Eq. (47) is obtained as,

Φ(η)=Exp(−αkη)M[k−n,Γ,(d−1)Sc2α2Exp(−αη)]M[k−n,Γ,(d−1)Sc2α2], (54)

And the wall mass flux is,

−Φη(0)=αk+Sc(d−1)(k−n)2ΓαM[1+k−n,Γ+1,(d−1)Sc2α2]M[k−n,Γ,(d−1)Sc2α2]. (55)

2.6 General Power-Law Mass Flux

In this section, the general condition is assumed with the wall concentration by a power law dependence on both time and distance −D∂C∂y=mwxn(1−γt)m−12 , where n,m∈R . Now define the dimensionless concentration as follows:

C=C∞+mwDνxn(1−γt)mH(η), (56)

Use Eq. (56) in Eq. (4) for γ=−1 will give,

Hηη+Sc(af+12η)Hη−Sc(anfη+m−aβ)H=0. (57)

With B.Cs as,

Hη(0)=−1,H(∞)=0, (58)

Eq. (57) is the same as Eq. (46), therefore their solutions are similar. We can obtain the solution of Eq. (57) as,

H(η)=C1[(d−1)Sc2α2]kExp(−αkη)M[k−n,Γ,(d−1)Sc2α2Exp(−αη)], (59)

On applying B.C as in Eq. (58) to Eq. (59), we obtain the solution of Eq. (57) as follows:

H(η)=2ΓαExp(−αkη)M[k−n,Γ,(d−1)Sc2α2Exp(−αη)]2α2kΓM[k−n,Γ,(d−1)Sc2α2]+Sc(k−n)(d−1)M[k−n+1,Γ+1,(d−1)Sc2α2], (60)

The current work with nanoparticles dispersed in the base fluid is well agreement with the investigation of Fang et al. [9] in the absence of nanoparticles, porous media, stagnation point parameter and chemical reaction parameter.

3  Results and Discussion

The examination of unsteady stagnation point flow over porous media with mass transpiration and mass transfer with chemical reaction for Cu‐Al2O3/H2O hybrid nanofluid is carried out to observe several results. The momentum and mass transfer problem are combined to form the system of PDEs (1) to (4), then the system is converted into system of ODEs (11) to (12) via similarity transformations. Then the governing ODEs are solved analytically to obtain the solution for velocity and concentration profiles in exponential and hypergeometric forms. Four different cases are considered for the concentration profile as constant wall concentration, uniform mass flux, general power law wall concentration and general power law mass flux. The effect of different physical parameters such as Darcy number (Da−1) , mass transpiration parameter (VC) , stretching/shrinking parameter (d) , chemical reaction parameter (β) , Schmidt number (Sc) on velocity and concentration profile is examined under different situations. These effects are observed with the help of graphical representation of physically interested parameters for the solid volume fraction of Al2O3 nanoparticle (φ1) which is taken as 0.1 and that of Cu nanoparticle (φ2) is fixed at 0.04.

Fig. 2 demonstrates the solution domain α versus d for different values of VC . It can be observed that, as the mass transpiration decreases from suction to injection, the solution domain will expand for negative values of d.

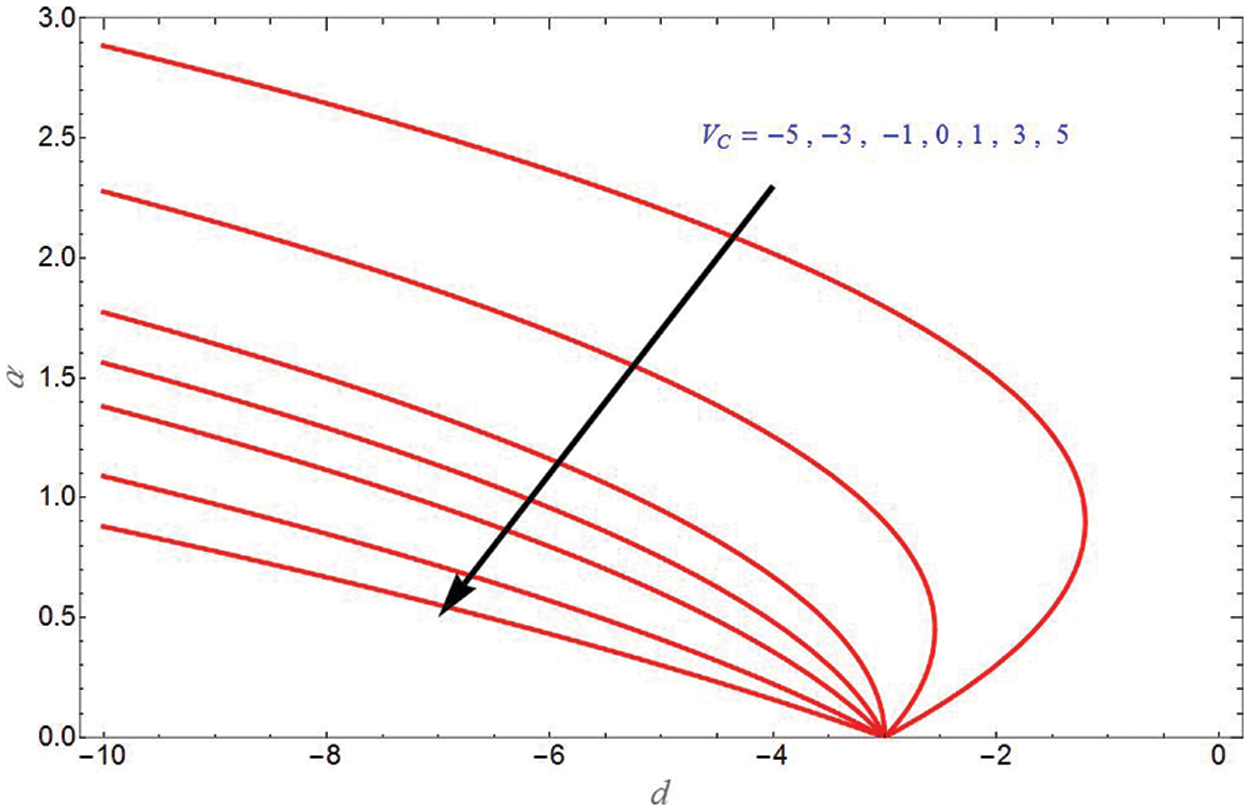
Figure 2: α vs. stretching/shrinking parameter d for different values of mass transpiration parameter VC

Fig. 3 depicts the transverse velocity due to stretching sheet and different values of VC in Fig. 3a. It shows that transverse velocity increases with increase in VC . Fig. 3b demonstrates the transverse velocity for different values of Da−1 and it will increase with increase in Da−1 .

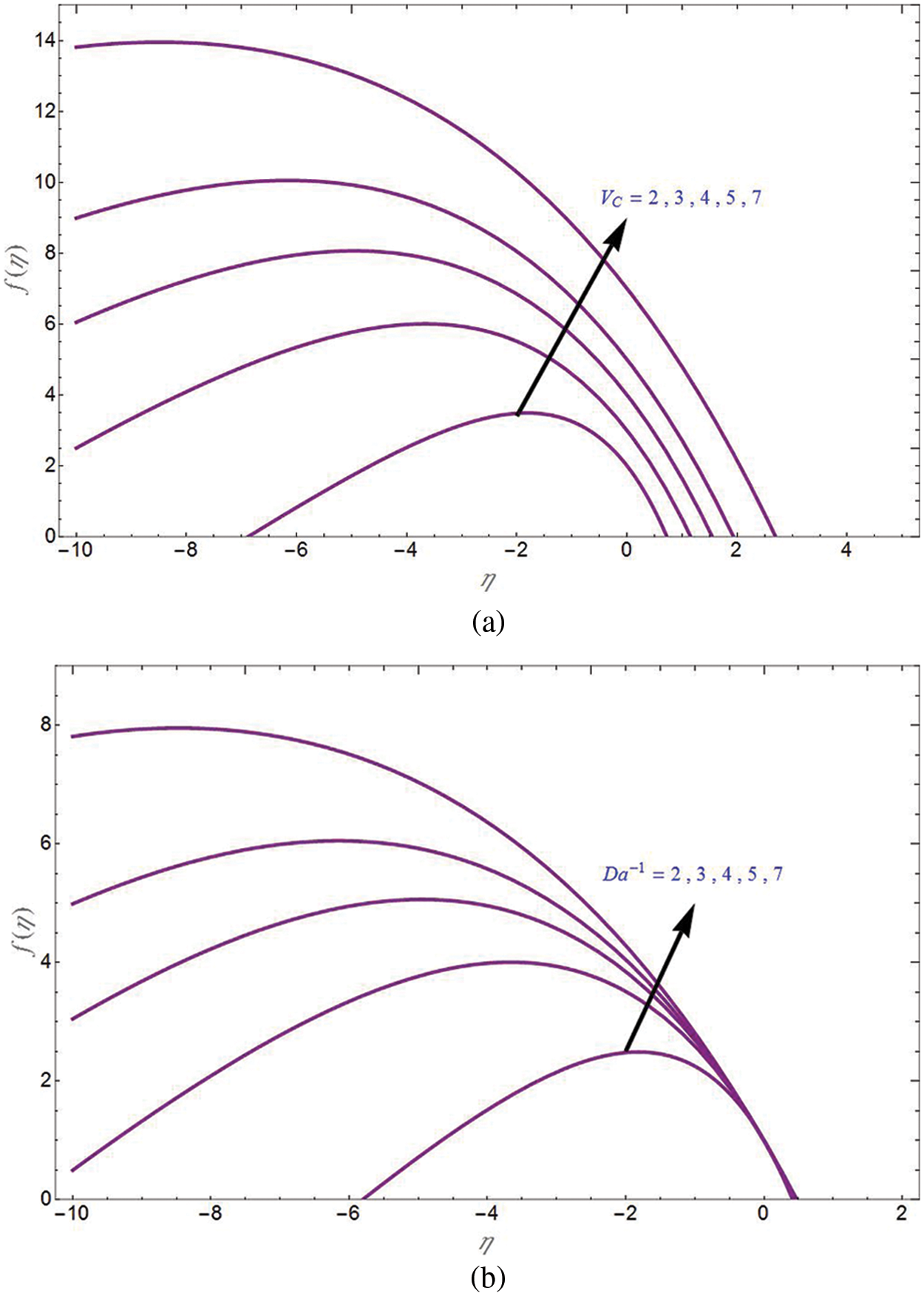
Figure 3: Transverse velocity f(η) for different values of VC in (a) and Da−1 in (b)

Fig. 4a is the plot for axial velocity due to shrinking sheet (d=−4) with various values of VC . In this situation, axial velocity is negative and it is decreases with increase in mass transpiration from injection to suction. Furthermore, Fig. 4b is the plot for axial velocity due to stretching sheet (d=2) with various values of injection parameter. In this situation axial velocity is positive and it is increased with increase in injection parameter. Fig. 5 is depicted for axial velocity due to shrinking sheet (d=−4) with various values of Da−1 . In this condition axial velocity is negative and it is decreased with increase in Da−1 for both suction and injection cases. Fig. 6 investigates the axial velocity due to shrinking sheet with various values of shrinking sheet parameter. As the shrinking sheet parameter increases, the axial velocity will decrease in both suction and injection cases.

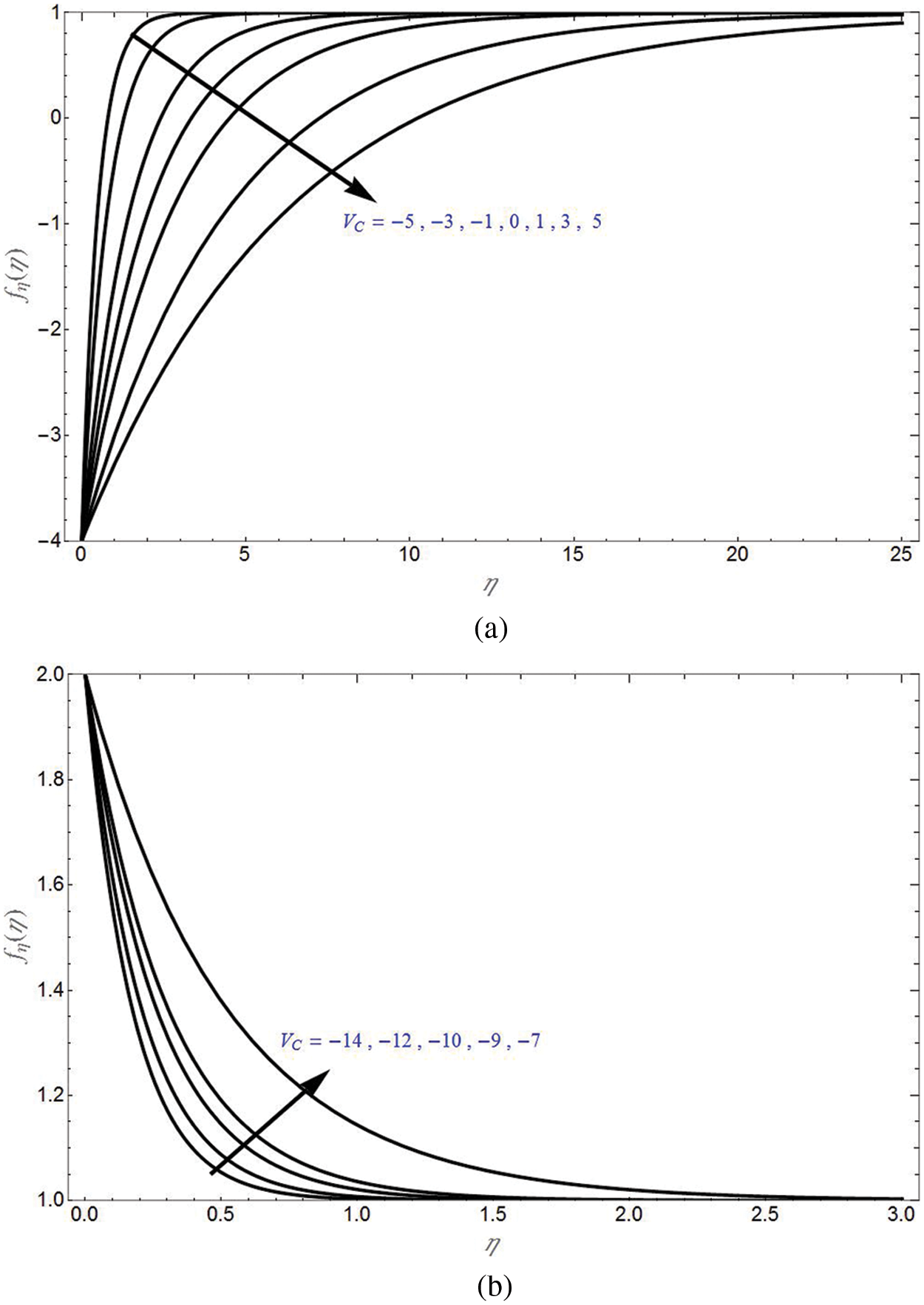
Figure 4: Axial velocity fη(η) for different values of VC for shrinking sheet in (a) and stretching sheet in (b)

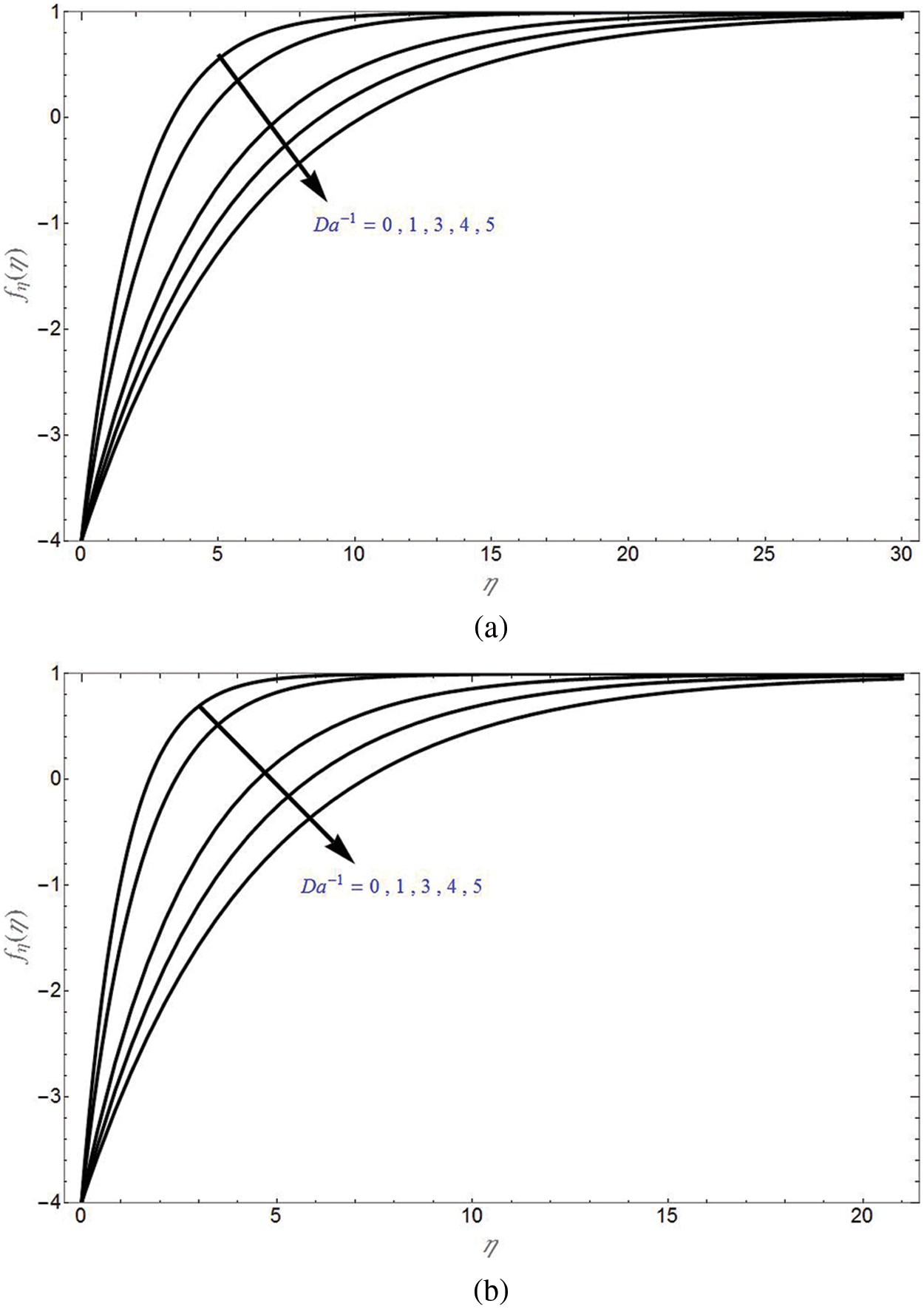
Figure 5: Axial velocity fη(η) for different values of Da−1 due to shrinking sheet for suction case (VC=1) in (a) and injection case (VC=−1) in (b)

Figure 6: Axial velocity fη(η) for different values of shrinking sheet parameter for suction case (VC=1) in (a) and injection case (VC=−1) in (b)

The concentration profiles for different values of shrinking sheet parameter are demonstrated in Fig. 7 for suction and non-permeability cases in Figs. 7a and 7b, respectively. It can be seen that ϕ(η) will decrease with increase in shrinking sheet parameter. Initially, ϕ(η) will decrease upto certain value of η and then become constant to 0.

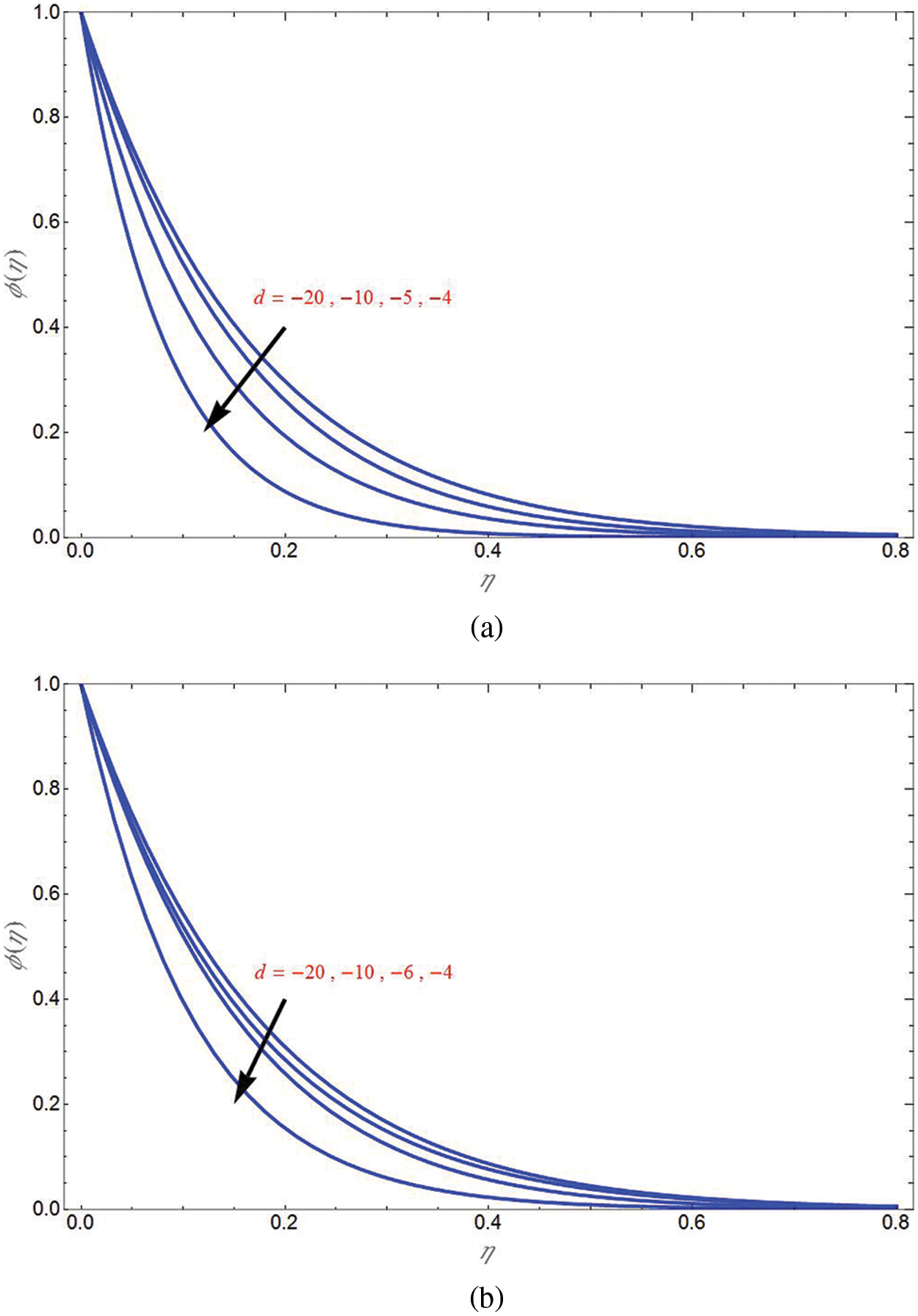
Figure 7: Concentration profile ϕ(η) for different values of shrinking sheet parameter for suction case (VC=1) in (a) and non-permeability case (VC=0) in (b)

The concentration profile for different values of β is demonstrated in Fig. 8 for non-permeability and injection case in Figs. 8a and 8b, respectively. It can be seen that ϕ(η) will decrease with increase in β .

Figure 8: Concentration profile ϕ(η) for different values of β due to shrinking sheet parameter for non-permeability case (VC=0) in (a) and injection case (VC=−1) in (b)

The concentration profile for different values of mass transpiration parameter due to shrinking sheet (d=−4) is demonstrated in Fig. 9. It can be seen that ϕ(η) will decrease with increase in mass transpiration from injection to suction.

Figure 9: Concentration profile ϕ(η) for different values of suction/injection parameter due to shrinking sheet parameter

The concentration profile of mass flux case for different values of shrinking sheet parameter is demonstrated in Fig. 10 for suction, non-permeability and injection cases, respectively in Figs. 10a–10c. It can be seen that h(η) will decrease with increase in shrinking sheet parameter. Initially, h(η) will decrease upto certain value of η and then become constant to 0. On compare, injection case has more mass transfer than non-permeable case and non-permeable case has more mass transfer than suction case and the difference is very less in this case.

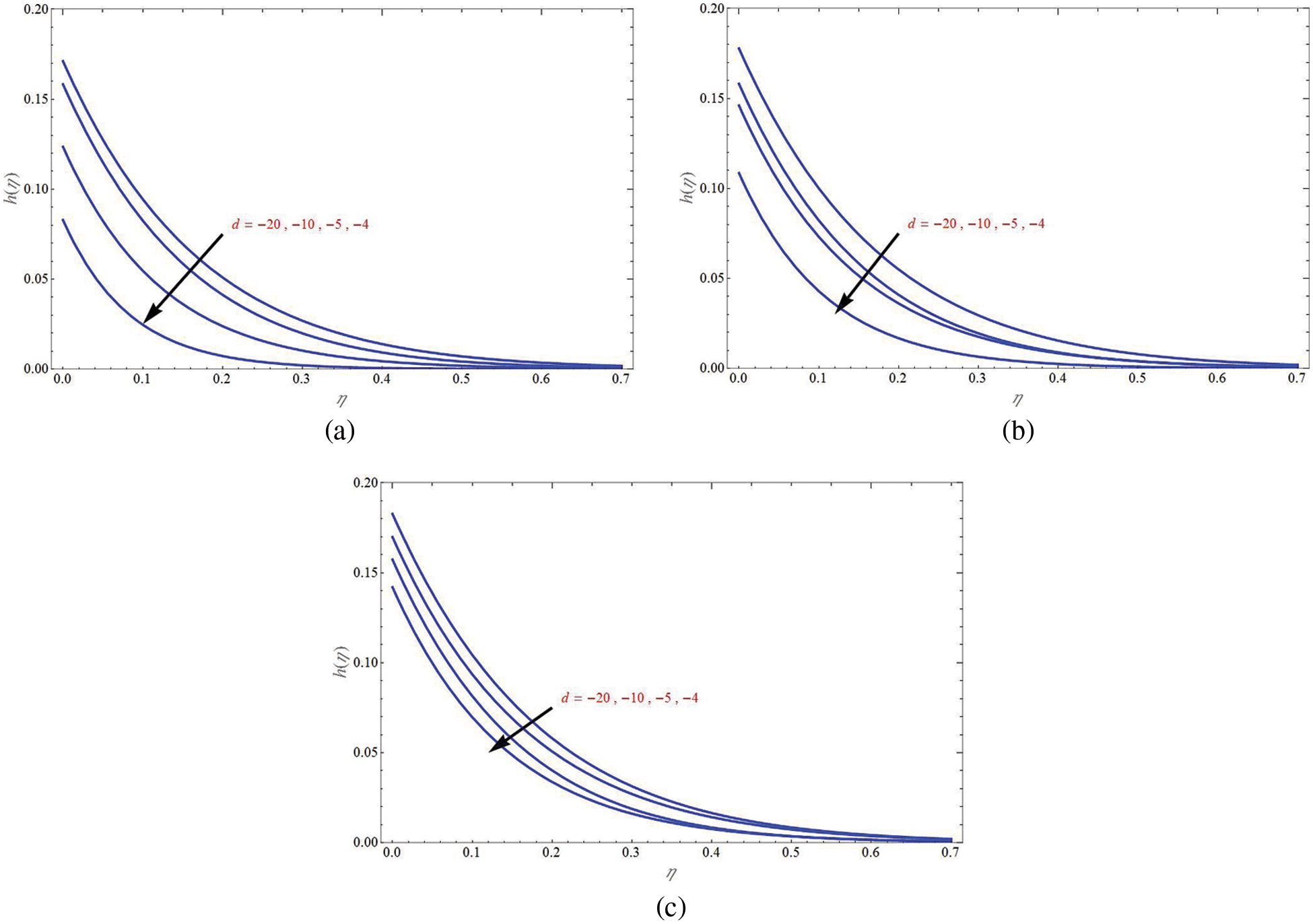
Figure 10: Concentration profile h(η) of mass flux case for different values of shrinking sheet parameter for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

The concentration profile of mass flux case for different values of β due to shrinking sheet (d=−4) is demonstrated in Fig. 11 for suction, non-permeability and injection case in Figs. 11a–11c, respectively. It can be seen that h(η) will decrease with increase in β . On compare, injection case has more mass transfer than non-permeable case and non-permeable case has more mass transfer than suction case and the difference is greater in this case.

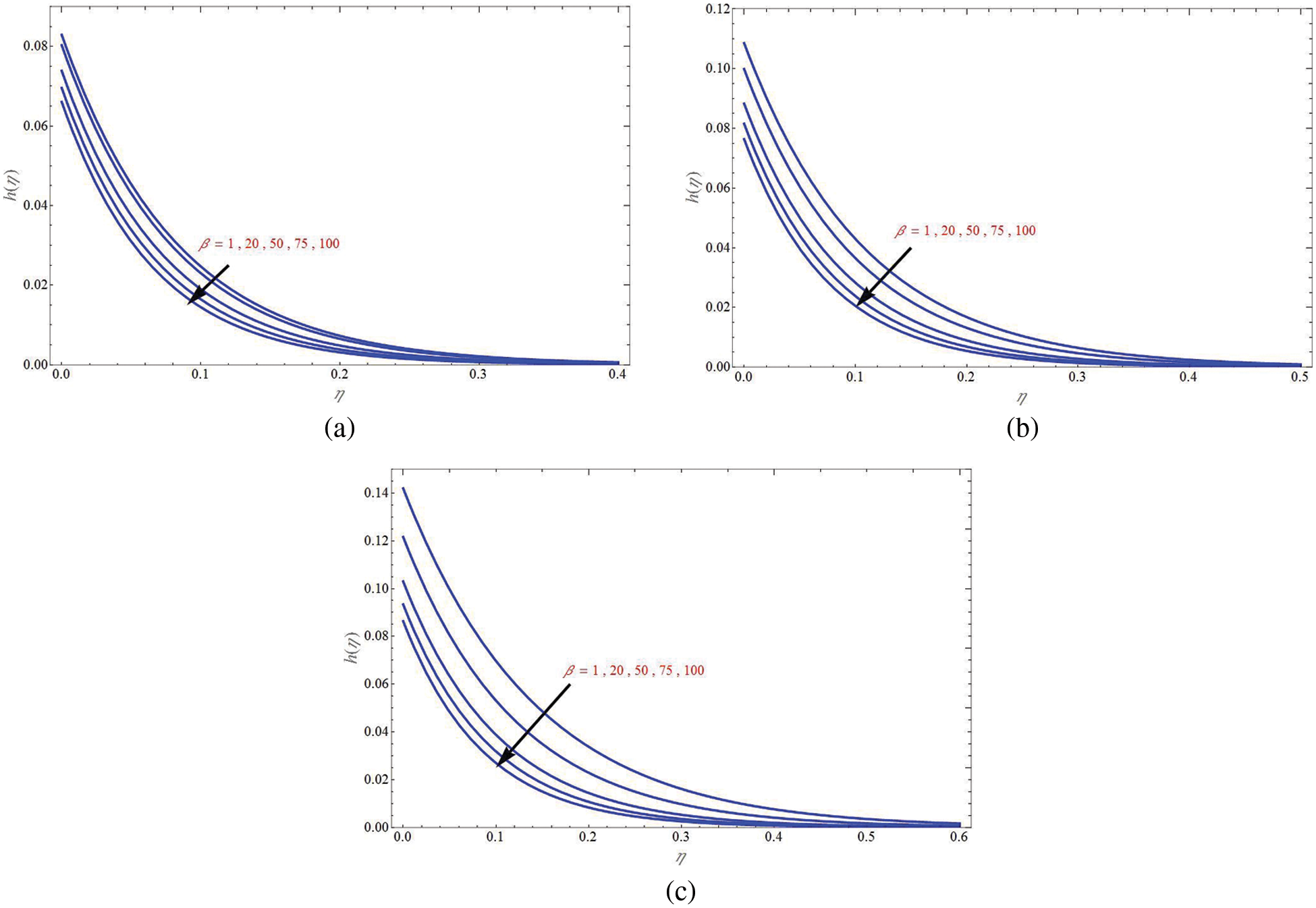
Figure 11: Concentration profile h(η) of mass flux case for different values of β due to shrinking sheet for suction case (VC=1) in (a) non-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

The concentration profile of mass flux case for different values of mass transpiration parameter due to shrinking sheet (d=−4) is demonstrated in Fig. 12. It can be seen that h(η) will decrease with increase in mass transpiration from injection to suction. Injection case has more transfer than suction case.

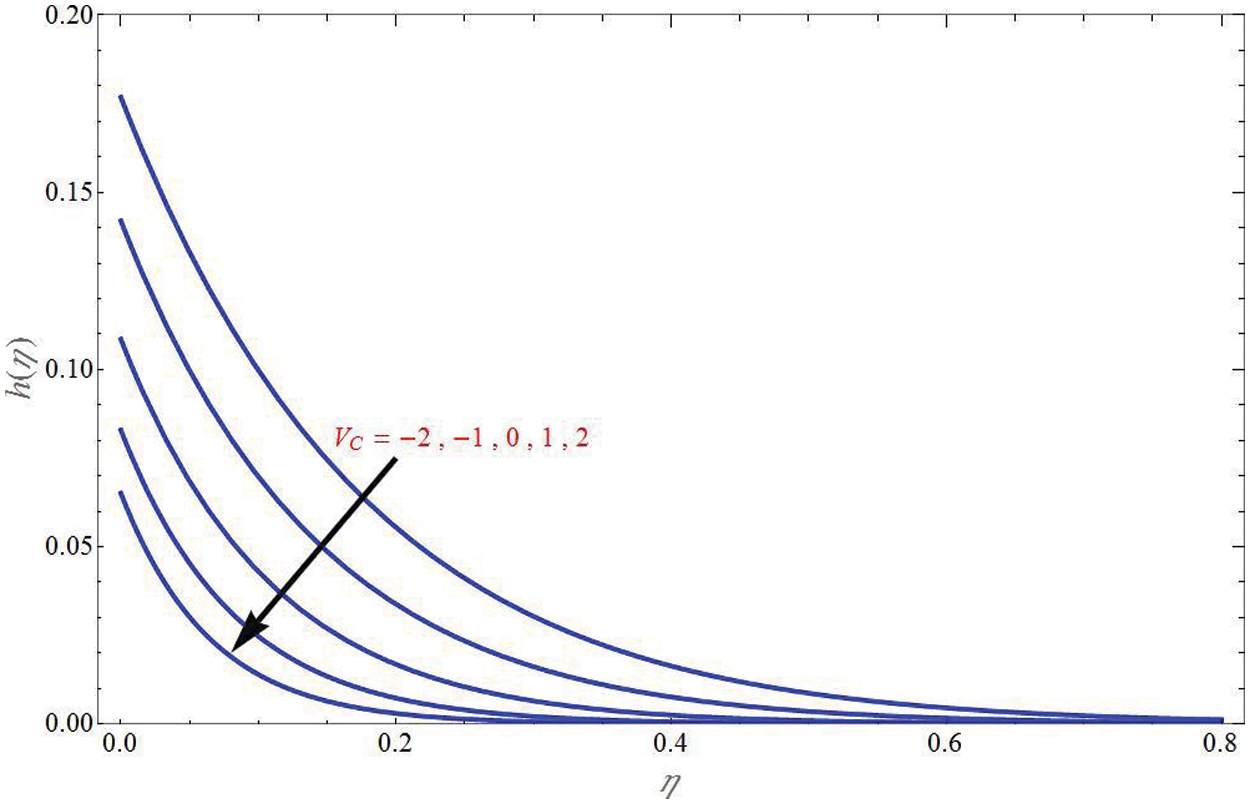
Figure 12: Concentration profile h(η) of mass flux case for different values of VC due to shrinking sheet

The concentration profile of mass flux case for different values of Sc due to shrinking sheet (d=−4) is demonstrated in Fig. 13 for suction, non-permeability and injection case in Figs. 13a–13c, respectively. It can be seen that h(η) will decrease with increase in Sc . By a comparison study, it can be found that injection case has more mass transfer than non-permeable case and non-permeable case has more mass transfer than suction case and the difference is more in this case also.

Figure 13: Concentration profile h(η) of mass flux case for different values of Schmidt number (Sc) due to shrinking sheet for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

The concentration profile of mass flux case for different values of Da−1 due to shrinking sheet (d=−4) is demonstrated in Fig. 14 for suction, non-permeability and injection case respectively in Figs. 14a–14c. It can be seen that h(η) will decrease with increase in Da−1 .

Figure 14: Concentration profile h(η) of mass flux case for different values of Da−1 due to shrinking sheet for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

Fig. 15 shows the general power law wall concentration profile for different values of shrinking sheet parameter for suction, non-permeability and injection cases in Figs. 15a–15c, respectively. It can be seen that Φ(η) will increase with increase in shrinking sheet parameter. Initially Φ(η) decreases upto certain value of η and then become constant to 0.

Figure 15: General power law wall concentration profile Φ(η) for different values of shrinking sheet parameter for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

Furthermore, Fig. 16 demonstrates the general power law wall concentration profile for different values of β due to shrinking sheet (d=−4) for suction, non-permeability and injection case respectively in Figs. 16a–16c. It can be seen that Φ(η) will decrease with increase in β .

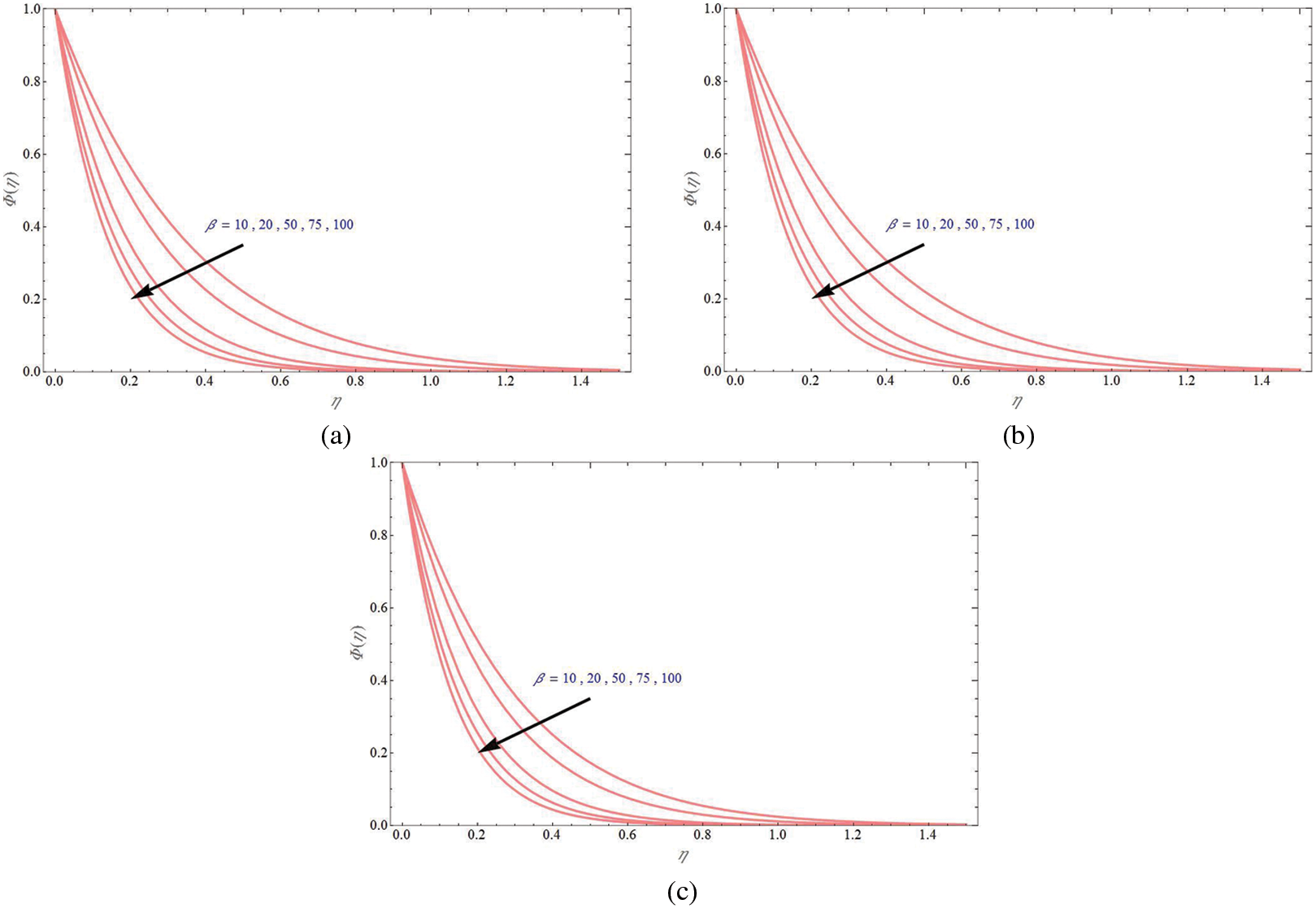
Figure 16: General power law wall concentration profile Φ(η) for different values of β due to shrinking sheet parameter for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

The general power law wall concentration profile for different values of mass transpiration parameter due to shrinking sheet (d=−4) is demonstrated in Fig. 17. It can be seen that Φ(η) will increase with increase in mass transpiration from injection to suction and it seems that suction case has more transfer than injection case.

Figure 17: The general power law wall concentration profile Φ(η) for different values of VC due to shrinking sheet

The general power law wall concentration profile for different values of Sc due to shrinking sheet (d=−4) is demonstrated in Fig. 18 for suction, non-permeability and injection case respectively in Figs. 18a–18c. It can be seen that Φ(η) will decrease with increase in Sc .

Figure 18: The general power law wall concentration profile Φ(η) for different values of Schmidt number (Sc) due to shrinking sheet for suction case (VC=1) in (a) no-permeability case (VC=0) in (b) and injection case (VC=−1) in (c)

Finally, Figs. 19 and 20 demonstrate the stream line graphs for upper branch solution and lower branch solution, respectively for some values of time t = 0.1, 0.5, 1. Stretching velocity of the wall is away from the origin since stream velocity is towards the origin. It can be seen that as the time increases, the stagnation point is moving away from the origin and towards the positive y direction.

Figure 19: Stream line graphs for upper branch solution keeping VC = −6, d = −1, K = 1, in (a) t=0.1 , in (b) t=0.5 and in (c) t=1

Figure 20: Stream line graphs for lower branch solution keeping VC=−6,d=−1,K=1 , in (a) t=0.1 , in (b) t=0.5 and in (c) t=1

4  Conclusion

The current work examined the unsteady stagnation point HNF flow over porous sheet with mass transpiration and mass transfer with chemical reaction. The momentum and mass transfer problem are solved analytically to obtain the solution for velocity and concentration profiles in exponential form and hypergeometric form respectively. The concentration profile is obtained for four different cases such as constant wall concentration, uniform mass flux, general power law wall concentration and general power law mass flux. The effect of different physical parameters like Darcy number (Da−1) , mass transpiration parameter (VC) , stretching/shrinking parameter (d) , chemical reaction parameter (β) , Schmidt number (Sc) on velocity and concentration profile is examined under different situations. The observations are as follows:

•   The solution domain will expand as mass transpiration decreases for shrinking sheet case.

•   Transverse velocity increases with increase in VC and Da−1 .

•   Axial velocity decreases with increase in mass transpiration and it decreases with increase in Da−1 for both suction and injection cases.

•   The axial velocity will decrease as the shrinking sheet parameter increases both in suction and injection cases.

•   Concentration profile ϕ(η) will decrease with increase in shrinking sheet parameter or chemical reaction parameter or mass transpiration.

•   The concentration profile of mass flux case h(η) will decrease with increase in shrinking sheet parameter, chemical reaction parameter, mass transpiration, Schmidt number or inverse Darcy number.

•   Injection case had more mass transfer than suction case.

•   The general power law wall concentration profile Φ(η) will increase with increase in shrinking sheet parameter or mass transpiration and it will decrease with increase in chemical reaction parameter or Schmidt number.

Acknowledgement: The author T. Anusha is thankful to Council of Scientific and Industrial Research (CSIR), New Delhi, India for financial support in the form of Junior Research Fellowship: File No. 09/1207(0003)/2020-EMR-I.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Crane, L. J. (1970). Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP, 21(4), 645–647. DOI 10.1007/BF01587695. [Google Scholar] [CrossRef]

 2.  Wang, C. Y. (1984). The three-dimensional flow due to a stretching flat surface. Physics of Fluids, 27, 1915–1917. [Google Scholar]

 3.  Aly, E. H., Pop, I. (2020). MHD flow and heat transfer near stagnation point over a stretching/shrinking surface with partial slip and viscous dissipation: Hybrid nanofluid versus nanofluid. Powder Technology, 367(1), 192–205. DOI 10.1016/j.powtec.2020.03.030. [Google Scholar] [CrossRef]

 4.  Aly, E. H., Pop, I. M. (2019). MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. International Journal of Numerical Methods for Heat and Fluid Flow, 29(9), 3012–3038. DOI 10.1108/HFF-12-2018-0794. [Google Scholar] [CrossRef]

 5.  Turkyilmazoglu, M. (2011). Multiple solutions of heat and mass transfer of MHD slip flow for the viscoelastic fluid over a stretching sheet. International Journal of Thermal Sciences, 50(11), 2264–2276. DOI 10.1016/j.ijthermalsci.2011.05.014. [Google Scholar] [CrossRef]

 6.  Anusha, T., Huang, H. N., Mahabaleshwar, U. S. (2021). Two dimensional unsteady stagnation point flow of Casson hybrid nanofluid over a permeable flat surface and heat transfer analysis with radiation. Journal of Taiwan Institute of Chemical Engineers, 127(8), 79–91. DOI 10.1016/j.jtice.2021.08.014. [Google Scholar] [CrossRef]

 7.  Anusha, T., Mahabaleshwar, U. S., Sheikhnejad, Y. (2021). An MHD of nanofluid flow over a porous stretching/shrinking plate with mass transpiration and Brinkman ratio. Transport in Porous Media, 142(1–20), 333–352. DOI 10.1007/s11242-021-01695-y. [Google Scholar] [CrossRef]

 8.  Mahabaleshwar, U. S., Anusha, T., Hatami, M. (2021). The MHD Newtonian hybrid nanofluid flow and mass transfer analysis due to super-linear stretching sheet embedded in porous medium. Scientific Reports, 11(1), 1–17. DOI 10.1038/s41598-021-01902-2. [Google Scholar] [CrossRef]

 9.  Fang, T. G., Wang, F. J. (2020). Momentum and heat transfer of a special case of the unsteady stagnation point flow. Applied Mathematics and Mechanics, 41(1), 51–82. DOI 10.1007/s10483-020-2556-9. [Google Scholar] [CrossRef]

10. Mahabaleshwar, U. S., Sneha, K. N., Huang, H. N. (2021). An effect of MHD and radiation on CNTS-water based nanofluid due to a stretching sheet in a Newtonian fluid. Case Studies in Thermal Engineering, 28(2), 101462. DOI 10.1016/j.csite.2021.101462. [Google Scholar] [CrossRef]

11. Siddheshwar, P. G., Mahabaleshwar, U. S., Andersson, H. I. (2013). A new analytical procedure for solving the non-linear differential equation arising the stretching sheet problem. International Journal of Applied Mechanics and Engineering, 18(3), 955–964. [Google Scholar]

12. Suresh, S., Venkitaraj, K., Selvakumar, P., Chandrasekar, M. (2012). Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Experimental Thermal and Fluid Science, 38, 54–60. [Google Scholar]

13. Suresh, S., Venkitaraj, K., Selvakumar, P., Chandrasekar, M. (2011). Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids and Surface A, 388, 41–48. [Google Scholar]

14. Momin, G. G. (2013). Experimental investigation of mixed convection with water-Al2O3 & hybrid nanofluid in inclined tube for laminar flow. International Journal of Scientific and Technology Research, 2, 195–202. [Google Scholar]

15. Mallikarjun, P., Murthy, R. V., Mahabaleshwar, U. S., Lorenzini, G. (2019). Numerical study of mixed convective flow of a couple stress fluid in a vertical channel with first order chemical reaction and heat generation/absorption. Mathematical Modelling of Engineering Problems, 6(2), 175–182. [Google Scholar]

16. Mahabaleshwar, U. S., Vishalakshi, A. B., Azese, M. N. (2022). The role of Brinkman ratio on non-Newtonian fluid flow due to a porous shrinking/stretching sheet with heat transfer. European Journal of Mechanics–B Fluids, 92, 153–165. [Google Scholar]

17. Mahabaleshwar, U. S., Vishalakshi, A. B., Andersson, H. I. (2022). Hybrid nanofluid flow past a stretching/shrinking sheet with thermal radiation and mass transpiration. Chinese Journal of Physics, 75, 152–168. [Google Scholar]

18. Nakhchi, M. E., Hatami, M., Rahmati, M. (2021). Effects of CuO nano powder on performance improvement and entropy production of double-pipe heat exchanger with innovative perforated turbulators. Advanced Powder Technology, 32, 3063–3074. [Google Scholar]

19. Nakhchi, M. E., Esfahani, J. A. (2021). Numerical investigation of turbulent CuO-water nanofluid inside heat exchanger enhanced with double V-cut twisted tapes. Journal of Thermal Analysis and Calorimetry, 145, 2535–2545. [Google Scholar]

20. Zainal, N. A., Nazar, R., Naganthran, K., Pop, I. M. (2020). Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alexandria Engineering Journal, 60, 915–926. [Google Scholar]

21. Khan, U., Shafiq, A., Zaib, A., Baleanu, D. (2020). Hybrid nanofluid on mixed convective radiative flow from an irregular variably thick moving surface with convex and concave effects. Case Studies in Thermal Engineering, 21, 100660. [Google Scholar]

22. Sarkar, J., Ghosh, P., Adil, A. (2015). A review on hybrid nanofluids: Recent research, development and applications. Renewable and Sustainable Energy Reviews, 43, 164–177. [Google Scholar]

23. Vishalakshi, A. B., Mahabaleshwar, U. S., Sarris, I. E. (2022). An MHD fluid flow over a porous stretching/shrinking sheet with slips and mass transpiration. Micromachines, 13(1), 116. [Google Scholar]

24. Sneha, K. N., Mahabaleshwar, U. S., Bennacer, R., Ganaoui, M. E. L. (2021). Darcy Brinkman equations for hybrid dusty nanofluid flow with heat transfer and mass transpiration. Computation, 9(11), 118. [Google Scholar]

25. Jalali, H., Abbassi, H. (2020). Analysis of the influence of viscosity and thermal conductivity on heat transfer by Al2O3-water nanofluid. Fluid Dynamics and Materials Processing, 16(2), 181–198. DOI 10.32604/fdmp.2020.07804. [Google Scholar] [CrossRef]

26. Bhandari, A. (2019). Radiation and chemical reaction effects on nanofluid flow over a stretching sheet. Fluid Dynamics and Materials Processing, 15(5), 557–582. DOI 10.32604/fdmp.2019.04. [Google Scholar] [CrossRef]