An Automatic Deep Neural Network Model for Fingerprint Classification

1  Introduction

Fingerprint recognition is one of the most extensively studied fields in biometrics. Recently, it has many applications, such as airport security, law enforcement, mobile access, and authentication. Passwords or ID cards have been used for security purposes for identifying individuals and controlling access. However, with the advancement in technology and the widespread presence of hackers, using personal identification numbers (PIN) does not guarantee security. Moreover, it is easy to steal, lose, or forget. Hence, using biometric traits such as a fingerprint is safer. It is unique; two people do not have the same fingerprint, including identical twins. It remains permanent and stable during a person’s whole life. Therefore, we propose a system for fingerprint recognition. Almost ten years ago, in criminal cases, an automatic fingerprint identification system (AFIS) was used to identify people using their fingerprints available in a large database. For this application and others, as mentioned earlier, we faced challenges related to performance. The detection accuracy for smaller objects is still much lower than that of larger objects [1].

Several fingerprint recognition methods exist, and minutiae matching is the most often used method. Minutiae are the bifurcations and endings of the ridges that form fingerprint images (see Fig. 1). These features are not unique to one person; we all have them in our fingerprints. However, the difference is in their distribution. The precise position and direction of the ridge endings and bifurcations can distinguish one person from another.

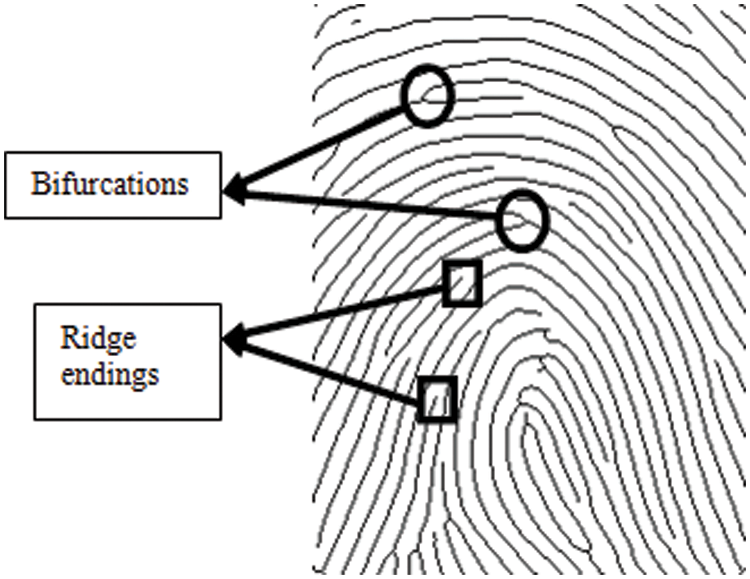
Figure 1: Unique characteristics (minutiae) of the fingerprint image; circles denote ridge bifurcations and squares denote ridge endings

There are many techniques to identify fingerprints: Fuzzy Logic (FL), Neural Networks (NN), and Genetic Algorithms (GA). These algorithms fall under Artificial Intelligence (AI), as listed in Tab. 1. There are also nonartificial intelligence methods like statistical techniques [2] for fingerprint recognition. We can combine the two methods (AI and statistical techniques) to efficiently classify fingerprints. Recently, the deep neural network (DNN) has shown efficiency in completing several tasks; hence, it is used in this study for fingerprint identification.

Several papers have been written on the minutiae extraction stage because of its importance. Here, we discuss the overall network, not just this stage, and explain how it can be successfully automated. The architecture of our network has two main stages. The first stage is feature extraction which mainly depends on convolutional layers. The second stage is a classifier, which can recognize or classify the fingerprint image using the outcome features extracted from the first stage. These two stages are illustrated in detail in Section 4.

The contributions of our paper are as follows:

•   Theoretically, we discuss the principle of the network depth, specifying the features and size of input images and the principle of the residual network.

•   Practically, an automatic system based on a residual convolution network is proposed with efficient performance for fingerprint recognition.Hence, we can control the overall network (parameters and depth), achieving our goal of best accuracy.

In Section 2, some recent studies on fingerprint recognition algorithms based on DNN have been discussed. Section 3 discusses the principles of this network based on previous studies. Section 4 introduces our system in detail, its overall architecture, and how it solves the previous studies’ disadvantages. Our experimental results and comparisons supported by charts are presented in Section 5. Finally, Section 6 summarizes the conclusion of the study.

2  Related Work

Fattahi et al. [6] presented the architecture of a model that recognizes damaged fingerprints using Convolutional Short-Term Memory Networks for forensics. Khan et al. [7] proposed a model that could classify rolled, plain, and latent fingerprint samples using a convolutional neural network (CNN) to facilitate the matching process of fingerprints. Tertychnyi et al. [8] used the VGG16-based deep network to classify low-quality fingerprint images resulting from dryness, physical damage, wetness, the existence of dots, and blurriness. Peralta et al. [9] proposed an approach to fingerprint classification using CNN and the recognition of low-quality fingerprints. Zhang et al. [10] distinguished between live fingerprints and fake ones by residual convolutional nets for protection from spoof attacks. Nahar et al. [11] proposed people recognition from their fingerprint images using ResNet50. It is a deep network with high accuracy. Our study also uses residual networks. However, our network achieves higher performance in less time, and it has the advantage of using automatic techniques. Many professional algorithms for object detection have emerged. Li et al. [12] proposed a Hierarchical Convolutional Neural Network (HCNN) for image classification. HCNNs consist of multiple subnetworks that are used to classify images progressively. Chang et al. [13] presented an improved deep-learning network, You only look once, version 3 (Yolov3), a clever recognition algorithm. Kumar et al. [14] proposed an automatic system to detect the existence of face masks using deep learning and image processing algorithms. Cao et al. [15] presented an improved network-inspired NN to solve object rotation problems.

For the minutiae extraction, Nguyen et al. [16] proposed a universal minutiae extractor based on a modified U-shaped network for segmentation. Zhou et al. [17] proposed a network consisting of two stages. In the first stage, a network produces initial candidate patches of minutiae; in the second stage, another network can extract the direction and precise minutia location of each patch. Although the feature extraction stage is essential in recognition systems, it is still an intermediate stage, unlike in our paper, which presents the complete fingerprint recognition system.

Shehu et al. [18] proposed a deep CNN that classifies three types of alterations: Z-cut, obliteration, and central rotation in the fingerprint image. This study used the SOCO database as we had used. Alterations classification is important, but the classification of people is more important and useful in real life. So, we did something to get the system to recognize individuals from their fingerprints. This is discussed in detail in the next section.

The all previous studies cannot be suitable for all kinds of datasets because of the unified network problem. However, our model can do that because it changes its network according to accuracy. Moreover, the previous studies do not achieve the best performance that led to the design of the proposed methodology.

3  Materials and Methods

3.1 Data Collection and System Implementation

We used the SOCOFing dataset [19] for training and testing to demonstrate the efficiency of our system. We divided our dataset into three sets—training, validation, and testing in the ratio of 7:2:1. The original dataset was divided into Z-cut, obliteration (Obl), central rotation alterations (CR), and real fingerprints. There are some samples of the dataset in Fig. 2. Our model was evaluated for classifying four categories or alterations, yielding a test accuracy of 0.965 and test loss of 0.098. However, because people’s classification was applied in real life, we altered the dataset to classify according to people and not categories and split it into a split-folders library. It was easy and automatic; instead of a person splitting it manually. It saved time and effort. We split our data files into individual persons such that every folder of a person had his samples. All the preprocessing steps were also automatic without manual intervention.

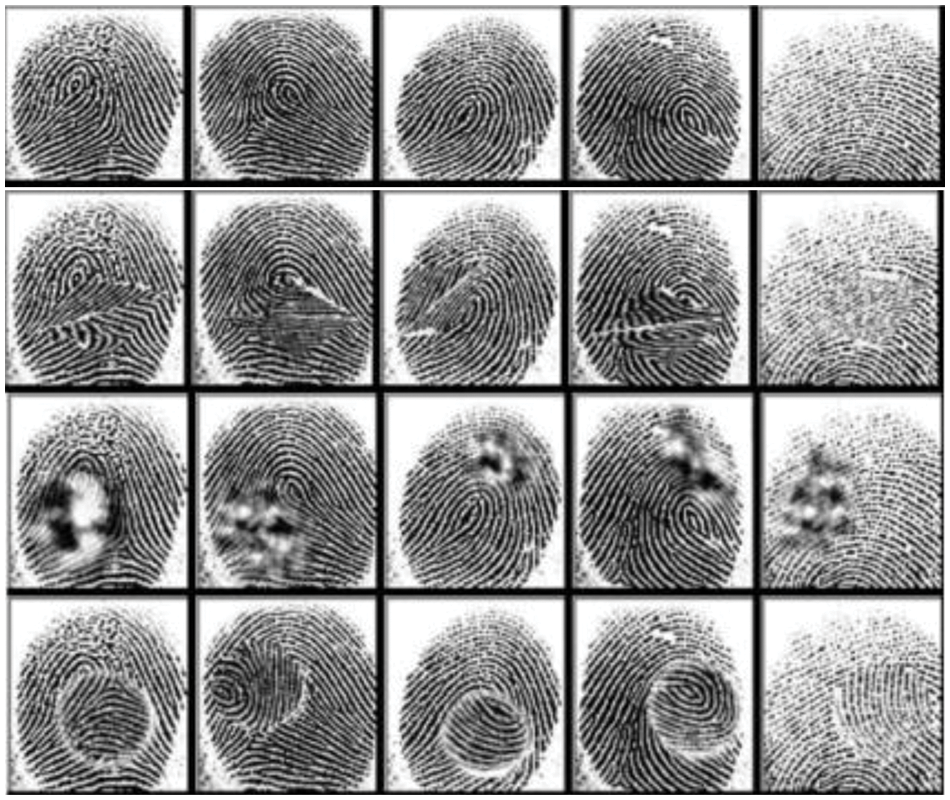
Figure 2: Some examples of fingerprint images in the dataset; real, Z-cut, obliteration and central rotation, respectively

We resized all the images in the dataset to 100 × 100 pixels; we then padded all the images to 106 × 106 pixels. This was the only preprocessing step to standardize the dimensions of all the images.

Our dataset consisted of fingerprint images of 600 subjects. Every subject had ten samples of his ten fingers giving a total output of 6000 fingerprint samples.

The last three categories in Fig. 2 represent the different types of alterations. This empowers our model to recognize distorted samples and match them with their real subject. Furthermore, some samples had changed in real life and become distorted due to many factors, so distorted fingers were applied more. Every alteration of the three we mentioned is around 6000 samples, resulting in 17,934 altered images with simple parameter settings. There are three settings—easy, medium, and hard. After dividing the dataset by subject, we randomly selected 100 subjects to generate the set (10 × 100 × 4 = 4000 images) divided into training, validation, and testing, as shown in Tab. 2.

We used the Python 3.8 version, Anaconda environment, and Jupyter Notebook for the implementation. We used Keras and TensorFlow libraries. We first trained and tested our model on the Kaggle website, but we alternatively used the Anaconda environment because of its limited memory and run time. Our network had two tasks to perform. One was to extract features; another was to classify the input image. Feature extraction was performed by the conv layers automatically. We used the “sparse_categorical_cross-entropy” loss and “Adam” optimizer for the classification task.

3.2 Preliminaries

In Fig. 3, one of the most important stages in the recognition or classification system is feature extraction. This stage can be implemented manually or automatically. The classical method uses the histogram of oriented gradients (HOG) features, which have many steps like preprocessing, calculating gradients, calculating a histogram of gradients, block normalization, and creating HOG description vectors. Then, we used a classifier such as support vector machines (SVM) or NN. Our system uses a CNN owing to its ability to extract features of input images automatically without human intervention, which saves time and effort. The feature map is a representation of the resulting image feature.

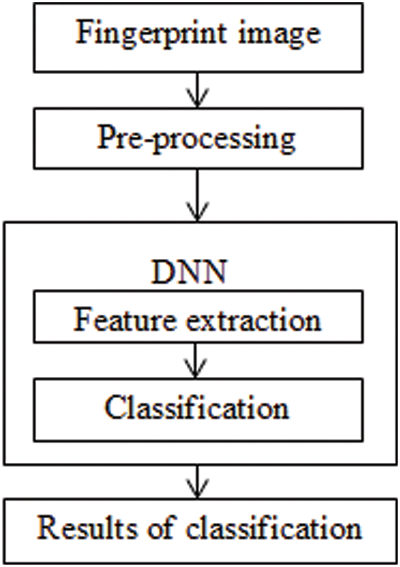
Figure 3: Main structure of the fingerprint classification system

Deep learning is a black-box technique, but the concept is that the network’s early layers can detect low-level features [20] (like colors, edges, etc.), and the later layers of the network can detect high-level features (like shapes and objects). Adding so many layers to a deep network is important to extract more complex features. We used this example to clarify these complex features; a person is composed of his head, hands, and legs. His head is composed of the eyes, nose, and mouth. His eyes are composed of edges and circles. The network must be deep enough to learn these features at different levels (see Fig. 4). Also, adding more conv layers to large-scale images is useful in learning features, and it decreases error and increases accuracy.

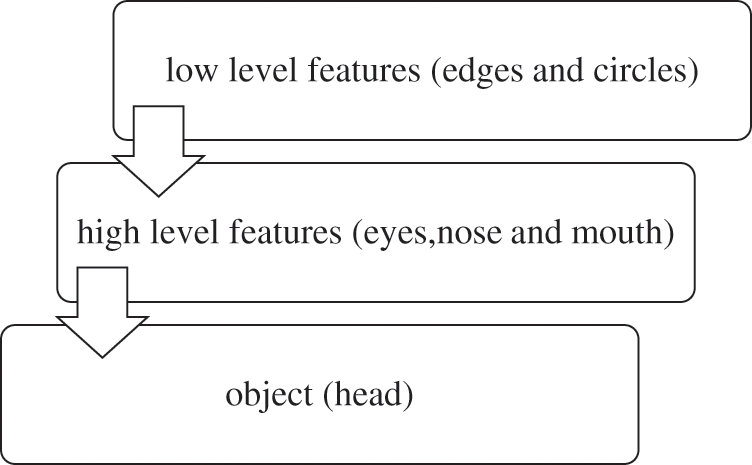
Figure 4: Hierarchical representation of the features

The image of a fingerprint is composed of dark lines. The important features of these lines are minutiae, which are low-level features. Furthermore, the size of fingerprint images is often small compared to natural ones (images of persons, animals, etc.). We can use shallow networks to extract minutiae for fingerprint recognition. Therefore, we can specify our network’s depth based on the complexity of the features and the size of the dataset images.

Our network is a residual CNN inspired by ResNet50 [11]. Then, we decrease the number of conv layers to learn minutiae features.

Despite the importance of adding layers to learn more features, there is a maximum threshold for depth in the CNN model [21]. The plot in Fig. 5 shows that the training error of the 20-layer is smaller than that of the 56-layer network.

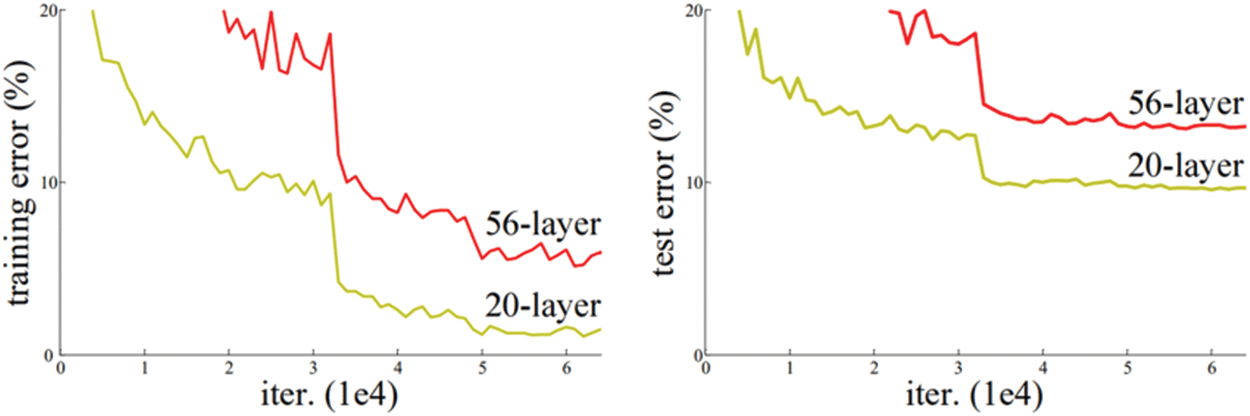
Figure 5: Training error on the left side and the test error on the right side in two cases, 56-layer and 20-layer networks on the CIFAR-10 dataset [21]

The failure of 56-layer CNN could be blamed on the famous vanishing/exploding gradient problem [22]. Before the residual technique, the very deep nets (100–1000 layers) could not converge during training; instead of adding more layers, we used residual convolutional networks, which alleviated the problem of training very deep networks and degradation problems [21]. So, our network classifying fingerprints did not have to be very deep, as our automatic system ensured that. This system will be discussed in the next section.

4  The Proposed Model

4.1 The Automatic System

For most networks, all the parameters are determined by constant values, for example, ResNet50 uses 64 filters in the primary stage. Why do we not start with fewer or more filters? Similarly with several layers, why do we choose a specified architecture whereas another achieves better results? In this research, we solved this conflict by using an automatic system. It is created automatically without any intervention by people, and it chooses to start with 32 filters and a specified number of layers which achieves the best accuracy.

After simple preprocessing, as shown in Fig. 6, we determined that as an initial number, the number of filters should be two or the user could input this number. Then, the system updates itself until it gets the best architecture with the best number of filters. In the first stage, our ResNet used 7 × 7 convolutions with stride 2, and the convolution process was implemented via the following equation:

(I∗K)xy=∑m−0k1−1∑q−0k2−1∑c=1nckm,q,cIx+m,y+qc+b (1)

where I is the input image, its dimensions are W, H for width and height, respectively. nc denotes the number of image channels. K is the kernel matrix with k1 * k2 dimensions. b represents a bias value for each kernel K. x = 0,…,H and y = 0,…,W.

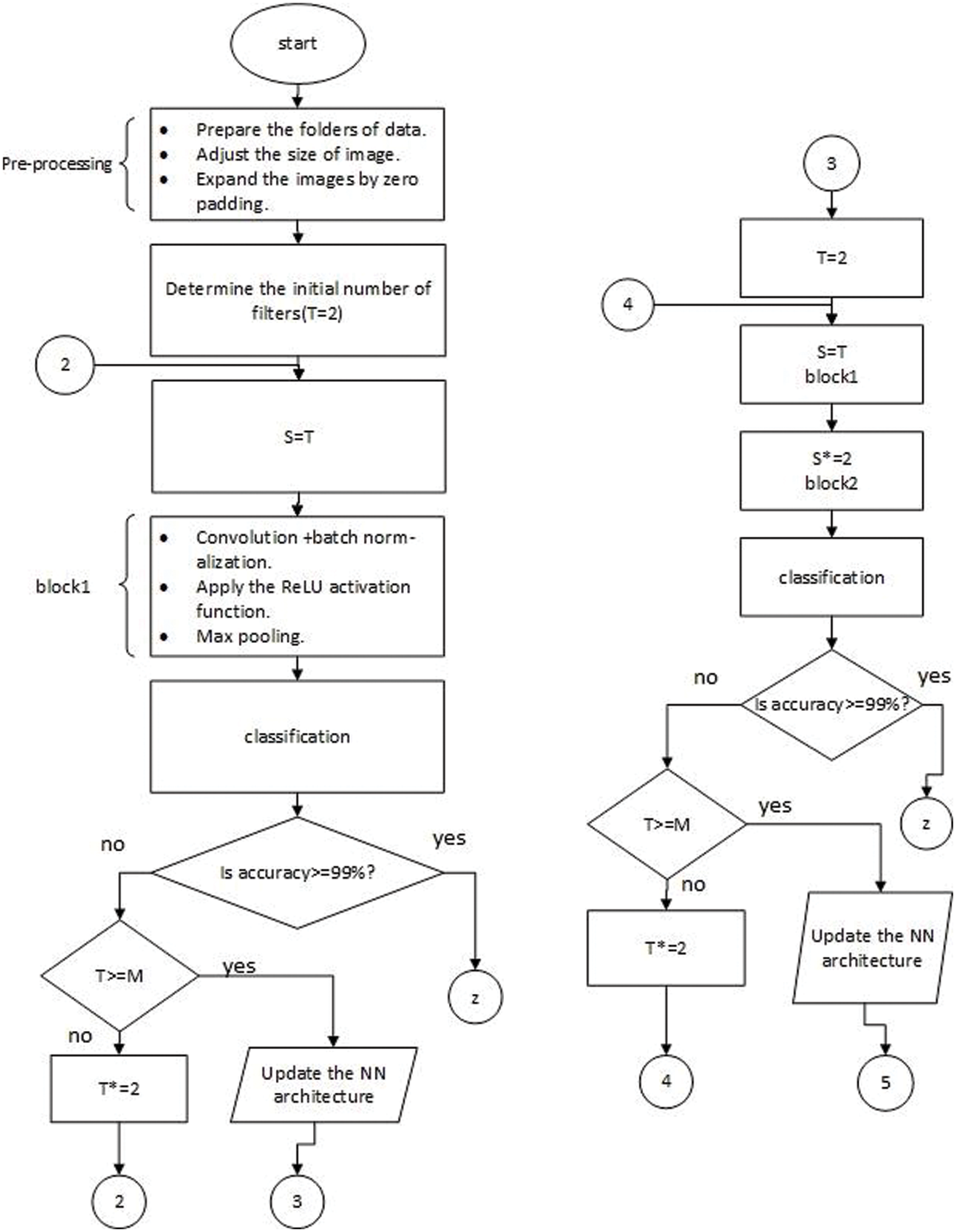
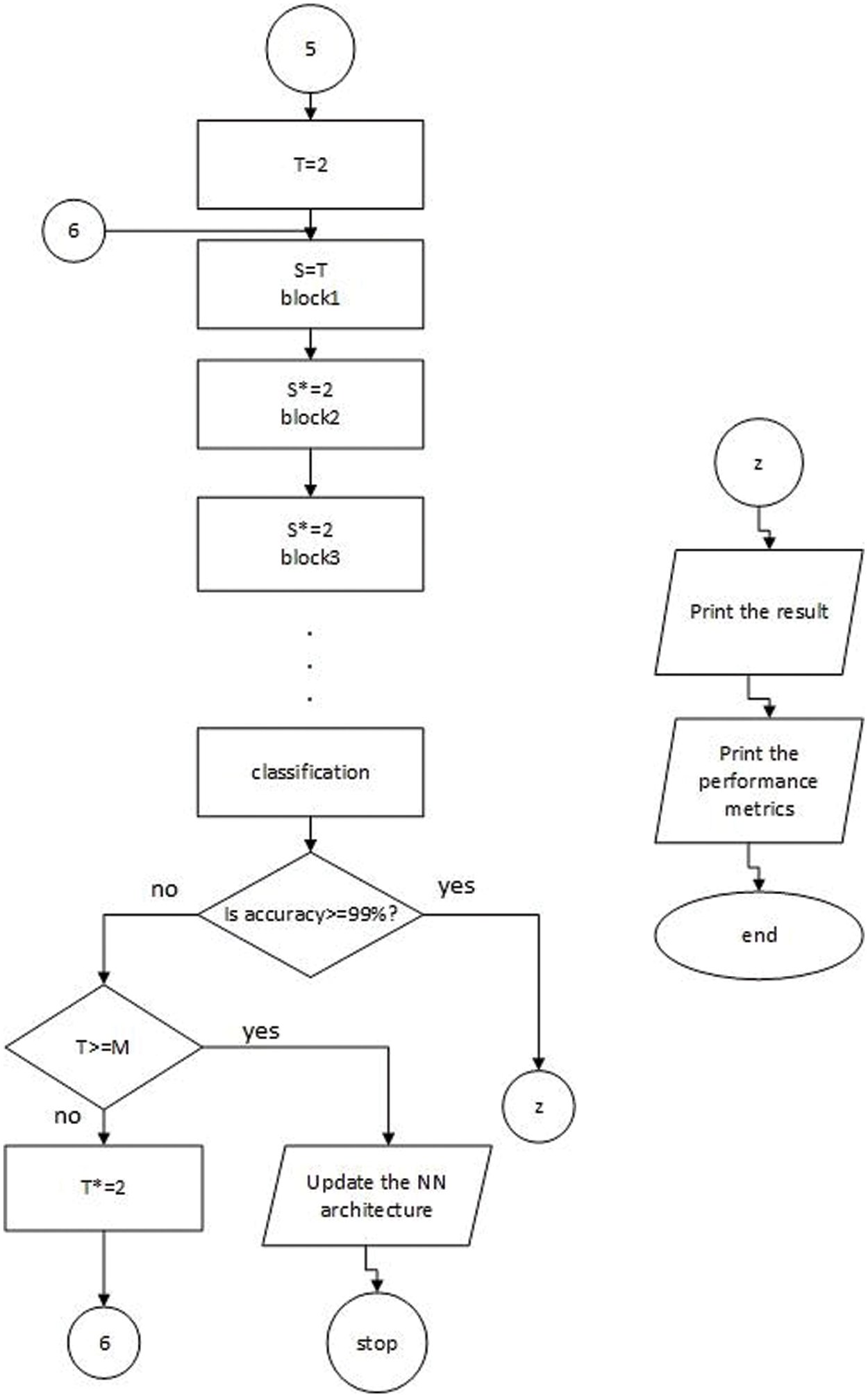
Figure 6: Detailed structure of the automatic system: Numbers 2, 4, and 6 represent looping in the same architecture, numbers 3 and 5 represent updating to another architecture, z denotes printing results, and T, S, and M denote the initial number of filters, filter number in the conv layer, and the maximum no. of initial filters, respectively

The dimensions of the output matrix can be calculated from the following equations:

nH=⌊nHprev+2p−fs+1⌋;s>0 (2)

nW=⌊nWprev+2p−fs+1⌋;s>0 (3)

Here, nH,nW denote the height and width of the output convolved image, and nHprev , nWprev denote the image height and width of the previous layer, respectively. f is the filter size, either width or height, as it is a square filter, p denotes the padding value, and s denotes the stride.

The main goal of the convolutional operation is to extract features and produce a feature map much smaller than the input fingerprint image.

Then max-pooling layer is implemented with a (3, 3) window size and two strides. The following equations calculate the dimensions of the image after pooling layers:

nH=⌊nHprev−fs+1⌋;s>0 (4)

nW=⌊nWprev−fs+1⌋;s>0 (5)

These two equations are applied for either average pooling or max one for the pooling process. After that, the downsampling occurs by convolution layers and one average pooling layer at the end. The outcome of the flattened layer would be 100, which is nourished straightforwardly into a dense layer (softmax). In this way, the network can assign the fingerprint image to the class it belongs.

In addition to the initial number of filters, this automatic system also allows the user to input epochs and iterations. Therefore, our model can control and specify these parameters (number of layers, filter number, epochs, and iterations). In Fig. 6, M and T represent the maximum initial number (no.) of filters and initial no. of filters, respectively. We determine M = 64; if T >= 64, the system updates NN architecture.

Notice that the number of filters in our system is 2n

when n = 1 no. of filters = 2,

n = 2 no. of filters = 4,

n = 3 no. of filters = 8 and so on.

This is because the experiments prove that when the no. of filters equals 2n , this achieves the best accuracy. Therefore, we chose to update no. of filters by twice as much. The threshold used depends on test accuracy.

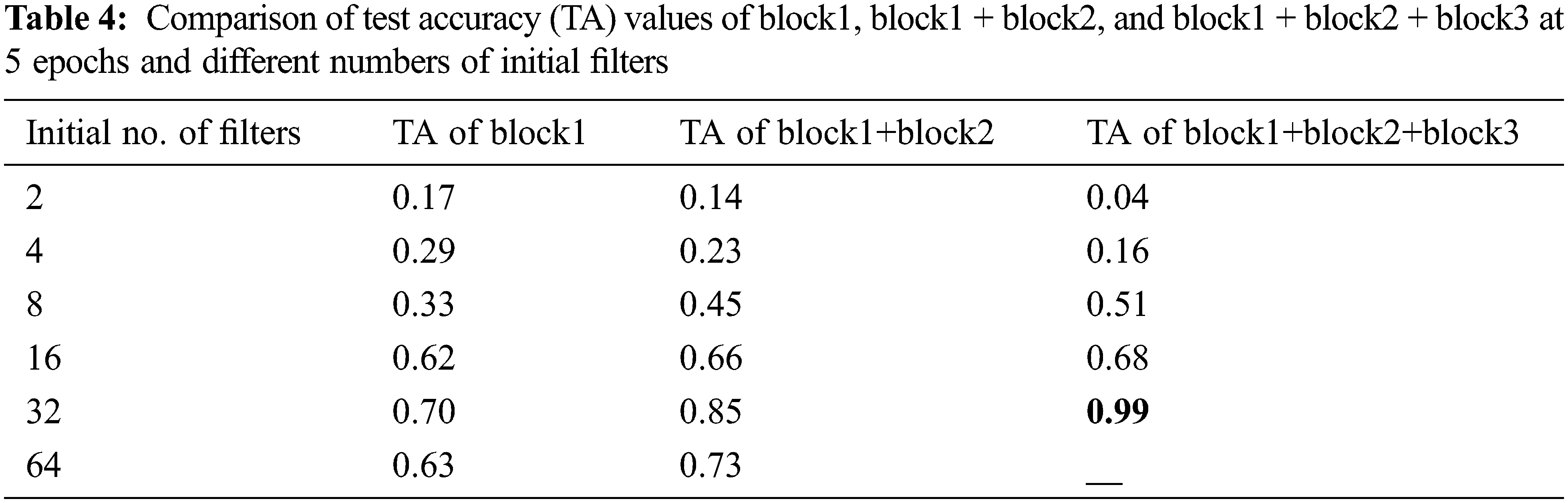
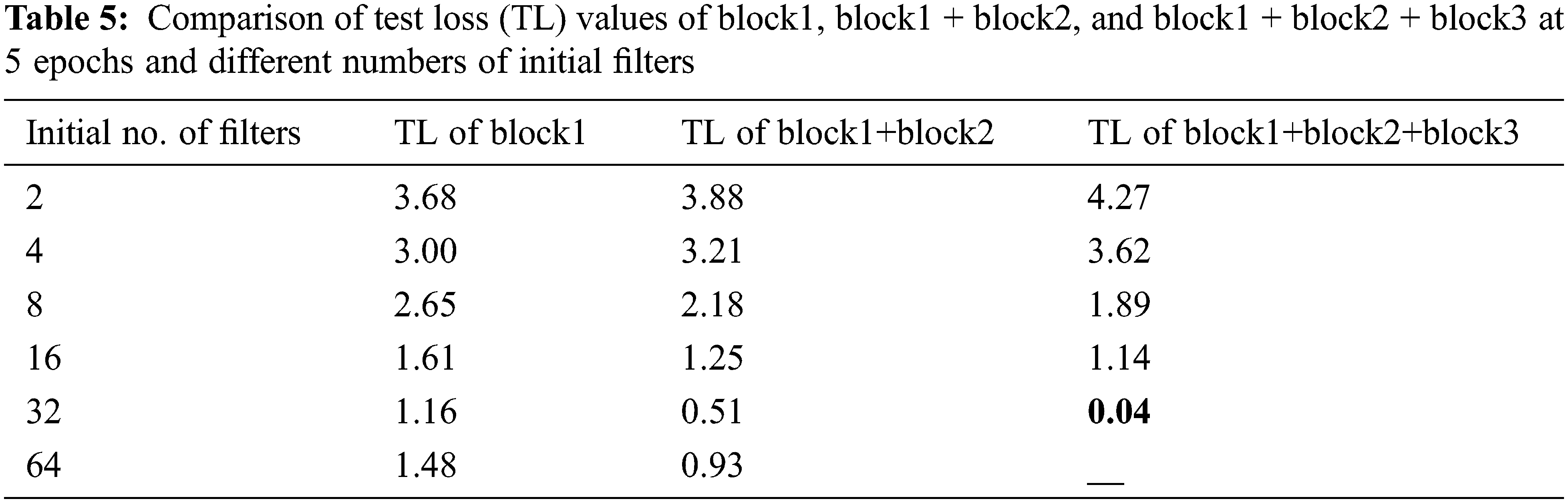
Although our system stops at block 3 when it achieves 99% test accuracy as shown in Tab. 4, the structure in Fig. 6 continues at this point to make the automatic system applicable to any goal and dataset. The last network with the best parameters is presented in the experiments and results section. Block 2, block 3, or any later block consists of an identity block and conv block discussed in detail in the next section.

4.2 Residual Neural Network

We designed the following model to solve the drawbacks of the studies discussed in Section 2. Counter to the plain network, a sequence of traditional conv layers followed by fully connected layers, the residual nets have shortcut connections adding the output from the previous layer to the convolutional layer ahead through element-wise add operation. This operation is performed on two corresponding feature maps, channel by channel. The resulting feature map is fed to the activation function in Fig. 7.

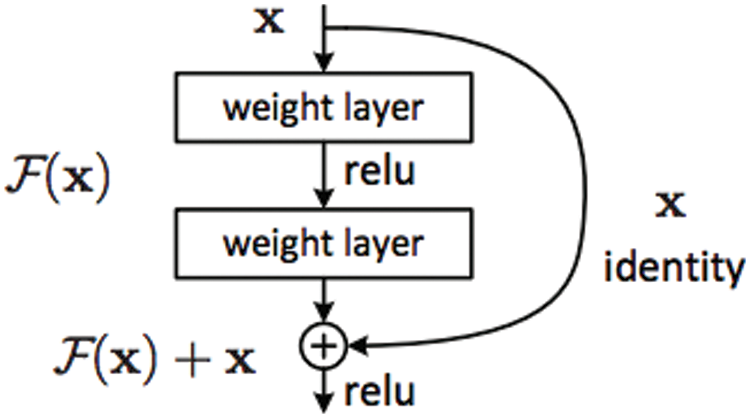
Figure 7: The building block of residual net [21]: X denotes the input of the first layer, and F(X) denotes the ReLU function where F(X) * weight = F(X); weight is constant

We used two residual blocks in our network—identity and convolutional blocks, as shown in Fig. 8. Each of them has two conv layers; each conv layer is followed by the batch normalization layer [23] and then the activation function. We chose a rectified linear unit activation function (ReLU) [24].

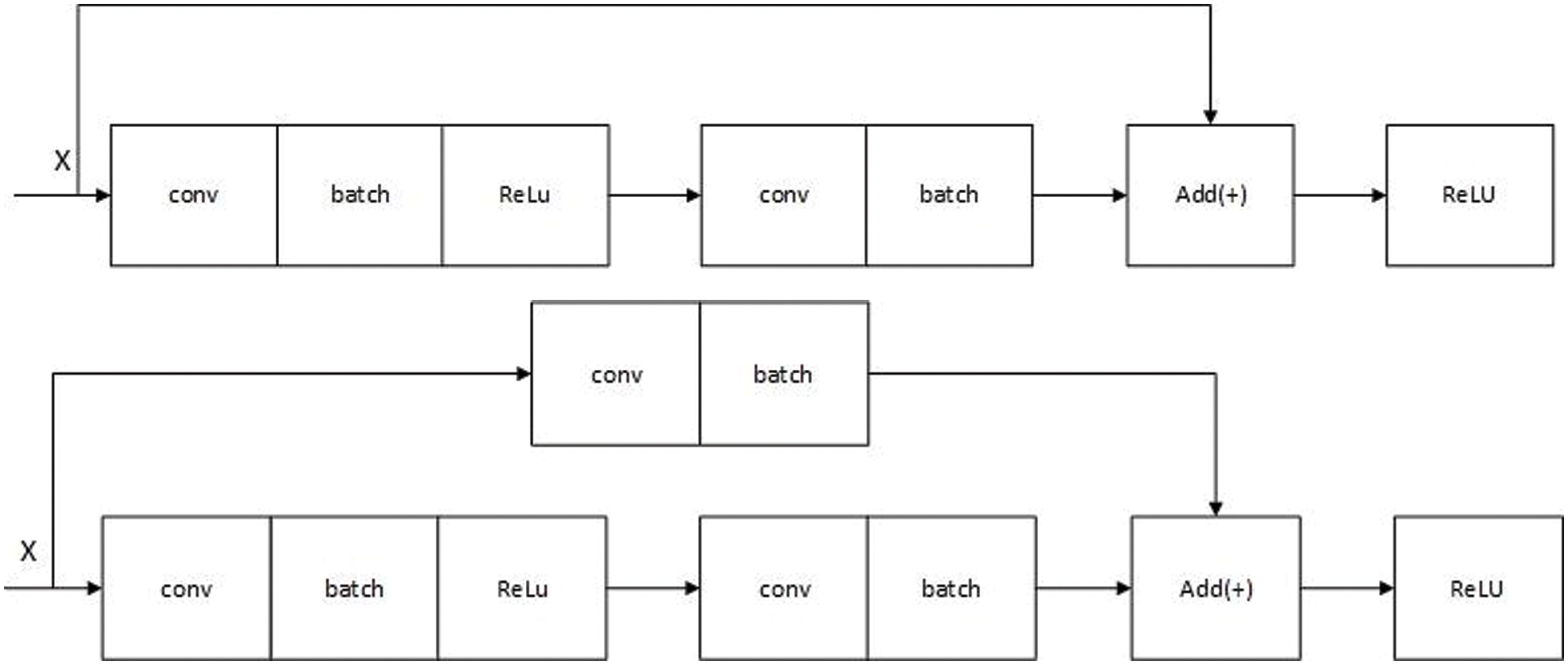
Figure 8: The first figure represents the identity block, and the figure below is the conv block where conv denotes the convolution layer, batch denotes the batch normalization layer, and X is the input of the first layer

The difference between the two blocks is the shortcut connection. The skipped connection of the identity block does not contain any parameters. It adds the two feature maps, but in the conv block, there are convolutional and batch normalization operations before the adding step. See the following figures:

The function of the identity block is:

ol+2=r(zl+2+ol) (6)

where r represents the RELU function, and function z represents the convolutional and batch normalization processes. o denotes the output of the layer assigned ( l ). l is the index of the layer.

We designed the equation of the conv block as follows:

ol+2=r(zl+2+z(ol)) (7)

The additional convolutional and batch normalization processes are represented by function z.

The dimensions of the two feature maps should be the same to implement the element-wise add operation. Hence, we use the padding is the “same” not “valid” to preserve the dimensions, and the stride is 1. This is for the identity block.

In the Conv block, the stride of the first conv layer is 2 to shrink the spatial resolution of the feature map. The stride of the next conv layer in this block is one, and the padding is “same.” In the shortcut connection, we implement the conv layer with stride 2 to make the two images in the same dimension. This step is responsible for reducing the dimensions of the feature map.

For the classification loss, we use sparse categorical cross-entropy as follows:

J(w)=−1N∑i=1N⁡(yilog⁡(y^i)+(1−yi)log⁡(1−y^i)) (8)

where w refers to model parameters, i is the sample size, yi is the true label for the ith sample, y^i is the predicted label for the ith input data, N is the sample size.

We used an adaptive moment optimizer to train the network (ADAM) [25], with a learning rate of 0.001 and an exponential decay rate of 0.9 and 0.999 for the 1st and 2nd moment estimates, respectively.

5  Experiments and Results

This section is divided into three subsections. First, we display our experiments implemented. Second, the final and best network is presented after applying the automatic system. Finally, we present the model results.

First, we implemented the ResNet50 model; it had good accuracy, but this model was not fast and required many epochs, unlike our model, which achieved better accuracy in the earlier epochs, conforming to the deep learning principle.

Then, the LeNet network [26] was implemented with the ReLU activation function as an example of a simple CNN, not a residual one. The accuracy was high, but it was still lower than our model, proving that our choice of the residual CNN is suitable for our data and goal. In the original LeNet architecture, you may find that the Tanh activation function was used, but we used ReLU instead of Tanh for good accuracy. Next, the MobileNet model [27] was implemented as an example of a light weight DNN. This model uses depthwise separable CNN [28–43].

Tab. 3 compares the three algorithms above and our algorithm. The four algorithms used the same SOCOFing dataset. The table clarifies that our algorithm has the highest test accuracy, F1_score and Recall and the least test loss. Furthermore, our algorithm has the least no. of parameters, conforming to the low complexity compared with other algorithms. The comparison chart between the four algorithms is shown in Fig. 9.

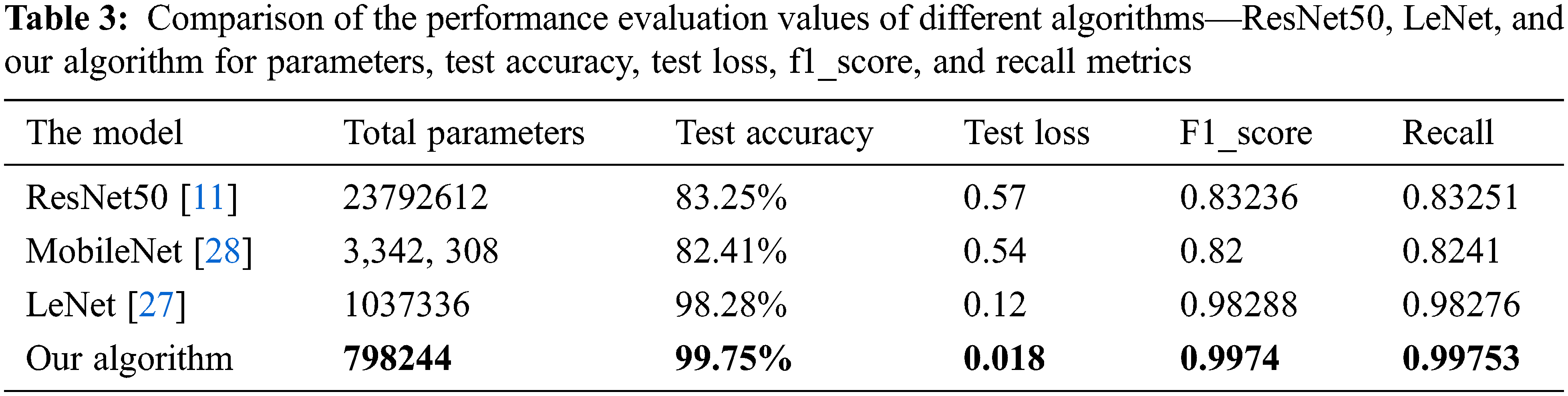
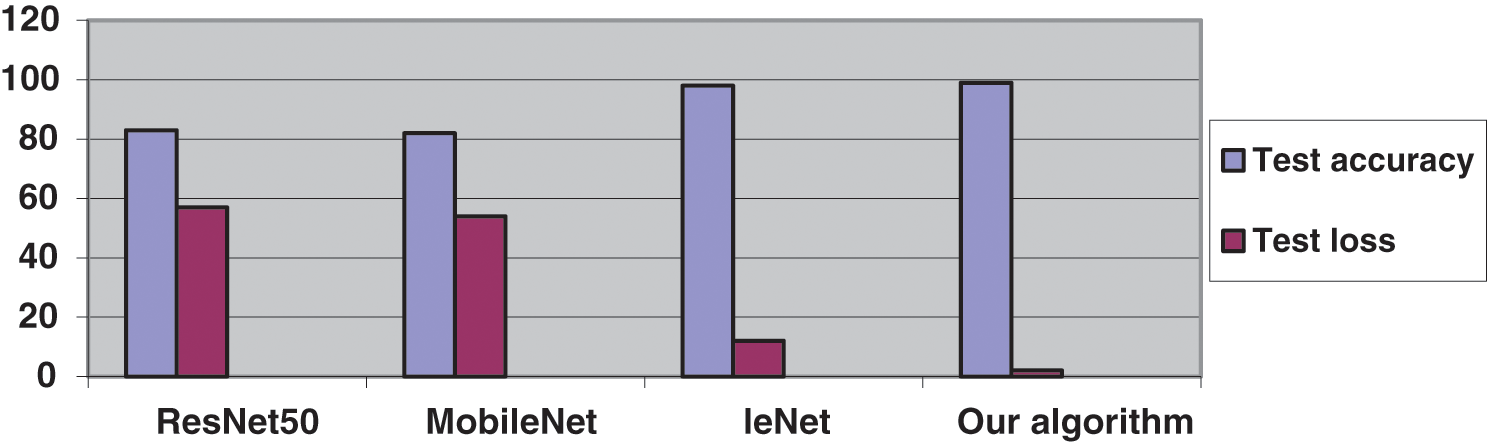
Figure 9: Comparison chart between the four algorithms, where the blue for accuracy and the purple for loss

Also, we tried the VGG-16 model [23], but it failed, and its implementation was not complete due to the small size of fingerprint images that do not suit very deep networks like VGG. As we mentioned earlier, these very deep networks are more suitable for large-scale images.

From these experiments, we could show that the advantages of our model are as follows:

•   The system is completely automatic and guarantees the best accuracy.

•   It is fast and works on the dataset without complex preprocessing stages.

•   It is easy to implement, and the network is not very deep.

•   It can recognize a person from any ten of his/her fingers, not just his/her thumb. Furthermore, it can recognize distorted samples.

Fig. 10 shows the last network architecture reached after applying the automatic system. In this figure, notice that all the kernel size of the convolutional layers in our net is 3 × 3 except the first conv layer, which has 32 filters and the stride equals 2, which has a 7 × 7 kernel size. The best value of the initial number of filters is 32. The window size and stride are (2, 2) for the average pooling layer. The dotted arrow represents the conv block. However, the ordinary one represents the identity block. In our step-by-step figure, every conv layer is followed by a batch normalization layer and uses a ReLU activation function. Our goal is to have our model automatically specify those parameters based on accuracy. Tab. 4 compares test accuracy (TA) values of block1, block1 + block2, and block1 + block2 + block3 at 5 epochs and different numbers of initial filters whereas Tab. 5 compares test loss (TL) values of block1, block1 + block2, and block1 + block2 + block3 at 5 epochs and different numbers of initial filters.

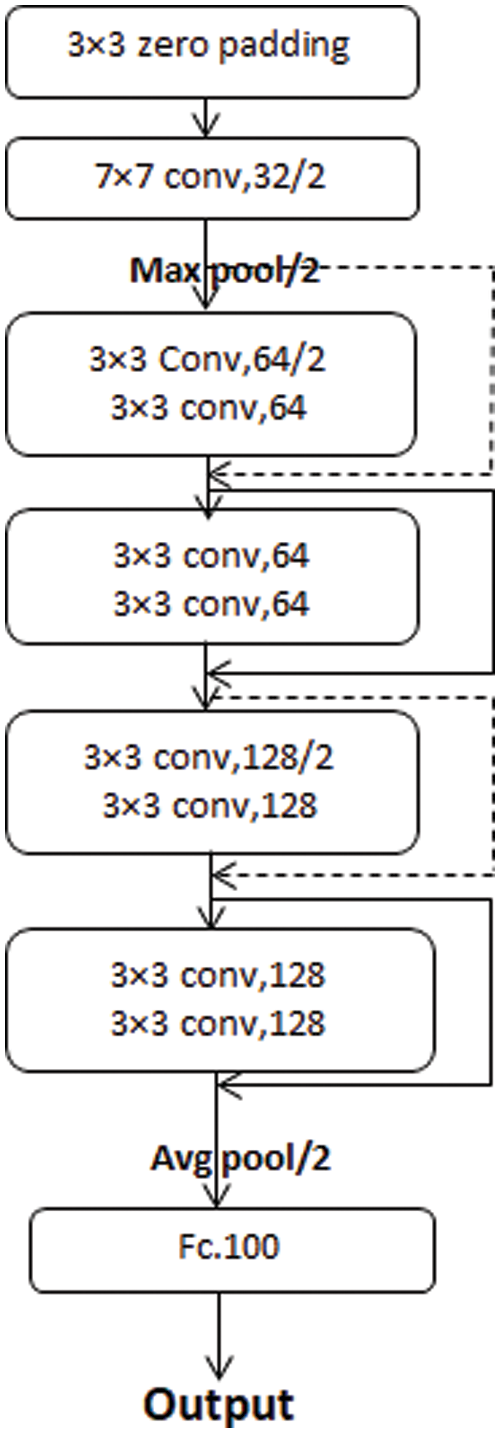
Figure 10: Step-by-step architecture of the best network where the conv denotes the convolutional layer, the max pool is the max-pooling layer, Avg pool is the average pooling layer, and Fc is a fully connected layer

We get this successful network after the following comparisons:

Notice that in each architecture, the value of test accuracy increases gradually until a specific point where it starts to decrease. However, using three blocks, we achieved the condition (99%), then the system stops.

The two previous tables show the most successful architecture for our goal and dataset, which contains 3 blocks and begins with 32 filters.

We used four performance metrics for evaluation—accuracy, loss, f1_score, and recall, which evaluated our model on our datasets and showed how successfully it classified the fingerprint samples. Tab. 6 shows the results of our model when applied to the dataset in easy, medium, and hard settings. In Fig. 11, the network’s accuracy and loss curves in the training and testing stages make it clear that there is not the overfitting problem.

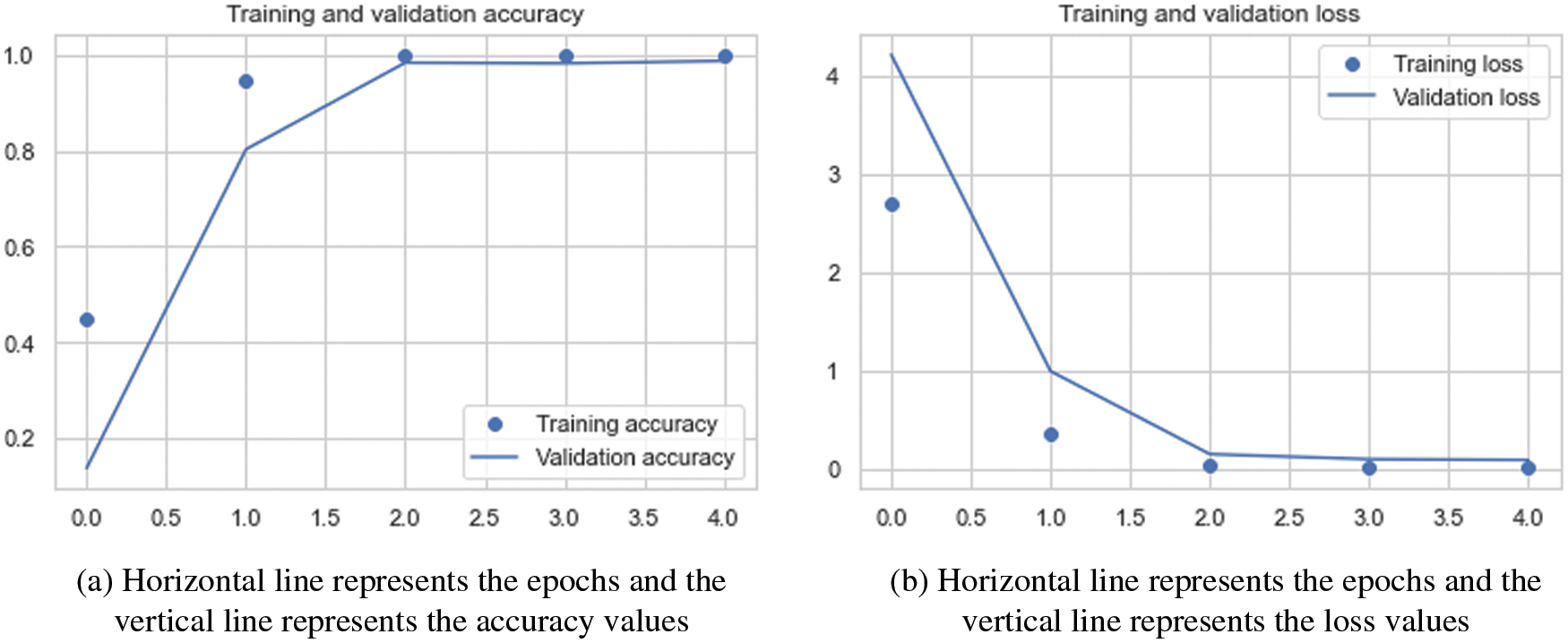
Figure 11: Accuracy and loss curves in the training and validation stages

6  Conclusion

We proposed a new and automatic system for fingerprint recognition, a residual convolutional neural network creating itself and achieving the highest performance. Our algorithm is substantially more efficient and faster than the other algorithms. Another useful aspect of this paper is the principle we have proposed, whereby the network should be deep according to the complexity of the features and the size of the images. We came to this conclusion after analyzing the properties of fingerprint images and previous convolutional neural network-based algorithms on fingerprints. Future work on the proposed fingerprint recognition algorithm will include: (1) attempting to automate the entire network by controlling all model parameters; (2) applying our algorithm to larger datasets; (3) implementing the algorithm to recognize other fingerprint types, like partial and latent fingerprints.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R54), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Data Availability Statement: The dataset is freely available in [19] at the following link https://www.kaggle.com/ruizgara/socofing

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R54), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. Zhang, J. Hu, F. Li, X. Ding, A. K. Sangaiah et al., “Small object detection via precise region-based fully convolutional networks,” Computers, Materials and Continua, vol. 69, no. 2, pp. 1503–1517, 2021. [Google Scholar]

 2.  R. Kumar, P. Chandra and M. Hanmandlu, “Statistical descriptors for fingerprint matching,” International Journal of Computer Applications, vol. 59, no. 16, pp. 24–27, 2012. [Google Scholar]

 3.  I. Iancu, N. Constantinescu and M. Colhon, “Fingerprints identification using a fuzzy logic system,” International Journal of Computers Communications and Control, vol. 5, no. 4, pp. 525–531, 2010. [Google Scholar]

 4.  K. M. Sagayam, D. N. Ponraj, J. Winston, J. C. Yaspy, D. E. Jeba et al., “Authentication of biometric system using fingerprint recognition with Euclidean distance and neural network classifier,” International Journal of Innovative Technology and Exploring Engineering (IJITEE), vol. 8, no. 4, pp. 766–771, 2019. [Google Scholar]

 5.  P. Balakrishnan, “Genetic algorithm for fingerprint matching,” WSEAS Transactions on Information Science and Applications, vol. 3, no. 4, pp. 1–14, 2006. [Google Scholar]

 6.  J. Fattahi and M. Mejri, “Damaged fingerprint recognition by convolutional long short-term memory networks for forensic purposes,” in 2021 IEEE 5th Int. Conf. on Cryptography, Security and Privacy (CSP), Zhuhai, China, IEEE, pp. 193–199, 2021. [Google Scholar]

 7.  A. I. Khan and M. A. Wani, “A common convolutional neural network model to classify plain, rolled and latent fingerprints,” International Journal of Biometrics, vol. 11, no. 3, pp. 257–273, 2019. [Google Scholar]

 8.  P. Tertychnyi, C. Ozcinar and G. Anbarjafari, “Low-quality fingerprint classification using deep neural network,” IET Biometrics, vol. 7, no. 6, pp. 550–556, 2018. [Google Scholar]

 9.  D. Peralta, I. Triguero, S. García, Y. Saeys, J. M. Benitez et al., “On the use of convolutional neural networks for robust classification of multiple fingerprint captures,” International Journal of Intelligent Systems, vol. 33, no. 1, pp. 213–230, 2018. [Google Scholar]

10. Y. Zhang, D. Shi, X. Zhan, D. Cao, K. Zhu et al., “Slim-ResCNN: A deep residual convolutional neural network for fingerprint liveness detection,” IEEE Access, vol. 7, no. 4, pp. 91476–91487, 2019. [Google Scholar]

11. P. Nahar, S. Tanwani and N. S. Chaudhari, “Fingerprint classification using deep neural network model resnet50,” International Journal of Research and Analytical Reviews (IJRAR), vol. 5, no. 4, pp. 1521–1537, 2018. [Google Scholar]

12. C. Li, F. Miao and G. Gao, “A novel progressive image classification method based on hierarchical convolutional neural networks,” Electronics, vol. 10, no. 24, pp. 3183, 2021. [Google Scholar]

13. L. Chang, Y. -T. Chen, J. Wang and Y. L. Chang, “Modified yolov3 for ship detection with visible and infrared images,” Electronics, vol. 11, no. 5, pp. 739, 2022. [Google Scholar]

14. T. A. Kumar, R. Rajmohan, M. Pavithra, S. A. Ajagbe, R. Hodhod et al., “Automatic face mask detection system in public transportation in smart cities using IoT and deep learning,” Electronics, vol. 11, no. 6, pp. 904, 2022. [Google Scholar]

15. J. Cao, C. Bao, Q. Hao, Y. Cheng and C. Chen, “LPNet: Retina inspired neural network for object detection and recognition,” Electronics, vol. 10, no. 22, pp. 2883, 2021. [Google Scholar]

16. V. H. Nguyen, J. Liu, T. H. B. Nguyen and H. Kim, “Universal fingerprint minutiae extractor using convolutional neural networks,” IET Biometrics, vol. 9, no. 2, pp. 47–57, 2020. [Google Scholar]

17. B. Zhou, C. Han, Y. Liu, T. Guo and J. Qin, “Fast minutiae extractor using neural network,” Pattern Recognition, vol. 103, no. 4, pp. 107273, 2020. [Google Scholar]

18. Y. I. Shehu, A. Ruiz-Garcia, V. Palade and A. James, “Detection of fingerprint alterations using deep convolutional neural networks,” in Int. Conf. on Artificial Neural Networks, Island of Rhodes Greece, Springer, pp. 51–60, 2018. [Google Scholar]

19. Y. I. Shehu, A. Ruiz-Garcia, V. Palade and A. James, “Sokoto coventry fingerprint dataset,” arXiv: 1807.10609, 2018. [Google Scholar]

20. J. Wang, Y. Wu, S. He, P. K. Sharma, X. Yu et al., “Lightweight single image super-resolution convolution neural network in portable device,” KSII Transactions on Internet and Information Systems (TIIS), vol. 15, no. 11, pp. 4065–4083, 2021. [Google Scholar]

21. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, IEEE, pp. 770–778, 2016. [Google Scholar]

22. Y. Bengio, P. Simard and P. Frasconi, “Learning long-term dependencies with gradient descent is difficult,” IEEE Transactions on Neural Networks, vol. 5, no. 2, pp. 157–166, 1994. [Google Scholar]

23. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Int. Conf. on Machine Learning, Lille, France, pp. 448–456, 2015. [Google Scholar]

24. G. Lin and W. Shen, “Research on convolutional neural network based on improved ReLU piecewise activation function,” Procedia Computer Science, vol. 131, no. 3, pp. 977–984, 2018. [Google Scholar]

25. U. M. Khaire and R. Dhanalakshmi, “High-dimensional microarray dataset classification using an improved adam optimizer (IAdam),” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 11, pp. 5187–5204, 2020. [Google Scholar]

26. Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [Google Scholar]

27. A. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang et al., “Mobilenets: Efficient convolutional neural networks for mobile vision applications,” arXiv: 1704.04861, 2017. [Google Scholar]

28. M. K. Hasan, M. T. Jawad, A. Dutta, M. A. Awal, M. A. Islam et al., “Associating measles vaccine uptake classification and its underlying factors using an ensemble of machine learning models,” IEEE Access, vol. 9, no. 12, pp. 119613–119628, 2021. [Google Scholar]

29. M. Masud, P. Singh, G. S. Gaba, A. Kaur, R. Alroobaea et al., “CROWD: Crow search and deep learning based feature extractor for classification of Parkinson’s disease,” ACM Transactions on Internet Technology (TOIT), vol. 21, no. 3, pp. 1–18, 2021. [Google Scholar]

30. K. Deb, M. Abouhawwash and J. Dutta, “Evolutionary multi-criterion optimization: 8th international conference,” in EMO 2015, Proceedings, Part II, Springer International Publishing, Cham, Guimarães, Portugal, pp. 18–33, 2015. [Google Scholar]

31. A. Nayyar, S. Tanwar and M. Abouhawwash, Emergence of Cyber Physical System and IoT in Smart Automation and Robotics: Computer Engineering in Automation, Germany: Springer, 2021. [Google Scholar]

32. A. Garg, A. Parashar, D. Barman, S. Jain, D. Singhal et al., “Autism spectrum disorder prediction by an explainable deep learning approach,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1459–1471, 2022. [Google Scholar]

33. M. Abouhawwash and K. Deb, “Karush-kuhn-tucker proximity measure for multi-objective optimization based on numerical gradients,” in Proc. of the 2016 on Genetic and Evolutionary Computation Conf. Companion, ACM, Denver Colorado USA, pp. 525–532, 2016. [Google Scholar]

34. A. H. El-Bassiouny, M. Abouhawwash and H. S. Shahen, “New generalized extreme value distribution and its bivariate extension,” International Journal of Computer Applications, vol. 173, no. 3, pp. 1–10, 2017. [Google Scholar]

35. A. H. El-Bassiouny, M. Abouhawwash and H. S. Shahen, “Inverted exponentiated gamma and its bivariate extension,” International Journal of Computer Application, vol. 3, no. 8, pp. 13–39, 2018. [Google Scholar]

36. A. H. El-Bassiouny, H. S. Shahen and M. Abouhawwash, “A new bivariate modified weibull distribution and its extended distribution,” Journal of Statistics Applications & Probability, vol. 7, no. 2, pp. 217–231, 2018. [Google Scholar]

37. M. Abouhawwash and M. A. Jameel, “KKT proximity measure versus augmented achievement scalarization function,” International Journal of Computer Applications, vol. 182, no. 24, pp. 1–7, 2018. [Google Scholar]

38. H. S. Shahen, A. H. El-Bassiouny and M. Abouhawwash, “Bivariate exponentiated modified weibull distribution,” Journal of Statistics Applications & Probability, vol. 8, no. 1, pp. 27–39, 2019. [Google Scholar]

39. M. Abouhawwash and M. A. Jameel, “Evolutionary multi-objective optimization using benson’s karush-kuhn-tucker proximity measure,” in Int. Conf. on Evolutionary Multi-Criterion Optimization, East Lansing, Michigan, USA, Springer, pp. 27–38, 2019. [Google Scholar]

40. M. Abouhawwash, M. A. Jameel and K. Deb, “A smooth proximity measure for optimality in multi-objective optimization using benson’s method,” Computers \& Operations Research, vol. 117, no. 2, pp. 104900, 2020. [Google Scholar]

41. M. Abouhawwash, K. Deb and A. Alessio, “Exploration of multi-objective optimization with genetic algorithms for PET image reconstruction,” Journal of Nuclear Medicine, vol. 61, no. 1, pp. 572–572, 2020. [Google Scholar]

42. P. Singh, M. Masud, M. S. Hossain and A. Kaur, “Cross-domain secure data sharing using blockchain for industrial IoT,” Journal of Parallel and Distributed Computing, vol. 156, no. 3, pp. 176–184, 2021. [Google Scholar]

43. A. Ali, H. A. Rahim, J. Ali, M. F. Pasha, M. Masud et al., “A novel secure blockchain framework for accessing electronic health records using multiple certificate authority,” Applied Sciences, vol. 11, no. 21, pp. 1–14, 2021. [Google Scholar]