Adaptive Cyber Defense Technique Based on Multiagent Reinforcement Learning Strategies

1  Introduction

In human society, learning is an essential component of intelligent behavior. However, each agent need not learn everything from scratch through their discovery. Instead, agents can exchange information and knowledge with each other and learn from their peers or teachers either directly or indirectly. When a task is too large for a single agent to handle, multiple agents may cooperate to accomplish the task. Applying this idea to the area of computer security opens the door to a new perspective on this debate. Do multiple agents have sufficient incentive to cooperate? What would cooperative multiple agents learn in the process? Will this cooperation result in quick and easy learning of attacker behavior? What insights can we glean from the success or failure of agents that learn to cooperate? Answering these questions would help us to re-evaluate current security solutions.

In our application, an agent can be any tool, software, and/or appliances used for monitoring, detection, and prediction such as the System Information and Event Monitoring (SIEM) solution, Endpoint Detection and Response (EDR), and a threat intelligence platform. Agent cooperation means all agents that are deployed and used to protect the monitored environment must cooperate to minimize the risk. They can cooperate by integrating and their findings can be correlated by a centralized system.

Evaluation of the security of information technology systems considers the interactions between a defender and an attacker. Attackers and defenders have opposite goals, where attackers aim, for example, to find vulnerabilities and exploit them. On the other hand, defenders aim to deploy robust and secure systems to reduce the attack surface, and this process usually starts by learning the attackers’ behaviors.

Current security solutions are mostly static and demand a long process to reconfigure if reconfiguration is even possible [1]. This gives attackers a sufficient amount of time to explore and exploit vulnerable systems. Defending against different types of attacks cannot be perfectly achieved by static security techniques. This motivates the recent study of adaptive cyber defense (ACD) which creates a changing attack surface based on information collected from an interactive environment. ACD-based solutions are promising to the configuration stativity and homogeneity problem [2–5] and are the most similar to human learning because the adaptive solutions can learn from their own experience by exploring and exploiting the unknown environment [6]. However, for better utilization of this advantage, we believe deploying multiple cooperating agents for the sake of increasing the quality of learning is essential, especially in real-time and adversarial environments.

In this paper, we focus on investigating whether multiple agents should cooperate or work independently to achieve a shared goal. We use the multiarmed bandits (MAB) decision-making strategy to show that multiple agents cooperate to increase their revenue. The objectives of the multiagent are first, to gather a body of useful information that when combined can draw a complete picture of the system threats. The second objective is to employ the optimal defense policy that could result in increased system security and a reduced attack surface.

In this paper, we do not consider a specific attack surface. However, we consider the attacker can penetrate the environment by compromising a machine and then have full accessibility to the environment. That said, the attacker then can apply a full cyber-attack kill chain [7] covering internal reconnaissance, initial access, foothold establishment, lateral movement, and data exfiltration.

This information can be related to a system’s vulnerabilities, threats, malicious activities, and security policy. We formulate the multiagent cooperation using a multiagent reinforcement learning strategy (MARL). An agent is loosely defined as a program that can exercise an individual’s or organization’s authority, work autonomously toward a goal, and meet and interact with other agents and their environments [8,9].

We consider developing a learning-based defense that performs superior reconnaissance and possesses greater understanding than a randomized defense policy. The idea is that multiagents sense and provide information from an interactive environment to make changes to the system’s configuration every so often based on observed and shared knowledge, which should reduce the attacker’s chances of success. Our contributions in this paper can be summarized as follows:

•   We provide insight into how multiplayer MAB is a desirable strategy for players’ cooperation.

•   We demonstrate how multiagents can learn and communicate regarding sharing useful information and cooperating to protect a targeted system and increase their rewards.

•   We deploy a game-theory-based solution to minimize the attacker’s rewards.

•   We implement our approach in a real OpenStack system to validate our defense strategy.

The rest of the paper is organized as follows. In Section 2, the related work is presented. The system model and problem formulation are presented in Section 3. Section 4 describes our approach. Finally, Section 5 concludes this paper.

2  Related Work

Nicholas et al. [10] show that most multiagents have a common setting. As individuals, they have incomplete information about the environment, no centralized control, and the information is distributed and decentralized throughout the environment. Pamait et al. [11] detailed two features of multiagent learning: (a) the search space in multiagent learning can be unusually large because it addresses problem domains involving multiple agents, and due to the interaction of those multiple agents, small changes in learned behaviors can often result in unpredictable changes in the resulting macro-level (“emergent”) properties of the multiagent group as a whole; and (b) multiple learners can be involved in multiagent learning, where each learns and adapts in the context of others.

Ming [12] reported that if cooperation is performed intelligently, each agent can benefit from other agents’ instantaneous information, episodic experience, and learned knowledge. They identified three means of cooperation among multiple agents: (a) agents can share instantaneous information such as sensation, actions, or rewards; (b) they can communicate episodes, which are sequences of sensation, action, and reward that have been experienced by agents; and finally, (c) agents can share the learned decision policies. In [4], Xiaorui et al. surveyed several papers that applied reinforcement learning to cybersecurity research issues. In [13], Aidin et al. modeled the interactions between two players (i.e., the attacker and defender [Anti-Virus]), in a game-theoretic fashion by applying deep reinforcement learning instead of directly deriving a solution based on the mixed-strategy Nash equilibrium analytics [14].

In [15,16], reinforcement learning methods were demonstrated to be effective in various intrusion detection system (IDS) applications. However, the authors elaborated on the drawbacks of anomaly-based and signature-based detection techniques. The authors then demonstrated a reinforcement learning-based IDS where a collaboration of reinforcement learning methods, including rule learning and log correlation techniques, enables the system to choose more appropriate log files in searching for traces of the attack. In [17], Ravindra et al. proposed a multiagent intelligent system utilizing reinforcement learning and an influence diagram. The proposed approach enables immediate responses against complex attacks where all agents learn from shared information within the environment. However, the proposed approach was not implemented to show how the agents can share information and reduce the attack surface. Abhishek et al. [18] proposed a filtering scheme to detect corrupted measurements and mitigate the effects of adversarial errors through state-based information, where the information obtained at each state is considered as input to decide if a current state is damaged and whether a new state should be generated.

Although the idea of utilizing reinforcement learning and multiple agents in cybersecurity has been discussed in previous research, we believe our proposed approach can act as a starting point for other papers interested in sequential dynamic games.

3  System Model and Problem Formulation

3.1 Motivation Scenario

Current security solutions such as IDSs, intrusion prevention systems (IPSs), and firewalls are designed to monitor incoming traffic and observe patterns of activity in user accounts and to generate alerts if unusual activity is detected. These methods are “static” and cannot prevent possible information attacks beforehand. Typically, they use predefined filtering rules to prevent illegal network access; however, implementing effective intrusion detection capability is an elusive goal that cannot be solved easily or with a single mechanism.

For instance, firewalls do not inspect the contents of incoming traffic. Thus, if a valid application contains malicious content such as viruses or worms they will not be detected. Furthermore, firewalls or system guards cannot stop denial-of-service attacks and are ineffective in detecting internal attacks. IDSs are designed to initiate detection of network intruders or hackers. IDSs usually audit records, network packets, or any other observable activities to detect abnormal activities in the system or check them against known intrusion patterns (signatures). The signature-based intrusion detection method does not work against new or unknown forms of attack. The anomaly intrusion detection method is ineffective in detecting inside attacks. Thus, any intrusion detection system that employs only one of these methods will detect only a limited range of intrusions [19].

Furthermore, many sophisticated attacks, such as advanced persistent threats (APTs), have emerged with a variety of different attack forms. APTs employ a wide range of sophisticated reconnaissance and information-gathering tools, as well as attack tools and methods [7]. However, existing deployed security systems are generally optimized for processing a large amount of system data (e.g., event logs) and are, therefore, highly automated. This makes the detection of sophisticated, intelligent, and complex attacks difficult. Although these systems can identify individual characteristics of an attack, it is often necessary to perform an additional investigation of complex attacks to reveal all malicious activities. Thus, due to the stealthy nature of APT attacks, where the sequence of malicious activities is performed at low frequency, any proposed security system must be robust and able to accurately reveal important hidden details in the system that can lead to detecting intelligent malicious activities.

Therefore, with the variety of possible defensive mechanisms and different detection techniques that can be deployed to handle the aforementioned threats, a decision-making system that gathers information from multiple agents becomes a necessary component for the following reasons:

a)   Different detection techniques analyze different portions of enterprise traffic (e.g., network traffic and system data) with different goals.

b)   Different recommended security solutions issued by different security agents may enhance security risk assessment when they are combined.

c)   Peer relationships among cooperative multiple agents are needed when different administrations manage portions of an enterprise network or distinct and separate networks [5].

d)   Multiple agents can provide diversity in task handling—for example, having specialized agents focused on specific classes of intrusion, such as coordinated attacks that occur over long periods from multiple sources.

3.2 Reward Modeling

MAB is often used in dynamic decision-making systems to investigate the trade-off between exploring and exploiting. It is presented with multiple slot machines, where, in each turn, the player can pull the arm of one of the slot machines and receive a reward. Each arm is associated with observation, transition, and reward. The player can play multiple trials to explore or exploit a system. Once they have explored the system, they have to decide whether to exploit the found-well-paying-arm or to approach another set of alternatives (arms) to maximize the total payoff.

The model in the literature is often introduced as a player who visits a casino and attempts to maximize their profits by pulling the arms of different K “bandits” (a.k.a. slot machines). The player has to choose between K bandits over many T turns. In each turn t∈{1, …, T} , they will select one of the bandits n∈{1, …, K} , which then results in a reward cn,t from pulling its arm. This reward is decided upon by the slot machine n. In this paper, we study a related problem in which two players pull the arms of an MAB, and each maximizes their reward.

Multiplayer MABs have seen limited study in terms of gaining insights into multiagent cooperation in the recent literature. In [20] and [21] the authors investigated a multiplayer MAB in which at each time epoch, users compete for arms of the MAB that yield independent and identically distributed (i.i.d.) rewards for each pull. In this way, the players collectively and quickly learn the best arms, even with no direct information sharing, by inferring the best actions based on the action profiles of other players. In both works, the authors establish the policies that enforce a degree of “fairness” between players and come up with lower bounds with respect to overall regret of the system. Although they do not explicitly use the MAB formulation, [22] investigated cooperation in a cognitive system with learning. Similarly, they found lower bounds on system regret with respect to throughput.

3.2.1 Multiplayer MAB

In this subsection, we begin by formulating the two-player MAB. At each time epoch t, the system state for an n-bandit problem-is given by the vector X= (X1)X=(X1,   X2,  …,  Xn) , where X is the state of the ith bandit. Each player at each time epoch has n actions available, corresponding to each arm of the bandit. Letting N=(1,  …,  n) under action a∈N , the system transitions from X=(X1,   Xa,  …,  Xn) to X′=(X1,   X′a,  …,  Xn) according to the Markov process of arma guided by transition matrix Y, and the player who engaged in the action receives a reward cXa′ . Letting π be a policy that maps the system state and letting X under action a∈N , the expected reward for Player 1 in a t epoch game is generated by Eq. (1)

maxπ1⁡E[∑k=1tβk(−1)k+1+12cXπ1(Xk)k] (1)

where Xk is the system state at time k and β ∈(0, 1] acts as a discounting factor. Note that the above equation is nonzero only at odd epochs, which implies that Player 1 plays first. Furthermore, we suppress the dependence of X  on the policy since we will eventually show how to compute optimal strategies and payoffs in a dynamic programming formulation. Now, from the perspective of a single player, since we model this game assuming each player is rational and self-interested, their optimal strategies and expected payoffs can be modeled using a restless MAB (RMAB).

Lemma 3.1 (RMAB Formulation). Each player’s optimal strategy and expected payoff can be modeled using an RMAB.

Proof. Since each player is rational and tries to maximize their expected reward, at time t, the system state transitions from X to X′ according to Player 1’s optimal action a, after which Player 2 chooses an optimal action that changes the system state to X′′ . We can model this as an RMAB where, from the perspective of Player 1, after any given action, each state of the system changes with probability 1 to a state where each action other than the optimal action for Player 2 yields a reward of −∞ and the reward for choosing the optimal action for Player 2 yields a reward of 0, which transitions the system into a state that again can yield rewards for Player 1. This is an RMAB since, after each action, the multiple arms of the system change state and is possible since Player 2 is assumed to act optimally. This formulation gives us some insight into the difficulty of the problem. RMABs themselves are in general NP-hard and PSPACE-hard to approximate (see [23] for complexity details and proofs). Furthermore, to generate the RMAB environment, the optimal policy for another player must be established, which further adds to the complexity of the system. However, in small problem instances, our problem still maintains computational tractability. We solve the system through the following dynamic program that operates backward in time. Thus, the optimal policy for Player i is determined by the dynamic program as shown in Eq. (2)

Vti=mina∈𝒩∑X′YX,X′(cXa′+β2∑X′′YX′,X′′Vt−1i (X′′)  (2)

with terminating state V0i (X)=0 and where the outer summation is with respect to player i ′s action and the inner summation is with respect to the opposite player’s optimal action. Thus, in solving for Vt1 , we must solve Vt2 and Vt−11 , and solving for Vt2 requires solving Vt−11 and Vt−12 since we assume Player 1 plays before Player 2.

3.2.2 Birth Processes

Suppose that each arm i of our MAB operates as a pure birth process with retirement and its states are labeled s1,i . . . smi,i as in Fig. 1. In this way, each state transitions only to itself and the state ahead of it with positive probability, and after the state has reached smi,i , it is retired and can no longer be used as an action. For this reason, we assume a dummy arm that generates zero rewards and has infinite states so that the players always have a valid action.

Figure 1: One arm of the MAB under a pure birth process. The arrows signify a positive probability of transition after a “pull” of the MAB. We assume that the arm retires after transitioning to smi,i

In such a scenario, it would seem that the first player has an advantage over the second player since they always have the option of waiting available to them, effectively “passing” their turn. Indeed, this turns out to be true in the case of pure birth processes but is not necessarily true in the more general setting.

Lemma 3.2 (Player 1 Advantage). Player 1 receives a larger cumulative reward than Player 2.

Proof. The proof is immediate, noting that if there were any advantage to passing the first turn, Player 1 could simply choose to pull the dummy arm and delay their turn. Player 2 then either delays or obtains a reward that is discounted by β from what Player 1 could have achieved.

In some applications, it is natural that the system experiences decreasing rewards over time for each arm. This type of problem arises when each arm of the MAB experiences a positive probability of degrading each time it is used. In the case of a system that experiences pure degradation, we find that the optimal policies for both players are myopic.

Lemma 3.3 (Decreasing Rewards). If Cj,i > Cj+1,i  for each i∈ 𝒩 and j ∈ {1, …, mi},  each player’s strategy is myopic.

Proof. The proof is obvious because each time an arm is pulled, the system state is worse for both players. Since the entire system is degrading, any action will not yield a state for that player that is better than the current state, which is the only incentive for not following a myopic discipline. Thus, both players must play greedily. In this paper, we apply the reward modeling to an application where attacker and defender obviously do not have to cooperate.

A pure birth process only experiences positive rewards when the system transitions to the final period (i.e., when smi−1,i→smi,i can be used to model events like job completion). However, in a two-player game, the player who brings the system to state smi−1,i may be penalized since the other player, to maximize their rewards, may bring the system to smi,i and take the completion rewards instead of the first player, regardless of past efforts. Thus, for the purpose of designing a “fair” process for multiple players, we modify such a modeling technique and let cmi−1,i=cmi,i with the transition probability of smi−1,i→smi,i=1.

Lemma 3.4 (Final State Rewards)

If Cj,i=0 if j≠mi or mi−1 and cmi,i=cmi−1,i>0 with the probability of smi−1,i→smi,i=1,  in an infinite horizon setting, both players will choose to prioritize the same arm until it is retired.

Proof. The proof is obtained by a sample path argument. Suppose both players choose any policies that are myopic when a state is in smi−1,i (which guarantees a reward of discounted cmi,i ). In a given path, suppose the first reward a player receives βtcmi,i is for transitioning smi−2,i→smi−1,i at time t. This guarantees the other player a reward of βt+1cmi,i on the next epoch. If it took τ<t “pulls” of class i to obtain this state, the rewards are increased to βτcmi,i and βτ+1cmi,i , respectively, if both players work together without reducing their future rewards (by working together in the future in a similar manner). This proves the assertion.

3.3 Reinforcement Learning (RL) Model

RL is used in cooperative multiagent systems for different problems [24]. In this paper, we formulate the RL in MAB fashion, where multiagents are attempting to protect a virtualization networking system in cloud computing and maximize the utility through learning from acting in their environment.

In the real world, the multiagents (i.e., security agents), for example, IDS agent, IPS agent, firewall agent, and cybersecurity threat intelligence (CTI) agent, do not have to directly communicate to learn from each other. Instead, they can provide their observations (explorations) to a single point (e.g., the security operation center [SOC]). That said, we consider multiagents to work independently and each agent can be configured to observe intrusions within its coverage; for example, having an IDS configured to monitor either network traffic or system events to detect any intrusion that matches predefined rules. In this case, if any suspicious activities are observed, then alerts will be generated. However, the security team usually will deal with this alert as a single event. Another issue is that this alert might be a false positive that could consume resources to figure out. With this same perspective, all other agents may result in heavy resource consumption if not integrated. Therefore, applying RL can utilize different reported alerts to increase the coverage and minimize the attack surface. In the following Eq. (3), we can see how to maximize the value of each state based on actions taken and on rewards.

V∗(s)←∑s′τ(s, a, s′) ×[R(s, a, s′)+δV∗(s′)] (3)

The interactions between multiagents can drastically increase the complexity with their action space. However, investigating this point is beyond the scope of this paper.

For the goal of deploying MAB in our research area, we make the following assumptions on the model:

•   Instead of having multiple agents explore and exploit, we decouple exploration and exploitation.

•   Agents can still explore the system and report their findings to a centralized defender; in our system, this task is assigned to the SOC.

•   Agents’ observations are collected and processed by the SOC.

•   The SOC can either exploit or wait for other explorations.

•   The SOC calculates the global reward based on the received explorations from system security agents.

In each round of this game, every agent chooses an action a from its finite set of individual actions (action space). In the learning process, these actions are executed simultaneously, and the reward that corresponds to the joint action is exchanged with the centralized security center. A more formal account of this type of problem was given by [25]. The security center should explore the use of moves that have been attempted and exploit those for which the confidence of receiving a large reward is relatively high. Thus, the reward of the taken previous action ap can be formed by a score that can be used to decide whether to explore or exploit. This cooperative game is designed based on an RL strategy. It concerns how to map specific process conditions and then select a suitable policy to distribute learned malicious activities (rewards) to maximize some notion of long-term reward to satisfy process performance goals.

Assume the multiagents act simultaneously, where each agent monitors different parts of the network to lead to an immediate reinforcement that is used to build confidence in selecting optimal countermeasures and policies. These interactions between the security center and its environment, through its embedded agents, run continuously, to help the security center learn a decision-making strategy that maximizes the total reward. Afterward, the security center can start implementing a sequence of actions based on the side information learned from the environment. More formally, given a set of possible side information values Y, a set of possible actions Y, and a set of reward functions R ⊂ {r : y ×a→R} at each time epoch, the agent can learn some side information yt ∈Y . Then, they can take an action at ∈A  based on the gain, while the environment simultaneously chooses a reward function rt ∈R . Consequently, the agent will receive a reward rt(yt, rt) .

The action selection strategy is an important step to avoid taking random action; for example, the ε−greedy  strategy treats all of the actions, apart from the best action, equivalently. However, we could select an action with a weighted probability depending on the value of {EV(action)}. This is known as soft-max action selection, and the common approach to use is the Boltzmann strategy [26] which states that an agent chooses an action to perform in the next iteration of the game with a probability that is based on the agent’s current estimate of the usefulness of that action, denoted by EV(action) in this Eq. (4) [27]:

P(action)=expEV (action)T∑action′∈ AiexpEV (action′)T (4)

where T>0 is the temperature specifying how randomly actions should be chosen. When T is high, actions are chosen with almost equal probabilities. However, when the temperature is reduced, the highest-valued actions are more likely to be chosen, and in the limit of T→0 , the best action is always chosen. The expected cumulative regret for Boltzmann exploration is also linear.

One of the greatest advantages of the ε−greedy strategy is that the information about the value of other actions can be taken into consideration. For example, if multiple actions are available to Agent x, for example, three actions, when applying the ε−greedy strategy, two of the three actions are estimated to be nonoptimal and considered equally. However, the Boltzmann strategy considers that the actions are weighted by their relative value, which helps the security center to select the most promising action.

Fig. 2 presents the idea of deploying an interactive environment where multiple agents send their observations to the security center. This model helps in learning and detecting malicious activities in the monitored environment. It consists of several interrelated security modules (multiagent) {agenti, …, agentn} . These multiagents generate intrusion alerts based on their assigned tasks and configurations. For example, if an EDR is deployed then it can be configured to monitor any intrusion at the system level. In addition, other received alerts from other deployed agents can increase confidence once all alerts are correlated at the security center. The security center inspects all received alerts to extract useful information about attacker movements in the system, such as their target, preferences, and launched attacks. Also, extracted information along with system static information “vulnerabilities” can assist the security center to evaluate the countermeasure deployment process at present t. This helps us to analyze the attacks that occurred since the last countermeasure deployment at time t−1 and deploy a new countermeasure if necessary.

Figure 2: Multiagent and security center interaction

Developing observations (i.e., a knowledge base) can help in taking future actions and also avoiding reprocessing of the same actions that harm the global reward. The security center can update the knowledge base if new knowledge is observed. The knowledge base consists of reward tables, actions that have been taken, system responses, previous state, and the current state. Since the security center has a global view of all working agents and their responsibilities in terms of their tasks and which parts of the system they monitor, updates to any agent’s configuration, if necessary, can be based on the knowledge base. MARL problems are often framed in the context of Markov games, where n agents cooperate in an environment with shared states. For simplicity, in this model, we consider the game theory-based problem between cooperating multiagents (represented by a defender and an attacker).

4  Implementation and Evaluation

4.1 Game Theory Model

Since cyberspace involves various cyber components, reliable cyber security requires taking into consideration the interactions among these components. Thus, the decision space increases considerably, with many what-if scenarios when the system is large [4]. Therefore, game theory has been demonstrated to be effective in solving large-scale problems. This is due to the ability to examine many scenarios to derive the best policy for each player [28].

Since our multiagents are formed to only explore and report their findings to the centralized security center, as discussed in Section 3.3, we consider the game theory-based problem between the centralized security center (defender) and an (attacker) to establish a 2-player dynamic game model. The defender and attacker interact in an adversarial environment involving defense solutions and attack events. Thus, the defender and the attacker can repeatedly change their defense and attack strategies. To simplify the analysis, this paper supposes that each player is only a single player (attacker or defender). However, the defender is based on multiagents that are collaboratively working together following the concept in Lemma 4.3. The multiagents only can explore, as aforementioned, and the centralized security center (i.e., the single defender), can exploit based on the received information.

A multiagent game for two agents can be defined by the tuple ( S , A1 , A2 , R , τ , δ ). The variables that are present in this tuple are defined as follows:

•    S={s1, s2, s3, …, sk} are the finite states of the game.

•    A1={a11, a12, …, a1m } represents the possible finite action set for Agent x, “the defender.”

•    A2={a21, a22, …, a2n} is the finite action set for Agent y.

•    τ is the next state of the game provided Players x and y take actions ax and ay in state s based on the received communication messages.

•    R(s, a)=(Rx(s, ax), …, Ry(s, ay)  is the reward value for taking action ax by Agent x.

•    δ →(0, 1] is the discount factor for future discount rewards.

Player 1 will try to maximize his expected discounted reward, while Player 2 will try to select actions that minimize the expected reward for Player 1. We consider the min-max expected reward for a Markov game. We can represent the expected value in the discounted Markov game as follows when the attacker has available actions ai∈A1 and the administrator has available actions aj∈A2 .

4.2 Value Iteration and Q-Learning

In this subsection, we present the analysis algorithms that model the defender’s behavior. We design two algorithms (Algorithm 4.1 and Algorithm 4.2) to model the defender’s strategy, namely, the value iteration algorithm and Q-learning algorithm. The algorithm for discounted reward shows a generalized idea of a policy that the defender will take to learn the attacker’s exploration and exploitation in the system. However, if the transition function is not known, then the function Q(s, a) can be obtained through the Q-learning algorithm to obtain the transition function through some processes, where the defender can improve his knowledge by extracting useful information from reported alerts. Thus, at each time step in the sequence, the defender chooses an action to incorporate the knowledge about previously experienced states. Therefore, as the attacker takes multiple actions (attack sequences), the defender (utilizing deployed MAS) will receive alerts indicating if the attacker succeeded in penetrating into the environment.

4.3 Implementation

To implement the actual modified value iteration, it is necessary to solve a linear program for each state after obtaining the updated Q values. However, this process becomes computationally inefficient for large networks. Thus, two assumptions are made that provide us with an approximate strategy for the players. First, we restrict the attacker to select a pure strategy (i.e., π (s) ∀ s has the value of 1 for only one action a∈A2 that it can execute in certain states and zero for all other actions). Second, we consider that the defender has observability of the attacker’s action and thus only uses action pairs (a1,  a2) with respect to the min-max strategy.

To evaluate this approach, we consider the game theory-based problem between the security solution system (i.e., defender) and an attacker to establish a 2-player dynamic game model. To simplify the analysis, this paper supposes each player is only a single player. However, for the defender, two sources of threat information are selected. First, we utilize and collect the cybersecurity incidents information that is usually obtained from the SOC, and in this scenario, we consider, as shown in Fig. 3, multiple distributed SOCs (SOC-Di), where each is deployed in a network segment (i) and reports to the centralized SOC-Brain. In the SOC-Brain, all received alerts are correlated for the goal of increasing the defender’s global rewards and decreasing the attacker’s reward. Second, we utilize the CTI program, which may provide additional information on ongoing threats inside the environment. Thus, when the information received from both SOC-Brain and CTI is combined, it can increase the protection rewards by enhancing the knowledge of the system administrators (security teams) to understand ongoing threats to their organization.

Figure 3: System architecture

To model the game, we design the environment depicted in Fig. 3 where we use an OpenStack SDN-based environment with few virtual machines (VMs) in two different network segments (tenants). In each segment, we deploy (a) Ubuntu 16.04, (b) Windows and vulnerable machine, and (c) metasploitable and centralized SOC-D. We assume that the attacker’s goal is to obtain root-level privileges on the targeted VMs by penetrating into the system and exploiting existing vulnerabilities such as buffer-overflow. We assume the attacker is compromising an Ubuntu machine with user-level privileges on it. He or she uses this VM as a starting point (foothold) to perform lateral movement. The attacker starts with information gathering (internal reconnaissance) and conducts an nmap scan to enumerate the vulnerable system and network services that are present on the host and the target VM. Our deployed IDS inside the SOC-Di can observe such incidents and generate and send alerts to the SOC-Brain.

Our experimental environment contains multiple vulnerable services such as Mutillidae owasp, Damn Vulnerable Web Application (DVWA), Metasploitable, and BadStore. Utilizing these vulnerabilities helps us to emulate attackers’ behavior and also allows us to monitor the environment at the network level using a network-based IDS. In addition, another virtual machine hosts Samba, WordPress, FTP, MySQL, and Nexus. Each VM, therefore, has packet- and log-capturing abilities. A stack-based Elasticsearch-Logstash-Kibana (ELK) log server was used for log storage and filtering.

Utilizing our deployed CTI, we can observe the vulnerability-related information from open sources, such as discussions on hacking forums, about an existing vulnerability on aforementioned services and how it can be exploited. In addition, we gather vulnerability information from well-known vulnerability databases such as Common Vulnerabilities and Exposures (CVE) which is deployed in our SOC environment. The advantage of utilizing CTI is showing what vulnerabilities active actors are discussing and how they exploit them. Furthermore, we can reflect this scenario on our multiagent interaction, where we sum up multiple alerts, resulting from multiple actions taken by the attacker, to detect ongoing attacks. The optimal goal is to minimize the reward of the attacker using a min-max strategy. The system administrator should be able to select the optimal countermeasure once they collect significant information on incidents within the organization. The collected incident information helps the administrator to model the attacker’s policy. Thus, necessary countermeasures can be taken to minimize the expected utility for the attacker.

4.4 Evaluation

We conducted Markov game cost-benefit analysis for the two players (attacker and defender). As shown in Fig. 4, the reward value for the attacker decreases as we utilize value iteration and Q-learning algorithms by observing and collecting alerts from multiple sources (agents). This means the defender increases his attack surface coverage. In our implementation, we collect incident information from different sources, as presented in Fig. 4 (i.e., CTI, SOC-Di, and SOC-Brain). The CTI provides more details on vulnerabilities that were discussed in open-source platforms such as the dark web. We utilized TorBot which is an open-source tool for the dark web. However, such intelligence may not lead to accurate detection or prediction of an attack if it is considered separately. In addition, each distributed SOC-Di is configured to monitor its local segmentation. However, their coverage is not efficient when they work separately as shown in Fig. 4 where we can notice the attacker’s reward is still high. However, when we react to the alerts received from multiple sources that are combined and correlated, we can notice that, as shown in Fig. 4, the Q-learning shows how the attacker’s reward decreases over time. This is due to the ability to learn the attacker’s behavior via multiagent RL.

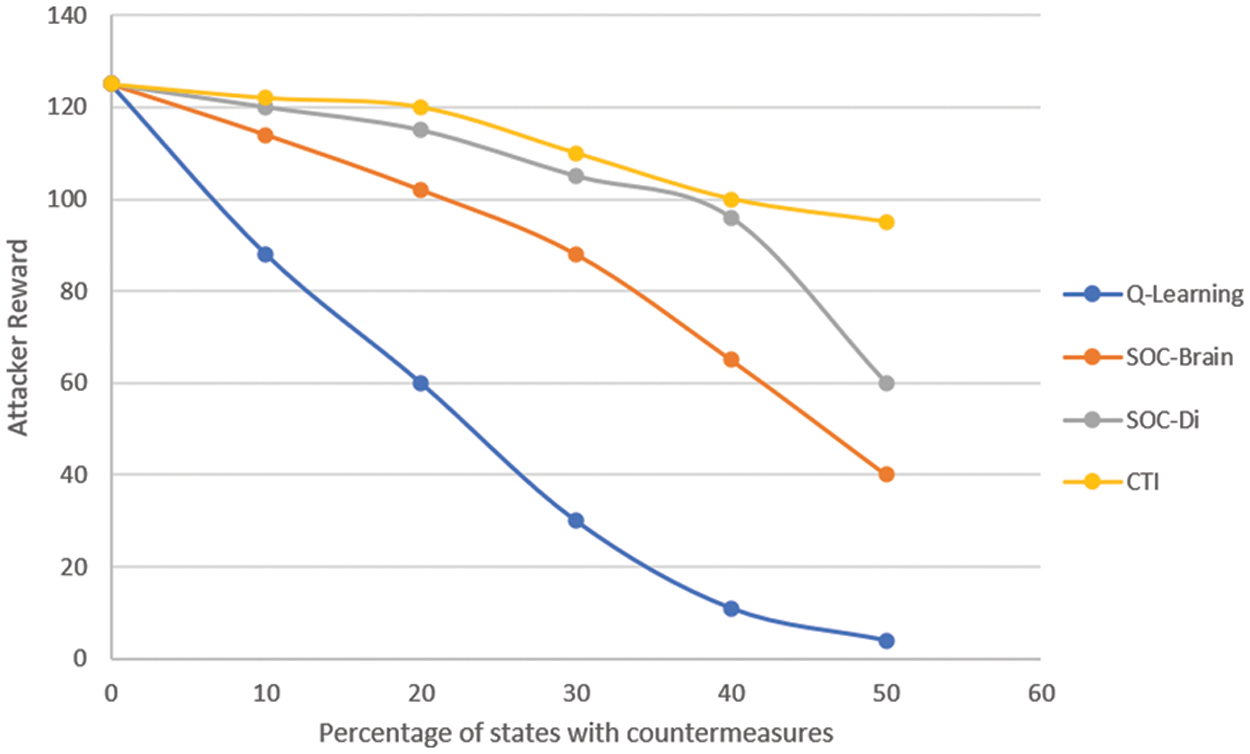
Figure 4: Attacker decreasing rewards over time

5  Conclusion

To gain an understanding of how players cooperate or fail to cooperate in dynamic games, we formulated a two-player MAB and provided various results, such as conditions for myopic optimality, the first player’s advantage, and an environment that fosters cooperation between two players. Moreover, many of these preliminary results appear to be generalizable to more players. Additionally, the framework of this problem can act as a starting point for other researchers interested in sequential dynamic games.

We further presented a multiagent RL model where we deployed n agents cooperating in an environment to minimize the attacker’s rewards. We presented a game theory-based problem between the attacker and defender to perform a cost-benefit and min-max strategy. Our solution is deployed on an OpenStack-based environment consisting of two tenants with the configuration of a centralized SOC inside each tenant and a centralized SOC. Our approach showed that cooperating agents are a promising solution to minimize the attacker’s exploration surface and rewards. In future work, we plan to address the limitation of this work which is how to model the game when the number of players increases. In addition, we further need to explore the complexity concerning reward distribution over an increased number of players.

Acknowledgement: This work was funded by the Deanship of Scientific Research (DSR), University of Jeddah, under Grant No. (UJ-22-DR-1). The authors, therefore, acknowledge with thanks DSR financial support.

Funding Statement: This work is funded by the Deanship of Scientific Research (DSR), the University of Jeddah, under Grant No. (UJ-22-DR-1).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. Minghui, Z. Hu and P. Liu, “Reinforcement learning algorithms for adaptive cyber defense against heartbleed,” in Proc. First ACM Workshop on Moving Target Defense, Scottsdale, AZ, USA, vol. 2, no. 6, pp. 51–58, 2014. [Google Scholar]

2. H. White, “Trustworthy cyberspace: Strategic plan for the federal cyber security research and development program,” Report of the National Science and Technology Council, Executive Office of the President, vol. 4, no. 9, pp. 674–719, 2011. [Google Scholar]

3. S. Bradley, G. A. Moreno, A. Mellinger, J. Camara and D. Garlan, “Architecture-based self-adaptation for moving target defense,” Carnegie Mellon University Pittsburgh, USA, vol. 3, no. 8, pp. 3474–3499, 2014. [Google Scholar]

4. Z. Xiaorui, H. Wu, W. Sun, A. Song and S. K. Jha, “A fast and accurate vascular tissue simulation model based on point primitive method,” Intelligent Automation and Soft Computing, vol. 27, no. 3, pp. 873–889, 2021. [Google Scholar]

5. Z. Xiaorui, X. Chen, W. Sun and X. He, “Vehicle re-identification model based on optimized DenseNet121 with joint loss,” Computers Materials & Continua, vol. 67, no. 3, pp. 3933–3948, 2021. [Google Scholar]

6. N. T. Thi and V. J. Reddi, “Deep reinforcement learning for cyber security,” IEEE Transactions on Neural Networks and Learning Systems, vol. 67, no. 3, pp. 387–432, 2019. [Google Scholar]

7. A. Alshamrani, S. Myneni, A. Chowdhary and D. Huan, “A survey on advanced persistent threats: Techniques, solutions, challenges, and research opportunities,” IEEE Communications Surveys & Tutorials, vol. 21, no. 2, pp. 1851–1877, 2019. [Google Scholar]

8. J. Wayne, “Intrusion detection with mobile agents,” Computer Communications, vol. 25, no. 15, pp. 1392–1401, 2002. [Google Scholar]

9. N. T. Thi and V. J. Reddi, “Deep reinforcement learning for cyber security,” IEEE Transactions on Neural Networks and Learning Systems, vol. 2, no. 8, pp. 1–17, 2019. [Google Scholar]

10. J. Nicholas, K. Sycara and M. Wooldridge, “A roadmap of agent research and development,” Autonomous Agents and Multi-Agent Systems, vol. 1, no. 1, pp. 7–38, 1998. [Google Scholar]

11. L. Pamait and S. Luke, “Collaborative multi-agent learning: A survey,” Department of Computer Science, George Mason University, Technical Report, vol. 3, no.7, pp. 78–98, 2003. [Google Scholar]

12. T. Ming, “Multi-agent reinforcement learning: Independent vs. cooperative agents,” in Proc. Tenth Int. Conf. on Machine Learning, Amherst, MA, USA, vol. 3, no.7, pp. 330–337, 1993. [Google Scholar]

13. F. Aidin, U. Challita, W. Saad and N. B. Mandayam, “Robust deep reinforcement learning for security and safety in autonomous vehicle systems,” in Proc. 2018 IEEE 21st Int. Conf. on Intelligent Transportation Systems (ITSC), Maui, HI, USA, vol. 3, no. 5, pp. 307–312, 2018. [Google Scholar]

14. D. Constantinos, P. W. Goldberg and C. H. Papadimitriou, “The complexity of computing a nash equilibrium,” SIAM Journal on Computing, vol. 39, no. 1, pp. 195–259, 2009. [Google Scholar]

15. J. Anirudh and S. Hossen, “Analysis of network intrusion detection system with machine learning algorithms (deep reinforcement learning algorithm),” Faculty of Computing, Blekinge Institute of Technology, vol. 371, no. 79, pp. 567, 2018. [Google Scholar]

16. D. Bhagyashree and A. Hazarnis, “Intrusion detection system using log files and reinforcement learning,” International Journal of Computer Applications, vol. 45, no. 19, pp. 28–35, 2012. [Google Scholar]

17. B. Ravindra, S. Mahajan and P. Kulkarni, “Cooperative machine learning for intrusion detection system,” International Journal of Scientific and Engineering Research, vol. 5, no. 1, pp. 1780–1785, 2014. [Google Scholar]

18. G. Abhishek and Z. Yang, “Adversarial reinforcement learning for observer design in autonomous systems under cyber attacks,” Arxiv Preprint Arxiv, 1809.06784, 2018. [Google Scholar]

19. M. H. Kuo, “An intelligent agent-based collaborative information security framework,” Expert Systems Applications, vol. 32, no. 2, pp. 585–598, 2007. [Google Scholar]

20. L. Keqin and Q. Zhao, “Distributed learning in multi-armed bandit with multiple players,” IEEE Transactions on Signal Processing, vol. 58, no. 11, pp. 5667–5681, 2010. [Google Scholar]

21. L. Keqin and Q. Zhao, “Decentralized multi-armed bandit with multiple distributed players,” IEEE Information Theory and Applications Workshop (ITA), vol. 4, no. 6, pp. 1–10, 2010. [Google Scholar]

22. A. Animashree, N. Michael and A. Tang, “Opportunistic spectrum access with multiple users: Learning under competition,” in Proc. IEEE Int. Conf. on Computer Communications INFOCOM, San Diego, CA, USA, vol. 2, no. 5, pp. 1–9, 2010. [Google Scholar]

23. P. Christos and J. N. Tsitsiklis, “The complexity of optimal queueing network control,” in Proc. IEEE 9th Annual Conf. on Structure in Complexity Theory, Amsterdam, Netherlands, vol. 2, no. 8, pp. 318–322, 1994. [Google Scholar]

24. P. Liviu and S. Luke, “Cooperative multi-agent learning: The state of the art,” Autonomous Agents and Multi-Agent Systems, vol. 11, no. 3, pp. 387–434, 2005. [Google Scholar]

25. F. Drew and D. K. Levine, “The theory of learning in games,” Journal of Economic Perspectives, vol. 2, no. 4, pp. 151–168, 1998. [Google Scholar]

26. K. L. Pack, M. L. Littman and A. W. Moore, “Reinforcement learning: A survey,” Journal of Artificial Intelligence Research, vol. 4, no. 7, pp. 237–285, 1996. [Google Scholar]

27. K. Spiros and K. Daniel, “Reinforcement learning of coordination in cooperative mas,” in Proc. 18th National Conf. on AI, Alberta, Canada, ACM Press, pp. 326–331, 2002. [Google Scholar]

28. Z. Quanyan and S. Rass, “Game theory meets network security: A tutorial,” in Proc. 2018 ACM SIGSAC Conf. on Computer and Communications Security, Toronto, Canada, pp. 2163–2165, 2018. [Google Scholar]