 Open Access
Open Access
ARTICLE
Two-Sided Matching Decision Making with Multi-Attribute Probabilistic Hesitant Fuzzy Sets
1 School of Mathematics and Statistics, Heze University, Heze, 274015, China
2 School of Management, Shanghai University of Engineering Science, Shanghai, 201620, China
3 School of Information Management, Jiangxi University of Finance and Economics, Nanchang, 330013, China
* Corresponding Author: Qi Yue. Email:
Intelligent Automation & Soft Computing 2023, 37(1), 849-873. https://doi.org/10.32604/iasc.2023.037090
Received 23 October 2022; Accepted 13 February 2023; Issue published 29 April 2023
Abstract
In previous research on two-sided matching (TSM) decision, agents’ preferences were often given in the form of exact values of ordinal numbers and linguistic phrase term sets. Nowdays, the matching agent cannot perform the exact evaluation in the TSM situations due to the great fuzziness of human thought and the complexity of reality. Probability hesitant fuzzy sets, however, have grown in popularity due to their advantages in communicating complex information. Therefore, this paper develops a TSM decision-making approach with multi-attribute probability hesitant fuzzy sets and unknown attribute weight information. The agent attribute weight vector should be obtained by using the maximum deviation method and Hamming distance. The probabilistic hesitancy fuzzy information matrix of each agent is then arranged to determine the comprehensive evaluation of two matching agent sets. The agent satisfaction degree is calculated using the technique for order preference by similarity to ideal solution (TOPSIS). Additionally, the multi-object programming technique is used to establish a TSM method with the objective of maximizing the agent satisfaction of two-sided agents, and the matching schemes are then established by solving the built model. The study concludes by providing a real-world supply-demand scenario to illustrate the effectiveness of the proposed method. The proposed method is more flexible than prior research since it expresses evaluation information using probability hesitating fuzzy sets and can be used in scenarios when attribute weight information is unclear.Keywords
Two-sided matching decision-making (TSMDM) consists of two sides of matching agents and belongs to the decision-making problems [1], which was first proposed and applied by Gale and Shapley in a study of matchmaking and college admission [2]. The agent, also called as the intermediary, is what determines the result of the matching process but does not actually participate in the matching process directly. The matching agents could play various roles in various scenarios requiring decision-making [3]. If you search or buy a product online today, you will find more of the same products on the website tomorrow; this indicates that the matching system has automatically matched you as a potential customer. Both sides of matching agents participate in the matching process, and using a given matching technique, all matching agents are evaluated by those on the other side. The formation of a perfect matching scheme which is satisfied by all matching agents must be facilitated by the intermediary based on the preferences or evaluations provided by the matching agent.
TSMDM is now used in a wide range of fields, such as marriage matching problems [4,5], colleges admissions [6], volunteer team dispatching [7], human resource management [8], economic management matching [9], public-private partnership [10], and knowledge service matching [11]. The two-sided matching theory has been used in a variety of areas recently, along with the development of the market economy and the level of science and technology. For instance, Wu et al. [12] studied the supply-demand issue in transport services and developed the corresponding TSMDM method. Wang et al. [13] has developed a novel matching method for solving the freight source matching problem. Liu et al. proposed a unique TSMDM method with the objective of achieving satisfying matching between surgeons and patients [14]. For the purpose of resolving the existing house seller-buyer matching problem, Jiang et al. [15] proposed a novel TSMDM.
Meantime, a significant number of scholars have studied the multi-attribute TSMDM problem. For instance, Jiang et al. [16] proposed a multi-objective non-linear model to address one-shot multi-attribute exchange problems. Based on the Choquet integral aggregation operator, a novel TSMDM method was developed by Liang et al. [17], which was used to solve the multi-attribute TSMDM problems considering q-Rung Orthopair fuzzy information. Liang et al. [18] developed a novel TSMDM model based on the strict order number information. In light of multi-granularity probabilistic linguistic MARCOS, Lu et al. [19] proposed a multi-attribute two-sided matching method.
Some researchers studied the TSMDM problem with complete or partial preference ordering in the previous studies. For instance, Pu et al. [20] proposed a novel TSMDM method under the goal of maximizing intermediary revenue and overall agent satisfaction. Fan et al. [21] studied the TSMDM problem with uncertain preference ordinal and proposed the corresponding TSMDM model. A novel TSMDM method was developed by Chen et al. [22] after studying the TSMDM problem in perspective of psychological behaviors. Qin et al. [23] proposed an optimization method for resolving the TSMDM problem with incomplete weak preference ordering. To express the evaluation information in the practical TSMDM problem, linguistic evaluation was also applied. For instance, Lin et al. [24] studied the multi-attribute TSMDM problems with 2-tuple linguistic information and proposed a new TSMDM method. Considering the multi-granular HFLTSs environment, Zhang et al. [25] developed a comprehensive TSMDM method considering the stable one-to-one matching constraints.
Researches conducted by many scholars have provided sufficient solutions for the two-sided matching problem under different scenarios. However, decision-makers find it difficult to deliver precise and concise information given the complexity of the real world. In certain situations, decision-makers are unable to convey the whole significance of the evaluation information. To describe the evaluation information, several fuzzy information express tools would be employed, such as interval numbers, fuzzy numbers, hesitant fuzzy sets, intuitionistic fuzzy sets [26] and others.
PHFS, which is an important extended form of the hesitant fuzzy set and a close and effective combination of membership degree and probability distribution information, was first proposed by Zhu [27]. Probabilistic hesitating fuzzy sets, as compared to HFS, are more capable of dealing with and explain the information of preference evaluation in complex decision-making situations. In real world, significant and vital decisions are usually made by the group which consists of multiple members. Due to the inaccurate estimations and lack of expertise, the evaluation information provided by experts may have different assessment values. Therefore, the information of the probabilistic hesitant fuzzy element (PHFE) may be used to express the overall opinion formed by these different evaluation results. For instance, suppose a company invites ten experts to evaluate a scheme (score between [0, 1]), and let’s say that six of the ten experts give the scheme a score of 0.5 and four experts give it a score of 0.7. The evaluation information can be provided by the PHFE
The rest of this paper is organized as follows. Some preliminaries about TSMDM and PHFS will be presented in Section 2. The proposed problem is explained in Section 3, and builds the framework for the proposed method. In Section 4, a case is provided to demonstrate the effectiveness of the proposed method. Additionally, Section 4 explains the characteristics of the proposed TSMDM method. Finally, the main contributions of the proposed method are presented in Section 5.
The concept of two-sided matching is given in this section, and then some related theories of PHFSs are introduced, including the concept, operation rules, score function and aggregation operation. Finally, it discusses the distance measure of PHFSs and TOPSIS method.
Two matching agent sets, A and B, are given in this subsection. Let
Definition 1 [35]. Suppose
Then,
2.2 Probabilistic Hesitant Fuzzy Sets
HFS was first proposed by Torra [26] and further expressed in mathematical symbol by Xia et al. [36]. Unlike other extensions of the fuzzy set, HFS allows the membership degree of an element to a set presented by several possible values, which can express the uncertain information more comprehensively. However, the probability of each membership degree is the same. To better represent the preference information, by incorporating probability to describe the preference information in HFS, Zhu [27] proposed the concept of PHFS. Compared with HFSs, the following PHFSs can reserve more original information.
Definition 2 [27,32]. Let X be a fixed set. Then, a PHFS on X is
Remark 1: In Definition 2,
Remark 2: In Definition 2, the PHFE
Definition 3 [27,32]: Let
i)
ii)
iii)
iv)
v)
Definition 4 [27,32]: Let
According to the score function, the deviation function is defined by:
According to the score functions, we can compare PHFEs
if
if
if
2.3 Aggregation Operators and Distance Measures for PHFEs
Zhang et al. [32] proposed the probabilistic hesitant fuzzy weighted averaging (PHFWA) operator and the probabilistic hesitant fuzzy weighted geometric (PHFWG) operator, both of which are very useful in decision-making using probabilistic hesitant fuzzy information.
Definition 5 [32]. Let
These two operators can transform the fuzzy decision information of the decision makers into aggregated decision information to identify the best option out of all feasible choices.
The definitions of the Hamming distance and the Euclidean distance of PHFEs are given as follows:
Definition 6 [29]. Let
where
Remark3: In most cases,
Definition 7 [29]. The probabilistic hesitant fuzzy Positive Ideal Solution (PIS) is given as:
2.4 The TOPSIS Method for PHFS
The TOPSIS method, which was first proposed by Hwang and Yoon, is essential for processing information from multi-attribute evaluations and is a topic of much scholarly discussion [37]. According to the PHFSs Hamming distance measure and the basic idea of traditional TOPSIS method, let
The closeness coefficients C for each alternative are calculated for both, the distance
3 The Approach of TSMDM with PHFSs Information
In this section, the TSMDM problem with PHFSs is introduced and a novel TSMDM method is proposed.
Two agent sets are given in the two-sided matching problem which is addressed in this paper. Considering the fuzziness of the thinking of the matching subject and the disparity in knowledge organization, the evaluation information given by the two-sided agent is presented in the form of PHFS, and the attribute weight information given is also incomplete. The problem studied in this paper is to promote the formation of equitable bilateral matching results based on the information of probabilistic hesitancy fuzzy sets given by two-sided agents. The main notations used in this section are presented as follows:
For the matching object
3.2 The Maximizing Deviation Method to Obtain the Weights of Attribute
Weight plays an essential role in reaching a reasonable decision result. The matching subject is unable to provide a comprehensive attribute weight vector due to the diversity and fuzziness of the information in the real decision-making environment. At the same time, Wang [38] puts forward a maximum deviation method to determine the attribute weight, and the core idea is to give the attribute weight based on the evaluation information given by the decision-maker. Some models will be proposed to determine the attribute weight vector for a two-sided agent based on the maximum deviation method.
In relation to the
The total deviation among
We can evaluate the total variance between
Then, a constrained condition
Therefore, a model for computing the attribute weight for
By using the Lagrange multiplier method and normalizing the weight vector, we have
Similar to that, the attribute weight vector for
Furthermore, the matrices
First, the Hamming distance measure between the comprehensive evaluation of each matching agent and their corresponding positive and negative ideal evaluation is calculated, that is:
Then, the closeness coefficients of each matching agent could be computed by:
The degree of divergence within the matching agent sets could clearly be observed in the closeness coefficients of each matching. For the matching agent
Additionally, a TSMDM model could be developed to obtain the best matching. Suppose
In model (16), formula (a) and formula (b) aim to maximize the overall satisfaction. And formula (c) and formula (d) refer to the one-to-one matching constrains.
We apply the linear weighted method to solve the multi-objective optimization model, and thus model (17) could be constructed as follows:
where
In conclusion, the steps of the proposed TSMDM approach can be summed up as follows (see Fig. 1 below):
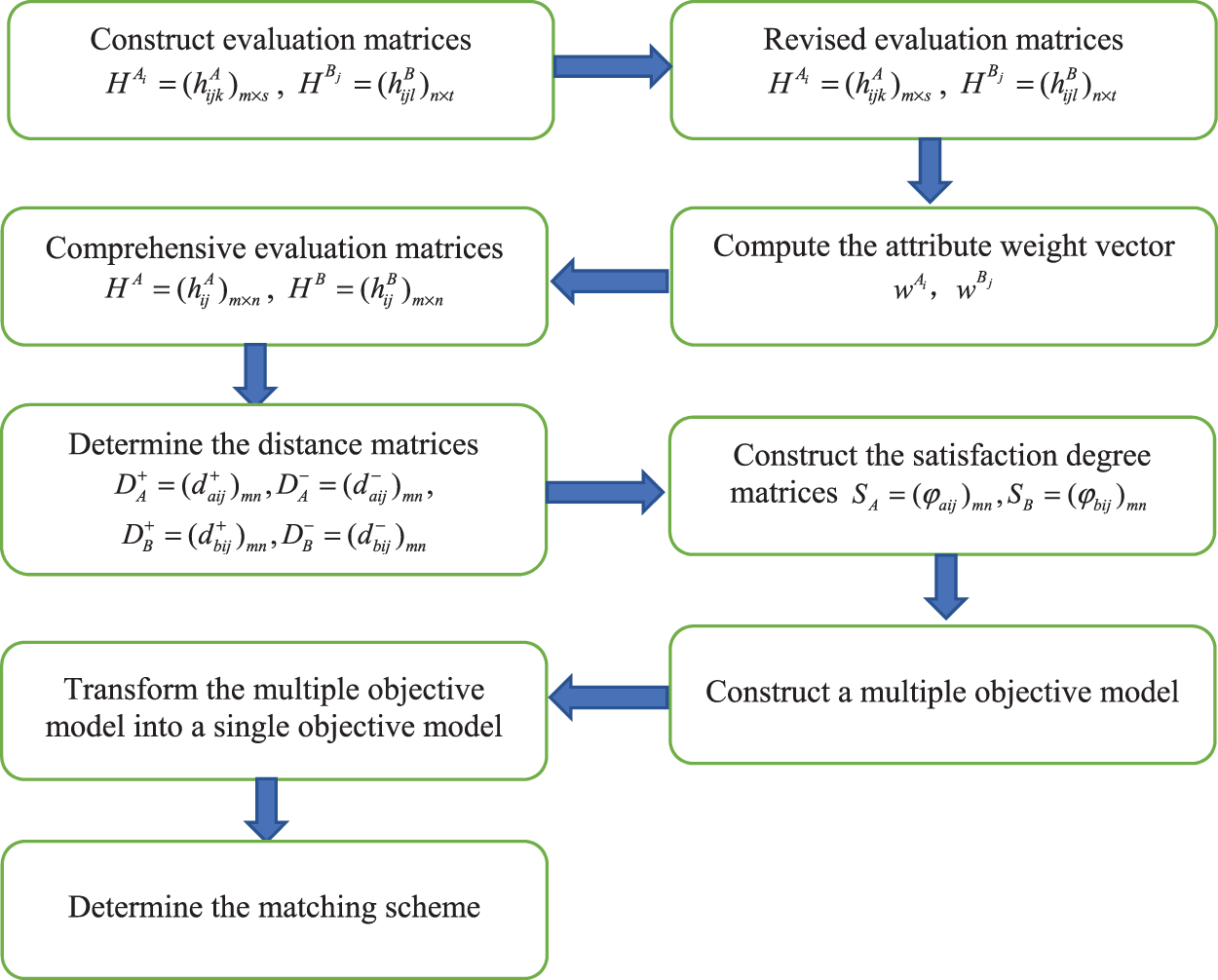
Figure 1: The procedure of two-sided matching

Step 1: Construct evaluation matrices
Step 2: Compute the attribute weight vector
Step 3: According to the Eq. (3), transform evaluation matrices
Step 4: According to Eq. (13), determine the distance matrix
Step 5: Construct the satisfaction degree matrices
Step 6: Construct model (16) based on the satisfaction matrix
Step 7: Determine the matching scheme bysolving model (17).
4 Illustrative Example and Discussion
To demonstrate the proposed approach, an example of lunch supply and demand matching is provided in this section.
Because of operational constraints and limited space, primary schools are unable to provide lunch for both students and teachers. Therefore, their lunch supply needs to be outsourced and completed by external catering companies. The local education authority of a city intends to provide lunch to students in three primary schools in order to improve public service and reduce chances for students to leave school. The local education authority conducts a comprehensive survey of the situation and information summary of the actual activity, and invites five catering companies to bid for three primary schools. An enterprise can only bid effectively in one school for a prolonged period of time due to the financial strain and service quality. To establish a compatible match and maintain a stable, strong partnership that benefits both sides, the local education authority makes the three primary schools
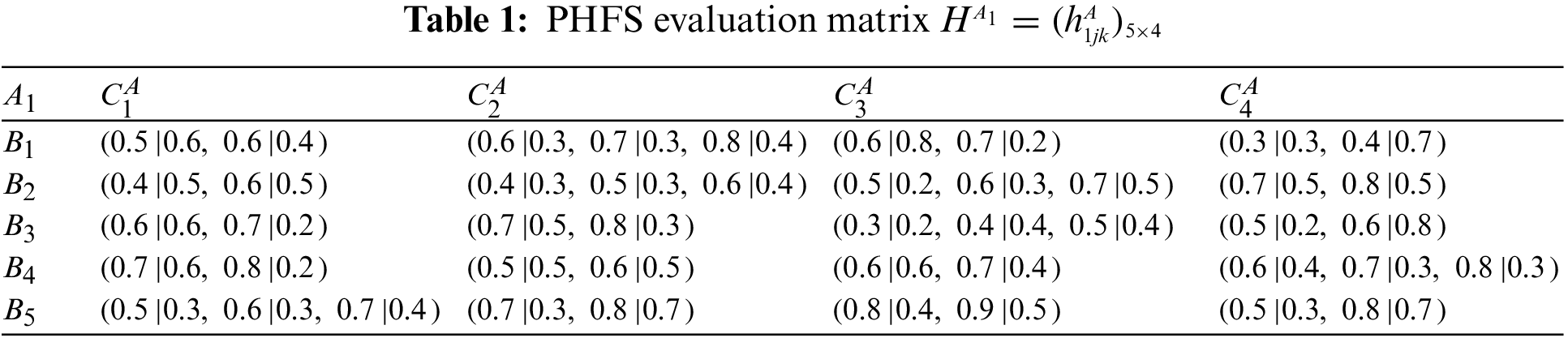
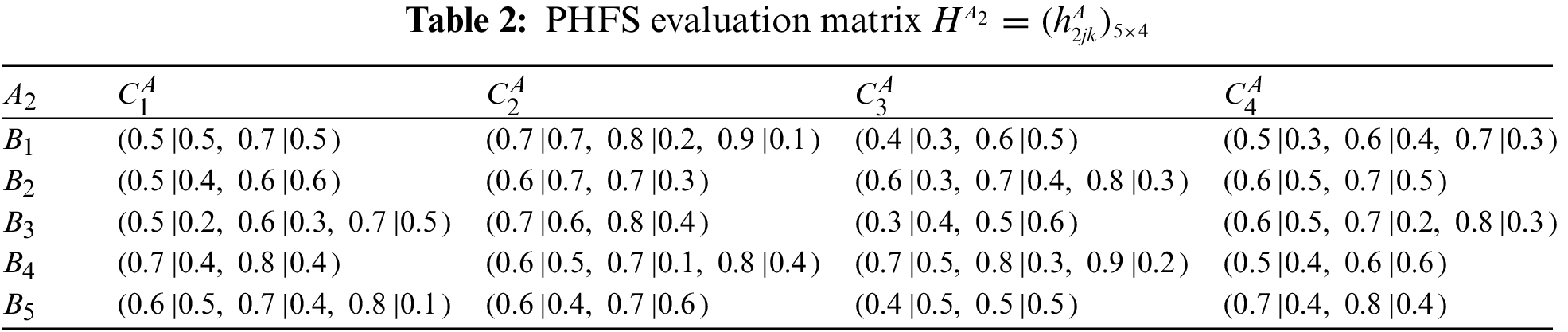
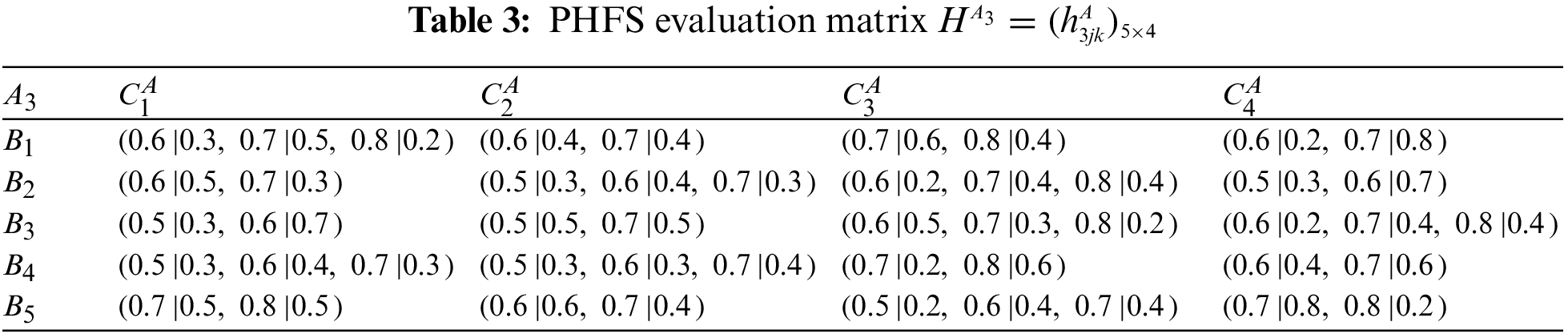





Step 1: Construct evaluation matrices.
At the same time, there are differences in the number of membership elements among different PHFEs. Decision-makers are therefore considered to be risk-averse. Based on this, the PHFE, which has a smaller number of membership degrees, is added with the minimal value, and the probability of each additive value is 0. In accordance with the revised method of Definition 1, the PHFE of PHFS evaluation matrix can be revised, and then the PHFS evaluation matrices can be modified and shown in Tables 9–16.

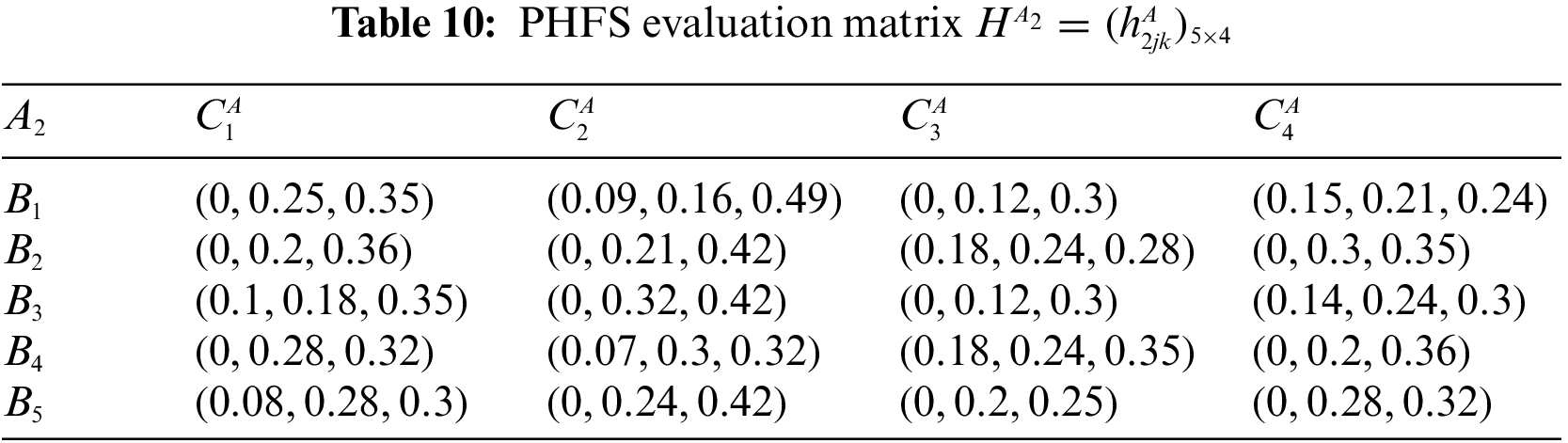
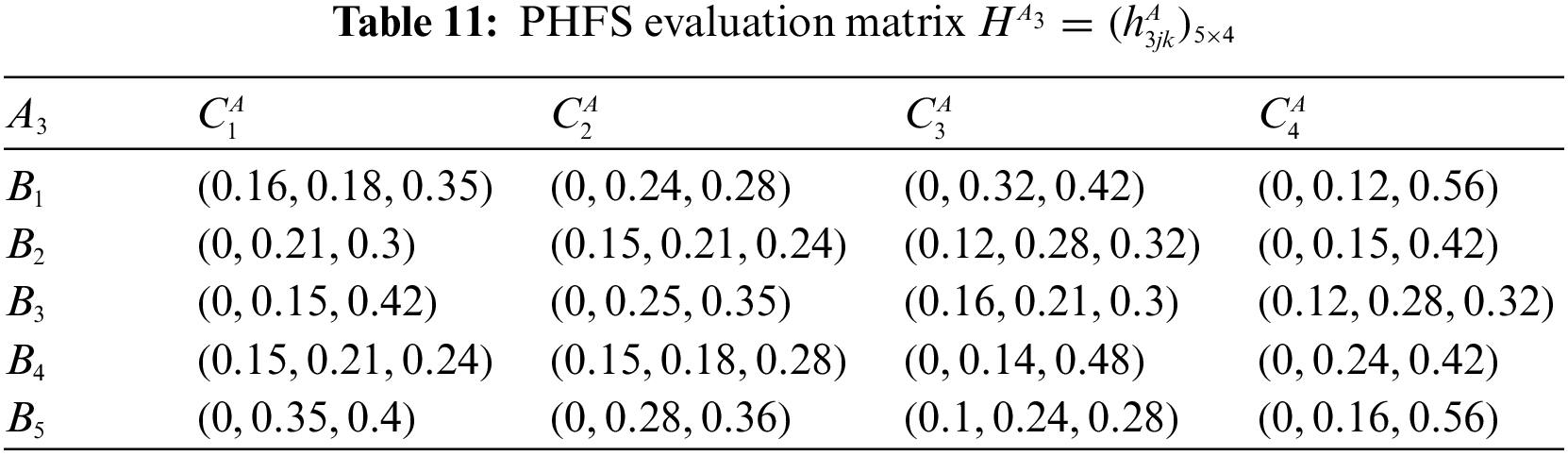
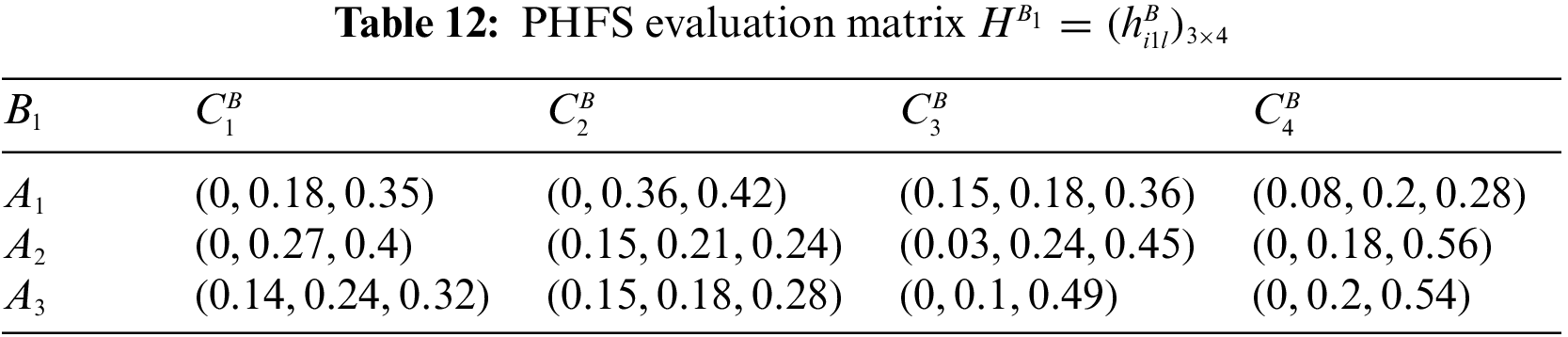
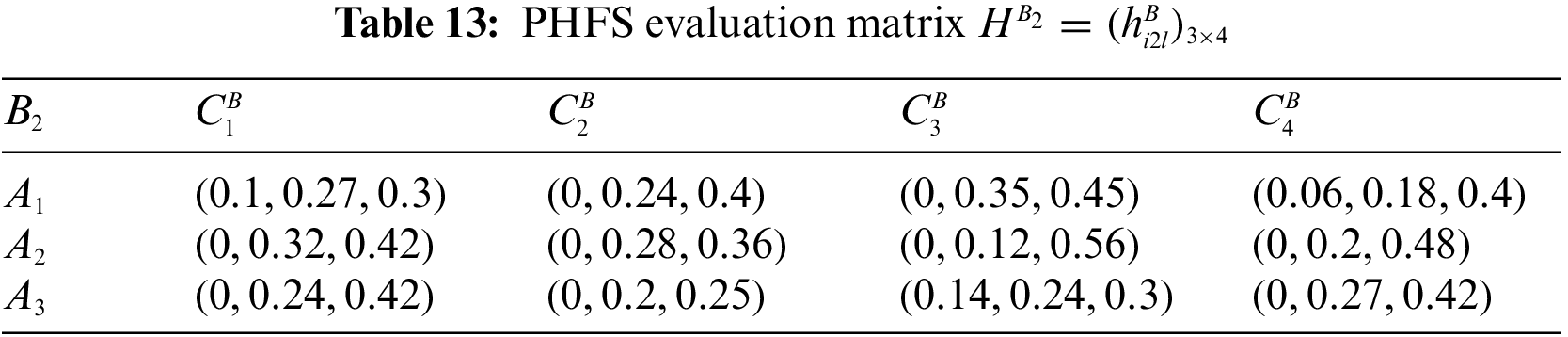
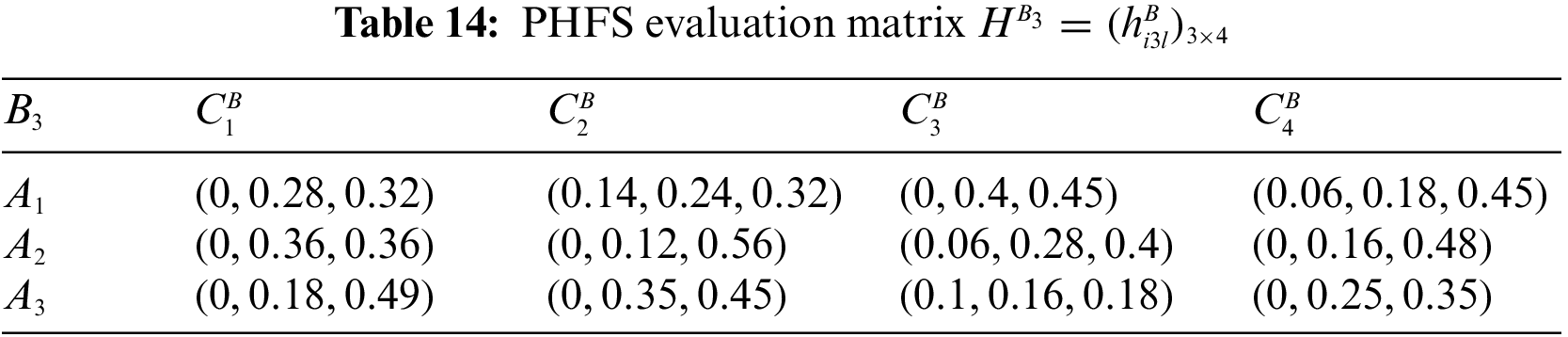

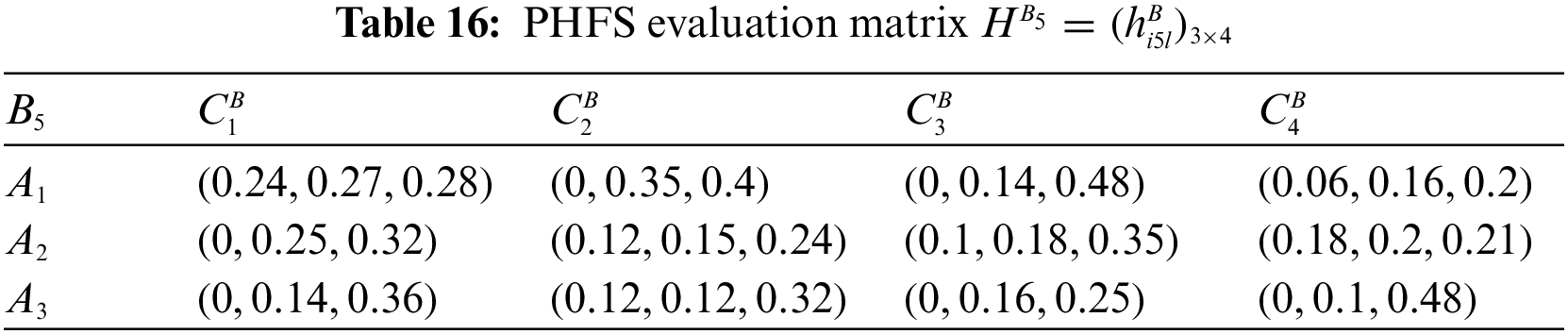
Step 2: Compute the attribute weight vector.
Matching is performed by the municipal education bureau/commission using probabilistic hesitant fuzzy evaluation matrices. The information regarding how much each attribute weighs in the evaluation is not provided by two-sided agents. In accordance with the above given steps, the weight information of each attribute can be calculated by Eqs. (12) and (13), that is:
Step 3: Comprehensive evaluation matrices.
On this basis, the comprehensive assessment
Therefore, the comprehensive assessment
The comprehensive PHFS evaluation information of the primary schools can be obtained, as shown in matrix
Step 4: To calculate the distance.
Owing to the number of each PHFE is not equal for
Step 5: Construct the satisfaction degree matrices.
According to the satisfaction degree formula, the satisfaction degree of the matching agent
Step 6–7: Construct the model and solve it.
Based on the satisfaction matrices
The optimization model can be solved by utilizing the Lingo 11 software, so that we can get
4.2 Sensitivity Analysis and Discussion
To better illustrate the impact of the weights
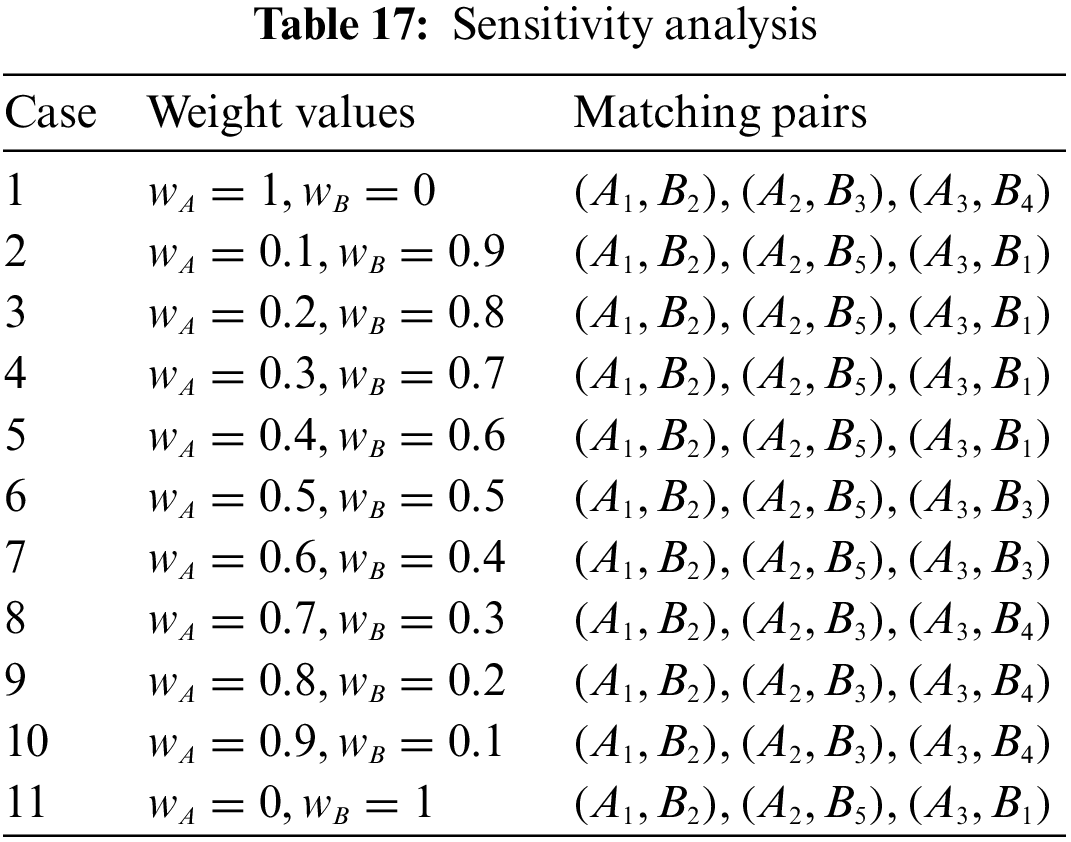
The matching objects can express their evaluations more flexibly in PHFS since the decision-maker may hesitate while describing the preference evaluation information. As can be observed, in comparison to the matching objects, information on their assessments is provided in triangular intuitionistic fuzzy sets [39], hesitant fuzzy numbers [40] and intuitionistic fuzzy numbers [8], the method proposed in this paper has more advantages.
Furthermore, the tendency of the object function value Z from cases 1–3 is displayed in Fig. 2. The tendency of the matching scheme
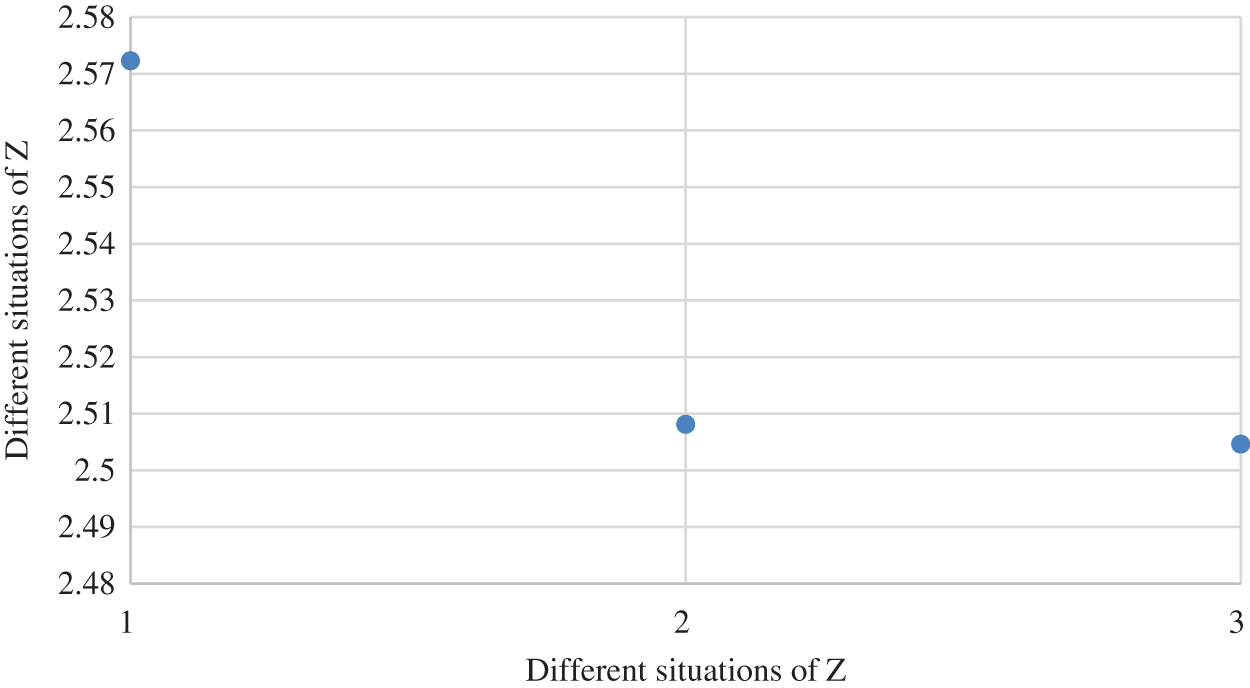
Figure 2: The object function value Z from cases 1–3
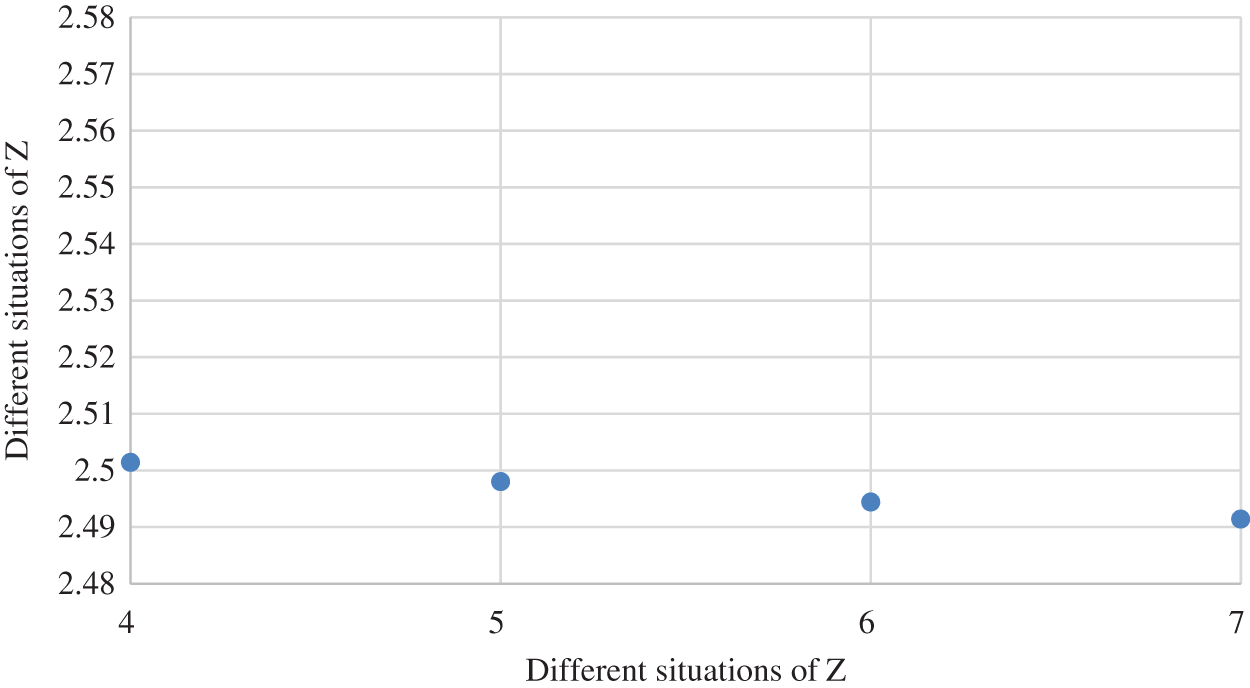
Figure 3: The object function value Z from cases 4–7
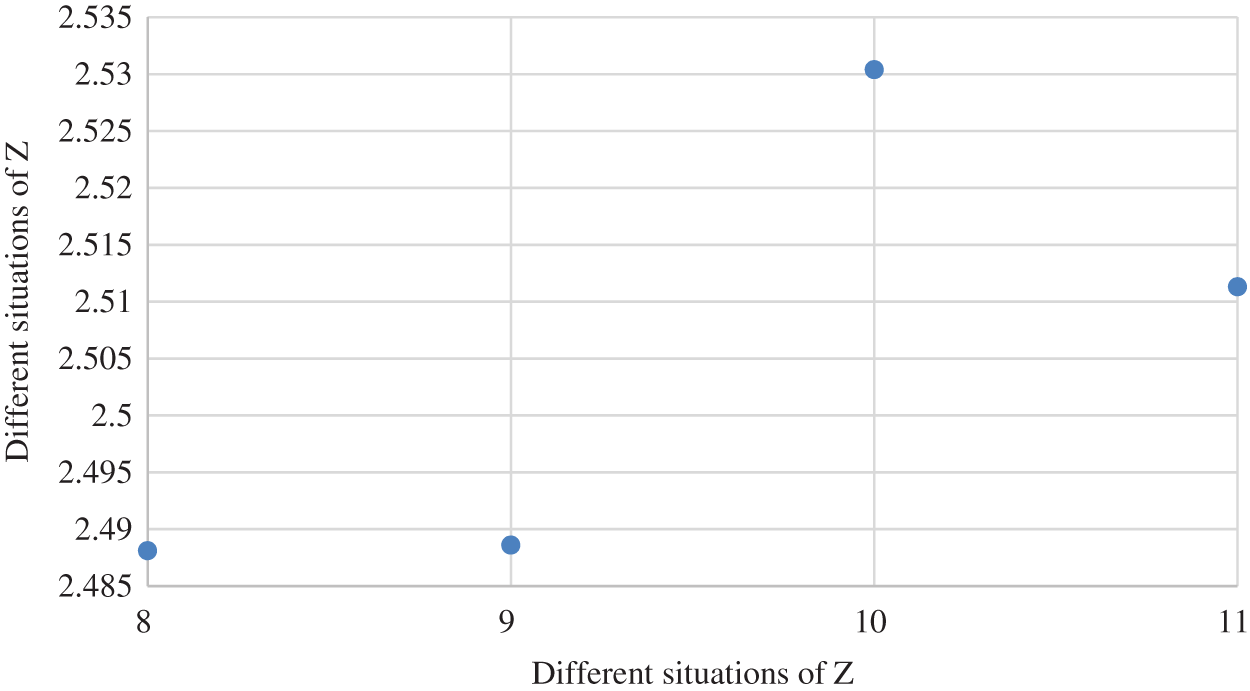
Figure 4: The object function value Z from cases 8–11
From Figs. 2 to 4, the paper analyzes the role of two-sided agent weight values on the objective function value, as displayed in Fig. 5. As the weight of the two-sided agent changes from cases 1–2, the object function drops significantly. As the weight changes from cases 2 to 9, the function value gradually decreases until it reaches its lowest point in case 9. However, from cases 9–11, results show that the value of object functioninitially rises and then falls.
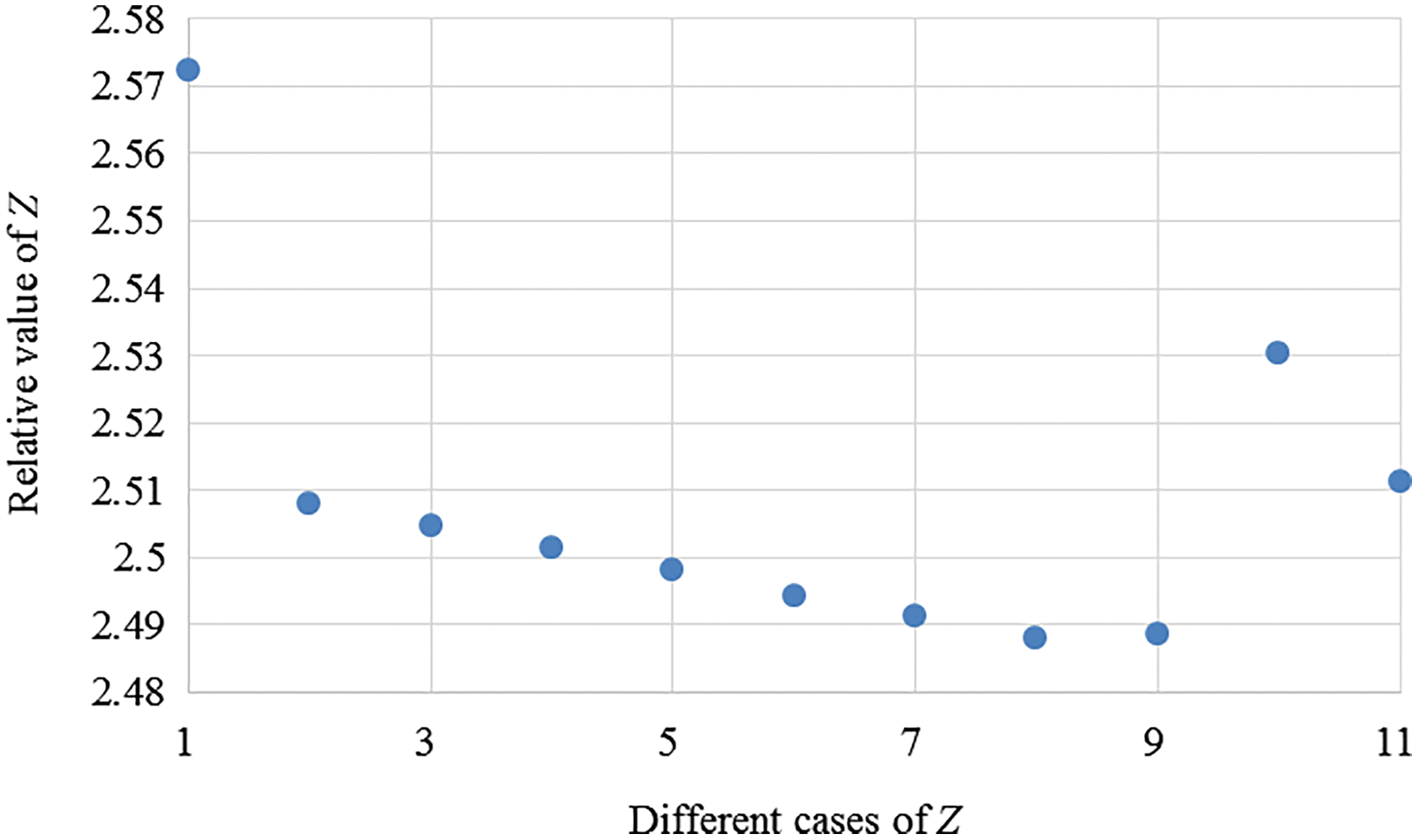
Figure 5: The object function value Z from cases 1–11
The tendency of matching scheme
Figure 6: The matching scheme
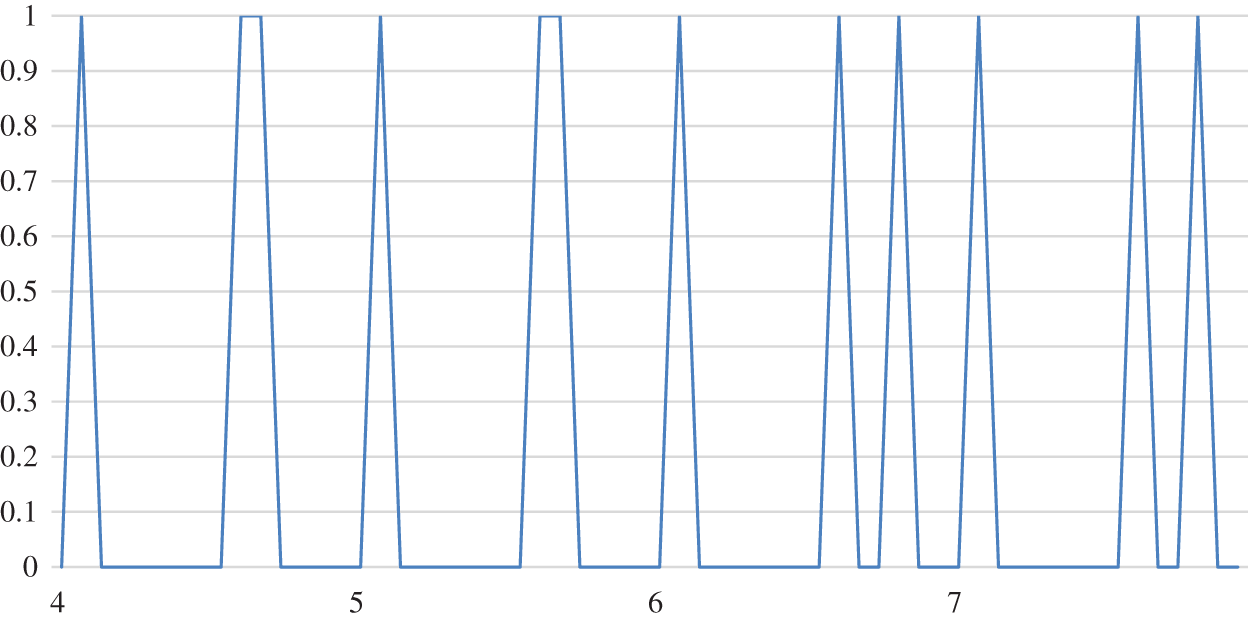
Figure 7: The matching scheme
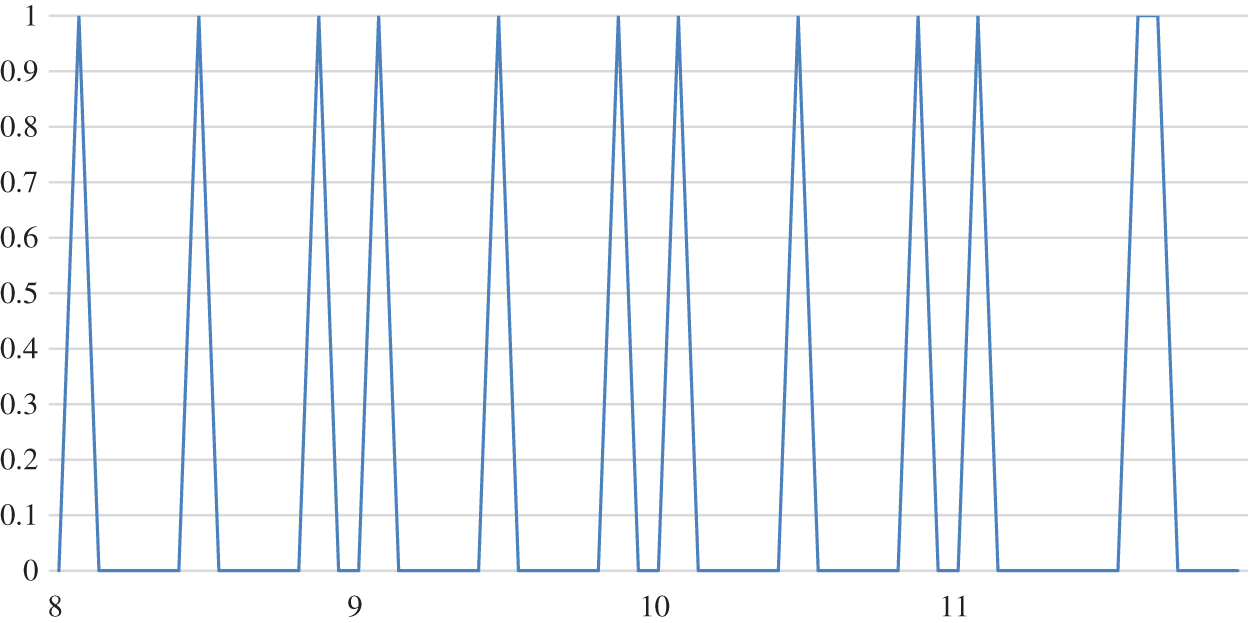
Figure 8: The matching scheme
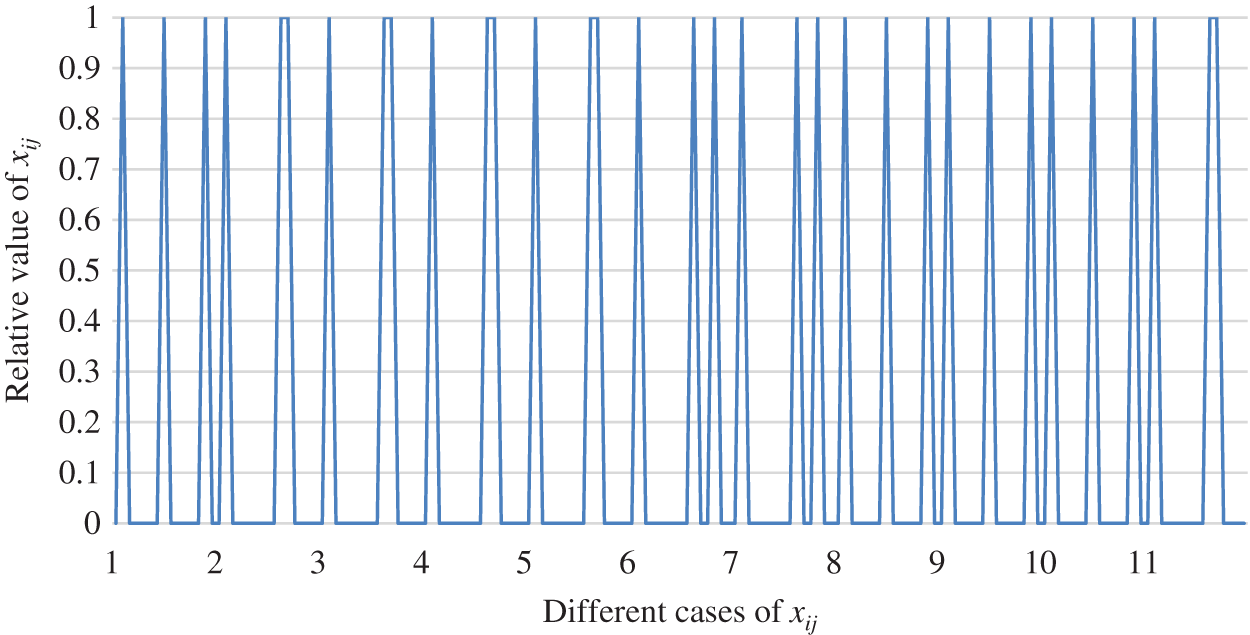
Figure 9: The matching scheme
From Figs. 6 to 8, the function of two-sided agent weight values on the matching scheme is examined in the paper. Fig. 9 shows an overall comparison. It can be concluded that the matching results slightly changes with the change in the two-sided agent’s weight. Therefore, it is clear that the weight of the two-sided agent plays no significant role in the change of the matching scheme.
The tendency of the relationship between object function value Z and matching scheme
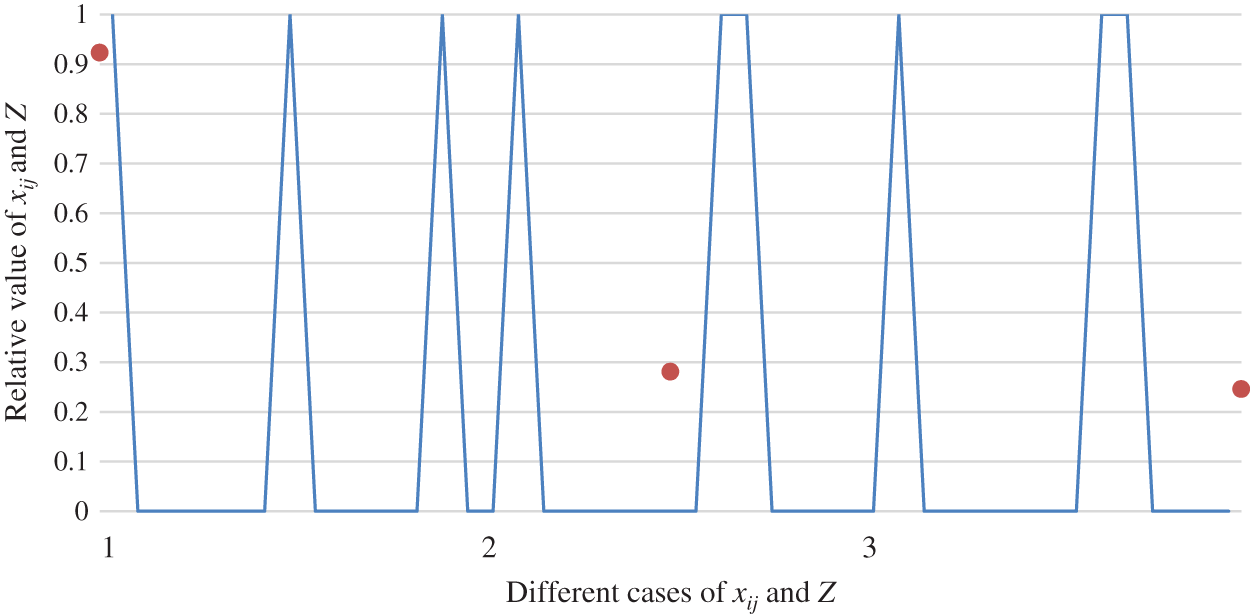
Figure 10: The relationship between object function value Z and matching scheme
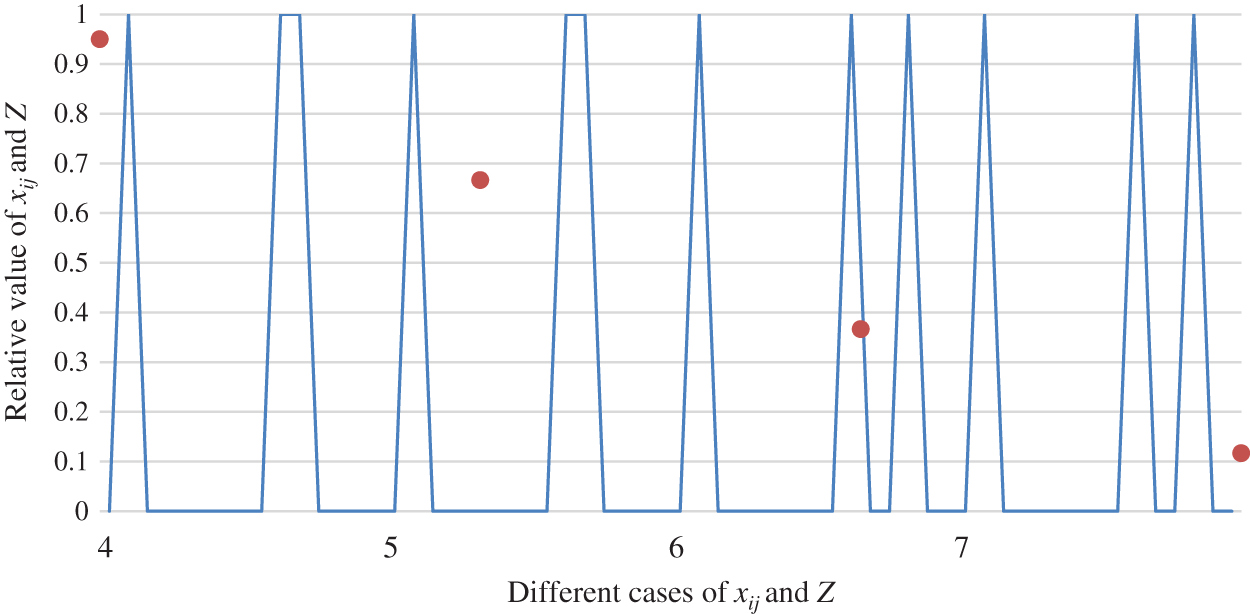
Figure 11: The relationship between object function value Z and matching scheme
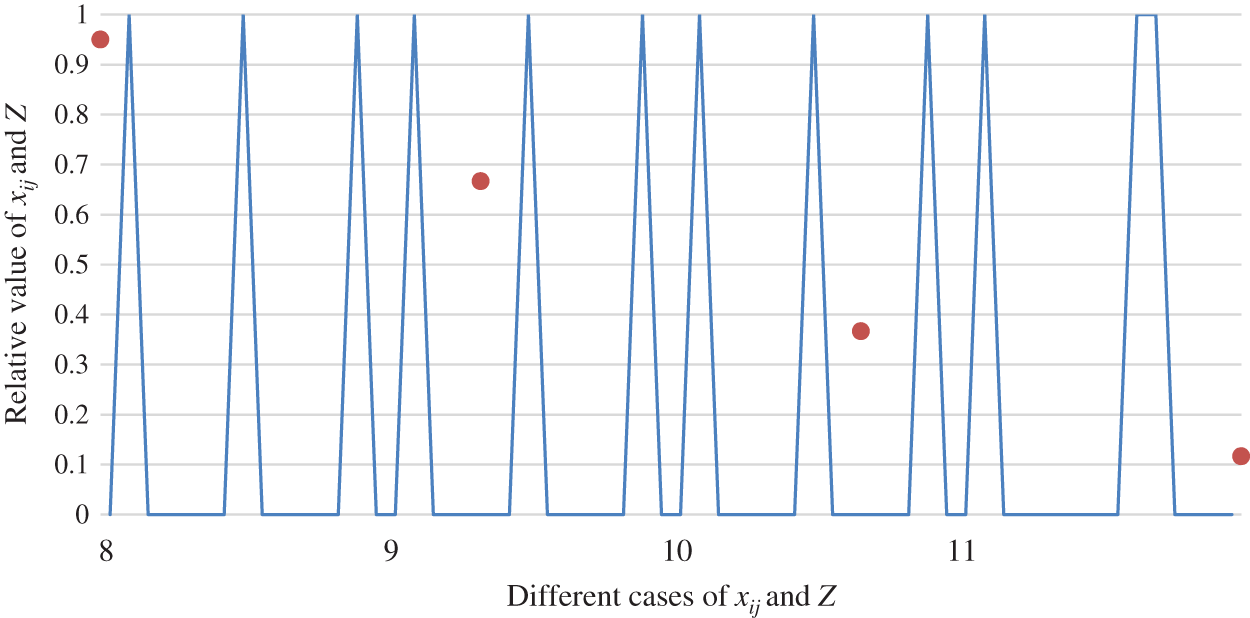
Figure 12: The relationship between object function value Z and matching scheme
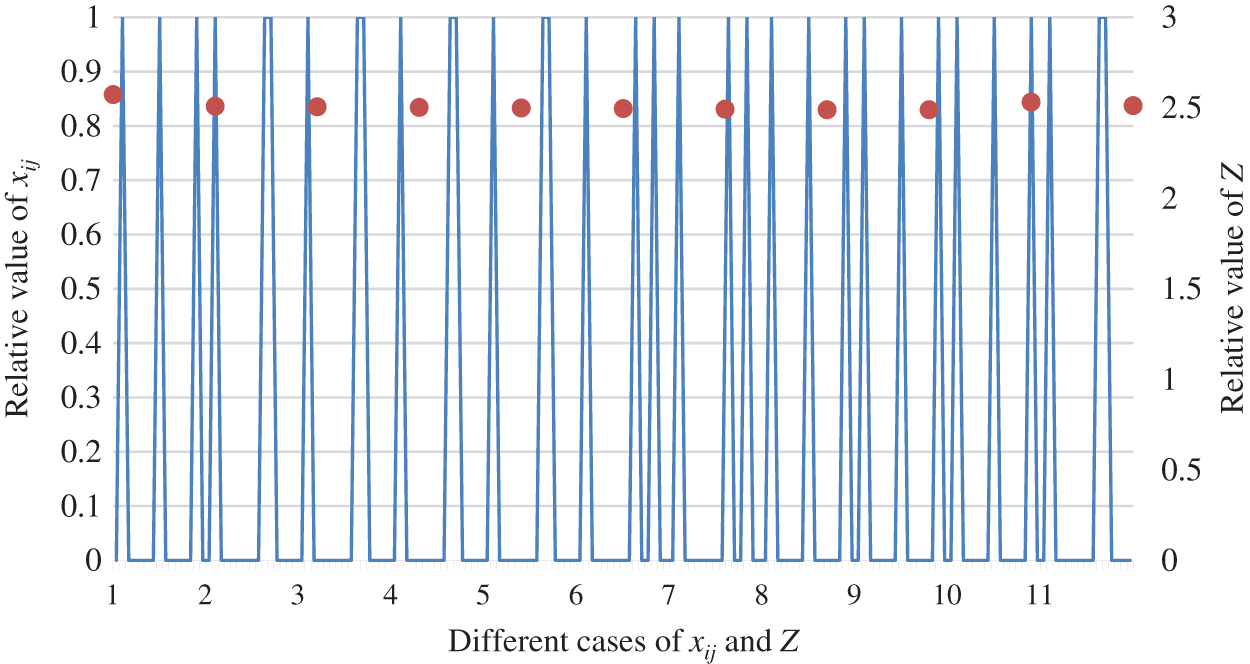
Figure 13: The relationship between object function value Z and matching scheme
As shown in Figs. 10 to 12, the paper analyzes the role of two-sided agent weight values on the objection function value and matching scheme. Fig. 13 displays the overall comparison. This leads to the conclusion that a key factor in the change in the value of the objection function is the weight of the two-sided agent. However, the result reveals that the weight of the two-sided agent has no vital role in the change of matching scheme.
Firstly, to better illustrate the advantages of the proposed method for handling fuzzy preference information, the paper compares the proposed method with the one given in [35]. In Reference [35], the score function is applied to the preference information provided by two-sided agents. Table 18 shows the matching results resulting from two methods. As can be seen in Table 18, there are many differences in the bilateral matching scheme obtained by the above two separate methods. Compared with the method used in reference [35] to process fuzzy preference information, the distance metric applied in this paper accurately processes the preference evaluation information given by matching agents, thus avoiding the loss and misunderstanding of preference information.
Second, in contrast to the traditional TSM research, the methodology used in this paper retains complete information while taking into account hesitant fuzziness and the corresponding probability when evaluating matching objects, making the evaluation more scientific and reasonable, and the results under the probability hesitation fuzzy environment correspond to reality.
Third, multiple attributes are considered, and their weights are calculated by using the maximum deviation method, which can ensure a scientific matching result. Simultaneously, the satisfaction of TSM is acquired by the closeness coefficients of each matching subject, making the entire process more interpretable.
In this paper, the TSMDM approach, by considering the attribute of matching objects under probability hesitant fuzzy environment, is developed. The main contributions of this paper are as follows: First, the PHFS is applied to describe the evaluation information provided by matching agents, and the weight vector is incomplete. Second, attribute weight vectors for matching objects are determined using the Hamming distance measures of PHFSs and the extended maximum deviation method based on the unknown weight and probability hesitant fuzzy environment of each matching object. Third, agent satisfaction degrees are gained in accordance with the multi-attribute probability hesitant fuzzy sets comprehensive assessments by using PHFOWA operator. Additionally, the relative closeness coefficient is used to calculate the satisfaction degrees of matched agents. Finally, we build a TSMDM model with the intention of maximizing the overall satisfaction of matching agents, and then the best matching result is determined by solving the constructed TSMDM model with linear weighted method. Overall, the proposed TSMDM approach not only has great potential for application in some real-world TSMDM scenarios, but it could also enhance the theoretical framework for the study of TSMDM problems. The psychology and expectations of the matching subjects when the evaluation information is provided, which is also a future research direction, are not taken into account in this paper. In terms of future research, the future research direction could be presented as follows: (1) For some TSMDM problems, matching objects may provide more evaluation value in hybrid formats, such as the PHFS, probability interval-valued hesitant fuzzy set (PIVHFS) and PHFLTS. In the meanwhile, the matching agents might provide insufficient attribute information. Hence, it could be useful to carry on the discussion of the TSMDM issues with multiple fuzzy information and insufficient attribute values. (2) In the TSMDM process, each matching individual should determine the automatic matching of recommended matching alternatives in the evolutionary environment as a result of the development of artificial intelligence computing systems. In light of these conditions, it could be necessary to develop a novel TSMDM method.
Acknowledgement: The authors would like to thank the editor and anonymous reviewers for their valuable comments and suggestions, thus improving the version of this article.
Funding Statement: This work is supported by the National Natural Science Foundation in China (Yue Qi, Project No. 71861015).
Conflicts of Interest: The authors declare that they have no conflicts of interest regarding the present study.
References
1. Z. Zhang, X. Kou, W. Yu and Y. Gao, “Consistency improvement for fuzzy preference relations with self-confidence: An application in two-sided matching decision making,” Journal of the Operational Research Society, vol. 72, no. 8, pp. 1914–1927, 2021. [Google Scholar]
2. D. Gale and L. S. Shapley, “College admissions and the stability of marriage,” The American Mathematical Monthly, vol. 69, no. 1, pp. 9–15, 1962. [Google Scholar]
3. J. Chang, H. Li and B. Z. Sun, “Matching knowledge suppliers and demanders on a digital platform: A novel method,” IEEE Access, vol. 7, pp. 21331–21342, 2019. [Google Scholar]
4. K. Alexander, “A necessary and sufficient condition for uniqueness consistency in the stable marriage matching problem,” Economics Letters, vol. 178, pp. 63–65, 2019. [Google Scholar]
5. E. M. Fenoaltea, I. B. Baybusinov, J. Y. Zhao, L. Zhou, and Y. C. Zhang, “The stable marriage problem: An interdisciplinary review from the physicist’s perspective,” The Stable Marriage Problem: An Interdisciplinary Review from the Physicist’s Perspective, vol. 917, pp. 1–79, 2021. [Google Scholar]
6. A. E. Roth, “The college admissions problem is not equivalent to the marriage problem,” Journal of Economic Theory, vol. 36, no. 2, pp. 277–288, 1985. [Google Scholar]
7. S. Q. Chen, L. Zhang, H. L. Shi and Y. M. Wang,“Two-sided matching model for assigning volunteer teams to relief tasks in the absence of sufficient information,” Knowledge-Based Systems, vol. 232, no. 28, pp. 1–18, 2021. [Google Scholar]
8. D. J. Yu and Z. S. Xu, “Intuitionistic fuzzy two-sided matching model and its application to personnel-position matching problems,” Journal of the Operational Research Society, vol. 71, no. 2, pp. 312–321, 2020. [Google Scholar]
9. Y. M. Miao, R. Du, J. Lin and J. C. Westland, “A Two-sided matching model in the context of B2B export cross-border e-commerce,” Electronic Commerce Research, vol. 19, no. 4, pp. 841–861, 2019. [Google Scholar]
10. R. Liang, C. Z. Wu, Z. H. Sheng and X. Y. Wang, “Multi-criterion two-sided matching of public–private partnership infrastructure projects: Criteria and methods,” Sustainability, vol. 10, no. 1178, pp. 1–22, 2018. [Google Scholar]
11. Y. Liu and K. W. Li, “A Two-sided matching decision method for supply and demand of technological knowledge,” Journal of Knowledge Management, vol. 21, no. 3, pp. 592–606, 2017. [Google Scholar]
12. T. Wu, M. B. Zhang, X. Tian, S. Y. Wang and G. W. Hua, “Spatial differentiation and network externality in pricing mechanism of online car hailing platform,” International Journal of Production Economics, vol. 219, no. 1, pp. 275–283, 2020. [Google Scholar]
13. Z. H. Wang, Y. Y. Li, F. Gu, J. F. Guo and X. J. Wu, “Two-sided matching and strategic selection on freight resource sharing platforms,” Physica A: Statistical Mechanics and its Applications, vol. 559, pp. 125014, 2020. [Google Scholar]
14. Y. Liu, Z. P. Fan and Y. P. Jiang, “Satisfied surgeon-patient matching: A model-based method,” Quality & Quantity, vol. 52, no. 6, pp. 2871–2891, 2018. [Google Scholar]
15. Y. P. Jiang, Z. P. Fan, H. M. Liang and M. H. Sun, “An optimization approach for existing home seller-buyer matching,” Journal of the Operational Research Society, vol. 70, no. 2, pp. 237–254, 2018. [Google Scholar]
16. Z. Z. Jiang, W. H. Ip, H. Lau and Z. P. Fan, “Multi-objective optimization matching for one-shot multi-attribute exchanges with quantity discounts in e-brokerage,” Expert Systems with Applications, vol. 38, no. 4, pp. 4169–4180, 2011. [Google Scholar]
17. D. C. Liang, Y. J. Zhang and W. Cao, “q-rung orthopair fuzzy choquet integral aggregation and its application in heterogeneous multi criteria two-sided matching decision making,” International Journal of Intelligent Systems, vol. 34, pp. 3275–3301, 2019. [Google Scholar]
18. D. C. Liang, X. He, Z. S. Xu and J. H. Li, “Multi-attribute strict two-sided matching methods with interval-valued preference ordinal information,” Journal of Experimental & Theoretical Artificial Intelligence, vol. 34, no. 4, pp. 545–569, 2021. [Google Scholar]
19. J. L. Lu and J. Ni,“A Multi-attribute two-sided matching decision method based on multi-granularity probabilistic linguistic MARCOS,” Mathematical Problems in Engineering, vol. 34, no. 3, pp. 1–16, 2022. [Google Scholar]
20. P. Pu, G. H. Yuan, “Two-sided matching model considering multi-information fusion of stakeholders,” Expert Systems with Applications, vol. 212, pp. 118784, 2023. [Google Scholar]
21. Z. P. Fan, M. Y. Li and X. Zhang, “Satisfied two-sided matching: A method considering elation and disappointment of agents,” Soft Computing, vol. 22, no. 21, pp. 7227–7241, 2018. [Google Scholar]
22. X. Chen, J. Wang, H. M. Liang and J. Han, “Hesitant multi-attribute two-sided matching: A perspective based on prospect theory,” Journal of Intelligent and Fuzzy Systems, vol. 36, no. 3, pp. 6343–6358, 2019. [Google Scholar]
23. J. Qin, S. Fan, H. Liang, C. C. Li and Y. C. Dong, “Two-sided matching decision-making in an incomplete and heterogeneous context: A optimization-based method,” International Journal of Computational Intelligence Systems, vol. 15, no. 23, pp. 1–15, 2022. [Google Scholar]
24. Y. Lin, Y. M. Wang and K. S. Chin, “An enhanced approach for two-sided matching with 2-tuple linguistic multi-attribute preference,” Soft Computing, vol. 23, no. 17, pp. 7977–7990, 2019. [Google Scholar]
25. Z. Zhang, J. Gao, Y. Gao and W. Yu, “Two-sided matching decision making with multi-granular hesitant fuzzy linguistic term sets and incomplete criteria weight information,” Expert Systems with Applications, vol. 168, pp. 1–12, 2021. [Google Scholar]
26. V. Torra,“Hesitant fuzzy sets,” International Journal of Intelligent Systems, vol. 25, no. 6, pp. 529–539, 2010. [Google Scholar]
27. B. Zhu, “Decision making methods and applications based on preference relations,” Ph.D. Dissertation, University of Southeast University, Nanjing, 2014. [Google Scholar]
28. X. D. Liu, Z. W. Wang, S. T. Zhang and Y. F. Chen, “Investment decision making along the B & R using critic approach in probabilistic hesitant fuzzy environment,” Journal of Business Economics and Management, vol. 21, no. 6, pp. 1683–1705, 2020. [Google Scholar]
29. J. Gao, Z. S. Xu and H. C. Liao, “A dynamic reference point method for emergency response under hesitant probabilistic fuzzy environment,” International Journal of Fuzzy Systems, vol. 19, no. 5, pp. 1261–1278, 2017. [Google Scholar]
30. Q. Y. Ding, Y. M. Wang and M. Goh, “TODIM dynamic emergency decision-making method based on hybrid weighted distance under probabilistic hesitant fuzzy information,” International Journal of Fuzzy Systems, vol. 23, pp. 474–491, 2021. [Google Scholar]
31. J. P. Liu, C. Huang, J. S. Song, P. C. Du and F. F. Jin, “Group decision making based on the modified probability calculation method and DEA cross-efficiency with probabilistic hesitant fuzzy preference relations,” Computers & Industrial Engineering, vol. 156, pp. 1–15, 2021. [Google Scholar]
32. S. Zhang, Z. S. Xu and Y. He, “Operations and integrations of probabilistic hesitant fuzzy information in decision making,” Information Fusion, vol. 38, no. 2, pp. 1–11, 2017. [Google Scholar]
33. J. Ding, Z. S. Xu and N. Zhao, “An interactive approach to probabilistic hesitant fuzzy multi-attribute group decision making with incomplete weight information,” Journal of Intelligent & Fuzzy Systems, vol. 32, pp. 2523–2536, 2017. [Google Scholar]
34. Z. Su, Z. S. Xu, H. Zhao, Z. N. Hao and B. Chen,“Entropy measures for probabilistic hesitant fuzzy information,” IEEEAccess, vol. 7, pp. 65714–65727, 2019. [Google Scholar]
35. Q. Yue and L. L. Zhang, “Two-sided matching for hesitant fuzzy numbers in smart intelligent technique transfer,” Mechanical Systems and Signal Processing, vol. 139, pp. 1–11, 2020. [Google Scholar]
36. M. M. Xia and Z. S. Xu, “Hesitant fuzzy information aggregation in decision-making,” International Journal of Approximate Reasoning, vol. 52, no. 3, pp. 395–407, 2011. [Google Scholar]
37. F. Y. Zhong and Y. C. Deng, “Audit risk evaluation method based on TOPSIS and choquet fuzzy integral,” American Journal of Industrial and Business Management, vol. 10, pp. 815–823, 2020. [Google Scholar]
38. Y. M. Wang, “Using the method of maximizing deviations to make decision for multiindices,” Systems Engineering and Electronics, vol. 8, no. 3, pp. 21–26, 1997. [Google Scholar]
39. Q. Yue, W. C. Zhou and W. Hu, “A new theory of triangular intuitionistic fuzzy sets to solve the two-sided matching problem,” Alexandria Engineering Journal, vol. 63, pp. 57–73, 2022. [Google Scholar]
40. N. Xiang, Y. J. Dou, B. Y. Xin, K. W. Yang and Y. J. Tan, “High-end equipment: An improved two-sided based S&M matching and a novel pareto refining method considering consistency,” Expert Systems with Applications, vol. 202, pp. 1–12, 2022. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools