A Technical Note for a Shor’s Algorithm by Phase Estimation

1  Introduction

The most famous quantum algorithm is the Shor’s algorithms that is dedicated to integer factorization and that received a considerable amount of attention due to its possible application in the cryptanalysis field. The algorithm proposes a super-polynomial execution speedup as regards the classical resolution on classical computers. The RSA encryption method lies on the hypothesis that it is exponentially harder to factor large numbers that achieving a multiplication ensuring secure send of information online. Shor’s factoring algorithm uses an efficient combination of regular and quantum computers, i.e., a hybrid computing approach where the regular computers and the quantum ones are paired into an iterative process [1]. Such approaches received a lot of attention leading to several variational algorithms including but not limited to QAOA [2,3].

Feynman has been the very first researcher considering that quantum mechanics could be more efficient computationally than a Turing machine considering that a computer based on quantum mechanics should avoid the expensive computation required for simulation on a classical computer. The question has been addressed first by [4] proving that some problems can be solved fast to optimality using quantum computers. In 1994 [5] introduced a circuit using an oracle to solve a problem (i.e., a black-box that can be checked) requiring a polynomial time since it requires an exponential time on a classical non quantum computer. Shor [6] introduced a quantum computer algorithm for factoring a integer number N undirectly by computing the order of an element a in the multiplicative group (modN) considering the lower integer l/al≡1modN. He defines a new promising approach to factor a number into a product of primes and his proposal resulted in a significant improvement of the factoring algorithms efficiency. The corner stone of the Shor’s algorithm is the modular exponentiation that is the most computational component (in time and space) of Shor’s algorithm [7].

2  Proposition

Finding a factor of N (N is an odd number) requires a method to compute the order l of a where a is a random integer number/a∈[2;N−1]:

al≡1modN

al−1≡0modN

If l is an even number we have: (al/2−1).(al/2+1)≡0modN.

And the Euclidean algorithm of [8] can be used to compute the gcd(al2−1;N) and gcd(al2+1;N) giving the two dividers of N. If l is an odd number, it is possible to investigate both the even numbers l−1 and l+1. Our work propose an architecture where the computation of the order of an element a in the multiplicative group (modN) is replaced by the computation of the order of a in the phase additive group (mod2π). The Quantum Circuit defines a probability phase distribution that aggregates probabilities on phases that indirectly model order of a. The measurement gates jointly gives a float value that defines the phase that will permit to find the order of a with a high probability through further classical post-processing. The sampling of the probability distribution permits to create a heap χ of set of phases (step 5 to 8 in algorithm 1). The post-processing consists in iteratively considering the phases registered in χ which may gives on order of a: li=χi×N.

If li≡0mod2 the post-processing consists in computing both gcd(ali/2−1;N) and gcd(ali/2+1;N) which define two dividers of N and that are saved into the set of divider of N referred to as ℘. If li is an odd number, both the even number li−1 and the even number li+1 are investigated for giving factors of N.

Note that the “necessary” conditions at steps 8, 9 and 24 have to be design over considerations of the objective function that could be, but not limited to: 1) computation of one divider only; 2) computation of a fixed number of dividers; 3) computation of all dividers.

2.1 Shor’s Quantum Circuit Based on Phase

Given a, to find l such that al≡1modN, the circuit Fig. 1 is based on the following considerations. First we find p the lowest power of 2 such that 2p=q satisfy 2p>N+1 and we compute n the lowest power of 2 such that 2n>a.

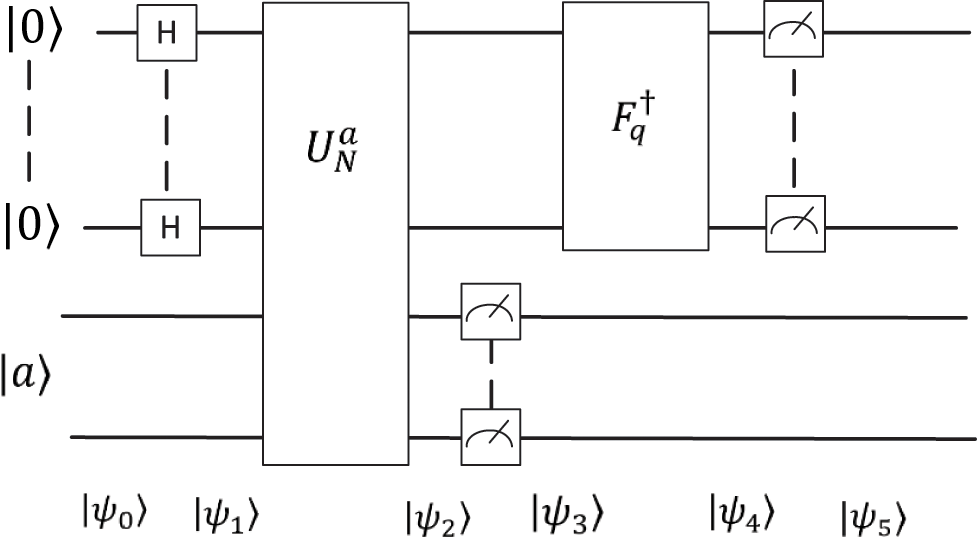
Figure 1: Quantum circuit

The second step is easy since its entails is putting each qubit of the first register into the superposition 12(|0⟩+|1⟩) and to compute almodN in the second register leaving the circuit in the state:

|ψ⟩=1q.∑j=0q−1|j⟩⊗|a⟩(1)

The most computational quantum part of the classical Shor’s algorithm is the modular exponentiation UNa that achieves the transformation to its quantum input:

UNa.|l⟩⊗|y⟩=|l⟩⊗|y⊕(almodN)⟩

with0≤l<q,0≤y<2n(2)

The Hadamard gates on the first q qubits creates a superposition of number l before application of the modular exponentiation.

|ψ2⟩=UNa.(1q∑j=0q−1|j⟩⊗|0⟩⊗n)(3)

|ψ2⟩=UNa.(1q∑j=0q−1|j⟩⊗|0…0⟩)(4)

|ψ2⟩=1q∑j=0q−1|j⟩⊗|0→⊕almodN⟩(5)

Classical modular exponentiations are based on: 1) controlled multiplier/accumulator [9,10]; 2) quantum divider based on the algorithm introduced by [11].

We propose to replace the modular exponentiation UNa by UNφa that achieves the transformation to its quantum input in:

UNφa.|l⟩⊗|y⟩=|l⟩⊗|y⊗φalmod2π

with0≤l<q,0≤y<2n(6)

The Hadamard gates at the first q qubits have created a superposition of number l before application of the modular exponentiation.

|ψ2⟩=UNφa.(1q∑j=0q−1|j⟩⊗|0⟩⊗n)(7)

|ψ2⟩=UNφa.(1q∑j=0q−1|j⟩⊗|0…0⟩)(8)

|ψ2⟩=1q∑j=0q−1|j⟩⊗|0→⊕φalmod2π⟩(9)

The classical post-processing of the measurement in the computational basis after the Inverse Quantum Fourier Transform (QFT† block) is a sampling procedure that gives with high probability the period of the function f(l)=φalmod2π.

During post-processing, all the phases φa are saved into a pool χ of phases and all phases are iteratively investigated to check if the phase can permit to obtain one divider:

For all li=χi×N/li≡0mod2, compute v1=ali/2−1 and v2=ali/2+1 and next p1=gcd(v1;N) and p2=gcd(v1;N). p1 and p2 are both dividers of N.

For all li=χi×N/li≡1mod2, compute v1=a(li+1)/2−1, v2=a(li+1)/2+1, v3=a(li−1)/2−1, v4=a(li−1)/2+1. Compute next p1=gcd(v1;N), p2=gcd(v2;N), p3=gcd(v3;N) and p4=gcd(v4;N) that are dividers of N.

2.2 Quantum Fourier Transformation

For p qubits, q=2p defines 2p basis vectors and the Quantum Fourier Transformation is:

Fq(|k⟩)=X|k⟩=12n∑j=02n−1e2.π.i.k.j2n.|l⟩(10)

Fq(|k⟩)=X|k⟩=1q∑j=0q−1e2.π.i.k.j2n.|l⟩(11)

Fq(|k⟩)=X|k⟩=1q∑j=0q−1ωk.j.|j⟩avecωk.j=e2.π.i.k.j2n(12)

By consequence

Fq†(|k⟩)=1q∑j=0q−1ω−k.j.|j⟩(13)

2.3 Modular Exponentiation of the Phase:UNφa

The design uses q=2p qubits to represents l, a controlled qubit for the Inverse Fourier Transformation, n qubits to represents a and a controlled qubit required by UNφa (Fig. 2).

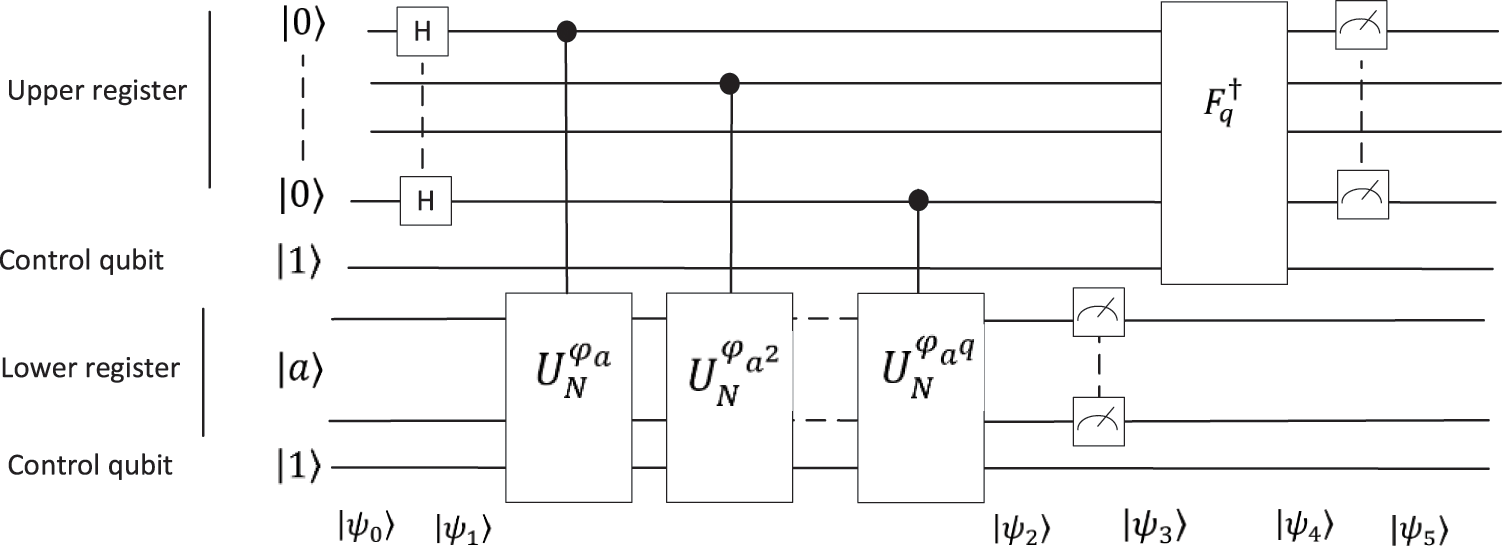
Figure 2: Design of the exponentiation circuit using controlled modular phase

The design uses q controlled-U (CU) block, and each block referred to as UNφa2j is a controlled modular 2.π multiplier of its input (the lower quantum register) by constant φa by (2j−1modN). Each block is controlled by the corresponding |lj⟩ qubit of the upper quantum register.

Definition of φa2j

Let us note φa=2.πN.a

The phase of a is: φa2j=(2j−1modN).2.πN.a

The modular exponentiation UNφak requires the iterative computation of

φa1, φa2,φa4,φa8,…,φak,…

i.e., the computation of φa20, φa21,φa22,φa23,…,φa2p−1,φa2p,…

We note

φa2p=φa2p−1+∑k=12p−1φa=φa2p−1+2p−1.φa

For example with a=3, we have φa=2.πN.3, φa2=2.πN.3+2.πN.3 and

φa4=2.πN.3+2.πN.3+2.πN.3+2.πN.3

φa4=φa2+22−1.φa=φa2+2.φa

We have next:

φa8=φa4+22.φa=φa4+4.φa=8.φa

φa16=φa8+23.φa=φa8+8.φa=16.φa

Definition of UNφak

A controlled UNφak block is based on the application of CP(α) conditional phase rotation gates that need to be repeated a logarithmic number of times regarding to N and next on the application of the Inverse Fourier Transformation (Fig. 3). The diagonal symmetric controlled gate CP(α)is used to induce a phase on the state of the target qubit number n depending on the control qubit state.

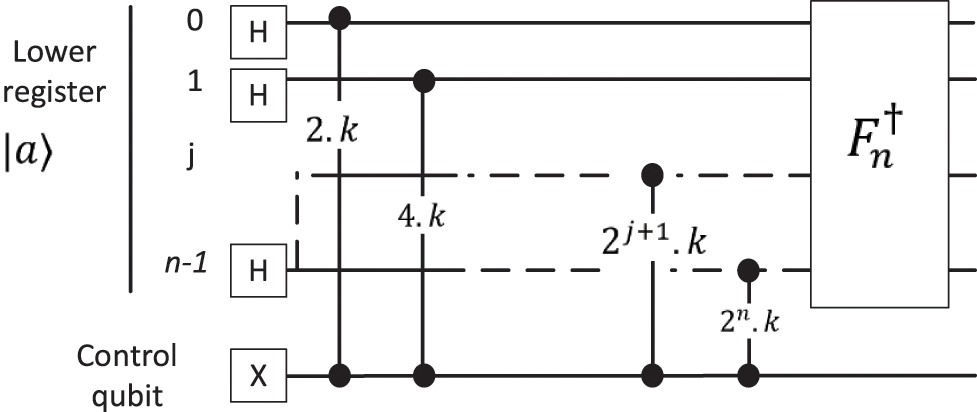
Figure 3: Design of UNφak

Matrix representation of CP(α) for two qubits

CP(α)=|0⟩⟨0|⊗I+|1⟩⟨1|⊗P=(100001000010000eα)(14)

n consecutive applications of CP(α) gates are required for defining a n-qubit quantum number

|b⟩=|bn−1⟩|bn−2⟩…|b1⟩|b0⟩(15)

that is transformed by a simple uncontrolled Inverse Quantum Fourier Transformation into a quantum state

|φak⟩=|φakn−1⟩|φakn−2⟩|φakn−3⟩…|φak0⟩(16)

We have:

Fn(|b⟩)=12n∑j=02n−1e2.π.i.b.j2n.|j⟩

and the individual jth qubit |φakj⟩ of |φak⟩:

|φakj⟩=12(|0⟩+e2.π.i.b2j|1⟩)

3  Experimentation

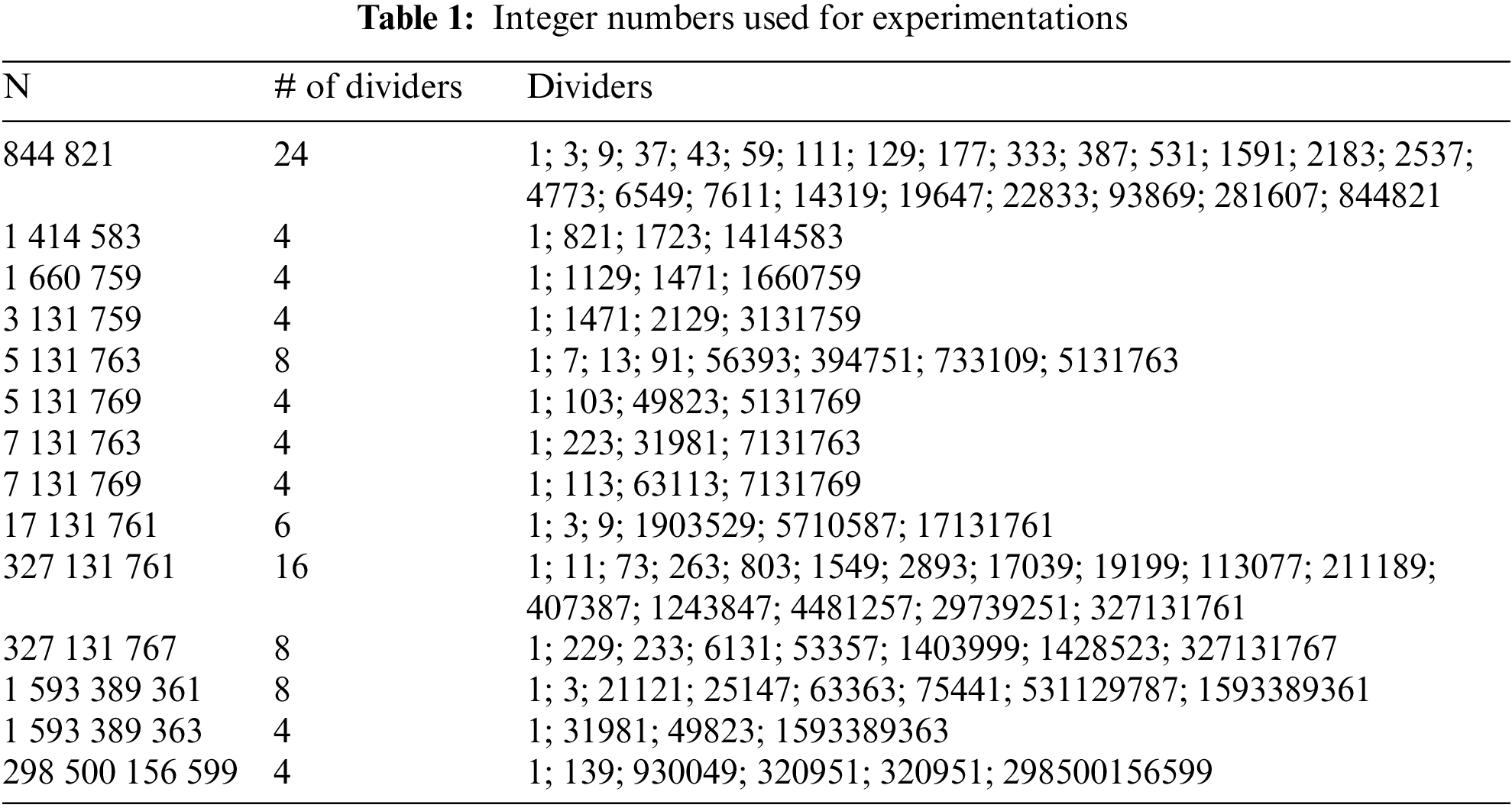
With the following examples, the objective is to illustrate the performances of this phase based Shor’s algorithm on both simulator and physical quantum optimizer. Experiments are achieved considering 5 large numbers (introduced in Table 1) with a number of dividers that varies from 4 to 24.

The number of qubits required depends on both N and a: the experiments on the simulator are limited to 32 qubits and the experiments on quantum optimizer are limited to 124 qubits that is the largest IBM physical quantum optimizer available. A number with many dividers should be easier to factor in the sense that one circuit execution should permit to obtain several dividers in one sampling run. Note that for a theoretical point of view, the value of a should be defined at random but from a practical point of view, an efficient implementation should investigate small values first to obtain smaller circuits.

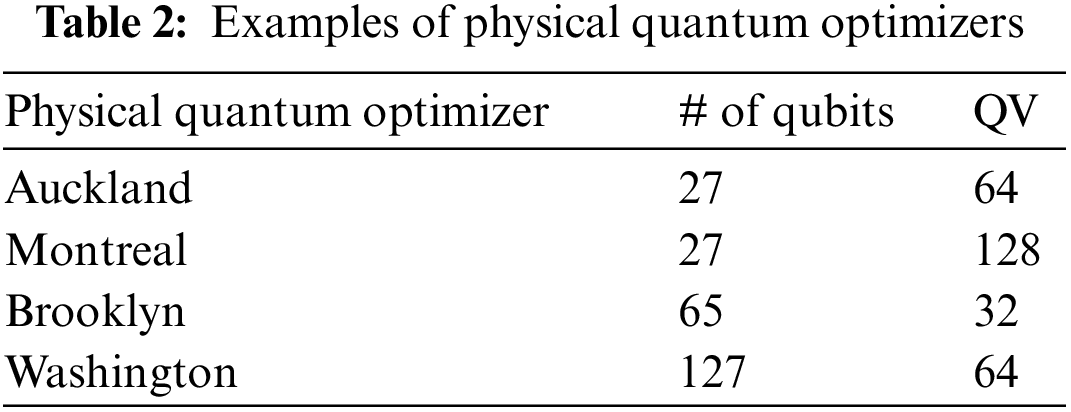
Experiments have been achieved on the Brooklyn Quantum Physical Optimizers introduced in Table 2 and has been chosen taking into account the individual optimizers availabilities and the total pending jobs involved in experiments with the potential to lead the results in acceptable delays at the particular moment. Note that preliminary experiments achieved on Auckland, Montreal and Washington quantum optimizers push us into considering that very similar results should be obtained. Let us note that the Brooklyn physical quantum optimizer is not the best one in term of number of qubits and it is not the more efficient as regards the quantum volume.

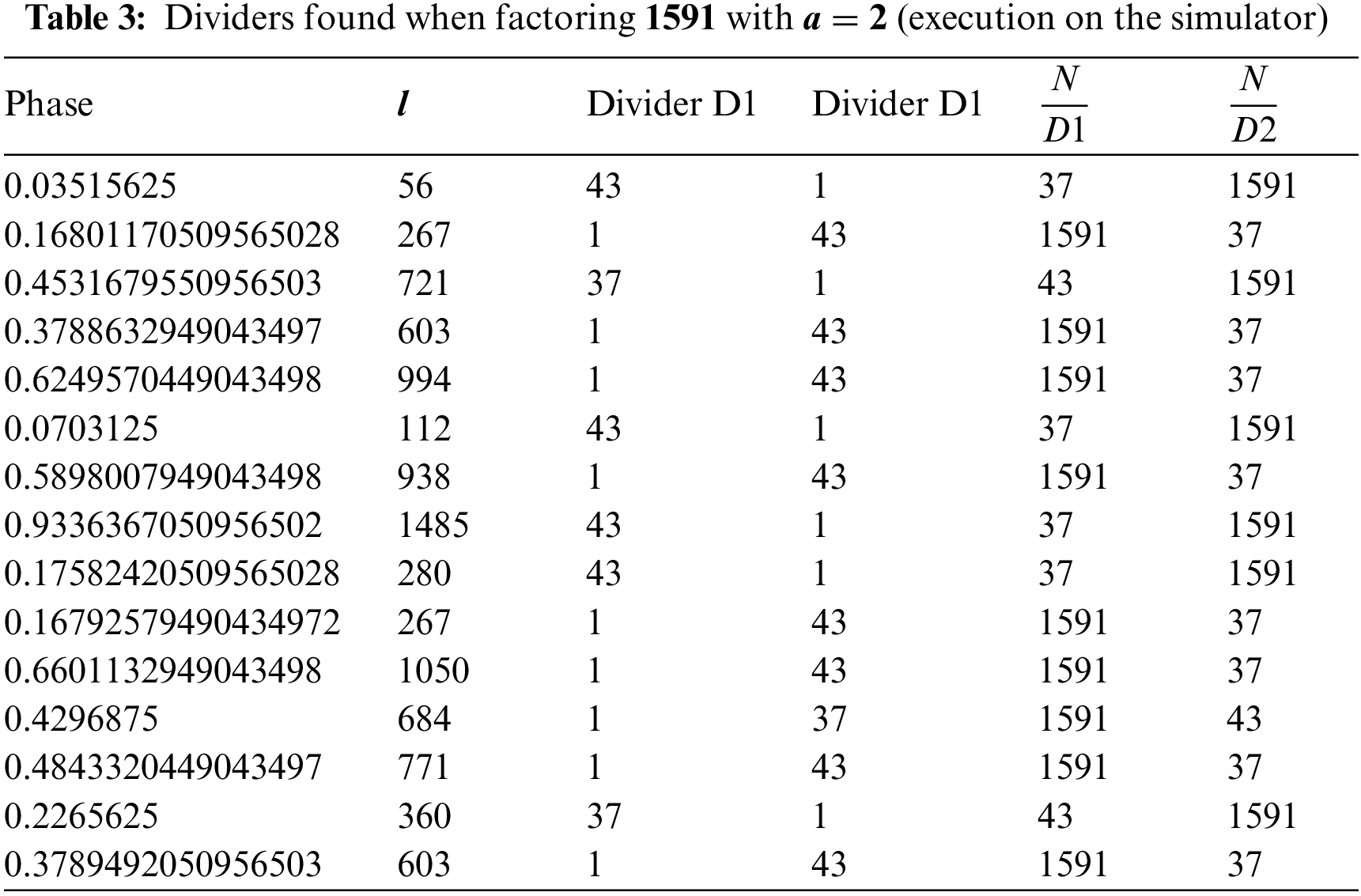
3.1 Numerical Experiments with 1591

For the small N=1591 the probability distribution of l are plotted on Fig. 4. The values l=37, l=43 could occurred when factoring 1591 if a were chosen to be 2 for example. The graphic concerns small N and small a values to make the plot distinguishable but very similar structures of probabilities can be observed for every N and a values. Note that the probabilities plotted on Fig. 4 are related to an execution on the Brooklyn Physical Quantum Optimizer are based on 1500 samplings.

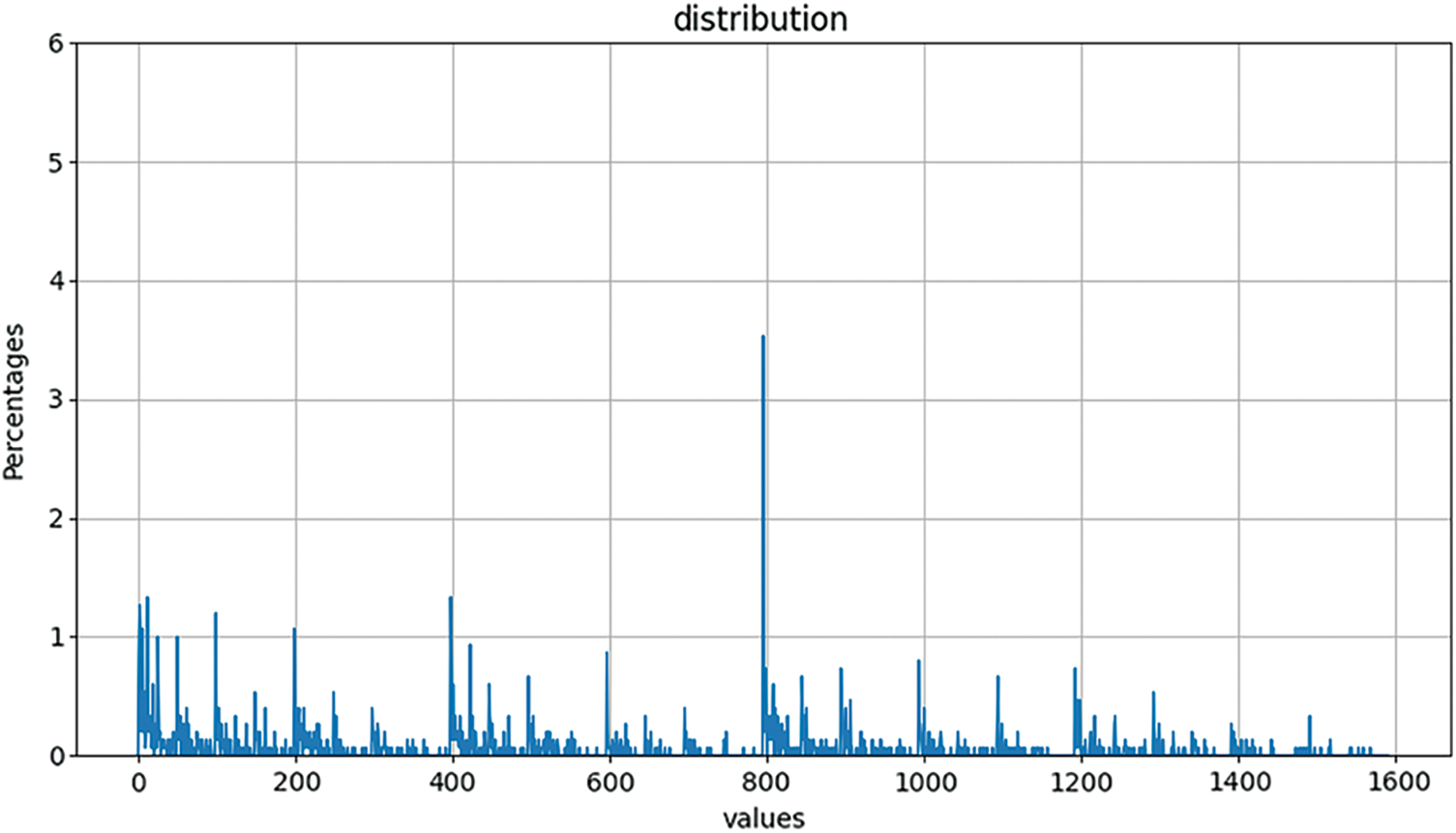
Figure 4: The probability P to observe values giving N=1591 and a=2 (execution on Brooklyn physical quantum optimizer)

The phases in χ define possible values of l for al such that l should be the order of a. Table 3 gives the observed value of both the phase and of l obtained when factoring 1591 with a=2: the post-processing enables us to obtain the two non-trivial dividers of 1541 namely 43 and 37. Execution on the Brooklyn gives quite different probabilities but the observed phase value permits to obtain the dividers 43 and 37.

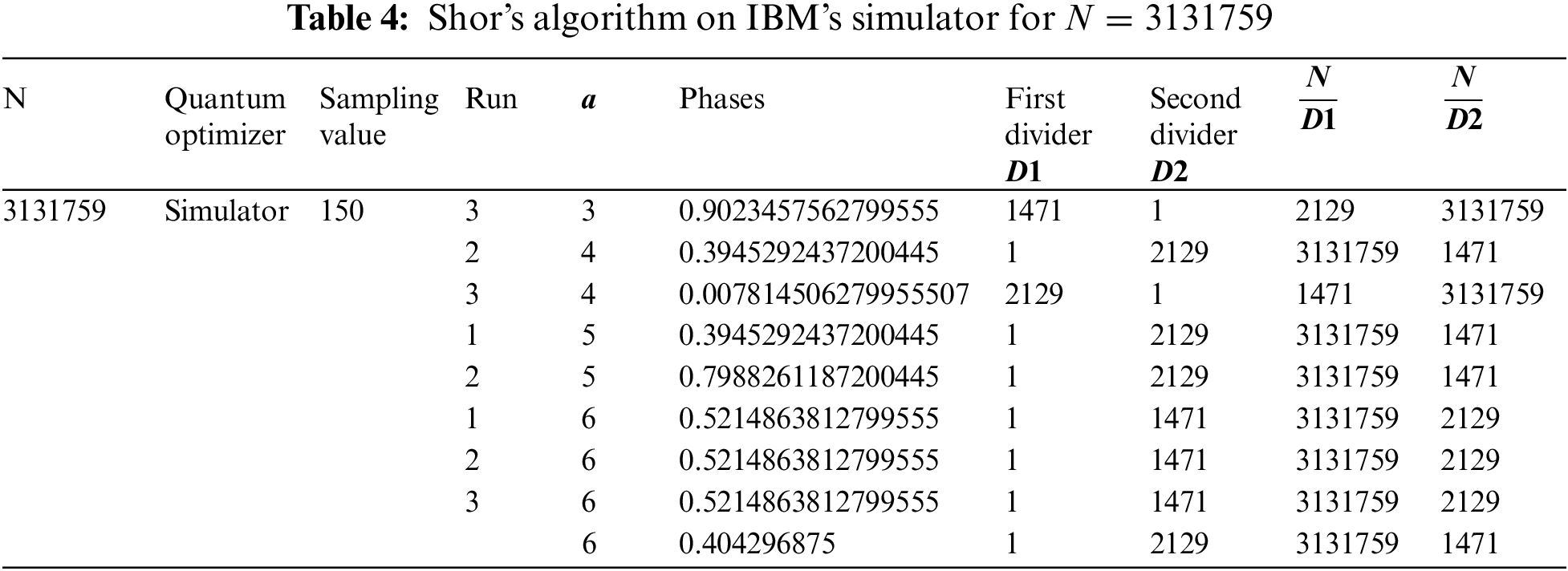
3.2 Numerical Experiments on Simulator when Factoring 3 131 759

Execution of the simulator for N=3131759 has been achieved for several values of a and permits to retrieve several dividers depending on the run. With a=2 the runs are unsuccessful and the run 3 with a=3 succeeds retrieving 1471 and 2129 (Table 4). Note that the number of measurements (150 here) should be increased to obtain more consistent results between runs.

3.3 Numerical Experiments for 3 Numbers: Dividers Obtained for 3 Small Numbers

Table 5 gives the observed values of the phase and the dividers obtained when factoring 844 821 with a=2 during a single run. The results are compliant with the results provided by the simulator and the algorithm succeeds in computing a large part of the dividers. Experiments for 1 414 583 have been achieved with one run for value of a varying from 2 to 5 and the two dividers are identified with a=5.

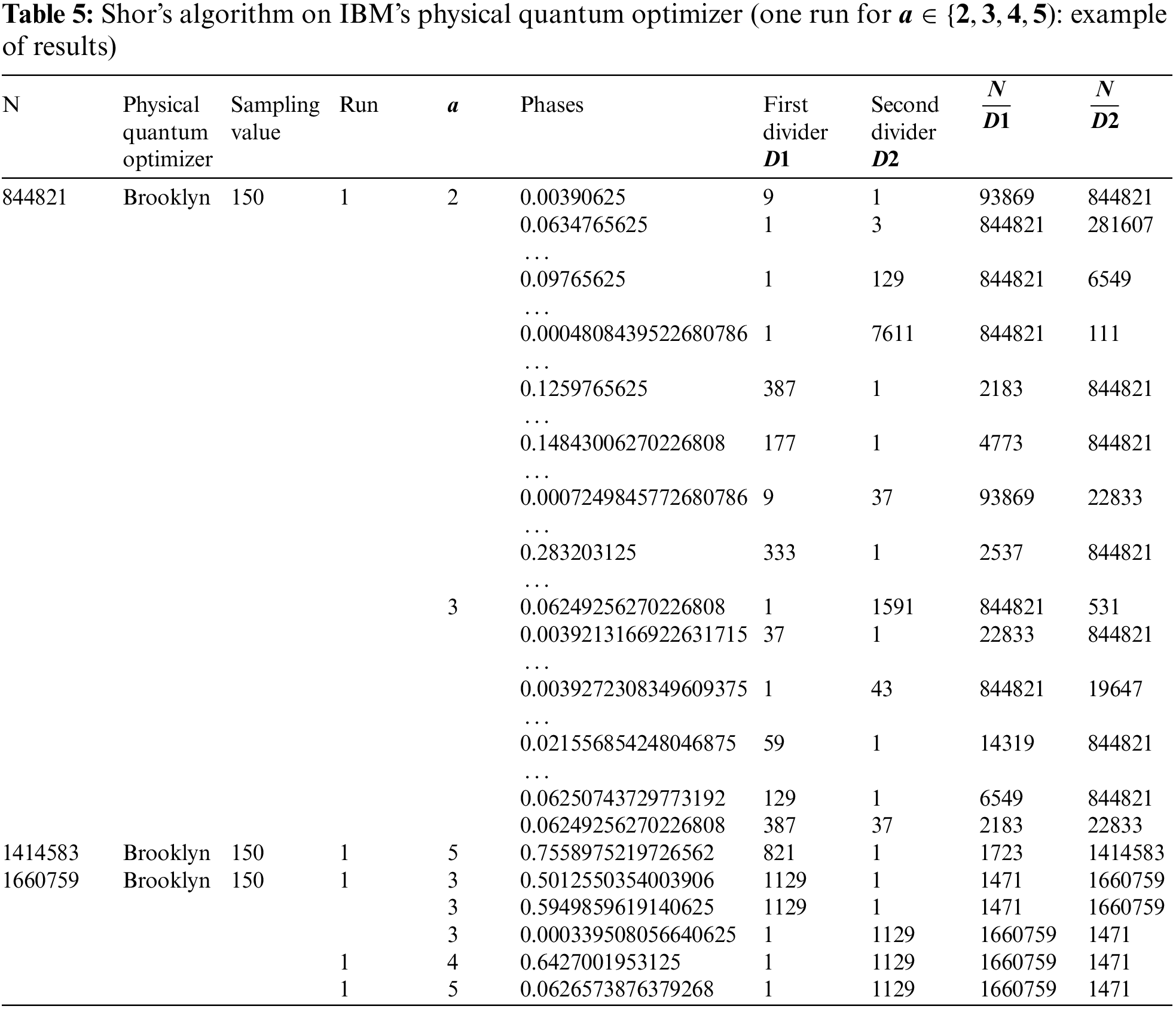
The last number 1660759 has two non-trivial dividers only (1471 and 1129) that are found for a=3,4,5 by the algorithm in one single run as stressed in Table 5.

3.4 Numerical Experiments on IBM Programmable Noisy Quantum Optimizer for Large Number

An attempt for 3 131 759 factorization is achieved with 5 run and a = 2 and it succeeds leading to non-trivial dividers i.e., 1471 and 2129 (Table 6). Note that 5 131 763 can be factorized on the Physical Quantum Optimizer and that a single run with a=2 gives several dividers including 1, 7, 13, 91, 56393, 733109, 394751 and 5 131 763. The algorithm succeeds in factoring 5 131 769 with a=2. Computation of the dividers of both 7 131 763 and 7 131 769 succeed for small value of a as stressed in Table 6.

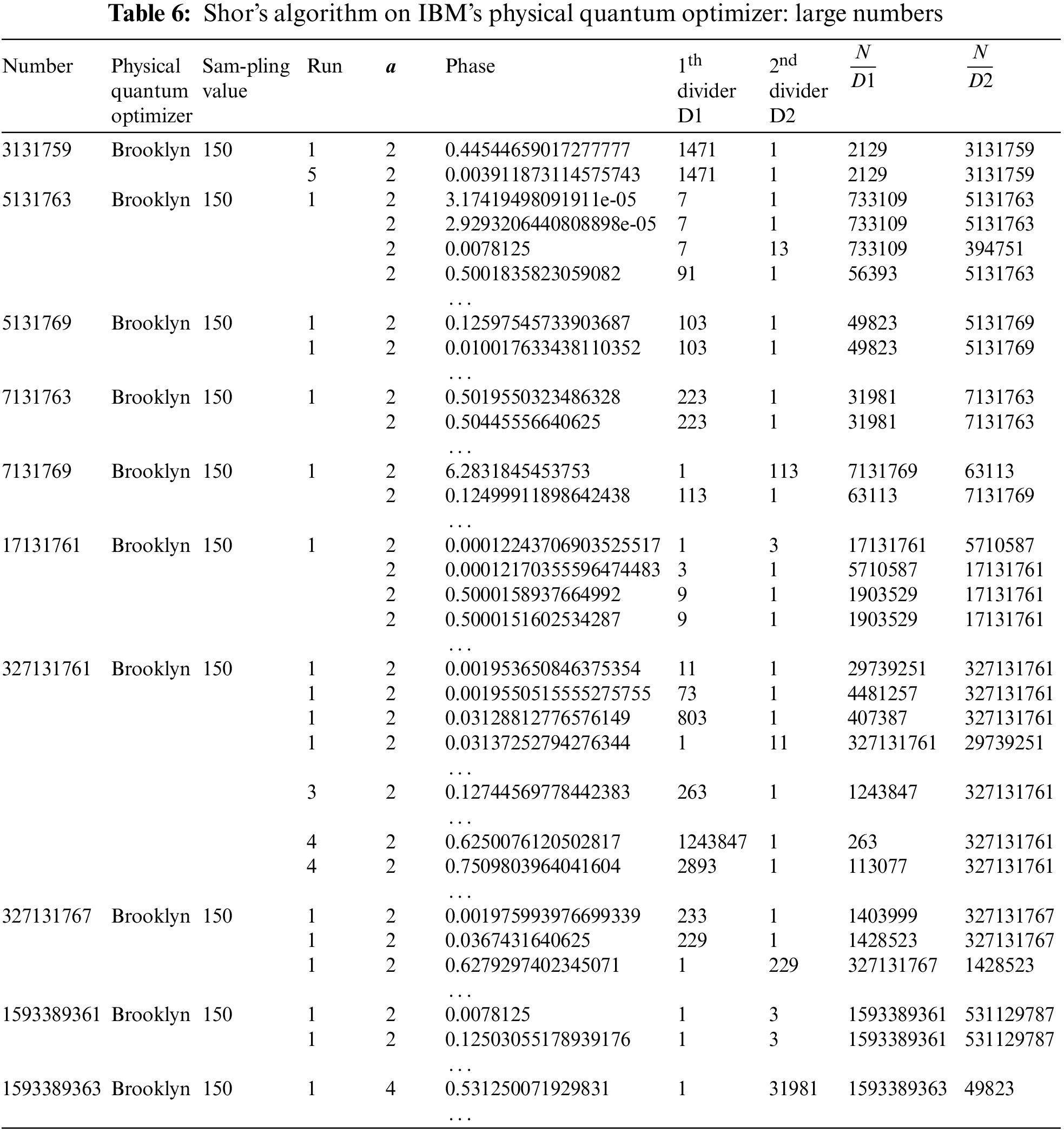
The algorithm succeeds in factoring the large number 327 131 761 and using several run (5 runs are used in the experiments) several dividers are computed including large dividers. Note that the sampling parameters could have to be tune considering a balance between runs and number of sampling efforts.

Half of the dividers of 327 131 767 are computing on a single run for a=2 including the non-trivial dividers 229, 233, 1 403 999 and 1 428 523. For number greater that 1.109, the algorithm succeeds as stressed on Table 6 where the two dividers of 1593389363 are obtained for a=4 with a single run.

3.5 Extra Experiments with Very Large Numbers

Experiments have been carried out with the following numbers 298500156599, 23750433609940 4000, 237504336099404013, and 237504336099404017 that require more than 60 qubits.

To conclude, a set of experiments have been achieved on the Washington physical quantum optimizer using

N=157858237504336099404013

N=237515785823750433609940401323457

N=23751578582375043360994040132345711

N=237515785823750433609940401323451157

N=237515785823750433609940401323451151

N=2375157858237504336099404013234511517

All the results are introduced in Table 7 and confirm the approach efficiency.

4  Concluding Remarks

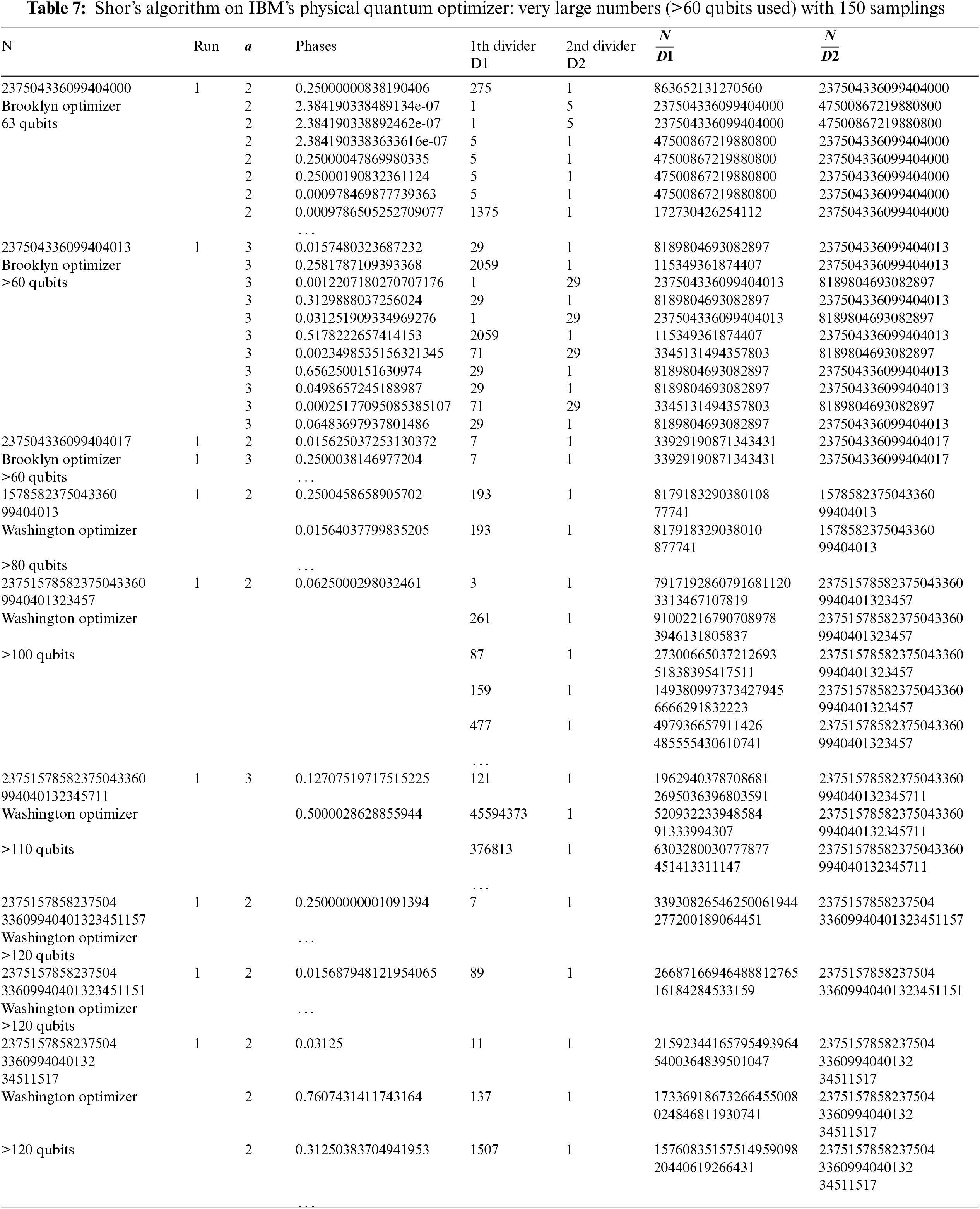
Considering the factorization of a large constant is a challenging problem that can be addressed using a modular multiplier based on phases to build block of a modular exponentiation circuit. Such approach is theoretically accurate taking advantages of the well-known phase definition (φa2j=(2j−1modN).2.πN.a) and particularly useful.

Because of the effectiveness of our models for modular computation that defines compact circuit in both number of qubits and number of gates, our model has permit successful experimentations on physical quantum optimizer for very large integer numbers requiring circuit with more than 100 qubits. The promise of quantum physical optimizers with more than 1000 qubits in 2023 offers interesting perspectives. However, the tests carried out in many fields do not yet conclude about quantum supremacy.

Acknowledgement: Thanks to E. Bourreau for constant support and help in quantum computing research activities.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Sahoo, A. Kumar Mandal, P. Kanti Samanta, I. Basu and P. Roy, “A critical overview on quantum computing,” Journal of Quantum Computing, vol. 2, no. 4, pp. 181–192, 2020. [Google Scholar]

2. E. Farhi and J. Goldstone, A Quantum Approximate Optimization Algorithm. Report MIT-CTP/4610. arXiv:1411.4028v1. 2014. [Google Scholar]

3. M. Medvidović and G. Carleo, “Classical variational simulation of the quantum approximate optimization algorithm,” npj Quantum Inf., vol. 7, no. 1, pp. 101, 2021. https://doi.org/10.1038/s41534-021-00440-z [Google Scholar] [CrossRef]

4. D. Deutsch and R. Jozsa, “Rapid solutions of problems by quantum computation,” in Proc. of the Royal Society of London A, vol. 439, pp. 553–558, 1992. https://doi.org/10.1098/rspa.1992.0167 [Google Scholar] [CrossRef]

5. D. R. Simon, “On the power of quantum computation,” in Proc. of the 35th Annual Symp. on Foundations of Computer Science, Santa Fe, pp. 116–123, 1994. https://doi.org/10.1109/SFCS.1994.365701 [Google Scholar] [CrossRef]

6. P. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” in Proc. of the 35th Annual Symp. on Foundations of Computer Science, Santa Fe, NM, 1994. https://arXiv:quant-ph/9508027 [Google Scholar]

7. A. Pavlidis and D. Gizopulous, “Fast quantum modular exponentiation architecture for shor’s factoring algorithm,” Quantum Information and Computation, vol. 14, no. 7–8, pp. 649–682, 2014. [Google Scholar]

8. D. E. Knuth, The Art of Computer Programming, Second Edition ed., vol. 2: Semi-numerical Algorithms. Addison-Wesley, 1981. https://www-cs-faculty.stanford.edu/~knuth/taocp.html [Google Scholar]

9. T. G. Draper, “Addition on a quantum computer,” arXiv preprint quant-ph/0008033. 2000. [Google Scholar]

10. S. Beauregard, “Circuit for Shor’s algorithm using 2n+3 qubits,” Quantum Information and Computation, vol. 3, pp. 175–185, 2003. [Google Scholar]

11. T. Granlund and P. L. Montgomery, “Division by invariant integers using multiplication,” in Proc. of the ACM SIGPLAN, Conf. on Programming Language Design and Implementation (PLDI), Orlando Florida USA, vol. 29, pp. 61–72, 1994. [Google Scholar]