A Review of Experimental Research on the Mode I Fracture Behavior of Bamboo

1  Introduction

The construction industry is one of the industries with the greatest environmental impact, accounting for 39% of global carbon emissions, with steel and concrete, the two commonly used building materials, dominating [1–3]. Therefore, there is an urgent search for low-carbon, environmentally friendly alternative materials [4,5]. Bamboo is a highly sustainable and eco-friendly building material, widely distributed in Asia, Africa and Latin America, which is receiving considerable attention because of its high yield, fast growth and excellent mechanical properties [6–8]. To solve the disadvantages of restricted size, irregular shape and radial gradient variation of mechanical properties of raw bamboo, a number of bamboo-based composite materials, i.e., engineered bamboo materials, have been developed using composite and recombinant technologies.

Engineered bamboo includes bamboo mat plywood, bamboo scrimber/parallel bamboo stand lumber (PBSL) [9,10], laminated bamboo lumber (LBL) [11–13], laminated flattened-bamboo lumber (LFBL) [14,15] and Glubam [16], among which PBSL and LBL are the two most widely used. The production process of PBSL is as follows: after defibering, the original bamboo is separated into fiber bundles, which are then reconstituted, and glued together with adhesive (Fig. 1a). LBL is made by splitting the original bamboo and shaving off the excess to take the bamboo strips of equal thickness in the middle, then gluing and laminating these bamboo strips together (Fig. 1b). These two materials retain the excellent mechanical properties of bamboo and can also be freely changed in size for processing into large-size and various-shaped components.

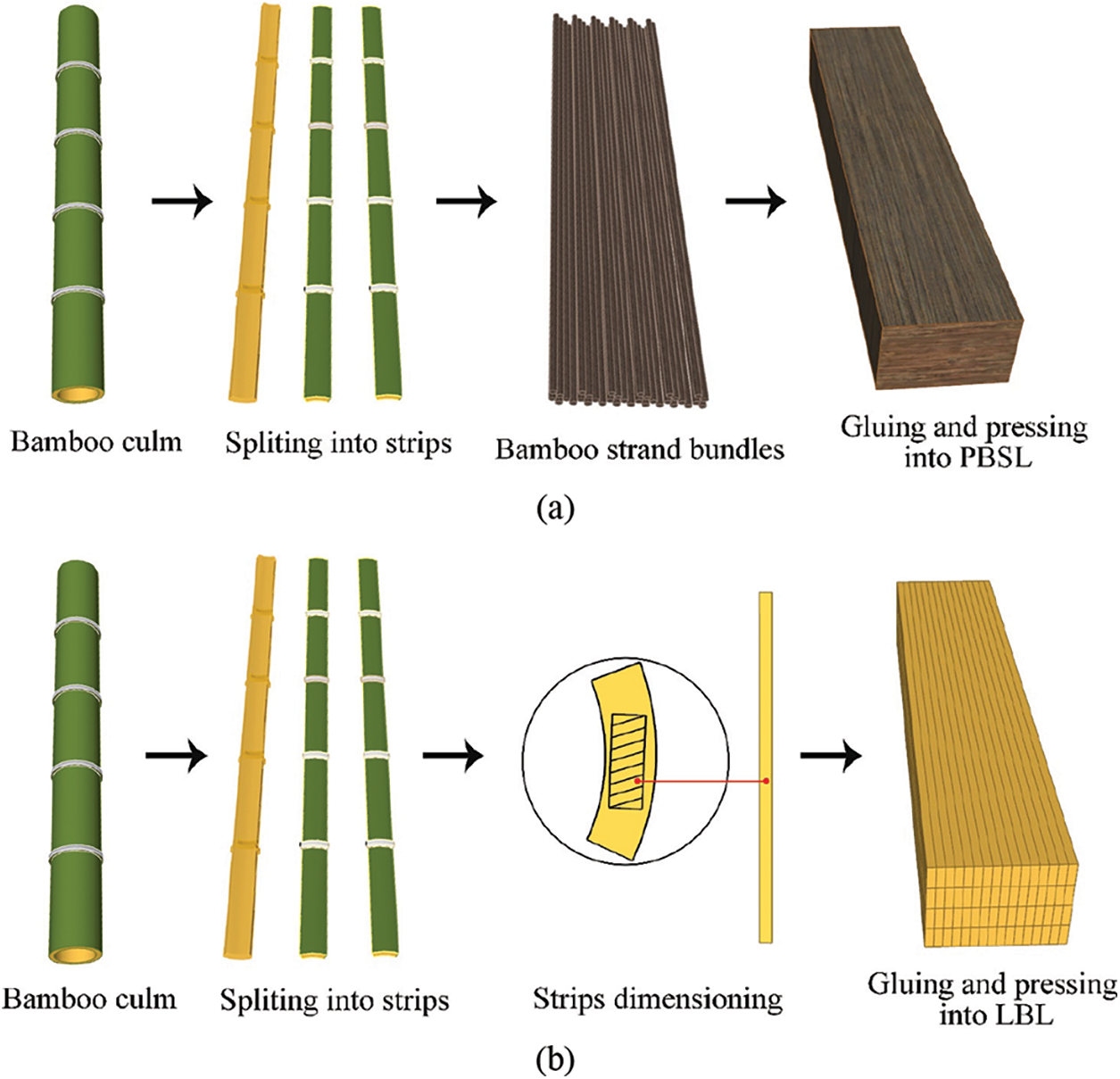
Figure 1: The manufacturing processes of the two most common engineered bamboo [9,11]: (a) The manufacturing process of PBSL [9]; (b) The manufacturing process of LBL [11]

The fiber bundles of bamboo are connected by a matrix (ground tissue) consisting of parenchyma cells, so their interfacial strength is low. Especially in the process of processing into engineered bamboo, bubbles and pores will inevitably exist, which leads to the splitting along the grain direction easily [17,18]. The studies [19–22] show that, under the action of external forces, the stiffness degradation and load capacity reduction caused by crack extension are the main factors for the damage of bamboo members, and the fracture failure of the material is the main damage mode at the ultimate state. Therefore, the application of fracture mechanics method to study the failure of the bamboo and analyze its fracture mechanism is crucial to the design of the members and the safety of the structures.

In practice, materials are often in complex stress situations. Irwin et al. [23–25] were the first to propose that cracks can be classified into three modes according to the crack loading characteristics: Mode I, opening mode, Mode II, slipping mode, and Mode III, tearing mode (as shown in Fig. 2). Among them, Mode I cracks possess the lowest resistance to extension and require the minimum energy for crack initiation, therefore, Mode I cracks are the most prone to extension [26], while the other two modes of cracks are often appeared on the basis of compounding with Mode I [27–29].

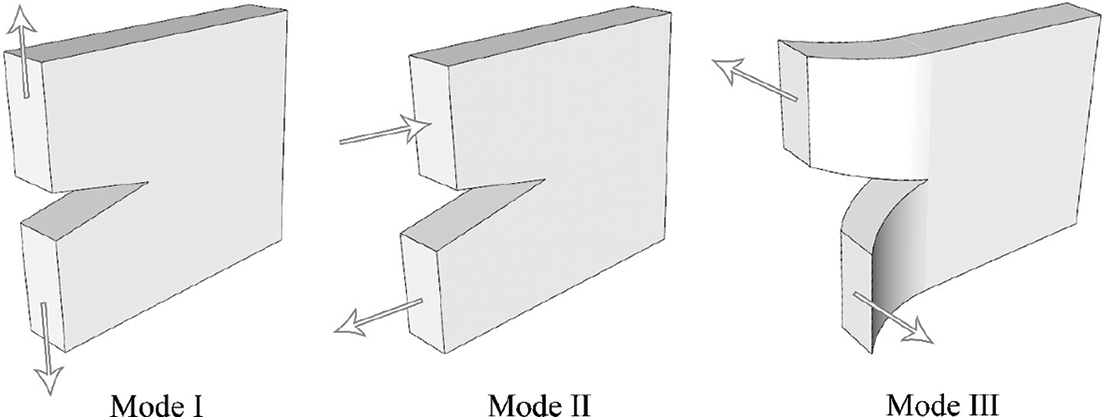
Figure 2: Three modes of cracks [23]

As mentioned above, the Mode I fracture characteristics of both raw bamboo and engineered bamboo are the focus of research on their material mechanical properties. According to the published test results and theories, this study introduces the Mode I fracture behavior of bamboo in detail. The objectives are to clarify the connection between microscopic damage and fracture mechanism, compare the fracture toughness of different bamboo products, and evaluate the characteristics of different test methods and theoretical calculation methods, so as to provide reference for the future development of bamboo fracture test standards and structural safety design.

2  Brief Introduction to Fracture Mechanics Theory

Strength design methods based on elastic mechanics cannot characterize the strength of structures with cracks; therefore, relevant fracture criteria based on fracture mechanics methods are needed to study the damage of defective materials and structures [20–22]. Fracture mechanics theory is established on the basis of linear elastic fracture theory, that is, fracture occurs without significant crack extension, and the member is brittle damaged. Linear elastic fracture mechanics (LEFM) mainly studies brittle fracture and the case of small-scale plastic deformation near the crack tip. With the development of production technology, such high toughness materials as bamboo, bamboo-based composite materials and wood-based composites are widely used, and their plastic zone length at the crack tip can no longer be ignored, which drives the development of elastic-plastic fracture theory.

2.1 Linear Elastic Fracture Mechanics (LEFM)

In explaining the fracture behavior of the material, Inglis [30] assumed that the infinite flat plate contains an elliptical hole traversing it, and when the length of the short axis of the elliptical hole tends to zero, the hole becomes a crack of length equal to the long axis of the ellipse. At this point, if analyzed according to the continuum theory of elastic mechanics, the maximum stress at the long-axis end of the hole is given by Eq. (1) [30].

σA=limb→0⁡σ(1+2ab)→∞ (1)

where a is the length of the semi-long axis of the elliptical penetration hole, b is the length of the semi-short axis of the elliptical penetration hole, and σ is the applied stress of the material. It can be seen that when the ellipse is infinitely close to the crack, the crack tip stress solution has singularity, i.e., the crack tip stress field will tend to infinity, indicating that the materials containing the crack can withstand a load of 0, which is unrealistic.

The above stress-based fracture paradox prompted Griffith [31] to take the lead in analyzing the fracture process from an energy perspective, proposing that the damage of a solid with defects is caused by initial crack extension rather than by material yielding and he argued that the necessary condition for brittle fracture to occur under static conditions is that the energy released in the crack-end region is equal to the energy required to form the crack area, thus establishing the basic framework of brittle fracture theory. In order to overcome the singularity at the crack tip, Irwin [32] introduced the concepts of strain energy release rate (G) and stress intensity factor (K) on the foundation of Griffith’s theory, and proposed the K criterion for judging brittle fracture: the stress intensity factor K is to characterize the degree of stress concentration at the crack tip of the crack-containing material, and when K reaches its critical value, the crack begins to extend. The energy release rate G is equivalent to K in describing the ability of a material to resist fracture, i.e., crack extension occurs when G reaches the critical strain energy release rate (GIC). Critical stress intensity factor (KIC) and GIC, generally referred to as fracture toughness, are inherent properties of the material and can be measured by standard tests.

2.2 Non Linear Elastic Fracture Mechanics (Non-LEFM)

The fracture behavior of a material with a plastic extension region at the crack tip cannot be accurately described by the LEFM, requiring the inclusion of some correction conditions. Initially, when considering the effect of the plastic zone of the crack tip, it was thought that the stiffness of the structure with a crack would be slightly weaker than that obtained by the linear elastic method, and therefore the result from linear elastic fracture was corrected by increasing the crack length and reducing the stiffness, which is called the equivalent crack length (ECL) method, first proposed by Irwin [33].

Based on extensive experiments, Wells [34] proposed that nonlinear fracture can be determined by crack opening displacement (COD) and established the COD criterion. Similarly, the crack tip opening displacement (CTOD) method [35] can measure the plastic deformation near the crack tip when the cracked material fractures. Some scholars [36–38] also developed a fracture covariate based on the plasticity total theory to describe the fracture energy-J integral, which is independent of the path, and the crack starts to extend when J reaches a critical value (JIC). JIC can be regarded as a material constant under certain conditions, and its value is determined depending on the loading method and the specimen size.

It is thereby clear that the criterion for judging material fracture is not singular, but multiple parameters can be considered, and these parameters are interconvertible. Table 1 shows a summary of the classical fracture criteria [22].

Theoretically, the fracture mechanics theory is still suitable for bamboo and its composites, but the fracture mechanism of these materials is very complex, causing difficulties in solving the stress field near the crack tip. The stress-strain relationships for fracture damage in bamboo given in many studies cannot be recognized widely, and there is no unified theory to describe the fracture mechanism of bamboo for the time being. Therefore, a combination of microscopic analysis and mechanical response behavior is essential to deeply analyze the fracture behavior of bamboo.

3  Mode I Fracture in the Transverse Direction

Unlike isotropic materials such as concrete and steel [39,40], bamboo and its composites are typical orthogonal anisotropic materials, whose fracture characteristics depend on the crack location and crack extension direction, so their fracture parameters are different in each direction to be discussed separately, as shown in Fig. 3 [41–43]. The orientation of the engineered bamboo material is defined according to the direction of the bamboo strip units. The crack location is depicted by a combination of two letters shaped like “TL”, the first letter indicates the crack opening direction, and the second letter indicates the crack extension direction. Transverse fracture indicates that the crack extends in the T-direction or R-direction, essentially the fibers at the crack tip are pulled off. Due to the strong tensile strength of the bamboo fibers [44], the transverse fracture toughness of the bamboo material is also high. The most common method for transverse Mode I fracture tests are the three-point bending (TPB) method and the single-edge notched beam (SENB) method [45,46].

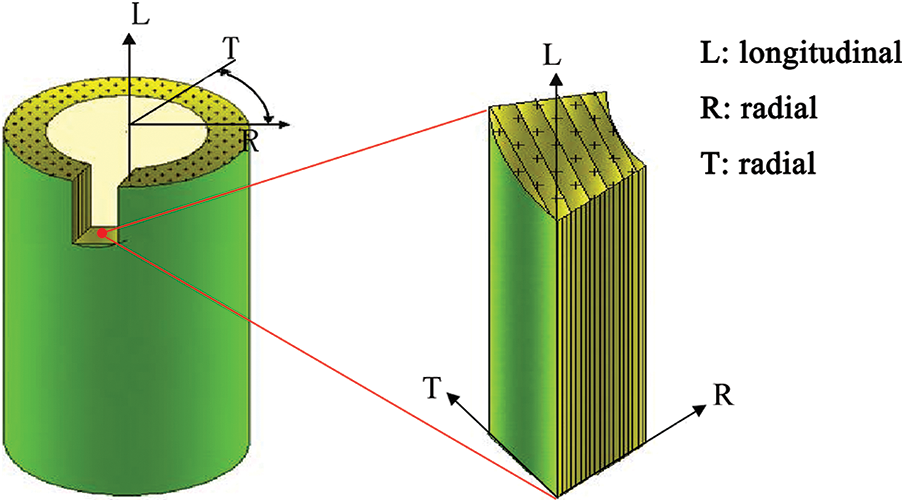
Figure 3: Three-direction definition of bamboo [41]

3.1 Tests with Three-Point Bending (TPB)

The TPB method does not require notching on the specimen, but only the pivot points at the ends of the beam and loading in the middle part (as shown in Fig. 4) This method is mostly used by scholars for in situ observation of fiber dynamics during transverse fracture of bamboo [47–49].

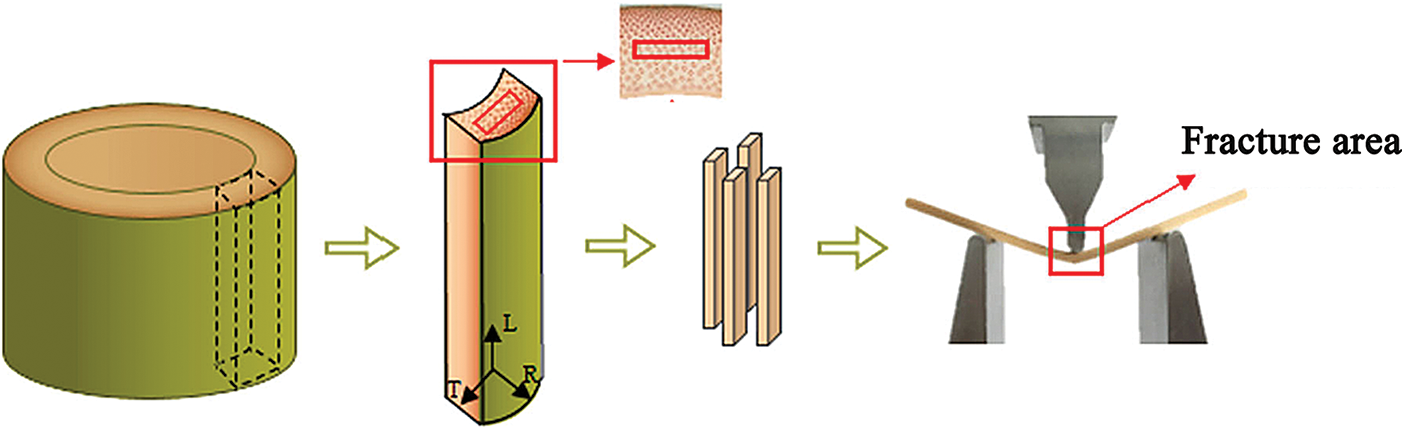
Figure 4: Three-point bending (TPB) test diagram [49]

Due to the gradual increase of fibers along the radial direction of the raw bamboo (Fig. 5a), An et al. [50] tested the three-point bending fracture behavior of two years old moso bamboo (Phyllostachys edulis) with dense-fiber layer upward and downward, respectively, and presented the corresponding load displacement curves (Fig. 5b); the three-point bending strength for specimens with dense fiber layer downward of 139.6 MPa was higher than that with dense fiber layer upward of 93.6 MPa, resulting from that the former’s damage mode is fiber fracture, while the latter’s damage mode was fiber pulled out of the matrix.

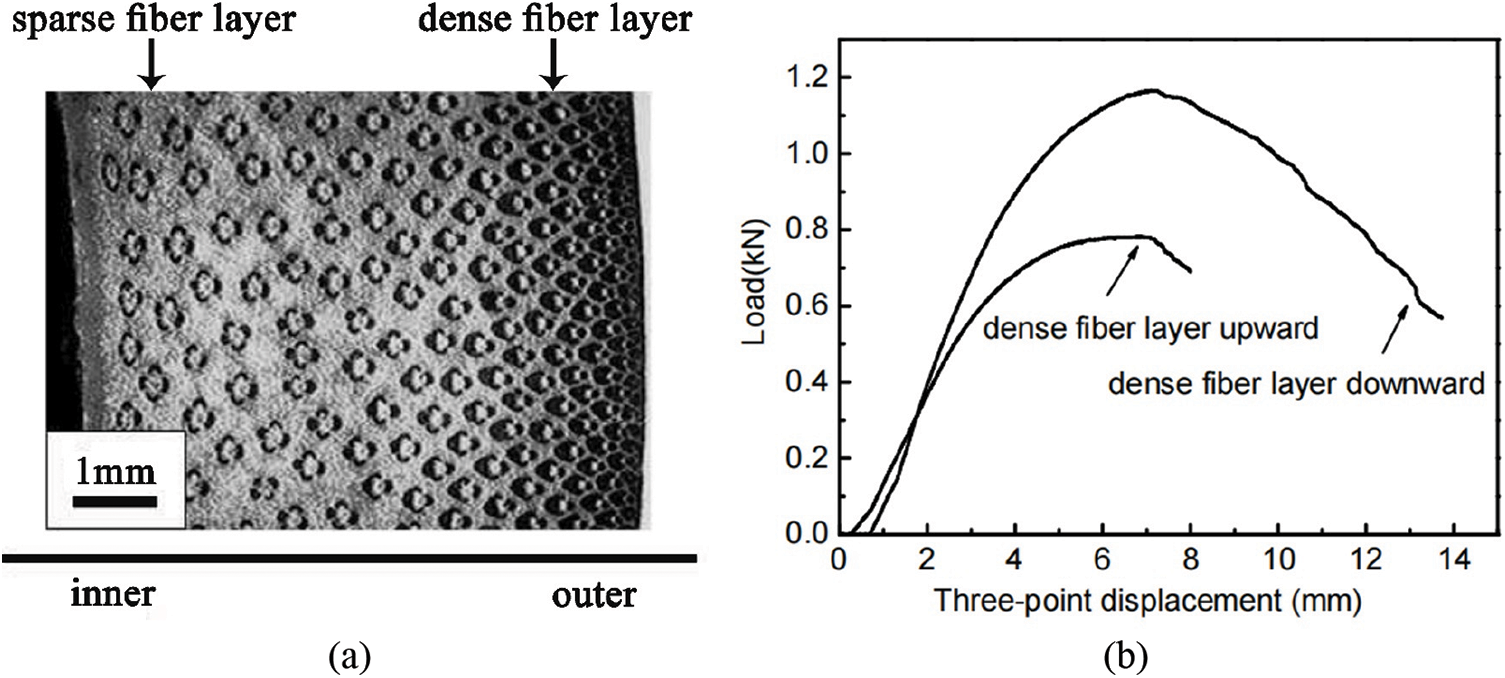
Figure 5: Three-point bending test with different locations of dense fiber layers [50]: (a) Bamboo fiber distribution; (b) Load-displacement carves

A similar study on moso bamboo (Phyllostachys edulis) was done by Chen et al. [51] using the acoustic emission (AE) system, three types of bending fracture behaviors were observed in the internodes region of bamboo: matrix (parenchyma cell) disruption, fiber dissociation (fiber-matrix and fiber-fiber wall dissociation), and fiber fracture; likewise, the bending fracture of bamboo in the radial direction did not possess symmetry, and this asymmetry increased as moisture increased (Fig. 6). By the same method [52], they also tested the asymmetry to the moso bamboo node: the flexural strength and average fracture energy of the specimens with bending direction from out to inner skin (dense layer downward) were much higher than those with bending direction from inner to outer skin (dense layer upward), respectively: 175 MPa, 2.76 MJ·m−3, 100 MPa, 0.94 MJ·m−3.

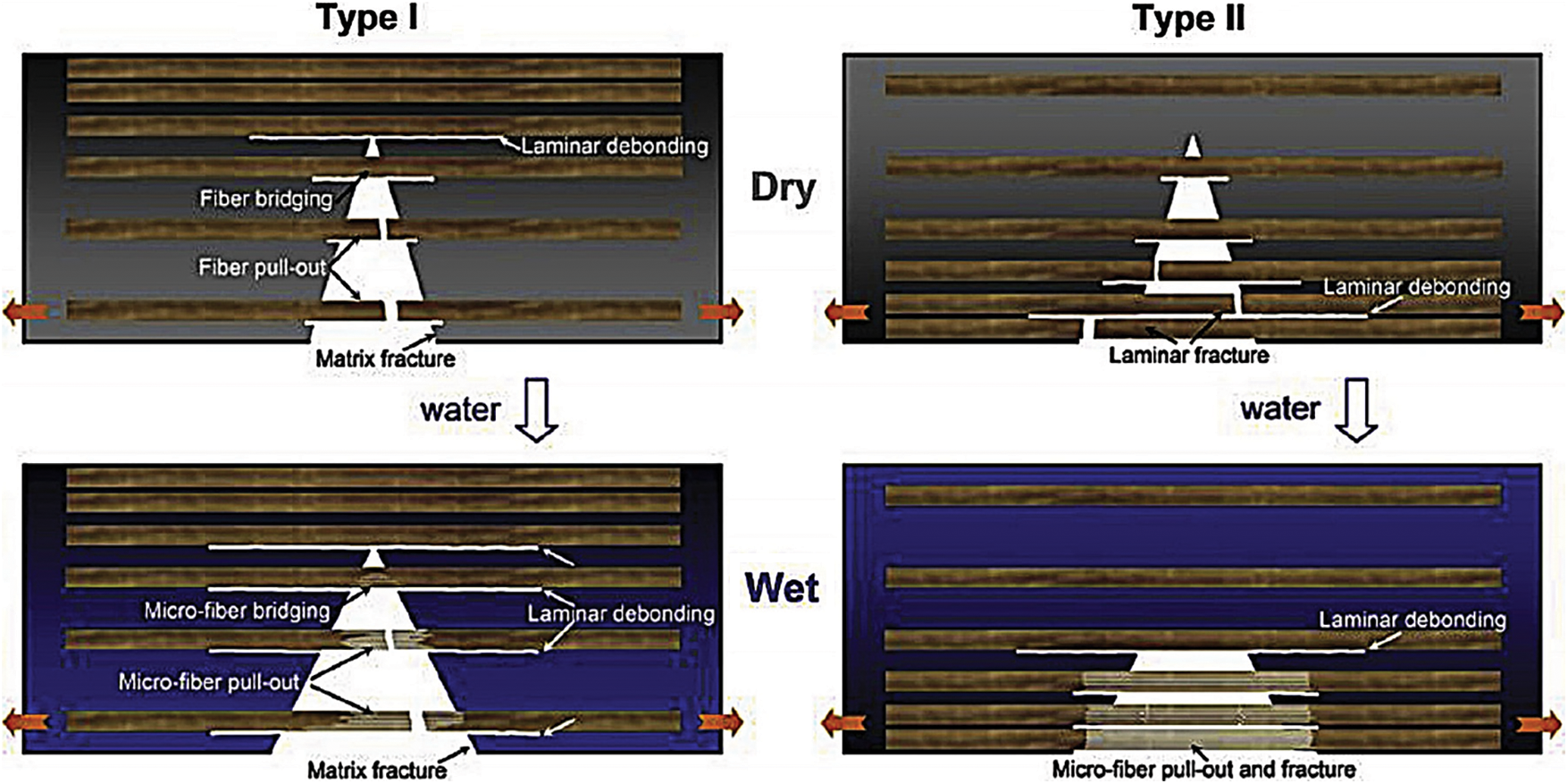
Figure 6: Effects of the gradient hierarchical fibrous structure and water on the flexural fracture behaviors and toughening mechanisms within natural bamboo [51]

The delamination patterns of fiber bundles are also shown in the study of Chen et al. [49]. They analyzed the fracture characteristics of fibers using microscopic techniques; it was found that cracks extend in a tortuous manner; the smooth and delaminated fracture of fibers occurred in the tensile layer, while three fracture modes, namely tiny cracks around the loading head, localized fiber tensile cracks and delamination between fibers were observed in the compression layer. The damage modes described in the above studies almost cover all the damage modes of bamboo fibers during bending fracture. In another paper, Chen et al. [53] identified three main types of fracture based on the six kinds of fiber cell wall structure (Fig. 7): brittle fracture in fibers with small diameters and few layers; alternating changes in microfiber angle and decreasing layer thickness with increasing number of layers leading to a fracture transition from brittle to ductile or splitting tensile damage; and pits have little effect on fracture behavior.

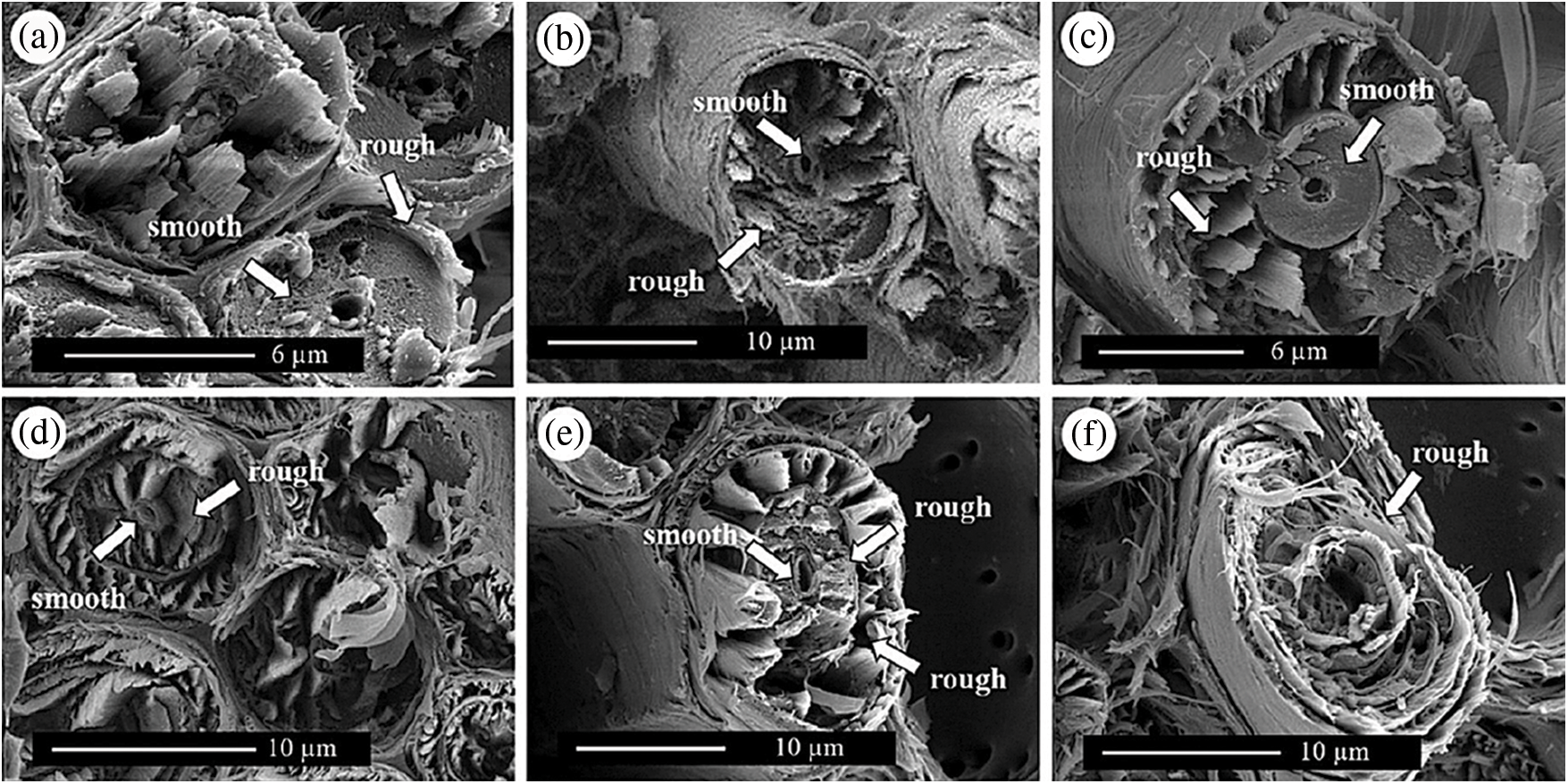
Figure 7: Six kinds of fiber cell wall structure [53]

The weak interfaces between bamboo fiber layers have a great influence on the fracture properties. Using synchrotron radiation microcomputed tomography and scanning electron microscopy (SEM), Liu et al. [54] investigated the bending fracture behaviors of moso bamboo (Phyllostachys pubescens), and the important fracture characteristics of matrix cracking, interface debonding, fiber bridging and cell wall splitting were found; it was proved that the rational weak interfaces had the positive effect on the fracture toughness of fiber-reinforced bamboo. Zou et al. [55] also applied in-situ observation on the fracture behavior of 6-year old natural bamboo (Phyllostachys edulis) under three-point bending, and found that when bamboo fractured transversely, cracks propagated across parenchyma cell, combined with crack bridging and fiber pull-out. As shown in Fig. 8, this crack bridging and fiber pull-out were also observed in the study by Liu et al. [56].

Figure 8: Crack bridging and fiber pull-out [56]

The damage modes mentioned above in the literatures basically cover all the damage modes in the transverse fracture process of bamboo, which are summarized in Table 2. In situ observation of the transverse fracture process of bamboo by TPB method combined with SEM is the key to analyze the microscopic mechanism of bamboo fracture damage and improve the understanding of fiber fracture behavior. In general, fibers are the key factor to bear the load and hinder the crack extension, whose cell wall structures significantly influence the fracture characteristics of bamboo; the weak interfaces make bamboo transversely highly tough, and the delamination of fiber bundles caused by them can further retard the fracture; and the gradient variability of raw bamboo leads to significant differences in fracture behavior between its outer layers and inner layers.

3.2 Tests with Single-Edge Notched Beam (SENB)

As shown in Fig. 9, the single-edge notched beam (SENB) method requires pre-cutting treatment in the middle of the bottom of the beam, and then perform three-point bending or four-point bending loading, which can test the fracture toughness of a variety of materials [57–59].

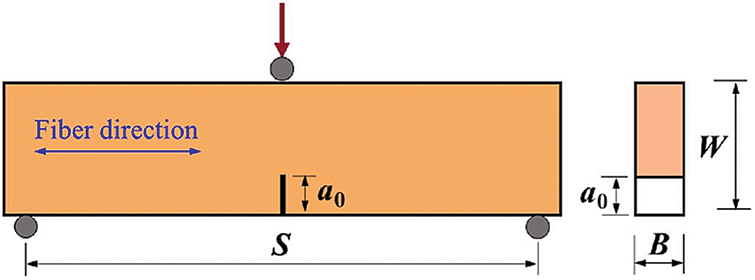
Figure 9: Single-edge notched beam (SENB) test diagram [57], where, a0 is the prefabricated crack length, B is the specimen thickness, W is the specimen height, and S is the effective specimen length (span)

The most commonly used method to solve for the transverse fracture toughness of bamboo is as follows: the load-displacement curve is obtained by testing the crack opening displacement (COD) value and the 95% stiffness correction method is used to solve for the critical load to calculate the stress intensity factor. Under SENB test, Xu et al. [60] tested the COD of moso bamboo specimens in the LT direction with a/W values between 0.45 and 0.55; the critical load was determined by the 95% stiffness correction method; the average fracture toughness (expressed as critical stress intensity factor—KIC) calculated according to American Society for Testing and Materials—ASTM E399-09 was 16.05 MPa·m1/2 and the maximum fracture toughness reached 17.39 MPa·m1/2. This study analyzed the transverse Mode I fracture characteristics of bamboo from the aspect of stress intensity factor, which provides a reference for future research on the fracture behavior of bamboo-based composites, but the load-COD curve of each specimen was not clearly given in the paper.

By the same method, Xu [41] also tested the mean fracture toughness of LBL in the LT direction of 4.65 MPa·m1/2, finding the anisotropy of LBL was not as pronounced as in the raw bamboo; and in this literature, the measured average fracture toughness of moso bamboo in LT direction was 4.16 MPa·m1/2 which differed considerably from the results of reference [60], and it is speculated that the difference may be caused by the different densities of bamboo from various height. Liu et al. [61] compared the fracture properties of fir and moso bamboo by testing COD, finding that the Mode I fracture toughness of bamboo varied from inner to outer and generally higher than fir.

The boundary effect model (BEM) is a new numerical method developed after the finite element method, which has the advantages of few unknowns of the unit and simple data preparation. Some scholars use this method to calculate the fracture parameters of engineered bamboo materials. Liu et al. [62] used a boundary effect model and normal distribution analysis to determine the transverse Mode I quasi-brittle fracture toughness of bamboo composited by bamboo fiber bundles and a water-soluble phenol formaldehyde—PF resin under SENB test. In this study, the fiber bundles were considered as an “aggregate” and the average diameter of the bundles (G) was observed to be 0.4 mm by microscopic images. As the fiber bundle diameter increases, the fracture toughness also increases, with an average fracture toughness of 7.96 MPa·m1/2. Xie et al. [63] used the same approach to investigate the role of size effects on the fracture parameters of bamboo scrimber and confirmed that the BEM solutions of the fracture parameters were not affected by size effects, leading to average values of 216.4 MPa and 16.76 MPa·m1/2 for tensile strength and transverse Mode I fracture toughness, respectively.

In addition, the quasi-brittle fracture process of the bamboo-based fiber composite was explained in Liu’s study [62], including initial cracking before loading, followed by independent microcrack extension in the matrix without the bottom fibers damage, resulting in deformation and softening behavior, after which the fictitious crack from the microcrack in the matrix developed to its critical length of 1.5 G and the bottom fiber bundles fractured under peak load (Fig. 10). The normal distribution analysis applied in this study, covering all the experimental scattering points, allowed the results to reach a reliability in line with expectations.

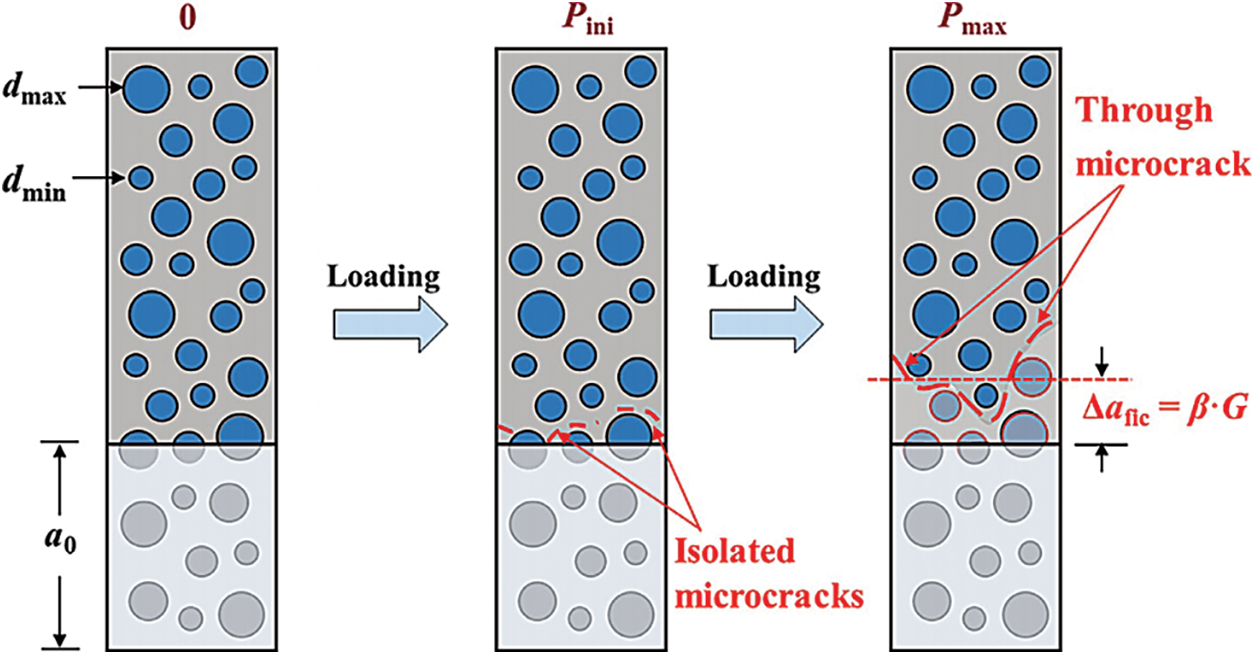
Figure 10: Schematic graphs of quasi-brittle fracture process of bamboo-based fiber composites [62], where, d is the diameter of the fiber bundle, a0 is the initial crack length, Pini is the initial-cracking load, Pmax is the peak load, Δafic is the critical crack length, βav is the average discrete number, and G is the average grain size

The information on the transverse Mode I fracture parameters provided in the above studies are summarized in Table 3. Combined with the fracture damage mechanism revealed in Section 3.1, it is clear that the significant difference in fracture toughness between outer layers and inner layers of the raw bamboo is caused by the difference in fiber density, while the engineered bamboo eliminates this difference after reassembling; There are few studies on the transverse fracture properties of LBL, and the existing studies lack the comparison of LBL in LT and LR direction; even for the same material, the fracture toughness shown in different studies varies greatly, and the tensile strength and fracture toughness do not show obvious correlation, so the effects of bamboo age, extraction part, moisture content, adhesive kinds and processing technology on the transverse Mode I fracture properties need to be further studied in depth.

3.3 Tension Tests

In addition to the above two methods, uniaxial tension has also been studied to test the transverse I fracture toughness of bamboo (some will be notched on one side of the specimen) [64–66]. Reynolds et al. [64] examined the effect of different anticorrosive treatments on the fracture properties of LBL, revealing that the critical strain energy release rate was much lower for caramelized materials than for bleached ones, and that the fracture behavior of bleached materials more closely resembled that of raw bamboo; the bleached bamboo was stronger under tension—a load under which failure is dominated by fracture, while caramelized bamboos behaved more strongly in compression—at such loads, failure was determined by yield strength. By detecting the behavior of moso bamboo nodes internally during tensile fracture via AE, Chen et al. [65,66] found a much lower volumes of fracture behaviors and a higher percentage of fiber dissociation and matrix damage in bamboo node due to its hierarchical fibrous woven structure, the coarse fiber bundles, high volumes of fibers, fiber pull-out and crack deflections constituted a reinforcement mechanism within bamboo nodes.

The TPB method is mainly used to observe the internal microstructure of bamboo during transverse fracture, so as to establish the connection among toughening mechanism, damage mode and fracture performance; this method cannot visually and accurately measure the transverse Mode I fracture toughness of the material because there is no prefabricated notch on the specimen, resulting in the initial damage not necessarily arising from the transverse crack at the bottom center (most of the time the damage occurs first in the internal matrix). The SENB has the well-established standard test methods, in which the tip of the prefabricated crack is the first to break when loaded due to the stress concentration, forming a transverse extension of the crack, thus enabling the measurement of transverse Mode I fracture parameters. Future research should focus on the observation of crack extension in the SENB method and clarify the fracture toughness of bamboo in different states in combination with the microscopic dynamics of fibers and matrix.

4  Mode I Fracture in the Parallel-to-Grain Direction

Bamboo and engineered bamboo are fiber-reinforced materials, and their tensile strength in the parallel-to-grain direction is much higher than that in the transverse direction. Without sufficient resistance, cracks are more likely to extend in the parallel-to-grain direction, and damage often occurs in the weak substrate, so the fracture characteristics in this direction are very important mechanical properties of bamboo and engineered bamboo. The current methods for testing the Mode I fracture properties in the parallel-to-grain direction are mainly the compact tension (CT) method [45] and the double cantilever beam (DCB) method [67], as shown in Fig. 11.

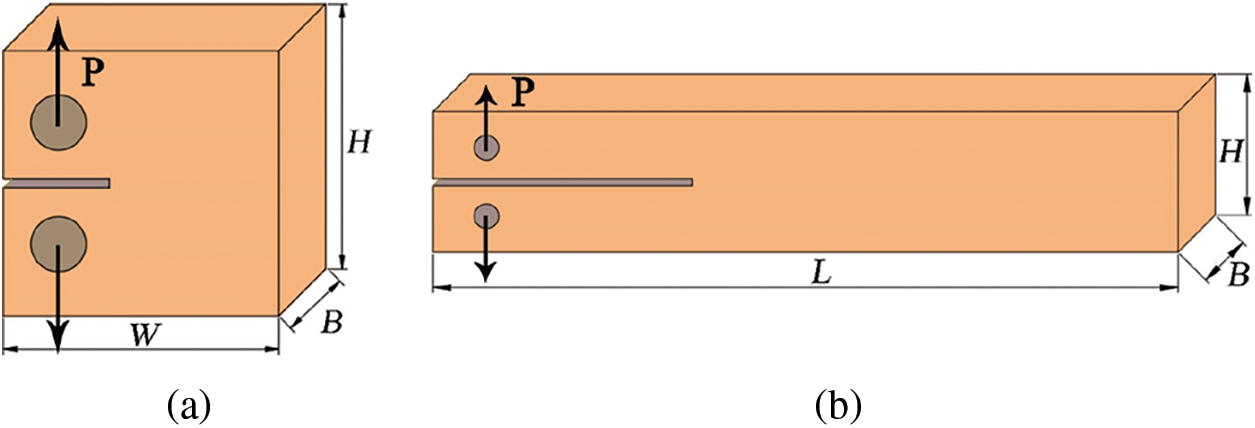
Figure 11: Test methods of Mode I fracture in parallel-to-grain direction [45,67]: (a) Schematic of the compact tension (CT) method [45]; (b) Schematic of the double cantilever beam (DCB) method [67]. Where, P is the load, W is the width of CT specimen, L is the length of DCB specimen, H is the specimen height

4.1 Tests with Compact Tension (CT) Method

Compact tensile method is to punch holes in the prefabricated crack end of the specimen and then use the U-shaped fixture for tensile, with the advantages of small specimen size and simple test operation. This test method is very mature to calculate the fracture parameters through the test data directly by applying the theoretical formula of fracture toughness given in the standards, as shown in Eqs. (2) and 3 [45].

KQ=(PQ/BW1/2)×f(a/W) (2)

where, PQ is the critical load; B was the specimen thickness; W is the effective width of specimen; a is the crack length, and f (a/W) is the geometric factor of the compact tension specimen, calculated according to Eq. (3).

f(x)=(2+x)×0.886+4.64(x)−13.32(x)2+14.72(x)3−5.6(x)4(1−x)1.5 (3)

The development of new materials has been the focus of attention, and some scholars have conducted compact tensile tests on various emerging bamboo-based composites [68–70]. Wong et al. [71] investigated the effect of fiber length and content on the fracture behavior of short bamboo fiber reinforced thermosetting polyester resin (Reservol P 9509) using the CT method. The results showed that: When the fiber length was 4 mm, the increase in fiber content decreased the fracture toughness, while effective fiber reinforcement was observed for fiber lengths of 7 and 10 mm; the highest fracture toughness was achieved when the fiber length and content were 10 mm and 50 vol%, with an increase of 340% compared to pure polyester. This study provides an important reference for the future development of bamboo fiber-reinforced thermosetting polyester resin composites.

A bamboo mat plywood (“Reservol P-9509 unsaturated polyester” as the matrix material and “Gigantochloa scortechinii bamboo strips” in a woven form) was introduced and tested for its fracture properties under different fiber orientations (Fig. 12) in the study by Ali et al. [72], obtaining a fracture toughness of 4.85 MPa·m1/2 for horizontal fiber orientation and 8.33 MPa·m1/2 for vertical fiber orientation. It can be demonstrated that the fracture toughness of this composite material is comparable to the transverse fracture toughness of some engineered bamboo materials, which is due to the longitudinal and transverse fibers that effectively retard the crack expansion, and this material has good prospects for application in the fields of building walls and other fields.

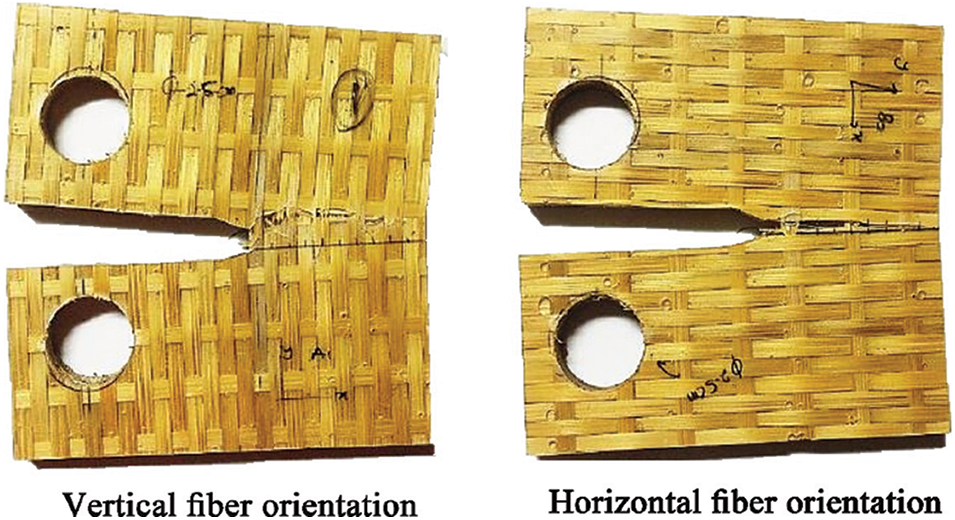
Figure 12: Fiber orientations of bamboo mat plywood [72]

To CT tests on PBSL of different thicknesses, both Li et al. [73] and Wu et al. [74] calculated the fracture toughness in the RL and TL directions using the stress intensity factor as shown in Eq. (2). Wu’s paper gives the typical load-tension displacement curve as shown in Fig. 13a. The curve has a section with decreasing slope, so the critical load PQ should be calculated according to the 95% stiffness correction method given in the test standard, while in Li’s study, the critical load PQ is directly replaced by the ultimate load, which may lead to errors in the results.

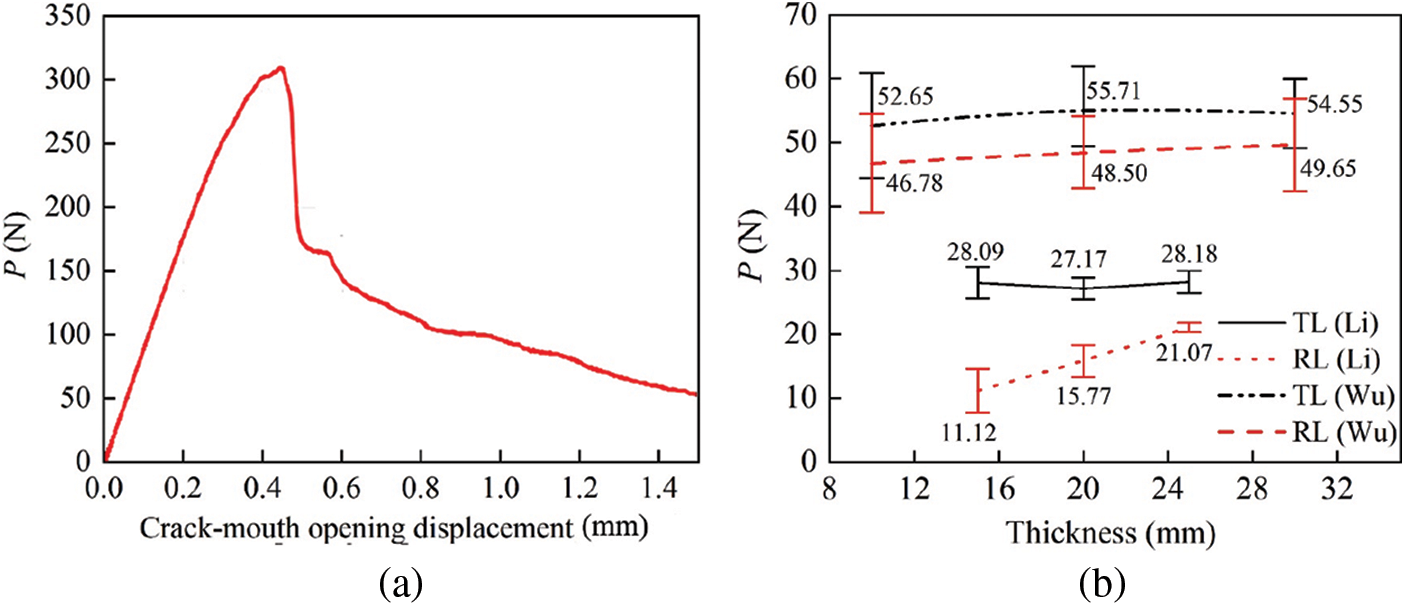
Figure 13: Fracture parameters in the literature [73] and literature [74]: (a) Typical load displacement curve of CT specimen [74]; (b) Comparison of fracture toughness [73,74], where, P is the load; in “TL” and “RL”, the first letter indicates the crack opening direction, and the second letter indicates the crack extension direction

Fig. 13b compares the fracture toughness of the specimens with different orientations and thicknesses in these two papers, and it can be seen that: the fracture toughness of the RL specimens improves remarkably with increasing specimen thickness, and all of them are lower than that of the TL specimens, while the fracture toughness of the TL specimens does not change obviously with thickness; the average fracture toughness of all TL specimens tested by Wu et al. [74] was 1.95 times higher than that of Li et al. [73] while that of RL specimens was 3.02 times higher, 54.31, 27.81, 48.31 and 15.99 MPa·m1/2, respectively. The reasons for such differences may be due to different densities, moisture contents, and processing processes. Therefore, the material processing conditions and experimental conditions should be controlled as uniform as possible in future studies.

Testing Mode I fracture by the CT method is simple and efficient, and similar to it is the wedge splitting method [75,76]. However, both methods have a short ligament zone, which makes it more difficult to meet the accuracy requirements when considering the detection of crack lengths during fracture testing, so a longer specimen is required to further understand the toughening mechanism of bamboo.

4.2 Tests with Double Cantilever Beam (DCB) Method

The DCB method is actually the compliance method or energy method, and according to the strain energy release rate (G) criterion proposed by Griffith [31] and Irwin [23], the value of G corresponding to any length of crack extension can be obtained, as shown in Eq. (4) [77,78]. There are several commonly used methods for theoretical analysis of the strain energy release rate in the Mode I fracture DCB test, namely, beam theory (BT), modified beam theory (MBT), compliance calibration (CC) method, and modified compliance calibration (MCC) method. Using each method to solve Eq. (4), the resulting equations for G are summarized in Table 4.

To the relationship between the G and the crack extension length (a) of PBSL using different theoretical methods, Zhu [22] concluded that: the crack length correction value Δ in MBT method had no obvious pattern; the compliance coefficient n in CC method was between 2 and 3 (different from 3 in BT) with a tendency to increase as the initial compliance increased; in MCC method, the modified compliance coefficient A was between 20 and 40; the critical strain energy release rate GIC calculated using BT method is larger, while the results of the other three methods differed slightly at the early stage of crack opening and basically overlapped at the later stage. The study by Toygar et al. [82] also showed that the MBT, CC, and MCC methods had good agreement.

By BT method, Shao et al. [83] performed DCB tests on moso bamboo and calculated the average critical strain energy release rate GIC of 358 J/m2. The results also indicated that the crack was self-similar without fiber bridging and there was no significant difference in GIC between specimens of different heights. In contrast, the DCB test by Chen et al. [84] showed that fiber bridging phenomenon was present when the extension of moso bamboo (Phyllostachys pubescens) occurred along the parallel-to-grain direction. As shown in Fig. 14, the fiber bridging phenomenon exists between fiber bundles and fiber bundles, matrix and fiber bundles, matrix and matrix, and this phenomenon will impact the Mode I fracture toughness of bamboo in the parallel-to-grain direction.

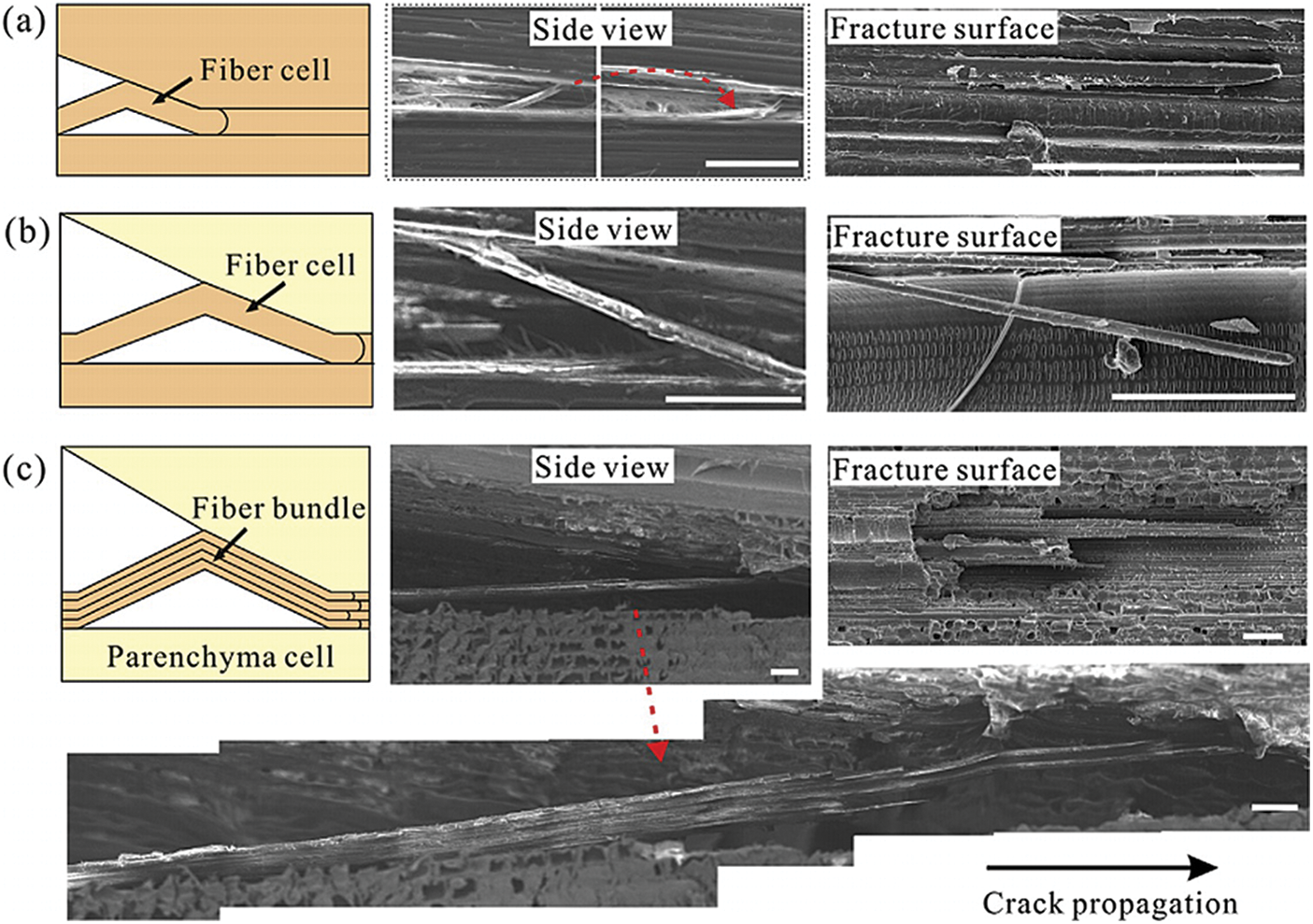
Figure 14: Bridging phenomenon of moso bamboo fibers [84]: (a) between fiber bundles and fiber bundles; (b) between fiber bundles and matrix; (c) between matrix and matrix. Scales in all SEM images are 100 mm

For PBSL, Shen et al. [85] concluded that the fiber bridging region is created when the crack begins to extend (Fig. 15); the strain energy release rate gradually increases to the steady-state fracture toughness as the length of the bridging region increases, and the length between the initial crack length and the crack length that corresponds to the steady-state fracture toughness is referred to as the steady-state bridging region length. In this case, G will be affected by the initial crack length, so the DCB test results of Shen et al. [85] indicate that the R(G-a) curve is not a material property PBSL. Liu et al. [86] performed DCB tests on LBL in the RL direction, and no significant fiber bridging was observed during the tests. At the front end of the crack tip, the nonlinear response was relatively small and negligible, and the damage mode of the material was mainly based on brittle fracture.

Figure 15: Fiber bridging phenomenon in PBSL [85]

The self-similarity of crack extension is an important property of I fracture, which means that the members are in the same state after crack extension to the equal length regardless of the initial crack length. Both the results of DCB test on PBSL by Zhu [22] and on LBL by Sheng [20] showed self-similarity, i.e., the load displacement curves of specimens with different initial crack lengths overlapped in the descending section, and the critical strain energy release rates of both materials were not affected by the initial crack length; the fracture energy would tend to a stable value after the plastic zone at the crack tip developed sufficiently, i.e., the fracture toughness, which is an inherent property of the material. This conclusion is contrary to that of the literature [85].

It has been demonstrated that when the fracture process zone (FPZ) length is short, the crack extension length can be studied by the linear elastic fracture mechanics method [87,88]; however, for many composite materials, the FPZ zone is long due to the toughening mechanism arising from microcrack extension, bridging, and void connecting, when linear elastic fracture mechanics is no longer applicable to the fracture analysis of such materials [89,90]. Sheng [20] used virtual crack closure technique (VCCT) and cohesive zone modeling (CZM) for finite element analysis of Mode I fracture behavior of LBL and investigated the effect of DCB specimen width on the G of Mode I interlaminar fracture. The feasibility of both finite element methods was verified. However, VCCT analysis is relatively stable, and the results are easy to converge, so it can also be used to analyze the fracture behavior of materials when the fracture nonlinearity is not obvious. Other scholars have also used these two methods to perform finite element analysis on DCB specimens of PBSL [91] and LBL [92], and the conclusions reached were consistent with Sheng [20].

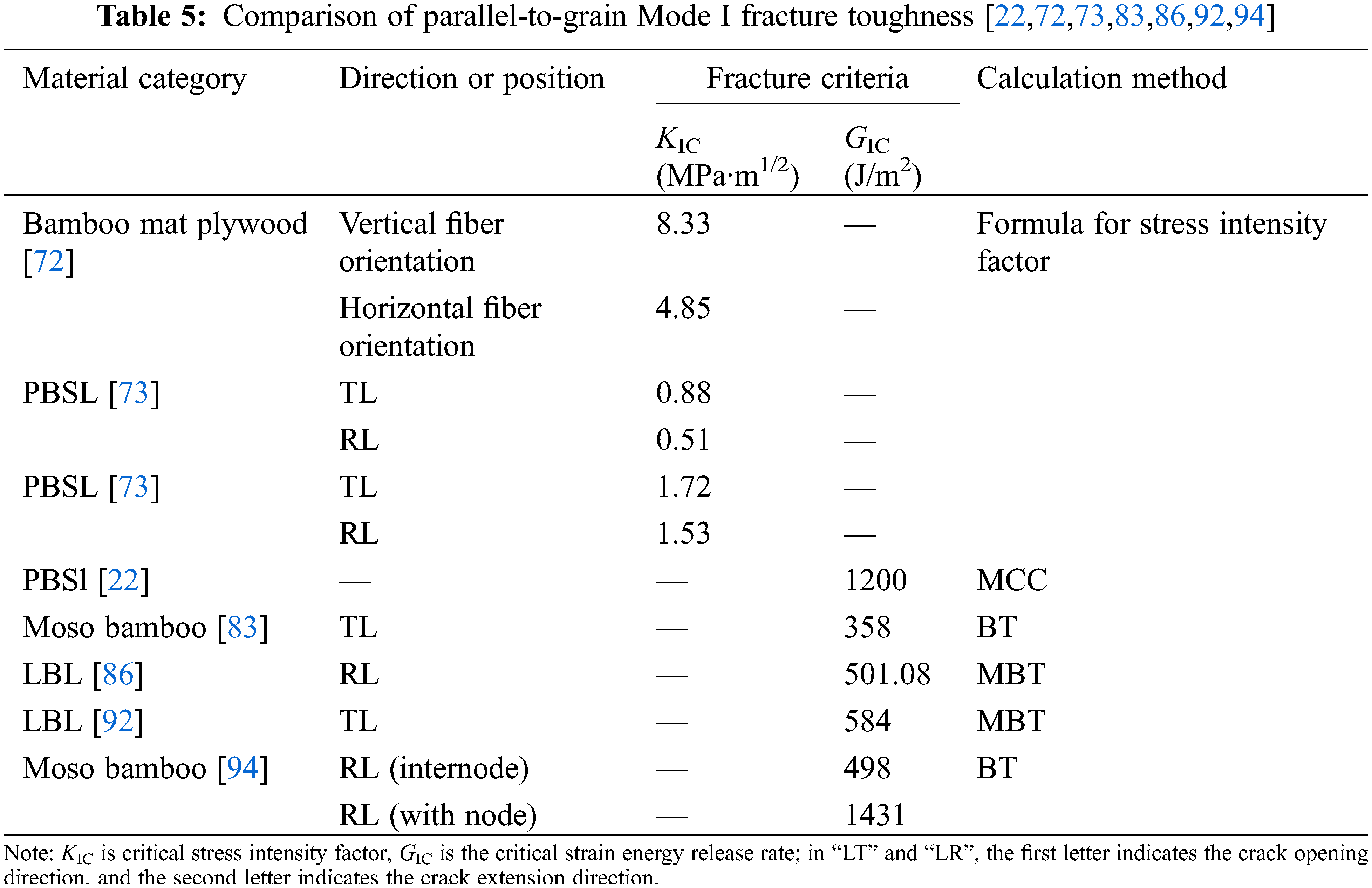
In addition to size, which affects the Mode I critical strain energy release rate of bamboo, bamboo nodes, moisture content, and age also have an effect [93,94]. As shown in Table 5, the fracture toughness of bamboo in the TL direction is higher than that in the RL direction, and the fracture toughness of PBSL is generally higher than that of LBL, which is due to the fact that the processing method of sparing and then regluing the fibers makes the PBSL denser and therefore has a higher cracking energy.

CT test is similar to DCB test, except that the DCB specimen is longer in the length direction, i.e., perpendicular to the loading direction, and the CT specimen is taller in the height direction, i.e., the loading direction. Due to the role of toughening mechanism in the fracture process, there is a non-negligible FPZ in bamboo fracture, while the crack extension of CT specimen is short, which cannot fully reflect the fracture characteristics of bamboo. As for bamboo and wood, which are quasi-brittle materials, the fracture resistance curve measured by the DCB test is more complete to describe the fracture mechanism. In order to avoid the deflection of specimen, DCB method requires a superior fabrication process to ensure the accuracy of specimen size and prefabricated crack location.

5  Final Considerations

This paper reviews the current status of experimental research on Mode I fracture characteristics of bamboo and engineered bamboo, classifying the research methods for transverse and parallel-to-grained Mode I fracture, and comparing the characteristics of different theoretical calculation methods and the fracture toughness of different bamboo materials.

(1)   The main methods for testing Mode I transverse fracture are three-point bending (TPB) method and single-edge notched beam (SENB) method. TPB method is mainly used to observe the internal microstructure of bamboo, so as to establish the connection between toughening mechanism, damage modes and fracture performance; SENB method can measure the fracture parameters of bamboo. The damage modes of transverse fracture include matrix cracking, interfacial debonding, fiber bridging and splitting of the cell wall. The fiber is the key factor to bear the load and hinder the crack extension, whose cell wall greatly influences the fracture properties of bamboo; the presence of weak interface makes bamboo transversely highly tough, and the delamination of fiber bundles caused by it can further retard the fracture.

(2)   The test methods for parallel-to-grain Mode I fracture are compact tension (CT) method and double cantilever beam (DCB) method. The CT method is efficient and simple but cannot fully reflect the crack extension process of bamboo, and DCB method is the most widely used and suitable method for testing the Mode I fracture characteristics of bamboo. The theoretical methods of modified beam theory (MBT), compliance calibration (CC) and modified compliance calibration (MCC) are used to calculate the critical strain energy release rate (GIC) with a high degree of agreement, while the toughening mechanism of fracture process zone (FPZ) caused by microcrack extension, bridging and void connecting make the analysis of bamboo fracture process difficult, and virtual crack closure technique (VCCT) and cohesive zone modeling (CZM) are feasible finite element analysis methods.

(3)   The age of bamboo, moisture content, loading direction, bamboo specie, the presence of bamboo nodes, the sampled region of the stem or stalk and processing technology can cause deviation of test results, so the existing experimental studies cannot give the certain range of fracture toughness for each material, so more experimental studies with strict control of the above conditions are needed to establish a unified set of standards in the future. Moreover, most of the existing studies are on parallel bamboo stand lumber (PBSL), but laminated bamboo lumber (LBL) are better than PBSL in terms of low cost and simple processing. Therefore, more Mode I fracture tests should be conducted on LBL in the future, especially on the fracture behavior of adhesive surfaces.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 51878354 & 51308301); the Natural Science Foundation of Jiangsu Province (Nos. BK20181402 & BK20130978); 333 Talent High-Level Project of Jiangsu Province; Qinglan Project of Jiangsu Higher Education Institutions; and the Ministry of Housing and Urban-Rural Science Project of Jiangsu Province under Grant (No. 2021ZD10). Any research results expressed in this paper are those of the writer(s) and do not necessarily reflect the views of the foundations.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. WGBC (2019). The building and construction sector can reach net zero carbon emissions by 2050. London, UK: World Green Building Council. [Google Scholar]

2. Ponzo, F. C., Antonio, D. C., Nicla, L., Nigro, D. (2021). Experimental estimation of energy dissipated by multistorey post-tensioned timber framed buildings with anti-seismic dissipative devices. Sustainable Structures, 1(2), 000007. https://doi.org/10.54113/j.sust.2021.000007 [Google Scholar] [CrossRef]

3. Guo, A., Sun, Z. H., Feng, H., Shang, H., Sathitsuksanoh, N. (2022). State-of-the-art review on the use of lignocellulosic biomass in cementitious materials. Sustainable Structures, 3(1), 000023. https://doi.org/10.54113/j.sust.2023.000023 [Google Scholar] [CrossRef]

4. Xiao, F., Wu, Y. Q., Zuo, Y. F., Peng, L., Li, W. H. et al. (2021). Preparation and bonding performance evaluation of bamboo veneer/foam aluminum composites. Journal of Forestry Engineering, 6(3), 35–40. https://doi.org/10.13360/j.issn.2096-1359.202009024 [Google Scholar] [CrossRef]

5. Zhou, Y. H., Huang, Y. J., Sayed, U., Wang, Z. (2021). Research on dynamic characteristics test of wooden floor structure for gymnasium. Sustainable Structures, 1(1), 000005. https://doi.org/10.54113/j.sust.2021.000005 [Google Scholar] [CrossRef]

6. Lei, W. C., Zhang, Y. M., Yu, W. J., Yu, Y. L. (2021). The adsorption and desorption characteristics of moso bamboo induced by heat treatment. Journal of Forestry Engineering, 6(3), 41–46. https://doi.org/10.13360/j.issn.2096-1359.202010008 [Google Scholar] [CrossRef]

7. Chaowana, K., Wisadsatorn, S., Chaowana, P. (2021). Bamboo as a sustainable building material—culm characteristics and properties. Sustainability, 13(13), 7376. https://doi.org/10.3390/su13137376 [Google Scholar] [CrossRef]

8. Liu, K. W., Jayaraman, A., Shi, Y. J., Harries, K., Yang, J. et al. (2022). Bamboo: A very sustainable construction material–2021 international online seminar summary report. Sustainable Structures, 2(1), 000015. https://doi.org/10.54113/j.sust.2022.000015 [Google Scholar] [CrossRef]

9. Liu, J., Zhou, A. P., Sheng, B. L., Liu, Y. Y., Sun, L. W. (2021). Effect of temperature on short-term compression creep property of bamboo scrimber. Journal of Forestry Engineering, 6(2), 64–69. https://doi.org/10.13360/j.issn.2096-1359.202006003 [Google Scholar] [CrossRef]

10. Oh, S. (2022). Experimental study of bending and bearing strength of parallel strand lumber (PSL) from Japanese larch veneer strand. Journal of the Korean Wood Science and Technology, 50(4), 237–245. https://doi.org/10.5658/WOOD.2022.50.4.237 [Google Scholar] [CrossRef]

11. Sharma, B., Eley, D., Emanuel, O., Brentnall, C. (2021). Mechanical properties of laminated bamboo designed for curvature. Construction and Building Materials, 300(8), 123937. https://doi.org/10.1016/j.conbuildmat.2021.123937 [Google Scholar] [CrossRef]

12. Li, H. T., Gao, T. Y., Cheng, G. S., Lorenzo, R. (2022). Evaluation on the pin groove compressive performance of laminated bamboo lumber at different angles. Cellulose, 30, 557–573. https://doi.org/10.1007/s10570-022-04920-z [Google Scholar] [CrossRef]

13. Dauletbek, A., Li, H., Xiong, Z., Lorenzo, R. (2021). A review of mechanical behavior of structural laminated bamboo lumber. Sustainable Structures, 1(1), 000004. https://doi.org/10.54113/j.sust.2021.000004 [Google Scholar] [CrossRef]

14. Li, Y. J., Lou, Z. C. (2021). Progress of bamboo flatten technology research. Journal of Forestry Engineering, 6(4), 14–23. https://doi.org/10.13360/j.issn.2096-1359.202012021 [Google Scholar] [CrossRef]

15. Chen, Y., Li, H. T., Yang, D., Lorenzo, R., Yuan, C. G. et al. (2022). Experimental evaluation of the dowel-bearing strength of laminated flattened-bamboo lumber perpendicular to grain. Construction and Building Materials, 350(1), 128791. https://doi.org/10.1016/j.conbuildmat.2022.128791 [Google Scholar] [CrossRef]

16. Wei, Y., Zhou, M. Q., Chen, D. J. (2015). Flexural behaviour of glulam bamboo beams reinforced with near-surface mounted steel bars. Materials Research Innovations, 19(sup1), S1-98–S1-103. https://doi.org/10.1179/1432891715Z.0000000001377 [Google Scholar] [CrossRef]

17. Yang, L., Zhou, A. P., Huang, D. S., He, C. (2016). Determination of mode-I fracture parameters of parallel strand bamboo based on VIC-3D technology. Journal of Nanjing Tech University (Natural Science Edition), (5), 100–104+110. https://doi.org/10.1007/s00226-013-0591-2 [Google Scholar] [CrossRef]

18. Cook, J., Gordon, T. E. (1964). A mechanism for the control of crack propagation in all-brittle systems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 282(1391), 508–520. https://doi.org/10.1098/rspa.1964.0248 [Google Scholar] [CrossRef]

19. Huang, D. S., Zhou, A. P., Bian, Y. L. (2013). Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams. Construction and Building Materials, 44, 585–592. https://doi.org/10.1016/j.conbuildmat.2013.03.050 [Google Scholar] [CrossRef]

20. Sheng, B. L. (2021). Experimental and analytical study on intralaminar/interlaminar fracture of laminated veneer bamboo under Mode I loading. Nanjing, China: Nanjing Forestry University. https://doi.org/10.27242/d.cnki.gnjlu.2021.000012 [Google Scholar] [CrossRef]

21. Yuan, K. Y. (2019). Experimental study on mode I fracture energy of parallel strand bamboo. Nanjing, China: Nanjing Forestry University. https://doi.org/10.27242/d.cnki.gnjlu.2019.000273 [Google Scholar] [CrossRef]

22. Zhu, Y. (2020). Experimental research on mode I fracture of parallel strand bamboo: Detection of crack tip and measurement of fracture toughness. Nanjing, China: Nanjing Forestry University. https://doi.org/10.27242/d.cnki.gnjlu.2020.000244 [Google Scholar] [CrossRef]

23. Irwin, G. R. (1956). Onset of fast crack propagation in high strength steel and aluminum alloys. Sayamore Research Conference Proceedings, 2, 289–305. [Google Scholar]

24. Irwin, G. R., Paris, P. C. (1971). Fundamental aspects of crack growth and fracture. Engineering Fundamentals and Environmental Effects, 243(1), 1–46. https://doi.org/10.1016/B978-0-12-449703-0.50006-0 [Google Scholar] [CrossRef]

25. Irwin, G. R., Wells, A. A. (1965). Continuum-mechanics view of crack propagation. Metallurgical Reviews, 10(1), 223–270. https://doi.org/10.1179/mtlr.1965.10.1.223 [Google Scholar] [CrossRef]

26. Feng, W., Tang, Y. C., He, W. M., Wei, W. B., Yang, Y. M. (2022). Mode I dynamic fracture toughness of rubberised concrete using a drop hammer device and split Hopkinson pressure bar. Journal of Building Engineering, 48(1), 103995. https://doi.org/10.1016/j.jobe.2022.103995 [Google Scholar] [CrossRef]

27. Bocca, P., Carpinteri, A., Valente, S. (1991). Mixed mode fracture of concrete. International Journal of Solids and Structures, 27(9), 1139–1153. https://doi.org/10.1016/0020-7683(91)90115-V [Google Scholar] [CrossRef]

28. Fang, K., Ren, L., Jiang, H. Q. (2021). Development of Mode I and Mode II fracture toughness of cemented paste backfill: Experimental results of the effect of mix proportion, temperature and chemistry of the pore water. Engineering Fracture Mechanics, 258(5), 108096. https://doi.org/10.1016/j.engfracmech.2021.108096 [Google Scholar] [CrossRef]

29. Wang, Y. L., Wang, W. G., Zhang, B. H., Li, C. Q. (2020). A review on mixed mode fracture of metals. Engineering Fracture Mechanics, 235(6), 107126. https://doi.org/10.1016/j.engfracmech.2020.107126 [Google Scholar] [CrossRef]

30. Inglis, C. E. (1913). Stress in a plate due to the presence of cracks and sharp comers. Institution of Naval Architects, 55, 219–230. [Google Scholar]

31. Griffith, A. A. (1921). The phenomena of rupture and flow in solid. Philosophical Transaction of Royal Society of London, 221(582–593), 163–197. https://doi.org/10.1098/rsta.1921.0006 [Google Scholar] [CrossRef]

32. Irwin, G. R. (1957). Analysis of stresses and strains near the end of a crack traversing a plate. Journal of Applied Mechanics, 24(3), 361–364. https://doi.org/10.1115/1.4011547 [Google Scholar] [CrossRef]

33. Irwin, G. R. (1958). Fracture strength relative to onset and arrest of crack propagation. Proceedings of the American Society for Testing Material, 58, 640–657. [Google Scholar]

34. Wells, A. A. (1963). Application of fracture mechanics at and beyond general yielding. British Welding Journal, 10, 563–570. [Google Scholar]

35. Newman Jr, J. C., James, M. A., Zerbst, U. (2003). A review of the CTOA/CTOD fracture criterion. Engineering Fracture Mechanics, 70(3–4), 371–385. https://doi.org/10.1016/S0013-7944(02)00125-X [Google Scholar] [CrossRef]

36. Rice, J. R. (1968). A path independent integral and the approximate analysis of strain concentration by notches and cracks. Journal of Applied Mechanics, 35(2), 379–386. https://doi.org/10.1115/1.3601206 [Google Scholar] [CrossRef]

37. Hutchinson, J. (1968). Singular behaviour at the end of a tensile crack in a hardening material. Journal of the Mechanics and Physics of Solids, 16(1), 13–31. https://doi.org/10.1016/0022-5096(68)90014-8 [Google Scholar] [CrossRef]

38. Rice, J. R., Rosengren, G. (1968). Plane strain deformation near a crack tip in a power-law hardening material. Journal of the Mechanics and Physics of Solids, 16(1), 1–12. https://doi.org/10.1016/0022-5096(68)90013-6 [Google Scholar] [CrossRef]

39. Chen, C., Fan, X. Q., Chen, X. D. (2020). Experimental investigation of concrete fracture behavior with different loading rates based on acoustic emission. Construction and Building Materials, 237(6063), 117472. https://doi.org/10.1016/j.conbuildmat.2019.117472 [Google Scholar] [CrossRef]

40. Frómeta, D., Parareda, S., Lara, A., Molas, S., Casellas, D. et al. (2020). Identification of fracture toughness parameters to understand the fracture resistance of advanced high strength sheet steels. Engineering Fracture Mechanics, 229, 106949. https://doi.org/10.1016/j.engfracmech.2020.106949 [Google Scholar] [CrossRef]

41. Xu, M. M. (2014). Mode I fracture toughness of moso bamboo and glued bamboo. Beijing, China: Chinese Academy of Forestry. https://doi.org/10.7666/d.Y2629829 [Google Scholar] [CrossRef]

42. Li, H. T., Xu, W., Chen, C., Yao, L. S., Lorenzo, R. (2022). Temperatures influencing on the bending performance of laminated bamboo lumber. Journal of Materials in Civil Engineering ASCE. https://doi.org/10.1061/(ASCE)MT.1943-5533.0004730 [Google Scholar] [CrossRef]

43. Li, H. T., Chen, B., Fei, B. H., Li, H., Xiong, Z. H. et al. (2022). Mechanical properties of aramid fiber reinforced polymer confined laminated bamboo lumber column under cyclic loading. European Journal of Wood and Wood Products, 80(5), 1057–1070. https://doi.org/10.1007/s00107-022-01816-4 [Google Scholar] [CrossRef]

44. Wang, F., Shao, Z. P. (2020). Study on the variation law of bamboo fibers’ tensile properties and the organization structure on the radial direction of bamboo stem. Industrial Crops and Products, 152(4), 112521. https://doi.org/10.1016/j.indcrop.2020.112521 [Google Scholar] [CrossRef]

45. ASTM E399 (2020). Standard test method for translaminar fracture toughness of laminated and pultruded matrix composite materials. Philadelphia, Pennsylvania, USA: American Society of Testing Materials. [Google Scholar]

46. BS 5447 (1977). Methods of test for plane strain fracture toughness. London, UK: British Standards Institution. [Google Scholar]

47. Fadlelmola, A. B. F. A., Chen, Z., Du, Y., Ma, R., Ma, J. (2021). Experimental investigation and design method on a lightweight bamboo-concrete sandwich panel under bending load. Structures, 34(1239), 856–874. https://doi.org/10.1016/j.istruc.2021.08.030 [Google Scholar] [CrossRef]

48. Zhang, T. C., Wang, A. L., Wang, Q. S., Guan, F. R. (2019). Bending characteristics analysis and lightweight design of a bionic beam inspired by bamboo structures. Thin-Walled Structures, 142(3), 476–498. https://doi.org/10.1016/j.tws.2019.04.043 [Google Scholar] [CrossRef]

49. Chen, M. L., Ye, L., Wang, G., Fang, C. H., Dai, C. P. et al. (2019). Fracture modes of bamboo fiber bundles in three-point bending. Cellulose, 26(13), 8101–8108. https://doi.org/10.1007/s10570-019-02631-6 [Google Scholar] [CrossRef]

50. An, Y. L., Liu, Z. M., Wang, G., Wu, W. J. (2011). Three-point bending fracture behaviors of bamboo. In: Advanced materials research, vol. 261, pp. 464–468. https://doi.org/10.4028/www.scientific.net/AMR [Google Scholar] [CrossRef]

51. Chen, G. W., Luo, H. Y., Wu, S. J., Guan, J., Luo, J. et al. (2018). Flexural deformation and fracture behaviors of bamboo with gradient hierarchical fibrous structure and water content. Composites Science and Technology, 157(2), 126–133. https://doi.org/10.1016/j.compscitech.2018.01.034 [Google Scholar] [CrossRef]

52. Chen, G. W., Luo, H. Y. (2021). Asymmetric flexural process and fracture behaviors of natural bamboo node with gradient discontinuous fibers. Composites Communications, 24, 100647. https://doi.org/10.1016/j.coco.2021.100647 [Google Scholar] [CrossRef]

53. Chen, M. L., Dai, C. P., Liu, R., Lian, C. P., Yuan, J. et al. (2020). Influence of cell wall structure on the fracture behavior of bamboo (Phyllostachys edulis) fibers. Industrial Crops and Products, 155(1), 112787. https://doi.org/10.1016/j.indcrop.2020.112787 [Google Scholar] [CrossRef]

54. Liu, H. R., Peng, G. Y., Chai, Y., Huang, A. Y., Jiang, Z. H. et al. (2019). Analysis of tension and bending fracture behavior in moso bamboo (Phyllostachys pubescens) using synchrotron radiation micro-computed tomography (SRμCT). Holzforschung, 73(12), 1051–1058. https://doi.org/10.1515/hf-2018-0275 [Google Scholar] [CrossRef]

55. Zou, L. H., Li, X. D. (2021). In situ observation of fracture behavior of bamboo culm. The Minerals, Metals & Materials Society, 73(6), 1705–1713. https://doi.org/10.1007/s11837-021-04661-7 [Google Scholar] [CrossRef]

56. Liu, H. R., Wang, X. Q., Zhang, X. B., Sun, Z. J., Jiang, Z. H. (2016). In situdetection of the fracture behaviour of moso bamboo (Phyllostachys pubescens) by scanning electron microscopy. Holzforschung, 70(12), 1183–1190. https://doi.org/10.1515/hf-2016-0003 [Google Scholar] [CrossRef]

57. Liu, W., Hu, X. Z., Yuan, B. Y., Xu, F., Huang, J. K. (2020). Tensile strength model of bamboo srimber by 3-pb fracture test on the basis of non-LEFM. Composites Science and Technology, 198, 108295. https://doi.org/10.1016/j.compscitech.2020.108295 [Google Scholar] [CrossRef]

58. Xie, J., Liu, Y., Yan, M. L., Yan, J. B. (2022). Mode I fracture behaviors of concrete at low temperatures. Construction and Building Materials, 323, 126612. https://doi.org/0.1016/j.conbuildmat.2022.126612 [Google Scholar]

59. Ayatollahi, M. R., Bahrami, B., Mirzaei, A. M., Yahya, M. Y. (2019). Effects of support friction on mode I stress intensity factor and fracture toughness in SENB testing. Theoretical and Applied Fracture Mechanics, 103, 102288. https://doi.org/10.1016/j.tafmec.2019.102288 [Google Scholar] [CrossRef]

60. Xu, M. M., Wu, X. M., Liu, H. R., Sun, Z. J., Song, G. G. et al. (2014). Mode I fracture toughness of tangential moso bamboo. BioResources, 9(2), 2026–2032. https://doi.org/10.15376/biores.9.2.2026-2032 [Google Scholar] [CrossRef]

61. Liu, H. R. (2010). Study on the properties and mechanism of fracture in bamboo. Beijing, China: Chinese Academy of Forestry. https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CDFD0911&filename=2010264591.nh [Google Scholar]

62. Liu, W., Yu, Y., Hu, X. Z., Han, X. Y., Xie, P. (2019). Quasi-brittle fracture criterion of bamboo-based fiber composites in transverse direction based on boundary effect model. Composite Structures, 220(41–48), 347–354. https://doi.org/10.1016/j.compstruct.2019.04.008 [Google Scholar] [CrossRef]

63. Xie, P., Liu, W., Hu, Y. C., Meng, X. M., Huang, J. K. (2020). Size effect research of tensile strength of bamboo scrimber based on boundary effect model. Engineering Fracture Mechanics, 239, 107319. https://doi.org/10.1016/j.engfracmech.2020.107319 [Google Scholar] [CrossRef]

64. Reynolds, T. P., Sharma, B., Serrano, E., Gustafsson, P. J., Ramage, M. H. (2019). Fracture of laminated bamboo and the influence of preservative treatments. Composites Part B: Engineering, 174(4), 107017. https://doi.org/10.1016/j.compositesb.2019.107017 [Google Scholar] [CrossRef]

65. Chen, G. W., Luo, H. Y. (2020). Effects of node with discontinuous hierarchical fibers on the tensile fracture behaviors of natural bamboo. Sustainable Materials and Technologies, 26, e00228. https://doi.org/10.1016/j.susmat.2020.e00228 [Google Scholar] [CrossRef]

66. Chen, G. W., Luo, H. Y., Yang, H. Y., Zhang, T., Li, S. J. (2018). Water effects on the deformation and fracture behaviors of the multi-scaled cellular fibrous bamboo. Acta Biomaterialia, 65(1), 203–215. https://doi.org/10.1016/j.actbio.2017.10.005 [Google Scholar] [PubMed] [CrossRef]

67. ASTM D5528 (2013). Standard test method for mode I interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites. Philadelphia, Pennsylvania, USA: American Society of Testing Materials. [Google Scholar]

68. Khan, Z., Yousif, B. F., Islam, M. (2017). Fracture behaviour of bamboo fiber reinforced epoxy composites. Composites Part B: Engineering, 116(3), 186–199. https://doi.org/10.1016/j.compositesb.2017.02.015 [Google Scholar] [CrossRef]

69. Almeida-Fernandes, L., Silvestre, N., Correia, J. R., Arruda, M. R. T. (2020). Fracture toughness-based models for damage simulation of pultruded GFRP materials. Composites Part B: Engineering, 186(3), 107818. https://doi.org/10.1016/j.compositesb.2020.107818 [Google Scholar] [CrossRef]

70. Konukcu, A. C., Quin, F., Zhang, J. (2021). Effect of growth rings on fracture toughness of wood. European Journal of Wood and Wood Products, 79(6), 1495–1506. https://doi.org/10.1007/s00107-021-01738-7 [Google Scholar] [CrossRef]

71. Wong, K. J., Zahi, S., Low, K. O., Lim, C. C. (2010). Fracture characterization of short bamboo fiber reinforced polyester composites. Materials & Design, 31(9), 4147–4154. https://doi.org/10.1016/j.matdes.2010.04.029 [Google Scholar] [CrossRef]

72. Ali, A., Rassiah, K., Othman, F., Lee, H. P., Tay, T. E. et al. (2016). Fatigue and fracture properties of laminated bamboo strips from Gigantochloa scortechinii polyester composites. BioResources, 11(4), 9142–9153. https://doi.org/10.15376/biores.11.4.9142-9153 [Google Scholar] [CrossRef]

73. Li, X. Z., Yao, B., Xu, J. M., Ren, H. Q. (2018). Investigation on Mode I interlaminar fracture toughness of Recombinant Bamboo. Wood Processing Machinery, 29(4), 4–7, +23. https://doi.org/10.13594/j.cnki.mcjgjx.2018.04.002 [Google Scholar] [CrossRef]

74. Wu, G. F., Gong, Y. C., Zhong, Y., Ren, H. Q. (2019). Determination and simulation of the Mode I fracture toughness of bamboo scrimber. BioResources, 14(3), 6811–6821. https://doi.org/10.15376/biores.14.3.6811-6821 [Google Scholar] [CrossRef]

75. Stanzl-Tschegg, S. E., Tan, D. M., Tschegg, E. K. (1995). New splitting method for wood fracture characterization. Wood Science and Technology, 29(1), 31–50. https://doi.org/10.1007/BF00196930 [Google Scholar] [CrossRef]

76. Samadi, S., Jin, S., Gruber, D., Harmuth, H. (2021). A comparison of two damage models for inverse identification of mode I fracture parameters: Case study of a refractory ceramic. International Journal of Mechanical Sciences, 197(4), 106345. https://doi.org/10.1016/j.ijmecsci.2021.106345 [Google Scholar] [CrossRef]

77. Tobata, Y., Naito, K., Tanks, J. (2022). Investigation of a critical separation criterion for mode I-Governed fracture of basalt fiber/polypropylene rods via a modified double cantilever beam test. Composite Structures, 279(10), 114778. https://doi.org/10.1016/j.compstruct.2021.114778 [Google Scholar] [CrossRef]

78. Moazzami, M., Ayatollahi, M. R., Akhavan-Safar, A., de Freitas, S. T., Poulis, J. A. et al. (2022). Effect of cyclic aging on mode I fracture energy of dissimilar metal/composite DCB adhesive joints. Engineering Fracture Mechanics, 271(1), 108675. https://doi.org/10.1016/j.engfracmech.2022.108675 [Google Scholar] [CrossRef]

79. Williams, J. G. (1988). On the calculation of energy release rates for cracked laminates. International Journal of Fracture, 36(2), 101–119. https://doi.org/10.1007/BF00017790 [Google Scholar] [CrossRef]

80. Nairn, J. A. (2006). On the calculation of energy release rates for cracked laminates with residual stresses. International Journal of Fracture, 139(2), 267–293. https://doi.org/10.1007/s10704-006-0044-0 [Google Scholar] [CrossRef]

81. Kondo, K. (2007). Analysis of potential energy release rate of composite laminate based on timoshenko beam theory. Key Engineering Materials, 334, 513–516. https://doi.org/10.4028/www.scientific.net/KEM.334-335.513 [Google Scholar] [CrossRef]

82. Toygar, M. E., Maleki, F. K. (2016). The temperature and pre-crack length effects on delamination resistance of woven GFRP sandwich composites. Mechanics, 22(5), 331–336. https://doi.org/10.5755/j01.mech.22.5.16229 [Google Scholar] [CrossRef]

83. Shao, Z. P., Fang, C. H., Tian, G. L. (2009). Mode I interlaminar fracture property of moso bamboo (Phyllostachys pubescens). Wood Science and Technology, 43(5), 527–536. https://doi.org/10.1007/s00226-009-0265-2 [Google Scholar] [CrossRef]

84. Chen, Q., Dai, C. P., Fang, C. H., Chen, M. L., Zhang, S. Q. et al. (2019). Mode I interlaminar fracture toughness behavior and mechanisms of bamboo. Materials & Design, 183(4), 108132. https://doi.org/10.1016/j.matdes.2019.108132 [Google Scholar] [CrossRef]

85. Shen, Y. R., Huang, D. S., Chui, Y. H., Dai, C. P. (2019). Fracture of parallel strand bamboo composite under mode I loading: DCB test investigation. Advances in Materials Science and Engineering. https://doi.org/10.1155/2019/7657234 [Google Scholar] [CrossRef]

86. Liu, Y. Y., Sheng, B. L., Huang, D. S., Zhou, A. P. (2021). Mode-I interlaminar fracture behavior of laminated bamboo composites. Advances in Structural Engineering, 24(4), 733–741. https://doi.org/10.1177/1369433220965270 [Google Scholar] [CrossRef]

87. Fan, M., Yi, D. K., Xiao, Z. M. (2015). Fracture analysis for a sub-interface Zener-Stroh crack in a bi-material plate under small-scale yielding condition. Theoretical and Applied Fracture Mechanics, 76, 60–66. https://doi.org/10.1016/j.tafmec.2015.01.003 [Google Scholar] [CrossRef]

88. Xie, D., Biggers Jr, S. B. (2006). Strain energy release rate calculation for a moving delamination front of arbitrary shape based on the virtual crack closure technique. Part I: Formulation and validation. Engineering Fracture Mechanics, 73(6), 771–785. https://doi.org/10.1016/j.engfracmech.2005.07.013 [Google Scholar] [CrossRef]

89. Ural, A., Krishnan, V. R., Papoulia, K. D. (2009). A cohesive zone model for fatigue crack growth allowing for crack retardation. International Journal of Solids and Structures, 46(11–12), 2453–2462. https://doi.org/10.1016/j.ijsolstr.2009.01.031 [Google Scholar] [CrossRef]

90. de Moura, M. F. S. F., Chousal, J. A. G. (2006). Cohesive and continuum damage models applied to fracture characterization of bonded joints. International Journal of Mechanical Sciences, 48(5), 493–503. https://doi.org/10.1016/j.ijmecsci.2005.12.008 [Google Scholar] [CrossRef]

91. Liu, M. K., Zhou, A. P., Liu, Y. Y., Sheng, B. L. (2020). Numerical simulation analysis of parallel strand bamboo type I fracture using extended finite element method. Journal of Forestry Engineering, (6), 49–56. https://doi.org/10.13360/j.issn.2096-1359.201912018 [Google Scholar] [CrossRef]

92. Liu, Y. Y., Huang, D. S., Sheng, B. L. (2021). Experimental study and numerical simulation on mode-I interlaminar fracture behavior of laminated bamboo. Journal of Building Structures, 44(1). https://doi.org/10.14006/j.jzjgxb.2021.0263 [Google Scholar] [CrossRef]

93. Hao, Z., Yang, S. T. (2017). Determination of type I fracture energy between layers of Phyllostachys pubescens. Journal of Green Science and Technology, (12), 219–223. https://doi.org/10.16663/j.cnki.lskj.2017.12.088 [Google Scholar] [CrossRef]

94. Wang, F. L., Shao, Z. P., Wu, Y. J., Wu, D. (2014). The toughness contribution of bamboo node to the mode I interlaminar fracture toughness of bamboo. Wood Science and Technology, 48(6), 1257–1268. https://doi.org/10.1007/s00226-013-0591-2 [Google Scholar] [CrossRef]