A Fault Feature Extraction Model in Synchronous Generator under Stator Inter-Turn Short Circuit Based on ACMD and DEO3S

1  Introduction

As one of the most important machines in electricity production, the synchronous generators directly influence the stability and the safety of the electric power system. However, due to the complex operating environment, the generator is facing the challenge of frequent faults. Stator inter-turn short circuit, which is often caused by insulation damage, is a kind of common electrical fault in generator sets. Such fault will lead to the unbalance of the three-phase voltages and even damage the components [1]. According to the relevant investigation, the probability of such failure is as high as 30% [2]. Therefore, it is significant to explore effective methods in particular for early detection on stator short circuit fault.

Many scholars have studied the fault diagnosis methods for generators and contributed to a series of academic achievements. These existing methods for detecting the generator faults are mostly based on electrical parameters such as the currents and voltages [3–5]. For instance, Bouzid et al. [6] used the negative sequence current as the indicator to diagnose stator faults, but they ignored the influence of the inherent asymmetry inside the electric machines. Ma et al. [7] proposed a method according to the phase-angle of branch current in synchronous condensers. However, the branch current in synchronous condensers is not so easy to obtain in real conditions. Wang et al. [8] proposed the combined diagnosis method by employing both the negative sequence current difference and the double frequency component of the radial stator vibration for the stator inter-turn short circuit fault. This study is a typical work which fully used the vibration signal by the frequency spectrum, while with a great pity it did not propose the effective model to extract the fault feature obviously. In this work, however, the proposed model is useful to extract not only double frequency component but also 4f, 6f (f is the fundamental electrical frequency) characteristic frequency, which shows better effect than simple spectrum analysis in reference [8]. In addition, the method in reference [7] only has simulation analysis because the current sensor is hard to be installed due to the space limitation at the outlet of stator windings. The fault diagnosis method in this paper has been verified by experiment on MJF-30-6 generator. Benefit from the simple installation of sensors, the vibration signal is easy to be obtained. Thus, the diagnosis method based on vibration is more practical in engineering.

In fact, the vibration signal of the generator contains a lot of faulty information, which can efficiently be used to diagnose faults. He [1] analyzed the vibration characteristics of stator and rotor in synchronous generators under different kinds of faults, and found that the amplitudes of 2f, 4f and 6f (f refers to the fundamental electrical frequency) components of stator vibration will be increased obviously when stator short circuit fault occurs. Hegde et al. [9] adopted the vibration signature analysis to reveal the features of inter-turn short circuit faults. Liang et al. [10] analyzed the stator vibration and current to detect the fault in permanent magnet synchronous motor (PMSM). The aforementioned studies showed that the stator vibration features are effective and sometimes pretty convenient for the fault detection in generators.

In order to extract the fault features of the stator inter-turn short circuit, the study of the processing method for vibration signal is necessary. Actually, the vibration signal processing technology has a long-term development in the field of rotating machinery fault diagnosis [11–15]. For example, EMD (empirical mode decomposition) and EEMD (ensemble empirical mode decomposition) are used in many fields related to the fault diagnosis model [16–21]. However, most of the fault diagnosis researches focus on the mechanics. For instance, the rolling bearing and gearbox vibration processing shows the obvious characteristics as a result of contact-impact. As for the generator, the vibration of the stator is caused by the pulsating magnetic pull, and the fault features are so weak that it would be easily submerged in environmental noise. Therefore, it is essential to study the method for suppressing the impact of the noise.

By far, scholars have tried a lot of ways to optimize the existing methods. Aiming at the chirp signal, variational nonlinear chirp mode decomposition (VNCMD) was proposed by Chen et al. [22], which is essentially a generalization of variational mode decomposition (VMD) method. To achieve the adaptively decomposition of the chirp signal, the adaptive chirp mode decomposition (ACMD) was proposed by Chen et al. [23] which employed a greedy algorithm to catch each signal component individually. Wang et al. [24] used ACMD to realize the fault detection in rolling bearings. Their work proves the effectiveness of ACMD in vibration signal analysis. As for the demodulation technique, the Hilbert transform can be used for machine diagnosis [25]. Potamianos et al. [26] compared Hilbert transform with the energy operator method for the signal demodulation, and found that the energy operator has a faster adaptation due to its instantaneous nature. Xu et al. [27] realized the diagnosis of rolling bearings based on the demodulation energy operator of symmetrical differencing (DEO3S). The study of Wu et al. [28] and Shen et al. [29] also presented the effectiveness of DEO3S in machinery fault diagnosis. To quantify the feature of the signal, permutation entropy is usually applied. Permutation entropy (PE) algorithm was proposed by Bandt et al. [30] to detect the randomness and the dynamic mutation. Zhang et al. [31] used the permutation entropy (PE) as the parameter to detect the bearing faults. Liu et al. [32] employed PE to improve the algorithm of rolling bearing fault diagnosis.

In this paper, the method of ACMD is introduced to decompose the stator vibration signal in synchronous generator. Combining with the demodulation technique of DEO3S, a hybrid model based on ACMD and DEO3S is proposed. The model applied ACMD to obtain the optimal mode of the original signal, and acquired the envelop spectrum of the optimal mode which contains the fault feature by DEO3S. Finally, the fault feature is extracted. The main contributions of the work are as follows:

(1)   Aiming at the stator inter turn short circuit fault, many existed diagnosis methods are based on electrical parameters. Few people considered vibration to diagnose this fault. After sufficient study of the vibration of generator and the fault characteristic, the vibration signal of the stator is introduced to detect the electrical fault in this study;

(2)   The effectiveness of ACMD in signal decomposition and DEO3S in signal demodulation is illustrated according to the comparative analysis. In order to highlight the effect of ACMD in signal decomposition, EEMD is carried out. Moreover, the traditional Hilbert transform is applied as a contrast to highlight the ability of DEO3S;

(3)   The hybrid model for stator inter-turn short circuit in synchronous generator is verified. The experiment on MJF-30-6 generator is designed to test the proposed model based on ACMD_DEO3S. CD-21C speed sensor is used to collect the vibration signal of the stator. The normal signal and the fault signal are both collected and analyzed.

The remainder of this paper is constructed as follows: A brief introduction of the method based on ACMD and DEO3S is introduced in Section 2, while Section 3 gives the simulation study using the simulating signal to extract the weak features in noisy environments. In Section 4, the experiment on the MJF prototype generator and the analysis result are employed to demonstrate the effectiveness of the proposed method. Finally, Section 5 concludes the main work of this paper.

2  Brief Introduction of the Main Theory

2.1 Review of ACMD

Adaptive chirp mode decomposition (ACMD) uses a greedy algorithm to estimate the signal components. It can convert broadband nonlinear chirp signal into narrowband signal. Actually, the vibration signal collected on generator exists modulation phenomenon inevitably. Thus, the characteristic of ACMD is significant to the signal of generator. The process of the decomposition is as follows [23]. For one signal component, the problem in Eq. (1) should be solved.

minmi(t),ni(t),fp(t)⁡{‖m¨i‖22+‖n¨i‖22+α‖s(t)−si(t)‖22}s.t.{s(t)=∑i=1Ksi(t)si(t)=mi(t)cos⁡[2π∫0tfp(τ)dτ]+ni(t)sin⁡[2π∫0tfp(τ)dτ] (1)

where s(t) is the original signal, si(t) is the i-th chirp mode of s(t), ‖s(t)−si(t)‖22 indicates the remaining energy after removing the currently estimated component, α > 0 is a weight coefficient, fp(t) is the instantaneous frequency of the i-th chirp mode, mi(t) and ni(t) are the corresponding demodulated signals of si(t).

For a series of the digital signal with N samples, the discrete form of Eq. (1) can be described as

minui,fi⁡{‖Θui‖22+α‖s−Giui‖22} (2)

where Θ=[ΩΩ] , Ω is a second-order difference matrix, ui=[miT,niT] with miT=[mi(t0),⋯,mi(tN−1)]T , niT=[ni(t0),⋯,ni(tN−1)]T and siT=[si(t0),⋯,si(tN−1)]T .

Gi=[Ci,Si] (3)

Ci=diag[cos⁡(φi(t0)),⋯,cos⁡(φi(tN−1))] (4)

Si=diag[sin⁡(φi(t0)),⋯,sin⁡(φi(tN−1))] (5)

where φi(t)=2π∫0tfi(τ)dτ .

Eq. (2) indicates that, given a frequency function fi(t) (or matrix Gi), the vector ui (created by the demodulated signals) can be estimated by solving a l2-regularized least-squares problem. Thus, the above problem can be solved through an iterative algorithm that alternately updates the vector ui. For the j-th iteration, the vector ui is updated as

uij=[mijnij]=argmin{‖Θui‖22 + α‖s−Gijui‖22}ui=[1αΘTΘ+(Gij)TGij]−1(Gij)Ts (6)

where Gij is constructed with the instantaneous frequencies, and the superscript j stands for the iteration number.

Then the mode can be estimated as

sij=Gijuij (7)

The difference ξ between the modes in two adjacent iterations can be obtained as

ξij=‖sij−sij−1‖22/‖sij−sij−1‖22‖sij‖‖sij‖22 (8)

The above decomposition steps would operate iteratively until the difference value is within the given stopping criterion. After that, the estimated mode can be obtained.

2.2 Introduction of DEO3S

The reason of the stator vibration in generator is periodic pulsating magnetic force. In this paper, DEO3S is considered to be the tool of restoring the periodic shock signal. The process of demodulation energy operator of symmetrical differencing (DEO3S) is as follows [27]. Assuming that x(t) is a time signal

x(t)=acos⁡(ωt) (9)

where a, ω are the amplitude and the frequency of x(t), respectively.

Teager energy operator is defined as

ψ(x)=x˙2−x⋅x¨ (10)

and the discrete form for a time series x(n) can be described as

ψ[x(n)]=x2(n)−x(n−1)⋅x(n+1) (11)

where ψ(x) is the sum of kinetic energy and potential energy, thus this definition is called energy operator.

Combining with Eq. (9), we can obtain

{ψ(x)=a2ω2ψ(x˙)=a2ω4 (12)

According to Eq. (12), the amplitude and the frequency of x(t) can be expressed as

{ω=ψ(x˙)ψ(x)a=ψ(x)ψ(x˙) (13)

DEO3S is developed on the basis of the above energy operator. Firstly, the symmetric differential sequence y(n) is defined as

y(n)=[x(n+1)−x(n)]+[x(n)−x(n−1)]2=x(n+1)−x(n−1)2 (14)

The new difference sequence is obtained by smoothing y(n) as

y~(n)=x(n+1)−2x(n)+x(n−1)4 (15)

Substitute Eqs. (14) and (15) into Eq. (11)

ψ~[x(n)]=ψ[x(n+1)]+2ψ[x(n)]+ψ[x(n−1)]4 (16)

According to Eq. (16), the energy operator based on DEO3S is obtained by taking ψ[x(n)] as the input with the transfer function H(z) = z(1+2z−1+z−2)/4, thus its estimated amplitude would be

a(n)≈2ψ[x(n)]ψ[x(n+1)−x(n−1)] (17)

2.3 Process of the Hybrid Model

In this part, the detailed steps of the proposed model are described. For the stator vibration signal in a synchronous generator, the following steps are performed to extract the feature frequencies under the stator inter-turn short circuit fault. Steps 1 and 2 are the signal preprocessing to select proper parameters.

Step 1: Conduct Fourier transform to obtain the peak frequency of the signal;

Step 2: Preprocess the original signal. Calculate the PE values of the DEO3S envelope of ACMD estimated modes in time domain to decide the weighting coefficient;

Step 3: Input the original signal and proper parameters to ACMD to acquire the optimal mode;

Step 4: Obtain the DEO3S envelop spectrum of the optimal mode.

The process is as Fig. 1.

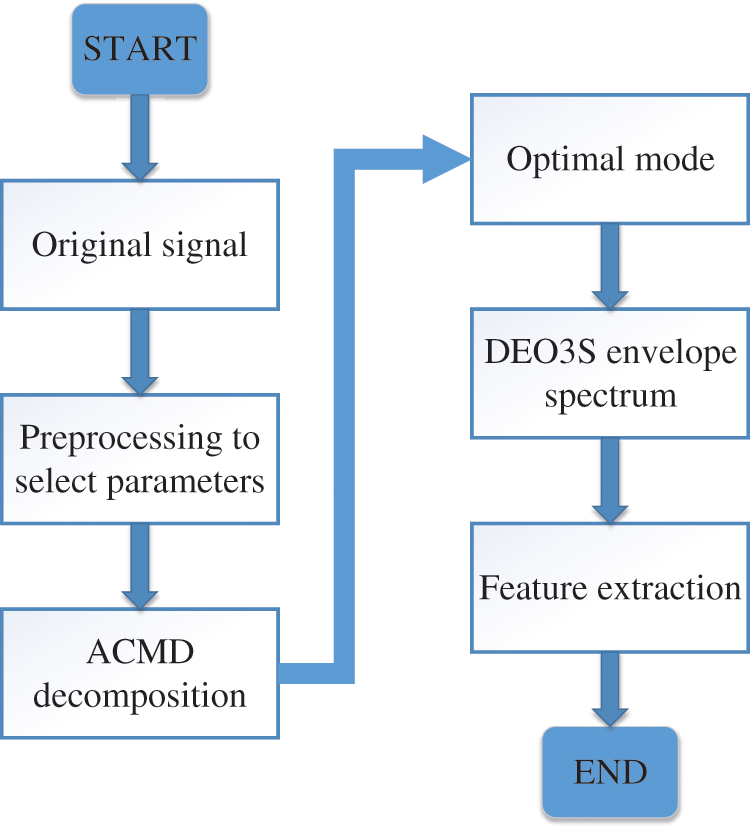
Figure 1: Process of the proposed model

3  Research of Simulating Signal

3.1 Brief Introduction of the Simulating Signal

In this section, a simulating vibration signal of the stator in a synchronous generator under the stator inter-turn short circuit fault is studied. It can be suggested from reference [1] that the amplitudes at 2f0, 4f0 and 6f0 (f0 = 50 Hz is the fundamental frequency of generator) will be increased as the fault occurs. But in fact, these characteristic frequencies are easy to be submerged in noise. In order to simulate the fault signal with noises, a simulating signal x(t) is designed as

x(t)=Am0+A0cos⁡(2πf0t+φ0)+A1cos⁡(2πf1t+φ1)+A2cos⁡(2πf2t+φ2)+A3cos⁡(2πf3t+φ3)+n(t) (18)

where Am0 is the DC component contained in x(t); Aicos(2πfit+φi) refers to the four main components of the vibration signal to simulate the characteristic frequencies of the stator inter-turn short circuit fault; n(t) is a Gaussian white noise with a signal-to-noise ratio of 40 dB. The amplitudes A2 and A3 are set to a small value to simulate the condition in which these two components are submerged by noise. Meanwhile, different phases φi are set to avoid beat vibration. The sampling frequency fs is 5,000 Hz and the sample number N is 16,384. The detailed parameters of the simulating signal are shown in Table 1, while the time-domain wave and the frequency spectrum of the simulating signal are shown in Fig. 2.

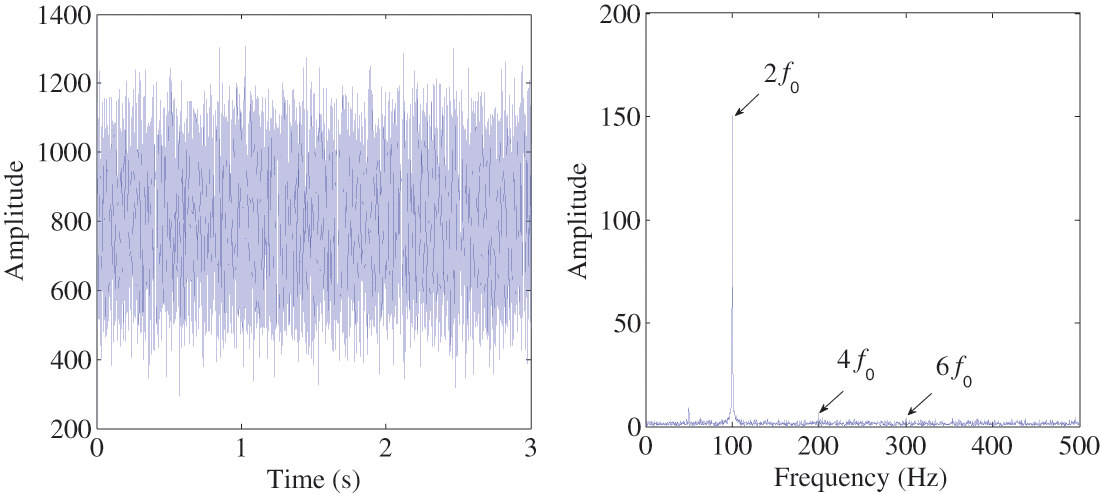
Figure 2: Simulating signal

It can be seen in Fig. 2 that the time-domain wave is out of order and no useful fault information is displayed. The peak at 2f0 can be easily selected, because the vibration signal of generator is usually dominated in the double frequency component. However, the components of 4f0 and 6f0 which represent the fault information cannot be recognized in the spectrum, so the fault category cannot be accurately identified only by the double frequency component.

3.2 Parameter Selection and Fault Feature Enhancement of ACMD

In order to highlight the fault characteristics contained in the original signal, the method of ACMD described in Section 2.1 is employed. The key point of the application of ACMD method is how to select the appropriate decomposition parameters, i.e., the initial instantaneous frequency fp and the weighting coefficient α, to obtain the optimal mode. The research shows that the values of fp and α have a very obvious influence on the estimated mode of ACMD.

In reference [23], the peak frequency of the signal is suggested as the choice of the initial instantaneous frequency of ACMD. In our study, the peak frequency of the vibration signal, which is double-frequency at 100 Hz, can be easily obtained from the spectrum due to its predominance in the vibration signal regardless there is a fault or not. Therefore, the double-frequency component is selected as the initial instantaneous frequency of ACMD. According to reference [23], the weight factor α mainly affects the bandwidth of the estimated mode, and α is usually set from 0.0001 to 0.1. The optimal mode estimated by ACMD for the simulating signal and its spectrum are shown in Fig. 3. Compared Fig. 3 with Fig. 2, ACMD does not show an obvious superiority. Although the fault feature is not shown up, the influence of the noise on the signal analysis is reduced.

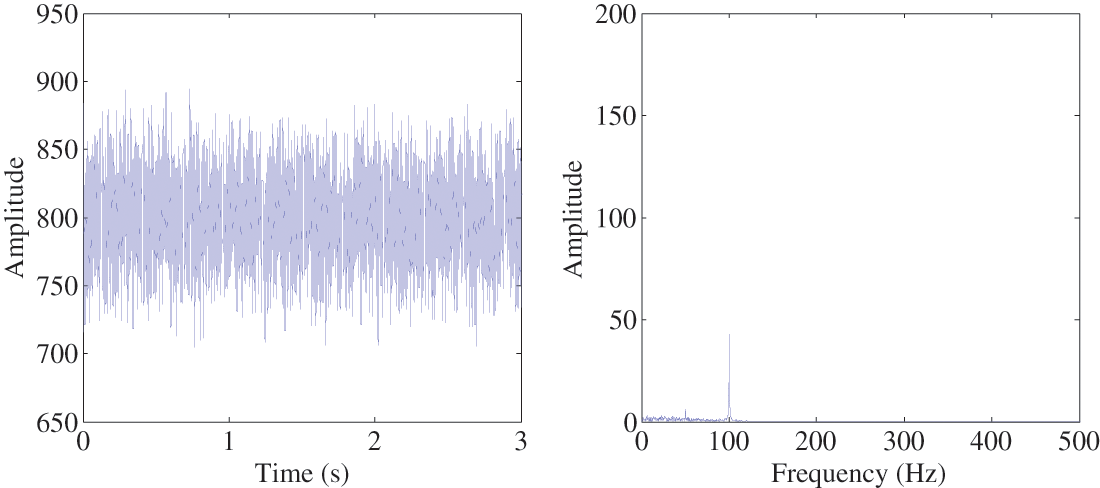
Figure 3: The optimal mode estimated by ACMD and its frequency spectrum

The envelop curve of the signal usually includes more information of fault, thus the Hilbert envelope spectrum of the estimated mode above with fp = 100 Hz and different α of 0.1, 0.01, 0.001 and 0.0001 are obtained, as shown in Fig. 4. Unfortunately, the 4f0 and 6f0 components of the original signal cannot be recognized in any Hilbert envelope spectrum.

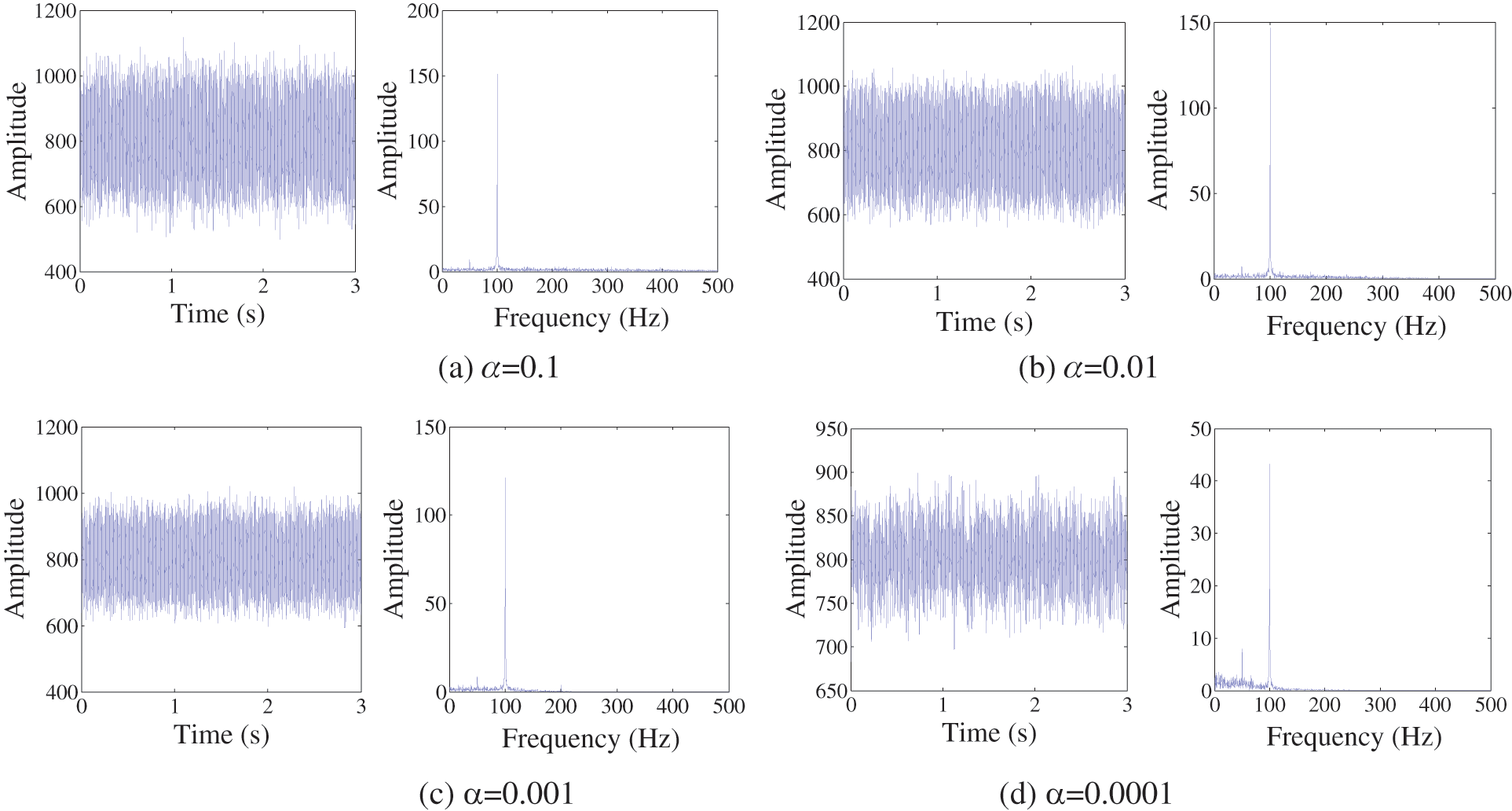
Figure 4: Hilbert envelope spectrum of the estimated modes by ACMD under different α

It can be concluded that Hilbert envelope is not suitable for such original signal, so a better envelope method is requested. In this paper, an alternative demodulation method called DEO3S is used to envelope the estimated modes of ACMD. Compared with the traditional Hilbert demodulation method, DEO3S has a high sensitivity to the weak fault feature, which shows the potential ability in the diagnosis of rotating machines. The DEO3S envelope spectrums of the estimated modes of ACMD with different α values are shown in Fig. 5.

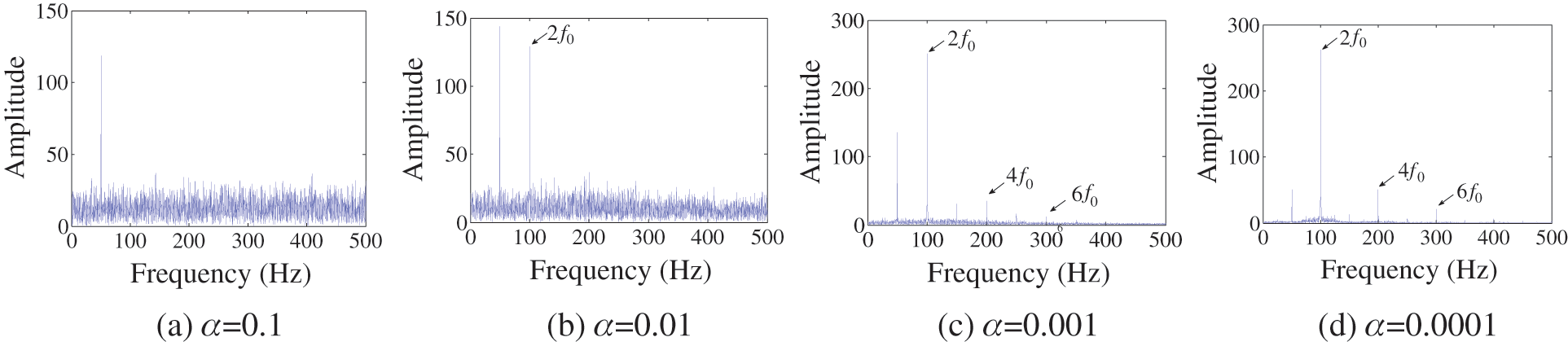
Figure 5: Comparison of DEO3S envelope spectrum of the estimated mode by ACMD with different α

It can be seen from Fig. 5a that the characteristic components are submerged in the envelope spectrum with α = 0.1. When α = 0.01, only the f0 and 2f0 components can be identified, as shown in Fig. 5b. Although the characteristic components can be found when α = 0.001, as shown in Fig. 5c, they obviously suffer from the disturbing frequencies of 150 Hz and 250 Hz which have the similar amplitudes. The spectrum in Fig. 5d shows the best envelope effect because its characteristic frequency components are very prominent and the influence of noise is suppressed. Thus, 0.0001 would be the optimal value of the weighting coefficient α. The optimal parameters are fp = 100 Hz, α = 0.0001.

The above analysis shows that the weighting coefficient α will influent the optimal mode obtained by ACMD, so as to influent the performance of DEO3S envelop spectrum indirectly. However, when using the proposed method to deal with the real signal of a generator, it is unlikely to analyze every DEO3S envelop spectrum under different α. Thus, it is significant to select a proper index to evaluate the DEO3S envelop signal under different α.

In order to achieve the best decomposition effect, the permutation entropy (PE) is introduced to quantify the effect of the signal decomposition. PE is able to indicate the confusion degree of the original signal. In theory, the higher the degree of the signal confusion is, the greater the possibility of failure will be. Therefore, the distribution of the spectral lines is expected to be clearer, which means a lower complexity of the series [33]. The detailed calculation of PE can be learned in reference [30]. In this paper, DEO3S is applied to calculate the envelope for the estimated mode by ACMD. Thus, the PE values of the DEO3S envelope under different weight factor values of α are calculated, and the result is shown in Fig. 6. As illustrated in Fig. 6, the PE value when α = 0.0001 is the smallest. This result is the same as the previous analysis in Fig. 5, so it is proved that PE can be used to evaluate the DEO3S envelop signal under different α, further as the selection basis of the parameter of ACMD.

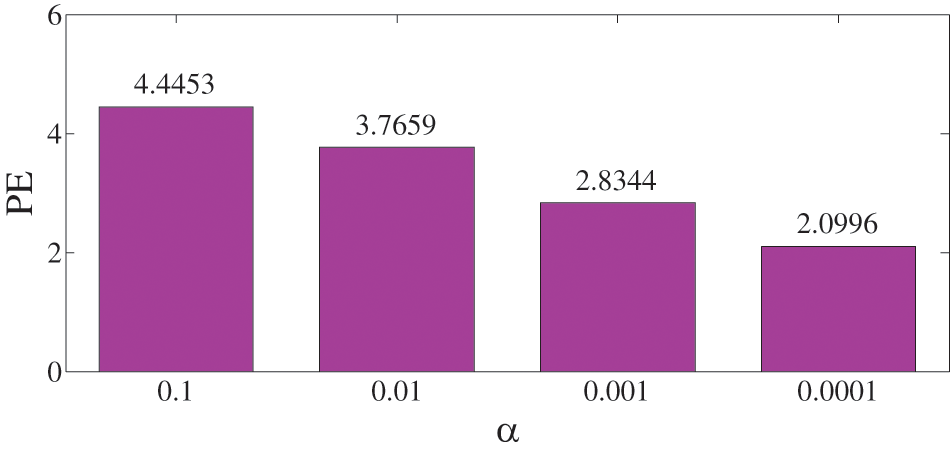
Figure 6: PE values of the envelope under different weighting coefficient

3.3 Discussion of the Demodulation Result

In this part, the result of ACMD_DEO3S method was presented to solve the problem of fault feature extraction. As a reference, EEMD was also used to evaluate the mode and the envelop. The comparison with different methods is shown in Fig. 7.

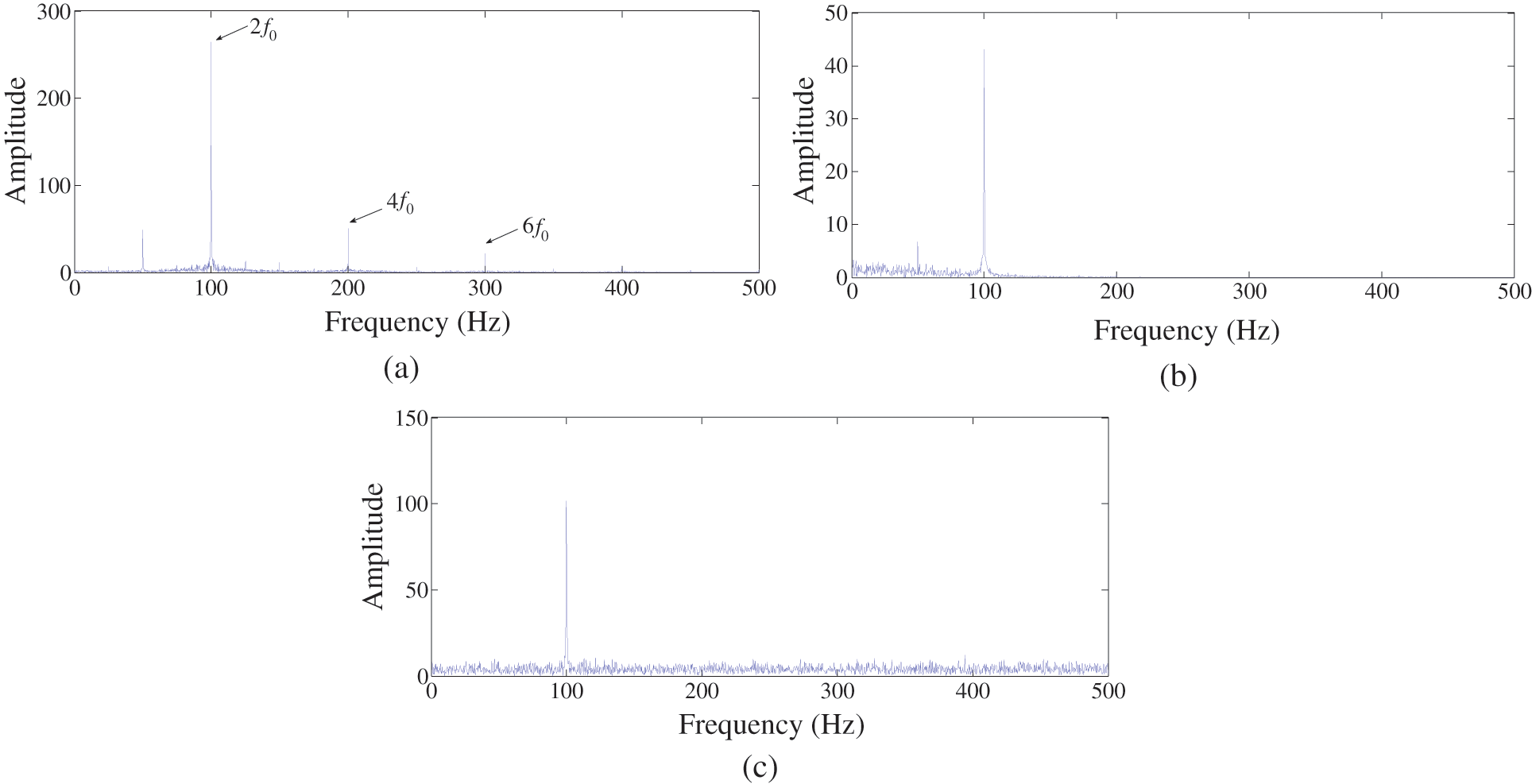
Figure 7: Comparison of the proposed method and the traditional methods: (a) ACMD_DEO3S envelop spectrum; (b) ACMD_Hilbert envelop spectrum; (c) EEMD_DEO3S envelop spectrum

It can be seen in Fig. 7a that the characteristic frequencies are extracted with clear spectrum lines by the ACMD_DEO3S method. Compared with the traditional decomposition and demodulation methods, ACMD_DEO3S has a higher sensitivity to the weak signal which shows the potential application in fault diagnosis with vibration signal. In Fig. 7b, Eigenfrequency components of 4f, 6f cannot be found based on ACMD_Hilbert envelop spectrum. In Fig. 7c, based on the EEMD_DEO3S method, only 2f can be found obviously. Eigenfrequency components of 4f, 6f are submerged in noise. Even the fundamental frequency of 50 Hz is also not extracted. It can be discovered that the EEMD method cannot realize the detection of the feature frequencies. In summary, the study of simulating signal provides an idea of detecting weak impact.

4  Experimental Verification

4.1 Acquisition of the Vibration Signal

In order to verify the effectiveness of the proposed method, the experiment on MJF-30-6 prototype generator was conducted in this section. The appearance of the experimental equipment and the schematic diagram of stator and rotor slots are shown in Figs. 8a and 8b. The CD-21C speed sensor with the sensitivity of 30 mV/mm/s was installed in the vertical direction on the stator outer circular surface to acquire the vibration signal, as illustrated in Fig. 8c. The sampling frequency was set to 5,000 Hz, while the number of samples was 32,768. The main parameters of the generator are listed in Table 2.

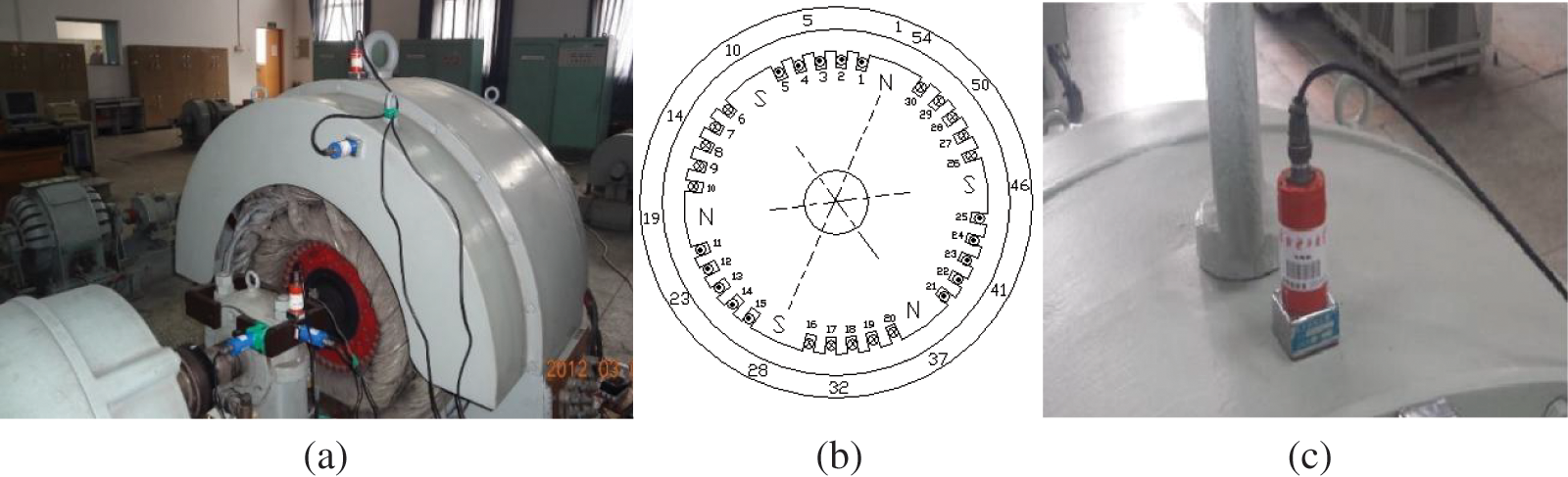
Figure 8: Experimental equipment, (a) appearance of the experimental equipment; (b) schematic diagram of stator and rotor slots; (c) installation method of speed sensor

4.2 Signal Processing and Result Analysis

The original vibration signal of the stator and its frequency spectrum under normal condition and the stator short circuit fault are shown in Figs. 9a and 9b, respectively. According to reference [1], the normal signal of the stator should contain only the 2f0 component in theory. However, the real condition is so complicated that the obtained signal includes many noisy components. Meanwhile, the fault frequencies of 4f0 and 6f0 are not easy to obtain from the spectrum, as shown in Fig. 9b. Although the amplitude of the normal signal is smaller than that of the fault signal, the characteristic fault frequencies and the noise components cannot be distinguished.

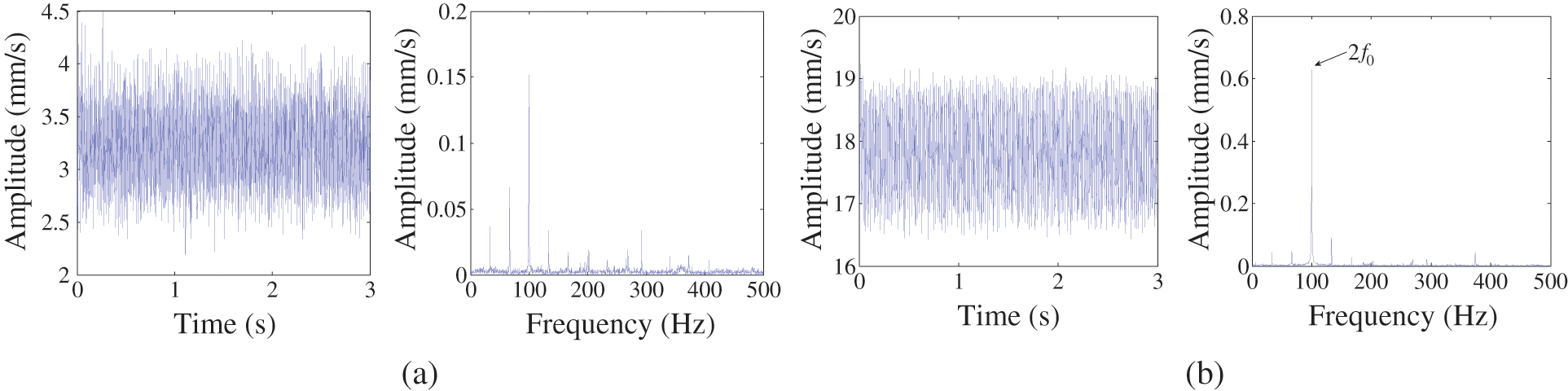
Figure 9: The original vibration signal of the stator fault and its frequency spectrum

Next, the proposed ACMD_DEO3S method was applied to the fault signal. Since the peak frequency of 100 Hz can be recognized from the frequency spectrum in Fig. 9, 100 Hz was selected to be the instantaneous frequency of ACMD. Afterward, PE values of the estimated mode envelop under different weight factor values of α were calculated. To enhance the accuracy, the section is expanded to 0.000001~0.1, and the results are shown in Fig. 10.

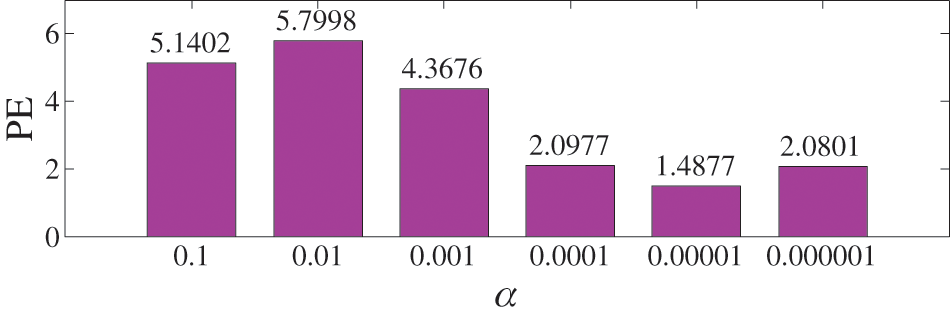
Figure 10: PE values of the estimated mode envelop under different α

It can be seen that the PE value is the smallest when α is set to 0.00001. Thus, 0.00001 is selected to be the optimal value of the weight factor. Then, the optimal mode and its frequency spectrum can be obtained, as indicated in Fig. 11.

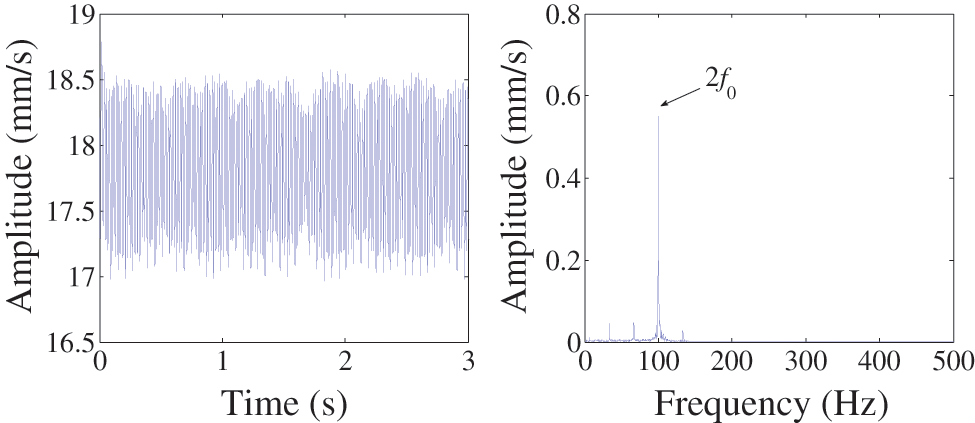
Figure 11: Optimal mode estimated by ACMD and its frequency spectrum

Although the 4f0 and 6f0 components are not found in the spectrum of the optimal mode, these components can be found in DEO3S envelop spectrum, as shown in Fig. 12a.

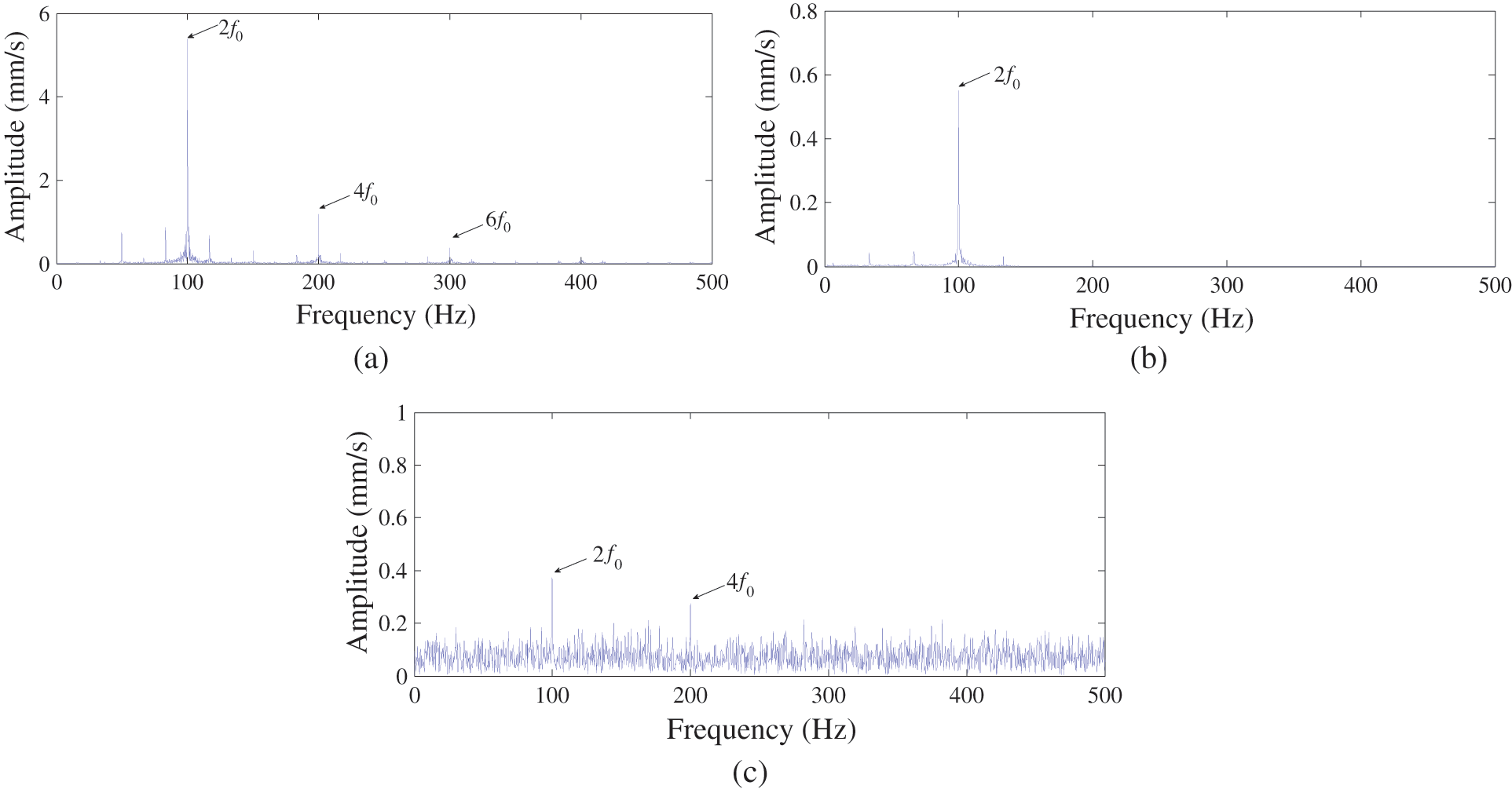
Figure 12: Comparison of ACMD_DEO3S spectrum and other methods, (a) ACMD_DEO3S result in this paper (b) Traditional Hilbert envelop based on ACMD_Hilbert (c) EEMD_DEO3S method result

In order to verify the priority of the proposed method, alternative methods were conducted. However, it can be suggested from Fig. 12b that the traditional Hilbert envelop is able to extract the 2f0 component, while the 4f0 and 6f0 components cannot not be extracted. EEMD is a good adaptive decomposition method which is widely used in the field of fault diagnosis. However, the result of EEMD_DEO3S in Fig. 12c shows that the 4f0 and 6f0 components are hard to be identified. Therefore, the proposed method in this paper is better than others aiming in the feature extraction under the stator inter-turn short circuit fault.

The amplitudes of the characteristic components in the fault signal are shown in Table 3, which can be used to quantify the effect of the fault feature extraction.

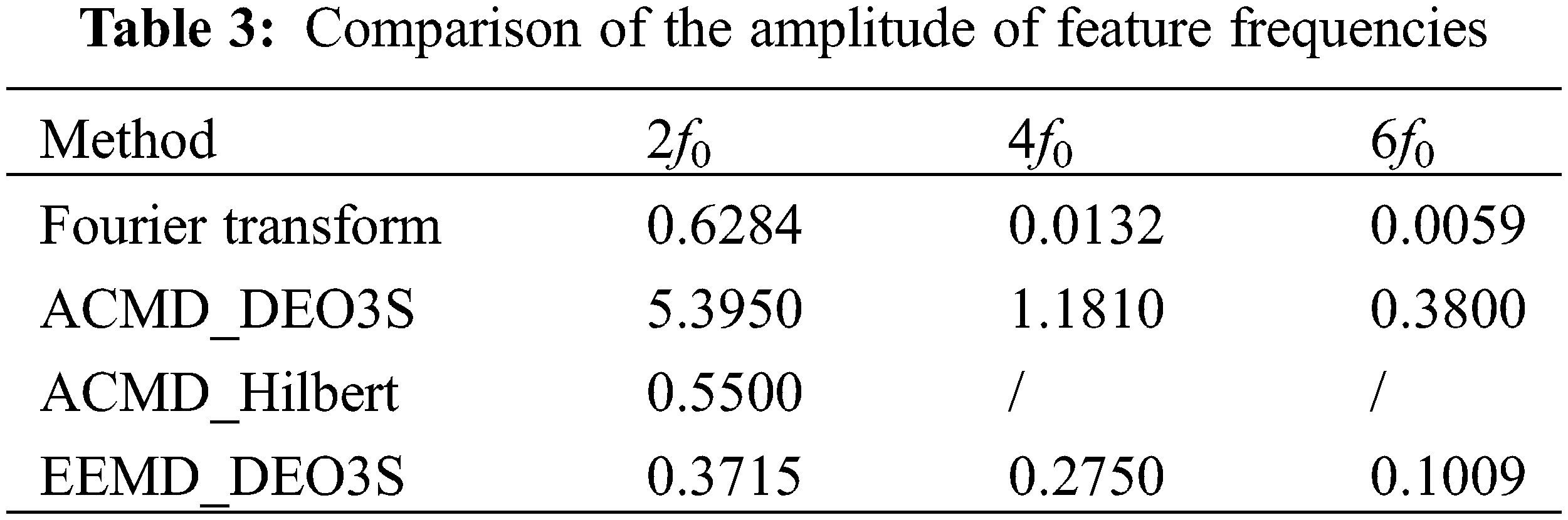
It can be seen from Table 3 that the proposed ACMD_DEO3S method enhances the amplitude of 2f0, 4f0 and 6f0 components by 8.6, 8.6 and 64.4 times, respectively. This result shows that the method of ACMD_DEO3S is effective to enhance the key vibration features of the stator short circuit fault according to the quantitative analysis on the enhancement times of amplitude. After the conduction of the proposed method, the comparison of the normal and the stator short circuit fault signal are shown in Fig. 13.

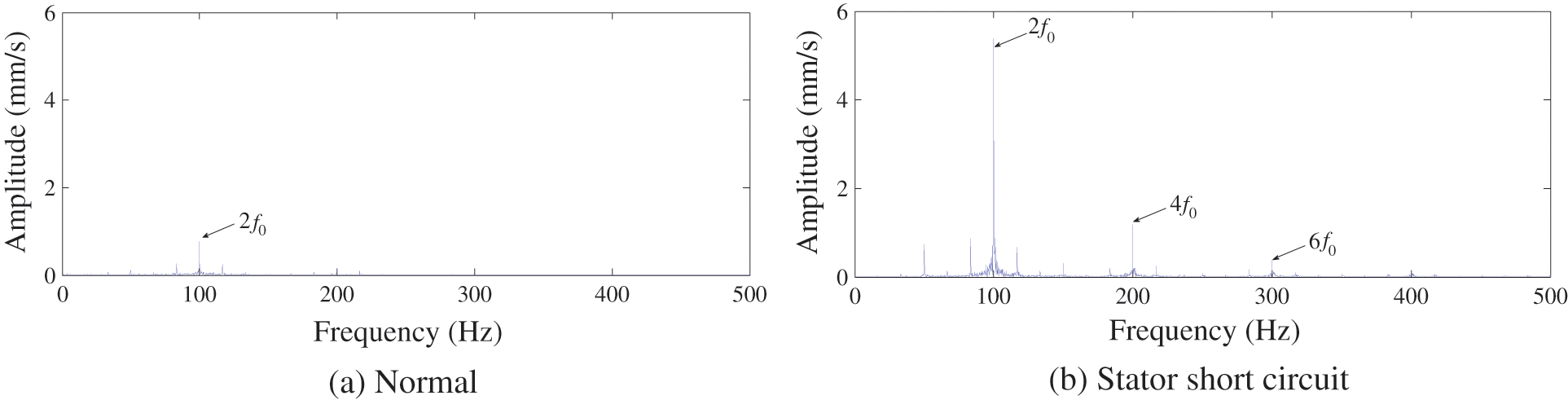
Figure 13: Comparison of the normal signal result and stator short circuit result

Although the noise has some influence on the result, we can easily recognize that the 2f0 component of the normal signal is the prominent one. The result is consistent with the description in reference [1]. This is an important reference for the fault diagnosis of the generator. The comparison of the amplitude values between the normal and the faulty signals are shown in Table 4. It can be seen that the 2f0, 4f0 and 6f0 components in the faulty case are respectively increased by 7.0, 7.5 and 16.4 times, respectively, with respect to the normal condition. This result shows that the stator inter-turn short circuit fault will significantly intensify the vibration amplitudes of the characteristic frequencies, which can be used as a faulty feature. reference [1] also pointed out that f0, 2f0, 3f0 and 4f0 will enhance when rotor inter-turn short circuit occurs. Some components are coincident, so it needs comprehensive research and judgment to diagnose. For example, 3f0 and 6f0 can be the basis. Besides, it can be concluded that the proposed method of ACMD_DEO3S is able to improve the fault diagnosis by comparing with other methods according to the data in Tables 3 and 4.

5  Conclusion

In this paper, a new approach to detect the stator inter-turn short circuit fault in synchronous generators called ACMD_DEO3S is proposed. The method uses ACMD to decompose the original vibration signal and employs DEO3S to obtain the envelop spectrum of the optimal mode. The proposed method can extract the weak characteristic in noise of the simulating signal, and the characteristic of the real signal in a generator is also extremely impact by noise. Thus, the research of the simulating signal which contains weak impact in noise shows the latent capacity of the method to realize fault diagnosis of generator. Moreover, the experiment on the MJF-30-6 prototype generator validates the effectiveness of the method. The main conclusions of the results are as follows:

(1)   The vibration signal of the stator processed by the proposed method is useful to diagnose the stator inter-turn short circuit fault based on the characteristics component variations.

(2)   Comparing with the proposed ACMD_DEO3S model, the result based on EEMD_DEO3S is almost illegible and the result based on ACMD_Hilbert lacks the information of 4f0 and 6f0, which highlights a more superior ability of the proposed ACMD_DEO3S method to extract the characteristic frequencies of 2f0, 4f0 and 6f0.

(3)   The quantitative analysis shows that the amplitudes of the characteristic frequencies will be increased by significant multiples after processing. It can be a support for the theoretical analysis that 2f0, 4f0 and 6f0 would raise when the stator short circuit fault occurs.

In our next step, we would propose more approaches to diagnose other types of generator faults such as rotor inter-turn short circuit, air-gap eccentricity, and even the mixed fault based on vibrations.

Funding Statement: This work is supported in part by the National Natural Science Foundation of China (52177042), Natural Science Foundation of Hebei Province (E2020502031), the Fundamental Research Funds for the Central Universities (2017MS151), Suzhou Social Developing Innovation Project of Science and Technology (SS202134), and the Top Youth Talent Support Program of Hebei Province ([2018]-27).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. He, Y. L. (2012). Analysis on mechanical and electrical characteristics of generator under air gap eccentricity and winding short circuit composite faults (Ph.D. Thesis). North China Electric Power University, China. [Google Scholar]

2. Wei, S. R., Wu, R., Fu, Y., Wang, J., Zhou, B. et al. (2019). Inter-turn short circuit fault identification of stator winding for offshore DFIG based on positive sequence impedance angel. Automation of Electric Power Systems, 43(12), 165–171. [Google Scholar]

3. Bensaoucha, S., Brik, Y., Moreau, S., Bessedik, S. A., Ameur, A. (2021). Induction machine stator short-circuit fault detection using support vector machine. COMPEL–The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 40(3), 373–389. https://doi.org/10.1108/COMPEL-06-2020-0208 [Google Scholar] [CrossRef]

4. Zorig, A., Kia, S. H., Chouder, A., Rabhi, A. (2022). A comparative study for stator winding inter-turn short-circuit fault detection based on harmonic analysis of induction machine signatures. Mathematics and Computers in Simulation, 196(5), 273–288. https://doi.org/10.1016/j.matcom.2022.01.019 [Google Scholar] [CrossRef]

5. Zaparoli, I. O., Rabelo Baccarini, L. M., Lamim Filho, P. C. M., Batista, F. B. (2020). Transient envelope current analysis for inter-turn short-circuit detection in induction motor stator. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42(2), 1–12. [Google Scholar]

6. Bouzid, M. B. K., Champenois, G. (2012). New expressions of symmetrical components of the induction motor under stator faults. Institute of Electrical and Electronics Engineers Transactions on Industrial Electronics, 60(9), 4093–4102. [Google Scholar]

7. Ma, H. Z., Jiang, M. Y., Li, C. Y., Chen, Z. F., Tang, X. Z. (2021). New fault diagnosis method for stator winding inter turn short circuit in synchronous condensers. Electric Machines and Control, 25(9), 35–45. https://doi.org/10.15938/j.emc.2021.09.005 [Google Scholar] [CrossRef]

8. Wang, D. Y., Gu, H. G., Wei, S. R., Wu, R., Fu, Y. (2020). Diagnosis of inter-turn short-circuit fault in stator windings of DFIG based on mechanical and electrical signal fusion. Automation of Electric Power System, 44(9), 171–178. [Google Scholar]

9. Hegde, V., Rao, M. G. S. (2017). Detection of stator winding inter-turn short circuit fault in induction motor using vibration signals by MEMS accelerometer. Electric Power Components and Systems, 45(13), 1463–1473. https://doi.org/10.1080/15325008.2017.1358777 [Google Scholar] [CrossRef]

10. Liang, H., Chen, Y., Liang, S., Wang, C. (2018). Fault detection of stator inter-turn short-circuit in PMSM on stator current and vibration signal. Applied Sciences, 8(9), 1677. https://doi.org/10.3390/app8091677 [Google Scholar] [CrossRef]

11. Sun, Y., Li, S., Wang, X. (2021). Bearing fault diagnosis based on EMD and improved Chebyshev distance in SDP image. Measurement, 176(17), 109100. https://doi.org/10.1016/j.measurement.2021.109100 [Google Scholar] [CrossRef]

12. Cicone, A., Liu, J., Zhou, H. (2016). Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Applied and Computational Harmonic Analysis, 41(2), 384–411. https://doi.org/10.1016/j.acha.2016.03.001 [Google Scholar] [CrossRef]

13. Meyer, A. (2022). Vibration fault diagnosis in wind turbines based on automated feature learning. Energies, 15(4), 1514. https://doi.org/10.3390/en15041514 [Google Scholar] [CrossRef]

14. Attoui, I., Oudjani, B., Boutasseta, N., Fergani, N., Bouakkaz, M. S. et al. (2020). Novel predictive features using a wrapper model for rolling bearing fault diagnosis based on vibration signal analysis. International Journal of Advanced Manufacturing Technology, 106(7), 3409–3435. https://doi.org/10.1007/s00170-019-04729-4 [Google Scholar] [CrossRef]

15. Chen, G., Wang, Z. (2012). A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components. Mechanical Systems and Signal Processing, 28(3), 258–279. https://doi.org/10.1016/j.ymssp.2011.02.002 [Google Scholar] [CrossRef]

16. Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H. et al. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454(1971), 903–995. https://doi.org/10.1098/rspa.1998.0193 [Google Scholar] [CrossRef]

17. Zhang, Y. F. (2021). Prediction of bank stock price based on PCA-EMD-LSTM model (Master Thesis). Lanzhou University, China. [Google Scholar]

18. Zhang, Y. Q., Chen, Q. Z., Jiang, W. J., Liu, X. F., Shen, L. et al. (2021). Photovoltaic power prediction model based on EMD-PCA-LSTM. Acta Energiae Solaris Sinica, 42(9), 62–69. [Google Scholar]

19. Wu, Z., Huang, N. E. (2004). A study of the characteristics of white noise using the empirical mode decomposition method. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 460(2046), 1597–1611. https://doi.org/10.1098/rspa.2003.1221 [Google Scholar] [CrossRef]

20. Chen, Y., Dong, Z., Wang, Y., Su, J., Han, Z. et al. (2021). Short-term wind speed predicting framework based on EEMD-GA-LSTM method under large scaled wind history. Energy Conversion and Management, 227(4), 113559. https://doi.org/10.1016/j.enconman.2020.113559 [Google Scholar] [CrossRef]

21. Zou, P., Hou, B., Jiang, L., Zhang, Z. (2020). Bearing fault diagnosis method based on EEMD and LSTM. International Journal of Computers Communications & Control, 15(1), 1–14. [Google Scholar]

22. Chen, S., Dong, X., Peng, Z., Zhang, W., Meng, G. (2017). Nonlinear chirp mode decomposition: A variational method. Institute of Electrical and Electronics Engineers Transactions on Signal Processing, 65(22), 6024–6037. https://doi.org/10.1109/TSP.2017.2731300 [Google Scholar] [CrossRef]

23. Chen, S., Yang, Y., Peng, Z., Wang, S., Zhang, W. et al. (2019). Detection of rub-impact fault for rotor-stator systems: A novel method based on adaptive chirp mode decomposition. Journal of Sound and Vibration, 440(26), 83–99. https://doi.org/10.1016/j.jsv.2018.10.010 [Google Scholar] [CrossRef]

24. Wang, X., Tang, G., Yan, X., He, Y., Zhang, X. et al. (2021). Fault diagnosis of wind turbine bearing based on optimized adaptive chirp mode decomposition. Institute of Electrical and Electronics Engineers Sensors Journal, 21(12), 13649–13666. https://doi.org/10.1109/JSEN.2021.3071164 [Google Scholar] [CrossRef]

25. Feldman, M. (2011). Hilbert transform in vibration analysis. Mechanical Systems and Signal Processing, 25(3), 735–802. https://doi.org/10.1016/j.ymssp.2010.07.018 [Google Scholar] [CrossRef]

26. Potamianos, A., Maragos, P. (1994). A comparison of the energy operator and the Hilbert transform approach to signal and speech demodulation. Signal Processing, 37(1), 95–120. https://doi.org/10.1016/0165-1684(94)90169-4 [Google Scholar] [CrossRef]

27. Xu, Y. B., Cai, Z. Y. (2017). Application of demodulation energy operator of symmetrical differencing and empirical wavelet transform in bearing fault diagnosis. Journal of Electronic Measurement and Instrumentation, 31(8), 1247–1256. https://doi.org/10.13382/j.jemi.2017.08.013 [Google Scholar] [CrossRef]

28. Wu, Y. G., Li, J. (2018). Bearing fault diagnosis for booster fan with differential-based empirical mode decomposition. Science & Technology of Baotou Steel, 44(4), 68–71. [Google Scholar]

29. Shen, M. J., Gao, H. Y., Zhang, S. J., Yang, J. W., Wu, R. (2021). Fault diagnosis of rolling bearings based on CEEMD and demodulation energy operator of symmetrical differencing. Light Industry Machinery, 39(4), 62–67. [Google Scholar]

30. Bandt, C., Pompe, B. (2002). Permutation entropy: A natural complexity measure for time series. Physical Review Letters, 88(17), 174102. https://doi.org/10.1103/PhysRevLett.88.174102 [Google Scholar] [PubMed] [CrossRef]

31. Zhang, X., Liang, Y., Zhou, J. (2015). A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement, 69, 164–179. https://doi.org/10.1016/j.measurement.2015.03.017 [Google Scholar] [CrossRef]

32. Liu, P., Lin, Z., Zhang, M., Gu, Y. (2021). Fault diagnosis of rolling bearing based on permutation entropy optimized maximum correlation kurtosis deconvolution. IOP Conference Series: Materials Science and Engineering, 1043, 022029. [Google Scholar]

33. He, Y. L., Sun, K., Wang, T., Wang, X., Tang, G. (2021). Fault diagnosis of generator interturn short circuit fault based on variational mode decomposition and refined composite multiscale dispersion entropy. Electric Power Automation Equipment, 41(3), 164–172. [Google Scholar]