 Open Access
Open Access
ARTICLE
Performance Evaluation of Damaged T-Beam Bridges with External Prestressing Reinforcement Based on Natural Frequencies
1 Henan Zhonggong Design & Research Group Co., Ltd., Zhengzhou, 450000, China
2 School of Civil Engineering, Zhengzhou University, Zhengzhou, 450001, China
* Corresponding Author: Panxu Sun. Email:
(This article belongs to the Special Issue: Advanced Data Mining in Bridge Structural Health Monitoring)
Structural Durability & Health Monitoring 2025, 19(2), 399-415. https://doi.org/10.32604/sdhm.2024.056250
Received 17 July 2024; Accepted 29 September 2024; Issue published 15 January 2025
Abstract
As an evaluation index, the natural frequency has the advantages of easy acquisition and quantitative evaluation. In this paper, the natural frequency is used to evaluate the performance of external cable reinforced bridges. Numerical examples show that compared with the natural frequencies of first-order modes, the natural frequencies of higher-order modes are more sensitive and can reflect the damage situation and external cable reinforcement effect of T-beam bridges. For damaged bridges, as the damage to the T-beam increases, the natural frequency value of the bridge gradually decreases. When the degree of local damage to the beam reaches 60%, the amplitude of natural frequency change exceeds 10% for the first time. The natural frequencies of the first-order vibration mode and higher-order vibration mode can be selected as indexes for different degrees of the damaged T-beam bridges. For damaged bridges reinforced with external cables, the traditional natural frequency of the first-order vibration mode cannot be used as the index, which is insensitive to changes in prestress of the external cable. Some natural frequencies of higher-order vibration modes can be selected as indexes, which can reflect the reinforcement effect of externally prestressed damaged T-beam bridges, and its numerical value increases with the increase of external prestressed cable force.Keywords
Nomenclature
| FRP | Fiber-reinforced polymer |
| FE | Finite element |
| ω | Natural frequency of first-order vibration mode (unit: rad/s) |
| f | Natural frequency of first-order vibration mode (unit: Hz) |
| E | Elastic modulus |
| | Mass per unit length |
| I | Moments of inertia |
| N | Equivalent horizontal prestress |
| l0 | Actual length of the external cable |
| θ | Angle of the segmented line external cable |
With the damage of in-service bridges, many bridges have been reinforced to ensure structural safey [1–3]. Some reinforcement schemes have been adopted, such as fiber polymer reinforcement [4], steel plate reinforcement [5], beam section enlargement [6], shape memory alloy reinforced bars [7], etc. After reinforcement, the performance of the damaged bridge can be improved and the service life is extended.
Due to weak lateral stiffness, some in-service T-beam bridges have developed diseases, such as beam cracking and large vibration displacement. Hag-Elsafi et al. [8] reinforced a T-beam bridge with bonded fiber-reinforced polymer (FRP) laminates and conducted instrument and load tests on the bridge to evaluate the effectiveness of the FRP reinforcement system. Gao et al. [9] introduced a new active reinforcement method for bridges-prestressed steel wire rope modified polyurethane cement, which can effectively reduce the occurrence of cracks and improve the bending resistance. Aryan et al. [10] used FRP composite materials to reinforce T-beams. The reinforcement technology increased the shear bearing capacity of ordinary beams and high-strength beams by 37% and 20%, respectively, and improved the ductility of the beams before failure. Chen [11] proposed a bonded steel plate reinforcement method and finally conducted static load tests to evaluate the effectiveness of bridge reinforcement. Wu et al. [12] used three external T-beams for reinforcement and conducted failure tests on the reinforced T-beams. The cracking load of T-beams has been improved, and the development speed of cracks has been slowed down. Huang et al. [13] proposed a method of widening and strengthening longitudinal and transverse beams. After bridge reinforcement, the load distribution factor of the side beams decreased by 63.92%. The load distribution factor at the fulcrum increased by 30% after reinforcement. Farouk et al. [14] studied the bending beam reinforcement of an inverted T-shaped concrete bridge, and the bearing capacity increased by 44.0%. Shi et al. [15] used steel wire rope as a reinforcement material for the negative bending moment area of T-beams and evaluated the reinforcement effect by comparing the flexural bearing capacity using the layered method. The above research indicated that in terms of statistics, some common reinforcement schemes could effectively improve the bearing capacity of in-service T-beam bridges.
The dynamic performance of bridges is equally important to the static performance, which is directly related to the relative stiffness of the bridges. Some dynamic characteristic indexes are adopted to evaluate the dynamic performance, such as natural frequency, modal curvature, damping ratio, etc. [16]. Compared with some common indexes, the natural frequency has the advantages of easy acquisition, intuitive reflection of structural health status, quantitative evaluation, and real-time monitoring, which can evaluate the performance of T-beam bridges [17,18]. Abedin et al. [19] demonstrated that the natural frequency of bridges undergoes significant changes after fracture, and the degree of change can be effectively detected through bridge frequency monitoring. Li et al. [20] applied this indicator to damage identification of T-beam bridges, analyzed the changes in the first-order natural frequency. Wei et al. [21] validated that using the natural frequency vector method can accurately identify the damage location, but it requires a large amount of computation. Jiang et al. [22] used the natural frequency to evaluate the prestressed carbon fiber plate reinforcement effect. When there is significant damage or overall reinforcement to the in-service bridges, the natural frequency of the first-order vibration mode changes significantly, which can effectively evaluate the dynamic performance. For locally reinforced bridges, the further investigation is needed to determine the effectiveness of using only the natural frequency of the first-order vibration mode.
Compared with other reinforcement methods, the external prestressing reinforcement method, as one of the commonly used methods for strengthening old bridges, has the advantages of easy construction, easy detection, strong applicability, and improved shear resistance [23–26]. Due to these significant advantages, the external prestressing reinforcement method is widely used in the reinforcement of damaged bridges. With the increase of prestressing force, the natural frequencies of prestressed beams have an increasing trend [27]. In this paper, the natural frequencies are used to evaluate the performance of damaged T-beam bridges with external prestressing reinforcement. Compared with the traditional natural frequency of the first-order vibration mode, the changes in some natural frequencies of higher-order vibration modes are more significant for damaged T-beam bridges. The natural frequencies can be selected as indexes for different degrees of the damaged T-beam bridges. Besides, the traditional natural frequency of the first-order vibration mode cannot be used as the index of locally reinforced T-beam bridges, which is insensitive to changes in the prestress of the external cable. Some natural frequencies of higher-order vibration modes can be selected as indexes, which can reflect the reinforcement effect of externally prestressed damaged T-beam bridges, and its numerical value increases with the increase of external prestressed cable force. In Section 2, based on the natural vibration characteristics of external prestressed cables with segmented lines, analyze the natural frequency of T-beams reinforced with external prestressed cables under different prestress levels. In Section 3, the performance of damaged T-beam bridges and externally reinforced T-beam bridges were analyzed using first-order and higher-order natural frequencies, respectively. Section 4 summarizes the relationship between natural frequency and damage and reinforcement performance of T-beam bridges based on engineering examples.
2 Analysis of the Natural Vibration Characteristics of T-Beams Reinforced with External Prestressed Cables with Segmented Lines
2.1 The Natural Frequency of the External Prestressed Cable with a Segmented Line
The external prestressed cable is in a segmented line shape, with a calculated length of 30 m. The external prestressed cable adopts finished bundle OVM GJ15-3 is made of 1860-grade steel stranded wire. The cross-sectional area is 420 mm2. According to the product manual, the yielding strength of the external prestressed cable is 1860 MPa and the braking force is 782 kN. The dimension is shown in Fig. 1. ANSYS software is used for finite element (FE) analysis [28]. Using LINK8 elements in ANSYS software to simulate external prestressed cables, the application of prestressing is achieved by changing the numerical value of initial strain in the real constant. The FE model of the external prestressed cable is shown in Fig. 2. The steel anchor blocks are installed at the two ends of the external cable, and the two ends of the external cable are fixed. Four steering gears are installed at the segmented points of the external cable, and the degrees of freedom in the Z-axis direction are constrained. The simulation method of limiting its Z-direction displacement at the corner and forming the corner through height difference is adopted. After convergence verification, the element size has reached the convergence effect at 0.2 m, so the element length is taken as 0.2 m when dividing the grid. The elastic modulus E is taken as 1.95 × 1011 Pa and the unit mass is 4.7 kg/m.

Figure 1: Dimension of the external prestressed cable (unit: cm)

Figure 2: FE model of the external prestressed cable
By FE simulation, the first 5 natural frequencies of the external prestressed cable are obtained. The first 5 natural frequencies refer to the first 5 minimum non-zero natural frequencies of the prestressed cable during the vibration process, as shown in Table 1. With the increase of external prestress, the natural frequencies gradually increase.

2.2 The Natural Vibration Frequency of T-Beams Reinforced with External Prestressed Cables of a Segmented Line Type
The external prestressed cables are arranged in a segmented line shape, with both ends fixed at the T-beam bridge. The cross-section of the T-beam is shown in Fig. 3, and the layout diagram of the T-beam with external prestressed cable is shown in Fig. 4. The elastic modulus of reinforced concrete material is 3.45 × 1010 Pa, with a density of 2500 kg/m3 for the T-beam. The external prestressed cable is the same as the one in Section 2.1.

Figure 3: Cross section of the T-beam (unit: mm)

Figure 4: Layout diagram of external prestressed cables (unit: cm)
The boundary condition of a continuous T-beam in the transverse vibration plane is a fixed connection. Rayleigh’s method is based on the conservation of energy, ignoring the influence of damping [29,30]. The sum of strain energy and kinetic energy remains constant.
The dynamic displacement of the beam is
The velocity of the beam is
where
The strain energy of free vibration response is [31]
where I is moments of inertia for the beam.
The kinetic energy of the free vibration of a beam is [32]
According to the conservation of energy, it can be concluded that
where
Using the virtual work method for solving, the system can be decomposed into two statically indeterminate structures, namely
By taking the derivative of Eq. (6) and substituting it into Eq. (5), the natural frequency of the first-order vibration mode for the fixed end beam can be obtained as
where EI is the equivalent material stiffness.
For the simplified theoretical calculation of the natural frequency of prestressed equal-section T beams, the prestressed beam can be regarded as an isotropic material. The equivalent stiffness method is used to modify the calculated stiffness of the beam, and the projection method is used. The horizontal equivalent stiffness can be expressed as
where N is the external axial compressive force [33],
The equivalent calculated span can be expressed as
where
The first-order natural frequency of the T-beam reinforced with external prestressed cables of the segmented line type can be calculated using Eq. (7).
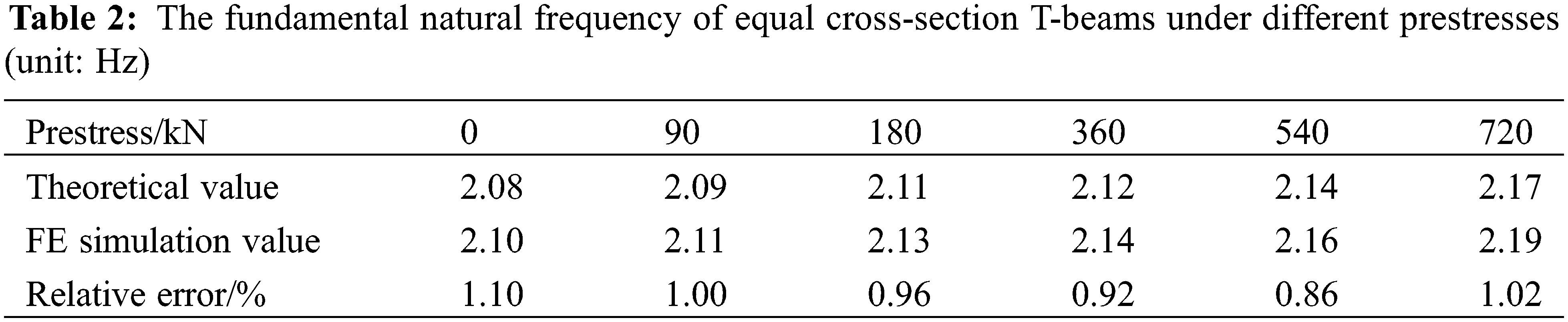
For T-beams reinforced with external prestressed cables, a prestressed force of 90 kN is applied to the reinforcement, and the natural frequency is simulated and analyzed. On this basis, adjust the size of the prestressing force, observe the influence of natural frequencies, and apply prestressing forces of 180, 360, 540 and 720 kN, respectively.
In ANSYS software, SOLID45 elements are used to simulate reinforced concrete T-beams, and LINK8 elements are used to simulate external prestressed cables. The two ends of the T-beam are fixed. The FE simulation results are shown in Table 2. As shown in Table 2, with the increase of prestress, the natural frequency of the first mode of vibration of a constant cross-section T-beam gradually increases. The maximum relative error between the theoretical calculation results and the numerical simulation results is 1.10%, which can prove the correctness of the FE method.
3 Performance Evaluation of Damaged T-Beam Bridges Strengthened with External Prestressing based on Natural Frequency
3.1 The Natural Frequency of Damaged T-Beam Bridges
The natural frequency can be used as one of the indicators to evaluate the damage to bridges. When there is a damaged area in the bridge, the decrease in local stiffness can cause local softening of the structure, resulting in a decrease in the stiffness of the entire bridge and a decrease in its natural frequency, thereby affecting the vibration characteristics. Therefore, by comparing the natural frequency changes before and after damage, the health status of the bridge can be preliminarily evaluated.
The T-beam bridge of the Lianhuo Expressway is an example, which is shown in Fig. 5. The bridge is a five-span continuous beam bridge. The bottom and both ends of the bridge are fixed constraints. The structure diagram of the T-beam bridge is shown in Fig. 6. The bridge has a total of 5 spans, each of which is 50 m, consisting of 5 T-beams with a length of 250 m. The elastic modulus of reinforced concrete material is 3.45 × 1010 Pa. The density is 2500 kg/m3. The elastic modulus of external prestressed cables is 1.95 × 1011 Pa. The density is 7921 kg∙m−3. Firstly, simulate a non-destructive T-beam bridge without external prestressing cables.

Figure 5: Site pictures of the T-beam bridge of Lianhuo Expressway

Figure 6: Structure diagram of the T-beam bridge
The FE model of the Lianhuo Expressway bridge uses solid elements and the calculating amount is large, which is not applied for modal analysis of engineering structures. To improve computing efficiency, the FE model of the Lianhuo Expressway bridge uses a combination of solid elements and beam elements. The T-beams use BEAM188 element. Firstly, to verify the effectiveness of beam elements, the FE models of T-beams are established based on the SOLID45 element and BEAM188 element, respectively. The natural frequencies of the first three-order vibration modes are shown in Table 3. The results show that the maximum relative error is 2.3%. The calculation results of the BEAM188 element are approximately equal to those of the SOLID45 element.

In ANSYS software, SOLID45 elements are adopted to simulate bridge piers, BEAM188 elements are used to simulate beams, and LINK8 elements are used to simulate external prestressed cables. To ensure the accuracy of the analysis results, the 5 m beam element is used to establish a T-beam bridge model, as shown in Fig. 7. The total number of elements is 26,119. The element information of the FE model is shown in Table 4.

Figure 7: FE model diagram of T-beam bridge

Compared to non-destructive bridges, the local stiffness of damaged bridges will be reduced. When a bridge is damaged or aged due to cracks, corrosion, fatigue damage, etc., such local damage can lead to a decrease in the stiffness of the structure. Overall, the crack damage has an impact on reducing stiffness in beams. Therefore, a simple simulation method is adopted and the damages within the concrete of the girders are simulated by decreasing the values of the elastic modulus. Therefore, when constructing a damaged T-beam bridge model, the elastic modulus at the beam support, one-third, and midspan should be reduced based on the non-destructive T-beam bridge model. The elastic modulus gradually decreases from the initial value E = 3.45 × 1010 Pa to 0.2 E, with each decrease of 0.2 E, to simulate damaged bridges with different damage locations and degrees. Extract the first 21 natural frequencies of non-destructive T-beam bridges and damaged T-beam bridges for comparative analysis, as shown in Fig. 8, and the relative errors are shown in Tables 5–7.

Figure 8: Changes in natural frequency of T-beam bridges with different damage locations



Taking the damaged T-beam bridge at the midspan as an example, as shown in Table 7. As the damage to the T-beam increases, the natural frequency value of the bridge gradually decreases. When the damage level at the midspan of the T-beam reaches 60%, the amplitude of the natural frequency change exceeds 10% for the first time. Taking the first natural frequency as an example, when the midspan damage of the T-beam reaches 80%, the amplitude of the first natural frequency change is less than 11%, and at this time, the high-order frequencies are all above 15%.
Compared with the damage at the midspan of the beam, there is a slight difference in the amplitude of natural frequency variation when the beam is damaged at the support and 1/3 position of the beam, but the overall pattern is consistent. For example, when the degree of damage at 1/3 of the beam reaches 60%, the amplitude of natural frequency change exceeds 10% for the first time. When the degree of damage to the beam at the support reaches 40%, the amplitude of the 21st natural frequency change exceeds 10%, but only this first mode exceeds 10% and is within a higher order range. When the degree of damage to the beam at the support reaches 60%, the amplitude of the natural frequency change mostly exceeds 10%.
The above conclusions indicate that using natural frequency as an indicator to evaluate the overall performance of T-beam bridges has an intuitive and easily obtainable advantage. However, when the local damage is less than 20%, the amplitude of natural frequency variation is less than 5%, indicating that the natural frequency is not sensitive to relatively small damage.
3.2 The Natural Frequency of Damaged T-Beam Bridges with External Prestressing Reinforcement
The T-beam bridge of the Lianhuo Expressway is reinforced with external prestressing, as shown in Fig. 9. The finished strands OVM are used for external prestressed cables GJ15-31860 grade steel stranded wire. The elastic modulus is 1.95 × 1011 Pa and the density is 7921 kg/m3. The external prestressed cables are arranged in a segmented line shape, with both ends fixed at the ends of the T-beam bridge, and one external prestressed cable is arranged on each beam.

Figure 9: T-beam bridge of Lianhuo Expressway with external prestressing reinforcement
The T-beam bridge is assumed with 80% midspan damage. The application of prestressing is achieved by setting the initial strain in the real constant, and the prestressing force increases from 90 to 540 kN, with each increase of 90 kN. The natural vibration frequency of the bridge reinforced with external cables under different prestress and midspan damage is shown in Fig. 10, and the relative error is shown in Table 8. When the prestressing force is 450 and 540 kN, the maximum increase amplitude reaches 6.07% and 7.50%, respectively. The results show that local reinforcement has a relatively great effect on the local stiffness, which can change the modal parameter of the corresponding high-order vibration mode. The natural frequency of the first-order vibration mode for the damaged T-beam bridge strengthened with external prestressing reinforcement has little change. When the prestress is large, the natural frequency of the high-order vibration mode can be used to evaluate the performance of damaged T-girder bridges with external prestressing reinforcement. Secondly, the maximum amplification occurs in the fourth mode of vibration, and when the mode reaches a certain order, the amplitude of the high-order natural frequency value of the reinforced bridge decreases.

Figure 10: Natural frequency of reinforced bridge with midspan damage under different prestressing forces

The natural frequency is an important index of performance evaluation. In this paper, the natural frequencies are used to evaluate the T-beam bridge with varying degrees of damage. Then the performance of damaged T-beam bridges with external prestressing reinforcement is analyzed. Some conclusions are as follows:
(1) As the damage to the T-beam increases, the natural frequency value of the bridge gradually decreases. When the degree of local damage to the beam reaches 60%, the amplitude of the natural frequency of first-order vibration mode change exceeds 10% for the first time. When the local damage of the T-beam is within 20%, the amplitude of the natural frequency change is less than 5%, indicating that the natural frequency is not sensitive to relatively small damage.
(2) Compared with the natural frequency of first-order vibration mode, the changes in some natural frequencies of higher-order vibration modes are more significant. Namely, the changes in local stiffness have a greater impact on the corresponding higher-order vibration modes. The natural frequencies of the first-order vibration mode and higher-order vibration mode can be selected as indexes for different degrees of the damaged T-beam bridges.
(3) The traditional natural frequency of the first-order vibration mode cannot be used as the index, which is insensitive to changes in the prestress of the external cable. When the prestressing force is greater than 450 kN, the maximum increase amplitude of the natural frequency of higher-order vibration mode is greater than 5%. Some natural frequencies of higher-order vibration modes can be selected as indexes, which can reflect the reinforcement effect of externally prestressed damaged T-beam bridges, and its numerical value increases with the increase of external prestressed cable force.
At present, only preliminary finite element analysis for the performance evaluation of damaged T-beam bridges with external prestressing reinforcement based on natural frequencies is conducted. In further work, the material parameters will be further adjusted based on on-site testing. Combining with fracture mechanics theory and local fine mesh technology, a FE model of local cracks will be constructed based on the cracking of the T-beam bridge on site. Then the effectiveness of the proposed method can be verified based on site testing data. Besides, the geometric parameters of modal deformation will be introduced, which can combine with natural frequencies to finely evaluate the performance.
Acknowledgement: None.
Funding Statement: The research has been supported by Henan Province Science and Technology Research Funding Project (No. 222102320129) and the Key Research Project of Henan Higher Education Institutions (Grant Nos. 22A560004, 22A56005).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Menghui Hao and Panxu Sun; data collection: Shanshan Zhou; analysis and interpretation of results: Yongchao Han, Zhanwei Zhu and Jiajun Fan; draft manuscript preparation: Menghui Hao, Qiang Yang and Panxu Sun. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Formisano A, Felitti M, Oliveto F, Mendicino L. The robustness of reinforced concrete tied arch bridges: a case study. Struct Concrete. 2023;24:4504–14. doi:10.1002/suco.202200374. [Google Scholar] [CrossRef]
2. Wang Y, Yu T, Zhang L, Yin L, Wu Y, Chen B. Fatigue performance of rib beam bridge slabs reinforced with polyurethane concrete based on the damage theory. Buildings. 2022;12:704. doi:10.3390/buildings12060704. [Google Scholar] [CrossRef]
3. Yuan S, Chen W, Yang F, He T, Liu G. Reinforcement analysis of rigid hangers for existing old arch bridges: a case study of ling bridge. Int J Steel Struct. 2019;19(6):1743–54. doi:10.1007/s13296-019-00242-2. [Google Scholar] [CrossRef]
4. Wu B, Zhou Y, Yin X, Lin Z, Zhou Z. The anti-arch inhibition effect of multispan continuous girder bridge strengthened with prestressed CFRP plates. Structures. 2022;35:845–55. doi:10.1016/j.istruc.2021.11.055. [Google Scholar] [CrossRef]
5. Jiang T, Wang H, Zhang Z, Qin S, Xu F. The disease and reinforcement of slanting cross shaped arch bridge. Eng Fail Anal. 2018;94:447–57. doi:10.1016/j.engfailanal.2018.08.025. [Google Scholar] [CrossRef]
6. Tan YB, He XW, Shi L, Zheng S, Zhang Z, Wang XS. Reinforcement effect evaluation on dynamic characteristics of an arch bridge based on vehicle-bridge coupled vibration analysis. Comp Model Eng Sci. 2022;131(2):1041–61. doi:10.32604/cmes.2022.018543. [Google Scholar] [CrossRef]
7. Mao JZ, Jia DG, Yang ZL, Xiang NL. Seismic performance of concrete bridge piers reinforced with hybrid shape memory alloy (SMA) and steel bars. J Earthq Tsunami. 2020;14(1):2050001. doi:10.1142/S1793431120500013. [Google Scholar] [CrossRef]
8. Hag-Elsafi O, Alampalli S, Kunin J. In-service evaluation of a reinforced concrete T-beam bridge FRP strengthening system. Compos Struct. 2004;64(2):179–88. doi:10.1016/j.compstruct.2003.08.002. [Google Scholar] [CrossRef]
9. Gao HS, Sun QS. Static field test on flexural behavior of reinforced concrete T-beam bridge strengthened with MPC-PSWR. Int J Struct Integr. 2020;11(3):515–31. doi:10.1108/IJSI-09-2019-0089. [Google Scholar] [CrossRef]
10. Aryan H, Gencturk B, Alkhrdaji T. Shear strengthening of reinforced concrete T-beams with anchored fiber-reinforced polymer composites. J Build Eng. 2023;73:106812. doi:10.1016/j.jobe.2023.106812. [Google Scholar] [CrossRef]
11. Chen H. An experimental study on bearing capacity of simply supported T-beam bridge strengthened with steel plates. In: 6th International Conference on Minerals Source, Geotechnology and Civil Engineering (MSGCE 2021), 2021 Apr 8–11; Guangzhou, China. [Google Scholar]
12. Wu JY, Jiang XJ, Wang LY. Study on the destructive test of T-beam strengthened by external prestressing. J Phys. 2020;1549:22110. doi:10.1088/1742-6596/1549/2/022110. [Google Scholar] [CrossRef]
13. Huang LP, Cao SG, Chang ZG, Zhang XC, Huang YZ. Load distribution factor before and after widening of existing T-beam bridges. J Eng Sci Technol Rev. 2017;10:90–6. doi:10.25103/jestr.103.13. [Google Scholar] [CrossRef]
14. Farouk K, Elafandy T, Abdelrahman A. Strengthening of inverted T-concrete bridge bent beams with insufficient ledge reinforcement. Ain Shams Eng J. 2023;14(6):102106. doi:10.1016/j.asej.2022.102106. [Google Scholar] [CrossRef]
15. Shi J, Duan J, Cheng Y. Research on reinforcement design based on a T-beam bridge. In: 1st International Conference on Environment Prevention and Pollution Control Technology (EPPCT), 2018 Nov 09–11; Tokyo, Japan. [Google Scholar]
16. Tarozzi M, Pignagnoli G, Benedetti A. Evaluation of the residual carrying capacity of a large-scale model bridge through frequency shifts. J Civ Struct Health Monit. 2022;12(4):931–41. doi:10.1007/s13349-022-00586-0. [Google Scholar] [CrossRef]
17. Chiaia B, Marasco G, Ventura G, Quirini CZ. Customised active monitoring system for structural control and maintenance optimisation. J Civ Struct Health Monit. 2020;10(2):267–82. doi:10.1007/s13349-020-00382-8. [Google Scholar] [CrossRef]
18. Cai YX, Zhang K, Ye ZJ, Liu C, Lu KJ, Wang LB. Influence of temperature on the natural vibration characteristics of simply supported reinforced concrete beam. Sensors. 2021;21(12):4242. doi:10.3390/s21124242. [Google Scholar] [PubMed] [CrossRef]
19. Abedin M, Mehrabi AB. Bridge damage identification through frequency changes. In: Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, 2021 Mar 22–26. doi:10.1117/12.2581136. [Google Scholar] [CrossRef]
20. Li S. Analysis of influence of bridge deck damage on first order natural frequency of simply supported T-beam bridge. Vibroeng Proc. 2021;36(3):43–8. doi:10.21595/vp.2021.21846. [Google Scholar] [CrossRef]
21. Wei Z, Song X, Lu W. Research on structural damage identification by use of no inversion algorithm of frequency. In: International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), 2020 Jan 11–12; Vientiane, Laos. [Google Scholar]
22. Jiang F, Zhang Z, Guo W. Effect evaluation of prestressed carbon fiber plate reinforced bridges in critical condition. Appl Mech Mater. 2014;587–589:1477–82. doi:10.4028/www.scientific.net/AMM.587-589.1477. [Google Scholar] [CrossRef]
23. Yu TL, Tian LL, Ma Q. The shear resistant effect of RC beam strengthened with SWR external prestressing under dead load level when strengthening. Adv Mater Res. 2011;243–249(6):5576–81. doi:10.4028/www.scientific.net/AMR.243-249.5576. [Google Scholar] [CrossRef]
24. Zhang KX, Qi TY, Li DC, Xue XW, Wu FY, Liu XF. Research on innovative reinforcement of prestressed T-beam bridge. Int J Struct Integr. 2021;12(6):922–37. doi:10.1108/IJSI-11-2020-0117. [Google Scholar] [CrossRef]
25. Sun Z, Sun Q, Li J, Yang S. Field experimental study on external prestressing reinforcement of a 420m PC continuous beam bridge. Civ Eng J-Staveb Obz. 2023;32(1):94–107. doi:10.14311/CEJ.2023.01.0008. [Google Scholar] [CrossRef]
26. Hu B, Yang J, Sun Q, Zhang C. Experimental study on real bridge before and after simple-supporting to continuous reinforced concrete hollow slab. Civ Eng J-Staveb Obz. 2023;32(2):188–202. doi:10.14311/CEJ.2023.02.0015. [Google Scholar] [CrossRef]
27. Noble D, Nogal M, O’Connor A, Pakrashi V. The effect of prestress force magnitude and eccentricity on the natural bending frequencies of uncracked prestressed concrete beams. J Sound Vibr. 2016;365:22–44. doi:10.1016/j.jsv.2015.11.047. [Google Scholar] [CrossRef]
28. Fish J, Belytschko T. A first course in the finite element method. New York: John Wiley & Sons Inc.; 2007. p. 392–405. [Google Scholar]
29. Clough RW, Penzien J. Dynamics of structures. New York: McGraw-Hill; 1993. p. 149–60. [Google Scholar]
30. Wang SX, He JJ, Fan J, Sun PX, Wang DW. A time-domain method for free vibration responses of an equivalent viscous damped system based on a complex damping model. J Low Freq Noise V A. 2023;42(3):1531–40. doi:10.1177/14613484231157514. [Google Scholar] [CrossRef]
31. Guan H, Ni K, Ma H, Xiong Q, Wang W, Wang H. Dynamic modeling and verification of rotating compressor blade with crack based on beam element. Appl Math Model. 2024;133:367–93. doi:10.1016/j.apm.2024.05.019. [Google Scholar] [CrossRef]
32. Sun PX, Wang SX, Yan YD, Wang DW. Numerical methods for time-domain responses of the frequency-independent damped system. Int J Struct Stab Dy. 2024;24(14):2450151. doi:10.1142/S0219455424501517. [Google Scholar] [CrossRef]
33. Bonopera M, Chang KC, Chen CC, Sung YC, Tullini N. Experimental study on the fundamental frequency of prestressed concrete bridge beams with parabolic unbonded tendons. J Sound Vibr. 2019;455:150–60. doi:10.1016/j.jsv.2019.04.038. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools