Cable-Stayed Bridge Model Updating Based on Response Surface Method

1  Introduction

During the establishment of the finite element model (FEM), uncertainties in terms of subjectivity, geometry, materials, and other aspects lead to a particular deviation between the initial FEM and the actual bridge structure [1]. In scenarios where high accuracy is demanded, such as in bridge health monitoring and condition assessment, the initial FEM hardly suffices for the application. Consequently, research on FEM updating methods has become a prominent issue at present. To date, scholars from both China and abroad have proposed numerous model updating methods, among which two categories are more commonly employed. One is the sensitivity method based on sensitivity analysis, and the other is the response surface model (RSM) method based on Analysis of Variance [2]. Both of these methods hinge on algorithmic optimization. Due to its operability and computational efficiency, the bridge model updating method based on the response surface has garnered significant attention from scholars. The RSM method was proposed by Box and Wilson in 1951, and this method utilizes statistical concepts through specific experimental designs to convert implicit functional relationships into simple explicit functional relationships.

Lu et al. [3] put forward a combination of RSM and genetic algorithm (GA) for model updating, and the numerical example results of supported beams demonstrated that the method worked well and achieved reasonable results. Subsequently, GA was used to update the parameters by minimizing the objective function. Zhu et al. [4] proposed a FEM updating method that combined the RSM with the GA. They utilized the GA to optimize the design parameters of the scientific test frame, which improved the computational efficiency. Ji et al. [5] proposed a more practical and faster method of combining the RSM and the Fmincon algorithm (FA) for the correction of the FEM of a new, improved box girder bridge with corrugated steel webs. This method used the RSM to define the response that minimized the discrepancy between the measured data and the predictions of the FEM. Ma et al. [6] proposed a multi-scale FEM updating method for steel-tube-concrete composite truss bridges based on RSM. Wang et al. [7] introduced the robust estimation method into the response surface optimization solution process, which improved the reliability of the response surface model updating. Dong et al. [8] combined the peak picking (PP) method and the random subspace identification (SSI) method with the RSM method to identify the environmental vibration test results of a prestressed concrete continuous girder bridge to achieve an accurate modification of FEM of the continuous girder bridge. The corrected model could reflect the current situation of the actual bridge. Zhao et al. [9] introduced a radial basis function into the RSM as an augmentation term of the polynomial function of the objective function, which resulted in a higher fitting accuracy of the RSM and led to a substantial improvement in the convergence speed and accuracy of the optimized solution of the model. Luo et al. [10] proposed a structural damage identification method based on the combination of RSM updating and cloud model similarity metric. The method took the first five orders of the intrinsic frequency of a 5-story steel frame as the response and adopted the central composite design method to establish the response surface model. To quantify the measurement noise of the structural response, the numerical properties of the cloud model were introduced, and the accuracy of the RSM was improved through a filtering process. Fang et al. [11] and Perera successfully carried out model updating of structures by using a quadratic polynomial function as the response surface function and by applying the D-optimal design of experiments to the RSM.

In the future, more and more algorithms will be combined with the RSM, such as wavelet neural networks, nature-inspired algorithms [12,13], which will simplify calculations and complex structures. The research objects of bridge model updating methods can be broadly classified into two categories [14]. One is the updating method based on static load test results; the other is the updating method based on dynamic response data. Han et al. [15] utilized the RSM to modify the continuous beam bridge model through static and dynamic tests, thus overcoming the limitations of relying solely on static or dynamic test data. Zhang et al. [16] employed the actual monitoring dynamic characteristic parameters to formulate the response surface equation and objective function suitable for cable-stayed bridge model updating. They also explored the correlation of weight coefficients within the objective function. Xu et al. [17] selected the parameters of steel strand stay cables to be corrected and combined the measured data to construct the objective function. Then, they used the RSM to update the cable-stayed bridge model. Shimpi et al. [18] proposed a response surface-based model updating method for two-story arcade heritage bridges. They chose the third-order modal frequencies as the response parameters and obtained a highly precise bridge response surface model, successfully ascertaining that Bridge No. 493 had sustained damage. Chen et al. [19] proposed a novel FEM updating method for structural dynamics with uncertainty. It used quadratic polynomials to construct the RSM between frequencies and updating parameters; that is, it conducted FEM updating based on dynamic responses and verified the feasibility of this method. Sarehati et al. [20] used modal frequencies and mode shapes as state parameters to establish a response surface model. They conducted comparative verification through the numerical model of a supported beam and the laboratory-tested steel frame. This proved that this response surface model was an adequate substitute for the FEM used for damage detection. Kadir et al. [21] updated the original finite element model based on the results of in-situ dynamic tests using the RSM. This method reduced the computational workload and furnished more stable results for the bridge assessment work. The static load test demands substantial manpower and material resources, and the field test conditions are relatively harsh. In contrast, the dynamic load test, which uses environmental excitation to obtain dynamic response data, is more convenient and expeditious. Numerous studies have been conducted on finite element updating based on static data, wherein the response values typically comprise deflections and strains. When the model is updated based on dynamic test data, the response values usually involve mode frequencies and shapes. Given the convenience of measuring response data via environmental excitation, this paper focuses on the response data based on dynamic responses.

2  The Basic Principle of Model Updating Based on RSM

The response surface method (RSM) is based on experimental design and statistical analysis, leveraging statistical theories. It can transform the implicit functional relationship between the original input parameters and the output responses into an explicit approximate functional relationship via a limited number of experiments. This resultant relationship is called the RSM and is also known as the “model of models.” The crux of the RSM lies in the appropriate selection of parameters and responses within the system. The experimental design should be carried out within a rational scope. The response values of the sample points in the experimental design can be acquired through experiments or calculations. Subsequently, statistical analysis techniques were applied to analyze and fit the actual experimental data, thus constructing a response surface model that mirrors the relationship between the input parameters and the output responses. The RSM astutely substitutes the traditional finite element model for repetitive, iterative computations by constructing the response surface model. Consequently, it does away with the onerous process of invoking the finite element model in each iteration. It substantially curtails the workload of finite element simulation, boosts computational efficiency, and safeguards computational accuracy.

The fundamental procedures of the RSM chiefly encompass determining the response surface function, identifying parameters, carrying out experimental design, constructing the response surface model, and verifying its accuracy.

In this paper, a cable-stayed bridge was taken as the engineering object, and the first ten-order frequencies were utilized as the updating target to probe into the accuracy and effectiveness of the updating method based on the response surface model. The technical route of this paper is shown in Fig. 1.

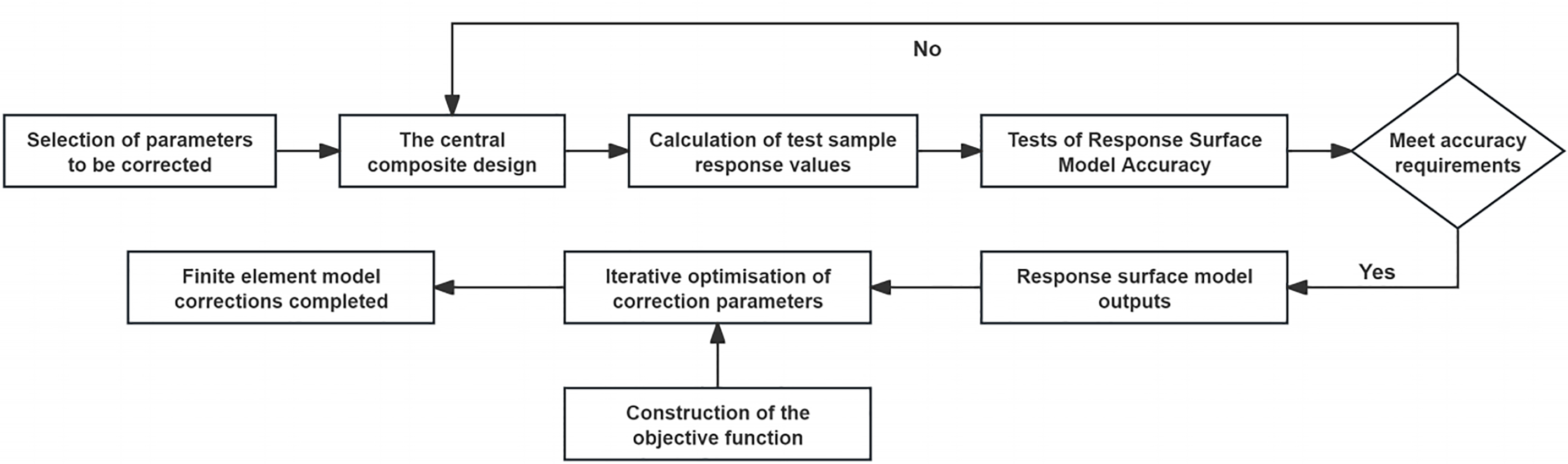
Figure 1: Flowchart of model correction based on RSM

2.1 Updating Parameters and the Selection of the Corresponding Parameters

The selection of updating parameters constitutes a crucial step in the successful updating of FEM. The suitability of the selected update parameters significantly impacts both the correction accuracy and the correction efficiency of the model update. This step mainly depends on understanding structural principles, sound engineering judgment, and test objectives. Therefore, the selection of updating parameters is mainly grounded in prior experience and sensitivity analysis of parameters. We usually choose the modulus of elasticity, density, Poisson’s ratio, damping ratio, friction coefficient, and bearing stiffness of each part of the bridge materials as the updating parameters.

2.2 Central Composite Design

Currently, the commonly used experimental design methods in civil engineering include full-factorial design, uniform design, central composite design, and Latin hypercube design. The full-factorial design method is a basic experimental method with relatively intuitive logic. As the number of parameters to be corrected increases, the number of experiments increases exponentially (if there are n parameters to be corrected and the number of levels for each component is L, the number of experiments is m = Ln), so the full-factorial design method does not apply to complex FEM. The uniform design method focuses on the uniform distribution of experimental sample points within the research interval, and other factors may be ignored. Regarding the Latin hypercube design method, the number of sample points must exceed that of parameters, which is likely to lead to a relatively large workload for generating the sample set.

The central composite design method is one of the most commonly used design methods in RSM, and it combines the partial factorial experimental design method with the interpolated node method to increase the number of sample points within a distance of ±δ on the principle that they are over the center point and parallel to the coordinate axis. The center composite test consists of center, cubic, and axial points with k parameters to be corrected. The number of cubic points is 2k; the cubic points are used to estimate the linear and interaction terms but not the bending. The axial points are on the axis of the test space with a total number of 2k, and the (0, 0) coordinates are the center points, which are used to check the bending, and the two-factor center composite test is shown in Fig. 2.

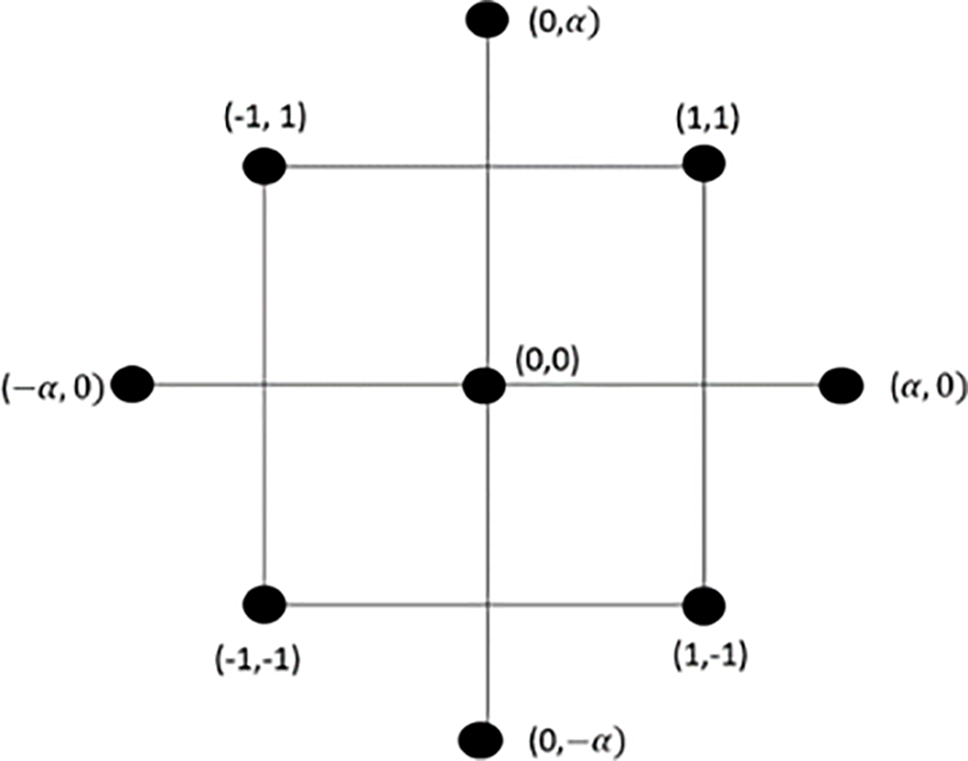
Figure 2: Two-factor central composite design diagram

The central composite design method features a uniform distribution of test points, which overcomes the deficiency of only outputting linear relationships between variables and factors. It can effectively expand the design space to obtain higher-order information, with the advantages of simple design and fewer trials. The central composite method design test has a very high advantage over other test design methods, making the test results more accurate. Hence, the test design method used in this paper is the central composite method.

2.3 Response Surface Function (RSF)

The choice of the mathematical functions for the RSM is crucial to the overall response surface analysis method, and the type of function chosen determines the accuracy of the subsequent corrections [22]. For large-scale structures, finite element calculations’ structural inputs and outputs are often complex and exhibit a certain degree of nonlinearity. Thus, the RSM is generally required to reflect the structure of the input-output relationship and simplify the calculation process. The RSM method smartly substitutes the traditional FEM for repeated iterative calculations by constructing a response surface model, and it is especially vital to express the relationship between design parameters and the response using a reasonable function mapping within an acceptable accuracy range. The RSM demands the selection of an appropriate RSF, which is directly related to the success of the problem solution.

Polynomial functions are more widely used in response surfaces owing to their strong nonlinear ability and simple forms. Two aspects need to be considered when choosing a suitable response surface function. Firstly, the function expression should comprehensively reflect the correlation between the input parameters and the output values. Secondly, a relatively straightforward function expression should be chosen as it can reduce the workload associated with the parameters to be corrected and regression analysis. Generally, second-order and third-order polynomials meet the accuracy requirements for representing the relationship between the parameters to be corrected and the response values. In the finite element model updating of bridges, the most prevalently utilized response surface function models are first-order polynomials and second-order polynomials.

First-order polynomials are mostly used for fitting simple linear relationships. Higher-order polynomials are mostly used for fitting complex nonlinear relationships between structural responses and parameters. Among them, second-order polynomials are the most widely adopted because they can achieve a good balance between fitting accuracy and computational efficiency. Li et al. [23] fitted the response surface equations of the parameters to be corrected and the objective function, with and without considering the parameter cross terms, respectively, and obtained the explicit equations between them and the optimal values of the parameters to be corrected. Their results indicated that the updating effect was better when the parameter cross terms were considered during the updating process. Therefore, this paper chose second-order complete polynomials as the RSF, as shown in Eq. (1).

y^=β0+∑i=1kβixi+∑i=1kβiixi2+∑i∑jβijxixj+ε,(1)

where y^ is the response surface function; β0 is the constant term to be determined; βi is the primary term to be coefficient; βii and βij are the quadratic terms to be determined; xi and xj denote the correction parameters of the structure; k denotes the number of coefficients to be determined; ε is the higher order error and ε∼N(0,σ2).

3  Project Overview

This paper uses a cable-stayed bridge on a provincial expressway as the engineering background. The main bridge’s span arrangement is (108 + 180 + 108) m. The bridge tower and cable-stayed cables are located in the medial strip. The whole bridge adopts nine pairs of cables. The height of the bridge tower is 435 m. The main girder cross-section is a prestressed variable section box girder with a single box and three chambers. The elevation of the cable-stayed bridge is shown in Fig. 3.

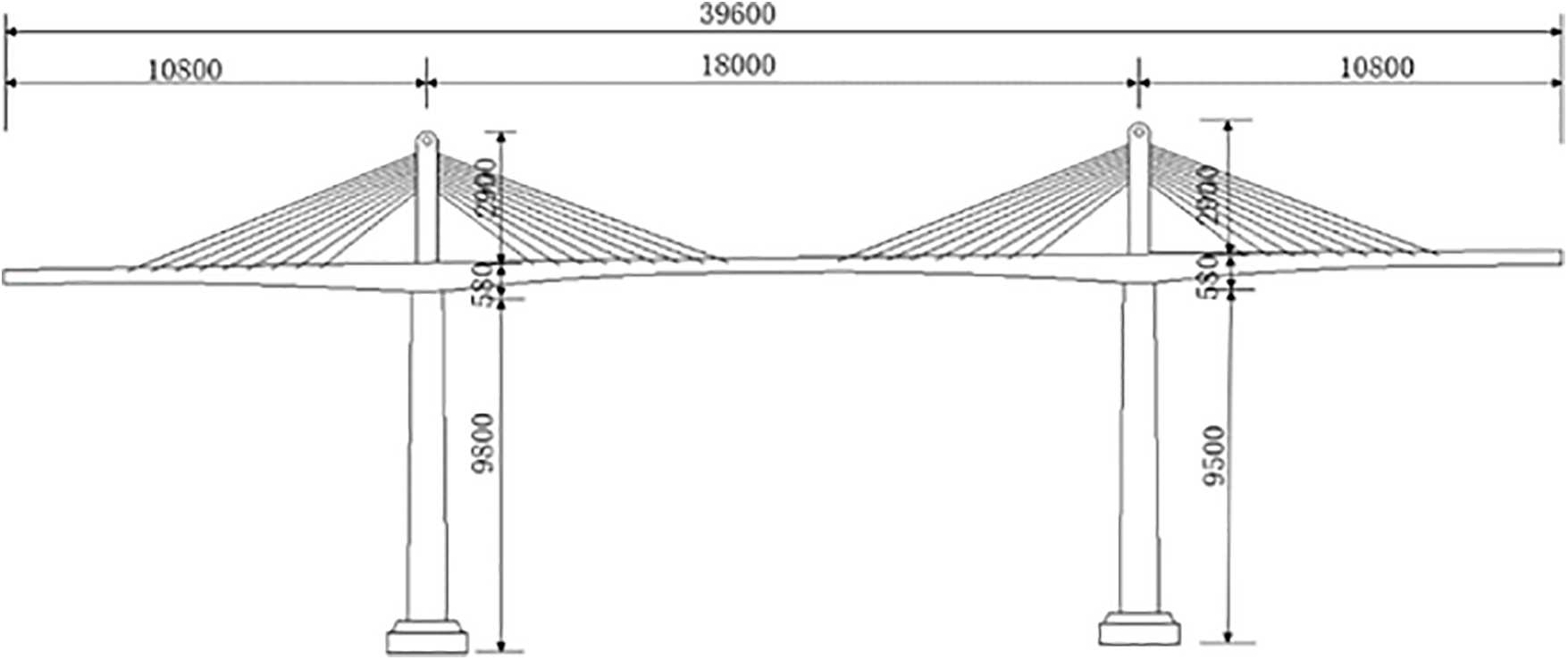
Figure 3: Elevation of the cable-stayed bridge (unit: cm)

The girder at the abutment is 5.8 m high with a 1.1 m thick base plate, and the girder at the middle section of the span is 3 m high with a 0.32 m thick base plate. The girder height and footing thickness of the girder section between piers vary according to a quadratic parabola.

The equation for the variation of beam height (H) is given in Eq. (2).

H=x2842×2.8+3.(2)

The variation equation for the thickness of the base plate (D) is given in Eq. (3).

D=x2842×0.78+0.32.(3)

The equation for the variation of the base plate width (B) is given in Eq. (4).

B=18.8275−H2.(4)

According to the drawings, the main girder is divided into 29 kinds of single-box, three-compartment sections. The standard girder section of the main girder is shown in Fig. 4, and the cross-section of the cable tower is shown in Fig. 5. The piers are divided into 20 cross-sections, and the piers are variable section thin-walled hollow piers. The transverse bridge dimensions remain constant, and the longitudinal pier cross-section dimensions change according to the 80:1 inclination. The wall thickness at the middle of the pier is 1.2 m, and Wall thicknesses at the top and bottom of the pier are thickened to 1.8 and 2.2 m, respectively. The cross-section of the bridge piers is shown in Fig. 6. As shown in the image, the right abutment data is in parentheses, the left abutment data is outside parentheses, and the rest of the dimensions are common to both.

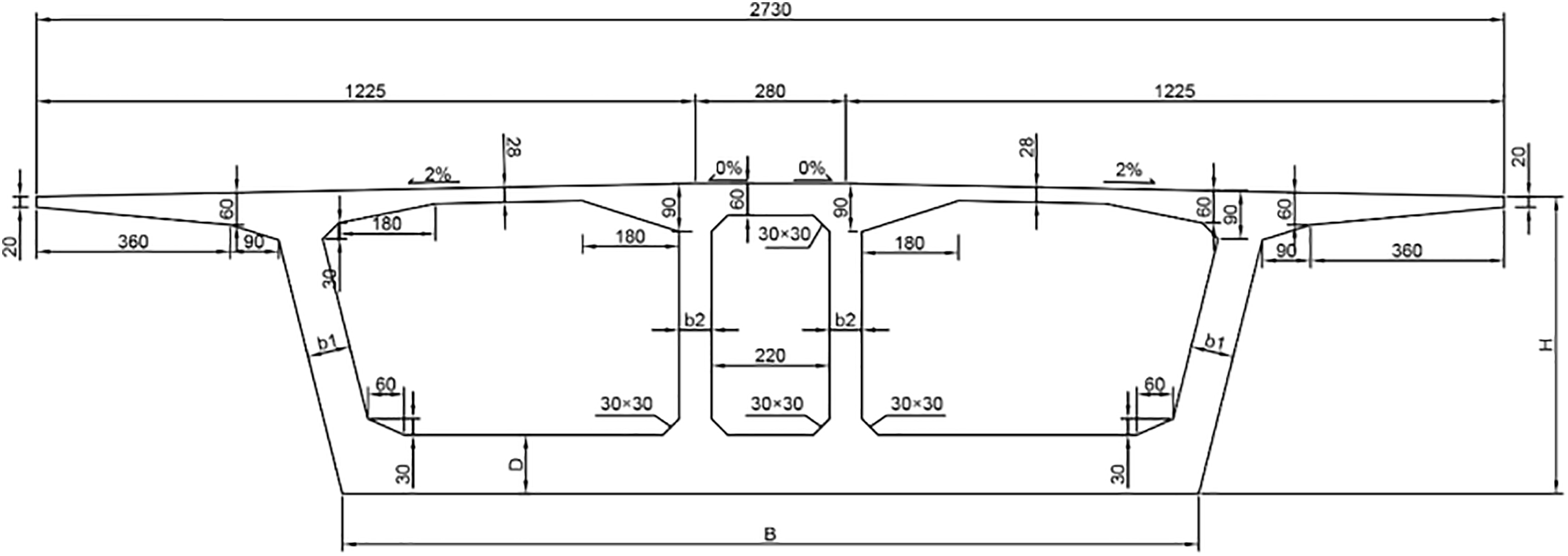
Figure 4: The standard girder section of the main girder (unit: cm)

Figure 5: The cross-section of the cable tower (unit: cm)

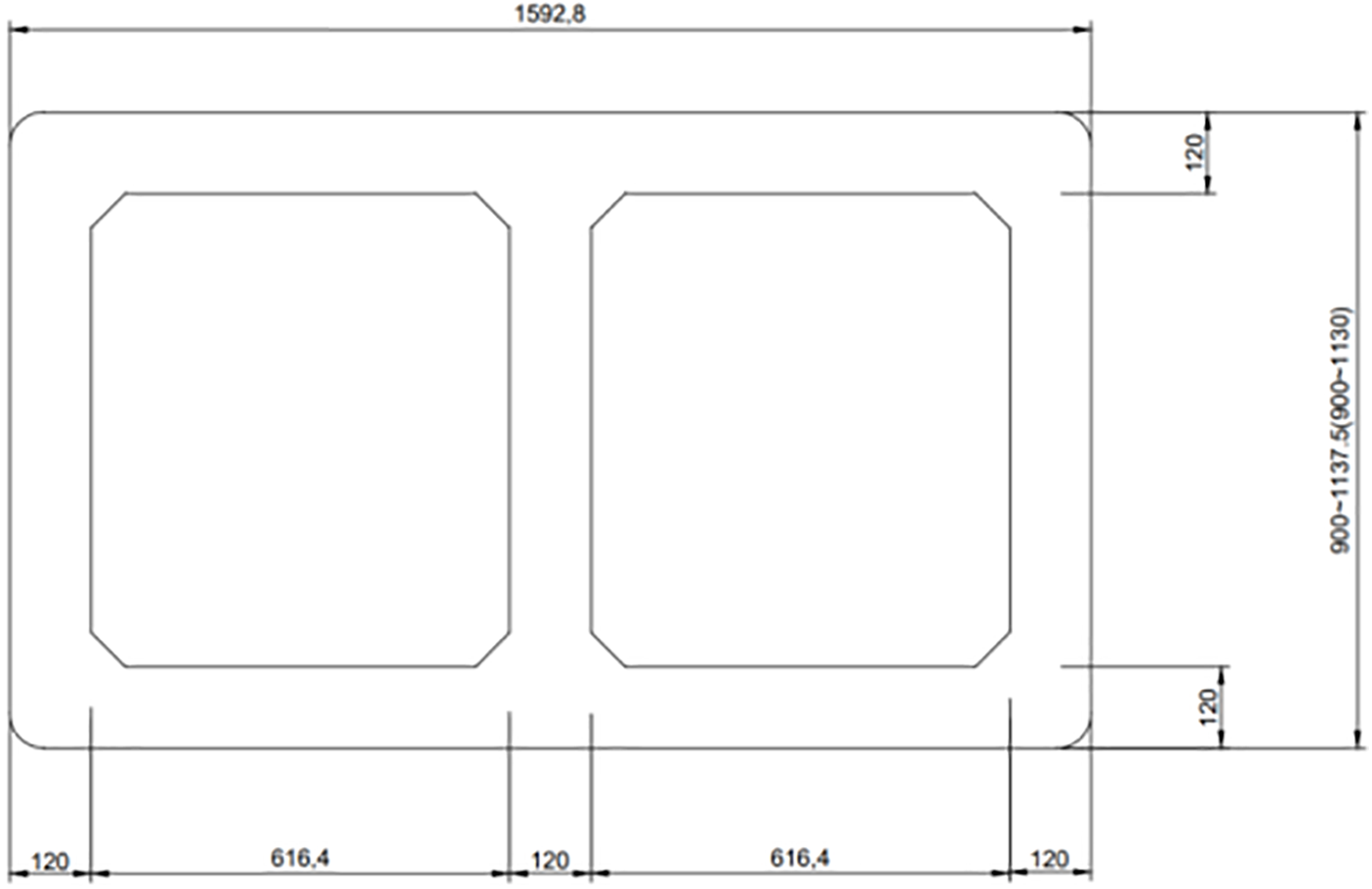
Figure 6: The cross-section of the bridge piers (unit: cm)

4  Establishment of Initial FEM and Analysis of Measured Data

4.1 Establishment of Initial FEM

In this paper, according to the bridge design drawings, the cable-stayed bridge FEM was established and analyzed with the finite element software ANSYS based on the actual situation. The entire bridge deck was modeled in the form of a fishbone girder, as shown in Fig. 7, where the longitudinal girder and the transverse stiffeners are crossed in the shape of a “fishbone.” The transverse rigid arm connects the centroid of the beam’s cross-section and cable end to transfer the load. The advantage of the “fishbone” mode is that the mass and the stiffness of the bridge deck system can be concentrated in the central node. Connecting the center of gravity of the beam section and the cable node through the stiffening arm makes the stiffness modeling of the main girder more accurate.

Figure 7: Fishbone-shaped main beam

The main material parameters and their corresponding components of the initial FEM are shown in Table 1.

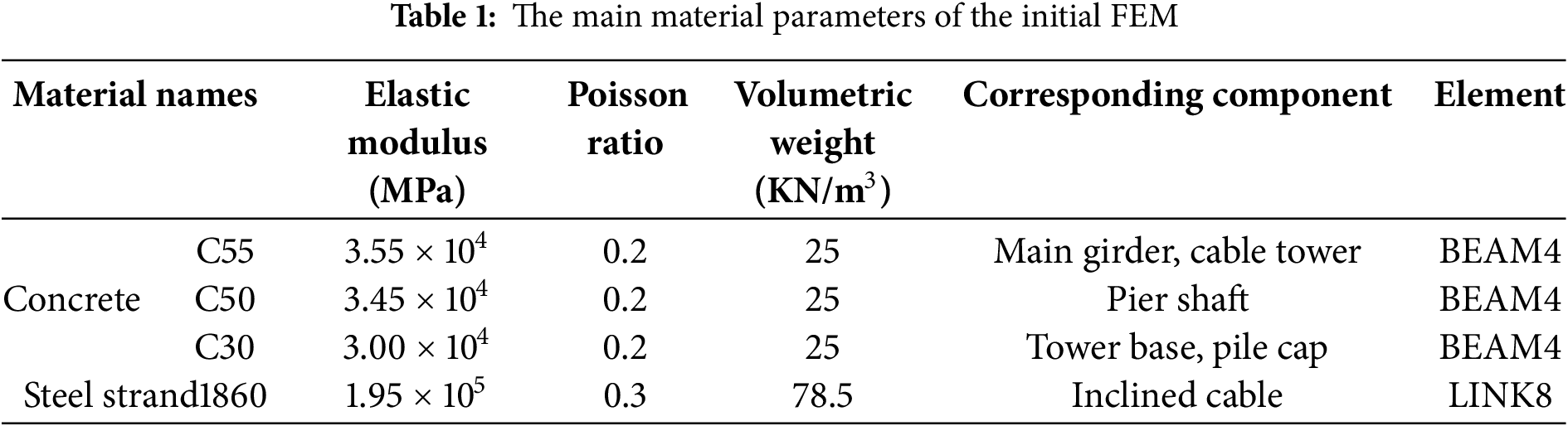
The main girder, cable tower, and pier of the bridge are simulated by the BEAM4 element, which is a uniaxial force unit that can withstand tension, compression, bending, and torsion, and this unit has six degrees of freedom at the nodes, which are the linear and angular displacements in the X, Y, and Z directions. The cable is simulated by the LINK8 element, a three-dimensional rod unit that can only withstand tension and compression, and the unit has three degrees of freedom at each node: displacement in the X, Y, and Z directions. The initial FEM of the cable-stayed bridge is shown in Fig. 8.

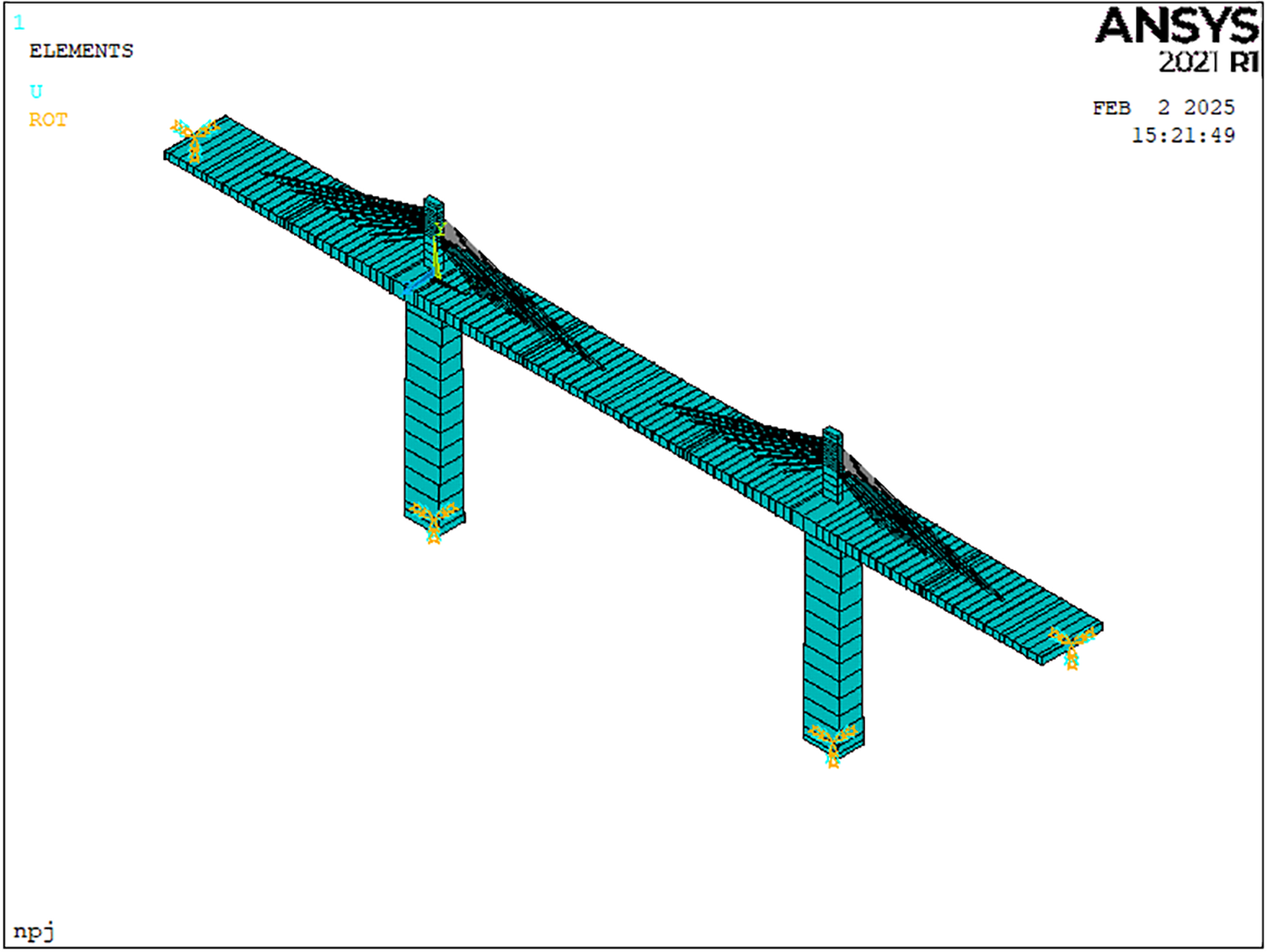
Figure 8: The initial FEM of cable-stayed bridge

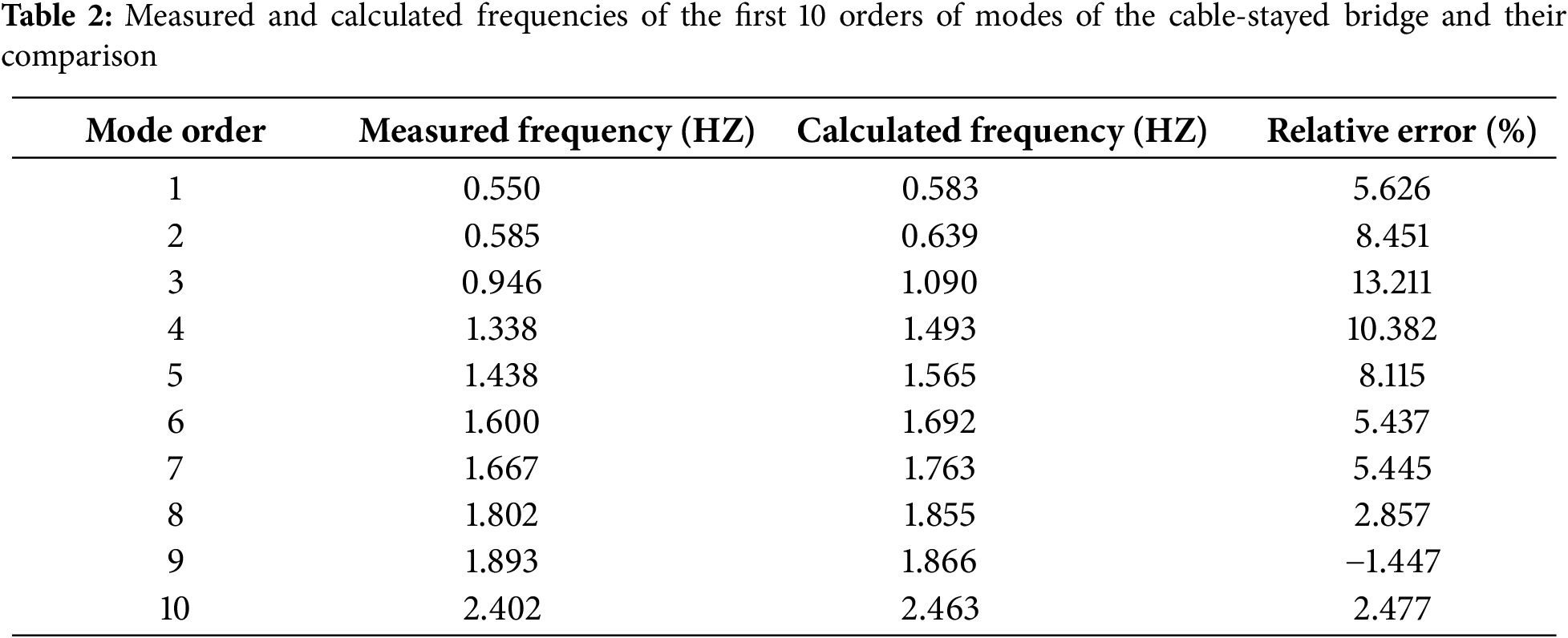
This paper calculated the first ten modes of the cable-stayed bridge. The first five vibration modes are shown in Fig. 9, and the first ten vibration frequencies are listed in Table 2.

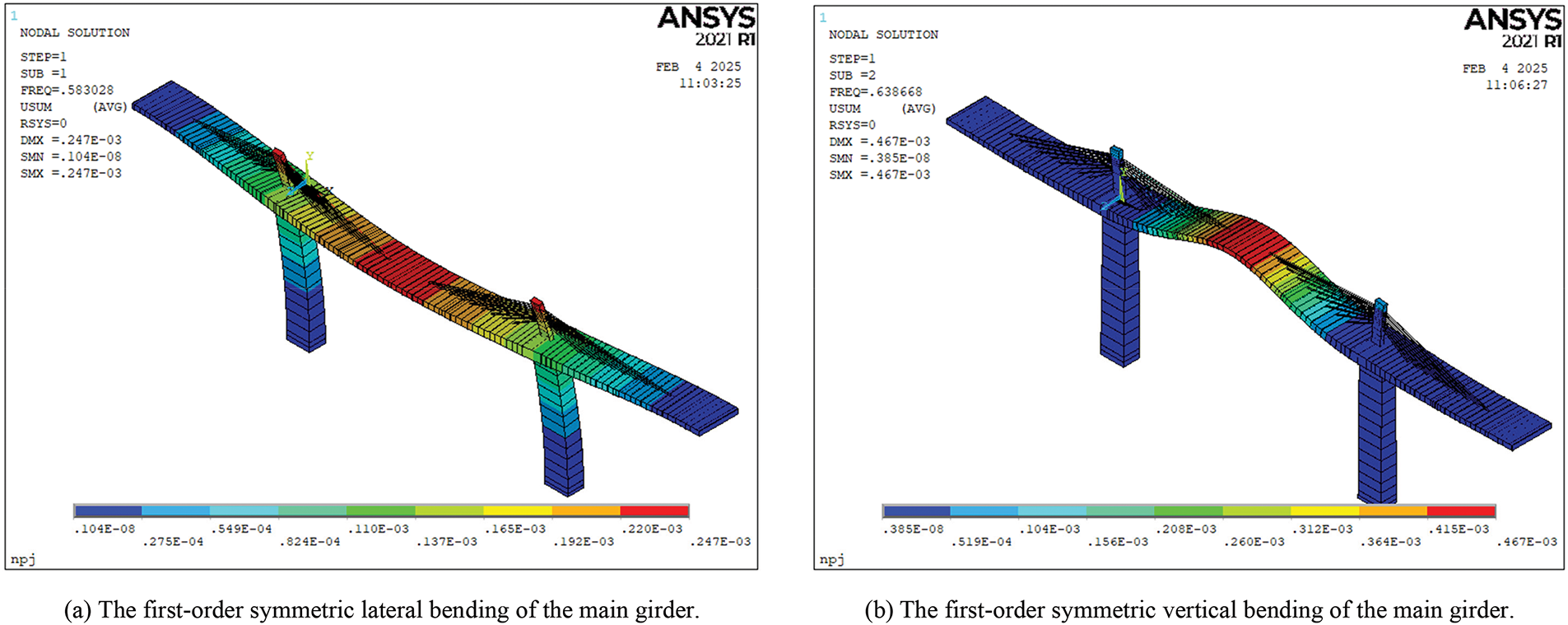
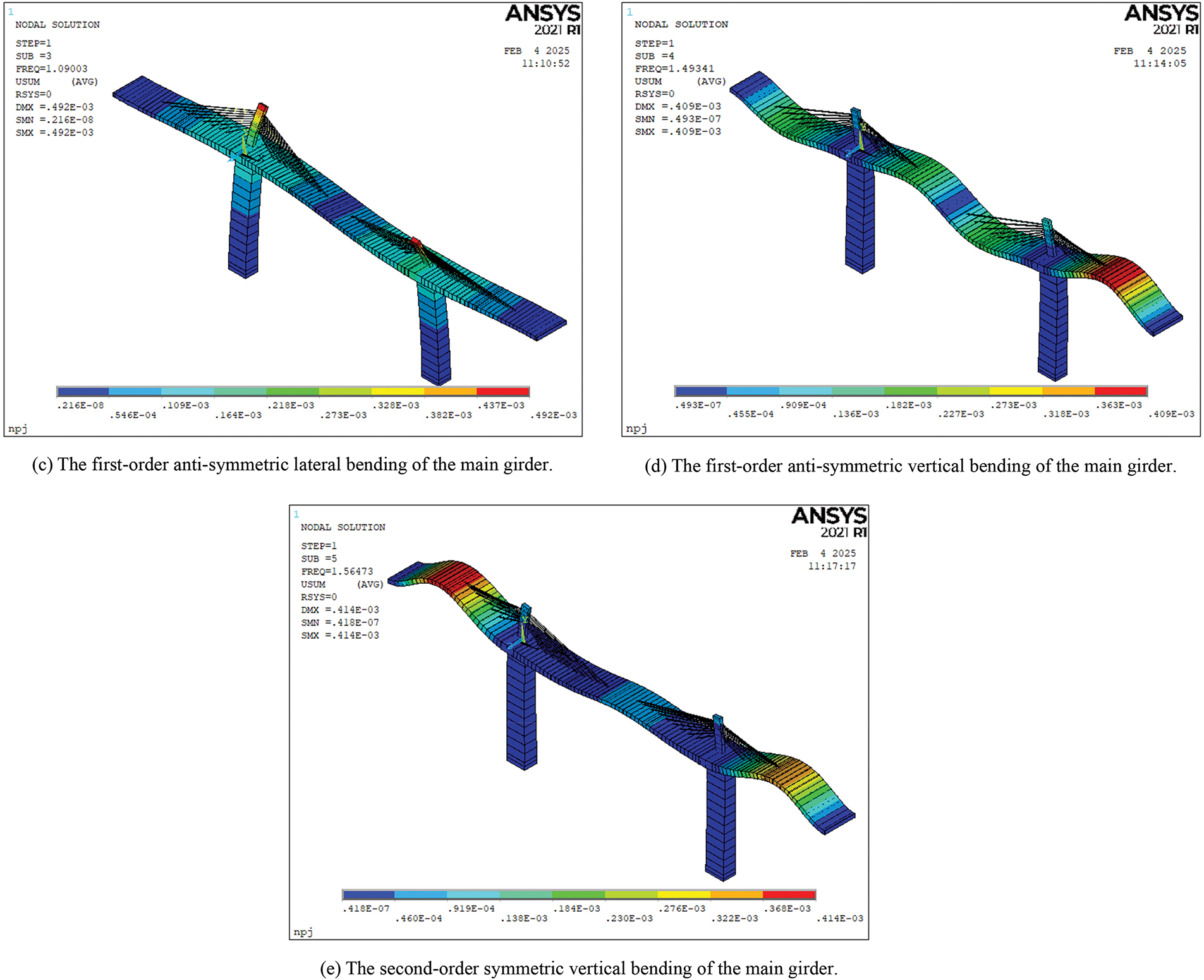
Figure 9: The first five-order frequency-vibration mode diagrams

4.2 Analysis of Measured Data

The monitoring contents of the bridge monitoring system used in this paper include vibration monitoring, cable force monitoring, and deflection monitoring. There are nine unidirectional acceleration sensors, and the layout diagram of sensor measuring points is shown in Fig. 10.

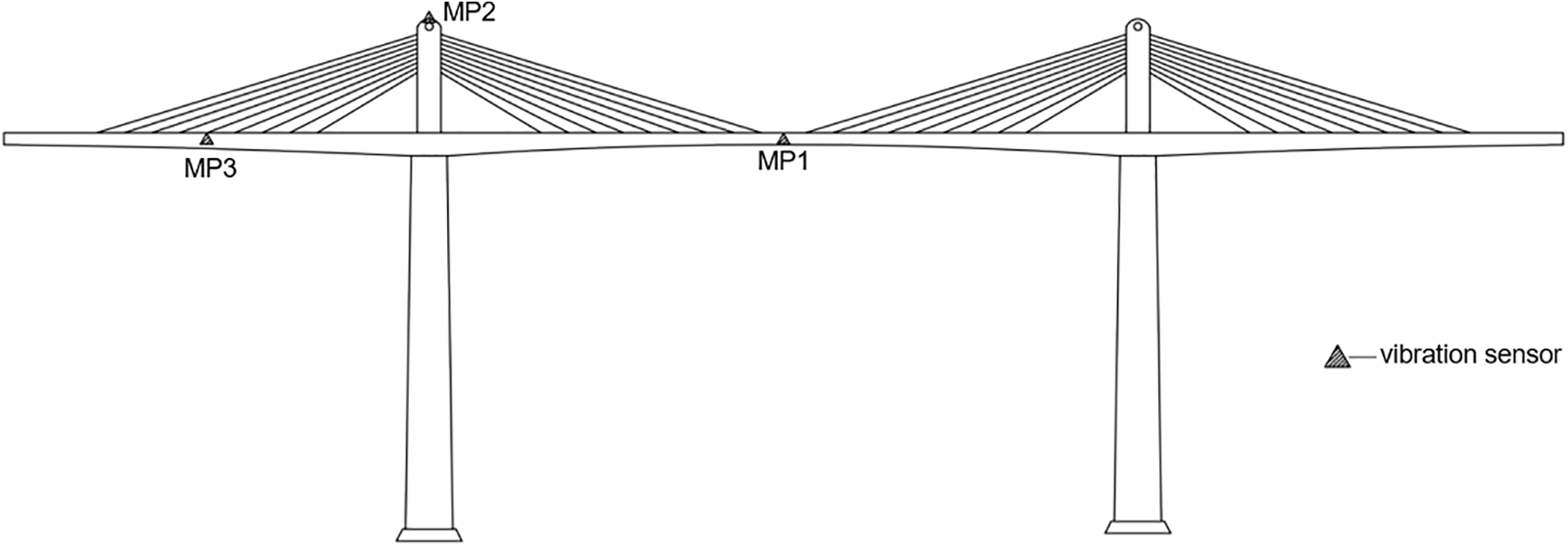
Figure 10: Layout diagram of sensor measuring points

The traditional Bayesian Fast Fourier Transform (FFT) method is susceptible to adverse conditions and may fail to converge under such circumstances. Li et al. [24] devised an Expectation-Maximization (EM) algorithm for calculating the second-order Taylor approximation of the logarithmic posterior probability density function (PDF) at the local maximum. When the traditional algorithm fails to converge in modal analysis, this method can substitute for the conventional one and enhance computational efficiency. Compared with the traditional algorithm, the improved Bayesian Fast Fourier Transform (FFT) algorithm can identify structural responses with greater accuracy and higher efficiency.

In light of the theory underlying the improved Bayesian FFT algorithm, the acceleration monitoring data of the cable-stayed bridge from the first quarter of 2021, which is presently accessible and closest to the bridge’s initial state, was chosen to perform modal analysis on the measured vibrations of the cable-stayed bridge.

The modal analysis was conducted using ANSYS to obtain the first 10 orders of modes of the cable-stayed bridge. The measured and calculated frequencies of the first 10 orders of modes of cable-stayed bridges and their comparison are shown in Table 2, except for the third-order modes with the largest relative error of 13.211%, and the fourth-order modes with a relative error of 10.382%. The relative error of the rest of the modes is less than 10%.

5  FEM Updating of Cable-Stayed Bridge Based on RSM

5.1 Selection of Updating Parameters

In this paper, we initially select certain parameters based on experience. Subsequently, through parameter sensitivity analysis, we select the parameters with higher sensitivity to update.

When multiple correction parameters are within the structure, their units are not identical. Eq. (5) can be employed to calculate the dimensionless sensitivity values to avoid this kind of interference. This facilitates an intuitive evaluation of the degree of influence the updated parameters exert on the state variables.

∂F∂p=(F″−F′)Δp/(p0+Δp),(5)

where p represents the parameter to be corrected, p0 is the initial value of the parameter to be corrected, Δp is the slight change amount of the parameter to be corrected, and F is the state parameter of the structure. When p=p0, the state variable F′ in this case can be calculated through ANSYS. Keeping other parameters unchanged and making a small change to the parameter to be corrected p, that is, p=p0+Δp, the state variable F′, in this case, can also be calculated through ANSYS.

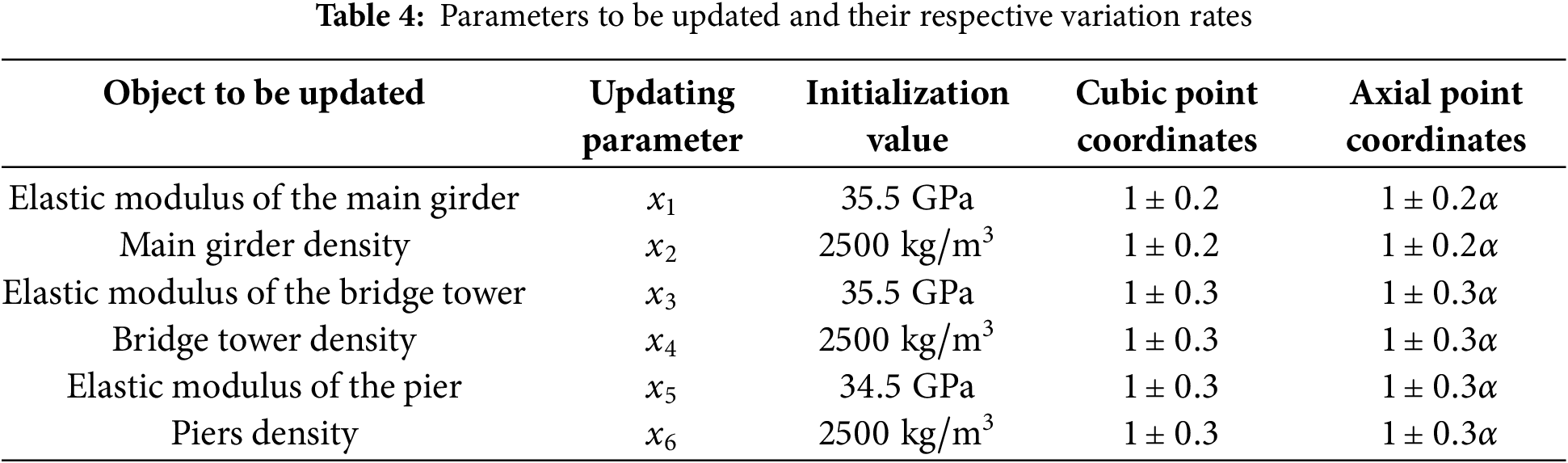
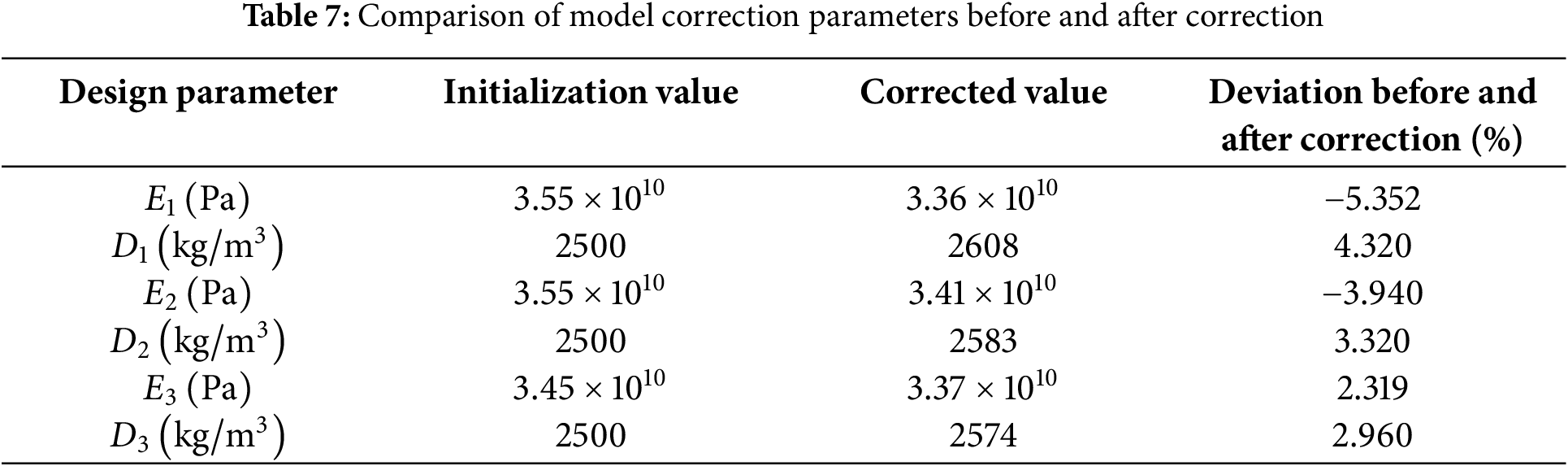
Initially, the elastic modulus and density of main girders, bridge towers, abutments, and diagonal cables were chosen as the parameters to be updated. Specifically, the elastic modulus and density of the main girder are E1 and D1, and the elastic modulus and density of the bridge tower are E2 and D2. The elastic modulus and density of the bridge abutment are E3 and D3. The elastic modulus and density of the diagonal cable are E4 and D4. By employing the parameter perturbation method, each of the eight preliminarily screened parameters to be corrected was increased by 10% to analyze their sensitivities to the first 10 orders of frequencies. The original values and perturbed values of the parameters to be updated are shown in Table 3. The frequency sensitivity analyses of each parameter are shown in Fig. 11. When the parameter analysis is based on sensitivity, the parameter with high sensitivity is usually selected as the parameter to be updated, because the high sensitivity parameter controlled the objective function. In contrast, the low sensitivity parameter tends to increase the model error. Consequently, the elastic modulus and density of the main girder, bridge tower, and abutment are selected as the parameters to be updated.

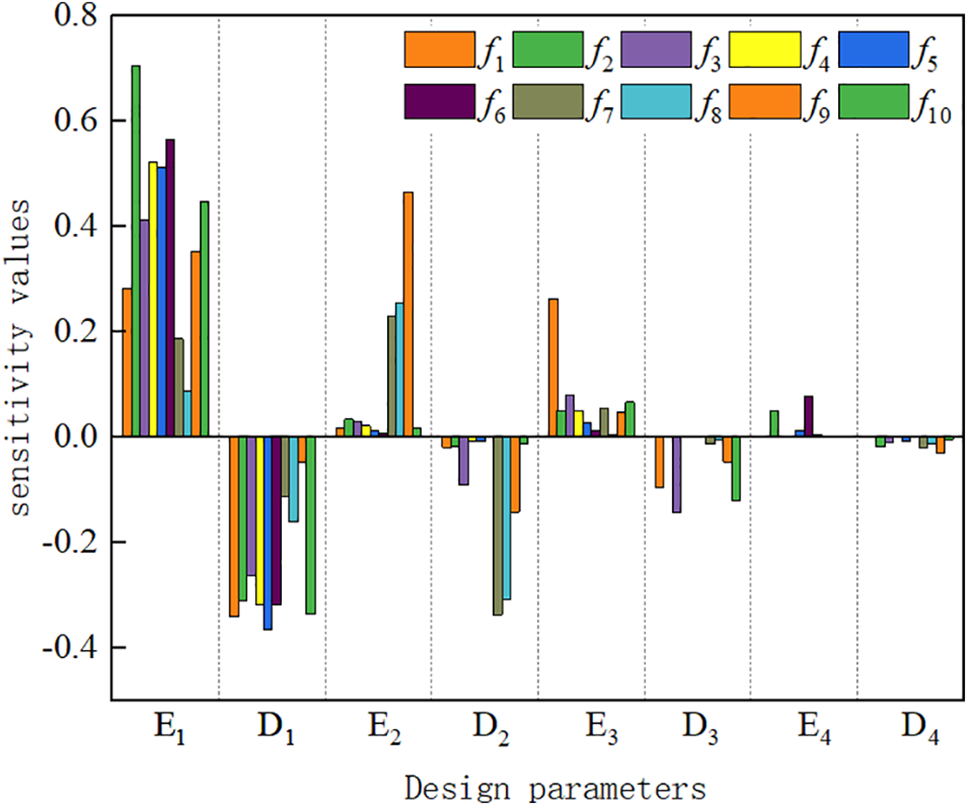
Figure 11: Frequency sensitivity analysis of each parameter

5.2 Experimental Design and Response Surface Fitting

By comparison, the frequency of cable-stayed bridges exhibits a higher sensitivity to the parameters of the main girders. Therefore, the variation rates of the density and elastic modulus of the main girders are 1±0.2, while those of the remaining parameters are 1±0.3, and parameters to be updated and their respective variation rates are shown in Table 4.

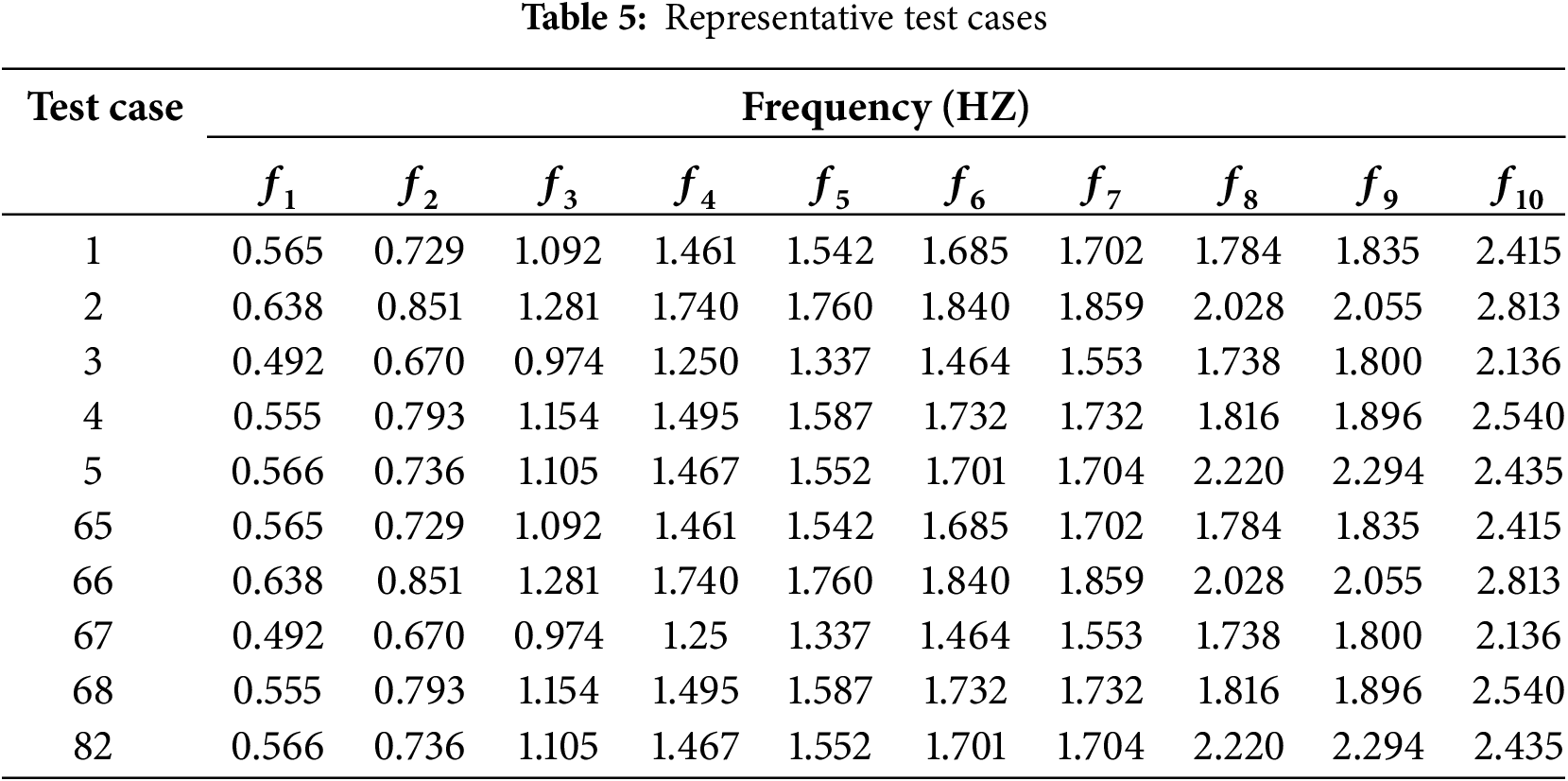
To establish the response surface equations, the central composite design method is used to devise the experimental conditions for the response surface. Given that there are six parameters to be corrected, the number of factors is thus six. There are 64 cubic points and 12 axial points, with the value of α being 2.828. The finite element analysis results for each representative test case are shown in Table 5, where cases 1 to 64 are cubic points, cases 65 to 76 are axial points, and cases 77 to 82 are center points. The calculated results in Table 5 are used to construct the response surface equations.

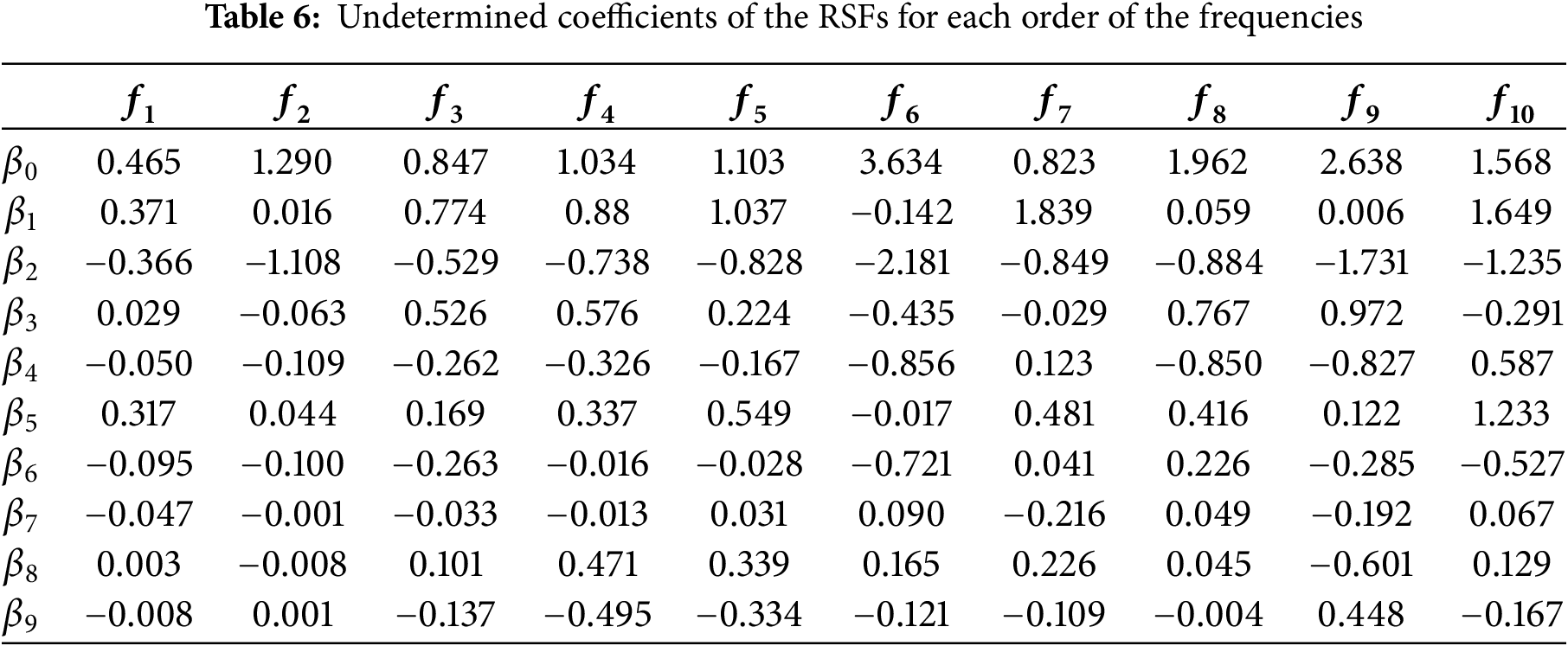
According to the calculation and analysis results of the FEM under each test case, the least squares method is adopted to regress the undetermined coefficients βi in the response surface equations, and the βl˙ of the RSFs for each order of the frequencies are shown in Table 6.

5.3 Comparison of Updating Results

This paper utilized the measured first 10 order frequencies of the bridge structure and the corresponding first 10 order frequencies obtained from the response surface calculation. It calculated the sum of the squares of their relative errors as the objective function. The relative error of the frequency was adopted as the objective function rather than the absolute error. This was mainly due to the consideration that the magnitudes of frequencies of each order vary, aiming to avoid the error resulting from inconsistent weighting magnitudes. The constructed objective function was given as in Eq. (6).

y=min∑i=18(fAi−fEifEi)2.(6)

Here, fEi is the measured value of the frequency, and fAi is the calculated value of the response surface of the frequency, and i=1,2,…,8. Once the objective function has been constructed, iterative optimization can be carried out to seek the objective function’s minimum value under the parameters’ constraints. This paper conducted optimization iteration on the MATLAB platform using the sequential quadratic programming method. The percentage error of the objective function values between two adjacent model updates during the optimization iteration process was used to judge whether convergence had been achieved. If the percentage error of the objective function value was less than 1% for two consecutive times and this situation occurs twice in a row, it was deemed that convergence has been reached. Then, the optimal values of the design parameters can be obtained. The comparison of the model updating parameters before and after correction is shown in Table 7.

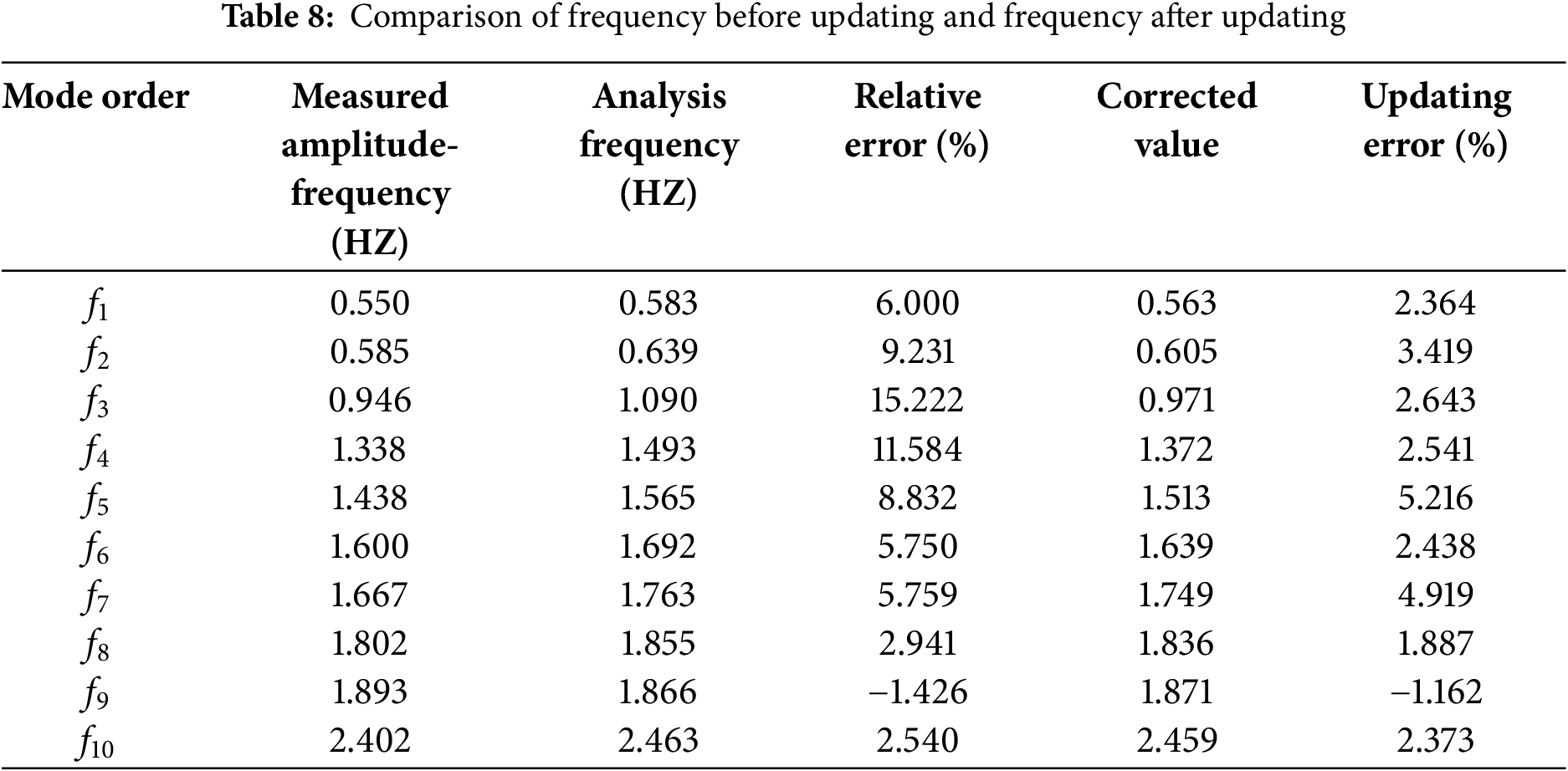
The comparison between the pre-updating frequency and the post-updating frequency is shown in Table 8. It could be seen that after the model update, the vibration frequency values calculated by the finite element method (FEM) were closer to those monitored from the actual bridge structure. Through the model updating, the absolute error values between the vibration frequency values calculated by the FEM and the monitored ones changed from ranging between 1.426% and 15.222% to a range of 1.162% and 5.216%. The most significant error occurred in the third-order vibration frequency, which decreased from 15.222% to 2.643%, thus showing better agreement with the actual vibration frequency value.

6  Conclusion

This paper developed a dynamic model updating method for cable-stayed bridges predicated on the RSM, thereby achieving the FEM updating of cable-stayed bridges.

(1) Crucial issues about the dynamic model updating of cable-stayed bridges were addressed, including the establishment of response surface equations, the solution of the objective function, and the implementation of the optimization algorithm. Subsequently, the general procedure for the dynamic model updating of cable-stayed bridges was deduced.

(2) The error between the modal frequency value computed by the modified finite element method (FEM) and the modal frequency value monitored from the actual bridge structure was reduced from the range of 1.426% to 15.222% down to the range of 1.162% to 5.216%. Notably, for the third-order vibration frequency, the error was decreased from 15.222% to 2.643%. The results show that the modified FEM with the response surface method is much more accurate than the actual bridge structure.

In recent years, the RSM has found extensive application in bridge and structural engineering domains. Particularly in the FEM updating of cable-stayed bridges and suspension bridges, it has demonstrated a robust development momentum. This study offers a valuable reference for future endeavors concerning FEM updating of large and complex structures. It aids subsequent research in deepening the comprehension of model modification for cable-stayed bridges. It enriches the reservoir of knowledge outcomes, possessing strong practicality and promising application prospects in engineering practice.

Simultaneously, the proposed methodology’s limitations should be addressed in our forthcoming work. In this paper, we mainly focused on the finite elements of cable-stayed bridges based on frequency, and future research will involve the concurrent selection of multiple static and dynamic responses for updating, to further compare and validate the correction results.

Acknowledgement: The authors gratefully acknowledge Shandong Hi-Speed Engineering Test Co., Ltd., for providing monitoring data and bridge design information.

Funding Statement: This study was supported by the National Natural Science Foundation of China (NNSFC) (Grant no. 12272148).

Author Contributions: The authors confirm their contribution to the paper as follows: data analysis: Yao Lu; finite element modeling: Xintong Huo; data collection: Guangzhen Qu; modal analysis: Yanjun Li; thesis planning and guidance: Lei Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Due to the nature of this research, participants did not agree that their data should be shared publicly, so supporting data is unavailable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang YX, Yang FL, Chen D. Application of improved response surface method in finite element model updating of bridge structure. J Highw Transp Res Dev. 2020;37(10):83–91+133 (In Chinese). [Google Scholar]

2. Shan DS, Li Q, Khan I, Zhou XH. A novel finite element model updating method based on substructure and response surface model. Eng Struct. 2015;103:147–56. doi:10.1016/j.engstruct.2015.09.006. [Google Scholar] [CrossRef]

3. Lu D, Cai CS. Bridge model updating using response surface method and genetic algorithm. J Bridge Eng. 2010;15(5):553–64. [Google Scholar]

4. Zhu QY, Han QK, Liu JG, Yu CS. High-accuracy finite element model updating a framed structure based on response surface method and partition modification. Aerospace. 2023;10(1):79. doi:10.3390/aerospace10010079. [Google Scholar] [CrossRef]

5. Ji W, Shao TY. Finite element model updating for improved box girder bridges with corrugated steel webs using the response surface method and fmincon algorithm. KSCE J Civil Eng. 2021;25(2):586–602. doi:10.1007/s12205-020-0591-3. [Google Scholar] [CrossRef]

6. Ma YP, Liu YJ, Liu J. Multi-scale finite element model updating of CFST composite truss bridge based on response surface method. China J Highw Transp. 2019;32(11):51–61. doi:10.1061/9780784483565.084. [Google Scholar] [CrossRef]

7. Wang XG, Dang LT, Ma M. A robust estimation method for response surface model updating based on vibration frequency. J Highw Transp Res Dev. 2022;39(2):77–84. [Google Scholar]

8. Dong F, Shi ZQ, Zhong RM, Jin N. FE model updating of continuous beam bridge based on response surface method. Buildings. 2024;14(4):960. doi:10.3390/buildings14040960. [Google Scholar] [CrossRef]

9. Zhao Y, Zhang JJ, Li DS, Zhou DC, Xin DB. Finite element model updating of bridge structures based on improved response surface methods. Struct Contr Health Monit. 2023;2488951:1–16. doi:10.1155/2023/2488951. [Google Scholar] [CrossRef]

10. Luo YP, Zheng JL, Yuan M, Wang LK, Guo X, Liu JL. Structural damage identification using the similarity measure of the cloud model and response surface-based model updating considering the uncertainty. J Civil Struct Health Monit. 2022;12:1067–81. doi:10.1007/s13349-022-00598-w. [Google Scholar] [CrossRef]

11. Fang SE, Perera R. Damage identification by response surface based model updating using D optimal design. Mech Syst Signal Process. 2011;25(2):717–33. doi:10.1016/j.ymssp.2010.07.007. [Google Scholar] [CrossRef]

12. He HF, Zeng BJ, Zhou YL, Song YY, Zhang TN, Su H, et al. Bridge model updating based on wavelet neural network and wind-driven optimization. Sensors. 2023;23(22):1–24. doi:10.3390/s23229185. [Google Scholar] [PubMed] [CrossRef]

13. Jiménez-Alonso JF, Suzana E, Duvnjak I, Caetano SED. Evolutionary game theory-based finite element model updating of a moveable cable-stayed footbridge. J Civil Struct Health Monit. doi:10.1007/s13349-024-00865-y. [Google Scholar] [CrossRef]

14. Ereiz S, Duvnjak, Jiménez-Alonso JF. Review of finite element model updating methods for structural applications. Structures. 2022;41:684–723. doi:10.1016/j.istruc.2022.05.041. [Google Scholar] [CrossRef]

15. Han JP, Luo YP. Static and dynamic finite element model updating of a rigid frame-continuous girders bridge based on response surface method. Adv Mater Res. 2013;639-640:992–7. doi:10.4028/www.scientific.net/AMR.639-640.992. [Google Scholar] [CrossRef]

16. Zhang LY, Wang B, Wang BJ, Chen K, Lv JM. A method for modifying dynamic model of cable-stayed bridge based on response surface method. J Highw Transp Res Dev. 2022;39(8):46–52. [Google Scholar]

17. Xu SZ, Ma YG, Zhang H. Parametric updating of steel strand stay cable force calculation model based on response surface method. Adv Civ Eng. 2023;2023(1):1–12. doi:10.1155/2023/6611232. [Google Scholar] [CrossRef]

18. Shimpi V, Sivasubramanian MVR, Singh SB. Integrating response surface methodology and finite element analysis for model updating and damage assessment of multi-arch gallery masonry bridges. Sadhana-Acad P Eng S. 2024;49(33):1–18. doi:10.1007/s12046-023-02363-1. [Google Scholar] [CrossRef]

19. Chen XQ, Shen ZP, Liu XE. Structural dynamics model updating with interval uncertainty based on response surface model and sensitivity analysis. Inverse Probl Sci Eng. 2018;27(10):1425–41. doi:10.1080/17415977.2018.1554656. [Google Scholar] [CrossRef]

20. Umar S, Bakhary N, Abidin ARZ. Response surface methodology for damage detection using frequency and mode shape. Measurement. 2018;115:258–68. doi:10.1016/j.measurement.2017.10.047. [Google Scholar] [CrossRef]

21. Kadir O, Mehmet FY, Barlas OC. Assessment of an old reinforced concrete open-spandrel arch railway bridge. Structures. 2022;44:284–94. doi:10.1016/j.istruc.2022.08.018. [Google Scholar] [CrossRef]

22. Yang FL. Finite element model updating of bridge structure based on response surface-linear decreasing weight particle swarm optimization algorithm [M.E. thesis]. China: Chang’an University; 2022 (In Chinese). [Google Scholar]

23. Li YQ, Liu XH, Chen ZL, Zhang H. Cable-stayed bridge model updating based on cable force response surface method. J Railw. 2021;43(2):168–74 (In Chinese). [Google Scholar]

24. Li BB, Au S-K. An expectation-maximization algorithm for Bayesian operational modal analysis with multiple (possibly close) modes. MSSP. 2019;132:490–511. [Google Scholar]