Sensitive Analysis on the Compressive and Flexural Strength of Carbon Nanotube-Reinforced Cement Composites Using Machine Learning

1  Introduction

Carbon nanotube-reinforced cement composites have gained growing attention in construction materials due to their strong mechanical behavior [1–4]. Carbon nanotubes (CNTs), with their high tensile strength, electrical conductivity, and heat resistance, have been found to improve the compressive and flexural strength of cement-based materials [5–7]. Many studies have examined how these nanotubes contribute to better strength and internal structure [8–10]. Makar et al. [11] shared early observations and possible applications of cement composites containing carbon nanotubes. Liew et al. [12] provided an overview of the mechanical performance of these materials and suggested possible uses in construction. Ramezani et al. (2022) reviewed the progress and pointed out ongoing challenges in their practical use.

Work has also been done to study how these composites behave under pressure and how their internal structure changes with the addition of nanotubes [13–16]. Manzur et al. [17] studied the use of carbon nanotube-reinforced cement as a repair material, suggesting its usefulness in extending the life of concrete structures. Konsta-Gdoutos et al. [18] emphasized the need for even dispersion of the nanotubes, since clumping reduces their ability to reinforce the material. Parveen et al. [19] introduced a method to improve nanotube distribution, which helped both internal structure and strength. The effect of nanotube size has also been studied in depth. Manzur et al. [20] showed that different nanotube sizes change compressive strength significantly. Luo et al. [21] studied how these composites are made and how they respond to cracking. Manzur and Yazdani [22] explored the impact of various parameters, including the concentration of nanotubes and how they are dispersed, and found that these factors had a noticeable effect on the results. Fakhim et al. [23] worked on how to prepare the material and improve its internal structure using multiwalled carbon nanotubes. Guan et al. [24] looked into how these composites perform under early-age freezing conditions, focusing on both structure and strength. Huang et al. [25] studied how curing time affects the compressive and flexural strength of these materials.

Previously, while many experimental studies have been done on the behavior of structures and materials, various numerical investigations have also been conducted [26–29]. In this regards, recent numerical work on CNT composites has looked at how machine learning can support the study of carbon nanotube-reinforced cement composites. Bagherzadeh and Shafighfard [30] and Li et al. [31] used ensemble-based machine learning models to assess material characteristics. Talayero et al. [32] carried out both computer-based predictions and lab testing to study the strength of these composites. Adel et al. [33] used machine learning models that are easier to interpret and applied them to predict mechanical behavior. Kalogeris et al. [34] applied optimization methods to improve how these materials perform in structural settings. Although many of these studies offer detailed findings on different aspects of carbon nanotube-reinforced cement composites, there is still a lack of work that looks at how several variables together influence strength, especially with the support of large datasets. Most existing studies focus on only a few inputs or study a limited range of conditions. There is also not enough use of data analysis tools that can test several factors at once and explain how much each one matters.

This study addresses that issue by testing four main factors: the machine learning model used, the data preprocessing method, and the effect of constituent materials on both compressive and flexural strength. This is because, in structural design, compressive strength determines axial load capacity, while flexural strength dictates bending and crack resistance. Hence, both these properties are fundamental for durability and safety in concrete elements. The investigated features are studied on two levels, globally through feature importance which quantifies each input’s contribution to predictive performance, and locally through partial dependence analysis which allows depicting the marginal effect of one feature on the model output. To carry this out, a total of ninety-nine model combinations are tested. These include eleven machine learning algorithms and nine different data preprocessing techniques. Each model is fine-tuned, and results are compared. The goal is to find out which inputs matter most and how they influence the predicted strength. This work offers a detailed look at how various factors affect the strength of carbon nanotube-reinforced cement composites. Accordingly, the contributions of this study include a systematic comparison of nine data-preprocessing methods and a comprehensive evaluation of eleven machine-learning algorithms, which is an area that has not previously been explored in carbon nanotube-reinforced cement composite research.

2  Materials and Method

2.1 Investigated Parameters and Developed Database

The dataset utilized in this study includes experimental results that were obtained from Huang et al. [2]. This dataset was subjected to quality screening where outliers were identified via the interquartile range method (representing less than 2% of observations) and removed. In general, the dataset includes 114 distinct mixtures each tested for compression and flexure. It encompasses wide and diverse mixtures spanning cement types 1–2, water/cement ratios of 0.20–0.50, CNT contents of 0–0.80 wt%, tube diameters from 4–60 nm, lengths of 1–250 μm, and curing times of 3–28 days, providing a broad basis for robust model training and sensitivity analysis. Table 1 details the descriptive statistics for the selected data. Furthermore, Fig. 1 depicts the correlation analysis between the input variables and the outputs of the dataset. Besides, the strengths’ distributions were examined as shown in Fig. 2.

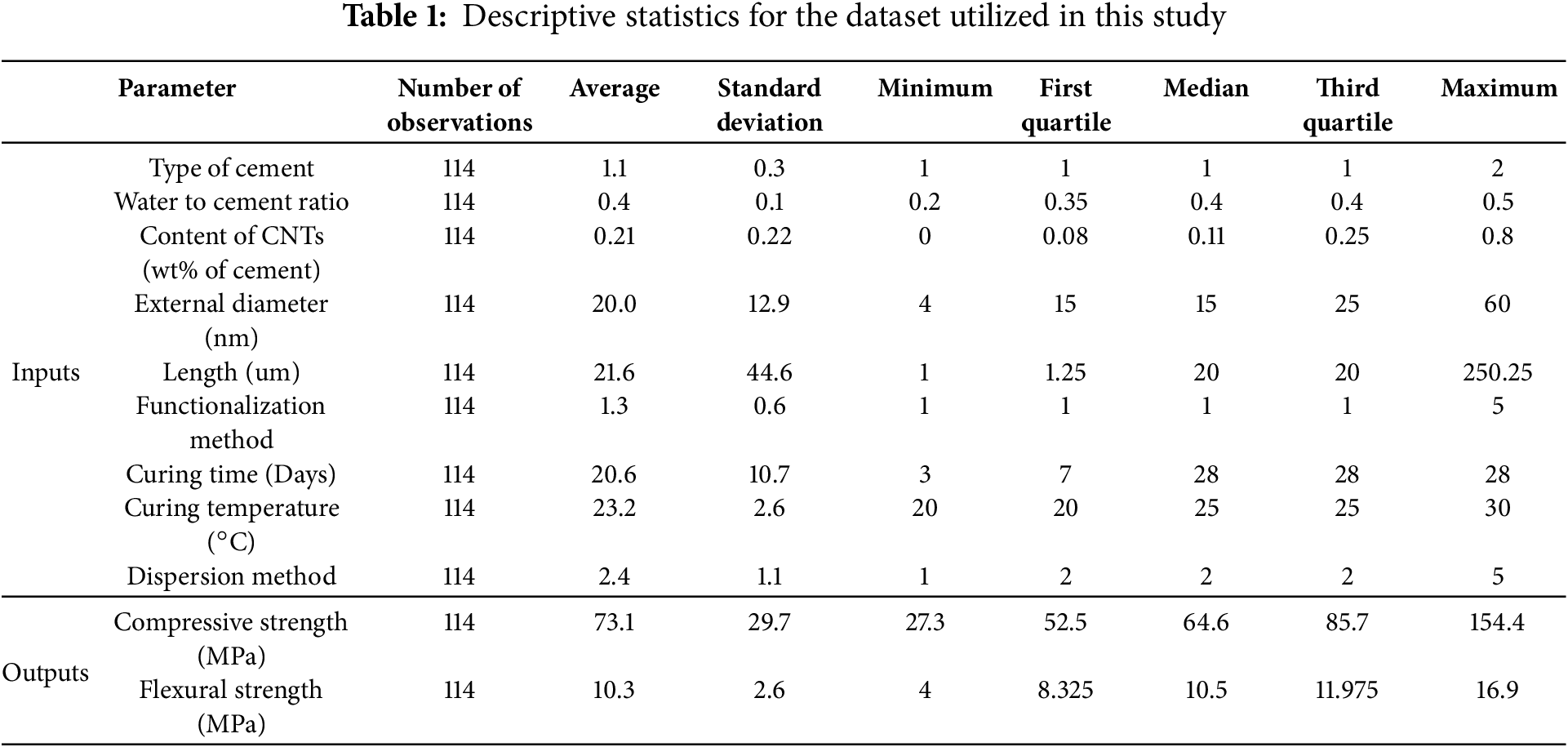
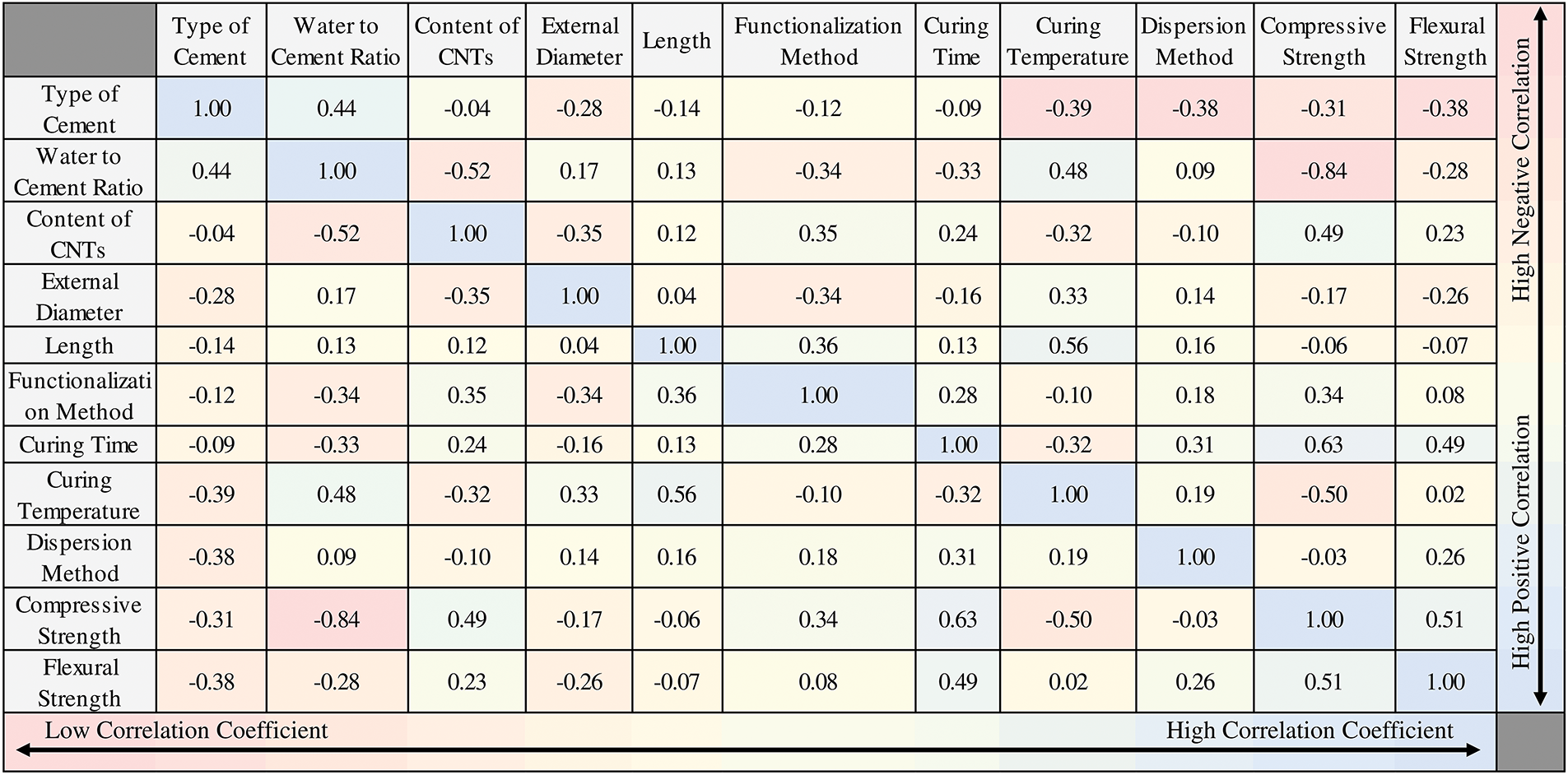
Figure 1: Features-features and features-outputs pair-wise statistical correlation

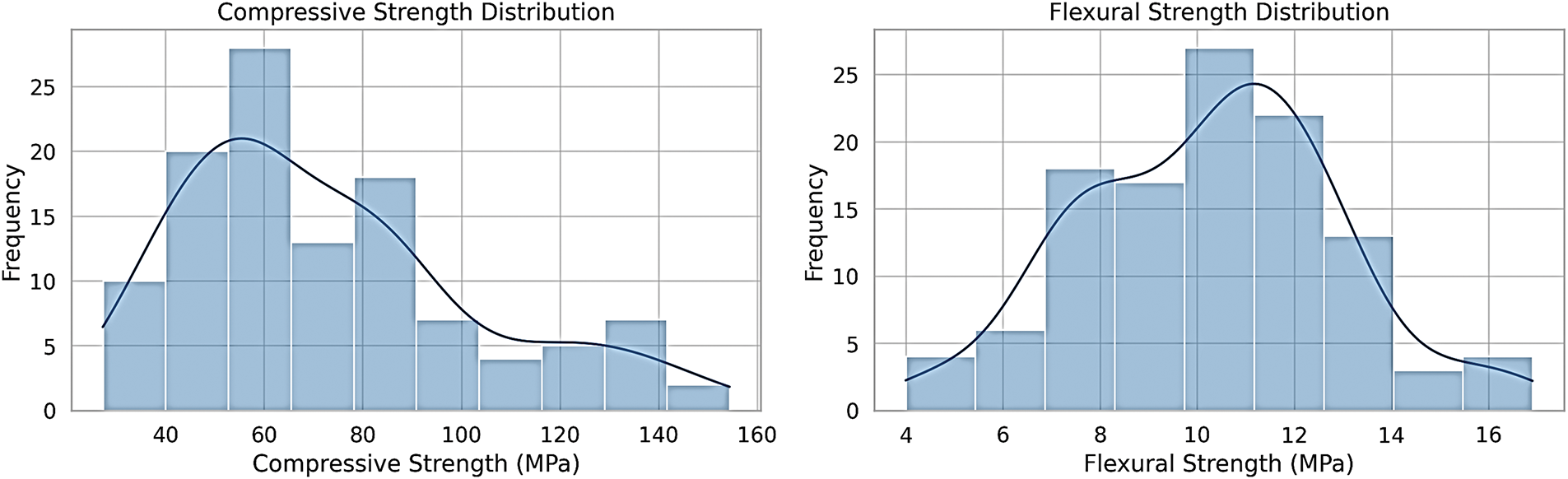
Figure 2: Distribution of the strengths in the collected database

2.2 Regression Models

Machine learning models are indispensable in the data analysis and predictive modeling of construction materials [35–39]. Each method comes with its own characteristics, robustness, and practical applications. Accordingly, eleven algorithms were selected in this study to represent three complementary paradigms: (1) linear models, which offer interpretable baselines and address multicollinearity; (2) tree-based methods, capable of capturing complex nonlinear interactions with minimal preprocessing; and (3) ensemble boosters, which achieve high accuracy by sequentially correcting errors through gradient or adaptive boosting.

Multiple linear regression (MLR) is a fundamental way for correlating a single dependent variable with multiple independent variables [40]. This model is particularly significant in interdisciplinary studies where the variables are interdependent. Tranmer and Elliot [41] highlight its applicability, mathematically represented as given in Eq. (1).

Y=βX+ε(1)

where Y=[y1,…,yn]T is the output; X=[x1,1…x1,k⋮⋱⋮xn,k…xn,k] is the input matrix for n observations and k inputs; β=[β1,…,βk]T represents the coefficients to be estimated; ε=[ε1,…,εk]T represents the random errors.

The ordinary least squares estimator is expressed as follows:

β=(XTX)−1XTY(2)

Having established the baseline with multiple linear regression, the next step is to incorporate penalization to address multicollinearity and overfitting via Ridge, Lasso, and ElasticNet. In general, the Ridge regression modifies MLR by adding a regularization term to the loss function, aimed at controlling model complexity. McDonald [42] notes that this approach effectively addresses multicollinearity and improves predictive accuracy by shrinking the regression coefficients. The ridge estimator is given by:

β^∗=(XTX+αIp)−1XTY(3)

where β^∗ is the ridge estimator; α>0 is the complexity parameter that controls the amount of shrinkage and ensures that E[(β^∗−β)T(β^∗−β)]<E[(β^−β)T(β^−β)]; Ip is the identity matrix.

Ridge regression optimizes a penalized residual sum of squares using the ℓ2 regularization norm:

minβ=‖βX−y‖22+α‖β‖22(4)

Lasso regression extends ridge regression by allowing some coefficients to be reduced to zero, facilitating variable selection. This is particularly useful in high-dimensional datasets to avoid overfitting and enhance interpretability. The optimization criterion is:

minβ=12nsamples‖βX−y‖22+α‖β‖1(5)

ElasticNet regression, described by Zou and Hastie [43], combines the penalties of both ridge and lasso regressions into a single framework, balancing variable selection and multicollinearity correction. It is particularly effective in datasets with high predictor correlations or more predictors than observations. The objective function is:

minβ=12nsamples‖βX−y‖22+αρ‖β‖1+α(1−ρ)2‖β‖22(6)

where ρ is a parameter that is utilized to control the convex combination of ℓ1 and ℓ2.

Bayesian ridge regression applies a probabilistic approach by imposing a prior distribution on the coefficients, which is beneficial under uncertainty [44,45]. The Bayesian framework allows for coefficient estimation in uncertain conditions:

P(β,Σε|Y,X)∝P(Y|X,β,Σε)P(β,Σε)(7)

Bedoui and Lazar [46] enhanced this model with an empirical Bayesian approach and a ridge penalty:

min(‖βX−Y‖22+α‖β‖22)(8)

Indeed, a common method nowadays to capture nonlinear relationships and interactions without explicit feature engineering is to employ tree-based algorithms. Decision trees (DTs) offer a non-parametric method for segmenting data based on specific decision criteria, emulating human decision logic [47]. When assessing stiffness modifiers, DTs highlight the relative importance of various factors hierarchically. The DT model splits the dataset recursively, assigning a basic mathematical model to each segment and organizing them into a tree structure [48]. The dataset Qm for node m with Nm samples are split into:

Qmleft(θ)={(x,y)|xi≤tm}(9)

Qmright(θ)=Qm/Qmleft(θ)(10)

The quality of each split is assessed using a loss function H():

G(Qm,θ)=NmleftNmH(Qmleft(θ))+NmrightNmH(Qmright(θ))(11)

The optimal split parameters θ∗ are chosen to minimize the loss function:

θ∗=argminθG(Qm,θ)(12)

Random forest (RF) models improve upon decision trees by aggregating multiple trees and synthesizing their outcomes [49]. RF mitigates overfitting by using numerous tree predictors, each based on randomly selected variables. The ensemble of trees enhances prediction reliability and precision:

m^(x)=1M∑jm^j(x)(13)

where M denotes the ensemble’s total tree count; m^j represents the prediction from an individual tree within the ensemble.

Extremely randomized trees (ERT), or Extra Trees, introduce more randomness in node splits than RF models [50]. This method randomly selects cut points, capturing unpredictable patterns and reducing model variance, though it may slightly increase bias.

Adaptive boosting (AB) combines several simple learners to create a more accurate composite model [51]. AB iteratively adjusts new trees to focus on misclassified data points, enhancing accuracy on complex datasets. The initial estimator f(x) ais trained on the dataset, and subsequent models adjust weights based on prior errors. The composite model H(x) is defined as:

H(x)=v∑k=1N(ln1αk)g(x)(14)

where v represents the learning rate; αk denotes the significance attributed to each weak learner, determined as per Eq. (15); g(x) signifies the median output across all αkfk(x).

αk=ei1−ei(15)

Gradient boosting (GB) builds trees sequentially, with each tree correcting the errors of its predecessor using gradient descent. GB is valuable for handling complex data structures and nonlinear variable interactions. The GB model’s forecasted output is:

y^i=FM(xi)=∑m=1Mhm(xi)(16)

where M represents the aggregate number of estimators; hm is a singular weak learner. The architecture of the GB model leverages a greedy algorithm, as given in Eq. (17).

Fm(x)=Fm−1(x)+argminh∈H∑i=1nL[yi,Fm−1(xi)+h(xi)](17)

where h(x) symbolizes the foundational estimator; L(⋅) denotes the loss function, with its negative gradient presented in Eq. (18).

gm=−∂L[y,Fm−1(x)]∂Fm−1(x)(18)

Extreme gradient boosting (XGB) is an advanced, scalable approach that enhances decision trees with thorough regularization, reducing overfitting. XGB is adept at managing diverse data types and distributions, making it effective for predicting stiffness modifiers and understanding variable interactions. The objective function is:

Obj=∑i=1nL[y^i,yi)]+∑i=1nω(ft)(19)

where L(⋅) signifies the model’s loss function, focusing on model bias reduction; ω represents a regularization parameter intended to curb the model’s complexity.

2.3 Data Preprocessing Models

Indeed, there are many ways to preprocess data that can help make regression models more accurate and easier to understand [52,53]. This section explains various common methods. Each method works well in different situations based on the type of data and the model being used.

Standardization adjusts the data so that it has a mean of zero and a standard deviation of one. This is helpful when features are measured in different units or have different ranges. Bringing everything to a similar scale can improve how well some algorithms work, especially ones like logistic regression and support vector machines that assume data is normally distributed.

Normalization changes the scale of the data so that each feature falls between 0 and 1 [54]. It is especially helpful for models that are sensitive to the size of the input values, such as neural networks and k-nearest neighbors. This keeps any single feature from having too much influence just because of its larger range.

Discretization turns continuous values into categories by splitting the range into intervals. This can be helpful when converting numbers into groups, especially when trying to model patterns that are easier to capture with categories rather than continuous values.

Polynomial feature creation involves adding new features by raising existing variables to powers or multiplying them together. This helps when the relationship between the inputs and the output is not linear. Adding squared or interaction terms allows the model to pick up on more complex patterns. But it also increases the number of features, which can lead to overfitting. Regularization is often used to manage this.

Principal component analysis (PCA) reduces the number of features while keeping most of the useful information [55,56]. It does this by creating new variables that are combinations of the originals and that explain as much of the variation in the data as possible [57,58]. PCA can make models simpler and reduce the chance of overfitting by cutting down on the number of features.

Kernel PCA is a variation of PCA that works better with nonlinear data [59]. It first transforms the data using a kernel function and then applies PCA. This approach can reveal useful patterns in data where simple PCA falls short.

Backward elimination starts with all features in the model and removes the least useful ones step by step [60]. This keeps the model from becoming too complex while still aiming for good prediction results. It works well when there are many variables and some of them are strongly related to each other.

Forward selection does the opposite. It begins with no features and adds the most useful ones one by one. The process stops when adding more features no longer improves the model. This is a good choice when there are many possible inputs and testing every combination would take too much time.

2.4 Model Development Approach

As noted earlier, a broad set of machine learning models and data processing methods was applied to find the most effective way to estimate the properties of concrete reinforced with carbon nanotubes. The study followed a clear and structured approach to develop and adjust predictive models based on the given data. The process began by loading the dataset and splitting it into training and testing portions, with 70% of the data used for training and 30% reserved for testing. Several data preparation techniques were used, including standardization, normalization, discretization, and generating polynomial features, as previously outlined. This setup helped check whether the models could produce reliable predictions on new data, which is essential given the uncertainty often present in numerical modeling [61–63]. A range of regression models was used, including multiple linear regression, ridge regression, and lasso regression, all within a supervised learning setup. Model parameters were tuned using grid search, which tested different configurations to identify the best-performing ones. The models were judged using several evaluation measures: the correlation coefficient (R), normalized root mean square error (NRMSE), and normalized mean absolute error (NMAE). These measures helped identify which models gave the most accurate predictions under various preprocessing settings. Results were reviewed for both training and testing sets, and the predicted values were compared with actual ones through visual plots. The full process was outlined in the pseudo-code shown in Fig. 3.

Figure 3: Pseudocode for the developed machine learning models

2.5 Sensitivity Analyses Using Machine Learning

Feature importance and partial dependence are useful tools for understanding how each input affects the model’s predictions. Feature importance measures how much a feature adds to the model’s ability to make good predictions. For example, in models based on decision trees, this can be calculated by checking how much a feature helps reduce impurity, like Gini or entropy, across all the trees. This kind of analysis makes it easier to see which features the model depends on the most. It helps to narrow down the variables that really matter in the prediction process. Partial dependence plots show how changing the value of one feature affects the prediction, while keeping everything else the same. The model’s predictions are averaged across all values of the other features. These plots reveal whether a feature has a simple or more complex relationship with the predicted output. They are especially helpful when trying to understand how a model reacts to different values of a feature. Looking at these plots gives a clearer picture of what drives the model’s decisions, and can help make better choices based on its predictions.

3  Concrete Properties Estimation Using Machine Learning

3.1 Compressive Strength

This study used machine learning models to improve how well the compressive strength of carbon nanotube-reinforced cement composites could be predicted. Fig. 4 illustrates the performance assessment of the developed models, which include 99 combinations of 11 machine learning algorithms and 9 data preprocessing techniques. The metrics used for evaluation were the R coefficient, NRMSE, NMAE, and A10 score.

Figure 4: Performance assessment of the investigated models developed for predicting the compressive strength of concrete with CNTs

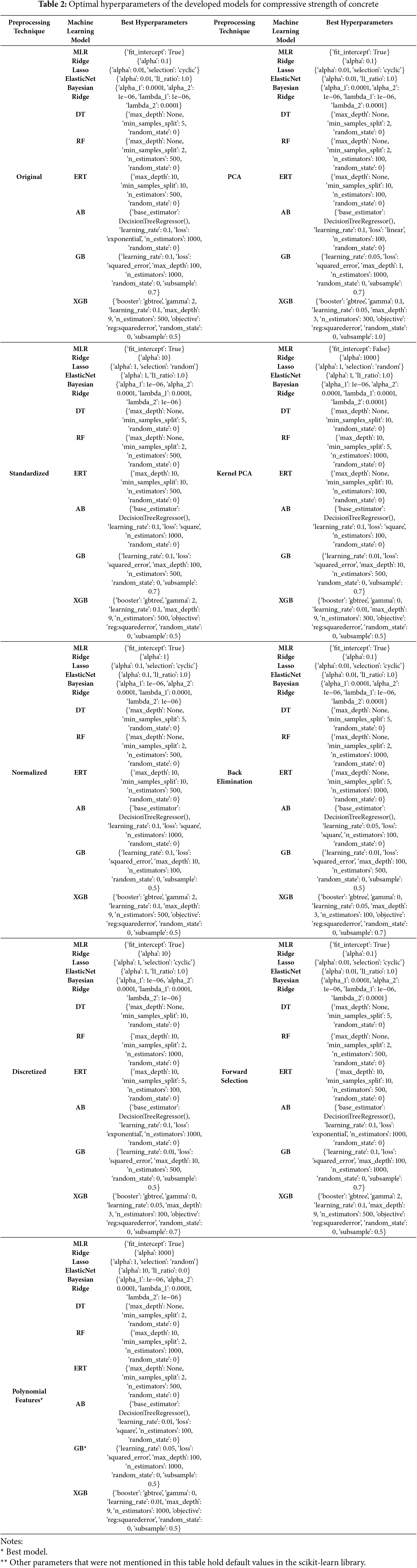
The GB model combined with polynomial features was considered the best-performing model, achieving an R value of 95%, an NRMSE of 9%, an NMAE of 5%, and an A10 score of 77%. In contrast, the Ridge model with polynomial features yielded the worst results, with an R value of 85%, an NRMSE of 15%, an NMAE of 12%, and an A10 score of 23%. Among the models without data preprocessing, the RF model performed the best, underscoring the significant role of appropriate data preprocessing in enhancing model accuracy. Fig. 5 benchmarks these machine learning models against the Original + MLR case, representing the simplest form of prediction. The use of advanced machine learning models significantly improved estimation performance. For training cases, the optimal model (GB with polynomial features) improved the R value by 9%, reduced the NRMSE by 75%, lowered the NMAE by 100%, and increased the A10 score by 93% compared to the Original + MLR case. For testing cases, the improvements were also substantial, with a 1% increase in R value, a 6% decrease in NRMSE, a 24% reduction in NMAE, and a 69% increase in the A10 score. These findings justify the use of advanced machine learning models for predicting the compressive strength of CNT-reinforced concrete. The scatter and residual plots in Fig. 6 further illustrate the superiority of the optimal model. The plots compare the predicted vs. actual values and the residuals for both the Original + MLR case and the optimal Gradient Boosting with polynomial features case. The optimal model demonstrates less scatter and a closer alignment with the equality line in the predicted vs. actual plot, as well as more centralized residuals around the zero line, indicating better prediction accuracy and consistency. Table 2 provides the optimal hyperparameters for the developed models, derived through a 10-fold grid search cross-validation process. This comprehensive optimization ensured that the models achieved their best possible performance given the data and the chosen algorithms.

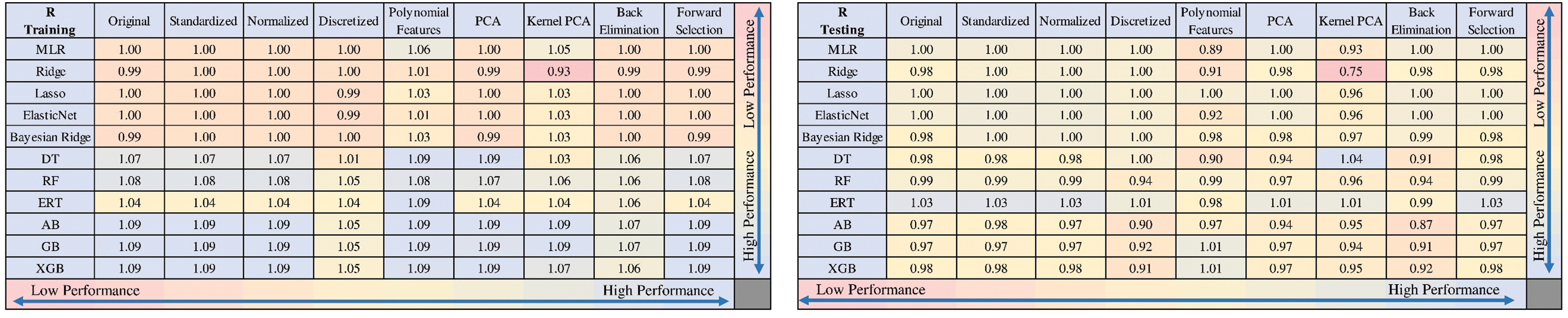
Figure 5: Benchmarking the developed models for predicting the compressive strength of CNT-reinforced concrete against the Original + MLR case

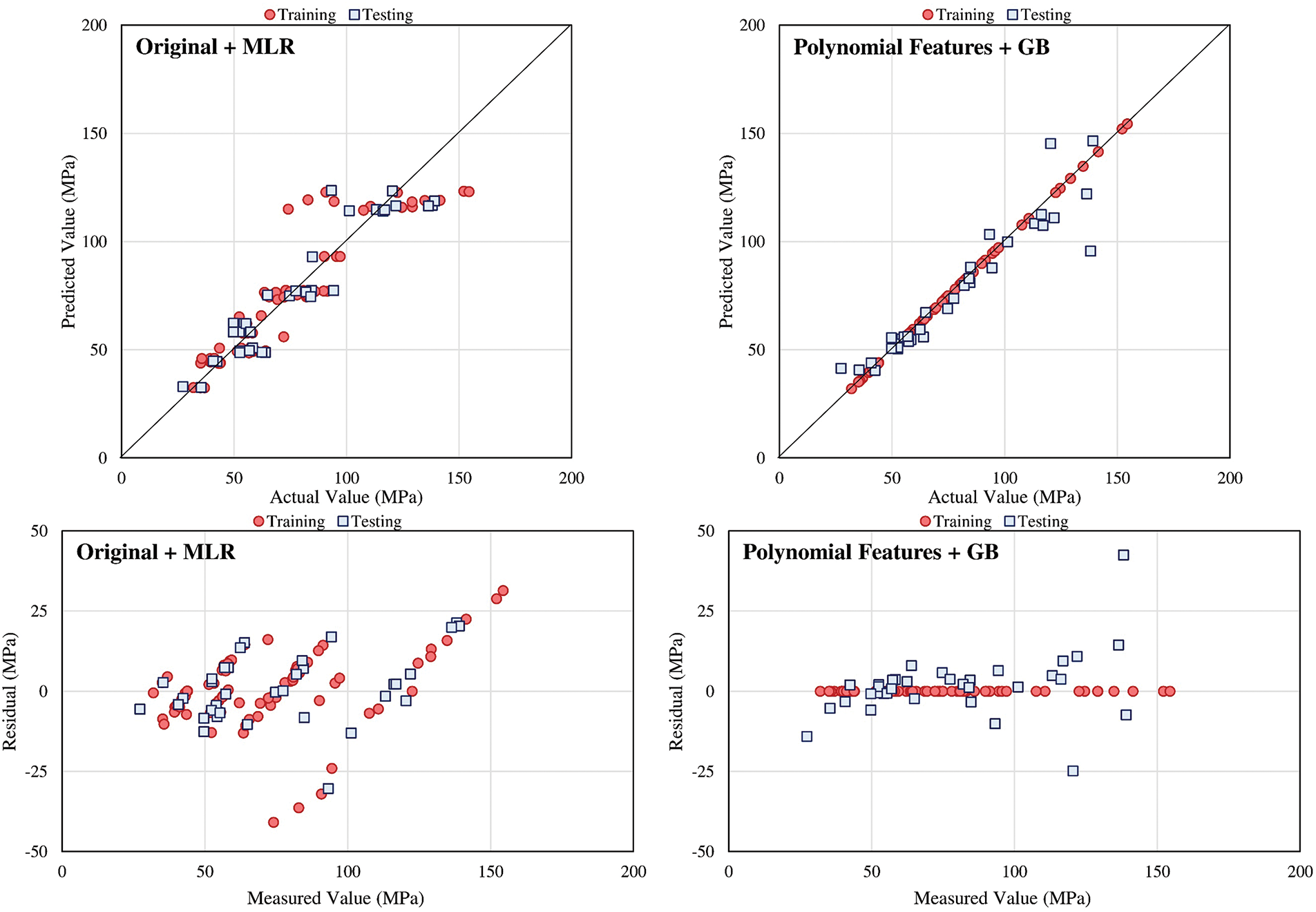
Figure 6: Scatter and residual plots of the best case for estimating the compressive strength of concrete with CNTs against the Original + MLR case

3.2 Flexural Strength

Similar methods were applied in predicting the flexural strength of cement composites containing carbon nanotubes. Fig. 7 displays the performance assessment of the 99 model combinations. The ERT model with PCA preprocessing was the best-performing combination, achieving an R value of 89%, an NRMSE of 10%, an NMAE of 6%, and an A10 score of 69%. Conversely, the MLR model combined with kernel PCA preprocessing performed the worst, with an R value of 74%, an NRMSE of 80%, an NMAE of 78%, and an A10 score of 0%. The best model without data preprocessing was once again the Random Forest model.

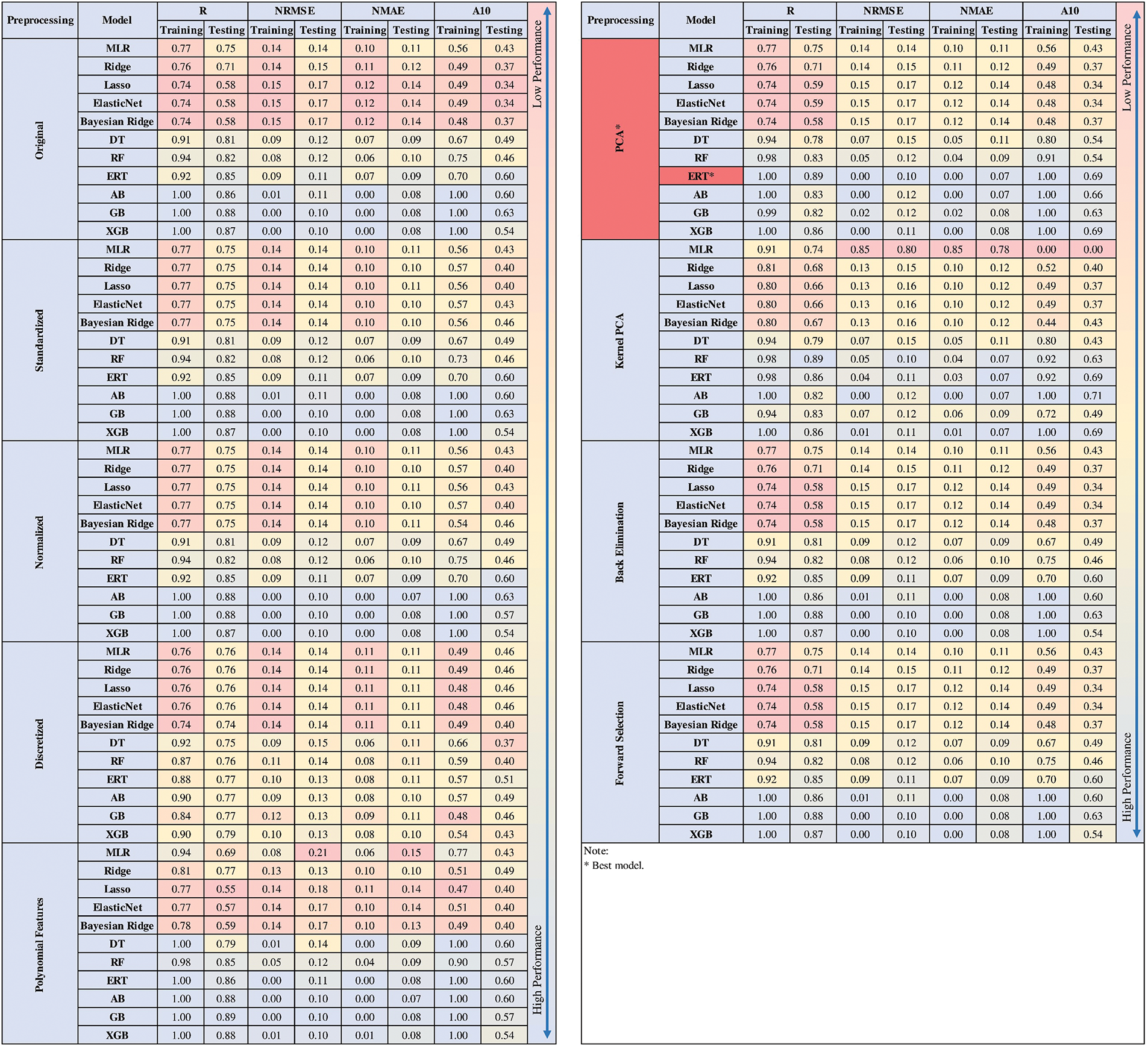
Figure 7: Performance of the models developed for estimating the flexural strength of concrete with CNTs

Fig. 8 benchmarks these models against the Original + MLR case. The advanced machine learning models significantly enhanced the prediction accuracy for flexural strength as well. The optimal ERT with the PCA model showed improvements in the R value by 29%, NRMSE by 100%, NMAE by 100%, and A10 score by 80% for training cases. For testing cases, the improvements were 18% in R value, 30% in NRMSE, 34% in NMAE, and 60% in A10 score compared to the Original + MLR case. These improvements highlight the efficacy of advanced machine learning techniques in accurately predicting the flexural strength of CNT-reinforced concrete.

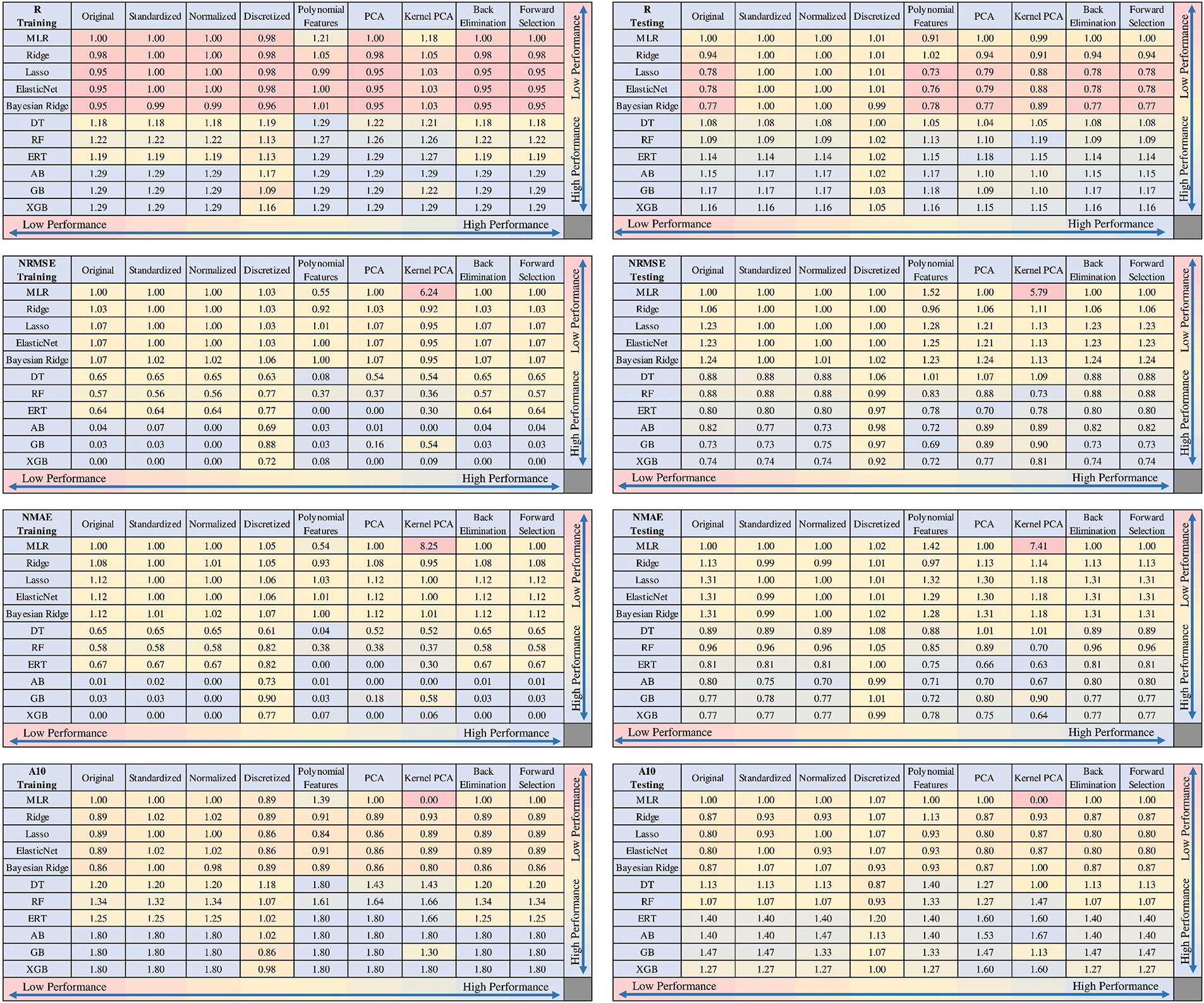
Figure 8: Benchmarking the models for estimating the flexural strength of CNT-reinforced concrete against the Original + MLR case

Fig. 9 presents the scatter and residual plots for the best model compared to the Original + MLR case. The optimal ERT with the PCA model shows less scatter and a closer fit to the equality line in the predicted vs. actual plot, as well as more centralized residuals around the zero line, indicating superior prediction accuracy and reliability. Table 3 details the optimal hyperparameters for the models predicting flexural strength, obtained through an extensive 10-fold grid search cross-validation process.

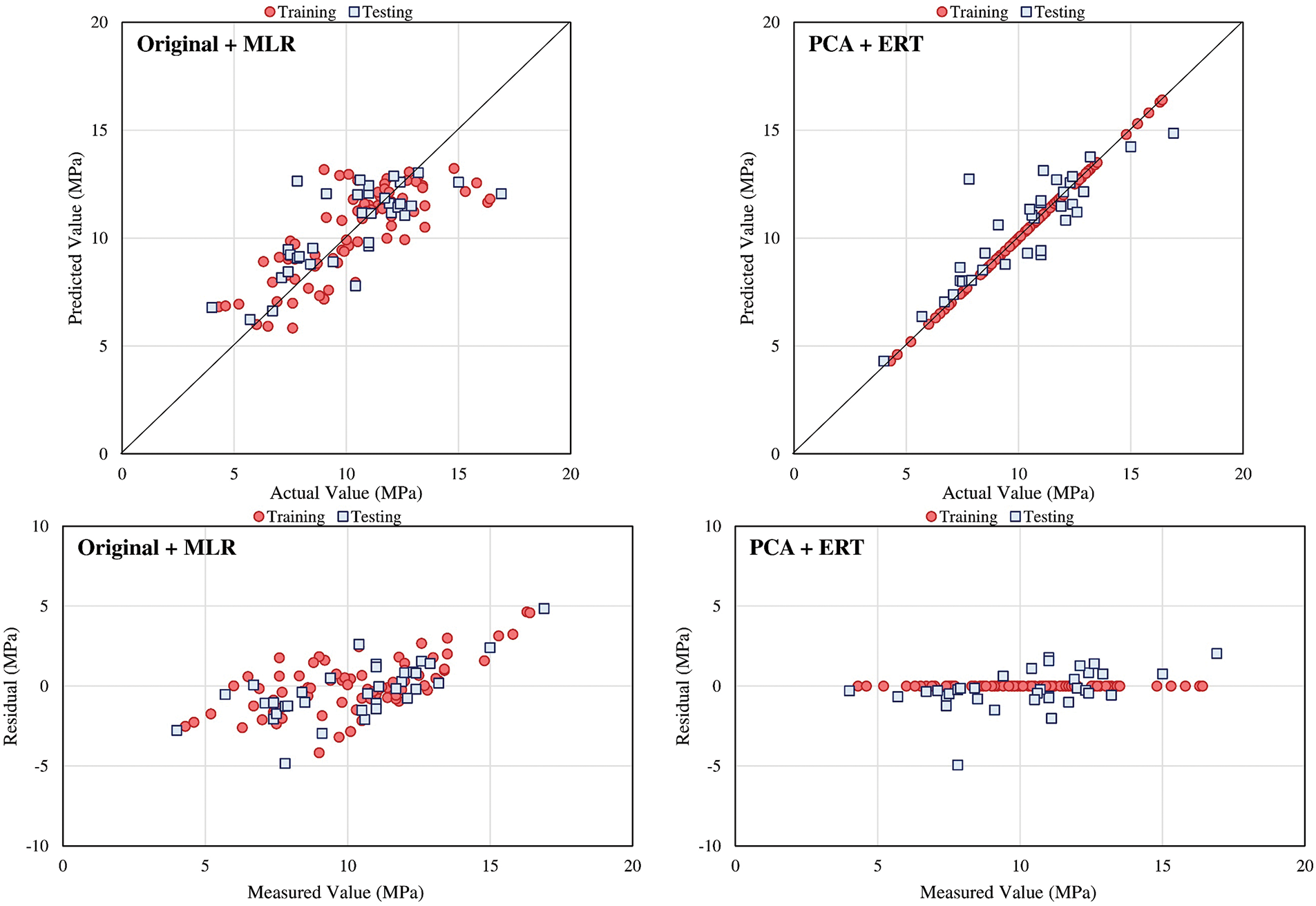
Figure 9: Scatter and residual plots of the best case for estimating the flexural strength of concrete with CNTs against the Original + MLR case

4  Machine Learning-Based Sensitivity Analysis

The sensitivity analysis based on machine learning was carried out to determine which factors most strongly affect the strengths of cement composites reinforced with carbon nanotubes in compression and flexure. This analysis relied on the top-performing machine learning models trained on the raw data, which helped maintain the original relationships among the variables and supported reliable evaluation. The decision tree model was used for compressive strength, while the gradient boosting model was chosen for flexural strength, as both showed the highest performance scores when compared to other configurations that included data preprocessing. The reasoning behind this approach stems from the fact that pairing a model with a preprocessing method can result in an opaque system, where the path from input to output becomes difficult to trace or explain. For compressive strength, the feature importance results shown in Fig. 10 indicate that the water-to-cement ratio plays the most dominant role, contributing 69.84% of the total influence. This outcome supports established theory, as the water-to-cement ratio has long been recognized as a central factor in determining how strong concrete becomes. When this ratio is lower, it typically results in higher compressive strength, as the reduced amount of water leads to less porosity and better bonding among cement particles. Curing time also showed a strong influence, with a contribution of 14.08%, as it directly affects the cement hydration process, which controls how strength develops as the material sets. The presence of CNTs, contributing 6.48% to the feature importance, further enhances the compressive strength by providing additional reinforcement and improving the composite’s microstructure.

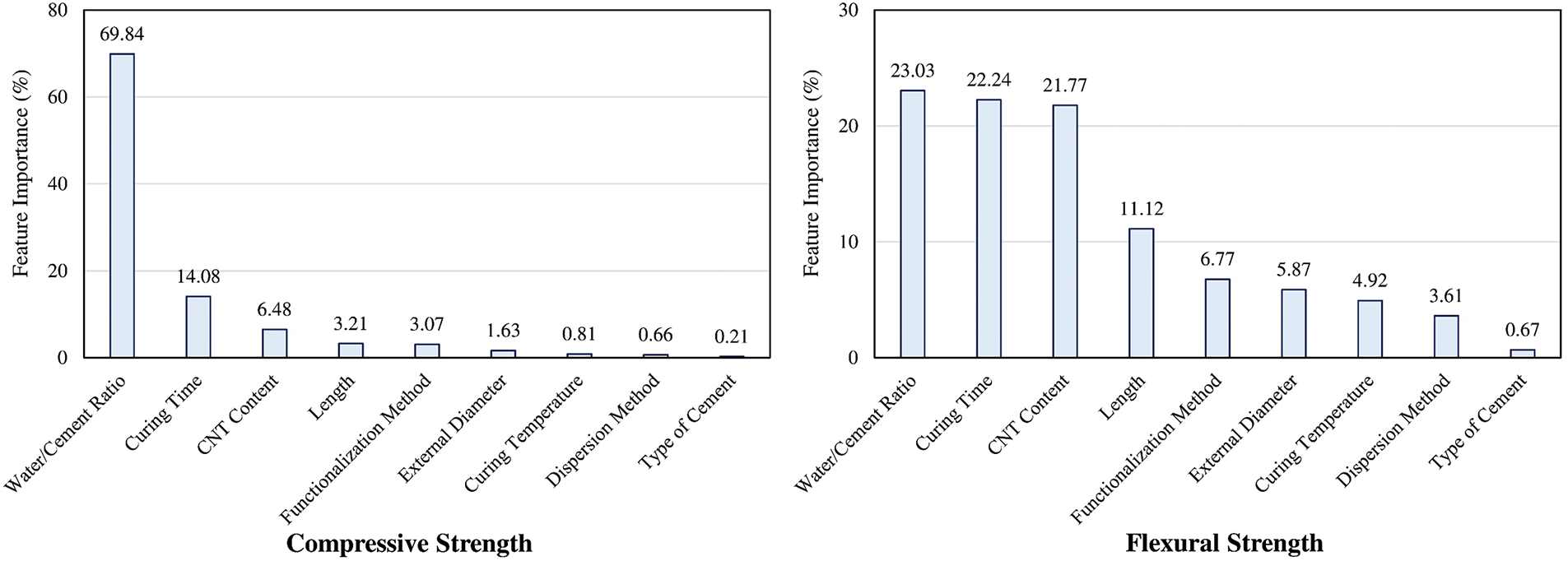
Figure 10: Feature importance analysis for the compressive and flexural strength cases

The partial dependence plots in Fig. 11 further elucidate the impact of these parameters. The plot for the water/cement ratio shows a clear negative correlation with compressive strength, confirming that a lower ratio results in higher strength. The CNT content plot indicates that an optimal range of CNT concentration exists, beyond which the benefits plateau or even diminish, likely due to agglomeration issues that can negatively affect the composite’s uniformity. The curing time plot demonstrates a positive correlation, with strength increasing significantly up to a certain period, beyond which the gains are marginal.

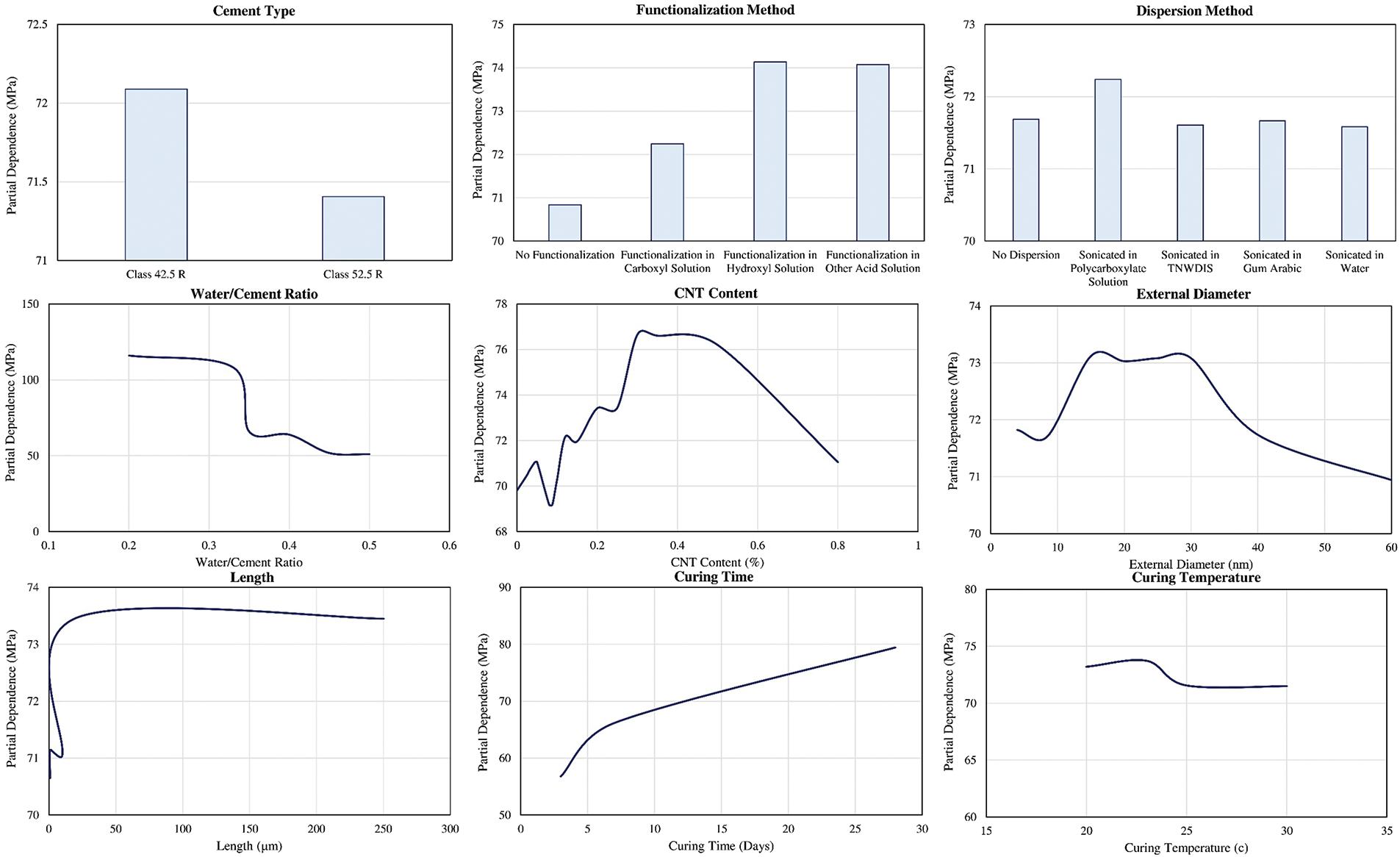
Figure 11: Partial dependence plots for the compressive strength of concrete

For flexural strength, the feature importance analysis in Fig. 9 reveals a more balanced distribution among the top factors. The water/cement ratio (23.03%), curing time (22.24%), and CNT content (21.77%) are nearly equally influential. This balanced importance suggests that flexural strength is affected by a combination of factors, each contributing significantly to the overall performance. The theoretical basis for these findings lies in the nature of flexural strength, which is sensitive to both the composite’s ductility and the quality of the cement matrix. The partial dependence plots in Fig. 12 provide further insights. The water/cement ratio plot indicates a nonlinear relationship with flexural strength, where both very high and very low ratios can be detrimental. This observation can be attributed to the dual requirement of adequate hydration and maintaining structural integrity, which are critical for flexural performance. The CNT content plot highlights the importance of achieving a uniform dispersion of CNTs, as higher concentrations can enhance the composite’s toughness and crack resistance, but only if the dispersion is adequate. The curing time plot, similar to compressive strength, shows that prolonged curing enhances flexural strength, emphasizing the role of complete hydration and internal curing in developing flexural properties. The sensitivity analysis also reveals interesting contrasts between the factors influencing strengths. While the water/cement ratio and curing time are significant for both properties, their relative importance and the nature of their influence differ. For compressive strength, the water/cement ratio has an overwhelming impact, overshadowing other factors. In contrast, for flexural strength, multiple factors contribute more evenly, reflecting the complex interplay between ductility, toughness, and matrix quality. The role of CNTs is another area where differences are observed. In compressive strength, CNT content is moderately important, suggesting that while CNTs enhance strength, other factors like the water/cement ratio and curing time are more critical. For flexural strength, CNT content is nearly as important as the water/cement ratio and curing time, highlighting the significant role of CNTs in enhancing the toughness and crack resistance of the composite. Therefore, these results have reflected theoretical and practical implications. From a theoretical perspective, the findings confirm the critical roles of water/cement ratio and curing time in determining the mechanical properties of cement composites. The importance of CNT content, especially for flexural strength, highlights the potential of nanomaterials to enhance composite performance. The nonlinear relationships observed in the partial dependence plots align with the complex nature of composite materials, where optimal ranges exist for various parameters. Practically, these insights can guide the design and optimization of CNT-reinforced cement composites. For instance, optimizing the water/cement ratio and curing conditions can significantly enhance both strengths. Additionally, achieving uniform CNT dispersion is crucial for realizing the full benefits of CNT reinforcement. These findings can inform guidelines for mix design, curing protocols, and quality control in the production of advanced cement composites. The feature importance analysis provides specific recommendations for optimizing the properties of CNT-reinforced cement composites. For compressive strength, it is recommended to focus on maintaining a low water/cement ratio, ensuring adequate curing time, and optimizing CNT content within a specific range. These factors are paramount in achieving high compressive strength. For flexural strength, a balanced approach is necessary, considering the water/cement ratio, curing time, and CNT content collectively to enhance toughness and crack resistance. The detailed partial dependence plots offer further practical insights. For instance, the optimal water/cement ratio for compressive strength is around 0.2 to 0.3, beyond which the benefits diminish. Similarly, for flexural strength, maintaining the water/cement ratio within a moderate range (0.3 to 0.4) is crucial. For CNT content, an optimal range is identified, typically around 0.025 to 0.05 wt%, beyond which agglomeration can negatively impact the composite’s performance.

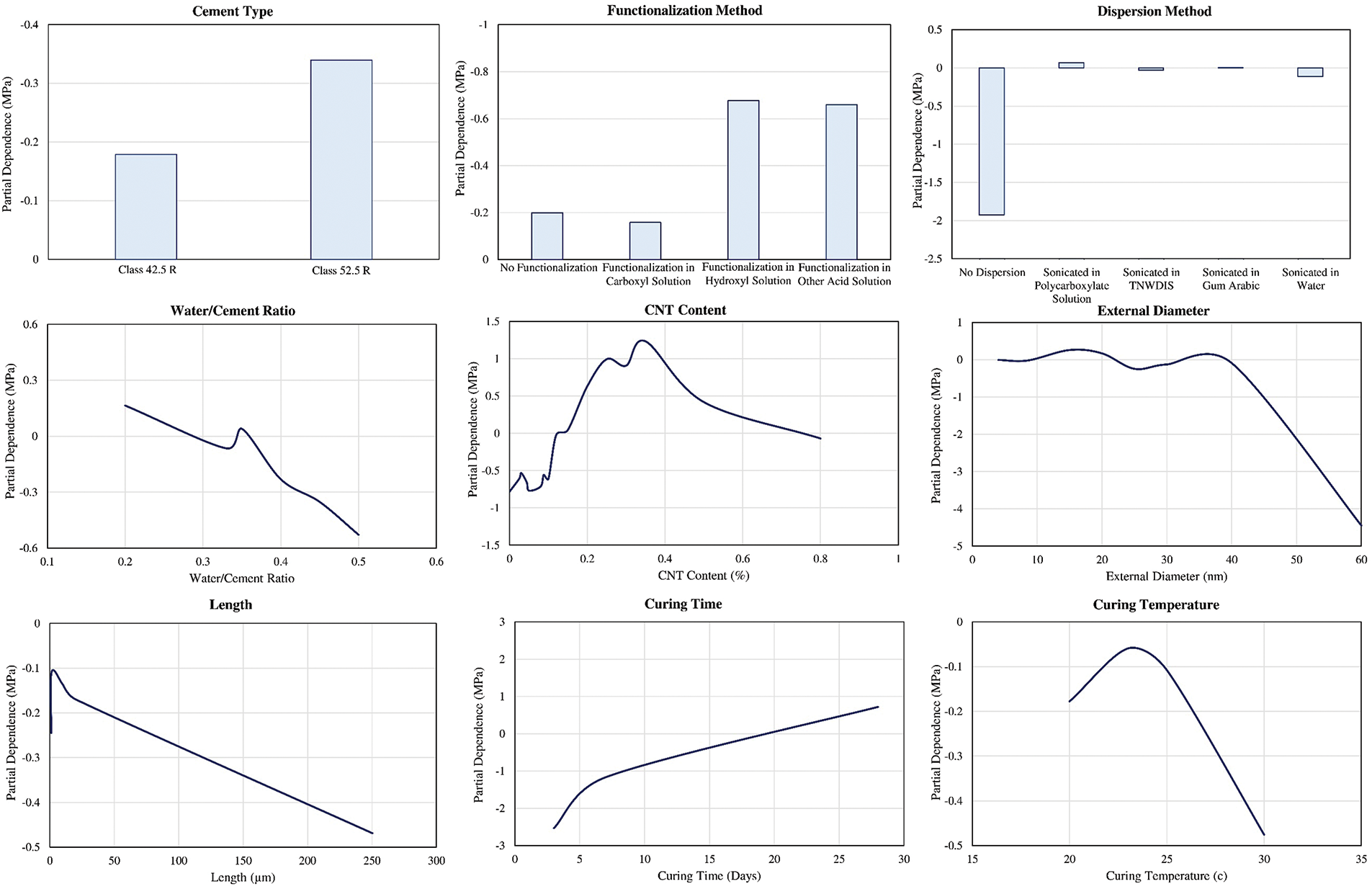
Figure 12: Partial dependence plots for the flexural strength of concrete

Indeed, existing literature confirms some of the results observed in this sensitivity analysis. For instance, Kim et al. [64] observed a drop in the strengths of concrete with the increase in the water to cement ratio. Adhikary et al. [65] discussed an increasing and then dressing trend in the effect of CNT content on the strengths of the composite. This trend was confirmed experimentally by Vesmawala et al. [66] with a value of 0.4% being the optimum for the compressive strength of concrete, which is similar to the results obtained in this study. Kang et al. [67] reported a very similar trend to the one obtained in this study for the relation between the curing time and the compressive strength of the composite mixture. These observations confirm the consistency of the results obtained in this study with the existing literature.

5  Conclusion

This study focused on closing the current gap in understanding how different factors influence the strength of cement composites reinforced with carbon nanotubes. Although many studies have been carried out in this area, most have not examined these materials using large datasets, which are better suited for capturing the full range of variable interactions. This work applied machine learning to run a sensitivity analysis, aiming to improve prediction of mechanical properties while also identifying which parameters have the strongest effect. The models developed in this process were chosen based on performance and consistency, allowing for more dependable results. The findings help clarify which factors matter most when designing these composites for structural use. This kind of understanding supports more reliable design practices for construction materials made with carbon nanotubes. The main outcomes of this study are listed below:

1.    For predicting compressive strength, the GB model combined with polynomial features provided the best estimation results, achieving an R value of 95%, an NRMSE of 9%, an NMAE of 5%, and an A10 score of 77%. This model significantly outperformed others by accurately capturing the complex interactions within the data.

2.    For predicting flexural strength, the ERT model with PCA preprocessing yielded the best results, with an R value of 89%, an NRMSE of 10%, an NMAE of 6%, and an A10 score of 69%. This combination effectively leveraged the benefits of dimensionality reduction and robust ensemble learning to enhance prediction accuracy.

3.    The water-to-cement ratio emerged as the most significant factor influencing both strengths. For compressive strength, a lower ratio led to higher strength due to reduced porosity and improved bonding. For flexural strength, a moderate ratio was crucial, balancing adequate hydration with structural integrity.

4.    Curing time significantly impacted both strengths. Extended curing periods improved the hydration process, resulting in better development of mechanical properties. The optimal curing period was identified as at least 28 days.

5.    The content of CNTs played a crucial role, especially in flexural strength, where it significantly enhanced the composite’s toughness and crack resistance. However, an optimal range of CNT concentration was necessary to avoid issues related to agglomeration.

6.    Advanced data preprocessing methods combined with machine learning approaches significantly improved the predictive accuracy of strengths compared to simpler models. The GB with polynomial features for compressive strength and ERT with PCA for flexural strength were identified as the best-performing models.

7.    The findings confirmed the theoretical understanding of the critical roles of water/cement ratio, curing time, and CNT content in determining mechanical properties. Practically, these insights guide the optimization of mix design, curing protocols, and quality control for CNT-reinforced cement composites, promoting the development of more durable and resilient construction materials.

Finally, based on feature importance and partial dependence results, this study recommends a water/cement ratio of 0.20–0.30 for optimal compressive strength, a CNT content of 0.025–0.05 wt% to maximize flexural performance without agglomeration issues, and a minimum curing period of 28 days to ensure full hydration. While this study provides valuable insights, it also has limitations. The dataset used, although comprehensive, may not encompass all possible variations of CNT-reinforced cement composites. Future studies should consider a broader range of compositions and conditions to validate and extend the findings. Additionally, the machine learning models employed, while effective, could be further refined with larger datasets and more advanced techniques. Future research should also explore the long-term performance and durability of CNT-reinforced cement composites under various environmental conditions. Investigating the effects of different types of CNT functionalization and dispersion methods on mechanical properties can provide deeper insights into optimizing these advanced materials. Moreover, accounting for the interaction between the features when doing a sensitivity analysis would be another key area that can be studied in the future.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Ahed Habib, Mohamed Maalej, Samir Dirar, M. Talha Junaid, and Salah Altoubat; analysis and interpretation of results: Ahed Habib, Mohamed Maalej, Samir Dirar, M. Talha Junaid, and Salah Altoubat; draft manuscript preparation: Ahed Habib, Mohamed Maalej, and Samir Dirar; manuscript review & editing: M. Talha Junaid and Salah Altoubat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kim GM, Nam IW, Yang B, Yoon HN, Lee HK, Park S. Carbon nanotube (CNT) incorporated cementitious composites for functional construction materials: the state of the art. Compos Struct. 2019;227(1980–2015):111244. doi:10.1016/j.compstruct.2019.111244. [Google Scholar] [CrossRef]

2. Huang JS, Liew JX, Liew KM. Data-driven machine learning approach for exploring and assessing mechanical properties of carbon nanotube-reinforced cement composites. Compos Struct. 2021;267(2):113917. doi:10.1016/j.compstruct.2021.113917. [Google Scholar] [CrossRef]

3. Liu B, Sun J, Zhao J, Yun X. Hybrid graphene and carbon nanotube-reinforced composites: polymer, metal, and ceramic matrices. Adv Compos Hybrid Mater. 2024;8(1):1. doi:10.1007/s42114-024-01074-3. [Google Scholar] [CrossRef]

4. Zhang F, Feng C, Fan Y, Hang Z, Zhang J, Liu H. Experiment and micromechanical modelling on electrical conductivity of curved carbon nanotube reinforced porous cement composites. J Adv Concr Technol. 2025;23(3):152–67. doi:10.3151/jact.23.152. [Google Scholar] [CrossRef]

5. Nitodas SS, Shah R, Das M. Research advancements in the mechanical performance and functional properties of nanocomposites reinforced with surface-modified carbon nanotubes: a review. Appl Sci. 2025;15(1):374. doi:10.3390/app15010374. [Google Scholar] [CrossRef]

6. Elbakyan L, Zaporotskova I. Polypropylene modified with carbon nanomaterials: structure, properties and application (a review). Polymers. 2025;17(4):517. doi:10.3390/polym17040517. [Google Scholar] [PubMed] [CrossRef]

7. Lee H, Yu W, Loh KJ, Chung W. Self-heating and electrical performance of carbon nanotube-enhanced cement composites. Constr Build Mater. 2020;250(4):118838. doi:10.1016/j.conbuildmat.2020.118838. [Google Scholar] [CrossRef]

8. Gao FF, Zhao Y, Wang WD, Shi YL. Study on microstructure evolution mechanism of concrete containing carbon nanotubes subjected to different heating-cooling regimes: experiments and molecular dynamics simulation. Constr Build Mater. 2025;458(5):139625. doi:10.1016/j.conbuildmat.2024.139625. [Google Scholar] [CrossRef]

9. Piao R, Cui Z, Jeong JW, Yoo DY. Optimal multi-walled carbon nanotube dosage for improving the mechanical and thermoelectric characteristics of ultra-high-performance fiber-reinforced concrete. Constr Build Mater. 2025;462(7):139927. doi:10.1016/j.conbuildmat.2025.139927. [Google Scholar] [CrossRef]

10. Wang X, Zhong J, Sun Y. Innovative strategy to reduce autogenous shrinkage in alkali-activated slag using hydrophilic carbon nanotube sponge. Compos Part B Eng. 2025;299:112447. doi:10.1016/j.compositesb.2025.112447. [Google Scholar] [CrossRef]

11. Makar J, Margeson J, Luh J. Carbon nanotube/cement composites-early results and potential applications. In: Proceedings of the 3rd International Conference on Construction Materials: Performance, Innovations and Structural Implications; 2005 Aug 22–24; Vancouver, BC, Canada. [Google Scholar]

12. Liew KM, Kai MF, Zhang LW. Carbon nanotube reinforced cementitious composites: an overview. Compos Part A Appl Sci Manuf. 2016;91(6348):301–23. doi:10.1016/j.compositesa.2016.10.020. [Google Scholar] [CrossRef]

13. Ramezani M, Dehghani A, Sherif MM. Carbon nanotube reinforced cementitious composites: a comprehensive review. Constr Build Mater. 2022;315(1):125100. doi:10.1016/j.conbuildmat.2021.125100. [Google Scholar] [CrossRef]

14. Wang X, Zhong J. Revisiting the effects of carbon nanotube agglomerates in cement. Carbon. 2025;231:119710. doi:10.1016/j.carbon.2024.119710. [Google Scholar] [CrossRef]

15. Modi A, Sahu C, Ahuja M, Chakroborty S, Gaur NK. Carbon-nanotube-reinforced 3D and 4D printable conductive polymer composites. In: Moharana S, Sahu BB, Satpathy SK, Chakroborty S, editors. Polymer nanocomposites for 3D, 4D and 5D printing. Singapore: Springer; 2025. p. 187–212. doi:10.1007/978-981-96-4214-4_8. [Google Scholar] [CrossRef]

16. Lee SH, Lee YJ, Kim JH, Han SJ, Kim KS. Localized damage detection using UHPFRC sensors with carbon nanotubes: experimental study and applications. J Build Eng. 2025;103:112117. doi:10.1016/j.jobe.2025.112117. [Google Scholar] [CrossRef]

17. Manzur T, Yazdani N, Emon MAB. Potential of carbon nanotube reinforced cement composites as concrete repair material. J Nanomater. 2016;2016(2142):1421959. doi:10.1155/2016/1421959. [Google Scholar] [CrossRef]

18. Konsta-Gdoutos MS, Metaxa ZS, Shah SP. Highly dispersed carbon nanotube reinforced cement based materials. Cem Concr Res. 2010;40(7):1052–9. doi:10.1016/j.cemconres.2010.02.015. [Google Scholar] [CrossRef]

19. Parveen S, Rana S, Fangueiro R, Paiva MC. Microstructure and mechanical properties of carbon nanotube reinforced cementitious composites developed using a novel dispersion technique. Cem Concr Res. 2015;73(2):215–27. doi:10.1016/j.cemconres.2015.03.006. [Google Scholar] [CrossRef]

20. Manzur T, Yazdani N, Emon MAB. Effect of carbon nanotube size on compressive strengths of nanotube reinforced cementitious composites. J Mater. 2014;2014(1):960984. doi:10.1155/2014/960984. [Google Scholar] [CrossRef]

21. Luo JL, Duan Z, Xian G, Li Q, Zhao T. Fabrication and fracture toughness properties of carbon nanotube-reinforced cement composite. Eur Phys J Appl Phys. 2011;53(3):30402. doi:10.1051/epjap/2010100449. [Google Scholar] [CrossRef]

22. Manzur T, Yazdani N. Effect of different parameters on properties of multiwalled carbon nanotube-reinforced cement composites. Arab J Sci Eng. 2016;41(12):4835–45. doi:10.1007/s13369-016-2181-8. [Google Scholar] [CrossRef]

23. Fakhim B, Hassani A, Rashidi A, Ghodousi P. Preparation and microstructural properties study on cement composites reinforced with multi-walled carbon nanotubes. J Compos Mater. 2015;49(1):85–98. doi:10.1177/0021998313514873. [Google Scholar] [CrossRef]

24. Guan X, Bai S, Li H, Ou J. Mechanical properties and microstructure of multi-walled carbon nanotube-reinforced cementitious composites under the early-age freezing conditions. Constr Build Mater. 2020;233(6348):117317. doi:10.1016/j.conbuildmat.2019.117317. [Google Scholar] [CrossRef]

25. Huang J, Rodrigue D, Guo P. Flexural and compressive strengths of carbon nanotube reinforced cementitious composites as a function of curing time. Constr Build Mater. 2022;318(7):125996. doi:10.1016/j.conbuildmat.2021.125996. [Google Scholar] [CrossRef]

26. Habib A, Houri AA, Habib M, Elzokra A, Yildirim U. Structural performance and finite element modeling of roller compacted concrete dams: a review. Lat Am J Solids Struct. 2021;18(4):e376. doi:10.1590/1679-78256467. [Google Scholar] [CrossRef]

27. Tarabin M, Maalej M, Altoubat S, Talha Junaid M. Review of the bond behavior between reinforcing steel and engineered cementitious composites. Structures. 2023;55(2):2143–56. doi:10.1016/j.istruc.2023.07.025. [Google Scholar] [CrossRef]

28. Talha Junaid M, Khennane A, Kayali O. Investigation into the effect of the duration of exposure on the behaviour of GPC at elevated temperatures. MATEC Web Conf. 2014;11:01003. doi:10.1051/matecconf/20141101003. [Google Scholar] [CrossRef]

29. John SK, Cascardi A, Verre S, Nadir Y. RC-columns subjected to lateral cyclic force with different FRCM-strengthening schemes: experimental and numerical investigation. Bull Earthq Eng. 2025;23(4):1561–90. doi:10.1007/s10518-025-02100-5. [Google Scholar] [CrossRef]

30. Bagherzadeh F, Shafighfard T. Ensemble machine learning approach for evaluating the material characterization of carbon nanotube-reinforced cementitious composites. Case Stud Constr Mater. 2022;17(10):e01537. doi:10.1016/j.cscm.2022.e01537. [Google Scholar] [CrossRef]

31. Li Y, Li H, Jin C, Shen J. The study of effect of carbon nanotubes on the compressive strength of cement-based materials based on machine learning. Constr Build Mater. 2022;358(7):129435. doi:10.1016/j.conbuildmat.2022.129435. [Google Scholar] [CrossRef]

32. Talayero C, Aït-Salem O, Gallego P, Páez-Pavón A, Merodio-Perea RG, Lado-Touriño I. Computational prediction and experimental values of mechanical properties of carbon nanotube reinforced cement. Nanomater. 2021;11(11):2997. doi:10.3390/nano11112997. [Google Scholar] [PubMed] [CrossRef]

33. Adel H, Palizban SMM, Sharifi SS, Ilchi Ghazaan M, Korayem AH. Predicting mechanical properties of carbon nanotube-reinforced cementitious nanocomposites using interpretable ensemble learning models. Constr Build Mater. 2022;354(1):129209. doi:10.1016/j.conbuildmat.2022.129209. [Google Scholar] [CrossRef]

34. Kalogeris I, Pyrialakos S, Kokkinos O, Papadopoulos V. Stochastic optimization of carbon nanotube reinforced concrete for enhanced structural performance. Eng Comput. 2023;39(4):2927–43. doi:10.1007/s00366-022-01693-8. [Google Scholar] [CrossRef]

35. Habib A, Yildirim U. Estimating mechanical and dynamic properties of rubberized concrete using machine learning techniques: a comprehensive study. Eng Comput. 2022;39(8):3129–78. doi:10.1108/ec-09-2021-0527. [Google Scholar] [CrossRef]

36. Shrif M, Al-Sadoon ZA, Barakat S, Habib A, Mostafa O. Optimizing gene expression programming to predict shear capacity in corrugated web steel beams. Civ Eng J. 2024;10(5):1370–85. doi:10.28991/cej-2024-010-05-02. [Google Scholar] [CrossRef]

37. Al Houri A, Habib A, Al Sadoon ZA. Artificial intelligence-based design and analysis of passive control structures: an overview. J Soft Comput Civ Eng. 2025;9(3):145–82. [Google Scholar]

38. Habib A, Yildirim U. Proposing unsupervised clustering-based earthquake records selection framework for computationally efficient nonlinear response history analysis of structures equipped with multi-stage friction pendulum bearings. Soil Dyn Earthq Eng. 2024;182(3):108732. doi:10.1016/j.soildyn.2024.108732. [Google Scholar] [CrossRef]

39. Habib M, Habib A, Albzaie M, Farghal A. Sustainability benefits of AI-based engineering solutions for infrastructure resilience in arid regions against extreme rainfall events. Discov Sustain. 2024;5(1):278. doi:10.1007/s43621-024-00500-2. [Google Scholar] [CrossRef]

40. Nassif N, Talha Junaid M, Hamad K, Al-Sadoon Z, Altoubat S, Maalej M. Performance-based prediction of shear and flexural strengths in fiber-reinforced concrete beams via machine learning. Struct Eng Int. 2024;34(4):651–6. doi:10.1080/10168664.2024.2310520. [Google Scholar] [CrossRef]

41. Tranmer M, Elliot M. Multiple linear regression. Cathie Marsh Cent Census Surv Res. 2008;5(5):1–5. [Google Scholar]

42. McDonald GC. Ridge regression. Wires Comput Stat. 2009;1(1):93–100. doi:10.1002/wics.14. [Google Scholar] [CrossRef]

43. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol. 2005;67(2):301–20. doi:10.1111/j.1467-9868.2005.00503.x. [Google Scholar] [CrossRef]

44. Habib A, Yildirim U. Simplified modeling of rubberized concrete properties using multivariable regression analysis. Mater Constr. 2022;72(347):e289. doi:10.3989/mc.2022.13621. [Google Scholar] [CrossRef]

45. Zhao H, Ding Y, Meng L, Qin Z, Yang F, Li A. Bayesian multiple linear regression and new modeling paradigm for structural deflection robust to data time lag and abnormal signal. IEEE Sens J. 2023;23(17):19635–47. doi:10.1109/JSEN.2023.3294912. [Google Scholar] [CrossRef]

46. Bedoui A, Lazar NA. Bayesian empirical likelihood for ridge and lasso regressions. Comput Stat Data Anal. 2020;145:106917. doi:10.1016/j.csda.2020.106917. [Google Scholar] [CrossRef]

47. Nassif N, Al-Sadoon ZA, Hamad K, Altoubat S. Cost-based optimization of shear capacity in fiber reinforced concrete beams using machine learning. Struct Eng Mech. 2022;83(5):671–80. [Google Scholar]

48. Loh WY. Classification and regression trees. Wiley Interdiscip Rev Data Min Knowl Discov. 2011;1(1):14–23. doi:10.1002/widm.8. [Google Scholar] [CrossRef]

49. Al-Sadoon ZA, Alotaibi E, Omar M, Arab MG, Tahmaz A. AI-driven prediction of tunneling squeezing: comparing rock classification systems. Geotech Geol Eng. 2024;42(3):2127–49. doi:10.1007/s10706-023-02665-5. [Google Scholar] [CrossRef]

50. Geurts P, Ernst D, Wehenkel L. Extremely randomized trees. Mach Learn. 2006;63(1):3–42. doi:10.1007/s10994-006-6226-1. [Google Scholar] [CrossRef]

51. Habib A, Yildirim U, Habib M. Applying kernel principal component analysis for enhanced multivariable regression modeling of rubberized concrete properties. Arab J Sci Eng. 2023;48(4):5383–96. doi:10.1007/s13369-022-07435-8. [Google Scholar] [CrossRef]

52. Habib A, Barakat S, Al-Toubat S, Junaid MT, Maalej M. Developing machine learning models for identifying the failure potential of fire-exposed FRP-strengthened concrete beams. Arab J Sci Eng. 2024;2024(1):1–16. doi:10.1007/s13369-024-09497-2. [Google Scholar] [CrossRef]

53. Habib A, Junaid MT, Dirar S, Barakat S, Al-Sadoon ZA. Machine learning-based estimation of reinforced concrete columns stiffness modifiers for improved accuracy in linear response history analysis. J Earthq Eng. 2025;29(1):130–55. doi:10.1080/13632469.2024.2409865. [Google Scholar] [CrossRef]

54. Huang L, Qin J, Zhou Y, Zhu F, Liu L, Shao L. Normalization techniques in training DNNs: methodology, analysis and application. IEEE Trans Pattern Anal Mach Intell. 2023;45(8):10173–96. doi:10.1109/TPAMI.2023.3250241. [Google Scholar] [PubMed] [CrossRef]

55. Wold S, Esbensen K, Geladi P. Principal component analysis. Chemom Intell Lab Syst. 1987;2(1–3):37–52. doi:10.1016/0169-7439(87)80084-9. [Google Scholar] [CrossRef]

56. Greenacre M, Groenen PJF, Hastie T, D’Enza AI, Markos A, Tuzhilina E. Principal component analysis. Nat Rev Meth Primers. 2022;2(1):100. doi:10.1038/s43586-022-00184-w. [Google Scholar] [CrossRef]

57. Hasan BMS, Abdulazeez AM. A review of principal component analysis algorithm for dimensionality reduction. J Soft Comput Data Min. 2021;2(1):20–30. doi:10.30880/jscdm.2021.02.01.003. [Google Scholar] [CrossRef]

58. Habib M. Quantifying topographic ruggedness using principal component analysis. Adv Civ Eng. 2021;2021(1):3311912. doi:10.1155/2021/3311912. [Google Scholar] [CrossRef]

59. Habib M, Bashir B, Alsalman A, Bachir H. Evaluating the accuracy and effectiveness of machine learning methods for rapidly determining the safety factor of road embankments. Multidiscip Model Mater Struct. 2023;19(5):966–83. doi:10.1108/mmms-12-2022-0290. [Google Scholar] [CrossRef]

60. Chan JY, Leow SMH, Bea KT, Cheng WK, Phoong SW, Hong ZW, et al. Mitigating the multicollinearity problem and its machine learning approach: a review. Mathematics. 2022;10(8):1283. doi:10.3390/math10081283. [Google Scholar] [CrossRef]

61. Mina D, Forcellini D. Soil-structure interaction assessment of the 23 November 1980 irpinia-Basilicata earthquake. Geosciences. 2020;10(4):152. doi:10.3390/geosciences10040152. [Google Scholar] [CrossRef]

62. Fiamingo A, Bosco M, Massimino MR. The role of soil in structure response of a building damaged by the 26 December 2018 earthquake in Italy. J Rock Mech Geotech Eng. 2023;15(4):937–53. doi:10.1016/j.jrmge.2022.06.010. [Google Scholar] [CrossRef]

63. Forcellini D. A 3-DOF system for preliminary assessments of the interaction between base isolation (BI) technique and soil structure interaction (SSI) effects for low-rise buildings. Structures. 2024;59(2):105803. doi:10.1016/j.istruc.2023.105803. [Google Scholar] [CrossRef]

64. Kim S, Piao R, Lee SK, Oh T, Chun B, Jeong JW, et al. Thermoelectric cement-based composites containing carbon nanotubes (CNTseffects of water-to-cement ratio and CNT dosage. Case Stud Constr Mater. 2024;21(6):e03861. doi:10.1016/j.cscm.2024.e03861. [Google Scholar] [CrossRef]

65. Adhikary SK, Rudžionis Ž, Rajapriya R. The effect of carbon nanotubes on the flowability, mechanical, microstructural and durability properties of cementitious composite: an overview. Sustainability. 2020;12(20):8362. doi:10.3390/su12208362. [Google Scholar] [CrossRef]

66. Vesmawala GR, Vaghela AR, Yadav KD, Patil Y. Effectiveness of polycarboxylate as a dispersant of carbon nanotubes in concrete. Mater Today Proc. 2020;28(18):1170–4. doi:10.1016/j.matpr.2020.01.102. [Google Scholar] [CrossRef]

67. Kang J, Al-Sabah S, Théo R. Effect of single-walled carbon nanotubes on strength properties of cement composites. Materials. 2020;13(6):1305. doi:10.3390/ma13061305. [Google Scholar] [PubMed] [CrossRef]