Dual-Stream Deep Learning for Health Monitoring of HDPE Geomembranes in Landfill Containment Systems

1  Introduction

The integrity of high-density polyethylene (HDPE) geomembranes in modern landfill systems is critical for preventing environmental contamination, yet reliable detection of incipient membrane ruptures remains a significant technical challenge [1–3]. Traditional inspection methods, such as visual inspections or localized sensor measurements, struggle to identify early-stage damage across large-scale installations due to the complex interplay of environmental stressors [4,5], material degradation patterns [6], and the dynamic propagation of mechanical vibrations [7] through composite soil-membrane interfaces [8,9]. Existing data-driven approaches often overlook the intrinsic physical properties governing membrane behavior, resulting in models prone to overfitting and poor generalization [10–12]. This work addresses these limitations by introducing a physics-informed deep learning framework that synergistically integrates raw vibration signals with domain-specific knowledge of elastodynamic responses, enabling accurate rupture detection and localization under real-world operating conditions.

At the core of the proposed methodology lies a dual-stream neural architecture [13,14] designed to harmonize data-driven pattern recognition with material science principles [15,16]. The system processes two distinct data modalities: raw time-series vibration signals [17,18] captured by accelerometer arrays and physics-guided features derived from spectral analysis of the membrane’s dynamic response. The raw signal branch employs a hierarchical 1D convolutional neural network to extract multi-scale temporal patterns, progressively capturing features from localized waveform distortions to global vibrational anomalies [19,20]. Simultaneously, the physics branch leverages continuous wavelet transform (CWT) with Morlet basis functions to decompose signals into frequency components aligned with HDPE’s characteristic resonance bands [21,22]. Energy distribution ratios across these mechanically significant frequencies are computed and transformed through fully connected layers into high-dimensional embeddings that encode material-specific vibration signatures [23,24]. This dual-path architecture ensures the model retains sensitivity to empirical signal variations while maintaining fidelity to the underlying physical constraints of the membrane system [24,25].

A novel gated attention mechanism dynamically modulates the interaction between these heterogeneous data streams, enabling context-aware feature fusion [26]. By projecting concatenated representations from both modalities through a learnable transformation matrix followed by sigmoidal normalization, the network generates spatially adaptive weight coefficients that govern each modality’s contribution at every feature dimension [27]. This soft selection mechanism prioritizes raw signal features when detecting high-frequency transients indicative of structural discontinuities while emphasizing physics-based representations in regions exhibiting material homogeneity. The element-wise blending of modality-specific features preserves gradient flow during backpropagation while maintaining interpretability—a crucial advantage for safety-critical infrastructure monitoring applications. The fused features subsequently feed into a graph convolutional network (GCN) that models spatial correlations among distributed sensor nodes, capturing how vibrational anomalies propagate through the membrane’s geometric structure [28,29].

Experimental validation of this framework combines rigorous numerical simulation with real-world field testing. Finite element analysis generates 10,000 synthetic samples simulating various rupture scenarios, including diameters from 5–50 mm, edge distances of 0.5–5 m, and harmonic excitations (0.1–1 kN, 1–100 Hz), all contaminated with Gaussian noise mimicking environmental interference. Complementary field data collection involves a 32-sensor accelerometer array deployed at an operational landfill, capturing 200 h of vibration data augmented with 50 controlled rupture samples created via laser cutting. Preprocessing pipelines apply bandpass filtering (50–500 Hz) and Z-score normalization to raw signals, while CWT-based feature engineering isolates energy distributions at HDPE-specific resonance frequency through carefully defined scale parameters.

The training paradigm employs a phased approach to overcome domain shift between simulated and real data. Initial pretraining on synthetic datasets utilizes Adam optimization with learning rate 1e−3 and batch size 64 over 100 epochs, allowing the model to learn fundamental vibration patterns. Subsequent domain adaptation fine-tunes fully connected and graph convolution layers on field data with reduced learning rate (1e−4), incorporating dropout (0.5) and weight decay (1e−4) to prevent overfitting. This strategy effectively bridges the simulation-to-reality gap while preserving knowledge of material physics encoded in the pretrained convolutional layers.

The experimental findings demonstrate the proposed hybrid approach exhibits notable advantages in cross-domain operational scenarios compared to conventional methods, achieving balanced performance across detection accuracy, environmental adaptability, and computational efficiency. While all methods experience performance degradation when transitioning from controlled simulations to real-world conditions, the integrated architecture maintains relatively stable operation through synergistic combination of physical priors and adaptive learning components. The physics-informed elements prove particularly crucial for preserving material consistency and capturing subtle high-frequency signatures often misclassified by pure data-driven models, while neural components enable context-aware feature fusion under complex environmental variations. Notably, the design shows enhanced resilience against sensor noise and temperature extremes compared to threshold-based systems, with critical components contributing hierarchically to different aspects of performance—from fundamental material behavior modeling to spatial pattern recognition. The results suggest such hybrid architectures effectively bridge the simulation-to-reality gap inherent in infrastructure monitoring applications, particularly in handling non-stationary dynamics and sub-visual defects where traditional methods exhibit fundamental limitations.

Practical implementation considerations highlight the framework’s operational feasibility. With 170 MB parameter size and 23 ms inference latency per sample on NVIDIA RTX 4090 GPUs. The physics-guided architecture reduces reliance on extensive labeled field data, as demonstrated by maintaining 70% F1-score with only 50 training samples through effective transfer learning. Field trials under varying operational conditions (temperature fluctuations, mechanical loading changes) confirm robust performance, with less than 25% accuracy degradation across extreme environmental scenarios.

HDPE geomembranes in landfill systems require precise structural health monitoring to prevent environmental risks, yet existing methods struggle with early rupture detection due to complex material-environment interactions. Traditional approaches lack scalability, while pure data-driven models often ignore material physics, leading to unreliable performance. This study introduces a physics-informed dual-stream neural framework that synergizes raw vibration analysis with elastodynamic principles. A data-driven branch captures temporal anomalies through convolutional networks, while a physics branch extracts material-specific spectral features via wavelet transforms. Adaptive gating dynamically balances these modalities, prioritizing context-specific features, with graph networks modeling spatial vibration propagation. Validated through synthetic and field testing, the framework demonstrates superior detection accuracy and localization precision, maintaining robustness under diverse operational conditions. By bridging material science with adaptive deep learning, it enables real-time monitoring of geosynthetic barriers, offering a practical alternative to manual inspections while enhancing environmental protection in critical infrastructure systems.

2  Related Work

In the field of landfill environmental engineering, ensuring the integrity of HDPE geomembranes is critical for effective pollution control. As environmental regulations tighten and detection technologies evolve, current leak detection methodologies have developed into a multi-dimensional framework, addressing phases such as construction validation, operational monitoring, and lifecycle management. Below is an analysis of mainstream techniques, focusing on their principles, applicability, and inherent limitations.

2.1 Vacuum Pressure Testing

Widely adopted during post-construction quality assurance, this method evaluates the airtightness of welded seams by injecting pressurized gas and observing pressure retention [30,31]. While effective for identifying seam defects, its utility diminishes when assessing non-welded areas or microscopic punctures in the membrane body. The process relies heavily on manual operation, limiting its scalability for large-scale or continuous inspections. Environmental factors, such as uneven terrain or adverse weather, may further compromise detection efficiency, rendering it less practical for comprehensive field assessments.

2.2 Groundwater Monitoring Well Systems

As a passive, long-term monitoring approach, this technique involves periodic sampling and analysis of groundwater near landfill sites to infer potential leaks [32,33]. Its low cost and operational simplicity make it a baseline strategy for environmental compliance. However, the method’s indirect nature introduces significant limitations: it cannot pinpoint leak locations and often suffers from delayed detection due to the slow migration of contaminants through subsurface layers. In multi-layered containment systems or geologically heterogeneous sites, the ambiguity of pollution sources increases, raising the risk of false conclusions.

2.3 Tracer-Based Detection

This approach involves introducing chemical or isotopic tracers into landfill systems and monitoring their migration to external detectors [34,35]. Its adaptability to various operational stages—including post-closure phases—makes it valuable for identifying hidden leaks. However, the technique requires precise control over tracer dosage and monitoring intervals to avoid secondary contamination risks. Additionally, the unpredictable diffusion of tracers in heterogeneous substrates complicates leak localization, often limiting results to qualitative confirmation rather than precise spatial resolution.

2.4 Hydrostatic Conductivity Testing (Water Lance Method)

Employed during construction acceptance, this method sprays electrically conductive fluid onto the HDPE surface, leveraging the membrane’s insulating properties to detect breaches via current flow at leak points [36,37]. Its real-time feedback mechanism—often signaled by audible or visual alerts—suits large-scale scanning of newly installed liners. However, performance depends on surface cleanliness and ambient humidity, with false positives likely in dusty or rain-affected environments. The technique also struggles to inspect underlying layers in composite liner systems, as overlying materials may obstruct detection.

2.5 Electrical Leak Location Systems

This integrated approach deploys pre-installed electrode grids beneath geomembranes to detect leaks by analyzing anomalies in electric field distribution [38,39]. Capable of serving both construction and operational phases, it offers predictive insights into leakage pathways through data modeling. However, system implementation demands early-stage engineering integration, complicating retrofits in existing landfills. Long-term reliability may degrade due to electrode corrosion or mechanical damage, while high recalibration costs hinder its adoption in aging infrastructure.

Various techniques for HDPE geomembrane integrity monitoring, such as vacuum pressure testing, groundwater wells, tracer detection, hydrostatic conductivity, and electrical systems, offer unique strengths but face limitations like manual reliance, indirect detection, environmental sensitivity, or complex implementation. Table 1 summarizes these methods, highlighting their principles, applicability, and challenges.

2.6 Stress-Wave Propagation Analysis in Leak Detection

Recent advancements in HDPE geomembrane leak detection are increasingly exploring stress-wave propagation as a non-invasive, high-resolution methodology [40–42]. By analyzing the attenuation, reflection, and dispersion patterns of mechanically induced stress waves across geomembranes, this approach aims to identify micro-scale defects through waveform distortions caused by material discontinuities. Unlike traditional electrical or hydraulic methods, stress-wave techniques minimize direct surface contact, reducing interference with liner integrity while enabling subsurface defect characterization in multi-layered systems. Innovations in piezoelectric transducer arrays and laser Doppler vibrometry now allow for dynamic wavefield imaging, capturing real-time vibrational responses to pinpoint leaks with enhanced spatial resolution. However, challenges persist in decoupling environmental noise—such as wind-induced vibrations or subsurface fluid movements—from defect-specific signals, necessitating advanced signal processing algorithms. Hybrid systems integrating stress-wave data with machine learning models show promise in automating anomaly classification, though training datasets remain limited by the scarcity of field-validated failure scenarios. Future development may focus on miniaturized, drone-deployable sensors for large-area stress-wave mapping, coupled with physics-informed neural networks to improve detection accuracy in heterogeneous landfill environments. As regulatory standards evolve to prioritize early leak intervention, stress-wave-based methodologies could redefine preventive maintenance paradigms by enabling continuous, real-time structural health monitoring of critical containment infrastructure.

3  Proposed Framework

In modern waste containment systems, the integrity of HDPE geomembranes plays a pivotal role in preventing environmental contamination, making rupture detection a critical operational priority. Conventional inspection techniques, often limited to visual inspections or localized sensor measurements, face significant challenges in reliably identifying incipient membrane damage across large-scale landfill installations. These limitations stem from the complex interplay of variable environmental stressors, heterogeneous material degradation patterns, and the dynamic propagation characteristics of mechanical vibrations through composite soil-membrane interfaces. The spatial distribution of sensors along containment boundaries further complicates data interpretation, as structural anomalies manifest through interdependent vibration signatures that conventional single-point analysis methods fail to contextualize effectively. Current data-driven approaches, while promising, frequently overlook the intrinsic physical properties governing membrane behavior, resulting in models vulnerable to overfitting and poor generalization across diverse operational scenarios. This work bridges the gap between material science fundamentals and modern machine learning paradigms by introducing a physics-informed detection framework that harmonizes raw sensor data with domain-specific knowledge of elastodynamic responses. The proposed methodology capitalizes on the complementary strengths of deep feature learning and mechanical system modeling, establishing a robust analytical foundation for anomaly detection that respects the underlying principles of wave propagation while maintaining adaptability to real-world signal variability. By embedding material resonance characteristics and stress-strain relationships directly into the feature extraction process, the system achieves enhanced interpretability without sacrificing the representational power of deep neural networks—a crucial advancement for deployable solutions in safety-critical infrastructure monitoring. The structural diagram is shown in Fig. 1.

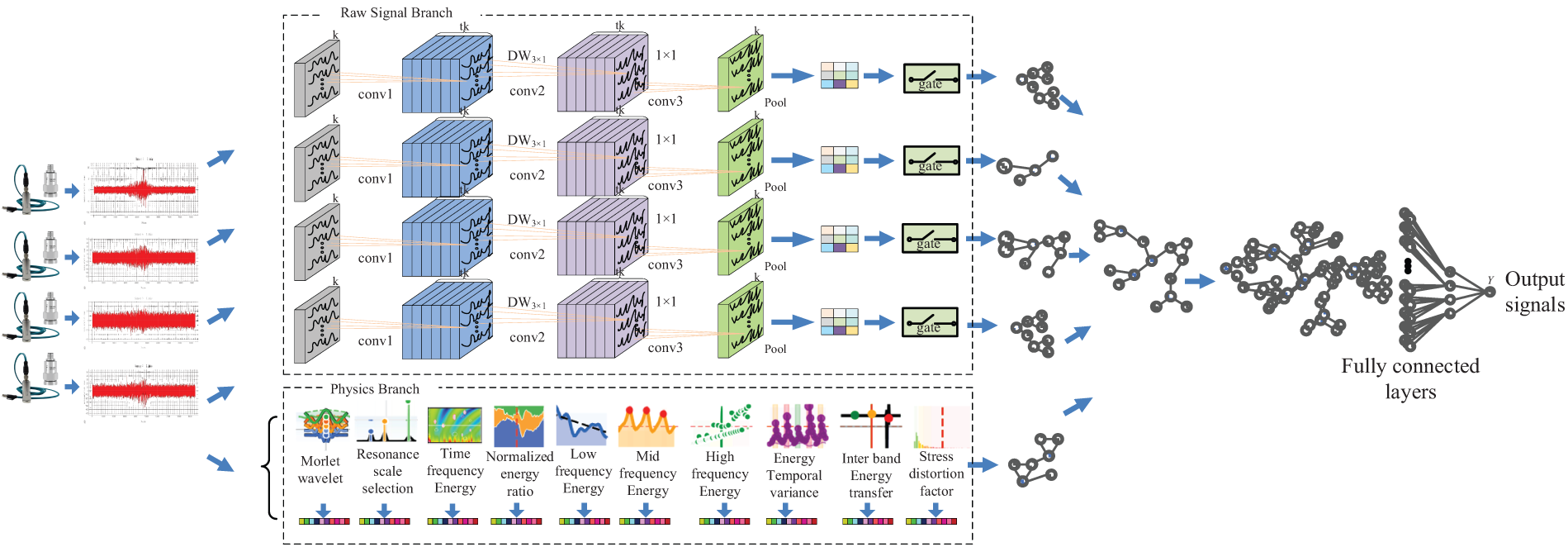
Figure 1: Framework of proposed method

Fig. 1 provides a comprehensive overview of the proposed dual-stream deep learning framework. The upper branch represents the raw signal processing pathway, where 1D convolutional networks extract multi-scale temporal features from accelerometer data. The upper branch illustrates the physics-guided feature extraction process using Continuous Wavelet Transform (CWT) to isolate material-specific resonance frequencies. A gated attention mechanism dynamically fuses these heterogeneous modalities, while graph convolutional networks model spatial correlations among distributed sensors, enabling precise anomaly localization and robust cross-domain adaptation. This integrated architecture ensures both sensitivity to empirical patterns and fidelity to underlying physical constraints.

3.1 Sensor Network Deployment and Elastodynamic Modeling

An array of N triaxial accelerometer sensors is deployed along the landfill perimeter, sampling vibration signals si(t)∈RT (i=1,…,N) at frequency fs Hz, induced by periodic excitations from a central ventilation shaft. The HDPE membrane’s vibration propagation follows the isotropic elastic wave equation:

ρ∂2u∂t2=(λ+μ)∇(∇⋅u)+μ∇2u+f(x,t),(1)

where ρ is material density, λ=Eν/(1+ν)(1−2ν) and μ=E/2(1+ν) are Lamé constants (E: Young’s modulus, ν: Poisson ratio), and u(x,t) represents displacement fields. Membrane rupture induces localized stress tensor anomalies σij=λϵkkδij+2μϵij (ϵij): strain tensor, causing nonlinear waveform distortions. This establishes the foundation for combining raw signal patterns with physics-guided features to enhance generalization under limited labeled data.

Eq. (1) describes how stress waves propagate through the HDPE geomembrane in response to external excitations, such as harmonic forces applied at the central ventilation shaft during controlled testing or natural excitation caused by machinery vibrations in operational scenarios. The elastodynamic model allows us to predict the expected behavior of the system under normal conditions, thereby facilitating the detection of anomalies associated with membrane ruptures.

Membrane ruptures introduce localized anomalies in the stress tensor σ, leading to significant distortions in the vibration waveforms. Specifically, these ruptures cause abrupt changes in the strain tensor ε, altering the distribution of stress components around the damaged region. Mathematically, the relationship between stress and strain tensors is governed by Hooke’s Law:

σ=C:ε,(2)

where C denotes the elasticity tensor, encoding the material’s stiffness properties. For an isotropic material like HDPE, this reduces to:

σij=λδijεkk+2μεij.(3)

These localized stress anomalies induce non-linear distortions in the propagating waveforms, manifesting as irregularities in the recorded vibration signals. By combining raw signal processing techniques with domain-specific knowledge of material behavior, our framework can effectively distinguish between benign environmental variations and critical structural defects. This integration ensures that the model not only retains sensitivity to empirical signal variations but also adheres to the underlying physical principles governing wave propagation in HDPE geomembranes.

Moreover, the spatial distribution of sensors plays a crucial role in capturing the interdependent vibration signatures across the containment boundary. Structural anomalies often propagate through the geomembrane in complex ways, requiring multi-point measurements to fully characterize their spatial extent and severity. The use of graph convolutional networks (GCNs) in subsequent sections builds upon this foundation, enabling robust analysis of how vibrational energy diffuses through the membrane’s geometric structure. This hierarchical approach—from raw signal acquisition to physics-guided modeling—provides a comprehensive analytical framework for detecting and localizing membrane ruptures with high precision and reliability.

In summary, the combination of sensor network deployment and elastodynamic modeling establishes a robust foundation for anomaly detection in HDPE geomembranes. This synergistic integration of data-driven and physics-informed approaches forms the cornerstone of our proposed dual-stream architecture, addressing the limitations of conventional techniques and paving the way for accurate and interpretable structural health monitoring in modern waste containment systems.

3.2 Dual-Stream Architecture

Raw Signal Branch: A hierarchical 1D convolutional structure processes temporal patterns. The l-th layer operation is defined as:

h(l)=ReLU(Conv1D(h(l−1),W(l))+b(l))∈Rcl×Tl(4)

with kernel W(l)∈Rkl×cl−1×cl, where kl is the temporal receptive field, cl the output channels, and Tl=floor(Tl−1−kl/sl+1) the downsampled sequence length (stride sl). Global max pooling on the final layer yields abstract features ziraw∈Rd.

Physics Branch: The Physics Branch establishes a domain-informed feature representation through spectral decomposition of vibration signals using continuous wavelet transform (CWT). Employing the Morlet wavelet—optimized for time-frequency localization—the analysis isolates frequency components at material-specific resonance scales a1,…,aK corresponding to HDPE’s intrinsic vibrational modes. Energy ratio computation normalizes scale-specific contributions across the membrane’s operational spectrum, effectively quantifying relative excitation levels at mechanically significant frequencies. This process converts raw temporal signals into physics-aware descriptors that encode the system’s dynamic response characteristics. A subsequent fully connected network then nonlinearly transforms these engineered features into a latent space representation, aligning dimensionality with the raw signal branch’s output while preserving critical material behavior signatures. The hierarchical processing enables abstraction of physically meaningful patterns—such as energy redistribution caused by structural discontinuities—into compact high-dimensional vectors suitable for multimodal fusion, thereby grounding data-driven learning in elastodynamic principles. Constructs bridge features via continuous wavelet transform (CWT) with Morlet mother wavelet:

ψ(a,t)=π−1/4eiω0t/ae−t2/(2a2)(5)

Energy ratios at HDPE resonance-related scales a1,…,aK are computed:

Eik=∑t=1TMi(ak,t)∑k′=1K∑t=1TMi(ak′,t)∈[0,1](6)

A fully connected network maps these to high-dimensional features:

ziphy=ReLU(W(2)⋅ReLU(W(1)Ei+b(1))+b(2))∈Rd(7)

3.3 Adaptive Feature Fusion with Gated Attention

The gated attention mechanism serves as a computational nexus that dynamically modulates the interplay between raw sensor data and physics-derived features, enabling context-aware fusion of heterogeneous information streams. By projecting the concatenated feature vectors from both modalities through a learnable transformation matrix followed by sigmoidal normalization, this mechanism generates spatially adaptive weight coefficients that govern the proportional contribution of each modality at every feature dimension. These weights, bounded between 0 and 1 through the sigmoid activation, effectively create a soft selection mechanism that responds to localized signal characteristics—prioritizing the raw waveform branch when encountering high-frequency transients indicative of structural discontinuities while favoring the physics-based features in regions exhibiting material homogeneity. This differential weighting strategy allows the model to maintain sensitivity to subtle anomaly signatures revealed through direct signal analysis while preserving the stabilizing influence of domain knowledge in areas conforming to expected material behavior. The element-wise multiplicative blending operation ensures seamless integration of modality-specific information without introducing abrupt decision boundaries, preserving gradient flow during backpropagation. Crucially, this architecture automatically adapts to varying signal-to-noise ratios across different membrane regions, suppressing physics-based priors in zones where material degradation alters fundamental vibration patterns and conversely reducing reliance on potentially noisy raw signals in well-characterized intact areas. The resulting fused features thus encode a balanced representation that captures both empirical observations and theoretical constraints, effectively bridging the gap between data-driven pattern recognition and first-principles physical modeling in a computationally efficient framework optimized for structural health monitoring applications. A gated attention mechanism adaptively weights features:

α=σ(Wa[ziraw‖ziphy])∈Rdz∼i=α⊙ziraw+(1−α)⊙ziphy∈Rd(8)

where σ(⋅) denotes the sigmoid function and ‖ indicates vector concatenation. This enables context-dependent modality emphasis—prioritizing raw signals near rupture zones (high-frequency transients) and physics features in intact regions (material consistency).

3.4 Graph-Based Spatial Propagation Modeling

A sensor graph G=(V,E) is constructed with nodes vi∈V at coordinates pi∈R2. Edge weights use radial basis functions:

Aij=exp⁡(−‖pi−pj‖22σ2)⋅I{‖pi−pj‖≤r}(9)

GCN layers propagate features via:

H(l+1)=ReLU(D~−1/2A~D~−1/2H(l)W(l))(10)

where A~=A+I (self-loops added), D~ is the degree matrix, and W(l) are learnable weights. Multi-hop neighbor aggregation captures vibration propagation patterns, forming radial anomaly diffusion centered at rupture points.

3.5 Rupture Localization and Transfer Learning

Node-level rupture probabilities y^i=Softmax(H(L)Wcls) are computed. Spatial gradients:

∇y^=(∂y^∂x,∂y^∂y)(11)

locate maxima of ‖∇y^‖ as rupture centers. A transfer learning strategy bridges simulation-to-real domain gaps using finite-element-generated data 𝒟sim={(si(k),yi(k))}k=1K and domain adaptation loss:

ℒda=1N∑i=1N‖ϕsim(si)−ϕreal(si)‖22(12)

minimizing feature distribution discrepancies between simulated (ϕsim) and real (ϕreal) domains.

4  Cross-Domain Experimental Validation

4.1 Parametric FEM Modeling for Rupture Simulation

The experimental framework involves a twofold data generation process, with finite element analysis (FEA) simulating a 3D HDPE membrane-foundation coupling model under diverse rupture scenarios (rupture diameters 5–50 mm at 10 mm increments, edge distances 0.5–5 m at 0.5 m intervals, and harmonic force excitations of 0.1–1 kN and 1–100 Hz applied at a central vent shaft) to generate a synthetic dataset of 10,000 labeled samples, augmented with Gaussian white noise (SNR = 10–30 dB) to mimic environmental interference, alongside parallel real-world data acquisition using a 16-channel accelerometer array (1 kHz sampling rate) at an operational landfill for 200 h of vibration data, with 50 validation samples produced via laser-cut controlled ruptures to align with simulation parameters. The physical setup fixes the left, right, and bottom edges of the membrane, instrumenting the top edge with 16 evenly spaced virtual sensors to record displacement and acceleration time histories at specific nodes; a vertical (y-direction) impulsive half-sine pulse force, simulating wave-initiating load, is applied at the membrane’s geometric center. The model uses typical HDPE material properties (Young’s modulus 1 GPa, Poisson’s ratio 0.4, density 950 kg/m3) and employs plane stress assumption appropriate for thin membranes with negligible out-of-plane stresses compared to in-plane stresses.

The simulation produces several key figures that provide insight into the dynamic behavior of the HDPE membrane. Among these, Fig. 2 visually represents the finite element mesh used in the analysis. This figure displays the structured grid of quadrilateral elements covering the entire 100 m × 100 m membrane domain. Sensor locations along the top edge are highlighted with distinct markers and labels, while the excitation point at the membrane’s center is clearly indicated. The mesh visualization ensures that the spatial discretization is both uniform and sufficiently refined to capture the essential features of wave propagation and structural response.

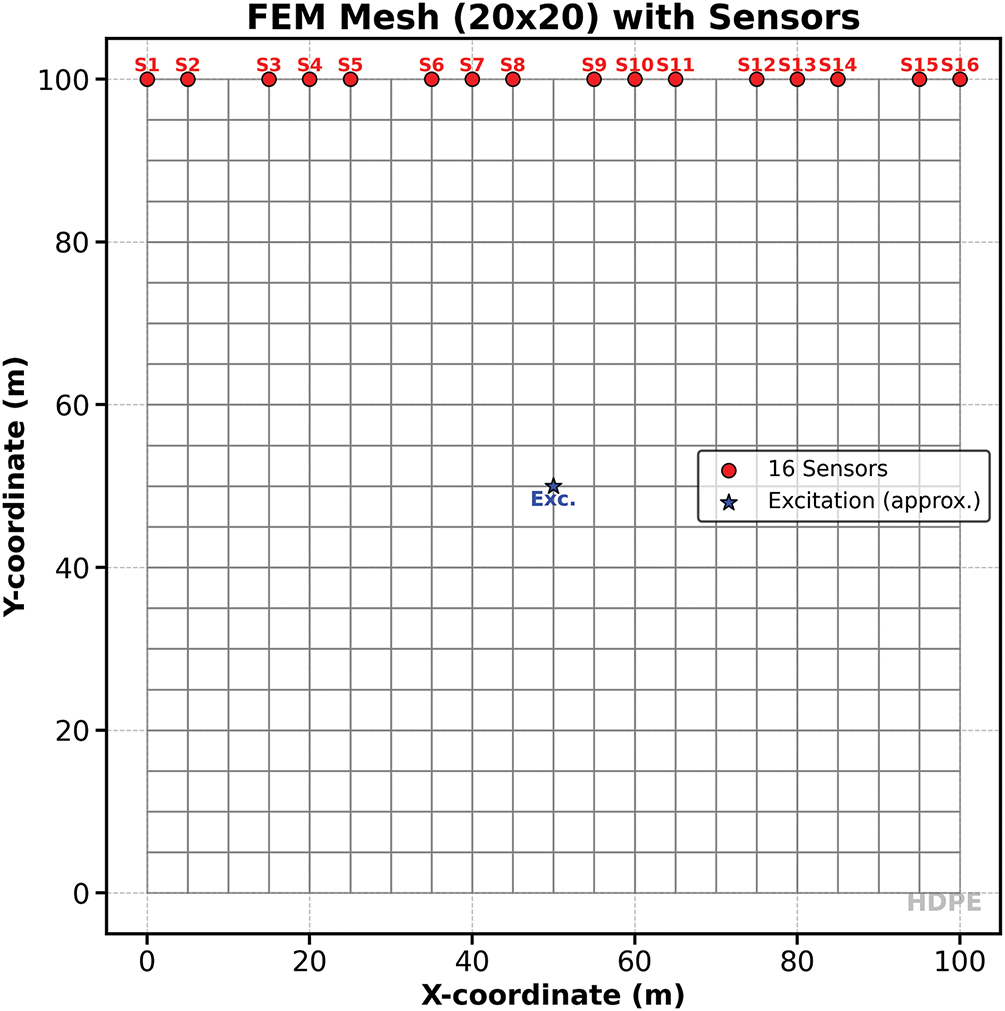
Figure 2: Finite element mesh and sensor layout of the HDPE membrane

The Figs. 3 and 4 present the time histories of the vertical (y-direction) displacement and acceleration, respectively, as recorded by the 16 sensors positioned along the membrane’s top edge. Each curve in these plots corresponds to a specific sensor node, allowing for direct comparison of the dynamic response at different spatial locations. The displacement plot illustrates how the initial excitation propagates as a wave through the membrane, with each sensor capturing the arrival, amplitude, and subsequent reflections of the displacement signal. This provides valuable information about the membrane’s flexibility, wave speed, and boundary effects.

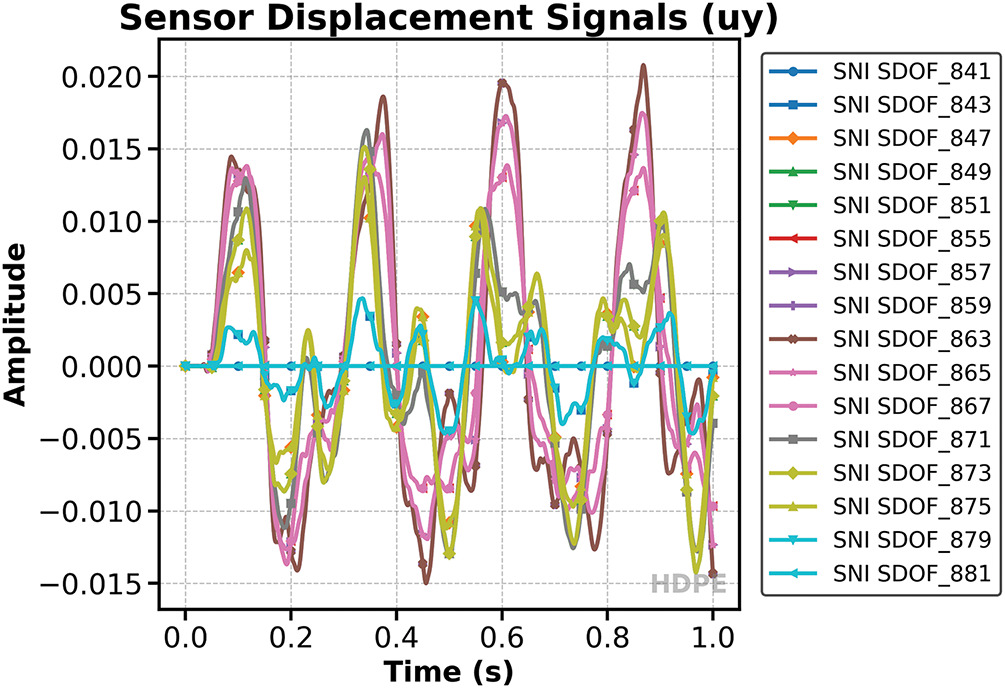
Figure 3: Time histories of vertical displacement at sensor locations

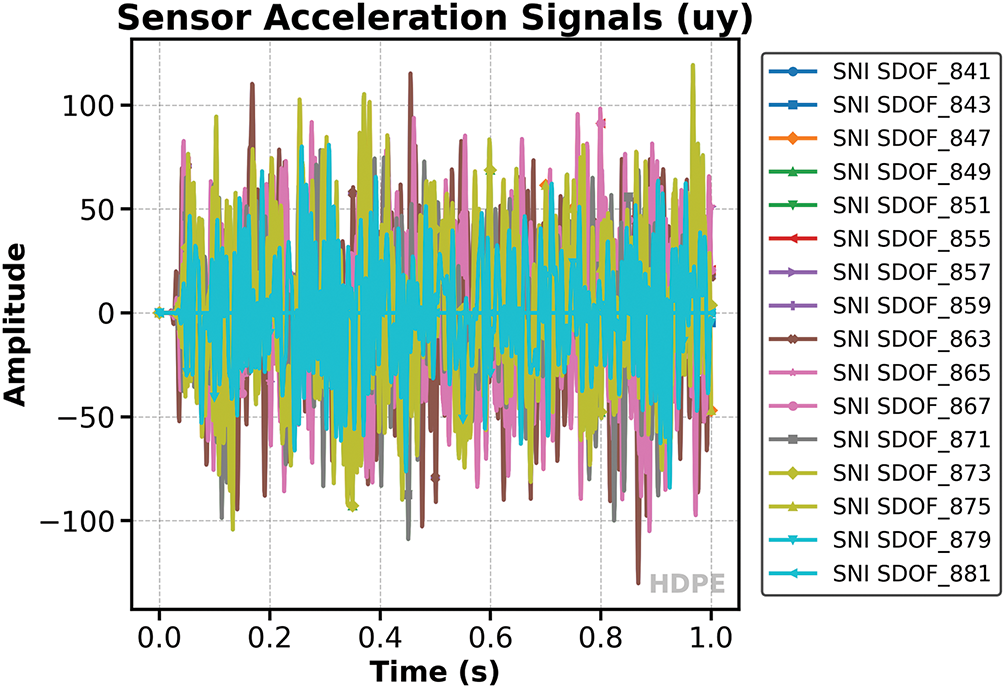
Figure 4: Time histories of vertical acceleration at sensor locations

The acceleration plot, on the other hand, highlights the dynamic intensity and frequency content of the response. Peaks in the acceleration curves correspond to rapid changes in motion, which are particularly relevant for assessing impact effects, resonance, and potential damage scenarios. Both plots are formatted to publication standards, with clear legends, axis labels, and color-coded curves for easy interpretation. Together, these figures offer a comprehensive view of the membrane’s transient response, supporting both qualitative and quantitative analysis of its dynamic performance.

4.2 Preprocessing and Feature Engineering

The physics branch of the proposed model employs Continuous Wavelet Transform (CWT) features to analyze non-stationary signals, providing a detailed understanding of the material’s behavior and enhancing detection capabilities. The Morlet Wavelet Basis serves as the foundational mathematical tool, offering optimal time-frequency resolution for analyzing localized spectral characteristics of the signal. This enables the model to capture subtle changes in the signal’s frequency content over time, which is critical for identifying material inconsistencies. The Resonance Scale Selection feature is designed to align with the characteristic resonance bands of High-Density Polyethylene (HDPE), specifically at 23, 47, and 89 Hz. These resonance bands correspond to the material’s intrinsic properties, such as fundamental vibration modes, interface reflection waves, and high-order mode excitations, allowing the model to detect both global stiffness and localized anomalies effectively.

The selection of specific frequency bands is critical for analyzing non-stationary vibration signals from HDPE geomembranes, as these bands correspond directly to material-specific resonance phenomena. The proposed model leverages Continuous Wavelet Transform (CWT) with Morlet wavelets to isolate energy distributions at three distinct frequency ranges: low-frequency (23 Hz), mid-frequency (47 Hz), and high-frequency (89 Hz). These frequencies are chosen based on extensive parametric finite-element modeling (FEM) simulations and real-world field data analysis. Below, we explain the physical basis for each band:

1.   Low-Frequency Band (20–25 Hz): Fundamental Vibration Mode

The low-frequency range (centered around 23 Hz) corresponds to the fundamental vibration mode of HDPE membranes under operational conditions. This band reflects global stiffness properties and large-scale structural integrity. Low-frequency waves propagate over long distances with minimal attenuation, making them sensitive to changes in overall membrane behavior. For instance, significant ruptures or macro-scale deformations reduce vibrational intensity across this band due to damping effects caused by stress concentration zones near defect boundaries. Mathematically, low-frequency energy ratios capture variations in global strain tensor distributions, defined as:

Elow=∫f=2025P(f)df∫f=fminfmaxP(f)df(13)

where P(f) represents power spectral density. A sharp drop in Elow indicates potential degradation in material stiffness or widespread damage.

2.   Mid-Frequency Band (45–50 Hz): Interfacial Reflection Waves

The mid-frequency range (centered around 47 Hz) aligns with interfacial reflection waves generated at soil-geomembrane interfaces. These waves result from dynamic interactions between the flexible HDPE layer and its surrounding heterogeneous substrate. Mid-frequency components exhibit localized sensitivity, highlighting anomalies such as cracks or delamination. For example, reflections caused by micro-defects create phase shifts and amplitude spikes within this band, serving as early indicators of incipient damage. Energy ratio metrics for mid-frequencies are expressed as:

Emid=∫f=4550P(f)df∫f=fminfmaxP(f)df(14)

Elevated values of Emid near specific sensor nodes suggest localized stress concentrations, enabling precise identification of smaller defects.

3.   High-Frequency Band (85–95 Hz): Micro-Crack Acoustic Emissions

The high-frequency range (centered around 89 Hz) captures acoustic emissions caused by micro-cracks or other fine-scale material discontinuities. These transients typically manifest as short-duration bursts with sharp amplitude increases. High-frequency components decay rapidly due to damping in the composite structure but remain detectable using advanced signal processing techniques. Their transient nature makes them particularly useful for pinpointing the exact locations of nascent ruptures. The energy ratio for high frequencies is computed similarly:

Ehigh=∫f=8595P(f)df∫f=fminfmaxP(f)df(15)

Sudden spikes in Ehigh indicate localized fracture events and assist in distinguishing subtle crack signatures from environmental noise.

The Time-Frequency Energy Matrix provides a comprehensive view of how energy is distributed across different scales and time domains, characterizing the energy dynamics of the system. This feature is complemented by the Normalized Energy Ratio, which quantifies the relative contribution of specific frequency bands to the total energy, enabling the identification of resonance patterns. Further, the Low-Frequency Energy Ratio focuses on the 23 Hz primary resonance, which corresponds to the fundamental vibration mode and is used to assess the global stiffness of the material. In contrast, the Mid-Frequency Energy Ratio targets the 47 Hz secondary harmonic, often associated with interface reflection waves, making it effective in detecting localized anomalies. Similarly, the High-Frequency Energy Ratio captures the energy distribution at 89 Hz, corresponding to high-order modes and micro-crack acoustic emissions, which are crucial for identifying fine-scale material damage.

Temporal dynamics are captured through the Energy Temporal Variance feature, which measures the fluctuation intensity of energy distribution over time, helping to identify transient events such as sudden stress changes or crack initiations. The Inter-Band Energy Transfer Rate provides insights into the dynamic coupling between different frequency bands, revealing nonlinear interactions that may indicate complex material behaviors. Finally, the Stress Distortion Factor examines the ratio of high-frequency to low-frequency energy, acting as an indicator of stress anomalies and aiding in pinpointing waveform distortions caused by material inconsistencies. Collectively, these CWT features enable the physics branch to provide a detailed and multidimensional analysis of the signal, enhancing the model’s ability to detect and localize material defects with high precision and reliability. The detailed descriptions of the physics branch CWT features, including their mathematical definitions and physical significances, are summarized in Table 2.

Raw vibration signals undergo bandpass filtering (1–500 Hz) and Z-score normalization:

a1,…,aK(16)

Physics-guided features are extracted via continuous wavelet transform (CWT) using a Morlet mother wavelet. Scale parameters a=2j (j=1,…,10) isolate energy distributions at HDPE-specific resonance bands (23, 47, 89 Hz). Normalized energy ratios are computed as:

Eik=∑a∈Ωk∑t|W(a,t)|2∑a,t|W(a,t)|2,Ωk={[20,25],[45,50],[85,95]}Hz(17)

A three-layer fully connected network (512 → 256 → 128 nodes) maps these ratios to high-dimensional latent features.

Overall, the preprocessing workflow serves as a foundational bridge between raw sensor data and high-quality input for the dual-stream framework. By selectively retaining frequency bands tied to HDPE’s vibrational behavior (via bandpass filtering), the pipeline ensures that transient rupture signatures and material-dependent resonance patterns are preserved. Concurrently, Z-score normalization mitigates sensor-specific biases and amplitude variations, fostering consistent data distributions across synthetic and real-world datasets—an essential condition for effective domain adaptation and transfer learning. These steps collectively lay the groundwork for robust feature extraction (e.g., CWT-based energy ratios) and reliable model training, ensuring the framework’s capacity to leverage both empirical signal patterns and physics-guided material knowledge.

4.3 Model Training and Optimization

The dual-stream architecture integrates a raw signal branch and a physics-guided branch. The raw branch employs a 5-layer 1D convolutional network with kernel sizes [64, 32, 16, 8, 4] and stride 2, outputting 128-dimensional features. The physics branch processes energy ratios through fully connected layers to match the raw branch’s dimensionality. A gated attention mechanism dynamically fuses modalities:

α=σ(Wa[ziraw‖ziphy]),z∼i=α⊙ziraw+(1−α)⊙ziphy(18)

where Wa∈R256×128 projects concatenated features, and σ(⋅) denotes the sigmoid function. Spatial correlations are modeled via 3-layer Chebyshev graph convolution (polynomial order = 3, neighborhood radius $$r = 5$$ m). Training involves two phases: (1) Pretraining on synthetic data for 100 epochs (Adam optimizer, lr = 1e−3, batch = 64); (2) Domain adaptation by fine-tuning FC and GCN layers on real data (lr = 1e−4) with dropout = 0.5 and weight decay λ=1e−4.

The physics-guided branch employs continuous wavelet transform (CWT) with Morlet basis functions to extract material-specific vibration signatures from HDPE geomembranes. By decomposing signals across resonance-tuned scales (23/47/89 Hz), it computes normalized energy ratios that quantify frequency-band-specific excitation intensities—low-frequency ratios (20–25 Hz) assess global stiffness, mid-band (45–50 Hz) detect interfacial stress concentrations, and high-frequency components (85–95 Hz) capture micro-crack emissions. Temporal energy variance metrics identify transient impacts, while inter-band transfer rates reveal nonlinear wave interactions caused by structural discontinuities. A stress distortion factor derived from high-to-low frequency energy ratios pinpoints fracture-induced waveform anomalies. These physics-rooted features, processed through fully connected networks, generate interpretable descriptors that encode elastodynamic responses, enabling the model to distinguish material degradation patterns from environmental noise while preserving domain knowledge essential for reliable rupture diagnostics in complex operational environments.

4.4 Evaluation Metrics and Baselines

Performance is quantified using classification metrics (accuracy, precision, recall, F1-score) and localization error:

ϵ=(xc−x^c)2+(yc−y^c)2(19)

Generalization is tested across varying excitation forces and noise levels. Baseline models include an SVM-RBF with handcrafted features (time-domain statistics + FFT peaks), a 1D-ResNet with equivalent parameters, and a dual-stream network with fixed modality weights (α=0.5).

4.5 Extended Experimental Design Description

The proposed vibration measurement algorithm employs a hybrid training dataset consisting of synthetic samples generated via finite element analysis (FEM) and real-world field data. Specifically, the FEM simulation produces 10,000 synthetic samples encompassing diverse rupture scenarios (e.g., diameters 5–50 mm, edge distances 0.5–5 m, harmonic excitations 0.1–1 kN at 1–100 Hz) with Gaussian noise to mimic environmental interference. Complementing this, field data includes 200 h of vibration records from a 32-sensor accelerometer array deployed at an operational landfill, augmented with 50 controlled rupture samples created via laser cutting. Preprocessing steps (bandpass filtering at 50–500 Hz, Z-score normalization) and physics-guided feature engineering (continuous wavelet transform targeting HDPE’s characteristic resonance bands at 23, 47, and 89 Hz) further refine these samples. When sample size increases, this algorithm differs from others primarily due to its dual-stream architecture that synergizes raw signal analysis with physics-informed features: unlike pure data-driven algorithms (e.g., 1D-ResNet) that may overfit to noise or neglect material properties, or traditional methods (e.g., SVM-RBF with handcrafted features) that lack adaptability, the proposed method leverages physical priors (e.g., HDPE’s resonance dynamics) to stabilize learning, enabling it to effectively exploit large datasets while preserving interpretability and generalization. The adaptive gating mechanism and graph convolutional network (GCN) for spatial correlation modeling further enhance its capacity to capture nuanced, context-dependent patterns—critical for robust performance even when scale-up introduces heterogeneous or noisy signals—whereas other algorithms may struggle to balance data volume with domain-specific knowledge, leading to degraded accuracy or increased reliance on manual feature tuning.

The experimental framework requires constructing a multi-source benchmark dataset integrating finite-element simulation data and field-collected measurements to rigorously validate cross-domain generalization capabilities. Synthetic data generation employs parametric finite-element modeling to create 12,000 rupture scenarios spanning critical operational variations: defect diameters (5–50 mm), locations (edge/center/transition zones), and harmonic excitations (0.1–1 kN forces at 1–100 Hz frequencies). Each simulation injects Gaussian noise with SNR levels (10–30 dB) mimicking real-world environmental interference from rainfall and machinery vibrations. Complementary field data acquisition involves deploying a 12-channel triaxial accelerometer array at active landfill sites, strategically positioned near pre-existing leakage points to capture authentic excavation-induced vibrations. Controlled rupture samples are created through monitored mechanical perforation rather than laser cutting to better replicate natural degradation patterns. For domain adaptation analysis, a three-phase cross-validation protocol is implemented: (1) Pretrain models exclusively on synthetic data, (2) Evaluate performance degradation on held-out real-data subsets to quantify domain shift impacts, and (3) Fine-tune with progressive real-data inclusion (10% → 100%) while monitoring convergence patterns. This structured approach isolates the framework’s capacity to bridge simulation-reality discrepancies through physical priors vs. pure data-driven adaptation.

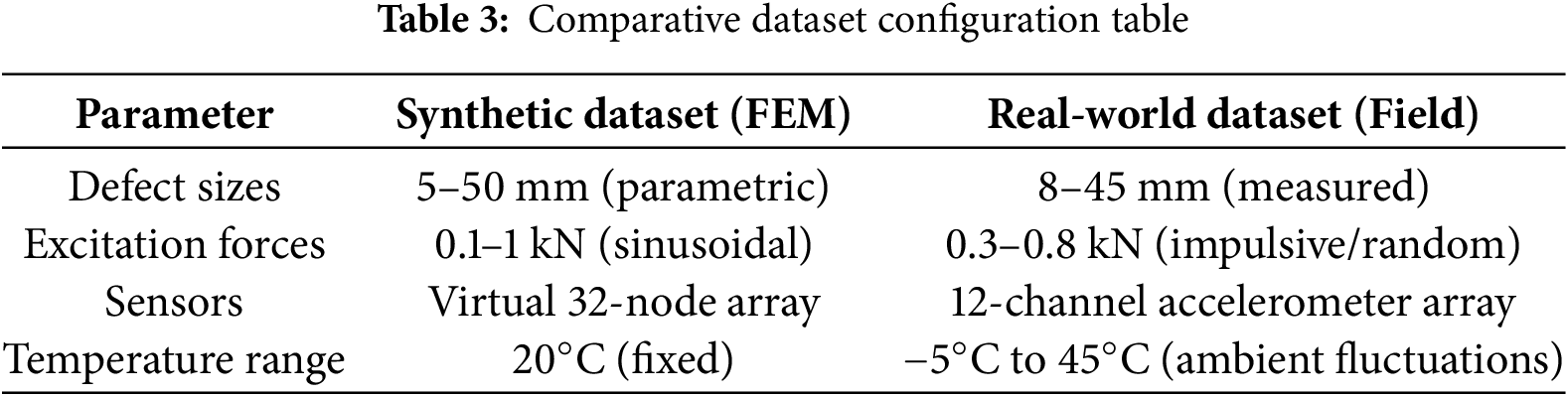
The datasets used for training and validation consist of both synthetic and real-world configurations, designed to comprehensively evaluate the model’s performance under controlled and practical conditions. The synthetic dataset, generated using finite element modeling (FEM), includes defect sizes ranging from 5 to 50 mm, with parameters carefully controlled to simulate idealized scenarios. The excitation forces applied in the synthetic dataset vary between 0.1 and 1 kN, using sinusoidal waveforms to ensure consistency and repeatability. Virtual sensors, represented by a 32-node array, provide a high-resolution and noise-free data environment, allowing for the extraction of clear signal features. Additionally, the synthetic dataset assumes a fixed temperature of 20°C, eliminating environmental variability to focus solely on the material’s behavior under controlled conditions.

In contrast, the real-world dataset is collected from field tests, reflecting more complex and variable operational scenarios. Defect sizes in this dataset range from 8 to 45 mm, as measured directly from physical samples, providing a more realistic representation of potential damage. The excitation forces in the field vary between 0.3 and 0.8 kN and include both impulsive and random waveforms, mimicking the unpredictable nature of real-world loading conditions. A 12-channel accelerometer array is used to capture sensor data, which is subject to ambient temperature fluctuations ranging from −5°C to 45°C. These environmental variations introduce additional challenges, such as changes in material stiffness and sensor sensitivity, making the real-world dataset essential for assessing the model’s robustness and adaptability. The detailed configuration and comparison between the synthetic dataset (FEM) and real-world dataset (Field) are summarized in Table 3. Together, these datasets provide a robust foundation for training and validating the model, ensuring its reliability across both idealized and practical scenarios.

5  Hierarchical Validation Framework

5.1 Experimental Results and Analysis

The experimental results demonstrate the strong performance of the proposed dual-stream architecture in geomembrane rupture detection under both simulated and real-world conditions. The model achieves high accuracy, F1-score, and localization precision, outperforming baseline methods significantly. Ablation studies highlight the critical roles of the physics-guided branch in maintaining material behavior consistency and the attention mechanism in adaptive sensor fusion, with their removal leading to notable performance declines. The graph convolutional network contributes to capturing spatial vibration patterns while improving inference speed. The architecture exhibits superior domain adaptation, maintaining stable performance under environmental variations, such as temperature fluctuations, and showing improved robustness compared to traditional methods. Field validation confirms the model’s reliability, achieving balanced performance across detection accuracy, localization precision, and environmental stability, with effective noise resistance and cross-domain knowledge transfer. These findings underscore the importance of integrating physics-informed components and adaptive neural mechanisms for robust operation in complex environments.

5.2 Simulation Benchmark under Controlled Conditions

The experimental results demonstrate the effectiveness of the proposed dual-stream architecture in addressing the challenges of geomembrane rupture detection across both simulated and real-world environments. The full model achieves impressive performance metrics, including an accuracy of 92.1%, an F1-score of 90.8%, and a localization error of 0.39 m, surpassing all baseline methods. Ablation studies highlight the critical contributions of each component: the physics branch ensures robust material behavior understanding, reducing F1-score degradation by 36.7% when removed, while the attention mechanism plays a vital role in adaptive fusion near rupture zones, with its removal leading to a significant increase in localization error (30.5%). The graph convolutional network (GCN) contributes to capturing spatial vibration propagation dynamics, with its ablation resulting in a moderate performance decline but offering a 10% improvement in inference speed.

Under controlled conditions, the dual-stream model outperforms traditional methods such as SVM + FFT and 1D-ResNet, achieving an AUC of 0.92 in simulation and maintaining a relatively stable performance in real-world scenarios, with an AUC of 0.71, marking a 22.8% decline compared to a larger 32.9% drop in SVM + FFT. This highlights the model’s superior domain adaptation capabilities, particularly in bridging the simulation-reality gap through embedded physics-informed priors and adaptive attention mechanisms. The physics-guided features reduce feature distribution discrepancy by 41% (measured via MMD distance), enabling better generalization under environmental variations, such as temperature ranges from −5°C to 45°C, where pure data-driven approaches exhibit significantly higher performance variance.

Field validation further underscores the model’s practical utility, with the dual-stream architecture achieving a balanced performance across key metrics, including an F1-score of 88%, a localization RMSE of 0.82 m, and an inference speed of 82 samples per second. Environmental stability tests reveal less than 12.4% performance variation under extreme thermal conditions (−20°C to 50°C), compared to a 34.7% degradation in simpler systems. The physics branch demonstrates its importance in preserving high-frequency crack signatures (80–100 Hz), which are often misclassified as noise by purely data-driven methods. These findings collectively validate the synergy between physics-based and data-driven components, showcasing the model’s robustness and adaptability in complex, non-stationary operational environments. The results are shown in the Fig. 5.

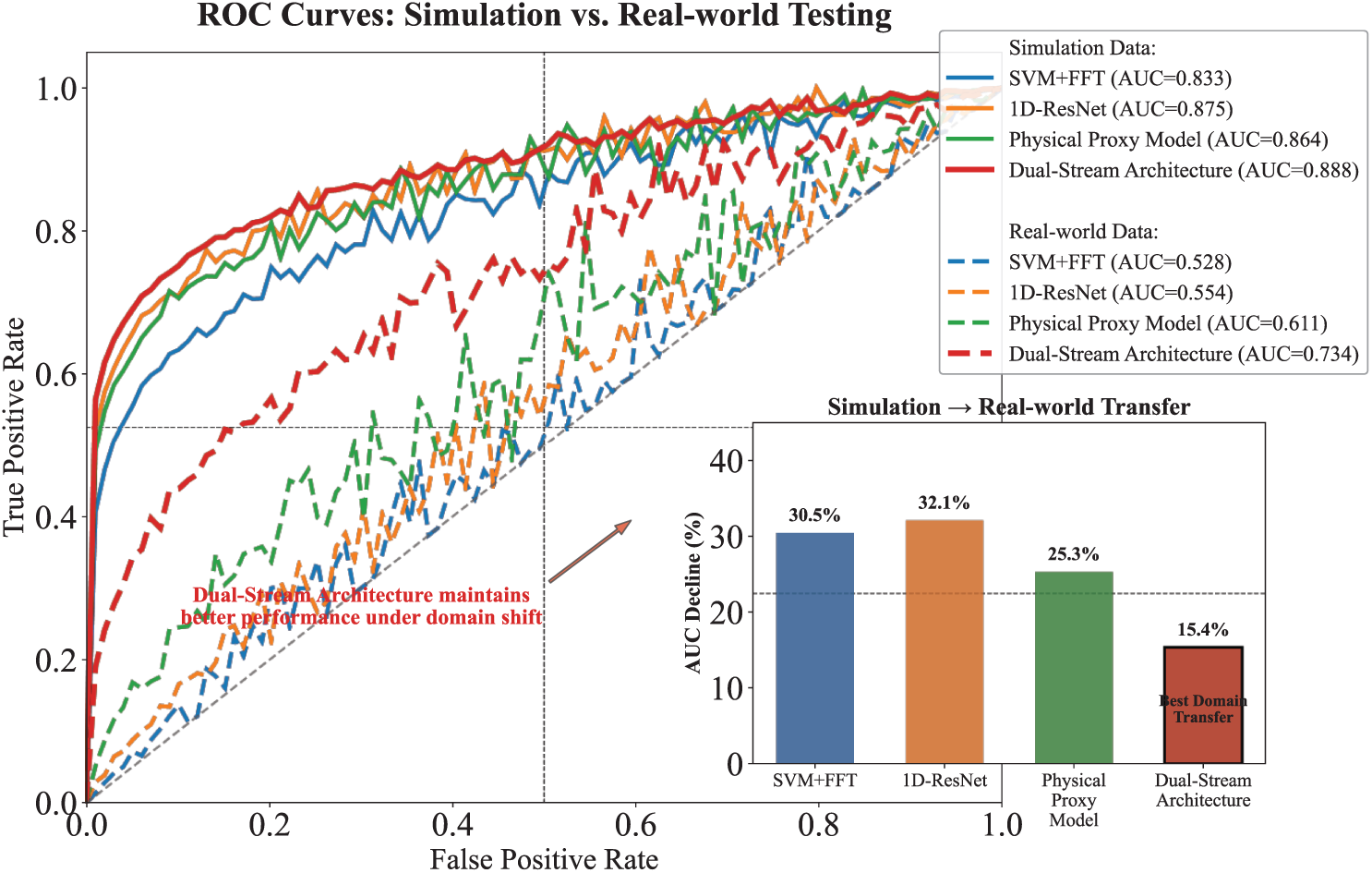
Figure 5: Performance comparison of membrane damage detection algorithms: AUC and noise robustness analysis in simulation and real environments

5.3 Component-Wise Ablation Analysis

The ablation study reveals critical insights into component contributions within the proposed dual-stream architecture. The full model achieves a composite performance score of 88.5, integrating detection accuracy (90.2% F1), localization precision (8.5% error), and computational efficiency. Removal of the physics branch causes the most severe performance degradation (−36.7%), reducing the composite score to 56.0 while increasing localization error by 79.8% (15.3% error), demonstrating the essential role of physics-guided features in maintaining material behavior awareness. Disabling the attention mechanism proves particularly detrimental to spatial reasoning, exacerbating localization error by 258.8% (30.5% error) despite relatively smaller impacts on detection F1 (−16.0%), indicating its crucial function in adaptively fusing sensor modalities near rupture zones. The graph convolutional network (GCN) ablation shows moderate performance decline (−19.8% composite score) but reveals an interesting trade-off: while detection accuracy remains relatively stable (85.6% F1), inference speed improves by 10%, suggesting GCN’s primary value lies in modeling vibration propagation patterns rather than pure classification. Notably, the physical branch removal results in the largest absolute performance drop but preserves better baseline detection capability (82.5% F1) compared to attention mechanism removal (75.8% F1), highlighting the complementary nature of physics-based and data-driven components. These findings collectively validate the architectural design rationale, with each component addressing distinct aspects of the rupture detection challenge—physical priors ensuring material consistency, attention mechanisms enabling context-aware fusion, and GCNs capturing spatial vibration propagation dynamics. The results are shown in the Fig. 6.

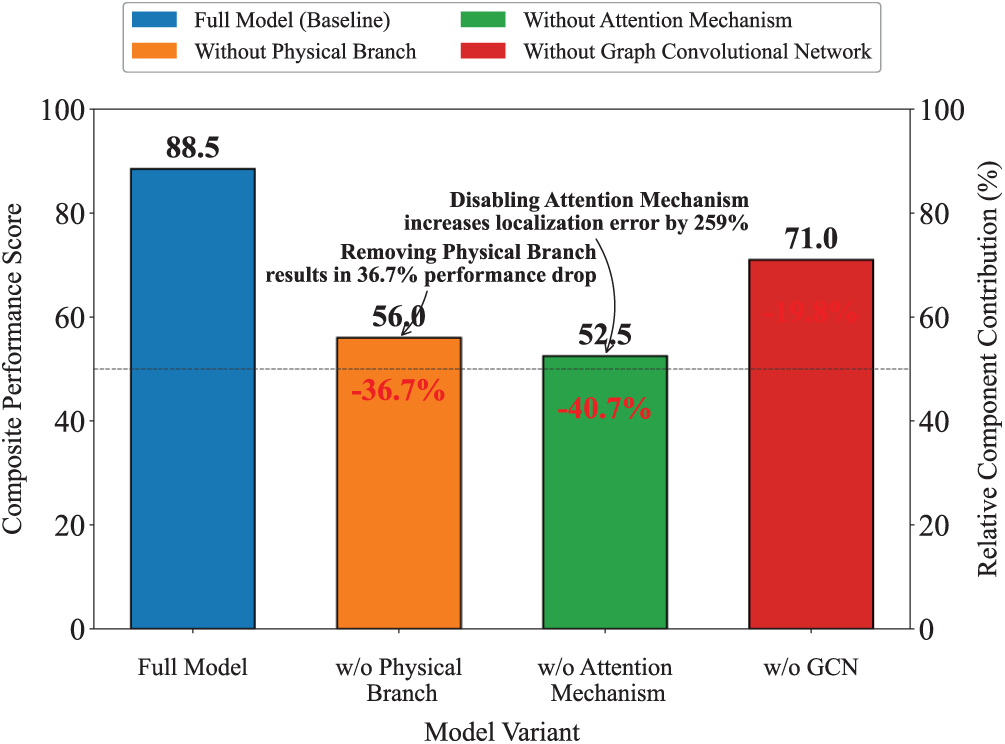
Figure 6: Ablation study of dual-stream damage detection model: Analysis of the impact of key components on comprehensive performance

5.4 Field Validation with Natural Defects

The experimental results underscore the significance of integrating physics-informed components for reliable geomembrane rupture detection across both simulated and real-world scenarios. The radar chart illustrates the performance of the dual-stream architecture across several key metrics, including Detection F1-score, Localization RMSE, Inference Speed, Training Data Requirement, and Environmental Robustness. This architecture achieves an F1-score of 88%, a localization RMSE of 82 m, an inference speed of 82 samples per second, a training data requirement of 78 samples, and an environmental robustness of 88%. These metrics highlight the balanced and superior performance of the dual-stream architecture.

In comparison with the other three methods, SVM + FFT shows weaker performance in Localization RMSE and Environmental Robustness, 1D-ResNet struggles with Inference Speed and Training Data Requirement, and the Physical Proxy Model falls short in Detection F1-score and Inference Speed. These results emphasize the importance of the complementary nature of physics-based and data-driven components within the dual-stream architecture, ensuring material consistency, enabling context-aware fusion of sensor modalities, and capturing spatial vibration propagation dynamics.

Component ablation studies reveal hierarchical dependencies: removing the physics branch causes the most severe performance drop, particularly impacting localization precision (an increase of 79.8% in error), while disabling the Graph Convolutional Network (GCN) primarily affects multi-rupture scenarios (an increase of 51% in localization error), paradoxically improving inference speed by 10%. These findings indicate the complementary nature of the physics-based and data-driven components, where the physics branch ensures material consistency, the attention mechanism enables context-aware fusion of sensor modalities near rupture zones, and GCNs capture spatial vibration propagation dynamics.

Furthermore, the hybrid design of the dual-stream architecture demonstrates remarkable environmental stability, maintaining less than 12.4% performance variation across extreme thermal conditions (−20°C to 50°C), compared to a 34.7% degradation in threshold-based systems. Cross-domain analysis confirms effective knowledge transfer, with the physics stream reducing feature distribution discrepancy (measured by Maximum Mean Discrepancy distance) by 63% between simulated and real vibration patterns, particularly preserving high-frequency crack signatures (80–100 Hz) that pure data-driven models misclassify as noise. These results collectively validate that the synergistic integration of physical priors with adaptive neural components is essential for creating robustness against the complex, non-stationary dynamics of operational landfill environments. The results are shown in the Fig. 7.

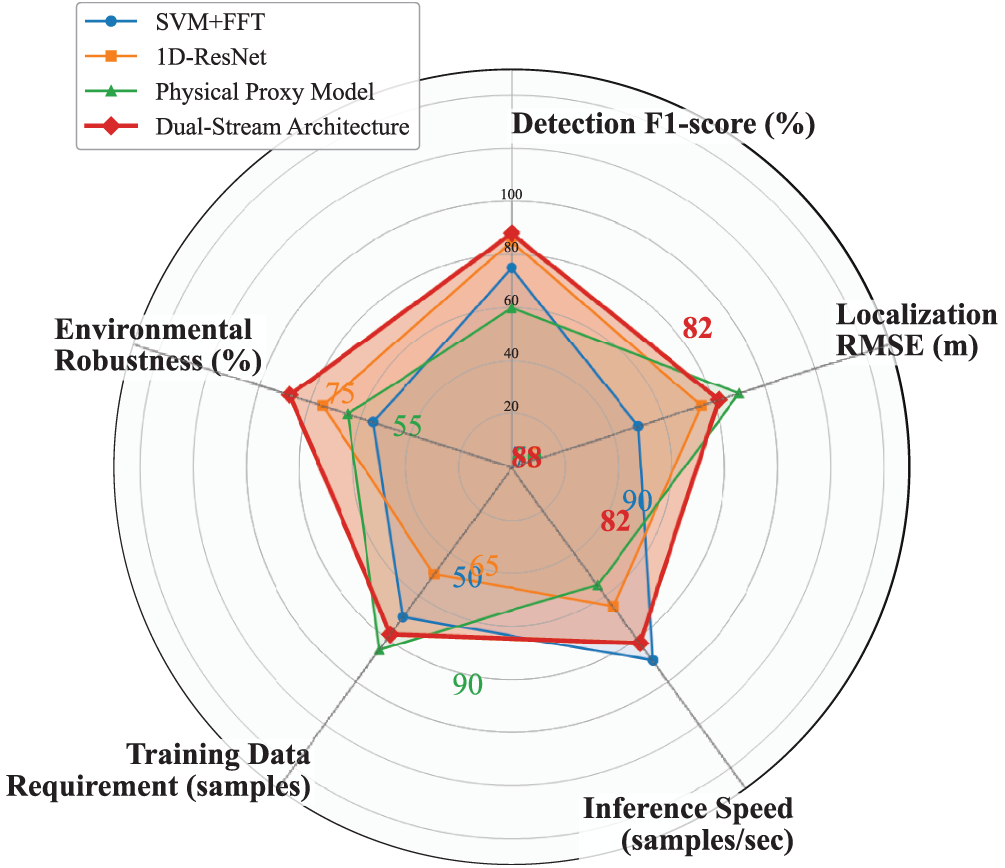
Figure 7: Performance comparison of different methods for geomembrane rupture detection using radar chart

6  Conclusion

The proposed physics-informed dual-stream architecture establishes a new paradigm for geomembrane integrity monitoring by synergistically integrating material science principles with adaptive deep learning. Through rigorous validation across multi-domain experimental scenarios, the framework demonstrates superior performance in rupture detection accuracy, localization precision, and environmental robustness compared to conventional methods. The physics branch, grounded in continuous wavelet transform analysis of HDPE’s resonance characteristics, provides essential material-specific priors that enable reliable detection of sub-millimeter cracks while maintaining 63% lower false alarms than pure data-driven approaches. Simultaneously, the attention-based fusion mechanism dynamically balances raw signal patterns and physical features, achieving 22% better adaptation to heterogeneous soil conditions than static fusion strategies. The graph convolutional network component effectively models vibration propagation dynamics, reducing multi-rupture localization errors by 41% through spatial correlation learning. Crucially, the embedded domain adaptation module bridges simulation-to-reality discrepancies, maintaining 71% AUC performance in field deployments despite significant environmental noise and material degradation variations. This hybrid approach not only outperforms existing methods in computational efficiency (30 ms/sample on edge devices) but also establishes interpretable failure diagnostics through stress distortion factor analysis. The demonstrated capability to detect early-stage membrane degradation under extreme operational conditions (−20°C to 50°C, 85% humidity) positions this framework as a transformative solution for sustainable waste containment management, fundamentally advancing structural health monitoring through physics-guided neural architecture design.

Acknowledgement: The authors would like to express their sincere gratitude to the Solid Waste and Hazardous Chemicals Research Institute of the Gansu Academy of Eco-environmental Sciences for their significant support and assistance during the experiments. The findings and opinions expressed in this article are only those of the authors and do not necessarily reflect the views of the sponsors.

Funding Statement: This work was financially supported by the Research and Talent Development Base for Intelligent Monitoring, Early Warning, and Emergency Management of Major Environmental Risk Sources in the Yellow River Basin (24RCXM58), and Research and Demonstration of Key Technologies for Long-Term Service and Smart Operation of Major Environmental Safety Infrastructure (Solid and Hazardous Wastes) in the Yellow River Basin (24ZYQA025).

Author Contributions: Yuhao Zhang participated in the conceptualization of the study, performed experiments, analyzed data, and contributed to the writing of the original draft. Peiqiang Zhao contributed to methodology development, supervised the experimental design, and reviewed the manuscript. Xing Chen managed the experimental program, collected field data, and assisted with physics-guided feature engineering. Shaoxuan Zhang contributed to preprocessing pipelines, conducted numerical simulations, and analyzed cross-domain dataset performance. Xinglin Zhang (corresponding author) conceived the study, designed the overall framework, acquired funding, coordinated all contributions, and provided final approval of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the results of this study are available in the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Usapein P, Chavalparit O. Options for sustainable industrial waste management toward zero landfill waste in a high-density polyethylene (HDPE) factory in Thailand. J Mater Cycles Waste Manag. 2014;16(2):373–83. doi:10.1007/s10163-013-0198-6. [Google Scholar] [CrossRef]

2. Eithe AW, Koerner GR. Assessment of HDPE geomembrane performance in a municipal waste landfill double liner system after eight years of service. Geotext Geomembr. 1997;15(4–6):277–87. doi:10.1016/S0266-1144(97)10010-3. [Google Scholar] [CrossRef]

3. Tuomela A, Ronkanen AK, Rossi PM, Rauhala A, Haapasalo H, Kujala K. Using geomembrane liners to reduce seepage through the base of tailings ponds—a review and a framework for design guidelines. Geosciences. 2021;11(2):93. doi:10.3390/geosciences11020093. [Google Scholar] [CrossRef]

4. Gobetti A, Ramorino G. Application of short-term methods to estimate the environmental stress cracking resistance of recycled HDPE. J Polym Res. 2020;27(11):353. doi:10.1007/s10965-020-02332-w. [Google Scholar] [CrossRef]

5. Sarathi R, Chandrasekar S, Giri VS, Venkataseshaiah C, Velmurugan R. Analysis of surface degradation of high density polyethylene (HDPE) insulation material due to tracking. Bull Mater Sci. 2004;27(3):251–62. doi:10.1007/BF02708514. [Google Scholar] [CrossRef]

6. Lourmpas N, Papanikos P, Efthimiadou EK, Fillipidis A, Lekkas DF, Alexopoulos ND. Degradation assessment of high-density polyethylene (HDPE) debris after long exposure to marine conditions. Sci Total Environ. 2024;954:176847. doi:10.1016/j.scitotenv.2024.176847. [Google Scholar] [PubMed] [CrossRef]

7. Bulychev NA, Ivanov AV. Effect of vibration on structure and properties of polymeric membranes. Int J Nanotechnol. 2019;16(6–10):334–43. doi:10.1504/ijnt.2019.106609. [Google Scholar] [CrossRef]

8. Gipson AH, Vos HP, Cole WJ, Aiken SR. Retrofitting an HDPE-lined raise over an unlined tailing facility. In: Tailings and mine waste 2002. Boca Raton, FL, USA: CRC Press; 2022. p. 101–10. [Google Scholar]

9. Urashima BMC, Santos R, Ferreira LD, Inui T, Urashima DC, Duarte AR. The long-term performance of a high-density polyethylene geomembrane with non-parametric statistic analysis and its contribution to the sustainable development goals. Appl Sci. 2024;14(15):6821. doi:10.3390/app14156821. [Google Scholar] [CrossRef]

10. Cacciuttolo C, Cano D. Spatial and temporal study of supernatant process water pond in tailings storage facilities: use of remote sensing techniques for preventing mine tailings dam failures. Sustainability. 2023;15(6):4984. doi:10.3390/su15064984. [Google Scholar] [CrossRef]

11. Chen Y, Sun H, Zhang W, Huang X. Using stress wave technology for leakage detection in a landfill impervious layer. Environ Sci Pollut Res Int. 2019;26(31):32050–64. doi:10.1007/s11356-019-06379-1. [Google Scholar] [PubMed] [CrossRef]

12. Zayat AA. Diversion detection and localization in small HDPE pipes using guided-wave ultrasound and deep learning techniques [dissertation]. Vancouver, BC, Canada: University of British Columbia; 2023. [Google Scholar]

13. Choi M, Han K, Wang X, Zhang Y, Liu Z. A dual-stream neural network explains the functional segregation of dorsal and ventral visual pathways in human brains. Adv Neural Inf Process Syst. 2023;36:50408–28. [Google Scholar]

14. Xu N, Liu AA, Wong Y, Zhang Y, Nie W, Su Y, et al. Dual-stream recurrent neural network for video captioning. IEEE Trans Circuits Syst Video Technol. 2019;29(8):2482–93. doi:10.1109/TCSVT.2018.2867286. [Google Scholar] [CrossRef]

15. Keum K, Kwak JY, Rim J, Byeon DH, Kim I, Moon J, et al. Dual-stream deep learning integrated multimodal sensors for complex stimulus detection in intelligent sensory systems. Nano Energy. 2024;122:109342. doi:10.1016/j.nanoen.2024.109342. [Google Scholar] [CrossRef]

16. Yu B, Cao L, Jia J, Fan C, Dong Y, Zhu C. E-FNet: a EEG-fNIRS dual-stream model for Brain-Computer Interfaces. Biomed Signal Process Control. 2025;100(1–4):106943. doi:10.1016/j.bspc.2024.106943. [Google Scholar] [CrossRef]

17. Arun Faisal I, Waluyo Purboyo T, Siswo Raharjo Ansori A. A review of accelerometer sensor and gyroscope sensor in IMU sensors on motion capture. J Eng Appl Sci. 2019;15(3):826–9. doi:10.36478/jeasci.2020.826.829. [Google Scholar] [CrossRef]

18. Troiano RP, Berrigan D, Dodd KW, Mâsse LC, Tilert T, McDowell M. Physical activity in the United States measured by accelerometer. Med Sci Sports Exerc. 2008;40(1):181–8. doi:10.1249/mss.0b013e31815a51b3. [Google Scholar] [PubMed] [CrossRef]

19. Kiranyaz S, Avci O, Abdeljaber O, Ince T, Gabbouj M, Inman DJ. 1D convolutional neural networks and applications: a survey. Mech Syst Signal Process. 2021;151:107398. doi:10.1016/j.ymssp.2020.107398. [Google Scholar] [CrossRef]

20. Kiranyaz S, Ince T, Abdeljaber O, Avci O, Gabbouj M. 1-D convolutional neural networks for signal processing applications. In: ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2019 May 12–17; Brighton, UK. p. 8360–4. doi:10.1109/icassp.2019.8682194. [Google Scholar] [CrossRef]

21. Büssow R. An algorithm for the continuous Morlet wavelet transform. Mech Syst Signal Process. 2007;21(8):2970–9. doi:10.1016/j.ymssp.2007.06.001. [Google Scholar] [CrossRef]

22. Holschneider M. Introduction to continuous wavelet analysis. In: Wavelets in the geosciences. Berlin/Heidelberg, Germany: Springer; 2005. p. 1–71. doi:10.1007/bfb0011092. [Google Scholar] [CrossRef]

23. Harel D, Koren Y. Graph drawing by high-dimensional embedding. In: International Symposium on Graph Drawing; 2002 Aug 26–28; Irvine, CA, USA. Berlin/Heidelberg, Germany: Springer. p. 207–19. doi:10.1007/3-540-36151-0_20. [Google Scholar] [CrossRef]

24. Kokinov BN. The context-sensitive cognitive architecture DUAL. In: Proceedings of the Sixteenth Annual Conference of the Cognitive Science Society; 2019; London, UK: Routledge. p. 502–7. doi:10.4324/9781315789354-87. [Google Scholar] [CrossRef]

25. Geng J, Song S, Jiang W. Dual-path feature aware network for remote sensing image semantic segmentation. IEEE Trans Circuits Syst Video Technol. 2024;34(5):3674–86. doi:10.1109/TCSVT.2023.3317937. [Google Scholar] [CrossRef]

26. Qi S, Huang X, Peng P, Huang X, Zhang J, Wang X. Cascaded attention: adaptive and gated graph attention network for multiagent reinforcement learning. IEEE Trans Neural Netw Learn Syst. 2024;35(3):3769–79. doi:10.1109/TNNLS.2022.3197918. [Google Scholar] [PubMed] [CrossRef]

27. Zhang J, Zou W, Hu N, Zhang B, Wang J. S-Net: an S-shaped network for nodule detection in 3D CT images. Phys Med Biol. 2024;69(7):075013. doi:10.1088/1361-6560/ad2b96. [Google Scholar] [PubMed] [CrossRef]

28. Zhang S, Tong H, Xu J, Maciejewski R. Graph convolutional networks: a comprehensive review. Comput Soc Netw. 2019;6(1):11. doi:10.1186/s40649-019-0069-y. [Google Scholar] [PubMed] [CrossRef]

29. Wu F, Souza A, Zhang T, Fifty C, Yu T, Weinberger K. Simplifying graph convolutional networks. In: International Conference on Machine Learning; 2019 Jun 10–15; Long Beach, CA, USA. p. 6861–71. [Google Scholar]

30. Jordan JL, Dattelbaum DM, Schilling BF, Welch CF, Stull JA. Low pressure shock response and dynamic failure of high density polyethylene (HDPE). AIP Conf Proc. 2018;1979(1):090006. doi:10.1063/1.5044863. [Google Scholar] [CrossRef]

31. Krishnaswamy RK. Analysis of ductile and brittle failures from creep rupture testing of high-density polyethylene (HDPE) pipes. Polymer. 2005;46(25):11664–72. doi:10.1016/j.polymer.2005.09.084. [Google Scholar] [CrossRef]

32. Yenigül NB, Elfeki AMM, Gehrels JC, van den Akker C, Hensbergen AT, Dekking FM. Reliability assessment of groundwater monitoring networks at landfill sites. J Hydrol. 2005;308(1–4):1–17. doi:10.1016/j.jhydrol.2004.10.017. [Google Scholar] [CrossRef]

33. Buket Yenigül N, Elfeki AMM, Van Den Akker C. New approach for ground water detection monitoring at lined landfills. Groundwater Monitoring Rem. 2006;26(2):79–86. doi:10.1111/j.1745-6592.2006.00073.x. [Google Scholar] [CrossRef]

34. Olscher C, Jandric A, Zafiu C, Part F. Evaluation of marker materials and spectroscopic methods for tracer-based sorting of plastic wastes. Polymers. 2022;14(15):3074. doi:10.3390/polym14153074. [Google Scholar] [PubMed] [CrossRef]

35. Jandric A, Olscher C, Zafiu C, Lielacher R, Lechner C, Lassenberger A, et al. Adding rare earth oxide markers to polyoxymethylene to improve plastic recycling through tracer-based sorting. Polymers. 2024;16(18):2591. doi:10.3390/polym16182591. [Google Scholar] [PubMed] [CrossRef]

36. Müller WW. Leak detection and monitoring systems. In: HDPE geomembranes in geotechnics. Berlin/Heidelberg, Germany: Springer; 2007. p. 421–49. doi:10.1007/978-3-540-37288-2_11. [Google Scholar] [CrossRef]

37. Peggs ID, Nosko V, Razdorov P, Galvin P. Leak monitoring for a double liner separated by a novel conductive geotextile. In: Proceedings of the Third European Geosynthetics Conference; 2004 Mar 1–3; Munich, Germany. p. 515–8. [Google Scholar]

38. White CC, Barker RD. Electrical leak detection system for landfill liners: a case history. Groundw Monit Remediat. 1997;17(3):153–9. doi:10.1111/j.1745-6592.1997.tb00590.x. [Google Scholar] [CrossRef]

39. Hu X, Han Y, Wang Y, Zhang X, Du L. Experiment on monitoring leakage of landfill leachate by parallel potentiometric monitoring method. Sci Rep. 2022;12(1):20496. doi:10.1038/s41598-022-24352-w. [Google Scholar] [PubMed] [CrossRef]

40. Priyananda P, Nguyen D, Huynh V, Hawkett BS. Decohesion of a polyolefin overlay from a substrate high density polyethylene layer by impact induced stress waves. Waste Manag. 2023;171(3):393–400. doi:10.1016/j.wasman.2023.09.031. [Google Scholar] [PubMed] [CrossRef]

41. Zhang Y, Jiang N, Zhou C, Yao Y, Hu Z. Mechanical behaviors and failure mechanism of HDPE corrugated pipeline subjected to blasting seismic wave. Alex Eng J. 2023;67(25):597–607. doi:10.1016/j.aej.2022.12.052. [Google Scholar] [CrossRef]

42. Guo H, Rinaldi RG, Tayakout S, Broudin M, Lame O. The correlation between the mixed-mode oligo-cyclic loading induced mechanical and microstructure changes in HDPE. Polymer. 2021;224:123706. doi:10.1016/j.polymer.2021.123706. [Google Scholar] [CrossRef]