A Novel Quantitative Detection of Sleeve Grouting Compactness Based on Ultrasonic Time-Frequency Dual-Domain Analysis

1  Introduction

Prefabricated building systems have become the mainstream construction method in modern civil engineering due to their high industrial construction efficiency and excellent environmental performance throughout their entire lifecycle [1]. In the connection of prefabricated components, the grouting sleeve is the core force transmitting component, and its internal compactness directly determines the overall collaborative performance, seismic energy dissipation mechanism, and service life durability evolution of the structure [2–4]. Therefore, the quantitative detection research of the grouting compactness of the sleeve has key engineering value.

The existing experimental research has clearly identified the serious harm of sleeve defects. Xiao et al. [5] confirmed through quasi-static tests on prefabricated shear walls, and Cao et al. [6] confirmed through full-scale structural tests that if there are honeycomb defects or segregation layers inside the sleeve, it will cause a nonlinear reduction of 30%–45% in the stiffness of structural nodes, intensify the hysteresis curve pinching effect, and reduce the energy dissipation coefficient by 0.15–0.25. Moreover, it is easy to cause unforeseeable brittle failure under the action of earthquakes with excessive fortification compactness, highlighting the necessity of precise detection of compactness.

Further research has been conducted to verify the fatal effects of defects on bridge structures subjected to cyclic loads. Cao et al. [7] found in the cyclic loading test of bridge piers and columns that when the grouting compactness is below 90%, the hysteresis area of the piers and columns decreases by 40%, and there is a significant slip section in the skeleton curve; The corrugated pipe grouting test conducted by Chu et al. [8] also showed that insufficient compaction can reduce the displacement ductility coefficient of the structure by more than 40%, directly threatening the seismic safety of the bridge. The common problems between the above-mentioned buildings and bridge scenes provide the core engineering basis for the quantitative detection of the compactness of sleeve grouting, which is the focus of this study.

The sleeve grouting compactness is a core indicator for ensuring the seismic performance and durability of prefabricated concrete structures, and its defects in grouting sleeves may result in a 30%–50% decrease in structural load-bearing capacity [9,10]. Traditional testing methods, such as drilling and coring, are destructive and inefficient, which makes nondestructive testing technology a research hotspot. The current research has formed a technical system with signal acquisition technology, a feature extraction method, and an intelligent diagnosis model as the core. However, the accurate detection under complex working conditions still faces multiple challenges [11,12].

In terms of signal acquisition technology, ultrasonic testing is widely used in structural nondestructive testing. Liu et al. [13] proposed a bridge prestressed bellow grouting detection method based on random forest (RF) feature selection and genetic algorithm optimized support vector machine (GA-SVM). By collecting the vibration signals of multiple physical field sensors, a defect classification accuracy of 92.3% is achieved. Li et al. [14] developed an ultrasonic detection method based on wavelet packet energy. By changing the energy of high-frequency components, the defect positioning accuracy of ±1.5 mm was achieved. Liu et al. [15] combined elastic inverse time shift imaging technology to further improve the defect visualization resolution to a sub-millimeter level. In terms of acoustic emission (AE) technology, Ma et al. [10] proposed the detection method of acoustic emission energy characteristic parameters, and found that when the compactness was less than 70%, the proportion of high-frequency (100–200 kHz) energy increased significantly; Zhang et al. [16] realized the full cycle tracking from crack initiation to propagation through the joint monitoring of acoustic emission and ultrasonic. In terms of piezoelectric sensor technology, Wu et al. [11] verified the feasibility of monitoring the grouting process, and Jiang et al. [17] optimized the sensor layout scheme through finite element simulation, so that the defect positioning accuracy reached ±2 cm. In addition, in terms of microwave detection technology, Zheng et al. [18] established the correlation model between compactness and dielectric constant based on the change of RF s parameter, and the experiment showed that the change rate of S parameter was linearly correlated with porosity (R2 = 0.89).

In the field of signal processing and feature extraction, wavelet analysis has become the mainstream tool. Cao et al. [19] proposed the wavelet packet energy ratio change index (ERCR) and established a linear relationship with porosity (R2 = 0.91); Xiao et al. [20] built a time domain dimensionless feature parameter set (such as peak factor and pulse factor) to improve the recognition rate of small defects (<5 mm) to 90%. Janeliukstis et al. [21] realized the multi-damage location of beam structures through wavelet transform, but did not solve the problem of noise suppression. In terms of time-frequency analysis, Zhang et al. [22] used wavelet packet denoising and energy spectrum analysis combined with a support vector machine to achieve an 85.6% detection accuracy of grouting defects of prefabricated columns. At the same time, in view of the nonstationarity (signal superposition caused by multi-interface reflection) and multimodal characteristics (P-wave and S-wave coexistence) of the ultrasonic signal of the grouting sleeve, Hilbert Huang transform (HHT)—its empirical mode decomposition (EMD) can separate the intrinsic mode function (IMF) of different frequencies to eliminate signal interference is introduced in this paper; Hilbert spectrum can characterize the change of instantaneous frequency and amplitude, which provides a theoretical basis for subsequent extraction of HEP, and solves the problem that traditional Fourier transform cannot process non-stationary signals.

In terms of an intelligent diagnosis model, machine learning and deep learning technology significantly improve the detection accuracy. Liu et al. [13] combined with an RF-GA-SVM model to achieve 92.3% classification accuracy under complex conditions; Li et al. [23] developed a guided wave detection model driven by deep learning, and the recognition accuracy of the half-grouted sleeve reached 94.2%. Liu et al. [24] realized an 88.7% recognition rate of insufficient grouting (<80%) based on a BP neural network, but there is a problem of over-fitting. Lei et al. [25] applied the intelligent classification method to mechanical fault diagnosis, but did not consider the multi-condition migration scenario.

To sum up, there are many problems in the existing sleeve grouting compactness detection methods. For example, the above detection method can only judge whether there are grouting defects but cannot detect the defect rate. Single-sensor technology is easily affected by the discreteness of concrete materials. Li et al. [26] pointed out that the amplitude of the acoustic emission signal is negatively correlated with the strength of concrete. In traditional signal processing, it is challenging to capture weak defect features, which must be combined with multi-source information fusion technology [16,27]. In addition, three-dimensional defect characterization [12], multi-physical field coupling mechanisms [16], and environmental temperature influence [28] still need to be further explored. Although the finite element simulation of Jiang et al. [17] optimized the sensor layout, it did not consider the actual construction error. Therefore, the detection method of sleeve grouting compactness still needs further research [29,30].

In practical applications, there are many methods to detect sleeve grouting compactness. However, there are still relatively few methods to detect sleeve grouting compactness quantitatively. With the advantages of high-frequency harmonic detection ability, signal stability, and high precision, ultrasonic technology shows excellent potential in the field of sleeve grouting compactness detection. To realize the quantitative detection of sleeve grouting compactness, a novel quantitative detection method based on a comprehensive DI is established using ultrasonic technology and eight characteristic parameters (including time-frequency KU and FF, etc.). The contributions of this study are as follows:

(1)   Combined with eight characteristic parameters (including KU and FF, etc., in the time-frequency domain), a novel quantitative detection method based on comprehensive defect index DI was established for the quantitative detection of sleeve grouting compactness.

(2)   The selected characteristic parameters can effectively reflect whether there are defects in the grouting sleeve and provide a reliable basis for the subsequent quantitative evaluation of defects.

(3)   The defect detection method of grouting sleeve based on multi-characteristic parameters in the time-frequency domain is proposed, which breaks through the limitations of the traditional single-parameter detection system.

(4)   There are two types of grouting sleeves, for which the novel DI quantitative detection proposed has good universality.

The remaining part of the article is structured as follows. Section 2 introduces the design and implementation of the test, including two sub-sections: the construction and parameter design of the gradient defect specimen system, and the construction and parameter optimization of the ultrasonic testing system. Section 3 features parameter selection and construction, including three sub-sections: time domain dimensionless parameter sensitivity analysis and application, wavelet packet energy entropy feature extraction, and Hilbert energy peak feature extraction. Section 4 constructs the comprehensive defect index DI. Section 5 is the analysis of the experimental results of ultrasonic multi-characteristic parameter detection, including two sub-sections: the analysis of the response law of characteristic parameters to grouting defects, and the quantitative characteristics and defect degree characterization of the comprehensive defect index DI. Finally, Section 6 summarizes the research conclusions and discussions.

2  Experimental Design and Implementation

2.1 Gradient Defect Specimen System Construction and Parameter Design

To establish a mapping relationship between the sleeve grouting compactness and characteristic parameters, this study first constructed a gradient defect sample system. By precisely controlling the defect level, a reliable sample basis was provided for subsequent experiments. This study focuses on high-performance cement-based grout as the core material, which is provided by Qingdao Zhuo Neng da Construction Technology Co., Ltd. The component design follows the principle of composite synergistic effect, ensuring the material’s excellent performance under extreme water-to-cement ratios. Laboratory tests demonstrate that the material exhibits excellent performance under a 0.11 water-cement ratio, with an initial flow of ≥300 mm, a two-hour flow loss of ≤5%, and a 3-day compressive strength exceeding 36.5 MPa. The 28-day volume expansion rate is stabilized within the range of 0.02% to 0.04%.

As shown in Fig. 1, the slurry preparation uses a two-stage mechanical stirring process. Firstly, add 70% of the total dry material to the mixing barrel and stir at a low speed of 150 ± 10 rpm for 90 s to form a primary dispersion system. Then, add the remaining 30% of dry material in three batches and gradually increase the speed to 220 ± 10 rpm, continue stirring for 240 s. Finally, as shown in Fig. 2, the slurry is left to stand for 180 s for defoaming treatment; as shown in Fig. 3, compressive test specimens are prepared. Through this stirring process and subsequent static defoaming treatment, bubbles in the slurry can be effectively removed, thereby improving the uniformity of the slurry and ensuring that it meets stability requirements.

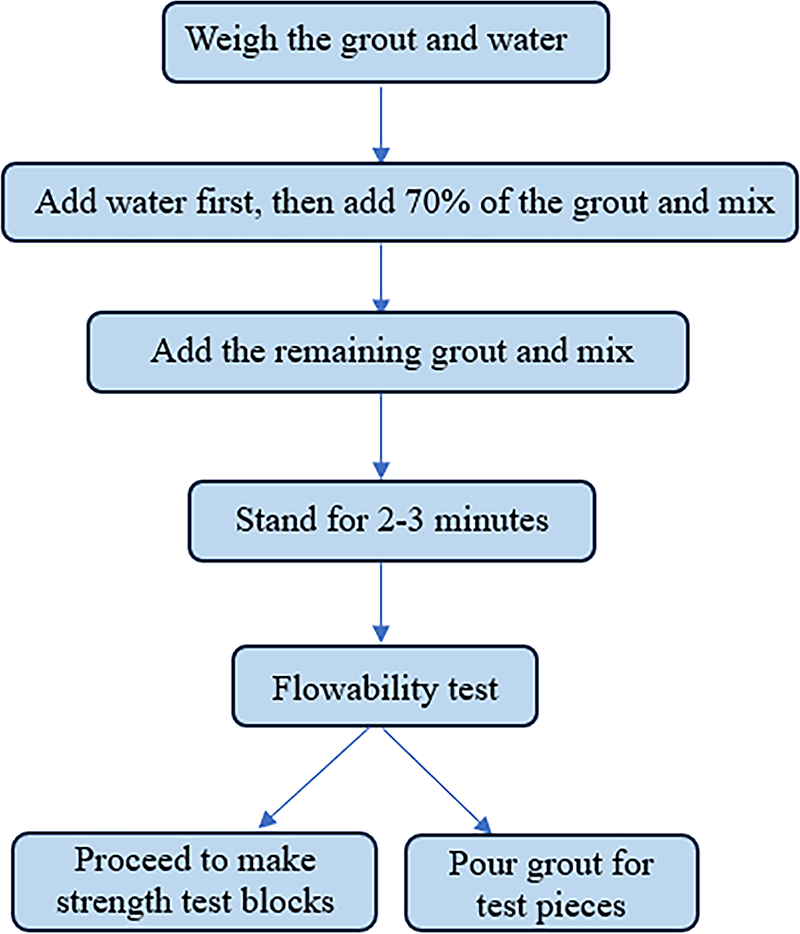
Figure 1: Production process

Figure 2: Grouting material

Figure 3: Compressive specimens

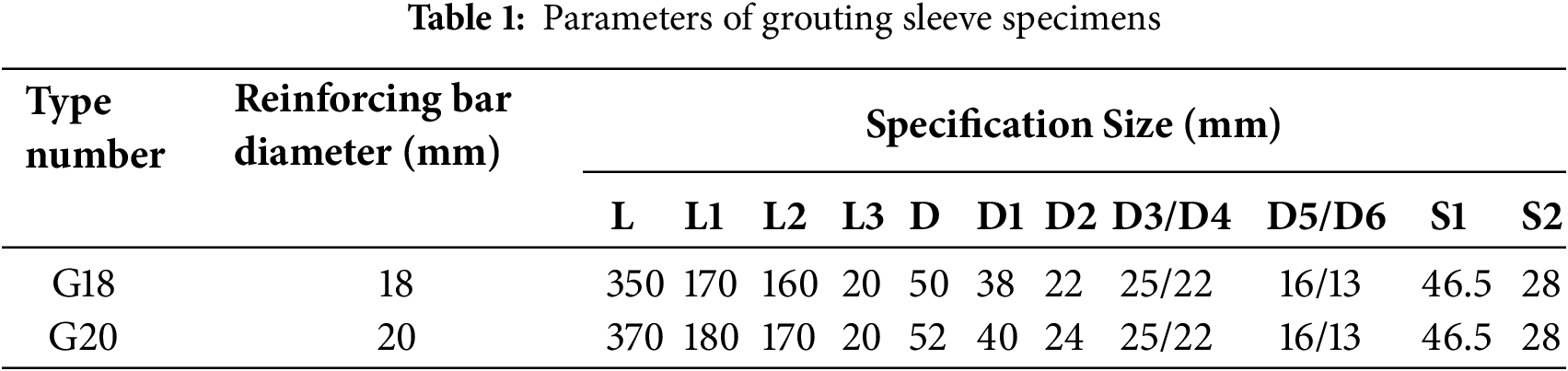
Based on the principles of orthogonal experimental design, this study selected two types of grouting sleeves and prepared samples with gradient defects to construct a research system with two types and four defects. Selecting the GT4 series G18 (Φ18 mm) and G20 (Φ20 mm) grouting sleeves as the experimental carriers. Its internal structure is shown in Fig. 4, and the key dimensions are shown in Table 1. L is the total length of the sleeve; L1, L2, and L3 are the lengths of different parts of the sleeve; D is the inner diameter, D1–D6 are the diameters of the other sections; S1 and S2 are the specific dimensions of both ends of the sleeve.

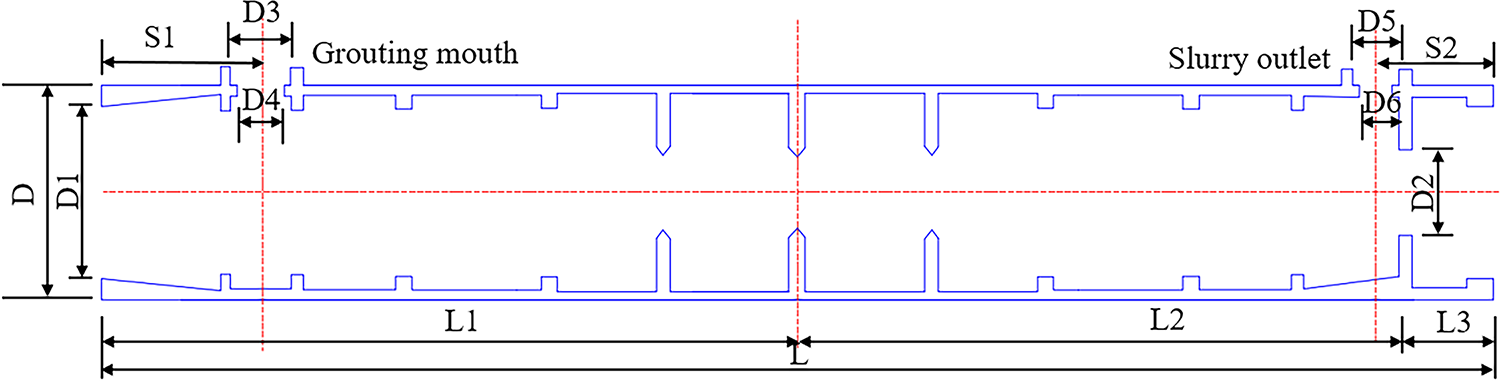
Figure 4: Internal structure of grouting sleeve

Before grouting, insert both ends of the reinforcing bars into the grouting sleeves and secure them with sealing plugs to prevent the reinforcing bars from shifting and the grout from leaking out. The sleeve grouting compactness is precisely controlled by the mass method, and the compactness grades are shown in Fig. 5. The specific steps are as follows: Before grouting, weigh the total mass of the sleeve, internal reinforcing bars, and sealing plug (denoted as M1); After grouting is complete, weigh the total mass again (denoted as M2); Finally, calculate the actual mass of grout injected based on the mass difference; The theoretical grouting quality of defect free grouting sleeves is based on the difference between the completed grouting and the pre grouting. The compactness P of the no-defect grouting sleeve can be calculated using the following formula:

P=M2−M1(1)

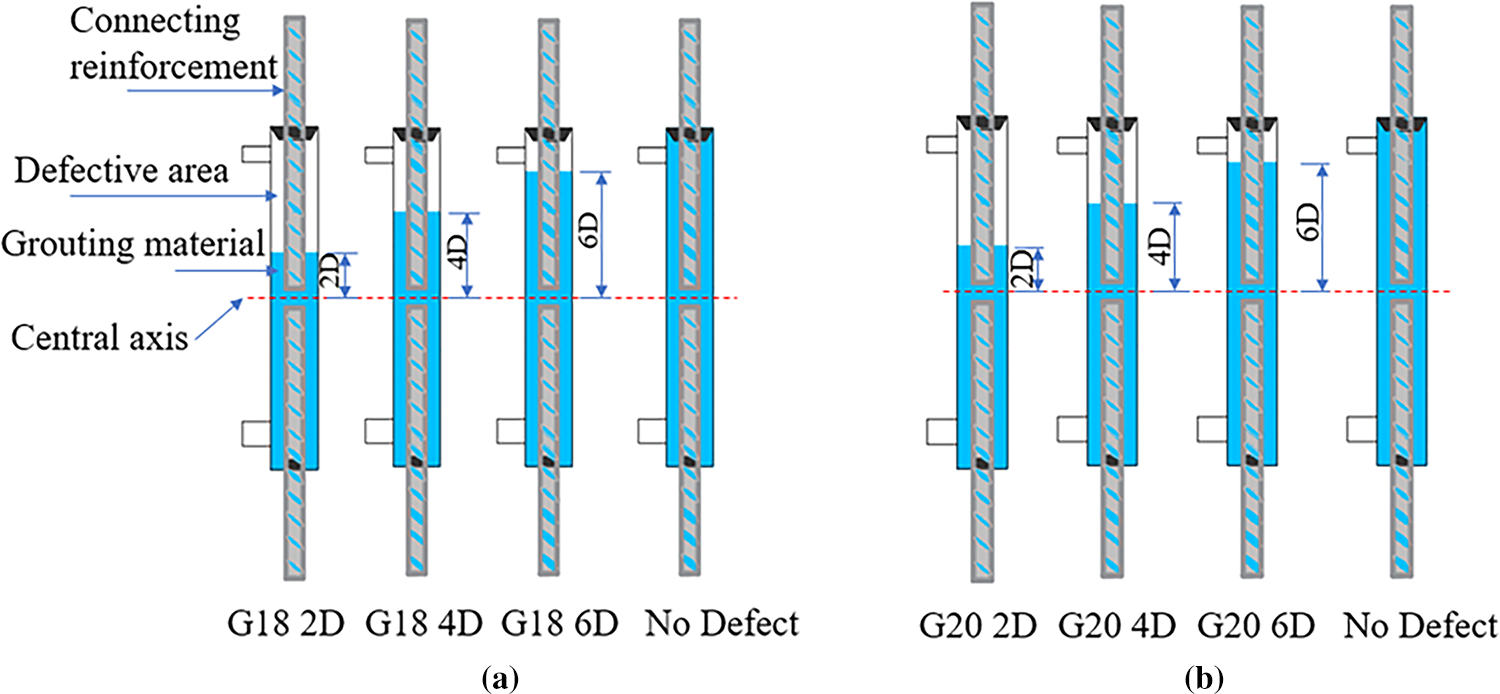
Figure 5: Grouting sleeve defect diagram. (a) G18 (b) G20

2D Grouting Sleeve Compactness:

P1=14P(2)

4D Grouting Sleeve Compactness:

P2=12P(3)

6D Grouting Sleeve Compactness:

P3=34P(4)

After grouting, the specimens were cured in a standard curing room at 20 ± 0.5°C and relative humidity (RH) of 95 ± 3% for 28 days, with daily temperature and humidity inspections to ensure environmental stability. Through the construction of the above system and parameter design, a reliable test piece foundation was provided for subsequent experiments.

2.2 Ultrasonic Inspection System Construction and Parameter Optimization

As shown in Fig. 6, this study establishes an ultrasonic detection system based on the principle of pulse reflection. The aim is to obtain information on the three-dimensional spatial acoustic field distribution within the grouting sleeve, utilizing the reflective properties of ultrasound at the interface of the medium. The system consists of a signal generator, power amplifier, digital oscilloscope, and piezoelectric sensor. The configuration of each component is as follows: the signal generator uses a Ding Sheng SDG1022X series function/arbitrary waveform generator, with a sampling rate of 150 MSa/s and a bandwidth of ≤200 MHz, capable of meeting the requirements for high-frequency harmonic detection; the power amplifier is the An Tai ATA-101B/105B, with a gain of 20 dB and a signal-to-noise ratio of ≥70 dB; its linearity ensures signal transmission fidelity, meeting the voltage requirements for driving PZT sensors; the digital oscilloscope uses the Ding Sheng SDS1202X-C dual-channel digital oscilloscope, with a bandwidth of 200 MHz, a storage depth of 14 Mpts, vertical resolution of 12 bits, and its segmented storage technology enables high-fidelity signal capture. The ultrasonic transducer uses a PZT5-type lead zirconate titanate ceramic sensor, as shown in Fig. 7, with dimensions of 10 mm3 ∗ 10 mm3 ∗ 1 mm3, Curie temperature of 350°C, electromechanical coupling coefficient kt = 0.52, relative permittivity ε33T/ε0 = 2000 ± 10%, and center frequency of 1.98 MHz (–6 dB bandwidth 1.2–2.8 MHz). The excitation signal used in this study was a single-cycle sine wave with a center frequency of 200 kHz and peak-to-peak value of 5 V to ensure signal stability and detection accuracy.

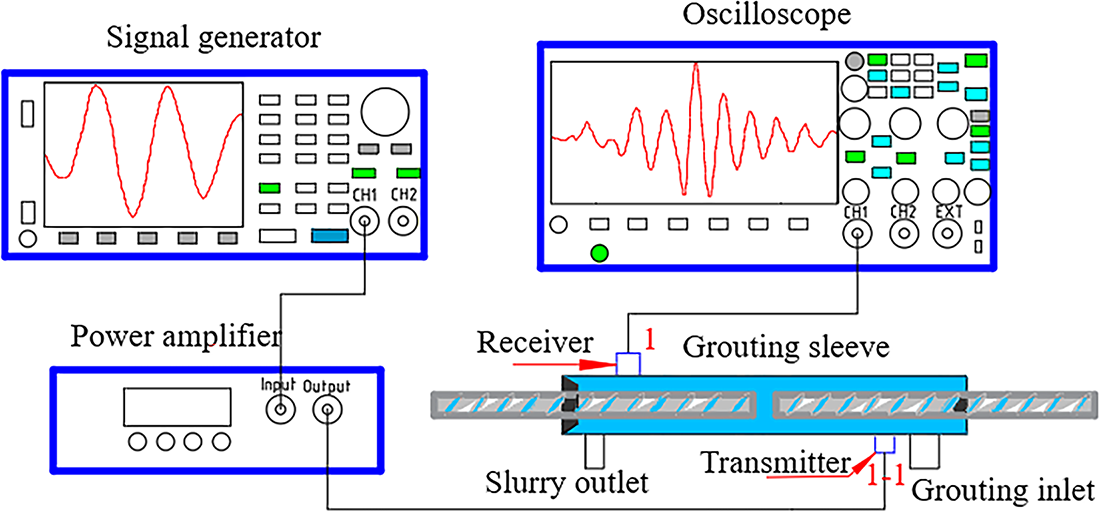
Figure 6: Ultrasonic testing system

Figure 7: PZT piezoceramics

As shown in Fig. 8, based on the principle of optimizing the spatial resolution of the sound field, an orthogonal detection network was constructed on the surface of the sleeve. Four groups (PZT1–PZT4) are uniformly arranged along the circumference of the sleeve, with a center to center distance of 160 ± 0.5 mm between each transmitter (Tx) and receiver (Rx), forming four independent detection paths in sequence. The distance between the center of the sensor and the grouting port and the outlet is 30 ± 1 mm, and the radial angle between the axis and the sleeve is 45° (error ≤ 0.5°); Medical Vaseline (purity ≥ 99%) is selected as the coupling agent, with a coating thickness of 0.2 ± 0.05 mm to ensure acoustic impedance matching and reduce signal attenuation.

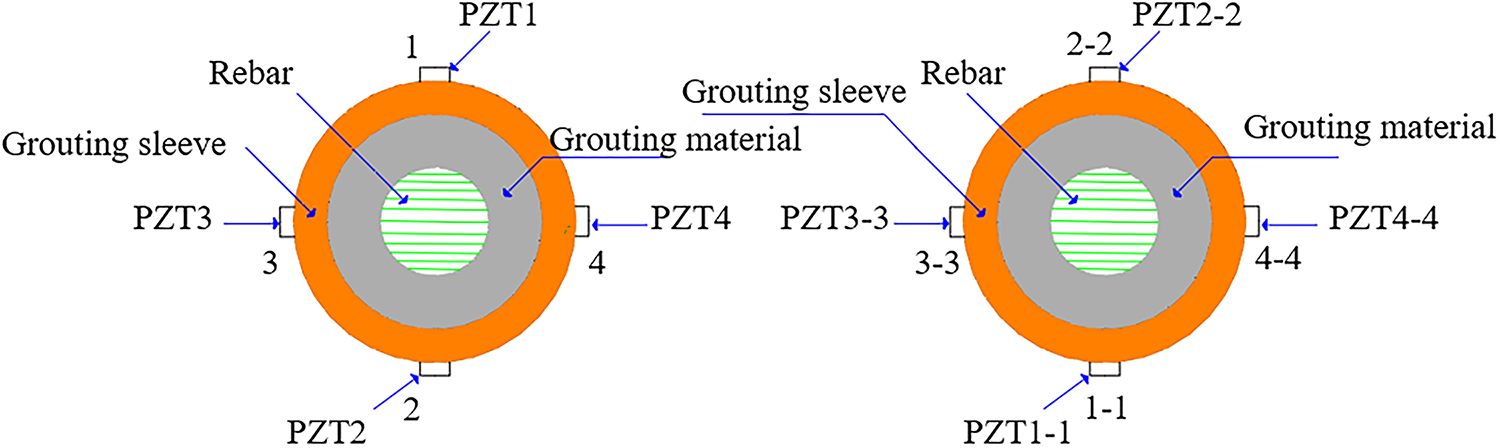
Figure 8: Space layout of grouting sleeve multi-path detection. (a) Left side view of pulp outlet (b) Right side view of grouting port

As shown in Fig. 9, each type of precast grouting sleeve contains four different compactness levels. As shown in Fig. 10, for these precast sleeves with different compactness levels, we used a multipath cross-detection method to obtain three-dimensional acoustic field distribution information inside the sleeve.

Figure 9: Grouting sleeve

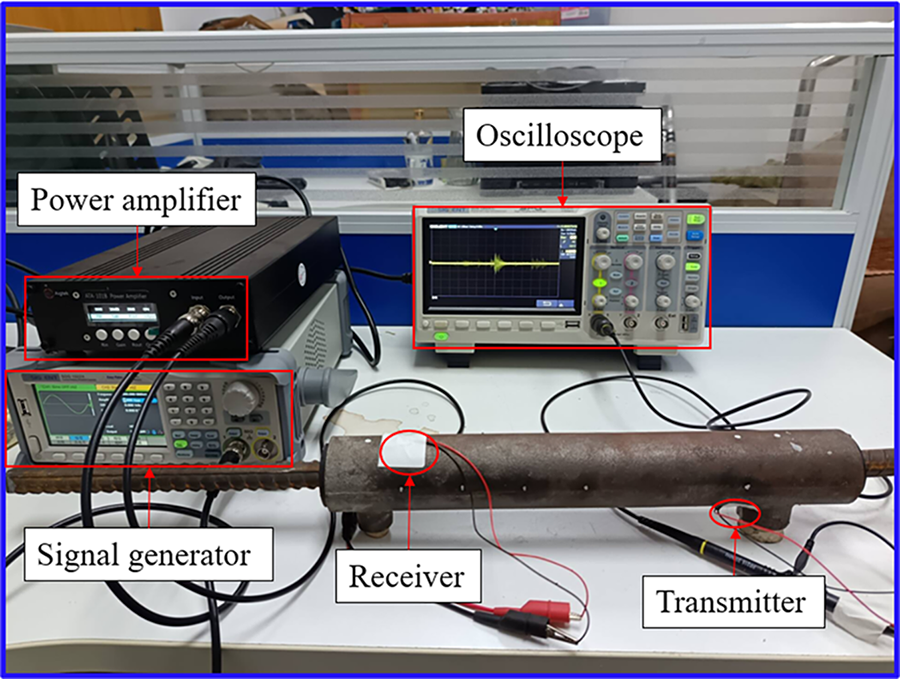
Figure 10: Detection system

The specific acquisition parameter settings are shown in Table 2.

It should be noted that the reasonable configuration of parameters is crucial for improving signal quality and detection accuracy. By employing a transmitter-receiver position rotation strategy, the reliability and reproducibility of the detection results were effectively improved. Through the aforementioned hardware configuration, detection network design, and parameter optimization, the ultrasonic detection system developed in this study can accurately capture the acoustic characteristics of the fill level inside the grouting sleeves, providing high-quality experimental data support for subsequent fill level identification and quantitative analysis.

3  Feature Parameter Selection and Construction

3.1 Time-Domain Dimensionless Parameter Sensitivity Analysis with Applications

Time-domain dimensionless parameters have significant advantages in the field of ultrasonic nondestructive testing. This is mainly due to their insensitivity to signal amplitude, which can more accurately reflect the waveform and statistical characteristics of the signal. In the practical application of grouting sleeve testing, these characteristic parameters can effectively capture signal changes caused by grouting defects, providing key evidence for the accurate assessment of grouting compactness. This study carefully selected six time-domain dimensionless parameters: KU, SK, FF, CF, IF, and CLF. These parameters are committed to building a multidimensional feature space. These parameters were derived from different mathematical dimensions, a comprehensive characterization of ultrasonic signals. Together, they form a multiscale feature description system for ultrasonic signals, providing rich and multidimensional criteria for the quantitative detection of sleeve grouting compactness. Specifically, the KU reflects the sharpness of the signal distribution by calculating the fourth-order central moment of the signal, which is highly sensitive to impact defects; The SK is based on the third-order central moment to characterize the asymmetry of signal distribution, which can be used to identify local damage such as internal cracks in materials and provide strong support for early detection of defects; The FF is defined as the ratio of the RMS value of the signal to the absolute mean value, which can effectively reflect the uniformity of the signal energy distribution, thus providing an essential reference for assessing the grout compactness; The CF quantifies the transient shock component of the signal by calculating the peak-to-average ratio, and the IF quantifies the transient shock component of the signal by the peak-to-peak ratio, both of which provide richer information for precise localization and assessment of defects; The CLF uses the ratio of the peak value to the square root amplitude, which has a unique advantage in the early detection of weak defects, and is able to effectively capture the weak changes in the signal, providing an essential basis for the early assessment of grout compactness.

Assuming that the vibration signals collected in each sampling period are ui (i = 1, 2, 3, ..., N), N denotes the number of sampling points of the vibration signal in a single sampling period. Based on these signals, the mean (u¯), standard deviation (σ), and the above time-domain dimensionless characteristic parameters of the signals can be calculated, the specific formula is a classical statistical expression, which has been derived in detail in references [19,20]. This study directly cites the calculation results.

3.2 Wavelet Packet Energy Entropy Feature Extraction

In the field of non-stationary signal feature extraction, wavelet packet decomposition (WPD) is a cutting-edge technology. Compared to traditional wavelet transforms, it demonstrated significant advantages. It decomposes low-frequency approximation coefficients and high-frequency detail coefficients through bidirectional recursion, overcomes the symmetry constraints of classical wavelet transforms in frequency domain partitioning, and achieves adaptive multi-resolution analysis of the signal frequency domain. This full-band decomposition mechanism significantly improves the flexibility and accuracy of non-stationary signal feature extraction and can capture signal characteristics in different frequency bands more precisely. As shown in Fig. 11, wavelet packet decomposition generates a complete binary tree structure, with each node uniquely identified by its decomposition path through binary encoding, corresponding to the time-frequency energy distribution of the signal within a specific frequency band. This structure can analyze signals in more detail, thereby extracting more valuable information.

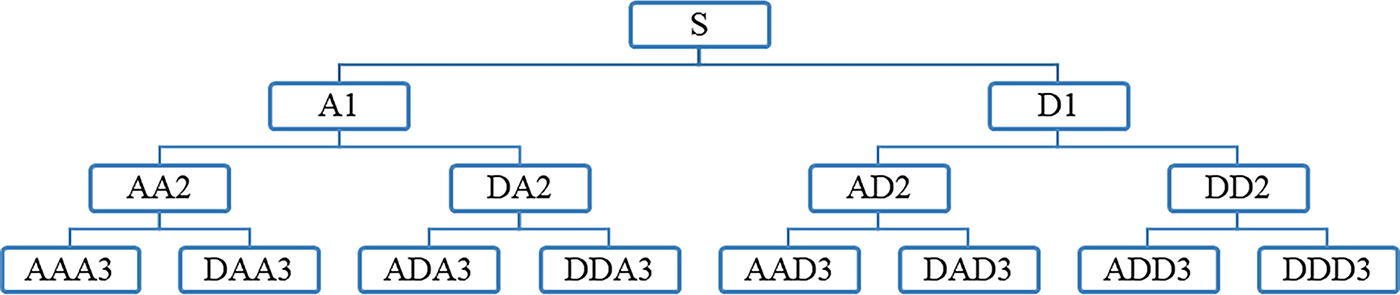
Figure 11: Schematic diagram of three-level wavelet packet decomposition

In Fig. 11, S represents the original ultrasonic signal to be decomposed, A represents the low frequency, and D represents the high frequency. The decomposition relationship can be expressed as follows:

S=AAA3+DAA3+ADA3+DDA3+AAD3+DAD3+ADD3+DDD3(5)

Based on wavelet packet decomposition, WPEE serves as a feature extraction tool, offering a new perspective for signal characterization by quantifying the complexity of the energy distribution across different frequency bands. The introduction of energy entropy not only compensates for the inadequacy of single-frequency or time-domain features but also effectively captures the non-stationary characteristics of the signal, providing a more comprehensive means of analysis for the non-destructive testing of complex engineering structures. By combining wavelet packet decomposition with energy entropy analysis, this study further optimizes the accuracy and reliability of signal feature extraction, laying a solid theoretical foundation for subsequent quantitative detection of compactness.

When ultrasound signals propagate in the defect sleeve, energy will be transferred to the high frequency band [10], resulting in uneven energy distribution in different frequency bands, and energy entropy can quantify this unevenness through energy probability; Energy entropy is an important measure of information entropy that characterizes the complexity of energy distribution, defined as Eq. (6) [19]:

H(x)=−∑i=1nP(xi)ln⁡P(xi)i=1,2,…,n(6)

where P(xi) is the probability of a random event being generated, reflecting the energy share of the signal in the ith frequency band.

In the process of ultrasonic testing for the sleeve grouting compactness, WPEE serves as an effective signal analysis method, reflecting the distribution characteristics of signal energy. The ultrasonic wave is affected by the internal structure of the grout sleeve in the process of propagation, and the distribution of signal energy is closely related to the compactness of the sleeve. WPEE quantifies the distribution of signal energy across different frequency bands, effectively characterizing the complexity and uniformity of the signal. Specifically, when defects exist inside the grout sleeve, the energy distribution of the ultrasonic signal changes. WPEE can sensitively detect these changes, thereby providing important evidence for the detection and evaluation of compactness.

3.3 Hilbert Energy Peak Feature Extraction

Based on the field of non-stationary signal processing, the combination of empirical modal decomposition (EMD) and Hilbert transform is an effective means of signal feature extraction. In 1998, Huang and other scholars proposed the empirical modal decomposition method, the basic principle of which is to decompose the signal into the intrinsic modal functions (IMFs) at different frequencies and a residual component. Each IMF component must satisfy two conditions: first, the number of extreme points of the function and the number of zero crossing points are equal, with a difference of at most 1; second, the average value of the upper and lower envelopes formed by the extreme points is zero.

Assuming that the original signal is X(t), after wavelet threshold denoising preprocessing, n eigenmode function components and residual components are obtained by EMD decomposition, denoted as Eq. (7) [14]:

X(t)=∑i=1nCi(t)+r(t)(7)

where Ci(t) is the IMF component, r(t) is the residual component.

Next, the Hilbert transform is applied to each IMF component to obtain the corresponding Hilbert spectrum. The formula is shown in Eq. (8) [14]:

H(ω,t)=Re∑jnaj(t)ei∫ωj(t)dt(8)

where Re is the fundamental part of the complex number and aj(t) is the instantaneous amplitude and instantaneous frequency of the jth IMF component, respectively.

Based on the Hilbert transform, the Hilbert energy ES(ω) can be defined as the integral of the amplitude squared over time, expressed as the energy accumulated at each frequency over the entire length of time, formulated as in Eq. (9) [15]:

ES(ω)=∫0TH2(ω,t)dt(9)

where T is the time length of the signal.

Ultimately, based on the Hilbert energy ES(ω) defined by Formula (9), take its maximum value as the Hilbert energy (HEP), as in Eq. (10) [15]:

E=max(ES(ω))(10)

The HEP feature constructed by the above method can effectively reflect the signal changes triggered by the internal defects of the grouting sleeve and provide an essential basis for the quantitative assessment of grouting compactness.

4  Comprehensive Defect Indicator DI Construction and Quantitative Assessment of Grout Compactness

In ultrasonic non-destructive testing, quantitative analysis of signal characteristics is crucial for accurately assessing sleeve grouting compactness. This study innovatively proposes the comprehensive evaluation standard of “defect index” based on the signal response characteristics of the ultrasonic oblique measurement method. By integrating multi-dimensional signal features in time-frequency domain, quantifying the difference between defect signals and reference signals, not only avoids the limitations of traditional single parameters, but also forms a unified judgment scale through mathematical design, shifting the evaluation of compactness from subjective judgment to objective calculation, and ultimately achieving accurate characterization of sleeve grouting compactness, providing scientific basis for quantitative detection of compactness and engineering acceptance.

Specifically, the mathematical definition of the comprehensive discrimination index DI is as shown in Eq. (11):

DI=∑k=14(|Sd,k−Si,k|Si,k)2(11)

Among them:

Si,k indicates the ultrasonic signal characteristic parameters of the kth group in a no defect state;

Sd,k represents the ultrasonic signal characteristic parameters of the channel corresponding to the defective sleeve under different compactness conditions (2D, 4D, and 6D);

k = 1, 2, 3, 4; correspond to different acquisition groups.

5  Ultrasound Multi-Featured Parameter Detection Experiment Results Analysis

5.1 Characteristic Parameter Response Law Analysis on Grouting Defects

This study, using ultrasonic testing technology, systematically investigates the response patterns of characteristic parameters of different types of grouting sleeves under various grouting compactness conditions. This investigation aims to establish a quantitative relationship between characteristic parameters and grout compactness, thereby providing a reliable basis for the quantitative detection of grouting compactness. The experiment used an ultrasonic testing system to test two types of grouting sleeves, G18 and G20; the test subjects covered parallel test pieces with different degrees of compactness. To ensure the accuracy and stability of experimental data, we keep the parameters of each excitation signal consistent. This approach can effectively reduce the impact of signal fluctuations on experimental results and ensure the comparability of waveform parameters. Figs. 12 and 13 show the four groups of signals collected from each specimen of G18 and G20 types, respectively, and the calculated characteristic parameter index values.

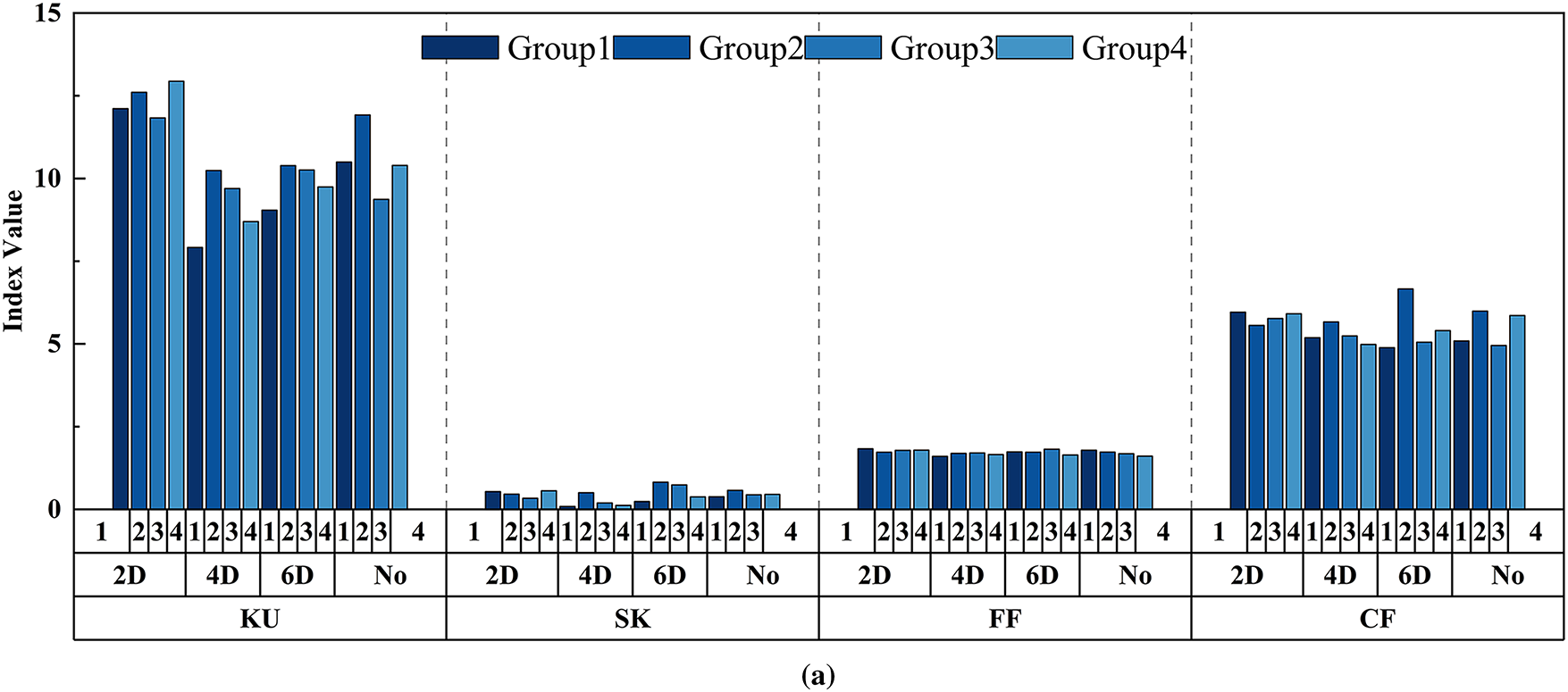
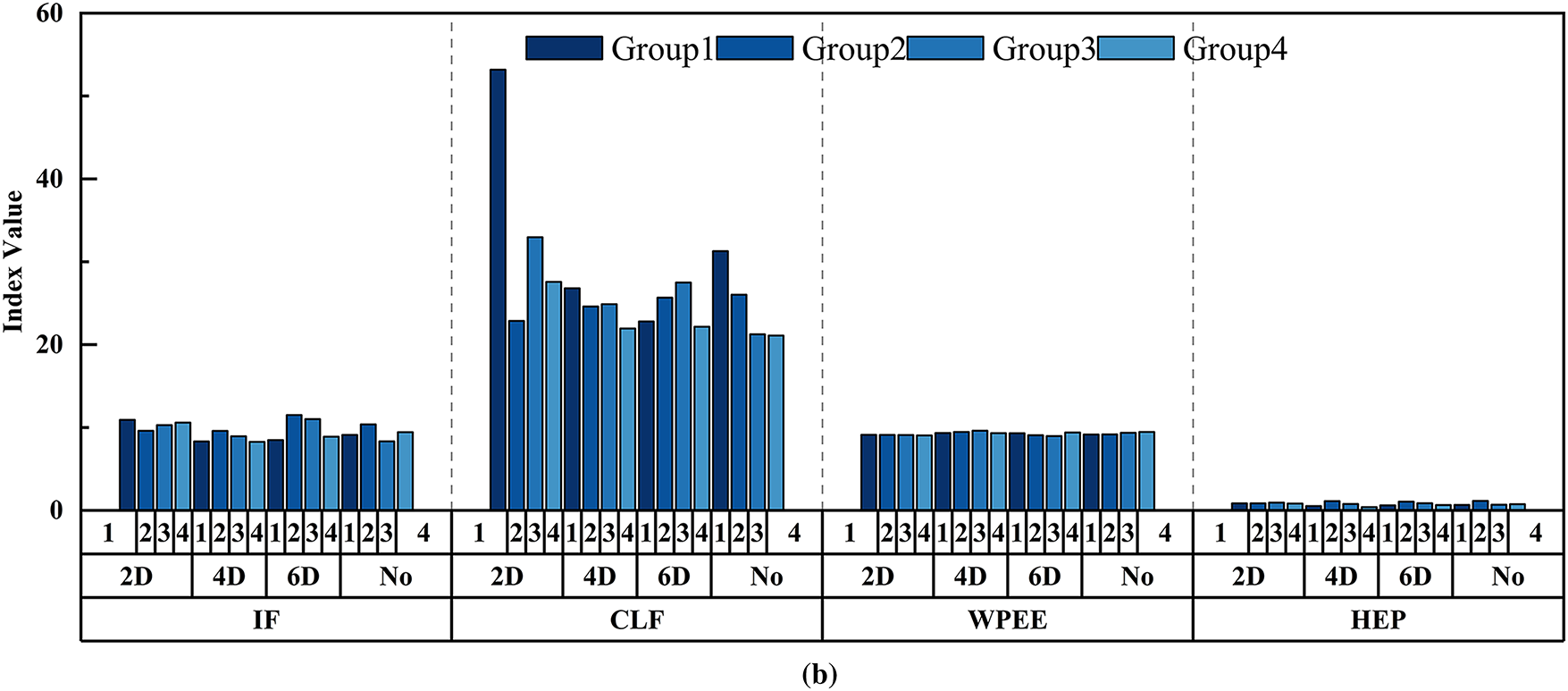
Figure 12: Characteristic parameter index values of G18 grouting sleeve under different grouting compactness. (a) KU, SK, FF, and CF characteristic parameter index values (b) IF, CLF, WPEE, and HEP characteristic parameter index values

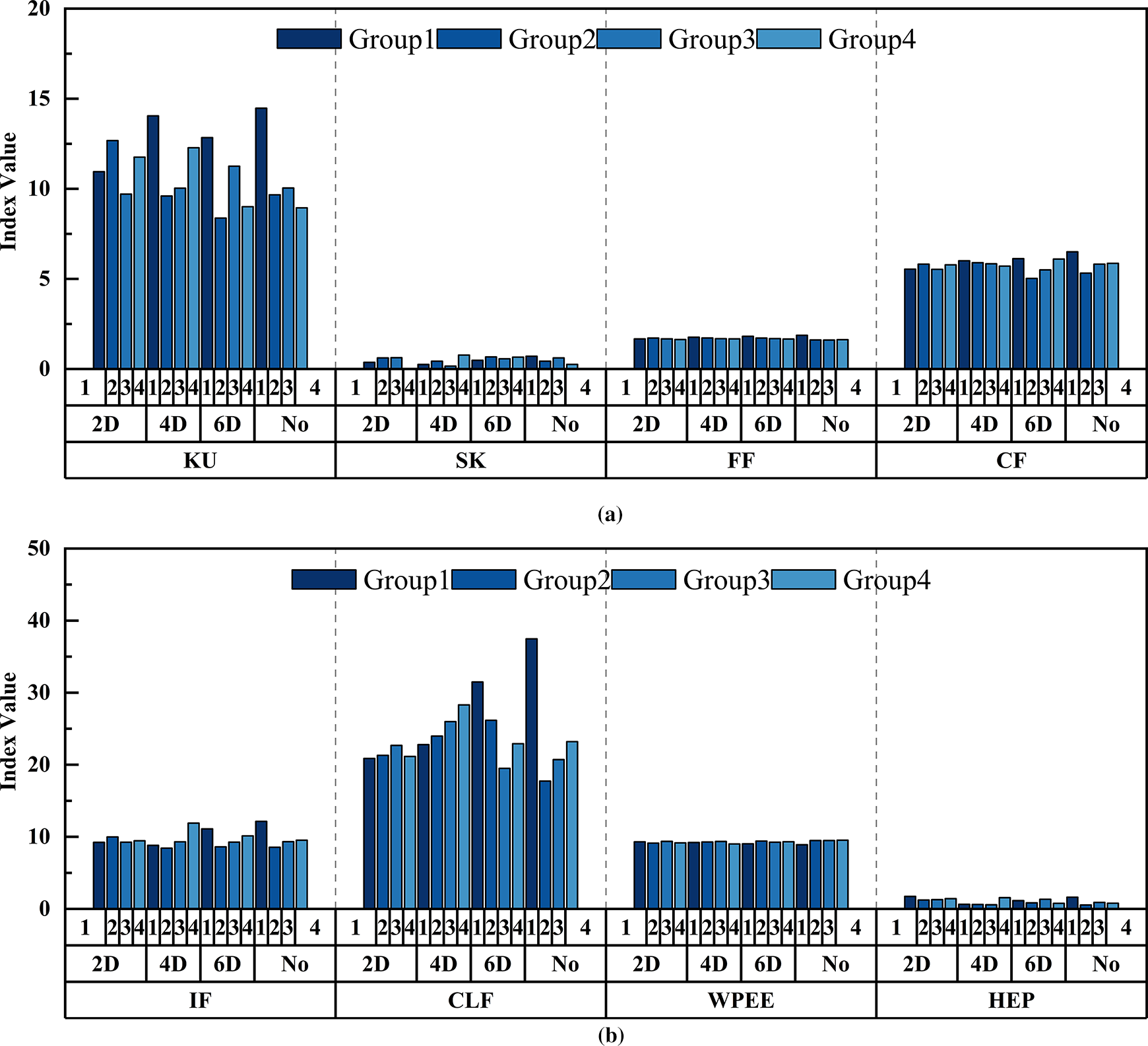
Figure 13: Characteristic parameter index values of G20 grouting sleeve under different grouting compactness. (a) KU, SK, FF, and CF characteristic parameter index values (b) IF, CLF, WPEE, and HEP characteristic parameter index values

Taking the G18 type defect free grouting sleeve parallel specimen as the research object, first prepare the specimen according to the process described in Section 2.1, and then carry out data collection work. Four sets of data were collected for each specimen, and eight characteristic parameters were calculated based on them. The results are shown in the Table 3.

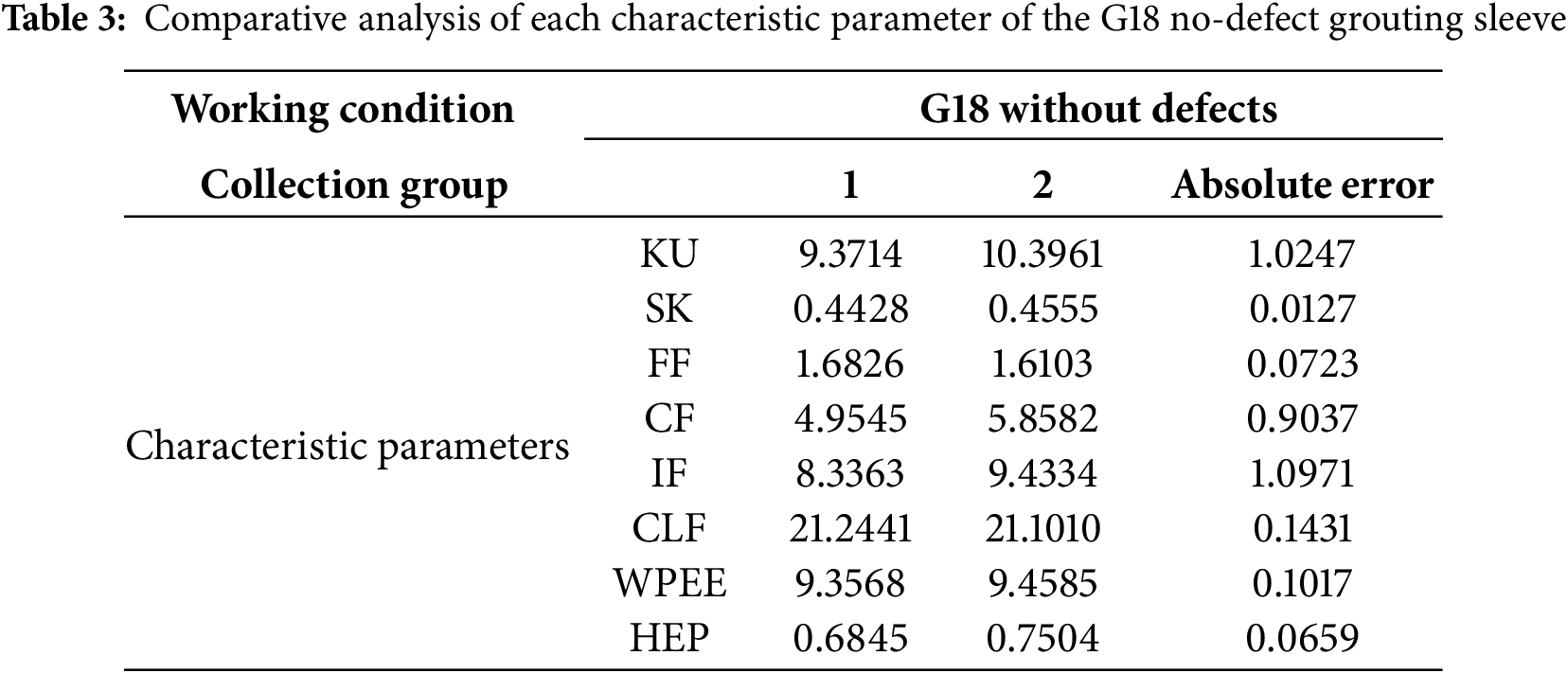
The absolute error of all characteristic parameters is controlled within 1%, indicating that under the same operating conditions, the characteristic parameters of parallel specimens have good consistency, and the experimental data have high reliability and repeatability. Based on the above results, this study selected the average data of characteristic parameters calculated from four sets of data for each specimen under the same operating conditions as the analysis basis. This method effectively improves the representativeness and stability of the data, providing a solid data foundation for establishing the mapping relationship between grouting compactness and feature parameters in the future, and helping to achieve accurate identification and quantitative detection of grouting compactness.

Fig. 14 shows the index values of various characteristic parameters for two types of grouting sleeves with and without defects. From this, it can be found that the trends in the characteristic parameter indices of the two types of grouting sleeves show a high degree of consistency. Under no-defect conditions, most characteristic parameter values are significantly lower than those in the defective state. In the case of defects, the index values of each characteristic parameter vary with different levels of compactness.

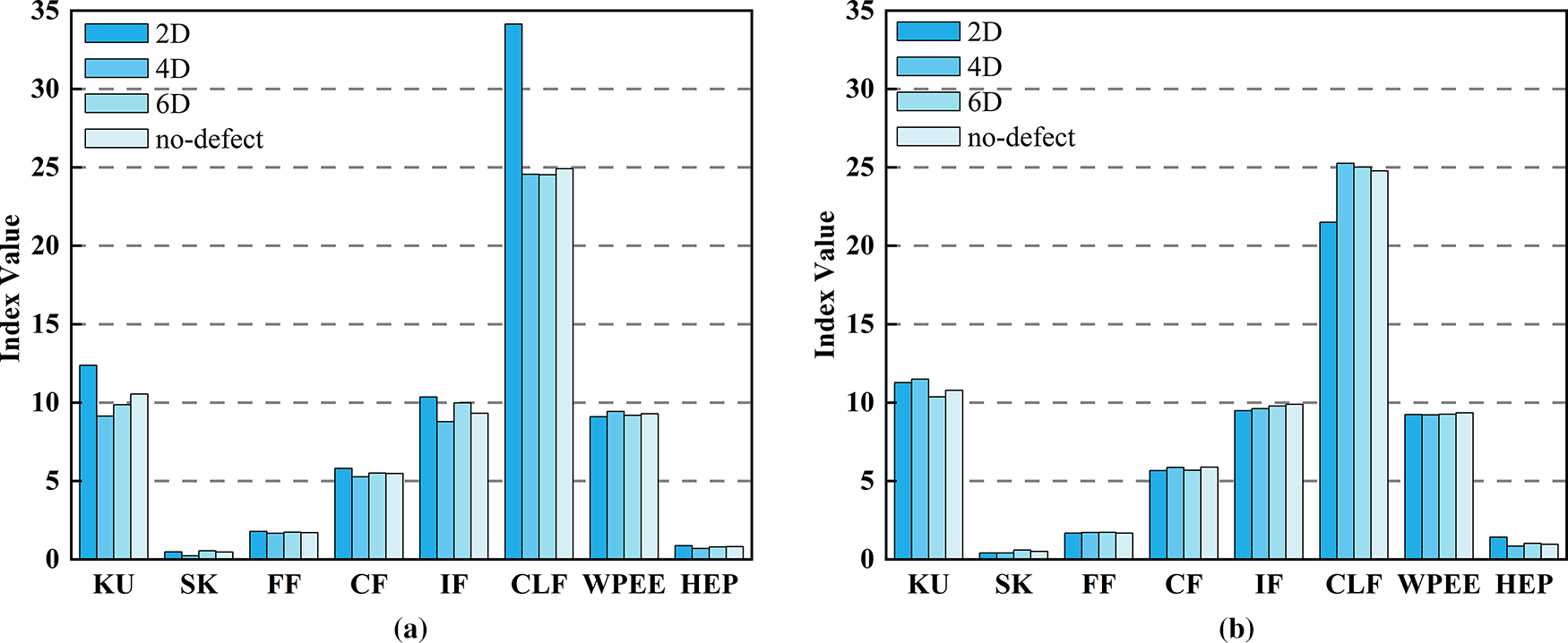
Figure 14: Characteristic parameter index values of different types of grouting sleeves under different grouting compactness. (a) Type G18 (b) Type G20

At the same time, there are differences in the structural dimensions between the G18 and G20 types. The G20 type has a relatively larger inner diameter and length. This may result in more complex effects of the medium on the ultrasonic signal during propagation, which makes its characteristic parameters more sensitive to changes in sleeve grouting compactness. In addition, there may be slight differences in material properties between the two types of sleeves. These differences can further affect the propagation speed and attenuation of ultrasonic signals, which may have a certain impact on the test results.

After verifying the reliability of the experimental data, we conducted further analysis of the variation patterns of different characteristic parameters with and without defects. Select feature parameters with high values for the three types of indicators, including KU, IF, and CLF, for analysis.

By analyzing the three working conditions of KU, IF, and CLF, and comparing the characteristic parameter index values of the G18 type grouting sleeve connecting steel bar with a diameter of 18 mm and the G20 type grouting sleeve connecting steel bar with a diameter of 20 mm, it can be concluded that: Under the KU condition, the distribution trends of the corresponding index values for each defect (2D, 4D, 6D, no-defect) of the two types of sleeves are similar, indicating that the influence of sleeve diameter on the signal under this condition has a certain consistency. When ultrasonic waves propagate in sleeves of different diameters, the type of action of the defect under this condition is similar; The difference in CLF working conditions is most prominent, with the 2D defect index values in G18 sleeve being much higher than other defect types, while the values of various defect types in G20 sleeve are closer, reflecting the significant influence of diameter on the ultrasonic signal characteristics of defect recognition under CLF working conditions.

In summary, in actual engineering projects, the compactness of the sleeve can be detected to a certain extent based on different characteristic parameters. However, it should be noted that the accuracy and reliability of this method may be affected by various factors, such as material properties, defect types, and sensor layout. Therefore, in actual applications, comprehensive evaluation and verification should be conducted based on specific circumstances.

5.2 Quantitative Characteristics and Defect Degree Characterization of Comprehensive Defect Index DI

After analyzing the response patterns of characteristic parameters of grouting defects, this study further quantifies the intrinsic relationship between defect severity and grout compactness. Additionally, a comprehensive defect index DI evaluation system based on multiple feature parameters was constructed. By comprehensively analyzing multiple feature parameters, the system achieves a quantitative assessment of defects in grouting sleeves and provides a scientific basis for the quantitative analysis of grout compactness.

In the study presented in Section 5.1, we identified a specific correlation between the characteristic parameters of each grouting sleeve model and the compactness of the grouting. Based on this, the DI index primarily quantifies the differences between defect signals and reference signals in the time-frequency domain. This enables the accurate and objective characterization of the severity of defects in grouting sleeves and allows for their effective application in standardized assessments of different models and levels of grout compactness.

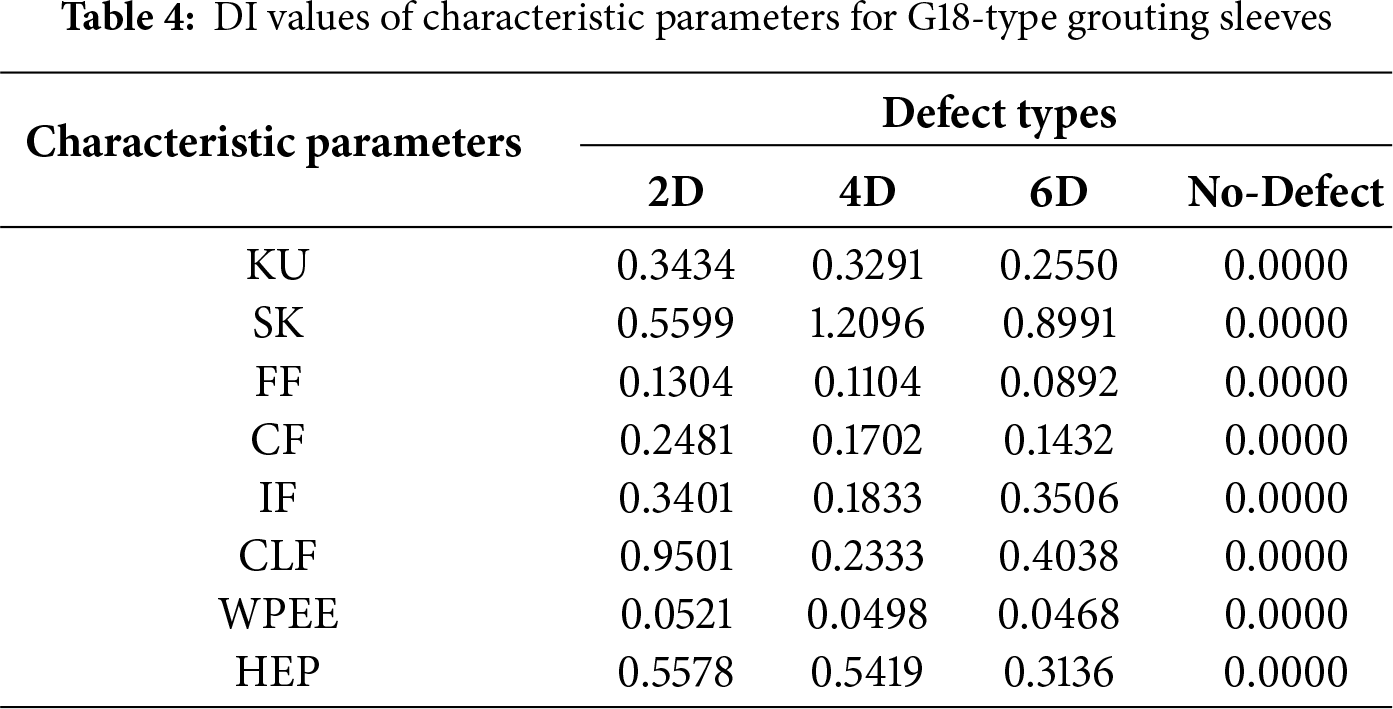
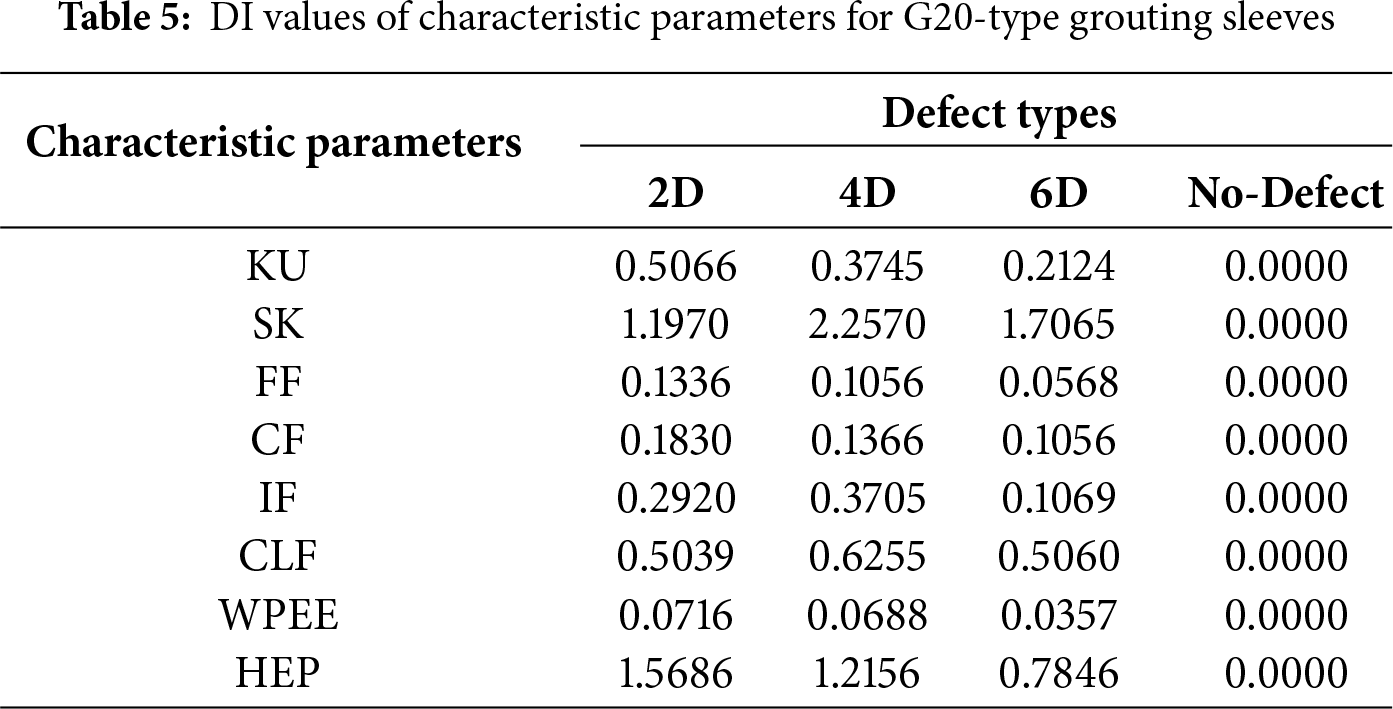
Tables 4 and 5 demonstrate the DI values of each characteristic parameter for the G18 and G20 types of grouting sleeves, respectively. Among these characteristic parameters, the DI values of the KU, FF, CF, WPEE, and HEP all exhibit a linear decay with the increase in medium compactness inside the sleeve. This phenomenon is attributed to the fact that the way the ultrasonic signal interacts with the medium in the propagation path changes significantly as the medium’s compactness increases. Specifically, the increase in medium density reduces the ultrasonic signal encountered during the propagation process at the reflection interface, and the refraction path tends to stabilize. At the same time, the absorption effect is relatively enhanced, resulting in signal energy attenuation. This attenuation process causes the signal’s adequate amplitude to decrease, and the peak amplitude is also reduced. At the same time, with the increase in compactness, the energy distribution of the ultrasonic signal becomes more uniform, the energy difference in the frequency bands is gradually reduced, and the energy distribution of the entire signal tends to become dispersed from a centralized state. In addition, the increase in saturation may also reduce the overall intensity of the ultrasonic signal, making the distribution of the signal’s energy on the time axis more uniform. Consequently, the instantaneous energy peak is no longer as prominent as it was when the saturation was lower. Together, these changes result in a linear decay of the characteristic parameters of the ultrasonic signal, such as the KU, FF, CF, WPEE, and HEP, with increasing saturation.

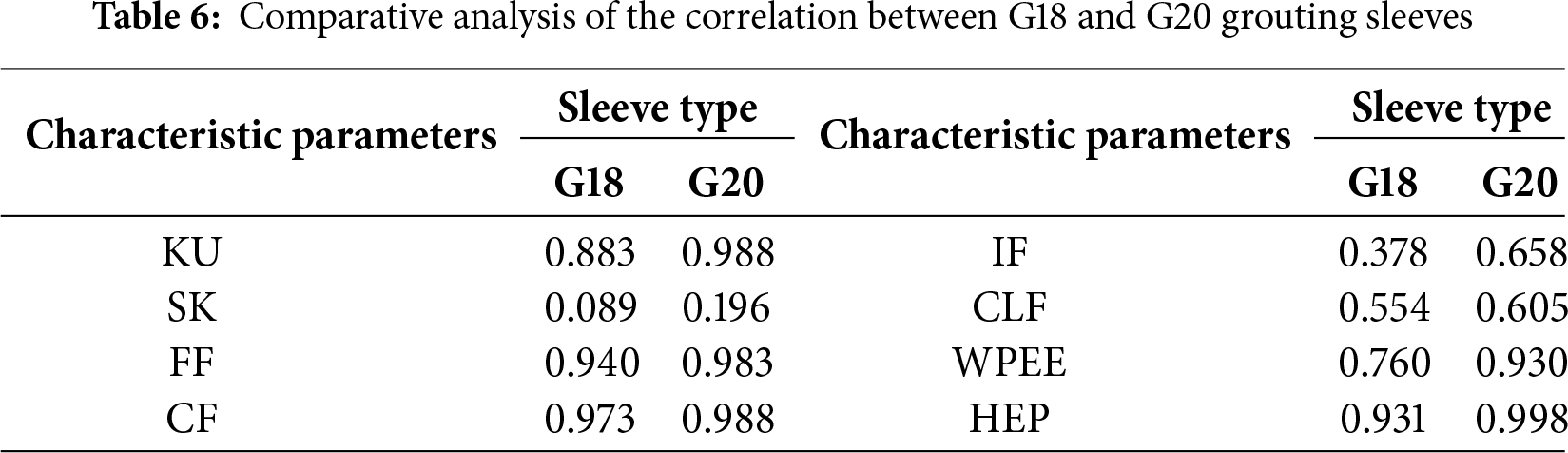
As shown in Figs. 15 and 16, a significant correlation between DI and grouting compactness was verified by linear fitting. As shown in Table 6, the goodness-of-fit R2 values for the KU, FF, CF, WPEE, and HEP DI values were all significantly higher than 0.80 for the two types of grouting sleeves. This result indicates that the DI values of these characteristic parameters have a very high correlation with the sleeve grouting compactness, further confirming that using the DI values of these characteristic parameters to assess sleeve grouting compactness defects quantitatively is reasonable and practical.

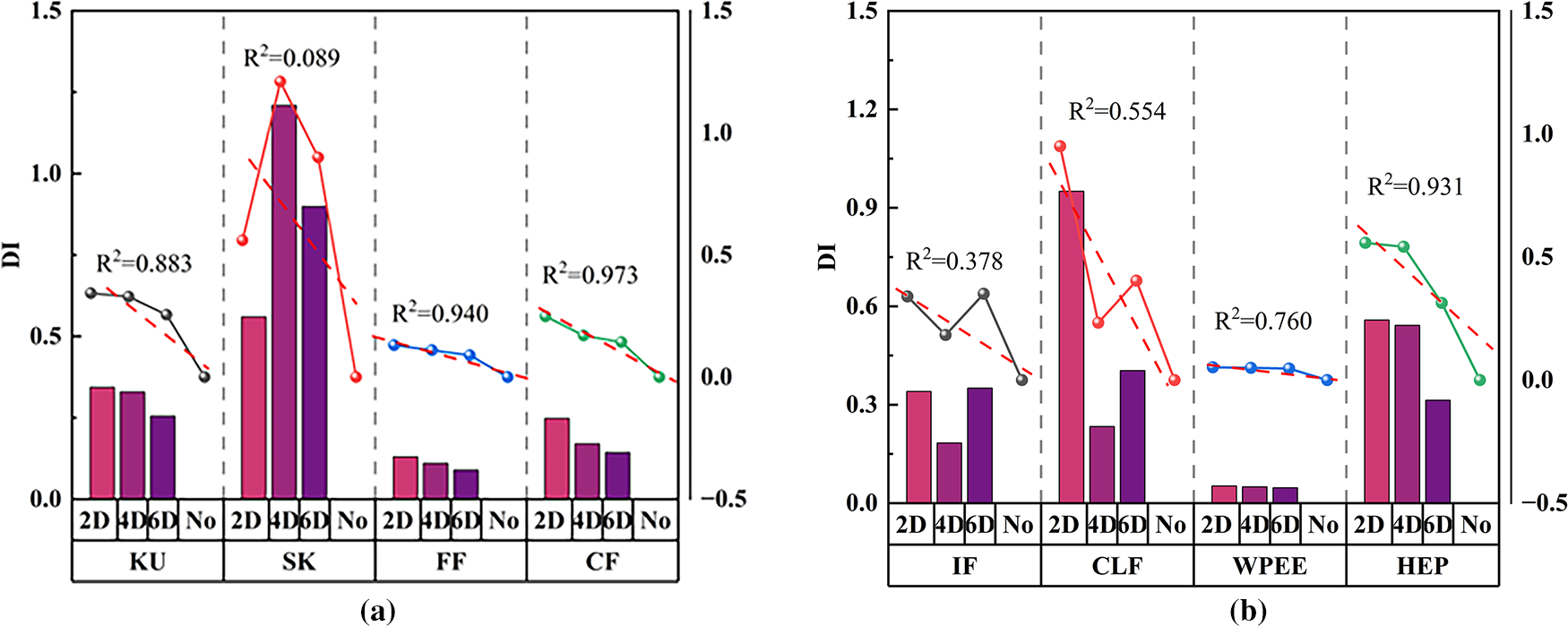
Figure 15: DI values and correlation of various characteristic parameters of G18 grouting sleeve under different grouting compactness levels. (a) KU, SK, FF, and CF DI values and correlations (b) IF, CLF, WPEE, and HEP DI values and correlations

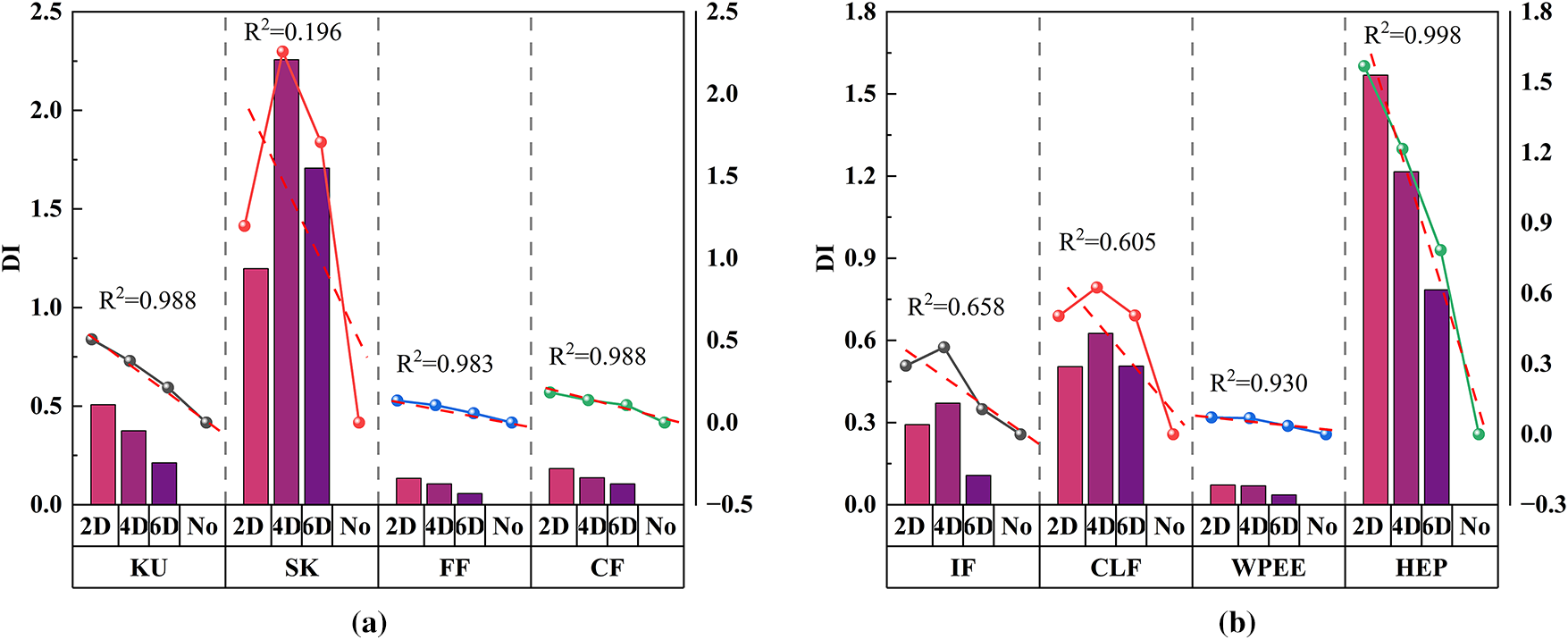
Figure 16: DI values and correlation of various characteristic parameters of G20 grouting sleeve under different grouting compactness levels. (a) KU, SK, FF, and CF DI values and correlations (b) IF, CLF, WPEE, and HEP DI values and correlations

In examining the type of the relationship between the KU, FF, CF, WPEE, and HEP and DI values for the two types of grouted sleeves (G18 and G20), we found that the decay trend of the G20 type specimens was greater than that of the G18 type, which suggests that the compactness of the G20 type sleeve is more sensitive to the DI values. Based on ultrasound theory, the larger the inner diameter of the G20 sleeve, the greater the deviation of sound wave reflection angle, the longer the propagation distance, the more severe the energy attenuation, and the amplification of parameter differences. Therefore, DI is more sensitive to compactness. However, the two types of grouted sleeves were very close in terms of decay trend and decay rate, and the DI values were roughly comparable. To determine more intuitively whether the grouting sleeve type has a significant effect on the relationship between DI value and grouting compactness, we fit the DI values of the two grouting sleeve types under different characteristic parameter types. The fitting results are shown in Fig. 17.

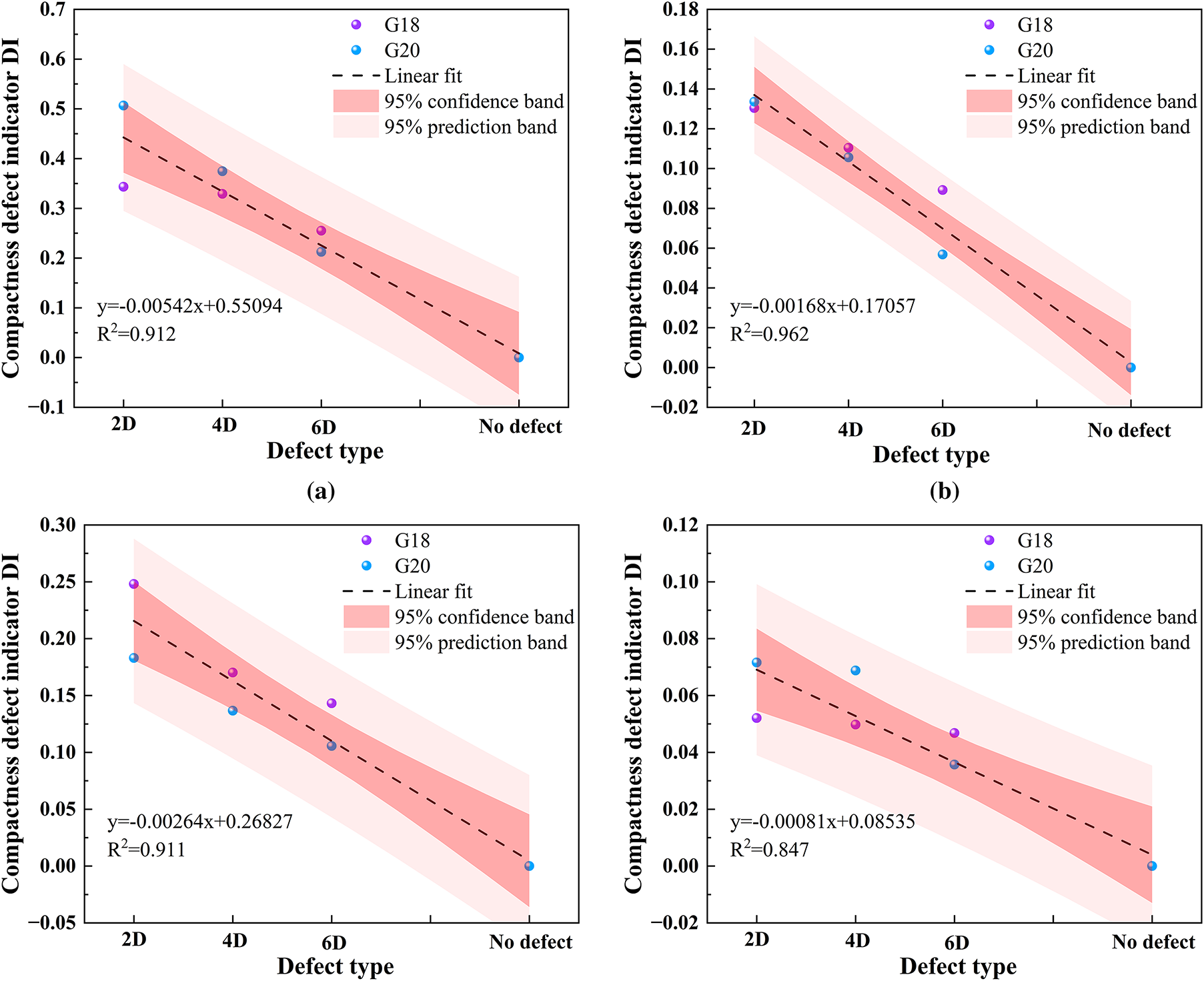
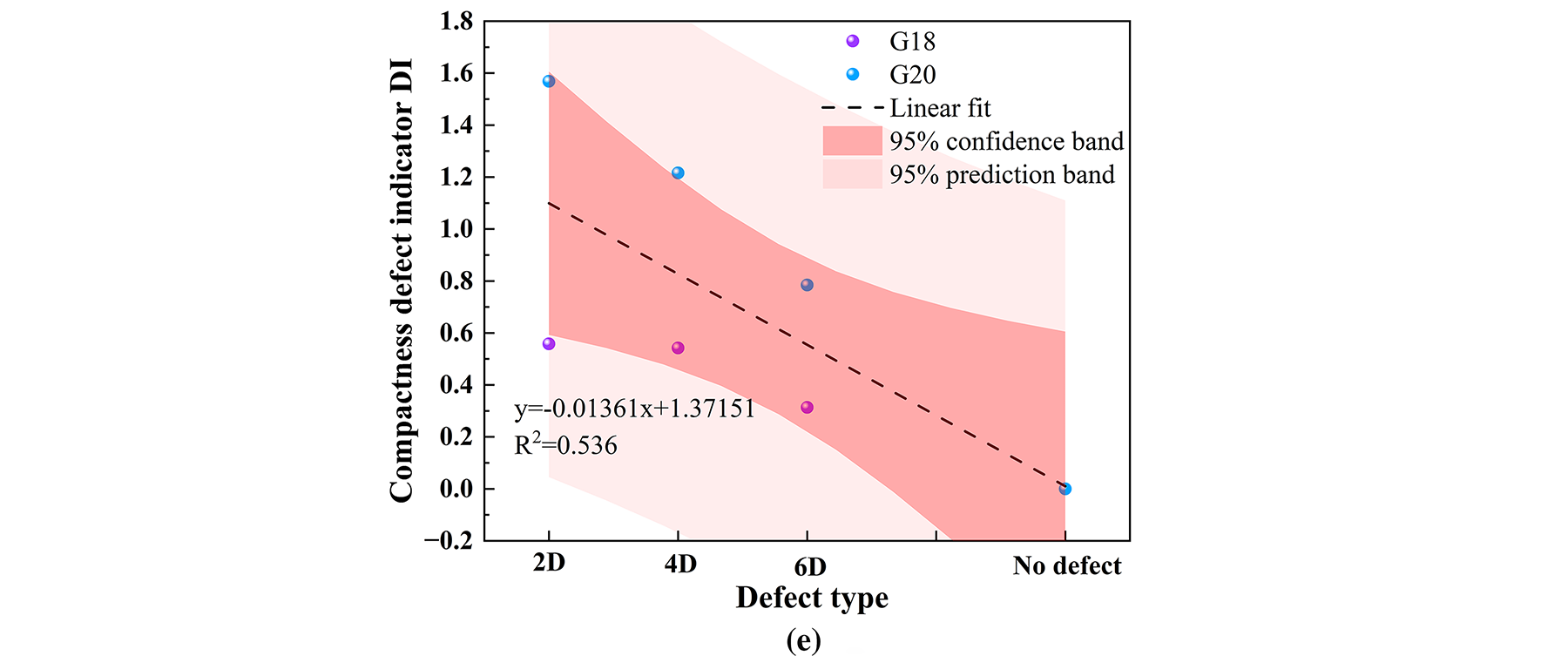
Figure 17: DI value fitting of grouting sleeves under different characteristic parameter types. (a) DI value fitting of KU (b) DI value fitting of FF (c) DI value fitting of CF (d) DI value fitting of WPEE (e) DI value fitting of HEP

It can be observed that through linear function fitting, the relationship model between grouting compactness and DI value of different types of grouting sleeves under different characteristic parameter models is obtained. Specifically, the goodness of fit of KU, FF, CF, and WPEE were 0.912, 0.962, 0.911, and 0.847, respectively, indicating that the fitting effect was good, which could well reflect the relationship between grouting compactness and DI value. However, the goodness of fit of the HEP is only 0.536, and the dispersion is high, perhaps due to the HEP being more sensitive to local defects in the ultrasonic propagation path, and the small differences in the distribution of 2D/4D/6D defects in the experiment, the response of HEP to density is unstable which cannot well reflect the relationship between grouting compactness and DI value.

Compared to traditional semi-nondestructive testing methods, ultrasonic excitation signals can actively excite the test signal to achieve complete non-destructive testing. This method is easier to operate and more suitable for practical engineering applications. In actual projects, if the raw materials and grouting methods used are identical to those in this test, the test results can be directly referenced and used to guide the testing of sleeve grouting compactness. However, there are differences in raw materials or grouting methods. In that case, it is necessary to prepare sleeve specimens with different grouting compactness gradients under various grouting methods in the laboratory, according to the on-site construction process and material requirements. These specimens must include sleeves with 100% grouting compactness. Subsequently, these sleeve specimens were tested according to the method proposed in this study, and their KU, FF, CF, WPEE, and HEP, as well as the DI value, were calculated to establish a relationship type between different grouting compactness and DI value. This will provide reliable data support for testing the grout compactness of unknown sleeves at the construction site.

6  Conclusions and Discussions

This study explores a novel quantitative detection method based on ultrasonic time-frequency dual-domain analysis, establishing a mapping relationship between sleeve grouting compactness and characteristic parameters. Samples of G18 and G20 grouting sleeves with gradient defects were prepared, including 2D, 4D, 6D defects (where D is the diameter of the grouting sleeve) and no-defect. By combining eight characteristic parameters (including KU and FF, etc.), a novel quantification method with a comprehensive defect index (DI) was established. The main conclusions and discussions are as follows:

(1)   The selected 8 feature parameters can effectively distinguish between defect and no defect states. Under non defect conditions, the feature parameter values are significantly lower than those under defect conditions. Among the selected 8 feature parameters (KU, SK, FF, CF, IF, CLF, WPEE, HEP), KU, FF, CF, WPEE, HEP are strongly correlated with grouting compactness (R2 > 0.8); The comprehensive defect index DI established based on these parameters has a good linear fit with the compactness of G18 and G20 sleeves (goodness of fit 0.847–0.962), which can effectively quantify the level of compactness.

(2)   The comprehensive defect index DI has good universality in G18 and G20 casing (linear goodness of fit 0.847–0.962). Compared with the single-parameter evaluation method [20], DI integrates multidimensional information and reduces the misjudgment rate caused by single-parameter noise interference. At the same time, the sensitivity of G20 casing defects is relatively high, indicating that the size of the casing structure affects the detection effect and needs to be considered in the actual detection process.

(3)   The orthogonal detection network and multi-parameter fusion method proposed in this article break through the limitations of traditional single-parameter detection systems. Compared with single path detection, orthogonal layout improves the spatial resolution of the sound field, and three-dimensional sound field data can more accurately locate defect positions; multi-parameter fusion avoids the one sidedness of single parameter evaluation and is of great significance in improving the reliability of detection results.

The proposed method still has room for improvement: (1) The current methods are mainly based on domestic sleeve specifications and grouting material standards. To further adapt to international standards, future work can conduct verification tests on internationally recognized sleeve specifications and grouting material characteristics in different regions, forming a database covering mainstream international products and providing more comprehensive data support for the implementation of regulatory provisions. (2) The current method is still based on the traditional parameter-driven detection PDB concept, focusing on defect quantification but not related to the resilience requirements of the entire lifecycle of the structure, while the current cutting-edge methods have been guided by resilience as the core [31]. Future research needs to combine relevant studies [32,33] to conduct quasi-static and vibration table tests on sleeve defect structures, and establish a mapping model for toughness indicators such as DI index and displacement ductility coefficient; Referring to the resilience driven detection optimization approach [34], the DI index is incorporated into the structural resilience assessment system, so that the detection results directly serve the needs of disaster resistance, loss reduction, and restoration throughout the entire process, enhancing the engineering application value of the method.

Acknowledgement: Thanks to all team members for their work and contributions.

Funding Statement: This work is supported in part by the National Natural Science Foundation of China Grant 11962006 and the Natural Science Foundation of Jiangxi Province of China Grant 20232BAB204067.

Author Contributions: The authors confirm their contribution to the paper as follows: Longqi Liao: conceptualization, methodology, software, validation, visualization, writing—original draft, writing—review & editing. Jing Li: conceptualization, software. Yuhua Li: conceptualization, investigation. Yuemin Wang: conceptualization, investigation. Jinhua Li: conceptualization, writing—review & editing, supervision, data curation, funding acquisition. Liyuan Cao: conceptualization, data curation, investigation, writing—review & editing. Chunxiang Li: conceptualization, investigation, writing—review & editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of the study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhang P, Li Y, Zhu X, Xu S, Guan P, Liu W, et al. Research on sleeve grouting density detection based on the impact echo method. Struct Durab Health Monit. 2024;18(2):143–59. doi:10.32604/sdhm.2024.046986. [Google Scholar] [CrossRef]

2. Du Y, Sun X, Yang J, Wu Z, Bian D. Research on the sleeve grouting fullness testing of prefabricated structures based on piezoelectric method. KSCE J Civ Eng. 2024;28(5):1928–46. doi:10.1007/s12205-024-1410-z. [Google Scholar] [CrossRef]

3. Cao D, Pan Z, Zhen G. Effects of grouting defects on seismic behavior of full-scale precast reinforced concrete shear wall. J Build Eng. 2023;76(3):107216. doi:10.1016/j.jobe.2023.107216. [Google Scholar] [CrossRef]

4. Bianchi D, Mayrhofer E, Gröschl M, Betz G, Vernes A. Wavelet packet transform for detection of single events in acoustic emission signals. Mech Syst Signal Process. 2015;64:441–51. doi:10.1016/j.ymssp.2015.04.014. [Google Scholar] [CrossRef]

5. Xiao S, Wang Z, Li X, Harries KA, Xu Q, Gao R. Study of effects of sleeve grouting defects on the seismic performance of precast concrete shear walls. Eng Struct. 2021;236:111833. doi:10.1016/j.engstruct.2020.111833. [Google Scholar] [CrossRef]

6. Cao D, Pan Z, Zhang Z, Zeng B. Experimental and numerical study on detection of sleeve grouting defect with impact-echo method. Structures. 2023;52(1):632–50. doi:10.1016/j.istruc.2023.03.137. [Google Scholar] [CrossRef]

7. Cao D, Pan Z, Zhang Z, Zeng B. Defect detection of grouting sleeve connection with energy ratio change in frequency domain. Appl Acoust. 2024;221(1):110037. doi:10.1016/j.apacoust.2024.110037. [Google Scholar] [CrossRef]

8. Chu F, Cao Y, Qi GZ, Gao L. Experimental study of bellows duct grouting compactness with quantitative detection. Appl Mech Mater. 2014;716–717:322–7. doi:10.4028/www.scientific.net/amm.716-717.322. [Google Scholar] [CrossRef]

9. Yu A, Li X, Fu F, Chen X, Zhang Y. Detection of sleeve grouting compactness based on acoustic emission technology. Materials. 2023;16(4):1455. doi:10.3390/ma16041455. [Google Scholar] [PubMed] [CrossRef]

10. Ma Y, Li S, Wu Y, Wang D, Liu M. Acoustic emission testing method for the sleeve grouting compactness of fabricated structure. Constr Build Mater. 2019;221:800–10. doi:10.1016/j.conbuildmat.2019.06.124. [Google Scholar] [CrossRef]

11. Wu C, Yang C, Ma S, Xu X. Feasibility study on grouting compactness detection in sleeves using piezoelectric transducers. Appl Sci. 2020;10(1):149. doi:10.3390/app10010149. [Google Scholar] [CrossRef]

12. Nakahata K, Kawamura G, Yano T, Hirose S. Three-dimensional numerical modeling of ultrasonic wave propagation in concrete and its experimental validation. Constr Build Mater. 2015;78:217–23. doi:10.1016/j.conbuildmat.2014.12.049. [Google Scholar] [CrossRef]

13. Liu H, Chen C, Guo Z, Xia Y, Yu X, Li S. Overall grouting compactness detection of bridge prestressed bellows based on RF feature selection and the GA-SVM model. Constr Build Mater. 2021;301:124323. doi:10.1016/j.conbuildmat.2021.124323. [Google Scholar] [CrossRef]

14. Li Z, Zheng L, Chen C, Long Z, Wang Y. Ultrasonic detection method for grouted defects in grouted splice sleeve connector based on wavelet pack energy. Sensors. 2019;19(7):1642. doi:10.3390/s19071642. [Google Scholar] [PubMed] [CrossRef]

15. Liu H, Qi Y, Chen Z, Tong H, Liu C, Zhuang M. Ultrasonic inspection of grouted splice sleeves in precast concrete structures using elastic reverse time migration method. Mech Syst Signal Process. 2021;148:107152. doi:10.1016/j.ymssp.2020.107152. [Google Scholar] [CrossRef]

16. Zhang L, Fang Z, Tang Y, Li H, Liu Q. Characterization of damage progress in the defective grouted sleeve connection using combined acoustic emission and ultrasonics. Sensors. 2022;22(21):8579. doi:10.3390/s22218579. [Google Scholar] [PubMed] [CrossRef]

17. Jiang T, Zheng J, Huo L, Song G. Finite element analysis of grouting compactness monitoring in a post-tensioning tendon duct using piezoceramic transducers. Sensors. 2017;17(10):2239. doi:10.3390/s17102239. [Google Scholar] [PubMed] [CrossRef]

18. Zheng X, Qi J, Shi W, Wang C, Yuan B. Grouting sleeve fullness detection method based on microwave radio frequency S parameter. In: Proceedings of the 2019 Photonics & Electromagnetics Research Symposium-Fall (PIERS-Fall); 2019 Dec 17–20; Xiamen, China. p. 1895–900. doi:10.1109/piers-fall48861.2019.9021824. [Google Scholar] [CrossRef]

19. Cao D, Pan Z, Zhang Z, Zeng B. Study on non-destructive testing method of grouting sleeve compactness with wavelet packet energy ratio change. Constr Build Mater. 2023;389:131767. doi:10.1016/j.conbuildmat.2023.131767. [Google Scholar] [CrossRef]

20. Xiao H, Huang Y. Detection of grout sleeve defects based on the time domain dimensionless indicators of component signals. J Build Eng. 2023;65:105795. doi:10.1016/j.jobe.2022.105795. [Google Scholar] [CrossRef]

21. Janeliukstis R, Rucevskis S, Wesolowski M, Chate A. Multiple damage identification in beam structure based on wavelet transform. Procedia Eng. 2017;172:426–32. doi:10.1016/j.proeng.2017.02.023. [Google Scholar] [CrossRef]

22. Zhang X, Zhou D, Tang H, Han X. Experimental study of grout defect identification in precast column based on wavelet packet analysis. Int J Distrib Sens Netw. 2019;15(11):155014771988959. doi:10.1177/1550147719889590. [Google Scholar] [CrossRef]

23. Li Z, Li D, Chen Y. Deep learning-based guided wave method for semi-grouting sleeve detection. J Build Eng. 2022;46:103739. doi:10.1016/j.jobe.2021.103739. [Google Scholar] [CrossRef]

24. Liu H, Liu J, Wang Y, Xia Y, Guo Z. Identification of grouting compactness in bridge bellows based on the BP neural network. Structures. 2021;32:817–26. doi:10.1016/j.istruc.2021.02.069. [Google Scholar] [CrossRef]

25. Lei Y, He Z, Zi Y. Application of an intelligent classification method to mechanical fault diagnosis. Expert Syst Appl. 2009;36(6):9941–8. doi:10.1016/j.eswa.2009.01.065. [Google Scholar] [CrossRef]

26. Li S, Liu X, Ma Y, Zhang L, Feng H. Influence of grouted sleeve and concrete strength of fabricated shear wall on acoustic emission detection method for sleeve compactness. J Build Eng. 2021;43:102541. doi:10.1016/j.jobe.2021.102541. [Google Scholar] [CrossRef]

27. Xu B, Fan X, Wang H, Zhou S, Wang C, Chen H, et al. Experimental study on grout defects detection for grouted splice sleeve connectors using stress wave measurement. Constr Build Mater. 2021;274:121755. doi:10.1016/j.conbuildmat.2020.121755. [Google Scholar] [CrossRef]

28. Li S, Yao Z, Wang L, Ma L, He Y, Ban X. Research on the factors influencing the seismic performance of grouting sleeve assembled double-column piers. J Sens. 2024;2024:6938870. doi:10.1155/2024/6938870. [Google Scholar] [CrossRef]

29. Zhou ZZ, Wu HY, Tan CJ, Xing Y, Gao RD. Comparison and a case study of test methods for sleeve grouting fullness in precast bridge piers. in: Life-cycle civil engineering: innovation, theory and practice. London, UK: CRC Press; 2021. p. 971–6. doi:10.1201/9780429343292-128. [Google Scholar] [CrossRef]

30. Xu B, Chen H, Xia S. Numerical study on the mechanism of active interfacial debonding detection for rectangular CFSTs based on wavelet packet analysis with piezoceramics. Mech Syst Signal Process. 2017;86:108–21. doi:10.1016/j.ymssp.2016.10.002. [Google Scholar] [CrossRef]

31. Elettore E, Freddi F, Latour M, Rizzano G. Design and analysis of a seismic resilient steel moment resisting frame equipped with damage-free self-centering column bases. J Constr Steel Res. 2021;179:106543. doi:10.1016/j.jcsr.2021.106543. [Google Scholar] [CrossRef]

32. Mata R, Nuñez E, Forcellini D. Seismic resilience of composite moment frames buildings with slender built-up columns. J Build Eng. 2025;111:113532. doi:10.1016/j.jobe.2025.113532. [Google Scholar] [CrossRef]

33. Xu G, Guo T, Li A, Zhang H, Wang K, Xu J, et al. Seismic resilience enhancement for building structures: a comprehensive review and outlook. Structures. 2024;59:105738. doi:10.1016/j.istruc.2023.105738. [Google Scholar] [CrossRef]

34. Forcellini D. Quantification of the seismic resilience of bridge classes. J Infrastruct Syst. 2024;30(3):04024016. doi:10.1061/jitse4.iseng-2376. [Google Scholar] [CrossRef]