A Fixed-Point Iterative Method for Discrete Tomography Reconstruction Based on Intelligent Optimization

1  Introduction

The purpose of tomography is usually to reconstruct some physical objects through projection. The reconstruction algorithm plays an important role in the fields of medicine, image processing and computed tomography. Discrete tomography(DT) is essentially a function formed by reconstructing discrete values from multiple projection directions [1]. DT regards the reconstructed object as a limited set of pixels, and the slope of the straight line along the projection direction should be a rational number. The framework studied in this work is a two-dimensional lattice, that is, the reconstructed object is an image. From a long history, this field is gradually developed by multiple branches of mathematics. The combination of binary matrices is one example. Ensuring that the reconstructed result is equal to the original object is an important task of tomographic reconstruction. A core problem of DT is to reconstruct (0–1) discrete matrix from multiple directions Herman et al. [2] introduced relevant applications and theories for this problem. Weber et al. [3] focused on reconstructing binary functions, this approach extends the linear programming relaxation of combinatorial optimization problems proposed by previous researchers from a small number of X-ray projections from a small number of X-ray projections to the objective function of quadratic smooth a priori, and can calculate the solution that biases the reconstruction to the region with spatial coherence by any interior point solution method. The image reconstruction problem forms a 0–1 discrete matrix through ray projection, which can be expressed in the form of integer programming.

Linear integer programming model is widely used in combinatorial optimization and emergency management. Haghani et al. [4] modeled the emergency vehicle scheduling as an integer programming model to solve the problem of reasonable vehicle routing in the case of serious traffic congestion, and the vehicle routing was flexibly scheduled using real-time traffic data by studying the optimization model. Considering that the rescue route is blocked due to various uncertain traffic accidents, Chai et al. [5] and others proposed a reliable integer programming model to calculate the travel time required for the whole rescue route and optimize the allocation of emergency resources. Cao et al. [6] designed an emergency organization optimization strategy based on branch and bound method to solve the sustainability problem in the disaster response decision optimization system. Huibregtse et al. [7] designed and developed an optimized evacuation instruction framework by using a fixed-point formula, to better optimize the evacuation efficiency of traffic. Dulebenets et al. [8] constructed an integer programming model to guarantee smooth evacuation of people and avoid congestion when disasters occur, and it was combined with heuristic algorithm to reduce the total traveling salesman time of individual evacuation to a certain extent, for optimizing the final evacuation plan. French et al. [9] avoided floating-point data calculation by using fixed-point algorithm, and only processed integer data, to reduce the processing time in aerial positioning and optimize the imaging system.

This reconstruction problem is a NP hard problem. Graph partition [10] and quadratic knapsack problem [11] are also classical NP combinatorial optimization problems. Dang et al. [12,13] proposed a fixed-point iterative method to solve such problems. This method can find an integer point in any type of polyhedron. This fixed-point algorithm has been widely used in the reassignment of aircraft disturbed by aviation. A large number of flights are disturbed and cannot operate according to the original plan due to the emergency bad weather. Wu et al. [14] and others used the distributed integer programming to re-optimize the aircraft allocation based on the fixed-point iterative method for calculating the feasible route. With a slight modification of this method, all integer points in the polyhedron can be further obtained, and then multiple feasible solutions can be obtained. At present, this method has effectively solved many integer programming problems. When solving large-scale integer programming problems, this method can better reflect its effectiveness compared with the previous traditional methods. Our future work can focus on the implementation of fixed-point iterative method with distributed computing, and distributed problemshave been widely used in some aspects, such as distributed permutation flow shop scheduling problem. A multi-point iterative greedy algorithm is proposed in [15] to solve this problem. If the problem is not improved after a certain number of continuous iterations, then the restart strategy is adopted to minimize the factory completion time. A mixed integer linear model is established in [16], and the search ability is improved by an improved artificial bee colony algorithm. The heuristic method based on greedy rules proposed in [17] can also effectively solve this problem. Therefore, distributed computing will occupy an important position in the future work.

In the process of solving the DT problem, if its reconstruction problem can be rewritten into the form of integer programming, this problem can be effectively solved by the fixed-point iterative method. On the basis of algorithm proposed by Aardal et al. [18,19], we transform the DT problem into an integer programming system. Branch and bound method is a classical method, which can solve integer programming systems. Its characteristic is that it can quickly obtain the optimal solution. However, the numerical results show that the fixed-point iterative method is more effective and feasible than the two methods mentioned above especially in the case of high dimension.

The fixed-point algorithm proposed in this study has been widely used in the rapid response of emergency management in smart city, such as flight delay, fire and other emergencies. On the basis of this fixed-point theory, an integer programming algorithm is proposed to quickly solve the integer programming of new scheduling under emergencies for providing support for the development of smart city and its core algorithms. It can also provide a new idea and method for the research of integer programming.

The rest of the paper can be divided into the following sections. Section 2 introduces the problem and model of DT reconstruction. In Section 3, LLL(Lenstra-Lenstra-LovaszLattice) algorithm is briefly described, and DT problem is transformed into polyhedron judgment problem through this algorithm. Section 4 shows the calculation principle and workflow of Dang fixed point iterative method. In Section 5, the experimental data are obtained by running MATLAB and then compared with those of the branch and bound method. Section 6 summarizes this work and puts forward the future prospects.

2  Problem Statement and Model

DT essentially re-establishes the function with known discrete range, which is based on the projection along a certain direction. Reconstruction of discrete (0–1) matrix from multiple projections is a key step in the study of DT problem [20].

The following model is more intuitive and clearly shows the essence of the reconstructed object. This model does not involve any prior knowledge related to the reconstructed object. In general, the reconstruction results produced by this model are not the only solution.

Let f:Ω⊂R2→R,y↦f(y) be an unknown attenuation function. This study establishes a discrete model similar to that in Fig. 1, which can more intuitively describe the reconstruction of f. The function f can be represented by its value xj∈{0,1}, j=1,2,⋯,n, x=(x1,x2,⋯,xn)T, in a square pixel. We define f(y)=∑j=1nxjΦj(y)=⟨x,Φ(y)⟩, Φ(y)=(Φ1(y),Φ2(y),⋯,Φn(y))T, where if and only if y is within the jth pixel range, then the value of Φj(y) is 1 and 0 at other positions. Several rays i=1,2,⋯,m intersect with Ω, the contribution aij of each pixel j forms a projection matrix A of m×n, and the ith component bi of vector b represents the total attenuation along the ith ray. In this study we ignore any “noise” generated in the imaging process, and we default the projection ray, point source and detector to the ideal state.

Figure 1: Discrete model of DT reconstruction problem [3]

The imaging process is shown in Fig. 1. The DT problem can usually be simplified to a 0/1 integer linear programming system in the following form:

Ax=b(1)

We find x∈{0,1}n that satisfies Eq. (1), where the coefficient matrix A∈Nm×n of the equations is composed of m rows and n columns, and b∈Nm is an m-dimensional column vector. The model described above is widely used in the research of material science. For example, when studying crystal materials, the lattice formed by atoms of crystal solids can be transformed into integer point lattice through modeling. Then, obtaining all atoms on a line by using electron microscope technology is relatively easy, and the calculated number can be used as the component of vector b to participate in the operation of (1). Therefore, after the abovementioned integer linear equations are solved, the problem of image reconstruction can be solved.

However, in the actual calculation process, the solution of (1) is difficult to find smoothly. The scale of this kind of problem is NP hard. In fact, nearly no suitable solution to solve this problem is available in practical application.

The problem of n-dimensional scale corresponds to the number of atoms contained in the reconstructed object, which is a huge number that is difficult to calculate, regardless of scene application. For example, the most common daily water contains at least 1023 atoms per milliliter. Previous research and calculation show that relevant algorithms are available for solving integer linear programming, but they are time consuming and costly.

Multiple solutions of (1) may be available, but only one solution matching is possible in the actual reconstruction object. Usually, some optimization algorithms are used to solve this problem, but this way increases the computational difficulty of the problem to a certain extent. The solution obtained by calculation can only approximate the actual value in any case. A more accurate approximation can be achieved by increasing the number of projection directions, but this way will undoubtedly increase the scale of the problem again.

This study presents a new solution to problem (1), which avoids the abovementioned difficulties to a certain extent. The purpose is to clarify the computational theory in DT. The characteristics and basic idea of the new algorithm (based on 2D) are as follows:

1.    Any possible situation is included in the established calculation model.

2.    The projection ray only occurs in one direction with a certain slope, such that only one integer point can be generated on this line at most.

3.    Each projection ray to be solved is expressed as linear Diophantine equation ax+by=c, where x,y∈Z, a,b,c∈R. The coefficients a and b in different linear equations are proportional to each other or the same, that is, the slope of the straight line is the same.

All the solutions obtained by calculation are the accurate reconstruction of the processed object.

3  Transformation of the DT Problem into a Polyhedron Judgement Problem

In [18,19], an LLL [21] based reduction method is proposed, which can transform problem (1) into a polyhedron judgment problem.

If a base c1,c2,⋯,ch of Rh exists in subset L of n-dimensional vector space Rh, where h is a positive integer, then it can be called lattice, such that

L={∑j=1hαjcj,αj∈Z,1≤j≤h}(2)

In this way, c1,c2,⋯,ch can be called a base of L, and the rank of L is h. Then the determinant of L can be defined as the following form:

d(L)=|det(c1,c2,⋯,ch)|(3)

where cj is expressed as a column vector. The result of this determinant is a positive real number, which is independent of the selection of the base.

Given that the relationship between c1,c2,⋯,ch is linearly independent, these linearly independent column vectors cj, 1≤j≤h are orthogonalized into cj∗, 1≤j≤h by an algorithm for deriving orthogonal vectors, that is, Gram-Schmidt orthogonalization rule. Matrices C=(c1,c2,⋯,ch) and C∗=(c1∗,c2∗,⋯,ch∗) are composed of column vectors cj and cj∗, respectively. The definition of vector cj∗ can be summarized as follows:

cj∗=cj−∑k=1j−1μkjck∗,j=1,2,⋯,h(4)

where

μkj=(ck∗,cj)(ck∗,ck∗),k=1,2,⋯,j−1(5)

where (,) represents the inner product of two ordinary vectors on Rh. The relationship between cj∗ and cj is that the former is the orthogonal projection of the latter on ∑k=1j−1Rck, and∑k=1j−1Rck=∑k=1j−1Rck∗,1≤j≤h. Therefore, through the operation of the abovementioned rules, the obtained c1,c2,⋯,ch is the orthogonal basis on Rh.

Notably, C∗ is not the base of L in general, because all the values of μkj are not integral. The following is the definition of approximate orthogonal basis.

Let a set of linearly independent vector groups C=(c1,c2,⋯,ch) be a basis of L, and a new set of bases C∗=(c1∗,c2∗,⋯,ch∗) is obtained through Schmidt orthogonalization. If the following conditions are met, then C is called reduced basis.

|μjk|≤12,1≤k≤j≤h(6)

and

‖cj∗+μj,j−1cj−1∗‖2≥34‖cj−1∗‖2,1<j≤h(7)

‖‖ in the formula represents the ordinary Euclidean length. The constant 34 in the inequality is not necessarily a fixed value, it can be randomly selected, and its value can be replaced by any other real number 14<n<1.

To obtain the reduced basis of the lattice given according to the original basis, a polynomial time algorithm is introduced below. Its components are size reductions and interchanges.

Size reduction: If the condition of inequality (6) is not satisfied for any index k and j, 1≤k≤j≤h, the value of cj can be re expressed by cj−μ^jkck, where μ^jk is the approximate integer rounded by μjk.

Interchange: If j for some indexes does not meet the requirements in (7), the vectors cj and cj+1 can be swapped.

After the abovementioned description, the process of base reduction algorithm can be summarized as follows (Fig. 2).

Figure 2: Base reduction algorithm

Based on the abovementioned base reduction algorithm, given two suitable and relatively independent positive integers N1 and N2, they should be sufficiently large compared with the input.

Then we consider the following matrix B=(bj)1≤j≤n+1, in which any column vectors are linearly independent:

B=(I(n)0(n×1)0(1×n)N1N2A−N2b)(8)

where I(n) represents n-dimensional identity matrix, 0(n×1) represents an zero matrix, which is n×1-dimensional, A represents aij in the reconstructed model, and b represents bi in the abovementioned model. For lattice B, a new matrix is obtained by applying the LLL basis reduction algorithm of polynomial, which can be re expressed as the following formula:

B′=(X0(n×(n−m))xd0(1×(n−m))N10(m×(n−m))0(m×1))(9)

where X0=(x01,x02,…,x0n−m) is the general solution of (1), that is, Ax0j=0, j=1,2,…,n−m. xd is its special solution, and Axd=b.Then problem (1) can be transformed into solving the following inequality:

If a vector exists, then

λ∈Zn−ms.t.−xd≤X0λ≤I(n−m)×1−xd(10)

Through the above analysis, we successfully transform problem (1) into problem (10), that is, to judge whether there are integer points exist in the polyhedron is determined. We use the fixed-point iteration method [9,10] to solve it. If integer points exist, then a solution exists; otherwise no solution exists. We will describe this method in detail in the next section.

4  The Fixed-Point Iterative Method

Let

P={x∈Rb|Dx+Gw≤dforsomew∈Rp}(11)

where D∈Ra×b is an a×b matrix with b≥2, where the elements are integers, G∈Ra×p an a×p matrix, and d a vector of Ra. In this study, we assume that P is a region with wide dimensions and upper and lower bounds. For a real number α, we use ⌊α⌋ to represent the largest integer rounded to the left of α. For x=(x1,x2,…,xb)T∈Rb, let ⌊x⌋=(⌊x1⌋,⌊x2⌋,…,⌊xb⌋)T.

Let xmax=(x1max,x2max,…,xbmax)T with xjmax=maxx∈Pxj, j=1,2,…,b, andxmin=(x1min,x2min,…,xbmin)T, with xjmin=minx∈Pxj, j=1,2,…,b. Then xmin≤x≤xmax for all x∈P. Let D(P)={x∈Zb|xl≤x≤xu}. where xu=⌊xmax⌋ and xl=⌊xmin⌋ , therefore, all integer points, which are in P, are in D(P). In the general case, we assume that xl<xmin(let xil=ximin−1 if xil=ximin for some i∈N). For z∈Rb and k∈N0, let p(z,k)={x∈P|xi=zi,1≤i≤kandxi≤zi,k+1≤i≤b}.

An integer point is given as the initial point y∈D(P) with y1>x1l; We introduce a method to judge whether an integer point x∗∈P with x∗≤ly exists, which is the fixed-point iterative. The pseudo code for a particular algorithm is illustrated in Fig. 3.

Figure 3: Pseudo code of specific algorithm

The basic idea of solving the abovementioned integer problem involves the incremental mapping, which is from finite lattice to itself. Except for the integer points in polyhedron P, all other integer points can be mapped to the first point in P, which is smaller than them in the lexicographical order of xl. After the abovementioned incremental mapping steps, all integer points in the polyhedron are fixed points. We present an integer point as the initial point, find an integer point in the polyhedron by this method, or prove that no such point exists in the polyhedron in finite iterations.

5  Numerical Results

After the analysis in the second section, we can conclude that the DT problem is a special case of the market split problem [22]. The problem of market segmentation is defined as that a company supplies several products to retailers, and allocates retailers to the two departments D1 and D2 in the company. Thus D1 can grasp 40% of the market occupied by each product of the company, and D2 can grasp the remaining 60%. If the product cannot be divided in proportion completely and accurately, then the proportion error of the division will be minimized. The market segmentation problem can be expressed by a set of mathematical methods of 0–1 linear programming:

∃x∈{0,1}:Ax=d(12)

where A=(aij)∈Zh×k and d∈Zh.

In this section, we take market split problem as an example to show the relevant numerical results of solving problem (1). Given any real number m, the expression of n is n=10(m−1), the elements in the coefficient matrix A are integers randomly selected from [0,99], and each component of vector b is calculated by bi=⌊12∑j=1naij⌋, 1≤i≤m. Let N1=1000 and N2=10000 in the computation. Through the abovementioned examples, we compare the method introduced in this study with the branch and bound method, which are two classical algorithms to solve integer programming problems. We also analyze the number of iterations and time required by the two algorithms to solve the problem.

The design idea of the fixed-point algorithm is to give a polyhedron and define an incremental mapping from the problem lattice to the lattice itself in combination with the incremental mapping principle. In that way, the integer points outside the polyhedron are mapped to the feasible integer points in the polyhedron that are smaller than the dictionary order of the integer points. When the feasible solution is not satisfied, the next round of iteration is conducted. The algorithm is terminated until a feasible solution is found or no feasible solution is found. The basic idea of branch and bound method is to select different branch variables and sub-problems for branching. Usually, all feasible solution spaces are gradually decomposed into smaller subsets. When the subset limit after branching exceeds the known feasible solution value, the branching is terminated to reduce the search range until the feasible solution is found.

In the numerical expression in the following table, define “NumLPs” represents the number of traversal nodes during the iteration of a specific algorithm, “F” indicates whether the specific method is feasible for solving the example, including the following three cases. “Feasible” means that an integer solution can be obtained by calculating an instance, otherwise it is represented by “Infeasible”. We use the fixed-point iterative method and branch-and-bound method introduced in this study to solve the problems of m=3, n=20, m=4, n=30 and m=5, n=40. Table 1 illustrates the numerical outcomes of m=3 and n=20 problem, Table 2 presents the outcomes of m=4 and n=30 problem, and the outcomes of the problem with m=5 and n=40 are shown in Table 3. Figs. 4–6 show the comparison of the number of nodes traversed by the fixed-point iterative method and the branch-and-bound method for the three dimensional problems mentioned above, respectively, which show the computational effects and performance of the two algorithms more clearly and intuitively.

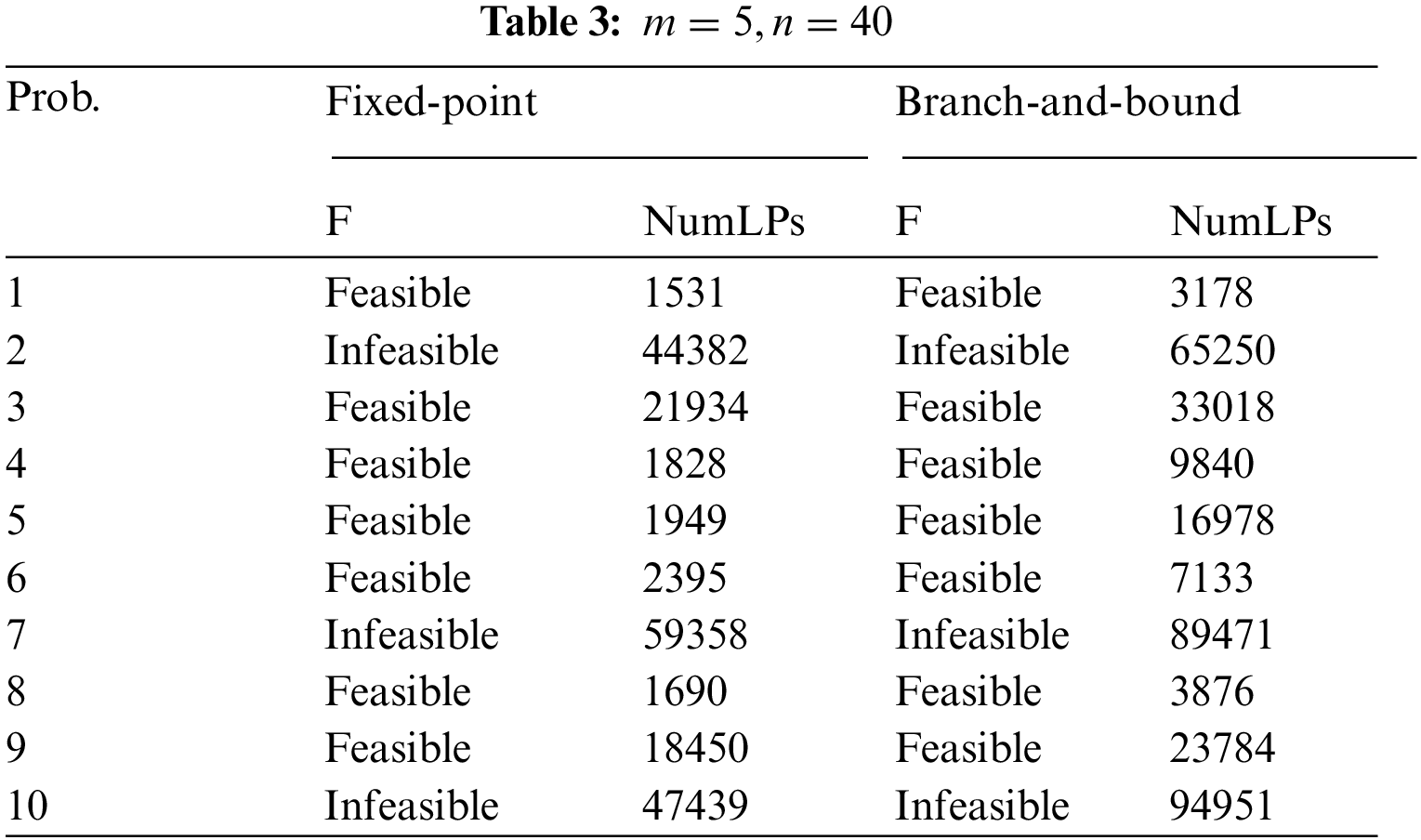
Figure 4: Comparison of the number of traversal nodes with m = 3 and n = 20

Figure 5: Comparison of the number of traversal nodes with m = 4 and n = 30

Figure 6: Comparison of the number of traversal nodes with m = 5 and n = 40

The three groups of experimental values mentioned above show that the method studied in this paper can effectively solve the problem of DT. In the case of m=3, n=20 in Table 1, there is no significant difference between the fixed-point iterative method and the branch and bound method in solving this problem, and the results can be obtained within 5 s, although the number of nodes traversed by the branch and bound method in the iteration is slightly larger than that of the fixed-point iterative method. Table 2 shows that, when the dimension of the problem increases to m=4, n=30, the fixed-point iterative method can generally end the solution process of the problem in 200 s and obtain the feasible solution. The number of nodes traversed by the branch-and-bound method in computing the feasible solution is about twice or more than that of the fixed-point iteration method because the dimension is so high at this point. In the two dimensional cases mentioned above, branch-and-bound and fixed-point iterative methods are effective in computing feasible solutions to the problem without considering the number of traversed nodes. Finally, when m=5, n=40, as shown in Table 3, the branch-and-bound method does not solve the problem in some cases. If the fixed-point iterative method is feasible without considering the length of time, the time to solve this problem may be longer or even several hours due to the different parameters selected in different examples. Therefore, we choose to terminate the iteration of the algorithm for solving this instance and mark it “Infeasible”. For the fixed-point iterative method, if the time consumption is ignored, it can solve the reconstruction model of DT problem with any dimension.

From the data of the three charts mentioned above with increasing dimension, the number of nodes traversed in the process of obtaining the result through fixed-point iteration is about 40% higher than that of branch and bound method. With the continuous increase in dimension, the advantage of fixed-point iteration method in traversing less nodes is more prominent, which also verifies the efficiency of this algorithm.

The comparison and analysis of the three tables mentioned above, indicate that solving the problem becomes increasingly difficult when the dimension of the problem increases due to the limited computing power of a single computer. If the fixed-point iterative method can be in a distributed implementation and multiple computers are used to solve this problem at the same time, then even higher dimensional problems can be solved with relatively less time consumption. Therefore, our future work direction will be to realize the distributed computing of fixed-point iterative method.

After the two methods mentioned above are compared, we change the fixed-point iterative method in simple steps to change the initial point of its iteration for forming an inverse iterative process. For the three types of problems in Tables 1–3, the fixed-point iterative method before and after changing the initial point is used to calculate each example. The number of iterations required in the process of calculating whether the problem has a solution is recorded in Fig. 7, the data show that changing the initial point of iteration will not affect the feasibility and effectiveness of the fixed-point iterative method proposed in this study.

Figure 7: Iterative effect of different initial points

6  Conclusions and Future Prospects

This study presents a new method that can effectively solve the reconstruction problem of the DT model. The solution procedure is divided into two steps. First, the reconstruction problem is changed into a polyhedron judgment problem on the basis of LLL-based reduction algorithm. Second, the fixed point iteration method of integer programming is used to solve the polyhedron judgment problem in the previous step. The calculation results of specific examples are compared and analyzed between this method and branch and bound method. The results show that the fixed point iteration method has more advantages in solving this kind of problem which is embodied in the optimization of time and the number of traversal nodes.

However, the dimension of the problem examples involved in this study is not particularly high. Thus, the latent advantages of this method are not thoroughly reflected. With the continuous increase in the problem dimension, this method can be realized by distributed approach in the future. This solution process will reduce considerable time consumption through utilizing multiple slave computers working at the same time.

Funding Statement: This research was funded by the NSFC under Grant Nos. 61803279, 71471091, 62003231 and 51874205, in part by the Qing Lan Project of Jiangsu, in part by the China Postdoctoral Science Foundation under Grant Nos. 2020M671596 and 2021M692369, in part by the Suzhou Science and Technology Development Plan Project (Key Industry Technology Innovation) under Grant No. SYG202114, in part by the Natural Science Foundation of Jiangsu Province under Grant No. BK20200989, and Postdoctoral Research Funding Program of Jiangsu Province.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Pagani, S. M. (2019). Local uniqueness under two directions in discrete tomography: A graph-theoretical approach. International Symposium on Mathematical Morphology and Its Applications to Signal and Image Processing, pp. 96–107. Cham: Springer. [Google Scholar]

 2.  Herman, G. T., Kuba, A. (2012). Discrete tomography: Foundations, algorithms, and applications. New York, USA: Springer Science & Business Media. [Google Scholar]

 3.  Weber, S., Schnorr, C., Hornegger, J. (2003). A linear programming relaxation for binary tomography with smoothness priors. Electronic Notes in Discrete Mathematics, 12(2), 243–254. DOI 10.1016/S1571-0653(04)00490-1. [Google Scholar] [CrossRef]

 4.  Haghani, A., Hu, H., Tian, Q. (2003). An optimization model for real-time emergency vehicle dispatching and routing. 82nd Annual Meeting of the Transportation Research Board, Washington DC, USA. [Google Scholar]

 5.  Chai, G., Cao, J., Huang, W., Guo, J. (2018). Optimized traffic emergency resource scheduling using time varying rescue route travel time. Neurocomputing, 275(1), 1567–1575. DOI 10.1016/j.neucom.2017.09.086. [Google Scholar] [CrossRef]

 6.  Cao, C., Li, C., Yang, Q., Zhang, F. (2017). Multi-objective optimization model of emergency organization allocation for sustainable disaster supply chain. Sustainability, 9(11), 2103. DOI 10.3390/su9112103. [Google Scholar] [CrossRef]

 7.  Huibregtse, O., Flötteröd, G., Bierlaire, M., Hegyi, A., Hoogendoorn, S. (2011). Optimization of evacuation instructions as a fixed-point problem. Swiss Transport Research Conference, Ascona, Swirzerland. [Google Scholar]

 8.  Dulebenets, M. A., Pasha, J., Abioye, O. F., Kavoosi, M., Ozguven, E. E. et al. (2019). Exact and heuristic solution algorithms for efficient emergency evacuation in areas with vulnerable populations. International Journal of Disaster Risk Reduction, 39(2), 101114. DOI 10.1016/j.ijdrr.2019.101114. [Google Scholar] [CrossRef]

 9.  French, J. C., Balster, E. J. (2013). A fast and accurate orthorectification algorithm of aerial imagery using integer arithmetic. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7(5), 1826–1834. DOI 10.1109/JSTARS.2013.2292009. [Google Scholar] [CrossRef]

10. Wu, Z., Karimi, H. R., Dang, C. (2019). An approximation algorithm for graph partitioning via deterministic annealing neural network. Neural Networks, 117(5), 191–200. DOI 10.1016/j.neunet.2019.05.010. [Google Scholar] [CrossRef]

11. Wu, Z., Jiang, B., Karimi, H. R. (2020). A logarithmic descent direction algorithm for the quadratic knapsack problem. Applied Mathematics and Computation, 369(1), 124854. DOI 10.1016/j.amc.2019.124854. [Google Scholar] [CrossRef]

12. Dang, C., Ye, Y. (2015). A fixed point iterative approach to integer programming and its distributed computation. Fixed Point Theory and Applications, 2015(1), 1–15. DOI 10.1186/s13663-015-0429-8. [Google Scholar] [CrossRef]

13. Dang, C. (2010). An increasing-mapping approach to integer programming based on lexicographic ordering and linear programming. The Ninth International Symposium on Operations Research and Its Applications. Lecture Notes in Operations Research, vol. 12, pp. 55–60. Chengdu-Jiuzhaigou, China. [Google Scholar]

14. Wu, Z., Li, B., Dang, C., Hu, F., Zhu, Q. et al. (2017). Solving long haul airline disruption problem caused by groundings using a distributed fixed-point computational approach to integer programming. Neurocomputing, 269(1), 232–255. DOI 10.1016/j.neucom.2017.02.091. [Google Scholar] [CrossRef]

15. Mao, J. Y., Pan, Q. K., Miao, Z. H., Gao, L. (2021). An effective multi-start iterated greedy algorithm to minimize makespan for the distributed permutation flowshop scheduling problem with preventive maintenance. Expert Systems with Applications, 169(1), 114495. DOI 10.1016/j.eswa.2020.114495. [Google Scholar] [CrossRef]

16. Meng, T., Pan, Q. K. (2021). A distributed heterogeneous permutation flowshop scheduling problem with lot-streaming and carryover sequence-dependent setup time. Swarm and Evolutionary Computation, 60(9), 100804. DOI 10.1016/j.swevo.2020.100804. [Google Scholar] [CrossRef]

17. Huang, J. P., Pan, Q. K., Miao, Z. H., Gao, L. (2021). Effective constructive heuristics and discrete bee colony optimization for distributed flowshop with setup times. Engineering Applications of Artificial Intelligence, 97(2), 104016. DOI 10.1016/j.engappai.2020.104016. [Google Scholar] [CrossRef]

18. Aardal, K. I. (1997). An algorithm for solving a diophantine equation with lower and upper bounds on the variables, vol. 1997. Utrecht University, Berlin, Heidelberg: Information and Computing Sciences. [Google Scholar]

19. Aardal, K., Bixby, R. E., Hurkens, C. A., Lenstra, A. K., Smeltink, J. W. (2000). Market split and basis reduction: Towards a solution of the Cornuéjols-Dawande instances. INFORMS Journal on Computing, 12(3), 192–202. DOI 10.1287/ijoc.12.3.192.12635. [Google Scholar] [CrossRef]

20. Dahl, G., Flatberg, T. (2009). Reconstructing (0, 1)-matrices from projections using integer programming. Computational Optimization and Applications, 42(1), 141–154. DOI 10.1007/s10589-007-9116-y. [Google Scholar] [CrossRef]

21. Lenstra, A. K., Lenstra, H. W., Lovász, L. (1982). Factoring polynomials with rational coefficients. Mathematische Annalen, 261(4), 515–534. DOI 10.1007/BF01457454. [Google Scholar] [CrossRef]

22. Wu, Z., Dang, C., Zhu, C. (2013). Solving the market split problem using a distributed computation approach. 2013 IEEE International Conference on Information and Automation (ICIA), pp. 1252–1257. Yinchuan, China, IEEE. [Google Scholar]