Improved Adaptive Iterated Extended Kalman Filter for GNSS/INS/UWB-Integrated Fixed-Point Positioning

1  Introduction

During the construction phase of the construction project, various measurements must be carried out, such as the measurement of known length, the measurement of known angle, the measurement of the plane position of building detail points, etc. The premise of these measurements is that the control points of the construction site must be accurately measured [1–3]. Therefore, the accurate measurement of control points becomes the basis for completing the project construction with high quality.

To further improve position information accuracy, many works have been done, which mainly include two aspects: data fusion model and data fusion filtering algorithm [4]. In the data fusion model, in order to overcome the shortcoming of the global navigation satellite system (GNSS), the inertial navigation system (INS) has been used to be fused with the solution of the GNSS. And the most widely used example is the loosely-integrated localization model. For example, the GNSS/INS loosely processing strategy has been proposed in [5]. In [6], the loosely-integrated model is investigated, and then used to the indoor pedestrian tracking. In this model, the most obvious advantage of this model is that it is easy to achieve [7,8]. It should be pointed out that the loosely integrated localization scheme is hard to avoid introducing the positioning error of the combined subsystem [9,10]. In order to overcome this problem, the tightly integrated localization scheme has been proposed [10]. For example, in [11], the scheme for coupling foot-mounted inertial measurement unit (IMU) and radio frequency identification (RFID) measurements. To the data fusion filter, the Kalman filter (KF) has been widely used in this field [12–15]. It should be emphasized that the KF is suitable for the linear model. To deal with the nonlinear problem, some attempts based on the extended KF (EKF) have been proposed [16]. However, although the EKF is able to face nonlinear system, the truncation error caused by the first-order Taylor expansion will still affect the final filtering accuracy.

To continuously improve the localization accuracy, an adaptive iterated EKF (AIEKF) for fixed-point positioning integrating GNSS, INS and ultra wide band (UWB) is proposed. In our method, the switched GNSS and UWB measurement is used as the measurement of the proposed filter. For data fusion, the expectation-maximization (EM) based IEKF is used as the forward filter; Then, the Rauch-Tung-Striebel smoother is used for the IEKF filter’s results smoothing. Tests illustrate the effectiveness of the proposed AIEKF.

The contribution of this paper mainly includes the following two parts:

•   An improved localization model is proposed to fuse the INS-based and the switched GNSS-based and UWB-based distance tightly. In this model, when the GNSS data is available, the INS-based and GNSS-based distances are used by the data fusion filter, which is able to provide the fixed-point position. When the GNSS is unavailable, the INS-based and UWB-based distances are employed to fuse the fixed-point position, which is used to compensate for the outage of the GNSS.

•   An AIEKF algorithm is designed with a forward filter of expectation-maximization (EM) based IEKF and a backward smoother of R-T-S. To this method, the IEKF method is used to reduce the truncation error caused by nonlinear systems. Meanwhile, the EM method is employed by the IEKF to estimate the noise statistics. Moreover, the threshold is used to improve the adaptability of the algorithm. Finally, the R-T-S smoothing method is used to smooth the output of the IEKF filter, which can improve the localization accuracy.

2  The Integrated Positioning Scheme

This section introduces the positioning scheme integrating GNSS/INS/UWB (G-I-U) firstly. Secondly, the state equation and measurement equation based on the integrated scheme will be designed.

2.1 The Improved Positioning Scheme for Fusing the INS, UWB, and GNSS Measurement Tightly

The structure of the G-I-U-integrated positioning scheme is shown in Fig. 1. In this scheme, the GNSS, INS, and UWB work in parallel. The GNSS estimates the distances d1,2,…,gG between the control point and the satellite. Here, the g means the number of the satellite. Meanwhile, the UWB estimates the distances d1,2,…,qU between the control point and the UWB reference node (RN). The INS is used to provide the INS-derived position PoI. All the measurement mentioned above are input to the proposed improved AIEKF, which will be investigated in following section. Finally, the improved AIEKF outputs the position Po.

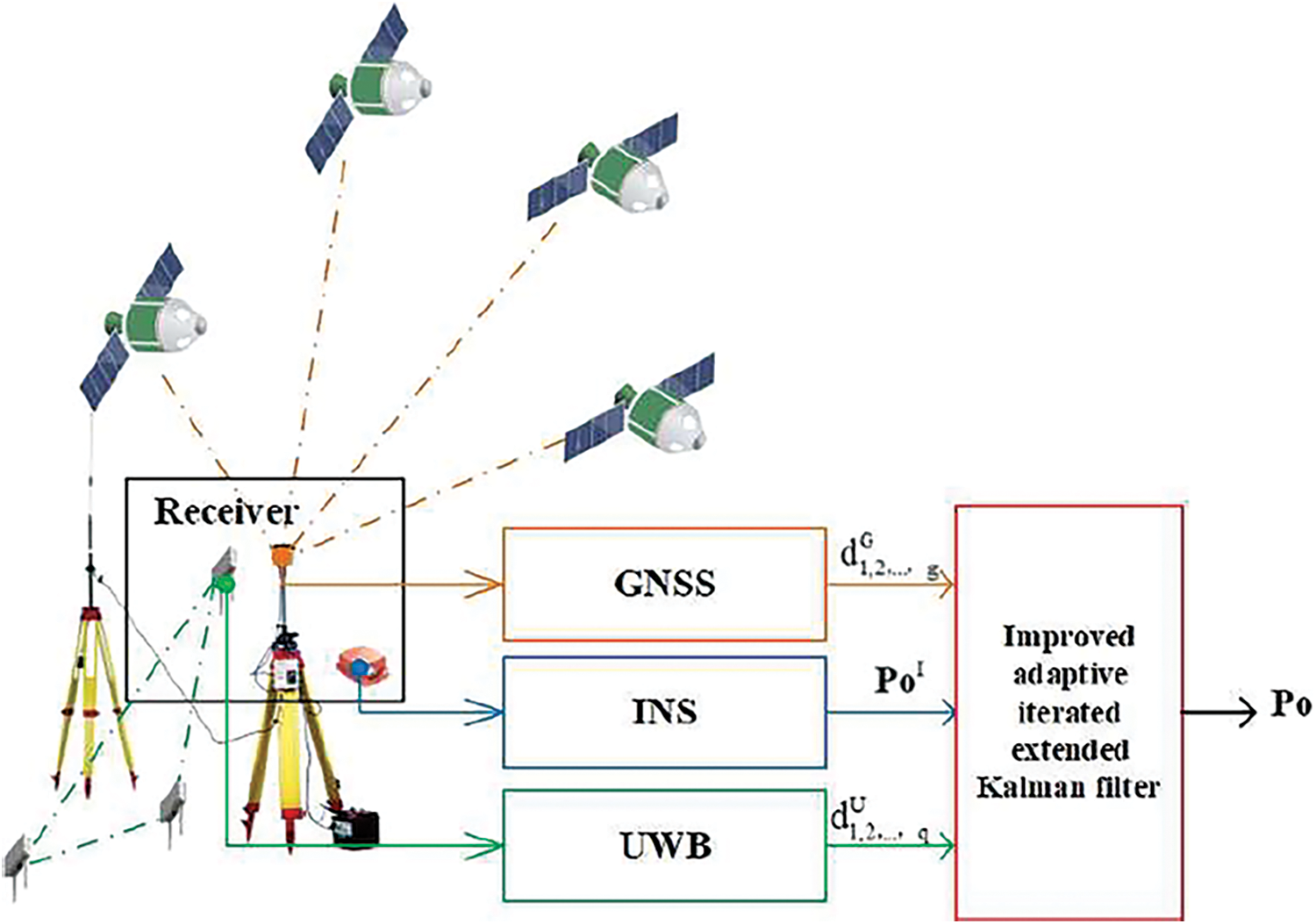
Figure 1: The improved positioning scheme for fusing the INS, UWB, and GNSS measurement tightly

2.2 The State Equation and Measurement Equation for the Proposed Improved Filter

In this subsection, the state equation and measurement equation for the proposed improved filter will be designed. The stated equation of the proposed improved filter which will be introduced in the next section is listed as Eq. (1).

[δPxt−δVxt−δPyt−δVyt−]=Xt−=[1ΔT000100001ΔT0001][δPxt−1δVxt−1δPyt−1δVyt−1]+wt=AXt−1+w,(1)

where (δPxt,δPyt) means the INS’s position error in directions east (E) and north (N) at time t; (δVxt,δVyt) means the INS’s velcity error in E and N directions at time t; ΔT means the sample time; and wt∼(0,Q) means noise in system.

To the measurement equation, when the GNSS data is available, the measurement equation can be derived as follows:

(di,tI)2−(di,tG)2=((PxtI−PxiG)2+(PytI−PyiG)2)−((PxtG−PxiG)2+(PytG−PyiG)2)=(PxtI−PxiG)2−(PxtG−PxiG)2+(PytI−PyiG)2−(PytG−PyiG)2=(PxtI+PxtG−2PxiG)δPx+(PytI+PytG−2PyiG)δPy=(PxtI+PxtI−δPx−2PxiG)δPx+(PytI+PytI−δPy−2PyiG)δPy=2(PxtI−PxiG)δPx+2(PytI−PyiG)δPy−((δPx)2+(δPy)2)=hiG(Xt−),i∈[1,g],(2)

where (PxtI,PytI) means the INS’s position in E and N directions at time t; (PxiG,PyiG) means the ith satellite’s position in E and N directions; thus, the measurement equation when the GNSS data is available can be listed in the following equation.

[(d1I)2−(d1G)2(d2I)2−(d2G)2⋮(dgI)2−(dgG)2]⏟ytG=[h1G(Xt−)h2G(Xt−)⋮hgG(Xt−)]⏟hG(Xt−)+vtG,(3)

where vtG∼(0,R) means the measurement noise; similar to Eq. (2), when the UWB data is available, we can get the following equation:

(di,tI)2−(di,tU)2=((PxtI−PxiU)2+(PytI−PyiU)2)−((PxtU−PxiU)2+(PytU−PyiU)2)=(PxtI−PxiU)2−(PxtU−PxiU)2+(PytI−PyiU)2−(PytU−PyiU)2=(PxtI+PxtU−2PxiU)δPx+(PytI+PytU−2PyiU)δPy=(PxtI+PxtI−δPx−2PxiU)δPx+(PytI+PytI−δPy−2PyiU)δPy=2(PxtI−PxiU)δPx+2(PytI−PyiU)δPy−((δPx)2+(δPy)2)=hiU(Xt−),i∈[1,q],(4)

where (PxiU,PyiU) means the ith UWB’s position in E and N directions; thus, the measurement equation when the UWB data is available can be written as:

[(d2I)2−(d1U)2(d2I)2−(d2U)2⋮(dgI)2−(dgU)2]⏟ytU=[h1U(Xt−)h2U(Xt−)⋮hqU(Xt−)]⏟hU(Xt−)+vtU,(5)

where vtU∼(0,R) means the measurement noise.

3  The Improved AIEKF with Switch Measurement

Based on the models (1)(3)(5), the improved AIEKF with switch measurement will be designed in this section. The iterated extended Kalman filter (IEKF) with switch measurement is listed in the Algorithm 1. In this method, we employ the switch measurement. When the GNSS data is available, we employ the GNSS data as the measurement. When the GNSS data is unavailable, we employ the UWB data as the measurement. Moreover, it should be noted that the IEKF performance in the Algorithm 1 depends on the accuracy of the noise statistics. Thus, we should improve the noise statistics accuracy.

For more accurate noise statistics, we improve the Algorithm 1, and the improved IEKF is listed in the Algorithm 1 based on the models (1)(3)(5) is in the 2nd Algorithm. The 2nd Algorithm shows that the improved algorithm employs the adaptive updating of noise statistics (lines 18–19), which is used to provide the noise statistics adaptively. Moreover, in order to achieve adaptive iteration, we employ the Mahalanobis distance [17] (line 17), which is listed in Eq. (7). Finally, the localization accuracy is improved by employing the R-T-S method (lines 27–32). The structure of the improved IEKF based on the models (1)(3)(5) is shown in Fig. 2.

D(t)=(yt−h(Xt(j))−Ht(j)(Xt−−Xt(j)))T(Rt(j))−1(yt−h(Xt(j))−Ht(j)(Xt−−Xt(j))),(6)

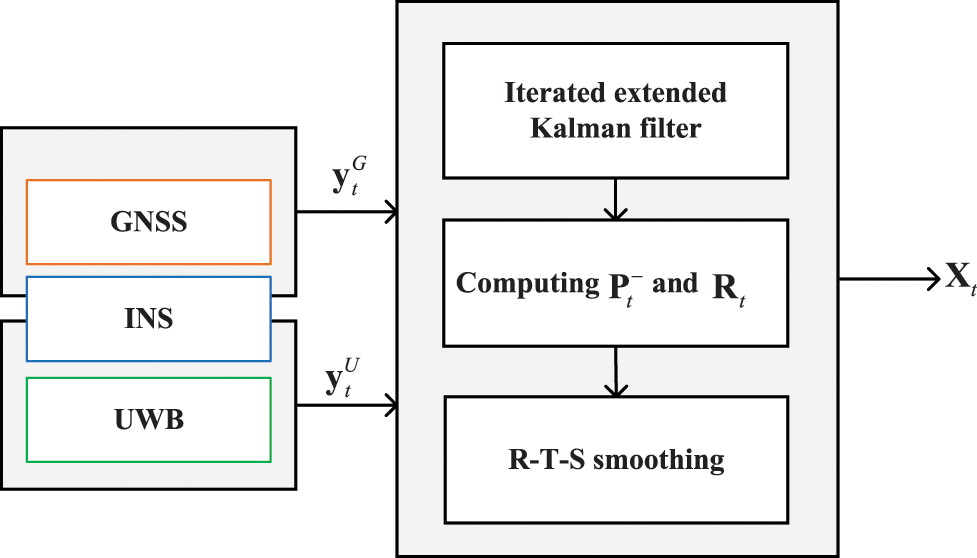
Figure 2: The structure of the improved IEKF based on the models (1)(3)(5)

4  Test

This section verifies the proposed improved AIEKF performance. First, the experimental configuration is introduced. Second, the localization error is compared.

4.1 Setting of the Test

In this work, one test has been done in the University of Jinan, China. In the test, we employ the GPS to provide the GNSS’s solution, meanwhile, the UWB is used to provide the UWB’s solution. The structure of experimental platform is shown in Fig. 3. In this work, we employ one GPS receiver, one UWB localization system (includes blind node (BN) and reference node (RN)), and one inertial measurement unit (IMU). We fix the GPS receiver and the UWB BN on the known coordinate. To the filter, we set the threshold=0.005 and N=5 in Algorithm 2, we set the parameter of the proposed improved AIEKF as follows:

X0=[0000]T,(7)

P0=[1000010000100001],(8)

Q0=[ΔT24ΔT200ΔT210000ΔT24ΔT200ΔT21],(9)

R0=[4.600005.900006.200004.8]×10−3.(10)

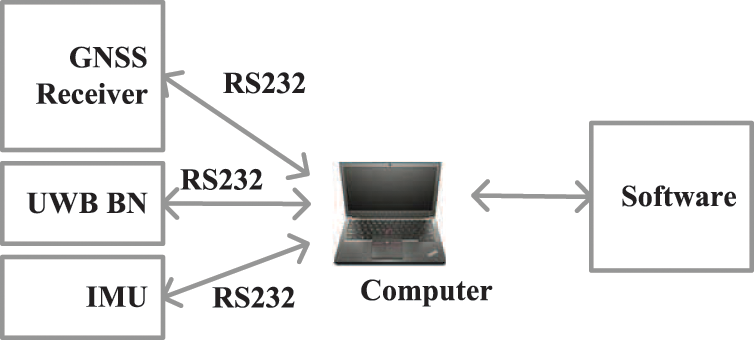
Figure 3: The structure of experimental platform

4.2 Localization Error

In this subsection, the localization error of the proposed method will be compared with the EKF and the traditional IEKF to verify the performance. Figs. 4 and 5 show the position estimated by the GNSS + UWB, EKF, the traditional IEKF, and the proposed improved AIEKF (E and N directions). It should be pointed out that we employ the fixed-point testing in this paper, thus the reference position used in this work are (0, 0). Moreover, in the test, we employ the GNSS + UWB to represent the original data of the sensor. From the figures, one can infer that all the methods mentioned above can provide the positioning accuracy, the EKF and the traditional IEKF perform similarly in directions E and N. Since in this test, the zero is the reference value in E and N directions, and we can see that the estimations of the proposed improved AIEKF are close to zero in E and N directions. Thus, we can conclude that the localization accuracy of the proposed AIEKF has a lower error than the EKF and the traditional IEKF.

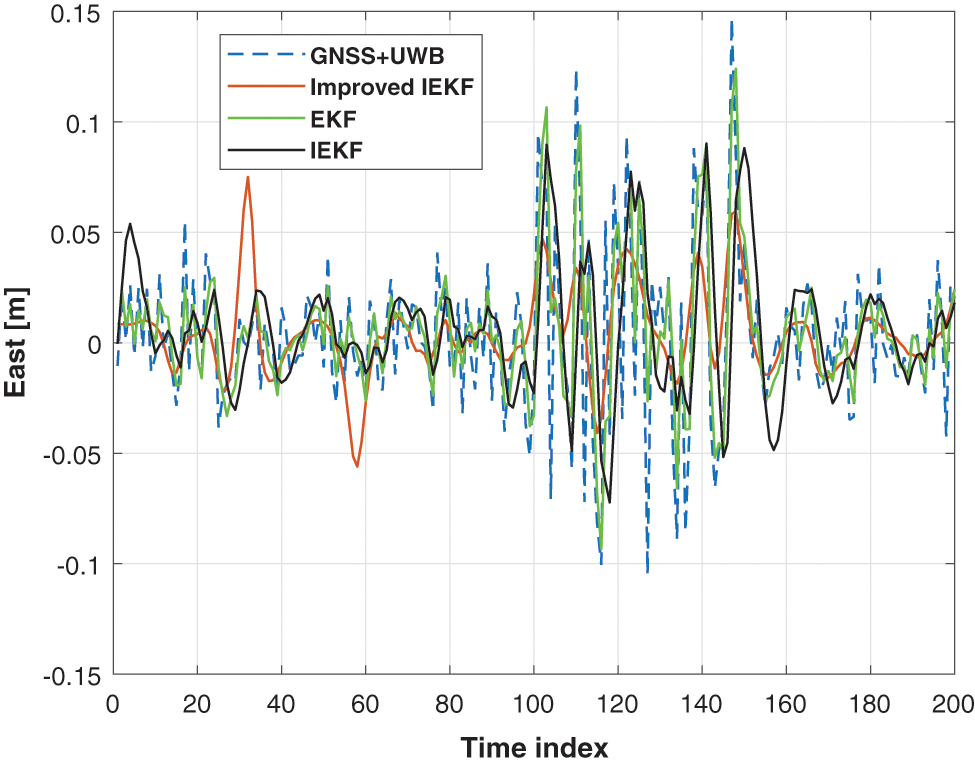
Figure 4: The east position given by the GNSS + UWB vs. EKF vs. the traditional IEKF, and the proposed improved AIEKF

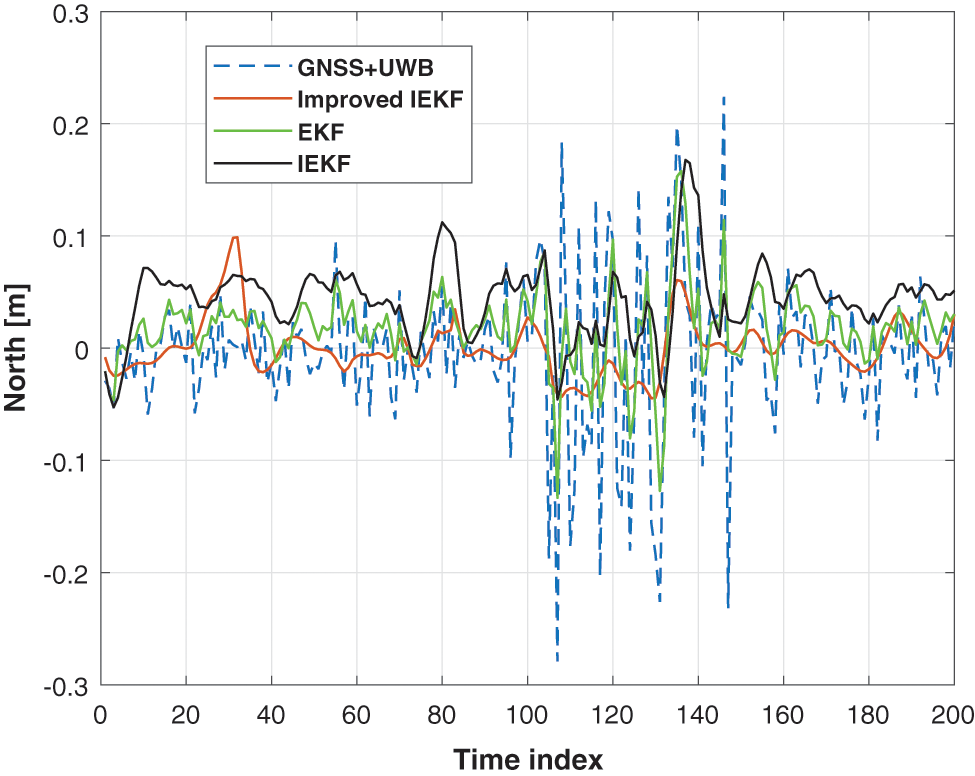
Figure 5: The north position given by the GNSS + UWB vs. EKF vs. the traditional IEKF, and the proposed improved AIEKF

Moreover, to further prove the accuracy of our improved AIEKF, the absolute position errors in E and N directions of the EKF, the traditional IEKF, and the proposed improved AIEKF are shown in Figs. 6 and 7. Those results shows that our improved AIEKF has the smallest localization error when compared with the EKF and the traditional IEKF. The cumulative distribution function (CDF) of the position errors of the EKF, the traditional IEKF, and the proposed improved AIEKF are shown in Fig. 8. Those results shows that the position error of the proposed improved AIEKF is about 0.05 m, and those value of the EKF and the traditional IEKF are 0.08 and the 0.06 m respectively. The root mean square errors (RMSEs) of the position produced by the EKF, the traditional IEKF, and the proposed improved AIEKF are shown in Table 1. As it shows, the RMSEs of the position given by the EKF in E and N directions are 0.0299 and 0.0392 m, respectively. And those values of the proposed method are 0.0194 and 0.0240 m, respectively, which are improved by about 35.12% and 38.78%, respectively when compared with the EKF. And it is easy to see that there is a significant error in the north direction for traditional IEKF. Therefore, it can be concluded that our new method is effective.

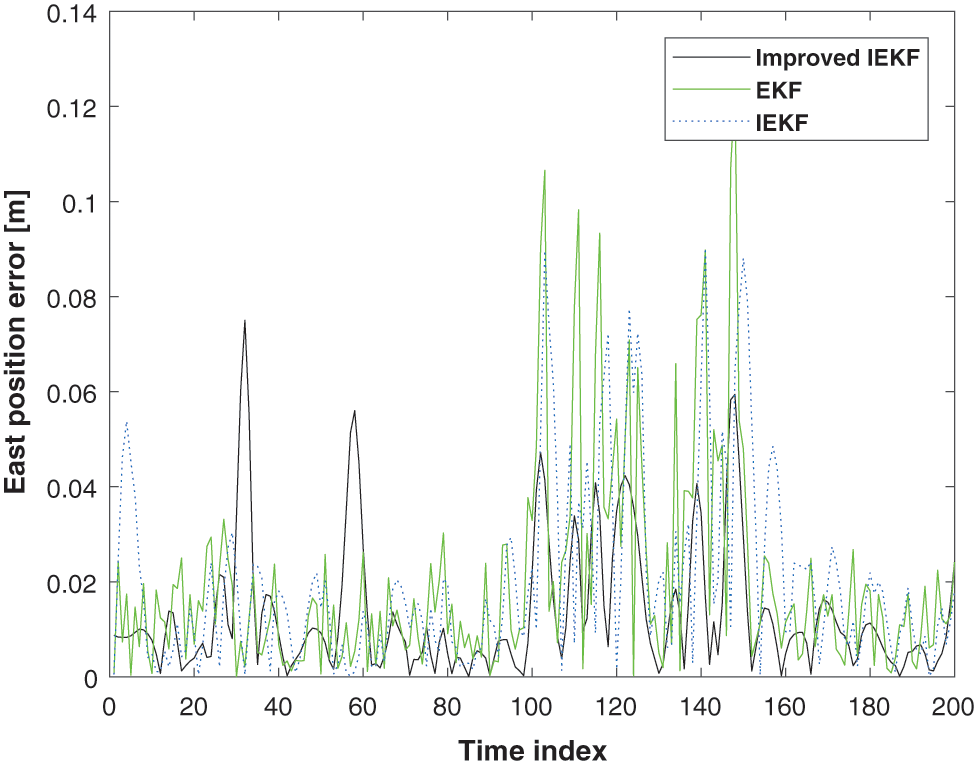
Figure 6: The absolute direction E position error given by the EKF vs. traditional IEKF vs. the proposed improved AIEKF

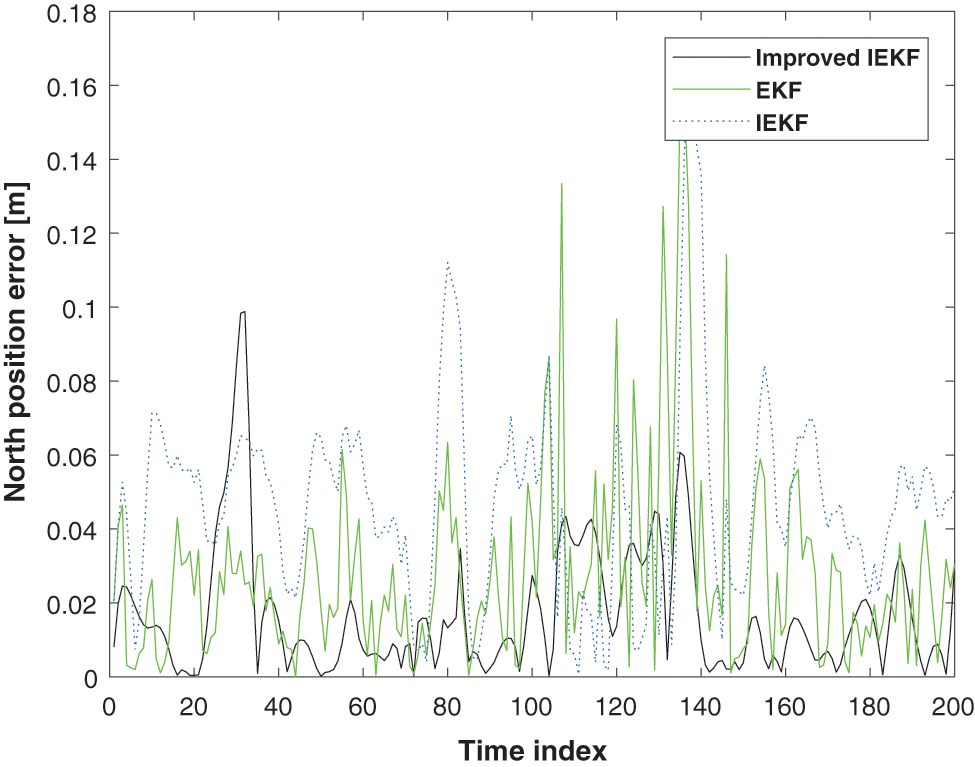
Figure 7: The absolute direction N position error given by the EKF vs. the traditional IEKF vs. the proposed improved AIEKF

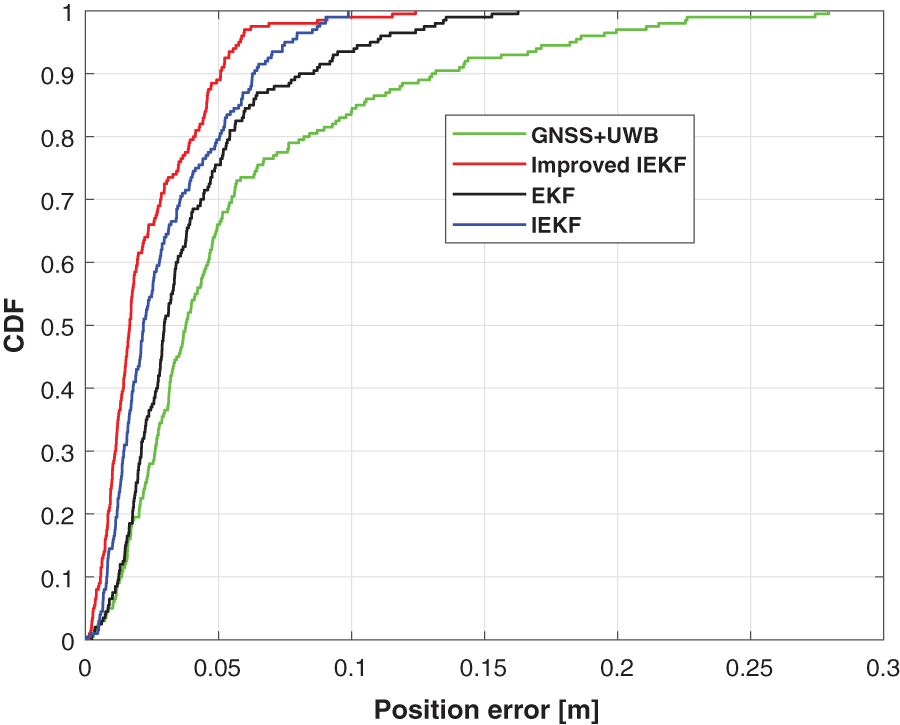
Figure 8: The CDF of the position errors of the EKF vs. the traditional IEKF vs. the proposed improved AIEKF

4.3 The Number of Iterations of the Proposed Improved AIEKF Algorithm

In this subsection, we will investigate the number of iterations of the proposed algorithm. The number of iterations of the proposed improved AIEKF is shown in Fig. 9. From the figure, we can see that the number of iterations changes from 1 to 5, which shows that the proposed method can adjust iteration number adaptively.

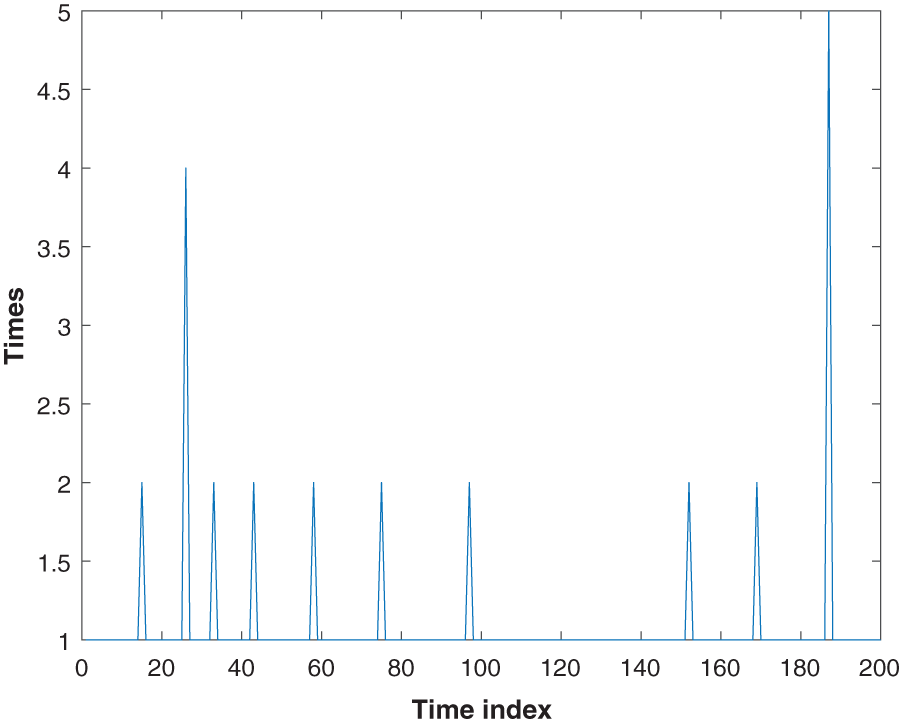
Figure 9: The number of iterations of the proposed improved AIEKF

5  Conclusion

In this work, an improved localization scheme is proposed to fuse the INS-based and the switched GNSS-based and UWB-based distance tightly. Moreover, an AIEKF algorithm is designed with a forward filter of expectation-maximization (EM) based IEKF and a backward smoother of R-T-S.

Funding Statement: This work was supported in part by the Shandong Natural Science Foundation under Grant ZR2020MF067.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Pealoza, G. A., Formoso, C. T., Saurin, T. A. (2021). A resilience engineering-based framework for assessing safety performance measurement systems: A study in the construction industry. Safety Science, 142(5), 105364. [Google Scholar]

 2.  Peñaloza, G. A., Saurin, T. A., Formoso, C. T. (2019). Monitoring complexity and resilience in construction projects: The contribution of safety performance measurement systems. Applied Ergonomics, 82, 102978. DOI 10.1016/j.apergo.2019.102978. [Google Scholar] [CrossRef]

 3.  Xu, Y., Shmaliy, Y. S., Ma, W., Jiang, X., Guo, H. (2021). Improving tightly LiDAR/Compass/Encoder-integrated mobile robot localization with uncertain sampling period utilizing EFIR filter. Mobile Networks and Applications, 26(5), 1–9. [Google Scholar]

 4.  Zhou, B., Zhuang, Y., Cao, Y. (2020). On the performance gain of harnessing non-line-of-sight propagation for visible light-based positioning. IEEE Transactions on Wireless Communications, 19(7), 4863–4878. DOI 10.1109/TWC.7693. [Google Scholar] [CrossRef]

 5.  Shi, B., Wang, M., Wang, Y., Bai, Y., Yang, F. (2021). Effect analysis of GNSS/INS processing strategy for sufficient utilization of urban environment observations. Sensors, 21(2), 620. DOI 10.3390/s21020620. [Google Scholar] [CrossRef]

 6.  Bu, L., Yong, Z., Yuan, X. (2017). Indoor pedestrian tracking by combining recent INS and UWB measurements. 2017 International Conference on Advanced Mechatronic Systems (ICAMechS), Xiamen, China. DOI 10.1109/ICAMechS.2017.8316479. [Google Scholar] [CrossRef]

 7.  Jiang, H., Shi, C., Li, T., Dong, Y., Jing, G. (2021). Low-cost GPS/INS integration with accurate measurement modeling using an extended state observer. GPS Solutions, 25(1), 1–15. DOI 10.1007/s10291-020-01053-3. [Google Scholar] [CrossRef]

 8.  Chen, C., Chang, G. (2021). PPPLib: An open-source software for precise point positioning using GPS, BeiDou, Galileo, GLONASS, and QZSS with multi-frequency observations. GPS Solutions, 25(1), 1–7. [Google Scholar]

 9.  Xu, Y., Ahn, C. K., Shmaliy, Y. S., Chen, X., Li, Y. (2018). Adaptive robust INS/UWB-integrated human tracking using UFIR filter bank. Measurement, 123, 1–7. DOI 10.1016/j.measurement.2018.03.043. [Google Scholar] [CrossRef]

10. Xu, Y., Shmaliy, Y. S., Ahn, C. K., Shen, T., Zhuang, Y. (2021). Tightly-coupled integration of INS and UWB using fixed-lag extended UFIR smoothing for quadrotor localization. IEEE Internet of Things Journal, 8(3), 1716–1727. DOI 10.1109/JIoT.6488907. [Google Scholar] [CrossRef]

11. Ruiz, A. J., Granja, F. S., Honorato, J. P., Rosas, J. G. (2011). Accurate pedestrian indoor navigation by tightly coupling foot-mounted IMU and RFID measurements. IEEE Transactions on Instrumentation and Measurement, 61(1), 178–189. DOI 10.1109/TIM.2011.2159317. [Google Scholar] [CrossRef]

12. Qin, J., Wang, J., Shi, L., Kang, Y. (2020). Randomized consensus-based distributed kalman filtering over wireless sensor networks. IEEE Transactions on Automatic Control, 66(8), 3794–3801. DOI 10.1109/TAC.2020.3026017. [Google Scholar] [CrossRef]

13. Zhao, S., Huang, B. (2020). Trial-and-error or avoiding a guess? Initialization of the kalman filter. Automatica, 121, 109184. DOI 10.1016/j.automatica.2020.109184. [Google Scholar] [CrossRef]

14. Zhao, S., Shmaliy, Y. S., Liu, F. (2016). Fast kalman-like optimal unbiased FIR filtering with applications. IEEE Transactions on Signal Processing, 64(9), 2284–2297. DOI 10.1109/TSP.2016.2516960. [Google Scholar] [CrossRef]

15. Xu, Y., Cao, J., Shmaliy, Y. S., Zhuang, Y. (2021). Distributed kalman filter for UWB/INS integrated iedestrian localization under colored measurement noise. Satellite Navigation, 2(1), 1–10. DOI 10.1186/s43020-021-00053-z. [Google Scholar] [CrossRef]

16. Xu, X., Sun, Y., Tian, X., Zhou, L., Li, Y. (2021). A double-EKF orientation estimator decoupling magnetometer effects on pitch and roll angles. IEEE Transactions on Industrial Electronics, 69(2), 2055–2066. DOI 10.1109/TIE.2021.3060652. [Google Scholar] [CrossRef]

17. Pak, J. M., Ahn, C. K., Shi, P., Lim, M. T. (2016). Self-recovering extended kalman filtering algorithm based on model-based diagnosis and resetting using an assisting FIR filter. Neurocomputing, 173, 645–658. DOI 10.1016/j.neucom.2015.08.011. [Google Scholar] [CrossRef]