Novel Analysis of Two Kinds Hybrid Models in Ferro Martial Inserting Variable Lorentz Force Past a Heated Disk: An Implementation of Finite Element Method

Nomenclature:

1  Introduction

Nanoparticles dispersed in the base fluid can improve the thermos-physical properties of nanofluids. Nanofluids outperform other working fluids in thermal conductivity and convective heat transfer. As a result, there has been an increase in the study of nanofluids in thermal systems in recent years. The shape of nanoparticle influences nanofluid-based thermal systems and hydraulic performance. The influence of nanoparticle shape on the performance of single-particle and hybrid nanofluid flows in various thermal environments has received a lot of attention. The thermophysical properties of nanofluids containing various-shaped nanoparticles have received much attention. The introduction summarizes various studies on the heat transfer characteristics of single-particle nanofluids with various particle shapes. Thermal energy conservation is gaining popularity to reduce heat loss while increasing heat transfer. Researchers are increasingly turning to nanofluids because conventional working fluids have limited improvement potential in heat transfer systems. The heat transfer of nanofluids in thermal systems such as tubes has received much attention. Algehyne et al. [1] studied the thermal transport of a Maxwell hybrid nanofluid on an infinitely stretchable vertical porous sheet. Hybrid nanofluids can be used to track thermal transport. A non-Fourier heat flux model can be used to exploit thermal failure. External heat sources must also be taken into account. The mathematical formulation of the model is based on a coupled nonlinear partial differential equations system. The partial differential equations model was converted to an ordinary differential equations model using transformations. Finite elements are then used to solve the nonlinear ordinary differential equations system. A grid-independent survey and a comparative analysis confirm the approach and solution’s dependability. The physical properties of the solution are investigated and recorded concerning several relevant variables. The higher the number in Forchheimer and Darcy’s porous numbers, the slower the motion. Rather than nanofluids, hybrid nanostructures accelerate thermal growth. Hybrid nanoparticles have a much thicker momentum layer than nanoparticles. A pseudo-plastic model with tri-hybrid nanoparticles was used by Hou et al. [2] to model the thermal energy and solute transport problems to improve heat transfer. Thermal and solute transport was governed by the well-known Fourier and Fick’s laws. The coupled partial differential equations system was simplified using the boundary layer theory. The modeled partial differential equations were transformed into ordinary differential equations using a similarity transformation and then numerically solved using a Finite Element Procedure. The result was compared to many other factors. There is also a survey without grids. The fluid was discovered to be hotter than the tri-hybrid nanoparticles. The temperature and concentration of the fluid increased as the Dufour number increased. The fluid temperature increased as the heat generation parameter and Eckert numbers increased. The buoyancy force and porosity parameters were used to polarize the fluid velocity. Wang et al. [3] used a porous model of a stretched surface to study heat and mass transfer. The relationship between Darcy Forchheimer and the Forchheimer family is mentioned. Cattaneo and Christov’s double diffusion theories are used to derive the thermal and mass transport expressions. The thermal conductivity of tri-hybrid nanoparticles embedded in a pseudo-plastic material is also investigated. The phenomenon of boundary layers is the basis for this complicated model. Correlation can be used to convert tri-hybrid nanoparticle model partial differential equations to ordinary differential equations. Ordinary differential equations that have been transformed cannot be solved precisely. The numerical problem is solved using the finite element method. The researchers compare their findings to those previously published to ensure their approach is valid. To summarize, this research shows how finite element methods can solve complex engineering problems. Nanoparticles are also required to improve thermal performance and control mass diffusion. Hou et al. [4] investigated heat and mass transport in a pseudo-plastic model with Soret and Dufour effects over a porous surface with entropy analysis. The thermal energy and solute transport problems were modeled using heat generation/absorption and chemical reactions, including tri-hybrid nanoparticles to improve heat transfer. Thermal and solute transport was governed by the well-known Fourier and Fick’s laws. Using Cartesian coordinates and boundary layer theory, a set of coupled partial differential equations was simplified in the physical model. The modeled PDEs were transformed into corresponding ODEs using a similarity transformation and then numerically solved using the Finite Element Procedure. The result was compared to several other factors. There is also a survey without grids. The fluid was discovered to be hotter than the tri-hybrid nanoparticles. The temperature and concentration of the fluid increased as the Dufour number increased. The fluid temperature increased as the heat generation parameter and Eckert numbers increased. The buoyancy force and porosity parameters were used to polarize the fluid velocity. Hou et al. [5] studied a porous stretched surface with a hydromagnetic Carreau–Yasuda liquid, the effects of Soret and Dufour. Heat generation/absorption, viscous dissipation, and joule heating have significant effects. A chemical reaction can be seen during mass transportation. The conductivity of the Carreau–Yasuda liquid was investigated. PDEs were the governing laws in their early stages. The ODEs were then solved using the FEM (Finite Element Method). Grid-independent analysis was used to assess the methodology chosen. When parameter values were increased, significant physical effects were discovered. The rates of heat and mass transfer were calculated and discussed in detail. Nazir et al. [6] investigated the thermal efficiency of MoS2 SiO2 Williamson fluid with nano-sized hybrid particles. The Williamson fluid is thought to be thermally relaxed. These properties reduce the fluid’s temperature field. The fluid-particle resistive force controls the boundary layer. The resistive forces of Darcy and Forchheimer can also be compared. A hybrid nanofluid may be used to improve heat transfer. Hybrid nanofluid produces less heat than mono nanofluid. Relaxation impairs one’s ability to focus. Just as heat-generating chemical reactions affect temperature, they also affect mass mobility. It transports mass and heat better than a mono nanofluid. Using hybrid nanofluid instead of nanofluid as a heat-conducting material can significantly improve cooling system efficiency. Nazir et al. [7] have considered the Carreau-Yasuda model. Carreau and Yasuda’s shear rate-dependent model is used numerically to predict fluid flow dynamics. The use of hybrid nanostructures improves two-dimensional heat transfer. The pure Carreau-Yasuda fluid and the fluid with nanostructures are compared. The numerical simulations are carried out by the FEM software, which saves the results as graphs and numerical data. In both types of fluids, the wall shear stress is proportional to the magnetic field intensity. As the temperature of fluid rises, the heat transfer rate decreases due to Ohmic dissipation. The heat transfer rate of a hybrid nanofluid decreases faster than that of a mono nanofluid. The concentration profile clearly shows that generative reactions behave differently from destructive reactions. The Weissenberg number increases the fluid motion proclivity. In a hybrid nanofluid, the diffusion of wall movement has a more significant effect than the diffusion of solid boundary movement in a mono nanofluid. Rayleigh convection slows atom and ion movement in mono nano and hybrid nanofluids. Shear stress increases as the magnetic field strength increases. MHD fluids have higher shear stress at the wall than non-MHD fluids. Changes in magnetic field intensity have an impact on temperature profiles. The magnetic force causes electrons to slow down. As a result, boosting the magnetic field’s strength reduces convective heat energy transport. The melting parabolic stretched surface to focus on Powell–Eyring fluid flow was discussed by Chu et al. [8]. Boundary layer theory contains flow rheology expressions. In this study, similarity transformations were used to convert PDEs to ODEs. These transformed ODEs were solved using the finite element method, including the symbolic computational. The grid-independent analysis demonstrates the utility and effectiveness of FEM. The surface drag and heat transfer coefficients show that the FEM is accurate and dependable. The nonlinear problem method is highly effective and can be applied to various nonlinear problems. The magnetic parameter is not inversely proportional to the thermal profile, but the Prandtl number behaves inversely. Waqas et al. [9] bio-convective flow of modified viscoelastic second grade and handled the complex equations numerically. They found that higher values of the Peckelt number reduce the density profile of microorganism. Nazir et al. [10] investigated the thermal performance of tri-hybrid nanomaterial in Sisko martial involving variable thermal properties. They implemented a numerical approach to obtain numerical results. Algehyne et al. [11] investigated the effects of thermal transport on a pseudo-plastic material by heating and stretching a porous sheet. To stimulate energy conservation, heat generation and absorption are used. Prandtl’s boundary-layer approach was used to model the phenomenon in Cartesian coordinates to make the problem easier to understand. The rheology is modeled using nonlinear coupled PDEs. Similarity transformation is used to convert these derived PDEs to ODEs. The converted ODEs with their new parameters were numerically approximated using the finite element method. In this study’s limiting case, it was discovered that the obtained solution was consistent with previously published findings. The finite element method is an excellent method for solving nonlinear problems in mathematical modeling, among other things. Hafeez et al. [12] created it to use a system of partial differential equations to simulate the thermal and solute properties of the Casson liquid in a Darcy porous medium. Convective boundary conditions determine how models behave in these situations. A 108-tolerance finite element method is used to solve these problems numerically. The subject of discussion is a mathematical algorithm (also known as a finite element approach). There is apparent convergence of 300 elements. Computer simulations study flow dynamics, heat transfer, and mass transport. The effects of temperature and concentration gradients on mass and heat energy transport are studied using simulations. It is fascinating to watch the numbers for Dufour and Soret change over time. Abdelmalek et al. [13] performed both the numerical and parametric analysis, as evidenced by their simulations. Suspending hybrid nanostructures significantly improved thermal conductivity and mass transport. When thermal radiation is increased, the temperature drops significantly. The Weissenberg parameter affects the velocity of a Carreau liquid in a magnetic field. Specie diffusion from the wedge into the fluid increases when the chemical reaction is generative; the opposite trend occurs when the chemical reaction is destructive. Imran et al.’s [14] research focused on the unsteady two-dimensional flow of a second-grade hybrid nanofluid over a stretchable moving horizontal porous plate. The entropy of the system is taken into account. The magnetic field and Joule heating are also considered. This experiment uses silicon carbide and titanium oxide nanoparticles dispersed in oil. Small particles (such as spheres, bricks, tetrahedrons, and platelets) are also studied for their shape factors. PDEs are represented mathematically by accounting for Joule heating and viscous dissipation effects. The current PDEs are converted into ODEs using MATLAB’s bvp4c (shooting) scheme. The effects of various physical constraints on momentum and temperature fields are graphed and numerically investigated. Manzoor et al.’s [15] work on improving heat transfer in industrial and engineering applications has piqued the interest of researchers. For example, in heat exchangers and electronic devices, the rate of thermal transport is critical. Oil, water, and ethylene glycol are examples of low thermal conductivity base fluids. Hybrid convective heat transfer has a wide range of manufacturing applications. Researchers investigated heat transfer in hybrid nanoparticles with magnetic dipoles using blood as a base fluid. Using similarity transformations, the flow problem of PDEs can be transformed into the structure of nonlinear ODEs. Several recent contribution covering the modeling of physical aspects are covered in [16–21] and references therein. Mahbood et al. [22] developed a system for performing his calculations. The MHD couple stress fluid was studied in greater depth using the fourth–fifth-order Runge–Kutta–Fehlberg equations, including nonlinear thermal radiation, velocity slip, and entropy generation. Mahbood et al. [23] investigated the heat and mass transfer properties of a Brinkmann-type nanofluid flow composed of sodium alginate and Fe3O4 in a vertical rotating frame. The Runge-Kutta Fehlberg method (RKF-45) solves dimensionless nonlinear partial differential equations. Ayub et al. [24] investigated the second-order slip phenomenon and the flow of cross nanofluids that comes to a halt at a certain point using a spectral relaxation method. Brownian motion, joules, viscous heating, thermophoresis, and mixed convection are all considered. The way MHD transferred heat was studied by Shah et al. [25]. Thermal conductivity allows a nanofluid to pass through using thermophoresis, Brownian motion, and a binary chemical reaction in cylindrical coordinates. The velocity and activation energy of nanofluid are determined using perpendicular magnetic dipole field measurements. Wang et al. [26] estimated numerical consequences of traveling waves in terms of chemical kinetics using equations of time-fractional fishers. Some recently published contributions are mentioned in [27–32].

Available studies ensure that no report is presented on heat and mass transport for axisymmetric flow produced due to the stretching of a heated rotating disk with Yamada Ota hybrid and Hamilton Crosser models containing the variable properties via finite element scheme. This work fills this gap. Section 1 contains the comprehensive literature review, modeling is covered in Section 2 and the scheme is explained in Section 3 and implemented, the obtained solution is discussed in detail in Section 4 and important results are highlighted in Section 5.

2  Formulation of the Developed Model

The model is prepared using the following assumptions:

■   A rheology of Ferro-fluid is considered;

■   A axisymmetric heated disc is taken out;

■   Variable magnetic field and variable wall temperature is addressed;

■   Yamada Ota hybrid and Hamilton Crosser models are used;

■   Viscous dissipation and Joule heating influences are observed;

■   Motion of fluid particles is induced using the movement of wall;

■   Thermal properties regarding nanoparticles are inserted;

■   An efficient approach based on the finite element method is used;

■   Chemical reaction is occurred into mass species;

■   Non constant thermal conductivity and non-constant mass diffusion are addressed;

■   Fig. 1 represents the flow behavior of the current model.

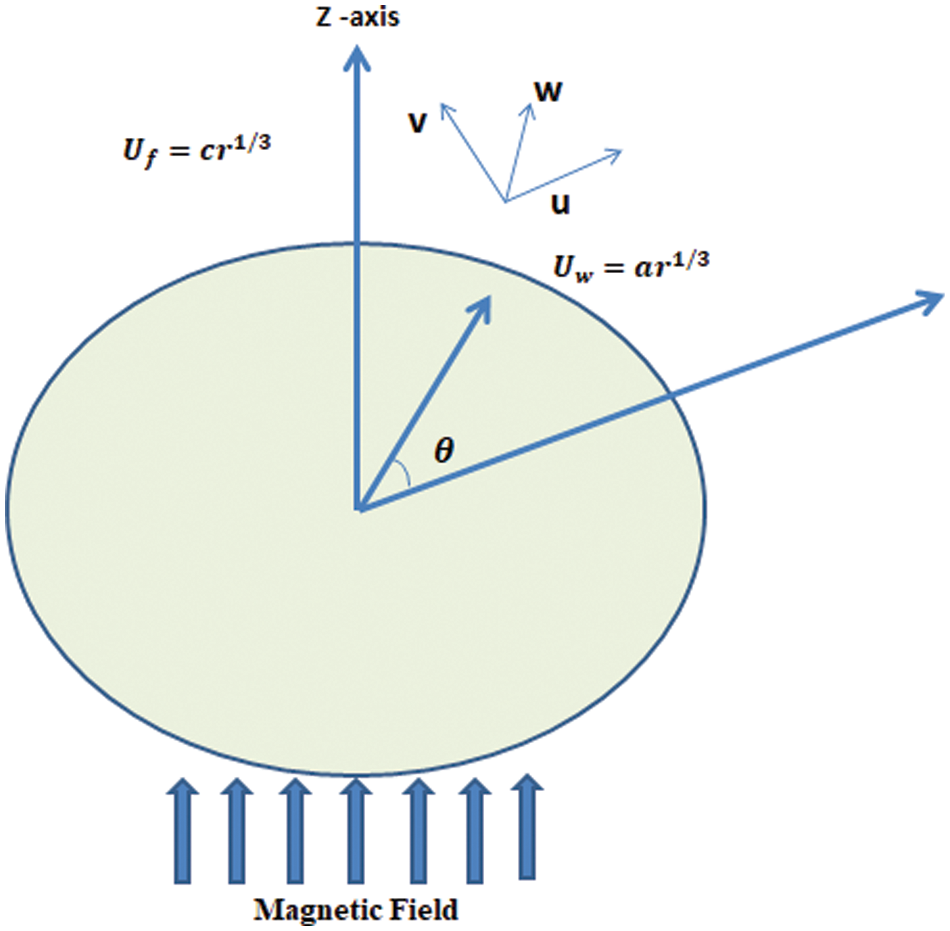
Figure 1: Geometry of model

A variable magnetic field [0,0,B0dr−1/3] is imposed at surface of wall. It is noticed that fluidic motion is generated by stretching surface in the radial direction along with velocity Uw=ar1/3 whereas ambient fluid is generated with velocity uf=cr1/3. The formulated PDEs which present the continuity equation, momentum, heat and mass transport are derived via boundary layer approximations and these obtained PDEs [29,31,32] are

∂u∂r+ur+∂w∂r=0,(1)

u∂u∂r+w∂u∂z−uf∂uf∂r=r−23B02σhybridd2ρhybrid(uf−u)+νhybrid∂2u∂z2,(2)

u∂T∂r+w∂T∂z=1(ρCp)hybrid∂∂z(k(T)∂T∂z)+r−23B02σd2ρhybridu2+1(ρCp)hybrid(∂u∂z)2,+Q(ρCp)hybrid(T−T∞),(3)

u∂C∂r+w∂C∂z=∂∂z(D(T)∂C∂z)−r−23k0(C−C∞).(4)

Implication of desired boundary conditions [29] is considered as

u=ar1/3,w=0,C=Cw,T=Tw:z=0,u→uf,C→C∞,T→T∞:z→∞.(5)

Hybrid correlations among nanoparticles [30] are delivered as in Table 1.

ρhybrid=[(1−ϕ2){(1−ϕ1)ρf+ϕ1ρs1}]+ϕ2ρs2(ρCp)hybrid=[(1−ϕ2){(1−ϕ1)(ρCp)f+ϕ1(ρCp)s1}]+ϕ1(ρCp)s2{ks1+(n−1)kf−(n−1)ϕ1(kf−ks2)ks1+(n−1)kf−ϕ1(ks2−kf)}=kbfkf},(6)

μhybrid=(1−ϕ2)2.5μf(1−ϕ1)2.5,knfkf={ks+(n+1)kf−(n−1)ϕ(kf−ks)ks+(n−1)kf+ϕ(kf−ks)}khybridkhybrid={ks2+(n−1)kbf−(1−n)ϕ2(ks2−kbf)ks2+(n−1)kbf−ϕ2(kbf−ks2)}{ks2+(n−1)kbf−(1−n)ϕ2(ks2−kbf)ks2+(n−1)kbf−ϕ2(kbf−ks2)}=khybridkbf},(7)

khybridkbf={ks2kbf+ω+ωϕ2(1−ks2kbf)ks2kbf+ω+ϕ2(1−ks2kbf)}ω=2ϕ215LDfor cylindrical particleω=2ϕ215for spherical particle},(8)

khybridkbf={ks1kf+ω+ωϕ1(1−ks1kf)ks1kf+ω+ϕ1(1−ks1kf)}ω=2ϕ215LDfor cylindrical particleω=2ϕ215for spherical particles},(9)

Similarity variables [29] are

u=ar1/3f′,η=(aνf)1/2r−1/3z,θ=T−TwTw−T∞w=−(aνf)12r−1/3[53f−13ηf′],φ=C−CwCw−C∞.(10)

Thermal conductivity and mass diffusion are functions of temperature [31] which are addressed as

k(T)=khybrid[1+ϵ1(T−T∞Tw−T∞)],D(T)=Dhybrid[1+ϵ2(T−T∞Tw−T∞)].(11)

Using similarity variables in system of PDEs and obtained ODEs [29] are

f′′′−νfνhnf13f′f′+νfνhnf53ff′′+13A2+M2(A−f′)=0.(12)

(1+ϵ1θ)θ′′+ϵ1θ′2+kf(ρCp)hnfkhnf(ρCp)f53Prf′θ′−kf(ρCp)hnfkhnf(ρCp)f13Prf′θr+(1−ϕ2)−2.5kf(1−ϕ1)2.5khnfEcPrf′f′+(1−ϕ2)−2.5kf(1−ϕ1)2.5khnfPrEcf′′f′′+kfkhnfHsPrθ=0,(13)

(1+ϵ2θ)φ′′+ϵ2θ′φ′+(1−ϕ2)−2.5Sc(1−ϕ1)2.553f′φ′−(1−ϕ2)−2.5Sc(1−ϕ1)2.513f′φ−(1−ϕ2)−2.5Sc(1−ϕ1)2.5Kcφ=0.(14)

Dimensionless boundary conditions [29] are

θ(η)=1,φ(η)=1,f(η)=A,f′(0)=1:η=0,θ(η)=0,φ(η)=0,f′(η)=1:η=∞.(15)

Dimensionless parameters are derived as

Pr=μf(Cp)fkf,Ec=a2CpdT0,Sc=νfDf,Kc=k0a,M2=σfd2B02aρf,A=ca.

Drag force coefficient for Ferro-fluid [29,32] is

Cf=(1−ϕ2)−2.5(1−ϕ1)−2.5Re12f′′(0).(16)

Temperature gradient and rate of mass diffusion under hybrid nanofluid and variable properties are modeled [29,32] as

NU=−1Re−12kfkhybrid(1+ϵ1)θ′(0),(17)

SH=−(1−ϕ2)−2.5(1−ϕ1)−2.5Re−12(1+ϵ2)φ′(0).(18)

3  Numerical Procedure

Model problem along with boundary conditions is simulated by an efficient technique called finte element method. Numberious computational fluid dynamics problems are solved by FEM. It is noticed that code regarding finite element method is designed on MAPLE 18. Moreover, Maple is known as numerical and symobolic computing enviroment. It deals with numberious areas, such as numerical analysis, data processing, symobilc mathematics and visulizations. Basicscally, six steps of FEM are discussed here and these steps are skecched by Fig. 2.

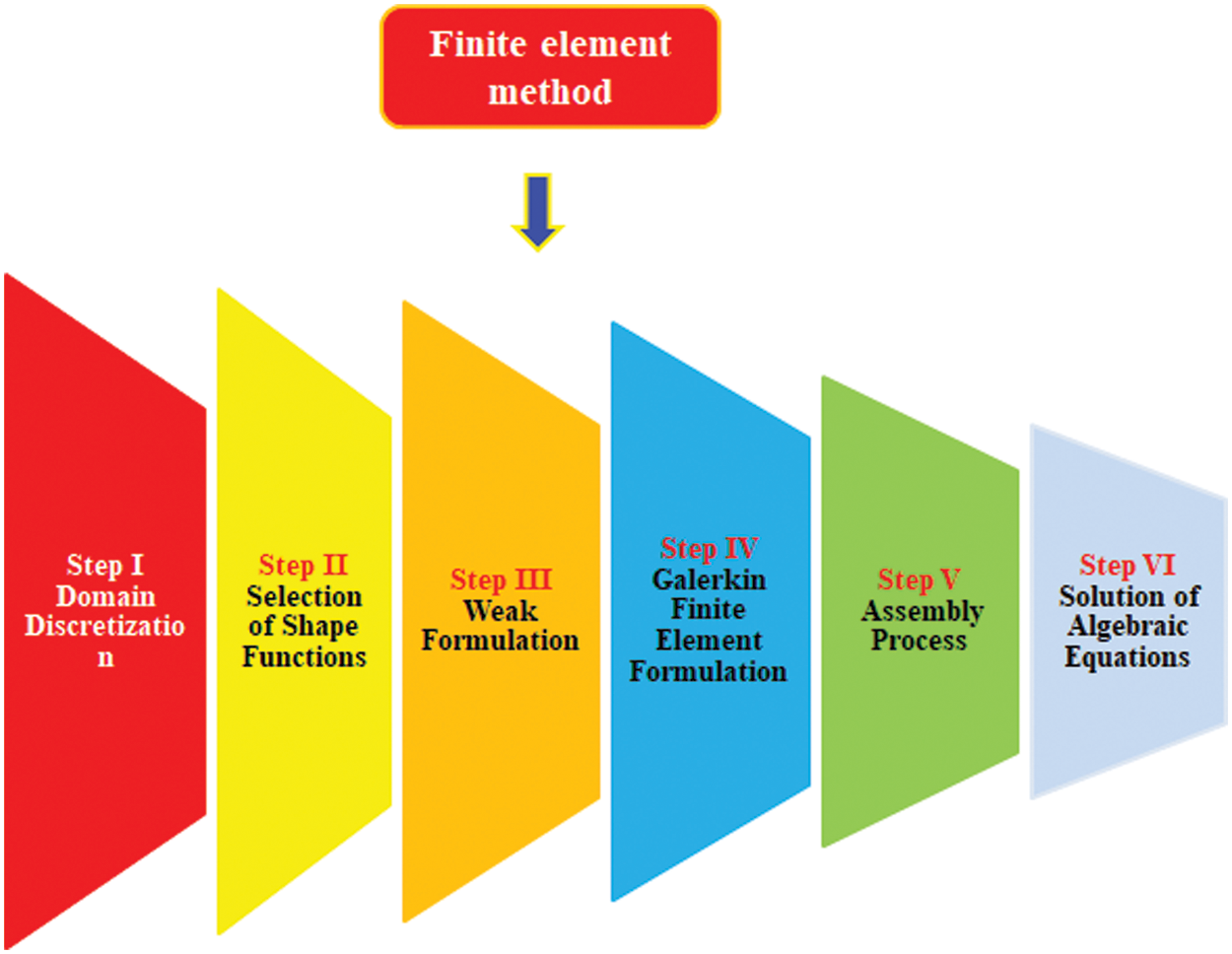
Figure 2: Illustration of FEM’s steps

Step I: The subdomains are obtained by dividing the domain into elements which are connected with neighboring elements at nodes. The discretization of the elements gives approximation solution over each element rather than over whole domain and approximation solution is considered as a linear polynomial.

Step II: The shape functions are orthogonal nodal basis which possess the property Kronecker delta. The approximation solution is obtained from the product of shape functions. The linear shape functions are used here.

Step III: The weak formulation of the transformed problem is covered in this step.

Step IV: The elements stiffness matrix is generated due to using of Galerkin approach in weak form whereas concept of assembly process is helped to generate elements stiffness matrices.

Step V: Finally, a global stiffness matrix is obtained via assembly process. Picard linearization method is used to linearize the system of non-linear equations.

Step VI: Finally, algebraic equations are achieved using the Picard linearization method. Code is designed in MAPLE 18. The table is tabulated to check the convergence of the developed analaysis. It is observed that outcomes regarding concentration, velocity and temperature profiles at the mid of each element are simulated in the Table 2. Moreover, the number of elements is increased against velocity, temperature and concentration profiles and obtained outcomes are noticed. It is found that the results of velocity, temperature and concentration profiles are not changed after 300 elements. Therefore, the results of the developed model are converged at 300 elements and all numerical and graphical simulations are obtained for 300 elements.

4  Results and Discussion

Mass diffusion and heat energy in Ferro-fluid including variable properties are analyzed in the heated disk. Yamada Ota hybrid and Hamilton Crosser models are inserted. Heat source and Joule heating are observed along with chemical reaction. The feature based on the stagnation point is studied. A complex model is developed while the complex model is simulated with the help of a numerical approach called the finite element method. The ranges of dimensionless parameters 0.001≤M≤0.4,≤,0≤A≤0.3,206≤Pr≤208,−1.8≤Hs≤0.3,0.0≤Sc≤0.8,0.0≤Kc≤0.8,0.0≤Ec≤2.0,0.0≤ϵ1≤1.5,0.0≤ϵ1≤1.7 are used in simulations. Variation in various parameters is accumulated on flow, mass diffusion and heat energy which are explained below.

4.1 Consequences Regarding Flow and Thermal Energy

In this subsection, flow analysis and heat energy analysis are studied vs. various parameters. It is mentioned that two kinds of models regarding the hybrid approach are studied. Moreover, solid curves are plotted for representation of the Yamada Ota hybrid approach while Hamilton Crosser is captured to address the consequence of the Hamilton Crosser model. Fig. 3 is addressed to predict the behavior of the magnetic number on velocity curves. It is investigated that flow becomes slow down vs. higher impact of the magnetic parameter. It is because Lorentz force is applied along the vertical direction of the heated disk. Therefore, flow is slowed down due to negative Lorentz force. Physically, the magnetic parameter is formulated using the concept of Lorentz force in momentum equations. It is noticed that the magnetic parameter is implemented along perpendicular direction on the wall. Therefore, the fluid becomes significantly viscous and the thickness associated with momentum layers decreases. The role of the Eckert number is implemented on the temperature field presented in Fig. 4. Maximum amount of heat energy is gained vs. higher impact of Eckert number. It is studied that appearance of Eckert number is produced because of viscous dissipation. More heat dissipates when Eckert number is increased. Therefore, direct proportional relation is estimated among heat energy and Eckert number. Moreover, maximum production regarding thermal energy is generated for the Yamada Ota hybrid model rather than heat energy for the case Hamilton Crosser hybrid model. Eckert number is a dimensionless number formulated due to in viscous dissipation in the energy equation. An increment in Eckert number results in viscous dissipation which is enhanced. Hence, heat energy is significantly dissipated when the Eckert number is increased. Fluid particles gain more heat energy vs. the impact of Eckert number. Fig. 5 addresses an impact of heat source parameter on thermal curves. Thermal curves are plotted for positive numerical values as well as negative values of heat source parameter. It is investigated that negative numerical values for heat source parameter are predicted for heat absorption while positive numerical values for heat source parameter are observed for heat generation phenomenon. It is observed that the heat generation parameter is implemented at the wall of the surface. Hence, thermal energy can be adjusted against the variation in heat source parameter. Moreover, thickness related to thermal layers is enhanced against higher numerical values of heat source number. The observation of magnetic parameter on heat energy curves is analyzed in Fig. 6. It is observed that heat energy is enhanced into fluidic particles when magnetic parameter is increased. The occurrence of magnetic parameter on heat energy is generated due to applying the impact of Joule heating. Physically, the Joule heating process is occurred by interaction among moving fluidic particles that make current. Thermal layers thickness is reduced when the magnetic parameter is increased. Moreover, maximum production regarding thermal energy is generated for Yamada Ota hybrid model rather than heat energy for the case Hamilton Crosser hybrid model.

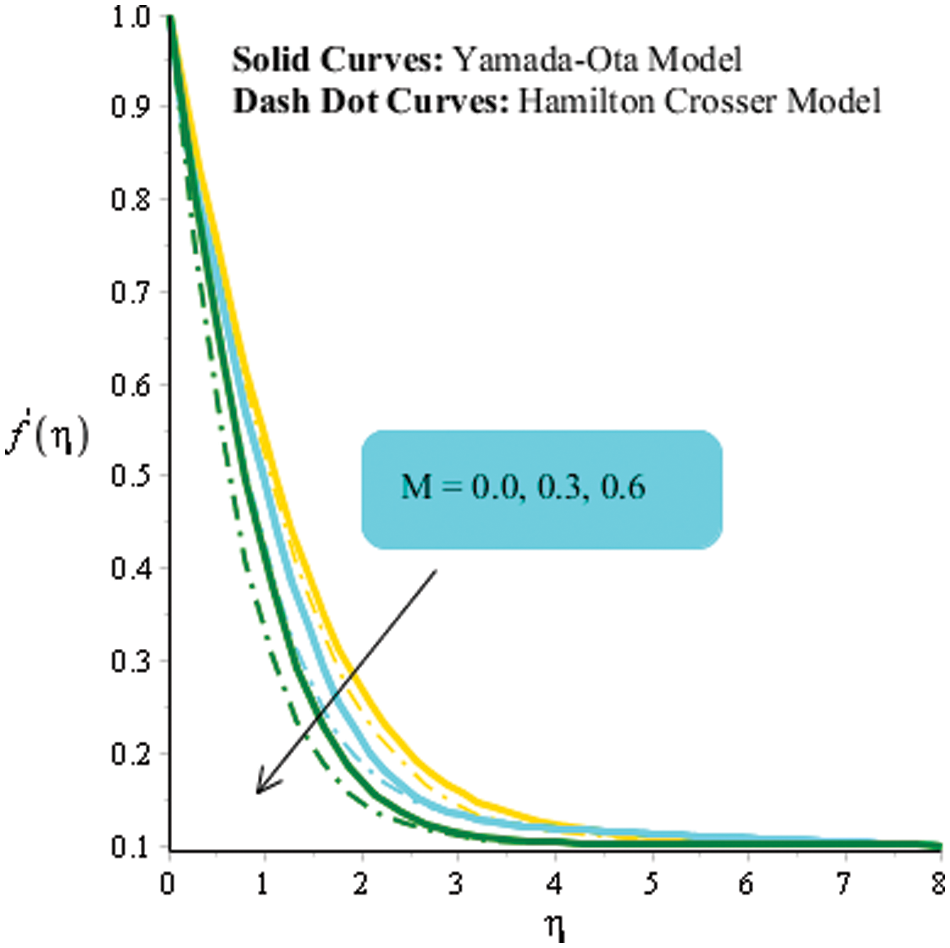
Figure 3: An influence of M on velocity curves when Pr=208,A=0.0,ϵ1=0.03,ϵ2=0.08,Ec=1.4,Hs=−1.8,Sc=0.7,Kc=0.3

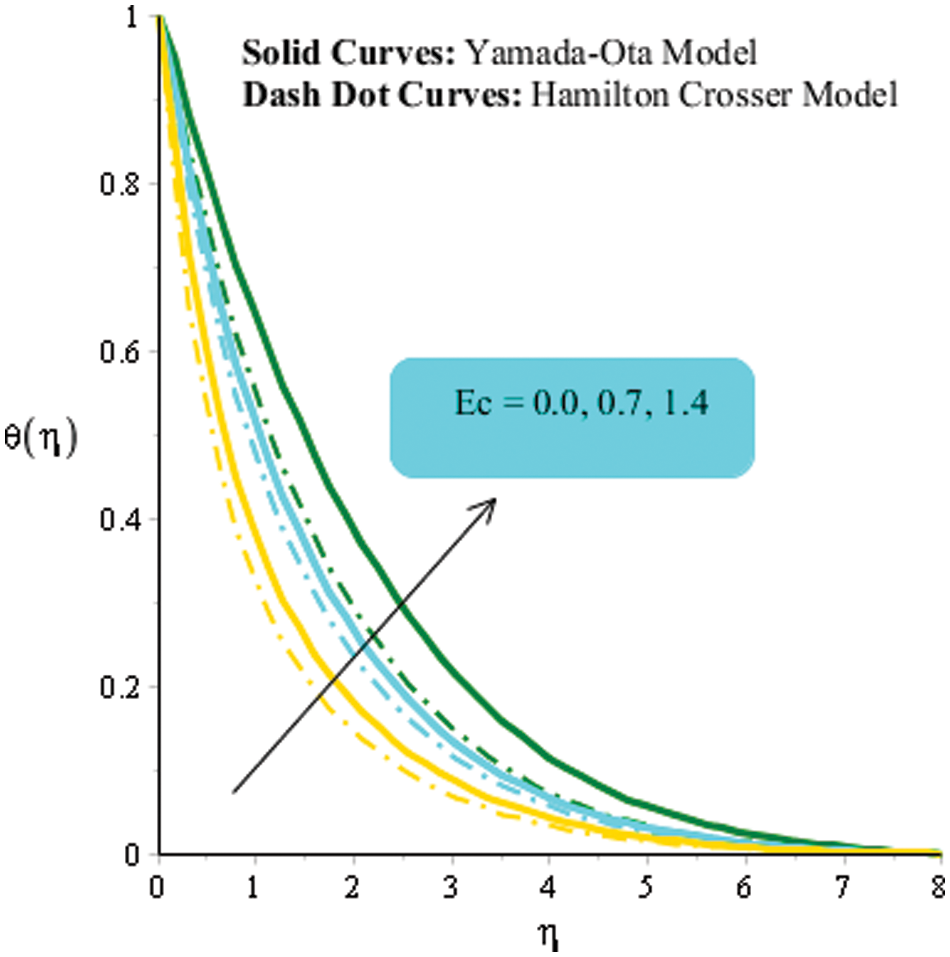
Figure 4: An influence of Ec on thermal curves when M=0.001,Pr=206,A=0.0,ϵ1=0.04,ϵ2=0.08,Hs=−1.4,Sc=0.7,Kc=0.4

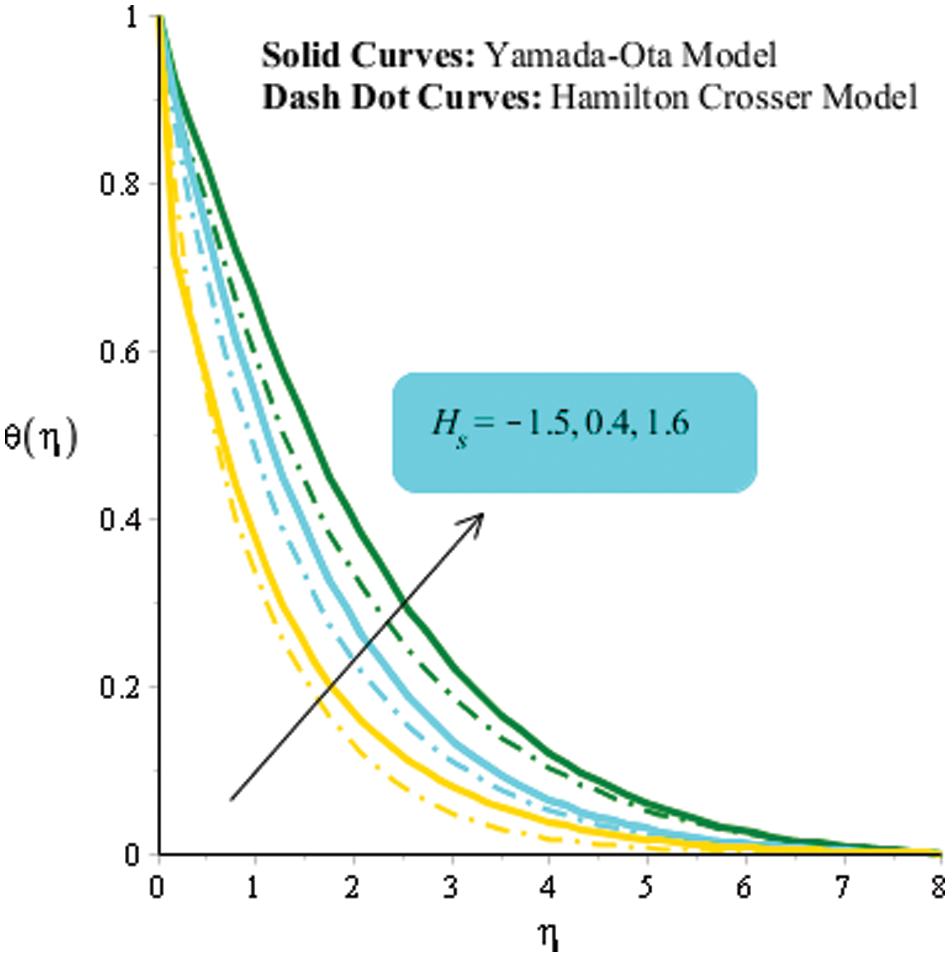
Figure 5: An influence of Hs on thermal curves when M=0.03,Pr=206,A=0.0,ϵ1=0.02,ϵ2=0.08,Ec=1.4,Sc=0.7,Kc=0.2

Figure 6: An influence of M on thermal curves when Pr=206,A=0.0,ϵ1=0.02,ϵ2=0.08,Ec=1.4,Hs=−1.4,Sc=0.7,Kc=0.2

4.2 Consequences Regarding Mass Diffusion

Figs. 7–9 are plotted to determine influences of Sc,Kc and ϵ2 on concentration field including models related to Hamilton Crosser and Yamada Ota hybrid models. Fig. 7 is addressed the effect of Schmidt number on concentration field. It is estimated that Curves associated with concentration field are declined vs. an impact of Schmidt number. This is because Schmidt number is ratio among momentum and mass diffusivities. Therefore, an inversely proportional relation is investigated vs. an impact of Schmidt number. Schmidt number is known as dimensionless number. Mathematically, Sc(=νfDf) is formulated mass diffusion equation. Hence, ration among νf and Df is called Schmidt number. Moreover, maximum production regarding concentration is generated for the Yamada Ota hybrid model rather than concentration for the case Hamilton Crosser hybrid model. Fig. 8 is prepared to predict the amount regarding concentration vs. chemical reaction number. Diffusion into fluid particles becomes slowed down when the chemical reaction parameter is increased. The chemical reaction number is known as coefficient of temperature based on the concentration field. It can be visualized by variation in Kc. It is observed that Kc<0 is the case when solute particles are generated during the chemical reaction. Such kind of chemical reaction is known as a generative chemical reaction. Further, the chemical reaction is called destructive chemical reaction when solute is used in chemical reaction. The role of ϵ2 on mass diffusion is investigated by Fig. 9. It is noticed that process of mass diffusion is enhanced when ϵ2 is increased. Mathematically, variable mass diffusion number has direct relation against temperature difference. Further, ϵ2 is the dimensionless parameter, which is formulated variable mass diffusion in mass diffusion equation. Mass diffusion for the case of ϵ2=0 is higher than mass diffusion for the case of ϵ2≠0. Thickness associated with mass diffusion is enhanced vs. higher numerical values of ϵ2.

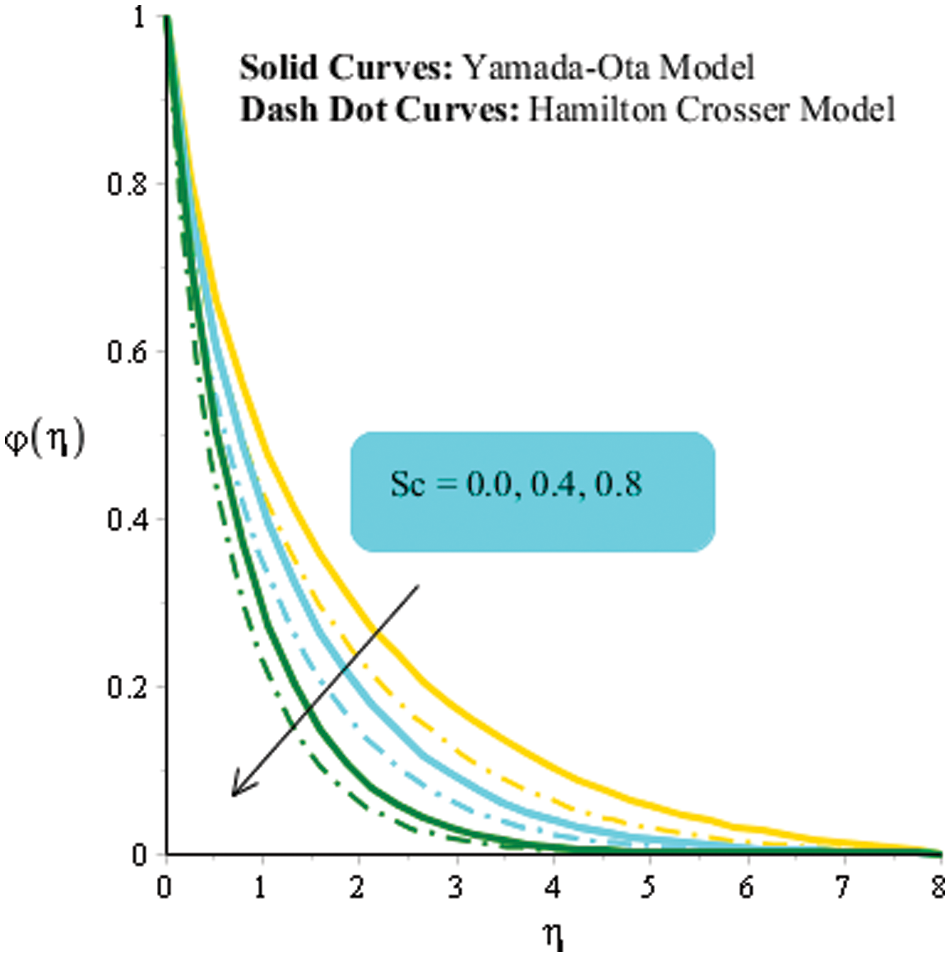
Figure 7: An influence of Sc on concentration curves when M=0.04,Pr=206,A=0.0,ϵ1=0.02,ϵ2=0.08,Ec=1.4,Hs=−1.4,Kc=0.8

Figure 8: An influence of Kc on concentration curves when M=0.001,Pr=206,A=0.0,ϵ1=0.02,ϵ2=0.08,Ec=1.9,Hs=−1.4,Sc=0.9

Figure 9: An influence of ϵ2 on concentration curves when M=0.3,Pr=209,A=0.0,ϵ1=0.02,Ec=1.4,Hs=−1.8,Sc=0.7,Kc=0.2

4.3 Investigation of Nusselt Number, Flow Rate and Sherwood Number

Table 3 investigates numerical aspects of Nusselt number, flow rate and Sherwood number against the variation in magnetic number, heat source parameter, Dufour number and Schmidt number. Flow rate, mass diffusion rate and heat energy rate are declined when the heat source parameter and magnetic parameter are increased. But heat transfer rate and mass diffusion rate are boosted against argument numerical values of Dufour number.

5  Conclusions

Dispersion of hybrid nanoparticles is carried out in this research with variable properties for the fluid flow through a heated disc. The arising problem is tackled numerically. The remarkable findings are:

■   Ferro-fluid flow and heat energy for the case of the Yamada Ota hybrid model are higher than for the case of the Hamilton Crosser hybrid model;

■   Convergence of the present problem is ensured by 300 elements;

■   Developing a model is applicable to printing process, electronic devices, temperature measurements, engineering process and food making;

■   Heat energy is boosted against variation in Eckert number and heat source number, but production regarding thermal energy is declined vs. variation in Joule heating process;

■   The amount of mass species is reduced vs. incline impacts of chemical reaction and Schmidt parameter;

■   Mass diffusion rate and thermal energy rate are increased against variation in magnetic parameter, but mass diffusion rate and thermal energy rate are declined vs. heat source number.

Availability of Data and Material: The data used to support this study are included in the Manuscript.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Algehyne, E. A., El-Zahar, E. R., Elhag, S. H., Bayones, F. S., Nazir, U. et al. (2022). Investigation of thermal performance of Maxwell hybrid nanofluid boundary value problem in vertical porous surface via finite element approach. Scientific Reports, 12(1), 1–12. DOI 10.1038/s41598-022-06213-8. [Google Scholar] [CrossRef]

 2.  Hou, E., Wang, F., Nazir, U., Sohail, M., Jabbar, N. et al. (2022). Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines, 13(2), 201. DOI 10.3390/mi13020201. [Google Scholar] [CrossRef]

 3.  Wang, F., Nazir, U., Sohail, M., El-Zahar, E. R., Park, C. et al. (2022). A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory. Nanotechnology Reviews, 11(1), 834–845. DOI 10.1515/ntrev-2022-0050. [Google Scholar] [CrossRef]

 4.  Hou, E., Hussain, A., Rehman, A., Baleanu, D., Nadeem, S. et al. (2021). Entropy generation and induced magnetic field in pseudoplastic nanofluid flow near a stagnant point. Scientific Reports, 11(1), 1–25. DOI 10.1038/s41598-018-33214-3. [Google Scholar] [CrossRef]

 5.  Hou, E., Wang, F., El-Zahar, E. R., Nazir, U., Sohail, M. (2021). Computational assessment of thermal and solute mechanisms in Carreau-Yasuda hybrid nanoparticles involving soret and dufour effects over porous surface. Micromachines, 12(11), 1302. DOI 10.3390/mi12111302. [Google Scholar] [CrossRef]

 6.  Nazir, U., Sadiq, M. A., Nawaz, M. (2021). Non-fourier thermal and mass transport in hybridnano-williamson fluid under chemical reaction in forchheimer porous medium. International Communications in Heat and Mass Transfer, 127, 105536. DOI 10.1016/j.icheatmasstransfer.2021.105536. [Google Scholar] [CrossRef]

 7.  Nazir, U., Abu-Hamdeh, N. H., Nawaz, M., Alharbi, S. O., Khan, W. (2021). Numerical study of thermal and mass enhancement in the flow of Carreau-Yasuda fluid with hybrid nanoparticles. Case Studies in Thermal Engineering, 27, 101256. DOI 10.1016/j.csite.2021.101256. [Google Scholar] [CrossRef]

 8.  Chu, Y. M., Nazir, U., Sohail, M., Selim, M. M., Lee, J. R. (2021). Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal and Fractional, 5(3), 119. DOI 10.3390/fractalfract5030119. [Google Scholar] [CrossRef]

 9.  Waqas, H., Khan, S. U., Hassan, M., Bhatti, M. M., Imran, M. (2019). Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. Journal of Molecular Liquids, 291, 111231. DOI 10.1016/j.molliq.2019.111231. [Google Scholar] [CrossRef]

10. Nazir, U., Saleem, S., Al-Zubaidi, A., Shahzadi, I., Feroz, N. (2022). Thermal and mass species transportation in tri-hybridized sisko martial with heat source over vertical heated cylinder. International Communications in Heat and Mass Transfer, 134, 106003. DOI 10.1016/j.icheatmasstransfer.2022.106003. [Google Scholar] [CrossRef]

11. Algehyne, E. A., El-Zahar, E. R., Sohail, M., Nazir, U., AL-bonsrulah, H. A. et al. (2021). Thermal improvement in pseudo-plastic material using ternary hybrid nanoparticles via non-Fourier’s law over porous heated surface. Energies, 14(23), 8115. DOI 10.3390/en14238115. [Google Scholar] [CrossRef]

12. Hafeez, M. B., Sumelka, W., Nazir, U., Ahmad, H., Askar, S. (2021). Mechanism of solute and thermal characteristics in a Casson hybrid nanofluid based with ethylene glycol influenced by soret and dufour effects. Energies, 14(20), 6818. DOI 10.3390/en14206818. [Google Scholar] [CrossRef]

13. Abdelmalek, Z., Nazir, U., Nawaz, M., Alebraheem, J., Elmoasry, A. (2020). Double diffusion in carreau liquid suspended with hybrid nanoparticles in the presence of heat generation and chemical reaction. International Communications in Heat and Mass Transfer, 119, 104932. DOI 10.1016/j.icheatmasstransfer.2020.104932. [Google Scholar] [CrossRef]

14. Imran, M., Yasmin, S., Waqas, H., Khan, S. A., Muhammad, T. et al. (2022). Computational analysis of nanoparticle shapes on hybrid nanofluid flow due to flat horizontal plate via solar collector. Nanomaterials, 12(4), 663. DOI 10.3390/nano12040663. [Google Scholar] [CrossRef]

15. Manzoor, U., Imran, M., Muhammad, T., Waqas, H., Alghamdi, M. (2021). Heat transfer improvement in hybrid nanofluid flow over a moving sheet with magnetic dipole. Waves in Random and Complex Media, 1–15. DOI 10.1080/17455030.2021.1991602. [Google Scholar] [CrossRef]

16. Rasool, G., Zhang, T., Chamkha, A. J., Shafiq, A., Tlili, I. et al. (2019). Entropy generation and consequences of binary chemical reaction on MHD Darcy–Forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy, 22(1), 18. DOI 10.3390/e22010018. [Google Scholar] [CrossRef]

17. Alghamdi, M., Wakif, A., Thumma, T., Khan, U., Baleanu, D. et al. (2021). Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a darcy-brinkman porous structure bounded vertically by an irregular slender surface. Case Studies in Thermal Engineering, 28, 101428. DOI 10.1016/j.csite.2021.101428. [Google Scholar] [CrossRef]

18. Rasool, G., Shafiq, A., Hussain, S., Zaydan, M., Wakif, A. et al. (2022). Significance of Rosseland’s radiative process on reactive Maxwell nanofluid flows over an isothermally heated stretching sheet in the presence of Darcy–Forchheimer and lorentz forces: Towards a new perspective on Buongiorno’s model. Micromachines, 13(3), 368. DOI 10.3390/mi13030368. [Google Scholar] [CrossRef]

19. Shafiq, A., Mebarek-Oudina, F., Sindhu, T. N., Rasool, G. (2021). Sensitivity analysis for Walters-B nanoliquid flow over a radiative Riga surface by RSM. Scientia Iranica, 29(3), 1236–1249. [Google Scholar]

20. Jamshed, W., Nisar, K. S., Ibrahim, R. W., Shahzad, F., Eid, M. R. (2021). Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. Journal of Materials Research and Technology, 14, 985–1006. DOI 10.1016/j.jmrt.2021.06.031. [Google Scholar] [CrossRef]

21. Shahzad, F., Jamshed, W., Sajid, T., Nisar, K. S., Eid, M. R. (2021). Heat transfer analysis of MHD rotating flow of Fe3O4 nanoparticles through a stretchable surface. Communications in Theoretical Physics, 73(7), 075004. DOI 10.1088/1572-9494/abf8a1. [Google Scholar] [CrossRef]

22. Mabood, F., Yusuf, T. A., Bognár, G. (2020). Features of entropy optimization on MHD couple stress nanofluid slip flow with melting heat transfer and nonlinear thermal radiation. Scientific Reports, 10(1), 1–13. DOI 10.1038/s41598-020-76133-y. [Google Scholar] [CrossRef]

23. Mabood, F., Yusuf, T. A., Rashad, A. M., Khan, W. A., Nabwey, H. A. (2021). Effects of combined heat and mass transfer on entropy generation due to MHD nanofluid flow over a rotating frame. Computers, Materials & Continua, 66(1), 575–587. DOI 10.32604/cmc.2020.012505. [Google Scholar] [CrossRef]

24. Ayub, A., Shah, S. Z. H., Sabir, Z., Rao, N. S., Sadat, R. et al. (2022). Spectral relaxation approach and velocity slip stagnation point flow of inclined magnetized cross-nanofluid with a quadratic multiple regression model. Waves in Random and Complex Media, 1–25. DOI 10.1080/17455030.2022.2049923. [Google Scholar] [CrossRef]

25. Shah, S. L., Ayub, A., Dehraj, S., Wahab, H. A., Sagayam, K. M. et al. (2022). Magnetic dipole aspect of binary chemical reactive cross nanofluid and heat transport over composite cylindrical panels. Waves in Random and Complex Media, 1–24. DOI 10.1080/17455030.2021.2020373. [Google Scholar] [CrossRef]

26. Wang, F., Khan, M. N., Ahmad, I., Ahmad, H., Abu-Zinadah, H. et al. (2022). Numerical solution of traveling waves in chemical kinetics: Time-fractional fishers equations. Fractals, 30(2), 2240051. DOI 10.1142/S0218348X22400515. [Google Scholar] [CrossRef]

27. Wang, F., Sohail, M., Nazir, U., El-Zahar, E. R., Park, C. et al. (2022). An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial. Nanotechnology Reviews, 11(1), 1620–1632. DOI 10.1515/ntrev-2022-0100. [Google Scholar] [CrossRef]

28. Sohail, M., El-Zahar, E. R., Mousa, A. A. A., Nazir, U., Althobaiti, S. et al. (2022). Finite element analysis for ternary hybrid nanoparticles on thermal enhancement in pseudo-plastic liquid through porous stretching sheet. Scientific Reports, 12(1), 1–13. [Google Scholar]

29. Alharbi, S. O. (2021). Numerical computing for axisymmetric transport phenomenon in carreau liquid using variable conductance models. Journal of Thermal Analysis and Calorimetry, 145(1), 161–172. DOI 10.1007/s10973-020-09510-4. [Google Scholar] [CrossRef]

30. Gul, H., Ramzan, M., Nisar, K. S., Mohamed, R. N., Ghazwani, H. A. S. (2022). Performance-based comparison of Yamada–Ota and Hamilton–Crosser hybrid nanofluid flow models with magnetic dipole impact past a stretched surface. Scientific Reports, 12(1), 1–11. DOI 10.1038/s41598-021-04019-8. [Google Scholar] [CrossRef]

31. Nazir, U., Saleem, S., Nawaz, M., Sadiq, M. A., Alderremy, A. A. (2020). Study of transport phenomenon in carreau fluid using Cattaneo–Christov heat flux model with temperature dependent diffusion coefficients. Physica A: Statistical Mechanics and its Applications, 554, 123921. DOI 10.1016/j.physa.2019.123921. [Google Scholar] [CrossRef]

32. Bhandari, A. (2022). Influence of the diameter of the magnetic core and surfactant thickness on water carrying iron (iii) oxide ferrofluid flow over a rotating disk. Waves in Random and Complex Media, 1–20. DOI 10.1080/17455030.2022.2046299. [Google Scholar] [CrossRef]