On Some Ev-Degree and Ve-Degree Dependent Indices of Benes Network and Its Derived Classes

1  Introduction

A classic and helpful strategy is to attach various graphs to objects that may be an algebraic structure, a chemical structure of a drug, or a network, which assists in understanding certain features of the objects. Various graph parameters can be associated with the properties of the structure under examination which leads to a deeper study of its theory. These properties may include the algebraic properties of the zero divisor graphs and the physio chemical properties of the chemical structures. By adopting this strategy, several researchers studied different objects such as algebraic objects [1], pysio-chemical properties of chemical structures [2–4], drugs used for breast cancer treatment [5], and interconnection networks [6]. The analysis of networks, such as Butterfly network [7], Benes network [8,9], Interconnection network [6,10] and David-derived network [11] through similar approach, is one of the most recent developments in the field of graph theory.

The class of topological indices (TIs) is a significant class of parameters associated with graphs. Many TIs have been introduced and studied during the last fifty years. Among the class of degree dependent TIs, the Zagreb indices (ZIs) introduced in [12], vastly studied due to the ability to estimate the π-electron energy is still a topic of interest [13] after 5 decades. Another degree dependent graph parameter, used in mathematical chemistry is known as Randíc index (RI). The details regarding its applications and its different variants are presented in [14]. Furthermore, the geometric-arithmetic (GA) index was formulated [15] in an attempt to exceed the Randíc index in terms of predicting ability. Its chemical use and mathematical characteristics drew scientists to examine it further in [16]. Another significant index, known as Atom bond connectivity index (ABC-index) was put forward by Estrada and was used for investigating stain energy and stability of cycloalkanes and linear alkanes, see [17–20]. Another graph invariant, having connections with eigen values of graphs was introduced in [21] and is a topic of interest till now known as Harmonic index (HI). In [22], Chellali et al. introduced some new degrees of a vertex in a graph, known as ve-degree and ev-degree. Mathematical notions related to these degrees were also studied by Horoldagva et al. [23]. The ZIs and RI, based on ev-degree and ve-degree notions, are formulated in [24–27] and it was analyzed that predicting ability of ve-degree ZI has improved as compared to its classical version. For more developments on the study of TIs, see [28–32].

Butterfly graphs are the associated graphs of Fast Fourier Transforms (FFT) networks which are especially effective in performing the FFT. The butterfly network is constructed by a sequence of switch stages and connector patterns that allow ′n′ different configurations. The ′n′ outputs should be connected to ′n′ inputs. Furthermore, the Benes network obtained by attaching back-to-back butterfly networks is known for permutation routing [8]. These networks are key multistage interconnection networks with appealing communication network topologies [9]. The graph associated to s-dimensional butterfly network consists of vertex set V with elements [v, i] in which v is an s-bit binary number representing the row of the node and 0≤i≤s. The edge between any two vertices [v, i] and [v′, i′] exists if and only if i′=i+1 and either (1) v=v′ or (2) v, v′ differ in exactly the ith bit. Clearly, for |V(BF(s))|=2s(s+1) and |E(BF(s))|=s2s+1. Further, an s dimensional Benes network is obtained by connecting back-to-back butterflies BF(s). An s-dimensional Benes network is denoted by B(s), for example B(3) is shown in Fig. 1. Further, |V(B(s))|=2s(2s+1) and |E(B(s))|=s2s+2. For more regarding the structure and construction of butterfly and benes networks, we refer readers to [6]. By keeping in view the importance of these networks, Hussain et al. recently introduced some families of graphs obtained by Horizontal and vertical identifications of Benes network. These new graphs are known as Horizontal Cylindrical (HCB(s)) and Vertical Cylindrical (VCB(s)) Benes network. In these networks, |V(HCB(s))|=(2s−1)(2s+1), |V(VCB(s))|=2s+1s, |E(HCB(s))|=2s(2s+1−1) and |E(VCB(s))|=2s+2s. For the complete details regarding the structures HCB(s) and VCB(s), see Figs. 2 and 3 [33,34].

Figure 1: 3-dimentional Benes network

Figure 2: Normal representation of VCB(3)

Figure 3: Normal representation of HCB(3)

2  Preliminaries

Let G(V,E) denotes a connected graph having V as a vertex set and E as an edge set. For u∈V, the degree u, denoted by d(u) is the cardinality of edges incident to it. For any u,v∈V, the vertices u, v are called adjacent if there is e∈E with e=uv. For u∈V its open neighborhood, denoted by N(u), is defined as: N(u)={v∈V:thereexistse∈Ewithe=uv} and the closed neighborhood N[u]={u}∪N(u). For uv=e∈E, its ev-degree is the cardinality of the vertices in N[u]∪N[v] and the ve-degree of v∈V is the cardinality of N[v]. The ev-degree of e and ve-degree of u are denoted by dev(e) and dve(u), respectively. In Table 1, we include the formulae of ev-degree and ve-degree dependent variants of the well known TIs discussed above.

3  Ev-Degree Dependent Topological Indices for Bensen Networks and Its Derived Classes

In this section, we prove analytical formulae for the ev-degree dependent TIs for B(s), VCB(s) and HCB(s). The formulae have been established through partition of the vertex sets of B(s), VCB(s) and HCB(s) on the basis of ev-degree as shown in Tables 2–4. We start with the following theorem for B(s).

Theorem 3.1. For an s-dimensional Benes network B(s), we have:

(i) Mev(B(s))=2s+2(64s−28).

(ii) Rev(B(s))=2s+2(16+s8−1).

Proof.

By using Table 2, we compute the ev-degree based indices for Benes network as follows:

(i)

Mev(B(s))=∑e∈E(B(s))dev(e)2=(6)2(2s+2)+(8)2(s)2s+2−2s+2=2s+2(64s−28).

(ii)

Rev(B(s))=∑e∈E(B(s))dev(e)−12=(6)−12(2s+2)+(8)−12(s)2s+2−2s+2=2s+2(16+s8−1).

Now, we continue to prove the ev-degree dependent TIs for VCB(s) in the next theorem.

Theorem 3.2. For VCB(s), the Mev(VCB(s)) and Rev(VCB(s)) are given as:

(i) Mev(VCB(s))=2s+9⋅s.

(ii) Rev(VCB(s))=2s+32⋅s.

Proof. (i) From Table 3 and the definition of Mev, we have:

Mev(VCB(s))=∑e∈E(VCB(s))dev(e)2=(8)2(2)(s)(2s+2)=2s+9s.

(ii) From Table 3 and the definition of Rev, we have:

Rev(VCB(s))=∑e∈E(VCB(s))dev(e)−12=(8)−12(2)(r)(2s+2)=2s+32⋅s.

We conclude the results of this section by proving the ev-degree dependent TIs for HCB(s):

Theorem 3.3. For HCB(s), the Mev(HCB(s)) and Rev(HCB(s)) are given as:

(i) Mev(HCB(s))=2s+7(2s−1)+320s−138.

(ii) Rev(HCB(s))=162s+2+s2s[6+245+6+2]+47+22−126−810+23+62.

Proof. (i) From Table 4 and the definition of Mev, we have:

Mev(HCB(s))=∑e∈E(HCB(r))dev(e)2=(6)2(2r+2−12)+(7)2(4)+(8)2(4)+(8)2(4)(s−1)(ss−3)+(9)2(2)+(10)2(8)(s−1)+(12)2(2)(s−1)=2s+7+2s(256s−256)+320s−138,

which upon simplification gives the required result.

(ii) From Table 4 and the definition of Rev, we have:

Rev(HCB(s))=∑e∈E(HCB(r))dev(e)−12=(6)−1/2(2r+2−12)+(7)−1/2(4)+(8)−1/2(4)+(8)−1/2(4)(s−1)(ss−3)+(9)−1/2(2)+(10)−1/2(8)(s−1)+(12)−1/2(2)(s−1)=162r+2+22s2s+1282s[48+810+13]s+47+22−126−810+23+62,

which upon simplification gives the required result.

Now, we present an example of the results proved in this section:

Example 3.1. By taking s=4 in Theorem 3.1, Theorem 3.2 and Theorem 3.3, we obtain the values of ev-degree based TIs for B(4), VCB(4) and HCB(4) as shown in Table 5:

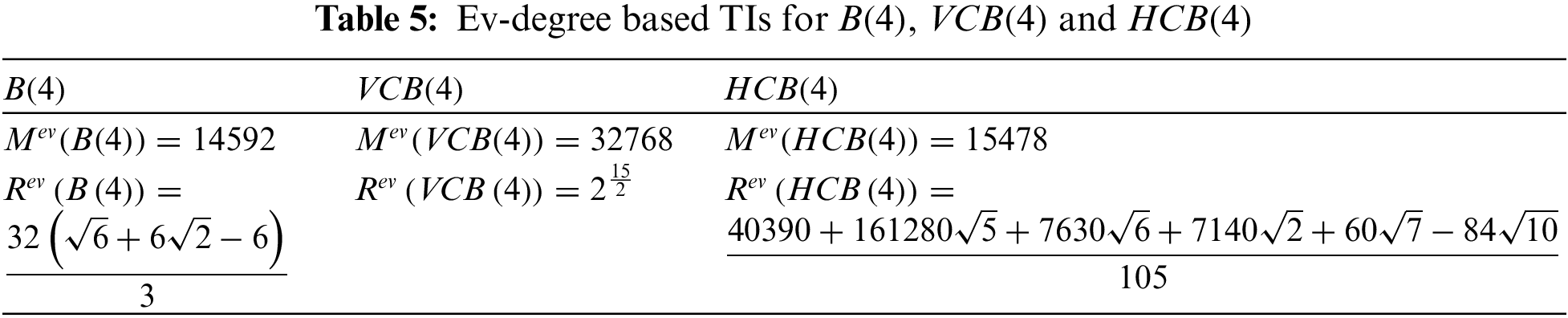
4  Ve-Degree Dependent Topological Indices for Bensen Networks and Its Derived Classes

In this section, we develop formulae for the ve-degree dependent TIs for B(s), VCB(s) and HCB(s). The key to obtaining these formulae is to obtain partition the edge set of B(s), VCB(s) and HCB(s) on the basis of ve-degrees of the end vertices of each edge as shown in Tables 6–8.

Theorem 4.1. For B(s), the ve-degree dependent TIs M1αve(B(s)), M1βve(B(s)), M2ve(B(s)), Rve(B(s)), ABCve(B(s)), GAve(B(s)), Hve(B(s)) and χve(B(s)) are given as:

(i) M1αve(B(s))=32.2s(16s−11).

(ii) M1βve(B(s))=2s+2(32s−16).

(iii) M2ve(B(s))=2s+2(256s−224).

(iv) Rve(B(s))=2s+2[196+1192+s16−18].

(v) ABCve(B(s))=2s+2[296+7192+2s4−22].

(vi) GAve(B(s))=2s+2[265+8314+s−2].

(vii) Hve(B(s))=2s+2[13280+s16].

(viii) χve(B(s))=2s+2[125+s814+122].

Proof. (i) From Table 6 and the definition of M1αve, we have:

M1αve(B(s))=∑v∈V(B(s))dve(v)2=(8)22s+1+(12)22s+1+(16)2(2s−3)2s=2s+1(208)+512s2s−7682s,

which upon simplification gives the required formula.

(ii) The Table 6 and the formula for M1βve yields:

M1βve(B(s))=∑uv∈E(B(s))(dve(u)+dve(v))=(12+8)2s+2+(12+16)2s+2+(16+16)(s2s+2−2s+3)=2s+2(32s−16).

(iii) The Table 6 and the formula for M2ve yields:

M2ve(B(s))=∑uv∈E(B(s))(dve(u)dve(v))=(12)(8)2s+2+(12)(16)2s+2+(16)(16)(s2s+2−2s+3)=2s+2(256s−224).

(iv) The Table 6 and the formula for Rve gives:

Rve(B(s))=∑uv∈E(B(s))((dve(u)dve(v)))−1/2=((12)(8))−1/22s+2+((12)(16))−1/22s+2+((16)(16))−1/2(s2s+2−2s+3)=2s+2[196+1192+s16−18].

(v) The Table 6 and the formula for ABCve yields:

ABCve(B(s))=∑uv∈E(B(s))dve(u)+dve(v)−2dve(u)dve(v)=12+8−2(12)(8)2s+2+12+16−2(12)(16)2s+2+16+16−2(16)(16)(s2s+2−2s+3)=2s+2[296+7192+2s4−22].

(vi) The Table 6 and the formula for GAve yields:

GAve(B(s))=∑uv∈E(B(s))2dve(u)dve(v)dve(u)+dve(v)=2(12)(8)12+82s+2+2(12)(16)12+162s+2+2(16)(16)16+16(s2s+2−2s+3)=2s+2[265+8314+s−2].

(vii) The Table 6 and the formula for Hve yields:

Hve(B(s))=∑uv∈E(B(s))2dve(u)+dve(v)=212+82s+2+212+162s+2+216+16(s2s+2−2s+3)=2s+2[13280+s16].

(viii) Lastly, the Table 6 and the formula for χve gives:

χve(B(s))=∑uv∈E(B(s))(dve(u)+dve(v))−1/2=(12+8)−1/22s+2+(12+16)−1/22s+2+(16+16)−1/2(s2s+2−2s+3)=2s+2[125+127s42+122],

which upon simplification gives the required formula.

By using the Table 7 and the formulae of TIs defined in Table 1, we get the following results for the VCB(s).

Theorem 4.2. For VCB(s), ve-degree dependent TIs M1αve(B(s)), M1βve(B(s)), M2ve(B(s)), Rve(B(s)), ABCve(B(s)), GAve(B(s)), Hve(B(s)) and χve(B(s)) are given as:

(i) M1αve(VCB(s))=256s2s+1.

(ii) M1βve(VCB(s))=32s2s+2.

(iii) M2ve(VCB(s))=256s2s+2.

(iv) Rve(VCB(s))=s162s+2.

(v) ABCve(VCB(s))=2s42s+2.

(vi) GAve(VCB(s))=s2s+2.

(vii) Hve(VCB(s))=s162s+2.

(viii) χve(VCB(s))=s422s+2.

By using the Table 8 and the formulae of TIs defined in Table 1, we get the following results for the HCB(s).

Theorem 4.3. For HCB(s), the ve-degree dependent TIs M1αve(B(s)), M1βve(B(s)), M2ve(B(s)) and Rve(B(s)) are given as:

(i) M1αve(HCB(s))=2s(512s−352)+816s.

(ii) M1βve(HCB(s))=(16s+409)2s+3+128s−88.

(iii) M2ve(HCB(s))=(8s−7)2s+7+3040s−2932.

(iv) Rve(HCB(s))=[s8+23+6−32122]2s+1+[223−4728]s+6210+4130+27−56+113+114+436−423+321−4717+272+1421+135+4314−15456.

(v) ABCve(HCB(s))=[32s16+56+723−2]2s+1+[4173−7324+147+446314]s+631210+423130+2227+1056+2913+3014+43036−5683+8173−7322+33+231414+24272+2337221+4335−104634.

(vi) GAve(HCB(s))=[s+265+437−2]2s+1+[828817+450423+2826−14]s+1221031+813023+411211+420829+222415+421615−3228834+437+239221+433637+353−1050423−46−83+30.

(vii) Hve(HCB(s))=63522s+3[s8−14]−788521436s−17.57077354.

(viii) χve(HCB(s))=[s22+15+17−12]2s+1+[s22+1634+114+84]s+631+822−25+429+1230−107−3234−214+12+437+13−2046+27+72.

Now, we conclude the section by including the following example:

Example 4.1. By taking s=4 in Theorem 4.1, Theorem 4.2 and Theorem 4.3, we obtain the values of ve-degree based TIs for B(4), VCB(4) and HCB(4) as shown in Table 9:

5  Graphical Analysis

We proceed further with our obtained formulae in previous section to study graphical patterns in the values of TIs of B(s), HCB(s) and HCB(s). In Figs. 4–6, the patterns of ZI(VE), RI(VE), ABC-I(VE), GA-(VE) and HI(VE) (on y-axis), where the value of s has been taken on x-axis, for B(s), HCB(s) and VCB(s) have been presented. All the figures show the rapid rise in the values of each TI for B(s), HCB(s) and HCB(s) with the rise in the value of s. The trends in Fig. 4 (L) show that the HCB(s) attains higher values of ZI(VE), whereas values of ZI(VE) for VCB(s) remain between B(s) and HCB(s). Similar trend for RI(VE) has been shown in Fig. 4 (R). In Fig. 5 (L), it can be seen that the values of ABC-I(VE) show different behaviours as in case of ZI(VE) and RI(VE). The ABC-I(VE) attains lowest values for HCB(s), whereas values for B(s) remain between VCB(s) and HCB(s). Furthermore, the trend for HI(EV) is shown in Fig. 5 (R). In the case of GA(VE), the values for B(s) remain the highest and the values for VCB(s) remain between the values of B(s) and HCB(s), see Fig. 6.

Figure 4: Graphical comparison between ZI(VE) on left (L) and RI(VE) on right (R) of B(s), HCB(s) and HCB(s)

Figure 5: Graphical comparison between ABC(VE) on left (L) and HI(VE) on right (R) of B(s), HCB(s) and HCB(s)

Figure 6: Graphical comparison between GA-I(VE) of B(s), HCB(s) and HCB(s)

6  Conclusion

The study of newly formed networks is always a fascinating topic. Using B(s), several novel networks such as HCB(s) and VCB(s) have been defined through identifications in [33] and further investigated in [34]. Furthermore, the ev-degree and the ve-degree of these structures were not investigated yet. In the current work, we constructed the ev-degree based partition of the vertex set and the ve-degree based partition of the edge set for these networks. Through these partitions, we developed formulae for several ev-degree and ve-degree based TIs for B(s), HCB(s) and VCB(s) in terms of the parameter s. Further, we presented the comparative analysis of the values of ZI(VE), RI(VE), ABC-I(VE), GA-I(VE) and HI(VE) for B(s), HCB(s) and VCB(s). It is observed that similar patterns have been developed for ZI(VE) and RI(VE), whereas the other three TIs produce different trends.

Acknowledgement: The authors are thankful to their respective institutes.

Funding Statement: This work is partially supported by the National Natural Science Foundation of China (Grant No. 61702291); China Henan International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Selvakumar, K., Gangaeswari, P., Arunkumar, G. (2022). The wiener index of the zero-divisor graph of a finite commutative ring with unity. Discrete Applied Mathematics, 311, 72–84. DOI 10.1016/j.dam.2022.01.012. [Google Scholar] [CrossRef]

 2.  Yang, Y., Liu, H., Wang, H., Fu, H. (2015). Subtrees of spiro and polyphenyl hexagonal chains. Applied Mathematics and Computation, 268, 547–560. DOI 10.1016/j.amc.2015.06.094. [Google Scholar] [CrossRef]

 3.  Oz, M. S., Cangul, I. N. (2022). Enumeration of independent sets in benzenoid chains. MATCH Communications in Mathematical and in Computer Chemistry, 88, 93–107. DOI 10.46793/match.88-1.093o. [Google Scholar] [CrossRef]

 4.  Yang, Y., Sun, X. J., Cao, J. Y., Wang, H., Zhang, X. D. (2020). The expected subtree number index in random polyphenylene and spiro chains. Discrete Applied Mathematics, 285, 483–492. DOI 10.1016/j.dam.2020.06.013. [Google Scholar] [CrossRef]

 5.  Bokhary, S. A. U. H., Adnan, Siddiqui, M. K., Cancan, M. (2021). On topological indices and qspr analysis of drugs used for the treatment of breast cancer. Polycyclic Aromatic Compounds. DOI 10.1080/10406638.2021.1977353. [Google Scholar] [CrossRef]

 6.  Imran, M., Hayat, S., Mailk, M. Y. H. (2014). On topological indices of certain interconnection networks. Applied Mathematics and Computation, 244, 936–951. DOI 10.1016/j.amc.2014.07.064. [Google Scholar] [CrossRef]

 7.  Liu, X. C., Gu, Q. P. (2002). Multicasts on wdm all-optical butterfly networks. Journal of Information Science and Engineering, 18(6), 1049–1058. [Google Scholar]

 8.  Beneš, V. E. (1965). Mathematical theory of connecting networks and telephone traffic. New York: Academic Press. [Google Scholar]

 9.  Manuel, P. D., Abd-El-Barr, M. I., Rajasingh, I., Rajan, B. (2008). An efficient representation of benes networks and its applications. Journal of Discrete Algorithms, 6(1), 11–19. DOI 10.1016/j.jda.2006.08.003. [Google Scholar] [CrossRef]

10. Xu, J. (2013). Topological structure and analysis of interconnection networks. New York: Springer. [Google Scholar]

11. Imran, M., Baig, A. Q., Ali, H. (2016). On topological properties of dominating david derived networks. Canadian Journal of Chemistry, 94(2), 137–148. DOI 10.1139/cjc-2015-0185. [Google Scholar] [CrossRef]

12. Gutman, I., Trinajstić, N. (1972). Graph theory and molecular orbitals. total φ-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), 535–538. DOI 10.1016/0009-2614(72)85099-1. [Google Scholar] [CrossRef]

13. Chen, C., Liu, M., Gu, X., Das, K. C. (2022). Extremal augmented Zagreb index of trees with given numbers of vertices and leaves. Discrete Mathematics, 345(4), 112753. DOI 10.1016/j.disc.2021.112753. [Google Scholar] [CrossRef]

14. Randić, M. (2008). On history of the randić index and emerging hostility toward chemical graph theory. MATCH Communications in Mathematical and in Computer Chemistry, 59(5), 5–124. [Google Scholar]

15. Vukicevic, D., Furtula, B. (2009). Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. Journal of Mathematical Chemistry, 46(4), 1369–1376. DOI 10.1007/s10910-009-9520-x. [Google Scholar] [CrossRef]

16. Aouchiche, M., El Hallaoui, I., Hansen, P. (2020). Geometric-arithmetic index and minimum degree of connected graphs. MATCH Communications in Mathematical and in Computer Chemistry, 83, 179–188. [Google Scholar]

17. Estrada, E., Torres, L. A., Rodríguez, L., Gutman, I. (1998). An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian Journal of Chemistry, 37, 849–855. [Google Scholar]

18. Estrada, E. (2001). Generalization of topological indices. Chemical Physics Letters, 336(3–4), 248–252. DOI 10.1016/S0009-2614(01)00127-0. [Google Scholar] [CrossRef]

19. Das, K. C., Gutman, I., Furtula, B. (2011). On atom-bond connectivity index. Chemical Physics Letters, 511(4–6), 452–454. DOI 10.1016/j.cplett.2011.06.049. [Google Scholar] [CrossRef]

20. Gutman, I., Tošović, J., Radenković, S., Marković, S. (2012). On atom-bond connectivity index and its chemical applicability. Indian Journal of Chemistry, 51, 690–694. [Google Scholar]

21. Zhong, L. (2012). The harmonic index for graphs. Applied Mathematics Letters, 25(3), 561–566. DOI 10.1016/j.aml.2011.09.059. [Google Scholar] [CrossRef]

22. Chellali, M., Haynes, T. W., Hedetniemi, S. T., Lewis, T. M. (2017). On ve-degrees and ev-degrees in graphs. Discrete Mathematics, 340(2), 31–38. DOI 10.1016/j.disc.2016.07.008. [Google Scholar] [CrossRef]

23. Horoldagva, B., Das, K. C., Selenge, T. A. (2019). On ve-degree and ev-degree of graphs. Discrete Optimization, 31, 1–7. DOI 10.1016/j.disopt.2018.07.002. [Google Scholar] [CrossRef]

24. Süleyman, E. (2017). A new tool for qspr researches: Ev-degree randić index. Celal Bayar University Journal of Science, 13(3), 615–618. [Google Scholar]

25. Sahin, B., Ediz, S. (2018). On ev-degree and ve-degree topological indices. Iranian Journal of Mathematical Chemistry, 9(4), 263–277. [Google Scholar]

26. Lee, J. R., Hussain, A., Fahad, A., Raza, A., Qureshi, M. I. et al. (2022). On ev and ve-degree based topological indices of silicon carbides. Computer Modeling in Engineering & Sciences, 130(2), 871–885. DOI 10.32604/cmes.2022.016836. [Google Scholar] [CrossRef]

27. Zahra, N., Ibrahim, M. (2022). A study of ve and ev degree based topological indices of transition metal tetra-cyano benzene structure. Alexandria Engineering Journal, 61(8), 6409–6417. DOI 10.1016/j.aej.2021.12.001. [Google Scholar] [CrossRef]

28. Deepika, T., Lokesha, V. (2020). Computing discrete adriatic indices of probabilistic neural network. European Journal of Pure and Applied Mathematics, 13(5), 1149–1161. DOI 10.29020/nybg.ejpam.v13i5.3712. [Google Scholar] [CrossRef]

29. Ranjini, P., Lokesha, V., Cangül, I. N. (2011). On the Zagreb indices of the line graphs of the subdivision graphs. Applied Mathematics and Computation, 218(3), 699–702. DOI 10.1016/j.amc.2011.03.125. [Google Scholar] [CrossRef]

30. Shwetha Shetty, B., Lokesha, V., Ranjini, P. (2015). On the harmonic index of graph operations. Transactions on Combinatorics, 4(4), 5–14. [Google Scholar]

31. Lokesha, V., Deepika, T., Ranjini, P., Cangul, I. (2017). Operations of nanostructures via, and indices. Applied Mathematics and Nonlinear Sciences, 2(1), 173–180. DOI 10.21042/AMNS.2017.1.00014. [Google Scholar] [CrossRef]

32. Das, K. C., Çevik, A. S., Cangul, I. N., Shang, Y. (2021). On sombor index. Symmetry, 13(1), 140. DOI 10.3390/sym13010140. [Google Scholar] [CrossRef]

33. Hussain, A., Numan, M., Naz, N., Butt, S. I., Aslam, A. et al. (2021). On topological indices for new classes of benes network. Journal of Mathematics, 2021, 6690053. DOI 10.1155/2021/6690053. [Google Scholar] [CrossRef]

34. Wang, W., Nisar, A., Fahad, A., Qureshi, M. I., Alameri, A. (2022). Modified Zagreb connection indices for benes network and related classes. Journal of Mathematics, 2022, 8547332. DOI 10.1155/2022/9347942. [Google Scholar] [CrossRef]