Comparative Analysis of Pythagorean MCDM Methods for the Risk Assessment of Childhood Cancer

1  Introduction

Childhood cancer is the leading cause of death in children, especially in low and middle-income countries. Their likelihood of survival heavily rests on the country where they live. The chance of curing childhood cancer in high-income countries is above eighty percent, whereas in low and in middle-income countries, it is a mere forty-five percent. This difference in curing rate owes to many factors, such as late diagnosing and cancer diagnosed at its late stages due to unavailability of resources, cost of treatment (the treatment cost is rather high in later stages), or incorrect diagnostics and inappropriate treatment. The survival rate can be increased if low and in middle-income countries improve the access to necessary medicines and technologies. Generally speaking, the most productive way to reduce the effects of childhood cancer is by effective and evidence-based therapy with appropriate nurturing care.

The chances of curing childhood cancer, and the cost of treatment with lesser suffering, can be improved if it is identified early, and appropriate treatment is provided immediately. A correct diagnosis is required to treat childhood cancer efficiently with the right treatment, which may include surgeries, radiotherapy, and chemotherapy. For early diagnosing, we should consider the following three aspects:

1.    Parents should know about childhood cancer so that they can perceive its symptoms and consult a medical expert.

2.    The medical expert should be skilled enough and investigate the case promptly in order to cater for the right treatment.

3.    The patient has accessibility to the right treatment at right time.

When someone is diagnosed with cancer, the chances of recovery and survival increase if it is detected in an early stage, even with the least amount of financial and physical suffering. The low- and middle-income countries should run education campaigns for parents with the help of competent doctors so that in the presence of symptoms in any child, their parents can respond without delay. This task requires the joint effort of civil society and non-governmental organizations. In 2018, the World Health Organization launched a global initiative on cancer in children. As part of this initiative, they provided governments with professional guidance and support to maintain high-quality childhood cancer programs. They aim to increase childhood cancer survival rates, and by 2030 that rate should be at least sixty percent.

Medical information is very sensitive and contains many uncertainties. Every expert may have their personal opinion on a health record, and it may become rather difficult to make an accurate diagnostic based on these reports. In such uncertain situations, fuzzy logic can play an important role in making decisions among different alternative diagnostics. Many extensions of fuzzy sets theory have been proposed [1,2]. In fact research has provided many medical applications that have taken advantage of different fuzzy approaches [3,4], and of models of vague knowledge born from alternative narratives [5]. Feng et al. [6,7] generalized intuitionistic fuzzy soft sets and related multi attribute decision making methods. By inspiration of these applied studies, we have selected a powerful and flexible model for the representation of undertain knowledge. It has been popularized by Yager et al. [8,9], who coined the term Pythagorean fuzzy sets (PFSs). PFSs improve the performance of intuitionistic fuzzy sets, which for each alternative, provide a fuzzy assessment of both membership (μ) and nonmembership (ν) in such a way that μ+ν≤1. In PFSs however, assessments that meet the relaxed condition μ2+ν2≤1 are acceptable. The PFS model has become one of the most influential notions in fuzzy modeling, since it allows us to accept more uncertain appraisals than the intuitionistic fuzzy or fuzzy sets, and consequently, its applications are potentially wider. The next summary of recent results testifies to this claim.

Yucesan et al. [10] presented the ideas of Pythagorean fuzzy analytic hierarchy method and Pythagorean fuzzy method for order decision by comparison to the ideal solution, in order to present an exact decision-making technique for estimating hospital service quality. Guleria et al. [11] proposed a new (R, S)-norm discriminant measure of Pythagorean fuzzy sets and proved some interesting features. Their monotonicity with respect to the parameters R&S were studied too. This information measure is utilized in some problems related to medical diagnosis or pattern recognition. Extensions and hybrid models based on PFSs have been put forward too. Rahman [12] extended the spirit of some popular aggregation operators to the more general framework of interval-valued Pythagorean fuzzy numbers, thus producing the so-called GIVPFWA, GIVPFOWA, and GIVPFHA operators. They discussed their properties, and argued that their generalized operators are more reliable and accurate than the existing aggregation operators. Zulqarnain et al. [13] proposed the averaging and geometric operators of Pythagorean fuzzy hypersoft sets. They also introduced a novel TOPSIS method in this new environment. They applied this methodology to a case-study of selection of multipurpose masks for protection against COVID-19. Yue et al. [14] proposed novel score function of hesitant fuzzy numbers and prove the validity of this function using an example. Yue [15] proposed a novel bilateral matching (BM) decision-making method for knowledge innovation management considering the matching willingness of bilateral enterprises. Ejegwa [16] improved composite relation for Pythagorean fuzzy sets and applied it to medical diagnosis. Many other decision-making methods have been suggested in the literature [17–25].

The following targets motivate the research contained in this article:

1.    Early diagnosis of cancer in children can reduce overall mortality and expense of treatment, which ultimately reduces the patient’s suffering.

2.    Effective handling of vague and uncertain data in a medical context is required.

3.    Get opinions of available medical experts and decide the final treatment.

4.    Contribution towards WHO’s goal of increasing survival from childhood cancer by least sixty percent before 2030.

Concerning these issues, our contribution to this study is described below:

1.    We develop a novel decision-making system to determine childhood cancer risk at its early stages, thus increasing the survival rate.

2.    We use the Pythagorean fuzzy sets (PFS) for decision-making because it is very close to human thinking. It is characteristic of simultaneously focusing on the degree of truth, the degree of non-membership, and the degree of indeterminacy of each alternative to make it more powerful.

3.    We design algorithms to demonstrate the entire performance of the model. In addition, we determine their respective time complexities.

The rest of this paper is structured as follows. Section 2 discusses preliminary work. Section 3 describes the main contributions of the paper. Then Section 4 performs a comparative analysis. Section 5 concludes the proposed work and lays out some future directions for research.

2  Preliminaries

This section summarizes some of the introductory concepts that need to be followed to completely benefit from this study. First we overview technical concepts that will help us formulate our theoretical model. Then we summarize some facts about its prospective application (namely, identification of childhood cancer).

2.1 Pythagorean Fuzzy Set [8]

Let Z be a universal set. Then, a Pythagorean fuzzy set S over Z is a set of ordered triples indexed by Z, which adopts the following form: S={<z,μS(z),νS(z)>|z∈Z}, where the functions μS(z):Z⟶[0,1] and νS(z):Z⟶[0,1] respectively define the degree of membership and the degree of non-membership of z ∈ Z to S, and the inequalities 0≤(μS(z))2+(νS(z))2≤1 hold for each z ∈ Z. The figure πS(z)=1−[μS(z))2+(νS(z))2] defines the degree of indeterminacy of z ∈ Z to S. Observe πS(z)∈[0,1], and πS(z)=0 whenever (μS(z))2+(νS(z))2=1. We represent the set of all PFSs over Z by PFS(Z).

2.2 Pythagorean Fuzzy Relation [16]

Let U and V be two nonempty sets. A Pythagorean fuzzy relation (PFR), L, from U to V is a PFS over U × V. It is characterized by a membership function, μR, and a nonmembership function, νL that meet the corresponding bounds. A PF relation or PFR from U to V is denoted by L(U→V ).

2.3 Pythagorean Fuzzy-Technique for Order of Preference by Similarity to Ideal Solution (PF-TOPSIS) Method [20]

The PF-TOPSIS method uses linguistic terms and Pythagorean fuzzy numbers (PFNs) to represent the relative importance of experts and criteria. These linguistic terms and PFNs are predefined and used to rate any expert or criteria. The following equation is used to calculate the weight in crisp form for any Pythagorean fuzzy evaluation. Assume that Pn=[μn,νn,πn] is a Pythagorean Fuzzy Number (PFN), then its weight can be calculated by using the following formula:

σn=μn+πn(μn/(μn+νn))∑l=1k(μl+πl(μl/(μl+νl))).(1)

Notice that the sum of all weights should be equal to 1.

Suppose that Zn=(zij(n))l×m denotes the Pythagorean Fuzzy Decision Matrix (PFDM) of the nth expert having weight σn. The following formula is used to aggregate all PFDMs with the assistance of the Pythagorean Fuzzy Aggregated Averaging (PFWA) operator: for each i = 1, 2, 3, ..., l, j = 1, 2, 3, ..., m,

zij=(1−∏n=1k(1−(μijn)2)σn,∏n=1k(νijn)σn,∏n=1k(1−(μijn)2)σn−(∏n=1k(λijn)σn)2).(2)

Let Pjn=[μjn,νjn,πjn] be the Pythagorean fuzzy number assigned to the criteria Rj, then the weighted aggregated PFDM against each criteria Rj can be calculated as

zij=(μSi(Rj).μP(Rj),νSi2(Rj)+νP2(Rj)−νSi2(Rj).νP2(Rj),(3)

and πSiP(Rj)=1−μSi(Rj)⋅μP(Rj)−νSi2(Rj)−νP2(Rj)+νSi2(Rj)⋅νP2(Rj).

Let B1 and B2 be the sets of benefit-type and cost-type criteria, respectively.

The Pythagorean Fuzzy Positive Ideal Solution (PFPIS) S+ and Pythagorean Fuzzy Negative Ideal Solution (PFNIS) S− can be obtained as: S+={⟨Rj,μS+P,νS+P⟩|Rj∈C,j=1,2,....,m},

S−={⟨Rj,μS−P,νS−P⟩|Rj∈C,j=1,2,....,m}, where

μS+P(Rj)={max1≤i≤lμSiP(Rj),if Rj∈B1,min1≤i≤lμSiP(Rj),if Rj∈B2,(4)

λS+P(Rj)={min1≤i≤lνSiP(Rj),if Rj∈B1,max1≤i≤lνSiP(Rj),if Rj∈B2,(5)

μS−P(Rj)={min1≤i≤lμSiP(Rj),if Rj∈B1,max1≤i≤lμSiP(Rj),if Rj∈B2,(6)

λS−P(Rj)={max1≤i≤lνSiP(Rj),if Rj∈B1,min1≤i≤lνSiP(Rj),if Rj∈B2.(7)

The following formula is used to calculate the distance of each alternative from PFPIS and PFNIS:

E(Si,S+)=12m∑j=1m[(μSiP2(Rj)−μS+P2(Rj))2+(νSiP2(Rj)−νS+P2(Rj))2+(πSiP2(Rj)−πS+P2(Rj))2],(8)

E(Si,S−)=12m∑j=1m[(μAiP2(Rj)−μS−P2(Rj))2+(νSiP2(Rj)−νS−P2(Rj))2+(πSiP2(Rj)−πS−P2(Rj))2].(9)

The relative closeness value of each choice Si is calculated as follows:

Yi+=E(Si,S−)E(Si,S+)+E(Si,S−),i=1,2,....,l.(10)

The maximum relative closeness value is the best choice among all possible choices.

2.4 Pythagorean Fuzzy-Entropy (PF-Entropy) Method [21]

According to [21], the following equation computes the entropy T(P) of any criteria represented by a Pythagorean Fuzzy Number (PFN) P:

T(P)=1n∑i=1n[T∗(Pi)+πp(zi)−πp(zi)T∗(Pi)],(11)

where, T∗(pi)=1−|μp(zi)−νp(zi)|.

The score function K(P) of such P can be defined as follows:

K(P)=(μP)2−(νP)2.(12)

The weighted entropy of each criteria is calculated using the next equation:

wj=1−Tjn−∑j=1nTj.(13)

2.5 Pythagorean Fuzzy Power Weighted Average (PFPWA) [21,22]

The support of two PFNs is calculated using the next formula:

Support(Pij,Pik)=1−d(Pij,Pik),j,k=1,2,...,n.(14)

The distance between two PFNs can be calculated using the following normalized Hamming distance:

d(Pij,Pik)=(|(μij)2−(μik)2|+|(νij)2−(νik)2|)2,j,k=1,2,...,n.(15)

The formula for the weighted support is as follows:

M(Pij)=∑k=1nωjSupport(Pij,Pik),(16)

and we compute the weights γij associated with the PFN Pij as

γij=ωj(1+M(Pij))∑j=1nωj+(1+M(Pij)),(17)

where i = 1, 2, ..., m, j = 1, 2, ...,n, γij≥0, and ∑j=1nγij=1.

The Pythagorean Fuzzy Power Weighted Geometric (PFPWG) operator is as follows:

PFPWG=(∏j=1n(μij)γij,1−∏j=1n(1−(νij)2)γij).(18)

Let P=(μ,ν) be a PFN. Then a score function S of P, a PFN, can be defined by the expression:

Score(P)=12(1+μ2+ν2)∈[0,1].(19)

2.6 Major Factors of Childhood Cancer [26,27]

Many studies have tried to identify the causes of childhood cancer. Some factors are related to the environment, such as radiation exposure and chemical exposure. Some are lifestyle-related, such as drugs, alcohol, cell phone use, and smoking. Some children inherit DNA changes from a parent that increase their risk of a certain type of cancer. Here we list possible risk factors for childhood cancer with a small description of each factor.

Gender (S1): Gender can be male or female.

Age (S2): The age of a child is considered between 0 and 19 years.

Height (S3): The height of a child.

BMI (S4): The body mass index (BMI) is a measure of body fat according to height and weight.

Drugs (S5): A medication is a drug used to diagnose, cure, treat, or prevent disease.

Alcohal (S6): It is a substance that contains the recreational drug ethanol, alcohol is made by fermentation of fruits, grains, or any source of sugar.

Cell Phone Usage (S7): The use of cell phones on a daily basis.

Pagets Disease (S8): It is a bone disease that disrupts the body’s normal recycling process, in which new bone tissue gradually replaces old bone tissue. Over time, the disease can cause compromised bones to become weak and distorted.

Genetic Disposition (S9): There is an increased chance of acquiring a specific disease based on a person’s ancestral genes.

Smoking (S10): The habit of inhaling and exhaling tobacco or drug smoke.

Blood Disorder (S11): These are conditions that affect the blood’s ability to function.

Birth Defects (S12): It is a disease that, despite its cause, is present at birth. Birth defects can appear as disabilities that can be physical, mental, or developmental in nature.

Immunity (S13): Immunity is the capability of multi-cellular organisms to resist harmful microorganisms.

Auto Immune Diseases (S14): It is a disease in which your immune system unintentionally attacks your body.

Certain Syndromes(S15): Any syndrome already present in children such as Down syndrome, Li-Fraumeni syndrome, etc.

Race (S16): Identification of a group of people.

Certain Radiation Exposure (S17): Exposed to certain electromagnetic radiation, or living in the vicinity of a source of electromagnetic radiation.

Certain Chemical Exposure (S18): Exposure to certain chemicals or polluted groundwater used for drinking.

Socioeconomic Status (S19): A family’s financial status in society.

2.7 Types of Childhood Cancers

Children and teenagers tend to get different types of childhood cancers. The most common childhood cancers are discussed below:

Leukemia (D1): It is bone marrow and blood cancer. Twenty-eight percent of childhood cancer cases fall into this category.

Brain and spinal cord tumors (D2): The second most common cancer in children is the brain and spinal cord cancer. In this type of cancer, abnormal growth in tissues of the brain and spinal cord is seen causing headache, nausea, vomiting, blurred vision, and difficulty in walking and holding objects. About 26 children develop this type of cancer every year.

Neuroblastoma (D3): Neuroblastoma begins in the early forms of nerve cells seen in a developing egg or fetus. About 6 percent of cancers in adolescents are neuroblastomas. This type of cancer occurs in newborns and adolescents. It is uncommon in children over 10 years of age. Neuroblastomas mostly occur in and around the adrenal glands. However, neuroblastomas can develop in other areas of the stomach and ribs, neck, and near the spine where there are clusters of nerve cells.

Wilms Tumor (D4): Wilms’ tumor begins in one or, rarely, both kidneys. It is usually found in children around 3 to 4 years of age and is rare in more mature children and adults. Wilms’ tumor accounts for around 5 percent of childhood cancers. Its symptoms are fever, pain, nausea, or loss of appetite.

Lymphomas (D5): It is a disease that attacks infection-fighting cells in the immune system. These cells are called lymphocytes. These cells are found in the lymph nodes, spleen, thymus gland, bone marrow, and other parts of the body. In this disease, abnormal growth of lymphocytes has been observed. Symptoms include weight loss, fever, sweats, fatigue, and lumps under the skin in the neck, armpits, or groin area.

Retinoblastoma (D6): This type of cancer is related to the eyes. It is a rare type of cancer in which a child could not distinguish the colors of light, also had impaired vision and sensitive eyes. The pupil of the eyes becomes large.

Rhabdomyosarcoma (D7): It is an intrusive and very dangerous cancer that originates from skeletal muscle cells. It is widely believed to be a childhood disease as the vast majority of cases found are under the age of 18. It is about 3 percent of childhood cancers.

Bone Cancer (D8): This type of cancer usually occurs in older children. This type of cancer causes severe bone pain all the time. The bones become weak and can also be broken. In some cases, weight loss is also observed.

3  Pythagorean Fuzzy Model of Childhood Cancer

To make the proposed Pythagorean model more understandable, consider the block diagram shown in Fig. 1. The proposed model uses nineteen symptoms as inputs. For each input, a linguistic variable is defined in the Pythagorean fuzzy number. There may be n experts, but we’re only picking three experts here. Their expertise is represented by PFNs. Symptom PFNs and expert weights are input to PF-TOPSIS, PF-entropy, and PFPWG blocks. In these blocks, the algorithm of each approach is executing and generating its final outputs. We compare the results of each method and highlight the signal output. The results of these three methods should be the same.

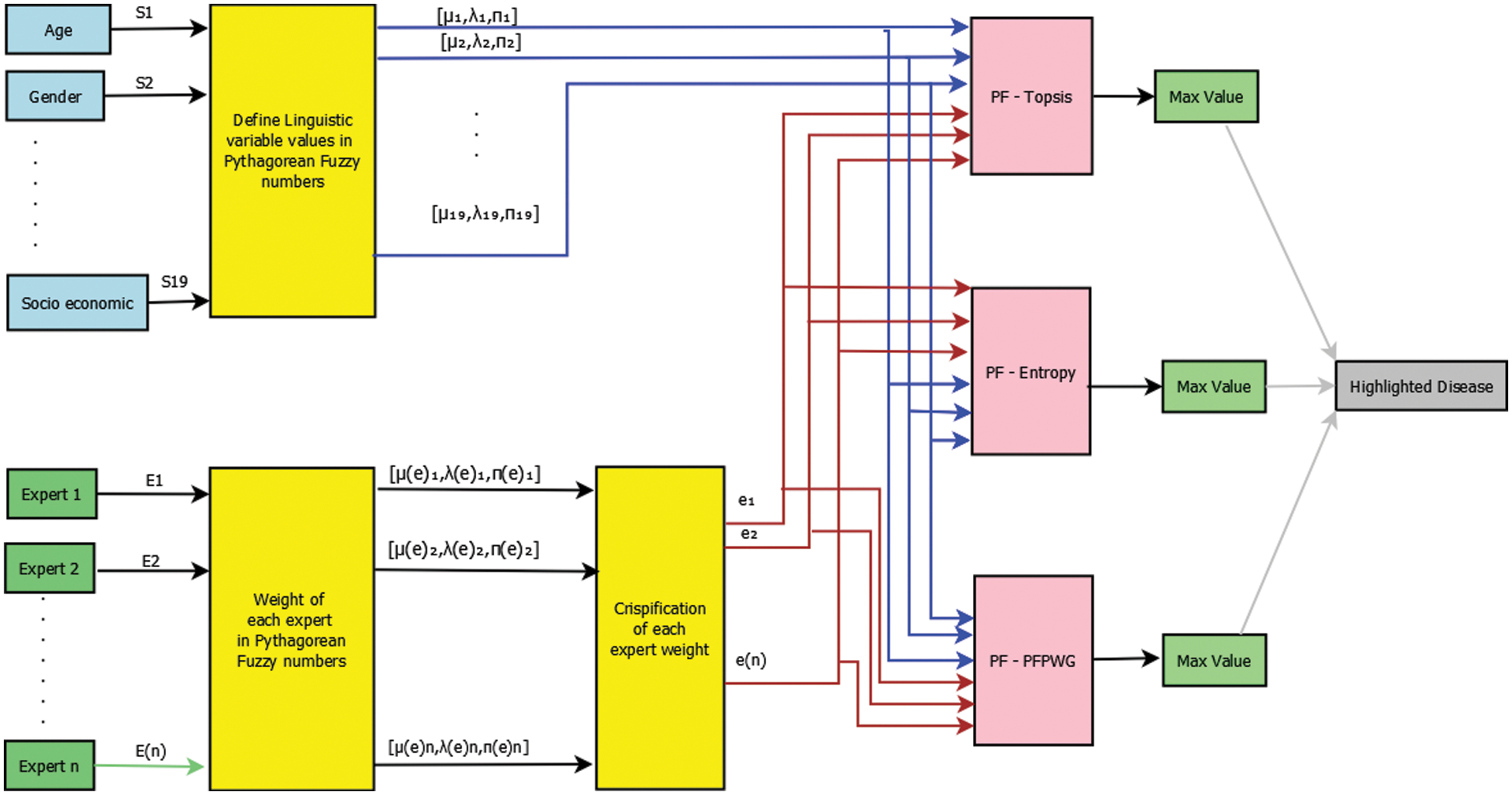
Figure 1: Block diagram of risk assessment of childhood cancer

3.1 Algorithm for Risk Assessment of Childhood Cancer

In this subsection, we write all of the instructions that must be followed to obtain final results for any input. Each algorithm takes certain inputs and produces certain outputs. There are seven sub-algorithms of the PF-TOPSIS algorithm, namely, Algorithm A, Algorithm B, Algorithm C, Algorithm D, Algorithm E, Algorithm F, and Algorithm G. Each sub-algorithm shows each step of the TOPSIS process. We also write the net time complexity of every algorithm.

3.1.1 Algorithm: PF-TOPSIS

Input: Two-dimensional arrays containing expert's weights, and decision matrix of each expert. Output: Highlighted type of cancer.

Algorithm-A: Weights of experts

Input: Two dimensional arrays EWmem[ ][ ], EWnmem[ ][ ], and EWpi[ ][ ] containing Experts weights, and membership, non-membership, and indeterminate parts of PFNs.

Algorithm-B: Pythagorean decision matrix (PDM)

Input: Pythagorean decision matrices of all experts, and weight of each expert.

Algorithm-C: Symptom's weight

Input: Pythagorean symptom's weight matrix, and expert's weights.

Algorithm-D: Weighted aggregated PDM

Input: Pythagorean Symptom's weight matrix, and Pythagorean decision matrices.

Algorithm-E: PFPIS and PFNIS

Input: Weighted aggregated decision matrix.

Algorithm-F: Distance PIS NIS

Input: Positive ideal and negative ideal solutions. Weighted aggregated decision matrix.

Algorithm-G: Relative Closeness

Input: Distance of each disease from positive and negative ideal solutions.

After aggregating all complexities, we get the final time complexity of the PF-TOPSIS algorithm, which is O(loe). If l ≈ o ≈ e ≈ n then wecan say that net time complexity is O(n3).

3.1.2 Algorithm: Entropy

Algorithm PF-Entropy shows the set of instructions that need to follow to find the final results of each childhood cancer.

Input: Aggregated decision matrix and symptom's weight matrix.

3.1.3 Algorithm: PFPWG

Algorithm-PFPWG shows the set of instructions of PFPWG decision-making techniques.

3.2 Example of Risk Assessment of Childhood Cancer

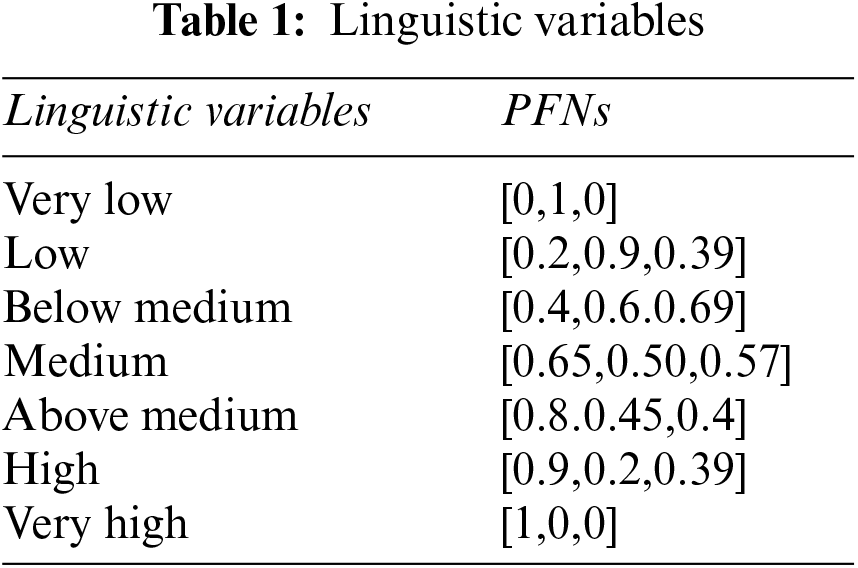
To understand the working of the above algorithm, consider the following example and apply the PF-TOPSIS method to it. The PFNs against each linguistic variable are shown in Table 1. Table 1 shows the linguistic variables for all inputs.

3.2.1 Pythagorean Fuzzy Topsis

We shall first show how a decision can be made with the application of the steps described in Section 3.1.1.

Step 1: We are taking opinions from three medical experts, E1, E2, and E3, and the credibility of each expert is high, above medium, and medium, depending upon their experience, qualification, and research. The rating of each medical expert is calculated using Eq. (1) and Table 1. The ratings of E1, E2, and E3 are 0.375, 0.325, and 0.3, respectively [20].

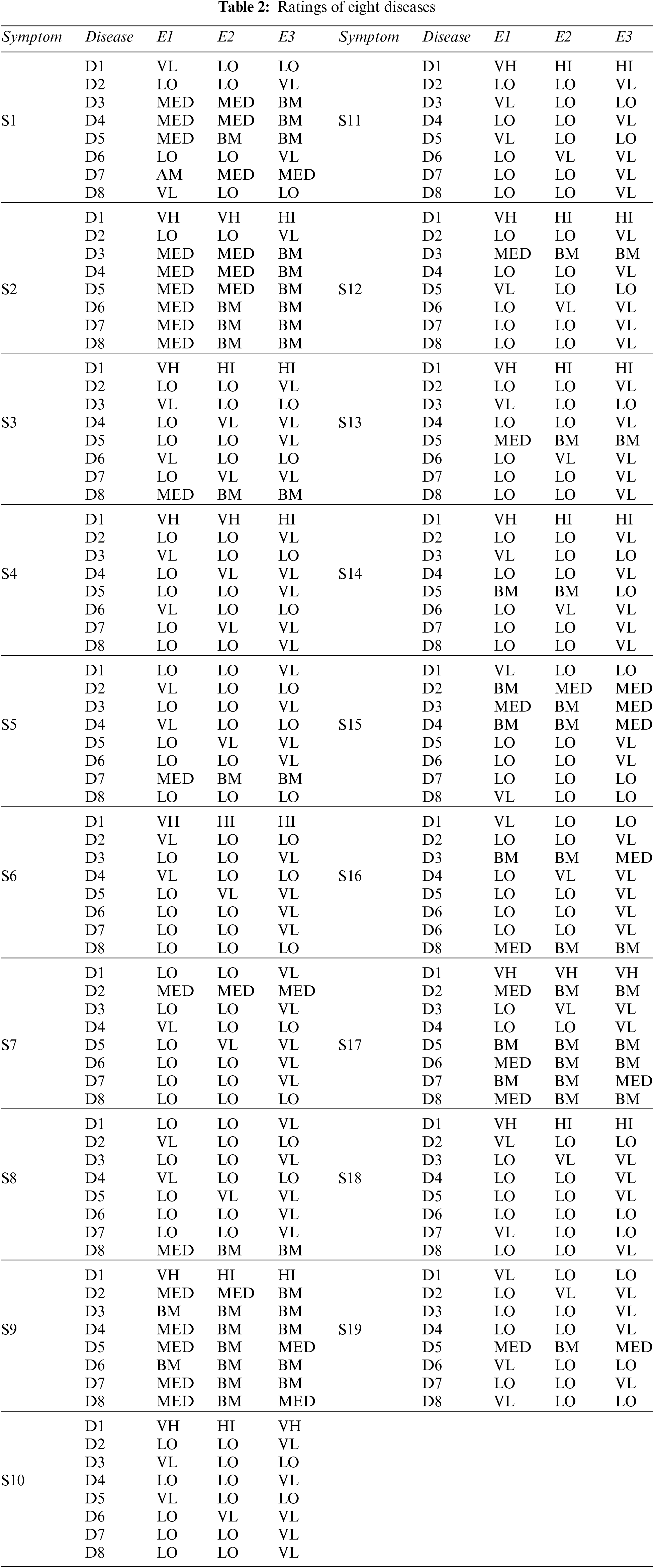
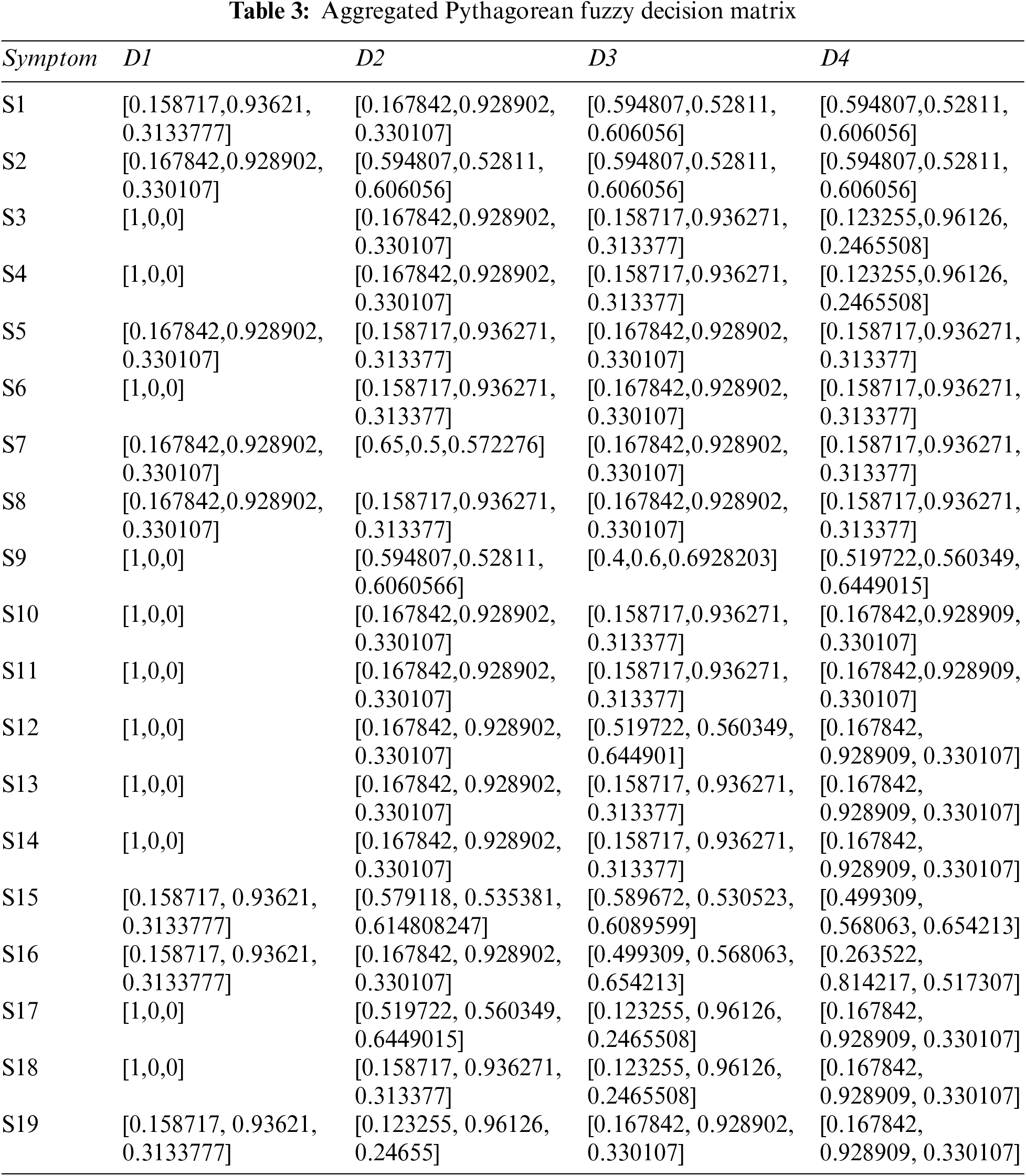
Step 2: The Pythagorean Fuzzy Decision Matrix shows ratings of eight diseases by the experts in relation to nineteen symptoms. This step is completed using Tables 1 and 2, and Eq. (2). The result of this step is shown in Tables 3 and 4.

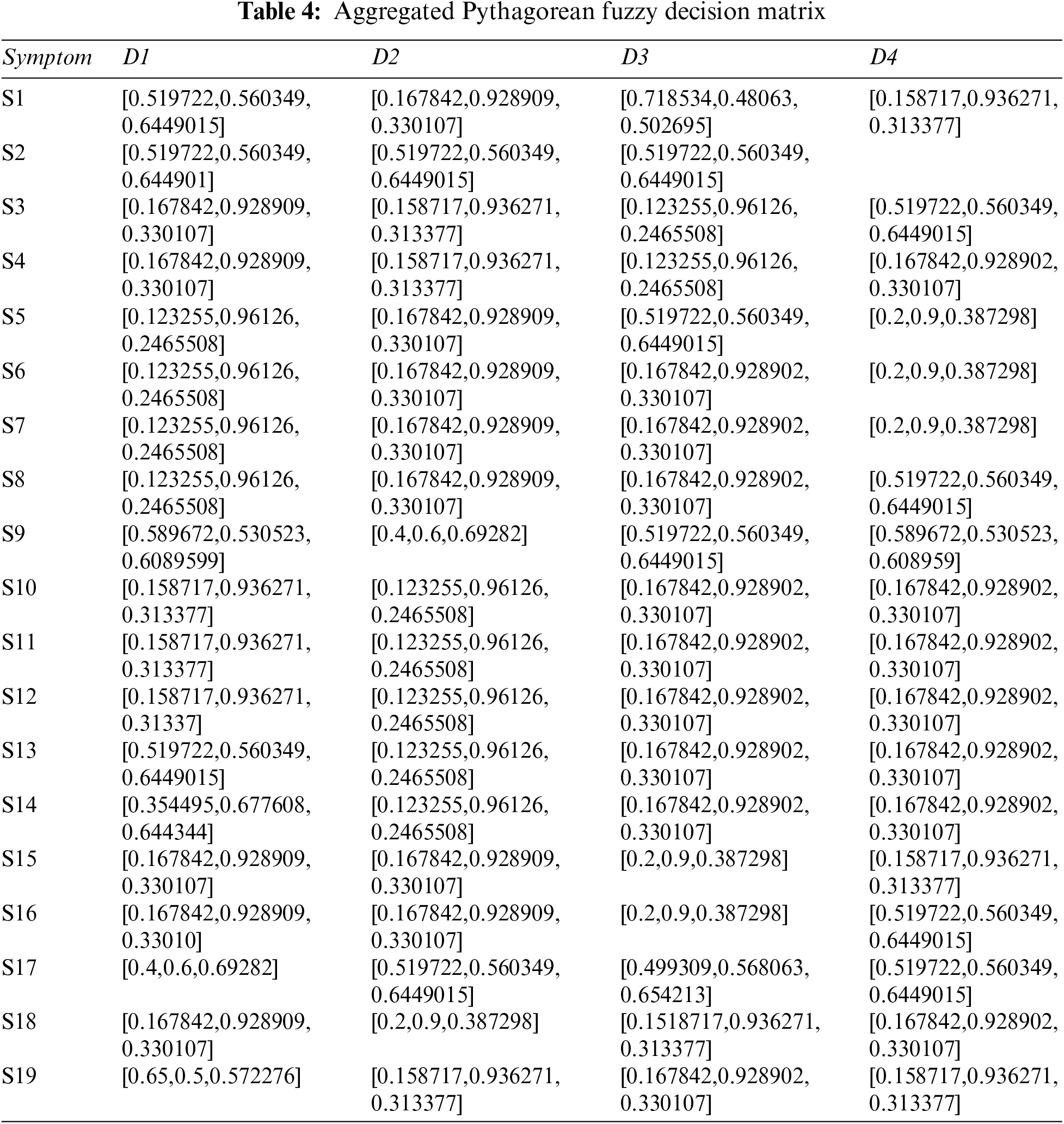
Step 3: Determine the weight of each symptom using Table 5, and Eq. (2). The result of this step is shown in Table 6.

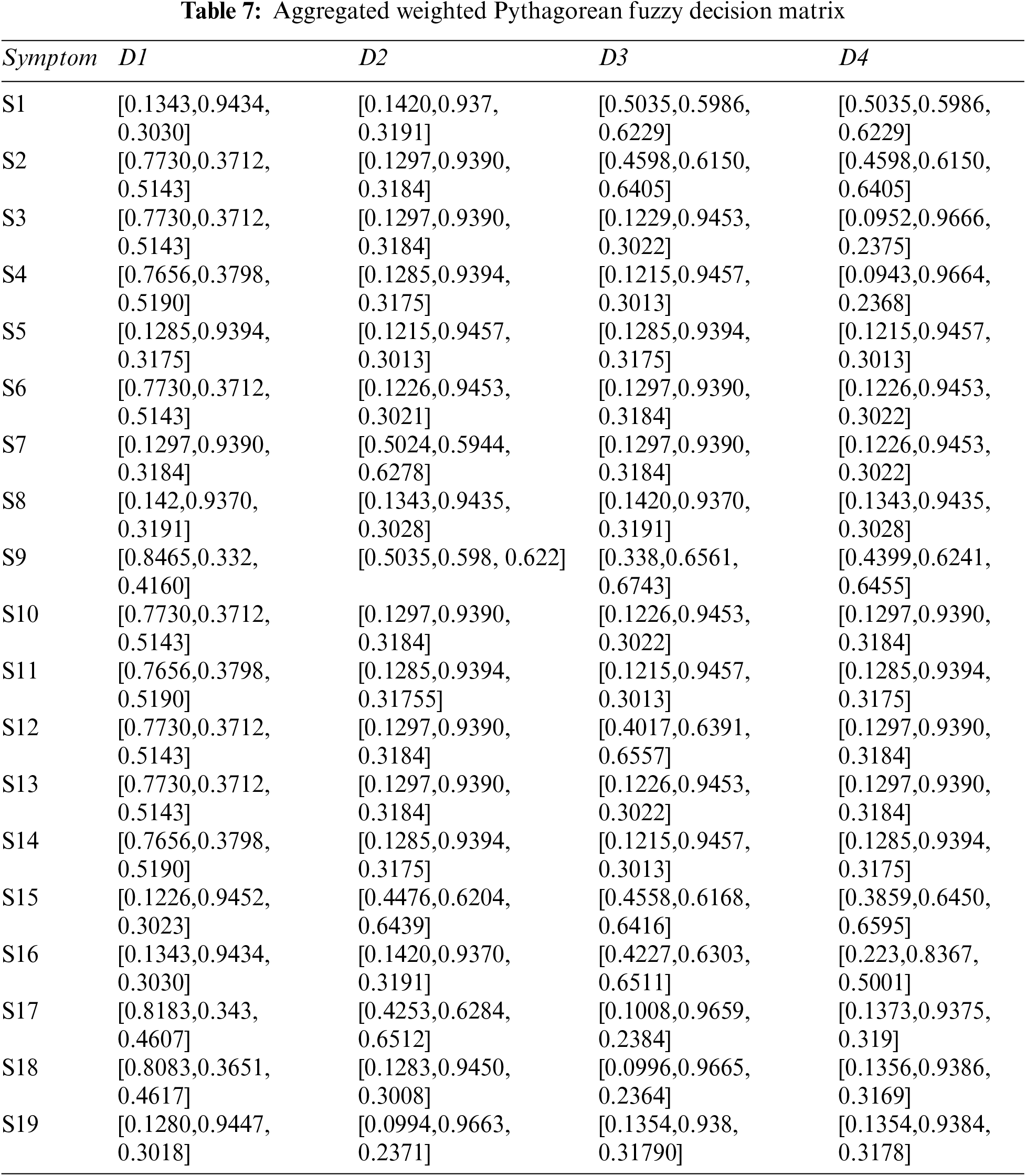
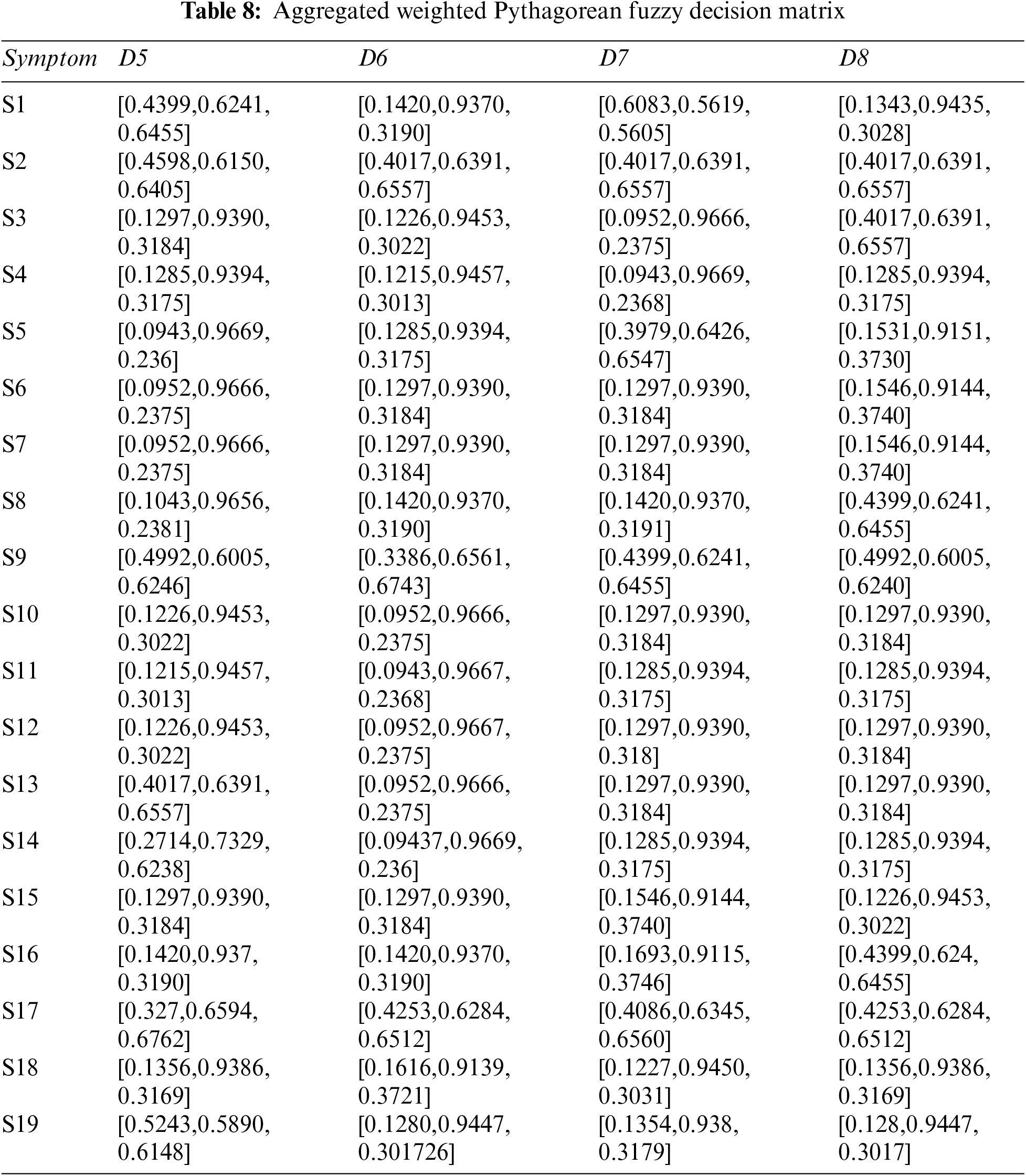
Step 4: Constructing aggregated weighted PFDM using Eq. (3), and Tables 3, 4, and 6. The results are shown in Tables 7 and 8.

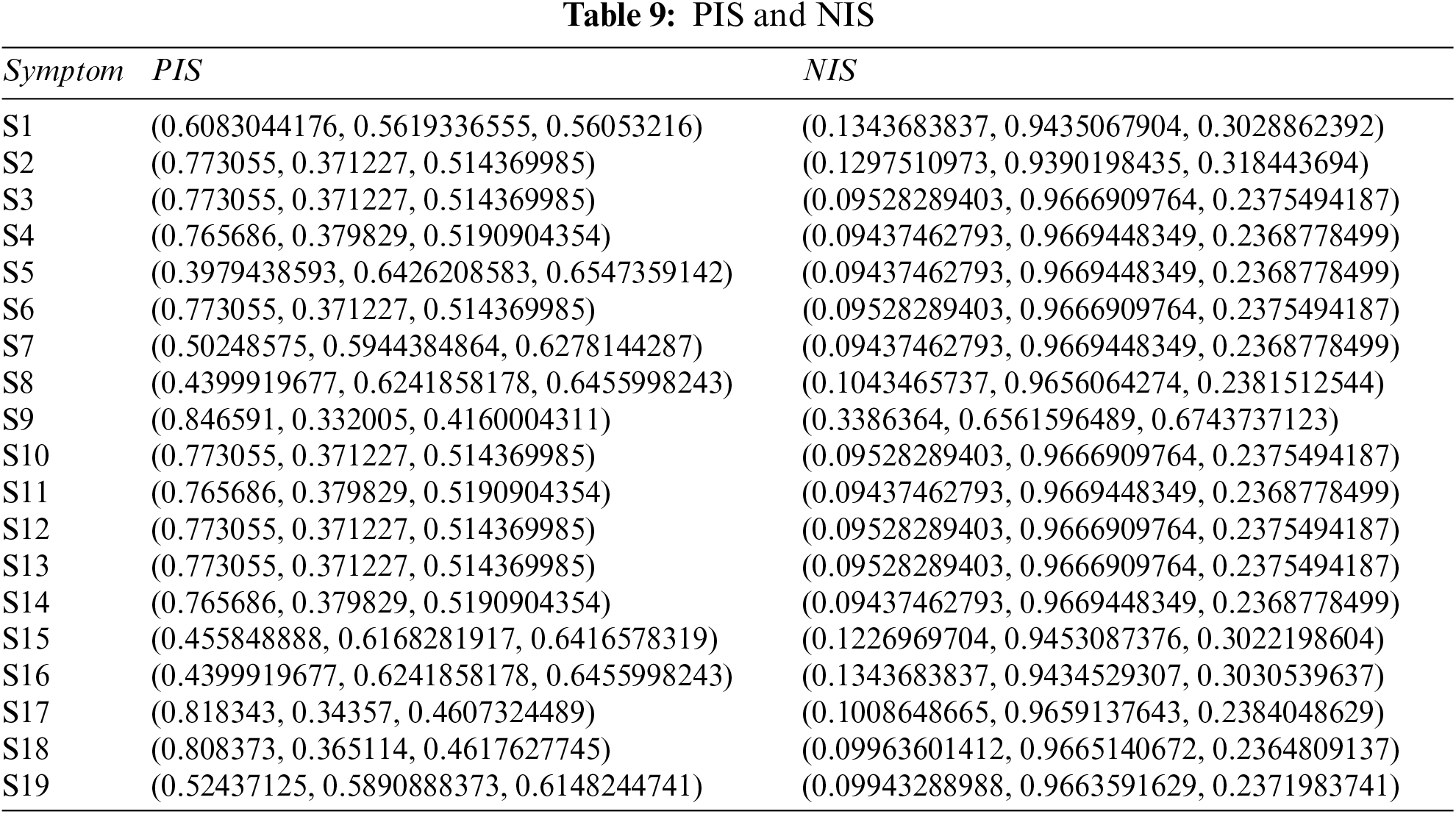
Step 5: Table 9 shows the results of PFPIS and PFNIS using Eqs. (4)–(7), and Tables 7 and 8.

Step 6: Find distance of each disease with respect to PIS and NIS using Eqs. (8) and (9), and Tables 7 and 8.

Step 7: Now apply Eq. (10) on Table 10 to calculate the relative closeness of each disease.

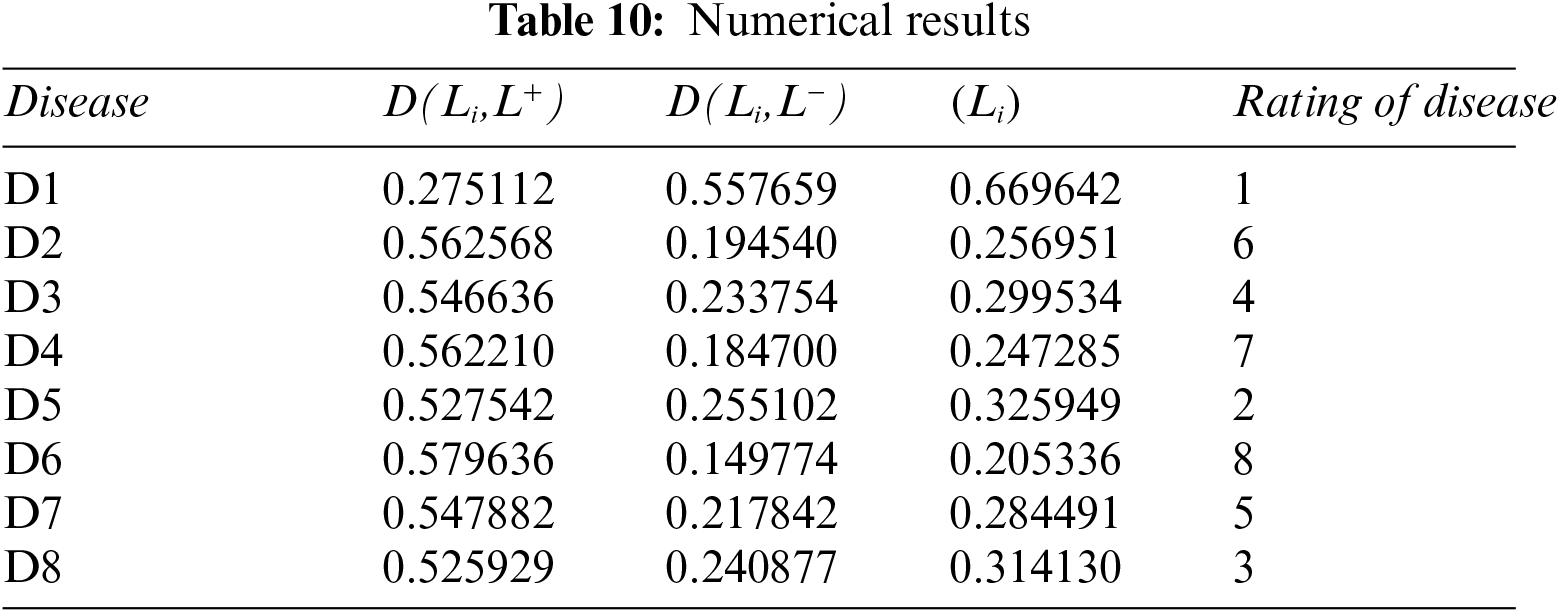
Step 8: The maximum value is D1 disease.

3.2.2 Pythagorean Fuzzy Entropy Method

Now we evaluate the same inputs with our second methodology (cf., Section 3.1.2). The step-by-step calculations of this algorithm are as follows:

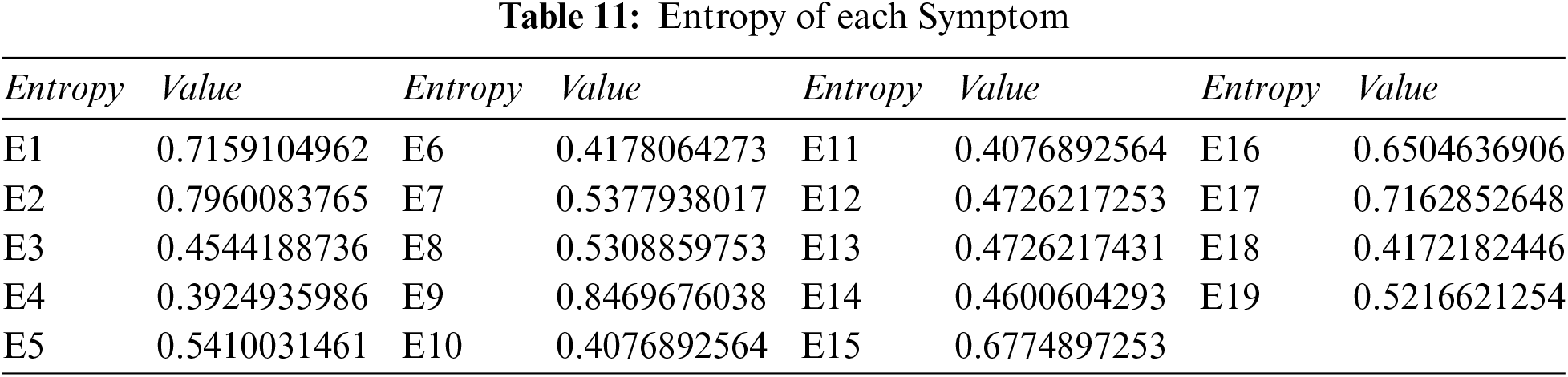
Step 1: Compute the overall entropy of each criterion using Tables 3 and 4, and Eq. (11).

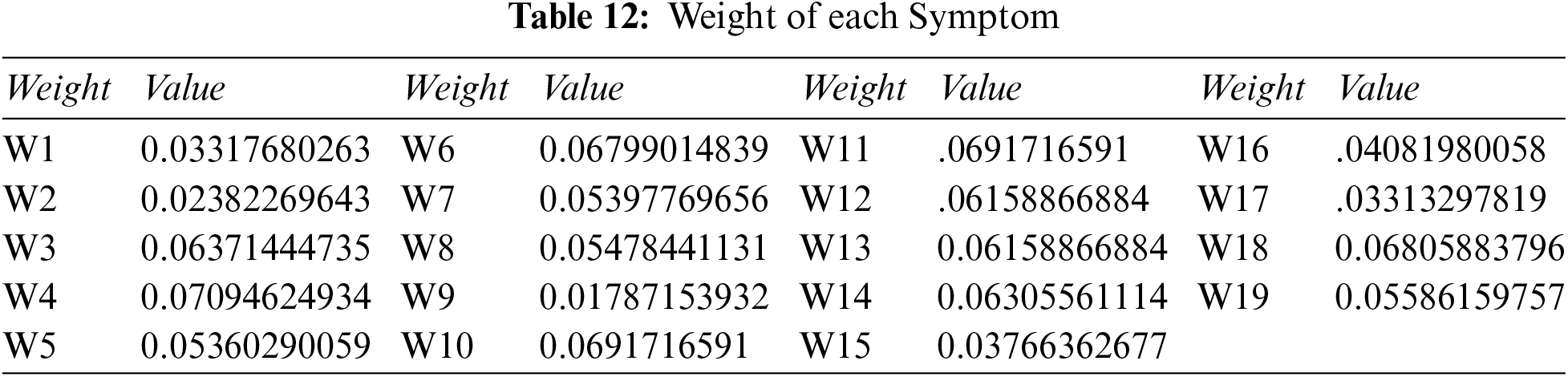
Step 2: Compute the overall weight of each symptom: we use Tables 6 and 11, and Eq. (13), to get Table 12.

Step 3: Determine the Pythagorean fuzzy PIS γ+ and NIS γ− of each alternative using Eqs. (4)–(7), and Tables 3 and 4. The PIS and NIS results are shown in Table 13.

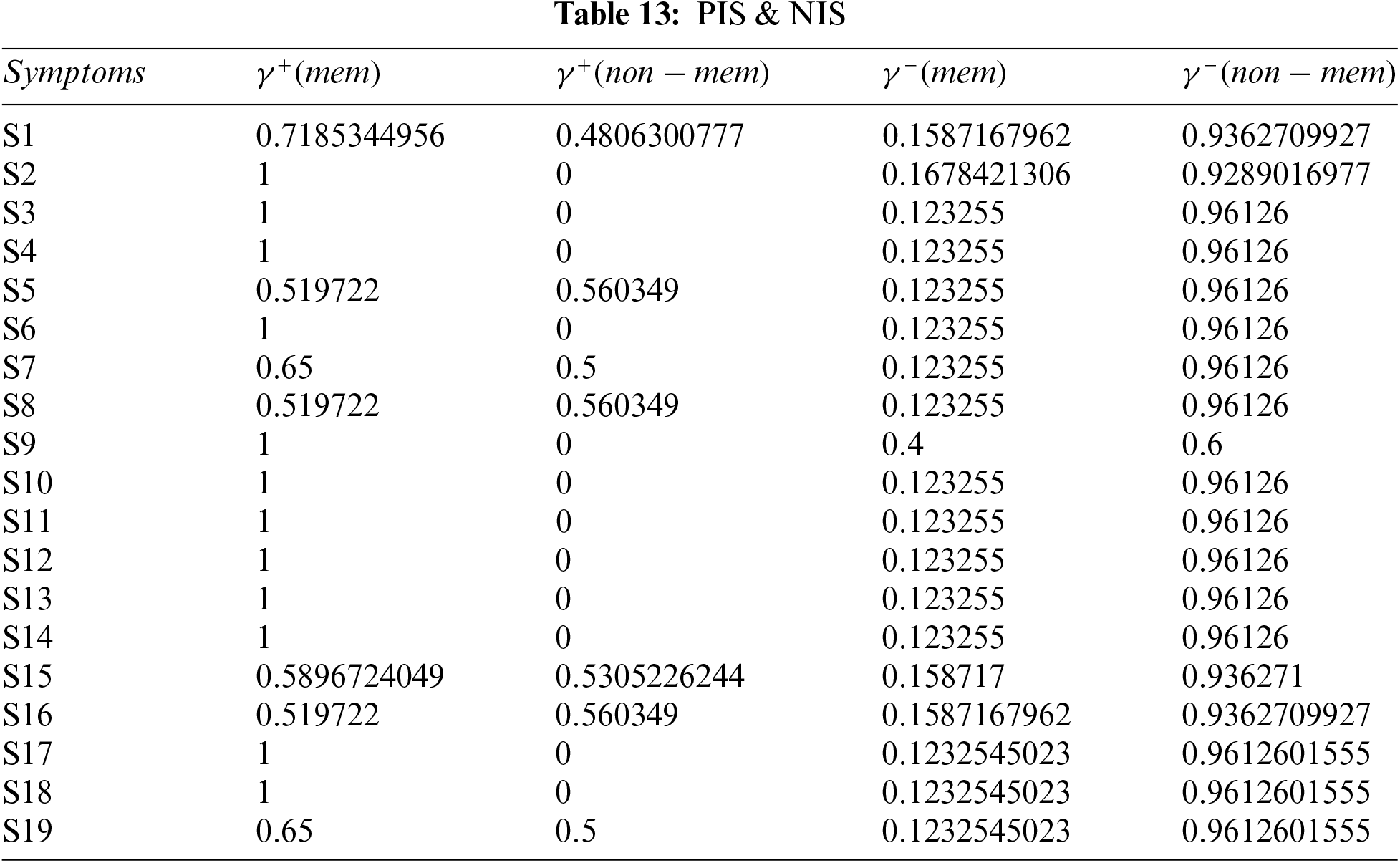
Step 4: Calculate the distance between alternatives using Tables 12 and 13.

Step 5: Calculate the relative degree of closeness of each alternative using Eq. (10), and Table 14. Table 15 shows the relative closeness of each disease.

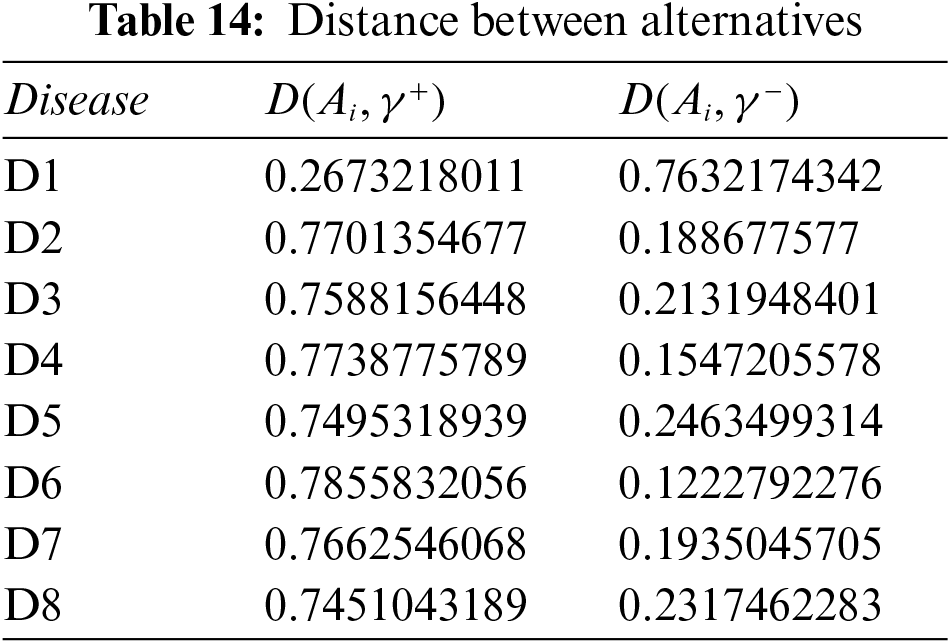
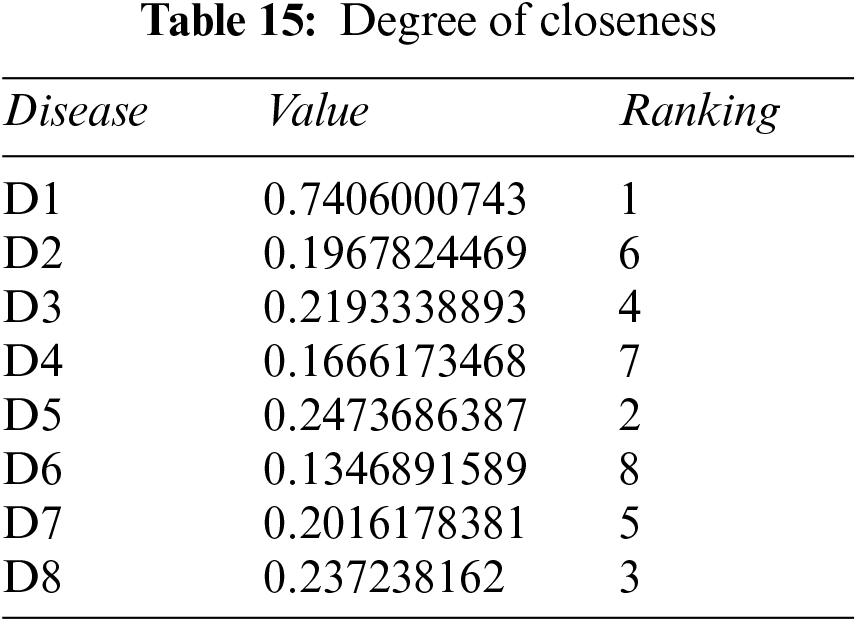
Step 6: Rank all alternatives Ai according to relative closeness ϕ(Ai) of each alternative. The highest value is of D1.

3.2.3 Pythagorean Fuzzy Power Weighted Geometric Method (PFPWG)

We consider the same example again, but now we follow the PFPWG algorithm (cf., Section 3.1.3) to find the final result.

Step 1: Calculate the supports using distance and support formulas–Eqs. (15) and (14), with Tables 3 and 4.

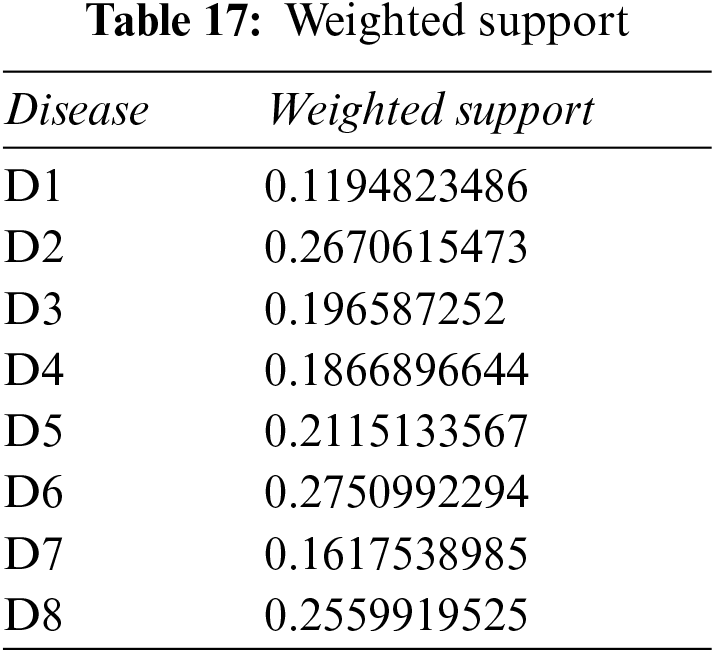
Step 2: Calculate the weighted support using Tables 12, 16, and Eq. (16).

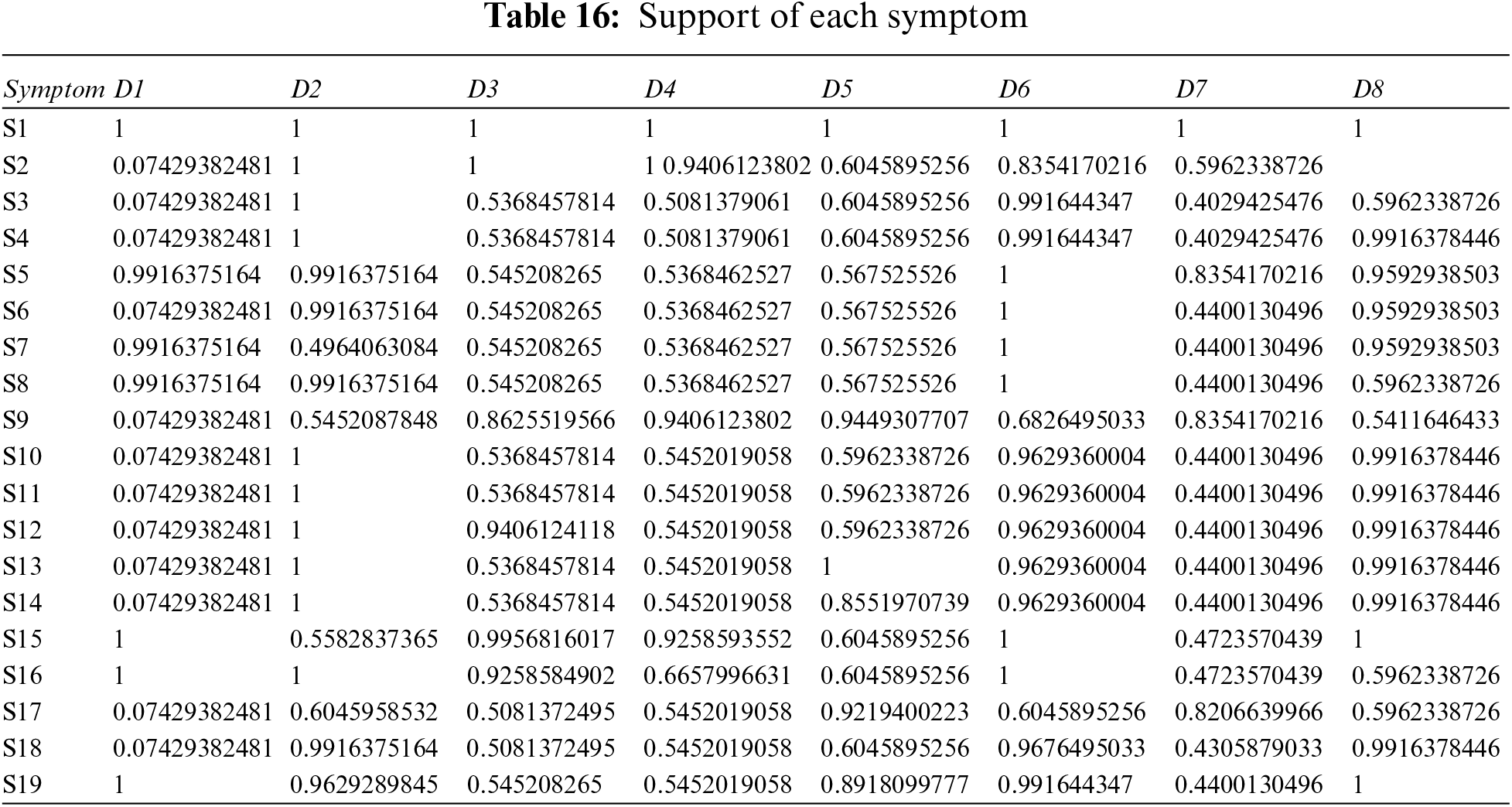
Step 3: Use Table 2 and Eq. (1) to get crisp weight of each symptom.

Step 4: Use Eq. (17), plus Tables 16, 17 and 18, to determine the weight associated with PFNs.

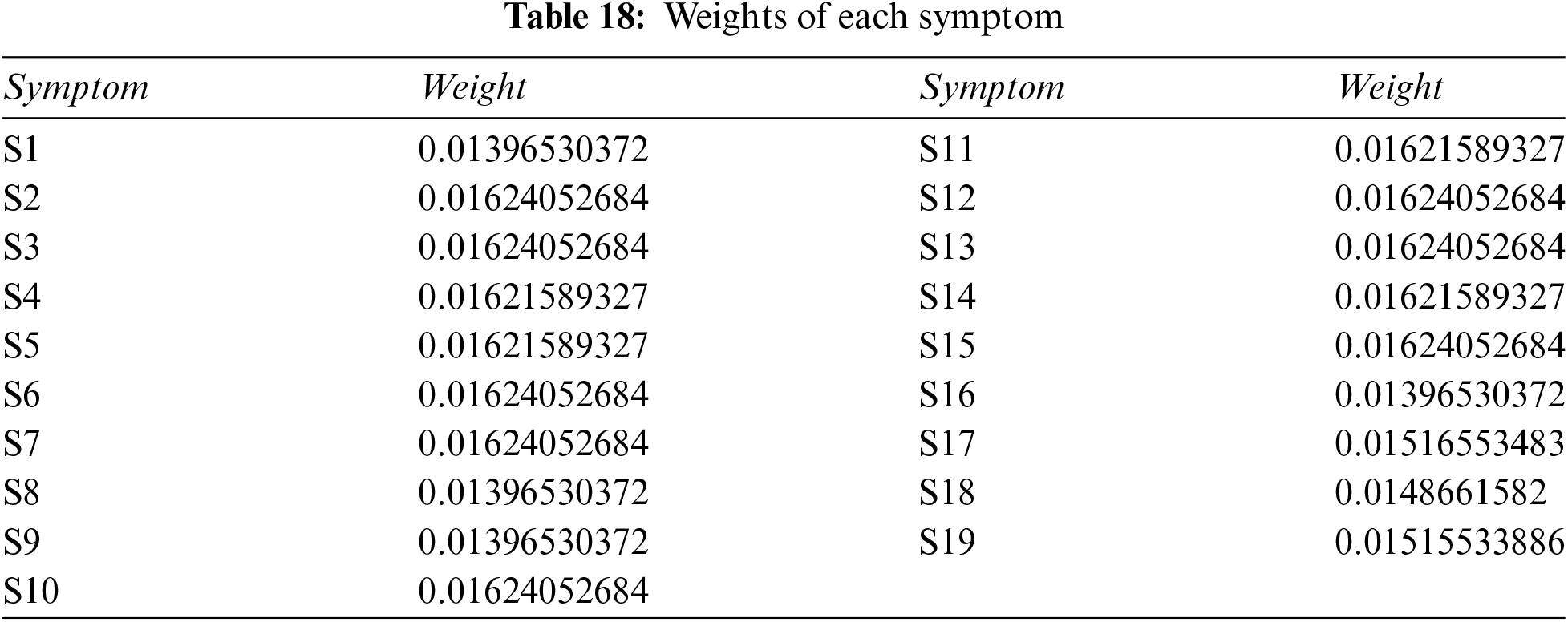
Step 5: Apply the PFPWG operator using Eq. (18), and Tables 19, 3, and 4.

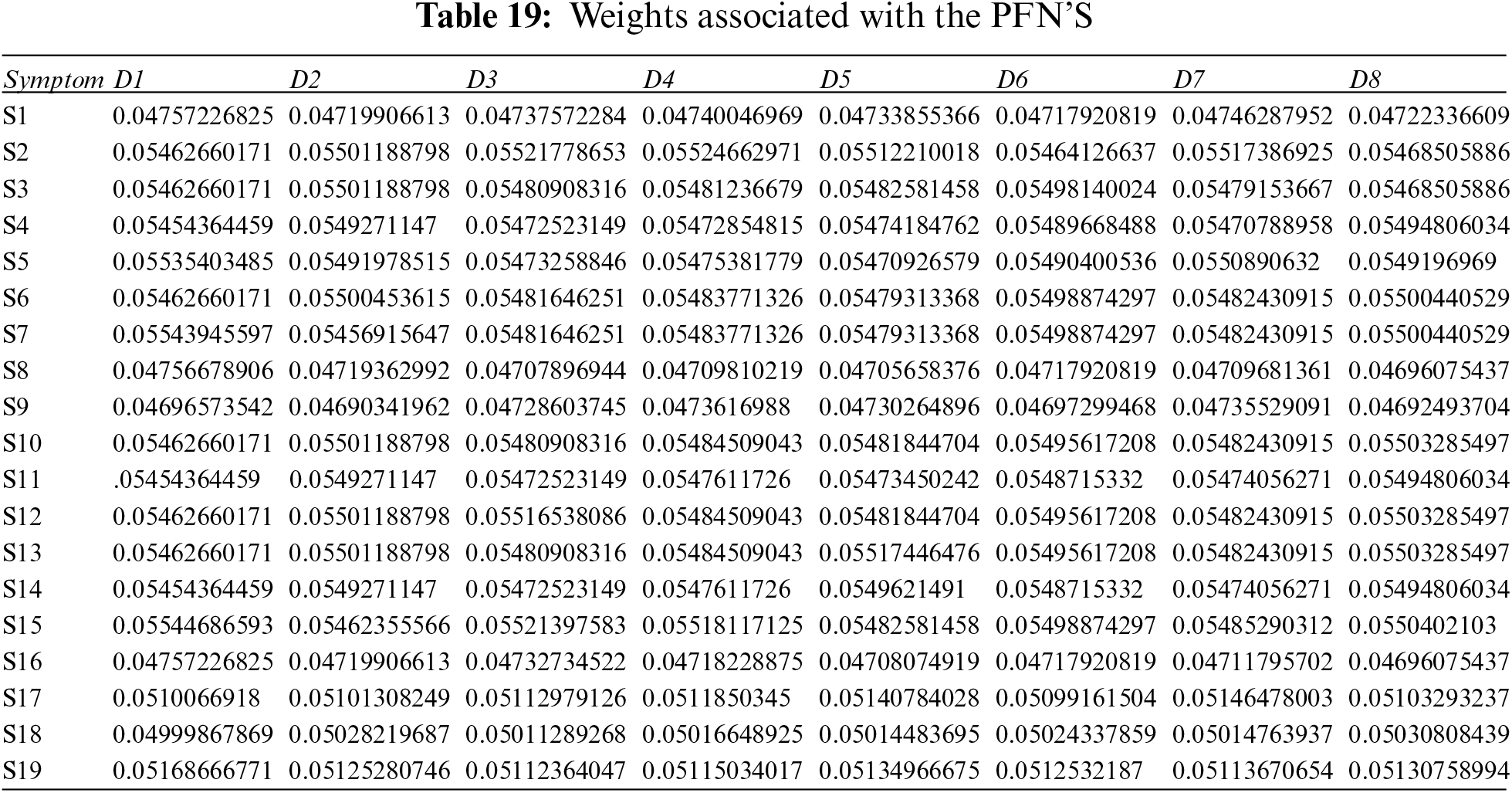
Step 6: Calculate the scores of the overall PFNs using Eq. (19) and Tables 20 and 21.

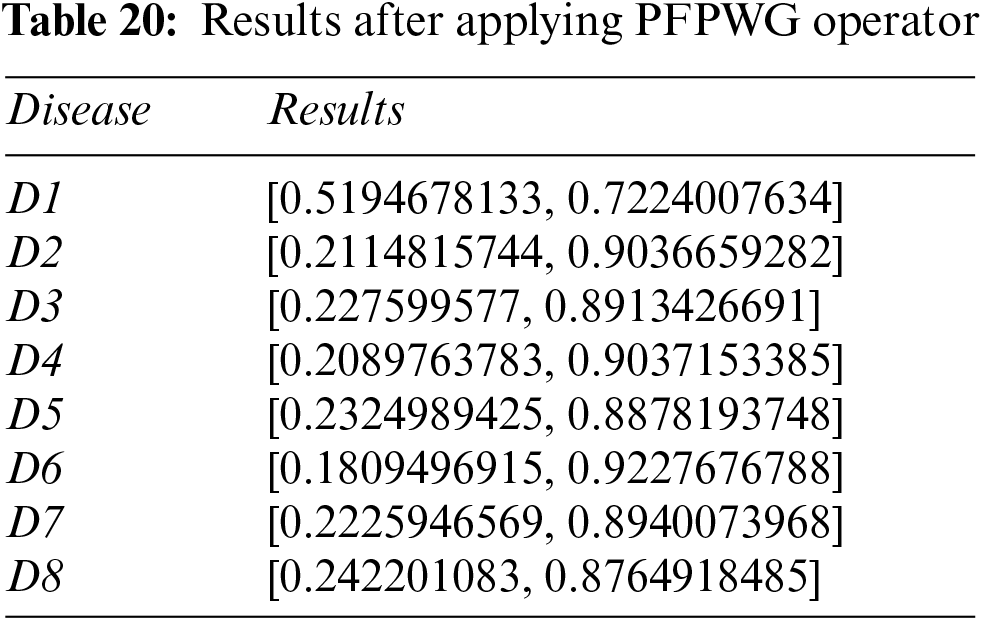
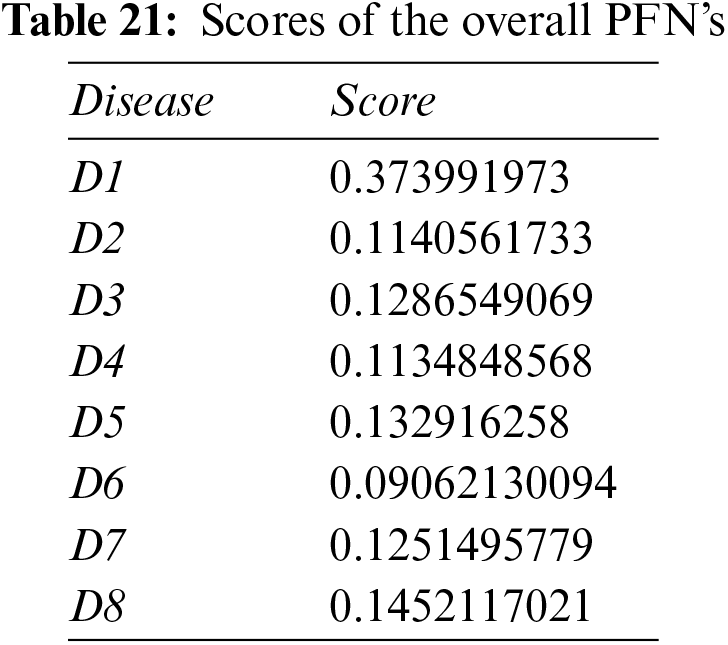
Step 7: Disease D1 is pinpointed again.

We confirm that each approach highlights the same disease based on the patient record provided.

4  Comparative Analysis

In this section, we compare the results of the Pythagorean Fuzzy TOPSIS (PF-TOPSIS), the Pythagorean Fuzzy Entropy (PF-Entropy), and the PFPWG method. To do this, we took ten different data sets and applied PF-TOPSIS, PF-Entropy, and the PFPWG techniques. The results obtained from each technique are represented by drawing bar graphs. In Fig. 2, the results of PF-TOPSIS are displayed. The eight diseases are shown in different eight colors. The length of each bar shows its value obtained from the PF-TOPSIS method. In Fig. 3, the results of the PF entropy are displayed. In this figure, eight diseases are also represented by different colors, and the length of the bar shows the value of each disease for each data set obtained from PF entropy method. Fig. 4 shows the results of the PFPWG method.

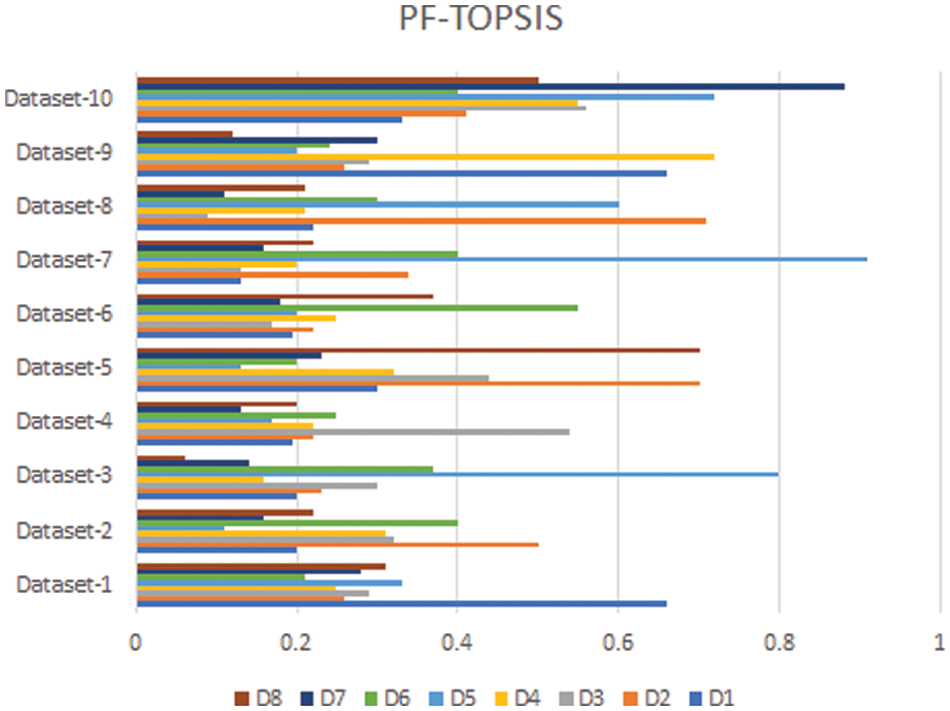
Figure 2: PF-TOPSIS Results

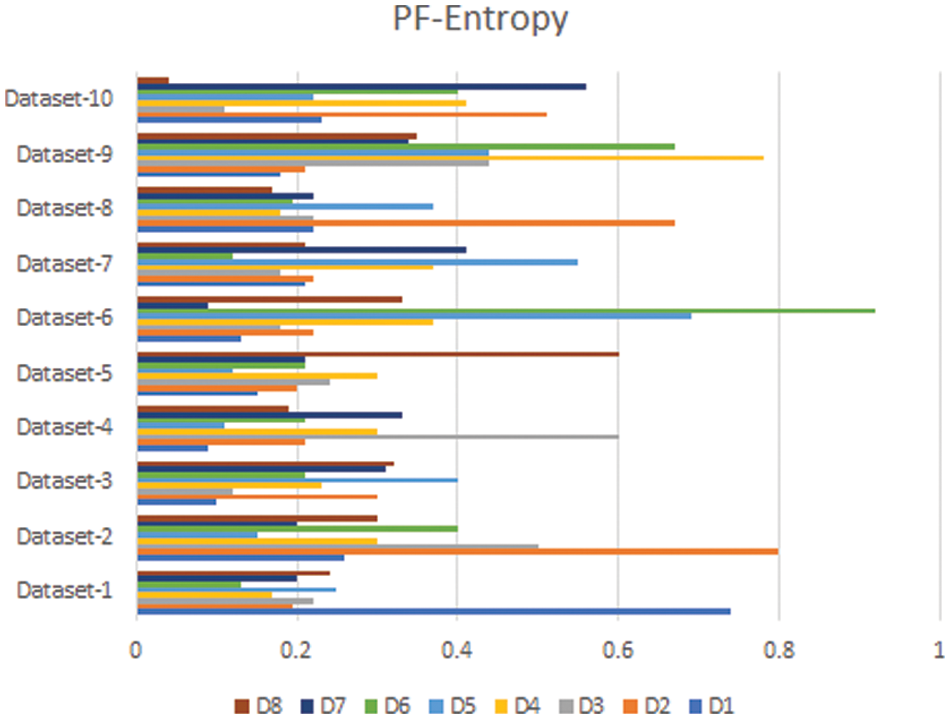
Figure 3: PF-Entropy Results

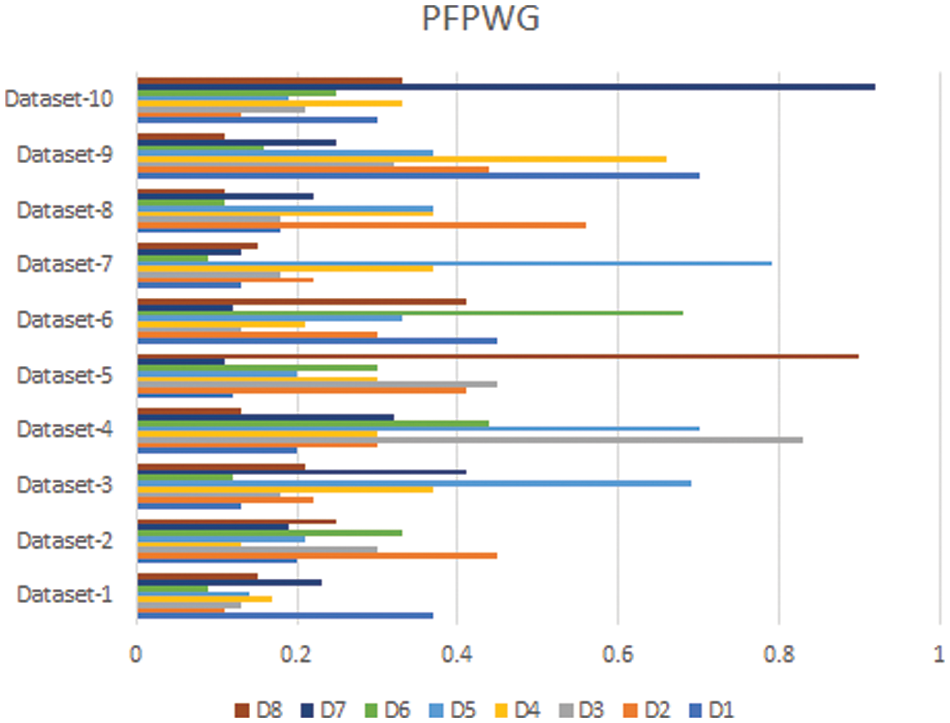
Figure 4: PFPWG Results

Now we compare these three bar charts for each data set. We can see that the data set 1,2,3,4,5,6,7,8,9, highlighted D1, D2, D1, D4, D8, D6, D1, D2, D1, and D7 diseases, respectively. We can see that each approach highlights the same disease based on the provided patient’s records, which testifies the authenticity of our model.

5  Conclusion and Future Work

According to the World Health Organization (WHO), around 400,000 children are diagnosed with cancer each year and the rate of cure in low and middle-income countries is only 45 percent, which is highly unsatisfactory. To improve this percentage, WHO has launched a global initiative and provided appropriate professional guidance and resources. Their goal is to increase the survival rate up to sixty percent by the end of 2030. To help achieve this goal, we have proposed a novel model that allows doctors to diagnose the type of childhood cancer early, so that appropriate treatment can be given at the right time. This ultimately reduces the physical and financial suffering of the patient and their parents. Our model takes nineteen symptoms as inputs and determines the type of cancer. We have used Pythagorean fuzzy decision-making techniques for diagnostic purposes. We designed three algorithms, namely, Pythagorean fuzzy TOPSIS method, Pythagorean fuzzy entropy, and PFPWG. We have determined their respective time complexities. To test them, we have taken ten data sets and compared the results of the different approaches. Also, we have set forth a numerical example to make each of their steps understandable.

There are many other applications where decision-making takes place and our approaches can provide assistance. Our system is applicable when data is fuzzy and decisions must be made. So, some future directions of our work are discussed below:

Industrial automation and Industry 4.0: In Industry 4.0, we connect the devices through the internet to make a network of different things. Then through the proposed approach, the different manufacturing parts of the machines can be controlled without human intervention. We can use our proposed model in Industry 4.0 to make intelligent decisions by taking into account all parameters and making the manufacturing process more productively and efficiently.

Precision agriculture: We need various decision-making systems to automate traditional farming to increase the yields and reduce the potential risks. With our model, precision farming can be made more efficient and productive. We can make timely decisions, and automate the decision process. Through this approach, an irrigation system can be improved, and water wastage could be reduced. Our proposed approach can be useful for designing a pest control system that helps the farmer to save crops from pests timely. This approach can also be useful to monitor soil pH and other ingredients, which require for the proper growth of the crops. Through this procedure, farmers can decide the right amount of fertilizers for the field.

Computer aided diagnosis: These systems help doctors to analyze the medical images and highlight diseases based on symptoms. The proposed approach can help doctors to early detect the chances of any disease, which could happen in the future due to the patient’s routine or changes in his body and enable the doctor to prevent it from spreading more by proper medication or therapies.

Classroom monitoring: The proposed approach could be beneficial for monitoring students’ activities in a large classroom and concluding which student is not attentive in class or how much students in the class are attentive.

Data Availability: No data were used to support this study.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under Grant No. (R.G.P.2/48/43).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.   Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

 2.   Atanassov, K., Gargov, G. (1998). Elements of intuitionistic fuzzy logic. Fuzzy Sets and Systems, 95(1), 39–52. DOI 10.1016/S0165-0114(96)00326-0. [Google Scholar] [CrossRef]

 3.   Habib, S., Akram, M. (2019). Medical decision support systems based on fuzzy cognitive maps. International Journal of Biomathematics, 12(6), 1950069–34, DOI 10.1142/S1793524519500694. [Google Scholar] [CrossRef]

 4.   Habib, S., Butt, M. A., Akram, M., Smarandache, F. (2020). A neutrosophic clinical decision-making system for cardiovascular diseases risk analysis. Journal of Intelligent & Fuzzy Systems, 39(5), 7807–7829. DOI 10.3233/JIFS-201163. [Google Scholar] [CrossRef]

 5.   Alcantud, J. C. R., Varela, G., Santos-Buitrago, B., Santos-García, G., Jiménez, M. F. (2019). Analysis of survival for lung cancer resections cases with fuzzy and soft set theory in surgical decision making. PLoS One, 14, 1–17. DOI 10.1371/journal.pone.0218283. [Google Scholar] [CrossRef]

 6.   Feng, F., Fujita, H., Ali, M. I., Yager, R. R., Liu, X. (2019). Another view on generalized intuitionistic fuzzy soft sets and related multiattribute decision making methods. IEEE Transactions on Fuzzy Systems, 27(3), 474–488. DOI 10.1109/TFUZZ.2018.2860967. [Google Scholar] [CrossRef]

 7.   Feng, F., Zheng, Y., Sun, B., Akram, M. (2021). Novel score functions of generalized orthopair fuzzy membership grades with application to multiple attribute decision making. Granular Computing, 7, 95–111. DOI 10.1007/s41066-021-00253-7. [Google Scholar] [CrossRef]

 8.   Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]

 9.   Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222–1230. DOI 10.1109/TFUZZ.2016.2604005. [Google Scholar] [CrossRef]

10.  Yucesan, M., Gul, M. (2020). Hospital service quality evaluation: An integrated model based on pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Computing, 24(5), 3237–3255. DOI 10.1007/s00500-019-04084-2. [Google Scholar] [CrossRef]

11.  Guleria, A., Bajaj, R. K. (2020). Pythagorean fuzzy (R, S)-norm discriminant measure in various decision making processes. Journal of Intelligent & Fuzzy Systems, 38(1), 761–777. DOI 10.3233/JIFS-179447. [Google Scholar] [CrossRef]

12.  Rahman, K. (2021). The new generalized averaging aggregation operators and their application on group decision making problem base on interval-valued pythagorean fuzzy numbers. Annals of Optimization Theory and Practice, 4(1), 87–102. DOI 10.22121/AOTP.2021.285741.1066. [Google Scholar] [CrossRef]

13.  Zulqarnain, R. M., Siddique, I., Jarad, F., Ali, R., Abdeljawad, T. (2021). Development of TOPSIS technique under pythagorean fuzzy hypersoft environment based on correlation coefficient and its application towards the selection of antivirus mask in COVID-19 pandemic. Complexity, 6634991. DOI 10.1155/2021/6634991. [Google Scholar] [CrossRef]

14.  Yue, Q., Zhang, L. (2020). Two-sided matching for hesitant fuzzy numbers in smart intelligent technique transfer. Mechanical Systems and Signal Processing, 139, 106643. DOI 10.1016/j.ymssp.2020.106643. [Google Scholar] [CrossRef]

15.  Yue, Q. (2022). Bilateral matching decision-making for knowledge innovation management considering matching willingness in an interval intuitionistic fuzzy set environment. Journal of Innovation & Knowledge, 7(3), 100209. DOI 10.1016/j.jik.2022.100209. [Google Scholar] [CrossRef]

16.  Ejegwa, P. A. (2020). Improved composite relation for pythagorean fuzzy sets and its application to medical diagnosis. Granular Computing, 5(2), 277–286. DOI 10.1007/s41066-019-00156-8. [Google Scholar] [CrossRef]

17.  Akram, M., Habib, A., Alcantud, J. C. R. (2021). An optimization study based on dijkstra algorithm for a network with trapezoidal picture fuzzy numbers. Neural Computing and Applications, 33, 1329–1342. DOI 10.1007/s00521-020-05034-y. [Google Scholar] [CrossRef]

18.  Akram, M., Luqman, A., R., Alcantud, J. C. (2021). Risk evaluation in failure modes and effects analysis: Hybrid TOPSIS and ELECTRE I solutions with pythagorean fuzzy information. Neural Computing and Applications, 33(11), 5675–5703. DOI 10.1007/s00521-020-05350-3. [Google Scholar] [CrossRef]

19.  Luqman, A., Akram, M., Alcantud, J. C. R. (2021). Digraph and matrix approach for risk evaluations under pythagorean fuzzy information. Expert Systems with Applications, 170, 114518. DOI 10.1016/j.eswa.2020.114518. [Google Scholar] [CrossRef]

20.  Akram, M., Dudek, W. A., Ilyas, F. (2019). Group decision-making based on pythagorean fuzzy TOPSIS method. International Journal of Intelligent Systems, 34(7), 1455–1475. DOI 10.1002/int.22103. [Google Scholar] [CrossRef]

21.  Xu, T. T., Zhang, H., Li, B. Q. (2020). Pythagorean fuzzy entropy and its application in multiple-criteria decision-making. International Journal of Fuzzy Systems, 22(5), 1552–1564. DOI 10.1007/s40815-020-00877-y. [Google Scholar] [CrossRef]

22.  Feng, J., Zhang, Q., Hu, J. (2020). Group generalized pythagorean fuzzy aggregation operators and their application in decision making. IEEE Access, 8, 138004–138020. DOI 10.1109/ACCESS.2020.3010718. [Google Scholar] [CrossRef]

23.  Ye, J. (2015). An extended TOPSIS method for multiple attribute group decision making based on single valued neutrosophic linguistic numbers. Journal of Intelligent & Fuzzy Systems, 28(1), 247–255. DOI 10.3233/IFS-141295. [Google Scholar] [CrossRef]

24.  Ye, J. (2009). Application of extension theory in misfire fault diagnosis of gasoline engines. Expert Systems with Applications, 36(2), 1217–1221. DOI 10.1016/j.eswa.2007.11.012. [Google Scholar] [CrossRef]

25.  Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for interval-valued pythagorean fuzzy so set with their application to solve multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. DOI 10.32604/cmes.2022.019408. [Google Scholar] [CrossRef]

26.  Johnston, W. T., Erdmann, F., Newton, R., Steliarova-Foucher, E., Schuz, J. et al. (2021). Childhood cancer: Estimating regional and global incidence. Cancer Epidemiology, 71, 101662. DOI 10.1016/j.canep.2019.101662. [Google Scholar] [CrossRef]

27.  Spector, L. G., Pankratz, N., Marcotte, E. L. (2015). Genetic and nongenetic risk factors for childhood cancer. Pediatric Clinics of North America, 62(1), 11–25. DOI 10.1016/j.pcl.2014.09.013. [Google Scholar] [CrossRef]