Performance Analysis of RIS Assisted NOMA Networks over Rician Fading Channels

1  Introduction

As a promising multiple access technology in the next generation wireless communication network, non-orthogonal multiple access (NOMA) has the ability to tremendously enhance the spectral and energy efficiency [1,2]. The distinguishing feature of NOMA is that multiple users with different quality-of-service requirements are served by exploiting the superposition coding scheme in the same time/frequency/code resource block [3–5]. In [6,7], the authors have proved that the outage probability and ergodic rate of NOMA can be better than that of conventional orthogonal multiple access (OMA). Zhu et al. [8] have proposed an optimal power allocation scheme learned by adopting the deep deterministic policy gradient algorithm in multiple-input multiple-output NOMA vehicular edge computing.

Recently, reconfigurable intelligent surface (RIS) has been regarded as a promising technology for the next generation wireless communication, which can improve the spectral and energy efficiency of future wireless communication networks in a cost-effective way [9–11]. Specifically, RIS is a low-cost planar array composed of a large number of reconfigurable passive elements, in which the amplitude and phase of the incident signal for each element can be changed independently [12,13]. By adjusting the amplitude and phase coefficients of RIS elements through programmable controller, the electromagnetic signal can be reconfigured to significantly enhance the signal quality and the coverage of wireless communication [14]. Compared with the conventional relaying technology, the advantage of RIS is that the passive reflection does not consume energy and it does not generate self-interference in full duplex (FD) mode [15]. The RIS-empowered multiuser uplink communication system has been investigated in [16], in which a channel estimation framework based on the parallel factor decomposition has been proposed to unfold the resulting cascaded channel model. In [17], the authors have studied the downlink wireless communication system, in which the transmit beamforming and the RIS have been jointly optimized to maximize the energy efficiency of the system. A new joint design of the transmit beamforming and the phase shifting of the RIS has been proposed in [18], in which the sum rate of the multiuser system has been maximized by using deep reinforcement learning (DRL). In [19], the multiuser communication system assisted by RIS has been considered, in which the power allocation and the phase shifting of the RIS have been jointly optimized to minimize the sum transmit power. Considering RIS-empowered terahertz band communications, a DRL-based hybrid beamforming scheme has been proposed in [20] to improve the communication coverage.

1.1 Related Work

Since both RIS and NOMA can greatly improve the spectrum and energy efficiency, it is critical to study their combined advantages to further enhance the spectrum and energy efficiency of future wireless communication networks. In [21], a simple RIS-NOMA transmission scheme has been designed, in which the outage performance of the cell-edge user has been improved with the assistance of RIS in a NOMA system. In [22], the authors have investigated the performance of RIS-NOMA networks in terms of the outage probability, ergodic rate, and energy efficiency by exploiting 1-bit coding scheme. The effects of coherent phase shifting and random phase shifting on outage performance for RIS-NOMA networks have been investigated in [23]. By designing the passive beamforming weights, the authors in [24] have investigated the outage probability and ergodic rate of prioritized user for RIS-NOMA. The RIS reflection with discrete phase shifting for RIS-NOMA and RIS-OMA has been analyzed in [25]. In [26], a novel NOMA solution with RIS partitioning has been proposed to reduce the transmission interference. Considering the impact of the direct link from the base station (BS) to users on the network performance, the outage behaviors of multiple RISs-assisted NOMA networks have been studied by using discrete phase shifting in [27]. The authors in [28] have examined the outage performance of RIS-NOMA networks under presence of hardware impairment. In [29], the outage probability and ergodic rate of RIS-aided uplink and downlink NOMA networks have been investigated by employing continuous phase shifting. The authors in [30] have studied RIS assisted downlink NOMA networks, in which the performance of the networks has been analyzed by using the coherent phase shifting.

1.2 Motivation and Contributions

As mentioned in the above works, compared with the conventional relaying technology, the RIS is capable of reflecting the incident signal transmitted from the transmitter to the receiver in FD mode without self-interference and energy consumption, which not only enhances the spectrum and energy efficiency, but also has a very low cost. Therefore, the integration of RIS and NOMA can further improve the spectrum and energy efficiency of the next generation wireless communication networks. Furthermore, the current literature on RIS-NOMA mainly concentrates on the optimization problem, but the research on performance analysis is not enough. Compared with conventional NOMA systems, the performance analysis of RIS-NOMA systems is more complex and challenging owing to the influence of the RIS. These motivate us to study the performance of RIS assisted NOMA systems, which provides an important theoretical basis for deployment of RIS in the future.

In this paper, we consider a RIS assisted NOMA network, in which a pair of NOMA users in a cell cannot directly receive signals from the BS due to the obstruction of obstacles, and each user needs the help of a RIS. Moreover, we comprehensively analyze the performance of RIS-NOMA networks in terms of the outage probability, ergodic rate, and system throughput. The primary contributions of this paper are summarized as follows:

•   We derive the closed-form and asymptotic expressions for the outage probability of a pair of NOMA users over Rician fading channels for the proposed RIS-assisted NOMA network. To gain further insight, we obtain the diversity orders of the pair of NOMA users for RIS-NOMA network according to the asymptotic analyses at high signal-to-noise ratio (SNR). We observe that the diversity orders of the pair of NOMA users depend on the number of reflecting elements and Rician factor.

•   We compare the outage performance of the pair of users for RIS-NOMA and RIS-OMA networks. We demonstrate that the outage performance of RIS-NOMA outperforms that of RIS-OMA. We prove that the RIS-NOMA network is capable of improving outage performance with increasing the number of reflecting elements and Rician factor.

•   We derive the exact and asymptotic expressions for the ergodic rate of the pair of NOMA users over Rician fading channels for our proposed RIS-NOMA network. To approximate the exact ergodic rate, we also derive the exact and asymptotic upper bound expressions for the ergodic rate of the nearby user. Based on theoretical analyses, we obtain the high SNR slopes for the ergodic rate of the pair of NOMA users. We observe that the throughput ceiling appears in the ergodic rate of the distant user at high SNR. We demonstrate that the superiority of RIS-NOMA over RIS-OMA in terms of the ergodic rate. We evidence that the ergodic rate of RIS-NOMA becomes larger with the increase of the number of reflecting elements.

•   We analyze the system throughput of our proposed RIS-NOMA network in two transmission modes. In delay-limited transmission mode, we observe that the system throughput of RIS-NOMA converges to a constant at high SNR. Furthermore, we prove that the proposed RIS-NOMA is capable of enhancing the system throughput compared to RIS-OMA. In delay-tolerant transmission mode, we evidence that the proposed RIS-NOMA can achieve a larger system throughput than RIS-OMA at high SNR. Moreover, we confirm that as the number of reflecting elements increases, the system throughput of RIS-NOMA can be significantly improved in the two transmission modes.

The main notations used in this paper are explained as follows. Cx×y denotes the space of x×y complex-valued matrices. VH represents the conjugate-transpose of V. fX(⋅) and FX(⋅) mean the probability density function (PDF) and cumulative distribution function (CDF) of random variable X, respectively. diag(⋅) denotes a diagonal matrix. Pr(⋅) denotes the probability. E(⋅) and D(⋅) stand for the expectation and variance, respectively.

2  System Model

Consider a two-RIS assisted NOMA network with one single-antenna BS and two single-antenna users as shown in Fig. 1, in which the BS sends the superposed signals to the pair of NOMA users by means of two RISs. Assume that there is no direct link between the BS and each NOMA user due to strong attenuation, and each NOMA user needs a RIS to assist in communicating with the BS. D1 and D2 are the nearby user and the distant user, respectively. R1 and R2 are RISs corresponding to D1 and D2, respectively. Each RIS has K reflecting elements. The reflecting phase shifting matrix of Rn is denoted by ϑn=diag(βejθn1,…,βejθnk,…,βejθnK), n∈{1,2}, where β∈[0,1] and θnk∈[0,2π) represent the amplitude coefficient and the phase shift of the k-th reflecting element of the RIS, respectively.

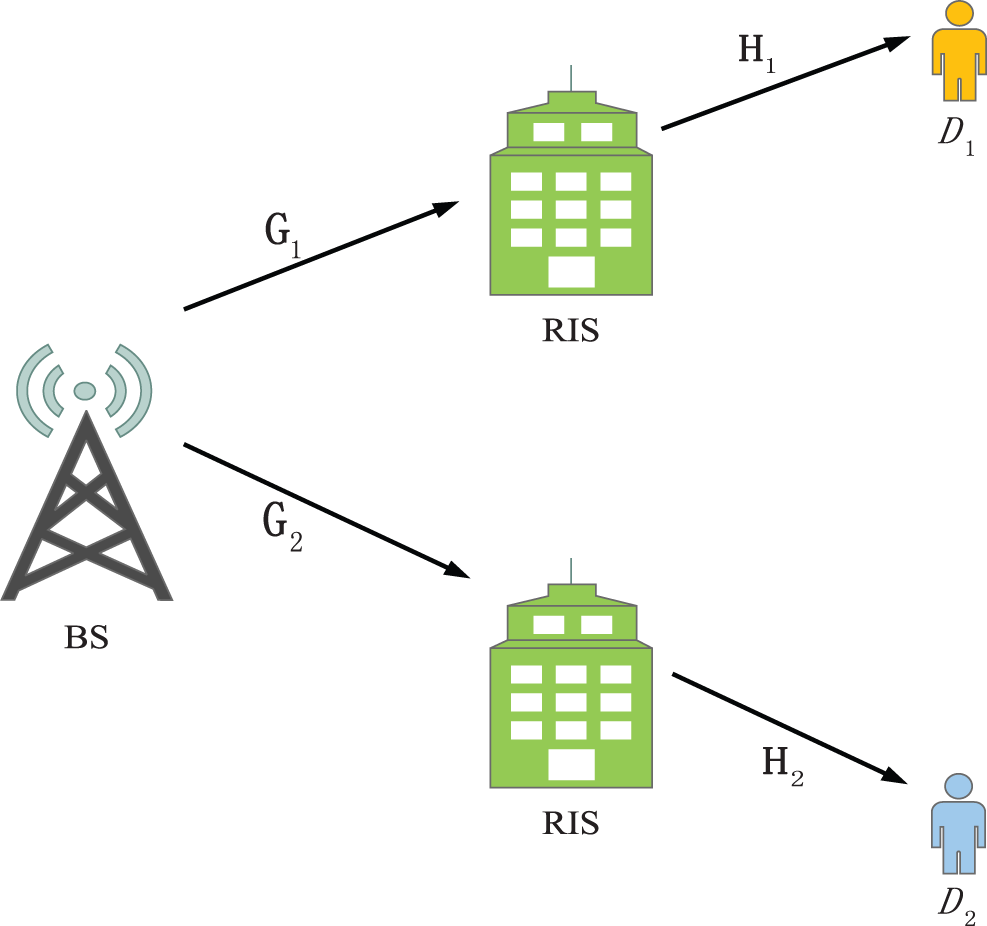
Figure 1: System model of RIS assisted downlink NOMA networks

2.1 Channel Model

It is assumed that the channel state information of all channels is completely known at the BS. The complex channel coefficients from the BS to Rn and from Rn to Dn are represented by Gn∈CK×1 and Hn∈CK×1, respectively. Assume that the wireless links for RIS-NOMA networks are modeled as Rician fading channels. The cascade channel gains from the BS to Rn and from Rn to Dn can be expressed as HnHϑnGn. The channel coefficient matrixes can be written as

Gn=[Gn1,…,Gnk,…,GnK]H,(1)

and

Hn=[Hn1,…,Hnk,…,HnK]H,(2)

where the channel coefficients from the BS to the k-th reflecting element of Rn and from the k-th reflecting element of Rn to Dn are respectively given by

Gnk=αn,1k(κκ+1+1κ+1G~nk),(3)

and

Hnk=αn,2k(κκ+1+1κ+1H~nk).(4)

Defining αn,1k=ηdn,1−α, αn,2k=ηdn,2−α, dn,1 and dn,2 are the distances from the BS to Rn and from Rn to Dn, respectively. κ, α, and η are the Rician factor, path loss exponent, and frequency dependent factor, respectively. The fading gains G~nk and H~nk follow complex Gaussian distribution with zero mean and unit variance, i.e., G~nk∼CN(0,1) and H~nk∼CN(0,1).

2.2 Signal Model

Based on the superposition coding scheme, the BS broadcasts superposed signal s=a1Pbs1+a2Pbs2 to D1 and D2, where Pb means the normalized transmit power of the BS, sn represents the unit power signal transmitted to Dn with an denoting the power allocation factor of Dn. For simplicity, we assume a fixed power allocation between two users. The optimized power sharing between non-orthogonal users can further enhance the system performance of RIS-NOMA networks, which will be studied in future work. For user fairness, the power allocation factor satisfies a2>a1 with a1+a2=1. The received signals at D1 and D2 are respectively given by

yD1=H1Hϑ1G1(a1Pbs1+a2Pbs2)+nD1,(5)

and

yD2=H2Hϑ2G2(a1Pbs1+a2Pbs2)+nD2,(6)

where nDn represents the additive white Gaussian noise with the mean power N0 at Dn. On the basis of the successive interference cancellation (SIC) principle, the signal of D2 is detected first at D1. The received signal-to-interference-plus-noise ratio (SINR) at D1 to detect signal s2 of D2 is given by

γD1→s2=ρ|H1Hϑ1G1|2a2ρ|H1Hϑ1G1|2a1+1,(7)

where ρ=PbN0 is the transmit SNR. After performing SIC, the signal of D1 is detected at D1. The received SINR of detecting signal s1 of D1 at D1 can be given by

γD1→s1=ρ|H1Hϑ1G1|2a1.(8)

The signal of D2 is directly detected by treating the signal of D1 as interference at D2. The received SINR of D2 to detect its own signal can be given by

γD2→s2=ρ|H2Hϑ2G2|2a2ρ|H2Hϑ2G2|2a1+1.(9)

2.3 RIS-OMA

For comparison, we regard the RIS-OMA scheme as the benchmark, in which the BS sends information to two OMA users through two RISs in two time slots. In each time slot, signal sn is transmitted from the BS to Dn by utilizing Rn. The observation at Dn is given by

yn,DnOMA=HnHϑnGnPbsn+nDn.(10)

The received SINR at Dn for detecting its own signal can be given by

γn,Dn→snOMA=ρ|HnHϑnGn|2.(11)

2.4 Channel Statistics

In order to achieve optimal performance, we use the coherent phase shift design. For the wireless communication links of RIS-NOMA networks, our goal is to optimize the channel by adjusting the amplitude and phase of the RIS to achieve the optimal channel gain for each user. For the BS-RIS-Dn link, we maximize |HnHϑnGn|=|∑k=1KβGnkHnkejθnk|, where Gnk and Hnk are the k-th element of Gn and Hn, respectively. In order to achieve maximization, the sum of the phase of GnkHnk and the phase shift θnk of the k-th reflecting element of the RIS is equal to zero. Therefore, we have

|HnHϑnGn|=∑k=1K|GnkHnk|,(12)

where β=1 without loss of generality.

The channel coefficients Gnk from the BS to the k-th reflecting element and Hnk from the k-th reflecting element to Dn follow Rician distribution, hence the probability density function (PDF) of cascade Rician channel Xnk=|GnkHnk| in [31] is expressed as

fXnk(x)=1αn,1αn,2∑i=0∞∑j=0∞4xi+j+1(κ+1)i+j+2κi+j(i!)2(j!)2e2κ(αn,1αn,2)−i+j+12Ki−j[2x(κ+1)αn,1αn,2],(13)

where Kν(⋅) denotes the modified Bessel function of the second kind with order ν [32]. The mean and variance of Xnk are respectively written as

μn=E(Xnk)=παn,1αn,24(1+κ)[L12(−κ)]2,(14)

and

Ωn=D(Xnk)=αn,1αn,2{1−π216(1+κ)2[L12(−κ)]4},(15)

where L12(⋅) represents the Laguerre polynomial and L12(κ)=e12κ[(1−κ)K0(−κ2)−κK1(−κ2)].

3  Outage Probability

In communication systems, the outage probability can be defined as the probability that the outage occurs for a user when the information rate of the user is lower than its target rate. The outage probability is a widely used system performance metric in fixed-rate transmission systems. In this section, the outage performance of downlink RIS-NOMA networks is investigated.

3.1 Outage Probability of D1

By using the SIC scheme at nearby user D1, the signal of distant user D2 is detected first, and then its own signal is detected. Therefore, when both signals s1 and s2 cannot be successfully detected by D1, an outage occurs for D1. Based on Eqs. (7) and (8), the outage probability of D1 for RIS-NOMA networks can be expressed as

PD1=1−Pr(γD1→s1>γth1,γD1→s2>γth2),(16)

where γth1=2r1−1 and γth2=2r2−1 represent the target SNRs with r1 and r2 denoting the target rates of D1 and D2 to detect signals s1 and s2, respectively. The outage probability of D1 is derived in the following theorem.

Theorem 3.1. Under Rician fading channels, the closed-form expression for the outage probability of D1 for RIS-NOMA networks can be approximated as

PD1≈1Γ(Kμ12Ω1)γ(Kμ12Ω1,μ1λΩ1),(17)

where λ≜max(λ1,λ2), λ1=γth1ρa1, λ2=γth2ρ(a2−a1γth2) with a2>a1γth2, μ1=πα1,1α1,24(1+κ)[L12(−κ)]2, Ω1=α1,1α1,2{1−π216(1+κ)2[L12(−κ)]4}, γ(α,x)=∫0xe−ttα−1dt is the lower incomplete Gamma function [32], and Γ(z)=∫0∞e−ttz−1dt is the gamma function [32].

Proof: See Appendix A.

Remark 3.1. From Eq. (17), it is observed that the approximate outage probability of D1 for RIS-NOMA is subject to ρ, K, κ, and α when the target SNR and the power allocation coefficient are fixed. Specifically, increasing ρ, K, κ, and α, the approximate outage probability of D1 for RIS-NOMA decreases. As a result, the outage performance of D1 for RIS-NOMA can be enhanced.

3.2 Outage Probability of D2

On account of the NOMA principle, the signal of D2 is directly detected at distant user D2. Thus the outage occurs for D2 when signal s2 cannot be successfully detected by D2. In view of Eq. (9), the outage probability of D2 for RIS-NOMA networks can be expressed as

PD2=Pr(γD2→s2<γth2).(18)

The outage probability of D2 is derived in the following theorem.

Theorem 3.2. Under Rician fading channels, the closed-form expression for the outage probability of D2 for RIS-NOMA networks can be approximated as

PD2≈1Γ(Kμ22Ω2)γ(Kμ22Ω2,μ2λ2Ω2),(19)

where μ2=πα2,1α2,24(1+κ)[L12(−κ)]2 and Ω2=α2,1α2,2{1−π216(1+κ)2[L12(−κ)]4}.

Proof: See Appendix B.

Remark 3.2. From Eq. (19), it can be seen that the approximate outage probability of D2 for RIS-NOMA depends on ρ, K, κ, and α. Similarly, as ρ, K, κ, and α increase, the approximate outage probability of D2 for RIS-NOMA decreases. Consequently, the outage performance of D2 for RIS-NOMA can be improved.

3.3 Outage Probability of Dn for RIS-OMA

For RIS-OMA networks, Dn detects its own signal sn in each time slot. Hence the outage occurs for Dn when its own signal cannot be successfully detected. According to Eq. (11), the outage probability of Dn for RIS-OMA networks can be expressed as

PDnOMA=Pr(γn,Dn→snOMA<γthnOMA),(20)

where γthnOMA=22rnOMA−1 is the target SNR with rnOMA being the target rate of Dn to detect signal sn. The derivation process of the outage probability for RIS-OMA networks is similar to that of RIS-NOMA networks. The outage probability of Dn for RIS-OMA networks can be provided in the following corollary.

Corollary 3.1. Under Rician fading channels, the closed-form expression for the outage probability of Dn for RIS-OMA networks can be approximated as

PDnOMA≈1Γ(Kμn2Ωn)γ(Kμn2Ωn,μnτnΩn),(21)

where τn=γthnOMAρ.

3.4 Diversity Analysis

In communication systems, the diversity order can be defined as the slope of the outage probability at high SNR. The diversity order describes the speed at which the outage probability decreases with the transmit SNR, which is usually used to evaluate the outage performance of wireless communication networks. The diversity order can be expressed as

d=−limρ→∞log⁡(PD∞(ρ))log⁡(ρ).(22)

In order to obtain further insights, the approximate results of the outage probability are analyzed at high SNR, which can be used to determine the diversity order. The asymptotic outage probabilities of D1 and D2 at high SNR for RIS-NOMA networks can be provided in the following corollary.

Corollary 3.2. Based on Eqs. (17) and (19), when ρ→∞, the asymptotic expressions for outage probability of D1 and D2 for RIS-NOMA networks can be respectively given by

PD1∞≈Ω1Kμ121Γ(Kμ12Ω1)(μ1λΩ1)Kμ12Ω1,(23)

and

PD2∞≈Ω2Kμ221Γ(Kμ22Ω2)(μ2λ2Ω2)Kμ22Ω2.(24)

Proof: Applying the series representation [32], when ρ→∞, we have λ→0 and λ2→0, by extracting the first term (n=0) of series representation, the high SNR approximate expressions can be given by

γ(Kμ12Ω1,μ1λΩ1)≈Ω1Kμ12(μ1λΩ1)Kμ12Ω1,(25)

and

γ(Kμ22Ω2,μ2λ2Ω2)≈Ω2Kμ22(μ2λ2Ω2)Kμ22Ω2.(26)

Substituting Eqs. (25) and (26) into Eqs. (17) and (19), respectively, Eqs. (23) and (24) can be obtained. The proof is completed.

Remark 3.3. From Eqs. (23) and (24), it can be observed that the asymptotic outage probabilities of D1 and D2 for RIS-NOMA are related to ρ, K, κ, and α. Hence the asymptotic outage probabilities of D1 and D2 for RIS-NOMA increase with the increase of ρ, K, κ, and α at high SNR.

Substituting Eqs. (23) and (24) into Eq. (22), the diversity orders of D1 and D2 for RIS-NOMA networks can be respectively calculated as

dD1=−limρ→∞log⁡(PD1∞(ρ))log⁡(ρ)=Kμ122Ω1,(27)

and

dD2=−limρ→∞log⁡(PD2∞(ρ))log⁡(ρ)=Kμ222Ω2.(28)

Remark 3.4. From Eqs. (27) and (28), we can observe that the diversity orders of D1 and D2 for RIS-NOMA are influenced by the number of reflecting elements of RIS, the Rician factor, and the path loss exponent.

Remark 3.5. It can be observed that the diversity orders increase as K, κ, and α increase. The outage probability curve becomes steeper with the increase of the diversity order, resulting in the faster convergence of the outage probability. Therefore, increasing the diversity order can improve the outage performance of RIS-NOMA at high SNR.

Remark 3.6. Similarly, the diversity order of Dn for RIS-OMA is Kμn22Ωn, which is also in connection with K, κ, and α.

3.5 Delay-Limited System Throughput

The system throughput is an important performance metric in wireless communication systems. The research on system throughput is of great significance for practical implementation. In the delay-limited transmission mode, the information is transmitted from the BS to users at a constant rate, which leads to outage due to the influence of the wireless fading channels. Therefore, the system throughput depends on the outage probability in the delay-limited transmission mode. The delay-limited system throughput of RIS-NOMA is expressed as

RDL=(1−PD1)r1+(1−PD2)r2,(29)

where PD1 and PD2 are the outage probabilities from Eqs. (17) and (19), respectively.

4  Ergodic Rate

The ergodic rate is a commonly used system performance metric in adaptive-rate transmission systems. In this section, the ergodic rates of two users for RIS-NOMA networks are analyzed.

4.1 Ergodic Rate of D1

Based on SIC principle, if D1 can successfully detect the signal of D2, the achievable rate of D1 can be given by RD1=log⁡(1+γD1→s1). On account of Eq. (8), the ergodic rate of D1 for RIS-NOMA networks is expressed as

RD1erg=E[log⁡(1+γD1→s1)].(30)

The ergodic rate of D1 is obtained in the following theorem.

Theorem 4.1. Under Rician fading channels, the exact expression for the ergodic rate of D1 for RIS-NOMA is calculated as

RD1erg=ρa1ln⁡2∫0∞Γ(ω1+1)−γ(ω1+1,yυ1)(1+ρa1y)Γ(ω1+1)dy,(31)

where ω1=Kμ12Ω1−1 and υ1=Ω1μ1.

Proof: See Appendix C.

Remark 4.1. From Eq. (31), we can observe that the ergodic rate of D1 for RIS-NOMA is dependent on ρ, K, κ, and α when the target SNR and the power allocation coefficient are constants. More specifically, with the increase of ρ, K, κ, and α, the ergodic rate of D1 for RIS-NOMA increases.

4.2 Ergodic Rate of D2

Assuming that D2 can detect its own signal s2, the achievable rate of D2 can be given by RD2=log⁡(1+γD2→s2). In virtue of Eq. (9), the ergodic rate of D2 for RIS-NOMA networks is expressed as

RD2erg=E[log⁡(1+γD2→s2)].(32)

The ergodic rate of D2 is obtained in the following theorem.

Theorem 4.2. Under Rician fading channels, the approximate expression for the ergodic rate of D2 for RIS-NOMA is calculated as

RD2erg≈πLln⁡2∑l=1La21−tl22a1+a2(tl+1)[1−1Γ(ω2+1)γ(ω2+1,1υ2tl+1ρa1(1−tl))],(33)

where tl=cos⁡(2l−12Lπ), ω2=Kμ22Ω2−1, and υ2=Ω2μ2.

Proof: See Appendix D.

Remark 4.2. From Eq. (33), it is observed that the ergodic rate of D2 for RIS-NOMA is related to ρ, K, κ, and α. Similarly, the ergodic rate of D2 for RIS-NOMA increases with ρ, K, κ, and α.

4.3 Ergodic Rate of Dn for RIS-OMA

For RIS-OMA networks, since Dn can detect its own signal sn, the achievable rate of Dn can be given by RDn,OMA=12log⁡(1+γn,Dn→snOMA). According to Eq. (11), the ergodic rate of Dn for RIS-OMA networks can be expressed as

RDn,OMAerg=E[12log⁡(1+γn,Dn→snOMA)].(34)

Similar to the derivation process of Eq. (31), the ergodic rate of Dn can be presented in the following corollary.

Corollary 4.1. Under Rician fading channels, the exact expression for the ergodic rate of Dn for RIS-OMA is given by

RDn,OMAerg=ρ2ln⁡2∫0∞Γ(ωn+1)−γ(ωn+1,yυn)(1+ρy)Γ(ωn+1)dy.(35)

4.4 Slope Analysis

Similar to the diversity order, the high SNR slope can be defined as the slope of the ergodic rate at high SNR, which describes how fast the ergodic rate increases with the transmit SNR. The high SNR slope can be expressed as

S=limρ→∞RD,erg∞(ρ)log⁡(ρ).(36)

To gain deep insights into the system performance, the approximate ergodic rate at high SNR is studied, which can be used to calculate the high SNR slope. However, the approximate ergodic rate of D1 at high SNR cannot be obtained from Eq. (31). For the convenience of analyses, the upper bound for the ergodic rate of D1 can be derived in the following theorem.

Theorem 4.3. Under Rician fading channels, the upper bound for the ergodic rate of D1 for RIS-NOMA can be calculated as

RD1,UBerg=log⁡(1+ρa1((Kμ1)2+KΩ1)).(37)

Proof: Based on Eq. (30), by adopting the Jensen’s inequality, the upper bound for the ergodic rate of D1 can be given by

RD1erg=E[log⁡(1+|H1Hϑ1G1|2ρa1)]≤log⁡(1+ρa1E(|H1Hϑ1G1|2)).(38)

On the basis of Eq. (12), the upper bound for the ergodic rate of D1 can be expressed as

RD1,UBerg=log⁡(1+ρa1E(|X1|2)).(39)

According to Eqs. (14) and (15), the upper bound for the ergodic rate of D1 can be calculated as

RD1,UBerg=log⁡(1+ρa1(E2(X1)+D(X1)))=log⁡(1+ρa1((Kμ1)2+KΩ1)).(40)

Hence Eq. (37) can be obtained. The proof is completed.

Remark 4.3. From Eq. (37), we can observe that the upper bound for the ergodic rate of D1 for RIS-NOMA is related to ρ, K, κ, and α. Specifically, the upper bound for the ergodic rate of D1 for RIS-NOMA increases with ρ, K, κ, and α.

The asymptotic upper bound for the ergodic rate of D1 at high SNR for RIS-NOMA networks can be provided in the following corollary.

Corollary 4.2. Based on Eq. (37), when ρ→∞, the asymptotic upper bound for the ergodic rate of D1 for RIS-NOMA can be given by

RD1,UBerg,∞=log⁡(ρa1((Kμ1)2+KΩ1)).(41)

Remark 4.4. From Eq. (41), we can observe that the asymptotic upper bound for the ergodic rate of D1 for RIS-NOMA depends on ρ, K, κ, and α. Similarly, increasing ρ, K, κ, and α, the asymptotic upper bound for the ergodic rate of D1 for RIS-NOMA increases at high SNR.

Substituting Eq. (41) into Eq. (36), the high SNR slope of D1 for RIS-NOMA networks can be calculated as

SD1=limρ→∞RD1,UBerg,∞(ρ)log⁡(ρ)=1.(42)

Remark 4.5. From Eq. (42), we can observe that the high SNR slope of D1 for RIS-NOMA is a non-zero value. This implies that the ergodic rate of D1 for RIS-NOMA tends to infinity at high SNR. The higher the high SNR slope, the steeper the ergodic rate curve, which results in the faster convergence of the ergodic rate. Hence the ergodic rate increases with the increase of the high SNR slope.

The asymptotic ergodic rate of D2 at high SNR for RIS-NOMA networks can be presented in the following corollary.

Corollary 4.3. Based on Eq. (32), when ρ→∞, the asymptotic ergodic rate of D2 for RIS-NOMA can be calculated as

RD2erg,∞=log⁡(1+a2a1).(43)

Proof: With the aid of Eqs. (9) and (12), we can obtain

limρ→∞γD2→s2=limρ→∞ρ|H2Hϑ2G2|2a2ρ|H2Hϑ2G2|2a1+1=limρ→∞ρ|X2|2a2ρ|X2|2a1+1=a2a1.(44)

In view of Eq. (32), when ρ→∞, the asymptotic ergodic rate of D2 can be calculated as

RD2erg,∞=limρ→∞E[log⁡(1+γD2→s2)]=E[log⁡(1+limρ→∞γD2→s2)]=log⁡(1+a2a1).(45)

Hence Eq. (43) can be obtained. The proof is completed.

Remark 4.6. From Eq. (43), it can be observed that the asymptotic ergodic rate of D2 for RIS-NOMA is a constant when the power allocation coefficient is fixed. Hence the asymptotic ergodic rate of D2 for RIS-NOMA remains unchanged at high SNR.

Substituting Eq. (43) into Eq. (36), the high SNR slope of D2 for RIS-NOMA networks can be calculated as

SD2=limρ→∞RD2erg,∞(ρ)log⁡(ρ)=0.(46)

Remark 4.7. From Eq. (46), it can be observed that the high SNR slope of D2 for RIS-NOMA is zero. This means that the ergodic rate of D2 for RIS-NOMA is a constant. Hence the ergodic rate of D2 for RIS-NOMA converges to a throughput ceiling at high SNR.

Similar to the derivation process of Eq. (37), the upper bound for the ergodic rate of Dn for RIS-OMA networks can be obtained in the following corollary.

Corollary 4.4. Under Rician fading channels, the upper bound for the ergodic rate of Dn for RIS-OMA is given by

RDn,OMAerg,UB=12log⁡(1+ρ((Kμn)2+KΩn)).(47)

The asymptotic upper bound for the ergodic rate of Dn at high SNR for RIS-OMA networks can be provided in the following corollary.

Corollary 4.5. Based on Eq. (47), when ρ→∞, the asymptotic upper bound for the ergodic rate of Dn for RIS-OMA can be given by

RDn,OMAerg,UB,∞=12log⁡(ρ((Kμn)2+KΩn)).(48)

Remark 4.8. Substituting Eq. (48) into Eq. (36), the high SNR slope of Dn for RIS-OMA networks is equal to 12.

4.5 Delay-Tolerant System Throughput

In the delay-tolerant transmission mode, the information is transmitted from the BS to users at any constant rate, which is subject to the channel conditions of the users. Hence the delay-tolerant system throughput of RIS-NOMA is expressed as

RDT=RD1erg+RD2erg,(49)

where RD1erg and RD2erg are the ergodic rates from Eqs. (31) and (33), respectively.

5  Numerical Results

In this section, numerical results are presented to evaluate the performance of RIS-NOMA networks over Rician fading channels. The effects of the Rician factor, the number of reflecting elements of the RIS, and the pass loss exponent on the performance of RIS-NOMA networks are discussed. The accuracy of the derived theoretical results can be verified by Monte Carlo simulations. In order to compare the performance with the RIS-NOMA networks, the conventional RIS-OMA networks are also provided. Without loss of generality, the power allocation factors of two users are set to a1=0.2 and a2=0.8, the target rates of two users are set to r1=0.0005 bits per channel use (BPCU) and r2=0.002 BPCU. In order to simplify the calculation, we adopt the normalized distance for dimensionless physical quantity. It is assumed that the distances from the BS to R2 and from R2 to D2 are normalized to unity. The normalized distances from BS to R1 and R2, from R1 to D1, and from R2 to D2 are set to d1,1=0.4, d2,1=0.5, d1,2=0.4, and d2,2=0.5, respectively. For clarity, the main parameters used for numerical results are summarized in Table 1.

5.1 Outage Probability

Fig. 2 plots the outage probabilities of two users vs. the transmit SNR for RIS-NOMA networks. The parameters are set to K=8, κ=−10 dB, and α=2. We can observe that the accurate outage probability curves given by Monte Carlo simulations are in good agreement with the derived theoretical outage probability results for RIS-NOMA networks, which verifies the accuracy of the derived theoretical outage probability results. It can be observed that the outage performance of RIS-NOMA networks is better than that of RIS-OMA networks. The reason is that RIS-NOMA can provide services for multiple users in the same time slot by adopting the superposition coding scheme, while RIS-OMA can only provide services for one user in each time slot. One can observe that the asymptotic outage probability curves converge to the derived theoretical results in the high SNR regime, which also demonstrates the accuracy of the theoretical analysis. As can be observed that the outage probability decreases with the increase of the transmit SNR. One can make the following observation from figure that the outage probabilities of two users converge to zeros in the high SNR regime and thus the non-zero diversity order can be obtained.

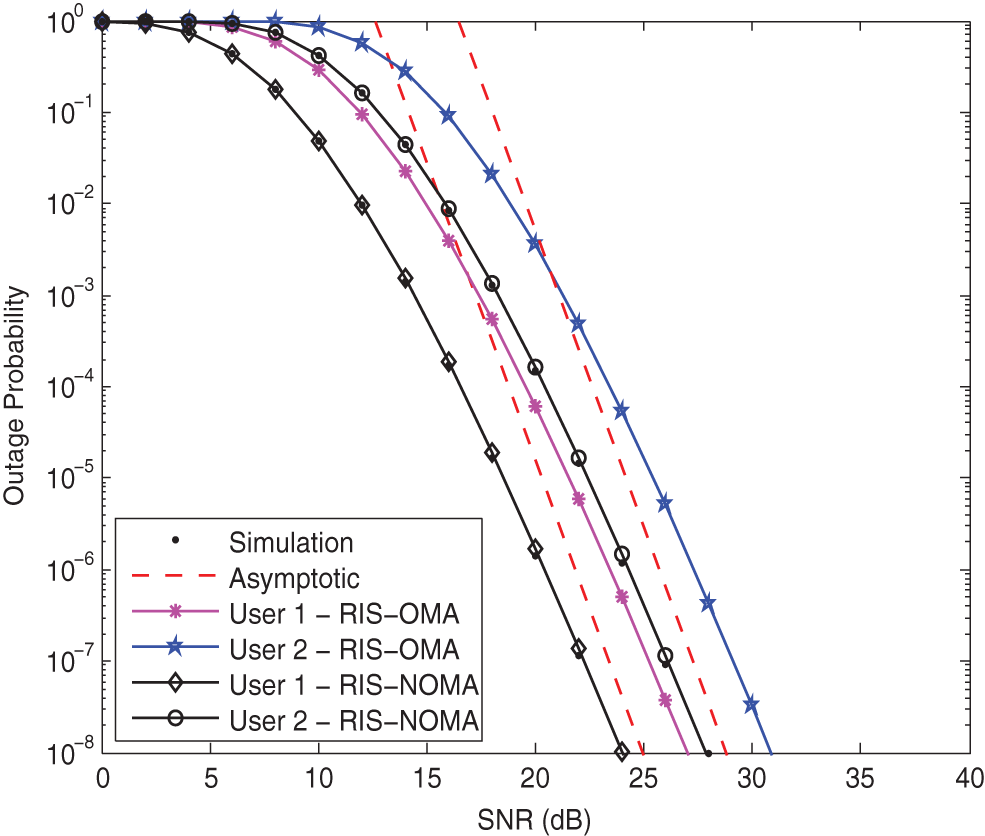
Figure 2: Outage probability vs. the transmit SNR when K = 8, κ = −10 dB, and α = 2

Fig. 3 plots the outage probabilities of two users vs. the transmit SNR with different K for RIS-NOMA networks. The parameters are set to κ=−10 dB and α=2. It is observed that the outage probabilities of two users for RIS-NOMA decrease with increasing the number of reflecting elements K, thus the outage performance for RIS-NOMA can be improved. The reason is that the diversity orders of two users for RIS-NOMA depend on the number of reflecting elements.

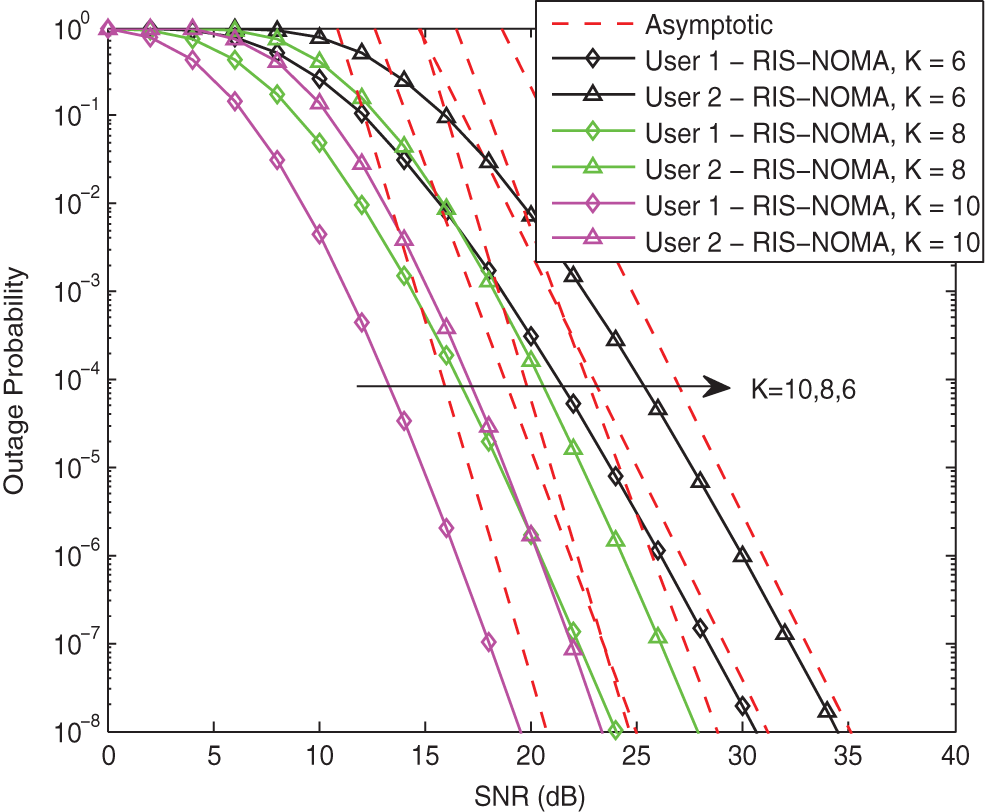
Figure 3: Outage probability vs. the transmit SNR with different K when κ = −10 dB and α = 2

In order to explain the influence of the Rician factor on the outage performance of RIS-NOMA networks, Fig. 4 plots the outage probabilities of two users vs. the transmit SNR with different κ for RIS-NOMA networks. The parameters are set to K=8 and α=2. As can be seen from the figure that as the value of the Rician factor κ increases, the outage probabilities of two users for RIS-NOMA reduce, hence the outage performance of RIS-NOMA becomes better. This is due to the fact that the diversity orders of two users for RIS-NOMA are related to the value of the Rician factor. The reason behind this phenomenon is that there are a large number of LoS components of Rician fading channels, which greatly improves the outage performance of RIS-NOMA networks.

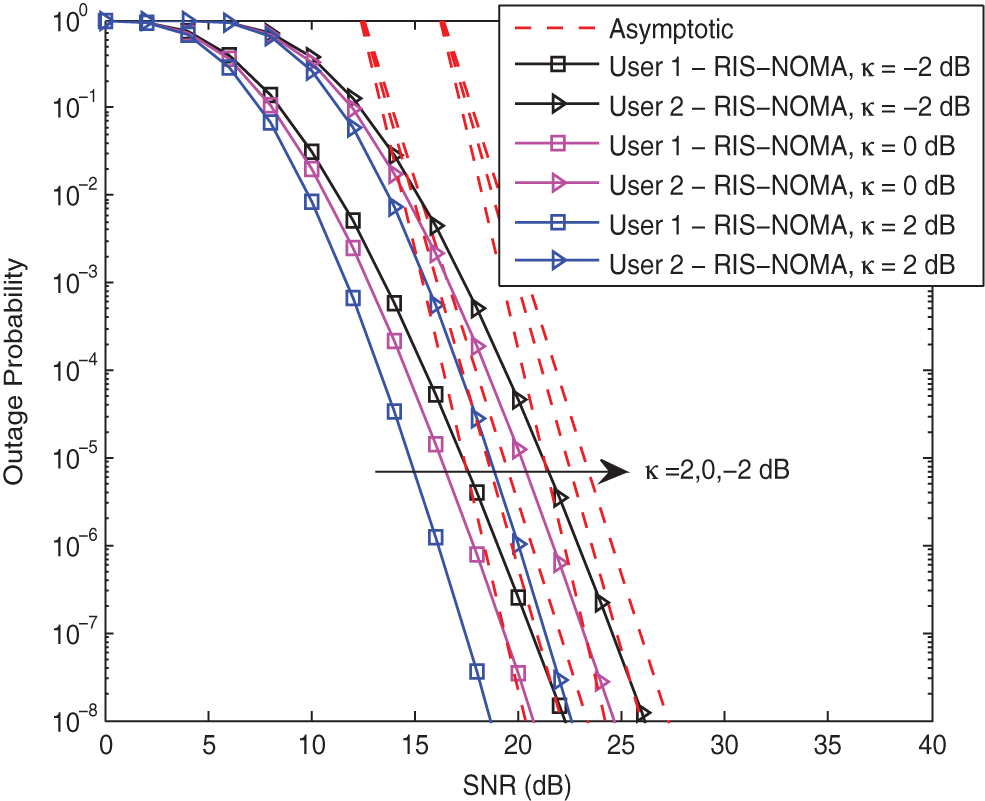
Figure 4: Outage probability vs. the transmit SNR with different κ when K = 8 and α = 2

To further illustrate the impact of the path loss exponent on the outage performance of RIS-NOMA networks, Fig. 5 plots the outage probabilities of two users vs. the transmit SNR with different α for RIS-NOMA networks. The parameters are set to K=8 and κ=−10 dB. It can be seen that the outage probabilities of two users for RIS-NOMA increase significantly with the decrease of the path loss exponent α, therefore the outage performance for RIS-NOMA deteriorates sharply. This is because that the path loss exponent reflects the number of obstacles in the propagation environment.

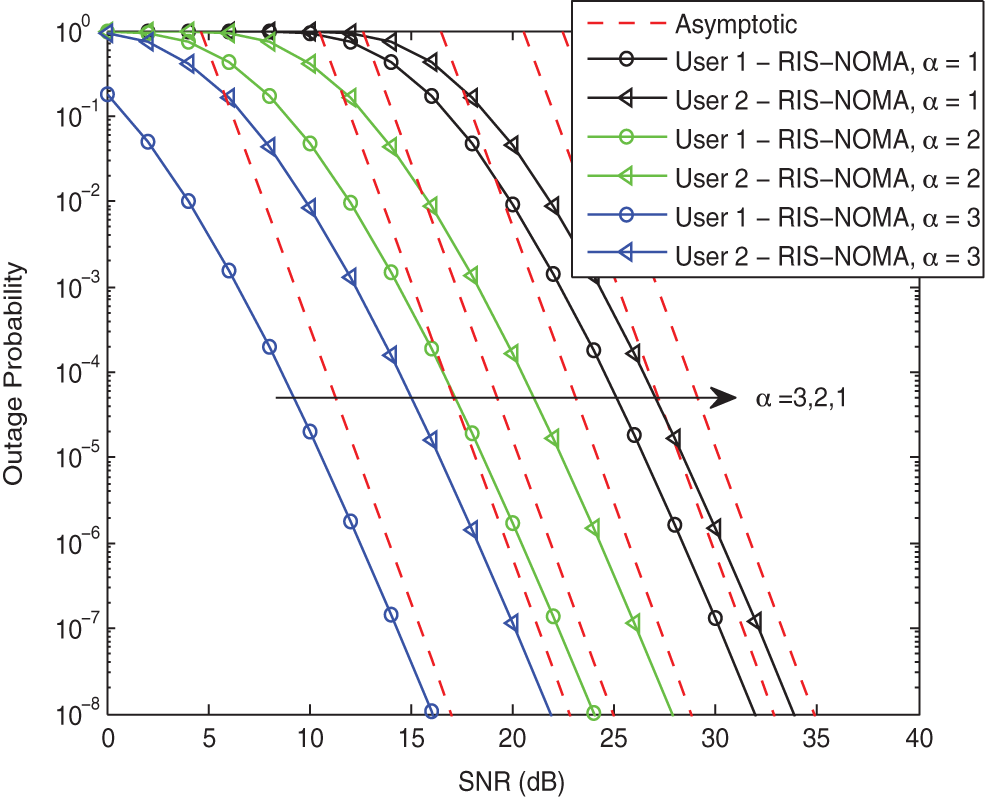
Figure 5: Outage probability vs. the transmit SNR with different α when K = 8 and κ = −10 dB

5.2 Ergodic Rate

Fig. 6 plots the ergodic rates of two users vs. the transmit SNR for RIS-NOMA networks. The parameters are set to K=20, κ=−10 dB, and α=2. We can see from the figure that the Monte Carlo simulation ergodic rate curves are completely consistent with the derived theoretical ergodic rate results for RIS-NOMA, which demonstrates the accuracy of the derived theoretical ergodic rate results. Another observation is that the upper bound curve for ergodic rate of D1 is very close to the derived theoretical ergodic rate. As can be observed from this figure that the ergodic rate of D2 converges to a throughput ceiling at high SNR and therefore leads to a zero high SNR slope. The important observation is that the ergodic rate of D1 for RIS-NOMA is higher than that of D1 for RIS-OMA at high SNR. The reason is that the high SNR slope of D1 for RIS-NOMA exceeds that of D1 for RIS-OMA. On the other hand, the ergodic rate of D2 for RIS-NOMA is lower than that of D2 for RIS-OMA at high SNR. This is because that D2 for RIS-NOMA has a smaller the high SNR slope compared with D2 for RIS-OMA.

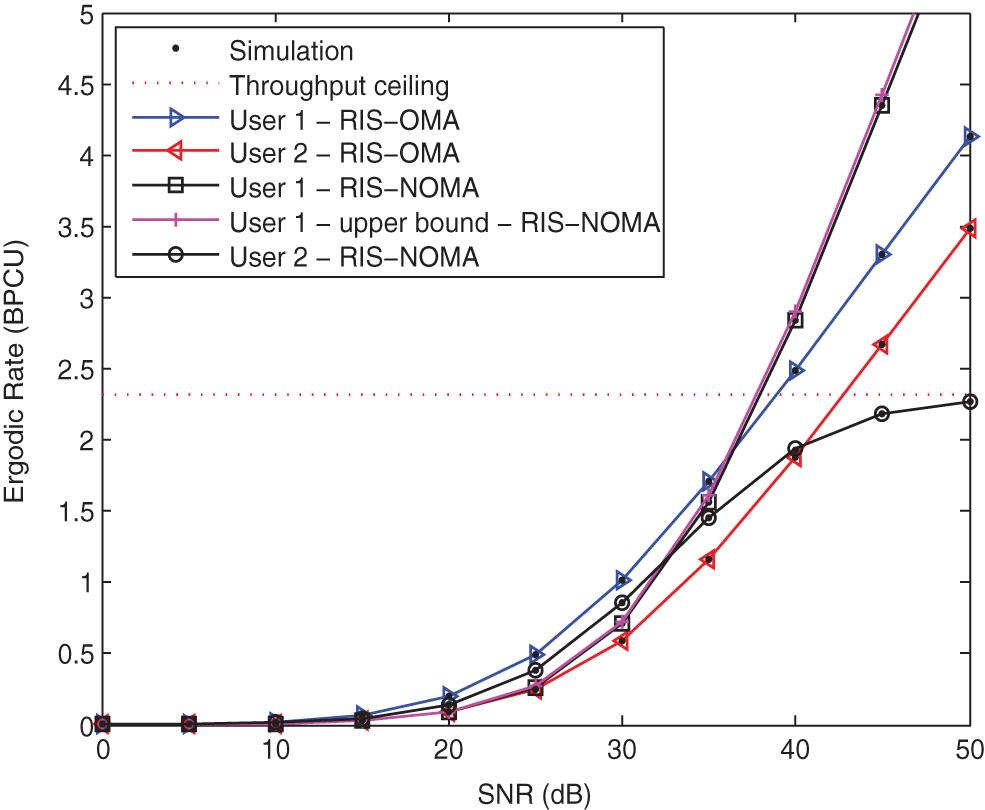
Figure 6: Ergodic rate vs. the transmit SNR when K = 20, κ = −10 dB, and α = 2

Considering the influence of the number of reflecting elements on the ergodic performance of RIS-NOMA networks, Fig. 7 plots the ergodic rates of two users vs. the transmit SNR with different K for RIS-NOMA networks. The parameters are set to κ=−10 dB and α=2. We can observe from the figure that the ergodic rates of two users for RIS-NOMA increase as the number of reflecting elements K increases. Another observation is that the ergodic rate of D1 is extremely large with respect to that of D2 for RIS-NOMA with the increase of the number of reflecting elements. This is due to the fact that there is a throughput ceiling at high SNR for the ergodic rate of D2 for RIS-NOMA.

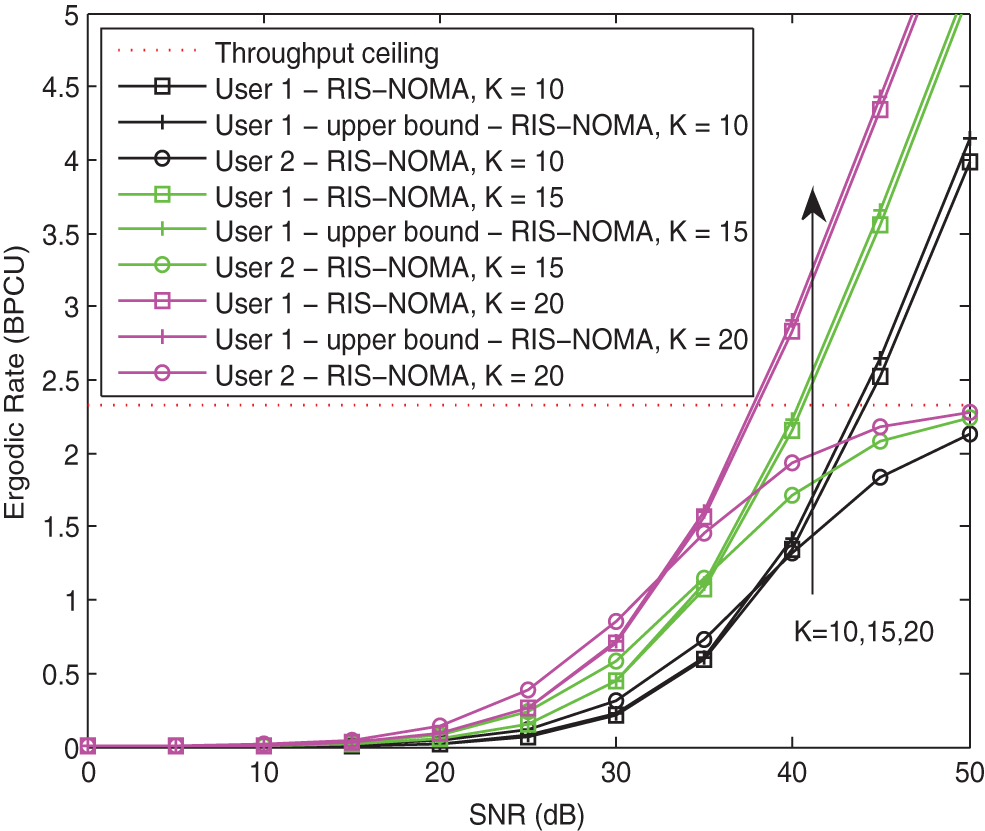
Figure 7: Ergodic rate vs. the transmit SNR with different K when κ = −10 dB and α = 2

5.3 System Throughput

Fig. 8 plots the system throughput vs. the transmit SNR with different K for RIS-NOMA networks in delay-limited transmission mode. The parameters are set to κ=−10 dB and α=2. It can be seen that RIS-NOMA is capable of enhancing the system throughput compared to RIS-OMA. The reason is that the system throughput depends on the outage probability in delay-limited transmission mode. One can make the following observation from figure that the system throughput of RIS-NOMA converges to a constant at high SNR. This phenomenon indicates that the system throughput no longer increases with the increase of SNR when it reaches a fixed value at high SNR. Another observation is that as the number of reflecting elements increases, the system throughput of RIS-NOMA can be significantly improved.

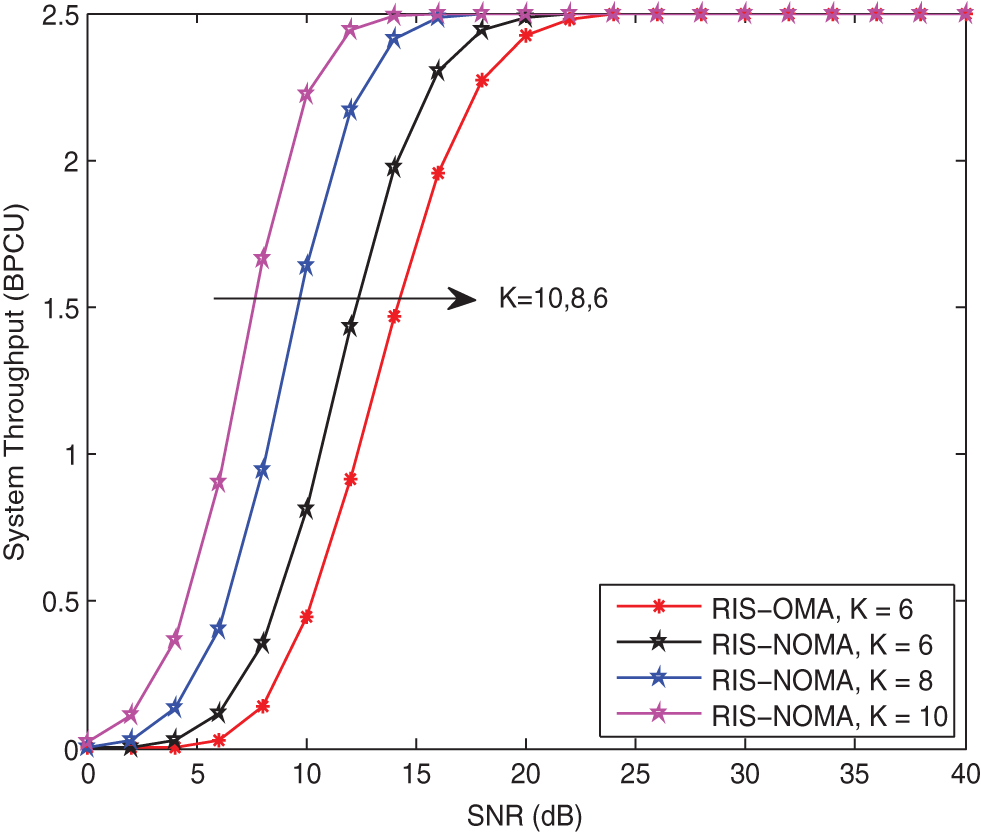
Figure 8: System throughput in delay-limited transmission mode vs. the transmit SNR with different K when κ = −10 dB and α = 2

As a further advance, Fig. 9 plots the system throughput vs. the transmit SNR with different K for RIS-NOMA networks in delay-tolerant transmission mode. The parameters are set to κ=−10 dB and α=2. It can be observed that RIS-NOMA can achieve a larger system throughput than RIS-OMA at high SNR. The main reason behind this is that the system throughput is related to the ergodic rate in delay-tolerant transmission mode. It is observed from the figure that the system throughput of RIS-NOMA becomes larger with increasing the number of reflecting elements.

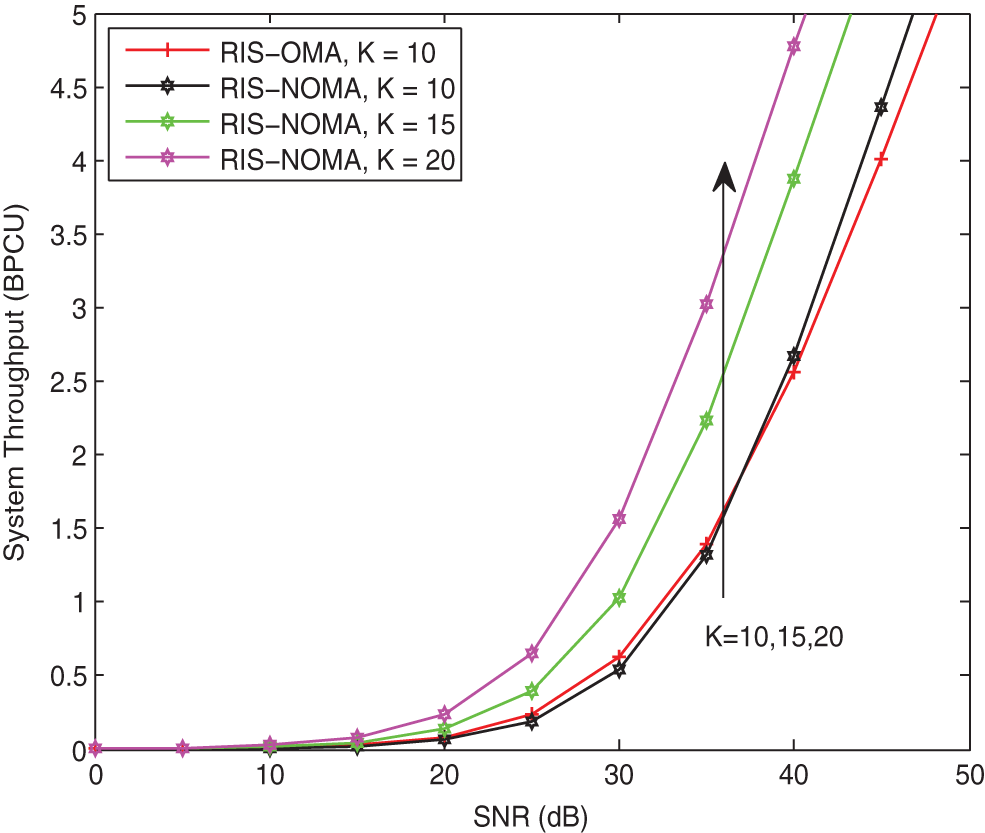
Figure 9: System throughput in delay-tolerant transmission mode vs. the transmit SNR with different K when κ = −10 dB and α = 2

6  Conclusion

In this paper, the system performance of RIS-assisted downlink NOMA communication networks has been investigated in terms of the outage probability, ergodic rate, and system throughput over Rician fading channels. The exact and asymptotic expressions for the outage probability and ergodic rate of two users for RIS-NOMA networks have been derived. Based on the theoretical analyses, the diversity orders and high SNR slopes of the two users have been obtained at high SNR. In addition, the system throughputs of RIS-NOMA networks have been derived in delay-limited and delay-tolerant transmission modes. Simulation results have indicated that the outage probability and ergodic rate of RIS-NOMA outperform that of RIS-OMA. It has been shown that the system throughput of RIS-NOMA is superior to that of RIS-OMA. Moreover, it has been demonstrated that the system performance of RIS-NOMA networks becomes better with increasing the number of reflecting elements and Rician factor. Based on this work, we will consider extending the research to multiple users in the future. In addition, optimized power allocation and multiple antennas of device nodes are also promising research directions.

Funding Statement: This work was supported in part by the Key R&D Program of Zhejiang Province under Grant No. 2020C05005, in part by the National Natural Science Foundation of China under Grants U2033215, 91738301, 91538202, and 91638301, in part by the Program for New Century Excellent Talents in University under Grant NCET-09-0025, and in part by the Fundamental Research Funds for the Central Universities. The work of C. Huang was partially supported by the China National Key R&D Program under Grant 2021YFA1000500, National Natural Science Foundation of China under Grant 62101492, Zhejiang Provincial Natural Science Foundation of China under Grant LR22F010002, Distinguished Young Scholars of the National Natural Science Foundation of China, Ng Teng Fong Charitable Foundation in the form of ZJU-SUTD IDEA Grant, Zhejiang University Education Foundation Qizhen Scholar Foundation, and Fundamental Research Funds for the Central Universities under Grant 2021FZZX001-21. The work of X. Yue was supported by the National Natural Science Foundation of China under Grant 62071052 and the R&D Program of Beijing Municipal Education Commission under Grant KM202011232003.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Ding, Z., Liu, Y., Choi, J., Sun, Q., Elkashlan, M. et al. (2017). Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Communications Magazine, 55(2), 185–191. DOI 10.1109/MCOM.35. [Google Scholar] [CrossRef]

 2.  Shirvanimoghaddam, M., Dohler, M., Johnson, S. J. (2017). Massive non-orthogonal multiple access for cellular IoT: Potentials and limitations. IEEE Communications Magazine, 55(9), 55–61. DOI 10.1109/MCOM.2017.1600618. [Google Scholar] [CrossRef]

 3.  Liu, Y., Qin, Z., Elkashlan, M., Ding, Z., Nallanathan, A. et al. (2017). Non-orthogonal multiple access for 5G and beyond. Proceedings of the IEEE, 105(12), 2347–2381. DOI 10.1109/JPROC.2017.2768666. [Google Scholar] [CrossRef]

 4.  Islam, S. M. R., Avazov, N., Dobre, O. A., Kwak, K. (2017). Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Communications Surveys and Tutorials, 19(2), 721–742. DOI 10.1109/COMST.2016.2621116. [Google Scholar] [CrossRef]

 5.  Montalban, J., Scopelliti, P., Fadda, M., Iradier, E., Desogus, C. et al. (2018). Multimedia multicast services in 5G networks: Subgrouping and non-orthogonal multiple access techniques. IEEE Communications Magazine, 56(3), 91–95. DOI 10.1109/MCOM.2018.1700660. [Google Scholar] [CrossRef]

 6.  Ding, Z., Yang, Z., Fan, P., Poor, H. V. (2014). On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Processing Letters, 21(12), 1501–1505. DOI 10.1109/LSP.97. [Google Scholar] [CrossRef]

 7.  Yue, X., Qin, Z., Liu, Y., Kang, S., Chen, Y. (2018). A unified framework for non-orthogonal multiple access. IEEE Transactions on Communications, 66(11), 5346–5359. DOI 10.1109/TCOMM.2018.2842217. [Google Scholar] [CrossRef]

 8.  Zhu, H., Wu, Q., Wu, X. J., Fan, Q., Fan, P. et al. (2022). Decentralized power allocation for MIMO-NOMA vehicular edge computing based on deep reinforcement learning. IEEE Internet of Things Journal, 9(14), 12770–12782. DOI 10.1109/JIOT.2021.3138434. [Google Scholar] [CrossRef]

 9.  Liu, Y., Liu, X., Mu, X., Hou, T., Xu, J. et al. (2021). Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Communications Surveys and Tutorials, 23(3), 1546–1577. DOI 10.1109/COMST.2021.3077737. [Google Scholar] [CrossRef]

10. Zhang, Z., Xiao, Y., Ma, Z., Xiao, M., Ding, Z. et al. (2019). 6G wireless networks: Vision, requirements, architecture, and key technologies. IEEE Vehicular Technology Magazine, 14(3), 28–41. DOI 10.1109/MVT.10209. [Google Scholar] [CrossRef]

11. Pan, C., Ren, H., Wang, K., Kolb, J. F., Elkashlan, M. et al. (2021). Reconfigurable intelligent surfaces for 6G systems: Principles, applications, and research directions. IEEE Communications Magazine, 59(6), 14–20. DOI 10.1109/MCOM.001.2001076. [Google Scholar] [CrossRef]

12. Huang, C., Zappone, A., Alexandropoulos, G. C., Debbah, M., Yuen, C. (2019). Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Transactions on Wireless Communications, 18(8), 4157–4170. DOI 10.1109/TWC.7693. [Google Scholar] [CrossRef]

13. Huang, C., Hu, S., Alexandropoulos, G. C., Zappone, A., Yuen, C. et al. (2020). Holographic MIMO surfaces for 6G wireless networks: Opportunities, challenges, and trends. IEEE Wireless Communications, 27(5), 118–125. DOI 10.1109/MWC.7742. [Google Scholar] [CrossRef]

14. Zhou, G., Pan, C., Ren, H., Wang, K., Nallanathan, A. (2020). A framework of robust transmission design for IRS-aided MISO communications with imperfect cascaded channels. IEEE Transactions on Signal Processing, 68, 5092–5106. DOI 10.1109/TSP.2020.3019666. [Google Scholar] [CrossRef]

15. Wu, Q., Zhang, R. (2020). Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Communications Magazine, 58(1), 106–112. DOI 10.1109/MCOM.35. [Google Scholar] [CrossRef]

16. Wei, L., Huang, C., Alexandropoulos, G. C., Yuen, C., Zhang, Z. et al. (2021). Channel estimation for RIS-empowered multi-user MISO wireless communications. IEEE Transactions on Communications, 69(6), 4144–4157. DOI 10.1109/TCOMM.2021.3063236. [Google Scholar] [CrossRef]

17. Yang, Z., Chen, M., Saad, W., Xu, W., Shikh-Bahaei, M. et al. (2022). Energy-efficient wireless communications with distributed reconfigurable intelligent surfaces. IEEE Transactions on Wireless Communications, 21(1), 665–679. DOI 10.1109/TWC.2021.3098632. [Google Scholar] [CrossRef]

18. Huang, C., Mo, R., Yuen, C. (2020). Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning. IEEE Journal on Selected Areas in Communications, 38(8), 1839–1850. DOI 10.1109/JSAC.49. [Google Scholar] [CrossRef]

19. Yang, Z., Xu, W., Huang, C., Shi, J., Shikh-Bahaei, M. (2021). Beamforming design for multiuser transmission through reconfigurable intelligent surface. IEEE Transactions on Communications, 69(1), 589–601. DOI 10.1109/TCOMM.26. [Google Scholar] [CrossRef]

20. Huang, C., Yang, Z., Alexandropoulos, G. C., Xiong, K., Wei, L. et al. (2021). Multi-hop RIS-empowered terahertz communications: A DRL-based hybrid beamforming design. IEEE Journal on Selected Areas in Communications, 39(6), 1663–1677. DOI 10.1109/JSAC.2021.3071836. [Google Scholar] [CrossRef]

21. Ding, Z., Poor, H. V. (2020). A simple design of IRS-NOMA transmission. IEEE Communications Letters, 24(5), 1119–1123. DOI 10.1109/COML.4234. [Google Scholar] [CrossRef]

22. Yue, X., Liu, Y. (2022). Performance analysis of intelligent reflecting surface assisted NOMA networks. IEEE Transactions on Wireless Communications, 21(4), 2623–2636. DOI 10.1109/TWC.2021.3114221. [Google Scholar] [CrossRef]

23. Ding, Z., Schober, R., Poor, H. V. (2020). On the impact of phase shifting designs on IRS-NOMA. IEEE Wireless Communication Letters, 9(10), 1596–1600. DOI 10.1109/LWC.5962382. [Google Scholar] [CrossRef]

24. Hou, T., Liu, Y., Song, Z., Sun, X., Chen, Y. et al. (2020). Reconfigurable intelligent surface aided NOMA networks. IEEE Journal on Selected Areas in Communications, 38(11), 2575–2588. DOI 10.1109/JSAC.49. [Google Scholar] [CrossRef]

25. Zheng, B., Wu, Q., Zhang, R. (2020). Intelligent reflecting surface-assisted multiple access with user pairing: NOMA or OMA? IEEE Communications Letters, 24(4), 753–757. DOI 10.1109/COML.4234. [Google Scholar] [CrossRef]

26. Khaleel, A., Basar, E. (2022). A novel NOMA solution with RIS partitioning. IEEE Journal of Selected Topics in Signal Processing, 16(1), 70–81. DOI 10.1109/JSTSP.2021.3127725. [Google Scholar] [CrossRef]

27. Cheng, Y., Li, K. H., Liu, Y., Teh, K. C., Karagiannidis, G. K. (2021). Non-orthogonal multiple access (NOMA) with multiple intelligent reflecting surfaces. IEEE Transactions on Wireless Communications, 20(11), 7184–7195. DOI 10.1109/TWC.2021.3081423. [Google Scholar] [CrossRef]

28. Hemanth, A., Umamaheswari, K., Pogaku, A. C., Do, D. T., Lee, B. M. (2020). Outage performance analysis of reconfigurable intelligent surfaces-aided NOMA under presence of hardware impairment. IEEE Access, 8, 212156–212165. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

29. Cheng, Y., Li, K. H., Liu, Y., Teh, K. C., Vincent Poor, H. (2021). Downlink and uplink intelligent reflecting surface aided networks: NOMA and OMA. IEEE Transactions on Wireless Communications, 20(6), 3988–4000. DOI 10.1109/TWC.2021.3054841. [Google Scholar] [CrossRef]

30. Gong, X., Huang, C., Yue, X., Liu, F., Yang, Z. (2022). Performance analysis for reconfigurable intelligent surface assisted downlink NOMA networks. IET Communications, 16(13), 1593–1605. DOI 10.1049/cmu2.12375. [Google Scholar] [CrossRef]

31. Simon, M. K. (2006). Probability distributions involving gaussian random variables. USA: Springer. [Google Scholar]

32. Gradshteyn, I. S., Ryzhik, I. M. (2000). Table of integrals, series and products. 6th edition. New York, NY, USA: Academic Press. [Google Scholar]

33. Primak, S., Kontorovitch, V., Lyandres, V. (2004). Stochastic methods and their applications to communications: Stochastic differential equations approach. West Sussex, UK: Wiley. [Google Scholar]

34. Hildebrand, B. F. (1987). Introduction to numerical analysis. New York, NY, USA: Dover. [Google Scholar]

Appendix A: Proof of Theorem 1

Substituting Eqs. (7) and (8) into Eq. (16), based on Eq. (12), the outage probability of D1 for RIS-NOMA networks is expressed as

PD1=1−Pr(|H1Hϑ1G1|2>λ1,|H1Hϑ1G1|2>λ2)=1−Pr(|H1Hϑ1G1|2>max(λ1,λ2))=1−Pr(|H1Hϑ1G1|2>λ)=Pr(∑k=1K|G1kH1k|<λ),(A.1)

where λ≜max(λ1,λ2), λ1=γth1ρa1, and λ2=γth2ρ(a2−a1γth2) with a2>a1γth2.

Applying the series of Laguerre polynomials [33], the PDF of X1=∑k=1K|G1kH1k| is approximated as

fX1(x)≈xω1(υ1)ω1+1Γ(ω1+1)exp⁡(−xυ1),(A.2)

where ω1=Kμ12Ω1−1 and υ1=Ω1μ1.

Substituting Eq. (A.2) into Eq. (A.1), the outage probability of D1 can be approximated as

PD1=Pr(X1<λ)≈∫0λxω1(υ1)ω1+1Γ(ω1+1)exp⁡(−xυ1)dx=1(υ1)ω1+1Γ(ω1+1)∫0λxω1e−xυ1dx.(A.3)

Using t=xυ1, the outage probability of D1 is expressed as

PD1≈1Γ(ω1+1)∫0λυ1tω1e−tdt.(A.4)

Applying the lower incomplete Gamma function [32], the outage probability of D1 can be calculated as

PD1≈1Γ(ω1+1)∫0λυ1t(ω1+1)−1e−tdt=1Γ(ω1+1)γ(ω1+1,λυ1)=1Γ(Kμ12Ω1)γ(Kμ12Ω1,μ1λΩ1),(A.5)

where Ω1=α1,1α1,2{1−π216(1+κ)2[L12(−κ)]4} and μ1=πα1,1α1,24(1+κ)[L12(−κ)]2. Thus, Eq. (17) can be obtained. The proof is completed.

Appendix B: Proof of Theorem 2

Substituting Eq. (9) into Eq. (18), the outage probability of D2 for RIS-NOMA networks can be expressed as

PD2=Pr(ρ|H2Hϑ2G2|2a2ρ|H2Hϑ2G2|2a1+1<γth2)=Pr(|H2Hϑ2G2|2<λ2)=Pr(∑k=1K|G2kH2k|<λ2),(B.1)

where the last equality holds because of Eq. (12).

Similarly, the PDF of X2=∑k=1K|G2kH2k| by utilizing the series of Laguerre polynomials can be approximated as

fX2(x)≈xω2(υ2)ω2+1Γ(ω2+1)exp⁡(−xυ2),(B.2)

where ω2=Kμ22Ω2−1 and υ2=Ω2μ2.

Substituting Eq. (B.2) into Eq. (B.1), using u=xυ2, the outage probability of D2 can be approximated as

PD2=Pr(X2<λ2)≈∫0λ2xω2(υ2)ω2+1Γ(ω2+1)exp⁡(−xυ2)dx=1Γ(ω2+1)∫0λ2υ2uω2e−udu.(B.3)

By referring to the lower incomplete Gamma function, the outage probability of D2 can be calculated as

PD2≈1Γ(ω2+1)γ(ω2+1,λ2υ2)=1Γ(Kμ22Ω2)γ(Kμ22Ω2,μ2λ2Ω2),(B.4)