Numerical Simulation about the Characteristics of the Store Released from the Internal Bay in Supersonic Flow

1  Introduction

In order to keep the fighter airplane smooth, reduce air resistance and radar scattering cross section, improve stealth performance, increase mobility and avoid the serious aerodynamic heating problem of the store under supersonic conditions, the store is embedded in the internal bay [1–3]. However, this will make the flow field between the store and the internal bay complex. In addition, there is aerodynamic interference between the store and the internal bay when the store falls, so it is difficult to predict the motion trajectory of the store. If the store is separated in an unsafe way, its hit rate will be reduced, and it may even collide with the internal bay [4]. Therefore, it is necessary to study the separation of the store.

In the study of separation characteristics, Johnson et al. [5] and Davis et al. [6] simulated the separation of the internal storage through numerical simulation and wind tunnel experiments. It is found that the motion trajectory of the internal store will change at different time under the same launch conditions, which is caused by the unsteady flow field of the internal bay. Some scholars [7–12] have studied the hybrid complex variable element-free Galerkin (HCVEFG) method, which can improve computational efficiency. The research of Westmoreland [13] showed that applying appropriate ejection force to the store is conducive to the separation. Stallings [14] studied the separation of the store by wind tunnel experiment. The experimental results show that the presence of hatch will affect the pitching moment of store after leaving the internal bay. For the external store, the research of Mizrahi et al. [15,16] suggested that the rolling motion in the separation process of external store is affected by the relation between the ejection period and the low structural frequencies of the wing. A similarity law between the separation of a heavy store and the unsteady wind tunnel free flight tests of air-launch rockets was derived, is can be used to the research of the separation of a heavy store [17,18]. A modeling method based reduced order model for external store separation is proposed, which can make high fidelity predictions for both surface pressure and shear stress distributions at minimal computational cost [19,20].

At present, the research at home and abroad mainly focuses on cavity flow control about the control devices, including passive control and active control. The internal bay is one of the typical applications of cavity flow. For the passive control method, the flow field is usually controlled by changing the geometry of the cavity, such as slanted aft wall [21,22], adding the spoiler of different shapes [23,24], and passive resonant absorbers [25]. The active control method is to inject energy into the shear layer and cavity flow field, such as leading edge blowing [26,27], mass-injection [28,29], actuators [30], micro-jets [31]. For the influence of flow control on the separation characteristics of the store, the research of Guo et al. [32] indicated that the cylindrical spoiler and leading edge blowing are conducive to the safe separation of the internal bay with the Ma = 3.5. To improve the separation characteristics of the internal store, Song et al. [33,34] installed a cuboid control device at the leading edge of the internal bay.

With the further and faster development of fighter airplanes, the engineering application background of the separation of the store at high Mach number (Ma = 4) is wider and wider. Based on the research progress at home and abroad, the research on the store separation mainly focuses on the subsonic and transonic fields. Although several scholars have begun to study the store separation in supersonic flow, there are few researches on the store separation with Ma > 3. Whether the effect of initial launching conditions on the separation of the store at high Mach number is same as that at low Mach number and whether the control measures can improve the separation characteristics of the store at high Mach number need to be studied. In this paper, based on an unstructured grid Realizable k−ε simulation method coupled with equation with six degrees of freedom has been proved that it can well simulate the motion trajectory of the store through the calculation example verification. Then the influence of different initial conditions on the separation of the store and whether the control measures can improve the separation characteristics of the store are analyzed by using a validated numerical simulation method.

2  Numerical Method

A three-dimensional compressible flow solver based on an unstructured mesh technique is used for numerical simulation. The overset grid method and the Realizable k−ε turbulence model coupled with equation with six degrees of freedom are used to calculate the motion trajectory of the store released from the internal bay. For spatial discretization, the second-order TVD (Total Variation Diminishing) scheme is adopted. The dual time step method is used for time discretization.

The governing equation is the Navier-Stokes equation, which is expressed in the three-dimensional rectangular coordinate system [35] is as follows:

∂Q∂t+∂(Fi−Gi)∂x+∂(Fg−Gg)∂y+∂(Fh−Gh)∂z=S⋅(1)

In Eq. (1), Q is a vector of conserved variables, S⋅ is a vector of source terms, F is vectors of convective flux, G is vectors of viscous flux, and their definition forms are as follows:

Q=[Eρρuρvρw]T(2)

Fi=[(E+P)uρuρu2+Pρvuρwu]TFg=[(E+P)vρvρuvρv2+Pρwv]TFh=[(E+P)wρwρuwρvwρw2+P]T(3)

Gi=[Θx0τxxτxyτxz]TGg=[Θy0τyxτyyτyz]TGh=[Θz0τzxτzyτzz]T(4)

Θx=uτxx+vτxy+wτxz+kTxΘy=uτyx+vτyy+wτyz+kTyΘz=uτzx+vτzy+wτzz+kTz(5)

k=CpμPr(6)

In Eqs. (2)–(6), ρ represents the gas density, P represents the pressure, E represents the internal energy, v=(u,v,w) represents the velocity in the three coordinate axis directions of the rectangular coordinate system, respectively. τ is the viscous stress tensor. k is the thermal conductivity. Cp is the constant pressure specific heat capacity Pr is the number of Prandtl. T is the temperature. Eq. (7) is introduced to close the equations:

P=nRT,E=Pγ−1+12ρ(u2+v2+w2)(7)

where the value of specific heat ratio γ is 1.4. When heat conduction and body force are not considered, the integral form of N-S equation is expressed as Eq. (8)

∂∂t∫ΩWdΩ+∮∂Ω(Fc−Fv)dS=0(8)

where ∂Ω is the boundary of control body Ω. dS is the unit area of ∂Ω. n=(nx,ny,nz) is the unit normal vector. Fc, Fv represent convective flux and viscous flux in integral form, respectively.

Fc=[ρVρuV+nxPρvV+nyPρwV+nzP(ρE+p)V],Fv=[0nxτxx+nxτxy+nxτxznxτyx+nxτyy+nxτyznxτzx+nxτzy+nxτzznxΘx+nxΘy+nxΘz](9)

V is normal velocity of dS which is expressed as Eq. (10).

V=v⋅n=u⋅nx+v⋅ny+w⋅nz(10)

Realizable k−ε turbulence model has been proven to be able to simulate different types of flows, such as rotating uniform shear flow, jet flow, boundary layer flow, mixed flow, and flow separation. Compared with the standard k−ε turbulence model, the Realizable k−ε turbulence model has better performance in dealing with strong streamline bending, vortex and rotation [36]. Therefore, the Realizable k−ε turbulence model is more suitable for simulating the flow field of the store with complex shapes. The transport equation of the Realizable k−ε is as follows:

∂∂t(ρk)+∂∂xi(ρkuj)=∂∂xi[(μ+μtσk)∂k∂xj]+Gk+Gb−ρε−YM+Sk(11)

∂∂t(ρε)+∂∂xj(ρεuj)=∂∂xj[(μ+μtσε)∂ε∂xj]+ρC1Sε−ρC2ε2k+vε+C1εεkC3εGb+Sε(12)

C1=max(0.43,ηη+5),η=Skε(13)

Among them, C1ε=1.44, C2=1.9, C3ε=0.09, σk=1.0, σε=1.2, the turbulent kinetic energy generated by the velocity gradient is denoted by Gk, the turbulent kinetic energy generated by buoyancy is denoted by Gb, and the contribution of pulsation expansion in compressible turbulence is denoted by YM, Sk and Sε depend on the specific calculation conditions [36].

Where

μt=ρCμk2ε,Cμ=1A0+AskU∗ε(14)

U∗=SijSij+Ω~ijΩ~ij,Ω~ij=Ωij−2εijkωk,Ωij=Ω¯ij−εijkωk(15)

where Ω¯ij is the mean rate-of-rotation tensor viewed in a rotating reference frame with the angular velocity ωk. The model of constants A0 and As are as follows:

A0=4.04,As=6cos⁡ϕ,ϕ=13arccos⁡(6W)(16)

W=SijSjkSkjS~,S~=SijSij,Sij=12(∂uj∂xi+∂ui∂xj)(17)

For high Mach number flow, the influence of compressibility on turbulence is reflected in YM

YM=ρε2M2(18)

The motion trajectory of the store is solved by solving six-degree-of-freedom equation, in which the equation of motion of the centroid is as follows:

{fx=m(vx⋅+vzωy−vyωz)fy=m(vy⋅+vxωz−vzωx)fz=m(vz⋅+vyωx−vxωy)(19)

{Mx=ωx⋅Ixx−ωz⋅Izx−ωyωz(Izz−Iyy)−ωxωyIzxMy=ωy⋅Iyy−ωxωz(Ixx−Izz)−(ωx2−ωz2)IzxMz=ωz⋅Izz−ωx⋅Izx+ωxωy(Iyy−Ixx)+ωyωzIzx(20)

The relationship between attitude angle and angular velocity is given by Eq. (21)

{θ⋅=ωycos⁡γ−ωzsin⁡γφ⋅=(ωysin⁡γ+ωzcos⁡γ)/cos⁡θγ⋅=ωx+tan⁡θ(ωysin⁡γ+ωzcos⁡γ)(21)

{f=fxi+fyj+fzkM=Mxi+Myj+Mzkω=ωxi+ωyj+ωzk(22)

where f and M are the resultant force and resultant moment, respectively. m is the mass. I is moment of inertia. v and ω the linear velocity and angular velocity, respectively. θ, φ and γ are the pitch angle, yaw angle, and roll angle, respectively. From these three equations, the attitude and motion trajectory of the store released from the internal bay can be obtained.

3  Numerical Modeling

For the internal bay, the length the width and the depth are 5.32, 0.5, 0.5 m, respectively. The length of the store is 4.8 m, the position of centroid is 2.3 m away from the center point of the tail of the store, and the overall mass of the store is 1040 kg. The moment of inertia around the X axis is 32 kg⋅m2, and the moment of inertia around the Y and Z axes is 1580 kg⋅m2. Two different shape control measures are adopted to improve the separation characteristics of the store. Among them, the cylindrical rod control measure is installed on the front plate of the internal bay, and another control measure is to change the aft wall to slanted wall. The geometric dimensions of the two passive control measures are shown in Fig. 1.

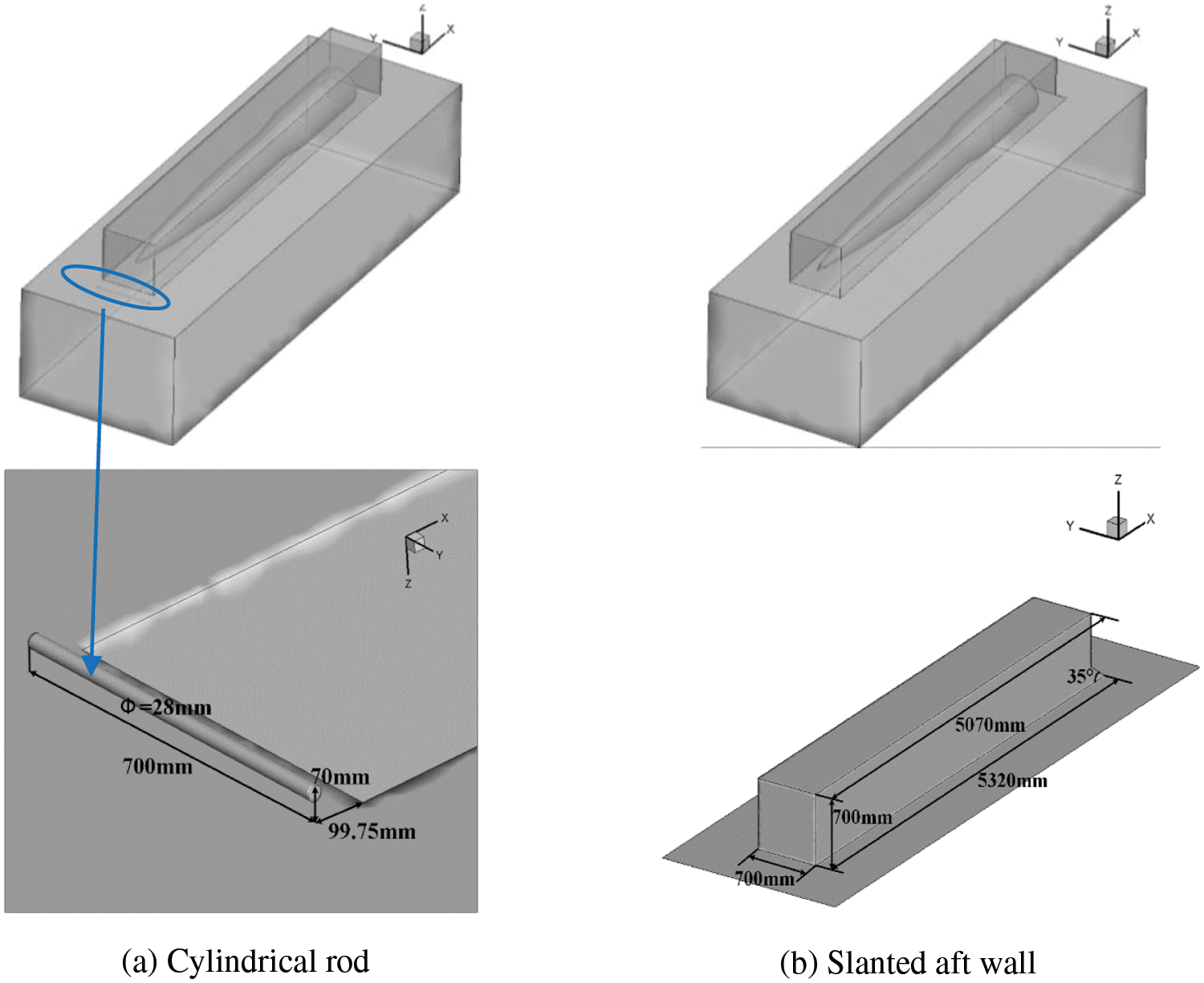
Figure 1: The geometric dimensions of the two control measures

To understand the influence of centroid position, launching height, initial velocity and different control measures on the separation characteristics of store, a total of six conditions are calculated in which the Mach number of free stream flow is 4 and the angle of attack is 0°. The detailed parameter value of each condition is shown in Table 1.

The overset grid includes background grid and component grid which are generated independently. Then the CFD++ software is used to combine the two sets of grids together to establish the topological relationship by “digging holes”. The grids inside the internal bay, the store and the place where the store is to fall are densified, and the total number of grids is 3.34 million. To ensure the accuracy of hole excavation and interpolation, the ratio of the size of the background grid and the grid of the store at the junction should be kept between 1–1.2. The spatial dimension of grid is 3D. The characteristic inlet/outlet boundary is adopted for the external boundary of the overall calculation domain, the internal bay and the surface of the store are set as adiabatic non slip wall boundary, and the overset boundary is adopted for the external boundary of the store. The time step is 2.5 × 10−4  s and the calculation step is 1000. The total calculation time of internal store falling is 0.25 s the grid used for calculation is shown as Fig. 2.

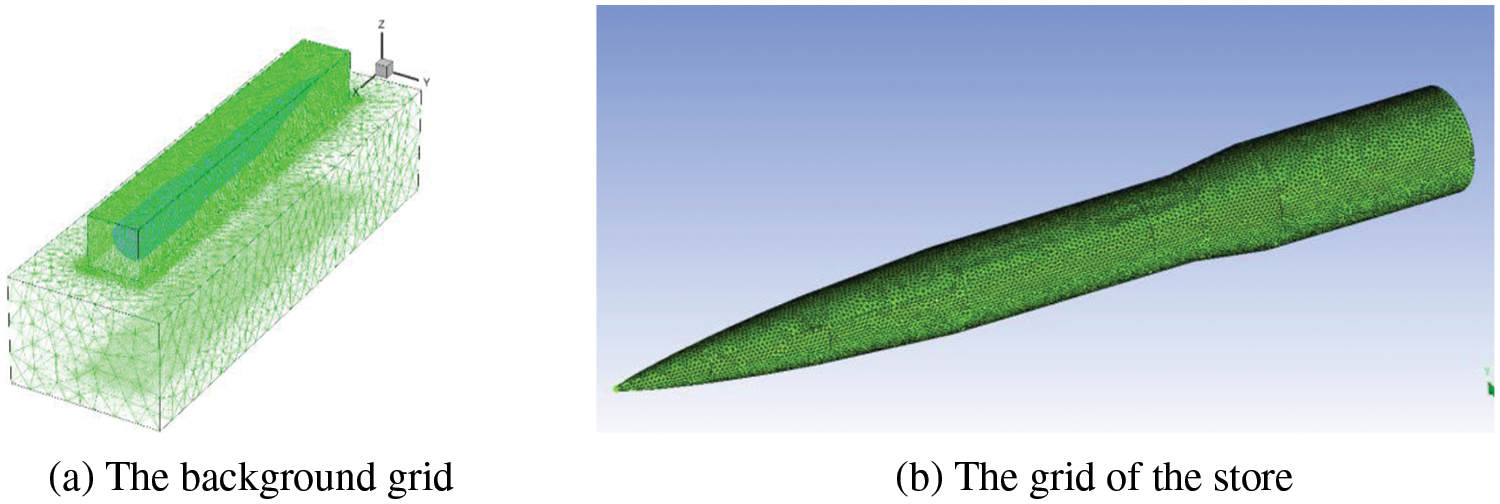
Figure 2: The grid used for calculation

4  Model Validation and Analysis of Numerical Simulation Results

The model in the literature [37] is selected as a verification example for investigating the accuracy of the numerical simulation method. According to the experiment condition, the store is launched by ejection which is subjected to a vertical downward ejection force and a pitching moment. The values of these two parameters are 53388 N and 12140 N⋅m, respectively. The length and the diameter of the store are 3.38 and 0.508 m, the position of centroid is 1.42 m away from the tip of the head of the store, and the overall mass of the store is 907.2 kg. The moment of inertia around the X axis is 27 kg⋅m2, and the moment of inertia around the Y and Z axes is 488 kg⋅m2.

The numerical simulation method and mesh division are same as the above. Fig. 3 gives the attitude angle of the store at different time. It can be seen that the pitch angle at first increases which is cause by the ejection force. After the ejection force is removed, the pitch angle decreases due to the effect of gravity and aerodynamic force. The calculated results are consistent with the experimental values quite well, which also increases the reliability of the numerical method.

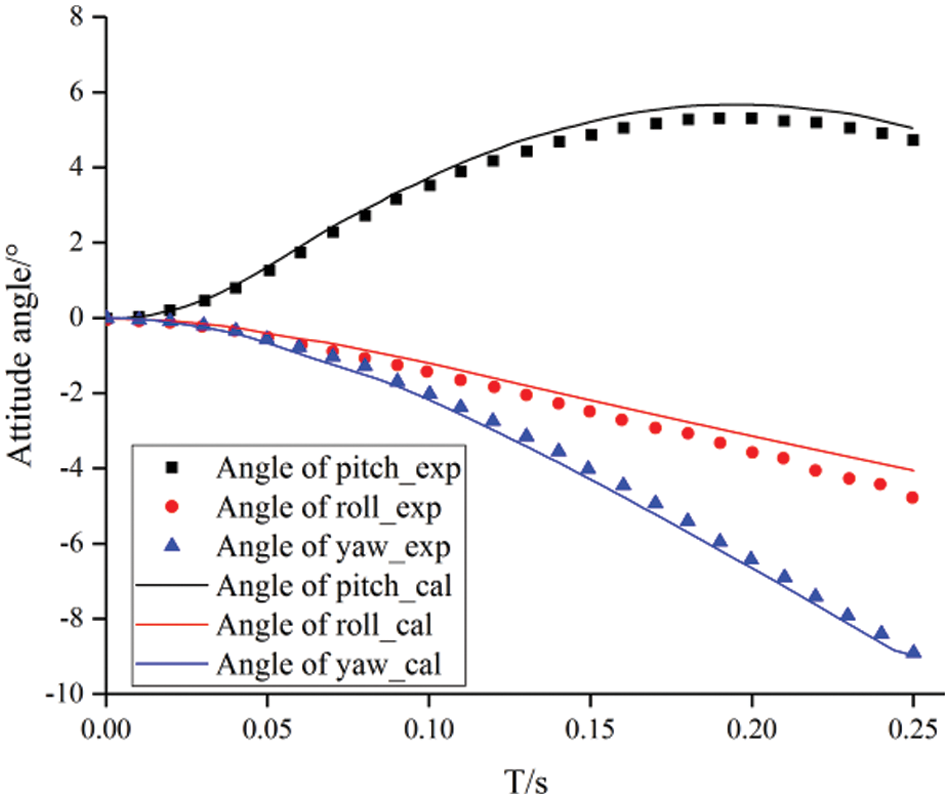
Figure 3: Comparison of calculated results and experimental values

The separation quality of the store can be divided into two types: safe separation and unsafe separation. Unsafe separation can be divided into two cases: one case is that the distance between the store and the internal bay decreases gradually due to the change of attitude angle and motion trajectory. Another case is the direct collision between the store and the internal bay after separation. These two situations should be avoided. The safe separation should achieve the conditions of small change of attitude angle, leave quickly from the flow field and no collision with the internal bay.

Compared with condition 1 (Reference centroid), the position of centroid has been moved horizontally forward along the X-axis by 0.65 m in the condition 2 (The position of centroid moves forward), in which the centroid of condition 1 is recorded as the reference centroid. Fig. 4 compares the attitude angles of the store at different centroid positions. The store under the two conditions has a certain degree of pitch when it released from the internal bay. It can be found that the pitch angel of the store whose centroid moves forward at 0–0.4 s is greater, while the pitch angle of the store with reference centroid after 0.4 s is greater. As for the yaw angle and roll angle, there is little different between two conditions. In general, the position of centroid will affect the separation of the store, so it should be considered in the design.

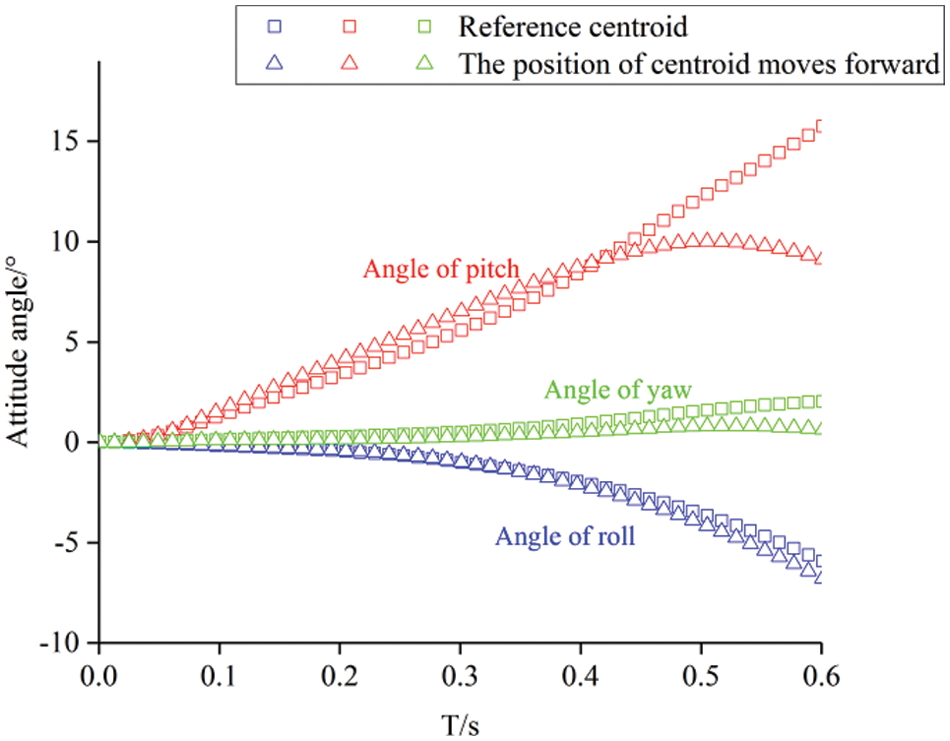
Figure 4: Comparison of the attitude angles of the store at different centroid positions

There are two methods for the separation of the store, one is gravity launch, the other is ejection launch. One of the differences between the two methods is that the ejected store has an initial velocity when falling. Fig. 5 compares attitude angle and motion trajectory of the store with different initial velocity in which the time interval of the store falling is 0.1 s. It can be seen the attitude angle of the store with initial velocity = 3 m/s is slightly larger, which means that the aerodynamic interference of the flow field of the internal bay to the store does not weaken with the increase of velocity. However, the time for the store with velocity = 3 m/s to leave the flow field of the internal bay is shortened, so the effect time of aerodynamic interference on the store will be reduced which means that the probability of collision between the store and the wall of the internal bay is reduced. Due to the initial velocity = 0 m/s, the store released by gravity will leave the flow field of the internal bay for a long time, which may lead to large attitude and even collision with the wall of the internal bay under strong aerodynamic interference. Therefore, the store with an initial velocity is conducive to the separation.

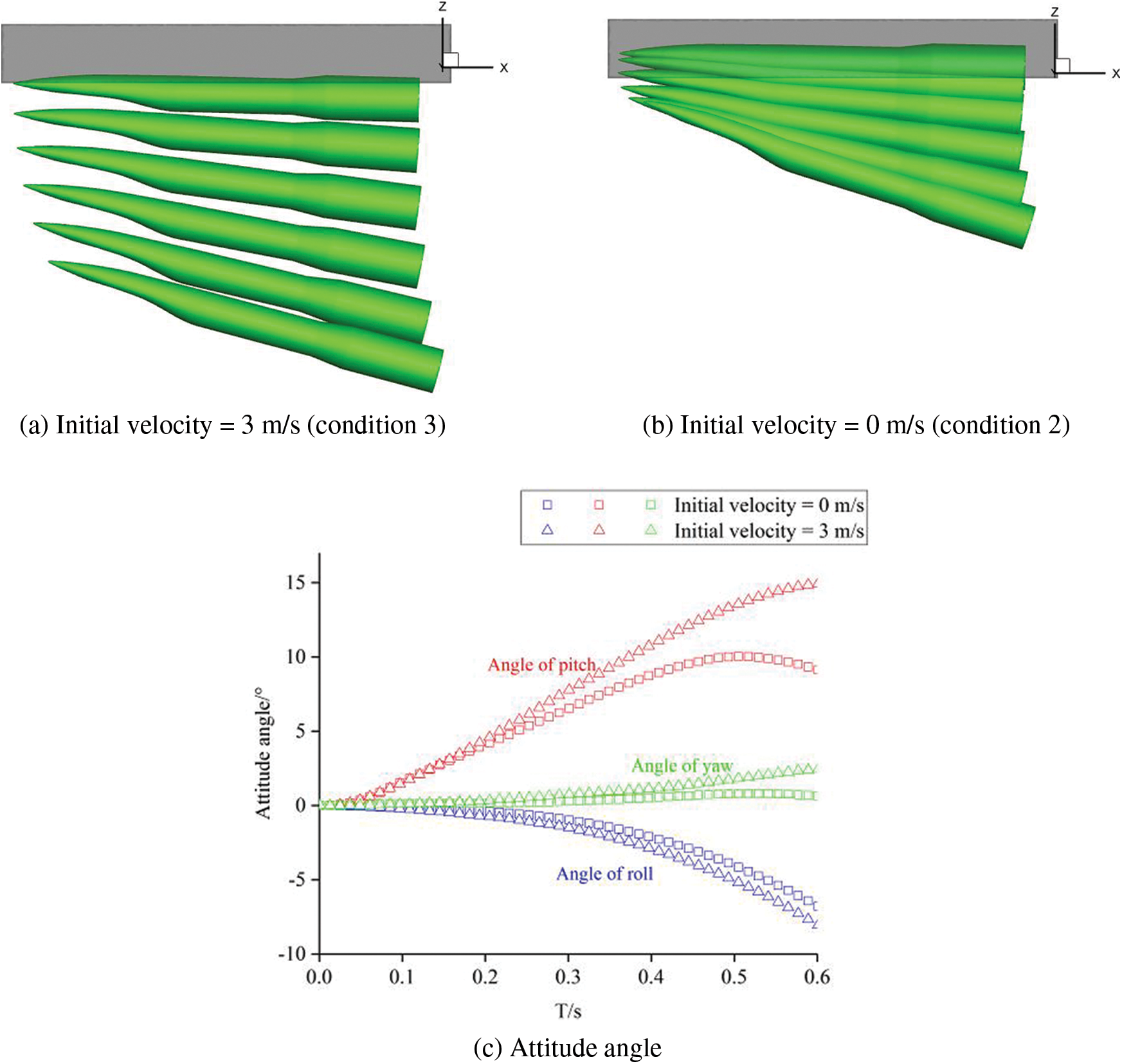
Figure 5: Comparison of the motion trajectory of the store with different initial velocity

The only difference between condition 1 (20 km) and condition 4 (25 km) is that launching height of the store is different. Fig. 6 shows the comparison of attitude angles of the store at different launching heights. It is found that the pitch angle, yaw angle and roll angle of store at launching height of 25 km are less than that of 20 km. Compared with the altitude of 20 km, the air density at the altitude of 25 km is relatively low, so the aerodynamic force of the store is relatively small when falling, and the influence of the flow field of the internal bay on the store will be weakened accordingly. Consequently, the lower the height, the worse the launch environment of the store, which may cause unsafe separation.

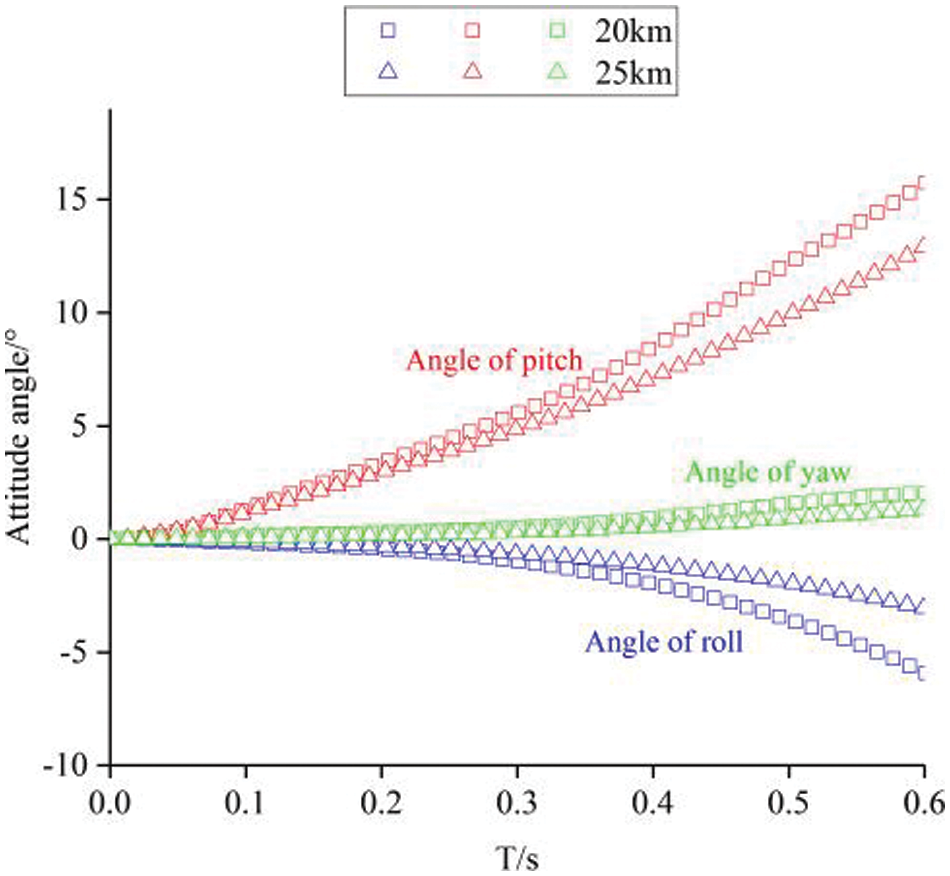
Figure 6: Comparison of attitude angles of the store at different altitude

The comparison of attitude angle among the cylindrical rod (condition 5) slanted aft wall (condition 6) and “clean” internal bay (condition 4) is shown as Fig. 7. It is concluded that two control measures improve the separation characteristics of the store to a certain extent. Cylindrical rod and slanted aft wall make the store fall more smoothly. Among them, the more obvious is the improvement of pitch angle. For the “clean” internal bay, the maximum pitch angle of the store is 13°, while the maximum pitch angle of the store with slanted aft wall and cylindrical rod are 2.5° and 2.7°. These two control measures are to improve the flow field of the internal bay, so as to obtain a better attitude in the process of releasing and separating the store. The control measure of slanted aft wall is better than that of cylindrical rod.

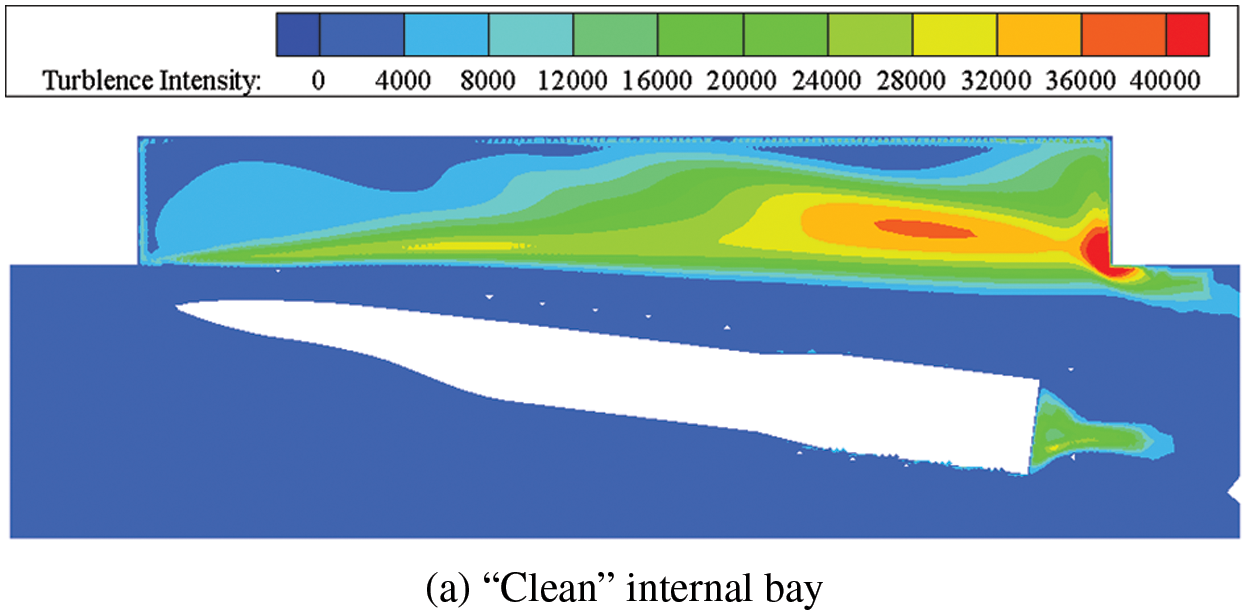
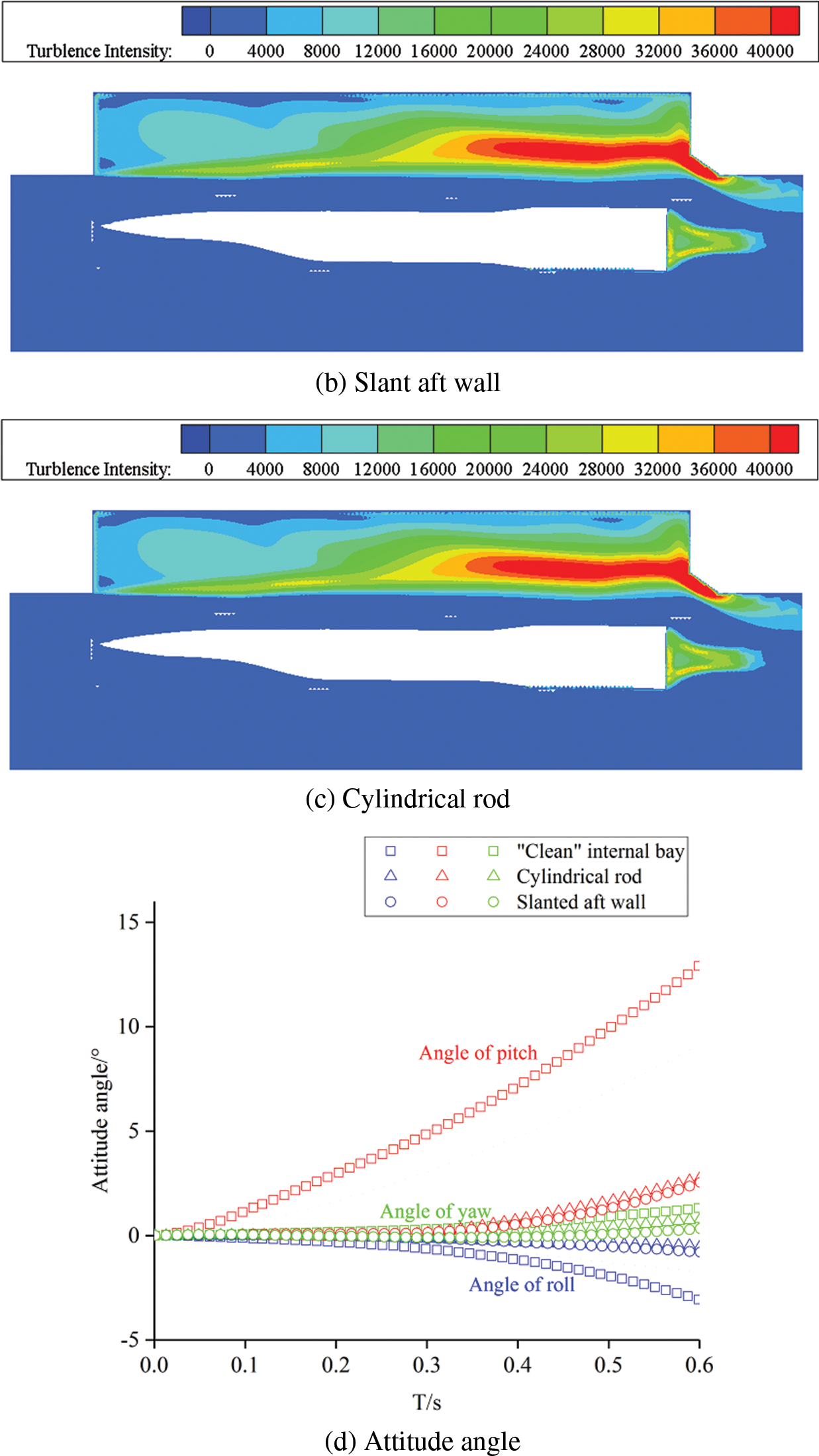
Figure 7: Comparison of the attitude angle of the store with different control measures

5  Conclusions

In this paper, the realizable k−ε turbulence model coupled with the equation with six degrees of freedom is used to simulate the separation of the store under different centroid, height, initial velocity and control measure. It can be concluded that:

(1)   The position of the centroid will affect the separation of the store, which needs to be considered in the design.

(2)   The higher the height, the smaller the air density, and the aerodynamic force on the store will become smaller. Therefore, increasing the launching height is conducive to the separation of the store.

(3)   The store leaves the internal bay faster with an initial velocity, and reduces the probability of collision with the wall.

(4)   The cylindrical rod and the slanted aft wall can improve the attitude of the store, and make it fall more smoothly. The pitch angle of the store falling can be reduced by about 10° by two control measures.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Wang, G., Chen, X., Xing, Y., Zeng, Z. (2017). Multi-body separation simulation with an improved general mesh deformation method. Aerospace Science and Technology, 71, 763–771. DOI 10.1016/j.ast.2017.10.027. [Google Scholar] [CrossRef]

    2. Bacci, D., Saddington, A. J., Bray, D. (2019). The effect of angle of attack on the aeroacoustic environment within the weapons bay of a generic UCAV. Aerospace Science and Technology, 93, 1–14. DOI 10.1016/j.ast.2019.105315. [Google Scholar] [CrossRef]

    3. Loupy, G. J., Barakos, G. N., Taylor, N. J. (2018). Store release trajectory variability from weapon bays using scale-adaptive simulations. AIAA Journal, 56(2), 752–765. DOI 10.2514/1.J056485. [Google Scholar] [CrossRef]

    4. Song, W., Dong, J. G., Lu, W., Jiang, Z. H. (2021). Trajectory and attitude deviations for internal store separation due to unsteady and quasi-steady test method. Chinese Journal of Aeronautics, 35(2), 74–81. DOI 10.1016/j.cja.2021.03.007. [Google Scholar] [CrossRef]

    5. Johnson, R. A., Stanek, M. J., Grove, J. E. (2008). Store separation trajectory deviations due to unsteady weapons bay aerodynamics. 46th AIAA Aerospace Sciences Meeting and Exhibit, pp. 188. Nevada. DOI 10.2514/6.2008-188. [Google Scholar] [CrossRef]

    6. Davis, M. B., Pat, Y., Smith, B. R. (2009). Store trajectory response to unsteady weapons bay flow fields. 47th AIAA Aerospace Sciences Meeting, pp. 547. Florida. DOI 10.2514/6.2009-547. [Google Scholar] [CrossRef]

    7. Cheng, H., Peng, M. J., Cheng, Y. M. (2018). The dimension splitting and improved complex variable element-free galerkin method for 3-dimensional transient heat conduction problems. International Journal for Numerical Methods in Engineering, 114(3), 321–345. DOI 10.1002/nme.5745. [Google Scholar] [CrossRef]

    8. Cheng, H., Peng, M. J., Cheng, Y. M. (2017). A hybrid improved complex variable element-free galerkin method for three-dimensional potential problems. Engineering Analysis with Boundary Elements, 84, 52–62. DOI 10.1016/j.enganabound.2017.08.001. [Google Scholar] [CrossRef]

    9. Cheng, H., Peng, M. J., Cheng, Y. M. (2017). A fast complex variable element-free galerkin method for three-dimensional wave propagation problems. International Journal of Applied Mechanics, 9(6), 1750090. DOI 10.1142/S1758825117500909. [Google Scholar] [CrossRef]

  10. Cheng, H., Peng, M. J., Cheng, Y. M. (2018). A hybrid improved complex variable element-free galerkin method for three-dimensional advection-diffusion problems. Engineering Analysis with Boundary Elements, 97, 39–54. DOI 10.1016/j.enganabound.2018.09.007. [Google Scholar] [CrossRef]

  11. Cheng, H., Peng, M. J., Cheng, Y. M., Meng, Z. J. (2020). The hybrid complex variable element-free galerkin method for 3D elasticity problems. Engineering Structures, 219, 110835. DOI 10.1016/j.engstruct.2020.110835. [Google Scholar] [CrossRef]

  12. Cheng, H., Peng, M. J. (2022). The improved element-free galerkin method for 3D helmholtz equations. Mathematics, 10, 14. DOI 10.3390/math10010014. [Google Scholar] [CrossRef]

  13. Westmoreland, W. S. (2009). Trajectory variation due to an unsteady flow field. 47th AIAA Aerospace Sciences Meeting, pp. 550. Florida. DOI 10.2514/6.2009-550. [Google Scholar] [CrossRef]

  14. Stallings, L. R. (2015). Store separation from cavities at supersonic flight speeds. Journal of Spacecraft & Rockets, 20(2), 129–132. DOI 10.2514/3.28368. [Google Scholar] [CrossRef]

  15. Mizrahi, I., Raveh, D. E. (2018). An investigation of wing elasticity effects on store separation based on computational fluid dynamics. Atmospheric Flight Mechanics Conference, pp. 2831. Georgia. DOI 10.2514/6.2018-2831. [Google Scholar] [CrossRef]

  16. Mizrahi, I., Raveh, D. E. (2019). Wing elasticity effects on store separation. Journal of Aircraft, 56(3), 1231–1249. DOI 10.2514/1.C035204. [Google Scholar] [CrossRef]

  17. Xue, F., Wang, H., Jiang, Z., Wang, Y. C. (2020). Derivation and verification of a similarity law for wind-tunnel free-flight tests of heavy-store separation. Acta Astronautica, 174, 123–130. DOI 10.1016/j.actaastro.2020.04.061. [Google Scholar] [CrossRef]

  18. Xue, F., Wang, Y., Qin, H. (2019). Derivation and validation of wind tunnel free-flight similarity law for store separation from aircraft. Aerospace Science and Technology, 97, 1–9. DOI 10.1016/j.ast.2019.105614. [Google Scholar] [CrossRef]

  19. Peters, N. J., Wissink, A., Ekaterinaris, J. (2021). A mode based reduced order model for supersonic store separation. AIAA Aviation Forum, pp. 2548. Florida. DOI 10.2514/6.2021-2548. [Google Scholar] [CrossRef]

  20. Peters, N. J., Wissink, A., Ekaterinaris, J. (2022). A mode based reduced order model for rotorcraft store separation. AIAA Scitech Forum, pp. 312. San Diego. DOI 10.2514/6.2022-0312. [Google Scholar] [CrossRef]

  21. Ren, Z. X., Wang, B., Hu, B., Zheng, L. X. (2018). Numerical analysis of supersonic flows over an aft-ramped open-mode cavity. Aerospace Science and Technology, 78, 427–437. DOI 10.1016/j.ast.2018.05.003. [Google Scholar] [CrossRef]

  22. Wu, Z. Y., Gao, Z. X., Jiang, C. W., Lee, C. H. (2019). An in-depth numerical investigation of a supersonic cavity-ramp flow with DDES method. Aerospace Science and Technology, 89, 253–263. DOI 10.1016/j.ast.2019.03.055. [Google Scholar] [CrossRef]

  23. Bennett, G. J., Okolo, P. N., Zhao, K., Philo, J., Guan, Y. Y. et al. (2019). Cavity resonance suppression using fluidic spoilers. AIAA Journal, 57(2), 706–720. DOI 10.2514/1.J057407. [Google Scholar] [CrossRef]

  24. Liu, Y., Shi, Y., Tong, M., Zhao, F., Chen, B. Q. (2019). Aeroacoustic investigation of passive and active control on cavity flowfields using delayed detached eddy simulation. International Journal of Aerospace Engineering, 2019(5), 1–9. DOI 10.1155/2019/2650842. [Google Scholar] [CrossRef]

  25. Roberts, D. A., Macmanus, D. G., Johnson, R. A., Grove, J. E., Birch, T. J. et al. (2015). Passive attenuation of modal cavity aeroacoustics under supersonic and transonic conditions. AIAA Journal, 53(7), 1861–1877. DOI 10.2514/1.J053564. [Google Scholar] [CrossRef]

  26. Kim, D. H., Choi, J. H., Kwon, O. J. (2015). Detached eddy simulation of weapons bay flows and store separation. Computers & Fluids, 121, 1–10. DOI 10.1016/j.compfluid.2015.07.022. [Google Scholar] [CrossRef]

  27. Sun, Y. Y., Liu, Q., Cattafesta, N. C., Ukeiley, L. S., Taira, K. (2019). Effects of sidewalls and leading-edge blowing on flows over long cuboid cavities. AIAA Journal, 57(1), 106–120. DOI 10.2514/1.J057413. [Google Scholar] [CrossRef]

  28. Wang, X., Yang, D., Liu, J., Zhou, F. Q. (2020). Control of pressure oscillations induced by supersonic cavity flow. AIAA Journal, 58(60), 1–8. DOI 10.2514/1.J059014. [Google Scholar] [CrossRef]

  29. Chen, B., Wang, Y. (2021). Active aerodynamic noise control research for supersonic aircraft cavity by nonlinear numerical simulation. International Journal of Electrical Engineering Education, pp. 1–15. DOI 10.1177/0020720921996589. [Google Scholar] [CrossRef]

  30. Webb, N., Samimy, M. (2017). Control of supersonic cavity flow using plasma actuators. AIAA Journal, 55(10), 3346–3355. DOI 10.2514/1.J055720. [Google Scholar] [CrossRef]

  31. Sahoo, D., Annaswamy, M., Alvi, F. (2007). Active store trajectory control in supersonic cavities using micro-jets and low-order modeling. AIAA Journal, 45(3), 516–531. DOI 10.2514/1.18007. [Google Scholar] [CrossRef]

  32. Guo, L., Wang, C., Bin, Y., Xie, Y. K., Tong, M. B. (2015). Investigation on characteristics of store release from internal bay in supersonic flow under flow control. Acta Aeronautica et Astronautica Sinica, 36(6), 1752–1761 (in Chinese). DOI 10.7527/S1000-6893.2014.0325. [Google Scholar] [CrossRef]

  33. Song, W., Ai, B. C., Zhao, X. J., Jiang, Z. H., Lu, W. (2020). Influence of control device on store separation from an open cavity. Aerospace Science and Technology, 106(3), 106–117. DOI 10.1016/j.ast.2020.106117. [Google Scholar] [CrossRef]

  34. Song, W., Ai, B. C. (2021). Analysis of aircraft-store compatibility for internal weapons separation. Aerospace Science and Technology, 110(5), 528–538. DOI 10.1016/j.ast.2021.106528. [Google Scholar] [CrossRef]

  35. Blazek, J. (2001). Computational fluid dynamics: Principles and applications. Computational Fluid Dynamics Principles & Applications, 14(1), 134–143. DOI 10.1002/9780470727225.ch1. [Google Scholar] [CrossRef]

  36. Zhu, S. Q. (2018). Numerical investigations on the missile separation and its flow control. University of Science & Technology, Nanjing, China. [Google Scholar]

  37. Panagiotopoulos, E. E., Kyparissis, S. D. (2010). CFD transonic store separation trajectory predictions with comparison to wind tunnel investigations. International Journal of Engineering, 3(6), 538–553. [Google Scholar]