Some Topological Values of Supramolecular Chain of Different Complexes of N-Salicylidene-L-Valine

1  Introduction

Medicine manufacturing has grown rapidly in recent years and that has resulted in the production of an enormous number of novel drugs. Consequently, a considerable number of efforts is required to investigate the pharmacological, chemical, and biological properties of these recently synthesized drugs that makes this enormous workload much more clustered and fussier. Sufficient scientific assistance, equipment and reagents are necessary for the evaluation of their performance and shortcomings of the existing drugs. Furthermore, the lack of research funding in underdeveloped countries makes it further difficult to investigate the performance of these drugs. Literature suggests an inextricable relationship between the molecular structures of the drugs to their corresponding pharmacodynamic and chemical properties. The identification of the topological indices by quantifying the measures of molecular structures of a drug, can help the pharmaceutical researchers to predict the therapeutic performance of that drug. Advantageously, this can reduce the efforts and time required to optimize the pharmacological, chemical, and biological performance of the drugs. Thus, the mathematical methods computing the topological indices are of great importance in predicting the pharmacological properties of drugs. For the computation studies regarding the evaluation of topological indices of a drug, the chemical structure of a medication is mathematically represented as a graph atom represented by vertex and bond between the atoms represented by an edge. Suppose a drug’s structure represented by a graph G, with vertices (atoms) and edges (chemical bonds). Here, the topological index is a real-valued function used to transform the drug’s molecular composition to specified numerical values that are unique to a particular molecular structure. Literature is enriched by many of the significant indices for assessment of the pharmacological and chemical properties of the molecules in the past 40 years. For example, the discovery of these topological indices has found their applications in molecular graphs, nano materials, pharmaceutical and engineering fields. In literature, the topological properties of the metal-organic compounds [1] engineered nanostructures [2,3], silicon carbide [4], titanium-based nanostructures [5], organic structures [6], nanotubes [7–9], etc., have been reported. The ABC indices [10,11] have employed for some chemical structures and predicting the performance of the dendrimers/honeycomb network in the terms of their topological indices [12].

Mammalian essential amino acid among the twenty-amino acids of the protein is Lv which is a glycogen. Several coordination modes towards metal ions and extraordinary coordination capacity has seen by a carboxylate ligand with a chiral Schiff base NsLv synthesize from salicylaldehyde and Lv. Such metal complexes bearing ligands have been extensively used for both laboratory scale research and industrial scale [13–17]. An effective reagent for DNA cleavage, enantio-selective reaction catalysts and chiral fluorescent molecular sensors are the potential applications of these chiral metal complexes. Organotin compounds have an extensive range of applications in medicines, Synthesis of chemical compounds, catalysis and material science [18]. Furthermore, carboxylate ligands in organotin complexes have attracted huge attention owing to their well diverse structures, high cytotoxic and catalytic activities [19–21]. Potential biological and optical properties have been reported for NsLv organotin complexes [16,22,23]. There are many chemical ways reported to synthesize them either with a potassium or oxide mixing a chlorine with sodium and potassium, or NsLv.

Let ϑ be a simple, loopless, linked molecular graph with a set of vertex values V(ϑ) and edge set E(ϑ). Order and size of molecular graph is shown by |V(ϑ)|=r and |E(ϑ)|=s. The degree d(v) of a vertex v is a total number of edges that are incident on it. A molecular descriptor, also referred as a topological structure index, is a mathematical formula that yields a numerical value associated with some molecular structure. The formulas for topological indices discussed in this article are listed below, along with their citations.

Definitions:

In 1975, the Chemist Milan Randić [24] proposed a topological index

R1(ϑ)=∑rs∈E(ϑ)1d(r)d(s)(1)

R2(ϑ)=∑rs∈E(ϑ)1d(r)d(s)(2)

The expression of harmonic index [25] is,

H(ϑ)=∑rs∈E(ϑ)2d(r)+d(s)(3)

The expression of sum-connectivity index [26] is,

SCI(ϑ)=∑rs∈E(ϑ)1d(r)+d(s)(4)

The expression of atom-bond-connectivity index [27] is,

ABC(ϑ)=∑rs∈E(ϑ)d(r)+d(s)−2d(r)d(s)(5)

The expression of geometric-arithmetic index [28] is,

GA(ϑ)=∑rs∈E(ϑ)2d(r)d(s)d(r)+d(s)(6)

The expression of reduced reciprocal Randić index [29] is,

RRR(ϑ)=∑rs∈E(ϑ)(d(r)−1)(d(s)−1)(7)

2  Sc in Dialkyltin Complex-2 of NsLv (C2,ω)

The four forms of sc found in dialkyltin are complexes 2, 3, 4, and 5 of NsLv. This section will go over complex-2. Complex-2 of NsLv is one of the dialkyltin sc complexes ω units that are identical, the second unit is blended with the aid of a vertex with the first unit, and its miles further producing a series of ω units [30], Fig. 1 shows the molecular structure of this. Fig. 2 depicts the generalized ω the unit graph of this molecular shape is derived from the chemical structure in discern 1 by [30]. This chain contains a variety of bonds, including single-degree, two-degree, three-degree, four-degree, and five-degree bonds (vertices). Additionally, Table 1 represents the edge type with their end vertices degree and also the number of repetitions (frequency) of that edge, which is very useful for our computations. The order and size of C2,ω, are |V(C2,ω)|=21ω, |E(C2,ω)|=25ω−2, respectively.

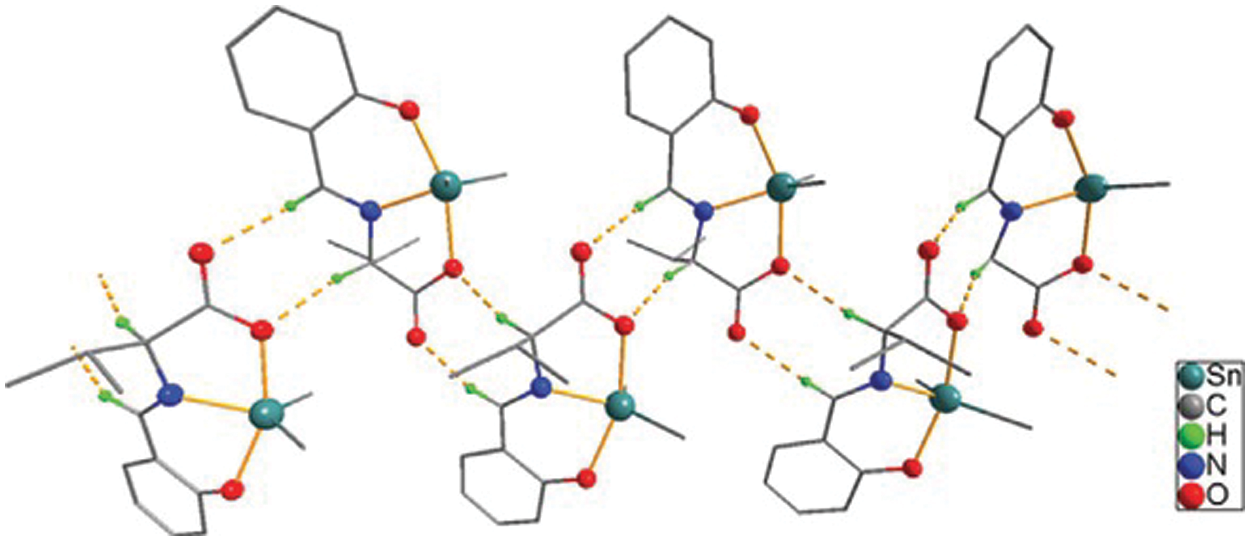
Figure 1: Chemical structure of the sc in NsLv dialkyltin complex-2

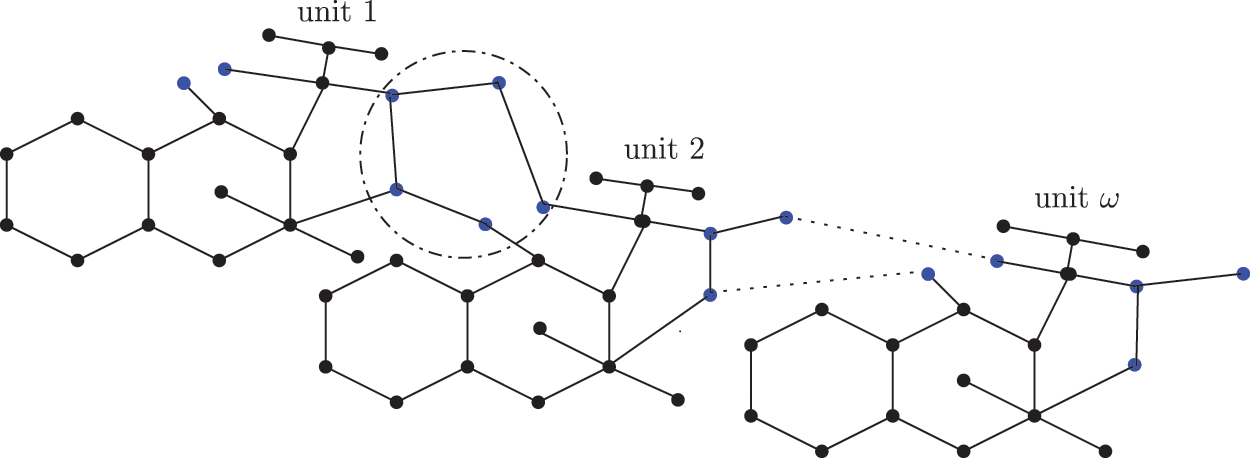
Figure 2: Sc in dialkyltin complex-2 of NsLv

Theorem 2.1. If C2,ω, with ω≥1 if a sc graph in NsLv dialkyltin complex-2 exists, then the first definition of the Randić index is,

R1(C2,ω)=4.112ω+0.125

Proof. By applying the first definition of the Randić index and Table 1

R1(C2,ω)=(4ω−1)12×2+(6ω−2)12×3+(2ω+2)11×3+(1)11×4+(3ω)13×4+(4ω−1)13×3+(2ω)11×5+(ω+1)12×5+(2ω−1)13×5+(ω−1)12×4.

After simplifying the previous equation, we get the following result:

R1(C2,ω)=4.112ω+0.125

Theorem 2.2. If C2,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-2 exists, the harmonic index is,

H(C2,ω)=9.375ω−0.53

Proof. By applying the expression of the harmonic index and Table 1

H(C2,ω)=(4ω−1)22+2+(6ω−2)22+3+(2ω+2)21+3+(1)21+4+(3ω)23+4+(4ω−1)23+3+(2ω)21+5+(ω+1)22+5+(2ω−1)23+5+(ω−1)22+4.

After simplifying the previous equation, we get the following result:

H(C2,ω)=9.375ω−0.53

Theorem 2.3. If C2,ω, with ω≥1 if a sc graph in NsLv dialkyltin complex-2 exists, then the second definition of the Randić index is,

R2(C2,ω)=9.877ω−0.29

Proof. By applying the second definition of the Randić index and Table 1

R2(C2,ω)=(4ω−1)12×2+(6ω−2)12×3+(2ω+2)11×3+(1)11×4+(3ω)13×4+(4ω−1)13×3+(2ω)11×5+(ω+1)12×5+(2ω−1)13×5+(ω−1)12×4.

After simplifying the previous equation, we get the following result:

R2(C2,ω)=9.877ω−0.29

Theorem 2.4. If C2,ω, with ω≥1 if a sc graph in NsLv dialkyltin complex-2 exists, then the sum-connectivity index is,

SCI(C2,ω)=10.756ω−0.738

Proof. By applying the expression of the sum-connectivity index and Table 1

SCI(C2,ω)=(4ω−1)12+2+(6ω−2)12+3+(2ω+2)11+3+(1)11+4+(3ω)13+4+(4ω−1)13+3+(2ω)11+5+(ω+1)12+5+(2ω−1)13+5+(ω−1)12+4.

After simplifying the previous equation, we get the following result:

SCI(C2,ω)=10.756ω−0.738

Theorem 2.5. If C2,ω, with ω≥1 if a sc graph in NsLv dialkyltin complex-2 exists, then the Atom-Bond-Connectivity index is,

ABC(C2,ω)=17.767ω−0.921

Proof. By applying the expression of the Atom-Bond-Connectivity index and Table 1

ABC(C2,ω)=(4ω−1)2+2−22×2+(6ω−2)2+3−22×3+(2ω+2)1+3−21×3+(1)1+4−21×4+(3ω)3+4−23×4+(4ω−1)3+3−23×3+(2ω)1+5−21×5+(ω+1)2+5−22×5+(2ω−1)3+5−23×5+(ω−1)2+4−22×4.

After simplifying the previous equation, we get the following result:

ABC(C2,ω)=17.767ω−0.921

Theorem 2.6. If C2,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-2 exists, then the geometric-arithmetic index is,

GA(C2,ω)=23.844ω−2.433

Proof. By applying the expression of the geometric-arithmetic index and Table 1

GA(C2,ω)=(4ω−1)22×22+2+(6ω−2)22×32+3+(2ω+2)21×31+3+(1)21×41+4+(3ω)23×43+4+(4ω−1)23×33+3+(2ω)21×51+5+(ω+1)22×52+5+(2ω−1)23×53+5+(ω−1)22×42+4.

After simplifying the previous equation, we get the following result:

GA(C2,ω)=23.844ω−2.433

Theorem 2.7. If C2,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-2 exists, then the reduced reciprocal Randić index is,

RRR(C2,ω)=37.219ω−8.388

Proof. By applying the expression of the reduced reciprocal Randić index and Table 1

RRR(C2,ω)=(4ω−1)(2−1)(2−1)+(6ω−2)(2−1)(3−1)+(2ω+2)(1−1)(3−1)+(1)(1−1)(4−1)+(3ω)(3−1)(4−1)+(4ω−1)(3−1)(3−1)+(2ω)(1−1)(5−1)+(ω+1)(2−1)(5−1)+(2ω−1)(3−1)(5−1)+(ω−1)(2−1)(4−1).

After simplifying the previous equation, we get the following result:

RRR(C2,ω)=37.219ω−8.388

3  Sc in Dialkyltin Complex-3 of NsLv (C3,ω)

The sc in dialyltin has four different forms of complexes, which are referred to as complexes 2, 3, 4, and 5 of NsLv. Complex-3 will be discussed in this section. Complex-3 of NsLv is one of the sc complexes in dialkyltin ω same gadgets, where the second unit is joined via a vertex to the first unit, and it produces a sequence of ω units, Fig. 3 shows the molecular graph of this. Fig. 4 displays the parameter ω unit graph of this molecular structure generalised from the chemical structure [30]. This chain comprises a variety of bonds, including single degree, 2, 3, and 6 degree bonds (vertices). Also, Table 2 represents the sort of edge with their end vertices degree and also the number of repetition (frequency) of that edge which is very useful in support of our computational work. The order and size of C3,ω, are |V(C3,ω)|=26ω, |E(C3,ω)|=30ω−1, respectively.

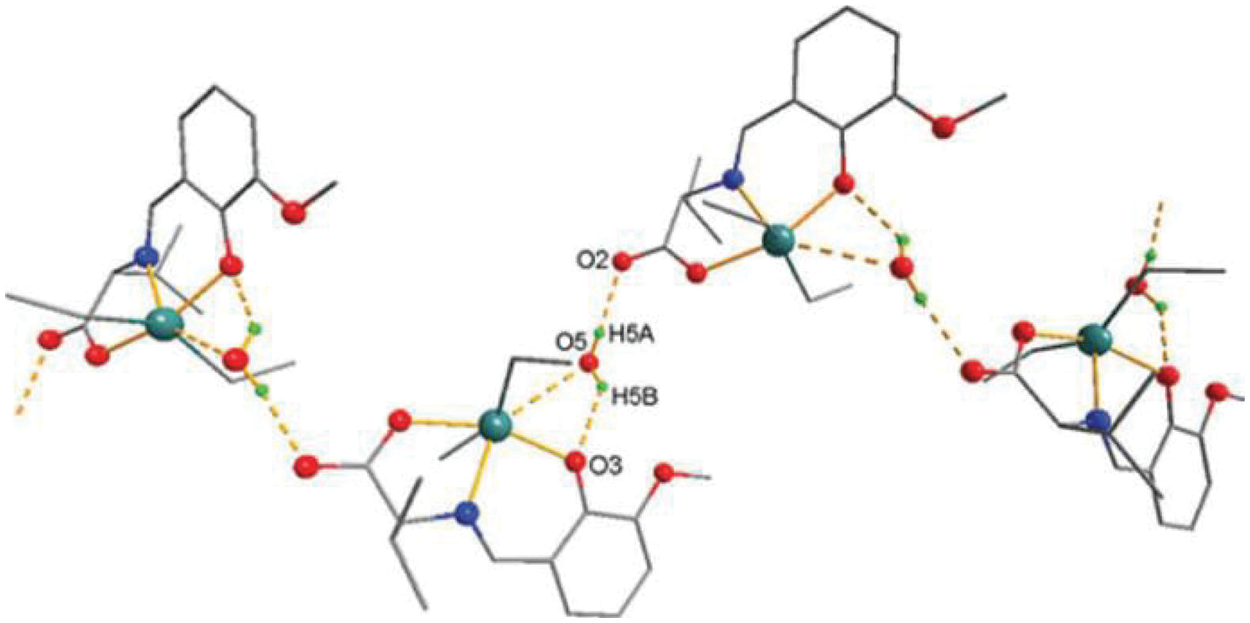
Figure 3: Chemical structure of the sc in the NsLv dialkyltin complex-3

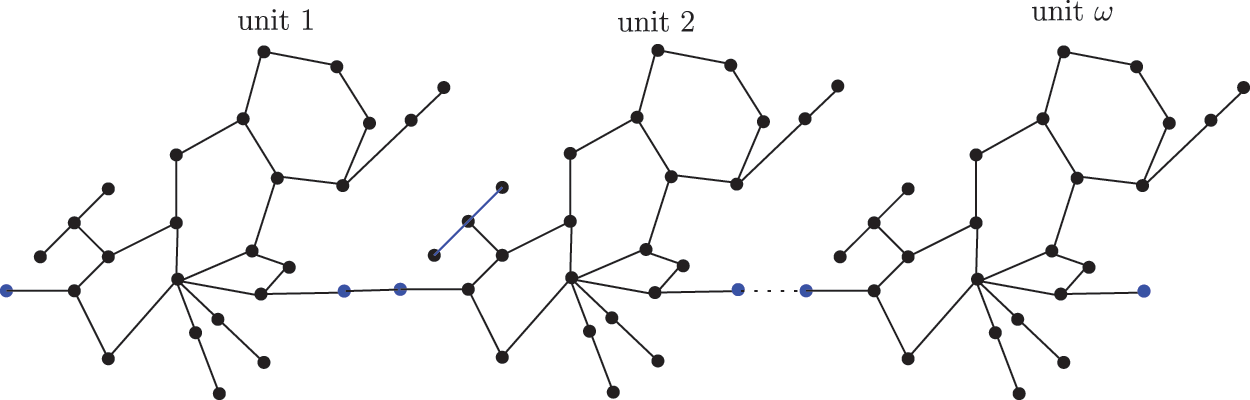
Figure 4: Sc in the dialkyltin complex-3 of NsLv

Theorem 3.1. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the first definition of the Randić index is,

R1(C3,ω)=5.655ω+0.084

Proof. By applying the first definition of the Randić index and Table 2

R1(C3,ω)=(3ω)11×2+(10ω−2)12×3+(3ω−1)12×2+(6ω)13×3+(2ω+2)11×3+(3ω)12×6+(3ω)13×6.

After simplifying the previous equation, we get the following result:

R1(C3,ω)=5.655ω+0.084

Theorem 3.2. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the harmonic index is,

H(C3,ω)=11.416ω−0.3

Proof. By applying the expression of the harmonic index and Table 2

H(C3,ω)=(3ω)21+2+(10ω−2)22+3+(3ω−1)22+2+(6ω)23+3+(2ω+2)21+3+(3ω)22+6+(3ω)23+6.

After simplifying the previous equation, we get the following result:

H(C3,ω)=11.416ω−0.3

Theorem 3.3. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the second definition of the Randić index is,

R2(C3,ω)=12.422ω−0.162

Proof. By applying the second definition of the Randić index and Table 2

R2(C3,ω)=(3ω)11×2+(10ω−2)12×3+(3ω−1)12×2+(6ω)13×3+(2ω+2)11×3+(3ω)12×6+(3ω)13×6.

After simplifying the previous equation, we get the following result:

R2(C3,ω)=12.422ω−0.162

Theorem 3.4. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the sum-connectivity index is,

SCI(C3,ω)=13.207ω−0.394

Proof. By applying the expression of the sum-connectivity index and Table 2

SCI(C3,ω)=(3ω)11+2+(10ω−2)12+3+(3ω−1)12+2+(6ω)13+3+(2ω+2)11+3+(3ω)12+6+(3ω)13+6.

After simplifying the previous equation, we get the following result:

SCI(C3,ω)=13.207ω−0.394

Theorem 3.5. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the Atom-Bond-Connectivity index is,

ABC(C3,ω)=20.927ω−0.489

Proof. By applying the expression of the Atom-Bond-Connectivity index and Table 2

ABC(C3,ω)=(3ω)1+2−21×2+(10ω−2)2+3−22×3+(3ω−1)2+2−22×2+(6ω)3+3−23×3+(2ω+2)1+3−21×3+(3ω)2+6−22×6+(3ω)3+6−23×6.

After simplifying the previous equation, we get the following result:

ABC(C3,ω)=20.927ω−0.489

Theorem 3.6. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the geometric-arithmetic index is,

GA(C3,ω)=28.77ω−1.226

Proof. By applying the expression of the geometric-arithmetic index and Table 2

GA(C3,ω)=(3ω)21×21+2+(10ω−2)22×32+3+(3ω−1)22×22+2+(6ω)23×33×3+(2ω+2)21×31+3+(3ω)22×62+6+(3ω)23×63+6.

After simplifying the previous equation, we get the following result:

GA(C3,ω)=28.77ω−1.226

Theorem 3.7. If C3,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-3 exist, then the reduced reciprocal Randić index is,

RRR(C3,ω)=45.334ω−3.828

Proof. By applying the expression of the reduced reciprocal Randić index and Table 2

RRR(C3,ω)=(3ω)(1−1)(2−1)+(10ω−2)(2−1)(3−1)+(3ω−1)(2−1)(2−1)+(6ω)(3−1)(3−1)+(2ω+2)(1−1)(3−1)+(3ω)(2−1)(6−1)+(3ω)(3−1)(6−1).

After simplifying the previous equation, we get the following result:

RRR(C3,ω)=45.334ω−3.828

4  Sc in Dialkyltin Complex-4 of NsLv (C4,ω)

The sc in dialkyltin has four different forms of complexes, which are referreed as complexes 2, 3, 4, and 5 of NsLv. Complex-4 will be discussed in this section. Complex-4 of NsLv is one of the sc complexes in dialkyltin ω equal devices, where the second one unit blended via a vertex with the first unit and its miles similarly developing with a sequence of parameter ω units. Fig. 5 suggests the generalized ω unit graph of this molecular shape from the chemical structure given in Fig. 6 by [30]. This chain comprises a variety of bonds, including single degree, 2, 3, and 5 degree bonds (vertices). Also, Table 3 represents the edge type with their end vertices degree and also the number of repetition (frequency) of that edge which is very useful in support of our computation. The order and size of C4,ω, are |V(C4,ω)|=28ω, |E(C4,ω)|=31ω−1, respectively.

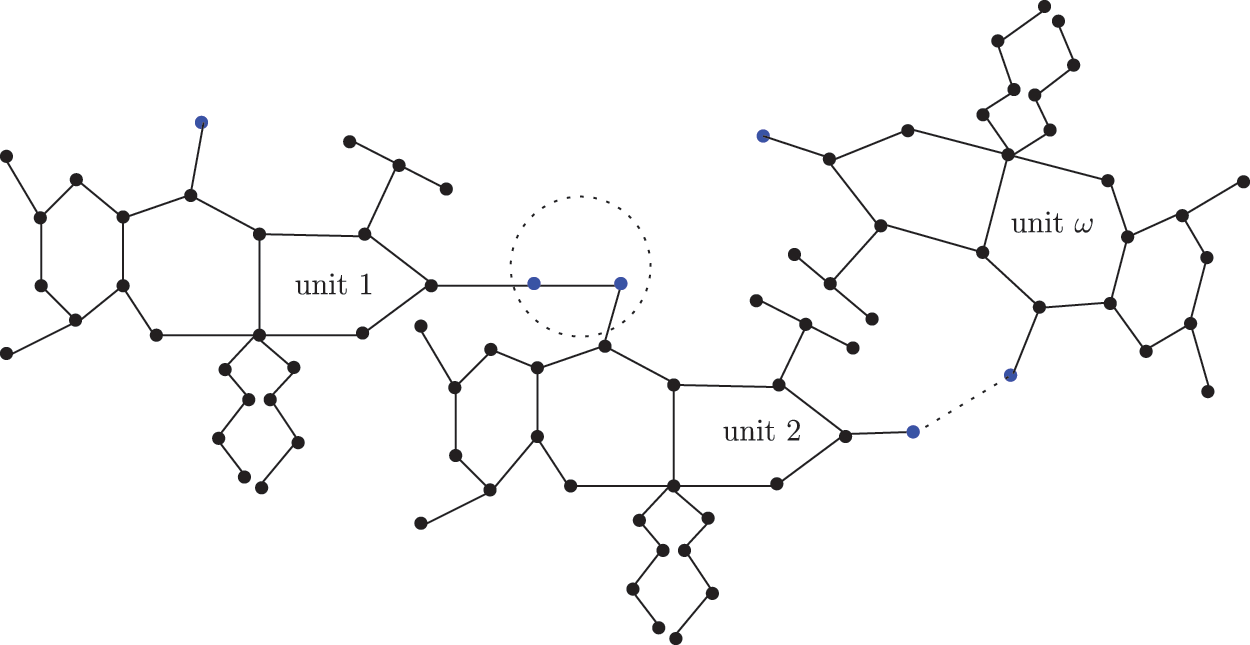
Figure 5: Sc in dialkyltin complex-4 of NsLv

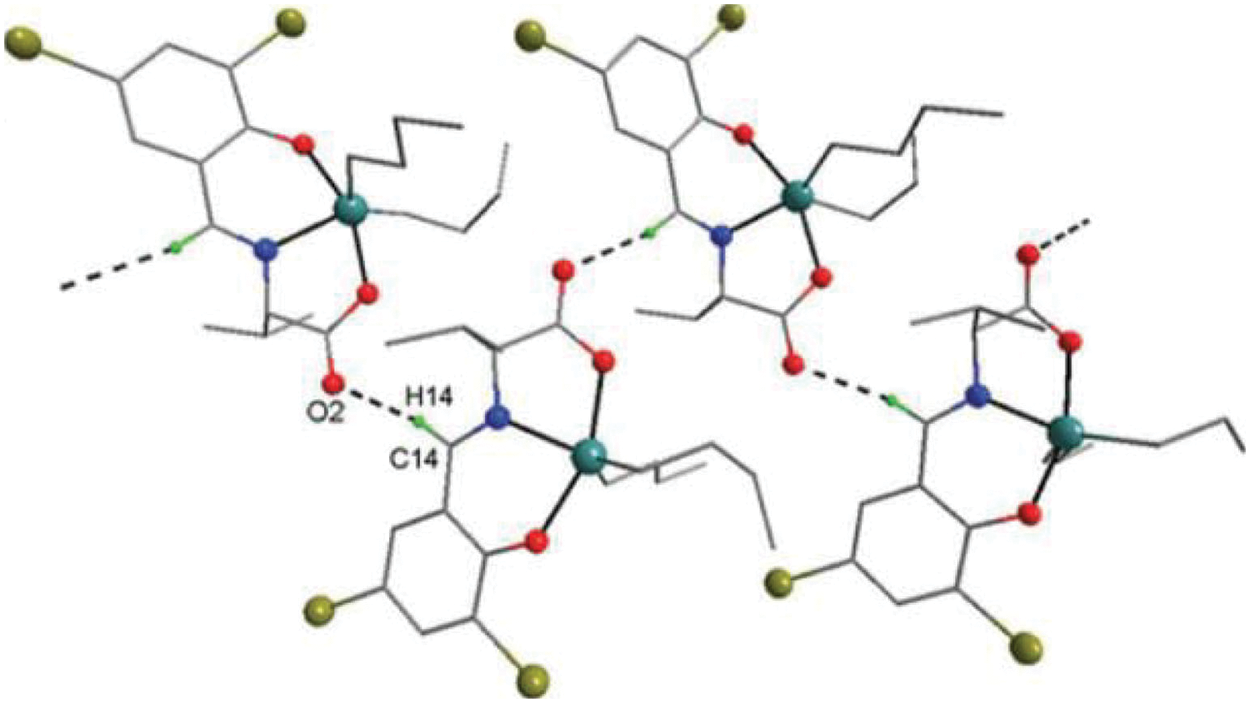
Figure 6: Chemical structure of the sc in NsLv dialkyltin complex-4

Theorem 4.1. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the first definition of the Randić index is,

R1(C4,ω)=6.153ω+0.084

Proof. By applying the first definition of the Randic index and Table 3

R1(C4,ω)=(4ω+2)11×3+(8ω−2)12×3+(7ω)13×3+(2ω)11×2+(5ω−1)12×2+(4ω)12×5+(ω)13×5.

After simplifying the previous equation, we get the following result:

R1(C4,ω)=6.153ω+0.084

Theorem 4.2. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the harmonic index is,

H(C4,ω)=12.759ω−0.3

Proof. By applying the expression of the harmonic index and Table 3

H(C4,ω)=(4ω+2)21+3+(8ω−2)22+3+(7ω)23+3+(2ω)21+2+(5ω−1)22+2+(4ω)22+5+(ω)23+5.

After simplifying the previous equation, we get the following result:

H(C4,ω)=12.759ω−0.3

Theorem 4.3. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the second definition of the Randić index is,

R2(C4,ω)=13.339ω−0.162

Proof. By applying the second definition of the Randić index and Table 3

R2(C4,ω)=(4ω+2)11×3+(8ω−2)12×3+(7ω)13×3+(2ω)11×2+(5ω−1)12×2+(4ω)12×5+(ω)13×5.

After simplifying the previous equation, we get the following result:

R2(C4,ω)=13.339ω−0.162

Theorem 4.4. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the sum-connectivity index is,

SCI(C4,ω)=13.953ω−0.394

Proof. By applying the expression of the sum-connectivity index and Table 3

SCI(C4,ω)=(4ω+2)11+3+(8ω−2)12+3+(7ω)13+3+(2ω)11+2+(5ω−1)12+2+(4ω)12+5+(ω)13+5

After simplifying the previous equation, we get the following result:

SCI(C4,ω)=13.953ω−0.394

Theorem 4.5. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the Atom-Bond-Connectivity index is,

ABC(C4,ω)=21.991ω−0.489

Proof. By applying the expression of the Atom-Bond-Connectivity index and Table 3

ABC(C4,ω)=(4ω+2)1+3−21×3+(8ω−2)2+3−22×3+(7ω)3+3−23×3+(2ω)1+2−21×2+(5ω−1)2+2−22×2+(4ω)2+5−22×5+(ω)3+5−23×5.

After simplifying the previous equation, we get the following result:

ABC(C4,ω)=21.991ω−0.489

Theorem 4.6. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the geometric-arithmetic index is,

GA(C4,ω)=29.761ω−1.226

Proof. By applying the expression of the geometric-arithmetic index and Table 3

GA(C4,ω)=(4ω+2)21×31+3+(8ω−2)22×32+3+(7ω)23×33+3+(2ω)21×21+2+(5ω−1)22×22+2+(4ω)22×52+5+(ω)23×53+5.

After simplifying the previous equation, we get the following result:

GA(C4,ω)=29.761ω−1.226

Theorem 4.7. If C4,ω, with ω≥1 if a sc graph in the NsLv dialkyltin complex-4 exist, then the reduced reciprocal Randić index is,

RRR(C4,ω)=41.14ω−3.828

Proof. By applying the expression of the reduced reciprocal Randić index and Table 3

RRR(C4,ω)=(4ω+2)(1−1)(3−1)+(8ω−2)(2−1)(3−1)+(7ω)(3−1)(3−1)+(2ω)(1−1)(2−1)+(5ω−1)(2−1)(2−1)+(4ω)(2−1)(5−1)+(ω)(3−1)(5−1).

After simplifying the previous equation, we get the following result:

RRR(C4,ω)=41.14ω−3.828

5  Discussion

Topological indices are seen as a useful mechanism for investigating chemical characteristics and their own planned graphs through concepts of vertices and edges. The behaviour of a certain structure and graphs can be seen using topological indices, which provide numerical numbers. The current part compares seven degree based topological indices of our table-based structure, with matching graphs created by using a range of values 1 to 7 for the parameter ω in the seventh topological indices. Fig. 7 shows a plot of seven degree-based topological indices form the sc in dialkyltin complex-2 of NsLv (C2,ω) made from the data in Table 4. The plots grow in size in a linear pattern; the harmonic index, the second definition of the Randić index, and the sum-connectivity index are fairly close to each other, but the first definition of the Randić index moves extremely sharply among the others. Fig. 8 shows a visualisation of seven degree-based topological indices for the structure of the sc in the NsLv dialkyltin complex-3 (C3,ω) based on the values in Table 5. The plots grow in size in a linear pattern; the harmonic index, the second definition of the Randić index, and the sum-connectivity index are fairly close to each other, but the first definition of the Randić index moves extremely sharply among the others. It is reasonable to believe that the first definition of the Randić index is more appropriate for studying our chosen structure than the others. Fig. 9 shows a visualisation of seven degree-based topological indices for the structure of the sc in NsLv dialkyltin complex-4 (C4,ω) based on the values in Table 6. The plots grow in size in a linear pattern; the harmonic index, the second definition of the Randić index, and sum-connectivity index are fairly close to each other, but the first definition of the Randić index moves extremely sharply among the others. It is reasonable to believe that the first definition of Randić index is more appropriate for studying our chosen structure than the others.

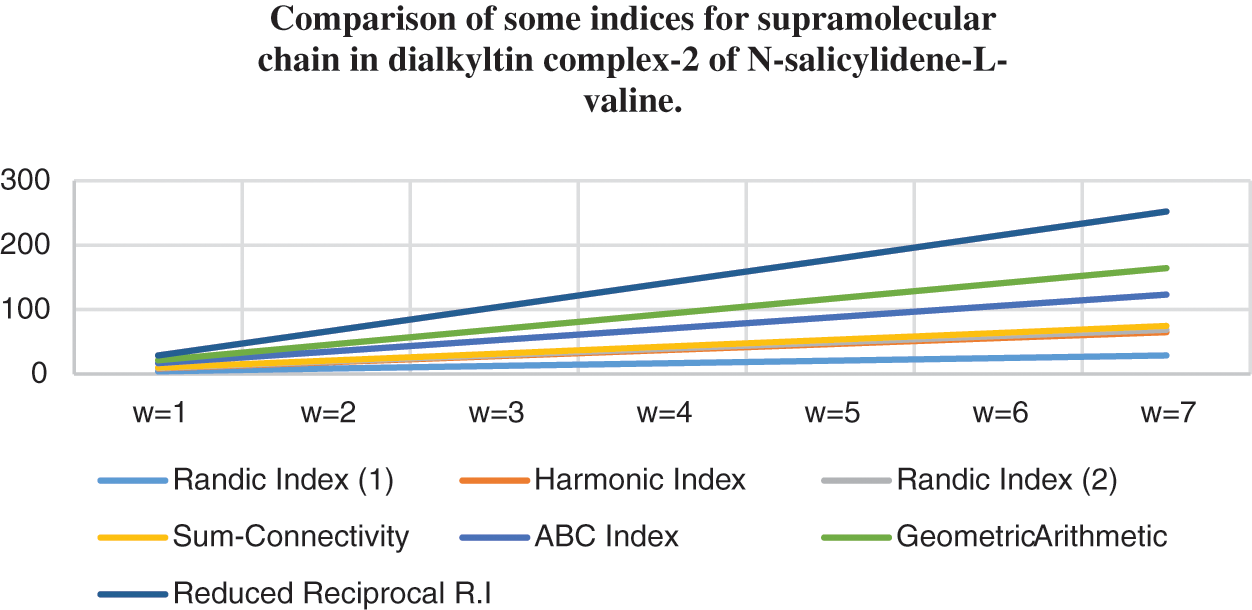
Figure 7: Correlation of some indices for sc in the dialkyltin complex-2 of NsLv

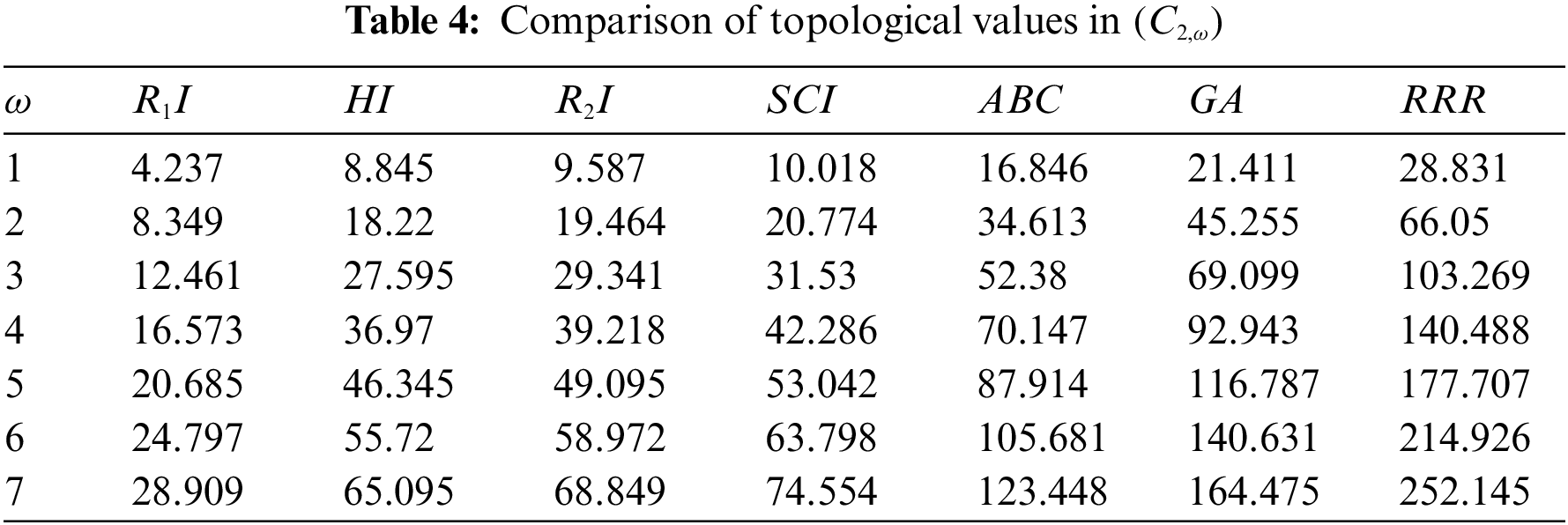
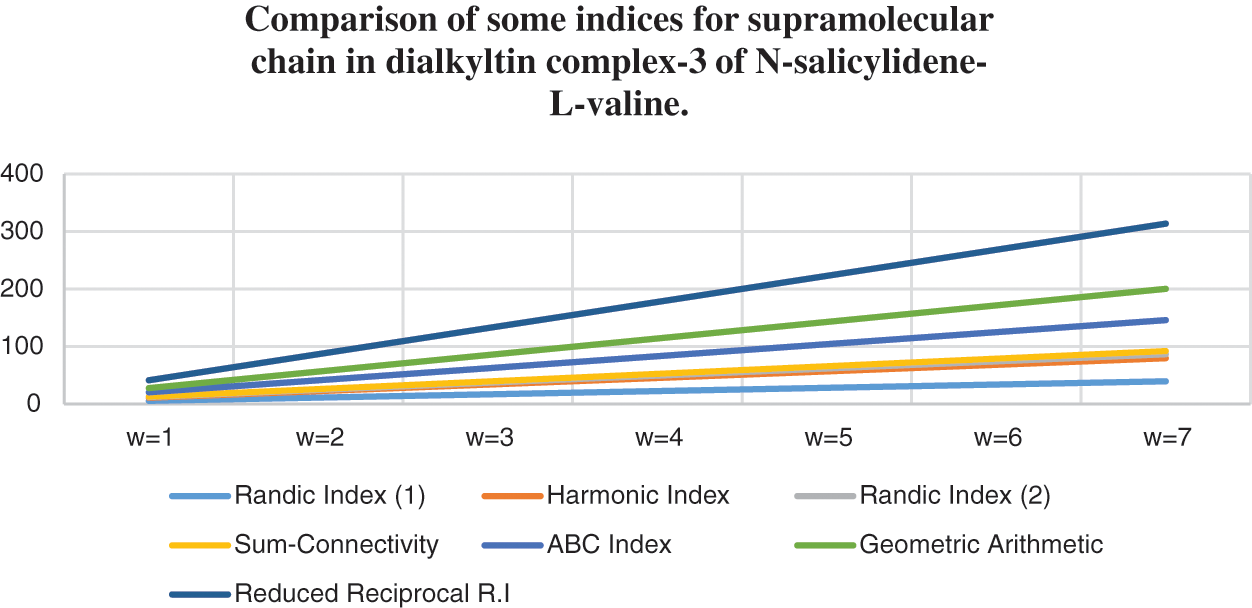
Figure 8: Correlation of some indices for sc in the dialkyltin complex-3 of NsLv

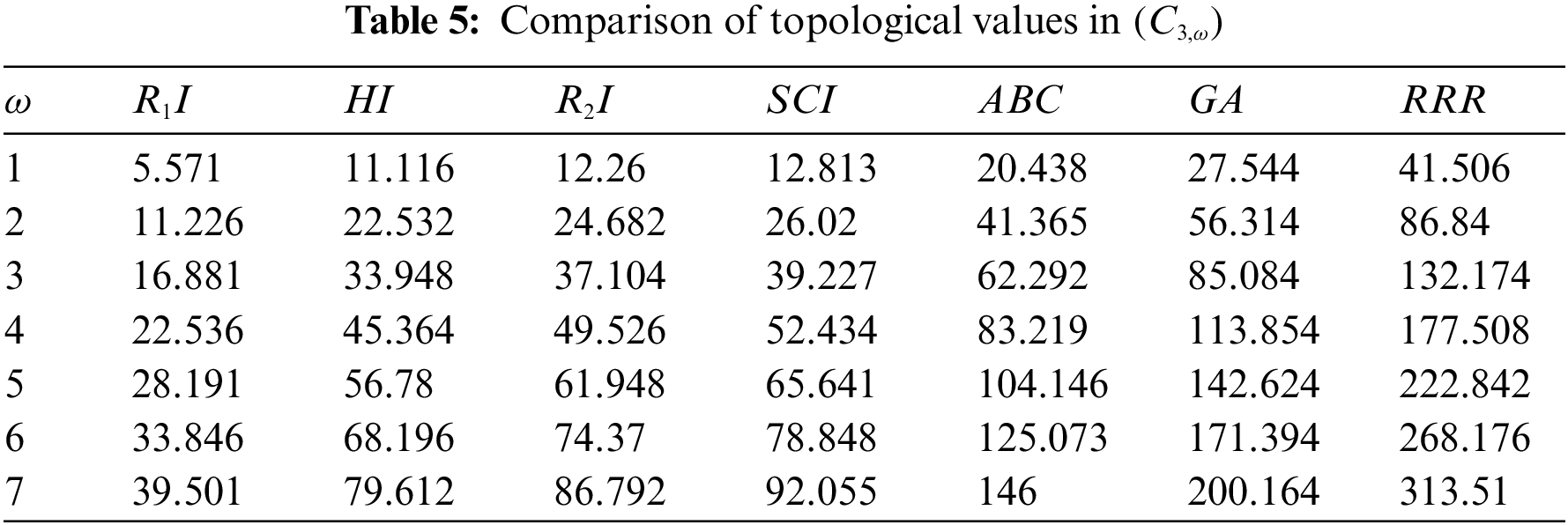
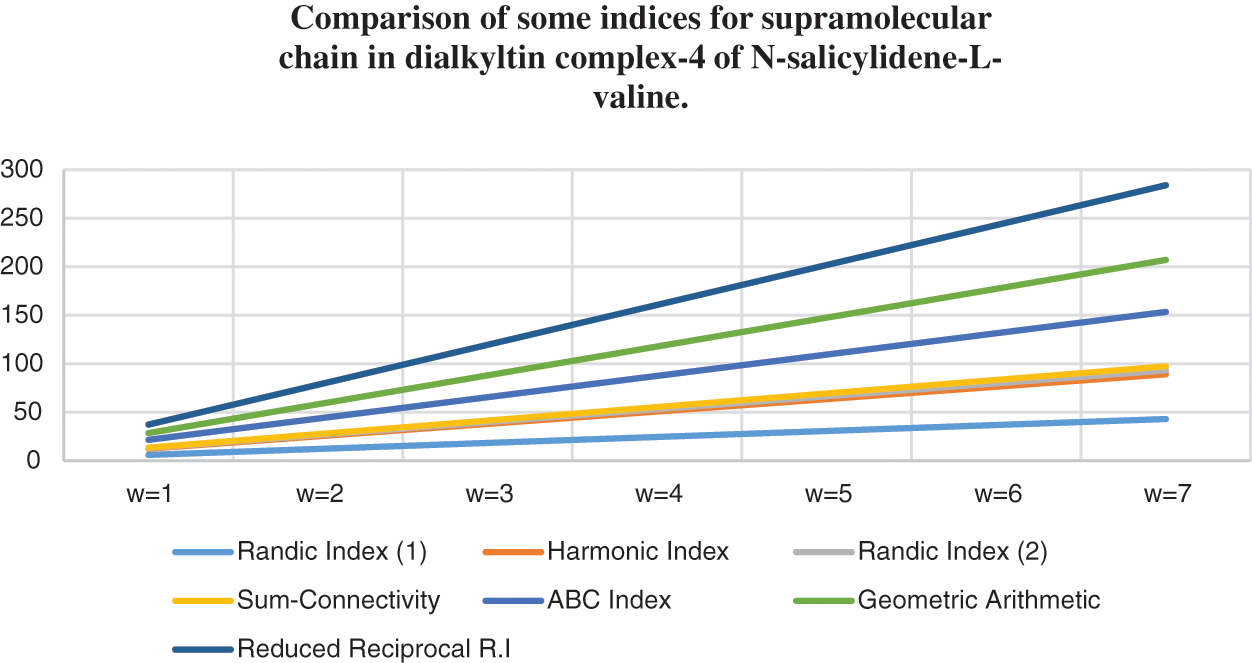
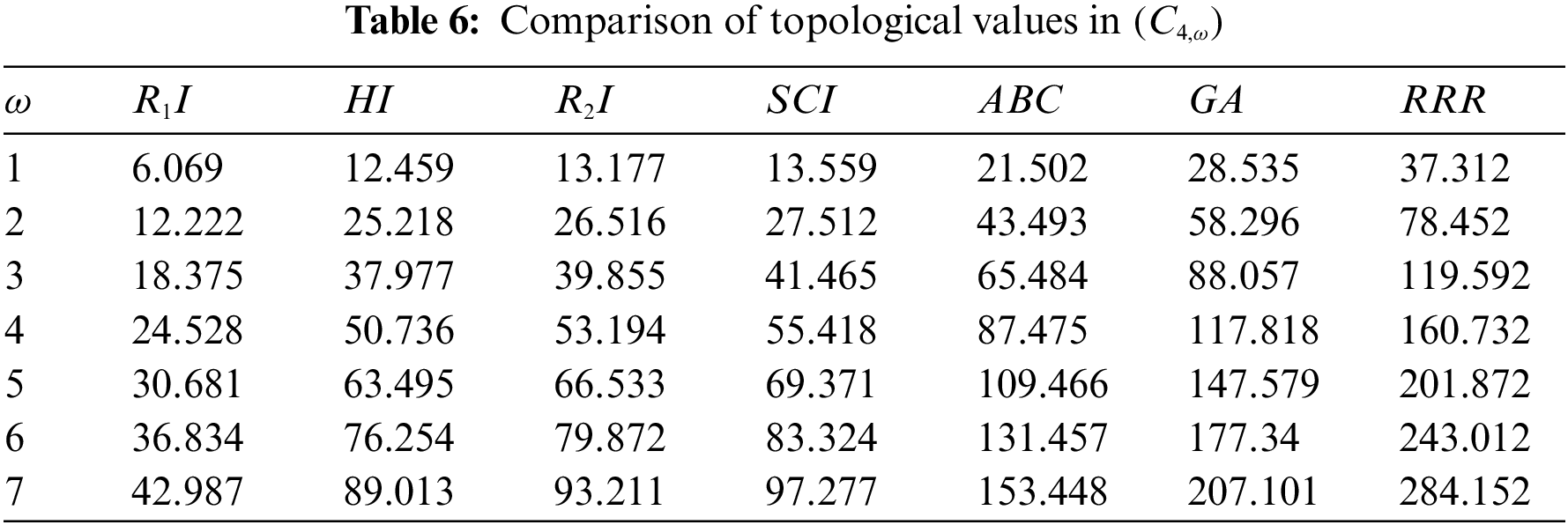
Figure 9: Correlation of some indices for sc in the dialkyltin complex-4 of NsLv

6  Conclusion

This study focused on chemical composition known as a sc in the dialkyltin complexes-2, 3, and 4 of NsLv using computational methods. To examine the behaviour of our chosen structures, we reviewed some relevant topological indices such as the first and second definitions of the Randić index, the harmonic index, the sum-connectivity index, the abc index, the geometric-arithmetic index, and the reduced reciprocal Randić index. Furthermore, we conducted a comparative analysis by selecting specific values for an arbitrary parameter ω associated to the structures and analysing them.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Hong, G., Gu, Z., Javaid, M., Awais, H. M., Siddiqui, M. K. (2020). Degree-based topological invariants of metal-organic networks. IEEE Access, 8, 68288–68300. DOI 10.1109/ACCESS.2020.2985729. [Google Scholar] [CrossRef]

    2. Nadeem, M. F., Zafar, S., Zahid, Z. (2016). On topological properties of the line graphs of subdivision graphs of certain nanostructures. Applied Mathematics and Computation, 273, 125–130. [Google Scholar]

    3. Nadeem, I., Shaker, H., Hussain, M., Naseem, A. (2019). Topological indices of para-line graphs of V-phenylenic nanostructures. Open Mathematics, 17, 260–266. [Google Scholar]

    4. Cai, Z. Q., Rauf, A., Ishtiaq, M., Siddiqui, M. K. (2020). On ve-degree and ev-degree based topological properties of silicon carbide Si2⊣C3⊣||[p,q]. Polycyclic Aromatic Compounds, 42(2). DOI 10.1080/10406638.2020.1747095. [Google Scholar] [CrossRef]

    5. Zhang, J., Siddiqui, M. K., Rauf, A., Ishtiaq, M. (2020). On ve-degree and ev-degree based topological properties of single walled titanium dioxide nanotube. Journal of Cluster Science, 32, 821–832. [Google Scholar]

    6. Nadeem, M. F., Imran, M., Muhammad, H., Siddiqui, H. M. A., Azeem, M. et al. (2021). Topological aspects of metal-organic structure with the help of underlying networks. Arabian Journal of Chemistry, 14(6), 103157. [Google Scholar]

    7. Shabbir, A., Nadeem, M. F., Mukhtar, S., Raza, A. (2020). On edge version of some degree-based topological indices of HAC5C7[p,q] and VC5C7[p,q] nanotubes. Polycyclic Aromatic Compound, 42(3), 849–865. DOI 10.1080/10406638.2020.1753220. [Google Scholar] [CrossRef]

    8. Nadeem, M. F., Azeem, M., Muhammad, H., Siddiqui, H. M. A. (2021). Comparative study of Zagreb indices for capped, semi-capped and uncapped carbon naotubes. Polycyclic Aromatic Compound, 42(6). DOI 10.1080/10406638.2021.1890625. [Google Scholar] [CrossRef]

    9. Nadeem, M. F., Azeem, M., Farman, I. (2021). Comparative study of topological indices for capped and uncapped carbon nanotubes. Polycyclic Aromatic Compound, 42(7), 4666–4683. DOI 10.1080/10406638.2021/1903952. [Google Scholar] [CrossRef]

  10. Gao, W., Wang, W. F., Jamil, M. K., Farooq, R., Farahani, M. R. (2016). Generalized atom-bond connectivity analysis of several chemical molecular graphs. Bulgarian Chemical Communications, 48(3), 543–549. [Google Scholar]

  11. Gao, W., Younas, M., Farooq, A., Virk, A. U. R., Nazeer, W. (2018). Some reverse degree-based topological indices and polynomials of dendrimers. Mathematics, 6(10), 214–220. [Google Scholar]

  12. Hayat, S., Malik, M. A., Imran, M. (2015). Computing topological indices of honeycomb derived networks. Romanian Journal of Information Science and Technology, 18, 144–165. [Google Scholar]

  13. Belokon, Y., Maleev, V. I., Kataev, D., Saveleva, T. F., Skrupskaya, T. V. et al. (2009). Chiral ion pairs in catalysis: Lithium salts of chiral metallo-complex anions as catalysts for asymmetric C-C bond formation. Tetrahedron: Asymmetry, 20(15), 1746–1752. [Google Scholar]

  14. Chen, C. T., Bettigeri, S., Weng, S. S., Pawar, V. D., Lin, Y. H. et al. (2007). Asymmetric aerobic oxidation of α hydroxy acid derivatives by C4-symmetric, vanadate-centered, tetrakisvanadyl(V) clusters derived from N-salicylidene-αaminocarboxylates. The Journal of Organic Chemistry, 72(22), 8175–8185. [Google Scholar]

  15. Chen, C. T., Lin, J. S., Kuo, J. H., Weng, S. S., Cuo, T. S. et al. (2004). Site-selective DNA photocleavage involving unusual photoinitiated tautomerization of chiral tridentate vanadyl (V) complexes derived from N-salicylidene alpha-amino acids. Organic Letters, 6(24), 4471–4474. [Google Scholar]

  16. Ucar, A., Findik, M., Bingol, H., Guler, E., Ozcan, E. (2017). Organometallic chiral schiff base for EnantioSelective fluorescent recognition of methionine. Chemical Papers, 71(10), 1855–1862. [Google Scholar]

  17. Yu, J., Jiang, H. J., Zhou, Y., Luo, S. W., Gong, L. Z. (2015). Sodium salts of anionic chiral cobalt(III) complexes as catalysts of the Enantioselective povarov reaction. Angewandte Chemie, 54(38), 11209–11213. [Google Scholar]

  18. Davies, A. G., Gielen, M., Pannell, K. H., Tiekink, E. R. T. (2008). Tin chemistry: Fundamentals, frontiers, and applications. Journal of the American Chemical Society, 15, 752. [Google Scholar]

  19. Arjmand, F., Parveen, S., Tabassum, S., Pettinari, C. (2014). Organotin antitumor compounds: Their present status in drug development and future perspectives. Inorganica Chimica Acta, 423, 26–37. [Google Scholar]

  20. Banti, C. N., Hadjikakou, S. K., Sismanoglu, T., Hadjiliadis, N. (2019). Anti-proliferative and antitumor activity of organotin(IV) compounds. An overview of the last decade and future perspectives. Journal of Inorganic Biochemistry, 194, 114–152. [Google Scholar]

  21. Tian, L. J., Chen, L. X., An, W. G., Liu, X. C. (2019). Diorganotin complexes of N-[4-(diethylamino) salicylidene]-L-tryptophane: Syntheses, structures and properties. Chinese Journal of Structural Chemistry, 38, 1977–1985. [Google Scholar]

  22. Beltran, H., Zamudio, L., Percino, T. M., Baca, R. S., Farfan, N. (2003). One-step preparation, structural assignment, and X-ray study of 2,2-di-n-butyl- and 2,2-diphenyl-6-aza-1,3-dioxa-2-stannabenzocyclononen-4-ones derived from amino acids. Chemistry (Weinheim an Der Bergstrasse, Germany), 9(10), 2291–2306. [Google Scholar]

  23. Yao, Y., Yang, M., Zheng, X., Tian, L. (2017). Synthesis, characterization, and cytotoxic activity of triphenyltin complexes of N-(5-bromosalicylidene)-α-amino acids. Main Group Metal Chemistry, 40(3−4), 93–99. [Google Scholar]

  24. Randić, M. (1975). On characterization of molecular branching. Journal of the American Chemical Society, 97, 6609–6615. [Google Scholar]

  25. Zhong, L. (2012). The harmonic index for graphs. Applied Mathematics Latters, 25, 561–566. [Google Scholar]

  26. Zhou, B., Trinajstić, N. (2010). On general sum-connectivity index. Journal of Mathematical Chemistry, 47, 210–218. [Google Scholar]

  27. Xing, R., Zhou, B., Dong, F. (2011). On atom-bond connectivity index of connected graphs. Discrete Applied Mathematics, 159(15), 1617–1630. DOI 10.1016/j.dam.2011.06.004. [Google Scholar] [CrossRef]

  28. Das, K. C., Gutman, I., Furtula, B. (2011). On the first geometric-arithmetic index of graphs. Discret Applied Mathematics, 159, 2030–2037. [Google Scholar]

  29. Manso, F. C. G., Junior, H. S., Bruns, R. E., Rubira, A. F., Muniz, E. C. (2012). Development of a new topological index for the prediction of normal boiling point temperatures of hydrocarbons. Journal of Molecular Liquids, 165, 125–132. [Google Scholar]

  30. Tian, L., Wang, R., Zhang, J., Zhong, F., Qiu, Y. (2020). Synthesis and structural characterization of dialkyltin complexex of N-salicylidene-L-valine. Main Group Metal Chemistry, 43(1), 138–146. [Google Scholar]