Metric Basis of Four-Dimensional Klein Bottle

1  Introduction

Due to its inherent simplicity, graph theory has a wide range of applications in different fields of sciences, such as engineering, physical, social, and biological sciences, and in diverse other areas. A graph can be used to represent relatively any physical situation involving discrete objects and the relationships among them, despite the restrictions of the dimension. The three and four-dimensional mathematical topologies were discussed with graph theoretical concepts [1–5] and showed the two-dimensional shapes [6] with the physical and chemical properties [1,2], and different transformations [4].

After the idea of the Möbius strip was developed in 1858, German mathematician Felix Klein described Klein’s bottle in 1882. It is a non-orientable surface with four dimensions and without any boundary. The Möbius strip can be embedded in the three-dimensional Euclidean space R3, but the Klein bottle cannot be embeddable. It is a four-dimensional object and is only embedded in R4. Fig. 2 shows the two-dimensional view of the Klein bottle and Fig. 1 the three-dimensional view of Klein bottle. For different shapes and views of this interesting topology, we refer to [3].

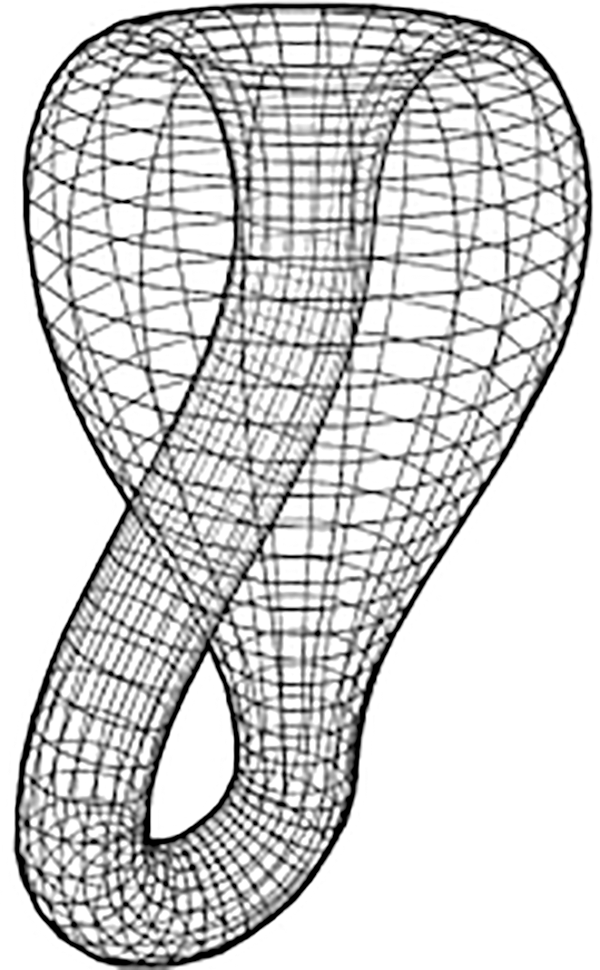
Figure 1: Klein bottle

Figure 2: Immersed Klein bottles in the Science Museum in London

Let (V,G) be a simple connected graph and B be a ordered subset of V, if each point v∈V is uniquely determined by the distances d(v,b) for some b∈B, then B is called a metric basis of (V,G). The minimum cardinality among all metric basis of V described as the metric dimension of (V,G), denoted by dim(G) [7]. Slater [8] introduced the concept of locating set (metric dimension), later Harary et al. [9] described this idea as a resolving set for a graph. Consequently, it is found in many other disciplines, most cited of them are, robot navigation, in the form of solutions of mastermind games, pattern recognition and drug discovery in pharmacological field [10–13].

Recently, the metric dimension of different spaces, including n-dimensional Euclidean space, hyperbolic space, spherical space, and Riemann surfaces, has been computed in [7]. Further continuation of this work has some generalizations in [14,15] and computed the metric dimension of manifolds, orbit spaces, and-dimensional geometric spaces. Moreover, the n-dimensional structures are discussed in [6] and [16] and computed the metric dimension of different types of Möbius strips. Metric dimension and other resolving parameters are discussed in [17]. Metric dimensions of some cycle-related and convex polytope-related graphs are discussed in [18]. Resolving sets for computer-related graphs are found in [19]. Metric dimensions for the wheel and its extended version of the graph are found in [20]. For interesting recent studies, see [21,22]. The complexity of metric dimension and finding metric basis or resolving set are found in [23,24].

Different graph-theoretical work has been done on the algebraic topological structure Klein bottle and discussed within the frame of combinatorial topology. The finding of topological symmetries between the torus and Klein bottles is studied in [25]; the algebraic topology of the Klein bottle is discussed in [1]; the Klein bottle in terms of labeling is studied in [2] for physical properties; chemical properties in terms of topological indices have been studied in [4]; embeddings of numerous networks in the Klein bottle have been studied in [26]. Motivated by all this combinatorial work on the Klein bottle, we found a metric basis and proved that this topological structure has a constant metric basis.

A few preliminaries and results are discussed in Section 2, the construction of the Klein bottle in graph theory perspective is discussed in Section 3, the metric basis and metric dimension are computed in Section 4, and the conclusion is drawn in the last section.

2  Preliminaries and Results

Following are few useful notations, definitions and literature which are necessary for our main results.

Definition 2.1: A simple connected graph G=(V,E) with vertex and edge set V and E, respectively, two vertices a1,a2∈V, the distance d(a1,a2) between vertices a1 and a2 is the count of edges between them.

Definition 2.2: A vertex a∈V is said to distinguish two vertices a1 and a2, if d(a,a1)≠d(a,a2). A set B⊂V is called a metric basis of G, if any pair of distinct vertices of G is distinguished by some element of B, and its cardinality is the metric dimension of G, denoted by dim(G).

Definition 2.3: The minimum number of edges χ between two vertices a1,a2 of a cycle (sub) graph is called as χ-size gap between a1,a2.

Now the following are a few findings from the literature and are necessary for the conclusion of our main results.

Theorem 2.4: [27] Let G be a simple connected graph with dim(G)=2 and let {a1,a2}⊂V(G) be a metric basis of G, then the degree of both a1,a2 is at most 3 and there exists a unique shortest path between a1,a2.

For further recent metric-based parameter and the extension of this work can be found in [28,29], in which the authors discussed chemical properties and an interconnection network.

3  Klein Bottle

Fig. 2 shows the graphical view of the Klein bottle, it is constructed by square grid of g×h-points, by identifying the right and left most vertices of the grid, after that, twisting this newly tube with 180∘ and identifying the upper and lowermost vertices of the tube and at the end merge the four corner vertices is shown in Fig. 2.

This can also be defined as a non-orientable surfaces, with a cross-cap number of 2 and an edge number of 0. It can be easily constructed from Möbius bands (for simplicity, only half-twisted Möbius joints will be considered herewith), connecting the remaining open edges in a “parallel” manner, i.e., performing the same operation involved in transforming a rectangle into a cylinder until the structure is completely glued to a one-sided surface. The construction of the typical physical model of a Klein bottle is comparable. A variety of variations on this topological topic can be seen in a collection of hand-blown glass Klein bottles on exhibition at the Science Museum in London. The bottles were created by Alan Bennett for the museum in 1995, construction shown in Fig. 2 given by [30].

Fig. 3 shows the grid view of the Klein bottle with order gh and it is a 4-regular graph. M-vertices denotes the mirror-vertices (M={xbg+1:1≤b≤h−1}),T-vertices denotes the twist-vertices (T={xa:2≤a≤g}),Gr-vertices denotes the grid-vertices (Gr={xbg+a+1:1≤b≤h−1,1≤a≤g−1}) and x1 is the identical vertex for simplicity we assume it in T-vertices.

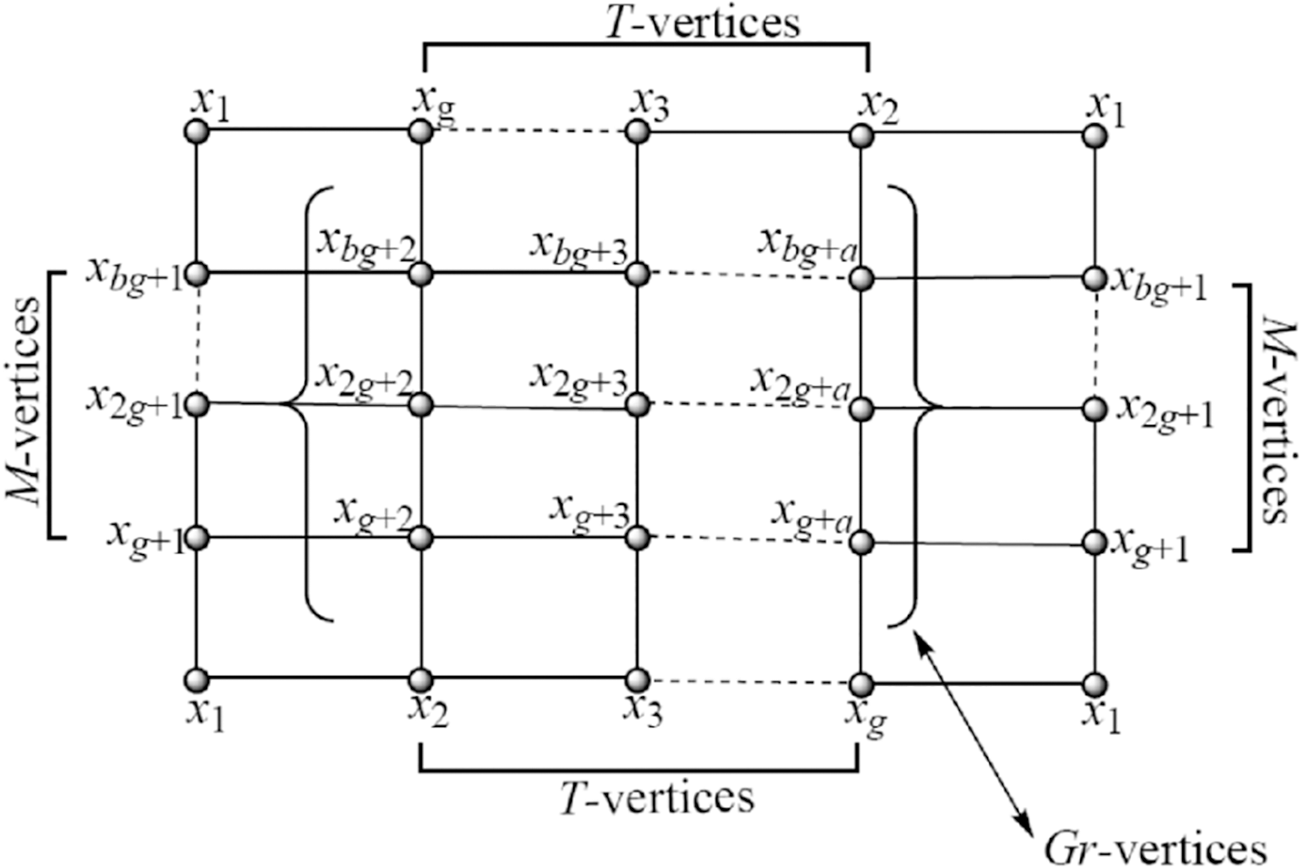
Figure 3: The grid view of KB(g,h) graph

4  Results

In this section, we determine the metric basis of the Klein bottle, KB(g,h), and proved that Kleiin bottle has constant metric dimension.

Theorem 4.1: For g odd h even, and h odd, the metric dimension of KB(g,h) is 3, where g,h≥3.

Proof. To prove dim(KB(g,h))≤3 we split the proof into the following two cases:

Case 1: h is odd

Assume the basis set B={x1,x2,xg(h−1)+22}, following are the vector representations:

r(xa|B)=(d(xa,x1),d(xa,x2),d(xa,xg(h−1)+22)),a=1,2,…,gh.(1)

Now, splitting the vector shown in Eq. (1) in components, the first component is Eqs. (2) to (4), the second component is from Eqs. (5) to (8) and the last component is from Eqs. (9) to (11).

d(xa,x1)={a−1if a=1,2,…,⌊g+22⌋g−a+1if a=⌊g+42⌋,…,g.(2)

d(xgb+1,x1)={bif b=1,2,…,⌊h2;⌋h−bif b=⌊h+22⌋,…,h−1.(3)

d(xgb+a+1,x1)={a+bif a=1,2,…,⌊g2⌋, b=1,2,…,⌊h2⌋;g−a+bif a=⌊g+22⌋,…,g−1, b=1,2,…,⌊h2⌋;g+a−bif a=1,2,…,⌊g2⌋, b=⌊h+22⌋,…,h−1;g+h−b−aif a=⌊g+22⌋,…,g−1, b=⌊h+22⌋,…,h−1.(4)

d(xa,x2)={|a−2|if a=1,2,…,⌊g+42⌋;g−a+2if a=⌊g+62⌋,…,g.(5)

d(xgb+1,x2)={b+1if b=1,2,…,⌊h−12⌋;h−b+1if b=⌊h+12⌋,…,h−1.(6)

When g>h

d(xgb+a+1,x1)={a+bif a=1,2,…,⌊g2⌋, b=1,2,…,⌊h2⌋;g−a+bif a=⌊g+22⌋,…,g−1, b=1,2,…,⌊h2⌋;h−b+aif a=1,2,…,⌊g2⌋, b=⌊h+22⌋,…,h−1;g+h−a−bif a=⌊g+22⌋,…,g−1, b=⌊h+22⌋,…,h−1.(7)

When g≤h

d(xgb+a+1,x1)={a+b−1if a=1,2,…,g−1, b=1,2,…,⌈h−22⌉;h2+a−1if a=1,2,…,⌊g2⌋,b=h2  andh=even;h2+g−a−1if a=⌊g+22⌋,…,g−1, b=⌊h2⌋andh=even;g+h−a−b−1if a=1,2,…,g−1, b=⌈h2⌉,…,h−1.(8)

d(xa,xg(h−1)+22)={h−12+a−1if a=1,2,…,⌊g+22⌋;h+12+g−aif a=⌊g+42⌋,…,g.(9)

d(xgb+1,xg(h−1)+22)=|gb+1−g(h−1)+22g|,if b=1,2,…,h−1.(10)

For b=1,2,…,h−1;

d(xgb+a+1,xg(h−1)+22)={|gb+1−g(h−1)+22g|−a+gif a=1,2,…,⌊g2⌋;|gb+1−g(h−1)+22g|+aif a=⌊g+22⌋,…,g−1.(11)

Case 2: g≥3,h≥2,h is even and g is odd

If we assume the basis set B={x1,xg+12,x3g+12}, the following are the vector representations:

r(xa|B)=(d(xa,x1),d(xa,xg+12),d(xa,x3g+12)),a=1,2,…,gh(12)

Now again splitting the vector shown in Eq. (12) in components, the first component is Eqs. (2)–(4), the second component is from Eqs. (13)–(15) and the last component is from Eqs. (16)–(18).

d(xa,xg+12)=|a−g+12|,if a=1,2,…,g.(13)

d(xgb+1,xg+12)={g−12+bif b=1,2,…,h2;g+2h−2b−12if b=h+22,…,h−1.(14)

d(xgb+a+1,xg+12)={|2a−g+12|+bif a=1,2,…,g−1, b=1,2,…,h−22;2a+h−22if a=1,2,…,g−12,b=h2;h−2a+2g+22if a=g+12,…,g−1, b=h2;|2a−g−12|−b+hif a=1,2,…,g−1, b=h+22,…,h−1.(15)

d(xa,x3g+12)={|a−g+12|+1if a=1,2,…,g+12,h=2;|a−g+32|+1if a=g+32,…,g,h=2;|a−g+12|+1if a=1,2,…,g,h≥4.(16)

d(xgb+1,x3g+12)={g−32+bif b=1,2,…,h2;g+12+h−bif b=h+22,…,h−1.(17)

d(xgb+a+1,x3g+12)={|a−g−12|+b−1if a=1,2,…,g−1, b=1,2,…,h2;|a−g+12|+h−bif a=1,2,…,g−1, b=h+22,…,h−1.(18)

As the vector representations of all vertices of KB(g,h) given in Eq. (1) are distinct, hence dim(KB(g,h))≤3.

To prove the reverse inequality that dim(KB(g,h))≥3. On contrary, it becomes dim(KB(g,h))=2, that is not possible because in Theorem 2.4 the vertices candidate for metric basis must have maximum degree three and the Klein bottle is four regular graphs, which implies that dim(KB(g,h))≥3 and concluded that dim(KB(g,h))=3.

Theorem 4.2: For g≥4,h=2 and h≥6, and g≥8,h=4 where g,h are even, the metric dimension of KB(g,h) is 4.

Proof. To prove dim(KB(g,h))≤4 we split the proof into following three cases:

Case 1: g≥4,h=2,g is even.

If we assume the basis set B={x1,x2,xg+22,xg+2}, following are the vector representations:

r(xa|B)=(d(xa,x1),d(xa,x2),d(xa,xg+22),d(xa,xg+2)),a=1,2,…,gh.(19)

Now, splitting the vector shown in Eq. (19) in components, the first component is Eqs. (2)–(4), the second component is from Eqs. (5)–(8), the third component is from Eqs. (20)–(22) and the last component is from Eqs. (23)–(25).

d(xa,xg+22)=|a−g+22|,if a=1,2,…,g.(20)

d(xgb+1,xg+22)={b+g2if b=1,2,…,h2;g2+h−bif a=h+22,…,h−1.(21)

d(xgb+a+1,xg+22)={|a−g2|+bif a=1,2,…,g−1, b=1,2,…,h2;|a−g2|−b+hif a=1,2,…,g−1, b=h+22,…,h−1.(22)

d(xa,xg+2)={2if a=1;a−1if a=2,3,…,g+22;h−2+aif a=g+42,…,g.(23)

d(xgb+1,xg+2)=b,if b=1,2,…,h−1.(24)

d(xgb+a+1,xg+2)={a+b−2if a=1,2,…,g+22, b=1,2;g−a+bif a=g+42,…,g−1,b=1,2;a+b−2if a=1,2,…,g2, b=3;g−a+1if a=g+22,…,g−1, b=3.(25)

Case 2: g≥4,h≥6,g,h are even

If we assume the basis set B={x1,xg+22,x3g+42,x5g2}, the following are the vector representations:

r(xa|B)=(d(xa,x1),d(xa,xg+22),d(xa,x3g+42),d(xa,x5g2)),a=1,2,…,gh.(26)

Now again splitting the vector shown in Eq. (26) in components, the first component is Eqs. (2)–(4), the second component is from Eqs. (20)–(22), the third component is from Eqs. (27)–(29) and the last component from Eqs. (30)–(32).

d(xa,x3g+42)={g2if a=1;|g+42−a|+1if a=2,3,…,g.(27)

d(xgb+1,x3g+42)={g−42+bif b=1,2,…,h+22;g2+h−bif b=h+42,…,h−1.(28)

d(xgb+a+1,x3g+42)={|a−g+22|+b−1if a=1,2,…,g−1, b=1,2,…,h2;|a−g−22|+h2if a=1,2,…,g2, b=h+22;|a−g+22|+h2if a=g+22,…,g−1, b=h+22;|a−g−22|+h−b+1if a=1,2,…,g−1, b=h+42,…,h−1.(29)

d(xa,x5g2)=|g2−a|+2,if a=1,2,3,…,g.(30)

d(xgb+1,x5g2)={|g−2b−22|+2if b=1,2,…,h+42;g+22+h−bif b=h+62,…,h−1.(31)

d(xgb+a+1,x5g2)={|b−2|+|a−g−22|if a=1,2,…,g−1, b=1,2,…,h+22;|a−g+22|+h−b+2if a=1,2,…,g−1, b=h+42,…,h−1.(32)

Case 3: g≥8,h=4,g is even

If we assume the basis set B={x2,xg,xg+2,x2g}, following are the vector representations with respect to B:

r(xa|B)=(d(xa,x2),d(xa,xg),d(xa,xg+2),d(xa,x2g)),a=1,2,…,gh(33)

Once again splitting the vector shown in Eq. (33) in components, the first component is Eqs. (5)–(8), the second component is from Eqs. (34)–(36), the third component is from Eqs. (23)–(25) and the last component is from Eqs. (37)–(39).

d(xa,xg)={aif a=1,2,…,g2;g−aif a=g+22,…,g.(34)

d(xgb+1,xg)={2if b=1,3;3if b=2.(35)

d(xgb+a+1,xg)={3−b+aif a=1,2,…,g−42+b, b=1,2,3;b+g−a−1if a=g−22+b,…,g−1, b=1,2,3.(36)

d(xa,x2g)={a+1if a=1,2,…,g2;g−a+1if a=g+22,…,g.(37)

d(xgb+1,x2g)=b,if b=1,2,3.(38)

d(xgb+a+1,x2g)={b+aif a=1,2,…,g−22, b=1,2;a+1if a=1,2,…,g−22+b, b=3;b+g−a−2if a=g2,…,g−1, b=1,2,3.(39)

As the vector representations of all vertices of KB(g,h) given in Eqs. (19), (26) and (33) are distinct, hence dim(KB(g,h))≤4.

To prove the reverse inequality that dim(KB(g,h))≥4. On contrary, it becomes dim(KB(g,h))=3, following are cases in the support of this claim.

Case 1: Due to the construction of the Klein bottle the twisted vertices are shown in Fig. 2. If the set T={xa:1≤a≤g} is chosen as basis set B′⊂T, with cardinality three and indices can be i′,i″,i‴, then it is resulting in the same distance with respect to the B′, vertices adjacent to x2-vertex and these are xg+2 and xgh, this case leads us to decision that B′⊂T. The possibilities of vertices in B′ can be with any gap-size and those gap-size possibilities are in the form of indices i′,i″,i′,i‴, and i″,i‴ can be apart from 0 to g−2 distinct numbers, such as i′=1,i″=2,i‴=8=g, similarly, i′=1,i″=7,i‴=8=g, and same as with all possibilities of i′,i″,i‴ in their respective domain, it will be end up on at least two vertices with the same distance.

Case 2: As shown in Fig. 2 the mirror vertices M={xgb+1:1≤b≤h−1} have symmetry with the twisted vertices T, so the symmetry resulted in the same distance, and when we choose mirror vertices in the basis set for example, let B′⊂M with cardinality three and having possible gap via indices, it implies d(x2|B′)=d(xg|B′). So, this case also leads to contradiction and it is not providing single possible vertex set with cardinality three as a candidate for the basis set of the Klein bottle.

Case 3: In the basis set, vertices belong to the grid i.e., Gr={xgb+a+1:1≤a≤g−1,1≤b≤h−1}. If Bb′⊂Gr with three cardinality with corresponding to Bb′, then the same distance in two vertices d(xα|Bb′)=d(xβ|Bb′), where α and β are both adjacent to at least one of the element of Bb′. Here b-index on Bb′ denotes that Bb′ contains vertices on each level or layer of grid. Analogously, if without the restriction on b-index and Bb′⊂Gr with |Bb′|=3, then the same distance of two vertices d(xT|B′)=d(xg|B′). This also implies a contradiction.

Case 4: In this case, we consider that if basis set with one vertex belongs to the mirror vertices and two vertices from twisted vertex set. If B′={xi′,xi″,xi‴:1≤i′,i″≤g,i‴∈gb+1,1≤b≤h−1}, then the same distance will be in vertices d(xT|B′)=d(xg|B′).

Case 5: Now, the basis set B′={xi′,xi″,xi‴:i′,i″∈gb+a+1,i‴∈gb+1,1≤a≤g−1,1≤b≤h−1}, then the two vertices gave same distances are d(xα|B′)=d(xβ|B′), where α=1,2 and β=g+2,g+3,…,2g,gh.

Case 6: Now, for the basis set B′={xa,xgb+1,xgb+a+1:1≤a≤g−1,1≤b≤h−1}⊂V(KB(g,h)), with cardinality three, there must exist two vertices with the same distances towards B′ and leads to contradiction and this time d(xα|B′)=d(xα′|B′), where α=g+2,g+3,…,2g or its symmetrical vertices that are α′=g(h−1)+1,…,gh−1,gh.

All the cases resulted in contradiction and indicate that B′ with three cardinality is not possible which implied that dim(KB(g,h))≠3 and this further concluded that for g≥4,h=2,h≥6 and g≥8,h=4 with g,h are even, dim(KB(g,h))=4.

Theorem 4.3: For g=4,6 and h=4, the metric dimension of KB(g,h) is 5.

Proof. To prove dim(KB(g,h))≤5, assume the basis set B and following are the vector representations with respect to B={x1,x2,xg+22,xg+1,xg+2}:

r(xa|B)=(d(xa,x1),d(xa,x2),d(xa,xg+22),d(xa,xg+1),d(xa,xg+2)),a=1,2,…,gh.(40)

Now, splitting the vector shown in Eq. (40) in components, the first component is Eqs. (2)–(4), the second component is from Eqs. (5)–(8), the third component is from Eqs. (20)–(22), the fourth component is from Eqs. (41)–(43), and the last component is from Eqs. (44)–(46).

d(xa,xg+1)={aif a=1,2,…,g+22;2+g−aif a=g+42,…,g.(41)

d(xgb+1,xg+1)=b−1,if b=1,2,3.(42)

d(xgb+a+1,xg+1)={b+a−1if a=1,2,…,g2, b=1,2,3;b+g−a−1if a=g+22+b,…,g−1, b=1,2,3.(43)

d(xa,xg+2)={2if a=1;a−1if a=2,3,…,g+42;2+g−aif a=g+62,…,g.(44)

d(xgb+1,xg+2)=b,if b=1,2,…,h−1.(45)

d(xgb+a+1,xg+2)={b+a−2if a=1,2,…,g+22, b=1,2,…,h−1;b+1if a=g+42+b,…,g−1, b=1,2,…,h−1.(46)

As the given vector representations of all vertices of KB(g,h) in Eq. (40) are distinct, hence dim(KB(g,h))≤5.

To prove the reverse inequality that dim(KB(g,h))≥5. On contrary, it becomes dim(KB(g,h))=4, following discussion in the support of this claim.

Case 1: For the specific values of g=4,6 and h=4. We will have only two possibilities from them. Firstly, we choose B′⊂T with four cardinality, then due to the symmetry position of vertices, two symmetrical vertices have the same distance d(xg+1|B′)=d(xg(h−1)+1|B′), and when B′⊂M, then d(x2|B′)=d(xg|B′). If B′⊂Gr with four cardinality, then the same distance either d(x1|B′)=d(xgh|B′) or d(xg|B′)=d(xg+1|B′). Now, analogously B′={xa,xgb+1,xgb+a+1:1≤a≤g−1,1≤b≤h−1}⊂V(KB(g,h)), with |B′|=4, from the possibilities of ghC4 two vertices exist which have the same distance corresponding to the chosen basis set and this leads to the contradiction and resulted in dim(KB(g,h))≠4, furthermore, when g=4,6,h=4, it implies that dim(KB(g,h))=5.

5  Conclusion

To extend the research from a 3-dimensional structure to a four-dimensional structure, we studied the metric basis of the Klein bottle and proved that the Klein bottle has a constant metric dimension for the variation of all its parameters. Although the metric basis is in variation in 3 and 4 values when changing the values of its parameter g, and h, it remains constant and unchanged with respect to its order or number of vertices. The methodology of determining the metric basis or locating set is totally based on the distances of a graph. Therefore, we proved the main theorems in the distance forms. Varying the square g-vertically and h-horizontally in the Klein bottle does not affect its metric basis. Moreover, the final view of metric basis and metric dimension with different possibilities and combinations of g,h in the following Table 1.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Ajmal, M., Kwun, Y. C., Nazeer, W., Munir, M., Kang, S. M. (2017). Some algebraic polynomials and topological indices of generalized prism and toroidal polyhex networks. Symmetry, 9(1). https://doi.org/10.3390/sym9010005 [Google Scholar] [CrossRef]

2. Pu, Q., Numan, M., Butt, S. I., Asif, M., Rafique, F. et al. (2019). Cyclic super magic labellings for toroidal and Klein-bottle fullerenes. IEEE Access, 7, 145928–145933. https://doi.org/10.1109/ACCESS.2019.2943368 [Google Scholar] [CrossRef]

3. Séquin, C. H. (2013). On the number of Klein bottle types. Journal of Mathematics and the Arts, 7, 51–63. https://doi.org/10.1080/17513472.2013.795883 [Google Scholar] [CrossRef]

4. Zuo, X., Liu, J. B., Iqbal, H., Ali, K., Rizvi, S. T. R. (2020). Topological indices of certain transformed chemical structures. Journal of Chemistry, 2020. https://doi.org/10.1155/2020/3045646 [Google Scholar] [CrossRef]

5. Heydarpour, M., Maghsoudi, S. (2021). On the metric dimension of certain metric manifolds. Bulletin of the Iranian Mathematical Society, 47, 649–657. https://doi.org/10.1007/s41980-020-00404-7 [Google Scholar] [CrossRef]

6. Nadeem, M. F., Azeem, M., Khalil, A. (2021). The locating number of hexagonal möbius ladder network. Journal of Applied Mathematics and Computing, 66, 149–165. https://doi.org/10.1007/s12190-020-01430-8 [Google Scholar] [CrossRef]

7. Bau, S., Beardon, A. F. (2013). The metric dimension of metric spaces. Computational Methods and Function Theory, 13, 295–305. https://doi.org/10.1007/s40315-013-0024-0 [Google Scholar] [CrossRef]

8. Slater, P. J. (1975). Leaves of trees. Proceeding of the 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Congressus Numerantium, vol. 14, pp. 549–559. Boca Raton, Florida, Florida Atlantic University. [Google Scholar]

9. Harary, F., Melter, R. A. (1976). On the metric dimension of a graph. Ars Combinatoria, 2, 191–195. [Google Scholar]

10. Chvatal, V. (1983). Mastermind. Combinatorica, 3, 325–329. https://doi.org/10.1007/BF02579188 [Google Scholar] [CrossRef]

11. Khuller, S., Raghavachari, B., Rosenfeld, A. (1996). Landmarks in graphs. Discrete Applied Mathematics, 70(3), 217–229. https://doi.org/10.1016/0166-218X(95)00106-2 [Google Scholar] [CrossRef]

12. Melter, R. A., Tomescu, I. (1984). Metric bases in digital geometry. Computer Vision Graphics and Image Processing, 25, 113–121. https://doi.org/10.1016/0734-189X(84)90051-3 [Google Scholar] [CrossRef]

13. Chartrand, G., Sebö, L. A., Tannier, E. (2004). On metric generators of graphs. Mathematics and Operational Research, 29(2), 383–393. https://doi.org/10.1287/moor.1030.0070 [Google Scholar] [CrossRef]

14. Heydarpour, M. (2016). On metric orbit spaces and metric dimension. Topology and its Application, 214, 94–99. https://doi.org/10.1016/j.topol.2016.10.004 [Google Scholar] [CrossRef]

15. Heydarpour, M., Maghsoudi, S. (2015). The metric dimension of metric manifolds. Bulletin of the Australian Mathematical Society, 91(3), 508–513. https://doi.org/10.1017/S0004972714001129 [Google Scholar] [CrossRef]

16. Ali, M., Ali, G., Imran, M., Baig, A. Q., Shafiq, M. K. (2012). On the metric dimension of Möbius ladders. Ars Combinatoria, 105, 403–410. [Google Scholar]

17. Azeem, M., Nadeem, M. F. (2021). Metric-based resolvability of polycyclic aromatic hydrocarbons. European Physical Journal Plus, 136(395). https://doi.org/10.1140/epjp/s13360-021-01399-8 [Google Scholar] [CrossRef]

18. Zhang, Y., Gao, S. (2020). On the edge metric dimension of convex polytopes and its related graphs. Journal of Combinatorial Optimization, 39(2), 334–350. https://doi.org/10.1007/s10878-019-00472-4 [Google Scholar] [CrossRef]

19. Shao, Z., Wu, P., Zhu, E., Chen, L. (2018). On metric dimension in some hex derived networks. Sensors, 19(1), 94. https://doi.org/10.3390/s19010094 [Google Scholar] [PubMed] [CrossRef]

20. Siddiqui, H. M. A., Imran, M. (2014). Computing the metric dimension of wheel related graphs. Applied Mathematics Computation, 242, 624–632. https://doi.org/10.1016/j.amc.2014.06.006 [Google Scholar] [CrossRef]

21. Lewis, H. R., Garey, M. R., Johnson, D. S. (1983). Computers and intractability. A guide to the theory of np-completeness. Journal of Symbolic Logic, 48(2), 498–500. https://doi.org/10.2307/2273574 [Google Scholar] [CrossRef]

22. Liu, J. B., Zafari, A., Zarei, H. (2020). Metric dimension, minimal doubly resolving sets and the strong metric dimension for jellyfish graph and cocktail party graph. Complexity, 2020. https://doi.org/10.1155/2020/9407456 [Google Scholar] [CrossRef]

23. Caceres, J., Hernando, C., Mora, M., Pelayo, I. M., Puertas, M. L. et al. (2007). On the metric dimension of cartesian product of graphs. SIAM Journal on Discrete Mathematics, 21(2), 423–441. https://doi.org/10.1137/050641867 [Google Scholar] [CrossRef]

24. Hauptmann, M., Schmied, R., Viehmann, C. (2012). Approximation complexity of metric dimension problem. Journal of Discrete Algorithms, 14, 214–222. https://doi.org/10.1016/j.jda.2011.12.010 [Google Scholar] [CrossRef]

25. Putz, M. V., Ori, O. (2020). Topological symmetry transition between toroidal and Klein bottle graphenic systems. Symmetry, 12(8). https://doi.org/10.3390/sym12081233 [Google Scholar] [CrossRef]

26. Shabbir, A. (2014). Fault-tolerant designs in lattice networks on the Klein bottle. Electronic Journal of Graph Theory and Applications, 2(2), 99–109. https://doi.org/10.5614/ejgta [Google Scholar] [CrossRef]

27. Liu, J. B., Nadeem, M. F., Siddiqui, H. M. A., Nazir, W. (2019). Computing metric dimension of certain families of toeplitz graphs. IEEE Access, 7, 126734–126741. https://doi.org/10.1109/ACCESS.2019.2938579 [Google Scholar] [CrossRef]

28. Sharma, S. K., Bhat, V. K., Raza, H. (2022). On mixed metric dimension of polycyclic aromatic hydrocarbon networks. Chemical Papers, 76, 4115–4128. https://doi.org/10.1007/s11696-022-02151-x [Google Scholar] [CrossRef]

29. Prabhu, S., Manimozhi, V., Arulperumjothi, M., Klavžar, S. (2002). Twin vertices in fault-tolerant metric sets and fault-tolerant metric dimension of multistage interconnection networks. Applied Mathematics and Computation, 420. https://doi.org/10.1016/j.amc.2021.126897 [Google Scholar] [CrossRef]

30. “Strange surfaces: New ideas”. Science Museum London. https://201708014.azurewebsites.net/index.php?q=oKipp7eAc2SWr3HmtNTZ4JzJqsRgwuHce-fP2bV-t92crMa5mNjf47OsadCfpprPvcrJkJM [Google Scholar]