An Effective Neighborhood Solution Clipping Method for Large-Scale Job Shop Scheduling Problem

1  Introduction

Job shop scheduling problem (JSSP) is one of the most important combinatorial optimization problems in the field of operational research and management science [1]. As one of the most classic scheduling problems, it widely exists in the fields of aerospace, transportation, and automotive processing. JSSP can be briefly described as a set of jobs to be processed on a set of machines, and each job has to go through all machines in a certain order. It is a well-known NP-hard problem, when the number of jobs increases, the difficulty of solving the problem exponentially increases. In the past few decades, JSSP has been studied by a significant number of researchers. But even the most efficient state-of-the-art method cannot ensure the acquisition of the optimal solution to the JSSP problem and becomes time-consuming as the size of the problem increases. Hence, there is still much work to be done on addressing large-scale JSSP.

Currently, many effective methods use local search methods with embedded neighborhood structures to enhance the local search capability of the methods, such as biased random-key genetic algorithm (BRKGA) [2], Tabu search/path relinking algorithm (TSPR) [3], Tabu search algorithm with a new neighborhood structure (TSED) [4], Knowledge-Based Multiobjective Memetic Algorithm (MOMA) [5], and variable neighborhood descent hybrid genetic algorithm (VND-hGA) [6]. Some of these algorithms are currently the most effective methods, such as BRKGA and TSPR, which improved the upper bounds of benchmark instances. From the existing literature, the results of the benchmark have been updated with the proposal of effective neighborhood structures, meaning that the neighborhood structure of JSSP plays a crucial role in the local search method. During the development of the neighborhood structure, it seems that the size of the neighborhood structure has a significant impact on the efficiency of local search. Large-size neighborhood structures may reduce the efficiency of the local search approach, while the properly-size neighborhood structure will improve the efficiency of the method. For instance, in comparison with N4 [7], N5 [8], and N6 [9], the exploitation and efficiency of neighborhood structure N1 [10] are inhibited because it spends a lot of time making unfruitful moves [7]. On the other hand, after erasing several unfruitful movements from N4, N6 is more constrained than N4 and is currently one of the most effective and efficient neighborhood structures [4]. Therefore, reducing the number of unfruitful moves to improve the quality of the neighborhood solution set has a positive impact on improving the efficiency of the algorithm.

To obtain a more efficient local search procedure, a neighborhood solution clipping method is proposed based on the domain knowledge of JSSP. It can reduce the computational cost of the algorithm by avoiding the search for unfruitful moves. Besides, a genetic Tabu search algorithm with neighborhood clipping (GTS_NC) is developed to solve large-scale JSSP. The main contributions of this paper are as follows:

(1) This work mined the domain knowledge of the neighborhood structure of JSSP that provided a deeper exploration of the characteristics of the JSSP.

(2) Based on the domain knowledge of JSSP, a neighborhood solution clipping method is developed to improve the efficiency of the local search method by avoiding the generation of unimproved neighborhood solutions.

(3) A feasible neighborhood solution determination method is proposed to distinguish feasible neighborhood solutions from infeasible ones.

The remainder of this paper is organized as follows. Section 2 reviews relevant literature. Section 3 is the problem formulation. Section 4 proposes the detail of GTS_NC. Section 5 shows the computational results and comparisons. Finally, Section 6 summarizes the research and discusses future research directions.

2  Literature Review

JSSP is a kind of typical machine scheduling problem that a huge amount of literature has been published within the last six decades [1]. In a general way, algorithms for JSSP can be grossly classified into two categories: exact algorithms and approximation algorithms. Since exact algorithms have encountered difficulties in solving JSSP with more than 250 operations in a reasonable time, approximation algorithms provide a quite good alternative for the JSSP [4]. More recently, swarm intelligence and evolutionary algorithms are widely used to solve JSSP, such as genetic algorithm [11,12], Differential evolution algorithm [13], Tabu search algorithm [3,4,14], Coral Reef optimization [15], Memetic algorithm [16,17], Artificial bee colony algorithm [18], Artificial algae algorithm [19], Jaya algorithm [20], and Hybrid algorithms [21–23].

From the existing literature, it appears that the increase in the size of the problem leads to an increase in the computational consumption of the algorithm, thus reducing its efficiency of the algorithm. Hence, local search methods based on neighborhood structure, which can obtain high-quality local optimal solutions, have received increasing attention for their advantage in improving the exploration capability of the algorithm. For example, a new neighborhood structure with adaptive GA is developed in [22], in which crossover probability (Pc) and mutation probability (Pm) can be adjusted based on the dispersion of the fitness of the population in the evolution. In [24], an artificial bee colony algorithm adopted with five neighborhood structures is proposed for solving a profit-oriented and energy-efficient disassembly sequencing problem. Mohanmmad et al. [25] developed a hybrid algorithm that combines global equilibrium search, path relinking, and Tabu search to solve the JSSP. The neighborhood structure N6 is applied in the Tabu search framework. Cheng et al. [26] presented a Hybrid evolutionary algorithm which incorporated a Tabu search with neighborhood structure N7. The approach identifies a better upper bound of two instances, SWV06 and SWV08. Nagata et al. [27] presented a local search-based method that works in partial solution space for solving the JSSP. The local search procedure applied with neighborhood structure N6 is performed in a partial solution space where the current solution is represented as a partial schedule. Zobolas et al. [28] presented a hybrid metaheuristic method consisting of differential evolution, variable neighborhood search, and genetic algorithm.

In addition to the solving of JSSP, neighborhood structure-based local search methods are also widely used to solve other types of scheduling problems. For example, Li et al. [29] developed a new neighborhood search method for solving the permutation flow shop scheduling problem (PFSP). Zhang et al. proposed a variable neighborhood search using four neighborhood structures is proposed to solve the dynamic flexible job shop scheduling problems (DFJSP) [30]. Fan et al. [31] developed an improved genetic algorithm with a modified k-insertion neighborhood structure for solving flexible job shop scheduling problem (FJSP) considering reconfigurable tools with limited auxiliary modules. They also proposed a Tabu search embedded with three neighborhood operators to solve FJSP [32]. In fact, every approach that improves the best-known solutions of famous benchmark instances is developed with neighborhood structures, such as BRKGA [2], TSPR [3], and novel memetic algorithms [16]. The BRKGA, which combined with neighborhood structure N5, improved the best-known solution for 57 instances of well-known benchmarks. The TSPR algorithm, which is embedded with neighborhood structure N7, improved the best-known solution for 49 instances of well-known benchmarks. Besides, the neighborhood structure N7 is also used in the novel memetic algorithm [16], which improved the best-known solutions for 3 instances of well-known benchmarks. Thus, it is obvious that the neighborhood structures of JSSP play an essential role in the process of finding a high-quality optimal solution.

The development of neighborhood structures can be summarized as follow. In 1992, it is verified that the permutation of non-critical operations cannot improve the objective function and may create infeasible solutions. Subsequently, researchers developed neighborhood structure N1, which brought the attention of researchers to the study of the critical path of the scheduling solution. Combined simulated annealing with N1, the algorithm can find a better optimal solution than other effective approximation approaches at that time. As N1 includes a great number of unimproved moves, it is observed that unless the job-predecessor of operation u or the job successor of operation v is on the critical path, the interchange containing u and v cannot reduce the makespan [33]. This theory strongly supports the development of neighborhood structures. For instance, neighborhood structure N4 is developed based on N1 by erasing the interchange of adjacent pair of critical operations and inserting an operation to either the front or the rear of the critical block. It combined with the Tabu search algorithm improves the best-known upper bound for 5 of the seven open benchmark problems. Similarly, the neighborhood structure N5 is designed based on N4, which only concerns the exchange of operations in the front and the back of the critical block. Computational experiment shows it is competitive in terms of computational consumption. To date, neighborhood structure N6 is the most effective neighborhood structure. It is properly optimized on the basis of N4, which maintains an abundant set of neighborhood solutions compared with N5. The algorithm embedded with N6 obtains the optimal solution of LA27 (unknown before) and improved most of the TD and LA instances. After the development of N6, researchers are still focusing on developing efficient neighborhood structures, such as Zhang et al. [4] proposed neighborhood structure N7, which extends N6 by moving either the first or the last operation of the critical block into the internal operation within the block. Zhao [34] proposed a multi-operation joint movement neighborhood structure, it can exchange up to 3 pairs of operations simultaneously. Xie et al. [35] developed a new neighborhood structure N8, which considers the movement of critical operations outside the critical block on the basis of N7.

The development of neighborhood structure reveals that the size of neighborhood structure is closely related to the quality and efficiency of local search. Large-scale neighborhood structure enables adequate exploration of the solution space, but the computational cost increases at the same time. Even the most efficient neighborhood structure N6 still contains a number of neighborhood solutions that are generated by invalid operations movements. Therefore, it is necessary to develop a JSSP domain knowledge-based method that can recognize and clip the unimproved neighborhood solutions to improve the efficiency of the algorithm.

In summary, this research proposed an algorithm named GTS_NC for solving large-scale JSSP. The details of the proposed method will be given in the following sections.

3  Problem Formulation

Job shop scheduling problem can be described as n jobs processed on m machines; each job has to go through all machines in a certain order. A job’s processing on a machine indicates an operation of the job, and its duration is a given constant. It is an NP-hard problem. The constraints of JSSP are as follows: (i) the processing sequence of operations of each job is prescribed. (ii) each machine can process at most one job at a time. (iii) each operation can be processed on at most one machine at a time. The objective is to minimize the makespan.

It is useful to formulate JSSP with disjunctive graph G = (N, A, E) including node set N, conjunctive arc set A (directed), and disjunctive arc set E (undirected) [4]. N is contained by all operations nodes, a dummy start node s, and a dummy end node e. The directed arc (i, j) of A shows the sequence constraints of operations where the length depends on the duration of operation i. The selected direction of the arc (i, j) of E decides the processing order of jobs on each machine. S denotes the set of selections of edge set E, which will instead of E get a solution Ds = (N, A∪S). A feasible solution Ds corresponds to an acyclic set S, that no directed cycle exists in the directed graph. Furthermore, if L(u, v) denotes the longest path from u to v, then the L(s, e) of Ds is equal to the makespan of the schedule. Thus, in the disjunctive graph of JSSP, the objective function is to find the acyclic set S that minimizes the longest path from s to e.

4  Proposed GTS_NC Method

4.1 Text Layout Neighborhood Solution Clipping Method

The neighborhood structure is a specific perturbation that can obtain a set of similar solutions. It usually considers a pair of operations u and v processed on the same machine, and both of them belong to the critical path of the solution (v processed after u). When u is moved right after v, we will call the perturbation a forward interchange. When v is moved before u, we will call the perturbation a backward interchange. As neighborhood structures focus on the design of movement rules, the lack of control over the quality of neighborhood solutions reduces the local search efficiency. Therefore, this paper proposes a neighborhood solution clipping method that can improve the efficiency of the local search method by avoiding the generation of unimproved neighborhood solutions.

To demonstrate our properties clearly, related symbols are identified as follows: For any operation u, denoting α(u) as the job-predecessor operation and γ(u) as the job-successor operation, respectively [9]. Also, β(u) means the machine-predecessor operation, and δ(u) means the machine-successor operation of operation u, respectively.

A neighborhood solution clipping method is well-designed in this section. We state these methods with proof as follows:

Proposition 1. For feasible scheduling, if the movement between a pair of critical operations of a solution cannot reduce the start time of at least one critical block, then the makespan of the solution will not reduce.

Proof. Suppose there are n critical blocks in solution S, and the start processing time of each critical block i is denoted as ci with length li, thus the makespan of S is equal to cn + ln. Solution S’ is obtained after the interchange of solution S. Since no critical block is advanced and the length li of each critical block will not change after a within-the-block interchange. Therefore, the longest path of S’ from s to e is at least equal to cn + ln, which means the makespan of S’ cannot be less than S.

Then we explore conditions, where an interchange on operation u and v is guaranteed, but cannot reduce the makespan.

Proposition 1.1. For a feasible scheduling S, v is the first operation in critical block, if α(u) is completed after the starting time of v, then the backward interchange of operation u before v cannot reduce the makespan.

Proof. Suppose solution S’ is obtained after the backward interchange of S. The makespan of S can be described as L(s, v) + pv + L(v, e) or L(s, u) + pu + L(u, e). Then move u to the front of v, the start time of u is the completion time of α(u) due to the sequence constraints. Thus, the makespan of S’ is max{L(s, v)’ + pv + L(v, e)’, L(s, u)’ + pu + L(u, e)’}. Where L(s, u)’ = L(s, α(u)) + pα(u), L(u, e)’ = pv + L(v, e)’, L(v, e)’ = L(v, e) − pu, so L(s, u)’ + pu + L(u, e)’ = L(s, α(u)) + pα(u) + pu + pv + L(v, e) − pu = L(s, α(u)) + pα(u) + pv + L(v, e). Since α(u) is completed after the starting time of v in S, L(s, v) ≤ L(s, α(u)) + pα(u). Hence L(s, α(u)) + pα(u) + pv + L(v, e) ≥ L(s, v) + pv + L(v, e), which means a new longest path is created and the makespan of S’ cannot be less than S confirms the Proposition 1.1 (see Fig. 1).

Figure 1: The backward interchange of operation u

Proposition 1.2. For a feasible scheduling S, v is the last operation in critical block, if γ(u) processed on the same machine before γ(v), then the forward interchange of operations u in critical block cannot reduce the makespan.

Proof. Suppose solution S’ is obtained after the backward interchange of S. The makespan of S can be described as L(s, v) + pv + L(v, e). Then move u right after v that obtain solution S’ which makespan is max{L(s, v)’ + pv + L(v, e)’, L(s, u)’ + pu + L(u, e)’}, where L(s, v)’ = L(s, v) − pu, L(v, e)’ = L(v, e), L(s, u)’ = L(s, v)’ + pv, because γ(u) processed on the same machine before γ(v), so the processing of γ(u) is delayed due to the delay of u, L(u, e)’ ≥ pγ(u) + L(v, e). Hence L(s, u)’ + pu + L(u, e)’ ≥ L(s, v) − pu + pv + pu + pγ(u) + L(v, e) = L(s, v) + pv + pγ(u) + L(v, e) ≥ L(s, v) + pv + L(v, e). It means a new operation is added and the makespan of S’ cannot be less than S confirms the Proposition 1.2 (see Fig. 2).

Figure 2: The forward interchange of operation u

Both proposition 1.1 and 1.2 can be used to decrease the size of N6 and N7. In addition, consider N7 has more perturbations than N6 with the forward interchange of the first operation and the backward interchange of the last operation in each critical block, another two propositions should be concerned as follows.

Proposition 1.3. For a feasible schedule S, u is the first operation in the critical block, if α(δ(u)) (if it exists) is completed after the starting time of u, then the forward interchange of operation u cannot reduce the makespan.

Proof. Suppose solution S’ is obtained after the backward interchange of S. After the backward interchange of u, δ(u) will be the first operation of the critical block of S’. If α(δ(u)) (if it exists) is completed after the starting time of u, the start time of the critical block will be delayed due to the sequence constraints between α(δ(u)) and δ(u). Because the interchange will not change the length of the critical block, all the critical blocks behind will be delayed. According to Proposition 1, the makespan of S’ cannot be less than S (see Fig. 3).

Figure 3: The forward interchange of operation u

Proposition 1.4. For an active scheduling S, u is the last operation in the critical block, if γ(β(u)) (if it exists) is processed on the same machine before γ(u) (if it exists), then the backward interchange of operations u in the critical block cannot reduce the makespan.

Proof. Suppose solution S’ is obtained after the backward interchange of S. After the forward interchange of u, β(u) will be the last operation of the critical block of S’. If γ(β(u)) (if it exists) is processed on the same machine before γ(u), all the operations between γ(β(u)) and γ(u) will be added into the critical block containing γ(u), the start time of γ(u) will be delayed due to the sequence constraint of β(u) and γ(β(u)). Considering no operation is removed from the critical path, the makespan of S’ cannot be less than S (see Fig. 4).

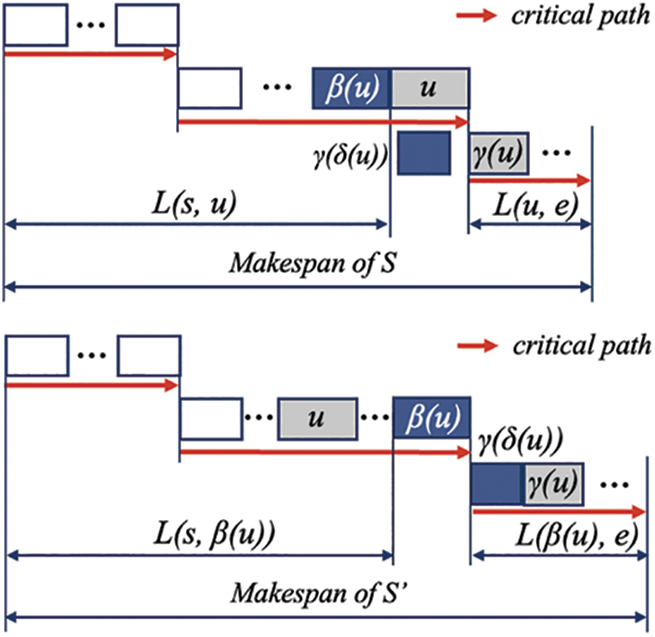
Figure 4: The backward interchange of operation u

4.2 Feasible Neighborhood Solution Determination Method

The determination of feasible neighborhood solutions involves the efficiency of local search methods because infeasible neighborhood solutions cannot provide a referable recommendation for the scheduling scheme. In order to distinguish a feasible neighborhood solution from an infeasible one, two propositions proposed by Balas et al. [9] are shown as follows:

Proposition 2. If two operations u and v to be performed on the same machine are both on the critical path P(s, e), and L(v, e) ≥ L(γ(u), e), then a forward interchange on u and v yields an acyclic complete selection.

Proposition 3. If two operations u and v to be performed on the same machine are both on the critical path P(s, e), and L(s, u) + pu ≥ L(s, α(v)) + pα(v), then a backward interchange on u and v yields an acyclic complete selection.

Although both of the propositions can ensure the feasible of the obtained neighborhood solutions, it was found to be inadequate for obtaining all acyclic solutions. As shown in Fig. 5a, the scheduling problem consists of 5 jobs and 4 machines (Ji,j means the j-th operation of job i). The critical path of each solution is signed with red bold line. Solution S’ is a neighborhood solution of S by backward interchange on J2,2 and J4,3. According to proposition 2, the backward interchange will lead to an infeasible solution because the L(J4,3, e) = p4,4, L(J2,3, e) = p2,4, L(J4,3, e) ≤ L(J2,3, e). In fact, however, the backward interchange corresponding to a feasible solution, and the Gantt chart of S’ is shown in Fig. 5b. The reason is the length between the start node and end node to each operation cannot fully map the sequential connection relationship of the operations. Therefore, in this paper, a new theorem is developed to determine the feasible neighborhood solutions (see Fig. 6). For an operation u, we define a front operation set FSu and back operation set BSu, separately. The FSu includes operation u’s α(u), β(u), FSα(u), and FSβ(u) (if exits). The BSu includes operation u’s γ(u), δ(u), BSγ(u) and BSδ(u) (if exits). Consider a feasible solution S:

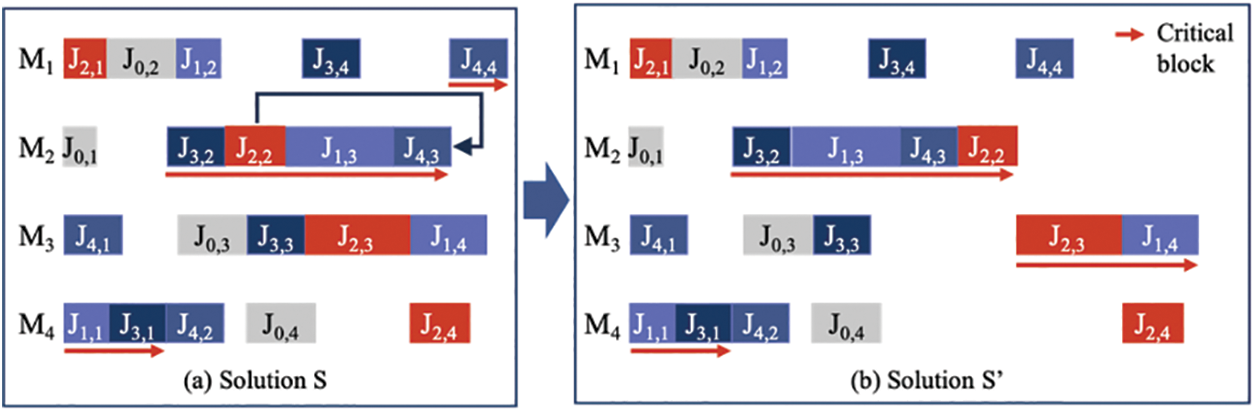
Figure 5: A counter-example for proposition 2. (a) Gantt chart of solution S. (b) Gantt chart of solution S’

Figure 6: Example of the back operation set BSγ(u) of an individual

Proposition 4. If a critical path P(s, e) containing u and v, and v ∉ BSγ(u), then move u to the back of v yields an acyclic complete selection.

Proof. By contradiction: suppose there is a feasible solution S, if v ∉ BSγ(u) for operation u and v on the critical path, then moving u to the back of v creates a cycle C in the disjunctive graph. Because the interchange of u and v deletes the direct arc from u to v on the machine, creating a direct arc (v, u) and a cycle, (v, u) ∈ C, there exists a path in Ds from u to v. Hence Ds exists a direct arc from u to another operations l1,…,lk connect with v. In this case, v must belong to BSγ(u) which is contrary to the assumption.

Proposition 5. If a critical path P(s, e) containing u and v, and u ∉ FSα(v), then moving v to the front of u yields an acyclic complete selection.

Proof. By contradiction: suppose there is a feasible solution S, if u ∉ FSα(v) for operation u and v on the critical path, then moving v to the front of u creates a cycle C in the disjunctive graph. Because the interchange of u and v deletes the direct arc from u to v on the machine, creating a direct arc (v, u) and a cycle, (v, u) ∈ C, there exists a path in Ds from u to v. Hence Ds exists a direct arc from v to another operations l1,…,lk connect with u. In this case, u must belong to FSα(v) which is contrary to the assumption.

The procedure of distinguishing feasible neighborhood solutions by existing method and the proposed method is shown in Fig. 7.

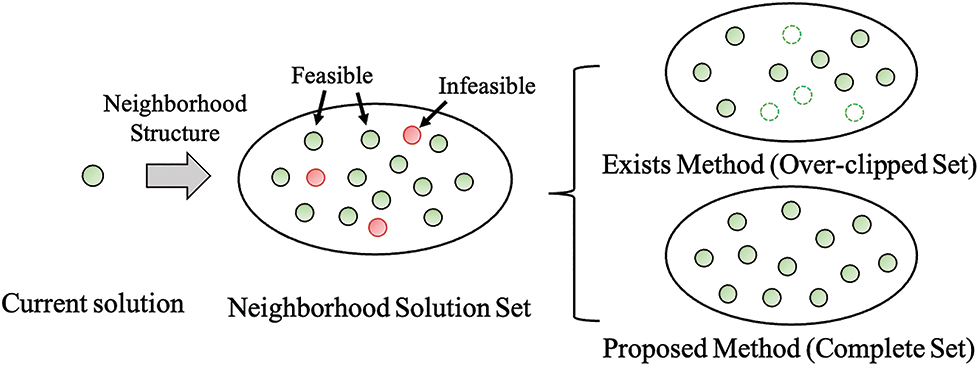
Figure 7: The procedure of filtering feasible neighborhood solutions

4.3 Framework of the Proposed GTS_NC Algorithm

In this paper, the hybrid algorithm [36] is combined with the proposed neighborhood solution clipping method for solving JSSP. The workflow and details of GTS_NC can be seen in Algorithm 1 which is composed of selection, crossover, mutation, and Tabu search. Each solution is encoded by a vector whose size is equal to the total number of operations and generated randomly. Besides, two-generation selection operators are adopted, an elitist selection scheme and a tournament selection scheme. In the elitist selection scheme, the best pr×popsize solutions will be selected from solutions randomly chosen. In the tournament selection scheme, a number of individuals (pt×popsize) will be maintained through randomly chosen tn solutions from the population and keep the one with the best fitness. Then, the crossover scheme contains precedence operation crossover (POX) and job-based crossover (JBX) [36]. The mutation scheme contains swapping mutation and neighborhood mutation methods [36]. The Tabu search algorithm [4] is adopted as local search algorithm. To enhance the diversity of the Tabu search and avoid premature convergence of the algorithm, we improve the Tabu search algorithm with a memory pool to save the best-unchosen neighborhood solution in each iteration. In addition, a random solution will be generated if the size of the neighborhood solution set is less than two. The workflow of the Tabu search algorithm is shown in Fig. 8.

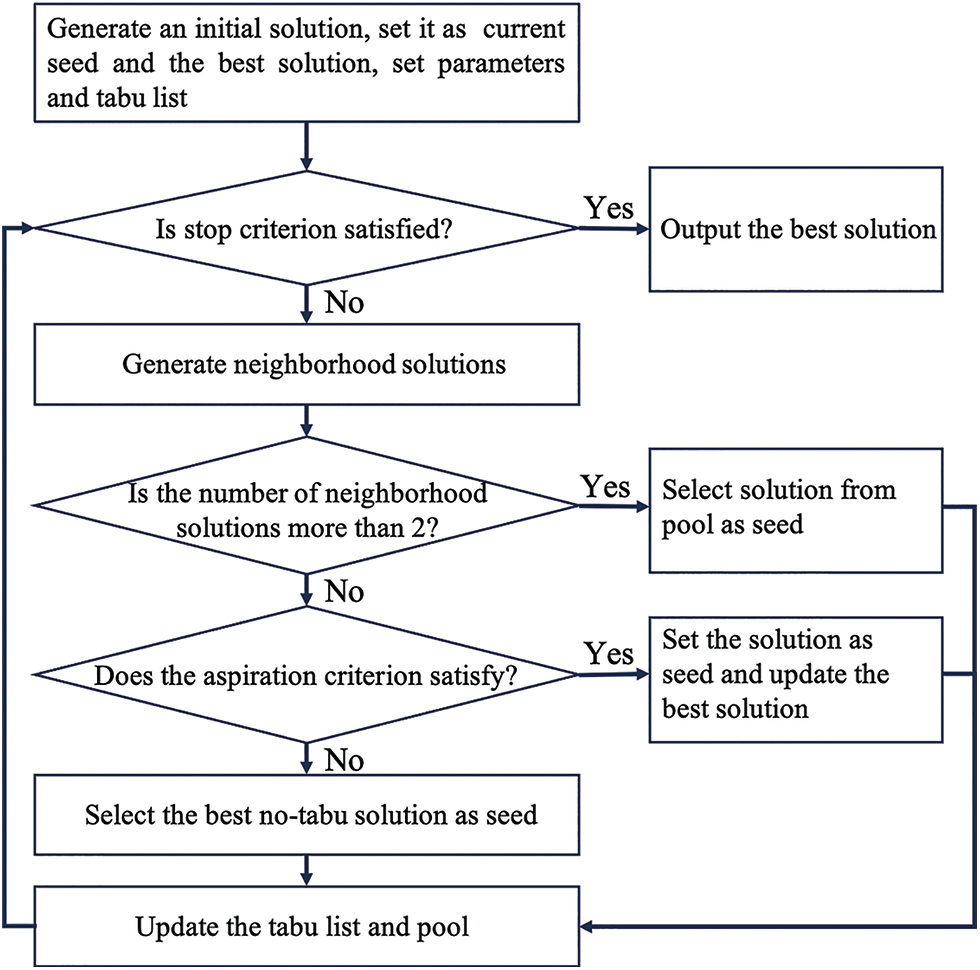
Figure 8: Tabu search workflow

5  Results and Discussion

In this section, three experiments are set to verify the proposed feasible neighborhood solution determination method, the neighborhood solution clipping method, and the proposed GTS_NC algorithm, respectively.

Experiment 1 compares the proposed feasible neighborhood solution determination method with the state-of-the-art feasible solution definition method [4] according to the average quantity of feasible neighborhood solutions obtained for each benchmark instance problem. Experiment 2 tests the effectiveness of the proposed neighborhood solution clipping method by the local search algorithm. Experiment 3 tests the performance of the proposed GTS_NC algorithm by comparing it with other algorithms. All the best solutions are recorded. The famous LA benchmark instance [37] was adopted to evaluate the performance of the proposed algorithm. The objective of this paper is to minimize makespan.

The proposed GTS_NC algorithm was coded in C++ and implemented on a computer with an Apple M1 with 16.0 GB of RAM memory.

5.1 Parameters Setting

The parameters of GTS_NC are the same as their basic papers, respectively (see Table 1) [4,36].

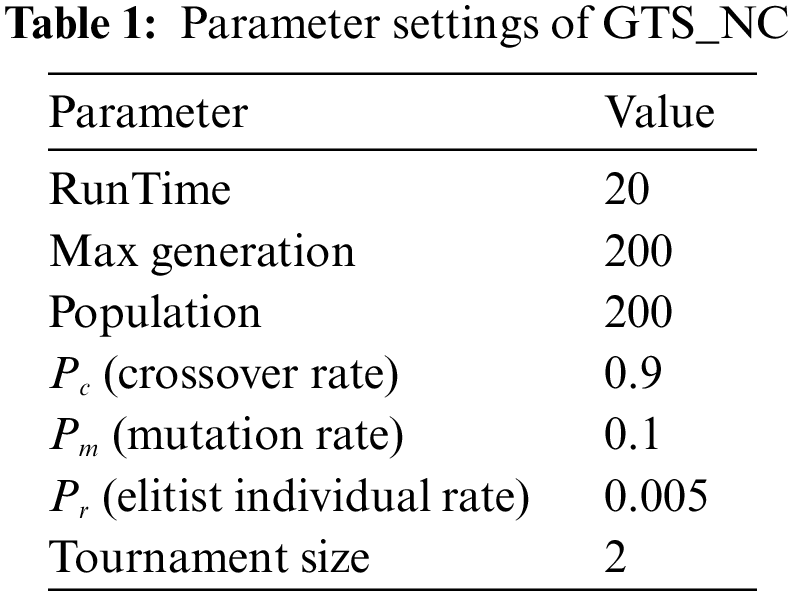
The maximum iteration size maxTS was 10000 and a dynamic tabu list was used [4], which length dynamically changed from Lmin to Lmax (Lmin = l, Lmax = [1.4 −1.5l], where if n ≤ 2m, then the maximal extreme value Lmax = [1.4l]. Otherwise, Lmax = [1.5l]). The parameters of GTS_NC were shown in Table 1 (n × m means the problem contains n jobs and m machines).

5.2 Experiment 1

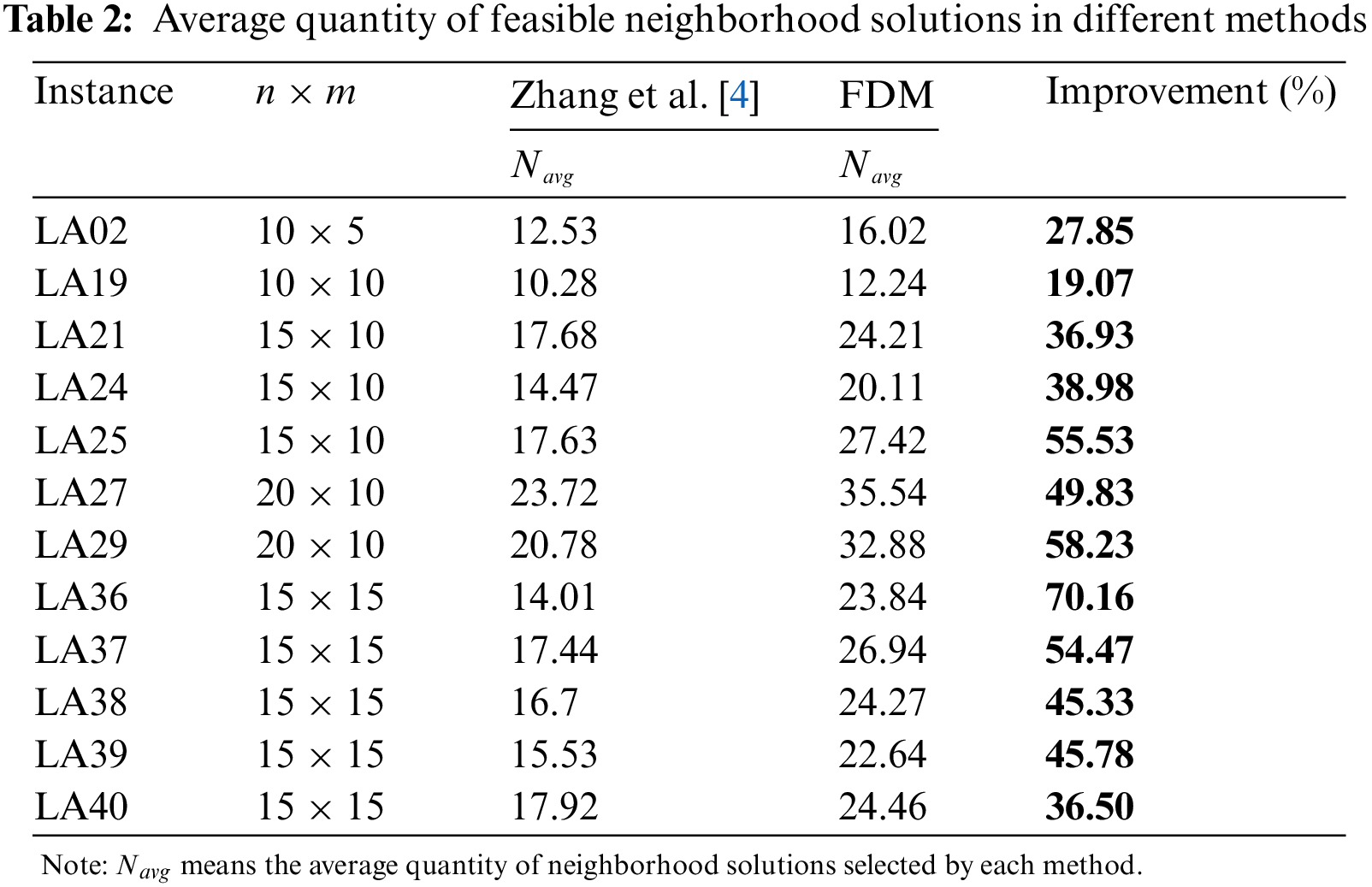
To validate the performance of the suggested feasible neighborhood solution determination method (denoted as FDM), it is compared with the basic version of the proposition proposed by Zhang et al. [4]. The comparison is performed in terms of the average quantity of feasible neighborhood solutions (Navg). The experimental can be described as follows.

Firstly, for each problem, 2000 feasible initial solutions were randomly generated, and their neighborhood solutions were generated by neighborhood structure N7. Then, for each initial solution, record the number of its feasible neighborhood solutions selected by feasible solution definition methods. Finally, the average quantity of feasible neighborhood solutions for each problem was compared to show the determination ability of each method. In particular, each selected neighborhood solution was decoded to verify its feasibility.

The reported results are demonstrated in Table 2. The outcomes demonstrated that the proposed method is more competitive than the proposition proposed by Zhang et al. [4] for all twelve benchmark test problems. It means that the proposed feasible neighborhood solution determination method has obvious advantages in mapping the JSSP.

5.3 Experiment 2

To validate the performance of the proposed neighborhood solution clipping method, the Tabu search embedded and unembedded neighborhood solution clipping method is compared. The widely used neighborhood structure N6 was adopted here. LA instances which contain at least 150 operations are considered in this paper. The maximum generation of Tabu search is 10000. Each of the problems is tested 10 times independently.

The comparison results are demonstrated in Table 3. Table 3 represents, name of problem instances, size of the problem that represents number of jobs × number of machines, the makespan of the best known solutions (Cmax) obtained by TSN6 (TS unembedded with neighborhood solution clipping method), the average makespan of the best known solutions (Cavg) obtained by TSN6, the shortest (Tmin) and average computational cost (Tavg) of TSN6, and the values of the best known solutions obtained by TSN6_NC (TS embedded with neighborhood solution clipping method).

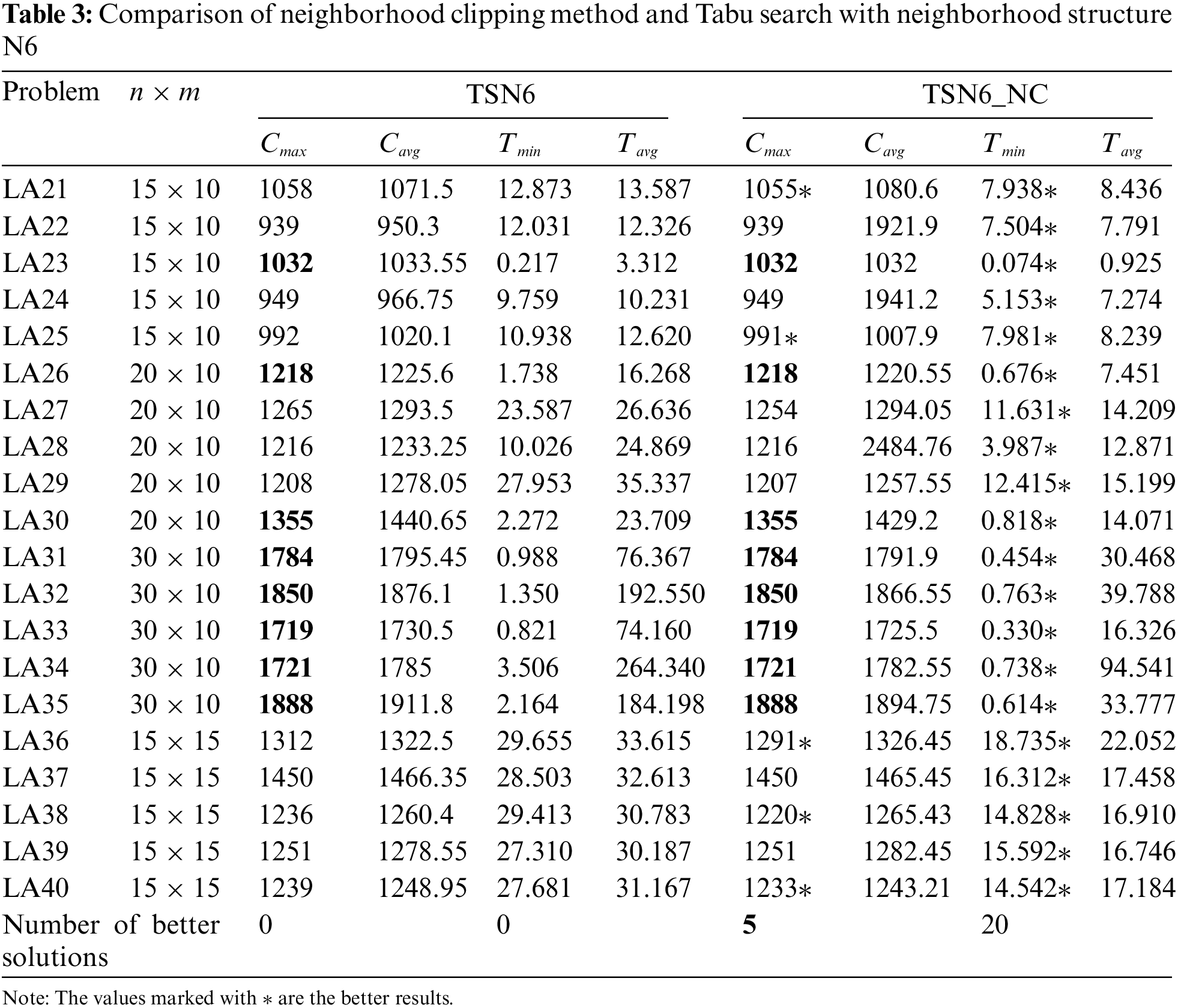
In Table 3, the bolded results are the optimal Cmax, others marked by * are the better Cmax and better Tmin. As shown in Table 3, the TSN6_NC obtained seven better optimal solutions than TSN6 (21, 25, 27, 29, 36, 38 and 40). Moreover, TSN6_NC gets 34 problems with lower computational cost. For instance, TSN6 require 27.9 s on solving LA29, but TSN6_NC requires 12.4 s to get better solution. The convergence curves of TSN6 and TSN6_NC are shown in Fig. 9. From the reported results in Table 3, it is obvious that the suggested algorithm TSN6_NC produces more efficient results in terms of best makespan and computational time. In Particular, the advantage of the proposed algorithm in terms of computational time become more pronounces as the size of the problem increases, as shown in Table 4. The obtained results show that proposed neighborhood solution clipping method produces more efficiency results as compared to the Tabu search unembedded with it.

Figure 9: Convergence curves of the TSN6 and TSN6_NC for LA problems

5.4 Experiment 3

To validate the efficiency of the proposed algorithm GTS_NC (applied with neighborhood structure N6), LA instances that contain at least 150 operations are considered in this paper. The obtained results are compared with the following significant approaches for solving JSSP as available in the literature:

1.    teaching-learning-based optimization (TLBO) algorithm [38],

2.    upper-level algorithm (UPLA) [39],

3.    genetic algorithm with improved local search techniques (mXLSGA) [11],

4.    mXLSGA with Frequency Analysis (GIFA) Operator (GIFA-mXLSGA) [12],

5.    the proposed approach unembedded with the neighborhood solution clipping method (GTS).

The comparison results with all the considered algorithms are depicted in Table 5. Table 5 represents the name of problem instances, the size of the problem, the upper bound of the problem, the makespan value (Cmax) of the best solution obtained by each algorithm, the CPU time of GTS and GTS_NC, and relative percentage error (RPE) with respect to Cmax. Here, PRE is calculated using the following Eq. (1):

RPE=100×(Cmax−UB)/UB(1)

The reported results for LA instances for TLBO, UPLA, mXLSGA, GIFA-mXLSGA, GTS and GTS_NC are shown in Table 5. From the reported results in Table 5, it is obvious that the suggested algorithm GTS_NC produces more efficient results in terms of best makespan and RPE in comparison with TLBO, UPLA, mXLSGA, GIFA-mXLSGA, and GTS. Besides, GTS_NC has an obvious advantage in computational time.

Further, to analyze the convergence characteristics of the proposed GTS_NC algorithm, it is applied to the LA25 instance and the average makespan is recorded during the generations and computational time. The obtained results are depicted in Fig. 10. The proposed GTS_NC algorithm converges very fast and finds the optimal solution very rapidly as shown in Fig. 10. The Gantt chart of the best solution of LA25 obtained by the proposed approach is shown in Fig. 11.

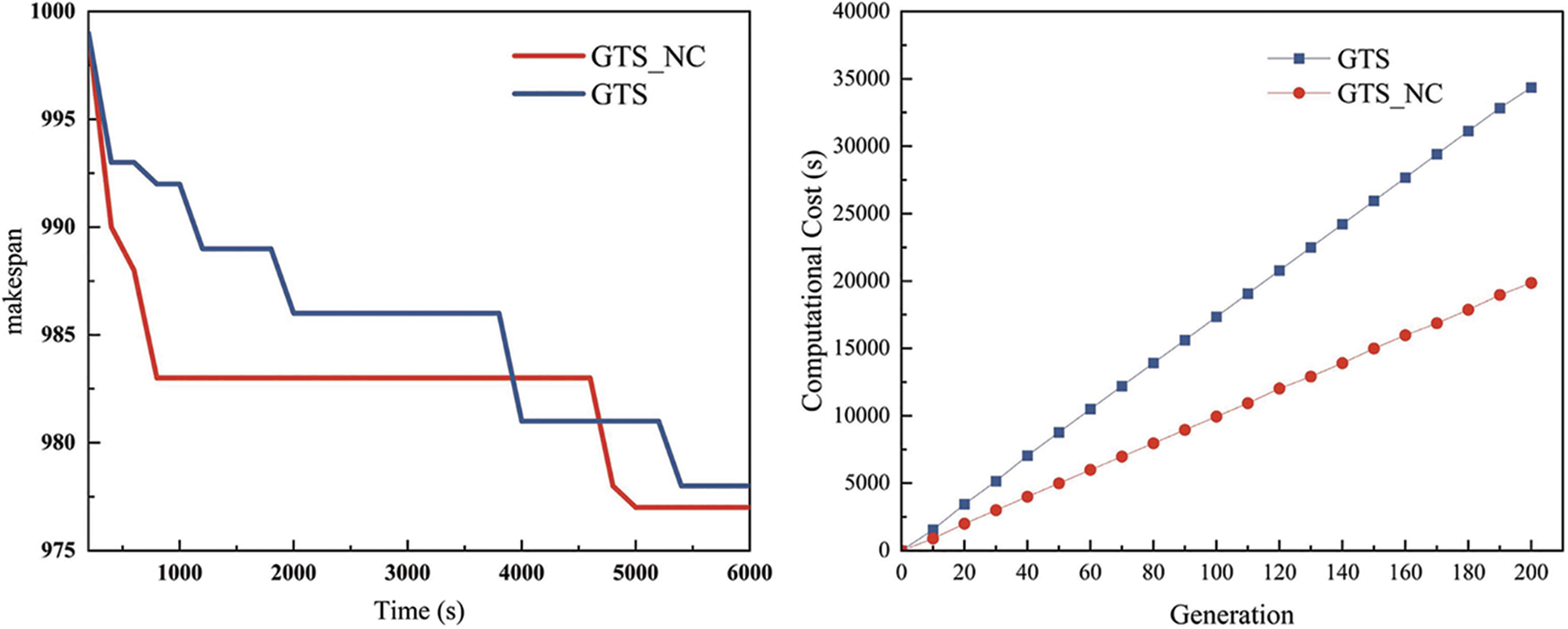
Figure 10: Convergence characteristics of LA25

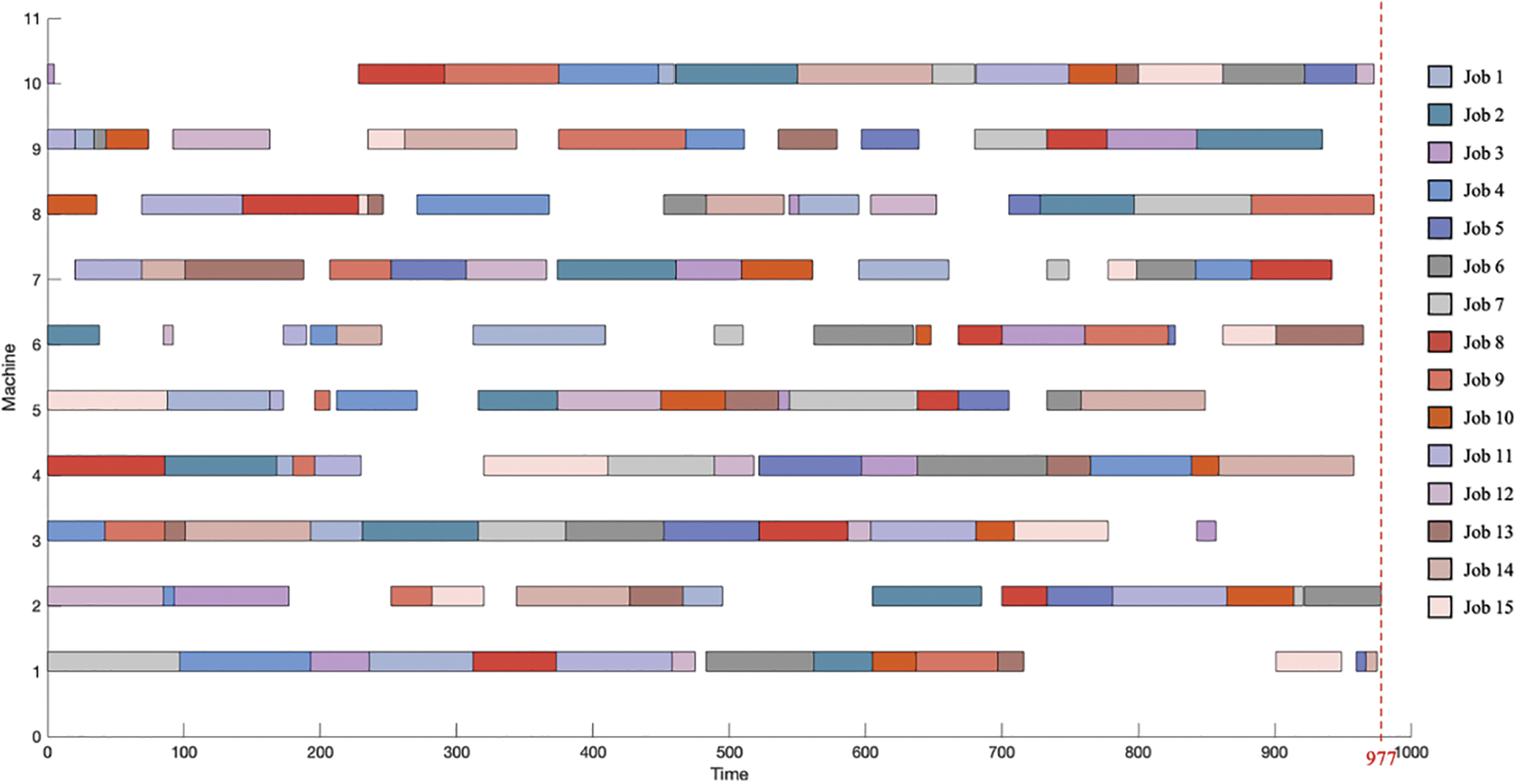
Figure 11: Gantt chart of the best solution of LA25

5.5 Discussion

From the computational results, the proposed GTS_NC can obtain the best results for most problems. Embedded with the neighborhood solution clipping method, GTS_NC shows strong competitiveness in terms of computational time. And the proposed feasible neighborhood solution determination method was verified so that it can accurately distinguish feasible neighborhood solutions from infeasible ones, and achieves a better mapping relationship with the JSSP.

The reasons are as follows. Firstly, the neighborhood solution clipping method was proposed based on the characteristic of movement of operations in the critical block, so it can accurately avoid the calculation for unimproved neighborhood solutions to save computational time. Secondly, the proposed feasible neighborhood solution determination method was designed based on the precedence constraints between operations, which provides a more comprehensive view of all feasible solutions by directly checking for constraint satisfaction. However, there is also a disadvantage of the proposed neighborhood solution clipping method, the decrease in the neighborhood solution set will limit the diversification of the local search procedure. Therefore, this method will perform better when combined with strategies that increase the diversity of the population.

6  Conclusions

In this paper, a hybrid algorithm that consisted of a Genetic algorithm and Tabu search with a clipping method is proposed for solving large-scale JSSP. A neighborhood solution clipping method is developed and embedded in Tabu search, which can improve the efficiency of the local search by clipping the calculation for unimproved neighborhood solutions. Moreover, a feasible neighborhood solution determination method is developed, which can accurately distinguish feasible neighborhood solutions from infeasible ones. Both of the methods are based on the domain knowledge of JSSP.

The proposed GTS_NC is tested on LA benchmark instance and compared with several algorithms. The computational results obtained in experiments demonstrate the efficiency of the proposed GTS_NC algorithm, which is significantly superior to the other reported methods. In the future, the proposed algorithm can be extended to solve other scheduling problems, such as flexible job shop scheduling problems, dynamic scheduling problems, and so on.

Funding Statement: This work is supported by National Natural Science Foundation for Distinguished Young Scholars of China (under the Grant No. 51825502).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Xiong, H. G., Shi, S. Y., Ren, D. N., Hu, J. J. (2022). A survey of job shop scheduling problem: The types and models. Computers & Operations Research, 142(2), 105731. https://doi.org/10.1016/j.cor.2022.105731 [Google Scholar] [CrossRef]

2. Gonçalves, J. F., Resende, M. G. C. (2014). An extended Akers graphical method with a biased random-key genetic algorithm for job-shop scheduling. International Transactions in Operational Research, 21(2), 215–246. https://doi.org/10.1111/itor.12044 [Google Scholar] [CrossRef]

3. Peng, B., Lü, Z. P., Cheng, T. C. E. (2015). A tabu search/path relinking algorithm to solve the job shop scheduling problem. Computers & Operations Research, 53(3), 154–164. https://doi.org/10.1016/j.cor.2014.08.006 [Google Scholar] [CrossRef]

4. Zhang, C. Y., Li, P. G., Guan, Z. L., Rao, Y. Q. (2007). A tabu search algorithm with a new neighborhood structure for the job shop scheduling problem. Computers & Operations Research, 34(11), 3229–3242. https://doi.org/10.1016/j.cor.2005.12.002 [Google Scholar] [CrossRef]

5. Lu, C., Zhang, B., Gao, L., Yi, J., Mou, J. H. (2021). A knowledge-based multiobjective memetic algorithm for green job shop scheduling with variable machining speeds. IEEE Systems Journal, 16(1), 844–855. https://doi.org/10.1109/JSYST.2021.3076481 [Google Scholar] [CrossRef]

6. Liu, Z. F., Wang, J. L., Zhang, C. X., Chu, H. Y., Ding, G. Z. et al. (2021). A hybrid genetic-particle swarm algorithm based on multilevel neighbourhood structure for flexible job shop scheduling problem. Computers & Operations Research, 135(2), 105431. https://doi.org/10.1016/j.cor.2021.105431 [Google Scholar] [CrossRef]

7. Amico, M. D., Trubian, M. (1993). Applying tabu-search to job-shop scheduling problem. Annals of Operations Research, 41(3), 231–252. https://doi.org/10.1007/BF02023076 [Google Scholar] [CrossRef]

8. Nowicki, E., Smutnicki, C. (1996). A fast taboo search algorithm for the job shop problem. Management Science, 42(6), 797–813. https://doi.org/10.1287/mnsc.42.6.797 [Google Scholar] [CrossRef]

9. Balas, E., Vazacopoulos, A. (1998). Guided local search with shifting bottleneck for job shop scheduling. Management Science, 44(2), 262–275. https://doi.org/10.1287/mnsc.44.2.262 [Google Scholar] [CrossRef]

10. Laarhoven, P. V., Aarts, E., Lenstra, J. (1992). Job shop scheduling by simulated annealing. Operations Research, 40(1), 113–125. https://doi.org/10.1287/opre.40.1.113 [Google Scholar] [CrossRef]

11. Monique, S. V., Orides, M. J., Rodrigo, C. (2020). A modified genetic algorithm with local search strategies and multi-crossover operator for job shop scheduling problem. Sensors, 20(18), 5440. https://doi.org/10.3390/s20185440 [Google Scholar] [PubMed] [CrossRef]

12. Monique, S. V., Orides, M. J., Rodrigo, C. (2022). A new frequency analysis operator for population improvement in genetic algorithms to solve the job shop scheduling problem. Sensors, 22(12), 4561. https://doi.org/10.3390/s22124561 [Google Scholar] [PubMed] [CrossRef]

13. Hu, R., Wu, X., Qian, B., Mao, J. L., Jin, H. P. (2022). Differential evolution algorithm combined with uncertainty handling techniques for stochastic reentrant job shop scheduling problem. Complexity, 2022, 9924163. https://doi.org/10.1155/2022/9924163 [Google Scholar] [CrossRef]

14. Ge, Y., Wang, A. M., Zhao, Z. J., Ye, J. R. (2019). A tabu-genetic hybrid search algorithm for job-shop scheduling problem. E3S Web of Conferences, 95, 04007. https://doi.org/10.1051/e3sconf/20199504007 [Google Scholar] [CrossRef]

15. Abdel-Kader, R. F. (2022). Modified coral reef optimization methods for job shop scheduling problems. Applied Sciences, 12(19), 9867. https://doi.org/10.3390/app12199867 [Google Scholar] [CrossRef]

16. Constantino, O. H., Segura, C. (2022). A parallel memetic algorithm with explicit management of diversity for the job shop scheduling problem. Applied Intelligence, 53(1), 1–13. https://doi.org/10.1007/s10489-021-02406-2 [Google Scholar] [CrossRef]

17. Gao, L., Zhang, G. H., Zhang, L. P., Li, X. Y. (2011). An efficient memetic algorithm for solving the job shop scheduling problem. Computers & Industrial Engineering, 60(4), 699–705. https://doi.org/10.1016/j.cie.2011.01.003 [Google Scholar] [CrossRef]

18. Sharma, N., Sharma, H., Sharma, A. (2018). Beer froth artificial bee colony algorithm for job-shop scheduling problem. Applied Soft Computing, 68(2), 507–524. https://doi.org/10.1016/j.asoc.2018.04.001 [Google Scholar] [CrossRef]

19. Abdelmonem, M. I., Mohanmed, A. T. (2022). An improved artificial algae algorithm integrated with differential evolution for job-shop scheduling problem. Journal of Intelligent Manufacturing, 12(1), 151. https://doi.org/10.1007/s10845-021-01888-8 [Google Scholar] [CrossRef]

20. He, L. J., Li, W. F., Chiong, R., Abedi, M., Cao, Y. L. et al. (2021). Optimising the job-shop scheduling problem using a multi-objective Jaya algorithm. Applied Soft Computing, 111(1), 107654. https://doi.org/10.1016/j.asoc.2021.107654 [Google Scholar] [CrossRef]

21. Alkhatteb, F., Abed-alguni, B. H., AI-rousan, M. H. (2022). Discrete hybrid cuckoo search and simulated annealing algorithm for solving the job shop scheduling problem. The Journal of Supercomputing, 78(4), 4799–4826. https://doi.org/10.1007/s11227-021-04050-6 [Google Scholar] [CrossRef]

22. Liang, Z. Y., Liu, M., Zhong, P. S., Zhang, C. (2021). Application research of a new neighbourhood structure with adaptive genetic algorithm for job shop scheduling problem. International Journal of Production Reaserch, 61(2), 362–381. https://doi.org/10.1080/00207543.2021.2007310 [Google Scholar] [CrossRef]

23. Liang, Z. Y., Zhong, P. S., Zhang, C., Liu, M., Liu, J. M. (2021). An improved adaptive genetic algorithm for job shop scheduling problem. International Conference on Intelligent Equipment and Special Robots, vol. 1212722. Qingdao, China. [Google Scholar]

24. Lu, Q., Ren, Y. P., Jin, H. Y., Meng, L. L., Li, L. et al. (2020). A hybrid metaheuristic algorithm for a profit-oriented and energy-efficient disassembly sequencing problem. Robotics and Computer-Integrated Manufacturing, 61, 101828. https://doi.org/10.1016/j.rcim.2019.101828 [Google Scholar] [CrossRef]

25. Mohanmmad, M. N., Farhad, K. (2012). A GES/TS algorithm for the job shop scheduling. Computers & Industrial Engineering, 62(4), 946–952. https://doi.org/10.1016/j.cie.2011.12.018 [Google Scholar] [CrossRef]

26. Cheng, T. C. E., Peng, B., Lü, Z. P. (2016). A hybrid evolutionary algorithm to solve the job shop scheduling problem. Annals of Operation Research, 242(2), 223–237. https://doi.org/10.1007/s10479-013-1332-5 [Google Scholar] [CrossRef]

27. Nagata, Y., Ono, I. (2018). A guided local search with iterative ejections of bottleneck operations for the job shop scheduling problem. Computers & Operations Research, 90(3), 60–71. https://doi.org/10.1016/j.cor.2017.09.017 [Google Scholar] [CrossRef]

28. Zobolas, G. I., Tarantillis, C. D., Ioannou, G. (2009). A hybrid evolutionary algorithm for the job shop scheduling problem. Journal of Operational Research Society, 60(2), 221–235. https://doi.org/10.1057/palgrave.jors.2602534 [Google Scholar] [CrossRef]

29. Li, Y., Li, X. Y., Gao, L., Fu, L., Wang, C. Y. (2022). An effective critical path based method for permutation flow shop scheduling problem. Journal of Manufacturing Systems, 63(5), 344–353. https://doi.org/10.1016/j.jmsy.2022.04.005 [Google Scholar] [CrossRef]

30. Zhang, C. J., Zhou, Y., Peng, K. K., Li, X. Y., Lian, K. L. et al. (2021). Dynamic flexible job shop scheduling method based on improved gene expression programming. Measurement and Control, 54(7–8), 1136–1146. https://doi.org/10.1177/0020294020946352 [Google Scholar] [CrossRef]

31. Fan, J. X., Zhang, C. J., Liu, Q. H., Shen, W. M., Gao, L. (2022). An improved genetic algorithm for flexible job shop scheduling problem considering reconfigurable machine tools with limited auxiliary modules. Journal of Manufacturing Systems, 62(1), 650–667. https://doi.org/10.1016/j.jmsy.2022.01.014 [Google Scholar] [CrossRef]

32. Fan, J. X., Shen, W. M., Gao, L., Zhang, C. J., Zhang, Z. (2021). A hybrid Jaya algorithm for solving flexible job shop scheduling problem considering multiple critical paths. Journal of Manufacturing Systems, 60(1), 298–311. https://doi.org/10.1016/j.jmsy.2021.05.018 [Google Scholar] [CrossRef]

33. Matsuo, H., Suh, C. J., Sullivan, R. S. (1989). A controlled search simulated annealing method for general job shop scheduling problem. Annals of Operations Research, 21(1), 85–108. https://doi.org/10.1007/BF02022094 [Google Scholar] [CrossRef]

34. Zhao, S. K. (2020). Research on multi-operation joint movement neighborhood structure of job shop scheduling problem. Journal of Mechanical Engineering, 56(13), 192–206. https://doi.org/10.3901/JME.2020.13.192 [Google Scholar] [CrossRef]

35. Xie, J., Li, X. Y., Gao, L., Gui, L. (2022). A new neighborhood structure for job shop scheduling problems. International Journal of Production Research, 61(7), 2147–2161. https://doi.org/10.1080/00207543.2022.2060772 [Google Scholar] [CrossRef]

36. Li, X. Y., Gao, L. (2016). An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. International Journal of Production Economics, 174(19), 93–110. https://doi.org/10.1016/j.ijpe.2016.01.016 [Google Scholar] [CrossRef]

37. Hurink, J. L., Jurisch, B., Thole, M. (1994). Tabu search for the job shop scheduling problem with multi-purpose machines. Operations Research Spektrum, 15(4), 205–215. https://doi.org/10.1007/BF01719451 [Google Scholar] [CrossRef]

38. Keesari, H. S., Rao, R. V. (2014). Optimization of job shop scheduling problems using teaching-learning-based optimization algorithm. Opsearch, 51(4), 545–561. https://doi.org/10.1007/s12597-013-0159-9 [Google Scholar] [CrossRef]

39. Pongchairesrks, P. (2019). A two-level metaheuristic algorithm for the job-shop scheduling problem. Complexity, 2019, 8683472. [Google Scholar]