Activation Redistribution Based Hybrid Asymmetric Quantization Method of Neural Networks

1  Introduction

Artificial intelligence with deep convolutional neural networks has made significant breakthroughs in many fields, which will be widely used in the aerospace field, such as situational awareness [1], intelligent obstacle avoidance [2], and remote sensing image in-orbit detection [3]. The biggest challenge for applying artificial intelligence in the aerospace field is that these artificial intelligence algorithms based on deep convolutional neural networks require a lot of memory and computational cost. In order to efficiently deploy neural networks on embedded devices, several model compression methods have been widely explored. Quantization is an essential technique for adopting deep neural networks in energy- and memory-constrained devices.

This paper is focused on Integer-only quantization for inference. Quantization is a method of quantizing the high-precision parameters of the neural network into low-precision parameters in a finite set, thereby speeding up the computation. High-precision parameters have a more extensive dynamic range, so the 32-bit floating-point data type is usually used in training. After training, in order to reduce the size of the neural network algorithm, the 32-bit floating-point neural network is quantized to an 8-bit or even lower bit integer network.

How to quantize a floating-point network to an integer network requires designing a proper mapping method. Quantization usually results in a loss of accuracy due to information lost. How to improve the accuracy of the quantized neural network considering hardware efficiency is the key problem that needs to be solved. A good quantization mapping method should resolve the two following questions to improve the deployment performance.

The first question is the trade-off between the accuracy of the quantized neural network and the difficulty of deployment and implementation. The simpler the mapping strategy is, the easier and faster the deployment on embedded devices will be, but the loss of accuracy will increase. The more complex the mapping strategy is, the lower the loss of accuracy will be. However, the deployment on embedded devices will be more difficult and result in enormous computational overhead. The commonly used quantization method is symmetric quantization for easy implementation on embedded devices. This method works well only for symmetric distributions, but most distributions of the neural networks are asymmetric.

The second question is the trade-off between range and quantization resolution, which significantly influences quantization parameters’ computation. The larger the clipping range is, the lower the data clipping loss will be. However, the quantization resolution will be lower. The smaller the data clipping range is, the higher the quantization resolution will be, but the data clipping loss will be greater. Range and quantization resolution affect each other, and there is no suitable method to guide how to balance them.

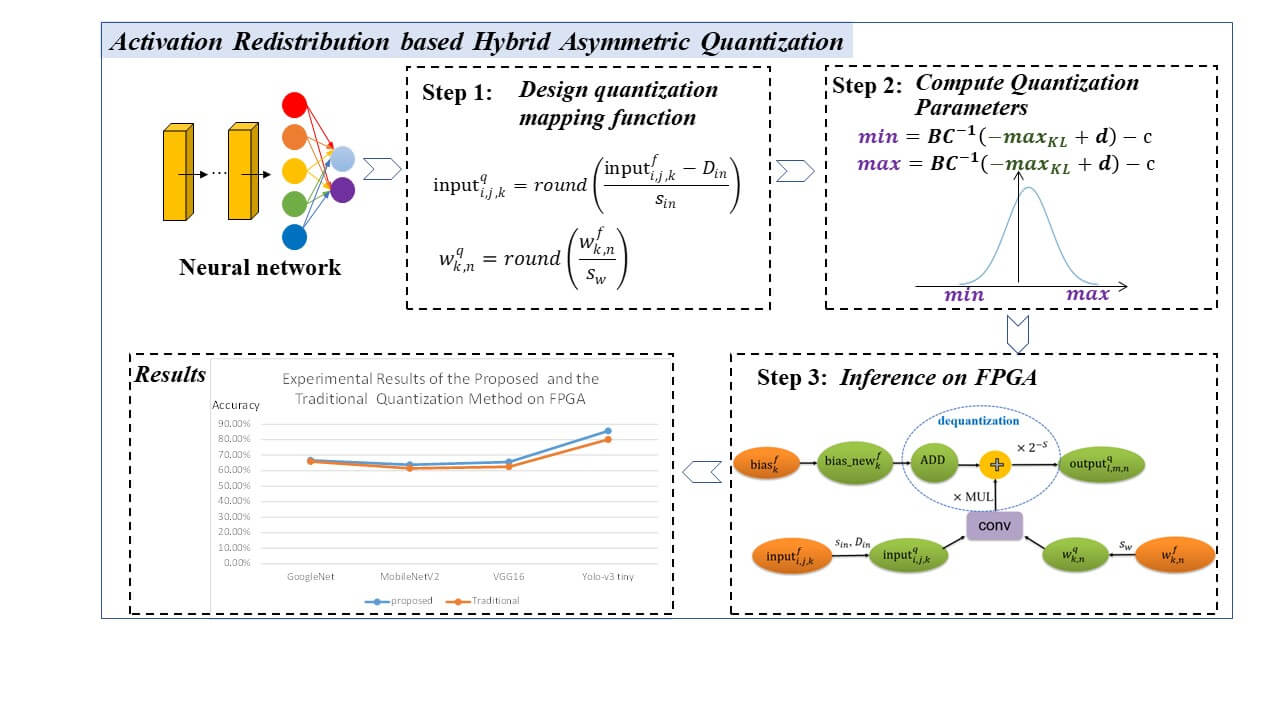
We propose an activation redistribution hybrid asymmetric quantization mapping method for Integer-only inference to resolve these two questions. Our contribution can be listed as follows:

Firstly, we propose a hardware-friendly hybrid asymmetric quantization method for Integer-only inference of neural networks, of which the activation uses asymmetric activation quantization and the weights use symmetric quantization. The proposed method can avoid the additional data-dependent computation, achieve higher accuracy without any computational overhead on embedded accelerators, and resolve the contradiction between the accuracy of the quantized neural network and the ease of deployment and implementation.

Secondly, we introduce an activation redistribution method to compute the quantization parameters achieving lower quantization error. This method has no restrictions on data distribution, and can get the balance between range and quantization resolution.

2  Related Works

Most of the existing quantization approaches asymmetric quantization or symmetric quantization [4]. The asymmetric quantization function is as follows:

r=f(Q)=s⋅Q+D(1)

Q=f−1(r)=round(r−Ds)(2)

where f and f−1 are the quantization mapping function, f−1 is the inverse function of f, round is the rounding operation, r is the floating point real value, Q is the integer value after quantization, s and D are quantization parameters. s is the scaling factor, and D is the zero point, chosen such that the 0 value would exactly map to quantized values.

Symmetric quantization is a simplified version of the general asymmetric case [5]. The symmetric quantizer restricts the quantization parameter D to 0 [6].

On the one hand, different quantization mapping functions are applicable for different data distributions. The data distributions of each layer in the neural network are not same. Figs. 1 and 2 illustrate the activation distributions for each convolutional layer in the Yolo-v3 tiny model. We divide the data distributions into two categories: one is approximately symmetric, as shown in Fig. 2, and the other is asymmetric, as shown in Fig. 1. Symmetric quantization is much simpler and hardware-friendly, but is only effective for symmetric distribution. The asymmetric quantization does not require the data distribution to be symmetric around zero, but it is more expressive because there is an extra quantization parameter D and a computational overhead. The activation distributions of twelve convolutional layers (layer 3, layer 5, layer 7, layer 9, layer 11, layer 13, layer 14, layer 15, layer 16, layer 21-1, layer 21-2, layer 23) are asymmetric. Only two activation distributions of convolutional layers (layer 1 and layer 19) are approximately symmetric. Most activation distributions of the Yolo-v3 tiny model for detection are asymmetric, so the traditional symmetric quantization method suffers from a considerable loss of accuracy for the small target detection tasks.

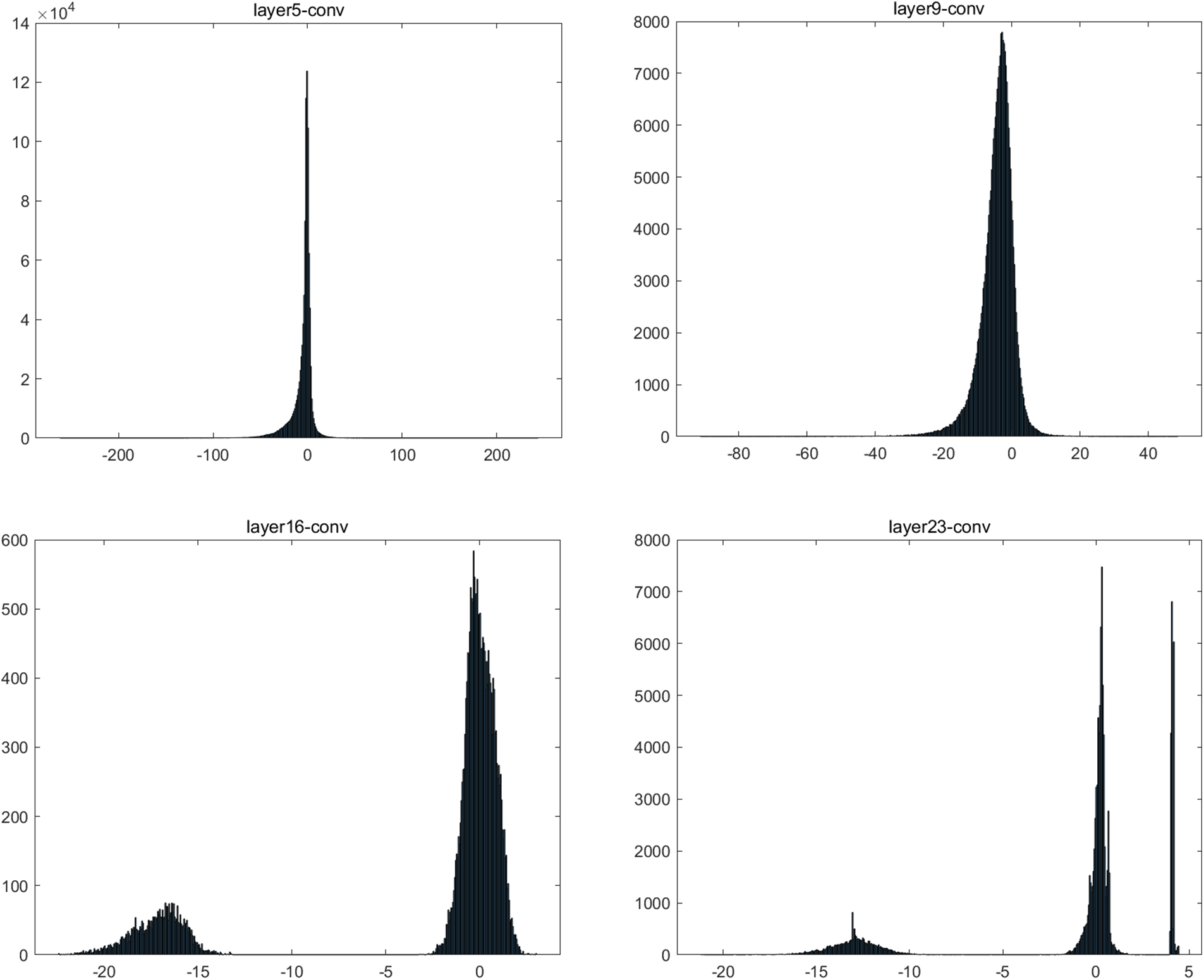
Figure 1: The activation distributions of four representative convolutional layers (layer 5, layer 9, layer 16, layer 23) of the Yolo-v3 tiny model for detection. These activation distributions are asymmetric. The horizontal axis is the activation value, and the vertical axis is the activation density

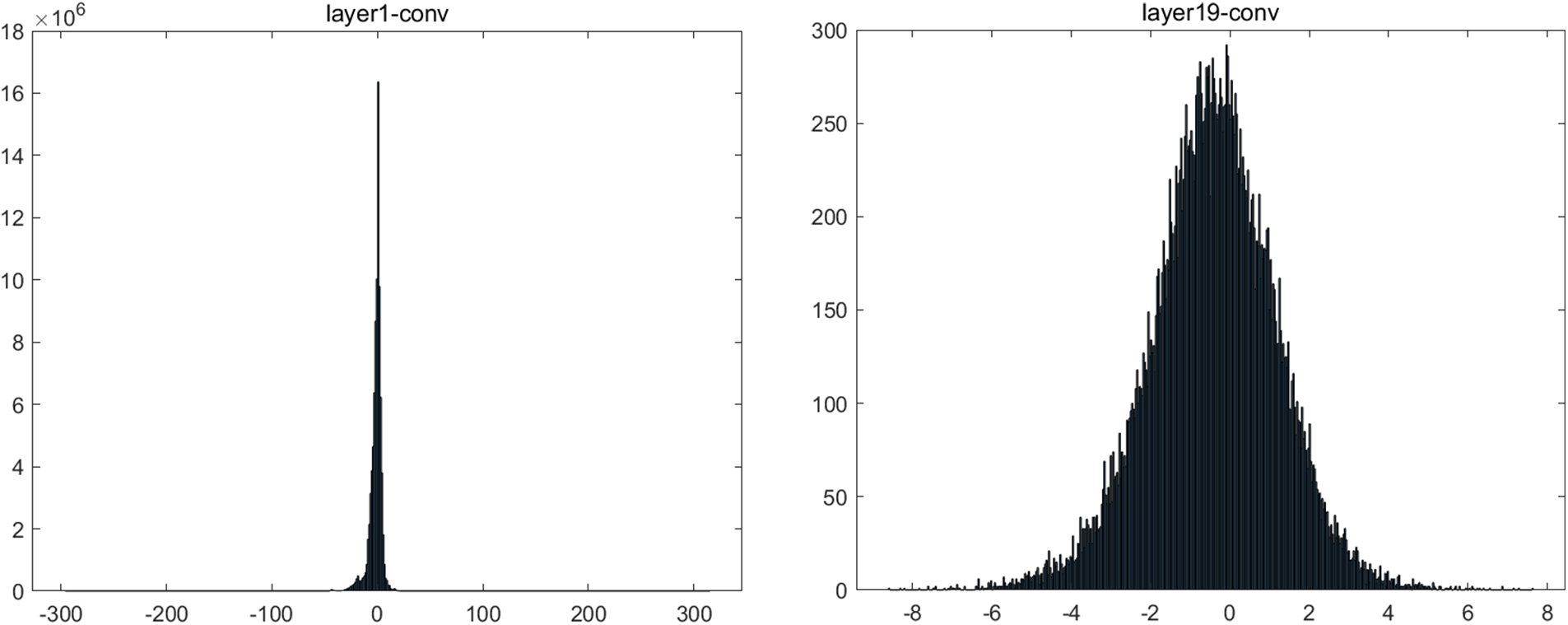
Figure 2: The activation distributions of two convolutional layers (layer 1 and layer 19) of the Yolo-v3 tiny model for detection. These activation distributions are approximately symmetric. The horizontal axis is the activation value, and the vertical axis is the activation density

On the other hand, the quantization parameters are very important for both asymmetric and symmetric quantization and affect the performance of the quantized neural network. The quantization parameters depend on the clipping range, and the scaling factors divides the given range of real values into a number of partitions. Usually, a series of calibrations are used as the input of a neural network to compute the typical range of activations [7,8]. A straightforward choice is to use the min/max of the data for the clipping range [7], which may unnecessarily increase the range and reduce the quantization resolution. One approach is to use the i-th largest/smallest value instead of the min/max value as the clipping range [9]. Another approach is to select the clipping range by some kinds of information loss between the original real values and the quantized values [10,11], including KL divergence [12,13], Mean Squared Error (MSE) [14–17], or entropy [18]. There are other methods to get the clipping range by learning the clipping range during training, including PACT [19], LQNets [20], LSQ [21], and LSQ+ [22]. When computing the data clipping range by KL, MSE, or other methods between the original real value and the quantized value, the absolute value of the data is first taken. Therefore, the data distribution in the range of positive and negative values cannot be effectively measured, and there is a problem of wasting the dynamic range of the data. At the same time, simply and directly taking the maximum and minimum values as the clipping thresholds cannot reflect the data distribution. So for the hybrid asymmetric quantization mapping strategy, there is no suitable method to compute the clipping range.

Therefore, the data distribution is not taken consideration in the current one-size-fits-all quantization methods, and there is no guiding principle on how to choose the most suitable method to compute the clipping range, so the current quantization methods cannot adapt to different neural network structures, and perform poorly for tasks with higher accuracy requirement.

3  Design

3.1 Overall Design Scheme

We propose an activation redistribution hybrid asymmetric quantization method for Integer-only inference of neural networks with simplicity and efficient implementation to hardware. The activation uses asymmetric activation quantization and the weights use symmetric quantization that avoids the additional data-dependent computation. A neural network usually consists of various layers, including the convolutional layer, the relu layer, the leaky-relu layer, the relu6 layer, the sigmoid layer, the tanh layer, and the FC layer, etc. We propose a hybrid asymmetric quantization method for neural networks and the corresponding method to compute the quantization parameters. For the computationally expensive layers, including the convolutional layer and the FC layer, we propose how to effectively quantize these layers according to the hybrid quantization parameters. For the non-linear layers, such as the relu layer, the leaky-relu layer, the relu6 layer, the sigmoid layer, etc, we propose a quantization template. All the non-linear layers can be quantized according to this template.

3.2 The Hybrid Asymmetric Integer-Only Quantization Method

In order to take into account the inference speed, accuracy, and convenience of the deployment for a quantized neural network, we propose a hybrid quantization method with asymmetric activation quantization and symmetric weight quantization. So the quantization mapping functions of the activation and weights are:

inputi,j,kq=round(inputi,j,kf−Dinsin)(3)

wk,nq=round(wk,nfsw)(4)

where inputi,j,kf is the activation of the neural network, wk,nf represents the weights of the k-th input channel and the n-th output channel, inputi,j,kq is the quantized input and wk,nq is the quantized weight, sw is the quantization parameter of the weights, sin and Din are the quantization parameters of the convolution input.

For the computationally expensive layers, including the convolutional layer and the FC layer, we propose how to effectively quantize these layers according to the hybrid quantization parameters. The quantization of the FC layer is as same as the convolutional layer.

For the non-linear layers, such as the relu layer, the leaky-relu layer, the relu6 layer, the sigmoid layer, etc., we propose a quantization template. All the non-linear layers can be quantized according to this template. The proposed method can achieve higher accuracy without any execution time overhead on embedded accelerators.

3.2.1 The Method to Quantize the Convolutional Layer

How to quantize the convolutional layer needs to be inferred from the computational principles of the convolutional layer. The computation principle of the convolutional layer is:

∑(inputi,j,kf⋅wk,nf)+biaskf=outputl,m,nf(5)

where biaskf is the k-th bias of the convolutional layer, and outputm,n,lf is the output of the convolutional layer. All the above data types are floating-point.

According to the computation principle of the convolution layer and the proposed hybrid asymmetric quantization strategy, how to quantize the convolutional layer can be inferred. The activations of the convolutional layer (including the input and output) adopt asymmetric quantization mapping, and the weights of the convolutional layer adopt symmetric quantization mapping. The computation principle of the quantization for the convolutional layer is:

{(sin⋅swsout⋅2S)(∑(inputi,j,kf−Dinsin⋅wk,nfsw))+biaskf+Din⋅∑wk,nf−Doutsout⋅2S}⋅2−S=outputl,m,nf−Doutsout(6)

where sout and Dout are the quantization parameters of the convolution output, and S is the shift parameter for the inference process of the convolution layer.

The method to quantize the convolutional layer can be divided into 5 steps according to Eq. (6), as shown in Algorithm 1. Algorithm 1 is based on Eq. (6), and Eq. (6) illustrates how to get the integer output of the convolution layer from the integer input and the integer weights. In Eq. (6), the integer output is represented as outputl,m,nf−Doutsout, the integer input is represented as inputi,j,kf−Dinsin,and the integer weight is represented as wk,nfsw. inputi,j,kf−Dinsin and wk,nfsw should be on the left side of Eq. (6), outputl,m,nf−Doutsout should be on the right side of Eq. (6), and in order to make both sides of Eq. (6) equal and involve only integer arithmetic, we can get that the left side of Eq. (6) should be {(sin⋅swsout⋅2S)(∑(inputi,j,kf−Dinsin⋅wk,nfsw))+biaskf+Din⋅∑wk,nf−Doutsout⋅2S}⋅2−S on the basis of Eq. (5). The first step to quantize the convolutional layer is to compute the hybrid asymmetric quantization parameters, including sin, Din, sw, sout and Dout. The second step is to quantize the floating-point activations and weights into integer with the hybrid asymmetric quantization parameters according to Eqs. (7)–(10). The third step is to execute the multiplication and accumulation operations of the integer activations and weights, which is represented as conv in Fig. 3. The fourth step is to compute the dequantization parameters, including shift parameter S, multiplication parameter MUL, and addition parameter ADD. Dequantization is the procedure proposed in this paper to get the integer convolutional output from the results of the third step. The Dequantization procedure consists of multiplication, addition and shift. The last step is to complete the dequantization on the results of the third step in order of multiplying, adding and shifting. The multiplier is MUL. Adding uses parameter ADD, means Adding ADD. Shifting uses parameter S, means Multiplying 2−S, so 2−S can be implemented with an efficient bit-shift. The procedure for quantizing the convolutional layer is shown in Fig. 3.

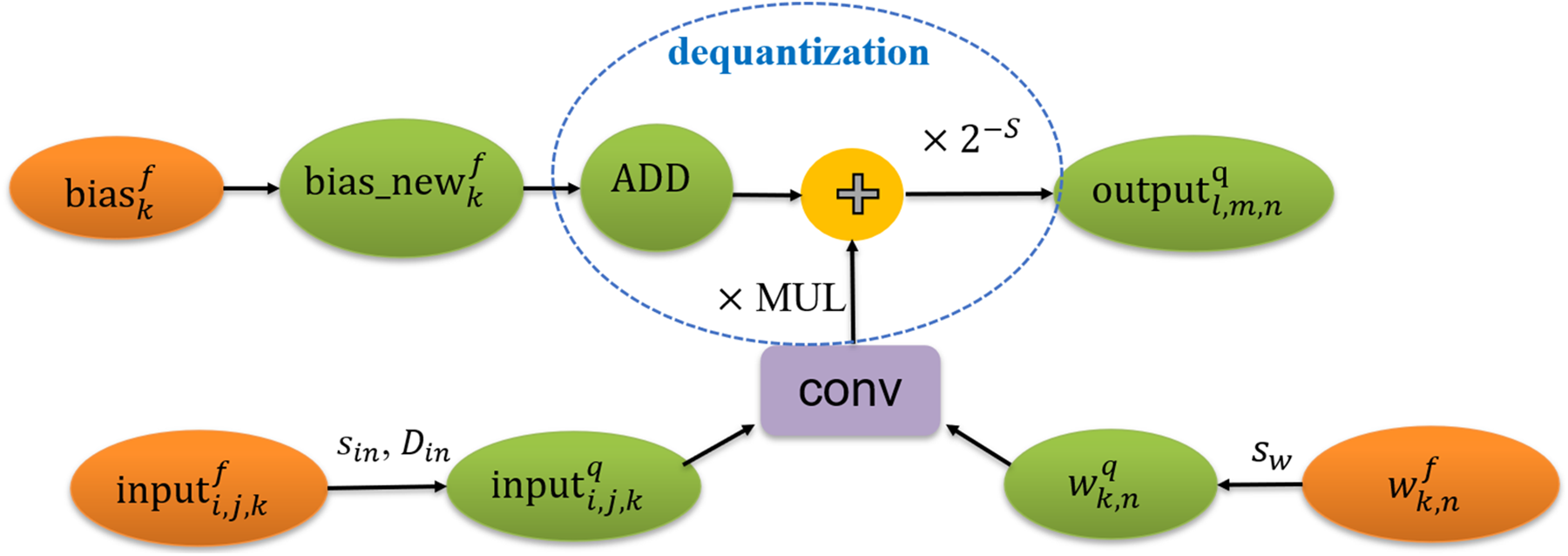
Figure 3: The procedure for quantizing the convolutional layer

In step 2, inputi,j,kf and outputm,n,lf are clipped according to their respective thresholds, as shown in Eqs. (7) and (8), and then they are quantized to integer according to Eqs. (9) and (10). MAX in Eqs. (7) and (8) is to take the maximum value and MIN in Eqs. (7) and (8) is to take the minimum value.

In step 4, the shift parameter S, multiply parameter MUL, and add parameter ADD are computed according to Eqs. (11)–(14). A convolution layer has several groups of dequantization parameters, the number of dequantization parameters is the same as the number of output channels. We should convert the floating-point biases of a convolutional layer to add parameters. In order to simplify the process of inference, we modify the floating-point biases biaskf to bias_newkf, thereby accelerating the inference speed of the convolutional layer. ∑wk,nf is the sum of the weights in units of output channels, that is, how many output channels there are, how many ∑wk,nf values are computed.

3.2.2 The Method to Quantize the Non-Linear Layers

This section introduces how to quantize the non-linear layers. We propose a quantization template for the non-linear layers. All the non-linear layers can be quantized according to this template. We introduce how to quantize the relu layer, the leaky-relu layer, the relu6 layer, the sigmoid layer, and the tanh layer according to the proposed quantization template.

The computation principle of the nonlinear layers can be expressed as:

outputl,m,nf=F(inputi,j,kf,x)(15)

where F is the function of a non-linear layer, x is the fixed floating-point real value. For the relu layer and the leaky-relu layer, x is 0. For the relu6 layer, x is 6. The floating-point input is represented by inputi,j,kf, and the floating-point output is represented by outputl,m,nf.

The quantization method of the non-linear layers is based on the lookup table. The proposed quantization template to compute the lookup table for the non-linear layers is:

outputl,m,nq=round(f−1(F(f(inputi,j,kq),round(x−Doutsout))))(16)

where f is the quantization mapping function as in Eq. (1), f−1 is the inverse function of mapping function f as in Eq. (2), the integer input is represented by inputi,j,kq, and the integer output is represented by outputl,m,nq.

How to use the proposed quantization template to compute the lookup tables for the relu layer, the leaky-relu layer, the relu6 layer, the sigmoid layer and the tanh layer is shown in Table 1. Negative_slope is the parameter of the leaky-relu layer.

3.3 The Method to Compute Quantization Parameters

This section introduces how to compute the hybrid asymmetric quantization parameters. Select several pictures as the calibration set to compute the quantization parameters for the neural network. The method to compute quantization parameters is divided into two steps. The first step is to get the clipping thresholds, and the second step is to compute the quantization parameters according to the clipping thresholds. The clipping thresholds significantly influence quantization parameters’ computation.

The method to compute the clipping thresholds should balance the trade-off between range and quantization resolution. Whether the data clipping thresholds are determined by KL, MSE or other methods between the original real values and the quantized values, there is a problem of wasting the dynamic range of the data. Because these methods are on the premise that data distribution is symmetric. But most of the activation distributions are asymmetric. These methods take the absolute value of the data first when computing the clipping range, and then select the data thresholds by a certain measurement method. The operation of taking the absolute value makes these methods unable to truly reflect the data distribution both in the positive and negative range. The quantization of non-negative activations may be less effective at this point because the clipping range includes values that never appear in the input.

In order to adopt asymmetric activation distributions, and balance the trade-off between range and quantization resolution, we propose an activation redistribution method to compute the clipping thresholds achieving lower quantization error, because this method takes data distribution into consideration. The optimal clipping range for the input is [minin,maxin], the optimal clipping range for the output is [minout,maxout], the threshold of the weights is thw. The procedure for computing these clipping thresholds is shown in Algorithm 2 and Fig. 4.

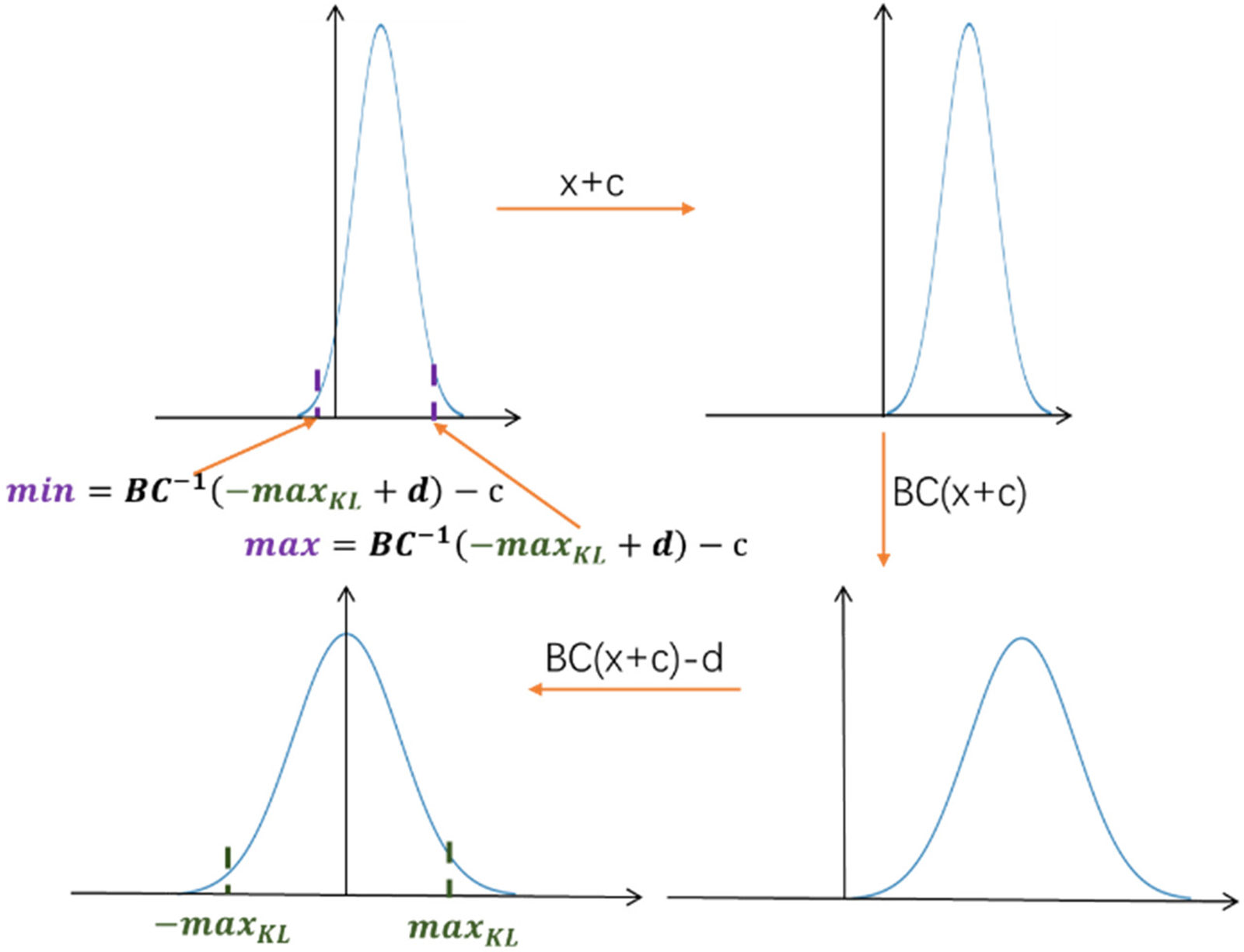
Figure 4: The activation redistribution method to compute the optimal clipping thresholds

Fig. 4 shows how to get the clipping thresholds [minin,maxin] of the input. c is a constant to ensure that the input is positive. All of the inputs plus c, and then transform the input into a gaussian-like distribution by Box-Cox, which is represented as BC in Fig. 4. d is a constant to ensure that the transformed gaussian-like distribution is symmetric. We use KL divergence to balance the trade-off between range and quantization resolution. Get the clipping thresholds [−maxKL,maxKL] by KL divergence [10] of the symmetric gaussian-like distribution. In this way, the data both in the positive and negative range is taken into consideration. At last, get [minin,maxin] by the inverse transformation of Box-Cox, which is represented as BC−1.

As can be seen from the above figure, when the data distribution is not symmetrical around 0, for example, the negative values are small, then the data thresholds determined by the KL divergence are not suitable, because the threshold selected for the negative value area is affected by the positive value, which cannot match the actual data distribution of negative values. The proposed method transforms an asymmetric and skewed activation distribution into a gaussian-like distribution, then get the clipping thresholds by KL divergence, and finally gets the final clipping range by the inverse transformation.

How to compute the quantization parameters according to the clipping thresholds is as follows. The quantization parameters sin, Din,sout, Dout, sw of a layer are computed according to Eqs. (18)–(22).

sin=maxin−minin2bwin−1(18)

Din=minin−maxin2bwin−1⋅round((2bwin−1−1)⋅minin+2bwin−1⋅maxinminin−maxin)(19)

sout=maxout−minout2bwout−1(20)

Dout=minout−maxout2bwout−1⋅round((2bwout−1−1)⋅minout+2bwout−1⋅maxoutminout−maxout)(21)

sw=thw2bww−1−1(22)

where bwin, bwout and bww are the bit width of input, output and weight, of which 8 is commonly used.

4  Implementation and Experimental Results

The purpose of the experiments is to verify the effectiveness of the proposed hybrid asymmetric Integer-only quantization method.

4.1 Experimental Setting

The neural networks adopted in the experiments are the image classification models and the small target detection model. All of the neural networks are quantized to INT8.

Firstly, the experiments are implemented on the TIANJI NPU3.0 neural network accelerator proposed by Xi’an Microelectronics Technology Institute [24] and Cambricon MLU220 [25]. TIANJI NPU3.0 accelerator is implemented based on Xilinx ZCU102 FPGA, with self-controllable IP and application development tool chain [26]. The FPGA is Zynq UltraScale + XCZU9EG, and there are 2520 DSP slices, and the DDR4 in the programmable logic is 4 Gb. MLU220 is Based on the Cambrian MLUv02 architecture. The theoretical peak performance is 8TOPS and the power consumption is 8.25 W. These two accelerators can be widely used in edge computing scenarios to support diverse AI applications. The image classification models and the small target detection model are deployed on the neural network accelerators, and the speed and accuracy are verified. The purpose of the experiments is to verify the effectiveness of the proposed hybrid asymmetric Integer-only quantization method on embedded devices. The expected experimental results are that the proposed quantization method can improve the accuracy without affecting the speed on embedded devices compared with the traditional symmetric quantization method adopted by most embedded neural network accelerators.

Secondly, we compare the proposed method with PyTorch and NNI [27] on image classification models and the small target detection model, and the accuracy is verified on software. The CPU is Intel(R) Core(TM) i7-8700K, 3.70 GHz, and the GPU is NVIDIA GeForce GTX1070. In order to get the experimental results conveniently, software with fake-quantization [28] modules is used to simulate the accuracy on the neural network accelerator. Fake-quantization models quantization errors in the forward passes. The reason to apply fake-quantization is to quickly simulate the effects of quantization using simulated quantization operations. Codes will be available on https://github.com/ycjcy/Hybrid-Asymmetric-Quantization, from which the experimental results of the proposed method, PyTorch, and NNI can be obtained. The purpose of the experiments is to verify the effectiveness of the proposed hybrid asymmetric quantization method with the state-of-art. The expected experimental results are that the proposed hybrid asymmetric quantization method can improve the accuracy compared with PyTorch and NNI.

4.2 Dataset

The dataset for image classification application is ImageNet. ImageNet is an image database organized according to the WordNet hierarchy, in which each node of the hierarchy is depicted by hundreds and thousands of images. The dataset has been instrumental in advancing computer vision and deep learning research.

The dataset for is small target detection application is HRSID. HRSID is a dataset for ship detection, semantic segmentation, and instance segmentation tasks in high-resolution SAR images. The dataset contains 5604 SAR images with resolutions of 0.5, 1, and 3 m.

4.3 Evaluation Metrics

In order to verify the accuracy of quantification methods extensively, we evaluate two aspects of quantization errors. One is the quantization error of a particular layer. The second is the overall quantization error of a model.

For the first aspect of quantization error, there are no ideal metrics that can perfectly measure the quantization error. Different metrics reflect the quantization error from different points. We adopt the following three metrics to measure the quantization error, including Manhattan distance, Euclidean distance, and Signal to Noise Ratio. The range of Manhattan distance and Euclidean distance is 0 to +∞, and the range of Signal to Noise Ratio is −∞ to +∞. The smaller the Manhattan distance and the Euclidean distance are, the lower the error will be. The higher the signal-to-noise ratio is, the lower the error will be.

•   Manhattan distance (sum of the absolute values of the difference between the original real values and the corresponding floating-point values after quantization):

d1=∑i=1i=t|ri−qi|(23)

•   Euclidean distance (the square root of the sum of the square of the difference between the original real values and the corresponding floating-point values after quantization):

d2=∑i=1i=t(ri−qi)2(24)

•   Signal to Noise Ratio:

SQNR=10⋅log10⁡(∑i=1i=tri2∑i=1i=t(ri−qi)2)(25)

where ri is the original real value of floating point, qi is the corresponding real value after quantization, and the size of the input or output data is t.

For the second aspect of quantization error, the evaluation metrics are the accuracy metrics of that model. For image classification application, we use Top-1 Accuracy (the one with the highest probability must be exactly the expected answer). For small target detection application, we use mAP (Mean Average Precision). The calculation of mAP is the same as in the internationally renowned target detection competition PASCAL VOC Challenge.

4.4 Baseline

Firstly, we use a traditional symmetric quantization method as a baseline. This method adopts symmetric quantization for both activation and weights, with the clipping range determined by KL divergence. This method is adopted by most embedded neural network accelerators, such as Nvidia’s TensorRT [12], TVM [13], etc.

Secondly, as a baseline, we compare the proposed method with PyTorch and NNI on PC. PyTorch supports INT8 quantization compared to typical FP32 models allowing for a 4x reduction in the model size and a 4x reduction in memory bandwidth requirements. Hardware support for INT8 computations is typically 2 to 4 times faster compared to FP32 computing. PyTorch supports multiple approaches to quantize a deep learning model. In most cases, the model is trained in FP32 and then the model is converted to INT8. In addition, there are three functions in PyTorch to compute the clipping range. The torch.quantization.observer module in Pytorch integrates three calibration strategies, including MinMaxObserver, MovingAverageMinMaxObserver, and HistogramObserver. There is no guide on how to get the most suitable strategy. The easiest way (and the default option in Pytorch) is to directly take the minimum and maximum values by the MinMaxObserver function. The method in NNI to compute the clipping range is also to take the minimum and maximum values.

4.5 Results

4.5.1 Results on FPGA

•   Classification Application

The models used for image classification are GoogleNet, MobileNetV2, and VGG16. For fair comparison and ease of reproducibility, we use well-trained models on the ImageNet dataset. For image classification application, we test Top-1 Accuracy and FPS (How many frames can be processed per second).

TIANJI NPU3.0 accelerator runs at a frequency of 200M. The resources consumption on FPGA of TIANJI NPU3.0 is shown in Table 2, including LUT, FlipFlops, Block RAMs and DSPs.

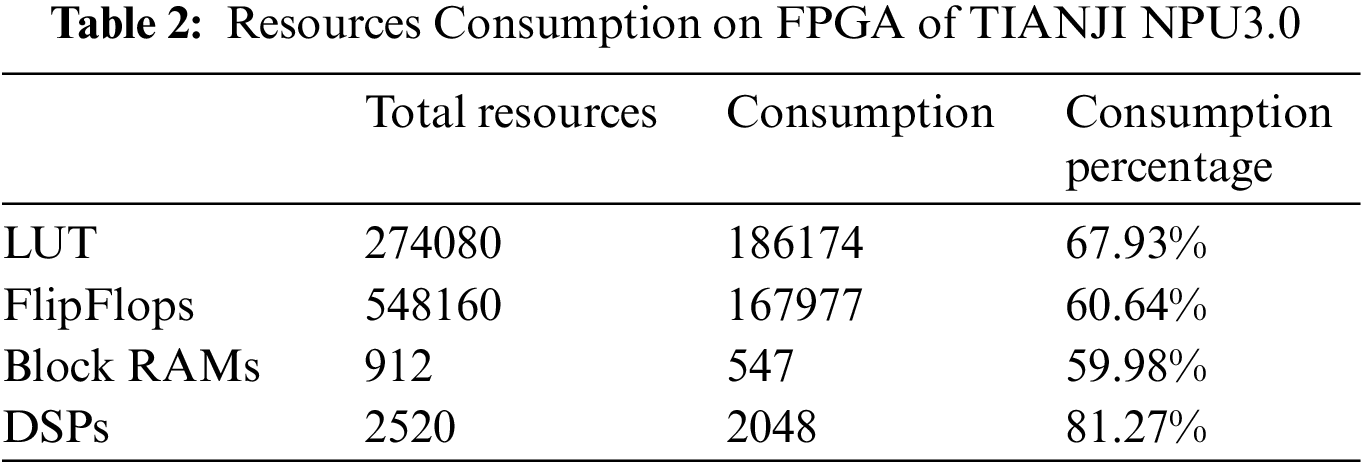
The results for the classification application on TIANJI NPU3.0 are shown in Table 3. A basic requirement of inference on TIANJI NPU3.0 is that it permits implementation of all arithmetic using only integer arithmetic operations, so it is a big challenge for the quantization method to reduce the accuracy loss. The proposed method ensures that all the layers of the neural network are inferenced by integer. For the three classification models, the FPS of the proposed hybrid asymmetric quantization method is the same as the FPS of the traditional symmetric quantization method. So the proposed hybrid asymmetric quantization method can improve the classification accuracy by an average of 2.02% without affecting the speed on FPGA. It can meet the accuracy requirements of image classification tasks.

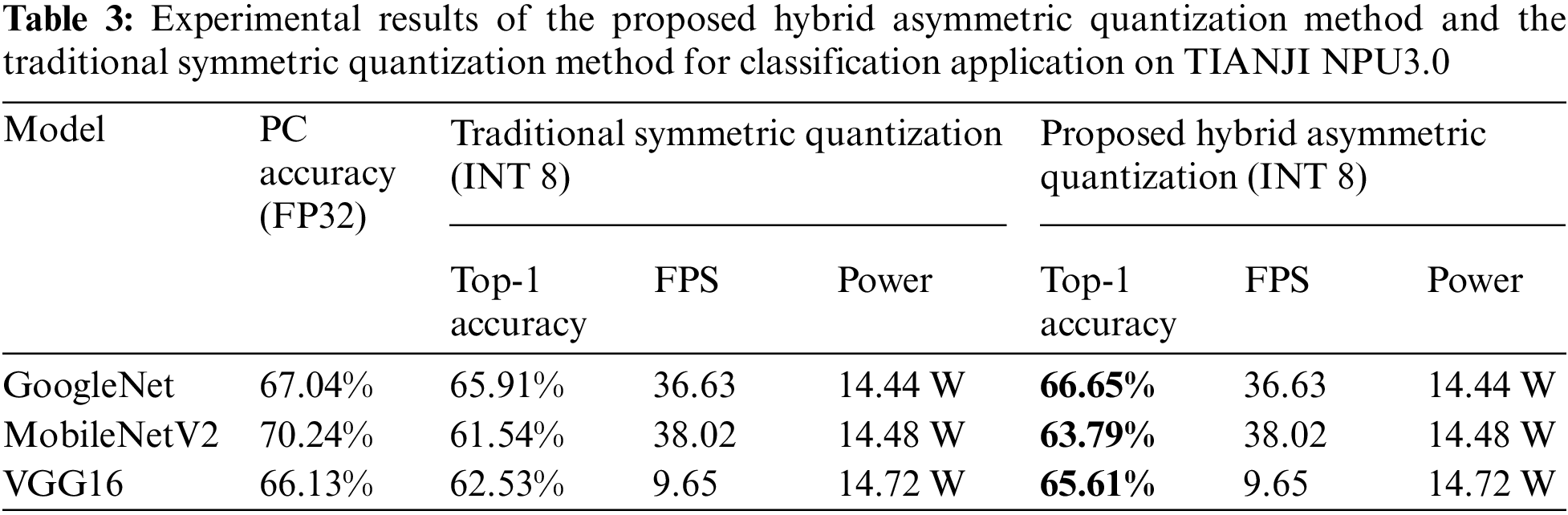
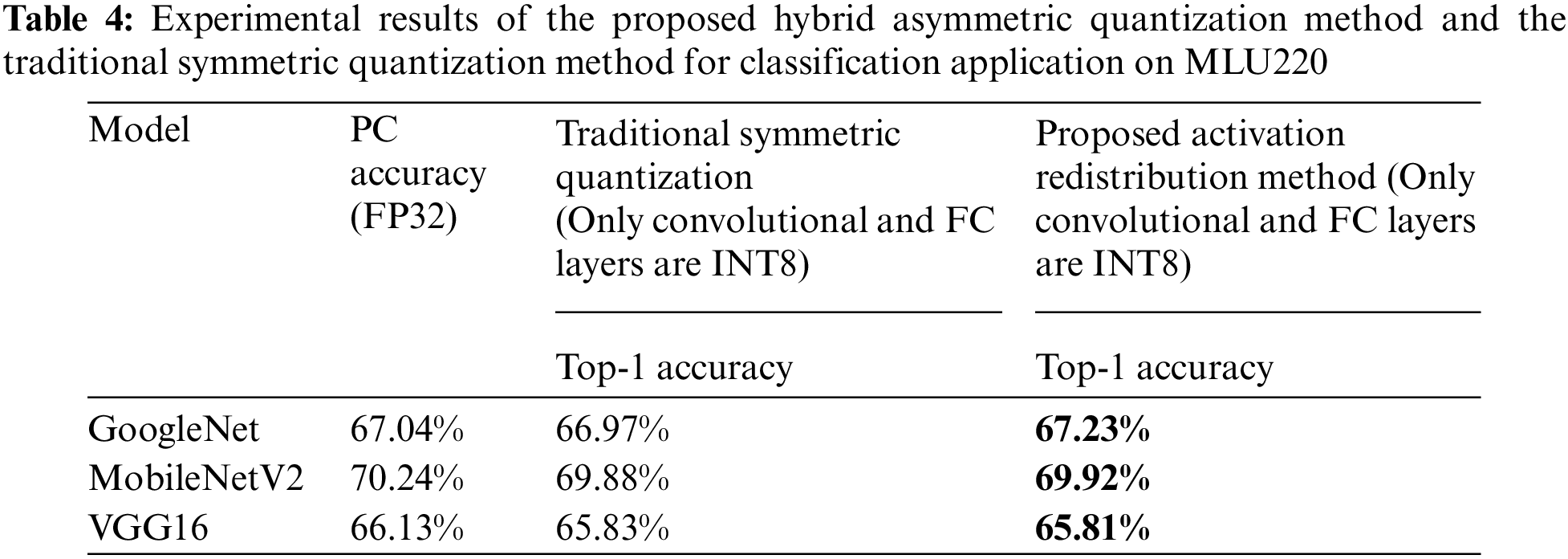
The results for the classification application on MLU220 are shown in Table 4. MLU220 only supports symmetric quantization, and only convolutional layers and FC layers can be quantized to INT8, others types of layers are all executed in FP32. The traditional method on MLU220 to compute the clipping range is to take the minimum and maximum values. We compare the proposed activation redistribution method with the traditional method on MLU220. The methods proposed in this paper are all computed offline and do not increase the computational overhead of the embedded devices, which is the same as other traditional methods. It is valid for different embedded devices,because this method proposes a new way to compute quantization parameters from a mathematical point of view, which has no effect on embedded devices.

•   Small Target Detection Application

The small target detection task is very challenging because the loss of accuracy is very sensitive to quantization. The model we choose for this small target detection task is Yolo-v3 tiny, a typical object detection model that has been widely adopted.

The experimental results measuring the quantization error of convolutional layers and relu layers for the small target detection application on TIANJI NPU3.0 are shown in Tables 5 and 6. It can be seen that the Manhattan distance and the Euclidean distance of the proposed hybrid asymmetric method are lower, and the signal-to-noise ratio SQNR of the proposed hybrid asymmetric method is higher.

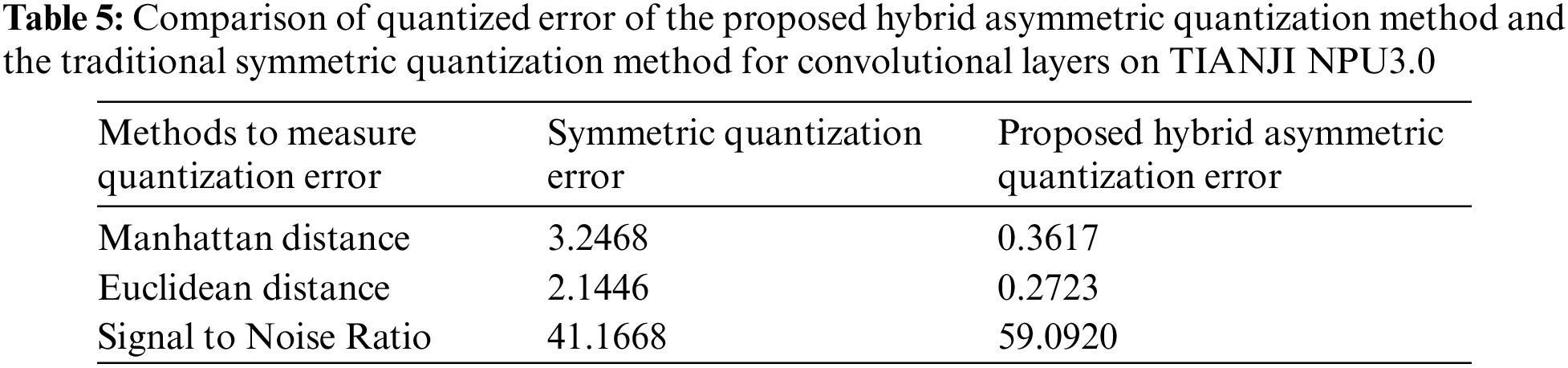
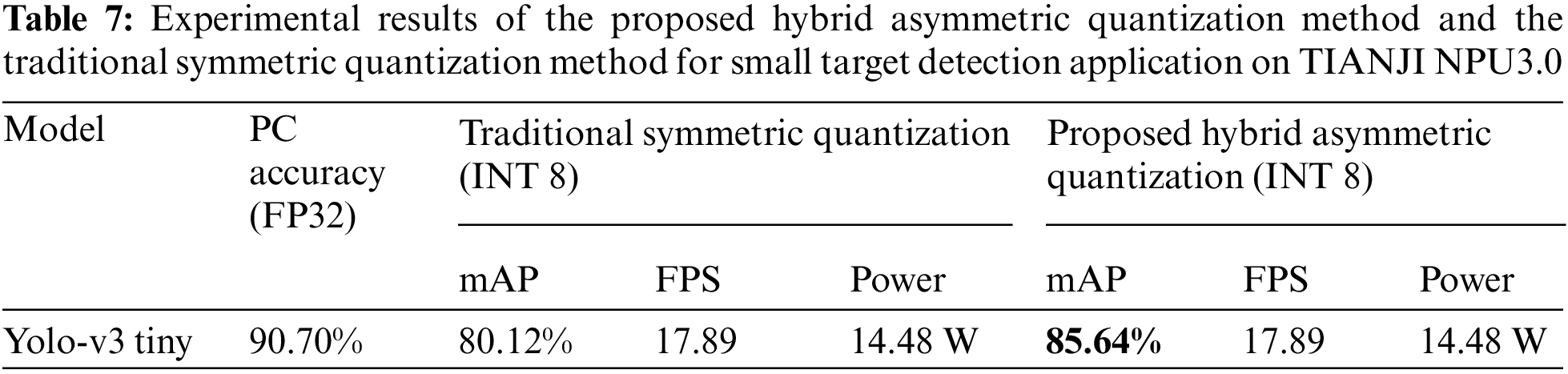
The speed and accuracy experimental results for the small target detection application on TIANJI NPU3.0 are shown in Fig. 5 and Table 7. For the small target detection model, the FPS of the proposed hybrid asymmetric quantization method is the same as the FPS of the traditional symmetric quantization method. So the proposed hybrid asymmetric quantization method can improve the detection accuracy by 5.52% without affecting the speed on embedded devices. It can meet the accuracy requirements of small object detection tasks.

Figure 5: Small object detection on HRSID dataset

The results for the small target detection application on MLU220 are shown in Table 8. The proposed activation redistribution method can improve the detection accuracy from 82.67% to 82.83%.

4.5.2 Results on PC

•   Classification Application

The models used for image classification to compare with PyTorch and NNI are the same as Section 4.5.1. The evaluation metric is Top-1 Accuracy. There are three ways in PyTorch to compute the clipping range, including MinMax, MovingAverage, and Histogram. We compare the proposed hybrid asymmetric quantization method with PyTorch and NNI, and compare the proposed activation redistribution method with MinMax, MovingAverage, and Histogram in PyTorch on fake-quantization software.

The results for the classification application are shown in Table 9 and Fig. 6. For the three classification models, the accuracy of the proposed hybrid asymmetric quantization method (66.85%, 67.38%, 66.26%) is the highest compared with PyTorch (66.50%, 66.82%, 65.22%) and NNI (66.74%, 66.50%, 65.20%). At the same time, there are three ways in PyTorch and NNI to compute the clipping range. For different models, the best strategy of PyTorch and NNI to compute the clipping range is different. The proposed activation redistribution method outperforms the three strategies of PyTorch and NNI.

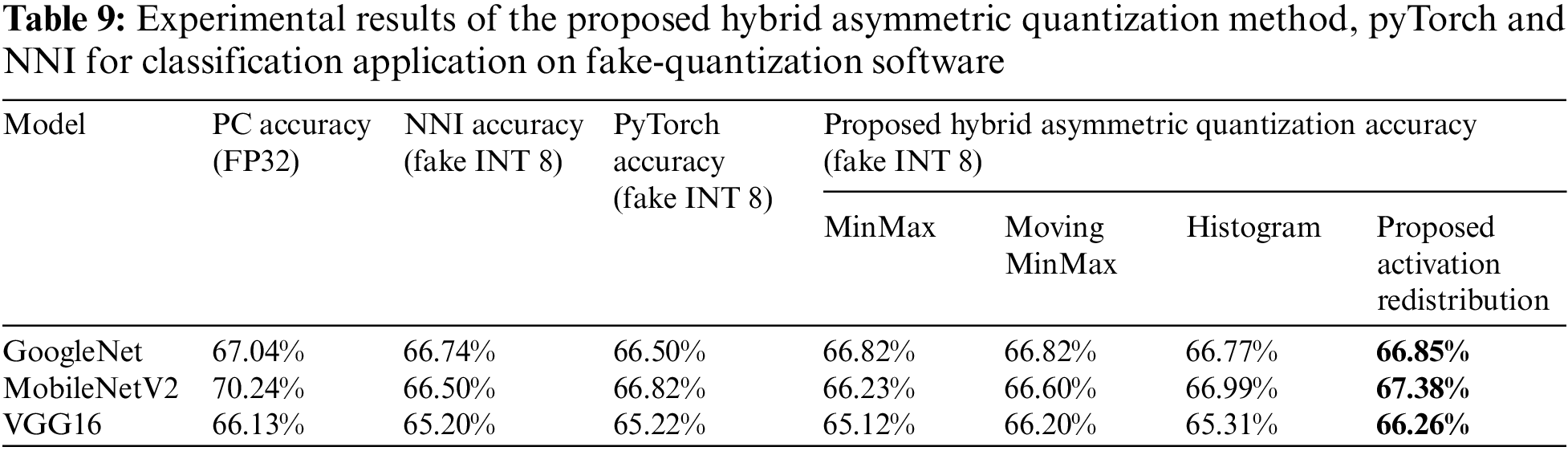
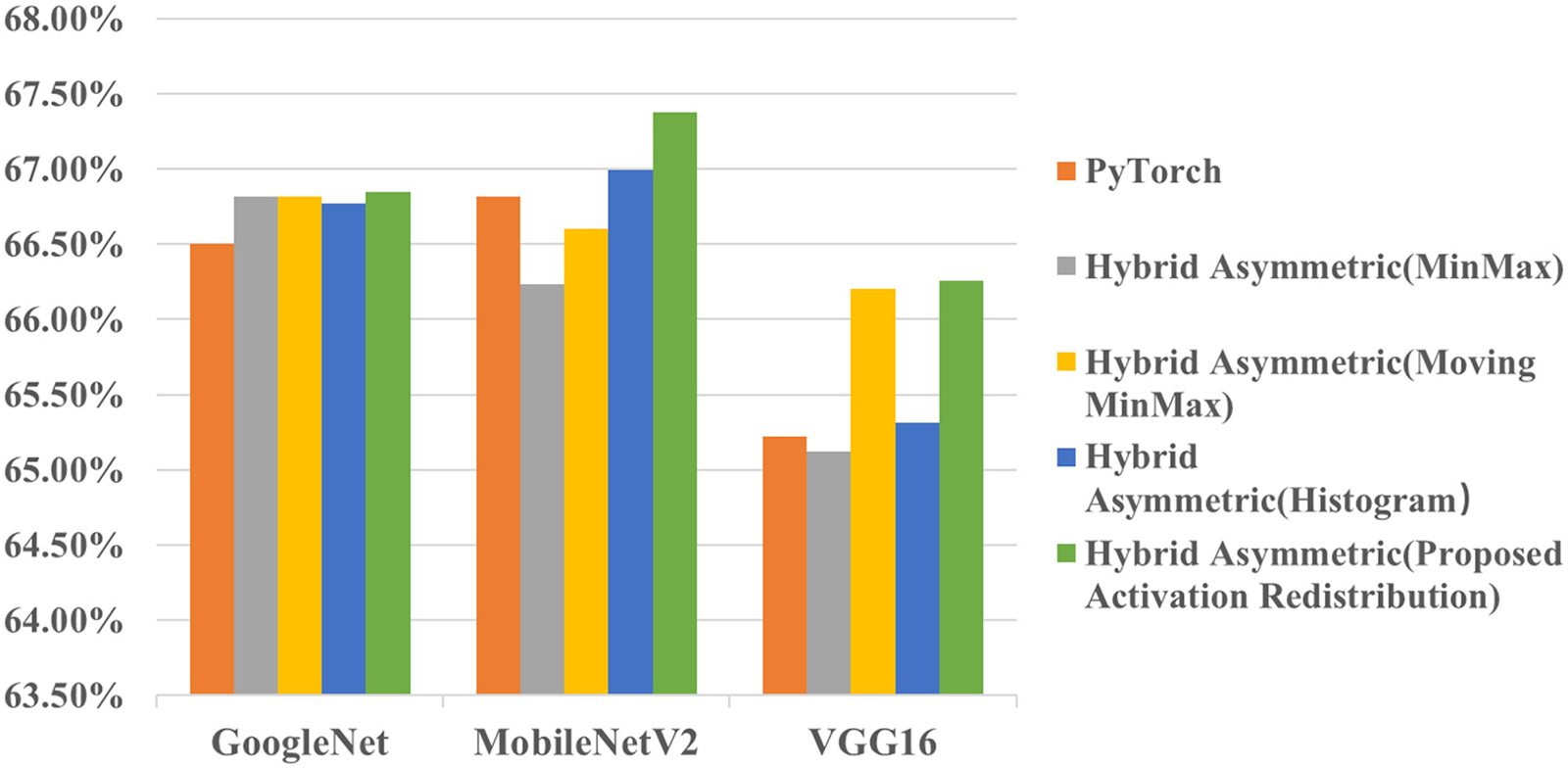
Figure 6: Comparison of the proposed method and PyTorch for image classification application. The vertical axis is the Top-1 Accuracy

•   Small Target Detection Application

The model used for small target detection to compare with PyTorch is the same as Section 4.5.1. The evaluation metric is mAP. We compare the proposed hybrid asymmetric quantization method with PyTorch, and compare the proposed activation redistribution method with MinMax, MovingAverage, and Histogram in PyTorch on fake-quantization software.

The results for small target detection model application are shown in Table 10. The proposed hybrid asymmetric quantization method can improve the detection accuracy compared with PyTorch.

5  Conclusion and Future Directions

We propose an activation redistribution hybrid asymmetric quantization method for Integer-only inference of neural networks. This method is suitable for both symmetric distributions and asymmetric distributions. When the proposed hybrid asymmetric Integer-only quantization method is applied to classification models, we can achieve an average accuracy improvement up to 2.02% compared with the traditional symmetric quantization method. When the proposed hybrid asymmetric Integer-only quantization method is applied to Yolo-v3 tiny model for detection, the accuracy improvement is 5.52% compared with the traditional symmetric quantization method. So, our method can make the neural networks quickly and easily deployed on the resource-constrained embedded devices.

For further work, we believe that making the distribution more friendly to quantization is a promising research direction to improve the quantization performance further.

Acknowledgement: The Authors acknowledge the support received from the Qian Xuesen Youth Innovation Foundation of China Aerospace Science and Technology Corporation under grant 2022JY51.

Funding Statement: The Qian Xuesen Youth Innovation Foundation from China Aerospace Science and Technology Corporation (Grant Number 2022JY51).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Lu Wei, Zhong Ma; data collection and experiment: Chaojie Yang; analysis and interpretation of results: Lu Wei, Chaojie Yang; draft manuscript preparation: Lu Wei, Zhong Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the accessible website https://github.com/ycjcy/Hybrid-Asymmetric-Quantization.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Tang, L., Ma, Z., Li, S., Wang, Z. X. (2022). The present situation and developing trends of space-based intelligent computing technology. Microelectronics & Computer, 39(4), 1–8. https://doi.org/10.19304/J.ISSN1000-7180.2021.1229 [Google Scholar] [CrossRef]

2. Zhou, X. S., Wu, W. L. (2021). Unmanned system swarm intelligence and its research progresses. Microelectronics & Computer, 38(12), 1–7. https://doi.org/10.19304/J.ISSN1000-7180.2021.1171 [Google Scholar] [CrossRef]

3. Uçar, F., Korkmaz, D. (2020). A ship detector design based on deep convolutional neural networks for satellite images. Sakarya University Journal of Science, 24(1), 197–204. [Google Scholar]

4. Gholami, A., Kim, S., Dong, Z., Yao, Z., Mahoney, M. W. et al. (2021). A survey of quantization methods for efficient neural network inference. arXiv preprint arXiv.2103.13630. [Google Scholar]

5. Nagel, M., Fournarakis, M., Amjad, R. A., Bondarenko, Y., Baalen, M. V. et al. (2021). A white paper on neural network quantization. arXiv preprint arXiv:2106.08295. [Google Scholar]

6. Li, Y., Dong, X., Wang, W. (2020). Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks. arXiv preprint arXiv:1909.13144. [Google Scholar]

7. Jacob, B., Kligys, S., Chen, B., Zhu, M. L., Tang, M. et al. (2018). Quantization and training of neural networks for efficient integer-arithmetic-only inference. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2704–2713. Salt Lake City, UT, USA. [Google Scholar]

8. Yao, Z. W., Dong, Z., Zheng, Z., Gholaminejad, A., Yu, J. et al. (2020). HAWQV3: Dyadic neural network quantization. arXiv preprint arXiv:2011.10680. [Google Scholar]

9. McKinstry, J. L., Esser, S. K., Appuswamy, R., Bablani, D., Arthur, J. V. et al. (2018). Discovering low-precision networks close to full-precision networks for efficient embedded inference. arXiv preprint arXiv:1809.04191. [Google Scholar]

10. Krishnamoorthi, R. (2018). Quantizing deep convolutional net-works for efficient inference: A whitepaper. arXiv preprint arXiv:1806.08342. [Google Scholar]

11. Wu, H., Judd, P., Zhang, X., Isaev, M., Micikevicius, P. et al. (2020). Integer quantization for deep learning inference: Principles and empirical evaluation. arXiv preprint arXiv:2004.09602. [Google Scholar]

12. Migacz, S. (2017). 8-bit inference with TensorRT. GPU Technology Conference, vol. 2, pp. 7. https://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf [Google Scholar]

13. Chen, T., Moreau, T., Jiang, Z., Zheng, L., Yan, E. (2018). TVM: An automated end-to-end optimizing compiler for deep learning. 13th fUSENIXg Symposium on Operating Systems Design and Implementation (fOSDIg 18), pp. 578–594. Carlsbad, CA, USA. [Google Scholar]

14. Choukroun, Y., Kravchik, E., Yang, F., Kisilev, P. (2019). Low-bit quantization of neural networks for efficient inference. ICCV Workshops, pp. 3009–3018. Seoul, Korea. [Google Scholar]

15. Shin, S., Hwang, K., Sung, W. (2016). Fixed-point performance analysis of recurrent neural networks. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 976–980. Shanghai, China. [Google Scholar]

16. Sung, W., Shin, S., Hwang, K. (2015). Resiliency of deep neural networks under quantization. arXiv preprint arXiv:1511.06488. [Google Scholar]

17. Zhao, R., Hu, Y. W., Dotzel, J. (2019). Improving neural network quantization without retraining using outlier channel splitting. arXiv preprint arXiv:1901.09504. [Google Scholar]

18. Park, E., Ahn, J., Yoo, S. (2017). Weighted-entropy-based quantization for deep neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5456–5464. Honolulu, Hawaii. [Google Scholar]

19. Choi, J., Zhuo, W., Venkataramani, S., Chuang, I. J., Gopalakrishnan, K. (2018). PACT: Parameterized clipping activation for quantized neural networks. arXiv preprint arXiv:1805.06085. [Google Scholar]

20. Zhang, D., Yang, J., Ye, D., Hua, G. (2018). LQ-Nets: Learned quantization for highly accurate and compact deep neural networks. European Conference on Computer Vision (ECCV), pp. 373–390. Munich, Germany. [Google Scholar]

21. Esser, S., McKinstry, J. L., Bablani, D., Appuswamy, R., Modha, D. S. (2019). Learned step size quantization. arXiv preprint arXiv:1902.08153. [Google Scholar]

22. Bhalgat, Y., Lee, J., Nagel, M., Blankevoort, T., Kwak, N. (2020). LSQ+: Improving low-bit quantization through learnable offsets and better initialization. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 696–697. [Google Scholar]

23. Box G.E., P., Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society: Series B (Methodological), 26(2), 211–243. https://doi.org/10.1111/j.2517-6161.1964.tb00553.x [Google Scholar] [CrossRef]

24. Jiao, F., Ma, Y., Bi, S. Y., Ma, Z. (2022). Design of instruction control system for neural network accelerator. Microelectronics & Computer, 39(8), 78–85. [Google Scholar]

25. Cambricon (2023). https://www.cambricon.com [Google Scholar]

26. Ma, Y., Bi, S. Y., Jiao, F., Ma, Z. (2021). A CNN accelerator with high bandwidth storage. Chinese invention patent, CN20210921363.9. [Google Scholar]

27. Microsoft (2022). Neural network intelligence (version v2.10). https://github.com/microsoft/nni [Google Scholar]

28. Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M. et al. (2017). Quantization and training of neural networks for efficient integer-arithmetic-only inference. arXiv preprint arXiv:1712.05877. [Google Scholar]