 Open Access
Open Access
ARTICLE
Effect of Blasting Stress Wave on Dynamic Crack Propagation
1 Key Laboratory for Old Bridge Detection & Reinforcement Technology of the Ministry of Transportation, Beijing, 100088, China
2 School of Mechanics and Civil Engineering, China University of Mining and Technology, Beijing, 100083, China
3 MOE Key Laboratory of Deep Underground Science and Engineering, School of Architecture and Environment, Sichuan University, Chengdu, 610065, China
* Corresponding Author: Liyun Yang. Email:
Computer Modeling in Engineering & Sciences 2024, 138(1), 349-368. https://doi.org/10.32604/cmes.2023.028197
Received 04 December 2022; Accepted 16 May 2023; Issue published 22 September 2023
Abstract
Stress waves affect the stress field at the crack tip and dominate the dynamic crack propagation. Therefore, evaluating the influence of blasting stress waves on the crack propagation behavior and the mechanical characteristics of crack propagation is of great significance for engineering blasting. In this study, ANSYS/LS-DYNA was used for blasting numerical simulation, in which the propagation characteristics of blasting stress waves and stress field distribution at the crack tip were closely observed. Moreover, ABAQUS was applied for simulating the crack propagation path and calculating dynamic stress intensity factors (DSIFs). The universal function was calculated by the fractal method. The results show that: the compressive wave causes the crack to close and the reflected tensile wave drives the crack to initiate and propagate, and failure mode is mainly tensile failure. The crack propagation velocity varies with time, which increases at first and then decreases, and the crack arrest occurs due to the attenuation of stress waves and dissipation of the blasting energy. In addition, crack arrest toughness is smaller than the crack initiation toughness, applied pressure waveforms (such as the peak pressure, duration, waveforms, wavelengths and loading rates) have a great influence on DSIFs. It is conducive to our deep understanding or the study of blasting stress waves dominated fracture, suggesting a broad reference for the further development of rock blasting in engineering practice.Keywords
Nomenclature
| CP | P-wave speed |
| CS | S-wave speed |
| Ed | Elastic modulus |
| μd | Poisson’s ratio |
| ρ | Density |
| ρ0 | Reference density |
| V | Relative volume |
| D | Detonation speed |
| Pcj | Detonation pressure |
| A, B, R1, R2, ω | Basic parameters of equation of state |
| C0∼C6 | Coefficients of linear polynomial equation of state |
| E | Internal energy per unit volume |
| k | Volume modulus |
During the excavation of underground engineering, such as mining [1,2] and tunnel [3], rock mass often bears different forms of dynamic loads, like earthquakes, impacts, and blasts, which can all cause typical dynamic fracture problems. Furthermore, blast loads are more common and complex than impact loads in rock engineering. The propagation of blasting stress waves in a fractured rock mass will induce crack propagation and lead to the instability of the rock mass structure. Therefore, it is necessary to study the propagation characteristics of blasting-induced stress waves and crack dynamic behavior induced by blasting loads in rock mass for engineering blasting design and improving blasting efficiency and reducing disaster, which is of great significance to engineering practice.
It is well known that the dynamic fracture is a very complex problem, and existing studies are mainly focused on the dynamic crack propagation behavior of rocks or rock-like materials, namely, the crack initiation, propagation and fracture toughness [4–6]. In fact, it is also worth noting the focus on the stress wave dominated fracture in actual engineering. Stress wave influences the stress field at the crack tip and causes stress concentration at the crack tip, which then drives the crack initiation. Experimentally, Knauss et al. [7] studied the influence of stress waves on dynamic crack propagation behavior using PMMA specimens. Dally [8] and Rossmanith et al. [9,10] adopted dynamic photoelastic method to study the action of blasting-induced stress waves on crack initiation and propagation. Additionally, Split Hopkinson Pressure Bar (SHPB) test [11,12] is also a recommended research method, while the small specimen size used in the test may cause the reflected stress waves to arrive at the crack tip before crack initiation, which is greatly unfavorable for studying the dynamic crack propagation behavior. In this regard, Zhu et al. [3,13] improved the SHPB device to study the dynamic fracture behavior of large-size specimens. Recently, Chen et al. [14] applied a new specimen to study stress wave-dominated the dynamic fracture. Lang et al. [15] indicated that the interaction of stress waves generated by blasting or excavation disturbance with cracks or joints significantly affected the mechanical behavior of a rock mass with some pre-existing cracks, and studied the effect of reflected stress wave on dynamic crack propagation and arrest behavior of sandstone specimens under impact loading. Qiu et al. [16] proposed a theory of distorted caustics patterns under blasting-induced stress waves to accurately measure the stress intensity factors and study the influence of blasting stress waves on crack propagation behavior. Yang et al. [17,18] studied the interaction between blasting-induced stress waves and dynamic crack. Chen et al. [19] studied the interaction process between the oblique incident blasting stress waves and the prefabricated crack and stress field at the crack tip by the photoelastic method. Wang et al. [20,21] studied the process of crack propagation induced by explosion stress waves in rock mass with open joints and filled defects by the digital laser dynamic caustics experiment.
However, the experiment may suffer from some limitations due to the transient and invisible nature of stress waves, which are often complicated and changeable, unable to record the whole process, yielding unstable results and only qualitative analysis. Numerical simulation can easily reflect the whole process of crack propagation, so it is necessary to reproduce the experimental effect and results by numerical method [22–26]. Sang et al. [22] applied pressure waveforms on the finite element model to study the dynamic fracture process in rock. Niu et al. [27] studied effects of the duration and amplitude of incident stress waves on the rock failure pattern. But their studies just concentrated on the influence of rising and falling time on fracture propagation, with the nature of the action of stress waves on the pre-existing crack being unclear.
Therefore, it is necessary to conduct a more in-depth study on the propagation characteristics of blasting stress waves and dynamic crack behavior caused by blasting stress waves. To this end, this paper combines ANSYS/LS-DYNA with ABAQUS to capture crack tip stress and displacement as well as calculate DSIFs, which offers a detailed analysis of the blasting stress waves loaded on a PMMA fracture specimen. The results can provide some basic knowledge for the study of blasting stress waves dominated fracture.
2 Numerical Modelling and Material Parameters
Finite element method (FEM) has been generally applied in simulating rock blasting, which can provide the full field data of blasting and obtain a better insight into the highly complex interaction process between stress wave and crack. Thus, in this section, ANSYS/LS-DYNA and HYPERMES software were employed to simulate the propagation characteristics of blasting stress waves and capture the stress evolution near the crack tip. The calculation termination time is approximately 800 μs and the time step is set to 1 μs, the adopted system of unit is cm-g-μs. The numerical model will be established according to a previous experiment with Polymethyl methacrylate (PMMA) conducted by Wan et al. [28], which considered the specimen with edge notch. While the specimen without edge notch was adopted for study in this paper.
2.1 Specimen Geometric Dimension
PMMA, which is similar to brittle rock in dynamic fracture characteristics, can better simulate the brittle fracture behavior of rock with defects [29]. The specimen is designed to be enough large in size and has enough space for crack propagation. The dimensions of the PMMA specimen without edge notch shown in Fig. 1 are 600 mm × 500 mm × 10 mm, and the length of the pre-existing crack is 200 mm and the width is 1 mm. The borehole is located in the middle of the upper boundary of the specimen and radius is 3.5 mm. The charge has a radius of 2 mm and is ignited to provide dynamic load on the borehole wall. The parameters of PMMA used in the numerical simulation are obtained from the literature [28], as listed in Table 1.

Figure 1: Schematic of PMMA specimen with a pre-existing crack

2.2.1 Element and the Selection of Algorithms
The solid164 element is applied to the PMMA, explosive and air. PMMA adopts Lagrange algorithm. As the air and explosive deform greatly in the process of blasting, Arbitrary Lagrangian-Eulerian (ALE) algorithm is applied for the explosive and air, which avoids the numerical calculation difficulties caused by serious distortion and achieves the dynamic analysis of fluid-structure coupling. Air and explosive are bound in an element algorithm by *ALE_MULTI_MATERIAL_GROUPA keyword. In addition, in modelling, it is necessary to separate grids for explosive and air and give their own equations of state.
2.2.2 Material Parameters and the Equation of State
To calculate the detonation products, explosives need to be defined by the keyword *MAT_HIGH_EXPLOSIVE_BURN in conjunction with the John-Wilkins-Lee (JWL) equation of state. The JWL equation, expressed in terms of the pressure of detonation product.
where P represents pressure generated by the explosion; V represents the relative volume; E represents the internal energy per unit volume; A, B, R1, R2, ω are basic parameters. The relevant parameters [28] have been presented in Table 2, where ρ represents density of explosive, D represents detonation speed, Pcj represents detonation pressure.

The air medium was considered, as shown in Fig. 2, which was added by the keyword *MAT_NULL. Linear polynomial equation of state was adopted for air and the keyword *EOS_LINEAR_PLOYNOMIAL was used, and can be expressed as
where C0∼C6 represent the coefficients; P represents the detonation pressure; E represents the internal energy per unit volume;

Figure 2: The meshes of the specimen and local meshes around the borehole and crack tip
PMMA was described by adding keywords *MAT_ELASTC and linear equation of state. The linear equation of state of PMMA is as follows:
where P represents the pressure; k represents the volume modulus; ρ/ρ0 represents the density ratio between the deformation state and initial state, respectively.
A geometric model was established by Proe 5.0. Then, it was imported into Hpermesh software for pre-processing on meshing and adding keywords. A single-layer solid grid was employed to mesh the model, Fig. 2 illustrates the meshes of the specimen and local meshes near the borehole and pre-existing crack in the model, where the borehole was divided into 22 equal parts and the model was meshed into 644270 elements in total. Time step was set as 1 μs and maximum mesh size is not more than 1 cm. The explosive grid and the air grid are shared-nodes at the interface. The reflection boundaries were employed in all sides and a normal constraint was imposed in the thickness direction of specimen. Then, ANSYS/LS-DYNA was used for the numerical calculation [31].
2.3.1 Propagation of the Blasting Stress Waves
Ls-prepost for post-processing to view the simulation results, Fig. 3 presents the pressure contours at different times as a result of the explosive detonation, which indicates propagation process of the blasting stress waves. After being ignited, the explosive produces shock wave on the borehole wall and causes it deformed, then diffuses outward and attenuates in a circular shape into a stress wave, including a leading compressive wave and a trailing tensile wave as shown in Fig. 3. After blasting, the pre-existing crack is subject to the joint action of compressive waves and tensile waves. The blasting stress waves propagate freely and approach the crack tip continuously before t = 90 μs. When t = 90 μs, the compressive wave arrives at the crack tip at first, and followed by the tensile wave. At t = 130 μs, blasting stress wave reaches the left and right free boundaries of the specimen. Then, it is reflected back and transformed into the tensile stress wave at t = 140 μs. When t = 210 μs, blasting stress wave reaches the lower boundary of the specimen and then is reflected, producing reflected tensile wave can be seen at t = 220 μs. Subsequently, these stress waves propagate gradually and then superimpose together. As the blasting energy dissipates, the stress waves decay quickly with time at the later stage.

Figure 3: Blasting-induced pressure contours
2.3.2 Stress Evolution at the Crack Tip
The transient stress field induced by blasting is influenced by the propagation of a stress wave. To analyze the stress distribution of the crack tip, combined with propagation characteristics of stress wave, Fig. 4 displays pressure-time curve at the crack tip, where the positive value of pressure shows the compressive stress, while the negative value shows the tensile stress. As mentioned previously in Fig. 3, it can be found that, from Fig. 4, the compressive wave arrives at the crack tip at first and then acts on it. After 150 μs, the tensile waves reflected from the left and right boundaries reach the crack tip, the tensile area at the crack tip is formed at about 180 μs shown in Fig. 3. At about 175 μs, the tensile stress of pre-existing crack tip in Fig. 4 reaches the maximum as well. It can be inferred that the crack will initiate and propagate at this time. Thereafter, second tensile apperas due to reflection from the lower boundary of the specimen. After that, the pressure at the crack tip oscillates around 0 with the stress wave propagating through the pre-existing crack as shown in the dashed box. As shown in Fig. 3, with the increase of time, the crack is influenced by complex stress waves, such as the trailing tensile waves, reflected tensile waves, and p-wave and s-wave scattered from the crack tip, where these stress waves encounter and then superimpose together. However, in contrast to the initial stress waves, amplitudes of these superposition stress waves are so smaller, and have very little effect on the dynamic propagation behavior of the pre-existing crack. Therefore, they are not considered in this study. In addition, it should be pointed out that, under the action of these waves, the stress field at the crack tip varies with time, resulting in the pre-existing crack initiation and propagation eventually, which will be discussed later.

Figure 4: Pressure time curve at the crack tip
3 Crack Initiation and Propagation
3.1 Crack Propagation Path by XFEM
The extended finite element method (XFEM) in ABAQUS is adopted to simulate the crack propagation along any path, the maximum principal stress failure criterion is regard as the criterion of damage initiation. And the damage evolution of the fracture criterion based on energy method is used to simulate the crack propagation. In previous numerical investigations, the blasting load was usually represented by a pressure-time history curve [32,33]. Hu et al. [34] studied the loading form of blasting stress wave with an equivalent pressure wave to represent the blasting load. Therefore, the pressure-time history curve as shown in Fig. 5, obtained from the previous experiment [28], is applied on the borehole wall to simulate the blasting loading, which is roughly triangular in shape. Where the peak value of pressure is about 84 MPa and the duration is 55 μs, both the ascending and descending times are about 20 μs. The lower boundary of the model is fixed, as shown in Fig. 6a.

Figure 5: Dynamic load applied on the blasthole wall

Figure 6: Finite element model and crack propagation path
The analyses in Section 2 show that the stress field of crack tip was markedly affected by the blasting stress waves, this implies that the fracture processes are closely associated with the stress waves induced by blasting. Fig. 6 displays the crack propagation path and fracture mode of the specimen. It can be found from Figs. 6b–6d that the crack propagates approximately along a straight line, which is basically consistent with blasting experiment result under the same condition [28] except for crack propagation length. That is, the mode I fracture caused by tensile stress plays a leading role in the dynamic crack propagation process. However, the propagation length of the pre-existing crack is not very long due to the small blasting pressure applied. If the charge weight is too large, the specimen will be seriously damaged, which is not conducive to the study of dynamic crack propagation behavior.
Fig. 7 displays the local magnified view of crack propagation path with time. Note that in the figure, only a portion of the model is presented due to the limitation of view field. The location of the crack tip can be determined from Fig. 7, and the part below the red dashed line is the propagation length of the pre-existing crack. It can be observed that the crack initiation and propagation start at approximately 175 μs, at this time, the tensile stress of crack tip reaches the maximum as described in Section 2.3.2, denoting that tensile stress tends to promote the crack initiation and propagation but the compressive waves lead to crack closure. Since the compressive waves occur before the tensile waves, it can be deduced that the crack is compressed at first and then pulled to crack under the loading of blasting stress waves. Thereafter, the crack gradually propagates downward, forming a vertical crack, which is due to the action of the tensile stress induced by tensile waves. Nevertheless, when blasting stress waves attenuate to a certain extent, it will be not sufficient to support the crack propagating and the crack propagation length is limited to a final length of 40 mm.

Figure 7: Local magnified view of crack propagation path with time
3.2 Crack Propagation Length and Velocity
Based on the local magnified view of the crack propagation path in Fig. 7, the crack propagation length and crack propagation velocity can be calculated. According to the length and the fracture time of each element, the crack propagation length and propagation velocity as function of time are obtained shown in Fig. 8, which shows the crack propagation velocity is not a constant and is relatively low at the initial stage. This is because the crack cannot initiate immediately under the action of compressive waves. While the crack propagation velocity increases rapidly after crack initiation and then reaches a maximum value of 925.9 m/s. After that, the energy at the crack tip gradually decreases with attenuation of stress waves, the crack propagation velocity gradually decreases as well, and the crack arrest occurs in the end. Fig. 9 displays the variation curve of crack propagation velocity with crack propagation length. The crack propagation velocity fluctuates greatly with crack propagation length, and slows down finally until the crack arrest. The crack initiation velocity is 135.1 m/s and the average crack propagation velocity is 488.11 m/s.

Figure 8: Crack propagation velocity and length vs. time

Figure 9: Crack propagation velocity vs. crack propagation length
3.3 Fractal Characteristics of the Crack Propagation Path
The crack propagation path is often irregular, resulting in rough fracture surface. And the crack propagation path of brittle materials has fractal characteristics. To further study the instability of crack propagation path, fractal theory is employed to analyze the characteristics of crack propagation path. Binarization method is adopted to process the crack propagation path obtained by numerical simulation, as shown in Fig. 10a. It can be found that, on the whole, the crack travels slightly curved and approximately a straight line, indicating that the failure mode is mode I fracture during blasting.

Figure 10: Fractal dimension method of crack propagation path (a) Binarization process (b) Fractal dimension calculation by the box counting method (c) Linear fitting in the double logarithmic coordinate system
The box counting method is adopted to calculate the fractal dimension of crack propagation path [35]. Although there are many ways to calculate fractal dimension, the box counting method is simple and convenient to use. The formula [36] is shown in Eq. (4):
After processing with box counting method, δ and N(δ) can be given. And a linear correlation can be obtained, as shown in Fig. 10c. The slope of the fitting line is Df, and the negative value is the fractal dimension D. Thus, the fractal dimension of the crack propagation path can be calculated as 2.0285 and the correlation coefficient R2 = 0.9994 > 0.98, which manifests that the result is consistent with the fractal law.
DSIF is an important parameter to predict dynamic crack propagation behavior, which is different from static stress intensity factor. The DSIF
where CR is Rayleigh wave speed, Cd is P wave speed. When V = 0, k (0) = 1, which indicates DSIF does not need to be multiplied by the universal function, that is, the universal function is 1 and static stress intensity factor is equal to the DSIF at crack initiation and arrest. When V = CR, k(CR) = 0. This shows when the crack propagates at Rayleigh wave speed, the DSIF is 0.
Substituting Eq. (6) into Eq. (8), is expressed as
ABAQUS has been widely applied in calculating stress intensity factors [3,13], because of its accuracy. The displacement extrapolation method according to crack tip opening displacement is employed to calculate stress intensity factor in this paper. Based on the specimen size and loading condition, the finite element model was established. The area near the crack tip was meshed by six-node triangular element CPS6, and the other areas were meshed by eight-node quadrilateral element CPS8. Fig. 11 shows the mesh division of finite element model, where a total of 42863 elements are meshed in the model.

Figure 11: Finite element mesh model applied in calculating the DSIFs
4.2 Displacement Extrapolation Method
The stress intensity factors were calculated according to displacement extrapolation method. Firstly, the opening displacement of crack tip can be gained by the established finite element model, as shown in Fig. 11.
Based on the fracture mechanics theory [43], the displacement near the crack tip in the x direction in Fig. 11 is as follows:
where
It is known that, from Eq. (12),
Assuming the stress intensity factors at points A, B and O in Fig. 11 are respectively

Figure 12: CPS6 elements and the displacements at the crack tip
Accordingly, the stress intensity factor
Finally, according to Eq. (7), the calculated stress intensity factor is multiplied by the velocity universal function, which is the DSIF.
Fig. 13 shows the change curves of DSIFs with time calculated by the displacement extrapolation method. At crack initiation, as shown in Fig. 13a, the compressive wave reaches the crack tip at about 90 μs, and lasts about 31 μs from 90 to121 μs. During this, the DSIFs at the crack tip are negative. After that, the DSIFs become positive, indicating the stress field at the crack tip varies from compressive into tensile, then reaches its maximum value of 7.16 MPa⋅m1/2 at 188 μs. According to the Sections 2 and 3, crack initiation occurs at approximately175 μs, and the crack initiation velocity is zero, the universal function k(V) = 1, the corresponding critical DSIF is 4.48 MPa⋅m1/2, which is the crack initiation toughness. Fig. 13a shows that crack initiation occurs before the DSIF reaches the maximum value of 7.16 MPa⋅m1/2.

Figure 13: The DSIFs evolution with time
It has been pointed out in Section 3.3 that the DSIF is related to the velocity function. To calculate the DSIFs at crack propagation, at t = 199 μs, the crack propagation length is 10 mm in Fig. 7 and the original crack length is 200 mm. The average crack propagation velocity is 428.6 m/s. Similarly, it is assumed that the original length of the crack is 210 mm before the blasting load is applied. The finite element model can be established by ABAQUS. Then, the blasting load curve is applied on the borehole wall, and the stress intensity factors at crack propagation are calculated, as shown by the solid curve in Fig. 13b. Based on the velocity universal function Eq. (9), the obtained k(V) is 0.738, and then the DSIFs at the crack tip are obtained by Eq. (8), which are presented in the dashed curve in Fig. 13b. Thus, when t = 199 μs, the corresponding critical DSIF is 5.19 MPa⋅m1/2.
When t = 301.9 μs, the crack propagation length is 34 mm. The finite element model is established, and then the blasting load curve is applied to the borehole wall. The DSIFs calculated are shown as the solid curve in Fig. 13c. At this time, the crack propagation velocity is 66.8 m/s, so the velocity universal function k(V) = 0.962(≈1), and the difference of DSIF is only 3.8% compared with that at crack arrest. Then, the DSIFs are calculated by Eq. (8), and which are presented as the dashed curve in Fig. 13c. And the critical DSIF is 2.12 MPa⋅m1/2 at t = 301.9 μs, which is smaller than the crack initiation toughness 4.48 MPa⋅m1/2.
4.3.2 Effect of Blasting Stress Wave Characteristics on DSIFs
To further analyze the influence of the loading form of blasting stress waves on the DSIFs at the pre-exsiting crack tip, such as the peak pressure, duration, waveforms, wavelengths and loading rates were taken into account, and the corresponding DSIFs were calculated, respectively, as shown in Figs. 14 and 15.
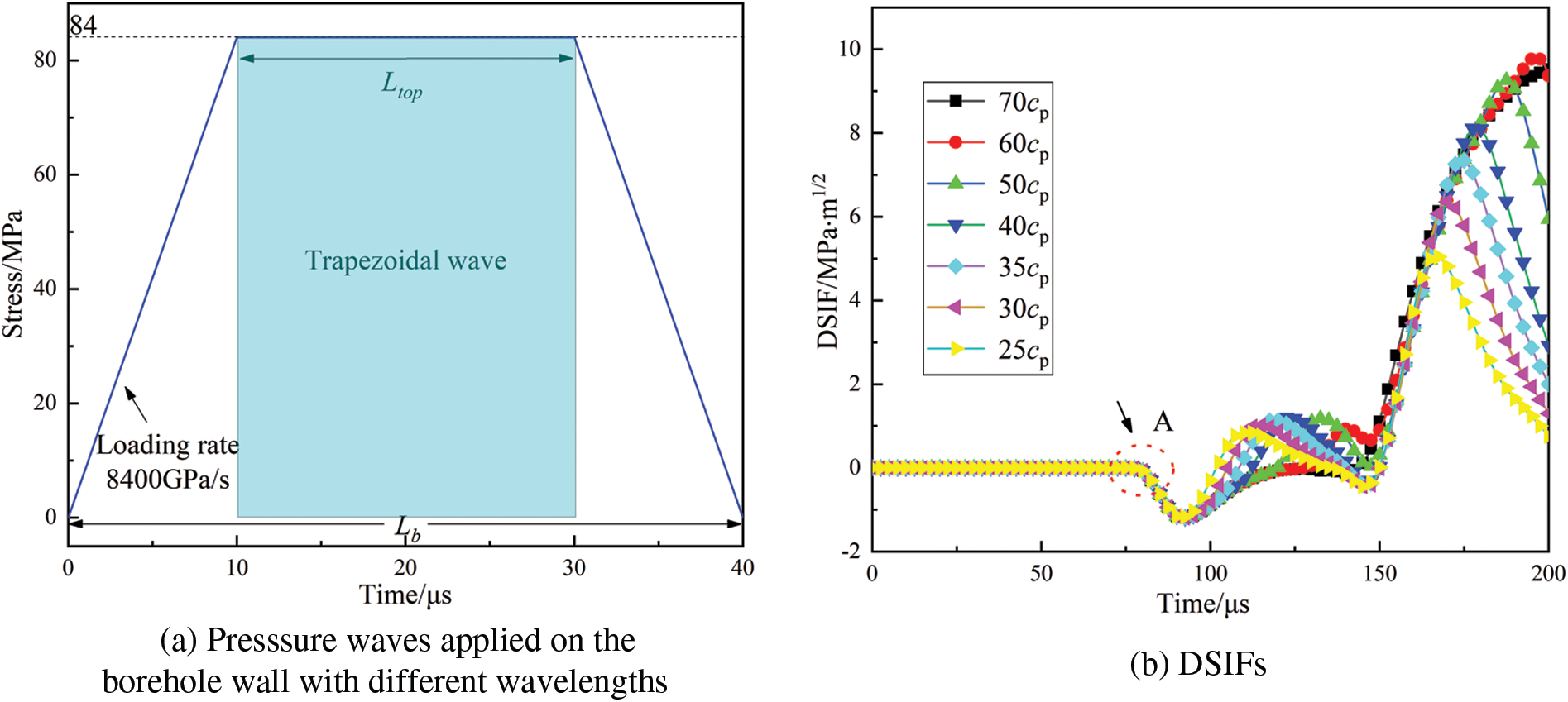
Figure 14: Waveforms and DSIFs with a constant loading rate of 8400 GPa/s

Figure 15: Waveforms and DSIFs with a constant wavelength of 40cp
A blasting-induced wave is usually simplified in numerical studies, such as a half-cycle sinusoidal, triangular or rectangular stress wave. Hence, the original loading wave curve in Fig. 5 is simplified as a trapezoidal loading wave shown in Fig. 14a, and then the trapezoidal loading wave is applied to the borehole wall for numerical simulation. The peak pressure of the trapezoidal wave is kept as 84 MPa. Correspondingly, the top platform length Ltop changes equally when the wavelength Lb is changed; the wavelength is the product of wave travel time and wave propagation velocity in specimen, i.e., Lb = tcp. The loading rate is defined as the slope of linear ascending segment of the loading stress curve, as shown in Fig. 14a. In which the rising and falling times of the trapezoidal wave are 10 μs, so the loading rate is 8400 GPa/s. For the trapezoidal wave of different wavelengths, it can be seen that the curves of DSIFs exhibit a similar trend in Fig. 14b, but there are differences in the peak values. As the wavelength increases, the location where the peak values appear gradually moves to the right, the time of DSIFs reaching its peak value is delayed, while the peak value is larger, because duration of the trapezoidal loading wave increases. When the wavelength is short, the top platform is also short, the duration of the trapezoidal loading wave decreases, so it also starts to decay earlier. Point A shows that the time of the compressive wave arriving at the crack tip is unchanged, because the wavefront part of trapezoidal wave is the same, that is, the time of the stress waves attaining its peak is the same, which is 10 μs. In addition, the propagation velocity of the compressive wave in the PMMA is the same, and the propagation distance to the crack tip is also the same. When the wavelength is 20cp, the pressure waveform transforms into the triangular loading wave. This case will be discussed further in the following section.
To clarify the influence of loading rate and applied pressure waveforms on the DSIFs at the pre-exsiting crack tip, the pressure waveforms, as shown in Fig. 15a, were applied to the borehole wall, respectively. The wavelength of 40cp, the peak of loading waves of 84 MPa and the duration 40 μs remain unchanged. As the top platform length Ltop increased in the range of 0 to 40cp, and the loading rate changes accordingly. The waveforms are regarded as the special triangular loading wave, trapezoidal loading wave and rectangular loading wave, through adjusting the rising time and falling time, which are varied between 10 and 20 μs, the increased loading rate reduces the rising time and falling time, as shown in Fig. 15a. Although various loading wave curves with the same peak pressure are applied on the borehole wall, the stress field in the model varies significantly with increasing loading rate, resulting in different DSIFs.
As can be seen from Fig. 15a, the stress wave reaches the peak pressure early with the larger loading rate. At lower loading rates, the peak pressure lasts only a short time, even to zero. In Fig. 15b, the time of DSIFs achieving the peak is almost not affected by the loading rate, but the larger the loading rate is, the larger the DSIFs are. When the loading rate is infinite, the DSIFs curve becomes distorted, indicating that the wave propagation in the specimen is unstable, and this case does not exist in reality. For trapezoidal wave and triangular wave with the same wavelength and peak pressure, the trapezoidal wave arrives at the peak stress of 84 MPa at first, the larger the DSIFs are, thus, the crack initiation is earlier. That is, the larger the loading rate is, the earlier the crack initiates.
On the basis of the analysis above, it can be concluded that the DSIFs at the pre-exsiting crack tip are related to the amplitude of applied pressure wave, wavelength, waveform, loading rate and duration, the reason being that the stress field at the crack tip is affected by blasting stress waves. Therefore, the dynamic crack behavior should be evaluated considering the characteristics of stress waves.
The blasting-induced stress wave plays a significant role in crack propagation behavior. Numerical simulation based on ANSYS/LS-DYNA and ABAQUS was performed in PMMA specimens, reproducing the entire process of dynamic crack propagation, and the influence of characteristics of applied pressure wave on DSIFs was analyzed.
The compressive wave causes the crack to close and the reflected tensile wave from the free boundary drives the crack to initiate and propagate, and the failure mode of the specimen is mainly tensile failure. Under blasting-induced stress waves, the crack propagation velocity is not constant. Owing to the attenuation of stress waves and the dissipation of the blasting energy, the crack propagation velocity decreases and crack arrest occurs at the later stage. Furthermore, the crack arrest toughness is smaller than the crack initiation toughness. Peak pressure, duration, waveforms, wavelengths and loading rates significantly affect DSIFs.
The study provides a reference for the study of dynamic crack behavior under blasting stress waves. In future studies, the action of various waves, incidence angle and in-situ stress will be considered for optimizing blast designs.
Acknowledgement: This research was supported by the National Natural Science Foundation of China and the Fundamental research funds for Central Universities.
Funding Statement: This research was supported by the National Natural Science Foundation of China (No. 52227805) and the Fundamental Research Funds for Central Universities (No. 2022JCCXLJ01). Awards were granted to the author Liyun Yang.
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Huizhen Liu, Liyun Yang; data collection: Meng Wang, Duanying Wan; analysis and interpretation of results: Huizhen Liu, Liyun Yang, Zheming Zhu; draft manuscript preparation: Huizhen Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: None.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Xue, Y., Liu, J., Ranjith, P. G., Gao, F., Xie, H. et al. (2022). Changes in microstructure and mechanical properties of low-permeability coal induced by pulsating nitrogen fatigue fracturing tests. Rock Mechanics and Rock Engineering, 55(12), 7469–7488. https://doi.org/10.1007/s00603-022-03031-2 [Google Scholar] [CrossRef]
2. Xue, Y., Ranjith, P. G., Chen, Y., Cai, C., Gao, F. et al. (2023). Nonlinear mechanical characteristics and damage constitutive model of coal under CO2 adsorption during geological sequestration. Fuel, 331, 125690. https://doi.org/10.1016/j.fuel.2022.125690 [Google Scholar] [CrossRef]
3. Zhou, L., Zhu, Z., Dong, Y., Fan, Y., Zhou, Q. et al. (2019). The influence of impacting orientations on the failure modes of cracked tunnel. International Journal of Impact Engineering, 125, 134–142. https://doi.org/10.1016/j.ijimpeng.2018.11.010 [Google Scholar] [CrossRef]
4. Funatsu, T., Kuruppu, M., Matsui, K. (2014). Effects of temperature and confining pressure on mixed-mode (I–II) and mode II fracture toughness of Kimachi sandstone. International Journal of Rock Mechanics & Mining Sciences, 67, 1–8. https://doi.org/10.1016/j.ijrmms.2013.12.009 [Google Scholar] [CrossRef]
5. Haeri, H., Shahriar, K., Marji, M. F., Moarefvand, P. (2014). Experimental and numerical study of crack propagation and coalescence in pre-cracked rock-like disks. International Journal of Rock Mechanics and Mining Sciences, 67(4), 20–28. https://doi.org/10.1016/j.ijrmms.2014.01.008 [Google Scholar] [CrossRef]
6. Aliha, M., Ayatollahi, M. R. (2014). Rock fracture toughness study using cracked chevron notched Brazilian disc specimen under pure modes I and II loading–A statistical approach. Theoretical & Applied Fracture Mechanics, 69, 17–25. https://doi.org/10.1016/j.tafmec.2013.11.008 [Google Scholar] [CrossRef]
7. Knauss, W. G., Ravi-Chandar, K. (1985). Some basic problems in stress wave dominated fracture. International Journal of Fracture, 27(3–4), 127–143. https://doi.org/10.1007/BF00017963 [Google Scholar] [CrossRef]
8. Dally, J. W. (1980). An introduction to dynamic photoelasticity. Experimental Mechanics, 20(12), 409–416. [Google Scholar]
9. Rossmanith, H. P., Fourney, W. L. (1982). Fracture initiation and stress wave diffraction at cracked interfaces in layered media I. Brittle/brittle transition. Rock Mechanics, 14(4), 209–233. https://doi.org/10.1007/BF01596617 [Google Scholar] [CrossRef]
10. Rossmanith, H. P., Shukla, A. (1981). Dynamic photoelastic investigation of interaction of stress waves with running cracks. Experimental Mechanics, 21(11), 415–422. https://doi.org/10.1007/BF02327143 [Google Scholar] [CrossRef]
11. Li, J. C., Li, N. N., Li, H. B., Zhao, J. (2017). An SHPB test study on wave propagation across rock masses with different contact area ratios of joint. International Journal of Impact Engineering, 105(7), 109–116. https://doi.org/10.1016/j.ijimpeng.2016.12.011 [Google Scholar] [CrossRef]
12. Liu, K., Zhang, Q. B., Wu, G., Li, J. C., Zhao, J. (2019). Dynamic mechanical and fracture behaviour of sandstone under multiaxial loads using a triaxial Hopkinson bar. Rock Mechanics and Rock Engineering, 52, 2175–2195. https://doi.org/10.1007/s00603-018-1691-y [Google Scholar] [CrossRef]
13. Wang, X. M., Zhu, Z. M., Wang, M., Ying, P., Zhou, L. et al. (2017). Study of rock dynamic fracture toughness by using VB-SCSC specimens under medium-low speed impacts. Engineering Fracture Mechanics, 181, 52–64. https://doi.org/10.1016/j.engfracmech.2017.06.024 [Google Scholar] [CrossRef]
14. Chen, S., Osovski, S. (2018). A new specimen for growing dynamic cracks along a well defined path using stress wave loading. Engineering Fracture Mechanics, 191, 102–110. https://doi.org/10.1016/j.engfracmech.2018.01.027 [Google Scholar] [CrossRef]
15. Lang, L., Qin, Y., Tang, H., Zhu, Z., Li, H. et al. (2023). Effect of reflected stress wave on dynamic crack propagation and arrest behavior of sandstone specimens under impact loading. Theoretical and Applied Fracture Mechanics, 123, 103720. https://doi.org/10.1016/j.tafmec.2022.103720 [Google Scholar] [CrossRef]
16. Qiu, P., Yue, Z. W., Ju, Y., Zhao, J. (2020). Characterizing dynamic crack-tip stress distribution and evolution under blast gases and reflected stress waves by caustics method. Theoretical and Applied Fracture Mechanics, 108, 102632. https://doi.org/10.1016/j.tafmec.2020.102632 [Google Scholar] [CrossRef]
17. Yang, R. S., Xu, P., Chen, C. (2019). Interaction between blast stress waves and cracks. Explosion and Shock Waves, 39(8), 1–11. [Google Scholar]
18. Ding, C. X., Yang, R. S., Feng, C. (2021). Stress wave superposition effect and crack initiation mechanism between two adjacent boreholes. International Journal of Rock Mechanics and Mining Sciences, 138, 104622. https://doi.org/10.1016/j.ijrmms.2021.104622 [Google Scholar] [CrossRef]
19. Chen, C., Yang, R. S., Xu, P., Ding, C. X. (2022). Experimental study on the interaction between oblique incident blast stress wave and static crack by dynamic photoelasticity. Optics and Lasers in Engineering, 148(3),106764. https://doi.org/10.1016/j.optlaseng.2021.106764 [Google Scholar] [CrossRef]
20. Wang, Y. B., Ren, B., Wang, D. C. (2021). Research on the process of crack growth induced by explosion stress waves in rock masses with open joints. Theoretical and Applied Fracture Mechanics, 115, 103038. https://doi.org/10.1016/j.tafmec.2021.103038 [Google Scholar] [CrossRef]
21. Wang, Y. B., Dong, J. Q., Wang, Z. Y., Zhao, Y. B. (2021). Analysis of the expansion process of cracks caused by blasting stress waves in a PMMA medium with filled defects. Materials Today Communications, 27, 102396. https://doi.org/10.1016/j.mtcomm.2021.102396 [Google Scholar] [CrossRef]
22. Sang, H. C., Kaneko, K. (2004). Influence of the applied pressure waveform on the dynamic fracture processes in rock. International Journal of Rock Mechanics and Mining Sciences, 41(5), 771–784. https://doi.org/10.1016/j.ijrmms.2004.02.006 [Google Scholar] [CrossRef]
23. Fan, H., Li, S. (2017). A peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads. Computer Methods in Applied Mechanics & Engineering, 318, 349–381. https://doi.org/10.1016/j.cma.2017.01.026 [Google Scholar] [CrossRef]
24. Ren, B., Fan, H., Bergel, G. L., Regueiro, R. A., Lai, X. et al. (2015). A peridynamics-SPH coupling approach to simulate soil fragmentation induced by shock waves. Computational Mechanics, 55(2), 287–302. https://doi.org/10.1007/s00466-014-1101-6 [Google Scholar] [CrossRef]
25. Lai, X., Ren, B., Fan, H., Li, S., Wu, C. T. et al. (2015). Peridynamics simulations of geomaterial fragmentation by impulse loads. International Journal for Numerical and Analytical Methods in Geomechanics, 39(12), 1304–1330. https://doi.org/10.1002/nag.2356 [Google Scholar] [CrossRef]
26. Fan, H., Bergel, G. L., Li, S. (2016). A hybrid peridynamics–SPH simulation of soil fragmentation by blast loads of buried explosive. International Journal of Impact Engineering, 87. https://doi.org/10.1016/j.ijimpeng.2015.08.006 [Google Scholar] [CrossRef]
27. Niu, L. L., Zhu, W. C., Cheng, Z., Guan, K., Qin, T. (2017). Numerical simulation on excavation-induced damage of rock under quasi-static unloading and dynamic disturbance. Environmental Earth Sciences, 76(17), 614. https://doi.org/10.1007/s12665-017-6955-4 [Google Scholar] [CrossRef]
28. Wan, D. Y., Zhu, Z. M., Liu, R. F., Liu, L. J. F. (2019). Measuring method of dynamic fracture toughness of mode I crack under blasting using a rectangle specimen with a crack and edge notches. International Journal of Rock Mechanics and Mining Sciences, 123, 104104. https://doi.org/10.1016/j.ijrmms.2019.104104 [Google Scholar] [CrossRef]
29. Rossmanith, H. P., Daehnke, A., Nasmillner, R. E. K., Kouzniak, N., Ohtsu, M. et al. (2010). Fracture mechanics applications to drilling and blasting. Fatigue and Fracture of Engineering Materials and Structures, 20(11), 1617–1636. https://doi.org/10.1111/j.1460-2695.1997.tb01515.x [Google Scholar] [CrossRef]
30. Gao, X. N., Wu, Y. J. (2015). Numerical calculation of TNT explosion and its influencing factors. Chinese Journal of Explosives & Propellants, 38(3), 32–39. [Google Scholar]
31. Dong, J. K., Sirijaroonchai, K., El-Tawil, S., Naaman, A. E. (2010). Numerical simulation of the split Hopkinson pressure Bar test technique for concrete under compression. International Journal of Impact Engineering, 37(2), 141–149. https://doi.org/10.1016/j.ijimpeng.2009.06.012 [Google Scholar] [CrossRef]
32. Donze, F. V., Bouchez, J., Magnier, S. A. (1997). Modeling fractures in rock blasting. International Journal of Rock Mechanics & Mining Sciences, 34, 1153–1163. https://doi.org/10.1016/S1365-1609(97)80068-8 [Google Scholar] [CrossRef]
33. Zhu, W. C., Niu, L. L., Wei, J., Bai, Y., Wei, C. H. (2013). Numerical simulation on rock failure process under combined static and dynamic loading. Proceedings of the 1st International Conference on Rock Dynamics and Applications, London, Taylor & Francis Group. [Google Scholar]
34. Hu, X. D., Zhao, G. F., Deng, X. F., Hao, Y. F., Fan, L. F. et al. (2018). Application of the four-dimensional lattice spring model for blasting wave propagation around the underground rock cavern. Tunnelling and Underground Space Technology, 82, 135–147. https://doi.org/10.1016/j.tust.2018.08.006 [Google Scholar] [CrossRef]
35. Xie, H. P., Sanderson, D. J. (1986). Fractal effects of crack propagation on dynamic stress intensity factors and crack velocities. International Journal of Fracture, 74, 29–42. https://doi.org/10.1007/BF00018573 [Google Scholar] [CrossRef]
36. Peng, R. D., Xie, H. P., Yang, J. U. (2004). Computation method of fractal dimension for 2-D digital image. Journal of China University of Mining & Technology, 33(1), 19–24. https://doi.org/10.3321/j.issn:1000-1964.2004.01.005 [Google Scholar] [CrossRef]
37. Bhat, H. S., Rosakis, A. J., Sammis, C. G. (2012). A micromechanics based constitutive model for brittle failure at high strain rates. Journal of Applied Mechanics, 79(3), 39–37. https://doi.org/10.1115/1.4005897 [Google Scholar] [CrossRef]
38. Rose, L. (1976). On the initial motion of a Griffith crack. International Journal of Fracture, 12(6), 829–841. https://doi.org/10.1007/BF00034622 [Google Scholar] [CrossRef]
39. Freund, L. B., Hutchinson, J. W. (2006). Dynamic fracture mechanics. Journal of Applied Mechanics, 59(1), 245. [Google Scholar]
40. Ravi-Chandar, K. (2004). Dynamic fracture. Amsterdam: Elsevier. [Google Scholar]
41. Freund, L. B. (1990). Dynamic fracture mechanics. Cambridge: Cambridge University Press. [Google Scholar]
42. Zhang, C. G., Cao, F., Li, L., Zhou, Y., Huang, R. Q. et al. (2016). Determination of dynamic fracture initiation, propagation, and arrest toughness of rock using SCDC specimen. Chinese Journal of Theoretical and Applied Mechanics, 48(3), 624–635. https://doi.org/10.6052/0459-1879-15-349 [Google Scholar] [CrossRef]
43. Zehnder, A. T. (2012). Fracture mechanics. Ithaca, USA: Cornell University. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools