Mechanism of Thermally Radiative Prandtl Nanofluids and Double-Diffusive Convection in Tapered Channel on Peristaltic Flow with Viscous Dissipation and Induced Magnetic Field

Nomenclature

1  Introduction

The peristalsis flow of many physical fluids is significant natural phenomena that has vast industrial and medical applications. Peristalsis is the extension and condensation that naturally occurs on longitudinal walls of expandable chamber or tube. Human anatomy has numerous examples of the phenomenon among various organs such as stomach, large & small intestine, and others. The substances and liquids in human body move through peristalsis flow, hence the food digestion within gastrointestinal track, release of sperms and ovum by reproductory organs, blood circulation, lymph secretion and flow in lymphatic vessels, waste excretion through bladder and secretion of numerous hormones are all owe to the peristalsis. The same phenomenon is the life deriving force in plants too. Peristalsis extension and condensation appear in phloem relocation through sucrose suction within tubules. Other naturally occurring phenomena include propelling movements of insects. Moreover, in manufacturing industries, the phenomenon is implemented in devising medical equipment such as machines to pump blood, dialysis apparatus, finger pump machines, lung machinery and heart apparatuses. These applications attract the attention of many researchers to explore the peristaltic flow in human anatomy. In addition, its practical utility led many researchers and scientists like mathematicians, physicists, engineers to investigate the phenomenon actively and intensely. Some significant studies are referred in [1–10].

Another field of recent investigation is magneto-science which is the combination of biological systems and medical science with implications of a magnetic field. Many magnetic devices are available in the market like an instrument for cell segregation, bio-waste transportation equipment, gastrointestinal control through an induced magnetic field, drug targeting and trafficking devices, cancer cell control and destruction mechanism build through an alternating magnetic field are some of the examples of implication of the phenomenon in medical industry. Extension of this phenomenon is induced magnetic field (IMF) which is a supplementary magnetic flux induced upon electrically charged fluid with an external magnetic field. This occurrence owes to the effect of greater magnetic Reynolds number. IMF is applied in both medical and manufacturing industries, some of the examples include geophysics equipment, in MRI machines, glass production, electric MHD generators, etc. In medicine, the phenomenon has applications such as IMF combined with blood flows used in blood pumping, cardiac problems, and many other biological applications. Numerous studies have been conducted to theoretically and mathematically examine the phenomenon. Few recent works can be seen in [11–15].

Recently, researchers are engaged in exploring the techniques to ameliorate the thermos-physical qualities of fluids. One such technique is the addition of minute particles with increased heat conductivity [16]. If a liquid contains a large particle or nanoparticle, it cannot be stable and develop resistance to flow. If such kinds of fluids are injected into the human body, it will result in clotting and roughness. While nanoparticles ranging from 1–100 nm in a suspension can envelope more area with an increased coefficient of conduction and convection. Nanoparticles have vast engineering applications. Whereas in medicine, nanofluids are used in targeted drug transfer for cancer therapies and treatments. Kothandapani et al. [17] investigated the peristaltic nanofluids flow under magnetic flux and thermal radiation. While the numerous impacts of Jeffrey nanofluid with peristalsis have been examined by Reddy et al. [18]. Ramesh et al. [19] further explored the phenomenon with couple stress fluid having magnetic flux and heat transfer. Recent literature on nanofluid flow has been listed as [20–27].

Thermal and concentration gradients involve in the process of double diffusion. The model was proposed by Aifanties [28] in 1976, according to which a concentration gradient is produced in a thermal mixture with sustained temperature difference. The phenomenon is useful in medical, engineering, and industrial solutions. Diffusion convection in peristaltic flow has numerous applications in the field of biomedicine. The cumulative impact of thermophoresis with Brownian motion under the magnetic force upon dual nonlinear thermal radiation was examined by Raju et al. [29]. Similarly, Ganesan et al. [30] explored the impact on non-Newtonian fluids. Further investigations on the flow of non-Newtonian fluid under double-diffusive convection are referred to in references [31–37].

The multiple advantages of thermal radiation impacts include the temperature control of a system, varying rate of heat transmission, thermal boundary layer control and regulating the structure of thermal layer. The investigation of Siddheshwar et al. [38] covers MHD flow with heat transfer of viscoelastic fluid over tense sheet in induced radiation. Aliakbar et al. [39] have examined the viscoelastic fluid flow through linear suspended sheet under the conditions of Maxwellian fluid and cross magnetic field. Similarly, Bataller [40] studied the flow of condensed second-grade liquid for non-isothermal stretched sheet with irregular heat production and absorption. Asha et al. [41] further explored the thermal radiation impact on Jeffrey’s liquid peristaltic flow with double diffusion having gold nanoparticles. Whereas another study conducted by Farooq et al. [42] focused on hybrid nanomaterials of the peristaltic process of viscous liquid including slip effects, entropy increase and erratic radiation. Recent research on the topic is mentioned in references [43–49].

The impact of viscous dissolution on the rate of heat exchange is a notable energy source for continuous heat transfer. The quality and excellence of viscous dissolution are determined by whether the plate being used is heated or cooled. The material after heat processing mobile in wind rollers and feed rollers, and material produced through electronic chips, glass fibre, paper manufacturing, cooling of metals, etc., are examples of the process. Other related studies on viscous dissipation on peristalsis flow are given in [50–55].

In lieu of the above discussed implications of viscous dissipation, thermal radiation, nanofluid and double diffusion convection, the current investigation is to study the cumulative impact of viscous dissipation, thermal radiation, double diffusion convection on peristaltic flow of Prandtl nanofluid under induced magnetic flux in a tapered asymmetric channel. The present study in broader perspective deals with the blood circulation in vessels supposition of wall properties thermal radiation. The partial differential equation system has been resolved to couple ordinary differential equations through the lubrication method. The resultant equation is mathematically computed and then the resultant analysis is depicted graphically with altered parameters.

2  Mathematical Model

The following assumptions and approximations are used for the mathematical modelling of the present work:

•   Two-dimensional and directional flow.

•   Tapered asymmetric channel.

•   Rosseland diffusion approximation for thermal radiation.

•   Prandtl nanofluid.

•   Induced magnetic field.

Let us assume the peristalsis of two-dimensional Prandtl nanofluid along the channel with width 2α. The flow originates like a sinusoidal wave propagation diffused with constant speed c along with asymmetric tapered channel. H1=Y and H2=Y are taken as the left and right walls of the tapered channel, respectively. The impact of thermal radiation, double diffusion convection, and viscous dissipation is assumed in the heat exchange. Then temperature, solute concentration, and nanoparticle volume fraction at the left and right walls are represented as T0,C0,Θ0 and T1,C1,Θ1, respectively. The velocity field, for two-dimensional & two-directional flow, is defined as V=(U(X,Y,t),V(X,Y,t),0). Moreover, an outer cross-uniform persistent magnetic field H~0, induced magnetic field H~1+(hX(X,Y,t),H0+hY(X,Y,t),0) and cumulative magnetic field H~+(hX(X,Y,t),H0+hY(X,Y,t),0) are considered. The schematic illustration of the problem is defined in Fig. 1.

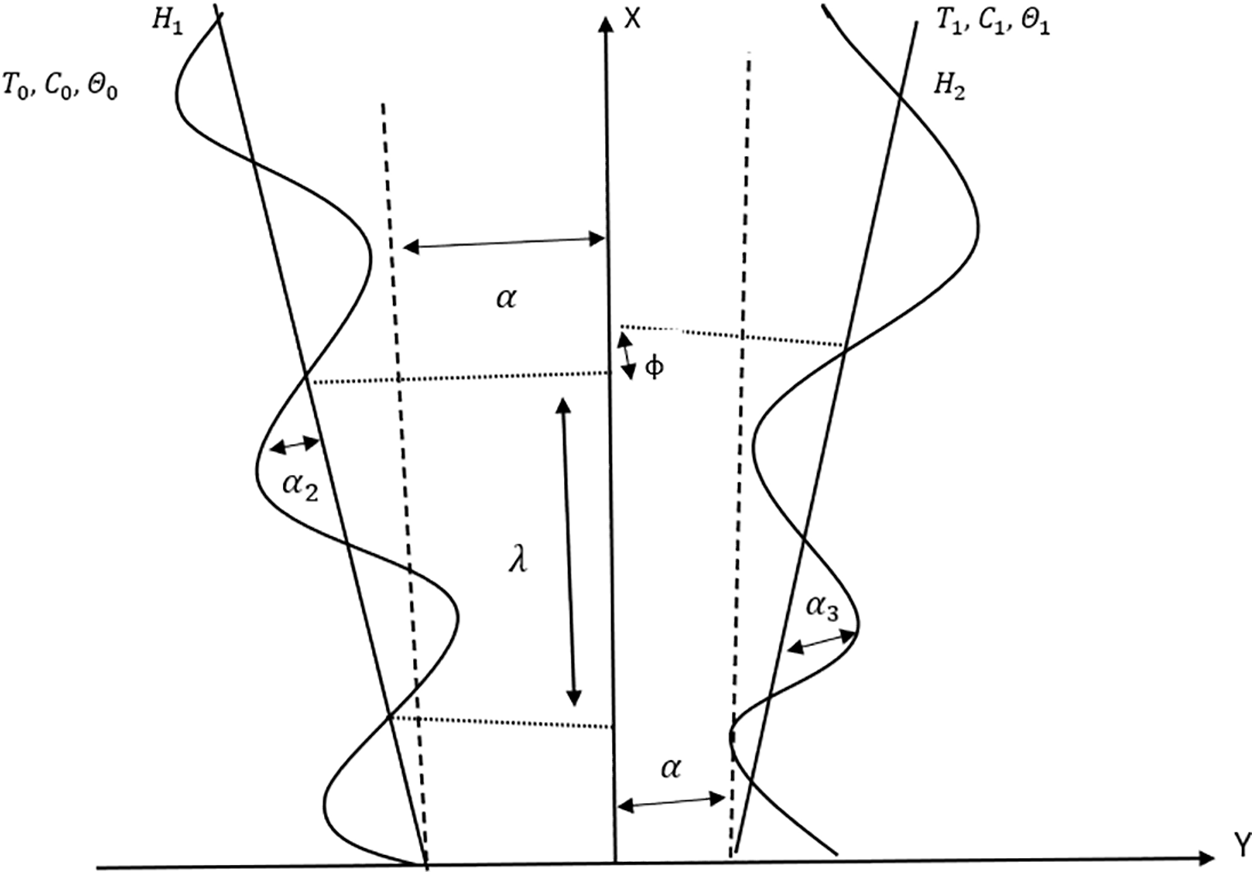
Figure 1: Schematic illustration of the problem

The tapered channel’s left (H1) and right (H2) walls for a fixed reference frame are defined by [10,17]

Y=H1=−α−α1X−α2 sin[2πλ(X−ct)+φ]=(left wall),

Y=H2=α+α1X+α3 sin[2πλ(X−ct)]=(right wall),(1)

here α stands for channel half-width, α1(α1<<1) indicates a non-uniform constant for tapered channel, α2 and α3 are amplitudes of the left and right walls respectively, t indicates time, c is the wave’s phase speed, λ indicates wavelength, the phase difference φ lying between [0,π]. Also α2,α3,α, and φ satisfy the condition α22+α32+2α2α3 cos φ≤(2α)2.

For the Prandtl fluid, the Cauchy stress tensor is denoted by [37]

τ=−pI+S,(2)

S=[A~η0 sin−1[|∇ V|B~]|∇V|]∇V,(3)

where I is identity tensor, p stands for pressure, S stands for extra stress tensor for Prandtl fluid, (A~,B~) stands for material constants of Prandtl fluid.

The equations describing an incompressible, Prandtl nanofluid in laboratory frame (X,Y) under the mechanism of double diffusivity convection, an induced magnetic field, radiation parameter and viscous dissipation are defined by [31]

∂U∂X+∂V∂Y=0,(4)

ρf(∂∂t¯+U∂∂X+V∂∂Y)U=−∂p∂X+∂SXX∂X+∂SXY∂Y+μe(hX∂hX∂X+hY∂hX∂Y+H0∂hX∂Y)

−μe2(∂H+2∂X)+g{(1−Θ0)ρf0{βT(T−T0)+βC(C−C0)}−(ρp−ρf0)(Θ−Θ0)},(5)

ρf(∂∂t¯+U∂∂X+V∂∂Y)V=−∂p∂Y+∂SYX∂X+∂SYY∂Y−μe2(∂H+2∂Y)+μe(hX∂hY∂X+hY∂hY∂Y+H0∂hY∂Y),(6)

(ρc)f(∂∂t~+U∂∂X+V∂∂Y)T=k(∂2T∂X2+∂2T∂Y2)+(ρc)p{DB(∂Θ∂X∂T∂X+∂Θ∂Y∂T∂Y)(DTT0)[(∂T∂X)2+(∂T∂Y)2]}+DTC(∂2C∂X2+∂2C∂Y2)−∂qr∂Y+(SXX∂U∂X+SXY(∂U∂Y+∂V∂X)+SYY∂V∂Y),(7)

(∂∂t~+U∂∂X+V∂∂Y)C=Ds(∂2C∂X2+∂2C∂Y2)+DCT(∂2T∂X2+∂2T∂Y2),(8)

(∂∂t~+U∂∂X+V∂∂Y)Θ=DB(∂2Θ∂X2+∂2Θ∂Y2)+(DTT0)(∂2T∂X2+∂2T∂Y2),(9)

where ρf0,g,βC,ρf,βT,(ρc)p,ρp,T,C,Θ,DB,Ds,DCT,(ρc)f,k,DTC,DT, symbolizes density of fluid at T0, acceleration, volumetric solutal expansion coefficient, density of base fluid, volumetric thermal expansion of a fluid, heat capacity of nanoparticle, particles density, temperature, concentration, nanoparticle volume fraction, Brownian diffusion, solutal diffusively, Soret diffusively, fluid heat capacity, thermal conductivity, Dufour diffusively, and thermophoretic diffusion, respectively.

The radiative flux for radiation (qr), stipulated in Eq. (7), is calculated by employing the Rosseland diffusion approximation and is given as [48]

qr=−4σ∗3k∗∂T4∂Y,(10)

Since significant radiation limit is considered in this investigation. So, if temperature variations inside the flow path are negligibly small, T4 is linear representation of temperature function and is modified by performing the Taylor expansion on T4 about T0 as shown below:

T4=T04+4T03(T−T0)+6T02(T−T0)2+…,(11)

By ignoring the higher powers of T (higher that first) in (T−T0), we get

T4=−3T04+4T03T,(12)

From Eqs. (10) and (12), we get

qr=−16σ∗T033k∗∂T∂Y,(13)

∂qr∂Y=−16σ∗T033k∗∂2T∂Y2,(14)

where σ∗ represents Stefan-Boltzmann constant, and k∗ represents Rosseland mean absorption.

x=Xλ, m0=α2α, u=Uc, δ=αλ, m1=α3α, p=α2pη0cλ, t=ct¯λ, M2=Re RmS12, h1=H1α,

 y=Yα,v=Vc,m2=α1λα, Re=ρfcαη0, Θ=T−T0T1−T0, Rm=σμeαc, Br=EcPr,υ=η0ρf,

Φ¯=ΦH0α, Sxx=λSXXη0c, Sxy=αSXYη0c, Syy=αSYYη0c, γ=C−C0C1−C0, Pr=(ρc)f υk, Ln=υDB,

pm=p+12Re δμe(H+)2ρc2,Ω=Θ−Θ0Θ1−Θ0,Le=υDs,NCT=DCT(T1−T0)(C1−C0)Ds, u=∂ψ∂y,

S1=H0cμeρ,v=−δ∂ψ∂x, hy=−δ∂Φ∂x, NTC=DCT(C1−C0)k(T1−T0),Nb=(ρc)pDB(Θ1−Θ0)k,

  Nt=(ρc)pDT(T1−T0)T0k, GrF=g(ρp−ρf)(Θ1−Θ0)η0cα2,Grc=(1−Θ0)ρfβc(C1−C0)α2gη0c,

Grt=gα2(1−Θ0)ρfβT(T1−T0)η0c, Rd=−16σ∗T033k∗.(15)

Using Eq. (15), Eq. (4) is automatically satisfied, but Eqs. (5) to (9) along with Eq. (14) in wave frame becomes

Re δ(ψty+ψyψxy−ψxψyy)=−∂pm∂x+δ2∂Sxx∂x+∂Sxy∂y−Re S12Φyy−Re S12δ(ΦyΦxy−ΦxΦyy)+GrtΘ+Grcγ−GrFΩ,(16)

Re δ3(ψtx+ψxψxy−ψyψxx)=−∂pm∂y+δ2∂Sxy∂x+δ∂Syy∂y+Re δ2S12Φyy−Re S12δ3(ΦyΦxx−ΦxΦxy),(17)

Re δ(Θt+ψyΘx−ψxΘy)=1Pr(Θyy+δ2Θxx)+NTC(δ2γxx+γyy)+RdΘyy+Ec(δ2Sxxψxy+Sxy(ψyy−δ2ψxx)−δSyyψxy)+Nb(δ2ΩxΘx+ΩyΘy)+Nt(δ2(Θx)2+(Θy)2),(18)

Re δLe(γt+ψyγx−ψxγy)=(δ2γxx+γyy)+NCT(δ2Θxx+Θyy),(19)

Re δLn(Ωt+Ωxψy−Ωyψx)=(δ2Ωxx+Ωyy)+NtNb(δ2Θxx+Θyy),(20)

ψy−δ(ψyΦx−ψxΦy)+1Rm(Φyy+δ2Φxx)=E,(21)

where Rm stands for magnetic Reynolds numbers, γ signifies solutal (species) concentration, Le stands for Lewis number, Ω signifies nanoparticle fraction, S1 stands for Strommer’s number, E represents electric field, Grt signifies thermal Grashof numbers, Ln represents nanofluid Lewis number, Pr indicates Prandtl number, Grc denotes solutal Grashof numbers, Nt indicates thermophoresis parameter, NTC represents Dufour parameter, Nb indicates Brownian motion, GrF stands for nanoparticle Grashof numbers, NCT denotes Soret parameter, Re denotes Reynolds number, Θ stand for temperature, and pm is total pressure in the fluid, which is the sum of magnetic and ordinary pressure.

Now considering the hypotheses of a long wavelength (δ<<1) and a small but finite Reynolds number, the Eqs. (16) to (21) becomes

0=−∂p∂x+∂Sxy∂y+Re S12Φyy+GrtΘ+Grcγ−GrFΩ,(22)

−∂p∂y=0,(23)

∂2Θ∂y2+NTCPr∂2γ∂y2+NbPr(∂Θ∂y∂Ω∂y)+NtPr(∂Θ∂y)2+RdPr∂2Θ∂y2

+Br(ξ(∂2ψ∂y2)2+χ6(∂2ψ∂y2)4))=0,(24)

∂2γ∂y2+NCT∂2Θ∂y2=0,(25)

∂2Ω∂y2+NtNb∂2Θ∂y2=0,(26)

Φyy=Rm(E−∂ψ∂y),(27)

Now omitted pressure from Eqs. (22) and (23), the equation for the stream function becomes

∂2Sxy∂y2−Re S12Rm∂2ψ∂y2+Grt∂Θ∂y+Grc∂γ∂y−GrF∂Ω∂y=0,(28)

where

Sxy=ξ∂2ψ∂y2+χ6(∂2ψ∂y2)3,(29)

where ξ=A~η0B~ and χ=ξc2B~2α denotes Prandtl fluid constraints.

The non-dimensional form of the boundary conditions is

ψ=−F2 at y=h1(x)=−1−m2x−m0 sin[2π(x−t)+φ],

ψ=F2 at y=h2(x)=1+m2x+m1 sin[2π(x−t)],

∂ψ∂y=0 at y=h1(x)=−1−m2x−m0 sin[2π(x−t)+φ],

∂ψ∂y=0 at y=h2(x)=1+m2x+m1 sin[2π(x−t)],(30)

Θ=0,  Ω=0,  γ=0, at y=h1(x),(31)

Θ=1,  Ω=1,  γ=1, at y=h2(x),(32)

Φ=0 at y=h1(x) and y=h2(x).(33)

Volume flow rate:

When a period T=λ/c is taken into consideration, the time-averaged flow at fixed point X is given by

Q1=1T∫0TQ1¯dt.(34)

we now acquire

Q1=q+α2c sin[2πλ(X−ct¯)]+α3c sin[2πλ(X−ct¯)+φ].(35)

where q=∫H1H2u(x,y)dy is the wave frame’s dimensional volume flow rate. Using non-dimensional mean flows Q in wave frame and F in laboratory frame, we have

F=Q1cα, Q=qcα,(36)

F(X,t)=Q+m0 sin[2π(x−t)]+m1 sin[2π(x−t)+φ],(37)

where

F=∫h1h2u dy=∫h1h2∂ψ∂ydy=ψ(h2)−ψ(h1).(38)

The pressure rise per wave length Δp are described by

Δp=∫01∫01(∂p∂x)y=0dxdt.(39)

3  Methodology of Solutions and Discussion

Numerical simulations are necessary because there are few cases for which analytic solutions can be found. Numerical simulations give us an alternative way to comprehend the issue and the solution without squandering the study’s actual resources. We can have a thorough grasp of the flow circumstances by employing contemporary technologies, such as software like MATHEMATICA, MATLAB, and ANSYS. The coupled and non-linear properties of the Eqs. (22)–(28) make it difficult to evaluate the exact solutions. Thus, using MATHEMATICA’s built-in command ND-Solve, the regressive equations are numerically solved. Solutions are used to calculate temperature, pressure gradients, concentration, pressure rises, nanoparticle volume fraction, magnetic force function, and streamlines for various flow parameters.

The biophysical and graphical significance of various flow parameters on Prandtl nanofluids flow in a tapered channel are examined in Figs. 2 to 11. The temperature effects on Brinkman number Br, Brownian motion Nb, and Prandtl number Pr are explored in Figs. 2a–2c. It is evident from Fig. 2a that the Brinkman number Br has an increasing influence on temperature. The fundamental cause of the temperature rise is that as Br values rise, shear flow resistance also rises. This causes more heat to be generated owing to viscous dissipation effects, which raises the fluid’s temperature. The enhancing Brownian motion values also cause an increase in the temperature profile (see Fig. 2b). It is noticeable that forces exerted on nanometer-sized particles are stochastic forces that accelerate the particle’s Brownian motion. As a result of the intense stochastic force, the base fluid’s internal energy has increased, because of which the temperature profile has risen. From Fig. 2c, it is depicted that the temperature increases with an increase in Prandtl numbers Pr because of the potent effects of viscous dissipation. The graphs in Figs. 3a–3d explore how Concentration affects the Brinkman number Br, Brownian motion Nb, Dufour parameter (NCT), and Prandtl number Pr. It can be shown in Fig. 3a that the concentration of fluid particles significantly reduces as the impact of Brinkman number Br increases. Similar effects are observed in the cases of Brownian motion Nb, Dufour NTC number and Prandtl number Pr. As seen in Fig. 3b, Nb has a declining impact on nanoparticle concentration, causing the concentration distribution to drop due to the huge transport of nanoparticles from a hot to a cold location. Fig. 3c shows that raising the Dufour number NCT increases fluid heat transfer, which affects the fluid’s viscosity by reducing the temperature difference between the wall and the fluid. The concentration of nanoparticles falls as a result. Fig. 3d shows that increasing the Prandtl number causes a decrease in the concentration of nanoparticles. Figs. 4a to 4d illustrate the graphic evolution of the nanoparticle fraction for varying values of Brownian motion Nb, Brinkman number Br, thermophoresis Nt and Prandtl number Pr. It is illustrated in Fig. 4a that the increasing impact of Brownian motion Nb causes nanoparticle fraction to rise. Physically, the Brownian motion index is enhanced because of the simultaneous random motion of the fluid and nanoparticles, which raises the fluctuations of the nanoparticle volume fraction. Opposite effects are noticed for the case of Br,Nt and Pr. It is noted from Figs. 4b to 4d that enhancing impact of Br,Nt and Pr causes the decrease in nanoparticle fraction.

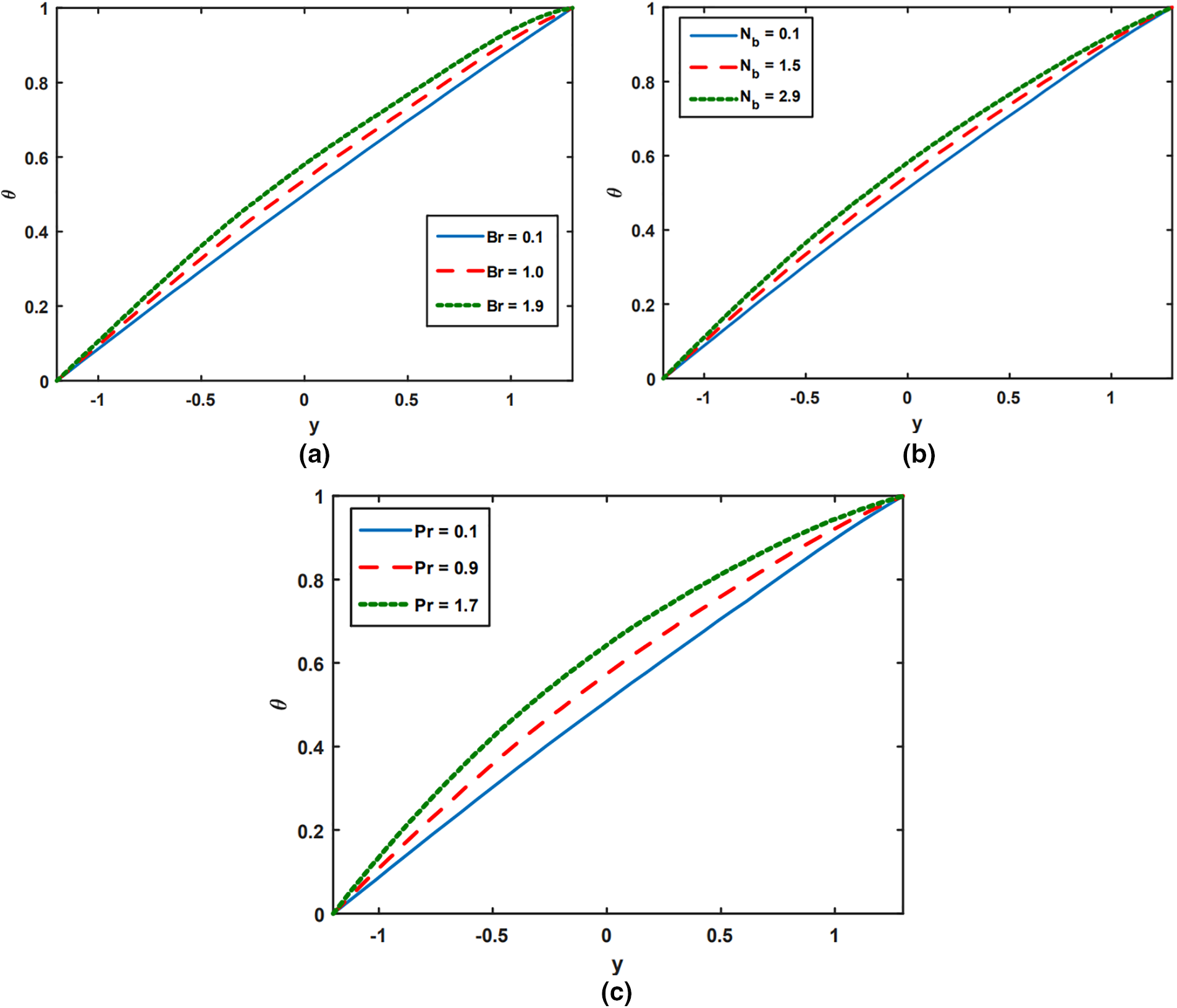
Figure 2: Temperature distribution for varying values of Br, Nb, and Pr

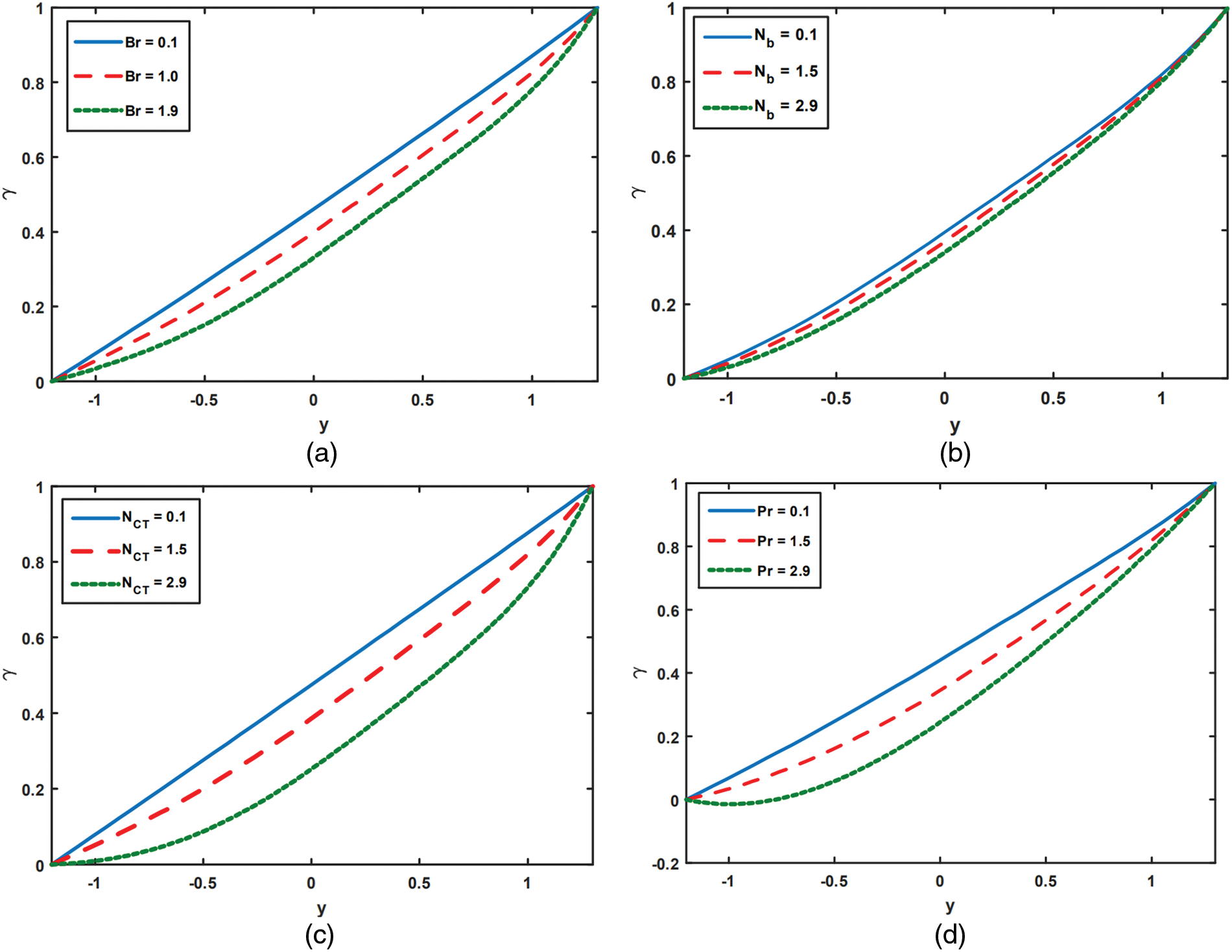
Figure 3: Concentration analysis for varying values of Br,Nb,NCT, and Pr

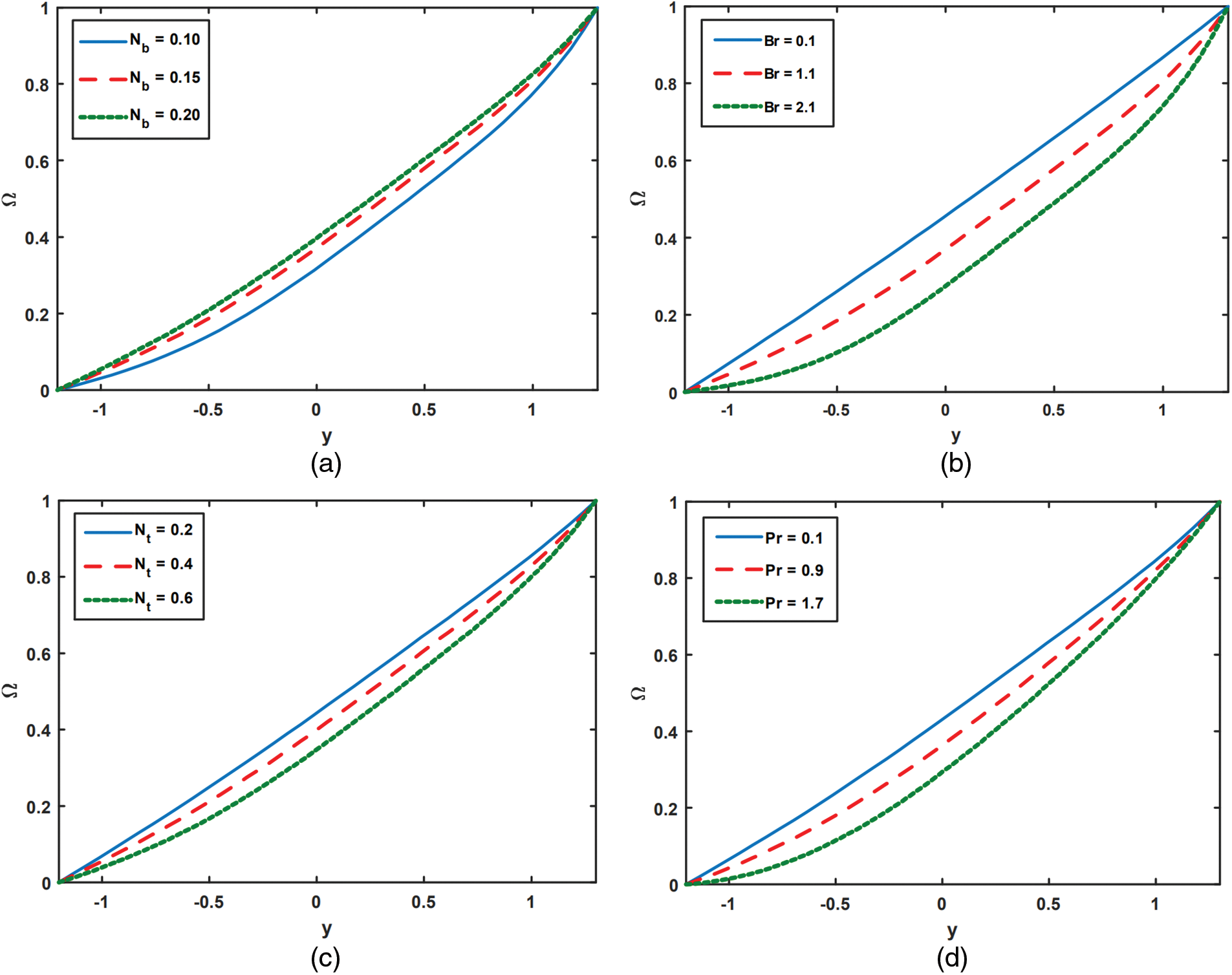
Figure 4: Analysis of Nb,Br,Nt and Pr on nanoparticle fraction

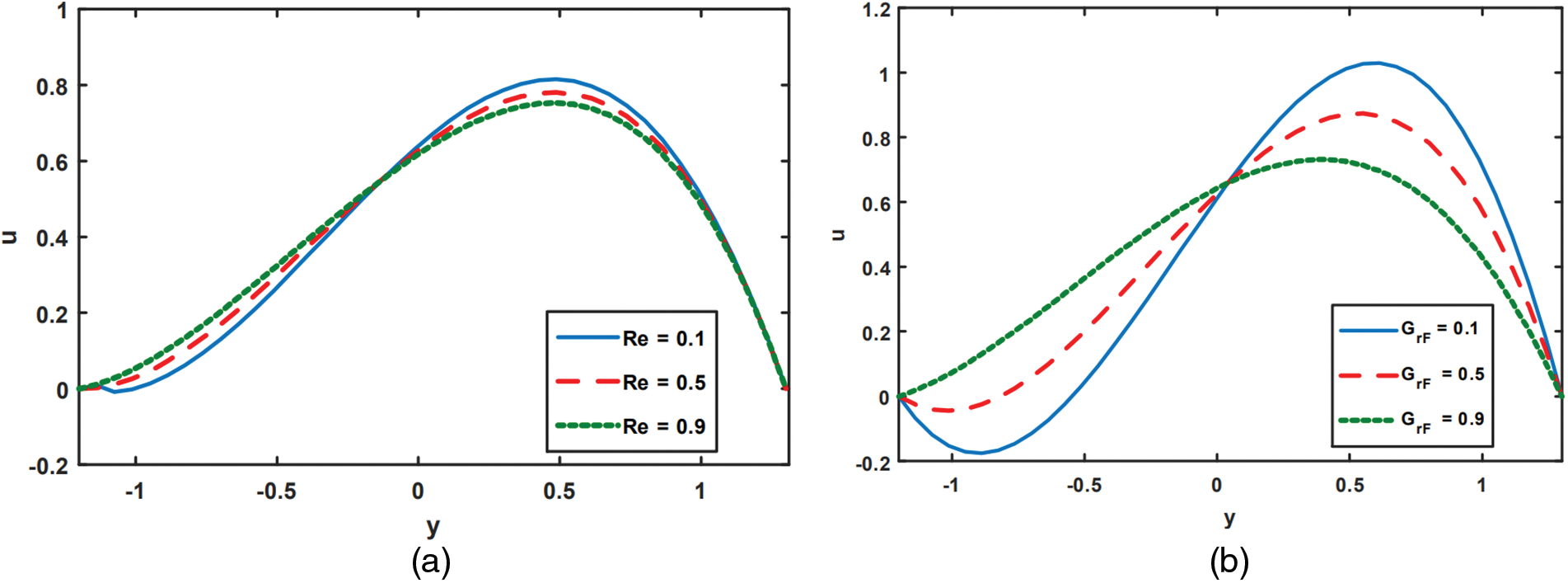
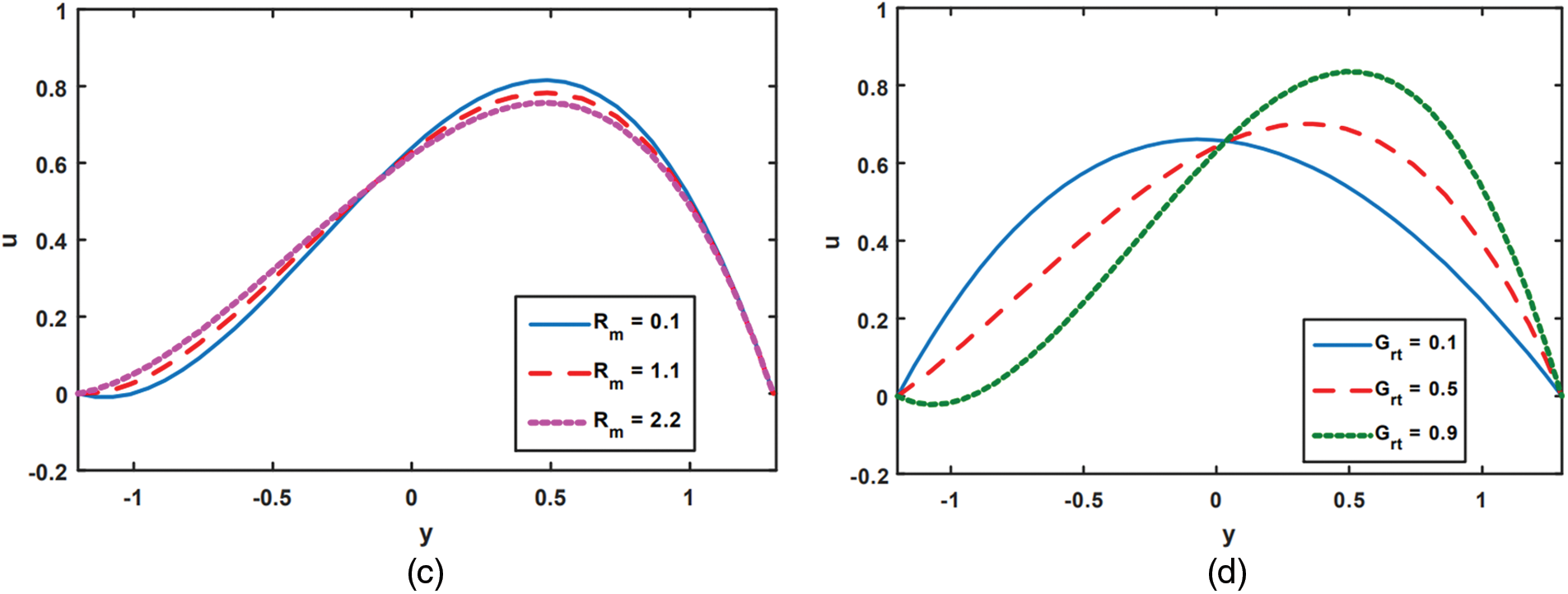
Figure 5: Effect of velocity for varying values of Re,GrF,Rm and Grt

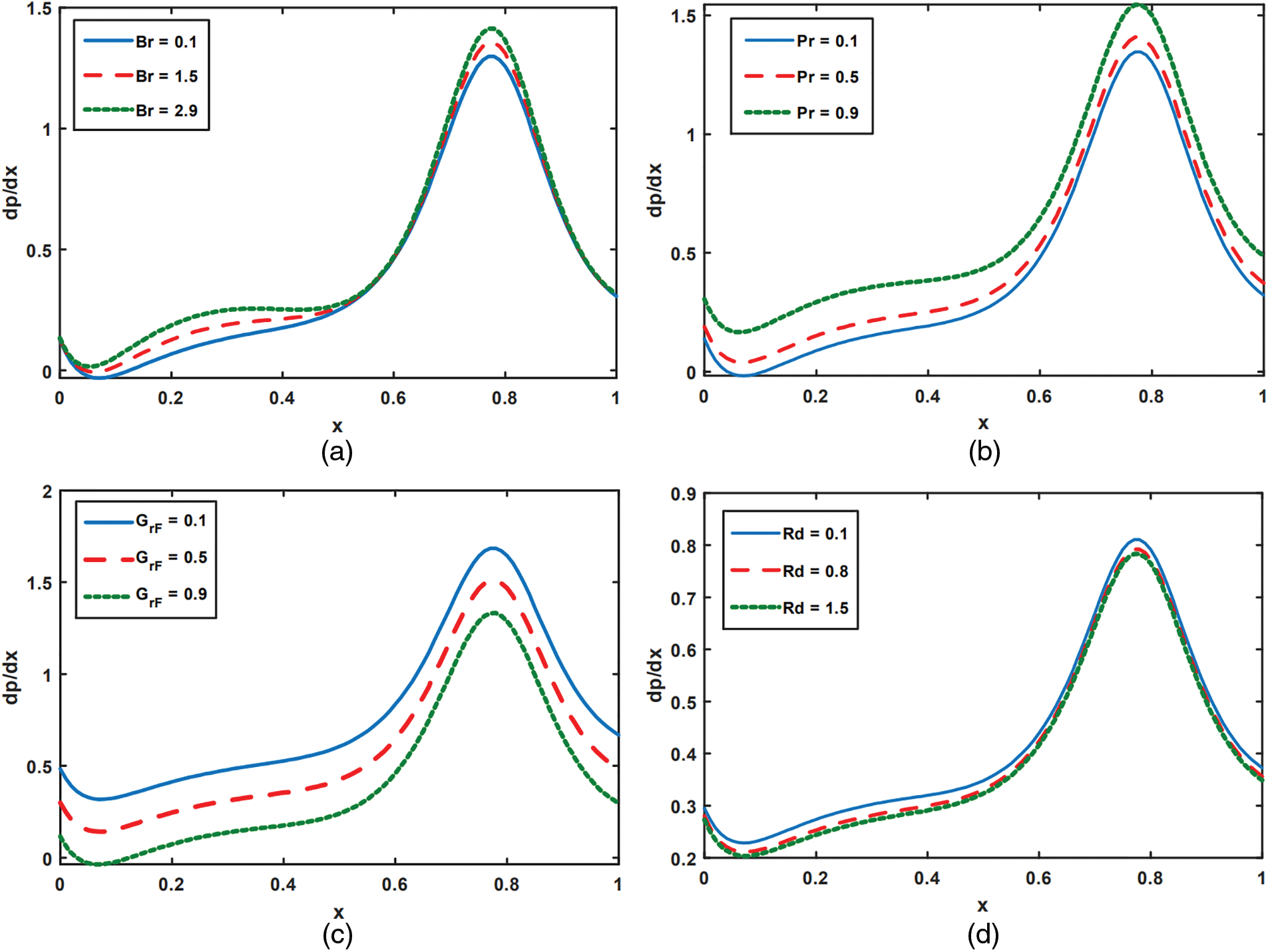
Figure 6: Analysis of Br,Pr,GrF, and Rd on pressure gradient

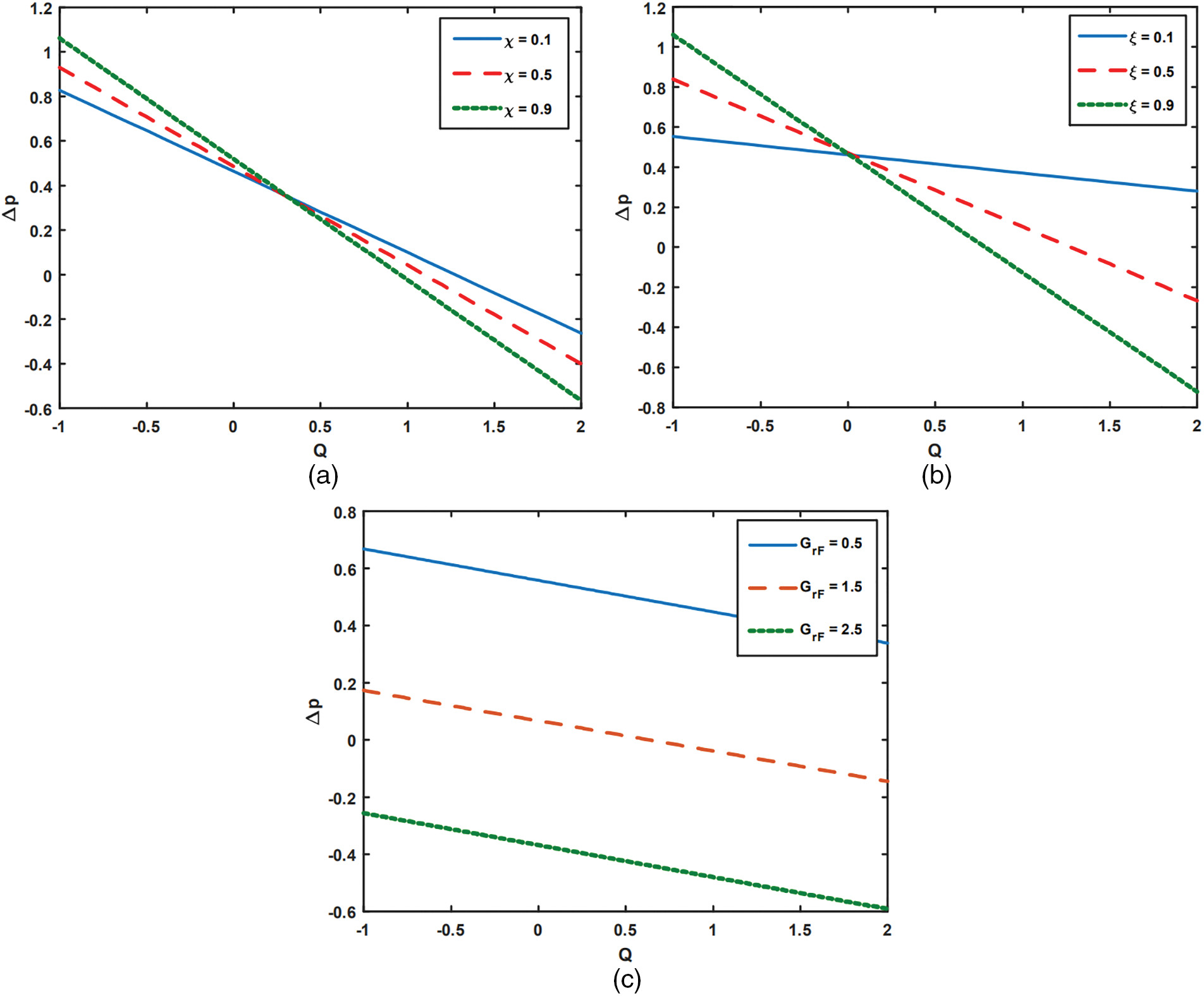
Figure 7: Impact of χ, ξ, and GrF on pressure rise

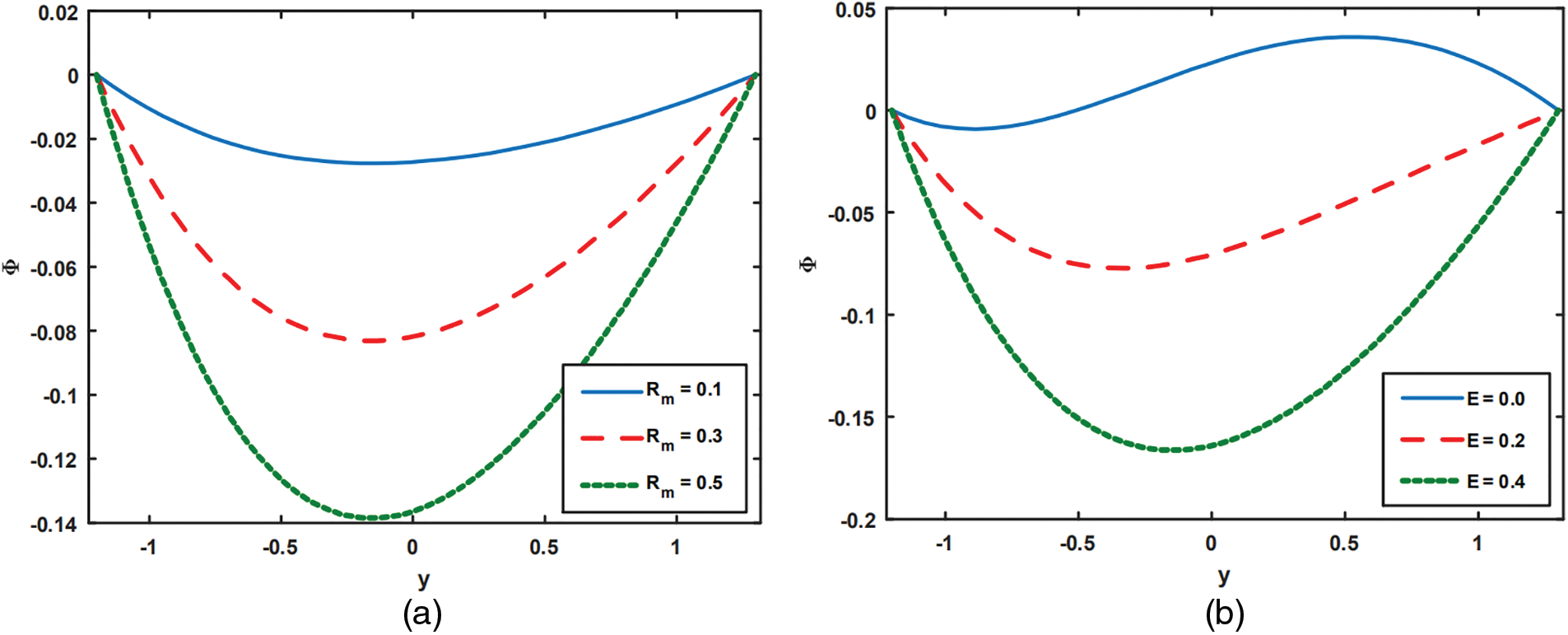
Figure 8: Analysis of Rm and E on magnetic force function

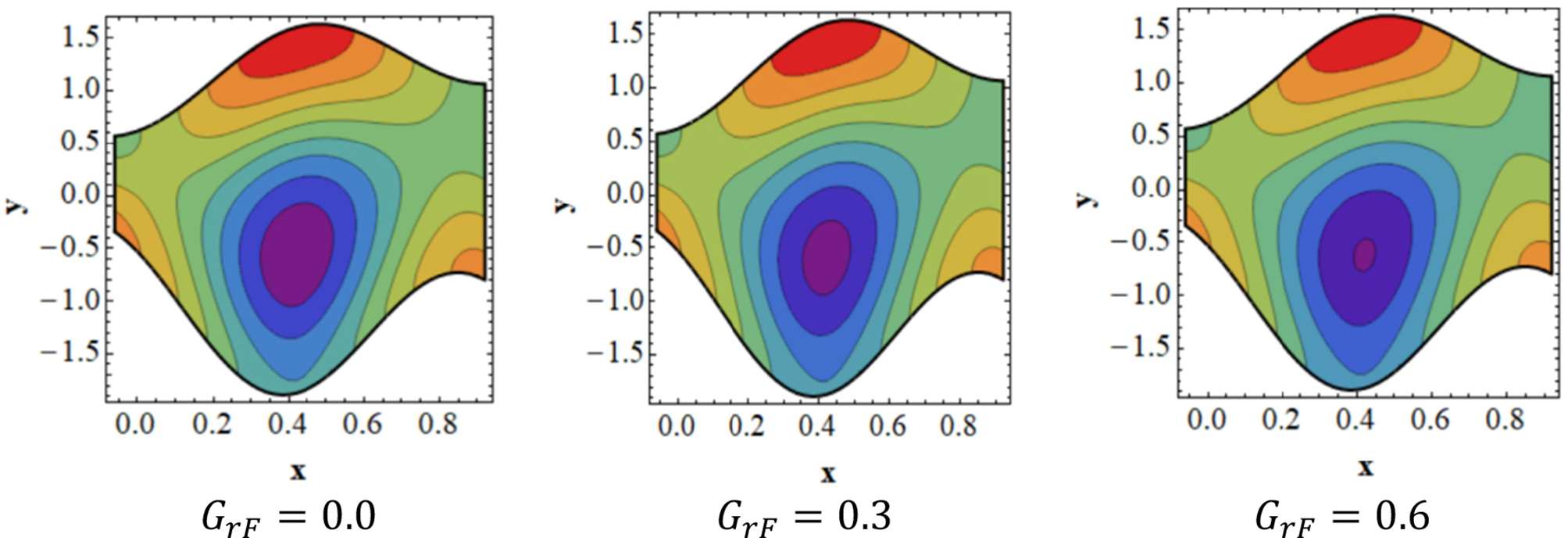
Figure 9: Analysis of GrF on streamlines

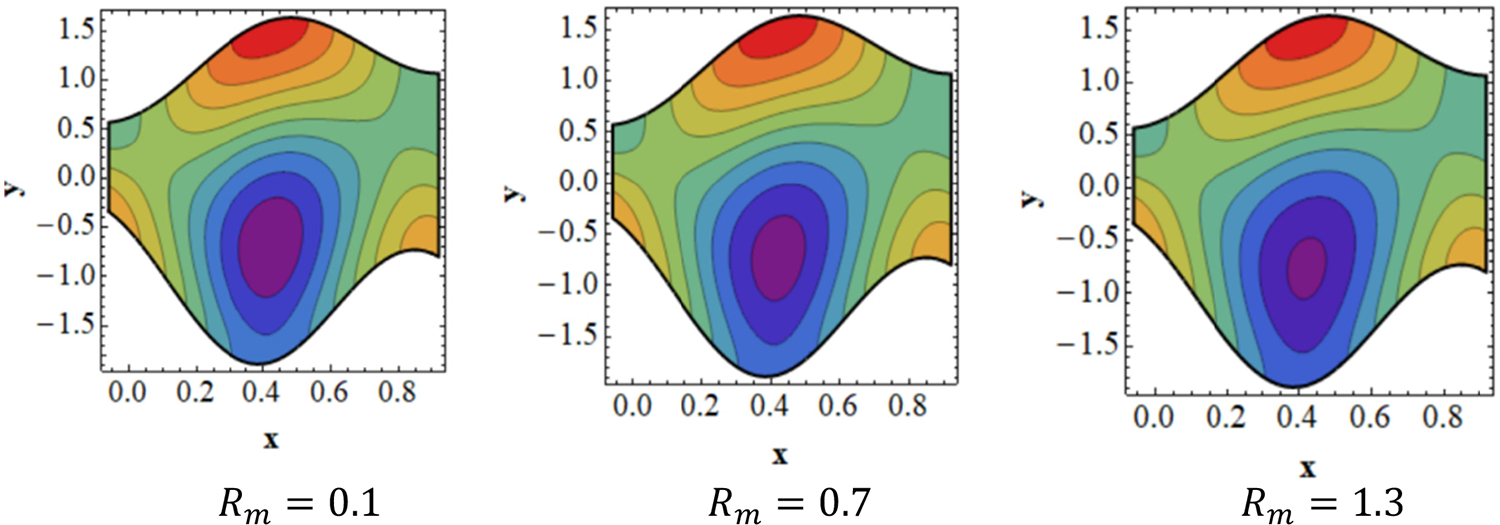
Figure 10: Analysis of Rm on streamlines

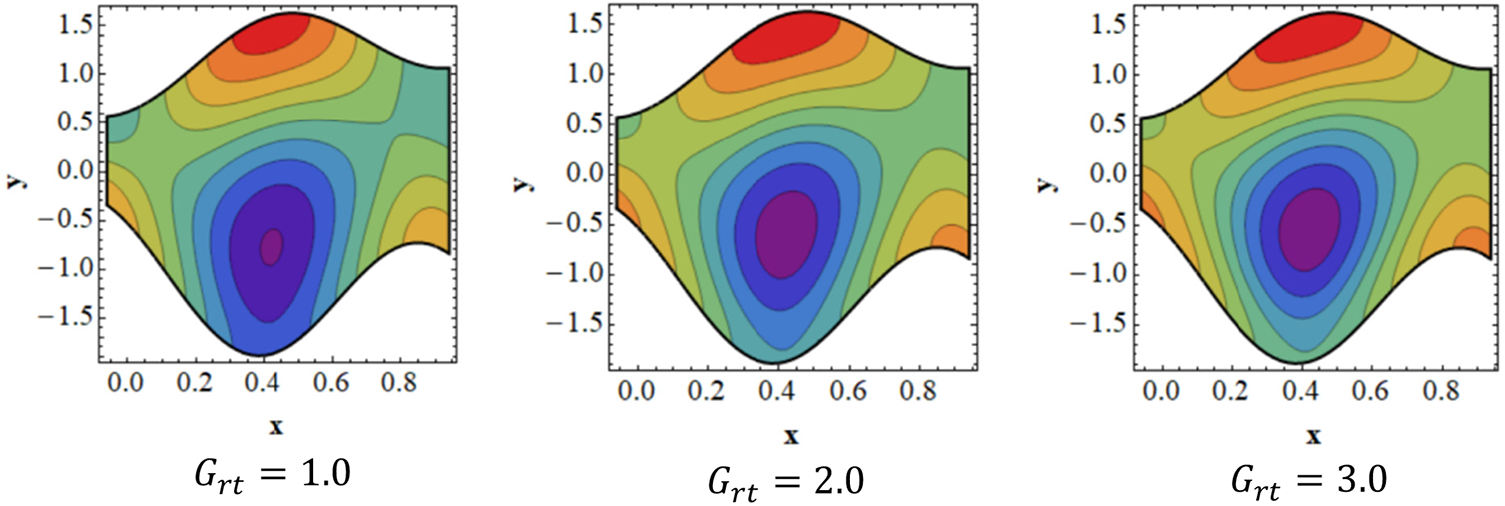
Figure 11: Analysis of Grt on streamlines

Figs. 5a to 5d depict the effects of various Reynold number Re, nanoparticle Grashof numbers GrF, magnetic Reynolds number Rm and thermal Grashof number Grt on flow velocity. It is noted in Fig. 5a that the flow of velocity enhances in the region y∈[−1.2,0] due to the increasing impact of Reynolds number. Physically, viscous forces become less significant as the Reynolds number rises, which reduces the propagation of velocity defects in the flow field. The opposite effects are noted in the region y∈[0,1.3]. In this region, flow velocity increases due to the increasing impact of Re. As demonstrated seen in Figs. 5b and 5c, enhancing the effect of nanoparticle Grashof numbers GrF and Reynolds number Rm causes the fluid velocity to increase when y∈[−1.2,0] but decrease when y∈[0,1.3]. The opposite characteristic is observed for the case of thermal Grashof number Grt. The flow velocity drops when y∈[−1.2,0] but increases when y∈[0,1.3] due to increasing impact of Grt  (see Fig. 5d).

Figs. 6a to 6d are provided to illustrate how Br, Pr, GrF, and Rd affect pressure gradients. The pressure gradient widens as the impact of Br and Pr increases (see Figs. 6a and 6b) but opposite impact is noted for the case of GrF, and Rd. The pressure gradient drops as GrF, and Rd increases (see Figs. 6c and 6d). Figs. 7a to 7c describe the outcomes of pressure rises on non-Newtonian parameters (χ and ξ), and nanoparticle Grashof number GrF. To investigate the characteristic of pressure rise, pumping regions are split into the following categories: (a) when Q>0,Δp>0 the peristaltic zone occurs, where peristalsis oscillations govern pressure and fluid movement along their line of propagation; (b) when Q>0,Δp<0 the augmented zone occurs, where peristaltic push pressure boosts flow; (c) when Q<0,Δp>0 the retrograde zone exists, In this case, peristalsis is opposing the flow and (d) when Δp=0 free pumping region exist. Here peristalsis walls are the only cause of flow in this region. It is noted in Figs. 7a and 7b that the pressure rise increases in the retrograde region due to the increasing impact of non-Newtonian parameters (χ and ξ) but opposite effects are noted in peristaltic, augmented, and free pumping regions. Here pressure rise drops. It is noted in Fig. 7c that the pressure rise decreases in all the regions of peristaltic due to the increasing behaviour of GrF. Figs. 8a and 8b are shown to highlight the analysis of Rm and E on the magnetic force function. It is to be observed in Figs. 8a and 8b that as Rm and E have a greater impact, the magnetic force function’s magnitude values grow.

To examine how trapping affects peristaltic flow, streamlines for GrF, Rm, and Grt are created. The streamlines are analyzed in Figs. 9 and 10 for varying values of nanoparticle Grashof GrF and magnetic Reynolds number Rm. It is shown that as the influence of the nanoparticle Grashof GrF and magnetic Reynolds number Rm grows, the size of the confined bolus decreases. By considering the thermal Grashof number, the opposite effects are observed (see Fig. 11). The thermal Grashof number (Grc) here causes the confined bolus to grow in size.

4  Conclusion

In this article, we attempted to simultaneously link the consequences of thermal radiation and viscous dissipation with the influence of double diffusion convection on the peristaltic flow of magnetohydrodynamic Prandtl nanofluids in an asymmetric tapered channel. In our investigation, the equations governing the flow are developed using the preexisting constraints of long wavelength and low Reynolds values. Finally, reduced equations are solved numerically to achieve a comparative evaluation. It is observed that by raising Brinkman number the temperature of fluid flow increases because shear flow resistance increases. Furthermore, it is noted that increasing Brownian motion values accelerates the movement of nanoparticles along the fluid wall, which increases the temperature. Another important finding is that due to the massive transit of nanoparticles from a hot to a cool, site Brownian motion has a diminishing effect on nanoparticle concentration, causing the concentration distribution to decrease. It is noted that by raising the effects of Reynolds number, viscous forces become less significant, which reduces the propagation of velocity defects in the flow field. Moreover, it is observed that by growing the influence of the nanoparticle Grashof and magnetic Reynolds number, the size of the confined bolus decreases.

Acknowledgement: Authors gratefully acknowledge technical and financial support from Ministry of Education and University of Hafr Al Batin, Saudi Arabia.

Funding Statement: This research work was funded by Institutional Fund Projects under No. (IFP-A-2022-2-5-24) by Ministry of Education and University of Hafr Al Batin, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Y. K., S. A., A. A.; data collection: K. S., A. R., A. A.; analysis and interpretation of results: S. A., M. A., K. S.; draft manuscript preparation: S. A., A. R., Y. K.; funding: Y. K., A. A. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No data was used for the research described in the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Latham, T. W. (1966). Fluid motion in a peristaltic pump (M.S. Thesis). MIT, Cambridge, MA. [Google Scholar]

2. Tripathi, D., Bég, O. A., Gupta, P. K., Radhakrishnamacharya, G., Mazumdar, J. (2015). DTM simulation of peristaltic viscoelastic biofluid flow in asymmetric porous media: A digestive transport model. Journal of Bionic Engineering, 12, 643–655. [Google Scholar]

3. Sreenadh, S., Komala, K., Srinivas, A. N. S. (2017). Peristaltic pumping of a power–Law fluid in contact with a Jeffrey fluid in an inclined channel with permeable walls. Ain Shams Engineering Journal, 8, 605–611. [Google Scholar]

4. Mishra, M., Rao, A. R. (2003). Peristaltic transport of a Newtonian fluid in an asymmetric channel. Zeitschrift fur Angewandte Mathematik und Physik (ZAMP), 54, 532–550. [Google Scholar]

5. Nadeem, S., Akram, S. (2009). Peristaltic transport of a hyperbolic tangent fluid model in an asymmetric channel. Zeitschrift für Naturforschung A, 64(9–10), 559–567. [Google Scholar]

6. Ali, N., Abbasi, A., Ahmad, I. (2015). Channel flow of Ellis fluid due to peristalsis. AIP Advances, 5, 097214. [Google Scholar]

7. Mekheimer, K. S. (2002). Peristaltic transport of a couple stress fluid in a uniform and non-uniform channel. Biorheology, 39, 755–770. [Google Scholar] [PubMed]

8. Ellahi, R., Riaz, A., Nadeem, S., Ali, M. (2012). Peristaltic flow of Carreau fluid in a rectangular duct through a porous medium. Mathematical Problems in Engineering, 2012, 329639. [Google Scholar]

9. Vajravelu, K., Sreenadh, S., Devaki, P., Prasad, K. V. (2011). Mathematical model for a Herschel-Bulkley fluid flow in an elastic tube. Central European Journal of Physics, 9, 1357–1365. [Google Scholar]

10. Hayat, T., Akram, J., Zahir, H., Alsaedi, A. A. (2019). Peristaltic motion of Sisko fluid in an inclined asymmetric tapered channel with nonlinear radiation. Journal of Thermal Analysis and Calorimetry, 138, 545–558. [Google Scholar]

11. Vishnyakov, I., Pavlov, K. B., (1972). Peristaltic flow of a conductive liquid in a transverse magnetic field. Magnetohydrodynamics, 8, 174–178. [Google Scholar]

12. Munawar, S., Saleem, N. (2020). Second law analysis of ciliary pumping transport in an inclined channel coated with Carreau fluid under a magnetic field. Coatings, 10, 240. [Google Scholar]

13. Ellahi, R., Riaz, A., Sohail, S., Mushtaq, M. (2013). Series solutions of magnetohydrodynamic peristaltic flow of a Jeffrey fluid in eccentric cylinders. Journal of Applied Mathematics & Information Sciences, 7, 1441–1449. [Google Scholar]

14. Ellahi, R., Bhatti, M. M., Riaz, A., Sheikholeslami, M. (2014). Effects of magnetohydrodynamics on peristaltic flow of Jeffery fluid in a rectangular duct through a porous medium. Journal of Porous Media, 17, 143–157. [Google Scholar]

15. Akram, S., Nadeem, S. S., Hanif, M. (2013). Numerical and analytical treatment on peristaltic flow of Williamson fluid in the occurrence of induced magnetic field. Journal of Magnetism and Magnetic Materials, 346, 142–151. [Google Scholar]

16. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab: Argonne, IL, USA. [Google Scholar]

17. Kothandapani, M., Prakash, J. (2015). Effects of thermal radiation parameter and magnetic field on the peristaltic motion of Williamson nanofluids in a tapered asymmetric channel. International Journal of Heat and Mass Transfer, 81, 234–245. [Google Scholar]

18. Reddy, M. G., Makinde, O. D. (2016). Magnetohydrodynamic peristaltic transport of Jeffrey nanofluid in an asymmetric channel. Journal of Molecular Liquids, 223, 1242–1248. [Google Scholar]

19. Ramesh, K., Devakar, M. (2015). Magnetohydrodynamic peristaltic transport of couple stress fluid through porous medium in an inclined asymmetric channel with heat transfer. Journal of Magnetism and Magnetic Materials, 394, 335–348. [Google Scholar]

20. Rahman, S. U., Ellahi, R., Nadeem, S., Zia, Q. M. Z. (2016). Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. Journal of Molecular Liquids, 218, 484–493. [Google Scholar]

21. Akram, S., Nadeem, S. (2014). Significance of nanofluid and partial slip on the peristaltic transport of a Jeffrey fluid model in an asymmetric channel with different wave forms. IEEE Transactions on Nanotechnology, 13, 375–385. [Google Scholar]

22. Akram, S. (2014). Effects of nanofluid on peristaltic flow of a Carreau fluid model in an inclined magnetic field. Heat Transfer Asian Research, 43, 368–383. [Google Scholar]

23. Bhatti, M. M., Zeeshan, A., Ellahi, R. (2017). Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvascular Research, 110, 32–42. [Google Scholar] [PubMed]

24. Patil, P. M., Shankar, H. F. (2022). Heat transfer attributes of Al2O3–Fe3O4/H2O hybrid nanofluid flow over a yawed cylinder. Propulsion and Power Research, 11, 416–429. [Google Scholar]

25. Ali, A., Barman, A., Das, S. (2022). EDL aspect in cilia-regulated bloodstream infused with hybridized nanoparticles via a microtube under a strong field of magnetic attraction. Thermal Science and Engineering Progress, 36, 101510. [Google Scholar]

26. Patil, P. M., Benawadi, S. (2022). Shape effects on the mixed convective hybrid nanoliquid flow over a rough slender cylinder with convective condition. Waves in Random and Complex Media, https://doi.org/10.1080/17455030.2022.2143930 [Google Scholar] [CrossRef]

27. Abbas, N., Shatanawi, W., Shatnawi, T. A. M. (2023). Thermodynamic study of radiative chemically reactive flow of induced MHD sutterby nanofluid over a nonlinear stretching cylinder. Alexandria Engineering Journal, 70, 179–189. [Google Scholar]

28. Aifanties, E. C. (1976). Continuum basis for diffusion in regions with multiple diffusivities. Journal of Applied Physics, 50, 1334–1338. [Google Scholar]

29. Raju, A., Ojjela, O., Kambhatla, P. K. (2020). The combined effects of induced magnetic field, thermophoresis and Brownian motion on double stratified nonlinear convective-radiative Jeffrey nanofluid flow with heat source/sink. Journal of Analysis, 28, 503–532. [Google Scholar]

30. Ganesan, S., Vasanthakumari, R. (2020). Influence of magnetic field and thermal radiation on peristaltic motion with double-diffusive convection in Jeffery nanofluids. Heat Transfer, 49, 2025–2043. [Google Scholar]

31. Bég, O. A., Tripathi, D. (2011). Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: A bio-nanoengineering model, proceedings of the institution of mechanical engineers. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, 225, 99–114. [Google Scholar]

32. Alolaiyan, H., Riaz, A., Razaq, A., Saleem, N., Zeeshan, A. et al. (2020). Effects of double diffusion convection on third grade nanofluid through a curved compliant peristaltic channel. Coatings, 10(2), 154. [Google Scholar]

33. Asha, S. K., Sunitha, G. (2020). Thermal radiation and hall effects on peristaltic blood flow with double diffusion in the presence of nanoparticles. Case Studies in Thermal Engineering, 17, 100560. [Google Scholar]

34. Sharma, A., Tripathi, D., Sharma, R. K., Tiwari, A. K. (2019). Analysis of double diffusive convection in electroosmosis regulated peristaltic transport of nanofluids. Physica A: Statistical Mechanics and its Applications, 535, 122148. [Google Scholar]

35. Akram, S., Afzal, Q. (2020). Effects of thermal and concentration convection and induced magnetic field on peristaltic flow of Williamson nanofluid in inclined uniform channel. European Physical Journal Plus, 135, 857. [Google Scholar]

36. Akram, S., Athar, M., Saeed, K., Razia, A., Muhammad, T. (2023). Hybridized consequence of thermal and concentration convection on peristaltic transport of magneto Powell-Eyring nanofluids in inclined asymmetric channel. Mathematical Methods in the Applied Sciences, 46, 11462–11478. [Google Scholar]

37. Akram, S., Athar, M., Saeed, K. (2021). Hybrid impact of thermal and concentration convection on peristaltic pumping of Prandtl nanofluids in non-uniform inclined channel and magnetic field. Case Studies in Thermal Engineering, 25, 100965. [Google Scholar]

38. Siddheshwar, P. G., Mahabaleshwar, U. S. (2005). Effects of radiation and heat source on MHD flow of a viscoelastic liquid and heat transfer over a stretching sheet. International Journal of Non-Linear Mechanics, 40, 807–820. [Google Scholar]

39. Aliakbar, V., Pahlavan, A. A., Sadeghy, K. (2009). The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets. Communications in Nonlinear Science and Numerical Simulation, 14, 779–794. [Google Scholar]

40. Bataller, R. C. (2007). Viscoelastic fluid flow and heat transfer over a stretching sheet under the effects of a non-uniform heat source, viscous dissipation and thermal radiation. International Journal of Heat and Mass Transfer, 50(15–16), 3152–3162. [Google Scholar]

41. Asha, S. K., Sunitha, G. (2019). Influence of thermal radiation on peristaltic blood flow of a Jeffrey fluid with double diffusion in the presence of gold nanoparticles. Informatics in Medicine Unlocked, 17, 100272. [Google Scholar]

42. Farooq, S., Khan, M. I., Waqas, M., Hayat, T., Alsaedi, A. (2020). Transport of hybrid type nanomaterials in peristaltic activity of viscous fluid considering nonlinear radiation, entropy optimization and slip effects. Computer Methods Programs Biomed, 184, 105086. [Google Scholar]

43. Mahmoud, M. A. A. (2007). Thermal radiation effects on MHD flow of a micropolar fluid over a stretching surface with variable thermal conductivity. Physica A: Statistical Mechanics and its Applications, 375, 401–410. [Google Scholar]

44. Mahantesh, M. N., Vajravelu, K., Abel, M. S. (2011). Heat transfer in MHD viscoelastic boundary layer flow over a stretching sheet with thermal radiation and non-uniform heat source/sink. Communications in Nonlinear Science and Numerical Simulation, 16, 3578–3590. [Google Scholar]

45. Jamshed, W., Devi, S. S. U., Goodarzi, M., Prakash, M., Nisar, K. S. et al. (2021). Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Studies in Thermal Engineering, 26, 101160. [Google Scholar]

46. Jamshed, W., Nisar, K. S., Gowda, R. J. P., Kumar, R. N., Prasannakumara, B. C. (2021). Radiative heat transfer of second grade nanofluid flow past a porous flat surface: A single-phase mathematical model. Physica Scripta, 96, 064006. [Google Scholar]

47. Reddy, M. G., Padma, P., Shankar, B., Gireesha, B. J. (2016). Thermal radiation effects on MHD stagnation point flow of nanofluid over a stretching sheet in a porous medium. Journal of Nanofluids, 5, 753–764. [Google Scholar]

48. Nisar, Z., Hayat, T., Muhammad, K., Ahmed, B., Aziz, A. (2023). Significance of Joule heating for radiative peristaltic flow of couple stress magnetic nanofluid. Journal of Magnetism and Magnetic Materials, 581, 170951. [Google Scholar]

49. Hayat, T., Ahmed, B., Abbasi, F. M., Alsaedi, A. (2019). Numerical investigation for peristaltic flow of Carreau–Yasuda magneto-nanofluid with modified Darcy and radiation. Journal of Thermal Analysis and Calorimetry, 137, 1359–1367. [Google Scholar]

50. Abou-zeid, M. (2016). Effects of thermal-diffusion and viscous dissipation on peristaltic flow of micropolar non-Newtonian nanofluid: Application of homotopy perturbation method. Results in Physics, 6, 481–495. [Google Scholar]

51. Haile, E., Shankar, B. (2014). Heat and mass transfer through a porous media of MHD flow of nanofluids with thermal radiation, viscous dissipation and chemical reaction effects. American Chemical Science Journal, 4, 828–846. [Google Scholar]

52. Li, P., Abbasi, A., El-Zahar, E. R., Farooq, W., Hussain, Z. et al. (2022). Hall effects and viscous dissipation applications in peristaltic transport of Jeffrey nanofluid due to wave frame. Colloid and Interface Science Communications, 47, 100593. [Google Scholar]

53. Yassen, M. F., Mahrous, Y. M., Nazeer, M., Pasha, A. A., Hussain, F. et al. (2021). Theoretical study of transport of MHD peristaltic flow of fluid under the impact of viscous dissipation. Waves in Random and Complex Media. https://doi.org/10.1080/17455030.2022.2078519 [Google Scholar] [CrossRef]

54. Channakote, M. M., Kalse, V. D. (2022). Combined convective and viscous dissipation effects on peristaltic flow of Ellis fluid in non uniform tube. Journal of Naval Architecture and Marine Engineering, 19, 1–12. [Google Scholar]

55. Sadaf, H., Nadeem, S. (2017). Analysis of combined convective and viscous dissipation effects for peristaltic flow of Rabinowitsch fluid model. Journal of Bionic Engineering, 14, 182–190. [Google Scholar]