Crashworthiness Design and Multi-Objective Optimization of Bionic Thin-Walled Hybrid Tube Structures

1  Introduction

Thin-walled structures are widely used as energy absorbers in the automotive, rail transport, and aerospace industries due to their superior impact resistance [1–3]. The deformation mechanism of these structures can be classified as progressive buckling, depending on the geometry, type of load, and boundary conditions [4], tube inversion [5,6], shrinkage [7], expansion [8], or splitting [9,10]. They are utilized in many engineering structures to dissipate the kinetic energy of impact during collisions.

The impact resistance of thin-walled tubes is related to the material properties, wall thickness, cross-sectional configuration, geometric defects, and other factors [11–15]. Of these factors, the cross-sectional configuration plays a vital role in the design of energy absorbers. The energy absorption capacity of thin-walled tubes can be significantly improved by making appropriate changes to the cross-sectional configuration [16,17]. For example, Alavi Nia et al. [18] compared the performance of circular, square, triangular, and conical cross-sections under axial quasi-static loading and determined that circular cross-sections had the highest specific energy absorption of these different cross-sections.

Although thin-walled tubes are widely used as energy absorbers in safety applications due to their lightweight and progressive deformation, they have some disadvantages. These include high initial peak load at the start of deformation, low energy absorption efficiency, and instability during crash impacts [19], among other problems. To solve these problems, many novel configurations, such as the multi-angle [20], multi-cell [21,22], and other structural profiles [23], have been introduced into thin-walled structures. For example, Liu et al. [24] investigated the deformation pattern and energy absorption efficiency of polygonal tubes with a star cross-section. They found that the specific energy absorption (SEA) of star tubes is slightly better than that of polygonal tubes. Zhang et al. [25] proposed a bionic thin-walled tube inspired by the microstructure of bamboo and beetle forewings. The finite element model of the bionic thin-walled tube was validated experimentally.

The inversion of thin-walled tubes results in an ideal deformation energy absorption pattern. Stable crushing forces, long strokes, and low initial force peaks can be achieved during inversion. Stable braking forces and long strokes are considered good indicators of an energy-absorbing structure. Several researchers have investigated the impact resistance parameters of circular tubes in internal and external inversions through theoretical, experimental, and numerical simulations [26–32]. Rezvani et al. [33] proposed a tube overturning model with a trigger mechanism press-fitted to the bottom of the circular tube. They showed that this approach prevents the sudden application of loads to the main part of the structure and the passengers in the event of an accident. Chahardoli et al. [34] developed a device to produce an inward flip of the truncated conical by squeezing downwards through a hollow cylinder with a cap below. Once the truncated conical is fully inverted, both structures are subjected to simultaneous progressive folding, and experimental results indicate that the specific energy of the proposed absorber is increased compared to conventional absorbers.

Materials and structures from natural organisms show superior mechanical and multifunctional properties of lightweight, high-strength, and impact-resistant [35,36], which has attracted attention in the field of structural bionics. As a result, many researchers have studied thin-walled tubes with biconically inspired characteristics. For instance, Huang et al. [37] designed a hierarchical topological tubular honeycomb. Their numerical and theoretical results indicated that the topological honeycomb has better energy absorption capacity than traditional honeycombs. Gong et al. [38] designed a lotus-inspired bionic multi-cell tube (LBMT) and found that the LBMT exhibits superior energy absorption behavior than traditional multi-cell tubes.

In the above literature, much attention has been focused on the quasi-static or dynamic compression of multicellular tubes. In addition, mainly by folding deformation to absorb energy; however, there is little research on the crashworthiness of thin-walled shell structures with combined geometries, Gupta et al. [39] introduced several types of composite tube structures and concluded that the change of geometry affects the collapse process, and the thickness and semi-apical angle influence the flip mode of the conical tube, but the structural deformation mechanism and parametric analysis need further research.

This study proposes a bamboo-inspired straight conical tube (BSCT) structure with a bulkhead based on bamboo knots to make the conical tube turn outward stably and improve the energy absorption capacity of the thin-walled tube. It compares the crashworthiness of BSCT with a straight conical tube (SCT). The multi-objective optimization problem of the structure with a modified bulkhead is solved using the Non-dominated Sorting Genetic Algorithm-II (NSGA-II), and the results showed that the BSCT achieves good results in terms of initial peak force. In contrast, the bulkhead in the middle of the structure can effectively improve the specific energy absorption.

2  Materials and Methods

2.1 Geometry

Since bamboo possesses excellent mechanical properties, this study draws inspiration from bamboo joints and introduces a bulkhead structure directly in the straight and conical tubes. Fig. 1 shows the finite element model of the BSCT, and all the geometric features of the tube are represented by five parameters: t is thickness; R is the radius under the conical tube; r is the radius of the straight tube; A is the length of the straight tube; B is the length of the conical tube.

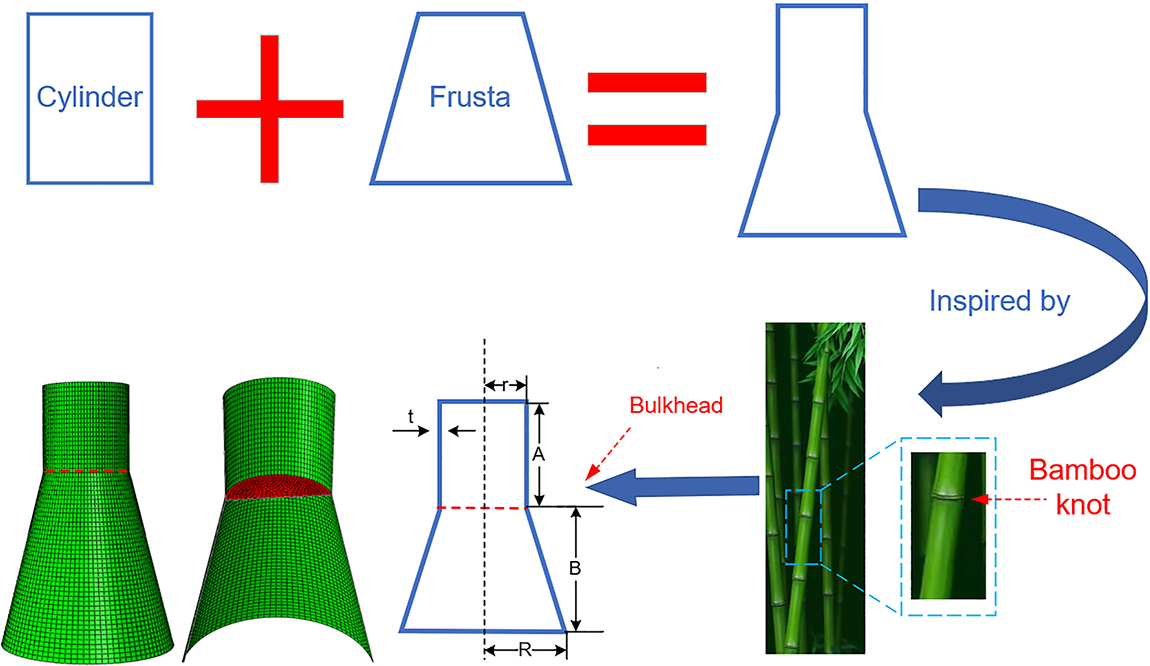
Figure 1: The inspiration for the BSCT

2.2 Crashworthiness Parameters

The energy absorption (EA) represents the total energy absorption that is dissipated during the crushing process, and it is defined as follows:

EA=∫0lmaxF(s)ds(1)

where F(s) is the crushing force and lmax is the crushing distance (or effective stroke).

The SEA is defined as the ratio of the EA to the mass of the structure.

SEA=EAm(2)

The PCF is the peak stress, and for general energy-absorbing structures, PCF usually occurs at the beginning stage and is termed IPCF (initial peak crushing force). However, the discontinuity of straight conical tube structures generates two peak stresses during the deformation of the combined tube. These need to be discussed separately for excellent energy absorbers. The IPCF should be minimized for effective protection. The second peak stress occurs when the conical tube is folded together with the straight tube after it has been turned outwards and is called the SPCF (second peak crushing force).

2.3 Material Properties

A standard elastic-plastic intrinsic model was employed to simulate the large deformation of the tube during the crushing process. The material of the tube is aluminum alloy Al-6063-T5. Fig. 2 depicts the actual stress and plastic strain data.

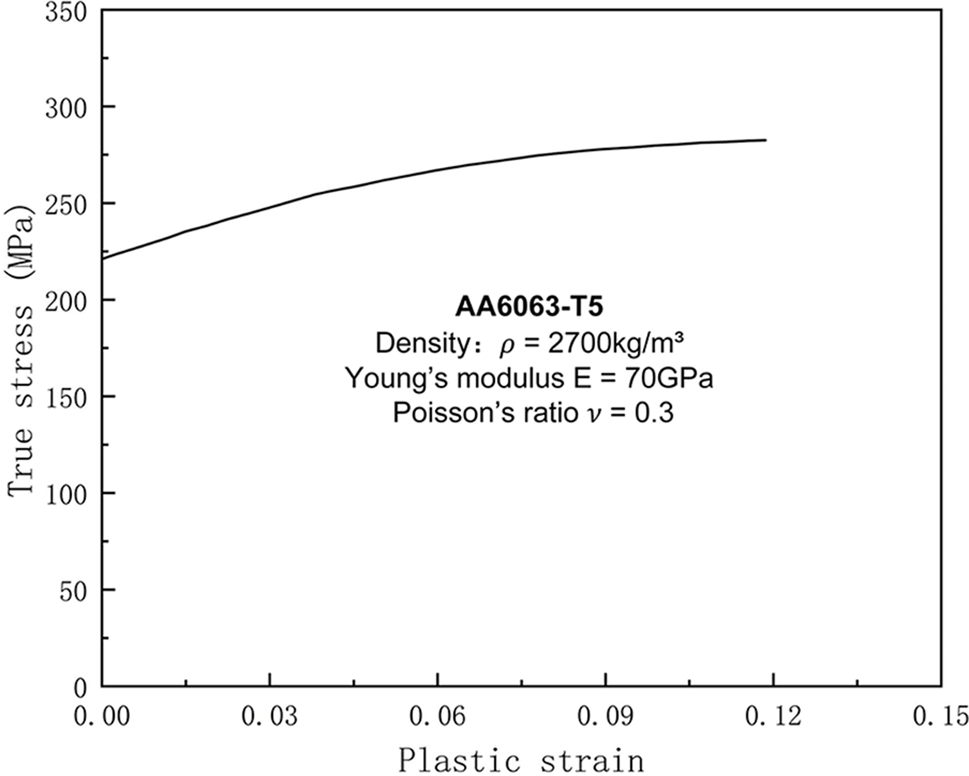
Figure 2: True stress-true plastic strain curve for the aluminum AL-6063-T5 [40]

Due to the insensitivity of Al-6063-T5 material to strain rate [41], the inertial effect of low-velocity impacts has a negligible effect on the crashworthiness of the structure. Hence, quasi-static tests are widely applied to verify the energy absorber for low-velocity impacts (10 m/s) [42–44]; they are also used in this study.

2.4 Finite Element Method

The commercial finite element software ABAQUS/ EXPLICIT is often used as an effective solver for numerical simulation experiments. The impact model consists of a rigid plate, a tube structure, and a supporting rigid plate (Fig. 3), with the mass of the impact rigid plate set to 600 kg. The impact distance is 96 mm, which is 80% of the height of the column (H = 120 mm). The impact plate velocity is always downwards, and all the degrees of freedom of the supporting rigid plate are fixed. In addition, the thin-walled structure is simulated using a four-node simplified integral shell element (S4R) with five integration points along the thickness direction. The model uses general contact to describe the interaction effects, and the friction coefficient is set to 0.2 [24].

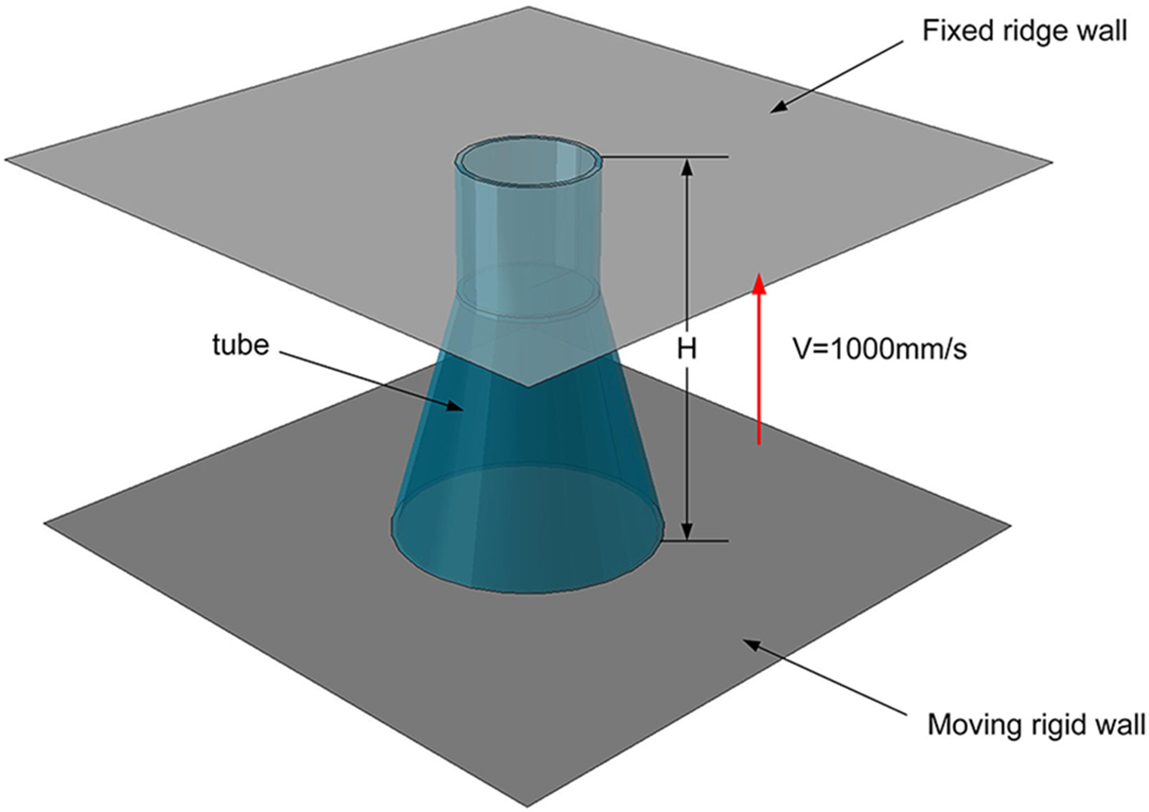
Figure 3: Schematic of impact model

The convergence of the mesh sizes was obtained by mesh sensitivity analysis. Therefore, the dimensions t = 2 mm, r = 20 mm, R = 40 mm, A = 40 mm, and B = 80 mm were chosen to compare the EA and IPCF for six different sets of mesh sizes to determine the optimum mesh size for the model.

Fig. 4 indicates that the mesh size has little influence on the PCF but significantly affects the EA. It also exhibits that the mesh size impacts the energy absorption, and it requires more time to calculate the same model with too small a mesh size. Table 1 compares absorbed energy and peak initial force for different mesh sizes. It shows that when the mesh size is 1.5 mm, the initial peak crushing force error is only 0.27%, and the absorbed energy error is 1.44% compared to the 1 mm. Therefore, a mesh size of 1.5 mm is the best choice, considering the computational cost and accuracy balance.

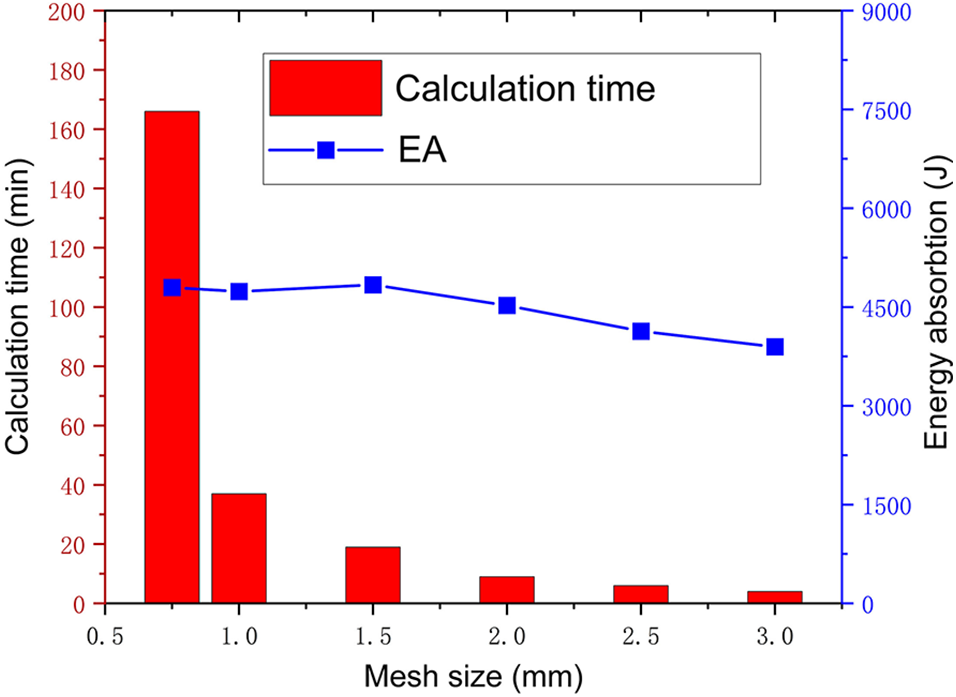
Figure 4: Mesh sensitivity analysis for the BSCT

2.5 Verification of the FE Model

In order to guarantee accuracy, the experimental results in [39] were utilized to validate the FE model. The experiments were conducted at 10 mm/min speed under quasi-static compression. The crushing speed was increased to 1 mm/s in the simulations to improve the efficiency of the structure analysis and reduce the computational cost.

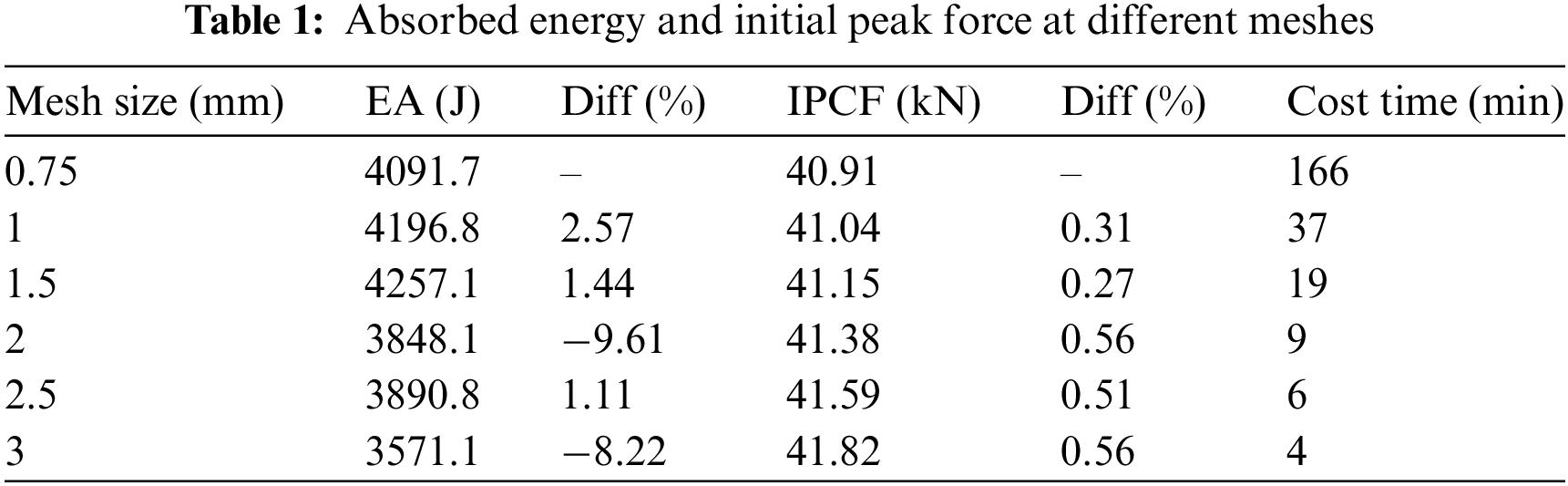
Fig. 5 shows that the total kinetic energy is 1% of the total internal energy, less than the critical threshold. Therefore, quasi-static loading scenarios can amplify the crushing velocity, and the dynamic effects can be neglected [45]. Fig. 6 indicates that the deformation results of finite element simulation are consistent with the deformation results of previous experimental studies. In addition, the force-displacement curves obtained from the numerical calculation results in this study agree with the experimental tests, and the curves’ similarity is represented in the amplitude and waveform. The small differences can be due to the uniform thickness used in the finite element model, the manufacturing accuracy of the test specimens, or material defects. This indicates that the accuracy of the finite element model is acceptable to investigate the energy absorption characteristics of the straight conical tube. The following simulations are set up the same way as the above verification, with the same boundary and loading conditions but different shapes and material properties of the structure. Therefore, the following simulations can be performed with acceptable accuracy based on these parameters.

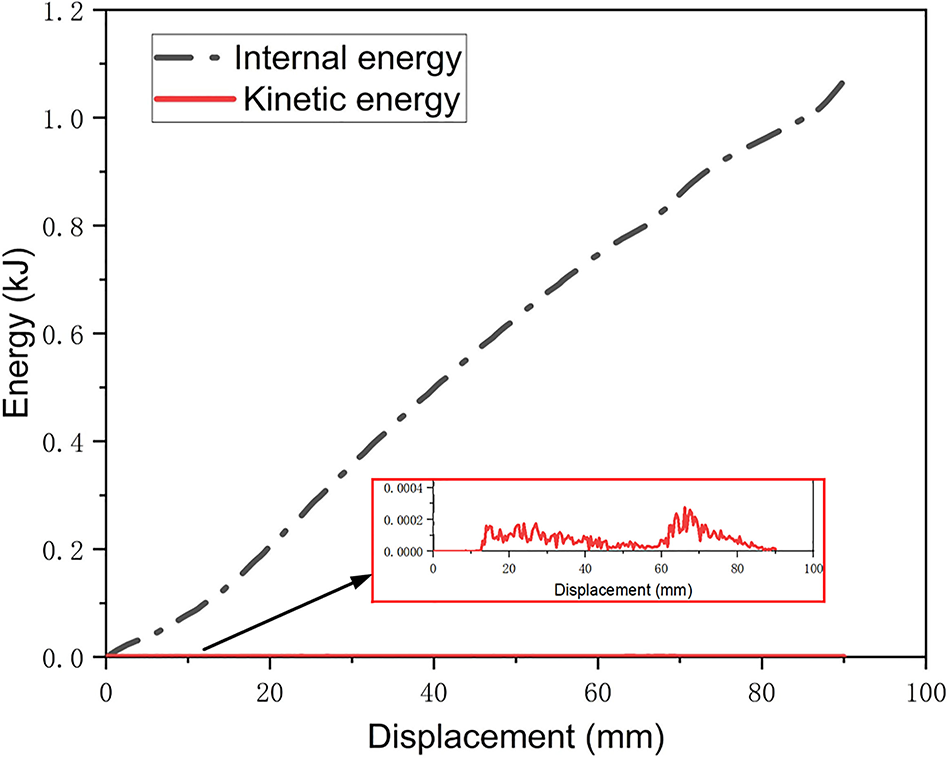
Figure 5: Kinetic and internal energies of the FE model of the tube

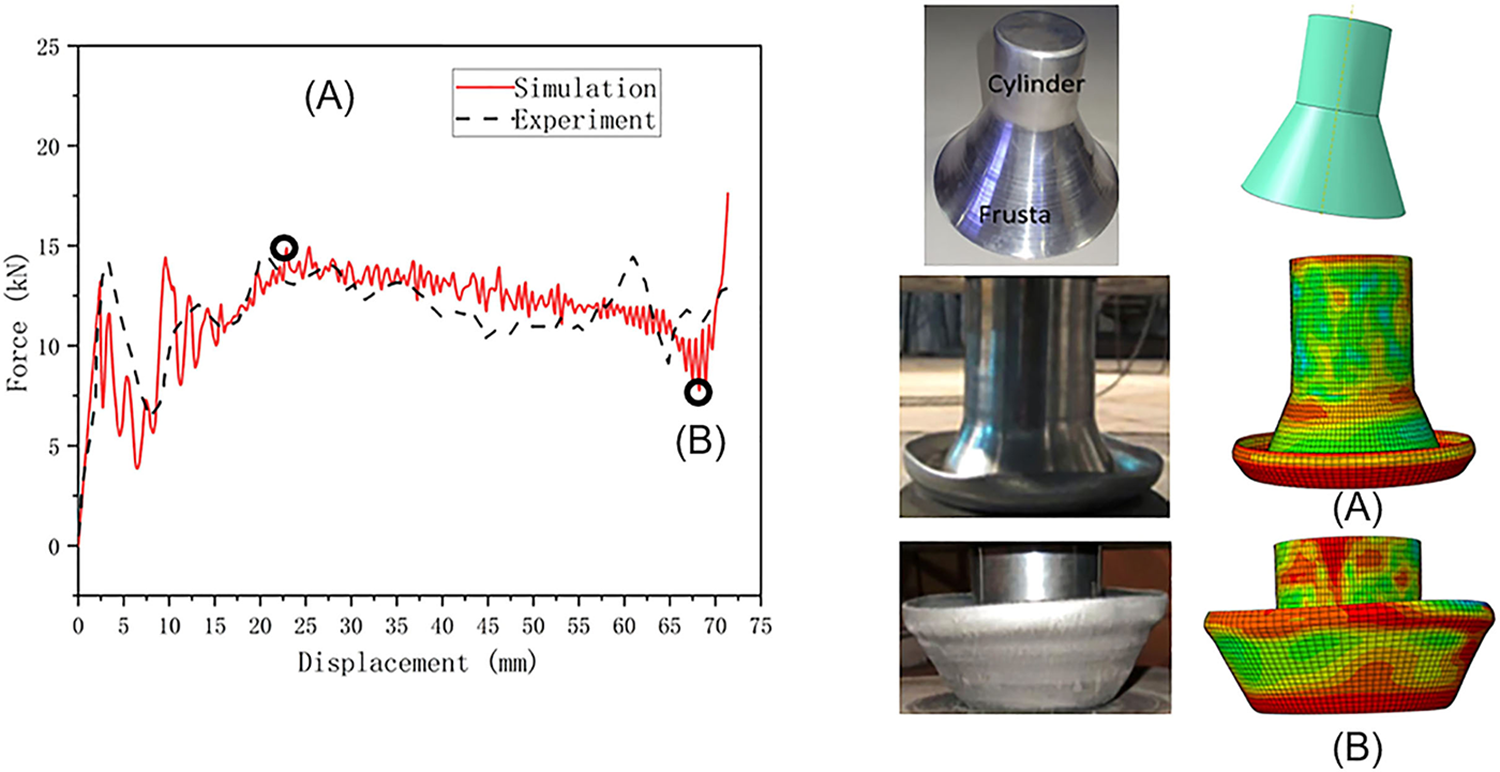
Figure 6: Numerical and experimental results [39] comparison of tubes under quasi-static oblique loadings

3  Results and Discussion

3.1 Influence of Bulkhead on the BSCT

Fig. 7 depicts the deformation of the BSCT and SCT. The SCT collapses internally at the junction during compressions, causing the conical tube to flip inwards and then fold with the straight tube after the flip. In contrast, the BSCT starts to flip outwards at the lower end during compression and then folds with the straight tube after the flip is complete.

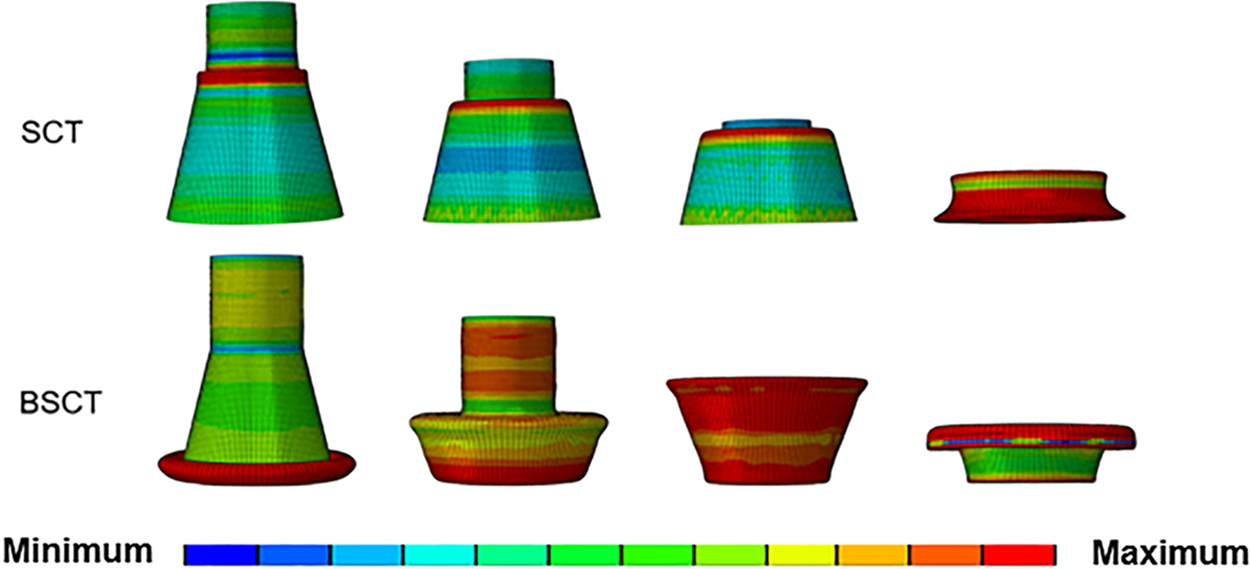
Figure 7: Deformation diagram of BSCT and SCT

Fig. 8 compares the energy absorption and force-displacement curves for BSCT and SCT. It can be concluded that the IPCF of BSCT is 46.34 kN, the IPCF of SCT is 53.24 kN, and the difference is 6.9 kN. The SPCF of BSCT is 113.47 kN, the SCT is 145.02 kN, and the difference is 31.55 kN. The energy absorption curve shows that both have a turning point; the energy absorbed by BSCT is 5025 J, and the energy absorbed by SCT is 3510 J. The difference between the two is 1515 J, an increase of 30.15%. In addition, the BSCT straight tapered tube with a bulkhead has a lower peak force, higher energy absorption, and superior crashworthiness characteristics compared to the SCT without a bulkhead.

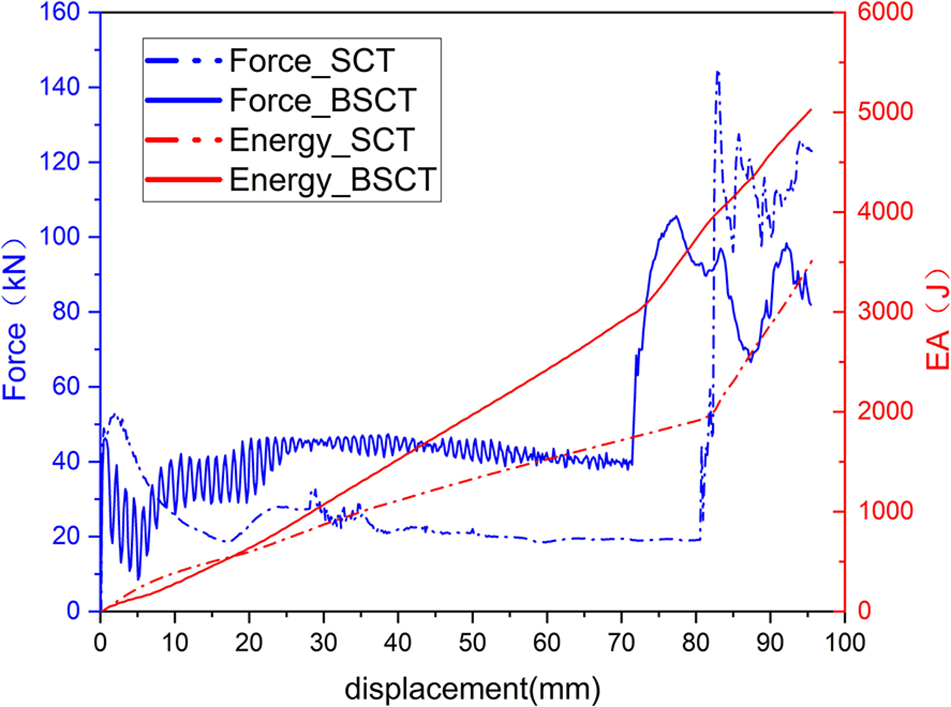
Figure 8: Force displacement and energy absorption curves

The reason is that BSCT has a partition reinforcement at the connection between the straight tube and the conical tube so that the force of the whole tube is relatively stable. During the pressure, it does not yield from the middle, resulting in the inward flip of the conical tube, and the case of external inversion can produce more significant plastic deformation, and this deformation allows for greater energy absorption. Moreover, the IPCF and SPCF with the bulkhead are small, indicating that the bulkhead's introduction improves the structure's crashworthiness.

3.2 Trim the Bulkhead

Fig. 9 demonstrates that the bulkhead does not directly bear the load in the deformation process but strengthens the stability of the stressed structure and does not directly participate in the compression and collapse deformation. It considers digging holes in the bulkhead to reduce the weight of the bulkhead and further improve the SEA. The diameter of the circular hole dug in the bulkhead is 0%, 25%, 50%, 75%, and 100% of the radius of the straight tube.

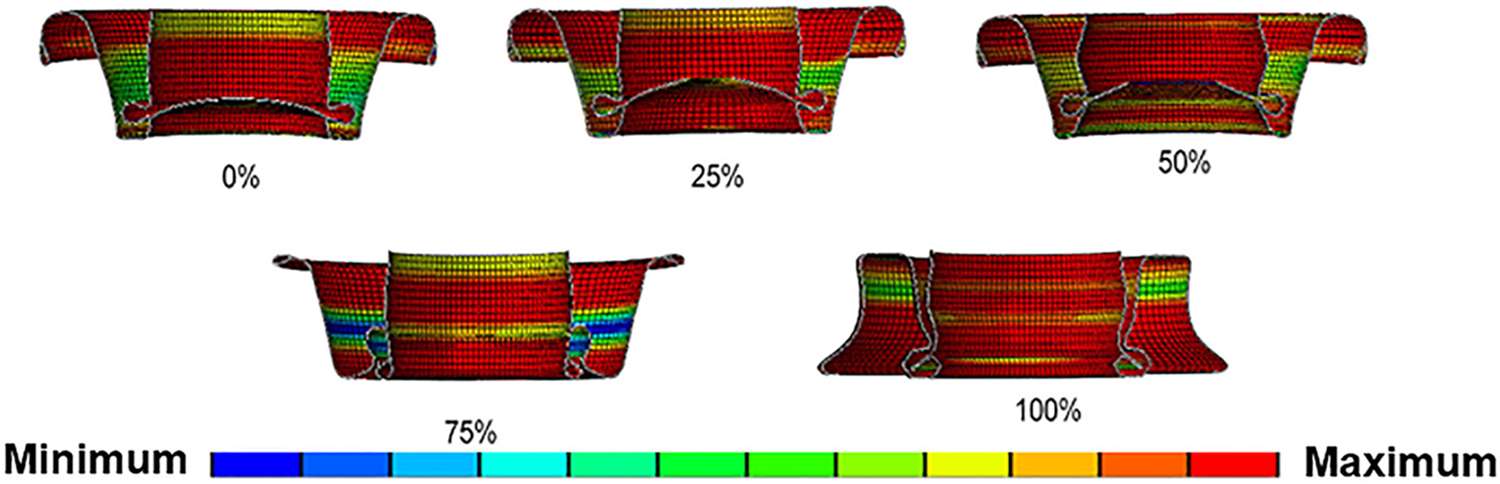
Figure 9: BSCT deformation diagrams for different digging radiuses

Fig. 10a indicates that the appropriate openings improve the absorption performance of the SEA due to the reduction of the structure's mass and the fact that the bulkhead’s function does not fail.

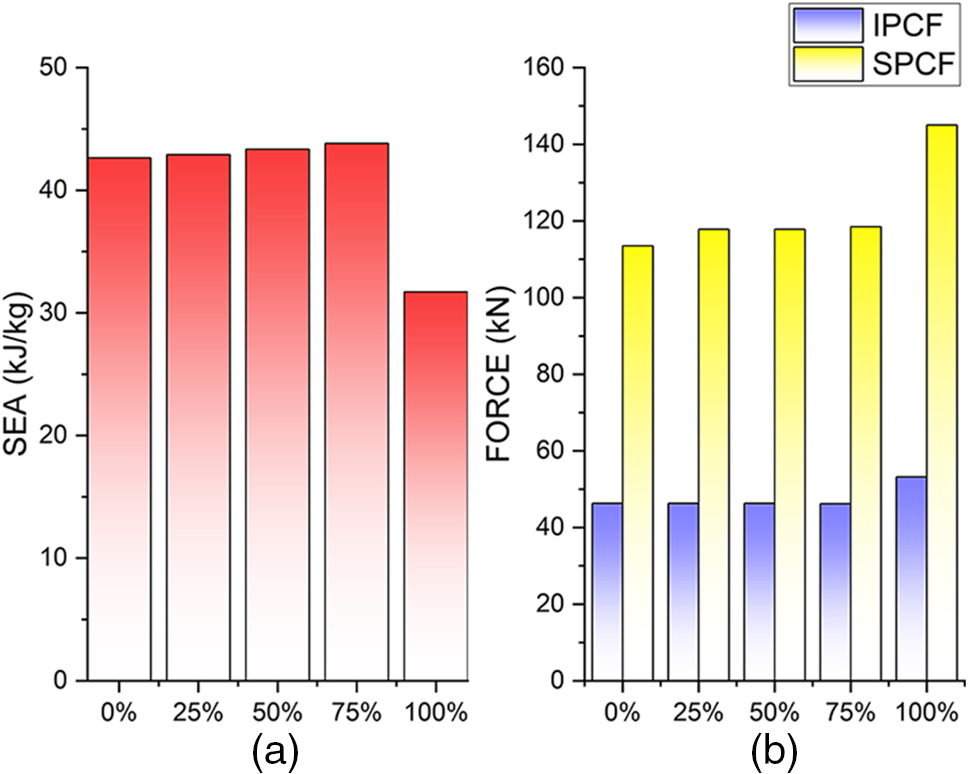
Figure 10: Comparison of (a) SEA and (b) peak forces for different digging ratios

Fig. 10b demonstrates that the initial peak stresses are not significantly different when the bulkhead is present but are significantly greater when the bulkhead is absent.

3.3 Comparison of Conventional Round Tubes and BSCT for the Same Mass

Five different cross-sectional tubes were chosen to compare the SEA of different cross-sectional tubes. Fig. 11a compares the BSCT with the other cross-sectional tubes, which differ only in cross-sectional dimensions for the same wall thickness and mass. The SEA of the BSCT is 26.85% higher than the SEA of the circular cross-section tube. Fig. 11b shows that the peak stress of the BSCT is lower than all four other cross-section tubes, and the initial peak stress is 40.26% lower than the circular cross-section comparison.

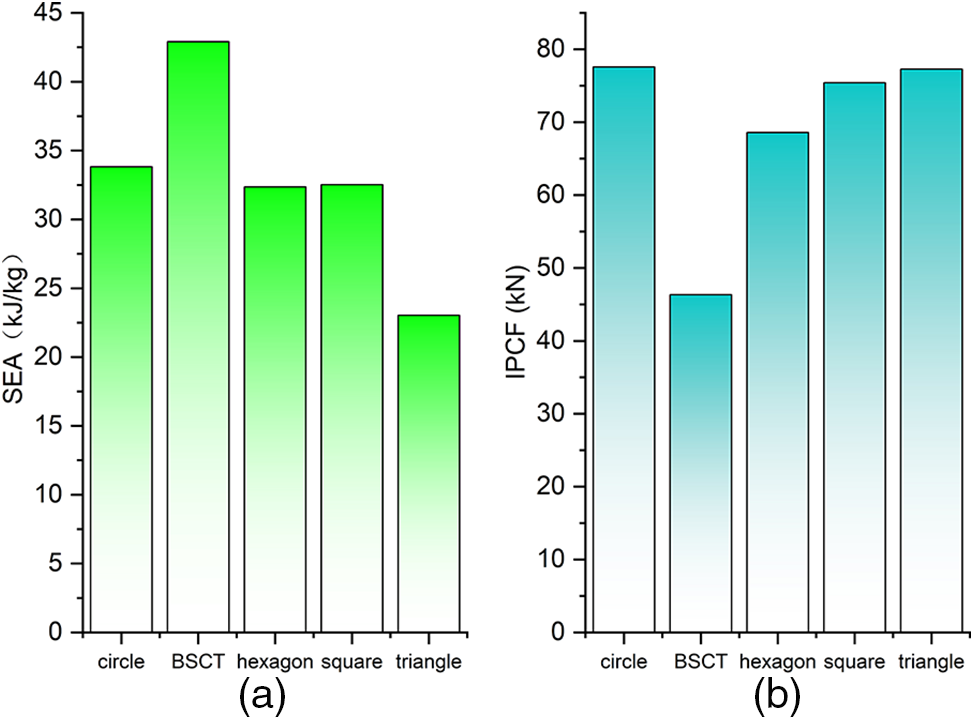
Figure 11: Comparison of (a) SEA and (b) peak forces for different cross-sectional tubes

3.4 Design Optimization

3.4.1 Multi-Objective Optimization Problem

As an ideal energy absorber, the structure should dissipate more of the kinetic energy of the impact while minimizing the peak reaction force. Therefore, SEA, IPCF, and SPCF were chosen as the three objective functions in optimizing the impact resistance. Wall thickness, straight tube radius, and conical tube radius are sensitive to the impact resistance of the straight conical tube and were therefore selected as design variables. The final selected optimization model has a circular hole diameter cut in the bulkhead of 75% of the straight tube radius.

The problem of optimizing the design for crashworthiness can be written as follows:

{Max SEA=f(t,r,R)Min IPCF=f(t,r,R)Min SPCF=f(t,r,R)s.t.1 mm≤t≤3 mm20 mm≤r≤40 mm40 mm≤R≤60 mm(3)

To clarify, the optimization process employed in this study is described in brief detail below. Sampling points were initially selected from different combinations of the design variables shown in Fig. 12. These structures were then modeled and analyzed in ABAQUS to extract the crashworthiness criteria SEA and PCF. The objective functions for the crashworthiness criteria SEA and PCF were then obtained based on the dimensions of thickness and radius by generating approximate models using the input (i.e., t and r and R) and output (i.e., SEA and PCF) data. If the accuracy of these functions is adequate, the best combination of thickness and radius is determined by minimizing and maximizing the objective functions of PCF and SEA, respectively, using an undominated ranking genetic algorithm. Otherwise, new sampling points are selected from the space of design variables shown in it. The above process is repeated multiple times until an optimal point is reached.

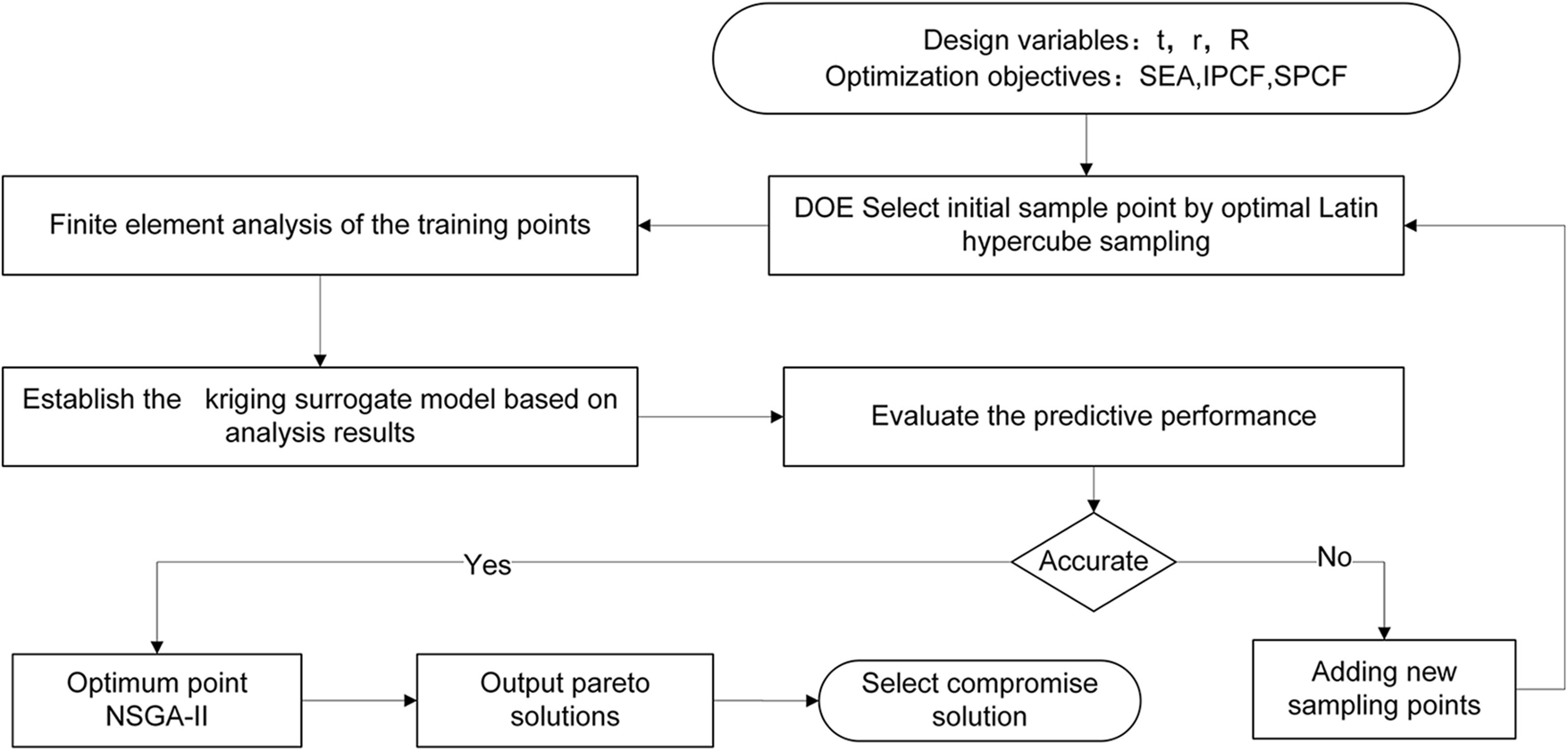
Figure 12: Flowchart of optimization

3.4.2 Design of Experiment and Surrogate Model

Due to interaction effects, obtaining an analytical formulation of the objective function concerning the shape and material parameters is challenging. As an alternative, surrogate modeling techniques, such as Kriging modeling, have proven effective and are widely used in crashworthiness design [46]. In practice, surrogate modeling techniques start with data samples from specific training points. Design of experiments (DOE) is a method that addresses how to select training points effectively, and commonly used methods are complete factorial design, orthogonal arrays, central composite design, Box-Behnken, Latin hypercube design, and optimal Latin hypercube design. This study uses optimal Latin hypercube sampling (OLHS) to generate training points. It has the advantage of effective space-filling capability, fitting non-linear responses, and good space-filling and equilibrium compared to Latin hypercube sampling.

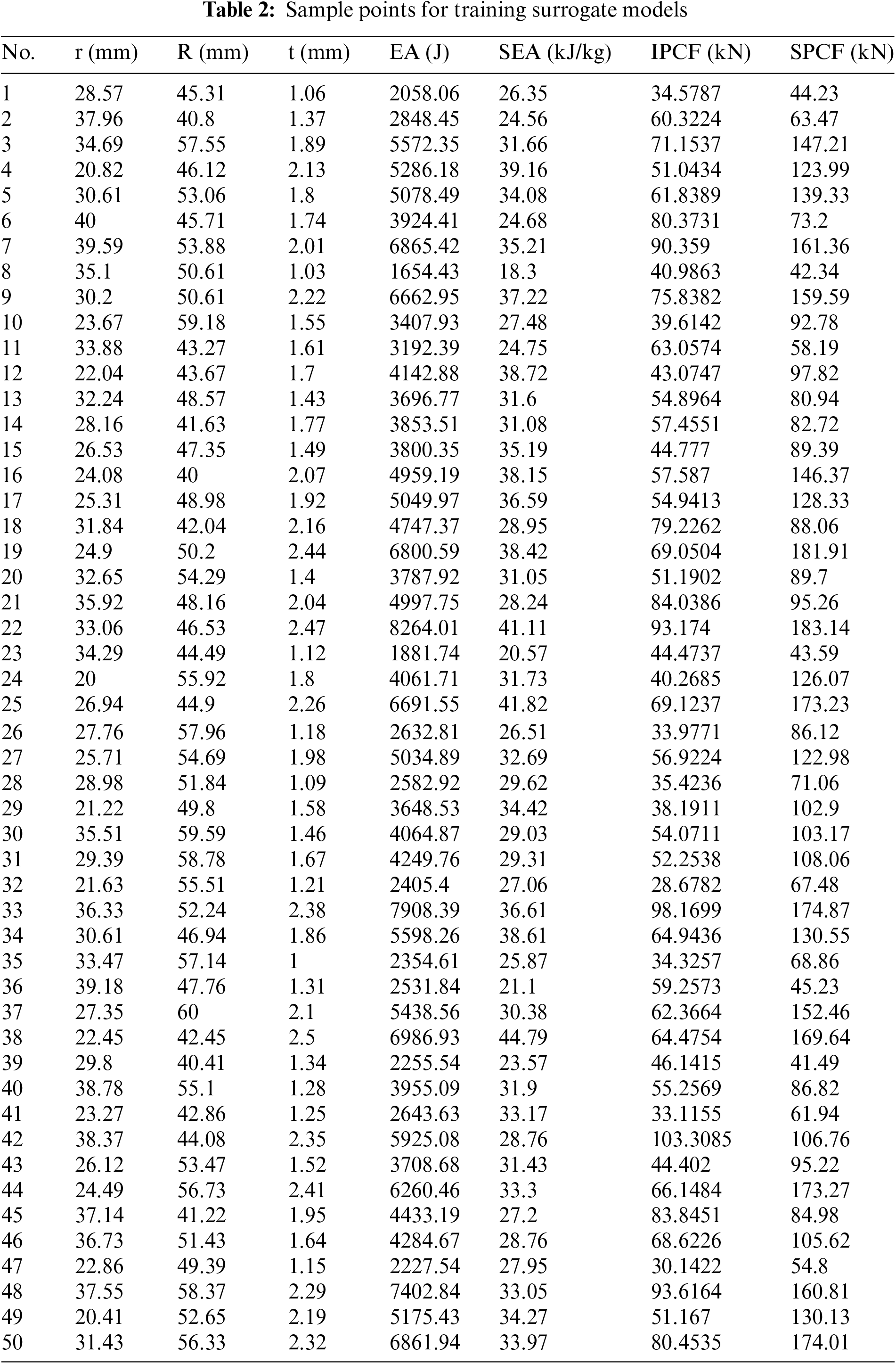
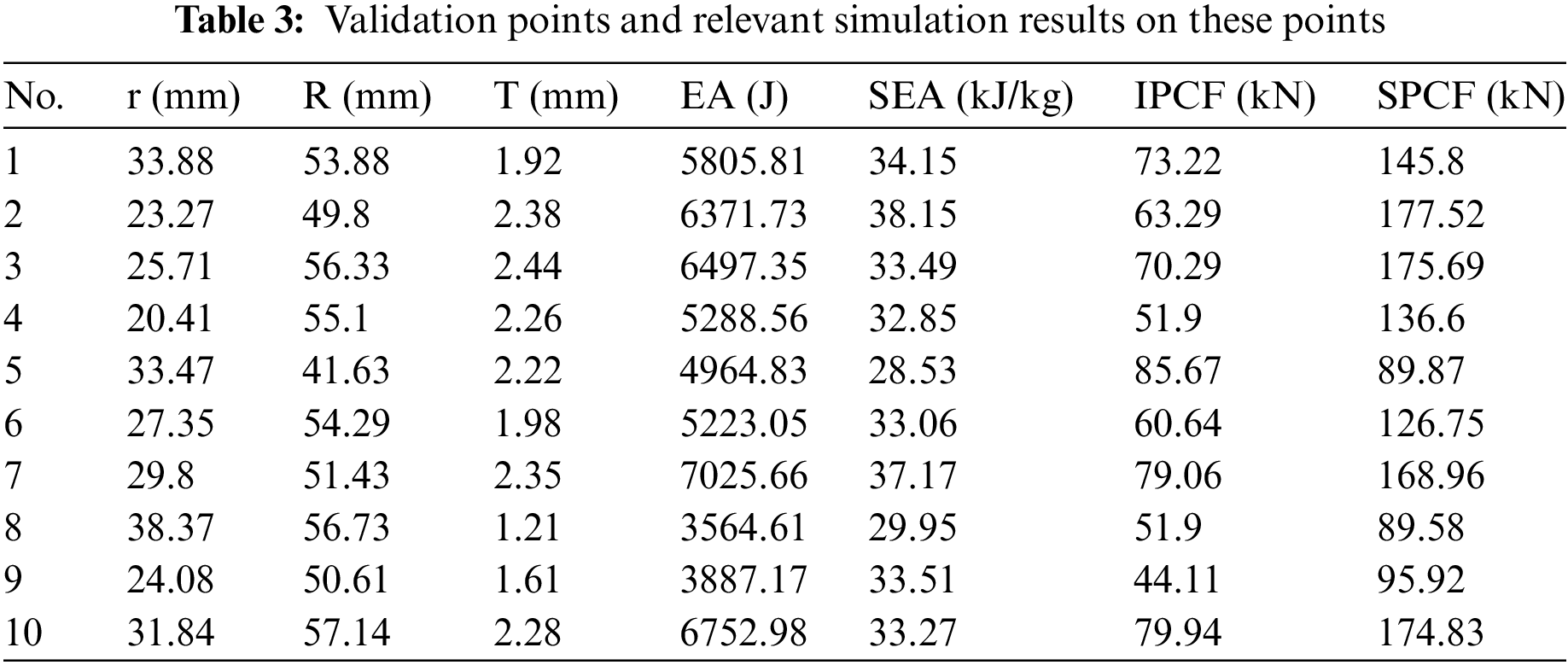
A Kriging surrogate model was then built to approximate the SEA and PCF to ensure that the surrogate model met the accuracy requirements and to assess the surrogate model's accuracy. Fig. 13 depicts the spatial distribution of these sample points. The training point data are detailed in Table 2, and the validation point data are listed in Table 3.

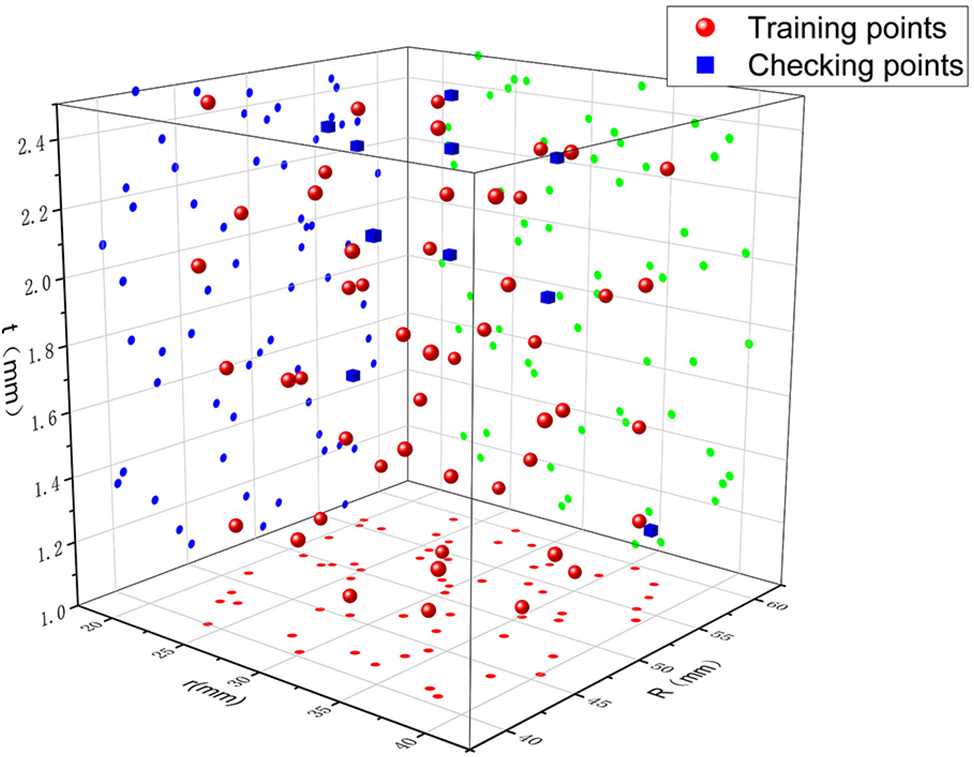
Figure 13: Sample points for testing the Latin hypercube design

3.4.3 Evaluation of Surrogate Model Fit Accuracy Indicators

R2=1−∑i=1n(yi−y∧i)2∑i=1n(yi−yi¯)2(4)

RAAE=∑i=1n|yi−y∧i|n×1n−1∑i=1n(yi−y∧i)(5)

RMAE=max(|y1−y∧1|,|y2−y∧2|,…,|yn−y∧n|)1n−1∑i=1n(yi−y∧i)(6)

RMSE=1n∑i=1n(yi−y∧i)2(7)

where yi is the actual value; y∧i is the predicted value; yi¯ is the mean of the sample points; n is the number of samples.

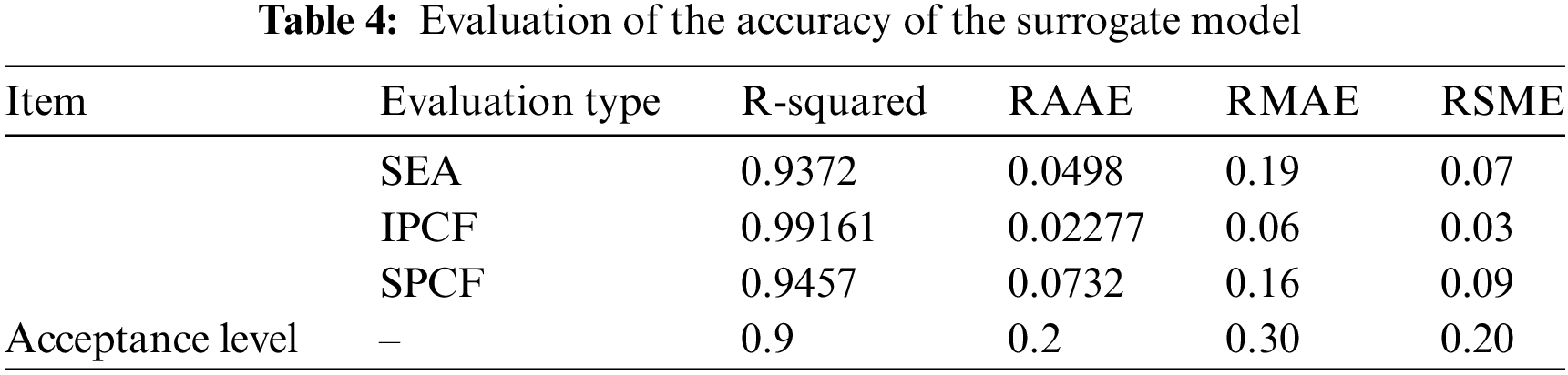
For R2, the closer the value is to 1, the higher its accuracy. For the assessment metrics, RSME, RAAE and RMAE, the closer the value is to 0, the higher its accuracy. Table 4 indicates that the fitted accuracies are all within acceptable limits, illustrating the reliability of the surrogate models.

3.4.4 Optimization Algorithm

This study utilizes the Non-Dominated Sorting Genetic Algorithm (NSGA-II) [42] to search for the Pareto frontier of these two conflicting objectives. The algorithm is based on the principle of fast, non-dominated sorting.

The non-dominated set can be obtained using the elite non-dominated sort and the crowded distance sort. The non-dominated fronts are generated after each generation. Finally, the non-dominated set is obtained by iterative convergence to form the Pareto front. This algorithm effectively solves collision-resistant design problems [43,44]. Table 5 lists the optimization calculation parameters.

3.4.5 Pareto Front

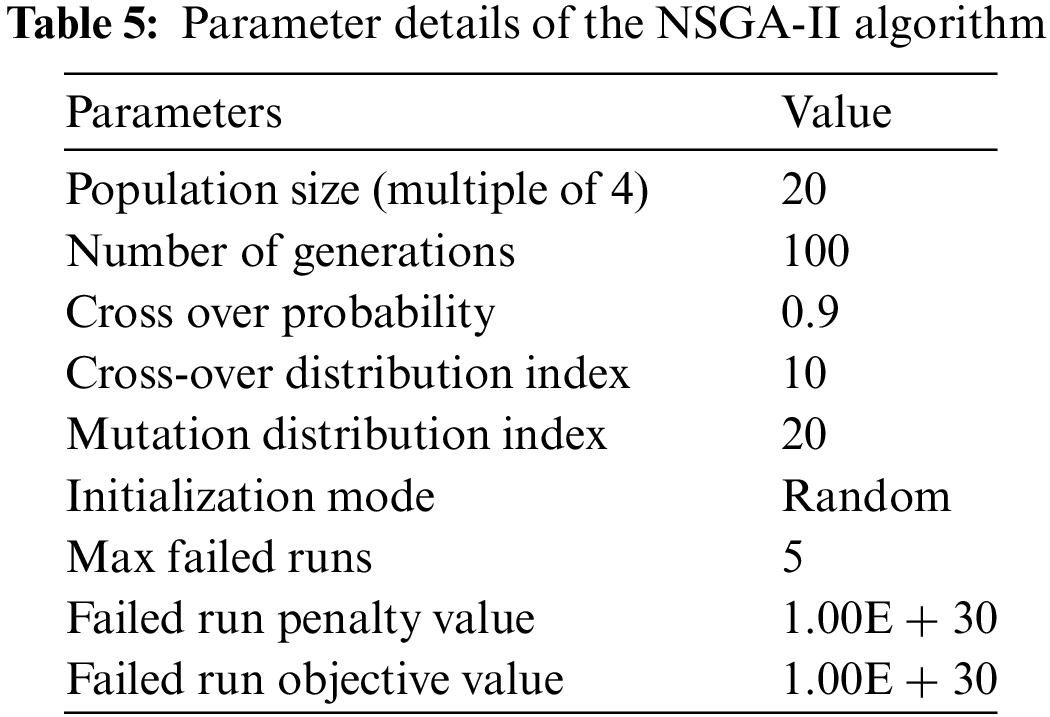
Fig. 14 depicts the Pareto front of the bionic straight conical tube obtained by multi-objective optimization, and it is clear that there is an intense conflict between the two optimization objectives, PCF and SEA. The designer can choose the optimal design at the Pareto front based on the actual engineering design requirements. This research selected three sample points, and the geometric parameters are listed in Table 6. When only SEA is considered, Case 3 has a straight tube radius of 22.16 mm and a conical tube radius of 43.40 mm with a wall thickness of 2.47 mm. The surrogate model predicts that the optimum SEA point is 44.72 kJ/kg; the actual value obtained by the finite element model is 43.97 kJ/kg.

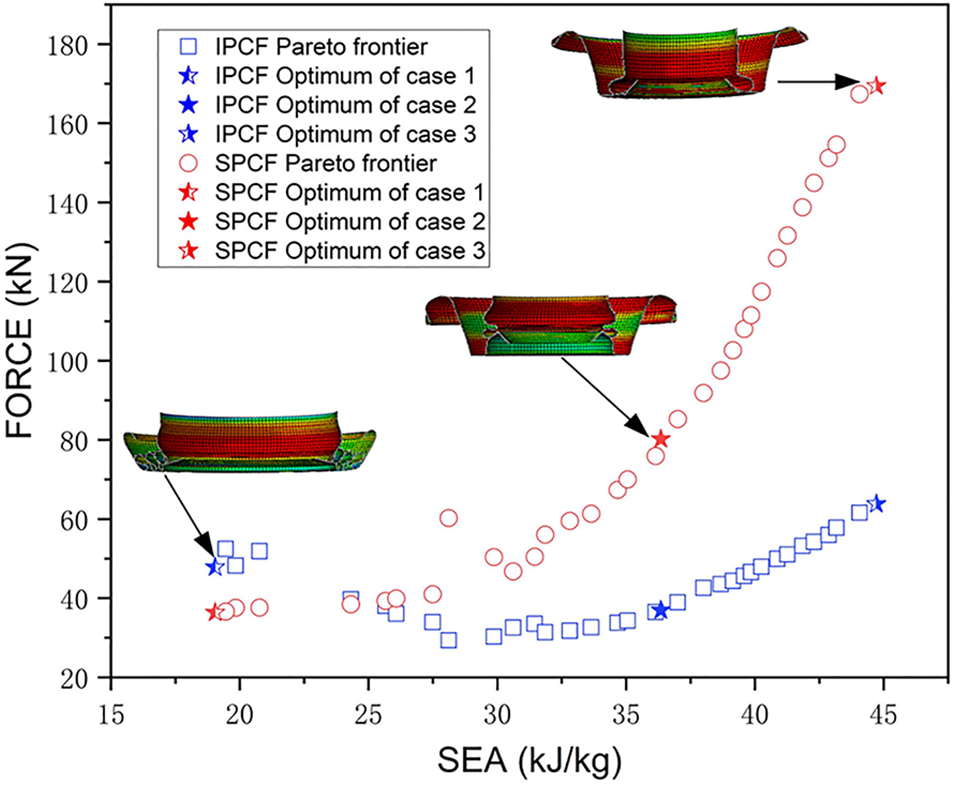
Figure 14: Pareto frontiers from the BSCT

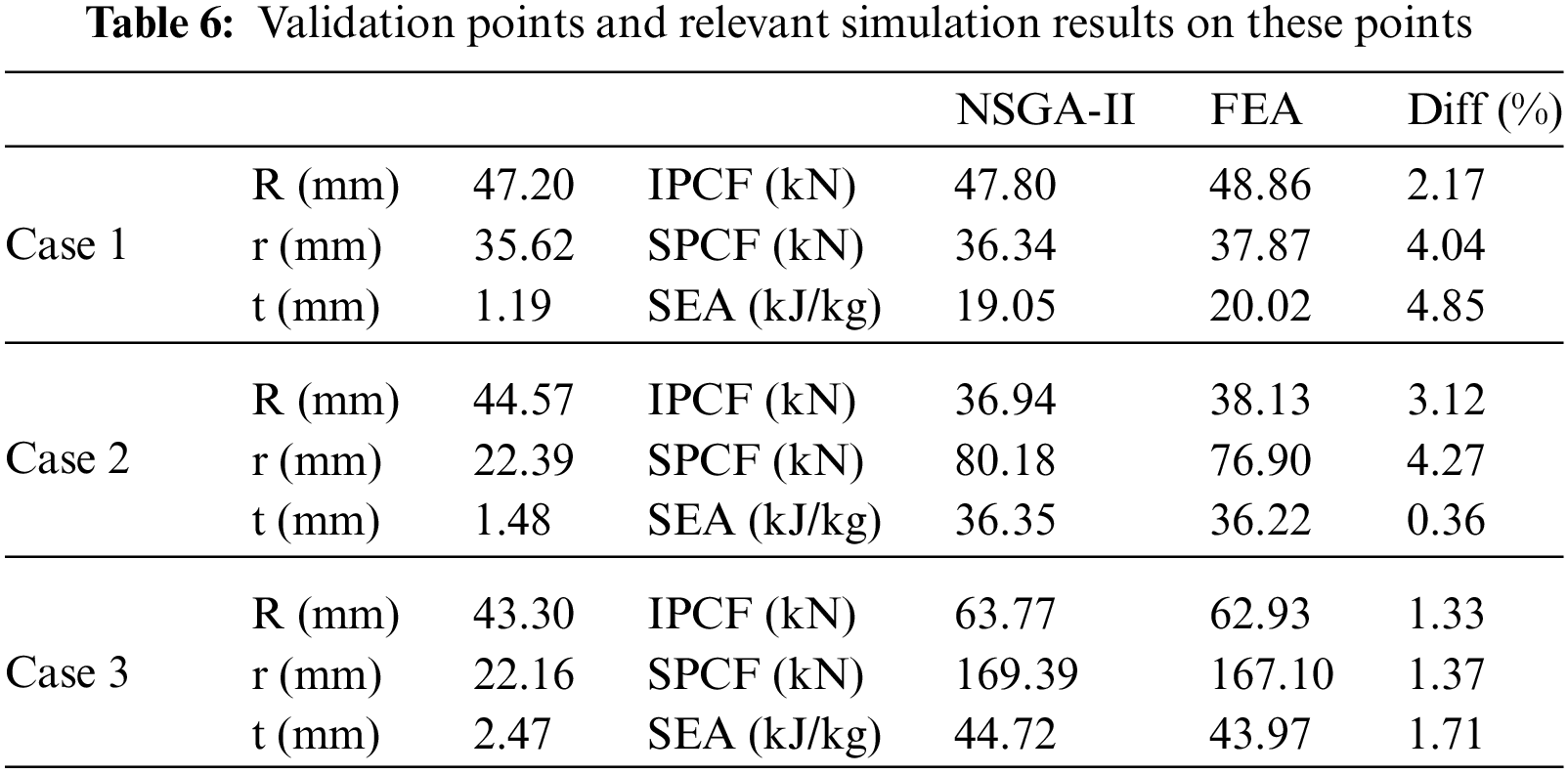
On the other hand, if only the PCF is considered, the optimal Case 1 is obtained, in which the optimized tube configuration is a straight tube radius of 35.62 mm and a conical tube radius of 47.20 mm with a wall thickness of 1.19 mm, and the IPCF, SPCF, and SEA for this design are 47.80 kN, 36.34 kN, and 19.05 kJ/kg, respectively.

In addition, a compromise solution, Case 2, is considered, which balances the PCF and SEA to a certain extent. The radius of the straight tube in Case 2 is 22.39 mm, the radius of the conical tube is 44.57 mm, the wall thickness of the tube is 1.48 mm, and the thickness of the tube is 1.5 mm. When the tube wall is thin, the SEA value is low, and the initial force peak is the maximum peak force. In contrast, as the wall thickness increases, the straight conical tube shows prominent graded energy absorption characteristics, and the second force peak is higher than the initial force peak.

A comparison of the finite element results with the surrogate model results is provided. The errors are within 5%, all within reasonable limits. The accuracy of the optimization results is verified.

4  Conclusion

This study proposes a BSCT structure with a bulkhead based on bamboo knots. It investigates the impact of the bulkhead on energy absorption with openings in the bulkhead and considers the effect of tube geometry on crashworthiness. Finally, multi-objective optimization is employed to enhance the crashworthiness of the BSCT structures. Within its limitation, the following conclusions can be drawn:

1.    The BSCT passes through the discontinuity of the tube structure; first, the conical tube undergoes a flip, which produces a lower peak force. Then, the conical tube flip collapses with the straight tube, and the folding stage contributes to a higher stress plateau. This enhances the structure's energy-absorbing capacity. The SEA increases by 26.85% for the same mass compared to the circular cross-section tube.

2.    The outward flip of the conical tube exhibits a lower PCF and a higher SEA than the inward flip of the conical tube, as the outward flip induces greater plastic deformation. Also, the BSCT that produces the outward-flip case absorbs 30.15% more energy than the SCT that produces the inward-flip case.

3.    The bulkhead is a key factor influencing the impact resistance characteristics of BSCT. It suppresses the inward collapsing deformation mode, and trimming the bulkhead can further improve the energy absorption efficiency.

4.    The SEA and PCF rise with an increasing thickness, and the BSCT exhibits significant gradient energy absorption characteristics, with the second peak crushing force higher than the initial peak crushing force.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Pingfan Li; data collection: Pingfan Li; analysis and interpretation of results: Pingfan Li; draft manuscript preparation: Pingfan Li, Jiumei Xiao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that supports the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study. And the pictures cited in this article have been licensed.

References

1. Alghamdi, A. A. A. (2001). Collapsible impact energy absorbers: An overview. Thin-Walled Structures, 39(2), 189–213. [Google Scholar]

2. Baroutaji, A., Sajjia, M., Olabi, A. G. (2017). On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments. Thin-Walled Structures, 118, 137–163. [Google Scholar]

3. Magliaro, J., Altenhof, W., Alpas, A. T. (2022). A review of advanced materials, structures and deformation modes for adaptive energy dissipation and structural crashworthiness. Thin-Walled Structures, 180, 109808. [Google Scholar]

4. Albak, E. İ. (2021). Crashworthiness design and optimization of nested structures with a circumferentially corrugated circular outer wall and inner ribs. Thin-Walled Structures, 167, 108219. [Google Scholar]

5. Niknejad, A., Moeinifard, M. (2012). Theoretical and experimental studies of the external inversion process in the circular metal tubes. Materials & Design, 40, 324–330. [Google Scholar]

6. Yu, X., Qiu, X., Yu, T. X. (2015). Analysis of the free external inversion of circular tubes based on deformation theory. International Journal of Mechanical Sciences, 100, 262–268. [Google Scholar]

7. Li, J., Gao, G., Guan, W., Wang, S., Yu, Y. (2018). Experimental and numerical investigations on the energy absorption of shrink circular tube under quasi-static loading. International Journal of Mechanical Sciences, 137, 284–294. [Google Scholar]

8. Yan, J., Yao, S., Xu, P., Peng, Y., Shao, H. et al. (2016). Theoretical prediction and numerical studies of expanding circular tubes as energy absorbers. International Journal of Mechanical Sciences, 105, 206–214. [Google Scholar]

9. Guan, W., Gao, G., Yu, Y., Zhuo, T. (2020). Theoretical, experimental and numerical investigations on the energy absorption of splitting multiple circular tubes under impact loading. Thin-Walled Structures, 155, 106916. [Google Scholar]

10. Huang, X., Lu, G., Yu, T. X. (2002). On the axial splitting and curling of circular metal tubes. International Journal of Mechanical Sciences, 44(11), 2369–2391. [Google Scholar]

11. Isaac, C. W., Oluwole, O. (2016). Energy absorption improvement of circular tubes with externally press-fitted ring around tube surface subjected under axial and oblique impact loading. Thin-Walled Structures, 109, 352–366. [Google Scholar]

12. Hao, W., Xie, J., Wang, F., Liu, Z., Wang, Z. (2017). Analytical model of thin-walled corrugated tubes with sinusoidal patterns under axial impacting. International Journal of Mechanical Sciences, 128–129, 1–16. [Google Scholar]

13. Liu, Q., Ma, J., He, Z., Hu, Z., Hui, D. (2017). Energy absorption of bio-inspired multi-cell CFRP and aluminum square tubes. Composites Part B: Engineering, 121, 134–144. [Google Scholar]

14. Li, Z., Ma, W., Hou, L., Xu, P., Yao, S. (2020). Crashworthiness analysis of corrugations reinforced multi-cell square tubes. Thin-Walled Structures, 150, 106708. [Google Scholar]

15. Song, J., Xu, S., Zhou, J., Huang, H., Zou, M. (2021). Experiment and numerical simulation study on the bionic tubes with gradient thickness under oblique loading. Thin-Walled Structures, 163, 107624. [Google Scholar]

16. Ghahremanzadeh, Z., Pirmohammad, S. (2023). Crashworthiness performance of square, pentagonal, and hexagonal thin-walled structures with a new sectional design. Mechanics of Advanced Materials and Structures, 30(12), 2353–2370. [Google Scholar]

17. Gong, C., Bai, Z., Hu, Y. (2023). Crushing behaviors of novel multi-cell square tubes and its hierarchical multi-cell structures under axial loading. Mechanics of Advanced Materials and Structures, 30(15), 3156–3171. [Google Scholar]

18. Alavi Nia, A., Haddad Hamedani, J. (2010). Comparative analysis of energy absorption and deformations of thin walled tubes with various section geometries. Thin-Walled Structures, 48(12), 946–954. [Google Scholar]

19. Tang, Z., Liu, S., Zhang, Z. (2012). Energy absorption properties of non-convex multi-corner thin-walled columns. Thin-Walled Structures, 51, 112–120. [Google Scholar]

20. Qiu, N., Gao, Y., Fang, J., Feng, Z., Sun, G. et al. (2015). Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases. Finite Elements in Analysis and Design, 104, 89–101. [Google Scholar]

21. Chen, W., Wierzbicki, T. (2001). Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption. Thin-Walled Structures, 39(4), 287–306. [Google Scholar]

22. Pirmohammad, S., Esmaeili Marzdashti, S. (2018). Crashworthiness optimization of combined straight-tapered tubes using genetic algorithm and neural networks. Thin-Walled Structures, 127, 318–332. [Google Scholar]

23. Wu, S., Sun, G., Wu, X., Li, G., Li, Q. (2017). Crashworthiness analysis and optimization of fourier varying section tubes. International Journal of Non-Linear Mechanics, 92, 41–58. [Google Scholar]

24. Liu, W., Lin, Z., He, J., Wang, N., Deng, X. (2016). Crushing behavior and multi-objective optimization on the crashworthiness of sandwich structure with star-shaped tube in the center. Thin-Walled Structures, 108, 205–214. [Google Scholar]

25. Zhang, L., Zhong, Y., Tan, W., Gong, C., Hu, Y. et al. (2022). Crushing characteristics of bionic thin-walled tubes inspired by bamboo and beetle forewing. Mechanics of Advanced Materials and Structures, 29(14), 2024–2039. [Google Scholar]

26. Zhang, X., Cheng, G., Zhang, H. (2009). Numerical investigations on a new type of energy-absorbing structure based on free inversion of tubes. International Journal of Mechanical Sciences, 51(1), 64–76. [Google Scholar]

27. Gupta, N. K., Mohamed Sheriff, N., Velmurugan, R. (2008). Analysis of collapse behaviour of combined geometry metallic shells under axial impact. International Journal of Impact Engineering, 35(8), 731–741. [Google Scholar]

28. Niknejad, A., Tavassolimanesh, A. (2013). Axial compression of the empty capped-end frusta during the inversion progress. Materials & Design, 49, 65–75. [Google Scholar]

29. Mohammadiha, O., Ghariblu, H. (2016). Crush response of variable thickness distribution inversion tubes under oblique loading. Thin-Walled Structures, 109, 159–173. [Google Scholar]

30. Liu, Y., Qiu, X., Yu, T. X. (2018). A theoretical model of the inversion tube over a conical die. Thin-Walled Structures, 127, 31–39. [Google Scholar]

31. Zhang, J., Ye, Y., Zhu, Y., Yuan, H., Qin, Q. et al. (2020). On axial splitting and curling behaviour of circular sandwich metal tubes with metal foam core. International Journal of Solids and Structures, 202, 111–125. [Google Scholar]

32. Guo, H., Zhang, J. (2023). Expansion of sandwich tubes with metal foam core under axial compression. Journal of Applied Mechanics, 90(5), 051008. [Google Scholar]

33. Rezvani, M. J., Souzangarzadeh, H. (2020). Effects of triggering and polyurethane foam on energy absorption of thin-walled circular tubes under the inversion process. Journal of Energy Storage, 27, 101071. [Google Scholar]

34. Chahardoli, S., Shabanzadeh, M., Marashi, S. M. (2022). Introducing a new mechanism for energy absorption through simultaneous inversion-folding process. International Journal of Crashworthiness, 27(1), 92–106. [Google Scholar]

35. Wu, J., Zhang, Y., Zhang, F., Hou, Y., Yan, X. (2021). A bionic tree-liked fractal structure as energy absorber under axial loading. Engineering Structures, 245, 112914. [Google Scholar]

36. Zhang, Y., Wang, J., Wang, C., Zeng, Y., Chen, T. (2018). Crashworthiness of bionic fractal hierarchical structures. Materials & Design, 158, 147–159. [Google Scholar]

37. Huang, F., Zhou, X., Zhou, D., Tao, Y. (2023). Crashworthiness analysis of bio-inspired hierarchical circular tube under axial crushing. Journal of Materials Science, 58(1), 101–123. [Google Scholar]

38. Gong, C., Hu, Y., Bai, Z. (2023). Crashworthiness analysis and optimization of lotus-inspired bionic multi-cell circular tubes. Mechanics of Advanced Materials and Structures, 30(24), 4996–5014. [Google Scholar]

39. Gupta, P. K., Sahu, R. R. (2018). A study on mechanics of collapse of combined geometry metallic shells. Thin-Walled Structures, 126, 48–57. [Google Scholar]

40. Ha, N. S., Pham, T. M., Hao, H., Lu, G. (2021). Energy absorption characteristics of bio-inspired hierarchical multi-cell square tubes under axial crushing. International Journal of Mechanical Sciences, 201, 106464. [Google Scholar]

41. Zhang, Y., Lu, M., Sun, G., Li, G., Li, Q. (2015). On functionally graded composite structures for crashworthiness. Composite Structures, 132, 393–405. [Google Scholar]

42. Deng, X., Qin, S., Huang, J. (2022). Crashworthiness analysis of gradient hierarchical multicellular columns evolved from the spatial folding. Materials & Design, 215, 110435. [Google Scholar]

43. Fu, J., Liu, Q., Liufu, K., Deng, Y., Fang, J. et al. (2019). Design of bionic-bamboo thin-walled structures for energy absorption. Thin-Walled Structures, 135, 400–413. [Google Scholar]

44. Zhang, Y., He, N., Song, X., Chen, T., Chen, H. (2020). On impacting mechanical behaviors of side fractal structures. Thin-Walled Structures, 146, 106490. [Google Scholar]

45. Ha, N. S., Pham, T. M., Chen, W., Hao, H., Lu, G. (2021). Crashworthiness analysis of bio-inspired fractal tree-like multi-cell circular tubes under axial crushing. Thin-Walled Structures, 169, 108315. [Google Scholar]

46. Zheng, G., Wu, S., Sun, G., Li, G., Li, Q. (2014). Crushing analysis of foam-filled single and bitubal polygonal thin-walled tubes. International Journal of Mechanical Sciences, 87, 226–240. [Google Scholar]