A Novel Fractional Dengue Transmission Model in the Presence of Wolbachia Using Stochastic Based Artificial Neural Network

Nomenclature

1  Introduction

Dengue fever is widespread, with an approximated 3.9 billion people at threat and 390 million new dengue infections estimated each year [1]. The female Aedes aegypti and Aedes albopictus mosquitoes are the main vectors spreading dengue infection [2]. The virus that causes dengue has four serotypes: DEN1, DEN2, DEN3, and DEN4, with a probable fifth strain recently discovered [3]. Recent progress has been made in the development of dengue vaccines that provide protection against four strains of the virus. For example, the first vaccine called Dengvaxia has been approved in many countries. Other dengue vaccine candidates like TAK-003 and TV003/TV005 are also in development [4–6].

Dengue is transmitted to people through the bite of a dengue-infected female mosquito. The extrinsic incubation period (EIP) is the time it takes for the dengue virus to multiply in a mosquito’s body before it can reach the salivary glands and be transmitted to a human through a bite. Factors such as temperature, humidity, and rainfall affect the length of the EIP. A comprehensive approach that includes these factors can help to reduce the EIP of dengue virus in mosquitoes and ultimately reduce the transmission of the disease. Only mosquitoes that survive the EIP are capable of transmitting the virus to humans [7].

Wolbachia, a bacterium, is present in certain mosquito species and about 60% of all groups of insects. The potential use of Wolbachia-infected mosquitoes as an alternative approach to control dengue transmission. While vaccines and insecticides are effective, they have limitations such as incomplete protection and adverse effects on the environment. In contrast, Wolbachia-infected mosquitoes have shown promise in reducing dengue transmission in field trials by preventing the virus from being transmitted to humans. This method appears to have fewer environmental impacts and a lower likelihood of insecticide-resistant mosquito populations developing [8]. Wolbachia is transferred through vertical transmission and changes the reproductive phenotype of potentially infected insects, providing the bacterium a reproductive advantage over uninfected insects. Depending on the insect species and Wolbachia strain, the reproductive phenotype displayed might lead to feminization, male death, parthenogenesis, or, most frequently, cytoplasmic incompatibility. Cytoplasmic incompatibility (CI) is the characteristic of Wolbachia that is critical for the invasion of population and perseverance because it provides a reproductive advantage to female mosquitoes that carry Wolbachia [9]. Fractional models can capture the behavior of a system when classical differential equations fail, especially when memory effects or long-range interactions are present. To obtain the results in non-integer order we use the fractional model. Compared to ordinary differential equations, fractional differential equations can describe more complex dynamics and can be formulated in various ways, such as in terms of Caputo or Riemann-Liouville fractional derivatives. Fractional mathematical models can help to better understand the dynamics of Wolbachia transfer and how it affects the invasion of dengue.

The theory of fractional derivatives has a wide range of applications in medicine, finance, engineering, physics, and many other fields [10–12]. Many researchers analyzed a wide range of complicated phenomena based on the fractional derivatives, Kilicman et al. [13] worked on the SIR fractional model for dengue transmission, Jajarmi et al. [14] investigated a fractional mathematical model for dengue fever, Qureshi et al. [15] analyzed the derivatives of fractional-order. Zafar et al. [16] analyzed the fractional model for the Human papillomavirus (HPV). The Caputo derivatives are easier to utilize than the other fractional derivative concepts. The definition of Caputo derivative as defined in [11] is:

Dtαf(t)=1γ(n−α)∫0tfn(s)ds(t−s)α−n+1

where α represents the order of the differential and α∈(n−1,n), n is an integer.

An artificial neural network (ANN) is a method for simulating biological neural activity using mathematics. The essential mathematical principles of an artificial neural network employing an artificial neuron are multiplication, summation, and activation. At the start of the neuron, the input values are multiplied by the specified weights. The sum function, which adds all weighted inputs and biases, is located in the middle layer of the artificial neuron. The summation of previously weighted inputs and bias is sent via an activation function, also known as a transfer function, at the end of an artificial neuron [17].

In ANN, an activation function is utilized to provide nonlinear features. In a neural network, the yn are input variables, wn are the weights, and fn shows the output in Fig. 1. Using a multilayer perceptron (MLP), the number of hidden units can be optimized. The number mentioned in the hidden layer shows how many neurons were utilized in the network [18].

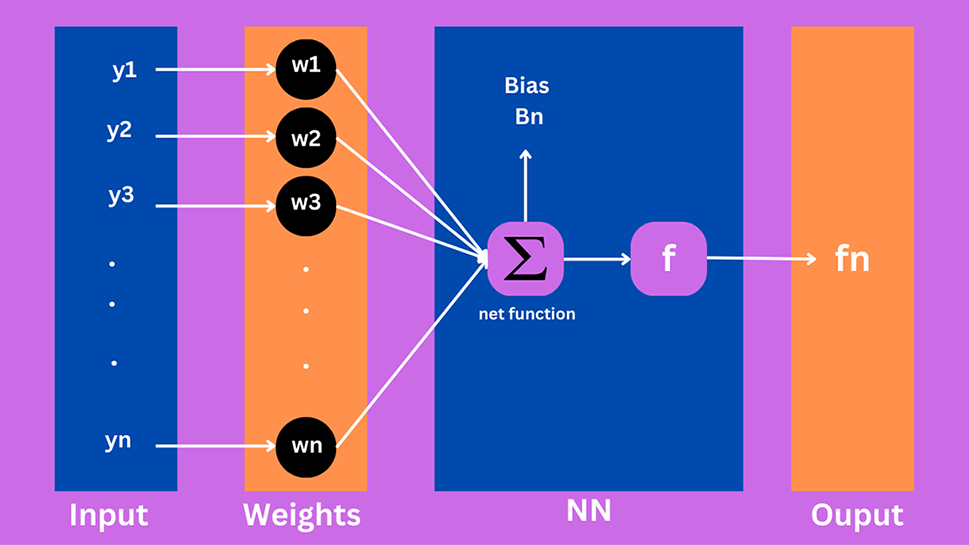
Figure 1: Proposed structure for the neuron

In literature, many fractional-order mathematical models along with artificial neural network approach models for real-world problems have been proposed utilizing the ANNs approach. Pornsawad et al. [19] analyze fractional-order mathematical differential equations for the backward heat problems by developing neural networks procedure. Qu et al. [20] analyzed the stability of the Caputo fractional-order derivative by utilizing the cellular neural network approach. Sabir et al. [21] analyzed the fractional order mathematical model of computer viruses by employing the Levenberg approach. Ghazizadeh et al. [22] studied the fractional order inverse problem with the estimation of relaxation time by utilizing the neural network approach. Souayeh et al. [23] utilized the Bayesian regularization approach to understand the Allee effect on the food chain supply. Umar et al. [24] investigated the neural network approach for analyzing the behavior of the nonlinear coronavirus model. Noinang et al. [25] worked on a system of magnetohydrodynamic (MHD) past over an inclined plate by utilizing the artificial neural network approach. Zhuang et al. [26] analyzed parameter estimation of inverse problem heat conduction problem in a composite medium utilizing Levenberg-Marquardt. Sabir et al. [27] studied nonlinear singular second-order delay differential equation utilizing the ANN approach.

The aim of this work was to develop and numerically solve a fractional dengue transmission model (FDTM) with Wolbachia using neural network. In the present model, we incorporated Wolbachia-infected mosquitoes along with Wolbachia-free mosquitoes and humans. The impact of vertical transmission probability on the persistence of dengue transmission in humans and mosquitoes has been analyzed using the Levenberg-Marquardt neural network (LM-NN) approach. The convergence and accuracy of the proposed LM-NN technique have been checked through mean square error, regression analysis plots, and state transition results. The results obtained from the proposed LM-NN approach for FDTM have been compared with the reference solutions obtained using the Adams-Bashforth-Moulton (ABM) method and they were found to be in good agreement.

2  Mathematical Model

A fractional dengue transmission model in the presence of Wolbachia is developed to observe the dynamics of dengue between humans and mosquitoes. The model consists of 12 compartments, namely, susceptible human (Sh), exposed human (Eh), infectious (Ih), recovered human (Rh), susceptible Wolbachia-infected mosquitoes Sw, Wolbachia-infected mosquitoes that are exposed but not yet infected Ew, Wolbachia-infected mosquitoes that are Infectious to dengue virus Iw, and the aquatic stage (eggs, larvae, pupae) of the Wolbachia-infected mosquitoe Aw. Similarly, Wolbachia-free mosquito compartments are denoted with Sn, En, In, and An. The subscript w stands for Wolbachia-carrying mosquitoes, subscript n represents Wolbachia-free mosquitoes, and the subscript h denotes the human classes. The death rates of Wolbachia-carrying and Wolbachia-free mosquitoes are denoted by μw and μn, respectively. Wolbachia-infected mosquitoes have a higher death rate than that of Wolbachia-free mosquitoes. This leads to reduced dengue virus load in Wolbachia-carrying mosquitoes and a lower probability of transmission from Wolbachia-carrying mosquitoes to humans than for Wolbachia-free mosquitoes. The maturation rate of Wolbachia-carrying aquatic mosquitoes to become adult Wolbachia-carrying mosquitoes is denoted with ηρw, where η denotes the probability of becoming Wolbachia-infected mosquitoes and 1−η is the probability for the Wolbachia-free mosquitoes.

The reproduction rate of Wolbachia-carrying and Wolbachia-free mosquitoes are denoted by ϕw and ϕn, respectively. It has been observed that Wolbachia can cause a bendy proboscis, which inhibits feeding and results in a reduction in the biting rate. This decreased biting rate also accounts for the fact that some Wolbachia-carrying mosquitoes are efficiently not infected by dengue because of the viral replication limitation, resulting in a lower transmission rate from humans (i.e., βwτn<βnτn) [28].

The model flowchart is given in Fig. 2.

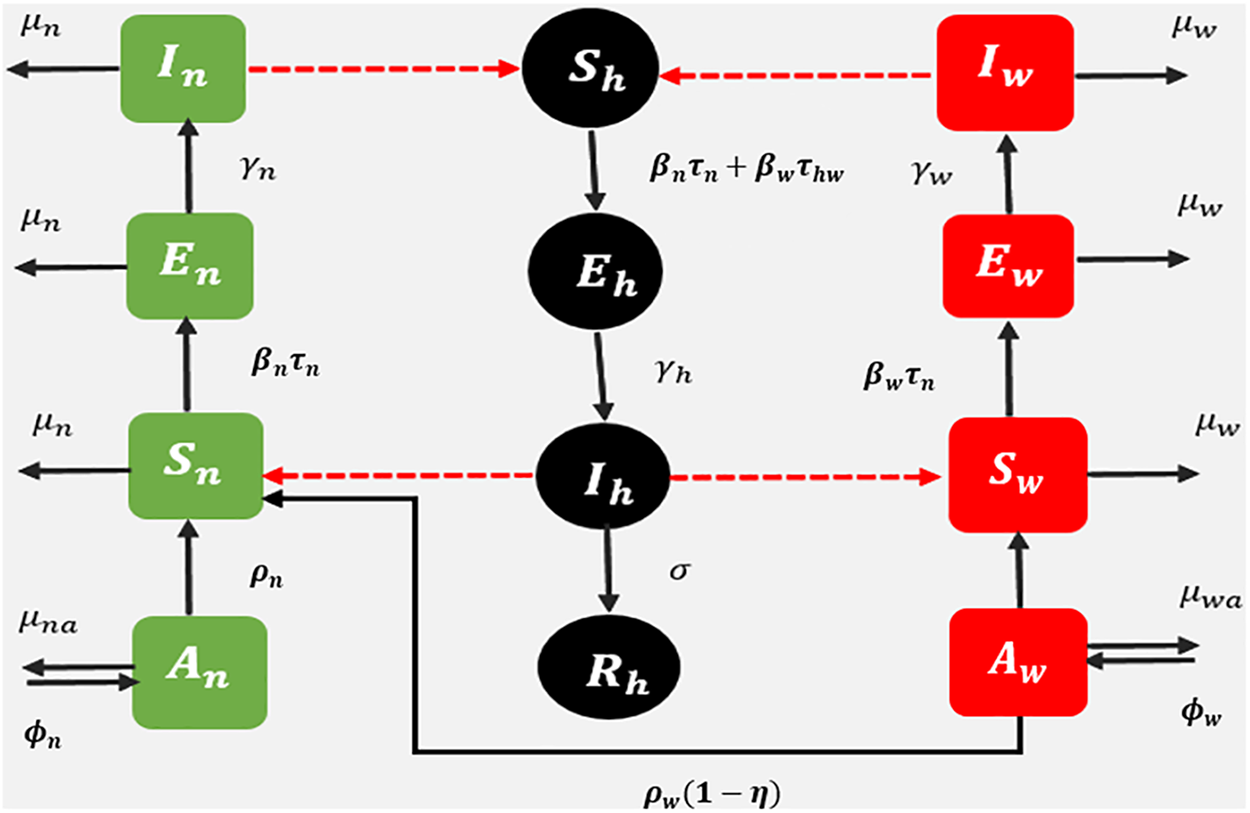
Figure 2: Schematic diagram: fractional dengue transmission model (FDTM) when Wolbachia-carrying and Wolbachia-free mosquitoes are present. Dashed lines represent disease transmission and solid lines show population progression

All the parameters that appear in model (1) are defined in Table 1. The FDTM model in the presence of Wolbachia is given below:

{DtαSh=μ−βnτnLInSh−βwτhwLIwSh−μSh,DtαEh=βnτnLInSh+βwτhwLIwSh−γhEh−μEh,DtαIh=γhEh−σIh−μIh,DtαRh=σIh−μRh,DtαAn=ϕn(Sn+En+In)22(Sn+En+In+Sw+Ew+Iw)(1−(An+Aw))−(ρn+μna)An,DtαSn=ρnAn2+(1−η)ρwAw2−(βnτnIh+μn0)Sn,DtαEn=(βnτnIn)Sn−(γn+μn0)En,DtαIn=γnEn−μn0In,DtαAw=ϕwSw+Ew+Iw2(1−(An+Aw))−(ρw+μwa)Aw,DtαSw=ρwηAw2−(βwτnIh+μw0)Sw,DtαEw=βwτnIhSw−(γw+μw0)Ew,DtαIw=γwEw−μw0Iw.(1)

3  Methodology

In this section, we explained the proposed Levenberg-Marquardt neural network (LM-NN) method that is used to solve the FDTM model (1). The Pseudocode of the proposed LM-NN technique is also given in Table 2. The construction of neuron is given in Fig. 3. The details of steps involved in utilizing the LM-NN technique to solve the FDTM model in the presence of Wolbachia given in Fig. 4.

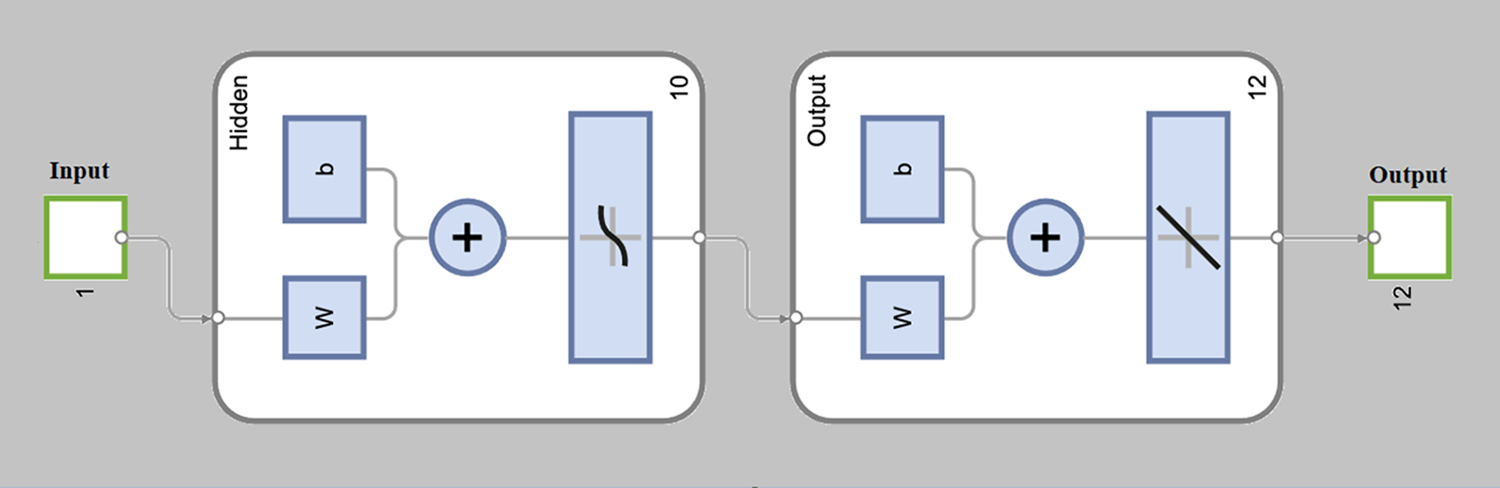
Figure 3: Construction of single neuron

Figure 4: Flowchart for solving the FDTM model in the presence of Wolbachia using the proposed LM-NN technique

The novel properties of the proposed research work is as follows:

•   Levenberg-Marquardt neural network (LM-NN) is based on a backpropagation process with a novel methodology or design is created for solving the fractional-order model (1) dealing with Wolbachia carrying and Wolbachia-free mosquitoes with humans.

•   For the fractional dengue transmission model (FDTM), a stochastic-based back propagated numerical Levenberg-Marquardt neural network (LM-NN) procedure is utilized to obtain the best-approximated solution.

•   Adams-Bashforth-Moulton (ABM) numerical method has been employed to generate the reference dataset.

•   Numerical results obtained from the proposed LM-NN technique show good agreement with the reference solutions achieved using the ABM method.

•   The reliability and consistency of the proposed LM-NN approach are investigated through statistical analysis.

•   The best performance of the proposed LM-NN technique is analyzed using regression analysis (RA) plots, mean square error (MSE) graphs, fitness curves, and state transitions (STs) for different classes.

•   Error analysis performed for different classes of FDTM is used to check the accuracy of the proposed LM-NN technique.

4  Numerical Simulations

This section describes the numerical simulations based on the outcomes of three scenarios of the nonlinear fractional dengue transmission model (FDTM) performed with the suggested LM-NN approach. The simulations were conducted on scenarios with only Wolbachia-free mosquitoes present, both Wolbachia-free and Wolbachia-carrying mosquitoes present, and only Wolbachia-carrying mosquitoes present. The mathematical structure for each case is given as:

4.1 Case-1: Only Wolbachia-Free Mosquitoes Persist

For this case, we consider the following values of the parameters α=0.4, η=0.6, μ=1(70)(365), τn=0.2614, τw=0.2614, τhw=0.1307, βn=0.63, βw=0.5985, μn0=1/14, σ=1/5, ρw=1/10, ρn=1/10, ϕn=1.25, ϕw=1.1875, γw=1/10, γh=1/5.5, γn=1/10, μwa=1/14, μna=1/14, μw0=1/14, L = 3, with initial condition Sh(0)=1−Eh(0)−Ih(0)−Rh(0), Eh(0)=2(1.5×105), Ih(0)=0, Rh(0)=0, Sn(0)=0.1326, En(0)=0, In(0)=0, An(0)=0.0138, Sw(0)=0.9400, Ew(0)=0, Iw(0)=0, Aw(0)=0.7535, then the resulting model (1) takes the following form:

{Dt0.4Sh=1(70)(365)−(0.63)(0.2614)(3)InSh−(0.63)(0.1307)(3)IwSh−1(70)(365)Sh,Dt0.4Eh=(0.63)(0.2614)(3)InSh+(0.5985)(0.1307)(3)IwSh−(1/5.5)Eh−1(70)(365)Eh,Dt0.4Ih=(1/5.5)Eh−(1/5)Ih−1(70)(365)Ih,Dt0.4Rh=(1/5)Ih−1(70)(365)Rh,Dt0.4An=(1.25)(Sn+En+In)22(1−(An+Aw))−(1/10+1/14)An,Dt0.4Sn=(1/10)An2+(1−0.6)(1/10)Aw2−((0.63)(0.2614)Ih+(1/14))Sn,Dt0.4En=((0.63)(0.2614)In)Sn−(1/10+1/14)En,Dt0.4In=(1/10)En−(1/14)In,Dt0.4Aw=(1.1875)(Sw+Ew+Iw)2(1−(An+Aw))−(1/10+1/14)Aw,Dt0.4Sw=(1/10)(0.8)Aw2−((0.5985)(0.2614)Ih+114)Sw,Dt0.4Ew=(0.5985)(0.2614)IhSw−(1/10+114)Ew,Dt0.4Iw=(1/10)Ew−114Iw.

4.2 Case-2: Both Type of Mosquitoes Wolbachia-Free and Wolbachia-Carrying Persist

For this case, the parameter values being examined are α=0.6, η=0.8, μ=1(70)(365), τn=0.2614, τw=0.2614, τhw=0.1307, βn=0.63, βw=0.5985, μn0=1/14, σ=1/5, ρw=1/10, ρn=1/10, ϕn=1.25, ϕw=1.1875, γw=1/10, γh=1/5.5, γn=1/10, μwa=1/14, μna=1/14, μw0=1/14, L = 3, with initial condition Sh(0)=1−Eh(0)−Ih(0)−Rh(0), Eh(0)=2(1.5×105), Ih(0)=0, Rh(0)=0, Sn(0)=0.1326, En(0)=0, In(0)=0, An(0)=0.0138, Sw(0)=0.9400, Ew(0)=0, Iw(0)=0, Aw(0)=0.7535, then the model (1) becomes:

{Dt0.6Sh=1(70)(365)−(0.63)(0.2614)(3)InSh−(0.5985)(0.1307)(3)IwSh−1(70)(365)Sh,Dt0.6Eh=(0.63)(0.2614)(3)InSh+(0.5985)(0.1307)(3)IwSh−(1/5.5)Eh−1(70)(365)Eh,Dt0.6Ih=(1/5.5)Eh−(1/5)Ih−1(70)(365)Ih,Dt0.6Rh=(1/5)Ih−1(70)(365)Rh,Dt0.6An=(1.25)(Sn+En+In)22(Sn+En+In+Sw+Ew+Iw)(1−(An+Aw))−(1/10+1/14)An,Dt0.6Sn=(1/10)An2+(1−0.8)(1/10)Aw2−((063)(0.2614)Ih+(1/14))Sn,Dt0.6En=((0.63)(0.2614)In)Sn−(1/10+1/14)En,Dt0.6In=(1/10)En−(1/14)In,Dt0.6Aw=Rw(Sw+Ew+Iw)2(1−(An+Aw))−(1/10+1/14)Aw,Dt0.6Sw=(1/10)(0.8)Aw2−((0.5985)(0.2614)Ih+114)Sw,Dt0.6Ew=(0.5985)(0.2614)IhSw−(1/10+114)Ew,Dt0.6Iw=(1/10)Ew−114Iw.

4.3 Case-3: Only Wolbachia-Carrying Mosquitoes Persist

Similarly, after putting the values of parameters in the model (1) α=0.8, η=1, μ=1(70)(365), τn=0.2614, τw=0.2614, τhw=0.1307, βn=0.63, βw=0.5985, μn0=1/14, σ=1/5, ρw=1/10, ρn=1/10, ϕn=1.25, ϕw=1.1875, γw=1/10, γh=1/5.5, γn=1/10, μwa=1/14, μna=1/14, μw0=1/14, L = 3, with initial condition Sh(0)=1−Eh(0)−Ih(0)−Rh(0), Eh(0)=2(1.5×105), Ih(0)=0, Rh(0)=0, Sn(0)=0.1326, En(0)=0, In(0)=0, An(0)=0.0138, Sw(0)=0.9400, Ew(0)=0, Iw(0)=0, Aw(0)=0.7535, then the model (1) is expressed in the following form:

{Dt0.8Sh=1(70)(365)−0.6302614(3)InSh−(0.5985)(0.1307)(3)IwSh−1(70)(365)Sh,Dt0.8Eh=(0.63)(0.2614)(3)InSh+(0.5985)(0.1307)(3)IwSh−(1/5.5)Eh−1(70)(365)Eh,Dt0.8Ih=(1/5.5)Eh−(1/5)Ih−1(70)(365)Ih,Dt0.8Rh=(1/5)Ih−1(70)(365)Rh,Dt0.8An=(1.25)(Sn+En+In)22(Sn+En+In+Sw+Ew+Iw)−(1/10+1/14)An,Dt0.8Sn=(1/10)An2+(1−1)(1/10)Aw2−((0.5985)(0.2614)Ih+1/14)Sn,Dt0.8En=((0.63)(0.2614)In)Sn−(1/10+1/14)En,Dt0.8In=(1/10)En−(1/14)In,Dt0.8Aw=Rw(Sw+Ew+Iw)2(1−(An+Aw))−(1/10+1/14)Aw,Dt0.8Sw=(1/10)(1)Aw2−((0.5985)(0.2614)Ih+114)Sw,Dt0.8Ew=(0.5985)(0.2614)IhSw−(1/10+114)Ew,Dt0.8Iw=(1/10)Ew−114Iw.

The numerical results of the FDTM model is obtained through LM-NN technique which is implemented in MATLAB using the built-in package ‘nftool’ together with 10 neurons. To train the model using the Levenberg method, we used 80% of the data for training purposes, 10% of the data is used for validation and the remaining 10% of the data is used for testing. Fig. 3 shows the structure of a single neuron used for the best solution of the FDTM. The MSE performance for training, validation, and testing along with the number of epochs and gradient are presented in Table 3.

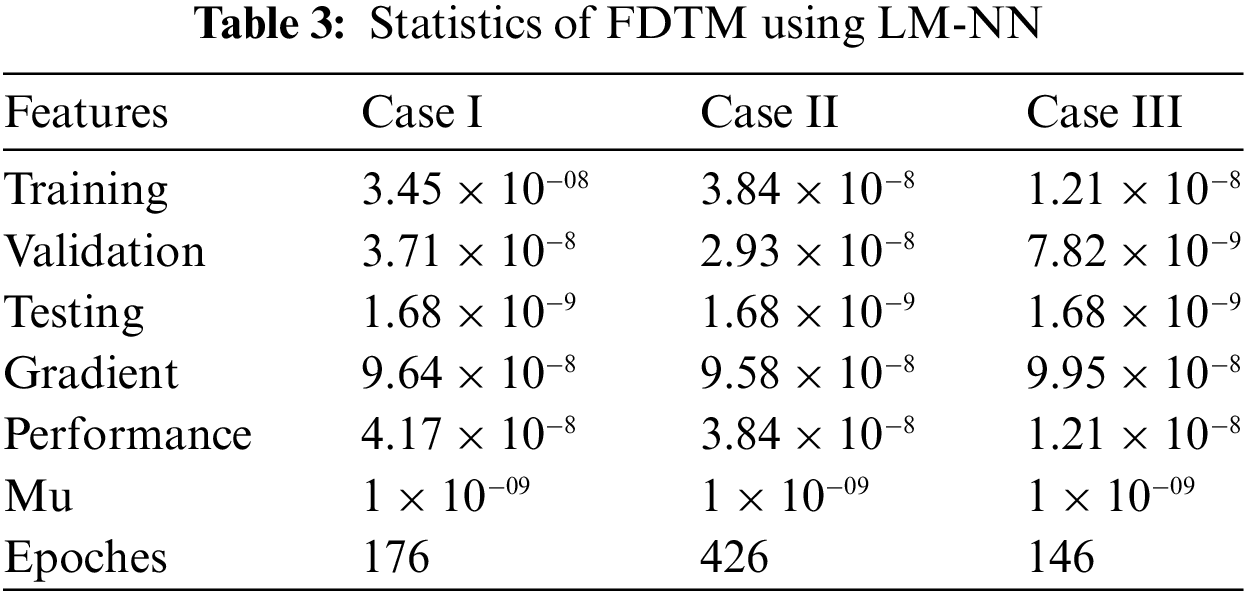
The mean square error results obtained from the proposed neural network approach for each scenario of the FDTM are presented in Fig. 5. At epochs 176, 426, and 146 the mean square error is very small and the best performance values are 9.90×10−09, 5.21×10−09 and 5.29×10−09, respectively.

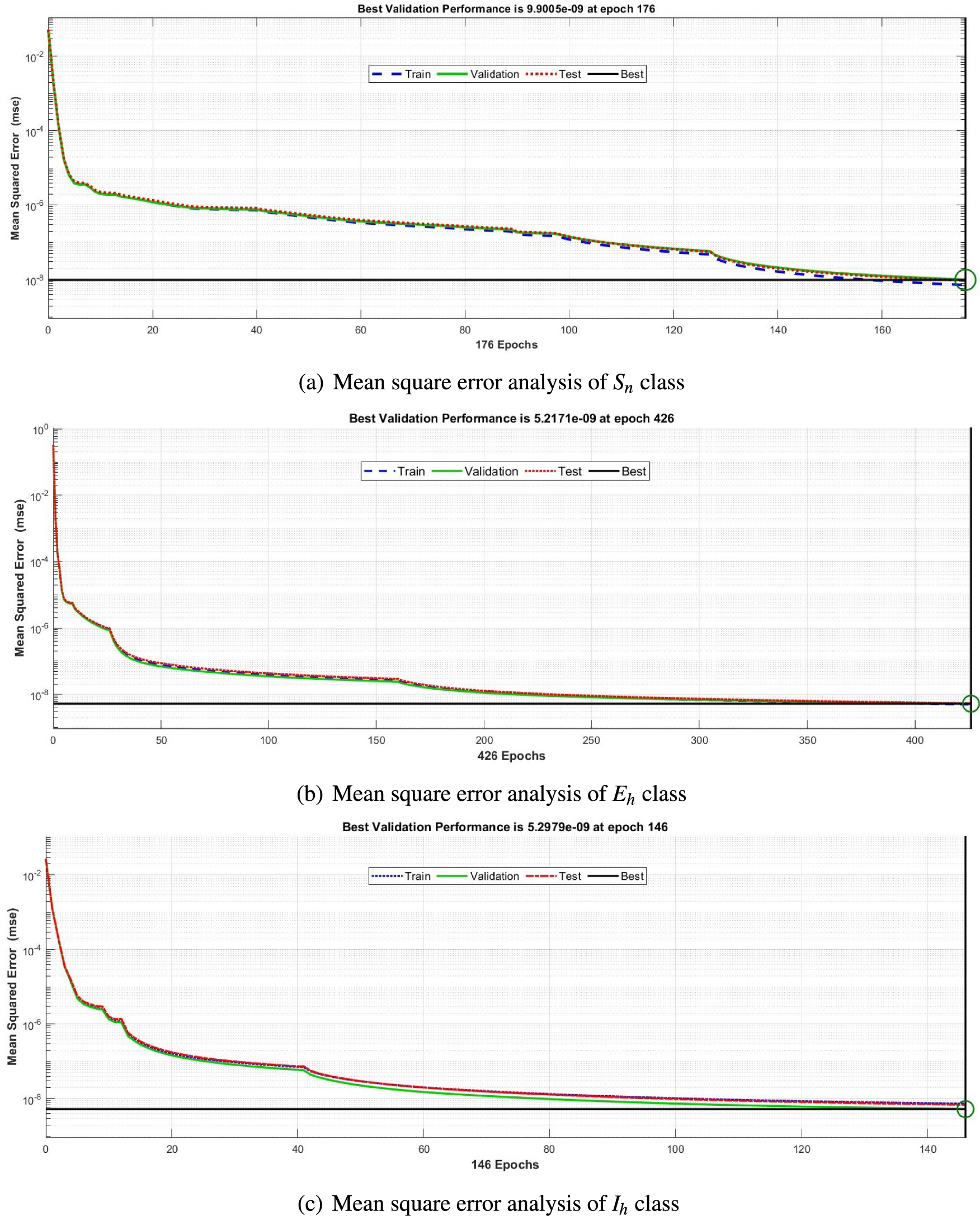
Figure 5: Mean square error analysis for FDTM

Figs. 6–8 present the graphs of gradient, Mu, and validation performances of the proposed LM-NN to solve the fractional dengue transmission model (FDTM). The values of gradient, and Mu, for Case I are 9.7776×10−08, 1×10−11, for Case II the values range 9.9631×10−08, 1×10−10, and for Case III these values are 9.6248×10−08, 1×10−10. These values of gradient, Mu, and validation performances indicate the convergence and accuracy of the proposed LM-NN to solve the fractional dengue transmission model (FDTM). The fitting curve values for each case of the FDTM model are also shown in Figs. 9–11. These graphs show good agreement between the solution obtained from LM-NN and the reference solution.

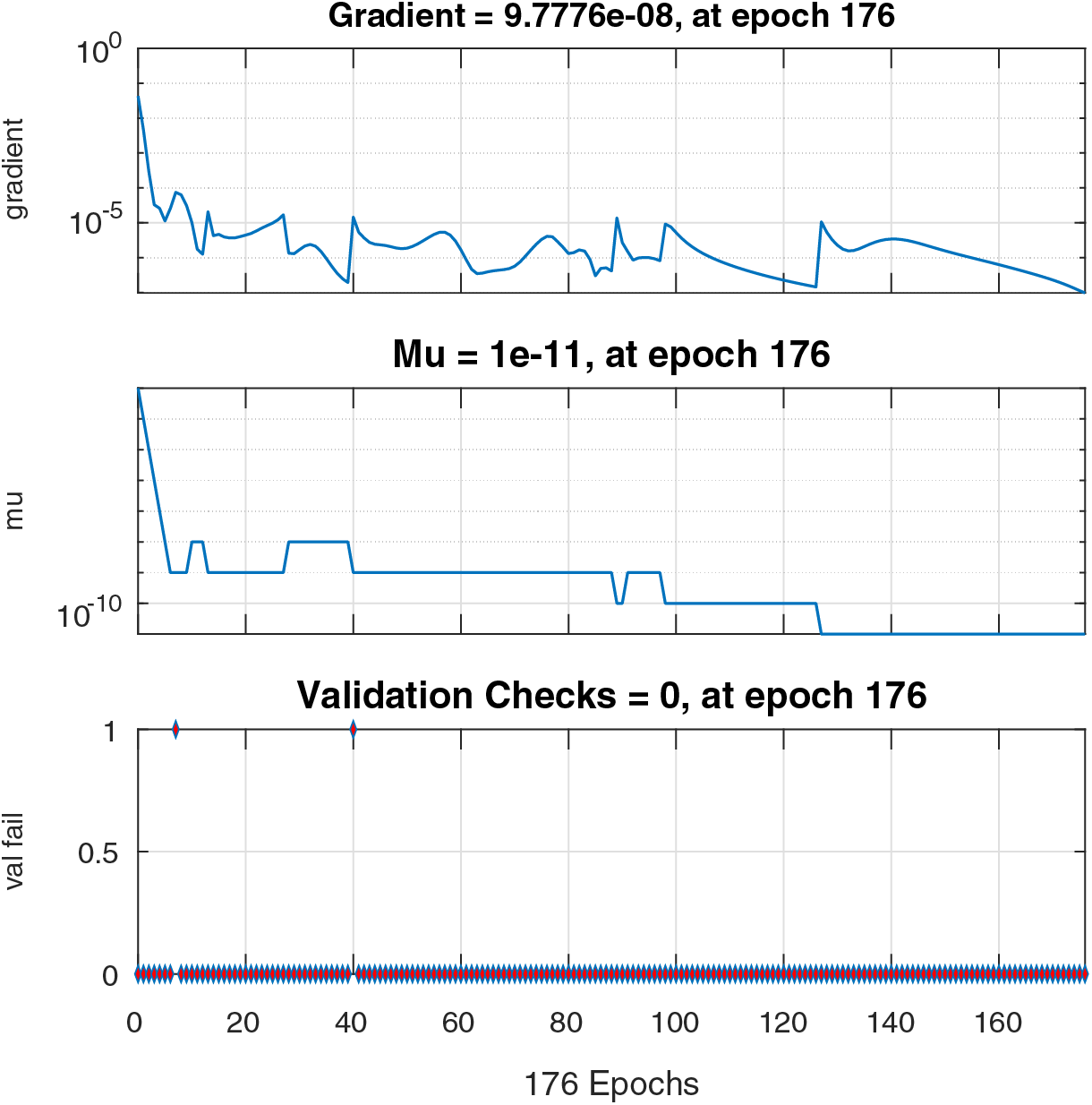
Figure 6: Case I: state transitions for FDTM

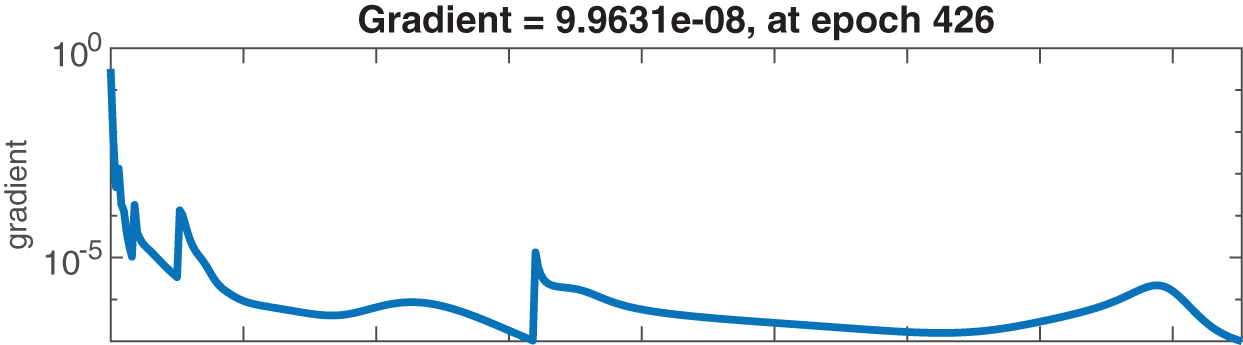
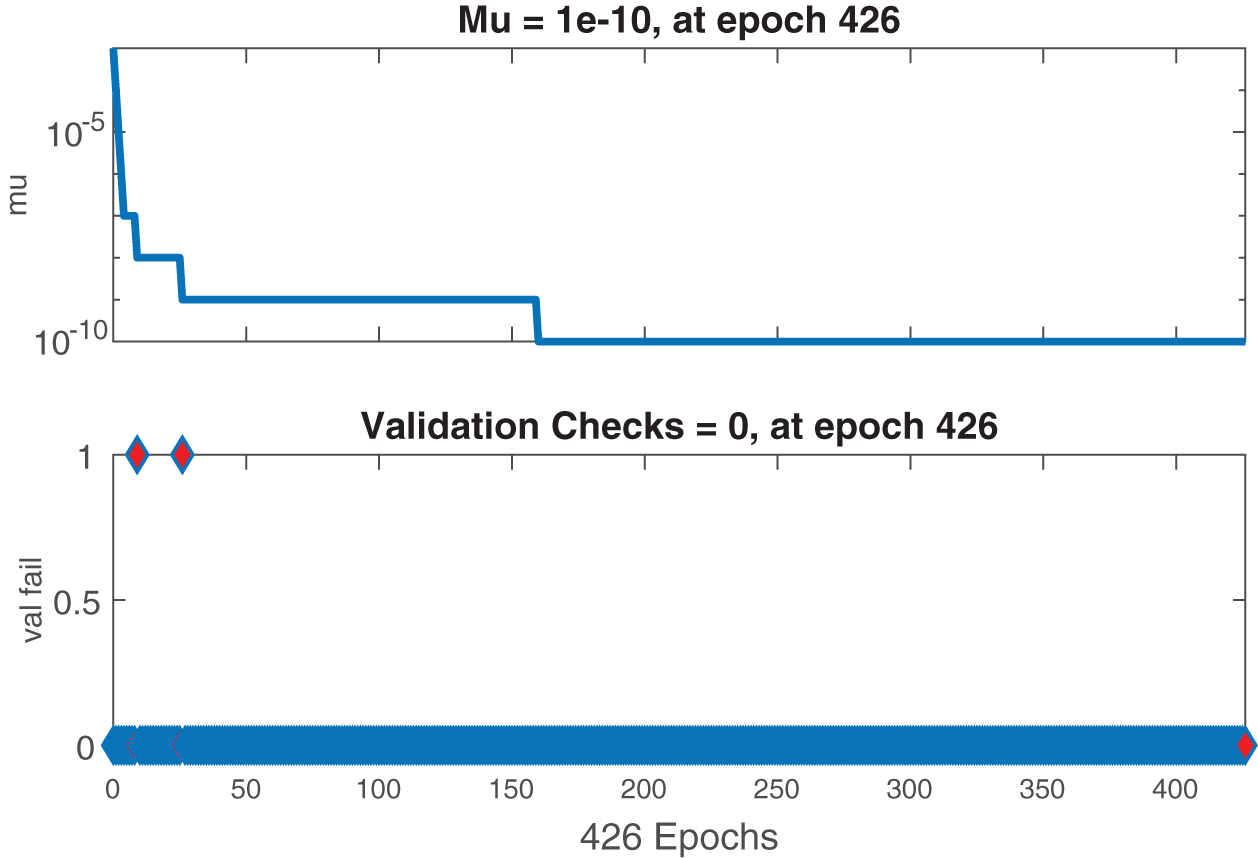
Figure 7: Case II: state transitions for FDTM

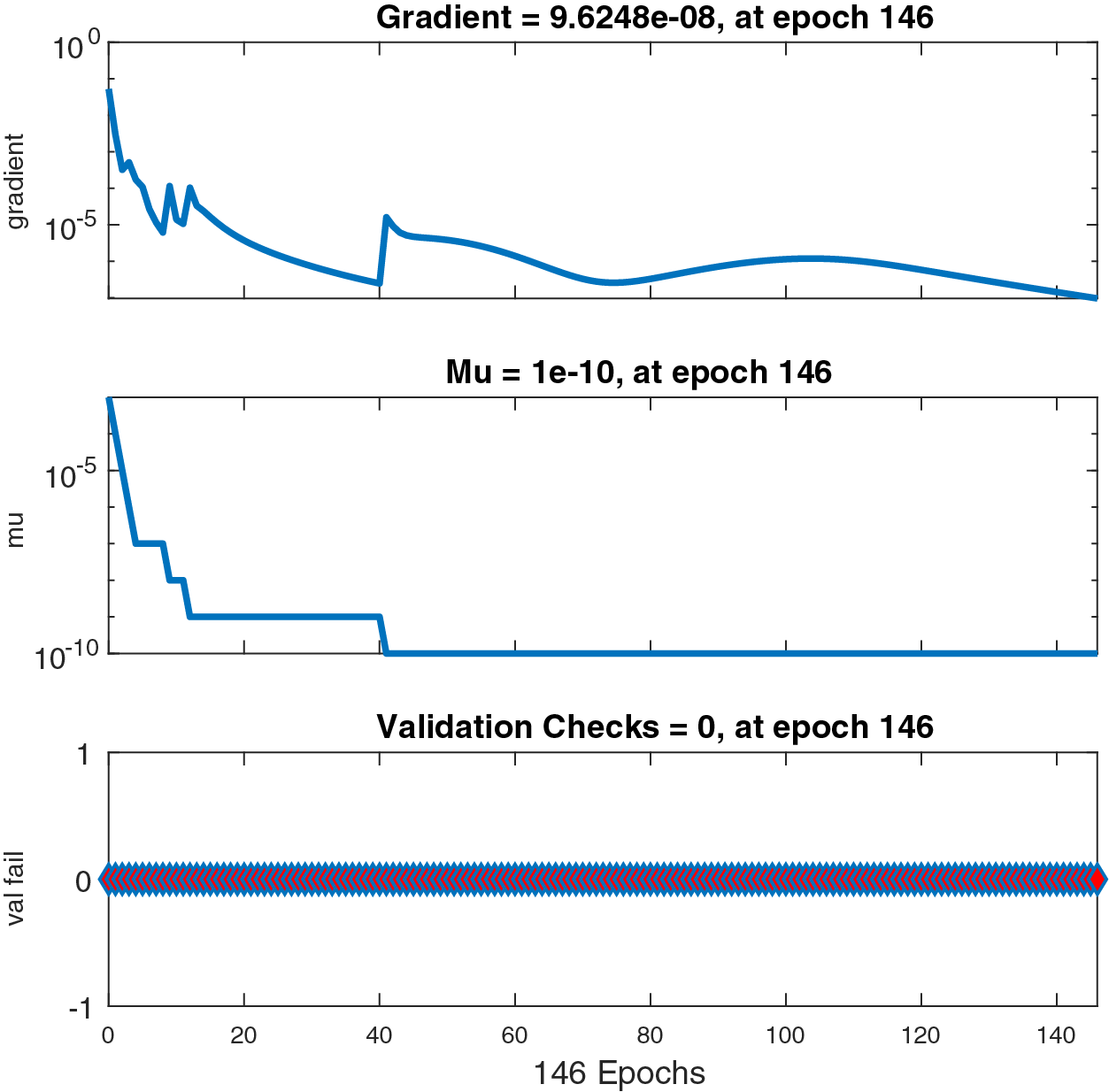
Figure 8: Case III: state transitions for FDTM

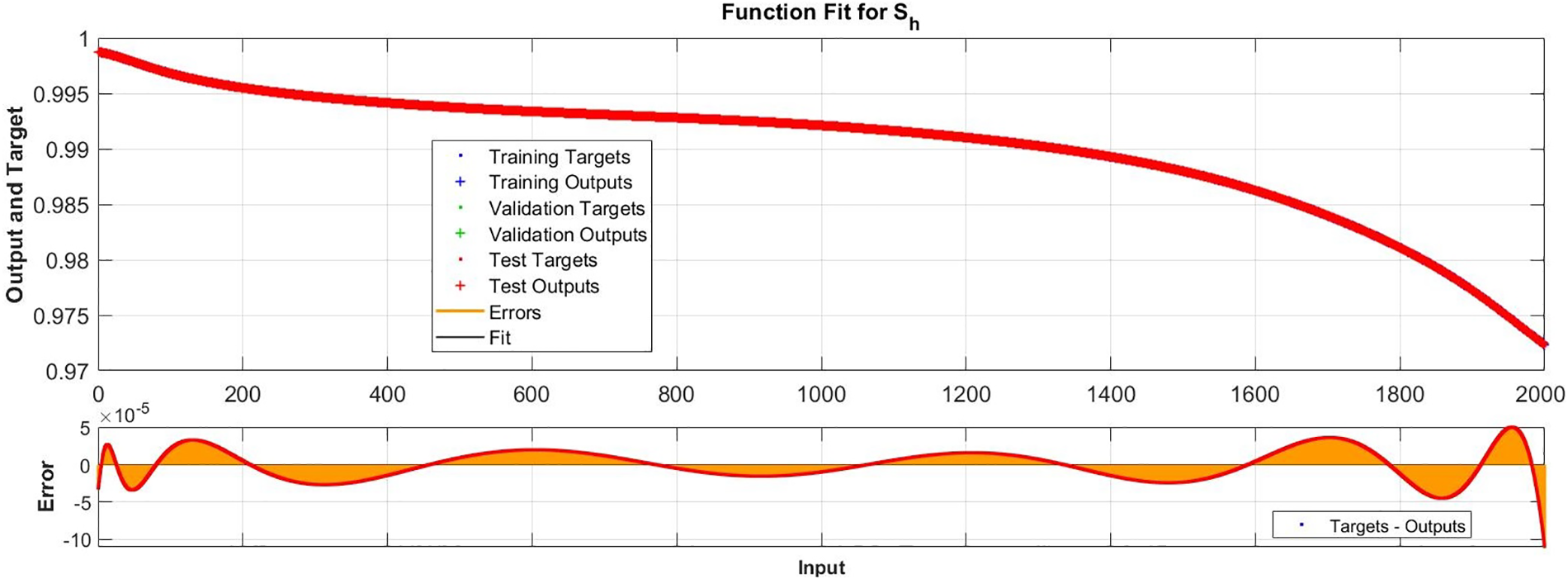
Figure 9: Case I: comparison of the outcomes through LM-NN for solving FDTM

Figure 10: Case II: comparison of the outcomes through LM-NN for solving FDTM

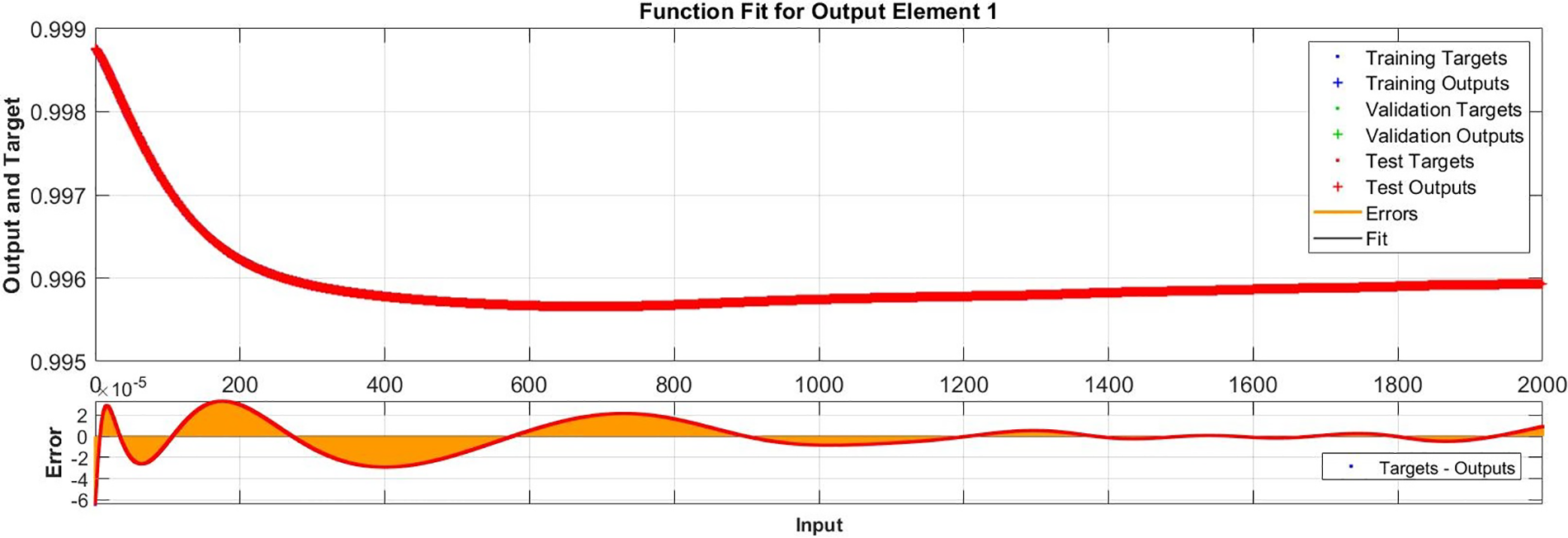
Figure 11: Case III: comparison of the outcomes through LM-NN for solving FDTM

Regression is a graphical representation of the precision of the LM-NN solution to the reference values for training, validation, and testing points separately. A straight line represents an available reference solution in these plots, while dots or small circles represent LM-NN results. The numerical value of regression can also be used to assess the computation’s accuracy and precision. R = 1 indicates that the LM-NN solution is very near to the reference values, whereas R = 0 indicates that the relationship between the reference and the LM-NN solution is very weak. The regression plots are shown in Figs. 12–14. From the regression plots, we observe that R value is 1 for all the three different cases. The testing, validation, and training plots demonstrate that the developed LM-NN technique is efficient for solving the FDTM model.

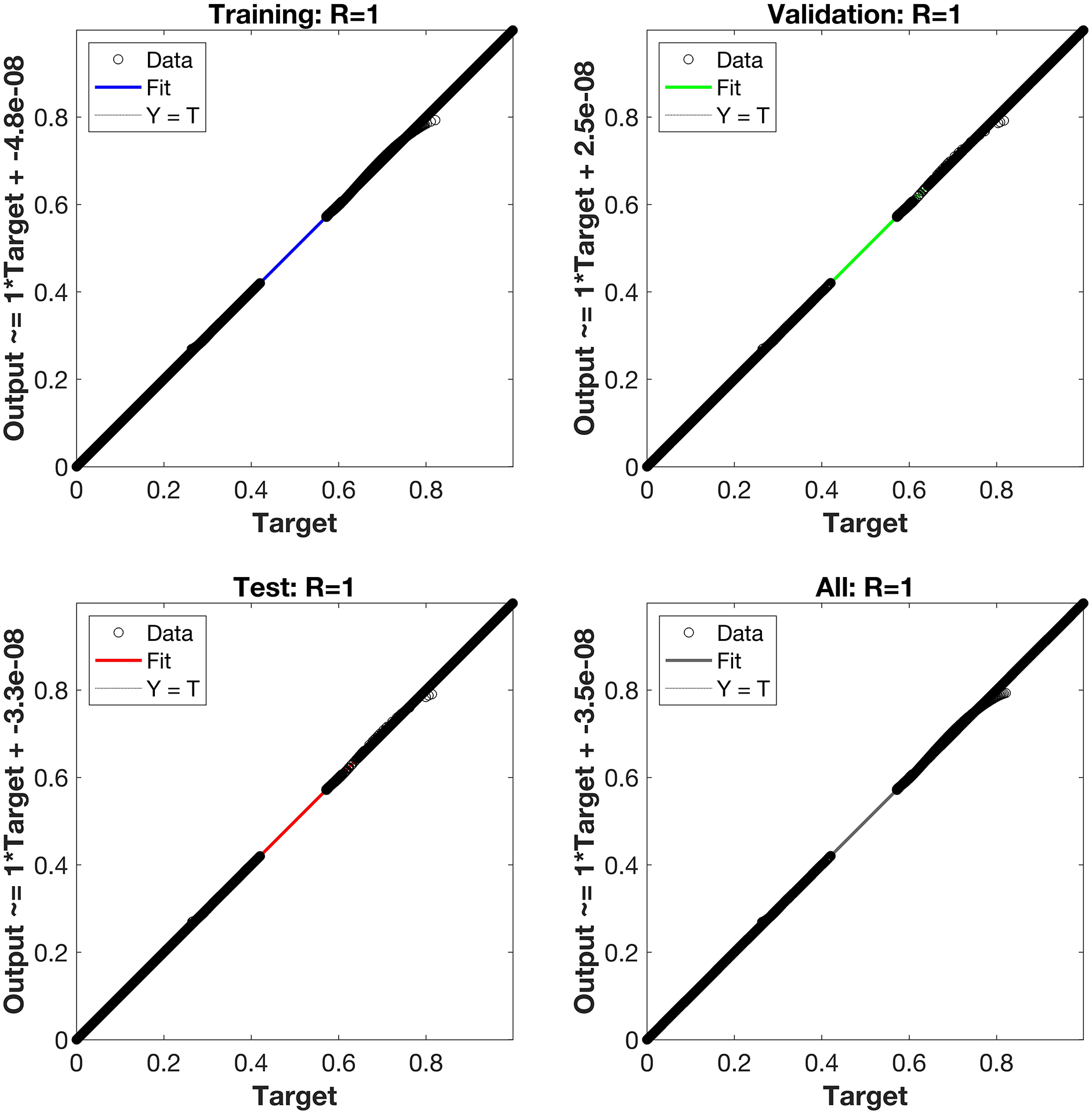
Figure 12: Case I: regression plots utilizing the LM-NN solving the FDTM

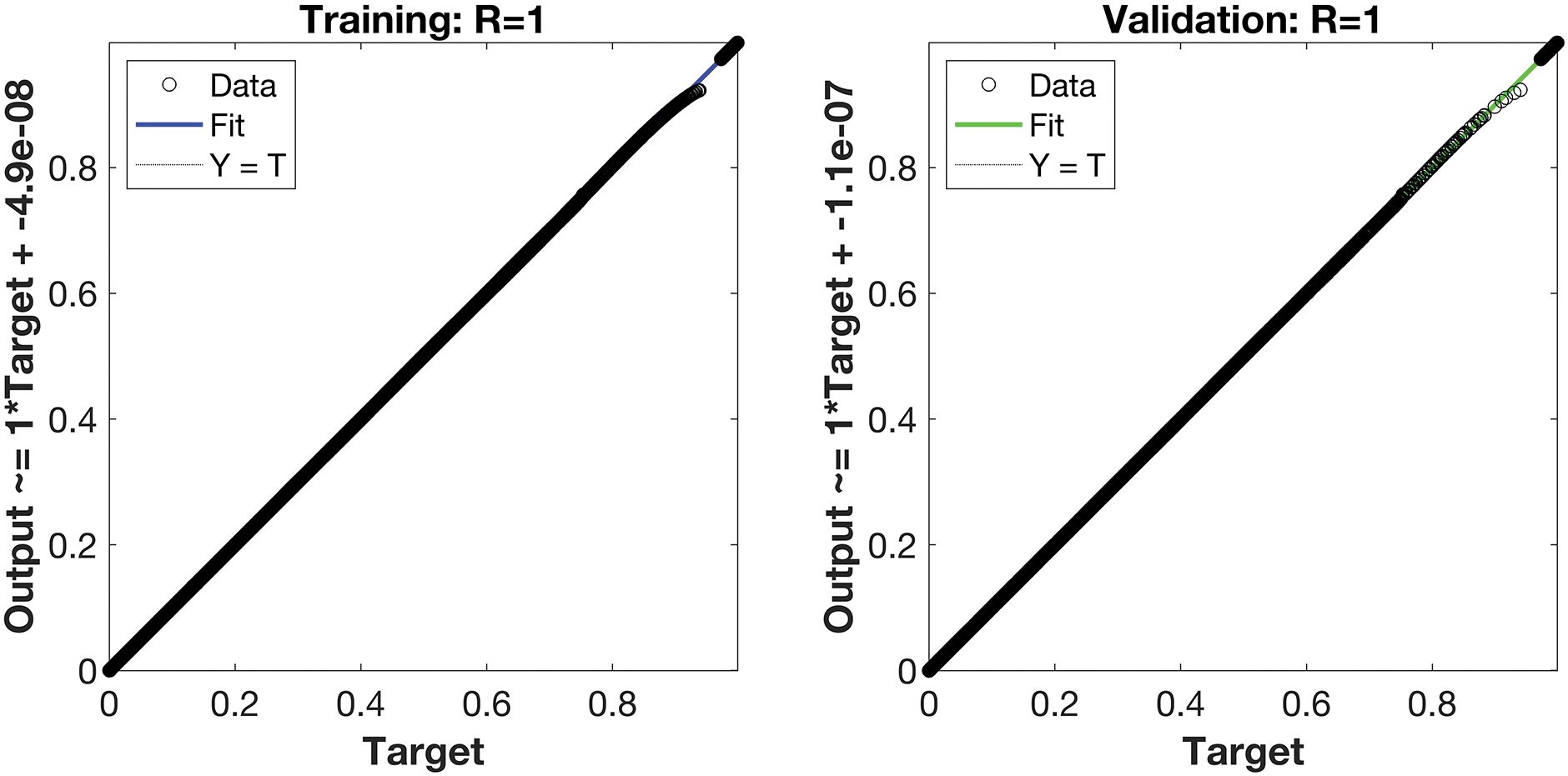
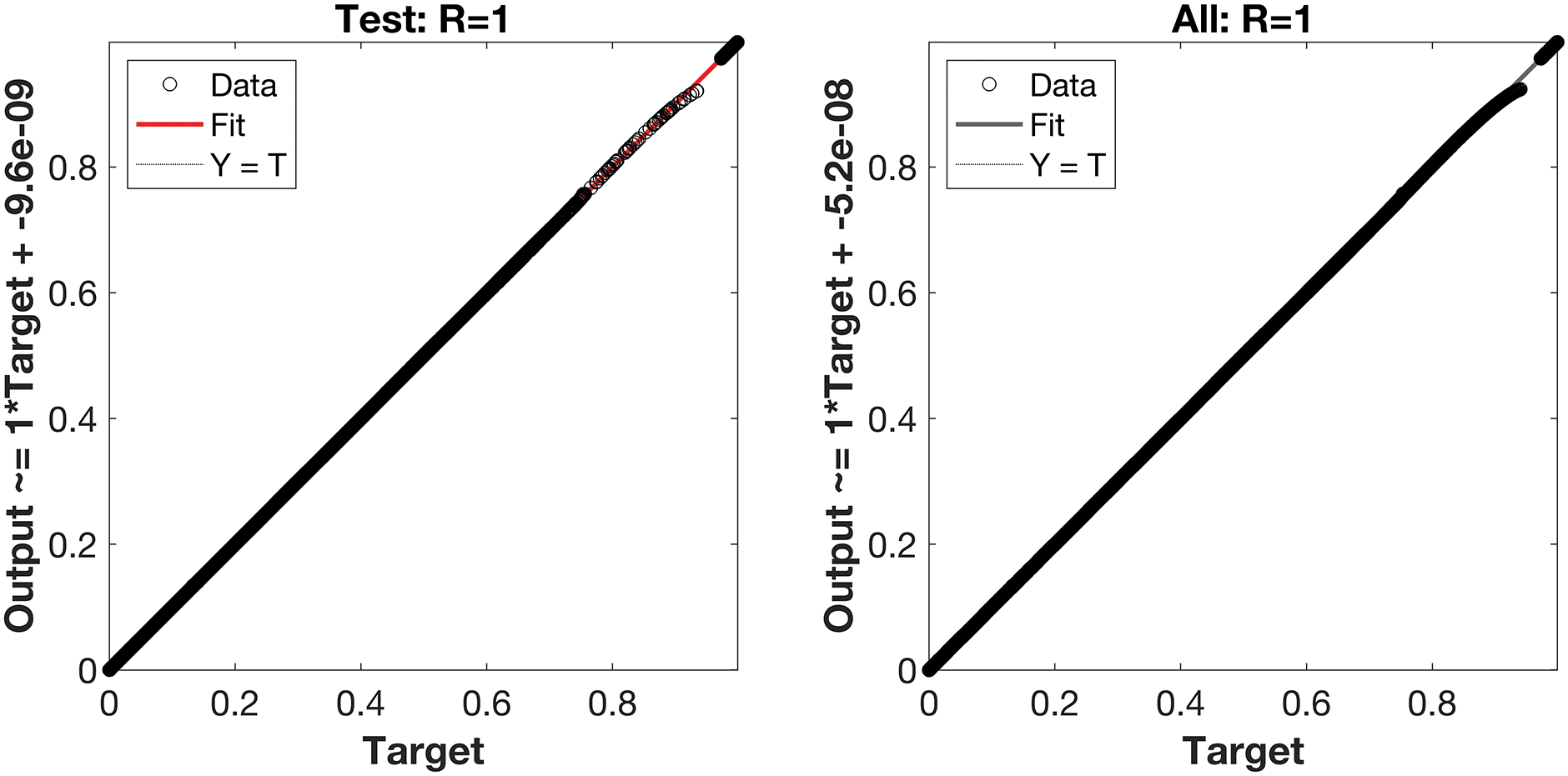
Figure 13: Case II: regression plots utilizing the LM-NN solving the FDTM

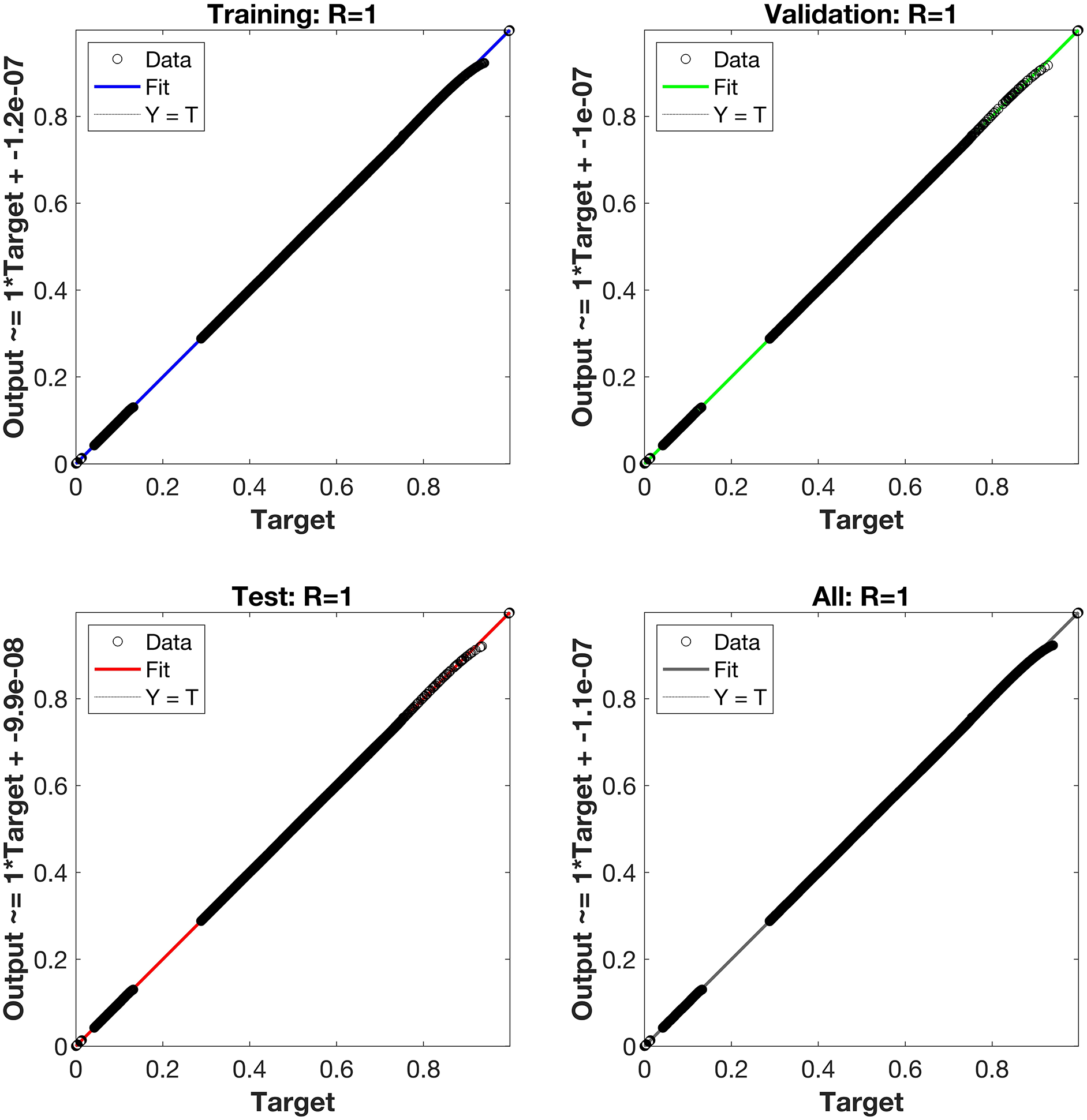
Figure 14: Case III: regression plots utilizing the LM-NN solving the FDTM

Fig. 15 illustrates the comparison of the numerical results of model (1) using the ABM approach to the solution of the FDTM using the LM-NN technique. Fig. 15a shows the comparison of the Sn class for three different cases, similarly Figs. 15b–15d represent the comparison of the classes Sw, Eh and Ih, respectively. Fig. 15 shows that the numerical results obtained using the LM-NN technique lie on the target solution lines. The perfect matching of the results shows that the proposed stochastic approach for solving the FDTM is accurate and reliable. The Fig. 15 shows the impact of varying levels of vertical transmission of Wolbachia on mosquito populations and dengue transmission. In case-1 and case-2, of Fig. 15a populations of Wolbachia-free mosquitoes persist, while in case-3, populations of Wolbachia-free mosquitoes decrease with increasing vertical transmission probability of Wolbachia. Fig. 15b shows the population of Wolbachia-carrying mosquitoes increases with increasing vertical transmission probability of Wolbachia and decreases with decreasing vertical transmission probability. Fig. 15c has shown that when η=0.6 ( case-1), the number of exposed humans are high. Since for η=0.6, only Wolbachia-uninfected mosquitoes persist, so the number of exposed humans is high compared to when we have Wolbachia-free along with Wolbachia-infected (case-2). The number of exposed humans decreases significantly when η=1 (case-3). Fig. 15d shows the rate of dengue infection in humans is highest at a vertical transmission probability of 0.6, but decreases when the vertical transmission (η) probability is grows up. For example in case-2 vertical transmission probability is 0.8 and in case-3 vertical transmission probability is 1, the dengue infection dropped down, respectively.

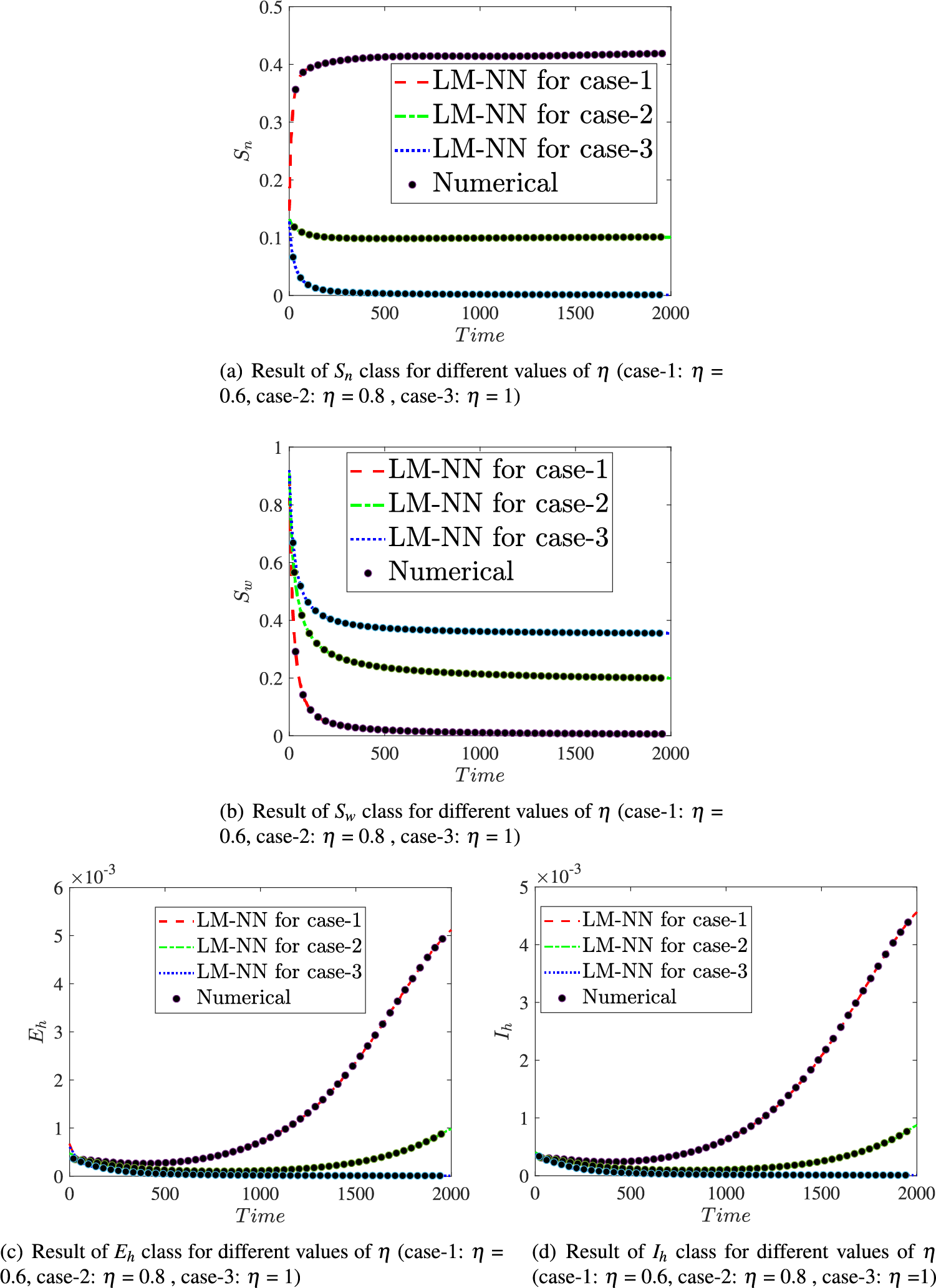
Figure 15: Comparison values of the presented LM-NN and the reference solutions for solving the FDTM

Error plots were generated for three different scenarios involving the classes Sn, Eh, and Ih. The error analysis used a reference dataset (obtained from the Adams-Bashforth-Moulton method) and the best-approximated solution of the FDTM model solved by the Levenberg-Marquardt Neural Network (LM-NN) approach. The error plot for the susceptible non-Wolbachia Sn class has been provided in Fig. 16a, exposed human Eh provided in Fig. 16b, and infected human Ih class presented in Fig. 16c and their range is up to 10−4.

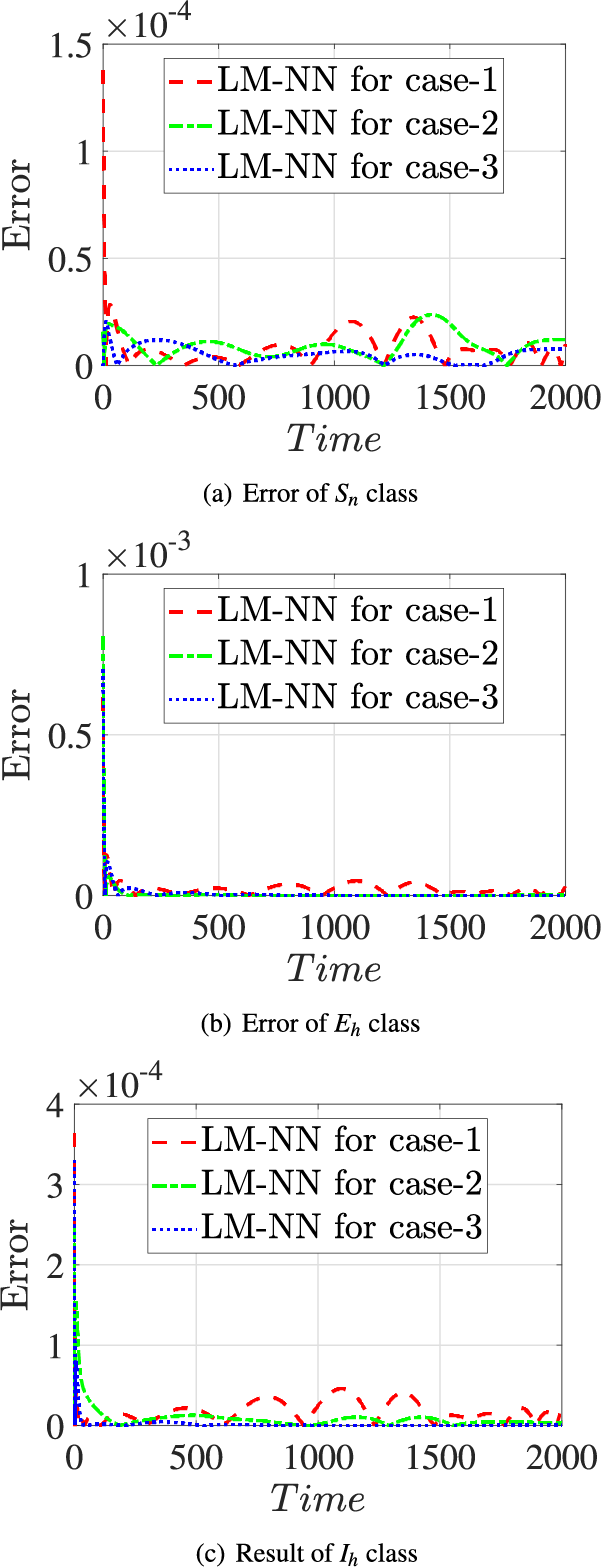
Figure 16: Error values of the presented LM-NN and the reference solutions for solving the FDTM

5  Conclusion

The purpose of this research study was to develop the fractional dengue transmission model (FDTM) in the presence of Wolbachia-carrying mosquitoes. The model incorporated the vertical transmission of Wolbachia in mosquitoes. In this study, we proposed the numerical solution of the fractional dengue transmission model (FDTM) using the stochastic-based Levenberg-Marquardt neural networks (LM-NN) technique. The FDTM model was solved using the Adams-Bashforth-Moulton (ABM) technique to create a reference dataset. The created dataset was used for training (80%), testing (10%), and validation (10%) of the proposed LM-NN technique with 10 hidden layers of neurons. The graphs of mean square error were presented for three different cases, when Wolbachia-free mosquitoes persist only (η=0.6), when both types of mosquitoes persist (η=0.8), and when only Wolbachia-infected mosquitoes persist (η=1). The reduction in dengue occurs when the vertical transmission probability of Wolbachia increases in mosquitoes. The accuracy of the proposed Levenberg-Marquardt neural networks (LM-NN) technique is assessed by comparing results obtained from the proposed LM-NN technique with the reference solutions. The plots of state transitions, fitness curves, error, and regression analysis were also presented. These results suggest the accuracy and reliability of the proposed LM-NN technique.

Acknowledgement: The authors are thankful to the anonymous reviewers for improving this article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: SJ, IA, and DB; methodology: ZF; analysis and interpretation of results: SJ, IA, ZF, and DB; draft manuscript preparation: SJ, IA, ZF, and DB; validation: SJ and DB; review and editing: IF and ZF. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Bhatt, S., Gething, P. W., Brady, O. J., Messina, J. P., Farlow, A. W. et al. (2013). The global distribution and burden of dengue. Nature, 496(7446), 504–507. [Google Scholar] [PubMed]

2. Adekunle, A. I., Meehan, M. T., McBryde, E. S. (2019). Mathematical analysis of a wolbachia invasive model with imperfect maternal transmission and loss of wolbachia infection. Infectious Disease Modelling, 4, 265–285. [Google Scholar] [PubMed]

3. Normile, D. (2013). First new dengue virus type in 50 years. Health. https://doi.org/10.1126/article.24052 [Google Scholar] [CrossRef]

4. Vaccine, D. (2018). WHO position paper–September 2018. The Weekly Epidemiological Record, 93, 457–476. [Google Scholar]

5. de Silva, A. (2023). Safety of dengue vaccine? Clinical Infectious Diseases, 76(2), 371–372. [Google Scholar] [PubMed]

6. Tricou, V., Low, J. G., Oh, H. M., Leo, Y. S., Kalimuddin, S. et al. (2020). Safety and immunogenicity of a single dose of a tetravalent dengue vaccine with two different serotype-2 potencies in adults in singapore: A phase 2, double-blind, randomised, controlled trial. Vaccine, 38(6), 1513–1519. [Google Scholar] [PubMed]

7. Tjaden, N. B., Thomas, S. M., Fischer, D., Beierkuhnlein, C. (2013). Extrinsic incubation period of dengue: Knowledge, backlog, and applications of temperature dependence. PLoS Neglected Tropical Diseases, 7(6), e2207. [Google Scholar] [PubMed]

8. Dorigatti, I., McCormack, C., Nedjati-Gilani, G., Ferguson, N. M. (2018). Using wolbachia for dengue control: Insights from modelling. Trends in Parasitology, 34(2), 102–113. [Google Scholar] [PubMed]

9. Turelli, M. (2010). Cytoplasmic incompatibility in populations with overlapping generations. Evolution, 64(1), 232–241. [Google Scholar] [PubMed]

10. Fatmawati, Jan, R., Khan, M. A., Khan, Y., Ullah, S. et al. (2020). A new model of dengue fever in terms of fractional derivative. Mathematical Biosciences and Engineering, 17(5), 5267–5288. [Google Scholar] [PubMed]

11. Ahmad, S., Javeed, S., Ahmad, H., Khushi, J., Elagan, S. et al. (2021). Analysis and numerical solution of novel fractional model for dengue. Results in Physics, 28, 104669. [Google Scholar]

12. Srivastava, H., Saad, K. M., Khader, M. (2020). An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos, Solitons & Fractals, 140, 110174. [Google Scholar]

13. Hamdan, I. N., Kilicman, A. (2018). A fractional order sir epidemic model for dengue transmission. Chaos, Solitons & Fractals, 114, 55–62. [Google Scholar]

14. Jajarmi, A., Arshad, S., Baleanu, D. (2019). A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A: Statistical Mechanics and its Applications, 535, 122524. [Google Scholar]

15. Qureshi, S., Atangana, A. (2019). Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Physica A: Statistical Mechanics and its Applications, 526, 121127. [Google Scholar]

16. Zafar, Z. U. A., Hussain, M., Inc, M., Baleanu, D., Almohsen, D. et al. (2022). Fractional-order dynamics of human papillomavirus. Results in Physics, 34, 105281. [Google Scholar]

17. Suzuki, K. (2011). Artificial neural networks: Methodological advances and biomedical applications,pp. 1–376. UK: InTech. [Google Scholar]

18. Alhakami, H., Umar, M., Sulaiman, M., Alhakami, W., Baz, A. (2022). A numerical study of the dynamics of vector-born viral plant disorders using a hybrid artificial neural network approach. Entropy, 24(11), 1511. [Google Scholar] [PubMed]

19. Pornsawad, P., Böckmann, C., Panitsupakamon, W. (2022). The levenberg–marquardt regularization for the backward heat equation with fractional derivative. Electronic Transactions on Numerical Analysis, 57, 67–79. [Google Scholar]

20. Qu, H., Zhang, T., Zhou, J. (2020). Global stability analysis of S-asymptotically ω-periodic oscillation in fractional-order cellular neural networks with time variable delays. Neurocomputing, 399, 390–398. [Google Scholar]

21. Sabir, Z., Raja, M. A. Z., Mumtaz, N., Fathurrochman, I., Sadat, R. et al. (2022). An investigation through stochastic procedures for solving the fractional order computer virus propagation mathematical model with kill signals. Neural Processing Letters, 55(2), 1783–1797. [Google Scholar]

22. Ghazizadeh, H. R., Azimi, A., Maerefat, M. (2012). An inverse problem to estimate relaxation parameter and order of fractionality in fractional single-phase-lag heat equation. International Journal of Heat and Mass Transfer, 55(7–8), 2095–2101. [Google Scholar]

23. Souayeh, B., Sabir, Z., Hdhiri, N., Al-Kouz, W., Alam, M. W. et al. (2022). A stochastic bayesian regularization approach for the fractional food chain supply system with allee effects. Fractal and Fractional, 6(10), 553. [Google Scholar]

24. Umar, M., Sabir, Z., Raja, M. A. Z., Shoaib, M., Gupta, M. et al. (2020). A stochastic intelligent computing with neuro-evolution heuristics for nonlinear sitr system of novel COVID-19 dynamics. Symmetry, 12(10), 1628. [Google Scholar]

25. Noinang, S., Sabir, Z., Javeed, S., Raja, M. A. Z., Ali, D. et al. (2022). A novel stochastic framework for the mhd generator in ocean. Computers, Materials & Continua, 73(2), 3383–3402. [Google Scholar]

26. Zhuang, Q., Yu, B., Jiang, X. (2015). An inverse problem of parameter estimation for time-fractional heat conduction in a composite medium using carbon–carbon experimental data. Physica B: Condensed Matter, 456, 9–15. [Google Scholar]

27. Sabir, Z., Guirao, J. L., Saeed, T. (2021). Solving a novel designed second order nonlinear Lane–Emden delay differential model using the heuristic techniques. Applied Soft Computing, 102, 107105. [Google Scholar]

28. Ndii, M. Z., Hickson, R. I., Allingham, D., Mercer, G. (2015). Modelling the transmission dynamics of dengue in the presence of wolbachia. Mathematical Biosciences, 262, 157–166. [Google Scholar] [PubMed]

29. Junsawang, P., Zuhra, S., Sabir, Z., Raja, M. A. Z., Shoaib, M. et al. (2022). Numerical simulations of vaccination and wolbachia on dengue transmission dynamics in the nonlinear model. IEEE Access, 10, 31116–31144. [Google Scholar]