Effect of Bogie Cavity End Wall Inclination on Flow Field and Aerodynamic Noise in the Bogie Region of High-Speed Trains

1  Introduction

Over the past decades, the high-speed railway has developed rapidly in the world due to its advantages of high efficiency, energy conservation, environmental friendliness, and safety. Nowadays, the operation speed of high-speed trains in many countries can achieve 300 km/h and people are still making efforts for further improvement. For example, the “CR450 technology innovation project” carried out in China aims to further improve the train operation speed to 400 km/h. To achieve this goal, many technical challenges need to be addressed, especially problems related to train aerodynamics [1–4], one of which is the aerodynamic noise control [5,6]. The high-speed train noise mainly includes rolling noise and aerodynamic noise. It is generally believed that the aerodynamic noise increases faster with running speed than rolling noise. When the train speed exceeds 300 km/h, the contribution of the aerodynamic noise should not be ignored any longer. Therefore, aerodynamic noise control has been an important consideration during the design of trains with operation speeds higher than 300 km/h [5,6].

The aerodynamic noise control of high-speed trains can be boiled down to the control of the main aerodynamic noise sources. The bogie region, especially the first bogie of the head car, is one of the most important aerodynamic noise sources of high-speed trains [7–10]. To better understand the generation mechanism of the aerodynamic noise in the bogie region and grasp its characteristics, several experimental and numerical studies have been conducted. Lauterbach et al. [7] tested the aerodynamic noise of a 1:25 scaled model of an ICE train in the wind tunnel and found that the bogie region is the primary source of aerodynamic noise in the frequency range below 5000 Hz (corresponding to 200 Hz for full-scale model), showing certain characteristics of cavity noise. Meskine et al. [8] simulated the aerodynamic noise of a full-scale train model based on the Lattice Boltzmann Method (LBM) and pointed out that the aerodynamic noise in the bogie region is related to the interaction between the shear layer falling off at the leading edge of the bogie cavity and the solid parts inside the cavity, as well as the cavity rear wall. Besides, affected by the boundary layer beneath the train, the airflow velocity beneath the train decreases gradually along the direction from the head car to the tail car, which is considered to be the reason that the aerodynamic noise generated by the foremost bogie is much higher than that of other bogies. Iglesias et al. [11] tested the aerodynamic noise of 1:7 scaled bogie models with different configurations in an anechoic wind tunnel and concluded that the components exposed to the free stream are the main aerodynamic noise sources of the bogie region.

In terms of aerodynamic noise control of the bogie region, adding side skirts is the most widely used measure. The side skirts eliminate the discontinuity of train side walls and also have certain sound insulation effects [12,13]. The numerical and experimental studies in references [14–16] show that the side skirts are also beneficial for reducing the aerodynamic drag of the bogie region and mitigating slipstream induced by the train.

The aerodynamic noise in the bogie region is also closely related to the airflow beneath the train. In recent years, the management of the underbody flow of high-speed trains has also been a hotspot in studies on train aerodynamic performance optimization. Zhang et al. [17] investigated the influence of bogie cut outs’ angles on the aerodynamic performance of high-speed trains and proposed a new compound mode of bogie cut outs, which could reduce the aerodynamic drag of a three-car model by 2.92%. However, this scheme is not symmetrical for the head car and tail car. Considering the feature of the two-way operation of high-speed trains, additional mechanisms are required to realize the deformation of the bogie cavity end walls when the running direction is reversed. Guo et al. [18] studied the effect of the clearance under the cowcatcher on the aerodynamic performance of high-speed trains. They found that a smaller clearance reduces the aerodynamic drag of the front part of the train body and strengths the negative lift while increasing the drag of the middle and rear parts as well as the positive lift. In reference [19], Liu et al. proposed a method of installing small deflectors upstream of the leading edge of the bogie cavity to optimize the underbody flow and reduce the aerodynamic drag of high-speed trains. Their numerical results show that the deflectors can reduce the impact of underbody flow on the bogie by guiding the airflow to the ground, thus producing a significant drag-reduction effect. By further optimizing the installation positions of the deflectors, the maximum drag reduction effect of about 12% can be obtained. The numerical results of Yao et al. [20] further suggest that the introduction of such small deflectors also has a positive effect on reducing aerodynamic noise in the bogie region. In summary, the current studies on the flow control of train underbody flow mostly focus on the reduction of aerodynamic drag, while the aerodynamic noise control of the bogie region has not received equal attention. The effects and corresponding mechanisms of altering the shape parameters of train bottom structures, such as the bogie cavity and cowcatcher, on aerodynamic noise in the bogie region remain unclear, necessitating further investigation.

The presence of the bogie cavity makes the flow in the bogie region present certain cavity flow characteristics. Many experimental and numerical studies have shown that the shapes of the front and rear walls of the cavity are key factors that affect the pressure fluctuation inside the cavity [21–24]. However, these studies were mainly conducted on clean cavity models (no object in the cavity). The differences in the Mach number of incoming flow and geometry size of the cavities also make their flow characteristics significantly different from that in the bogie region [25]. The presence of the bogie will cause a coupling effect with the cavity. The aerodynamic noise control of the bogie region needs a suppression of the random noise induced by turbulent fluctuation over a wide frequency range, rather than the tonal noise caused by flow induced oscillation. Besides, for high-speed trains, the feature of two-way operation is also an important factor that needs to be considered in the optimization of the shape of the bogie cavity. To sum up, it is necessary to conduct a detailed analysis of the effect of the cavity end wall shape on the flow field and aerodynamic noise in the bogie region.

In this paper, the detached eddy simulation (DES) method is employed in combination with Ffowcs Williams-Hawkings (FW-H) equation to investigate the effect of bogie cavity end wall inclination on flow field and aerodynamic noise in the bogie region. The numerical study is conducted on a simplified cavity-bogie model first, including five cases obtained by changing the inclination angles of the front and rear end walls of the cavity. The influence regularity and corresponding mechanism are revealed by comparing and analyzing the flow field and acoustic results of the five cases. After that, the noise reduction strategy determined based on the simulation results of the simplified cavity-bogie model is applied to a three-car marshalling train model to verify its effectiveness when applied to the real train. The relevant results contribute to a deeper understanding of the flow field and aerodynamic noise characteristics in the bogie region and could provide valuable reference for the aerodynamic noise control of high-speed trains.

2  Numerical Methods

2.1 DDES Model

DES is the most widely used turbulence model in the prediction of aerodynamic noise generated by intricate geometry structures. DES is a kind of hybrid model. Its basic idea is to solve the boundary layer in near wall region by Reynolds Averaged Navier-Stokes (RANS) model, and to solve the large-scale vortex motion by large eddy simulation (LES) model in the separation region [26]. Based on the original DES model, two variants have been proposed successively, namely the delayed detached eddy simulation (DDES) and the improved delayed detached eddy simulation (IDDES), to address the issues of grid-induced separation and log-layer mismatch [27–30]. Based on our previous test of the turbulence models, the DDES model based on the shear stress transport (SST) k−ω model is chosen to numerically solve the unsteady flow field in the bogie region in current research.

2.2 FW-H Equation

The FW-H equation is the theoretical description of sound generated by the interaction between moving objects and fluid, as depicted in Eq. (1) [31].

1c02∂2∂t2[p′H(f)]−∇2[p′H(f)]=∂∂t[ρ0vnδ(f)]−∂∂xi[pijn^jδ(f)]+∂2∂xi∂xj[TijH(f)](1)

where c0 is the speed of sound, t is time, p′ is sound pressure, xi,i=1,2,3 is the Cartesian coordinate component, f=0 is the equation of the source surface, H(⋅) is the Heaviside function, ρ0 is the density of fluid in undisturbed area, vn is the projection of the surface velocity of the source in the outer normal direction, pij=(p−p0)δij−σij is the fluid compressive stress tensor, p is pressure, p0 is the pressure of fluid in undisturbed area, σij represents the viscous stress and can be ignored in most cases, n^j is the unit outer normal vector of the source surface, ∇ is the Nabla operator, Tij is the Lighthill stress tensor. According to the idea of acoustic analogy, the three terms on the right-hand side in Eq. (1) are monopole source term, dipole source term, and quadrupole source term, respectively.

In the current study, the quadrupole source term is neglected, which is a classical assumption for low Mach number flow. Besides, the numerical simulation is based on wind tunnel mode, the train is a static rigid surface, so the monopole source term is also 0. That is, the far-field noise only includes the contribution of the dipole source term. By using the Green’s function in free space, the sound pressure at far field point x can be expressed as [32]

p′(x,t)=14π∫f=0(p˙n^ir^ic0r+pn^ir^ir2)retdS(2)

where r is the distance between the source point and the receiver, r^i is the unit vector in the direction that the source point points to the receiver, the superscript dot represents the time derivative, and the subscript ret represents the relevant variables evaluated at the emission time τ=t−r/c0.

3  Simplified Cavity-Bogie Model

3.1 Geometry Model, Computational Domain, and Boundary Conditions

The simulation is first conducted on a simplified cavity-bogie model, which is 1:8 scaled with respect to the real bogie, as shown in Fig. 1. The bogie model has been simplified to some extent but is still sufficient to reflect the geometric characteristics of a real bogie [33]. The cavity in the model is extracted from the bogie region of the mid car of a high-speed train model. It is convenient to modify the inclination angles of the front and rear end walls of the cavity on this model without involving changes in other structures so as to better compare the influence caused by the changing of the inclination angles of the front and rear end walls of the cavity.

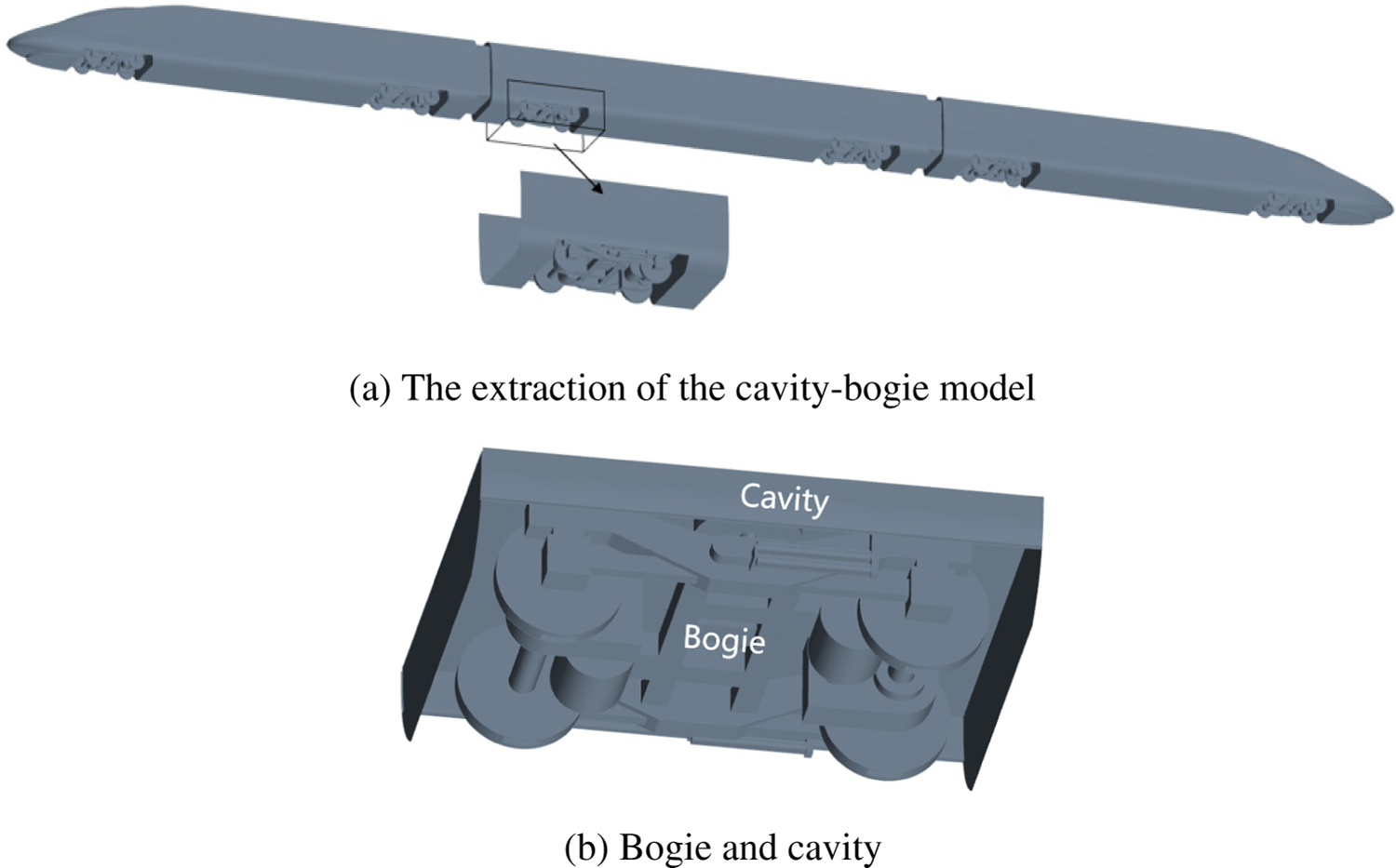
Figure 1: The simplified cavity-bogie model

By adjusting the inclination angles of the front and rear end walls of the cavity, five schemes of the bogie cavities are established, as shown in Fig. 2 and Table 1. In case0 (base model), the front and rear walls of the cavity are both kept upright with an inclination of 0°. In case1 and case3, the front walls of the cavities are inclined forward by 30° and 45°, respectively, and the rear walls are kept upright. In case2 and case4, the front walls of the cavities are kept upright, and the rear walls are inclined backward by 30° and 45°, respectively.

Figure 2: Cavity end wall inclination

The computational domain established for this simplified cavity-bogie model is shown in Fig. 3. The boundary conditions of the domain are also marked in Fig. 3. The inlet of the domain is set as the velocity inlet with an inflow velocity of 97.22 m/s. The outlet of the domain is set as the pressure outlet with 0 gauge pressure. The ground and track surfaces are set as moving walls with the moving velocity equal to the inflow velocity. Both sides of the computational domain are set as symmetry boundaries. The top surface of the domain is set as the wall without friction.

Figure 3: Computational domain for the simplified cavity-bogie model (not to scale)

3.2 Mesh Generation

The trimmed mesh is used to discrete the computational domain. The surface grid size of the bogie and cavity is controlled within 0.375–1.5 mm, and the maximum grid size of the domain is 192 mm. To simulate the flow in the near wall region accurately, 15 layers of fine prism layer mesh with an initial height of 0.01 mm and a stretching ratio of 1.2 are generated on the train surface. Several blocks are established for local refinement of the volume mesh. The volume grids with 1.5 mm size are adopted for the refinement of the bogie region. By modifying the surface grid size of the bogie components, three sets of meshes are generated for the mesh independence test, which are named as mesh1-mesh3 in turn. The total number of volume cells of them are 15 million, 22 million and 29 million, respectively. Fig. 4 presents the grid distribution around the bogie region in mesh2.

Figure 4: Grid distribution around the bogie region in mesh2

3.3 Solver Setup

The Mach number in the current simulation is less than 0.3, so the air is considered as a gas with constant density. The segregated flow solver based on the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm is adopted to solve the discretized flow governing equations. The convection term is discretized by a hybrid scheme of second-order upwind and central differencing [26,34], and the diffusion term is discretized by the second-order scheme. The second-order hybrid Gauss-least square method is used for gradient calculation [26]. The second-order implicit method is adopted for time marching with a time step size of 0.00005 s. For a second-order spatial scheme, based on the principle of containing 10–15 points per time period to resolve the wave amplitude, it is expected that the noise components up to 2000 Hz can be accurately analyzed [26]. The simulation of an unsteady flow field is carried out with a convergent steady-state solution obtained by RANS simulation as an initial field. The total simulation time of the unsteady flow field is 0.4 s, and the FW-H solver is activated when the transient simulation reaches 0.2 s for far field noise signal calculation.

4  Validation of the Mesh Strategy and Numerical Methods

4.1 Mesh Independence Test

The time-averaged and fluctuating value of the pressure coefficient Cp (Cp=(p−p0)/(12ρ0u02), u0 is the free stream velocity 97.22 m/s) on a line probe beneath the bogie cavity calculated based on the three sets of meshes are compared for mesh independence test, as shown in Fig. 5. For time-averaged values, the calculation results of the three sets of meshes show good consistency. However, regarding the fluctuating value, its convergence during the refinement of the volume mesh is slightly worse than that of the time-averaged value, but the results of mesh2 seem to match better with that of mesh3. Considering both the accuracy and resource consumption of the simulation, the mesh parameters of mesh2 are used in the following simulations.

Figure 5: Results of the mesh independence test

4.2 Simple Bogie Case Validation

The simple bogie model proposed by Zhu [12] is selected to validate the numerical methods in current research further. This model is composed of two wheelsets and a simple side frame without central structure and is 1:10 scaled, with the axle diameter d equal to 17.5 mm and the wheel diameter D equal to 92 mm, as shown in Fig. 6a.

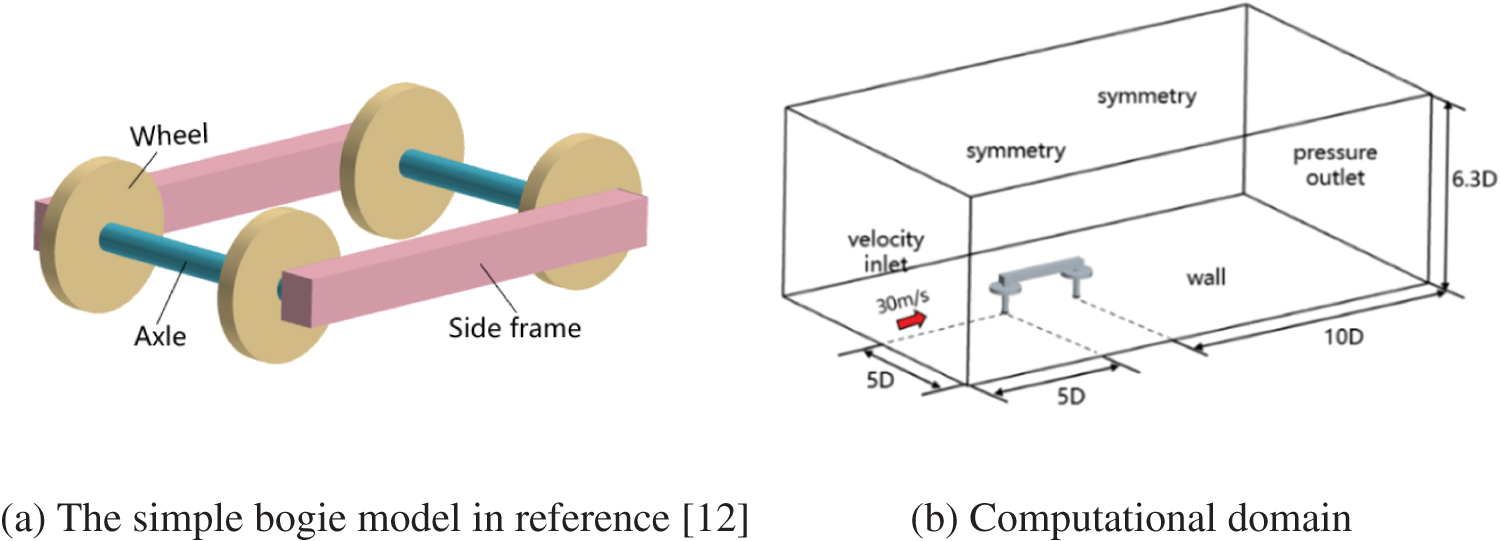
Figure 6: The simple bogie model and computational domain

The wind tunnel test in reference [12] was conducted on a half-bogie model. To match the configuration of the wind tunnel test, the numerical simulation is also conducted on a half-bogie model. The corresponding computational domain and boundary conditions are shown in Fig. 6b. The mesh for this case is generated based on the mesh strategy of mesh2 in Section 3.2, and the number of volume cells is about 3.9 million. The far field noise results of the measurement point named as “top microphone” in reference [12] is used to validate the numerical results. The specific coordinates of the microphone location can also be found in reference [12]. Fig. 7 presents the comparison between the spectrum results of the current simulation and the wind tunnel test. As can be seen, the numerical results and test results are in good agreement in spectrum shape and dominant frequency. The peak frequency in the wind tunnel test results is 314 Hz and that predicted in the current simulation is 307 Hz. This peak corresponds to the main frequency of the lift fluctuation of the wheelsets. Furthermore, the usage of the wall boundary condition at the bottom of the domain improves the overestimation of sound pressure level at the dominant frequency caused by the usage of symmetry boundary condition in reference [12]. In general, the numerical results are in good agreement with the test results, which proves again that the mesh strategy and numerical methods in current research are reliable.

Figure 7: Simulation and wind tunnel test results of the far field noise of the simple bogie

5  Results of the Simplified Cavity-Bogie Model

5.1 Flow Characteristics

Fig. 8 shows the time-averaged velocity vector diagrams on the mid-section of the bogie region. These results clearly show the path of the underbody flow entering and exiting the bogie cavity. For all the models, airflow separation occurs at the leading edge of the bogie cavity, leading to the formation of a shear layer. Subsequently, the airflow crosses the front of the bogie cavity and rolls up into the cavity. The airflow entering the cavity slowly recirculates towards the front of the cavity, ultimately rolling downwards and exiting the cavity under the influence of the cavity front wall, merging with the high-speed airflow beneath the train. In case0, the shear layer starts to rise up after crossing the middle of the bogie, while in case1 and case3, the inclined front wall makes the position where the airflow rises up move upstream. The airflow beneath the front wheelset has already exhibited a noticeable trend of moving upward. As for case2 and case4, the differences between the flow field results of them and that of case0 are primarily observed at the rear of the bogie cavity. In contrast to that the airflow beneath the bogie impacts almost vertically on the cavity rear wall in case0, the inclined rear walls in case2 and case4 appear to play a certain guiding role, a clear deflection of the streamlines toward the outside of the cavity can be observed. This is expected to alter the flux distribution of the airflow entering and flowing outside the cavity, making more airflow flow outside instead of entering the cavity.

Figure 8: Velocity vector diagrams in the bogie region

Fig. 9 illustrates the time-averaged pressure distribution in the bogie region. As can be observed, compared with the base model, both the area and magnitude of positive pressure at the lower part of the bogie increase in case1 and case3. This indicates that the inclined cavity front wall leads to a stronger impact from the underbody flow on the lower part of the bogie. In case2 and case4, there is no significant difference in the pressure distribution at the lower part of the bogie compared with the base model. However, there is a noticeable decrease in positive pressure at the lower part of the cavity rear wall, suggesting that the inclined rear wall is beneficial to attenuate the impact from the airflow on the rear wall of the bogie cavity.

Figure 9: Time-averaged pressure distribution in the bogie region

5.2 Dipole Source

For Eq. (2), under the condition of acoustic far-field, the approximation in Eq. (3) holds true.

p′(x,t)≈14π∫f=0(p˙n^ir^ic0r)retdS(3)

Based on Eq. (3) and the concept of correlation function, the sound power W of the surface dipole sources can be expressed as [35–38]

W=112πρ0c03∫S[p˙(y,t)]2¯Ac(y)dS(4)

where Ac(y) is the correlation area of point y on source surface. The integrated term in Eq. (4) can be regarded as the sound power density of the dipole sources. The changing rate of pressure vs. time reflects the intensity of the dipole source and Ac(y) reflects the correlation between the fluctuating pressure of point y and that of its surrounding points.

Fig. 10 presents the distribution of the root mean square value of pressure derivative vs. time (dp/dt)rms in the bogie region. In all the cases, the highest (dp/dt)rms values appear at the lower and lateral surface of the bogie, the rear wall of the bogie cavity and the carbody surface that connects to the cavity rear wall. In case0, the dipole source intensity at the rear of the bogie is significantly higher than that at the front of the bogie. In case1 and case3, the (dp/dt)rms values on front wheelset, front traction motor and front gearbox exhibit a significant increase compared with that in case0, especially in case3, while the (dp/dt)rms values on the rear wall of the cavity are almost the same as that in case0. In case2 and case4, the (dp/dt)rms values at the front of the bogie are basically the same as that in case0, while the (dp/dt)rms values on the rear wall of the bogie cavity show a notable decrease and this decrease in case4 is much more obvious. In summary, the forward inclination of the front end wall of the bogie cavity increases the intensity of dipole sources at the front part of the bogie, while the inclination of the rear end wall of the bogie cavity could reduce the dipole source intensity on the cavity rear wall.

Figure 10: (dp/dt)rms distribution in the bogie region

The pressure fluctuation on the solid surface is typically induced by the interaction between vortex structures and the solid wall. To analyze the influence mechanism of the bogie cavity end wall inclination on the intensity and distribution of dipole sources in the bogie region, Fig. 11 shows an instantaneous vorticity distribution on the mid-section of the bogie region. In all the cases, a jet shear layer forms at the leading edge of the bogie cavity and convects with the airflow beneath the train. Due to the velocity difference between the airflow inside and outside the cavity, the shear layer exhibits Kelvin-Helmholtz instability. When the velocity difference reaches a certain limit, the shear layer begins to form a series of swinging vortex structures. These vortex structures continue to grow, eventually roll up and invade into the cavity. The velocity vector diagrams in Fig. 8 also approximately illustrate the motion trajectory of the vortex structures.

Figure 11: Instantaneous vorticity distribution in the bogie region

In case0, the shear layer could span the front components of the bogie, mainly interacting with the rear part of the bogie and the rear wall of the cavity. As a result, there are fewer vortex structures at the front of the cavity and the flow field there is relatively stable. In case1 and case3, the inclined front wall makes the position where the shear layer loses stability and rolls up move upstream, which enlarges the influence area of the shear vortices. In Fig. 11, it can be observed that the vorticity magnitudes at the front of the bogie cavity in case1 and case3 are much higher than that in case0, indicating that the interaction between the shear vortex structures and the front part of the bogie is intensified. This is the reason for the increase of the dipole source intensity on front wheelset, front traction motor and front gear box increase in case1 and case3. In case2 and case4, when the airflow passes through the rear wall of the cavity, due to the flow guiding effect of the inclined rear wall, the vortex structures mostly flow out of the cavity rather than invade into the cavity, which could effectively weaken the interaction between the vortex structures and the cavity rear wall. Therefore, in case2 and case4, the (dp/dt)rms values on the cavity rear wall are significantly reduced compared with that in case0.

The relationship between correlation area Ac(y) and correlation scale lc(y) of point y on the source surface meets

Ac(y)∝lc2(y)(5)

For broadband noise, considering that the turbulent fluctuating pressure on the surface of the sound source propagates at convective velocity, thus

lc(y)∝Uc(y)(6)

where Uc(y) is the convective velocity of point y. To simplify the calculation, it is generally assumed that the ratio of the convective velocity Uc(y) to the airflow velocity U(y) is a constant value [35,37,38]. Therefore, the flow velocity in the near wall region can be used as an index to approximately characterize the correlation area [38].

Fig. 12 shows the surface flow velocity (the velocity value at the cell center of the first layer grids outside the wall) distribution in the bogie region in each case. It suggests that the highest surface airflow velocity occurs at the lower surface of the traction motor, gearbox, and wheels, because these areas are close to the high-speed airflow outside the cavity. Compared with the base model, the airflow velocity at the lower part of the front wheelset, front traction motor and front gear box in case1 and case3 slightly increases, the flow velocity at the lower part of the cavity rear wall in case2 and case4 slightly increases. Overall, the difference in surface flow velocity in the bogie region among the five cases is not as obvious as that in surface (dp/dt)rms.

Figure 12: Surface flow velocity distribution in the bogie region

5.3 Far Field Noise

As depicted in Fig. 13, nine measurement points on the track side are defined for the evaluation of far field noise, denoted as p1–p9. Each measurement point is positioned at a lateral distance of 2.5 m from the track centerline and shares an equivalent height with that from the geometry center of the bogie to the ground. The distance between two adjacent measurement points is 1 m.

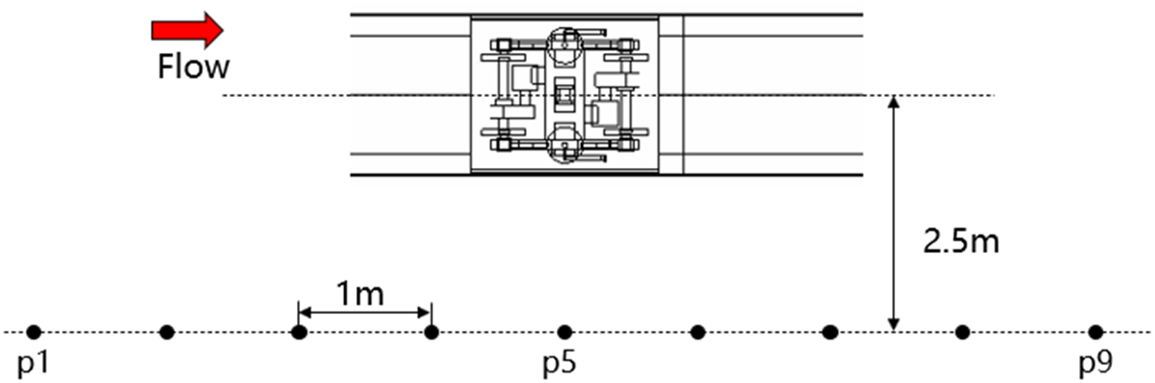
Figure 13: Arrangement of the measurement points (not to scale)

Fig. 14a presents the overall sound pressure level (OASPL) results of the base model (case0) with different components used as source surfaces. As depicted in Fig. 14a, the far-field noise is primarily contributed by the bogie at p4, p5, and p6, while at other measurement points, it is predominantly influenced by the bogie cavity. The difference in radiation characteristics between the bogie and bogie cavity can be elucidated by referring to the dipole source identification results in Fig. 10. For the bogie itself, the strongest dipole sources are distributed on its lower and lateral surfaces. Hence, for measurement points on the track side, the variation in OASPL is approximately consistent with the variation of distance between the source surface and receivers. For the bogie cavity, the strongest dipole sources are located on its rear wall, so it mainly radiates noise to the forward and backward direction of the bogie region and contributes little to the measurement points on both sides of the bogie region.

Figure 14: OASPL results at measurement points p1–p9

Fig. 14b illustrates the comparison of OASPL results at p1–p9 measurement points with the bogie and cavity together set as source surface. It is evident that the OASPL results for case1 are essentially equivalent to those of case0. Notably, in case3, the OASPL results reach their highest levels, approximately 1 dB higher than those observed in case0 at p4–p6. Conversely, both case2 and case4 exhibit significant reductions in OASPL compared to case0, particularly noticeable at measurement points p1–p3 and p7–p9 where there is a reduction of 2–4 dB in OASPL.

Figs. 14c and 14d further illustrate the OASPL results with the bogie and bogie cavity used as source surfaces, respectively. It can be seen that the aerodynamic noise generated by the bogie itself in case3 is about 1 dB higher than that in case0. This corresponds to the enhancement of dipole source intensity at the front of the bogie observed in Fig. 10. In addition, the aerodynamic noise generated by the bogie cavity in case2 and case4 is significantly reduced compared with that in case0, especially at measurement points p1–p3 and p7–p9. This corresponds to the decrease of dipole source intensity on cavity rear wall observed in Fig. 10. As the aerodynamic noise in the bogie region is mainly contributed by the bogie cavity at p1–p3 and p7–p9, the most significant aerodynamic noise reduction effect of the bogie region also appears at these positions.

Fig. 15 presents the spectrum results of aerodynamic noise in the bogie region at measurement points p2 and p5 (limited by sampling time, the noise components below 100 Hz are considered to be inaccurate and are not shown). As shown in Fig. 15, the aerodynamic noise energy in the bogie region is mainly concentrated in the frequency range below 2000 Hz. According to the similarity law of aeroacoustics, the aerodynamic noise energy in the bogie region of a full-scale model is mainly concentrated in the frequency range below 250 Hz. At p2, the inclined front walls in case1 and case3 contribute to an increase in noise levels in the bogie region in the frequency range of 100–200 and 800–1000 Hz, resulting in a slight increase of OASPL. Conversely, the inclined rear walls in case2 and case4 could effectively mitigate aerodynamic noise in the bogie region over a wide frequency range (200–2000 Hz), leading to a significant reduction in OASPL. At p5, an increase in noise in the frequency range of 100–200 and 800–1000 Hz in case1 and case3 can also be observed, especially in case3. Due to the negligible contribution of the bogie cavity to the total noise at p5, no obvious noise reduction behavior is observed in the spectrum results of case2 and case4.

Figure 15: Spectrum results at p2 and p5

6  Results of the Three-Car Marshalling Model

The simulation results of the simplified cavity-bogie model suggest that inclining the rear wall of the bogie cavity appears to be a promising measure for reducing aerodynamic noise in the bogie region. However, further confirmation is required to assess its effectiveness when applied to the foremost bogie region of a real train. On the one hand, the presence of the head streamlined surface and cowcatcher makes the incoming flow state of the foremost bogie region of the real train somewhat different from that of the simplified cavity-bogie model. On the other hand, additional validation is imperative to ascertain whether the two-way operation of the train will exert any influence on the efficacy of noise reduction. In this section, the aforementioned noise reduction strategy is applied to a three-car marshalling model to further substantiate its effectiveness. The model configurations are depicted in Fig. 16. In the optimized model, the first bogie cavity of the head car features a rear wall inclined at an angle of 45°, while maintaining symmetrical bogie cavity structures between the head car and tail car.

Figure 16: Three-car marshalling model

The same mesh strategy as mesh2 in Section 3.2 is used for the three-car marshalling model and the corresponding number of volume cells is approximately 120 million. Fig. 17 shows the grid distribution around the train model. For the three-car marshalling model, due to the increase of the model length, longer running time is required for transient simulation to ensure the full development of the transient flow field. After initializing the transient simulation with a converged steady field, the transient simulation is initially run for 0.3 s with a time step size of 0.0001 s, then the time step size is switched to 0.00005 s and the simulation is run to 0.4 s. Finally, maintaining the time step size of 0.00005 s, the simulation is run for another 0.2 s to calculate the far field noise.

Figure 17: Grid distribution of the three-car marshalling model

Fig. 18 shows the distribution of surface dipole sources ((dp/dt)rms) of the two three-car marshalling models. As can be seen, the dipole source intensity in the foremost bogie region is much higher than that of other bogies. In the foremost bogie region of the optimized model, the intensity of dipole sources on the rear wall of the bogie cavity and the carbody surface connects to it exhibits a significant attenuation compared with that of the original model, which is similar to the simulation results of the simplified cavity-bogie models.

Figure 18: (dp/dt)rms distribution in the bogie region of the three-car marshalling model

The far field noise generated by the bogies and cavities of the two three-car marshalling models are further calculated. The arrangement of the far field noise measurement points is shown in Fig. 19. The height of the measurement points from the ground is the same as the height of the geometry center of the bogie from the ground.

Figure 19: Arrangement of the far field noise receivers for the three-car marshalling model

As shown in Fig. 20, for far field noise calculation, two source configurations are considered for the foremost bogie region, referred to as “Train head” and “Bogie region”. The former encompasses the head streamlined surface, cowcatcher, bogie, and bogie cavity, whereas the latter only comprises the bogie and its cavity. As for other bogies, only the source configuration named as “Bogie region” is considered.

Figure 20: Definition of source surfaces

Fig. 21 presents the OASPL results of the original model and optimized model at q1–q16. According to the results in Fig. 21, the following conclusions can be drawn. Firstly, for most measurement points, there is no obvious difference between the results of the source configurations of Train head and Bogie region1. Only at q4 that is located at the side of the Bogie region1, the head streamlined surface has a relatively significant contribution. Secondly, on both sides of the track, the noise generated by the Train head or Bogie region1 is significantly higher than the noise radiated by the other sources. At downstream measurement points such as q10 and q11 that are far away from the Bogie region1, the total noise is still dominated by the Bogie region1. Besides, a notable phenomenon is that the noise generated by Bogie region6 seems to be higher than that of Bogie region2 to Bogie region5. Especially at q12–q16, Bogie region6 is the main contributor to the total noise. Similar results were reported by Li et al. in reference [9]. They found that the pressure and velocity fluctuation around the last bogie of the tail car are stronger than those of the bogies in the middle position. One possible reason for this phenomenon is that the Bogie region6 is close to the train tail, and the flow structures there are different from those of the other bogies, but there is not sufficient evidence to confirm this view, so further research is needed in the future.

Figure 21: OASPL results of the three-car marshalling model

Fig. 22 further compares the far-field noise results of the original model and the optimized model with the Train head and Bogie region1 used as source surfaces, respectively. The noise reduction effect (OASPLoriginal–OASPLoptimized) is also presented in Fig. 22, which suggests that the most obvious noise reduction effect appears at measurement points q7-q16 that are located downstream of the foremost bogie, and the noise reduction effect becomes increasingly significant along the direction from q7 to q16. At these points, the OASPL can be reduced by 0.5 to 1.5 dB. However, at measurement points q3, q4, and q5 that are located at the side of Bogie region1, the OASPL results are almost unchanged, consistent with the sound radiation characteristics of the bogie cavity shown in previous results. In addition, a comparison is also made between the OASPL results of the two models with the Bogie region6 used as source surface and the results show that there is little difference between the results of the two models (the difference in OASPL is not separately listed in the paper).

Figure 22: Noise reduction effects

In general, the far field noise results of the three-car marshalling model further confirm the effectiveness of inclining the rear wall of the bogie cavity in aerodynamic noise reduction of the bogie region. This kind of effectiveness is reflected in the suppression of noise radiated by the bogie cavity, while having limited impact on the noise generated by the bogie itself. Considering that the measurement points located at the side of the bogie exhibit higher noise level and the noise at these positions is mainly contributed by the bogie itself, further investigation is imperative to explore measures to mitigate the aerodynamic noise generated by the bogie itself, as well as their integration with noise control measures for the bogie cavity, in order to achieve a comprehensive aerodynamic noise reduction in the bogie region.

7  Conclusions

In this paper, the influence regularity and mechanism of the bogie cavity end wall inclination on flow field and aerodynamic noise characteristics in the bogie region are numerically studied. The simulation is first conducted on a simplified cavity-bogie model, including five cases with different cavity end wall inclination angles. By comparing and analyzing the five cases’ flow field and acoustic results, a noise reduction strategy is determined and subsequently applied to the foremost bogie region of a three-car marshalling model to verify its effectiveness when applied to the real train. The results indicate that variations of the inclination angles of the bogie cavity’s front and rear end walls can significantly affect the aerodynamic noise in the bogie region and have different influence mechanisms. The inclined front wall makes the position where the shear layer rolls up move upstream and enlarges the influence area of the shear vortices, which intensifies the interaction between the shear vortex structures and the front wheelset, front motor, and front gearbox, thereby increasing the aerodynamic noise generated by the bogie itself. The inclined rear wall has certain flow guiding effects, making more vortex structures flow out of the cavity, which could effectively weaken the interaction between the vortex structures and the rear wall of the bogie cavity and reduce the aerodynamic noise generated by the bogie cavity over a wide frequency range. The far-field noise results of the three-car marshalling model further validate the efficacy of inclining the rear end wall in mitigating aerodynamic noise in the bogie region. This effectiveness is primarily observed in attenuating noise emitted by the bogie cavity while having a limited impact on the noise generated by the bogie itself. A noise reduction of 0.5 to 1.5 dB can be achieved in the main sound radiation direction of the bogie cavity. Considering that the measurement points located at the side of the bogie have higher noise level and the noise at these positions is mainly contributed by the bogie itself, further investigation is needed to explore measures to reduce the aerodynamic noise generated by the bogie itself, as well as their integration with noise control measures for the bogie cavity, in order to achieve a comprehensive aerodynamic noise reduction in the bogie region.

Acknowledgement: For the successful completion of this paper, the authors of this paper expresses their sincere gratitude to the research institutions where the participants work.

Funding Statement: This work was supported by National Natural Science Foundation of China (12172308) and National Key Research and Development Program of China (2020YFA0710902).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jiawei Shi, Jiye Zhang; data collection: Jiawei Shi; analysis and interpretation of results: Jiawei Shi, Jiye Zhang; draft manuscript preparation: Jiawei Shi, Jiye Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Dai, Z., Li, T., Zhang, W., Zhang, J. Y. (2023). Research progress of aerodynamic multi-objective optimization on high-speed train nose shape. Computer Modeling in Engineering & Sciences, 137(2), 1419–1459. https://doi.org/10.32604/cmes.2023.028198 [Google Scholar] [CrossRef]

2. Dai, Z. Y., Li, T., Deng, J., Zhou, N., Zhang, W. H. (2022). Effect of the strip spacing on the aerodynamic performance of a high-speed double-strip pantograph. Vehicle System Dynamics, 60(10), 3358–3374. [Google Scholar]

3. Wei, L., Zeng, J., Gao, H., Qu, S. (2022). On-board measurement of aerodynamic loads for high-speed trains negotiating transitions in windbreak walls. Journal of Wind Engineering and Industrial Aerodynamics, 222, 104923. [Google Scholar]

4. Chen, Z. W., Ni, Y. Q., Wang, Y. W., Wang, Y. W., Wang, S. M. et al. (2022). Mitigating crosswind effect on high-speed trains by active blowing method: A comparative study. Engineering Applications of Computational Fluid Mechanics, 16(1), 1064–1081. [Google Scholar]

5. Thompson, D. J. (2008). Railway noise and vibration: Mechanisms, modelling and means of control. Oxford: Elsevier Science. [Google Scholar]

6. Thompson, D. J., Iglesias, E. L., Liu, X. W., Zhu, J. Y., Hu, Z. W. (2015). Recent developments in the prediction and control of aerodynamic noise from high-speed trains. International Journal of Rail Transportation, 3(3), 119–150. [Google Scholar]

7. Lauterbach, A., Ehrenfried, K., Loose, S., Wagner, C. (2012). Microphone array wind tunnel measurements of Reynolds number effects in high-speed train aeroacoustics. International Journal of Aeroacoustics, 11(3–4), 411–446. [Google Scholar]

8. Meskine, M., Perot, F., Kim, M. S. (2013). Community noise prediction of digital high speed train using LBM. 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany. [Google Scholar]

9. Li, Z. M., Li, Q. L., Yang, Z. G. (2022). Flow structure and far-field noise of high-speed train under ballast track. Journal of Wind Engineering and Industrial Aerodynamics, 220, 104858. [Google Scholar]

10. Li, M., Deng, T., Wang, D., Xu, F., Xiao, X. et al. (2022). An experimental investigation into the difference in the external noise behavior of a high-speed train between viaduct and embankment sections. Shock and Vibration, 2022, 8827491. [Google Scholar]

11. Iglesias, E. L., Thompson, D. J., Smith, M., Kitagawa, T., Yamazaki, N. (2017). Anechoic wind tunnel tests on high-speed train bogie aerodynamic noise. International Journal of Rail Transportation, 5(2), 87–109. [Google Scholar]

12. Zhu, J. (2015). Aerodynamic noise of high-speed train bogies (Ph.D. Thesis). University of Southampton, UK. [Google Scholar]

13. Kurita, T., Kikuchi, Y., Yamada, H., Ido, A., Murata, K. et al. (2012). Reduction of noise generated from lower part of Shinkansen cars by sound absorption. Journal of Mechanical Systems for Transportation and Logistics, 5(1), 1–13. [Google Scholar]

14. Wang, J., Minelli, G., Dong, T., Chen, G., Krajnović, S. (2019). The effect of bogie fairings on the slipstream and wake flow of a high-speed train. An IDDES study. Journal of Wind Engineering and Industrial Aerodynamics, 191, 183–202. [Google Scholar]

15. Wang, J., Gao, G., Li, X., Liang, X., Zhang, J. (2019). Effect of bogie fairings on the flow behaviours and aerodynamic performance of a high-speed train. Vehicle System Dynamics, 58(6), 890–910. [Google Scholar]

16. Kwak, M., Lee, Y., Lee, J., Cho, J., Kim, K. H. (2012). Experimental study on aerodynamic drag characteristics by train underbody shape variation. 30th AIAA Applied Aerodynamics Conference, New Orleans, USA. [Google Scholar]

17. Zhang, J., Wang, J., Wang, Q., Xiong, X., Gao, G. (2018). A study of the influence of bogie cut outs’ angles on the aerodynamic performance of a high-speed train. Journal of Wind Engineering and Industrial Aerodynamics, 175, 153–168. [Google Scholar]

18. Guo, Z., Liu, T., Xia, Y., Liu, Z. (2022). Aerodynamic influence of the clearance under the cowcatcher of a high-speed train. Journal of Wind Engineering and Industrial Aerodynamics, 220, 104844. [Google Scholar]

19. Liu, W., Ji, Z., Guo, D., Yang, G., Zhou, G. et al. (2022). Effects of bottom deflectors on aerodynamic drag reduction of a high-speed train. Acta Mechanica Sinica, 38(5), 321251. [Google Scholar]

20. Yao, Y., Sun, Z., Li, G., Yang, G., Prapamonthon, P. et al. (2022). Aerodynamic optimization using passive control devices near the bogie cabin of high-speed trains. Acta Mechanica Sinica, 38(9), 321363. [Google Scholar]

21. Lawson, S. J., Barakos, G. N. (2011). Review of numerical simulations for high-speed, turbulent cavity flows. Progress in Aerospace Sciences, 47(3), 186–216. [Google Scholar]

22. Nayyar, P., Barakos, G., Badcock, K., Kirkham, D. (2005). Analysis and control of transonic cavity flow using DES and LES. 35th AIAA Fluid Dynamics Conference and Exhibit, vol. 2005. Toronto, Canada. [Google Scholar]

23. Luo, K., Zhu, W., Xiao, Z., Weng, Z., Deng, L. et al. (2018). Investigation of spectral characteristics by passive control methods past a supersonic cavity. AIAA Journal, 2018, 1–18. [Google Scholar]

24. Guo, Z., Liu, P., Guo, H. (2021). Control effect on deep cavity noise by slanted walls at low mach numbers. Journal of Vibration and Control, 27(9–10), 998–1008. [Google Scholar]

25. Kim, H., Hu, Z., Thompson, D. J. (2020). Effect of cavity flow control on high-speed train pantograph and roof aerodynamic noise. Railway Engineering Science, 28, 54–74. [Google Scholar]

26. STAR-CCM+ User Guide (Version 12.04) (2017). Siemens PLM software. [Google Scholar]

27. Spalart, P. R. (1997). Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. Proceedings of First AFOSR International Conference on DNS/LES, pp. 137–147. Ruston, USA. [Google Scholar]

28. Menter, F. R., Kuntz, M., Langtry, R. (2003). Ten years of industrial experience with the SST turbulence model. Turbulence, Heat and Mass Transfer, 4(1), 625–632. [Google Scholar]

29. Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. k. et al. (2006). A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics, 20(3), 181–195. [Google Scholar]

30. Shur, M. L., Spalart, P. R., Strelets, M. K., Travin, A. (2008). A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. International Journal of Heat and Fluid Flow, 29(6), 1638–1649. [Google Scholar]

31. Williams, J. F., Hawkings, D. L. (1969). Sound generation by turbulence and surfaces in arbitrary motion. Philosophical Transactions of the Royal Society of London Series A, 264(1151). [Google Scholar]

32. Farassat, F. (2007). Derivation of formulations 1 and 1A of farassat. 20070010579. NASA Langley Research Center. [Google Scholar]

33. Dong, T., Liang, X., Krajnović, S., Xiong, X., Zhou, W. (2019). Effects of simplifying train bogies on surrounding flow and aerodynamic forces. Journal of Wind Engineering and Industrial Aerodynamics, 191, 170–182. [Google Scholar]

34. van de Ven, T., Louis, J., Palfreyman, D., Mendonca, F. (2009). Computational aeroacoustic analysis of a 1/4 scale G550 nose landing gear and comparison to NASA and UFL wind tunnel data. 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), vol. 2009. Miami, USA. [Google Scholar]

35. King III, W. F. (1977). On the role of aerodynamically generated sound in determining wayside noise levels from high speed trains. Journal of Sound and Vibration, 54(3), 361–378. [Google Scholar]

36. Kim, S. E., Dai, Y., Koutsavdis, E., Sovani, S., Kadam, N. et al. (2003). A versatile implementation of acoustic analogy based noise prediction method in a general-purpose CFD code. 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head, USA. [Google Scholar]

37. Heller, H. H., Dobrzynski, W. M. (1978). Unsteady surface pressure characteristics on aircraft components and far-field radiated airframe noise. Journal of Aircraft, 15(12), 809–815. [Google Scholar]

38. Phan, V. L., Tanaka, H., Nagatani, T., Wakamatsu, M., Yasuki, T. (2017). A CFD analysis method for prediction of vehicle exterior wind noise. SAE International Journal of Passenger Cars-Mechanical Systems, 10(1), 286–299. [Google Scholar]