Privacy-Preserving Federated Deep Learning Diagnostic Method for Multi-Stage Diseases

1  Introduction

In medicine, multi-stage diseases refer to diseases that can be divided into different stages or periods during their development process. These stages may have different pathological characteristics, clinical manifestations, and prognoses. The staging of multi-stage diseases can be based on physiological processes, pathological features, clinical symptoms, imaging results, and other aspects of the disease. The diagnosis of multi-stage diseases also requires multiple types of data to support it, such as clinical symptoms, physical signs, laboratory test data, imaging data, histopathological data, and genetic data. In addition, doctors need to have comprehensive medical knowledge and experience. To assist doctors in diagnosis, improve diagnostic accuracy, speed up the diagnosis process, and provide personalized treatment, artificial intelligence algorithms can be used for intelligent diagnosis and treatment. Traditional artificial intelligence algorithms require the consolidation of patient data from different sources for modeling and prediction, which can easily lead to the leakage of patients’ medical records, genetic information, and other sensitive data. To protect patients’ privacy data in intelligent diagnosis, we need to combine federated learning techniques to design a federated intelligent diagnosis method for multi-stage diseases.

The concept of federated learning was first introduced by Google in 2016 [1]. Since then, it has received continuous attention and become a research hotspot in the field of machine learning. It can realize the safe sharing of data between different organizations. Federal learning includes horizontal federated learning (HFL), vertical federated learning (VFL) and federal transfer learning (FTL).

For vertical federated learning, it can be divided into two architectures: the architecture with coordinator and the architecture with de coordinator. Yang et al. [2] implemented a vertical federal logical regression algorithm with a coordinator, which approximated the loss function and gradient function with second-order Taylor, and then used homomorphic encryption to calculate privacy protection. This method uses the first-order random gradient descent algorithm, which requires a large number of communication rounds. Therefore, in order to reduce the communication cost, Yang et al. [2] proposed a vertical logic regression framework based on quasi Newton method. However, these two methods are aimed at binary classification. In order to expand vertical federated learning, Feng et al. [3] proposed a VFL framework for multiple participants and multiple classifications. Yang et al. [4] proposed a vertical logic regression framework for de coordinator, which effectively protects privacy and improves the accuracy of the classifier. Hardy et al. [5] proposed a three-party end-to-end logistic regression, which consists of a trusted arbiter and two other parties, where the coordinator’s tasks include computing the training loss and generating homomorphic encryption key pairs for privacy protection.

However, the arbiter-based architecture poses privacy risks as the arbiter has the potential to leak information about the participating parties. Furthermore, the existing algorithms for arbiter-free architectures are mainly focused on conventional machine learning, such as logistic regression and boosting trees. However, the diagnosis of multi-stage diseases requires the integration of various multimodal data for inference. Therefore, this paper aims to investigate an arbiter-free algorithm for vertical deep neural networks, eliminating the need for a third-party arbiter and enabling collaborative participants to engage in federated training of deep neural networks. Our main contributions are as follows.

This paper proposes a vertical federated deep neural network approach and provides a detailed description of its three-layer model’s secure forward and backward propagation processes. By introducing homomorphic encryption during the propagation process, it can operate without the involvement of a third-party arbiter.

This paper proposes a hardware acceleration solution for our federated deep neural network is designed based on finite field arithmetic chips. This approach effectively addresses the challenges of multimodal data in the diagnosis of multi-stage diseases, the privacy leakage issue in vertical federated learning, and the computational burden of encryption operations in federated learning.

The method referred to in this article is named the Vertical Deep Neural Network (VDNN). The article has conducted complexity analysis and security assessment of this method, demonstrating its feasibility and security. Through comparative experiments with the method in reference [6], this paper proves the better performance of the proposed method in terms of communication overhead and program execution time. The method presented in this paper achieves a more balanced computation load between the Guest and Host parties, resulting in improved performance.

The rest of this paper is organized as follows. Section 2 introduces the preliminary knowledge of homomorphic encryption and the basic knowledge of deep neural networks. Section 3 discusses the specific method of vertical deep neural networks without an arbiter and provides complexity and security analysis. Then, in Section 4, we present a detailed comparative experiment between our federated modeling VDNN model and the model in reference [6] on commonly used datasets. Finally, Section 5 summarizes this work.

2  Related Works

Alzheimer’s disease is a typical multi-stage disease. Saleem et al. [7] summarized the application of machine learning in the diagnosis of Alzheimer’s disease and found that neuroimaging data, electroencephalogram (EEG) data, and genomic data can improve the accuracy of Alzheimer’s disease diagnosis. These data are large-scale and high-dimensional multimodal data, and ordinary machine learning methods struggle to handle such complex multimodal data. Therefore, neural networks that can directly process multimodal data are necessary for this type of multi-stage disease. Furthermore, to achieve a privacy-preserving intelligent diagnostic method, it is crucial to focus on implementing privacy-preserving deep neural networks.

Liu et al. [8] presented the federated forest algorithm, which is a VFL method with coordinator based on random forest. The structure of the global federated forest model is stored in a decentralized manner, the central server retains the complete structure information of the global model, and the node information is stored in each participant in a decentralized manner. The method presented in this paper eliminates the central server, reducing the risk of data leakage. Zhang et al. [6] decomposed the forward and backward propagation of neural networks into four distinct steps and proposed a privacy-preserving architecture that enables collaborative parties to effectively federated train deep learning models. For ease of expression, in this paper, this method is referred to as the Fate Deep Neural Network (FDNN).

Our work focuses on the forward and backward propagation processes of deep neural networks. We introduce encrypted noise in both the forward and backward propagation processes and use homomorphic encryption methods for parameter updates. This allows vertical deep neural networks to achieve lossless joint modeling while protecting data privacy. Additionally, our approach is insensitive to the neural network structure and can effectively solve various multi-class and non-linear problems. Furthermore, we implement a hardware-level Paillier algorithm that supports decimals and negative numbers based on a large finite field arithmetic chip, enhancing the security of encryption and decryption during the interaction process.

3  Preliminaries

3.1 Homomorphic Encryption

In the vertical federated learning scenario, both the Guest and the Host in the collaborative modeling process each hold part of the private data, and the traditional encryption mechanism cannot perform computing operations on the undecrypted encrypted data. Therefore, in order to calculate the gradient required for model training, the Guest and Host need to disclose some private information. Homomorphic encryption (HE) [9,10], an asymmetric encryption technique widely used in privacy computing, can solve this problem by allowing any third party to operate on encrypted data. We perform calculations on the homomorphically encrypted data, and after decrypting the calculation results, the decrypted results match the results of the calculations performed directly on the plaintext. The concept of HE was first proposed in 1978 [11] to protect the private data of banks. According to the number and types of ciphertext calculations, homomorphic encryption can be divided into: Partial Homomorphic Encryption (PHE), Somewhat Homomorphic Encryption (SHE), Fully Homomorphic Encryption (FHE).

The PHE technique only supports a single type of homomorphic computation (additive or multiplicative homomorphism), RSA [12] is a widely used PHE algorithm that follows multiplicative homomorphism and its security is based on the factorization of the product of two large prime numbers question. GM proposed the first probabilistic public key encryption scheme Goldwasser-Micali [13], which is based on the quadratic residual difficulty problem with multiplicative homomorphism. In 1985, Elgama [14] proposed a new public key encryption scheme, which improved the original Diffie-Hellman key exchange algorithm, and its security was based on the discrete logarithm problem. Benaloh [15] proposed an extension of the GM algorithm, using the encryption mode of block encryption instead of bitwise encryption. In 1999, Paillier proposed a SHE algorithm based on the composite residual problem [16], which satisfies the additive homomorphism. This algorithm is also a commonly used algorithm in the follow-up research field.

There are four definitions for the homomorphic properties of homomorphic encryption algorithms:

Additive homomorphism: without needing to know the value of x,y, Enc(x+y) can be calculated by Enc(x) and Enc(y), and satisfies C(Enc(x),Enc(y))=Enc(x+y) that the function C represents any operation. The “ENC” signifies the corresponding ciphertext after encryption.

Multiplicative homomorphism: without needing to know the value of x,y, Enc(x×y) can be calculated by Enc(x) and Enc(y), and it is satisfied C(Enc(x),Enc(y))=Enc(x×y) that the function C represents any operation.

Hybrid multiplicative homomorphism: without needing to know the value of x, Enc(x×y) can be calculated from Enc(x) and y, and satisfy C(Enc(x),y)=Enc(x×y) that the function C represents any operation.

Fully homomorphic encryption FHE scheme: if the HE encryption function Enc satisfies consistency for all Boolean circuits, then the scheme is called a fully homomorphic encryption FHE scheme.

3.2 Paillier Encryption

Among different homomorphic encryption algorithms, the SHE schemes has excellent performance in terms of execution efficiency and construction complexity, so it is widely used. Meanwhile, the vertical LR models mainly involve addition and multiplication when calculating gradients for parameter update. Therefore, this paper adopts the famous SHE algorithm Paillier [16], which is based on the difficult problem of compound residual classes and has been widely used in electronic voting and biometric applications, and its encryption and decryption efficiency can be controlled at the millisecond level, which can meet the encryption and decryption operations and ciphertext computing operations of ciphertext in this paper. The encryption and decryption mechanism of Paillier homomorphic encryption algorithm is as follows:

Key generation process: the Paillier algorithm is a homomorphic encryption algorithm under the public key encryption system, so before using the Paillier algorithm, a pair of public and private keys needs to be constructed. First, randomly select two sums of large prime numbers p and q, and the greatest common divisor of pq and (p−1)(q−1) is 1. Define N=pq, λ as the least common multiple of (p−1)(q−1). Then randomly select an integer g∈Z N2*, let µ=(L(gλmodN2))−1, where the function L(x)=(x−1)/N. The final pair of public key and private key is generated, where the public key Pk is represented as (N,g) and the private key Sk is represented as λ.

Encryption process: after generating the public/private key pair, we can use the Paillier public key Pk=(N,g) for encryption. First, define the plaintext to be encrypted by m Paillier 0≤m≤N. Select a random integer r, and match 0<r<N, r and N coprime, r∈Z N2*. Using “E” to represent the encryption function, the plaintext m becomes:

c=E(m,r)=gm⋅rNmodN2(1)

It is worth noting here that for the same plaintext, Paillier’s algorithm can get different ciphertexts, which makes it have the semantic security of ciphertexts. This is because in the encryption process, even if the same public key Pk=(N,g) is used for encryption, when we pick different random numbers r, the obtained ciphertext will also be different, but decryption can restore the original plaintext m.

Decryption process: using the private key Sk=λ, the ciphertext c can be decrypted to obtain the plaintext:

m=D(c)=L(cλmodN2)⋅µmodN(2)

Select integers r1 and r2 at random, encrypt plaintext m1 to obtain ciphertext E(m1)=gm1⋅r1NmodN2, and encrypt plaintext m2 to obtain ciphertext E(m2)=gm2⋅r2NmodN2, so we get:

E(m1)⋅E(m2)&=gm1⋅r1N⋅gm2⋅r2NmodN2=gm1+m2⋅(r1⋅r2)N⋅mod⋅N2=E(m1+m2)(3)

Therefore, Paillier’s algorithm has additive homomorphism and mixed multiplicative homomorphism, that is, for a given ciphertext E(m1), E(m2) and integer k∈Z N have:

E(m1)⋅E(m2)=E(m1+m2)(4)

Ek(m1)=E(km1)(5)

3.3 Deep Neural Network and Backpropagation

Deep Neural Networks (DNN) simulate the working principles of the biological neural system. It treats inputs as electrical signals between neuron connections, where the importance of different connections corresponds to the weight values of different inputs. DNN can be divided into three categories: (1) Feedforward deep networks, constructed by multiple encoder layers, typical examples include multilayer perceptron and convolutional neural networks. (2) Feedback deep networks, constructed by multiple decoder layers, typical examples include HSC level sparse coding grid and deconvolutional networks. (3) Bidirectional deep networks, each layer can contain either an encoder or a decoder, or a combination of both, typical examples include stacked autoencoders, deep Boltzmann machines, and DBN deep belief networks. For feedforward deep networks, the training process of the model can be divided into two steps: forward propagation and backward propagation [17].

Forward propagation is the prediction process of the DNN model for the input. The input information flows in the same direction, from the input layer through the hidden layers, and finally reaches the output layer. There are no closed loops in the network model structure. During the forward propagation process, each neuron in the neural network takes the dot product of the outputs of all the neurons in the upper layer and its own weight vector, and then passes through an activation function to obtain the output of that neuron.

The backpropagation algorithm (BP) is the process of updating model parameters to minimize the value of the objective function. By using the chain rule of differentiation, the partial derivatives of the loss function with respect to each model parameter can be calculated, and these derivatives are then used to update the corresponding parameters. After iteratively performing forward propagation and backpropagation, the loss function gradually converges. Therefore, before using the BP algorithm, it is necessary to determine the loss function to measure the difference between the predicted labels of the model and the true labels of the samples.

4  Vertical Deep Neural Network without Arbiter

This paper proposes a vertical deep neural network algorithm, called Vertical DNN (VDNN), which can effectively achieve lossless joint modeling while protecting data privacy. VDNN is insensitive to the neural network structure and can address multi-class and non-linear problems.

In the scenario of vertical federated linear modeling, the participating party Host possesses data features XH=x1,x2,…,xk, while the initiating party Guest possesses data features XG=xk+1,xk+2,…,xI, where k represents the number of data features of the participating party and (I−k) represents the number of data features of the initiating party. Both parties jointly train a vertical DNN model consisting of a bottom layer, an interaction layer, and a top layer, as shown in Fig. 1. We can perform secure data exchange at the interaction layer to address the issue of information leakage during the forward and backward propagation processes. For the parameters in the neural network model, the Host party holds the interaction layer parameters WH and keeps them confidential from the Guest party. The Guest party holds the interaction layer parameters WG and the parameters of the top layer model, keeping them confidential from the Host party. Here, the parameters WG=w(k+1)1,…,w(k+1)J,w(k+2)1,…,w(k+2)J,…,wI1,…,wIJ and the parameters WH=w11,…,w1J,w21,…,w2J,…,wk1,…,wkJ. J represents the total number of neurons in the input layer of the top layer model, and wij represents the linear coefficient from the i-th neuron in the interaction layer to the j-th neuron in the input layer of the top layer model.

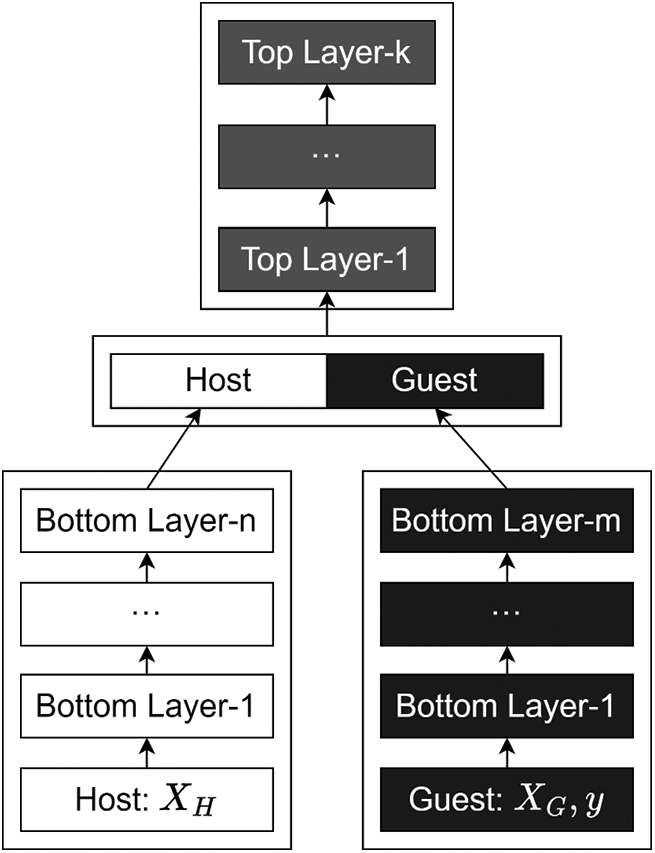
Figure 1: Vertical DNN model

The secure forward propagation and secure backward propagation processes of the VDNN algorithm will be presented below, and their timing is illustrated in Figs. 2 and 3.

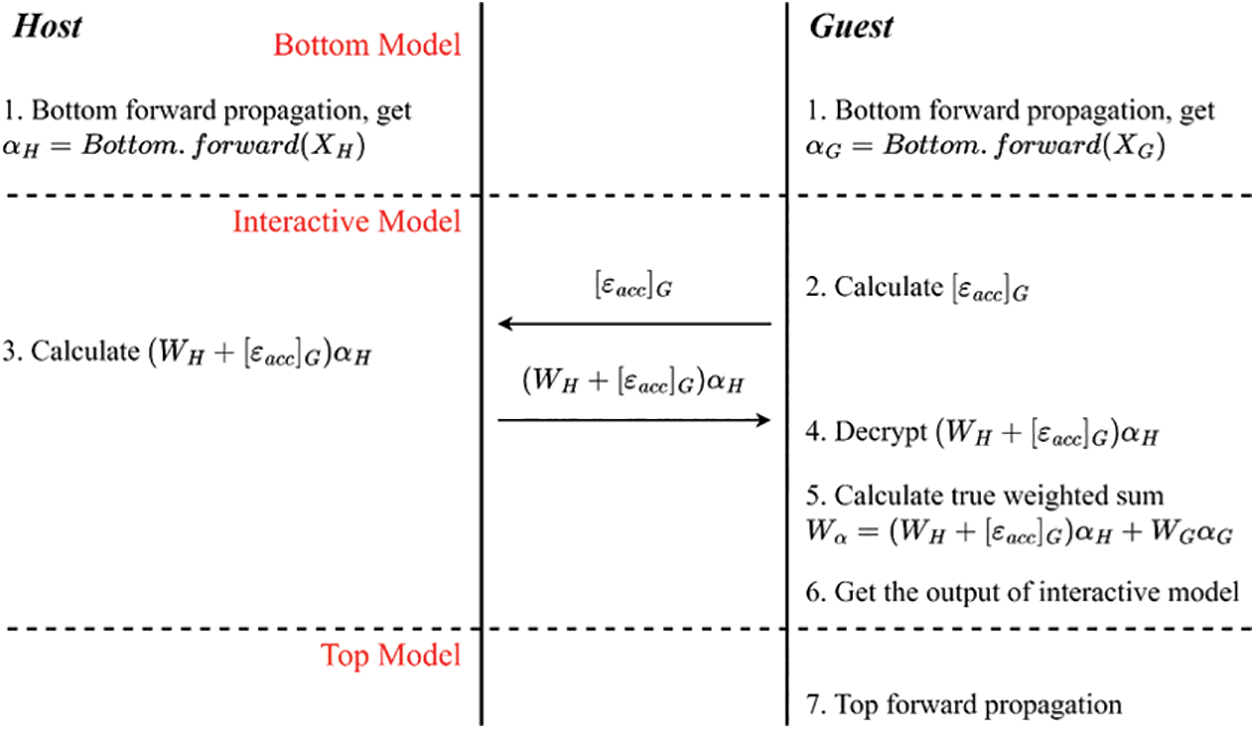
Figure 2: VDNN secure forward propagation timing diagram

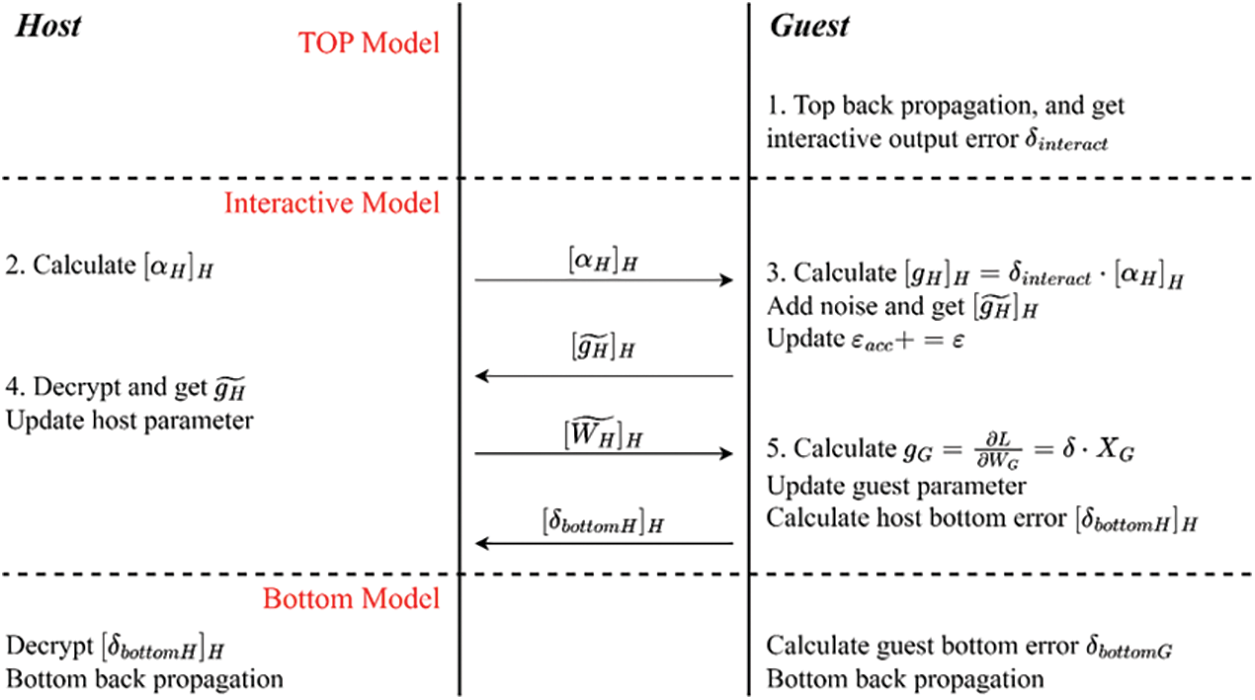
Figure 3: VDNN secure backward propagation timing diagram

The improved secure forward propagation process is as follows:

a)   The Host and Guest parties respectively use XH and XG as inputs to their own bottom layer models and perform the forward propagation process of the bottom layer models, obtaining the outputs αH and αG of the bottom layer models.

b)   The Guest party computes the encrypted accumulated noise [εacc]G and sends it to the Host party.

c)   The Host party receives and computes the encrypted weighted value (WH+[εacc]G)αH and sends it to the initiating party Guest.

d)   The Guest party decrypts the encrypted weighted value (WH+[εacc]G)αH using the private key of the Host party, obtaining the true weighted value (WH+εacc)αH of the Host party. Therefore, the Guest party can compute the true weighted value Wα=(WH+εacc)αH+WGαG and use the computed result to obtain the output of the interaction layer’s activation function, and then continue with the forward propagation process of the top layer model.

Improved secure backward propagation process is as follows:

a)   The Host party computes the encrypted data [αH]H and WHH and sends them to the Guest party.

b)   The Guest party receives and computes the encrypted gradient value [gH]H=[∂L/∂WH]H=δinteract⋅αHH in the Host party’s interaction layer. It generates random noise ε, computes the encrypted gradient value with noise [gH]H+ε/η=δinteract⋅αHH+ε/η, and the encrypted bottom layer intermediate error b. [δbottom]H=δinteract⋅([WH]H+[εacc]H). It sends [gH]H and [δbottom]H to the Host party and updates the accumulated noise [εacc]H+=ε, where η is the learning rate.

c)   The Host party receives the encrypted gradient value with noise [gH]H=[∂L/∂WH]H+ϵ/η=δinteract⋅αHH+ϵ/η, decrypts it to obtain the gradient value with noisegH=∂L/∂WH+ε/η=δinteract⋅αH+ε/η, and updates the parameters in the Host party’s interaction layer using the decrypted result: [WH]H=[WH]H−η⋅gH. Then, it performs the bottom layer backward propagation process using δbottom.

d)   The Guest party computes its own gradient value in the interaction layer gG=∂L/∂WG=δinteract⋅αG and updates the parameters in the Host party’s interaction layer using the computed result: WG=WG−η⋅gG. Then, it performs the bottom layer backward propagation process using δbottom=δinteract⋅WG.

4.1 Hardware Acceleration for Paillier

The computation of the Paillier algorithm involves a significant amount of finite field arithmetic, including modular addition, modular multiplication, and modular exponentiation of large integers and prime numbers. When the key length of Paillier is set to 1024 bits, the CPU needs to perform modular addition, modular multiplication, and modular exponentiation operations on 2048-bit data. Since the CPU is not specifically designed for large finite field arithmetic operations, these computations consume a substantial amount of CPU power and slow down the modeling process. Therefore, we propose the use of dedicated finite field arithmetic chips to accelerate the computations of the Paillier algorithm.

The Paillier hardware module is shown in Fig. 4. Our hardware module communicates with the host computer via the Peripheral Component Interconnect express (PCIe) interface. The PCIE communication module receives algorithm instructions and data from the host computer, performs byte order conversion to convert big-endian data to little-endian data, and then sends the data and instructions to the Paillier algorithm controller.

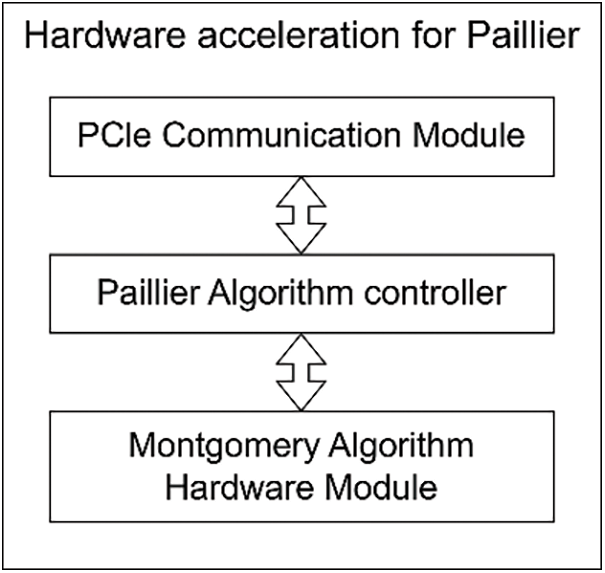
Figure 4: Hardware acceleration for Paillier

The Paillier algorithm controller generates corresponding control byte streams and data byte streams based on the received encryption and decryption instructions, and sends the byte streams to the Montgomery algorithm hardware module.

In the Montgomery algorithm hardware module, the module performs specific computational steps on the data based on the control bytes, thereby completing the Paillier encryption and decryption operations.

Finally, the module returns the computed result data byte stream to the Paillier algorithm controller, which then sends it back to the host computer via the PCIE module. With this, we have successfully completed the hardware implementation of the Paillier algorithm.

4.2 Complexity Analysis

Equations in display format are separated from the paragraphs of the text. Equations should be flushed to the left of the column. Equations should be made editable. Displayed equations should be numbered consecutively, using Arabic numbers in parentheses. See Eq. (1) for an example. The number should be aligned to the right margin.

The VDNN model consists of a bottom layer, an interaction layer, and a top layer model. The bottom layer model involves participants executing the parameter update process locally, using their own local data features as input. This layer plays a role in extracting data features and reducing data dimensions. The output of the bottom layer model serves as the input for the interaction layer model. Therefore, unlike the VLR algorithm, the VDNN model is not sensitive to the feature dimensions of the input dataset. Additionally, the top layer model is not sensitive to the DNN model architecture. It can choose any loss function, activation function, and optimizer. This is because during the backpropagation process of the top layer model, according to the chain rule of differentiation, the error of each layer is related to the error and weight of the previous layer.

During the training of the entire vertical federated model, participants perform encrypted computations and exchanges in the interaction layer. Therefore, the computational complexity and communication efficiency of the vertical deep neural network (VDNN) algorithm depend to some extent on the model structure of the interaction layer, specifically the values of interact_in and interact_out, which represent the number of input and output nodes in the interaction layer, respectively. The following analysis will focus on the computational complexity and communication complexity of the interaction layer in the VDNN algorithm.

For ease of description, let us assume that the batch size for each iteration is batch_size=n, the number of output nodes in the bottom layer model is bottom_outG=bottom_outH=m, the interact_in of the interaction layer model is 2m, and interact_out is l. Let α and β represent the computational cost of performing one 1024-bit exponentiation and one 2048-bit multiplication operation during the encryption and decryption process, respectively. Let γ and δ represent the computational cost of performing one homomorphic addition and one homomorphic scalar multiplication operation.

In the secure forward propagation algorithm, the computational cost of encryption and decryption operations for the Guest is mlα+(m+n)lβ. In the secure backward propagation algorithm, the computational cost of encryption and decryption operations for the Host is (n+l)mα+(n+2l)mβ. Throughout the VDNN algorithm, the Guest needs to perform 2ml homomorphic addition operations and 2nml homomorphic scalar multiplication operations, while the Host needs to perform ml homomorphic addition operations and nml homomorphic scalar multiplication operations.

In the FDNN algorithm, the Host is responsible for encryption and decryption operations on intermediate results, while the Guest performs homomorphic computations in the ciphertext domain. The computational time complexity of both algorithms is shown in Table 1. It can be seen that the VDNN algorithm has a more balanced computational time complexity, with comparable computational tasks for both the Guest and the Host. This eliminates the need for both parties to wait for each other’s computation results during the model update process, resulting in shorter program execution time.

In each iteration of the VDNN algorithm, the number of ciphertexts that need to be transmitted between participants is 2 nm+3 ml+nl. It can be observed that the communication cost and computational cost of the VDNN algorithm are influenced by the parameters m, l, and n, but are not sensitive to the input data dimension. At the same time, the number of output nodes m in the bottom layer model for both the Guest and the Host also affects the feature extraction performance of the bottom layer model, which in turn affects the classification performance of the VDNN model. Therefore, when setting the hyperparameters bottom_outG, bottom_outH, and interact_out, a balance needs to be struck between communication efficiency and classification performance.

4.3 Security Analysis

In the forward propagation and backward propagation processes, the outputs of the bottom layer model, αH and αG, as well as the intermediate error δinteract in the interaction layer, need to be encrypted or noise-added before being sent to other participants. Otherwise, malicious attackers may collect these intermediate results and infer the privacy information of other participants. In this section, we will analyze the security of the vertical deep neural network algorithm VDNN from two aspects.

Security of Guest’s label data and feature data. Secure forward propagation and secure backward propagation constitute the iterative update process of the VDNN algorithm. Step 2 of secure forward propagation and step 3 of secure backward propagation involve sending data from the Guest to the Host. In step 2 of secure forward propagation, the Host learns the encrypted accumulated noise [εacc]G, removes the noise from its own parameters, and sends the real encrypted weighted value (WH+[εacc]G)αH to the initiating party. Since the Host does not know the Guest’s private key information, it cannot decrypt the ciphertext. In step 3 of secure backward propagation, after decrypting the received encrypted values, the Host can obtain gH∼=∂L/∂WH+ε/η=δinteract⋅αH+ε/η and δbottomH=δinteract⋅(WH∼+εacc), where δinteract is the intermediate error calculated by the Guest in the interaction layer, ε is the random noise added by the Guest, and εacc is the cumulative value of ε. All three values are kept secret from the Host, so the Host cannot determine the value of δinteract by solving a system of linear equations.

Security of Host’s feature data. Step 3 of secure forward propagation and step 2 of secure backward propagation involve sending data from the Host to the Guest. In step 3 of secure forward propagation, the Guest decrypts and obtains the real weighted value (WH+εacc)αH from the Host. Since αH is the output of the Host’s bottom layer model and the Guest does not know the value of WH, the Guest cannot infer any additional information. In step 2 of secure backward propagation, the Host calculates the encrypted data [αH]H and [WH∼]H to send to the initiating party. Since the Guest does not have the Host’s private key information, it cannot decrypt the data and can only perform ciphertext computations, ensuring security.

5  Experimental Results and Analysis

5.1 Experimental Datasets

To test the performance of the VDNN methods, experiments were conducted on two widely used datasets. Each dataset was divided into two parts based on their features, with Guest and Host having a subset of features each, and only Guest having access to the labels. The datasets are:

Dataset 1: Default credit dataset, which collected credit card data from a Taiwan bank from April to September 2005. It is a binary classification problem on default payment, with 30,000 samples and 24 data features, including payment history, demographic factors, credit data, billing information, etc. The dataset is split longitudinally, with Guest having 13 data features and labels, and Host having 10 data features.

Dataset 2: Vehicle scale dataset, which is divided into four categories based on the vehicle contour data features. It consists of 846 data samples and 18 data features related to vehicle contours. After vertical splitting the dataset, the Guest has 9 data features and labels, while the Host has 9 data features.

5.2 Experimental Design

The paper implements the vertical deep neural network algorithm VDNN without an arbiter and the heterogeneous neural network algorithm FDNN from [6] as a control using TensorFlow. In the neural network model, bottom_outG and bottom_outH represent the number of output nodes in the bottom layer models of the Guest and Host, respectively. interact_in represents the number of input nodes in the interaction layer, and interact_out represents the number of output nodes in the interaction layer. Therefore, interact_in=bottom_outG+bottom_outH. The paper sets bottom_outG=bottom_outH=6 for the bottom layer models, interact_in=12, and interact_out=4 for the interaction layer model. The optimizer chosen is Nadam, with hyperparameters lr=0.001 and clipnorm=1. For dataset 1, the batch size is set to 500, and the maximum number of iterations is MAX=5. For dataset 2, the batch size is 846, and the maximum number of iterations is MAX=500.

The experimental environment for the models was a computer with 3.10 GHz (8 CPUs) and 16 GB RAM. Different models and hyperparameters can achieve different classification results for classification tasks, but this paper focused on the overall system and did not focus on the performance of the models themselves. Therefore, the same hyperparameters were used to compare different solutions horizontally.

Common evaluation metrics for machine learning models include accuracy, precision, recall, and F1-Score, etc. In addition, as a federated learning model, continuous communication is often required among the participating parties to exchange model update information. Therefore, the total communication volume is also an important metric to consider, as it will affect the network cost and minimum bandwidth required for deploying the model in practice. Therefore, this paper evaluates and compares the performance of the VDNN and FDNN algorithms based on metrics such as accuracy, AUC, F1-Score, program running time, and the total transmission volume (TV) between the participating parties during the model training process.

The total transmission volume TV=SendG+ReceiveG. where SendG and ReceiveG represent the total amount of data sent and received by the Guest, respectively, measured in MB. A smaller value of the total transmission volume indicates higher communication efficiency of the algorithm.

5.3 Experimental Analysis

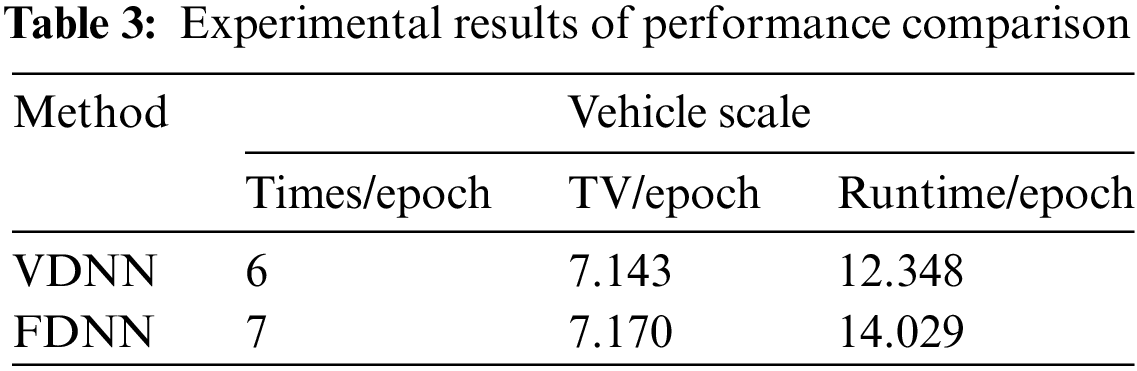
We compared and analyzed the performance of the VDNN and FDNN algorithms based on metrics such as accuracy, AUC, F1-Score, program running time, and the total transmission volume (TV) between the participating parties during the model training process. The results showed that under the same model parameters and experimental environment, the VDNN method achieved better classification performance, faster running time, and higher communication efficiency. Table 2 presents the classification comparison results of the VDNN and FDNN models on Dataset 1 and Dataset 2. Figs. 5–7 show the convergence curves of accuracy, loss function, and F1-Score for both models during the model training process. It can be observed that the VDNN model avoided local optima on Dataset 2, resulting in higher classification accuracy. From Table 3, it can be seen that the VDNN model required 6 interactions between the Guest and Host for each iteration, while the FDNN model required 7 interactions. The total transmission volume (TV) and program running time of the VDNN model were both superior to those of the FDNN model.

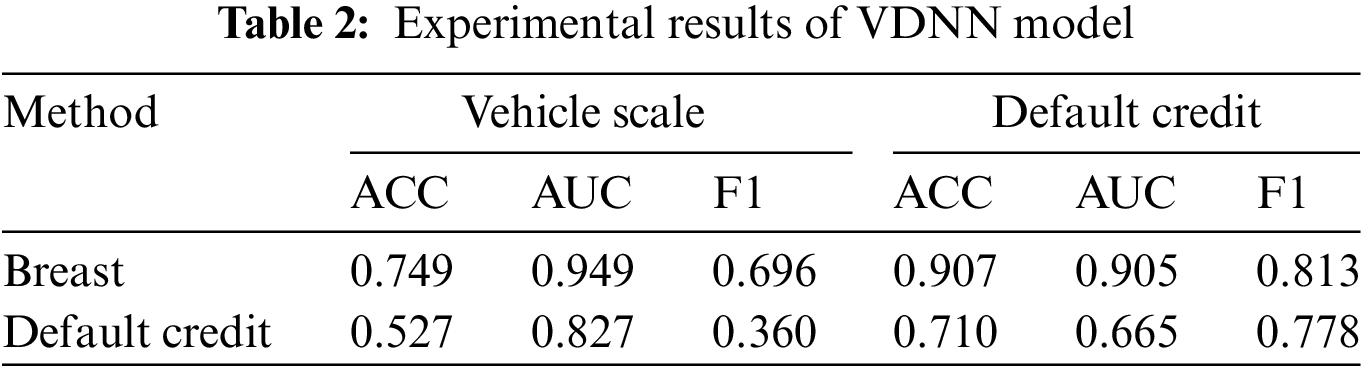
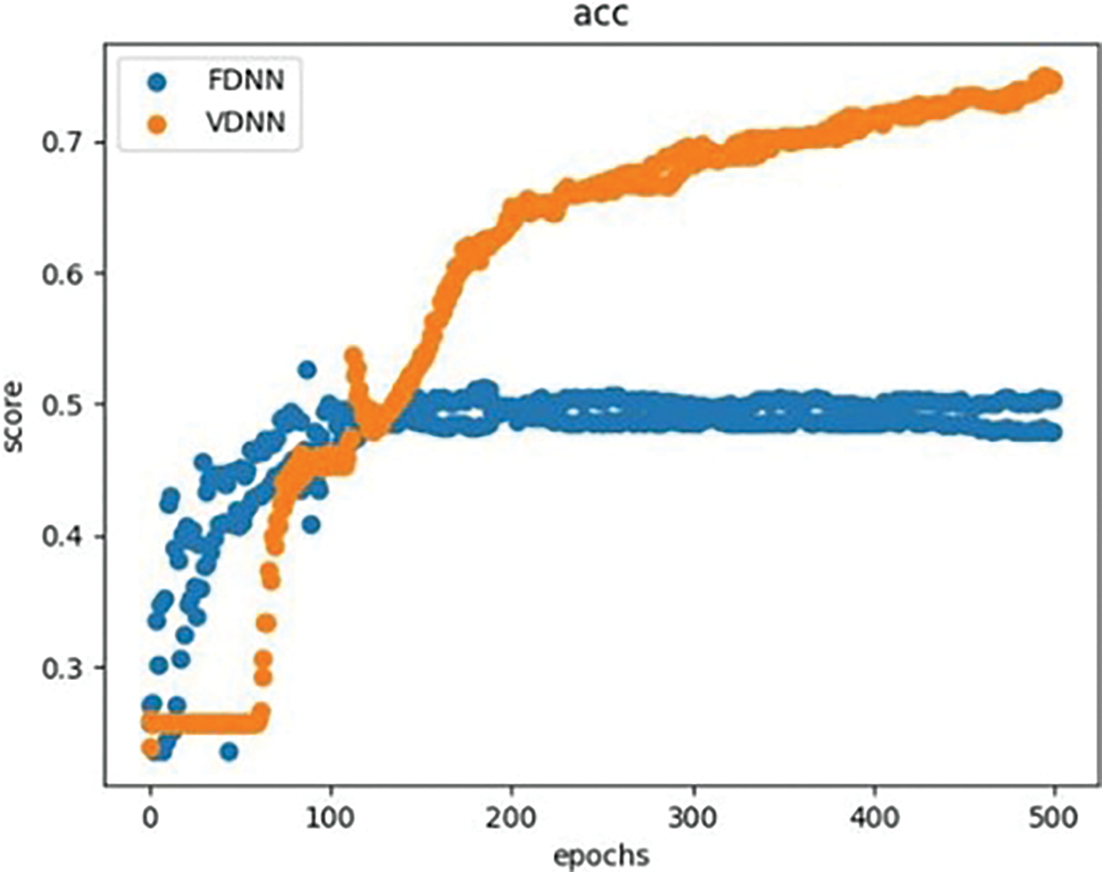
Figure 5: Comparison of ACC curve for VDNN

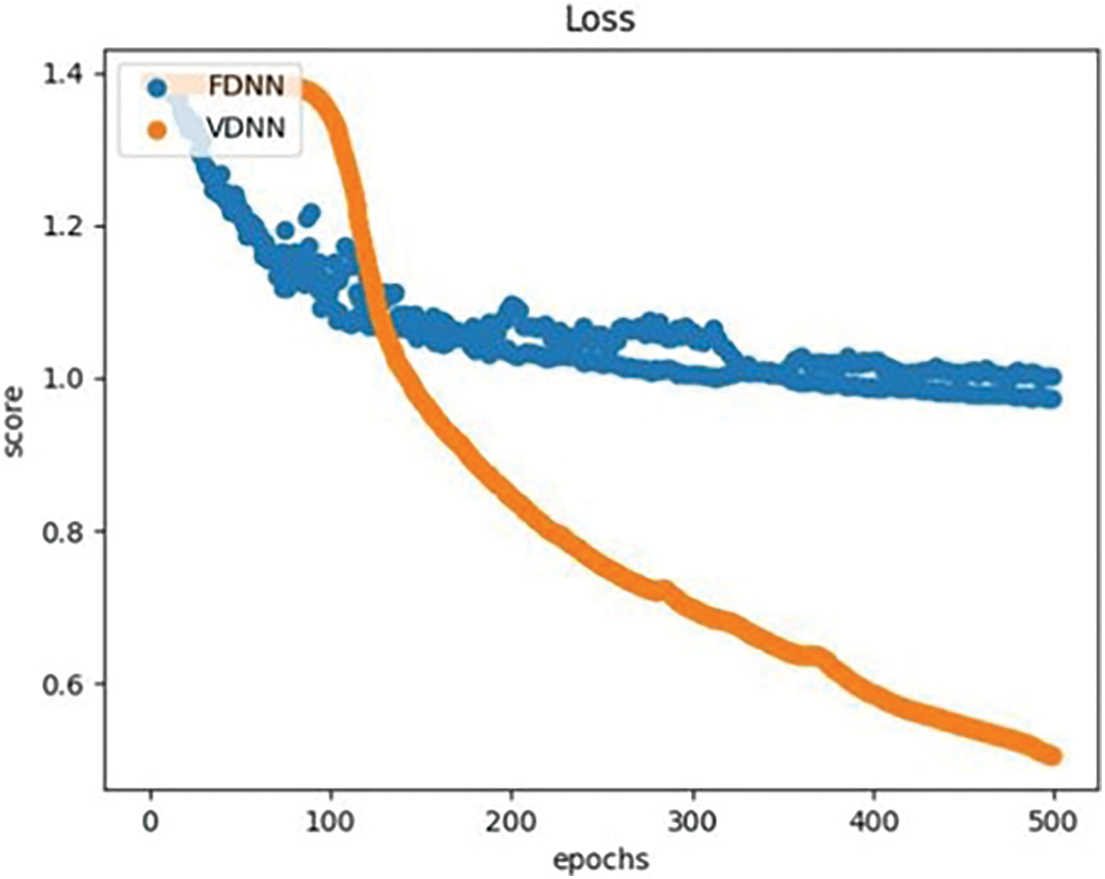
Figure 6: Comparison of loss curve for VDNN

Figure 7: Comparison of F1 curve for VDNN

6  Conclusions

This paper firstly introduces the concept of homomorphic encryption algorithm, and then focuses on the key generation, encryption and decryption process and homomorphic properties of Paillier encryption algorithm, and gives the correctness proof of Paillier algorithm. Furthermore, this paper introduces the forward and backward propagation algorithms of deep neural networks, detailing the steps of adding noise and applying homomorphic encryption in both forward and backward propagation. The security and complexity of the method are analyzed. Finally, comparative experiments are conducted between the proposed method and the FDNN method. The experimental results demonstrate that the VDNN method achieves better classification performance, faster runtime, and superior communication efficiency. The VDNN method can be applied to federated modeling of multimodal data in medical scenarios, which is highly beneficial for intelligent diagnosis of multi-stage diseases. However, even with chip acceleration, the modeling speed of the VDNN method still lags behind that of traditional centralized data modeling. Future work should focus on further enhancing the computational speed of vertical federated modeling.

Acknowledgement: The authors thank the support from the central government and the Harbin Manufacturing Technology Innovation Talent Project.

Funding Statement: This research was funded by the National Natural Science Foundation, China (No. 62172123), the Key Research and Development Program of Heilongjiang (Grant No. 2022ZX01A36), the Special Projects for the Central Government to Guide the Development of Local Science and Technology, China (No. ZY20B11), the Harbin Manufacturing Technology Innovation Talent Project (No. CXRC20221104236).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Jinbo Yang and Lailai Yin; Data curation, Wanjuan Xie; Formal analysis, Jinbo Yang; Funding acquisition, Jiaxing Qu; Investigation, Wanjuan Xie; Methodology, Jinbo Yang and Lailai Yin; Project administration, Jiaxing Qu; Resources, Hai Huang; Software, Jinbo Yang and Lailai Yin; Supervision, Hai Huang; Validation, Jinbo Yang; Writing–original draft, Jinbo Yang; Writing–review & editing, Hai Huang.

Availability of Data and Materials: The data comes from publicly available datasets on Kaggle, including the Default of Credit Card Clients Dataset and the vehicle scale Data Set.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. McMahan, B., Moore, E., Ramage, D., Hampson, S., Arcas, B. A. Y. (2017). Communication-efficient learning of deep networks from decentralized data. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, pp. 1273–1282. Fort Lauderdale, FL, USA. https://proceedings.mlr.press/v54/mcmahan17a.html [Google Scholar]

2. Yang, K., Fan, T., Chen, T., Shi, Y., Yang, Q. (2019). A quasi-newton method based vertical federated learning framework for logistic regression. https://doi.org/10.48550/arXiv.1912.00513 [Google Scholar] [CrossRef]

3. Feng, S., Yu, H. (2020). Multi-participant multi-class vertical federated learning. https://doi.org/10.48550/arXiv.2001.11154 [Google Scholar] [CrossRef]

4. Yang, S., Ren, B., Zhou, X., Liu, L. (2019). Parallel distributed logistic regression for vertical federated learning without third-party coordinator. https://doi.org/10.48550/arXiv.1911.09824 [Google Scholar] [CrossRef]

5. Hardy, S., Henecka, W., Ivey-Law, H., Nock, R., Patrini, G. et al. (2017). Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption. https://doi.org/10.48550/arXiv.1711.10677 [Google Scholar] [CrossRef]

6. Zhang, Y., Zhu, H. (2020). Additively homomorphical encryption based deep neural network for asymmetrically collaborative machine learning. https://doi.org/10.48550/arXiv.2007.06849 [Google Scholar] [CrossRef]

7. Saleem, T. J., Zahra, S. R., Wu, F., Alwakeel, A., Alwakeel, M. et al. (2022). Deep learning-based diagnosis of Alzheimer’s disease. Journal of Personalized Medicine, 12(5), 815. https://doi.org/10.3390/jpm12050815 [Google Scholar] [PubMed] [CrossRef]

8. Liu, Y., Liu, Y., Liu, Z., Liang, Y., Meng, C. et al. (2022). Federated forest. IEEE Transactions on Big Data, 8(3), 843–854. https://doi.org/10.1109/TBDATA.2020.2992755 [Google Scholar] [CrossRef]

9. Fang, H., Qian, Q. (2021). Privacy preserving machine learning with homomorphic encryption and federated learning. Future Internet, 13(4), 94. https://doi.org/10.3390/fi13040094 [Google Scholar] [CrossRef]

10. Pulido-Gaytan, B., Tchernykh, A., Cortés-Mendoza, J. M., Babenko, M., Radchenko, G. et al. (2021). Privacy-preserving neural networks with Homomorphic encryption: Challenges and opportunities. Peer-to-Peer Networking and Applications, 14(3), 1666–1691. https://doi.org/10.1007/s12083-021-01076-8 [Google Scholar] [CrossRef]

11. Rivest, R. L., Adleman, L. M., Deaouzos, M. L. (1978). On data banks and privacy homomorphisms. Foundations of Secure Computation, 4, 169–179. [Google Scholar]

12. Rivest, R. L., Shamir, A., Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), 120–126. https://doi.org/10.1145/359340.359342 [Google Scholar] [CrossRef]

13. Goldwasser, S., Micali, S. (1982). Probabilistic encryption & how to play mental poker keeping secret all partial information. Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing, pp. 365–377. New York, NY, USA. https://doi.org/10.1145/800070.802212 [Google Scholar] [CrossRef]

14. Elgamal, T. (1985). A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transactions on Information Theory, 31(4), 469–472. https://doi.org/10.1109/TIT.1985.1057074 [Google Scholar] [CrossRef]

15. Benaloh, J. (1994). Dense probabilistic encryption. Selected areas of cryptography. https://www.microsoft.com/en-us/research/wp-content/uploads/1999/02/dpe.pdf (accessed 10/08/2023). [Google Scholar]

16. Paillier, P. (1999). Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (Ed.) Proceedings of the 17th International Conference on Theory and Application of Cryptographic Techniques, pp. 223–238, Berlin, Heidelberg, Springer-Verlag. https://doi.org/10.1007/3-540-48910-X_16 [Google Scholar] [CrossRef]

17. Singh, A. K., Kumar, B., Singh, S. K., Ghrera, S. P., Mohan, A. (2018). Multiple watermarking technique for securing online social network contents using back propagation neural network. Future Generation Computer Systems, 86, 926–939. https://doi.org/10.1016/j.future.2016.11.023 [Google Scholar] [CrossRef]