A Coupled Thermomechanical Crack Propagation Behavior of Brittle Materials by Peridynamic Differential Operator

1  Introduction

The investigation of the problem involving brittle material fracture caused by thermal deformations and thermal stresses due to thermal loading is highly meaningful. When temperature fluctuations lead to thermal stresses surpassing the material’s strength threshold, it triggers the initiation of microcracks within the structure. These microcracks gradually propagate, evolving into macroscopic fractures, ultimately culminating in structural failure. Brittle materials and structures frequently experience diverse temperature loads, including rapid cooling or heating, thereby inducing intricate thermally driven deformations and fractures, elevating the risk of structural failure. Notably, recent years have witnessed extensive investigations into the physical and mechanical characteristics of brittle materials, such as granite [1] and ceramics [2], under thermomechanical conditions.

Over the past few decades, researchers have investigated the cracking behaviors of granites and ceramics under thermal shocks, employing various experimental, theoretical, and numerical methods to predict thermal shock cracking patterns in brittle solids. Early experimental studies on thermal shock cracking patterns in ceramic materials date back to the 1950s. Kingery [3] introduced the fracture criterion of critical stress, utilizing the maximum thermal stress for determining the initiation of thermal shock cracks. Nied [4] investigated thermal shock resulting from sudden surface heating in an edge-cracked plate and juxtaposed it with the opposite thermal shock condition of surface cooling. Shao et al. [5–8] conducted real-time investigations on the thermal shock crack propagation of ceramic through water quenching, employing translucent ceramic and high-speed imaging. Geyer et al. [9] conducted an experimental study on thermally induced parallel edge cracks in a half-plane of brittle material. Besides, Liu et al. [1] examined the physical and mechanical properties of granite and sandstone samples following high-temperature treatment, revealing distinct responses to temperature in each rock type. Fan et al. [10] demonstrated that elevated temperatures lead to internal mineral expansion, generating significant thermal stress even in the absence of external constraints. Zhu et al. [11] investigated the impact of thermal cyclic treatment on granite, revealing increased microcrack generation, leading to deterioration and weakening of physical and mechanical properties, as observed through laboratory tests. These materials, commonly employed in high-temperature contexts [12], exhibit inherent material heterogeneity, rendering their thermomechanical behaviors intricate and challenging to comprehend. Despite substantial advancements in comprehending the thermomechanical properties of brittle materials through experiments [10,13,14], certain damage-related behaviors, such as crack propagation, remain elusive. The need for precise physical models and numerical forecasts has become pressing.

The crack initiation and propagation under thermal shock is quite a rapid and highly complicated process. Besides the experimental and theoretical methods, numerical method is considered as a useful approach to understand the mechanism of multiple thermal shock cracks, which plays an important role in thermomechanical analysis. Traditional approaches rooted in continuum mechanics, such as phase field models (PFM) [15], have been developed to dissect intricate dynamic crack propagation trajectories in brittle materials subjected to thermomechanical loads [16]. Besides, Boundary element method (BEM) [17] was employed to reproduce multiple crack patterns of brittle solids in quenching tests; Finite element method (FEM) [18] was used to investigate the effect of heterogeneity on fracture behaviors of ceramic slabs subjected to thermal shocks. The extended finite element method (XFEM) [19] was applied to numerically analyze crack oscillating propagation in glass plates subjected to thermal shocks. However, despite the successful reproduction of multiple crack initiation and propagation in brittle materials under thermal shocks using the aforementioned numerical methods, they still require external techniques such as remeshing, external failure criteria, and supplementary constitutive models.

The peridynamics framework, introduced by Silling [20], presents a promising alternative that overcomes the limitations of numerical methods grounded in continuum mechanics. In comparison to previous numerical methods, such as PMF, FEM, and XFEM, the primary advantage of peridynamics lies in the fact that its governing equations of motion inherently accommodate the presence of discontinuities in the deformation field [21]. Peridynamic governing equations are formulated in integral form, with interactions defined by bonds [21]. This framework allows the discontinuous damage behavior of points to be quantified through the tally of broken bonds, obviating the need for an additional fracture criterion. Bond-based peridynamics (BB PD) [20] was the initial version to emerge within the peridynamics theory framework, distinguished by its clear concepts and ease of implementation. However, BB PD has inherent limitations, including constraints associated with the Poisson’s ratio and limited capabilities in analyzing plastic deformation. To address these limitations, Silling et al. [22] extended BB PD to state-based peridynamics (SB PD), comprising ordinary state-based peridynamics (OSB PD) and non-ordinary state-based peridynamics (NOSB PD). In addition to these three variants, peridynamic differential operator (PDDO) [23] introduces a non-local interaction mechanism in the Taylor series expansion. This innovation establishes a more generalized peridynamics theoretical framework and provides a broader and more versatile approach to non-local theories.

Peridynamics, as a nonlocal reformulation of continuum mechanics theory, introduces a nonlocal integral operator in its equation of motion, replacing the stress divergence term in classical continuum mechanics with pairwise force density [21]. This unique approach has attracted attention from researchers exploring nonlocal operators. Bergel et al. [24] extended peridynamics to total and updated Lagrangian approaches, demonstrating convergence to local operators in finite deformation contexts. Researchers like Yan et al. [25] developed a higher-order nonlocal continuum theory within updated Lagrangian particle hydrodynamics, focusing on accurate and stable simulations of complex three-dimensional multiphase flows. Yu et al. [26] contributed to the field by developing and analyzing nonlocal discrete differential operators, showcasing their convergence to local operators and computational performance. In a comparative study, Kan et al. [27] explored two types of nonlocal differential operators derived from the Taylor series expansion of nonlocal interpolation and the nonlocal operator theory in peridynamic theory. Furthermore, Ren et al. [28] addressed shock wave-induced soil fragmentation by developing a nonlocal PD-smoothed particle hydrodynamics (SPH) coupling, demonstrating successful simulations.

Peridynamics has emerged as a valuable tool for analyzing the dynamic crack propagation mechanisms in thermomechanically loaded brittle materials. Notable contributions have been made in this realm. Kilic et al. [29] employed the uncoupled thermomechanical peridynamics model to simulate crack propagation modes in a quenched glass plate. D’Antuono et al. [30] studied thermal shock-induced crack propagation behaviors in a brittle slab using the weakly coupled thermomechanical OSB PD model. Giannakeas et al. [31] explored the effects of hot and cold shock in brittle materials using a coupled thermomechanical model that combined BB PD with finite element methods. Chu et al. [32] proposed a BB PD model to accurately describe the dynamic behavior of ceramics under impact loading, considering brittle response, softening plasticity, and strain-rate effects. Bazazzadeh et al. [33] developed an adaptive grid refinement thermo-mechanical PD model. Zhang et al. [34] proposed a novel BB PD model to investigate the thermomechanical behavior of quasi-brittle materials. Prakash et al. [35] applied PD to model microstructural mechanics, revealing multiple toughening mechanisms and demonstrating increased fracture toughness in glass ceramics compared to traditional glass. Additionally, Wang et al. [36] investigated thermal crack processes in rocks using a coupled thermomechanical BB PD approach, and extended the model to simulate thermal crack behaviors in a nuclear pellet while examining crack branch instability in brittle solids. Rabczuk et al. [37] proposed a dual-horizon PD formulation for fracture in granular and rock-like materials, eliminating the need for explicit crack surface representation and addressing complex fracture patterns. Wang et al. [38] introduced shear failure into the coupled thermomechanical OSB PD model, effectively simulating thermal crack behavior in rocks. Yang et al. [39] investigated the thermal fracture characteristics of granite subjected to thermal cycling treatment using a fully coupled OSB PD thermomechanical model. Yang et al. [39,40] investigated thermal-mechanical fracturing behaviors in granite post thermal cycling using a fully coupled OSB PD, examining crack evolution under varied temperatures and fissure angles. Feng et al. [41] introduced a BB PD with shear deformation to simulate complex compression/shear failure in heterogeneous rocks under uniaxial compression. Despite notable advancements in coupled thermomechanical modeling, there remains a need for further developments in numerical studies concerning the thermal crack propagation behavior of brittle materials using peridynamics.

This study presents a comprehensive approach by formulating coupled thermomechanical governing equations. The classical differential thermomechanical equations’ local spatial derivatives are replaced with non-local integral forms derived from the PDDO. The model’s effectiveness is exemplified through two numerical examples investigating thermomechanical fracturing behaviors in brittle materials. The first example employs the Shuffle algorithm to accurately capture granite’s inherent heterogeneity, probing crack behaviors during thermal cycling treatments. The second example introduces the Weibull distribution to simulate ceramic’s heterogeneity, quantifying crack expansion during ceramic slab quenching. Remarkably, the PDDO model’s predictions align well with other numerical and experimental outcomes, validating the efficacy of this fully coupled thermomechanical approach.

This innovative methodology unlocks new avenues for exploring the intricate thermal crack propagation behavior of materials like granite and ceramics. By integrating the PDDO into classical thermomechanical equations, it provides a deeper understanding of the initiation and progression of microcracks under thermal stress, with significant implications for structural integrity in various applications. This approach offers a distinctive perspective on fracture mechanics, enriching the comprehension of material behavior under thermal loading conditions.

The paper’s structure is organized as follows: Section 2 introduces the complete simulation framework. Section 3 outlines the numerical implementation details. Section 4 is dedicated to modeling the first numerical example, while Section 5 focuses on the second numerical example. Finally, Section 6 presents the conclusions drawn from the study.

2  Fully Coupled Thermomechanics Model

2.1 Classical Thermomechanical Equations

The thermomechanical coupled equations in classical continuum mechanics are

ρcvT˙=kT∇2T−α(3λ+2μ)T0ε˙kk+STρu¨=∇⋅σ+b(1)

where ε˙kk is the volumetric strain rate, u is displacement tensor, T is the temperature, T0 is the reference temperature, b is the body force density vector, σ is the Cauchy stress tensor, α(3λ+2μ) is the thermal modulus, α is the coefficient of thermal expansion, ST is a source term,∇ is the gradient operator, ∇⋅() is a divergence operator, E is Young’s modulus, ν is Poisson’s ratio, λ=Eν(1+ν)(1−2ν),μ=E2(1+ν) are Lame’s constants.

The component form of Cauchy stress tensor σ for isotropic linear thermoelasticity can be written as

σij=2μεij+(λεkk−α(3λ+2μ)(T−T0))δij(2)

where εij,εkk are the components of the strain tensor, δij is the Kronecker symbol. The dummy indexes i,j equal to 1, 2, 3 for 3D-problems, 1, 2 for 2D-problems, and 1 for 1D-problems.

Expressing the strain component as the displacement component

σij=μ(ui,j+uj,i)+(λukk−α(3λ+2μ)(T−T0))δij(3)

The thermomechanical coupling equation expressed in terms of the partial derivatives of the displacement components can be written as

{ρcv∂T∂t=kT∂2T∂x2−α(3λ+2μ)T0∂∂t(∂uk∂xk)+STρ∂2ui∂t2=μ∂2ui∂xk2+(λ+μ)∂2uk∂xk∂xi−α(3λ+2μ)∂(T−T0)∂xi+bi(4)

2.2 PDDO Equations

The inception of peridynamic theory was pioneered by Silling [20]. Subsequently, Madenci et al. [23] presented a comprehensive PD definition, known as the PDDO. PDDO is frequently employed to deduce an integral non-local expression for local derivatives of arbitrary order [42,43], a derivation rooted in the Taylor series expansion, as depicted below:

f(x+ξ)−f(x)=ξ1∂f(x)∂x1+ξ2∂f(x)∂x2+12!ξ1∂f2(x)∂x12+12!ξ2∂f2(x)∂x22+ξ1ξ2∂2f(x)∂x1∂x2+R(2,x)(5)

where ξ=x′−x is the relative position vector, R(2,x) is the remainder.

Here, an orthogonality property of PD function is introduced and constructed.

g2P1P2(ξ)=a00P1P2ω(| ξ |)+a10P1P2ω(| ξ |)ξ1+a01P1P2ω(| ξ |)ξ2+20P1P2ω(| ξ |)ξ12+a02P1P2ω(| ξ |)ξ22                   +a11P1P2ω(| ξ |)ξ1ξ2(6)

where ω(|ξ|) is the weight function, associated with each term ξ in the polynomial expansion. It can be used to measure the strength of the influence of the integral points in the defined horizon. The weight function between two points is usually used to describe the process of interaction strength of points, which is not a physical quantity in the experiment.

Based on the orthogonal nature of the PD function, the partial derivative can be as follows:

∂fP1+P2(x)∂x1P1∂x2P2=∫Hxf(x+ξ)g2P1P2(ξ)dVx′(7)

The orthogonality property of the PD function can be expressed as

∫Hxξ1n1ξ2n2g2P1P2(ξ)dVx′=n1!n2!δn1P1δn2P2(8)

The unknown coefficients, a can be determined from the solution of

∑q1=02∑q2=02−q1A(n1n2)(q1q2)aq1q2P1P2=bn1n2P1P2(9)

The coefficient matrix can be constructed as

{A(n1n2)(q1q2)=∫Hxω(|ξ|)ξ1n1+q1ξ2n2+q2dVx′bn1n2P1P2=n1!n2!δn1P1δn2P2(10)

By solving for the unknown coefficients of this equation a, the PD functions g2P1P2(ξ) can be constructed.

After determining the PD functions, the first- and second-order derivatives can be expressed as

{∂f∂x1∂f∂x2}=∫Hx(f(x+ξ)−f(x)){g210(ξ)g201(ξ)}dVx′{∂2f∂x12∂2f∂x22∂2f∂x1∂x2}=∫Hx(f(x+ξ)−f(x)){g220(ξ)g202(ξ)g211(ξ)}dVx′(11)

2.3 Non-Local Integral Formulation of Fully Coupled Thermomechanics

The conventional thermodynamic Eq. (4), expressed in terms of displacement components, is augmented by substituting the local spatial derivatives with their corresponding non-local integral forms derived from the PDDO. As a result, the thermal diffusion equation can be formulated as follows:

ρcv∂T∂t=kT∫Hx(T(x+ξ)−T(x))(g220(ξ)+g202(ξ))dVx′−α(3λ+2μ)T0∂∂t(∫Hx(u1(x+ξ)−u1(x))g210(ξ)dVx′+∫Hx(u2(x+ξ)−u2(x))g201(ξ)dVx′)+ST(x,t)(12)

The equations of motion in two directions can be formulated as

ρ∂2u1∂t2=(λ+2μ)∫Hx(u1(x+ξ)−u1(x))g220(ξ)dVx′+μ∫Hx(u1(x+ξ)−u1(x))g202(ξ)dVx′+(λ+μ)∫Hx(u2(x+ξ)−u2(x))g211(ξ)dVx′−α(3λ+2μ)∫Hx((T−T0)(x+ξ)−(T−T0)(x))g210(ξ)dVx′+b1(x,t)(13)

ρ∂2u2∂t2=μ∫Hx(u2(x+ξ)−u2(x))g220(ξ)dVx′+(λ+2μ)∫Hx(u2(x+ξ)−u2(x))g202(ξ)dVx′+(λ+μ)∫Hx(u1(x+ξ)−u1(x))g211(ξ)dVx′−α(3λ+2μ)∫Hx((T−T0)(x+ξ)−(T−T0)(x))g201(ξ)dVx′+b1(x,t)(14)

The PDDO model substitutes differentiation in the original equation with spatial integration, effectively circumventing the singularity issue inherent in continuous medium mechanics.

3  Numerical Implementation

3.1 Spatial and Temporal Integration

In peridynamic simulations, spatial integrations can be assessed through a single-point Gaussian quadrature scheme, coupled with mesh-free particle discretization [21]. Fig. 1 illustrates the distribution of collocation points and family shapes within a 2D analysis. Note that the horizon can vary across individual points. In the subsequent simulations section, a symmetric horizon was used, meaning that the left and right family points have equal weight on the target points. Any asymmetric properties are a result of asymmetric family points, whether they exhibited symmetric or asymmetric characteristics as individual points.

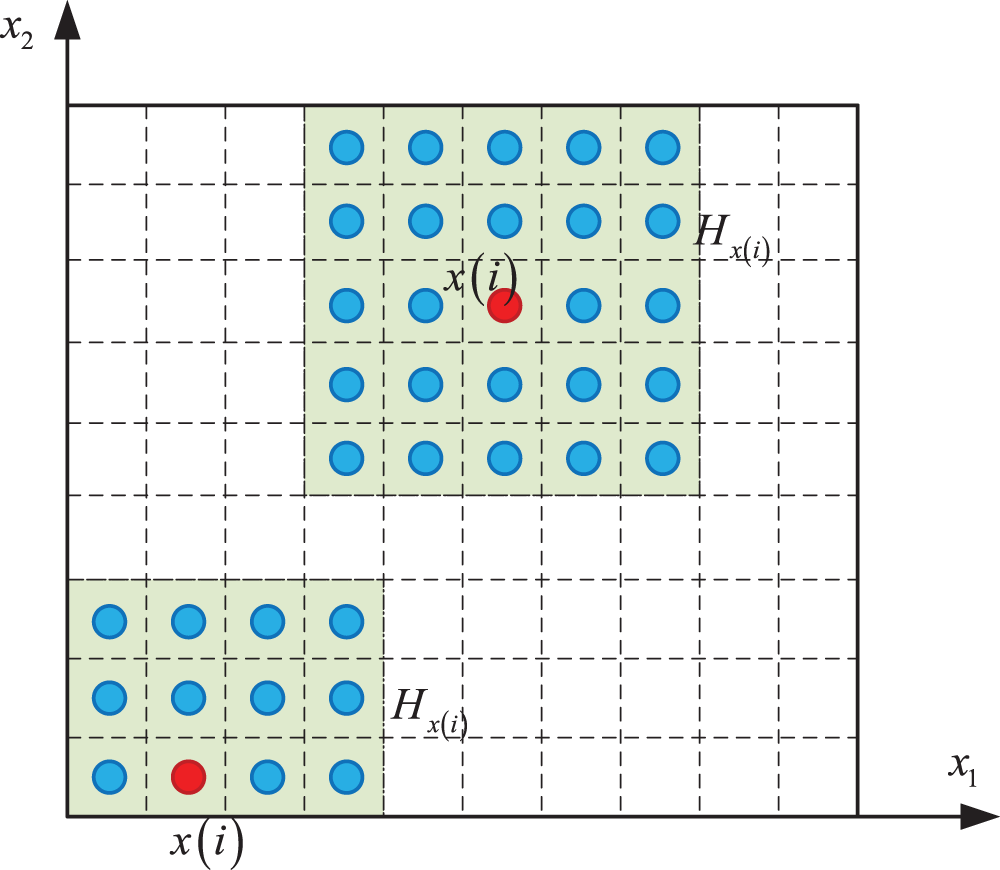
Figure 1: Schematic of 2D-spatial discretization

Explicit time integration is employed to numerically solve the coupled PDDO thermomechanical equations. Specifically, for 2D problems, the discretization of the thermal diffusion equation can be represented as

Tkn+1−TknΔt=kTρcv∑j=1NK(g220+g202)[Tjn−Tkn]ΔVj−α(3λ+2μ)ρcvT0{∑j=1NKg210[u1,jn−u1,kn]ΔVj/Δt−∑j=1NKg210[u1,jn−1−u1,kn−1]ΔVj/Δt}−α(3λ+2μ)ρcvT0{∑j=1NKg201[u2,jn−u2,kn]ΔVj/Δt−0∑j=1NKg201[u2,jn−1−u2,kn−1]ΔVj/Δt}(15)

where Δt is the calculated time step of the thermal diffusion equation, n is the time step, j is the point within the horizon of the point i, NK is the total number of points, Vj is the approximate volume of the point, the actual volume of the 2D-dimensional matter point when using the orthogonal homogenization discretization is Vj=|Δx|2, Δx is the length of the matter point. To ensure the accuracy of the integration, the amount of integration of the substance material needs to be modified [44].

The motion equations can be discretized respectively as

ρu1,kn+1−2u1,kn+u1,kn−1(Δt)2=(λ+2μ)∑j=1NKg220[u1,jn−u1,kn]ΔVj+μ∑j=1NKg202[u1,jn−u1,kn]ΔVj+(λ+μ)×∑j=1NKg211[u2,jn−u2,kn]ΔVj−α(3λ+2μ)∑j=1NKg210[(T−T0)jn−(T−T0)kn]ΔVj(16)

ρu2,kn+1−2u2,kn+u2,kn−1(Δt)2=(λ+2μ)∑j=1NKg202[u2,jn−u2,kn]ΔVj+μ∑j=1NKg220[u2,jn−u2,kn]ΔVj+(λ+μ)×∑j=1NKg211[u1,jn−u1,kn]ΔVj−α(3λ+2μ)∑j=1NKg210[(T−T0)jn−(T−T0)kn]ΔVj(17)

3.2 Numerical Implementation

In the peridynamics approach, the numerical model is discretized into numerous points, and the structural motion and deformation are characterized by non-local interactions among these points. Fig. 2 schematically illustrates the heat conduction mode, highlighting the distinction between non-local and conventional local forms. In non-local peridynamics, the interaction model is fundamentally different from conventional local theories. Instead of focusing solely on immediate neighboring contact points, non-local peridynamics consider interactions between a central material point and all other material points within a specified horizon range. This approach is particularly effective in scenarios like fracture mechanics, where classical continuum mechanics, reliant on local interactions, often falls short.

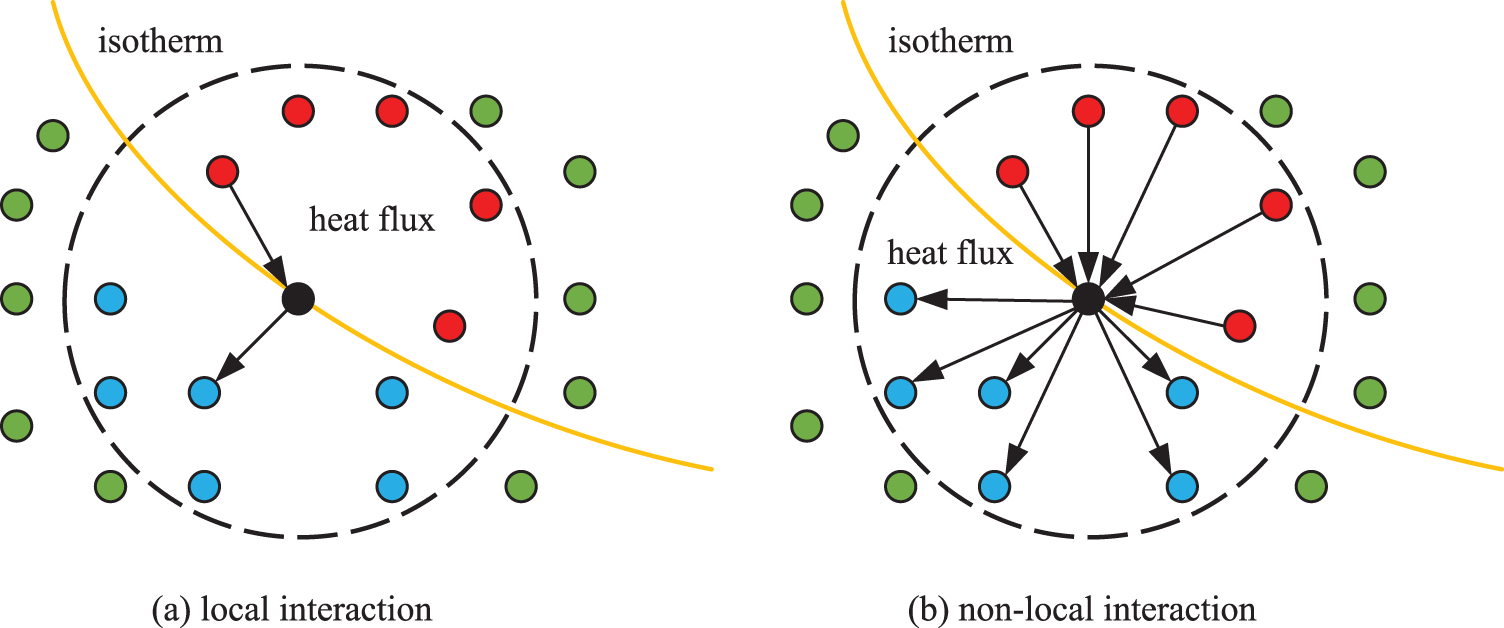
Figure 2: Schematic of heat conduction mode

Among the various non-local methods, the PDDO stands out, sharing the stage with other approaches such as General Particle Dynamics (GPD) [45]. These non-local methods are united by their capacity to handle long-range interactions and spatially distributed forces phenomena that traditional local theories cannot adequately address. PDDO, in particular, differentiates itself by employing integral equations without spatial derivatives, concentrating on the nonlocal interactions within the horizon of a material. This method provides a more comprehensive understanding of material behaviors, especially in contexts involving complex mechanical interactions. The advantage of non-local integral forms, compared to conventional local formulations, lies in their ability to capture the inherently non-local physics associated with microscopic scales [46,47].

Bonds connecting two points are commonly employed to depict the progression of damage accumulation, crack initiation, and propagation. To characterize the state of these bonds, Silling et al. [21] introduced a scalar-valued function linked to their historical evolution.

μ(ξ,t)={1s(t′,ξ)<s0,0<t′<t0other(18)

where s0 is the critical stretch, related to the fracture energy release rate G0 of materials and peridynamic horizon size δ. Its value for 2D problems can be defined as [48]

s0=G0[6πμ+169π2(λ−2μ)]δ(19)

Fig. 3 shows the influence of cracks on heat transfer. The presence of cracks results in a decreased thermal conductivity, as interactions between points passing through the cracks become ineffective in the system.

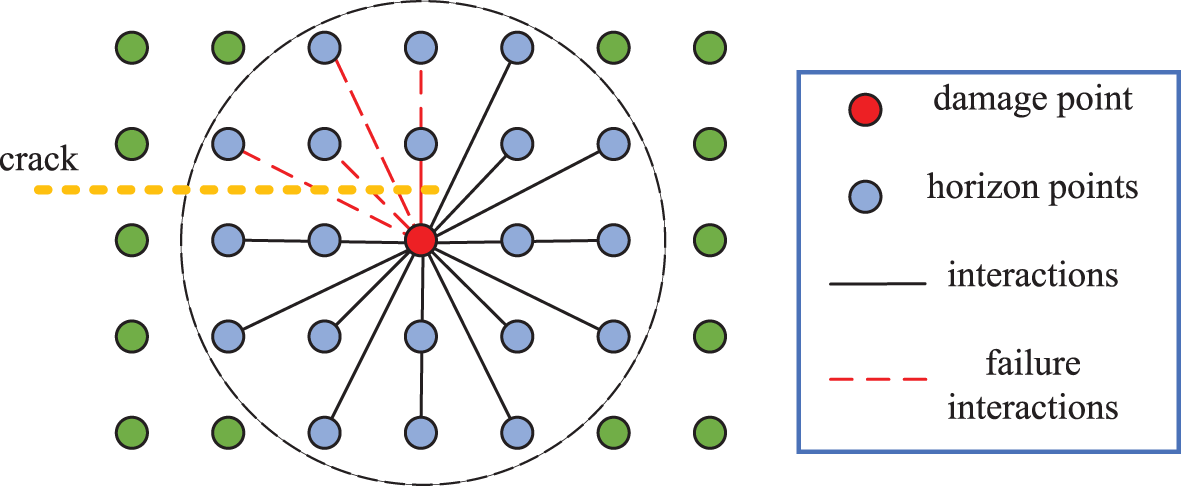
Figure 3: Crack effect on the heat transfer

Von Neumann stability analysis has revealed a substantial disparity between the time steps suitable for thermal diffusion and mechanical deformation, with the former being significantly larger [49]. To address this discrepancy, explicit multiscale time integration schemes [30,50,51] are introduced, as depicted in Fig. 4, to effectively manage the unequal time steps inherent in thermomechanical coupled problems.

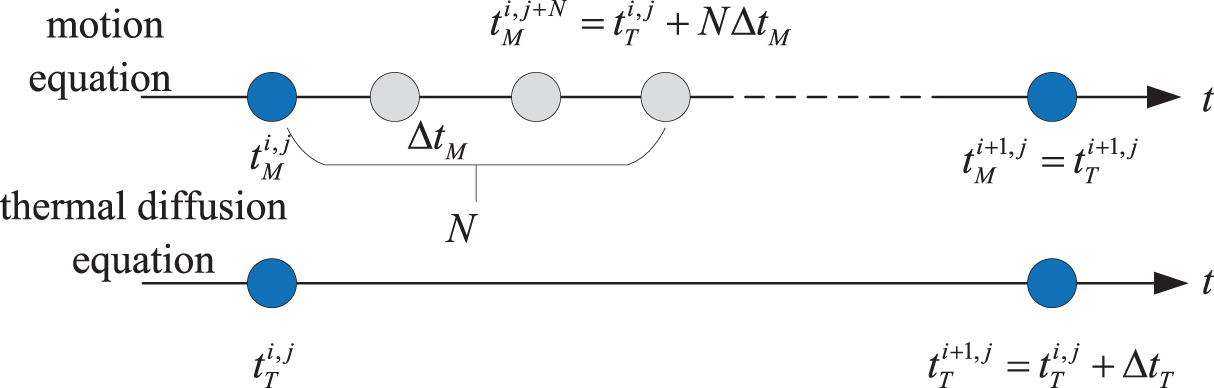
Figure 4: Explicit multi-scale time integration scheme

The numerical algorithm for addressing the thermomechanical coupled problem is visually outlined in Fig. 5, encompassing three distinct phases: pre-processing, thermomechanical computation, and post-processing. Within the thermomechanical component, the initial stage involves thermal diffusion analysis, after which, upon a single step, the temperature is presumed to reach a steady-state condition. Subsequently, mechanical deformation analysis is carried out until the system attains the predetermined steady deformation state. Following this, the subsequent step of thermal diffusion analysis commences.

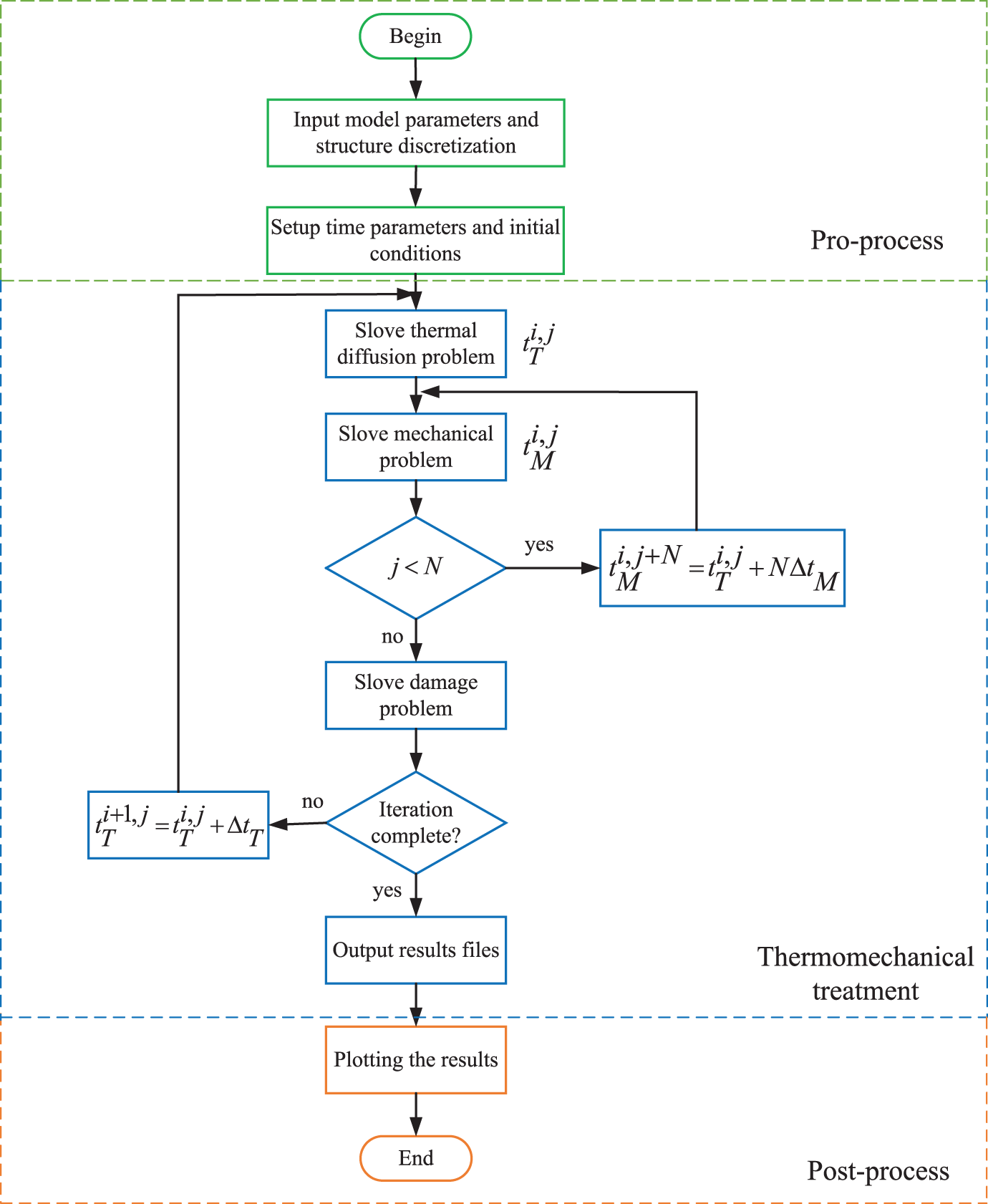
Figure 5: Numerical algorithm

4  Thermal Cycling Treatment on Granite

4.1 Shuffle Algorithm

Heterogeneity represents a prevalent attribute of rock materials. It has been established that under high temperature, thermal cracking is induced by the non-uniform thermal expansion coefficient between different minerals, even without external constraints [10]. Consequently, the Shuffle algorithm is incorporated to simulate the inherent heterogeneity of rock materials [39]. As illustrated in Fig. 6, the Shuffle algorithm is commonly employed to transform an ordered array into an unordered one, randomly assigning each element of the original array to any position within the rearranged array with equal probability.

Figure 6: (a) The initial array; (b) the re-sorted array

Table 1 presents the mineral types, their respective contents, and the corresponding thermal expansion coefficients for the granites. Throughout the subsequent numerical simulations, the properties of individual components remain constant and do not vary with temperature. As depicted in Fig. 6a, an array of relevant parameters is initially assigned, aligning with the mineral types and their contents within the granite material. Subsequently, the parameter information array undergoes reordering via the Shuffle algorithm, illustrated in Fig. 6b, resulting in the final parameter information array. Fig. 7 visualizes the ultimate distribution of thermal expansion coefficients associated with each material point.

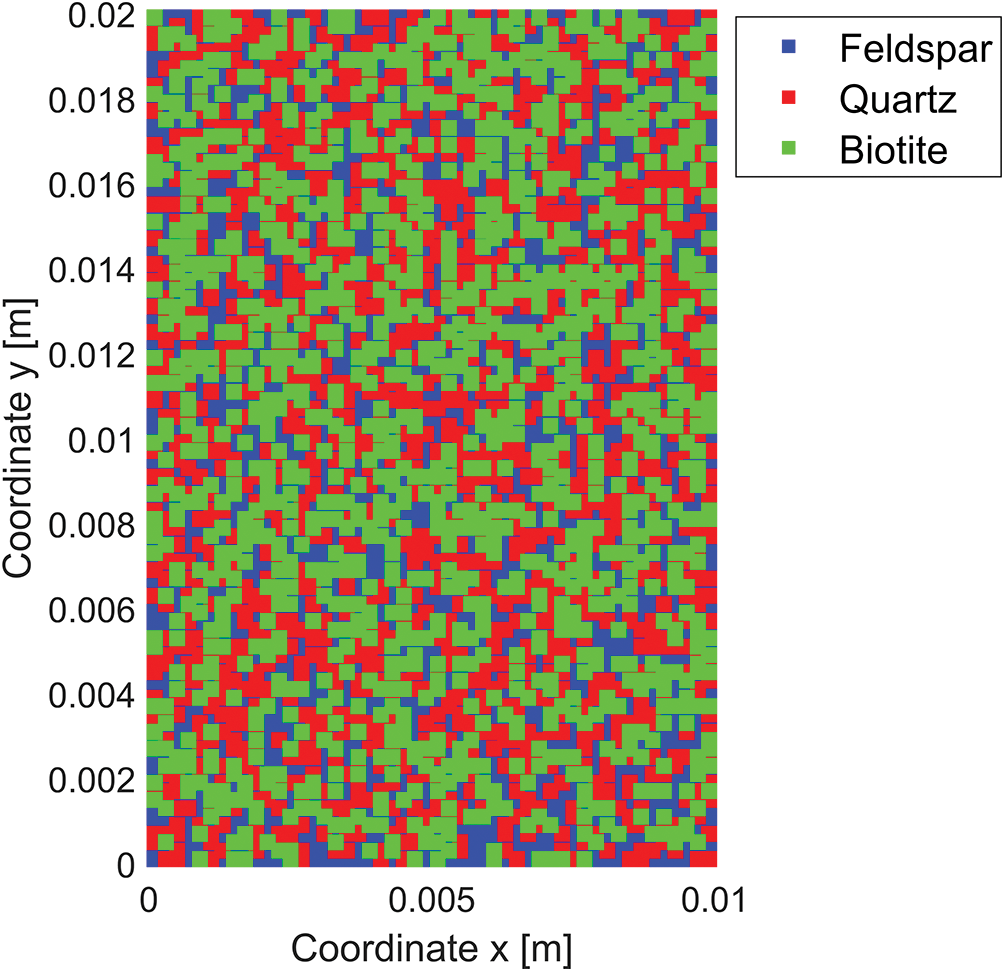
Figure 7: Thermal expansion coefficient distribution

4.2 Results and Comparisons

To validate the efficacy of the proposed thermomechanical coupling approach, we conducted simulations to investigate damage behavior resulting from incompatible expansion between various minerals within granite materials under thermal cycling conditions. The granite specimen measures 10 mm in length and 20 mm in height, with boundaries free from any displacement constraints. The temperature boundaries of the model surface, similar to the imposition of the convection condition, heat can be imposed in the form of a rate of heat generation per point in the boundary layer. The heating rate of the boundary layer is 0.2∘C/step, corresponding to the thermal time step of 2.5×10−2  s/step, can be converted to 8∘C/s. The test temperatures selected are 500∘C and 1000∘C. A temperature monitoring point at the center of the specimen records the entire thermal cycling treatment process. Table 2 provides details regarding the PD discretization, thermal, and mechanical parameters employed in the numerical simulations, considering material properties as temperature-independent.

Fig. 8 shows the temperature curve at the center of the numerical specimen. The thermal treatment involves an initial stage of infrared radiation heating followed by a subsequent natural cooling phase, designed to explore the crack behavior of granite during thermal cycling treatment. The simulation spans 1040 s, and at the point when the numerical simulation time reaches 520 s, the temperature within the core area has attained 480.78∘C, marking the beginning of the cooling process.

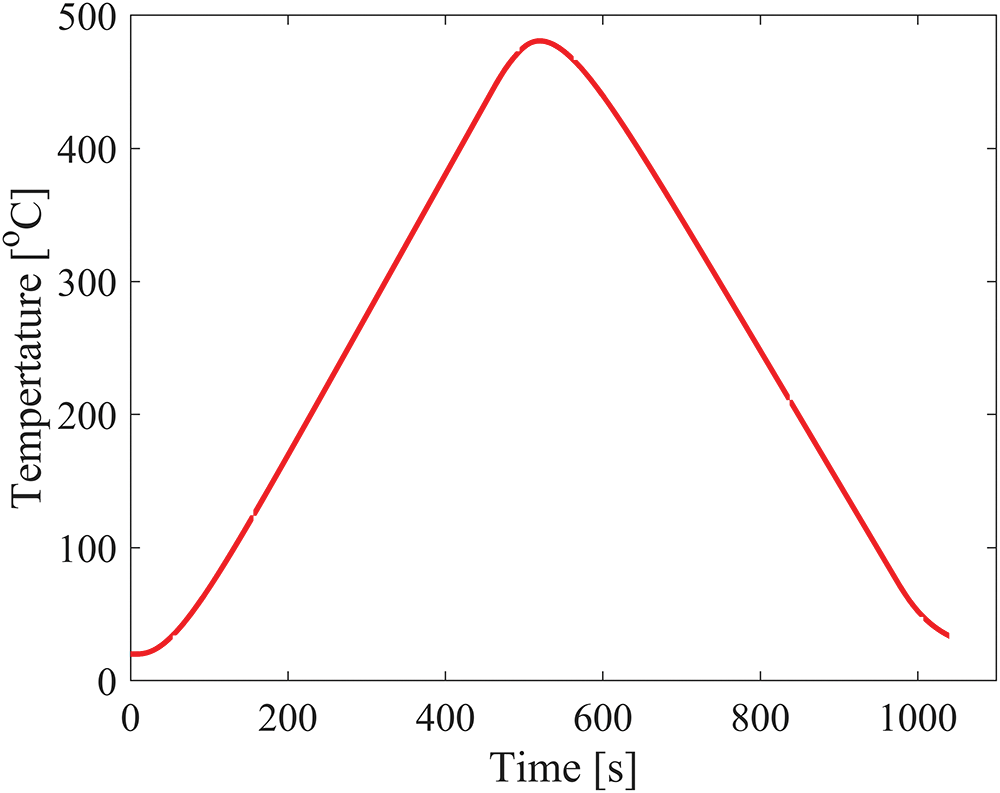
Figure 8: Temperature curve at the center of the numerical specimen

The evolution of crack propagation patterns, temperature distributions, and horizontal displacement profiles at various time steps for loading temperatures of 500∘C and 1000∘C is presented in Figs. 9 and 10. The different colors in the crack propagation patterns represent the damage values, as defined in Eq. (18). The color red in the figures indicates the material point is fully damaged, while the color blue represents the material point is undamaged. Initially, when the numerical model undergoes heating, minimal damage occurs due to the small compression displacement caused by the initial temperature change (t = 40 s). With continuous heating, the temperature differential between the surface and core regions steadily increases, leading to the emergence of numerous microcrack patterns at the four boundaries. These cracks progressively extend from the boundaries towards the interior (t = 120 s or t = 200 s). As the numerical model continues to heat towards the maximum temperature, crack propagation persists towards the center, with new cracks continuously emerging at the boundaries (t = 520 s or t = 1000 s). During the early stages of the cooling process, temperature-induced displacement transitions from compression to tension (t = 600 s or t = 1040 s). Subsequently, as the surface temperature decreases further, tensile displacement occurs at the model’s surface. In this phase, damage at the boundaries intensifies, and crack propagation no longer extends into the interior (t = 1040 s or t = 2000 s).

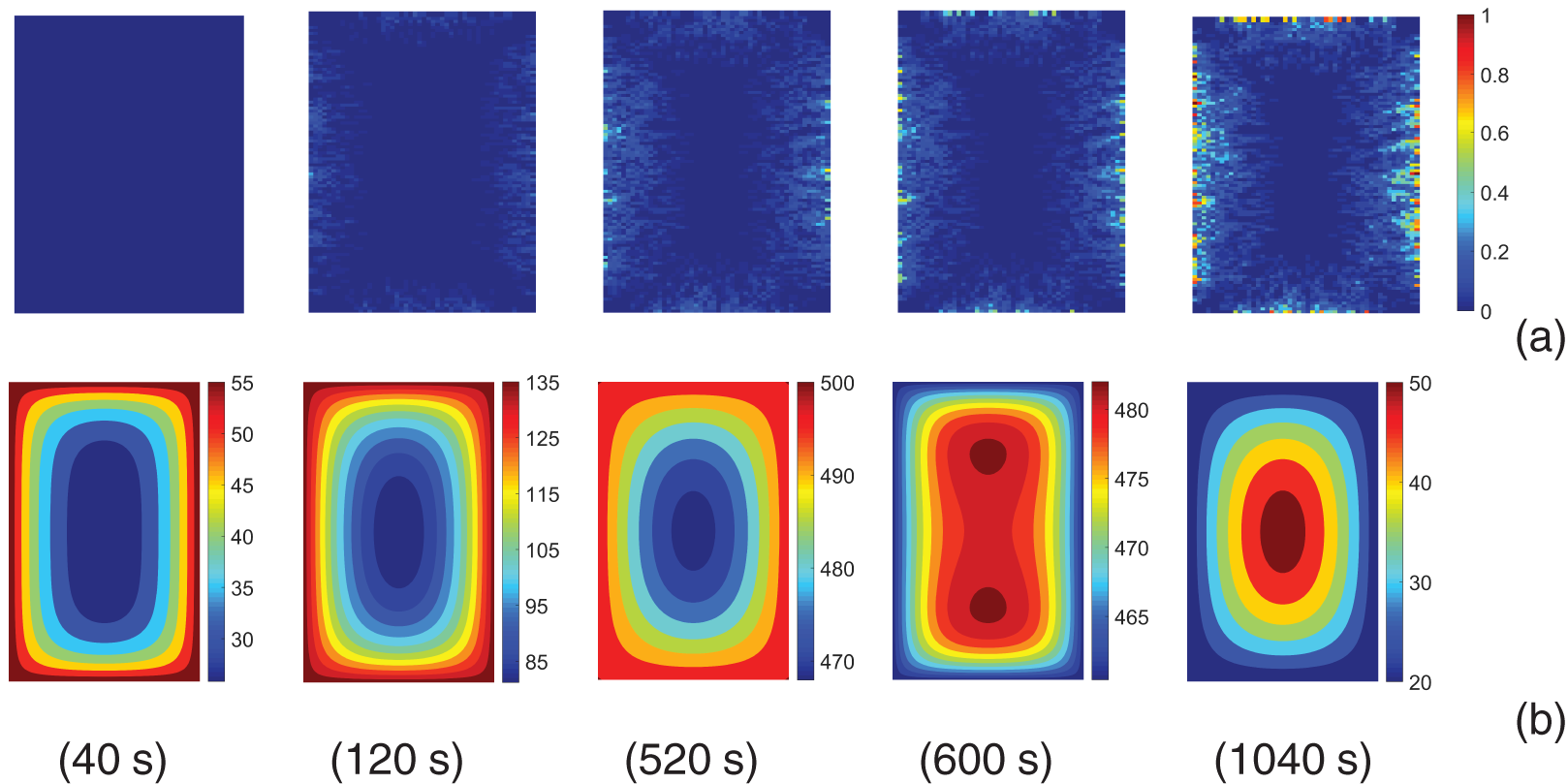
Figure 9: (a) Crack propagation patterns; (b) temperature distributions under 500∘C

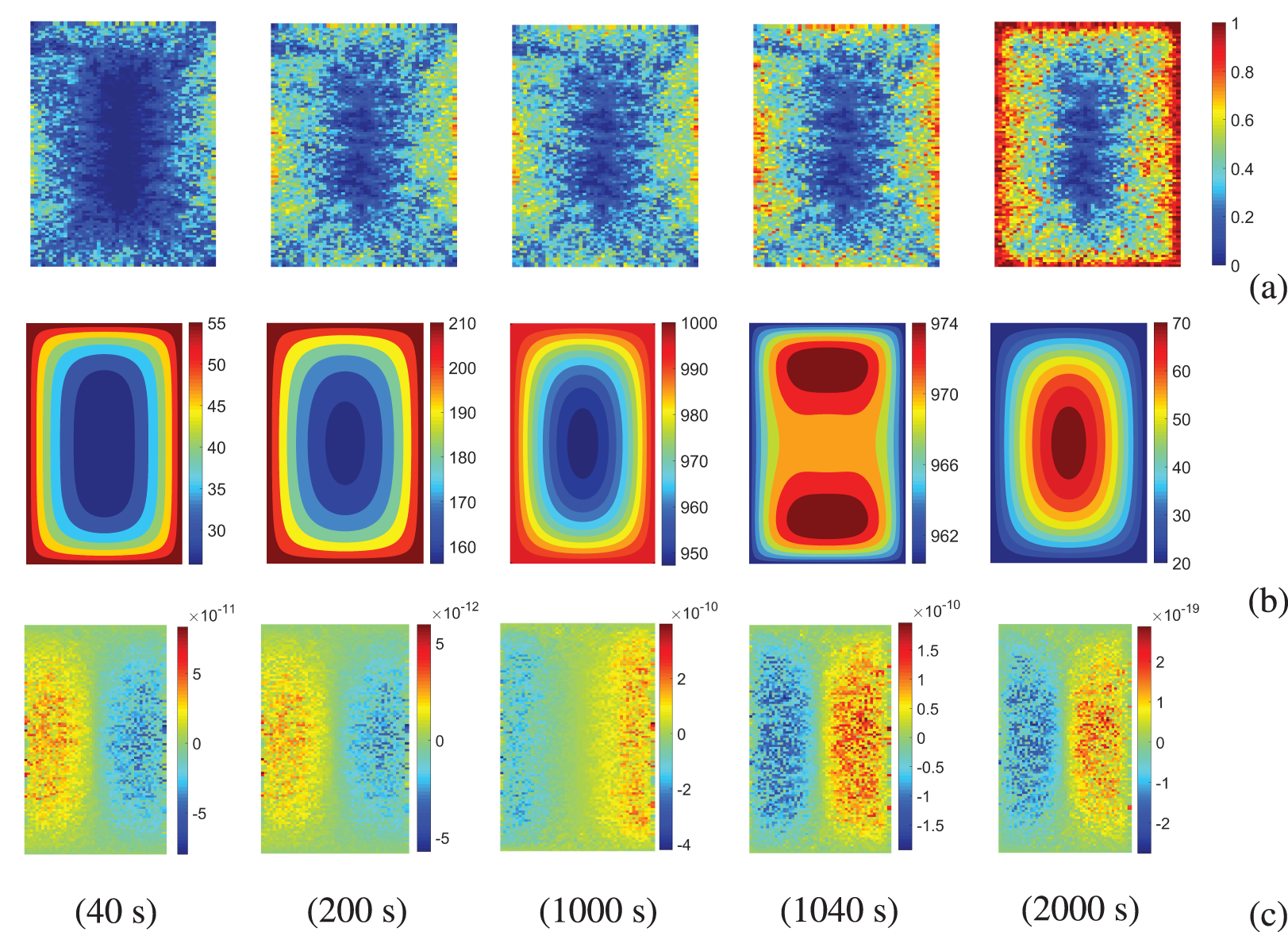
Figure 10: (a) Crack propagation patterns; (b) temperature distributions and (c) horizontal displacement distributions under 1000∘C

Fig. 11 shows the temperature distribution along the horizontal axis, with solid lines representing the heating stage and dashed lines representing the cooling stage. The presence of cracks should result in temperature discontinuities. However, this discontinuity in Figs. 9 and 10b is not particularly pronounced. It is mainly reflected in the non-smooth variations of temperature, and the entire temperature field lacks evident discontinuity. This is likely due to cracks predominantly occur at the edges, without notably pronounced penetrating fractures.

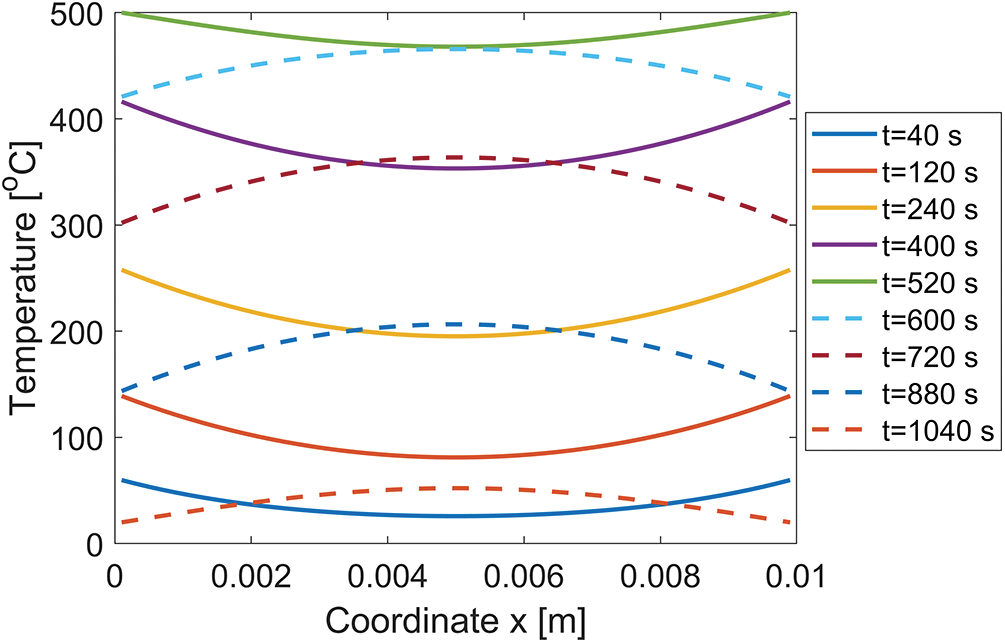
Figure 11: Temperature distribution along the horizontal axis at various times under 500∘C

For comparative purposes, experimental and previous numerical results are presented in Fig. 12. It is apparent that the damage models and crack paths across these results exhibit striking similarities. However, it is worth noting that neither the Shuffle algorithm nor other algorithms can precisely replicate the actual microstructure of granite material. Consequently, the distribution of cracks in the numerical simulation results may not entirely align with the observations derived from experimental data.

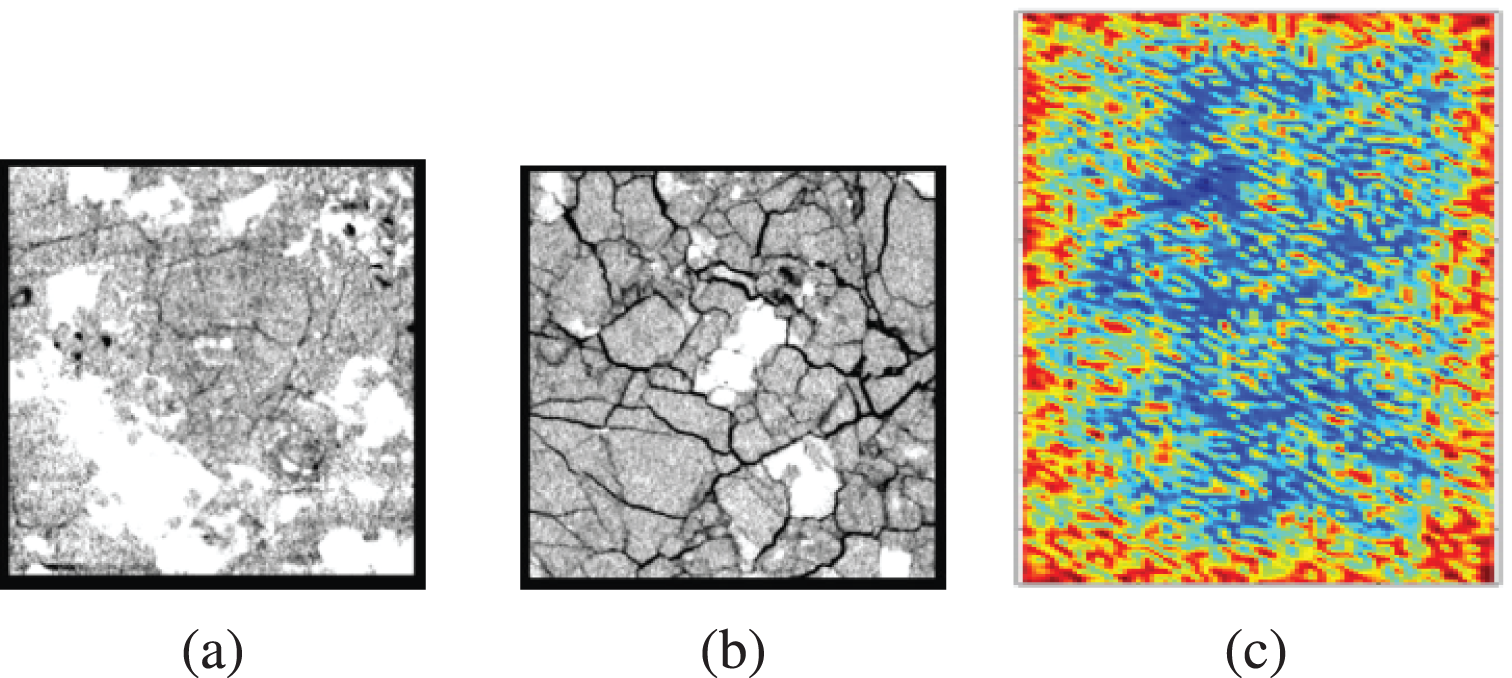
Figure 12: Crack paths predicted by different methods: (a) experimental result under 500∘C [10]; (b) experimental result under 1000∘C [10]; (c) numerical result of crack [39] (Copyright obtained)

5  Ceramic Slab in Quenching

5.1 Characteristics of Fracture Process

Focusing on an Al2O3 ceramic plate subjected to a quench test, we compare the crack paths predicted by the PD model with published numerical and experimental results. The quench test represents a standard scenario for examining thermal shock-induced damage, involving a brittle ceramic plate composed of Al2O3 powder. In this test, the plate is initially heated to a high temperature of approximately 300∘C and subsequently immersed in a 20∘C water bath. As the temperature rapidly decreases, the specimen’s surface experiences significant contraction, resulting in the development of surface cracks that propagate towards the interior. The material parameters for the ceramic plate are detailed in Table 3, and the geometric parameters and boundary conditions are illustrated in Fig. 13.

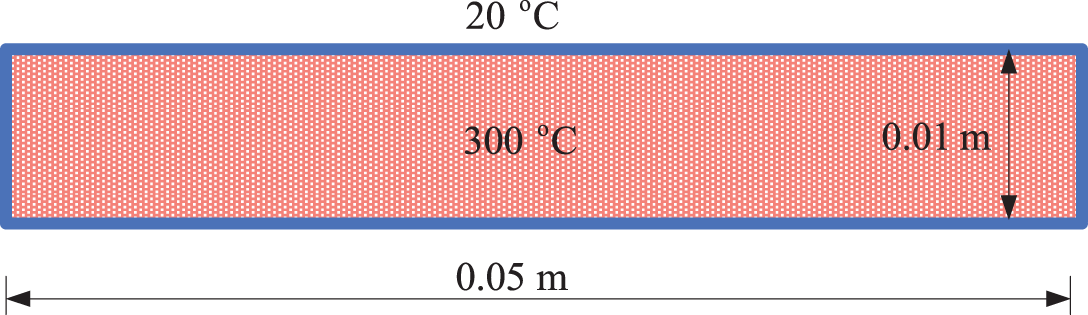
Figure 13: Schematic diagram of Al2O3 ceramic slab

For our simulations, we choose a point spacing of Δx=2×10−4 m, and the horizon size can be determined by δ=3Δx. The time steps for the thermal diffusion equation are set at 5×10−4 s, while the time steps for the motion equation are specified as 1×10−9 s.

The crack propagation patterns at different time instants are presented in Fig. 14. During the initial cooling phase, notable temperature variations occur at the free surfaces where the thermal load is applied. Consequently, microcracks are initiated at the edges of the ceramic slab, and these initial cracks are predominantly parallel (Fig. 14a). Subsequently, due to the temperature gradient between the surface and the interior of the brittle ceramic slab, significant tensile forces persist at the boundaries. This leads to the expansion of some cracks towards the interior of the slab (Figs. 14b and 14c).

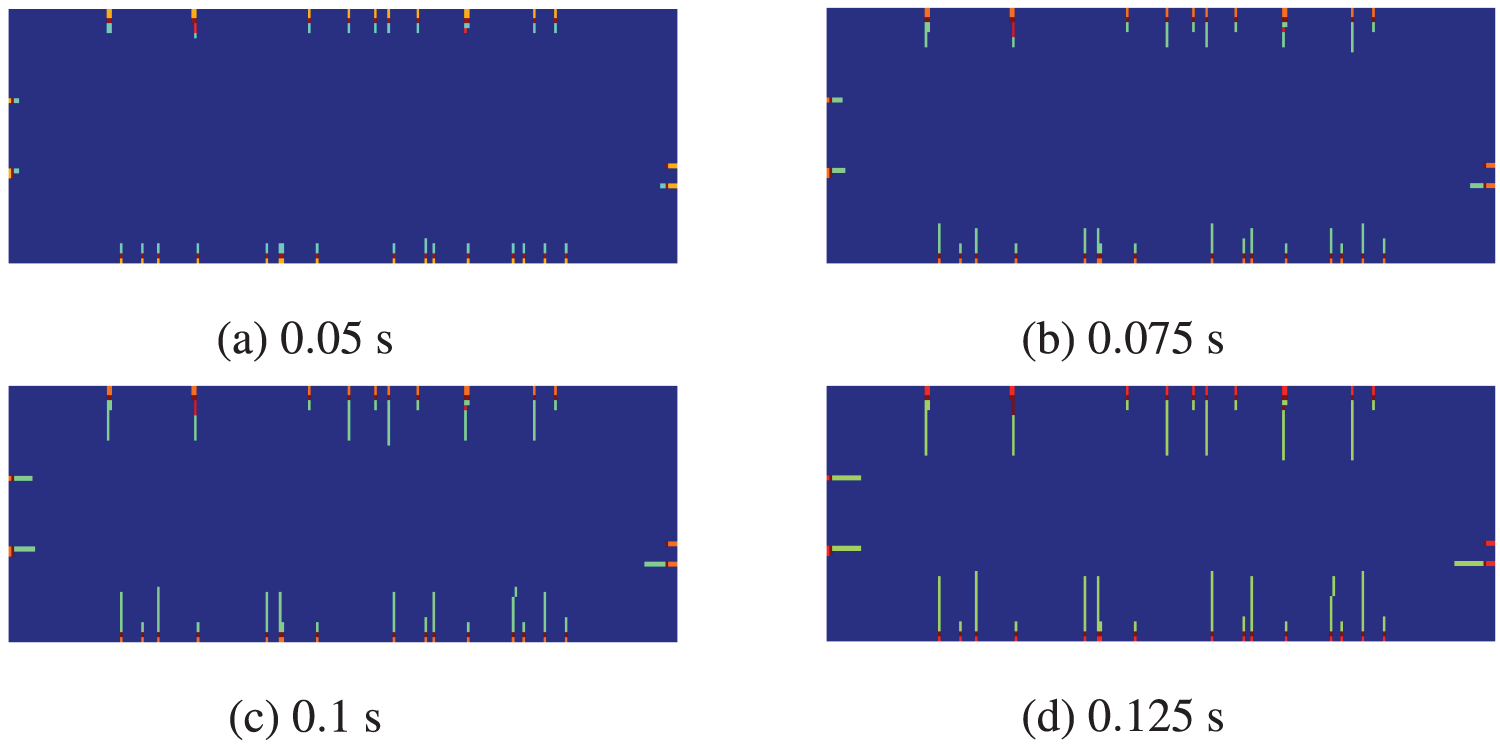
Figure 14: Crack initiation and propagation patterns

Finally, as the temperature continues to decrease, the cooling effect advances towards the interior of the thin plate, reducing the temperature differential. As a result, some cracks cease to propagate while others continue to extend to a certain length (Fig. 14d).

Figs. 15 and 16 depict the temperature and vertical displacement distributions at various time points. Notably, the temperature and vertical displacement patterns on both sides of the crack exhibit discontinuous distributions, reflecting the inherent non-local characteristics of peridynamics. Highlighting that conventional local algorithms, such as the Distinct Element Method, struggle to capture the temperature jump across the crack surface when simulating thermomechanical coupling problems [52].

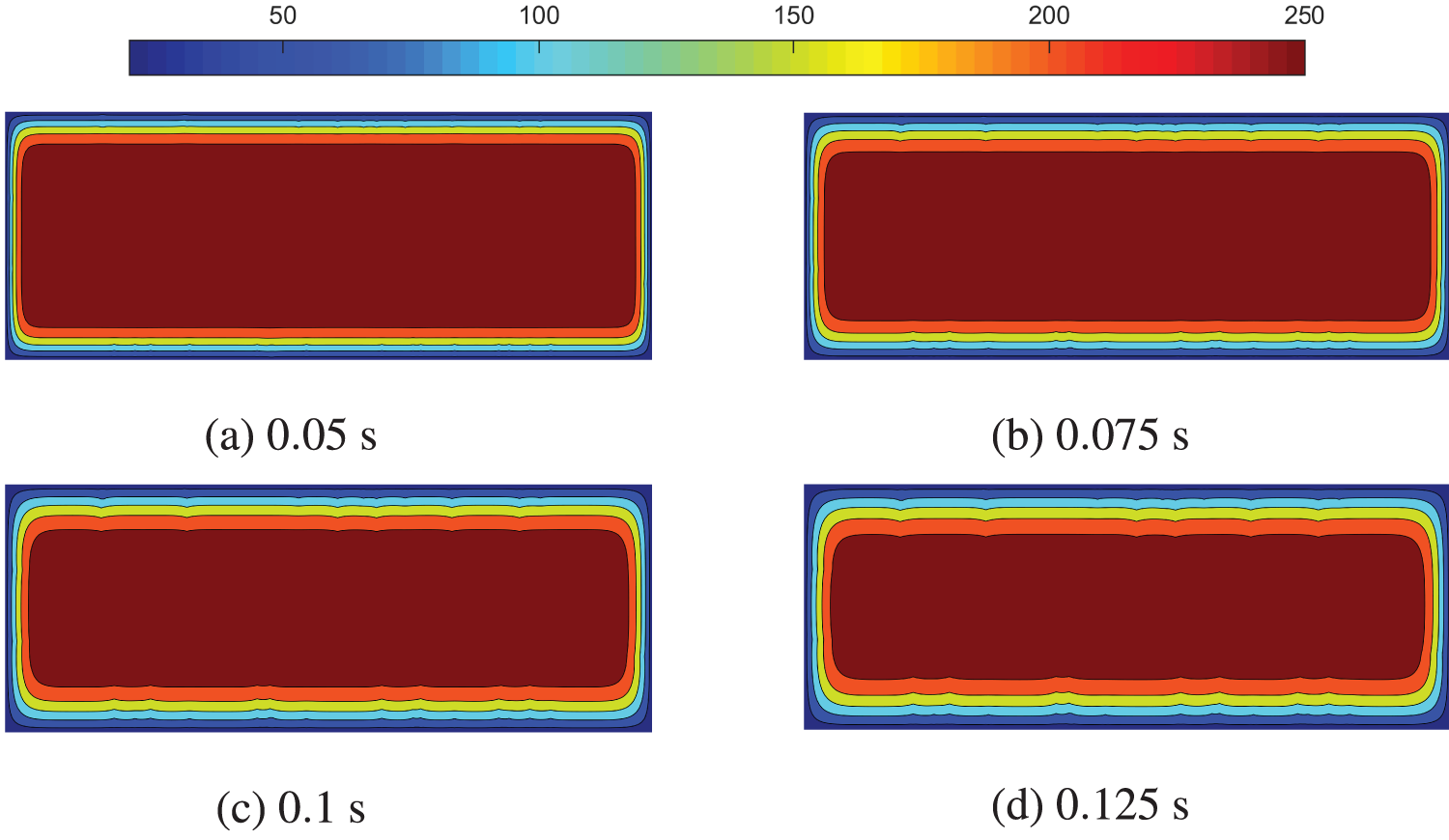
Figure 15: Temperature distribution

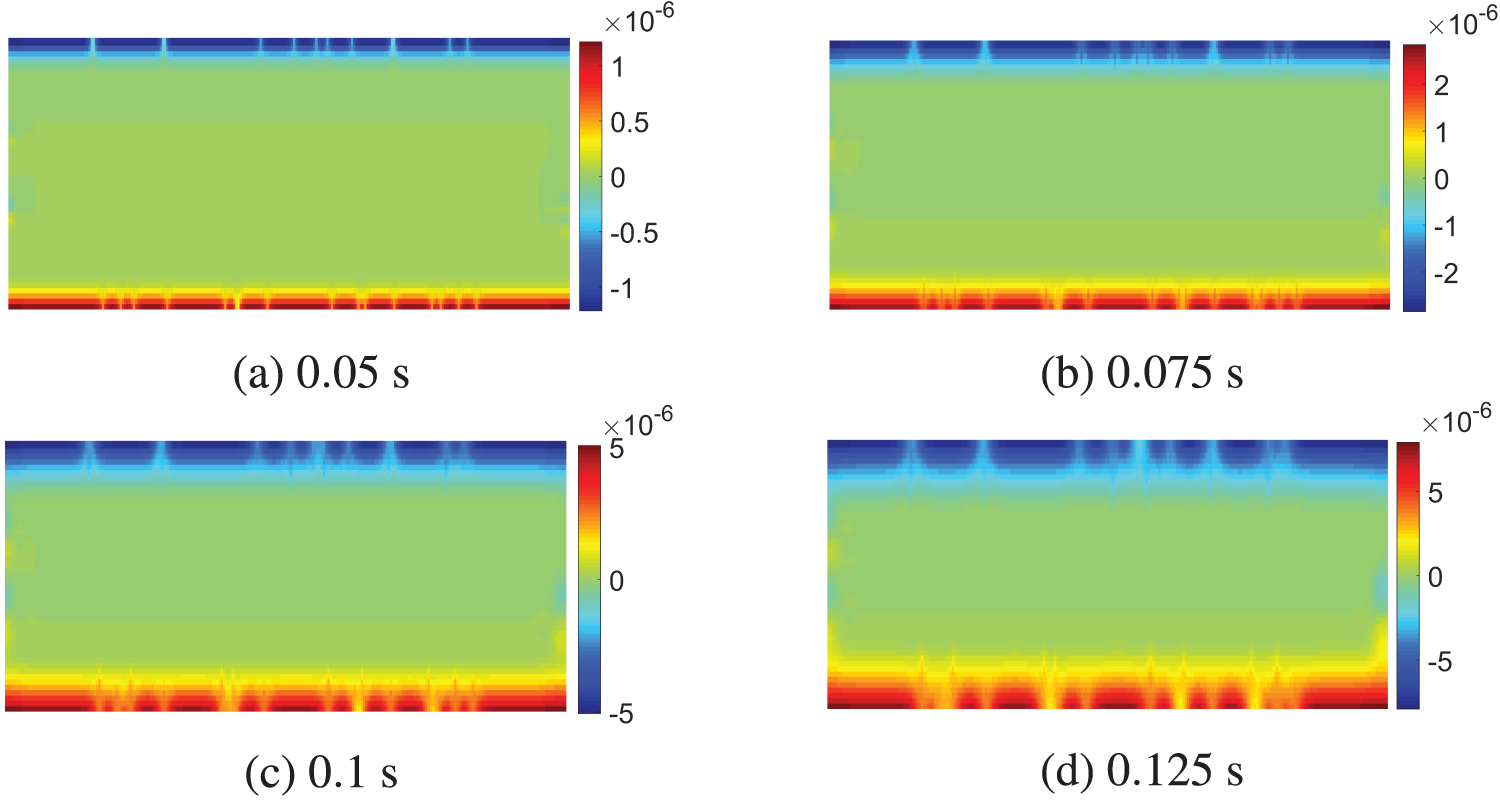
Figure 16: Vertical displacement distribution

5.2 Fracture Simulations Considering Heterogeneity

Heterogeneity represents a significant characteristic of ceramic materials, and exploring its impact on crack morphology is crucial. To account for material heterogeneity, we introduce the Weibull distribution [53]. This distribution is employed to model the heterogeneous properties of the ceramic material. The Weibull distribution is defined as

φ(a)=ma0(aa0)m−1exp⁡[−(aa0)m](20)

where φ(a) is a statistical distribution density function, a is the mechanical property, such as fracture energy release rate, a0 is the average value of the mechanical property and m is the homogeneity level index, which indicates the heterogeneity of a material.

Fig. 17 visually portrays the distribution of fracture energy release rates, the probability density function following the Weibull distribution, and statistical information related to fracture energy release rates. These statistics are provided for two numerical models generated with the same exponential value, m = 5.

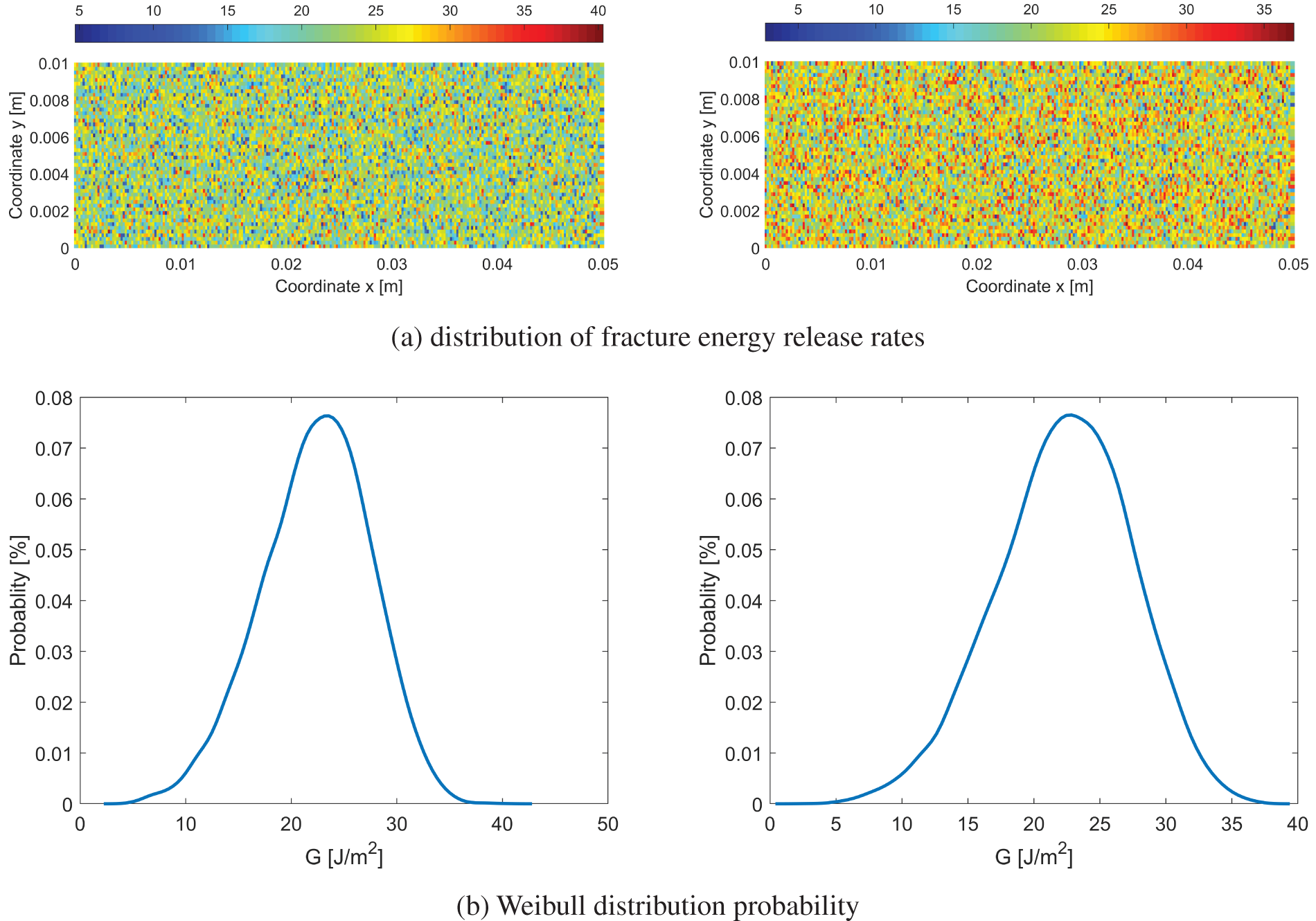
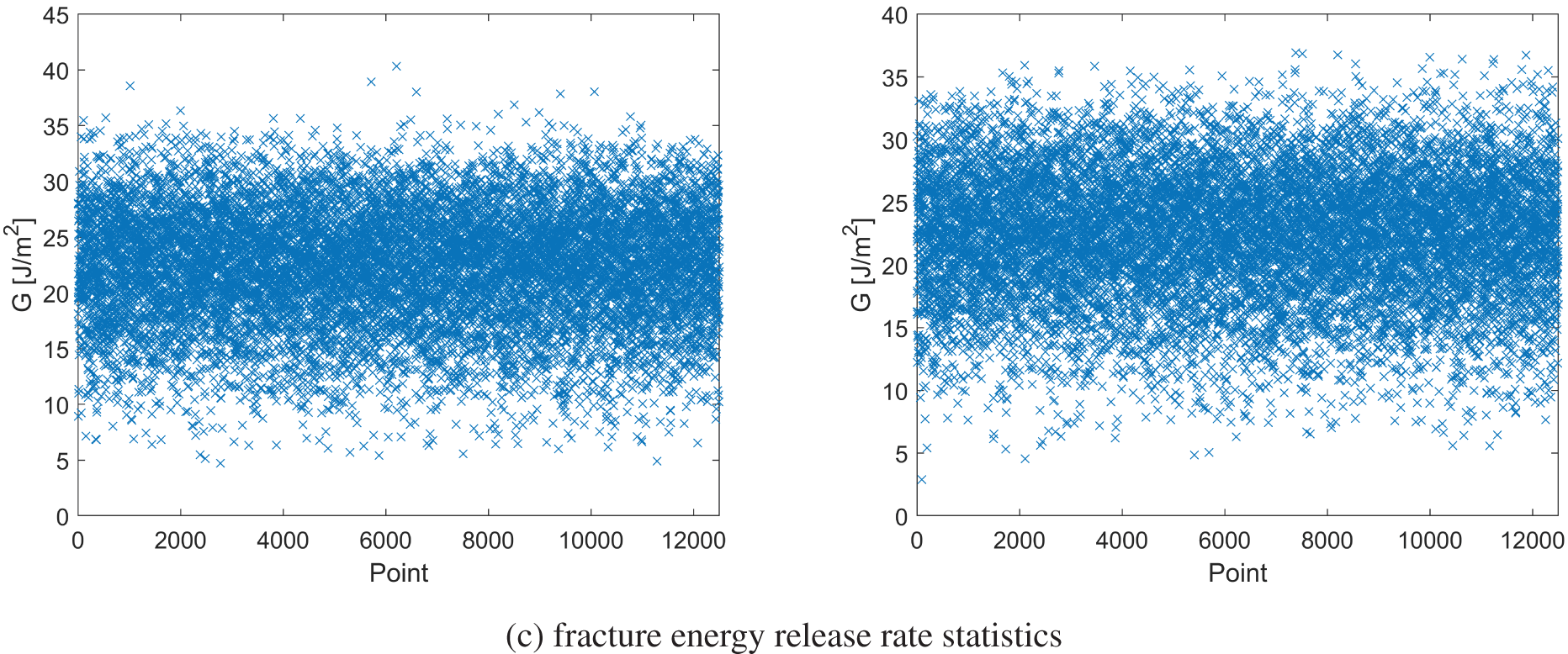
Figure 17: Random fracture energy release rate (left side: model 1; right side: mode 2)

The ultimate thermal crack path is depicted in Figs. 18a and 18b. When compared to the findings presented in Fig. 14, there are evident slight oscillations and deflections in the crack paths. Fig. 18 also includes previously published experimental and numerical results. Through a comparative analysis of these results, the following conclusions can be drawn: during the initial cooling phase, multiple microcracks first manifest at the edges of the ceramic slab. These microcracks originate from the edges and gradually propagate towards the interior. Initially, these microcracks are nearly parallel, but as they extend, they exhibit variations in length.

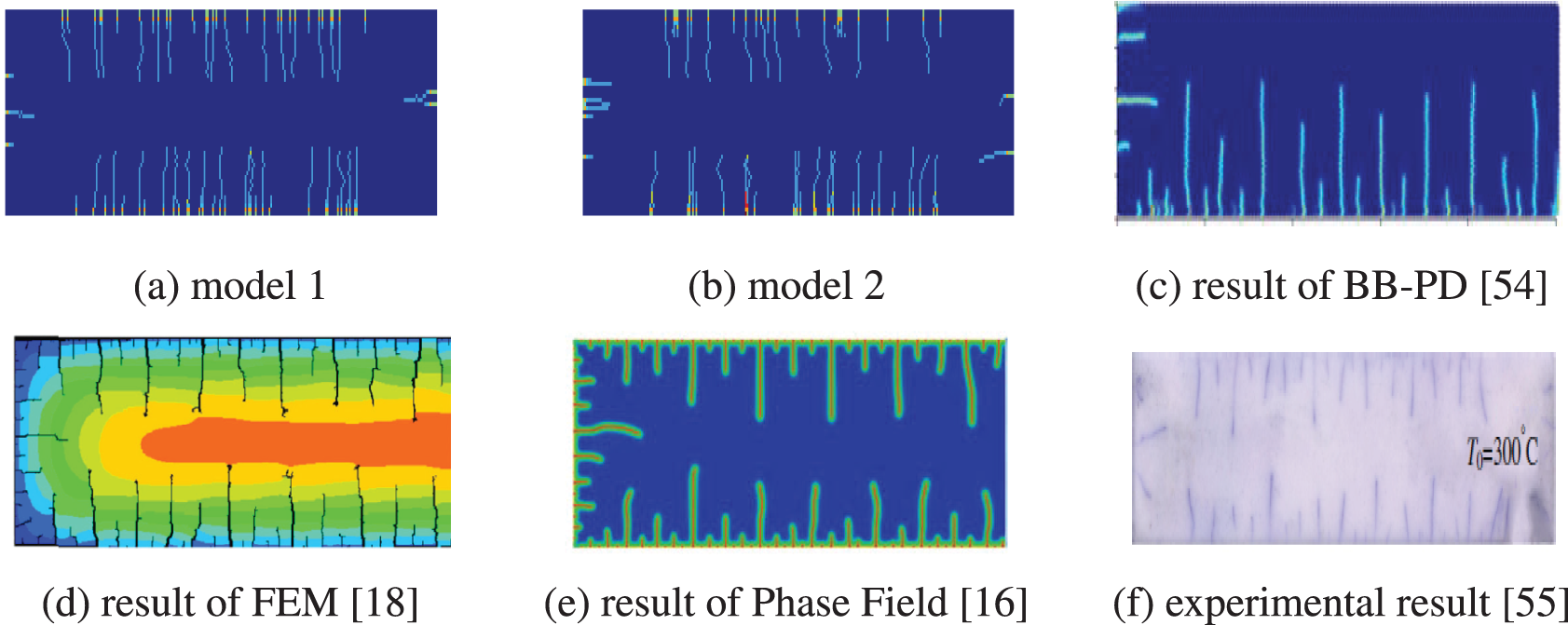
Figure 18: Crack paths predicted by different methods (Copyright obtained) [16,18,54,55]

5.3 Limiations of the PDDO-Based Fully Coupled Thermomechanical Model

It is also noteworthy that this study has three main limitations of the PDDO-based model in quantifying thermomechanical brittle fracturing phenomena. First, the weight function ω(|ξ|) is chosen empirical, which should be further explored for various conditions. Second, the horizon is determined by specified data δ=3Δx, and the quantitative relationship between horizon and media needs to be established in the future. Third, non-local property leads to the calculation time of the PDDO-based model being much higher than that of the local model. Fast algorithms for solving the PDDO-based model need to be further investigated.

6  Conclusions

This study introduces a fully coupled thermomechanical model that efficiently addresses thermomechanical brittle fracturing phenomena in granite and ceramic materials by substituting the classical local spatial derivatives with the non-local integral formulation derived from PDDO. The model’s predictions have been rigorously validated against existing numerical and experimental data. Based on the obtained results, the following key conclusions can be drawn:

(1) The PDDO transforms continuum mechanics equations into non-local integral form, eliminating the need for extra calibration. Cracks naturally propagate without added fracture criteria in the PDDO model, mitigating issues of traditional continuum-based numerical methods. This innovative approach holds the potential for advancing fracture mechanics analyses.

(2) During the thermal cycling of granite, microcracks initiate at boundaries and progress inwards, persisting through both heating and cooling stages. Additionally, the quenching of ceramic slabs sees surface-initiated microcracks gradually extending inward. While initially parallel, crack lengths eventually vary. These findings deepen our understanding of material fracture behavior under thermal stress.

(3) The employed multi-rate explicit time integration scheme effectively resolves diverse time-scale challenges in multi-physics systems. Additionally, the application of the Shuffle algorithm and Weibull distribution efficiently captures the inherent heterogeneity of brittle materials. These techniques contribute significantly to advancing our understanding of material behavior.

Acknowledgement: The authors would like to extend their gratitude to the reviewers for their valuable suggestions, which significantly enhanced the quality of this paper. The authors also acknowledge the support provided by the University Natural Science Foundation of Jiangsu Province and the National Natural Science Foundation of China.

Funding Statement: This work was supported by the University Natural Science Foundation of Jiangsu Province (Grant No. 23KJB130004), the National Natural Science Foundation of China (Grant Nos. 11932006, U1934206, 12172121, 12002118).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: T.L., Q.Z.; data collection: T.L.; analysis and interpretation of results: T.L., X.G., Q.Z.; draft manuscript preparation: T.L., X.G., Q.Z. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and codes that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, S., Xu, J. (2015). An experimental study on the physico-mechanical properties of two post-high-temperature rocks. Engineering Geology, 185, 63–70. [Google Scholar]

2. Gupta, A., Talha, M. (2015). Recent development in modeling and analysis of functionally graded materials and structures. Progress in Aerospace Sciences, 79, 1–14. [Google Scholar]

3. Kingery, W. D. (1955). Factors affecting thermal stress resistance of ceramic materials. Journal of the American Ceramic Society, 38(1), 3–15. [Google Scholar]

4. Nied, H. (1987). Thermal shock in an edge-cracked plate subjected to uniform surface heating. Engineering Fracture Mechanics, 26(2), 239–246. [Google Scholar]

5. Shao, Y., Xu, X., Meng, S., Bai, G., Jiang, C. et al. (2010). Crack patterns in ceramic plates after quenching. Journal of the American Ceramic Society, 93(10), 3006–3008. [Google Scholar]

6. Shao, Y., Zhang, Y., Xu, X., Zhou, Z., Li, W. et al. (2011). Effect of crack pattern on the residual strength of ceramics after quenching. Journal of the American Ceramic Society, 94(9), 2804–2807. [Google Scholar]

7. Shao, Y., Song, F., Liu, B., Li, W., Li, L. et al. (2017). Observation of ceramic cracking during quenching. Journal of the American Ceramic Society, 100(2), 520–523. [Google Scholar]

8. Shao, Y., Liu, B., Wang, X., Li, L., Wei, J. et al. (2018). Crack propagation speed in ceramic during quenching. Journal of the European Ceramic Society, 38(7), 2879–2885. [Google Scholar]

9. Geyer, J. F., Nemat-Nasser, S. (1982). Experimental investigation of thermally induced interacting cracks in brittle solids. International Journal of Solids and Structures, 18(4), 349–356. [Google Scholar]

10. Fan, L., Gao, J., Wu, Z., Yang, S., Ma, G. (2018). An investigation of thermal effects on micro-properties of granite by x-ray ct technique. Applied Thermal Engineering, 140, 505–519. [Google Scholar]

11. Zhu, Z., Tian, H., Mei, G., Jiang, G., Dou, B. (2020). Experimental investigation on physical and mechanical properties of thermal cycling granite by water cooling. Acta Geotechnica, 15, 1881–1893. [Google Scholar]

12. Bobaru, F. (2007). Designing optimal volume fractions for functionally graded materials with temperature-dependent material properties. Journal of Applied Mechanics, 74, 861–874. [Google Scholar]

13. Zhang, W., Sun, Q., Hao, S., Geng, J., Lv, C. (2016). Experimental study on the variation of physical and mechanical properties of rock after high temperature treatment. Applied Thermal Engineering, 98, 1297–1304. [Google Scholar]

14. Yang, S., Jing, H., Huang, Y., Ranjith, P., Jiao, Y. (2014). Fracture mechanical behavior of red sandstone containing a single fissure and two parallel fissures after exposure to different high temperature treatments. Journal of Structural Geology, 69, 245–264. [Google Scholar]

15. de Borst, R., Verhoosel, C. V. (2016). Gradient damage vs phase-field approaches for fracture: Similarities and differences. Computer Methods in Applied Mechanics and Engineering, 312, 78–94. [Google Scholar]

16. Chu, D., Li, X., Liu, Z. (2017). Study the dynamic crack path in brittle material under thermal shock loading by phase field modeling. International Journal of Fracture, 208, 115–130. [Google Scholar]

17. Tarasovs, S., Ghassemi, A. (2014). Self-similarity and scaling of thermal shock fractures. Physical Review E, 90(1), 012403. [Google Scholar]

18. Tang, S., Zhang, H., Tang, C., Liu, H. (2016). Numerical model for the cracking behavior of heterogeneous brittle solids subjected to thermal shock. International Journal of Solids and Structures, 80, 520–531. [Google Scholar]

19. Menouillard, T., Belytschko, T. (2011). Analysis and computations of oscillating crack propagation in a heated strip. International Journal of Fracture, 167, 57–70. [Google Scholar]

20. Silling, S. A. (2000). Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48(1), 175–209. [Google Scholar]

21. Silling, S. A., Askari, E. (2005). A meshfree method based on the peridynamic model of solid mechanics. Computers & Structures, 83(17–18), 1526–1535. [Google Scholar]

22. Silling, S. A., Epton, M., Weckner, O., Xu, J., Askari, E. (2007). Peridynamic states and constitutive modeling. Journal of Elasticity, 88, 151–184. [Google Scholar]

23. Madenci, E., Barut, A., Futch, M. (2016). Peridynamic differential operator and its applications. Computer Methods in Applied Mechanics and Engineering, 304, 408–451. [Google Scholar]

24. Bergel, G. L., Li, S. (2016). The total and updated lagrangian formulations of state-based peridynamics. Computational Mechanics, 58, 351–370. [Google Scholar]

25. Yan, J., Li, S., Kan, X., Zhang, A. M., Lai, X. (2020). Higher-order nonlocal theory of updated lagrangian particle hydrodynamics (ULPH) and simulations of multiphase flows. Computer Methods in Applied Mechanics and Engineering, 368, 113176. [Google Scholar]

26. Yu, H., Li, S. (2021). On approximation theory of nonlocal differential operators. International Journal for Numerical Methods in Engineering, 122(23), 6984–7012. [Google Scholar]

27. Kan, X., Yan, J., Li, S., Zhang, A. M. (2021). On differences and comparisons of peridynamic differential operators and nonlocal differential operators. Computational Mechanics, 68, 1349–1367. [Google Scholar]

28. Ren, B., Fan, H., Bergel, G. L., Regueiro, R. A., Lai, X. et al. (2014). A peridynamics-SPH coupling approach to simulate soil fragmentation induced by shock waves. Computational Mechanics, 55, 287–302. [Google Scholar]

29. Kilic, B., Madenci, E. (2009). Prediction of crack paths in a quenched glass plate by using peridynamic theory. International Journal of Fracture, 156, 165–177. [Google Scholar]

30. D’Antuono, P., Morandini, M. (2017). Thermal shock response via weakly coupled peridynamic thermo-mechanics. International Journal of Solids and Structures, 129, 74–89. [Google Scholar]

31. Giannakeas, I. N., Papathanasiou, T. K., Bahai, H. (2018). Simulation of thermal shock cracking in ceramics using bond-based peridynamics and fem. Journal of the European Ceramic Society, 38(8), 3037–3048. [Google Scholar]

32. Chu, B., Liu, Q., Liu, L., Lai, X., Mei, H. (2020). A rate-dependent peridynamic model for the dynamic behavior of ceramic materials. Computer Modeling in Engineering & Sciences, 124(1), 151–178. https://doi.org/10.32604/cmes.2020.010115 [Google Scholar] [CrossRef]

33. Bazazzadeh, S., Mossaiby, F., Shojaei, A. (2020). An adaptive thermo-mechanical peridynamic model for fracture analysis in ceramics. Engineering Fracture Mechanics, 223, 106708. [Google Scholar]

34. Zhang, H., Liu, L., Lai, X., Mei, H., Liu, X. (2022). Thermo-mechanical coupling model of bond-based peridynamics for quasi-brittle materials. Materials, 15(20), 7401. [Google Scholar] [PubMed]

35. Prakash, N., Deng, B., Stewart, R. J., Smith, C. M., Harris, J. T. (2022). Investigation of microscale fracture mechanisms in glass-ceramics using peridynamics simulations. Journal of the American Ceramic Society, 105(6), 4304–4320. [Google Scholar]

36. Wang, Y., Zhou, X., Kou, M. (2018). Peridynamic investigation on thermal fracturing behavior of ceramic nuclear fuel pellets under power cycles. Ceramics International, 44(10), 11512–11542. [Google Scholar]

37. Rabczuk, T., Ren, H. (2017). A peridynamics formulation for quasi-static fracture and contact in rock. Engineering Geology, 225, 42–48. [Google Scholar]

38. Wang, Y., Zhou, X. (2019). Peridynamic simulation of thermal failure behaviors in rocks subjected to heating from boreholes. International Journal of Rock Mechanics and Mining Sciences, 117, 31–48. [Google Scholar]

39. Yang, Z., Yang, S., Chen, M. (2020). Peridynamic simulation on fracture mechanical behavior of granite containing a single fissure after thermal cycling treatment. Computers and Geotechnics, 120, 103414. [Google Scholar]

40. Yang, Z., Yang, S., Tian, W. (2021). Peridynamic simulation of fracture mechanical behaviour of granite specimen under real-time temperature and post-temperature treatments. International Journal of Rock Mechanics and Mining Sciences, 138, 104573. [Google Scholar]

41. Feng, K., Zhou, X. (2022). Peridynamic simulation of the mechanical responses and fracturing behaviors of granite subjected to uniaxial compression based on ct heterogeneous data. Engineering with Computers, 39, 1–23. [Google Scholar]

42. Gu, X., Zhang, Q., Madenci, E. (2019). Refined bond-based peridynamics for thermal diffusion. Engineering Computations, 36(8), 2557–2587. [Google Scholar]

43. Anicode, S. V. K., Madenci, E., Phan, N. (2023). A unified method to simulate electrodeposition and galvanic corrosion using the peridynamic differential operator. Computer Methods in Applied Mechanics and Engineering, 408, 115968. [Google Scholar]

44. Yu, K. (2011). Enhanced integration method for the peridynamic theory (Ph.D. Thesis). Kansas State University, USA. [Google Scholar]

45. Yao, W., Zhou, X., Dias, D., Jia, Y., Li, Y. (2023). Frictional contact and stick-slip: Mechanism and numerical technology. International Journal of Solids and Structures, 274, 112289. [Google Scholar]

46. Du, Q., Gunzburger, M., Lehoucq, R. B., Zhou, K. (2013). A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Mathematical Models and Methods in Applied Sciences, 23(3), 493–540. [Google Scholar]

47. Luciani, J., Mora, P., Virmont, J. (1983). Nonlocal heat transport due to steep temperature gradients. Physical Review Letters, 51(18), 1664. [Google Scholar]

48. Bobaru, F., Foster, J. T., Geubelle, P. H., Silling, S. A. (2016). Handbook of peridynamic modeling. Boca Raton, Florida: CRC Press. [Google Scholar]

49. Chen, W., Gu, X., Zhang, Q., Xia, X. (2021). A refined thermo-mechanical fully coupled peridynamics with application to concrete cracking. Engineering Fracture Mechanics, 242, 107463. [Google Scholar]

50. Gear, C. W., Wells, D. R. (1984). Multirate linear multistep methods. BIT Numerical Mathematics, 24(4), 484–502. [Google Scholar]

51. Seny, B., Lambrechts, J., Toulorge, T., Legat, V., Remacle, J. F. (2014). An efficient parallel implementation of explicit multirate runge-kutta schemes for discontinuous galerkin computations. Journal of Computational Physics, 256, 135–160. [Google Scholar]

52. Huang, H., Spencer, B., Hales, J. (2014). Discrete element method for simulation of early-life thermal fracturing behavior in ceramic nuclear fuel pellets. Nuclear Engineering and Design, 278, 515–528. [Google Scholar]

53. Tang, C., Yang, Y. (2012). Crack branching mechanism of rock-like quasi-brittle materials under dynamic stress. Journal of Central South University, 19(11), 3273–3284. [Google Scholar]

54. Wang, Y., Zhou, X., Kou, M. (2019). An improved coupled thermo-mechanic bond-based peridynamic model for cracking behaviors in brittle solids subjected to thermal shocks. European Journal of Mechanics-A/Solids, 73, 282–305. [Google Scholar]

55. Jiang, C., Wu, X., Li, J., Song, F., Shao, Y. et al. (2012). A study of the mechanism of formation and numerical simulations of crack patterns in ceramics subjected to thermal shock. Acta Materialia, 60(11), 4540–4550. [Google Scholar]