Phase-Field Simulation of Sintering Process: A Review

1  Introduction

Sintering is a well-established technique in the powder metallurgy industry [1,2]. Some materials with high melting points, such as ceramics and refractory metals like tungsten, are challenging to process using conventional casting methods. However, they can be easily processed through sintering technology [3,4]. Understanding the mechanisms behind structural densification and microstructural evolution during the sintering process holds significant importance for evaluating the performance of sintered products. To achieve this, various methods for simulating the sintering process have been proposed [5–7]. On one hand, macroscopic finite element models based on continuum theory can accurately predict the spatial distribution of stress and strain in the structure during the sintering process [8–10]. However, these methods require direct tracking of grain interfaces during sintering, involving solving coupled equations for grain boundary and surface diffusion. Due to the disappearance of pores or grain boundaries during the sintering process, significant changes occur in the microstructural topology, adding to the complexity of the problem and imposing limitations on such models [11–13]. On the other hand, simulation methods that do not require direct interface tracking include molecular dynamics simulations [14,15], Monte Carlo simulations [16–19], cellular automata [20,21], and phase-field methods [22–24]. These methods have found increasingly widespread application in simulating the sintering process, offering advantages in terms of not requiring direct interface tracking.

The phase-field method eliminates the need for direct interface tracking by indirectly reflecting the evolution of microstructures through variations in order parameters. As a result, it possesses unique advantages in simulating microstructural evolution [25,26]. The application of the phase-field method has become increasingly widespread in various fields such as materials science [27,28]. Several review articles have summarized the use of the phase-field method in the development of novel materials [29,30]. Others have focused on its application in simulating material fracture behavior [31,32], and some have elucidated its application in simulating microstructural evolution under complex conditions [33,34]. However, there is a limited number of literature reviews specifically addressing the application of the phase-field method in sintering simulations. With the continuous development of additive manufacturing technologies like selective laser sintering, there is a pressing need for comprehensive models in this area to provide theoretical guidance for advanced manufacturing techniques.

This article provides a comprehensive overview of the latest research advancements in phase-field sintering models, as shown in Fig. 1. In Section 2, a summary of energy-based phase-field sintering models is presented. Commencing with the introduction of the fundamental phase-field sintering model, subsequent discussions address models that incorporate considerations for interface energy anisotropy, anisotropic diffusion mechanisms, and the rigid motion of sintering particles. Additionally, a compilation of phase-field sintering models is provided, exploring their coupling with other physical fields such as stress/strain fields, viscous flow, temperature fields, and external electric fields. Lastly, an overview is presented for multi-component and multi-physics coupled phase-field sintering models. Section 3 introduces phase-field sintering models based on the grand potential. Moving on to Section 4, an exploration of entropy-based phase-field sintering models is conducted. Section 5 provides insights into the research progress of phase-field simulations in the additive manufacturing field. Section 6 outlines the numerical solution methods for phase-field models. In conclusion, Section 7 summarizes the article and outlines prospects for future research directions.

Figure 1: Schematic representation of different phase-field models (PFM) for sintering

2  Energy-Based Phase-Field Sintering Model

2.1 Fundamental Formulation of the Phase-Field Sintering Model

In the phase-field method, the evolution of microstructural changes is typically represented through a set of continuous order parameters that vary over time and space. These order parameters exhibit continuous and rapid changes within the interface region, implicitly capturing variations in the geometric structure of the interface. This approach avoids the direct tracking of interface geometry. The order parameters within the phase-field framework can be broadly categorized into two types: conservation order parameters and non-conservation order parameters. In the context of phase-field sintering models, the most common type of conservation order parameter is the concentration field or mass density field. As illustrated in Fig. 2, a mass density value of ρ=1 signifies a sintered solid at that location, while ρ=0 indicates a pore or air. Given the necessity to uphold the law of mass conservation throughout microstructural evolution, this type of order parameter is referred to as a conservation order parameter. Conversely, the other category, non-conservation order parameters, exclusively convey structural and crystallographic orientation information at specific spatial locations. For instance, in Fig. 2, the order parameter η1=1 indicates the presence of grain 1 at a given location, whereas η2=1 denotes the occupation of that location by grain 2.

Figure 2: Schematic representation of two types of order parameters in the phase-field model [35]. Copyright (2014), with permission from Elsevier

The evolution of conservation order parameters is governed by the Cahn-Hilliard diffusion equation [36], whereas the evolution of non-conservation order parameters is determined by the Allen-Cahn equation [37]:

∂ρ∂t=∇⋅[M∇δFδρ](1)

∂ηi∂t=−LδFδηi(2)

In the above equations, L denotes the kinetic coefficient associated with grain boundary migration, M represents the material diffusion coefficient, and F signifies the system’s free energy. Typically, the system’s free energy can be expressed as a function of these two types of order parameters [38,39]:

F=∫V[f(ρ,η)+12κρ|∇ρ|2+12∑i=1Nκη|∇ηi|2]dV(3)

where f(ρ,η) stands for the free energy density of the system, κρ and κη represent the gradient energy coefficients.

Based on this model, Kumar et al. [40] initially simulated the sintering process of two unequal-sized circular particles. As shown in Fig. 3, the sintering process begins with the contact of the two particles. In the initial stage of sintering (from normalized time 0 to 0.01), there is no significant change in the sizes of the two particles; only the neck between them grows continuously. In the mid-stage of sintering (from normalized time 0.01 to 0.5), the neck size remains constant while the size of the smaller particle gradually decreases, and the larger particle coarsens. Once the normalized time 0.5 is reached, the grain boundaries start migrating towards the smaller particle at a slower speed, causing an increase in the shrinkage rate of the smaller particle. As the sintering progresses to the final stage (from normalized time 0.5 to 1.0), the rapid movement of the grain boundaries leads to a rapid reduction in the sizes of both the neck and the smaller particle until they disappear. The driving force for grain boundary migration is jointly determined by the changes in the bulk free energy and the interfacial energy during the sintering process. In the initial stage of grain boundary migration, the reduction in bulk free energy generates the migration driving force, while the increase in interfacial energy with the growth of the grain boundary size generates migration resistance, resulting in a low grain boundary movement speed. As the grain boundary progressively encircles the smaller particle, the migration resistance gradually turns into a migration driving force, leading to a rapid increase in grain boundary movement speed during the later stages of sintering.

Figure 3: Sintering evolution of two circular particles with different sizes in phase-field simulation, where red numbers indicate normalized time [40]. Copyright (2010), with permission from Elsevier

Choudhuri et al. [41] systematically investigated the influence of curvature on microstructural evolution during the sintering process using models involving two, three, and four particles. They pointed out that flat grain boundaries and solid surfaces do not affect the three stages of sintering. Local curvature only impacts the degree of coarsening of the sintering neck, and the effect of grain boundary energy on the length of the sintering neck is greater than that of surface energy. Kang et al. [42] employed the phase-field method to explore the microwave sintering mechanisms of different metal materials. They conducted microwave sintering simulations for two metal materials, Ti and Al, which exhibit distinct electromagnetic properties. They found that the sintering rate of Ti is significantly higher than that of Al. Theoretical analysis indicated that the heat generated by eddy current losses during the sintering process leads to differing heating efficiencies on the surfaces of the two metal particles. This discrepancy results in a larger surface diffusion rate for Ti compared to Al. Additionally, moving charges experience a Lorentz force directed toward the particle’s interior in a magnetic field, which hinders bulk diffusion. As the induced current is greater for Al, its bulk diffusion rate is slower. The combined effects of these factors result in a faster sintering rate for Ti. Yan et al. [43] conducted simulations on the sintering mechanism of Ti6Al4V powder particles during the preheating process in electron beam additive manufacturing. Initially, a heat flow model was employed to simulate potential liquid-phase sintering during the preheating process. The study revealed that partially molten particles retained their spherical shape due to surface tension, indicating scarce occurrence of liquid-phase sintering during preheating. Subsequently, the phase-field method was applied to simulate the solid-phase sintering process that might take place during preheating. It was observed that the preheating temperature significantly influences the growth of the sintering neck. The simulations highlighted that solid-phase sintering predominantly governs particle behavior during preheating, aligning with experimental observations.

In phase-field sintering models, it is common to introduce various dynamic parameters, which can impact the accuracy of simulation results. Mukherjee et al. [44] investigated the influence of grain boundary mobility and material diffusion coefficients on the microstructural evolution of nanoporous spherical aggregates. As depicted in Fig. 4, when the grain boundary mobility L is relatively low, stable grain boundaries can form between grains on the exterior of the aggregate. The internal pores within the aggregate remain interconnected, diffusing outward through surface diffusion. Individual grains inside the aggregate gradually dissolve due to Ostwald ripening, ultimately giving rise to a hollow shell structure. Conversely, with an increase in the grain boundary diffusion coefficient MGB, the rate of grain boundary diffusion filling the pores becomes faster than Ostwald ripening. This leads to the eventual formation of a completely dense inner sphere within the aggregate.

Figure 4: Comparison of sintering evolution morphologies of nanospherical aggregates with different grain boundary mobilities and diffusion coefficients [44]. Copyright (2010), with permission from American Chemical Society

Apart from dynamic parameters, the influence of pores on grain growth during the sintering process has also been extensively studied. Ahmed et al. [45] investigated the effect of pores on grain growth in porous CeO2. They highlighted that pores impose resistance at grain boundaries, hindering grain boundary motion and thereby suppressing grain growth. As pores move with the grain boundaries, their shapes continuously change. As shown in Fig. 5, pores may detach from the interfaces and enter the interior of grains (enclosed within hexagonal frames) or convert from internal voids within grains to pores at grain boundaries (enclosed within square frames). Pores at the junctions of four grains or three grains tend to evolve into pores at the junction of two grains (enclosed within diamond frames). Moreover, voids at the junction of two grains may combine with other grain boundaries, forming multiphase boundary pores (enclosed within square frames). With an increasing pore fraction, the growth rate of grain boundaries shifts gradually from being controlled by the grain boundaries to being governed by pores. Therefore, for accurately determining grain growth rates, it is crucial to consider factors such as pore fraction, pore size, and pore location of the microstructure within phase-field simulations. Du et al. [46] investigated the deformation of pores during the sintering process. They found that the presence of pores enhances grain coarsening in their vicinity, accompanied by changes in the pore shapes. Circular and square pores initially evolve into approximately circular polygonal pores, while rectangular and elliptical pores eventually transform into elliptical pores. Grain boundaries intersecting with the pore surface gradually become perpendicular to the pore surface. With an increase in the curvature radius of the pores, the influence of grain coarsening on pore shape diminishes. Hötzer et al. [47] investigated changes in the pores between grain boundaries in three-dimensional ideal hexagonal grain structures. They observed three relationships between pores and grain boundaries during grain growth: constant attachment, partial separation, and complete separation. These relationships are significantly influenced by the initial positions of the pores. Similar to the two-dimensional case, in the three-dimensional scenario, voids at the junction of four grains initially detach from one grain, then separate from another grain, forming pores at the junction of two grains. These ultimately evolve into internal pores within the grains. The distance between the voids does not affect this process. Liu et al. [48] simulated the grain growth in the later stages of sintering for porous ceramics. Their results indicated that, when the number of voids remains constant, larger voids lead to faster grain growth. On the other hand, when the pore fraction remains constant and the number of voids increases, resulting in smaller voids, the grain growth rate slows down. These conclusions align with Zener’s hypothesis of the critical grain size. In another study [49], they examined the sintering process of a porous ceramic with a pore fraction of 25.6%. They found that in the initial stages of sintering, grain boundary diffusion and surface diffusion are the dominant mechanisms. The rate of sintering neck thickening obtained from the phase-field simulation also matched the results of classical sintering theory analysis. Rehn et al. [50] conducted similar research and found that for ceramics with low pore fractions, the number of pores dominates grain growth resistance. However, at higher pore fractions, pore size becomes the primary factor in grain growth resistance. Compared to pores with a uniform size distribution, pores with a random size distribution generate greater grain growth resistance. This finding aligns with simulations by Berry et al. [51] in the context of solid-state sintering of UO2.

Figure 5: Pore motion evolution at various times in phase-field simulation of porous CeO2 [45]. Copyright (2016), with permission from Springer

Additionally, microstructures obtained through phase-field simulations can be imported into other models to further simulate changes in their physical properties. For instance, Wang et al. [52] first employed phase-field simulations to investigate the evolution of porous structures in two-dimensional ceramic films under various sintering conditions. They then utilized resistor network models and effective medium theories to calculate their electrical conductivity. They discovered significant changes in the electrical transport properties of ceramic films under different sintering conditions, highlighting the significant role of phase-field sintering simulations in the development and optimization of advanced ceramic structures. Abdeljawad et al. [53] combined the phase-field sintering model with an electrochemical battery model to study the impact of sintering-induced coarsening of Ni in porous anode materials composed of Ni and ZrO2 on the electrochemical performance of solid oxide fuel cells. By obtaining the structural characteristics of the anode material through phase-field simulations and using them as initial conditions for the electrochemical battery model, they assessed the cell’s performance. The results indicated that the grain size and proportion of Ni and ZrO2 significantly influence the stability of the microstructure and electrochemical performance of the cell.

In addition to using the mass density field as a non-conserved order parameter, Asp et al. [54] proposed a phase-field sintering model based on vacancy diffusion. This model, compared to the most basic phase-field sintering model, does not have any fundamental differences. The key distinction lies in defining the non-conserved order parameter as the vacancy content. In this model, the sintered region is characterized by a low vacancy content, the surrounding pores have a high vacancy content, and the vacancy content at interfaces varies continuously between these two extremes. The model then employs the common thermal vacancy model found in crystals to derive the energy expression for the structure. The results of dual-particle sintering simulations using this model demonstrate that it can achieve consistent results with traditional phase-field sintering models.

2.2 Phase-Field Sintering Model with Anisotropic Interfacial Energy

During the sintering process, the anisotropy of grain boundary energy between grains with different orientations can lead to significant variations in the final sintered morphology [55]. To simulate the directional growth of plate-like Al2O3 particles, Shinagawa et al. [56] employed ellipsoidal functions to calculate the gradient energy coefficients:

κi={11+δ⋅[1−δcos⁡(2(θ−θ0))]πi+(θm−θ0)≤θ≤π(i+1)−(θm−θ0)cos⁡θcos⁡θm⋅[1−δcos⁡(2(θ−θ0))]πi−(θm−θ0)≤θ≤πi+(θm−θ0)(4)

In the equation above, κi represents the gradient energy coefficient for the ith grain, θ0=πi/N is the orientation angle of that grain, δ is a constant indicating the degree of anisotropy, and θm=π/6 is introduced to prevent structural instability caused by strong anisotropy. θ is the grain boundary angle and can be expressed as:

θ=tan−1⁡[∂ηi/∂y∂ηi/∂x](5)

According to crystal growth theory, the grain boundary mobility L can be expressed as a function of the driving force for grain growth Δg:

L={L0h<0,1≤hL0exp⁡(2−2/h)0.25≤h<10.01L00≤h≤0.25(6)

h=ΔgΔgc=2γVmΔgc(1r∗−1r)(7)

where Δgc is the critical driving force, r is the effective radius calculated based on grain area, r∗ is the critical radius, and γ is the grain boundary energy.

Fig. 6 illustrates the grain growth morphology at the same time step with isotropic (δ=0) and anisotropic (δ=0.4) grain boundary energies. In contrast to the uniform growth of polygonal grains with isotropic grain boundary energy, the growth under anisotropic mechanism tends to occur in a fixed direction, resulting in the formation of plate-like grains. Additionally, when the grain boundary energy becomes anisotropic, the grain growth exponent changes from 2 to 5, indicating a significantly reduced growth rate. Moreover, when the initial grain size distribution is broader, a larger number of plate-like grains are formed. Li et al. [57] employed a three-dimensional phase-field method to simulate the evolution of tungsten carbide (WC) grain morphology caused by interface energy anisotropy during the sintering process. With progressing simulation time, spherical grains quickly transform into polyhedra composed of multiple facets to minimize the system’s free energy. The lower interface energy facets expand continuously, eventually forming prismatic grains. Furthermore, when the ratio of interface energy σ011¯0/σ101¯0 is 1.6, prismatic grains with a truncated cross-section can be formed, aligning with experimental results observed in low-carbon alloys. When this ratio exceeds 2, the simulated grain morphology becomes fully prismatic, consistent with experimental results observed in high-carbon alloys.

Figure 6: Phase-field simulation of polycrystalline morphology of Al2O3 at the same time step with (a) isotropic and (b) anisotropic grain boundary energies [56]. Copyright (2016), with permission from Elsevier

2.3 Phase-Field Sintering Model with Anisotropic Diffusion Mechanism

During the sintering process, material diffusion often occurs along specific directions. Deng [58] proposed a phase-field sintering model that incorporates direction-dependent diffusion, suggesting that surface and grain boundary diffusion only occur along the tangent direction of the interfaces. Specifically, they extended the scalar diffusion coefficient into a tensor form:

M=MsfTsf+MgbTgb+MatI(8)

Tsf=I−nsf⊗nsf(9)

Tgb=I−ngb⊗ngb(10)

where I represents the identity tensor, nsf=∇ρ|∇ρ| is the unit normal vector on the surface, and ngb=∇ηi−∇ηj|∇ηi−∇ηj| is the unit normal vector on the grain boundary.

Fig. 7 illustrates a comparison of sintering morphologies between the cases with and without direction-dependent diffusion mechanisms for two hexagonal grains. It can be observed that under the scalar diffusion mechanism, although the grain surfaces gradually smooth out, the overall grain morphology deviates significantly from the sintering equilibrium state. In contrast, under the tensor diffusion mechanism, both surface and grain boundary diffusion drive the interface curvatures to become consistent, leading to the formation of the sintering equilibrium state. This alignment with theoretical predictions highlights the significant importance of considering the tensor form of material diffusion mechanisms for the accuracy of the phase-field sintering model. Chockalingam et al. [59] also employed a tensor diffusion mechanism to investigate the sintering process of silver nanoparticles. Fig. 8 compares the phase-field simulation results with experimental data from Asoro et al. [60]. It can be observed that the density field obtained from the phase-field simulation closely matches the experimental results. However, the predicted grain dihedral angles deviate significantly from the experimental results. In the experiment, the dihedral angle remains acute from 0 to 15 min, whereas the phase-field simulation’s dihedral angle gradually increases from an acute to an obtuse angle. This discrepancy can be attributed to the phase-field simulation not accounting for the potential influence of carbon impurities on the silver particle surfaces in the experiment, leading to differences in diffusion coefficients and resulting in deviations from the experimental results. Additionally, considering factors such as silver particle size and sintering temperature, they obtained results that were consistent with the experimental findings.

Figure 7: Sintering morphological changes of two hexagonal grains under (a) scalar and (b) tensor diffusion mechanisms [58]. Copyright (2012), with permission from J-STAGE

Figure 8: Morphological changes of two equally sized silver particles sintered at 400°C for 15 min: (a–c) experimental results, (d–f) phase-field simulation results [59]. Copyright (2016), with permission from Elsevier

Guo et al. [61] investigated the anomalous grain growth observed in the late stage of sintering in porous UO2 pellets. They found that, under the tensor diffusion mechanism, the evolution of the microstructure is also influenced by the volume fraction of pores and the size of pores. When the pore volume fraction is high, grain growth is significantly inhibited, while at lower pore volume fractions, grain growth remains unaffected. Additionally, smaller pore sizes may lead to more pronounced anomalous grain growth at low pore volume fractions. Wei et al. [62] used the phase-field method to simulate the densification of Al2O3-ZrO2 ceramics during sintering. They simultaneously considered three types of order parameters: density field, composition field, and grain orientation field. The results showed that a higher initial relative density leads to larger average grain size and density in the sintered ceramics. On the other hand, a higher volume fraction of ZrO2 results in smaller density and average grain size of the sintered product. Overall, the average grain size is more sensitive to these factors. Ahmed et al. [63] also statistically analyzed the grain growth exponent of porous CeO2 ceramics during sintering under the tensor diffusion mechanism. The phase-field simulation results showed that for fully dense CeO2 ceramics, the relationship between the average grain size and sintering time follows a parabolic curve, consistent with theoretical predictions for grain growth controlled by grain boundaries. When the pore volume fraction is increased to 1%, the obtained grain growth exponent is 2.5, indicating a competition between pore-controlled and grain boundary-controlled grain growth. When the pore volume fraction is further increased to 4%, the grain growth exponent increases to 4, indicating dominance of pore-controlled grain growth. Under the tensor diffusion mechanism, with increasing pore density, the transition from grain boundary-controlled to pore-controlled grain growth occurs. This phenomenon has also been observed in the phase-field simulation of UO2 particle sintering [35,64]. Sun et al. [65] conducted further simulations of the sintering process for different shapes of UO2 particles. They found that initial spherical morphology of ceramic powders is more conducive to effective sintering. In a related study, Jing et al. [66] investigated the influence of the ratio of surface diffusion coefficient to grain boundary diffusion coefficient, denoted as Msf/Mgb, on the neck growth during sintering. They observed that a larger Msf/Mgb ratio leads to faster neck growth. With prolonged sintering time, all simulation outcomes converge to a consistent level of densification, indicating that the impact of Msf/Mgb on the degree of structural densification is minimal.

2.4 Phase-Field Sintering Model with Particle Rigid Motion

During the sintering process, the free surfaces and grain boundaries serve as sources and sinks for vacancies, respectively. The vacancy or mass diffusion caused by them leads to the rigid-body motion of grains, ultimately resulting in macrostructural contraction and densification. To address the limitations of phase-field sintering models in simulating grain rigid-body motion, Kazaryan et al. [67] were the first to consider the additional contribution of grain rigid-body motion to mass flux. Specifically, they modified the Cahn-Hilliard equation that governs the evolution of the local density field as follows:

∂ρ∂t=∇⋅[M∇δFδρ−ρv](11)

In the above equation, v represents the local velocity. Within the grains, the local velocity is equivalent to the rigid-body motion velocity of the grains, whereas at the grain boundaries, the local velocity needs to be solved based on the steady-state condition (∂ρ/∂t)gb=0. Fig. 9 compares the evolution of an initial circular pore within two grains with and without the rigid-body correction term. It can be observed that with the introduction of the rigid-body motion correction term, the pore size continuously contracts, and the degree of microstructural densification increases, which aligns well with the theoretical solution proposed by Pan et al. [12]. On the other hand, when not considering grain rigid-body motion, the pore only relaxes into an elliptical shape without significant size contraction.

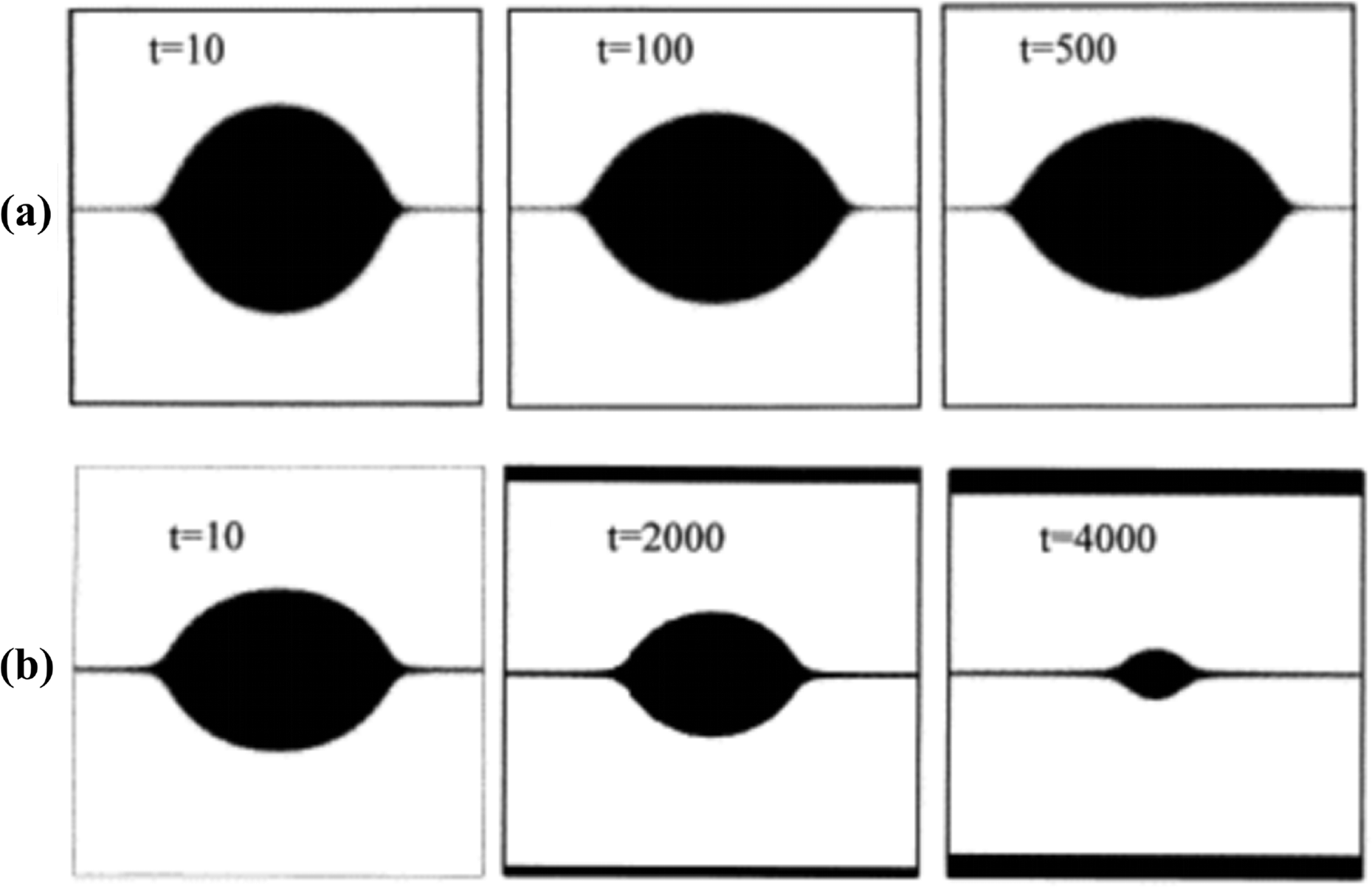
Figure 9: Variations in pore morphology: (a) without considering rigid motion and (b) introducing rigid motion [67]. Copyright (1999), with permission from Elsevier

The model proposed by Kazaryan et al. [67] treats the local velocity as an independent variable and does not explicitly couple the grain rigid-body motion with the phase-field order parameter. Wang [68] further developed a phase-field sintering model based on both grain translational and rotational rigid-body motion. Initially, he introduced an advection velocity field vtotal to describe the collective rigid-body motion of all grains within the microstructure:

vtotal=∑αvadv(α)=∑α[vt(α)+vr(α)](12)

where vt(α) and vr(α) represent the translational and rotational velocities of the α grain, respectively. For each grain, the local effective force inducing its own rigid-body motion is given by:

dF(α)=κ∑α≠β(ρ−ρ0)δ[∇η(α)−∇η(β)]d3r(13)

δ={1,ifη(α)⋅η(β)≥c0,otherwise(14)

Here, κ represents the local effective force constant, ρ0 is the equilibrium value of the density field at the grain boundaries, and c is the threshold determining the grain boundary region. From the above expression, it can be observed that the local effective force is only generated at the grain boundaries, with the magnitude of the force determined by the gradient difference of the order parameter at the grain boundaries. The magnitude of the local effective force experienced by adjacent grains is equal, but their directions are opposite, satisfying the principle of action and reaction.

By globally integrating the local effective force, the resultant force and torque experienced by the α grain can be further obtained as follows:

F(α)=∫VdF(α)(15)

T(α)=∫V[r−rc(α)]×dF(α)(16)

where rc(α) is the position vector of the center of mass of the α grain. Due to the dissipative nature of grain motion during sintering, the translational and rotational constants mt and mr are introduced, and the translational and rotational velocities of the α grain can be obtained as follows, considering the grain size V(α):

vt(α)=mtV(α)F(α)η(α)(17)

vr(α)=mrV(α)T(α)×[r−rc]η(α)(18)

Finally, the Cahn-Hilliard equation and the Allen-Cahn equation are modified as follows:

∂ρ∂t=∇⋅[M∇δFδρ−ρvtotal](19)

∂η(α)∂t=−LδFδη(α)−∇⋅[η(α)vadv(α)](20)

Based on the aforementioned model, Biswas et al. [69] investigated the specific changes in the rigid body motion velocities of two tungsten metal particles during the sintering process. They found that the particle size, relative positions, and distribution of surrounding pores have a significant impact on the translational and rotational velocities of sintering particles, leading to distinct microstructures. For instance, Fig. 10 compares the distribution of rigid body motion velocities for two equally-sized particles and two particles with different sizes at 1800 K temperature. When the particle sizes are the same, the particles maintain equal magnitudes of translational velocities in opposite directions. The translational velocities in the vertical direction and the rotational velocities around the center of mass are negligible, while the translational velocities in the horizontal direction cause the particles to move towards the grain boundary, promoting structural densification. When particle sizes are unequal, the smaller particle exhibits a greater translational velocity, while the larger particle has a larger rotational velocity around the center of mass. The translational velocities also consistently forces the particles to move towards the grain boundary, accelerating the disappearance of the smaller particle.

Figure 10: Comparison of particle rigid motion velocities between same-size particles and unequal-size particles: (a and b) horizontal velocity component, (c and d) vertical velocity component, (e and f) rotational velocity about the center of mass [69]. Copyright (2018), with permission from Springer

Seiz et al. [70], on the other hand, neglected the influence of rigid body rotational velocities and simulated the sintering process of a finite-length, equally-sized linear particle chain. The results indicated that simulations without considering rigid motion exhibited lower degrees of densification. With increasing chain length, the extent of structural densification also changed, contradicting theoretical analyses. In contrast, simulations that accounted for particle rigid motion displayed characteristics of densification that were independent of chain length, aligning with theoretical predictions. Shi et al. [71] systematically compared the effects of rigid body translational and rotational motion on different stages of the sintering process for a system of three particles. They discovered that translational motion could transport material from within the particles to the grain boundaries and pore regions, promoting neck growth and pore shrinkage. The diminishing magnitude of the effective force driving this rigid body motion throughout sintering led to an influence limited to the initial and intermediate stages. In comparison to translational effects, particle rotation around their centers of mass had virtually no impact on sintering outcomes, making it possible to disregard particle rotation in phase-field sintering simulations.

Molecular dynamics simulations provide the most detailed insights into the solid-state sintering process but are limited to simulating sintering of only a few particles, making accurate predictions of microstructure densification challenging [14,72]. On the other hand, methods based on continuum mechanics can predict changes in the overall geometry of the entire workpiece at a macroscopic scale but lack the ability to provide effective information about the grain shapes within the microstructure [73]. Serving as a bridge between these two approaches, it is crucial to simulate the sintering process within representative volume elements containing hundreds to thousands of particles using phase-field simulations [74–76]. However, directly representing all particles with different order parameters incurs significant computational costs. To mitigate these costs and accelerate computation speed, in multiscale phase-field sintering simulations, the same order parameter is often used to represent multiple particles that do not directly contact each other [77]. Specifically, akin to solving the graph coloring problem, order parameters are initially assigned based on the particles’ initial positions. During the evolution process, a grain tracking algorithm promptly reallocates order parameters to particles with the same order parameter that may come into contact. By employing a very limited number of order parameters, the solution for hundreds or even thousands of particles can be efficiently achieved [74]. Termuhlen et al. [75] simulated the densification process of a large 3D structure containing 2968 particles and found that the introduction of rigid body motion could promote the coordinated coalescence of regularly packed particles, resulting in a significant increase in pore tortuosity and accelerating structural densification.

In addition to the aforementioned models, alternative methods have been proposed by researchers to calculate particle rigid body motion during the sintering process. For instance, Shinagawa [78] combined the phase-field model with the discrete element method, utilizing the discrete element approach to compute the rigid body motion term in the phase-field equation. The rigid body motion driving forces required in the discrete element calculations were related to particle surface curvature and sintering neck width, which could be evaluated through phase-field simulations. Ivannikov et al. [79] also introduced another model based on the assumption of rigid particles and elastic contacts to compute rigid body motion during the sintering process of two particles. By comparing the sintering morphology of two titanium particles obtained from phase-field simulations with experimental results, they validated the reliability of their model.

2.5 Phase-Field Sintering Model with Stress/Strain Field

During the sintering process, internal stresses often exist within the microstructure. To address this, it is necessary to couple the phase-field sintering model with the mechanical equilibrium equations. Initially, elastic strain εijel is defined as the difference between total strain εijtotal and the intrinsic strain εij0 arising from lattice misfit, thermal strain, and other factors [80]:

εijel=εijtotal−εij0(21)

Combining with Hooke’s law, the equilibrium equation can be further derived:

∇⋅(Cijklεklel)+bm=0(22)

In this context, Cijkl represents the position-dependent elastic constants, and bm corresponds to the volumetric force term. Assuming an externally applied stress of σija, the elastic strain energy can be derived as follows:

fel=12∫VCijklεijelεkleldV−∫VσijaεijeldV(23)

Due to the distinct mechanical properties between the solid structure and the pores during the sintering process, the overall elastic energy of the microstructure can be interpolated from the density field considering both the solid and pore contributions:

Fel=h(ρ)felbulk+(1−h(ρ))felvoid(24)

Subsequently, incorporating the elastic energy into the total free energy of the microscale system and solving the phase-field equations alongside the mechanical equilibrium equations achieves the coupling between the stress field and the phase-field.

Building upon the aforementioned model, Biswas et al. [80] conducted simulations of the sintering morphology of pure metallic tungsten particles under the influence of pressure. To simplify the analysis, they assumed the absence of intrinsic strain within the microstructure during the sintering process. In the case of two-dimensional simulations, they applied loads by imposing displacement boundary conditions at the microstructure boundaries, as illustrated in Fig. 11a. The normal displacements were set to zero along the bottom edge and the lateral sides, while a time-dependent displacement boundary condition was applied only along the upper boundary. Fig. 11b presents the evolving shape of circular particles during the sintering process. The interplay of surface diffusion and grain boundary diffusion leads to a gradual reduction in internal porosity within the particles. Since the particles on the sides have larger surface areas compared to the central particle, the pores on the sides close earlier. Under the compressive load, the initially circular particle shapes gradually transform into ellipsoidal shapes, indicating the significant influence of external loads on the morphology of sintered particles.

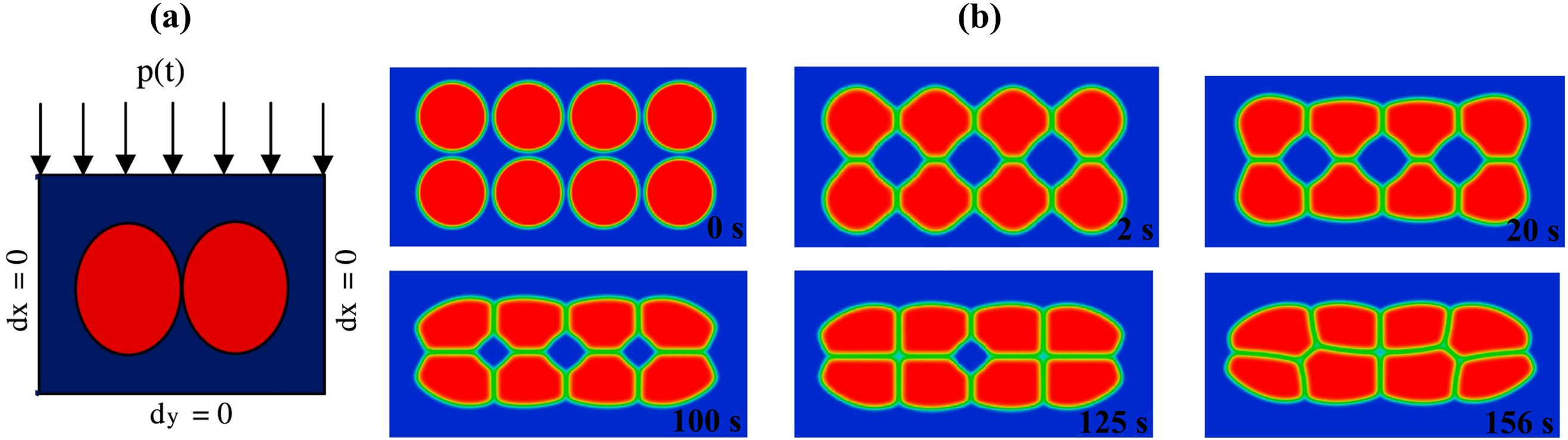
Figure 11: Phase-field simulation of tungsten particles under pressure: (a) applied displacement boundary conditions in 2D simulation; (b) sintering morphologies of tungsten particles at different times [80]. Copyright (2016), with permission from Elsevier

Jiang et al. [81] investigated the impact of externally applied stress on pore size during the sintering process of UO2. They observed that with increasing external stress, the pore size within the microstructure tends to enlarge, indicating that stress promotes further absorption of vacancies by nearby pores. Under the same external stress conditions, the pore sizes at grain boundaries were significantly larger than those within the grains. This phenomenon is attributed to the higher concentration of vacancies at grain boundaries, which accelerates the growth of inter-grain pores. As the magnitude of external stress increases, stress concentration near the pores becomes more pronounced. Jing et al. [82] further investigated the influence of elastic anisotropy on the growth of ceramic grains in cubic crystals. When the anisotropy factor is positive (C12+2C44<C11), the lower elastic strain energy density along the diagonal direction disrupts the uniform growth mechanism of grains, resulting in elongation along the 45° direction. Conversely, when the anisotropy factor is negative, grains tend to form columnar structures due to the lower elastic strain energy density along the axial direction. Dzepina et al. [83] proposed an effective contact force algorithm to simulate the elastic deformation of particles in phase-field sintering simulations. Simulations involving multiple diamond particles subjected to compression revealed that compressive stress causes spherical particles to undergo contact flattening. This leads to the transformation of elastic energy within the particles into surface energy, further enhancing the degree of microstructural densification.

2.6 Phase-Field Sintering Model with Viscous Flow

Unlike solid-state sintering in crystalline materials, viscous sintering does not involve the formation of grain boundaries between particles. Instead, densification in viscous sintering occurs through material viscous flow. In order to simulate the sintering process of amorphous materials, Yang et al. [84] introduced the viscous flow term into the phase-field sintering model. Initially, the total free energy of the system is given by:

Π=∫V[12mmix|v|2+f(ρ)+12kρ|∇ρ|2]dV(25)

where ρ and v represent the phase-field order parameter and the velocity vector field of viscous flow, respectively. mmix stands for the mixed mass density determined jointly by the surrounding medium and sintered powder, while kρ is the gradient energy coefficient. Since the driving force for viscous sintering arises from energy dissipation during the viscous flow process, the energy dissipation theorem is introduced:

∂Π∂t=−∫V2μ(ρ)‖∇v+(∇v)T2‖2dV(26)

Here, μ(ρ) represents the viscosity of the mixed system. Under the incompressibility assumption, the governing equation for viscous sintering is derived using the energy variational approach as follows:

∂ρ∂t=∇⋅[M∇δΠδρ]−∇⋅(vρ)(27)

mmix[∂v∂t+(v⋅∇)v]=−∇p+∇⋅[μ(ρ)(∇v+(∇v)T)]−∇⋅(∂Π∂∇ρ⊗∇ρ)(28)

∇⋅v=0(29)

The first equation introduces a correction term for convective flux in the Cahn-Hilliard equation. The second equation employs the incompressible Stokes equation with the inclusion of surface tension effects to describe the motion of viscous mass flow. The final equation represents the incompressibility of the evolving system.

Based on this model, simulations of the sintering process for polyamide 12 (PA12) particles were conducted. As shown in Fig. 12, the phase-field simulation employed a multi-particle ring chain consistent with experimental conditions. As the sintering process progresses, the stretching of the ring chain leads to an increase in the distance between the two particles marked by white rectangles. Simultaneously, the area of voids within the chain decreases, aligning with the observed experimental outcomes. However, there is a discrepancy from the experimental results, as the simulation does not exhibit pronounced mutual approach between the two bottommost horizontal spheres in the chain during the sintering process. This difference may stem from varying initial contact angles between closely spaced particles in the phase-field simulation and the experimental setup. Krivilyov et al. [85] conducted simulations of the consolidation process of hydroxyl iron powder and found that viscous flow leads to significant shear stress on the surface of pores, impeding their movement. This is in strong contrast to the motion of pores in sintering of crystalline materials. By simulating the sintering process of complex geometrical structures, they further confirmed the reliability of the aforementioned viscous sintering model.

Figure 12: Comparison of sintering morphologies of PA12 particles: (a) phase-field simulation and (b) experimental observation [84]. Copyright (2018), with permission from the American Ceramic Society

2.7 Phase-Field Sintering Model with Temperature Field

During the sintering process, there may also be variations in temperature within the microstructure. As a result, thermal conduction during sintering needs to be taken into account:

∇⋅(∇kT)+Q=ρcp∂T∂t(30)

where T represents the temperature field, k and cp denote thermal conductivity and specific heat capacity, respectively, ρ stands for density, and Q represents the heat source term.

Based on this model, Zhang et al. [86] simulated the influence of particle size distribution on the structural porosity and density of aluminum powder particles during laser powder bed fusion. Through simulations of sintering processes involving aluminum powder particles with varying initial sizes, they observed that smaller powder particles contribute to the formation of sintering necks and densification of the structure. Furthermore, blending smaller particles with larger ones in larger-sized powders helps in reducing the structural porosity. Additionally, they investigated the motion of He and Xe gas pores within the microstructure of UO2 under non-isothermal conditions [87]. Due to the significantly lower thermal conductivities of these gases compared to UO2, large temperature gradients were observed near the gas pores. Fig. 13 illustrates a comparison between simulations considering and not considering the low thermal conductivity of Xe gas pores. The figure displays the positions of gas pores and the distribution of the temperature field within the microstructure. It can be observed that when not considering the low thermal conductivity of Xe gas pores, the temperature gradients within the Xe gas pores and the UO2 matrix remain consistent. However, in simulations accounting for the low thermal conductivity of Xe gas pores, larger temperature gradients appear within the pores, leading to faster movement of the gas pores towards regions of higher temperature. Furthermore, they also conducted simulations on selective laser sintering of 316L stainless steel powder, titanium powder, and nickel powder, observing that increasing laser power or reducing scanning speed promotes the growth of sintering necks [88,89]. Experimental comparisons indicate that the phase-field model incorporating temperature field evolution accurately predicts the distribution of temperature fields and variations in microstructural morphology during selective laser sintering. Rizza et al. [90] simulated the morphological changes in electron beam-melted Ti6Al4V powder under different temperature histories. They found that both temperature history and powder geometry influence the sintering rate and neck size. Moreover, the sintering neck size predicted by the phase-field simulation differed by around 9% from the experimental values, which could be further reduced through reasonable adjustment of calculation parameters. Nandy et al. [91] simulated the process of selective laser sintering for AlSi10Mg powder, revealing that the growth rate of grains increases with rising temperature gradient, highlighting the significant role of temperature gradient in the evolution of sintering structures.

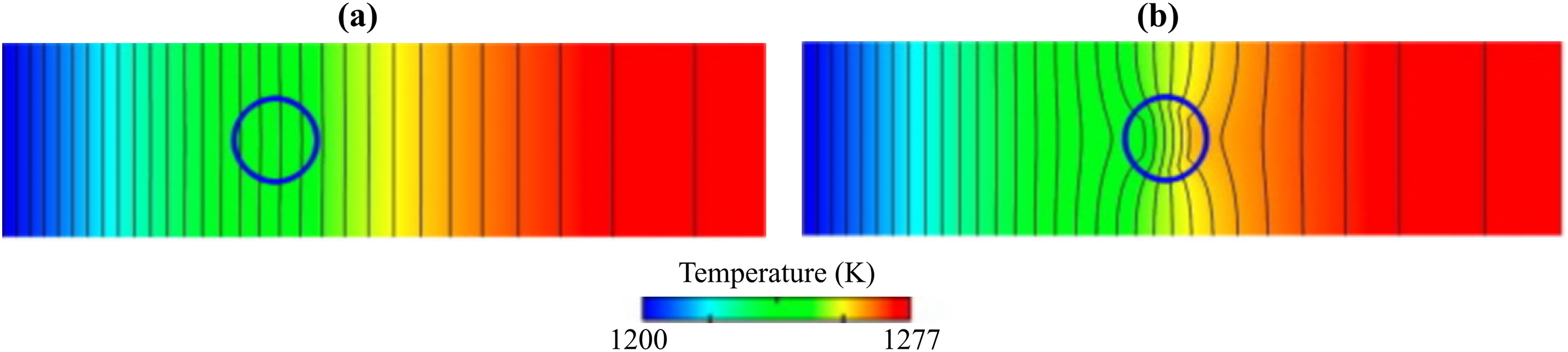
Figure 13: Position of pores and temperature field distribution: (a) without considering and (b) considering low thermal conductivity of pores in simulation [87]. Copyright (2012), with permission from Elsevier

2.8 Phase-Field Sintering Model with External Electric Field

Jiang et al. [92] incorporated an external electric field into the phase-field sintering model to investigate the phenomenon of electrical migration of silver during the sintering process. When an external electric field is applied, the free energy density induced by the electrostatic field is given by:

fem=NaeZρψVm(31)

In the above equation, Na represents Avogadro’s constant, e stands for the elementary charge of an electron, Z denotes the effective charge, Vm represents the molar volume, and ρ and ψ correspond to the mass density field and electric potential field, respectively. By incorporating the free energy induced by the electrostatic field into the phase-field model, the evolution equation for the order parameter under the influence of an external electric field can be obtained. The electric potential field can then be determined by solving the Laplace’s equation:

∇⋅[σ(ρ)⋅∇ψ]=0(32)

where σ(ρ) represents the local electrical conductivity determined by the mass density field.

Fig. 14 illustrates the morphological evolution of porous silver under the influence of a bottom-up electric current, showcasing scenarios where the ratio of surface energy to grain boundary energy is respectively 1 and 1.44. It is evident that the application of an external electric field induces upward migration of both grain boundaries and pores along the direction of the current. As the ratio of these two interface energies increases, the average grain size enlarges, and the velocity of pore migration accelerates. A significant aggregation of pores near the cathode leads to mutual pore connectivity, resulting in the separation of solid silver from the cathode. Analyzing the distribution of current density in the two scenarios depicted in panels (b) and (d) of Fig. 14, it becomes evident that the current density predominantly concentrates at the surfaces of pores and along the grain boundaries that connect these pores. In the later stages of the sintering process, the accumulation of pores near the cathode narrows the effective path for current flow towards the cathode, leading to a more concentrated cathode current density. This phenomenon may even lead to structural discontinuity, causing failures due to the narrowing and disruption of the current pathway toward the cathode.

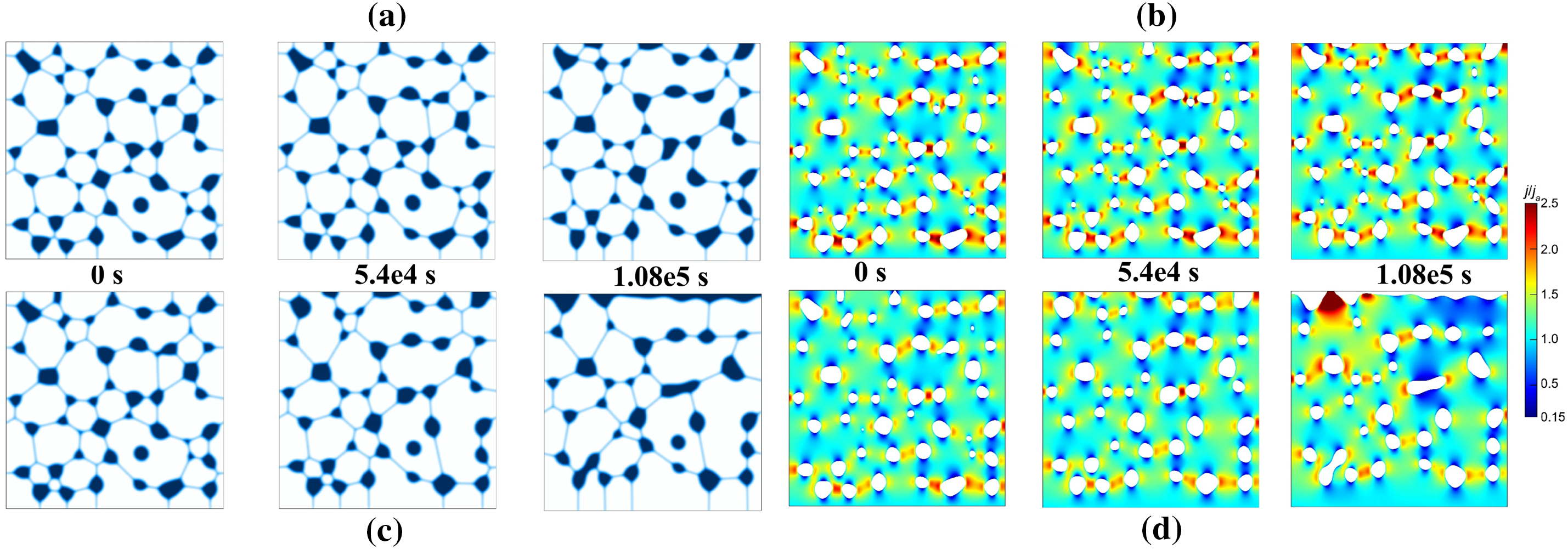
Figure 14: Microstructure evolution after applying current with the surface energy to grain boundary energy ratio of (a) 1.0 and (c) 1.44, along with (b) and (d) current density distributions [92]. Copyright (2022), with permission from Springer

Park et al. [93] investigated the influence of current on the sintering morphology of intermetallic compounds Cu6Sn5 and Cu3Sn in Cu/Sn solder joints. In the absence of current, multiple fan-shaped grains of similar sizes formed in the Cu6Sn5 layer, while the Cu3Sn layer exhibited elongated grain structures. The morphology of these intermetallic compounds varied depending on the direction of the applied current. For instance, when the current flowed from top to bottom, the growth of certain Cu6Sn5 grains occurred, leading to more significant grain size variations. Additionally, the layer thickness of the intermetallic compounds increased, indicating that local current could facilitate grain growth. Conversely, when the current flowed from bottom to top, the growth of the intermetallic compounds was suppressed.

2.9 Multiphase and Multicomponent Phase-Field Sintering Model

In addition to sintering models for pure substances, Zhang et al. [94] developed a phase-field sintering model for multiphase powder systems. Assuming a microstructure composed of N distinct phases and involving M different material components, the total free energy of the system can be defined as follows:

F=∫V[∑i=1Nh(ϕi)fi(Ci,1,......Ci,M−1)+∑i=1N∑j>iN(wi,jϕiϕj−εij22∇ϕi⋅∇ϕj)]dV(33)

In this equation, h(ϕi) represents the interpolation function of the order parameter, fi(Ci,1,…,Ci,M−1) denotes the free energy density of phase i composed of the component fields (Ci,1,…,Ci,M−1), wi,j signifies the two-phase coupling energy coefficient, and εij stands for the gradient energy coefficient. At each local position within the system, the chemical potential of the same material component in different phases is equal:

∂f1∂C1,p=∂f2∂C2,p=...=∂fN∂CN,p=μp,p=1,2,...,M−1(34)

The solute composition at that position is given by:

Cp=∑i=1NϕiCi,p,p=1,2,...,M−1(35)

The evolution equations are given by:

∂ϕi∂t=−∑j≠iNLij(δFδϕi−δFδϕj)(36)

∂Cp∂t=∇∑q=1M−1Mpq∇δFδCp(37)

Based on this model, they investigated the sintering process of Fe-Cu powder. As shown in Fig. 15a, iron particles are typically mixed with smaller copper particles, with copper particles adhering to the surface of iron particles. As sintering progresses, copper particles gradually form necks with iron particles and are eventually completely absorbed by the iron particles. Neck formation is observed even between larger iron particles. The evolution of the copper concentration field in Fig. 15b indicates that, initially, copper concentration is highest in the copper particles at the surface; as copper particles are progressively absorbed by iron particles, copper concentration gradually diffuses from the surface to the interior of iron particles. After a longer simulation time, the copper concentration becomes uniform within the iron particles. These phenomena cannot be simulated by pure material sintering models. Similarly, Ravash et al. [95] employed a similar model to study the evolution of grain morphology in the late stage of sintering for binary liquid-phase systems in three dimensions. By varying the ratio of solid-solid interfacial energy to solid-liquid interfacial energy, as well as the volume fraction of the solid phase, they analyzed the dominant mechanisms for grain coarsening. When the ratio of the two interfacial energies is 2.5, increasing the volume fraction of the solid phase significantly reduces the thickness of the liquid film between sintered particles. The liquid phase forms a network structure enveloping isolated grains, and grain coarsening is governed by Ostwald ripening of solid particles. When the ratio of the two interfacial energies decreases to 2, the liquid phase extensively infiltrates the solid phase, leading to mutual contact between grains. With increasing volume fraction of the solid phase, the number of grain boundaries formed by grain-to-grain contacts increases. When the solid-solid interfacial energy equals the solid-liquid interfacial energy, solid particles are almost fully connected, with only a few isolated liquid regions at triple grain junctions. At this point, grain growth is primarily driven by grain boundary migration.

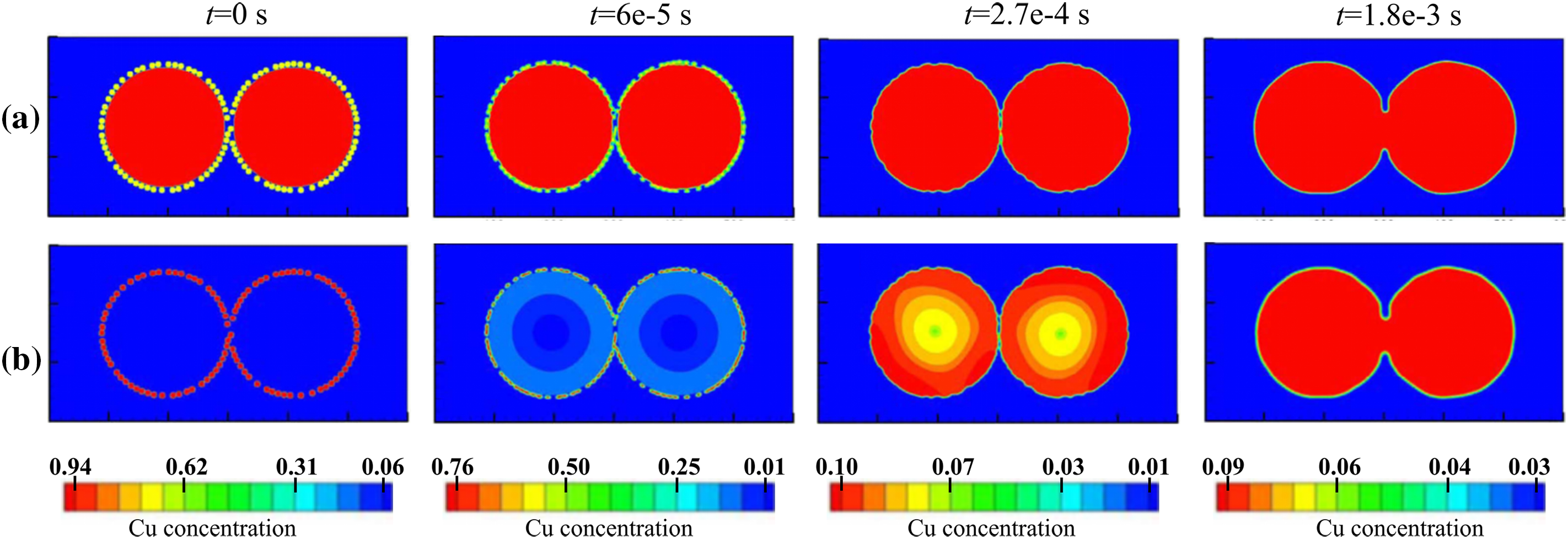
Figure 15: Evolution of (a) sintering morphologies of Fe-Cu particles and (b) the distribution of Cu concentration at different times [94]. Copyright (2014), with permission from Elsevier

Davis et al. [96] investigated the morphological evolution of metal catalysts in porous structures of solid oxide fuel cell anodes. As the volume fraction of the catalyst increases, a transition from isolated particles to semi-continuous network structures and ultimately to fully continuous percolating structures between the catalysts is observed. This transition significantly impacts the performance of fuel cells. Cheng et al. [97] conducted phase-field simulations to study the phenomenon of liquid phase migration in WC-Co cemented carbide liquid-phase sintering. The results revealed that liquid phase migration involves two processes: rapid separation of solid particles and substance diffusion, both of which contribute to grain growth. When the ratio of solid-solid interfacial energy to solid-liquid interfacial energy satisfies the wetting condition, rapid separation of solid particles occurs, consistent with experimental findings. This serves to qualitatively validate the reliability of phase-field simulations. Zhou et al. [98] investigated the growth of Al2O3 grains containing pores and second-phase nanoparticles. They found that, with a fixed nanoparticle size, an increased number of nanoparticles favors the formation of finer and more homogeneous Al2O3 grain structures. However, once the nanoparticle content reaches a certain threshold, clustering of nanoparticles within the grains occurs, leading to a decline in material properties. When nanoparticle content is fixed, reducing the nanoparticle size results in smaller final Al2O3 grain sizes. Yu et al. [99] simulated the precipitation and microstructural evolution of over-saturated Al2O3/ZrO2 solid solution powders, observing the formation of elongated Al2O3 precipitates interconnected within a ZrO2 matrix. This aligned well with experimental observations. Liu et al. [100] simulated the sintering process of two-phase porous structures, discovering that the addition of a second phase would act as a pinning effect on the grain boundary migration of the matrix phase, hindering its growth. This effect strengthened with increasing second phase content, and the closure of pores during sintering primarily depended on the diffusion of the second phase. Villanueva et al. [101] introduced a velocity field representing liquid flow within a multi-phase and multi-component phase-field sintering model, capturing the dynamic features of the sintering process. By simulating the evolution of two solid particles connected by a central liquid bridge, they found that rapid wetting induced two vortices in the bridge’s velocity field, resulting in a weak attractive force between the particles. As sintering progressed, rapid wetting and capillary forces led to the detachment of the liquid bridge between the particles, intensifying the attraction between them. In the later stages of sintering, a weak repulsive force developed between the solid particles, which did not significantly affect the overall densification of the microstructure.

2.10 Multiphysics-Coupled Phase-Field Sintering Model

In addition to coupling with individual physical fields as mentioned earlier, phase-field sintering simulations can also readily couple with multiple physical fields. For instance, Yan et al. [102] extended the classical thermo-mechanical-coupled diffusion equation from equilibrium to non-equilibrium conditions. By combining it with the phase-field method, they simulated the fully coupled thermo-mechanical-diffusion process during non-isothermal conditions. Through derivation, the free energy density for fully coupled thermo-elastic-diffusion of isotropic materials is given by:

f(T,εij,c,{ηi})=f0(c,{ηi})+ρcp2T0T2+12Cijklεijεkl−β1δijεijT−β2δijεijc−aTc(38)

β1=(3λ+2μ)αT(39)

β2=(3λ+2μ)αc(40)

In the above equation, f0(c,ηi) represents the energy term determined by the order parameters in the phase-field model, ρ, cp, and T0 denote density, specific heat capacity, and reference temperature, respectively. a stands for the thermal diffusion constant, while λ and μ are Lame constants. β1 and β2 represent the coefficients of thermal expansion and diffusion-induced expansion, respectively. By solving the momentum equation expressed in terms of displacement ui, the coupled strain field is obtained:

μui,jj+(λ+μ)uj,ij−β1T,i−β2ρc,i+Fi=ρ∂2ui∂t2(41)

By solving the Fourier heat conduction equation, the coupled temperature field is obtained:

ρcp∂T∂t+β1T∂εij∂t+aTρ∂c∂t=(kT,i),i(42)

The evolution of the order parameter is determined by the phase-field equation.

Building upon the aforementioned model, Tan et al. [103] further investigated the influence of driving forces induced by concentration gradients, strain gradients, and temperature gradients on the sintering process of SiC particles. Fig. 16a depicts the boundary conditions applied in the simulation, where the left and right sides experience constant compressive stress and linearly increasing temperature over time, while the top and bottom boundaries are stress-free and adiabatic. Fig. 16b illustrates the evolution of microstructural concentration fields and sintered particle morphology during the hot pressing sintering process. As sintering progresses, the contact neck radius gradually increases, leading to a reduction in neck curvature, and subsequently causing the intermediate pores to shrink. Moreover, the study revealed that both the concentration gradient-induced and strain gradient-induced driving forces decrease rapidly with sintering advancement. When the heating rate is higher, the sintering duration is shorter, resulting in a faster reduction of these two driving forces. In contrast, for temperature gradient-induced driving force, higher heating rates correspond to a greater driving force initially, but as sintering proceeds, this force demonstrates a trend of increasing and then decreasing.

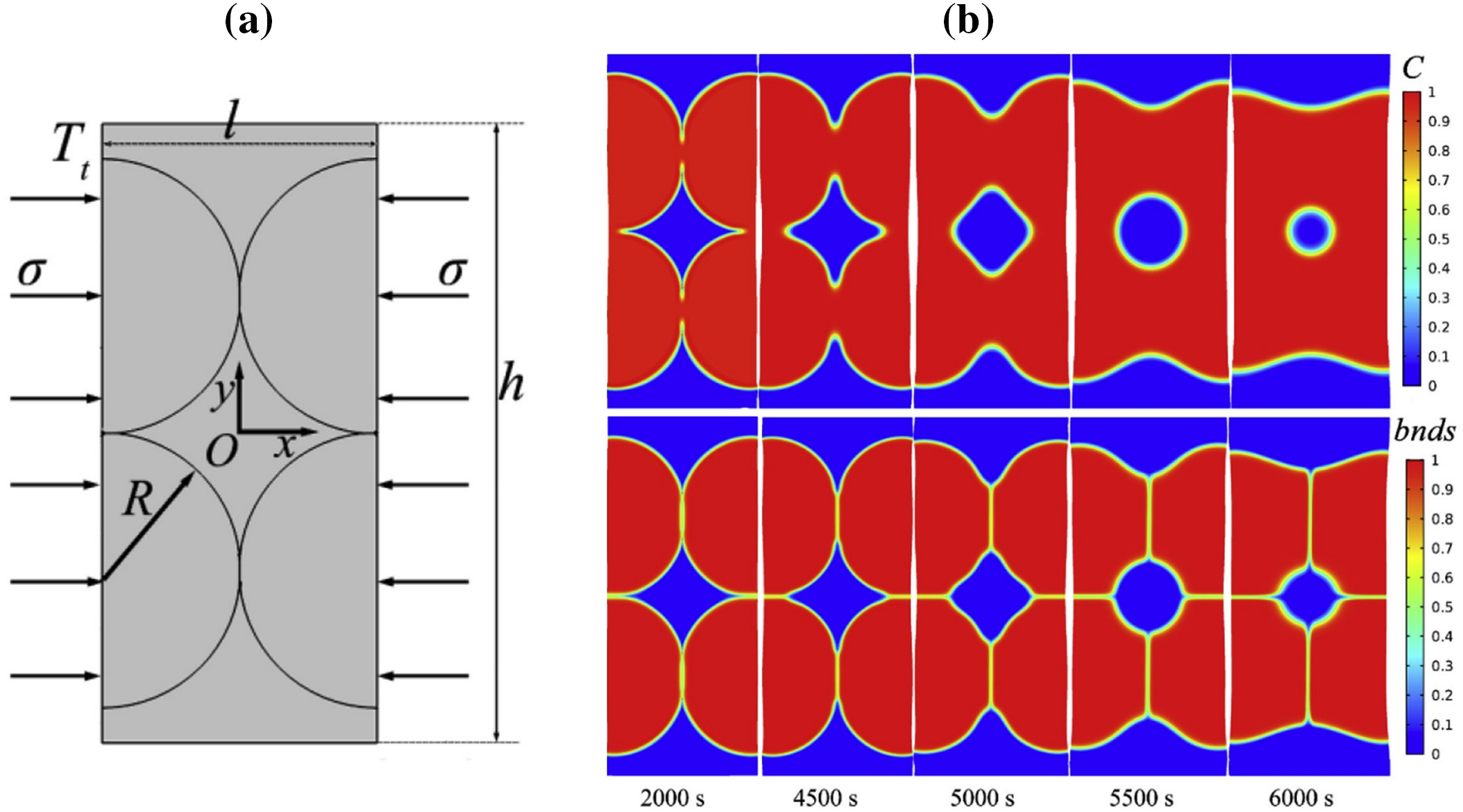
Figure 16: Benchmark of the thermo-mechanical-diffusion coupled phase-field sintering model: (a) boundary conditions of the simulation setup; (b) evolution of concentration field and SiC particle morphology during sintering [103]. Copyright (2020), with permission from Elsevier

Shulin et al. [104] established a thermo-mechano-electro-diffusion coupled phase-field sintering model to investigate the sintering densification of SiC under current-assisted and stress-assisted conditions. Simulation results indicated that higher heating rates lead to faster structural densification rates, without significantly affecting the final degree of densification. During sintering, there was a noticeable concentration of current density at the sintering neck, resulting in a much greater material diffusion rate in the neck compared to other regions. These findings were consistent with observations from sintering experiments. Liu et al. [105] proposed a multi-physics coupled model to simulate the evolution of pores during the selective laser melting process of Ti6Al4V. The velocity field of the liquid phase was described by the incompressible Navier-Stokes equations, while considering the compressibility of the gas phase that leads to density variations, necessitating the introduction of a variable fluid density in the Navier-Stokes equations. Unlike traditional sintering models, they employed the Cahn-Hilliard equation exclusively to describe the evolution of the solid-liquid interface, omitting changes in grain morphology within the solid phase. Simulation results from the phase-field approach demonstrated that during the laser exposure, all pores exhibited significant movement speeds. Pores in the middle of the molten pool congregated, while upper pores moved to the molten pool’s surface and escaped. Following laser removal, solidification began at the molten pool’s bottom and gradually extended upward. Due to rapid solidification, certain pores became trapped within the solidified region as it grew.

3  Grand Potential Phase-Field Sintering Model

In energy-based phase-field sintering models, limitations arise due to the influence of excess chemical potential on interfacial energy and interface thickness. Typically, this leads to very thin equilibrium interfaces, which pose significant computational costs when simulating the evolution of large-scale microstructures. Therefore, researchers have introduced phase-field models based on grand potential minimization [106]. This approach decouples interfacial energy and interface thickness by projecting the thermodynamic energy in the grand potential space. It allows for independent adjustment of bulk and interfacial properties, rendering the interface thickness independent of the driving force. As a result, this methodology enables efficient simulations of the evolution of large-scale microstructures [106,107].

For a microstructure with n solid-phase order parameters η→={η1,η2,...,ηn} and one gas-phase order parameter ϕ, the grand potential functional of the system can be defined as follows:

Ω=∫V[ωb(η→,ϕ)+ωgb(∇η→,∇ϕ)+hs(ϕ)ωs+hv(ϕ)ωv]dV(43)

where ωs and ωv are the grand potential energy densities of the solid phase and gas phase, respectively, ωb and ωgb are the contributions from the bulk and the interface, and hs(ϕ) and hv(ϕ) are the interpolation functions. Assuming the vacancy concentrations in the solid phase and gas phase are cs and cv, respectively, we can further derive the chemical potential of vacancies [108,109]:

μ=Va∂fs(cs)∂cs=Va∂fv(cv)∂cv(44)

where fs(cs) and fv(cv) are the free energy densities of the solid phase and gas phase, respectively, and Va is the atomic volume of the material. As a result, in addition to the non-conserved order parameters η→ and ϕ evolving according to the Allen-Cahn equations, the evolution equation for the chemical potential with respect to time is given by [106]:

∂μ∂t=1χ[∇⋅(χD∇μ)−1Va∂c∂t∂ϕ∂t](45)

where c is the total concentration satisfying the law of mass conservation, χ is the sensitivity coefficient, and D is the diffusion tensor.

Hötzer et al. [110] employed the grand potential phase-field model to investigate the neck evolution of Al2O3 particles under different diffusion mechanisms. Fig. 17 compares the simulated geometries of sintering necks with four diffusion mechanisms (volume diffusion: v; grain boundary diffusion: gb; surface diffusion: s). It can be observed that the evolution of the neck during sintering is significantly influenced by the diffusion mechanism. Simulations involving surface diffusion yield longer sintering necks, while simulations involving only volume diffusion result in slower neck growth. Furthermore, simulations involving surface diffusion achieve greater structural densification. Comparing with simulations involving only volume diffusion, although grain boundary diffusion can enhance structural densification, it is confined to the limited grain boundary regions, thus having a limited impact on the degree of densification. Greenquist et al. [111] used the grand potential phase-field model to simulate the sintering process of multiple UO2 particles in three dimensions. In this work, they employed anisotropic diffusion tensors to represent different diffusion mechanisms, indirectly reflecting the influence of rigid body motion on the sintering morphology. By simulating 113 randomly distributed spherical UO2 particles with sizes consistent with experiments and using a sintering temperature consistent with experiments, they observed that within the first 6 h, sintering necks quickly formed between the UO2 particles. Larger particles continually absorbed smaller ones, leading to changes in their own morphology. With increasing sintering temperature and simulation time, these particles eventually aggregated into nearly spherical complete particles with a relative density close to 100%. This result demonstrates that the grand potential phase-field model can accurately describe the rate of structural densification during the sintering process without introducing rigid body motion terms. By solely changing the diffusion mechanism, it offers clear advantages compared to traditional energy-based phase-field models.

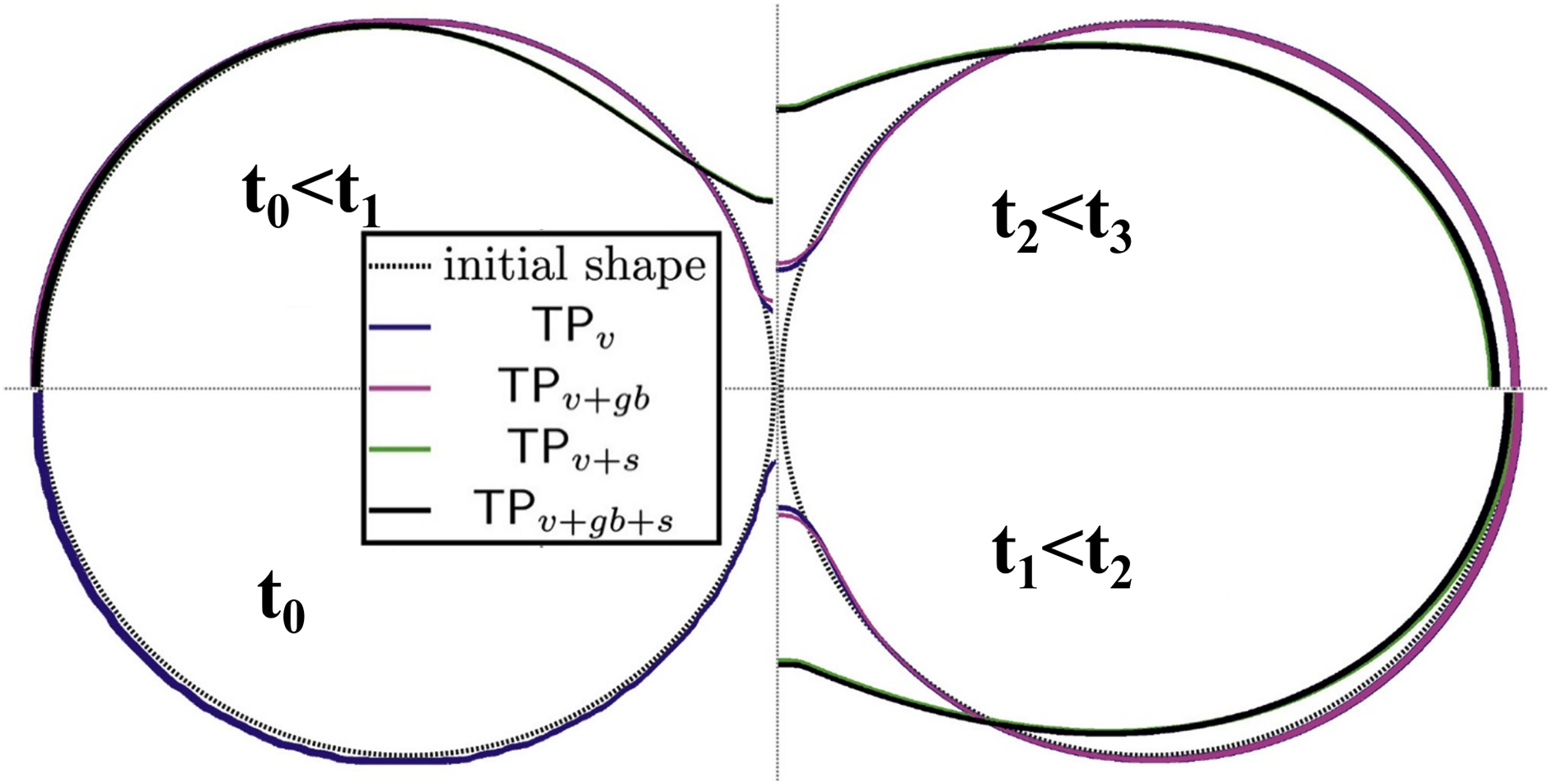
Figure 17: Comparison of grain geometries under different diffusion mechanisms [110]. Copyright (2019), with permission from Elsevier

Aagesen et al. [112] showcased the capability of the grand potential phase-field model in simulating the morphologies of second-phase particles at three-grain junctions and along grain boundaries. As shown in Fig. 18, four parent-phase particles with a hexagonal structure are distributed with periodic boundary conditions, and circular second-phase particles are situated at three-grain junctions and along grain boundaries. After a brief evolution, the second-phase particles at grain boundaries transform into convex lens shapes, while those at three-grain junctions form triangular shapes composed of curved arcs. These morphological differences arise from the energy balance between interfaces. As the structure further evolves, the second-phase particles at three-grain junctions gradually coarsen, accompanied by the continuous reduction of second-phase particles at grain boundaries. This selective coarsening is due to curvature differences that result in chemical potential gradients at different positions, leading to the transfer of material from grain boundaries to three-grain junctions. Additionally, the second-phase particles strongly pin the grain boundaries, hindering the growth of parent-phase grains. Azizi et al. [113] utilized the grand potential model to simulate the grain growth of binary AlSi alloy during selective laser sintering. Simulation results of single-layer powder sintering indicate that the grains mainly consist of columnar dendrites, aligning well with experimental outcomes. Greenquist et al. [108] employed a grand potential model to simulate the influence of two dopants, Mn and Cr, on the sintering behavior of UO2. The simulation outcomes revealed that compared to pure UO2 sintering, UO2 doped with Mn exhibited a faster densification rate and an increased average grain size. Additionally, the simulated density ratio of UO2 doped with Cr compared to pure UO2 sintering closely matched experimental results, thereby affirming the accuracy of the model.

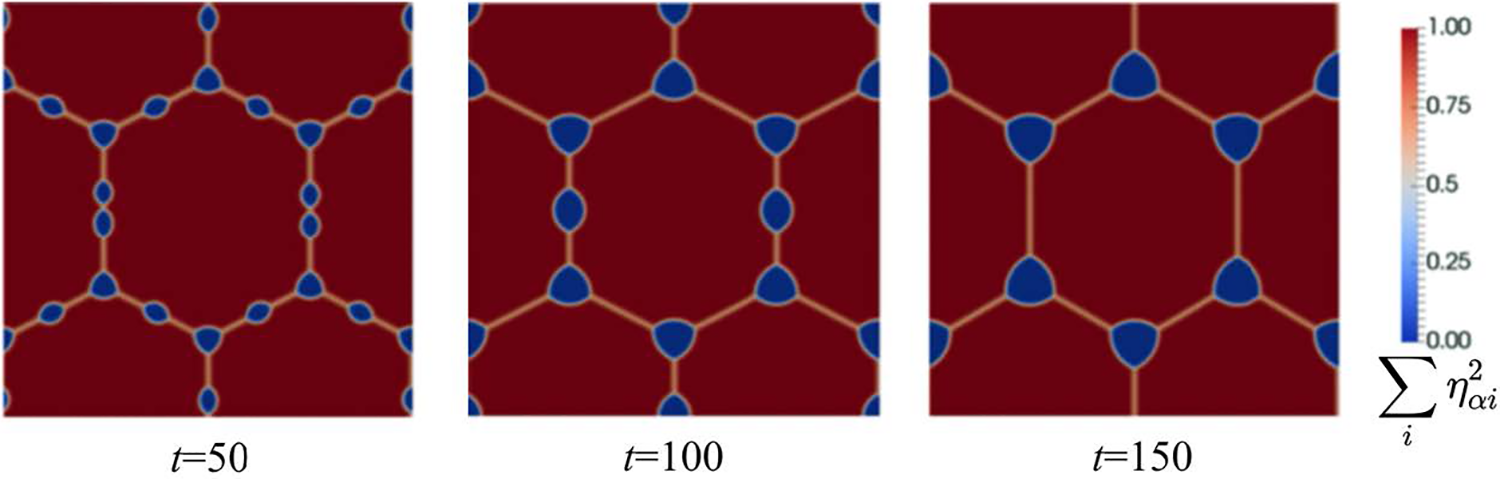
Figure 18: Morphology distribution of matrix and second-phase particles at different times [112]. Copyright (2018), with permission from American Physical Society

4  Entropy-Based Phase-Field Sintering Model

According to the Legendre transformation, the relationship between the free energy density f(φ,T) and the entropy density s(e,φ) of a system at finite temperature is given by [114]:

f(φ,T)=infe[e−Ts(e,φ)](46)

s(e,φ)=infT[eT−f(φ,T)T](47)

where φ is the phase-field order parameter, and e is the internal energy density. Based on the above relation, the free energy in the phase-field model can be rewritten as:

F(T,φ)=∫V[infe(e−Ts(e,φ))+12κ|∇φ|2]dV=infe[E(e)−TS(e,φ)](48)

E(e)=∫VedV(49)

S(e,φ)=∫V[s(e,φ)−12κT|∇φ|2]dV(50)

When φ is a non-conserved order parameter, the Allen-Cahn equation can be rewritten as:

∂φ∂t=−LδF(T,φ)δφ=TLδS(e,φ)δφ(51)

When φ is a conserved order parameter, the Cahn-Hilliard equation is then rewritten as:

∂φ∂t=−∇⋅[M∇(TδSδφ)](52)

Yang et al. [115] derived a non-isothermal phase-field model based on the microstructure’s entropy density functional to simulate the effect of temperature gradients on sintering structure evolution. To be more specific, by extending the entropy functional into the sintering model, the microstructure’s free energy functional can be represented as:

F=∫V[f(T,ρ,{ηi})+12Tκρ|∇ρ|2+12Tκη∑i=1N|∇ηi|2]dV(53)

The evolution equation for the conserved order parameter ηi is given by:

∂ηi∂t=−LδFδηi=−L[∂f∂ηi−κη(T∇2ηi+∇ηi⋅∇T)](54)

The evolution equation for the non-conserved order parameter ρ is:

∂ρ∂t=∇⋅[M⋅∇(δFδρ)−δFδρM~⋅∇TT](55)

In the given equation, M and M~ represent the diffusion tensors for mass diffusion and thermo-phoretic diffusion, respectively. The terms on the right-hand side, the first and second terms, correspondingly depict the diffusion flux caused by Fickian diffusion and thermal-phoretic effects. The heat conduction equation with the introduction of the heat source term Qe is expressed as follows:

cr∂T∂t+∂e∂ρ∂ρ∂t+∑i=1N∂e∂ηi∂ηi∂t=∇⋅(k⋅∇T)+Qe(56)

where cr and k stand for the specific heat and the thermal conductivity tensor, respectively.

In the sintering process, various competing physical mechanisms exist within the microstructure. Grain coarsening and densification are the two most significant mechanisms [75]. At the beginning of sintering, atoms from the free surface and grain boundaries tend to migrate to the concave neck regions between adjacent particles to reduce the system’s free energy. As sintering progresses, driven by the energy difference on surfaces with different curvatures, atoms diffuse from surfaces of smaller particles with high surface curvature to those of larger particles with low surface curvature, leading to a phenomenon known as Ostwald ripening. For particles within the solid, atoms diffuse from convex to concave surfaces of grain boundaries, resulting in an increase in average grain size, i.e., grain growth. Ostwald ripening and grain growth are the primary mechanisms contributing to grain coarsening. Due to the lower interfacial energy of grain boundaries compared to free surfaces, as the free surface decreases, the system evolves to increase the grain boundary area. With an increase in the neck area between particles, local atomic flux causes mutual attraction between particles, leading to structural densification. Additionally, under non-isothermal conditions such as laser selective sintering, the mechanism of how local temperature gradients affect structural densification remains controversial. Young et al. [116,117] were the first to discuss the driving effect of temperature gradients, suggesting that thermophoretic diffusion is more conducive to mass transfer than curvature-driven diffusion, promoting structural densification. Johnson [118] pointed out that temperature gradients parallel to the grain boundary direction cannot drive material diffusion, rendering the impact of thermophoresis on structural densification negligible. Biesuz et al. [119] evaluated the strength of these two mechanisms during the sintering process. They noted that thermophoretic effects are not significant in the early stages of sintering. However, in the mid and late stages of sintering, thermophoretic effects become a key factor influencing structural densification.

Traditional energy-based phase-field sintering models encounter challenges in capturing the intricate physical effects influenced by temperature gradients. Yang et al. [115] conducted simulations of non-isothermal sintering processes for multiple particles in a three-dimensional scenario and compared the results with conventional isothermal sintering simulations. Fig. 19 illustrates the temporal evolution of local relative density along the temperature gradient direction for the sintered region in both scenarios. In the non-isothermal sintering model, owing to the combined effects of Fickian diffusion and thermal-phoretic phenomena, a noticeable material migration from the low-temperature end to the high-temperature end occurred within the microstructure. This resulted in a reduction of relative density to zero at coordinates 2–6 at the conclusion of sintering, while the relative density at coordinates 34–38 approached nearly 100%. On the other hand, in the isothermal sintering model, the local density of the microstructure remained stable throughout the entire sintering process, experiencing only slight decreases at coordinates 10–14 and 30–34, and slight increases at coordinates 18–26. These variations in relative density were attributed to material migration induced by local curvature effects. Liang et al. [120] addressed this issue by employing a thermodynamically consistent non-isothermal phase-field model to investigate the impact of temperature gradients and curvature on the direction of grain boundary migration during sintering. Fig. 20 illustrates the competitive relationship between temperature gradients and curvature in influencing grain boundary movement under non-isothermal conditions. In Fig. 20a, the locally significant curvature results in curvature-driven forces causing the grain boundary to move to the left. In contrast, in Fig. 20b, with decreasing curvature-driven force, temperature gradients induce the grain boundary to move to the right.

Figure 19: Evolution of structural relative density with sintering time in (a) non-isothermal and (b) isothermal phase-field models [115]. Copyright (2020), with permission from Elsevier

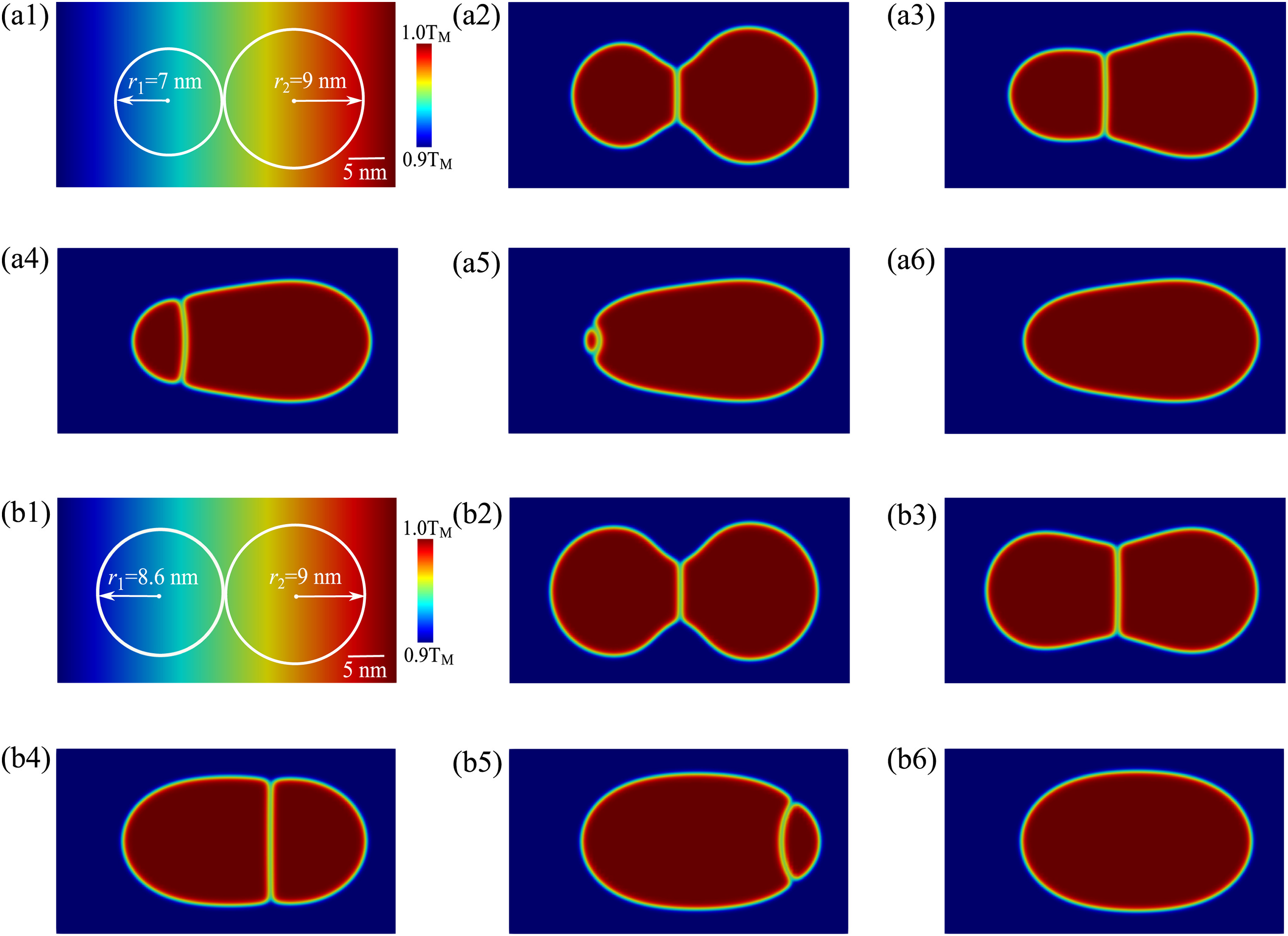
Figure 20: Mechanisms of grain boundary movement under non-isothermal conditions: (a) dominance of curvature-driven forces leading to leftward movement, and (b) dominance of temperature gradients inducing rightward movement [120]. Copyright (2023), with permission from Elsevier

Furthermore, Yang et al. extended this methodology to simulate laser selective area sintering and laser selective area melting additive manufacturing processes for 316L stainless steel powders. They also considered the influence of capillary effects on molten flow and the reciprocal impact of molten flow on heat conduction [121,122]. Wang et al. [123], building upon the aforementioned non-isothermal phase-field sintering model, further considered the impact of locally varying velocity due to the combined influence of particle rigid motion and molten flow during the sintering process. Simulation outcomes demonstrated that using a thinner powder layer thickness was conducive to reducing porosity in the sintered product. When particle size disparity was small, an increase in overall thermal conductivity and a larger laser heating region were achieved, resulting in decreased structural porosity. Li et al. [124] examined the effect of scanning laser beams on the heating and melting rate of individual Ti powder particles. They found that higher laser power and narrower beam size accelerated the melting rate of Ti powder. However, the choice of scanning speed needed to be moderate; excessively fast speeds led to incomplete powder melting, while overly slow speeds caused excessive vaporization due to elevated liquid-phase temperatures.

5  Phase-Field Simulation in Additive Manufacturing

Metal additive manufacturing involves multiple physical processes such as heat and mass transfer, phase transformation, grain growth, and molten metal flow. The complexity of the influencing factors in microstructure evolution poses challenges for alloy design and performance control in additive manufacturing [125–127]. The phase-field method utilizes order parameters to describe various complex microstructures, including gas/liquid/solid phases, grain shapes/orientations, and can directly incorporate field variables describing various physical processes (such as stress/strain, melt velocity, temperature, concentration, electric/magnetic fields, etc.). This method demonstrates significant advantages in structural simulation and mechanistic exploration during the additive manufacturing process. This is crucial for improving the quality of additive manufacturing products and minimizing costs [85,128].

Flint et al. [129] incorporated the temperature gradient effect into a phase-field model to simulate the evolution of grain morphology during the melting process of Ti6Al4V alloy induced by a high-energy-density heat source in laser welding. They found that a sufficiently large temperature gradient could drive grain boundary migration, leading to migration of the grain boundary towards the direction of the temperature gradient. This model contributes to a better understanding of the evolution of solid boundaries in powder bed fusion additive manufacturing processes. In the realm of electron beam melting (EBM) for Ti6Al4V, Liu et al. [130] established a multiscale model to explore the evolution mechanisms of grain structures in specific locations during the metal alloy additive manufacturing process. The macroscopic heat response in the EBM process was simulated using the finite element method. By inputting the extracted thermal information into a temperature-related phase-field model, the authors accurately predicted physical processes such as grain extension and selective growth at the mesoscale, showing good consistency with experimentally observed grain textures.

In another study involving selective laser sintering of 200 stainless steel particles [131], the researchers systematically explored the effects of laser power and scanning speed on structural characteristics such as porosity, surface morphology, temperature distribution, and changes in grain geometry. They validated the quantitative relationship between sintering rate, structural densification, and laser input energy. Fig. 21 illustrates the distribution of powder morphology and temperature field in the powder bed under simulated conditions with different laser powers and scanning speeds [131]. The temperature field distribution on the surface of the powder bed is highly non-uniform under laser heating: at the leading edge of the moving beam, isotherms are densely packed, and once the beam has scanned through, the isotherms become sparse. When both laser power and scanning speed are low (15 W, 100 mm/s), there are numerous insufficiently fused particles in the microstructure, resulting in a low structural density. In contrast, at lower scanning speeds and higher laser power (30 W, 100 mm/s), the powder particles are completely agglomerated, forming a nearly fully dense structure. Additionally, with a fixed laser power (20 W), lower scanning speeds (from 150 to 80 mm/s) lead to higher structural density.

Figure 21: Distribution of powder morphology and temperature field in the powder bed under various laser powers and scanning rates in simulation [132]. Copyright (2019), with permission from Springer

Developing a phase-field model to simulate the additive manufacturing process in a powder bed, Lu et al. [132] provided insights into phenomena observed by varying laser power and scanning speed. The work determined relationships between porosity, grain density, and process parameters, offering valuable guidance for the precise control of defects in additive manufacturing. Wang et al. [123] developed a multiscale framework to study the layer-by-layer densification behavior of powder during solid-state metal laser sintering. Based on a three-dimensional heat transfer model of powder, they first determined the macroscopic heat response during laser processing. Subsequently, by inputting the thermal response information into a non-isothermal phase-field model, they simulated the layer-by-layer densification process of 316L stainless steel powder. They found that the lowest porosity was achieved when the particle size ratio was 0.4 and the blending ratio was 0.6. Conducting phase-field simulations of the laser selective melting process for porous materials, Zhou et al. [133] integrated finite element methods to evaluate mechanical properties and residual stresses of the obtained microstructure. The analysis revealed that under high laser power and low scanning speed, partial melting of the powder occurred, reducing the microstructure’s porosity and ultimately enhancing its mechanical properties. Azizi et al. [113] utilized phase-field simulations to investigate the influence of print direction on the microstructural evolution of laser-sintered AlSi10Mg alloy. They found that controlling the print direction could promote the transition of grain morphology from columnar grains to equiaxed grains, aligning with experimental observations.

6  Numerical Solution of Phase-Field Equations

The phase-field model consists of a set of nonlinear partial differential equations (PDEs), and these equations typically lack analytical solutions, necessitating numerical solutions through various methods [32,134,135]. Currently, the most common numerical solution methods include finite difference method, finite element method, and spectral method.

Finite difference method involves replacing the differential forms with difference forms to handle the system of nonlinear PDEs. This method has a relatively simple discretization process, straightforward data preprocessing, ease of programming, and parallel computation. However, it demands a high level of conformity to the simulation region shape, making it suitable mainly for simulations with simple shapes. Additionally, it exhibits poor flexibility and boundary adaptability [136,137]. The explicit and implicit formats are two commonly used formats in finite difference methods for solving partial differential equations [138]. The explicit format has simple iteration and high computational efficiency but is limited by grid and time step requirements, resulting in lower accuracy. On the other hand, the implicit format has lower demands on grid and time step, with higher accuracy and stability. However, solving a large system of higher-order linear equations significantly reduces computational efficiency [139].

Finite element method involves partitioning the entire region into a finite number of non-overlapping grids, commonly referred to as finite elements. These elements are interconnected through nodes, and the method proceeds by applying variational principles and partial interpolation to obtain approximate solutions for each element. Subsequently, through iterative solving, the results of all elements are combined to obtain the finite element solution for the entire region [140–143]. The flexibility and adaptability of the finite element method are significant, but it poses challenges in terms of program design and involves complexities in data preparation, along with potential issues of data oscillations during computation [143,144]. For phase-field equations, the phase parameter changes most rapidly at the interface, making it crucial to refine the finite element grid in these regions. Adaptive recognition and refinement of these areas can be achieved by comparing the magnitudes of the phase parameter gradients [145]. The time spent on adaptive grid refinement involves two main aspects: the time for grid generation and the actual computation time. An ideal adaptive grid refinement algorithm should minimize the time spent on grid generation and focus more on computation. The grid should not be overly refined to avoid a substantial increase in computational time due to a large number of grids. Additionally, regions far from the interface need timely coarsening of the grid [146,147].

Spectral methods approximate the solution of partial differential equations by expanding it into a finite series of smooth functions, known as the approximate spectral series of the solution. The number of terms in the series directly determines the accuracy of this method [148]. For solving functions with periodic boundary conditions, the use of Fourier series and harmonic series is more convenient. Spectral methods share a similar solving philosophy with finite element methods, but their distinction lies in the fact that spectral methods seek a smooth approximation of the true solution by summing a set of functions defined across the entire domain, while finite element methods approximate the solution by summing simple functions in segmented domains. With the development of fast Fourier transforms, the computational complexity of spectral methods has been reduced, leading to a substantial decrease in computational costs [149]. Particularly in the simulation of three-dimensional phase-fields, both finite difference and finite element methods require a sufficient number of grid points to achieve a solution. In contrast, spectral methods can achieve higher solution accuracy without the need for as many grid points [150].

7  Summary and Outlooks

The phase-field method has undoubtedly become one of the core approaches for simulating the microstructure evolution in sintering processes. Energy-based phase-field sintering models easily achieve coupling with other physical fields by introducing additional energy terms into the free energy functional. Meanwhile, phase-field models based on the minimization of the grand potential decouple interfacial energy and interface thickness by projecting the thermodynamic energy in grand potential space. This enables the independent adjustment of properties at bulk and interface regions, making the interface thickness independent of the driving force. Consequently, these models are effective in simulating the evolution of large microstructures. Additionally, phase-field sintering models based on entropy increase can capture non-isothermal effects, such as local temperature gradients, playing a significant role in simulations of additive manufacturing processes like laser selective sintering. The following briefly outlines some challenges and opportunities in this research field.

Supplementing phase-field model parameters. The accuracy of phase-field simulations is closely tied to the precision of various material parameters used in the model. In the context of additive manufacturing simulations, the accuracy of thermodynamic parameters related to temperature becomes particularly crucial. Due to a lack of necessary thermodynamic data, current phase-field simulations in additive manufacturing predominantly focus on pure metals and a limited set of binary alloys, to some extent falling short of meeting the material requirements for metal additive manufacturing. For various diffusion coefficients, it is essential to supplement measurements through experimental means and complement them with methods such as first-principles calculations and molecular dynamics simulations.

Quantitative validation of phase-Field simulation results. It is imperative to thoroughly utilize existing additive manufacturing experimental results to quantitatively validate the predicted microstructural morphologies from phase-field simulations. Conducting phase-field simulations with materials and processing parameters consistent with additive manufacturing experiments and characterizing the additive manufacturing samples through scanning electron microscope or transmission electron microscope, among other techniques, facilitates the validation of the phase-field model. Through quantitative comparisons between simulation results and experimental observations, there is an opportunity for substantial improvement in the phase-field model, numerical methods, and model parameters.

Multiscale simulation in phase-field modeling results. For additive manufacturing processes, there exist multiscale challenges in both physical phenomena and the scale of the study, encompassing micro, meso, and macro scales. Establishing a quantitative relationship between composition-process-microstructure-performance is essential for developing high-performance additive manufacturing alloys. Phase-field simulations can predict the crystal organization, grain size, orientation, and various defects within additive manufacturing products, establishing a quantitative relationship between composition-process-microstructure. However, these micro-scale characteristics may not directly reflect the macroscopic performance of the additive manufacturing component. The results from phase-field simulations can be employed as inputs for macroscopic scale simulations, enabling accurate assessment of the mechanical performance of additive manufacturing products and determining the quantitative relationship between microstructure-performance.

Full-scale phase-field simulations. As mentioned earlier, the physically rich phase-field models can quantitatively and accurately simulate the evolution of microstructures under highly non-equilibrium additive manufacturing conditions, with a high degree of fidelity. However, this richness also results in a substantial computational burden, making it extremely challenging to achieve full-scale phase-field simulations on additive manufacturing components. Emerging exascale heterogeneous (CPU + GPU) high-performance computing frameworks and enhanced computational methods can be utilized for large-scale, high-fidelity simulations of microstructure evolution. This extends the applicability of phase-field simulations beyond the scale of representative volume units to enable full-scale simulations on the continuum of additive manufacturing components.

Integration of phase-field simulation with data-driven methods. In the metal additive manufacturing process, considering only the melt pool involves multiple complex physical processes such as wetting, capillarity, surface tension, Marangoni convection, melt pool dynamics, and phase transitions. The accurate mechanisms and evolution laws of these physical changes need validation and summarization through additive manufacturing practices, making it challenging to entirely predict and generalize using phase-field control equations alone. In the future, leveraging methods like machine learning to analyze additive manufacturing data can help infer unknown physical mechanisms.

Acknowledgement: The authors acknowledge the support from the High Performance Computing Platform of Nanjing University of Aeronautics and Astronautics, China. We are also thankful for the insightful comments from anonymous reviewers, which have greatly improved this manuscript.

Funding Statement: This work was partially supported by the National Science and Technology Major Project, China (No. J2019-IV-0014-0082), the National Key Research and Development Program of China (No. 2022YFB4600700), the National Overseas Youth Talents Program, China, the Research Fund of State Key Laboratory of Mechanics and Control for Aerospace Structures, China (No. MCMS-I-0422K01), and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions, China.

Author Contributions: Ming Xue: Conceptualization, Investigation, Data curation, Writing—original draft. Min Yi: Conceptualization, Investigation, Resources, Supervision, Project administration, Funding acquisition, Writing—original draft & review & editing.

Availability of Data and Materials: Data will be made available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Moya JS, Baudín C, Miranzo P. Sintering. In: Encyclopedia of physical science and technology. 3rd ed. New York: Academic Press; 2003. p. 865–78. [Google Scholar]

2. Kang SJL. Sintering processes. In: Sintering. Oxford: Butterworth-Heinemann; 2005. p. 3–8. [Google Scholar]

3. Blackford JR. Sintering and microstructure of ice: a review. J Phys D. 2007;40(21):R355. doi:10.1088/0022-3727/40/21/R02. [Google Scholar] [CrossRef]

4. Greenquist I, Tonks MR, Zhang Y. Review of sintering and densification in nuclear fuels: physical mechanisms, experimental results, and computational models. J Nucl Mater. 2018;507:381–95. doi:10.1016/j.jnucmat.2018.03.046. [Google Scholar] [CrossRef]

5. Ivannikov V, Thomsen F, Ebel T, Willumeit-Römer R. Coupling the discrete element method and solid state diffusion equations for modeling of metallic powders sintering. Comput Part Mech. 2023;10(2):185–207. doi:10.1007/s40571-022-00486-6. [Google Scholar] [CrossRef]

6. Thomsen F, Hofmann G, Ebel T, Willumeit-Römer R. An elementary simulation model for neck growth and shrinkage during solid phase sintering. Materialia. 2018;3:338–46. doi:10.1016/j.mtla.2018.08.031. [Google Scholar] [CrossRef]

7. Li H, Zhang LP, Zhang YX, Fu XL, Shao XJ, Du J. A peridynamic approach for the evaluation of metal ablation under high temperature. Comput Model Eng Sci. 2023;134(3):1997–2019. doi: 10.32604/cmes.2022.020792. [Google Scholar] [CrossRef]

8. Olevsky EA. Theory of sintering: from discrete to continuum. Mater Sci Eng R Rep. 1998;23(2):41–100. doi:10.1016/S0927-796X(98)00009-6. [Google Scholar] [CrossRef]

9. Jagota A, Mikeska KR, Bordia RK. Isotropic constitutive model for sintering particle packings. J Am Ceram Soc. 1990;73(8):2266–73. doi:10.1111/jace.1990.73.issue-8. [Google Scholar] [CrossRef]

10. Rojek J, Nosewicz S, Maździarz M, Kowalczyk P, Wawrzyk K, Lumelskyj D. Modeling of a sintering process at various scales. Procedia Eng. 2017;177:263–70. doi:10.1016/j.proeng.2017.02.210. [Google Scholar] [CrossRef]

11. Olevsky EA, Tikare V, Garino T. Multi-Scale Study of Sintering: a review. J Am Ceram Soc. 2006;89(6):1914–22. doi:10.1111/jace.2006.89.issue-6. [Google Scholar] [CrossRef]

12. Pan J. Modelling sintering at different length scales. Int Mater Rev. 2003;48(2):69–85. doi:10.1179/095066002225010209. [Google Scholar] [CrossRef]

13. Riedel H, Kozák V, Svoboda J. Densification and creep in the final stage of sintering. Acta Metall Mater. 1994;42(9):3093–3103. doi:10.1016/0956-7151(94)90407-3. [Google Scholar] [CrossRef]

14. Ding L, Davidchack RL, Pan J. A molecular dynamics study of sintering between nanoparticles. Comput Mater Sci. 2009;45(2):247–56. doi:10.1016/j.commatsci.2008.09.021. [Google Scholar] [CrossRef]

15. Zhang Z, Fu G, Wan B, Su Y, Jiang M. Research on sintering process and thermal conductivity of hybrid nanosilver solder paste based on molecular dynamics simulation. Microelectron Reliab. 2021;126:114203. doi:10.1016/j.microrel.2021.114203. [Google Scholar] [CrossRef]

16. Marvel CJ, Riedel C, Frazier WE, Rollett AD, Rickman JM, Harmer MP. Relating the kinetics of grain-boundary complexion transitions and abnormal grain growth: a Monte Carlo time-temperature-transformation approach. Acta Mater. 2022;239:118262. doi:10.1016/j.actamat.2022.118262. [Google Scholar] [CrossRef]

17. Yan W, Melville J, Yadav V, Everett K, Yang L, Kesler MS, et al. A novel physics-regularized interpretable machine learning model for grain growth. Mater Des. 2022;222:111032. doi:10.1016/j.matdes.2022.111032. [Google Scholar] [CrossRef]

18. Raether F, Seifert G. Modeling Inherently Homogeneous Sintering Processes. Adv Theory Simul. 2018;1(5):1800022. doi:10.1002/adts.v1.5. [Google Scholar] [CrossRef]

19. Guo Q, Hou H, Wang K, Li M, Liaw PK, Zhao Y. Coalescence of Al0.3CoCrFeNi polycrystalline high-entropy alloy in hot-pressed sintering: a molecular dynamics and phase-field study. npj Comput Mater. 2023;9(1):185. doi:10.1038/s41524-023-01139-9. [Google Scholar] [CrossRef]

20. Svyetlichnyy D, Krzyzanowski M, Straka R, Lach L, Rainforth WM. Application of cellular automata and lattice Boltzmann methods for modelling of additive layer manufacturing. Int J Numer Method H. 2018;28(1):31–46. doi:10.1108/HFF-10-2016-0418. [Google Scholar] [CrossRef]

21. Humenyuk LO, Lotysh VV, Rud VD. Computer model of sintering based on a cellular automation. Powder Metall Met Ceram. 1998;37(7):379–81. [Google Scholar]

22. Bejarano-Palma JA, Moshtaghioun BM, Cumbrera FL, Gomez-García D. On the role of the electric field in the last-stage sintering of ceramics: a phase-field modelling approach. Acta Mater. 2024;262:119422. doi:10.1016/j.actamat.2023.119422. [Google Scholar] [CrossRef]

23. Huang Z, Wang H, Chen L, Gomez H, Li B, Cao C. A meshfree phase-field model for simulating the sintering process of metallic particles for printed electronics. Eng Comput. 2023;35:129. doi:10.1007/s00366-023-01909-5. [Google Scholar] [CrossRef]

24. Cheng JJ, Xia Q, Kim JS, Li YB. An efficient linear and unconditionally stable numerical scheme for the phase field sintering model. Commun Nonlinear Sci Numer Simul. 2023;127:107529. doi:10.1016/j.cnsns.2023.107529. [Google Scholar] [CrossRef]

25. Chen LQ, Zhao Y. From classical thermodynamics to phase-field method. Prog Mater Sci. 2022;124:100868. doi:10.1016/j.pmatsci.2021.100868. [Google Scholar] [CrossRef]

26. Chen LQ. Phase-field models for microstructure evolution. Annu Rev Mater Sci. 2002;32(1):113–40. doi:10.1146/matsci.2002.32.issue-1. [Google Scholar] [CrossRef]

27. Moelans N, Blanpain B, Wollants P. An introduction to phase-field modeling of microstructure evolution. Calphad. 2008;32(2):268–94. doi:10.1016/j.calphad.2007.11.003. [Google Scholar] [CrossRef]

28. Steinbach I. Phase-field models in materials science. Model Simul Mat Sci Eng. 2009;17(7):073001. doi:10.1088/0965-0393/17/7/073001. [Google Scholar] [CrossRef]

29. Tonks MR, Aagesen LK. The phase field method: mesoscale simulation aiding material discovery. Annu Rev Mater Sci. 2019;49(1):79–102. doi:10.1146/matsci.2019.49.issue-1. [Google Scholar] [CrossRef]

30. Bui TQ, Hu X. A review of phase-field models, fundamentals and their applications to composite laminates. Eng Fract Mech. 2021;248:107705. doi:10.1016/j.engfracmech.2021.107705. [Google Scholar] [CrossRef]

31. Cervera M, Barbat GB, Chiumenti M, Wu JY. A comparative review of XFEM, mixed FEM and phase-field models for quasi-brittle cracking. Arch Comput Methods Eng. 2022;29(2):1009–83. doi:10.1007/s11831-021-09604-8. [Google Scholar] [CrossRef]

32. Zhuang X, Zhou S, Huynh GD, Areias P, Rabczuk T. Phase field modeling and computer implementation: a review. Eng Fract Mech. 2022;262:108234. doi:10.1016/j.engfracmech.2022.108234. [Google Scholar] [CrossRef]

33. Ansari TQ, Huang H, Shi SQ. Phase field modeling for the morphological and microstructural evolution of metallic materials under environmental attack. npj Comput Mater. 2021;7(1):143. doi:10.1038/s41524-021-00612-7. [Google Scholar] [CrossRef]

34. Li Y, Hu S, Sun X, Stan M. A review: applications of the phase field method in predicting microstructure and property evolution of irradiated nuclear materials. npj Comput Mater. 2017;3(1):16. doi:10.1038/s41524-017-0018-y. [Google Scholar] [CrossRef]

35. Ahmed K, Pakarinen J, Allen T, El-Azab A. Phase field simulation of grain growth in porous uranium dioxide. J Nucl Mater. 2014;446(3):90–9. [Google Scholar]

36. Cahn JW. On spinodal decomposition. Acta Metall. 1961;9(9):795–801. doi:10.1016/0001-6160(61)90182-1. [Google Scholar] [CrossRef]

37. Cahn JW, Allen SM. A microscopic theory for domain wall motion and its experimental verification in Fe-Al Alloy domain growth kinetics. J Phys Colloq. 1977;38:369–72. [Google Scholar]

38. Satpathy BB, Nandy J, Sahoo S. Investigation of consolidation kinetics and microstructure evolution of Al alloys in direct metal laser sintering using phase field simulation. Mater Sci Eng. 2018;338(1):012045. [Google Scholar]

39. Fan D, Chen LQ. Diffuse-interface description of grain boundary motion. Philos Mag Lett. 1997;75(4):187–96. doi:10.1080/095008397179615. [Google Scholar] [CrossRef]

40. Kumar V, Fang ZZ, Fife PC. Phase field simulations of grain growth during sintering of two unequal-sized particles. Mater Sci Eng. 2010;528(1):254–9. doi:10.1016/j.msea.2010.08.061. [Google Scholar] [CrossRef]

41. Choudhuri D, Blake L. Particle curvature effects on microstructural evolution during solid-state sintering: phenomenological insights from phase-field simulations. J Mater Sci. 2021;56(12):7474–93. doi:10.1007/s10853-021-05802-8. [Google Scholar] [CrossRef]

42. Kang D, Xu F, Hu X, Liu W, Dong B, Xiao Y. Analysis of evolution mechanism of metal microwave sintering based on phase field model and experimental verification with synchrotron computed tomography. Exp Mech. 2016;31(3):361–8. [Google Scholar]

43. Yan W, Ma W, Shen Y. Powder sintering mechanisms during the pre-heating procedure of electron beam additive manufacturing. Mater Today Commun. 2020;25:101579. doi:10.1016/j.mtcomm.2020.101579. [Google Scholar] [CrossRef]

44. Mukherjee R, Chakrabarti T, Anumol EA, Abinandanan TA, Ravishankar N. Thermal stability of spherical nanoporous aggregates and formation of hollow structures by sintering: a phase-field study. ACS Nano. 2011;5(4):2700–6. doi:10.1021/nn103036q. [Google Scholar] [PubMed] [CrossRef]

45. Ahmed K, Allen T, El-Azab A. Phase field modeling for grain growth in porous solids. J Mater Sci. 2016;51(3):1261–77. doi:10.1007/s10853-015-9107-9. [Google Scholar] [CrossRef]

46. Du L, Yang S, Zhu X, Jiang J, Hui Q, Du H. Pore deformation and grain boundary migration during sintering in porous materials: a phase-field approach. J Mater Sci. 2018;53(13):9567–77. doi:10.1007/s10853-018-2267-7. [Google Scholar] [CrossRef]

47. Ouml H, Tzer J, Rehn V, Rheinheimer W, Hoffmann MJ, Nestler B. Phase-field study of pore-grain boundary interaction. J Ceram Soc Jpn. 2016;124(4):329–39. doi:10.2109/jcersj2.15266. [Google Scholar] [CrossRef]

48. Liu M, Zhang R, Fang W, Zhang S, Qu X. Phase field simulation of sintering in two-phase porous microstructures. Acta Metall Sinica. 2012;48(10):1207–14. doi:10.3724/SP.J.1037.2012.00353. [Google Scholar] [CrossRef]

49. Liu LL, Gao F, Li B, Hu GX. Phase-field simulation of process in sintering ceramics. Adv Mat Res. 2010;154:1674–9. [Google Scholar]

50. Rehn V, Hötzer J, Rheinheimer W, Seiz M, Serr C, Nestler B. Phase-field study of grain growth in porous polycrystals. Acta Mater. 2019;174:439–49. doi:10.1016/j.actamat.2019.05.059. [Google Scholar] [CrossRef]

51. Berry BE, Millett PC. Phase-field simulations of the impact of bimodal pore size distributions on solid-state densification. J Nucl Mater. 2017;491:48–54. doi:10.1016/j.jnucmat.2017.04.050. [Google Scholar] [CrossRef]

52. Wang YZ, Liu YH, Ciobanu C, Patton BR. Simulating microstructural evolution and electrical transport in ceramic gas sensors. J Am Ceram Soc. 2000;83:2219–26. doi:10.1111/jace.2000.83.issue-9. [Google Scholar] [CrossRef]

53. Abdeljawad F, Völker B, Davis R, McMeeking RM, Haataja M. Connecting microstructural coarsening processes to electrochemical performance in solid oxide fuel cells: an integrated modeling approach. J Power Sources. 2014;250:319–31. doi:10.1016/j.jpowsour.2013.10.121. [Google Scholar] [CrossRef]

54. Asp K, Ågren J. Phase-field simulation of sintering and related phenomena: a vacancy diffusion approach. Acta Mater. 2006;54(5):1241–8. doi:10.1016/j.actamat.2005.11.005. [Google Scholar] [CrossRef]

55. Moelans N. New phase-field model for polycrystalline systems with anisotropic grain boundary properties. Mater Des. 2022;217:110592. doi:10.1016/j.matdes.2022.110592. [Google Scholar] [CrossRef]

56. Shinagawa K, Maki S, Yokota K. Phase-field simulation of platelike grain growth during sintering of alumina. J Eur Ceram Soc. 2014;34(12):3027–36. doi:10.1016/j.jeurceramsoc.2014.04.039. [Google Scholar] [CrossRef]

57. Li H, Du Y, Long J, Ye Z, Zheng Z, Zapolsky H, et al. 3D phase field modeling of the morphology of WC grains in WC-Co alloys: the role of interface anisotropy. Comput Mater Sci. 2021;196:110526. doi:10.1016/j.commatsci.2021.110526. [Google Scholar] [CrossRef]

58. Deng J. A phase field model of sintering with direction-dependent diffusion. Mater Trans. 2012;53(2):385–9. doi:10.2320/matertrans.M2011317. [Google Scholar] [CrossRef]

59. Chockalingam K, Kouznetsova VG, van der Sluis O, Geers MGD. 2D phase field modeling of sintering of silver nanoparticles. Comput Methods Appl Mech Eng. 2016;312:492–508. doi:10.1016/j.cma.2016.07.002. [Google Scholar] [CrossRef]

60. Asoro MA, Ferreira PJ, Kovar, D. In situ transmission electron microscopy and scanning transmission electron microscopy studies of sintering of Ag and Pt nanoparticles. Acta Mater. 2014;81: 173–83. doi:10.1016/j.actamat.2014.08.028. [Google Scholar] [CrossRef]

61. Guo Y, Liu Z, Huang Q, Lin CT, Du S. Abnormal grain growth of UO2 with pores in the final stage of sintering: a phase field study. Comput Mater Sci. 2018;145:24–34. doi:10.1016/j.commatsci.2017.12.057. [Google Scholar] [CrossRef]

62. Wei CY, Li SY. Microstructure evolution in sintering of alumina-zirconia ceramics simulated by a modified phase field method. Mater Sci Forum. 2012;715:788–93. [Google Scholar]

63. Ahmed K, Yablinsky CA, Schulte A, Allen T, El-Azab A. Phase field modeling of the effect of porosity on grain growth kinetics in polycrystalline ceramics. Model Simul Mat Sci Eng. 2013;21(6):065005. doi:10.1088/0965-0393/21/6/065005. [Google Scholar] [CrossRef]

64. Sun ZY, Wang YT, Liu WB. Phase-field simulation of the interaction between pore and grain boundary. Acta Metall Sinica. 2020;56(12):1643–53. [Google Scholar]

65. Sun Z, Yang C, Liu W. Phase field simulation of UO2 sintering process. Acta Metall Sin. 2020;56(9):1295–303. [Google Scholar]

66. He L, Zhao J, Jing X, Ni Y. Two-dimensional phase field simulation of porosity evolution in ceramic sintering process. J Inorg Mater. 2002;8(5):1078–82. [Google Scholar]

67. Kazaryan A, Wang Y, Patton BR. Generalized phase field approach for computer simulation of sintering: incorporation of rigid-body motion. Scr Mater. 1999;41(5):487–92. doi:10.1016/S1359-6462(99)00179-7. [Google Scholar] [CrossRef]

68. Wang YU. Computer modeling and simulation of solid-state sintering: a phase field approach. Acta Mater. 2006;54(4):953–61. doi:10.1016/j.actamat.2005.10.032. [Google Scholar] [CrossRef]

69. Biswas S, Schwen D, Tomar V. Implementation of a phase field model for simulating evolution of two powder particles representing microstructural changes during sintering. J Mater Sci. 2018;53(8):5799–5825. doi:10.1007/s10853-017-1846-3. [Google Scholar] [CrossRef]

70. Seiz M. Effect of rigid body motion in phase-field models of solid-state sintering. Comput Mater Sci. 2022;215:111756. doi:10.1016/j.commatsci.2022.111756. [Google Scholar] [CrossRef]

71. Shi R, Wood M, Heo TW, Wood BC, Ye J. Towards understanding particle rigid-body motion during solid-state sintering. J Eur Ceram Soc. 2021;41(16):211–31. doi:10.1016/j.jeurceramsoc.2021.09.039. [Google Scholar] [CrossRef]

72. Zhu H, Averback RS. Molecular dynamics simulations of densification processes in nanocrystalline materials. Mater Sci Eng A. 1995;204(1):96–100. [Google Scholar]

73. Mori K. Finite element simulation of powder forming and sintering. Comput Methods Appl Mech Eng. 2006;195(48):6737–49. [Google Scholar]

74. Peter M, Vladimir I, Christian C, Martin K. On the construction of an efficient finite-element solver for phase-field simulations of many-particle solid-state-sintering processes. Comput Mater Sci. 2024;231:112589. doi:10.1016/j.commatsci.2023.112589. [Google Scholar] [CrossRef]

75. Termuhlen R, Chatzistavrou X, Nicholas JD, Yu HC. Three-dimensional phase field sintering simulations accounting for the rigid-body motion of individual grains. Comput Mater Sci. 2021;186:109963. doi:10.1016/j.commatsci.2020.109963. [Google Scholar] [CrossRef]

76. Hierl H, Hötzer J, Seiz M, Reiter A, Nestler B. Extreme scale phase-field simulation of sintering processes. In: 2019 IEEE/ACM 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA), Denver, CO, USA; 2019; p. 25–32. [Google Scholar]

77. Miyoshi E, Takaki T, Ohno M, Shibuta Y, Sakane S, Shimokawabe T, et al. Ultra-large-scale phase-field simulation study of ideal grain growth. npj Comput Mater. 2017;3(1):25. doi:10.1038/s41524-017-0029-8. [Google Scholar] [CrossRef]

78. Shinagawa K. Simulation of grain growth and sintering process by combined phase-field/discrete-element method. Acta Mater. 2014;66:360–9. doi:10.1016/j.actamat.2013.11.023. [Google Scholar] [CrossRef]

79. Ivannikov V, Thomsen F, Ebel T, Willumeit-Römer R. Capturing shrinkage and neck growth with phase field simulations of the solid state sintering. Model Simul Mat Sci Eng. 2021;29(7):075008. doi:10.1088/1361-651X/ac1f87. [Google Scholar] [CrossRef]

80. Biswas S, Schwen D, Singh J, Tomar V. A study of the evolution of microstructure and consolidation kinetics during sintering using a phase field modeling based approach. Extreme Mech Lett. 2016;7:78–89. doi:10.1016/j.eml.2016.02.017. [Google Scholar] [CrossRef]

81. Jiang Y, Liu W, Sun Z, La Y, Yun D. Phase field simulation of hollow cavity evolution in UO2 under external stress. Acta Phys Sin. 2022;71(2):233–43. [Google Scholar]

82. Jing XN, Zhao JH, Subhash G, Gao XL. Anisotropic grain growth with pore drag under applied loads. Mater Sci Eng. 2005;412(2):271–8. [Google Scholar]

83. Dzepina B, Balint D, Dini D. A phase field model of pressure-assisted sintering. J Eur Ceram Soc. 2019;39(2–3):173–82. [Google Scholar]

84. Yang Q, Kirshtein A, Ji Y, Liu C, Shen J, Chen LQ. A thermodynamically consistent phase-field model for viscous sintering. J Am Ceram Soc. 2019;102(2):674–85. doi:10.1111/jace.2019.102.issue-2. [Google Scholar] [CrossRef]

85. Krivilyov MD, Mesarovic SD, Sekulic DP. Phase-field model of interface migration and powder consolidation in additive manufacturing of metals. J Mater Sci. 2017;52(8):4155–63. doi:10.1007/s10853-016-0311-z. [Google Scholar] [CrossRef]

86. Zhang Z, Yao XX, Ge P. Phase-field-model-based analysis of the effects of powder particle on porosities and densities in selective laser sintering additive manufacturing. Int J Mech Sci. 2020;166:105230. doi:10.1016/j.ijmecsci.2019.105230. [Google Scholar] [CrossRef]

87. Zhang L, Tonks MR, Millett PC, Zhang Y, Chockalingam K, Biner B. Phase-field modeling of temperature gradient driven pore migration coupling with thermal conduction. Comput Mater Sci. 2012;56:161–5. doi:10.1016/j.commatsci.2012.01.002. [Google Scholar] [CrossRef]

88. Zhang X, Liao Y. Microstructure evolution during solid-state selective laser sintering of metallic materials: a phase-field simulation. In: Int. Manufacturing Sci. and Eng. Conf., Erie, Pennsylvania, USA; 2019; p. 109–15. [Google Scholar]

89. Zhang X, Liao Y. A phase-field model for solid-state selective laser sintering of metallic materials. Powder Technol. 2018;339:677–85. doi:10.1016/j.powtec.2018.08.025. [Google Scholar] [CrossRef]

90. Rizza G, Galati M, Iuliano L. A phase-field study of neck growth in electron beam powder bed fusion (EB-PBF) process of Ti6Al4V powders under different processing conditions. Int J Adv Manuf Technol. 2022;123(3):855–73. [Google Scholar]

91. Nandy J, Sarangi H, Sahoo S. Microstructure evolution of AlSi10Mg in direct metal laser sintering using phase-field modeling. Adv Manuf. 2018;6(1):107–17. doi:10.1007/s40436-018-0213-1. [Google Scholar] [CrossRef]

92. Jiang H, Liang S, Wei C, Ke C. Phase field modelling of the electromigration behaviour in sintered silver. J Mater Res. 2022;37(14):2322–34. doi:10.1557/s43578-022-00635-w. [Google Scholar] [CrossRef]

93. Park MS, Gibbons SL, Arròyave R. Phase-field simulations of intermetallic compound evolution in Cu/Sn solder joints under electromigration. Acta Mater. 2013;61(19):7142–54. doi:10.1016/j.actamat.2013.08.016. [Google Scholar] [CrossRef]

94. Zhang RJ, Chen ZW, Fang W, Qu XH. Thermodynamic consistent phase field model for sintering process with multiphase powders. T Nonferr Metal Soc. 2014;24(3):783–9. doi:10.1016/S1003-6326(14)63126-5. [Google Scholar] [CrossRef]

95. Ravash H, Vanherpe L, Vleugels J, Moelans N. Three-dimensional phase-field study of grain coarsening and grain shape accommodation in the final stage of liquid-phase sintering. J Eur Ceram Soc. 2017;37(5):2265–75. doi:10.1016/j.jeurceramsoc.2017.01.001. [Google Scholar] [CrossRef]

96. Davis R, Haataja M. Microstructural stability of supported metal catalysts: a phase field approach. J Power Sources. 2017;369:111–21. doi:10.1016/j.jpowsour.2017.09.066. [Google Scholar] [CrossRef]

97. Cheng K, Zhang L, Schwarze C, Steinbach I, Du Y. Phase-field simulation of liquid phase migration in the WC-Co system during liquid phase sintering. International J Mater Res. 2016;107(4):309–14. doi:10.3139/146.111353. [Google Scholar] [CrossRef]

98. Zhou Y, Peng B. Phase field simulation of grain growth in Al2O3-based composite ceramic cutting tool materials containing second phase nanoparticles and pores. Mater Res Express. 2020;7(11):115202. doi:10.1088/2053-1591/abcb7d. [Google Scholar] [CrossRef]

99. Yu Y, Lin F, Zheng Y, Yu W, Liu X, Yuan Y, et al. High-density nanoprecipitation mechanism and microstructure evolution of high-performance Al2O3/ZrO2 nanocomposite ceramics. J Eur Ceram Soc. 2021;41(10):5269–79. doi:10.1016/j.jeurceramsoc.2021.04.034. [Google Scholar] [CrossRef]

100. Liu L, Gao F, Hu G, Liu J. Phase field study on grain growth and pore structure evolution in late-stage sintering of ceramics. J Northwest. 2012;30(2):234–8. [Google Scholar]

101. Villanueva W, Grönhagen K, Amberg G, Ågren J. Multicomponent and multiphase simulation of liquid-phase sintering. Comput Mater Sci. 2009;47(2):512–20. doi:10.1016/j.commatsci.2009.09.018. [Google Scholar] [CrossRef]

102. Yan Z, Zhang X, Tan S, Zhao Z. Numerical investigation on nonisothermal solid diffusion without phase transition using a full coupling theory combine with phase field method. Numer Heat Tr A-Appl. 2018;74(2):1018–31. doi:10.1080/10407782.2018.1469885. [Google Scholar] [CrossRef]

103. Tan S, Zhang X, Zhao Z, Wu Z. Driving force evolution in solid-state sintering with coupling multiphysical fields. Ceram Int. 2020;46(8):11584–11592. doi:10.1016/j.ceramint.2020.01.187. [Google Scholar] [CrossRef]

104. Tan S, Zhang X, Zhao Z, Wu Z, Zhang H. System simulation of multi-physical field coupling in electric current-assisted sintering. Powder Metall Tech. 2020;38(6):414–22. [Google Scholar]

105. Liu Y, Wang G, Zeng D. Prediction of pore evolution during selected laser melting solidification by a finite element-phase field model. Model Simul Mat Sci Eng. 2020;28(6):065004. doi:10.1088/1361-651X/ab9733. [Google Scholar] [CrossRef]

106. Plapp M. Unified derivation of phase-field models for alloy solidification from a grand-potential functional. Phys Rev E. 2011;84:031601. doi:10.1103/PhysRevE.84.031601. [Google Scholar] [CrossRef]

107. Choudhury A, Nestler B. Grand-potential formulation for multicomponent phase transformations combined with thin-interface asymptotics of the double-obstacle potential. Phys Rev E. 2012;85(2):021602. doi:10.1103/PhysRevE.85.021602. [Google Scholar] [CrossRef]

108. Greenquist I, Tonks M, Cooper M, Andersson D, Zhang Y. Grand potential sintering simulations of doped UO2 accident-tolerant fuel concepts. J Nucl Mater. 2020;532:152052. doi:10.1016/j.jnucmat.2020.152052. [Google Scholar] [CrossRef]

109. Kubendran Amos PG, Nestler B. Grand-potential based phase-field model for systems with interstitial sites. Sci Rep. 2020;10(1):22423. doi:10.1038/s41598-020-79956-x. [Google Scholar] [PubMed] [CrossRef]

110. Hötzer J, Seiz M, Kellner M, Rheinheimer W, Nestler B. Phase-field simulation of solid state sintering. Acta Mater. 2019;164:184–95. doi:10.1016/j.actamat.2018.10.021. [Google Scholar] [CrossRef]

111. Greenquist I, Tonks MR, Aagesen LK, Zhang Y. Development of a microstructural grand potential-based sintering model. Comput Mater Sci. 2020;172:109288. doi:10.1016/j.commatsci.2019.109288. [Google Scholar] [CrossRef]

112. Aagesen LK, Gao Y, Schwen D, Ahmed K. Grand-potential-based phase-field model for multiple phases, grains, and chemical components. Phys Rev E. 2018;98(2):023309. doi:10.1103/PhysRevE.98.023309. [Google Scholar] [PubMed] [CrossRef]

113. Azizi H, Provatas N, Mohammadi M. Phase-field simulation of microstructure evolution in direct metal laser sintered AlSi10Mg. In: TMS 2019 148th Annual Meeting & Exhibition Supplemental Proceedings, 2019; Switzerland: Springer International Publishing AG; p. 311–8. [Google Scholar]

114. Penrose O, Fife PC. Thermodynamically consistent models of phase-field type for the kinetic of phase transitions. Physica D. 1990;43(1):44–62. doi:10.1016/0167-2789(90)90015-H. [Google Scholar] [CrossRef]

115. Yang Y, Oyedeji TD, Kühn P, Xu BX. Investigation on temperature-gradient-driven effects in unconventional sintering via non-isothermal phase-field simulation. Scr Mater. 2020;186:152–7. doi:10.1016/j.scriptamat.2020.05.016. [Google Scholar] [CrossRef]

116. Young RM, McPherson R. Temperature-gradient-driven diffusion in rapid-rate sintering. J Am Ceram Soc. 1989;72(6):1080–1. doi:10.1111/jace.1989.72.issue-6. [Google Scholar] [CrossRef]

117. Olevsky EA, Froyen L. Impact of thermal diffusion on densification during SPS. J Am Ceram Soc. 2009;92(1):122–32. [Google Scholar]

118. Johnson DL. Comment on ‘temperature-gradient-driven diffusion in rapid-rate sintering’. J Am Ceram Soc. 1990;73(8):2576–8. doi:10.1111/jace.1990.73.issue-8. [Google Scholar] [CrossRef]

119. Biesuz M, Sglavo VM. Microstructural temperature gradient-driven diffusion: possible densification mechanism for flash sintering of zirconia? Ceram Int. 2019;45(1):1227–36. doi:10.1016/j.ceramint.2018.09.311. [Google Scholar] [CrossRef]

120. Liang C, Yin Y, Wang W, Yi M. A thermodynamically consistent non-isothermal phase-field model for selective laser sintering. Int J Mech Sci. 2023;259:108602. doi:10.1016/j.ijmecsci.2023.108602. [Google Scholar] [CrossRef]

121. Yang Y, Yi M, Xu B. Non-isothermal phase field simulation of microstructure in powder additive manufacturing. J Cent South Univ. 2020;51(11):3019–31. [Google Scholar]

122. Yang Y, Kühn P, Yi M, Egger H, Xu BX. Non-isothermal phase-field modeling of heat-melt-microstructure-coupled processes during powder bed fusion. JOM. 2020;72(4):1719–33. doi:10.1007/s11837-019-03982-y. [Google Scholar] [CrossRef]

123. Wang X, Liu Y, Li L, Yenusah CO, Xiao Y, Chen L. Multi-scale phase-field modeling of layer-by-layer powder compact densification during solid-state direct metal laser sintering. Mater Des. 2021;203:109615. doi:10.1016/j.matdes.2021.109615. [Google Scholar] [CrossRef]

124. Li JQ, Fan TH, Taniguchi T, Zhang B. Phase-field modeling on laser melting of a metallic powder. Int J Heat Mass Transf. 2018;117:412–24. doi:10.1016/j.ijheatmasstransfer.2017.10.001. [Google Scholar] [CrossRef]

125. Wang FC, Chen WP, Wang D, Hou H, Zhao YH. Phase-field modeling and experimental investigation for rapid solidification in wire and arc additive manufacturing. J Mater Res and Technology. 2024;28:4585–99. doi:10.1016/j.jmrt.2024.01.021. [Google Scholar] [CrossRef]

126. Baharin A, Yousef H, Bernd M. Predicting residual stresses in SLM additive manufacturing using a phase-field thermomechanical modeling framework. Comput Mater Sci. 2024;231:112576. doi:10.1016/j.commatsci.2023.112576. [Google Scholar] [CrossRef]

127. Li Y, Song YJ, Yang ZW, Jiang HJ, Liu BW. Temperature field in laser line scanning thermography: analytical calculation and experiment. Comput Model Eng Sci. 2023;137(1):1001–18. doi: 10.32604/cmes.2023.027072. [Google Scholar] [CrossRef]

128. Damien T, Hong L, Javier L. Phase-field modeling of microstructure evolution: recent applications, perspectives and challenges. Prog Mater Sci. 2022;123:100810. doi:10.1016/j.pmatsci.2021.100810. [Google Scholar] [CrossRef]

129. Flint TF, Panwisawas C, Sovani Y, Smith MC, Basoalto HC. Prediction of grain structure evolution during rapid solidification of high energy density beam induced re-melting. Mater Des. 2018;147:200–10. doi:10.1016/j.matdes.2018.03.036. [Google Scholar] [CrossRef]

130. Liu PW, Ji YZ, Wang Z, Qiu CL, Antonysamy AA, Chen LQ, et al. Investigation on evolution mechanisms of site-specific grain structures during metal additive manufacturing. J Mater Process Technol. 2018;257:191–202. doi:10.1016/j.jmatprotec.2018.02.042. [Google Scholar] [CrossRef]

131. Yang Y, Ragnvaldsen O, Bai Y, Yi M, Xu BX. 3D non-isothermal phase-field simulation of microstructure evolution during selective laser sintering. npj Comput Mater. 2019;5(1):81. doi:10.1038/s41524-019-0219-7. [Google Scholar] [CrossRef]

132. Lu LX, Sridhar N, Zhang YW. Phase field simulation of powder bed-based additive manufacturing. Acta Mater. 2018;144:801–9. doi:10.1016/j.actamat.2017.11.033. [Google Scholar] [CrossRef]

133. Zhou X, Yang Y, Bharech S, Lin B, Schroder J, Xu BX. 3D-multilayer simulation of microstructure and mechanical properties of porous materials by selective sintering. GAMM Mitteilungen. 2021;44(4):e202100017. doi:10.1002/gamm.v44.4. [Google Scholar] [CrossRef]

134. Sergiy R, Zhang YH, Lu J, Ciren P. A novel method for linear systems of fractional ordinary differential equations with applications to time-fractional PDEs. Comput Model Eng Sci. 2024;139(2):1583–1612. doi: 10.32604/cmes.2023.044878. [Google Scholar] [CrossRef]

135. Yuming C, Saima R, Khadija TK, Mustafa I, Zakia H, M.S. O. Analysis and numerical computations of the multi-dimensional, time-fractional model of Navier-stokes equation with a new integral transformation. Comput Model Eng Sci. 2023;136(3):3025–60. doi: 10.32604/cmes.2023.025470. [Google Scholar] [CrossRef]

136. Kaihua J, Amirhossein MT, Alain K. Isotropic finite-difference approximations for phase-field simulations of polycrystalline alloy solidification. J Comput Phys. 2022;457:111069. doi:10.1016/j.jcp.2022.111069. [Google Scholar] [CrossRef]

137. Yang J, Wang J, Tan Z. A simple and practical finite difference method for the phase-field crystal model with a strong nonlinear vacancy potential on 3D surfaces. Comput Math Appl. 2022;121:131–44. doi:10.1016/j.camwa.2022.07.012. [Google Scholar] [CrossRef]

138. Biner SB. Solving phase-field models with finite difference algorithms. In: Programming phase-field modeling. Cham: Springer International Publishing; 2017. p. 17–97. [Google Scholar]

139. Cao H, Sun Z. Two finite difference schemes for the phase field crystal equation. Sci China Math. 2015;58(11):2435–54. doi:10.1007/s11425-015-5025-1. [Google Scholar] [CrossRef]

140. Zhou SW, Rabczuk T, Zhuang XY. Phase field modeling of quasi-static and dynamic crack propagation: COMSOL implementation and case studies. Adv Eng Softw. 2018;122:31–49. doi:10.1016/j.advengsoft.2018.03.012. [Google Scholar] [CrossRef]

141. Hanen A, Jean-Jacques M, Corrado M. Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J Mech Phys Solids. 2009;57(8):1209–29. doi:10.1016/j.jmps.2009.04.011. [Google Scholar] [CrossRef]

142. Han F, Li ZB, Zhang JY, Liu ZY, Yao C, Han WP. ABAQUS and ANSYS implementations of the peridynamics-based finite element method (PeriFEM) for brittle fractures. Comput Model Eng Sci. 2023;136(3):2715–40. doi: 10.32604/cmes.2023.026922. [Google Scholar] [CrossRef]

143. Santillán D, Juanes R, Cueto-Felgueroso L. Phase field model of fluid-driven fracture in elastic media: immersed-fracture formulation and validation with analytical solutions. J Geophys Res Solid Earth. 2017;122(4):2565–89. doi:10.1002/jgrb.v122.4. [Google Scholar] [CrossRef]

144. Linchuan L, Jian W, Zhongwei H, Xiaochao J, Pin L, Tao Z, et al. Thermal analysis of turbine blades with thermal barrier coatings using virtual wall thickness method. Comput Model Eng Sci. 2023;134(2):1219–36. doi:10.32604/cmes.2022.022221. [Google Scholar] [CrossRef]

145. Freddi F, Mingazzi L. Adaptive mesh refinement for the phase field method: a FEniCS implementation. Appl Eng Sci. 2023;14:100127. [Google Scholar]

146. Abhinav GU, Meenu K, Tushar KM, Rajib C, Vinh PN. An adaptive mesh refinement algorithm for phase-field fracture models: application to brittle, cohesive, and dynamic fracture. Comput Methods Appl Mech Eng. 2022;399:115347. doi:/10.1016/j.cma.2022.115347. [Google Scholar] [CrossRef]

147. Weixin M, Yongxing S. A phase field model for the solid-state sintering with parametric proper generalized decomposition. Powder Technol. 2023;419:118345. doi:10.1016/j.powtec.2023.118345. [Google Scholar] [CrossRef]

148. Yoon S, Jeong D, Lee C, Kim H, Kim S, Lee HG, et al. Fourier-spectral method for the phase-field equations. Mathematics. 2020;8(8):1385. doi:10.3390/math8081385. [Google Scholar] [CrossRef]

149. Chen LQ, Shen J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput Phys Commun. 1998;108(2):147–58. [Google Scholar]

150. Dilshod D, Frank W. An effective Fourier spectral phase-field approach for ferroelectric materials. Comput Mater Sci. 2023;218:111928. doi:10.1016/j.commatsci.2022.111928. [Google Scholar] [CrossRef]