Energy-Saving Distributed Flexible Job Shop Scheduling Optimization with Dual Resource Constraints Based on Integrated Q-Learning Multi-Objective Grey Wolf Optimizer

1  Introduction

With the continuous development of the manufacturing industry, the flexible job shop scheduling problem (FJSP) has become one of the core problems in production scheduling. The increasing diversification of market demands and the shortening of product life cycles have prompted manufacturing enterprises to gradually shift from the traditional single-factory production pattern to the multi-factory collaborative production pattern. Under this pattern, optimizing the processing sequence of multiple jobs on multiple machines has become an important challenge for the manufacturing industry. To meet this challenge, the manufacturing industry has begun seeking more efficient and flexible scheduling schemes. The distributed flexible job shop scheduling problem (DFJSP) has thus become the focus of manufacturing industry and academia. Although many scholars have studied DFJSP, most of the previous research focused on machine constraints within the factories, with relatively little attention paid to worker constraints.

In actual production, the collaborative work of workers and machines is crucial to improving production efficiency. By considering the skills of workers and the characteristics of machines, resources can be allocated more rationally to avoid waste of resources [1]. Meanwhile, with the growing environmental issues, manufacturing enterprises have begun to pay attention to energy-saving manufacturing. As a specific measure of energy-saving manufacturing, energy-saving scheduling can minimize resource waste [2,3].

Therefore, the DFJSP with dual resource constraints (DFJSP-DRC) is investigated in this paper, with the objectives of minimizing makespan and total energy consumption. By considering the skills of workers and the characteristics of machines comprehensively, we construct a mathematical model of DFJSP-DRC, which enriches the existing DFJSP model and provides references for subsequent DFJSP research. Through considering the synergistic effect of worker and machine resources in actual production, this model not only enhances the practicality and applicability of scheduling theory but also provides new perspectives and tools to solve complex production scheduling problems.

It is difficult to get exact solutions using traditional mathematical methods. To obtain high-quality solutions, a novel and effective Q-learning-based multi-objective grey wolf optimizer (Q-MOGWO) is designed, which adds a local search strategy to multi-objective grey wolf optimizer (MOGWO) and uses a Q-learning strategy to dynamically adjust the local search strategy according to the population state. The main contributions of this paper are as follows:

(1) DFJSP-DRC is studied, and a multi-objective mathematical model aiming at minimizing the makespan and total energy consumption is established.

(2) A hybrid population initialization strategy is introduced to enhance the quality and diversity of the initial population, and an improved active decoding strategy that fully utilizes the public idle time of machines and workers is designed to transform solutions into efficient scheduling schemes.

(3) Two improved wolf predation strategies and a local search strategy based on Q-learning are proposed to extend the search space of solutions.

The rest of this paper is organized as follows: Section 2 describes the related works. Section 3 illustrates the multi-objective mathematical model of DFJSP-DRC. Section 4 details the proposed Q-MOGWO. Experiments in Section 5 evaluate the performance of Q-MOGWO. Section 6 provides the conclusions and future works.

2  Related Works

2.1 Distributed Flexible Job Shop Scheduling Problem

Some scholars have studied DFJSP with the objective of minimizing makespan [4–7]. Meanwhile, increasingly scholars pay attention to environmental issues, and DFJSP considering energy consumption is studied. Luo et al. [8] developed a mathematical framework for optimizing makespan, maximum workload, and total energy consumption of DFJSP. Du et al. [9] used a hybrid heuristic algorithm to optimize the makespan and total energy consumption for DFJSP considering crane transportation. Xu et al. [10] considered DFJSP, which requires operation outsourcing for some jobs, and established a mathematical model with four optimization objectives. Li et al. [11] proposed a two-stage knowledge-driven evolutionary algorithm to solve a multi-objective DFJSP with type-2 fuzzy processing time. The above studies can guide enterprises to realize energy-saving scheduling, but they only focus on machine resources and ignore worker resources. The role of workers is indispensable in the multi-variety and small-lot production model. Rational arrangement of workers can increase work efficiency and reduce costs [12].

To better simulate the real production scenario, both machines and workers should be considered in FJSP, which is referred to as the dual resource constrains flexible job shop scheduling problem (DRCFJSP). To solve the problem, Gong et al. [12] proposed a hybrid artificial bee colony algorithm with a specific local search strategy to expand the search space. Tan et al. [13] considered worker fatigue in DRCFJSP and proposed a multi-objective optimization model. Zhao et al. [14] proposed a hybrid discrete multi-objective imperial competition algorithm to solve DRCFJSP considering job transportation time and worker learning effects. Shi et al. [15] studied DRCFJSP, where employees are boredom-aware in allocating resources and scheduling tasks, and built a two-layer dictionary model to solve the problem. Luo et al. [16] used an improved mayfly algorithm based on the non-dominated sorting genetic algorithm-II (NSGA-II) structure to solve the DFJSP considering worker arrangements. Although the above literature considers both machine and worker resources in FJSP [17,18], few studies consider these resources in DFJSP. At the same time, the main optimization objective of the above literature research is makespan, and the objective of energy consumption is rarely considered.

2.2 Optimization Algorithms for DFJSP

The intelligent optimization algorithm is an effective method to solve different types of FJSP. Lin et al. [19] used a genetic algorithm with incomplete chromosome representation and shaded chromosomes to solve DFJSP. Li et al. [20] proposed an improved grey wolf optimizer for DFJSP. Xie et al. [21] proposed a hybrid genetic tabu search algorithm to address DFJSP. Li et al. [22] used an adaptive memetic algorithm to solve energy-saving DFJSP. Zhu et al. [23] applied a reformative memetic algorithm to address DFJSP considering order cancellations. Although various intelligent optimization algorithms have been employed to tackle scheduling problems, there are prevalent limitations, such as a lack of local search capability, the inability to ensure global optimal solutions, and difficulties in parameter adjustment.

Integrating reinforcement learning (RL) with intelligent optimization algorithms can effectively guide the intelligent optimization algorithms' search process, improve solution quality and accelerate convergence [24]. Several studies have combined RL and intelligent algorithms to solve scheduling problems. Cao et al. [25] suggested integrating a cuckoo search algorithm with RL modeling to address the scheduling problem in semiconductor terminal testing. Chen et al. [26] introduced a self-learning genetic algorithm for FJSP, incorporating state-action-reward-state-action (SARSA) and Q-learning as adaptive learning methods for intelligent adjustment of critical parameters. Cao et al. [27] introduced a cuckoo search algorithm based on the SARSA to solve the FJSP. Li et al. [28] used an RL-based multi-objective evolution algorithm based on decomposition (MOEA/D) to solve multi-objective FJSP with fuzzy processing time. Li et al. [29] proposed a Q-learning artificial bee colony algorithm with heuristic initialization rules, which uses Q-learning to prefer high-quality neighborhood structures.

The above literature proves that the combination of RL and intelligent optimization algorithms can help intelligent algorithms to find better solutions and accelerate convergence speed when solving various job shop scheduling problems. As a new intelligent optimization algorithm, MOGWO has been used to solve a variety of scheduling problems [30,31]. In addition, MOGWO has the advantages of fewer parameters, global search and strong adaptability, but it also lacks the ability of adaptive adjustment and local search. By combining the adaptive learning ability of Q-learning, MOGWO can dynamically adjust the search strategy, which can help MOGWO find a better solution in the complex search space. Therefore, the Q-MOGWO is designed to address the DFJSP-DRC in this study.

3  Description and Mathematical Modeling of DFJSP-DRC

3.1 Problem Definition

There are n jobs processed in p factories, and each factory is considered a flexible manufacturing unit. Job Ji contains ni operations. Every factory has m machines and w workers and jobs have processing sequence constraints. Workers have different skill levels and can operate different machines. The same machine is operated by different workers to process the same job will produce different processing times. Therefore, the DFJSP-DRC comprises four coupled subproblems: operation sequence, factory selection, machine selection and worker selection. To clarify the proposed problem, the following assumptions are considered: (1) All factories, machines, workers and jobs are available at 0 moment. (2) There are sequential constraints between different operations for one job. (3) Each job can be processed in multiple factories but only assigned to one factory for processing. (4) Each worker can operate multiple machines, and each machine can process multiple jobs. (5) There is no preemptive operation. (6) The machine breakdown and transportation time of jobs are not considered.

To explain DFJSP-DRC, Fig. 1 depicts a Gantt chart for an instance involving 4 jobs, 4 machines, 1 factory and 3 workers. Information for jobs processing is given in Table 1, in which ‘1/3’ indicates that the processing machine is M1, processing time is 3, and ‘-’ indicates that this worker cannot process this operation.

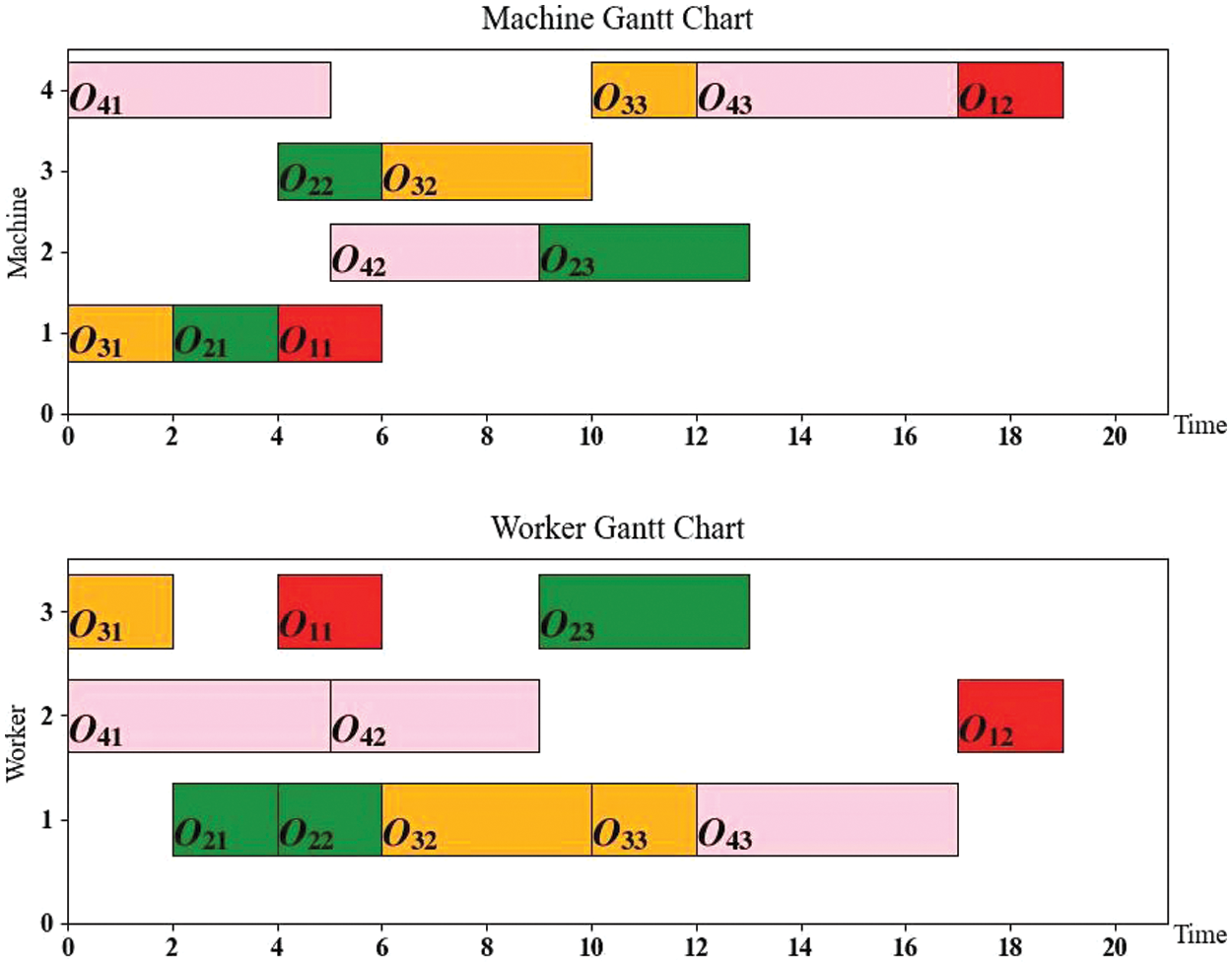
Figure 1: A Gantt chart of an instance

3.2 Mathematical Model of DFJSP-DRC

Based on the problem definition and assumptions in Section 3.1, the sets and indices, decision variables and parameters used in the mathematical model of DFJSP-DRC are as follows:

Sets and indices

i: Index of job

j: Index of operation

k: Index of machine

f: Index of factory

s: Index of worker

Mij: The set of available machines to operate Oij

Wijk: The set of available workers who can operate machine k for operation Oij

Fj: The set of available factories to operate Ji

Parameters

Ji: The i-th job

Mk: The k-th machine

Ws: The s-th worker

ni: Total number of operations for Ji

Oij: The j-th operation of Ji

Tijks: The processing time of Oij processed by worker s on machine k

STij: Start processing time of Oij

ETij: End processing time of Oij

Tijksf: The processing time of Oij processed by worker s on machine k in factory f

STijf: Starting processing time of Oij in factory f

ETijf: End processing time of Oij in factory f

cijks: Completion time of Oij on machine k by worker s

Ci: Completion time of Ji

Cmax: Makespan

Mek: Process energy consumption per unit time for machine k

Rek: Idle energy consumption per unit time for machine k

PE: Total processing energy consumption

IE: Total idle energy consumption

TEC: Total energy consumption

ε: A sufficiently sizeable positive number

Decision variables

Wif: 0-1 decision variables, take value 1 when Ji is processed in factory f; otherwise, the value is 0.

Xijksf: 0-1 decision variables, take value 1 when Oij is processed in factory f by worker s operating machine k; otherwise, the value is 0.

Yi'j'ijkf: 0-1 decision variables, take value 1 when Oij and Oi'j' are processed by machine k in factory f, Oi'j' is processed immediately before Oij; otherwise, the value is 0.

Zi'j'ijsf: 0-1 decision variables, take a value of 1 to indicate that Oij and Oi'j' are processed by worker s in factory f, Oi'j' is processed immediately before Oij; otherwise, the value is 0.

Combining the symbol description and problem definition, the mathematical model of DFJSP-DRC is developed:

f1=min(max(Ci))(1)

f2=min(TE)(2)

∑f=1pWif=1(3)

∑f=1p∑k=1m∑s=1wXijksf=1(4)

Ci≥cijks(5)

ETijkf−STijkf=∑k=1m∑s=1wXijksf⋅Tijksf(6)

STi(j+1)kf≥ETijk ′f(7)

STijf+ε(1−Yi ′j ′ijkf)≥ETi ′j ′f(8)

STijf+ε(1−Zi ′j ′ijsf)≥ETi ′j ′f(9)

STijf≥0(10)

ETijf≥0(11)

PE=∑f=1p∑i=1n∑j=1vi∑k=1m∑s=1wXijksf⋅Tijksf⋅Mek(12)

IE=∑f=1p∑i=1n∑j=1vi∑k=1m∑s=1wXijksf⋅(STijkf−ETi ′j ′kf)⋅Rek(13)

TEC=PE+IE(14)

where Eqs. (1) and (2) are the objectives of minimizing makespan and total energy consumption, respectively. Eq. (3) indicates that the job cannot be processed across factories. Eq. (4) indicates that only one worker operates one machine for each operation. Eq. (5) is the completion time of Ji. Eq. (6) indicates that the processing of each job cannot be interrupted. Eq. (7) denotes the presence of sequence constraints on the operations of the same job. Eq. (8) denotes that the same machine can only process a job at any moment. Eq. (9) indicates that the same worker can only process a job at any moment. Eq. (10) shows that machines and workers can start processing at 0 moment. Eq. (11) denotes that the start time and completion time of any operation are greater than or equal to 0. Eqs. (12)–(14) indicate the total processing energy consumption, total idle energy consumption and total energy consumption, respectively.

4  Q-MOGWO for DFJSP-DRC

4.1 The Canonical MOGWO

In the grey wolf optimizer (GWO), the grey wolf population is composed of four species based on social leadership mechanisms: α wolf, β wolf, δ wolf and ω wolves. In which α, β and δ are the first, second and third head wolves, and the rest of the wolves are ω. The ω wolves obey these head wolves. Hunting in the optimization process is directed by α, β and δ, ω follows head wolves in the pursuit of an optimal solution. The positions of α, β and δ are recorded after each iteration, and ω is guided to update its position accordingly.

MOGWO is built on GWO by adding two components. The first component is an archive that stores non-dominated Pareto optimal solutions acquired thus far. The second component is a leader selection strategy employed to aid in selecting α, β and δ as the leaders within the hunting process from the archive. The conventional MOGWO can be referred to in the literature [32].

4.2 Framework of the Proposed Q-MOGWO

The pseudo-code of Q-MOGWO is described in Algorithm 1. The main steps of Q-MOGWO include four-layer encoding, active decoding based on public idle time, hybrid initialization strategy, wolf pack search strategy and neighborhood structure based on Q-learning. The iteration of Q-MOGWO is as follows. Firstly, the initial population is generated by a hybrid initialization strategy and the head wolves are selected in the population. Secondly, the head wolves lead the evolution of the population, and the evolved population and the initial population are merged by the elite strategy to obtain the external archive and the new generation of population. Finally, the local search strategy based on Q-learning is applied to the external archive, and the external archive is updated by the elite strategy.

4.3 Four-Layer Encoding

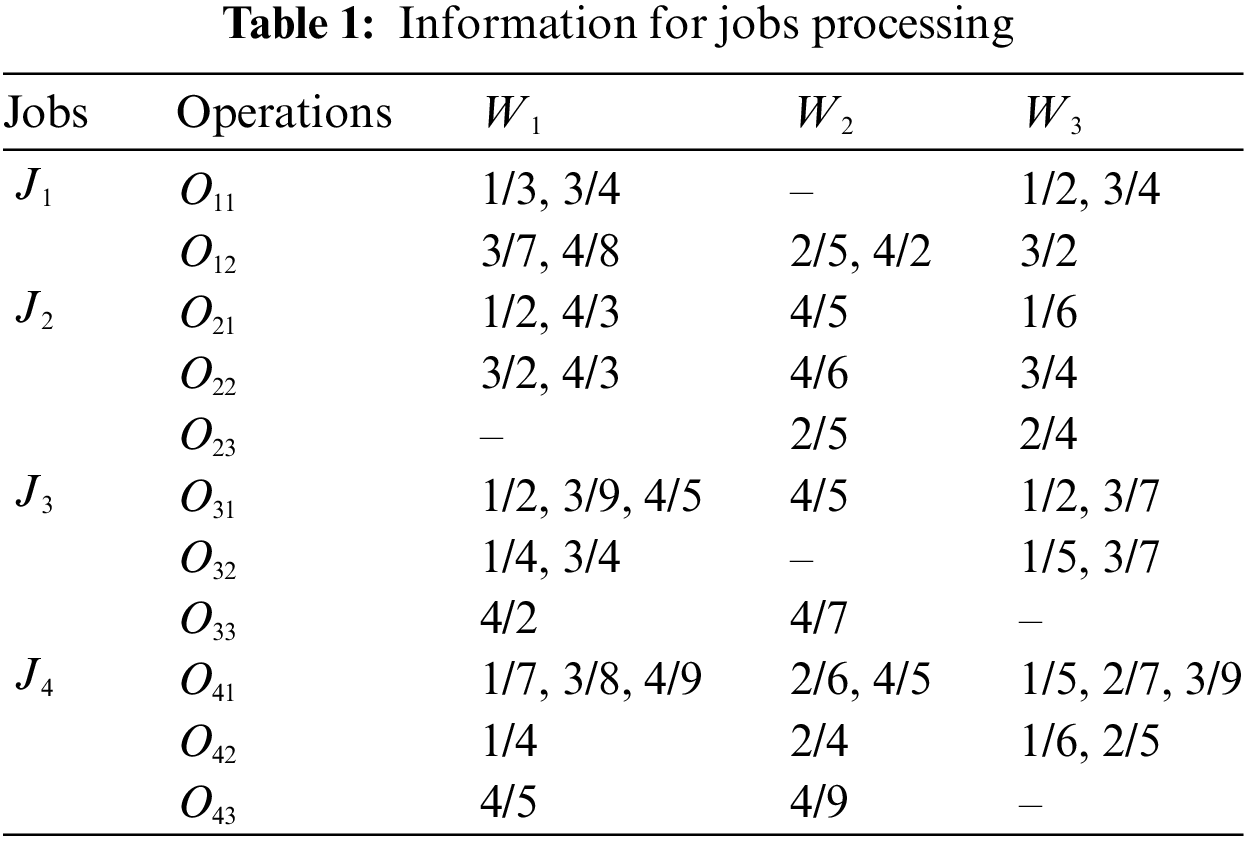
The feasible solutions for DFJSP-DRC are represented using a four-layer coding scheme, which includes vectors for the operations sequence (OS), factories sequence (FS), machines sequence (MS) and workers sequence (WS). A four-layer encoding scheme of 4 jobs and 3 factories is shown in Fig. 2. J1 and J4 have two operations, J2 and J3 have three operations. Each factory has three machines and two workers. OS consists of integers from 1 to n, and each integer i corresponds to Ji. The 2 in the fifth position indicates operation O22. The second layer is FS, in which each number represents the processing factory for each operation. The sequence length of FS is the same as the length of OS, and it is clear that J2 and J4 are processed in F1, J1 is processed in F2, J3 is processed in F3. The MS and WS structure is similar to the FS, with the third number in the MS and WS indicating that O41 is processed by machine 1 and worker 1.

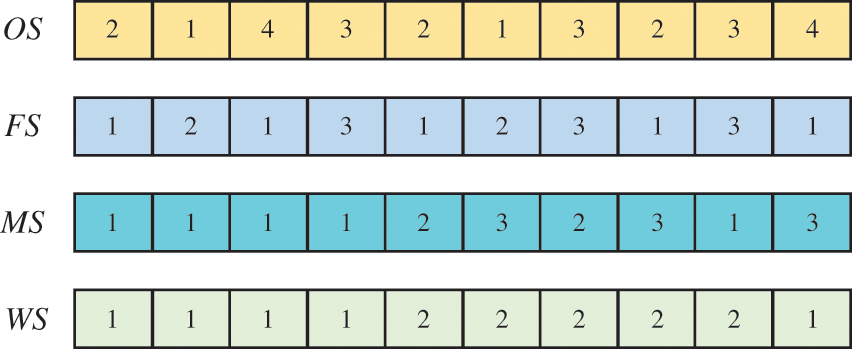
Figure 2: Schematic diagram of four-layer coding

4.4 Active Decoding Based on Public Idle Time

A good decoding strategy not only can rationalize the arrangement of jobs, machines and workers, but also obtain a high-quality scheduling scheme. Based on the literature of Kacem et al. [33], an improved active decoding strategy is devised, with the efficient use of the public idle time of machines and workers as its core. This reduces makespan by arranging processing jobs to the earliest public idle time slot. In the improved active decoding, it is necessary to determine whether the idle time of the current processing machine and the worker overlap and then determine the size of the overlap time and the processing time. When the two conditions are satisfied, the following two cases will appear. Algorithm 2 describes the pseudo-code for two cases.

Case 1: As shown in Fig. 3, the public idle processing time slot of a machine and a worker is [Ts, Te], Te–Ts≥Tijks and ETi(j-1)≥Ts. In this case, the processing time slot of the operation is denoted as [ETi(j-1), ETi(j-1)+Tijks].

Figure 3: Active decoding case 1

Case 2: As shown in Fig. 4, the public idle processing time slot of a machine and a worker is [Ts, Te], Te–Ts≥Tijks and Ts≥ETi(j-1). In this case, the processing time slot of the operation is denoted as [Ts, Ts+Tijks].

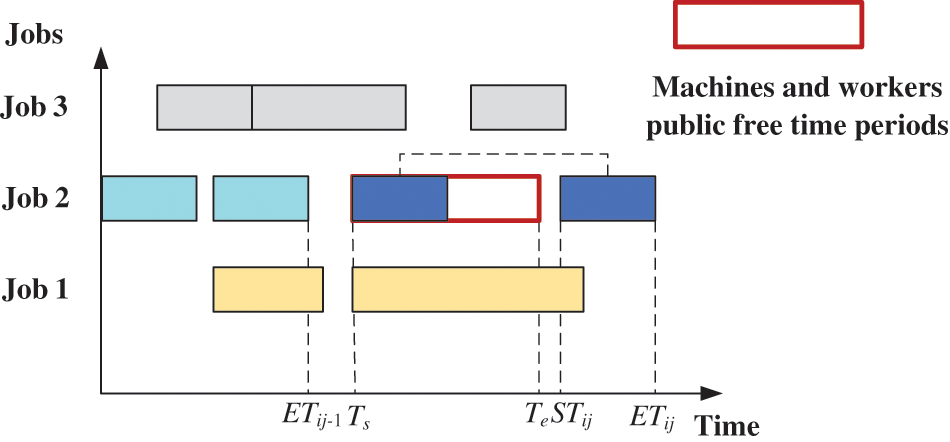
Figure 4: Active decoding case 2

4.5 Hybrid Initialization Strategy

(1) Initialization strategy for the OS. To ensure the diversity and randomness of the population, the initialization coding for OS adopts the positional ascending rule. Firstly, generate a list of basic OS. Secondly, generate a random number ranging from 0 to 1 for each element in the OS. Finally, the OS is rearranged in ascending order of these random numbers to obtain the initial OS.

(2) Initialization strategy for the FS. The following two strategies each account for 50% of the population size. The first strategy prioritizes the assignment to the factories with few jobs. One factory is randomly chosen if there are multiple optional factories for selection. The second strategy involves the random assignment of jobs to a factory.

(3) Initialization strategy for MS and WS. The processing time for the DFJSP-DRC depends on both the machine and the worker. Taking into account the time differences that arise from different operators using the same machine, a principle of machine-worker integration is formulated. First, determine the set of processing machines to operate, and then determine the available processing workers for each machine. For example, the available processing machines for O21 of J2 consist of M1 and M2. M1 and M2 can be operated by worker W1, and M2 can be operated by worker W2. The set of available machines and workers for O21 of J2 are [(M1, W1), (M2, W1) (M2, W2)]. Each operation has three strategies: randomly selecting a machine and worker, selecting the machine and worker combinations with the shortest processing time, and selecting the machine and worker combinations with the least energy consumption.

4.6 Wolf Pack Search Strategy

MOGWO mimics the grey wolf population predation strategy, utilizing the three head wolves to guide the position update of the population. However, this strategy cannot be applied directly to DFJSP-DRC. Therefore, in Q-MOGWO, the two modified search operators are adopted for global search to ensure the feasibility of the DFJSP-DRC solution. The social leadership mechanism proposed by Lu et al. [34] is used to obtain α, β and δ.

The first search operator comprises improved precedence operation crossover (IPOX) [35] and multiple point crossover (MPX). IPOX is performed for OS, where P1 and P2 represent the two paternal chromosomes that undergo crossover to generate offspring C1 and C2, as shown in Fig. 5. After the IPOX crossover is performed for the OS, MS and WS adopt MPX. MPX is a process in which multiple crossover points are randomly set up in two somatic chromosomes and then genes are exchanged, as shown in Fig. 6. If the case of infeasible solutions appears, machines and workers are randomly selected.

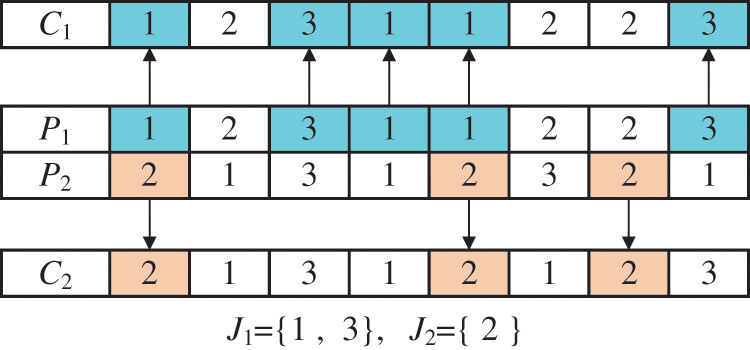
Figure 5: IPOX crossover

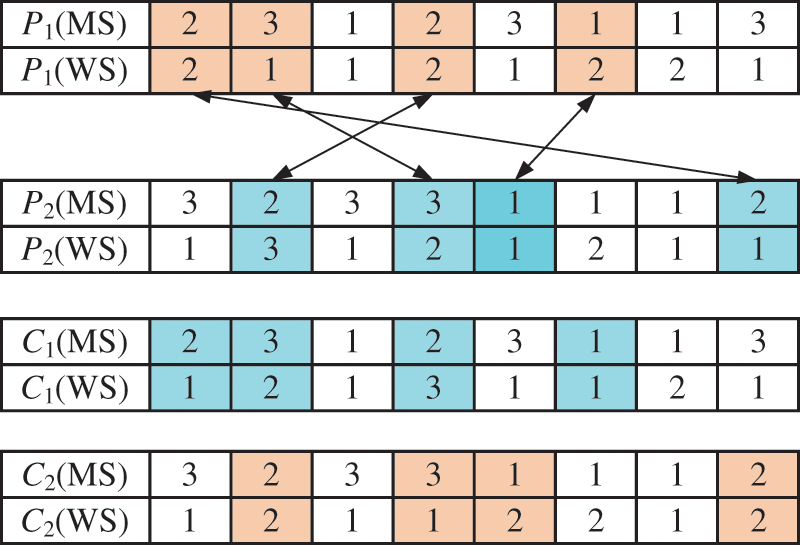
Figure 6: Multi-point intersection of machines and workers

The second search operator is the improved IPOX, which executes the crossover for OS, MS and WS, as shown in Fig. 7. Binding the three together while performing the crossover can avoid infeasible solutions.

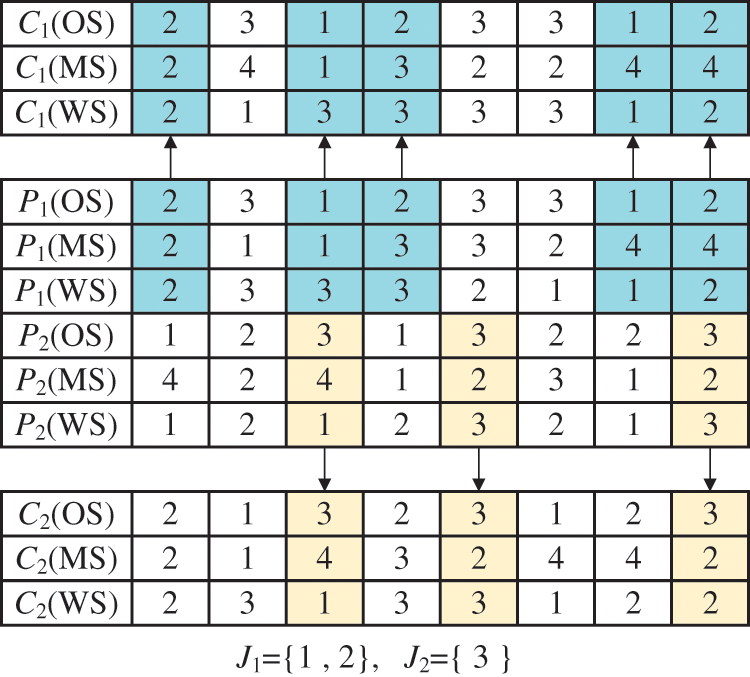
Figure 7: Improved IPOX operator

4.7 Neighborhood Structure Based on Q-Learning

4.7.1 Brief Introduction of Q-Learning

The main components of RL include agent, environment, actions, rewards and states. The agent in the RL algorithm gets as much reward as possible through trial and error of the environment. The agent takes action by its state St at time t within the environment, subsequently receiving a reward Rt+1 and transitioning to state St+1.

Q-learning is an effective algorithm that improves the solution diversity of the algorithm by choosing appropriate local search operators during iteration. Q-learning is a greedy algorithm where the agent selects the action with the highest Q value to maximize rewards. The agent can fine-tune the disparity between the actual and estimated Q values by computing the difference between them. Learning rate (a) and the discount factor (γ) are both in the range of 0 to 1, as γ approaches 0, the current state influences the Q value, and γ is more concerned with the future state as it approaches 1. The current state st can influence the later state st+1, and rt is the reward after performing an action at. The Q value is updated according to the Eq. (15).

Q(st,at)←Q(st,at)+α[rt+1+γmaxQ(st+1,a)−Q(st,at)](15)

4.7.2 Agent and Action Definition

In Q-MOGWO, the PF is the set of optimal solutions, which can reflect the comprehensive ability of the algorithm. Q-learning guides the algorithm to choose the optimal local search strategy. Therefore, the solution set in the external archive acts as an agent to reflect the success of the local search strategy.

4.7.3 State Definition

The state change can give feedback to the agent and determine whether the action performed can improve the overall quantity of the PF. In Q-MOGWO, MOGWO is viewed as the environment. To better construct the state of the environment, the comprehensive performance of the PF, and the other is the degree of excellence degree of the α are taken.

Whether or not the α is good depends on whether the α of the previous generation dominates the α of the current generation. The integrative performance of the PF is calculated by Inverse Generational Distance (IGD) [36]. IGD measures the diversity and convergence of PF. Eqs. (16) and (17) calculate IGD and ∆IGD, respectively:

IGD=∑x∈PF∗dist(x,PF)|PF∗|(16)

ΔIGD=IGDi−IGDi−1(17)

where PF* is the true frontier of the Pareto solution set, │PF*│ represents the total count of elements in PF*, meanwhile dist(x, PF) signifies the minimum Euclidean distance between point x and the closest element in PF. IGDi indicates the IGD value of the i-generation PF.

There are three outcomes of ∆IGD and two outcomes of α dominance in the iterative process, at thus. Six states can be obtained by combining these results: (1) State 1: ∆IGD > 0, αi does not dominate αi-1; (2) State 2: ∆IGD > 0, αi dominates αi-1; (3) State 3: ∆IGD = 0, αi dominates αi-1; (4) State 4: ∆IGD = 0, αi does not dominate αi-1; (5) State 5: ∆IGD < 0, αi dominates αi-1; (6) State 6: ∆IGD < 0, αi does not dominate αi-1.

4.7.4 Reward Definition

Upon performing an action, the agent receives a reward, which may be positive or negative. The definition of reward is as Eq. (18). The chosen action (local search strategy) is rewarded, and the Q-table is updated if PF exhibits superior overall performance; otherwise, the reward is set to 0.

Reward={2,ΔIGD<0;αidominatesαi−10,ΔIGD≥0;αi0doesnotdominate1,otherstates(18)

4.7.5 Q-Learning for Neighborhood Structure

Local search strategy is a crucial technique to improve resource utilization, but it consumes a lot of computing resources. Executing the local search strategy randomly leads to a low success rate. However, RL offers selection strategies to guide agents in choosing the local search strategy with the highest likelihood of success.

Based on the literature of Zhang et al. [37], this paper identifies two types of critical factories: one is related to the makespan and the other is related to the maximum energy consumption. For the local search strategy, two local search operators are proposed: (1) Remove a job from the critical factory and insert the job into the factory with the minimum makespan or energy consumption; (2) Reschedule the jobs in the critical factory.

Combining two different local search operators, three local search strategies are proposed. Local search strategy 1: Select the factory with the makspan. Local search strategy 2: Select the factory with the maximum energy consumption. Local search strategy 3: Randomly selected factory. According to the above description, an adaptive local search strategy based on Q-learning(Q-ALS) is designed, and Algorithm 3 provides the corresponding pseudo-code.

5  Experimental Results

A series of experimental instances are designed to assess Q-MOGWO’s performance. The Q-MOGWO and comparison algorithms are coded in Python on an Intel Core i7 8550 CPU @1.80 GHz and 8G RAM. To be fair, each algorithm collects the results after 20 independent runs and then calculates the average for performance comparison.

MOEA/D [38], MOGWO [32], NSGA-II [39] and memetic algorithm (MA) [40] are chosen to verify the Q-MOGWO effectiveness. Three multi-objective algorithmic measures: IGD, Spread [39] and Hyper Volume (HV) [41] are used to evaluate the obtained Pareto solutions. The IGD formulation is given in Section 4.7.3. The formulas for the other two metrics are as follows:

(1) Spread measures the degree of propagation between the found solutions, and its formula is:

Spread=∑j=1nodje+∑i=1|PF||di−d¯|∑j=1nodje+|PF|⋅d¯(19)

in Eq. (19), di represents the Euclidean distance between each point in the real PF and its nearest neighbor within the front. d¯ is the average of all di, the dje denotes the Euclidean distance between the extreme solution of the j-th objective and the boundary solution of the obtained PF. |PF| represents the number of points within the PF, while no stands for the number of objectives.

(2) HV serves as a metric for assessing the overall performance of an algorithm. It quantifies the volume or area within the objective space enclosed by the resulting non-dominant solution set and reference points. The formula of HV is:

HV(P,r)=∪X∈PPv(X,r)(20)

in Eq. (20), P represents the PF computed by the algorithm, r = (1, 1) is the reference point, and X denotes a normalized non-dominated solution in the PF. The variable v(X, r) signifies the volume of the hypercube formed by X and r. A higher HV indicates improved convergence and diversification of the algorithm.

5.1 Experimental Instances and Parameters Setting

For there is no specific instance of the DFJSP-DRC, the flexible job shop scheduling problem benchmark [42] is extended to consider production environments with 2, 3, and 4 factories, with the same number of machines and workers in each factory. 45 test instances are generated, and the worker machine information in each factory is shown in the link https://pan.baidu.com/s/1vIwX5MszpleEIm6pQ7XOFw?pwd=zxoi. Worker processing time Tijks is randomly generated within [Tij, Tij +δij], where the operation processing time Tij is given by the benchmarking algorithm and δij ∈ [2,8] [43]. The unit processing energy consumption of each machine ranges from 5 to 10, and the unit standby energy consumption with of each machine ranges from 1 to 5.

The parameter configuration affects the algorithm’s performance in solving the problem. Q-MOGWO contains three primary parameters: the length of the external archive (denoted by E), the maximum step (denoted by max-step), and the size of the population (denoted by N). Taguchi’s experimental approach can systematically assess parameter impact on algorithm performance, facilitating the identification of optimal parameter combinations. Therefore, the Taguchi experiment is used to obtain the optimal combination of the three parameters of Q-MOGWO. Each parameter exhibits three levels, and Table 2 displays the specific parameter values. The L9(34) orthogonal table is employed to conduct experiments based on the designated levels and the number of parameters.

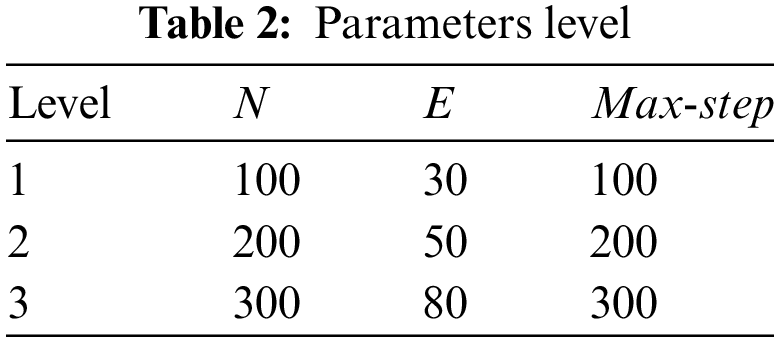
Q-MOGWO runs 20 times under each parameter combination to ensure fairness, and the average IGD values from these 10 runs are collected. Experiments are conducted on the Mk-3-01 instance, employing IGD to evaluate parameter combinations, as presented in Table 3. Fig. 8 illustrates the trend chart delineating each parameter level concerning the results outlined in Table 3. It can be observed that the optimal configuration for the parameter setting values is N = 300, E = 80, and max-step = 300.

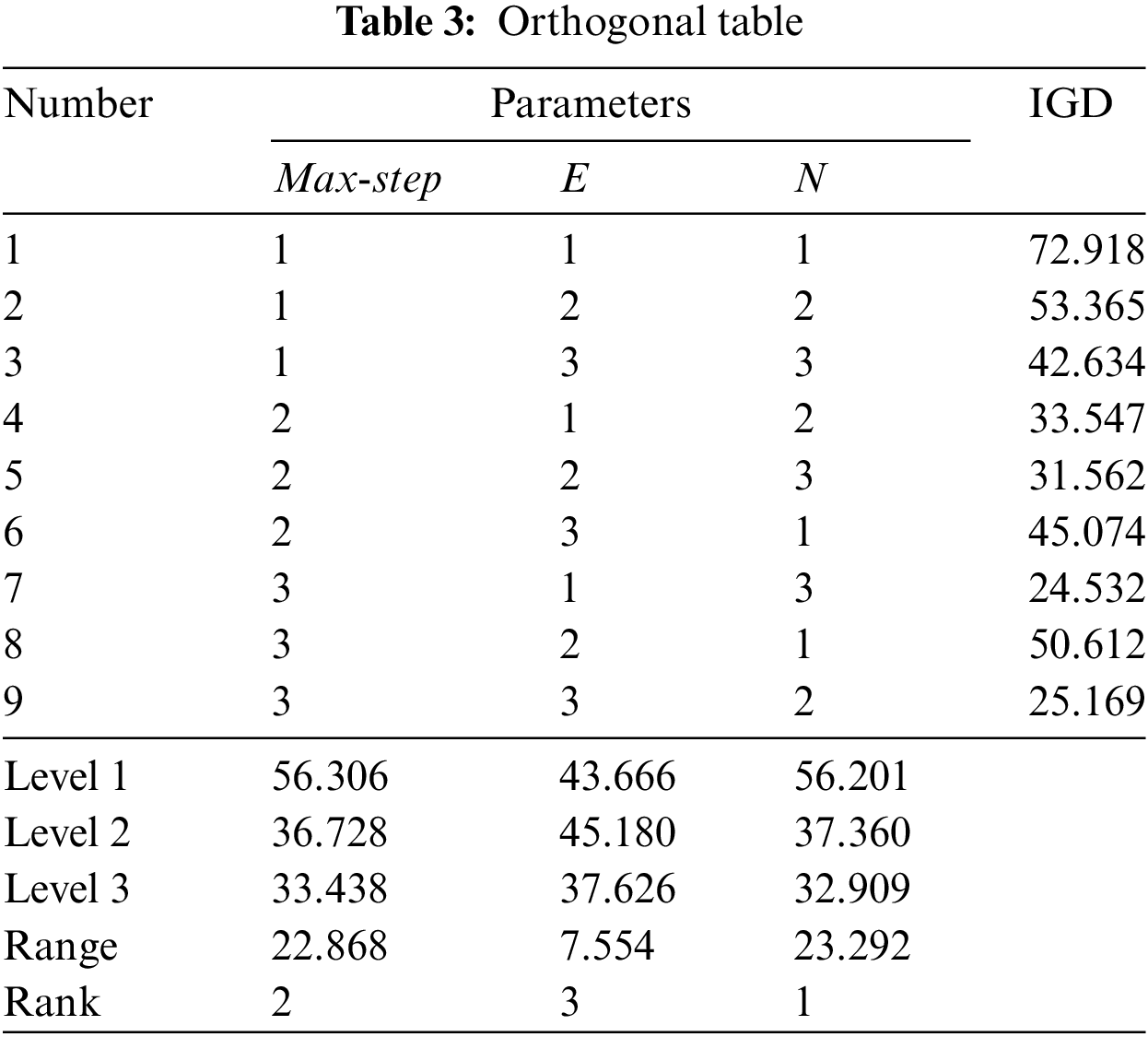
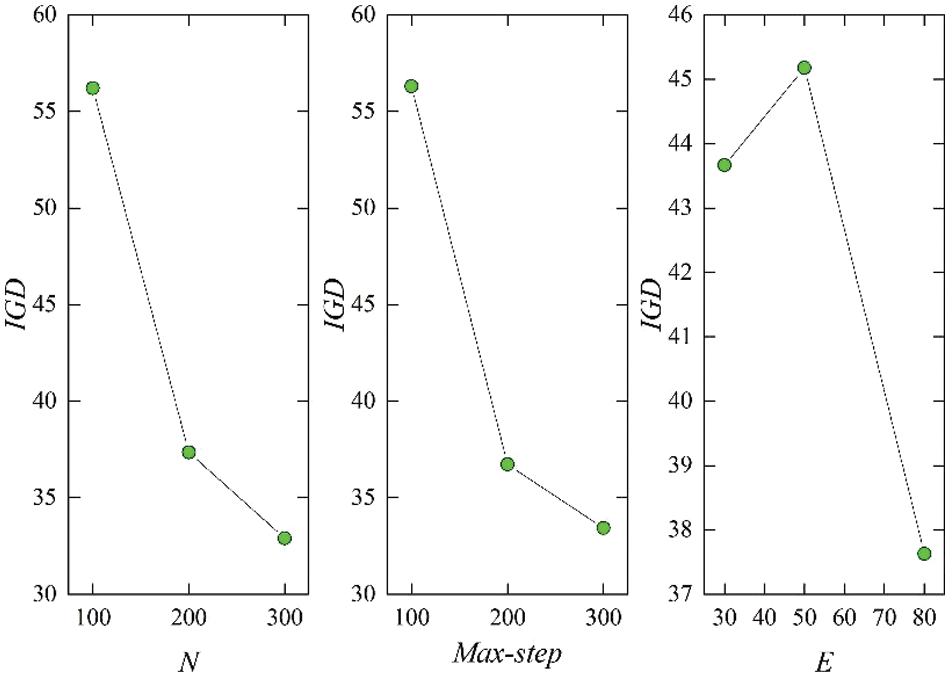
Figure 8: The trend chart of each parameter level

5.2 Effectiveness of the Proposed Strategy

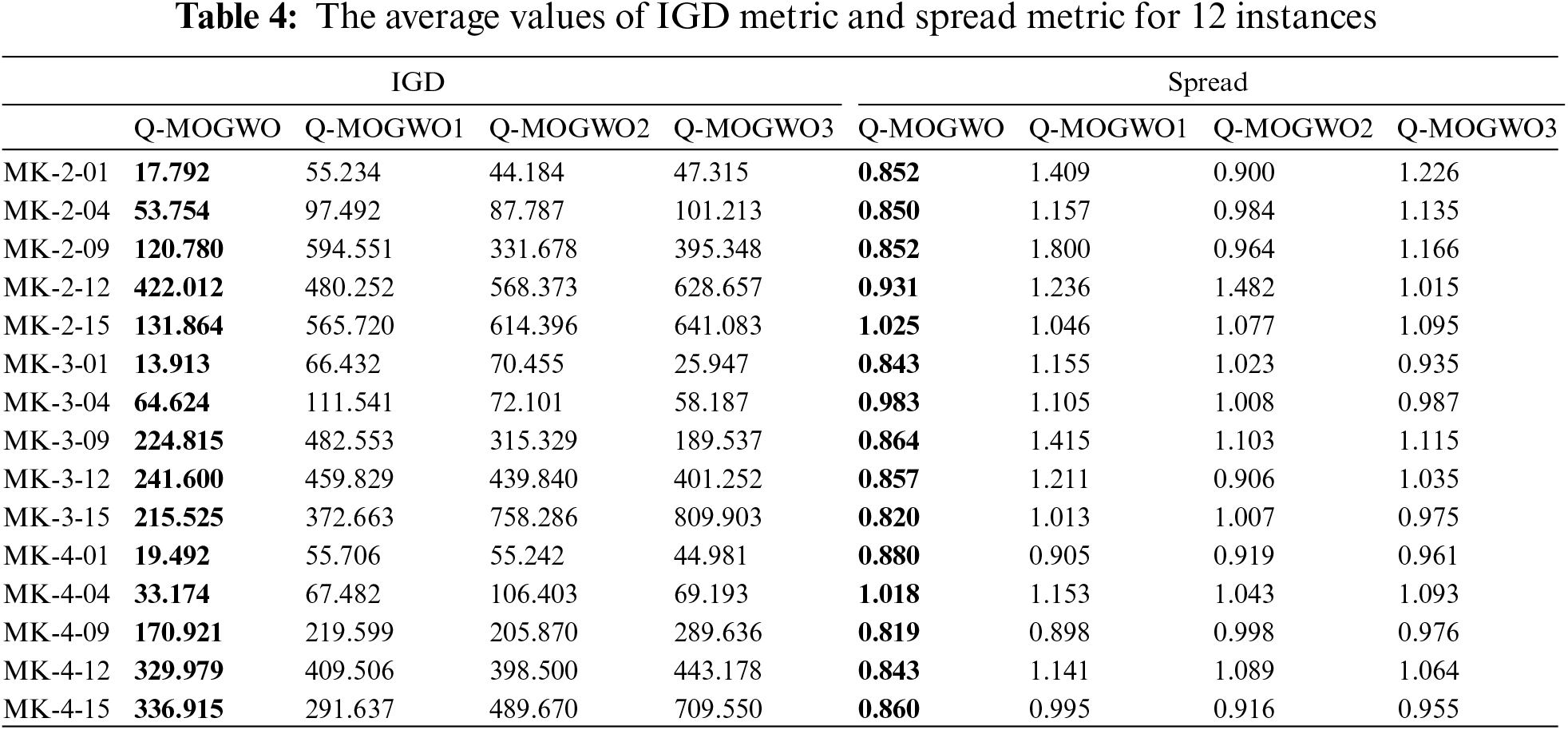
The proposed strategy’s effectiveness is validated through experiments on 15 instances. Algorithms Q-MOGWO1, Q-MOGWO2 and Q-MOGWO3 denote the local search strategy for the makespan factory, the maximum energy consumption factory and the randomized factory, respectively. The IGD and Spread values of Q-MOGWO, Q-MOGWO1, Q-MOGWO2 and Q-MOGWO3 are shown in Table 4. The better results are highlighted in bold for each instance. From Table 4, it can be seen that Q-MOGWO has lower IGD values compared with all the other three algorithms. Table 4 shows that Q-MOGWO has lower Spread values than all the other three algorithms. The Spread values correspond precisely to the IGD values. It can be seen clearly that the solutions identified through the RL selective local search strategy demonstrate superior breadth and comprehensive performance compared with those obtained via the deterministic local search strategy, thereby confirming the effectiveness of using RL to select critical factories.

5.3 Evaluation of the Proposed Q-MOGWO

To further evaluate the effectiveness of Q-MOGWO, four multi-objective optimization algorithms, MOEA/D, MA, NSGA-II and MOGWO, are selected as compared algorithms. Regarding the parameter setting of the compared algorithms, refer to the literature [44], and detailed data is shown in Table 5.

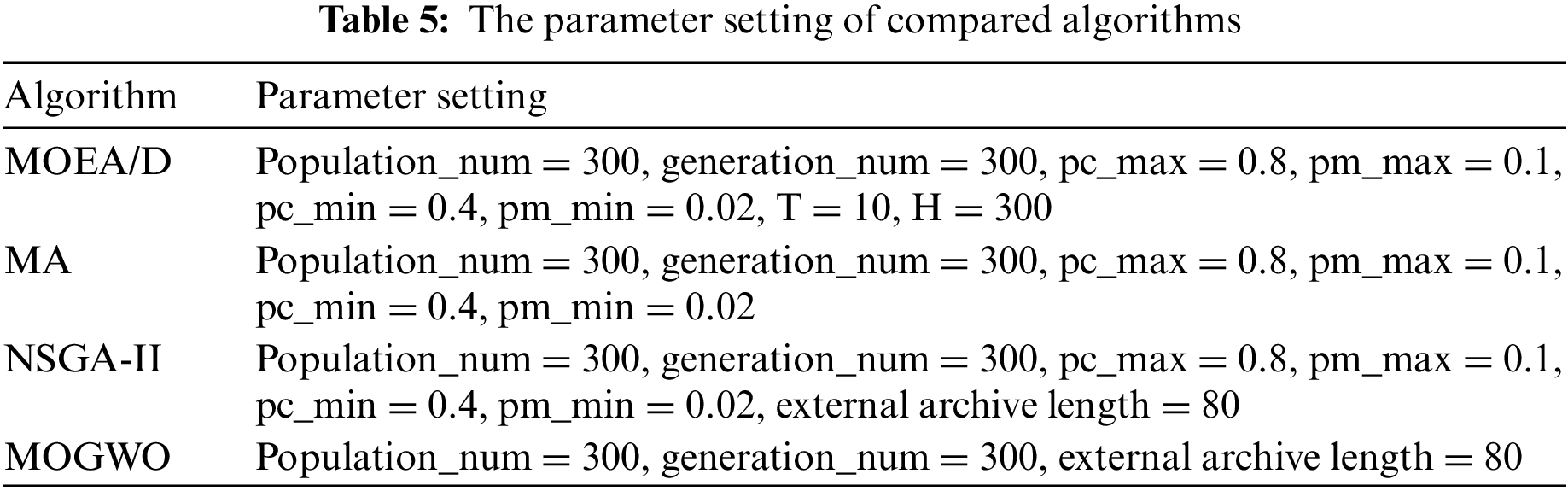
Tables 6 and 7 present the IGD and HV results. The better results are highlighted in bold for each instance. Table 6 reveals that Q-MOGWO consistently exhibits smaller average IGD values across all instances compared with other algorithms, indicating superior convergence and diversity in the solutions obtained by Q-MOGWO. Table 7 shows the average HV values for 45 instances, with Q-MOGWO consistently showing larger values compared with other algorithms. This proves that Q-MOGWO has better comprehensive performance and can obtain Pareto solutions with better coverage and distribution in the solution space. The IGD and HV results for 45 instances show that Q-MOGWO outperforms the compared algorithms. The boxplots of HV and IGD indicators are given in Figs. 9 and 10 to visualize the excellent performance of Q-MOGWO. Boxplots show that the Pareto solutions from Q-MOGWO consistently outperform those of compared algorithms, exhibiting superior maximum, minimum, median, and quartile values.

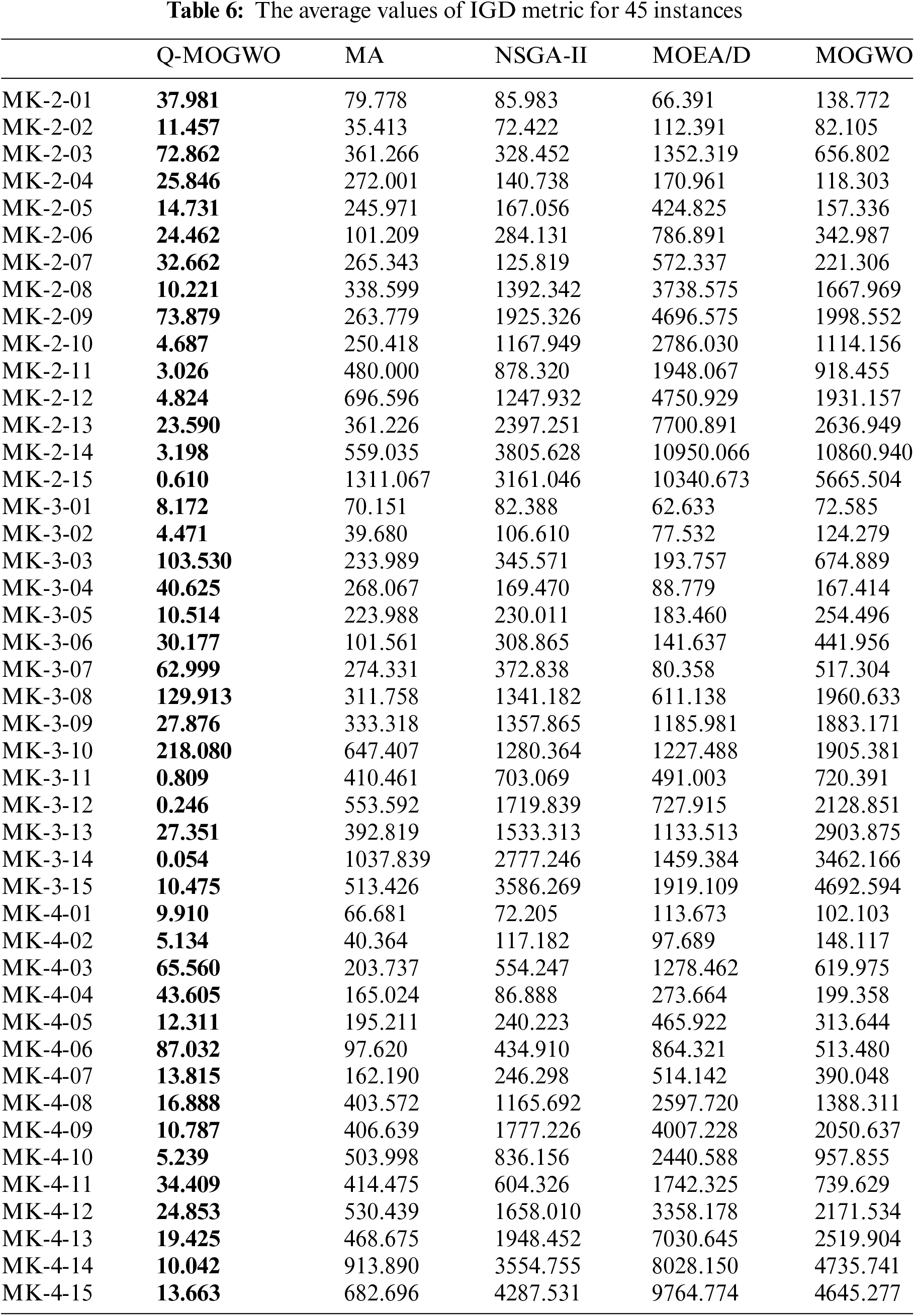
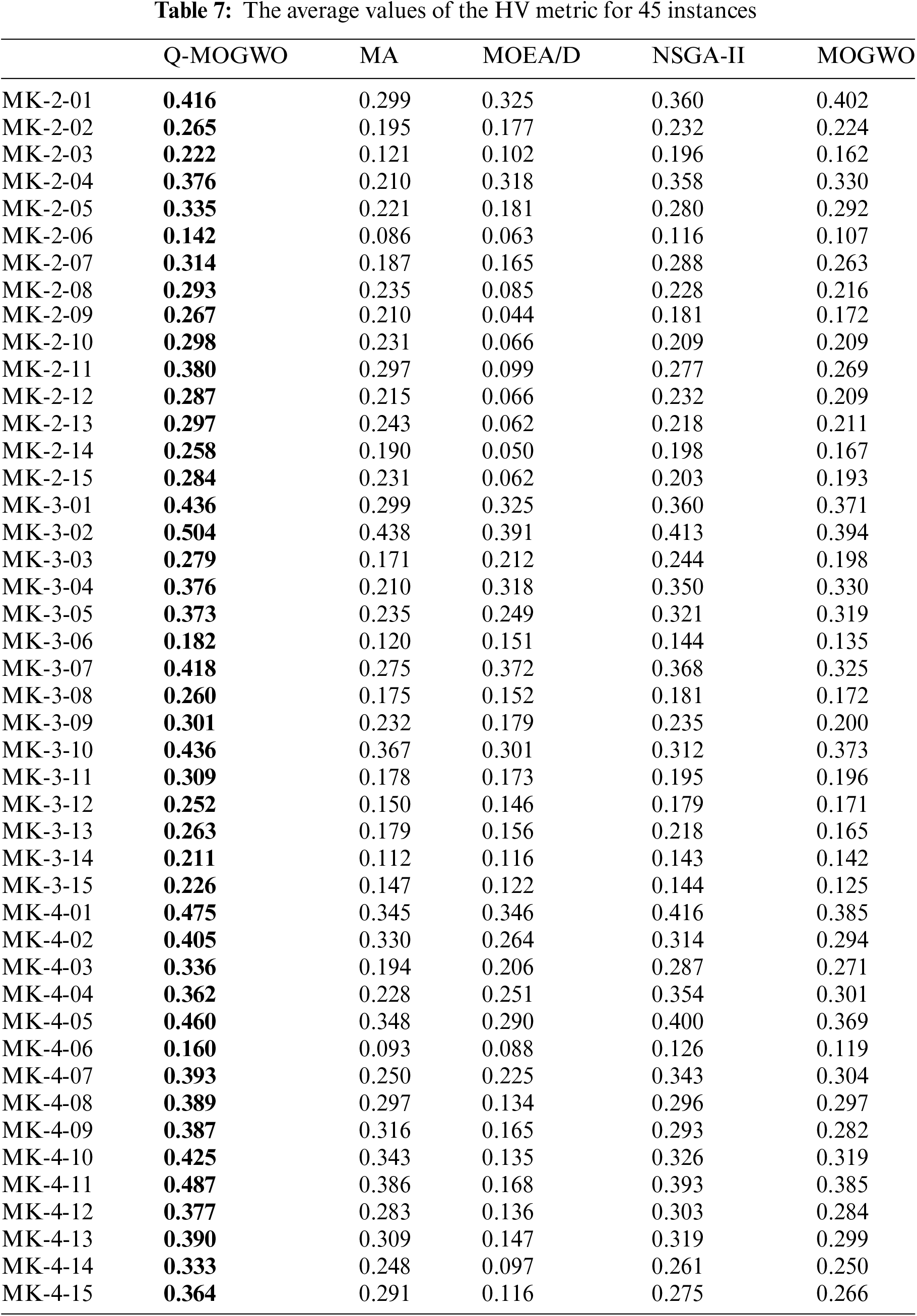
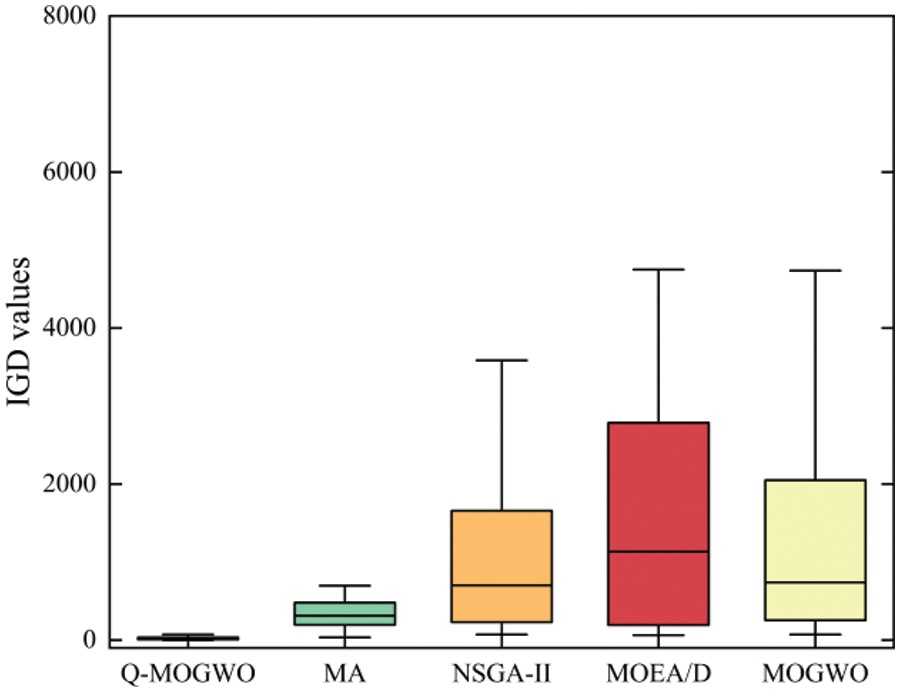
Figure 9: Experimental results of all algorithms for boxplot on the HV values

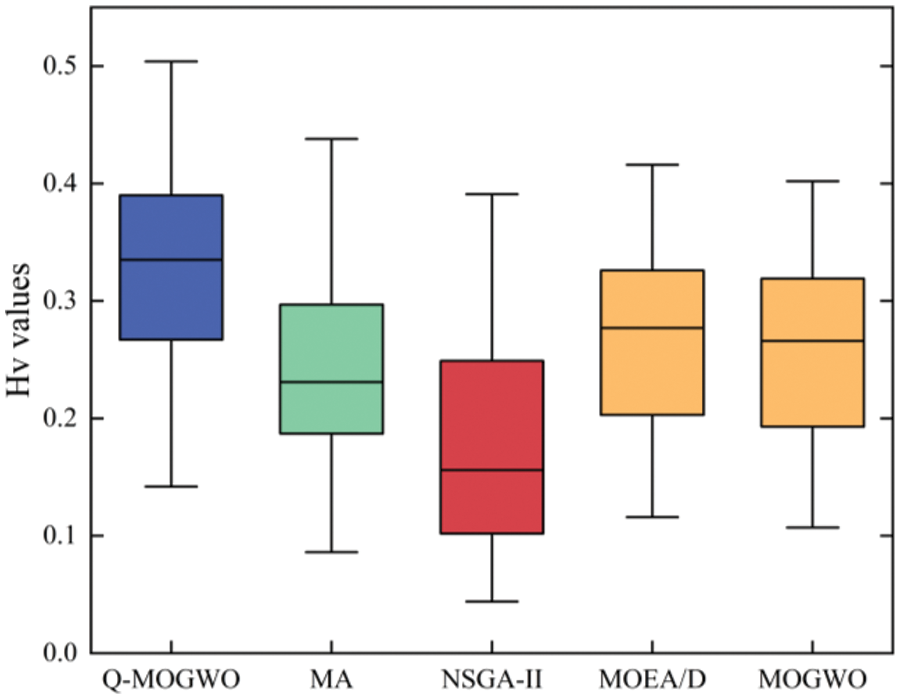
Figure 10: Experimental results of all algorithms for boxplot on the HV values

To visualize the performance of Q-MOGWO, NSGA-II, MOEA/D, MA and MOGWO, 6 instances (Mk-3-01, Mk-3-08, Mk-3-15, Mk-4-01, Mk-4-08, Mk-4-15) with different scales are selected, and the Pareto front obtained from one run of each algorithm for each selected instance is shown in Fig. 11. It can be observed that the Pareto front of Q-MOGWO is closer to the coordinate axis than that of compared algorithms, which indicates that the Pareto front of Q-MOGWO has better quality than that of compared algorithms.

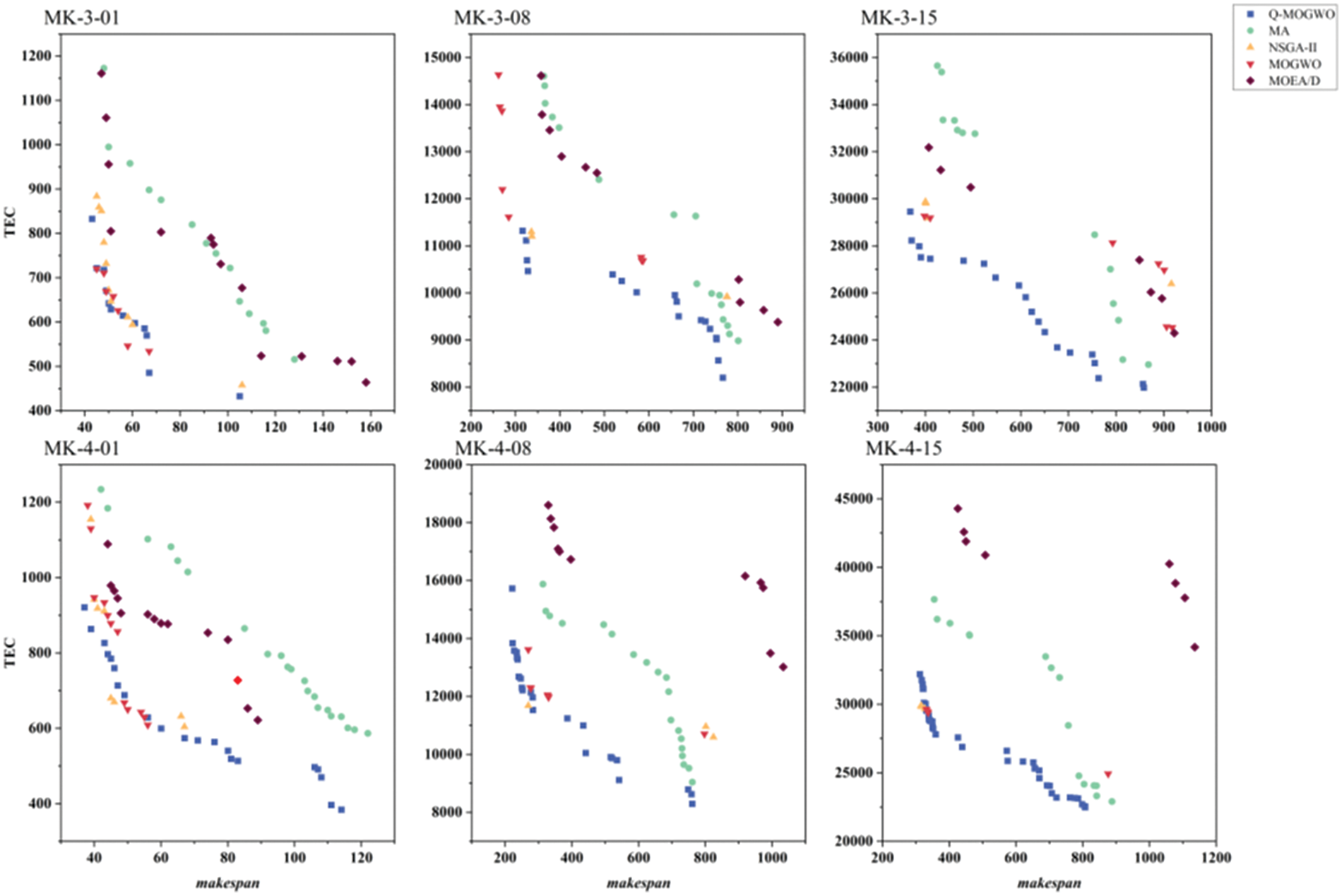
Figure 11: The Pareto fronts of selected instances for Q-MOGWO and compared algorithms

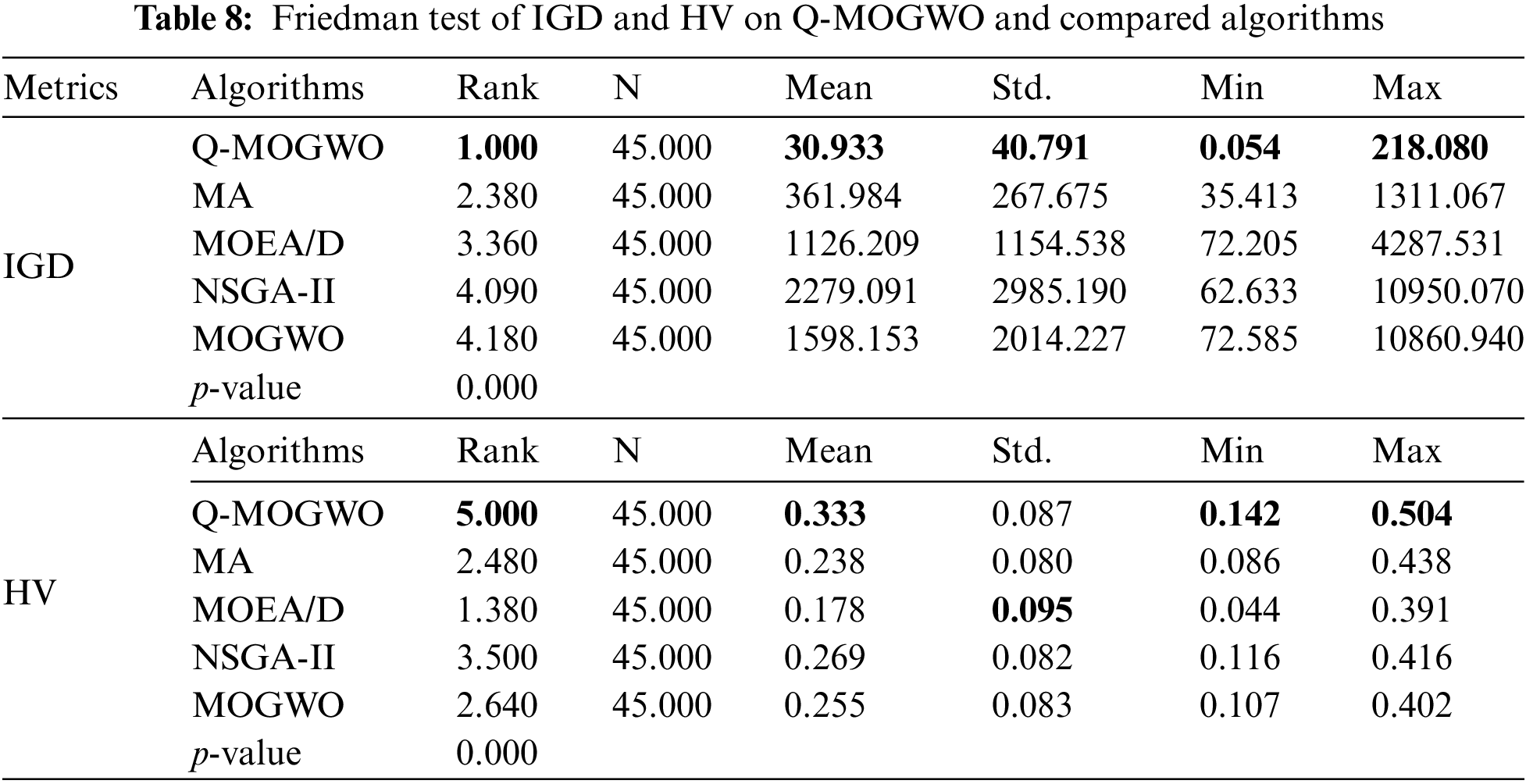
In addition, to further prove the effectiveness of Q-MOGWO, the IGD and HV values in Tables 6 and 7 are analyzed by Friedman’s statistical test with 95% confidence intervals, and the results are shown in Table 8. The better results are highlighted in bold for each instance. Table 8 indicates that the mean, standard deviation, minimum and maximum values of IGD and HV for Q-MOGWO surpass those of the compared algorithms. For a significance level of 0.05, the obtained p-value is 0, which proves that the performance of Q-MOGWO is significantly different from that of compared algorithms.

The experimental results show that Q-MOGWO outperforms the compared algorithms. The main reasons are as follows: (1) The hybrid population initialization strategy generates high-quality initial population and enhances global exploration of Q-MOGWO; (2) The active decoding strategy that effectively uses the public idle time of machines and workers decodes solutions to high-quality scheduling schemes; (3) According to the characteristics of the problem, two kinds of wolf predation strategies are designed to effectively explore the search space of solutions and increase the population diversity; (4) The Q-learning-based local search strategy enhances the local search capability and efficiency of Q-MOGWO, leading to accelerated convergence.

6  Conclusions and Future Work

In this paper, Q-MOGWO is proposed to solve the DFJSP-DRC with the objectives of minimizing makespan and total energy consumption. In Q-MOGWO, three scheduling rules are used to generate high-quality initial solutions, and an active decoding strategy converts solutions into reasonable scheduling schemes. Two predation strategies are designed to explore the unknown regions of solution space in the wolf predation phase. To improve the local search capability of Q-MOGWO, two kinds of neighborhood structures based on critical factories are designed. Through the effectiveness analysis, it can be found that the factory selection based on Q-learning significantly enhances the performance of Q-MOGWO. Especially when solving large-scale problems, Q-MOGWO is superior to the compared algorithms and has better non-dominated solutions.

The problem studied in this paper does not consider the impact of dynamic events on the scheduling schemes. Although worker resource is introduced, worker fatigue is not considered. Therefore, in future work, dynamic events such as machine failure and emergency order insertion will be considered, and worker fatigue will be introduced into the optimization objectives. In addition, some learning mechanisms will be introduced into the framework of Q-MOGWO to obtain stronger adaptability.

Acknowledgement: Thanks to three anonymous reviewers and the editors of this journal for providing valuable suggestions for the paper.

Funding Statement: This work was supported by the Natural Science Foundation of Anhui Province (Grant Number 2208085MG181); the Science Research Project of Higher Education Institutions in Anhui Province, Philosophy and Social Sciences (Grant Number 2023AH051063); and the Open Fund of Key Laboratory of Anhui Higher Education Institutes (Grant Number CS2021-ZD01).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Hongliang Zhang, Yi Chen and Gongjie Xu; data collection: Yuteng Zhang; analysis and interpretation of results: Hongliang Zhang, Yi Chen and Gongjie Xu; draft manuscript preparation: Hongliang Zhang, Yi Chen. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data generated in this paper are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Yu F, Lu C, Zhou J, Yin L. Mathematical model and knowledge-based iterated greedy algorithm for distributed assembly hybrid flow shop scheduling problem with dual-resource constraints. Expert Syst Appl. 2024;239:122434. doi:1016/j.eswa.2023.122434. [Google Scholar] [CrossRef]

2. He L, Chiong R, Li W, Dhakal S, Cao Y, Zhang Y. Multiobjective optimization of energy-efficient job-shop scheduling with dynamic reference point-based fuzzy relative entropy. IEEE Trans Industr Inform. 2022;18(1):600–10. doi:1109/tii.2021.3056425. [Google Scholar] [CrossRef]

3. Wang GG, Gao D, Pedrycz W. Solving multiobjective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans Industr Inform. 2022;18(12):8519–28. doi:1109/tii.2022.3165636. [Google Scholar] [CrossRef]

4. Meng LL, Zhang CY, Ren YP, Zhang B, Lv C. Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem. Comput Ind Eng. 2020;142:106347. doi:1016/j.cie.2020.106347. [Google Scholar] [CrossRef]

5. Sang YW, Tan JP. Intelligent factory many-objective distributed flexible job shop collaborative scheduling method. Comput Ind Eng. 2022;164:107884. doi:1016/j.cie.2021.107884. [Google Scholar] [CrossRef]

6. Tang H, Fang B, Liu R, Li Y, Guo S. A hybrid teaching and learning-based optimization algorithm for distributed sand casting job-shop scheduling problem. Appl Soft Comput. 2022;120:108694. doi:1016/j.asoc.2022.108694. [Google Scholar] [CrossRef]

7. Zhang ZQ, Wu FC, Qian B, Hu R, Wang L, Jin HP. A Q-learning-based hyper-heuristic evolutionary algorithm for the distributed flexible job-shop scheduling problem with crane transportation. Expert Syst Appl. 2023;234:121050. doi:1016/j.eswa.2023.121050. [Google Scholar] [CrossRef]

8. Luo Q, Deng QW, Gong GL, Zhang LK, Han WW, Li KX. An efficient memetic algorithm for distributed flexible job shop scheduling problem with transfers. Expert Syst Appl. 2020;160:113721. doi:1016/j.eswa.2020.113721. [Google Scholar] [CrossRef]

9. Du Y, Li JQ, Luo C, Meng LL. A hybrid estimation of distribution algorithm for distributed flexible job shop scheduling with crane transportations. Swarm Evol Comput. 2021;62:100861. doi:1016/j.swevo.2021.100861. [Google Scholar] [CrossRef]

10. Xu WX, Hu YW, Luo W, Wang L, Wu R. A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission. Comput Ind Eng. 2021;157:107318. doi:1016/j.cie.2021.107318. [Google Scholar] [CrossRef]

11. Li R, Gong WY, Wang L, Lu C, Jiang SN. Two-stage knowledge-driven evolutionary algorithm for distributed green flexible job shop scheduling with type-2 fuzzy processing time. Swarm Evol Comput. 2022b;74:101139. doi:1016/j.swevo.2022.101139. [Google Scholar] [CrossRef]

12. Gong GL, Chiong R, Deng QW, Gong X. A hybrid artificial bee colony algorithm for flexible job shop scheduling with worker flexibility. Int J Prod Res. 2020;58(14):4406–20. doi:1080/00207543.2019.1653504. [Google Scholar] [CrossRef]

13. Tan WH, Yuan XF, Wang JL, Zhang XZ. A fatigue-conscious dual resource constrained flexible job shop scheduling problem by enhanced NSGA-II: An application from casting workshop. Comput Ind Eng. 2021;160:107557. doi:1016/j.cie.2021.107557. [Google Scholar] [CrossRef]

14. Zhao P, Zhang H, Tang HT, Feng Y, Yin W. Research on flexible job-shop scheduling problem in green sustainable manufacturing based on learning effect. J Intell Manuf. 2022;33(6):1725–46. doi:1007/s10845-020-01713-8. [Google Scholar] [CrossRef]

15. Shi JX, Chen MZ, Ma YM, Qiao F. A new boredom-aware dual-resource constrained flexible job shop scheduling problem using a two-stage multi-objective particle swarm optimization algorithm. Inf Sci. 2023;643:119141. doi:1016/j.ins.2023.119141. [Google Scholar] [CrossRef]

16. Luo Q, Deng QW, Gong GL, Guo X, Liu X. A distributed flexible job shop scheduling problem considering worker arrangement using an improved memetic algorithm. Expert Syst Appl. 2022;207:117984. doi:1016/j.eswa.2022.117984. [Google Scholar] [CrossRef]

17. Meng LL, Zhang CY, Zhang B, Ren YP. Mathematical modeling and optimization of energy-conscious flexible job shop scheduling problem with worker flexibility. IEEE Access. 2019;7:68043–59. doi:1109/access.2019.2916468. [Google Scholar] [CrossRef]

18. He Z, Tang B, Luan F. An improved african vulture optimization algorithm for dual-resource constrained multi-objective flexible job shop scheduling problems. Sensors. 2023;23(1):90. doi:3390/s23010090. [Google Scholar] [PubMed] [CrossRef]

19. Lin CS, Lee IL, Wu MC. Merits of using chromosome representations and shadow chromosomes in genetic algorithms for solving scheduling problems. Robot Comput Integr Manuf. 2019;58:196–207. doi:1016/j.rcim.2019.01.005. [Google Scholar] [CrossRef]

20. Li XY, Xie J, Ma QJ, Gao L, Li PG. Improved gray wolf optimizer for distributed flexible job shop scheduling problem. Sci China Technol Sci. 2022;65(9):2105–15. doi:1007/s11431-022-2096-6. [Google Scholar] [CrossRef]

21. Xie J, Li X, Gao L, Gui L. A hybrid genetic tabu search algorithm for distributed flexible job shop scheduling problems. J Manuf Syst. 2023;71:82–94. doi:1016/j.jmsy.2023.09.002. [Google Scholar] [CrossRef]

22. Li R, Gong WY, Wang L, Lu C, Zhuang XY. Surprisingly popular-based adaptive memetic algorithm for energy-efficient distributed flexible job shop scheduling. IEEE Trans Cybern. 2023;53(12):8013–23. doi:1109/tcyb.2023.3280175. [Google Scholar] [PubMed] [CrossRef]

23. Zhu N, Gong GL, Lu D, Huang D, Peng NT, Qi H. An effective reformative memetic algorithm for distributed flexible job-shop scheduling problem with order cancellation. Expert Syst Appl. 2024;237:121205. doi:1016/j.eswa.2023.121205. [Google Scholar] [CrossRef]

24. Karimi-Mamaghana M, Mohammadi M, Meyer P, Karimi-Mamaghanb AM, Talbi E-G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur J Oper Res. 2022;296:393–422. doi:1016/j.ejor.2021.04.032. [Google Scholar] [CrossRef]

25. Cao ZC, Lin CR, Zhou MC, Huang R. Scheduling semiconductor testing facility by using cuckoo search algorithm with reinforcement learning and surrogate modeling. IEEE Trans Autom Sci Eng. 2019;16(2):825–37. doi:1109/tase.2018.2862380. [Google Scholar] [CrossRef]

26. Chen RH, Yang B, Li S, Wang SL. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput Ind Eng. 2020;149:106778. doi:1016/j.cie.2020.106778. [Google Scholar] [CrossRef]

27. Cao ZC, Lin CR, Zhou MC. A knowledge-based cuckoo search algorithm to schedule a flexible job shop with sequencing flexibility. IEEE Trans Autom Sci Eng. 2021;18(1):56–69. doi:1109/tase.2019.2945717. [Google Scholar] [CrossRef]

28. Li R, Gong W, Lu C. A reinforcement learning based RMOEA/D for bi-objective fuzzy flexible job shop scheduling. Expert Syst Appl. 2022;203:117380. doi:1016/j.eswa.2022.117380. [Google Scholar] [CrossRef]

29. Li HX, Gao KZ, Duan PY, Li JQ, Zhang L. An improved artificial bee colony algorithm with Q-learning for solving permutation flow shop scheduling problems. IEEE Trans Syst Man Cybern. 2023;53(5):2684–93. doi:1109/tsmc.2022.3219380. [Google Scholar] [CrossRef]

30. Lu C, Gao L, Pan Q, Li X, Zheng J. A multi-objective cellular grey wolf optimizer for hybrid flowshop scheduling problem considering noise pollution. Appl Soft Comput. 2019;75:728–49. doi:1016/j.asoc.2018.11.043. [Google Scholar] [CrossRef]

31. Lu C, Xiao S, Li X, Gao L. An effective multi-objective discrete grey wolf optimizer for a real-world scheduling problem in welding production. Adv Eng Softw. 2016;99:161–76. doi:1016/j.advengsoft.2016.06.004. [Google Scholar] [CrossRef]

32. Mirjalili S, Saremi S, Mirjalili SM, Coelho LdS. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst Appl. 2016;47:106–19. doi:1016/j.eswa.2015.10.039. [Google Scholar] [CrossRef]

33. Kacem I, Hammadi S, Borne P. Pareto-optimality approach for flexible job-shop scheduling problems: Hybridization of evolutionary algorithms and fuzzy logic. Math Comput Simul. 2002;60(3):245–76. doi:1016/S0378-4754(02)00019-8. [Google Scholar] [CrossRef]

34. Lu C, Gao L, Li XY, Xiao SQ. A hybrid multi-objective grey wolf optimizer for dynamic scheduling in a real-world welding industry. Eng Appl Artif Intell. 2017;57:61–79. doi:1016/j.engappai.2016.10.013. [Google Scholar] [CrossRef]

35. Zhang GH, Shao XY, Li PG, Gao L. An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Comput Ind Eng. 2009;56(4):1309–18. doi:1016/j.cie.2008.07.021. [Google Scholar] [CrossRef]

36. Czyzżak P, Jaszkiewicz A. Pareto simulated annealing—a metaheuristic technique for multiple-objective combinatorial optimization. J Multi-Criteria Dec. 1998;7(1):34–47. doi:1002/(SICI)1099-1360(199801)7:13.0.CO;2-6. [Google Scholar] [CrossRef]

37. Zhang GH, Xing KY, Cao F. Discrete differential evolution algorithm for distributed blocking flowshop scheduling with makespan criterion. Eng Appl Artif Intell. 2018;76:96–107. doi:1016/j.engappai.2018.09.005. [Google Scholar] [CrossRef]

38. Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput. 2007;11(6):712–31. doi:1109/tevc.2007.892759. [Google Scholar] [CrossRef]

39. Kalyanmoy D, Associate M, Sameer A, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97. doi:1109/4235.996017. [Google Scholar] [CrossRef]

40. Mencía R, Sierra MR, Mencía C, Varela R. Memetic algorithms for the job shop scheduling problem with operators. Appl Soft Comput. 2015;34:94–105. doi:1016/j.asoc.2015.05.004. [Google Scholar] [CrossRef]

41. Zitzler E, Thiele L. Multiobjective evolutionary algorithms a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput. 1999;3(4):257–71. doi:1109/4235.797969. [Google Scholar] [CrossRef]

42. Brandimarte P. Routing and scheduling in a flexible job shop by tabu search. Ann Oper Res. 1993;41:157–83. doi:1007/BF02023073. [Google Scholar] [CrossRef]

43. Cao XZ, Yang ZH. An improved genetic algorithm for dual-resource constrained flexible job shop scheduling. In: Fourth Int Conf Intell Comput Technol Automat. Shenzhen, China; 2011. p. 42–5. doi:1109/ICICTA.2011.18. [Google Scholar] [CrossRef]

44. Yuan MH, Li YD, Zhang LZ, Pei FQ. Research on intelligent workshop resource scheduling method based on improved NSGA-II algorithm. Robot Comput Integr Manuf. 2021;71:102141. doi:1016/j.rcim.2021.102141. [Google Scholar] [CrossRef]