 Open Access
Open Access
REVIEW
Topology, Size, and Shape Optimization in Civil Engineering Structures: A Review
1 Faculty of Civil and Environmental Engineering, Gdansk University of Technology, Gdansk, 80-223, Poland
2 Department of Computer Science, Modeling, Electronics and Systems Engineering, University of Calabria, Cosenza, 87036, Italy
3 Civil Engineering Department, University of Raparin, Rania, 46012, Iraq
4 Civil Engineering Department, Tishk International University, Erbil, 44001, Iraq
* Corresponding Authors: Ahmed Manguri. Email: ,
Computer Modeling in Engineering & Sciences 2025, 142(2), 933-971. https://doi.org/10.32604/cmes.2025.059249
Received 01 October 2024; Accepted 17 December 2024; Issue published 27 January 2025
Abstract
The optimization of civil engineering structures is critical for enhancing structural performance and material efficiency in engineering applications. Structural optimization approaches seek to determine the optimal design, by considering material performance, cost, and structural safety. The design approaches aim to reduce the built environment’s energy use and carbon emissions. This comprehensive review examines optimization techniques, including size, shape, topology, and multi-objective approaches, by integrating these methodologies. The trends and advancements that contribute to developing more efficient, cost-effective, and reliable structural designs were identified. The review also discusses emerging technologies, such as machine learning applications with different optimization techniques. Optimization of truss, frame, tensegrity, reinforced concrete, origami, pantographic, and adaptive structures are covered and discussed. Optimization techniques are explained, including metaheuristics, genetic algorithm, particle swarm, ant-colony, harmony search algorithm, and their applications with mentioned structure types. Linear and non-linear structures, including geometric and material nonlinearity, are distinguished. The role of optimization in active structures, structural design, seismic design, form-finding, and structural control is taken into account, and the most recent techniques and advancements are mentioned.Keywords
Optimization focuses on enhancing performance, and structural optimization involves designing a material assembly to withstand loads as efficiently as possible [1]. The theory of optimization is linked to both natural events and the human desire for a positive outcome [2]. Structural optimization approaches aim to discover the optimal design by balancing structural safety, material performance, and cost [3]. This field is a relatively new discipline with rapidly changing methodologies and focus [4,5]. Structural optimization resulted in a new era in structural engineering [6] since identifying the appropriate solution to a problem is critical for cost efficiency. Reducing weight can significantly lower manufacturing, transportation, and operational costs while enhancing material efficiency [7]. In addition, because the construction industry is a significant contributor to material use, energy usage, greenhouse gas emissions, and waste generation [8], the current design techniques aim to reduce the built environment’s energy consumption and carbon emissions to the lowest practicable level due to increasingly rigorous requirements [9]. Automated design processes that may guide structural design toward lower embodied carbon solutions are becoming more vital [10]. Structural optimization is crucial to lessen the built environment’s carbon footprint in light of the upcoming environmental catastrophe [11]. Minimizing whole-life energy results in adaptable solutions with a lower ecological impact than passive structures [12]. Optimized active structures have the potential to be sustainable as they use less material, consume less energy, and emit less Greenhouse gas GHGs over their lifespans [13].
According to Vanderplaats [2], the first analytical study in structural optimization was by Maxwell [14] and Michell [15]. This research establishes theoretical lower constraints on truss weight, contributing significantly to structural optimization and design. In addition, several studies were conducted to enhance analysis and design techniques by looking at recent advancements in computer analysis, mathematical research, and physical applications. These issues prompted the development of intelligent structures employing these assembly techniques. Using optimization to design structures is a crucial step toward the long-term growth of technology and structural designs [16]. Many design constraints, such as those pertaining to stiffness, frequency, and buckling load, may apply to a structure. Various standards for material deletion must be used based on the types of design constraints [17]. According to Xiao et al. [18], an ideal structural system design may include maximizing a system’s size, shape, or topology. Numerous studies have been conducted to optimize shapes and sizes. However, because of its complexities, topology optimization has received significantly less attention [19]. Size optimization focuses on adjusting the cross-sectional dimensions of structural components to minimize material usage without compromising structural integrity. In contrast, form optimization involves modifying the shapes of structural elements to enhance their performance. Additionally, topology optimization determines the optimal distribution of materials within a given design space.
Structural optimization approaches can be advanced through applications with other structural design and control fields. Research has been done to regulate uniform stress and shape while optimizing structures. Manguri et al. [20] employed interior point optimization with matrix condensation to regulate nodal displacements in pantographic structures. A computational technique was presented [21] for reducing material consumption in designing current spatial frame structures by prestressing only active members, considering shape control. Moreover, Saeed [22] presented an optimization-based technique to control the displacement of nonlinear pin-jointed assemblies. On the other hand, Wang et al. [13] concluded that using many materials can lead to a lighter design that performs better than one composed of a single material. They focused on applying optimization methodologies to multi-material structures because the methodology’s initial focus was on single-material designs. Moreover, a flexible form-finding strategy for tensegrity structures is discussed by Zhang et al. [23], emphasizing the restricted optimization challenge. In addition, Cai et al. [24] provided an optimization-based form-finding technique for regular and irregular tensegrity structures. Meanwhile, Brütting et al. [8] described structural optimization strategies for designing truss structures through reuse. They stated that reusing structural materials reduces waste, saves energy, and lowers the need for new materials. To overcome inefficiency in time-consuming and aesthetic knowledge, Qian et al. [25] introduced a self-sparse generative adversarial network (GAN), guaranteeing over 11% improvement in the Frechet inception distance (FID) score compared to traditional GAN approaches. In another study, Qian et al. [26] proposed That topology description functions enhanced the neural network (TDF-NN) to perform topology optimization 10 times faster than traditional approaches while enabling diverse structural designs for practical applications. In addition, an optimum number of actuators was used [27] to control the shape and buckling of truss structures. Similarly, Reference [28] used optimization in number actuators and actuation to control displacement and stress of truss structures.
Optimization techniques [13] are widely used in structural engineering with various structures and targets, such as truss structures [29–31], tensegrity structures [32–35], frame structures [36–39], reinforced concrete structures [40,41], origami structures [42,43] and pantographic structures [20]. However, there is a lack of review papers that focus on optimization techniques in structural engineering covering different techniques, structures, and applications; for this reason, this paper presents a comprehensive review of structural optimization techniques, including size, shape, topology, and multi-objective approaches and their applications for different types of structures such as truss, frames, and tensegrity. Such an article is essential for evaluating the improvement and widespread adoption of techniques with detailed comparisons in the face of theory and application. It is crucial to highlight how optimization techniques improve efficiency and reduce the environmental impacts of structures. Finally, Recent breakthroughs include using artificial intelligence and machine learning in optimization procedures with future directions covered in this article.
It is essential to emphasize that the literature review for this study was conducted using the highly reputable Web of Science database. This database was selected due to its broad coverage and rigorous selection criteria, ensuring the inclusion of only high-quality research. The review focused on the most recent developments in structural optimization over the past 20 years (2005–2024). A search strategy combining titles, topics, and keywords was applied to achieve a comprehensive and exhaustive collection of relevant studies. The primary search terms included ‘topology,’ ‘size,’ ‘shape,’ ‘optimization,’ ‘truss,’ ‘frame,’ ‘tensegrity,’ and ‘structures.’ Separate searches were performed for each type of structural optimization, using combinations such as ‘topology,’ ‘optimization,’ and ‘structures. Fig. 1 shows the distribution of literature according to years and Fig. 2 presents the correlation map of keywords based on literature that corresponds to topology, size, and shape optimization.
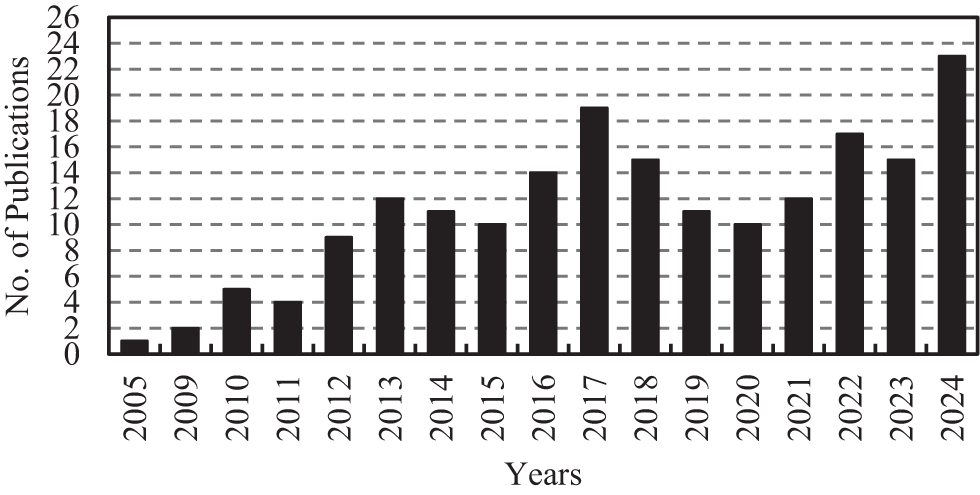
Figure 1: Classification of literature worked on structural optimization according to years
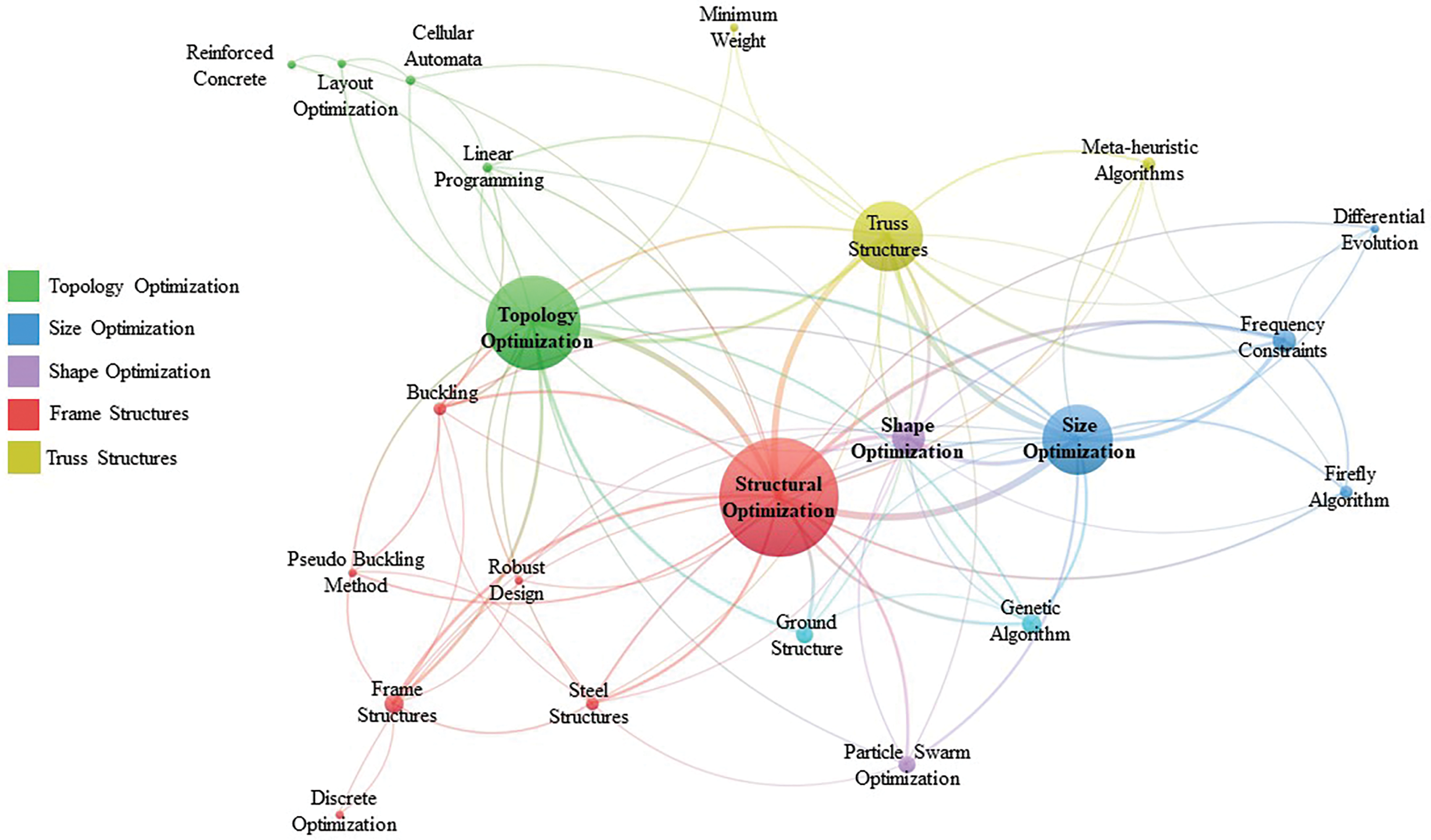
Figure 2: Correlation map of keywords based on literature
A truss is a structural system composed of small components connected at joints, typically at both ends of each member. Common architectural components used in trusses include metal bars, channels, wooden struts, and angles [16,44]. Given the widespread application of these structures, optimizing trusses can significantly influence flexibility, cost, environmental impact, and overall efficiency. This paper reviews various studies that focus on trusses, employing different optimization methods, as shown in Fig. 3. This section discusses the optimization of truss structures using these techniques.
Figure 3: Classification of literature worked on truss structure optimization
Topology optimization finds the optimal material distribution inside a design space. Topology optimization will be critical to provide solutions that increase stiffness and reduce weight without compromising structural functionality. In civil engineering, topology optimization has been used to design structures with the best possible material distribution, making the most use of available space and resources. Two examples of applications include complex support systems and the frames of high-rise buildings. The ground structure technique, developed in the 1960s, significantly enhanced topology optimization [45]. An interesting ground-structure-based representation for truss topology optimization is suggested by Shakya et al. [46]. Before designing the final trusses, the recommended diagram eliminates unnecessary components. Kinematically unstable and nonsensical zero-force components are examples of undesirable components. Also, a new strategy is suggested by Gao et al. [47] to produce ground structures based on primary stress trajectories that can be used in both regular and irregular design domains. The optimization model is a standard linear programming issue based on the plastic design handled by the interior point approach.
Asadpoure et al. [48] offered a method for considering manufacturing costs while optimizing the topology of light, rigid, periodic lattice structures. The regularized Heaviside step function approximates the number of elements in the design domain. Gradient-based optimization is made possible by the smoothness and differentiability of the cost function. The optimization will be more effective and faster when the analytical gradient of the functions is implemented [49]. Moreover, Tyburec et al. [50] offered a creative method for creating truss modules with little compliance through design and fabrication. To handle a variety of optimization challenges, modularity is essential. Besides, genetic algorithms used by Richardson et al. [51] enhance truss-like structures’ topology for both single- and multi-objective uses. The process has two phases: chromosomal repairs and producing stable individuals within the original population. In addition, Asadpoure et al. [52] provided a computational method based on known uncertainty and second-order statistics for optimizing structural topology. The technique combines a perturbation approach based on material characteristics and geometry with deterministic topology optimization to quantify uncertainty in structural stiffness. Similarly, a powerful topology optimization technique with discrete design parameters, material, and loading uncertainties was investigated for truss structures using Non-dominated Sorting GA-II (NSGA-II) by Richardson et al. [53]. The problem is defined by truss length, spatially correlated material stiffness, and load uncertainty. Also, Guo et al. [54] suggested a novel approach to truss-like continuous topology optimization under varying loads. The robust optimization formula minimizes the weighted sum of expectation and standard deviation for structural compliance within volume restrictions. According to this hypothesis, applied loads have independent and unexpected sizes and directions.
Furthermore, Zhang et al. [55] proposed a randomized optimization technique that considerably reduces the computational cost of designing truss and continuum topologies under varying loads. This technology lowers compliance under various load conditions and improves the layered minimum-end compliance topology by integrating density-based techniques with ground structure. On the other hand, Mashayekhi et al. [56] developed a Modified Gravitational Harmony Search Algorithm (MGHSA) that effectively enhances the topology of two- and three-layer grid layouts. The recommended solution worked well with respect to size optimization and topological concerns for double and triple-layer grid layouts. When compared to alternative meta-heuristic methods, MGHSA demonstrated strong competitiveness. While Nwe et al. [57] declared that, given a structural mass, the traditional approach to addressing a truss optimization problem is to minimize linear elastic strain energy. Based on this theory, the ideal solutions might produce thin members prone to buckling or giving way. Cai et al. [58] developed a Nominal Disturbing Force (NDF) technique to handle kinematic instability in the best-in-class truss assemblies. This method combines the ground structure approach with unstable nodes. It is suggested that a mixed-integer linear optimization model be used in conjunction with the NDF technique to reduce the weight of trusses with discontinuous cross-sectional areas. Constraints such as bar buckling, allowed stress, nodal displacement, bar crossing, and overlapping should be considered in this model, as shown in Fig. 4. The figure illustrates the domain (a) and the ground structure (b), considering neither kinematic stability (WNF) nor necessary conditions (WONC) (c). It also shows incorporating the Nominal Disturbing Force (NDF) approach while not considering necessary conditions (WNC) (d) and incorporating the Nominal Lateral Force (NLF) approach while not considering necessary conditions (WNC) (e). The figure also shows employing the Nominal Disturbing Force (NDF) approach without considering necessary conditions (WONC) (f).
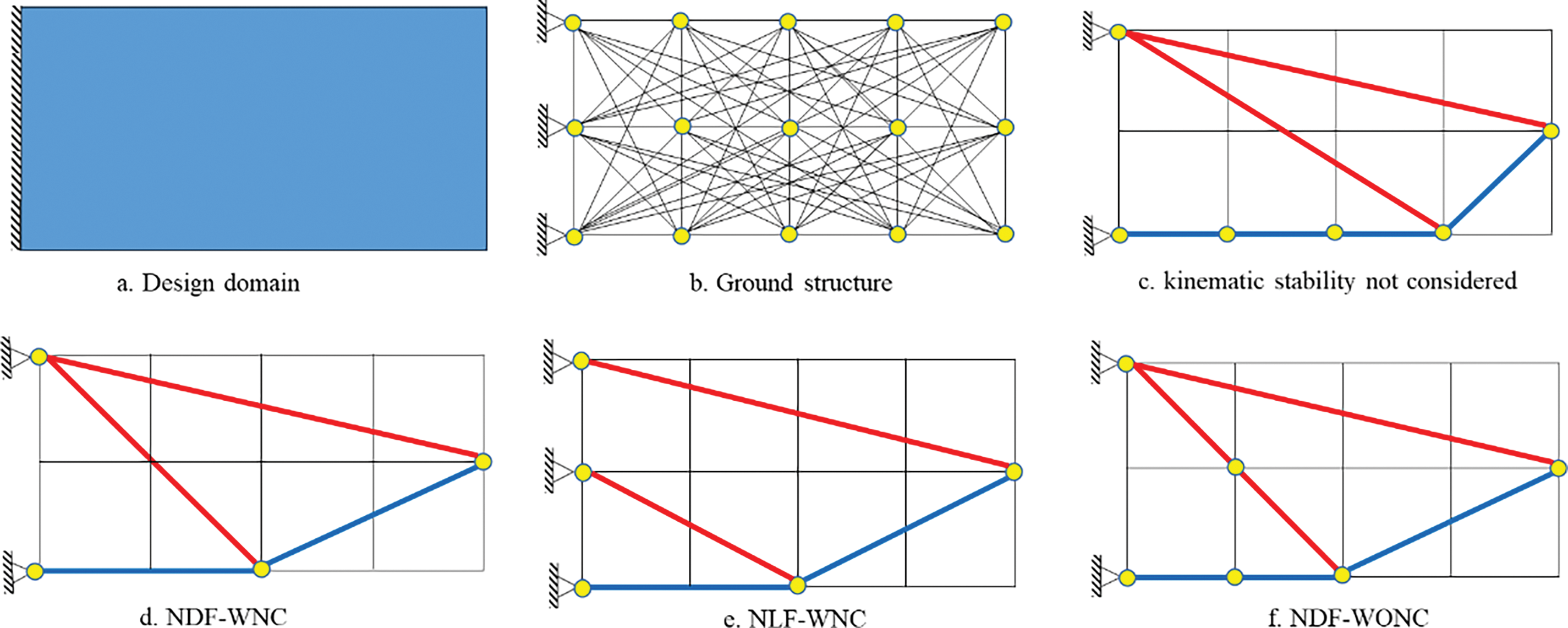
Figure 4: Cantilever beam optimization results (a. Design domain, b. round structure, c. kinematic stability not considered, d. NDF-WNC, e. NLF-WNC, f. NDF-WONC), adapted from [58]
To be optimal for practical applications, truss topologies need to consider both local and nodal buckling stability. Using widely used methods might result in processing that is highly costly or poorly conditioned optimization problems such as concavity; due to that, Cai et al. [59] provided two fundamental techniques: nominal Per Turbine Force (NPF) and acceptable stress iteration (ASI). Numerical examples show that nodal and local buckling stability significantly influence optimum designs. Also, Cai et al. [60] demonstrated that gradient-free Proportional Topology Optimization (PTO) may effectively enhance truss topology, which is considered unpredictable for static and dynamic loads. The objective function is estimated using the Univariate Dimension Reduction method and Gauss-type (UDRG) quadrature and the univariate dimension reduction approach to account for load uncertainty. The topology optimization of truss structures under unknown loads is reduced to a simple deterministic issue by using the UDRG approach. Moreover, He et al. [61] proposed a double-layer optimization (DLO) strategy to address the truss topology problem’s local buckling constraints. This method enables efficient calculation by considering local buckling limits as linear functions of optimized variables. Also, Ching et al. [10] suggested a technique for improving the topology of a two-material truss system to lessen global warming potential. New design variables are developed using the ground structure approach to regulate each truss component’s cross-sectional area and material composition. Moreover, Senatore et al. [62] provided a method for topology optimization of adaptive structures, which was the first of its kind to enable the development of flexible structures by optimizing both structural topology and actuator placement at the same time. This unique technique generates adaptive solutions that significantly outperform passive topology-optimized solutions. The study’s findings extend the domain applicability of flexible structures to design problems when stiffness is not the primary factor. Fig. 5 shows the relationship between actuation and structural topology may enhance solution quality by concurrently changing element size, actuator position, control instructions, and structural topology.
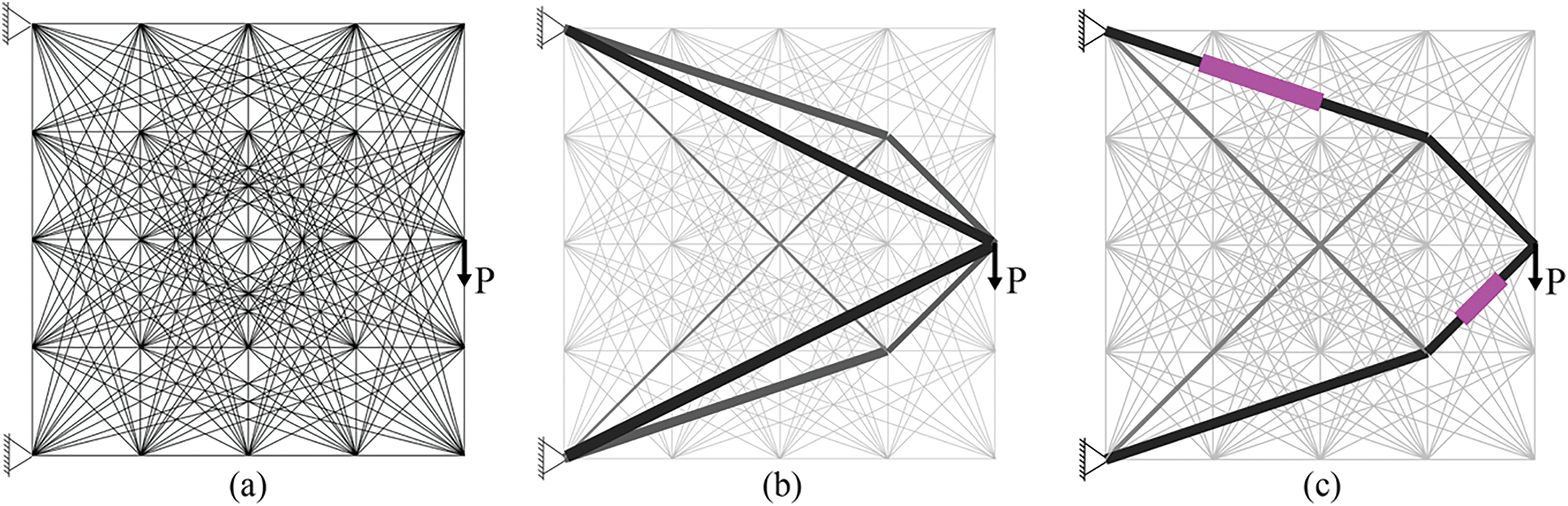
Figure 5: Ground structure (a), traditional (passive) solution (b), and adaptive solution (c) [62]
This subsection focuses on applications of topology optimization on non-linear structures, including geometry and material non-linearity. Descamps et al. [63] proposed a fast and reliable method for optimizing the geometry and topology of truss systems for various load scenarios. Recasting the issue with consistent substitutions can help fix topological and geometric differences. Stragiotti et al. [64] investigated maximum stress, local buckling limits, and volume reduction under various load conditions in 3D truss designs. It depends on the starting position and non-convex due to kinematic compatibility limitations and non-linearities from buckling. The proposed two-step optimization procedure minimizes the effect of the starting point on the optimized structure while solving numerical problems using a heuristic approach. Also, Leng et al. [65] described a new method of truss design optimization that prevents element intersection, as shown in Fig. 6. The intersection factor, element cross-sectional area, and local structural arrangement stability were computed using the Heaviside function and with application of Sequential Quadratic Programming (SQP) to solve the nonlinear optimization problems. Tangaramvong et al. [66] described a mathematical nonlinear programming (NLP) technique for improving the lowest-weight topology of truss-like structures. The process considers the properties of the material that become pliable under pressure and lead to bodily instability. Canelas et al. [67] presented a novel concept for optimizing interior points. This methodology uses failure probability as a direct measure of resilience, in contrast to earlier approaches. Adopting this technique is challenging because of its nonlinearity, nonconvexity, and complexity, which are all well-known issues in reliability-based design optimization. While Li et al. [68] offered a topology optimization technique that considers geometric nonlinearity for prestressed cable-truss constructions. They developed a multi-node cable element model using massive deformation kinematics theory that considers the geometric nonlinearity of prestress and external loads.
Figure 6: An explanation of element intersection in analytical adapted from geometry adapted from [65]
Applications of topology optimization that considered material nonlinearity were taken into account. Research by Fairclough et al. [69] intended to improve the fail-safe truss topology of plastic design. Damage is a moving circular zone with zero strength under the given load situation. New high-resolution criteria for “fail-safe” structure formation have been devised using stiff polymers and global reduction. The study examines how location, damage radius, and structural simplicity affect multi-span trusses, short cantilevers, and square cantilevers. Furthermore, the ground structure approach improves nonlinear topology for hyperelastic materials by including the total potential energy concept into both the target function and the equilibrium solution [70]. Kozłowski et al. [71] have a unique technique that optimizes the geometry and topology of planar trusses without the necessity of a ground structure by using virtual displacements and strain fields. Yang et al. [72] outlined a brand-new fail-safe topology optimization method for systems with many scales. Partial damage is considered in the structural design process both at the macro and micro levels. For fitting challenges, less complex models of partially damaged truss-like microstructures are used to save processing costs. They also concluded that heaviside projection also speeds up convergence and preserves a distinctive configuration. Rozvany et al. [73] examined plastically constructed multi-load, least-volume trusses and their significance in optimally designed trusses. Moreover, Zhang et al. [74] provided a helpful reduced-order modeling-based (ROM) filtering method to optimize two- and three-dimensional truss networks while considering nonlinear constitutive behavior under different load conditions. By optimizing for suitable load levels, the suggested method uses just truss members to create a displacement field devoid of artificial stiffness. Similarly, Zhang et al. [75] proposed an efficient multi-material topology optimization formula that solves structures with material nonlinearity. The proposed formulation, Zhang-Paulino-Ramos (ZPR) accommodates various materials with varying properties, allows for freely specified layers, and offers a generic volume limitation option, as shown in Fig. 7.

Figure 7: Initial material dispersal and the optimal structure for materials that share the whole domain adapted from [75]
In general, gradient-based optimizations are implemented for easy convergence and cost-effectiveness for linear techniques. In addition, GAs are implemented in multi-objective optimization, where strategies such as chromosomal repair and stability enhancement are employed to generate robust solutions through iterative population-based searches. Robust optimization frameworks have been included to handle load-impression uncertainties, using stochastic elements and Monte Carlo simulations to improve structural resilience. The application of advanced meta-heuristic algorithms like the (MGHSA) for non-linear techniques integrates principles from harmony search and gravitational optimization to solve complex, non-convex design problems. Moreover, (SQP) is discussed as an effective solver for handling nonlinear optimization with constraining local buckling regarding neural network applications, examination of architectures that utilize convolutional layers, and transfer learning techniques to optimize structural design processes by leveraging large datasets, enabling improved accuracy and reduced computational overhead.
Studies have demonstrated notable reductions in material usage while accomplishing objectives related to structural performance. Heuristic approaches like genetic algorithms and gradient-based approaches are examples of common methodologies. These approaches ensure both material economy and cost-effectiveness. Constructing lightweight truss bridges, which lower material costs without losing safety, is one well-known use of size optimization. Optimization research was conducted to minimize the weight of space structures by adding extra members in crucial locations [76]. Also, there are applications for using genetic algorithms to design truss structures for minimum weight [77–80]. Moreover, research was conducted to perform size optimization of truss structures using a metaheuristic algorithm [81,82], and by using the method of centers and force formulation [83]. Moreover, Kaveh et al. [30,84], presented optimization techniques for size optimization for truss structures using a swarm-based algorithm. While Kaveh et al. [85] presented a Hybrid Big Bang–Big Crunch (HBB–BC) optimization algorithm based on the Big Bang and Big Crunch hypothesis (BB-BC) to solve the truss optimization issue. One of the primary reasons why the size optimization problem was investigated more frequently than shape optimization, also known as geometry optimization in this context, was that it might occasionally be described as a linear programming problem [86].
Cheng et al. [87] described a novel use of the Harmony Search (HS) method. The hybrid harmonic search (HHS) technique replaces the randomization function with the global-best particle swarm optimization (PSO) and neighborhood search, maintaining the harmonic memory and pitch adjustment features of the HS algorithm. Furthermore, a new linear method is proposed to find the optimal weight arrangement for trussed structures subjected to self-weight and external loads [88]. The cross-sectional areas of the members are design variables. The force method determines inequality limits since isostatic structures require maximum and lowest axial stress. Moreover, Quyen et al. [89] provided a unique technique for optimizing truss size using the finite element approach. The purpose of truss weight reduction was achieved. Constraint criteria were developed to ensure the building conformed with equilibrium equations and standards for strength, stiffness, and compatibility. On the other hand, A novel and efficient method by combining border-search operator (BSO) and jump operator (JO) for optimizing spatial trusses has been created by Dizangian et al. [90]. First, an efficient random technique is used to find the global optimal point. Next, the initial local optimal point is discovered using a sensitivity-based technique to complete a series of evaluations.
An enhanced variant of the colliding bodies optimization (CBO) method, ECBO, is proposed by Kaveh et al. [91] to address problems such as delayed convergence and entrapment in local minima. Introducing chaos into metaheuristic algorithms is an effective way to improve their performance. Moreover, Flager et al. [92] examined the Fully Constrained Design (FCD) method for discrete component optimization in steel truss and frame systems. In contrast to other deterministic approaches, FCD does not need the first derivative of the goal and constraint functions in terms of design variables. A separate study uses an altered Heat Transfer Search Algorithm (HTS) version to improve truss designs [93]. Sizing optimization aims to reduce a structure’s weight while considering stress and displacement constraints. Another paper by Degertekin [94] presented two harmony search optimization techniques (EHS and SAHS) that perform better in robustness and convergence than traditional HS. It put the new methods for optimizing truss construction size to the test. Additionally, the newly created Marine Predators Algorithm (MPA) is used for the first time to improve the design of truss structures by Bodalal et al. [95]. Finally, because of its excellent performance and small number of performance factors, MPA is a reliable optimization metaheuristic for truss sizing issues.
Modified Simulated Annealing Algorithm (MSAA) is used by Millán-Páramo [96] to optimize the weight of truss structures with discrete size variables. MSSA is a more sophisticated version of the simulated annealing (SA) method. Moreover, Manguri et al. [97] described a new computing method that, when combined with the conventional force method, finds the optimal number of actuators to minimize the cost of producing the cross-sectional area of assemblies made up of pin-jointed structures. According to their findings, the most active members were chosen for prestressing to control the internal force of high-stress bars and distribute stress evenly throughout the structure. Because of the reduced stress in critical sections, the designers were able to employ smaller cross-sectional areas than before. The optimized results of their work are presented in Fig. 8. Furthermore, The objective of Sawada et al. [98] is to improve the accuracy ratio and convergence for the minimum-weight optimization of a discrete truss design by combining the unique randomized line search approach with GA. Another study [99] described a novel, ranked-based method for optimizing structure size. This approach uses violation-based sensitivity analysis and the borderline adaptive sliding technique (ViS-BLAST) on the feasible non-feasible (FNF) design space boundary.

Figure 8: The distorted shape of the standard and optimized 20-bar truss and the original structure’s shape [97]
Alkhraisat et al. [100] introduced the GWOM, a modified version of the grey wolf optimizer (GWO). The application of both discrete and continuous design factors optimizes the sizes of truss structures. The results show that mutation operators are successfully included in the GWO architecture to enhance exploration and exploitation capabilities while preventing local optima from becoming imprisoned. Moreover, Baghlani et al. [101] offered a teaching-learning-based optimization (TLBO) approach used to optimize the size of truss structures while addressing constraints efficiently. This method greatly enhanced the search for the perfect structure. The proposed technique can provide totally viable optimal designs. The resilience and quality of the solution are determined by the optimized structure’s geometry shown in Fig. 9, TLBO MS outperforms the other two variants, with TLBO-PF (penalty function) coming in second, then fly-back mechanism (TLBO-FB), as the results are shown graphically in Fig. 10. The study’s conclusions also show the success of the recommended TLBO-MS algorithm compared to other metaheuristic optimization methods.
Figure 9: 25-bar spatial truss structure [101]
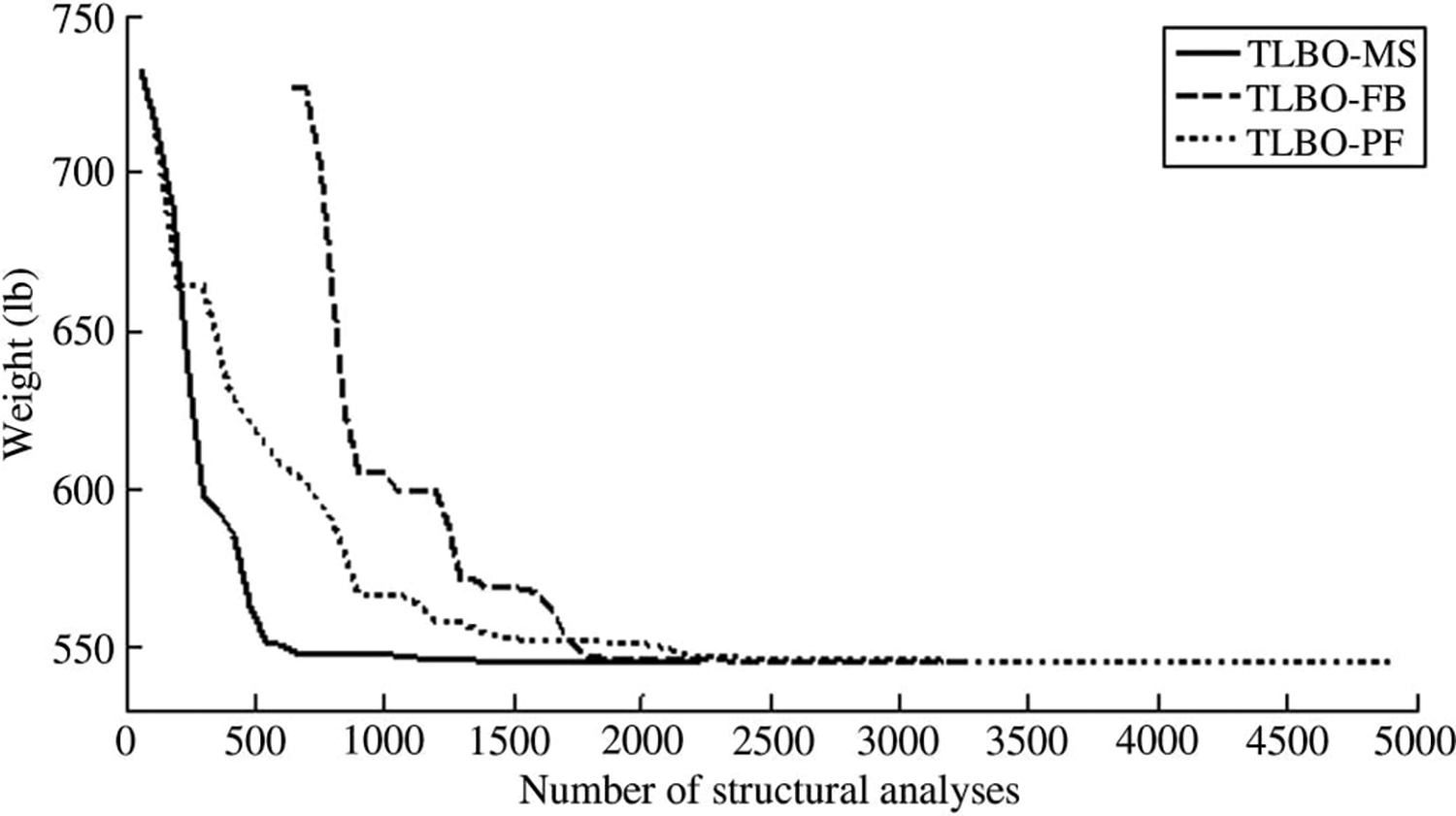
Figure 10: A comparison of the 25-bar spatial truss structure’s TLBO variants’ rates of convergence [101]
Since it is essential to optimize and manage natural frequencies in structures and prevent resonance, the computation of truss structure natural frequencies in various moods based on weight reduction has been highlighted in research by Joubari et al. [102] and stated that It’s not always the best course of action to optimize solely based on weight in several buildings that have sustained substantial damage from wind, earthquakes, or storms. Weight loss and natural frequency improvement have garnered much attention lately. The newly developed flower pollination algorithm lightens the truss framework’s load by Bekdaş et al. [103], considers the varied size of the design as well. The novel algorithm, which draws inspiration from the process of plants self-pollinating and cross-pollinating, has the potential to combine local and global searches efficiently. A novel approach to weight optimization of truss structures using continuous variables that is straightforward was presented by Kooshkbaghi et al. [104]. The artificial coronary circulation system algorithm (ACCS), a relatively recent metaheuristic method, improves the size of truss structures. The optical center point of populations is used in all iterations of the ACCS optimization technique. Degertekin et al. [105] optimized truss structures using a cutting-edge meta-heuristic search approach known as “teaching-learning-based optimization” (TLBO). The method makes connections between how optimization issues are solved and how students learn. Eleven additional well-known and strong solvers, as well as a discrete optimizer, called the Soccer League Competition (SLC) approach., have also been used in the search for a reliable and effective technique for optimizing truss designs are examined by Moosavian et al. [106] and statistical analysis is performed for them. Furthermore, optimization of the size of large-scale dome structures under dynamic restrictions is presented in [107]; the smallest size of design variables is discovered in the optimum design of these structures utilizing the Jaya approach. The design variables are the cross-sectional areas of the steel truss bar components.
Over the past 20 years, structural optimization problems have grown more difficult due to their severely non-linear design restrictions and complicated solution domains. This has prompted the creation and use of several cutting-edge metaheuristic algorithms [108]. Within the context of structural optimization, Awad [108] has used the recently announced political optimizer (PO) technique. To find the best balance between exploration and exploitation, the algorithm should split the search agents into political parties vying for control of seats (electoral districts). This strategy is based on the multiphase political framework prevalent in parliamentary democracies. Khatibinia et al. [109] resulted in the acceleration of the pace of convergence of the gravitational search algorithm (GSA) and the creation of the accelerated multi-gravitational search algorithm (AMGSA). Combining the breeder genetic algorithm (BGA) operator mutation and simplex crossover (SPX) the multi-gravitational search algorithm (MGSA) produces AMGSA, an algorithm with a high exploration-exploitation balance. Moreover, by Pham et al. [110] metaheuristic techniques were applied to provide a computationally efficient solution to the discrete variable truss problem. This new technique is called “k-nearest neighbor comparison,” or simply “k-NNC”. The k-NNC determines the value of a new design by comparing it to the k-closest designs (k-nearest neighbors) of an existing design in the population. In addition, Farshi et al. [83] presented a novel method for creating truss constructions with the least weight possible. The force notion is included in a center-point optimization algorithm. The design variables are the member cross-sectional areas and redundant forces measured for each loading scenario the structure encounters. The optimization method employs the greatest hyperspheres within the available space.
To sum-up, several hybrid optimization algorithms were introduced for size optimization and linear approaches, such as the (HHS), which combines elements from (PSO) to promote global search efficiency while maintaining the benefits of harmonic memory. Additionally, enhanced variants of metaheuristic methods like the (ECBO) utilize chaos theory to prevent entrapment in local optima. These modifications address common challenges in optimization, like slow convergence and local minima issues. For nonlinear approaches, cutting-edge algorithms like the Political Optimizer were included, which simulates the dynamics of political parties to balance exploration and exploitation phases, and the (AMGSA), which integrates genetic mutation and crossover techniques to enhance convergence speed. Furthermore, techniques such as (k-NNC) optimize discrete variable truss designs by leveraging proximity-based evaluations to guide the search process.
2.3 Topology and Size Optimization
Truss structure topology and size may be simultaneously optimized with the help of a probability-based regulating method provided by Mortazavi [111]. To minimize the number of ineffective repetitions, the suggested method focuses on topology or size action. It uses the Boolean characteristics of the topological variables to forecast the search algorithm’s behavior. In their paper, Faramarzi et al. [112] proposed a two-step procedure for size and topology optimization of two-dimensional truss designs. The topology problem was replaced with an appropriate size optimization problem to find the optimal truss topology. To preserve the topology found in the first phase, the optimal truss size has to be ascertained in the second. This presented a fresh difficulty for size optimization. Furthermore, Kaveh et al. [113] suggested a two-step process for optimizing two-dimensional truss designs regarding size and topology. A suitable size optimization problem was substituted for the topology issue to determine the ideal truss topology. The ideal truss size must be determined in the second phase to maintain the topology discovered in the first. This introduced a new level of difficulty to size optimization. Ali et al. [114] examined a combined strategy to increase the size and topology of structures under active management. A domain for the structure, load application sites, and support locations must be determined to attain the optimal structural topology. The optimal topology is reached by lowering the strain energy. Control system scaling and optimization are done iteratively once the optimal design has been determined. According to Brütting et al. [115], a formulation is provided for optimizing the size and topology of truss structures under stress and displacement constraints using mixed-integer linear programming (MILP) problems.
Assimi et al. [116] present a multi-objective genetic programming (GP) technique to optimize the topology and size of the truss. The aim is to find the optimal cross-sectional areas and connectivity between the nodes, subject to constraints like nodal deflections, maximum allowable stress in members, and kinematic stability, to arrive at a set of trade-off solutions that satisfy all optimization objective functions. Similarly, Su et al. [117] optimized the size and topology of the truss structure with a genetic algorithm. Individual identification and sparse node matrix encoding can save processing time by reducing pointless structural analysis. Furthermore, an adaptive multi-island search strategy for multi-objective optimization problem (AMISS-MOP) is developed to enhance the dissemination and convergence of non-dominated optimal solutions for multi-objective optimization problems. On the other hand, Kumar et al. [118] employed a discrete meta-heuristic (MH) technique to optimize the size and topology, thereby enhancing truss design performance. Heat transfer search (HTS), ant lion optimization (ALO), whale optimization (WOA), dragonfly algorithm (DA), and teaching–learning–based optimization (TLBO) are the five basic machine learning algorithms that are being studied. Also, the size and topological optimization of the truss structure was done by Lee et al. [119], QbHS (Quantum-based Harmony Search) is a recently suggested methodology combining classical HS (Harmony Search) approaches with quantum computing. In addition, by figuring out the best joint connectivity and cross-sectional areas, Assimi et al. [79] aimed to reduce the weight of the search space. For the structural optimization problem, the maximum allowable stress, deflection, and kinematic stability are utilized. This approach determines the optimal response by letting computer programs emerge from a variable-length representation of potential responses. Zhong et al. [120] provided the cooperative coevolutionary genetic algorithm with independent ground structures (CCGA-IGS) for simultaneously optimizing the topology and size of discrete structures.
In addition, Mortazavi [121] confirmed that the interactive fuzzy search algorithm (IFSA) can search for structural optimization problems and demonstrated the limitations of this class of optimization problems, including various natural frequencies. Furthermore, the structural dimensions and layout considerations are taken into consideration separately. Moreover, The Shuffled Shepherd Optimization algorithm (SSOA), a recently created meta-heuristic algorithm, was explored by Kaveh et al. [122] for its potential in structural layout optimization. Also, Jawad et al. [123] described a technique to optimize the combined size-layout of planar and spatial truss systems using a simulated bee colony. The Artificial Bee Colony algorithm (ABC) seeks to compete with honey bees’ intricate foraging techniques. The design variables of form optimization for the truss structure system are the joints’ nodal coordinates and the members’ cross-sectional areas.
To optimize the weight of truss constructions, an inventive, non-uniform cellular automated technique was introduced by El Bouzouiki et al. [124]. The method was evaluated on several benchmarking issues. The suggested approach (see Fig. 11) was quicker than previous techniques, but the results indicated it was still relatively competitive regarding structural weight. Moreover, the effectiveness of the proposed technique may be further enhanced by using the parallelism property of the Cellular Automata (CA) methods, which makes them ideal for resolving large-scale structure optimization problems. On the other hand, Moghaddam et al. [125] developed a practical plan that minimizes seismic damage to nonlinear truss-like structures while optimizing their size and topology. The approach explains a large percentage of the variability in ground motion. This is accomplished by closely evaluating each member’s Mean Annual Frequency of Exceedance (MAFE) in light of the relationships displayed and the results of the nonlinear analysis. The outcomes showed that the topology of the final structures and the cross-sectional values of the components are independent of the initial design and that the ultimate optimal design is constant throughout a range of beginning cross-sections.
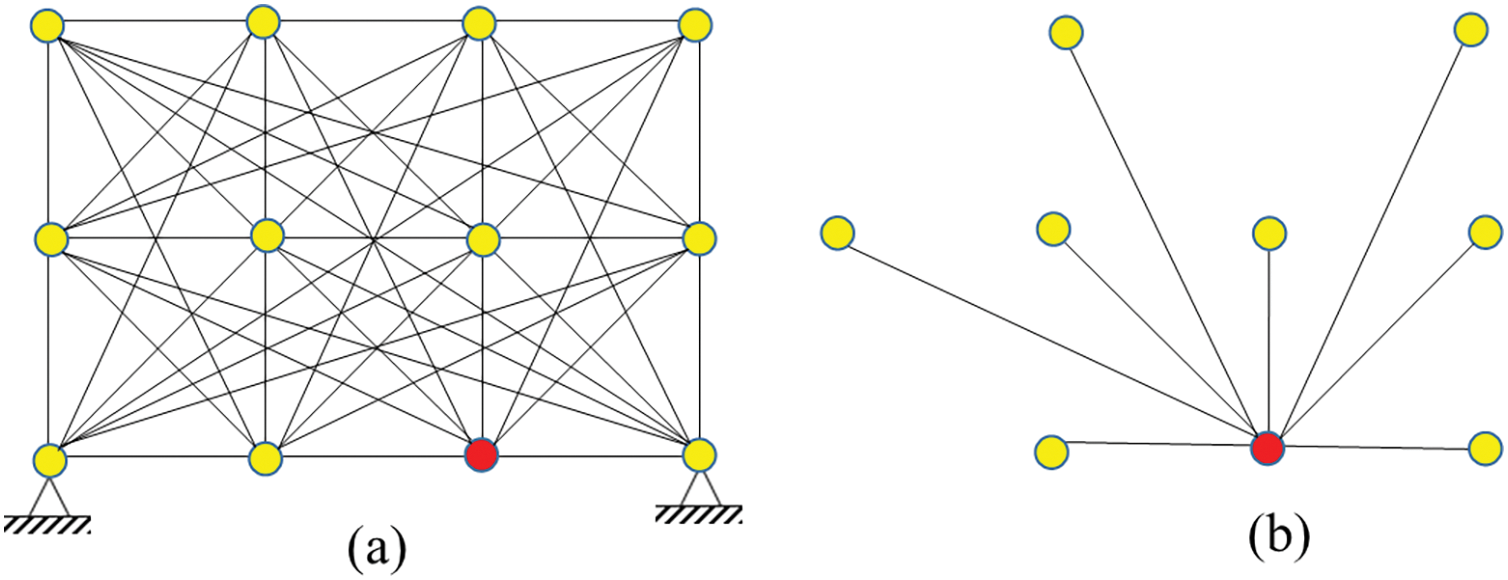
Figure 11: The representations of (a) Two-dimensional truss construction with non-uniform CA representation, and (b) the non-unform unit cell on the border adapted from [124]
Moreover, Avcı et al. [126] showed the effectiveness of the Improved Stochastic Ranking Evolution Strategy (ISRES) method for optimizing the size and design of benchmark truss structures. The results show how effectively the algorithm converges to optimal solutions, lowering the weight of the truss and satisfying complex design specifications. In addition, the electromagnetism-like mechanism algorithm and migration strategy (EM–MS) hybrid optimization approach is presented by Hosseinzadeh et al. [127]. The EM approach optimizes size in truss structure designs, and the migration strategy incorporates frequency constraints. Using the modified EM algorithm as a global optimizer, the hybrid approach under discussion guides the particles toward the region of the global optimum in the optimization problem’s solution space, and depending on this migration method, the particles can more quickly and efficiently explore their search zone. Kaveh et al. [128] provided an updated version of the spiral optimization algorithm (SPO) that maximizes the shapes and sizes of truss structures while accounting for different frequency constraints. One such technique is the hypotrochoid spiral optimization algorithm (HSPO), which has been proposed. To improve the accuracy of the results and the method’s capacity to break out of local optima, it reorganizes the search point movement operation and uses various tactics. Furthermore, The optimization of truss structure dimensions and arrangement is assessed using the newly developed Improved Vibrating Particles System (IVPS) method, which is an improved version of the VPS metaheuristic algorithm by Kaveh et al. [129]. The new technique almost always yielded results that were comparable, if not superior to, the best findings from its earlier complex algorithms. While Mortazavi et al. [130] examined how well the new particle swarm optimizer, called the integrated particle swarm optimization technique (iPSO), blends the improved fly-back mechanism with the weighted particle concept works.
Researchers used the probability space with boolean variables for linear approaches to improve the search and limit unnecessary iterations in complete optimization processes. Hybrid forms such as the (QbHS) incorporate the principles of optimization and quantum computing, enhancing the convergence and accuracy of the solution. Mixed techniques were also incorporated, and MILP and multi-objective genetic algorithms were used to improve topology and size while satisfying some constraints like nodal deflections, stress limits, and structural stability. For non-linear approaches, the most recent enhancements of meta-heuristic algorithms were underscored, which attempt to resolve the challenges related to the non-linear design space. For instance, the HSPO and IVPS algorithms employed near search dynamics to assist the HS takeover during local optima entrapment. Also, the iPSOM method employs weighted particles with a fly-back mechanism to solve optimization problems for structures’ dimensions and topology. These advanced algorithms allow for a balanced exploitation-exploration process, which is of utmost importance, especially for natural frequencies or dynamic loading conditions constrained designs. Incorporation of Cellular Automata, for instance, is a parallel method whereby optimization processes of large truss structures are made faster.
2.4 Shape and Size Optimization
The innovative bi-level hierarchical technique for optimizing member size and shape in both determinate and indeterminate truss systems is described by Flager et al. [131]. The method employs a novel algorithmic hierarchy: to optimize discrete sizing. The Fully Constrained Design (FCD) approach is paired with SEQOPT, a gradient-based optimization tool for continuous form variables. Lopez et al. [132] provided a unique way to enhance truss structure design while considering shape and size based on worldwide dependability. Response surface approximation, global optimization with the firefly approach, and global constraint formulation are used for reliability analysis. Also, using a job search-inspired (JSI) methodology and genetic operators of mutation, selection, and crossover, Serpik [133] proposed a meta-heuristic technique for the discrete optimization of truss size and form. Furthermore, an iterative approach to concurrently solve a size and form optimization sub-problem, subject to local stress constraints and Euler buckling, was proposed by Schwarz et al. [134] using Sequential Linear Programming (SLP).
To adhere to the SLP problem statement, a first-order Taylor expansion for the nodal movement and the buckling constraint is created. Cao et al. [135] stated that particle swarm optimization (EPSO) provided a better way to increase the size and form of truss constructions. The proposed EPSO combines partial swarm optimization (PSO) with a particle classification mechanism to reduce the need for extra structural studies throughout the optimization process while also increasing the computing efficiency of PSO-based structural optimization. To tackle the problem of early convergence in the traditional methods, Li et al. [136] proposed a novel PSO and integrated a structural design form optimization technique. Hosseini et al. [137] presented an approach to multi-objective optimization and asserted that, according to the statistics, the Multi-Objective Particle Swarm Optimization (MOPSO) technique generated more accurate answers. Moreover, the optimization of the size and form of truss structures is achieved by applying a recently developed method called ray optimization (RO) by Kaveh et al. [138]. Their optimization strategy aims to reduce the truss weight within the required bounds. SeyedOskouei et al. [139] used an advanced metaheuristic approach to deliver the optimum truss structural design. Using the Artificial Rabbit Optimization (ARO) approach, the algorithm’s principal search loop considers rabbits’ natural survival techniques, such as detour foraging and random hiding. The optimization of size and shape for several large-scale truss structures is investigated by Azizi et al. [140]. It uses the recently developed metaheuristic optimization method known as Chaos Game Optimization (CGO).
Optimizing the size and shape of truss structures is a complex task due to its NP-hard nature, highly nonlinear design constraints, and conflicting design variables [141]. The nonlinear relationship between nodal coordinates and cross-sectional areas further complicates optimization, particularly for large-scale truss structures. A costly optimization engineering challenge arises when the shape and bar size variables are connected, resulting in a multi-modal search space with dynamic limits [142]. Lieu et al. [143] gave rise to the Adaptive Hybrid Evolutionary Firefly Algorithm (AHEFA), which considers a range of frequency restrictions and optimizes the size and form of truss structures. The Differential Evolution (DE) and Firefly Algorithms (FA) are combined in this strategy. Moreover, Roulette Wheels Selection-elitist-Differential Evolution (RWeDE), an improved version of DE, was proposed by Ho-Huu et al. [144]. The proposed approach is a specific form of the DE algorithm with two modifications. Initially, rather than employing random selection, a Modified Roulette Wheel Selection (MRWS) with stochastic acceptance is utilized to choose members for the mutation phase. Also, Venkatesh Varma et al. [145] offered a comprehensive method for maximizing truss system size and shape while considering buckling limitations. The Change of Measure-Based Evolutionary Optimization (COMBEO) method, which manages complicated inequality constraints without violating them, is enhanced by this study.
The suggested approach uses a forward model to prevent buckling and capture the structure’s geometric nonlinear reactions. Jalili et al. [146] developed the Chaotic Biogeography-Based Optimization (CBBO) algorithm, which effectively optimizes by utilizing a combination of chaos theory and biogeography-based optimization (BBO). Huynh Van et al. [147] recommended the use of Gaussian Local Search (GLS) in combination with Enhanced Comprehensive Learning Particle Swarm Optimization (ECLPSO) to maximize the size and form of truss structures while respecting design constraints. On the other hand, Ma et al. [148] offered a technique for employing subset simulation to optimize size and shape design for discrete and continuous variables. A special adaptive conditional sampling technique is used to generate fresh conditional samples in addition to the component-wise Metropolis-Hasting approach. Furthermore, Bodalal [141] introduced an innovative human-based metaheuristic method for truss structural configuration optimization called the Heap-Based Optimizer (HBO). Search agents are logically structured into hierarchies based on their fitness ratings, similar to the Corporate Rank Hierarchy (CRH) concept. Fig. 12 illustrates the application of Bodalal [141]. Moreover, Seyed Taheri et al. [149] used the Enhanced Biogeography-Based Optimization (EBBO) method to optimize the form and dimensions of the truss system while respecting its intrinsic frequency constraints. Additionally, a completely new strategy was described by Ahrari et al. [150] that optimizes truss structures’ size and form simultaneously. A software known as the Fully Stressed Design (FSD) Evolution Strategy (FSD-ES) combines evolutionary algorithms’ wide global search capabilities with the well-known deterministic approach to entirely stressed design. In addition, a newly proposed metaheuristic method is suggested by Farshchin et al. [151] for optimization issues, including size, shape, and frequency restrictions.
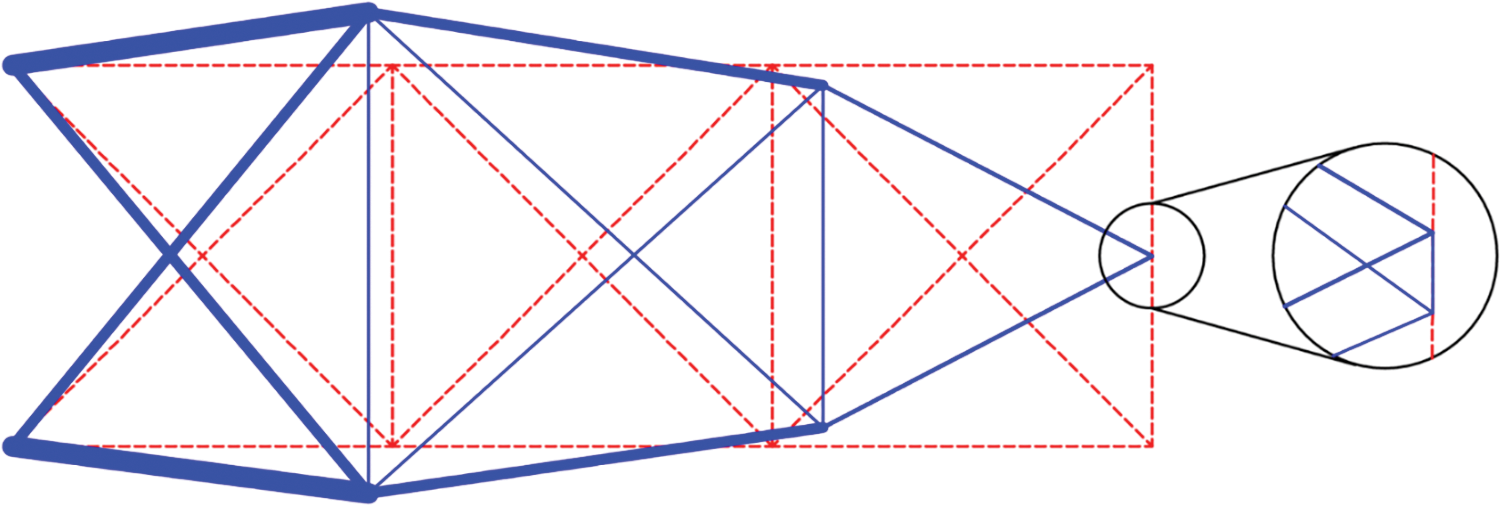
Figure 12: A. The best configuration for the 15-bar truss, B. detailed zoomed in for nodes 4 and 8 adapted from [141]
These optimization issues are thought to be very non-convex and non-linear. The suggested solution expands on using a single optimization process by utilizing many cooperative optimization processes. Moreover, for the first time, Miguel et al. [152] employed two of the most sophisticated metaheuristic algorithms developed in the last ten years, Harmony Search (HS) and Firefly Algorithm (FA), to optimize truss size and design under a variety of natural frequency limitations. However, the hybrid sine cosine firefly algorithm (HSCFA) is recommended to get better results with less finite element analysis. Meanwhile, to get better results with less finite element analysis, the Hybrid Sine Cosine Firefly Algorithm (HSCFA) is recommended by Tao et al. [153]. The Firefly Algorithm (FA) is analyzed, and the factors affecting its precision and computational effectiveness are revealed. Additionally, Teaching-Learning-Based Optimization (TLBO), a recently created methodology, was employed by Baghlani et al. [154].
Within the class of linear techniques, one such method is bi-level hierarchical optimization presented, wherein the fully constrained design is combined with SEQOPT to optimize both discrete and continuous variables. Other advanced meta-heuristics like (EPSO), (ARO), and (CGO) have further advanced the field by effectively searching much larger complex design spaces because of their classification mechanisms, natural survival strategies, and the principles of chaos, respectively. Within the non-linear optimization approaches, AHEFA and RWeDE combine evolutionary and swarm intelligence approaches to mitigate nonlinearity and achieve faster convergence with constraints. Likewise, (HBO) also adopts a hierarchical ranking model, while (TLBO) mimics learning processes to increase effectiveness in truss model exploration. Altogether, these techniques utilize a range of optimization functions and critical dimensions relevant to the design of trusses shapes and sizes.
2.5 Topology, Size, and Shape Optimization
Size, form, and topology are the three main categories structural optimization often falls into. In the past few decades, much work has gone into establishing methods for optimizing structures considering one or more of these aspects [155]. The most efficient truss optimization strategy takes topology, shape, and size (TSS) into account [156]. Dehghani et al. [157] introduced the future hybrid meta-heuristic algorithm CA-ICEA. The Imperialist Competitive Algorithm (ICA) was improved by the use of the Dolphin Echolocation algorithm (DE) and the Cellular Automata (CA) approach. The truss system’s size, topology, and layout were optimized using the suggested manner. The numerical results of the solved instance demonstrated the computational advantages of using the CA-ICEA approach to determine the best topology of large-scale skeletal systems. Degertekin et al. [158] provided an improved iteration of the Jaya Approach (JA) for optimizing discrete truss structures, taking into account topology, size, and placement. Discrete Advanced JA (DAJA) is a unique approach that generates a sequence of descending pathways around each candidate design to boost the population. In Miguel et al. [159], the Firefly Algorithm (FA) was used to optimize the truss structure’s topology, size, and shape simultaneously. The findings indicate that mixed variable optimization problems, a prevalent situation for these problems, are particularly well-suited to the technique. Potentially produce outcomes better than or equivalent to those reported in the literature of their paper, all at a reduced computing cost. Moreover, the integrated Particle Swarm Optimizer (iPSO) was suggested by Mortazavi et al. [160] as a way to optimize truss structures.
To solve simultaneous structural optimization issues, the iPSO effectively integrates the best aspects of the fly-back approach, weighted particle definition, and classic PSO into a single effective solution. Additionally, Carvalho et al. [161] examined fresh structural optimization problems using Generalized Differential Evolution 3 (GDE3) and presented some surprising but exciting results. Trade-off curves depict the number of unique cross-sectional areas employed in the solutions in relation to the ideal weights. The Jaya Algorithm (JA), a metaheuristic technique, is used by Degertekin et al. [162] to maximize the size and placement of truss structures. The outcomes demonstrate that JA can produce superior designs than other cutting-edge gradient-based and metaheuristic optimization techniques. In comparison, Tejani et al. [163] modified optimization using a framework for teaching and learning. To evaluate the efficacy of TLBO (MTLBO), it is utilized to simultaneously optimize the topology, form, and size of space and planar trusses. Stress, displacement, kinematic stability constraints, and discrete and continuous design factors are present in every benchmark challenge.
There are also nonlinear analysis applications in optimizing truss structures in this form. Souza et al. [164] provided a generic technique for optimizing transmission line tower topology, size, and shape. Stripped bracing may be readily incorporated using the recommended method. In every case studied, staggered bracing was shown to be the optimal design. The results show that the recommended strategy has much potential, but further research is still required. El Bouzouiki et al. [165] offered a bi-level non-uniform Cellular Automata (CA) method that may be employed to resolve the minimal weight optimization problem for truss designs in the case of stress and displacement constraints. Regarding the algorithms in this subsection, CA-ICEA outperformed the Imperialist Competitive Algorithm and Dolphin Echolocation and Cellular Automata for truss structure optimization. In another study, the Discrete Advanced Jaya Approach appears to improve the iteration process of the design candidate’s development to improve truss topology, design optimization, and size. As for trusses and related structures, researchers employed the Firefly Algorithm to optimize engineering structures with mixed variables. At the same time, another group of researchers integrated Particle Swarm Optimiser used PSO with combinations of weighted parameters to perform optimal topology, shape, and size optimization. For the nonlinear case, a bi-level Cellular Automata approach was used to optimize designs with a minimal weight that conforms to stresses and displacements. In addition, the details of most literature references about trusses and solvers are tabulated in Table 1.
A basic frame structure consists of joints and beams that are built to sustain specific loads [166]. Like truss structures, optimization is vital in designing frames, especially in lightweight frames and steel sections. In this part of the review, the different optimizations are focused on as classified in Fig. 13.
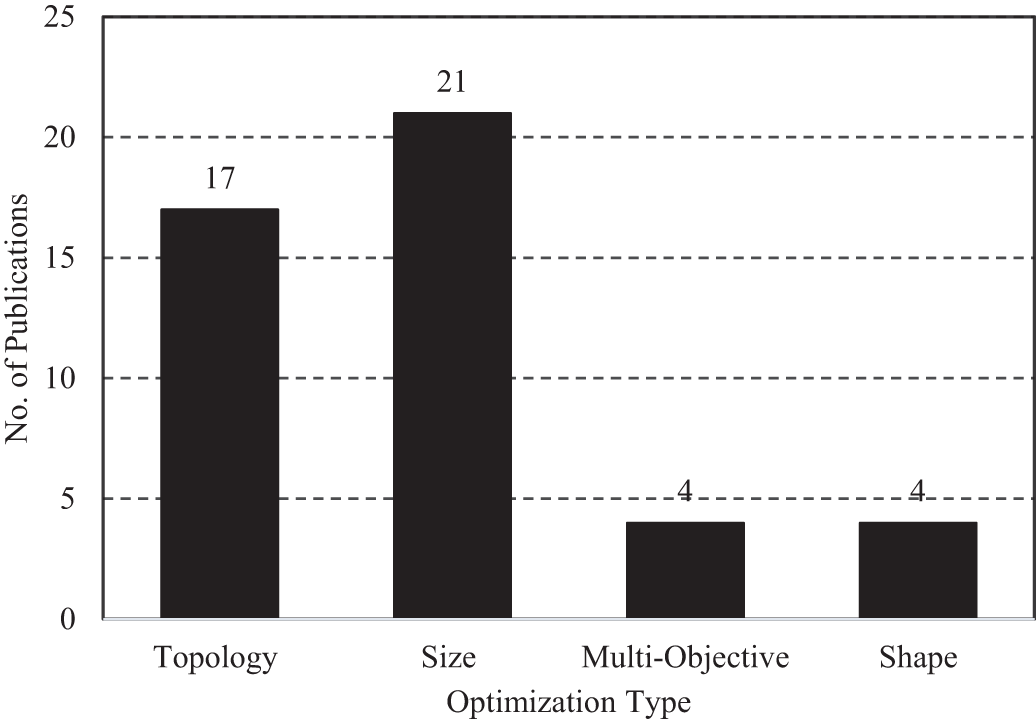
Figure 13: Classification of literature worked on frame structure optimization
Fu et al. [167] suggested a method to optimize the topology, materials, and beam types of complex structures made up of shells, bars, beams, or combinations of these; the extended ground structure is the basis for the optimization problem and is made up of different components or cross-sectional beams with other materials at each location. Kaveh et al. [36] demonstrated the process of utilizing Improved Ant Colony Optimization (IACO) to create planar steel structures. The process is divided into two stages: local search and global search. The findings demonstrate a considerable reduction in the computation time required for the improvement.
A periodic spaceframe structure is intended by Lim et al. [37] to maintain the highest torsional and flexural rigidities while maintaining the maximum mass. Once the spaceframe has been parametrized using its component unit cells, its shape, topology, and size as a generic structure should be optimized using multi-objective Genetic Algorithm (GA) (MOGA) optimization. Moreover, a performance-based optimum seismic design for frame structures is demonstrated by Kaveh et al. [168] using the Ant Colony Optimization (ACO) technique. A nonlinear analysis utilizing a basic computer-based push-over approach that considers first-order elastic and second-order geometric stiffness characteristics determines the structural response at different seismic performance levels. Yamada et al. [169] gave frequency limitations, and suggested a method that offers a locally optimum solution for frame topology optimization. The approach uses a nonlinear programming methodology to gradually reduce the relaxation value and solve a relaxation problem. For frame systems with unexpected geometric or material properties, a resilient topology optimization strategy is proposed in [170]. Based on a comparison of the resilient designs, the final designs exhibit greater load variety under both sources of uncertainty than deterministic designs. Also, Ahmadi et al. [171] offered a strategy for optimizing the topology of skeletal constructions with deficient structural components, even when the members are not perfectly straight. In addition, in [172], seismic analysis was performed on steel frame structures with brace configurations using topology optimization and a truss-like material model. The truss-like components in the first topology optimization design domain were chosen to match the original steel frame construction, establishing the first truss-like continuity.
In the face of geometric uncertainty, Changizi et al. [173] developed a practical stress-based topology optimization approach for frame systems. The suggested approach makes minimum assumptions about the lengths of the frame members and propagates uncertainty up to the response level defined as the highest anticipated value of von Mises stresses throughout the domain using the stochastic perturbation technique. Furthermore, the stress-based topology optimization method for steel frame structures with cross-sectional properties mapped from I-beam sections of a design manual is described in Changizi et al. [38] in a computationally efficient manner. Two methods were suggested to enhance frame gradient-based topology optimization. The structural design was initially based on actual data for components that were manufactured in factories. The significant variance in the data set was explained using quantile regression, which was also used to quantify the moment of inertia and other cross-sectional characteristics as a function of member cross-sectional area. A workable optimization strategy for the ideal seismic design of nonlinear truss structures is presented. For the optimal seismic design of non-linear truss systems, a feasible optimization approach is provided by Hajirasouliha et al. [174]. Uniform deformation may enhance the topology of rigid constructions subjected to seismic and gravitational forces. While each seismic excitation has its own ideal topology, one may reach practical results by averaging the best distribution patterns for a series of earthquakes.
Furthermore, Gao et al. [175] researched buckling constraint optimization of continuum structure topology. New methods, such as buckling load factors and volume, are being developed to decrease structural compliance. In [176], the goal was to construct the stiffest frame structure possible using hollow beam members using method of moving asymptotes (MMA) while accounting for the required load and stability. The proposed method may be used to build frame systems with beam members having distinct cross sections. Additionally, An approach for the topology optimization of multi-material active buildings is suggested by Wang et al. [13] to lessen its negative environmental effects, as shown in Fig. 14. The approach is based on the density-based topology optimization concept. Passive and active materials must be arranged as effectively as possible throughout the topology optimization approach while considering constraints and optimization goals. Changizi et al. [177] proposed a computationally efficient topology optimization technique for steel frame structures that incorporates user-defined safety factors against global and individual member instabilities. While Miyazu et al. [178] suggested an optimization method for creating flexible arch-supporting structures that lessen the acceleration response in the direction of the roof structure.
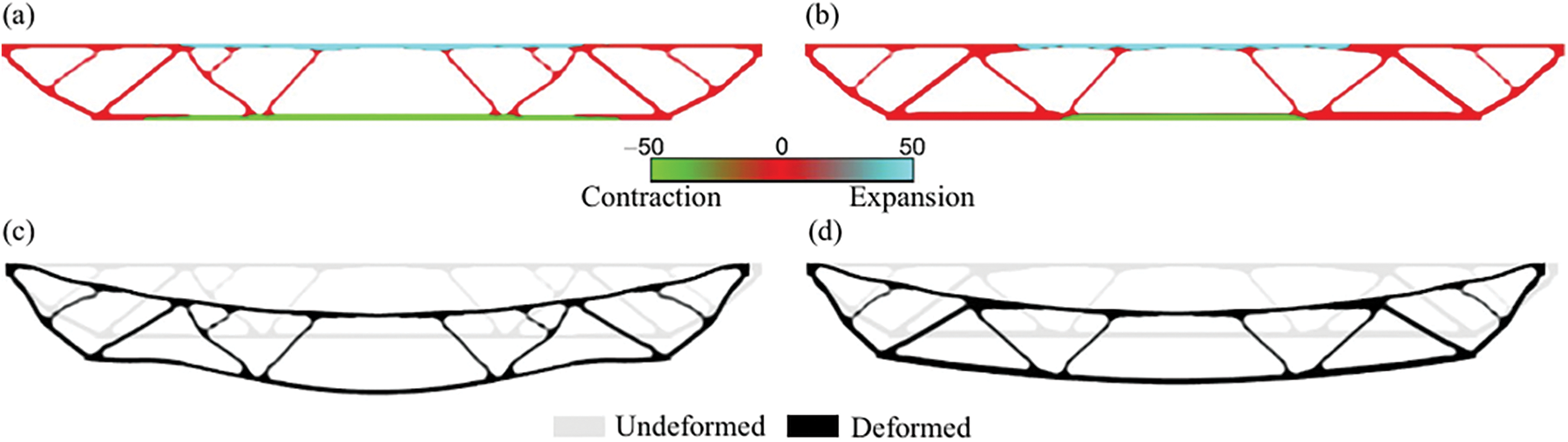
Figure 14: a and b exhibit the ideal designs for embodied and total energy savings, respectively, whereas c and d reflect the two structures’ final deformations. Actuation effects of active material in optimal active structures and the associated deformations [13]
In this subsection, Modern optimization techniques incorporate multi-objective strategies, such as genetic algorithms to balance rigidity and total mass in spaceframes or improved ant colony optimization to minimize computation time in 2D steel structure design and optimize local and global search. The seismic performance is evaluated with a push-over method considering dynamic loads, which optimizes the performance-based level to achieve an optimal frame for durability against seismic damage. Moreover, stress-based topology optimization, including stochastic perturbations that control uncertainties in structural parameters, has been conducted to enhance design reliability for steel frames. Adaptive methods such as (AIO) optimize structural topology with actuators’ location and control strategies to fulfil different load/performance actions and simultaneously meet different load and performance criteria. Further, they incorporate buckling limits and environmental effects through the optimization of material density or compliance, which results in structural designs that are lighter, more anti-fragile, stable, and resilient.
Research by Cui et al. [179] used nodal or elemental sensitivity data to develop a morphogenesis approach for spatially limited framed structures. As numerical examples demonstrate, this method effectively minimizes structural bending moments while producing structures that largely transfer external force via axial stress. While Shimoda et al. [180] described a non-parametric optimization approach for constructing solid, shell, and frame structures with strong shapes in the face of uncertainty. The suggested non-parametric form optimization method for robust design consists of four fundamental phases derived from structural eigenvalue analysis and gradient functions. Moreover, a two-phase genetic algorithm (GA) is proposed by Kociecki et al. [181] to conserve weight and build free-form steel space-frame roof structures using commercially available rectangular hollow structural sections (HSS), modifying the roof form, member and column sizes, and topology will increase structural efficiency.
Scale optimization of high-rise structures is complicated due to their discrete design elements, implicit optimization function, and expensive individual assessment [182]. A hybrid meta-heuristic approach that combines Particle Swarm Optimization (PSO) and Harris Hawk Optimization (HHO) is used by Mashayekhi et al. [183] to design Castellated beams. The desired purpose determines the whole cost, including construction and material expenses. Constrained functions have both geometric and coding limitations. A working set technique with interesting theoretical elements has been suggested by Verbart et al. [184] for size optimization problems in structures subjected to dynamic loads, with few variables but many restrictions. This method may improve the structural performance of frame structures subjected to various loads and stress limits. Moreover, An improved fireworks algorithm (IFWA) is suggested by Gholizadeh et al. [185] to lessen the shortcomings of the initial method. Also, Su et al. [186] recommended using standard member sizes in applying the Binary Comprehensive Learning Particle Swarm Optimization (BCLPSO) method to get the optimal design for nonlinear steel structures. Furthermore, Aydogdu et al. [187] offered four updated iterations of the well-known grasshopper optimization algorithm (GOA), which may be applied to tackle complex, large-scale, real-size steel truss and frame-building problems. GOA imitates the swarms of grasshoppers during their feeding. The objective is to improve the algorithmic performance of the GOA.
Moreover, Kaveh et al. [84] offered a revised iteration of the whale optimization technique to maintain a propensity toward balance in intensity and variation. This endeavor aims to improve and accelerate the convergence of the solution by stabilizing the original WOA formulation. The unique Extended Whale Optimization Algorithm (EWOA) is evaluated using truss and frame structure size optimization problems. Gholizadeh et al. [188] investigated and compared two distinct algorithms: the improved multiverse (IMV) algorithm for the discrete size and optimization of structures based on cosmology inspired by nature and the improved black hole (IBH). The numerical results show that the suggested improved algorithms outperform the metaheuristics mentioned in their literature. In addition, Kaveh et al. [189] introduced the Improved Shuffled-based Jaya (IS-Jaya) technique, a new iteration of the Jaya algorithm. The suggested technique simultaneously adds the concept of the shuffling process and a path out of local minima to the conventional Jaya algorithm. Furthermore, Ma et al. [190] present an interval size optimization for geometric analysis concerning beam structures based on beam theory. This optimization makes the beam construction lightweight and guarantees its lifetime. Moreover, the restricted size optimization based on the LRFD-AISC is carried out by Dede [191] utilizing the W-shape’s cross-sectional area and integer design variables.
The challenge’s goal is to find the minimum weight of the grillage assembly. Furthermore, the advantages of the two-phase GA optimization method and the technology provided by Kociecki et al. [192] include automation of the design process for complex and unique structures, reduced iterative design time, and more cost-effective design. Also, the optimization issue is represented by Van Mellaert et al. [193] as a Mixed-Integer Linear Programming (MILP) problem with structural analysis equations as constraints. Also, to enhance Teaching-Learning-Based Optimization (TLBO)’s performance, Quantum Teaching-Learning-Based Optimization, or QTLBO, is presented by Kaveh et al. [194]. Kaveh et al. [195] introduced Multi-Adaptive Harmony Search (MAHS), an enhanced Harmony Search technique. MAHS’s novel pitch-adjusting mechanism produces better results and faster convergence since the intensification and diversification stages of the optimization search process closely complement each other. While a non-parametric shape size optimization method was developed by Shimoda et al. [196] to alter the large-scale frame designs’ static deformation. The Lagrange multiplier approach, the material derivative method, and the adjoint variable method are theoretically used to determine this issue’s form gradient function, size gradient function, and optimality criterion.
In summary, high-rise structures are complex due to the nature of their design variables and, therefore, computationally expensive to optimize. Advanced hybrid algorithms (for example, combining Particle Swarm Optimization with Harris Hawk Optimization) address geometric and functional constraints for minimizing material cost and maximizing structural efficiency. Newer algorithms such as the (EWOA) and the (IS-Jaya) focus on systematic structural performance enhancement by finding stable solutions, thereby preventing reaching local minima. (MILP) effectively embeds structural constraints, and the Quantum and Multi-Adaptive, Harmony Search methods, improve convergence speed by balancing exploration and refinement while enhancing solution quality. Similar non-parametric shape optimization methods also help reduce weight, improve durability, and produce efficient large-scale structural designs. The types of optimizations and algorithms used to optimize different types of frame structures are tabulated in Table 2.
3.4 Multi-Objective Optimization
A Plasma Generation Optimization (PGO), a novel physics-based metaheuristic algorithm, was used by Kaveh et al. [197] to maximize the growth, organization, and structure of the skeletal system. PGO is utilized to mimic the creation of plasma, and the processes that go into making plasma are repeated. Six design examples illustrate how to assess PGO resilience and performance under different structural modifications. The optimization findings suggest that PGO could find the best solutions with fewer structural analyses. Zhao et al. [198] investigated a frame structure’s combined topology and size optimization problem, considering displacement, stress, and stability constraints. The study proposed a combined topology and size optimization approach for frame structures that prioritizes structural weight by balancing displacement, stress, and stability restrictions. In addition, Moghaddam et al. [125] offered a practical technique for optimizing the size and topology of nonlinear truss-like structures to survive seismic activity while accounting for a significant degree of uncertainty in ground motion. The best design solutions are produced by using an adaptive optimization technique. Also, Daneshfar et al. [199] investigated how to employ beam components in structural analysis models to optimize the size and topology of the frame structure according to the ground structure technique.
Tensegrity structures are light but stable systems composed of compression members called struts called in and tension components known as cables arranged to integrate their component parts in self-stressing equilibrium. The optimization in such structures is done to minimize total weight and enhance structural resistance. In a study about tensegrity robots, axial forces in cables attached to a tensegrity structure were calculated using a developed quadratic optimization (QO) approach [200]. In addition, a novel tensegrity sphere structure was introduced using spherical logarithmic spirals and Double Helix Tensegrity topology to optimize minimal mass under torsional loads [201]. Wang et al. [202] developed Total Energy Optimization (TEO) to enable the creation of minimal energy configurations for tensegrity implementing branch-and-bound (BNB), hybrid Quesada-Grossman (HQG), and mixed-integer sequential quadratic programming (MISQP). In addition, Masic et al. [32] are also concerned with designing tensegrity structures with the ideal mass-to-stiffness ratio. Also, particle swarm optimization is used by Yildiz et al. [203] to solve the prestress optimization and size of tensegrity booms.
Nonlinear finite element models of tensegrity structures and solution techniques provide an initial starting point. Additionally, Mills et al. [204] examined the appropriateness of intricate airplane wing designs and contrasted the structural performance of such designs with a typical conventional wing structure through simulation. In addition, a generalized objective function for the topology finding of tensegrity structures is proposed by Xu et al. [205], in order to quickly identify numerous tensegrity structures through a s and give selection priority to various members. Moreover, Wang et al. [206] investigated topology optimization based on mixed integer nonlinear programming (MINLP) to identify the optimal active tensegrity structure design; their typical benchmark examples demonstrated that topology-optimized active designs obtained using the proposed approach could consume less material than sizing-optimized active tensegrity designs, resulting in lighter structures.
Structural optimization for concrete structures minimizes total weight or improves the structural capacity against possible loads considering concrete codes. A nonlinear programming approach is implementing SQP to minimize the total cost of the reinforced concrete structure considering American Concrete Institute (ACI) 2005 code requirements [207]. Sirca Gene et al. [208] proposed a mixed integer-discrete nonlinear programming (MIDNLP) approach to minimize the total cost of precast prestressed reinforced concrete beams in bridges. Amir [209] proposed a topology optimization approach to reducing the total structural weight by minimizing the steel and concrete distribution, considering load-bearing capacity. A computational methodology proposed by [210] achieved 30% material savings while enhancing sustainability. In addition, a unique method based on topology optimization is given by Bruggi et al. [211] for the thoughtful placement of fiber reinforcement in masonry constructions. Rizzian et al. [212] offered a feasible numerical optimization method for comparing the seismic spectra and reactions to similar solicitations of a base-isolated and a traditional fixed-base reinforced concrete ordinary building, depending on what is appropriate for each scenario. Regarding optimization for improving structural stability, Khan et al. [210] used a diagonal approach to increase the systemic resistance of brick masonry structures with RC stiffeners. Also, Bondarabadi et al. [213] offered a unique cascade optimization strategy that minimizes the torsion of each RC structure narrative as a fitness function while satisfying the necessary constraints. In addition, Lee et al. [41] examined the stress interpolation function and the stress discrepancy problem to determine the best reinforcing layer design under in-plane load.
In this section we deal with the structural optimization conducted on engineering structures other than structural types mentioned above and we refer to the most significant studies conducted in structural optimization. A computational method based on a project algorithm (PA) was proposed to minimize self-deploying energy by considering the force density vector model [214]. In research by Gillman et al. [43], origami was used to generate auxetic metamaterials, and topology optimization provided an independent and reliable means of determining these structures. The potential value of formal structural optimization for foldable and deployable structure design was investigated in [215].
Similarly, the topology and size of geometrically nonlinear dome structures are modified in [216] to reduce total weight and joint displacements while maximizing load-carrying capacity. Moreover, Cucuzza et al. [217] optimized the guyed radio mast’s dimensions and design using a genetic algorithm, considering the effects of wind, ice, and seismic forces. They suggested a novel method for considering self-weight loading while improving structural topology in three spatial dimensions. Furthermore, Marotte Luz Filho et al. [218] proposed a new technique for optimizing structure topology in three spatial dimensions while considering self-weight loading. Also, Guo et al. [219] used movable bars to solve topology optimization in geometrically nonlinear three-dimensional structures. Moving morphable bars have fewer design variables due to their different geometrical forms, which speeds up convergence and improves processing efficiency. NURBS effectively optimized the design of elastic arches using an iso-geometric analysis based on non-uniform B-splines.
To sum-up the last three sections, the methods and optimization algorithms are briefly summarized. Advanced optimization algorithms for adaptive structures can enhance performance selections and efficiency. Total Energy Optimization (TEO) or particle swarm optimization (PSO) allows the determination of minimal energy configurations and prestress for tensegrity structures. Nonlinear solvers (Newton-Raphson method and augmented Lagrangian approaches) are used to tackle problems related to force density and deformation. Moving morphable bars (MMB) is a design variable in topology optimization that simplifies the topological problem and speeds up convergence. Focus on neural networks’ iterative-based management, especially convolutional neural networks (CNN), and the ability to predict optimal designs from large datasets using new approaches that result in designs without needing engineering experience. SQP reduces the use of materials, decreases costs, and applies nonlinear programming techniques to concrete. Seismic loading conditions are primarily considered when optimizing reinforcement layouts when designing structures, often coupled with gradient-based optimization integrated with a finite element model. Table 3 presents the objectives and optimization algorithms of various structural types presented in this section.
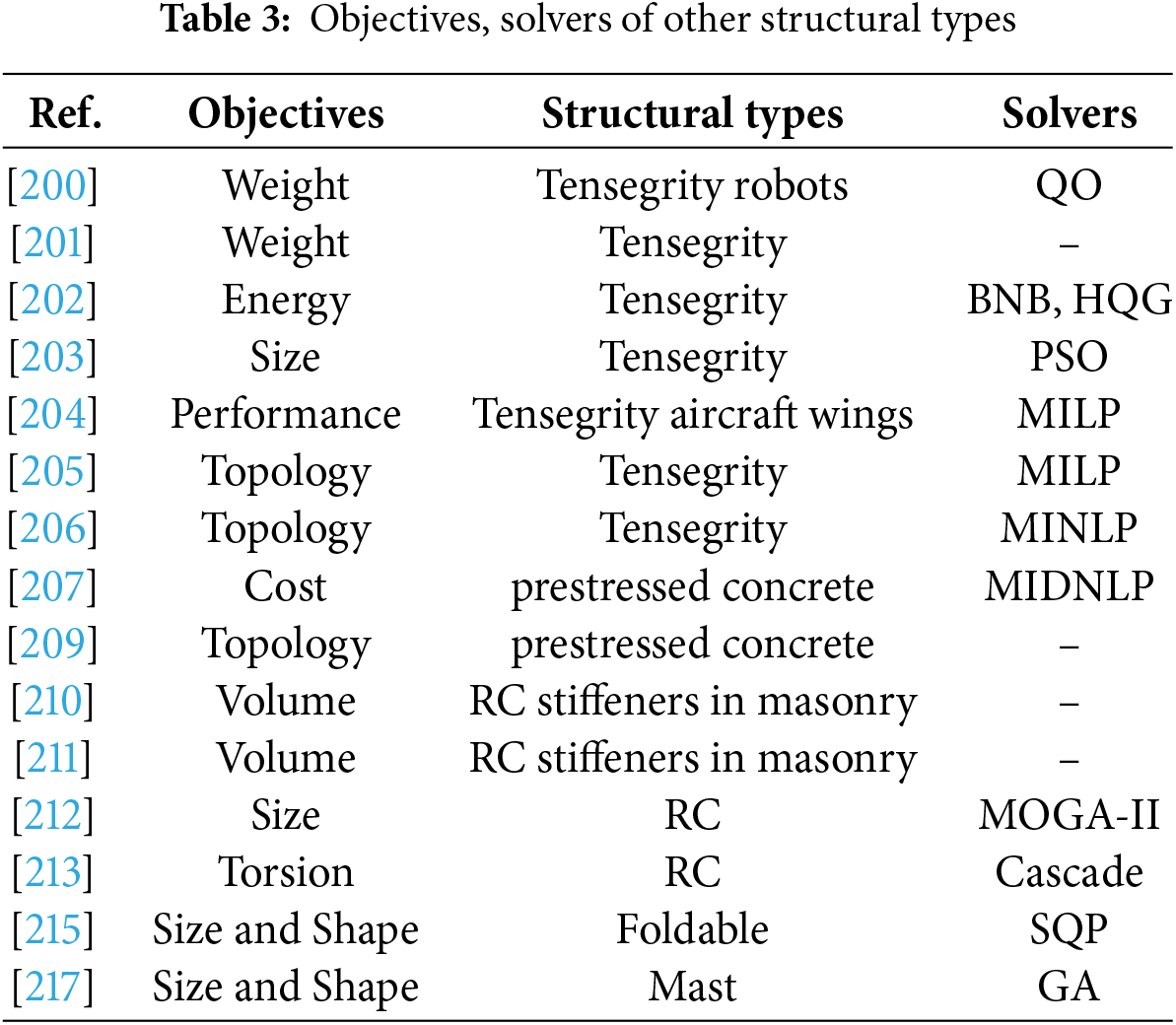
7 Recommendations for Future Studies
• Applying numerical gradient of the objective and constraint functions in case of gradient-based optimizations.
• Further enhancements to teaching-learning-based optimization methods.
• Exploration of adaptive teaching factors in various applications.
• Exploring more complex loading scenarios optimization and load combinations in topology.
• Further studies on structural optimization considering material nonlinearity and/or dynamic loadings.
• Investigating alternative methods for failure probability handling.
• Further investigations on structural optimization considering geometry and material uncertainties.
• Structural optimization techniques can be further developed through applications with other structural design and control disciplines. Form-finding, structural control, seismic design, active structures, and structural design all depend on optimization approaches.
• Since Artificial Intelligence (AI) is already contributing to growth in different sectors, we suggest establishing and expanding connections between AI and optimization in various structures to find new methods and significant applications in this area.
• The applications of machine learning techniques such as Artificial neural Networks, linear regression, Non-linear Regression, and Multi-linear Regression should be improved to achieve better results in structural optimization.
Applying optimization techniques is crucial for improving the effectiveness and performance of civil engineering constructions. Topology, size, and shape may all be enhanced to make an ideal structural system. Several studies were undertaken to optimize the forms and proportions. The literature leads to the following conclusions that can be made:
• By utilizing multi-objective optimization, size, shape, and topology, engineers may create more dependable, affordable, and high-performing designs. Given the impending environmental catastrophe, structural optimization is essential for reducing the built environment’s carbon footprint.
• In addition to boosting material efficiency, reducing weight may result in considerable cost savings on production, shipping, and operating expenditures. Furthermore, modern design strategies strive to minimize the energy consumption and carbon emissions of the built environment to the lowest feasible level, given the construction sector’s significant contributions to material usage, energy consumption, greenhouse gas emissions, and waste creation.
• The number of studies conducted on pin-jointed structures is higher than that on other structures like frames. This may be due to the fact that, the former are the simplest form of structural systems with less variables compared to frames.
• The most used optimization algorithms in the studies presented in this review implemented gradient-based optimization algorithms like SQP, MMA, and free gradient optimizers like GA, PSO, SA, ACO, DE, Artificial Bee Swarm (ABS), and GWO.
• Nowadays, machine learning techniques, such as supervised, unsupervised, and deep learning techniques, use a combination of gradient-based and non-gradient-based methods.
• Numerous studies exist in this field, so we had to select only a limited number of articles. Moreover, this review only considers papers published between 2005 and 2024; there are other significant articles published before the period
Acknowledgment: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contribution to the paper: study conception and design: All authors. Data collection: Ahmed Manguri, Hogr Hassan. Draft manuscript preparation: Ahmed Manguri, Hogr Hassan, Najmadeen Saeed, Robert Jankowski. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interests to report regarding the present study.
References
1. Christensen PW, Klarbring A. An introduction to structural optimization. Berlin, Germany: Springer Science & Business Media; 2008. [Google Scholar]
2. Vanderplaats GN. Structural optimization-past, present, and future. AIAA J. 1982;20(7):992–1000. doi:10.2514/3.51158. [Google Scholar] [CrossRef]
3. Bresolin JM, Pravia ZM, Kripka M. Discrete sizing and layout optimization of steel truss-framed structures with Simulated Annealing Algorithm. Steel Compos Struct Int J. 2022;44(5):603–17. doi:10.12989/scs.2022.44.5.589. [Google Scholar] [CrossRef]
4. Haftka RT, Gürdal Z. Elements of structural optimization. Berlin, Germany: Springer Science & Business Media; 2012. [Google Scholar]
5. Manguri A, Saeed N, Jankowski R. A review: structural shape and stress control techniques and their applications. Arch Comput Methods Eng. 2024;83(15):1191. doi:10.1007/s11831-024-10149-9. [Google Scholar] [CrossRef]
6. Kaveh A. Optimal structural analysis. Hoboken, NJ, USA: John Wiley & Sons; 2014. [Google Scholar]
7. Rothwell A. Optimization methods in structural design. Berlin, Germany: Springer; 2017. [Google Scholar]
8. Brütting J, Desruelle J, Senatore G, Fivet C. Design of truss structures through reuse. Structures. 2019;18(3):128–37. doi:10.1016/j.istruc.2018.11.006. [Google Scholar] [CrossRef]
9. Ajtayné Károlyfi K, Hajdú G, Rodaeva K, Szep J. Structural optimization of a steel truss for sustainability in parametric environment—a case study. Chem Eng Res Design. 2024;107:13–8. doi:10.3303/CET23107003. [Google Scholar] [CrossRef]
10. Ching E, Carstensen JV. Truss topology optimization of timber-steel structures for reduced embodied carbon design. Eng Struct. 2022;252(3):113540. doi:10.1016/j.engstruct.2021.113540. [Google Scholar] [CrossRef]
11. He L, Li Q, Gilbert M, Shepherd P, Rankine C, Pritchard T, et al. Optimization-driven conceptual design of truss structures in a parametric modelling environment. Structures. 2022;37(1):469–82. doi:10.1016/j.istruc.2021.12.048. [Google Scholar] [CrossRef]
12. Wang Y, Senatore G. Minimum energy adaptive structures-All-In-One problem formulation. Comput Struct. 2020;236(2):106266. doi:10.1016/j.compstruc.2020.106266. [Google Scholar] [CrossRef]
13. Wang Y, Sigmund O. Topology optimization of multi-material active structures to reduce energy consumption and carbon footprint. Struct Multidiscipl Optim. 2024;67(1):363. doi:10.1007/s00158-023-03698-3. [Google Scholar] [CrossRef]
14. Maxwell JC. The scientific papers of james clerk maxwell. Cambridge, UK: Cambridge University Press; 2011. [Google Scholar]
15. Michell AGMLVIII. The limits of economy of material in frame-structures. London Edinburgh Dublin Philos Mag J Sci. 1904;8(47):589–97. doi:10.1080/14786440409463229. [Google Scholar] [CrossRef]
16. Hassan HZ, Saeed NM. Advancements and applications of lightweight structures: a comprehensive review. Discover Civil Eng. 2024;1(1):47. doi:10.1007/s44290-024-00049-z. [Google Scholar] [CrossRef]
17. Xie YM, Steven GP. Basic evolutionary structural optimization. Evolutionary structural optimization. London: Springer London; 1997. p. 12–29. doi:10.1007/978-1-4471-0985-3_2. [Google Scholar] [CrossRef]
18. Xiao A, Wang B, Jin Y. Evolutionary truss layout optimization using the vectorized structure approach. In: 2013 IEEE Congress on Evolutionary Computation; 2013; Cancun, Mexico. p. 2879–86. doi:10.1109/CEC.2013.6557919. [Google Scholar] [CrossRef]
19. Martinez P, Marti P, Querin O. Growth method for size, topology, and geometry optimization of truss structures. Struct Multidiscip Optimiz. 2007;33(1):13–26. doi:10.1007/s00158-006-0043-9. [Google Scholar] [CrossRef]
20. Manguri A, Saeed N, Jankowski R. Controlling nodal displacement of pantographic structures using matrix condensation and interior-point optimization: a numerical and experimental study. Eng Struct. 2024;304:117603. doi:10.1016/j.engstruct.2024.117603. [Google Scholar] [CrossRef]
21. Manguri A, Saeed N, Kazemi F, Asgarkhani N, Szczepanski M, Jankowski R. Computational bar size optimization of single layer dome structures considering axial stress and shape disturbance. In: Mathematical modeling in physical sciences. Cham: Springer Nature Switzerland; 2024. doi:10.1007/978-3-031-52965-8_14. [Google Scholar] [CrossRef]
22. Saeed NM. Displacement control of nonlinear pin-jointed assemblies based on force method and optimization. AIAA J. 2022;60(2):1024–31. doi:10.2514/1.J060568. [Google Scholar] [CrossRef]
23. Zhang P, Zhou J, Chen J. Form-finding of complex tensegrity structures using constrained optimization method. Compos Struct. 2021;268:113971. doi:10.1016/j.compstruct.2021.113971. [Google Scholar] [CrossRef]
24. Cai J, Feng J. Form-finding of tensegrity structures using an optimization method. Eng Struct. 2015;104(4):126–32. doi:10.1016/j.engstruct.2015.09.028. [Google Scholar] [CrossRef]
25. Qian W, Xu Y, Li H. A self-sparse generative adversarial network for autonomous early-stage design of architectural sketches. Comput-Aided Civil Infrastruct Eng. 2022;37(5):612–28. doi:10.1111/mice.12759. [Google Scholar] [CrossRef]
26. Qian W, Xu Y, Li H. A topology description function-enhanced neural network for topology optimization. Comput-Aided Civil Infrastruct Eng. 2023;38(8):1020–40. doi:10.1111/mice.12933. [Google Scholar] [CrossRef]
27. Manguri A, Saeed N, Szczepanski M, Jankowski R. Buckling and shape control of prestressable trusses using optimum number of actuators. Sci Rep. 2023;13(1):3838. doi:10.1038/s41598-023-30274-y. [Google Scholar] [PubMed] [CrossRef]
28. Saeed NM, Manguri AA, Szczepanski M, Jankowski R, Haydar BA. Static shape and stress control of trusses with optimum time, actuators and actuation. Int J Civil Engi. 2023;21(3):379–90. doi:10.1007/s40999-022-00784-3. [Google Scholar] [CrossRef]
29. Lamberti L. An efficient simulated annealing algorithm for design optimization of truss structures. Comput Struct. 2008;86(19):1936–53. doi:10.1016/j.compstruc.2008.02.004. [Google Scholar] [CrossRef]
30. Kaveh A, Talatahari S. A particle swarm ant colony optimization for truss structures with discrete variables. J Constr Steel Res. 2009;65(8):1558–68. doi:10.1016/j.jcsr.2009.04.021. [Google Scholar] [CrossRef]
31. Gandomi AH, Talatahari S, Yang XS, Deb S. Design optimization of truss structures using cuckoo search algorithm. Struct Des Tall Spec Build. 2013;22(17):1330–49. doi:10.1002/tal.1033. [Google Scholar] [CrossRef]
32. Masic M, Skelton RE, Gill PE. Optimization of tensegrity structures. Int J Solids Struct. 2006;43(16):4687–703. doi:10.1016/j.ijsolstr.2005.07.046. [Google Scholar] [CrossRef]
33. Xu X, Wang Y, Luo Y, Hu D. Topology optimization of tensegrity structures considering buckling constraints. J Struct Eng. 2018;144(10):04018173. doi:10.1061/(ASCE)ST.1943-541X.0002156. [Google Scholar] [CrossRef]
34. Zhang J, Ohsaki M. Optimization methods for force and shape design of tensegrity structures. In: Proceedings of the 7th World Congresses of Structural and Multidisciplinary Optimization; 2007; Seoul, Republic of Korea. p. 40–9. [Google Scholar]
35. Su Y, Zhang J, Ohsaki M, Wu Y. Topology optimization and shape design method for large-span tensegrity structures with reciprocal struts. Int J Sol Structs. 2020;206(5):9–22. doi:10.1016/j.ijsolstr.2020.09.002. [Google Scholar] [CrossRef]
36. Kaveh A, Talatahari S. An improved ant colony optimization for the design of planar steel frames. Eng Struct. 2010;32(3):864–73. doi:10.1016/j.engstruct.2009.12.012. [Google Scholar] [CrossRef]
37. Lim J, You C, Dayyani I. Multi-objective topology optimization and structural analysis of periodic spaceframe structures. Mat Des. 2020;190(37):108552. doi:10.1016/j.matdes.2020.108552. [Google Scholar] [CrossRef]
38. Changizi N, Jalalpour M. Stress-based topology optimization of steel-frame structures using members with standard cross sections: gradient-based approach. J Struct Eng. 2017;143(8):04017078. doi:10.1080/0305215X.2016.1273912. [Google Scholar] [CrossRef]
39. Manguri A, Saeed N, Jankowski R. Deformation mitigation and twisting moment control in space frames. Structures. 2024;68(4):107227. doi:10.1016/j.istruc.2024.107227. [Google Scholar] [CrossRef]
40. Cui H, Xie L, Xiao M, Deng M. Conceptual design of reinforced concrete structures using truss-like topology optimization. Arch Civil Eng. 2022;68(3):523–37. doi:10.1002/nme.4253. [Google Scholar] [CrossRef]
41. Lee JW, Yoon GH. Stress based topology optimization of reinforcement structure under in-plane load. Comput Struct. 2017;191:115–28. doi:10.1016/j.compstruc.2017.05.009. [Google Scholar] [CrossRef]
42. Fuchi K, Diaz AR. Origami design by topology optimization. J Mech Des. 2013;135(11):111003. doi:10.1115/1.4025384. [Google Scholar] [CrossRef]
43. Gillman A, Fuchi K, Cook A, Pankonien A, Buskohl PR. Topology optimization for discovery of auxetic origami structures. In: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; 2018; Quebec City, QC, Canada. doi:10.1115/DETC2018-85732. [Google Scholar] [CrossRef]
44. Hibbeler RC, Tan K-H. Structural analysis. London, UK: Pearson Prentice Hall Upper Saddle River; 2006. [Google Scholar]
45. Tanskanen P. The evolutionary structural optimization method: theoretical aspects. Comput Methods Appl Mech Eng. 2002;191(47–48):5485–98. doi:10.1016/S0045-7825(02)00464-4. [Google Scholar] [CrossRef]
46. Shakya A, Nanakorn P, Petprakob W. A ground-structure-based representation with an element-removal algorithm for truss topology optimization. Struct Multidiscip Optimiz. 2018;58(2):657–75. doi:10.1007/s00158-018-1917-3. [Google Scholar] [CrossRef]
47. Gao G, Liu Z-Y, Li Y-B, Qiao Y-F. A new method to generate the ground structure in truss topology optimization. Eng Optimiz. 2017;49(2):235–51. doi:10.1080/0305215X.2016.1169050. [Google Scholar] [CrossRef]
48. Asadpoure A, Guest JK, Valdevit L. Incorporating fabrication cost into topology optimization of discrete structures and lattices. Struct Multidiscip Optimiz. 2015;51(2):385–96. doi:10.1007/s00158-014-1133-8. [Google Scholar] [CrossRef]
49. Manguri A, Magisano D, Jankowski R. Optimal shape and stress control of geometrically nonlinear structures with exact gradient with respect to the actuation inputs. Structures. 2024;70(1):107738. doi:10.1016/j.istruc.2024.107738. [Google Scholar] [CrossRef]
50. Tyburec M, Zeman J, Doškář M, Kružík M, Lepš M. Modular-topology optimization with Wang tilings: an application to truss structures. Struct Multidiscip Optimiz. 2021;63(3):1099–117. doi:10.1007/s00158-020-02744-8. [Google Scholar] [CrossRef]
51. Richardson JN, Adriaenssens S, Bouillard P, Filomeno Coelho R. Multiobjective topology optimization of truss structures with kinematic stability repair. Struct Multidiscip Optimiz. 2012;46(4):513–32. doi:10.1007/s00158-012-0777-5. [Google Scholar] [CrossRef]
52. Asadpoure A, Tootkaboni M, Guest JK. Robust topology optimization of structures with uncertainties in stiffness-Application to truss structures. Comput Struct. 2011;89(11–12):1131–41. doi:10.1016/j.compstruc.2010.11.004. [Google Scholar] [CrossRef]
53. Richardson JN, Coelho RF, Adriaenssens S. Robust topology optimization of truss structures with random loading and material properties: a multiobjective perspective. Comput Struct. 2015;154(1):41–7. doi:10.1016/j.compstruc.2015.03.011. [Google Scholar] [CrossRef]
54. Guo X, Zhou K, Shi S. Robust topology optimization of truss-like continuum structures under uncertain loads based on cloud model. Math Mechan Solids. 2024;29(2):370–85. doi:10.1177/10812865231196512. [Google Scholar] [CrossRef]
55. Zhang XS, de Sturler E, Paulino GH. Stochastic sampling for deterministic structural topology optimization with many load cases: density-based and ground structure approaches. Comput Meth Appl Mechd Eng. 2017;325(1):463–87. doi:10.1016/j.cma.2017.06.035. [Google Scholar] [CrossRef]
56. Mashayekhi M, Salajegheh E, Dehghani M. Topology optimization of double and triple layer grid structures using a modified gravitational harmony search algorithm with efficient member grouping strategy. Comput Struct. 2016;172(3):40–58. doi:10.1016/j.compstruc.2016.05.008. [Google Scholar] [CrossRef]
57. Nwe MTN, Guest JK. Topology optimization of truss structures considering stress and stability constraints. In: Structures Congress 2019. Reston, VA, USA: American Society of Civil Engineers; 2019. doi:10.1061/9780784482223.005. [Google Scholar] [CrossRef]
58. Cai Q, Feng R, Zhang Z, Wang X. Topology optimization of truss structure considering kinematic stability based on mixed-integer programming approach. Struct Multidiscip Optimiz. 2024;67(7):1–18. doi:10.1007/s00158-024-03827-6. [Google Scholar] [CrossRef]
59. Cai Q, Feng R, Zhang Z. Topology optimization of truss structure considering nodal stability and local buckling stability. Structures. 2022;40(4):64–73. doi:10.1016/j.istruc.2022.04.008. [Google Scholar] [CrossRef]
60. Cai J, Huang L, Wu H, Yin L. Topology optimization of truss structure under load uncertainty with gradient-free proportional topology optimization method. Structures. 2023;58:105377. doi:10.1016/j.istruc.2023.105377. [Google Scholar] [CrossRef]
61. He F, Feng R, Cai Q. Topology optimization of truss structures considering local buckling stability. Comput Struct. 2024;294(1):107273. doi:10.1016/j.compstruc.2024.107273. [Google Scholar] [CrossRef]
62. Senatore G, Wang Y. Topology optimization of adaptive structures: new limits of material economy. Comput Methods Appl Mech Eng. 2024;422(1):116710. doi:10.1016/j.cma.2023.116710. [Google Scholar] [CrossRef]
63. Descamps B, Filomeno Coelho R. A lower-bound formulation for the geometry and topology optimization of truss structures under multiple loading. Struct Multidiscip Optimiz. 2013;48(1):49–58. doi:10.1007/s00158-012-0876-3. [Google Scholar] [CrossRef]
64. Stragiotti E, Irisarri F-X, Julien C, Morlier J. Efficient 3D truss topology optimization for aeronautical structures. Struct Multidiscipl Optim. 2024;67(3):42. doi:10.1007/s00158-024-03739-5. [Google Scholar] [CrossRef]
65. Leng G, Duan B. Topology optimization of planar truss structures with continuous element intersection and node stability constraints. Proc Institut Mech Eng, Part C: J Mech Eng Sci. 2012;226(7):1821–31. doi:10.1177/0954406211427370. [Google Scholar] [CrossRef]
66. Tangaramvong S, Tin-Loi F. Topology optimization of softening structures under displacement constraints as an MPEC. Struct Multidiscip Optimiz. 2014;49(2):299–314. doi:10.1007/s00158-013-0985-7. [Google Scholar] [CrossRef]
67. Canelas A, Carrasco M, López J. Topology optimization of truss structures under failure probability using the Bernstein approximation. Comput Struct. 2024;296(4):107295. doi:10.1016/j.compstruc.2024.107295. [Google Scholar] [CrossRef]
68. Li X, Zhu J, Wang J, Zhang W. Topology optimization for prestressed cable-truss structure considering geometric nonlinearity. Struct Multidiscipl Optim. 2023;66(9):201. doi:10.1007/s00158-023-03646-1. [Google Scholar] [CrossRef]
69. Fairclough HE, He L, Asfaha TB, Rigby S. Adaptive topology optimization of fail-safe truss structures. Struct Multidiscipl Optim. 2023;66(7):148. doi:10.1007/s00158-023-03585-x. [Google Scholar] [CrossRef]
70. Ramos AS, Paulino GH. Convex topology optimization for hyperelastic trusses based on the ground-structure approach. Struct Multidiscip Optimiz. 2015;51(2):287–304. doi:10.1007/s00158-014-1147-2. [Google Scholar] [CrossRef]
71. Kozłowski G, Sokół T. Enhanced growth method for topology and geometry optimization of truss structures. Struct Multidiscip Optimiz. 2022;65(8):220. doi:10.1007/s00158-022-03317-7. [Google Scholar] [CrossRef]
72. Yang J, Su H, Li X, Wang Y. Fail-safe topology optimization for multiscale structures. Comput Struct. 2023;284:107069. doi:10.1016/j.compstruc.2023.107069. [Google Scholar] [CrossRef]
73. Rozvany GIN, Sokół T, Pomezanski V. Fundamentals of exact multi-load topology optimization-stress-based least-volume trusses (generalized Michell structures)–Part I: plastic design. Struct Multidiscip Optimiz. 2014;50(6):1051–78. doi:10.1007/s00158-014-1118-7. [Google Scholar] [CrossRef]
74. Zhang X, Ramos AS, Paulino GH. Material nonlinear topology optimization using the ground structure method with a discrete filtering scheme. Struct Multidiscip Optimiz. 2017;55(6):2045–72. doi:10.1007/s00158-016-1627-7. [Google Scholar] [CrossRef]
75. Zhang XS, Paulino GH, Ramos AS. Multi-material topology optimization with multiple volume constraints: a general approach applied to ground structures with material nonlinearity. Struct Multidiscip Optimiz. 2018;57(1):161–82. doi:10.1007/s00158-017-1768-3. [Google Scholar] [CrossRef]
76. Manguri A, Saeed N, Szczepański M, Jankowski R. Bending moment control and weight optimization in space structures by adding extra members in the optimal locations. Adv Sci Technol Res J. 2023;17:313–24. doi:10.12913/22998624/169573. [Google Scholar] [CrossRef]
77. Deb K, Gulati S. Design of truss-structures for minimum weight using genetic algorithms. Finite Elem Anal Design. 2001;37(5):447–65. doi:10.1016/S0168-874X(00)00057-3. [Google Scholar] [CrossRef]
78. Dede T, Bekiroğlu S, Ayvaz Y. Weight minimization of trusses with genetic algorithm. Appl Soft Comput. 2011;11(2):2565–75. doi:10.1016/j.asoc.2010.10.006. [Google Scholar] [CrossRef]
79. Assimi H, Jamali A, Nariman-Zadeh N. Sizing and topology optimization of truss structures using genetic programming. Swarm Evolution Computat. 2017;37(23–24):90–103. doi:10.1016/j.swevo.2017.05.009. [Google Scholar] [CrossRef]
80. Neeraja D, Kamireddy T, Kumar PS, Reddy VS. Weight optimization of plane truss using genetic algorithm. IOP Conf Ser: Mater Sci Eng. 2017;263:032015. doi:10.1088/1757-899X/263/3/032015. [Google Scholar] [CrossRef]
81. Kazemzadeh Azad S. Enhanced hybrid metaheuristic algorithms for optimal sizing of steel truss structures with numerous discrete variables. Struct Multidiscip Optimiz. 2017;55(6):2159–80. doi:10.1007/s00158-016-1634-8. [Google Scholar] [CrossRef]
82. Hasançebi O, Azad SK. Adaptive dimensional search: a new metaheuristic algorithm for discrete truss sizing optimization. Comput Struct. 2015;154(1):1–16. doi:10.1016/j.compstruc.2015.03.014. [Google Scholar] [CrossRef]
83. Farshi B, Alinia-Ziazi A. Sizing optimization of truss structures by method of centers and force formulation. Int J Solids Struct. 2010;47(18–19):2508–24. doi:10.1016/j.ijsolstr.2010.05.009. [Google Scholar] [CrossRef]
84. Kaveh A, Ghazaan MI. Enhanced whale optimization algorithm for sizing optimization of skeletal structures. Mech Based Des Struct Machines. 2017;45(3):345–62. doi:10.1080/15397734.2016.1213639. [Google Scholar] [CrossRef]
85. Kaveh A, Talatahari S. Size optimization of space trusses using Big Bang-Big Crunch algorithm. Comput Struct 2009;87(17–18):1129–40. doi:10.1016/j.compstruc.2009.04.011. [Google Scholar] [CrossRef]
86. Torii AJ, Lopez RH, Biondini F. An approach to reliability-based shape and topology optimization of truss structures. Eng Optimiz. 2012;44(1):37–53. doi:10.1080/0305215X.2011.558578. [Google Scholar] [CrossRef]
87. Cheng M-Y, Prayogo D, Wu Y-W, Lukito MM. A Hybrid Harmony Search algorithm for discrete sizing optimization of truss structure. Automat Construct. 2016;69(7):21–33. doi:10.1016/j.autcon.2016.05.023. [Google Scholar] [CrossRef]
88. Martins FAC, Avila JPJ, Silva MAD. A linear approach for sizing optimization of isostatic trussed structures subjected to external and self-weight loads. Int J Steel Struct. 2019;19(4):1146–57. doi:10.1007/s13296-018-0194-8. [Google Scholar] [CrossRef]
89. Quyen VTB, Van TTT, Khanh CQ. A new algorithm for size optimization of the truss structures using finite element method. IOP Conf Ser: Mater Sci Eng. 365:042055. doi:10.1088/1757-899X/365/4/042055. [Google Scholar] [CrossRef]
90. Dizangian B, Ghasemi MR. Border-search and jump reduction method for size optimization of spatial truss structures. Front Struct Civil Eng. 2019;13(1):123–34. doi:10.1007/s11709-018-0478-2. [Google Scholar] [CrossRef]
91. Kaveh A, Dadras A, Montazeran A. Chaotic enhanced colliding bodies algorithms for size optimization of truss structures. Acta Mechanica. 2018;229(7):2883–907. doi:10.1007/s00707-018-2149-8. [Google Scholar] [CrossRef]
92. Flager F, Soremekun G, Adya A, Shea K, Haymaker J, Fischer M. Fully constrained design: a general and scalable method for discrete member sizing optimization of steel truss structures. Comput Struct. 2014;140:55–65. doi:10.1016/j.compstruc.2014.05.002. [Google Scholar] [CrossRef]
93. Degertekin S, Lamberti L, Hayalioglu M. Heat transfer search algorithm for sizing optimization of truss structures. Latin Am J Soli Struct. 2017;14(3):373. doi:10.1590/1679-78253297. [Google Scholar] [CrossRef]
94. Degertekin S. Improved harmony search algorithms for sizing optimization of truss structures. Comput Struct. 2012;92(2):229–41. doi:10.1016/j.compstruc.2011.10.022. [Google Scholar] [CrossRef]
95. Bodalal R, Shuaeib F. Marine predators algorithm for sizing optimization of truss structures with continuous variables. Computation. 2023;11(5):91. doi:10.3390/computation11050091. [Google Scholar] [CrossRef]
96. Millán-Páramo C. Modified simulated annealing algorithm for discrete sizing optimization of truss structure. Jordan J Civ Eng. 2018;12(4):683–97. [Google Scholar]
97. Manguri A, Saeed N, Kazemi F, Szczepanski M, Jankowski R. Optimum number of actuators to minimize the cross-sectional area of prestressable cable and truss structures. Structures. 2023;47(3):2501–14. doi:10.1016/j.istruc.2022.12.031. [Google Scholar] [CrossRef]
98. Sawada K, Matsuo A, Shimizu H. Randomized line search techniques in combined GA for discrete sizing optimization of truss structures. Struct Multidiscip Optimiz. 2011;44(3):337–50. doi:10.1007/s00158-011-0629-8. [Google Scholar] [CrossRef]
99. Dizangian B, Ghasemi MR. Ranked-based sensitivity analysis for size optimization of structures. J Mech Des. 2015;137(12):121402. doi:10.1115/1.4031295. [Google Scholar] [CrossRef]
100. Alkhraisat H, Dalbah LM, Al-Betar MA, Awadallah MA, Assaleh K, Deriche M. Size optimization of truss structures using improved grey wolf optimizer. IEEE Access. 2023;11:13383–97. doi:10.1109/ACCESS.2023.3243164. [Google Scholar] [CrossRef]
101. Baghlani A, Makiabadi M, Maheri MR. Sizing optimization of truss structures by an efficient constraint-handling strategy in TLBO. J Comput Civ Eng. 2017;31(4):04017004. doi:10.1061/(ASCE)CP.1943-5487.0000642. [Google Scholar] [CrossRef]
102. Joubari MM, Pashaei M, Fathi A. Sizing optimization of truss structures under frequency constraints with artificial bee colony algorithm. J Math Comput Science. 2014;9(2):77–88. doi:10.22436/jmcs.09.02.01. [Google Scholar] [CrossRef]
103. Bekdaş G, Nigdeli SM, Yang X-S. Sizing optimization of truss structures using flower pollination algorithm. Appl Soft Comput. 2015;37(1):322–31. doi:10.1016/j.asoc.2015.08.037. [Google Scholar] [CrossRef]
104. Kooshkbaghi M, Kaveh A. Sizing optimization of truss structures with continuous variables by artificial coronary circulation system algorithm. Iran J Sci Technol Transact Civil Eng. 2020;44(1):1–20. doi:10.1007/s40996-019-00254-2. [Google Scholar] [CrossRef]
105. Degertekin S, Hayalioglu M. Sizing truss structures using teaching-learning-based optimization. Comput Struct. 2013;119:177–88. doi:10.1016/j.compstruc.2012.12.011. [Google Scholar] [CrossRef]
106. Moosavian N, Moosavian H. Testing soccer league competition algorithm in comparison with ten popular meta-heuristic algorithms for sizing optimization of truss structures. Int J Eng. 2017;30(7):926–36. doi:10.5829/idosi.ije.2017.30.07a.01. [Google Scholar] [CrossRef]
107. Tayfun D, Grzywiński M, Selejdak J. Continuous size optimization of large-scale dome structures with dynamic constraints. Struct Eng Mech. 2020;73(4):397–405. doi:10.12989/sem.2020.73.4.397. [Google Scholar] [CrossRef]
108. Awad R. Sizing optimization of truss structures using the political optimizer (PO) algorithm. Structures. 2021;33(1):4871–94. doi:10.1016/j.istruc.2021.07.027. [Google Scholar] [CrossRef]
109. Khatibinia M, Yazdani H. Accelerated multi-gravitational search algorithm for size optimization of truss structures. Swarm Evol Comput. 2018;38:109–19. doi:10.1016/j.swevo.2017.07.001. [Google Scholar] [CrossRef]
110. Pham H-A, Dang V-H, Vu T-C, Nguyen B-D. An efficient k-NN-based rao optimization method for optimal discrete sizing of truss structures. Appl Soft Comput. 2024;154(2):111373. doi:10.1016/j.asoc.2024.111373. [Google Scholar] [CrossRef]
111. Mortazavi A. A novel binomial strategy for simultaneous topology and size optimization of truss structures. Eng Optim. 2024;7(1):1–35. doi:10.1080/0305215X.2024.2349100. [Google Scholar] [CrossRef]
112. Faramarzi A, Afshar M. Application of cellular automata to size and topology optimization of truss structures. Scientia Iranica. 2012;19(3):373–80. doi:10.1016/j.scient.2012.04.009. [Google Scholar] [CrossRef]
113. Kaveh A, Mahdavi V. Colliding bodies optimization for size and topology optimization of truss structures. Struct Eng Mech. 2015;53(5):847–65. doi:10.12989/sem.2015.53.5.847. [Google Scholar] [CrossRef]
114. Ali A, Dhingra AK. Combined topology and sizing optimization of actively controlled structures. Eng Optimiz. 2015;47(1):55–71. doi:10.1080/0305215X.2013.868452. [Google Scholar] [CrossRef]
115. Brütting J, Senatore G, Fivet C. MILP-based discrete sizing and topology optimization of truss structures: new formulation and benchmarking. Struct Multidiscipl Optim. 2022;65(10):277. doi:10.1007/s00158-022-03325-7. [Google Scholar] [CrossRef]
116. Assimi H, Jamali A, Nariman-Zadeh N. Multi-objective sizing and topology optimization of truss structures using genetic programming based on a new adaptive mutant operator. Neural Comput Appl. 2019;31(10):5729–49. doi:10.1007/s00521-018-3401-9. [Google Scholar] [CrossRef]
117. Su R, Wang X, Gui L, Fan Z. Multi-objective topology and sizing optimization of truss structures based on adaptive multi-island search strategy. Struct Multidiscip Optimiz. 2011;43(2):275–86. doi:10.1007/s00158-010-0544-4. [Google Scholar] [CrossRef]
118. Kumar S, Tejani GG, Pholdee N, Bureerat S. Performance enhancement of meta-heuristics through random mutation and simulated annealing-based selection for concurrent topology and sizing optimization of truss structures. Soft Comput. 2022;26(12):5661–83. doi:10.1007/s00500-022-06930-2. [Google Scholar] [CrossRef]
119. Lee D, Shon S, Lee S, Ha J. Size and topology optimization of truss structures using quantum-based HS algorithm. Buildings. 2023;13(6):1436. doi:10.3390/buildings13061436. [Google Scholar] [CrossRef]
120. Zhong W, Su R, Gui L, Fan Z. Topology and sizing optimization of discrete structures using a cooperative coevolutionary genetic algorithm with independent ground structures. Eng Optimiz. 2016;48(6):911–32. doi:10.1080/0305215X.2015.1064119. [Google Scholar] [CrossRef]
121. Mortazavi A. Size and layout optimization of truss structures with dynamic constraints using the interactive fuzzy search algorithm. Eng Optimiz. 2021;53(3):369–91. doi:10.1080/0305215X.2020.1726341. [Google Scholar] [CrossRef]
122. Kaveh A, Zaerreza A. Size/layout optimization of truss structures using shuffled shepherd optimization method. Periodica Polytechnica Civil Eng. 2020;64(2):408–21. doi:10.3311/PPci.15726. [Google Scholar] [CrossRef]
123. Jawad FK, Ozturk C, Dansheng W, Mahmood M, Al-Azzawi O, Al-Jemely A. Sizing and layout optimization of truss structures with artificial bee colony algorithm. Structures. 2021. doi:10.1016/j.istruc.2021.01.016. [Google Scholar] [CrossRef]
124. El Bouzouiki M, Sedaghati R, Stiharu I. A non-uniform cellular automata framework for topology and sizing optimization of truss structures subjected to stress and displacement constraints. Comput Struct. 2021;242(5):106394. doi:10.1016/j.compstruc.2020.106394. [Google Scholar] [CrossRef]
125. Moghaddam H, Mohammadi A, Zare Golmoghany M. Size and topology optimization of truss-like structures under seismic excitations incorporating probabilistic aspects. Bull Earthq Eng. 2024;2024(10):1–28. doi:10.1007/s10518-024-01964-3. [Google Scholar] [CrossRef]
126. Avcı MS, Yavuz D, Ercan E, Nuhoğlu A. Efficient sizing and layout optimization of truss benchmark structures using ISRES algorithm. Appl Sci. 2024;14(8):3324. doi:10.3390/app14083324. [Google Scholar] [CrossRef]
127. Hosseinzadeh Y, Taghizadieh N, Jalili S. Hybridizing electromagnetism-like mechanism algorithm with migration strategy for layout and size optimization of truss structures with frequency constraints. Neural Comput Appl. 2016;27(4):953–71. doi:10.1007/s00521-015-1912-1. [Google Scholar] [CrossRef]
128. Kaveh A, Mahjoubi S. Hypotrochoid spiral optimization approach for sizing and layout optimization of truss structures with multiple frequency constraints. Eng Comput. 2019;35(4):1443–62. doi:10.1007/s00366-018-0675-6. [Google Scholar] [CrossRef]
129. Kaveh A, Khosravian M. Size/layout optimization of truss structures using vibrating particles system meta-heuristic algorithm and its improved version. Period Polytechnica Civ Eng. 2022;66(1):1–17. [Google Scholar]
130. Mortazavi A, Toğan V. Sizing and layout design of truss structures under dynamic and static constraints with an integrated particle swarm optimization algorithm. Appl Soft Comput. 2017;51(12):239–52. doi:10.1016/j.asoc.2016.11.032. [Google Scholar] [CrossRef]
131. Flager F, Adya A, Haymaker J, Fischer M. A bi-level hierarchical method for shape and member sizing optimization of steel truss structures. Comput Struct. 2014;131:1–11. doi:10.1016/j.compstruc.2013.10.004. [Google Scholar] [CrossRef]
132. Lopez RH, Torii AJ, Miguel LFF, De Cursi JES. An approach for the global reliability based optimization of the size and shape of truss structures. Mech Indus. 2015;16(6):603. doi:10.1051/meca/2015029. [Google Scholar] [CrossRef]
133. Serpik I. Discrete size and shape optimization of truss structures based on job search inspired strategy and genetic operations. Periodica Polytechnica Civil Eng. 2020;64(3):801–14. doi:10.3311/PPci.11840. [Google Scholar] [CrossRef]
134. Schwarz J, Chen T, Shea K, Stanković T. Efficient size and shape optimization of truss structures subject to stress and local buckling constraints using sequential linear programming. Struct Multidiscip Optimiz. 2018;58(1):171–84. doi:10.1007/s00158-017-1885-z. [Google Scholar] [CrossRef]
135. Cao H, Qian X, Chen Z, Zhu H. Enhanced particle swarm optimization for size and shape optimization of truss structures. Eng Optimiz. 2017;49(11):1939–56. doi:10.1080/0305215X.2016.1273912. [Google Scholar] [CrossRef]
136. Li Y, Peng Y, Zhou S. Improved PSO algorithm for shape and sizing optimization of truss structure. J Civil Eng Manag. 2013;19(4):542–9. doi:10.3846/13923730.2013.786754. [Google Scholar] [CrossRef]
137. Hosseini SS, Hamidi SA, Mansuri M, Ghoddosian A. Multi Objective Particle Swarm Optimization (MOPSO) for size and shape optimization of 2D truss structures. Periodica Polytechnica Civil Eng. 2015;59(1):9–14. doi:10.3311/PPci.7341. [Google Scholar] [CrossRef]
138. Kaveh A, Khayatazad M. Ray optimization for size and shape optimization of truss structures. Comput Struct. 2013;117:82–94. doi:10.1016/j.compstruc.2012.12.010. [Google Scholar] [CrossRef]
139. SeyedOskouei SL, Sojoudizadeh R, Milanchian R, Azizian H. Shape and size optimization of truss structure by means of improved artificial rabbits optimization algorithm. Eng Optim. 2024;56(12):1–30. doi:10.1080/0305215X.2024.2308577. [Google Scholar] [CrossRef]
140. Azizi M, Aickelin U, Khorshidi HA, Shishehgarkhaneh MB. Shape and size optimization of truss structures by Chaos game optimization considering frequency constraints. J Adv Res. 2022;41(1):89–100. doi:10.1016/j.jare.2022.01.002. [Google Scholar] [PubMed] [CrossRef]
141. Bodalal R. Combined size and shape optimization of truss structures using the heap-based optimizer (HBO) algorithm. Arab J Sci Eng. 2024;33:4871. doi:10.1007/s13369-024-09372-0. [Google Scholar] [CrossRef]
142. Etaati B, Neshat M, Dehkordi AA, Pargoo NS, El-Abd M, Sadollah A, et al. Shape and sizing optimisation of space truss structures using a new cooperative coevolutionary-based algorithm. Res Eng. 2024;21(24):101859. doi:10.1016/j.rineng.2024.101859. [Google Scholar] [CrossRef]
143. Lieu QX, Do DT, Lee J. An adaptive hybrid evolutionary firefly algorithm for shape and size optimization of truss structures with frequency constraints. Comput Struct. 2018;195:99–112. doi:10.1016/j.compstruc.2017.06.016. [Google Scholar] [CrossRef]
144. Ho-Huu V, Nguyen-Thoi T, Truong-Khac T, Le-Anh L, Vo-Duy T. An improved differential evolution based on roulette wheel selection for shape and size optimization of truss structures with frequency constraints. Neural Comput Appl. 2018;29(1):167–85. doi:10.1007/s00521-016-2426-1. [Google Scholar] [CrossRef]
145. Venkatesh Varma T, Sarkar S, Mondal G. Buckling restrained sizing and shape optimization of truss structures. J Struct Eng. 2020;146(5):04020048. doi:10.1061/(ASCE)ST.1943-541X.0002590. [Google Scholar] [PubMed] [CrossRef]
146. Jalili S, Hosseinzadeh Y, Kaveh A. Chaotic biogeography algorithm for size and shape optimization of truss structures with frequency constraints. Periodica Polytechnica Civil Eng. 2014;58(4):397–422. doi:10.3311/PPci.7466. [Google Scholar] [CrossRef]
147. Huynh Van T, Tangaramvong S, Muong S, Van P. Combined gaussian local search and enhanced comprehensive learning PSO algorithm for size and shape optimization of structures. Buildings. 2022;12(11):1976. doi:10.3390/buildings12111976. [Google Scholar] [CrossRef]
148. Ma Y-Z, Li H-S, Tee K-F, Yao W-X. Combined size and shape optimization of truss structures using subset simulation optimization. Proc Institut Mech Eng Part G: J Aeros Eng. 2018;233(7):2455–77. doi:10.1177/0954410018781464. [Google Scholar] [CrossRef]
149. Seyed Taheri SH, Jalili S. Enhanced biogeography-based optimization: a new method for size and shape optimization of truss structures with natural frequency constraints. Latin Am J Sol Struct. 2016;13:1406–30. doi:10.1590/1679-78252208. [Google Scholar] [CrossRef]
150. Ahrari A, Atai AA. Fully stressed design evolution strategy for shape and size optimization of truss structures. Comput Struct. 2013;123:58–67. doi:10.1016/j.compstruc.2013.04.013. [Google Scholar] [CrossRef]
151. Farshchin M, Camp CV, Maniat M. Optimal design of truss structures for size and shape with frequency constraints using a collaborative optimization strategy. Expert Syst Appl. 2016;66(7):203–18. doi:10.1016/j.eswa.2016.09.012. [Google Scholar] [CrossRef]
152. Miguel LFF, Fadel Miguel LF. Shape and size optimization of truss structures considering dynamic constraints through modern metaheuristic algorithms. Expert Syst Appl. 2012;39(10):9458–67. doi:10.1016/j.eswa.2012.02.113. [Google Scholar] [CrossRef]
153. Tao R, Yang X, Zhou H, Meng Z. Shape and size optimization of truss structures under frequency constraints based on hybrid sine cosine firefly algorithm. Comput Model Eng Sci. 2023;134(1):405–28. doi:10.32604/cmes.2022.020824. [Google Scholar] [CrossRef]
154. Baghlani A, Makiabadi MH. Teaching-learning-based optimization algorithm for shape and size optimization of truss structures with dynamic frequency constraints. Iranian J Sci Technol Transact A Sci. 2013;37:409–21. [Google Scholar]
155. Müller T, Van der Klashorst E. A quantitative comparison between size, shape, topology and simultaneous optimization for truss structures. Latin Am J Sol Struct. 2017;14(12):2221–42. doi:10.1590/1679-78253900. [Google Scholar] [CrossRef]
156. Ahrari A, Atai AA, Deb K. Simultaneous topology, shape and size optimization of truss structures by fully stressed design based on evolution strategy. Eng Optimiz. 2015;47(8):1063–84. doi:10.1080/0305215X.2014.947972. [Google Scholar] [CrossRef]
157. Dehghani M, Mashayekhi M, Sharifi M. An efficient imperialist competitive algorithm with likelihood assimilation for topology, shape and sizing optimization of truss structures. Appl Math Modell. 2021;93(2):1–27. doi:10.1016/j.apm.2020.11.044. [Google Scholar] [CrossRef]
158. Degertekin SO, Lamberti L, Ugur IB. Discrete sizing/layout/topology optimization of truss structures with an advanced Jaya algorithm. Appl Soft Comput. 2019;79:363–90. doi:10.1016/j.asoc.2019.03.058. [Google Scholar] [CrossRef]
159. Miguel LFF, Lopez RH, Miguel LFF. Multimodal size, shape, and topology optimisation of truss structures using the Firefly algorithm. Adv Eng Softw. 2013;56(3):23–37. doi:10.1016/j.advengsoft.2012.11.006. [Google Scholar] [CrossRef]
160. Mortazavi A, Toğan V. Simultaneous size, shape, and topology optimization of truss structures using integrated particle swarm optimizer. Struct Multidiscip Optimiz. 2016;54(4):715–36. doi:10.1007/s00158-016-1449-7. [Google Scholar] [CrossRef]
161. Carvalho JPG, Lemonge ACC, Hallak PH, Vargas DEC. Simultaneous sizing, shape, and layout optimization and automatic member grouping of dome structures. Structures. 2020;28(5):2188–202. doi:10.1016/j.istruc.2020.10.016. [Google Scholar] [CrossRef]
162. Degertekin SO, Lamberti L, Ugur IB. Sizing, layout and topology design optimization of truss structures using the Jaya algorithm. Appl Soft Comput. 2018;70(1):903–28. doi:10.1016/j.asoc.2017.10.001. [Google Scholar] [CrossRef]
163. Tejani G, Savsani V, Patel V, Bureerat S. Topology, shape, and size optimization of truss structures using modified teaching-learning based optimization. Adv Comput Des. 2017;2:313–31. doi:10.12989/acd.2017.2.4.313. [Google Scholar] [CrossRef]
164. Souza RRD, Fadel Miguel LF, Lopez RH, Miguel LFF, Torii AJ. A procedure for the size, shape and topology optimization of transmission line tower structures. Eng Struct. 2016;111(10):162–84. doi:10.1016/j.engstruct.2015.12.005. [Google Scholar] [CrossRef]
165. El Bouzouiki M, Sedaghati R, Stiharu I. Development of a non-uniform cellular automata framework for sizing, topology and layout optimization of truss structures. Eng Optim. 2024;56(12):1–32. doi:10.1080/0305215X.2024.2302571. [Google Scholar] [CrossRef]
166. Fredricson H, Johansen T, Klarbring A, Petersson J. Topology optimization of frame structures with flexible joints. Struct Multidiscip Optimiz. 2003;25(3):199–214. doi:10.1007/s00158-003-0281-z. [Google Scholar] [CrossRef]
167. Fu J, Huang H, Chen S, Zhang Y, An H. A topology, material and beam section optimization method for complex structures. Eng Optim. 2024:1–19. doi:10.1080/0305215X.2024.2357149. [Google Scholar] [CrossRef]
168. Kaveh A, Azar BF, Hadidi A, Sorochi FR, Talatahari S. Performance-based seismic design of steel frames using ant colony optimization. J Construct Steel Res. 2010;66(4):566–74. doi:10.1016/j.jcsr.2009.11.006. [Google Scholar] [CrossRef]
169. Yamada S, Kanno Y. Relaxation approach to topology optimization of frame structure under frequency constraint. Struct Multidiscip Optimiz. 2016;53(4):731–44. doi:10.1007/s00158-015-1353-6. [Google Scholar] [CrossRef]
170. Changizi N, Jalalpour M. Robust topology optimization of frame structures under geometric or material properties uncertainties. Struct Multidiscip Optimiz. 2017;56(4):791–807. doi:10.1007/s00158-017-1686-4. [Google Scholar] [CrossRef]
171. Ahmadi B, Jalalpour M, Asadpoure A, Tootkaboni M. Robust topology optimization of skeletal structures with imperfect structural members. Struct Multidiscip Optimiz. 2018;58(6):2533–44. doi:10.1007/s00158-018-2035-y. [Google Scholar] [CrossRef]
172. Qiao S, Han X, Zhou K, Ji J. Seismic analysis of steel structure with brace configuration using topology optimization. Steel Compos Struct. 2016;21(3):501–15. doi:10.12989/scs.2016.21.3.501. [Google Scholar] [CrossRef]
173. Changizi N, Kaboodanian H, Jalalpour M. Stress-based topology optimization of frame structures under geometric uncertainty. Comput Meth Appl Mech Eng. 2017;315(6):121–40. doi:10.1016/j.cma.2016.10.039. [Google Scholar] [CrossRef]
174. Hajirasouliha I, Pilakoutas K, Moghaddam H. Topology optimization for the seismic design of truss-like structures. Comput Struct. 2011;89(7–8):702–11. doi:10.1016/j.compstruc.2011.02.003. [Google Scholar] [CrossRef]
175. Gao X, Ma H. Topology optimization of continuum structures under buckling constraints. Comput Struct. 2015;157(5–6):142–52. doi:10.1016/j.compstruc.2015.05.020. [Google Scholar] [CrossRef]
176. Zhao L, Yi J, Zhao Z, Zhang Z, Han Y, Rong J. Topology optimization of frame structures with stress and stability constraints. Struct Multidiscipl Optim. 2022;65(9):268. doi:10.1007/s00158-022-03361-3. [Google Scholar] [CrossRef]
177. Changizi N, Jalalpour M. Topology optimization of steel frame structures with constraints on overall and individual member instabilities. Finite Eleme Anal Des. 2018;141(7):119–34. doi:10.1016/j.finel.2017.11.003. [Google Scholar] [CrossRef]
178. Miyazu Y, Ohsaki M, Tsuda S. Topology optimization of supporting structure for seismic response reduction of an arch. Sci China Technol Sci. 2016;59(6):852–61. doi:10.1007/s11431-016-6028-z. [Google Scholar] [CrossRef]
179. Cui C-Y, Jiang B-S. A morphogenesis method for shape optimization of framed structures subject to spatial constraints. Eng Struct. 2014;77(10):109–18. doi:10.1016/j.engstruct.2014.07.032. [Google Scholar] [CrossRef]
180. Shimoda M, Nagano T, Shi J-X. Non-parametric shape optimization method for robust design of solid, shell, and frame structures considering loading uncertainty. Struct Multidiscip Optimiz. 2019;59(5):1543–65. doi:10.1007/s00158-018-2144-7. [Google Scholar] [CrossRef]
181. Kociecki M, Adeli H. Shape optimization of free-form steel space-frame roof structures with complex geometries using evolutionary computing. Eng Appl Artif Intell. 2015;38(4):168–82. doi:10.1016/j.engappai.2014.10.012. [Google Scholar] [CrossRef]
182. Wan Y, Hu B, Yang Y, Jin F, Zhou J, Gao B. Discrete sizing optimization method based on dividing rectangles algorithm and local response surface for steel frame structures. J Build Eng. 2023;79:107826. doi:10.1016/j.jobe.2023.107826. [Google Scholar] [CrossRef]
183. Mashayekhi M, Mosayyebi S. A new hybrid Harris hawks optimization (HHO) and particle swarm optimization (PSO) algorithm for the design of castellated beams. Asian J Civil Eng. 2023;24(7):2121–39. doi:10.1007/s42107-023-00630-4. [Google Scholar] [CrossRef]
184. Verbart A, Stolpe M. A working-set approach for sizing optimization of frame-structures subjected to time-dependent constraints. Struct Multidiscip Optimiz. 2018;58(4):1367–82. doi:10.1007/s00158-018-2063-7. [Google Scholar] [CrossRef]
185. Gholizadeh S, Milany A. An improved fireworks algorithm for discrete sizing optimization of steel skeletal structures. Eng Optimiz. 2018;50(11):1829–49. doi:10.1080/0305215X.2017.1417402. [Google Scholar] [CrossRef]
186. Su R, Tangaramvong S, Van TH, Chaiwongnoi A, Song C. Binary comprehensive learning particle swarm optimization approach for optimal design of nonlinear steel structures with standard sizes. Buildings. 2023;13(8):1988. doi:10.3390/buildings13081988. [Google Scholar] [CrossRef]
187. Aydogdu I, Ormecioglu TO, Tunca O, Carbas S. Design of large-scale real-size steel structures using various modified grasshopper optimization algorithms. Neural Comput Appl. 2022;34(16):13825–48. doi:10.1007/s00521-022-07196-3. [Google Scholar] [CrossRef]
188. Gholizadeh S, Razavi N, Shojaei E. Improved black hole and multiverse algorithms for discrete sizing optimization of planar structures. Eng Optimiz. 2019;51(10):1645–67. doi:10.1080/0305215X.2018.1540697. [Google Scholar] [CrossRef]
189. Kaveh A, Hosseini SM, Zaerreza A. Improved Shuffled Jaya algorithm for sizing optimization of skeletal structures with discrete variables. Structures. 2021;29(4598):107–28. doi:10.1016/j.istruc.2020.11.008. [Google Scholar] [CrossRef]
190. Ma Y, Song X, Jia Q, Zhao Y, Lu S. Isogeometric interval size optimization of beam structures. Comput Methods Appl Mech Eng. 2022;395:115003. doi:10.1016/j.cma.2022.115003. [Google Scholar] [CrossRef]
191. Dede T. Jaya algorithm to solve single objective size optimization problem for steel grillage structures. Steel Compos Struct Int J. 2018;26(2):163–70. doi:10.12989/scs.2018.26.2.163. [Google Scholar] [CrossRef]
192. Kociecki M, Adeli H. Two-phase genetic algorithm for size optimization of free-form steel space-frame roof structures. J Construct Steel Res. 2013;90(5):283–96. doi:10.1016/j.jcsr.2013.07.027. [Google Scholar] [CrossRef]
193. Van Mellaert R, Mela K, Tiainen T, Heinisuo M, Lombaert G, Schevenels M. Mixed-integer linear programming approach for global discrete sizing optimization of frame structures. Struct Multidiscip Optimiz. 2018;57(2):579–93. doi:10.1007/s00158-017-1770-9. [Google Scholar] [CrossRef]
194. Kaveh A, Kamalinejad M, Hamedani KB, Arzani H. Quantum Teaching-Learning-Based Optimization algorithm for sizing optimization of skeletal structures with discrete variables. Structures. 2021;32(4):1798–819. doi:10.1016/j.istruc.2021.03.046. [Google Scholar] [CrossRef]
195. Kaveh A, Naeimi M. Sizing optimization of skeletal structures with a multi-adaptive harmony search algorithm. Sci Iran Trans A. 2015;22(2):345–66. [Google Scholar]
196. Shimoda M, Kameyama K, Shi J-X. Tailoring static deformation of frame structures based on a non-parametric shape-size optimization method. Int J Sol Struct. 2017;112:143–54. doi:10.1016/j.ijsolstr.2017.02.011. [Google Scholar] [CrossRef]
197. Kaveh A, Hosseini SM, Zaerreza A. Size, layout, and topology optimization of skeletal structures using plasma generation optimization. Iranian J Sci Technol, Transact Civil Eng. 2021;45(2):513–43. doi:10.1007/s40996-020-00527-1. [Google Scholar] [CrossRef]
198. Zhao L, Li Y, Cai J, Yi J, Zhou Q, Rong J. Integrated topology and size optimization for frame structures considering displacement, stress, and stability constraints. Struct Multidiscip Optimiz. 2024;67(4):48. doi:10.1007/s00158-024-03766-2. [Google Scholar] [CrossRef]
199. Daneshfar M, Hassani A, Aliha M, Berto F. Evaluating mechanical properties of macro-synthetic fiber-reinforced concrete with various types and contents. Streng Mat. 2017;49(5):618–26. doi:10.1007/s11223-017-9907-z. [Google Scholar] [CrossRef]
200. Sabelhaus AP, Li AH, Sover KA, Madden JR, Barkan AR, Agogino AK, et al. Inverse statics optimization for compound tensegrity robots. IEEE Robot Automat Letters. 2020;5(3):3982–9. doi:10.1109/LRA.2020.2983699. [Google Scholar] [CrossRef]
201. He J, Wang Y, Li X, Jiang H, Xie H, Zhou Y. Minimal mass optimization of tensegrity torsional structures. Compos Struct. 2024;345(7):118376. doi:10.1016/j.compstruct.2024.118376. [Google Scholar] [CrossRef]
202. Wang Y, Senatore G. Design of adaptive structures through energy minimization: extension to tensegrity. Struct Multidiscip Optimiz. 2021;64(3):1079–110. doi:10.1007/s00158-021-02899-y. [Google Scholar] [PubMed] [CrossRef]
203. Yildiz K, Lesieutre GA. Sizing and prestress optimization of Class-2 tensegrity structures for space boom applications. Eng Comput. 2022;38(2):1451–64. doi:10.1007/s00366-020-01111-x. [Google Scholar] [CrossRef]
204. Mills AS, Myszka DH, Woods DC, Joo JJ, Murray AP. The structural suitability of tensegrity aircraft wings. In: AIAA Scitech 2020 Forum; 2020; Orlando, FL, USA. doi:10.2514/6.2020-0480. [Google Scholar] [CrossRef]
205. Xu X, Huang S, Wang Y, Luo Y. A generalized objective function based on weight coefficient for topology-finding of tensegrity structures. Appl Mathe Modell. 2023;115(10):541–67. doi:10.1016/j.apm.2022.10.038. [Google Scholar] [CrossRef]
206. Wang Y, Han Z, Xu X, Luo Y. Topology optimization of active tensegrity structures. Comput Struct. 2024;305(4):107513. doi:10.1016/j.compstruc.2024.107513. [Google Scholar] [CrossRef]
207. Guerra A. Design optimization of reinforced concrete structures. USA: Colorado School of Mines; 2004. [Google Scholar]
208. Sirca Gene F, Adeli H. Cost optimization of prestressed concrete bridges. J Struct Eng. 2005;131(3):380–8. doi:10.1061/(ASCE)0733-9445(2005)131:3(380). [Google Scholar] [CrossRef]
209. Amir O. A topology optimization procedure for reinforced concrete structures. Comput Struct. 2013;114–115(12):46–58. doi:10.1016/j.compstruc.2012.10.011. [Google Scholar] [CrossRef]
210. Khan M, Ali M. Optimization of concrete stiffeners for confined brick masonry structures. J Build Eng. 2020;32(3):101689. doi:10.1016/j.jobe.2020.101689. [Google Scholar] [CrossRef]
211. Bruggi M, Milani G, Taliercio A. Design of the optimal fiber-reinforcement for masonry structures via topology optimization. Int J Sol Struct. 2013;50(13):2087–106. doi:10.1016/j.ijsolstr.2013.03.007. [Google Scholar] [CrossRef]
212. Rizzian L, Léger N, Marchi M. Multiobjective sizing optimization of seismic-isolated reinforced concrete structures. Procedia Eng. 2017;199:372–7. doi:10.1016/j.proeng.2017.09.044. [Google Scholar] [CrossRef]
213. Bondarabadi HAR, Kaveh A, Salimi P. Optimal design of shear walls for minimizing the structural torsion using cascade optimization algorithm. Period Polytechnica Civ Eng. 2024;68(2):588–99. doi:10.3311/PPci.23460. [Google Scholar] [CrossRef]
214. Li Q, Skelton RE, Yan J. Energy optimization of deployable tensegrity structure. In: Proceedings of the 30th Chinese Control Conference; 2011 Jul 22–24; Yantai, China. p. 2146–51. [Google Scholar]
215. Dai L, Guan F-L. Shape-sizing nested optimization of deployable structures using SQP. J Central South Univ. 2014;21(7):2915–20. doi:10.1007/s11771-014-2257-0. [Google Scholar] [CrossRef]
216. Tugrul T. Multiobjective size and topolgy optimization of dome structures. Struct Eng Mech. 2012;43(6):795–821. doi:10.12989/sem.2012.43.6.795. [Google Scholar] [CrossRef]
217. Cucuzza R, Rosso MM, Aloisio A, Melchiorre J, Giudice ML, Marano GC. Size and shape optimization of a guyed mast structure under wind, ice and seismic loading. Appl Sci. 2022;12(10):4875. doi:10.3390/app12104875. [Google Scholar] [CrossRef]
218. Marotte Luz Filho JM, Novotny AA. Topology optimization of three-dimensional structures subject to self-weight loading. Eng Comput. 2024;41(2):307–32. doi:10.1108/EC-11-2023-0791. [Google Scholar] [CrossRef]
219. Guo G, Zhao Y, Zuo W. Explicit and efficient topology optimization for three-dimensional structures considering geometrical nonlinearity. Adv Eng Softw. 2022;173:103238. doi:10.1016/j.advengsoft.2022.103238. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF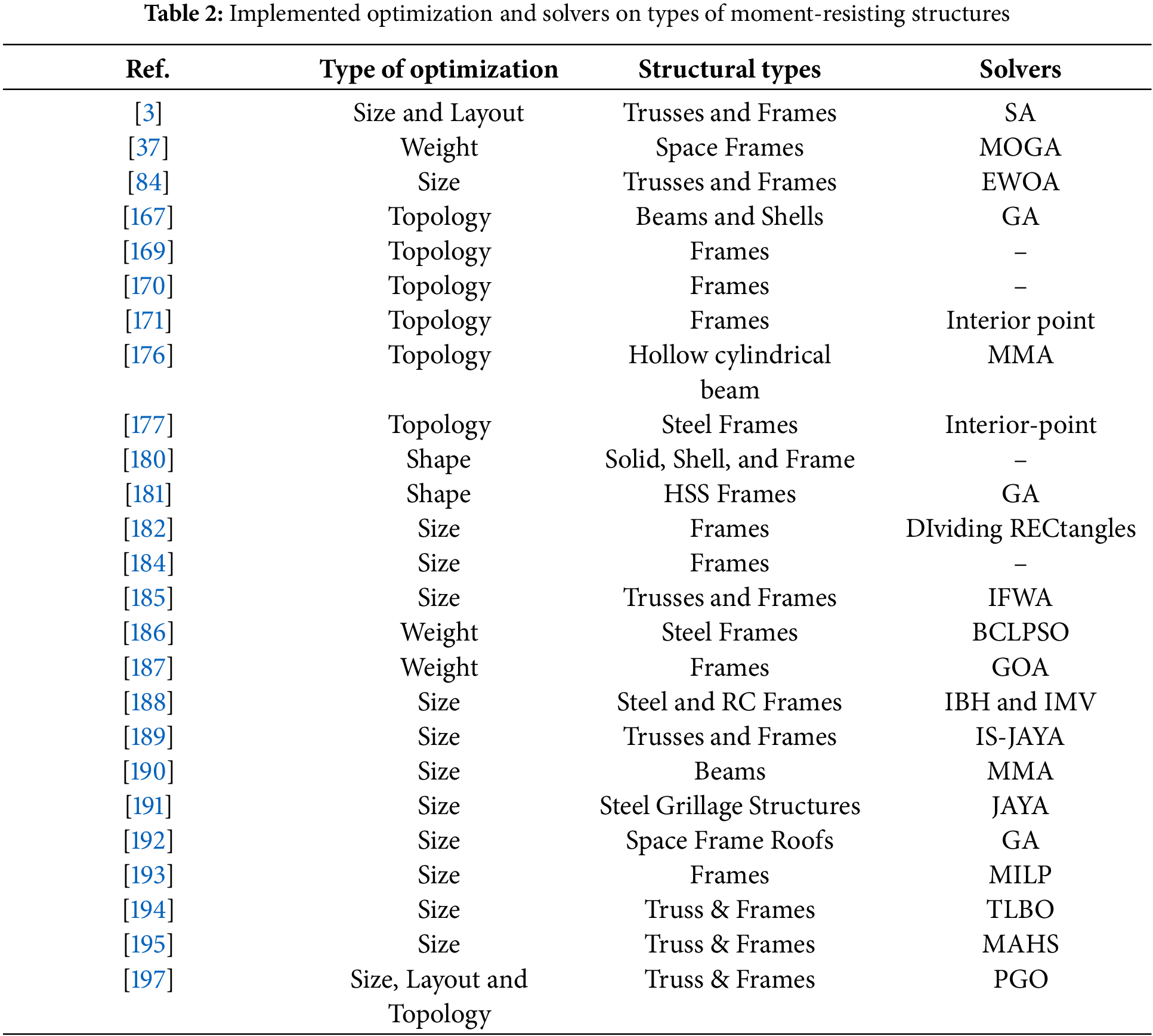
 Downloads
Downloads
 Citation Tools
Citation Tools