Hybrid DF and SIR Forwarding Strategy in Conventional and Distributed Alamouti Space-Time Coded Cooperative Networks

1  Introduction

Cooperative relaying schemes such as Amplify-and-Forward (AF) [1] and decode-and-forward (DF) [2] are designed to harness diversity gain by transmitting signals over multiple paths. The AF protocol performs well when the source-relay channel is strong, but it also amplifies noise along with the signal, which can degrade performance. In contrast, the DF protocol decodes the source message in the relay before forwarding it to the destination. However, this method assumes that the relay can always decode the message successfully, which is not guaranteed in practical networks and can result in error propagation. The performance of AF and DF protocols has been thoroughly analyzed in the literature, under various conditions [3–5]. To address the limitations of each protocol, adaptive relaying strategies have been proposed, combining the advantages of both AF and DF by dynamically switching between them according to channel conditions [6–8]. These hybrid AF-DF relay networks have been shown to outperform AF or DF alone by leveraging the benefits of both approaches.

To combat error propagation in cooperative communications, soft information relaying (SIR) appeared to be an effective solution that has been little studied in the literature and has been considered to combine both the soft signal representation in the AF protocol and the channel coding gain in the DF protocol. In [9], the authors demonstrated the ability of SIR to overcome error propagation at the relay node and proposed distributed coding schemes for soft re-encoding. Recently, the performance of coded cooperative communication employing SIR in multiple energy-harvesting (EH) relays was analyzed in [10], focusing on soft symbol modeling and optimizing the EH power-splitting ratio. Most studies on SIR assume binary phase shift keying (BPSK) modulation for inter-node communication, even though higher-order modulations are preferable when spectral efficiency is a priority. Models have been proposed to characterize the relationship between the forwarded soft estimated symbols at the relay and the correct BPSK source symbols. For example, in [11], the authors introduced a soft noise model, where log-likelihood-ratios (LLRs) were mapped to soft bits, and the resulting soft noise was modeled as non-zero-mean Gaussian noise. In [12], a soft fading model was proposed, characterizing errors as fading coefficients. Additionally, authors [13] extended the soft scalar model to higher-order pulse amplitude and quadrature amplitude modulations. It is important to note that model parameters were often computed offline or estimated via training sequences, which proved to be a limitation in practical implementations, as observed in studies like [11,12]. Furthermore, the soft symbol mapping for higher-order modulations generally relied on the soft mapping technique proposed in [14], used in low-complexity minimum mean squared error (MMSE) multi-user turbo detection. However, this mapping can be inadequate in soft relaying due to significant discrepancies between resulting points and hard input bit values.

Moreover, it was shown in the literature that cooperative diversity gains can be attained through distributed virtual antennas across different nodes in the network and hence the appearance of distributed space-time coding (DSTC) in cooperative networks [15]. This distributed approach leverages the spatial diversity from relay transmissions while preserving high spectral efficiency [16]. In several studies [17–20], space-time block codes (STBC) have been deployed in a distributed manner within cooperative networks, where DSTC was implemented using either AF or DF strategies. A hybrid AF-DF relaying scheme employing DSTC was proposed in [21], with a static assignment of AF and DF relays. Additionally, authors [22] introduced a hybrid decode-and-amplify-forward scheme in a distributed Alamouti-coded cooperative network, deriving the symbol error rate, outage probability, and an upper bound on the outage probability for flat fading Rayleigh channels.

This research addresses limitations inherent in traditional cooperative relaying techniques, particularly the vulnerability of DF to error propagation in challenging environments. The motivation behind the proposed hybrid DF-SIR strategy lies in its flexibility and adaptability in dynamic and variable channel conditions by switching between DF and SIR modes. This adaptability is particularly beneficial in low-energy and error-prone conditions, where traditional DF relaying can propagate errors if decoding fails. In addition, the integration of hybrid DF and SIR with DSTC remains unexplored. Combining these technologies could address several critical challenges, namely reducing error propagation, maximizing diversity gains, and adapting dynamically to variable channel conditions. The hybrid DF-SIR strategy can enhance error resilience in networks with changing channel qualities. This flexibility allows each relay to contribute to DSTC’s spatial diversity without running the risk of high error rates, even in weak channel conditions. Finally, Integrating DSTC with DF-SIR enhances diversity and resilience in challenging wireless settings. Despite significant advancements in cooperative relaying and distributed space-time coding (DSTC), the integration of hybrid DF-SIR with DSTC remains unexplored in cooperative networks, highlighting the novelty and potential impact of this approach.

Motivated by the need for more robust and adaptive cooperative communication strategies, particularly in challenging wireless environments, this paper proposes a novel hybrid DF-SIR (HDFSIR) strategy for both conventional and distributed Alamouti space-time coded cooperative networks. The key contributions of this work are:

•   We propose an opportunistic HDFSIR strategy for coded cooperative networks with EH relays. This practical relaying strategy effectively addresses the limitations of the DF protocol in cases where the source-relay channels are highly error-prone.

•   We derive closed-form expressions for the outage probability and symbol-error-rate (SER) of the coded cooperative network utilizing the HDFSIR strategy.

•   A novel method is introduced to estimate soft symbols for square M-quadrature amplitude modulation (QAM) modulation with Gray labeling, referred to as normalized LLR-based soft estimated symbol (NL-SES) mapping. A Rayleigh Gaussian model is proposed to characterize the complex soft estimated symbols, with model parameters determined online and transmitted to the destination, which is of practical significance.

•   We establish a hybrid DF and SIR relaying strategy within a distributed Alamouti space-time coded cooperative network and compute the outage probability based on the signal-to-noise-ratios (SNR) for different forwarding mode scenarios at the relay nodes.

The remainder of this paper is structured as follows. In Section 2, related works are presented. Section 3 presents the system model for the proposed communication scheme. The soft information relaying technique is detailed in Section 4. In Section 5, we derive the performance analysis in terms of outage probability for the coded cooperative communication with opportunistic relay selection using the HDFSIR strategy in multiple EH relays. Section 6 focuses on the estimation and modeling of soft symbols for M-QAM modulation. The SER of the coded cooperative communication applying the HDFSIR strategy is derived in Section 7. Section 8 introduces the HDFSIR forwarding strategy in a distributed Alamouti space-time coded cooperative network. Simulation results are presented in Section 9, and a conclusion is provided in Section 10.

2  Related Works

This paper proposes a hybrid DF-SIR strategy for coded cooperative networks. Extensive research exists on individual DF and AF relaying strategies, and several studies have explored the benefits of their hybrid combination. For instance, the authors in [23] investigated hybrid AF-DF relaying in cooperative networks to enhance diversity and spectral efficiency. Their findings reveal improved performance over pure AF or DF strategies. In [24], the authors investigate the exact analysis of a multi-hop multi-branch relaying network wherein the relays operate in hybrid AF-DF mode.

In addition, the exploration of hybrid relaying strategies incorporating both DF and AF techniques in conjunction with EH technologies has gained significant momentum in recent years. The authors in [25] provide a thorough performance analysis of hybrid DF-AF relaying networks, emphasizing the system’s ability to adapt relay strategies for improved throughput and reliability in the presence of EH components. They demonstrate how EH can empower wireless networks to sustain operations and optimize performance metrics in dynamic environments. In [26], the authors delve into hybrid AF-DF strategies within wireless EH networks, proposing optimized protocols that enhance energy efficiency without compromising the quality of service. Their work focuses on balancing the benefits of both relaying techniques to maximize overall network performance under constrained energy conditions. In [27], the authors adopt a game-theoretic approach to tackle resource allocation in hybrid relaying systems. Their work underscores the interplay between EH capabilities and strategic resource distribution, providing insights into maximizing network efficiency under competitive conditions. Several works have utilized rateless code (RC)-based dynamic decode-and-forward (DDF) relaying to enhance the performance of EH relay systems. For instance, authors [28] introduces a high-throughput wireless-powered relay network that optimizes time and power allocations, thereby balancing energy harvesting and relaying efficiency to boost throughput. Similarly, authors [29] explores RC-based DDF within SWIPT (Simultaneous Wireless Information and Power Transfer) multi-relay networks. This approach improves reliability and throughput by combining relay selection with rateless codes, which enables effective data transmission despite variable relay conditions. These methods provide useful insights for adaptive relaying in EH networks, demonstrating RC-based DDF’s potential for robust data delivery under fluctuating power conditions. Unlike the RC-based DDF strategy which focuses on incremental redundancy to improve reliability, the proposed hybrid DF-SIR approach directly mitigates error propagation by switching to SIR mode when decoding is unreliable. This switch reduces decoding overhead and processing requirements, making the proposed hybrid DF-SIR strategy suitable for EH networks where power conservation is essential.

Recent advancements in hybrid relaying strategies have explored the integration of DF and AF techniques with DSTC, aiming to enhance system performance in wireless networks. The authors in [30] conduct a comprehensive performance analysis of hybrid DF-AF relaying systems incorporating DSTC. Their findings reveal significant improvements in data throughput and reliability, highlighting the advantages of combining these techniques in challenging communication environments. In a complementary study [31], Wu et al. investigate cooperative strategies in hybrid DF-AF relaying systems that implement DSTC. Their work emphasizes the potential of cooperation among relays to optimize signal quality and increase coverage areas, thus enhancing overall system efficiency. They present simulation results demonstrating the effectiveness of their proposed cooperative strategies under various channel conditions. In [32], Tang et al. focus on the development of efficient protocols for hybrid DF-AF relaying combined with DSTC. Their work presents new protocol designs that not only improve data transmission rates but also enhance system robustness against interference and fading, forming a crucial contribution to the field of cooperative communications. These studies illustrate the growing body of literature addressing the intersection of hybrid DF-AF relaying and DSTC, underscoring their potential to advance wireless communication systems in terms of efficiency, reliability, and performance. However, these studies do not leverage soft information relaying, which is a key component of the proposed Hybrid DF-SIR strategy.

3  System Model

In this work, we consider a cooperative communication system consisting of a source node S, nR EH relay nodes denoted by R1,⋯,RnR, and a destination node D. The cooperation process occurs over two time-slots. During the first time-slot, the source node transmits a message to all relay nodes. It is assumed that the destination is outside the transmission range of the source node. The second time-slot is dedicated to the forwarding process, which begins after the source message has been decoded at the relays. If a relay successfully decodes the message, it operates in DF mode and is included in the set of DF relays. Otherwise, it switches to SIR mode and is included in the set of SIR relays (See the network model in Fig. 1a). The accuracy of the decoding process at each relay is verified using a cyclic redundancy check (CRC) code. An opportunistic relay selection strategy is applied, whereby only the relay that provides the best instantaneous SNR over the end-to-end channel is activated, choosing from either the DF or SIR relay sets.

Figure 1: (a) Network model, (b) Power splitting-based EH relay with HDFSIR forwarding strategy

In this work, we employ a power splitting-based EH scheme to manage the power of the received signal at the relays, as illustrated in Fig. 1b. The power of the source signal received at each relay is divided into two components by a power splitter: one component is used for decoding the source message, while the other is allocated to energize the message forwarding module. Let ρr denote the power splitting ratio (PSR) at relay Rr, which represents the fraction of the total received energy harvested for information forwarding. The remaining energy is dedicated to decoding the message. The source information sequence is expressed as u=(u1,…,uK), where K signifies the length of the information word. A binary channel code CS with rate RS=K/NS is employed at the source, where NS indicates the codeword length. The resulting codeword c=(c1,…,cNS) is then mapped to a modulated sequence x. The received sequence at the r-th relay node is given by:

ySRr=hSRrPSRrx+nSRr,(1)

where hSRr is the fading coefficient at the S−Rr link, and PSRr and nSRr represent, respectively, the average received power and the additive noise at the relay node Rr. The additive noise is modeled as a zero-mean Gaussian random variable with variance σn2. This work assumes quasi-static fading channels in which the fading coefficient remains constant throughout a block period and varies independently from one block to the next. These channels are modeled as normalized Rayleigh distributed random variables with a scale parameter of 1/2. Let PSD denote the received signal power at the destination node for a hypothetical direct link between the source node and the destination node. The SNR of the received signal at the EH relay node Rr, which is used for decoding the message, is expressed as:

γSRr=|hSRr|2(1−ρr)GSRrPSDσn2,(2)

where GSRr is the power gain of the S−Rr link, given by (dSD/dSRr)α. Here, dSD and dSRr represent the normalized distances between the source and destination nodes and the source and relay node Rr, respectively, while α is the path loss exponent. The transmit power allocated for information forwarding at relay Rr can be expressed as follows:

PRr=ρrν|hSRr|2GSRrPSD,(3)

where 0<ν<1 represents the EH conversion efficiency of the receiver, assumed to be constant across all relay nodes. The HDFSIR approach is motivated by its flexibility and adaptability to changing channel conditions, which is convenient in EH relay systems. It allows relays to switch between the DF and the SIR modes depending on decoding success, addressing the issue of error propagation in low-energy and unreliable environments.

In the subsequent sections, we first present the SIR strategy and then investigate the performance of the opportunistic hybrid DF-SIR strategy as an effective solution to address the issue of error propagation.

4  Soft Information Relaying

In this work, if a relay does not successfully decode the received message, it operates in SIR mode. In this case, the relay node Rr performs a Soft-Input-Soft-Output (SISO) decoding of the received message ySRr. The a-posteriori LLRs for the estimated information bits, denoted by L(u^Rr,t|ySRr) for 1≤t≤K, are calculated using a low-complexity Max-Log-MAP decoder, as described in [33]. Fig. 2a presents the histogram of the LLRs for a specific SNR per information bit, while Fig. 2b illustrates the corresponding normal Q-Q plot for the LLR distribution. A distribution is typically classified as Gaussian if the Q-Q plot aligns with the y=x line. However, it is clear that the Q-Q plot deviates significantly from the y=x line, indicating that the LLR distribution is non-Gaussian. Consequently, we hypothesize that the output LLRs from the SISO decoder are influenced not only by residual additive noise but also by quasi-static channel fading coefficients. This is because, while the channel decoding process tends to average out the Gaussian noise, the effects of channel fading persist partially even after decoding.

Figure 2: (a) Histogram of a relay soft encoder output LLRs for Eb/N0= 10 dB, (b) Normal Q-Q plot of the distribution

In this section, we adopt BPSK modulation, where the LLRs at the output of the relay SISO decoder are treated as soft symbols forwarded to the destination. These soft symbols are modeled using the Rayleigh-Gaussian LLR (RGL) model as follows [10]:

xRr,t=L(u^Rr,t|ySRr)=2hRrσnRr2(hRrxt+nRr,t),(4)

where xt∈{−1,1} represents the transmitted BPSK modulated symbol, hRr is a quasi-static Rayleigh-distributed fading coefficient, and nRr,t is Gaussian noise with zero mean and variance σnRr2. Using the moment method, the SNR at the output of the SISO decoder, denoted as γRr, is simply expressed as:

γRr=E24+14−12,(5)

where E2 is the second-order moment of the soft symbols (xRr,1,…,xRr,K). Each block of soft estimated symbols is normalized using a factor βRr, which remains constant during block transmission, and is calculated as follows:

βRr=1E{xRr2}=14γRr2+4γRr,(6)

where E{⋅} denotes the expected value operator. Higher-order modulation and its corresponding modeling are addressed in Section 6. At the destination, the received symbol at time t is given by:

yRrD,t=hRrDPRrGRrDβRrxRr,t+nRrD,t,(7)

where hRrD is the normalized quasi-static Rayleigh fading coefficient between relay Rr and the destination, GRrD=1/(RSdRrDα) accounts for path loss and coding rate at the destination, and nRrD,t is zero-mean additive white Gaussian noise with variance σn2. The distance dRrD refers to the normalized distance of the Rr−D link.

Based on (4), (6), and (7), the SNR of the equivalent end-to-end channel, denoted as γSRrD, is derived as:

γSRrD=γ¯RrDgSRrgRrDγRrγ¯RrDgSRrgRrD+γRr+1,(8)

where gSRr=|hSRr|2, gRrD=|hRrD|2, and γ¯RrD=ρrν(GSRr/dRrDα)(PSD/σn2). Note that gSRr, gRrD, and γRr are independent, exponentially distributed variables with parameters g¯SRr, g¯RrD, and γ¯Rr, where γ¯Rr is obtained by averaging γRr over number of blocks.

5  Performance of the Opportunistic HDFSIR Strategy in Coded Cooperative Communication with Multiple EH Relays

In this section, we analyze the performance of the opportunistic hybrid protocol HDFSIR, where a single relay Rsel is selected from two sets: one consisting of relays that successfully decode the received message using the DF protocol, and another consisting of relays using the SIR protocol. In order to ensure that the messages are decoded correctly at the relay Rr, the channel capacity of the S−Rr link, denoted by CSRr, should be no less than a threshold information rate per symbol R. Therefore, the set of candidate relays using the DF protocol is defined as:

ℛDF={r:CSRr=12log2⁡(1+γSRr)>R}.(9)

The received SNR at the destination, assuming error-free decoding at relay Rr, can be expressed as:

γRrD=gSRrgRrDγ¯RrD.(10)

Relay selection is based on maximizing the instantaneous SNR, i.e.,

Rsel=arg⁡maxr∈ℛSIR,j∈ℛDF⁡{γSRrD,γRjD},(11)

where ℛSIR is the set of relays using the SIR strategy. Outage in the coded cooperative scheme with the opportunistic HDFSIR strategy can occur in two distinct scenarios:

• Scenario 1: ℛDF≠∅. Outage occurs if the Rr−D link with the highest SNR among all relays in ℛDF is in outage, and the equivalent end-to-end link with the maximum SNR from the remaining relays is also in outage. The outage probability in this scenario is given by:

Pout(1)=∑k=1nR(nRk)∏r∈ℛDF,kP(γSRr>γth)P(γRrD<γth)⏟Ar∏r∉ℛDF,kP(γSRr<γth)P(γSRrD<γth)⏟Br=∑k=1nR(nRk)∏r∈ℛDF,kexp−γthg¯SRr⁡Ar∏r∉ℛDF,k(1−exp−γthg¯SRr)Br,(12)

where ℛDF,k is the set in (9) of size k and γth=22R−1 is the threshold SNR.

• Scenario 2: ℛDF=∅. All relays are in SIR forwarding mode. Outage occurs when the equivalent end-to-end link with the highest SNR is in outage. The outage probability for this scenario is given by:

Pout(2)=∏r=1nRP(γSRr<γth)P(maxr=1,…,nR⁡γSRrD<γth)=∏r=1nR(1−exp−γthγ¯SRr)P(γSRrD<γth)⏟Br.(13)

The probabilities Ar and Br are derived as follows:

Ar=P(γRrD<γth)=P(gSRrgRrD<γthγ¯RrD)=FgSRrgRrD(γthγ¯RrD),(14)

where:

FgSRrgRrD(γ)=1−P(gSRrgRrD>γ)=1−∫0∞P(gSRr>γx)fgRrD(x)dx=1−∫0∞exp−γg¯SRrx⁡1g¯RrDexp−xg¯RrD⁡dx=1−2γg¯rK1(2γg¯r),(15)

using ∫0∞exp−ax−b/x⁡dx=2b/aK1(2ab) [34], where K1(⋅) is the first-order modified Bessel function, and g¯r=g¯SRrg¯RrD.

Br=P(γSRrD<γth)=P(gSRrgRrD(γRr−γth)<ϕrγRr+1)=∫0γthfγRr(x)dx+∫γth∞FgSRrgRrD(ϕrx+1x−γth)fγRr(x)dx=1−exp−γthγ¯Rr+2γ¯Rr∫γth∞ϕrx+1g¯r(x−γth)K1(2ϕrx+1g¯r(x−γth))exp−xγ¯Rr⁡dx⏟Ir,(16)

where ϕr=γth/γ¯RrD. The integral Ir in (16) is not tractable, and therefore, the Monte Carlo method [35] is applied to obtain the following approximation:

Ir≈1NMC∑i=1NMCϕrxi+1g¯r(xi−γth)K1(2ϕrxi+1g¯r(xi−γth)),(17)

where xi,i=1,⋯,NMC, are NMC generated realizations from the distribution fγRr with xi>γth. Thus, the outage probability for coded cooperative communication using the HDFSIR protocol and relay selection in a multiple EH relays network is expressed as:

PoutHDFSIR-RS=Pout(1)+Pout(2).(18)

6  Soft Information Relaying for M-QAM: Soft Symbol Estimation and Modeling

Implementing soft information relaying for high-order modulation, such as M-QAM, can be challenging due to its complexity, which may hinder practical applications. However, high-order modulation is crucial when spectral efficiency is a priority. This section investigates the mapping characteristics of M-QAM to derive soft symbols from m=log2⁡(M) successive LLRs at the SISO decoder’s output, represented as (L(u^Rr,1|ySRr),⋯,L(u^Rr,K|ySRr)). Let 𝒮M={s1,⋯,sM} denote an M-ary symbol alphabet with ∑i=1Msi=0 and ∑i=1M|si|2=M. We will first describe the averaged soft estimated symbol (A-SES) mapping [14], based on the averaging of constellation points, and subsequently introduce NL-SES mapping, which leverages the decomposition of square M-QAM modulation into sub-modulations.

6.1 Averaged Soft Estimated Symbol Mapping

The A-SES mapping method has proven efficiency in low-complexity MMSE turbo multi-user detection. To determine the real and imaginary components of the soft estimated symbols at the relay, M-QAM modulation is viewed as a combination of two independent M-PAM modulations: one for the real part, denoted by the alphabet set 𝒮IM={sI,1,⋯,sI,M}, and the other for the imaginary part, represented by the alphabet set 𝒮QM={sQ,1,⋯,sQ,M}. The symbols in 𝒮IM and 𝒮QM are generated by applying the Gray code mapping rule [36] to bit sequences (i1,⋯,im2) and (q1,⋯,qm2), resulting in the symbols sI and sQ, respectively. These symbols are recursively determined as follows:

sI(i1,⋯,im2)=(1−2i1)(2m2−1d+sI(i2,⋯,im2)),(19)

sQ(q1,⋯,qm2)=(1−2q1)(2m2−1d+sQ(q2,⋯,qm2)),(20)

where sI(0)=sQ(0)=d, sI(1)=sQ(1)=−d, and d is the half minimum distance between two symbols, equal to 3/2(M−1) in the normalized M-QAM constellation. For 16-QAM modulation, the symbols in 𝒮I4 and 𝒮Q4 are generated from the PAM mapping of bit pairs (i1,i2) and (q1,q2) to the set {−3d,−d,d,3d}, where d=1/10.

Let (u^Rr,1,⋯,u^Rr,m) represent a block of estimated information bits corresponding to an M-QAM modulated symbol. The real and imaginary components of the soft estimated complex symbol to be transmitted over the Rr−D link are computed using the following expressions:

ℛ(xRr)=∑i1,⋯,im2sI(i1,⋯,im2)∏b=1,⋯,m2P(u^Rr,b=ib|ySRr),(21)

ℐ(xRr)=∑q1,⋯,qm2sQ(q1,⋯,qm2)∏b=1,⋯,m2P(u^Rr,b+m2=qb|ySRr),(22)

where ℛ(⋅) and ℐ(⋅) represent the real and imaginary components, respectively. The bit probabilities in (21) and (22) are calculated as P(uRr,b=0|ySRr)=expL(u^Rr,b|ySRr)⁡/(1+expL(u^b,Rr|ySRr)) and P(uRr,b=1|ySRr)=1/(1+expL(u^Rr,b|ySRr)).

6.2 Normalized LLR-Based Soft Estimated Symbol Mapping

To explain the proposed NL-SES mapping, we consider square 16-QAM modulation, which can be interpreted as the sum of two quadrature phase-shift keying (QPSK) sub-modulations. One is a primary QPSK sub-modulation with symbol amplitude 22d, and the other is a secondary QPSK sub-modulation with symbol amplitude 2d. Thus, each symbol in the 16-QAM constellation is a sum of a point from the primary sub-modulation and a point from the secondary sub-modulation.

To generalize, let M-QAM be a square modulation, where M=2m and m is even. Let (u^Rr,1,⋯,u^Rr,m) represent a block of estimated information bits corresponding to a modulated symbol. For each modulated symbol, the normalized LLRs of the estimated bits u^Rr,b,b=1,⋯,m, are defined as follows:

L¯(u^Rr,b)=L(u^Rr,b|ySRr)1m∑i=1mL(u^Rr,i)2.(23)

The real and imaginary components of the NL-SES mapping, according to square M-QAM modulation with Gray code labeling, are recursively defined as follows:

ℛ(xRr)=ℳm2(u^Rr,1,⋯,u^Rr,m2)=L¯(u^Rr,1)2m2−1d+sign(L¯(u^Rr,1))ℳm2−1(u^Rr,2,⋯,u^Rr,m2),(24)

ℐ(xRr)=ℳm2(u^Rr,m2+1,⋯,u^Rr,m)=L¯(u^Rr,m2+1)2m2−1d+sign(L¯(u^Rr,m2+1))ℳm2−1(u^Rr,m2+2,⋯,u^Rr,m),(25)

where ℳ(⋅) is a mapping function and ℳ1(u^)=L¯(u^)⋅d. The function sign(⋅) maps to +1 when the argument is positive and to −1 when it is negative. For 16-QAM modulation, ℛ(xRr)=L¯(u^Rr,1)⋅2d+sign(L¯(u^Rr,1))L¯(u^Rr,2)⋅d, and ℐ(xRr)=L¯(u^Rr,3)⋅2d+sign(L¯(u^Rr,3))L¯(u^Rr,4)⋅d.

6.3 Proposed Model for the Complex Soft Estimated Symbols

The complex soft estimated symbols xRr obtained using the A-SES or NL-SES mapping methods are modeled as follows:

xRr=ℛ(xRr)+jℐ(xRr)=hRrx+nRr,(26)

where x represents the correct modulated complex symbol, hRr is a Rayleigh distributed flat fading coefficient, and nRr is a symmetric zero-mean complex Gaussian noise with variance σnRr2/2 for each component. This model is referred to as the Rayleigh Gaussian (RG) model. The parameters hRr and σnRr2 are determined via the moment method and are given by the following expressions:

hRr2={E22+3E22−E42,E22≥E431,otherwise(27)

σnRr2=E2−hRr2,(28)

where E2 and E4 represent the second and fourth moments of the soft estimated symbols’ amplitude over a message block, respectively. The complex soft estimated symbols are normalized using a factor βRr, which remains constant during a block transmission and is computed as:

βRr=1E{|xRr|2}=1hRr2+σnRr2.(29)

It can be shown that the SNR of the end-to-end relay channel, based on the model in (26), is expressed similarly to (8), where γRr is substituted by hRr2/σnRr2, with hRr2 and σnRr2 defined in (27) and (28), respectively. The outage probability analysis for coded cooperative communication conducted in Section 6, in the context of BPSK modulation, can be extended to square M-QAM modulation using the corresponding model.

7  Symbol Error Rate Analysis of Coded Cooperative Scheme Applying HDFSIR Strategy with Single EH Relay

In this subsection, we derive the SER for the coded cooperative scheme utilizing the HDFSIR strategy with a single EH relay. The SER can be expressed as follows:

PSERHDFSIR=(1−PbSR)PSERRD+PbSRPSERSRD,(30)

where PbSR represents the bit error rate (BER) at the source-relay link after demodulation and channel decoding. PSERRD denotes the SER at the relay-destination link, assuming error-free decoding at the relay, while PSERSRD indicates the SER at the source-relay-destination channel under erroneous decoding at the relay while employing the SIR strategy. In this section, we omit the subscript r denoting the relay index, as we focus on a single relay scenario. The BER at the source-relay link post channel decoding can be tightly upper bounded using the limit-before-average technique proposed in [37], which is computed as follows:

PbSR≲1NMC∑i=1NMCmin{12,∑d=dminCSNS∑w=1KwAw,dCSP2,SR(d|xi)},(31)

where Aw,dCS refers to the number of codewords of weight d generated by the information words of weight w, and dminCS denotes the minimum distance of the code CS used at the source node. Additionally, P2,SR(d|xi) is the pairwise error probability of decoding an erroneous codeword c^ of weight d instead of the all-zero overall codeword, with xi representing NMC realizations generated according to the exponential distribution fγSR of the source-relay link SNR characterized by γ¯SR=(1−ρ)GSRPSD/σn2. Notably, the second term within the min{,} operation in (31) acts as the union bound on the BER when employing maximum likelihood decoding, as elaborated in [38], for a given SNR per transmitted symbol. The pairwise error probabilities for BPSK and M-QAM modulations are specified in [39]:

P2,SR(d|γ)=P(0→c^)={Q(dγ)forBPSK,2(M−1M)Q(3dγM−1)forM-QAM,(32)

where Q(⋅) is the Gaussian Q-function, which is approximated by Q(x)≃112e−x2/2+14e−2x2/3 [40]. Leveraging the findings in [41], the symbol error rates PSERRD and PSERSRD can be computed utilizing the cumulative distribution function (CDF) based approach as follows:

PSERX=ab2π∫0∞exp−bγγFγX(γ)dγ,(33)

where FγX(γ) denotes the CDF of the SNR per symbol at the relay-destination link for correctly decoding the message at the relay (X = RD) and for the CDF of the SNR per symbol at the end-to-end relaying channel when applying the SIR strategy in the case of erroneous decoding (X = SRD). The constants a and b are modulation-dependent, with a=0.5 and b=1 for BPSK, and a=2−2/M and b=3/(2M−2) for rectangular M-QAM. Following (10) and (15), we can express PSERRD as:

PSERRD=ab2π(∫0∞exp−bγγdγ−2γ¯RDg¯∫0∞exp−bγ⁡K1(2γγ¯RDg¯)dγ⏟I)=abπ(πb(limA→∞⁡erf(bA)−erf(b0))−2γ¯RDg¯I),(34)

where ∫BCexp−bγγdγ=πb(erf(bA)−erf(bC)). The resolution of the integral expression I is provided by Gradshteyn and Ryzhik [42] and is resolved as follows:

I=π2γ¯RDg¯bexp12γ¯RDg¯b⁡M−12,12(1γ¯RDg¯b)=π21γ¯RDg¯bF(32;2;1γ¯RDg¯b),(35)

where Mκ,μ(⋅) is the Whittaker function, defined in terms of the confluent hypergeometric function F(;;) [43]. Consequently, PSERRD is expressed as:

PSERRD=ab2π(limA→∞⁡erf(bA)−erf(0)−1γ¯RDg¯πbI).(36)

With similar manipulations as shown above, we can express the symbol error rate at the source-relay-destination channel PSERSRD in a similar manner. By combining the obtained results for PSERRD and PSERSRD in (30), we arrive at the final expression for the symbol error rate of the coded cooperative scheme applying the HDFSIR strategy.

8  Hybrid DF-SIR Strategy in Distributed Alamouti Space-Time Coded Cooperative Network

In this section, we analyze a cooperative network that consists of a source node S, two EH relay nodes R1 and R2, and a destination node D, all operating under the hybrid DF-SIR forwarding mode. Our focus is on symbols encoded using M-QAM modulation, which prompts us to adopt the RG model presented in (26). As depicted in Fig. 3, the transmission occurs in two phases, each comprising two time slots. During phase 1, the source S sends the symbols x1 and x2 to the relays. In phase 2, relays R1 and R2 use the Alamouti code to transmit in two time slots, effectively emulating a virtual multiple-input single-output system. The transmission scheme is summarized in Table 1, which illustrates the symbols transmitted by the source and the two relays across the four time slots in accordance with the Alamouti representation, where the asterisk refers to the complex conjugate.

Figure 3: Hybrid DF-SIR forwarding scheme in a distributed Alamouti space-time coded cooperative network, where the asterisk denotes the complex conjugate

We define Xi,j as the transmitted symbol during the second phase at time slot i from relay Rj, where i=1,2 and j=1,2. The symbol Xi,j depends on the forwarding mode and can be expressed as follows:

Xi,j={PRjxi,for DF mode,PRjβRj(hRjxi+nRj),for SIR mode,(37)

where PRj is the transmit symbol power at the EH relay Rj as given in (3), βRj is the normalization factor of the soft estimated symbols as detailed in (29), and hRj and nRj are defined in the proposed model for higher-order soft estimated symbols in Section 6. The received signal at the destination D during the two consecutive symbol periods can be expressed as follows:

y=[y1y2∗]=[h1−h2h2∗h1∗]⏟Heff[x1x2]+[w1w2∗]=c1x1+c2x2+w,(38)

where h1 and h2 are the equivalent fading coefficients for the links from R1 to D and from R2 to D, respectively. The vectors c1=(h1,h2∗)T and c2=(−h2,h1∗)T form the first and second columns of the effective matrix Heff of the Alamouti space-time code. The noise vector at the destination is denoted by w=(w1,w2∗)T, where wi represents the noise element resulting from the summation of the additive white Gaussian noise component nD,i at the relay-destination link, characterized by zero mean and variance σn2, and the equivalent combined noise from the relay after DF or SIR mode. The expressions for hj,j=1,2, and the resulting noise vector (w1,w2∗)T are dependent on the forwarding mode employed by relays R1 and R2, defined as follows:

hj=hRjDΓj(βRjhRj)(1−Θj),j=1,2,(39)

and

[w1w2∗]=[(1−Θ1)hR1Dζ1nR1−(1−Θ2)hR2Dζ2nR2+nD,1(1−Θ2)hR2D∗ζ2nR2+(1−Θ1)hR1D∗ζ1nR1+nD,2∗],(40)

where Γj=PRjGRjD, ζj=ΓjβRj, and

Θj={1,for DF mode,0,for SIR mode.(41)

The elements of the noise vector w are assumed to be independent and identically distributed (i.i.d.) with zero mean, leading to the expression for the noise covariance matrix:

E{wwH}=((1−Θ1)|hR1D|2ζ12σnR12+(1−Θ2)|hR2D|2ζ22σnR22+σn2⏟σeq2)I2,(42)

where (⋅)H denotes the Hermitian transpose of (⋅) and I2 is the 2×2 identity matrix.

At the receiver, due to the orthogonality of c1 and c2, we can decouple the transmitted symbols through beamforming applied to the received symbols y1 and y2∗. The expressions for the decoded symbols can be written as follows:

x~1=c1H||c1||y1=||c1||x1+c1H||c1||w⏟w~1,(43)

and

x~2=c2H||c2||y2∗=||c2||x2+c2H||c2||w⏟w~2,(44)

where ||ci||=|h1|2+|h2|2 represents the amplitude of ci for i=1,2. The estimates of the transmitted symbols x^1 and x^2 are determined by applying the maximum likelihood rule, which is expressed as x^i=arg⁡minx(|x~i−|h1|2+|h2|2x|2),i=1,2. The variance of the resulting noise w~i,i=1,2, can be computed as follows:

E{w~iw~i∗}=E{ciH||ci||wwHci||ci||}=E{σeq2ciHI2ci||ci||2}=σeq2.(45)

Thus, the SNR at the destination, utilizing the HDFSIR strategy with the distributed Alamouti space-time code and beamforming at the receiver, is given by:

γSRDDSTC=|hR1D|2Γ12(βR12hR12)(1−Θ1)+|hR2D|2Γ22(βR22hR22)(1−Θ2)(1−Θ1)|hR1D|2ζ12σnR12+(1−Θ2)|hR2D|2ζ22σnR22+σn2.(46)

It is obvious that the use HDFSIR in distributed Alamouti space-time coded cooperative network leads to a diversity gain regardless the operating mode of each relay, since the total power, as shown in the above equation, always made up of the sum of two parts, each power part comes from the corresponding relay be it in DF mode or in SIR mode.

The outage probability for the coded cooperative scheme utilizing the HDFSIR strategy and the distributed Alamouti space-time code is determined by four distinct scenarios, depending on the forwarding modes of relays R1 and R2. These scenarios are represented by the parameters (Θ1,Θ2), where (Θ1,Θ2)∈{0,1}2. The expression for the outage probability is given by:

PoutDSTC=P(γSR1<γth)P(γSR2<γth)P(γSRDSTBC<γth|Θ1=0,Θ2=0)+P(γSR1<γth)(1−P(γSR2<γth))P(γSRDSTBC<γth|Θ1=0,Θ2=1)+(1−P(γSR1<γth))P(γSR2<γth)P(γSRDSTBC<γth|Θ1=1,Θ2=0)+(1−P(γSR1<γth))(1−P(γSR2<γth))P(γSRDSTBC<γth|Θ1=1,Θ2=1).(47)

Currently, there are no analytical results available concerning the performance of the Hybrid DF-SIR relaying network when integrated with the distributed Alamouti space-time code. This is primarily due to the complexity of the statistical distribution of the resulting end-to-end SNR, which involves the products and sums of independent exponential random variables. Therefore, we will only present in the next section the experimental results to ascertain the appropriateness of the proposed relaying scheme.

9  Simulation Results

This section presents simulations evaluating the performance of the coded cooperative scheme, using the Hybrid DF-SIR strategy, and validating the earlier theoretical analysis. We established a comprehensive simulation environment to assess the scheme’s effectiveness. Table 2 summarizes the essential components and parameters of this simulation setup, providing clarity on the conditions under which the evaluations were performed.

The value of PSD/σn2 in the previous analysis is computed based on the SNR per information bit at the destination node, represented as Eb/N0, and is modified to (K/(NS+NCRC))(2Eb/N0), where NS is the length of the terminated code-word at the source node and NCRC is the number of additional CRC check bits, set to 16 for this work.

Fig. 4 illustrates the simulated and analytical outage performance of the coded cooperative schemes utilizing opportunistic DF, SIR, and HDFSIR strategies as the relays move away from the source toward the destination with nR=4. Here, the PSR is set to 0.5 for all relays, the SNR per information bit at the destination is Eb/N0=16 dB, and the threshold information rate is R=0.5 bit/sec/Hz. Notably, the trends in outage probability are consistent across all three forwarding strategies. The performance of the coded cooperative scheme using DF and SIR strategies can be explained as follows: the DF protocol demonstrates superior outage performance compared to the SIR strategy when the normalized distance dSRr is less than approximately 0.29. With a smaller distance between the source and relay nodes, the likelihood of error-free decoding at the relays increases due to higher received power. Consequently, more candidate relays are involved in the opportunistic DF relaying, enhancing outage performance by leveraging diversity. However, as the distance between the source and relay nodes increases, less energy is harvested at the relay, leading to a higher probability of erroneous decoding and reduced transmission power during the forwarding phase. This explains the observed degradation in outage probability performance as the relays approach the destination, which favors the SIR strategy. Even with low power levels and error-prone decoding at the relays, all available relays participate in the relay selection process. Furthermore, the application of the opportunistic HDFSIR protocol in the coded cooperative scheme consistently outperforms the DF and SIR strategies across all source-relay distances, with particularly pronounced advantages over the SIR strategy at small distances and the DF strategy at larger distances. This validates that the coded cooperative scheme employing the HDFSIR strategy effectively combines the strengths of both DF and SIR forwarding protocols for all relay positions.

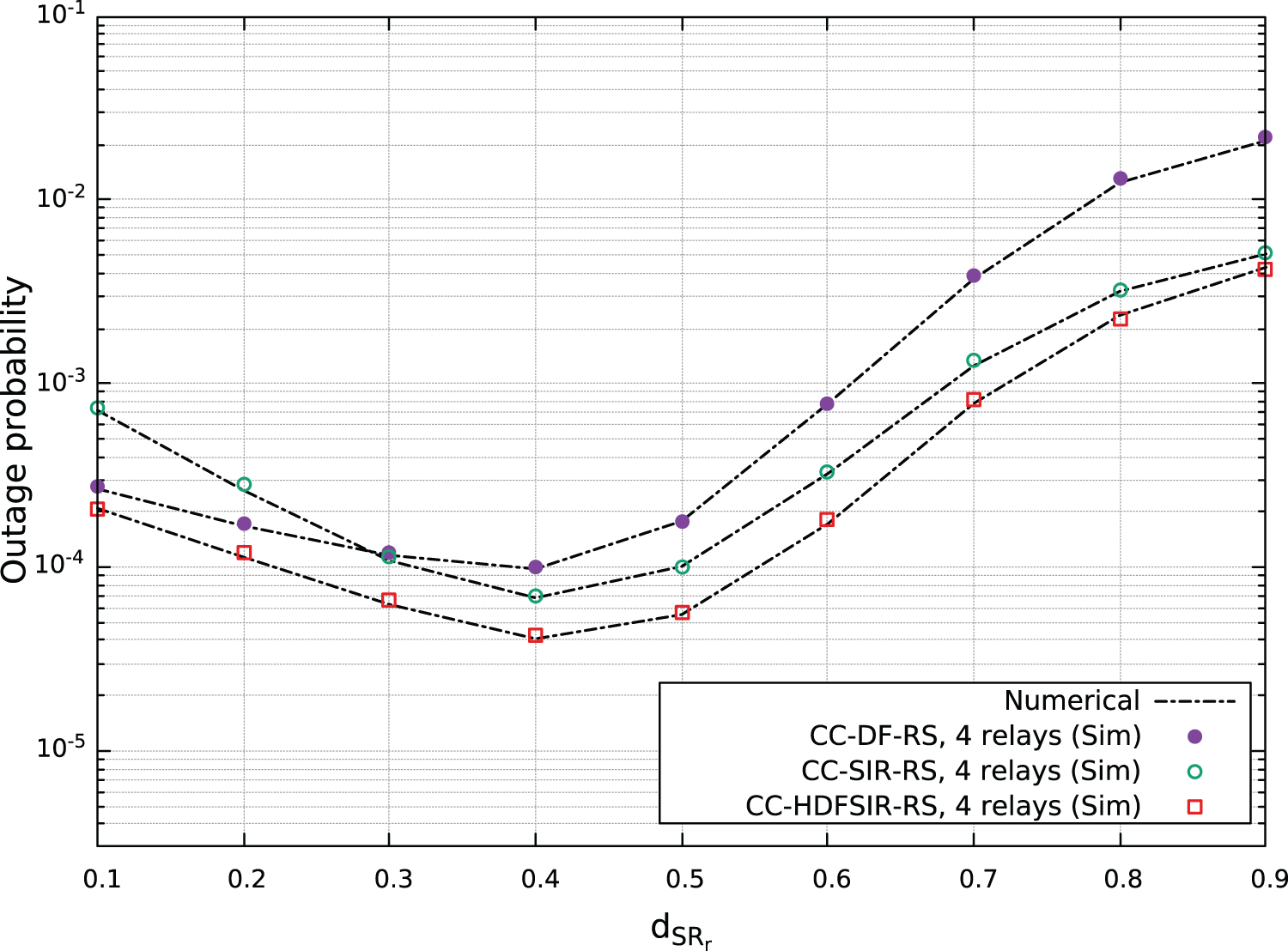
Figure 4: Numerical and simulated outage probability results of the coded cooperative schemes applying the DF, SIR, and HDFSIR strategies when varying dSRr, 4 relays, Eb/N0=16 dB, ρr=0.5 for all relays, and R=0.5 bit/sec/Hz

To evaluate the effectiveness of the proposed NL-SES mapping method, we compare the SER performance of the coded cooperative scheme using the SIR strategy with NL-SES mapping against that employing the A-SES mapping for QPSK and 16-QAM with Gray labeling. A single EH relay positioned at dSR=0.5 is considered. The forwarded soft estimated symbols are modeled using the RG model described in Section 6, with model parameters determined online at the relay for each block and subsequently transmitted to the destination for calculating LLRs. The linear combination of all soft information through A-SES mapping results in a loss of soft information, proving inefficient, as the resulting symbol may closely resemble a constellation point corresponding to a completely different symbol from the original input bits. This inefficiency accounts for the performance gap observed in Fig. 5 between the results obtained using A-SES mapping and those using the proposed NL-SES mapping for both QPSK and 16-QAM modulations. Additionally, the figure reveals that as the modulation order increases, the SIR strategy loses efficiency compared to the DF strategy, as the relative advantage of the SIR strategy with NL-SES mapping over the DF strategy when using QPSK diminishes when employing 16-QAM.

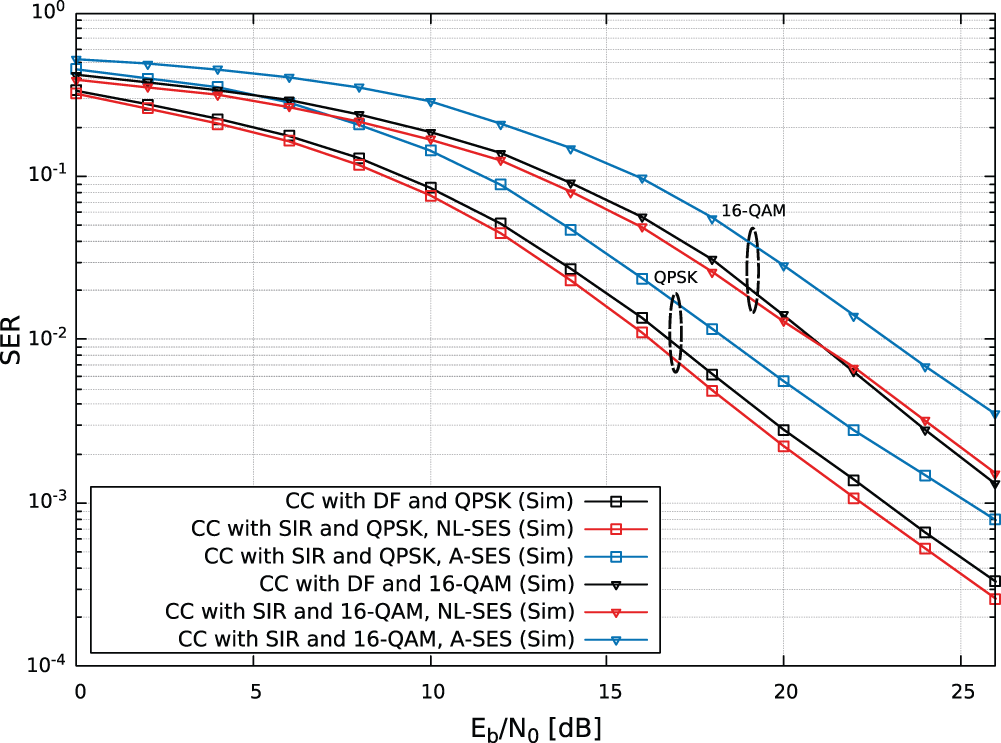
Figure 5: Simulated SER results of the coded cooperative scheme with SIR strategy applying the proposed NL-SES and the A-SES mapping methods for QPSK and 16-QAM modulations, ρ=0.5 and dSR=0.5

Subsequently, Fig. 6 displays the simulated and analytical SER vs. SNR per information bit Eb/N0 of the coded cooperative scheme using a single EH relay with the HDFSIR strategy, wherein only the NL-SES mapping is considered during SIR strategy application. Simulations are conducted for BPSK, QPSK, and 16-QAM. For BPSK, the forwarded soft symbols via the SIR strategy are derived by normalizing the LLRs at the output of the SISO decoder, modeled by the RGL model described in Section 4. The figure indicates a moderate discrepancy between analytical and simulated results when employing the SIR strategy for QPSK and 16-QAM, which can be attributed to information loss due to the RG model. However, it also shows that analytical results converge with simulated results at high SNRs. Additionally, a marginal gap favoring simulated results is observed at low SNRs for BPSK, which disappears at moderate and high SNRs.

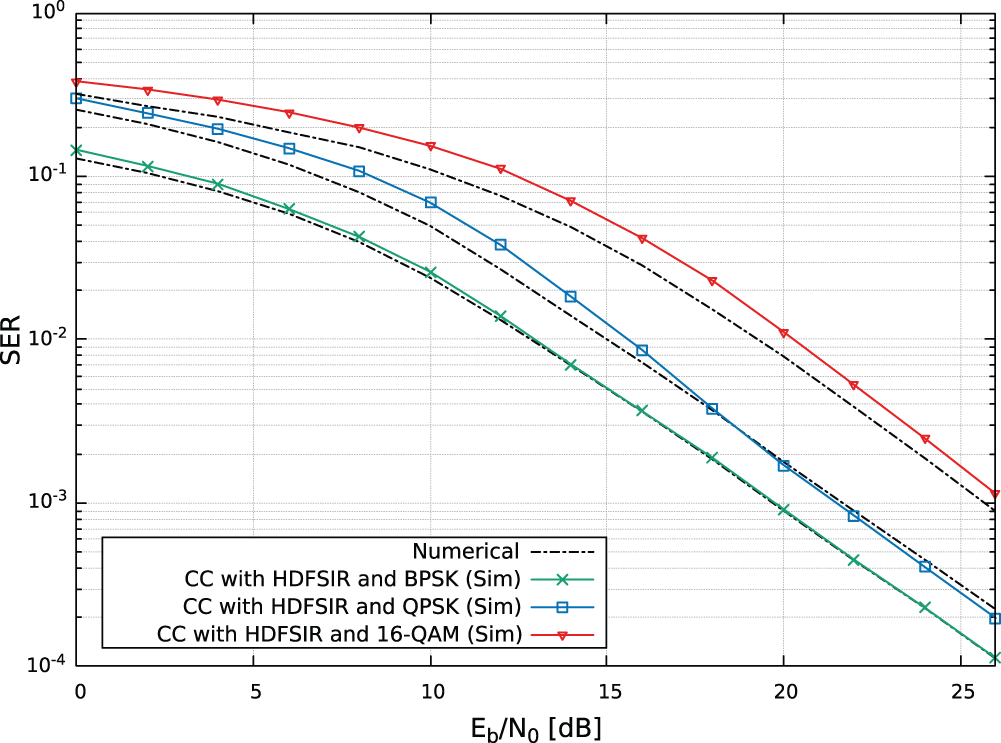
Figure 6: Numerical and simulated SER results of the coded cooperative scheme applying HDFSIR strategy for BPSK, QPSK, and 16-QAM modulations, ρ=0.5 and dSR=0.5

Finally, the simulation results for outage probability vs. SNR per information bit at the destination of the Alamouti DSTC coded cooperative scheme utilizing DF, SIR, and the proposed HDFSIR strategies are presented in Fig. 7. The results are obtained for a fixed threshold of information rate R=0.5 bit/sec/Hz, a PSR of ρ=0.5 for both relays, and QPSK modulation under two scenarios regarding relay location: scenario 1, where the relay nodes approach the source (dSR1=dSR2=0.3), and scenario 2, where the relay nodes approach the destination (dSR1=dSR2=0.7). As illustrated in Fig. 7, the outage probability of the cooperative network utilizing the HDFSIR strategy outperforms that of the DF and SIR strategies in both scenarios. Notably, the DF strategy performs better than the SIR strategy when the relays are closer to the source, whereas the opposite holds true as the relays move closer to the destination. This observation underscores that the proposed HDFSIR strategy effectively leverages the benefits of both the DF and SIR strategies to enhance performance across the entire range of SNR values, regardless of the relay positions.

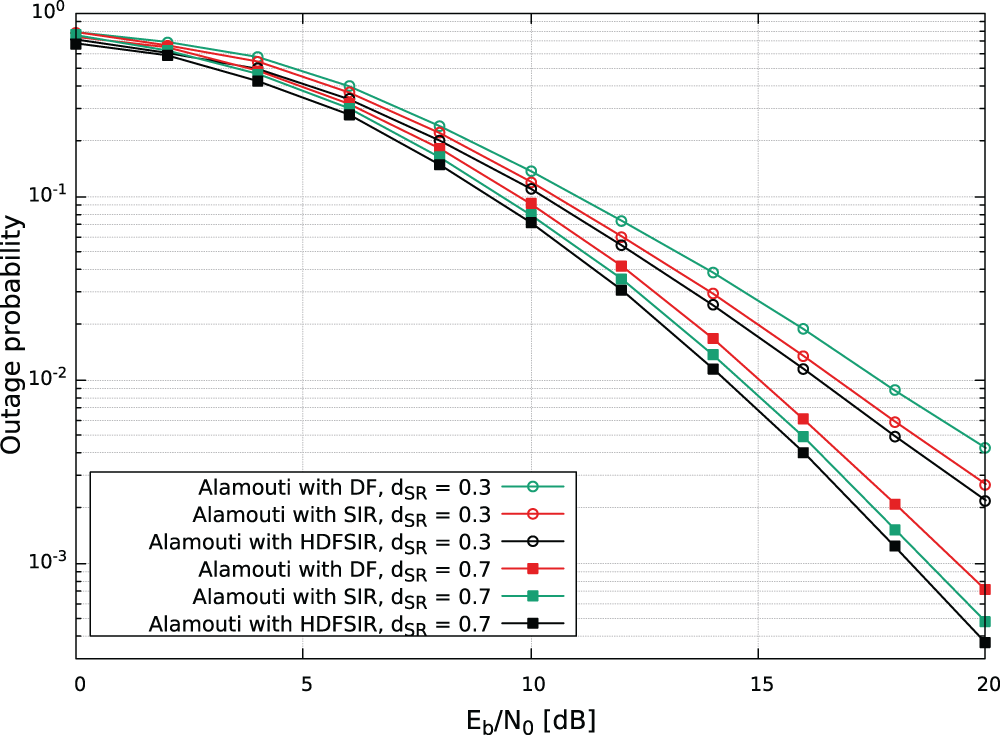
Figure 7: Simulated outage probability results of the coded cooperative scheme applying DF, SIR, and HDFSIR strategies with Alamouti DSTC coding for two different source-relay distances

10  Conclusion

In this paper, we presented a hybrid decode-and-forward and soft information relaying strategy to address error propagation in coded cooperative communication with multiple energy-harvesting relays. The proposed scheme differentiates relays based on decoding success: relays that fail to decode use SIR strategy, while those that decode successfully employ DF protocol. Analytical models were developed to derive closed-form expressions for the SNR of the equivalent end-to-end relaying channel, enabling opportunistic relay selection. Closed-form expressions for outage probability and SER were derived using the CDF-based method. Additionally, we introduced the NL-SES mapping method for efficient soft symbol estimation in square M-QAM modulation with Gray labeling, and we derived closed-form expressions for the symbol error rate using the CDF-based method. Lastly, by integrating distributed Alamouti space-time coding, we developed a hybrid DF-SIR protocol that further enhances performance compared to traditional DF or SIR-based DSTC.

Monte Carlo simulations validated the theoretical findings and demonstrated that the proposed HDFSIR protocol improves the performance of cooperative networks compared to using DF or SIR alone in both conventional and distributed Alamouti space-time coded cooperative networks. These improvements were particularly evident in challenging source-relay conditions where DF struggles. For the NL-SES mapping method, simulations revealed a significant SER gain of 3.5 dB at 10−3 compared to conventional averaging techniques for QPSK modulation. This numerical evidence highlights the effectiveness of NL-SES in improving soft symbol estimation accuracy.

Despite these promising results, this work has certain limitations. First, the analytical models assume perfect channel state information, which may not fully reflect practical scenarios. Second, the complexity of the NL-SES mapping and hybrid DF-SIR implementation, especially in distributed systems, could pose challenges for large-scale deployments. Third, the energy-harvesting model does not account for energy storage dynamics, which may affect performance under real-world conditions.

Future research could address these limitations by incorporating imperfect channel state information, more realistic EH models, and advanced channel coding schemes in order to develop practical applications. Additionally, extending the model to include energy accumulation at EH relays could enable more efficient power allocation during weak channel states, with potential benefits for throughput and outage probability within the HDFSIR framework. These directions offer exciting opportunities to further enhance the robustness and applicability of the proposed strategy in practical wireless networks.

Acknowledgement: The authors extend their appreciation to the Deanship of Graduate Studies and Scientific Research at Jouf University for funding this work.

Funding Statement: This work was funded by the Deanship of Graduate Studies and Scientific Research at Jouf University under grant No. (DGSSR-2024-02-02160).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Slim Chaoui, Omar Alruwaili; data collection: Slim Chaoui, Haifa Harrouch; analysis and interpretation of results: Slim Chaoui, Faeiz Alserhani; draft manuscript preparation: Slim Chaoui, Haifa Harrouch. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Popovski P, Yomo H. Wireless network coding by amplify-and-forward for bi-directional traffic flows. IEEE Commun Lett. 2007;11(1):16–8. doi:10.1109/LCOMM.2007.061436. [Google Scholar] [CrossRef]

2. Woldegebreal DH, Karl H. Network-coding-based adaptive decode and forward cooperative transmission in a wireless network: outage analysis. In: Proceeding of the 13th European Wireless Conference; 2007; Paris, France. [Google Scholar]

3. Ikki S, Ahmed MH. Performance analysis of cooperative diversity wireless networks over Nakagami-m fading channel. IEEE Commun Lett. 2007;11(4):334–6. doi:10.1109/LCOM.2007.348292. [Google Scholar] [CrossRef]

4. Sadek AK, Su W, Liu KR. Multinode cooperative communications in wireless networks. IEEE Trans Signal Process. 2006;55(1):341–55. doi:10.1109/TSP.2006.885773. [Google Scholar] [CrossRef]

5. Michalopoulos DS, Karagiannidis GK, Tombras GS. Symbol error probability of decode and forward cooperative diversity in Nakagami-m fading channels. J Frank Inst. 2008;345(7):723–8. doi:10.1016/j.jfranklin.2008.03.006. [Google Scholar] [CrossRef]

6. Huo Q, Liu T, Song L, Jiao B. All-participate hybrid forward cooperative communications with multiple relays. In: Proceedings of the 2010 International Conference on Wireless Communications & Signal Processing (WCSP); 2010; Suzhou, China: IEEE. p. 1–6. [Google Scholar]

7. Setiawan DP, Zhao HA. Performance analysis of hybrid AF and DF protocol for relay networks. In: Proceedings of the 2017 International Conference on Control, Electronics, Renewable Energy and Communications (ICCREC); 2017; Yogyakarta, Indonesia: IEEE. p. 207–11. [Google Scholar]

8. Bhattacharyya S, Kumar P, Sharma S, Darshi S, Almohammedi AA. A hybrid-combine-and-forward relaying scheme for network coded cooperative systems. In: Proceedings of the 2021 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS); 2021; Hyderabad, India: IEEE. p. 426–31. [Google Scholar]

9. Weitkemper P, Wübben D, Kühn V, Kammeyer KD. Soft information relaying for wireless networks with error-prone source-relay link. In: Proceedings of the of the 2008 7th International ITG Conference on Source and Channel Coding (SCC); 2008; Ulm, Germany: VDE. p. 1–6. [Google Scholar]

10. Chaoui S, Alruwaili O, Hamrouni C, Alutaybi A, Masmoudi A. On the performance of coded cooperative communication with multiple energy-harvesting relays and error-prone forwarding. Appl Sci. 2023;13(5):2910. doi:10.3390/app13052910. [Google Scholar] [CrossRef]

11. Li Y, Vucetic B, Tang Y, Zhou Z, Dohler M. Practical distributed turbo coding through soft information relaying. In: Proceeding of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications; 2005; Berlin, Germany: IEEE. vol. 4, p. 2707–11. doi:10.1109/PIMRC.2005.1651935. [Google Scholar] [CrossRef]

12. Azmi MH, Li J, Yuan J, Malaney R. LDPC codes for soft decode-and-forward in half-duplex relay channels. IEEE J Selected Areas Commun. 2013;31(8):1402–13. doi:10.1109/JSAC.2013.130805. [Google Scholar] [CrossRef]

13. Jayakody DN, Flanagan MF. A soft decode–compress–forward relaying scheme for cooperative wireless networks. IEEE Trans Veh Technol. 2015;65(5):3033–41. doi:10.1109/TVT.2015.2442459. [Google Scholar] [CrossRef]

14. Wang J, Poor HV. Iterative (turbo) soft interference cancellation and decoding for coded CDMA. IEEE Trans Commun. 1999;47(7):1046–61. doi:10.1109/26.774855. [Google Scholar] [CrossRef]

15. Jing Y, Hassibi B. Distributed space-time coding in wireless relay networks. IEEE Trans Wirel Commun. 2006;5(12):3524–36. doi:10.1109/TWC.2006.256975. [Google Scholar] [CrossRef]

16. Vajapeyam M, Mitra U. Performance analysis of distributed space-time coded protocols for wireless multi-hop communications. IEEE Trans Wirel Commun. 2010;9(1):122–33. [Google Scholar]

17. Duong TQ, Ha DB, Tran HA, Vo NS. Symbol error probability of distributed-Alamouti scheme in wireless relay networks. In: Proceedings of the VTC Spring 2008-IEEE Vehicular Technology Conference; 2008; Marina Bay, Singapore: IEEE. p. 648–52. [Google Scholar]

18. Shao Y, Wang L, Xue Y. Distributed alamouti protocol for full-duplex decode-and-forward relaying networks. IEEE Commun Lett. 2021;26(1):182–6. [Google Scholar]

19. Tayakout H, Bouchibane FZ, Boutellaa E. A new distributed-STBC scheme for cooperative relaying in wireless networks. In: Proceedings of the 2022 7th International Conference on Image and Signal Processing and their Applications (ISPA); 2022; Mostaganem, Algeria: IEEE. p. 1–5. [Google Scholar]

20. Murata H, Kuwabara A, Oishi Y. Distributed cooperative relaying based on space-time block code: system description and measurement campaign. IEEE Access. 2021;9:25623–31. [Google Scholar]

21. Touati S, Boujemaa H, Abed N. Static hybrid multihop relaying and two hops hybrid relaying using DSTC. Annals of telecommunications-annales des télécommunications. 2015;70:171–80. [Google Scholar]

22. Gurrala KK, Das S. Hybrid decode-amplify-forward (HDAF) scheme in distributed Alamouti-coded cooperative network. Int J Electron. 2015;102(5):725–41. [Google Scholar]

23. Zheng L, Zhang R. Hybrid amplify-and-forward/decode-and-forward relaying in cooperative networks. IEEE Trans Wirel Commun. 2011;10(11):3708–19. [Google Scholar]

24. Forghani AH, Al Hassan M, Ben Mabrouk I, Sultan A, Babar Rasheed M. Exact analysis of the multihop multibranch hybrid AF/DF relaying networks. Int J Commun Syst. 2020;33(15):e4549. [Google Scholar]

25. Zhou Q, Yang L, Zhang RD. Performance analysis of hybrid DF/AF relaying networks with energy harvesting. IEEE Trans Wirel Commun. 2023;22(5):3201–15. [Google Scholar]

26. Wang L, Lin S, Wu H. Hybrid relaying strategy in wireless energy harvesting networks: a DF and AF approach. IEEE Access. 2023;11:26589–601. [Google Scholar]

27. Chen M, Liu Z, Wang T. Resource allocation in hybrid relaying systems with energy harvesting: a game-theoretic approach. IEEE Trans Commun. 2022;70(11):7403–15. [Google Scholar]

28. Huang G, Tu W. A high-throughput wireless-powered relay network with joint time and power allocations. Comput Netw. 2019;160:65–76. [Google Scholar]

29. Huang G, Zhong Q, Zheng H, Zhao S, Tang D. Improving throughput in SWIPT-based wireless multirelay networks with relay selection and rateless codes. Dig Commun Netw. 2024;10(4):1131–44. doi:10.1016/j.dcan.2023.01.012. [Google Scholar] [CrossRef]

30. Liu Y, Zhao W, Tang H. Performance analysis of hybrid DF/AF relaying with distributed space-time coding. IEEE Trans Commun. 2023;71(2):1245–59. [Google Scholar]

31. Wu X, Li J, Huang Y. Cooperative strategies in hybrid DF/AF relaying systems with distributed space-time coding. IEEE Trans Wirel Commun. 2023;22(8):4967–79. [Google Scholar]

32. Tang L, Zhao M. Efficient protocols for hybrid DF/AF relaying and distributed space-time coding. IEEE Access. 2022;10:83985–95. [Google Scholar]

33. Papaharalabos S, Sweeney P, Evans BG. SISO algorithms based on Max-Log-MAP and Log-MAP turbo decoding. IET Commun. 2007;1(1):49–54. doi:10.1049/iet-com:20060090. [Google Scholar] [CrossRef]

34. Zwillinger D, Jeffrey A. Table of integrals, series, and products. Netherlands: Elsevier; 2007. [Google Scholar]

35. Barbu A, Zhu SC. Monte carlo methods. Singapore: Springer; 2020. Vol. 35. [Google Scholar]

36. Faloutsos C. Gray codes for partial match and range queries. IEEE Trans Softw Eng. 1988;14(10):1381–93. doi:10.1109/32.6184. [Google Scholar] [CrossRef]

37. Malkamaki E, Leib H. Evaluating the performance of convolutional codes over block fading channels. IEEE Trans Inf Theory. 1999;45(5):1643–6. doi:10.1109/18.771235. [Google Scholar] [CrossRef]

38. Viterbi AJ, Omura JK. Principles of digital communication and coding. USA: Courier Corporation; 2013. [Google Scholar]

39. Sklar B. Digital communications: fundamentals and applications. UK: Pearson; 2021. [Google Scholar]

40. Chiani M, Dardari D, Simon MK. New exponential bounds and approximations for the computation of error probability in fading channels. IEEE Trans Wirel Commun. 2003;2(4):840–5. doi:10.1109/TWC.2003.814350. [Google Scholar] [CrossRef]

41. McKay MR, Grant AJ, Collings IB. Performance analysis of MIMO-MRC in double-correlated Rayleigh environments. IEEE Trans Commun. 2007;55(3):497–507. doi:10.1109/TCOMM.2007.892450. [Google Scholar] [CrossRef]

42. Moll VH. Special integrals of gradshteyn and ryzhik. USA: CRC Press; 2015. [Google Scholar]

43. Schweizer W, Schweizer W. Confluent hypergeometric function. In: Special functions in physics with MATLAB. Switzerland: Springer; 2021. p. 91–9. [Google Scholar]