Ternary Hybrid Nanofluid with First and Second Order Velocity Slips: Dual Solutions with Stability Analysis

1  Introduction

The advanced thermal management methodology has forced robust research in nanofluid flow and enhanced the capabilities of heat transfer. The general context of hybrid nanofluids is that they are comprised of several suspended nanometal particles with a based fluid such as water, ethyl glycol, and kerosene [1]. The enhancement of thermal conductivity when incorporating two distinct nanometal particles called hybrid nanofluid has gathered significant attention from all over the world. Recently, the concept of integrating three different nanometal particles immersed in a based fluid called ternary hybrid nanofluids has been introduced to harvest greater thermal management efficiency. This claim is proven by the report done by Mumtaz et al. [2], which investigates the electromagnetohydrodynamic (EMHD) of ternary hybrid nanofluid towards a stretching curvature sheet. The combination of CuO, Al2O3, and TiO2 with based water gives out greater boundary layer thickness as well as amplifies the heat transferal ratio. It is also similar to the findings from Mishra et al. [3]. They found that the Al2O3-Cu-CNT with based water produced the most incredible values for heat transferal ratio compared to hybrid nanofluid. These findings are supported by Gasmi et al. [4], who also suggest that Cu-SiO2-ZrO2 with engine oil-based fluid produced a higher heat transferal ratio than hybrid nanofluid. All those researchers have proven in theory that there is a need to study the ternary hybrid nanofluid characteristics towards heat transferal ratio. Several other researchers have also agreed with this theory, such as Mohana et al. [5], using Fe3O4-Al2O3-ZnO/H2O as the ternary hybrid nanofluid, CuO-MgO-TiO2/water by Khan et al. [6] and Fahad et al. [7] implement Al2O3-CNT-graphene based water in their studies.

Recently, the research of nanofluid flow and heat transfer towards the stretch/shrink sheet has garnered much attention due to its wide-ranging application in industrial processes. Several examples of the application of this phenomenon are applied in manufacturing, cooling, and thin film optimization for solar panels, electronics, semiconductors, and optics [8]. Understanding fluid flow over surfaces is essential for enhancing processes in art, printing, semiconductors, and cooling systems. However, the study for ternary hybrid nanofluid flow and heat transfer over the stretch/shrink surfaces needs more information. Several researchers have attempted to investigate these matters successfully. For instance, Alharbi [9] reported with TiO2-Ag-ZnO/H2O as the ternary hybrid nanofluid, the heat transferal ratio diminished for the shrinking sheet, but the finding was the opposite for the stretching sheet. Mahmood et al. [10] reveal that the ternary hybrid nanofluid managed to improve the heat transferal ratio by more than 40% for both stretching and shrinking sheets. They consider Al2O3-Cu-TiO2/H2O to be the ternary hybrid nanofluid with suction effects on the system. Other than that, Mahabaleshwar et al. [11] claimed that the efficiency of the heat transferal ratio for dusty ternary hybrid nanofluid is better than that of dusty hybrid nanofluid. Several studies have been conducted on stretch/shrink sheets for ternary hybrid nanofluid flow, such as those by Ouyang et al. [12] using Maxwell ternary hybrid nanofluid, Mahmood et al. [13] applying Cu-Fe3O4-SiO2/SA and Jamrus et al. [14] utilizing titania-copper-alumina.

The no-slip boundary condition was employed in traditional fluid flow studies. This assumption is believed to be fictitious in the actual application world. The velocity slip concept on the fluid-solid interface has gained traction over the years. Many robust studies have been done to cater to first-order velocity slip’s influence. Even so, exploring second-order slip impacts is relatively limited and needs further investigation to elucidate its importance in thermal transportation. Uddin et al. [15] reported that the heat transferal ratio diminished as the second-order slip upsurged, but Vishnu Ganesh et al. [16] claimed that the temperature profile reduced as the second-order slip was gained for the stretching surface. Meanwhile, Usafzai [17] studied the second-order slip towards the axial velocity and found that the axial velocity upsurged with the second-order slip. Recent studies on second-order slip have been carried out by Mumtaz et al. [18], which suggests that the effect of first-order slip is outstanding compared to second-order slip and Bakar et al. [19] stated the heat transferal ratio is lowered as the second-order slip is amplified.

The existing literature reveals a theoretical gap in the study of ternary hybrid nanofluid flow and heat transfer over a stretch/shrink surface, particularly when considering the impacts of second-order slip. This study aims to address this gap by developing and numerically solving a mathematical model that incorporates these factors. Given the ability of the numerical solver to generate dual solutions for the boundary value problem, a stability analysis is required to evaluate the stability of these solutions. This analysis is crucial, as not all numerically obtained solutions are stable or reliable for practical applications despite being mathematically valid. Therefore, this study not only presents the mathematical model and its solutions but also offers guidance on controlling the flow dynamics and the transferal of heat. This control is achieved by manipulating parameters such as first- and second-order velocity slips and the stretching/shrinking parameter.

2  Mathematical Formulations

We consider the two-dimensional, steady, incompressible alumina + copper + silver/water nanofluid boundary layer flow along a permeable stretching/shrinking sheet, as shown in Fig. 1, where the Cartesian coordinates (x,y) are measured along the surface of the sheet and normal to it, respectively. The assumptions made are as follows:

•   The velocity of the stretching/shrinking sheet is uw(x)=ax, where a is constant.

•   The wall mass transfer velocity is vw=−avfS where positive S is for the case of suction.

•   The first and the second-order velocity slip factors are A1 and B1, respectively.

•   The temperature of the far field and at the surface are T∞ and Tw, respectively.

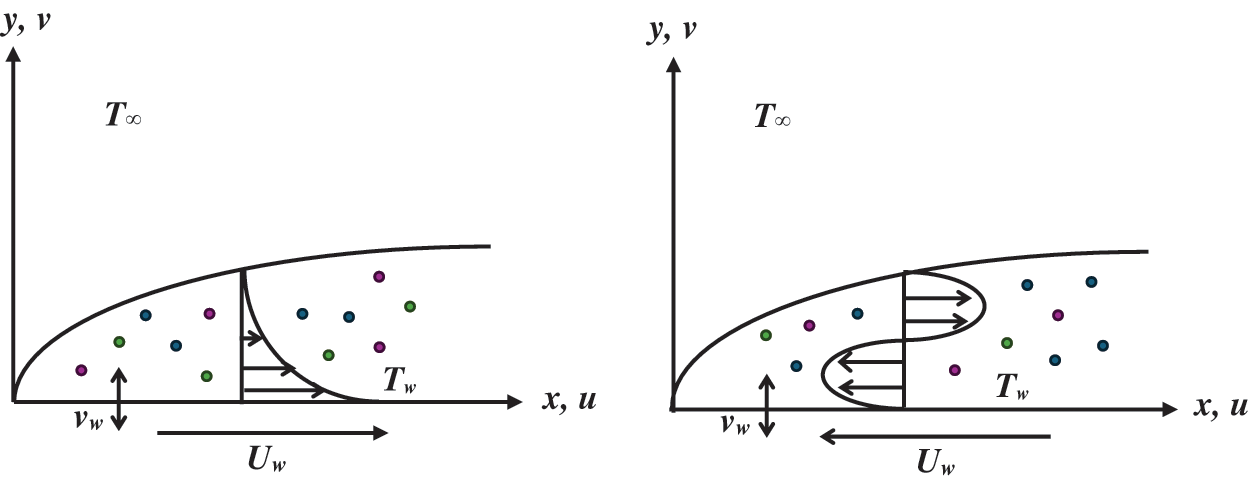
Figure 1: Model illustration

Given these assumptions, the governing model is formulated as follows (see [20–22]):

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y=μthnfρthnf∂2u∂y2,(2)

u=Uw(x)=λuw(x)+A1∂u∂y+B1∂2u∂y2,v=vw at y=0,u→0 as y→∞,u∂T∂x+v∂T∂y=kthnf(ρCp)thnf∂2T∂y2,T=Tw at y=0,T→T∞ as y→∞,(3)

where (u,v) are the velocity components along (x,y)—axes, and T is the temperature of the ternary hybrid nanofluid. Further, the formulations for the thermophysical properties of the ternary hybrid nanofluid are provided in Table 1. The chosen values for the thermophysical properties of the nanoparticles and the base fluid are tabulated in Table 2.

Next, the similarity variables are introduced, such that [22]:

u=axf′(η),v=−avff(η),T=θ(η)(Tw−T∞)+T∞,η=yavf.(4)

Applying the similarity variables from the model reduces the following boundary value problems in the form of ODEs, such that:

(μthnf/μfρthnf/ρf)f′′′−f′2+ff′′=0,f(0)=S,f′(0)=λ+Af′′(0)+Bf′′′(0),f′(∞)→0,(5)

1Pr(kthnf/kf(ρCp)thnf/(ρCp)f)θ′′+fθ′=0,θ(0)=1,θ(∞)→0(6)

Pr=(μCp)fkf,A=A1avf,B=B1avf.(7)

The model generates numerical solutions in the form of physical quantities, specifically, the skin friction coefficient Cf and the local Nusselt number Nux, defined as follows:

Cf=μthnfρfuw2(x)(∂u∂y)y=0,Nux=xkthnfkf(Tw−T∞)(−∂T∂y)y=0.(8)

Using Eqs. (4) and (8) transforms to:

Rex1/2Cf=μthnfμff′′(0),Rex−1/2Nux=−kthnfkfθ′(0).(9)

3  Stability Analysis

Since dual solutions are attainable, it is important to assess the stable nature carried by the solutions [26,27]. The procedure begins by considering the model to be unsteady or time dependent. Then, based on Eq. (4), the following new dimensionless variables with time, t are introduced:

u=ax∂f(η,τ)∂η,v=−avff(η,τ),T=θ(η,τ)(Tw−T∞)+T∞,η=yavf,τ=at,(10)

where τ is the dimensionless time variable. Thus, applying these variables, the boundary value problems can be rewritten as:

(μthnf/μfρthnf/ρf)∂3f∂η3+f∂2f∂η2−(∂f∂η)2−∂2f∂η∂τ=0,f(0,τ)=S,∂f(0,τ)∂η=λ+A∂2f(0,τ)∂η2+B∂3f(0,τ)∂η3,∂f(∞,τ)∂η→0,(11)

1Pr(kthnf/kf(ρCp)thnf/(ρCp)f)∂2θ∂η2+f∂θ∂η−∂θ∂τ=0,θ(0,τ)=1,θ(∞,τ)→0.(12)

Next, corresponding with Weidman et al. [27], the subsequent perturbation is allowed:

f(η,τ)=f0(η)+e−γτF(η,τ),θ(η,τ)=θ0(η)+e−γτG(η,τ),(13)

where γ is the eigenvalue parameter that will be generated, while F(η,τ) and G(η,τ) are small relative to f0(η) and θ0(η), respectively. Eq. (13) is substituted into Eqs. (11) and (12), and we set τ=0 (a steady flow) to see the growth or decay of the solution (13). Putting τ=0 leads us to F(η,0)=F0(η) and G(η,0)=G0(η). Finally, Eqs. (11) and (12) are transformed into:

(μthnf/μfρthnf/ρf)F0′′′+f0F0′′+F0f0′′−2f0′F0′+γF0′=0,F0=0,F0′(0)=λ+AF0′′(0)+BF0′′′(0), F0′(∞)→0,(14)

1Pr(kthnf/kf(ρCp)thnf/(ρCp)f)G0′′+f0G0′+F0θ0′+γG0=0,G0(0)=0,G0(∞)→0.(15)

The stability of the numerical solutions is assessed based on the smallest eigenvalue, denoted as γ1. If γ1 is positive (negative), there is an initial decay (growth), which signifies that the flow is stable (unstable). The possible range of eigenvalues can be established by resting the boundary condition at the far field [28], either F0(η) or G0(η). Hence, for this eigenvalue problem, F0′(η)=0 as η→∞ is rest and replaced with F0′′(η)=1 at η=0.

4  Results and Discussion

Similarity solutions for Eqs. (5) and (6) were obtained numerically, facilitated by MATLAB software. This solver, which utilizes a finite difference scheme and Lobatto III a formula with fourth-order accuracy [29], efficiently predicts solutions even when starting with arbitrary initial guesses. In this study, the boundary layer thickness is η∞=15, with constant suction strength set at S=2, and the properties of the nanoparticles, as well as the base fluid, are also kept constant as stated in Table 2 for the entire study (unless stated otherwise). Suitable initial guesses for the bvp4c solver and the remaining parameters are carefully selected to ensure the velocity and temperature profiles satisfy the boundary conditions while maintaining the relative tolerance error at 10−10 (zero tolerance). To utilize the bvp4c solver, it is necessary to convert Eqs. (5) and (6) into a first-order system. This can be accomplished by introducing new variables such that f=y(1),f′=y(2),f′′=y(3),θ=y(4),θ′=y(5). Hence, Eqs. (5) and (6) are rewritten as:

f′′′=1(μthnf/μfρthnf/ρf)(y(2)y(2)−y(1)y(3)),ya(1)−S,ya(2)−λ−Aya(3)−B((ρthnf/ρfμthnf/μf)(ya(2)ya(2)−ya(1)ya(3))),yb(2),(16)

θ′′=11Pr(kthnf/kf(ρCp)thnf/(ρCp)f)(−y(1)y(5)),ya(4)−1,yb(4),(17)

where ya refers to the boundary condition as η=0, and yb refers to the far field boundary condition, η→∞.

Further, to validate these numerical computations of the model in the solver, a comparison was made with an earlier study under the considered parameter configurations, as shown in Table 3. The findings demonstrate good agreement, as the values of the physical quantities are nearly identical. Therefore, it is believed that both the model and the numerical procedure employed are accurate.

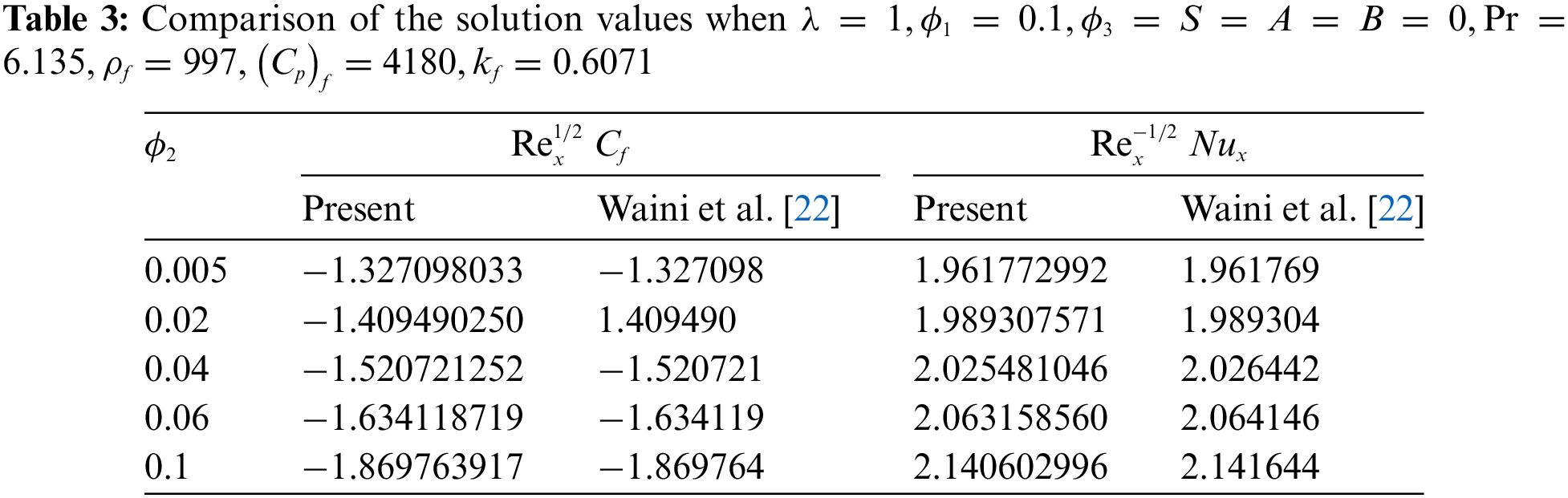
Figs. 2 and 3 illustrate the plots of Rex1/2Cf and Rex−1/2Nux for different types of nanofluids—(i) 1% alumina (mono) nanofluid, (ii) 1% alumina + 1% copper (hybrid) nanofluid, and (iii) 1% alumina + 1% copper + 1% silver (ternary hybrid) nanofluid—under varying values of λ when A=1,B=−1,S=2. Dual solutions are generated from the configurations, but they yield opposing trends of results. The first solution shows that the ternary hybrid nanofluid has the lowest Rex1/2Cf compared to the hybrid nanofluid, while the mono nanofluid exhibits the highest Rex1/2Cf among the three. Conversely, the second solution reveals the opposite trend. For Rex−1/2Nux (see Fig. 3), both solutions display similar patterns regarding the impact of different nanofluids, although the values from the first solution are higher than those from the second. The mono nanofluid results in the highest Rex−1/2Nux, whereas the ternary hybrid nanofluid shows the lowest. This contradicts the expectation that ternary hybrid nanofluids would provide the best heat transferal ratio. However, it should be noted that these observations pertain to cases with suction and velocity slips (both first and second order). Therefore, to consider ternary hybrid nanofluids in this context, the heat transferal ratio can be controlled through the adjustment of suction and velocity slip. In terms of boundary layer separation, the ternary hybrid nanofluid demonstrates the most delayed separation compared to the other two nanofluids, thereby maintaining laminar flow stability. This is evidenced by the extended range of λ and λc (refers to critical point value).

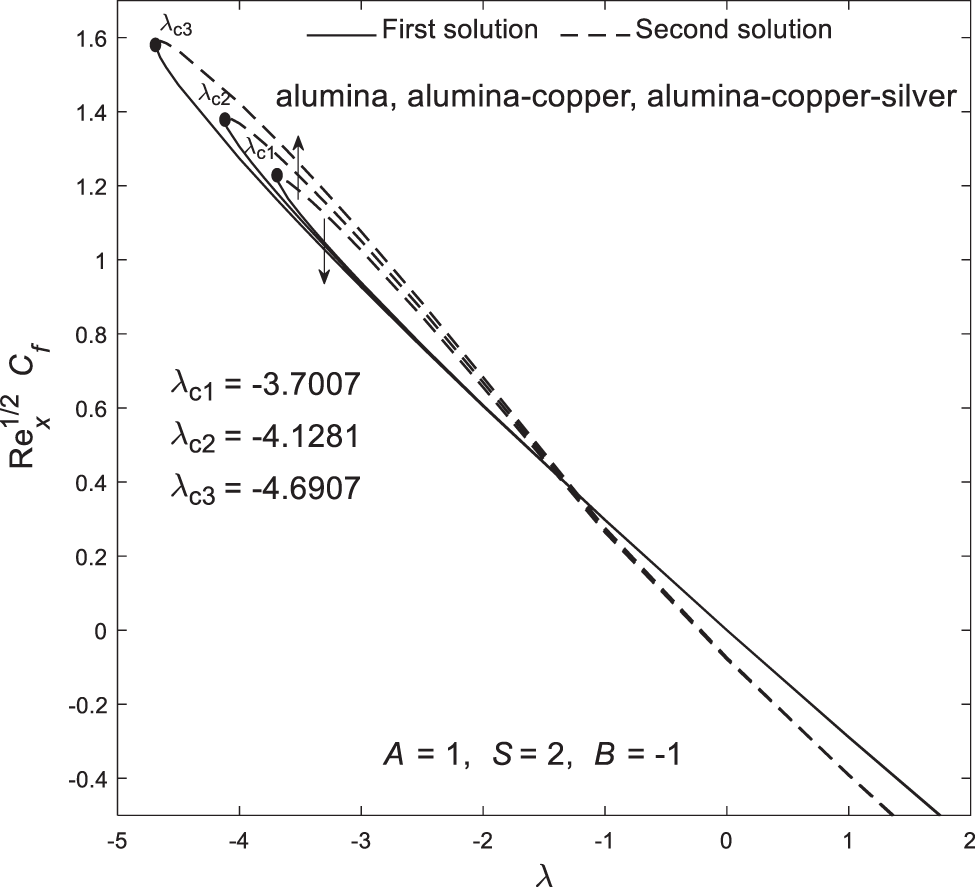
Figure 2: Plot of the skin friction coefficient Rex1/2 Cf for different nanofluids

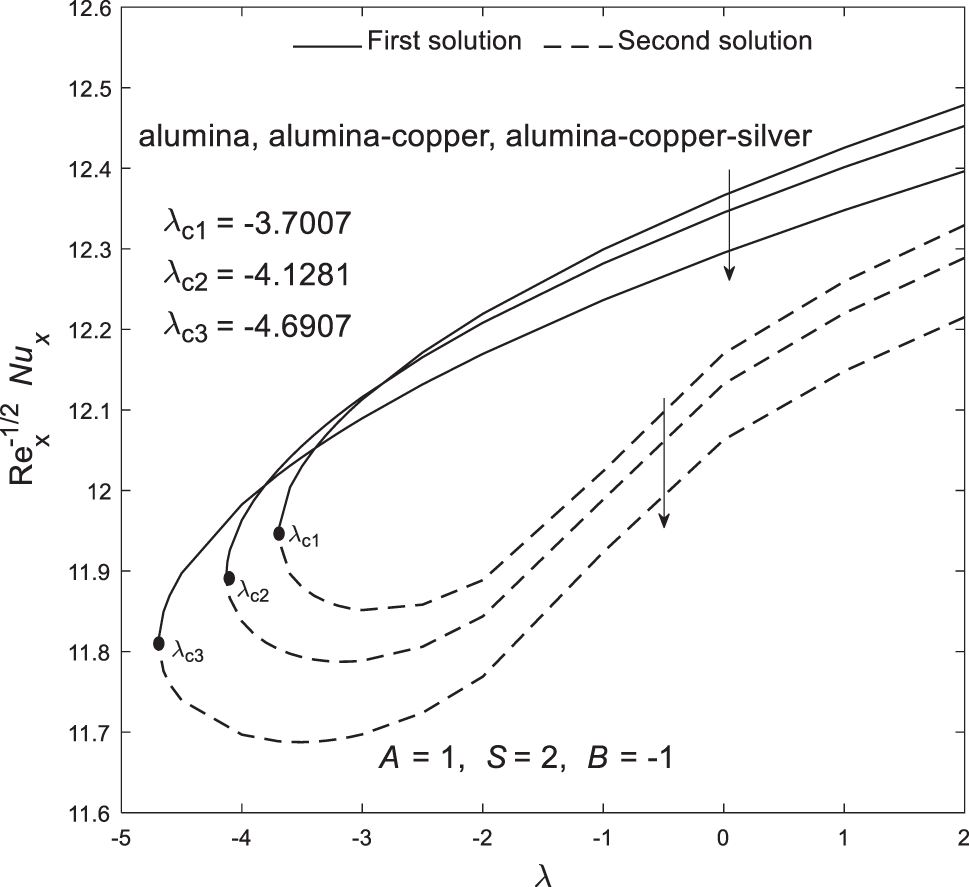
Figure 3: Plot of the local Nusselt number Rex−1/2 Nux for different nanofluids

The impact of A on Rex1/2Cf and Rex−1/2Nux under varying values of λ when B=−1,S=2 is shown in Figs. 4 and 5. Dual solutions were also obtained, both revealing the same pattern for the impact of A. An increase in A reduces Rex1/2Cf when considering a negative λ (shrinking sheet), while it increases Rex1/2Cf for a positive λ (stretching sheet). Besides, for Rex−1/2Nux, an increase in A raises the value for both solutions when the sheet is shrinking but decreases it when the sheet is stretching. The first solution yields higher values compared to the second. Regarding boundary layer separation, a higher value of A leads to the most delayed separation. This is because the velocity slip parameter physically allows the fluid near the surface to maintain higher momentum, which reduces viscous drag and promotes better flow attachment against adverse pressure gradients. Therefore, a suitably higher value of A enhances the heat transferal ratio and reduces skin friction when the surface is shrinking, while also maintaining laminar flow for a longer period.

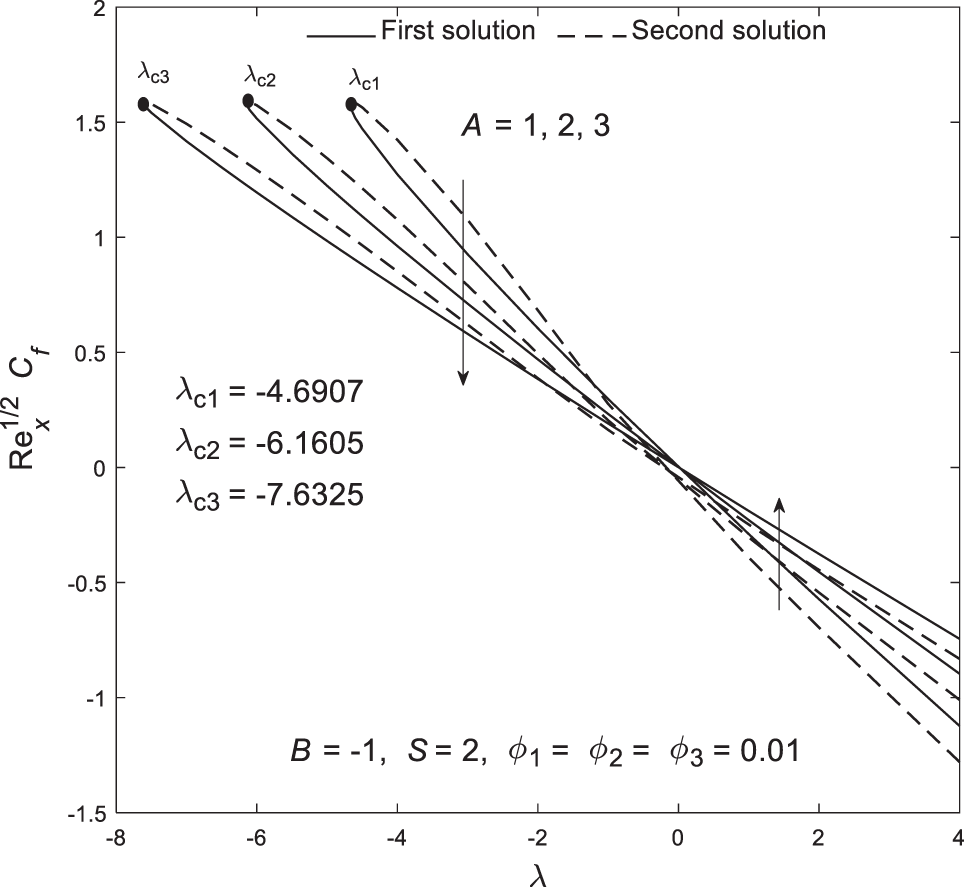
Figure 4: Plot of the skin friction coefficient Rex1/2 Cf for different velocity slip (first order)

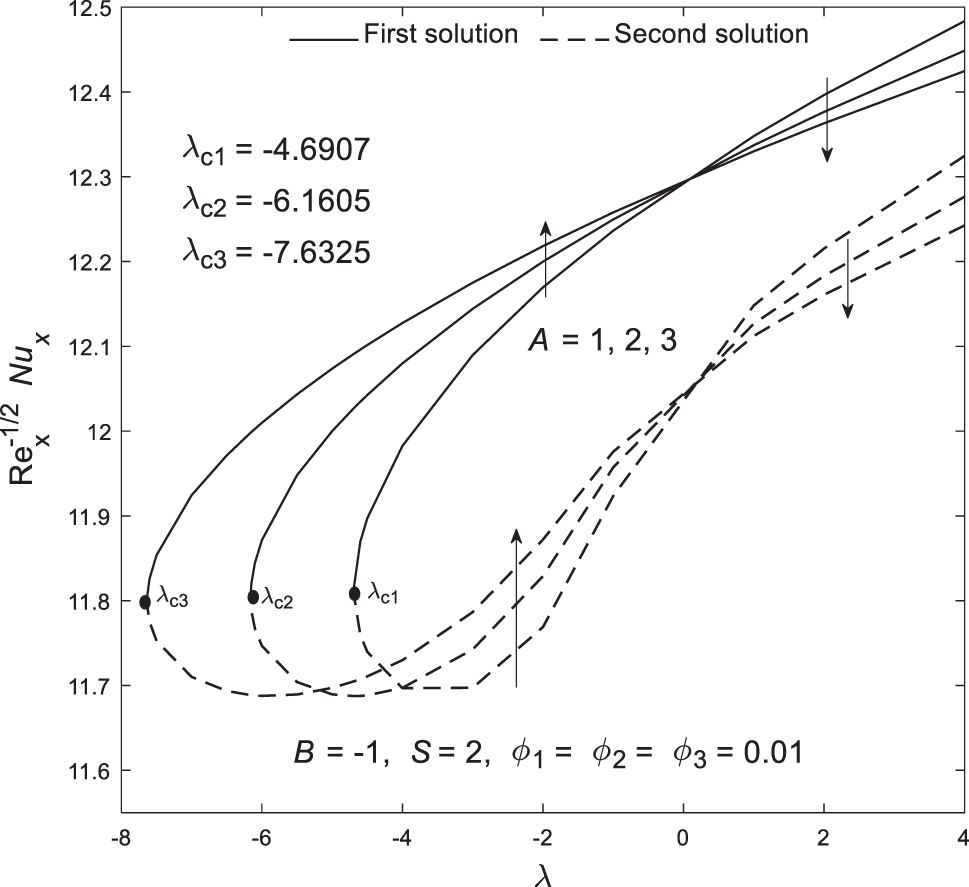
Figure 5: Plot of the local Nusselt number Rex−1/2 Nux for different velocity slip (first order)

Figs. 6 and 7 show the plots of Rex1/2Cf and Rex−1/2Nux for different imposition of B for varying value of λ when A=1,S=2. In this case, the value of B is considered negative, following recommendations from earlier studies by Waini et al. [25] and Turkyilmazoglu [30]. Increasing B from −3 to −2 to −1 results in an increment of Rex1/2Cf when the sheet is shrunk, while the opposite effect is observed when the sheet is stretched, with both solutions showing the same pattern. Meanwhile, Rex−1/2Nux decreases with increasing B when the sheet is shrunk but increases when the sheet is stretched. Additionally, boundary layer separation can be controlled by this parameter: to delay separation, a lower value of B should be used. Numerically, B=−3 is more effective in delaying separation compared to B=−1.

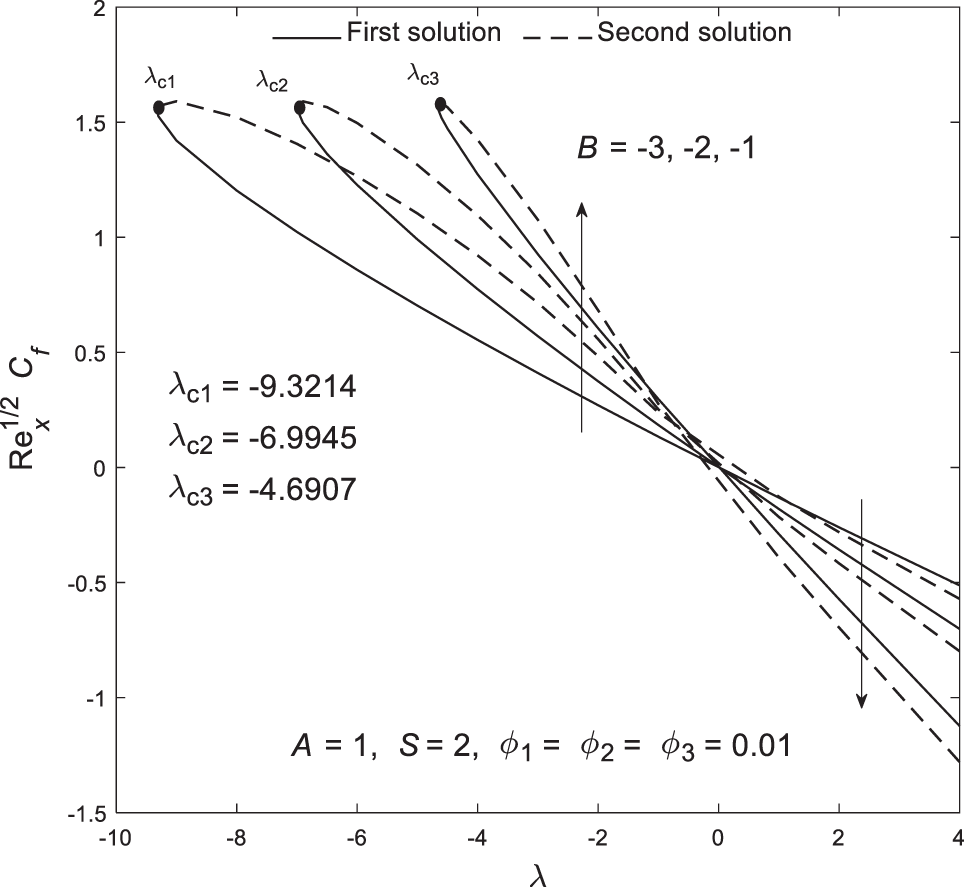
Figure 6: Plot of the skin friction coefficient Rex1/2 Cf for different velocity slip (second order)

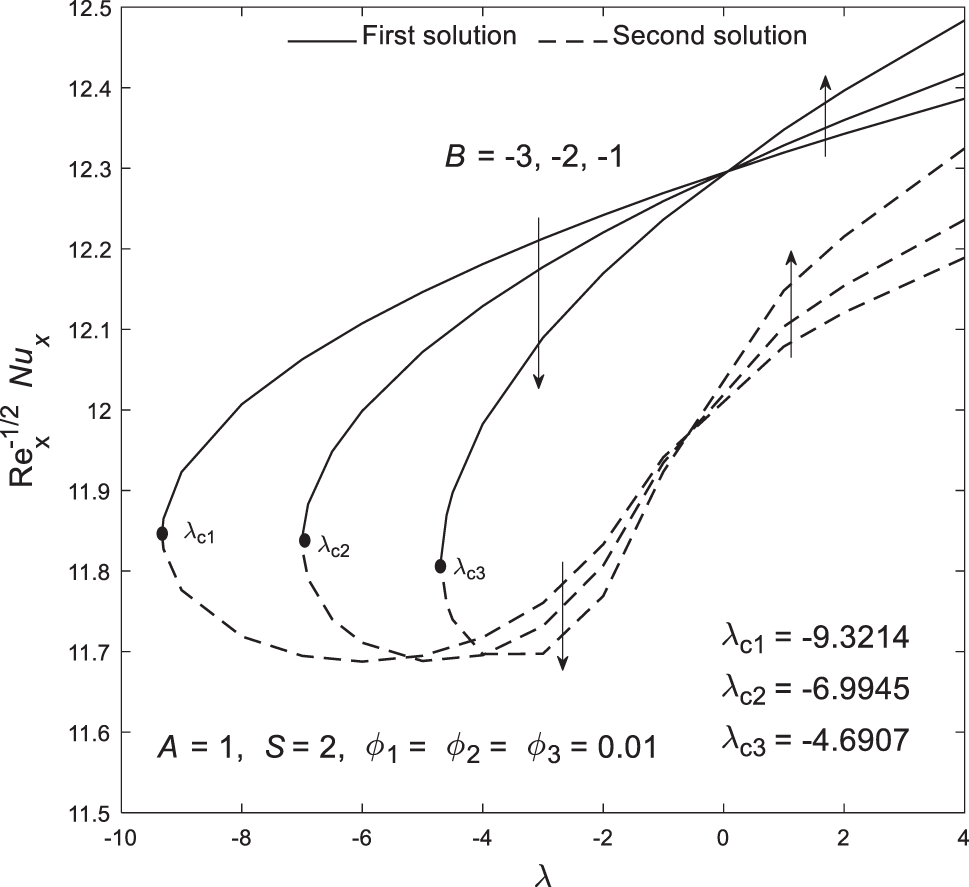
Figure 7: Plot of the local Nusselt number Rex−1/2 Nux for different velocity slip (second order)

Based on Figs. 2–7, all critical points are located within the shrinking region, suggesting that boundary layer separation is more likely to occur when the sheet shrinks. However, this phenomenon can be controlled and delayed by adjusting parameters such as velocity slip. Moreover, Figs. 8–13 illustrate the distribution of velocity f′(η) and temperature θ(η) for various parameter variations, specifically when the sheet is shrunk. The ternary hybrid nanofluid results in the highest velocity and has the thinnest momentum boundary layer compared to the hybrid and mono nanofluids (see Fig. 8) which are shown by the first solution. Conversely, the second solution reveals the opposite finding. Moreover, both solutions indicate that the ternary hybrid nanofluid results in the highest temperature and the thickest thermal boundary layer compared to the other two nanofluids (see Fig. 9). However, the first solution shows the thermal boundary layer to be thinner than the second solution’s results. In Figs. 10–13, the highest velocity and the thinnest momentum boundary layer are achieved with the highest value of A and the lowest value of B. This result is only true for the first solution. Conversely, the lowest temperature is observed with higher A and the lowest B. Thus, the presence of A can be considered as an effective factor for enhancing the cooling performance of the fluid system. Nevertheless, the second solution provided in Figs. 10 and 12 shows inconsistent findings across the ranges of η. Therefore, a stability analysis is required to evaluate the reliability of these numerical solutions.

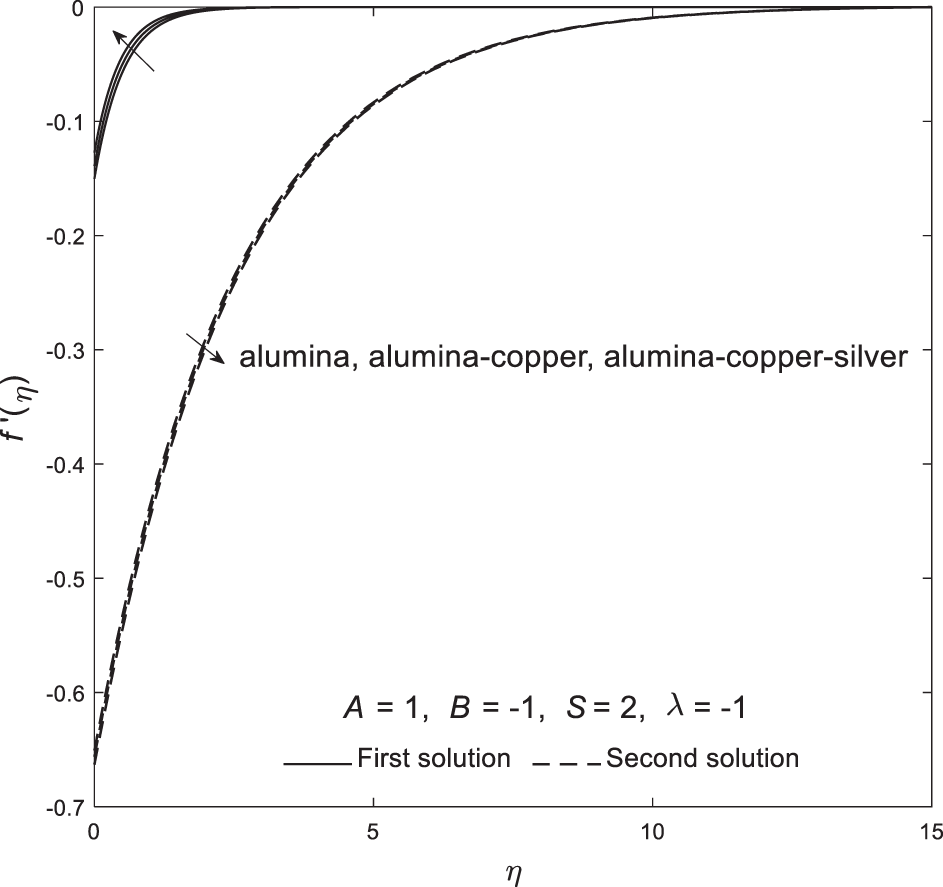
Figure 8: Plot of velocity f′(η) for different nanofluids

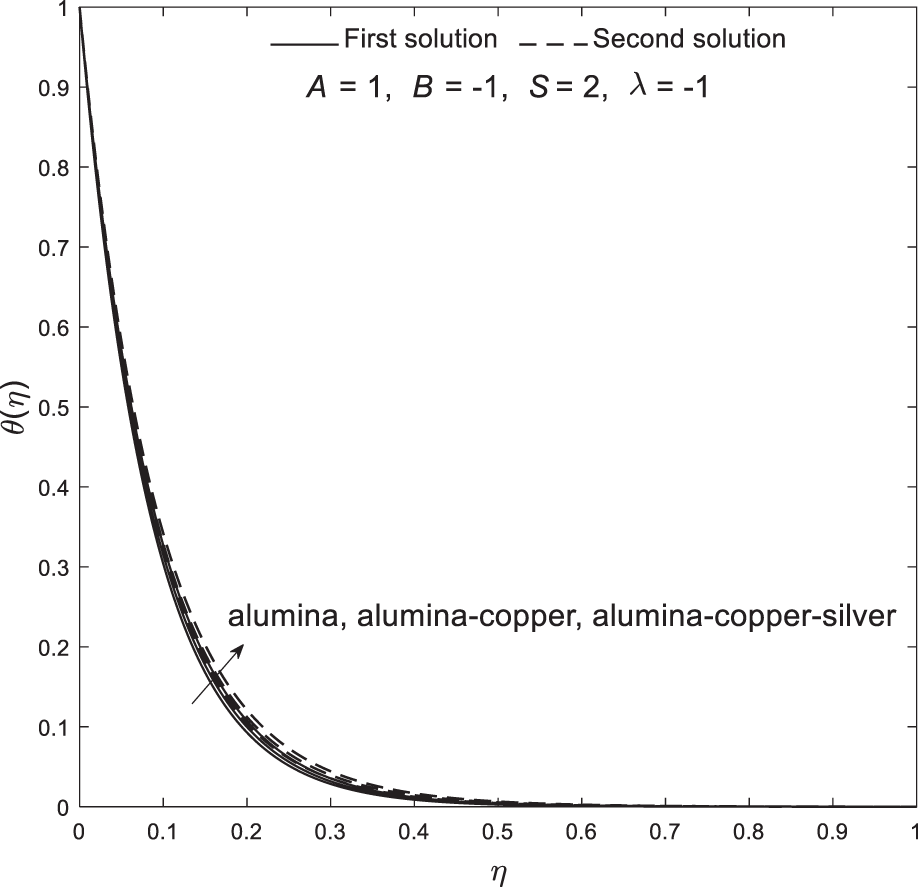
Figure 9: Plot of temperature θ(η) for different nanofluids

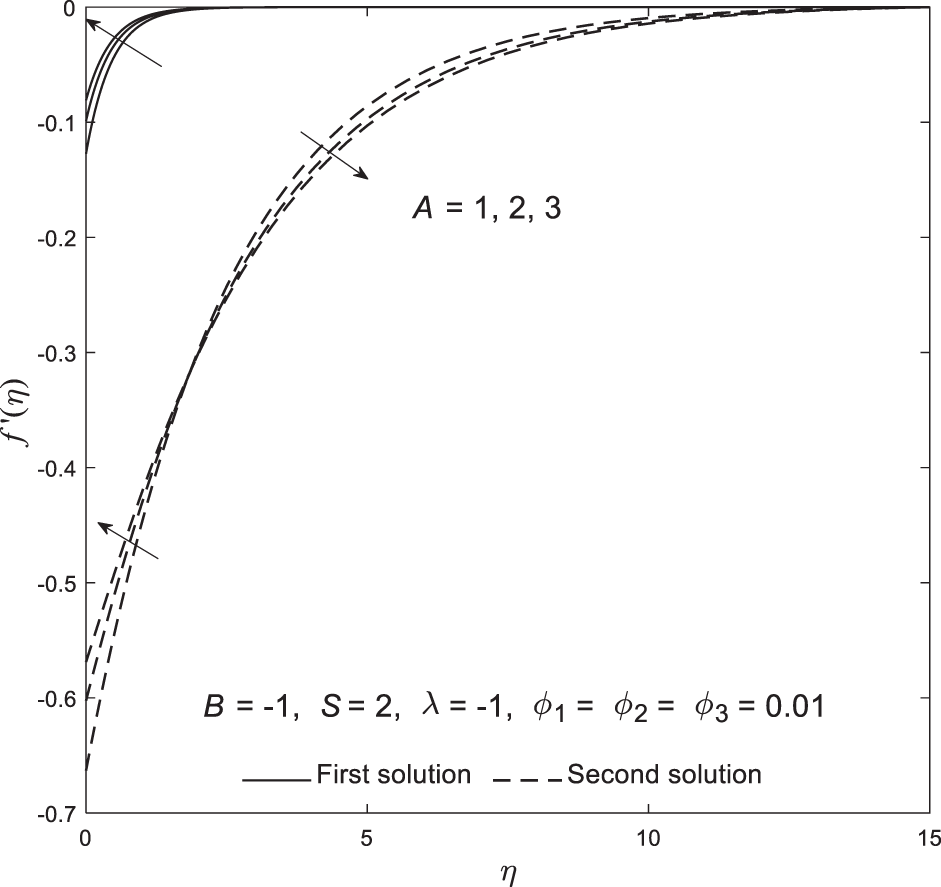
Figure 10: Plot of velocity f′(η) for varying values of velocity slip (first order) parameter

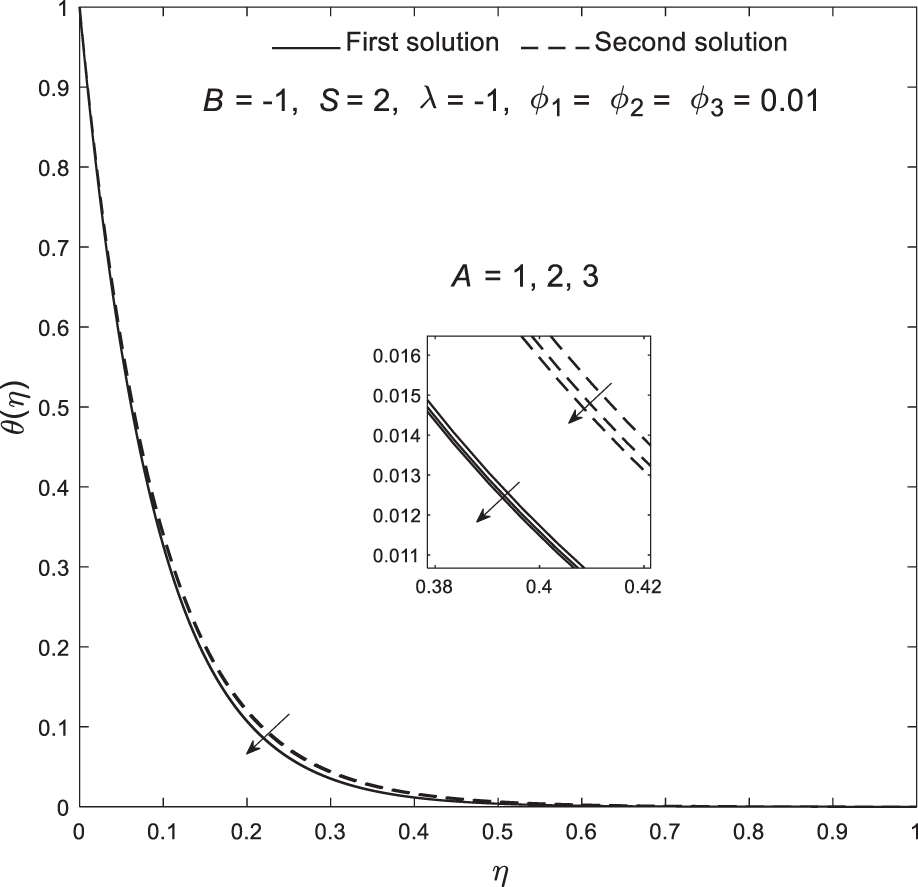
Figure 11: Plot of temperature θ(η) for varying values of velocity slip (first order)

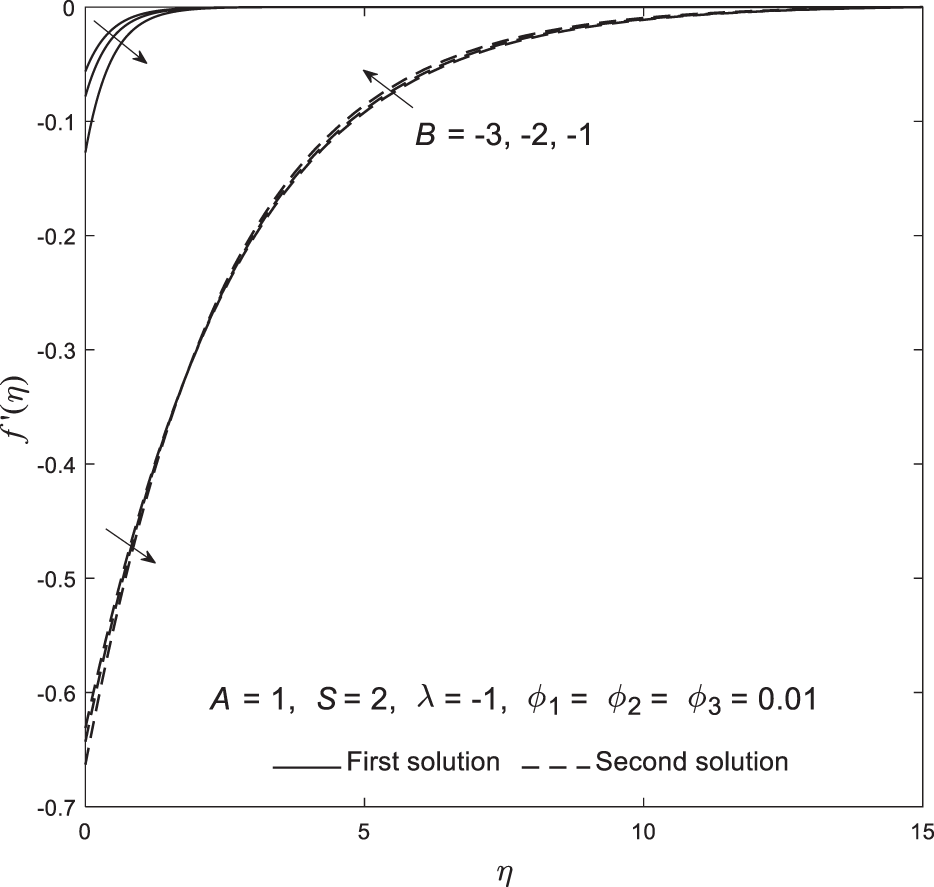
Figure 12: Plot of velocity f′(η) for varying values of velocity slip (second order)

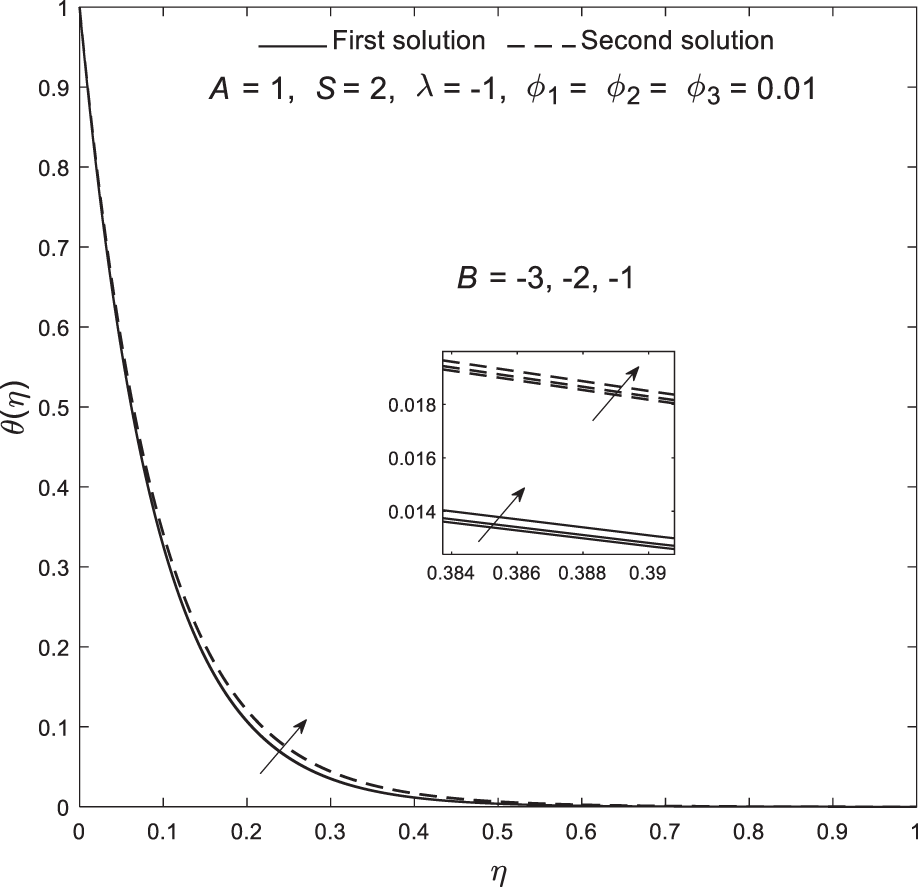
Figure 13: Plot of temperature θ(η) for varying values of velocity slip (second order)

For the stability analysis, Eqs. (14) and (15) were solved by relaxing and modifying a boundary condition of the far-field, which was declared in the previous section. These equations were computed using the bvp4c solver, and stability was assessed based on the smallest eigenvalues generated. According to Fig. 14, the first solution exhibits positive smallest eigenvalues, whereas the second solution shows negative smallest eigenvalues. This indicates that only one of the solutions is stable, that is the first one, and the findings from this solution are considered real throughout this study. Nonetheless, the second solution has been reported and discussed here just to provide comparative insights, explore potential instabilities, and guide future research.

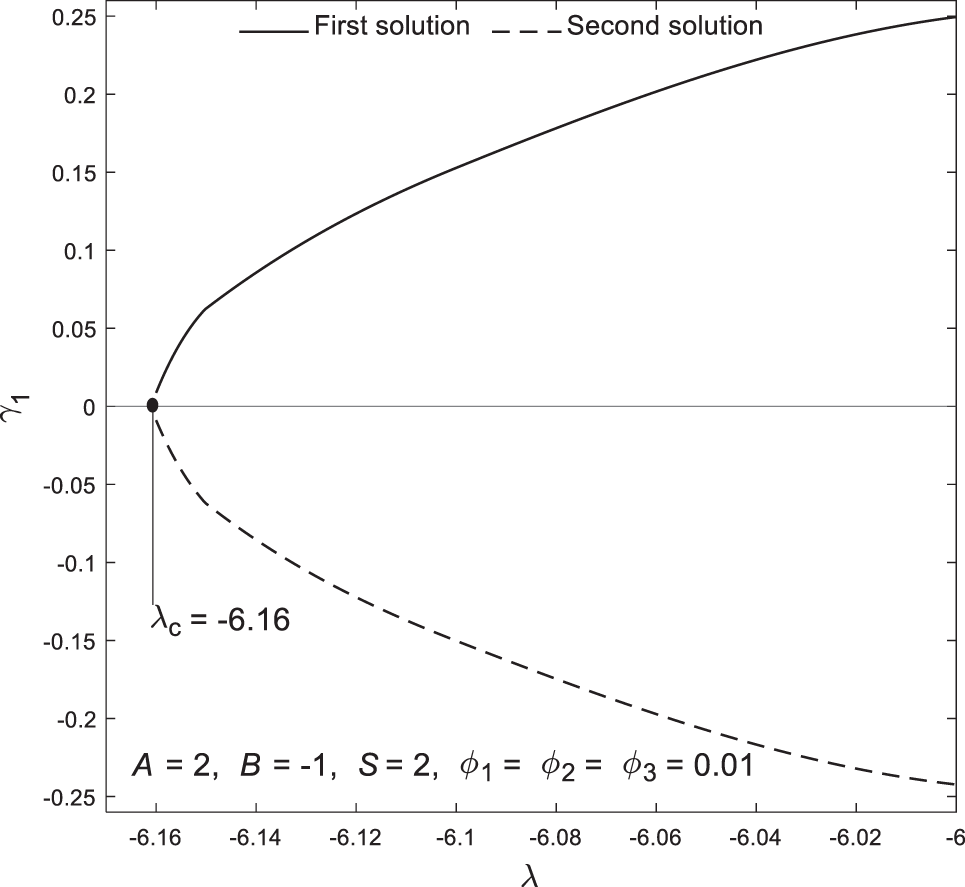
Figure 14: Plot of the smallest eigenvalue γ1 vs. λ for stability simulation

5  Conclusion

The model of alumina-copper-silver nanofluid flow past a permeable stretching/shrinking sheet with first and second-order velocity slip effects is formulated and solved in this study. Dual numerical solutions are obtained, but only the first solution has been assessed and confirmed as stable and dependable for flow control. From this stable solution, we analyzed the effects of various parameters on the skin friction coefficient and local Nusselt number, providing insights into how these parameters can be manipulated to control flow and enhance heat transfer. The recommendations for flow and heat transfer control can be deduced as follows:

•   Boundary layer separation can be delayed by configuring a suitably higher first-order velocity slip, whereas the second-order velocity slip has the opposite effect.

•   The ternary hybrid nanofluid achieves the most significant delay in boundary layer separation compared to the other two fluids.

•   The highest heat transferal ratio is achieved by increasing the first-order velocity slip when the sheet is shrunk, but the opposite effect occurs when the sheet is stretched. Conversely, the second-order velocity slip has the opposite effect: a higher heat transferal ratio is obtained when the sheet is stretched.

•   The ternary hybrid nanofluid model in this study exhibits a lower heat transferal ratio compared to the other two fluids, which contradicts the notion that ternary hybrid nanofluids would offer superior performance. However, this can be optimized by adjusting the stretching/shrinking parameter and velocity slip.

The conclusions drawn here are solely built upon the formulated model and the specific configuration of parameters and their considered ranges of values and may not apply to all cases. Overall, this research contributes to a better understanding of nanofluid behaviour and offers practical strategies for optimizing flow and heat transfer in engineering applications.

Acknowledgement: The authors acknowledged Universiti Putra Malaysia, Universiti Pertahanan Nasional Malaysia, Babeş-Bolyai University and the Academy of Romanian Scientists.

Funding Statement: The authors acknowledged Universiti Putra Malaysia for the Putra Grant that was received (GP-IPM 9787700). The work by Ioan Pop has been supported by Grant PN-III-P4-PCE-2021-0993, UEFISCDI, Romania.

Author Contributions: Nur Syahirah Wahid: Investigation, Methodology, Formal analysis, Writing—review & editing, Nor Ain Azeany Mohd Nasir: Writing—review & editing, Norihan Md Arifin: Supervision, Ioan Pop: Conceptualization, Writing—original draft preparation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Salahuddin T, Fatima G, Awais M, Khan M, Al Awan B. Adaptation of nanofluids with magnetohydrodynamic Williamson fluid to enhance the thermal and solutal flow analysis with viscous dissipation: a numerical study. Results Eng. 2024;21(3):101798. doi:10.1016/j.rineng.2024.101798. [Google Scholar] [CrossRef]

2. Mumtaz M, Islam S, Ullah H, Shah Z. Chemically reactive MHD convective flow and heat transfer performance of ternary hybrid nanofluid past a curved stretching sheet. J Mol Liq. 2023;390(4):123179. doi:10.1016/j.molliq.2023.123179. [Google Scholar] [CrossRef]

3. Mishra A, Rawat SK, Yaseen M, Pant M. Development of machine learning algorithm for assessment of heat transfer of ternary hybrid nanofluid flow towards three different geometries: case of artificial neural network. Heliyon. 2023;9(11):e21453. doi:10.1016/j.heliyon.2023.e21453. [Google Scholar] [PubMed] [CrossRef]

4. Gasmi H, Obalalu AM, Kaswan P, Khan U, Ojewola OB, Abdul-Yekeen AM, et al. Features of melting heat transfer in magnetized squeezing radiative flow of ternary hybrid nanofluid. Case Stud Therm Eng. 2024;61(1):104842. doi:10.1016/j.csite.2024.104842. [Google Scholar] [CrossRef]

5. Mohana CM, Kumar BR. Numerical and semi-analytical approaches for heat transfer analysis of ternary hybrid nanofluid flow: a comparative study. Math Comput Simul. 2024;226:66–90. doi:10.1016/j.matcom.2024.06.019. [Google Scholar] [CrossRef]

6. Khan SA, Imran M, Waqas H, Muhammad T, Yasmin S, Alhushaybari A. Numerical analysis of multiple slip effects on CuO/MgO/TiO-water ternary hybrid nanofluid with thermal and exponential space-based heat source. Tribol Int. 2024;197(4):109778. doi:10.1016/j.triboint.2024.109778. [Google Scholar] [CrossRef]

7. Fahad MK, Hasan MdJ, Ifraj NF, Chandra Dey D. Numerical investigation on the impact of different design arrangements of helical heat exchangers with varying cross-sections utilizing ternary hybrid nanofluids. Heliyon. 2024;10(14):e34481. doi:10.1016/j.heliyon.2024.e34481. [Google Scholar] [PubMed] [CrossRef]

8. Zeeshan A, Khalid N, Ellahi R, Khan MI, Alamri SZ. Analysis of nonlinear complex heat transfer MHD flow of Jeffrey nanofluid over an exponentially stretching sheet via three phase artificial intelligence and machine learning techniques. Chaos Soliton Fract. 2024;189(1):115600. doi:10.1016/j.chaos.2024.115600. [Google Scholar] [CrossRef]

9. Alharbi AA. Thermal analysis of heat transport in a slip flow of ternary hybrid nanofluid with suction upon a stretching/shrinking sheet. Case Stud Therm Eng. 2024;54(25–26):103965. doi:10.1016/j.csite.2023.103965. [Google Scholar] [CrossRef]

10. Mahmood Z, Eldin SM, Rafique K, Khan U. Numerical analysis of MHD tri-hybrid nanofluid over a nonlinear stretching/shrinking sheet with heat generation/absorption and slip conditions. Alex Eng J. 2023;76(4):799–819. doi:10.1016/j.aej.2023.06.081. [Google Scholar] [CrossRef]

11. Mahabaleshwar US, Maranna T, Pérez LM, Bognár GV, Oztop HF. An impact of radiation on laminar flow of dusty ternary nanofluid over porous stretching/shrinking sheet with mass transpiration. Results Eng. 2023;18(1):101227. doi:10.1016/j.rineng.2023.101227. [Google Scholar] [CrossRef]

12. Ouyang Y, Md Basir MF, Naganthran K, Pop I. Dual solutions in Maxwell ternary nanofluid flow with viscous dissipation and velocity slip past a stretching/shrinking sheet. Alex Eng J. 2024;105(157):437–48. doi:10.1016/j.aej.2024.07.093. [Google Scholar] [CrossRef]

13. Mahmood Z, Khan U, Saleem S, Rafique K, Eldin SM. Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and Lorentz force. J Magn Magn Mater. 2023;573(3):170654. doi:10.1016/j.jmmm.2023.170654. [Google Scholar] [CrossRef]

14. Jamrus FN, Waini I, Khan U, Ishak A. Effects of magnetohydrodynamics and velocity slip on mixed convective flow of thermally stratified ternary hybrid nanofluid over a stretching/shrinking sheet. Case Stud Therm Eng. 2024;55(66):104161. doi:10.1016/j.csite.2024.104161. [Google Scholar] [CrossRef]

15. Uddin MJ, Khan WA, Ismail AIMd. Melting and second order slip effect on convective flow of nanofluid past a radiating stretching/shrinking sheet. Propuls Power Res. 2018;7(1):60–71. doi:10.1016/j.jppr2018.01.003. [Google Scholar] [CrossRef]

16. Vishnu Ganesh N, Abdul Hakeem AK, Ganga B. Darcy-Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and ohmic dissipations effects. Ain Shams Eng J. 2018;9(4):939–51. doi:10.1016/j.asej.2016.04.019. [Google Scholar] [CrossRef]

17. Usafzai WK. Multiple exact solutions of second degree nanofluid slip flow and heat transport in porous medium. Therm Sci Eng Prog. 2023;40(4):101759. doi:10.1016/j.tsep.2023.101759. [Google Scholar] [CrossRef]

18. Mumtaz M, Islam S, Ullah H, Dawar A, Shah Z. A numerical approach to radiative ternary nanofluid flow on curved geometry with cross-diffusion and second order velocity slip constraints. Int J Heat Fluid Flow. 2024;105:109255. doi:10.1016/j.ijheatfluidflow.2023.109255. [Google Scholar] [CrossRef]

19. Bakar SA, Pop I, Md Arifin N. Unsteady flow of gyrotactic microorganisms with hybrid nanofluid and higher order slips using modified Buongiorno model. Int J Heat Fluid Flow. 2024;107(10):109378. doi:10.1016/j.ijheatfluidflow.2024.109378. [Google Scholar] [CrossRef]

20. Devi SU, Devi SA. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J Nigerian Math Soc. 2017;36:419–33. [Google Scholar]

21. Manjunatha S, Puneeth V, Gireesha BJ, Chamkha AliJ. Theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. J Appl Comput Mech. 2022;8(4):1279–86. doi:10.22055/jacm.2021.37698.3067. [Google Scholar] [CrossRef]

22. Waini I, Ishak A, Pop I. Hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking surface with a convective boundary condition. J Phys: Conf Ser. 2019;1366(1):012022. doi:10.1088/1742-6596/1366/1/012022. [Google Scholar] [CrossRef]

23. Jakeer S, Reddy SRR, Rashad AM, Lakshmi Rupa M, Manjula C. Nonlinear analysis of Darcy-Forchheimer flow in EMHD ternary hybrid nanofluid (Cu-CNT-Ti/water) with radiation effect. Forces Mech. 2023;10:100177. doi:10.1016/j.finmec.2023.100177. [Google Scholar] [CrossRef]

24. Ishak SS, Ilias MR, Kechil SA. Ternary hybrid nanofluids containing gyrotactic microorganisms with magnetohydrodynamics effect over a shrinking/stretching of the horizontal plate. J Adv Res Fluid Mech Therm Sci. 2023;109(2):102–230. doi:10.37934/arfmts.109.2.210230. [Google Scholar] [CrossRef]

25. Waini I, Ishak A, Pop I. Melting heat transfer of a hybrid nanofluid flow towards a stagnation point region with second-order slip. Proc Inst Mech Eng Part E J Process Mech Eng. 2021;235(2):405–15. doi:10.1177/0954408920961213. [Google Scholar] [CrossRef]

26. Merkin JH. On dual solutions occurring in mixed convection in a porous medium. J Eng Math. 1986;20(2):171–9. doi:10.1007/BF00042775. [Google Scholar] [CrossRef]

27. Weidman PD, Kubitschek DG, Davis AMJ. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int J Eng Sci. 2006;44(11–12):730–7. doi:10.1016/j.ijengsci.2006.04.005. [Google Scholar] [CrossRef]

28. Harris SD, Ingham DB, Pop I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp Porous Media. 2009;77(2):267–85. doi:10.1007/s11242-008-9309-6. [Google Scholar] [CrossRef]

29. Shampine LF, Kierzenka J, Reichelt MW. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. 2004;1–27. Available from: https://classes.engineering.wustl.edu/2009/spring/che512/bvp_paper.pdf. [Accessed 2024]. [Google Scholar]

30. Turkyilmazoglu M. Heat and mass transfer of MHD second order slip flow. Comput Fluids. 2013;71:426–34. doi:10.1016/j.compfluid.2012.11.011. [Google Scholar] [CrossRef]