 Open Access
Open Access
REVIEW
Plates, Beams and Shells Reinforced by CNTs or GPLs: A Review on Their Structural Behavior and Computational Methods
1 Department of Mechanical Engineering, Islamic Azad University, North Tehran Branch, Tehran, 16511-53311, Iran
2 Faculty of Mechanical Engineering, K.N. Toosi University of Technology, Tehran, 19991-43344, Iran
3 Faculty of Mechanical Engineering, University of Eyvanekey, Semnan, 99888-35918, Iran
* Corresponding Author: Kamran Asemi. Email:
Computer Modeling in Engineering & Sciences 2025, 142(2), 1351-1458. https://doi.org/10.32604/cmes.2025.060222
Received 27 October 2024; Accepted 08 January 2025; Issue published 27 January 2025
Abstract
Since the initial observation of carbon nanotubes (CNTs) and graphene platelets (GPLs) in the 1990 and 2000s, the demand for high-performance structural applications and multifunctional materials has driven significant interest in composite structures reinforced with GPLs and CNTs. Incorporating these nanofillers into matrix materials markedly enhances the mechanical properties of the structures. To further improve efficiency and functionality, functionally graded (FG) distributions of CNTs and GPLs have been proposed. This study presents an extensive review of computational approaches developed to predict the global behavior of composite structural components enhanced with CNT and GPL nanofillers. The analysis focuses on key structural elements, such as plate-type configurations, cylindrical and curved shells, and beams, emphasizing the computational techniques utilized to simulate their mechanical behavior. The utilization of three-dimensional elasticity theories and equivalent single-layer (ESL) frameworks, which are widely employed in the modeling and analysis of these composites, is comprehensively discussed. Additionally, the paper examines various mechanical performance aspects, including static, buckling, post-buckling, vibrational, and dynamic responses for the mentioned structures. The unique features of hybrid nanocomposites, combining CNTs and GPLs, are also analyzed. Furthermore, the study delves into the fabrication and processing techniques of these materials, with a particular focus on strategies to mitigate nanofiller agglomeration. The review extends to cover thermal and electrical properties, durability under environmental exposure, fatigue resistance, and vibration-damping characteristics. In conclusion, the paper underscores the necessity for ongoing advancements in computational modeling to facilitate improved design, analysis, and optimization of nanocomposite structures. Future research opportunities in this rapidly advancing domain are also outlined.Keywords
There has been a continuous pursuit of advanced materials and structures, particularly for composites. Advances in scientific research and manufacturing techniques have led to the development of modern composite materials with enhanced mechanical properties. The field of nanoscience, nanotechnology, and nanocomposites has flourished in recent years with the incorporation of carbon-based nanofillers. The significance of these materials has grown across various applications, including automotive, aerospace, packaging, electronics, biotechnology, flexible sensors, and numerous other sectors [1]. Following the discovery of the buckyball, a spherical molecule composed of pure carbon atoms, by Kroto et al. in 1985 [2], carbon nanotubes (CNTs) and graphene platelets (GPLs) emerged as prominent materials. Since the first report of a new type of finite carbon structure consisting of needle-like tube (Carbon nanotube) by Iijima in 1991 [3,4] and flat monolayer of carbon atoms tightly packed into a 2D honeycomb lattice (Graphene) by Novoselov et al. in 2004 [5,6], many researchers have explored various mechanical, physical, electrical, structural, and thermal properties of these new forms of carbon. Among the main carbon nanoparticles, graphene platelets (GPLs) and carbon nanotubes (CNTs) have attracted the most attention [7]. The superlative mechanical properties of CNT and GPL make them the best choice for composite reinforcement, significantly enhancing the base matrix when integrated as strengthening elements [8].
CNTs can be classified into two major types: single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs). SWCNTs consist of a single sheet of graphene rolled seamlessly to form a cylinder, with diameters around 1 nm and lengths up to centimeters. MWCNTs consist of multiple concentric cylinders; each separated by 0.35 nm and typically have diameters ranging from 2 to 100 nm and lengths of up to tens of microns. Graphene is a type of carbon allotrope composed of sp2-bonded carbon atoms, forming a two-dimensional hexagonal lattice that can be viewed as an unzipped SWCNT. Khoshraftar et al. [9] confirmed the previously discussed findings. As shown in Fig. 1, SWCNTs can be visualized as a single graphene sheet rolled into a continuous cylinder. On the other hand, MWCNTs consist of multiple concentric cylindrical layers of graphene sheets, aligned coaxially. These layers are held together by van der Waals forces between neighboring sheets, creating a hollow core. This unique structure differentiates SWCNTs from MWCNTs.

Figure 1: A schematic illustration showing the relationship and configuration of graphene, graphite, SWCNTs, and MWCNTs; Reprinted from Khoshraftar et al. [9], Nature, 2024, licensed under CC BY 4.0
CNTs possess an exceptionally high Young’s modulus of 1
The concept of functionally graded materials (FGMs) has modernized the application of nanofiller-reinforced composites. In FGMs, the weight fraction and distribution of the reinforcing material change gradually from the innermost to the outermost layers, offering enhanced performance compared to conventional composite materials. Given their high structural performance, carbon-based composite materials are highly sought after for modern smart engineering applications, including aerospace [7], marine science, water treatment [16], automotive [17], sports, and biomechanics. Due to their numerous beneficial properties and diverse applications, many researchers have explored various aspects of these valuable carbon-based nanofillers.
Several comparative studies have examined the characteristics of CNTs and GPLs reinforced composites. Li et al. [18] conducted a study comparing the mechanical properties of polymer composites reinforced with CNTs and graphene sheets. They found that composites reinforced with graphene sheets exhibited approximately 18% higher Young’s modulus, 8.7% higher tensile strength, and 5% higher surface crack energy compared to those reinforced with carbon nanotubes. Rafiee [19] investigated various mechanical properties, including Young’s modulus, ultimate tensile strength, fracture toughness, fracture energy, and fatigue crack propagation rate. Their results demonstrated that GPLs significantly enhance the mechanical properties of epoxy nanocomposites. Specifically, the Young’s modulus of a 0.1 wt.% GPL nanocomposite was 31% greater than that of pure epoxy, compared to a 3% increase for SWCNT composites. The ultimate tensile strength of the pristine epoxy improved by 40% with GPLs, while MWCNTs resulted in a 14% enhancement. Additionally, the fracture toughness of the GPL nanocomposite was 53% higher than that of the pristine epoxy, whereas MWCNTs provided only a 20% increase.
Given the growing interest in CNT and GPL-reinforced structures, numerous review articles have examined their various characteristics, including mechanical features [12,13,20–22], theoretical modeling [23,24], physical properties [25–27], agglomeration causes and solutions [8,28], fabrication methods [10,16], and thermal and electrical applications [29,30]. However, this paper focuses specifically on the structural mechanics of plate-type structures, beams, and cylindrical or curved shells reinforced with CNT and GPL nanoparticles. A schematic representation of each structural component is provided in Fig. 2. This review article, by tabulating the type of analysis, employed methodologies, and reinforcement types, serves as a valuable resource and database for the mechanics of carbonaceous nanocomposites. It covers their static and dynamic mechanical behavior, buckling and post-buckling responses, as well as free and forced vibration characteristics. Due to the wide range of analyses and geometries explored, the literature review is structured according to both geometric shape and type of analysis. Additionally, the paper presents a detailed comparison of computational methods used in these analyses, such as 3D elasticity and equivalent single layer (ESL) theories. Hybrid nanocomposites reinforced with a combination of CNTs and GPLs are also discussed. Moreover, the main processing techniques for preparing CNT- and GPL-reinforced composites and the significant production challenge, namely the agglomeration phenomenon, are explored. Further discussions cover the significance of CNTs and GPLs over porous structures, thermal and electrical properties, durability and resistance to environmental factors, fatigue behavior, as well as damping and vibration attenuation characteristics.
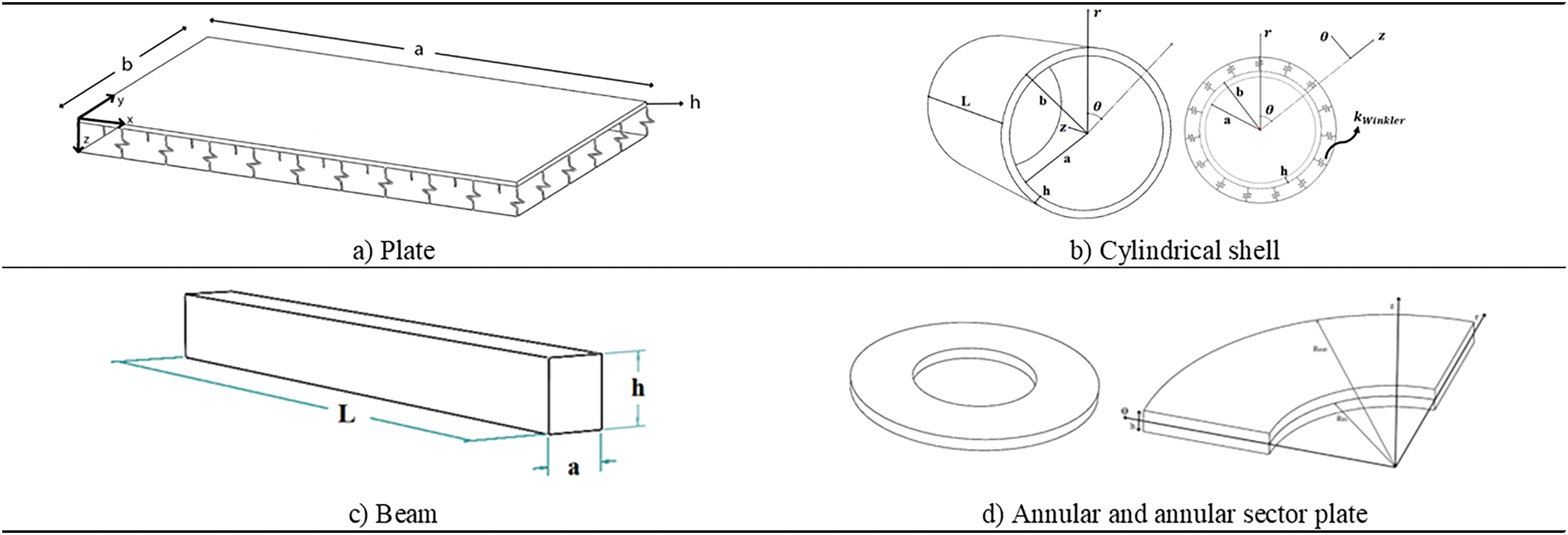
Figure 2: General geometries of structural components: a) Plate, b) Cylindrical shell, c) Beam, d) Annular and annular sector plate
2 Functionally Graded Materials (FGMs)
FGMs are advanced engineering materials designed for applications where conventional composites fall short and higher performance is required. In FGMs, which the concept was first introduced in 1984, the volume and distribution of the reinforcing material gradually change from the innermost to the outermost layers, offering advantages over traditional composites. Stress concentration typically arises at the interfaces of conventional laminate composites, often resulting in structural failure. FGMs address this issue by providing a continuous variation of material properties from one surface to another, effectively eliminating the stress concentration observed in traditional laminated composites [24]. FGMs provide opportunities to control material responses to static deformation, buckling and post-buckling, vibrational characteristics, corrosion, and dynamic loading [31]. The material properties of FG GPLs/CNTs RC elements vary along the thickness direction due to a layer-wise change in the weight fraction of nanofillers. This variation is dependent on the structure’s thickness.
Fig. 3 illustrates the five major patterns for nanofiller distribution in FG composites, which can be uniform, symmetric, or asymmetric. In the uniform distribution (UD) case, all layers have the same composition. The FG-X symmetric model features increased reinforcement in both the inner and outer layers. In contrast, the FG-O distribution pattern shows a higher concentration of reinforcement in the middle layers. The FG-V asymmetrical model includes greater reinforcement near one of the outer layers, while the FG-A model has a higher amount of reinforcement close to the other outer layer [32].
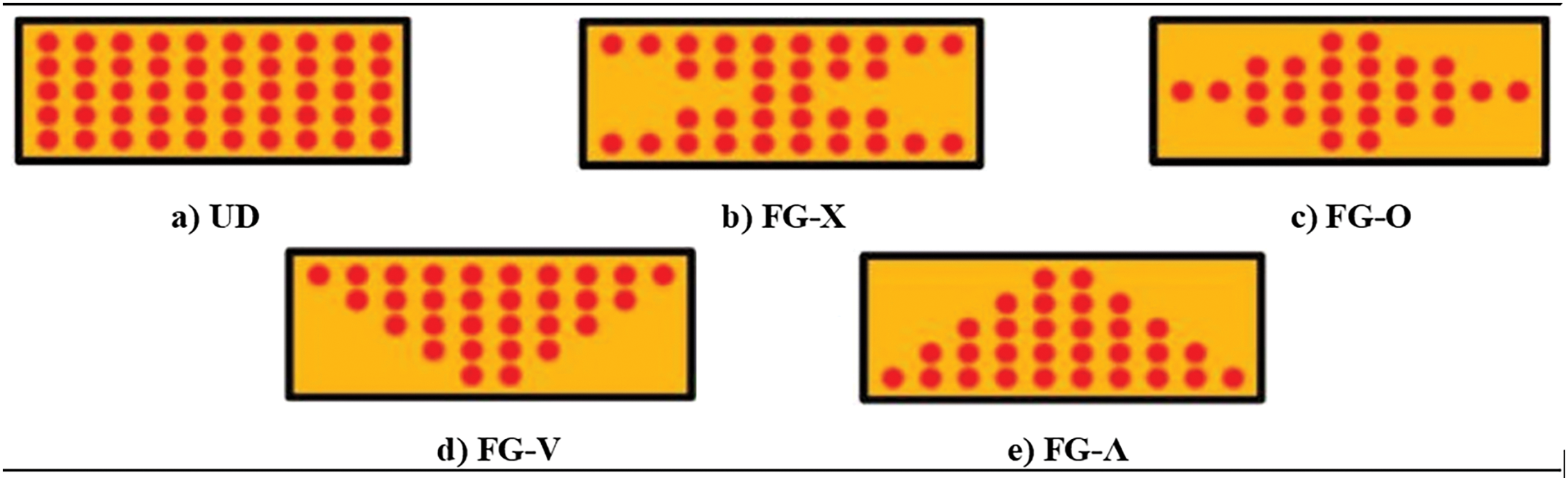
Figure 3: Various uniform and functionally graded distribution patterns of nanofiller reinforcing elements: a) UD, b) FG-X, c) FG-O, d) FG-V, e) FG-Λ
As will be discussed later, under nearly all conditions and for various types of structural analyses—including static, buckling, post-buckling, and free and forced vibrations—the top and bottom layers generally have the most significant impact on the stiffness of the structure. Consequently, the FG-X pattern results in the highest stiffness, while the FG-O pattern yields the lowest value. The UD and FG-V/FG-A patterns produce intermediate stiffness values, respectively.
3 Matrix Material of CNT or GPL RCs
Various matrices, including polymers, metals, and ceramics, are employed in CNT- or GPL-reinforced composites, enabling the tailoring of material properties to meet diverse application requirements such as lightweight structures, thermal management, and high-temperature performance. Polymer Matrix Composites (PMCs), Metal Matrix Composites (MMCs), and Ceramic Matrix Composites (CMCs) represent the primary classes of advanced composites, each with unique attributes tailored to specific applications.
PMCs offer excellent flexibility and lightweight characteristics, making them particularly suitable for aerospace and automotive applications. The incorporation of nanoparticles, such as CNTs or GPLs, significantly enhances the mechanical properties of PMCs, with improvements in modulus and hardness being especially notable due to the pronounced stiffness contrast between the polymeric matrix and the nano reinforcements. This high contrast facilitates efficient stress transfer at the nanoscale, leading to superior reinforcement efficiency compared to traditional fillers [33].
MMCs provide superior thermal and electrical conductivity, making them highly suitable for structural and electronic components in demanding environments. When reinforced with CNTs or GPLs, MMCs exhibit remarkable potential for enhanced mechanical as well as electrical properties. However, critical challenges must be addressed to fully realize their potential. The homogeneous distribution of fillers within the metal matrix is essential to avoid agglomeration, which can compromise performance. Additionally, the interfacial bonding between carbon-based fillers and the metal matrix plays a pivotal role in determining the composite’s mechanical strength and load transfer efficiency. Controlled interfacial reactions are required to optimize bonding without degrading the structural integrity of the fillers, ensuring their effectiveness as reinforcements [34].
CMCs have been developed to address the inherent brittleness and mechanical unreliability of monolithic ceramics, which, despite their high stiffness, strength, and excellent high-temperature stability, often fall short in demanding applications. By combining the intrinsic advantages of ceramics—such as corrosion resistance, lightweight properties, and electrical insulation—with reinforcements like CNTs or GPLs, CMCs exhibit enhanced toughness and thermal stability, making them highly suitable for harsh environments where metals and polymers fail. Graphene, in particular, offers advantages over CNTs due to its higher specific surface area and reduced tendency to tangle, enabling easier dispersion into ceramic matrices [35,36].
For CNT-reinforced composites, all three major matrix categories—PMCs, MMCs, and CMCs—have been extensively explored, each offering distinct advantages tailored to specific applications. In the case of polymer matrices, various polymers such as polystyrene (PS) [37], polypropylene (PP) [38], polyester [39], polyimide (PI) [40], polyaniline (PANI) [41], polypyrrole (PPY) [42], and polyvinyl alcohol (PVA) [43] have been used to incorporate CNTs, significantly enhancing their mechanical, thermal, and electrical properties while maintaining their lightweight and flexible characteristics. For metal matrices, CNTs have been successfully integrated into materials like aluminum (Al) [44–46], copper (Cu) [47], nickel (Ni) [48,49], magnesium (Mg) [50], and titanium (Ti) [51], leveraging their excellent electrical and thermal conductivity to create composites with superior strength and conductivity, suitable for high-performance structural and electronic applications. Ceramic matrices, including aluminum oxide (Al2O3) [52], titanium dioxide (TiO2) [53], magnesium aluminum spinel (MgAl2O4) [54], titanium nitride (TiN) [55], silicon carbide (SiC) [56], and silicon dioxide (SiO2) [57], have also been reinforced with CNTs. These combinations enhance the inherent high-temperature stability, wear resistance, and corrosion resistance of ceramics while addressing their brittleness, making them ideal for extreme environments and high-performance applications.
For GPL-reinforced composites, similar to CNTs, all three primary matrix types have been widely studied, offering tailored enhancements for a range of applications. In the polymer matrix category, GPLs have been integrated into polymers such as polymethyl methacrylate (PMMA) [58], waterborne polyurethane (WPU) [59], thermoplastic polyurethane (TPU) [60], poly(vinylidene fluoride) (PVDF) [61], polyethylene terephthalate (PET) [62], and polycarbonate (PC) [63], improving mechanical properties, thermal stability, and electrical conductivity while maintaining flexibility and ease of processing. For metal matrices, the incorporation of GPLs has been explored in materials like aluminum (Al) [64,65], copper (Cu) [66,67], nickel (Ni) [68,69], magnesium (Mg) [70,71], iron (Fe) [72], and nickel aluminide (Ni3Al) [73]. These combinations enhance the mechanical strength, thermal conductivity, and corrosion resistance of the metal matrix, making them highly suitable for applications in aerospace, automotive, and structural systems where performance under high stress and temperature is crucial. In ceramic matrix composites, the integration of GPLs into materials such as aluminum oxide (Al2O3) [74], silicon dioxide (SiO2) [75], zirconium dioxide (ZrO2) [76], silicon nitride (Si3N4) [77], silicon carbide (SiC) [78], and boron carbide (B4C) [79] offers significant improvements in toughness, thermal stability, and wear resistance, addressing the brittleness of ceramics while maintaining their superior high-temperature performance. These enhanced properties make GPL-reinforced CMCs ideal for demanding applications such as cutting tools, wear-resistant components, and structural materials in extreme environments.
Analytical and numerical computational techniques are pivotal in the analysis of composites reinforced with CNTs and GPLs. These methods are indispensable for accurately estimating mechanical properties, elucidating stress transfer mechanisms, and evaluating the interfacial bonding between the nanofillers and the matrix. For instance, molecular dynamics (MD) simulations provide a detailed understanding of atomic-scale interactions that govern the macroscopic behavior of composites, while FEA offers valuable insights into the distribution of stress within the material. Furthermore, computational fluid dynamics (CFD) plays a critical role in refining the processing and production stages by promoting uniform dispersion of nanoparticles. These computational methodologies and their practical applications make significant contributions to the development of efficient, high-performance composite materials, while reducing the need for extensive experimental testing.
3.1 Interfacial Bonding between the Nanoparticles and the Matrix
Interfacial bonding plays a crucial role in determining the mechanical performance of nanoparticle-reinforced composites, particularly in the case of CNT and GPL reinforcements. The strength of the interface between the nanofillers and the matrix directly influences how effectively mechanical loads are transferred across the composite material. To leverage the exceptional Young’s modulus and strength of CNTs and GPLs, it is essential that the mechanical load is efficiently transmitted from the matrix to the nanofillers, ensuring the reinforcement properties are fully utilized [13,80].
The reinforcement-matrix stress transfer mechanism and the interfacial strength are critical in enhancing the composite’s mechanical properties. A strong interfacial bond facilitates efficient stress transfer to the high-strength fillers, thereby strengthening the composite, but at the cost of reduced ductility. Conversely, weak interfaces can result in reduced strength and the potential for fillers pullout under low loads due to interface failure. Ensuring a homogeneous dispersion of CNTs or GPLs within the matrix is vital for maximizing interfacial contact area and optimizing mechanical properties. In such cases, each nanotube or graphene sheet is loaded individually, which allows for better utilization of their mechanical properties and contributes to toughening mechanisms [35].
In MMCs reinforced with carbon-based nanofillers, challenges arise from the density differences between the fillers and the matrix, as well as the high reactivity of metals like iron, aluminum, and titanium. Graphene’s planar structure and extensive interfacial contact area often lead to the formation of metal carbides during processing, which can negatively impact composite properties if not carefully controlled. However, pairing graphene with carbides such as B4C or SiC, or combining them with oxides like Al2O3 or ZrO2, has been shown to improve interfacial bonding and enhance the mechanical properties of CMCs [81–84].
To better understand and optimize these interfacial interactions, computational methods have become increasingly important. These techniques simulate stress transfer and evaluate interfacial bond strength, both of which are critical for enhancing composite performance. Studies have demonstrated how interface strength impacts the macroscopic behavior of reinforced composites using computational models as well as experimental investigations [85–88]. For example, molecular dynamics simulations have revealed the mechanical response and dislocation behaviors in graphene/iron composites, shedding light on the significant role of interfacial phenomena in determining overall performance [89]. Such findings highlight the necessity of incorporating interfacial bonding strength into computational models to accurately predict and improve the properties of nanocomposites.
4 Computational Acquisition of Material Properties
Several important methods are used to determine the effective mechanical properties of structures reinforced with GPLs and CNTs. Each method has its own advantages and disadvantages. For example, the rule of mixtures is a simple and advantageous approach but may lack accuracy and overlook the size of nanoparticles. The Mori-Tanaka and Halpin-Tsai methods offer better accuracy compared to the rule of mixtures. The extended Mori-Tanaka approach accounts for the agglomeration effect, which is a significant advantage, though it does not consider the size effects of nanoparticles, such as length, width, and thickness. On the other hand, the Halpin-Tsai method includes these dimensions and helps prevent agglomeration by choosing the maximum weight fraction of nanofillers based on experimental tests. Computational modeling serves as an essential tool for accurately predicting the material properties of structures reinforced with nanofillers. These approaches provide valuable insights into the mechanical behavior of nanocomposites, enabling more precise predictions of their performance under diverse loading scenarios. A detailed examination of these computational methodologies and their applications will be presented in the subsequent subsections.
The basic material properties can be estimated using the rule-of-mixture principle, which relies on a few assumptions. For particle-reinforced composites, it’s assumed that the particles are evenly spread throughout the matrix [90]. The effective mechanical properties of structures made from isotropic matrices and particle reinforcements can be assessed using the rule of mixtures as follows [91]:
In this context, E, ν, and ρ represent Young’s modulus, Poisson’s ratio, and density for reinforcements (R) and the matrix (m), respectively. V denotes the volume fraction of each component. For FGMs, reinforcements in each layer of the resultant composite are typically assumed to be randomly oriented and evenly distributed. Consequently, the rule of mixtures is often used to estimate properties like Poisson’s ratio and density. Additionally, other physical properties such as specific heat capacity and thermal expansion coefficient are approximated using this rule [92].
Because the rule of mixtures has limited accuracy, alternative methods are often used to approximate the elastic modulus. These methods will be discussed in the following sections.
Material properties of functionally graded carbon nanotube reinforced composites (FG-CNT RC) have been studied through both experimental and theoretical approaches [26,93–96]. In many mechanical theoretical analyses, the effective properties of composite materials-comprising an isotropic matrix and CNTs-are evaluated using the rule of mixtures. It is assumed that CNTs and the polymer are well-bonded and experience the same strain [97–99].
where
The effective mechanical properties of a structure reinforced with nanoparticles, based on the Mori-Tanaka approach, are determined based on coefficient of elasticity matrix as follows [101]:
where the subscripts m and r indicate the quantities of the matrix and the reinforcing phase, respectively. Also,
4.2.1 Considering Agglomeration in Mori-Tanaka Approach (Modified Mori-Tanaka)
Experimental results show that CNTs have low bending stiffness and high aspect ratios. These characteristics cause them to concentrate in spherical regions, termed ‘inclusions’, which have distinct elastic properties compared to the surrounding areas. Therefore, assuming a uniform distribution of CNTs within the matrix material is inaccurate. The total volume of CNTs, denoted by
where
Here,
The average volume fraction of CNTs in the matrix is defined as
where
In which
Km and Gm represent the bulk and shear moduli of the matrix material and can be expressed as follows:
Therefore, the Young’s modulus and Poisson’s ratio of the CNT-RC structure are given by:
4.3.1 Laminated FG-GPL RC Structure
To obtain mechanical properties of graphene reinforced laminated structures temperature dependent [103,104] and temperature independent [105] formulations is used. To determine the effective material properties of the laminated functionally graded graphene platelets reinforced composite (FG-GPL RC) structure, the Halpin-Tsai relations can be applied as follows [106,107]:
In the above equations,
Using the above equations, the elastic constants for a single-layer GPL RC with zigzag reinforcement (0-ply) can be determined for a specific volume fraction of GPLs. Additionally, for a composite material with armchair reinforcement of graphene (90°-ply), the matrix of elastic constants for the FG-GPL RC with 90°-ply can be obtained using transfer matrices [105].
Also, the thermal expansion coefficients in the longitudinal and transverse directions can be expressed as [104]:
where
To achieve a graded pattern for material properties, the FG-X type features a mid-plane symmetric graded distribution of graphene reinforcements, specified as [0.11/0.09/0.07/0.05/0.03]s. For the FG-O type, the graphene volume fractions are arranged as [0.03/0.05/0.07/0.09/0.11]s. Additionally, a uniformly distributed (UD) Graphene Reinforced Composite (GRC) laminated plate with the same thickness is used as a comparator, where each ply has a constant graphene volume fraction of
Shen [108] evaluated the values for

4.3.2 Multilayer FG-GPL RC Structures
The multilayer FG-GPL RC structure consists of
The subscripts (
The elastic modulus of the k-th layer, denoted by
The two parameters
The other two parameters,
where
The simple rule of mixtures is used to estimate the Poisson’s ratio and mass density of the k-th layer of the resulting composite structure.
Additionally, the rigidity modulus
In most cases, GPL nanofillers have basic dimensions of length
5 Theories for the Computational Modelling and Analysis of CNT and GPL RCs
For the analysis of composite plates and shells, both three-dimensional (3D) elasticity theory and equivalent single-layer (ESL) theories are commonly applied. While 3D elasticity theory provides a detailed representation of stress and strain distributions through the thickness, the ESL theories can be derived by making proper assumptions about these distributions. This simplification assumes equivalent properties for the entire layer, enabling efficient modeling with reduced computational complexity [111]. In this section, various established theories for analyzing composite plates and shells will be introduced, including Equivalent Single Layer theories—such as Classical Plate Theory (CPT), First-Order Shear Deformation Theory (FSDT), Third-Order Shear Deformation Theory (TSDT), Higher-Order Shear Deformation Theories (HSDTs), simplified approaches, and mixed theories—as well as three-dimensional elasticity theories and unified formulations.
The analysis of composite plates and shells often involves computational methods that balance accuracy and efficiency, particularly when addressing complex geometries and loading conditions. Finite element formulations based on Equivalent Single Layer theories, such as FSDT or HSDTs, are widely adopted for their reduced computational cost and ability to approximate global response effectively. However, these methods may exhibit limitations when capturing localized phenomena, such as through-thickness stress variations, delamination, or stress concentrations near discontinuities. In contrast, three-dimensional (3D) elasticity theory, which eliminates simplifying assumptions about through-thickness stress and strain distributions, provides a more comprehensive and accurate representation of these effects [112–114]. Despite its superior accuracy, 3D elasticity is computationally demanding, particularly for large-scale problems or complex geometries. This limitation often necessitates trade-offs between resolution and computational resources. Nonetheless, advancements in numerical techniques and computing power are making 3D elasticity increasingly viable, enabling its application to problems where ESL theories fall short, such as thick laminates or structures with significant heterogeneities [115–118].
Hereinafter, a comparative discussion of the features of the 3D elasticity and equivalent single-layer theories will be presented. Additionally, studies that have employed these theories to examine the mechanical properties of composite structures reinforced with CNTs or GPLs are summarized in tables according to each section. This compilation provides a valuable reference for assessing the applicability of these theories in the analysis of mechanical characteristics in composite materials.
Numerous researchers have studied the mechanical behavior of structures by employing various theories, including 2D and 3D elasticity theory. While 3D elasticity theory provides higher accuracy, it also incurs significant computational costs and increased implementation complexity. To address these challenges, the ESL theory has been proposed as a more efficient alternative. The 3D elasticity approach, though robust, often involves intricate and laborious mathematical formulations. To simplify these complexities, the plate and shell problems can be reduced to a 2D problem by assuming one dimension to be sufficiently smaller than the others, allowing for more practical computations while maintaining an acceptable degree of accuracy [20,119].
Three-dimensional (3D) elasticity theory is indispensable in addressing scenarios where through-thickness stress variations, interlaminar phenomena, or localized effects are critical to structural integrity and performance [120,121]. In mechanics, its rigorous formulation allows for precise characterization of stress singularities near geometric discontinuities, such as edges or cutouts, and accurate prediction of failure mechanisms like delamination and matrix cracking in composite structures. For thick laminates or structures subjected to complex loading, the inadequacies of ESL theories, including their reliance on predefined kinematic assumptions, often result in significant inaccuracies in the predicted response. Recent theoretical advancements, such as enriched finite element methods and variational multi-scale techniques, have enhanced the computational efficiency of 3D elasticity formulations while maintaining their accuracy [122,123]. Moreover, the integration of high-fidelity computational frameworks, such as isogeometric analysis and multi-resolution schemes, has provided a means to resolve fine-scale features without an excessive increase in computational cost. These advancements position 3D elasticity not only as a validation tool but also as a practical approach for solving complex engineering problems that demand a deeper understanding of the mechanics of composite materials and structures.
5.2 Equivalent-Single-Layer (ESL) Theories
As previously discussed, ESL theories are formulated by applying certain simplifying assumptions to the three-dimensional elasticity theory. These assumptions aim to reduce the complexity of the mathematical models while still capturing essential structural behavior. ESL theories streamline the analysis of composite structures by assuming a uniform distribution of stresses and strains across the thickness, allowing for more efficient computations without significantly compromising accuracy. This reduction is particularly beneficial when dealing with thin-walled structures, where the effects of shear and normal deformations can often be considered negligible. By leveraging these assumptions, ESL theories facilitate practical engineering applications, enabling the effective design and analysis of advanced materials such as functionally graded plates and shells.
5.2.1 Classical Plate Theory (CPT)
CPT, also referred to as Kirchhoff theory, represents the most basic ESL model, as it neglects both shear and normal deformation effects, making it suitable primarily for thin plates and shells. Based on the Kirchhoff-Love hypothesis, CPT assumes that straight lines normal to the midplane remain straight and perpendicular even after deformation. This simplified theory disregards shear and normal strains, as well as deformations, and is therefore applicable only in cases where these effects are negligible, such as in the analysis of thin structures.
Among ESL models, CPT is widely employed to predict the behavior of thin plates or shells due to its simplicity. Despite its limitations in accounting for shear and normal deformations, CPT can easily incorporate the effects of temperature variations, initial geometric imperfections, and geometric nonlinearities, making it versatile for various applications. While CPT may not capture shear and normal deformation effects, it still yields sufficiently accurate predictions for thin structures where these deformations play a minimal role, making it an efficient choice for such analyses [24,124].
5.2.2 Shear Deformation Theories
Among the shear deformation theories, the FSDT and the TSDT have been extensively utilized for the modeling and analysis of GPL or CNT reinforced composite plates and shells.
First-order shear deformation theory (FSDT)
FSDT, developed by Mindlin [125], considers a linear variation of in-plane displacements through the thickness, thus accounting for shear deformation effects. This theory requires a shear correction factor, which is influenced by geometric parameters, load conditions, and boundary constraints. Similar to Mindlin’s FSDT, the theory proposed by Reissner [126,127] also incorporates shear deformation effects, often referred to as “Reissner-Mindlin plates” or the “FSDT of Reissner.” However, it is important to note that Reissner’s theory is distinct from Mindlin’s approach [24]. Wang et al. [128] demonstrated that the bending relationships between Mindlin and Reissner quantities for general plate problems indicate that referring to Reissner’s theory as FSDT is misleading, as it implies a linear displacement variation through the thickness, which is not entirely accurate. Moreover, the inclusion of normal stress in Reissner’s theory distinguishes it from Mindlin’s theory, which omits normal stress effects. This difference highlights the nuanced complexities between these two shear deformation theories, emphasizing the need for careful application in structural analyses of plates and shells [129].
Higher-order shear deformation theory (HSDT)
The shear correction factor referenced in the FSDT subsection presents significant challenges in determination; therefore, HSDTs serve as an effective alternative. HSDTs are developed by expanding the displacement components in a power series along the thickness direction. By incorporating a sufficient number of terms in this series, HSDTs can yield accurate solutions for a wide range of structural problems. These theories take into account higher-order variations of both in-plane and transverse displacements, which allows for a more comprehensive representation of shear deformation, as well as the effects of normal deformation. This characteristic enables HSDTs to function as quasi-3D theories, offering enhanced accuracy for the analysis of plates and shells compared to first-order approaches. HSDTs can be formulated using either polynomial or non-polynomial shape functions, providing flexibility in modeling different material behaviors and geometries. This adaptability makes HSDTs particularly valuable for analyzing complex structures, such as functionally graded materials, where precise predictions of mechanical responses are crucial for effective design and application [24].
Third-order shear deformation theory (TSDT)
Reddy’s TSDT [130] is widely utilized for modeling plate and shell structures due to its advantageous combination of simplicity and accuracy. This theory incorporates the effects of transverse shear deformation and satisfies the zero-traction boundary conditions on the top and bottom surfaces of a plate, thereby eliminating the necessity for a shear correction factor. The displacement field formulated in Reddy’s theory closely resembles that of Levinson’s theory [131]; however, the governing equations of motion differ significantly. This divergence stems from Levinson’s reliance on the equilibrium equations of the FSDT, which are variationally inconsistent with the equations derived by Reddy. Consequently, Reddy’s TSDT provides a more comprehensive framework for accurately capturing the mechanical responses of plate and shell structures, especially in scenarios where shear deformation is a critical factor. This makes TSDT a preferred choice in engineering applications that require precise analysis of structural behavior [130,131].
It is widely recognized that HSDTs and quasi-3D theories, which are formulated by expanding displacement fields in a power series related to the thickness coordinate, are often computationally demanding. Each additional power of the thickness coordinate introduces an extra unknown variable into the model, thereby increasing the complexity of the analysis. Therefore, there is a critical necessity to simplify the existing HSDTs and quasi-3D theories or to devise new, more straightforward models that utilize fewer unknowns. Examples of simplified ESL theories include the simplified FSDT [132,133], the simplified TSDT [134], and the Refined Plate Theory (RPT) [135–138]. Other simplified approaches comprise four-unknown HSDTs [139–141], simplified nth-order shear deformation theories [142], four-unknown quasi-3D theories [143,144], five-unknown quasi-3D theories [145–149], and six-unknown quasi-3D theories [150]. These advancements seek to strike a balance between precision and computational efficiency, rendering them valuable alternatives for the analysis of plate and shell structures reinforced with advanced materials.
Mixed theories are developed to enhance the precision and accuracy of structural analysis while simultaneously reducing computational demands. One notable approach is the Principle of Virtual Displacements (PVD) [151,152], which treats the displacement components as primary variables. In this framework, the stress components are derived from the displacement components using strain-displacement relationships and constitutive equations. The Reissner Mixed Variational Theorem (RMVT) [153,154] was introduced by Reissner, positing two independent fields for displacements and transverse stresses. A key advantage of the RMVT over the PVD is its inherent ability to ensure the compatibility of displacements and the equilibrium conditions between adjacent layers. This “natural” satisfaction of compatibility and equilibrium is crucial for accurate modeling. Research indicates that mixed theories based on the RMVT tend to outperform those derived from the PVD in predicting the overall responses of FG plates, particularly regarding transverse stresses. This is attributed to the treatment of transverse stresses as primary variables in RMVT-based models, which contributes to more reliable predictions in structural performance [24].
The unified formulation introduced by Carrera [155–157] for composite structures represents a hierarchical approach that provides a comprehensive method for describing and implementing various plate and shell theories, as well as finite elements, in a cohesive manner. This methodology relies on a few fundamental nuclei, allowing for the straightforward development of multiple theories within the framework of the Carrera Unified Formulation (CUF). In the CUF, displacement variables are expanded in the thickness coordinate using Taylor’s series expansions of N-order, where N serves as a free parameter. This flexibility enables the formulation to encompass a wide range of plate and shell theories, facilitating their integration and application. The CUF has been extensively applied in the analysis of FG plates, leveraging both the Principle of Virtual Displacements (PVD) and the Reissner Mixed Variational Theorem (RMVT) as foundational approaches. This adaptability and breadth of application make the CUF a valuable tool in advancing the understanding and performance prediction of complex composite structures [158–160].
5.5 Comparison of Computational Methods
A comprehensive comparison of computational methods used for modeling and analyzing composite plates and shells highlights key trade-offs between precision and computational efficiency. 3D elasticity theory delivers the highest level of accuracy by thoroughly capturing stress variations throughout the thickness and addressing local phenomena such as delamination and stress concentrations. However, its computational demands and complexity render it less practical for large-scale problems or intricate geometries, unless coupled with advanced numerical approaches such as isogeometric analysis or multi-resolution methods. While these innovations enhance computational efficiency, they still do not achieve the speed of more straightforward methods. Conversely, ESL theories, including CPT, FSDT, and HSDTs, offer a compromise between computational efficiency and accuracy. ESL methods simplify the problem by assuming a uniform distribution of stress and strain across the thickness, making them highly efficient for thin structures or scenarios where shear deformation is not critical. Although ESL models are more effective in capturing shear deformations, they are less accurate in modeling through-thickness stresses or local effects, especially in thicker laminates or under complex loading conditions. Mixed theories provide a balanced solution by combining the strengths of both ESL and 3D elasticity. These methods introduce independent fields for displacements and stresses, improving accuracy without significantly increasing computational costs. Lastly, unified formulations, such as the CUF, offer a hierarchical framework that enables the modeling of multiple theories within a single structure. This flexibility makes unified formulations a promising choice for complex composite material analysis, allowing for customized solutions that align with the specific requirements of structural complexity and accuracy. Ultimately, the selection of a computational method depends on various factors, including the intricacy of the structure, the desired precision, and the computational resources available.
6 Structural Behavior and Computational Methods for Plates
In plates and shells theory, plates are flat, two-dimensional structural elements with a thickness much smaller than their other dimensions. They are designed to bear both out-of-plane and in-plane loads. Plate structures are crucial in mechanical engineering, commonly used for their ability to support loads and provide structural stability in bridges, buildings, aircraft, and machinery. Proper design and analysis of plate structures are essential to ensure they can handle intended loads without excessive deformation or failure. Table 6 summarizes numerous studies that investigate different aspects of CNT or GPL reinforced composite plates, focusing on their theoretical approaches.
Computational techniques are integral to understanding the complex behavior of composite plate structures subjected to various loading conditions. Methods such as 3D elasticity and equivalent single-layer (ESL) theories are widely employed to model static, dynamic, and buckling responses, achieving a balance between computational efficiency and accuracy. When combined with numerical methods, such as FEM, and analytical solution strategies, these approaches yield comprehensive insights into stress distributions, deformations, and stability, even in plates with intricate geometries or material heterogeneities. While ESL theories provide simplified yet effective models, 3D elasticity offers higher precision, albeit with increased computational requirements. Advances in numerical techniques and computational power are further enhancing the applicability of these methods to larger-scale and more complex problems. Applications of these computational approaches will follow in subsequent sections.
6.1.1 Static Response of CNT RC Plates
Several papers have examined the static responses of MWCNT and SWCNT reinforced composite plates [232–235]. The experimental results from Jamal-Omidi et al. [236] show that the Young’s modulus of nanocomposites with 0.1 and 0.25 wt.% SWCNTs increased by 10% and 18%, respectively. Ruan et al. [237] observed a significant improvement in the toughness of high-strength and high-modulus ultra-high molecular weight polyethylene (UHMWPE) films with the addition of 1 wt.% MWCNTs. Specifically, there was a 150% increase in strain energy density, a 140% increase in ductility, and up to a 25% increase in tensile strength.
Lei et al. [161] used the FSDT and the element-free kp-Ritz method to study the static bending responses of laminated SWCNT reinforced composite plates. They found that, compared to the effects of CNT volume fractions, plate width-to-thickness ratios, plate aspect ratios, and boundary conditions, the distribution of CNTs has minimal influence on the central deflections. Shen [97] investigated the impact of transverse uniform or sinusoidal loads in thermal environments on the nonlinear bending responses of simply supported FG SWCNT RC plates. Their findings confirm that the nonlinear bending characteristics are significantly affected by temperature rise, the nature of in-plane boundary conditions, transverse shear deformation, plate aspect ratio, and nanotube volume fraction. Alibeigloo [162], considered the static analysis of FG-CNT RC plates embedded in piezoelectric layers using the theory of elasticity, and observed that the effect of CNTs is more significant on the transverse quantities than on the in-plane quantities. Zhu et al. [163] introduced a numerical procedure using the FEM for analyzing the natural frequency and static bending of FG-CNT plates under various boundary conditions, applying the FSDT. Malekzadeh and Heydarpour [102] examined the static bending responses and natural frequencies of simply supported composite plates with FG-CNT RC layers, using the Navier-layer wise and Differential Quadrature Method (DQM). Natarajan et al. [164] employed HSDT and normal deformable plate theory for the static and natural frequency analysis of FG-CNT RC plates and sandwich plates with CNT-reinforced face sheets. Alibeigloo et al. [165] investigated the natural frequency and static bending behavior of FG CNT rectangular plates subjected to transverse uniform pressure under various boundary conditions, utilizing the DQM.
6.1.2 Static Response of GPL RC Plates
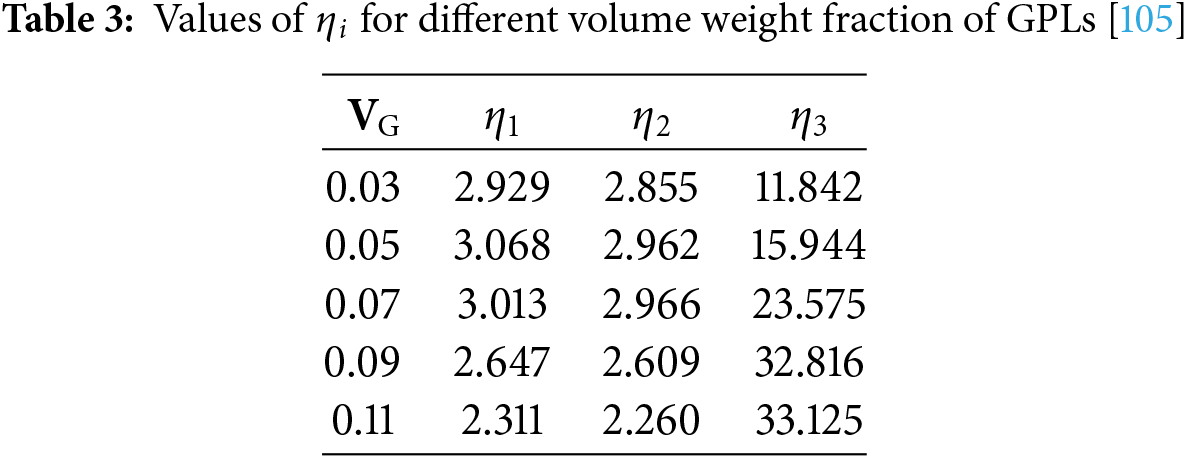
Song et al. [172] demonstrated in their bending analyses of FG-GPL RC plates that adding just 1.0 wt.% GPLs resulted in a central deflection of the FG-X plate that is only 17% of that of the pure epoxy plate. Thai et al. [173] also reported similar findings. They used a NURBS formulation based on four-variable refined plate theory, and observed that with a 1% addition of GPLs, the deflection decreased significantly by more than 80%, as shown in Fig. 4. García-Macías et al. [174] confirmed that, in the case of uniform distributions, polymers doped with 1% graphene nanoparticles can result in a reduction of over 85% in central deflection compared to the pristine polymer.
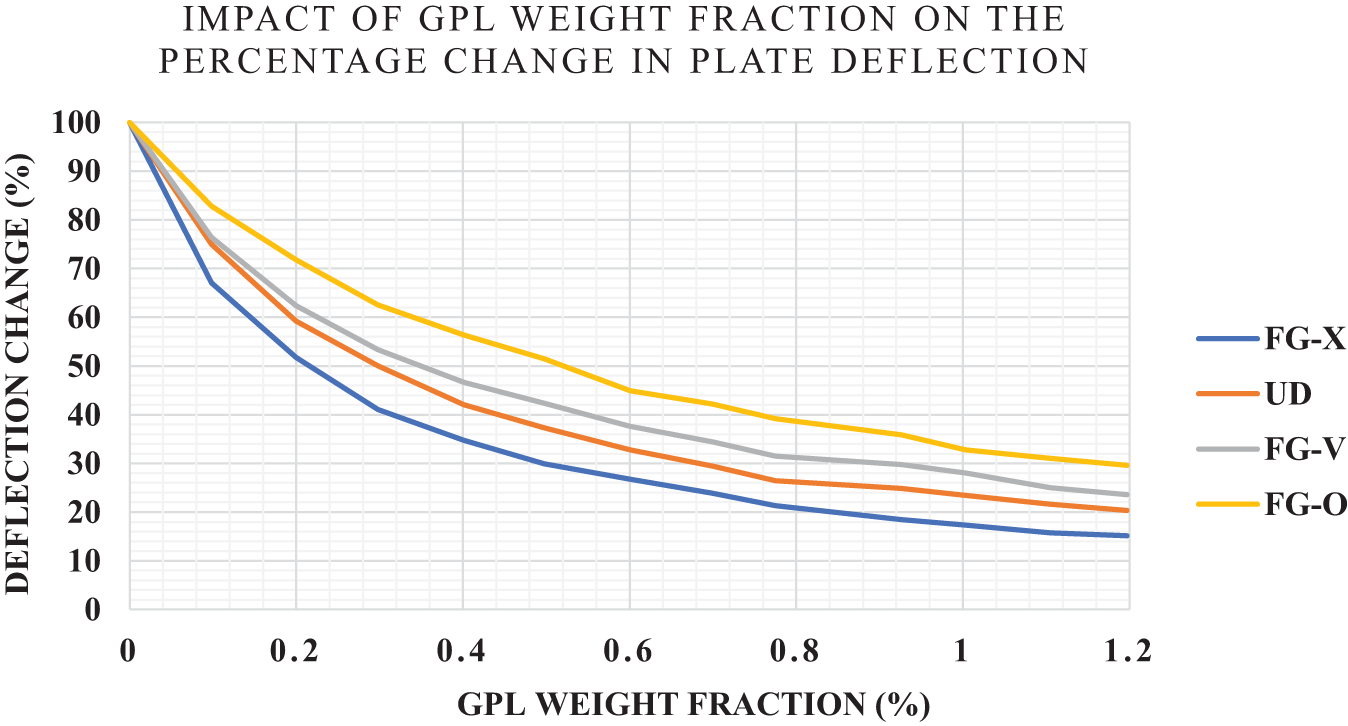
Figure 4: Impact of GPL weight fraction on the percentage change in plate deflection; Adopted from Thai [173]
Shen et al. [175] studied the thermal bending of a GRC plates using HSDT across different temperatures. They found that foundation stiffness, temperature increase, in-plane boundary conditions, and the magnitude of the initial compressive load significantly influence the nonlinear bending behavior of FG GRC laminated plates. Gholami et al. [176] performed a large deflection geometrically nonlinear analysis of multilayer FG-GPL RC rectangular plates using sinusoidal shear deformation plate theory. They discovered that the FG-X distribution pattern more effectively utilizes GPLs because the top and bottom surfaces experience greater bending. This results in enhanced overall plate stiffness and a reduction in maximum deflection. Zhao et al. [177] conducted a FE analysis on the nonlinear bending of FG nanocomposite trapezoidal plates reinforced with GPLs. They observed that increasing either of the two bottom angles of the trapezoidal plates reduces the nonlinear deflection. However, thermal loading negatively impacts nonlinear bending performance, particularly in the FG-X pattern.
6.2 Buckling and Post Buckling Response of Plates
6.2.1 Buckling Response of CNT RC Plates
Lei et al. [180,181] investigated the buckling behavior of FG-CNT RC plates under uniaxial and biaxial compression, using FSDT and a meshless kp-Ritz method to derive the buckling solutions. Their findings indicate that the buckling load parameters are enhanced by increasing the volume fraction and the plate length-to-thickness ratio. Additionally, the distribution type of CNTs also has a significant impact on the buckling strength of CNT RC plates. Zhang et al. [182,183] investigated the buckling behavior of skew plates reinforced with CNTs. In their first study [182], they established formulations based on FSDT and solved the governing equations using the element-free Improved Moving Least Squares-Ritz (IMLS-Ritz) method. They found that the skew angle significantly affects the intensity factors of the buckling load. In their second study [183], they utilized Reddy’s HSDT to examine the impact of the CNT orientation angle on the buckling load of a single-ply polymer-based CNT reinforced skew plate. Using carbon nanotubes as face sheets significantly affects the hydrothermal performance of the structure. Thang et al. [184] analyzed the thermal buckling behavior of sandwich plates and investigated how the nanocomposite face sheets influence the critical buckling load of these structures.
6.2.2 Buckling Response of GPL RC Plates
While investigating the biaxially compressed buckling and post-buckling behaviors of FG-GPL RC plates, Song et al. [190] observed that dispersing just 1.0 wt.% GPLs resulted in critical buckling loads for the FG-X plate that were up to 5.55 times higher than those of the neat epoxy plate. Their theoretical formulations were based on FSDT and von Kármán-type nonlinear kinematics, utilizing a two-step perturbation technique to determine the asymptotic post-buckling solutions. Geng et al. [191] examined the effect of circular cutouts on the buckling behavior of FG-GPL RC plates using FSDT, the minimum total potential energy principle, and a FE approach. Their results indicated that increasing the volume fraction of GPLs and the hole diameter enhanced the stability of the structure and increased the buckling load parameters. Shen et al. [108] investigated the effect of Pasternak and Winkler elastic foundations on the thermal buckling and post-buckling behavior of FG GRC laminated plates. Their results demonstrated that FG graphene reinforcement enhances both the buckling temperature and thermal post-buckling strength of the plates. Additionally, they found that the plate aspect ratio and foundation stiffness significantly influence the buckling behavior.
Wu et al. [192] studied the thermal buckling and post-buckling behavior of FG-GPL nanocomposite plates using FSDT and the principle of virtual displacements, solving the problem with a differential quadrature-based iteration technique. They examined the effects of the GPL width-to-thickness ratio and aspect ratio, finding that the width-to-thickness ratio has a more pronounced impact on behavior than the aspect ratio. Additionally, they investigated how the distribution pattern and weight fraction of GPL reinforcements affect the thermal buckling temperature of FG-GPL RC plates, as illustrated in Fig. 5. Kalhori et al. [193] employed TSDT and FEM to study the buckling behavior of orthogonally stiffened FG-GPL RC plates with a central circular cutout, embedded on elastic supports and subjected to in-plane normal and shear loads. They concluded that incorporating a set of stiffeners made from the same polymer as the PMMA matrix increased the critical buckling load by 41.8% while only adding 10.3% to the structure’s weight. Noorozi et al. [194] presented a mesh-free radial point interpolation method for the vibration and buckling analysis of FG-GPL RC perforated plates with central circular, square and elliptical cutouts under in-plane loading, based on HSDT.
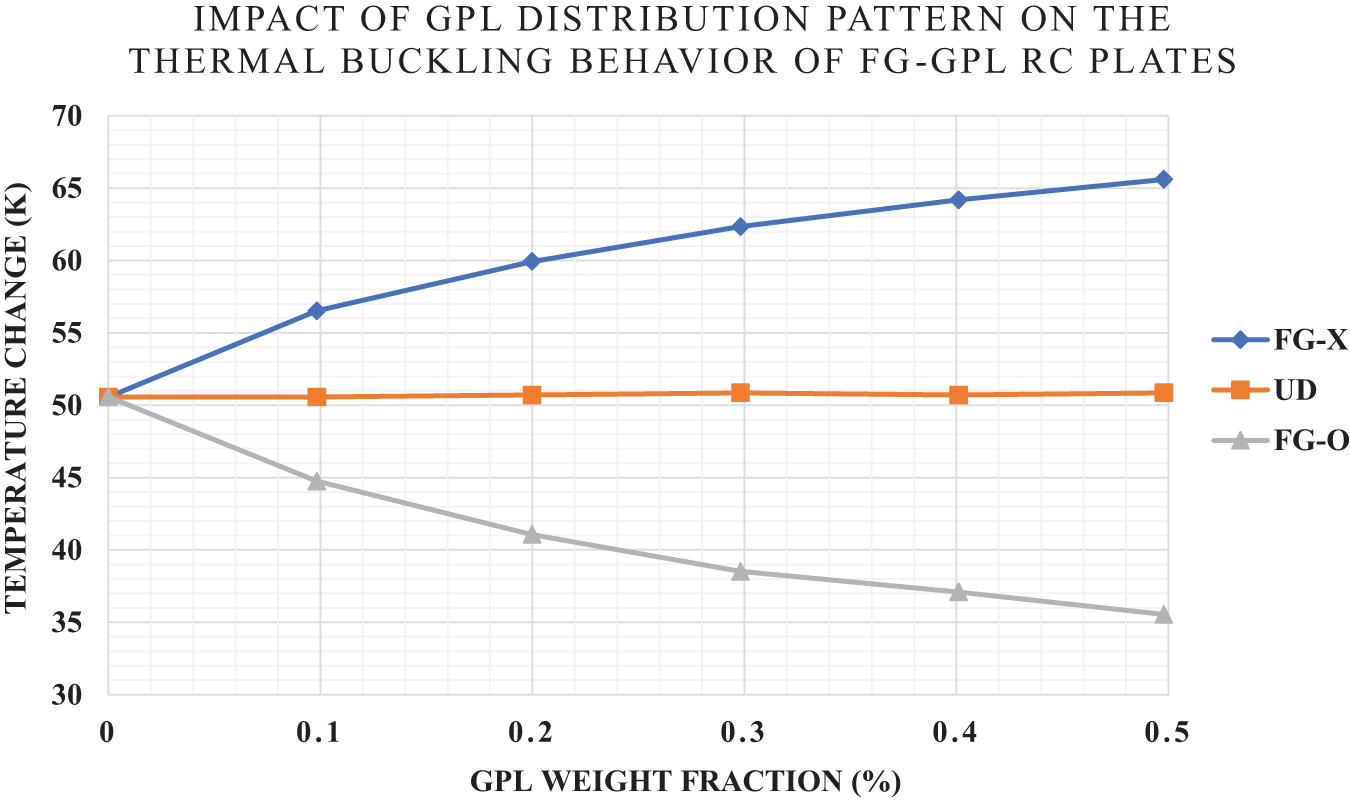
Figure 5: Impact of GPL distribution pattern on the thermal buckling behavior of FG-GPL RC plates; Adopted from Wu et al. [192]
Arefi et al. [195] presented the thermo-mechanical buckling behavior of FG-GPL RC micro plates and studied the size effect of graphene nanoplatelets based on modified strain gradient theory (MSGT).
6.3 Vibrational Response of Plates
6.3.1 Vibrational Response of CNT RC Plates
Various studies have been conducted on the vibrational characteristics of CNT RC plates [238–240]. Selim et al. [200] and Zhang et al. [201] investigated the free vibration of FG-CNT RC plates using Reddy’s HSDT and an element-free method, focusing on thermal [200] and mechanical effects [201], respectively. Hung et al. [202] utilized FSDT and the pb2-Ritz method for the free vibration analysis of laminated CNT RC plates. They found that increasing the carbon nanotube content in the polymeric matrix leads to higher plate frequencies. Additionally, they demonstrated that the effect of CNT volume fraction on fundamental frequencies is more significant in thin plates compared to thick plates. Lei et al. [203] analyzed the free vibration of laminated FG-CNT RC plates using FSDT and the kp-Ritz method. They concluded that CNTs distributed near the top and bottom surfaces are more effective in enhancing the stiffness of the structure than nanofillers located near the mid-plane of the composite material. Mehar et al. [204] investigated the free vibration of FG-CNT RC flat panels under a uniform thermal field, using temperature-dependent material properties along with HSDT, Green-Lagrange nonlinearity, and FEM. They observed that the nonlinear frequency responses decreased with increasing temperature load, as the stiffness of the FG-CNT RC panel diminishes with temperature rise. Bendenia et al. [205] reported on the deflections, stresses, and free vibration analysis of FG-CNT reinforced sandwich plates resting on a Pasternak elastic foundation, based on FSDT.
Wang et al. [206] conducted an investigation into the vibration and nonlinear bending of a sandwich sheet reinforced with carbon nanotubes, resting on a Pasternak foundation in a thermal environment. Their findings showed that the volume fraction of CNTs in the face sheets and the core-to-face sheet thickness ratio significantly affect the natural frequencies and the load–bending moment curves of the plate. Sharif Zarei et al. [207] utilized Mori-Tanaka’s approach to estimate the material properties of the face sheets and to account for the effect of carbon nanotube agglomeration in their study of the free vibration analysis of a nanocomposite sandwich plate resting on an orthotropic Pasternak foundation. Wang et al. [209] studied the nonlinear vibration of CNT-RC plates in thermal environments based on HSDT and employed a perturbation technique to solve the governing equations. Ansari et al. [210] conducted a natural frequency analysis of FG-CNT RC quadrilateral plates in thermal environments using elasticity theory. They found that the natural frequency decreases more significantly with a uniform temperature rise compared to a non-uniform temperature increase. Malekzadeh et al. [211] studied the vibration characteristics of composite plates with FG-CNT layers of arbitrary quadrilateral shape using FSDT and the DQM.
6.3.2 Vibrational Response of GPL RC Plates
This section presents several papers on the vibrational characteristics of FG plates reinforced with GPLs [241–243]. Song et al. [214] investigated the free and forced vibrations of FG-GPL RC plates using FSDT and a Navier solution-based technique. They found that the fundamental natural frequency of the plate with a 1.2% weight fraction of GPLs is approximately 160% higher for the FG-X distribution compared to that of the pristine epoxy plate. Additionally, they demonstrated that dispersing more square-shaped GPLs with fewer single graphene layers near the top and bottom surfaces of the plate is the most effective method for reinforcing the plate, leading to increased natural frequencies and significantly reduced dynamic deflections. Jafari et al. [215] studied the free vibration response of composite plates using a quasi-3D plate model. They demonstrated that a multilayer plate with at least 10 layers can be an excellent candidate for a multilayer FG material plate with continuous variation of properties. Reddy et al. [216] investigated the effect of various boundary conditions on the free vibration response of FG-GPL RC plates. They concluded that for a plate with 1% GPL reinforcement and simply supported boundary conditions using FG-X distribution, the percentage change in fundamental natural frequency increased from 121% for thick plates to 149% for thin plates. Conversely, for FG-O distribution, the percentage change decreased from 63% for thick plates to 54% for thin plates. Wang et al. [58] employed a molecular dynamics-based (MD) multiscale analysis to investigate the free vibration of laminated GRC, spanning from the atomic scale to macroscopic behavior. They confirmed that the elastic properties of graphene, including Young’s modulus, shear modulus, and Poisson’s ratio, are influenced by the chirality and size of the graphene. Saiah et al. [217] utilized FSDT, Lagrange’s equation, and FEM to demonstrate that FG-X laminated plates with a lower number of plies are the most effective for enhancing performance. In contrast, for FG-V, FG-Λ, or FG-O laminated plates, they suggested that a higher number of plies is the most effective approach for achieving improved performance. Bayat et al. [32] investigated the natural frequency analysis of orthogonally stiffened FG-GPL RC plate with circular cutout utilizing TSDT and FEM to achieve the desired solution. Kiani [218] studied the natural frequencies of FG-GPL RC laminated plates in thermal environments using a non-uniform rational B-spline (NURBS) formulation. Javani et al. [219] employed FSDT and DQM to investigate free vibration of FG-GPL RC T-shaped plates. In a comparative study, García-Macías et al. [174] demonstrated that adding graphene at a volume fraction of 0.05 increases the fundamental frequency of simply supported composite plates by up to five times that of the neat polymer, while CNTs only double this value.
6.4 Dynamic Instability of Plates
A limited number of studies have been conducted on the dynamic analysis of CNT [221,222] and GPL [228,244] reinforced composite plates under transient loads. Zhang et al. [221] analyzed the dynamic behavior of quadrilateral FG-CNT RC plates subjected to a transverse sudden dynamic load using FSDT and an element-free method. Their parametric study revealed that geometric and material properties—such as CNT distribution, volume fractions, side angles, area of the quadrilateral plates, width-to-thickness ratios, and various boundary conditions—primarily influence the vertical central displacement of the quadrilateral CNT RC plates. Selim et al. [222] investigated the impact behavior of FG-CNT RC plates based on Reddy’s HSDT using an element-free IMLS-Ritz model. They found that FG-X and FG-V types exhibit nearly the same peak contact force, which is the highest among the four considered distributions, while the FG-O type has the smallest peak contact force and the longest contact duration. Phung-Van et al. [223] studied the static and dynamic bending responses of FG-CNT RC plates with various boundary conditions using HSDT and iso-geometric analysis methods. Wang et al. [224] investigated the nonlinear dynamic bending behavior of FG-CNT plates supported on an elastic medium in thermal environments, based on von Karman assumptions and HSDT of plates. Kiani [227] investigated the effect of GPLs on the forced vibration response of composite plates subjected to a moving load, utilizing Ritz and Newmark methods.
7 Structural Behavior and Computational Methods for Shell Structures
Shells are curved, three-dimensional structural elements with a thickness relative to their other dimensions, designed to efficiently distribute loads. Unlike flat plates, shells can be cylindrical, spherical, or hyperbolic, enabling them to handle complex loading conditions effectively. Their curvature provides significant strength and stiffness, allowing them to withstand both in-plane and out-of-plane forces with minimal material use. Shells are commonly used in aerospace structures, pressure vessels, domes, and ship hulls, where weight and material efficiency are crucial. Studying shells involves distinct mathematical modelling to predict their behaviour under various loading conditions, ensuring safety and performance while optimizing design for engineering applications. Table 7 lists the literatures that studied the structural behavior of FG-CNT or GPL reinforced composite shells.
Computational modeling is crucial in analysing shell structures, providing reliable tools for predicting their behavior under various loading conditions. These models are widely applied to investigate mechanical behaviors such as buckling, post-buckling, vibrational responses, and dynamic instability, utilizing either ESL theories or 3D elasticity to evaluate deflections and stresses in composite shells. These approaches consider material distribution, loading scenarios, thermal effects, and structural imperfections. ESL theories, including FSDT, TSDT, and HSDTs, offer efficient solutions through simplified analysis, while 3D elasticity delivers more detailed and accurate representations of stress and strain distributions. The integration of these methods with FEM further enhances their predictive capabilities. These computational techniques are essential for optimizing the design and performance of shell structures in applications such as aerospace, pressure vessels, and civil infrastructure. Further applications of these methods will be provided in the following sections.
7.1.1 Static Response CNT RC Shells
A limited number of studies have been conducted on the static and bending responses of CNT reinforced cylindrical or curved shells [245–247]. Zghal et al. [245], using a discrete double directors shell finite element, studied the static behavior of FG-CNT RC shell structures. They claimed that the double directors shell element model enhances both accuracy and efficiency in predicting the static behavior of these nanostructures. Ansari et al. [246] performed a bending analysis of FG-CNT RC doubly curved truncated rhombic cones using TSDT and FEM. Their results indicate that the maximum deflection for all boundary conditions decreases by nearly 5% when the volume fraction of CNTs changes from 0.11 to 0.14, and a nearly 31% reduction is observed when the volume fraction increases from 0.14 to 0.17. Mehrabadi et al. [247] studied the stress analysis of FG open cylindrical shells reinforced with agglomerated carbon nanotubes using TSDT and 2D-GDQM. They found that increasing the volume fraction of CNTs can reduce the magnitude of radial and circumferential stresses on the inner surface. Huang et al. [248] applied a seven-unknown shear deformation theory and analytical procedure to investigate the static stability analysis of CNT reinforced polymeric composite doubly curved micro-shell panels. They demonstrated that spherical, elliptical, cylindrical, and hyperbolic panels exhibit progressively higher critical buckling loads. Djilali et al. [249] studied the large cylindrical deflection analysis of FG-CNT RC plates in thermal environments using HSDT and the minimization of total potential energy. Tornabene et al. [250] investigated the linear static response of nanocomposite shells reinforced with agglomerated carbon nanotubes using several distinct HSDTs and the GDQM. They concluded that the agglomeration of CNTs significantly influences the linear static response of nanoplates and nanoshells.
7.1.2 Static Response GPL RC Shells
Several papers have been published on the static responses of FG-GPL reinforced cylindrical or curved shells [254–257]. Van Do et al. [254] examined the static bending responses of multilayered composite cylindrical and spherical panels reinforced with GPLs using an iso-geometric analysis method combined with HSDT of shells. Their parametric studies, illustrated in Fig. 6, revealed that both the reinforcing graded pattern and the GPL weight fraction significantly affect the flexural and vibration behavior.

Figure 6: Dimensionless mid-point deflections
Safarpour et al. [255] analyzed the static responses of GPL reinforced truncated conical and cylindrical shells using the theory of elasticity and the DQM. They concluded that reinforcing the shell with a higher weight content of GPLs results in lower normal radial stress and displacement, thereby improving the bending characteristics of the shell. Arefi et al. [256] investigated the radial and axial displacements, along with various stress components, of GPL reinforced cylindrical shells subjected to thermo-mechanical loads. They concluded that increasing the weight fraction of GPL reinforcement does not significantly affect stress for a uniform distribution of reinforcement.
7.2 Buckling and Post Buckling Response of Shells
7.2.1 Buckling Response of CNT RC Shells
Axial [259,260,316] and torsional [261–263] buckling of CNT reinforced cylindrical shells have been investigated in several sources. Hajlaoui et al. [259] studied the buckling behavior of FG CNT reinforced shells using a solid-shell element based on a modified FSDT. Thang et al. [260] conducted a nonlinear buckling analysis of FG-CNT RC cylindrical shells with initial geometric imperfections using Donnell shell theory and the Galerkin procedure. They demonstrated that for the imperfect shell, the equilibrium paths begin to deflect as soon as the compressive load is applied. Ninh [261] investigated the thermal torsional post-buckling characteristics of FG-CNT reinforced cylindrical shells with surface-bonded piezoelectric layers using von Karman assumptions and the Galerkin method. Nam et al. [262] studied the nonlinear torsional buckling of FG CNT orthogonally reinforced cylindrical shells in a thermal environment. They found that the torsional load-bearing capacity of CNT orthogonally reinforced cylindrical shells is generally stronger than that of CNT longitudinally reinforced cylindrical shells. Shen [263] examined the torsional post-buckling behavior of SWCNT-reinforced cylindrical shells in thermal environments using a singular perturbation method combined with a two-step perturbation approach. Their findings reveal that the percentage reduction is approximately 57% for the thin FG-CNT RC shell when the temperature rises from
7.2.2 Buckling Response of GPL RC Shells
This section presents available papers on the normal [270–272,317] and torsional [273,274,279] buckling of GPL RC cylindrical shells. Wang et al. [270] investigated the eigenvalue buckling of FG cylindrical shells reinforced with GPLs using FEM. They discovered that the normalized buckling load is more sensitive to the length-to-thickness ratio of the shells than to other geometric ratios. Shen et al. studied the post-buckling behavior of FG-GPL RC laminated cylindrical panels under axial compression [271] and external pressure [272] in thermal environments. Their findings indicate that the GRC laminated cylindrical shell maintains a stable post-buckling equilibrium path under external pressure, while it exhibits an unstable path under axial compression. Sun et al. [273] studied the torsional buckling of FG-GPL RC cylindrical shells using Donnell’s shell theory and found that the effects of boundary conditions on the buckling behavior are highly dependent on the shell lengths, while they are nearly independent of the shell thicknesses. Wang et al. examined the torsional [274] and axial [275] buckling responses of FG-GPL RC cylindrical shells with cutouts using FEM. Fig. 7 shows how the weight fraction of GPLs, along with the distribution pattern, affects the critical buckling torque of FG-GPL RC cylindrical shell panels.
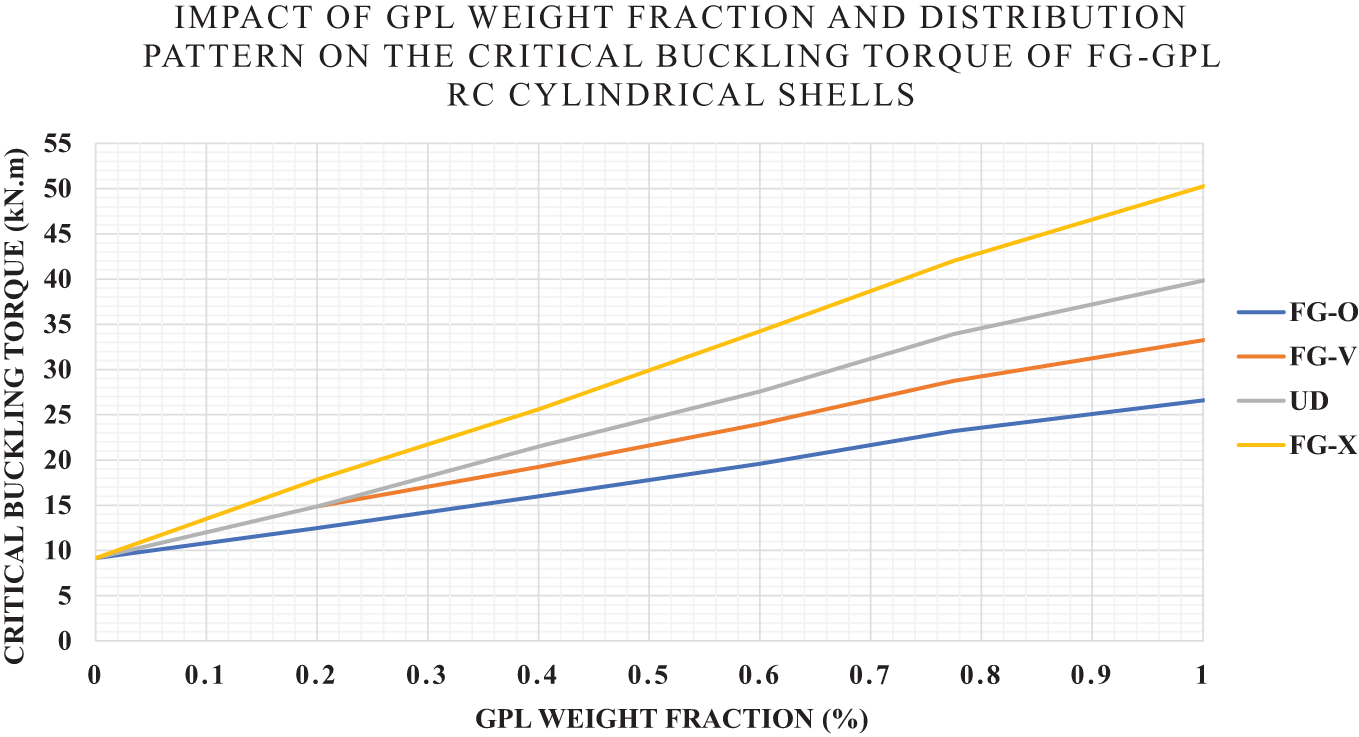
Figure 7: Effects of GPL weight fraction and distribution pattern on the critical buckling torque (
Liu et al. [276] investigated the buckling and free vibration of initially stressed FG-GPL RC cylindrical shells using both 2D and 3D elasticity theories. Their study, which made no assumptions about the deformation of the functionally graded graphene platelets reinforced composite (FG-GPLRC) cylindrical shells, appears to be highly accurate. Ansari et al. [277] conducted a post-buckling analysis of axially-loaded FG-GPL RC conical shells based on the FSDT and von Karman’s geometrically nonlinear relation, employing the variation differential quadrature method (VDQM) and Fourier series. Their results show that increasing the semi-vertex angle decreases the linear buckling loads.
7.3 Vibrational Response of Shells
7.3.1 Vibrational Response of CNT RC Shells
Several sources are available regarding the vibrational responses of conical, cylindrical, and curved shells [282–285]. Thomas et al. [282] analyzed the vibration characteristics of FG-CNT RC shell structures using Mindlin’s hypothesis. They concluded that incorporating CNTs enhances vibration and damping properties, as well as the overall dynamic performance of the structure. Song et al. [283] conducted a vibration analysis of FG-CNT RC cylindrical shells in thermal environments using Reddy’s HSDT and Hamilton’s principle and found that as the volume fraction of CNTs increases, the vibration amplitude of the FG-CNT reinforced cylindrical shell decreases. Kamarian et al. [284] performed a free vibration analysis of CNT RC conical shells based on the FSDT and GDQ technique. Their results indicate that when the volume fraction of CNT increases from 10% to 20%, the impact of the increasing mass on the system frequencies becomes more significant than that of the increasing stiffness, leading to an overall decrease in the natural frequencies of the structure. Kiani et al. [285] analyzed the free vibration characteristics of composite conical panels reinforced with FG-CNTs using FSDT and Donnell’s theory and found that the volume fraction of CNTs, the angles of embrace, and the boundary conditions significantly influence the fundamental frequencies of the structure. Tornabene et al. [286] explored the impact of agglomeration on the natural frequencies of FG-GPL RC doubly-curved shells using the CUF. They found that both the mass fraction and concentration of the agglomerated CNTs impact the stiffness of the structure. Banić et al. [287] examined the influence of Winkler-Pasternak foundations on the vibrational behavior of plates and shells reinforced with agglomerated carbon nanotubes, utilizing shear deformation theory and applying the GDQM. Their study explored various analytical methods to describe distinctive through-the-thickness volume fraction distributions, including power law, exponential, and Weibull functions.
7.3.2 Vibrational Response of GPL RC Shells
The vibrational behavior of GPL RC shells has been explored in several studies [318]. Liu et al. [276] examined the free vibration characteristics of initially stressed FG-GPL RC cylindrical shells and found that incorporating 1.5 wt.% of GPLs increased the natural frequency by 113% to 170% for the FG-X plate compared to a neat epoxy plate, depending on the shell’s inner radius. One of their cases is illustrated in Fig. 8, showing the effects of varying GPL weight fractions and distribution patterns on the percentage change in natural frequency.

Figure 8: Impact of GPL weight fraction and distribution pattern on the change in fundamental frequency of FG-GPL RC shell; Adopted from Liu et al. [276]
Dong et al. [291] presented an analytical study on the free vibration characteristics and dynamic responses of spinning FG-GRC thin cylindrical shells subjected to axial loads, based on Donnell’s nonlinear shell theory and Hamilton’s principle. Their results indicated that incorporating 1.0 wt.% of GPLs increases the nonlinear frequencies of forward-traveling waves in the cylindrical shell by 59.0% for the FG-X plate. Amirabadi et al. [292] scrutinized the free vibration behavior of rotating FG-GPL RC truncated thick conical shells using TSDT and GDQM. Their numerical examples indicated that GPLs with a larger surface area are more effective at reinforcing the structure. Baghbadorani et al. [293] studied the free vibration responses of FG-GPL RC cylindrical shells using FSDT and Donnell’s kinematic relations and found that an increase in shell length and a decrease in shell thickness lead to a reduction in frequencies. Ghabussi et al. [294] conducted a free vibration analysis of an electro-elastic GPL RC cylindrical shell surrounded by a viscoelastic foundation using a modified length-couple stress parameter.
Wang et al. [297] studied the nonlinear vibration of FG-GPL reinforced metal foam (GPLRMF) cylindrical shells using Hamilton’s principle and the Galerkin method. They found that the porosity coefficient, porosity distribution, and GPL patterns significantly impact the nonlinear vibration behavior of GPLRMF circular cylindrical shells. Jamalabadi et al. [295] conducted a nonlinear vibration analysis of FG-GPL conical panels supported by an elastic medium, using FSDT and GDQM. They demonstrated that for thicker panels, the effect of the elastic medium on the nonlinear response is more pronounced, significantly reducing the frequency ratio. Bidzard et al. [296] presented the effects of pressure and thermal environments on the nonlinear vibration characteristics of multilayer FG-GPL toroidal panels on a nonlinear elastic foundation, utilizing FSDT and employing FEM. Niu et al. [298] utilized the FSDT in conjunction with the Chebyshev-Ritz method to investigate the linear and nonlinear vibrations of GPL RC tapered plates and cylindrical panels. They concluded that, compared to the FG-O distribution pattern, the chaotic motion is delayed in the case of the FG-X distribution pattern.
7.4 Dynamic Instability of Shells
7.4.1 Dynamic Response of CNT RC Shells
The available sources on the dynamic behavior of CNT RC cylindrical shells are presented below [319]. Kiani [301] studied the dynamics of FG-CNT RC cylindrical panels subjected to moving loads using FSDT, the Ritz method, and the Gram-Schmidt process. Their findings indicate that a desired central deflection of the cylindrical panel can be achieved by using an appropriate distribution and volume fraction of CNTs. Asadi et al. [302] investigated the dynamic stability of a pressurized FG-CNT RC cylindrical shell interacting with supersonic airflow. They found that increasing the CNT volume fraction from 0.12 to 0.28 results in a significant increase of approximately 105% in the critical freestream static pressure. Jiao et al. [303] conducted dynamic buckling analyses of FG-CNTRC cylindrical shells under axial power-law time-varying displacement loads. Arumugam et al. [304] using HSDT and FEM investigated the damping characteristics of laminated composite cylindrical sandwich shells with a carbon nanotube-reinforced magnetorheological elastomer (CNT-MRE) core. Zhang et al. [305] examined the influence of impact loads on the dynamic responses of CNT RC cylindrical shells using Reddy’s HSDT and a linearized contact law.
7.4.2 Dynamic Response of GPL RC Shells
Several papers have examined the dynamical characteristics of GPL RC cylindrical and curved shells [320,321]. Wang et al. [310] investigated the nonlinear transient response of doubly curved shallow shells reinforced with GPLs subjected to blast loads, accounting for thermal effects using Hamilton’s principle, the nonlinear von Karman strain-displacement relationship, and HSDT. They found that the central deflection and shock resistance of the shell are significantly influenced by the weight fraction of GPLs. Shokrgozar et al. [311] analyzed the viscoelastic dynamic responses of a GPL RC cylindrical micro-shell using nonlocal strain gradient theory (NSGT) and GDQM. They found that at higher values of GPL weight fraction, the effect of the length scale factor on stability is more significant than at lower weight fractions. Guo et al. [320] examined the dynamical behavior of rotating matrix-cracked FG-GPL RC cylindrical shells using the element-free IMLS-Ritz method. Safarpour et al. [255] addressed the static and dynamic behavior of GPL RC truncated shell and plate structures within the frameworks of the theory of elasticity and the DQM. Heydarpour et al. [312] analyzed the effects of thermal shocks on rotating truncated conical shells reinforced with GPLs. Amirabadi et al. [313] presented a study on wave propagation in rotating FG-GPL-reinforced cylindrical shells based on TSDT.
8 Structural Behavior and Computational Methods for Beams
Beams are structural elements designed to support both axial and bending loads, with their length being significantly greater than their other dimensions. Their primary function is to resist bending moments and shear forces as well as axial load when utilized as columns and transferring loads from the point of application to their supports. The design and analysis of beams involve understanding their deflection, strength, and stability to ensure they can handle applied loads without failure. Buckling analysis of beams or columns under axial load is also crucial. The references on the structural responses of CNT- and GPL-RC beams, along with their corresponding computational methods and analysis types is provided in Table 8.
The analysis of structural behavior in reinforced composite beams relies heavily on computational methods, which address a wide range of responses, including static, buckling, vibrational, and dynamic behaviors. Numerical and analytical approaches provide robust frameworks for simulating these advanced materials. These computational techniques enable precise modeling of mechanical behaviors, including deflection, stress distribution, and thermal effects, under diverse loading conditions. Numerical solutions, such as FEA integrated with beam theories, effectively capture nanoscale phenomena like strain gradients and boundary effects, which are essential for accurate mechanical analysis. By employing these methods, researchers can optimize material configurations, corroborate experimental findings, and reliably predict the performance of CNT- and GPL-RC beams.
8.1.1 Static Response of CNT RC Beams
This section mentions papers investigating the bending responses of CNT-RC beams. Mayandi et al. [322] investigated the bending characteristics of FG-CNT reinforced polymer composite beams under non-uniform thermal loads. Vodenitcharova et al. [323] performed a bending analysis of a nanocomposite beam reinforced with a SWCNT using Euler-Bernoulli theory and the Airy stress-function method. They discovered that the inclusion of SWCNTs in the matrix leads to an increase in the radial deformation of the SWCNTs for the same bending angle. Talebizadehsardari et al. [324] examined the static bending response of a functionally graded polymer matrix composite (FG-PMC) curved beam reinforced with CNTs under sinusoidal and uniform loads, employing Timoshenko beam theory, higher-order strain gradient theory, and the Navier solution procedure. They concluded that higher axial stresses were achieved with uniform loadings compared to sinusoidal loadings. Kumar et al. [325] utilized ABAQUS software to study the stability behavior of curved FG-CNT beams with imperfections. Bending and vibration study of FG-CNT reinforced smart composite beams is presented by Kumar et al. [326]. Shen et al. [327] investigated the free vibrations, nonlinear bending, and post-buckling behavior of beams made of FG-CNT RC resting on an elastic foundation, utilizing HSDT under thermal conditions. Their results indicate that the CNT volume fraction significantly affects the load–deflection curves of beam bending, while its impact on the nonlinear-to-linear frequency ratios and thermal post-buckling load–deflection curves of CNTRC beams is less pronounced. Wuite et al. [328] analyzed the transient deflection and stress of composite beams reinforced with CNTs using Euler-Bernoulli theory. They discovered that applying a low volume fraction of nanotubes with a uniform distribution significantly increased the stiffness of these beams.
8.1.2 Static Response of GPL RC Beams
Several sources examining the bending of GRC beams are presented here. Wang et al. [332] utilized an improved TSDT and the Chebyshev-Ritz method for the bending analysis of FG-GPL RC beams. Feng et al. [333] scrutinized the nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed GPLs using Timoshenko beam theory and the von Karman nonlinear strain-displacement relationship. They found that dispersing more square-shaped GPLs with fewer single graphene layers near the top and bottom surfaces of the beam is the most effective approach to reducing bending deflections. Tam et al. [334] examined the impact of an open edge crack on the nonlinear bending of elastically restrained FG-GPL RC beams using FEM. They demonstrated that an increase in the crack depth ratio (CDR) and a rise in temperature weaken the structure, resulting in larger deflections. Karamanli et al. [335] performed a comparative analysis of the static bending responses of beams reinforced with GPLs vs. CNTs. Fig. 9 illustrates the effects of CNT volume fraction, GPL weight fraction, and the distribution patterns of CNTs and GPLs on the deflections of simply supported FG beams under uniform loads. The results show that increasing

Figure 9: Impact of CNT volume fraction, GPL weight fraction, and distribution patterns on the dimensionless deflection
8.2 Buckling and Post Buckling Response of Beams
8.2.1 Buckling Response of CNT RC Beams
Several notable studies on the buckling characteristics of CNT RC beams [384,385] are summarized below. Vodenicharova et al. [323], using the Airy stress-function method, studied the local buckling of a nanocomposite beam reinforced by SWCNTs. They discovered that in thicker matrix layers, the SWCNT buckles locally at smaller bending angles and greater flattening ratios. Fattahi et al. [386] investigated the buckling behavior of CNT RC beams, considering both short and long SWCNT reinforcements. Mayandi et al. [322] analyzed the buckling response of FG-CNT reinforced polymer composite beams under non-uniform thermal loads using FEM. They found that the critical buckling temperature is significantly influenced by the nature of the temperature variation and the type of functional grading of the CNTs. Murmu et al. [339] conducted a buckling analysis of a SWCNT embedded in Winkler and Pasternak elastic media using non-local elasticity and Timoshenko beam theory, applying the DQM. They found that, unlike the Winkler foundation model, the increase in critical buckling load is linear with the Pasternak foundation model. Nejati et al. [340] conducted a buckling and vibration analysis of FG-CNT RC beams under axial load. They found that both the critical buckling load and natural frequency increase when the concentrated spherical volume zone is enlarged or when the severity of the concentrated nanotube distribution is reduced.
Madenci et al. [341] analyzed the buckling response of FG CNT-reinforced polymer composite beams using both experimental and analytical methods. An improvement in the thermal buckling response of FG-CNT RC beams with temperature-dependent material properties resting on elastic foundations was reported by Bensaid et al. [342]. They demonstrated that the impact of the Pasternak layer on FG beams is more significant than that of the Winkler layer. Babaei et al. [343] developed a perturbation method for the thermal post-buckling analysis of shear-deformable FG-CNT RC beams with various boundary conditions. They showed that while the critical buckling temperature for pinned–pinned and clamped–roller beams is identical, their post-buckling responses are markedly different. Shafiei et al. [344] investigated the nonlinear free vibration and post-buckling behavior of FG-CNT RC beams on a nonlinear foundation. They emphasized the importance of performing a nonlinear analysis to accurately capture these behaviors. Imperfection sensitivity of thermal post-buckling behavior of FG-CNT RC beams was presented by Wu et al. [345]. They found that the location of imperfections significantly influences the sensitivity of thermal post-buckling to these imperfections.
8.2.2 Buckling Response of GPL RC Beams
Several examples of the buckling characteristics of GPL-reinforced beams are mentioned below. Yang et al. [349] analyzed the buckling and post-buckling behavior of FG-GPL RC beams using the FSDT of beams and a nonlinear algebraic system with the DQM. Their results demonstrated that GPLs with a large surface area and fewer single graphene layers offer better reinforcing effects. However, when the GPL aspect ratio and width-to-thickness ratio exceed 4 and 1000, respectively, both the critical buckling load and post-buckling path remain almost unchanged despite further increases in these ratios. Song et al. analyzed the buckling of edge-cracked FG multilayer graphene nanocomposite beams based on FSDT, including von Kármán geometric nonlinearity [350], and employed the differential quadrature method [351]. Wang et al. [352] studied the buckling and post-buckling behaviors of GPL-reinforced dielectric beams subjected to electrical voltage by employing Timoshenko beam theory and von Kármán nonlinearity. They found that these behaviors depend on the combined effects of the mechanical and dielectric properties of the composites, which are significantly influenced by the characteristics of GPLs and the applied electrical field. Eyvazian et al. [353] used the Chebyshev approach to analyze the thermal buckling and post-buckling behavior of rotating Timoshenko microbeams reinforced with graphene platelets. They found that, at the same temperature, increasing the rotational velocity leads to a higher post-critical deflection in the rotating GPLRC microbeam with clamped-simply (CS) boundary condition. Guo et al. [354] conducted a nonlinear thermal buckling instability analysis of a rotating nanocomposite beam reinforced with GPLs, utilizing the Chebyshev–Ritz scheme. Their study examined the effects of rotational velocity and distribution pattern on the beam’s performance.
8.3 Vibrational Response of Beams
8.3.1 Vibrational Response of CNT RC Beams
The vibrational behavior of CNT RC beams has been studied in several papers. Heshmati et al. [358] conducted a comprehensive study on the vibrational behavior of SWCNT RC beams using Timoshenko beam theory and FEM. They concluded that, due to the substantial impact of agglomeration phenomena, a uniform distribution of randomly oriented CNTs provides the most effective reinforcement. Vo-Duy et al. [359] employed FEM for the free vibration analysis of laminated FG-CNT RC beams. They demonstrated that the FG-X distribution results in the highest frequency, while the FG-O distribution leads to the lowest frequency in laminated FG-CNT RC beams. Wang et al. [360] employed the Timoshenko and the Euler beam theories for the vibration analysis of MWCNTs. Their comparison revealed that Euler beam theory significantly overpredicts frequencies, especially for small length-to-diameter ratios and higher vibration modes. They found that the Timoshenko beam model provides a more accurate representation in these cases. Lin et al. [361,362] investigated the vibration of CNT RC beams using first- and third-order beam theories. They found that the frequency parameters of the beams increase significantly when the CNT volume fraction varies from 0.12 to 0.17, while there is only a slight increase in frequency parameters when the CNT volume changes from 0.17 to 0.28.
Ke et al. [363] employed the Ritz method to study the nonlinear analysis of free vibrations of FG-CNT Timoshenko beams with linear and nonlinear CNT distribution in the thickness direction. Ansari et al. [364] analyzed the forced nonlinear vibrations of FG-CNT RC Timoshenko beams using the GDQM. They found that the amplitude peak decreases with increasing nanotube volume fraction or dimensionless damping parameter, while it increases with higher slenderness ratios or dimensionless transverse forces. Chahadhari et al. [365] provided a nonlinear analytical solution for the free vibrations of FG-CNT RC beams with various boundary conditions, using HSDT and supported by an elastic foundation in thermal environments. They demonstrated that incorporating an elastic foundation result in lower frequency ratios.
8.3.2 Vibrational Response of GPL RC Beams
Several available sources discuss the vibrational characteristics of GPL RC beams. Barati et al. [370] analyzed the forced vibration of nanocomposite beams reinforced with different distributions of GPLs in thermal environments by developing a higher-order refined beam element. They concluded that the resonance frequency decreases as the temperature increases.
Shahrjerdi et al. [371] studied the free vibration analysis of FG GRC beams with temperature-dependent properties using a spectral numerical method. They demonstrated that increasing beam thickness, graphene weight percentage, and the length and width of graphene platelets, as well as optimizing the distribution pattern, leads to higher vibrational frequencies. Song et al. [372] investigated the nonlinear free vibration of cracked FG-GPL RC beams in thermal environments using the framework of FSDT. They proved that the elastic rotational spring method is reliable for modeling the cracked sections of FG GPL RC laminated beams. Nonlinear natural frequencies of GPL-RC dielectric beams were performed by Wang et al. [373]. They found that increasing the electrical voltage results in an enhanced frequency ratio. Feng et al. [374] investigated the nonlinear free vibration of FG-GPL RC beams based on Hamilton’s principle, Timoshenko beam theory, and the von Kármán nonlinear strain-displacement relationship. They demonstrated that, for the same weight fraction, GPLs with a larger surface area and fewer single graphene layers provide better reinforcing effects.
8.4 Dynamic Responses of Beams
Bourada et al. [377] used FSDT to analyze the stability and dynamic responses of CNT-reinforced concrete beams resting on an elastic foundation. Yas et al. [378] investigated the dynamic analysis of FG-CNT RC beams under moving loads, utilizing Timoshenko and Euler–Bernoulli beam theories. They employed the Mori-Tanaka model to model the material properties of the resultant composite beam. Their study examined the effects of nanotube orientation, material distribution, moving load velocity, and different boundary conditions on the vibration analysis of the beams. Shen et al. [327] investigated the dynamic stability of FG-CNT RC beams. They derived the governing equations based on FSDT and converted them into a linear equation system using the squares difference method. Subsequently, they studied the effects of various factors, such as the volume fraction of carbon nanotubes, length-to-thickness ratio, and boundary conditions, on the dynamic stability of the beams.
9 Structural Behavior and Computational Methods for Annular Plates
Annular plates and disks are specialized types of circular plate structures, each serving unique functions in engineering applications. Annular plates, characterized by their ring-like shape with a central hole, are used in scenarios requiring support around a central void, such as in flanges, bearings, or circular supports. They are analysed for their ability to manage radial and tangential stresses while accommodating the effects of the central opening. On the other hand, disks are solid, flat circular plates that are often employed in components where uniform load distribution across a circular area is essential, such as in flywheels, brake discs, and pressure vessel components. Both annular plates and disks require precise structural analysis to ensure they can handle applied loads effectively, optimizing performance and safety in their respective applications. Table 9 provides an overview of studies that have investigated the mechanical responses of annular plate structures reinforced with CNT or GPL nanofillers.
The structural behavior of annular plates, particularly those reinforced with CNTs or GPLs, has been extensively studied through advanced computational approaches. Analytical and numerical methods, including FEM combined with ESL or 3D elasticity frameworks, are utilized to analyse their static, vibrational, buckling, and dynamic responses. These computational techniques enable detailed examinations of the influence of parameters such as temperature, geometry, and material distribution on the performance of these structures under thermal and mechanical loading conditions. This underscores the critical importance of computational methods in advancing the design and optimization of nanocomposite structures.
9.1 Static Response of Annular Plates
9.1.1 Static Response of CNT RC Annular Plates
The deflection responses of CNT RC annular and annular sector plates have been studied in limited papers. Babaei et al. [91] studied the static responses of FG-CNT RC annular sector plates resting on a viscoelastic foundation, applying Hamilton’s principle based on FSDT and FEM. Their results indicated that increasing the volume fraction of carbon nanotubes
9.1.2 Static Response of GPL RC Annular Plates
Several sources have studied the static bending characteristics of GPL RC annular sector plates [390–393,427]. Sobhy [390] conducted a piezoelectric bending analysis of GPL RC annular and circular sandwich nanoplates using DQM. They concluded that the solid circular plate experiences greater deflection than the annular plate. Additionally, they demonstrated that increasing the outer radius or reducing the inner radius widens the plate, resulting in increased deflection. Gholami et al. [391] studied the nonlinear bending response of polymeric composite annular plates reinforced with GPLs under transverse uniform and biharmonic loadings. They utilized the principle of virtual work, the variational differential quadrature (VDQ) method, and Reddy’s plate theory for their analysis. Yang et al. [392] utilized the Mian and Spencer method to obtain analytical solutions for investigating the 3D thermo-mechanical bending of FG-GRC circular and annular plates. They demonstrated that an increase in the total content of GPLs from 0% to 1% significantly reduces deflection and moderately increases radial stress, particularly in thin plates. Al-Furjan et al. [393] presented a non-polynomial framework for analyzing the bending responses of FG-GPL RC disks based on three-dimensional refined higher-order shear deformation theory (3D-RHOSDT) and DQM. They showed that the GPL RC disk exhibits superior bending and static behavior under a sinusoidal load pattern, while it demonstrates weaker performance under a uniform load pattern.
9.2 Buckling and Post Buckling Response of Annular Plates
9.2.1 Buckling Response of CNT RC Annular Plates
Several available literatures on the buckling responses of CNT RC annular and annular sector plates [394–397] are listed below. Ansari et al. [394] conducted in-plane and shear buckling analysis of FG-CNT RC annular sector plates based on TSDT using a numerical approach. They observed that plates with larger sector angles exhibit lower buckling loads, while those with a higher inner-to-outer radius ratio have higher buckling loads. Additionally, they demonstrated that an FG-X distribution plate with a CNT volume fraction (
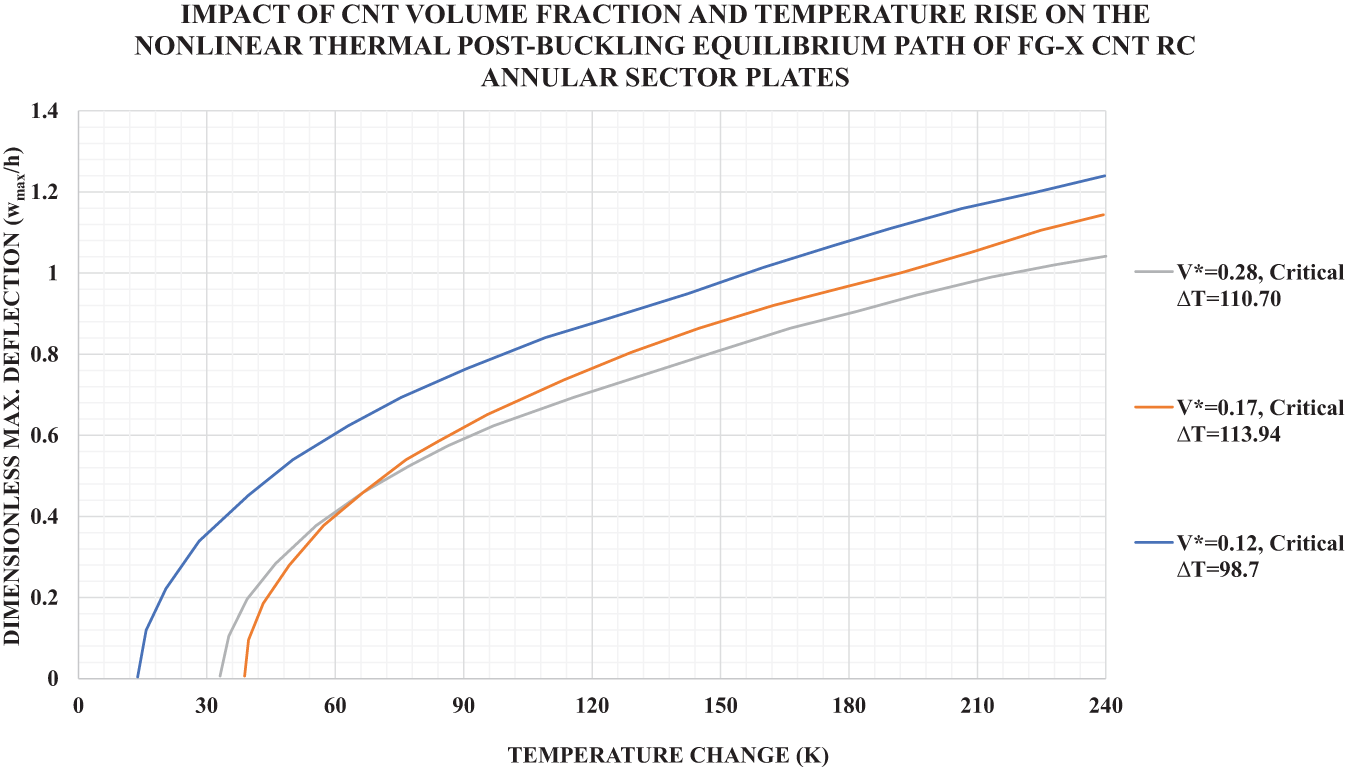
Figure 10: Effect of CNT volume fraction and temperature rise on the nonlinear thermal post-buckling equilibrium path of clamped FG-X CNT RC annular sector plates; Adopted from Gholami et al. [397]
9.2.2 Buckling Response of GPL RC Annular Plates
Several scholars have investigated the buckling and post-buckling responses of GPL RC annular plates [399–403]. Zhang et al. [399] studied the thermal and mechanical buckling of FG-GPL RC annular plates using HSDT and GDQM. Their results indicate that an increasing temperature gradient negatively affects the buckling response of the annular plate due to a decrease in structural stiffness. Allahkarami [400] examined the dynamic buckling of FG-GPL RC annular plates subjected to a periodic radial compressive load in a thermal environment using FSDT and Hamilton’s principle. They demonstrated that a rise in temperature leads to a lower pulsation frequency of the FG-GPL RC multilayer annular plate. Yang et al. [402,403] investigated the influence of thermal loads and elastic foundations on the buckling responses of GPL RC annular plates with piezoelectric/GPL RC layers. They found that as the weight fraction of GPLs decreases, the rise in critical buckling temperature tends to be lower. Based on FSDT and modified Halpin-Tsai approach, thermal buckling of FG-GPL RC annular sector plates was presented by Javani et al. [404]. They concluded that as the opening angle of the sector plate increases, the difference in critical buckling temperature diminishes.
9.3 Vibrational Responses of Annular Plates
9.3.1 Vibrational Responses of CNT RC Annular Plates
The vibrational characteristics of CNT RC annular and annular sector plates [395,409–411] are presented below. Civalek et al. [409] applied the discrete singular convolution method for the vibration analysis of CNT RC annular sector plates. Their results indicate that, due to the higher flexural stiffness of the FG-X pattern compared to other patterns, the FG-X pattern yields higher frequencies for all the studied cases. Beni [410] studied the free vibration analysis of annular sector sandwich plates with FG-CNT RC face sheets based on Carrera’s Unified Formulation. They concluded that an increase in the sector angle of the plate results in a decrease in natural frequencies. Zhong et al. [411] analyzed the vibration responses of FG-CNT RC circular, annular, and sector plates using the semi-analytical method developed by their research team. This approach incorporated modified Fourier series, FSDT, and the Ritz-variational energy method. Keleshteri et al. [412] and Mohammadzadeh-Keleshteri et al. [428] studied the nonlinear vibration response of FG-CNT annular sector plates with piezoelectric layers using FSDT of plates, von Karman strain-displacement assumptions, Hamilton’s principle, and the GDQM. The natural frequencies of viscoelastic fully symmetric systems with imperfect honeycomb core sandwich disks reinforced with multi-phase CNTs was presented by Al-Furjan et al. [413]. They concluded that increasing the CNT fraction in a multiphase sandwich disk can enhance the system’s frequency. Al-Furjan et al. [414] investigated the vibration behavior of an imperfect higher-order sandwich disk with a lactic core using the GDQ method. They demonstrated that incorporating an FG-X CNT RC laminated layer can significantly boost the frequency of the multiphase sandwich disk.
9.3.2 Vibrational Responses of GPL RC Annular Plates
Several available sources on the vibrational characteristics of GPL RC annular and annular sector plates [402,416–418,429] are presented in this section. Yang et al. [402] investigated the influence of thermal loads on the vibrational responses of GPL RC annular plates with piezoelectric/GPL RC layers. They indicated that imposing stricter boundary conditions at the outer radius or enlarging the inner radius can significantly increase the natural frequency. Habibi et al. [416] studied the vibrational characteristics of a FG-GPL RC viscoelastic thick annular plate using the fourth-order Runge-Kutta method and GDQM. They showed that at high values of the outer radius to inner radius ratio, this parameter significantly influences the frequency of the nanocomposite annular plate compared to lower values. Tao et al. [417] conducted an iso-geometric free vibration analysis of GPL RC laminated annular sector microplates based on a four-variable HSDT, von Karman large deflection assumptions, and modified couple stress theory (MCST). They found that increasing the sector angle from 30 to 75 degrees results in a significant decrease of approximately 51% in the fundamental frequency of the FG-X annular sector microplate. Wang et al. [418] analyzed the thermal vibration of FG-GPL RC annular plates under mechanical load using HSDT, Hamilton’s principle, and GDQM. They recommended applying a sinusoidal temperature rise pattern to mitigate the negative effects of temperature increase on the plate’s performance. Javani et al. [419] investigated the geometrically nonlinear free vibration of FG-GPL circular plates on a nonlinear elastic foundation based on FSDT and utilizing GDQM. They showed that the nonlinear component of the elastic foundation does not affect the linear frequencies, but as this factor increases, the nonlinear frequencies are enhanced.
9.4 Dynamic Responses of Annular Plates
A few studies have investigated the dynamic responses of annular sector plates reinforced by CNTs [91,422] or GPLs [400,424,425]. Frikha et al. [422] used a linear discrete double directors FE model based on a high-order displacement field distribution to compute transient center deflections of the studied annular structures. Their results indicated that the central deflection of FG-X annular plates decreases by approximately 40% when the volume fraction of CNTs increases from
10 Structural Behavior and Computational Methods for Hybrid Composites
Hybrid composite materials are engineered materials that combine two or more types of reinforcement, such as fibers or fillers, within a single matrix. This unique combination enhances the mechanical properties, such as strength, stiffness, and toughness, beyond what individual components could achieve. By integrating different materials, hybrid composites can exhibit tailored characteristics suitable for specific applications, including improved load-bearing capabilities, reduced weight, and enhanced resistance to environmental factors. The interplay between the various reinforcements allows for a synergistic effect, maximizing performance and expanding the potential uses of these advanced materials in industries like aerospace, automotive, and construction. In general, hybrid composite materials consist of multiple phases, where at least two reinforcement elements are integrated into a matrix to enhance the properties of the composite [430]. The demand for hybrid composites is significantly driven by developments in the automotive and transportation, aerospace and defense, marine, wind energy, and sporting goods industries [17].
The combination of GPLs and CNTs in polymer matrices leverages their complementary mechanical characteristics, creating a synergistic reinforcement mechanism that significantly enhances composite properties. The high aspect ratio and intrinsic stiffness of GPLs synergize with the axial strength and electrical conductivity of CNTs, leading to superior load transfer efficiency and multi-functional performance improvements. Experimental studies have demonstrated exceptional gains, such as a 950% improvement in fatigue life with optimized hybrid filler ratios, attributable to enhanced interfacial adhesion and tailored filler dispersion [431]. However, achieving this synergy is inherently challenging due to the propensity of nanofillers for agglomeration, driven by van der Waals forces and high surface energy. This necessitates advanced processing protocols, such as surface functionalization, conjugated polymer wrapping, or hybridization strategies, to mitigate agglomeration, ensure uniform dispersion, and maximize the effective stress transfer at the filler-matrix interface. Consequently, the fabrication of these hybrid nanocomposites requires meticulous optimization to balance dispersion quality, filler content, and processing conditions. The fabrication challenges and methods for preventing agglomeration will be discussed in detail in Section 12.
Due to the aforementioned exceptional chemical and physical properties of CNTs and GPLs—such as high stiffness, high strength, and low density—along with the proper tensile strength of carbon fibers, various researchers have explored metal [432] or polymer [433,434] matrix composite materials reinforced with CNTs or Carbon Fibers (CFs) [435–439]. On the mechanical characteristics of multilayered CNT/GPL/fiber/polymer hybrid composite plates several sources are available. Static [440,441] and vibrational [442,443] responses of cylindrical/curved shells and buckling [444] and vibration [445] analyses of plates is some of the available instances. However, few studies have explored the effect of GPL nanofillers on multiphase composite materials reinforced with fibers [446,447].
In this section, we discuss hybrid materials that incorporate CNTs or GPLs, the same configuration shown in Fig. 11. In recent years, hybrid nanocomposites reinforced with a combination of nanofillers, such as GPLs and CNTs within a matrix, have been developed [92,449,450]. Several researchers have examined various responses of these hybrid nanocomposites, as tabulated in Table 10. Hosseini [92] proposed a micromechanical model to determine the mechanical and thermal properties of a reinforced FG multilayer hybrid nanocomposite cylinder for thermoelastic wave propagation analysis with energy dissipation, employing Green–Naghdi theory. To calculate the modulus of elasticity for the hybrid nanocomposite material, they utilized the Halpin–Tsai micromechanical model, assuming that GPLs are distributed within a matrix containing CNTs. Additionally, the rule of mixtures was applied to determine the mass density and Poisson’s ratio of the FG multilayer GPLs-CNTs reinforced hybrid nanocomposite. Ghadiri Rad et al. [451] employed the element-free Galerkin (EFG) method in conjunction with Carrera’s Unified Formulation (CUF) as the CUF–EFG method for the buckling analysis of multilayer GPLs-CNTs-reinforced FG plates with cutouts and found that GPLs is far superior to CNTs in improving the buckling capacity of the nanocomposite plate. Zhao et al. [448] studied natural frequency characteristics of FG-GPL/CNT RC cylindrical shell based on FSDT of shells, Hamilton’s principle and FEM. As illustrated in Fig. 12, they found that the modulus of elasticity obtained from the case reinforced by only 0.5% of GPLs (
Figure 11: The schematic of the FG-O model of the hybrid nanocomposite illustrating the incorporation of both CNTs and GPLs within the same matrix; Reprinted from Zhao et al. [448] with permission from authors
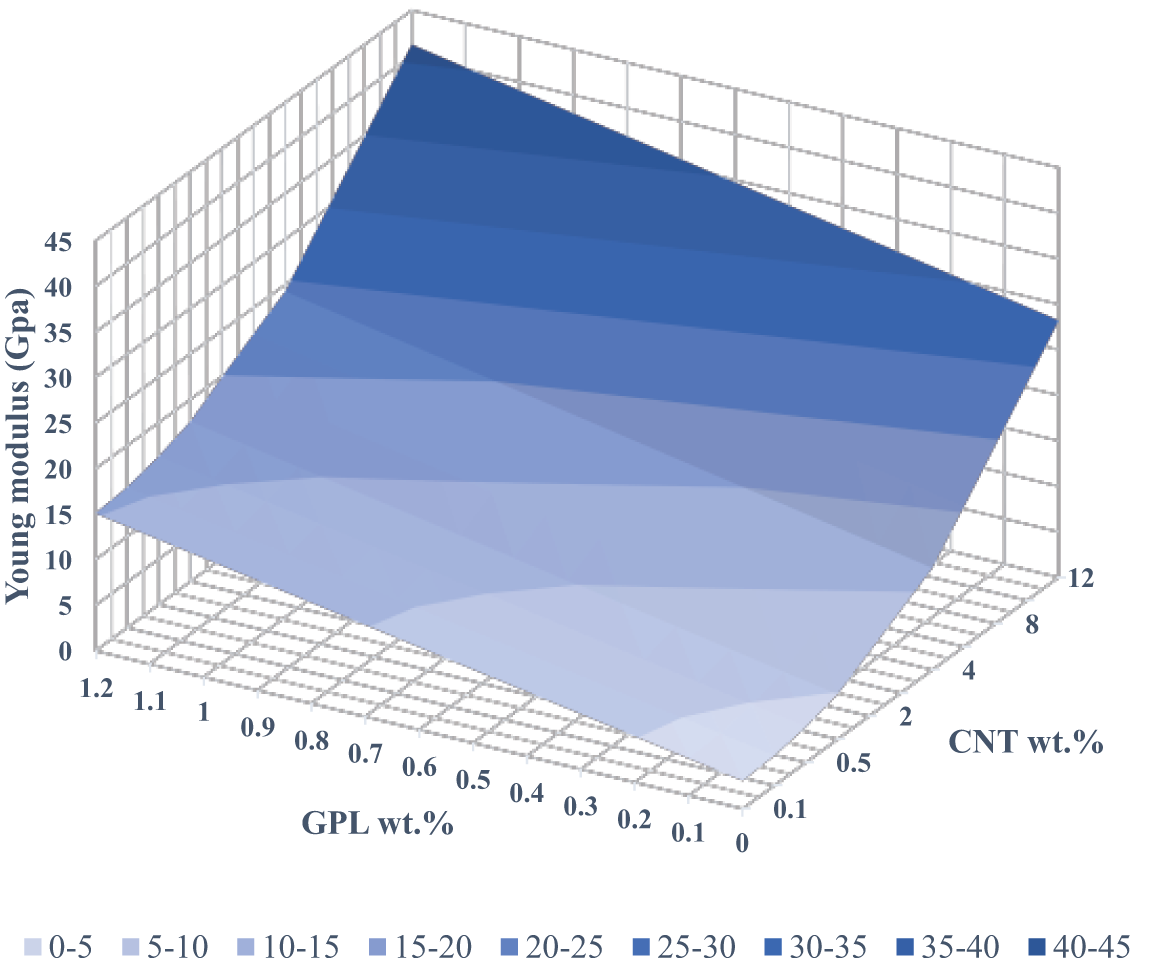
Figure 12: The effects of GPLs and CNTs weight fraction on the young modulus (
The synergistic effects of CNTs and GPLs have been investigated both experimentally and theoretically to improve the mechanical [454,455], electrical [456,457], thermal [458,459], and electromagnetic properties [460] of composites. For example, Wang et al. [461] demonstrated that the synergy arises due to the flexible nature of CNTs, which construct 3D hybrid architectures with GPLs. This architecture prevents the face-to-face aggregation of GPLs, thereby increasing the surface contact area with the epoxy matrix. Additionally, CNTs act as extended “tentacles,” entangling with polymer chains and enhancing the matrix-reinforcement interaction. Such hybrid structures provide significant mechanical reinforcement, including improvements in interfacial energy in filler composite laminates [461,462]. In the context of electrical conductivity, the hybridization of CNTs and GPLs has shown synergistic effects as well, with the electrical resistivity decreasing by up to three orders of magnitude when a homogenous dispersion of CNTs and GPLs is achieved in cementitious composites [463]. However, existing models face limitations, such as oversimplified assumptions regarding particle dispersion and matrix-interface interactions, which may not capture the complexities of real hybrid systems.
As demonstrated, computational approaches play a crucial role in analyzing the behavior of hybrid composites, particularly those incorporating CNTs and GPLs within a matrix. Both numerical and analytical methods enable precise predictions of mechanical, thermal, and dynamic properties, providing a comprehensive assessment of the material’s performance and characteristics. These techniques also address key challenges such as filler dispersion, particle agglomeration, and matrix-filler interactions, which are essential for optimizing the functionality of hybrid composites. By utilizing advanced computational tools, researchers can gain deeper insights into the responses of hybrid composites under varying loading conditions and environmental factors.
11 Porous Structures Reinforced by GPLs or CNTs
Porous materials are characterized by the presence of numerous voids or pores within their structure, which can significantly influence their physical and mechanical properties. These materials can be found in a wide range of applications, from construction and filtration to biomedical devices and insulation. The porosity allows for the absorption and transmission of fluids and gases, making porous materials ideal for applications such as water filtration, sound absorption, and thermal insulation. Within this category, porous functionally graded materials (P-FGMs) are a specialized type that exhibits a gradual variation in composition and microstructure, leading to a corresponding change in properties across the material. This gradient allows for enhanced performance in specific applications, such as thermal management, where different regions of the material can exhibit varying degrees of heat resistance or thermal conductivity. By carefully engineering the size, distribution, and connectivity of the pores, porous FGMs can be tailored to meet specific requirements, enhancing functionality while reducing weight and material usage in various industries.
Due to their valuable properties, including heat resistance, lightweight design, and excellent energy absorption, porous structures have been widely utilized in various engineering applications and pollutant sorption [464]. However, while the stiffness of porous structures significantly decreases due to the presence of internal cavities, incorporating carbon-based nanofillers [465] into the porous medium can considerably enhance the effective mechanical properties of the structure. To boost the efficiency and performance of structures, the concept of functionally graded porous structures reinforced with GPLs or CNTs is highly beneficial.
Porosity distribution patterns include functionally graded porosity distributions such as P-UD, P-X, P-O, P-V, and P-Λ. Their schematic geometrical characteristics is shown in Fig. 13. P-UD denotes a uniformly distributed porosity throughout the thickness of a structural member. In contrast, P-X and P-O represent symmetrical porosity distributions, with maximum and minimum porosity near the surfaces, respectively. Additionally, P-V and P-Λ are asymmetric porosity distribution patterns where one surface exhibits the lowest porosity, while the opposite surface has the highest porosity [466]. Many scholars have presented different analyses on functionally graded porous structural members reinforced by GPLs namely plates and annular plates [467–471], beams [472–474], and shells [475–478]. In general, the P-O porosity distribution exhibits the highest stiffness, while the P-X distribution demonstrates the lowest stiffness. The P-UD and P-V/P-Λ distributions yield intermediate stiffness values. It is evident that the stiffness of the structure has a direct relationship with its bending, buckling, and free vibration characteristics. Yas et al. [479] conducted a thermal buckling analysis of porous functionally graded nanocomposite beams reinforced with graphene platelets using the generalized differential quadrature method. Chen et al. [480] investigated the nonlinear vibration and post-buckling behavior of FG-GPL reinforced porous nanocomposite beams, employing Timoshenko beam theory and the Tsai-Halpin approach.
Figure 13: Porosity distributions and GPL dispersion patterns; Reprinted from Kiarasi et al. [465] with permission from authors
As seen, computational techniques are essential for elucidating the complex behavior of porous structures reinforced with carbon-based nanofillers, offering valuable insights into their mechanical, thermal, and vibrational properties. These approaches enable accurate predictions and optimization of material performance across a wide range of applications. Numerical and analytical methods, employing ESL theories or 3D elasticity, are utilized to model the behavior of functionally graded porous nanocomposites. These techniques allow for the investigation of various porosity distribution patterns and their influence on properties such as stiffness, bending, buckling, and vibration characteristics. Moreover, computational models provide a comprehensive understanding of how filler dispersion and porosity gradients affect overall material behavior under different loading and environmental conditions, contributing to the refinement and enhancement of material performance for engineering applications.
12 Other Characteristics and Applicability of CNTs and GPLs
The addition of CNTs and GPLs to composites enhances a wide range of properties, including mechanical strength, thermal conductivity, electrical conductivity, fatigue resistance, and durability. Both nanomaterials improve damping capabilities, impact resistance, and overall performance, making the composites more efficient, resilient, and suitable for demanding applications. Compared to traditional composites, those enhanced with GPLs and CNTs exhibit significantly improved thermal, electrical, and environmental properties. Traditional composites typically have low thermal conductivity, limiting their ability to dissipate heat, whereas GPLs and CNTs offer much higher thermal conductivity, enabling better heat distribution and thermal management. This makes composites with these nanomaterials ideal for high-performance applications where heat control is crucial. In terms of electrical properties, traditional composites are generally insulating or have poor conductivity, while the inclusion of CNTs, with their conductive networks, and GPLs, which enhance electron mobility, significantly improve electrical conductivity. This makes the modified composites more suitable for electronic and energy applications. Environmentally, both GPL- and CNT-enhanced composites are lighter than traditional composites, reducing overall weight and energy consumption in industries such as automotive and aerospace. Furthermore, these nanomaterials are more resistant to degradation than traditional fibres, offering improved durability and sustainability over time. In contrast to conventional composites, which are often limited by lower strength and conductivity, GPL- and CNT-modified composites demonstrate a marked performance improvement, although they may introduce challenges in processing and cost. In the following subsections, we provide a detailed review of the characteristics and applications of CNT- and GPL-reinforced composites that have received less attention in the field of structural mechanics and computational modelling.
In computational studies of CNT- and GPL-reinforced composites, various methods are utilized to model and predict the behavior of these advanced materials under diverse conditions. FEA is extensively employed to simulate mechanical, thermal, and electrical properties, enabling predictions of how these nanomaterials affect the overall composite performance. Additionally, MD simulations are used to investigate atomic-scale interactions, providing valuable insights into the dispersion, bonding, and stress transfer mechanisms between carbon-based fillers and polymer matrices. These simulations offer a deeper understanding of the molecular-level effects that improve properties such as thermal conductivity, electrical conductivity, and mechanical strength. Computational techniques also support the analysis of more complex behaviors, including vibration, damping, and fatigue resistance, within these nanocomposites. Furthermore, these approaches are essential for optimizing the distribution and alignment of CNTs and GPLs within the matrix, as the effectiveness of the fillers is significantly influenced by factors like orientation, dispersion, and aspect ratio. These computational tools are indispensable for designing high-performance composites tailored to meet the specific requirements of various applications, eliminating the need for costly trial-and-error experiments.
12.1 Thermal and Electrical Characteristics
As previously mentioned, GPLs and CNTs exhibit exceptional electrical and thermal properties, which are beneficial for reinforced materials. Both GPLs and CNTs possess electrical and thermal conductivities comparable to those of copper, making them particularly attractive for high-performance composite materials [11]. For example, their electrical conductivity can reach values as high as
12.1.1 Electrical Conductivity
Thermoplastic or thermoset polymers can be transformed into electrically conductive materials by incorporating conductive fillers, such as single- or multi-walled CNTs as well as GPLs. These fillers create conductive pathways within the polymer matrix, enabling the material to transition from an insulator to a conductor at a critical filler content [482]. In GPL- and CNT-reinforced polymer nanocomposites, this electrical transition is influenced by factors such as the dispersion state of the fillers, their aspect ratio, processing methods, curing conditions, temperature, filler structural quality, and loading content. Additionally, the overall electrical behavior depends on the distribution of individual fillers, the type of polymer used, the manufacturing process, and the presence of external electrical or magnetic fields [481,483–486]. Despite the promising potential of these fillers, blending CNTs and GPLs into polymers presents significant challenges when using traditional manufacturing techniques due to issues like agglomeration and uneven dispersion [487]. However, advancements in additive manufacturing (AM) have opened new possibilities for overcoming these challenges, enabling the production of electrically conductive parts with enhanced precision and control. Recent studies have demonstrated the successful application of CNT-based [488–492], graphene-based [493–495], and hybrid nanofillers [496–498] in producing conductive components, especially with advancements in additive manufacturing technologies [499,500].
Thermal conductivity is a critical property that can be significantly enhanced in polymer nanocomposites by incorporating high-thermal-conductivity nanofillers such as GPLs and CNTs. These carbon-based nanofillers can transform thermally insulating polymers into materials with improved thermal conduction capabilities. The covalent bonds formed between the nanofillers and the epoxy matrix facilitate effective phonon transport, which is essential for enhancing thermal conductivity [501]. Key geometrical features, including the interface thickness and the length of the reinforcements, also play a crucial role in determining the thermal properties of the final nanocomposite [501,502]. Among CNTs, MWCNTs tend to achieve the highest thermal conductivity in nanocomposites due to their relatively low interfacial area, which minimizes surface scattering and allows better heat transfer. In contrast, SWCNTs, with their larger surface area, suffer from greater electron and phonon boundary scattering, leading to a lower enhancement in conductivity [483]. The larger aspect ratio and diameter of MWCNTs make them more suitable for improving the thermal conductivity of nanocomposites, as they exhibit less surface scattering at the CNT–polymer interface. Most polymers exhibit thermal conductivities below 0.5
12.2 Durability and Resistance to Environmental Effects
One of the main challenges with neat epoxy resins is their low damage tolerance, which affects their long-term durability under service conditions [504]. However, the addition of carbon-based fillers, such as CNTs and GPLs, has been shown to significantly enhance the durability of these composites by improving mechanical performance and resistance to environmental conditions [505]. Several methods are available to analyze the durability of polymer composites, including hygrothermal aging (which accounts for temperature, time, and water or solution ingress), as well as physical and chemical aging. The retention of tensile strength under various environmental conditions can also be assessed. In general, mechanical, electrochemical, and durability degradation accelerates at elevated temperatures and is particularly pronounced under acidic conditions [506]. To address these issues, coatings made from CNT- or GPL-reinforced resin composites offer improved durability and resistance to harsh environments [507]. In addition to polymer matrices, CNT and GPL reinforcements have proven effective in enhancing the durability of various other composite systems. For example, metal matrix composites, such as Fe/steel reinforced with CNTs, demonstrate low maintenance costs, corrosion resistance, and improved mechanical properties like ductility and strength [508]. Cement-based composites reinforced with CNTs show enhanced dimensional stability (e.g., reduced shrinkage and creep) and durability against freezing, thawing, and corrosion [509]. Natural rubber composites incorporating CNTs and graphene oxide (GO) exhibit superior fatigue and durability properties [510,511], while graphene-reinforced aluminum matrix composites provide excellent corrosion resistance alongside high mechanical performance [512]. These examples confirm the efficiency of CNTs and GPLs in improving the durability and performance of reinforced composites in various applications.
Fatigue, defined as the progressive and localized damage that occurs when a material is subjected to cyclic axial, torsional, or flexural loading, is one of the primary causes of catastrophic failure in structural materials. Such failures can have serious, even tragic, consequences [513]. Improving the fatigue life of polymer composites is essential for enhancing their utility in various applications, particularly where long-term durability is required. However, epoxies, while widely used, have improper fracture toughness and fatigue resistance, which limits their reliability and service life [514,515]. While the influence of CNTs and GPLs on fatigue resistance is still underexplored in some areas [516,517], their potential for enhancing fatigue life is becoming evident. Engineering structures like wind turbines, which are subject to cyclic, random mechanical, thermal, and environmental loads, require materials that can sustain these stresses while maintaining stiffness and structural integrity [518]. The addition of CNTs and GPLs as nanofillers has been shown to significantly improve the fatigue life of polymer nanocomposites by preventing crack propagation, which slows down fracture in both impact and fatigue loading conditions [22,29,517,519].
Dai et al. [518] applied Paris’s law to study the fatigue behavior of CNT RCs, finding that CNTs positively affect shear and compressive strength, fracture toughness, and fatigue resistance. Ren et al. [520] also showed that SWCNTs outperformed carbon fiber-RC in terms of fatigue performance. Boroujeni et al. [521] reported an impressive 150% improvement in the fatigue life of carbon fiber-reinforced polymers (CFRPs) with patterned growth of MWCNTs. Similarly, Loos et al. [522] demonstrated a 1550% increase in the fatigue life of epoxy with a small amount of CNTs in the high-cycle, low-stress amplitude regime.
When comparing CNT RCs and GPL RCs, studies suggest that GPL-RC exhibit superior fatigue performance [22,523]. For instance, one report noted that the fatigue life was 27.4 times higher for GPL-RCs and 24 times higher for CNT-RCs [524]. Tareq et al. [525] showed that incorporating just 0.1 wt.% GPLs in an epoxy polymer matrix improved both mean and predicted fatigue life by 155% and 190%, respectively. Bortz et al. [526] observed that graphene-epoxy nanocomposites exhibited a fatigue life increase of 420% and 1580% compared to pure epoxy at stress amplitudes of 40 and 25 MPa, respectively. Shokrieh et al. [431], using displacement-controlled bending loading at 5 Hz, reported a 27.4-fold improvement in the fatigue life of nanocomposites with only 0.25 wt% GPLs compared to pristine epoxy. For hybrid nanocomposites, optimal fatigue performance was achieved with a combination of 0.2 wt.% graphene oxide (GO) and 0.04 wt.% CNTs, showing a remarkable 950% improvement in fatigue life due to the synergistic effects of GO-dispersed CNTs [527]. Mentioned studies demonstrate the potential of nanocomposites to further enhance fatigue resistance and extend the lifetime of polymer composites in demanding structural applications.
12.4 Damping and Vibration Attenuation Properties
Damping and vibration attenuation properties are essential for noise mitigation and vibration control in machines and structures. Materials used for this purpose need to combine high damping capacity with light weight and stiffness. In general, damping materials transform vibrations into heat energy [528]. Studies show that adding CNTs and GPLs to polymeric matrices enhances their damping capacity while retaining their mechanical strength [529,530]. Effective vibration damping is crucial for system performance, safety, and reliability, especially in control systems. While traditional metal matrix composites reinforced with whiskers or particles offer high strength and stiffness, they suffer from drawbacks such as high weight and limited damping capacity. Thus, the development of advanced materials that overcome these limitations is necessary [531]. CNTs and GPLs, due to their rich contacts and multiple energy dissipation pathways, have shown great potential for creating high-damping materials [532].
By incorporating CNTs and GPLs into polymer matrices, composites with improved damping capacities can be achieved without compromising mechanical strength or stiffness [533,534]. Experimental results confirm the positive effect of CNTs on the damping ratio of epoxy-based nanocomposites [535]. Dai et al. [528] reported more than a 350% increase in damping capacity with CNT additives in pure epoxy resins. Additionally, factors like the size and alignment of CNTs contribute to greater damping capacity [528]. MWCNTs have proven more effective than SWCNTs, showing up to a 700% increase in damping ratio compared to plain epoxy beams [534]. Koratkar et al. [536] observed a 200% increase in damping ratio with MWCNTs added to epoxy. Similarly, the influence of GPLs on the damping properties of polymer matrices is significant [530]. Rafiee et al. [537] found that the natural frequencies of nanocomposites increased with the concentration of GPLs, and an additional study by Rafiee et al. [538] reported a 26% increase in damping ratio for GPL-epoxy composites at 0.4 wt% GPL loading. Erkliğ et al. [539] investigated the vibration damping behavior of GPL-filled glass/carbon fiber hybrid composites and observed notable improvements based on varying GPL concentrations. Furthermore, Bulut et al. [540] demonstrated that incorporating GPLs into basalt/epoxy composites significantly enhanced their damping responses by up to 36%.
In is noteworthy that viscoelastic materials (VEMs) are commonly used for vibration damping, particularly in vibrating structures. VEMs dissipate energy effectively, though they tend to have low stiffness, leading to large shear strain. In contrast, CNT-reinforced composites can achieve significant damping without undergoing such high shear strain, making them advantageous compared to VEMs [541]. Overall, CNTs and GPLs are highly effective nanofillers for improving damping and vibration attenuation properties in polymer-based composites.
13 Production of Carbonaceous Nanocomposites
The production of carbon-based nanocomposites, particularly those reinforced with CNTs and GPLs, has attracted considerable interest due to their ability to enhance the mechanical, electrical, and thermal properties of polymer matrices. However, achieving uniform dispersion of these nanofillers within the polymer matrix remains a significant challenge, primarily due to the tendency of the nanofillers to agglomerate. Although theoretical expectations suggest that CNTs and GPLs should improve composite properties through their dispersion, the practical outcomes have been mixed. Some studies report improvements, while others emphasize the limitations associated with poor dispersion. This section explores the underlying causes of agglomeration, its effects on nanocomposite properties, and various strategies used to mitigate this issue. By examining techniques such as solvent-based approaches, mechanical dispersion, and functionalization, this discussion aims to offer insights into how these methods can optimize the performance of carbon-reinforced composites while minimizing agglomeration.
Computational methods have become indispensable for optimizing the fabrication processes of carbon-based nanocomposites, enabling more efficient and cost-effective production. These techniques are essential for predicting the dispersion, alignment, and interactions of nanofillers within polymer matrices. MD simulations are commonly employed to investigate the interaction forces between nanofillers and the polymer matrix at the atomic level, providing valuable insights into how processing parameters—such as temperature and shear stress—affect dispersion quality and the likelihood of agglomeration. Furthermore, CFD is used to model the flow behavior of nanocomposite slurry or melt during processing methods like extrusion, injection molding, or solution casting, helping to optimize parameters such as viscosity and shear rate to improve filler distribution. FEA is frequently applied to simulate the mechanical behavior of the composite during fabrication, predicting stress, strain, and deformation in processes like compression molding or injection molding. These simulations assist in selecting optimal processing conditions, such as curing temperatures and mixing speeds, to ensure uniform filler dispersion and minimize defects. Additionally, multi-scale modeling approaches predict the impact of processing on the macroscopic properties of the composite. These computational tools offer a more precise approach to nanocomposite fabrication, improving material performance and supporting the development of advanced materials for various industrial applications.
13.1 Agglomeration Phenomenon and Remedies
Agglomeration remains a significant challenge in the production of CNT- and GPL-reinforced composites, and this section will discuss reasons and methods to prevent this issue. Although the theoretical assumption is that the incorporation of CNT and GPL nanofillers should lead to uniform dispersion and improved nanocomposite properties, practical results remain inconclusive. Some studies have reported enhanced material performance following the addition of nanofillers [542,543], while others have observed no significant improvements [544,545], and in some cases, even a degradation in properties has been noted [546,547]. The issue of agglomeration becomes especially prominent when high concentrations of nanofillers are added, potentially leading to a deterioration in the properties of polymer-based nanocomposites [28]. Regardless of the production methods, matrix types, or chemical treatments employed, CNTs tend to agglomerate within the matrix [8]. Similarly, poor dispersion and the irreversible aggregation of graphene limit its broader application [548,549]. The reinforcing properties of carbon-based fillers such as CNTs and GPLs can only be fully realized if they are uniformly dispersed within the polymer matrix, with no agglomeration. Achieving this uniform dispersion is critical for maximizing the potential benefits of these nanofillers in composite materials.
The dispersion of carbonaceous nanofillers is a crucial factor that significantly affects the properties of nanocomposites. These nanomaterials exhibit a strong tendency to agglomerate due to the attractive van der Waals forces arising from their polarizable extended π-electron systems. Nanofillers such as GPLs and CNTs are particularly prone to agglomeration when dispersed in a polymer matrix [481]. The agglomerates formed are challenging to infiltrate with the matrix material, which often leads to potential defects in the resulting nanocomposite. Additionally, the large surface-to-volume ratio and unique chemical texture of nanofillers result in high surface energy [550]. When a polymer matrix is reinforced with carbon-based nanomaterials, this elevated surface energy promotes strong interfacial interactions, which can enhance the mechanical properties of the composite [551]. However, the presence of defects can actually reduce the van der Waals forces, thus improving their dispersion and interaction with polar materials [552]. This defect-induced reduction in agglomeration may enhance the overall performance of the nanocomposite by fostering better filler-matrix integration. Understanding and controlling the dispersion of these nanofillers is therefore critical to achieving the desired mechanical and functional improvements in polymer nanocomposites.
The process of breaking down agglomerates and distributing nanomaterials uniformly within matrices or solvents is known as dispersion [553]. The effectiveness of nanofiller dispersion is influenced by several key factors, including the length of the nanomaterials, their entanglement density, volume fraction, matrix viscosity, and the nature of the attractive forces between them. Preventing agglomeration is essential for achieving uniform dispersion, and several strategies can be employed to address this issue. These include the use of organic solvents and hybrid fillers to enhance the dispersion state, selecting appropriate dispersion and production techniques, and functionalizing the nanofillers [481]. Functionalization, in particular, modifies the surface chemistry of nanomaterials, reducing the van der Waals forces that cause agglomeration and promoting better interaction with the matrix. The following subsections will outline the processes that help prevent agglomeration of fillers, along with their specific advantages. These methods aim to improve the uniform distribution of nanofillers, which is critical for maximizing the performance and mechanical properties of nanocomposites.
The use of solvents for dispersing nanofillers [554], along with surfactants [555], plays a pivotal role in achieving well-dispersed nanofiller-reinforced polymer nanocomposites with enhanced properties [556]. Solvents are particularly effective due to their low viscosity, which helps reduce the overall viscosity of the polymer matrix. This reduction makes it easier to disperse nanofillers uniformly in a low-viscosity medium during the production process of nanocomposites [481]. While the decreased viscosity generally improves the dispersion of nanofillers, it may also have adverse effects on the mechanical properties of the composite. Issues such as reduced fracture strain, lower tensile strength, and a decline in Young’s modulus have been observed in some cases [557]. As a result, the use of solvents offers both advantages and disadvantages in terms of the final properties of polymer nanocomposites [558,559]. Achieving an optimal balance between improved dispersion and the preservation of mechanical characteristics is crucial for producing high-performance materials.
The physical dispersion method utilizes mechanical techniques to disperse agglomerated nanofillers without involving chemical reactions [64]. By applying external forces, such as sonication or mechanical stirring, or by using surfactant complexes, the dispersion of nanofillers within the polymer matrix can be optimized. Several mechanical dispersion methods, such as sonication [482], calendaring [560], ball milling [483], high-shear mixing (HSM) [561], and extrusion [561], are widely used to prevent agglomeration. Sonication is the most common approach, employing high-frequency sound waves to uniformly disperse both GPLs and CNTs nanofillers in polymer matrices [481,482,562]. Calendaring [563] uses a three-roll mill where shear forces are applied to disperse, mix, or homogenize viscous materials [481,482], while ball milling [564] reduces particle sizes to improve the dispersion of fillers [483,565]. High-shear mixing enhances filler distribution through intense mechanical forces [566,567], and extrusion achieves dispersion by mixing thermoplastic pellets with nanofillers, utilizing the shear flow generated by twin screws rotating at high speed [567]. In addition to these, other mechanical dispersion techniques like stirring and melt compounding are also effective in achieving uniform distribution of nanofillers in nanocomposites [568]. The success of these methods in preventing agglomeration is critical for ensuring that the nanofillers are well-integrated into the polymer matrix, thereby enhancing the overall properties and performance of the resulting nanocomposite materials.
Functionalization methods are crucial for improving the dispersion of nanofillers and preventing agglomeration, which is essential for enhancing the overall properties of nanocomposites. Surface modifications not only help control the spatial distribution of nanofillers but also facilitate better integration with matrix materials by enabling homogeneous dispersion [561]. The functionalization of GPLs and CNTs plays a pivotal role in improving dispersion and fostering stronger interactions between reinforcements and the polymeric matrix, leading to enhanced composite performance [569]. One critical factor in determining the properties of nanocomposites is the interfacial bond strength between the nanofillers and the matrix. Due to their smooth surfaces, GPLs and CNTs inherently form weak interfacial bonds with polymers, relying predominantly on van der Waals forces, which are insufficient for effective mechanical load transfer [13]. This weak bonding significantly limits the potential enhancement in mechanical properties that these nanofillers could provide. To overcome this limitation, various surface modification techniques, including chemical (covalent) and physical (non-covalent) functionalization, have been employed to enhance interfacial interactions. Chemical or covalent functionalization [566,570], such as the introduction of functional groups through acidic treatments in liquid phases [571], oxidation with amines [572], and fluorine [573], improves the chemical bonding between nanofillers and the polymer matrix. Additional methods, such as plasma [574], microwave irradiation [575], and the use of gas-phase chemicals [576,577], also enable the incorporation of functional groups that improve compatibility and bonding. On the other hand, physical or non-covalent functionalization [578–580], which includes techniques like polymer wrapping and surfactant adsorption, relies on weak but effective non-covalent interactions to disperse nanofillers without altering their intrinsic properties. These combined approaches lead to more efficient load transfer and significantly enhanced mechanical, electrical, and thermal properties of the nanocomposites.
The use of hybrid nano-fillers represents a promising approach for simultaneously improving the dispersion of GPLs and CNTs within a polymer matrix, while also enhancing the physical properties of the resulting hybrid nanocomposites. By combining different nanofillers, such as GPLs and CNTs, a synergistic effect is achieved, resulting in improved mechanical strength, electrical conductivity, and thermal stability [566,581]. One notable example of hybrid nano-fillers is the wrapping of nanofillers with conjugated polymers, which facilitates better dispersion and interaction within the matrix, further contributing to the enhanced performance of the composite material [582].
13.1.5 Theoretical Occurrence of Agglomerations
Theoretical models for predicting the occurrence of agglomerations and their impact on the mechanical properties of nanocomposites will briefly be discussed in this section. These frameworks help in understanding how interfacial properties between nanofillers influence the overall performance of the composite material. Several studies have developed theoretical approaches to address the effects of agglomeration on nanocomposites, particularly focusing on how these clusters of nanofillers alter the reinforcement efficiency and mechanical behavior. Researchers have applied these theories to various properties, including tensile and compressive strength [583–587], fracture toughness [588], electrical conductivity [589,590], and creep behavior [591–593].
13.2 Production and Fabrication
Reinforced polymer composites with nanofillers smaller than 100 nm have garnered significant attention for various industrial applications. Polymer nanocomposites demonstrate impressive performance and potential in this regard. They are typically easy to process and require only minimal nanofiller loading, resulting in property enhancements of the matrix that surpass those of traditional composites by several orders of magnitude [594]. Dispersion of CNTs and GPLs within a matrix poses significant challenges [595–600], necessitating the use of various processing methods for preparing carbon-based nanofiller-reinforced composites [600]. Bhattacharya [601] discussed various functionalization techniques and highlighted the impressive mechanical, electrical, and thermal properties of polymer matrix composites enhanced with carbon nanotubes, graphene, and clay as nanofillers. The degree of reinforcement is influenced by several factors, including the type of filler, the specific functional groups on the filler, the aspect ratio of the filler, the filler content, the polymer type, and the processing method. Achieving a uniform distribution of the nanofiller within the polymer matrix and ensuring strong interactions between the filler and the polymer are essential for effective reinforcement. However, at higher nanofiller concentrations, the properties of the composite tend to decline, indicating challenges in properly dispersing the fillers.
To avoid the agglomeration of CNTs caused by van der Waals interactions, Kaseem et al. [10] identified three processing methods for preparing Polystyrene/Carbon Nanotube (PS/CNT) composites: solution mixing, melt mixing, and in-situ polymerization. The solution mixing process involves three key steps: first, dispersing the CNTs in an appropriate solvent; second, combining this dispersion with a polymer solution; and third, recovering the composite through precipitation or by casting a film [602]. Due to the significant evaporation of solvent, solution mixing is impractical for large-scale production. In contrast, melt mixing is a versatile and widely used method for fabricating polymer systems, including polymer blends and composites. This technique is straightforward and compatible with existing polymer processing methods, such as extrusion, injection molding, and compression molding, making it suitable for large-scale industrial applications. For PS/CNT composites, CNTs are dispersed within the polymer matrix through the rheological shear stress and temperature applied during the compounding process. In-situ polymerization is another highly effective method for enhancing CNT dispersion and the interactions between CNTs and the polymer matrix. Typically, CNTs are initially mixed with monomers, and CNT/polymer composites are formed by polymerizing the monomers under specific conditions. Andrews et al. [603] discovered that in composites prepared through melt mixing with MWCNTs ranging from 2.5 to 25 vol.%, the Young’s modulus progressively increased from 1.9 to 4.5

Figure 14: (a) Flow stress-strain curves of PS/SWCNT composites with different SWCNT contents [604] and (b) Young’s modulus of PS/MWCNT composites with respect to MWCNT content [603]; Adopted from Refs. [603,604]
Practical methods for producing graphene-reinforced composites include chemical vapor deposition (CVD) and the exfoliation of graphite. However, the CVD method is not cost-effective or time-efficient enough to be commercially viable for large-scale production [605]. Compare to the CVD method, the exfoliation of graphite is gaining popularity due to its lower cost and reduced time requirements. Similar to CNT-RCs, the conventional methods used for producing exfoliated graphite-reinforced polymer composites include in-situ polymerization [606], solution mixing [607], and melt mixing [608]. In-situ polymerization and solution mixing aided by ultrasonication have demonstrated excellent results in achieving a highly homogeneous dispersion of graphite nanoplatelets. Roshan et al. [594] presented a cost-effective and efficient method for fabricating and characterizing graphene/poly(methyl methacrylate) (PMMA) composite flexible films using a one-pot alternate stirring sonication (OPASS) process.
In the case of additive manufacturing (AM), the selection of composite powder preparation methods significantly influences the dispersion quality of nanofillers and the resultant material performance [609]. For CNT-reinforced composites, wet mixing has gained attention due to its cost-effectiveness, though the dispersion quality can sometimes be limited [610]. Surface coating techniques offer moderate dispersion of CNTs on powder particle surfaces, which can improve uniformity to some extent [611,612]. Melt-compounding and ball milling methods [613,614], on the other hand, demonstrate notable advantages in enhancing laser energy absorption and accelerating powder fusion during processes such as selective laser sintering (SLS) [615], fused deposition modeling (FDM) [616,617], and vat photopolymerization (VP) [618]. Dissolution-precipitation methods have also been reported to enhance the thermal and electrical conductivities of CNT-reinforced composites, contributing to superior multifunctional properties [610,615].
For GPL-reinforced composites, surface coating remains a popular method, although it is solvent-intensive and may face challenges related to large-scale implementation [619,620]. Ball milling and melt-compounding approaches are widely adopted for improving dispersion uniformity, resulting in enhanced mechanical and thermal properties [621,622]. Similar to CNTs, GPL-reinforced composites benefit from AM techniques like SLS [623], FDM [624,625], and VP [626]. These methods offer varying levels of control over the structural integrity and distribution of fillers within the matrix. Therefore, understanding the advantages and limitations of each preparation technique is crucial for selecting an appropriate method based on specific performance requirements and intended applications [627].
Composite structures reinforced with CNTs or GPLs hold great promise for enhancing lightweight designs, which are particularly important in aerospace, automotive, marine, mechanical, and various other engineering applications. While numerous initial research studies have explored this topic, many issues remain to be addressed. As previously discussed, while there are several sources available on the fabrication of composite structures reinforced with carbon-based nanofillers, to the authors’ knowledge, no work has been reported on fabrication processes that facilitate the production of functionally graded structural elements, such as curved or cylindrical shells. Moreover, most analyses of nanocomposite structures reinforced with CNTs or GPLs have focused on elastic behaviors, including bending, buckling, post-buckling, vibrational, and dynamic analyses of beam, plate, and shell-type structures. There is a notable lack of research on plasticity, failure, and fracture analyses of these structures thus far. Additionally, hybrid nanocomposites reinforced with CNTs or GPLs present a significant opportunity for further investigation. Also, future research can explore the agglomeration effects and interactions of CNTs and GPLs in hybrid nanocomposites, as well as examine the production feasibility by considering interactions between various nanofiller types, such as fibers and nanofillers. Additionally, integrating agglomeration-related theories with micromechanical models to derive material properties would be a valuable area of investigation. Also, the synergistic effects between CNTs and GPLs need to be investigated theoretically to improve material behavior predictions, enabling optimized designs for structural reinforcement, multifunctional composites, and conductive materials. Addressing these gaps would be beneficial for the practical design of these advanced structures.
This review paper provides a thorough overview of the current state of structures reinforced with CNTs and GPLs, covering nearly all key structural aspects in this rapidly advancing field. It explores the mechanical behavior of structural components reinforced with GPLs or CNTs, including static loading, bending, dynamic responses, thermal and mechanical buckling, as well as vibrational properties. The analysis includes key structural elements such as plates, cylindrical and curved shells, beams, and annular sector plates. In addition, the paper offers an in-depth examination of studies on composite structures reinforced with GPLs or CNTs, with particular emphasis on the computational modeling techniques used to analyze these behaviors. A detailed review of analytical and numerical computational methods is provided, focusing on 3D elasticity and equivalent single-layer (ESL) theories, and the implementation of these models is also discussed. The review further covers research on functionally graded materials and the material properties of CNTs and GPLs. It investigates the role of CNTs and GPLs in improving the mechanics of porous structures and hybrid nanocomposites, as well as their thermal and electrical properties, environmental durability, fatigue resistance, and damping and vibration attenuation capabilities, highlighting the computational models used to predict and enhance these performance attributes. The paper also addresses the production and fabrication processes, with special attention given to the challenge of nanofiller agglomeration and solutions for predicting and mitigating this issue. Finally, it identifies key technical challenges, particularly in computational modeling, and outlines potential future research directions in this field.
Acknowledgement: The authors did not receive any assistance from individuals, institutions, or organizations that warrants acknowledgment.
Funding Statement: This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Author Contributions: Mohammad Javad Bayat: Writing—Original Draft, Resources, Software, Methodology, Investigation, Data Collection, Data Curation, Conceptualization. Amin Kalhori: Writing—Original Draft, Writing—Review & Editing, Resources, Visualization, Software, Methodology, Investigation, Data Collection, Data Curation, Conceptualization. Kamran Asemi: Conceptualization, Resources, Visualization, Data Curation, Investigation, Methodology, Supervision, Writing—Original Draft, Writing—Review & Editing. Masoud Babaei: Conceptualization, Data Curation, Data Collection, Investigation, Methodology, Writing—Original Draft. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: As the present article is the review article, therefore, no material is associated with the present study.
Ethics Approval: This study did not involve human participants, animals, or data requiring ethics approval.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Mohan VB, Lau KT, Hui D, Bhattacharyya D. Graphene-based materials and their composites: a review on production, applications and product limitations. Composit Part B: Eng. 2018;142:200–20. doi:10.1016/j.compositesb.2018.01.013. [Google Scholar] [CrossRef]
2. Kroto HW, Heath JR, O’Brien SC, Curl RF, Smalley RE. C60: buckminsterfullerene. Nature. 1985;318(6042):162–3. doi:10.1038/318162a0. [Google Scholar] [CrossRef]
3. Iijima S. Helical microtubules of graphitic carbon. Nature. 1991;354(6348):56–8. doi:10.1038/354056a0. [Google Scholar] [CrossRef]
4. Iijima S, Ichihashi T. Single-shell carbon nanotubes of 1-nm diameter. Nature. 1993;363(6430):603–5. doi:10.1038/363603a0. [Google Scholar] [CrossRef]
5. Geim AK, Novoselov KS. The rise of graphene. Nat Mat. 2007;6(3):183–91. doi:10.1038/nmat1849. [Google Scholar] [CrossRef]
6. Novoselov KS, Geim AK, Morozov SV, Jiang DE, Zhang Y, Dubonos SV, et al. Electric field effect in atomically thin carbon films. Science. 2004;306(5696):666–9. doi:10.1126/science.1102896. [Google Scholar] [CrossRef]
7. ShayanMehr M. Carbon nanostructures for reinforcement of polymers in mechanical and aerospace engineering. Aeros Polym Mat. 2022:61–84. doi:10.1002/9781119905264.ch3. [Google Scholar] [CrossRef]
8. Rubel RI, Ali MH, Jafor MA, Alam MM. Carbon nanotubes agglomeration in reinforced composites: a review. AIMS Mat Sci. 2019;6(5):756–80. [Google Scholar]
9. Khoshraftar Z, Ghaemi A, Hemmati A. Comprehensive investigation of isotherm, RSM, and ANN modeling of CO2 capture by multi-walled carbon nanotube. Sci Rep. 2024;14(1):5130. doi:10.1038/s41598-024-55836-6. [Google Scholar] [CrossRef]
10. Kaseem M, Hamad K, Ko YG. Fabrication and materials properties of polystyrene/carbon nanotube (PS/CNT) composites: a review. Eur Poly J. 2016;79:36–62. doi:10.1016/j.eurpolymj.2016.04.011. [Google Scholar] [CrossRef]
11. Shi G, Araby S, Gibson CT, Meng Q, Zhu S, Ma J. Graphene platelets and their polymer composites: fabrication, structure, properties, and applications. Adv Funct Mater. 2018;28(19):1706705. doi:10.1002/adfm.201706705. [Google Scholar] [CrossRef]
12. Yee K, Ghayesh MH. A review on the mechanics of graphene nanoplatelets reinforced structures. Int J Eng Sci. 2023;186(5):103831. doi:10.1016/j.ijengsci.2023.103831. [Google Scholar] [CrossRef]
13. Coleman JN, Khan U, Blau WJ, Gun’ko YK. Small but strong: a review of the mechanical properties of carbon nanotube-polymer composites. Carbon. 2006;44(9):1624–52. doi:10.1016/j.carbon.2006.02.038. [Google Scholar] [CrossRef]
14. Thostenson ET, Ren Z, Chou T-W. Advances in the science and technology of carbon nanotubes and their composites: a review. Composit Sci Technol. 2001;61(13):1899–912. doi:10.1016/S0266-3538(01)00094-X. [Google Scholar] [CrossRef]
15. Du J, Cheng HM. The fabrication, properties, and uses of graphene/polymer composites. Macromol Chem Phy. 2012;213(10–11):1060–77. doi:10.1002/macp.201200029. [Google Scholar] [CrossRef]
16. Ma L, Dong X, Chen M, Zhu L, Wang C, Yang F, et al. Fabrication and water treatment application of carbon nanotubes (CNTs)-based composite membranes: a review. Membranes. 2017;7(1):16. doi:10.3390/membranes7010016. [Google Scholar] [CrossRef]
17. Ravishankar B, Nayak SK, Kader MA. Hybrid composites for automotive applications-A review. J Reinfor Plast Compos. 2019;38(18):835–45. doi:10.1177/0731684419849. [Google Scholar] [CrossRef]
18. Li Y, Wang S, Wang Q, Xing M. A comparison study on mechanical properties of polymer composites reinforced by carbon nanotubes and graphene sheet. Compos Part B: Eng. 2018;133:35–41. doi:10.1016/j.compositesb.2017.09.024. [Google Scholar] [CrossRef]
19. Rafiee MA. Comparison of graphene with carbon nanotubes as a filler for epoxy composites. Graphene-based Composite Materials [ProQuest Dissertations & Theses]. Rensselaer Polytechnic Institute; 2011. Vol. 1, p. 58–73. ProQuest ID: 3476260. [Google Scholar]
20. Punera D, Kant T. A critical review of stress and vibration analyses of functionally graded shell structures. Compos Struct. 2019;210:787–809. doi:10.1016/j.compstruct.2018.11.084. [Google Scholar] [CrossRef]
21. Singh NP, Gupta V, Singh AP. Graphene and carbon nanotube reinforced epoxy nanocomposites: a review. Polymer. 2019;180:121724. doi:10.1016/j.polymer.2019.121724. [Google Scholar] [CrossRef]
22. Iqbal AA, Iqbal AP, Nuruzzaman DM. A review on fatigue fracture characteristics in graphene reinforced nanocomposites. Ain Shams Eng J. 2024;15(6):102730. doi:10.1016/j.asej.2024.102730. [Google Scholar] [CrossRef]
23. Ebrahimi F, Dabbagh A. A comprehensive review on modeling of nanocomposite materials and structures. J Comput Appl Mech. 2019;50(1):197–209. [Google Scholar]
24. Thai H-T, Kim S-E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos Struct. 2015;128(1):70–86. doi:10.1016/j.compstruct.2015.03.010. [Google Scholar] [CrossRef]
25. Kumar A, Sharma K, Dixit AR. Carbon nanotube-and graphene-reinforced multiphase polymeric composites: review on their properties and applications. J Mat Sci. 2020;55(7):2682–724. doi:10.1007/s10853-019-04196-y. [Google Scholar] [CrossRef]
26. Lu JP. Elastic properties of carbon nanotubes and nanoropes. Phys Rev Lett. 1997;79(7):1297–300. doi:10.1103/PhysRevLett.79.1297. [Google Scholar] [CrossRef]
27. Kumar A, Sharma K, Dixit AR. A review on the mechanical properties of polymer composites reinforced by carbon nanotubes and graphene. Carbon Letters. 2021;31(2):149–65. doi:10.1007/s42823-020-00161-x. [Google Scholar] [CrossRef]
28. Zeinedini A, Shokrieh MM. Agglomeration phenomenon in graphene/polymer nanocomposites: reasons, roles, and remedies. Appl Phys Rev. 2024;11(4):041301. doi:10.1063/5.0223785. [Google Scholar] [CrossRef]
29. Atif R, Shyha I, Inam F. Mechanical, thermal, and electrical properties of graphene-epoxy nanocomposites—A review. Polymers. 2016;8(8):281. doi:10.3390/polym8080281. [Google Scholar] [CrossRef]
30. Huang X, Jiang P, Tanaka T. A review of dielectric polymer composites with high thermal conductivity. IEEE Electr Insulat Magaz. 2011;27(4):8–16. doi:10.1109/MEI.2011.5954064. [Google Scholar] [CrossRef]
31. Borand G, Uzunsoy D. Fabrication of functionally graded few-layered graphene reinforced Al-4.5 Cu alloy by powder metallurgy. J Alloys Comp. 2022;923:166348. doi:10.1016/j.jallcom.2022.166348. [Google Scholar] [CrossRef]
32. Bayat MJ, Kalhori A, Babaei M, Asemi K. Natural frequency characteristics of stiffened FG multilayer graphene reinforced composite plate with circular cutout resting on elastic foundation. Int J Struct Stab Dyn. 2023;24(18):2450202. doi:10.1142/S021945542450202X. [Google Scholar] [CrossRef]
33. Naskar AK, Keum JK, Boeman RG. Polymer matrix nanocomposites for automotive structural components. Nature Nanotechnol. 2016;11(12):1026–30. doi:10.1038/nnano.2016.262. [Google Scholar] [CrossRef]
34. Bakshi SR, Lahiri D, Agarwal A. Carbon nanotube reinforced metal matrix composites-a review. Int Mat Rev. 2010;55(1):41–64. doi:10.1179/095066009X12572530170543. [Google Scholar] [CrossRef]
35. Cho J, Boccaccini AR, Shaffer MS. Ceramic matrix composites containing carbon nanotubes. J Mat Sci. 2009;44(8):1934–51. doi:10.1007/s10853-009-3262-9. [Google Scholar] [CrossRef]
36. Porwal H, Grasso S, Reece M. Review of graphene-ceramic matrix composites. Adv Appl Ceramics. 2013;112(8):443–54. doi:10.1179/174367613X13764308970581. [Google Scholar] [CrossRef]
37. Qian D, Dickey EC, Andrews R, Rantell T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene composites. App Phy Letters. 2000;76(20):2868–70. doi:10.1063/1.126500. [Google Scholar] [CrossRef]
38. Xie XI, Zhou XP, Tang J. Effect of maleic anhydride grafted SEBS on properties of polypropylene/carbon nanotube composites. China Synth Rubber Ind. 2002;25(1):46. [Google Scholar]
39. Kimura T, Ago H, Tobita M, Ohshima S, Kyotani M, Yumura M. Polymer composites of carbon nanotubes aligned by a magnetic field. Adv Mat. 2002;14(19):1380–3. [Google Scholar]
40. Jang J, Bae J, Yoon S-H. A study on the effect of surface treatment of carbon nanotubes for liquid crystalline epoxide-carbon nanotube composites. J Mat Chem. 2003;13(4):676–81. doi:10.1039/b212190e. [Google Scholar] [CrossRef]
41. Feng W, Bai X, Lian Y, Liang J, Wang X, Yoshino K. Well-aligned polyaniline/carbon-nanotube composite films grown by in-situ aniline polymerization. Carbon. 2003;41(8):1551–7. doi:10.1016/S0008-6223(03)00078-2. [Google Scholar] [CrossRef]
42. Xiao Q, Zhou X. The study of multiwalled carbon nanotube deposited with conducting polymer for supercapacitor. Electrochimica Acta. 2003;48(5):575–80. doi:10.1016/S0013-4686(02)00727-2. [Google Scholar] [CrossRef]
43. Cadek M, Coleman J, Barron V, Hedicke K, Blau W. Morphological and mechanical properties of carbon-nanotube-reinforced semicrystalline and amorphous polymer composites. Appl Phy Letters. 2002;81(27):5123–5. doi:10.1063/1.1533118. [Google Scholar] [CrossRef]
44. Singla D, Amulya K, Murtaza Q. CNT reinforced aluminium matrix composite-a review. Mat Today: Proc. 2015;2(4–5):2886–95. doi:10.1016/j.matpr.2015.07.248. [Google Scholar] [CrossRef]
45. Bakshi SR, Singh V, Balani K, McCartney DG, Seal S, Agarwal A. Carbon nanotube reinforced aluminum composite coating via cold spraying. Surf Coat Technol. 2008;202(21):5162–9. doi:10.1016/j.surfcoat.2008.05.042. [Google Scholar] [CrossRef]
46. Kuzumaki T, Miyazawa K, Ichinose H, Ito K. Processing of carbon nanotube reinforced aluminum composite. J Mater Res. 1998;13(9):2445–9. doi:10.1557/JMR.1998.0340. [Google Scholar] [CrossRef]
47. Dong S, Tu J, Zhang X. An investigation of the sliding wear behavior of Cu-matrix composite reinforced by carbon nanotubes. Mat Sci Eng: A. 2001;313(1–2):83–7. doi:10.1016/S0921-5093(01)00963-7. [Google Scholar] [CrossRef]
48. Shen G-R, Cheng Y-T, Tsai L-N. Synthesis and characterization of Ni-P-CNT’s nanocomposite film for MEMS applications. IEEE Transact Nanotech. 2005;4(5):539–47. doi:10.1109/TNANO.2005.851397. [Google Scholar] [CrossRef]
49. Chen C-S, Chen X-H, Li W-H, Xu L-S, Yi B. Effect of multi-walled carbon nanotubes as reinforced fibres on tribological behaviour of Ni-P electroless coatings. Diam Rela Mat. 2006;15(1):151–6. doi:10.1016/j.diamond.2005.09.004. [Google Scholar] [CrossRef]
50. Goh C, Wei J, Lee L, Gupta M. Simultaneous enhancement in strength and ductility by reinforcing magnesium with carbon nanotubes. Mat Sci Eng: A. 2006;423(1–2):153–6. doi:10.1016/j.msea.2005.10.071. [Google Scholar] [CrossRef]
51. Kuzumaki T, Ujiie O, Ichinose H, Ito K. Mechanical characteristics and preparation of carbon nanotube fiber-reinforced Ti composite. Adv Eng Mat. 2000;2(7):416–8. doi:10.1002/(ISSN)1527-2648. [Google Scholar] [CrossRef]
52. Inam F, Yan H, Reece MJ, Peijs T. Dimethylformamide: an effective dispersant for making ceramic-carbon nanotube composites. Nanotechnology. 2008;19(19):195710. doi:10.1088/0957-4484/19/19/195710. [Google Scholar] [CrossRef]
53. Sun J, Gao L. Development of a dispersion process for carbon nanotubes in ceramic matrix by heterocoagulation. Carbon. 2003;41(5):1063–8. doi:10.1016/S0008-6223(02)00441-4. [Google Scholar] [CrossRef]
54. Rul S, Lefèvre-Schlick F, Capria E, Laurent C, Peigney A. Percolation of single-walled carbon nanotubes in ceramic matrix nanocomposites. Acta Materialia. 2004;52(4):1061–7. doi:10.1016/j.actamat.2003.10.038. [Google Scholar] [CrossRef]
55. Jiang L, Gao L. Carbon nanotubes-metal nitride composites: a new class of nanocomposites with enhanced electrical properties. J Mat Chem. 2005;15(2):260–6. doi:10.1039/B409682G. [Google Scholar] [CrossRef]
56. Thostenson ET, Karandikar PG, Chou T-W. Fabrication and characterization of reaction bonded silicon carbide/carbon nanotube composites. J Phy D: Appl Phy. 2005;38(21):3962. doi:10.1088/0022-3727/38/21/020. [Google Scholar] [CrossRef]
57. Sivakumar R, Guo S, Nishimura T, Kagawa Y. Thermal conductivity in multi-wall carbon nanotube/silica-based nanocomposites. Scripta Materialia. 2007;56(4):265–8. doi:10.1016/j.scriptamat.2006.10.025. [Google Scholar] [CrossRef]
58. Wang J, Shi S, Yang J, Zhang W. Multiscale analysis on free vibration of functionally graded graphene reinforced PMMA composite plates. Appl Mathem Modell. 2021;98(4):38–58. doi:10.1016/j.apm.2021.04.023. [Google Scholar] [CrossRef]
59. Lee YR, Raghu AV, Jeong HM, Kim BK. Properties of waterborne polyurethane/functionalized graphene sheet nanocomposites prepared by an in situ method. Macromol Chem Phys. 2009;210(15):1247–54. doi:10.1002/macp.200900157. [Google Scholar] [CrossRef]
60. Liang J, Xu Y, Huang Y, Zhang L, Wang Y, Ma Y, et al. Infrared-triggered actuators from graphene-based nanocomposites. J Phys Chem C. 2009;113(22):9921–7. doi:10.1021/jp901284d. [Google Scholar] [CrossRef]
61. Ansari S, Giannelis EP. Functionalized graphene sheet—Poly (vinylidene fluoride) conductive nanocomposites. J Poly Sci Part B: Poly Phy. 2009;47(9):888–97. doi:10.1002/polb.21695. [Google Scholar] [CrossRef]
62. Zhang H-B, Zheng W-G, Yan Q, Yang Y, Wang J-W, Lu Z-H, et al. Electrically conductive polyethylene terephthalate/graphene nanocomposites prepared by melt compounding. Polymer. 2010;51(5):1191–6. doi:10.1016/j.polymer.2010.01.027. [Google Scholar] [CrossRef]
63. Kim H, Macosko CW. Processing-property relationships of polycarbonate/graphene composites. Polymer. 2009;50(15):3797–809. doi:10.1016/j.polymer.2009.05.038. [Google Scholar] [CrossRef]
64. Jeon C-H, Jeong Y-H, Seo J-J, Tien HN, Hong S-T, Yum Y-J, et al. Material properties of graphene/aluminum metal matrix composites fabricated by friction stir processing. Int J Precision Eng Manufact. 2014;15(6):1235–9. doi:10.1007/s12541-014-0462-2. [Google Scholar] [CrossRef]
65. Li Z, Fan G, Tan Z, Guo Q, Xiong D, Su Y, et al. Uniform dispersion of graphene oxide in aluminum powder by direct electrostatic adsorption for fabrication of graphene/aluminum composites. Nanotechnology. 2014;25(32):325601. doi:10.1088/0957-4484/25/32/325601. [Google Scholar] [CrossRef]
66. Xie G, Forslund M, Pan J. Direct electrochemical synthesis of reduced graphene oxide (rGO)/copper composite films and their electrical/electroactive properties. ACS Appl Mat Interf. 2014;6(10):7444–55. doi:10.1021/am500768g. [Google Scholar] [CrossRef]
67. Pavithra CL, Sarada BV, Rajulapati KV, Rao TN, Sundararajan G. A new electrochemical approach for the synthesis of copper-graphene nanocomposite foils with high hardness. Sci Rep. 2014;4(1):4049. doi:10.1038/srep04049. [Google Scholar] [CrossRef]
68. Kumar CP, Venkatesha T, Shabadi R. Preparation and corrosion behavior of Ni and Ni-graphene composite coatings. Mat Res Bulletin. 2013;48(4):1477–83. doi:10.1016/j.materresbull.2012.12.064. [Google Scholar] [CrossRef]
69. Kuang D, Xu L, Liu L, Hu W, Wu Y. Graphene-nickel composites. Appl Surf Sci. 2013;273:484–90. doi:10.1016/j.apsusc.2013.02.066. [Google Scholar] [CrossRef]
70. Rashad M, Pan F, Asif M, Tang A. Powder metallurgy of Mg-1% Al-1% Sn alloy reinforced with low content of graphene nanoplatelets (GNPs). J Industrial Eng Chem. 2014;20(6):4250–5. doi:10.1016/j.jiec.2014.01.028. [Google Scholar] [CrossRef]
71. Rashad M, Pan F, Tang A, Asif M, Aamir M. Synergetic effect of graphene nanoplatelets (GNPs) and multi-walled carbon nanotube (MW-CNTs) on mechanical properties of pure magnesium. J All Comp. 2014;603:111–8. doi:10.1016/j.jallcom.2014.03.038. [Google Scholar] [CrossRef]
72. Lin D, Liu CR, Cheng GJ. Single-layer graphene oxide reinforced metal matrix composites by laser sintering: microstructure and mechanical property enhancement. Acta Materialia. 2014;80:183–93. doi:10.1016/j.actamat.2014.07.038. [Google Scholar] [CrossRef]
73. Zhai W, Shi X, Yao J, Ibrahim AMM, Xu Z, Zhu Q, et al. Investigation of mechanical and tribological behaviors of multilayer graphene reinforced Ni3Al matrix composites. Comp Part B: Eng. 2015;70:149–55. doi:10.1016/j.compositesb.2014.10.052. [Google Scholar] [CrossRef]
74. Çelik Y, Çelik A, Flahaut E, Suvaci E. Anisotropic mechanical and functional properties of graphene-based alumina matrix nanocomposites. J Eur Cer Soc. 2016;36(8):2075–86. doi:10.1016/j.jeurceramsoc.2016.02.032. [Google Scholar] [CrossRef]
75. Chen B, Liu X, Zhao X, Wang Z, Wang L, Jiang W, et al. Preparation and properties of reduced graphene oxide/fused silica composites. Carbon. 2014;77:66–75. doi:10.1016/j.carbon.2014.05.004. [Google Scholar] [CrossRef]
76. Kwon S-M, Lee S-J, Shon I-J. Enhanced properties of nanostructured ZrO2-graphene composites rapidly sintered via high-frequency induction heating. Cer Int. 2015;41(1):835–42. doi:10.1016/j.ceramint.2014.08.042. [Google Scholar] [CrossRef]
77. Ramirez C, Figueiredo FM, Miranzo P, Poza P, Osendi MI. Graphene nanoplatelet/silicon nitride composites with high electrical conductivity. Carbon. 2012;50(10):3607–15. doi:10.1016/j.carbon.2012.03.031. [Google Scholar] [CrossRef]
78. Román-Manso B, Chevillotte Y, Osendi MI, Belmonte M, Miranzo P. Thermal conductivity of silicon carbide composites with highly oriented graphene nanoplatelets. J Eur Cer Soc. 2016;36(16):3987–93. doi:10.1016/j.jeurceramsoc.2016.06.016. [Google Scholar] [CrossRef]
79. Sedlák R, Kovalčíková A, Múdra E, Rutkowski Pł, Dubiel A, Girman V, et al. Boron carbide/graphene platelet ceramics with improved fracture toughness and electrical conductivity. J Eur Cer Soc. 2017;37(12):3773–80. doi:10.1016/j.jeurceramsoc.2017.04.061. [Google Scholar] [CrossRef]
80. Dilandro L, Dibenedetto A, Groeger J. The effect of fiber-matrix stress transfer on the strength of fiber-reinforced composite materials. Polym Compos. 1988;9(3):209–21. doi:10.1002/pc.750090308. [Google Scholar] [CrossRef]
81. Kumar HP, Xavior MA. Graphene reinforced metal matrix composite (GRMMCa review. Proce Eng. 2014;97:1033–40. doi:10.1016/j.proeng.2014.12.381. [Google Scholar] [CrossRef]
82. Young RJ, Kinloch IA. Graphene composites. In: Wiley Encyclopedia of Composites. Wiley; 2011. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781118097298.weoc102. [Google Scholar]
83. Hu Z, Tong G, Lin D, Chen C, Guo H, Xu J, et al. Graphene-reinforced metal matrix nanocomposites-a review. Mat Sci Technol. 2016;32(9):930–53. doi:10.1080/02670836.2015.1104018. [Google Scholar] [CrossRef]
84. Zhou B-Y, Fan S-J, Fan Y-C, Zheng Q, Zhang X, Jiang W, et al. Recent progress in ceramic matrix composites reinforced with graphene nanoplatelets. Rare Metals. 2020;39:513–28. doi:10.1007/s12598-019-01306-2. [Google Scholar] [CrossRef]
85. Markandan K, Chin JK, Tan MT. Recent progress in graphene based ceramic composites: a review. J Mat Res. 2017;32(1):84–106. doi:10.1557/jmr.2016.390. [Google Scholar] [CrossRef]
86. Zhong Z, Jiang X, Sun H, Wu Z, Yang L, Matamoros-Veloza A. Recent research on the optimization of interfacial structure and interfacial interaction mechanisms of metal matrix composites: a review. Adv Eng Mater. 2024;26(23):2401392. doi:10.1002/adem.202401392. [Google Scholar] [CrossRef]
87. Fan R, Zheng Q, Liu Y, Fan T. Insights into the interfacial bonding strength of TiB/Ti: a first principles study. J Appl Phys. 2019;126(3):035304. doi:10.1063/1.5109647. [Google Scholar] [CrossRef]
88. Wriggers P, Zavarise G, Zohdi T. A computational study of interfacial debonding damage in fibrous composite materials. Comput Mat Sci. 1998;12(1):39–56. doi:10.1016/S0927-0256(98)00025-1. [Google Scholar] [CrossRef]
89. Wang L, Jin J, Yang P, Li S, Tang S, Zong Y, et al. Effect of interfacial bonding on dislocation strengthening in graphene nanosheet reinforced iron composite: a molecular dynamics study. Comput Mater Sci. 2021;191:110309. doi:10.1016/j.commatsci.2021.110309. [Google Scholar] [CrossRef]
90. Tsai SW. Introduction to composite materials. 1st ed. New York: Routledge; 2018. doi:10.1201/9780203750148. [Google Scholar] [CrossRef]
91. Babaei M, Asemi K. Static, dynamic and natural frequency analyses of functionally graded carbon nanotube annular sector plates resting on viscoelastic foundation. SN Appl Sci. 2020;2:1–21. [Google Scholar]
92. Hosseini SM. Gaussian thermal shock-induced thermoelastic wave propagation in an FG multilayer hybrid nanocomposite cylinder reinforced by GPLs and CNTs. Thin-Walled Struct. 2021;166:108108. doi:10.1016/j.tws.2021.108108. [Google Scholar] [CrossRef]
93. Mohammadimehr M, Mohammadi-Dehabadi A, Alavi SA, Alambeigi K, Bamdad M, Yazdani R, et al. Bending, buckling, and free vibration analyses of carbon nanotube reinforced composite beams and experimental tensile test to obtain the mechanical properties of nanocomposite. Steel Compos Struct, Int J. 2018;29(3):405–22. doi:10.12989/scs.2018.29.3.405. [Google Scholar] [CrossRef]
94. Ruoff RS, Lorents DC. Mechanical and thermal properties of carbon nanotubes. Carbon. 1995;33(7):925–30. doi:10.1016/0008-6223(95)00021-5. [Google Scholar] [CrossRef]
95. Salvetat J-P, Bonard J-M, Thomson N, Kulik A, Forro L, Benoit W, et al. Mechanical properties of carbon nanotubes. Appl Phy A. 1999;69(3):255–60. doi:10.1007/s003390050999. [Google Scholar] [CrossRef]
96. Jamal-Omidi M, Sabour MH, ShayanMehr M, Sazesh S. Predicting Young’s modulus of CNT-reinforced polymers. Computat Mat Sci. 2015;108:34–7. doi:10.1016/j.commatsci.2015.06.007. [Google Scholar] [CrossRef]
97. Shen H-S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos Struct. 2009;91(1):9–19. doi:10.1016/j.compstruct.2009.04.026. [Google Scholar] [CrossRef]
98. Wang Z-X, Xu J, Qiao P. Nonlinear low-velocity impact analysis of temperature-dependent nanotube-reinforced composite plates. Compos Struct. 2014;108:423–34. doi:10.1016/j.compstruct.2013.09.024. [Google Scholar] [CrossRef]
99. Zhang L, Cui W, Liew K. Vibration analysis of functionally graded carbon nanotube reinforced composite thick plates with elastically restrained edges. Int J Mech Sci. 2015;103:9–21. doi:10.1016/j.ijmecsci.2015.08.021. [Google Scholar] [CrossRef]
100. Kiarasi F, Asadi A, Babaei M, Asemi K, Hosseini M. Dynamic analysis of functionally graded carbon nanotube (FGCNT) reinforced composite beam resting on viscoelastic foundation subjected to impulsive loading. J Computat Appl Mech. 2022;53(1):1–23. doi:10.22059/jcamech.2022.339008.693. [Google Scholar] [CrossRef]
101. Kiarasi F, Babaei M, Dimitri R, Tornabene F. Hygrothermal modeling of the buckling behavior of sandwich plates with nanocomposite face sheets resting on a Pasternak foundation. Contin Mech Thermodyn. 2021;33(4):911–32. doi:10.1007/s00161-020-00929-6. [Google Scholar] [CrossRef]
102. Malekzadeh P, Heydarpour Y. Mixed Navier-layerwise differential quadrature three-dimensional static and free vibration analysis of functionally graded carbon nanotube reinforced composite laminated plates. Meccanica. 2015;50(1):143–67. doi:10.1007/s11012-014-0061-4. [Google Scholar] [CrossRef]
103. Lin F, Xiang Y, Shen H-S. Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites-a molecular dynamics simulation. Compos Part B: Eng. 2017;111:261–9. doi:10.1016/j.compositesb.2016.12.004. [Google Scholar] [CrossRef]
104. Shen H-S, Xiang Y, Lin F. Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Comput Meth Appl Mech Eng. 2017;319:175–93. doi:10.1016/j.cma.2017.02.029. [Google Scholar] [CrossRef]
105. Babaei M, Kiarasi F, Tehrani MS, Hamzei A, Mohtarami E, Asemi K. Three dimensional free vibration analysis of functionally graded graphene reinforced composite laminated cylindrical panel. Proc Institut Mech Eng, Part L: J Mat: Des Appl. 2022;236(8):1501–14. doi:10.1177/14644207211073445. [Google Scholar] [CrossRef]
106. Asgari GR, Arabali A, Babaei M, Asemi K. Dynamic instability of sandwich beams made of isotropic core and functionally graded graphene platelets-reinforced composite face sheets. Int J Struct Stab Dyn. 2022;22(8):2250092. doi:10.1142/S0219455422500924. [Google Scholar] [CrossRef]
107. Khatounabadi M, Jafari M, Asemi K. Low-velocity impact analysis of functionally graded porous circular plate reinforced with graphene platelets. Waves Random Complex Media. 2022;38(3):1–27. doi:10.1080/17455030.2022.2091182. [Google Scholar] [CrossRef]
108. Shen H-S, Xiang Y, Lin F. Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin-Walled Structs. 2017;118(10):229–37. doi:10.1016/j.tws.2017.05.006. [Google Scholar] [CrossRef]
109. Zhou Y, Zhang Y, Nyasha Chirukam B, Li J, Lu C, Babaei M, et al. Free vibration analyses of stiffened functionally graded graphene-reinforced composite multilayer cylindrical panel. Mathematics. 2023;11(17):3662. doi:10.3390/math11173662. [Google Scholar] [CrossRef]
110. Kalhori A, Bayat MJ, Asemi K. Buckling response of functionally graded multilayer graphene. Front Mech Eng. 2023;9:1293713. doi:10.3389/fmech.2023.1293713. [Google Scholar] [CrossRef]
111. Reddy JN. Mechanics of laminated composite plates and shells: theory and analysis. 2nd ed. Boca Raton: CRC Press; 2003. doi:10.1201/b12409. [Google Scholar] [CrossRef]
112. Shariyat M, Behzad H, Shaterzadeh A. 3D thermomechanical buckling analysis of perforated annular sector plates with multiaxial material heterogeneities based on curved B-spline elements. Compos Struct. 2018;188(5):89–103. doi:10.1016/j.compstruct.2017.12.065. [Google Scholar] [CrossRef]
113. Shariyat M, Mohammadjani R. Three-dimensional dynamic stress and vibration analyses of thick singular-kernel fractional-order viscoelastic annular rotating discs under nonuniform loads. Int J Struct Stab Dyn. 2020;20(1):2050007. doi:10.1142/S0219455420500078. [Google Scholar] [CrossRef]
114. Behravan Rad A, Shariyat M. A three-dimensional elasticity solution for two-directional FGM annular plates with non-uniform elastic foundations subjected to normal and shear tractions. Acta Mechanica Solida Sinica. 2013;26(6):671–90. doi:10.1016/S0894-9166(14)60010-0. [Google Scholar] [CrossRef]
115. Shariyat M, Khosravi M, Ariatapeh MY, Najafipour M. Nonlinear stress and deformation analysis of pressurized thick-walled hyperelastic cylinders with experimental verifications and material identifications. Int J Press Vessel Piping. 2020;188(6):104211. doi:10.1016/j.ijpvp.2020.104211. [Google Scholar] [CrossRef]
116. Behzad H, Shaterzadeh A, Shariyat M. Thermal buckling analysis of functionally graded perforated annular sector plates using 3D elasticity theory. J Thermal Stress. 2017;40(12):1545–62. doi:10.1080/01495739.2017.1353895. [Google Scholar] [CrossRef]
117. Shariyat M, Mohammadjani R. Three-dimensional stress field analysis of rotating thick bidirectional functionally graded axisymmetric annular plates with nonuniform loads and elastic foundations. J Compos Mat. 2014;48(23):2879–904. doi:10.1177/00219983135033. [Google Scholar] [CrossRef]
118. Shariyat M, Yazdani Ariatapeh M. 3D hybrid semi-analytical creep, dissipation, and dynamic stress analyses of abruptly pressurized finite-length thick visco-hyperelastic cylinders. Acta Mechanica. 2023;234(12):6451–80. doi:10.1007/s00707-023-03717-w. [Google Scholar] [CrossRef]
119. Ghatage PS, Kar VR, Sudhagar PE. On the numerical modelling and analysis of multi-directional functionally graded composite structures: a review. Compos Struct. 2020;236:111837. doi:10.1016/j.compstruct.2019.111837. [Google Scholar] [CrossRef]
120. Shariyat M, Asemi K. 3D energy-based finite element elasticity approach for shear postbuckling analysis of functionally graded plates on elastic foundations. Compos Struct. 2016;152:579–91. doi:10.1016/j.compstruct.2016.05.057. [Google Scholar] [CrossRef]
121. Shariyat M, Asemi K. Three-dimensional non-linear elasticity-based 3D cubic B-spline finite element shear buckling analysis of rectangular orthotropic FGM plates surrounded by elastic foundations. Compos Part B: Eng. 2014;56(3):934–47. doi:10.1016/j.compositesb.2013.09.027. [Google Scholar] [CrossRef]
122. Asemi K, Shariyat M, Salehi M, Ashrafi H. A full compatible three-dimensional elasticity element for buckling analysis of FGM rectangular plates subjected to various combinations of biaxial normal and shear loads. Finite Elem Anal Des. 2013;74:9–21. doi:10.1016/j.finel.2013.05.011. [Google Scholar] [CrossRef]
123. Ghaznavi A, Shariyat M. Real time finite element simulation of thick and thin sandwich plate with viscoelastic core and embedded SMA wires. J Computat Appl Mech. 2022;53(2):219–43. doi:10.22059/JCAMECH.2022.337563.686. [Google Scholar] [CrossRef]
124. Kirchhoff G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. Journal Für Die Reine Und Angewandte Mathematik. 1850;1850(40):51–88. [Google Scholar]
125. Mindlin RD. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J Appl Mech. 1951 Mar;18(1):31–8. doi:10.1115/1.4010217. [Google Scholar] [CrossRef]
126. Reissner E. On bending of elastic plates. Quarter Appl Mathe. 1947;5(1):55–68. doi:10.1090/qam/20440. [Google Scholar] [CrossRef]
127. Reissner E. The effect of transverse shear deformation on the bending of elastic plates. J Appl Mech. 1945;12(2):A69–77. doi:10.1115/1.4009435. [Google Scholar] [CrossRef]
128. Wang CM, Lim G, Reddy J, Lee K. Relationships between bending solutions of Reissner and Mindlin plate theories. Eng Struct. 2001;23(7):838–49. doi:10.1016/S0141-0296(00)00092-4. [Google Scholar] [CrossRef]
129. Panc V. Theories of elastic plates. 1st ed. Dordrecht: Springer Science & Business Media; 1975. Series: Mechanics of Surface Structure. Originally published in Czech. Available from: https://link.springer.com/book/9789401019088. [Google Scholar]
130. Reddy JN. A simple higher-order theory for laminated composite plates. J Appl Mech. 1984;51(4):745–52. doi:10.1115/1.3167719. [Google Scholar] [CrossRef]
131. Levinson M. An accurate, simple theory of the statics and dynamics of elastic plates. Mech Res Commun. 1980;7(6):343–50. doi:10.1016/0093-6413(80)90049-X. [Google Scholar] [CrossRef]
132. Yu TT, Yin S, Bui TQ, Hirose S. A simple FSDT-based isogeometric analysis for geometrically nonlinear analysis of functionally graded plates. Finite Eleme Anal Des. 2015;96(18–19):1–10. doi:10.1016/j.finel.2014.11.003. [Google Scholar] [CrossRef]
133. Thai H-T, Choi D-H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos Struct. 2013;101(1–3):332–40. doi:10.1016/j.compstruct.2013.02.019. [Google Scholar] [CrossRef]
134. Thai H-T, Kim S-E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos Struct. 2013;96(7):165–73. doi:10.1016/j.compstruct.2012.08.025. [Google Scholar] [CrossRef]
135. Mechab I, Atmane HA, Tounsi A, Belhadj HA, Bedia EAA. A two variable refined plate theory for the bending analysis of functionally graded plates. Acta Mechanica Sinica. 2010;26(6):941–9. doi:10.1007/s10409-010-0372-1. [Google Scholar] [CrossRef]
136. Thai H-T, Choi D-H. A refined plate theory for functionally graded plates resting on elastic foundation. Compos Sci Technol. 2011;71(16):1850–8. doi:10.1016/j.compscitech.2011.08.016. [Google Scholar] [CrossRef]
137. Shimpi RP. Refined plate theory and its variants. AIAA J. 2002;40(1):137–46. doi:10.2514/2.1622. [Google Scholar] [CrossRef]
138. Thai H-T, Kim S-E. Free vibration of laminated composite plates using two variable refined plate theory. Int J Mech Sci. 2010;52(4):626–33. doi:10.1016/j.ijmecsci.2010.01.002. [Google Scholar] [CrossRef]
139. Mechab I, Mechab B, Benaissa S. Static and dynamic analysis of functionally graded plates using four-variable refined plate theory by the new function. Compos Part B: Eng. 2013;45(1):748–57. doi:10.1016/j.compositesb.2012.07.015. [Google Scholar] [CrossRef]
140. Tounsi A, Houari MSA, Benyoucef S. A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aeros Sci Technol. 2013;24(1):209–20. doi:10.1016/j.ast.2011.11.009. [Google Scholar] [CrossRef]
141. El Meiche N, Tounsi A, Ziane N, Mechab I. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. Int J Mech Sci. 2011;53(4):237–47. doi:10.1016/j.ijmecsci.2011.01.004. [Google Scholar] [CrossRef]
142. Yaghoobi H, Fereidoon A. Mechanical and thermal buckling analysis of functionally graded plates resting on elastic foundations: an assessment of a simple refined nth-order shear deformation theory. Compos Part B: Eng. 2014;62:54–64. doi:10.1016/j.compositesb.2014.02.014. [Google Scholar] [CrossRef]
143. Mantari J, Soares CG. A quasi-3D tangential shear deformation theory with four unknowns for functionally graded plates. Acta Mechanica. 2015;226:625–42. doi:10.1007/s00707-014-1192-3. [Google Scholar] [CrossRef]
144. Mantari J, Soares CG. Four-unknown quasi-3D shear deformation theory for advanced composite plates. Compos Struct. 2014;109:231–9. doi:10.1016/j.compstruct.2013.10.047. [Google Scholar] [CrossRef]
145. Mantari J, Soares CG. A trigonometric plate theory with 5-unknowns and stretching effect for advanced composite plates. Compos Struct. 2014;107(2):396–405. doi:10.1016/j.compstruct.2013.07.046. [Google Scholar] [CrossRef]
146. Thai H-T, Kim S-E. A simple quasi-3D sinusoidal shear deformation theory for functionally graded plates. Compo Struct. 2013;99(1):172–80. doi:10.1016/j.compstruct.2012.11.030. [Google Scholar] [CrossRef]
147. Bennoun M, Houari MSA, Tounsi A. A novel five-variable refined plate theory for vibration analysis of functionally graded sandwich plates. Mech Adv Mat Struct. 2016;23(4):423–31. doi:10.1080/15376494.2014.984088. [Google Scholar] [CrossRef]
148. Hebali H, Tounsi A, Houari MSA, Bessaim A, Bedia EAA. New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J Eng Mech. 2014;140(2):374–83. doi:10.1061/(ASCE)EM.1943-7889.0000665. [Google Scholar] [CrossRef]
149. Bessaim A, Houari MS, Tounsi A, Mahmoud S, Bedia EAA. A new higher-order shear and normal deformation theory for the static and free vibration analysis of sandwich plates with functionally graded isotropic face sheets. J Sandwich Struct Mat. 2013;15(6):671–703. doi:10.1177/1099636213498888. [Google Scholar] [CrossRef]
150. Zenkour AM. Simplified theory for hygrothermal response of angle-ply composite plates. AIAA J. 2014;52(7):1466–73. doi:10.2514/1.J052631. [Google Scholar] [CrossRef]
151. Mittelstedt C. Principle of virtual displacements. In: Structural mechanics in lightweight engineering. Cham: Springer; 2021. p. 371–403. doi:10.1007/978-3-030-75193-7. [Google Scholar] [CrossRef]
152. Como M. Virtual displacements principle, existence and uniqueness for elastic no tension bodies. Meccanica. 2017;52(6):1397–405. doi:10.1007/s11012-016-0480-5. [Google Scholar] [CrossRef]
153. Reissner E. On a mixed variational theorem and on shear deformable plate theory. Int J Num Meth Eng. 1986;23(2):193–8. doi:10.1002/nme.1620230203. [Google Scholar] [CrossRef]
154. Reissner E. On a certain mixed variational theorem and a proposed application. Int J Num Meth Eng. 1984;20(7):1366–8. doi:10.1002/nme.1620200714. [Google Scholar] [CrossRef]
155. Carrera E. A class of two-dimensional theories for anisotropic multilayered plates analysis. Atti della accademia delle scienze di Torino Classe di scienze fisiche matematiche e naturali. 1995;19:1–39. [Google Scholar]
156. Carrera E. A study of transverse normal stress effect on vibration of multilayered plates and shells. J Sou Vibrat. 1999;225(5):803–29. doi:10.1006/jsvi.1999.2271. [Google Scholar] [CrossRef]
157. Carrera E. Layer-wise mixed models for accurate vibrations analysis of multilayered plates. J Appl Mech. 1998;65(4):820–28. doi:10.1115/1.2791917. [Google Scholar] [CrossRef]
158. Carrera E, Giunta G, Petrolo M. Beam structures: classical and advanced theories. Hoboken: John Wiley & Sons; 2011. Avilable from: https://www.wiley.com/en-us/Beam+Structures%3A+Classical+and+Advanced+Theories-p-9781119951049. [Google Scholar]
159. Carrera E, Brischetto S, Nali P. Plates and shells for smart structures: classical and advanced theories for modeling and analysis. Torino, Italy: John Wiley & Sons; 2011. Avilable from: https://www.wiley.com/en-us/Plates+and+Shells+for+Smart+Structures%3A+Classical+and+Advanced+Theories+for+Modeling+and+Analysis-p-9781119951124. [Google Scholar]
160. Carrera E, Cinefra M, Petrolo M, Zappino E. Finite element analysis of structures through unified formulation. Hoboken: John Wiley & Sons; 2014. Avilable from: https://www.wiley.com/en-gb/Finite+Element+Analysis+of+Structures+through+Unified+Formulation-p-9781119941217. [Google Scholar]
161. Lei Z, Zhang L, Liew K. Analysis of laminated CNT reinforced functionally graded plates using the element-free kp-Ritz method. Compos Part B: Eng. 2016;84:211–21. doi:10.1016/j.compositesb.2015.08.081. [Google Scholar] [CrossRef]
162. Alibeigloo A. Static analysis of functionally graded carbon nanotube-reinforced composite plate embedded in piezoelectric layers by using theory of elasticity. Compos Struct. 2013;95(4):612–22. doi:10.1016/j.compstruct.2012.08.018. [Google Scholar] [CrossRef]
163. Zhu P, Lei Z, Liew KM. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos Struct. 2012;94(4):1450–60. doi:10.1016/j.compstruct.2011.11.010. [Google Scholar] [CrossRef]
164. Natarajan S, Haboussi M, Manickam G. Application of higher-order structural theory to bending and free vibration analysis of sandwich plates with CNT reinforced composite facesheets. Compos Struct. 2014;113:197–207. doi:10.1016/j.compstruct.2014.03.007. [Google Scholar] [CrossRef]
165. Alibeigloo A, Emtehani A. Static and free vibration analyses of carbon nanotube-reinforced composite plate using differential quadrature method. Meccanica. 2015;50(1):61–76. doi:10.1007/s11012-014-0050-7. [Google Scholar] [CrossRef]
166. Onvani D, Jafari A, Dehkordi MB. Carrera unified formulation for bending and free vibration analysis of sandwich plate with FG-CNT faces considering the both soft and stiff cores. Mech Adv Mat Struct. 2022;29(27):6718–32. doi:10.1080/15376494.2021.1983899. [Google Scholar] [CrossRef]
167. Hung P, Thai CH, Phung-Van P. Isogeometric bending and free vibration analyses of carbon nanotube-reinforced magneto-electric-elastic microplates using a four variable refined plate theory. Comput Struct. 2023;287(1–2):107121. doi:10.1016/j.compstruc.2023.107121. [Google Scholar] [CrossRef]
168. Cho J. Nonlinear bending analysis of FG-CNTRC plate resting on elastic foundation by natural element method. Eng Analy Bound Elem. 2022;141(8–10):65–74. doi:10.1016/j.enganabound.2022.05.008. [Google Scholar] [CrossRef]
169. Van Do VN, Lee C-H. Nonlinear bending analysis of carbon nanotube-reinforced composite plates in combined thermal and mechanical loading. Acta Mechanica. 2022;233(8):3365–91. doi:10.1007/s00707-022-03268-6. [Google Scholar] [CrossRef]
170. Li J, Lin J, Guan Y, Naceur H, Bao Y, Lu J, et al. Thermomechanical bending of functionally graded carbon nanotubes reinforced composite plate by meshless method. Polymer Compos. 2024; 45(14):13063–75. doi:10.1002/pc.28686. [Google Scholar] [CrossRef]
171. Kumar M, Rani R, Sarangi SK. Bending analysis of smart functionally graded CNT reinforced composite plates. Int Res J Adv Eng Manag (IRJAEM). 2024;2(5):1541–7. doi:10.47392/IRJAEM.2024.0209. [Google Scholar] [CrossRef]
172. Song M, Yang J, Kitipornchai S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos Part B: Eng. 2018;134(12):106–13. doi:10.1016/j.compositesb.2017.09.043. [Google Scholar] [CrossRef]
173. Thai CH, Ferreira A, Tran T, Phung-Van P. Free vibration, buckling and bending analyses of multilayer functionally graded graphene nanoplatelets reinforced composite plates using the NURBS formulation. Compos Struct. 2019;220(2):749–59. doi:10.1016/j.compstruct.2019.03.100. [Google Scholar] [CrossRef]
174. García-Macías E, Rodriguez-Tembleque L, Sáez A. Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos Struct. 2018;186:123–38. doi:10.1016/j.compstruct.2017.11.076. [Google Scholar] [CrossRef]
175. Shen H-S, Xiang Y, Lin F. Nonlinear bending of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations in thermal environments. Compos Struct. 2017;170:80–90. doi:10.1016/j.compstruct.2017.03.001. [Google Scholar] [CrossRef]
176. Gholami R, Ansari R. Large deflection geometrically nonlinear analysis of functionally graded multilayer graphene platelet-reinforced polymer composite rectangular plates. Compos Struct. 2017;180:760–71. doi:10.1016/j.compstruct.2017.08.053. [Google Scholar] [CrossRef]
177. Zhao Z, Feng C, Dong Y, Wang Y, Yang J. Geometrically nonlinear bending of functionally graded nanocomposite trapezoidal plates reinforced with graphene platelets (GPLs). Int J Mech Mat Des. 2019;15:791–800. doi:10.1007/s10999-019-09442-4. [Google Scholar] [CrossRef]
178. Guo W, Li Q, Babaei H. Nonlinear analysis of thermal-mechanical bending of laminated composite shallow arches reinforced with GPLs. Eng Anal Bound Elem. 2023;153:1–11. doi:10.1016/j.enganabound.2023.04.036. [Google Scholar] [CrossRef]
179. Zou Y, Kiani Y. Vibrations of nonlocal polymer-GPL plates at nanoscale: application of a quasi-3D plate model. Mathematics. 2023;11(19):4109. doi:10.3390/math11194109. [Google Scholar] [CrossRef]
180. Lei Z, Zhang L, Liew K. Buckling analysis of CNT reinforced functionally graded laminated composite plates. Compos Struct. 2016;152:62–73. doi:10.1016/j.compstruct.2016.05.047. [Google Scholar] [CrossRef]
181. Lei Z, Liew K, Yu J. Buckling analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method. Compos Struct. 2013;98:160–8. doi:10.1016/j.compstruct.2012.11.006. [Google Scholar] [CrossRef]
182. Zhang L, Lei Z, Liew K. Buckling analysis of FG-CNT reinforced composite thick skew plates using an element-free approach. Compos Part B: Eng. 2015;75(1):36–46. doi:10.1016/j.compositesb.2015.01.033. [Google Scholar] [CrossRef]
183. Zhang L, Ardestani MM, Liew K. Isogeometric approach for buckling analysis of CNT-reinforced composite skew plates under optimal CNT-orientation. Compos Struct. 2017;163(6348):365–84. doi:10.1016/j.compstruct.2016.12.047. [Google Scholar] [CrossRef]
184. Thang PT, Nguyen T-T, Lee J. A new approach for nonlinear buckling analysis of imperfect functionally graded carbon nanotube-reinforced composite plates. Compos Part B: Eng. 2017;127(6348):166–74. doi:10.1016/j.compositesb.2016.12.002. [Google Scholar] [CrossRef]
185. Kiani Y. Thermal post-buckling of temperature dependent sandwich plates with FG-CNTRC face sheets. J Thermal Stress. 2018;41(7):866–82. doi:10.1080/01495739.2018.1425645. [Google Scholar] [CrossRef]
186. Hu Z, Zhou C, Ni Z, Lin X, Li R. New symplectic analytic solutions for buckling of CNT reinforced composite rectangular plates. Compos Struct. 2023;303(16):116361. doi:10.1016/j.compstruct.2022.116361. [Google Scholar] [CrossRef]
187. Ipek C, Sofiyev A, Fantuzzi N, Efendiyeva SP. Buckling behavior of nanocomposite plates with functionally graded properties under compressive loads in elastic and thermal environments. J Appl Computat Mech. 2023;9(4):974–86. doi:10.22055/jacm.2023.43091.4019. [Google Scholar] [CrossRef]
188. Moradi Haghighi S, Alibeigloo A. Thermal buckling and vibrational analysis of carbon nanotube reinforced rectangular composite plates based on third-order shear deformation theory. J Eng Mech. 2023;149(6):04023026. doi:10.1061/JENMDT.EMENG-6875. [Google Scholar] [CrossRef]
189. Das S, Jana P. Buckling analysis of nonuniformly compressed rectangular FG-CNT reinforced laminated composite plate resting on elastic foundation: an analytical solution. Mech Adv Mater Struct. 2024;31(30):12699–720. doi:10.1080/15376494.2024.2327645. [Google Scholar] [CrossRef]
190. Song M, Yang J, Kitipornchai S, Zhu W. Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int J Mech Sci. 2017;131:345–55. doi:10.1016/j.ijmecsci.2017.07.017. [Google Scholar] [CrossRef]
191. Geng X, Zhao L, Zhou W. Finite-element buckling analysis of functionally graded GPL-reinforced composite plates with a circular hole. Mech Based Des Struct Mach. 2021;49(7):1028–44. doi:10.1080/15397734.2019.1707688. [Google Scholar] [CrossRef]
192. Wu H, Kitipornchai S, Yang J. Thermal buckling and postbuckling of functionally graded graphene nanocomposite plates. Mat Des. 2017;132(5696):430–41. doi:10.1016/j.matdes.2017.07.025. [Google Scholar] [CrossRef]
193. Kalhori A, Bayat MJ, Asemi K. Buckling analysis of stiffened functionally graded multilayer graphene platelet reinforced composite plate with circular cutout embedded on elastic support subjected to in-plane normal and shear loads. Res Eng. 2023;20(6348):101563. doi:10.1016/j.rineng.2023.101563. [Google Scholar] [CrossRef]
194. Noroozi AR, Malekzadeh P, Dimitri R, Tornabene F. Meshfree radial point interpolation method for the vibration and buckling analysis of FG-GPLRC perforated plates under an in-plane loading. Eng Struct. 2020;221(12):111000. doi:10.1016/j.engstruct.2020.111000. [Google Scholar] [CrossRef]
195. Arefi M, Bidgoli EM-R, Rabczuk T. Thermo-mechanical buckling behavior of FG GNP reinforced micro plate based on MSGT. Thin-Walled Struct. 2019;142(1):444–59. doi:10.1016/j.tws.2019.04.054. [Google Scholar] [CrossRef]
196. Kiani Y. NURBS-based isogeometric thermal postbuckling analysis of temperature dependent graphene reinforced composite laminated plates. Thin-Walled Struct. 2018;125:211–9. doi:10.1016/j.tws.2018.01.024. [Google Scholar] [CrossRef]
197. Jiao P, Chen Z, Ma H, Cheng Z, Gu Y, Tao W. Post-buckling behavior of rectangular multilayer FG-GPLRC plate with initial geometric defects subjected to non-uniform in-plane compression loads in thermal environment. Mech Adv Mat Struct. 2024;31(3):693–712. doi:10.1080/15376494.2022.2119313. [Google Scholar] [CrossRef]
198. Xu W, Han H, Li Q, Mollajafari M, Scott F. Layerwise formulation of poroelastic composite plate under pre-buckling and thermal shock loading. Compos Struct. 2023;304:116343. doi:10.1016/j.compstruct.2022.116343. [Google Scholar] [CrossRef]
199. Bo L, Wang H. Nonlinear dynamic buckling and multi-objective design optimisation of FG-GPLRP plates. Int J Mech Sci. 2023;256(4):108516. doi:10.1016/j.ijmecsci.2023.108516. [Google Scholar] [CrossRef]
200. Selim B, Zhang L, Liew K. Vibration analysis of CNT reinforced functionally graded composite plates in a thermal environment based on Reddy’s higher-order shear deformation theory. Compo Struct. 2016;156(6348):276–90. doi:10.1016/j.compstruct.2015.10.026. [Google Scholar] [CrossRef]
201. Zhang L, Selim B. Vibration analysis of CNT-reinforced thick laminated composite plates based on Reddy’s higher-order shear deformation theory. Compos Struct. 2017;160:689–705. doi:10.1016/j.compstruct.2016.10.102. [Google Scholar] [CrossRef]
202. Hung DX, Tu TM, Dai Hao T. Free vibration analysis of laminated CNTRC plates using the pb2-Ritz method. J Mech Eng (JMechE). 2021;18(1):213–32. doi:10.24191/jmeche.v18i1.15181. [Google Scholar] [CrossRef]
203. Lei Z, Zhang L, Liew K. Free vibration analysis of laminated FG-CNT reinforced composite rectangular plates using the kp-Ritz method. Compos Struct. 2015;127:245–59. doi:10.1016/j.compstruct.2015.03.019. [Google Scholar] [CrossRef]
204. Mehar K, Panda SK. Geometrical nonlinear free vibration analysis of FG-CNT reinforced composite flat panel under uniform thermal field. Compos Struct. 2016;143:336–46. doi:10.1016/j.compstruct.2016.02.038. [Google Scholar] [CrossRef]
205. Bendenia N, Zidour M, Bousahla AA, Bourada F, Tounsi A, Benrahou KH, et al. Deflections, stresses and free vibration studies of FG-CNT reinforced sandwich plates resting on Pasternak elastic foundation. Comput Conc Int J. 2020;26(3):213–26. doi:10.12989/cac.2020.26.3.213. [Google Scholar] [CrossRef]
206. Wang Z-X, Shen H-S. Nonlinear vibration and bending of sandwich plates with nanotube-reinforced composite face sheets. Compos Part B: Eng. 2012;43(2):411–21. doi:10.1016/j.compositesb.2011.04.040. [Google Scholar] [CrossRef]
207. Sharif Zarei M, Hajmohammad MH, Mostafavifar M, Mohammadimehr M. Influence of temperature change and humidity condition on free vibration analysis of a nano composite sandwich plate resting on orthotropic Pasternak foundation by considering agglomeration effect. J Sandw Struct Mate. 2017;7:1099636217735118. doi:10.1177/1099636217735118. [Google Scholar] [CrossRef]
208. Singh AK, Bhar A. Isogeometric FE analysis of CNT-reinforced composite plates: free vibration. SN Appl Sci. 2019;1(9):1010. doi:10.1007/s42452-019-1027-x. [Google Scholar] [CrossRef]
209. Wang Z-X, Shen H-S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Computat Mat Sci. 2011;50(8):2319–30. doi:10.1016/j.commatsci.2011.03.005. [Google Scholar] [CrossRef]
210. Ansari R, Shahabodini A, Shojaei MF. Vibrational analysis of carbon nanotube-reinforced composite quadrilateral plates subjected to thermal environments using a weak formulation of elasticity. Compos Struct. 2016;139:167–87. doi:10.1016/j.compstruct.2015.11.079. [Google Scholar] [CrossRef]
211. Malekzadeh P, Zarei A. Free vibration of quadrilateral laminated plates with carbon nanotube reinforced composite layers. Thin-Walled Struct. 2014;82:221–32. doi:10.1016/j.tws.2014.04.016. [Google Scholar] [CrossRef]
212. Avey M, Kadioglu F, Ahmetolan S, Fantuzzi N. Mathematical modeling and solution of nonlinear vibration problem of laminated plates with CNT originating layers interacting with two-parameter elastic foundation. J Braz Soc Mech Sci Eng. 2023;45(3):185. doi:10.1007/s40430-023-04016-0. [Google Scholar] [CrossRef]
213. Hoseinzadeh M, Pilafkan R, Maleki VA. Size-dependent linear and nonlinear vibration of functionally graded CNT reinforced imperfect microplates submerged in fluid medium. Ocean Eng. 2023;268:113257. doi:10.1016/j.oceaneng.2022.113257. [Google Scholar] [CrossRef]
214. Song M, Kitipornchai S, Yang J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos Struct. 2017;159:579–88. doi:10.1016/j.compstruct.2016.09.070. [Google Scholar] [CrossRef]
215. Jafari P, Kiani Y. Free vibration of functionally graded graphene platelet reinforced plates: a quasi 3D shear and normal deformable plate model. Compos Struct. 2021;275:114409. doi:10.1016/j.compstruct.2021.114409. [Google Scholar] [CrossRef]
216. Reddy RMR, Karunasena W, Lokuge W. Free vibration of functionally graded-GPL reinforced composite plates with different boundary conditions. Aeros Sci Technol. 2018;78:147–56. doi:10.1016/j.ast.2018.04.019. [Google Scholar] [CrossRef]
217. Saiah B, Bachene M, Guemana M, Chiker Y, Attaf B. On the free vibration behavior of nanocomposite laminated plates contained piece-wise functionally graded graphene-reinforced composite plies. Eng Struct. 2022;253(12):113784. doi:10.1016/j.engstruct.2021.113784. [Google Scholar] [CrossRef]
218. Kiani Y. Isogeometric large amplitude free vibration of graphene reinforced laminated plates in thermal environment using NURBS formulation. Comput Meth Appl Mech Eng. 2018;332:86–101. doi:10.1016/j.cma.2017.12.015. [Google Scholar] [CrossRef]
219. Javani M, Kiani Y, Eslami MR. Application of generalized differential quadrature element method to free vibration of FG-GPLRC T-shaped plates. Eng Struct. 2021;242(4):112510. doi:10.1016/j.engstruct.2021.112510. [Google Scholar] [CrossRef]
220. Zhang J, Li L. Free vibration of functionally graded graphene platelets reinforced composite porous L-shaped folded plate. Eng Struct. 2023;297:116977. doi:10.1016/j.engstruct.2023.116977. [Google Scholar] [CrossRef]
221. Zhang L, Xiao L, Zou G, Liew K. Elastodynamic analysis of quadrilateral CNT-reinforced functionally graded composite plates using FSDT element-free method. Compos Struct. 2016;148:144–54. doi:10.1016/j.compstruct.2016.04.006. [Google Scholar] [CrossRef]
222. Selim B, Zhang L, Liew K. Impact analysis of CNT-reinforced composite plates based on Reddy’s higher-order shear deformation theory using an element-free approach. Compos Struct. 2017;170:228–42. doi:10.1016/j.compstruct.2017.03.026. [Google Scholar] [CrossRef]
223. Phung-Van P, Abdel-Wahab M, Liew K, Bordas S, Nguyen-Xuan H. Isogeometric analysis of functionally graded carbon nanotube-reinforced composite plates using higher-order shear deformation theory. Compos Struct. 2015;123:137–49. doi:10.1016/j.compstruct.2014.12.021. [Google Scholar] [CrossRef]
224. Wang Z-X, Shen H-S. Nonlinear dynamic response of nanotube-reinforced composite plates resting on elastic foundations in thermal environments. Nonlin Dynam. 2012;70(1):735–54. doi:10.1007/s11071-012-0491-2. [Google Scholar] [CrossRef]
225. Xue T, Qin X, Wang Z, Schmidt R, Zhang S. Dynamic analysis of CNT functionally graded piezolaminated structures using third-order shear deformation theory. Mech Adv Mater Struct. 2023;31(22):5547–63. doi:10.1080/15376494.2023.2217550. [Google Scholar] [CrossRef]
226. Kumar R, Jana P. Vibration response of FG-CNTRC plate resting on non-homogeneous elastic foundation via a closed-form dynamic stiffness formulation. Structures. 2023;57:105203. doi:10.1016/j.istruc.2023.105203. [Google Scholar] [CrossRef]
227. Kiani Y. Influence of graphene platelets on the response of composite plates subjected to a moving load. Mech Based Des Struct Mach. 2022;50(4):1123–36. doi:10.1080/15397734.2020.1744006. [Google Scholar] [CrossRef]
228. Yang FL, Wang YQ, Liu Y. Low-velocity impact response of axially moving functionally graded graphene platelet reinforced metal foam plates. Aerosp Sci Technol. 2022;123:107496. doi:10.1016/j.ast.2022.107496. [Google Scholar] [CrossRef]
229. Lu SF, Xue N, Ma WS, Song XJ, Jiang X. Linear and nonlinear dynamics responses of an axially moving laminated composite plate reinforced with graphene nanoplatelets. Int J Struct Stab Dyn. 2024;10:2550036. doi:10.1142/S021945542450036X. [Google Scholar] [CrossRef]
230. Zhang X, Chen B, Shao Z, Wang Q, Xiang P. A novel stochastic calculation scheme for dynamic response analysis of FG-GPLRC plate subject to a moving load. Acta Mechanica. 2024;235(4):1803–22. doi:10.1007/s00707-023-03813-x. [Google Scholar] [CrossRef]
231. Tian Y, Li Q, Feng Y, Yu Y, Wu D, Chen X, et al. Nonlinear dynamic analysis of the functionally graded graphene platelets reinforced porous plate under moving mass. Thin-Walled Struct. 2023;183:110363. doi:10.1016/j.tws.2022.110363. [Google Scholar] [CrossRef]
232. Ansari MI, Kumar A, Fic S, Barnat-Hunek D. Flexural and free vibration analysis of CNT-reinforced functionally graded plate. Materials. 2018;11(12):2387. doi:10.3390/ma11122387. [Google Scholar] [CrossRef]
233. Ardestani MM, Zhang L, Liew K. Isogeometric analysis of the effect of CNT orientation on the static and vibration behaviors of CNT-reinforced skew composite plates. Comput Meth Appl Mech Eng. 2017;317(39–41):341–79. doi:10.1016/j.cma.2016.12.009. [Google Scholar] [CrossRef]
234. Mehar K, Panda SK. Thermoelastic analysis of FG-CNT reinforced shear deformable composite plate under various loadings. Int J Comput Methods. 2017;14(2):1750019. doi:10.1142/S0219876217500190. [Google Scholar] [CrossRef]
235. Singh SD, Sahoo R. Static and free vibration analysis of functionally graded CNT reinforced sandwich plates using inverse hyperbolic shear deformation theory. J Strain Anal Eng Des. 2021;56(6):386–403. doi:10.1177/0309324720957568. [Google Scholar] [CrossRef]
236. Jamal-Omidi M, ShayanMehr M. An experimental study on the nonlinear free vibration response of epoxy and carbon fiber-reinforced composite containing single-walled carbon nanotubes. J Vibrat Cont. 2018;24(19):4529–40. doi:10.1177/1077546317729628. [Google Scholar] [CrossRef]
237. Ruan S, Gao P, Yang XG, Yu T. Toughening high performance ultrahigh molecular weight polyethylene using multiwalled carbon nanotubes. Polymer. 2003;44(19):5643–54. doi:10.1016/S0032-3861(03)00628-1. [Google Scholar] [CrossRef]
238. Ansari MI, Kumar A, Barnat-Hunek D, Suchorab Z, Andrzejuk W, Majerek D. Static and dynamic response of FG-CNT-reinforced rhombic laminates. Appl Sci. 2018;8(5):834. doi:10.3390/app8050834. [Google Scholar] [CrossRef]
239. Singh SD, Sahoo R. Static and free vibration analysis of functionally graded CNT reinforced composite plates using trigonometric shear deformation theory. Structures. 2020;28:685–96. doi:10.1016/j.istruc.2020.09.008. [Google Scholar] [CrossRef]
240. Mehar K, Panda SK, Mahapatra TR. Thermoelastic nonlinear frequency analysis of CNT reinforced functionally graded sandwich structure. Euro J Mech-A/Solids. 2017;65:384–96. doi:10.1016/j.euromechsol.2017.05.005. [Google Scholar] [CrossRef]
241. Gholami R, Ansari R. Nonlinear stability and vibration of pre/post-buckled multilayer FG-GPLRPC rectangular plates. Appl Mathem Modell. 2019;65:627–60. doi:10.1016/j.apm.2018.08.038. [Google Scholar] [CrossRef]
242. Maji P, Rout M, Karmakar A. The thermo-elastic vibration of graphene reinforced composite stiffened plate with general boundary conditions. Structures. 2021;33:99–112. doi:10.1016/j.istruc.2021.04.029. [Google Scholar] [CrossRef]
243. Lin H, Cao D, Xu Y. Vibration, buckling and aeroelastic analyses of functionally graded multilayer graphene-nanoplatelets-reinforced composite plates embedded in piezoelectric layers. Int J Appl Mech. 2018;10(3):1850023. doi:10.1142/S1758825118500230. [Google Scholar] [CrossRef]
244. Bo L, Wang H. Nonlinear dynamic instability and multi-objective design optimization of the GPLR-FGP plate under biaxial impacts. Compos Struct. 2023;312:116854. doi:10.1016/j.compstruct.2023.116854. [Google Scholar] [CrossRef]
245. Zghal S, Frikha A, Dammak F. Static analysis of functionally graded carbon nanotube-reinforced plate and shell structures. Compos Struct. 2017;176:1107–23. doi:10.1016/j.compstruct.2017.06.015. [Google Scholar] [CrossRef]
246. Ansari MI, Kumar A. Bending analysis of functionally graded CNT reinforced doubly curved singly ruled truncated rhombic cone. Mech Based Des Struct Mach. 2019;47(1):67–86. doi:10.1080/15397734.2018.1519635. [Google Scholar] [CrossRef]
247. Mehrabadi SJ, Aragh BS. Stress analysis of functionally graded open cylindrical shell reinforced by agglomerated carbon nanotubes. Thin-Walled Struct. 2014;80(3):130–41. doi:10.1016/j.tws.2014.02.016. [Google Scholar] [CrossRef]
248. Huang Y, Karami B, Shahsavari D, Tounsi A. Static stability analysis of carbon nanotube reinforced polymeric composite doubly curved micro-shell panels. Arch Civil Mech Eng. 2021;21(4):139. doi:10.1007/s43452-021-00291-7. [Google Scholar] [CrossRef]
249. Djilali N, Bousahla AA, Kaci A, Selim MM, Bourada F, Tounsi A, et al. Large cylindrical deflection analysis of FG carbon nanotube-reinforced plates in thermal environment using a simple integral HSDT. Steel Compos Struct Int J. 2022;42(6):779–89. doi:10.12989/scs.2022.42.6.779. [Google Scholar] [CrossRef]
250. Tornabene F, Fantuzzi N, Bacciocchi M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos Part B: Eng. 2017;115(6):449–76. doi:10.1016/j.compositesb.2016.07.011. [Google Scholar] [CrossRef]
251. Ebrahimi F, Dabbagh A, Rastgoo A. Static stability analysis of multi-scale hybrid agglomerated nanocomposite shells. Mech Based Des Struct Mach. 2023;51(1):501–17. doi:10.1080/15397734.2020.1848585. [Google Scholar] [CrossRef]
252. Mallek H, Mellouli H, Said LB, Wali M, Dammak F, Boujelbene M. Bending and free vibration analyses of CNTRC shell structures considering agglomeration effects with through-the-thickness stretch. Thin-Walled Struct. 2023;191(1):111036. doi:10.1016/j.tws.2023.111036. [Google Scholar] [CrossRef]
253. Shokrollahi H, Emdadi Derabi M. Deformation of an open sandwich cylindrical shell with CNT reinforced faces using HDQ method. Arab J Sci Eng. 2024;49(5):1–16. doi:10.1007/s13369-024-09339-1. [Google Scholar] [CrossRef]
254. Van Do VN, Lee C-H. Static bending and free vibration analysis of multilayered composite cylindrical and spherical panels reinforced with graphene platelets by using isogeometric analysis method. Eng Struct. 2020;215:110682. doi:10.1016/j.engstruct.2020.110682. [Google Scholar] [CrossRef]
255. Safarpour M, Rahimi A, Alibeigloo A. Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM. Mech Based Des Struct Mach. 2020;48(4):496–524. doi:10.1080/15397734.2019.1646137. [Google Scholar] [CrossRef]
256. Arefi M, Moghaddam SK, Bidgoli EM-R, Kiani M, Civalek O. Analysis of graphene nanoplatelet reinforced cylindrical shell subjected to thermo-mechanical loads. Compos Struct. 2021;255(13):112924. doi:10.1016/j.compstruct.2020.112924. [Google Scholar] [CrossRef]
257. Van Do VN, Lee C-H. Isogeometric nonlinear bending and instability analysis of cylindrical composite shells reinforced with graphene platelets. Compos Struct. 2021;258:113401. doi:10.1016/j.compstruct.2020.113401. [Google Scholar] [CrossRef]
258. Cho J-R. Large amplitude vibration of FG-GPL reinforced conical shell panels on elastic foundation. Materials. 2023;16(17):6056. doi:10.3390/ma16176056. [Google Scholar] [CrossRef]
259. Hajlaoui A, Chebbi E, Dammak F. Buckling analysis of carbon nanotube reinforced FG shells using an efficient solid-shell element based on a modified FSDT. Thin-Walled Struct. 2019;144:106254. doi:10.1016/j.tws.2019.106254. [Google Scholar] [CrossRef]
260. Thang PT, Thoi TN, Lee J. Closed-form solution for nonlinear buckling analysis of FG-CNTRC cylindrical shells with initial geometric imperfections. Eur J Mech-A/Solids. 2019;73:483–91. doi:10.1016/j.euromechsol.2018.10.008. [Google Scholar] [CrossRef]
261. Ninh DG. Nonlinear thermal torsional post-buckling of carbon nanotube-reinforced composite cylindrical shell with piezoelectric actuator layers surrounded by elastic medium. Thin-Walled Struct. 2018;123(4):528–38. doi:10.1016/j.tws.2017.11.027. [Google Scholar] [CrossRef]
262. Nam VH, Trung N-T, Phuong NT, Duc VM, Hung VT. Nonlinear torsional buckling of functionally graded carbon nanotube orthogonally reinforced composite cylindrical shells in thermal environment. Int J Appl Mech. 2020;12(7):2050072. doi:10.1142/S1758825120500726. [Google Scholar] [CrossRef]
263. Shen H-S. Torsional postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Compos Struct. 2014;116:477–88. doi:10.1016/j.compstruct.2014.05.039. [Google Scholar] [CrossRef]
264. Mehar K, Panda SK, Devarajan Y, Choubey G. Numerical buckling analysis of graded CNT-reinforced composite sandwich shell structure under thermal loading. Compos Struct. 2019;216:406–14. doi:10.1016/j.compstruct.2019.03.002. [Google Scholar] [CrossRef]
265. Manh DT, Anh VTT, Nguyen PD, Duc ND. Nonlinear post-buckling of CNTs reinforced sandwich-structured composite annular spherical shells. Int J Struct Stab Dyn. 2020;20(2):2050018. doi:10.1142/S0219455420500182. [Google Scholar] [CrossRef]
266. Duc ND, Nguyen PD, Cuong NH, Van Sy N, Khoa ND. An analytical approach on nonlinear mechanical and thermal post-buckling of nanocomposite double-curved shallow shells reinforced by carbon nanotubes. Proc Institut Mech Eng, Part C: J Mech Eng Sci. 2019;233(11):3888–903. doi:10.1177/0954406218802921. [Google Scholar] [CrossRef]
267. Chakraborty S, Dey T. Thermomechanical buckling and wrinkling characteristics of softcore sandwich panels with CNT reinforced composite face sheets. Eur J Mech-A/Solids. 2023;98(6):104894. doi:10.1016/j.euromechsol.2022.104894. [Google Scholar] [CrossRef]
268. You Q, Hua F, Huang Q, Zhou X. Efficient analysis on buckling of FG-CNT reinforced composite joined conical-cylindrical laminated shells based on GDQ method under multiple loading conditions. Mech Adv Mater Struct. 2024;31(29):1–18. doi:10.1080/15376494.2024.2302327. [Google Scholar] [CrossRef]
269. Dong DT, Hieu PT, Duc VM, Phuong NT, Tien NV, Nam VH. Nonlinear buckling analysis of stiffened carbon nanotube-reinforced cylindrical shells subjected to external pressure in thermal environment. Mech Compos Mat. 2023;59(4):779–94. doi:10.1007/s11029-023-10131-9. [Google Scholar] [CrossRef]
270. Wang Y, Feng C, Zhao Z, Yang J. Eigenvalue buckling of functionally graded cylindrical shells reinforced with graphene platelets (GPL). Compos Struct. 2018;202(5):38–46. doi:10.1016/j.compstruct.2017.10.005. [Google Scholar] [CrossRef]
271. Shen H-S, Xiang Y, Fan Y. Postbuckling of functionally graded graphene-reinforced composite laminated cylindrical panels under axial compression in thermal environments. Int J Mech Sci. 2018;135:398–409. doi:10.1016/j.ijmecsci.2017.11.031. [Google Scholar] [CrossRef]
272. Shen H-S, Xiang Y. Postbuckling of functionally graded graphene-reinforced composite laminated cylindrical shells subjected to external pressure in thermal environments. Thin-Walled Struct. 2018;124:151–60. doi:10.1016/j.tws.2017.12.005. [Google Scholar] [CrossRef]
273. Sun J, Ni Y, Gao H, Zhu S, Tong Z, Zhou Z. Torsional buckling of functionally graded multilayer graphene nanoplatelet-reinforced cylindrical shells. Int J Struct Stab Dyn. 2020;20(1):2050005. doi:10.1142/S0219455420500054. [Google Scholar] [CrossRef]
274. Wang Y, Feng C, Zhao Z, Lu F, Yang J. Torsional buckling of graphene platelets (GPLs) reinforced functionally graded cylindrical shell with cutout. Compos Struct. 2018;197:72–9. doi:10.1016/j.compstruct.2018.05.056. [Google Scholar] [CrossRef]
275. Wang Y, Feng C, Zhao Z, Yang J. Buckling of graphene platelet reinforced composite cylindrical shell with cutout. Int J Struct Stab Dyn. 2018;18(3):1850040. doi:10.1142/S0219455418500402. [Google Scholar] [CrossRef]
276. Liu D, Kitipornchai S, Chen W, Yang J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos Struct. 2018;189(1):560–9. doi:10.1016/j.compstruct.2018.01.106. [Google Scholar] [CrossRef]
277. Ansari R, Torabi J, Hasrati E. Postbuckling analysis of axially-loaded functionally graded GPL-reinforced composite conical shells. Thin-Walled Struct. 2020;148(8):106594. doi:10.1016/j.tws.2019.106594. [Google Scholar] [CrossRef]
278. Liu Z, Tornabene F, Dimitri R, Babaei M. Numerical study of the buckling response of stiffened FG graphene-reinforced multilayer composite cylindrical panels. Processes. 2024;12(3):430. doi:10.3390/pr12030430. [Google Scholar] [CrossRef]
279. Mollaei S, Babaei M, Asemi K. Torsional buckling of functionally graded graphene reinforced composite laminated cylindrical panel. Arch Appl Mech. 2023;93(2):427–35. doi:10.1007/s00419-022-02132-2. [Google Scholar] [CrossRef]
280. Abbaspour F, Hosseini S. Thermal buckling of piezoelectric graphene platelets reinforced cylindrical microshells using Navier’s and meshless methods. Mech Based Des Struct Mach. 2023:1–20. doi:10.1080/15397734.2023.2260466. [Google Scholar] [CrossRef]
281. Cho J-R. Investigation of buckling behavior of cracked FG cylindrical panels reinforced by graphene platelets. Symmetry. 2023;15(12):2162. doi:10.3390/sym15122162. [Google Scholar] [CrossRef]
282. Thomas B, Roy T. Vibration analysis of functionally graded carbon nanotube-reinforced composite shell structures. Acta Mechanica. 2016;227(2):581–99. doi:10.1007/s00707-015-1479-z. [Google Scholar] [CrossRef]
283. Song Z, Zhang L, Liew K. Vibration analysis of CNT-reinforced functionally graded composite cylindrical shells in thermal environments. Int J Mech Sci. 2016;115(4):339–47. doi:10.1016/j.ijmecsci.2016.06.020. [Google Scholar] [CrossRef]
284. Kamarian S, Salim M, Dimitri R, Tornabene F. Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int J Mech Sci. 2016;108:157–65. doi:10.1016/j.ijmecsci.2016.02.006. [Google Scholar] [CrossRef]
285. Kiani Y, Dimitri R, Tornabene F. Free vibration study of composite conical panels reinforced with FG-CNTs. Eng Struct. 2018;172(1):472–82. doi:10.1016/j.engstruct.2018.06.006. [Google Scholar] [CrossRef]
286. Tornabene F, Fantuzzi N, Bacciocchi M, Viola E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos Part B: Eng. 2016;89:187–218. doi:10.1016/j.compositesb.2015.11.016. [Google Scholar] [CrossRef]
287. Banić D, Bacciocchi M, Tornabene F, Ferreira AJ. Influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl Sci. 2017;7(12):1228. doi:10.3390/app7121228. [Google Scholar] [CrossRef]
288. Cho J-R. Free vibration responses of functionally graded CNT-reinforced composite conical shell panels. Polymers. 2023;15(9):1987. doi:10.3390/polym15091987. [Google Scholar] [CrossRef]
289. Sobhani E. Vibrational characteristics of fastening of a spherical shell with a coupled conical-conical shells strengthened with nanocomposite sandwiches contained agglomerated CNT face layers and GNP core under spring boundary conditions. Eng Anal Bound Elem. 2023;146(10):362–87. doi:10.1016/j.enganabound.2022.10.035. [Google Scholar] [CrossRef]
290. Babaei MJ, Jafari AA. Effect of thermal environment on the free vibration of functionally graded carbon nanotubes cylindrical-conical shell. J Therm Stress. 2024;47(1):35–58. doi:10.1080/01495739.2023.2271525. [Google Scholar] [CrossRef]
291. Dong Y, Zhu B, Wang Y, Li Y, Yang J. Nonlinear free vibration of graded graphene reinforced cylindrical shells: effects of spinning motion and axial load. J Sou Vibrat. 2018;437:79–96. doi:10.1016/j.jsv.2018.08.036. [Google Scholar] [CrossRef]
292. Amirabadi H, Farhatnia F, Eftekhari SA, Hosseini-Ara R. Free vibration analysis of rotating functionally graded GPL-reinforced truncated thick conical shells under different boundary conditions. Mech Based Des Struct Mach. 2022;50(11):3821–52. doi:10.1080/15397734.2020.1822183. [Google Scholar] [CrossRef]
293. Baghbadorani AA, Kiani Y. Free vibration analysis of functionally graded cylindrical shells reinforced with graphene platelets. Compos Struct. 2021;276:114546. doi:10.1016/j.compstruct.2021.114546. [Google Scholar] [CrossRef]
294. Ghabussi A, Ashrafi N, Shavalipour A, Hosseinpour A, Habibi M, Moayedi H, et al. Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech Based Des Struct Mach. 2021;49(5):738–62. doi:10.1080/15397734.2019.1705166. [Google Scholar] [CrossRef]
295. Jamalabadi MYA, Borji P, Habibi M, Pelalak R. Nonlinear vibration analysis of functionally graded GPL-RC conical panels resting on elastic medium. Thin-Walled Struct. 2021;160(12):107370. doi:10.1016/j.tws.2020.107370. [Google Scholar] [CrossRef]
296. Bidzard A, Malekzadeh P, Mohebpour S. Influences of pressure and thermal environment on nonlinear vibration characteristics of multilayer FG-GPLRC toroidal panels on nonlinear elastic foundation. Compos Struct. 2021;259(15):113503. doi:10.1016/j.compstruct.2020.113503. [Google Scholar] [CrossRef]
297. Wang YQ, Ye C, Zu JW. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aeros Sci Technol. 2019;85(12):359–70. doi:10.1016/j.ast.2018.12.022. [Google Scholar] [CrossRef]
298. Niu Y, Yao M. Linear and nonlinear vibrations of graphene platelet reinforced composite tapered plates and cylindrical panels. Aerosp Sci Technol. 2021;115(2):106798. doi:10.1016/j.ast.2021.106798. [Google Scholar] [CrossRef]
299. Permoon M, Farsadi T, Askarian A. Vibration analysis of sandwich cylindrical shells made of graphene platelet polymer-viscoelastic–ceramic/metal FG layers. Funct Compos Struct. 2023;5(1):015004. doi:10.1088/2631-6331/acbd28. [Google Scholar] [CrossRef]
300. Saboori R, Ghadiri M. Nonlinear forced vibration analysis of PFG-GPLRC conical shells under parametric excitation considering internal and external resonances. Thin-Walled Struct. 2024;196(13):111474. doi:10.1016/j.tws.2023.111474. [Google Scholar] [CrossRef]
301. Kiani Y. Dynamics of FG-CNT reinforced composite cylindrical panel subjected to moving load. Thin-Walled Struct. 2017;111:48–57. doi:10.1016/j.tws.2016.11.011. [Google Scholar] [CrossRef]
302. Asadi H, Wang Q. Dynamic stability analysis of a pressurized FG-CNTRC cylindrical shell interacting with supersonic airflow. Compos Part B: Eng. 2017;118(15):15–25. doi:10.1016/j.compositesb.2017.03.001. [Google Scholar] [CrossRef]
303. Jiao P, Chen Z, Li Y, Ma H, Wu J. Dynamic buckling analyses of functionally graded carbon nanotubes reinforced composite (FG-CNTRC) cylindrical shell under axial power-law time-varying displacement load. Compos Struct. 2019;220(10):784–97. doi:10.1016/j.compstruct.2019.04.048. [Google Scholar] [CrossRef]
304. Arumugam AB, Subramani M, Dalakoti M, Jindal P, Selvaraj R, Khalife E. Dynamic characteristics of laminated composite CNT reinforced MRE cylindrical sandwich shells using HSDT. Mech Based Des Struct Mach. 2021;51(7):4120–36. doi:10.1080/15397734.2021.1950550. [Google Scholar] [CrossRef]
305. Zhang L, Song Z, Qiao P, Liew K. Modeling of dynamic responses of CNT-reinforced composite cylindrical shells under impact loads. Comput Meth Appl Mech Eng. 2017;313(2):889–903. doi:10.1016/j.cma.2016.10.020. [Google Scholar] [CrossRef]
306. Amirabadi H, Afshari H, Sarafraz M, Rahmani S. Effects of non-uniformity in thickness and volume fraction of agglomerated CNTs on the dynamics of a spinning CNT-reinforced nanocomposite truncated conical shell. Noise Vib Worldw. 2024;55(3):167–85. doi:10.1177/09574565241235330. [Google Scholar] [CrossRef]
307. Nguyen PD, Duc ND. A semi-analytical sinusoidal shear deformation theory for nonlinear dynamic response and vibration of CNT-FGM doubly curved shallow shells. Acta Mechanica. 2024;235(4):2077–112. doi:10.1007/s00707-023-03824-8. [Google Scholar] [CrossRef]
308. Mellouli H, Mallek H, Louhichi R, Wali M, Dammak F, Alharbi S. Dynamic analysis of piezolaminated shell structures reinforced with agglomerated carbon nanotubes using an enhanced solid-shell element. Eng Comput. 2023;40:2363–83. doi:10.1007/s00366-023-01923-7. [Google Scholar] [CrossRef]
309. Rahimi E, Sadeghian M, Golmakani ME. Nonlinear bending examination of nanocomposite cylindrical shell exposed to mechanical loads using dynamic relaxation method. Proc Instit Mech Eng, Part N: J Nanom, Nanoeng Nanosyst. 2024;44:23977914231215229. doi:10.1177/23977914231215229. [Google Scholar] [CrossRef]
310. Wang A, Chen H, Zhang W. Nonlinear transient response of doubly curved shallow shells reinforced with graphene nanoplatelets subjected to blast loads considering thermal effects. Compos Struct. 2019;225:111063. doi:10.1016/j.compstruct.2019.111063. [Google Scholar] [CrossRef]
311. Shokrgozar A, Ghabussi A, Ebrahimi F, Habibi M, Safarpour H. Viscoelastic dynamics and static responses of a graphene nanoplatelets-reinforced composite cylindrical microshell. Mech Based Des Struct Mach. 2022;50(2):509–36. doi:10.1080/15397734.2020.1719509. [Google Scholar] [CrossRef]
312. Heydarpour Y, Malekzadeh P, Dimitri R, Tornabene F. Thermoelastic analysis of rotating multilayer FG-GPLRC truncated conical shells based on a coupled TDQM-NURBS scheme. Compos Struct. 2020;235(8):111707. doi:10.1016/j.compstruct.2019.111707. [Google Scholar] [CrossRef]
313. Amirabadi H, Farhatnia F, Eftekhari SA, Hosseini-Ara R. Wave propagation in rotating functionally graded GPL-reinforced cylindrical shells based on the third-order shear deformation theory. Waves Rand Comp Media. 2023;33(2):345–71. doi:10.1080/17455030.2021.1880031. [Google Scholar] [CrossRef]
314. Hu H, Zhong R, Wang Q, Shi X. Spectro-Geometry dynamic analysis of FG-GPLRC cylindrical shell with periodically embedded dynamic vibration absorbers. Thin-Walled Struct. 2024;203(4):112243. doi:10.1016/j.tws.2024.112243. [Google Scholar] [CrossRef]
315. Ding H-X, She G-L. Nonlinear primary resonance behavior of graphene platelet-reinforced metal foams conical shells under axial motion. Nonl Dynam. 2023;111(15):13723–52. doi:10.1007/s11071-023-08564-x. [Google Scholar] [CrossRef]
316. Duc ND, Cong PH, Tuan ND, Tran P, Van Thanh N. Thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations. Thin-Walled Struct. 2017;115:300–10. doi:10.1016/j.tws.2017.02.016. [Google Scholar] [CrossRef]
317. Esmailpoor Hajilak Z, Pourghader J, Hashemabadi D, Sharifi Bagh F, Habibi M, Safarpour H. Multilayer GPLRC composite cylindrical nanoshell using modified strain gradient theory. Mech Based Des Struct Mach. 2019;47(5):521–45. [Google Scholar]
318. Liu D, Zhou Y, Zhu J. On the free vibration and bending analysis of functionally graded nanocomposite spherical shells reinforced with graphene nanoplatelets: three-dimensional elasticity solutions. Eng Struct. 2021;226:111376. doi:10.1016/j.engstruct.2020.111376. [Google Scholar] [CrossRef]
319. Zhang L, Lei Z, Liew K, Yu J. Static and dynamic of carbon nanotube reinforced functionally graded cylindrical panels. Compos Struct. 2014;111:205–12. doi:10.1016/j.compstruct.2013.12.035. [Google Scholar] [CrossRef]
320. Guo H, Du X, Żur KK. On the dynamics of rotating matrix cracked FG-GPLRC cylindrical shells via the element-free IMLS-Ritz method. Eng Anal Bound Elem. 2021;131:228–39. doi:10.1016/j.enganabound.2021.06.005. [Google Scholar] [CrossRef]
321. Hosseini SM, Zhang C. Coupled thermoelastic analysis of an FG multilayer graphene platelets-reinforced nanocomposite cylinder using meshless GFD method: a modified micromechanical model. Eng Anal Bound Elem. 2018;88:80–92. doi:10.1016/j.enganabound.2017.12.010. [Google Scholar] [CrossRef]
322. Mayandi K, Jeyaraj P. Bending, buckling and free vibration characteristics of FG-CNT-reinforced polymer composite beam under non-uniform thermal load. Proc Instit Mech Eng, Part L: J Mat: Des Appl. 2015;229(1):13–28. doi:10.1177/14644207134937. [Google Scholar] [CrossRef]
323. Vodenitcharova T, Zhang L. Bending and local buckling of a nanocomposite beam reinforced by a single-walled carbon nanotube. Int J Sol Struct. 2006;43(10):3006–24. doi:10.1016/j.ijsolstr.2005.05.014. [Google Scholar] [CrossRef]
324. Talebizadehsardari P, Eyvazian A, Asmael M, Karami B, Shahsavari D, Mahani RB. Static bending analysis of functionally graded polymer composite curved beams reinforced with carbon nanotubes. Thin-Walled Struct. 2020;157:107139. doi:10.1016/j.tws.2020.107139. [Google Scholar] [CrossRef]
325. Kumar P, Kumar A. Stability analysis of FGCNT beams with imperfections. Eng, Technol Appl Sci Res. 2023;13(4):11326–31. doi:10.48084/etasr.5949. [Google Scholar] [CrossRef]
326. Kumar M, Sarangi SK. Bending and vibration study of carbon nanotubes reinforced functionally graded smart composite beams. Eng Res Express. 2022;4(2):025043. doi:10.1088/2631-8695/ac76a0. [Google Scholar] [CrossRef]
327. Shen H-S, Xiang Y. Nonlinear analysis of nanotube-reinforced composite beams resting on elastic foundations in thermal environments. Eng Struct. 2013;56:698–708. doi:10.1016/j.engstruct.2013.06.002. [Google Scholar] [CrossRef]
328. Wuite J, Adali S. Deflection and stress behaviour of nanocomposite reinforced beams using a multiscale analysis. Compos Struct. 2005;71(3–4):388–96. doi:10.1016/j.compstruct.2005.09.011. [Google Scholar] [CrossRef]
329. Babar AB, Sahoo R. Static, buckling, and free vibration analysis of CNT reinforced composite beams with elastic foundation using IHSDT. J Vibrat Eng Technol. 2024;12(7):1–20. doi:10.1007/s42417-024-01349-5. [Google Scholar] [CrossRef]
330. Babar A, Sahoo R. Static, buckling, and free vibration responses of functionally graded carbon nanotube-reinforced composite beams with elastic foundation in non-polynomial framework. J Strain Anal Eng Des. 2024;59(5):03093247241234707. doi:10.1177/03093247241234707. [Google Scholar] [CrossRef]
331. Malekimoghadam R, Hosseini SA, Icardi U. Bending analysis of carbon nanotube coated-fiber multi-scale composite beams using the refined zigzag theory. Aerosp Sci Technol. 2023;138(23):108328. doi:10.1016/j.ast.2023.108328. [Google Scholar] [CrossRef]
332. Wang Y, Xie K, Fu T, Shi C. Bending and elastic vibration of a novel functionally graded polymer nanocomposite beam reinforced by graphene nanoplatelets. Nanomaterials. 2019;9(12):1690. doi:10.3390/nano9121690. [Google Scholar] [CrossRef]
333. Feng C, Kitipornchai S, Yang J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos Part B: Eng. 2017;110(7100):132–40. doi:10.1016/j.compositesb.2016.11.024. [Google Scholar] [CrossRef]
334. Tam M, Yang Z, Zhao S, Zhang H, Zhang Y, Yang J. Nonlinear bending of elastically restrained functionally graded graphene nanoplatelet reinforced beams with an open edge crack. Thin-Walled Struct. 2020;156:106972. doi:10.1016/j.tws.2020.106972. [Google Scholar] [CrossRef]
335. Karamanli A, Vo TP. Finite element model for carbon nanotube-reinforced and graphene nanoplatelet-reinforced composite beams. Compos Struct. 2021;264:113739. doi:10.1016/j.compstruct.2021.113739. [Google Scholar] [CrossRef]
336. Arshadi K, Arefi M. Out-of-plane strain included formulation for free vibration and bending analyses of a sandwich GPL-reinforced microbeam based on the MCST. J Vibrat Eng Technol. 2023;11(5):2199–214. doi:10.1007/s42417-022-00698-3. [Google Scholar] [CrossRef]
337. Songsuwan W, Prabkeao C, Wattanasakulpong N. On linear and nonlinear bending of functionally graded graphene nanoplatelet reinforced composite beams using Gram-Schmidt-Ritz method. Mech Based Des Struct Mach. 2023;51(10):5710–36. doi:10.1080/15397734.2021.2010571. [Google Scholar] [CrossRef]
338. Haghani A, Kiani Y. Closed form expressions for nonlinear analysis of FG-GPLRC beam under thermal loading: thermal postbuckling and nonlinear bending. Int J Struct Stab Dyn. 2024;24(2):2450016. doi:10.1142/S0219455424500160. [Google Scholar] [CrossRef]
339. Murmu T, Pradhan S. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physica E: Low-Dimens Syst Nanostruct. 2009;41(7):1232–9. doi:10.1016/j.physe.2009.02.004. [Google Scholar] [CrossRef]
340. Nejati M, Eslampanah A, Najafizadeh M. Buckling and vibration analysis of functionally graded carbon nanotube-reinforced beam under axial load. Int J Appl Mech. 2016;8(1):1650008. doi:10.1142/S1758825116500083. [Google Scholar] [CrossRef]
341. Madenci E, Özkılıç Y, Aksoylu C, Asyraf M, Syamsir A, Supian A, et al. Buckling analysis of CNT-reinforced polymer composite beam using experimental and analytical methods. Materials. 2023;16(2):614. doi:10.3390/ma16020614. [Google Scholar] [CrossRef]
342. Bensaid I, Kerboua B. Improvement of thermal buckling response of FG-CNT reinforced composite beams with temperature-dependent material properties resting on elastic foundations. Adv Aircraft Spacecraft Sci. 2019;6(3):207–23. doi:10.12989/aas.2019.6.3.207. [Google Scholar] [CrossRef]
343. Babaei H, Kiani Y, Reza Eslami M. Perturbation method for thermal post-buckling analysis of shear deformable FG-CNTRC beams with different boundary conditions. Int J Struct Stab Dyn. 2021;21(13):2150175. doi:10.1142/S0219455421501753. [Google Scholar] [CrossRef]
344. Shafiei H, Setoodeh AR. Nonlinear free vibration and post-buckling of FG-CNTRC beams on nonlinear foundation. Steel Compos Struct. 2017;24(1):65–77. doi:10.12989/scs.2017.24.1.065. [Google Scholar] [CrossRef]
345. Wu H, Kitipornchai S, Yang J. Imperfection sensitivity of thermal post-buckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Appl Mathem Modell. 2017;42:735–52. doi:10.1016/j.apm.2016.10.045. [Google Scholar] [CrossRef]
346. Houalef IE, Bensaid I, Saimi A, Cheikh A. An analysis of vibration and buckling behaviors of nano-composite beams reinforced with agglomerated carbon nanotubes via differential quadrature finite element method. Mech Adv Mat Struct. 2024;31(16):3798–816. doi:10.1080/15376494.2023.2185706. [Google Scholar] [CrossRef]
347. Sahu R, Harursampath D, Ponnusami SA. Continuum modeling of nonlinear buckling behavior of CNT using variational asymptotic method and nonlinear FEA. Mech Adv Mater Struct. 2023;31:5107–24. doi:10.1080/15376494.2023.2211971. [Google Scholar] [CrossRef]
348. Remil A, Belarbi M-O, Bessaim A, Houari MSA, Bouamoud A, Daikh AA, et al. An accurate analytical model for the buckling analysis of FG-CNT reinforced composite beams resting on an elastic foundation with arbitrary boundary conditions. Comput Concr. 2023;31(3):267. doi:10.12989/cac.2023.31.1.267. [Google Scholar] [CrossRef]
349. Yang J, Wu H, Kitipornchai S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos Struct. 2017;161(5696):111–8. doi:10.1016/j.compstruct.2016.11.048. [Google Scholar] [CrossRef]
350. Song M, Chen L, Yang J, Zhu W, Kitipornchai S. Thermal buckling and postbuckling of edge-cracked functionally graded multilayer graphene nanocomposite beams on an elastic foundation. Int J Mech Sci. 2019;161(15):105040. doi:10.1016/j.ijmecsci.2019.105040. [Google Scholar] [CrossRef]
351. Song M, Gong Y, Yang J, Zhu W, Kitipornchai S. Free vibration and buckling analyses of edge-cracked functionally graded multilayer graphene nanoplatelet-reinforced composite beams resting on an elastic foundation. J Sou Vibrat. 2019;458(5):89–108. doi:10.1016/j.jsv.2019.06.023. [Google Scholar] [CrossRef]
352. Wang Y, Feng C, Santiuste C, Zhao Z, Yang J. Buckling and postbuckling of dielectric composite beam reinforced with Graphene Platelets (GPLs). Aerosp Sci Technol. 2019;91:208–18. doi:10.1016/j.ast.2019.05.008. [Google Scholar] [CrossRef]
353. Eyvazian A, Zhang C, Alkhedher M, Muhsen S, Elkotb MA. Thermal buckling and post-buckling analyses of rotating Timoshenko microbeams reinforced with graphene platelet. Compos Struct. 2023;304(4):116358. doi:10.1016/j.compstruct.2022.116358. [Google Scholar] [CrossRef]
354. Guo M, Arvin H. Nonlinear thermal buckling instability analysis of a rotating nanocomposite beam reinforced with graphene platelet via the Chebyshev-Ritz scheme. Eng Anal Bound Elem. 2023;146(10):241–51. doi:10.1016/j.enganabound.2022.10.008. [Google Scholar] [CrossRef]
355. Patil HH, Pitchaimani J, Eltaher M. Buckling and vibration of beams using Ritz method: effects of axial grading of GPL and axially varying load. Mech Adv Mat Struct. 2024;31(16):3861–74. doi:10.1080/15376494.2023.2185711. [Google Scholar] [CrossRef]
356. Lv Y, Zhang J, Li L. Thermal buckling and postbuckling of functionally graded multilayer GPL-reinforced composite beams on nonlinear elastic foundations. Heliyon. 2023;9(9):e19549. doi:10.1016/j.heliyon.2023.e19549. [Google Scholar] [CrossRef]
357. Zhang L, Xu Z, Gao M, Xu R, Wang G. Static, dynamic and buckling responses of random functionally graded beams reinforced by graphene platelets. Eng Struct. 2023;291:116476. doi:10.1016/j.engstruct.2023.116476. [Google Scholar] [CrossRef]
358. Heshmati M, Yas M, Daneshmand F. A comprehensive study on the vibrational behavior of CNT-reinforced composite beams. Compo Struct. 2015;125(16):434–48. doi:10.1016/j.compstruct.2015.02.033. [Google Scholar] [CrossRef]
359. Vo-Duy T, Ho-Huu V, Nguyen-Thoi T. Free vibration analysis of laminated FG-CNT reinforced composite beams using finite element method. Front Struct Civil Eng. 2019;13(2):324–36. doi:10.1007/s11709-018-0466-6. [Google Scholar] [CrossRef]
360. Wang C, Tan V, Zhang Y. Timoshenko beam model for vibration analysis of multi-walled carbon nanotubes. J Sound Vib. 2006;294(4–5):1060–72. doi:10.1016/j.jsv.2006.01.005. [Google Scholar] [CrossRef]
361. Lin F, Xiang Y. Vibration of carbon nanotube reinforced composite beams based on the first and third order beam theories. Appl Math Model. 2014;38(15–16):3741–54. doi:10.1016/j.apm.2014.02.008. [Google Scholar] [CrossRef]
362. Lin F, Xiang Y. Numerical analysis on nonlinear free vibration of carbon nanotube reinforced composite beams. Int J Struct Stab Dyn. 2014;14(1):1350056. doi:10.1142/S0219455413500569. [Google Scholar] [CrossRef]
363. Ke L-L, Yang J, Kitipornchai S. Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos Struct. 2010;92(3):676–83. doi:10.1016/j.compstruct.2009.09.024. [Google Scholar] [CrossRef]
364. Ansari R, Shojaei MF, Mohammadi V, Gholami R, Sadeghi F. Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Compos Struct. 2014;113:316–27. doi:10.1016/j.compstruct.2014.03.015. [Google Scholar] [CrossRef]
365. Chaudhari VK, Lal A. Nonlinear free vibration analysis of elastically supported nanotube-reinforced composite beam in thermal environment. Procedia Eng. 2016;144:928–35. doi:10.1016/j.proeng.2016.05.119. [Google Scholar] [CrossRef]
366. Ghandehari MA, Masoodi AR, Panda SK. Thermal frequency analysis of double CNT-reinforced polymeric straight beam. J Vibrat Eng Technol. 2024;12(1):649–65. doi:10.1007/s42417-023-00865-0. [Google Scholar] [CrossRef]
367. Alimoradzadeh M, Akbaş Ş. Nonlinear free vibration analysis of a composite beam reinforced by carbon nanotubes. Steel Compos Struct. 2023;46(3):335–44. doi:10.12989/scs.2023.46.3.335. [Google Scholar] [CrossRef]
368. Sibtain M, Smith S, Yeganehmehr A, Ong OZS, Ghayesh MH. Vibrations of axially travelling CNT reinforced beams with clamped-clamped boundary condition and an elastic support. Procedia Struct Integ. 2023;45:132–9. doi:10.1016/j.prostr.2023.05.006. [Google Scholar] [CrossRef]
369. Masoodi AR, Ghandehari MA, Tornabene F, Dimitri R. Natural frequency response of FG-CNT coupled curved beams in thermal conditions. Appl Sci. 2024;14(2):687. doi:10.3390/app14020687. [Google Scholar] [CrossRef]
370. Barati MR, Shahverdi H. Finite element forced vibration analysis of refined shear deformable nanocomposite graphene platelet-reinforced beams. J Braz Soc Mech Sci Eng. 2020;42(1):1–14. doi:10.1007/s40430-019-2118-8. [Google Scholar] [CrossRef]
371. Shahrjerdi A, Yavari S. Free vibration analysis of functionally graded graphene-reinforced nanocomposite beams with temperature-dependent properties. J Braz Soc Mech Sci Eng. 2018;40(1):25. doi:10.1007/s40430-017-0943-1. [Google Scholar] [CrossRef]
372. Song M, Gong Y, Yang J, Zhu W, Kitipornchai S. Nonlinear free vibration of cracked functionally graded graphene platelet-reinforced nanocomposite beams in thermal environments. J Sound Vib. 2020;468:115115. doi:10.1016/j.jsv.2019.115115. [Google Scholar] [CrossRef]
373. Wang Y, Feng C, Wang X, Zhao Z, Romero CS, Yang J. Nonlinear free vibration of graphene platelets (GPLs)/polymer dielectric beam. Smart Mater Struct. 2019;28(5):055013. doi:10.1088/1361-665X/ab0b51. [Google Scholar] [CrossRef]
374. Feng C, Kitipornchai S, Yang J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng Struct. 2017;140:110–9. doi:10.1016/j.engstruct.2017.02.052. [Google Scholar] [CrossRef]
375. Zhang J, Yao Y. Strain gradient theory-based vibration analyses for functionally graded microbeams reinforced by GPL. Phys Scr. 2024;99(4):045966. doi:10.1088/1402-4896/ad3290. [Google Scholar] [CrossRef]
376. Bahranifard F, Malekzadeh P, Golbahar Haghighi MR. Large amplitude vibration of sandwich beams with GPLRC face sheets and porous core under moving load. Mech Based Des Struct Mach. 2024;52(3):1627–50. doi:10.1080/15397734.2022.2156884. [Google Scholar] [CrossRef]
377. Bourada F, Bousahla AA, Tounsi A, Bedia EA, Mahmoud S, Benrahou KH, et al. Stability and dynamic analyses of SW-CNT reinforced concrete beam resting on elastic-foundation. Comput Conc Int J. 2020;25(6):485–95. doi:10.12989/cac.2020.25.6.485. [Google Scholar] [CrossRef]
378. Yas M, Heshmati M. Dynamic analysis of functionally graded nanocomposite beams reinforced by randomly oriented carbon nanotube under the action of moving load. Appl Mathem Modell. 2012;36(4):1371–94. doi:10.1016/j.apm.2011.08.037. [Google Scholar] [CrossRef]
379. Ke L-L, Yang J, Kitipornchai S. Dynamic stability of functionally graded carbon nanotube-reinforced composite beams. Mech Adv Mat Struct. 2013;20(1):28–37. doi:10.1080/15376494.2011.581412. [Google Scholar] [CrossRef]
380. Abdelrahman AA, Esen I, Daikh AA, Eltaher MA. Dynamic analysis of FG nanobeam reinforced by carbon nanotubes and resting on elastic foundation under moving load. Mech Based Des Struct Mach. 2023;51(10):5383–406. doi:10.1080/15397734.2021.1999263. [Google Scholar] [CrossRef]
381. Eghbali M, Hosseini SA. On moving harmonic load and dynamic response of carbon nanotube-reinforced composite beams using higher-order shear deformation theories. Mech Adv Compos Struct. 2023;10(2):257–70. doi:10.22075/macs.2022.28205.1431. [Google Scholar] [CrossRef]
382. Wattanasakulpong N, Karamanli A, Vo TP. Nonlinear dynamic response of FG-GPLRC beams induced by two successive moving loads. Eng Anal Bound Elem. 2024;159(14):164–79. doi:10.1016/j.enganabound.2023.11.025. [Google Scholar] [CrossRef]
383. Ban H, Ni Z, Feng C. Parametric study on damped nonlinear vibration of FG-GPLRC dielectric beam with edge crack. Acta Mech. 2024;235(5):1–27. doi:10.1007/s00707-024-03866-6. [Google Scholar] [CrossRef]
384. Dash S, Chakraborty S, Dey T, Kumar R. Buckling and free vibration analysis of randomly distributed CNT reinforced composite beam under thermomechanical loading. Eur J Mech-A/Solids. 2022;96(4):104749. doi:10.1016/j.euromechsol.2022.104749. [Google Scholar] [CrossRef]
385. Zerrouki R, Karas A, Zidour M. Critical buckling analyses of nonlinear FG-CNT reinforced nano-composite beam. Adv Nano Res. 2020;9(3):211. doi:10.12989/anr.2020.9.3.211. [Google Scholar] [CrossRef]
386. Fattahi A, Safaei B. Buckling analysis of CNT-reinforced beams with arbitrary boundary conditions. Microsyst Technol. 2017;23(10):5079–91. doi:10.1007/s00542-017-3345-5. [Google Scholar] [CrossRef]
387. Keleshteri M, Asadi H, Aghdam M. Nonlinear bending analysis of FG-CNTRC annular plates with variable thickness on elastic foundation. Thin-Walled Struct. 2019;135(7):453–62. doi:10.1016/j.tws.2018.11.020. [Google Scholar] [CrossRef]
388. Sadeghian M, Palevicius A, Janusas G. Nonlocal strain gradient model for the nonlinear static analysis of a circular/annular nanoplate. Micromachines. 2023;14(5):1052. doi:10.3390/mi14051052. [Google Scholar] [CrossRef]
389. Ranjbar-Roeintan M. A circular plate with a central hole reinforced with agglomerated CNTs under impact loading. Multidiscip Model Mat Struct. 2023;19(5):876–96. doi:10.1108/MMMS-01-2023-0025. [Google Scholar] [CrossRef]
390. Sobhy M. Piezoelectric bending of GPL-reinforced annular and circular sandwich nanoplates with FG porous core integrated with sensor and actuator using DQM. Arch Civil Mech Eng. 2021;21(2):78. doi:10.1007/s43452-021-00231-5. [Google Scholar] [CrossRef]
391. Gholami R, Ansari R. Asymmetric nonlinear bending analysis of polymeric composite annular plates reinforced with graphene nanoplatelets. Int J Multiscale Comput Eng. 2019;17(1):45–63. doi:10.1615/IntJMultCompEng.2019029156. [Google Scholar] [CrossRef]
392. Yang B, Kitipornchai S, Yang Y-F, Yang J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl Math Modell. 2017;49:69–86. doi:10.1016/j.apm.2017.04.044. [Google Scholar] [CrossRef]
393. Al-Furjan M, Habibi M, Ghabussi A, Safarpour H, Safarpour M, Tounsi A. Non-polynomial framework for stress and strain response of the FG-GPLRC disk using three-dimensional refined higher-order theory. Eng Struct. 2021;228:111496. doi:10.1016/j.engstruct.2020.111496. [Google Scholar] [CrossRef]
394. Ansari R, Torabi J, Hassani R. In-plane and shear buckling analysis of FG-CNTRC annular sector plates based on the third-order shear deformation theory using a numerical approach. Comput Mathem Appl. 2018;75(2):486–502. doi:10.1016/j.camwa.2017.09.022. [Google Scholar] [CrossRef]
395. Ansari R, Torabi J, Shojaei MF. Buckling and vibration analysis of embedded functionally graded carbon nanotube-reinforced composite annular sector plates under thermal loading. Compos Part B: Eng. 2017;109(1):197–213. doi:10.1016/j.compositesb.2016.10.050. [Google Scholar] [CrossRef]
396. Torabi J, Ansari R, Hasrati E. Mechanical buckling analyses of sandwich annular plates with functionally graded carbon nanotube-reinforced composite face sheets resting on elastic foundation based on the higher-order shear deformation plate theory. J Sandw Struct Mat. 2020;22(6):1812–37. doi:10.1177/1099636218789617. [Google Scholar] [CrossRef]
397. Gholami R, Ansari R. Thermal postbuckling of temperature-dependent functionally graded nanocomposite annular sector plates reinforced by carbon nanotubes. Int J Struct Stab Dyn. 2021;21(2):2150026. doi:10.1142/S0219455421500267. [Google Scholar] [CrossRef]
398. Akbulut H, Bingöl M. Numerical and experimental buckling analysis for circular plates. Experiment Techn. 2024;48(3):439–48. doi:10.1007/s40799-023-00667-9. [Google Scholar] [CrossRef]
399. Zhang G, Xiao C, Rahimi A, Safarpour M. Thermal and mechanical buckling and vibration analysis of FG-GPLRC annular plate using higher order shear deformation theory and generalized differential quadrature method. Int J Appl Mech. 2020;12(2):2050019. doi:10.1142/S1758825120500192. [Google Scholar] [CrossRef]
400. Allahkarami F. Dynamic buckling of functionally graded multilayer graphene nanocomposite annular plate under different boundary conditions in thermal environment. Eng Comput. 2022;38(Suppl 1):583–606. doi:10.1007/s00366-020-01169-7. [Google Scholar] [CrossRef]
401. Wu H, Zheng Z, Guo J, Li L, Bao Y, Yang J. Axisymmetric thermal postbuckling of functionally graded graphene nanocomposite annular plates with various geometric imperfections. Thin-Walled Struct. 2023;185(1):110594. doi:10.1016/j.tws.2023.110594. [Google Scholar] [CrossRef]
402. Yang Y, Chen B, Lin W, Li Y, Dong Y. Vibration and symmetric thermal buckling of asymmetric annular sandwich plates with piezoelectric/GPLRC layers rested on foundation. Aerosp Sci Technol. 2021;110:106495. doi:10.1016/j.ast.2021.106495. [Google Scholar] [CrossRef]
403. Yang Y, Luo Q, J-a Li, Dong Y, Chen B, Li Y. Symmetric and asymmetric thermo-induced buckling and postbuckling of rotating GPLRC annular plates rested on elastic foundation. Eng Struct. 2022;259(1):114110. doi:10.1016/j.engstruct.2022.114110. [Google Scholar] [CrossRef]
404. Javani M, Kiani Y, Eslami M. Thermal buckling of FG graphene platelet reinforced composite annular sector plates. Thin-Walled Struct. 2020;148(6):106589. doi:10.1016/j.tws.2019.106589. [Google Scholar] [CrossRef]
405. Wang Y, Kiani Y. Asymmetric thermal stability in GPL reinforced composite circular plates on partial Winkler foundation. Int J Struct Stab Dyn. 2023;23(10):2350109. doi:10.1142/S0219455423501092. [Google Scholar] [CrossRef]
406. Nguyen TP, Dang TD, Bui TT, Vu MD, Le-Nguyen K, Pham TH, et al. Nonlinear thermo-mechanical axisymmetric stability of FG-GPLRC spherical shells and circular plates resting on nonlinear elastic medium. Ships Offsh Struct. 2024;19(6):820–30. doi:10.1080/17445302.2023.2214489. [Google Scholar] [CrossRef]
407. Zhou Q, Zhang JH, Zhao YG. Nonlinear buckling and postbuckling of circular plates reinforced with graphene platelets using the shooting method. Int J Struct Stab Dyn. 2024;24(1):2450001. doi:10.1142/S0219455424500019. [Google Scholar] [CrossRef]
408. Allahkarami F, Tohidi H. Axisymmetric postbuckling of functionally graded graphene platelets reinforced composite annular plate on nonlinear elastic medium in thermal environment. Int J Struct Stab Dyn. 2023;23(3):2350034. doi:10.1142/S0219455423500347. [Google Scholar] [CrossRef]
409. Civalek Ö, Baltacıoğlu AK. Vibration of carbon nanotube reinforced composite (CNTRC) annular sector plates by discrete singular convolution method. Compos Struct. 2018;203(4):458–65. doi:10.1016/j.compstruct.2018.07.037. [Google Scholar] [CrossRef]
410. Beni NN. Free vibration analysis of annular sector sandwich plates with FG-CNT reinforced composite face-sheets based on the Carrera’s Unified Formulation. Compos Struct. 2019;214(1):269–92. doi:10.1016/j.compstruct.2019.01.094. [Google Scholar] [CrossRef]
411. Zhong R, Wang Q, Tang J, Shuai C, Qin B. Vibration analysis of functionally graded carbon nanotube reinforced composites (FG-CNTRC) circular, annular and sector plates. Compo Struct. 2018;194:49–67. doi:10.1016/j.compstruct.2018.03.104. [Google Scholar] [CrossRef]
412. Keleshteri M, Asadi H, Wang Q. Large amplitude vibration of FG-CNT reinforced composite annular plates with integrated piezoelectric layers on elastic foundation. Thin-Walled Struct. 2017;120(10):203–14. doi:10.1016/j.tws.2017.08.035. [Google Scholar] [CrossRef]
413. Al-Furjan M, Habibi M, Ni J, Jung DW, Tounsi A. Frequency simulation of viscoelastic multi-phase reinforced fully symmetric systems. Eng Compu. 2022;38(Suppl 5):3725–41. doi:10.1007/s00366-020-01200-x. [Google Scholar] [CrossRef]
414. Al-Furjan M, Habibi M, Shan L, Tounsi A. On the vibrations of the imperfect sandwich higher-order disk with a lactic core using generalize differential quadrature method. Compos Struct. 2021;257(23):113150. doi:10.1016/j.compstruct.2020.113150. [Google Scholar] [CrossRef]
415. Emdadi M, Mohammadimehr M, Bargozini F. Vibration of a nanocomposite annular sandwich microplate based on HSDT using DQM. Multis Sci Eng. 2023;5(3):180–94. doi:10.1007/s42493-024-00096-9. [Google Scholar] [CrossRef]
416. Habibi M, Safarpour M, Safarpour H. Vibrational characteristics of a FG-GPLRC viscoelastic thick annular plate using fourth-order Runge-Kutta and GDQ methods. Mech Based Des Struct Mach. 2022;50(7):2471–92. doi:10.1080/15397734.2020.1779086. [Google Scholar] [CrossRef]
417. Tao C, Dai T. Isogeometric analysis for size-dependent nonlinear free vibration of graphene platelet reinforced laminated annular sector microplates. Eur J Mech-A/Solids. 2021;86:104171. doi:10.1016/j.euromechsol.2020.104171. [Google Scholar] [CrossRef]
418. Wang Y, Zeng R, Safarpour M. Vibration analysis of FG-GPLRC annular plate in a thermal environment. Mech Based Des Struct Mach. 2022;50(1):352–70. doi:10.1080/15397734.2020.1719508. [Google Scholar] [CrossRef]
419. Javani M, Kiani Y, Eslami M. Geometrically nonlinear free vibration of FG-GPLRC circular plate on the nonlinear elastic foundation. Compos Struct. 2021;261(1):113515. doi:10.1016/j.compstruct.2020.113515. [Google Scholar] [CrossRef]
420. Yang Y, Li J-A, Chen B, Dong Y, Li Y. Symmetric and asymmetric vibrations of rotating GPLRC annular plate. Int J Mech Sci. 2023;250(16):108282. doi:10.1016/j.ijmecsci.2023.108282. [Google Scholar] [CrossRef]
421. Zhou Q, Zhang J. Vibration analysis of shearable composite annular plates reinforced by graphene nanoplatelets using the differential quadrature method. Mech Compos Mat. 2024;60(1):117–34. doi:10.1007/s11029-024-10178-2. [Google Scholar] [CrossRef]
422. Frikha A, Zghal S, Dammak F. Dynamic analysis of functionally graded carbon nanotubes-reinforced plate and shell structures using a double directors finite shell element. Aerosp Sci Technol. 2018;78:438–51. doi:10.1016/j.ast.2018.04.048. [Google Scholar] [CrossRef]
423. Arshid E, Amir S, Loghman A, Civalek Ö. Aerodynamic stability and free vibration of FGP-Reinforced nano-fillers annular sector microplates exposed to supersonic flow. Thin-Walled Struct. 2024;197(26):111610. doi:10.1016/j.tws.2024.111610. [Google Scholar] [CrossRef]
424. Liu Z, Wu X, Yu M, Habibi M. Large-amplitude dynamical behavior of multilayer graphene platelets reinforced nanocomposite annular plate under thermo-mechanical loadings. Mech Based Des Struct Mach. 2022;50(11):3722–46. doi:10.1080/15397734.2020.1815544. [Google Scholar] [CrossRef]
425. Ma L, Liu X, Moradi Z. On the chaotic behavior of graphene-reinforced annular systems under harmonic excitation. Eng Comput. 2021;38(6):1–25. doi:10.1007/s00366-020-01210-9. [Google Scholar] [CrossRef]
426. Zhang Y-W, She G-L, Eltaher M. Nonlinear transient response of graphene platelets reinforced metal foams annular plate considering rotating motion and initial geometric imperfection. Aerosp Sci Technol. 2023;142(2):108693. doi:10.1016/j.ast.2023.108693. [Google Scholar] [CrossRef]
427. Liu D, Li Z, Kitipornchai S, Yang J. Three-dimensional free vibration and bending analyses of functionally graded graphene nanoplatelets-reinforced nanocomposite annular plates. Compos Struct. 2019;229:111453. doi:10.1016/j.compstruct.2019.111453. [Google Scholar] [CrossRef]
428. Mohammadzadeh-Keleshteri M, Asadi H, Aghdam M. Geometrical nonlinear free vibration responses of FG-CNT reinforced composite annular sector plates integrated with piezoelectric layers. Compos Struct. 2017;171(5):100–12. doi:10.1016/j.compstruct.2017.01.048. [Google Scholar] [CrossRef]
429. Bisheh H, Alibeigloo A, Safarpour M, Rahimi A. Three-dimensional static and free vibrational analysis of graphene reinforced composite circular/annular plate using differential quadrature method. Int J Appl Mech. 2019;11(8):1950073. doi:10.1142/S175882511950073X. [Google Scholar] [CrossRef]
430. Bouhfid N, Raji M, Boujmal R, Essabir H, Bensalah MO, Bouhfid R. Numerical modeling of hybrid composite materials. In: Modelling of damage processes in biocomposites, fibre-reinforced composites, and hybrid composites. Cambridge, UK: Woodhead Publishing; 2019. p. 57–101. [cited 2024 Nov 15]. Available from: https://shop.elsevier.com/books/modelling-of-damage-processes-in-biocomposites-fibre-reinforced-composites-and-hybrid-composites/jawaid/978-0-08-102289-4. [Google Scholar]
431. Shokrieh M, Esmkhani M, Haghighatkhah A. Flexural fatigue behaviour of carbon nanofiber/epoxy nanocomposites. Fatig Fract Eng Mat Struct. 2014;37(5):553–60. doi:10.1111/ffe.12137. [Google Scholar] [CrossRef]
432. Hassanzadeh-Aghdam M, Ansari R, Mahmoodi M. Micromechanical estimation of biaxial thermomechanical responses of hybrid fiber-reinforced metal matrix nanocomposites containing carbon nanotubes. Mech Mat. 2018;119:1–15. doi:10.1016/j.mechmat.2018.01.002. [Google Scholar] [CrossRef]
433. Bacciocchi M. Buckling analysis of three-phase CNT/polymer/fiber functionally graded orthotropic plates: influence of the non-uniform distribution of the oriented fibers on the critical load. Eng Struct. 2020;223:111176. doi:10.1016/j.engstruct.2020.111176. [Google Scholar] [CrossRef]
434. Kolahchi R, Zhu S-P, Keshtegar B, Trung N-T. Dynamic buckling optimization of laminated aircraft conical shells with hybrid nanocomposite martial. Aerosp Sci Technol. 2020;98:105656. doi:10.1016/j.ast.2019.105656. [Google Scholar] [CrossRef]
435. Ebrahimi F, Dabbagh A. Vibration analysis of multi-scale hybrid nanocomposite plates based on a Halpin-Tsai homogenization model. Compos Part B: Eng. 2019;173:106955. doi:10.1016/j.compositesb.2019.106955. [Google Scholar] [CrossRef]
436. Ghasemi AR, Mohandes M, Dimitri R, Tornabene F. Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos Part B: Eng. 2019;167:700–16. doi:10.1016/j.compositesb.2019.03.028. [Google Scholar] [CrossRef]
437. Hassanzadeh-Aghdam MK, Ansari R, Darvizeh A. Micromechanical analysis of carbon nanotube-coated fiber-reinforced hybrid composites. Int J Eng Sci. 2018;130(1):215–29. doi:10.1016/j.ijengsci.2018.06.001. [Google Scholar] [CrossRef]
438. Karimiasl M, Ebrahimi F, Mahesh V. Nonlinear forced vibration of smart multiscale sandwich composite doubly curved porous shell. Thin-Walled Struct. 2019;143(12):106152. doi:10.1016/j.tws.2019.04.044. [Google Scholar] [CrossRef]
439. Mohandes M, Ghasemi AR. A new approach to reinforce the fiber of nanocomposite reinforced by CNTs to analyze free vibration of hybrid laminated cylindrical shell using beam modal function method. Euro J Mech-A/Solids. 2019;73:224–34. doi:10.1016/j.euromechsol.2018.09.006. [Google Scholar] [CrossRef]
440. Emadi S, Badarloo B, Tayebikhorami S, Salehipour H, Civalek O. Geometrically nonlinear electro-thermo-static analysis of piezoelectric/CNT/GPL/fibre/polymer sandwich panels with double curvature resting on elastic foundation. Compos Struct. 2022;295(1):115844. doi:10.1016/j.compstruct.2022.115844. [Google Scholar] [CrossRef]
441. Shahmohammadi MA, Mirfatah SM, Emadi S, Salehipour H, Civalek Ö. Nonlinear thermo-mechanical static analysis of toroidal shells made of nanocomposite/fiber reinforced composite plies surrounded by elastic medium. Thin-Walled Struct. 2022;170:108616. doi:10.1016/j.tws.2021.108616. [Google Scholar] [CrossRef]
442. Mirfatah SM, Tayebikhorami S, Shahmohammadi MA, Salehipour H, Civalek Ö. Thermo-elastic damped nonlinear dynamic response of the initially stressed hybrid GPL/CNT/fiber/polymer composite toroidal shells surrounded by elastic foundation. Compos Struct. 2022;283(7):115047. doi:10.1016/j.compstruct.2021.115047. [Google Scholar] [CrossRef]
443. Ebrahimi F, Mahesh V. On nonlinear vibration of sandwiched polymer-CNT/GPL-fiber nanocomposite nanoshells. Thin-Walled Struct. 2020;146(8):106431. doi:10.1016/j.tws.2019.106431. [Google Scholar] [CrossRef]
444. Shahmohammadi MA, Azhari M, Salehipour H, Thai H-T. Buckling of multilayered CNT/GPL/fibre/polymer hybrid composite plates resting on elastic support using modified nonlocal first-order plate theory. Mech Based Des Struct Mach. 2022;52(3):1–26. doi:10.1080/15397734.2022.2164301. [Google Scholar] [CrossRef]
445. Salehipour H, Shahmohammadi MA, Folkow PD, Civalek O. An analytical solution for vibration response of CNT/GPL/fibre/polymer hybrid composite micro/nanoplates. Mech Adv Mater Struct. 2022:1–21. doi:10.1080/15376494.2022.2150916. [Google Scholar] [CrossRef]
446. Karbasizadeh A, Ghorbanpour Arani A, Niknejad S, Khoddami Maraghi Z. Free damped vibration analysis of sandwich plates with CNT-reinforced MRE core and laminated three-phase polymer/GPL/fiber face sheets. J Solid Mech. 2023. doi:10.22034/jsm.2022.1968033.1750. [Google Scholar] [CrossRef]
447. Ni Y, Zhang J, Sun J, Li Y, Tong Z, Zhou Z. Hygrothermal effects on the nonlinear buckling of functionally graded multilayer GPL-Fiber reinforced hybrid composite cylindrical shells. ZAMM-J Appl Mathem Mech/Zeitschrift Für Angewandte Mathematik Und Mechanik. 2023;103(2):e202200246. doi:10.1002/zamm.202200246. [Google Scholar] [CrossRef]
448. Zhao T, Bayat MJ, Kalhori A, Asemi K. Free vibration analysis of functionally graded multilayer hybrid composite cylindrical shell panel reinforced by GPLs and CNTs surrounded by Winkler elastic foundation. Eng Struct. 2024;308(18):117975. doi:10.1016/j.engstruct.2024.117975. [Google Scholar] [CrossRef]
449. Chandra Y, Flores ES, Scarpa F, Adhikari S. Buckling of hybrid nanocomposites with embedded graphene and carbon nanotubes. Physica E: Low-dimen Syst Nanostruct. 2016;83(4):434–41. doi:10.1016/j.physe.2016.01.021. [Google Scholar] [CrossRef]
450. Hosseini SM, Zhang C. Band structure analysis of Green-Naghdi thermoelastic wave propagation in a GPLs/CNTs-reinforced metamaterial with energy dissipation. Eng Struct. 2022;272(3):114984. doi:10.1016/j.engstruct.2022.114984. [Google Scholar] [CrossRef]
451. Ghadiri Rad MH, Hosseini SM. Application of the CUF-EFG method for buckling analysis of the multilayer GPLs-CNTs-reinforced FG plates with cutout. Mech Adv Mater Struct. 2022;31(3):1–17. doi:10.1080/15376494.2022.2116664. [Google Scholar] [CrossRef]
452. Żur KK, Mohammadi H, Kiani Y, Kondratiuk M. Nonlinear dynamics of nanocomposite beam-like aerospace structures. Eng Anal Bound Elem. 2024;165:105812. doi:10.1016/j.enganabound.2024.105812. [Google Scholar] [CrossRef]
453. Rad MHG, Hosseini SM. The modified CUF-EFG method for the dynamic analysis of GPLs-CNTs-reinforced FG multilayer thick cylindrical shells under shock loadings: a modified meshless implementation. Eng Anal Bound Elem. 2023;156(6):499–518. doi:10.1016/j.enganabound.2023.08.023. [Google Scholar] [CrossRef]
454. Li Y, Yang T, Yu T, Zheng L, Liao K. Synergistic effect of hybrid carbon nantube-graphene oxide as a nanofiller in enhancing the mechanical properties of PVA composites. J Mat Chem. 2011;21(29):10844–51. doi:10.1039/c1jm11359c. [Google Scholar] [CrossRef]
455. Li Y, Gao F, Xue Z, Luan Y, Yan X, Guo Z, et al. Synergistic effect of different graphene-CNT heterostructures on mechanical and self-healing properties of thermoplastic polyurethane composites. Mat Des. 2018;137:438–45. doi:10.1016/j.matdes.2017.10.018. [Google Scholar] [CrossRef]
456. Liu P, Li Y, Wu C, Liu C, Ma Y, Zhang Y, et al. Theoretical estimation on electrical conductivity, synergy effect and piezoresistive behavior for nanocomposites with hybrid carbon nanotube/graphene based on modified Bethe lattice method. Comput Mater Sci. 2022;202(37):110986. doi:10.1016/j.commatsci.2021.110986. [Google Scholar] [CrossRef]
457. Tang Z-H, Wang D-Y, Li Y-Q, Huang P, Fu S-Y. Modeling the synergistic electrical percolation effect of carbon nanotube/graphene/polymer composites. Compos Sci Technol. 2022;225:109496. doi:10.1016/j.compscitech.2022.109496. [Google Scholar] [CrossRef]
458. Yu J, Choi HK, Kim HS, Kim SY. Synergistic effect of hybrid graphene nanoplatelet and multi-walled carbon nanotube fillers on the thermal conductivity of polymer composites and theoretical modeling of the synergistic effect. Compos Part A: Appl Sci Manufact. 2016;88:79–85. doi:10.1016/j.compositesa.2016.05.022. [Google Scholar] [CrossRef]
459. Chen L, Sun Y-Y, Lin J, Du X-Z, Wei G-S, He S-J, et al. Modeling and analysis of synergistic effect in thermal conductivity enhancement of polymer composites with hybrid filler. Int J Heat Mass Trans. 2015;81(5):457–64. doi:10.1016/j.ijheatmasstransfer.2014.10.051. [Google Scholar] [CrossRef]
460. Zhou E, Xi J, Guo Y, Liu Y, Xu Z, Peng L, et al. Synergistic effect of graphene and carbon nanotube for high-performance electromagnetic interference shielding films. Carbon. 2018;133(9):316–22. doi:10.1016/j.carbon.2018.03.023. [Google Scholar] [CrossRef]
461. Wang P-N, Hsieh T-H, Chiang C-L, Shen M-Y. Synergetic effects of mechanical properties on graphene nanoplatelet and multiwalled carbon nanotube hybrids reinforced epoxy/carbon fiber composites. J Nanomat. 2015;2015(1):838032. doi:10.1155/2015/838032. [Google Scholar] [CrossRef]
462. Yang S-Y, Lin W-N, Huang Y-L, Tien H-W, Wang J-Y, Ma C-CM, et al. Synergetic effects of graphene platelets and carbon nanotubes on the mechanical and thermal properties of epoxy composites. Carbon. 2011;49(3):793–803. doi:10.1016/j.carbon.2010.10.014. [Google Scholar] [CrossRef]
463. Wang Y, Zhang L, Sun S. Cementitious composites modified by nanocarbon fillers with cooperation effect possessing excellent self-sensing properties. Nanotechnol Rev. 2024;13(1):20230226. doi:10.1515/ntrev-2023-0226. [Google Scholar] [CrossRef]
464. Gupta VK, Saleh TA. Sorption of pollutants by porous carbon, carbon nanotubes and fullerene-an overview. Environ Sci Pollut Res. 2013;20(5):2828–43. doi:10.1007/s11356-013-1524-1. [Google Scholar] [CrossRef]
465. Kiarasi F, Babaei M, Sarvi P, Asemi K, Hosseini M, Omidi Bidgoli M. A review on functionally graded porous structures reinforced by graphene platelets. J Computat Appl Mech. 2021;52(4):731–50. doi:10.22059/jcamech.2021.335739.675. [Google Scholar] [CrossRef]
466. Kiarasi F, Babaei M, Mollaei S, Mohammadi M, Asemi K. Free vibration analysis of FG porous joined truncated conical-cylindrical shell reinforced by graphene platelets. Adv Nano Res. 2021;11(4):361. doi:10.12989/anr.2021.11.4.361. [Google Scholar] [CrossRef]
467. Anamagh MR, Bediz B. Free vibration and buckling behavior of functionally graded porous plates reinforced by graphene platelets using spectral Chebyshev approach. Compos Struct. 2020;253(6):112765. doi:10.1016/j.compstruct.2020.112765. [Google Scholar] [CrossRef]
468. Arshid E, Khorshidvand AR. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin-Walled Struct. 2018;125(14):220–33. doi:10.1016/j.tws.2018.01.007. [Google Scholar] [CrossRef]
469. Bahaadini R, Saidi AR, Majidi-Mozafari K. Aeroelastic flutter analysis of thick porous plates in supersonic flow. Int J Appl Mech. 2019;11(10):1950096. doi:10.1142/S1758825119500960. [Google Scholar] [CrossRef]
470. Pourjabari A, Hajilak ZE, Mohammadi A, Habibi M, Safarpour H. Effect of porosity on free and forced vibration characteristics of the GPL reinforcement composite nanostructures. Comput Mathem Appl. 2019;77(10):2608–26. doi:10.1016/j.camwa.2018.12.041. [Google Scholar] [CrossRef]
471. Saidi AR, Bahaadini R, Majidi-Mozafari K. On vibration and stability analysis of porous plates reinforced by graphene platelets under aerodynamical loading. Compos Part B: Eng. 2019;164(4):778–99. doi:10.1016/j.compositesb.2019.01.074. [Google Scholar] [CrossRef]
472. Barati MR, Zenkour AM. Analysis of postbuckling of graded porous GPL-reinforced beams with geometrical imperfection. Mech Adv Mat Struct. 2019;26(6):503–11. doi:10.1080/15376494.2017.1400622. [Google Scholar] [CrossRef]
473. Wang Y, Zhang W. On the thermal buckling and postbuckling responses of temperature-dependent graphene platelets reinforced porous nanocomposite beams. Compos Struct. 2022;296(11):115880. doi:10.1016/j.compstruct.2022.115880. [Google Scholar] [CrossRef]
474. Kitipornchai S, Chen D, Yang J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mat Des. 2017;116:656–65. doi:10.1016/j.matdes.2016.12.061. [Google Scholar] [CrossRef]
475. Barati MR, Zenkour AM. Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech Adv Mat Struct. 2019;26(18):1580–8. doi:10.1080/15376494.2018.1444235. [Google Scholar] [CrossRef]
476. Habibi M, Mohammadi A, Safarpour H, Ghadiri M. Effect of porosity on buckling and vibrational characteristics of the imperfect GPLRC composite nanoshell. Mech Based Des Struct Mach. 2021;49(6):811–40. doi:10.1080/15397734.2019.1701490. [Google Scholar] [CrossRef]
477. Qin B, Wang Q, Zhong R, Zhao X, Shuai C. A three-dimensional solution for free vibration of FGP-GPLRC cylindrical shells resting on elastic foundations: a comparative and parametric study. Int J Mech Sci. 2020;187(11):105896. doi:10.1016/j.ijmecsci.2020.105896. [Google Scholar] [CrossRef]
478. Tariq M, Nisar S, Shah A, Akbar S, Khan MA, Khan SZ. Effect of hybrid reinforcement on the performance of filament wound hollow shaft. Compos Struct. 2018;184(1–4):378–87. doi:10.1016/j.compstruct.2017.09.098. [Google Scholar] [CrossRef]
479. Yas M-H, Rahimi S. Thermal buckling analysis of porous functionally graded nanocomposite beams reinforced by graphene platelets using Generalized differential quadrature method. Aerosp Sci Technol. 2020;107(2):106261. doi:10.1016/j.ast.2020.106261. [Google Scholar] [CrossRef]
480. Chen D, Yang J, Kitipornchai S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos Sci Technol. 2017;142:235–45. doi:10.1016/j.compscitech.2017.02.008. [Google Scholar] [CrossRef]
481. Atif R, Inam F. Reasons and remedies for the agglomeration of multilayered graphene and carbon nanotubes in polymers. Beilstein J Nanotechnol. 2016;7(1):1174–96. doi:10.3762/bjnano.7.109. [Google Scholar] [CrossRef]
482. Ma P-C, Siddiqui NA, Marom G, Kim J-K. Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites: a review. Compos Part A: Appl Sci Manufact. 2010;41(10):1345–67. doi:10.1016/j.compositesa.2010.07.003. [Google Scholar] [CrossRef]
483. Gojny FH, Wichmann MH, Fiedler B, Kinloch IA, Bauhofer W, Windle AH, et al. Evaluation and identification of electrical and thermal conduction mechanisms in carbon nanotube/epoxy composites. Polymer. 2006;47(6):2036–45. doi:10.1016/j.polymer.2006.01.029. [Google Scholar] [CrossRef]
484. Imran KA, Shivakumar KN. Enhancement of electrical conductivity of epoxy using graphene and determination of their thermo-mechanical properties. J Reinfor Plast Compos. 2018;37(2):118–33. doi:10.1177/0731684417736. [Google Scholar] [CrossRef]
485. Bao C, Guo Y, Song L, Kan Y, Qian X, Hu Y. In situ preparation of functionalized graphene oxide/epoxy nanocomposites with effective reinforcements. J Mat Chem. 2011;21(35):13290–8. doi:10.1039/C1JM11434D. [Google Scholar] [CrossRef]
486. Zhu Y, Su L, Deng J, Liang M, Xu C, Jiao Y, et al. Impact of GNP content on cure behaviors and diverse properties of epoxy composites modified with graphene nanoplatelets: a comprehensive study. Mater Today Commun. 2023;37:107014. doi:10.1016/j.mtcomm.2023.107014. [Google Scholar] [CrossRef]
487. Small WR, in het Panhuis M. Inkjet printing of transparent, electrically conducting single-walled carbon-nanotube composites. Small. 2007;3(9):1500–3. doi:10.1002/smll.200700110. [Google Scholar] [CrossRef]
488. Lim DD, Lee J, Park J, Choi W. High-resolution and electrically conductive three-dimensional printing of carbon nanotube-based polymer composites enabled by solution intercalation. Carbon. 2022;194:1–9. doi:10.1016/j.carbon.2022.03.042. [Google Scholar] [CrossRef]
489. Liu Y, Xiong W, Jiang L, Zhou Y. Precise 3D printing of micro/nanostructures using highly conductive carbon nanotube-thiol-acrylate composites. In: Laser 3D Manufacturing III. San Francisco, California, United States: SPIE; 2016. [Google Scholar]
490. Iervolino F, Bonessa A, Foti G, Levi M, Suriano R. Additive manufacturing of electrically conductive nanocomposites filled with carbon nanotubes. Adv Eng Mater. 2022;24(12):2200947. doi:10.1002/adem.202200947. [Google Scholar] [CrossRef]
491. Grossiord N, Loos J, Van Laake L, Maugey M, Zakri C, Koning CE, et al. High-conductivity polymer nanocomposites obtained by tailoring the characteristics of carbon nanotube fillers. Adv Funct Mat. 2008;18(20):3226–34. doi:10.1002/adfm.200800528. [Google Scholar] [CrossRef]
492. Abueidda DW, Al-Rub RKA, Dalaq AS, Younes HA, Al Ghaferi AA, Shah TK. Electrical conductivity of 3D periodic architectured interpenetrating phase composites with carbon nanostructured-epoxy reinforcements. Compos Sci Technol. 2015;118(5):127–34. doi:10.1016/j.compscitech.2015.08.021. [Google Scholar] [CrossRef]
493. Tilve-Martinez D, Neri W, Horaud D, Vukadinovic N, Berton B, Desmedt A, et al. Graphene oxide based transparent resins for accurate 3d printing of conductive materials. Adv Funct Mater. 2023;33(21):2214954. doi:10.1002/adfm.202214954. [Google Scholar] [CrossRef]
494. Sangermano M, Marchi S, Valentini L, Bon SB, Fabbri P. Transparent and conductive graphene oxide/poly (ethylene glycol) diacrylate coatings obtained by photopolymerization. Macromol Mat Eng. 2011;296(5):401–7. doi:10.1002/mame.201000372. [Google Scholar] [CrossRef]
495. Jakus AE, Secor EB, Rutz AL, Jordan SW, Hersam MC, Shah RN. Three-dimensional printing of high-content graphene scaffolds for electronic and biomedical applications. ACS Nano. 2015;9(4):4636–48. doi:10.1021/acsnano.5b01179. [Google Scholar] [CrossRef]
496. Liu H, Gao J, Huang W, Dai K, Zheng G, Liu C, et al. Electrically conductive strain sensing polyurethane nanocomposites with synergistic carbon nanotubes and graphene bifillers. Nanoscale. 2016;8(26):12977–89. doi:10.1039/C6NR02216B. [Google Scholar] [CrossRef]
497. Han H, Cho S. Fabrication of conducting polyacrylate resin solution with polyaniline nanofiber and graphene for conductive 3D printing application. Polymers. 2018;10(9):1003. doi:10.3390/polym10091003. [Google Scholar] [CrossRef]
498. Tsai S-C, Chen L-H, Chu C-P, Chao W-C, Liao Y-C. Photo curable resin for 3D printed conductive structures. Addit Manuf. 2022;51:102590. doi:10.1016/j.addma.2021.102590. [Google Scholar] [CrossRef]
499. Mu Q, Wang L, Dunn CK, Kuang X, Duan F, Zhang Z, et al. Digital light processing 3D printing of conductive complex structures. Add Manufact. 2017;18:74–83. doi:10.1016/j.addma.2017.08.011. [Google Scholar] [CrossRef]
500. Gallastegui A, Dominguez-Alfaro A, Lezama L, Alegret N, Prato M, Gómez ML, et al. Fast visible-light photopolymerization in the presence of multiwalled carbon nanotubes: toward 3D printing conducting nanocomposites. ACS Macro Letters. 2022;11(3):303–9. doi:10.1021/acsmacrolett.1c00758. [Google Scholar] [CrossRef]
501. Abdalla M, Dean D, Theodore M, Fielding J, Nyairo E, Price G. Magnetically processed carbon nanotube/epoxy nanocomposites: morphology, thermal, and mechanical properties. Polymer. 2010;51(7):1614–20. doi:10.1016/j.polymer.2009.05.059. [Google Scholar] [CrossRef]
502. Singh IV, Tanaka M, Endo M. Effect of interface on the thermal conductivity of carbon nanotube composites. Int J Therml Sci. 2007;46(9):842–7. doi:10.1016/j.ijthermalsci.2006.11.003. [Google Scholar] [CrossRef]
503. Li A, Zhang C, Zhang Y-F. Thermal conductivity of graphene-polymer composites: mechanisms, properties, and applications. Polymers. 2017;9(9):437. doi:10.3390/polym9090437. [Google Scholar] [CrossRef]
504. Yuan R, Wu S, Yu P, Wang B, Mu L, Zhang X, et al. Superamphiphobic and electroactive nanocomposite toward self-cleaning, antiwear, and anticorrosion coatings. ACS Appl Mat Interf. 2016;8(19):12481–93. doi:10.1021/acsami.6b03961. [Google Scholar] [CrossRef]
505. Bal S, Samal S. Carbon nanotube reinforced polymer composites—a state of the art. Bullet Mat Sci. 2007;30:379–86. doi:10.1007/s12034-007-0061-2. [Google Scholar] [CrossRef]
506. Uthaman A, Xian G, Thomas S, Wang Y, Zheng Q, Liu X. Durability of an epoxy resin and its carbon fiber-reinforced polymer composite upon immersion in water, acidic, and alkaline solutions. Polymers. 2020;12(3):614. doi:10.3390/polym12030614. [Google Scholar] [CrossRef]
507. Wang X, Tang F, Qi X, Lin Z. Mechanical, electrochemical, and durability behavior of graphene nano-platelet loaded epoxy-resin composite coatings. Compos Part B: Eng. 2019;176:107103. doi:10.1016/j.compositesb.2019.107103. [Google Scholar] [CrossRef]
508. Radhamani A, Lau HC, Ramakrishna S. Structural, mechanical and corrosion properties of CNT-304 stainless steel nanocomposites. Prog Nat Sci: Mat Internat. 2019;29(5):595–602. doi:10.1016/j.pnsc.2019.09.007. [Google Scholar] [CrossRef]
509. Ramezani M, Dehghani A, Sherif MM. Carbon nanotube reinforced cementitious composites: a comprehensive review. Constr Build Mater. 2022;315:125100. doi:10.1016/j.conbuildmat.2021.125100. [Google Scholar] [CrossRef]
510. Guo H, Ji P, Halász IZ, Pirityi DZ, Bárány T, Xu Z, et al. Enhanced fatigue and durability properties of natural rubber composites reinforced with carbon nanotubes and graphene oxide. Materials. 2020;13(24):5746. doi:10.3390/ma13245746. [Google Scholar] [CrossRef]
511. Guo H, Jerrams S, Xu Z, Zhou Y, Jiang L, Zhang L, et al. Enhanced fatigue and durability of carbon black/natural rubber composites reinforced with graphene oxide and carbon nanotubes. Eng Fract Mech. 2020;223:106764. doi:10.1016/j.engfracmech.2019.106764. [Google Scholar] [CrossRef]
512. Xie Y, Meng X, Chang Y, Mao D, Qin Z, Wan L, et al. Heteroatom modification enhances corrosion durability in high-mechanical-performance graphene-reinforced aluminum matrix composites. Adv Sci. 2022;9(23):e2104464. doi:10.1002/advs.202104464. [Google Scholar] [CrossRef]
513. Parente J, Santos P, Valvez S, Silva M, Reis P. Fatigue behaviour of graphene composites: an overview. Procedia Struct Integ. 2020;25:282–93. doi:10.1016/j.prostr.2020.04.033. [Google Scholar] [CrossRef]
514. Rafiee MA, Yavari F, Rafiee J, Koratkar N. Fullerene-epoxy nanocomposites-enhanced mechanical properties at low nanofiller loading. J Nanopart Res. 2011;13:733–7. doi:10.1007/s11051-010-0073-5. [Google Scholar] [CrossRef]
515. Callister WD Jr, Rethwisch DG. Fundamentals of materials science and engineering: an integrated approach. 5th ed. USA: John Wiley & Sons; 2020 [cited 2024 Nov 15]. Available from: https://www.wiley.com/en-gb/Fundamentals+of+Materials+Science+and+Engineering%3A+An+Integrated+Approach%2C+5th+Edition-p-9781119175506. [Google Scholar]
516. Loos MR, Schulte K. Is it worth the effort to reinforce polymers with carbon nanotubes? Macromol Theory Simulat. 2011;20(5):350–62. [Google Scholar]
517. Ismail AM, AL-Oqla FM, Risby M, Sapuan S. On the enhancement of the fatigue fracture performance of polymer matrix composites by reinforcement with carbon nanotubes: a systematic review. Carbon Letters. 2022;32(3):727–40. doi:10.1007/s42823-022-00323-z. [Google Scholar] [CrossRef]
518. Dai G, Mishnaevsky LJr. Carbone nanotube reinforced hybrid composites. Compos Part B: Eng, 78:349–60. doi:10.1016/j.compositesb.2015.03.073. [Google Scholar] [CrossRef]
519. Cui T, Mukherjee S, Sudeep PM, Colas G, Najafi F, Tam J, et al. Fatigue of graphene. Nature Mat. 2020;19(4):405–11. doi:10.1038/s41563-019-0586-y. [Google Scholar] [CrossRef]
520. Ren Y, Li F, Cheng H-M, Liao K. Tension-tension fatigue behavior of unidirectional single-walled carbon nanotube reinforced epoxy composite. Carbon. 2003;41(11):2177–9. doi:10.1016/S0008-6223(03)00248-3. [Google Scholar] [CrossRef]
521. Boroujeni AY, Al-Haik M. Carbon nanotube-Carbon fiber reinforced polymer composites with extended fatigue life. Compos Part B: Eng. 2019;164(12):537–45. doi:10.1016/j.compositesb.2018.11.056. [Google Scholar] [CrossRef]
522. Loos M, Yang J, Feke D, Manas-Zloczower I. Enhanced fatigue life of carbon nanotube-reinforced epoxy composites. Polymer Eng Sci. 2012;52(9):1882–7. doi:10.1002/pen.23145. [Google Scholar] [CrossRef]
523. Rafiee MA, Rafiee J, Srivastava I, Wang Z, Song H, Yu Z-Z, et al. Fracture and fatigue in graphene nanocomposites. Small. 2010;6(2):179. doi:10.1002/smll.200901480. [Google Scholar] [CrossRef]
524. Shokrieh M, Esmkhani M, Haghighatkhah A, Zhao Z. Flexural fatigue behavior of synthesized graphene/carbon-nanofiber/epoxy hybrid nanocomposites. Mat Des (1980–2015). 2014;62(7):401–8. doi:10.1016/j.matdes.2014.05.040. [Google Scholar] [CrossRef]
525. Tareq MS, Jony B, Zainuddin S, Al Ahsan M, Hosur MV. Fatigue analysis and fracture toughness of graphene reinforced carbon fibre polymer composites. Fati Fract Eng Mat Struct. 2021;44(2):461–74. doi:10.1111/ffe.13371. [Google Scholar] [CrossRef]
526. Bortz DR, Heras EG, Martin-Gullon I. Impressive fatigue life and fracture toughness improvements in graphene oxide/epoxy composites. Macromolecules. 2012;45(1):238–45. doi:10.1021/ma201563k. [Google Scholar] [CrossRef]
527. Li Y, Umer R, Isakovic A, Samad YA, Zheng L, Liao K. Synergistic toughening of epoxy with carbon nanotubes and graphene oxide for improved long-term performance. RSC Advances. 2013;3(23):8849–56. doi:10.1039/c3ra22300k. [Google Scholar] [CrossRef]
528. Dai RL, Liao WH. Fabrication, testing, and modeling of carbon nanotube composites for vibration damping. J Vibrati Acoustics. 2009;131(5):051004. doi:10.1115/1.3147126. [Google Scholar] [CrossRef]
529. Auad ML, Mosiewicki MA, Uzunpinar C, Williams RJ. Single-wall carbon nanotubes/epoxy elastomers exhibiting high damping capacity in an extended temperature range. Compos Sci Technol. 2009;69(7–8):1088–92. doi:10.1016/j.compscitech.2009.01.030. [Google Scholar] [CrossRef]
530. Katsiropoulos CV, Pappas P, Koutroumanis N, Kokkinos A, Galiotis C. Enhancement of damping response in polymers and composites by the addition of graphene nanoplatelets. Compos Sci Technol. 2022;227(3):109562. doi:10.1016/j.compscitech.2022.109562. [Google Scholar] [CrossRef]
531. Deng C, Wang D, Zhang X, Ma Y. Damping characteristics of carbon nanotube reinforced aluminum composite. Mater Lett. 2007;61(14–15):3229–31. doi:10.1016/j.matlet.2006.11.073. [Google Scholar] [CrossRef]
532. Zhao J, Wang F, Zhang X, Liang L, Yang X, Li Q, et al. Vibration damping of carbon nanotube assembly materials. Adv Eng Mater. 2018;20(3):1700647. doi:10.1002/adem.201700647. [Google Scholar] [CrossRef]
533. Suhr J, Zhang W, Ajayan PM, Koratkar NA. Temperature-activated interfacial friction damping in carbon nanotube polymer composites. Nano Letters. 2006;6(2):219–23. doi:10.1021/nl0521524. [Google Scholar] [CrossRef]
534. Rajoria H, Jalili N. Passive vibration damping enhancement using carbon nanotube-epoxy reinforced composites. Compos Sci Technol. 2005;65(14):2079–93. doi:10.1016/j.compscitech.2005.05.015. [Google Scholar] [CrossRef]
535. Khan SU, Li CY, Siddiqui NA, Kim J-K. Vibration damping characteristics of carbon fiber-reinforced composites containing multi-walled carbon nanotubes. Compos Sci Technol. 2011;71(12):1486–94. doi:10.1016/j.compscitech.2011.03.022. [Google Scholar] [CrossRef]
536. Koratkar NA, Wei B, Ajayan PM. Multifunctional structural reinforcement featuring carbon nanotube films. Compos Sci Techn. 2003;63(11):1525–31. doi:10.1016/S0266-3538(03)00065-4. [Google Scholar] [CrossRef]
537. Rafiee M, Nitzsche F, Labrosse M. Fabrication and experimental evaluation of vibration and damping in multiscale graphene/fiberglass/epoxy composites. J Compos Mat. 2019;53(15):2105–18. doi:10.1177/0021998318822708. [Google Scholar] [CrossRef]
538. Rafiee M, Nitzsche F, Labrosse MR. Processing, manufacturing, and characterization of vibration damping in epoxy composites modified with graphene nanoplatelets. Polymer Compos. 2019;40(10):3914–22. doi:10.1002/pc.25251. [Google Scholar] [CrossRef]
539. Erkliğ A, Younus B, Doğan NF, Alsaadi M, Bulut M, Sulaiman BH. Vibration damping properties of graphene nanoplatelets filled glass/carbon fiber hybrid composites. Int Polymer Process. 2023;38(2):145–53. doi:10.1515/ipp-2022-4241. [Google Scholar] [CrossRef]
540. Bulut M, Erkliğ A, Kanmaz P. Vibration-damping characterization of the basalt/epoxy composite laminates containing graphene nanopellets. Sci Eng Compos Mat. 2019;26(1):147–53. doi:10.1515/secm-2017-0380. [Google Scholar] [CrossRef]
541. Dai RL, Liao WH. Modeling of carbon nanotube composites for vibration damping. In: Proceedings of Nanosensors, Microsensors, and Biosensors and Systems 2007. Bellingham, WA, San Diego, CA, USA: SPIE; 2007. Vol. 6528, p. 64–73. doi:10.1117/12.716019. [Google Scholar] [CrossRef]
542. Corcione CE, Freuli F, Maffezzoli A. The aspect ratio of epoxy matrix nanocomposites reinforced with graphene stacks. Polymer Eng Sci. 2013;53(3):531–9. doi:10.1002/pen.23292. [Google Scholar] [CrossRef]
543. Ramos-Galicia L, Mendez L, Martínez-Hernández AL, Espindola-Gonzalez A, Galindo-Esquivel I, Fuentes-Ramirez R, et al. Improved performance of an epoxy matrix as a result of combining graphene oxide and reduced graphene. Int J Polym Sci. 2013;2013(1):493147. doi:10.1155/2013/493147. [Google Scholar] [CrossRef]
544. Li W, Dichiara A, Bai J. Carbon nanotube-graphene nanoplatelet hybrids as high-performance multifunctional reinforcements in epoxy composites. Compos Sci Technol. 2013;74(3):221–7. doi:10.1016/j.compscitech.2012.11.015. [Google Scholar] [CrossRef]
545. Yasmin A, Daniel IM. Mechanical and thermal properties of graphite platelet/epoxy composites. Polymer. 2004;45(24):8211–9. doi:10.1016/j.polymer.2004.09.054. [Google Scholar] [CrossRef]
546. Wong S-C, Sutherland EM, Uhl FM. Materials processes of graphite nanostructured composites using ball milling. Mat Manufact Process. 2006;21(2):159–66. [Google Scholar]
547. Wang X, Song L, Pornwannchai W, Hu Y, Kandola B. The effect of graphene presence in flame retarded epoxy resin matrix on the mechanical and flammability properties of glass fiber-reinforced composites. Compos Part A: App Sci Manufact. 2013;53:88–96. doi:10.1016/j.compositesa.2013.05.017. [Google Scholar] [CrossRef]
548. Liang A, Jiang X, Hong X, Jiang Y, Shao Z, Zhu D. Recent developments concerning the dispersion methods and mechanisms of graphene. Coatings. 2018;8(1):33. doi:10.3390/coatings8010033. [Google Scholar] [CrossRef]
549. Govindaraj P, Sokolova A, Salim N, Juodkazis S, Fuss FK, Fox B, et al. Distribution states of graphene in polymer nanocomposites: a review. Compos Part B: Eng. 2021;226:109353. doi:10.1016/j.compositesb.2021.109353. [Google Scholar] [CrossRef]
550. Jancar J, Douglas J, Starr FW, Kumar S, Cassagnau P, Lesser A, et al. Current issues in research on structure-property relationships in polymer nanocomposites. Polymer. 2010;51(15):3321–43. doi:10.1016/j.polymer.2010.04.074. [Google Scholar] [CrossRef]
551. Karger-Kocsis J, Mahmood H, Pegoretti A. Recent advances in fiber/matrix interphase engineering for polymer composites. Prog Mat Sci. 2015;73:1–43. doi:10.1016/j.pmatsci.2015.02.003. [Google Scholar] [CrossRef]
552. Lavagna L, Nisticò R, Musso S, Pavese M. Functionalization as a way to enhance dispersion of carbon nanotubes in matrices: a review. Mater Today Chem. 2021;20:100477. doi:10.1016/j.mtchem.2021.100477. [Google Scholar] [CrossRef]
553. Parveen S, Rana S, Fangueiro R. A review on nanomaterial dispersion, microstructure, and mechanical properties of carbon nanotube and nanofiber reinforced cementitious composites. J Nanomat. 2013;2013(1):710175. doi:10.1155/2013/710175. [Google Scholar] [CrossRef]
554. Ausman KD, Piner R, Lourie O, Ruoff RS, Korobov M. Organic solvent dispersions of single-walled carbon nanotubes: toward solutions of pristine nanotubes. J Phy Chem B. 2000;104(38):8911–5. doi:10.1021/jp002555m. [Google Scholar] [CrossRef]
555. Pang J, Xu G, Yuan S, Tan Y, He F. Dispersing carbon nanotubes in aqueous solutions by a silicon surfactant: experimental and molecular dynamics simulation study. Coll Surf A: Physicochem Eng Aspects. 2009;350(1–3):101–8. doi:10.1016/j.colsurfa.2009.09.011. [Google Scholar] [CrossRef]
556. Georgakilas V, Otyepka M, Bourlinos AB, Chandra V, Kim N, Kemp KC, et al. Functionalization of graphene: covalent and non-covalent approaches, derivatives and applications. Chem Reviews. 2012;112(11):6156–214. doi:10.1021/cr3000412. [Google Scholar] [CrossRef]
557. Loos MR, Coelho LAF, Pezzin SH, Amico SC. The effect of acetone addition on the properties of epoxy. Polímeros. 2008;18(1):76–80. doi:10.1590/S0104-14282008000100015. [Google Scholar] [CrossRef]
558. Lau K, Lu M, Cheung H, Sheng F, Li H. Thermal and mechanical properties of single-walled carbon nanotube bundle-reinforced epoxy nanocomposites: the role of solvent for nanotube dispersion. Compos Sci Technol. 2005;65(5):719–25. doi:10.1016/j.compscitech.2004.10.005. [Google Scholar] [CrossRef]
559. Hong S-G, Wu C-S. DSC and FTIR analysis of the curing behaviors of epoxy/DICY/solvent open systems. Thermochimica Acta. 1998;316(2):167–75. doi:10.1016/S0040-6031(98)00356-6. [Google Scholar] [CrossRef]
560. Rausch J, Zhuang R-C, Mäder E. Surfactant assisted dispersion of functionalized multi-walled carbon nanotubes in aqueous media. Compos Part A: Appl Sci Manuf. 2010;41(9):1038–46. doi:10.1016/j.compositesa.2010.03.007. [Google Scholar] [CrossRef]
561. Abdalla M, Dean D, Adibempe D, Nyairo E, Robinson P, Thompson G. The effect of interfacial chemistry on molecular mobility and morphology of multiwalled carbon nanotubes epoxy nanocomposite. Polymer. 2007;48(19):5662–70. doi:10.1016/j.polymer.2007.06.073. [Google Scholar] [CrossRef]
562. Krause B, Mende M, Pötschke P, Petzold G. Dispersability and particle size distribution of CNTs in an aqueous surfactant dispersion as a function of ultrasonic treatment time. Carbon. 2010;48(10):2746–54. doi:10.1016/j.carbon.2010.04.002. [Google Scholar] [CrossRef]
563. Schilde C, Nolte H, Arlt C, Kwade A. Effect of fluid-particle-interactions on dispersing nano-particles in epoxy resins using stirred-media-mills and three-roll-mills. Compos Sci Technol. 2010;70(4):657–63. doi:10.1016/j.compscitech.2009.12.021. [Google Scholar] [CrossRef]
564. Choi H, Shin J, Bae D. The effect of milling conditions on microstructures and mechanical properties of Al/MWCNT composites. Compos Part A: Appl Sci Manuf. 2012;43(7):1061–72. doi:10.1016/j.compositesa.2012.02.008. [Google Scholar] [CrossRef]
565. Tang L-C, Wan Y-J, Yan D, Pei Y-B, Zhao L, Li Y-B, et al. The effect of graphene dispersion on the mechanical properties of graphene/epoxy composites. Carbon. 2013;60(5696):16–27. doi:10.1016/j.carbon.2013.03.050. [Google Scholar] [CrossRef]
566. Sumfleth J, de Almeida Prado LA, Sriyai M, Schulte K. Titania-doped multi-walled carbon nanotubes epoxy composites: enhanced dispersion and synergistic effects in multiphase nanocomposites. Polymer. 2008;49(23):5105–12. doi:10.1016/j.polymer.2008.09.016. [Google Scholar] [CrossRef]
567. Shofner M, Rodríguez-Macías FJ, Vaidyanathan R, Barrera EV. Single wall nanotube and vapor grown carbon fiber reinforced polymers processed by extrusion freeform fabrication. Compos Part A: Appl Sci Manuf. 2003;34(12):1207–17. doi:10.1016/j.compositesa.2003.07.002. [Google Scholar] [CrossRef]
568. Villmow T, Pötschke P, Pegel S, Häussler L, Kretzschmar B. Influence of twin-screw extrusion conditions on the dispersion of multi-walled carbon nanotubes in a poly (lactic acid) matrix. Polymer. 2008;49(16):3500–9. doi:10.1016/j.polymer.2008.06.010. [Google Scholar] [CrossRef]
569. Vennerberg D, Rueger Z, Kessler MR. Effect of silane structure on the properties of silanized multiwalled carbon nanotube-epoxy nanocomposites. Polymer. 2014;55(7):1854–65. doi:10.1016/j.polymer.2014.02.018. [Google Scholar] [CrossRef]
570. Nayak RR, Lee KY, Shanmugharaj A, Ryu SH. Synthesis and characterization of styrene grafted carbon nanotube and its polystyrene nanocomposite. Euro Polymer J. 2007;43(12):4916–23. doi:10.1016/j.eurpolymj.2007.04.012. [Google Scholar] [CrossRef]
571. Peng H, Alemany LB, Margrave JL, Khabashesku VN. Sidewall carboxylic acid functionalization of single-walled carbon nanotubes. J American Chem Soc. 2003;125(49):15174–82. doi:10.1021/ja037746s. [Google Scholar] [CrossRef]
572. Wang Y, Iqbal Z, Malhotra SV. Functionalization of carbon nanotubes with amines and enzymes. Chem Phys Lett. 2005;402(1–3):96–101. doi:10.1016/j.cplett.2004.11.099. [Google Scholar] [CrossRef]
573. Lavskaya YV, Bulusheva L, Okotrub A, Yudanov N, Vyalikh D, Fonseca A. Comparative study of fluorinated single-and few-wall carbon nanotubes by X-ray photoelectron and X-ray absorption spectroscopy. Carbon. 2009;47(7):1629–36. doi:10.1016/j.carbon.2009.01.046. [Google Scholar] [CrossRef]
574. Utegulov ZN, Mast DB, He P, Shi D, Gilland RF. Functionalization of single-walled carbon nanotubes using isotropic plasma treatment: resonant Raman spectroscopy study. J Appl Phys. 2005;97(10):18. doi:10.1063/1.1913801. [Google Scholar] [CrossRef]
575. Wang Y, Iqbal Z, Mitra S. Rapidly functionalized, water-dispersed carbon nanotubes at high concentration. J American Chem Soc. 2006;128(1):95–9. doi:10.1021/ja053003q. [Google Scholar] [CrossRef]
576. Wang D, Wang K, Wu H, Luo Y, Sun L, Zhao Y, et al. CO2 oxidation of carbon nanotubes for lithium-sulfur batteries with improved electrochemical performance. Carbon. 2018;132(6):370–9. doi:10.1016/j.carbon.2018.02.048. [Google Scholar] [CrossRef]
577. Li M, Boggs M, Beebe TP, Huang C. Oxidation of single-walled carbon nanotubes in dilute aqueous solutions by ozone as affected by ultrasound. Carbon. 2008;46(3):466–75. doi:10.1016/j.carbon.2007.12.012. [Google Scholar] [CrossRef]
578. Li Z, Wang R, Young RJ, Deng L, Yang F, Hao L, et al. Control of the functionality of graphene oxide for its in epoxy nanocomposites application. Polymer. 2013;54(23):6437–46. doi:10.1016/j.polymer.2013.09.054. [Google Scholar] [CrossRef]
579. Yan Z, Yuexin D, Lu Y, Fengxia G. The dispersion of SWCNTs treated by dispersing agents in glass fiber reinforced polymer composites. Compos Sci Technol. 2009;69(13):2115–8. doi:10.1016/j.compscitech.2009.01.012. [Google Scholar] [CrossRef]
580. Lee JU, Huh J, Kim KH, Park C, Jo WH. Aqueous suspension of carbon nanotubes via non-covalent functionalization with oligothiophene-terminated poly (ethylene glycol). Carbon. 2007;45(5):1051–7. doi:10.1016/j.carbon.2006.12.017. [Google Scholar] [CrossRef]
581. Ma H, Tong L, Xu Z, Fang Z. Synergistic effect of carbon nanotube and clay for improving the flame retardancy of ABS resin. Nanotechnology. 2007;18(37):375602. doi:10.1088/0957-4484/18/37/375602. [Google Scholar] [CrossRef]
582. Haggenmueller R, Rahatekar SS, Fagan JA, Chun J, Becker ML, Naik RR, et al. Comparison of the quality of aqueous dispersions of single wall carbon nanotubes using surfactants and biomolecules. Langmuir. 2008;24(9):5070–8. doi:10.1021/la703008r. [Google Scholar] [CrossRef]
583. Rafiee R, Eskandariyun A. Predicting Young’s modulus of agglomerated graphene/polymer using multi-scale modeling. Compos Struct. 2020;245(12):112324. doi:10.1016/j.compstruct.2020.112324. [Google Scholar] [CrossRef]
584. Katsnelson M. Encyclopedia of condensed matter physics. 1st ed. Amsterdam: Elsevier; 2005. p. 1–3000. doi:10.1016/B0-12-227610-1. [Google Scholar] [CrossRef]
585. Li Z, Chu J, Yang C, Hao S, Bissett MA, Kinloch IA, et al. Effect of functional groups on the agglomeration of graphene in nanocomposites. Compos Sci Technol. 2018;163(5696):116–22. doi:10.1016/j.compscitech.2018.05.016. [Google Scholar] [CrossRef]
586. Ji X-Y, Cao Y-P, Feng X-Q. Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model Simul Mater Sci Eng. 2010;18(4):045005. doi:10.1088/0965-0393/18/4/045005. [Google Scholar] [CrossRef]
587. Rahnama EK, Ansari R, Hassanzadeh-Aghdam MK. Effect of graphene nano-additives on the fatigue limit of fiber-reinforced polymer hybrid composites—A micromechanical modeling procedure. Proc Inst Mech Eng, Part L: J Mat: Des Appl. 2024;238(6):1082–98. doi:10.1177/14644207231208180. [Google Scholar] [CrossRef]
588. Zeinedini A. Fracture toughness of graphene/polymer nanocomposites: well dispersion, agglomeration and toughening mechanisms. Theor Appl Fract Mech. 2024;131(24):104449. doi:10.1016/j.tafmec.2024.104449. [Google Scholar] [CrossRef]
589. Wang Y, Shan JW, Weng GJ. Percolation threshold and electrical conductivity of graphene-based nanocomposites with filler agglomeration and interfacial tunneling. J Appl Phys. 2015;118(6):1350. doi:10.1063/1.4928293. [Google Scholar] [CrossRef]
590. Du H, Zhang J, Fang C, Weng GJ. Modeling the evolution of graphene agglomeration and the electrical and mechanical properties of graphene/polypropylene nanocomposites. J Appl Polym Sci. 2023;140(2):e53292. doi:10.1002/app.53292. [Google Scholar] [CrossRef]
591. Acar A, Colak O, Correia J, Ahzi S. Cooperative-VBO model for polymer/graphene nanocomposites. Mech Mat. 2018;125(12):1–13. doi:10.1016/j.mechmat.2018.06.005. [Google Scholar] [CrossRef]
592. Hassanzadeh-Aghdam M. Evaluating the effective creep properties of graphene-reinforced polymer nanocomposites by a homogenization approach. Compos Sci Technol. 2021;209(11):108791. doi:10.1016/j.compscitech.2021.108791. [Google Scholar] [CrossRef]
593. Shokrieh Z, Shokrieh M, Zhao Z. A modified micromechanical model to predict the creep modulus of polymeric nanocomposites. Polymer Testing. 2018;65(18):414–9. doi:10.1016/j.polymertesting.2017.12.020. [Google Scholar] [CrossRef]
594. Roshan MJ, Jeevika A, Bhattacharyya A, Shankaran DR. One-pot fabrication and characterization of graphene/PMMA composite flexible films. Mat Res Bullet. 2018;105:133–41. doi:10.1016/j.materresbull.2018.04.034. [Google Scholar] [CrossRef]
595. Cha J, Jin S, Shim JH, Park CS, Ryu HJ, Hong SH. Functionalization of carbon nanotubes for fabrication of CNT/epoxy nanocomposites. Mat Des. 2016;95:1–8. doi:10.1016/j.matdes.2016.01.077. [Google Scholar] [CrossRef]
596. Dong X, Li B, Wei A, Cao X, Chan-Park MB, Zhang H, et al. One-step growth of graphene-carbon nanotube hybrid materials by chemical vapor deposition. Carbon. 2011;49(9):2944–9. doi:10.1016/j.carbon.2011.03.009. [Google Scholar] [CrossRef]
597. Eletskii AV, Iskandarova IM, Knizhnik AA, Krasikov DN. Graphene: fabrication methods and thermophysical properties. Phys Usp. 2011;54(3):227. doi:10.3367/UFNe.0181.201103a.0233. [Google Scholar] [CrossRef]
598. Galpayage Dona DG, Wang M, Liu M, Motta N, Waclawik E, Yan C. Recent advances in fabrication and characterization of graphene-polymer nanocomposites. Graphene. 2012;1(2):30–49. doi:10.4236/graphene.2012.12005. [Google Scholar] [CrossRef]
599. Zhang H, Feng PX. Fabrication and characterization of few-layer graphene. Carbon. 2010;48(2):359–64. doi:10.1016/j.carbon.2009.09.037. [Google Scholar] [CrossRef]
600. Jamal-Omidi M, ShayanMehr M. Improving the dispersion of SWNT in epoxy resin through a simple Multi-Stage method. J King Saud Univ-Sci. 2019;31(2):202–8. doi:10.1016/j.jksus.2018.01.007. [Google Scholar] [CrossRef]
601. Bhattacharya M. Polymer nanocomposites—a comparison between carbon nanotubes, graphene, and clay as nanofillers. Materials. 2016;9(4):262. doi:10.3390/ma9040262. [Google Scholar] [CrossRef]
602. Safadi B, Andrews R, Grulke E. Multiwalled carbon nanotube polymer composites: synthesis and characterization of thin films. J Appl Poly Sci. 2002;84(14):2660–9. doi:10.1002/app.10436. [Google Scholar] [CrossRef]
603. Andrews R, Jacques D, Minot M, Rantell T. Fabrication of carbon multiwall nanotube/polymer composites by shear mixing. Macromol Mat Eng. 2002;287(6):395–403. [Google Scholar]
604. Xie L, Xu F, Qiu F, Lu H, Yang Y. Single-walled carbon nanotubes functionalized with high bonding density of polymer layers and enhanced mechanical properties of composites. Macromolecules. 2007;40(9):3296–305. doi:10.1021/ma062103t. [Google Scholar] [CrossRef]
605. De S, Coleman JN. Are there fundamental limitations on the sheet resistance and transmittance of thin graphene films? ACS Nano. 2010;4(5):2713–20. doi:10.1021/nn100343f. [Google Scholar] [CrossRef]
606. Mo Z-L, Xie T-T, Zhang J-X, Zhao Y-X, Guo R-B. Synthesis and characterization of nanoGs-PPy/epoxy nanocomposites by in situ polymerization. Synth React Inorg, Metal-Organ Nano-Metal Chem. 2012;42(8):1172–6. doi:10.1080/15533174.2012.684259. [Google Scholar] [CrossRef]
607. Kuila T, Bose S, Hong CE, Uddin ME, Khanra P, Kim NH, et al. Preparation of functionalized graphene/linear low density polyethylene composites by a solution mixing method. Carbon. 2011;49(3):1033–7. doi:10.1016/j.carbon.2010.10.031. [Google Scholar] [CrossRef]
608. El Achaby M, Arrakhiz FE, Vaudreuil S, el Kacem Qaiss A, Bousmina M, Fassi-Fehri O. Mechanical, thermal, and rheological properties of graphene-based polypropylene nanocomposites prepared by melt mixing. Polymer Compos. 2012;33(5):733–44. doi:10.1002/pc.22198. [Google Scholar] [CrossRef]
609. Tan LJ, Zhu W, Zhou K. Recent progress on polymer materials for additive manufacturing. Adv Funct Mater. 2020;30(43):2003062. doi:10.1002/adfm.202003062. [Google Scholar] [CrossRef]
610. Bai J, Goodridge RD, Hague RJ, Song M, Okamoto M. Influence of carbon nanotubes on the rheology and dynamic mechanical properties of polyamide-12 for laser sintering. Polymer Test. 2014;36:95–100. doi:10.1016/j.polymertesting.2014.03.012. [Google Scholar] [CrossRef]
611. Gan X, Wang J, Wang Z, Zheng Z, Lavorgna M, Ronca A, et al. Simultaneous realization of conductive segregation network microstructure and minimal surface porous macrostructure by SLS 3D printing. Mat Des. 2019;178:107874. doi:10.1016/j.matdes.2019.107874. [Google Scholar] [CrossRef]
612. Yuan S, Zheng Y, Chua CK, Yan Q, Zhou K. Electrical and thermal conductivities of MWCNT/polymer composites fabricated by selective laser sintering. Compos Part A: Appl Sci Manufact. 2018;105:203–13. doi:10.1016/j.compositesa.2017.11.007. [Google Scholar] [CrossRef]
613. Lao S, Koo J, Moon T, Londa M, Ibeh C, Wissler G, et al. Flame-retardant polyamide 11 nanocomposites: further thermal and flammability studies. J Fire Sci. 2011;29(6):479–98. doi:10.1177/0734904111404658. [Google Scholar] [CrossRef]
614. Paggi R, Beal V, Salmoria G. Process optimization for PA12/MWCNT nanocomposite manufacturing by selective laser sintering. Int J Adv Manuf Technol. 2013;66(9-12):1977–85. doi:10.1007/s00170-012-4474-8. [Google Scholar] [CrossRef]
615. Bai J, Goodridge RD, Hague RJ, Song M. Improving the mechanical properties of laser-sintered polyamide 12 through incorporation of carbon nanotubes. Polymer Eng Sci. 2013;53(9):1937–46. doi:10.1002/pen.23459. [Google Scholar] [CrossRef]
616. Christ JF, Aliheidari N, Ameli A, Pötschke P. 3D printed highly elastic strain sensors of multiwalled carbon nanotube/thermoplastic polyurethane nanocomposites. Mat Des. 2017;131:394–401. doi:10.1016/j.matdes.2017.06.011. [Google Scholar] [CrossRef]
617. Meng S, He H, Jia Y, Yu P, Huang B, Chen J. Effect of nanoparticles on the mechanical properties of acrylonitrile-butadiene–styrene specimens fabricated by fused deposition modeling. J Appl Polym Sci. 2017;134(7):365. doi:10.1002/app.44470. [Google Scholar] [CrossRef]
618. Sandoval J, Soto K, Murr L, Wicker R. Nanotailoring photocrosslinkable epoxy resins with multi-walled carbon nanotubes for stereolithography layered manufacturing. J Mat Sci. 2007;42(1):156–65. doi:10.1007/s10853-006-1035-2. [Google Scholar] [CrossRef]
619. Ronca A, Rollo G, Cerruti P, Fei G, Gan X, Buonocore GG, et al. Selective laser sintering fabricated thermoplastic polyurethane/graphene cellular structures with tailorable properties and high strain sensitivity. Appl Sci. 2019;9(5):864. doi:10.3390/app9050864. [Google Scholar] [CrossRef]
620. Chen B, Davies R, Liu Y, Yi N, Qiang D, Zhu Y, et al. Laser sintering of graphene nanoplatelets encapsulated polyamide powders. Addit Manuf. 2020;35:101363. doi:10.1016/j.addma.2020.101363. [Google Scholar] [CrossRef]
621. Chen DZ, Lao S, Koo JH, Londa M, Alabdullatif Z. Powder processing and properties characterization of polyamide 11-graphene nanocomposites for selective laser sintering. University of Texas at Austin; 2010 [cited 2024 Nov 15]. Available from: https://repositories.lib.utexas.edu/items/c5c50a76-c445-48e7-8207-2639a8a5c8c3. [Google Scholar]
622. Gaikwad S, Tate J, Theodoropoulou N, Koo J. Electrical and mechanical properties of PA11 blended with nanographene platelets using industrial twin-screw extruder for selective laser sintering. J Compos Mat. 2013;47(23):2973–86. doi:10.1177/0021998312460560. [Google Scholar] [CrossRef]
623. Kim HC, Hahn HT, Yang YS. Synthesis of PA12/functionalized GNP nanocomposite powders for the selective laser sintering process. J Compos Mat. 2013;47(4):501–9. doi:10.1177/0021998312441812. [Google Scholar] [CrossRef]
624. Girdis J, McCaffrey M, Proust G. Additive manufacturing of carbon fiber and graphene-polymer composites using the technique of fused deposition modelling. University of Texas at Austin; 2016 [cited 2024 Nov 15]. Available from: https://repositories.lib.utexas.edu/items/1566659e-642d-40d2-b929-0154059b302d. [Google Scholar]
625. Zhu D, Ren Y, Liao G, Jiang S, Liu F, Guo J, et al. Thermal and mechanical properties of polyamide 12/graphene nanoplatelets nanocomposites and parts fabricated by fused deposition modeling. J Appl Polym Sci. 2017;134(39):45332. doi:10.1002/app.45332. [Google Scholar] [CrossRef]
626. Lin D, Jin S, Zhang F, Wang C, Wang Y, Zhou C, et al. 3D stereolithography printing of graphene oxide reinforced complex architectures. Nanotechnology. 2015;26(43):434003. doi:10.1088/0957-4484/26/43/434003. [Google Scholar] [CrossRef]
627. Yuan S, Shen F, Chua CK, Zhou K. Polymeric composites for powder-based additive manufacturing: materials and applications. Prog Polymer Sci. 2019;91:141–68. doi:10.1016/j.progpolymsci.2018.11.001. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF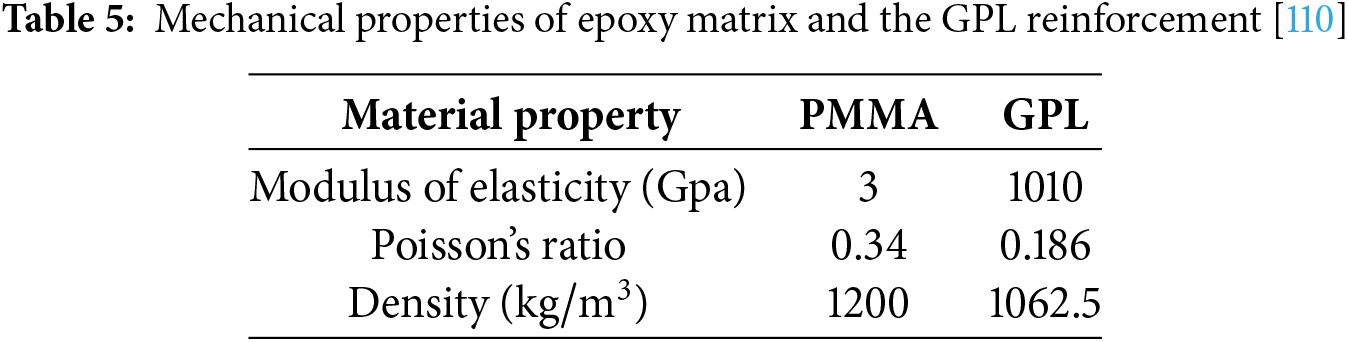




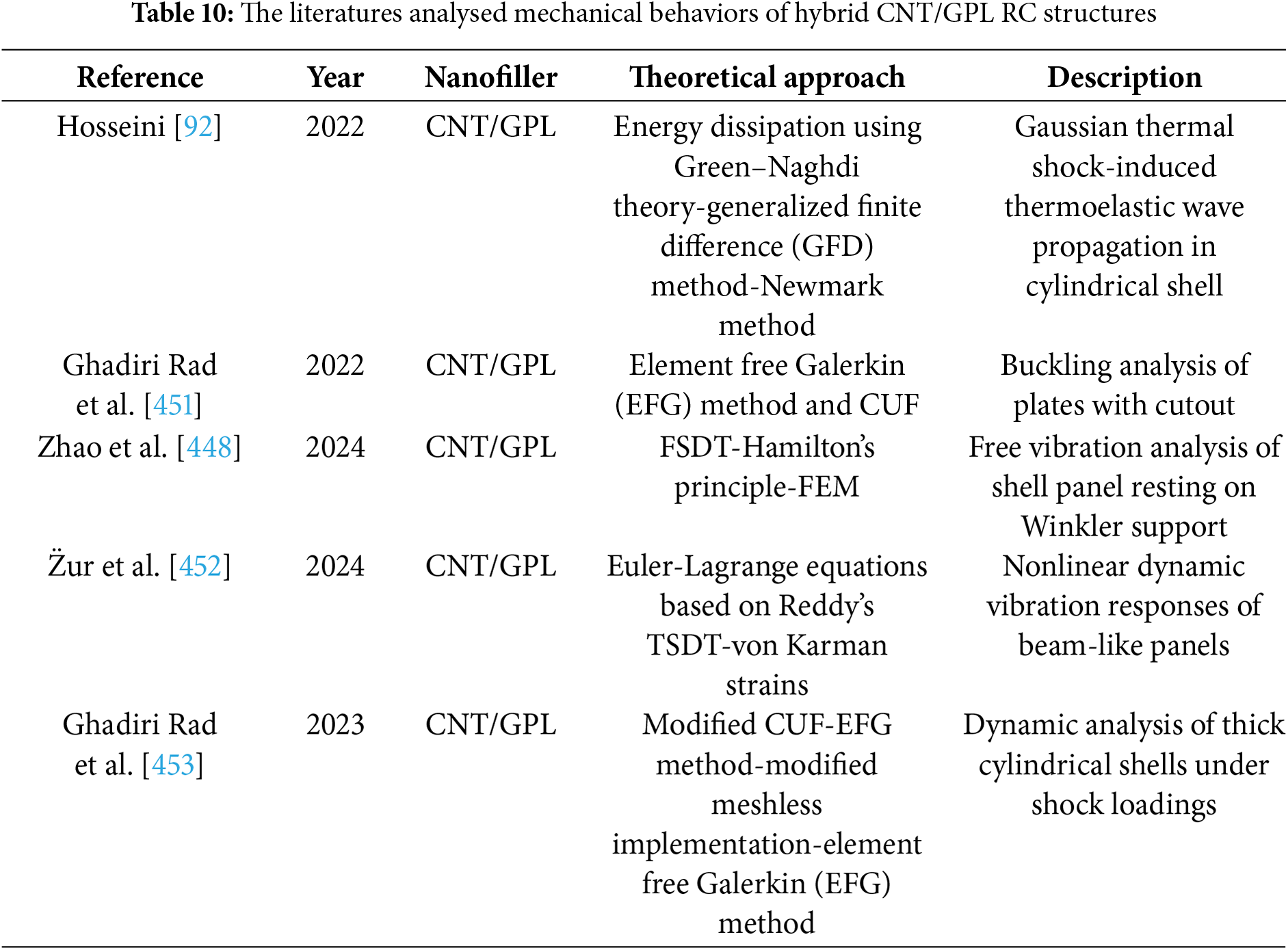
 Downloads
Downloads
 Citation Tools
Citation Tools