Enhanced Particle Swarm Optimization Algorithm Based on SVM Classifier for Feature Selection

1  Introduction

With the rapid progress of society and the economy, the era of big data is advancing steadily. Data collection and storage technology are widely utilized, and a massive amount of data has been accumulated. Against this background, extracting helpful information has proven challenging due to the sheer volume of data, its varying quality, and the diversity of data sources. Traditional data analysis methods, like hypothesis testing and regression analysis, can no longer handle large data sets. Even if some datasets are not significant in quantity, they cannot be analyzed using these methods due to the unique properties of the data. Therefore, to overcome these challenges, new techniques must be developed. Data mapping integrates classic data analysis tools with sophisticated algorithms to effectively process vast volumes of data and discover valuable knowledge within them. By applying data mapping techniques, hidden and helpful information and patterns can be extracted from massive databases. Thus, critical conclusions and trends can be drawn, helping people understand the data and make meaningful analyses and applications.

Feature selection (FS) is an instrumental part of Machine Learning (ML) and data mapping [1]. It can extract a valid set of features from a substantial quantity of redundant, noisy, and irrelevant information to raise the performance of learning algorithms, reduce computational expenses, improve the interpretability of models, and reduce the risk of over-fitting [2]. FS attempts to optimize the system for a particular metric by selecting N features from the available M features, where N < M.

Generally, FS methods have three categories [3]: filtering approach, embedding approach, and wrapping approach. First, independent of the specific learning algorithm, the filtering approach selects the most significant subset of features by assessing and ranking the features. The more common filtering approaches [4] are variance selection, mutual information method, chi-square test, etc. They all choose the top-ranked features by some law, and these guidelines can be based on statistical indicators, information theory, correlation coefficients, and so on. Filtering approaches are computationally simple and efficient, but they have several limitations. Due to their independence, they may not be able to capture the complex interactions between features; furthermore, focusing only on the attributes of the features themselves and the relationship with the target variables without considering the correlation between the features makes it impossible to discover the optimal subset of features for a given problem and data set. In practical applications, combining other FS approaches to obtain better results is frequently essential. Second, embedding approaches [5] perform feature selection simultaneously with model training and decide whether to select a feature or not by evaluating the importance or weight of the feature during the model training process. Embedding approaches have become familiar and effective in FS due to their advantages of automation, making full use of data, avoiding over-fitting, learning task adaptation, and reducing dimension catastrophe.

Finally, the core idea of the wrapping approach [6] is to convert the FS task into a subset search problem and to assess the effectiveness of various feature subsets using an evaluation metric. These evaluation criteria can be specific performance metrics of the learning algorithm or classifier, such as accuracy, mean square error, etc. Moreover, this approach can be combined with diverse classifiers, including the K-Nearest Neighbor method (KNN) [7], Decision Tree (DT) [8], Support Vector Machines (SVM) [9], and other similar techniques. Although these methods are computationally more expensive, they provide a more accurate measure of the impact of features on model performance and have more vital generalization ability. The wrapping approach generally utilizes optimization techniques to deal with the FS problem. The FS may be viewed as an optimization problem solved using existing optimization algorithms and techniques [10] and finding the near-optimal subset of features.

Meta-heuristic algorithms are extensively applied to solve FS problems by their extreme optimization search capability. In general, they randomly generate a group of initial solutions and then evaluate this group of solutions using an evaluation function to measure their performance [11] in the FS problem. Next, the algorithm undergoes a series of search strategies to refine the current solution through iteration. During each iteration, they adjust the state of the solution according to some rules and ways that approximate the optimal solution until the termination condition is reached or a predetermined result is satisfied. However, although each evaluated algorithm can perform well when considering some specific optimization problems, the No Free Lunch theorem [12] shows that no super-optimization technique can tackle all optimization problems. Hence, refining existing algorithms or inventing more capable ones is essential.

Particle Swarm Optimization (PSO) is a conventional meta-heuristic algorithm that takes inspiration from the foraging and social behavior of bird flocks [13]. Due to its relatively simple core thinking, PSO finds broad application in optimization problems. However, several challenges and limitations exist, such as being vulnerable to local optimization. Therefore, an enhanced particle swarm optimization is proposed in this paper. Meanwhile, the proposed algorithm is tested on two challenging test sets and applied to three engineering applications and six feature selection problems. The primary achievements of this paper are outlined as follows:

(1) Integrate the benefits of the Sand Cat Swarm Optimization (SCSO) into PSO and integrate two enhanced methodologies.

∎   The incorporation of the SCSO tackles the problem of restricted search breadth present in the original method, thereby greatly enhancing the algorithm’s ability to explore and reducing the likelihood of becoming ensnared in local optima.

∎   In the algorithm’s initial phase, the initial population’s random generation is discarded in favor of a more high-level Latin hypercube sampling strategy that permits particles to explore a broader range of the entire search space.

∎   Roundup search strategy is introduced so particles can more quickly determine the target’s location during the search process, significantly reducing the computational cost and increasing the optimization efficiency.

(2) Compare the suggested algorithm with other enhanced PSO and various algorithms on the CEC2020 and CEC2022 test suites.

(3) Self-adaptive Cooperative Particle Swarm Optimization (SCPSO) is tested against other excellent algorithms on three engineering application problems with satisfactory results.

(4) SCPSO has demonstrated its effectiveness in addressing six feature selection problems, producing subsets that exhibit high accuracy while containing only a limited number of features.

The following chapters are outlined: Section 2 introduces the improvement and optimization of PSO in recent years and the researchers’ settlement and study of the feature selection problem. Section 3 briefly describes the basic framework and optimization process of PSO and SCSO. In Section 4, the contents of the two enhanced strategies and the process of SCPSO are described in detail. Section 5 concentrates on verifying the performance of SCPSO on two test sets. Three real-world problems are chosen in Section 6 to test SCPSO’s ability to address the optimization problem further. The study of SCPSO to solve six feature selection problems is presented in Section 7. Section 8 offers a recapitulation and prospects.

2  Relevant Research

2.1 Research on PSO

Recently, continuous work has been done to improve PSO. In 2015, an SL-PSO proposed by Cheng et al. [14] incorporated a social learning mechanism into PSO and performed well on 40 low-dimensional issues and seven high-dimensional functions. HFPSO, a hybrid algorithm combining Firefly and Particle Swarm Optimization, proposed by Aydilek [15] in 2018, was tested on the CEC2015 and CEC2017 test suites in different dimensions as well as several engineering and mechanical design benchmark issues. The results showed that HFPSO provided fast and reliable optimized solutions with single peaks for computationally expensive numerical functions, simple multi-peak, mixed, and combined classes outperforming other algorithms. Moreover, researchers have also employed PSO in many real-world applications. The new hybrid genetic PSO proposed by Ha et al. [16] in 2020 obtains the advantages of both algorithms and achieves satisfactory results in allocating distributed generation in distribution grids. To enhance the operational efficacy of micro gas turbines under a wide range of operating conditions, Yang et al. [17], in 2021, developed an algorithm named HIPSO_ C.S. by combining PSO with the Cuckoo Search Algorithm.

2.2 Research on Feature Selection

As the optimization power of the meta-heuristic algorithms increases, so does the number of examples of their adoption for the FS algorithm. In the following, we will explore some of the studies in this domain. Zarita et al. [18] in 2016 proposed a wrapper’s Harmony Search Algorithm that successfully addressed the detection and prediction of epileptic seizures and enabled HS to discover a more reasonable solution within a limited time frame by varying the initialization process of HS and the improvisation of the solution. Desbordes et al. [19] applied a Genetic Algorithm to tackle the issue of the survival rate of patients after esophageal cancer treatment. The ultimate forecast outcomes were obtained as a subset of nine features, and the comparative findings indicated that the utilization of GA outperformed alternative approaches. Tu et al. [20] added the enhanced global optimal guidance strategy, adaptive cooperation strategy, and dispersed foraging strategy to Gray Wolf Optimization Algorithm (GWO) to obtain the multi-strategy ensemble GWO (MEGWO), which not only increases the local and global search ability of GWO but also enriches the species diversity. They also applied the MEGWO to 12 FS issues, which proves its reliability and utility in solving real-world issues. Meta-heuristic algorithms hold substantial significance in cancer prediction, and the enhanced Cuckoo search algorithm proposed by Malek et al. [21] can identify a reduced set of features while attaining superior classification accuracy. Besides, the binary teaching-based optimization algorithm [22], binary dandelion algorithm [23], and binary capuchin monkey search algorithm [24] came into being. It was adopted to solve the FS problem better.

3  PSO Overview

Particle Swarm Optimization [25], recognized as a leading meta-heuristic algorithm, was initially introduced by Eberhart and Kenned in 1995. PSO utilizes the biological flock model proposed by biologist Heppner to simulate birds’ feeding behavior. Assuming that there is one and only one piece of food in a defined area, a community of birds randomly seeks the food without knowing the exact location of the food, and the simplest and easiest to implement approach is to explore the vicinity of the bird nearest to the food. Consider each bird as a weightless and volume-less point mass in space, and each point mass is assigned a fitness value based on a particular function. Besides, velocity governs both the direction and distance of flight.

First, a uniform probability distribution function is deployed to randomly distribute each particle Pai={pai1,pai2,…,paiDim},(1≤i≤Nu) throughout the exploration space, and all the particles in the exploration space form a particle population POP={Pa1,Pa2,…PaNu} composed of Nu particles, with each particle represented as a Dim dimension vector; furthermore, the velocity Vei={vei1,vei2,…,veiDim} of each particle is randomly initialized with the specific formula shown below:

Pai=Lb+(Ub−Lb)⋅rand(0,1)(1)

Vei=Vemin+2⋅Vemax⋅rand(0,1)(2)

where Ub and Lb are the upper and lower bounds of all the population variables,Vemax,Vemin are the maximum and minimum values of the velocity of each particle. The fitness of each individual in the population is calculated using the function Fit, and the historical optimal position Pabesti of particle Pai, which can also be called the local optimal position, is given by the following formula:

Pabesti(t+1)={ Pabesti(t)F(Pai(t+1))≥F(Pabesti(t+1))Pai(t+1)F(Pai(t+1))<F(Pabesti(t+1))(3)

where t is the current iteration number. Finally, the location of the global best individual GPabest is determined by evaluating the fitness values of all particles in the population, i.e.,

F(GPabest)=min{F(Pabest1(t)),F(Pabest2(t)),…,F(PabestNu(t))}GPabest∈{Pabest1(t),Pabest2(t),…,PabestNu(t)}(4)

In the optimization process, the combination of two optimal values is applied to optimize the flight speed of each particle, which is then employed to adjust the velocity of each particle. The specific formula is presented below:

Vei(t+1)=ω⋅Vei(t)+a1⋅r1⋅(Pabesti(t)−Pai(t))+a2⋅r2⋅(GPabesti(t)−Pai(t))(5)

Pai(t+1)=Pai(t)+Vei(t)(6)

where a1=a2=0.5 are self-learning factor and group learning factor correspondingly, and r1,r2 are arbitrary numbers obeying a uniform distribution.

4  SCPSO Overview

The PSO algorithm’s principle is relatively simple, its structure is concise, and it can achieve fast convergence. This can significantly save computational costs for feature selection problems requiring high-dimensional data processing. However, the fast convergence characteristic also makes the algorithm prone to getting stuck in local optima, resulting in poor algorithm accuracy. Therefore, it is necessary to adopt enhancement strategies to improve the algorithm’s performance.

4.1 Latin Hypercube Sample Strategy

Most meta-heuristic algorithms adopt the technique of random initialization to obtain an initial population. However, this method is relatively low-level and highly prone to producing an unevenly distributed population, affecting the algorithm’s convergence rate and precision. The Latin hypercube sample technique is a statistical method of approximate random sampling from a multivariate distribution that produces as many uniformly distributed sample points as possible. He et al. added it to the Firework Algorithm to better solve the mixed polarity Reed-Muller (MPRM) logic loop area optimization problem [26]. The enhanced Atom Search Algorithm using a Latin hypercube sample is more stable and reliable in optimizing the extreme learning machine model [27]. So SCPSO uses the Latin hypercube sample strategy to make individuals among the starting population span across the whole search space to the greatest extent possible so that the distribution of individuals can be more rationalized, and the diversity of the population can be improved. Then, the specific processes for initializing SCPSO are outlined as follows:

(1) Determine the population size Nu and the dimension Dim.

(2) Divide the variable interval into Nu equally spaced non-overlapping subintervals.

(3) Randomly select one point in each dimension for each subinterval separately.

(4) Form an initial population from the randomly selected points.

Fig. 1 illustrates the comparison of the effects of the two initialization methods. From the figure, it is evident that the population obtained by the initialization of the Latin hypercube sample strategy has a more robust distribution, which makes it more beneficial to choose the sample points uniformly in all dimensions, making the dispersion of the initial population throughout the space more balanced and comprehensive. That initialized populations more uniformly and helps to increase population diversity. In contrast, random initialization possesses a distinctly short-periodic state with a less even distribution, which means that populations may cluster along specific directions in the search space while ignoring other possible search directions. This situation may limit the global search capability of the algorithm and lead to failure to achieve better optimization results.

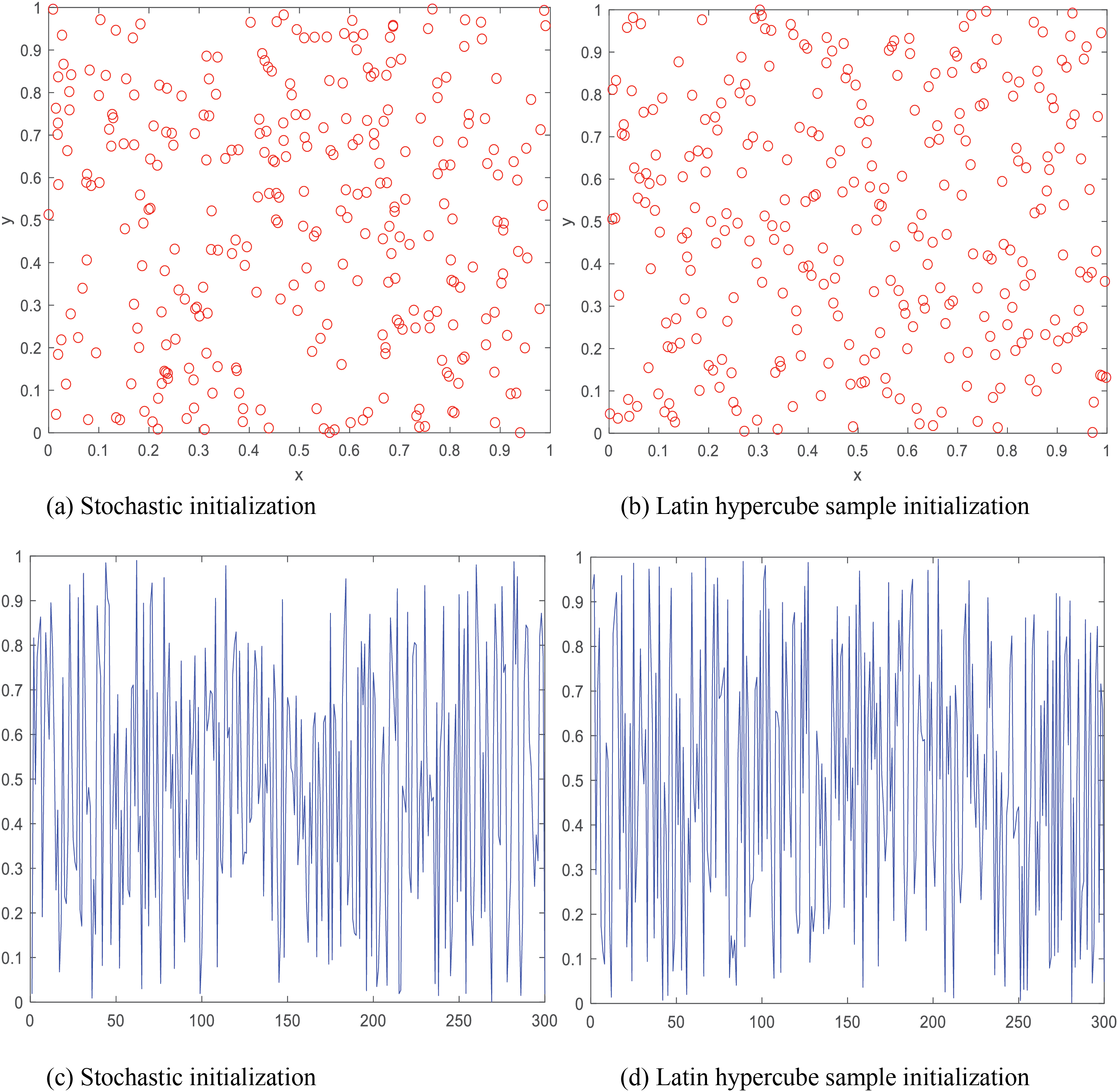
Figure 1: Comparison of the two initialization techniques

4.2 SCSO Strategy

Inspired by the foraging behavior of sand cats in desert environments, Amir Seyyedabbasi et al. introduced the Sand Cat Swarm Optimization [28]. Sand cats can efficiently locate and capture prey by exploiting their skill in detecting low-frequency noise. Like PSO, SCSO treats the prey position as the global optimal position and is divided into two mechanisms: search and attack.

4.2.1 Search Mechanism

Each sand cat utilizes its acute auditory sense to detect low-frequency vibrations below 2 kHz and locate prey throughout the exploration space. The specific modeling is as follows:

Pai(t+1)=ra⋅(GPabest(t)−rand(0,1)⋅Pai(t))(7)

ra=Ra×rand(0,1)(8)

Ra=SM−(SM×tT)(9)

where ra is the auditory sensitivity range of each sand cat. SM is a constant with a value of 2, T is the upper limit on the count of iterations for the entire search process, and Ra denotes the general sensitivity scope of the sand cat’s hearing, which linearly diminishes in value from 2 to 0 as the iterative process advances. Especially when Ra=0, ra=0, at which point the most recent position of the sand cat will also be adjusted to 0, is also in the search space. Furthermore, an adaptive balance factor R is proposed, which ranges from [0,2] and whose value is given by the following formula:

R=2×Ra×rand(0,1)−Ra(10)

4.2.2 Attack Mechanism

As the optimization procedure progresses, the sand cat in the exploration region automatically approaches the prey slowly and launches an attack on the targeted prey with the following formula:

Dist=|rand(0,1)⋅GPabest(t)−Pai(t)|(11)

Pai(t+1)=Pai(t)−ra⋅Dist⋅cos⁡(β)(12)

where Dist is the magnitude of displacement between the sand cat’s ideal position GPabest(t) and the current position Pai(t), β is an arbitrary angle that is between 0° and 360°. Through this mechanism, the orientation of the sand cat’s movement is determined by β. At this point, each member of the colony moves in a different circular put-up search in space.

4.2.3 Transition Mechanism

The implementation and transition of the process of SCSO search and attack on prey are determined by the parameter R. In the initial phase of the iteration, the value of Ra is large; when |R|>1, SCSO is in the exploring stage, and the sand cat explores broadly for potential targets within the exploration area. As the count of iterations grows, the value of Ra converges to 0 during the later phase of the iteration, at which point |R|>1, SCSO is in the exploitation phase, and the sand cat initiates an attack on the prey it is aiming at. The diagram of sand cat search and attack prey is displayed in Fig. 2. At this time, the specific formula is described below:

Pa(t+1)={ GPabest(t)−Dist⋅cos(β)⋅ra,|R≤1|;exploitationra⋅(GPabest(t)−rand(0,1)⋅Pa(t),|R≥1|;exploration (13)

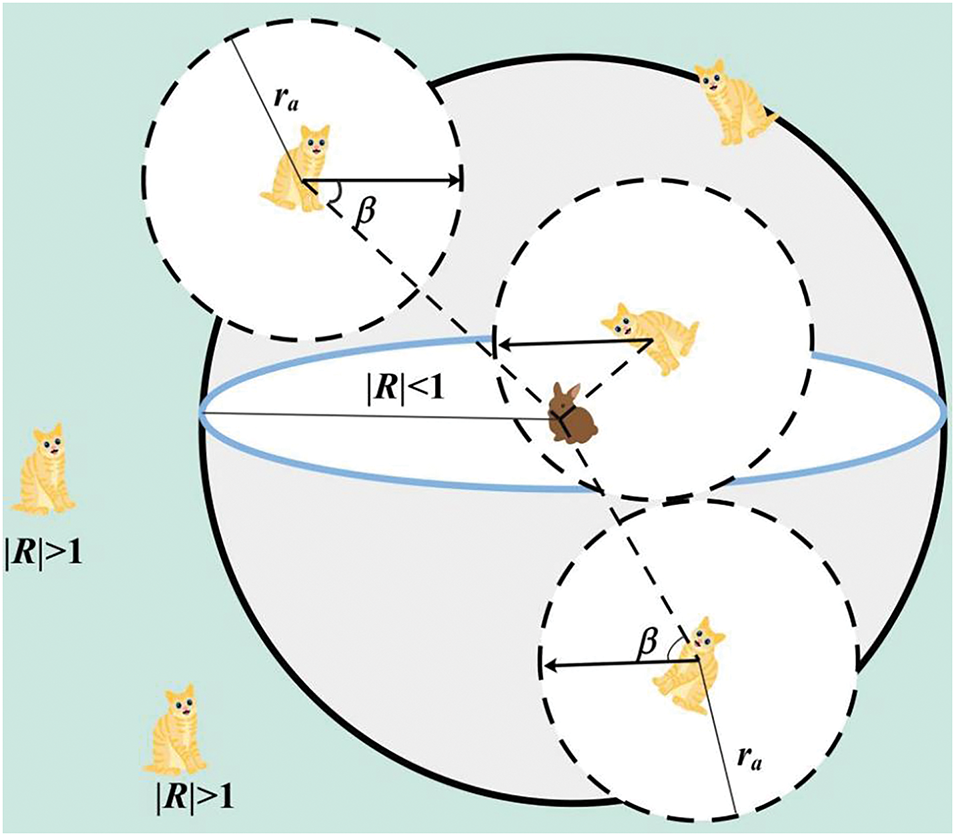
Figure 2: Diagram of sand cat search and attack prey

Once the algorithm finishes the PSO position update phase, it implements the SCSO position update formula. This crucial step effectively addresses the issue of limited search scope seen in the original approach, significantly improving the algorithm’s exploration capabilities and preventing it from getting trapped in local optima.

4.3 Roundup Search Strategy

Although the application of complex strategies enhances the accuracy of the solution, it may, to some extent, slow down the convergence speed of the algorithm. Drawing inspiration from how gray wolves round up food in the GWO [29], this paper refines the particle foraging exploration stage. Introducing the hierarchical idea of gray wolves, the leader chosen depending on the fitness size is nearer to the prey and is more capable of quickly recognizing the location of potential prey, and the leader leads the other particles to approach the target location gradually. That helps to improve exploration efficiency, thereby increasing the convergence speed of the algorithm. Usually, the number of leaders is kept in the top 10%. The specific modeling of individuals encircling prey is as follows:

Pam(t+1)=leaderm(t)−Bm⋅dism,m=1,2,…,Nu−leader(14)

Pa(t+1)=∑m=1Nu−leaderpam(t+1)Nu−leader(15)

where leader refers to the leader in the population, and Nu-leader refers to the number of leaders. dis is the spatial separation between the leader and the individual’s current. The specific equation is:

dism=|Cm⋅leaderm(t)−pa(t+1)|(16)

B and C are the two synergy coefficients, which are denoted as:

Bm=2b⋅r3−b(17)

Cm=2r4(18)

b=2−l⋅(tT)(19)

where B is designed to model the aggressive behavior of the particle toward its prey and its value is influenced by b. b exhibits a linear decline from 2 to 0 as the count of the iteration increases. r3, r4 are two random numbers in the range [0, 1]. Fig. 3 visualizes the particle updating its position according to the leader.

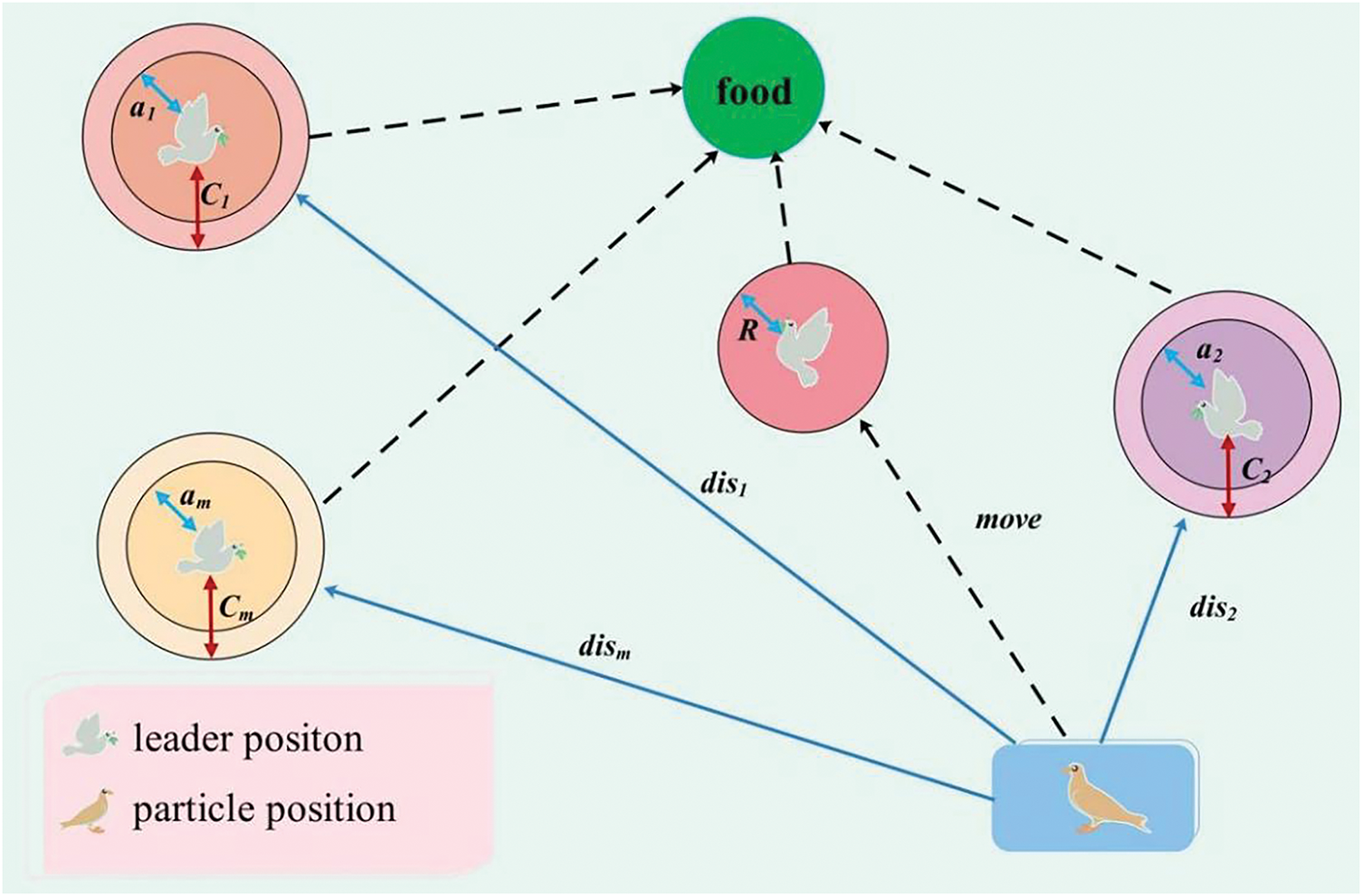
Figure 3: Diagram of the roundup search strategy

4.4 SCPSO

This section outlines the basic framework of SCPSO, where the PSO’s structure is reconstructed by adding the Latin hypercube sample strategy and the SCSO based on the roundup search strategy. Firstly, the Latin hypercube sampling strategy generates a population, and then the algorithm executes the PSO position update formula. Subsequently, the historical best position in PSO is passed as the initial point to SCSO, and SCSO’s position update is performed. Finally, the roundup search strategy will be integrated into the exploration phase of SCSO to improve the convergence speed of the algorithm.

The pseudo-code of SCPSO is also rendered in Algorithm 1. In addition, the flowchart in Fig. 4 visualizes more vividly the execution process of SCPSO.

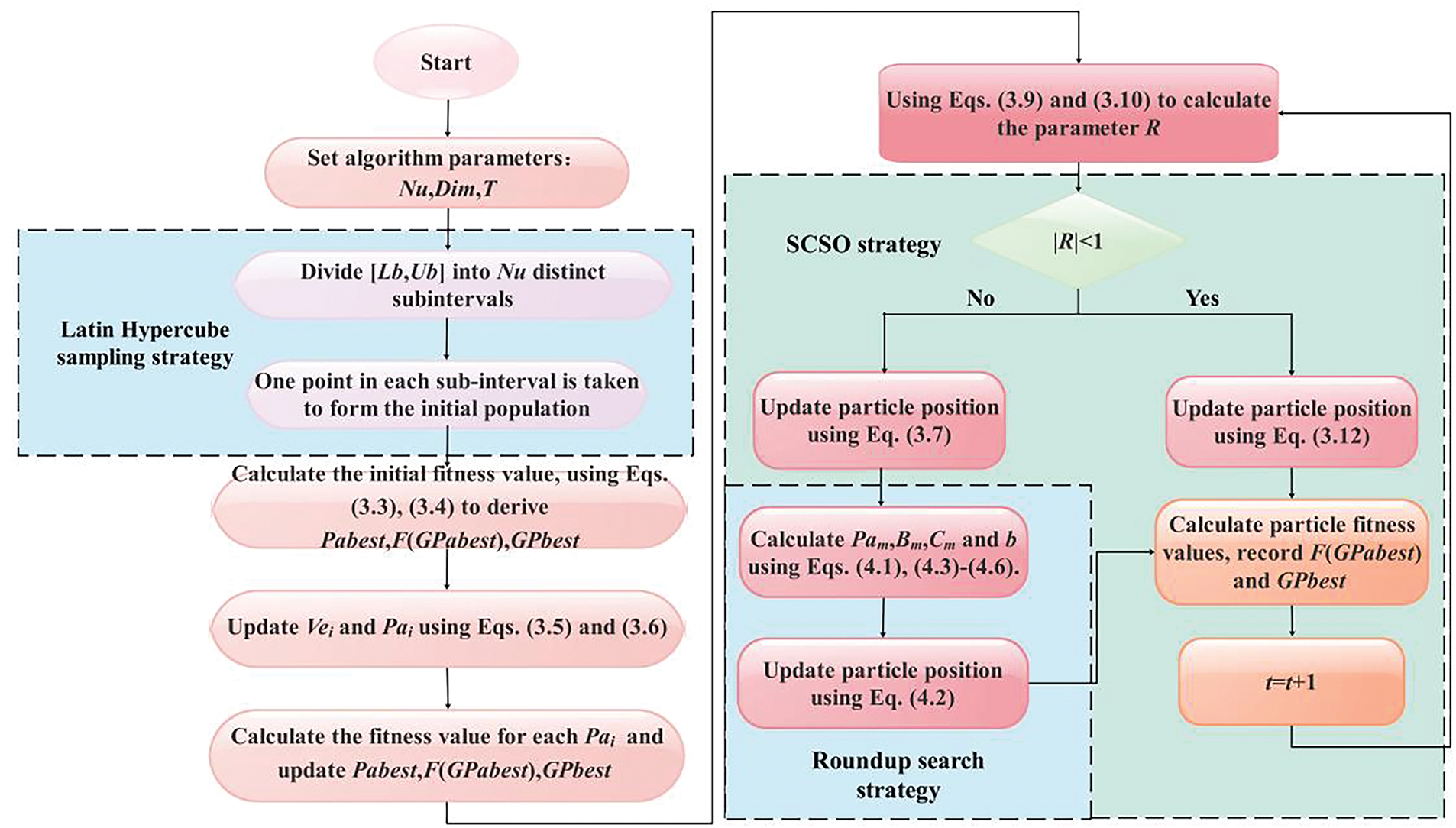
Figure 4: Flow chart of SCPSO

5  Trials and Analysis

Within this part, a series of numerical trials are conducted on SCPSO to evaluate its performance fairly. Firstly, we conduct a performance analysis on various strategies using nine benchmark functions. Secondly, SCPSO is evaluated against other modified PSO algorithms on the 30-dimension CEC2020 test suite [30] to test the efficiency of the strategies incorporated in this paper. Then, SCPSO is tested compared to other competitive algorithms on 10 and 20-dimension CEC2022 test suites [31]. Remarkably, the test functions in both the CEC2020 and CEC2022 test suites comprise a portion of the challenging test functions in the CEC2014 [32] and a portion of the CEC2017 [33] test suites. Moreover, they are all categorized into four parts: single-peak, fundamental, hybrid, and combined functions, encompassing a domain of −100 to 100 for all functions. Trials on such test suites are more adept at evaluating the proficiency of SCPSO in resolving diverse optimization issues.

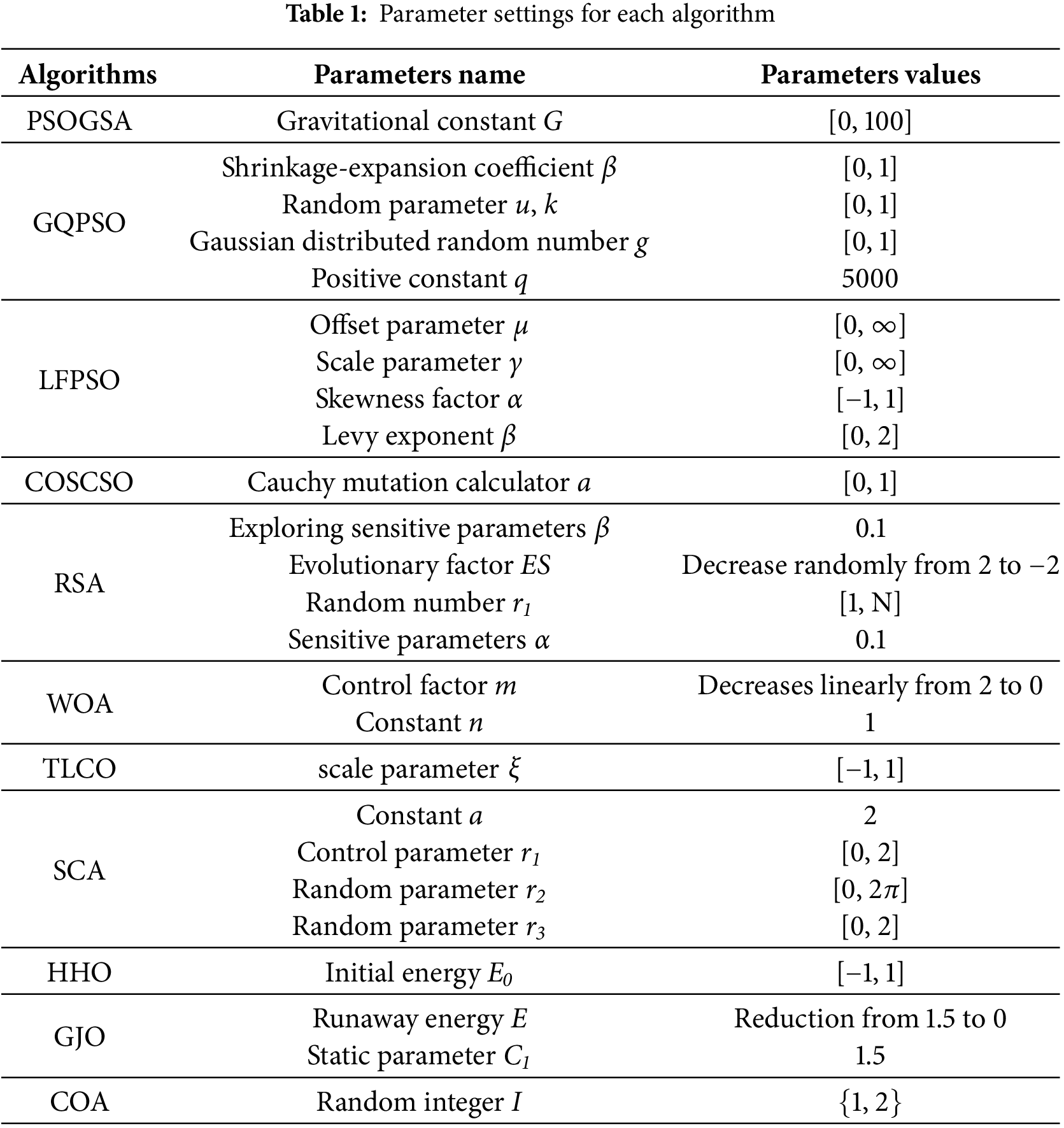
To reflect the impartiality of the trials and eliminate the interference of chance, the population size was set to 50 and the maximum limit of iterations was 1000. All algorithms were run 20 times. Table 1 shows the built-in parameters of the algorithms. Each trial was executed in a standardized environment.

Furthermore, to effectively compare the efficacy of distinct algorithms, it is measured in terms of four common quantitative metrics [34]:

(1)   Best value

Best={F1(GPabest),F2(GPabest),…,FRuns(GPabest)}

(2)   Worst value

Worst=max{F1(GPaworst),F2(GPaworst),…,FRuns(GPaworst)}

(3)   Average value

Average=∑k=1RunsFk(GPabest)Runs

(4)   Standard deviation

Std=1Runs−1∑k=1Runs(Fk(GPabest)−Average)2

where Fk(GPabest),Fk(GPaworst) are the optimal and worst values derived from one run of the algorithm, respectively. These two metrics demonstrate the accuracy of the algorithm. Taking the average value provides an overall indication of algorithm competence and mitigates the influence of random factors. The standard deviation, on the other hand, mirrors the degree of discretization of the data set. The robustness of the algorithm can be measured accordingly.

5.1 Performance Analysis of Strategies

The performance analysis of strategies is of great significance in studying optimization algorithms. By quantifying a strategy’s optimization effect, we can effectively evaluate its performance in terms of convergence speed, accuracy, and global search capability. In addition, the performance analysis can also evaluate the algorithm’s applicability and provide a basis for selecting appropriate strategies in practical application scenarios. Building on the foundation of Particle Swarm Optimization (PSO), we introduce a single strategy: PSO + LHS, which integrates the Latin hypercube sampling technique. Additionally, PSO + RSA denotes the version of PSO that employs the Roundup Search Strategy. Lastly, PSO + SCSO refers to the variant of PSO enhanced with the SCSO methodology. In addition, PSO and SCPSO are to compare with them. Table 2 records the statistics of the mean and standard deviation of PSO and its variants. Fig. 5 shows their convergence curves. Comprehensive figures and tables show that compared with the original PSO, PSO + LHS, and PSO + SCSO have a noticeable improvement in convergence accuracy and stability, which indicates that the Latin hypercube sampling technique and SCSO effectively improve the solution accuracy of PSO. However, it is worth noting that compared with the fast convergence of PSO, they are slightly slower in convergence. That indicates that the algorithm sacrifices part of the solution speed while jumping out of the local optimal solution and actively searching for the global optimal solution. PSO + RSA has a limited improvement of the accuracy of PSO in most functions and even has a specific inhibiting effect in individual functions. However, PSO + RSA retains the advantage of PSO’s fast convergence speed. Overall, SCPSO integrating three strategies is significantly better than the PSO variant with only a single strategy in most algorithms, both in terms of convergence accuracy and stability, and the convergence speed of SCPSO is moderate. That is mainly due to the cooperation between the Latin hypercube sampling technique and SCSO to improve the algorithm’s accuracy. Adding the Roundup Search Strategy also improves the algorithm’s overall convergence speed. However, the addition of the Roundup Search Strategy has a slight inhibiting effect on the overall accuracy of the algorithm for individual functions. Therefore, SCPSO is generally the best choice, but for practical problems requiring higher accuracy, readers can also consider PSO + LHS + SCSO.

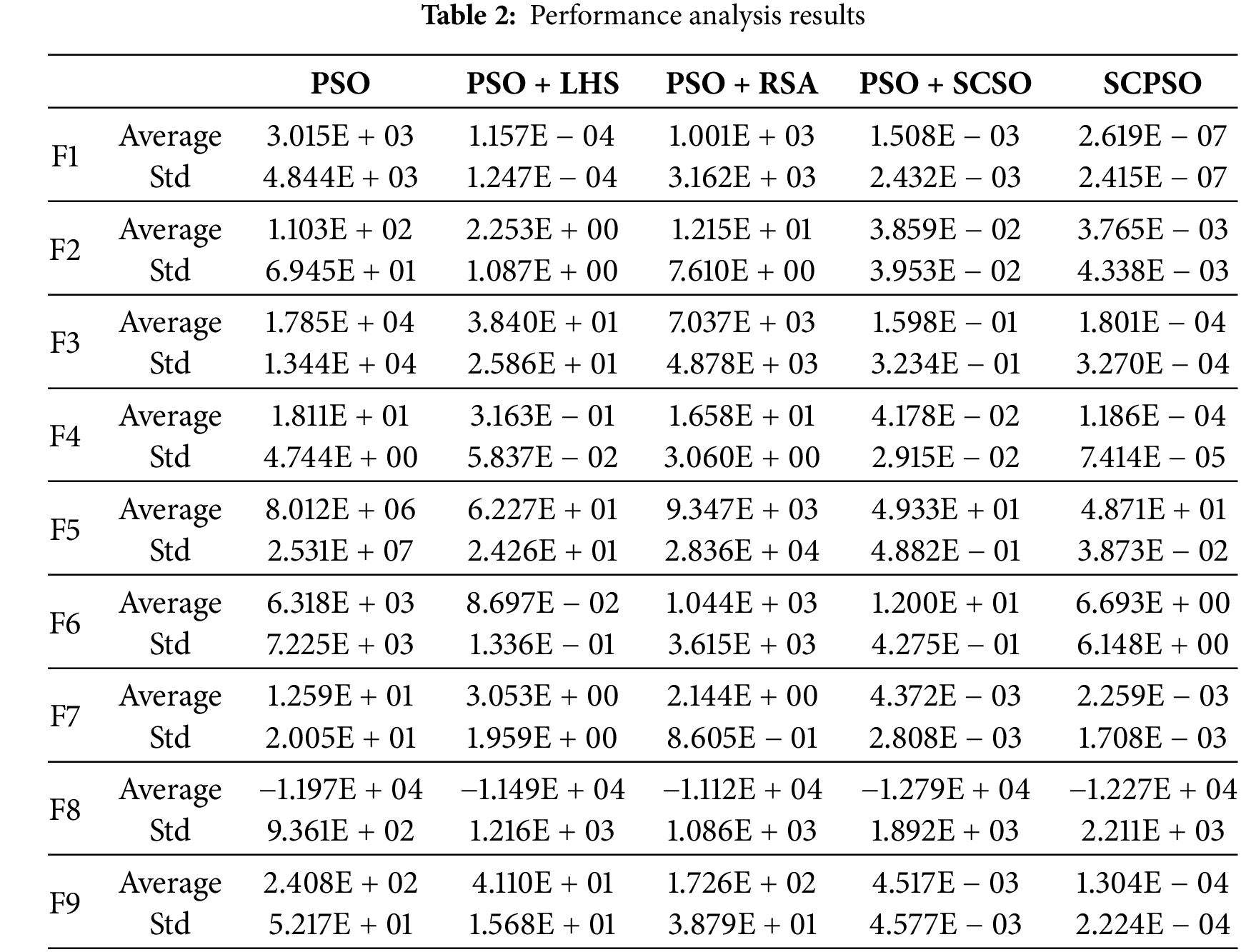
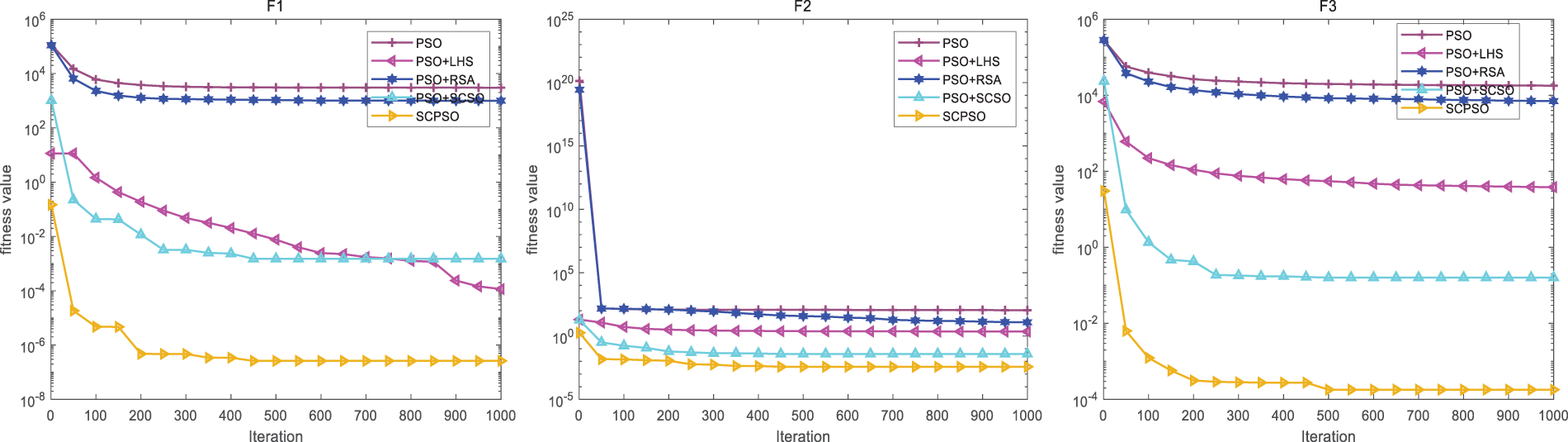
Figure 5: Convergence plot of SCPSO and PSO with a single strategy

5.2 Comparison and Analysis of SCPSO with Other Modified PSO

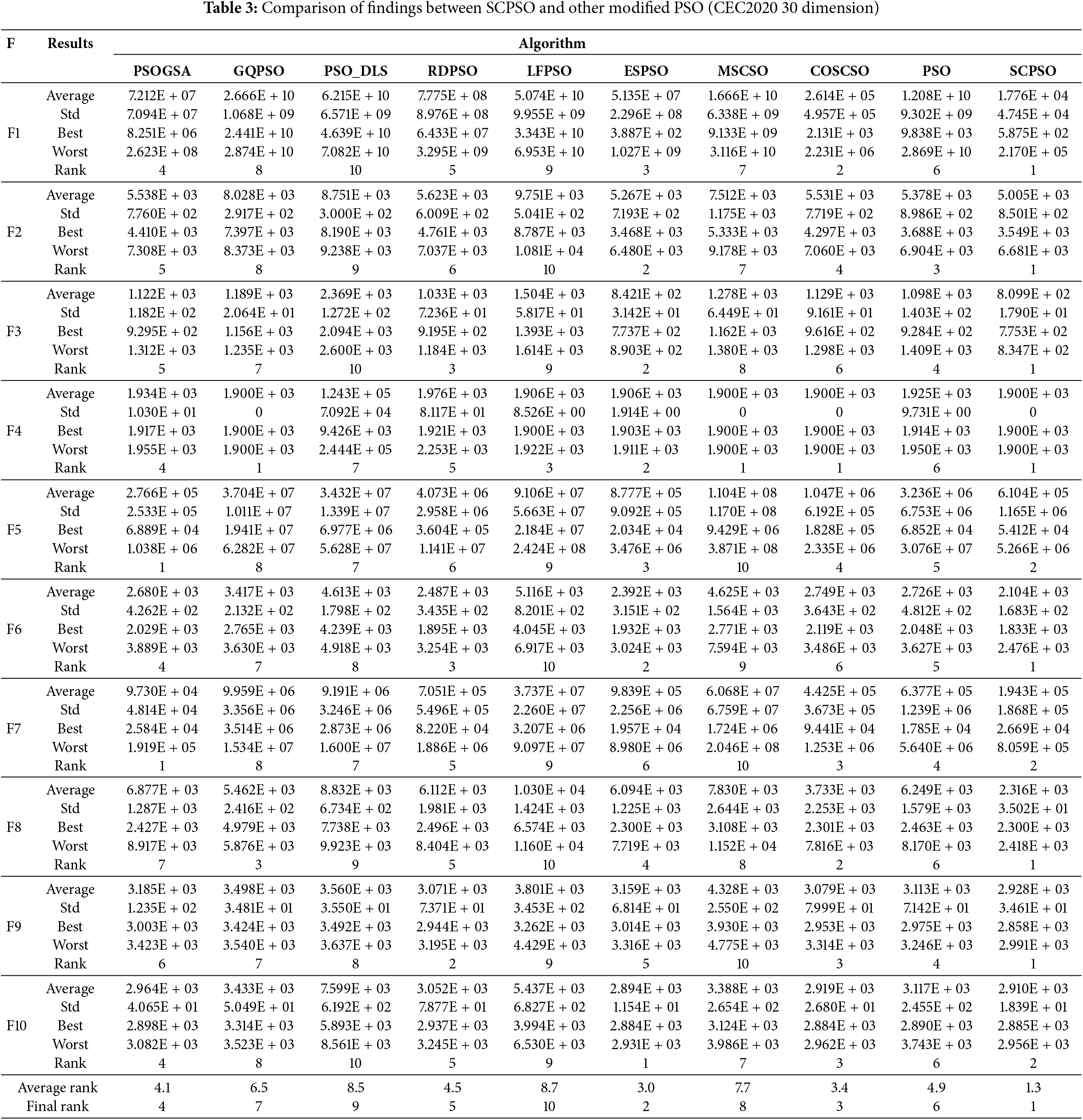
To assess the efficiency of SCPSO and investigate the effects of SCSO, the Latin hypercube sample strategy and roundup search strategy on PSO were used. In this part, SCPSO is tested against six other competitively modified versions of PSO and two improved versions of SCSO, in addition to comparing it with PSO on the 30-dimension CEC2020 test suite. The chosen algorithms are PSOGSA [35], GQPSO [36], PSO_DLS [37], RDPSO [38], LFPSO [39], ESPSO [40], MSCSO [41], COSCSO [42].

In Table 3, the results of the ten algorithms on the 30-dimensional CEC2020 test suite are meticulously compiled. SCPSO stands out as the front-runner, securing the top position on seven test functions. While it doesn’t quite outperform PSOGSA on F5 and F7, SCPSO still shows remarkable consistency and strong performance compared to the other algorithms. Notably, SCPSO demonstrates a clear edge on F1, F3, F4, F6, F8, and F9, where its results are consistently smaller than those of the other algorithms, reflecting its exceptional stability. The table further presents the algorithms’ average rankings and their final overall ranks, which are as follows: SCPSO > ESPSO > COSCSO > PSOGSA > RDPSO > PSO > GQPSO > MSCSO > PSO_DLS > LFPSO.SCPSO maintains an impressive lead with an average rank of 1.3, while ESPSO follows closely in second place with an average rank of 3.0. PSO lags in sixth place with an average rank of 4.9, demonstrating that the enhancements brought by SCSO hybridization give SCPSO a substantial edge in performance. This stark contrast in rankings highlights the effectiveness of SCPSO in delivering superior optimization results, establishing it as the top performer in this suite.

The Wilcoxon rank sum test [43], also known as the Wilcoxon signed rank test or Wilcoxon-Mann-Whitney test, is employed to compare two independent samples to see if there is a difference in their median. The Wilcoxon rank sum test p-value at the 95% significance level (α=0.05) with SCPSO as the control is tabulated in Table 4. Synthesizing the four significant indicators mentioned above, PSOGSA was significantly more potent than PSO on F5 and F7, and COSCSO was significantly superior to SCPSO on F10. ESPSO and PSO do not differ significantly from SCPSO at F2 and F5, respectively. Based on the data, SCPSO exhibits a significant superiority over the six modified versions of PSO and demonstrates a remarkable difference compared to the two enhanced SCSOs.

To better visualize the convergence performance of SCPSO during the iteration process, ten algorithms are qualitatively analyzed by the curve convergence plot given in Fig. 6. On observing the plot, the red curves on F1, F2, F3, F6, F7, F8, and F9 have distinctly lower minimums than those of the other modified algorithms. Moreover, except for F4 and F10, the convergence speed of SCPSO is rapidly accelerated when the iteration count reaches 400, and the precision is improved, which further suggests that it is wise to add SCSO to PSO.

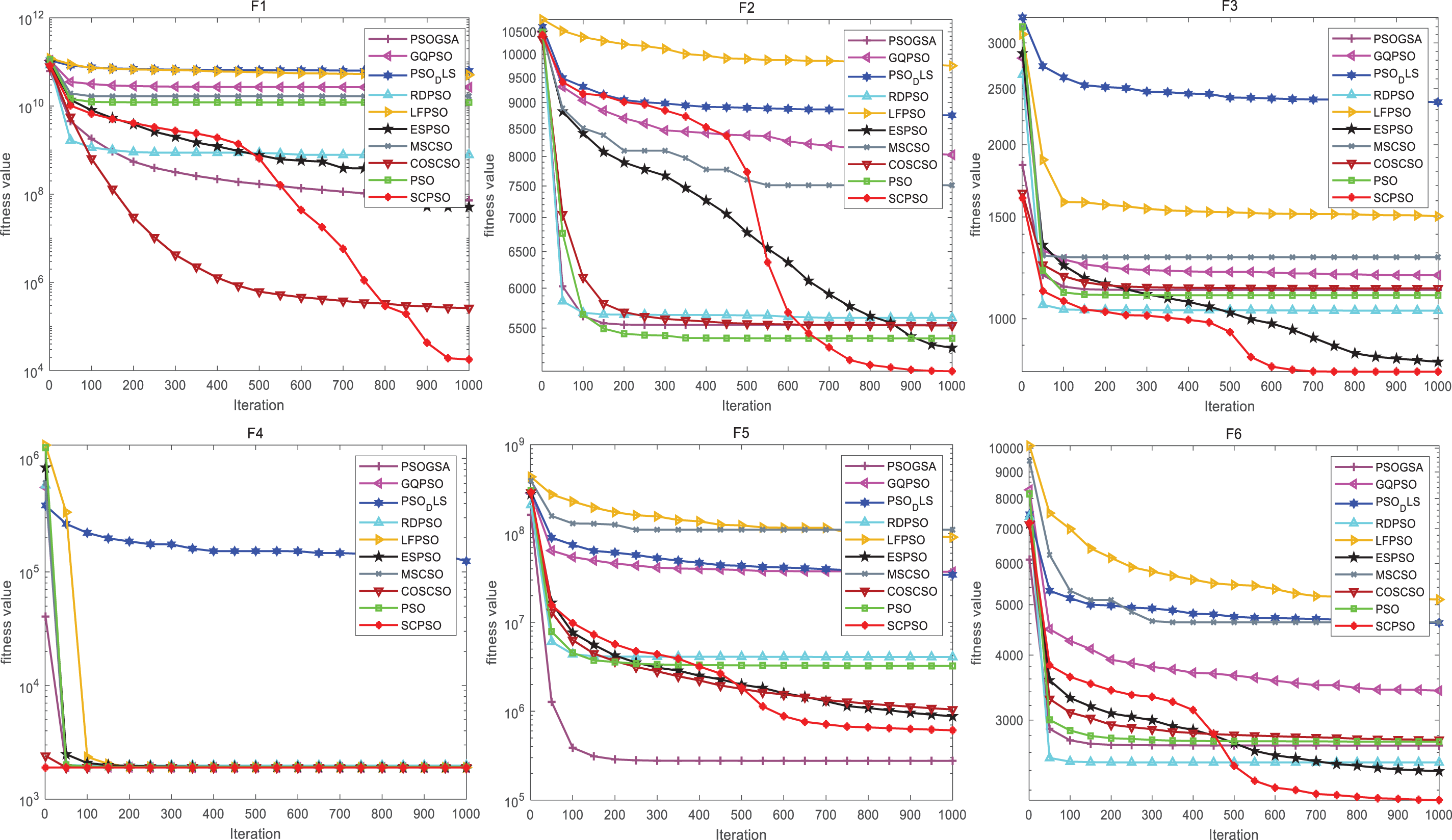
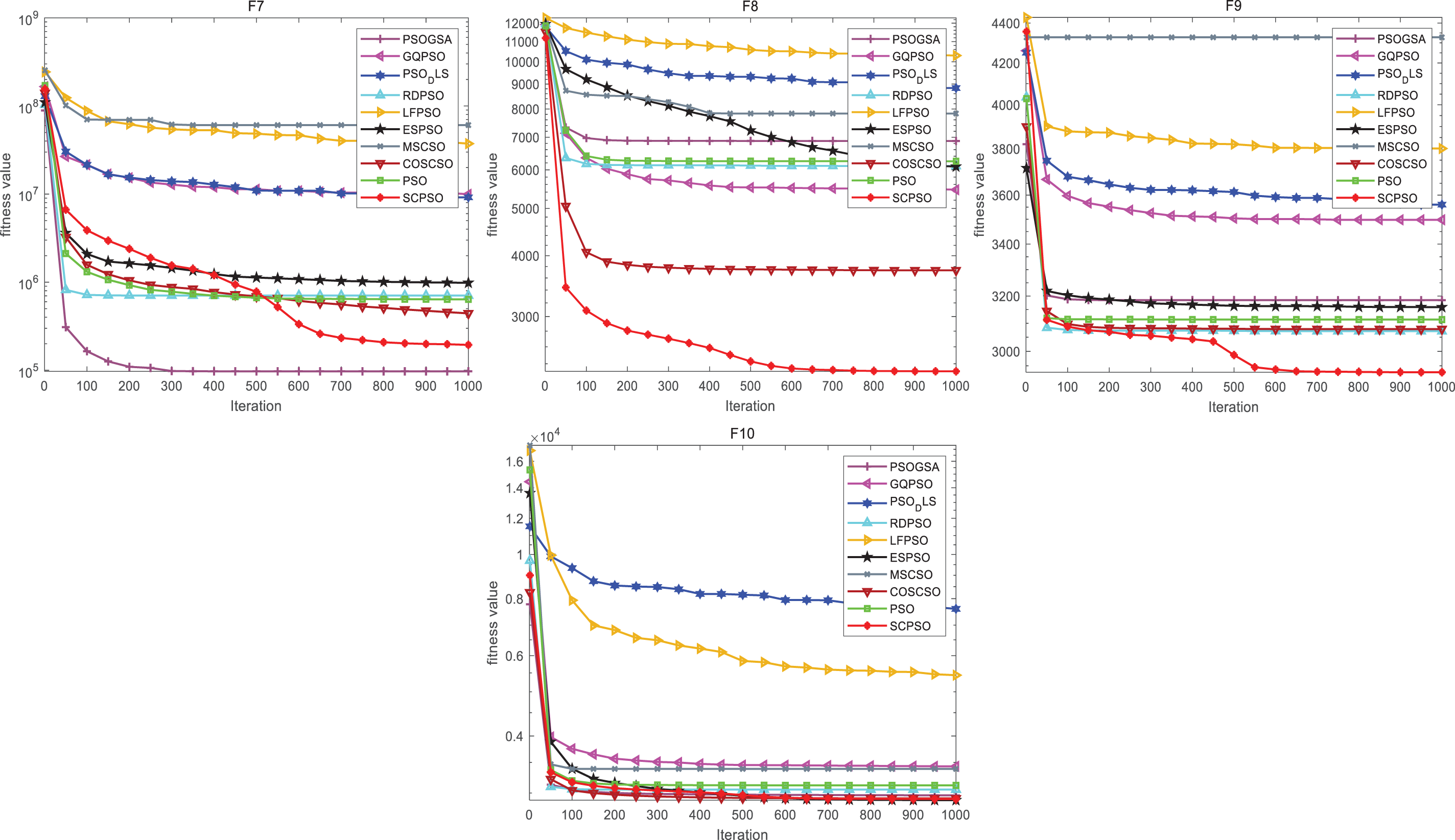
Figure 6: Convergence plot of SCPSO with other modified PSO (CEC2020 30 dimension)

Boxplot is a commonly available data visualization tool to display a data collection’s distribution and statistical characteristics. Fig. 7 exhibits a boxplot of SCPSO with other algorithms. Upon observation, except for F2, SCPSO has the smallest width of a rectangular box compared to other algorithms. That implies that SCPSO has a more centralized data distribution with a smaller range of outliers. In addition, SCPSO has the fewest outliers on all the test functions, which reveals that SCPSO performs more consistently in terms of performance and has stronger robustness compared to other modified algorithms. These findings provide us with more information about the advantages of SCPSO in data processing and optimization problems and give us more confidence to apply it in real-world scenarios.

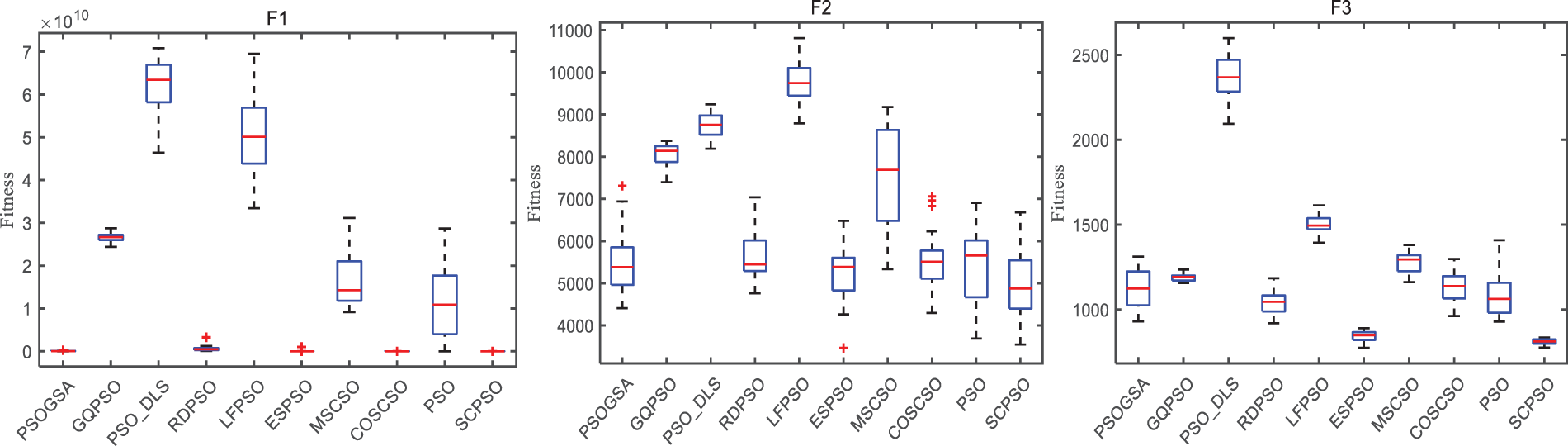
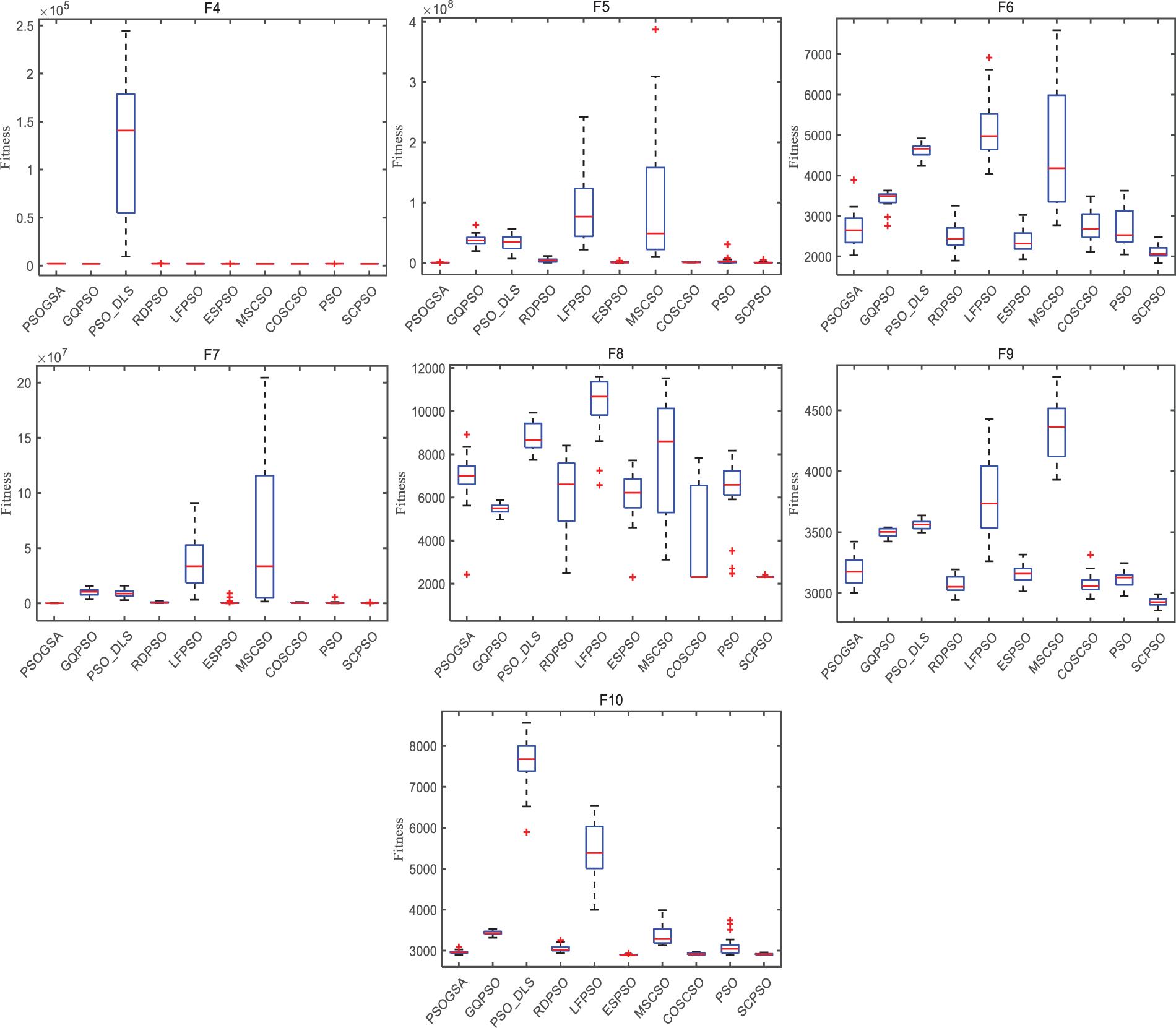
Figure 7: Boxplot of SCPSO with other modified PSO (CEC2020 30 dimension)

The following additions and summaries can be drawn by viewing the radar plot in Fig. 8 based on the rank of SCPSO vs. other modified PSO algorithms in the 30-dimension CEC2020 test suite. In the first place, it is evident from the radar plot that SCPSO encloses the smallest area, demonstrating that SCPSO performs best relative to other algorithms when evaluating the performance of multiple variables comprehensively. Secondly, it can be observed in the radar plot that the shaded area enclosed by the ESPSO is ranked second, but there is still a gap compared with the SCPSO.

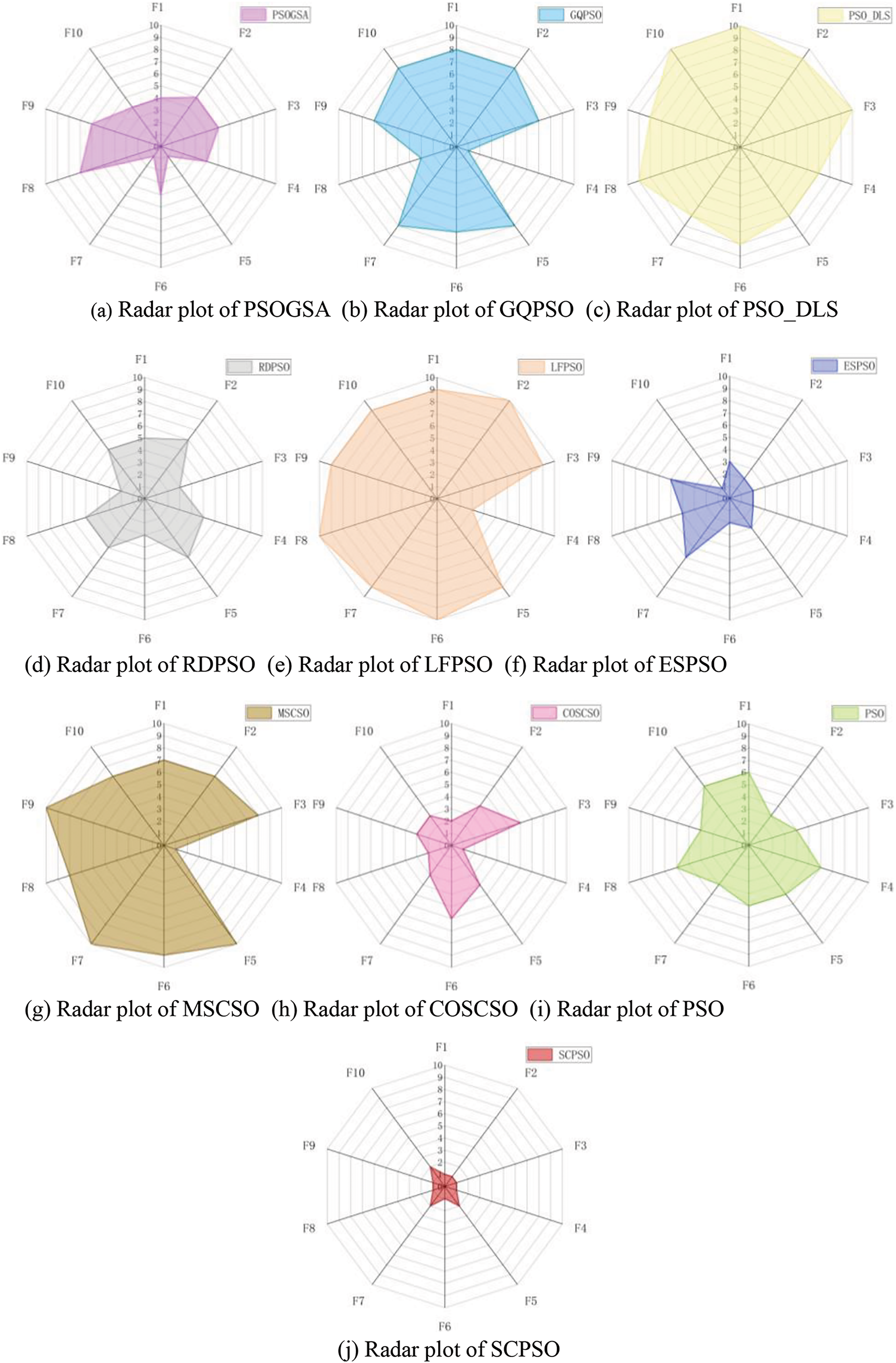
Figure 8: Radar plot of SCPSO with other modified PSO (CEC2020 30 dimension)

In summary, compared with other PSO variants, SCPSO has better convergence accuracy and stability, which is its most significant advantage. The rank sum test results also show that SCPSO outperforms other variants in accuracy. PSOGSA and GQPSO also performed well in multiple functions, achieving the second and third final rankings. The performance of LFPSO, PSO-DLS, and MSCSO could be improved, resulting in a lower final ranking.

5.3 Comparison and Analysis of SCPSO with Other Modified Algorithms

To more extensively evaluate the effectiveness of SCPSO in addressing intricate issues, researchers executed experiments in the newer and more challenging CEC2022 test suite involving two dimensions. In addition, SCPSO was compared with several competitive experimental algorithms besides PSO, including the Reptile search algorithm [44], Whale optimization algorithm (WOA) [45], Termite life cycle optimizer (TLCO) [46], Sine Cosine Algorithm (SCA) [47], Sand Cat Swarm Optimization (SCSO), Harris Hawk Optimizer (HHO) [48], Golden Jackal Optimizer (GJO) [49], and Coati Optimization Algorithm (COA) [50]. These algorithms represent the current cutting-edge methods in the field, so comparing them can reveal the advantages and characteristics of SCPSO.

Table 5 contains a collection of statistical findings for SCPSO and other algorithms on 10 dimensions. SCPSO ranks highest on 75% of the functions, which means that it performs excellently in solving these problems. However, on F1, although SCPSO and PSO have the same average, PSO has a minor standard deviation, implying that PSO slightly outperforms SCPSO regarding stability. Interestingly, on F6 and F10, SCPSO acts differently from the other functions, ranking 6th and 5th, respectively, and not dominating in standard deviation; there may be scope for improvement. Further research and analysis are necessary to determine the causes and find ways to improve.

What is more, the last part of Table 5 also counts the overall average rank, and judging from the statistics, the rank is from high to low: SCPSO > SCSO > PSO > HHO > GJO > SCA > WOA > TLCO > COA > RSA. As a result, SCPSO takes the lead with an average rank of 1.83. SCSO takes second place with an average rank of 3.58.

In addition, Table 6 provides the p-value results of the Wilcoxon rank sum test to explicitly demonstrate the statistical disparities between SCPSO and the other algorithms. The findings show that WOA, HHO, and COA significantly outperform SCPSO on F6. On F10, although the average values of TLCO, SCA, SCSO, and GJO are superior to those of SCPSO, the p-value reveals little variation between them and SCPSO. However, SCPSO excels on F1, F3, F4, F5, F7, F8, F9, F11, and F12. Therefore, SCPSO can solve the CEC2022 problem efficiently.

To present the convergence performance of SCPSO on the 10-dimension CEC2022 test suite more clearly and explicitly, Fig. 9 gives a convergence plot of SCPSO with other algorithms. We can draw the following conclusions by observing the plot’s trend. First, SCPSO exhibits a speedy rate of descent and reaches much lower nadirs on the F2, F5, F8, F9, F11, and F12 functions. That suggests that SCPSO has exceptional convergence performance in addressing these functions. Secondly, for F3, F7, and F11, although SCPSO’s rate of descent is not outstanding, it still obtains a superior solution after a certain level of convergence. That points to the fact that SCPSO may need more iterations on these functions to achieve the best results, but it still achieves satisfying convergence performance. Taken together, the superiority of SCPSO on the 10-dimension CEC2022 test suite is evident from the convergence curves in Fig. 9. It demonstrates fast descent rates and better nadir points in several functions, thus proving its effectiveness in solving these problems.

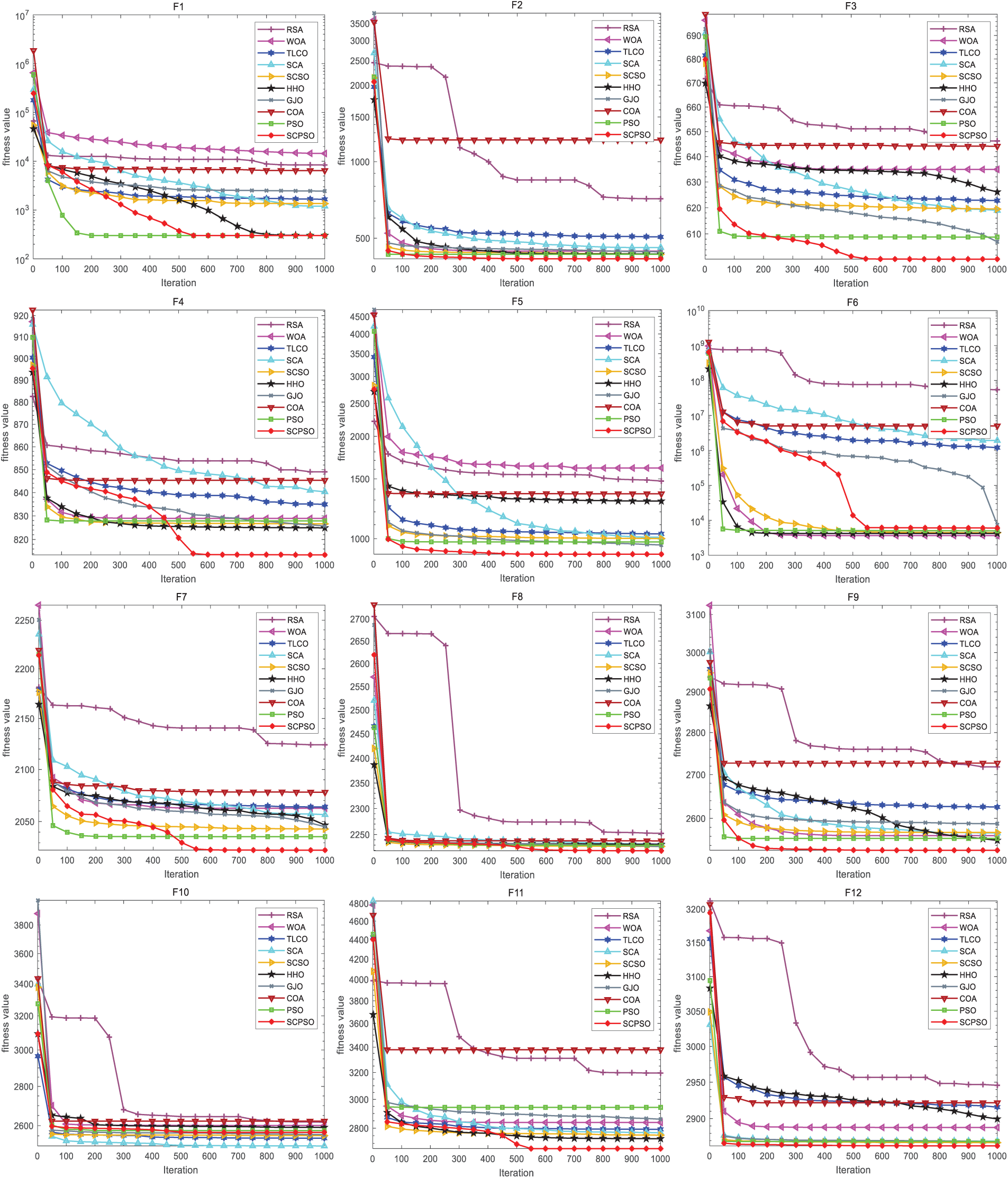
Figure 9: Convergence plot of SCPSO with other algorithms (CEC2022 10 dimension)

By comparing the boxplot of SCPSO with the other algorithms in Fig. 10, we can observe that on F1, F2, F3, F5, F7, F9, F11, and F12, SCPSO shows thinner boxes, signifying a more centralized distribution of fitness values for SCPSO. This more concentrated distribution implies that the performance of SCPSO is relatively stable on these functions. Simultaneously, we can also note the relatively small number of outliers in the SCPSO boxplot. Measurement errors, special conditions, or other factors may cause outliers. Thus, fewer outliers reflect a more stable and robust performance of SCPSO on these functions.

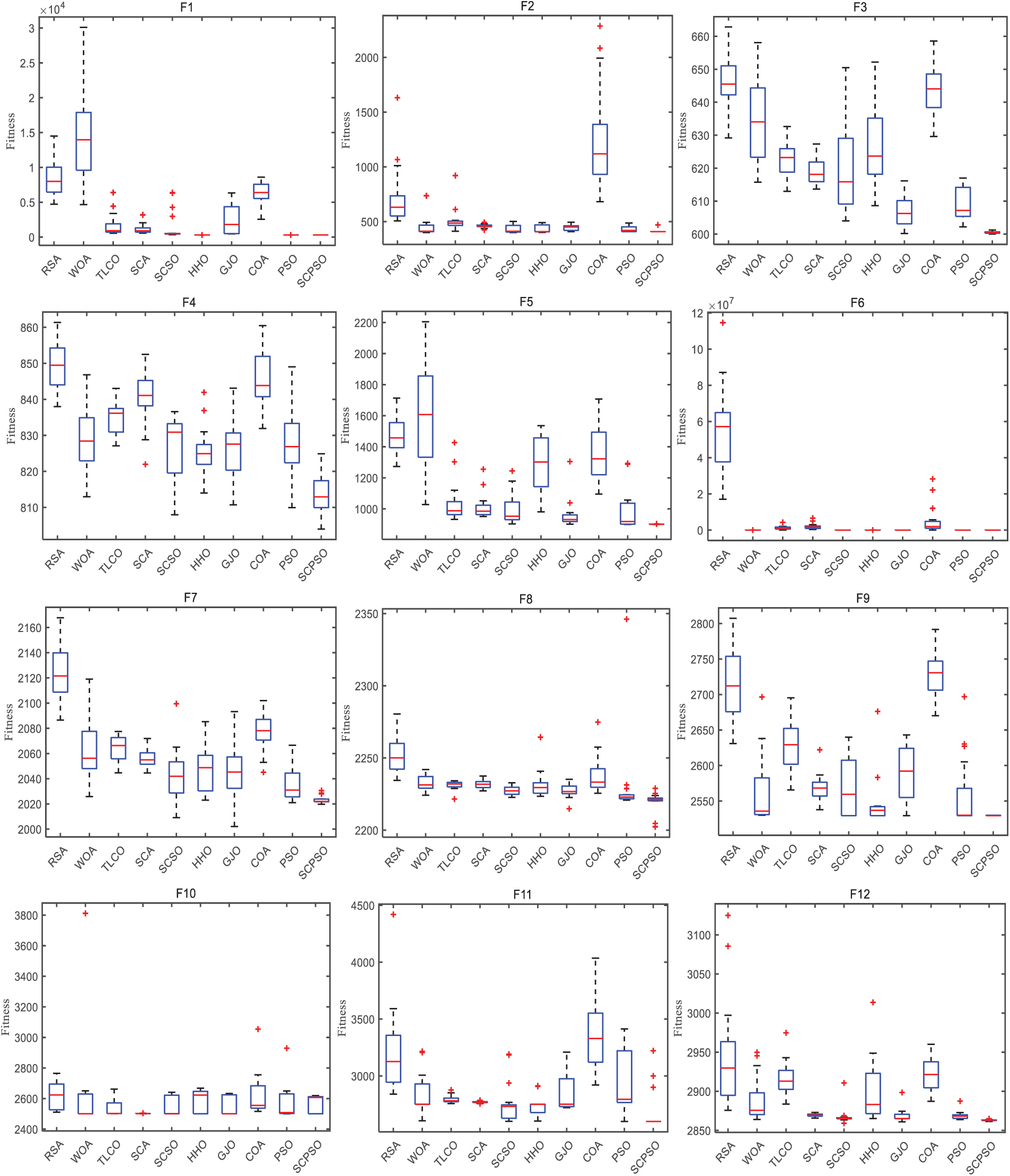
Figure 10: Boxplot of SCPSO with the other algorithms (CEC2022 10 dimension)

To investigate the dimension scaling capability of SCPSO further, SCPSO is measured on the 20dimension CEC2022 test suite. Table 7 contains a collection of statistical. Encouragingly, compared to its performance on 10 dimensions, SCPSO is ranked first on 83.3% of the functions and is only ranked 4th and 2nd on F10 and F11, respectively. Furthermore, SCPSO is ranked first on eight functions under average and standard deviation. That proves the excellence of SCPSO in terms of convergence and emphasizes its stability advantage. That implies that SCPSO can converge efficiently on high-dimensional problems and have excellent stability in outcomes. Depending on the statistical results, the rank of all the algorithms is SCPSO > HHO > SCSO = GJO > PSO > SCA > TLCO > WOA > RSA > COA. SCPSO holds the leading position with an average rank of 1.33. SCSO and GJO have the same average rank and are jointly listed in third place. In summary, SCPSO performs more prominently on higher dimensional problem.

Table 8 presents the p-value results from the Wilcoxon rank sum test applied to the 20-dimensional CEC2022 test suite. A closer look at the table reveals that while TLCO, SCA, and SCSO show a slight average advantage over SCPSO on F10, the p-value differences are minimal. That suggests these algorithms may marginally outperform SCPSO on specific functions, but the disparities are not statistically significant. In contrast, SCPSO consistently outshines most other algorithms, securing top positions across most test functions. It leads in terms of performance and claims the top spot in both the mean rank and overall ranking, reinforcing its dominance in optimization tasks.

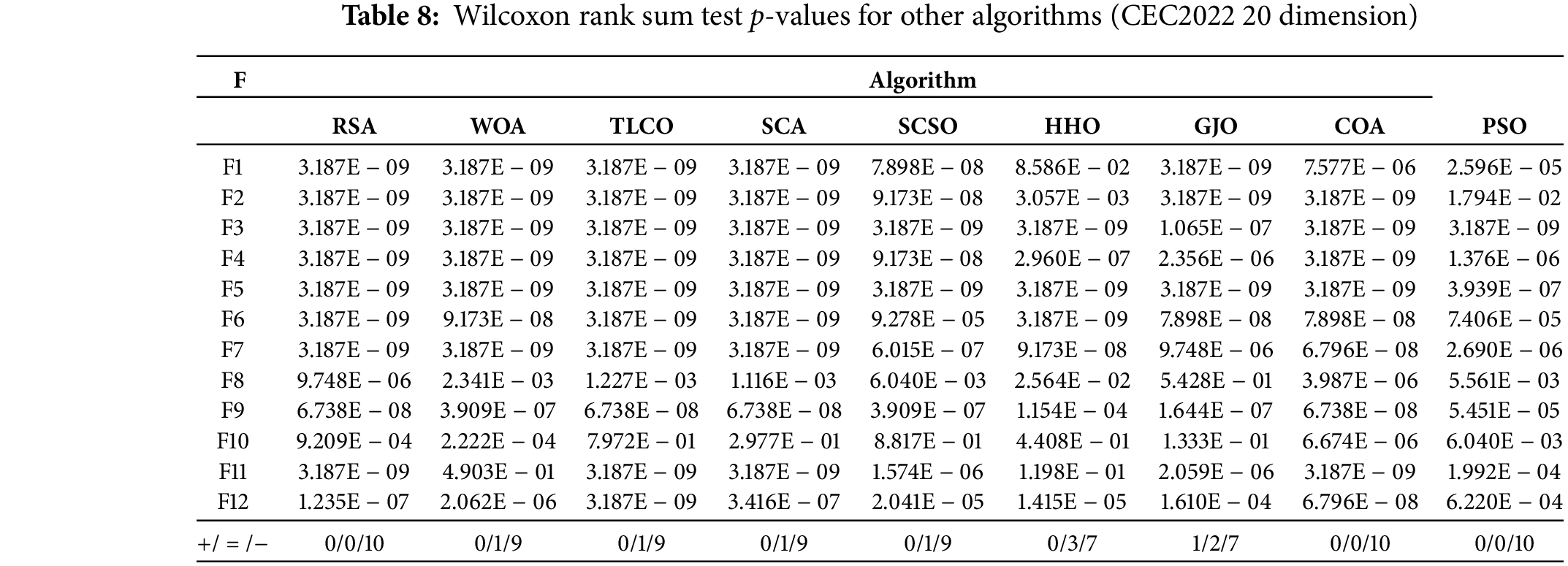
Figs. 11 and 12 contain convergence plots and boxplots of SCPSO and other algorithms on the 20-dimension CEC2022 test function. The convergence curve of SCPSO on the 20-dimension function decreases faster compared to that of the convergence plot in the 10-dimension case. Especially on F3, F4, F5, F6, and F7, SCPSO displays more notable advantages than other algorithms. Likewise, SCPSO has a relatively narrow box plot, which suggests it is relatively more stable and robust. A narrower box plot indicates that the algorithm has more consistent convergence performance across running instances and is more stable concerning parameter tuning and initial settings. Therefore, SCPSO performs better in solving these 20-dimensional function problems.

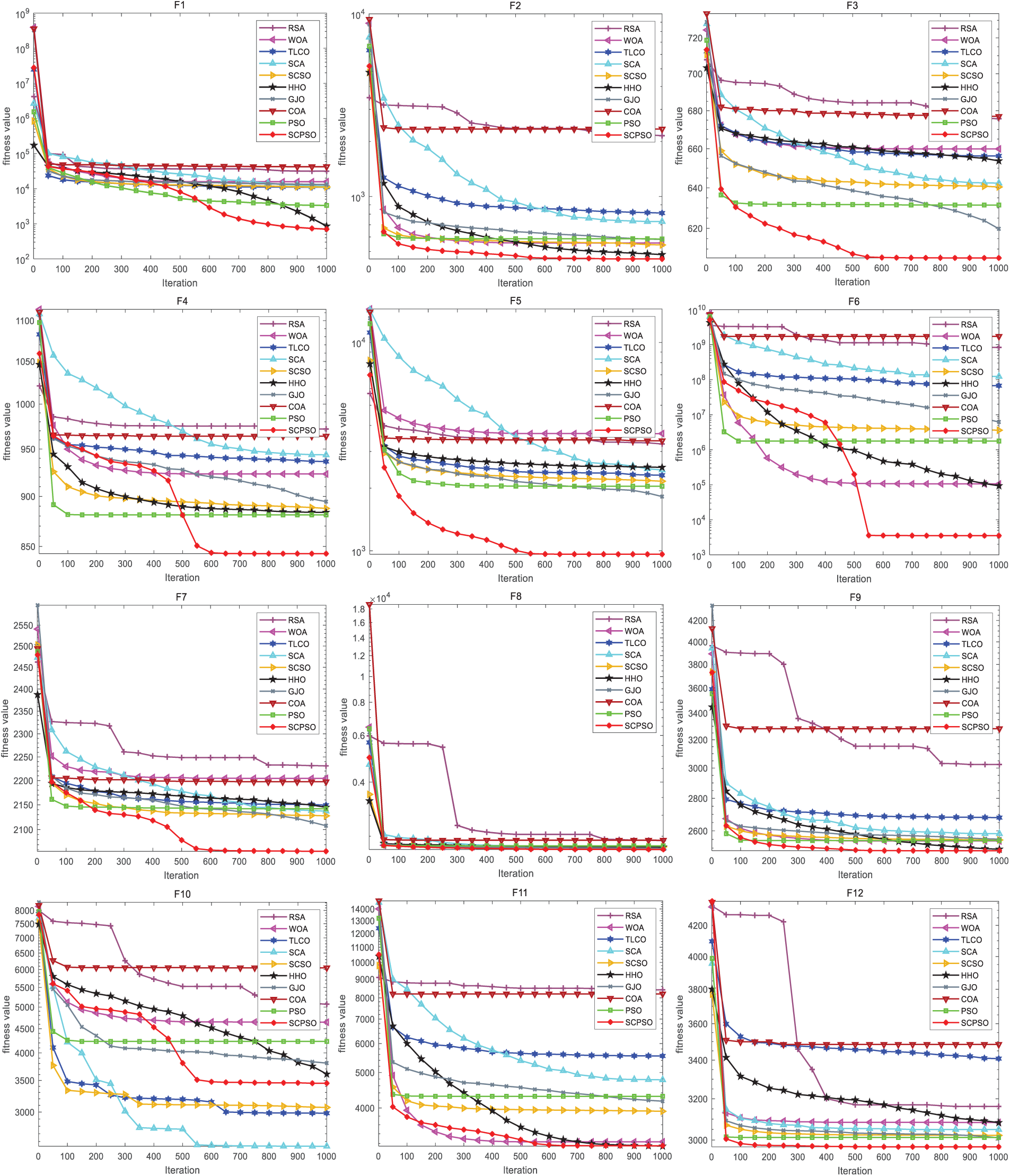
Figure 11: Convergence plot of SCPSO with other algorithms (CEC2022 20 dimension)

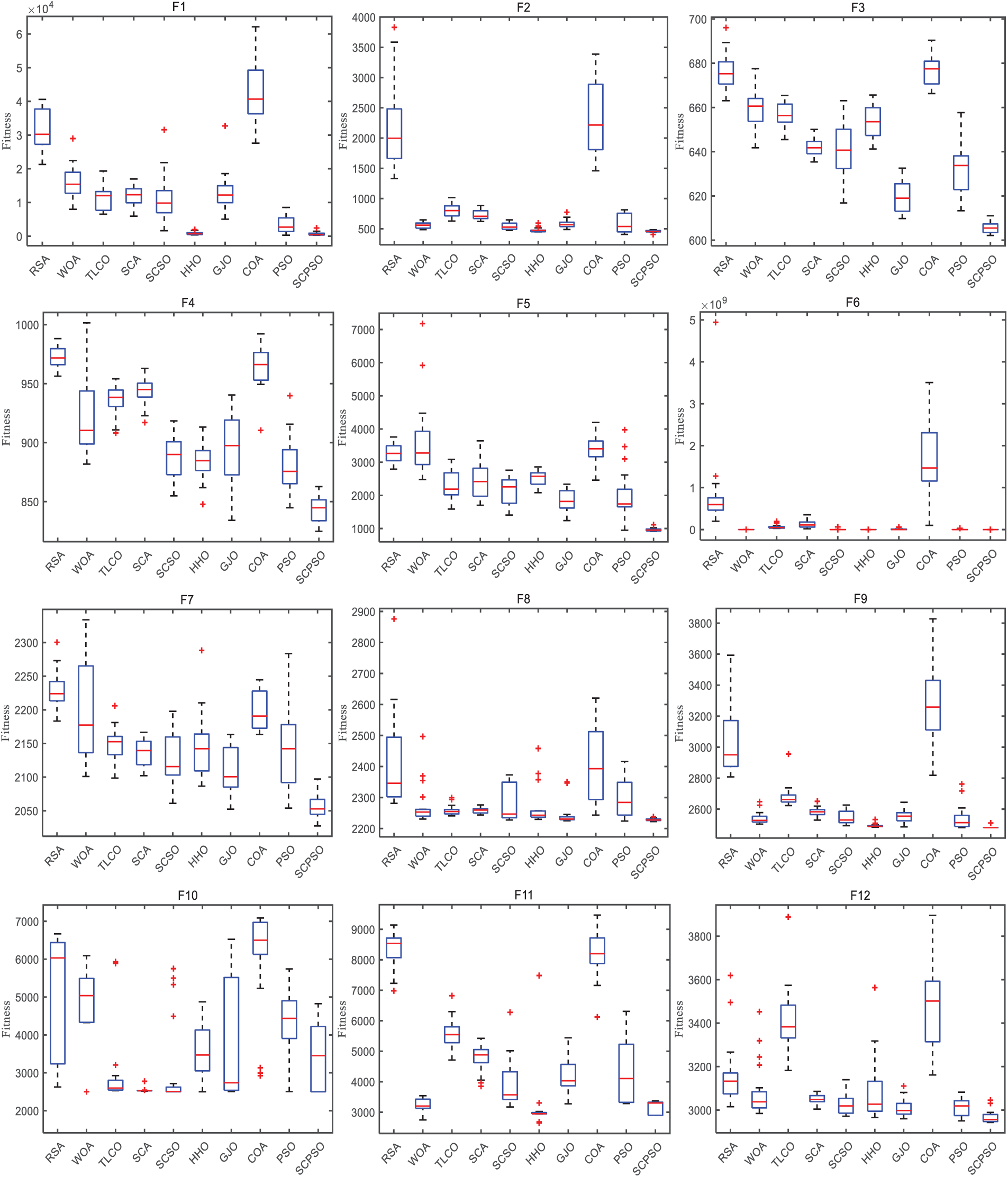
Figure 12: Boxplot of SCPSO with the other algorithms (CEC2022 20 dimension)

A radar plot according to the rank of SCPSO and other superior algorithms in the 10 and 20 dimensions of the CEC2022 test suite is plotted in Figs. 13 and 14. Observing the two sets of plots, SCPSO has the smallest area, and its image is more rounded in the 20 dimensions, demonstrating that SCPSO is more convergent and stable in the 20 dimensions of the test function. In addition, Fig. 15 visualizes the cumulative average ranks for the two dimensions. It again reveals that SCPSO provides an excellent output on both dimensions and the greater the dimension, the more enhanced the performance.

Figure 13: Radar plot of SCPSO with other algorithms (CEC2022 10 dimension)

Figure 14: Radar plot of SCPSO with the other algorithms (CEC2022 20 dimension)

Figure 15: Cumulative average rank of the 12 algorithms on two different dimensions

6  Engineering Issues

6.1 Alkylation Unit Optimization Issue

To further assess the capability of SCPSO in addressing intricate constrained optimization issues, it is applied to three challenging problems. These problems are the optimization of the alkylation unit, the vehicle side impact design problem, and the industrial refrigeration system design problem. To deal with these nonlinearly constrained problems, we introduce the concept of penalty function [51]. By transforming the constraints into penalty terms of the objective function, we can optimize unconstrained problems in SCPSO. In this approach, the algorithm evaluates the solution in each iteration and adjusts to the value of the penalty function to approximate the optimal solution. In this case, the population size is 30, the maximum count of iterations is 500, and the count of executions is 30.

The alkylation process [52] is an essential reaction common in the petroleum industry, and it finds extensive utility in the synthesis of alkylated products across various domains. In this process, an olefin feed (usually pure butene) is introduced into a reactor for reaction, a pure isobutane recycles, a 100% isobutene supplemental stream, and an acid catalyst. The product stream in the reactor is then processed through a fractionator to separate the isobutene and alkylation products, while the exhausted acid is discharged from the reactor. The design of the alkylation unit is diagrammed in Fig. 16. In this problem, there are 14 inequality constraints, and 7 variables Pa=[pa1,pa2,pa3,pa4,pa5,pa6,pa7] are involved. The profit maximization of the reaction system is achieved by considering various constraints comprehensively. The detailed model is as described below:

minf(Pa)=1.715pa1+0.035pa1pa6+4.0565pa3+10pa2−pa3pa5−3000(20)

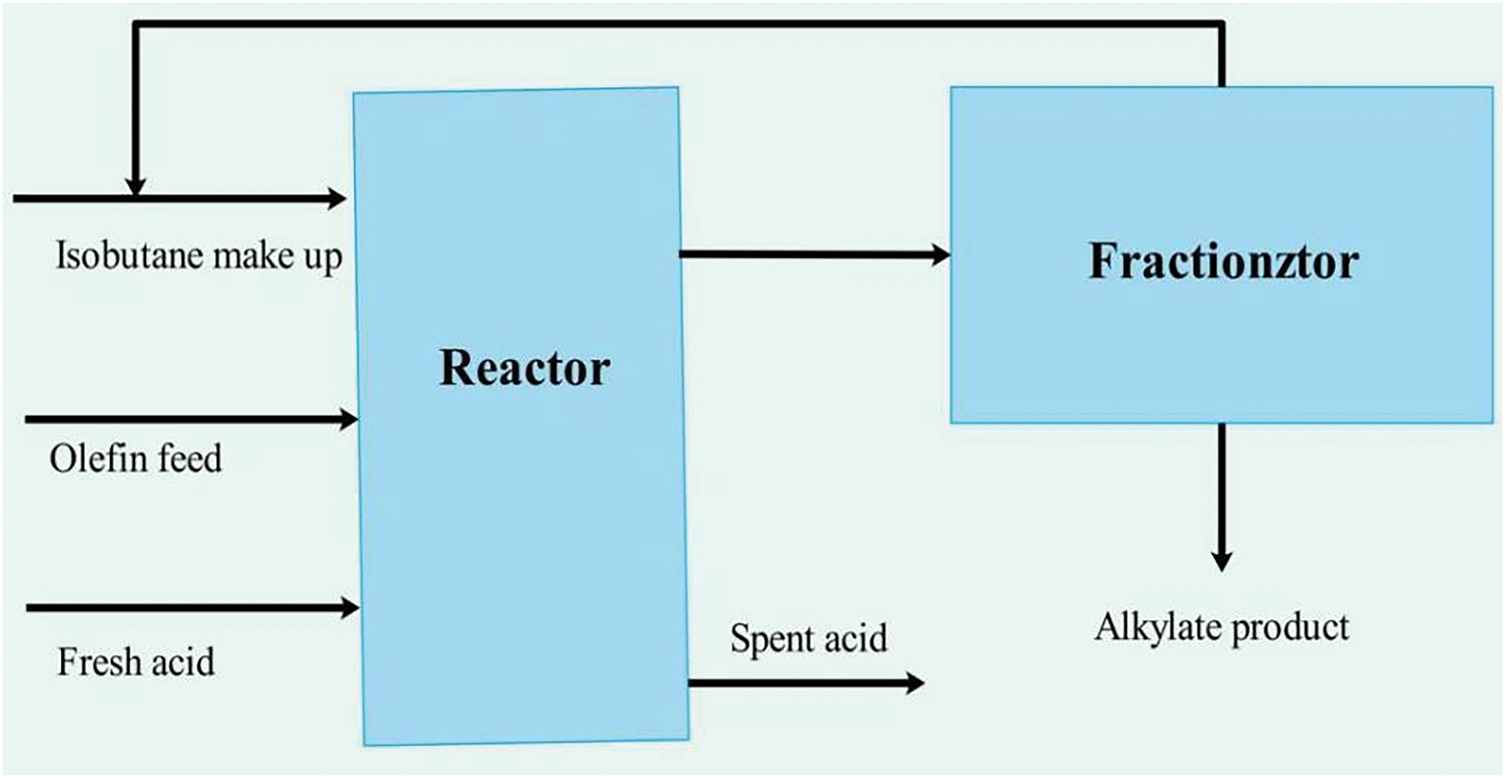
Figure 16: Design chart of the alkylation unit

Constraints:

g1(Pa)=0.0059553571pa62+0.88392857pa3pa1−0.1175625pa6−1,g2(Pa)=1.1088pa1pa3+0.1303533pa1pa6pa3−0.0066033pa1pa62pa3−1,g3(Pa)=0.00066173269pa62+0.017239878pa5−0.0056595559pa4−0.19120592pa6−1,g4(Pa)=56.85075pa5+1.08702pa6pa5+0.32175pa4pa5−0.32175pa62pa5−1,g5(Pa)=0.006198pa7+2462.3121pa2pa3pa4−25.125634pa2pa3−1,g6(Pa)=0.0016118996pa7+5000pa2pa3pa7−489510pa2pa3pa4pa7−1,g7(Pa)=44.333333pa5+0.33pa7pa5−1,g8(Pa)=0.022556pa5−0.007595pa7−1,g9(Pa)=0.00061pa3−0.0005pa1−1,g10(Pa)=0.819672pa1pa3+0.819672pa3−1,g11(Pa)=24500pa2pa3pa4−250pa2pa3−1,g12(Pa)=0.010204082pa4+0.000012244898pa3pa4pa2−1,g13(Pa)=0.0000625pa1pa6+0.0000625pa1−0.00007625pa3−1,g14(Pa)=1.22pa3pa1−pa6+pa1−1

Variables take values in the range:

1≤pa1≤2000,1≤pa2≤120,1≤pa3≤5000,85≤pa4≤93,90≤pa5≤95,3≤pa6≤12,145≤pa7≤162

The ten excellent algorithms used in this experiment are the Bird Search Algorithm [53], Aquila optimizer (AO) [54], SCSO, WOA, RSA, TLCO, SCA, Beluga whale optimization (BWO) [55], PSO, SCPSO. The optimal variables and outcomes of each algorithm for settling the alkylation unit problem are demonstrated in Table 9, from which we can see that SCPSO achieves the maximum profit. In addition, observing the statistical outcomes presented in Table 10, we can perceive that SCPSO has a smaller average and a minor standard deviation, suggesting that its results are more stable. That implies that SCPSO can achieve the optimal solution more reliably.

6.2 Automobile Lateral Crash Design Issue

The automobile lateral crash issue [56] is a constrained optimization problem. It aims to minimize the extent of passenger injuries in a collision by optimizing the crash resistance of the vehicle to meet vehicle market and regulatory side-impact standards and to provide adequate side-impact protection. According to the European Enhanced Vehicle Safety Council (EEVC) European vehicle side impact procedure, this paper performs optimization under eight constraints to minimize the vehicle weight. Among the variables is the thickness of the inside of the B-pillar (pa1), the B-pillar strengthening member (pa2), the inside of the floor (pa3), the cross member (pa4), the door beam (pa5), the door seat belt reinforcement (pa6), the roof truss beam (pa7), the material of the inside of the B-pillar (pa8), the inside of the floor (pa9), the stature of the impediment (pa10), and the batting slotting (pa11). The equation for this issue is:

minf(Pa)=1.98+4.9pa1+6.67pa2+6.98pa3+4.01pa4+1.78pa5+2.73pa7(21)

Constraints:

g1(Pa)=1.16−0.3717pa2pa4−0.00391pa2pa10−0.484pa3pa9+0.01343pa6pa10−1,g2(Pa)=0.261−0.0159pa1pa2−0.188pa1pa8−0.019pa2pa7+0.0144pa3pa5+0.0008757pa5pa10+0.08045pa6pa9+0.00139pa8pa11+0.00001575pa10pa11−0.32,g3(Pa)=0.214+0.00817pa5−0.131pa1pa8−0.0704pa1pa9+0.03099pa2pa6−0.018pa2pa7+0.0208pa3pa8+0.121pa3pa9−0.00364pa5pa6+0.0007715pa5pa10−0.0005354pa6pa10+0.00121pa8pa11−0.32.g4(Pa)=0.74−0.061pa2−0.163pa3pa8+0.001232pa3pa10−0.166pa7pa9+0.227pa22−0.32,g5(Pa)=28.98+3.818pa3−4.2pa1pa2+0.02070.001232pa5pa10+6.63pa6pa9−7.7a7pa8+0.32pa9pa10−32,g6(Pa)=33.86+2.95pa3+0.1792pa10−5.057pa1pa2−11pa2pa8−0.0215pa5pa10−9.98a7pa8+22pa8pa9−32,g7(Pa)=46.36−9.9pa2−12.9pa1pa8+0.1107pa3pa10−32,g8(Pa)=4.72−0.5pa4−0.19pa2pa3−0.0122pa4pa10+0.009325pa6pa10+0.000191pa112−4

Variables take values in the range:

0.5≤pa1,pa3,pa4≤1.5,0.45≤pa2≤1.35,0.875≤pa5≤2.625,0.4≤pa6,pa7≤1.2,0.192≤pa8,pa9≤0.345,−30≤pa10,pa11≤30

The following participated in this experiment: SCA, AO, Slime Mould Algorithm (SMA) [57], TLCO, Artificial Rabbits Optimization (ARO) [58], WOA, Seagull Optimization Algorithm (SOA) [59], Mountain Gazelle Optimizer (MGO) [60], PSO, and SCPSO. Based on the optimal results of the automobile lateral crash design issue presented in Table 11, SCPSO has performed better in solving this problem. Moreover, other statistical outcomes of each algorithm for solving the automobile lateral crash design issue are also provided in Table 12, which further demonstrates the superiority of SCPSO.

6.3 Industrial Refrigeration System Design Issue

Industrial refrigeration system [61] is a type of refrigeration equipment used in extensive industrial facilities and commercial buildings closely related to energy consumption. Therefore, the optimal design of an industrial refrigeration system plays a significant role in regulating energy consumption. This problem aims to find the minimum energy consumption under fifteen constraints and contains fourteen variables, which are formulated as follows:

minf(Pa)=63098.88pa2pa4pa12+5441.5pa22pa12+115055.5pa21.664pa6+6172.27pa22pa6+63098.88pa1pa3pa11+5441.5pa12pa11+115055.5pa11.664pa5+6172.27pa12pa5+140.53pa1pa11+70.26pa12+281.29pa1pa3+281.29pa32+14437pa81.8812pa120.3424pa10pa14−1pa12pa7pa9−1+20470.2pa72.893pa110.316pa12(22)

Constraints:

g1(Pa)=1.524pa7−1−1,g2(Pa)=1.524pa8−1−1,g3(Pa)=0.07789pa1−2pa7−1pa9−1,g4(Pa)=7.05305pa9−1pa12pa10pa8−1pa2−1pa14−1−1,g5(Pa)=0.0833pa13−1pa14−1,g6(Pa)=47.136pa20.333pa10−1pa12−1.333pa8pa132.119562.08pa132.1195pa12−1pa80.2pa10−1−1,g7(Pa)=0.04771pa10pa81.8812pa120.3424−1,g8(Pa)=0.0488pa9pa71.893pa110.316−1,g9(Pa)=0.0099pa1pa3−1−1,g10(Pa)=0.0193pa2pa4−1−1,g11(Pa)=0.0298pa1pa5−1−1,g12(Pa)=0.056pa2pa6−1−1,g13(Pa)=2pa9−1−1,g14(Pa)=2pa10−1−1,g15(Pa)=2pa11−1−1

Variables take values in the range:

0.001≤pai≤5,i=1,2,…,14

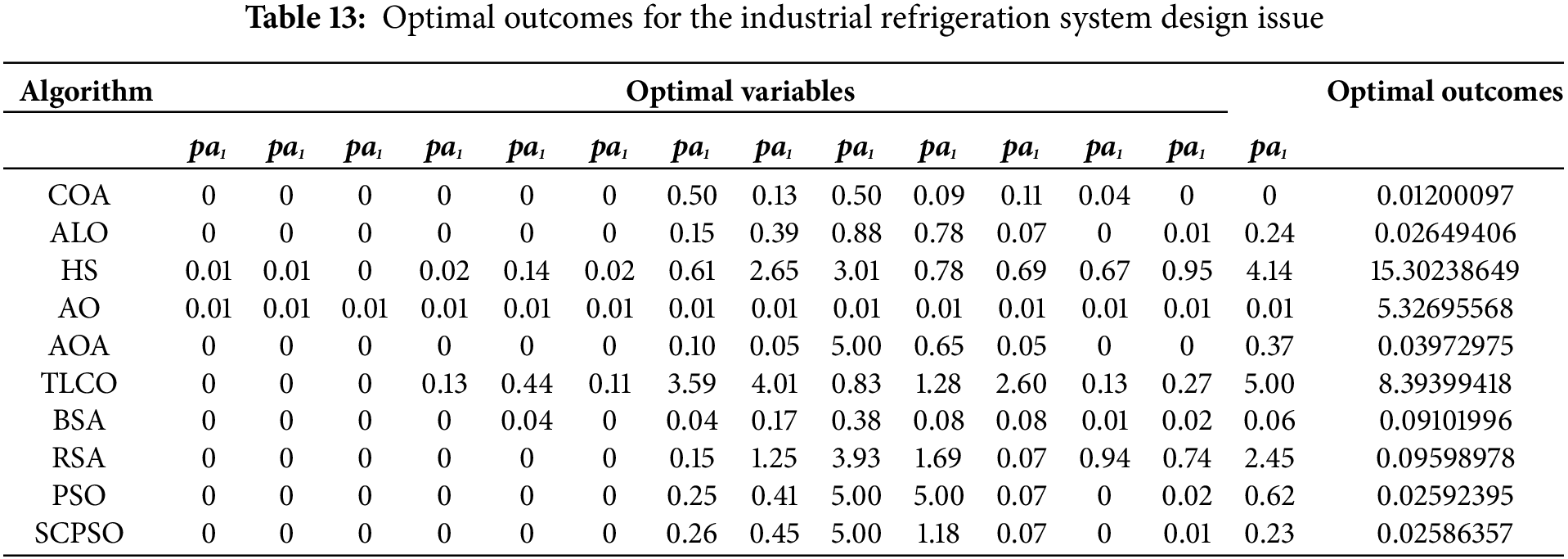
PSO and SCPSO that participated in the comparative experiments, as well as the COA, Ant Lion Optimizer (ALO) [62], Harmony Search Algorithm (HS) [63], AO, Arithmetic Optimization Algorithm (AOA) [64], TLCO, BSA, and RSA. The optimal results of the industrial refrigeration system design problem are provided in Table 13, from which it can be noted that the optimal value of SCPSO is closest to the desired result. Moreover, from the statistical outcomes of each algorithm for solving the industrial refrigeration system design issue in Table 14, SCPSO has the smallest mean value and is also in a distant second place regarding standard deviation.

7  Feature Selection

Feature selection (FS) [65] is a critical component of machine learning and data analysis, aiming to identify the most relevant subset of features from the raw data to build accurate and efficient predictive models. This process not only enhances model performance but also simplifies interpretation and reduces computational costs, making it essential for high-dimensional data applications. In this study, we leverage the Self-adaptive Cooperative Particle Swarm Optimization (SCPSO) algorithm to tackle the multi-objective FS problem effectively.

SCPSO is applied to achieve two main goals simultaneously: maximizing classification accuracy and minimizing the number of selected features. By balancing these objectives, SCPSO intelligently narrows down the feature space, identifying feature subsets that both maintain high predictive power and enhance efficiency. Through this approach, SCPSO demonstrates its ability to outperform other algorithms by selecting the most informative features that contribute to precise, generalizable models. This dual objective underscore the robustness of SCPSO in adapting to complex datasets, highlighting its value as a tool for both performance-driven and efficiency-oriented feature selection in machine learning tasks.

7.1 Modeling

Feature selection (FS) exemplifies a classic binary optimization challenge. In this context, each feature is represented by binary variables: a value of 1 indicates the feature is selected, while 0 signifies it is excluded. This binary transformation is fundamental to refining the feature subset and enhances interpretability in the optimization process. To robustly assess the performance of the binary FS algorithm, we employ 5-fold cross-validation, which partitions the data into training and test sets in five cycles, ensuring that the model’s reliability is consistently validated across varying data segments. This setup not only reinforces the robustness of the model but also minimizes overfitting. The core objective of FS is to strike a fine balance: minimizing the number of selected features while preserving, or even enhancing, classification accuracy. The fitness function is thus meticulously designed to reward minimal feature sets that maintain high predictive power. This approach emphasizes computational efficiency, reducing model complexity and enabling faster, more effective decision-making, especially in scenarios where high-dimensional data can obscure insights and overburden resources. In sum, this FS strategy allows the model to zoom in on the most informative features, stripping away the irrelevant ones and thus honing predictive accuracy with a lean, high-performing subset of data. To achieve this goal, the test function is set as:

Fit=γ1⋅err+γ2|R||N|(23)

where err represents the classification error rate of the selected classifier, |R| is the count of picked features in the data set, and |N| is the original count of features in the data set. γ1 as a penalty factor for controlling classification accuracy, γ2 as a factor identifying the count of picked features, and γ1∈[0,1],γ2=1−γ1. In this paper, set γ1=0.9,γ2=0.1.

7.2 Trials and Analysis

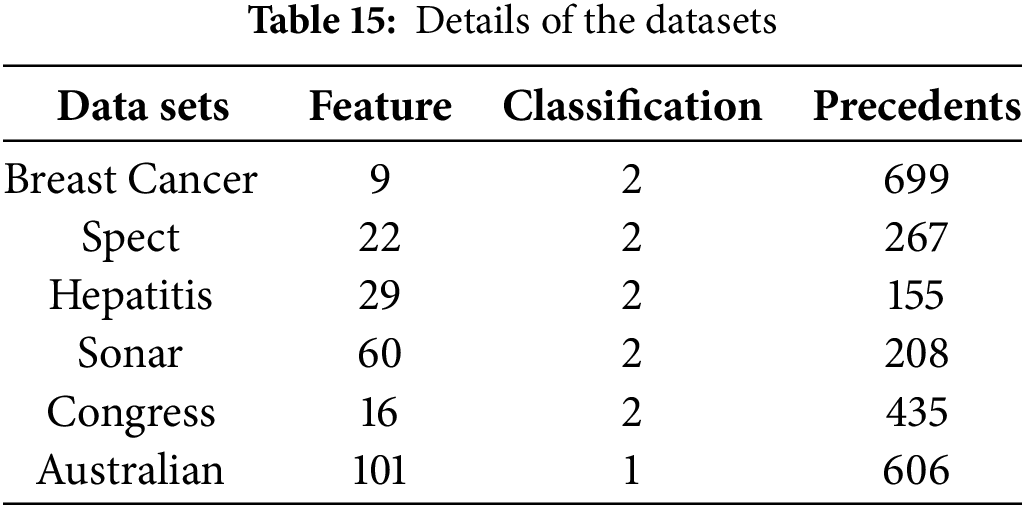
To showcase the superiority of SCPSO in settling specific feature selection issues. We use the SVM classifier for testing. Six standard test sets from the database published by the University of California, Irvine (UCI) for machine learning were used in the test experiment, and the main details of the datasets are summarized in Table 15. Breast Cancer: This dataset is usually used to classify breast cancer. The SPECT dataset is mostly used to study heart disease diagnosis. Hepatitis: This dataset is often used for the task of hepatitis-related classification. Sonar: This dataset is usually used to classify sonar signals. Congress: This dataset is usually used to study voting patterns. Australian: This dataset is mainly used for research related to financial or credit card applications. Comparisons with SCPSO were made with SMA, Differential evolution (DE) [66], Atom Search Optimization (ASO) [67], GWO, ACO, and Gravitational Search Algorithm (GSA) [68], besides PSO. In addition, the population size and the count of iterations were set to 20 and 100, and each data set was executed 20 times independently.

First, the data results of each algorithm on six test sets (including Breast Cancer, Spect, hepatitis, Sonar, Congress, and Australian) are presented in Table 16. In particular, it is worth noting that SCPSO has lower mean values than the other algorithms on all test sets, which reveals its superior performance in solving these issues. Additionally, the standard deviation is relatively small, which indicates that SCPSO also performs well in terms of stability. As a whole, the overall ranks of the algorithms are SCPSO > GSA > ASO > ACO > PSO > SMA = DE > GWO. SCPSO is ranked first with an average rank of 1, while PSO is ranked fifth with an average rank of 4.33, again emphasizing the introduced strategies’ importance and effectiveness. The excellent performance of SCPSO may be attributed to the efficiency and robustness of its optimization process, which enables it to find better feature combinations on complex datasets. The stable and high performance of GSA indicates its adaptability in handling different types of data. The relatively weak performance of PSO, SMA, DE, and GWO may be due to the lack of adaptability of these methods to different data feature distributions and complexity, resulting in poor results for some datasets.

In Fig. 17, we can view the convergence plot of each binary algorithm. Among them, the red curve represents the convergence trend of SCPSO. It is apparent from the observation that SCPSO converges more swiftly compared to other algorithms, and the minimum value reached is also the smallest. This observation further highlights the superiority of SCPSO in solving FS issues. Its fast convergence speed signifies that it can find the optimal subset of features more efficiently. At the same time, the minimum value reached indicates that it can find a more accurate prediction model. Not only that, the boxplot of SCPSO and the individual algorithms are also shown in Fig. 18, which also affirms the performance of SCPSO in terms of stability.

Figure 17: Convergence plot of each FS algorithm

Figure 18: Boxplot of each FS algorithm

Feature selection (FS) primarily aims to maximize classification accuracy. Table 17 presents each algorithm’s average classification accuracy and ranking across six datasets, with a bar plot in Fig. 19 visualizing these averages. Notably, SCPSO (Self-adaptive Cooperative Particle Swarm Optimization) shows varying effects depending on the dataset, with standout performance on several.SCPSO ranks first in solving Spect, hepatitis, Sonar, and Australian datasets, showcasing its ability to handle these tasks effectively. This consistent top-ranking highlights SCPSO’s robustness and adaptability, making it an ideal choice for complex feature selection problems in these domains. On the Breast Cancer dataset, SCPSO did not outperform SMA (Slime Mould Algorithm) and GSA (Gravitational Search Algorithm), but it still secured third place. This ranking indicates that SCPSO remains a competitive choice, even though other algorithms have a slight edge on this dataset. However, SCPSO ranks fifth on the Congress dataset, suggesting it faces challenges in addressing this data type. This result points to potential areas for SCPSO’s improvement and to develop optimized strategies tailored for Congress-type data.

Figure 19: Bar plot of the average classification accuracy of each algorithm

SCPSO excels across most datasets, but its relatively weaker performance in Congress highlights an opportunity to refine the algorithm and expand its versatility in feature selection applications.

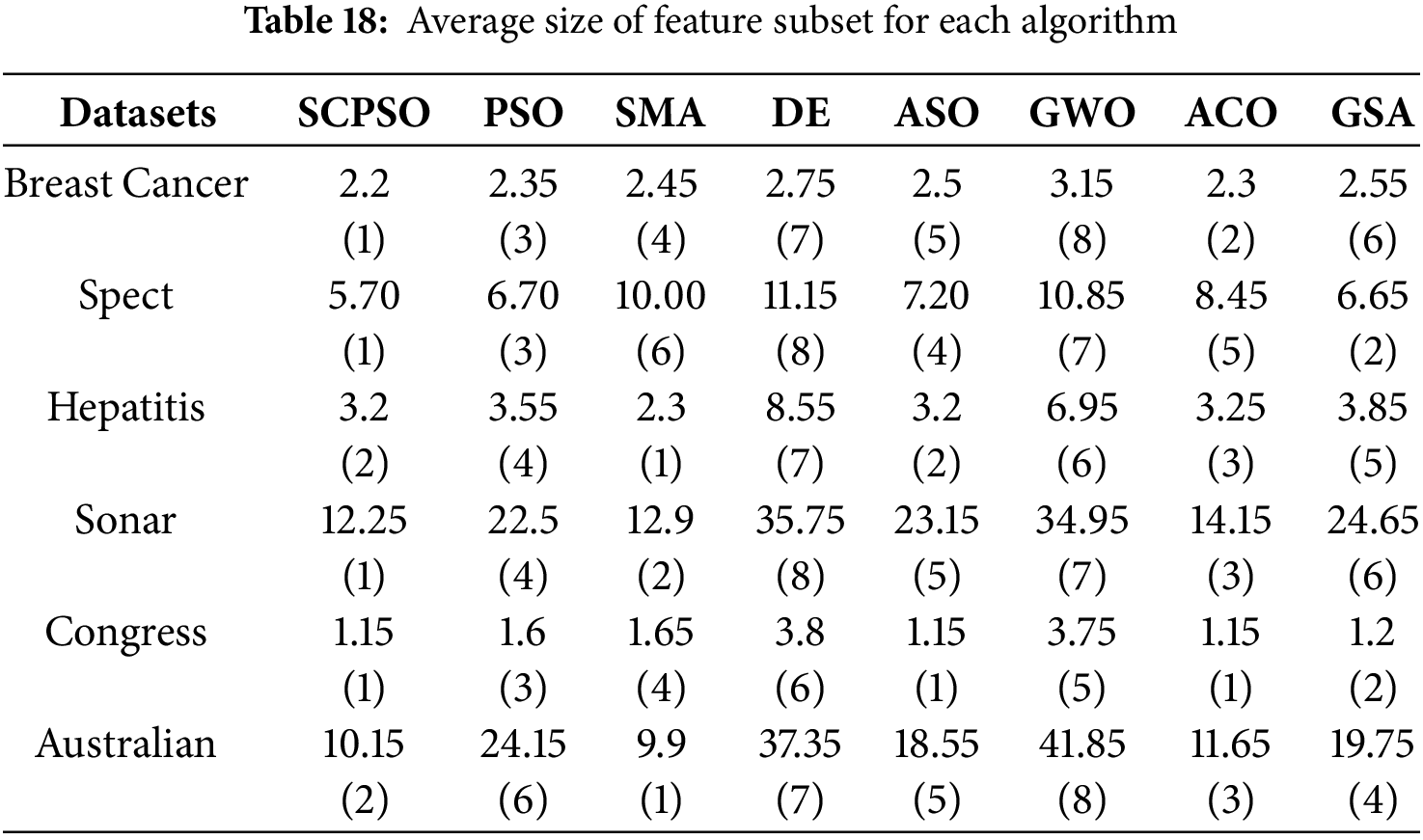
The second goal of the FS problem is to keep the number of features as small as possible. In Table 18, we collect the average size of the feature subset for the eight algorithms. These results show that all algorithms achieve some degree of reduction in the dimension of the original data set, i.e., successful feature selection. Specifically, with fewer features, SCPSO ranked first in Breast Cancer, Spect, Sonar, and Congress. Moreover, it is slightly inferior to SMA on hepatitis, Australian, and ranks second.

In summary, SCPSO iteratively selects features by evaluating the impact of feature subsets on model performance. To distinguish between related and unrelated features, the model reduces the probability of selecting features that contribute less to performance. That is achieved by strengthening particles that perform well (subsets with higher fitness) and punishing or abandoning particles that do not improve model performance. Therefore, as the iteration progresses, the algorithm will gradually converge to a feature set that contributes the most to prediction accuracy.

8  Conclusion and Future Direction

This paper presents an enhanced PSO algorithm called SCPSO. It demonstrates high convergence accuracy and stability on a complex CEC test suite and three engineering problems, proving its superb generalization ability and usefulness. He demonstrates its ability to reduce data dimensionality and improve model performance by selecting relevant features. The integration of SCSO into the traditional PSO framework is a key improvement that endows SCPSO with extended global search capabilities. This is attributed to SCSO’s ability to mimic the hunting behavior of sand cats, which are adept at detecting low-frequency vibrations to locate their prey, thus exploring the solution space more efficiently and reducing the likelihood of getting stuck in local optima.

Employing a Latin hypercube sampling strategy during the initialization phase has proven to be a strategic move. This approach ensures a more even distribution of the initial population in the search space, enhances population diversity, and provides broader coverage from the outset. This initialization technique is particularly effective in high-dimensional problems where random initialization may lead to clustering of solutions in some domains, ignoring others, and potentially missing the global optimum. In addition, inspired by the cooperative hunting behavior of Grey wolves, a roundup search strategy is introduced to accelerate the convergence of SCPSO. By selecting leaders based on fitness and allowing them to guide the group toward the goal, SCPSO demonstrates an improved ability to find optimal solutions quickly.

Improvements to the algorithm will continue in the future. On the one hand, although SCPSO has achieved some successes, the intake search strategy has been shown to improve the convergence speed but inhibit the accuracy of the solution on individual functions. Therefore, subsequent research can focus on finding better strategies. In addition, the transfer function helps to influence the way the algorithm navigates through the feature space, leading to changes in the quality and efficiency of feature selection. Therefore, more work needs to be done to measure the applicability of SCPSO in solving other FS problems using other transfer functions, such as the V-function. Finally, SCSO can be applied to more problems, such as UAV path planning, time series prediction, etc.

Acknowledgement: None.

Funding Statement: This work was supported by the Fundamental Research Funds for the Central Universities of China (No. 300102122105), the Natural Science Basic Research Plan in Shaanxi Province of China (2023-JC-YB-023).

Author Contributions: Xing Wang: Methodology, Software, Investigation, Formal analysis, Funding acquisition, Writing—original draft. Huazhen Liu: Data curation, Resources, Writing—original draft. Abdelazim G. Hussien: Visualization, Analysis, Supervision, Investigation. Gang Hu: Writing—review & editing, Supervision. Li Zhang: Conceptualization, Writing—review & editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ma X, Xu H, Liu Y, Zhang JZ. Class-specific feature selection using fuzzy information-theoretic metrics. Eng Appl Artif Intell. 2024;136(12):109035. doi:10.1016/j.engappai.2024.109035. [Google Scholar] [CrossRef]

2. Fan Y, Liu J, Tang J, Liu P, Lin Y, Du Y. Learning correlation information for multi-label feature selection. Pattern Recogn. 2024;145(8):109899. doi:10.1016/j.patcog.2023.109899. [Google Scholar] [CrossRef]

3. Mostafa RR, Ewees AA, Ghoniem RM, Abualigah L, Hashim FA. Boosting chameleon swarm algorithm with consumption AEO operator for global optimization and feature selection. Knowl-Based Syst. 2022;246(9):108743. doi:10.1016/j.knosys.2022.108743. [Google Scholar] [CrossRef]

4. Hu G, Zhong J, Wang X, Wei G. Multi-strategy assisted chaotic coot-inspired optimization algorithm for medical feature selection: a cervical cancer behavior risk study. Comput Biol Med. 2022;151(1):106239. doi:10.1016/j.compbiomed.2022.106239. [Google Scholar] [PubMed] [CrossRef]

5. Samieiyan B, MohammadiNasab P, Mollaei MA, Hajizadeh F, Kangavari M. Novel optimized crow search algorithm for feature selection. Expert Syst Appl. 2022;204(3):117486. doi:10.1016/j.eswa.2022.117486. [Google Scholar] [CrossRef]

6. Braik MS, Hammouri AI, Awadallah MA, Al-Betar MA, Khtatneh K. An improved hybrid chameleon swarm algorithm for feature selection in medical diagnosis. Biomed Signal Process Control. 2023;85(8):105073. doi:10.1016/j.bspc.2023.105073. [Google Scholar] [CrossRef]

7. Kamel SR, Yaghoubzadeh R. Feature selection using grasshopper optimization algorithm in diagnosis of diabetes disease. Inform Med Unlocked. 2021;26(12):100707. doi:10.1016/j.imu.2021.100707. [Google Scholar] [CrossRef]

8. Zadsafar F, Tabrizchi H, Parvizpour S, Razmara J, Lotfi S. A model for Mesothelioma cancer diagnosis based on feature selection using Harris hawk optimization algorithm. Comput Methods Programs Biomed Update. 2022;2(4):2022–100078. doi:10.1016/j.cmpbup.2022.100078. [Google Scholar] [CrossRef]

9. Yan H, Li Q, Tseng M, Guan X. Joint-optimized feature selection and classifier hyperparameters by salp swarm algorithm in piano score difficulty measurement problem. Appl Soft Comput. 2023;144:110464. doi:10.1016/j.asoc.2023.110464. [Google Scholar] [CrossRef]

10. Abd El-Mageed AA, Abohany AA, Elashry A. Effective feature selection strategy for supervised classification based on an improved binary Aquila optimization algorithm. Comput Ind Eng. 2023;181(4):109300. doi:10.1016/j.cie.2023.109300. [Google Scholar] [CrossRef]

11. Hu G, Yang R, Qin X, Wei G. MCSA: multi-strategy boosted chameleon-inspired optimization algorithm for engineering applications. Comput Method Appl Mech Eng. 2023;403(18):115676. doi:10.1016/j.cma.2022.115676. [Google Scholar] [CrossRef]

12. Hu G, Zheng Y, Abualigah L, Hussien AG. DETDO: an adaptive hybrid dandelion optimizer for engineering optimization. Adv Eng Inform. 2023;57(4):102004. doi:10.1016/j.aei.2023.102004. [Google Scholar] [CrossRef]

13. Chen Z, Cao H, Ye K, Zhu H, Li S. Improved particle swarm optimization-based form-finding method for suspension bridge installation analysis. J Comput Civil Eng. 2015;29(3):4014047 doi:10.1061/(ASCE)CP.1943-5487.0000354. [Google Scholar] [CrossRef]

14. Cheng R, Jin Y. A social learning particle swarm optimization algorithm for scalable optimization. Inform Sci. 2015;291(2):43–60. doi:10.1016/j.ins.2014.08.039. [Google Scholar] [CrossRef]

15. Aydilek IB. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl Soft Comput. 2018;66(2):232–49. doi:10.1016/j.asoc.2018.02.025. [Google Scholar] [CrossRef]

16. Ha MP, Nazari-Heris M, Mohammadi-Ivatloo B, Seyedi H. A hybrid genetic particle swarm optimization for distributed generation allocation in power distribution networks. Energy. 2020;209:118218. doi:10.1016/j.energy.2020.118218. [Google Scholar] [CrossRef]

17. Yang R, Liu Y, Yu Y, He X, Li H. Hybrid improved particle swarm optimization-cuckoo search optimized fuzzy PID controller for micro gas turbine. Energy Rep. 2021;7(1):5446–54. doi:10.1016/j.egyr.2021.08.120. [Google Scholar] [CrossRef]

18. Zainuddin Z, Lai KH, Ong P. An enhanced harmony search based algorithm for feature selection: applications in epileptic seizure detection and prediction. Comput Electr Eng. 2016;53(2):143–62. doi:10.1016/j.compeleceng.2016.02.009. [Google Scholar] [CrossRef]

19. Paul D, Su R, Romain M, Sébastien V, Pierre V, Isabelle G. Feature selection for outcome prediction in oesophageal cancer using genetic algorithm and random forest classifier. Comput Med Imag Grap. 2017;60(5):42–9. doi:10.1016/j.compmedimag.2016.12.002. [Google Scholar] [PubMed] [CrossRef]

20. Tu Q, Chen X, Liu X. Multi-strategy ensemble grey wolf optimizer and its application to feature selection. Appl Soft Comput. 2019;76(99):16–30. doi:10.1016/j.asoc.2018.11.047. [Google Scholar] [CrossRef]

21. Alzaqebah M, Briki K, Alrefai N, Brini S, Jawarneh S, Alsmadi MK, et al. Memory based cuckoo search algorithm for feature selection of gene expression dataset. Inform Med Unlocked. 2021;24(2):100572. doi:10.1016/j.imu.2021.100572. [Google Scholar] [CrossRef]

22. Khorashadizade M, Hosseini S. An intelligent feature selection method using binary teaching-learning based optimization algorithm and ANN. Chemometr Intell Lab Syst. 2023;240(5):104880. doi:10.1016/j.chemolab.2023.104880. [Google Scholar] [CrossRef]

23. Zhao Y, Dong J, Li X, Chen H, Li S. A binary dandelion algorithm using seeding and chaos population strategies for feature selection. Appl Soft Comput. 2022;125(5):109166. doi:10.1016/j.asoc.2022.109166. [Google Scholar] [CrossRef]

24. Braik M, Hammouri A, Alzoubi H, Sheta A. Feature selection based nature inspired capuchin search algorithm for solving classification problems. Expert Syst Appl. 2024;235(1):121128. doi:10.1016/j.eswa.2023.121128. [Google Scholar] [CrossRef]

25. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks; 1995; Perth, WA, Australia. Vol. 4, p. 1942–8. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

26. He Z, Pan Y, Wang K, Xiao L, Wang X. Area optimization for MPRM logic circuits based on improved multiple disturbances fireworks algorithm. Appl Math Comput. 2021;399(9):126008. doi:10.1016/j.amc.2021.126008. [Google Scholar] [CrossRef]

27. Hua L, Zhang C, Peng T, Ji C, Nazir MS. Integrated framework of extreme learning machine (ELM) based on improved atom search optimization for short-term wind speed prediction. Energ Convers Manage. 2022;252(30):115102. doi:10.1016/j.enconman.2021.115102. [Google Scholar] [CrossRef]

28. Seyyedabbasi A, Kiani F. Sand cat swarm optimization: a nature-inspired algorithm to solve global optimization problems. Eng Comput. 2023;39(4):2627–51. doi:10.1007/s00366-022-01604-x. [Google Scholar] [CrossRef]

29. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

30. Mohamed AW, Hadi AA, Mohamed AK, Awad NH. Evaluating the performance of adaptive gainingsharing knowledge based algorithm on CEC 2020 benchmark problems. In: 2020 IEEE Congress on Evolutionary Computation (CEC); 2020; Glasgow, UK. p. 1–8. doi:10.1109/CEC48606.2020.9185901. [Google Scholar] [CrossRef]

31. Yazdani D, Branke J, Omidvar MN, Li X, Li C, Mavrovouniotis M, et al. IEEE CEC 2022 competition on dynamic optimization problems generated by generalized moving peaks benchmark. arXiv:2106.06174. 2021. [Google Scholar]

32. Liang JJ, Qu BY, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. In: Technical report. Zhengzhou, China: Computational Intelligence Laboratory, Zhengzhou University. Singapore: Nanyang Technological University; 2014. [Google Scholar]

33. Awad N, Ali M, Liang J, Qu B, Suganthan P. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. In: Technical report; 2016. p. 5–8. [Google Scholar]

34. Hu G, Guo Y, Zhong J, Wei G. IYDSE: ameliorated Young’s double-slit experiment optimizer for applied mechanics and engineering. Comput Method Appl Mech Eng. 2023;412(1):116062. doi:10.1016/j.cma.2023.116062. [Google Scholar] [CrossRef]

35. Mirjalili S, Wang G, Coelho LDS. Binary optimization using hybrid particle swarm optimization and gravitational search algorithm. Neural Comput Appl. 2014;25(6):1423–35. doi:10.1007/s00521-014-1629-6. [Google Scholar] [CrossRef]

36. Coelho LS. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst Appl. 2010;37(2):1676–83. doi:10.1016/j.eswa.2009.06.044. [Google Scholar] [CrossRef]

37. Ye W, Feng W, Fan S. A novel multi-swarm particle swarm optimization with dynamic learning strategy. Appl Soft Comput. 2017;61(5):832–43. doi:10.1016/j.asoc.2017.08.051. [Google Scholar] [CrossRef]

38. Sun J, Wu X, Palade V, Fang W, Shi Y. Random drift particle swarm optimization algorithm: convergence analysis and parameter selection. Mach Learn. 2015;101(1–3):345–76. doi:10.1007/s10994-015-5522-z. [Google Scholar] [CrossRef]

39. Haklı H, Uğuz H. A novel particle swarm optimization algorithm with Levy flight. Appl Soft Comput. 2014;23(3):333–45. doi:10.1016/j.asoc.2014.06.034. [Google Scholar] [CrossRef]

40. Yapıcı H, Çetinkaya N. An improved particle swarm optimization algorithm using eagle strategy for power loss minimization. Math Probl Eng. 2017;2017(1):1063045. doi:10.1155/2017/1063045. [Google Scholar] [CrossRef]

41. Wu D, Rao H, Wen C, Jia H, Liu Q, Abualigah L. Modified sand cat swarm optimization algorithm for solving constrained engineering optimization problems. Mathematics. 2022;10(22):4350. doi:10.3390/math10224350. [Google Scholar] [CrossRef]

42. Wang X, Liu Q, Zhang L. An adaptive sand cat swarm algorithm based on cauchy mutation and optimal neighborhood disturbance strategy. Biomimetics. 2023;8(2):191. doi:10.3390/biomimetics8020191. [Google Scholar] [PubMed] [CrossRef]

43. Hu G, Zhong J, Zhao C, Wei G, Chang C. LCAHA: a hybrid artificial hummingbird algorithm with multi-strategy for engineering applications. Comput Method Appl Mech Eng. 2023;415(4):116238. doi:10.1016/j.cma.2023.116238. [Google Scholar] [CrossRef]

44. Abualigah L, Elaziz MAbd, Sumari P, Geem ZW, Gandomi AH. Reptile Search Algorithm (RSAa nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191(11):116158. doi:10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

45. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

46. Minh H, Sang-To T, Theraulaz G, Wahab MA, Cuong-Le T. Termite life cycle optimizer. Expert Syst Appl. 2023;213:119211. doi:10.1016/j.eswa.2022.119211. [Google Scholar] [CrossRef]

47. Abualigah L, Diabat A. Advances in sine cosine algorithm: a comprehensive survey. Artif Intell Rev. 2021;54(4):2567–608. doi:10.1007/s10462-020-09909-3. [Google Scholar] [CrossRef]

48. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: algorithm and applications. Future Gener Comput Syst. 2019;97:849–72. doi:10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

49. Chopra N, Ansari MM. Golden jackal optimization: a novel nature-inspired optimizer for engineering applications. Expert Syst Appl. 2022;198(5):116924. doi:10.1016/j.eswa.2022.116924. [Google Scholar] [CrossRef]

50. Dehghani M, Montazeri Z, Trojovská E, Trojovský P. Coati optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl-Based Syst. 2023;259(1):110011. doi:10.1016/j.knosys.2022.110011. [Google Scholar] [CrossRef]

51. Houssein EH, Hussain K, Abualigah L, Abd Elaziz M, Alomoush W, Dhiman G, et al. An improved opposition-based marine predators algorithm for global optimization and multilevel thresholding image segmentation. Knowl-Based Syst. 2021;229(1):107348. doi:10.1016/j.knosys.2021.107348. [Google Scholar] [CrossRef]

52. Kumar A, Wu G, Ali MZ, Mallipeddi R, Suganthan PN, Das S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol Comput. 2020;56:100693. doi:10.1016/j.swevo.2020.100693. [Google Scholar] [CrossRef]

53. Meng X, Gao XZ, Lu L, Liu Y, Zhang H. A new bio-inspired optimisation algorithm: bird Swarm Algorithm. J Exp Theor Artif Intell. 2016;28:673–87. doi:10.1080/0952813X.2015.1042530. [Google Scholar] [CrossRef]

54. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157(11):107250. doi:10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

55. Zhong C, Li G, Meng Z. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm. Knowl-Based Syst. 2022;251(1):109215. doi:10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]

56. Gu L, Yang RJ, Tho C, Makowskit M, Faruquet O, Li YLY. Optimisation and robustness for crashworthiness of side impact. Int J Vehicle Des. 2001;26(4):348–60. doi:10.1504/IJVD.2001.005210. [Google Scholar] [CrossRef]

57. Li S, Chen H, Wang M, Heidari AA, Mirjalili S. Slime mould algorithm: a new method for stochastic optimization. Future Gener Comput Syst. 2020;111(Suppl C):300–23. doi:10.1016/j.future.2020.03.055. [Google Scholar] [CrossRef]

58. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng Appl Artif Intel. 2022;114(4):105082. doi:10.1016/j.engappai.2022.105082. [Google Scholar] [CrossRef]

59. Dhiman G, Kumar V. Seagull optimization algorithm: theory and its applications for large-scale industrial engineering problems. Knowl-Based Syst. 2019;165(25):169–96. doi:10.1016/j.knosys.2018.11.024. [Google Scholar] [CrossRef]

60. Abdollahzadeh B, Gharehchopogh FS, Khodadadi N, Mirjalili S. Mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv Eng Softw. 2022;174(3):103282. doi:10.1016/j.advengsoft.2022.103282. [Google Scholar] [CrossRef]

61. Aydemir SB. Enhanced marine predator algorithm for global optimization and engineering design problems. Adv Eng Softw. 2023;184(2):103517. doi:10.1016/j.advengsoft.2023.103517. [Google Scholar] [CrossRef]

62. Mirjalili S. The ant lion optimizer. Adv Eng Softw. 2015;83:80–98. doi:10.1016/j.advengsoft.2015.01.010. [Google Scholar] [CrossRef]

63. Geem ZW, Kim JH, Loganathan GV. A new heuristic optimization algorithm: harmony search. Simul-t Soc Mod Sim. 2001;76:60–8. doi:10.1177/003754970107600201. [Google Scholar] [CrossRef]

64. Abualigah L, Diabat A, Mirjalili S, Elaziz MA, Gandomi AH. The arithmetic optimization algorithm. Comput Method Appl Mech Eng. 2021;376(2):113609. doi:10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]

65. Houssein EH, Oliva D, Celik E, Emam MM, Ghoniem RM. Boosted sooty tern optimization algorithm for global optimization and feature selection. Expert Syst Appl. 2023;213(168):119015. doi:10.1016/j.eswa.2022.119015. [Google Scholar] [CrossRef]

66. Price KV. Differential evolution. In: Handbook of optimization: from classical to modern approach. Berlin/Heidelberg: Springer; 2013. p. 187–214. [Google Scholar]

67. Zhao W, Wang L, Zhang Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl-Based Syst. 2019;163(4598):283–304. doi:10.1016/j.knosys.2018.08.030. [Google Scholar] [CrossRef]

68. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inform Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]