Optimization-Based Approaches to Uncertainty Analysis of Structures Using Non-Probabilistic Modeling: A Review

1  Introduction

1.1 Motivation

The significance of consideration of various uncertainties in the analysis and design of structural systems has been extensively recognized. Accordingly, many review articles are available on uncertainty analysis of structures as well as structural design under uncertainty, as referred to in Section 1.2. Moreover, a handbook [1], as well as monographs [2,3], have recently been published to comprehensively describe uncertainty quantification methods.

Roughly speaking, uncertainty modeling is categorized into probabilistic and non-probabilistic ones. Employing a non-probabilistic model of uncertainty, we usually attempt to find a bound for the structural response, to which uncertainty is propagated from the assumed non-probabilistic uncertainty in the parameters of a structural system. This attempt is naturally identified with solving a pair of optimization problems, each of which either maximizes or minimizes the structural response.

To the best of the authors’ knowledge, the present literature lacks a review of uncertainty structural analysis using non-probabilistic modeling from the perspective of numerical optimization. This paper aims to present an intensive review of this research area, where existing methods are categorized and surveyed by focusing on characteristics and differences of numerical optimization approaches employed in those methods.

1.2 Methods Covered by This Review

Suppose that a structural system involves some uncertain parameters, where a non-probabilistic model is adopted for the uncertain parameters. Consider a set of all possible values that the uncertain parameters can take. This set, usually supposed to be compact, is called the uncertainty set. An uncertainty model assumes only the hypothesis that the uncertainty parameters can be any element of the uncertainty set is sometimes called the unknown-but-bounded (or, uncertain-but-bounded) model. With this uncertainty model, we can formulate problems for finding upper and lower bounds for the uncertain structural response as a pair of two optimization problems; see Section 2.2 for the details. This paper provides a review on the methods that apply some optimization approaches to these optimization problems. As a closely related topic, the methods for quantitatively assessing the structural robustness are also reviewed.

Interval analysis has been developed to find a bound for solutions of linear and nonlinear problems with computational rounding errors as well as data uncertainties [4,5]. Interval arithmetic, which is a fundamental tool of interval analysis, is the arithmetic of compact intervals. There is a vast literature on applications of interval arithmetic to uncertainty analysis of structures, where each of the uncertain parameters is usually supposed to take any value in a given compact interval. These methods do not employ optimization methods to find bounds for the structural response, and are thereby out of the scope of this paper. For interval arithmetic-based methods as well as interval finite element methods, the reader is referred to the comprehensive reviews by references [6–9].

In this paper, we restrict ourselves to the case where the uncertainty set is a conventional set, and do not consider a fuzzy set. This is because we attempt to limit our discussion to optimization problems whose feasible sets are conventional. Reviews on uncertainty treatment using the fuzzy set theory can be found in references [6–12].

In probabilistic uncertainty modeling, the uncertain parameters are usually considered random variables. This paper does not treat models involving random variables. The reader is referred to Brevault et al. [13], Der Kiureghian [14] and Lemaire [15] for structural reliability, Acar et al. [11], Choi et al. [16], Hu [17], Hu et al. [18] and Valdebenito and Schueller [19] for reliability-based design optimization, Moens and Vandepitte [9] and Stefanou [20] for stochastic finite element methods, Faes et al. [21] for uncertainty analysis methods using probability boxes (p-boxes), Jiang et al. [22] for probability–interval hybrid models of uncertainty, Peherstorfer et al. [23] and Helton et al. [24] for multi-fidelity methods and sampling-based methods, respectively, for uncertainty analysis using probabilistic uncertainty modeling, and Xu et al. [25] for physics-informed machine learning approaches to reliability and system safety.

Uncertainty modeling based on the evidence theory is also out of scope of this paper; see Acar et al. [11] and Li et al. [10] for applications of the evidence theory to uncertainty analysis.

1.3 Organization

The remainder of this paper is organized as follows: In Section 2, we summarize the fundamentals of non-probabilistic modeling of uncertainty and analysis of uncertain structural responses, with clarifying their relations to optimization. In the subsequent sections, we provide reviews of the literature from the viewpoint of optimization methods adopted in numerical solutions: Nonlinear programming approaches are collected in Section 3, semidefinite programming approaches in Section 4, mixed-integer programming approaches in Section 5, MPCC (mathematical programming with complementarity constraints) approaches in Section 6, DC (difference-of-convex) algorithms in Section 7, robust optimization algorithms in Section 8, optimization methods using surrogate models and machine learning techniques in Section 9, and metaheuristics in Section 10. Section 11 presents a review of quantitative evaluation methods of robustness of structures under uncertainty. Section 12 collects applications of uncertainty analysis to data-driven computation in elasticity. Finally, several conclusions are drawn in Section 13.

2  Fundamental Formulations

This section briefly describes the fundamentals of uncertainty analysis using non-probabilistic uncertainty modeling. Section 2.1 introduces several concrete uncertainty models that are popularly used in the literature. Section 2.2 defines the bound for uncertain structural response, and discusses its relations to optimization formulations and algorithms.

2.1 Uncertainty Set

Consider a structural system involving uncertainty. We use d∈Rb to represent the structural design specification, where b is the number of design variables.

Let s∈Rk denote the uncertain parameter vector, where k is its dimension. Suppose that true s is unknown and that only a set of possible realizations of s is known. This set, denoted by S⊂Rk, is called the uncertainty set of s, and thereby our uncertainty model is described as s∈S. An uncertainty set is usually assumed to be compact. The following uncertainty sets are popular in the literature:

•   A set defined by some box constraints

S={s∈Rk∣l≤s≤u},(1)

        where l, u∈Rk are constant vectors (see Fig. 1). Uncertain parameter s∈S is sometimes referred to as the interval variable.

•   A polyhedron

S={s∈Rk∣As≤b},(2)

    where A∈Rm×k is a constant matrix, and b∈Rm is a constant vector (see Fig. 2). It is easy to see that (1) is a special case of (2) with

A=[−II],b=[−lu],m=2k.

    Another special case of (2) is

{s∈Rk∣l1≤s≤u1, l2≤Q(s−r)≤u2},

    where l1, l2, u1, u2, r∈Rk are constant vectors and Q∈Rk×k is a constant matrix. This model can be viewed as a generalization of (1) [26].

•   An ellipsoid

S={s∈Rk∣(s−s~)⊤Ω(s−s~)≤α},(3)

    where Ω∈Rk×k is a constant symmetric positive definite matrix, s~∈Rk is a constant vector, and α≥0 is a constant (see Fig. 3). It is worth noting that α is considered a parameter representing the magnitude of uncertainty; namely, a large value of α means that s can take values in a wide range, and α=0 means that s (=s~) is no longer uncertain. The center of the ellipsoid, s~, is regarded as the best estimate of s, and is sometimes called the nominal value of s.

    A slightly generalized ellipsoidal uncertainty model is

S′={s~+Fz∣‖z‖≤β},(4)

    where F∈Rk×h is a constant matrix with h≤k, β≥0 is a constant representing the magnitude of uncertainty, and ‖z‖ is the Euclidean norm of unknown vector z∈Rh, i.e., ‖z‖=z⊤z (see Fig. 4). If h=k and F is regular, then (4) can be rewritten equivalently as

S′={s∈Rk∣(s−s~)⊤F−⊤F−1(s−s~)≤β2},

    which coincides with the expression in (3) by putting

Ω=F−⊤F−1,α=β2.

•   Using the ℓp-norm (1≤p≤∞), we can generalize (4) as

Sp={s~+Fz∣‖z‖p≤β}.(5)

    Here, the ℓp-norm of z∈Rh is defined by

‖z‖p={(∑j=1h⁡|zj|p)1/pif 1≤p<∞,max{|z1|,…,|zh|}if p=∞.

    Note that (4) corresponds to the case with p=2. When p=1 or p=∞, Sp can be rewritten in the form of (2). Moreover, when p=∞ and F=diag(f) with h=k (i.e., F is a diagonal matrix, the vector of whose diagonal entries is f∈Rk), we have

S∞={s∈Rk∣s~−βf≤s≤s~+βf};

    namely, in this case S∞ can be identified with (1).

•   A multi-ellipsoid model defined by

si∈{si∈Rki∣(si−s~i)⊤Ωi(si−s~i)≤αi},i=1,…,r,

    where si∈Rki (i=1,…,r) are subvectors forming s as

s=[s1⋮sr].

Obviously, r=1 corresponds to the single ellipsoid model in (3). A special case with ni=1 (i=1,…,r) coincides with (1).

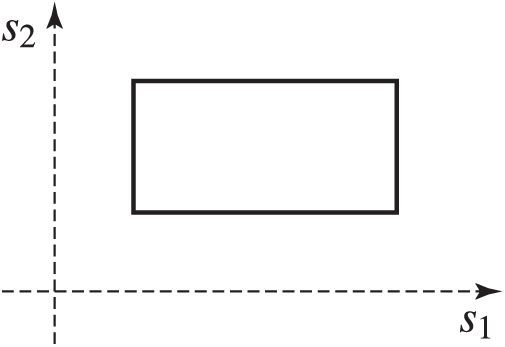
Figure 1: Uncertainty set defined by box constraints

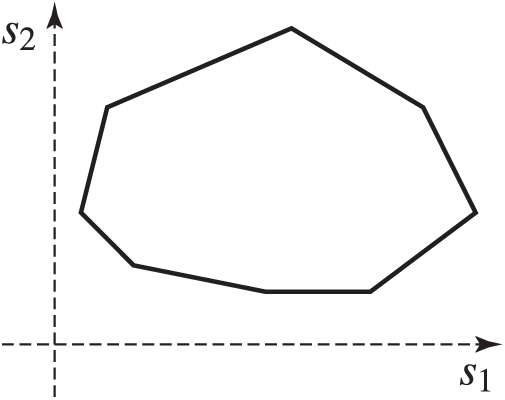
Figure 2: Polyhedral uncertainty set

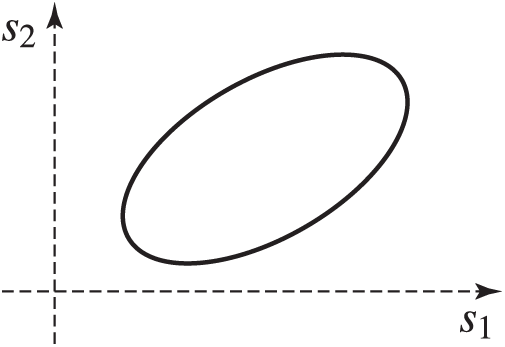
Figure 3: Ellipsoidal uncertainty set

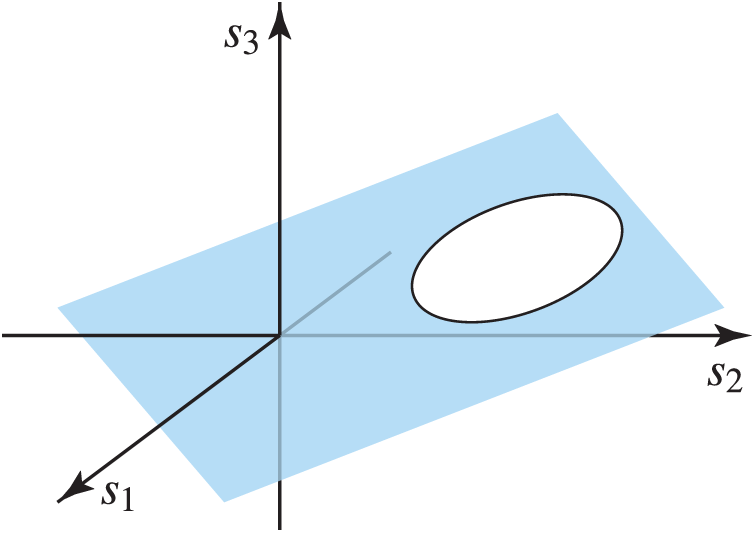
Figure 4: Ellipsoidal uncertainty set in a degenerated space

It is noteworthy that all the uncertainty sets collected above are closed convex sets.

2.2 Bound for Uncertain Structural Response

For given structural design d and uncertain parameter s, let

q(d;s),

denote the quantity of interest (QoI), i.e., the structural response on which we focus attention. Uncertainty analysis using non-probabilistic modeling aims to find a bound for QoI when s takes any possible value in the uncertainty set. Typically, we attempt to find q¯, q_∈R satisfying

q(d;s)∈[q_,q¯],∀s∈S,(6)

where q¯ and q_ are upper and lower bounds for QoI, respectively.

Exploring q¯ and q_ is essentially linked to solving the following optimization problems:

qmax:=maxs{q(d;s)∣s∈S},(7)

qmin:=mins{q(d;s)∣s∈S},(8)

where, qmax and qmin correspond to the minimum value of q¯ and the maximum value of q_, respectively. Namely, global optimal solutions of problems (7) and (8) provide the exact bound for QoI. A guarantee of global optimality can be obtained if problems (7) and (8) are convex optimization problems1 (see Table 1). Alternatively, if we can recast these two problems as mixed-integer (linear) programming problems, then the branch-and-bound method can find their global optimal solutions. Section 5 provides a review on the latter case.

If problems (7) and (8) are not convex optimization problems, a standard numerical optimization approach (i.e., the nonlinear programming) finds local optimal solutions. The literature on uncertainty analysis methods based on the nonlinear programming are collected in Section 3. It should be emphasized that the objective values of local optimal solutions (which are not globally optimal) do not satisfy (6) (see Fig. 5a). This is a crucially challenging issue in uncertainty analysis using non-probabilistic uncertainty modeling.

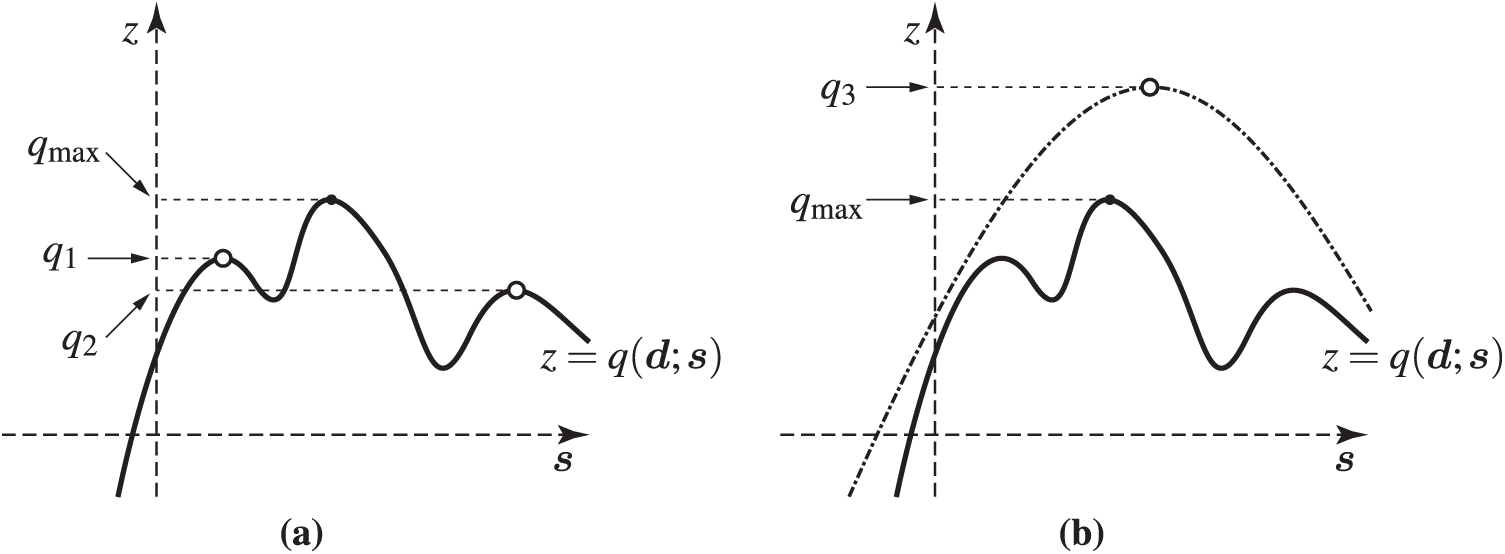
Figure 5: Underestimated and confidence upper bounds for QoI. (a) q1 and q2 are underestimated bounds obtained by the local optimization; (b) q3 is a confidence bound obtained by a convex relaxation of q(d;⋅)

A remedy is, instead of a direct application of the nonlinear programming approach, to make use of the specific problem structure in the process of optimization modeling and algorithm selection. Then one can often expect to obtain a high-quality local optimal solution, the objective value of which is sufficiently close to the global optimal value. As for specific optimization models, this paper covers mathematical programming with complementarity constraints in Section 6, difference-of-convex programming in Section 7, and robust optimization in Section 8.

Depending on the problem setting, the objective function q(d;⋅) of problems (7) and (8) is neither given as an explicit function nor represented by using (rather simple) governing equations, but for a given s∈S the value of q(d;s) can be evaluated only after numerical simulation. The maximum response displacement of an elastoplastic structure under the seismic load is an example. In such a case, the derivatives of q(d;⋅) are not directly available. Moreover, evaluation of q(d;s) itself is sometimes computationally expensive. A surrogate model constructed by a machine learning technique can be substituted for the objective function of problems (7) and (8). Section 9 reviews such methods.2 An alternative remedy is to use metaheuristics, e.g., evolutionary algorithms, which do not require the derivatives of the objective function. Use of metaheuristics can also be motivated by the purpose of avoiding convergence to a low-quality local optimal solution. Section 10 collects the literature using metaheuristics.

Another strategy is to construct tractable (often convex) optimization problems, the optimal values of which satisfy (6). For example, let U(d)⊆R×Rk be a convex set satisfying

{(t,s)∈R×Rk∣t≤q(d;s), s∈S}⊆U(d),

and consider the following convex optimization problem in variables t∈R and s∈Rk:

Maximizet,(9a)

subject to(t,s)∈U(d).(9b)

Solving this problem instead of problem (7), we obtain an upper bound for QoI, q¯, as its optimal value. We call problem (9) a relaxation problem of problem (7). A convex relaxation problem of problem (8) is constructed similarly. These two convex relaxation problems can be solved globally, which guarantees (6). In this sense, we refer to the bound obtained by such a method to as a confidence bound (see Table 1 and Fig. 5b). Section 4 reviews methods for finding confidence bounds.

As briefly viewed throughout this section, it is crucial to select an optimization model as well as an algorithm, depending on specific features of the setting of problems (7) and (8). In Sections 3–10, we classify the existing methods for uncertainty analysis according to differences in the employed optimization methods.

3  Nonlinear Programming Approaches

3.1 Overview

Nonlinear programming (NLP) basically attempts to find a local optimal solution of a (usually nonconvex) constrained or unconstrained optimization problem [29,30]. Therefore, when we apply an NLP approach to problems (7) and (8), the obtained solution may possibly correspond to underestimate of the exact bound of QoI; in other words, there exists no guarantee that the obtained bound includes [qmin,qmax]; see Table 1. It is worth noting that, in some of the literature reviewed below, the authors demonstrate the results of numerical experiments verifying that the solutions obtained by NLP approaches are sufficiently close to global optimal solutions by, e.g., performing the Monte Carlo simulation.

3.2 Methods

Tangaramvong et al. [31] consider the static equilibrium analysis of linear elastic skeletal structures, where the applied external forces, elastic modulus, and dimensions of the member cross-sections are supposed to be uncertain. They directly treat problems (7) and (8) as NLP problems.

Wu et al. [32] deal with functionally graded frame structures with interval uncertainties in the material constants, dimensions of the cross-sections of beams, and external forces. They treat a problem finding the maximum value of a nodal displacement or an internal member action in the linear elastic equilibrium analysis as an NLP problem. Similarly, Wu et al. [33] address frame structures consisting of a functionally graded porous material.

Wu et al. [34] perform uncertainty analysis in the linear elastic equilibrium analysis and the linear buckling analysis. They treat the problems finding the upper and lower bounds of a nodal displacement and linear buckling load factor as NLP problems, which were solved with a standard NLP solver. Wu et al. [35] also consider the problem finding the worst-case linear buckling load factor.

Fujita and Takewaki [36] perform robustness analysis of shear building models with passive viscous dampers by computing the extreme values of dynamic structural response. They construct the optimization problems that approximate problems (7) and (8) by using the second-order Taylor expansion, and solve the approximated problems with an NLP approach.

In the framework of plastic limit analysis, Tangaramvong et al. [37] suppose that the external forces and the yield limit of each structural component possess uncertainties following the interval model in (1).3 They first present a mixed-integer NLP formulation (more concretely, an NLP problem with 0–1 variables and continuous variables) for finding the worst-case limit load factor, and then solve its continuous relaxation which is in the form of NLP. Tangaramvong et al. [38] address the same uncertainty analysis problem with the scaled boundary finite method. They derive another NLP formulation from the upper bound theorem of limit analysis, where the inner product of the unknown nodal displacement vector and the uncertain nodal force vector appears as a nonconvex term.

3.3 Remarks and Future Perspectives

Although quality of the obtained solution cannot be evaluated in general, the NLP approach is sometimes adopted in structural uncertainty analysis. This is because NLP is a quite versatile framework, and formulating problems (7) and (8) as NLP problems is very often straightforward. Therefore, the NLP approach might continue to be used as a practical tool for structural uncertainty analysis.

It is also worth noting that all the literature cited in Section 3.2 adopt the interval uncertainty model (1), although the framework of NLP can deal with a more general uncertainty model involving nonlinear constraints. Other uncertainty models can possibly be used in future study.

4  Semidefinite Programming Approaches

4.1 Overview

Semidefinite programming (SDP) refers to a class of optimization problems which can be formulated in the following form:

Minimize∑j=1nbjxj,(10a)

subject toC−∑j=1nxjAj⪰0,(10b)

where b1,…,bn∈R are constants, A1,…,An, C∈Rm×m are constant symmetric matrices, and for symmetric matrix Z we write Z⪰0 to denote that Z is positive semidefinite (i.e., all the eigenvalues of Z are nonnegative).

SDP is convex optimization, which includes linear programming, (convex) quadratic programming, second-order cone programming, etc., as its special cases. We can obtain a global optimal solution of an SDP problem efficiently with a primal-dual interior-point method. The reader is referred to [39,40] for more details of SDP.

4.2 Uncertainty Analysis Using Semidefinite Programming

Guo et al. [41] deal with truss structures subjected to the uncertain static load, where the ellipsoidal uncertainty model in (3) is adopted. As for QoI, they consider the Euclidean norm of the displacement vector at a node or the compliance (i.e., the external work done by the static load). Finding the worst-case value (i.e., the maximum value) of QoI corresponds to maximizing a convex function over a convex set, which is difficult to solve globally. To overcome this difficulty, they derive an SDP relaxation by using the Lagrange duality.

Observe that problems (7) and (8) can be recast equivalently as follows:

Minimizel,u∈Ru−l,(11a)

subject toq(d;s)∈[l,u],∀s∈S.(11b)

In fact, at an optimal solution of this problem, u and l coincide with qmax and qmin, respectively. If we replace constraint (11b) with its sufficient condition, then by solving the reduced optimization problem we obtain upper and lower bounds for qmax and qmin, respectively (see Table 1). Moreover, if the sufficient condition corresponds to a convex constraint, then the reduced optimization problem can be solved efficiently and globally. This methodology can be extended from finding an interval to finding an ellipsoid, where an interval is regarded as an ellipsoid in R. Suppose that QoI is a vector, denoted by q(d;s)∈Rv, where v is its dimension. For instance, when QoI is the displacement vector at a node of a space truss, we have v=3. Let E(p)⊂Rv denote an ellipsoid, where p∈Rt is a parameter that determines the ellipsoid. Finding an ellipsoid representing a set of realizations of QoI is formally stated as follows:

Minimizep∈Rtℓ(p),(12a)

subject toq(d;s)∈E(p),∀s∈S,(12b)

where ℓ(p) is a measure of the size of an ellipsoid. Again, if we replace constraint (12b) with a sufficient condition that is easy to handle from the view point of numerical optimization, then by solving the resulting optimization problem we can obtain a confidence ellipsoid, which is guaranteed to include all possible realizations of QoI. This is the fundamental idea for developing the methods in [42–47] cited below, where a sufficient condition for (12b) is derived by using (a trivial part of) the S-lemma [48] (a.k.a. the S-procedure; see Appendix B in [40]).

For linear truss structures, Kanno and Takewaki [42,43] deal with uncertainty in the member stiffnesses and static load. They formulate an SDP problem for finding a confidence ellipsoid of the structural response.

Using the idea in [42,43], Du et al. [44] formulate an SDP problem for finding a bound for the sensitivity of QoI with respect to a member cross-section area. They use the obtained bound for reducing the computational cost of the mixed-integer programming (MIP) approach [49] to uncertainty analysis. See Section 5 for more details of Du et al. [44].

Kanno and Takewaki [45] apply the method in [42,43] developed for trusses to braced frames with uncertainty in brace stiffnesses. Moreover, Kanno and Takewaki [46] extend the method so that elastic structures in any structural forms can be dealt with, and perform numerical experiments on frame structures with uncertainty in beam stiffnesses. Kanno and Takewaki [47] present an extension to a dynamic problem. They handle steady-state responses of a damped structure subjected to uncertain harmonic driving load, and propose a method finding confidence bounds for the modulus and phase angle of the complex amplitude. The numerical experiments presented in [42,43,45–47] illustrate that the bounds obtained by these methods are sufficiently tight compared with the results of numerical simulation using many randomly generated uncertain parameter values.

In contrast, apart from the idea explained by using problem (12), Kang and Zhang [50] focus on construction of an ellipsoidal uncertainty set (3), where a set of observed samples of the uncertain parameters is supposed to be available. They use an SDP formulation for finding the minimum volume ellipsoid that include all the samples. As a preprocessing of this procedure, Bai et al. [51] propose an automatic method for detecting outliers from a given sample set.

Example 1. Consider the static equilibrium analysis of a linear elastic truss shown in Fig. 6. The lengths of horizontal and vertical members are 0.5m. The elastic modulus and nominal cross-sectional area of each member is 200GPa and 1000mm2, respectively. As the nominal load, a vertical external force of 1000kN is applied at the rightmost bottom node.

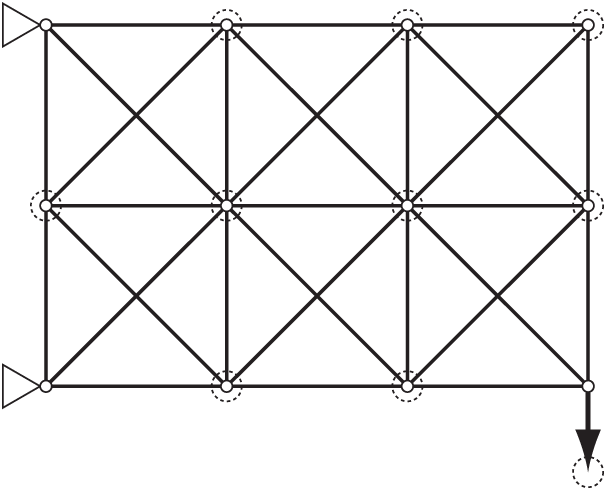
Figure 6: Planar truss used in Example 1

Both of the external forces and member stiffnesses possess uncertainty. Suppose that an uncertain external force vector, the norm of which is no greater than 100kN, is applied at each node, as depicted by the dotted circles in Fig. 6. The member cross-sectional area of each member is supposed to be in [900,1100]mm2.

Kanno and Takewaki [43] formulate an SDP problem for finding an ellipsoidal confidence bound. Fig. 7 shows the obtained bound for the displacement of each node, as well as the results of equilibrium analysis using randomly generated external forces and member cross-sectional areas. It is observed in Fig. 7 that the obtained ellipsoids provide quite tight bounds. ◼

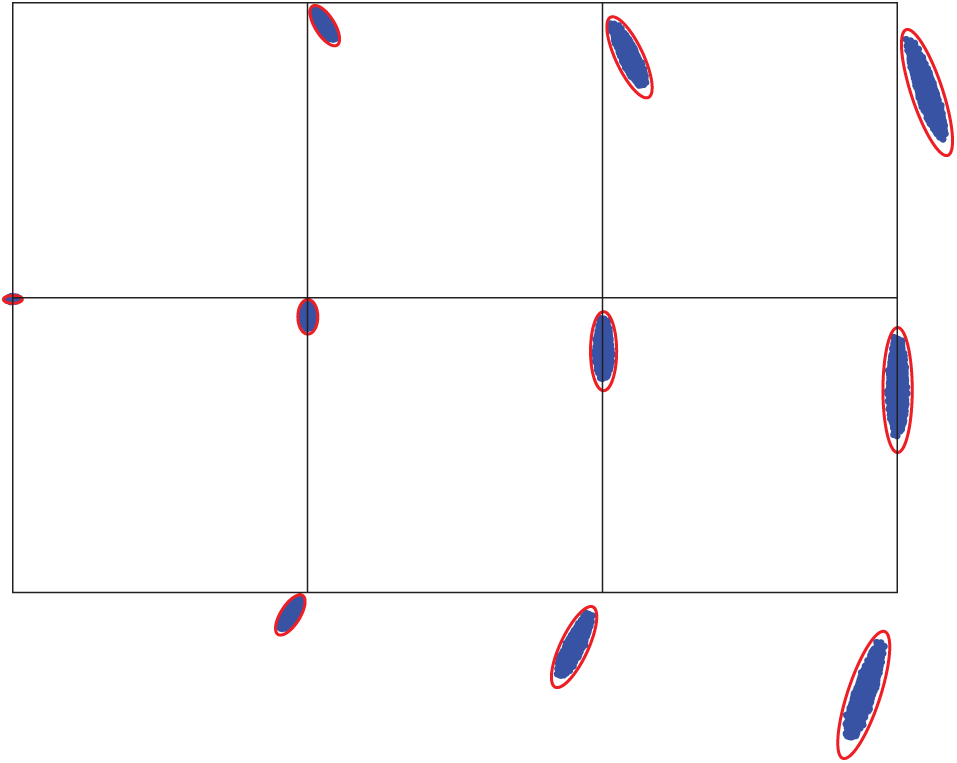
Figure 7: Ellipsoidal confidence bounds for the nodal displacements obtained by the SDP approach proposed by Kanno and Takewaki [43] (The displacements are amplified 10 times)

4.3 Robust Structural Optimization Using Semidefinite Programming

SDP and its extensions have also been applied to various worst-case robust optimization problems of structures.4

4.3.1 Linear Semidefinite Programming Approaches

Ben-Tal and Nemirovski [53] present an SDP formulation for the worst-case compliance minimization of trusses against uncertainty in the static load, where the ellipsoidal uncertainty set in (4) with s~=0 is employed. Calafiore and Dabbene [54] extend this SDP formulation to the case including s~≠0; see also eq. (8.2.15) in [55]. Variants of this formulation, in which the dependence of the uncertainty set on the truss design is taken into account, can be found in [56,57].

Hashimoto and Kanno [58] suppose that the nodal locations of trusses are uncertain, and formulate the worst-case compliance minimization. They propose a conservative SDP approximation for this optimization problem.

4.3.2 Nonlinear Semidefinite Programming Approaches

In problem (10), the left-side of constraint (10b) is an affine function of x1,…,xn. In contrast, when the left-side is a nonlinear (symmetric matrix-valued) function, the optimization problem is called a nonlinear SDP problem. To distinguish these two cases, problem (10) is sometimes called a linear SDP problem. It should be clear that nonlinear SDP is in general nonconvex optimization. Various solution methods, as well as diverse applications, have been proposed for nonlinear SDP [59].

For continuum topology optimization, it has been known that the worst-case compliance minimization against uncertainty in the static load can be formulated as the minimization of the maximum eigenvalue of a generalized eigenvalue problem [60,61] or a standard eigenvalue problem [62]. However, these maximum eigenvalue formulations are nonsmooth functions of the design variables. Especially, it is often that an optimal solution of minimization of the maximum eigenvalue has multiple eigenvalue, and the maximum eigenvalue at such an optimal solution is not differentiable [63]. Then standard nonlinear programming approaches are likely to fail to find an optimal solution, as actually observed in Thore [64].

Holmberg et al. [65] formulate this problem as a nonlinear SDP problem. Based on the Cholesky factorization of a symmetric positive semidefinite matrix, they recast the problem as a form of standard NLP. This avoids nonsmoothness in the maximum eigenvalue, and makes a standard NLP solver applicable. Thore [64] considers uncertainty in the boundary displacement, and formulate the worst-case compliance minimization as minimization of the maximum eigenvalue of a symmetric matrix. The nonlinear SDP approach in [65] is applicable to this optimization problem.

Aroztegui et al. [66] present a feasible direction interior-point method for solving nonlinear SDP problems, and apply it to the robust truss optimization problem in [53].

Kanno and Takewaki [67] consider truss optimization under the stress constraints, where the static load is supposed to be uncertain. Using the S-lemma [48], they show that this optimization problem can be reformulated as a nonlinear SDP problem, which is solved with a sequential SDP method; see Section 11.1 for more details.

Guo et al. [68] consider robust optimization of trusses against uncertainty in the member stiffnesses and the external forces. The method proposed in [68] can handle structural performance constraints that can be written in the form of quadratic inequalities of the nodal displacements. In a manner similar to [43] etc., they use (a trivial part of) the S-lemma [48] to obtain a tractable sufficient condition for the robust constraint, which yields a nonlinear SDP formulation of the worst-case robust optimization. Guo et al. [69] propose an augmented Lagrangian method for solving this nonlinear SDP problem.

Example 2. This example discusses the robust truss topology optimization against uncertainty in the static external load.

Consider the initial trusses shown in Fig. 8. As the nominal external load, a vertical downward force of 100kN is applied at the rightmost bottom node. The elastic modulus of the truss members is 20GPa. We minimize the compliance under the upper bound constraint on the structural volume, where the upper bounds for the problem settings in Fig. 8a,b are 4.2×106mm3 and 3.2×106mm3, respectively. Fig. 9 collects the optimal solutions, where the width of each member in the figures is proportional to its cross-sectional area.

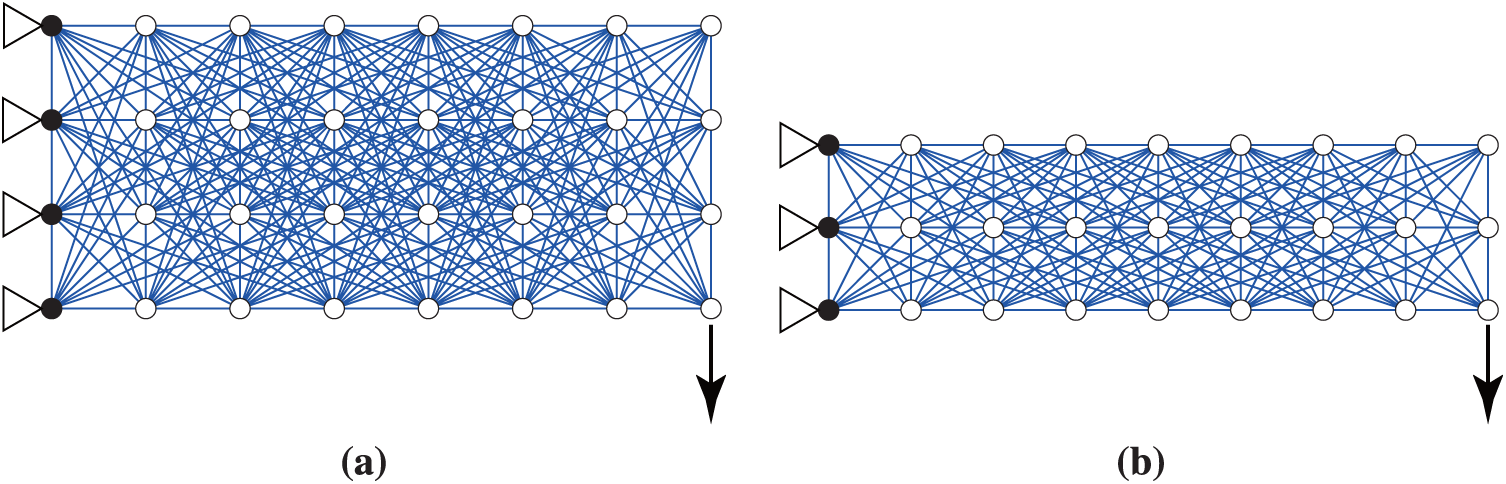
Figure 8: Problem settings used in Example 2. (a) 7×3 example; and (b) 8×2 example

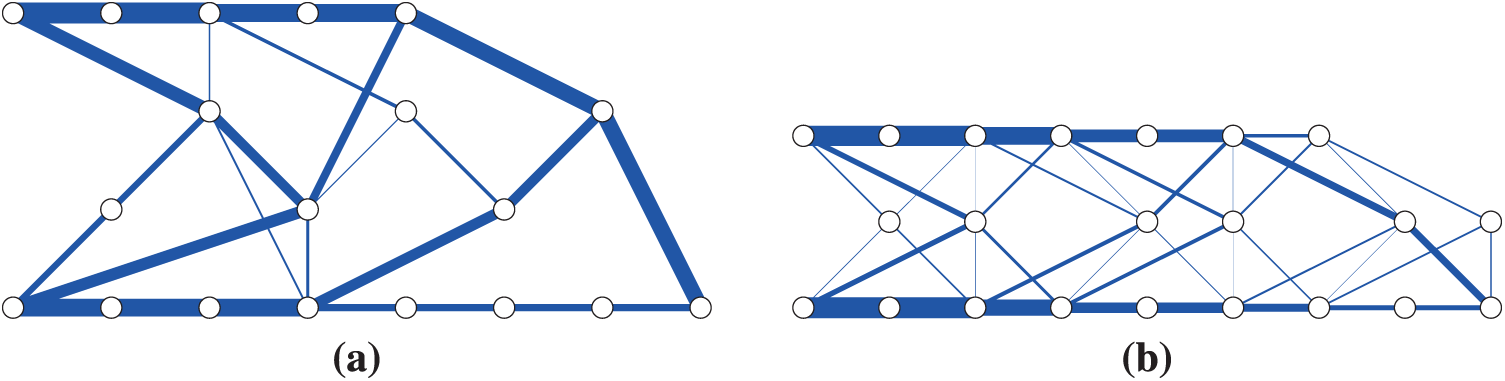
Figure 9: Optimal solutions of the compliance minimization for the nominal external load (Example 2). (a) 7×3 example; and (b) 8×2 example

As mentioned in Section 4.3.1, Ben-Tal and Nemirovski [53] formulate an SDP formulation to minimize the worst-case compliance (i.e., the maximum compliance) when the ellipsoidal uncertainty set is employed for the uncertain external load. In this formulation, it is required to specify a priori the nodes at which uncertain external forces are possibly applied. To enhance robustness of the solution, it may be natural to suppose that uncertain external forces can be applied at all the existing nodes at a solution. However, it is difficult to estimate the nodes that exist in a solution. For example, if we specify the nodes in Fig. 8 as the ones at which uncertain external forces are possibly applied, then all the nodes in the problem setting remain at the obtained solution, which is much different from the truss design in Fig. 9.

Another difficulty in robust truss topology optimization stems from treatment of a chain, which is a sequence of parallel members that are connected by nodes supported only in the direction of those members. As observed in Fig. 9, an optimal solution often has chains. When only the compliance is considered as the structural performance, the intermediate nodes in a chain can be removed as shown in Fig. 10. This procedure is called the hinge cancellation [70,71]. Note that the intermediate nodes in a chain are unstable. Therefore, if we suppose that uncertain external forces are applied at all the existing nodes in Fig. 9, then many thin bars are added to stabilize the intermediate nodes. In contrast, if we suppose that uncertain external forces are applied at all the existing nodes in Fig. 10, then such additional thin members are not needed.

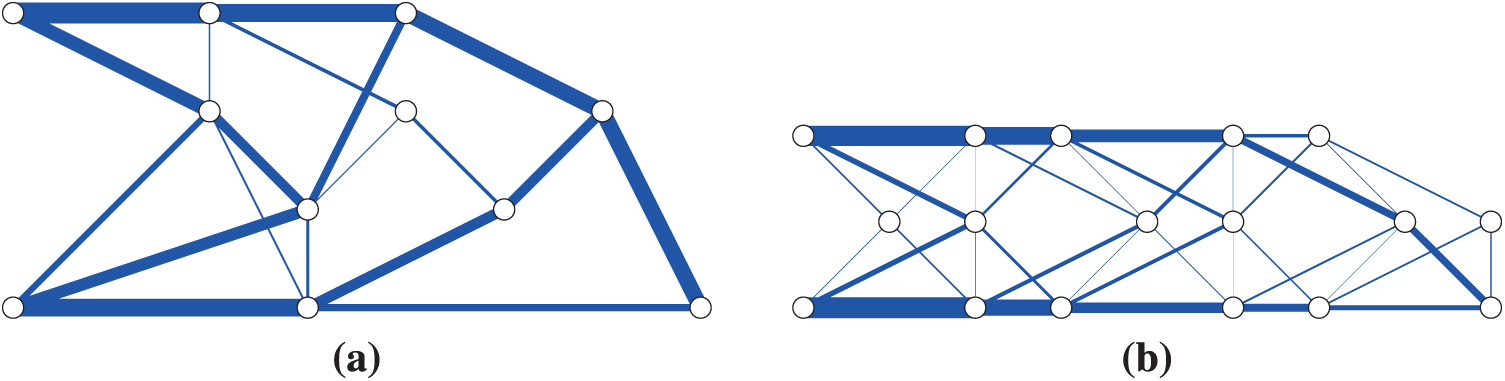
Figure 10: Final optimal designs obtained by applying the hinge cancellation to the solutions in Fig. 9 (Example 2). (a) 7×3 example; and (b) 8×2 example

Accordingly, to optimize the truss topology against uncertainty in the external load, it is necessary to consider a topology-dependent uncertainty set. Namely, the nodes at which uncertainty external forces are applied are the ones that exist in a solution and are not on a chain, although the robust optimal topology is not known a priori. Kanno [56] proposes an SDP with complementarity constraints to deal with this situation. Fig. 11 collects the robust optimal solutions obtained by the method proposed in [56]. It is worth noting that each solution in Fig. 11 has a different topology from the one in Fig. 10. ◼

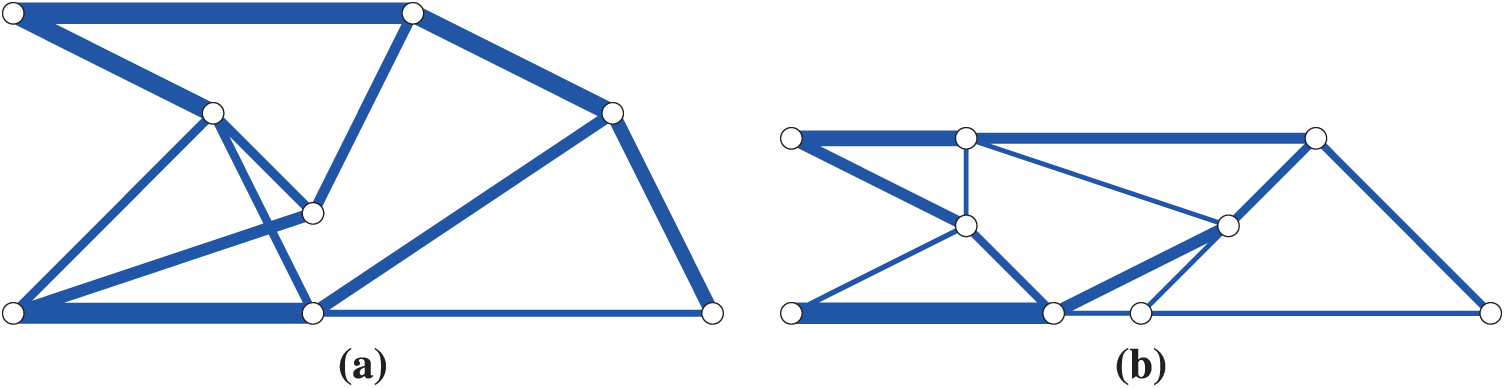
Figure 11: Optimal solutions of robust topology optimization obtained with the method proposed by Kanno [56] (Example 2). (a) 7×3 example; and (b) 8×2 example

4.4 Remarks and Future Perspectives

In general, SDP is a powerful optimization framework that can deal with quite strongly nonlinear constraints with guarantee of global optimality. Regarding structural uncertainty analysis, guarantee of conservativeness provided by the methods cited in Section 4.2 is attractive and unique. In contrast, formulating such a useful SDP problem is often not very straightforward; S-lemma [48] mentioned above, as well as the Rayleigh quotient theorem on eigenvalues [72], can be the key to the formulation. Once these mathematical tools are recognized by the community of structural uncertainty analysis, SDP approaches can possibly become more popular in this field.

Nonlinear SDP has various applications in structural optimization, other than robust optimization reviewed in Section 4.3. These include design optimization under the frequency constraint [73] and buckling constraint [74–76]. Future development of efficient algorithms for large-scale nonlinear SDP problems will expand the capability of nonlinear SDP approaches to structural uncertainty analysis as well as various structural optimization problems.

The moment-sum-of-squares hierarchy [77] is a successive SDP relaxations to solve a polynomial optimization problem globally, and has successfully been applied to structural optimization [78,79]. This method can possibly be applied to structural uncertainty analysis in future.

5  Mixed-Integer Programming Approaches

5.1 Overview

Mixed-integer programming (MIP) is a framework of global optimization, where some of the decision variables in an optimization problem can take only integer values while the others are treated as continuous variables [80,81]. This section deals with the following form of MIP:

Minimizec⊤x,(13a)

subject toAx≤b,(13b)

xj∈{0,1},j=1,…,l,(13c)

xj∈R,j=l+1,…,n.(13d)

Here, A∈Rm×n is a constant matrix, b∈Rm and c∈Rn are constant vectors, and l is a constant integer. Relaxing constraint (13c) as xj∈[0,1] (j=1,…,l) we obtain a linear programming problem, which can be solved globally. This guarantees that a global optimization of problem (13) is found by a branch-and-bound method. Practically, well-established solvers implementing branch-and-cut methods are available, e.g., CPLEX [82], SCIP [83], and Gurobi Optimizer [84]. Global optimality guaranteed by high-performance solvers is the key to the application of MIP to uncertainty analysis; namely, by recasting problems (7) and (8) as MIP problems, we can find qmax and qmin exactly (see Table 1).

5.2 Methods

Guo et al. [49] consider the static response (concretely, the nodal displacements and the member stresses) of a truss, where Young’s modulus of each member follows the interval uncertainty model in (1). It is shown that the structural response attains extreme value when every Young’s modulus takes either its upper or lower bound. By using this fact, Guo et al. [49] reformulate problems (7) and (8) as MIP problems, where the reformulation is based on the idea found in Stolpe and Svanberg [85].

The method proposed in [49] applies a standard MIP solver based on the branch-and-cut method to the MIP problem. Therefore, the size of problems that can be dealt with is limited, and large-scale problems cannot be solved from the practical point of view. To reduce the number of 0-1 variables in the MIP problem, Du et al. [44] make the following observation: If the sensitivity of QoI concerning a member cross-section area has the same sign for any element belonging to the uncertainty set, then the value of the cross-section area of that member at a globally optimal solution can be fixed (i.e., one can find whether the member cross-section area takes its lower or upper bound at a global optimal solution). To check the sign of the sensitivity, Du et al. [44] formulate an SDP problem providing a confidence bound of the sensitivity, based on the idea found in [42,43]. With this method, the number of unknown 0-1 variables is substantially reduced. In the numerical experiments, truss examples with up to 108 members were solved.

Kanno and Takewaki [86] consider uncertainty in the load in the plastic limit analyses of a truss, and attempt to find the worst-case load corresponding to the minimum limit load factor. They present an MIP formulation for this purpose and propose an algorithm combining the branch-and-bound method using the linear programming relaxation and the cutting plane method generating the disjunctive cuts. Similarly, the worst-case load detection for the limit analysis of frame structures can also be formulated as a MIP problem [87]. In [87], a standard MIP solver (CPLEX [82]) was used for solving the MIP problem.

Kanno [88] considers the plastic limit analysis of trusses under the unpredictable failure of some truss members. When only the number of deficient members is given, a MIP problem is formulated to detect the worst-case structural deficiency corresponding to the minimum limit load factor. In that formulation, 0-1 variables are used to represent whether each member is undamaged or damaged.

In the static equilibrium analysis of elastic skeletal structures, Kanno [89] focuses on uncertainty in the material behavior (i.e., the stress–strain relation). By using the result of the segmented least squares, an uncertainty set is determined as a set, the boundary of which is described by a pair of piecewise-linear inequalities. Then Kanno [89] presents MIP formulations for finding the maximum and minimum values of QoI.

Tangaramvong and Tin-Loi [90] consider the holonomic elastoplastic analysis of a structure under the multiple load case, and propose an optimization-based approach to finding the worst load combination corresponding to the maximum and minimum structural responses. The problem of finding the worst case is formulated as an MPCC problem with some continuous and 0-1 decision variables, where 0-1 variables are used to represent the load combination. By using a penalty approach to the complementarity constraints, Tangaramvong and Tin-Loi [90] reformulate this optimization problem as a mixed-integer nonlinear programming (MINLP) problem. Note that DICOPT, which is the solver used for solving this MINLP problem does not necessarily obtain a global optimal solution [91].

5.3 Remarks and Future Perspectives

MIP is a very attractive framework that can provide guarantee of the exactness of the obtained bound for QoI. The problem size that can be solved with a standard MIP solver within reasonable computational time has constantly been increasing. In contrast, reformulating a problem of interest into a MIP problem usually requires some know-hows. Some hints for the reformulation may be found in the literature on discrete structural optimization [92].

The MIP model in (13) has a linear objective function and linear constraints (other than the integrality constrtaints). This restriction limits the class of problems that can be handled. Nevertheless, MIP approaches are appreciated as it can provide benchmark examples for structural uncertainty analysis. Besides, in this decade, it has been recognized that mixed-integer second-order cone programming (MISOCP), which involves nonlinear constraints in a specific form is effective in some problems in structural optimization [93,94]. Attempt to apply MISOCP might shed new light on uncertainty analysis.

As seen in Section 5.2, MINLP is sometimes used for structural uncertainty analysis. Since guaranteeing global optimality for a MINLP problem is difficult, it is important to select an algorithm that can often find a feasible solution with a good objective value within reasonable computational time. Recent developement of MINLP algorithms, e.g., references [95–99], might extend applications of MILP to structural uncertainty analysis.

6  Mathematical Programming with Complementarity Constraints Approaches

6.1 Overview

Mathematical programming with complementarity constraints (MPCC) [100,101], or, more generally, mathematical programming with equilibrium constraints (MPEC) [102], is a special class of optimization problems. Since any feasible solution of an MPEC problem does not satisfy standard constraint qualifications, a (local) optimal solution of an MPEC problem does not necessarily satisfy the Karush–Kuhn–Tucker (KKT) condition. Therefore, conventional NLP approaches, which are designed to find a solution satisfying the KKT condition, are likely fail to find an optimal solution. Several special treatments for MPEC, including the regularization method, the reformulation and smoothing method, and the exact penalty method [102], have been proposed for application of a conventional NLP approach.

In uncertainty analysis, MPCC naturally arises when the governing equation of the structural response is formulated as a complementarity problem; the reader is referred to Facchinei and Pang [103] for the details of complementarity problems. Plasticity, contact, and friction are typical examples from which complementarity problems stem.

6.2 Methods

Tangaramvong et al. [104] consider a semi-rigid frame with uncertainty in the moment–rotation relation, and present an MPCC formulation finding a bound for the structural response.

For a holonomic (i.e., path-independent) elastoplastic analysis of a structure taking the second-order geometrical nonlinearity into account, Tangaramvong and Tin-Loi [90] formulate an MPCC problem with continuous and 0-1 decision variables to find the worst-case load combination. Similarly, Yang et al. [105] consider uncertainty in both the applied external forces and yield stresses.

Wu et al. [106] study the plastic limit analysis, where the external forces are supposed to be interval variables. Based on the upper bound theorem, they formulate the problem of finding the minimum limit load factor as an MPCC problem. The penalty for the complementarity constraints is adopted to transform the MPCC problem into a standard NLP problem.

6.3 Remarks and Future Perspectives

MPCC approaches can deal with uncertainty analysis of structures with nonsmoothness properties in the governing equations, e.g., plasticity, contact, and friction. Although a conventional NLP approach can be applied to an appropriately modified (i.e., regularized, reformulated and smoothened, penalized, etc.) MPCC problem, it is worth noting that the global optimality is not guaranteed. Therefore, the solution obtained by the approaches cited above can generally underestimate the structural response, i.e., it does not necessarily include the exact (i.e., tight) bound for QoI (see Table 1).

A remedy to obtain a high-quality solution of an MPCC problem is to use DC programming approaches [107–109], which, however, have not yet been adopted in structural uncertainty analysis to the authors’ knowledge. Moreover, it is known that a class of MPCC problems can be solved globally with MIP [110] or a branch-and-cut method [111]. Such a global optimization approach might be pursued in structural uncertainty analysis.

7  Difference-of-Convex Programming Approaches

7.1 Overview

In these two decades, difference-of-convex (DC) algorithm has been attracted significant attention in machine learning and data science [112,113]. A function is called a DC function if it can be expressed as a difference of two convex functions. A DC programming problem is a minimization problem of a DC function under constraints that some DC functions are no greater than zero. The DC algorithm is an algorithm proposed for DC programming, and is based on the affine minorization of the concave part of a DC function. It is known that the DC algorithm quite often converges to a global optimal solution of a DC programming problem [114,115].

7.2 Methods

To find a bound for the static response of an elastic structure with uncertainty, Li et al. [116] approximate g(x;s) in (7) and (8) as a quadratic function in terms of s by using the Taylor expansion, where S is defined by (1) (i.e., s is an interval variable). They apply the DC algorithm for solving the obtained optimization problem. It is worth noting that since the method is based on the Taylor expansion, it is not guaranteed that the actual structural response is included in the obtained bound, even if the DC algorithm finds a global optimal solution.

Li et al. [117] apply the same idea to the eigenvalue of free vibration of a structure with uncertainty.

7.3 Remarks and Future Perspectives

It is well known that a wide class of optimization problems can be treated with the DC programming, and the DC algorithm can often find a high-quality solution of a DC programming problem. Accordingly, there exists room to increase DC programming approaches to structural uncertainty analysis.

8  Robust Optimization Approaches

In the research field of mathematical optimization, robust optimization [55] is a methodology handling optimization problems involving non-probabilistic uncertainty, and has been studied extensively.

In the framework of limit analysis, Bleyer and Leclère [118] consider uncertainty in the yield surface, and apply the robust optimization methodology to the problem finding the worst-case limit load factor.

For the interval model updating, Callens et al. [119] adopt the scenario approach [120] proposed for robust optimization problems.

9  Surrogate Modeling-, Neural Network-, and Machine Learning-Based Optimization Approaches

When we analyze a complex system, it is often that the objective function q in problems (7) and (8) is not given in an explicit form, but the value of q(d;s) for fixed d and s can be evaluated only after numerical simulation or experiments. In such a case, surrogate models, neural networks, and other machine learning techniques are sometimes useful in predicting the objective function value in the course of optimization. Section 9.1 overviews surrogate models for uncertainty analysis, and Section 9.2 summarizes other machine learning techniques including neural networks. Although we divide these methods into two categories in accordance with the convention, from one point of view, both of them can be regarded essentially as approximation techniques of a function.

9.1 Surrogate Model

Suppose that the design variable d is fixed, and QoI q(d;⋅) is not given as an explicit function. We generate samples of the uncertain parameter s, a set of which is denoted by {sˇ1,…,sˇr}, where r is the number of generated samples. At each sample point, we can evaluate the value of QoI by, e.g., numerical simulation. Thus we obtain a pair of a sample point and a value of QoI. A set of those pairs, denoted by {(sˇ1,q(d;sˇ1)),…,(sˇr,q(d;sˇr))}, is called the training data. An approximation function of q(d;⋅) generated from the training data is called a response surface or surrogate model [121,122].

9.1.1 Polynomial Approximation

Polynomial approximation is one of the simplest surrogate model. Design of experiments is often used to generate a set of sample points [121].

Bai et al. [123] and Li et al. [124] (independently) adopt a quadratic polynomial without cross terms as a surrogate of the performance constraint function, and perform the robustness assessment (see also Section 11.2).

9.1.2 Radial Basis Function Network

Radial basis function (RBF) network [125] is a widely and successfully used surrogate model in, e.g., sequential approximate optimization [126].

Liu et al. [127] use the RBF network to approximate a static response of a linear elastic structure, where the material constants and applied load are uncertain. They obtain upper and lower bounds for the static response by maximizing and minimizing the output of the RBF network, respectively.

Xu et al. [128] consider the interval analysis of structures, where the so-called Taylor interval expansion model, i.e., the Taylor expansion of QoI concerning the interval variables, is employed. They use the RBF network to estimate the gradient and Hessian in the Taylor interval expansion model, and obtain upper and lower bounds for the natural frequency, displacement, and the stress of complex vehicle structures. A similar approach is described for the static structural response by Yao et al. [129].

Fang et al. [130] consider an inverse problem with uncertainty, where the system responses are given as interval variables and the unknown system internal parameters are estimated as interval variables. They present a double-loop optimization approach, and incorporate the RBF network to reduce its computational cost.

9.1.3 Kriging

Kriging (a.k.a. Gaussian process prediction) [131] is a probabilistic surrogate model that not only provides an estimate of QoI but also quantifies the uncertainty of the provided estimate.

Liu et al. [132] present a bidirectional sequential sampling approach for updating the Kriging model sequentially. They apply this approach to finding upper and lower bounds for dynamic response of structures with interval uncertainty.

Wang et al. [133] use a Kriging model as a surrogate of the performance constraint function to perform the robustness assessment (see also Section 11.2).

Li et al. [134] apply an adaptive Kriging method for solving a multi-objective optimization problem with interval uncertainty. An interval bound for each constraint function value is computed with the sequential quadratic programming (SQP).

Huang et al. [135] treat a situation in which an optimization problem involves uncertain interval parameters, and formulate a bi-objective optimization problem that minimizes the middle value and the width (or the radius) of the objective function. They use a Kinging model to solve this bi-objective optimization problem. Kriging is applied to a similar bi-objective optimization problem also by Cheng et al. [136].

9.1.4 Other Surrogate Models

Xu et al. [137] employ a surrogate model using the Chebyshev polynomials for optimization with interval design variables. Wang et al. [138] develop a Legendre polynomial expansion method for interval functions to solve optimization problems involving uncertain interval parameters. Wei et al. [139] use the Lagrange interpolation to analyze dynamic characteristics of a nonlinear oscillator with uncertain interval parameters.

9.2 Neural Network and Machine Learning

Machine learning techniques [140,141] have recently been utilized almost ubiquitously in science and engineering. Among others, deep learning, initiated by Hinton et al. [142], has attracted considerable attention. In uncertainty analysis, these techniques are often used to reduce the computational cost when the numerical simulation for evaluating QoI is computationally expensive.

9.2.1 Neural Network

Ma et al. [143] adopt a back-propagation neural network as a surrogate model for the ultimate strength of a laminated structure, and find upper and lower bounds of the surrogate model response with respect to uncertain interval parameters.

Wang et al. [144] train a feedforward neural network for predicting the structural response to uncertain interval parameters. They derive the gradient and Hessian from the neural network to obtain a sharp bound of the structural response under relatively large uncertainty. Wang et al. [145] compute the gradient of the structural response with a back-propagation neural network for efficient solution of an optimization problem involving uncertain interval parameters.

9.2.2 Deep Learning

Cui et al. [146] deal with the identification of the dynamic load applied to a structure involving uncertain interval parameters. They use the convolutional neural network (CNN) to reconstruct a bound for the unknown dynamic load.

Shi and Beer [147] use the deep neural network (DNN) as a surrogate model of the response of an aeronautical structure involving interval variables. They consider maximization and minimization of the output of DNN to predict upper and lower bounds for the structural response.

9.2.3 Bayesian Optimization

Cicirello and Giunta [148] employ the Bayesian optimization for evaluating upper and lower bounds for the QoI of an engineering system with interval uncertainty. The use of the acquisition function in Bayesian optimization can reduce the number of numerical simulations required to update the surrogate model, which is the Gaussian process regression.

Similarly, Dang et al. [149] utilize the Bayesian optimization, in combination with parallel computing, to further reduce the computational cost.

9.3 Remarks and Future Perspectives

To address complex structural systems, the importance of surrogate-based methods and machine learning techniques in structural uncertainty analysis inevitably continues to increase. Quality of the solution obtained by a surrogate-based method can highly depend on the sampling strategy. Similarly, the quality of the solution obtained by a machine-learning technique can highly depend on the training data, as well as the values of hyperparameters. Therefore, using these methods as black-boxes may yield inadequate result from the engineering point of view.

Most of machine learning methods for uncertainty analysis assume that sufficient data are available for training. Methods that are efficient when only limited data are available can be further explored.

10  Metaheuristics

10.1 Overview

The optimization problems (7) and (8), for finding the extreme values of QoI can be hard to solve, due to, e.g., some combinatorial property and/or difficulty in the computation of the derivatives of the objective and/or constraint functions. Metaheuristics are sometimes adopted in such a situation. Metaheuristics are a family of algorithmic strategies for finding quality solutions of non-specific difficult optimization problems [150–152], and often use nature-inspired ideas to explore diverse solutions different from the ones that are once obtained during the solution process. Application of metaheuristics often avoids convergence to a poor local optimal solution, but in general, does not give a guarantee on the optimality of obtained solutions.

10.2 Methods

Ma et al. [153] consider an interval uncertainty model in the microstructure of a material, and use the particle swarm optimization (PSO) to find effective quantities of the material.

Zhao et al. [154] deal with an identification problem, where the upper and lower bounds for the distributed load applied to a structure involving uncertainty are to be found. They employ the genetic algorithm (GA) with the Latin hypercube sampling.

Ma et al. [143] use a back-propagation neural network to construct a surrogate model for the ultimate strength of a laminated structure. Then the upper and lower bounds of the surrogate model response concerning uncertain intervals, parameters are explored by GA.

Jiang et al. [155] consider an optimization problem involving uncertain parameters in the objective and constraint functions, which can be viewed as a general form of (7) and (8). They use the Latin hypercube sampling and the quadratic polynomial responses surface approximation to construct an approximation optimization problem, and apply the intergeneration projection genetic algorithm (IP-GA) to solve the problem.

Shi and Beer [147] adopt DNN as a surrogate model for the response of an aeronautical structure with interval variables, and apply several metaheuristics, i.e., GA, PSO, the differential evolution (DE), and the simulated annealing (SA).

10.3 Remarks and Future Perspectives

Most advantage of metaheuristics is versability. One can use a software package without particular optimization modeling techniques. Moreover, metaheuristics can be applied to problems where the derivatives of objective and constraint functions are not available. However, the practical performance of metaheuristics in general depends on the values of the algorithmic parameters. Particular attention should be paid to this aspect.

One of the advantages of metaheuristics that has not been leveraged in uncertainty analysis is the potential to explore the Pareto frontier in a multi-objective optimization problem. Particularly, NSGA II (non-dominated sorting genetic algorithm II) [156] is a seminal method. Such an algorithm might be applied to an uncertainty analysis problem with multiple performance functions.

11  Robustness Quantification

This section collects the methods for quantitatively assessing the structural robustness by using a non-probabilistic uncertainty model. Section 11.1 provides a review on the approaches using the concept of robustness established in the info-gap theory [157]. Section 11.2 discuses some closely related concepts. Other robustness measures are outlined in Section 11.3.

11.1 Info-Gap Model and Robustness Function

Robustness function, which plays a pivotal role in the info-gap theory [157], is one of measures that can systematically quantify the robustness of a system possessing uncertainty. When we compare two system designs, a larger value of the robustness function means greater robustness.

The info-gap theory is a methodology for supporting decision making under uncertainty. It introduces a parameter, denoted by α (≥0), to represent the (unknown) magnitude of uncertainty. The uncertainty set, denoted by S^(α), is supposed to depend on α so that the uncertainty level increases as α increases. This model is called the info-gap uncertainty model, which is a family of sets satisfying the following two conditions (see Fig. 12):

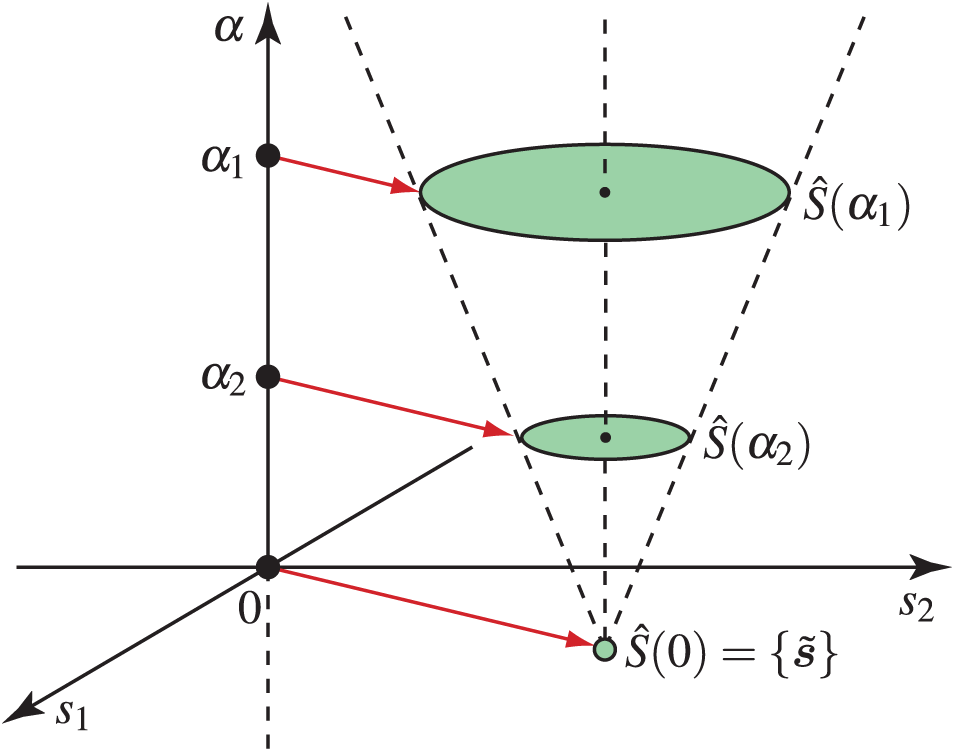
Figure 12: Info-gap uncertainty model

(i)   α1>α2 (≥0) implies S^(α1)⊇S^(α2).

(ii)   S^(0)={s~}, where s~∈Rk is the nominal value (or the best estimate) of uncertain parameter s.

For structural design d∈Rb, we use g(d;s) to denote its performance, where a small value of g(d;s) is supposed to be preferred over a large value. For given s∈S, the performance requirement (or the constraint) is written in the form

g(d;s)≤gc,(14)

where gc∈R is a critical value. For fixed α, s can take any value in Z^(α). The robust constraint requires that the performance requirement is satisfied for any realization of s, i.e.,

g(d;s)≤gc(∀s∈S^(α)).(15)

The robustness function, denoted by α^(d;gc) for given d and gc, is defined as the maximum value of α (≥0) such that the robust constraint is satisfied, i.e.,5

α^(d;gc)=maxα{α|g(d;s)≤gc (∀s∈S^(α))}.(16)

For two different designs d1, d2∈Rb, if we have α^(d1;gc)>α^(d2;gc), then we can conclude that d1 is more robust than d2. In this sense, the robustness function is defined by (16) serves as a quantitative measure of structural robustness. It is noteworthy that the robustness superiority between the given two designs can possibly reverse depending on the value of gc, which is known as the crossing of robustness curves [157].

Jaboviste et al. [158] compare the damping performance and robustness of two specific viscoelastic materials involved in a damper made of a steel frame and polymer inclusions. One material can show a very good damping performance, but the performance varies drastically depending on frequency and temperature. The other material has a less damping performance, and less frequency- and temperature-dependence. Robustness analysis based on the info-gap theory shows that the best choice can change depending on the critical performance.

Based on the info-gap theory, Kanno et al. [159] present a framework for evaluating seismic resilience of structures. They compare seismic-resistant structures and base-isolated structures, and illustrate that reversal of preference between these two structural systems can occur depending on the performance requirement.

Kuczkowiak et al. [160] present a method assessing the robustness of dynamic responses of a structure, against uncertainty in the identified modal model. As a performance requirement, the maximum response level at a certain frequency is required to be no greater than a critical value.

Conventionally, the calibration of a computer model adjusts model parameters so that the fidelity to measurements is maximized. Atamturktur et al. [161] formulate the model calibration as a bi-objective optimization problem that maximizes both the fidelity to measurements and the robustness to uncertainty in the model parameters.

Takewaki and Ben-Haim [162] consider a shear building model subjected to a stationary random base acceleration. They deal with uncertainties in both the load and structural model parameters, where uncertainty in the latter is represented with the info-gap model. They observe a trade-off relation between the functional performance of a structure and robustness to uncertainties.

The double impulse has widely been used to evaluate the critical response of an elastoplastic structure due to near-fault earthquake ground motions. Kanno and Takewaki [163] perform robustness assessment of an elastoplastic single-degree-of-freedom (SDOF) structure subjected to the double impulse input. The robustness function is evaluated analytically. Kanno et al. [164] further investigate the situation that the yield deformation and stiffness of a structure are supposed to be uncertain simultaneously. Fujita et al. [165] consider an SDOF elastic–perfectly plastic structure that is equivalent to an elastoplastic base-isolated high-rise building, and provide an analytic expression of the robustness function concerning the critical response against a near-fault ground motion.

Kanno and Takewaki [42] present a numerical method for computing a lower bound for the robustness function value of a truss structure, where the member stiffnesses and static external forces are supposed to be uncertain. They formulate the problem of finding a lower bound as the minimization of a quasi-convex function under convex constraints, and present a bi-section method using SDP. The stress constraints for the truss members are adopted as the performance requirement in the numerical examples.

Kanno and Takewaki [67] formulate the robustness maximization problem of structures, and propose an algorithm for solving it. They consider trusses with uncertain external load, and the stress constraints are chosen as the performance requirement. The robustness maximization problem is formulated as follows:

Maximizeα^(d;gc),subject tod∈D,

where D⊆Rb is the set of admissible structural designs. By using (16), we can rewrite this problem as

Maximizeα,(17a)

subject tog(d;s)≤gc(∀s∈S^(α)),(17b)

d∈D,(17c)

where d∈Rb and α∈R are variables to be optimized. Kanno and Takewaki [67] show that constraint (17b) can be reduced to a nonlinear matrix inequality, and present a sequential SDP method for solving the reduced problem.

Matsuda and Kanno [166] treat the limit analysis of trusses and frames, where uncertainty in the external forces is considered. A lower bound constraint on the limit load factor is chosen as the performance constraint. They show that the robustness function value can be computed by solving a linear programming (LP) problem. They also formulate a robust design optimization problem as a minimization problem of the structural volume under the performance requirement above, and show that this problem can be recast as an LP problem.

Tang et al. [167] formulate a reliability-based robust design optimization problem taking the epistemic uncertainty of design variables into account by using the info-gap theory, in conjunction with the reliability constraints involving random uncertainty.

11.2 Measures Closely Related to Info-Gap Robustness

Kang and Bai [168] define the robustness index as follows. Consider the performance requirement in (14), where we assume that g(d;⋅) is a continuous function. Suppose that uncertain parameter s belongs to the ellipsoidal model in (3). Then the corresponding info-gap uncertainty model is naturally defined by

S^(α)={s∈Rk∣(s−s~)⊤Ω(s−s~)≤α2},

where α (≥0) in (3) is replaced by α2 without loss of generality. We introduce variable v∈Rk through the variable transformation

s=s~+Ω−1/2v,(18)

where Ω−1/2=(Ω1/2)−1, and Ω1/2 is a symmetric matrix satisfying Ω1/2Ω1/2=Ω1/2. Define the info-gap uncertainty model of v by

V^(α)={v∈Rk∣‖v‖≤α},

to obtain the following equivalence relation:

s∈S^(α)⇔v∈V^(α).(19)

Moreover, following the variable transformation of (18), define g¯:Rb×Rk→R by

g¯(d;v)=g(d;s~+Ω−1/2v)−gc,

which yields

g(d;s)≤gc⇔g¯(d;v)≤0.(20)

Then Kang and Bai [168] define the robustness index by

ξ∗:=minv{‖v‖∣g¯(d;v)≥0}.(21)

We can see the direct link between the robustness function in (16) and the robustness index in (21) as follows:

ξ∗=minv,ξ{ξ∣g¯(d;v)≥0, ‖v‖≤ξ}=minv,ξ{ξ∣g(d;s~+Ω−1/2v)≥gc, v∈V^(ξ)}=mins,ξ{ξ∣g(d;s)≥gc, s∈S^(ξ)}=maxξ{ξ∣g(d;s)≤gc (∀s∈S^(ξ))}=α^(d;gc),(22)

where the first equality follows from the fact that minimizing ‖v‖ is equivalent to minimizing ξ under constraint ‖v‖≤ξ, the second equality is obtained by using (18) and (20), the third equality is obtained by using (19), the forth inequality follows from the continuity of g(d;⋅) and the fact that only one of the two assertions “∃s∈S^(ξ): g(d;s)≥gc” and “g(d;s)<gc (∀s∈S^(ξ))” can hold. Thus, Eq. (22) shows that the robustness index can essentially be identified with the robustness function. Similar treatments of robustness assessment can be found also in [50,123,169–171].

Kang and Bai [168] formulate a robust truss optimization problem based on the robustness index. It is worth noting that the optimization problem in the form of the right-side of (21) is dealt with in the performance measure approach (PMA) for reliability-based design optimization; see, for PMA, Hu et al. [18] and the references therein. Given this fact, Kang et al. [168] present an algorithm for solving their robust optimization problem.

The scale factor theory due to Li et al. [124] and Wang et al. [133] is also essentially identical to the info-gap theory.

11.3 Other Robustness Measures

Jiang et al. [172] define the following measure to quantify the robustness of structures. Consider the ellipsoidal uncertainty model in (3), where we put k=2. The performance constraint required for the structure is given by (14). For a compact set C⊂R2, we use |C| to denote its area (more precisely, its cardinality). Define ξ∈[0,1] by

ξ=|S∩{s∈R2∣g(d;s)≤gc}||S|,

which is the measure introduced by Jiang et al. [172]. In other words, ξ is the ratio of the area of the set of s with which the performance constraint is satisfied with the area of the set of all possible realizations of s. Note that Jiang et al. [172] call ξ the reliability with a non-probabilistic uncertainty model.

In finance, the conditional value-at-risk (CVaR) [173] is extensively used as a risk measure, which can compare the probability that an extreme event surpasses the critical value occurs, by taking the tail of the failure probability into account. Bleyer [174] adopts CVaR to estimate the effective properties of a heterogeneous elastic material with random microscopic properties. Optimization methods of structures considering CVaR can be found in Byun et al. [175], Byun and Royset [176], Chaudhuri et al. [177], and Rockafellar and Royset [178].

Considering uncertainty in feature degradation of a structure, Kanno and Ben-Haim [179] propose two measures of structural redundancy, called the strong redundancy and weak redundancy. Particularly, the strong redundancy is defined as the largest level of deficiency that can be tolerated at any place in a structure without violating the performance constraint.

11.4 Remarks and Future Perspectives

The framework of robustness assessment using the robustness function has been well established. However, evaluation of the robustness function value is in general not easy, and algorithmic aspects can further be studied. The difficulty arises from the fact that the robustness function value is defined essentially as the optimal value of a bi-level optimization problem, because Eq. (16) can be rewritten equivalently as

α^(d;gc)=maxα{α|max{g(d;s)∣s∈S^(α)}≤gc}.

It would be beneficial to identify some problem settings with which this bi-level optimization problem can be solved globally.

Study of direct maximization of the robustness of structures is very limited. Algorithmic developments of this issue are still in demand.

12  Uncertainty Analysis-Based Data-Driven Computational Mechanics

12.1 Overview

As one of the emerging topics in computational engineering, data-driven computational mechanics has received considerable attention. Consider the static equilibrium analysis of structures. The governing equations consist of (i) the compatibility relation between the strains and displacements, (ii) the force-balance equation between the stresses and external forces, and (iii) the constitutive law relating the stress to the strain. Among these three ingredients, (i) is determined from the geometric configuration of the structure, while (ii) is given as a physical law (derived from Newton’s law of motion). In contrast, (iii) is an empirical modeling of the material response, where usually the function form is firstly chosen and then the values of its parameters are calibrated to data of material experiments. Thus, (iii) possesses somewhat arbitrariness in nature. In this view, the seminal work of Kirchdoerfer and Ortiz [180] proposes a concept of data-driven computing in mechanics, which uses data of material response (i.e., pairs of observed stress and strain values) directly to predict the structural response, instead of using an empirically modeled conventional material constitutive law.

This section provides a review of applications of uncertainty analysis to data-driven computing in elasticity.

12.2 Methods

Guo et al. [181] initiated the data-driven computing using uncertainty analysis. Given a material data set, their method constructs an ellipsoidal uncertain set (3) that includes all the data points. Then they compute upper and lower bounds for QoI under the constraints that element stresses and strains satisfy (i) and (ii) and are included in the uncertainty set. Under the assumption of small deformation, the optimization problems for finding upper and lower bounds are formulated as convex optimization problems.

Kanno [182] attempts to give a physical interpretation to the bound obtained by this method. By using a fundamental property of the order statistics of the material data set, one can guarantee that, at least with a given confidence level, the probability that the structural response is included in the obtained bound is no smaller than a specified target reliability. It is worth noting that the notion of confidence level for the target reliability can be found in the reliability-based design optimization with an uncertain input probability distribution; see [183–186] and the references therein. Kanno [182] formulate LP problems for finding upper and lower bounds of QoI, where almost linear material response is considered. Kanno [187] applies this method for truss optimization with the guaranteed confidence level for a lower bound constraint on the probability that the compliance is no larger than the specified value, where the strong duality of LP is used to transform a bi-level optimization formulation into a single-level NLP problem. Kanno [89] extends the method in [182] to piecewise-linear material response, where MIP formulations for finding bounds for QoI are presented.

As mentioned above, Guo et al. [181] consider an uncertainty set including all the data points. This is reasonable when the material response is almost linear. If the material response is much different from a linear form and/or the given data set includes outliers, the bound obtained by their method can be very loose. To obtain a tight bound, Huang et al. [188] propose a method that constructs a polyhedral uncertainty set in (2) locally for each numerical integration point of the finite element method. They solve problems for finding upper and lower bounds for QoI with a sequential linear programming approach.

Example 3. Consider the pin-jointed structure shown in Fig. 13. The structure consists of 12 cables (depicted as thin lines) and 3 struts (depicted as thick lines) with 2.4863m in length. The top and bottom layers are triangles consisting of cables with 3m in length. The distance between these layers is 1.5m. The cross-sectional areas of the cables and struts are 500 and 1000mm2, respectively. To prevent the rigid-body motion, we fix 6 degrees of freedom of the nodal displacements of the bottom nodes. The vertical downward forces of λkN are applied at the top nodes, where λ is the load factor. Each cable and each strut has the initial strains 2×10−3 and −0.4×10−3, respectively.

Figure 13: Cable–strut structure used in Example 3

Fig. 14 shows the stress-strain data sets for cables and struts. Each data set consists of 150 data points. Data-driven computational mechanics aims to predict the structural response directly from these data sets. Particularly, an uncertainty analysis-based method provides a bound for the structural response. The method proposed by Kanno [89] guarantees that, at least a specified confidence level, the probability that the structural response is in the obtained bound is no smaller than a specified target reliability.

Figure 14: Data sets for Example 3. (a) Data set for cables; and (b) data set for struts

Fig. 15 shows the bounds for the vertical displacement of a top node, where the target reliability and specified confidence level are 1−ϵ=0.9 and 1−δ=0.95, respectively. ◼

Figure 15: Bounds for the nodal displacement of the cable–strut structure of Example 3. “◃” and “▹” denote the upper and lower bounds obtained by the method proposed by Kanno [89], respectively. “◻” denotes the reference solution

12.3 Remarks and Future Perspectives

Uncertainty analysis for data-driven computational mechanics is an emerging research topic. Many possibilities remain to be studied. For example, the existing methods are restricted to static equilibrium analysis of elastic structures. Extensions to dynamic problems, as well as inelastic structures, can be explored. Moreover, extensions to robustness assessment can be considered. Design optimization methods of structures other than trusses also remain as future research topics.

13  Conclusion

Attention to the analysis of structural systems involving uncertainty has increased dramatically in recent decades. Among others, uncertainty analysis using nonprobabilistic modeling has a close link to optimization. This paper has provided a comprehensive review of this field from the viewpoints of optimization modeling and algorithms. We can draw the following conclusions from this review:

•   Nonlinear programming approaches are popularly employed due to their ease of use and versatility, although they cannot guarantee the exactness/conservativeness of the obtained bound. The quality of the obtained bound may be examined by comparison with, e.g., results of the Monte Carlo simulation. However, such a direct comparison is usually possible only for small-scale problems, due to the computational cost of the compared methods.

•   Linear and nonlinear semidefinite programming approaches to find a conservative/exact bound were actively studied particularly in the late 2000s. Until today, these approaches have often been employed for worst-case robust optimization of structures. Moreover, they are crucial to structural uncertainty analysis as they provide confidence bounds for QoI.

•   The moment-sum-of-squares hierarchy is a successive of SDP relaxations to solve a polynomial optimization problem globally. Although its global optimal guarantee is attractive for structural uncertainty analysis, it has not yet been employed in this field to the best of the author’s knowledge.

•   Modeling with mixed-integer programming is attractive due to its guarantee of the exactness of the obtained bound. It can also provide benchmark examples for evaluating the other approaches. However, the problem settings for which mixed-integer programming is available are limited. Although, to the best of the authors’ knowledge, only mixed-integer programming with linear objectives and constraint functions have been used for uncertainty analysis, in general (nonlinear) convex optimization problems with discrete and continuous variables can now be dealt with by standard mixed-integer programming solver with reasonable computational cost. As a future direction of research, the application of such formulations to uncertainty analysis might expand a class of problems for which the exactness of the obtained bounds is guaranteed.

•   Other optimization models have also been used by emphasizing a focus on specific mathematical structures stemming from respective problem settings. This paper has presented reviews of the approaches based on mathematical programming with complementarity constraints (MPCC), difference-of-convex (DC) programming, and robust optimization.

•   The present literature lacks applications of global optimization approaches and DC programming approaches to MPCC-based structural uncertainty analysis.

•   Recently, surrogate models-based, neural networks-based, and machine learning techniques-based optimization approaches have widely spread in uncertainty analysis. They attempt to enhance the efficiency and accuracy of uncertainty analysis of complex systems. This trend of research will probably continue for a while.

•   The info-gap theory provides a systematic way to assess the robustness of structures. There exist non-probabilistic robustness measures inspired by reliability engineering, many of which can be essentially identified with the robustness function defined in the info-gap theory. This may suggest that the notion of robustness function is intuitively clear and natural from the engineering point of view. Existing methods for evaluating the robustness function values include explicit computations, nonlinear semidefinite programming approaches, optimization methods inspired by the performance measure approach in reliability engineering, etc.

•   Applying uncertainty analysis techniques to data-driven computing in mechanics is considered natural as material behavior inevitably and intrinsically possesses aleatory uncertainty (a.k.a. natural variability).

It should be clear again that this paper does not deal with the diverse methods for uncertainty analysis, overviewed in Section 1.2, other than optimization-based methods using non-probabilistic uncertainty modeling. Moreover, we have focused on optimization modeling of uncertainty analysis problems as well as solution algorithms, and thereby issues of uncertainty modeling have not been thoroughly discussed.

Acknowledgement: None.

Funding Statement: The work of the first author is partially supported by JSPS KAKENHI JP24K07747.

Author Contributions: The authors confirm the contributions to the paper as follows: study conception and design: Yoshihiro Kanno; reference collection: Yoshihiro Kanno; analysis and interpretation of the references: Yoshihiro Kanno and Izuru Takewaki; draft manuscript preparation: Yoshihiro Kanno; manuscript editing and revision: Yoshihiro Kanno and Izuru Takewaki. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The MATLAB codes used for the numerical examples in this paper are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1This is one of the reasons why all the uncertainty sets introduced in Section 2.1 are convex. It is also worth noting that the classical convex model approaches [27,28] often approximate q(d;⋅) as a linear function and adopt an ellipsoid in (3) as S, so that problems (7) and (8) can be solved explicitly.

2Prediction of QoI via a surrogate model or a machine learning method can both underestimate and overestimate the true value of QoI. This is because surrogate-based methods and machine-learning methods are not listed in Table 1.

3It is obvious that, in this problem setting, the worst case of the the limit load factor corresponds to the case that every yield limit takes its lower bound.

4There exist some different concepts, and accordingly diverse formulations, in robust design optimization in engineering, see [12,52]. Among others, we restrict ourselves to the concept based on the worst case, which optimizes the worst value of the objective function when the uncertainty parameters vary in a given uncertainty set.

5If g(d;s~) > gc, then we define α^(d;gc) = 0.

References

1. Ghanem R, Higdon D, Owhadi H, editors. Handbook of uncertainty quantification. Cham, Switzerland: Springer; 2017. [Google Scholar]

2. Soize C. Uncertainty quantification. Cham, Switzerland: Springer; 2017. [Google Scholar]

3. Sullivan TJ. Introduction to uncertainty quantification. Cham, Switzerland: Springer; 2015. [Google Scholar]

4. Alefeld G, Mayer G. Interval analysis: theory and applications. J Comput Appl Math. 2000;121:421–64. doi:10.1016/S0377-0427(00)00342-3. [Google Scholar] [CrossRef]

5. Neumaier A. Interval methods for systems of equations. Cambridge, UK: Cambridge University Press; 1990. [Google Scholar]

6. Faes M, Moens D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Arch Comput Methods Eng. 2020;2:633–71. doi:10.1007/s11831-019-09327-x. [Google Scholar] [CrossRef]

7. Moens D, Hanss M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: recent advances. Finite Elem Anal Des. 2011;47:4–16. doi:10.1016/j.finel.2010.07.010. [Google Scholar] [CrossRef]

8. Moens D, Vandepitte D. A survey of non-probabilistic uncertainty treatment in finite element analysis. Comput Methods Appl Mech Eng. 2005;194:1527–55. doi:10.1016/j.cma.2004.03.019. [Google Scholar] [CrossRef]

9. Moens D, Vandepitte D. Recent advances in non-probabilistic approaches for non-deterministic dynamic finite element analysis. Arch Comput Methods Eng. 2006;13:389–464. doi:10.1007/BF02736398. [Google Scholar] [CrossRef]

10. Li Y, Chen J, Feng L. Dealing with uncertainty: a survey of theories and practices. IEEE Trans Knowl Data Eng. 2013;25:2463–82. doi:10.1109/TKDE.2012.179. [Google Scholar] [CrossRef]

11. Acar E, Bayrak G, Jung Y, Lee I, Ramu P, Ravichandran SS. Modeling, analysis, and optimization under uncertainties: a review. Struct Multidiscipl Optim. 2021;64:2909–45. doi:10.1007/s00158-021-03026-7. [Google Scholar] [CrossRef]

12. Beyer H-G, Sendhoff B. Robust optimization—a comprehensive survey. Comput Methods Appl Mech Eng. 2007;196:3190–218. doi:10.1016/j.cma.2007.03.003. [Google Scholar] [CrossRef]

13. Brevault L, Balesdent M, Morio J. Aerospace system analysis and optimization in uncertainty. Cham: Springer; 2020. [Google Scholar]

14. Der Kiureghian A. Structural and system reliability. Cambridge, UK: Cambridge University Press; 2022. [Google Scholar]

15. Lemaire M. Structural reliability. London, UK: ISTE; 2009. [Google Scholar]

16. Choi S-K, Grandhi RV, Canfield RA. Reliability-based structural design. London, UK: Springer-Verlag; 2007. [Google Scholar]

17. Hu W. Design optimization under uncertainty. Cham, Switzerland: Springer; 2023. [Google Scholar]

18. Hu W, Cheng S, Yan J, Cheng J, Peng X, Cho H, et al. Reliability-based design optimization: a state-of-the-art review of its methodologies, applications, and challenges. Struct Multidiscipl Optim. 2024;67:168. doi:10.1007/s00158-024-03884-x. [Google Scholar] [CrossRef]

19. Valdebenito MA, Schuëller GI. A survey on approaches for reliability-based optimization. Struct Multidiscipl Optim. 2010;42:645–63. doi:10.1007/s00158-010-0518-6. [Google Scholar] [CrossRef]

20. Stefanou G. The stochastic finite element method: past, present and future. Comput Methods Appl Mech Eng. 2009;198:1031–51. doi:10.1016/j.cma.2008.11.007. [Google Scholar] [CrossRef]

21. Faes MGR, Daub M, Marelli S, Patelli E, Beer M. Engineering analysis with probability boxes: a review on computational methods. Struct Saf. 2021;93:102092. doi:10.1016/j.strusafe.2021.102092. [Google Scholar] [CrossRef]

22. Jiang C, Zheng J, Han X. Probability-interval hybrid uncertainty analysis for structures with both aleatory and epistemic uncertainties: a review. Struct Multidiscipl Optim. 2018;57:2485–502. doi:10.1007/s00158-017-1864-4. [Google Scholar] [CrossRef]

23. Peherstorfer B, Willcox K, Gunzburger M. Survey of multifidelity methods in uncertainty propagation, inference, and optimization. SIAM Rev. 2018;60:550–91. doi:10.1137/16M1082469. [Google Scholar] [CrossRef]

24. Helton JC, Johnson JD, Sallaberry CJ, Storlie CB. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab Eng Syst Saf. 2006;91:1175–209. doi:10.1016/j.ress.2005.11.017. [Google Scholar] [CrossRef]

25. Xu Y, Kohtz S, Boakye J, Gardoni P, Wang P. Physics-informed machine learning for reliability and systems safety applications: state of the art and challenges. Reliab Eng Syst Saf. 2023;230:108900. doi:10.1016/j.ress.2022.108900. [Google Scholar] [CrossRef]

26. Cao L, Liu J, Xie L, Jiang C, Bi R. Non-probabilistic polygonal convex set model for structural uncertainty quantification. Appl Math Model. 2021;89:504–18. doi:10.1016/j.apm.2020.07.025. [Google Scholar] [CrossRef]

27. Ben-Haim Y, Elishakoff I. Convex models of uncertainty in applied mechanics. New York, NY, USA: Elsevier; 1990. [Google Scholar]

28. Pantelides CP, Ganzerli S. Design of trusses under uncertain loads using convex models. J Struct Eng. 1998;124:318–29. doi:10.1061/(ASCE)0733-9445(1998)124:3(318). [Google Scholar] [CrossRef]

29. Luenberger DG, Ye Y. Linear and nonlinear programming. 3rd ed. New York, NY, USA: Springer; 2008. [Google Scholar]

30. Nocedal J, Wright SJ. Numerical optimization. 2nd ed. New York, NY, USA: Springer; 2006. [Google Scholar]

31. Tangaramvong S, Wu D, Gao W, Tin-Loi F. Response bounds of elastic structures in the presence of interval uncertainties. J Struct Eng. 2015;141:04015046. doi:10.1061/(ASCE)ST.1943-541X.0001297. [Google Scholar] [CrossRef]

32. Wu D, Gao W, Gao K, Tin-Loi F. Robust safety assessment of functionally graded structures with interval uncertainties. Compos Struct. 2017;180:664–85. doi:10.1016/j.compstruct.2017.08.011. [Google Scholar] [CrossRef]

33. Wu D, Liu A, Huang Y, Huang Y, Pi Y, Gao W. Mathematical programming approach for uncertain linear elastic analysis of functionally graded porous structures with interval parameters. Compos Part B: Eng. 2018;152:282–91. doi:10.1016/j.compositesb.2018.06.032. [Google Scholar] [CrossRef]

34. Wu D, Gao W, Song C, Luo Z. Mathematical programming approaches for interval structural behaviour and stability analysis. Comput Model Eng Sci. 2015;108:331–73. doi:10.3970/cmes.2015.108.331. [Google Scholar] [CrossRef]

35. Wu D, Gao W, Tangaramvong S, Tin-Loi F. Robust stability analysis of structures with uncertain parameters using mathematical programming approach. Int J Numer Methods Eng. 2014;100:720–45. doi:10.1002/nme.4758. [Google Scholar] [CrossRef]

36. Fujita K, Takewaki I. An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. Eng Struct. 2011;33:3299–310. doi:10.1016/j.engstruct.2011.08.029. [Google Scholar] [CrossRef]

37. Tangaramvong S, Tin-Loi F, Wu D, Gao W. Mathematical programming approaches for obtaining sharp collapse load bounds in interval limit analysis. Comput Struct. 2013;125:114–26. doi:10.1016/j.compstruc.2013.04.028. [Google Scholar] [CrossRef]

38. Tangaramvong S, Tin-Loi F, Song CM, Gao W. (eds.) Interval limit analysis within a scaled boundary element framework. ASME J Risk Uncertain Eng Syst Part B: Mech Eng. 2015;1:041004. doi:10.1115/1.4030471. [Google Scholar] [CrossRef]

39. Anjos MF, Lasserre JB, editors. Handbook on semidefinite, conic and polynomial optimization. New York, NY, USA: Springer; 2012. [Google Scholar]

40. Boyd S, Vandenberghe L. Convex optimization. Cambridge, UK: Cambridge University Press; 2004. [Google Scholar]

41. Guo X, Bai W, Zhang W. Confidence extremal structural response analysis of truss structures under static load uncertainty via SDP relaxation. Comput Struct. 2009;87:246–53. doi:10.1016/j.compstruc.2008.10.001. [Google Scholar] [CrossRef]

42. Kanno Y, Takewaki I. Robustness analysis of trusses with separable load and structural uncertainties. Int J Solids Struct. 2006;43:2646–69. doi:10.1016/j.ijsolstr.2005.06.088. [Google Scholar] [CrossRef]

43. Kanno Y, Takewaki I. Confidence ellipsoids for static response of trusses with load and structural uncertainties. Comput Methods Appl Mech Eng. 2006;196:393–403. doi:10.1016/j.cma.2006.04.007. [Google Scholar] [CrossRef]

44. Du J, Du Z, Wei Y, Zhang W, Guo X. Exact response bound analysis of truss structures via linear mixed 0-1 programming and sensitivity bounding technique. Int J Numer Methods Eng. 2018;116:21–42. doi:10.1002/nme.5913. [Google Scholar] [CrossRef]

45. Kanno Y, Takewaki I. Ellipsoidal bounds for static response of framed structures against interactive uncertainties. Interaction Multiscale Mech: Int J. 2007;1:103–21. doi:10.12989/imm.2008.1.1.103. [Google Scholar] [CrossRef]

46. Kanno Y, Takewaki I. Semidefinite programming for uncertain linear equations in static analysis of structures. Comput Methods Appl Mech Eng. 2008;198:102–15. doi:10.1016/j.cma.2008.04.003. [Google Scholar] [CrossRef]

47. Kanno Y, Takewaki I. Semidefinite programming for dynamic steady-state analysis of structures under uncertain harmonic loads. Comput Methods Appl Mech Eng. 2009;198:3239–61. doi:10.1016/j.cma.2009.06.005. [Google Scholar] [CrossRef]

48. Pólik I, Terlaky T. A survey of S-lemma. SIAM Rev. 2007;49:371–418. doi:10.1137/S003614450444614X. [Google Scholar] [CrossRef]

49. Guo X, Bai W, Zhang W. Extreme structural response analysis of truss structures under material uncertainty via linear mixed 0-1 programming. Int J Numer Methods Eng. 2008;76:253–77. doi:10.1002/nme.2298. [Google Scholar] [CrossRef]

50. Kang Z, Zhang W. Construction and application of an ellipsoidal convex model using a semi-definite programming formulation from measured data. Comput Methods Appl Mech Eng. 2016;300:461–89. doi:10.1016/j.cma.2015.11.025. [Google Scholar] [CrossRef]

51. Bai S, Li D, Kang Z. Construction of ellipsoid convex model of bounded uncertainties with outlier detection for application in non-probabilistic topology optimization. Comput Struct. 2024;296:107322. doi:10.1016/j.compstruc.2024.107322. [Google Scholar] [CrossRef]

52. Kanno Y. On three concepts in robust design optimization: absolute robustness, relative robustness, and less variance. Struct Multidiscipl Optim. 2020;62:979–1000. doi:10.1007/s00158-020-02503-9. [Google Scholar] [CrossRef]

53. Ben-Tal A, Nemirovski A. Robust truss topology design via semidefinite programming. SIAM J Optim. 1997;7:991–1016. doi:10.1137/S1052623495291951. [Google Scholar] [CrossRef]

54. Calafiore GC, Dabbene F. Optimization under uncertainty with applications to design of truss structures. Struct Multidiscipl Optim. 2008;35:189–200. doi:10.1007/s00158-007-0145-z. [Google Scholar] [CrossRef]

55. Ben-Tal A, El Ghaoui L, Nemirovski A. Robust optimization. Princeton, NJ, USA: Princeton University Press; 2009. [Google Scholar]

56. Kanno Y. Robust truss topology optimization via semidefinite programming with complementarity constraints: a difference-of-convex programming approach. Comput Optim Appl. 2018;71:403–33. doi:10.1007/s10589-018-0013-3. [Google Scholar] [CrossRef]

57. Yonekura K, Kanno Y. Global optimization of robust truss topology via mixed integer semidefinite programming. Optim Eng. 2010;11:355–79. doi:10.1007/s11081-010-9107-1. [Google Scholar] [CrossRef]

58. Hashimoto D, Kanno Y. A semidefinite programming approach to robust truss topology optimization under uncertainty in locations of nodes. Struct Multidiscipl Optim. 2015;51:439–61. doi:10.1007/s00158-014-1146-3. [Google Scholar] [CrossRef]

59. Yamashita H, Yabe H. A survey of numerical methods for nonlinear semidefinite programming. J Oper Res Soc Jpn. 2015;58:24–60. doi:10.15807/jorsj.58.24. [Google Scholar] [CrossRef]

60. Cherkaev E, Cherkaev A. Principal compliance and robust optimal design. J Elast. 2003;72:71–98. doi:10.1023/B:ELAS.0000018772.09023.6c. [Google Scholar] [CrossRef]

61. Cherkaev E, Cherkaev A. Minimax optimization problem of structural design. Computers and Struct. 2008;86:1426–35. doi:10.1016/j.compstruc.2007.05.026. [Google Scholar] [CrossRef]

62. Takezawa A, Nii S, Kitamura M, Kogiso N. Topology optimization for worst load conditions based on the eigenvalue analysis of an aggregated linear system. Comput Methods Appl Mech Eng. 2011;200:2268–81. doi:10.1016/j.cma.2011.03.008. [Google Scholar] [CrossRef]

63. Seyranian AP, Lund E, Olhoff N. Multiple eigenvalues in structural optimization problem. Struct Optim. 1994;8:207–27. doi:10.1007/BF01742705. [Google Scholar] [CrossRef]

64. Thore C-J. A worst-case approach to topology optimization for maximum stiffness under uncertain boundary displacement. Comput Struct. 2022;259:106696. doi:10.1016/j.compstruc.2021.106696. [Google Scholar] [CrossRef]

65. Holmberg E, Thore C-J, Klarbring A. Worst-case topology optimization of self-weight loaded structures using semi-definite programming. Struct Multidiscipl Optim. 2015;52:915–28. doi:10.1007/s00158-015-1285-1. [Google Scholar] [CrossRef]

66. Aroztegui M, Herskovits J, Roche JR, Bazán E. A feasible direction interior point algorithm for nonlinear semidefinite programming. Struct Multidiscipl Optim. 2014;50:1019–35. doi:10.1007/s00158-014-1090-2. [Google Scholar] [CrossRef]

67. Kanno Y, Takewaki I. Sequential semidefinite program for maximum robustness design of structures under load uncertainties. J Optim Theory Appl. 2006;130:265–87. doi:10.1007/s10957-006-9102-z. [Google Scholar] [CrossRef]

68. Guo X, Bai W, Zhang W, Gao X. Confidence structural robust design and optimization under stiffness and load uncertainties. Comput Methods Appl Mech Eng. 2009;198:3378–99. doi:10.1016/j.cma.2009.06.018. [Google Scholar] [CrossRef]

69. Guo X, Du J, Gao X. Confidence structural robust optimization by non-linear semidefinite programming-based single-level formulation. Int J Numer Methods Eng. 2011;86:953–74. doi:10.1002/nme.3083. [Google Scholar] [CrossRef]

70. Rozvany GIN. Difficulties in truss topology optimization with stress, local buckling and system stability constraints. Struct Optim. 1996;11:213–7. doi:10.1007/BF01197036. [Google Scholar] [CrossRef]

71. Achtziger W. Local stability of trusses in the context of topology optimization. Part I: exact modelling. Struct Optim. 1999;17:235–46. [Google Scholar]

72. Horn RA, Johnson CR. Matrix analysis. 2nd ed. New York, NY, USA: Cambridge University Press; 2013. [Google Scholar]

73. Yamada S, Kanno Y. Relaxation approach to topology optimization of frame structure under frequency constraint. Struct Multidiscipl Optim. 2016;53:731–44. doi:10.1007/s00158-015-1353-6. [Google Scholar] [CrossRef]

74. Kanno Y, Ohsaki M, Katoh N. Sequential semidefinite programming for optimization of framed structures under multimodal buckling constraints. Int J Struct Stab Dyn. 2001;1:585–602. doi:10.1142/S0219455401000305. [Google Scholar] [CrossRef]

75. Kočvara M. On the modelling and solving of the truss design problem with global stability constraints. Struct Multidiscipl Optim. 2002;23:189–203. doi:10.1007/s00158-002-0177-3. [Google Scholar] [CrossRef]

76. Kočvara M, Stingl M. Solving nonconvex SDP problems of structural optimization with stability control. Optim Methods Softw. 2004;19:595–609. doi:10.1080/10556780410001682844. [Google Scholar] [CrossRef]

77. Lasserre JB. The moment-SOS hierarchy: applications and related topics. Acta Numerica. 2024;33:841–908. doi:10.1017/S0962492923000053. [Google Scholar] [CrossRef]

78. Tyburec M, Kočvara M, Kružík M. Global weight optimization of frame structures with polynomial programming. Struct Multidiscipl Optim. 2023;66:257. doi:10.1007/s00158-023-03715-5. [Google Scholar] [CrossRef]

79. Tyburec M, Zeman J, Kružík M, Henrion D. Global optimality in minimum compliance topology optimization of frames and shells by moment-sum-of-squares hierarchy. Struct Multidiscipl Optim. 2021;64:1963–81. doi:10.1007/s00158-021-02957-5. [Google Scholar] [CrossRef]

80. Lee J, Leyffer S, editors. Mixed integer nonlinear programming. New York: Springer; 2012. [Google Scholar]

81. Wolsey LA. Integer programming. New York: John Wiley and Sons; 1998. [Google Scholar]

82. IBM ILOG. IBM ILOG CPLEX optimization studio. [cited 2025 Feb 17]. Available from: https://www.ibm.com/products/ilog-cplex-optimization-studio/. [Google Scholar]

83. Zuse Institute Berlin. SCIP: solving constraint integer programs. [cited 2025 Feb 17]. Available from: https://www.scipopt.org/. [Google Scholar]

84. Gurobi Optimization. Gurobi optimizer. [cited 2025 Feb 17]. Available from: https://www.gurobi.com/solutions/gurobi-optimizer/. [Google Scholar]

85. Stolpe M, Svanberg K. Modeling topology optimization problems as linear mixed 0–1 programs. Int J Numer Methods Eng. 2003;57:723–39. doi:10.1002/nme.700. [Google Scholar] [CrossRef]

86. Kanno Y, Takewaki I. Worst-case plastic limit analysis of trusses under uncertain loads via mixed 0–1 programming. J Mech Mater Struct. 2007;2:245–73. doi:10.2140/jomms. [Google Scholar] [CrossRef]

87. Kanno Y. Worst-case load in plastic limit analysis of frame structures. J Mech Mater Struct. 2013;8:415–39. doi:10.2140/jomms. [Google Scholar] [CrossRef]

88. Kanno Y. Worst scenario detection in limit analysis of trusses against deficiency of structural components. Eng Struct. 2012;42:33–42. doi:10.1016/j.engstruct.2012.04.012. [Google Scholar] [CrossRef]

89. Kanno Y. Data-driven confidence bound for structural response using segmented least squares: a mixed-integer programming approach. Jpn J Ind Appl Math. 2024;41:1501–34. doi:10.1007/s13160-024-00657-3. [Google Scholar] [CrossRef]

90. Tangaramvong S, Tin-Loi F. Automatic identification of the worst load combination for structural safety assessment using an optimization approach. Eng Struct. 2013;56:2287–98. doi:10.1016/j.engstruct.2013.08.036. [Google Scholar] [CrossRef]

91. GAMS Software GmbH. DICOPT. [cited 2025 Feb 17]. Available from: https://www.gams.com/latest/docs/S_DICOPT.html. [Google Scholar]

92. Stolpe M. Truss optimization with discrete design variables: a critical review. Struct Multidiscipl Optim. 2016;53:349–74. doi:10.1007/s00158-015-1333-x. [Google Scholar] [CrossRef]

93. Kanno Y. Damper placement optimization in a shear building model with discrete design variables: a mixed-integer second-order cone programming approach. Earthquake Eng Struct Dyn. 2013;42:1657–76. doi:10.1002/eqe.2292. [Google Scholar] [CrossRef]

94. Kanno Y. Mixed-integer second-order cone programming for global optimization of compliance of frame structure with discrete design variables. Struct Multidiscipl Optim. 2016;54:301–16. doi:10.1007/s00158-016-1406-5. [Google Scholar] [CrossRef]

95. Audet C, Le Digabel S, Montplaisir VR, Tribes C. Algorithm 1027: NOMAD version 4: nonlinear optimization with the MADS algorithm. ACM Trans Math Softw. 2022;48:35–22. doi:10.1145/3544489. [Google Scholar] [CrossRef]

96. Dahito M-A, Genest L, Maddaloni A, Neto J. A solution method for mixed-variable constrained blackbox optimization problems. Optim Eng. 2024;25:2093–148. doi:10.1007/s11081-023-09874-0. [Google Scholar] [CrossRef]

97. Kanno Y, Kitayama S. Alternating direction method of multipliers as a simple effective heuristic for mixed-integer nonlinear optimization. Struct Multidiscipl Optim. 2018;58:1291–5. doi:10.1007/s00158-018-1946-y. [Google Scholar] [CrossRef]

98. Müller J. MISO: mixed-integer surrogate optimization framework. Optim Eng. 2016;17:177–203. doi:10.1007/s11081-015-9281-2. [Google Scholar] [CrossRef]

99. Papalexopoulos TP, Tjandraatmadja C, Anderson R, Vielma JP, Belanger D. Constrained discrete black-box optimization using mixed-integer programming. Proc 39th Int Conf Mach Learn. 2022;162:17295–322. [Google Scholar]

100. Fukushima M, Luo Z-Q, Pang J-S. A globally convergent sequential quadratic programming algorithm for mathematical programs with linear complementarity constraints. Comput Optim Appl. 1998;10:5–34. doi:10.1023/A:1018359900133. [Google Scholar] [CrossRef]

101. Scholtes S. Convergence properties of a regularization scheme for mathematical programs with complementarity constraints. SIAM J Optim. 2001;11:918–36. doi:10.1137/S1052623499361233. [Google Scholar] [CrossRef]

102. Luo Z-Q, Pang J-S, Ralph D. Mathematical programs with equilibrium constraints. Cambridge: Cambridge University Press; 1996. [Google Scholar]

103. Facchine F, Pang J-S. Finite-dimensional variational inequalities and complementarity problems. Volumes I & II. New York: Springer-Verlag; 2003. [Google Scholar]

104. Tangaramvong S, Tin-Loi F, Yang C, Gao W. Interval analysis of nonlinear frames with uncertain connection properties. Int J Non Linear Mech. 2016;86:83–95. doi:10.1016/j.ijnonlinmec.2016.07.006. [Google Scholar] [CrossRef]

105. Yang C, Tangaramvong S, Gao W, Tin-Loi F. Interval elastoplastic analysis of structures. Comput Struct. 2015;151:1–10. doi:10.1016/j.compstruc.2014.12.004. [Google Scholar] [CrossRef]

106. Wu D, Gao W, Li G, Tangaramvong S, Tin-Loi F. Robust assessment of collapse resistance of structures under uncertain loads based on info-gap model. Comput Methods Appl Mech Eng. 2015;285:208–27. doi:10.1016/j.cma.2014.10.038. [Google Scholar] [CrossRef]

107. Jara-Moroni F, Pang J-S, Wächter A. A study of the difference-of-convex approach for solving linear programs with complementarity constraints. Math Program. 2018;169:221–54. doi:10.1007/s10107-017-1208-6. [Google Scholar] [CrossRef]

108. Le Thi HA, Pham Dinh T. On solving linear complementarity problems by DC programming and DCA. Comput Optim Appl. 2011;50:507–24. doi:10.1007/s10589-011-9398-y. [Google Scholar] [CrossRef]

109. Muu LD, Dinh QT, Le Thi HA, Tao PD. A new decomposition algorithm for globally solving mathematical programs with affine equilibrium constraints. Acta Math Vietnam. 2012;37:201–17. [Google Scholar]

110. Kleinert T, Labbé M, Ljubić I, Schmidt M. A survey on mixed-integer programming techniques in bilevel optimization. EURO J Comput Optim. 2021;9:100007. doi:10.1016/j.ejco.2021.100007. [Google Scholar] [CrossRef]

111. Yu B, Mitchell JE, Pang J-S. Solving linear programs with complementarity constraints using branch-and-cut. Math Program Comput. 2019;11:267–310. doi:10.1007/s12532-018-0149-2. [Google Scholar] [CrossRef]

112. Pham Dinh T, Le Thi HA. Recent advances in DC programming and DCA. In: Nguyen NT, Le Thi HA, editors. Transactions on computational collective intelligence XIII. Berlin: Springer-Verlag; 2014. p. 1–37. [Google Scholar]

113. Le Thi HA, Pham Dinh T. DC programming and DCA: thirty years of developments. Math Program. 2018;169:5–68. doi:10.1007/s10107-018-1235-y. [Google Scholar] [CrossRef]

114. Le Thi HA, Pham Dinh T. Solving a class of linearly constrained indefinite quadratic problems by D.C. algorithms. J Glob Optimiz. 1997;11:253–85. doi:10.1023/A:1008288411710. [Google Scholar] [CrossRef]

115. Le Thi HA, Pham Dinh T. The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Ann Oper Res. 2005;133:23–46. doi:10.1007/s10479-004-5022-1. [Google Scholar] [CrossRef]

116. Li Q, Qiu Z, Zhang X. Static response analysis of structures with interval parameters using the second-order Taylor series expansion and the DCA for QB. Acta Mech Sin. 2015;31:845–54. doi:10.1007/s10409-015-0501-y. [Google Scholar] [CrossRef]

117. Li Q, Qiu Z, Zhang X. Eigenvalue analysis of structures with interval parameters using the second-order Taylor series expansion and the DCA for QB. Appl Math Model. 2017;49:680–90. doi:10.1016/j.apm.2017.02.041. [Google Scholar] [CrossRef]

118. Bleyer J, Leclère V. Robust optimization applied to uncertain limit analysis. In: Garcea G, Weichert D, editors. Direct methods for limit state of materials and structures: advanced computational algorithms and material modelling. Cham, Switzerland: Springer; 2023. p. 225–42. [Google Scholar]

119. Callens R, Moens D, Faes M. Certified interval model updating using scenario optimization. In: AIAA SCITECH 2024 Forum; 2024 Jan; Orlando, FL, USA. [Google Scholar]

120. Campi MC, Garatti S. Introduction to the scenario approach. Philadelphia, PA, USA: SIAM; 2018. [Google Scholar]

121. Myers RH, Montgomery DC. Response surface methodology: process and product optimization using designed experiments. New York, NY, USA: John Wiley and Sons; 2002. [Google Scholar]

122. Koziel S, Leifsson L, editors. Surrogate-based modeling and optimization: applications in engineering. New York, NY, USA: Springer; 2013. [Google Scholar]

123. Bai YC, Han X, Jiang C, Bi RG. A response-surface-based structural reliability analysis method by using non-probability convex model. Appl Math Model. 2014;38:3834–47. doi:10.1016/j.apm.2013.11.053. [Google Scholar] [CrossRef]

124. Li Q, Wang J, Su G. A grasshopper optimization algorithm-based response surface method for non-probabilistic structural reliability analysis with an implicit performance function. Buildings. 2022;12:1061. doi:10.3390/buildings12071061. [Google Scholar] [CrossRef]

125. Broomhead DS, Lowe D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1988;2:321–55. [Google Scholar]

126. Kitayama S, Arakawa M, Yamazaki K. Sequential approximate optimization using radial basis function network for engineering optimization. Optim Eng. 2011;12:535–57. doi:10.1007/s11081-010-9118-y. [Google Scholar] [CrossRef]

127. Liu Y, Wang X, Wang L. Interval uncertainty analysis for static response of structures using radial basis functions. Appl Math Model. 2019;69:425–40. doi:10.1016/j.apm.2018.12.018. [Google Scholar] [CrossRef]

128. Xu X, Chen X, Liu Z, Zhang Y, Xu Y, Fang J, et al. A feasible identification method of uncertainty responses for vehicle structures. Struct Multidiscipl Optim. 2021;64:3861–76. doi:10.1007/s00158-021-03065-0. [Google Scholar] [CrossRef]

129. Yao Y, Wang L, Yang G, Xu F, Li L. A new interval perturbation method for static structural response bounds using radial basis neural network differentiation. J Mech Sci Technol. 2023;37:1389–400. doi:10.1007/s12206-023-0225-z. [Google Scholar] [CrossRef]

130. Fang H, Gong C, Li C, Li X, Su H, Gu L. A surrogate model based nested optimization framework for inverse problem considering interval uncertainty. Struct Multidiscipl Optim. 2018;58:869–83. doi:10.1007/s00158-018-1931-5. [Google Scholar] [CrossRef]

131. Rasmussen CE, Williams CKI. Gaussian processes for machine learning. Cambridge, UK: The MIT Press; 2006. [Google Scholar]

132. Liu Y, Wang X, Wang L. A dynamic evolution scheme for structures with interval uncertainties by using bidirectional sequential Kriging method. Comput Methods Appl Mech Eng. 2019;348:712–29. doi:10.1016/j.cma.2019.01.041. [Google Scholar] [CrossRef]

133. Wang J, Su G, Hao J. A dynamic Gaussian process surrogate model based on the grasshopper optimization algorithm for non-probabilistic reliability analysis of complex structures. Struct Infrastruct Eng. 2023;66:1–12. doi:10.1080/15732479.2023.2225509. [Google Scholar] [CrossRef]

134. Li F, Luo Z, Rong J, Zhang N. Interval multi-objective optimisation of structures using adaptive Kriging approximations. Comput Struct. 2013;119:68–84. doi:10.1016/j.compstruc.2012.12.028. [Google Scholar] [CrossRef]

135. Huang T, Song X, Liu M. A Kriging-based non-probability interval optimization of loading path in T-shape tube hydroforming. Int J Adv Manuf Technol. 2016;85:1615–31. doi:10.1007/s00170-015-8034-x. [Google Scholar] [CrossRef]

136. Cheng J, Liu Z, Qian Y, Zhou Z, Tan J. Non-probabilistic robust equilibrium optimization of complex uncertain structures. J Mech Des. 2020;142:021405. doi:10.1115/1.4044322. [Google Scholar] [CrossRef]

137. Xu F, Yang G, Wang L, Sun Q. Interval uncertain optimization for interior ballistics based on Chebyshev surrogate model and affine arithmetic. Eng Optim. 2020;53:1331–48. doi:10.1080/0305215X.2020.1790551. [Google Scholar] [CrossRef]

138. Wang L, Yang G, Li Z, Xu F. An efficient nonlinear interval uncertain optimization method using Legendre polynomial chaos expansion. Appl Soft Comput. 2021;108:107454. doi:10.1016/j.asoc.2021.107454. [Google Scholar] [CrossRef]

139. Wei S, Lan J-C, Ding H, Chen L-Q, Peng Z-K. A Lagrange surrogate-based approach for uncertain nonlinear oscillators. J Sound Vib. 2021;501:116075. doi:10.1016/j.jsv.2021.116075. [Google Scholar] [CrossRef]

140. Theodoridis S. Machine learning: a bayesian and optimization perspective. 2nd ed. London, UK: Academic Press; 2020. [Google Scholar]

141. Bishop CM. Pattern recognition and machine learning. New York, NY, USA: Springer-Verlag; 2006. [Google Scholar]

142. Hinton GE, Osindero S, Teh Y-W. A fast learning algorithms for deep belief nets. Neural Comput. 2006;18:1527–54. doi:10.1162/neco.2006.18.7.1527. [Google Scholar] [CrossRef]

143. Ma Y, Liu Z, Shi Q, Liu J, Geng X, Xue R. Interval prediction of ultimate strength for laminated composite structures using back-propagation neural network. Arch Appl Mech. 2022;92:1167–84. doi:10.1007/s00419-021-02097-8. [Google Scholar] [CrossRef]

144. Wang L, Chen Z, Yang G. An interval uncertainty analysis method for structural response bounds using feedforward neural network differentiation. Appl Math Model. 2020;82:449–68. doi:10.1016/j.apm.2020.01.059. [Google Scholar] [CrossRef]

145. Wang L, Chen Z, Yang G, Sun Q, Ge J. An interval uncertain optimization method using back-propagation neural network differentiation. Comput Methods Appl Mech Eng. 2020;366:113065. doi:10.1016/j.cma.2020.113065. [Google Scholar] [CrossRef]

146. Cui W, Jiang J, Sun H, Yang H, Wang X, Wang L, et al. Data-driven load identification method of structures with uncertain parameters. Acta Mech Sin. 2024;40:523138. doi:10.1007/s10409-023-23138-x. [Google Scholar] [CrossRef]

147. Shi Y, Beer M. Deep learning-driven interval uncertainty propagation for aeronautical structures. Chin J Aeronaut. 2024;37:71–86. doi:10.1016/j.cja.2024.05.009. [Google Scholar] [CrossRef]

148. Cicirello A, Giunta F. Machine learning based optimization for interval uncertainty propagation. Mech Syst Signal Process. 2022;170:108619. doi:10.1016/j.ymssp.2021.108619. [Google Scholar] [CrossRef]

149. Dang C, Wei P, Faes MGR, Valdebenito MA, Beer M. Interval uncertainty propagation by a parallel Bayesian global optimization method. Appl Math Model. 2022;108:220–35. doi:10.1016/j.apm.2022.03.031. [Google Scholar] [CrossRef]

150. Chopard B, Tomassini M. An introduction to methaheuristics for optimization. Cham, Switzerland: Springer; 2018. [Google Scholar]

151. Siarry P, editor. Methaheuristics. Cham, Switzerland: Springer; 2016. [Google Scholar]

152. Yang X-S. Engineering optimization: an introduction to methaheuristic applications. Hoboken, NJ, USA: John Wiley and Sons; 2010. [Google Scholar]

153. Ma J, Du W, Gao W, Wriggers P, Xue X. Multiscale finite element analysis of uncertain-but-bounded heterogeneous materials at finite deformation. Finite Elem Anal Des. 2018;149:15–31. doi:10.1016/j.finel.2018.06.001. [Google Scholar] [CrossRef]

154. Zhao H, Li X, Chen J. Distributed load identification for uncertain structure based on LHS-GA and improved L-curve method. Int J Comput Methods. 2021;18:2050022. doi:10.1142/S021987622050022X. [Google Scholar] [CrossRef]

155. Jiang C, Han X, Liu GP. A sequential nonlinear interval number programming method for uncertain structures. Comput Methods Appl Mech Eng. 2008;197:4250–65. doi:10.1016/j.cma.2008.04.027. [Google Scholar] [CrossRef]

156. Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput. 1999;3:257–71. doi:10.1109/4235.797969. [Google Scholar] [CrossRef]

157. Ben-Haim Y. Information-gap decision theory: decisions under severe uncertainty. 2nd ed. London, UK: Academic Press; 2006. [Google Scholar]

158. Jaboviste K, Sadoulet-Reboul E, Peyret N, Arnould C, Collard E, Chevallier G. On the compromise between performance and robustness for viscoelastic damped structures. Mech Syst Signal Process. 2019;119:65–80. doi:10.1016/j.ymssp.2018.08.061. [Google Scholar] [CrossRef]

159. Kanno Y, Fujita S, Ben-Haim Y. Structural design for earthquake resilience: info-gap management of uncertainty. Struct Saf. 2017;69:23–33. doi:10.1016/j.strusafe.2017.07.004. [Google Scholar] [CrossRef]

160. Kuczkowiak A, Cogan S, Ouisse M, Foltête E, Corus M. Experimental validation of an info-gap uncertainty model for a robustness analysis of structural responses. ASME J Risk Uncertain Eng Syst Part B: Mech Eng. 2020;6:030905. doi:10.1115/1.4047096. [Google Scholar] [CrossRef]

161. Atamturktur S, Liu Z, Cogan S, Juang H. Calibration of imprecise and inaccurate numerical models considering fidelity and robustness: a multi-objective optimization-based approach. Struct Multidiscipl Optim. 2015;51:659–71. doi:10.1007/s00158-014-1159-y. [Google Scholar] [CrossRef]

162. Takewaki I, Ben-Haim Y. Info-gap robust design with load and model uncertainties. J Sound Vib. 2005;288:551–70. doi:10.1016/j.jsv.2005.07.005. [Google Scholar] [CrossRef]

163. Kanno Y, Takewaki I. Robustness analysis of elastoplastic structure subjected to double impulse. J Sound Vib. 2016;383:309–23. doi:10.1016/j.jsv.2016.07.023. [Google Scholar] [CrossRef]

164. Kanno Y, Yasuda K, Fujita K, Takewaki I. Robustness of SDOF elastoplastic structure subjected to double-impulse input under simultaneous uncertainties of yield deformation and stiffness. Int J Non Linear Mech. 2017;91:151–62. doi:10.1016/j.ijnonlinmec.2017.02.013. [Google Scholar] [CrossRef]

165. Fujita K, Yasuda K, Kanno Y, Takewaki I. Robustness evaluation of elastic-plastic base-isolated high-rise buildings under critical double impulse. Front Built Environ. 2017;3:31. doi:10.3389/fbuil.2017.00031. [Google Scholar] [CrossRef]

166. Matsuda Y, Kanno Y. Robustness analysis of structures based on plastic limit analysis with uncertain loads. J Mech Mater Struct. 2008;3:213–42. doi:10.2140/jomms. [Google Scholar] [CrossRef]

167. Tang Y, Chen J, Wei J. A sequential algorithm for reliability-based robust design optimization under epistemic uncertainty. J Mech Des. 2012;134:014502. doi:10.1115/1.4005442. [Google Scholar] [CrossRef]

168. Kang Z, Bai S. On robust design optimization of truss structures with bounded uncertainties. Struct Multidiscipl Optim. 2013;47:699–714. doi:10.1007/s00158-012-0868-3. [Google Scholar] [CrossRef]

169. Luo Y, Kang Z, Luo Z, Li A. Continuum topology optimization with non-probabilistic reliability constraints based on multi-ellipsoid convex model. Struct Multidiscipl Optim. 2009;39:297–310. doi:10.1007/s00158-008-0329-1. [Google Scholar] [CrossRef]

170. Kang Z, Luo Y, Li A. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters. Strucrt Saf. 2011;33:196–205. doi:10.1016/j.strusafe.2011.03.002. [Google Scholar] [CrossRef]

171. Guo S-X, Lu Z-Z. A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters. Appl Math Model. 2015;39:1985–2002. doi:10.1016/j.apm.2014.10.026. [Google Scholar] [CrossRef]

172. Jiang C, Bi RG, Lu GY, Han X. Structural reliability analysis using non-probabilistic convex model. Comput Methods Appl Mech Eng. 2013;254:83–98. doi:10.1016/j.cma.2012.10.020. [Google Scholar] [CrossRef]

173. Rockafellar RT, Uryasev S. Optimization of conditional value-at-risk. J Risk. 2000;2:21–41. doi:10.21314/JOR.2000.038. [Google Scholar] [CrossRef]

174. Bleyer J. Risk-averse estimates of effective properties in heterogeneous elasticity. Comptes Rendus Mécanique. 2023;351:29–42. doi:10.5802/crmeca.171. [Google Scholar] [CrossRef]

175. Byun JE, de Oliveira W, Royset JO. S-BORM: reliability-based optimization of general systems using buffered optimization and reliability method. Reliab Eng Syst Saf. 2023;236:109314. doi:10.1016/j.ress.2023.109314. [Google Scholar] [CrossRef]

176. Byun JE, Royset JO. Data-driven optimization of reliability using buffered failure probability. Struct Saf. 2022;98:102232. doi:10.1016/j.strusafe.2022.102232. [Google Scholar] [CrossRef]

177. Chaudhuri A, Kramer B, Norton M, Royset JO, Willcox K. Certifiable risk-based engineering design optimization. AIAA J. 2022;60:551–65. doi:10.2514/1.J060539. [Google Scholar] [CrossRef]

178. Rockafellar RT, Royset JO. On buffered failure probability in design and optimization of structures. Reliab Eng Syst Saf. 2010;95:499–510. doi:10.1016/j.ress.2010.01.001. [Google Scholar] [CrossRef]

179. Kanno Y, Ben-Haim Y. Redundancy and robustness, or, when is redundancy redundant? J Struct Eng. 2011;137:935–45. doi:10.1061/(ASCE)ST.1943-541X.0000416. [Google Scholar] [CrossRef]

180. Kirchdoerfer T, Ortiz M. Data-driven computational mechanics. Comput Methods Appl Mech Eng. 2016;304:81–101. doi:10.1016/j.cma.2016.02.001. [Google Scholar] [CrossRef]

181. Guo X, Du Z, Liu C, Tang S. A new uncertainty analysis-based framework for data-driven computational mechanics. J Appl Mech. 2021;88:111003. doi:10.1115/1.4051594. [Google Scholar] [CrossRef]

182. Kanno Y. Computation-with-confidence for static elasticity: data-driven approach with order statistics. Zeitschrift Für Angewandte Mathematik Und Mechanik. 2023;103:e202100482. doi:10.1002/zamm.202100482. [Google Scholar] [CrossRef]

183. Cho H, Choi KK, Gaul NJ, Lee I, Lamb D, Gorsich D. Conservative reliability-based design optimization method with insufficient input data. Struct Multidiscipl Optim. 2016;54:1609–30. doi:10.1007/s00158-016-1492-4. [Google Scholar] [CrossRef]

184. Ito M, Kim NH, Kogiso N. Conservative reliability index for epistemic uncertainty in reliability-based design optimization. Struct Multidiscipl Optim. 2018;57:1919–35. doi:10.1007/s00158-018-1903-9. [Google Scholar] [CrossRef]

185. Jung Y, Cho H, Duan Z, Lee I. Determination of sample size for input variables in RBDO through bi-objective confidence-based design optimization under input model uncertainty. Struct Multidiscipl Optim. 2020;61:253–66. doi:10.1007/s00158-019-02357-w. [Google Scholar] [CrossRef]

186. Hao P, Yang H, Yang H, Zhang Y, Wang Y, Wang B. A sequential single-loop reliability optimization and confidence analysis method. Comput Methods Appl Mech Eng. 2022;399:115400. doi:10.1016/j.cma.2022.115400. [Google Scholar] [CrossRef]

187. Kanno Y. Non-parametric data-driven approach to reliability-based topology optimization of trusses under uncertainty of material constitutive law. J Adv Mech Design Syst Manuf. 2024;18:24–00223. doi:10.1299/jamdsm.2024jamdsm0064. [Google Scholar] [CrossRef]

188. Huang M, Liu C, Du Z, Tang S, Guo X. A sequential linear programming (SLP) approach for uncertainty analysis-based data-driven computational mechanics. Comput Mech. 2024;73:943–65. doi:10.1007/s00466-023-02395-8. [Google Scholar] [CrossRef]