 Open Access
Open Access
ARTICLE
Radiative Flow of Ag-Fe3O4/Water Hybrid Nanofluids Induced by a Shrinking/Stretching Disk with Influence of Velocity and Thermal Slip Conditions
1 Institute of Mathematics and Computer Science, University of Sindh, Jamshoro Sindh, 76080, Pakistan
2 KCAMS Khairpur Mir’s, Sindh Agriculture University, Tandojam Sindh, 70060, Pakistan
3 Department of Economics, College of Business Administration, King Saud University, Riyadh, 145111, Saudi Arabia
4 Department of Mathematics, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Saveetha University, Chennai, 602105, India
5 Department of Mathematics, Faculty of Science, Sakarya University, Serdivan/Sakarya, 54050, Turkey
* Corresponding Author: Umair Khan. Email:
Computer Modeling in Engineering & Sciences 2025, 143(1), 499-513. https://doi.org/10.32604/cmes.2025.061804
Received 03 December 2024; Accepted 13 February 2025; Issue published 11 April 2025
Abstract
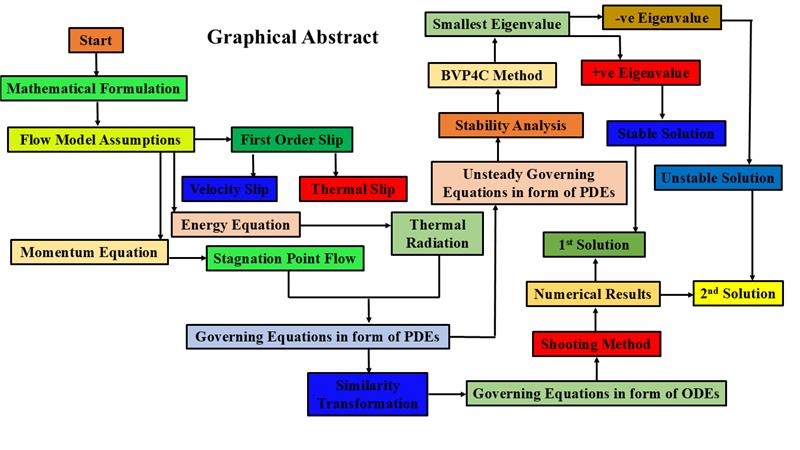
This paper discusses the model of the boundary layer (BL) flow and the heat transfer characteristics of hybrid nanofluid (HNF) over shrinking/stretching disks. In addition, the thermal radiation and the impact of velocity and thermal slip boundary conditions are also examined. The considered hybrid nano-fluid contains silver (Ag) and iron oxide (Fe3O4) nanoparticles dispersed in the water to prepare the Ag-Fe3O4/water-based hybrid nanofluid. The requisite posited partial differential equations model is converted to ordinary differential equations using similarity transformations. For a numerical solution, the shooting method in Maple is employed. Moreover, the duality in solutions is achieved for both cases of the disk (stretching () and shrinking ()). At the same time, a unique solution is observed for = 0. No solution is found for them at , whereas the solutions are split at the . Besides, the value of the is dependent on the . Meanwhile, the values of and intensified with increasing . Stability analysis has been applied using bvp4c in MATLAB software due to a dual solution. Furthermore, analysis shows that the first solution is stable and feasible physically. For the slip parameters, an increase in the velocity slip parameter increases the velocity and shear stress profiles while increasing the temperature profile in the first solutions. While the rise in thermal slip parameter reduces the temperature profile nanoparticle volume fractions increase it.Graphic Abstract
Keywords
The manufacturing sector has experienced significant advantages from using nanofluids, which possess highly favorable properties for heat transfer and heat conductivity. The employment of nanofluids has enabled these advantages. Traditional fluids like ethylene glycol, water, and lubricants have been commonly used in various industrial and technical processes with low thermal conductivity and heat transfer enhancement. To overcome these challenges, Choi et al. [1] introduced nanofluid that was prepared through the suspension of a different type of Nano-sized particle in the common traditional fluids later on, Kang et al. [2] investigated different aspects of Nano-fluid. The impact of Al2O3 and Cu nanoparticles on the flow and heat transfer characteristics in water-based Nano-fluids was examined by Lee et al. [3] experimentally. Although these Nano-fluidic systems complete many requirements of the modern engineering and industrial fields, investigators have always been in search of obtaining more and more effective Nano-fluidic systems. In this regard, for a few years, various studies have been performed to develop more effective types of the latest fluids dispersing various nanoparticles in a base fluid at a time which were named HNFs. The main purpose behind the preparation is to improve the heat-transferring capability as compared to common nanofluids by using different kinds of nanoparticles at the same time. Because of possessing enhanced thermal capabilities, such fluids can be used in various applications in medical, engineering, and industrial fields like as in solar heating systems, HVAC, cooling in transformers, MCHS (microchannel heat sink), and biomedical and electronic cooling [4]. Since the last many years, several investigators have been exploring different flow characteristics of HNF in the different geometrical shapes where their study have shown greater heat transfer capabilities of HNF as compared to common fluids/nanofluids [5–8]. Furthermore, CuO-water-based nanofluid and CuO-Ag water-based HNF in a vibrant cylindrical chamber were theoretically studied by Rajesh et al. [9]. The effects of Newton heating and MHD on HNF over-stretching sheets were studied by Devi et al. [10]. Nagoor et al. [11] investigated the flow characteristics of HNF numerically by using a bvp4c solutions technique over the revolving frame. Alempour et al. [12] examined the flow in a three-dimensional oval tube having circular types of the cross-sector. Their findings indicate an increase in friction and an increase in thermal characteristics due to changes in flow geometries. Three-dimensional MHD flows of HNF on a spinning disk were examined by Ouyang et al. [13].
To find the possibility that the fluid may slide on the solid’s surface, Navier presented a more general boundary condition (BC) in 1823. The slip BC was identified by Maxwell in 1879 using the gas kinetic theory [14,15]. Consequently, it is considered that the fluid velocity at the solid surface is directly proportional to the surface shear rate, with the constant proportionality having length dimensions [16]. The slip length is the imaginary distance inside a solid where the linear extrapolation of fluid velocity to zero. When fluid molecules behave differently at solid surfaces than when develop bulk in fluids, this phenomenon is called a slip condition in fluid mechanics [17]. Given their influence on fluid dynamics and properties, slip conditions are fundamental in a variety of contexts. In many different areas, slip conditions show an important character, such as in the design of efficient microfluidic systems [18], biomedical applications [19], nano-membranes, lab-on-a-chip devices, nanoscale sensors [20], thermal management systems, and improvement of oil extraction and transport processes [21]. They are also essential in designing blood vessels, biological tissues, drug delivery, blood flow, and biomedical systems [22]. Muhammad et al. [23] discovered that velocity slip parameters reduce SFC while examining HNF. Eid et al. [24] analyzed the Fe3O4-Cu/EG HNF, focusing on the impact of slip effects. Alharbi et al. [25] employed the slip effect on the ternary HNF and observed that the average velocity profile is raised as a result of improved slipping effects. In their statistical and theoretical study, Djoko et al. [26] examined the Navier-Stokes equations, which are subject to a BC related to power law slip. Moreover, Yasin et al. [27] worked on the peristalsis MHD Maxwell viscous-elastic fluid that is subject to slip conditions. Jamrus et al. [28] employed the Tiwari model to investigate the properties of a ternary HNF. To learn more about the uses of slip effects in various models of nanofluids and HNFs, readers can also check out the work done by [29–33] other related articles of Tiwari and Das’s model are also used by the researcher.
The main aim of this article is to study the flow and heat-transfer characteristics of Ag-Fe3O4/H2O HNF over stretched/shrinking disks with radiation and slip effects. This work was extended to the work done by Waini et al. [34]. The numerical investigations show duality in solutions due to which stability analysis is performed to check the feasibility of achieved solutions. The present work will be beneficial for researchers who want to work in the modern field of fluid mechanics of hybrid Nanofluid over disk which is rarely considered on a disk surface. On the other hand, this study also helps researchers how to deal with problems when more than one solution arises for the same value of parameter due to the non-linearity of the equations. The present study can be extended to ternary hybrid Nanofluid with non-Newtonian base Nanofluid with different boundary conditions over different geometrical phenomena.
There have been considered flow and heat transfer characteristics of Ag-Fe3O4/H2O hybrid nanofluid over stretching/shrinking disk. The following assumptions have been made:
• Thermal radiation effects are considered.
• The slip effect is also considered in the study.
• The flow phenomenon is described using a coordinate system, as shown in Fig. 1.
• The surface is set at
•
•
•
•
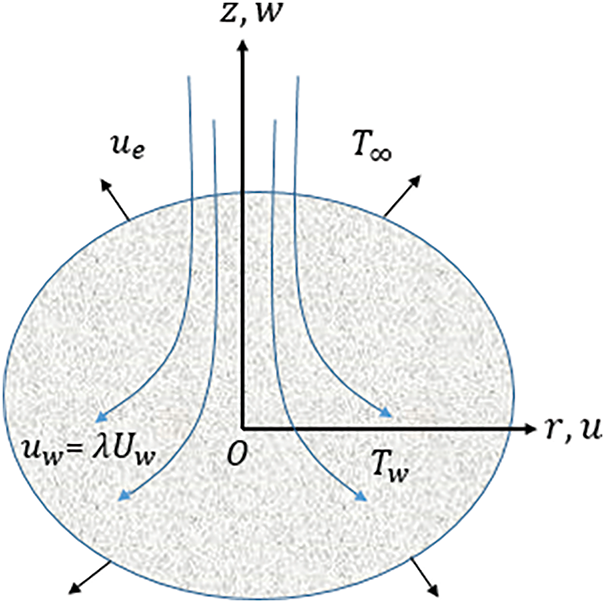
Figure 1: The flow phenomenon and coordinate system
The governing equations of the problem are written as:
Subject to BCs:
where u and w denote velocities components that are measured in directions of radial r and axial z. While,
where
To get similar solutions of the Eqs. (1)–(4), the following similarity transformation has been adopted as suggested by Waini et al. [34] and Weidman [35].
Substituting Eq. (8), Eqs. (2)–(4) have been transformed to ODEs as:
The reduced BCs are:
where
Furthermore, the SFC
Substituting Eq. (8) in Eq. (12), there is obtained
where
The numerical solution for the Eqs. (9)–(11) has been achieved by the applying shooting method in Maple software. The problem may be written as:
Subject to the boundary conditions:
where α1 and α2 are used for missing initial conditions. The results are obtained by shooting methods by adding shootlib functions in Maple software, whereas thermos-physical properties of the used nanoparticles are presented in Table 1 and defined in Table 2.
Whereas, f and hnf as a subscript indicate the base fluid and HNF, respectively.
The numerical investigation exhibits the existence of the dual nature of solutions across different ranges of the values of the particularly used parameters. To detect the viability of achieved solutions, there has been performed stability analysis as done by Merkin [36]. In this regard, Eqs. (2)–(4) are written into related unsteady form as:
The similarity transformation is modified as:
where
and boundary conditions are:
Following to the Weidman et al. [37], the steady solution
The functions
Subject to Boundary conditions are:
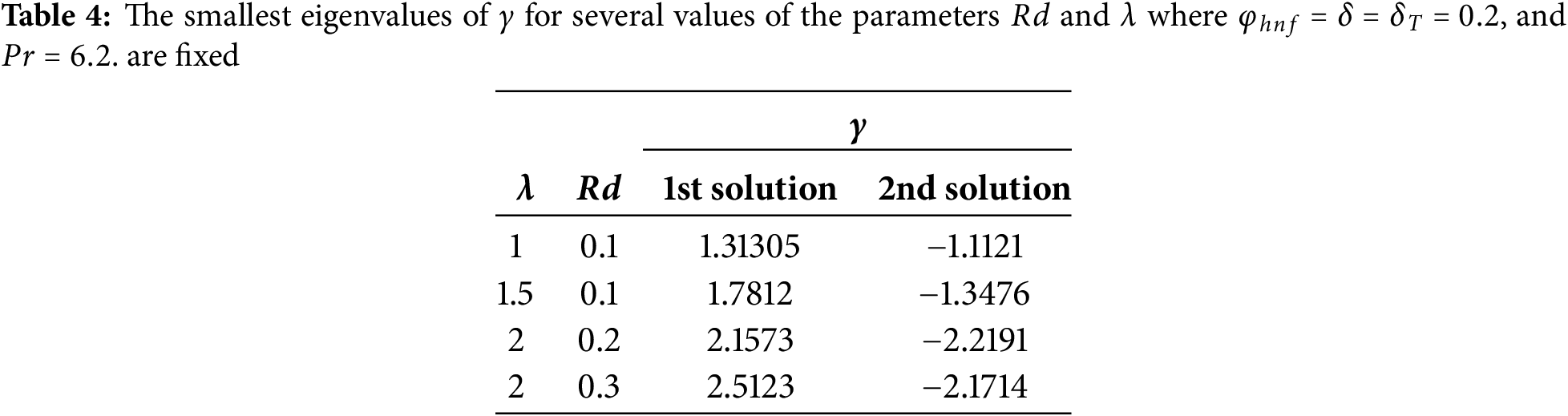
There are solved the above-linearized Eqs. (25) and (26) that are subject to conditions (27). Also, to achieve the smallest values
The numerical solution for a system of Eqs. (9) and (10) having boundary conditions in Eq. (11) is obtained by the shooting method in the software of Maple. The effects of nanoparticle volume fraction
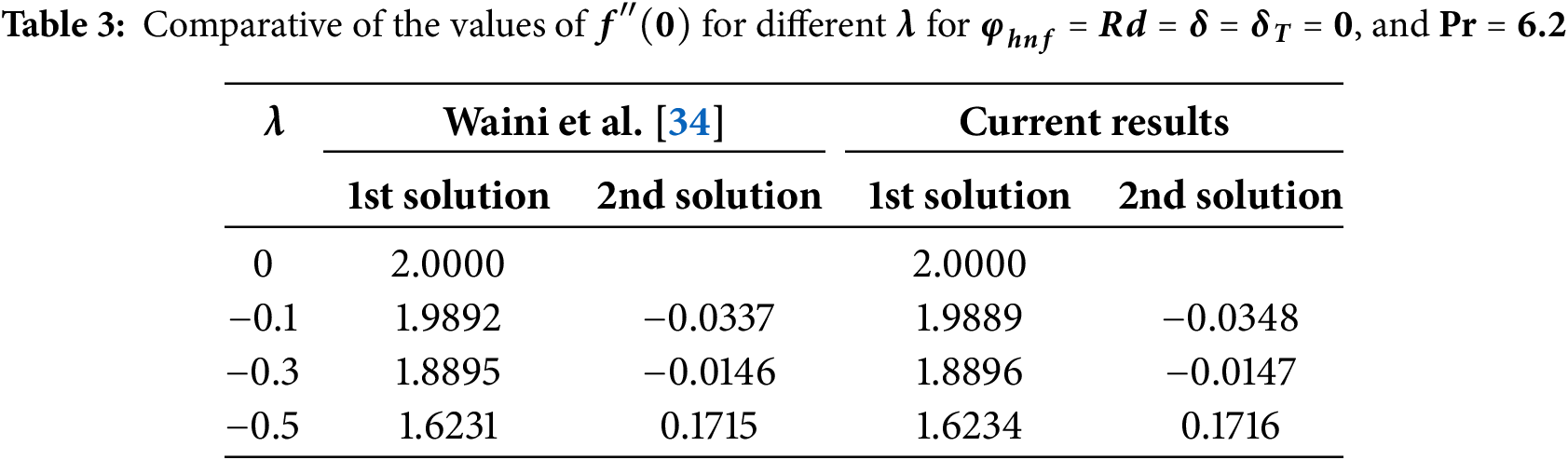
Furthermore, for the variation of the different physical parameters on SFC and Nusselt numbers along with velocity and temperature profiles dual solutions are achieved. To verify the feasibility of achieved solutions, there is performed stability analysis of solutions through the III-stage-Lobatto-IIIA formula that has been established in the bvp4c. The numerical values obtained through stability analysis are presented in Table 4, which indicates that the first solution is stable and physically feasible whose achieved eigenvalues are positive indicating continuity of the solutions. The second solution has been found unstable and physically impossible due to negative eigenvalues.
Additionally, the influences of various physical parameters on the SFC
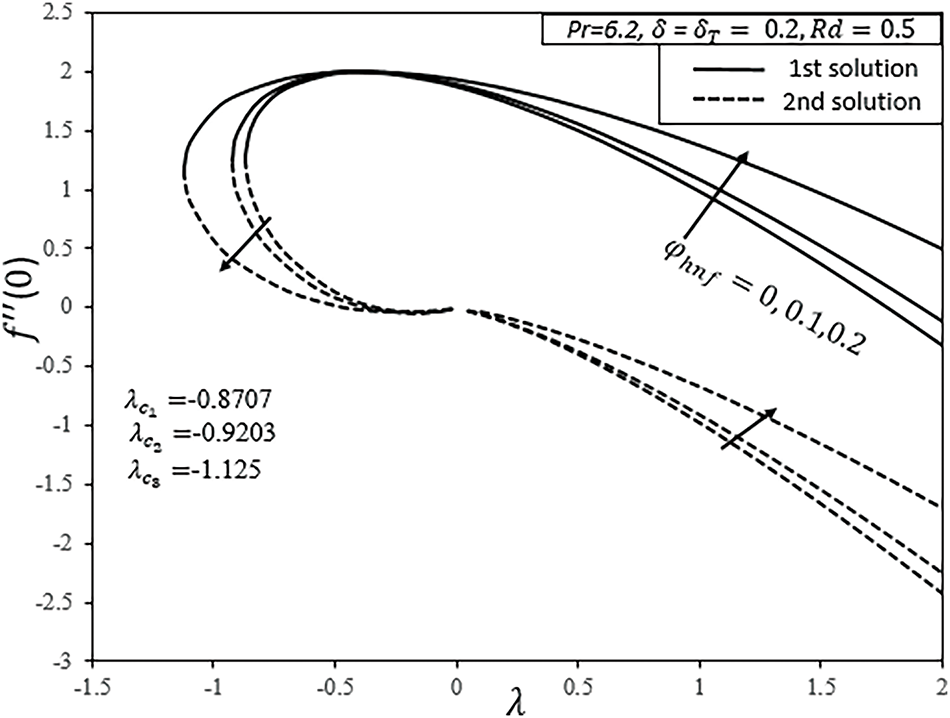
Figure 2: Variation of
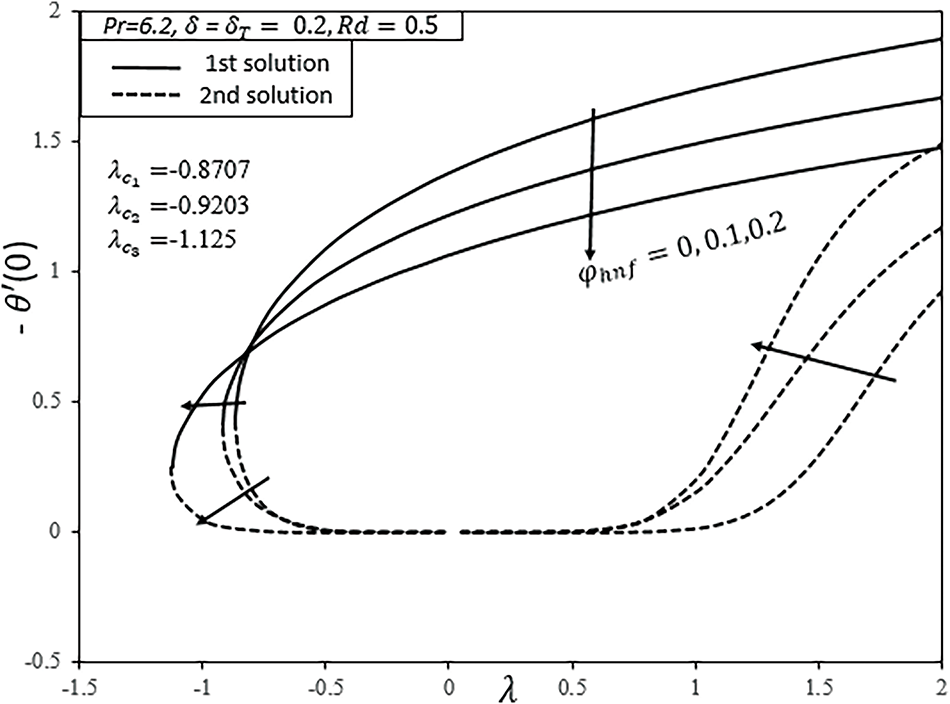
Figure 3: Variation of
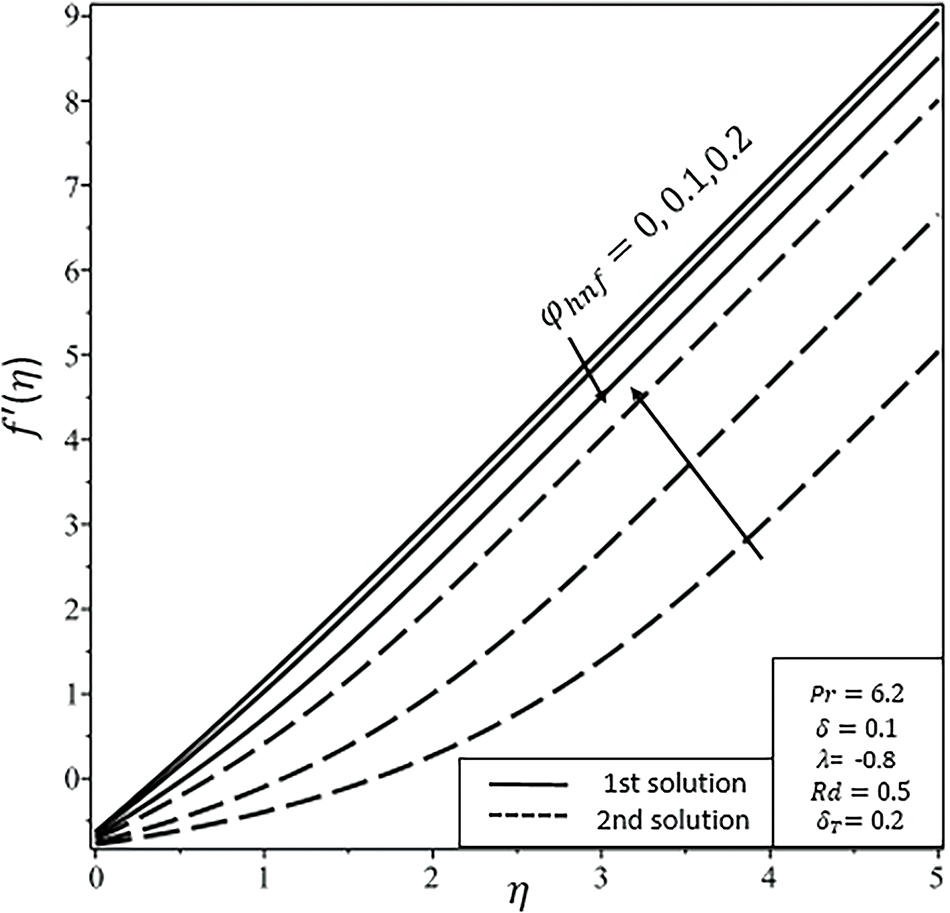
Figure 4: Velocity
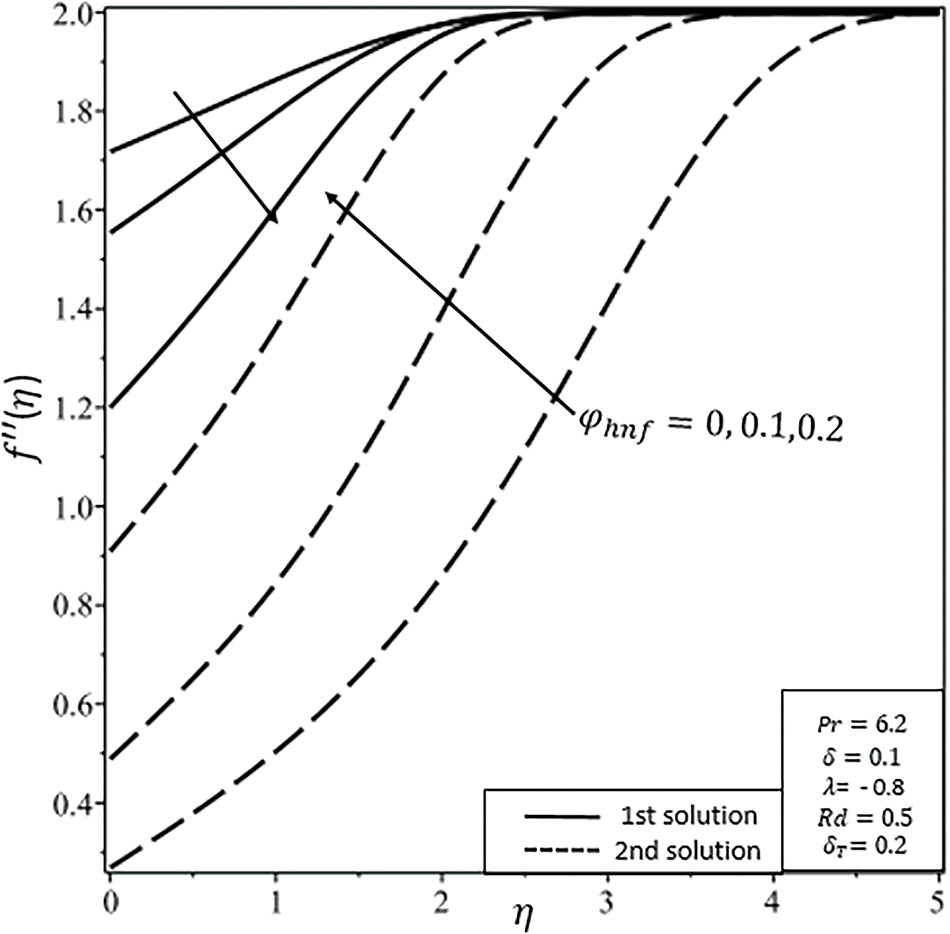
Figure 5: Shear stress
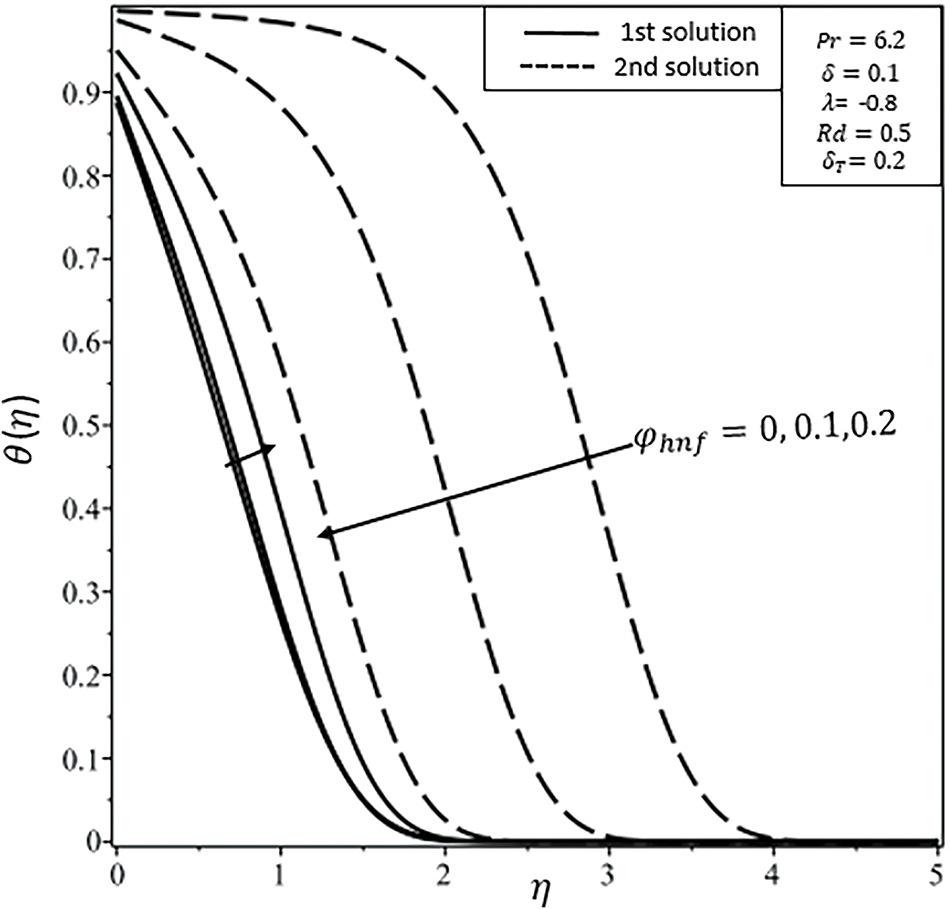
Figure 6: Temperature
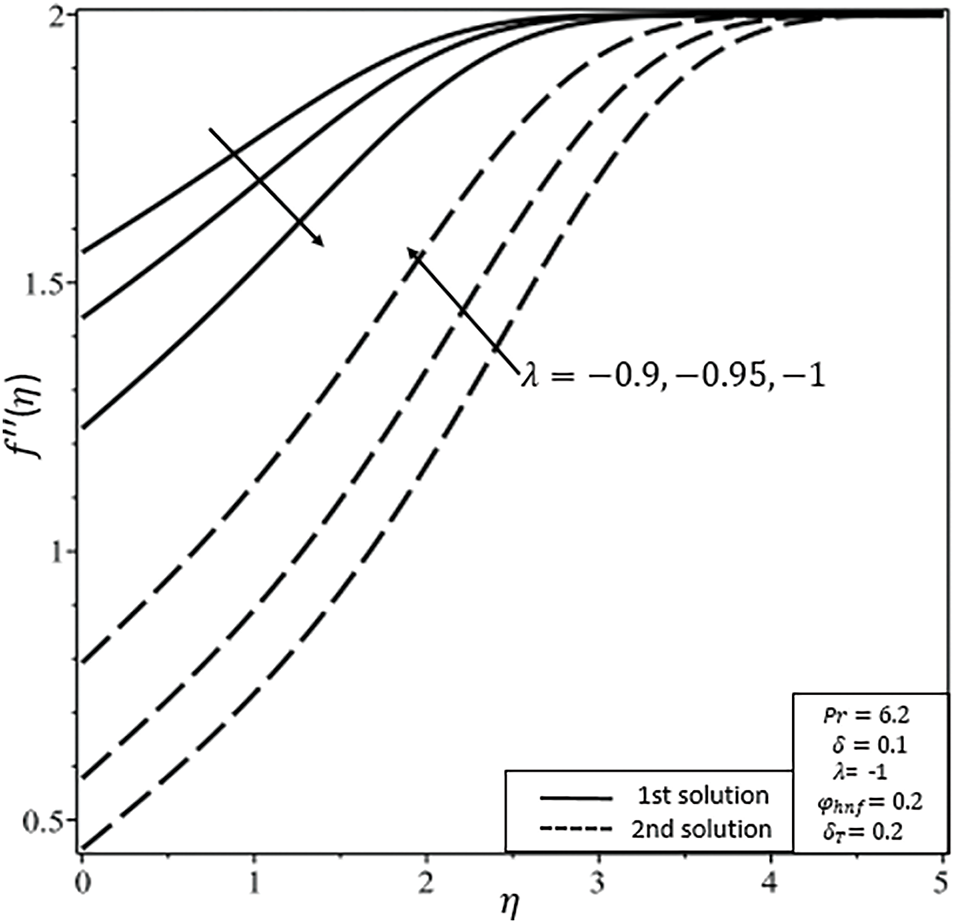
Figure 7: Shear stress
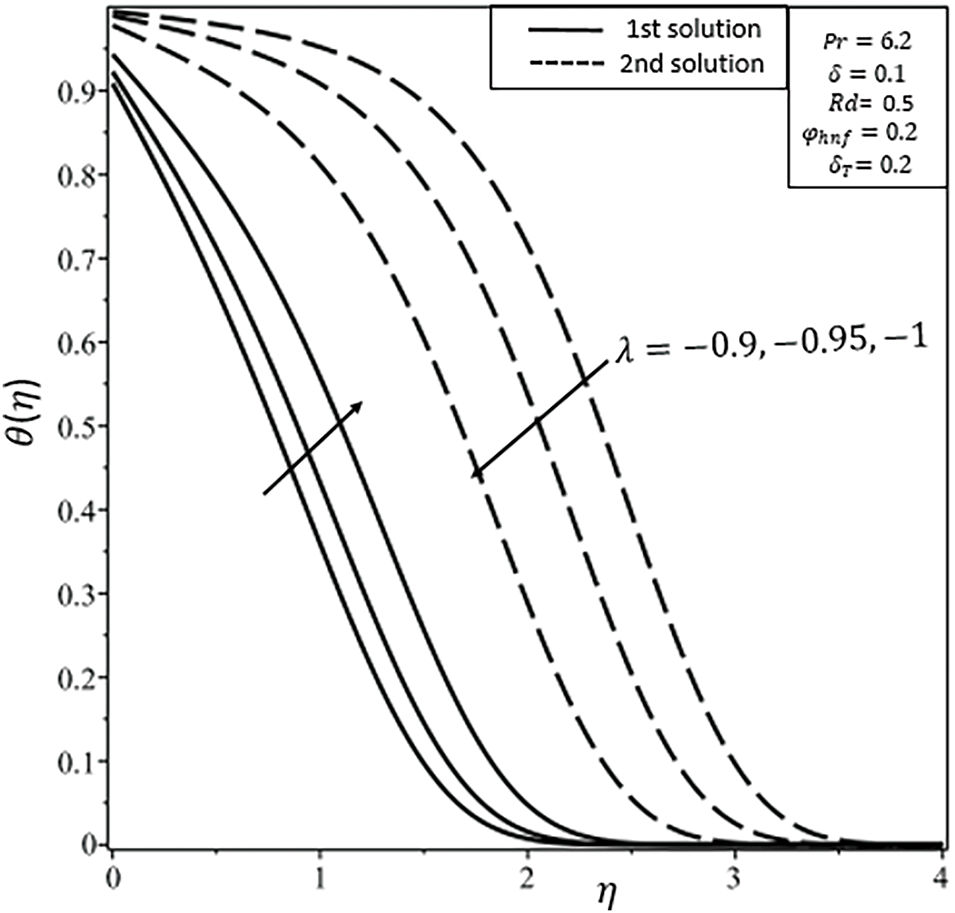
Figure 8: Temperature
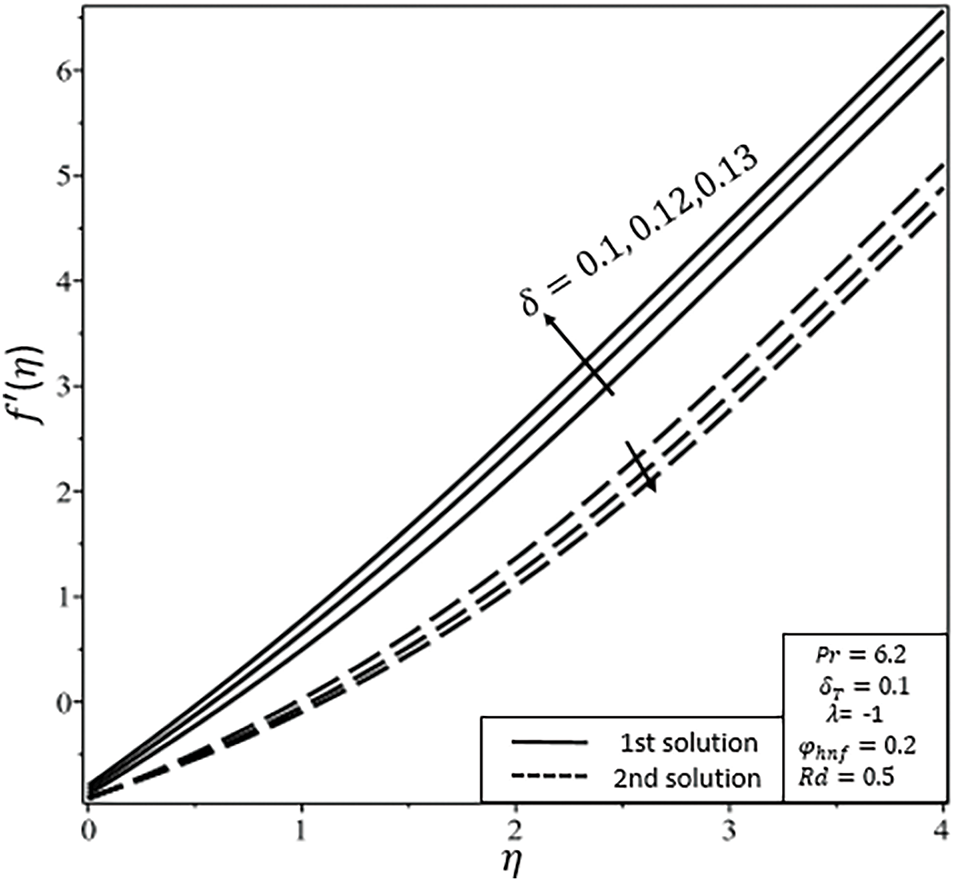
Figure 9: Velocity
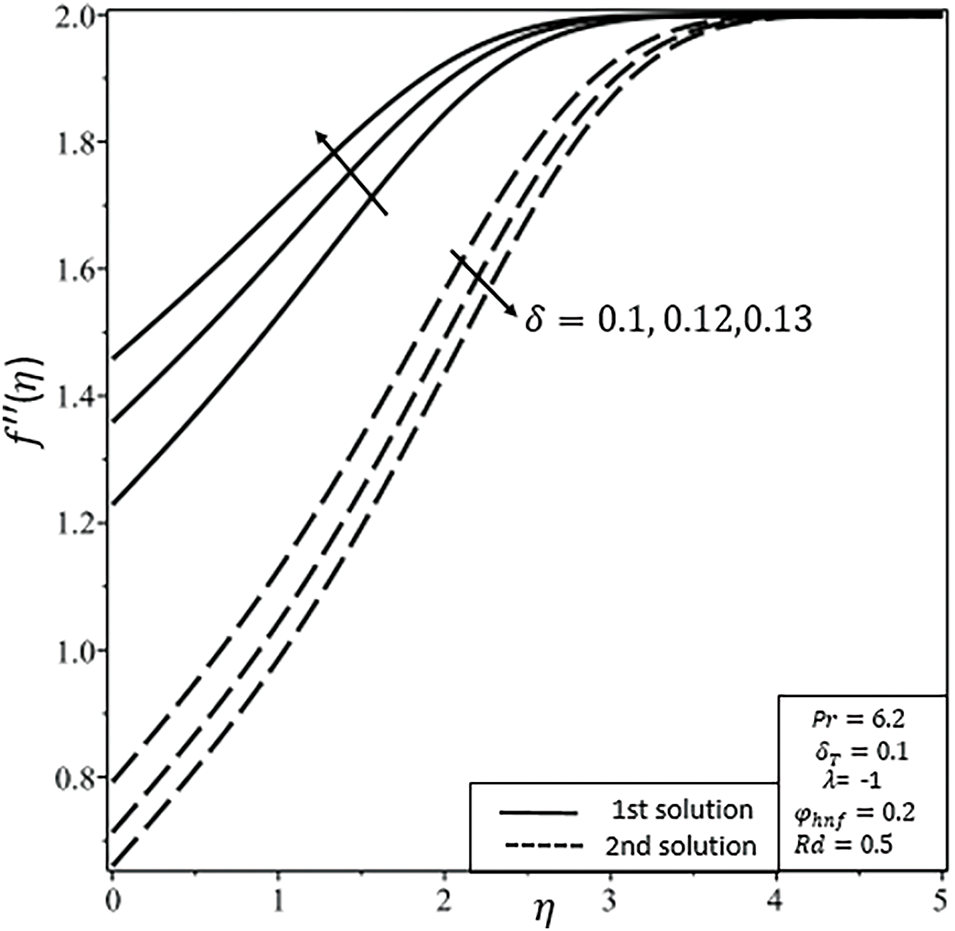
Figure 10: Shear stress
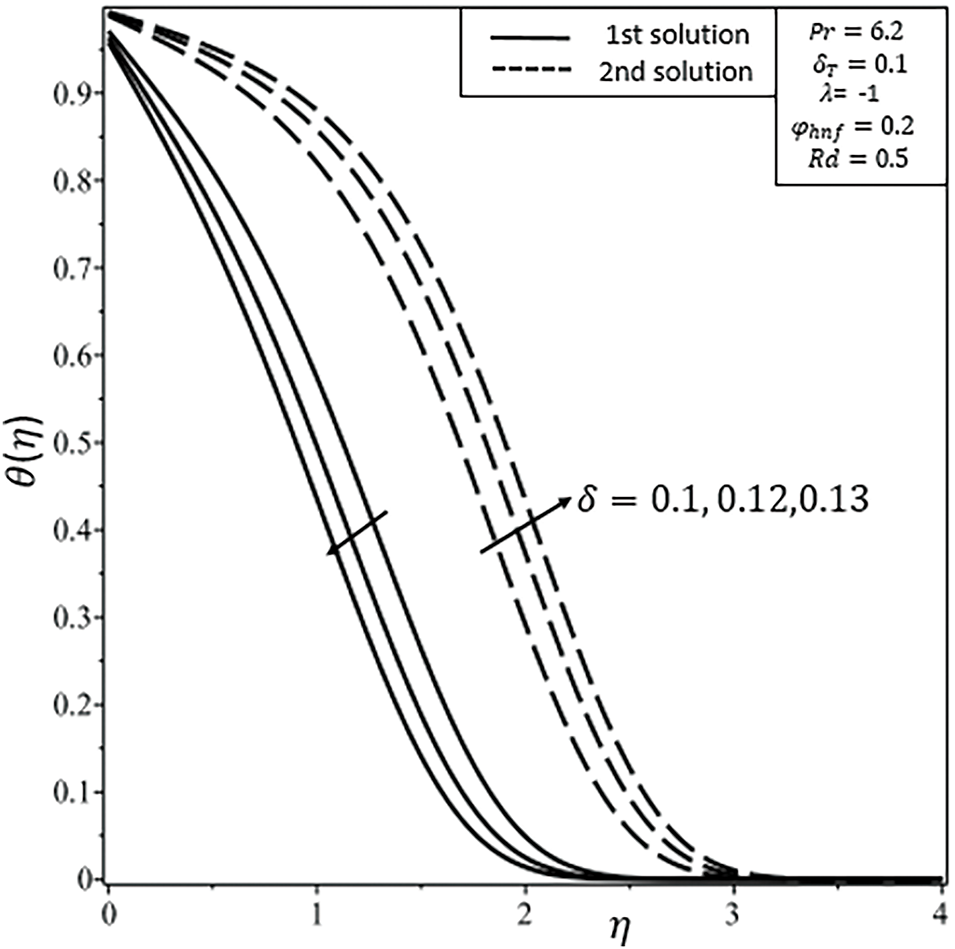
Figure 11: Temperature
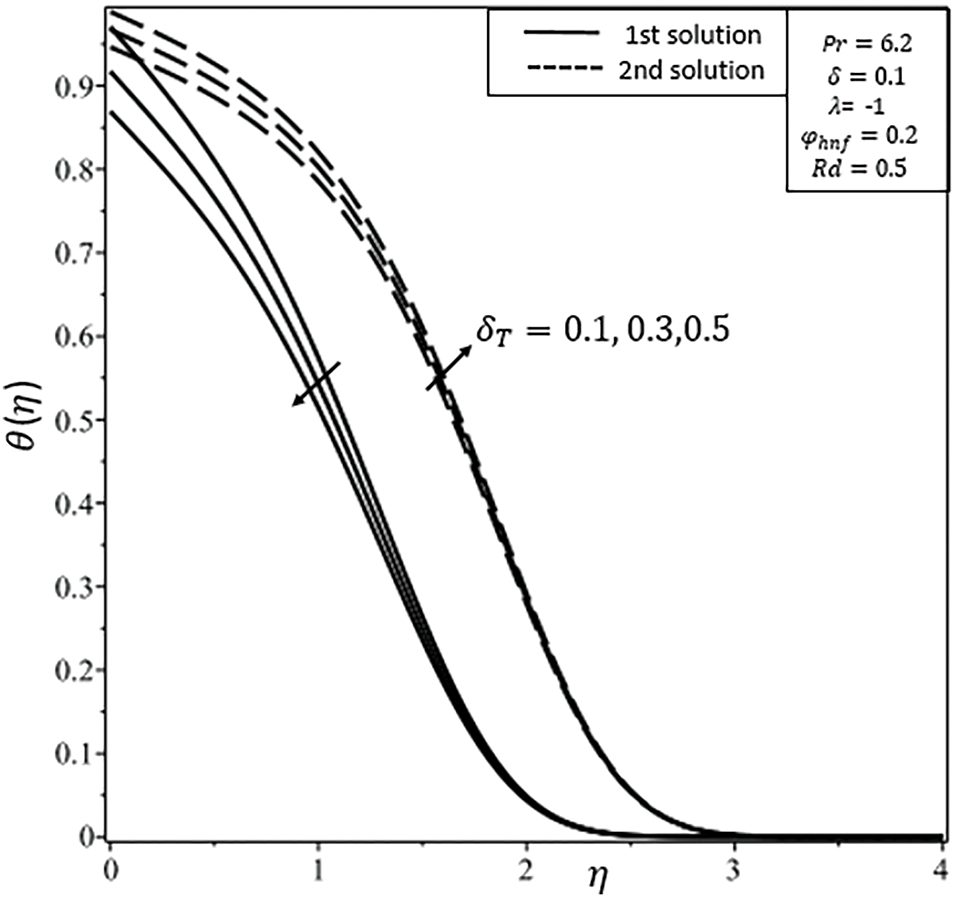
Figure 12: Temperature
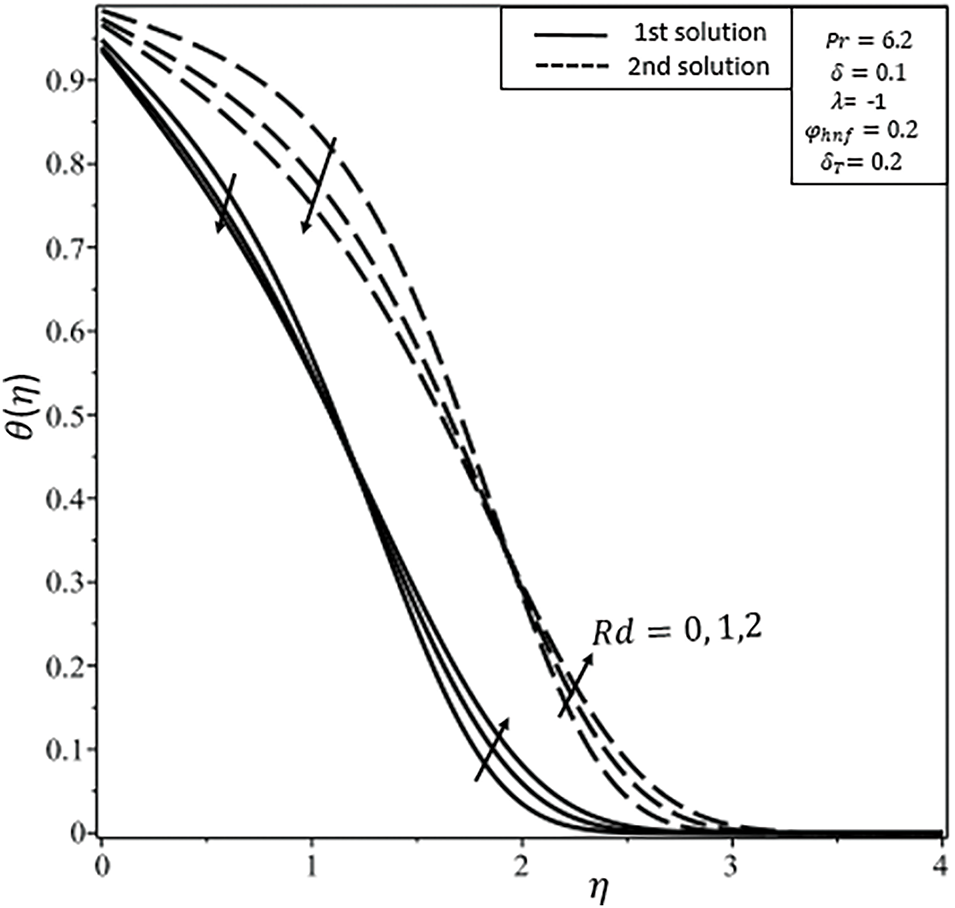
Figure 13: Temperature
The impact of nanoparticle volumetric fractions, denoted by
Figs. 4–6 show the combined effects of nanoparticles volumetric fraction of Ag and Fe2O4 nanoparticles on the velocity, shear stress, and temperature profiles of water-based HNF flow over the disk, respectively. Figs. 4 and 5 indicate that an increase in the rate of nanoparticles of Ag and Fe2O4 in water-based fluid raises velocity and shear stress profiles in the first (stable) solution. Fig. 6 demonstrates that the temperature profile and thermal boundary layer (BL) thickness rise throughout the flow in the first solution with an increase in nanoparticle volume fraction. Any increase in the rate of nanoparticles develops resistance in the flow because of increasing viscosity between flowing fluid layers, so, the velocity decreases and temperature rises [44].
Figs. 7 and 8 indicate the effects of shrinking parameters
Fig. 12 illustrates the influence of the thermal slip parameter (
Physically a higher thermal slip decreases the wall heat flux, aligns the fluid to retain more heat, and increases the temperature profile. The effect of thermal radiation
Due to the wide range of industrial applications of the Ag-Fe3O4/H2O hybrid nanofluid model, BL flow and heat transfer characteristics are considered over stretching/shrinking disk with thermal radiation and slip effects. The shooting method is employed to achieve the numerical solutions of the equations to analyze the effects of the different used parameters on the velocity profile, shear stress, and temperature profile. Moreover, stability analysis for the existing model has been performed due to the occurrence of duality in solutions. The main findings of the present study are given as follows:
• There are two solutions found, for
• The first solution exhibits stability and physical viability, whereas the second solution is deemed unstable.
• Notably, the skin friction coefficient (SFC) undergoes an increase for both stretching and shrinking scenarios, characterized by the parameter λ, as the volume fraction of nanoparticles rises.
• The Nusselt number decreases as the nanoparticle volume fraction increases for
• An increase in nanoparticle volume fractions decreases the velocity and shear stress profiles.
• A rise in the velocity slip parameter has a multifaceted effect, yielding enhancements in both velocity and shear stress profiles, while concurrently inducing a decline in the temperature profile.
• An increase in thermal slip parameter decreases the temperature profile but on the other hand, increasing nanoparticle volume fractions increases the temperature profile.
• An increase in radiation parameters at the start decreases the temperature profiles, but after that, it increases the temperature profile throughout the flow.
The present research has two primary limitations. Firstly, it focuses exclusively on cylindrical coordinates and HNF flow incorporating two nanoparticles, thermal radiation, and slip effects. Secondly, the study is restricted to examining two solutions, accompanied by a stability analysis.
Acknowledgement: The authors appreciate the support of the Researchers Supporting Project number (RSPD2025R997), King Saud University, Riyadh, Saudi Arabia.
Funding Statement: The authors received funding support from the Researchers Supporting Project number (RSPD2025R997), King Saud University, Riyadh, Saudi Arabia.
Author Contributions: Muhammad Zubair Mustafa, Sumera Dero: Conceptualization, Methodology, Software, Formal analysis, Validation, Writing—original draft. Liaquat Ali Lund: Writing—original draft, Data curation, Investigation, Visualization, Validation. Umair Khan: Conceptualization, Writing—original draft, Writing—review & editing, Supervision, Resources. Mehboob Ul Hassan: Validation, Investigation, Writing—review & editing, Formal analysis, Project administration, Funding acquisition, Software. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Umair Khan, upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Radial and axial directions (m) | |
| Stretching & shrinking velocity (m/s) | |
| u, w | Velocity components (m/s) |
| Surface velocity (m/s) | |
| Free stream velocity (m/s) | |
| Gravitational force (m/s2) | |
| T | Temperature (K) |
| Dimensionless Temperature | |
| Sheet temperature (K) | |
| Ambient temperature (K) | |
| Ag | Silver |
| Fe3O4 | Iron oxide |
| Volume fractions of nanoparticles (Ag) | |
| Volume fractions of nanoparticles (Fe3O4) | |
| Density of nanofluid (kg/m3) | |
| Heat capacitance (J/kg3.K) | |
| Dynamical viscosity (m2/s) | |
| Local Nusselt number | |
| Mean absorption coefficient (1/m) | |
| Thermal conductivity (W/m·K) | |
| Kinematic viscosity (m²/s) | |
| Stability transformed variable | |
| Radiative heat flux (W/m²) | |
| Local Reynolds number | |
| Thermal diffusivity (m2/s) | |
| Thermal conductivity (W/m·K) | |
| Similarity variable | |
| Thermal radiation | |
| Stream function | |
| Pr | Prandtl number |
| Shrinking/stretching parameter | |
| Constant of Stefan-Boltzmann (W/m2·K4) | |
| Unknown eigenvalue | |
| Electrical conductivity | |
| Dynamic viscosity fluid (Pa·s) | |
| Velocity slip parameter | |
| Thermal slip parameter | |
| Skin friction coefficient (SFC) |
References
1. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab. (ANLArgonne, IL, USA; 1995. Report No.: ANL/MSD/CP-84938; CONF-951135-29. [Google Scholar]
2. Kang HU, Kim SH, Oh JM. Estimation of thermal conductivity of nanofluids for the application of heat transfer fluids. Exp Heat Transf. 2006;19(3):181–91. doi:10.1080/08916150600619281. [Google Scholar] [CrossRef]
3. Lee S, Choi SS, Li SA, Eastman JA. Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transfer. 1999;121(2):280–9. doi:10.1115/1.2825978. [Google Scholar] [CrossRef]
4. Babar H, Ali HM. Towards hybrid nanofluids: preparation, thermophysical properties, applications, and challenges. J Mol Liq. 2019;281:598–633. doi:10.1016/j.molliq.2019.02.102. [Google Scholar] [CrossRef]
5. Babu JR, Kumar KK, Rao SS. State-of-art review on hybrid nanofluids. Renew Sustain Energy Rev. 2017;77:551–65. doi:10.1016/j.rser.2017.04.040. [Google Scholar] [CrossRef]
6. Dero S, Shaikh H, Talpur GH, Khan I, Alharbim SO, Andualem M. Influence of a Darcy-Forchheimer porous medium on the flow of a radiative magnetized rotating hybrid nanofluid over a shrinking surface. Sci Rep. 2021;11(1):1–16. doi:10.1038/s41598-021-03470-x. [Google Scholar] [PubMed] [CrossRef]
7. Hafeez A, Liu D, Khalid A, Du M. Melting heat transfer features in a Bödewadt flow of hybrid nanofluid (Cu− Al2O3/water) by a stretching stationary disk. Case Stud Therm Eng. 2024;59:104554. doi:10.1016/j.csite.2024.104554. [Google Scholar] [CrossRef]
8. Yang L, Ji W, Mao M, Huang JN. An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects. J Clean Prod. 2020;257:120408. doi:10.1016/j.jclepro.2020.120408. [Google Scholar] [CrossRef]
9. Rajesh V, Chamkha A, Kavitha M. Numerical investigation of Ag-CuO/water hybrid nanofluid flow past a moving oscillating cylinder with heat transfer. Math Methods Appl Sci. 2020. doi:10.1002/mma.6884. [Google Scholar] [CrossRef]
10. Devi SSU, Devi SA. Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can J Phys. 2016;94(5):490–6. doi:10.1139/cjp-2015-0799. [Google Scholar] [CrossRef]
11. Nagoor AH, Alaidarous ES, Sabir MT, Shoaib M, Raja MAZ. Numerical treatment for three-dimensional rotating flow of carbon nanotubes with Darcy-Forchheimer medium by the Lobatto IIIA technique. AIP Adv. 2020;10(2):025016. doi:10.1063/1.5135165. [Google Scholar] [CrossRef]
12. Alempour SM, AbbasianArani AA, Najafizadeh MM. Numerical investigation of nanofluid flow characteristics and heat transfer inside a twisted tube with elliptic cross section. J Therm Anal Calorim. 2020;140(3):1237–57. doi:10.1007/s10973-020-09337-z. [Google Scholar] [CrossRef]
13. Ouyang C, Akhtar R, Raja MAZ, Sabir MT, Awais M, Shoaib M. Numerical treatment with Lobatto IIIA technique for radiative flow of MHD hybrid nanofluid (Al2O3-Cu/H2O) over a convectively heated stretchable rotating disk with velocity slip effects. AIP Adv. 2020;10(5):055122. doi:10.1063/1.5143937. [Google Scholar] [CrossRef]
14. Maxwell J. A treatise on the kinetic theory of gases. Nature 1877;16:242–6. doi:10.1038/016242a0. [Google Scholar] [CrossRef]
15. Maxwell JC. Maxwell on molecules and gases. Cambridge, MA, USA: MIT Press; 1986. [Google Scholar]
16. Galea TM, Attard P. Molecular dynamics study of the effect of atomic roughness on the slip length at the fluid− solid boundary during shear flow. Langmuir. 2004;20(8):3477–82. doi:10.1021/la035880k. [Google Scholar] [PubMed] [CrossRef]
17. Squires TM, Quake SR. Microfluidics: fluid physics at the nanoliter scale. Rev Mod Phys. 2005;77(3):977. doi:10.1103/RevModPhys.77.977. [Google Scholar] [CrossRef]
18. Zhang J, Yan S, Yuan D, Alici G, Nguyen NT, Warkiani ME, et al. Fundamentals and applications of inertial microfluidics: a review. Lab Chip. 2016;16(1):10–34. doi:10.1039/C5LC01159K. [Google Scholar] [PubMed] [CrossRef]
19. Karniadakis G, Beskok A, Aluru N. Microflows and nanoflows: fundamentals and simulation. New York, NY, USA: Springer; 2006. [Google Scholar]
20. Bocquet L, Charlaix E. Nanofluidics, from bulk to interfaces. Chem Soc Rev. 2010;39(3):1073–95. doi:10.1039/B909366B. [Google Scholar] [PubMed] [CrossRef]
21. Cottin-Bizonne C, Barentin C, Charlaix E, Bocquet L, Barrat JL. Dynamics of simple liquids at heterogeneous surfaces: molecular-dynamics simulations and hydrodynamic description. Eur Phys J E. 2004;15(4):427–38. doi:10.1140/epje/i2004-10061-9. [Google Scholar] [PubMed] [CrossRef]
22. Yan L, Dero S, Khan I, Mari IA, Baleanu D, Nisar KS, et al. Dual solutions and stability analysis of magnetized hybrid nanofluid with joule heating and multiple slip conditions. Processes. 2020;8(3):332. doi:10.3390/pr8030332. [Google Scholar] [CrossRef]
23. Muhammad K, Hayat T, Alsaedi A, Ahmad B, Momani S. Mixed convective slip flow of hybrid nanofluid (MWCNTs + Cu + Waternanofluid (MWCNTs + Water) and base fluid (Watera comparative investigation. J Therm Anal Calorim. 2021;143(2):1523–36. doi:10.1007/s10973-020-09577-z. [Google Scholar] [CrossRef]
24. Eid MR, Nafe MA. Thermal conductivity variation and heat generation effects on magneto-hybrid nanofluid flow in a porous medium with slip condition. Waves Rand Comp Med. 2022;32(3):1103–27. doi:10.1080/17455030.2020.1810365. [Google Scholar] [CrossRef]
25. Alharbi AA. Thermal analysis of heat transport in a slip flow of ternary hybrid nanofluid with suction upon a stretching/shrinking sheet. Case Stud Therm Eng. 2024;54(25–26):103965. doi:10.1016/j.csite.2023.103965. [Google Scholar] [CrossRef]
26. Djoko JK, Koko J, Mbehou M, Sayah T. Stokes and Navier-Stokes equations under power law slip boundary condition: numerical Analysis. Comput Math Appl. 2022;128(7):198–213. doi:10.1016/j.camwa.2022.10.016. [Google Scholar] [CrossRef]
27. Yasin M, Hina S, Naz R. A modern study on peristaltically induced flow of Maxwell fluid considering modified Darcy’s law and Hall effect with slip condition. Alex Eng J. 2023;76:835–50. doi:10.1016/j.aej.2023.06.074. [Google Scholar] [CrossRef]
28. Jamrus FN, Ishak A, Waini I, Khan U. Radiative influence on axisymmetric ternary hybrid nanofluid flow with convective boundary conditions over a nonlinearly permeable stretching/shrinking disk. Int J Num Meth Heat Fluid Flow. 2024 Nov 26;34(12):4333–61. doi:10.1108/HFF-04-2024-0324. [Google Scholar] [CrossRef]
29. Rasool G, Xinhua W, Sun T, Hayat T, Sheremet M, Uddin A, et al. Recent advancements in battery thermal management system (BTMSa review of performance enhancement techniques with an emphasis on nano-enhanced phase change materials. Heliyon. 2024;10(17):e36950. doi:10.1016/j.heliyon.2024.e36950. [Google Scholar] [PubMed] [CrossRef]
30. Mahmood Z, Rafique K, Khan U, Abd El-Rahman M, Alharbi R. Analysis of mixed convective stagnation point flow of hybrid nanofluid over sheet with variable thermal conductivity and slip conditions: a model-based study. Int J Heat Fluid Flow. 2024;106(10):109296. doi:10.1016/j.ijheatfluidflow.2024.109296. [Google Scholar] [CrossRef]
31. Yadav S, Yadav S, Yadav PK. The mixed convection thermally radiated hybrid nanofluid flow through an inclined permeable shrinking plate with slip condition and inclined magnetic effect. Chin J Physics. 2024;89(3):1041–50. doi:10.1016/j.cjph.2023.12.039. [Google Scholar] [CrossRef]
32. Iqbal Z, Priya S, Hakeem AA, Ahammad NA, Fathima D, Nour MM, et al. Thermal convection and entropy generation analysis of hybrid nanofluid slip flow over a horizontal poignant thin needle with an inclined magnetic field: a numerical study. Mode Phy Lett B. 2024;38(5):2450004. doi:10.1142/S0217984924500040. [Google Scholar] [CrossRef]
33. Ali G, Kumam P, Sitthithakerngkiet K, Jarad F. Heat transfer analysis of unsteady MHD slip flow of ternary hybrid Casson fluid through nonlinear stretching disk embedded in a porous medium. Ain Shams Eng J. 2024;15(2):102419. doi:10.1016/j.asej.2023.102419. [Google Scholar] [CrossRef]
34. Waini I, Ishak A, Pop I. Agrawal flow of a hybrid nanofluid over a shrinking disk. Case Stud Therm Eng. 2021;25:100950. doi:10.1016/j.csite.2021.100950. [Google Scholar] [CrossRef]
35. Weidman P. Axisymmetric stagnation-point flow on a spiraling disk. Phys Fluids. 2014;26(7):073603. doi:10.1063/1.4887260. [Google Scholar] [CrossRef]
36. Merkin JH. On dual solutions occurring in mixed convection in a porous medium. J Eng Math. 1986;20(2):171–9. doi:10.1007/BF00042775. [Google Scholar] [CrossRef]
37. Weidman PD, Kubitschek DG, Davis AMJ. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int J Eng Sci. 2006;44(11–12):730–7. [Google Scholar]
38. Ahmad S, Ullah N, Nadeem S. Dual nature solutions for temperature-dependent transport properties of nanofluid flow with entropy generation. Numer Methods Partial Differ Eq. 2024;40(1):e22679. doi:10.1002/num.22679. [Google Scholar] [CrossRef]
39. Lund LA, Omar Z, Khan I, Dero S. Multiple solutions of Cu-C6H9NaO7 and Ag-C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J Cent South Univ. 2019;26(5):1283–93. doi:10.1007/s11771-019-4087-6. [Google Scholar] [CrossRef]
40. RamReddy C, Saran HL. Flow separation and stability analysis for aligned magnetic field in a porous medium saturated by a titanium alloy nanofluid. Int J Ambient Energy. 2024;45(1):2313136. doi:10.1080/01430750.2024.2313136. [Google Scholar] [CrossRef]
41. Wang J, Shah NA, Almutairi B, Kwon OK, Chung JD. Bvp4c approach and duality of hybrid nanofluid over extending and contracting sheet with chemical reaction and cross-diffusion effects. Results Phys. 2024;57:107362. doi:10.1016/j.rinp.2024.107362. [Google Scholar] [CrossRef]
42. Yahaya RI, Mustafa MS, Arifin NM, Pop I, Wahid NS, Ali FM, et al. Mixed convection hybrid nanofluid flow over a stationary permeable vertical cone with thermal radiation and convective boundary condition. ZAMM-J Appl Mathem Mech/Zeitschrift Für Angewandte Mathematik Und Mechanik. 2024;104(4):e202300428. doi:10.1002/zamm.202300428. [Google Scholar] [CrossRef]
43. Sohail M, Abodayeh K, Nazir U. Implementation of finite element scheme to study thermal and mass transportation in water-based nanofluid model under quadratic thermal radiation in a disk. Mech Time Depend Mater. 2024;28(3):1049–72. doi:10.1007/s11043-024-09736-x. [Google Scholar] [CrossRef]
44. Elboughdiri N, Nazir U, Saleem S, Ali MR. Impact of thermal energy efficiency based on kerosene oil movement through hybrid nano-particles across contracting/stretching needle. Case Stud Therm Eng. 2024;60(1):104775. doi:10.1016/j.csite.2024.104775. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF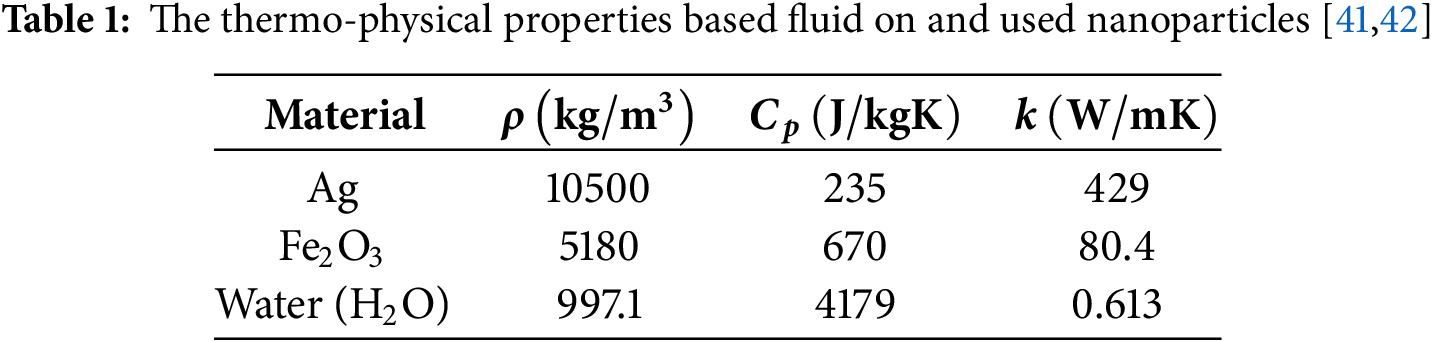

 Downloads
Downloads
 Citation Tools
Citation Tools