 Open Access
Open Access
ARTICLE
Numerical Treatments for a Crossover Cholera Mathematical Model Combining Different Fractional Derivatives Based on Nonsingular and Singular Kernels
1 Department of Mathematics, Faculty of Education, Sana’a University, Sana’a, 1247, Yemen
2 Mathematics Department, Faculty of Science, Al-Azhar University, Nasr-City, Cairo, 11651, Egypt
3 Mathematics Department, Faculty of Education, Abyan University, Abyan, Yemen
4 Ain Shams University Mathematics Department, Faculty of Science, Ain Shams University, Cairo, 11566, Egypt
* Corresponding Author: Seham M. AL-Mekhlafi. Email:
(This article belongs to the Special Issue: Analytical and Numerical Solution of the Fractional Differential Equation)
Computer Modeling in Engineering & Sciences 2025, 143(2), 1927-1953. https://doi.org/10.32604/cmes.2025.063971
Received 30 January 2025; Accepted 07 April 2025; Issue published 30 May 2025
Abstract
This study introduces a novel mathematical model to describe the progression of cholera by integrating fractional derivatives with both singular and non-singular kernels alongside stochastic differential equations over four distinct time intervals. The model incorporates three key fractional derivatives: the Caputo-Fabrizio fractional derivative with a non-singular kernel, the Caputo proportional constant fractional derivative with a singular kernel, and the Atangana-Baleanu fractional derivative with a non-singular kernel. We analyze the stability of the core model and apply various numerical methods to approximate the proposed crossover model. To achieve this, the approximation of Caputo proportional constant fractional derivative with Grünwald-Letnikov nonstandard finite difference method is used for the deterministic model with a singular kernel, while the Toufik-Atangana method is employed for models involving a non-singular Mittag-Leffler kernel. Additionally, the integral Caputo-Fabrizio approximation and a two-step Lagrange polynomial are utilized to approximate the model with a non-singular exponential decay kernel. For the stochastic component, the Milstein method is implemented to approximate the stochastic differential equations. The stability and effectiveness of the proposed model and methodologies are validated through numerical simulations and comparisons with real-world cholera data from Yemen. The results confirm the reliability and practical applicability of the model, providing strong theoretical and empirical support for the approach.Keywords
Cholera continues to pose a major public health challenge, particularly in endemic regions where sanitation and access to clean water are limited. According to Ali et al. [1], cholera remains a significant burden in many parts of the world, with periodic outbreaks contributing to considerable morbidity and mortality. Mathematical modeling has become an essential tool in understanding and predicting the spread of infectious diseases like cholera, offering insights that inform public health interventions and optimize resource allocation. Huppert and Katriel [2] emphasize the importance of mathematical frameworks in epidemiology, highlighting their capacity to simulate complex transmission dynamics and forecast outbreak patterns.
Recent advancements in mathematical modeling have incorporated fractional calculus to better represent the memory effects and hereditary properties inherent in disease transmission. Fractional-order models provide a more flexible and accurate description of epidemic processes compared to classical integer-order models, capturing the influence of past states on current disease progression. Lemos-Paião et al. [3] developed a cholera model with optimal control strategies, demonstrating how fractional dynamics can significantly enhance our understanding of disease spread and control measures. Similarly, the work by Lemos-Paião et al. [4] introduced an epidemic model for cholera that utilizes optimal control to manage treatment strategies, further illustrating the utility of fractional models in epidemiological applications.
Baleanu et al. [5] expanded on these approaches by proposing a generalized fractional model for real cholera outbreaks, incorporating stochastic components to account for the unpredictable nature of disease dynamics. Their model successfully captured the complexities observed in actual outbreaks, validating the effectiveness of fractional and stochastic approaches in improving predictive accuracy.
Fractional calculus has gained significant attention in recent years due to its ability to describe memory effects and hereditary properties in various physical and biological systems. Unlike classical integer-order derivatives, fractional derivatives provide a more generalized framework for modeling complex dynamical processes. In particular, special functions play a crucial role in solving fractional differential equations, offering analytical and numerical tools for applications in engineering, physics, and mathematical biology. The work presented in [6] explores the fundamental role of special functions in fractional models, highlighting their applicability in diverse scientific domains. Incorporating these special functions allows for more accurate representations of anomalous diffusion, viscoelastic materials, and population dynamics. This perspective aligns with our study, where fractional-order derivatives are employed to enhance the mathematical modeling of disease transmission and epidemiology, providing deeper insights into system behavior.
Building upon these foundational studies, this paper introduces a novel crossover cholera model that integrates multiple fractional derivatives with both singular and nonsingular kernels, bridging deterministic and stochastic processes to better reflect real-world conditions. The proposed model leverages three distinct types of fractional derivatives:
• Caputo-Fabrizio fractional derivative (nonsingular kernel) [7], known for its smooth memory effects and exponential decay properties.
• Caputo proportional constant fractional derivative (singular kernel) [8], capturing abrupt changes and reflecting more localized influences in the disease dynamics.
• Atangana-Baleanu fractional derivative (nonsingular kernel) [9], offering a more generalized representation of memory effects through Mittag-Leffler functions.
These derivatives are applied across four distinct time intervals, reflecting the various stages of cholera progression, from initial infection to outbreak resolution. By incorporating stochastic differential equations (SDEs) alongside fractional derivatives, the model accounts for the inherent randomness and uncertainty present in disease transmission, environmental factors, and population mobility.
This crossover model not only refines the predictive accuracy of cholera outbreaks but also extends the applicability of fractional calculus to broader epidemiological contexts. By addressing the limitations of traditional models and incorporating stochastic elements, the proposed framework contributes to the ongoing effort to mitigate the global impact of cholera through improved forecasting and intervention strategies.
These derivatives are applied across four distinct time intervals, reflecting the various stages of cholera progression, from initial infection to outbreak resolution. By incorporating stochastic differential equations (SDEs) alongside fractional derivatives, the model accounts for the inherent randomness and uncertainty present in disease transmission, environmental factors, and population mobility.
To ensure accurate numerical approximations, the model employs a combination of advanced numerical techniques:
• The approximation of Caputo proportional constant fractional derivative with Grünwald-Letnikov nonstandard finite difference method (CPC-GLNFDM) is applied to systems with singular kernels to achieve stable and accurate approximations [10].
• The Toufik-Atangana method was utilized for models involving nonsingular Mittag-Leffler kernels, ensuring convergence and minimizing computational error [11].
• Caputo-Fabrizio integral approximation and Lagrange polynomial interpolation applied to nonsingular exponential decay kernels, capturing the long-term behavior of the disease [11].
• The Milstein method is used for stochastic differential equations, providing precise approximations for random fluctuations in transmission dynamics [12].
The authors confirm that this study is original and has not been discussed before, and it is presented in this paper for the first time.
The structure of this study is as follows: Section 2 introduces key definitions of fractional derivatives, provides a brief overview of stochastic differential equations (SDEs), and outlines the numerical methods used to solve them. Section 3 presents the foundational model along with its mathematical analysis. Section 4 introduces a novel crossover model to describe the dynamics of cholera spread. This model integrates three fractional derivatives with both singular and nonsingular kernels, as well as SDEs across four distinct time intervals. The fractional derivatives employed include the Caputo-Fabrizio derivative (nonsingular kernel), the Caputo proportional constant derivative (singular kernel), and the Atangana-Baleanu derivative (nonsingular kernel). Section 5 details the application of four numerical methods to solve the proposed system and analyze its stability. Section 6 presents numerical simulations based on the proposed model, illustrating its performance and accuracy. Section 7 concludes the study by summarizing the key findings and highlighting the primary contributions of the research.
In this section, we go over some of the most important fractional calculus definitions that are used in the remainder of this research.
Definition 1. Let
where
Definition 2. Let
where
Definition 3. Let
Definition 4. [8] For
the normalizing function
where
Definition 5. The Caputo proportional fractional hybrid operator (CP) is generally defined as [8]:
where
Definition 6.The Caputo proportional constant fractional hybrid operator (CPC) can be defined as [8]:
where
Definition 7. According to Caputo, the Atangana Baleanu fractional derivative of the function
and the Riemann-Liouville Atangana Baleanu fractional derivative of the function
Here,
where
Milstein method
SDE can be approximated numerically using the Milstein method in mathematics. It bears the name of Milstein, who published it in 1974 [12]. To solve the following (SDE):
Using the Milstein method like this:
where
In this section, we introduce the basic cholera disease model as outlined in [3]. This model incorporates the following fundamental populations: quarantined individuals (
The parameters of the model are defined in Table 1, and the mathematical representation of the model is presented as follows:

In this study, we assume non-negative initial conditions for system (16):
3.2 Solutions’ Boundedness and Positivity
In the following, the domain
1. Human population domain
Biological Meaning: This constraint ensures that the total population remains within a biologically feasible limit, accounting for recruitment and death rates.
2. Bacterial population domain
Biological Meaning: This constraint reflects the balance between the contribution of bacteria to the environment (from infected individuals) and its natural decay. It ensures that the bacterial population remains within realistic ecological limits.
3. Combined domain
Biological Meaning: This domain ensures that the model operates within biologically meaningful constraints for both human and bacterial populations.
Lemma 1. The solutions of system (16) maintain non-negative values for all
Proof: We have
where
3.3 Analysis of Stability and Equilibrium Points
Equilibrium points represent steady-state conditions where the system remains unchanged over time. In the context of the cholera model, equilibrium points might represent scenarios where the disease has either been eradicated (disease-free equilibrium) or has reached a stable endemic state.
In the context of cholera models, the disease-free equilibrium (DFE) represents a state where the disease has been eradicated from the population.
It is produced when we set the L.H.S. system (16) to zero and put
The endemic equilibrium corresponds to a non-trivial solution where
First, we compute the fundamental reproduction factor
Proposition 1: Model (16)’s fundamental reproduction factor is:
Proof: Let
where:
Thus, since:
we have
The Jacobian matrix of
The Jacobian matrix of
Using the disease-free equilibrium
The model (16)’s fundamental reproduction factor is:
So, the proof is finished.
Now we prove the disease-free equilibrium
Theorem 2. The model (16)’s disease-free equilibrium (DFE)
1. Locally and asymptotically stable, provided that
2. If
Moreover, a critical case arises if:
Proof: The linearized system of model (16)’s characteristic polynomial is provided by:
To calculate the polynomial p’s roots, we possess that
That is:
According to Routh’s standard [15], the roots of the polynomial
Thus, if
else if
else
Proposition 2: The equations
where
which is possible if
Proof: The rate of transmission must be entirely positive in order for this equilibrium to be possible:
The fourth, third and second equilibrium equations of (16) are solved successively, and we discover
Next, we get
The final value of
It yields the fourth element of (20) as well as the first three through back substitution. Lastly, the practical value of
After rearranging and replacing the value of
Consequently,
Considering (21), and the reality that
Since all of the other coefficients and
4 The Piecewise Mathematical Model
The piecewise cholera mathematical model presented in this study enhances conventional epidemic modeling by employing sophisticated, multi-stage fractional differential equations to accurately capture the dynamics of cholera transmission. The model divides the progression of the disease into four distinct periods, each representing a critical stage in the spread of the infection. To reflect the unique characteristics of disease propagation at each stage, a different fractional derivative operator is applied within each interval.
In the initial phase
During the second phase
In the advanced stages of cholera, when
The stochastic cholera model for
By adopting this piecewise differential approach, the model offers a more realistic and comprehensive depiction of epidemic stages, significantly improving predictive insights into the progression and potential containment of cholera outbreaks.
The resulting system is expressed as follows:
with initial conditions
with initial conditions
with
where
5 Numerical Approach to Solving the Proposed Model
5.1 Numerical Scheme with Exponential Decay Kernel
Consider the hybrid fractional order derivatives equation that follows:
Rewriting the above equation as [11] is possible based on Caputo-Fabrizio’s definition integral (8):
We write (30) at
and at
where the normalization function
Using these equations’ various approaches, the following can be written [11]:
The following can be obtained by entering its Lagrange polynomial into the equation above:
and we get the following:
Calculating the integrals on the equation above’s right side is possible as:
Consequently, the following numerical scheme is:
Stability of Numerical Scheme with Exponential Decay Kernel
We employ spectral stability analysis to examine the stability of the specified numerical system. We presume that the function
With this approximation, we can rewrite the numerical Eq. (31) as follows [11]:
After simplifying, the recurrence relation becomes:
To achieve stability, the absolute values of the numerical coefficients in the recurrence relation must be less than or equal to
By rearranging the inequality as follows, we may obtain an upper bound for
Thus, stability is ensured if we select a time step
Consider the hybrid fractional order derivatives equation that follows:
The following is an expression for the relationship (10) [10]:
In this case,
and
Remark 1. If
Stability of CPC-GLNFDM
Consider a model test problem of linear fractional order delay differential equation [17] to examine the stability of the suggested approach (34).
Assuming that
we put
and
we get
we have
Accordingly, the suggested scheme is stable.
Let’s look at the Mittag-Leffler kernel Cauchy problem:
we transform (35) into
At the temporal point
and we write
The above equation can be expressed as follows once its Lagrange polynomial has been entered into (36) as an approximation of the function’s behavior
Thus, we get
and
we can calculate the above integrals in (37) as follows:
After entering these computations into (37), we obtain the numerical approximation [11]:
Stability of Toufik-Atangana Method
The stability of the Atangana-Baleanu method is examined by analyzing the errors arising from the numerical solution of the given Cauchy problem. Let’s begin with the general form of the Atangana-Baleanu fractional derivative in the Caputo sense, represented by [11]:
Applying this method to the equation
We proceed to obtain a stability criterion. Let
where
For the numerical scheme given in Eq. (38) to remain stable, the time step
This ensures that numerical errors remain controlled, preventing divergence in long-term simulations and ensuring stability by controlling the growth of numerical errors.
5.4 Numerical Methods for Solving the Crossover Model
We provide numerical methods for solving (22)–(29) in this section. Our method for addressing the ensuing linear crossover model is given as follows:
Now, to solve (39) as follows [11]:
To solve (40) as follows [10]:
and
To solve (41) as follows [11]:
To solve (42), we use the Milstein method as follows:
6 Discussion and Numerical Simulations
This section aims to validate the experimental results and analytical expressions derived in the previous sections. We utilize real-world data on cholera infections in Yemen, recorded between 27 April 2017, and 15 April 2018 [18]. The parameters and initial conditions used for the numerical simulations are outlined in Table 1.
All computations were performed using MATLAB 2021b on a PC equipped with an Intel(R) Core i7-3110M CPU (1.80 GHz) and 8 GB of RAM.
The numerical results for the proposed piecewise model are presented graphically:
• Fig. 1 illustrates a comparison between our numerical results and the actual data on cholera cases in Yemen. In this figure, we set
• Figs. 2–5 depict various scenarios comparing the simulated number of infected individuals to the real data. The numerical approximations closely match the observed cases, reinforcing the effectiveness of the proposed crossover model in accurately describing the spread of cholera in Yemen. Notably, our results surpass the accuracy of prior models presented in [3,5].
• Figs. 6 and 7 illustrate the influence of varying
• Fig. 8 reveals new dynamic behaviors under different values of

Figure 1: A comparison between real data and the classical model of cholera

Figure 2: A comparison between real data and the classical model of cholera and

Figure 3: A comparison between real data and the classical model of cholera and

Figure 4: A comparison between real data and the classical model of cholera and

Figure 5: A comparison between real data and the classical model of cholera and


Figure 6: Numerical behavior of the proposed model at different values of

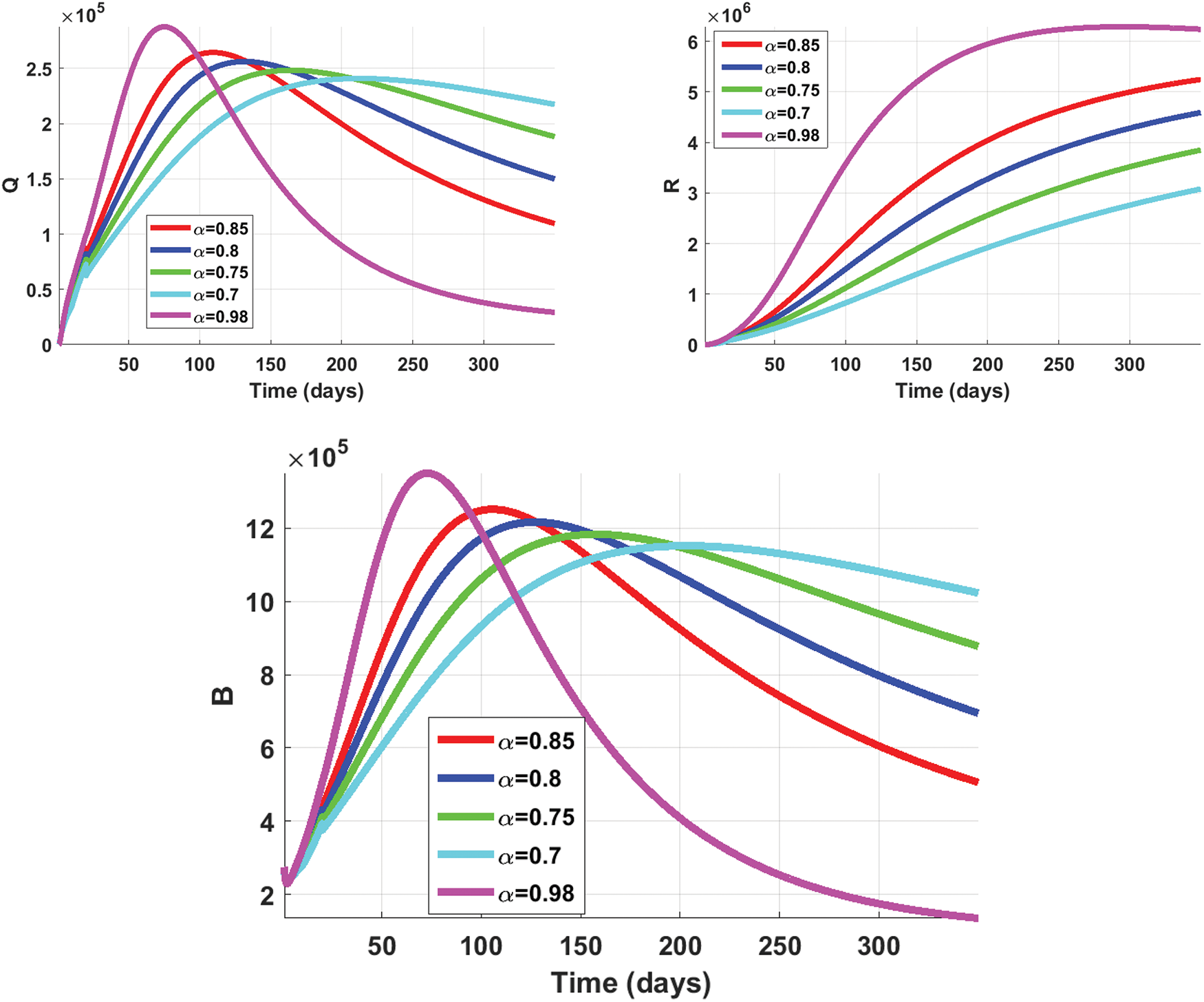
Figure 7: Numerical behavior of the proposed model at different values of


Figure 8: Numerical behavior of the proposed model at different values of
Overall, the proposed crossover model provides a robust and accurate framework for simulating the spread of cholera in Yemen, offering deeper insights into the complexity of infectious disease dynamics and surpassing the predictive capabilities of earlier models.
This study refined the mathematical model of cholera by incorporating a novel crossover framework. We integrated three distinct fractional derivatives—Caputo Fabrizio, Caputo proportional, and Atangana-Baleanu with SDEs to simulate the dynamics of the disease over four time intervals.
We employed CPC-GLNFDM for the numerical approximation of models with singular kernels, the Toufik-Atangana method for models with the Mittag-Leffler kernel, and the Milstein method for the SDEs. The stability of the proposed model was rigorously analyzed.
The results, validated against real data on cholera infections in Yemen from 27th April 2017, to 15 th April 2018, demonstrate that our model provides a more accurate approximation of the solution compared to previous studies. The integration of SDEs has significantly enhanced our understanding of the inherent randomness in infectious disease transmission, revealing diverse dynamic behaviors. This approach enables us to forecast disease trajectories from outbreak to resolution, capturing a broad spectrum of scenarios from deterministic crossovers to stochastic processes.
Piecewise crossover differential equations, combining fractional and stochastic elements, offer a powerful framework for modeling complex systems with time-varying dynamics. This approach has the potential to enhance our ability to model and predict the behavior of various real-world phenomena accurately.
Future research will focus on expanding the model to incorporate spatial heterogeneity and mobility patterns, which play a critical role in the spread of infectious diseases. Investigating the application of machine learning techniques to optimize parameter estimation and enhance predictive accuracy is another promising avenue. Additionally, we plan to apply this crossover modeling framework to other infectious diseases and environmental phenomena, aiming to uncover universal patterns in dynamic systems. Further exploration of multi-scale modeling, integrating micro and macro-level interactions, will provide deeper insights into disease dynamics and control strategies.
Acknowledgement: The authors wish to express sincere appreciation to the reviewers for their valuable comments, which significantly improved this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization, formal analysis, resources, software, supervision, writing—original draft, methodology, validation, writing—original draft, data collection: Seham M. Al-Mekhlafi. Conceptualization, supervision, visualization, resources: Kamal R. Raslan, Khalid K. Ali. Writing—original draft, methodology, data collection: Sadam H. Alssad. Funding acquisition, resources, visualization: Nehaya R. Alsenaideh. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the first and corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Ali M, Nelson AR, Lopez AL, Sack DA. Updated global burden of cholera in endemic countries. PLoS Negl Trop Dis. 2015;9(6):e0003832. doi:10.1371/journal.pntd.0003832. [Google Scholar] [PubMed] [CrossRef]
2. Huppert A, Katriel G. Mathematical modelling and prediction in infectious disease epidemiology. Clin Microbiol Infect. 2013;19(11):999–1005. doi:10.1111/1469-0691.12308. [Google Scholar] [PubMed] [CrossRef]
3. Lemos-Paião AP, Silva1 CJ, Torres DFM, Venturino E. Optimal control of aquatic diseases: a case study of Yemen’s cholera outbreak. J Optim Theory Appl. 2020;185(3):1008–30. doi:10.1007/s10957-020-01668-z. [Google Scholar] [CrossRef]
4. Lemos-Paião AP, Silva CJ, Torres DFM. An epidemic model for cholera with optimal control treatment. J Comput Appl Math. 2017;318(1):168–80. doi:10.1016/j.cam.2016.11.002. [Google Scholar] [CrossRef]
5. Baleanu D, Ghassabzade FA, Nieto JJ, Jajarmi A. On a new and generalized fractional model for the real cholera outbreak. Alex Eng J. 2022;61(11):9175–86. doi:10.1016/j.aej.2022.02.054. [Google Scholar] [CrossRef]
6. Singh H, Srivastava HM, Pandey RK. Special functions in fractional calculus and engineering. Boca Raton: CRC Press; 2023. [Google Scholar]
7. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl. 2015;1(2):73–85. [Google Scholar]
8. Baleanu D, Fernandez A, Akgül A. On a fractional operator combining proportional and classical differintegrals. Mathematics. 2020;8(3):360. doi:10.3390/math8030360. [Google Scholar] [CrossRef]
9. Atangana A, Baleanu D. New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm Sci. 2016;20(2):763–9. [Google Scholar]
10. Sweilam H, Al-Mekhlafi SM, Abou Hasan MM, Soliman T. New crossover lumpy skin disease: numerical treatments. Partial Differential Equations in Applied Mathematics. 2024;12(4):100986. doi:10.1016/j.padiff.2024.100986. [Google Scholar] [CrossRef]
11. Atangana A, Araz S. New numerical scheme with Newton polynomial: theory, methods, and applications. London, UK: Academic Press; 2021. [Google Scholar]
12. Mil’shtein GN. Approximate integration of stochastic differential equations. Theor Probab Appl. 1974;19(3):583–8. (In Russian). doi:10.1137/1119062. [Google Scholar] [CrossRef]
13. Podlubny I. Fractional differential equations. New York, NY, USA: Academic Press; 1999. [Google Scholar]
14. Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180:29–48. doi:10.1016/S0025-5564(02)00108-6. [Google Scholar] [PubMed] [CrossRef]
15. Hanif A, Butt AIK. Atangana-Baleanu fractional dynamics of dengue fever with optimal control strategies. AIMS Math. 2023;8(7):15499–535. doi:10.3934/math.2023791. [Google Scholar] [CrossRef]
16. Scherer R, Kalla S, Tang Y, Huang J. The Grünwald-Letnikov method for fractional differential equations. Comput Math Appl. 2011;62(3):902–17. doi:10.1016/j.camwa.2011.03.054. [Google Scholar] [CrossRef]
17. Rihan FA, Lakshmanan S, Hashish AH, Rakkiyappan R, Ahmed E. Fractional-order delayed predator prey systems with Holling type-II functional response. Nonlinear Dyn. 2015;80:777–89. doi:10.1007/s11071-015-1905-8. [Google Scholar] [CrossRef]
18. World Health Organization. Yemen: weekly cholera bulletins. [cited 2025 May 5]. Available from: https://www.who.int/emergencies/disease-outbreak-news/item/yemen-cholera. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools