 Open Access
Open Access
ARTICLE
Design of Chaos Induced Aquila Optimizer for Parameter Estimation of Electro-Hydraulic Control System
1 Department of Electrical and Computer Engineering, International Islamic University, Islamabad, 44000, Pakistan
2 Future Technology Research Center, National Yunlin University of Science and Technology, Yunlin, 64002, Taiwan
3 International Graduate School of Artificial Intelligence, National Yunlin University of Science and Technology, Yunlin, 64002, Taiwan
4 Department of Electronic Engineering, Fatima Jinnah Women University, Rawalpindi, 46000, Pakistan
5 Department of Information Technology, College of Computer and Information Technology, Taif University, Taif, 21944, Saudi Arabia
6 Institute of Public Administration, Jeddah, 21944, Saudi Arabia
* Corresponding Author: Naveed Ishtiaq Chaudhary. Email:
(This article belongs to the Special Issue: Advances in Swarm Intelligence Algorithms)
Computer Modeling in Engineering & Sciences 2025, 143(2), 1809-1841. https://doi.org/10.32604/cmes.2025.064900
Received 27 February 2025; Accepted 23 April 2025; Issue published 30 May 2025
Abstract
Aquila Optimizer (AO) is a recently proposed population-based optimization technique inspired by Aquila’s behavior in catching prey. AO is applied in various applications and its numerous variants were proposed in the literature. However, chaos theory has not been extensively investigated in AO. Moreover, it is still not applied in the parameter estimation of electro-hydraulic systems. In this work, ten well-defined chaotic maps were integrated into a narrowed exploitation of AO for the development of a robust chaotic optimization technique. An extensive investigation of twenty-three mathematical benchmarks and ten IEEE Congress on Evolutionary Computation (CEC) functions shows that chaotic Aquila optimization techniques perform better than the baseline technique. The investigation is further conducted on parameter estimation of an electro-hydraulic control system, which is performed on various noise levels and shows that the proposed chaotic AO with Piecewise map (CAO6) achieves the best fitness values of 2.873E−05, 1.014E−04, and 8.728E−03 at noise levels 1.300E−03, 1.300E−02, and 1.300E−01, respectively. Friedman test for repeated measures, computational analysis, and Taguchi test reflect the superiority of CAO6 against the state of the arts, demonstrating its potential for addressing various engineering optimization problems. However, the sensitivity to parameter tuning may limit its direct application to complex optimization scenarios.Keywords
Optimization techniques (OT) are applied in solving different problems related to science and engineering, such as wireless sensor networks [1], an electrically stimulated muscle model [2], leukemia cancer classification [3], nonlinear system identification [4], flow shop scheduling [5], feature selection [6], power system harmonics [7], agriculture [8], and renewable energy [9]. Machine learning assisted OT was also used for numerous applications, such as antenna design [10,11] and geometry [12], aircraft trajectories [13], and electronic packages and materials [14]. OT can be classified as swarm optimization techniques (SOT), evolutionary optimization techniques (EOT), physics-based optimization techniques (PBOT), and human-based optimization techniques (HBOT). In recent years, various optimizations have been proposed in each category. Some of them are given in Table 1.
The comparison between the advantages and disadvantages of some of the OT is given in Table 2.

Aquila Optimizer (AO) [35] is recently proposed OT, and its various variants were available in the literature [36] with applications in diversified fields such as optimal power flow [37], biomedical [38], text-to-speech conversion [39], anomaly detection [40], wireless sensor networks [41], generative adversarial networks [42], power transformers [43], fraud detection [44], autoregressive models [45], agriculture [46], distributed energy systems [47], image segmentation [48], vehicle cruise control system [49], automatic voltage regulator [50], Unmanned Aerial Vehicles [51], air fuel ratio system control [52], and PV systems [53]. Various improved variants of AO were also proposed such as fractional order chaotic oscillator-based AO [54], binary AO [55], local search enhanced AO [56], reinforcement learning based AO [57], chaotic mapping-based AO [58], adaptive AO [59], and chaotic opposition learning based AO [60].
Parameter identification is critical for precisely modeling electro-hydraulic control systems, as it includes defining system-specific parameters like viscosity, valve coefficients, and actuator dynamics to confirm accurate control [61]. Various techniques were proposed in the literature for its representation [62–64]. Autoregressive models are widely applied for the representation of linear and nonlinear systems [65]. For its identification, various techniques were present in the literature, such as the two-stage gradient [66], hybrid neural fuzzy [67], SOT [68], and momentum gradient descent [69]. Accurate identification improves the consistency and effectiveness of electro-hydraulic systems, empowering better control of various industrial systems [70].
In this work, an improved variant of AO, namely chaotic Aquila optimizer (CAO), is proposed by integrating the chaos theory [71–73] through ten well-known chaotic maps into narrow exploitation. Chaotic maps in AO are motivated by their ability to enhance exploration and exploitation dynamics, leveraging chaotic maps to introduce randomness. CAO is further applied to the parameter estimation of the electro-hydraulic control system. The performance of CAO is compared with the arithmetic optimization algorithm (AOA) [25], reptile search algorithm (RSA) [17] and whale optimization algorithm (WOA) [18]. The prominent features of this research work are:
• Integration of chaos theory with SOT-based AO is proposed for parameter estimation of the electro-hydraulic control system.
• The integration of chaotic maps in the narrowed exploitation of AO provides better performance than its baseline technique.
• Friedman test for repeated measures, convergence analysis, computational analysis, and Taguchi test recommend the precision of the proposed CAO in comparison with the state of the art.
The workflow is as follows: Section 2 comprises mathematical models of AO, CAO, and fitness definition. Section 3 provides an analysis of CEC and benchmark functions. Section 4 presents the investigation on the electro-hydraulic control system. Section 5 provides the concluding remarks.
This section provides mathematical model of Aquila Optimizer (AO), Chaotic Aquila Optimizer (CAO), fitness evaluation, and pseudo codes.
AO is a nature-inspired optimization technique involving four hunting strategies to catch prey. It starts with population initialization generated randomly for the upper and lower bounds of the given problem as shown in Eqs. (1) and (2).
here
here
In (
here
here
where
where
The pseudo code implementation of AO is shown in Algorithm 1.

2.2 Chaotic Aquila Optimizer (CAO)
Chaotic maps are integrated into OT to maximize its exploration and exploitation capabilities. These maps generate ergodic values used in OT for escaping the local minima. Moreover, they dynamically manage the smooth transitions between local and global search, which accelerates the convergence and maintains population diversity. In this work, the narrowed exploitation mechanism of AO is improved by integrating ten well-known chaotic maps into the QF of AO. These maps use chaotic values to balance the exploration and exploitation of AO and modulate transition timing based on search diversity. CAO is first tested on twenty-three mathematical and ten CEC benchmark functions having both unimodal and multimodal features, followed by a parameter estimation of EHCS. A brief comparison between AO and CAO is summarized in Table 3.

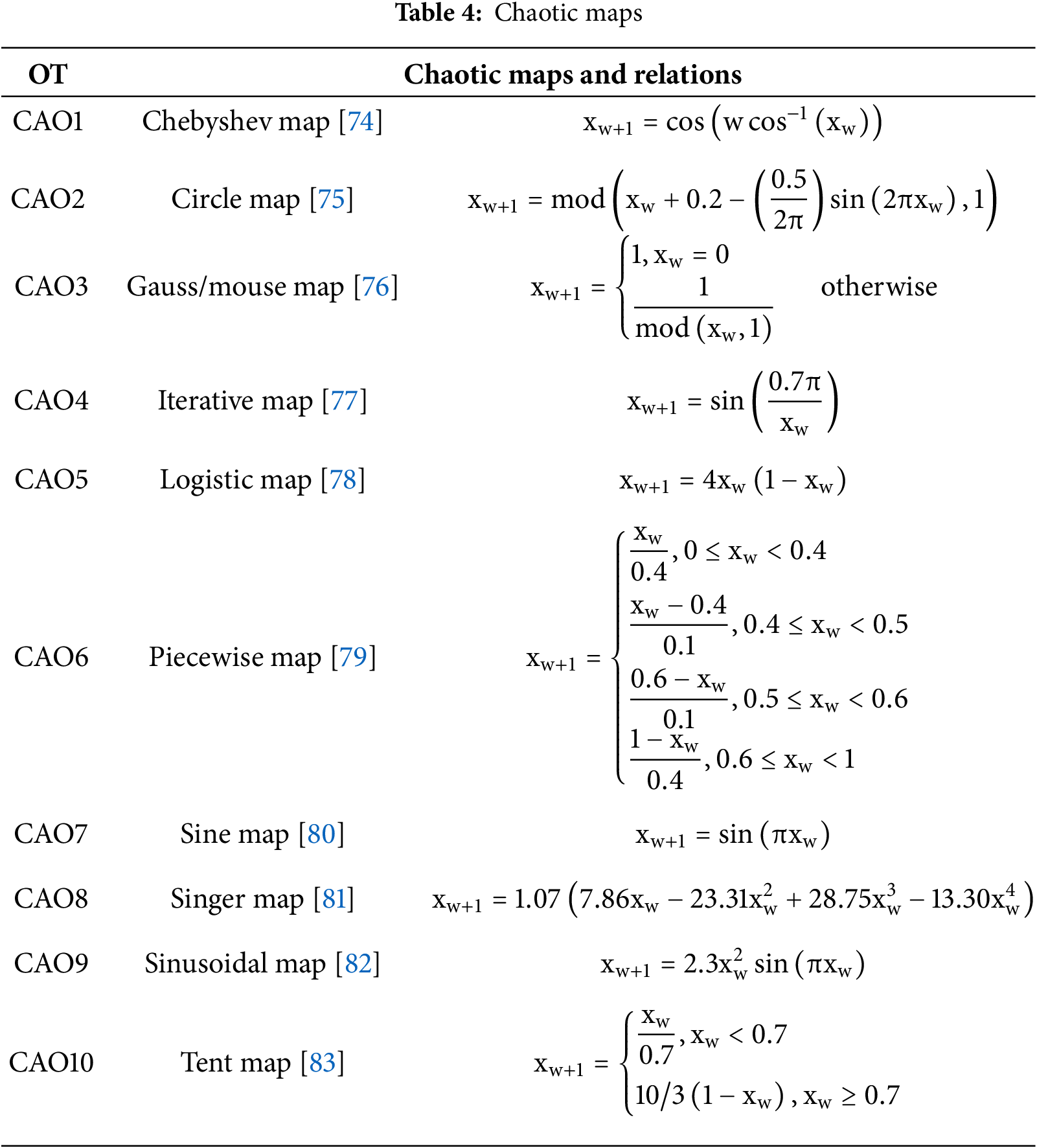
These details of these maps were given in Table 4.
These chaotic maps (
The pseudo code implementation of CAO is shown in Algorithm 2.

CAO is assessed by using the fitness evaluation as shown in Eq. (20).
where
This section provides the analysis of AO and its chaotic variants for mathematical benchmark and CEC functions.
3.1 Mathematical Functions Analysis
On 100 independent executions, the investigation for mathematical benchmark functions at
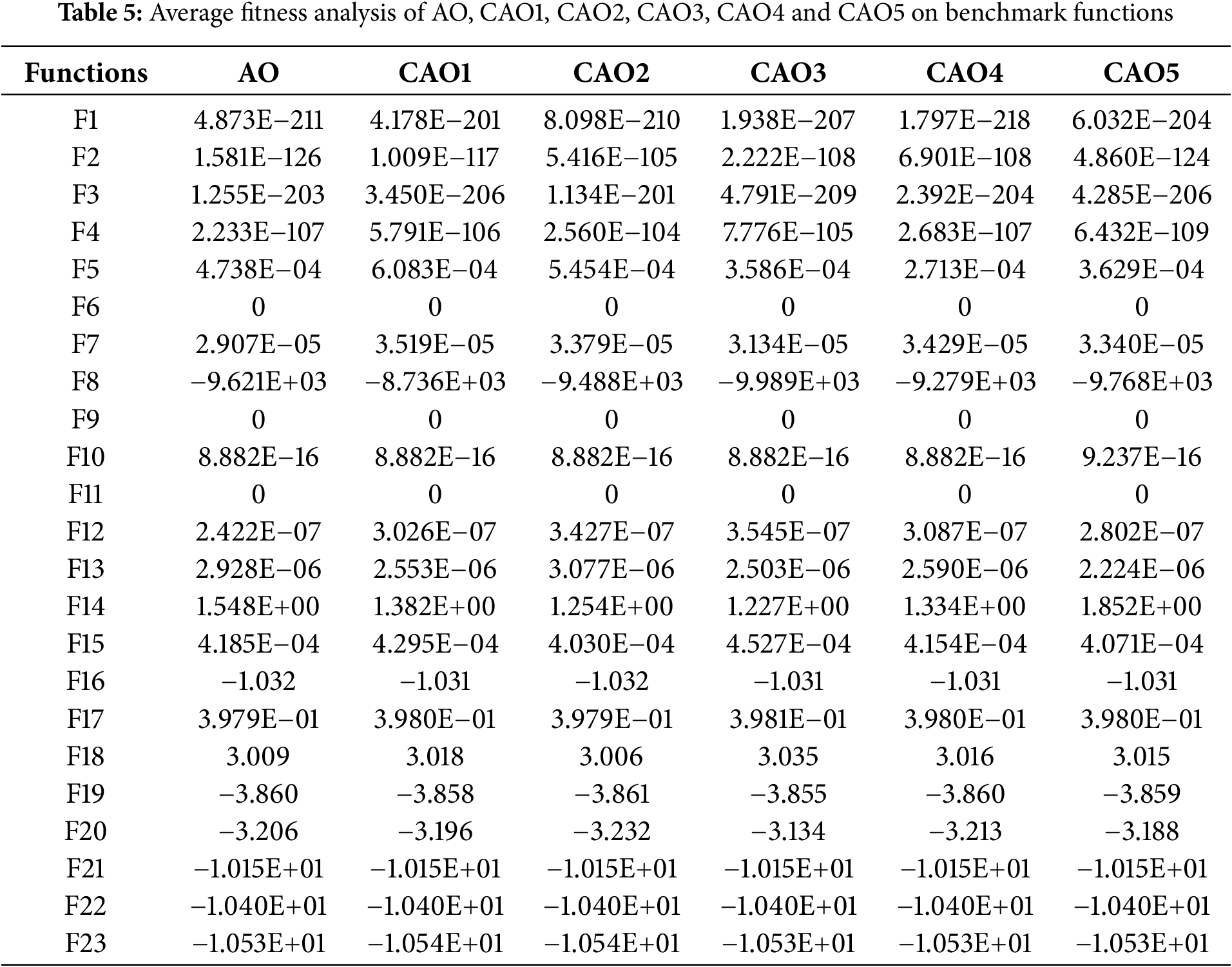
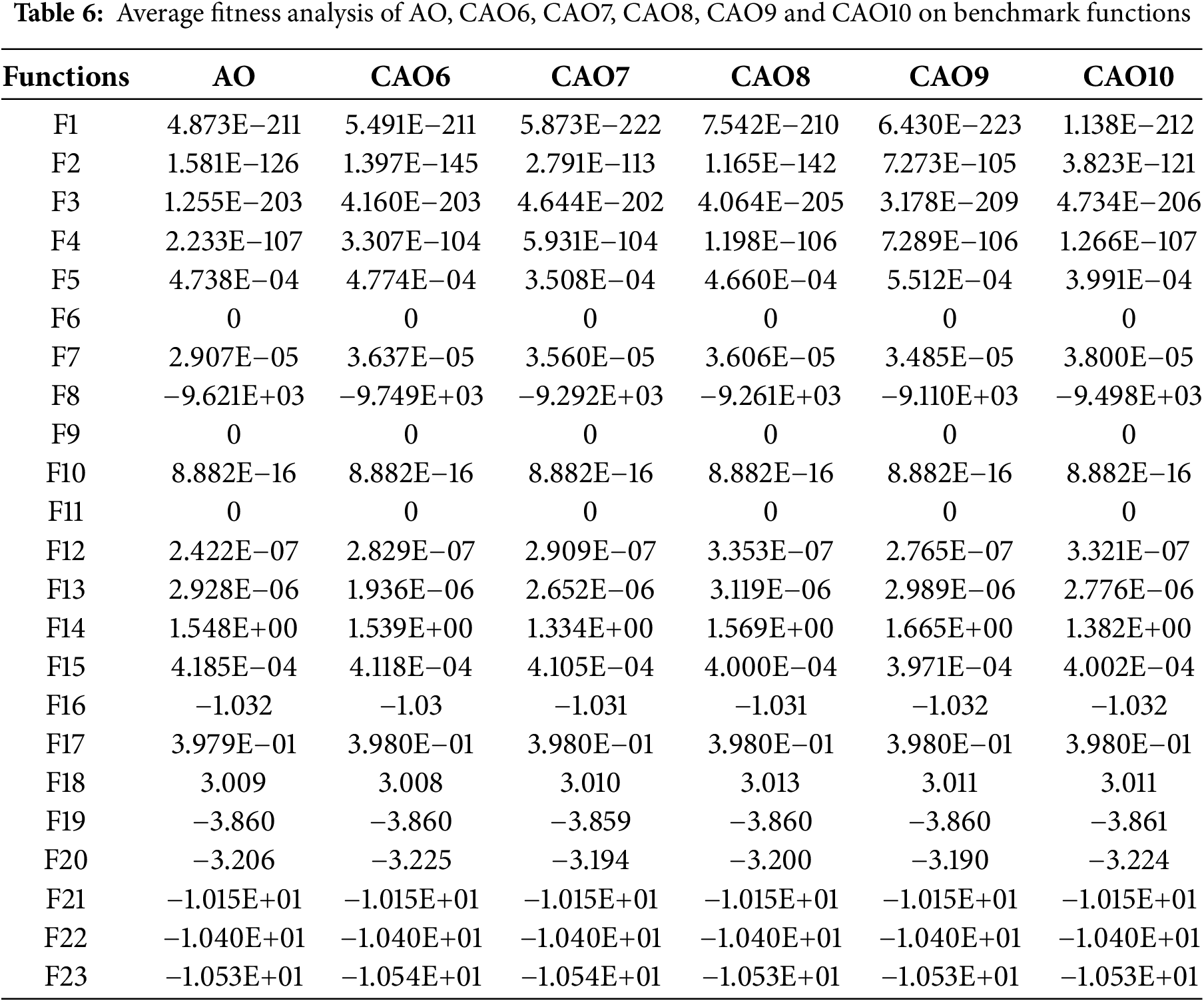
The convergence analysis of AO and CAO1-10 for mathematical functions is shown in Figs. 1–4 where legend is provided in Fig. 4. Fig. 1a–f shows the convergence for F1, F2, F3, F4, F5 and F6 functions. Similarly, Figs. 2a–f, 3a–f and 4a–e show the convergence for F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, and F23 functions, respectively. It is depicted from Figs. 1–4 that chaotic variants of AO show better convergence for these functions than AO.
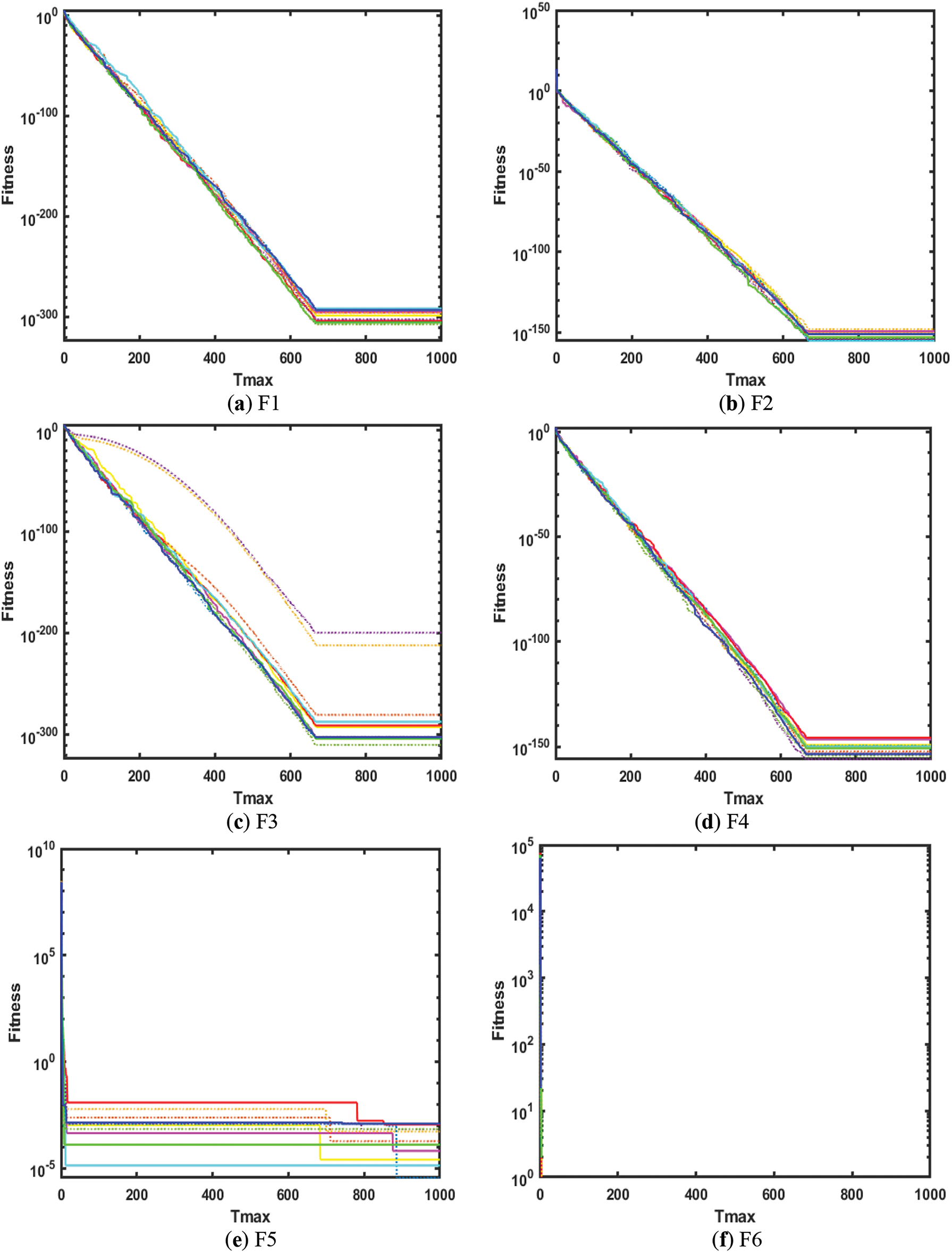
Figure 1: Convergence analysis on F1, F2, F3, F4, F5 and F6 mathematical functions
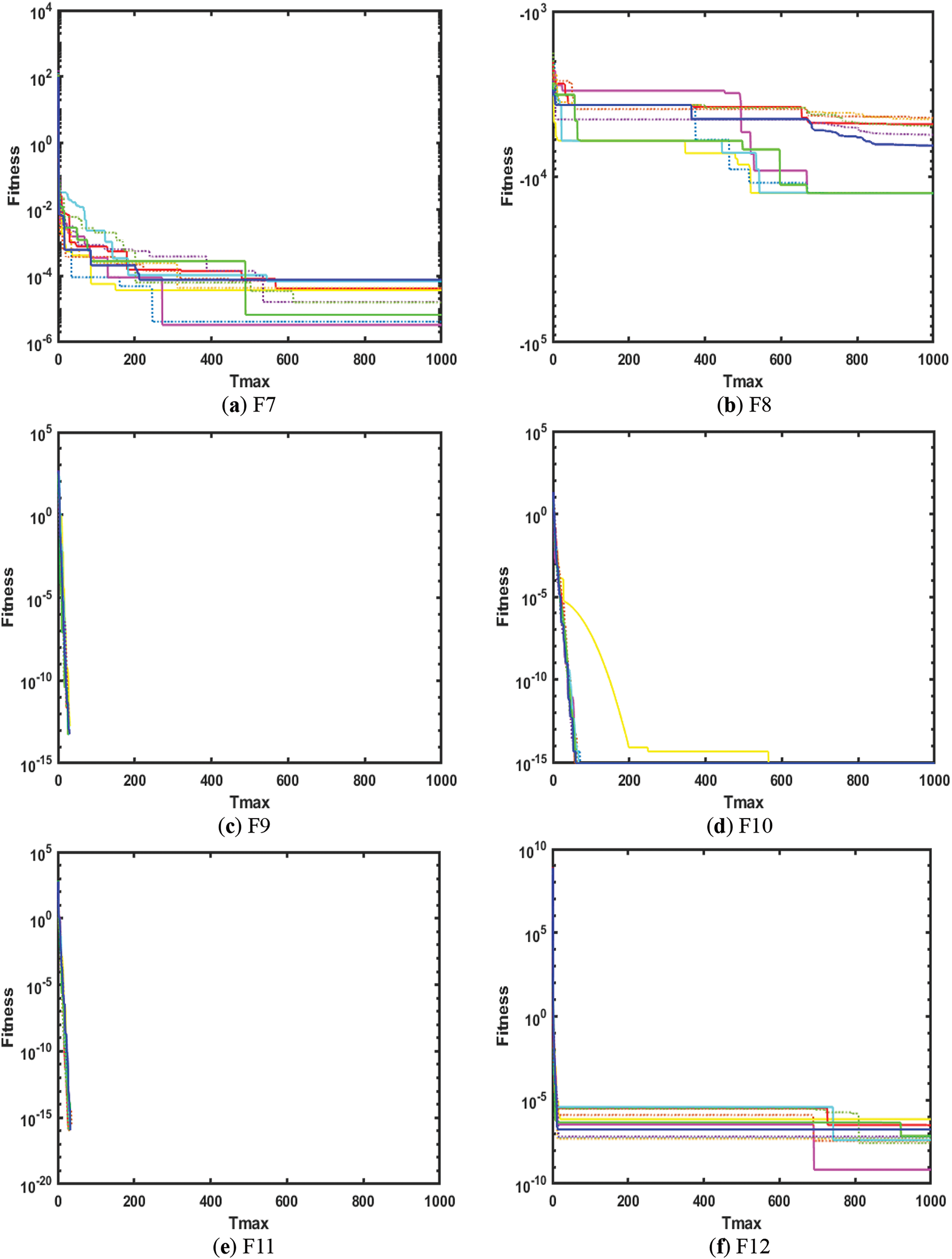
Figure 2: Convergence analysis on F7, F8, F9, F10, F11 and F12 mathematical functions

Figure 3: Convergence analysis on F13, F14, F15, F16, F17 and F18 mathematical functions
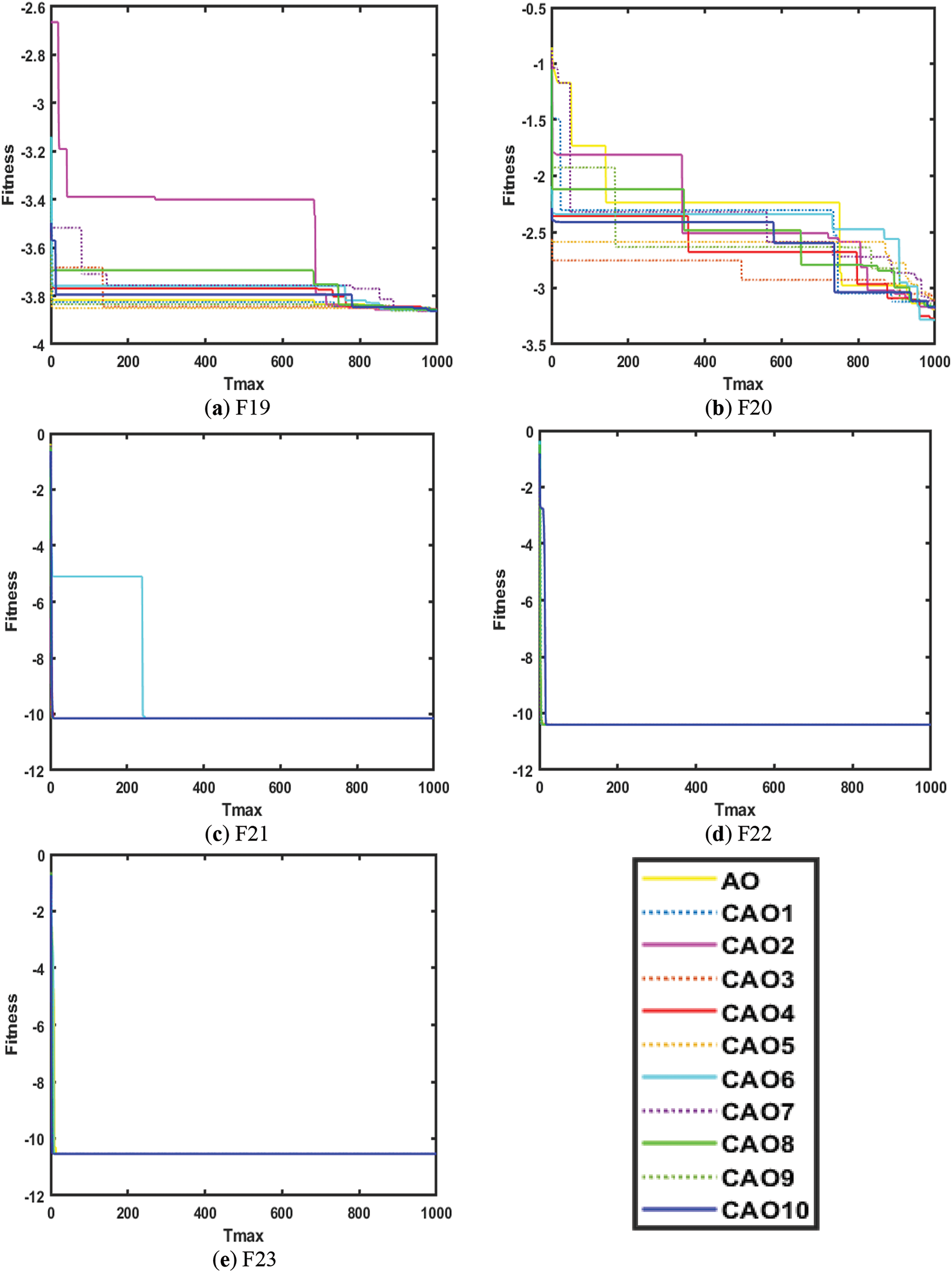
Figure 4: Convergence analysis on F19, F20, F21, F22 and F23 mathematical functions
On 100 independent executions, the investigation for the CEC2019 benchmark functions at
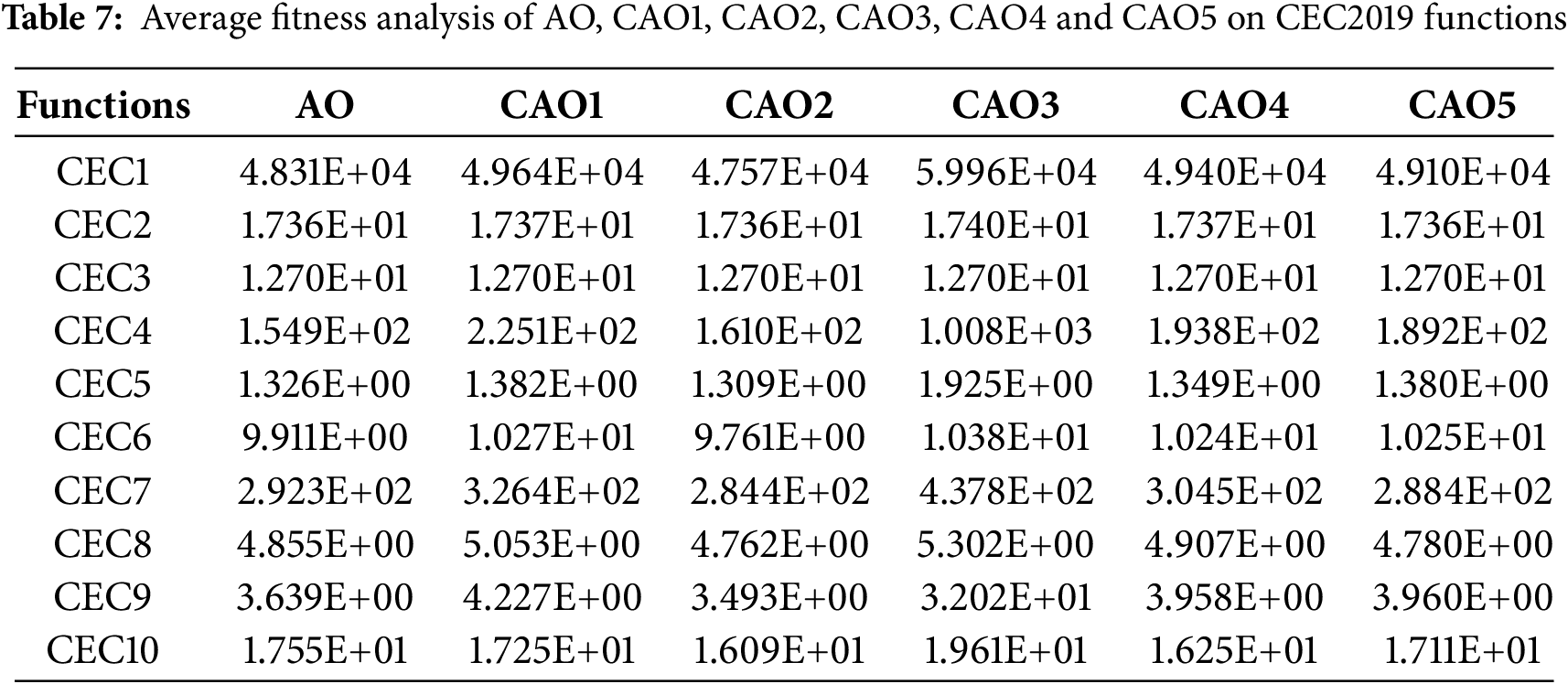
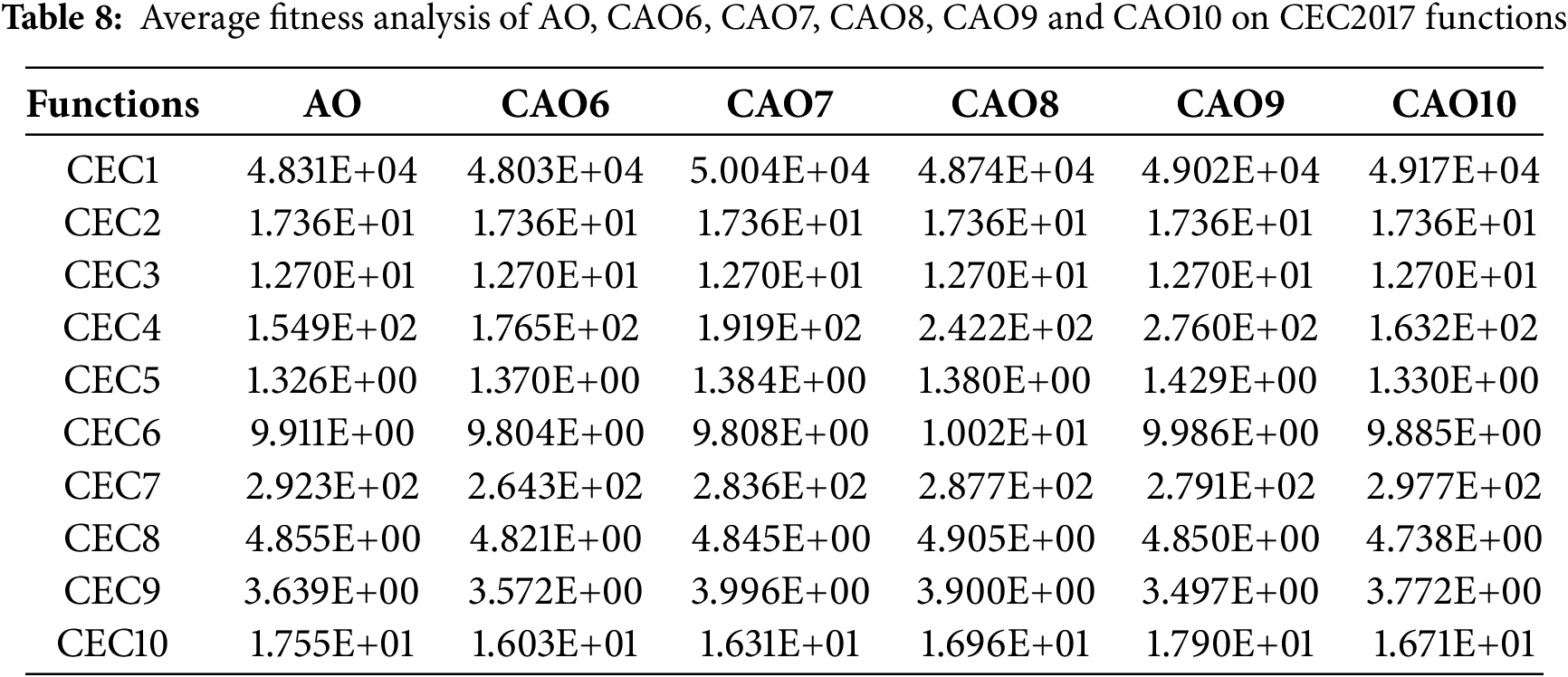
The convergence analysis of AO and CAO1-10 for CEC functions is shown in Figs. 5 and 6. Fig. 5a–e shows the convergence for CEC1, CEC2, CEC3, CEC4, and CEC5 functions, whereas Fig. 6a–e shows the convergence of CEC6, CEC7, CEC8, CEC9, and CEC10 functions, respectively. It is observed from Figs. 5 and 6 that chaotic variants of AO show better convergence for these functions than AO.
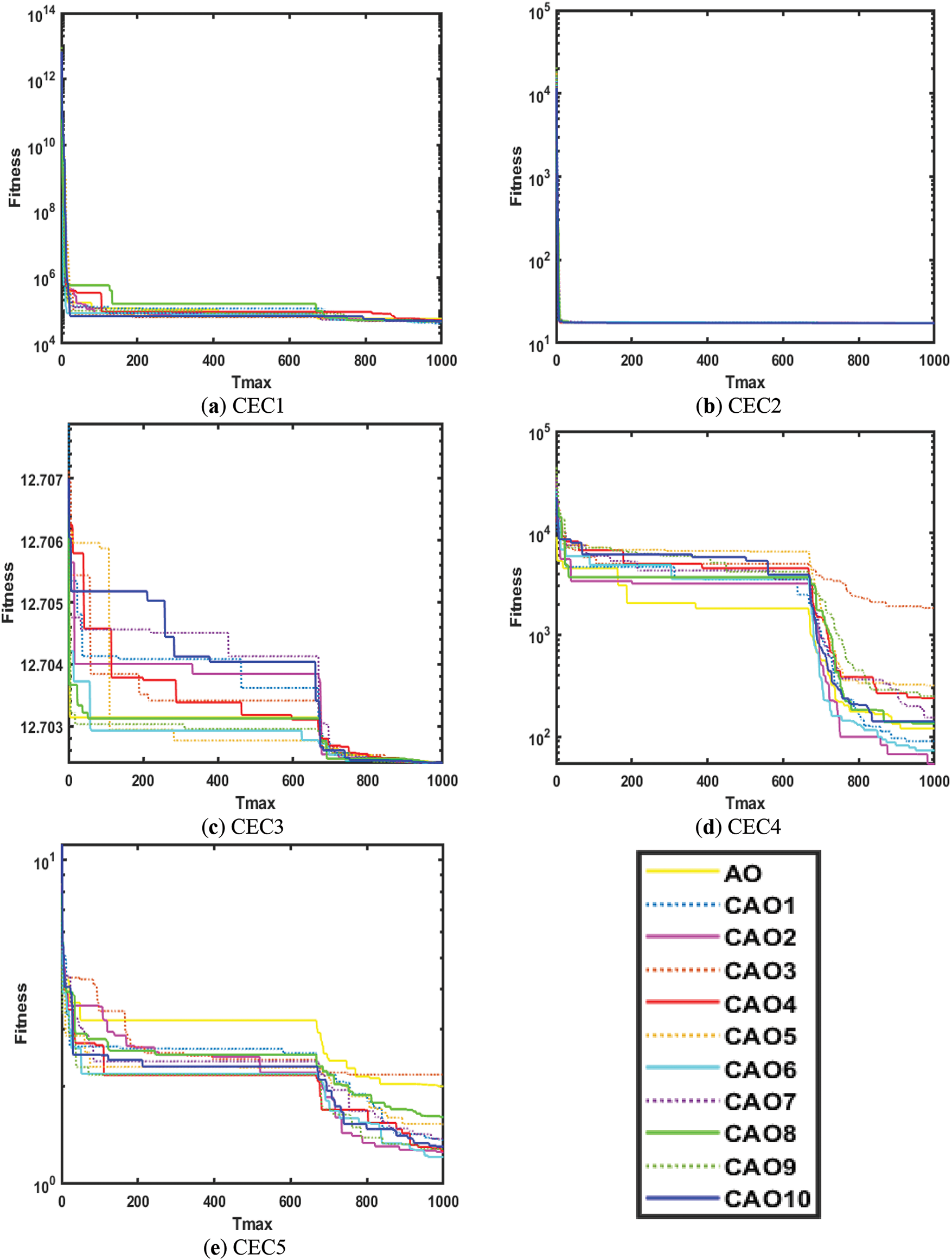
Figure 5: Convergence analysis on CEC1, CEC2, CEC3, CEC4 and CEC5 functions
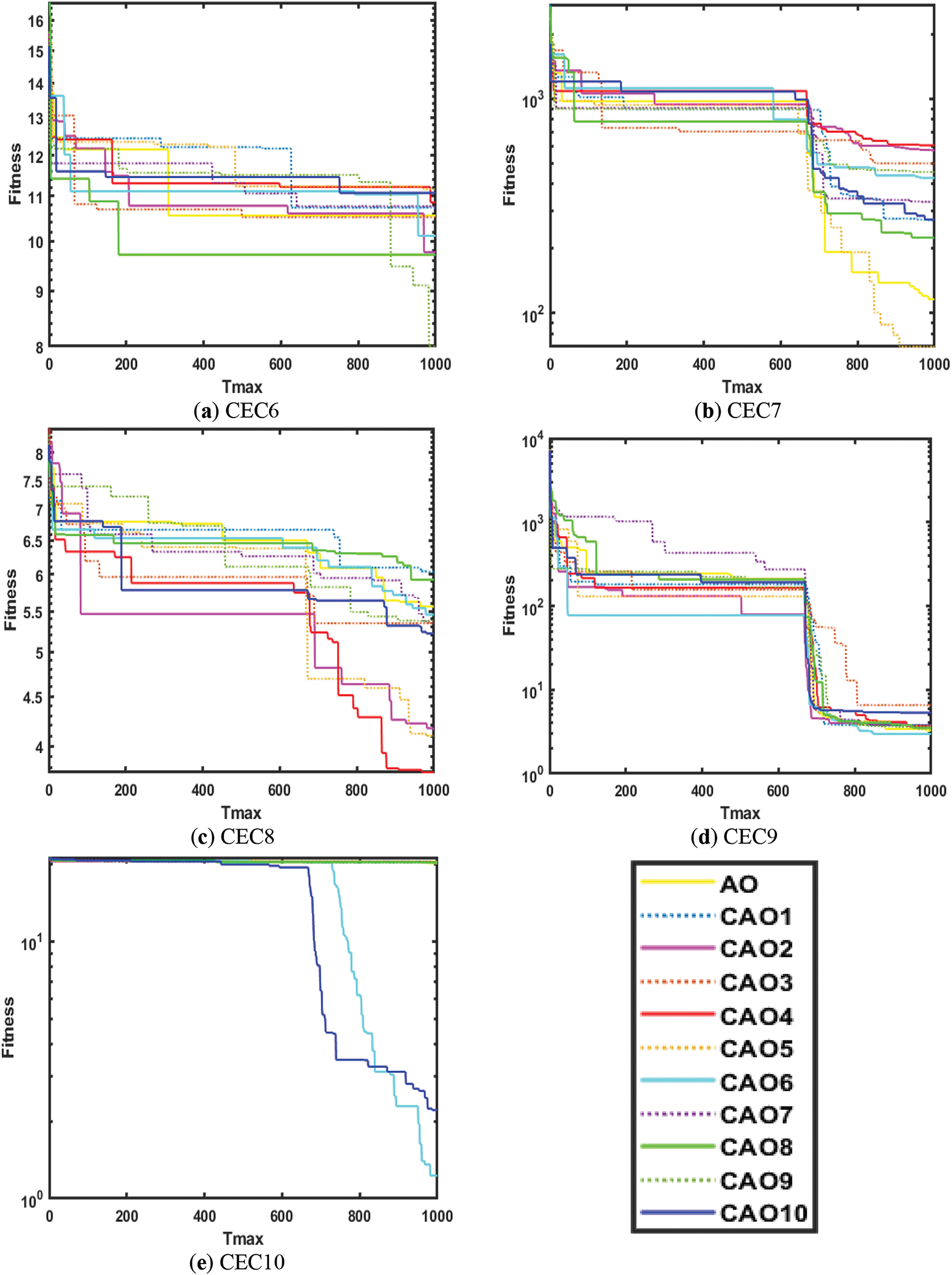
Figure 6: Convergence analysis on CEC6, CEC7, CEC8, CEC9 and CEC10 functions
The electro-hydraulic control system (EHCS) has been recently used in various applications [84]. It consists of an EH proportional valve and a valve-controlled asymmetric subsystem. It can be presented as a first-order model as shown in Eq. (21).
where
where
the simulations were performed at

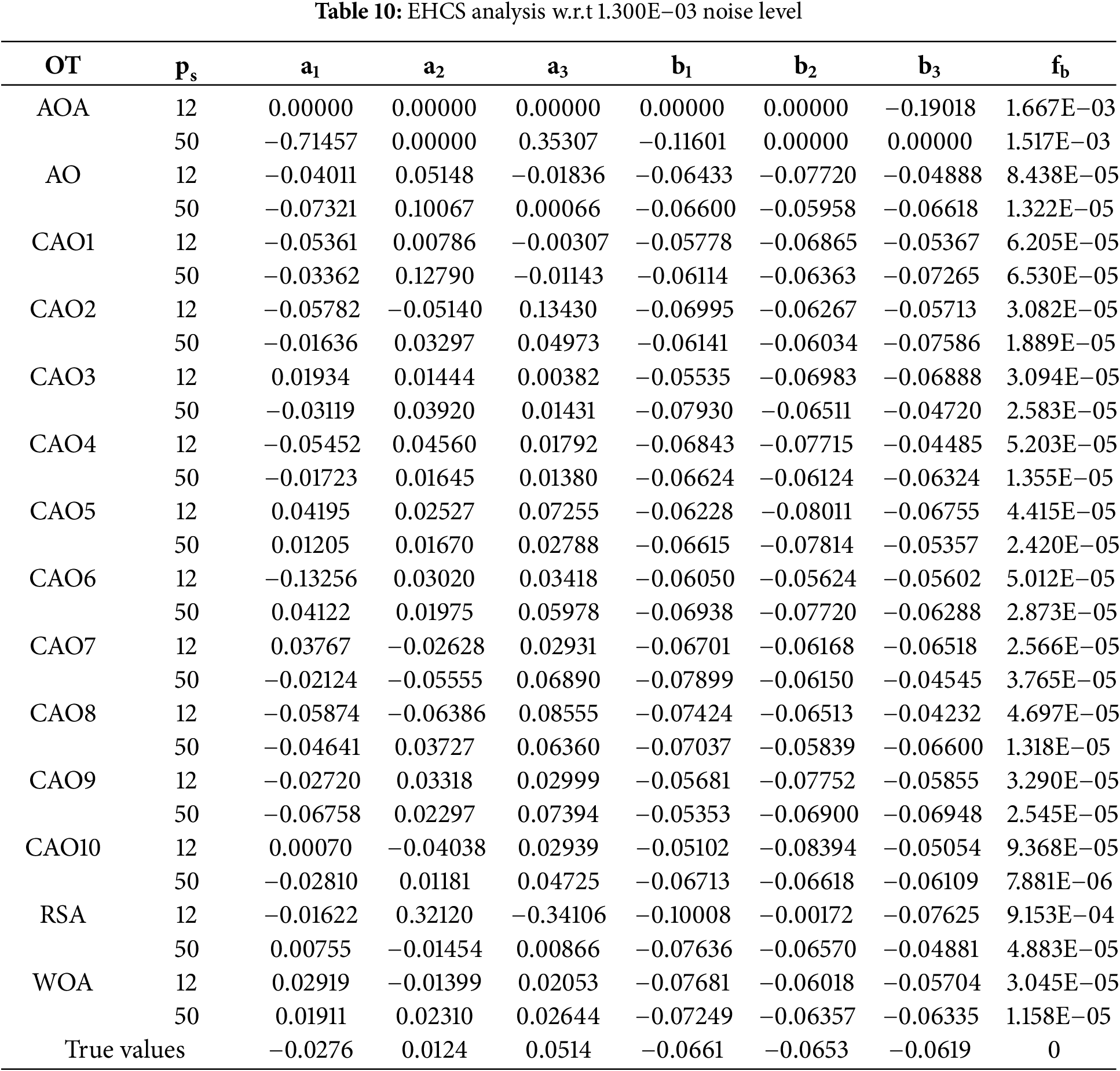
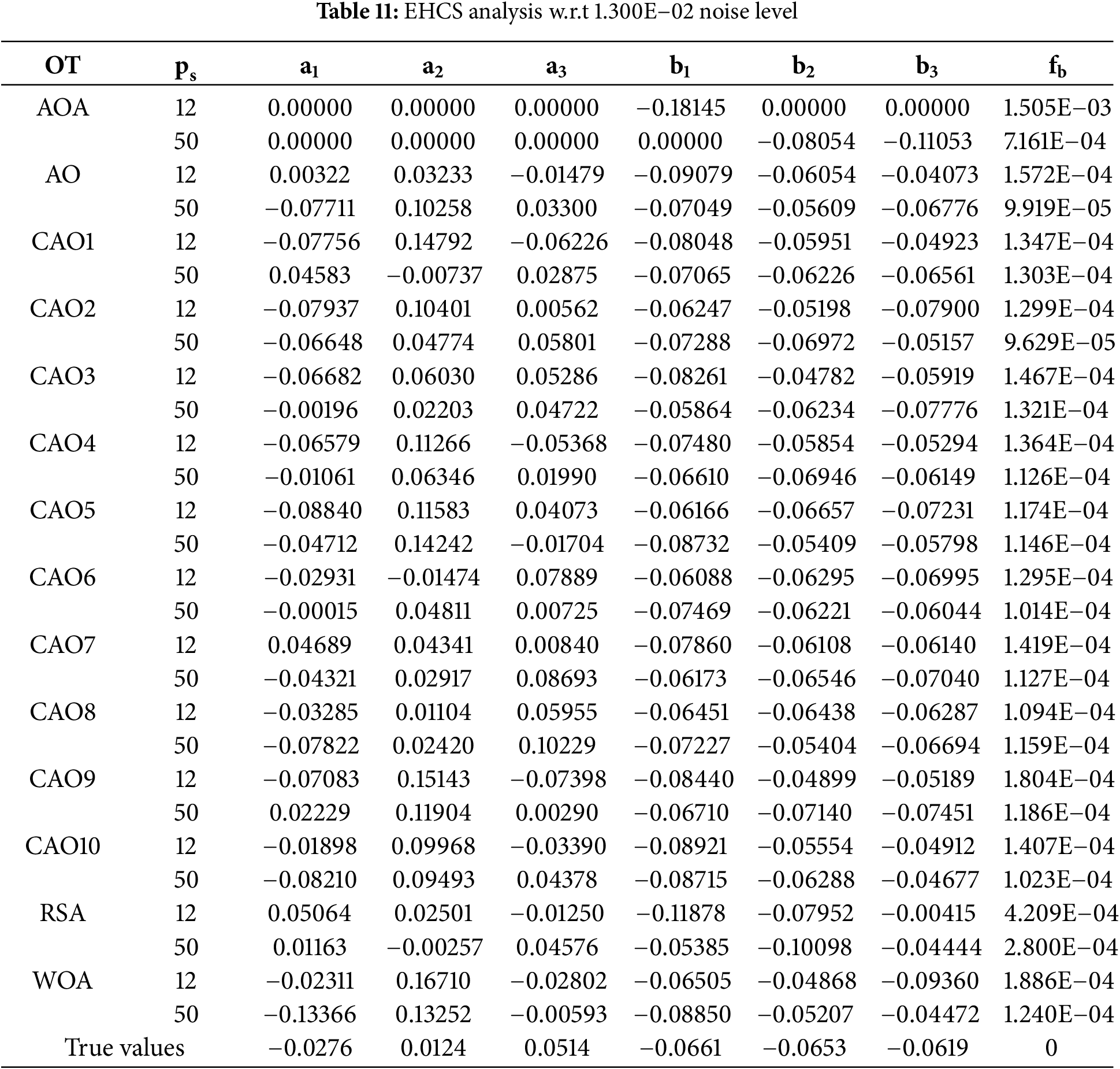
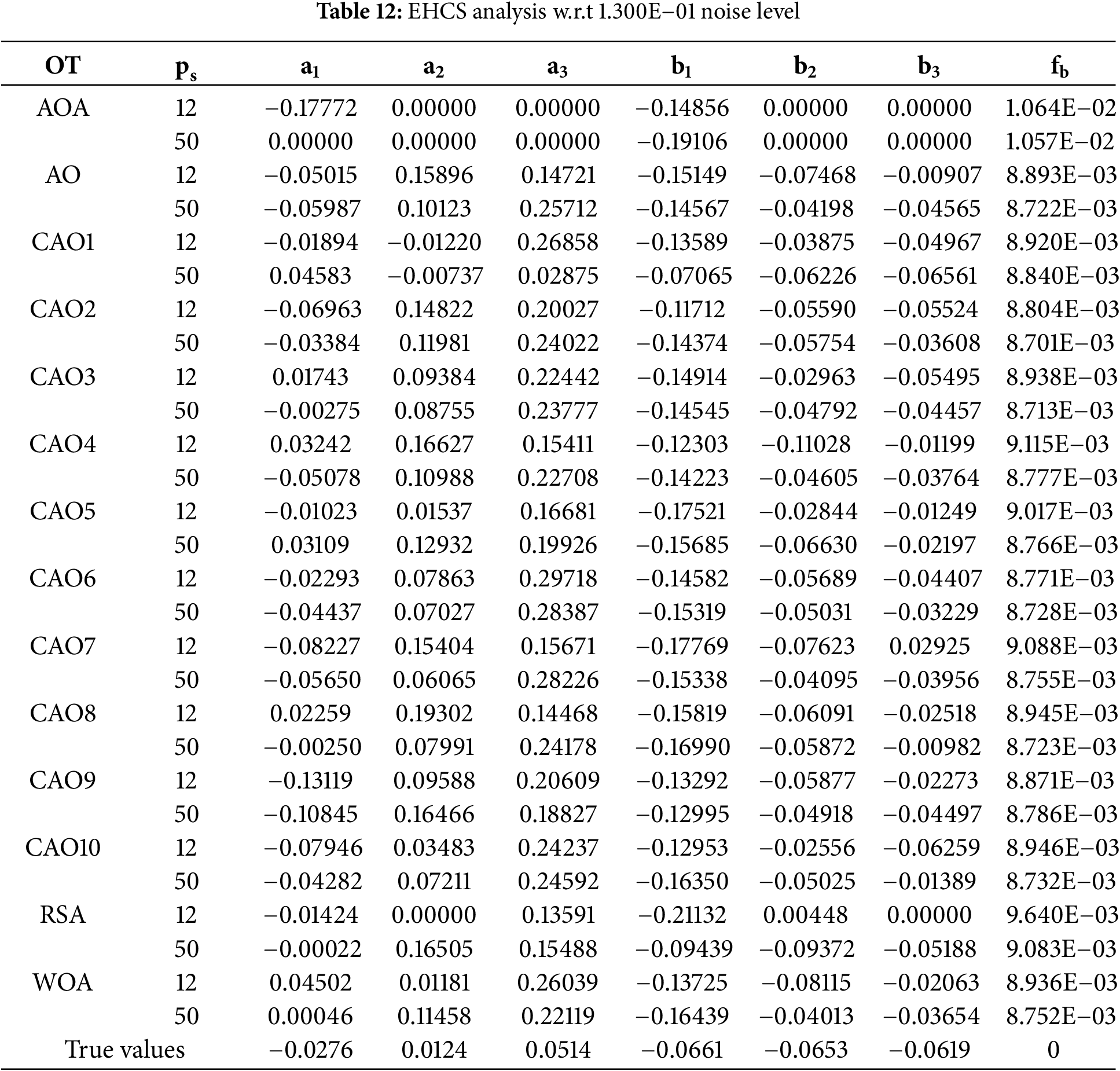
Tables 10–12 reflect the behavior of AO, CAO1-10, AOA, RSA, and WOA for true values, and best fitness (
The convergence analysis at
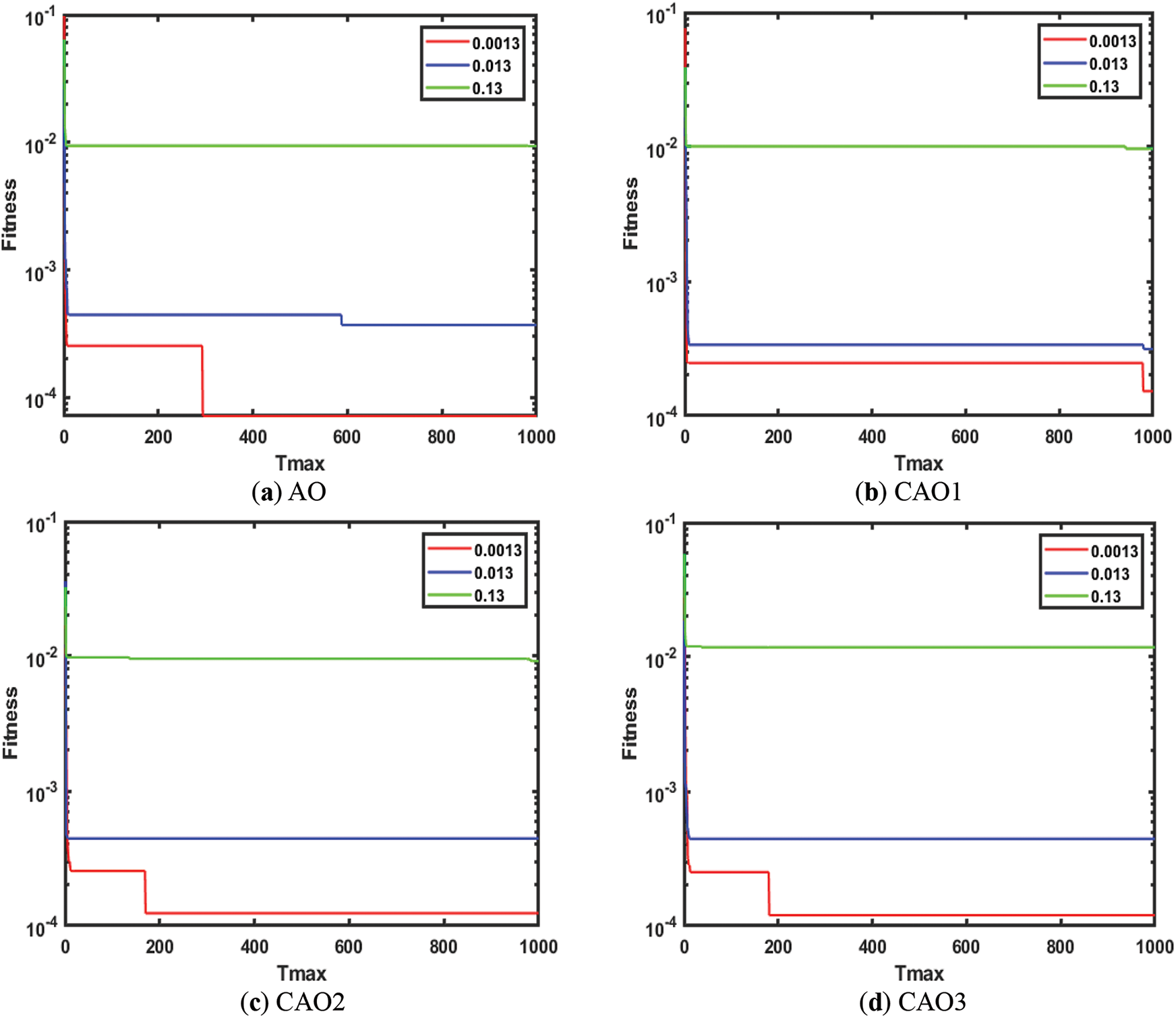
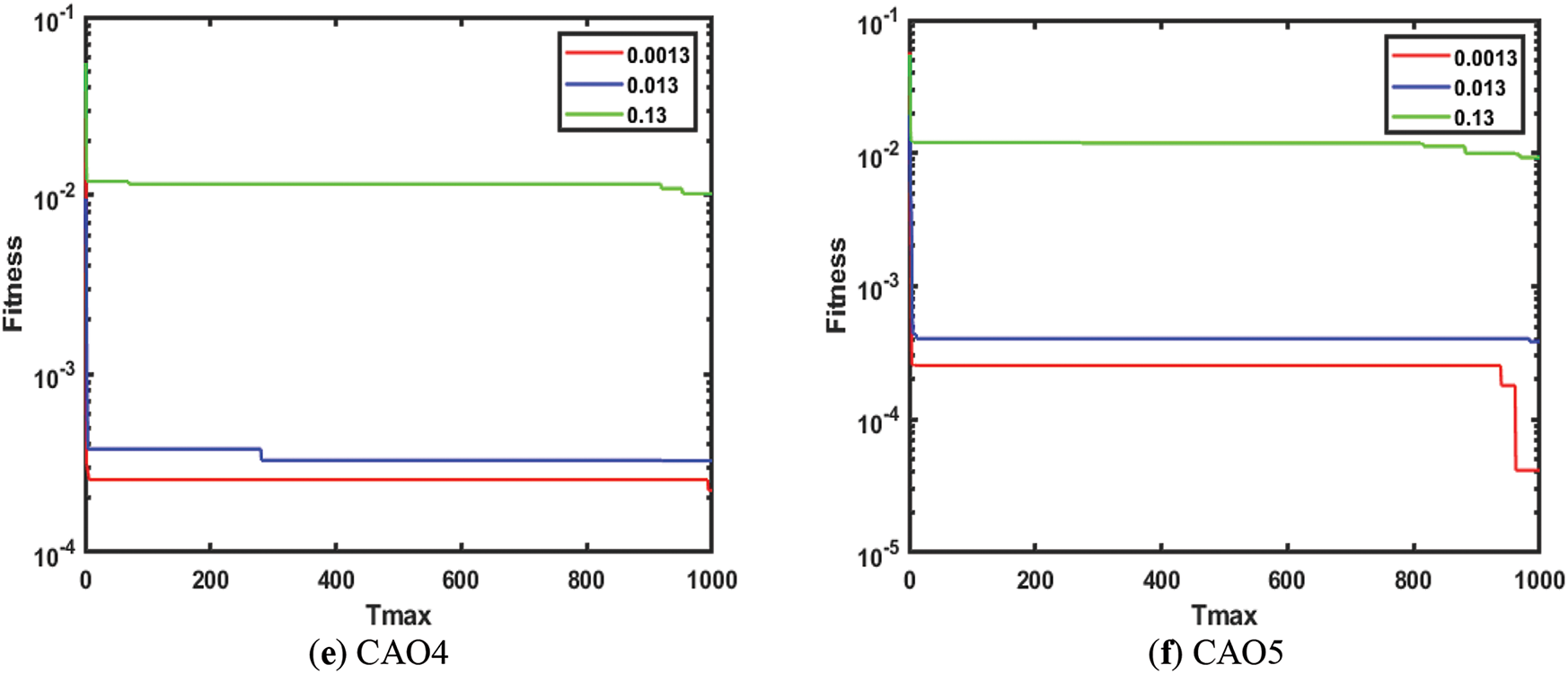
Figure 7: Performance of AO, and CAO1-5 for EHCS
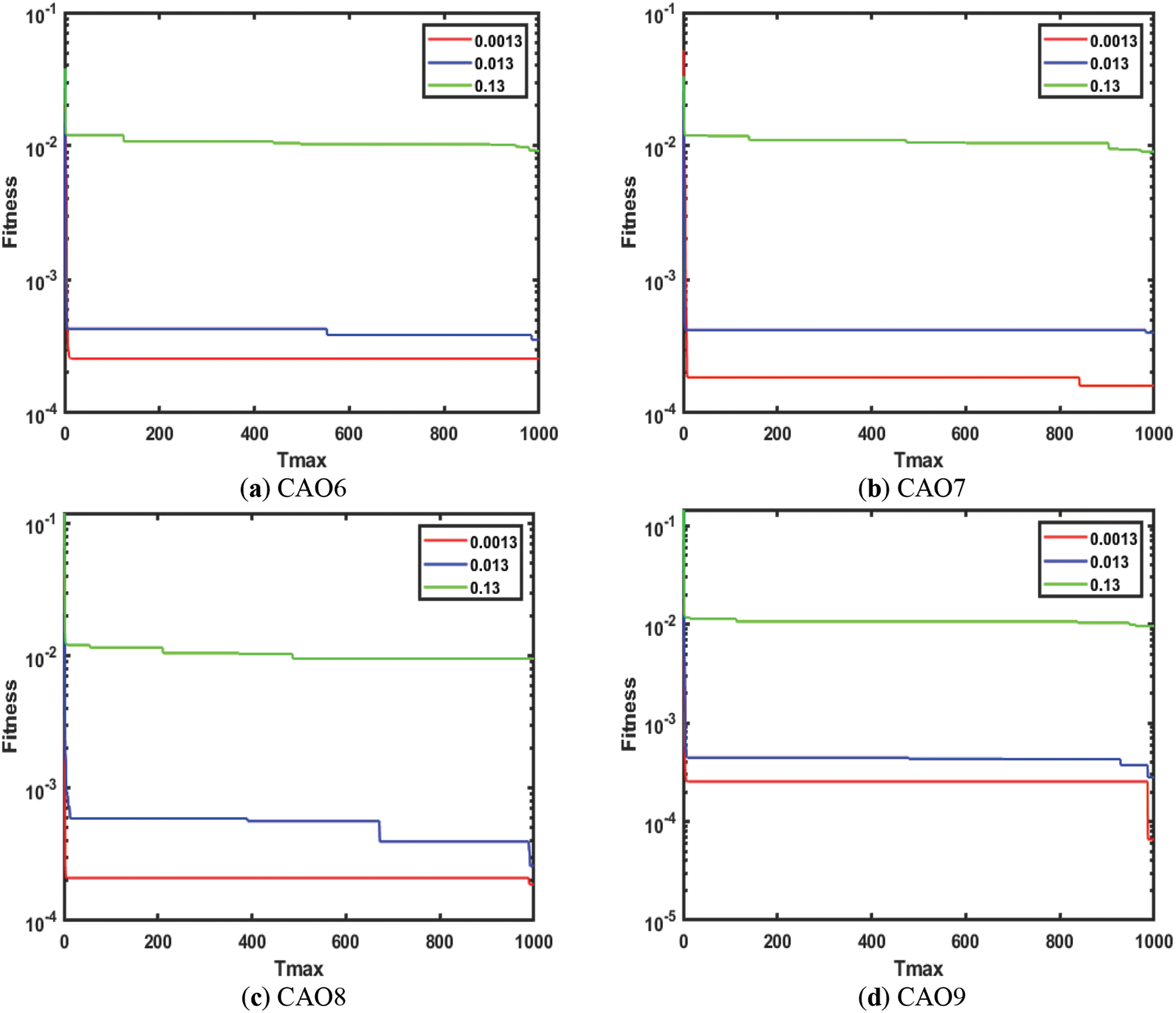

Figure 8: Performance of CAO6-10 and AOA for EHCS

Figure 9: Performance of RSA and WOA for EHCS
Figs. 10 and 11 show the convergence plots of AO, AOA, CAO1-10, RSA, and WOA at
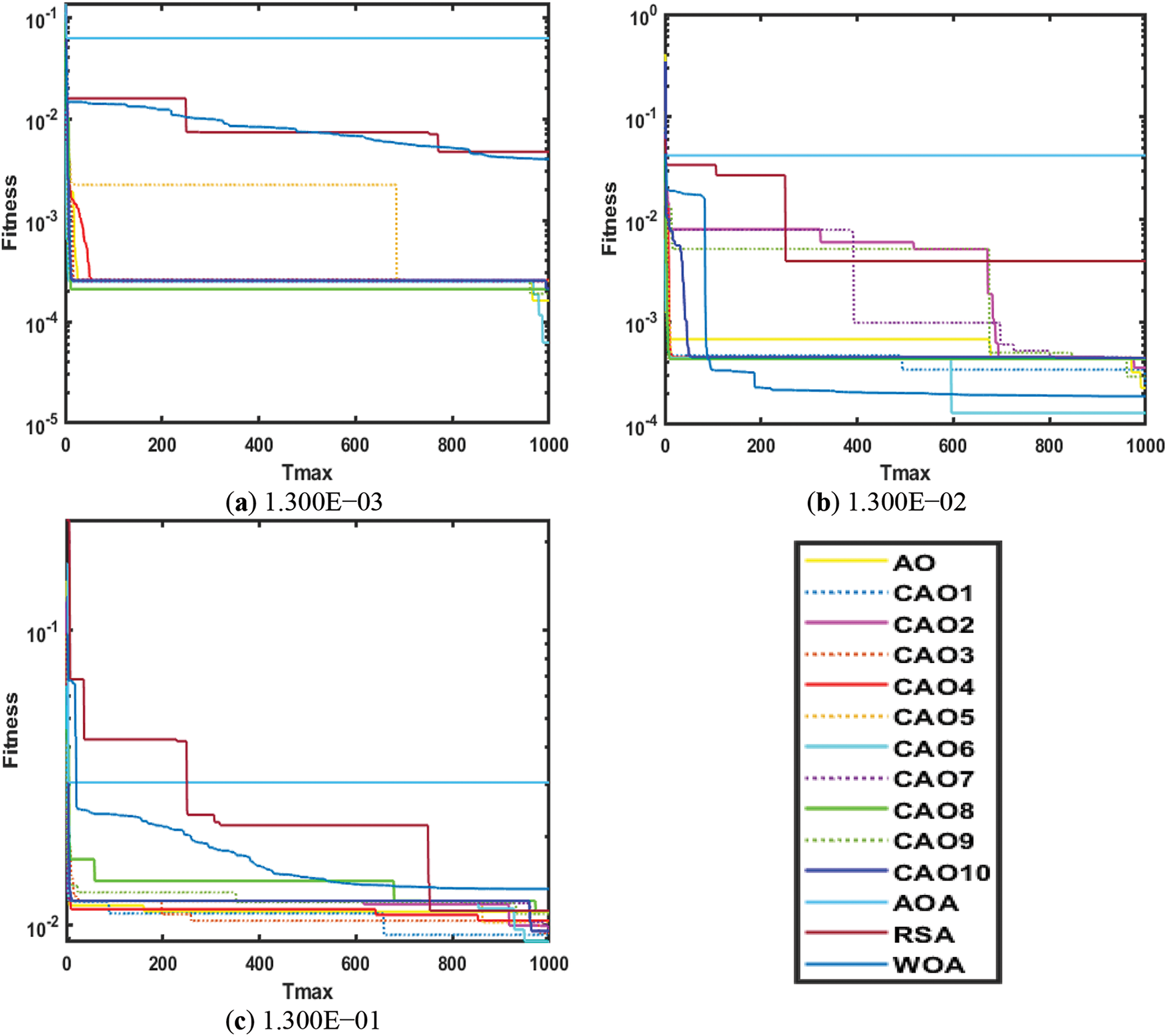
Figure 10: EHCS convergence analysis w.r.t noise at
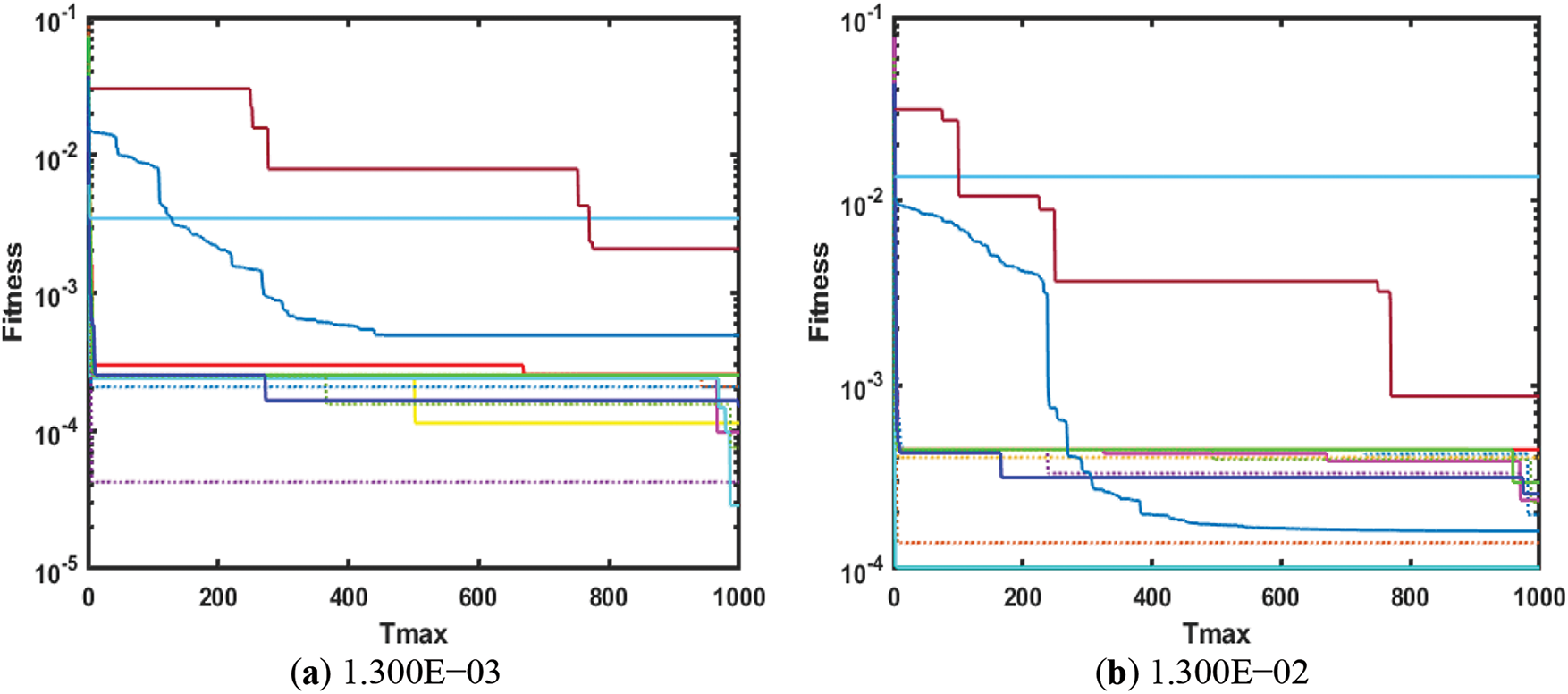
Figure 11: EHCS convergence analysis w.r.t noise at
The average computational time performance is measured on EHCS statistically on 100 independent runs at


The average fitness of AO, CAO1-10, AOA, RSA, and WOA for EHCS is shown in Fig. 12. It is observed from Fig. 12 that CAO6 achieves the lowest average fitness against AO, CAO1-5, CAO7-10, AOA, RSA, and WOA.
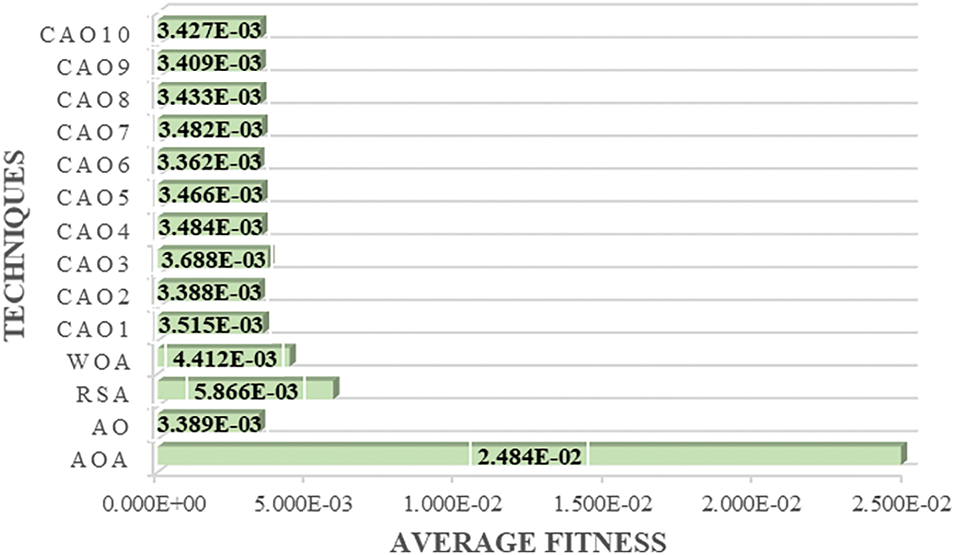
Figure 12: Average fitness of all OT’s w.r.t
To further assess the performance, the Friedman Test for repeated measures [72] is executed on average fitness values of CAO6, AO, AOA, RSA, and WOA with a significance level of 5.000E−02. The obtained p-value is 1.100E−04, indicating that CAO6 is statistically significant.
Figs. 13–15 show the Taguchi test [86] analysis of AO, CAO1-10, AOA, RSA, and WOA for EHCS at

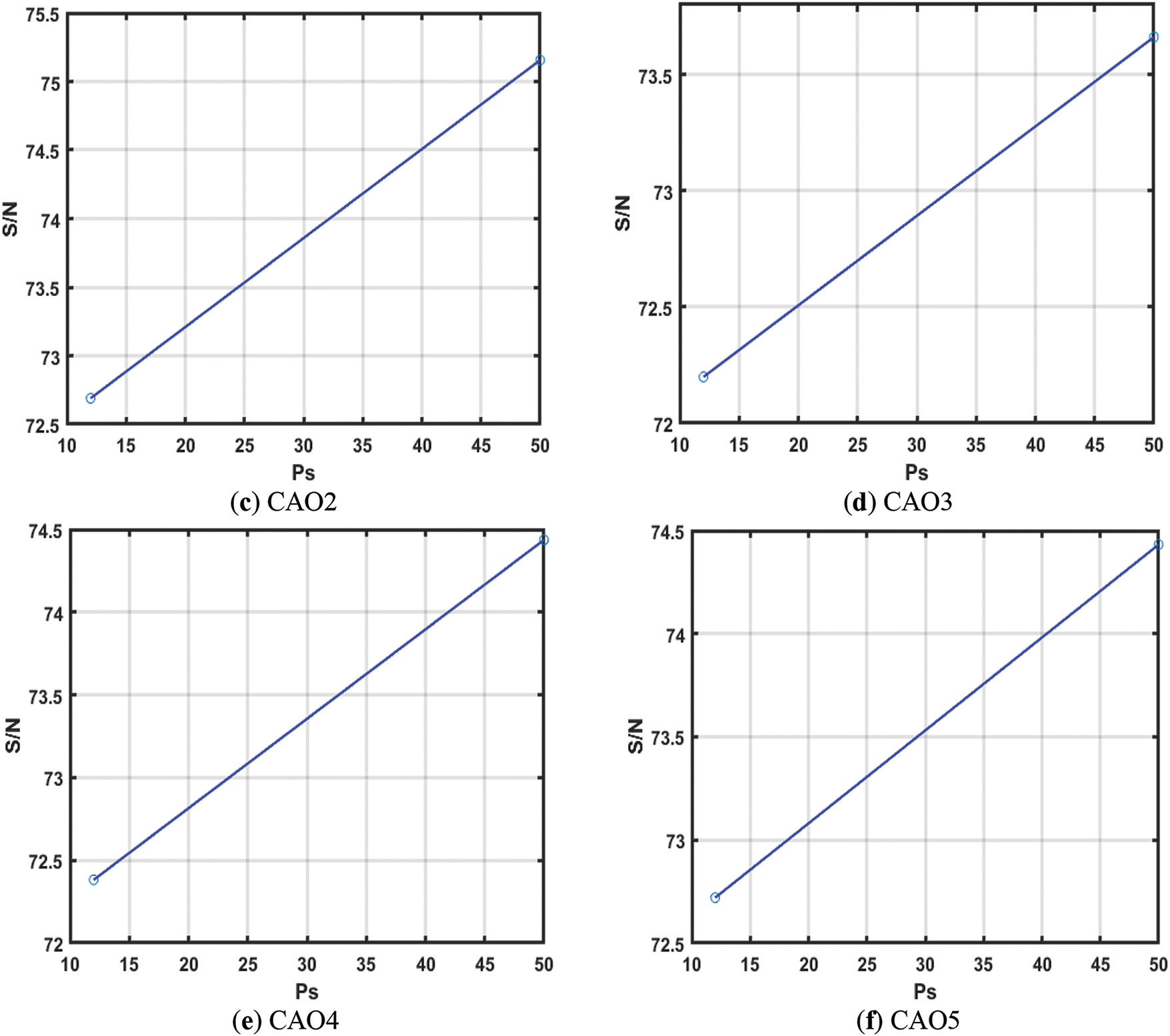
Figure 13: Taguchi analysis of AO, CAO1, CAO2, CAO3, CAO4 and CAO5 w.r.t
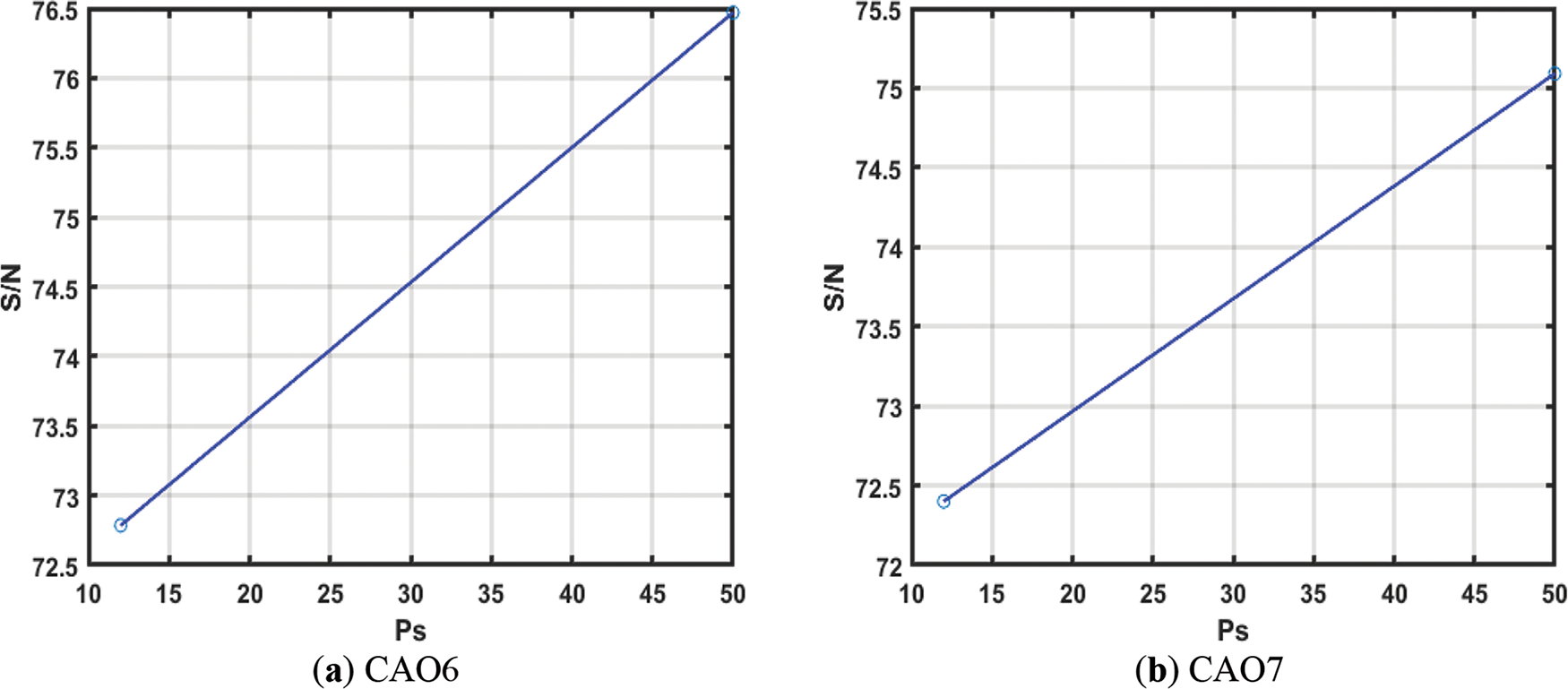
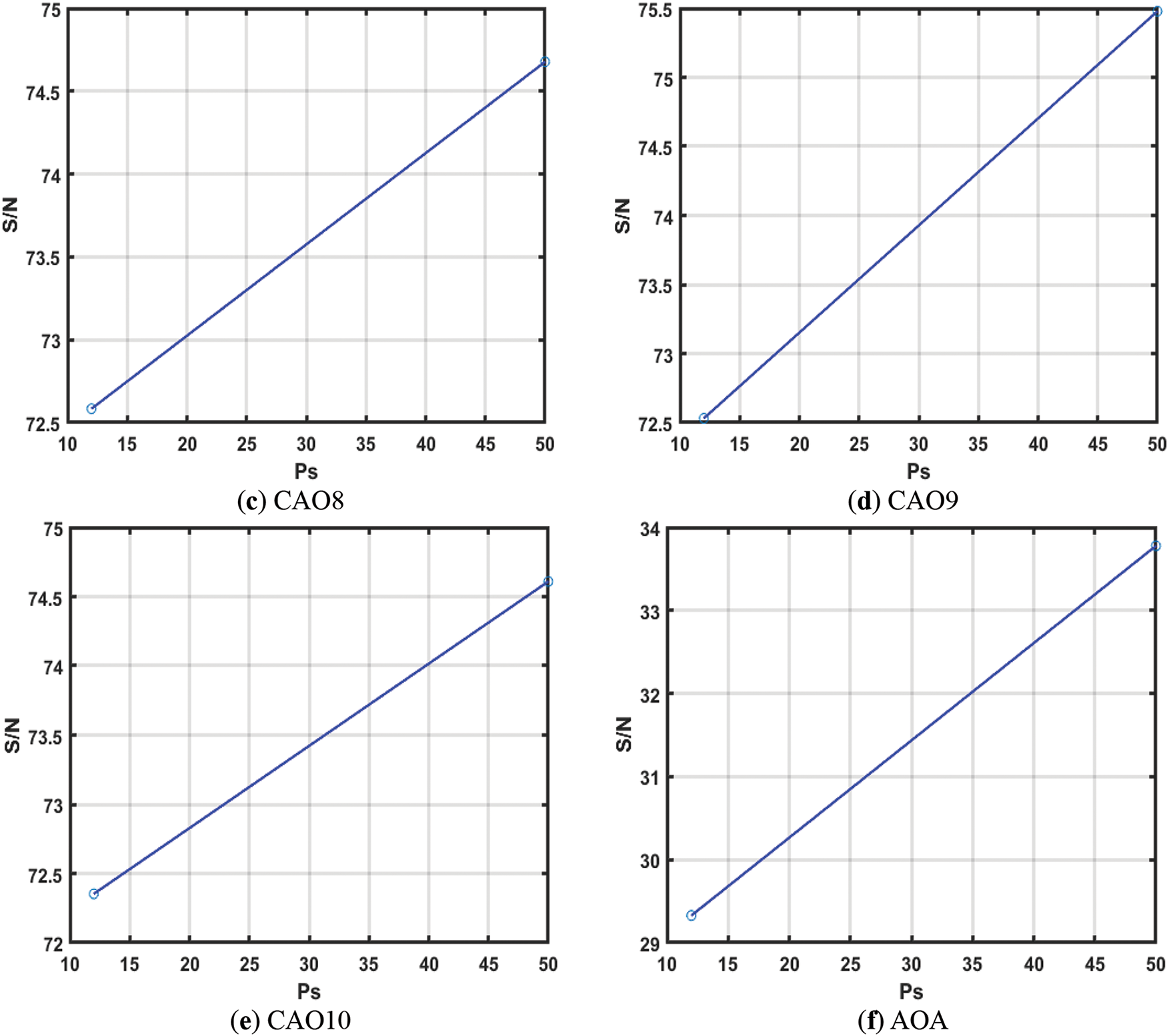
Figure 14: Taguchi analysis of CAO6, CAO7, CAO8, CAO9, CAO10 and AOA w.r.t
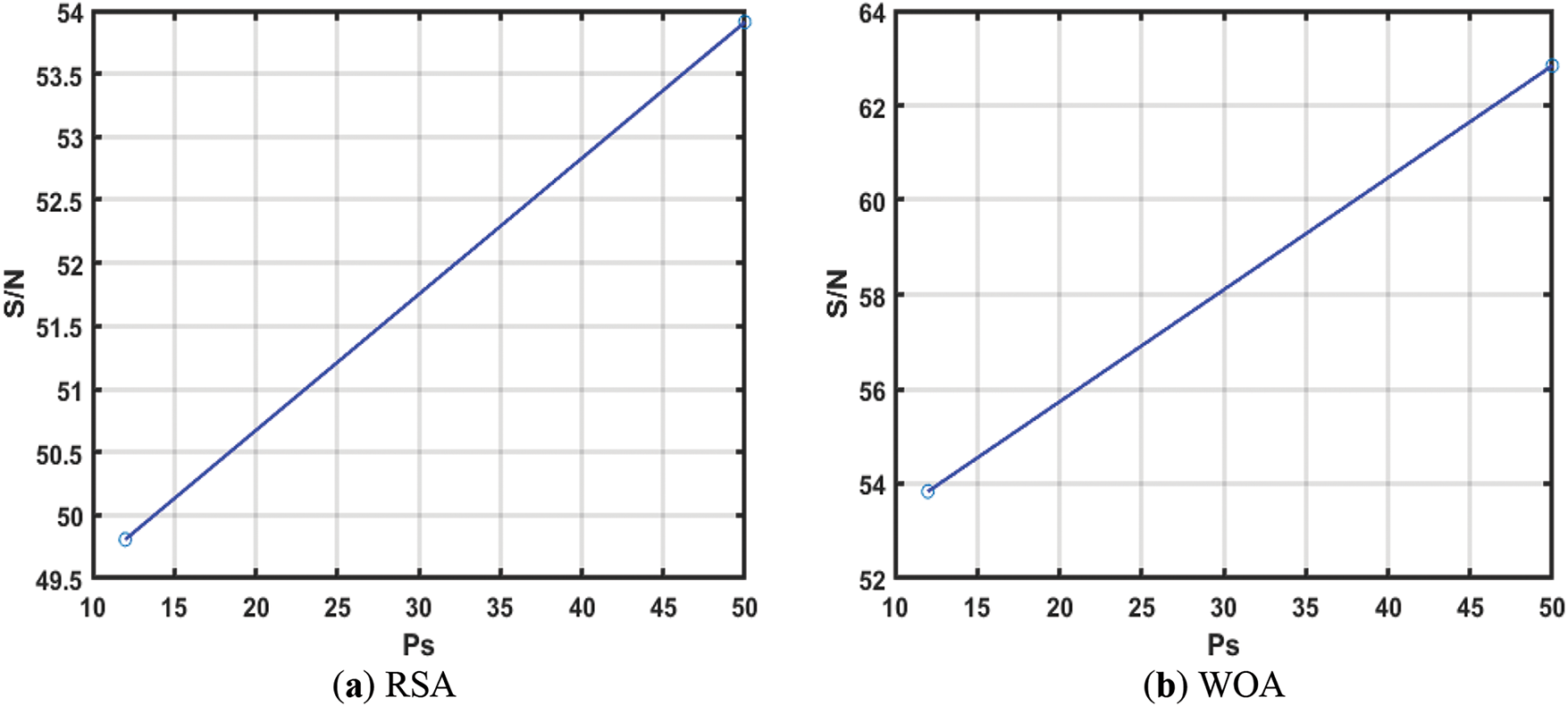
Figure 15: Taguchi analysis of RSA and WOA w.r.t
In this work, an improved variant of AO is proposed by integrating ten well-known chaotic maps in a narrowed exploitation mechanism. The proposed variant is applied for the parameter estimation of the electro-hydraulic control system, EHCS. Statistical analysis, Taguchi test, computational analysis, and Friedman test for repeated measures verify that AO with a chaotic piecewise map (CAO6) performs better than AO, CAO1, CAO2, CAO3, CAO4, CAO5, CAO7, CAO8, CAO9, CAO10, AOA, RSA, and WOA for parameter estimation of EHCS model. The proposed study achieves significant results. However, it may suffer from sensitivity to parameter tuning, limiting its effectiveness in other optimization problems. Future research could explore hybridizing the Chaotic Aquila Optimizer (CAO) with machine learning assisted algorithms, and parameter tuning strategies to enhance performance in complex optimization problems with extension to solve real-world problems in areas like renewable energy, biomedical systems, and industrial process control automation.
Acknowledgement: The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this project through project number (TU-DSPP-2024-52).
Funding Statement: This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-52).
Author Contributions: Conceptualization, Khizer Mehmood and Naveed Ishtiaq Chaudhary; Writing—original draft, Khizer Mehmood; Writing—review and edit, Naveed Ishtiaq Chaudhary and Muhammad Asif Zahoor Raja; Validation, Naveed Ishtiaq Chaudhary and Zeshan Aslam Khan; Visualization, Khalid Mehmood Cheema, Kaled M. Alshmrany and Sultan S. Alshamrani; Formal analysis, Khizer Mehmood, Khalid Mehmood Cheema and Zeshan Aslam Khan; Funding acquisition, Sultan S. Alshamrani and Kaled M. Alshmrany; Project administration, Sultan S. Alshamrani and Kaled M. Alshmrany. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Li S, Zhou Y, Luo Q. Enhanced multi-object dwarf mongoose algorithm for optimization stochastic data fusion wireless sensor network deployment. Comput Model Eng Sci. 2025;142(2):1955–94. doi:10.32604/cmes.2025.059738. [Google Scholar] [CrossRef]
2. Khan TA, Chaudhary NI, Hsu CC, Mehmood K, Khan ZA, Raja MAZ, et al. A gazelle optimization expedition for key term separated fractional nonlinear systems with application to electrically stimulated muscle modeling. Chaos Solitons Fractals. 2024;185(1):115111. doi:10.1016/j.chaos.2024.115111. [Google Scholar] [CrossRef]
3. Das S, Rout SK, Panda SK, Mohapatra PK, Almazyad AS, Jasser MB, et al. Marine predators algorithm with deep learning-based leukemia cancer classification on medical images. Comput Model Eng Sci. 2024;141(1):893–916. doi:10.32604/cmes.2024.051856. [Google Scholar] [CrossRef]
4. Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Raja MAZ. Parameter estimation of nonlinear systems: dwarf mongoose optimization algorithm with key term separation principle. J Ambient Intell Humaniz Comput. 2023;14(12):16921–31. doi:10.1007/s12652-023-04707-5. [Google Scholar] [CrossRef]
5. Wang Y, Jin H, Wang GG, Wang L. A bi-population cooperative discrete differential evolution for multiobjective energy-efficient distributed blocking flow shop scheduling problem. IEEE Trans Syst Man Cybern Syst. 2025;55(3):2211–23. doi:10.1109/TSMC.2024.3520320. [Google Scholar] [CrossRef]
6. Fatahi A, Nadimi-Shahraki MH, Zamani H. An improved binary quantum-based avian navigation optimizer algorithm to select effective feature subset from medical data: a COVID-19 case study. J Bionic Eng. 2024;21(1):426–46. doi:10.1007/s42235-023-00433-y. [Google Scholar] [CrossRef]
7. Cheema KM, Mehmood K, Chaudhary NI, Khan ZA, Raja MAZ, El-Sherbeeny AM, et al. Knacks of marine predator heuristics for distributed energy source-based power systems harmonics estimation. Heliyon. 2024;10(15):e35776. doi:10.1016/j.heliyon.2024.e35776. [Google Scholar] [PubMed] [CrossRef]
8. Song H, Wang J, Bei J, Wang M. Modified snake optimizer based multi-level thresholding for color image segmentation of agricultural diseases. Expert Syst Appl. 2024;255(8):124624. doi:10.1016/j.eswa.2024.124624. [Google Scholar] [CrossRef]
9. Cheema KM, Mehmood K, Chaudhary NI, Khan ZA, Raja MAZ. A nadeem, Knacks of evolutionary mating heuristics for renewable energy source-based power systems signal harmonics estimation. Int J Energy Res. 2024;1(1):8871266. doi:10.1155/2024/8871266. [Google Scholar] [CrossRef]
10. Wu Q, Cao Y, Wang H, Hong W. Machine-learning-assisted optimization and its application to antenna designs: opportunities and challenges. China Commun. 2020;17(4):152–64. doi:10.23919/JCC.2020.04.014. [Google Scholar] [CrossRef]
11. Akinsolu MO, Mistry KK, Liu B, Lazaridis PI, Excell P. Machine learning-assisted antenna design optimization: a review and the state-of-the-art. In: Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP); 2020 Mar 15–20; Copenhagen, Denmark. doi:10.23919/EuCAP48036.2020.9135936. [Google Scholar] [CrossRef]
12. Wu Q, Chen W, Yu C, Wang H, Hong W. Machine-learning-assisted optimization for antenna geometry design. IEEE Trans Antennas Propag. 2024;72(3):2083–95. doi:10.1109/TAP.2023.3346493. [Google Scholar] [CrossRef]
13. Xu Y, Wandelt S, Sun X, Yang Y, Jin X, Karichery S, et al. Machine-learning-assisted optimization of aircraft trajectories under realistic constraints. J Guid Control Dyn. 2023;46(9):1814–25. doi:10.2514/1.G007038. [Google Scholar] [CrossRef]
14. Bhatasana M, Marconnet A. Machine-learning assisted optimization strategies for phase change materials embedded within electronic packages. Appl Therm Eng. 2021;199(17–18):117384. doi:10.1016/j.applthermaleng.2021.117384. [Google Scholar] [CrossRef]
15. Abualigah L, Sheikhan A, Ikotun AM, Zitar RA, Alsoud AR, Al-Shourbaji I, et al. Particle swarm optimization algorithm: review and applications. Metaheuristic Optim Algorithms. 2024;1–14. doi:10.1016/B978-0-443-13925-3.00019-4. [Google Scholar] [CrossRef]
16. Wang GG, Deb S, Cui Z. Monarch butterfly optimization. Neural Comput Appl. 2019;31(7):1995–2014. doi:10.1007/s00521-015-1923-y. [Google Scholar] [CrossRef]
17. Abualigah L, Elaziz MA, Sumari P, Geem ZW, Gandomi AH. Reptile search algorithm (RSAa nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191(11):116158. doi:10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]
18. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]
19. Alzoubi S, Abualigah L, Sharaf M, Daoud MS, Khodadadi N, Jia H. Synergistic swarm optimization algorithm. Comput Model Eng Sci. 2024;139(3):2557–604. doi:10.32604/cmes.2023.045170. [Google Scholar] [CrossRef]
20. Price KV. Differential evolution. In: Zelinka I, Snášel V, Abraham A, editors. Handbook of optimization. Berlin/Heidelberg, Germany: Springer; 2013. p. 187–214. doi:10.1007/978-3-642-30504-7_8. [Google Scholar] [CrossRef]
21. Özcan N, Utku S, Berber T. Artificial circulation system algorithm: a novel bio-inspired algorithm. Comput Model Eng Sci. 2025;142(1):635–63. doi:10.32604/cmes.2024.055860. [Google Scholar] [CrossRef]
22. Simon D. Biogeography-based optimization. IEEE Trans Evol Comput. 2008;12(6):702–13. doi:10.1109/TEVC.2008.919004. [Google Scholar] [CrossRef]
23. Wang GG, Deb S, Coelho LDS. Earthworm optimisation algorithm: a bio-inspired metaheuristic algorithm for global optimisation problems. Int J Bio-Inspired Comput. 2018;12(1):1–22. doi:10.1504/IJBIC.2018.093328. [Google Scholar] [CrossRef]
24. Wang GG. Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018;10(2):151–64. doi:10.1007/s12293-016-0212-3. [Google Scholar] [CrossRef]
25. Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The arithmetic optimization algorithm. Comput Methods Appl Mech Eng. 2021;376(2):113609. doi:10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]
26. Bai J, Li Y, Zheng M, Khatir S, Benaissa B, Abualigah L, et al. A Sinh Cosh optimizer. Knowl-Based Syst. 2023;282(1):111081. doi:10.1016/j.knosys.2023.111081. [Google Scholar] [CrossRef]
27. Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl. 2016;27(2):495–513. doi:10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]
28. Rashedi E, Nezamabadi-pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]
29. Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S. Henry gas solubility optimization: a novel physics-based algorithm. Future Gener Comput Syst. 2019;101(4):646–67. doi:10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]
30. Askari Q, Younas I, Saeed M. Political optimizer: a novel socio-inspired meta-heuristic for global optimization. Knowl-Based Syst. 2020;195(5):105709. doi:10.1016/j.knosys.2020.105709. [Google Scholar] [CrossRef]
31. Emami H. Stock exchange trading optimization algorithm: a human-inspired method for global optimization. J Supercomput. 2022;78(2):2125–74. doi:10.1007/s11227-021-03943-w. [Google Scholar] [PubMed] [CrossRef]
32. Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput-Aided Des. 2011;43(3):303–15. doi:10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]
33. Askari Q, Saeed M, Younas I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst Appl. 2020;161(3):113702. doi:10.1016/j.eswa.2020.113702. [Google Scholar] [CrossRef]
34. Elsisi M. Future search algorithm for optimization. Evol Intell. 2019;12(1):21–31. doi:10.1007/s12065-018-0172-2. [Google Scholar] [CrossRef]
35. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-qaness MAA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157(11):107250. doi:10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]
36. Sasmal B, Hussien AG, Das A, Dhal KG. A comprehensive survey on Aquila optimizer. Arch Comput Methods Eng. 2023;30(7):4449–76. doi:10.1007/s11831-023-09945-6. [Google Scholar] [PubMed] [CrossRef]
37. Ahmadipour M, Murtadha Othman M, Bo R, Sadegh Javadi M, Mohammed Ridha H, Alrifaey M. Optimal power flow using a hybridization algorithm of arithmetic optimization and Aquila optimizer. Expert Syst Appl. 2024;235(4):121212. doi:10.1016/j.eswa.2023.121212. [Google Scholar] [CrossRef]
38. Ateeq Almutairi S. An optimized feature selection and hyperparameter tuning framework for automated heart disease diagnosis. Comput Syst Sci Eng. 2023;47(2):2599–624. doi:10.32604/csse.2023.041609. [Google Scholar] [CrossRef]
39. Alnfiai MM, Almalki N, Al-Wesabi FN, Alduhayyem M, Mustafa Hilal A, Ahmed Hamza M. Deep learning driven arabic text to speech synthesizer for visually challenged people. Intell Autom Soft Comput. 2023;36(3):2639–52. doi:10.32604/iasc.2023.034069. [Google Scholar] [CrossRef]
40. Ramachandran A, Gayathri K, Alkhayyat A, Malik RQ. Aquila optimization with machine learning-based anomaly detection technique in cyber-physical systems. Comput Syst Sci Eng. 2023;46(2):2177–94. doi:10.32604/csse.2023.034438. [Google Scholar] [CrossRef]
41. Agarwal N, Gokilavani M, Nagarajan S, Saranya S, Alsolai H, Dhahbi S, et al. Intelligent Aquila optimization algorithm-based node localization scheme for wireless sensor networks. Comput Mater Contin. 2023;74(1):141–52. doi:10.32604/cmc.2023.030074. [Google Scholar] [CrossRef]
42. Alghazzawi DM, Hamid Hasan S, Bhatia S. Optimized generative adversarial networks for adversarial sample generation. Comput Mater Contin. 2022;72(2):3877–97. doi:10.32604/cmc.2022.024613. [Google Scholar] [CrossRef]
43. Kari T, He Z, Rouzi A, Zhang Z, Ma X, Du L. Power transformer fault diagnosis using random forest and optimized kernel extreme learning machine. Intell Autom Soft Comput. 2023;37(1):691–705. doi:10.32604/iasc.2023.037617. [Google Scholar] [CrossRef]
44. Gouri Tekkali C, Natarajan K. Smart fraud detection in E-transactions using synthetic minority oversampling and binary Harris Hawks optimization. Comput Mater Contin. 2023;75(2):3171–87. doi:10.32604/cmc.2023.036865. [Google Scholar] [CrossRef]
45. Mehmood K, Chaudhary NI, Khan ZA, Raja MAZ, Cheema KM, Milyani AH. Design of Aquila optimization heuristic for identification of control autoregressive systems. Mathematics. 2022;10(10):1749. doi:10.3390/math10101749. [Google Scholar] [CrossRef]
46. Alahmari S, Yonbawi S, Racharla S, Laxmi Lydia E, Khairi Ishak M, Khalid Alkahtani H, et al. Hybrid multi-strategy Aquila optimization with deep learning driven crop type classification on hyperspectral images. Comput Syst Sci Eng. 2023;47(1):375–91. doi:10.32604/csse.2023.036362. [Google Scholar] [CrossRef]
47. Zhou Y, Chen Z, Gong Z, Chen P, Razmjooy S. The improved Aquila optimization approach for cost-effective design of hybrid renewable energy systems. Heliyon. 2024;10(6):e27281. doi:10.1016/j.heliyon.2024.e27281. [Google Scholar] [PubMed] [CrossRef]
48. Rajinikanth V, Mohamed Aslam S, Kadry S, Thinnukool O. Semi/fully-automated segmentation of gastric-polyp using Aquila-optimization-algorithm enhanced images. Comput Mater Contin. 2022;70(2):4087–105. doi:10.32604/cmc.2022.019786. [Google Scholar] [CrossRef]
49. Ekinci S, Izci D, Abualigah L, Zitar RA. A modified oppositional chaotic local search strategy based Aquila optimizer to design an effective controller for vehicle cruise control system. J Bionic Eng. 2023;20(4):1828–51. doi:10.1007/s42235-023-00336-y. [Google Scholar] [CrossRef]
50. Ekinci S, Izci D, Eker E, Abualigah L. An effective control design approach based on novel enhanced Aquila optimizer for automatic voltage regulator. Artif Intell Rev. 2023;56(2):1731–62. doi:10.1007/s10462-022-10216-2. [Google Scholar] [CrossRef]
51. Ma Y, Shao P, Liu X, Wang L. Collaborative trajectory planning for stereoscopic agricultural multi-UAVs driven by the Aquila optimizer. Comput Mater Contin. 2025;82(1):1349–76. doi:10.32604/cmc.2024.058294. [Google Scholar] [CrossRef]
52. Ekinci S, Izci D, Abualigah L. A novel balanced Aquila optimizer using random learning and Nelder-Mead simplex search mechanisms for air-fuel ratio system control. J Braz Soc Mech Sci Eng. 2023;45(1):68. doi:10.1007/s40430-022-04008-6. [Google Scholar] [CrossRef]
53. An D, Jia J, Cai W, Yang D, Lv C, Zhu J, et al. A novel Aquila optimizer based pv array reconfiguration scheme to generate maximum energy under partial shading condition. Energy Eng. 2022;119(4):1531–45. doi:10.32604/ee.2022.019284. [Google Scholar] [CrossRef]
54. Cavlak Y, Ateş A, Abualigah L, Elaziz MA. Fractional-order chaotic oscillator-based Aquila optimization algorithm for maximization of the chaotic with Lorentz oscillator. Neural Comput Appl. 2023;35(29):21645–62. doi:10.1007/s00521-023-08945-8. [Google Scholar] [CrossRef]
55. Baş E. Binary Aquila optimizer for 0–1 knapsack problems. Eng Appl Artif Intell. 2023;118(22):105592. doi:10.1016/j.engappai.2022.105592. [Google Scholar] [CrossRef]
56. Turgut E, Turgut MS. Local search enhanced Aquila optimization algorithm ameliorated with an ensemble of wavelet mutation strategies for complex optimization problems. Math Comput Simul. 2023;206:302–74. doi:10.1016/j.matcom.2022.11.020. [Google Scholar] [CrossRef]
57. Liu H, Zhang X, Zhang H, Li C, Chen Z. A reinforcement learning-based hybrid Aquila optimizer and improved arithmetic optimization algorithm for global optimization. Expert Syst Appl. 2023;224(11):119898. doi:10.1016/j.eswa.2023.119898. [Google Scholar] [CrossRef]
58. Verma M, Sreejeth M, Singh M, Babu TS, Alhelou HH. Chaotic mapping based advanced Aquila optimizer with single stage evolutionary algorithm. IEEE Access. 2022;10(4):89153–69. doi:10.1109/ACCESS.2022.3200386. [Google Scholar] [CrossRef]
59. Zhang Y, Xu X, Zhang N, Zhang K, Dong W, Li X. Adaptive Aquila optimizer combining niche thought with dispersed chaotic swarm. Sensors. 2023;23(2):755. doi:10.3390/s23020755. [Google Scholar] [PubMed] [CrossRef]
60. Wang Y, Xiao Y, Guo Y, Li J. Dynamic chaotic opposition-based learning-driven hybrid Aquila optimizer and artificial rabbits optimization algorithm: framework and applications. Processes. 2022;10(12):2703. doi:10.3390/pr10122703. [Google Scholar] [CrossRef]
61. Yang M, Yan G, Zhang Y, Zhang T, Ai C. Research on high efficiency and high dynamic optimal matching of the electro-hydraulic servo pump control system based on NSGA-II. Heliyon. 2023;9(3):e13805. doi:10.1016/j.heliyon.2023.e13805. [Google Scholar] [PubMed] [CrossRef]
62. Ling TG, Rahmat MF, Husain AR. System identification and control of an electro-hydraulic actuator system. In: Proceedings of the 2012 IEEE 8th International Colloquium on Signal Processing and its Applications; 2012 Mar 23–25; Malacca, Malaysia. doi:10.1109/CSPA.2012.6194696. [Google Scholar] [CrossRef]
63. Liang XW, Faudzi AAM, Ismail ZH. System identification and model predictive control using CVXGEN for electro-hydraulic actuator. Int J Integr Eng. 2019;11(4):166–74. doi:10.30880/ijie.2019.11.04.018. [Google Scholar] [CrossRef]
64. Izzuddin NH, Faudzi AAM, Johari MR, Osman K. System identification and predictive functional control for electro-hydraulic actuator system. In: Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS); 2015 Oct 18–20; Langkawi, Malaysia. doi:10.1109/IRIS.2015.7451600. [Google Scholar] [CrossRef]
65. Mehmood K, Chaudhary NI, Cheema KM, Khan ZA, Raja MAZ, Milyani AH, et al. Design of nonlinear marine predator heuristics for Hammerstein autoregressive exogenous system identification with key-term separation. Mathematics. 2023;11(11):2512. doi:10.3390/math11112512. [Google Scholar] [CrossRef]
66. Ding F, Lv L, Pan J, Wan X, Jin XB. Two-stage gradient-based iterative estimation methods for controlled autoregressive systems using the measurement data. Int J Control Autom Syst. 2020;18(4):886–96. doi:10.1007/s12555-019-0140-3. [Google Scholar] [CrossRef]
67. Li F, Zheng T, He N, Cao Q. Data-driven hybrid neural fuzzy network and ARX modeling approach to practical industrial process identification. IEEE/CAA J Autom Sin. 2022;9(9):1702–5. doi:10.1109/JAS.2022.105821. [Google Scholar] [CrossRef]
68. Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Raja MAZ, Milyani AH, et al. Dwarf mongoose optimization metaheuristics for autoregressive exogenous model identification. Mathematics. 2022;10(20):3821. doi:10.3390/math10203821. [Google Scholar] [CrossRef]
69. Tu Q, Rong Y, Chen J. Parameter identification of ARX models based on modified momentum gradient descent algorithm. Complexity. 2020;1(3):9537075. doi:10.1155/2020/9537075. [Google Scholar] [CrossRef]
70. Wu J, Wang F, Xu B, Sun Z. Characteristics study of electro-hydraulic load-sensing control system for mobile machines. Proc Inst Mech Eng Part J Automob Eng. 2023;237(9):2344–54. doi:10.1177/09544070221105386. [Google Scholar] [CrossRef]
71. Alatas B. Chaotic harmony search algorithms. Appl Math Comput. 2010;216(9):2687–99. doi:10.1016/j.amc.2010.03.114. [Google Scholar] [CrossRef]
72. Mehmood K, Khan ZA, Chaudhary NI, Cheema KM, Siddiqui B, Raja MAZ. Design of chaotic Young’s double slit experiment optimization heuristics for identification of nonlinear muscle model with key term separation. Chaos Solitons Fractals. 2024;189(20):115636. doi:10.1016/j.chaos.2024.115636. [Google Scholar] [CrossRef]
73. Turgut E, Turgut MS, Kırtepe E. Chaotic Aquila optimization algorithm for solving phase equilibrium problems and parameter estimation of semi-empirical models. J Bionic Eng. 2024;21(1):486–526. doi:10.1007/s42235-023-00438-7. [Google Scholar] [CrossRef]
74. Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Raja MAZ, Shu CM. Novel knacks of chaotic maps with Archimedes optimization paradigm for nonlinear ARX model identification with key term separation. Chaos Solitons Fractals. 2023;175(3):114028. doi:10.1016/j.chaos.2023.114028. [Google Scholar] [CrossRef]
75. Wang GG, Guo L, Gandomi AH, Hao GS, Wang H. Chaotic krill herd algorithm. Inf Sci. 2014;274(2):17–34. doi:10.1016/j.ins.2014.02.123. [Google Scholar] [CrossRef]
76. Alatas B. Chaotic bee colony algorithms for global numerical optimization. Expert Syst Appl. 2010;37(8):5682–7. doi:10.1016/j.eswa.2010.02.042. [Google Scholar] [CrossRef]
77. Turgut E, Turgut MS. Chaotic gradient based optimizer for solving multidimensional unconstrained and constrained optimization problems. Evol Intell. 2024;17(3):1967–2028. doi:10.1007/s12065-023-00876-6. [Google Scholar] [CrossRef]
78. Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Raja MAZ. Variants of chaotic grey wolf heuristic for robust identification of control autoregressive model. Biomimetics. 2023;8(2):141. doi:10.3390/biomimetics8020141. [Google Scholar] [PubMed] [CrossRef]
79. Gezici H, Livatyalı H. Chaotic harris hawks optimization algorithm. J Comput Des Eng. 2022;9(1):216–45. doi:10.1093/jcde/qwab082. [Google Scholar] [CrossRef]
80. Gharehchopogh FS, Nadimi-Shahraki MH, Barshandeh S, Abdollahzadeh B, Zamani H. CQFFA: a chaotic quasi-oppositional farmland fertility algorithm for solving engineering optimization problems. J Bionic Eng. 2023;20(1):158–83. doi:10.1007/s42235-022-00255-4. [Google Scholar] [CrossRef]
81. Wang GG, Deb S, Gandomi AH, Zhang Z, Alavi AH. Chaotic cuckoo search. Soft Comput. 2016;20(9):3349–62. doi:10.1007/s00500-015-1726-1. [Google Scholar] [CrossRef]
82. Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Zahoor Raja MA. Atomic physics-inspired atom search optimization heuristics integrated with chaotic maps for identification of electro-hydraulic actuator systems. Mod Phys Lett B. 2024;38(30):2450308. doi:10.1142/S0217984924503081. [Google Scholar] [CrossRef]
83. Wang GG, Hossein Gandomi A, Hossein Alavi A. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes. 2013;42(6):962–78. doi:10.1108/K-11-2012-0108. [Google Scholar] [CrossRef]
84. Elbayomy KM, Jiao ZX, Zhang HQ. PID controller optimization by GA and its performances on the electro-hydraulic servo control system. Chin J Aeronaut. 2008;21(4):378–84. doi:10.1016/S1000-9361(08)60049-7. [Google Scholar] [CrossRef]
85. Yan J, Li B, Guo G, Zeng Y, Zhang M. Nonlinear modeling and identification of the electro-hydraulic control system of an excavator arm using BONL model. Chin J Mech Eng. 2013;26(6):1212–21. doi:10.3901/CJME.2013.06.1212. [Google Scholar] [CrossRef]
86. Abedi Pahnehkolaei SM, Alfi A, Machado JAT. Particle swarm optimization algorithm using complex-order derivative concept: a comprehensive study. Appl Soft Comput. 2021;111(2):107641. doi:10.1016/j.asoc.2021.107641. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF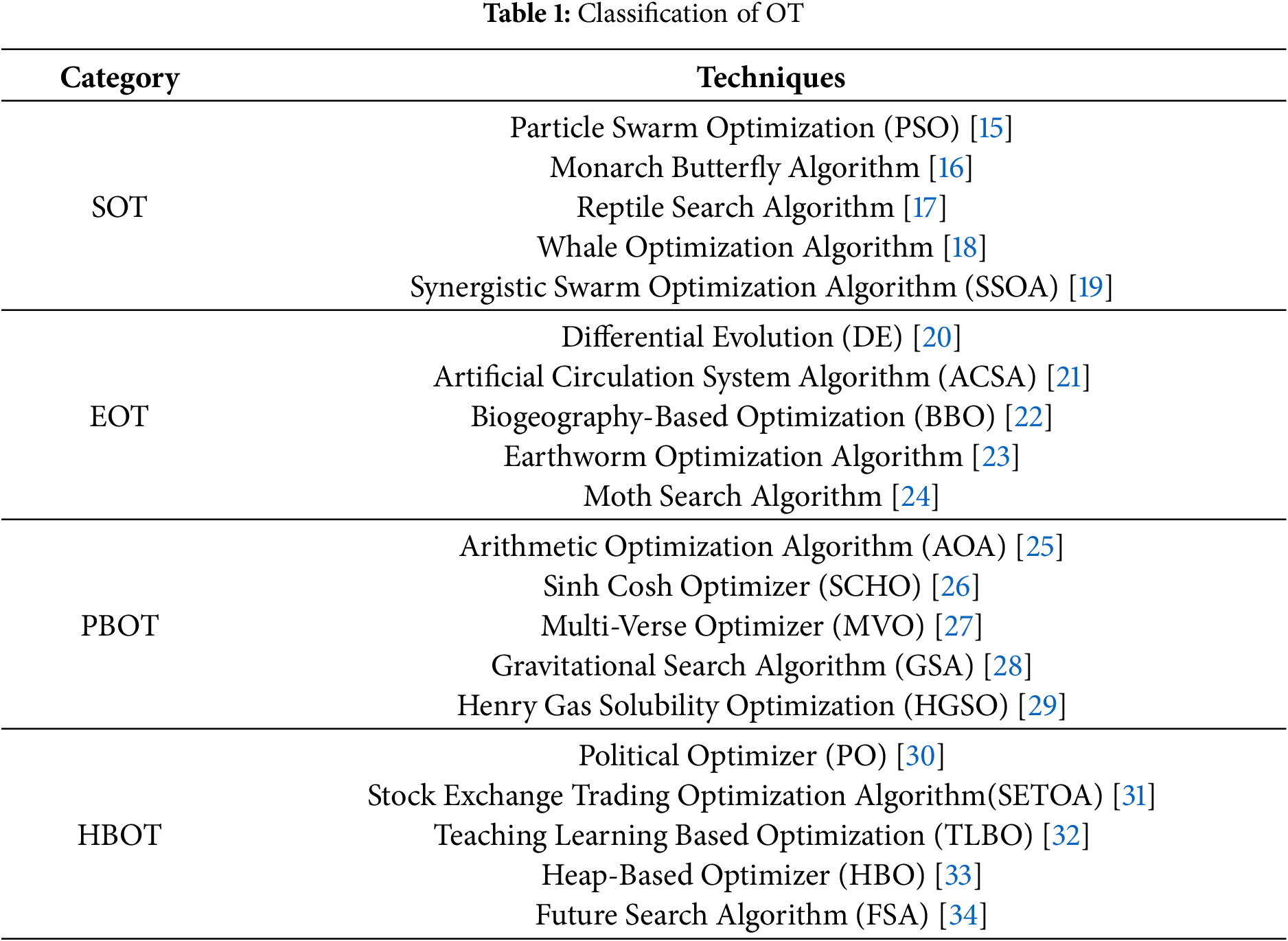
 Downloads
Downloads
 Citation Tools
Citation Tools