 Open Access
Open Access
ARTICLE
Epidemiological Modeling of Pneumococcal Pneumonia: Insights from ABC Fractal-Fractional Derivatives
1 Department of Mathematics, Faculty of Science, Al-Baha University, Al-Baha, 65779, Saudi Arabia
2 Department of Mathematics, College of Science, Qassim University, Buraidah, 51452, Saudi Arabia
3 Department of Mathematics and Computer Science, Faculty of Science, Beni-Suef University, Beni-Suef, 62521, Egypt
* Corresponding Author: Mohammed Althubyani. Email:
(This article belongs to the Special Issue: Recent Developments on Computational Biology-II)
Computer Modeling in Engineering & Sciences 2025, 143(3), 3491-3521. https://doi.org/10.32604/cmes.2025.061640
Received 29 November 2024; Accepted 20 May 2025; Issue published 30 June 2025
Abstract
This study investigates the dynamics of pneumococcal pneumonia using a novel fractal-fractional Susceptible-Carrier-Infected-Recovered model formulated with the Atangana-Baleanu in Caputo (ABC) sense. Unlike traditional epidemiological models that rely on classical or Caputo fractional derivatives, the proposed model incorporates nonlocal memory effects, hereditary properties, and complex transmission dynamics through fractal-fractional calculus. The Atangana-Baleanu operator, with its non-singular Mittag-Leffler kernel, ensures a more realistic representation of disease progression compared to classical integer-order models and singular kernel-based fractional models. The study establishes the existence and uniqueness of the proposed system and conducts a comprehensive stability analysis, including local and global stability. Furthermore, numerical simulations illustrate the effectiveness of the ABC operator in capturing long-memory effects and nonlocal interactions in disease transmission. The results provide valuable insights into public health interventions, particularly in optimizing vaccination strategies, treatment approaches, and mitigation measures. By extending epidemiological modeling through fractal-fractional derivatives, this study offers an advanced framework for analyzing infectious disease dynamics with enhanced accuracy and predictive capabilities.Keywords
Pneumococcal pneumonia, caused by Streptococcus pneumoniae, remains a significant global health issue, particularly affecting young children and the elderly. Despite medical advancements, it continues to contribute notably to morbidity and mortality worldwide. Traditional mathematical models, including classical and integer-order differential equations, have been employed to study disease dynamics, but these models often fail to account for nonlinear, long-memory effects and hereditary factors that influence disease transmission, immunity, and treatment responses. This lung disease, which can affect individuals of all ages, can manifest with varying severity, with some forms being non-airborne due to inhalation of harmful substances. While most pneumococcal toxins are harmless, certain strains can be extremely dangerous, leading to brain damage and hearing loss. Pneumococcal meningitis is the most severe form of illness, primarily affecting children under five, though it can also impact adults. The bacteria involved in pneumococcal infections can spread through the bloodstream, and while the mortality rate in children under five is around 1%, the elderly have a significantly higher mortality risk, with death rates around 5%. Pneumococcal pneumonia remains one of the leading causes of death in the elderly population.
Pneumococcal pneumonia, a major public health concern, has been extensively modeled using classical and fractional-order differential equations. However, existing models primarily rely on integer-order or Caputo fractional derivatives, which have limitations in capturing complex nonlocal memory effects, hereditary properties, and fractal-like transmission dynamics observed in real-world epidemiological data. These traditional models assume that disease progression depends only on current states, failing to incorporate long-term dependencies and memory effects, which are crucial for understanding infectious disease behavior. To address these limitations, we introduce a novel fractal-fractional Susceptible-Carrier-Infected-Recovered model formulated with the Atangana-Baleanu in Caputo (ABC) sense. Unlike classical or Caputo-based fractional models, the ABC derivative incorporates a non-singular Mittag-Leffler kernel, allowing for a more realistic representation of disease transmission.
A mathematical model of bacteremic Pneumococcal Pneumonia in young children (5-year-old) was developed by Ong’ala et al. [1] to describe the occurrence of this disease. They analyzed the transmission rates and paths between the carriers and the infected class, using the bifurcation theory and the stability of equilibrium points as a means of analyzing the transmission rates. Mochan et al. [2] provided a dynamic ordinary differential equation model of the host immunological response to bacterial Pneumococcal Pneumonia infection in Murine strains. Drusano et al. [3] investigated the efficacy of granulates in preventing bacterial growth and concluded that antibiotics play no part in this process. Ndelwa et al. [4] mathematically represented the dynamic features for the transmission of Pneumococcal Pneumonia, including screening and medicine, and analyzed the transmission and consequences. Kosasih et al. [5] analyzed a mathematical model of cough sounds using wavelet-based crackling detection to rapidly identify bacterial Pneumococcal Pneumonia in young patients. In 2016, César et al. [6] used a mathematical model for pediatric asthma and Pneumococcal Pneumonia over a large population. Based on the work of Marchello et al. [7], it was shown in 2016 that atypical bacterial infections were mostly responsible for the spread of respiratory illnesses such as coughing, bronchitis, and chronic obstructive pulmonary disease (COPD). In 2017, Cheng et al. [8] presented a dynamical mathematical model of the influenza A virus and Streptococcus pneumoniae. Kosasih and Abeyratne [9] provided a simple mathematical model illuminating the clinical analysis of measures for the diagnosis of childhood Pneumococcal Pneumonia and discussed the most common reasons why young infants in low-income areas of the world get Pneumococcal Pneumonia.
In 2018, a co-infection model for Pneumococcal Pneumonia and typhoid was presented by Tilahun et al. [10,11], and their defining connection in the face of a cure and therapeutic approaches was mathematically examined. With the use of mathematical properties of cough sounds, Raj et al. [12] examined the categorization of asthma and Pneumococcal Pneumonia in low-resource communities. Kizito and Tumwiine [13] produced a mathematical model that shows how microorganisms limit the spread of Pneumococcal Pneumonia. Vaccine formulation and treatment dynamics were also examined. Mbabazi et al. [14] looked into a nonlinear mathematical model that describes influenza A virus and Pneumococcal Pneumonia inside the host. A model of Pneumococcal Pneumonia-meningitis coinfection was developed by Tilahun [15], making use of some theorems and ordinary differential equations. Various strategies for eradicating diseases were outlined in detail. Dynamic mathematical models of Pneumococcal Pneumonia were evaluated by Diah and Aziz [16]. Pneumococcal Pneumonia risk was calculated using a different method. In 2019, Tilahun [17] developed a mathematical model of Pneumococcal Pneumonia and bacterial meningitis. A mathematical model of pneumococcal Pneumococcal Pneumonia with temporal delays was developed by Mbabazi et al. [18]. The effectiveness of the model was examined by Otoo et al. [19]. Models of respiratory diseases were presented in graphic form by Zephaniah et al. [20]. A coronavirus Pneumococcal Pneumonia outbreak was reported in Wuhan, China, by Ming et al. [21]. Based on clinical testing, Jung et al. [22] confirmed the findings and identified the pathogen responsible. A mathematical model of Pneumococcal Pneumonia-HIV co-infection was developed by Wafula et al. [23] based on anti-Pneumococcal Pneumonia treatments. Moreover, Oluwatobi and Erinle-Ibrahim, Ref. [24] examined the effects of Pneumococcal Pneumonia while explaining the presence of fundamental and effective reproduction numbers. In Sayed Saber et al. [25], the transmission dynamics of Pneumococcal Pneumonia were investigated using a fractional mathematical susceptible-vaccinated-carrier-infected-recovered model. Similar result on the Pneumonia diseases has been studied in [26].
Fractional-order models, particularly those using Caputo fractional derivatives, have been introduced to incorporate memory-dependent interactions into epidemiological dynamics. Fractal fractional dynamics are observed in various natural systems, including excitation-relaxation systems and natural oscillatory systems. Atangana and Qureshi [27] explore the modeling of chaotic attractors using fractal-fractional operators, focusing on their applicability to dynamical systems in the context of fractional calculus, see also [28–32]. Khalid et al. [33] propose the Modified Minimal Model for diabetes treatment strategies [34] and further investigate the use of fractal-fractional derivatives in diabetes modeling. Almutairi et al. [35] focus on the use of the fractal-fractional Atangana-Baleanu operator in modeling pneumonia, with detailed stability, statistical, and numerical analyses. Abodayeh et al. [36] highlight the use of efficient computational techniques in pneumonia modeling. Boukhouima et al. [37] study a fractional-order HIV infection model with functional response and cure rate, see also [38–40].
The application of fractional calculus in modeling dynamical systems has gained significant attention in recent years due to its ability to capture memory effects and complex dynamics more accurately than classical integer-order models. Several studies have demonstrated the effectiveness of fractional-order systems in various fields, including bioengineering, finance, and control theory [41–45]. For instance, Ref. [41] provides a comprehensive overview of fractional-order modeling and control applications, highlighting their advantages in representing real-world phenomena with hereditary properties. In the context of biological systems, fractional-order models have been particularly useful in describing glucose-insulin interactions. For example, Refs. [42,44] developed fractional-order models to analyze the dynamics of glucose-insulin regulation, demonstrating improved agreement with experimental data compared to traditional models. Similarly, epidemiological models have benefited from fractional calculus, as seen in [43,45], where fractional-order differential equations were used to model the spread of COVID-19, providing insights into transmission dynamics and stability.
Saber and Alahmari [46] discussed the modeling and mathematical analysis of zoonotic diseases, see also [47–49] presented additional advancements in zoonotic disease modeling. Althubyani and Saber [50] also contributed significantly to the understanding of complex dynamical systems. Several studies have demonstrated the effectiveness of fractional-order systems in various fields, including bioengineering, finance, and control theory [51].
The stability analysis of fractional-order systems has also been a key area of research. Theoretical frameworks such as those presented in [52,53] have been extended to fractional-order systems, enabling rigorous stability assessments. Additionally, chaos control in fractional-order chaotic systems has been explored in works such as [54], where the Burke-Shaw system was analyzed using fractal-fractional operators. The study of fractional-order systems is deeply rooted in both classical and modern mathematical frameworks.
Building on these theoretical underpinnings, Petras [55] systematized the modeling, analysis, and simulation of fractional-order nonlinear systems, bridging abstract mathematical theory with practical applications. Fractional calculus has further been applied to chaotic systems, including the Chua system [56], the Lorenz system [57], the Lü system [58], Burke-Shaw [59] and the Rössler system [60]. Recent studies, such as [61], have investigated chaos control in the fractional Newton-Leipnik system using different fractional derivatives. Further applications include disease modeling, where fractional derivatives have been used to study smoking epidemic model [62] and Chikungunya transmission [63] and typhoid fever dynamics [64]. The theoretical foundations of fractal-fractional differential equations have also been explored in [65], providing a mathematical basis for their application in complex systems. Additionally, fractal-fractional operators have been employed to analyze chaotic dynamics, as demonstrated in [66–68].
In this study, we present a fractal-fractional Atangana-Baleanu Caputo (ABC) derivative-order model that describes pneumococcal pneumonia transmission dynamics. The objective is to establish the existence and uniqueness of solutions and analyze the qualitative characteristics of the model. To capture actual disease behavior, we employ the fractal-fractional derivative of the Atangana-Baleanu equation and conduct a local and global stability analysis of steady states. Specifically, the basic reproductive number
Addressing the limitations of existing models, this study introduces a fractal-fractional Susceptible-Carrier-Infected-Recovered model using the ABC derivative. The ABC operator, with its non-singular Mittag-Leffler kernel, enhances epidemiological forecast accuracy by ensuring smooth transitions between disease states. Unlike previous models, this approach accounts for nonlocal effects and memory-dependent disease transmission, making it a more effective tool for studying pneumococcal pneumonia outbreaks. We establish the theoretical validity of the model by proving the existence and uniqueness of solutions. We conduct local and global stability assessments, and demonstrate the impact of memory and fractal structures through numerical simulations. Furthermore, we conduct a comprehensive sensitivity analysis using 3D visualizations to identify the most influential parameters affecting disease spread. By integrating a fractal-fractional calculus into epidemiological modeling, this study significantly enhances the predictive capability of disease transmission models, offering a more effective framework for intervention strategies.
To overcome the shortcomings of existing models, this study introduces a fractal-fractional Susceptible-Carrier-Infected-Recovered model using the Atangana-Baleanu in Caputo (ABC) derivative. The ABC operator, which is based on a non-singular Mittag-Leffler kernel, provides a more realistic representation of disease dynamics than previous fractional models. This approach ensures smoother transitions between disease states and enhances epidemiological forecast accuracy, making it a valuable tool for analyzing the long-term behavior of pneumococcal pneumonia outbreaks. We extend traditional pneumococcal pneumonia models by incorporating fractal-fractional operators, which account for nonlocal effects and memory-dependent disease transmission. We establish the existence and uniqueness of solutions, ensuring theoretical validity. We conduct local and global stability assessments to determine the conditions under which the disease persists or is eradicated. Unlike prior models, we employ numerical simulations based on the ABC operator to demonstrate the effects of memory and fractal structure on disease transmission. We conducted a comprehensive sensitivity analysis using 3D visualizations to identify the most influential parameters affecting disease spread. By integrating fractal-fractional calculus into epidemiological modeling, this study enhances the accuracy and predictive capability of disease transmission models, paving the way for more effective intervention strategies.
The novelty of our study lies in the integration of fractal and fractional dynamics. This better reflects real-world epidemic patterns, particularly in cases where transmission pathways are irregular and heterogeneous. This research applies fractal-fractional calculus to generalize traditional epidemiological models. Unlike classical differential equation models, which assume instantaneous effects and local interactions, the proposed approach accounts for long-memory behavior and nonlocal influences. This allows a more accurate representation of pneumococcal pneumonia dynamics, where past infections and immunity play a significant role in shaping future disease spread. Another crucial innovation is the incorporation of nonlinear, memory-dependent interactions into the modeling process. Classical epidemiological models often rely on simplified assumptions about disease transmission, ignoring the cumulative effects of immunity, delayed treatment response, and persistent infections. By integrating memory-dependent dynamics, this study provides a more comprehensive framework for understanding Pneumococcal Pneumonia progression and evaluating potential intervention strategies.
Mathematically, the study establishes the existence and uniqueness of solutions to the proposed model, ensuring its validity and applicability. Additionally, stability properties–including both local and global stability–are rigorously examined to determine the conditions under which disease persistence or eradication occurs. These theoretical foundations are essential for understanding the model’s behavior and implications for real-world disease control. To further illustrate the effectiveness of the proposed model, numerical simulations were conducted to analyze the impact of long-memory effects on disease spread. These simulations provide valuable insights into the transmission dynamics of pneumococcal pneumonia and demonstrate the advantages of fractal-fractional modeling in capturing complex epidemiological patterns. By comparing the results with classical models, the study highlights the significant improvements in accuracy and predictive capability offered by the fractal-fractional approach.
In previous studies on pneumococcal pneumonia dynamics, the limitations have primarily involved the use of classical integer-order models, which fail to capture the memory effects and fractal characteristics inherent in real-world biological systems. These models often assume homogeneous populations and instantaneous changes in disease progression, thereby oversimplifying the complex dynamics of reinfection, immunity decay, and bacterial carriage. This study aims to address these gaps by employing the Atangana-Baleanu Caputo (ABC) fractional operator, which incorporates memory effects and fractional-order parameters to provide a more comprehensive and accurate representation of pneumococcal pneumonia transmission dynamics.
The remainder of the paper is structured as follows: Section 2 provides preliminary definitions and a mathematical background. Section 3 introduces the pneumococcal pneumonia Susceptible-Carrier-Infected-Recovered model formulation with fractal-fractional derivatives. Sections 4 and 5 discuss the qualitative properties of the model, including stability analyses. Section 6 presents a sensitivity analysis of the basic reproduction number
Definition 1([51]). The Gamma function
Definition 2([51]). The Mittag-Leffler function is a generalization of the exponential function, while the gamma function is a generalization of the factorial function. The Mittag-Leffler function is defined as a power series expansion
where
The two-parameter generalization of the Mittag-Leffler function, which plays an important role in the fractional calculus, is defined by the series expansion
When
Definition 3([69,70]). Consider the fractal differentiable on
where
Definition 4([69,70]). The fractal-fractional integration operator are provided by
The parameter
When
• The Mittag-Leffler kernel simplifies to an exponential function, removing nonlocal memory effects.
• The fractional component vanishes, resulting in an integer-order derivative.
• The fractal properties disappear, causing the model to behave as a standard differential equation.
However, if
By integrating memory effects and fractal structures, our ABC-based model provides:
• More accurate predictions of outbreak dynamics, helping policymakers design better intervention strategies.
• Improved understanding of reinfection risks and long-term immunity, guiding vaccination campaigns.
• A more realistic assessment of treatment impact over time, aiding in antibiotic stewardship programs.
To help health practitioners grasp the importance of ABC operators, a simple analogy can be introduced:
Traditional models treat disease progression like flipping a switch–either you are infected or you are not. However, pneumococcal pneumonia leaves a lasting imprint on the body, much like a fading memory that still influences decisions. The ABC operator helps us mathematically capture this fading memory, allowing for a more realistic and accurate disease model.
The conditions
•
•
When
• The Mittag-Leffler kernel
• The AB-FF derivative reduces to the classical derivative, losing its fractional and fractal properties.
• The model no longer retains memory effects and behaves like a standard first-order differential equation.
• The fractional-order nature of the derivative disappears, meaning the system no longer retains past information.
• The fractal nature is lost, causing the system to behave as a regular differential equation without the complexity introduced by fractal geometry.
• The model transitions back to a standard integer-order system, eliminating the advantages of fractional calculus in capturing long-memory effects and nonlocal interactions.
Setting
3 Formulation of the Fractal-Fractional Model
The Susceptible-Carrier-Infected-Recovered model proposed by Abodayeh et al. in [36] describes the dynamics of a population divided into four compartments: The susceptible, who is at risk of acquiring Pneumococcal Pneumonia infection, is characterized by
For any given time
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
The governing equations of the model are as follows:
Here,
Assumptions and Motivations:
• Susceptible Population (
Assumption: Individuals who are susceptible to the disease are denoted by
– Motivation: In many epidemiological models, the susceptible population increases due to natural birth or migration. The loss of susceptible individuals occurs due to transmission, natural mortality, and movement into the recovered compartment.
•Carriers (
– Assumption: Carriers are individuals who are infected but do not exhibit symptoms. These individuals may transmit the disease to others and are important in the spread of the infection.
– Motivation: The rate at which susceptible individuals become carriers is given by
– Loss of carriers: Carriers can either develop symptoms and transition to the infected group or be removed from the population due to natural mortality, recovery, or vaccination. The parameter
Infected Population (
– Assumption: Infected individuals are those who exhibit symptoms and contribute to the disease spread. They can transition to recovery or death.
– Motivation: The term
– Loss of infected individuals: Infected individuals can recover with rate
Recovered Population (
– Assumption: Recovered individuals are those who have overcome the infection, either by recovering naturally or through vaccination. They can no longer transmit the disease.
– Motivation: The term
To obtain the model with the fractal-fractional derivative from the classical model of differential equations, you need to replace the standard first-order derivatives with the generalized fractal-fractional derivative
This is the model with the fractal-fractional derivatives, denoted as model (2). The transition from model (1) to model (2) is made by replacing the usual derivative
The ABC operator has become a crucial tool in fractal-fractional calculus, offering significant advantages for modeling complex systems with memory and hereditary properties, particularly in biological and epidemiological contexts. Its key benefits include incorporating memory effects through a non-singular Mittag-Leffler kernel, which realistically represents historical dependencies in disease dynamics, such as incubation periods and immune responses. The operator’s nonlocality ensures a comprehensive account of past states, surpassing classical derivatives in capturing infection progression and intervention effectiveness over time. Additionally, its flexibility across different orders allows for adaptable modeling of varying complexity levels, while its non-singular kernel enhances numerical stability, preventing singularities in simulations. The Atangana-Baleanu in Caputo (ABC) operator generalizes classical and fractional derivatives, making it a versatile framework for analyzing dynamic systems, with demonstrated success in modeling epidemic dynamics such as Pneumococcal Pneumonia. Traditional integer-order Susceptible-Carrier-Infected-Recovered models assume Markovian processes with instantaneous transitions, which fail to capture pneumococcal pneumonia’s memory effects, heterogeneous transmission, and long-tail recovery distributions. In contrast, the fractional-order Susceptible-Carrier-Infected-Recovered model using the AB operator in the Caputo sense addresses these limitations by incorporating memory effects into disease progression, allowing for non-exponential transmission and recovery rates, and improving data fitting to clinical observations. The Mittag-Leffler kernel further refines this approach by providing a smooth decay of memory effects, avoiding singularities, and ensuring a more accurate representation of pneumococcal pneumonia transmission and control dynamics.
This is the first study that applies the Atangana-Baleanu in Caputo (ABC) operators to model the dynamics of pneumococcal pneumonia. The novelty of this approach appears by incorporating fractal-fractional derivatives with a non-singular Mittag-Leffler kernel, which provides a more realistic representation of disease transmission compared to previous models using integer-order or Caputo derivatives.
4 Positivity, Existence and Uniqueness of the Model Solutions
By
Theorem 1. Model (3.2) has non-negative solutions if and only if
Proof. One has
To understand why
Based on Lemmas 5 and 6 in [37], all of the solutions to the model (2) have a semi-positive outcome. ▀
Model (2) can be stated as because the integration is differentiable.
with
Consider
with
Banach space
Establishing an operator
Assuming a nonlinear function
(H1) For all
(H2) For all
Theorem 2. Assume (H1) and (H2) are true. Let
Proof. There is no difference between
For any
To ensure that the homogeneity of the function is guaranteed, the operator
Consequently, as
Theorem 3. Suppose that (H1) and (H2) is true. If
Then the solution is unique, if it exists.
Proof. For
The total population at any time
To derive the equation for
Using the given system of equations, we have:
The resulting equation is:
At equilibrium (
Rearranging the equation gives:
The total population at equilibrium,
When
Implies
Lemma 1 ([36]). The Pneumococcal Pneumonia infection-free equilibrium
Theorem 4. The disease-free equilibrium
Proof. Consider the Lyapunov function:
From [53], applying the fractal-fractional derivative
Substituting the fractal-fractional system equations, we get:
At
Since this expression is negative for all
For
With
Lemma 2 ([36]). For
Lemma 3 ([36]). If
Theorem 5. The endemic equilibrium
Proof. Consider the Lyapunov function:
From [53], applying the fractal-fractional derivative
Substituting the fractal-fractional system equations, we get:
Since this expression is negative for all
6 Sensitivity Analysis of the Basic Reproduction Number
The sensitivity index of
The partial derivatives of
• For
• For
• For
• For
• For
• For
• For
The Basic Reproduction Number
The sensitivity indices for the parameters are computed as follows:
These sensitivity indices indicate the effect of parameter changes on the basic reproduction number
The sensitivity index quantifies how changes in each parameter of the model affect the basic reproduction number
Fig. 1 presents the sensitivity index analysis. The objective is to help readers quickly ascertain the parameters that significantly influence the spread of the disease in the population. By analyzing the sensitivity of model parameters, we can determine which factors have the most substantial impact on disease transmission dynamics. Parameters such as the transmission rate, recovery rate, and vaccination rate exhibit the highest sensitivity, indicating their crucial role in controlling disease spread. These sensitivity analyses offer valuable insights for public health interventions by identifying which parameters should be targeted for effective disease mitigation strategies.
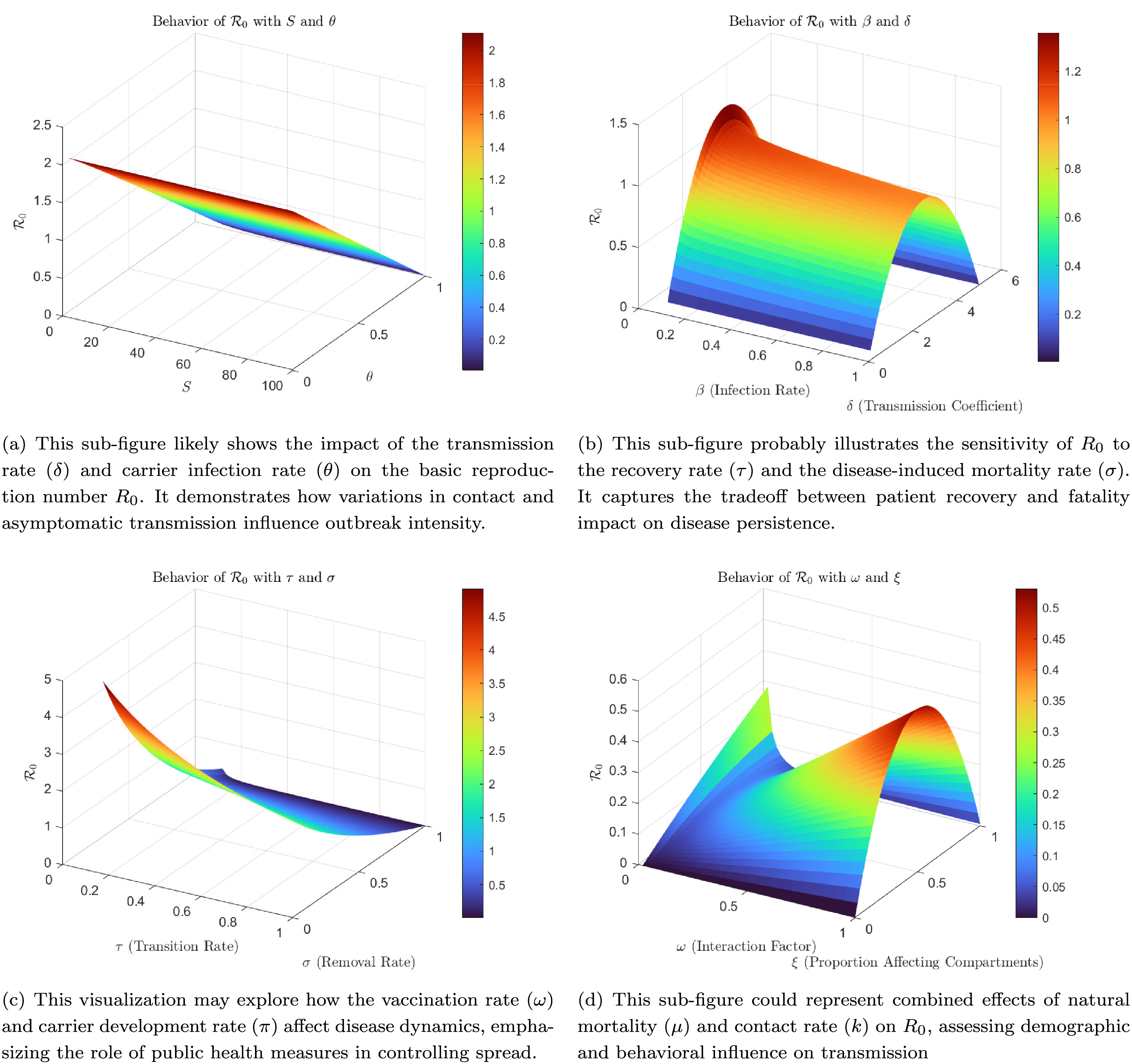
Figure 1: Sensitivity index analysis using 3D visualizations
7 Numerical Scheme of the Fractal-Fractional Pneumonia Model
Atangana-Baleanu fractal-fractional operators are implemented via Lagrangian piecewise interpolation for the proposed model. As in [72], consider system (3.2) in this case
The Antangana-Baleanu integral gives us
Replacing
Application of the two-step Lagrange polynomial yields
By using the Lagrange polynomial to solve the given problem, we obtain
Now solving the integral we get
Now replacing the value of
As a result, the numerical scheme above is
8 Numerical Simulations and Analysis
This section presents the numerical simulations of the pneumonia disease model, emphasizing the impact of fractional-order derivatives on disease dynamics. The results illustrate how different fractional orders influence the rate at which individuals transition through the compartments, demonstrating the nonlocal and memory-dependent nature of the fractal-fractional Atangana-Baleanu-Caputo (ABC) model. By incorporating memory effects, the model provides a more accurate representation of disease transmission dynamics, which classical integer-order models often fail to capture.
Fig. 2 presents the time series evolution of four key compartments–Susceptible
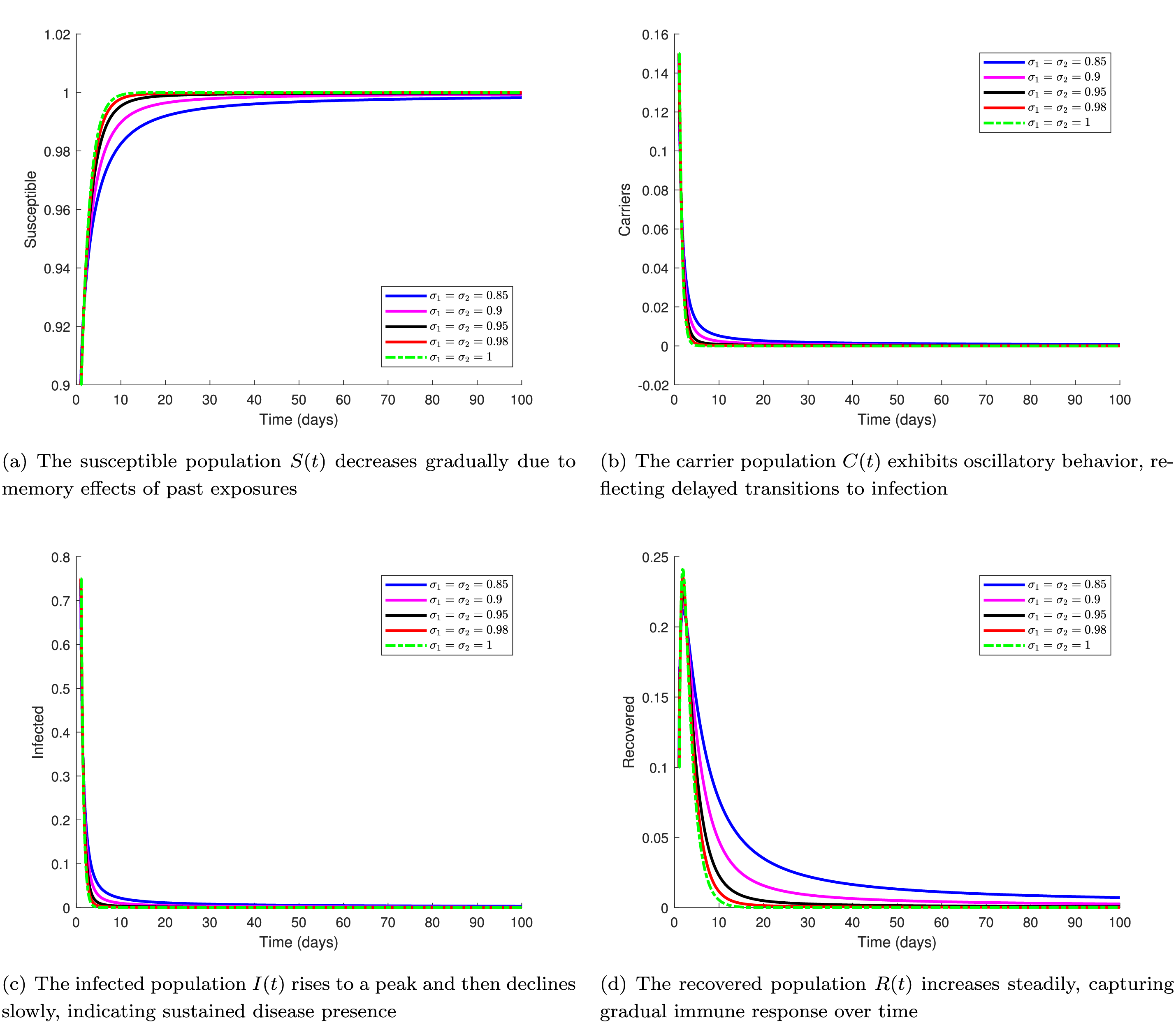
Figure 2: Time series of
Fig. 3 further investigates the impact of different fractional orders—
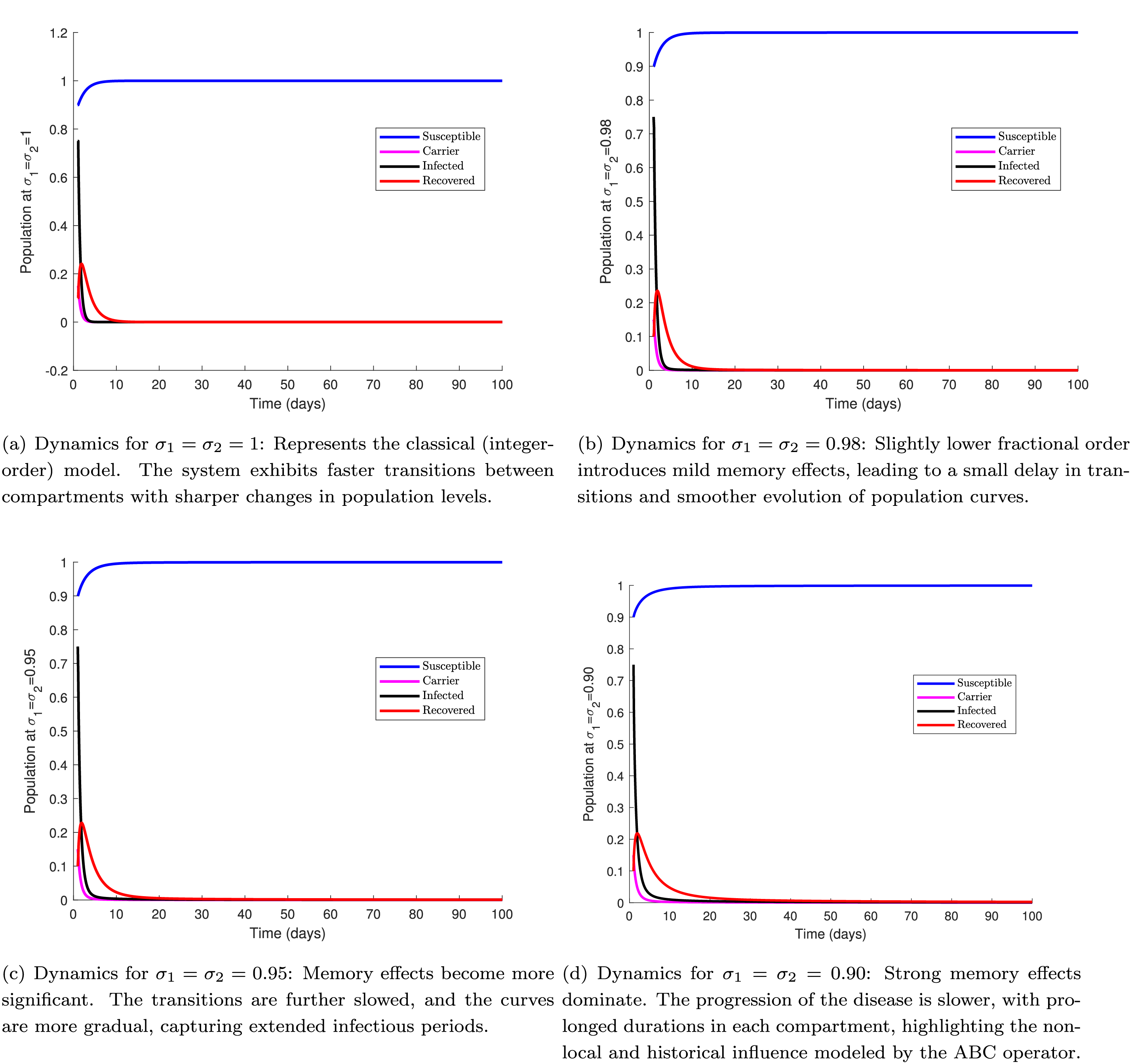
Figure 3: Dynamics of system (2.1) for
In summary, the numerical simulations validate the proposed approach, confirming its applicability in epidemiological studies. By incorporating fractional-order derivatives, the model offers a more comprehensive and realistic depiction of pneumonia transmission, providing valuable insights for disease control strategies and public health interventions.
This figure illustrates the impact of different fractional orders on the SCIR model dynamics using the Atangana–Baleanu–Caputo (ABC) operator. Each sub-figure corresponds to simulations with decreasing values of the fractional orders
The present study introduces a fractional-order Susceptible-Carrier-Infected-Recovered model using the ABC fractal-fractional derivative to explore the complex dynamics of pneumococcal pneumonia. By incorporating memory and nonlocal effects, the ABC operator extends traditional integer-order models and standard fractional derivatives. This approach allows for a more comprehensive representation of transmission dynamics, accounting for hereditary and incubation effects. Numerical simulations confirm that the ABC operator effectively captures equilibrium points and oscillatory behaviors, demonstrating its accuracy in modeling disease spread and mitigation. The ability of the fractional-order model to incorporate long-memory and nonlocal effects provides deeper insights into disease dynamics, particularly in scenarios involving complex temporal dependencies. Future research could focus on extending the model to include stochastic effects, exploring time-dependent parameters, or integrating additional compartments to study co-infections. Addressing computational challenges associated with the ABC operator would further enhance its applicability to real-world epidemiological studies. The parameter values used for simulation are summarized in Table 1. These include baseline rates for transmission, recovery, progression, and other key biological and epidemiological factors relevant to the SCIR model of pneumococcal pneumonia. The values were selected based on available literature and sensitivity considerations.

9.1 Depth and Clarity of the Findings
This study highlights the utility of the ABC operator in capturing complex disease dynamics through memory effects and hereditary properties. The findings show that the fractional-order Susceptible-Carrier-Infected-Recovered model, formulated with fractal-fractional derivatives, provides a more accurate representation of pneumococcal pneumonia dynamics compared to classical models. The derived basic reproduction number (
9.2 Implications for Public Health and Other Applications
The findings of this study have significant implications for public health strategies aimed at controlling pneumococcal pneumonia. By providing a framework that accounts for memory effects and long-term interactions, the model aids in predicting the outcomes of various interventions, such as vaccination and treatment campaigns. For instance, the model identifies critical thresholds where vaccination coverage can shift the system from an endemic to a disease-free state, emphasizing the importance of achieving high vaccination rates in vulnerable populations such as children under five and the elderly. Beyond pneumococcal pneumonia, the model’s adaptability to other infectious diseases is noteworthy. The incorporation of fractional-order dynamics makes it applicable to diseases with similar transmission patterns, such as tuberculosis and influenza. Policymakers can leverage these insights to design tailored interventions, optimize resource allocation, and predict the long-term impact of public health measures.
9.3 Integration of Theoretical and Numerical Analysis
The study effectively integrates theoretical stability analyses with numerical simulations, bridging the gap between mathematical derivations and real-world applications. The derivation of
9.4 Justification for the Use of ABC Operators in Pneumococcal Pneumonia Modeling
While the manuscript effectively highlights the mathematical advantages of the ABC operator, a clearer justification of its epidemiological relevance to pneumococcal pneumonia is needed–particularly for readers without a strong mathematical background, such as health practitioners and epidemiologists.
9.5 Memory Effects in Pneumococcal Pneumonia: Epidemiological Justification
Several key epidemiological characteristics of pneumococcal pneumonia align with the memory effects captured by ABC operators. Long-term carriage and transmission occur as many individuals harbor Streptococcus pneumoniae for extended periods without immediate symptoms, influencing future infection risks, which ABC operators model by allowing past bacterial load to affect present transmission rates. Delayed recovery and reinfection are also significant, as some patients take longer to recover due to immune suppression, prior infections, or antibiotic resistance; unlike classical models that assume instantaneous transitions, ABC operators smoothly represent the gradual return to health or the risk of reinfection. Additionally, waning immunity and vaccination implications are critical, as immunity from past infections or vaccines does not disappear abruptly but decays over time; the Mittag-Leffler function in the ABC operator realistically captures this process, refining vaccine strategies and improving long-term epidemiological forecasts.
9.6 Why Use Fractional and Fractal-Fractional Models for Pneumococcal Pneumonia?
Pneumococcal pneumonia exhibits memory-dependent and heterogeneous dynamics, meaning that factors such as past exposures, immunity levels, bacterial persistence, and environmental conditions significantly influence current and future disease progression. Classical models, which rely on integer-order derivatives, assume that disease state changes depend only on the present moment, thereby neglecting long-term dependencies and irregular disease spread patterns. To overcome these limitations, fractional and fractal-fractional models provide a more realistic approach by incorporating memory and fractal structures. Specifically, the Atangana-Baleanu-Caputo (ABC) operator, with its Mittag-Leffler kernel, enhances the accuracy of pneumococcal pneumonia models by accounting for memory decay and fractal characteristics.
The fractional component of the ABC operator ensures that past infections and immune responses gradually influence disease progression over time, rather than disappearing abruptly, while the fractal component captures nonlinear transmission dynamics influenced by population density, seasonal fluctuations, and variable immunity levels. This is particularly valuable for modeling superspreading events, dynamic contact rates, and memory-dependent treatment effects, including antibiotic resistance shaped by prior medication use. By integrating these aspects, the ABC-based fractional model enhances public health efforts by improving outbreak predictions, informing vaccination strategies, and providing a more realistic assessment of treatment impacts to support antibiotic stewardship programs.
This study provides an in-depth analysis of the Atangana-Baleanu Caputo (ABC) fractional operator and its application to pneumococcal pneumonia. The ABC operator integrates memory effects and fractal properties through its Mittag-Leffler kernel and incorporates two key parameters,
•
•
When
In the context of pneumococcal pneumonia, the ABC operator effectively captures nonlocal memory effects, reflecting the lasting biological imprint of prior infections and immune responses. By doing so, it enhances the modeling of reinfection risks, long-term immunity, and treatment impacts. These improvements aid policymakers in designing better intervention strategies, optimizing vaccination campaigns, and assessing the impacts of waning immunity over time.
In this study, we apply the Atangana-Baleanu Caputo (ABC) fractional operator to analyze the dynamics of pneumococcal pneumonia. The key objective is to illustrate, through numerical simulations and comparative analysis, how the fractional-order parameters
•
•
The results from the numerical simulations highlight the following key observations:
1. Impact of Memory Effects: When
2. Fractal Transmission Dynamics: Variations in
3. Reinfection and Immunity Decay: With fractional-order parameters
The manuscript emphasizes how the ABC operator, with its unique memory and nonlocal effects, captures key epidemiological phenomena such as delayed recovery, waning immunity, and prolonged bacterial carriage. Unlike classical models with integer-order derivatives, which consider only instantaneous state changes, ABC operators model the gradual decay of immunity and the lasting influence of past infections on current disease progression through the Mittag-Leffler function. These dynamics align closely with the memory-dependent transmission and recovery processes observed in pneumococcal pneumonia.
9.7 Comparison of the ABC Operator with Other Fractional Operators
To provide a comprehensive understanding, this section compares the ABC fractional operator with other fractional operators, such as Caputo-Fabrizio, Atangana-Seda, and Caputo, highlighting theoretical, numerical, and practical differences.
1. Theoretical Differences
• Memory Effects: The ABC fractional operator incorporates strong long-term memory effects through its Mittag-Leffler kernel, making it better suited to modeling hereditary and historical influences on disease dynamics. By contrast, the Caputo and Caputo-Fabrizio operators exhibit weaker or more limited memory effects.
• Nonlocal Behavior: The ABC fractional derivative accounts for nonlocal interactions, meaning that the current state of the disease depends on its entire past behavior. Caputo-based operators, by comparison, focus more on local interactions and instantaneous rates of change.
• Kernel Type: Unlike the exponential decay kernel of the Caputo-Fabrizio operator, the Mittag-Leffler kernel in the ABC operator decays more slowly, thus capturing the extended influence of past disease events and infections.
2. Numerical and Simulation Differences
• Rate of Disease Spread: Numerical simulations using the ABC operator often show slower decay rates due to strong memory effects, resulting in extended infectious periods compared to Caputo-based models.
• Long-Term Stability: ABC-based models may exhibit different equilibrium points or attractors due to the influence of fractional memory parameters (
• Parameter Sensitivity: ABC operator-based models demonstrate increased sensitivity to fractional-order parameters, allowing finer control over disease dynamics and improved calibration for mitigation strategies.
3. Practical Insights
• Reinfection and Immunity Decay: Due to its stronger memory effects, the ABC operator provides better insights into reinfection dynamics and waning immunity, thus informing vaccination strategies and booster shot timing.
• Realistic Disease Dynamics: The slow-decay nature of the Mittag-Leffler kernel captures real-world phenomena, such as prolonged bacterial carriage in pneumococcal pneumonia, which is difficult to model accurately with Caputo-Fabrizio or Atangana-Seda operators.
Overall, the enhanced memory, nonlocality, and long-term stability of the ABC fractional operator provide significant advantages for modeling complex disease dynamics, particularly in diseases with prolonged infectious periods and memory-dependent transmission patterns. By comparing different operators, this study demonstrates how the ABC operator’s unique properties contribute to more accurate and realistic epidemiological predictions.
9.8 Comparison of the Current Study with Previous Works
This study presents significant advancements over previous works, such as those by Abodayeh et al. [36] and Tilahun et al. [15], by introducing a fractal-fractional Susceptible-Carrier-Infected-Recovered model using the Atangana-Baleanu in Caputo (ABC) derivative, enabling a more biologically realistic representation of memory effects and nonlocal interactions. Unlike traditional models that assume a Markovian disease progression, this approach integrates memory-dependent dynamics, accounting for long-term immunity effects, reinfection risks, and delayed recovery periods. The study establishes the existence and uniqueness of solutions under the fractal-fractional framework, conducts local and global stability analyses, and provides rigorous numerical simulations based on the ABC operator. While Tilahun et al. focused on co-infections using ordinary and fractional differential equations, this work extends their study by applying fractal-fractional derivative frameworks to capture heterogeneous transmission dynamics, non-exponential recovery, and memory-driven interactions. Furthermore, it enhances pneumococcal pneumonia models by incorporating fractal-fractional operators to account for nonlocal effects in disease transmission and improves sensitivity analysis methods through 3D visualizations. Key contributions include the first application of ABC operators for pneumococcal pneumonia modeling, the use of non-singular Mittag-Leffler kernels for smoother epidemiological forecasts, and bridging theoretical and numerical modeling to ensure consistency between analytical predictions and computational results. In summary, this study extends and improves upon prior models by integrating fractal-fractional derivatives, memory effects, and numerical stability analysis, making it a more accurate and comprehensive framework for studying pneumococcal pneumonia transmission dynamics.
The following table (Table 2) presents sample numerical values that illustrate the system behavior under different fractional-order parameter settings: These numerical results demonstrate how the ABC fractional operator enhances the accuracy and realism of the pneumococcal pneumonia model. By incorporating memory effects and fractal properties through fractional-order parameters

This study presents a fractal-fractional Susceptible-Carrier-Infected-Recovered model utilizing the ABC derivative to investigate the intricate dynamics of pneumococcal pneumonia. By integrating memory and nonlocal effects, the ABC operator enhances traditional integer-order and standard fractional models, offering a more comprehensive framework for capturing disease transmission. This approach effectively accounts for hereditary and incubation effects, refining our understanding of epidemiological patterns. Theoretical analyses establish the existence and uniqueness of solutions, alongside local and global stability conditions that determine whether the disease persists or is eradicated. Numerical simulations further validate the model, demonstrating the significant influence of memory effects on disease spread. The results confirm that the ABC operator accurately characterizes equilibrium points and oscillatory behaviors, improving the precision of disease modeling and mitigation strategies. These findings underscore the critical role of fractional-order models in epidemiology, particularly in representing memory-dependent dynamics. The integration of these advanced mathematical techniques enhances forecasting capabilities and informs intervention strategies. Future research could extend this model by incorporating stochastic effects, time-dependent parameters, or additional compartments to study co-infections. Further exploration of computational methods may improve the model’s applicability to real-world epidemiological scenarios. By combining theoretical insights with numerical simulations, this study contributes to public health decision-making and highlights the transformative potential of fractional calculus in infectious disease modeling.
While the proposed SCIR model incorporating fractal-fractional derivatives provides a more flexible framework for capturing memory and hereditary effects in pneumococcal pneumonia dynamics, this work has several limitations. First, the parameter values are assumed constant and based on literature, which may not fully capture variability across different populations or settings. Second, the model does not explicitly account for age structure, seasonal effects, or spatial heterogeneity, which are important in respiratory disease transmission. Lastly, the numerical simulations are based on a specific fractional operator (ABC), and results may differ with alternative definitions. Future work may address these aspects to improve generalizability and predictive accuracy.
Acknowledgement: This article is derived from a research grant funded by the Research, Development, and Innovation Authority (RDIA)-Kingdom of Saudi Arabia-with grant number 12803-baha-2023-BU-R-3-1-EI.
Funding Statement: This article is derived from a research grant funded by the Research, Development, and Innovation Authority (RDIA)-Kingdom of Saudi Arabia-with grant number 12803-baha-2023-BU-R-3-1-EI.
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Mohammed Althubyani, Nidal E. Taha, Khdija O. Taha, Sayed Saber; Data collection: Nidal E. Taha, Khdija O. Taha, Rasmiyah A. Alharb, Sayed Saber; Analysis and interpretation of results: Mohammed Althubyani, Nidal E. Taha, Khdija O. Taha, Rasmiyah A. Alharb, Sayed Saber; Draft manuscript preparation: Mohammed Althubyani, Sayed Saber. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Ong’ala J, Oleche P, Mugisha JYT. Mathematical model for pneumonia dynamics with carriers. Int J Math Anal. 2013;7(50):2457–73. doi:10.12988/ijma.2013.35109. [Google Scholar] [CrossRef]
2. Mochan E, Swigon D, Ermentrout G, Luken S, Clermont GA. Mathematical model of intrahost pneumococcal pneumonia infection dynamics in murine strains. J Theor Biol. 2014;353:44–54. doi:10.1016/j.jtbi.2014.02.021. [Google Scholar] [PubMed] [CrossRef]
3. Drusano GL, Liu W, Fikes S, Cirz R, Robbins N, Kurhanewicz S, et al. Interaction of drug- and granulocyte-mediated killing of Pseudomonas aeruginosa in a murine pneumonia model. J Infect Dis. 2014;210(8):1319–24. doi:10.1093/infdis/jiu237. [Google Scholar] [PubMed] [CrossRef]
4. Ndelwa EJ, Kgosimore M, Massawe ES, Namkinga L. Mathematical modelling and analysis of treatment and screening of pneumonia. Mathem Theory Model. 2015;5(10):21–39. [Google Scholar]
5. Kosasih K, Abeyratne UR, Swarnkar V, Triasih R. Wavelet augmented cough analysis for rapid childhood pneumonia diagnosis. IEEE Trans Biomed Eng. 2015;62(4):1185–94. doi:10.1109/TBME.2014.2381214. [Google Scholar] [PubMed] [CrossRef]
6. César ACG, Nascimento LFC, Mantovani KCC, Vieira LCP. Fine particulate matter estimated by mathematical model and hospitalisations for pneumonia and asthma in children. Rev Paul Pediatr. 2016;34(1):18–23. doi:10.1016/j.rpped.2015.06.009. [Google Scholar] [PubMed] [CrossRef]
7. Marchello C, Dale AP, Thai TN, Han DS, Ebell MH. Prevalence of atypical pathogens in patients with cough and community-acquired pneumonia: a meta-analysis. Ann Fam Med. 2016;14(6):552–66. doi:10.1370/afm.1993. [Google Scholar] [PubMed] [CrossRef]
8. Cheng YH, You SH, Lin YJ, Chen SC, Chen WY, Chou WC, et al. Mathematical modeling of post coinfection with influenza A virus and Streptococcus pneumoniae, with implications for pneumonia and COPD-risk assessment. Int J Chron Obstruct Pulmon Dis. 2017;12:1973–88. doi:10.2147/COPD.S138295. [Google Scholar] [PubMed] [CrossRef]
9. Kosasih K, Abeyratne U. Exhaustive mathematical analysis of simple clinical measurements for childhood pneumonia diagnosis. World J Pediatr. 2017;13(5):446–56. doi:10.1007/s12519-017-0019-4. [Google Scholar] [PubMed] [CrossRef]
10. Tilahun GT, Makinde OD, Malonza D. Modelling and optimal control of pneumonia disease with cost-effective strategies. J Biol Dyn. 2017;11(2):400–26. doi:10.1080/17513758.2017.1337245. [Google Scholar] [PubMed] [CrossRef]
11. Tilahun GT, Makinde OD, Malonza D. Co-dynamics of pneumonia and typhoid fever diseases with cost-effective optimal control analysis. Appl Math Comput. 2018;316:438–59. doi:10.1016/j.amc.2017.07.063. [Google Scholar] [CrossRef]
12. Raj M, Reddy M, Mufeed M, Karthika S. HMM based cough sound analysis for classifying asthma and pneumonia in the pediatric population. Int J Pure Appl Math. 2018;118(18):609–16. [Google Scholar]
13. Kizito M, Tumwiine J. A mathematical model of treatment and vaccination interventions of pneumococcal pneumonia infection dynamics. J Appl Mathem. 2018;2018:1–16. doi:10.1155/2018/2539465. [Google Scholar] [CrossRef]
14. Mbabazi FK, Mugisha JYT, Kimathi M. Modeling the within-host coinfection of influenza A virus and pneumococcus. Appl Math Comput. 2018;339:488–506. doi:10.1016/j.amc.2018.07.031. [Google Scholar] [CrossRef]
15. Tilahun GT. Optimal control analysis of pneumonia and meningitis coinfection. Comput Math Methods Med. 2019;2019(1):1–15. doi:10.1155/2019/2658971. [Google Scholar] [PubMed] [CrossRef]
16. Diah IM, Aziz N. Stochastic modelling for pneumonia incidence: a conceptual framework. In: AIP Conference Proceedings. New York, NY, USA: AIP; 2019. Vol. 1, p. 1–3. [Google Scholar]
17. Tilahun GT. Modeling co-dynamics of pneumonia and meningitis diseases. Adv Different Equat. 2019;2019:149. doi:10.1186/s13662-019-2087-3. [Google Scholar] [CrossRef]
18. Mbabazi FK, Mugisha JY, Kimathi M. Hopf-bifurcation analysis of pneumococcal pneumonia with time delays. Abstr Appl Anal. 2019;2019:1–21. doi:10.1155/2019/3757036. [Google Scholar] [CrossRef]
19. Otoo D, Opoku P, Charles S, Kingsley AP. Deterministic epidemic model for (SVCSyCAsyIR) pneumonia dynamics, with vaccination and temporal immunity. Infect Dis Model. 2020;5:42–60. doi:10.1016/j.idm.2019.11.001. [Google Scholar] [PubMed] [CrossRef]
20. Zephaniah OC, Nwaugonma UIR, Chioma IS, Adrew O. A mathematical model and analysis of an SVEIR model for Streptococcus pneumonia with saturated incidence force of infection. Mathem Mode Applicat. 2020;5(1):16. doi:10.11648/j.mma.20200501.13. [Google Scholar] [CrossRef]
21. Ming WK, Huang J, Zhang CJ. Breaking down of healthcare system: mathematical modelling for controlling the novel coronavirus (2019-nCoV) outbreak in Wuhan, China. BioRxiv. 2020;1–18. doi:10.1101/2020.01.27.922443. [Google Scholar] [CrossRef]
22. Jung SM, Kinoshita R, Thompson RN, Linton NM, Yang Y, Akhmetzhanov AR, et al. Epidemiological identification of a novel pathogen in real-time: analysis of the atypical pneumonia outbreak in Wuhan, China, 2019–2020. J Clin Med. 2020;9(3):1–18. [Google Scholar]
23. Wafula NM, Kwach BO, Marani VN. Mathematical modeling and optimal control for controlling pneumonia-HIV coinfection. Int J Innovat Res Develop. 2021;10(1):138–44. doi:10.24940/ijird/2021/v10/i1/JAN21051. [Google Scholar] [CrossRef]
24. Oluwatobi KI, Erinle-Ibrahim LM. Mathematical modeling of pneumonia dynamics of children under the age of five. Research Square. 2021. doi:10.21203/rs.3.rs-194578/v1. [Google Scholar] [CrossRef]
25. Sayed Saber AM, Alghamdi GA, Alshehri KM. Mathematical modelling and optimal control of pneumonia disease in sheep and goats in Al-Baha region with cost-effective strategies. AIMS Math. 2022;7(7):12011–49. doi:10.3934/math.2022669. [Google Scholar] [CrossRef]
26. Saber S, Alahmari AA. Impact of fractal-fractional dynamics on pneumonia transmission modeling. European J Pure Appl Mathem. 2025;18(2):5901. doi:10.29020/nybg.ejpam.v18i2.5901. [Google Scholar] [CrossRef]
27. Atangana A, Qureshi S. Modeling attractors of chaotic dynamical systems with fractal-fractional operators. Chaos Soliton Fract. 2019;123:320–37. doi:10.1016/j.chaos.2019.04.020. [Google Scholar] [CrossRef]
28. Owolabi KM, Atangana A, Akgul A. Modelling and analysis of fractal-fractional partial differential equations: application to reaction-diffusion model. Alex Eng J. 2020;59(4):2477–90. doi:10.1016/j.aej.2020.03.022. [Google Scholar] [CrossRef]
29. Qureshi S, Rangaig NA, Baleanu D. New numerical aspects of Caputo-Fabrizio fractional derivative operator. Mathematics. 2019;7(4):374. doi:10.3390/math7040374. [Google Scholar] [CrossRef]
30. Qureshi S, Yusuf A, Ali Shaikh A, Inc M, Baleanu D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos. 2020;30(4):043106. doi:10.1063/1.5121845. [Google Scholar] [PubMed] [CrossRef]
31. Atangana A. Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex systems. Chaos Soliton Fract. 2017;102(5):396–406. doi:10.1016/j.chaos.2017.04.027. [Google Scholar] [CrossRef]
32. Alhazmi M, Saber S. Glucose-insulin regulatory system: chaos control and stability analysis via Atangana-Baleanu fractal-fractional derivatives. Alex Eng J. 2025;122(9911):77–90. doi:10.1016/j.aej.2025.02.066. [Google Scholar] [CrossRef]
33. Khalid IA, Haroon DS, Youssif MY, Saber S. Different strategies for diabetes by mathematical modeling: applications of fractal-fractional derivatives in the sense of Atangana-Baleanu. Results Phys. 2023;52(114):106892. doi:10.1016/j.rinp.2023.106892. [Google Scholar] [CrossRef]
34. Khalid IA, Haroon DS, Youssif MY, Saber S. Different strategies for diabetes by mathematical modeling: modified Minimal Model. Alex Eng J. 2023;80:74–87. doi:10.1016/j.aej.2023.07.050. [Google Scholar] [CrossRef]
35. Almutairi N, Saber S, Hijaz A. The fractal-fractional Atangana-Baleanu operator for pneumonia disease: stability, statistical and numerical analyses. AIMS Math. 2023;8(12):29382–410. doi:10.3934/math.20231504. [Google Scholar] [CrossRef]
36. Abodayeh K, Raza A, Rafiq M, Arif MS, Naveed M, Zeb Z, et al. Analysis of pneumonia model via efficient computing techniques. Comput Mater Contin. 2022;70(3):6073–88. doi:10.32604/cmc.2022.020732. [Google Scholar] [CrossRef]
37. Boukhouima A, Hattaf K, Yousfi N. Dynamics of a fractional order HIV infection model with specific functional response and cure rate. Int J Differ Equ. 2017;2017(SI1):1–8. doi:10.1155/2017/8372140. [Google Scholar] [CrossRef]
38. Kwambana-Adams BA, Mulholland EK, Satzke C. State-of-the-art in the pneumococcal field: proceedings of the 11th international symposium on pneumococci and pneumococcal diseases (ISPPD-11). Pneumonia. 2020;12(1):1–14. doi:10.1186/s41479-019-0064-y. [Google Scholar] [PubMed] [CrossRef]
39. Minucci SB, Heise RL, Reynolds AM. Review of mathematical modeling of the inflammatory response in lung infections and injuries. Front Appl Math Stat. 2020;6:36. doi:10.3389/fams.2020.00036. [Google Scholar] [CrossRef]
40. Huttinger ED, Boon NJ, Clarke TB, Tanaka RJ. Mathematical modeling of Streptococcus pneumonia colonisation, invasive infection and treatment. Front Physiol. 2017;8:115. doi:10.3389/fphys.2017.00115. [Google Scholar] [PubMed] [CrossRef]
41. Capponetto R, Dongola G, Fortuna L, Petras I. Fractional order systems: modelling and control applications. Singapore: World Scientific; 2010. [Google Scholar]
42. Ali Dokuyucu M, Celik E, Bulut H, Mehmet Baskonus H. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur Phys J Plus. 2018;133(3):92. doi:10.1140/epjp/i2018-11950-y. [Google Scholar] [CrossRef]
43. Veeresha P, Prakasha DG, Baskonus HM. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos. 2019 Jan 1;29(1):013119. doi:10.1063/1.5074099. [Google Scholar] [PubMed] [CrossRef]
44. Alshehri MH, Duraihem FZ, Alalyani A, Saber S. A Caputo (discretization) fractional-order model of glucose-insulin interaction: numerical solution and comparisons with experimental data. J Taibah Univ Sci. 2021;15(1):26–36. doi:10.1080/16583655.2021.1872197. [Google Scholar] [CrossRef]
45. Baskonus HM, Mekkaoui T, Hammouch Z, Bulut H. Active control of a chaotic fractional order economic system. Entropy. 2015;17:5771–83. doi:10.3390/e17085771. [Google Scholar] [CrossRef]
46. Saber S, Alahmari AA. Mathematical insights into zoonotic disease spread: application of the milstein method. European J Pure Appl Mathem. 2025;18(2):5881. doi:10.29020/nybg.ejpam.v18i2.5881. [Google Scholar] [CrossRef]
47. Althubyani M, Adam HDS, Alalyani A, Taha NE, Taha KO, Alharbi RA, et al. Understanding zoonotic disease spread with a fractional order epidemic model. Sci Rep. 2025;15(1):13921. doi:10.1038/s41598-025-95943-6. [Google Scholar] [PubMed] [CrossRef]
48. Adam HDS, Althubyani M, Mirgani SM, Saber S. An application of Newton’s interpolation polynomials to the zoonotic disease transmission between humans and baboons system based on a time-fractal fractional derivative with a power-law kernel. AIP Adv. 2025;15(4):045217. doi:10.1063/5.0253869. [Google Scholar] [CrossRef]
49. Saber S, Solouma E, Althubyani M, Messaoudi M. Statistical insights into zoonotic disease dynamics: simulation and control strategy evaluation. Symmetry. 2025;17(5):733. doi:10.3390/sym17050733. [Google Scholar] [CrossRef]
50. Althubyani M, Saber S. Hyers-ulam stability of fractal-fractional computer virus models with the Atangana-Baleanu operator. Fractal Fract. 2025;9(3):158. doi:10.3390/fractalfract9030158. [Google Scholar] [CrossRef]
51. Podlubny I. Fractional differential equations. Cambridge, MA, USA: Academic Press; 1999. [Google Scholar]
52. LaSalle JP. The stability of dynamic systems. Philadelphia, PA, USA: SIAM; 1976. [Google Scholar]
53. Vargas-De-León C. Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun Nonlinear Sci Numer Simul. 2015;24(1–3):75–85. doi:10.1016/j.cnsns.2014.12.013. [Google Scholar] [CrossRef]
54. Saber S. Control of chaos in the Burke-Shaw system of fractal-fractional order in the sense of Caputo-Fabrizio. J Appl Math Comput Mech. 2024;23(1):83–96. doi:10.17512/jamcm.2024.1.07. [Google Scholar] [CrossRef]
55. Petras I. Fractional-order nonlinear systems: modeling, analysis, and simulation. Berlin/Heidelberg: Germany, Springer-Verlag; 2011. [Google Scholar]
56. Hartley TT, Lorenzo CF, Qammer HK. Chaos in a fractional order Chua’s system. IEEE Transact Circ Syst I: Fundam Theory Applicat. 1995;42(6):485–90. doi:10.1109/81.404062. [Google Scholar] [CrossRef]
57. Wang XY, Song JM. Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control. Commun Nonlinear Sci Numer Simul. 2009;14(7):3351–7. doi:10.1016/j.cnsns.2009.01.010. [Google Scholar] [CrossRef]
58. Deng WH, Li CP. Chaos synchronization of the fractional Lü system. Physica A. 2005;353:61–72. doi:10.1016/j.physa.2005.01.021. [Google Scholar] [CrossRef]
59. Almutairi N, Saber S. Application of a time-fractal fractional derivative with a power-law kernel to the Burke-Shaw system based on Newton’s interpolation polynomials. MethodsX. 2024;12(5):102510. doi:10.1016/j.mex.2023.102510. [Google Scholar] [PubMed] [CrossRef]
60. Li CG, Chen G. Chaos and hyperchaos in the fractional-order Rössler equations. Physica A. 2004;341:55–61. doi:10.1016/j.physa.2004.04.113. [Google Scholar] [CrossRef]
61. Almutairi N, Saber S. On chaos control of nonlinear fractional Newton-Leipnik system via fractional Caputo-Fabrizio derivatives. Sci Rep. 2023;13(1):22726. doi:10.1038/s41598-023-49541-z. [Google Scholar] [PubMed] [CrossRef]
62. Veeresha P, Prakasha DG, Baskonus HM. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math Sci. 2019;13(2):115–28. doi:10.1007/s40096-019-0284-6. [Google Scholar] [CrossRef]
63. Yangla J, Abboubakar H, Dangbe E, Yankoulo R, Abba Ari AA, Damakoa I, et al. Fractional dynamics of a Chikungunya transmission model. Sci Afr. 2023;21:e01812. doi:10.1016/j.sciaf.2023.e01812. [Google Scholar] [CrossRef]
64. Abboubakar H, Regonne RK, Nisar KS. Fractional dynamics of typhoid fever transmission models with mass vaccination perspectives. Fract Fractional. 2021;5(2):149. doi:10.3390/fractalfract5040149. [Google Scholar] [CrossRef]
65. Atangana A, Akgul A, Owolabi KM. Analysis of fractal fractional differential equations. Alex Eng J. 2020;59(3):1117–34. doi:10.1016/j.aej.2020.01.005. [Google Scholar] [CrossRef]
66. Yan T, Muflih A, Youssif Mukhtar Y, Elhag Amna E, Aljohani Abdulrahman F, Sayed S. Analysis of a lorenz model using adomian decomposition and fractal-fractional operators. Therm Sci. 2024;28(6B):5001–9. [Google Scholar]
67. Alsulami A, Alharb RA, Albogami TM, Eljaneid NHE, Adam HDS, Saber S. Controlled chaos of a fractal-fractional Newton-Leipnik system. Therm Sci. 2024;29(6B):5153–60. [Google Scholar]
68. Alhazmi M, Dawalbait F, Aljohani A, Taha K, Adam H, Saber S. Numerical approximation method and chaos for a chaotic system in sense of Caputo-Fabrizio operator. Therm Sci. 2024;28(6B):5161–8. [Google Scholar]
69. Atangana A, Baleanu D. New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm Sci. 2016;20(2):763–9. doi:10.2298/TSCI151003158A. [Google Scholar] [CrossRef]
70. Abro KA, Atangana A. A comparative study of convective fluid motion in rotating cavity via Atangana-Baleanu and Caputo-Fabrizio fractal-fractional differentiations. Eur Phys J Plus. 2020;135(2):226. doi:10.1140/epjp/s13360-020-00136-x. [Google Scholar] [CrossRef]
71. Hefferman J, Smith R, Wahl L. Perspectives on the basic reproduction ratio. J R Soc Interface. 2005;2(4):281–93. doi:10.1098/rsif.2005.0042. [Google Scholar] [PubMed] [CrossRef]
72. Atangana A, Araz SI. New numerical scheme with newton polynomial: theory, methods, and applications. Cambridge, MA, USA: Academic Press; 2021. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools