 Open Access
Open Access
ARTICLE
Investigating the Link between Ascaris Lumbricoides and Asthma in Human with Analysis of Fractal Fractional Caputo-Fabrizio of a Mathematical Model
1 Department of Biology, College of Science, University of Duhok, Duhok, 42001, Iraq
2 Department of Mathematics, College of Science, University of Duhok, Duhok, 42001, Iraq
3 Department of Mathematics and Sciences, Prince Sultan University, Riyadh, 11586, Saudi Arabia
4 Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
5 Center for Applied Mathematics and Bioinformatics (CAMB), Gulf University for Science and Technology, Hawally, 32093, Kuwait
6 Department of Mathematics and Applied Mathematics, Sefako Makgatho Health Sciences University, Garankuwa, Medusa, 40204, South Africa
7 Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
* Corresponding Authors: Shayma Adil Murad. Email: ; Thabet Abdeljawad. Email:
(This article belongs to the Special Issue: Analytical and Numerical Solution of the Fractional Differential Equation)
Computer Modeling in Engineering & Sciences 2025, 143(3), 3377-3409. https://doi.org/10.32604/cmes.2025.064245
Received 09 February 2025; Accepted 29 April 2025; Issue published 30 June 2025
Abstract
Asthma is the most common allergic disorder and represents a significant global public health problem. Strong evidence suggests a link between ascariasis and asthma. This study aims primarily to determine the prevalence of Ascaris lumbricoides infection among various risk factors, to assess blood parameters, levels of immunoglobulin E (IgE) and interleukin-4 (IL-4), and to explore the relationship between ascariasis and asthma in affected individuals. The secondary objective is to examine a fractal-fractional mathematical model that describes the four stages of the life cycle of Ascaris infection, specifically within the framework of the Caputo-Fabrizio derivative. A case-control study was conducted that involved 270 individuals with asthma and 130 healthy controls, all of whom attended general hospitals in Duhok City, Iraq. Pulmonary function tests were performed using a micromedical spirometer. The presence of Ascaris lumbricoides antibodies-Immunoglobulin M (IgM), Immunoglobulin G (IgG), and Immunoglobulin E (IgE)-was detected using ELISA. Blood parameters were analyzed using a Coulter counter. The overall infection rate was (42.5%), with the highest rates observed among asthmatic men (70.0%) and rural residents (51.4%). Higher infection rates were also recorded among low-income individuals (64.3%) and those with frequent contact with the soil (58.6%). In particular, infected individuals exhibited a significant decrease in red blood cell count and hemoglobin concentration, while a marked increase in white blood cell count was recorded. In addition, levels of Immunoglobulin E (IgE) and interleukin-4 were significantly higher in the infected group compared to the controls. Effective disease awareness strategies that incorporate health education and preventive measures are needed. Exposure to Ascaris has been associated with reduced lung function and an increased risk of asthma. More research is required to elucidate the precise mechanisms that link Ascaris infection with asthma. Furthermore, the existence and uniqueness of solutions for the proposed model are investigated using the Krasnosel’skii and Banach fixed-point theorems. The Ulam-Hyers and Ulam-Hyers-Rassias stability types are explained within the framework of nonlinear analysis in -space. Finally, an application is presented, including tabulated results and figures generated using MATLAB to illustrate the validity of the theoretical findings.Keywords
Ascaris lumbricoides is a soil-transmitted parasite responsible for ascariasis. It ranks as the most prevalent parasitic helminth infection globally and causes significant health problems in humans, including lung diseases and intestinal obstructions [1]. The impact of this infection is particularly severe in impoverished populations that do not have access to clean water, sanitation, and hygiene facilities, especially in tropical and subtropical regions, due to the parasite’s life cycle relying on fecal soil contamination [2].
Beyond its substantial health implications, the migration of Ascaris larvae through the lungs can contribute to various pulmonary diseases, including asthma. In addition, chronic intestinal ascariasis can result in growth stunting, malnutrition, and severe abdominal pain [3]. The immune response to this parasite plays a role in the pathogenesis of allergic diseases, studies indicating that antibody responses to its proteins are linked to asthma symptoms [4]. According to [5], recent advances focus on understanding tissue-specific Type 2 immune responses to helminths, including the discovery of immune cells and cytokine pathways that contribute to immunity, tissue repair, and tolerance to parasites, as well as comparisons with immune-related diseases such as asthma and allergies. Upon exposure to allergens, crosslinking of IgE triggers the release of histamine, leukotrienes, and prostaglandins, leading to bronchoconstriction [6].
Pulmonary function tests are commonly used to assess lung function by measuring lung volumes and capacities. The connection between ascariasis and asthma remains unclear and is currently being investigated in regions that transition from high to low prevalence of helminthiasis [7]. Previous studies in Iraq have examined various aspects of ascariasis [8–10], while global research has been conducted in Brazil, Colombia, and Europe [11–13].
Recently, mathematical models and fractional calculus have been widely used to analyze the spread and control of infectious diseases, providing insight into epidemic dynamics, as demonstrated in studies on dengue infection [14] and breast cancer [15]. In [16], the authors analyze the dynamics of monkeypox in the UK and evaluate the impact of vaccination using a fractional mathematical model based on real data to inform effective disease control strategies. The stability of the Bcl-2/Bax ratio over time in reproductive cancer has been studied using Atangana-Baleanu fractional derivative operators, along with an investigation of the effect of the ABT-737 inhibitor on mitochondrial apoptosis through mathematical modeling and numerical simulations [17]. A fractal-fractional cancer model has been developed to examine the interactions between stem cells, effector cells, and tumor cells, both with and without chemotherapy, as well as to assess the role of chemotherapy in cancer treatment [18]. In addition, the study in [19] explored the effectiveness of seasonally timed treatment programs to control Ascaris lumbricoides infections using mathematical modeling for the four different stages of the life cycle of A. lumbricoides, intending to educate public health strategies by optimizing treatment schedules and maximizing the impact of intervention.
Over the years, fixed-point theory has become a crucial and effective tool for studying nonlinear phenomena. For example, the authors of [20] discussed that the Banach theorem has been utilized to establish the uniqueness, stability, and existence of stable solutions for the fractional-order mathematical model for cervical cancer in the sense of the Caputo-Fabrizio operator. Various fixed-point theorems and stability analyzes have been used to determine the conditions under which solutions exist and remain unique for different types of fractional differential problems; see [21–24]. Recently, stability has been an important topic in differential equations and guaranteeing that there is a close and exact solution. Several articles have been published related to Ulam-Hyers and Ulam-Hyers-Rassias stability; see [25–28]. Some researchers have begun to focus on the existence and stability of
Motivated by the above work, the objective of this study is to assess the relationship between ascariasis and asthma in humans. This research aims to increase public awareness about the health complications associated with this parasite, highlighting the importance of risk reduction and early treatment. Furthermore, by using fresh mathematical techniques, this study generalizes the model presented in [19] using the fractal-fractional Caputo-Fabrizio
with the initial conditions
Here, we present an analysis of the existence and uniqueness of a fractal-fractional Ascaris lumbricoides mathematical model by applying Banach’s contraction mapping principle and Krasnosel’skii’s fixed point theorem, along with the Hölder inequality in the
The structure of the manuscript is as follows: Section 1 presents the introduction and motivation. Section 2 outlines the materials and methods, while Section 3 displays the results. The definitions and fundamental concepts relevant to this study are introduced in Section 4. The fractal-fractional extension of the mathematical model for Ascaris infection is formulated in Section 5. The existence and uniqueness theorems for the fractal-fractional model are established in Section 6. The Ulam-Hyers and Ulam-Hyers-Rassias stability is analyzed in Section 7. Finally, the discussion and conclusion are provided in Sections 8 & 9, respectively.
This section outlines the study design, including participant grouping, laboratory procedures to detect ascariasis, serological tests for anti-Ascaris lumbricoides antibodies, data collection, and statistical analysis methods.
Patients: This study included 270 individuals with asthma and 130 controls who visited general hospitals in Duhok city, Iraq. A specialist physician confirmed the asthma diagnosis prior to the enrollment of patients in the study. The participants ranged in age from 15 to 80 years. A questionnaire was developed to collect information from each participant.
Pulmonary function tests: Pulmonary function tests (PFT) were conducted on all subjects using a MicroMedical Spirometer (MIR SpirolabIII Diagnostic Spirometer, Ltd., England), which is effective for accurate diagnosis of respiratory conditions such as asthma and pulmonary diseases. All participants underwent spirometry and received instructions to forcefully and continuously exhale into the instrument’s mouthpiece. This test was performed as a confirmatory diagnosis for asthma.
Blood Sample Collection: A volume of five milliliters of venous blood was collected from participants using a sterile syringe. One milliliter of this blood was placed in a tube containing anticoagulants for blood parameter analysis using the Coulter Count machine (Swelab, Germany). In [34], the remaining four milliliters was transferred to a second tube without anticoagulants, allowed to clot for 20 min, and then centrifuged for 10 min at 3000 rpm to obtain the serum. The collected serum was stored in sterile Eppendorf tubes at −20°C until it was needed for analysis in [35].
Measurement of blood parameters by Coulter Count machine: A volume of one milliliter of the blood sample was placed into a tube containing anticoagulant and analyzed using the Coulter Count machine to assess blood parameters [36].
Parasite examination: This study assessed A. lumbricoides using anti-A. lumbricoides IgM (AFG Bioscience, USA) and anti-E. granulosus IgG antibodies (AFG Bioscience, USA).
Serum total IgE measurement: The measurement of total IgE levels in serum was conducted using an ELISA kit (AFG Bioscience, USA), which allows for a quantitative assessment of human IgE in vitro. The procedure was carried out in accordance with the manufacturer’s guidelines.
Measurement of IL-4 using ELISA: In this study, interleukin-4 was measured using a kit (AFG Bioscience, USA), following the manufacturer’s guidelines. The optical density was recorded at 450 nm with a BioTek ELISA plate reader (USA). The procedure was carried out following the manufacturer’s guidelines.
Inclusion criteria: Subjects who agreed to participate in the current study were included.
Exclusion criteria: Individuals who declined to participate in this study, along with those suffering from infectious, non-infectious, chronic, and autoimmune diseases, were excluded.
Statistical analysis: All data were analyzed using the statistical program R and a chi-square test. Descriptive statistics included means, standard deviations, and ranges for numerical variables, along with frequencies (n) and percentages (
In this section, the results of the study are presented, including the distribution of ascariasis infection among different groups, the serological findings, and statistical analysis of the data.
A total of 400 subjects aged 15 to 80 years participated in this study, with 170 (42.5%) found to be infected with ascariasis. Among the infected cases, 45 individuals (26.5%) tested positive for anti-A. lumbricoides IgM antibodies, while 125 (73.5%) had IgG antibodies. The asthmatic group included 270 subjects and 130 controls. Within the asthmatic patients, 140 (51.9%) tested positive for ascariasis, while only 30 infections (23.1%) had been detected in the control group, as explained in Table 1.

Table 2 displays the distribution of various demographic characteristics between asthmatic and control subjects. Concerning asthmatic patients, the majority were male, with 170 cases (63.0%), while females made up 100 cases (37.5%). The age group with the highest occurrence was 48 to 58 years, accounting for (37.0%) of the cases, whereas only 8 cases (3.0%) observed in the 70 to 80-year age range. The data indicated that 160 cases (59.3%) from urban areas, in contrast to 110 cases (40.7%) from rural locations. A notable proportion of asthmatic patients had completed secondary education, totaling 190 cases (70.4%), compared to 16 cases (5.9%) among individuals with lower educational qualifications, within the asthmatic cohort, 160 cases (59.2%) ported having a low income, while 35 patients (13.0%) reported having a high income. In addition, 150 cases (55.6%) reported did not wash their hands before meals, while (44.4%) practiced hand washing. Finally, 140 asthmatic patients (51.9%) had exposure to soil, while 130 cases (48.1%) did not.

The analysis of ascariasis among the examined subjects is illustrated in Fig. 1. Out of 270 asthmatic patients, 140 (51.9%) tested seropositive for Ascaris, while 130 (48.1%) showed no infection.
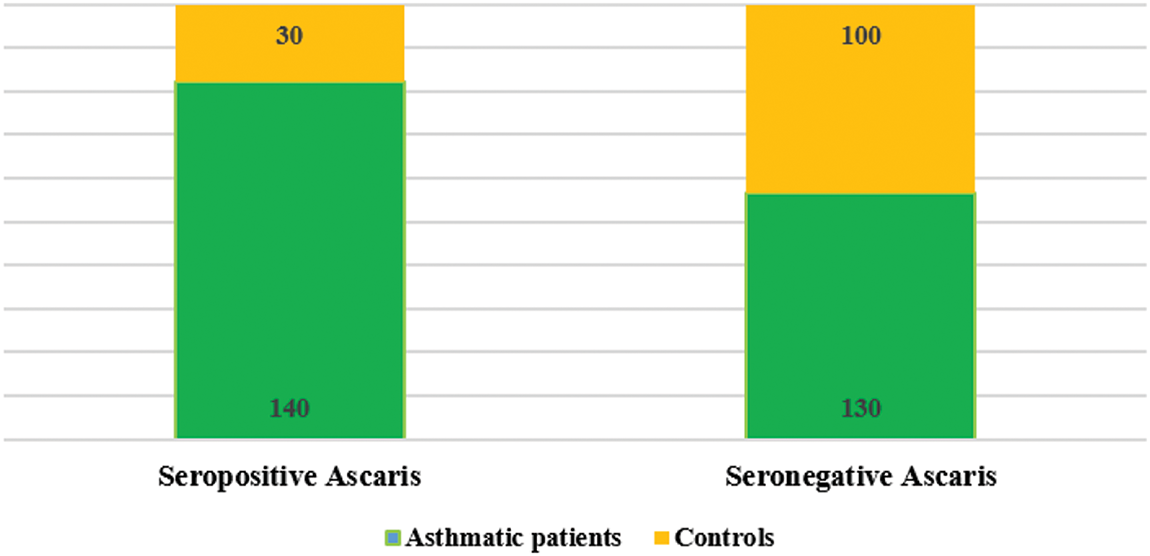
Figure 1: Distribution of ascariasis among examined individuals
Fig. 2 shows the sociodemographic features among individuals. Regarding asthmatic patients, males comprised the majority of cases of 170 (63.0%), followed by 100 females (37.0%). The highest cases belonged to age group 48–58 years represented 100 (37.0%) and the lowest found to be 8 (3.0%) as 70–80 years old. The rates of asthmatic patients from urban and rural areas accounted for (59.3%) and (40.7%), respectively. Secondary qualification reported 190 (70.4%) and illiterates 16 (5.9%). In terms of monthly income, 160 (59.2%) cases recorded a monthly income below 150.000 Dinars, and 35 subjects (13.0%) had more than 300.000 Dinars. About, 140 (51.9%) cases had a soil contact and 130 (48.1%) did not have it.
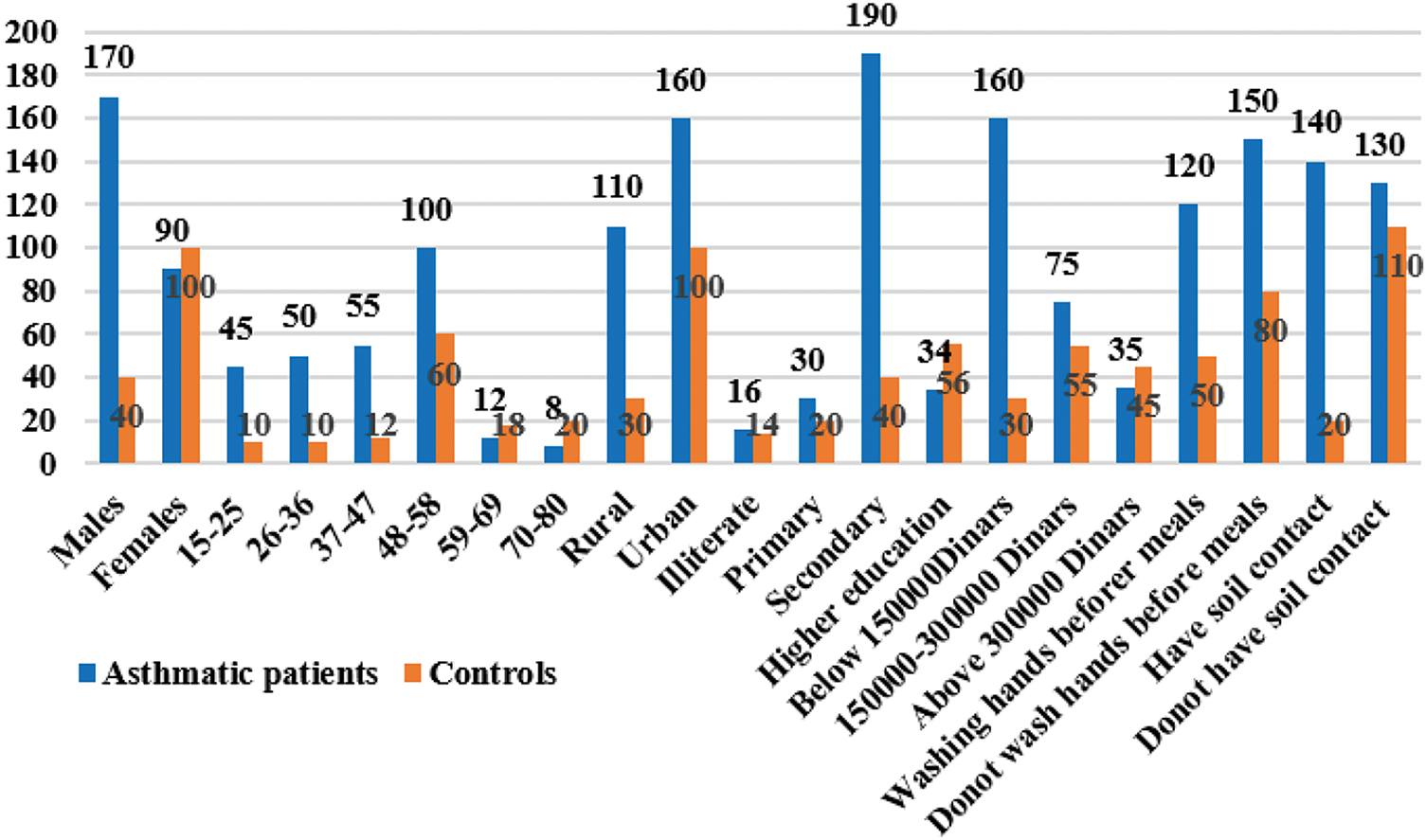
Figure 2: Demographic characters among subjects
Fig. 3 shows the infected and non-infected cases among asthmatic patients. About, the infection rate among males and females are 98 (70.0%) and 42 (30.0%), respectively. The age group 48–58 years old assessed 45 (32.1%) and 6 cases (4.3%) among 70–80 years old. Infected rural patients reported 72 (51.4%) and urban ones 68 (48.6%).
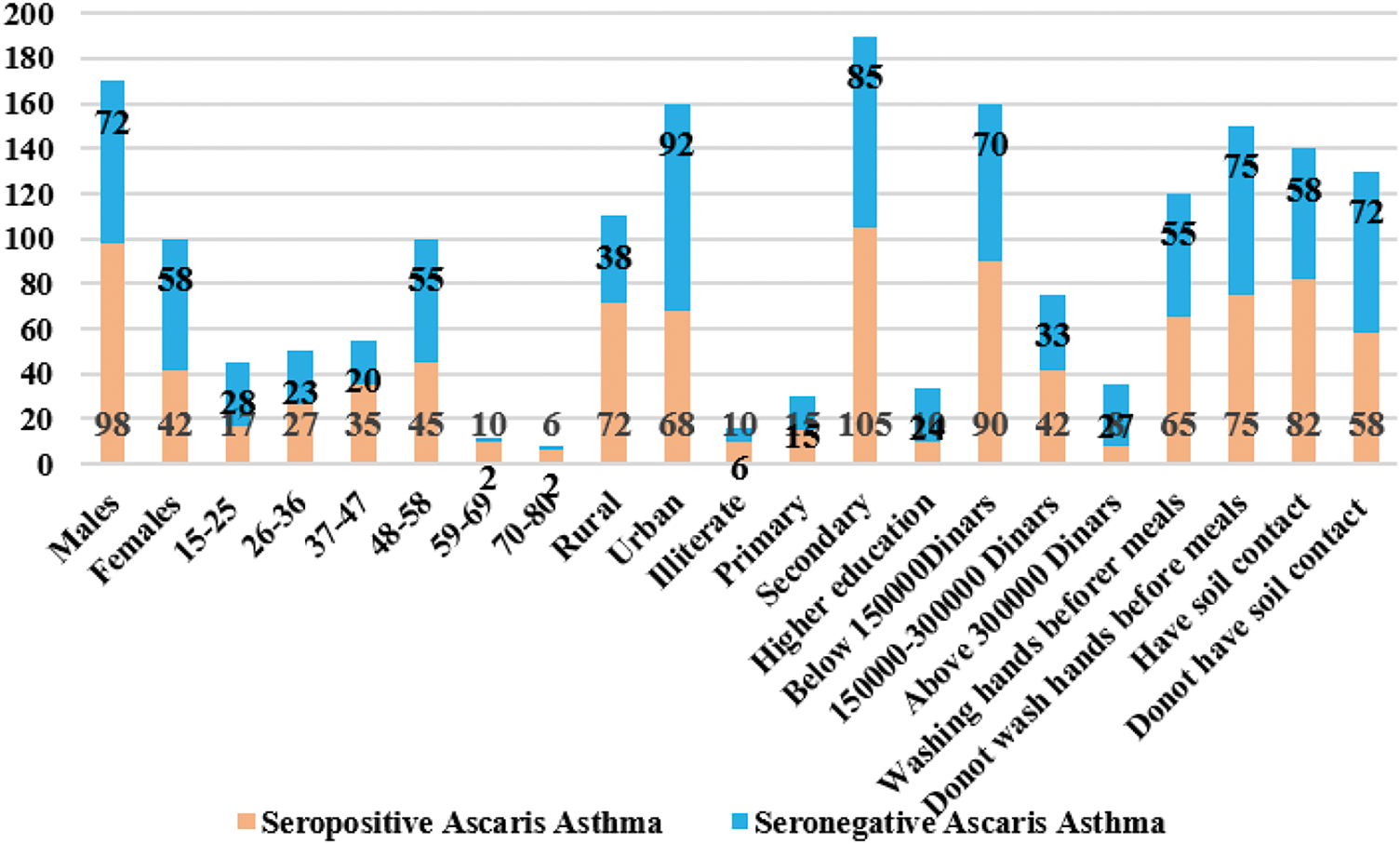
Figure 3: Cases of seropositive and seronegative ascariasis among asthmatic patients
Table 3 clarifies the prevalence of ascariasis according to various factors. About asthmatic patients, 98 males (70.0%) had been infected, while females constituted 42 cases (30.0%). The highest infection rate, at (32.1%), was observed in the 48–58 age group, whereas only (4.3%) of those aged 70–80 were infected. Infection rates in rural areas stood at (51.4%), compared to (48.6%) in urban settings. A significantly high rate of infection was found among individuals with secondary education, accounting for (75.0%), in contrast to just (7.1%) among those with higher education. Concerning monthly income, the majority of infections were found in the low-income group (64.3%), while only (5.7%) noted among high-income individuals. Also, the rate of infection was (53.6%) among subjects who did not practice hand washing, compared to (46.4%) among hand washing. Finally, individuals with soil contact had an infection rate of (58.6%), while those without such contact had a rate of (41.4%). All the studied risk factors had an association with infection with a

Table 4 presents the mean values

4 Fractional Calculus and Fundamental Concepts
This section introduces the fundamental definitions, lemmas, and prerequisite results that are crucial for developing the theoretical framework of the study.
The Caputo-Fabrizio derivative of order
Definition 1. [37] Let
where
According to Riemann’s definition, it is formulated as follows:
Then the corresponding Caputo Fabrizio integral is defined by
so that
and
However, it has been observed that
The fractal of order
It is clear that
Definition 2. [38,39] Suppose that
where
The fractal-fractional derivative in the Riemann sense with an exponential law is defined as
Definition 3. [39] Suppose that
where
Notice that for
Remark 4. Following [39], in Definition (3), the author selects the fractal order
Further, it is clear that
but not able to prove that
Due to this fact and Remark 4, the following new fractal fractional derivative with exponential law is defined in the Caputo sense as
Definition 5. Suppose that
The following lemma is crucial for advancing the solution representation of the system that describes the investigated model. The solution will satisfy the dynamic equation on both sides and verify the initial data.
Lemma 6. For
•
•
Proof. • From definition and (2), the result is
• From definition of the fractal fractional operators, (3), and that
Lemma 7. [40] The measurable function
Theorem 8. (Kolmogorov) [40]
Suppose
(A) The set
(B)
Lemma 9. (Hölder’s inequality) [40]
Let B be a measurable space and
Theorem 10. (Krasnosel’skii theorem) [41]. Let M be a closed, bounded, convex, and nonempty subset of a Banach space V. Let A and B be two operators such that
(1)
(2) A is compact and continuous;
(3) B is a contraction mapping.
Then there exists
Mathematical model of the dynamics of Ascaris infection
5 Fractal-Fractional Mathematical Model of Ascaris Infection
Mathematical modeling is an essential tool for effectively illustrating and understanding the epidemic models and intricacies of scientific phenomena. In this section, we discuss the mathematical model developed by [19] for the four stages of the A. lumbricoides life cycle, as described below.
with initial conditions
where B is ingestion or uptake rate seasonal;
The work mentioned above serves as our inspiration, as we examine the model (6) in the fractal-fractional sense, in the Caputo-Fabrizio
The functions
The fractal-fractional mathematical model (7) can be reformulated as the following problem
Lemma 11. Let
Proof. Applying the fractal-fractional integral
The solutions can be expressed as follows:
6 Existence and Uniqueness of Fractal-Fractional Model
This section focuses on studying the existence and uniqueness of the fractal-fractional model (8) under certain conditions. For a measurable function denoted by
In this case,
The assumptions below are fundamental to this analysis:
(
(
For simplicity, we define the notation as follows:
Lemma 12. The function
Proof.
In the same way
where
By including all equations, it concludes that
□
Theorem 13. Assume that
Proof. First, consider the operator
To derive the Banach fixed point theorem, defined the set:
Choose
for
Thus,
From (
which implies that
Hence,
Now, to prove that
Then,
If
The following result illustrates the application of Krasnosel’skii’s fixed point technique
Theorem 14. Assume that th condition (11) and (
Proof. Define the following operators based on Eqs. (9) and (10) as
Consider a set defined as
Let us observe that if
By the Lipschitz condition and Hölder’s inequality, the following result is obtained
By the same technique, one can have
This shows that the operators
Similarly, it follows that
Then,
where
If
Next, to prove that the operator
Then,
Therefore,
Then,
and
Since
Hence
Similarly
Hence
Then, by Theorem (8), it can be concluded that
7 Ulam-Hyers and Ulam-Hyers-Rassias Stability
This section is dedicated to establishing the stability for the problem (8) in the sense of Ulam-Hyers and Ulam-Hyers-Rassias. The following definitions and conditions are introduced.
Definition 15. The Eq. (8) is Ulam-Hyers stable, if there exists a positive real number
Definition 16. The Eq. (8) is Ulam-Hyers-Rassias-stable, if there exists a positive real number
for some non-negative function
(
Theorem 17. The fractal-fractional mathematical problem (8) is Ulam-Hyers-stable.
If
Proof. For
which give
For each
Then, using condition (11) and Hölder’s inequality, the results follow
Hence
Hence, the fractal fractional mathematical model (8) is Ulam-Hyers stable.
Theorem 18. Assume that
Proof. The solutions
which gives
Thus,
Using the same technique and considering condition (11) alongside Hölder’s inequality, it follows that
Then, the fractal fractional mathematical model (8) is Ulam-Hyers-Rassias-stable.
Example 19. To estimate the obtained results for the Banach contraction mapping and
The current study found a prevalence of ascariasis in Duhok city at an overall rate of (42.5%). This finding aligns with the results of [42] reported an Ascaris infection rate of (41.4%), and the authors in [12] found a similar prevalence of (43.3%). However, the current results differ from those of [11] and [43] reported infection rates of only (23.1%) and (6.25%), respectively. Also, the present study indicated that the infection rate among males was higher than in females, consistent with the findings of [44] showed that males had an infection rate of (59.0%) compared to (41.0%) for females. This is linked to the everyday participation of males in agricultural activities that bring them into contact with the soil. In contrast, Ref. [43] found a higher incidence of infection in females (57.1%) compared to males (42.9%), as most of their participants lived in rural areas and lacked knowledge of infection. The current findings also revealed a higher infection rate in rural residents compared to urban ones, with [45] reporting prevalence rates of (69.0%) in rural areas and (31.0%) in urban settings. This trend can be attributed to the limited access to sanitation facilities and healthcare in rural regions. However, some studies, like that of [46], reported that urban residents had a higher infection rate (16.5%) compared to rural residents (3.6%), attributing this to the high population density in urban areas and the lack of effective infection prevention and control strategies. This study found a link between poverty and increased exposure to parasitic infections due to inadequate clean water, poor sanitation, and crowded living conditions [45], supported the current results and investigated the infection rates among low-income and high-income patients, which (55.0%) and (18.0%), respectively. Ref. [47] noted that elevated IgE levels associated with Ascaris increase the risk of asthma by inducing larval migration through the lungs, leading to pulmonary infiltrates and airway obstruction [13] also found that elevated serum IgG antibody levels against Ascaris are associated with significantly reduced lung function and increased asthma symptoms. On the other hand, Ref. [9] provided contrasting results, suggesting that this parasite provokes an immune response in children, manifested by significant changes in white blood cell counts, eosinophils, and IgE; it did not have a substantial impact on pulmonary function tests (PFTs). Researchers found that the PFT results of asthmatic children were significantly worse than those of Ascaris-infected children, implying that the impairment in PFTs was primarily due to asthma rather than Ascaris infection. As well, Ref. [3] reported findings that contrasted with the current study, indicating no correlation between allergic reactions and parasitic infections in children. In terms of hematological parameters and IgE levels, the present study detected significant variations (
According to recent research, patients infected with A. lumbricoides showed reduced red blood cell counts and hemoglobin levels compared to the control group. Supporting this finding, Ref. [48] stated that infected individuals also exhibited lower red blood cell and hemoglobin concentrations. This decrease may be attributed to the parasite’s ability to cause hemolysis of red blood cells, resulting in a reduction in their overall number. Ascaris infection appears to be associated with elevated levels of white blood cells, eosinophils, IgE, and IL-4, reflecting an immune response similar to that seen in asthma [49] indicating that the immune response to helminthic parasites results in elevated levels of IgE, eosinophilia, interleukins 4, 5, and 13. In a similar vein, understanding the mathematical models that describe immune responses can benefit from a solid grasp of contraction mapping. Contraction mapping is fundamental in many areas of mathematics and applied sciences. Understanding their properties, particularly the importance of the contraction constant being less than 1, is crucial for ensuring convergence to a unique solution. Consequently, the contraction constant was examined in different cases, with the findings presented in tables and diagrams for further clarity.
To highlight the efficiency of the Banach contraction principle and the fractal-fractional Caputo-Fabrizio mathematical model of Ascaris lumbricoides in ensuring a unique solution, we will evaluate the values of the contraction parameters
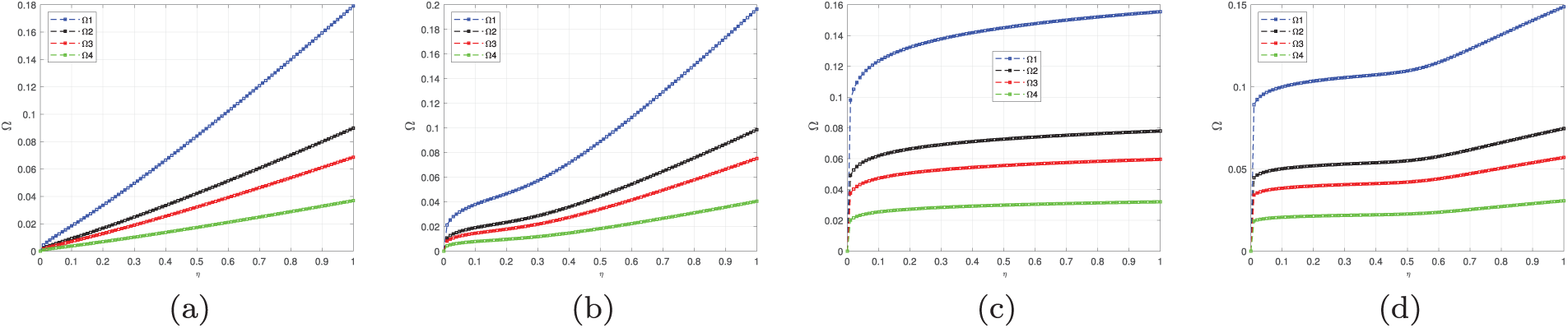
Figure 4: Behavior of the contraction parameters
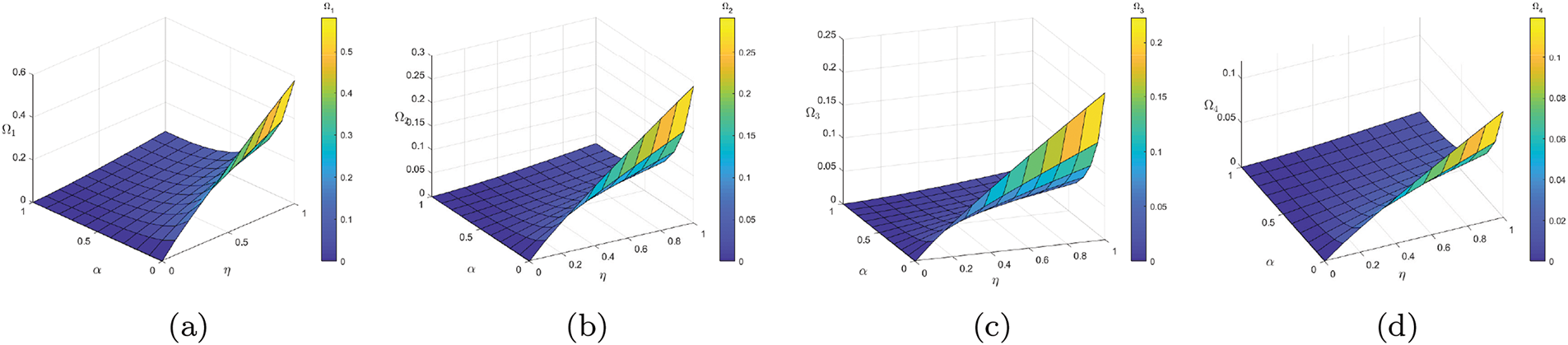
Figure 5: To show the efficiency of the Banach contraction principle and that the problem has a unique solution, the graphical 3D representation of the contraction parameter
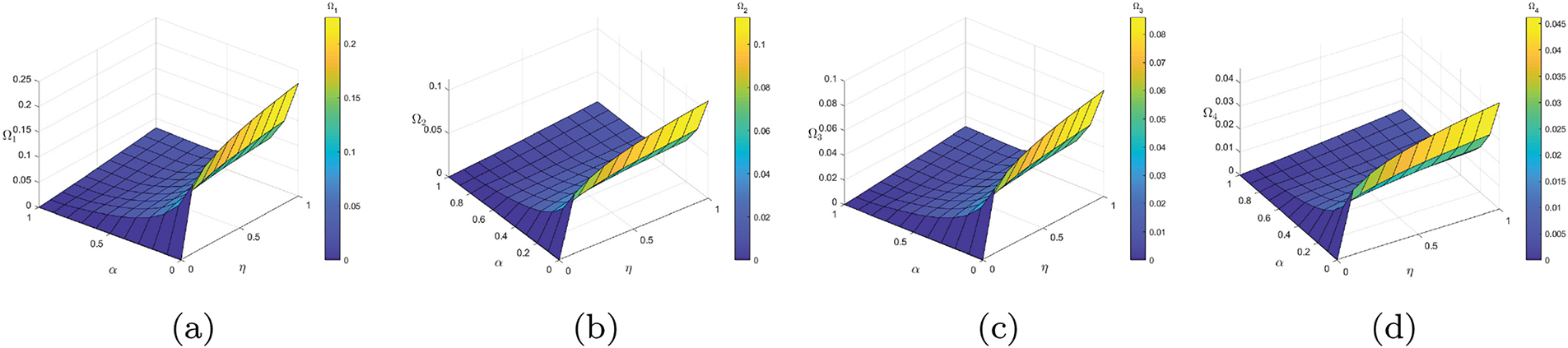
Figure 6: To explain the applicability of the Banach fixed theorem, Geometrical behaviour of
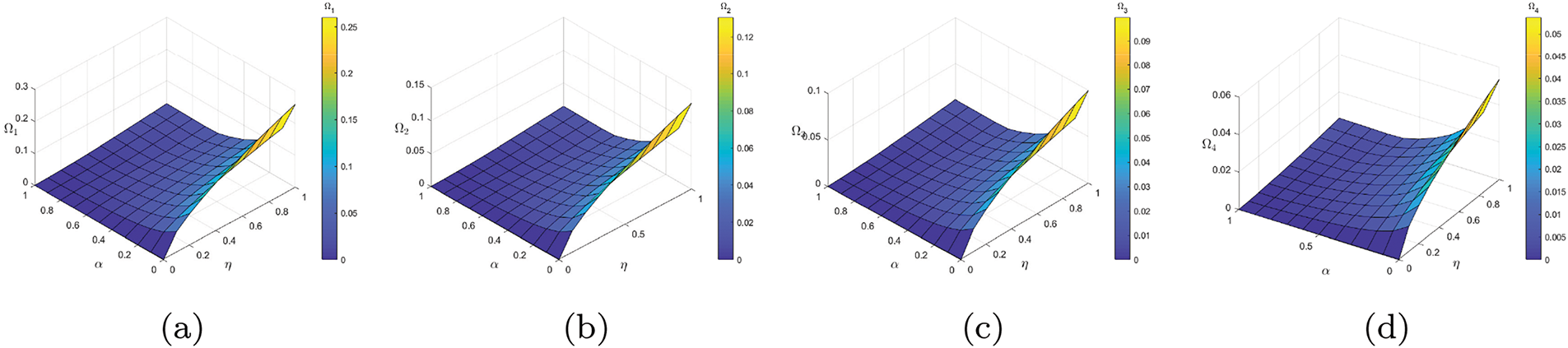
Figure 7: To establish a solution exists and there is only one solution to the mathematical model at selected points, the behavior of the parameters


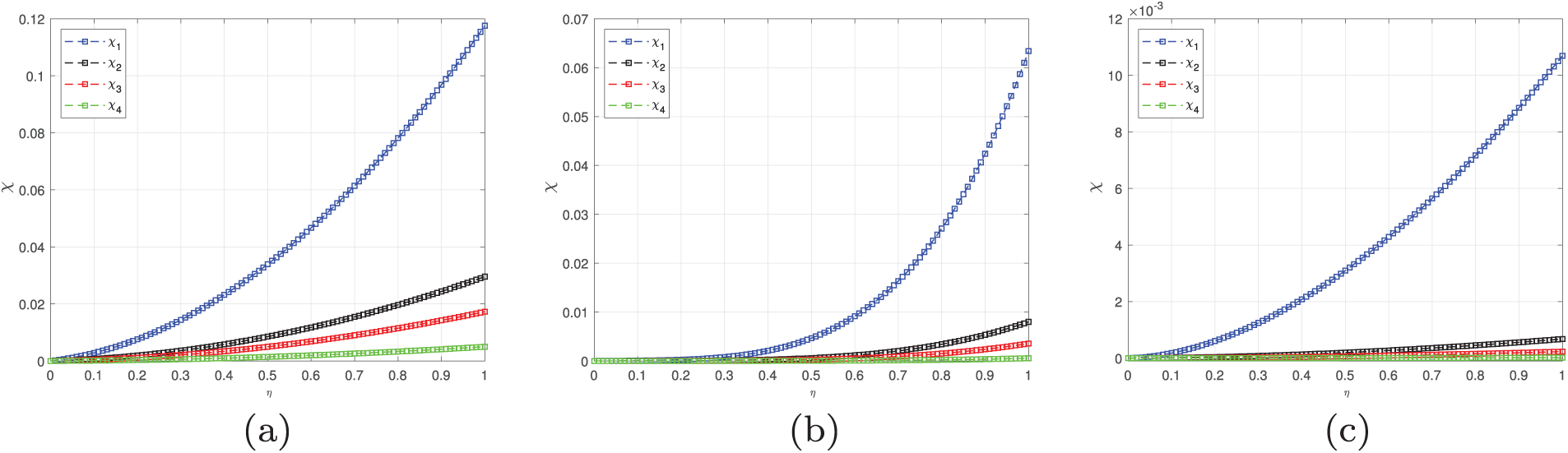
Figure 8: The visual analysis of
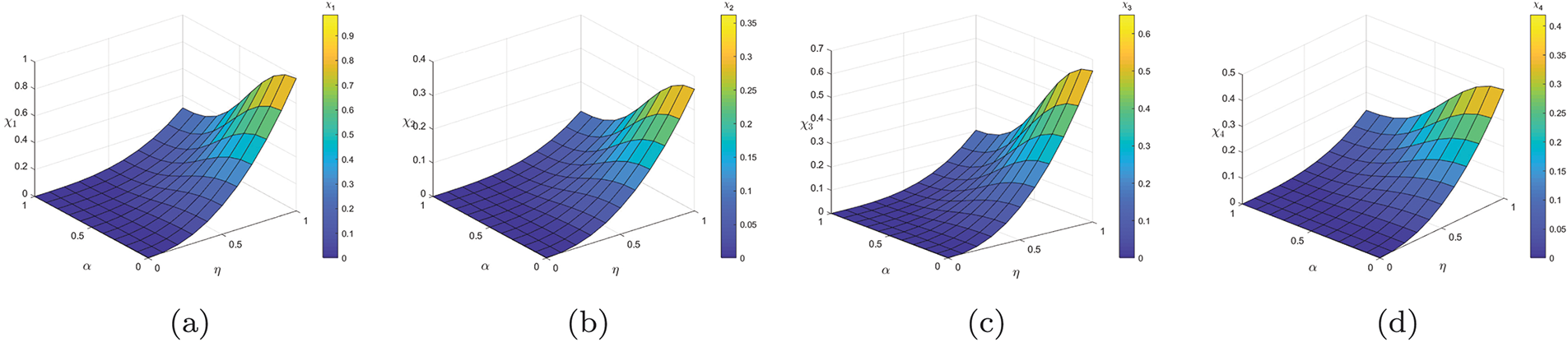
Figure 9: Graphical representation of the parameters
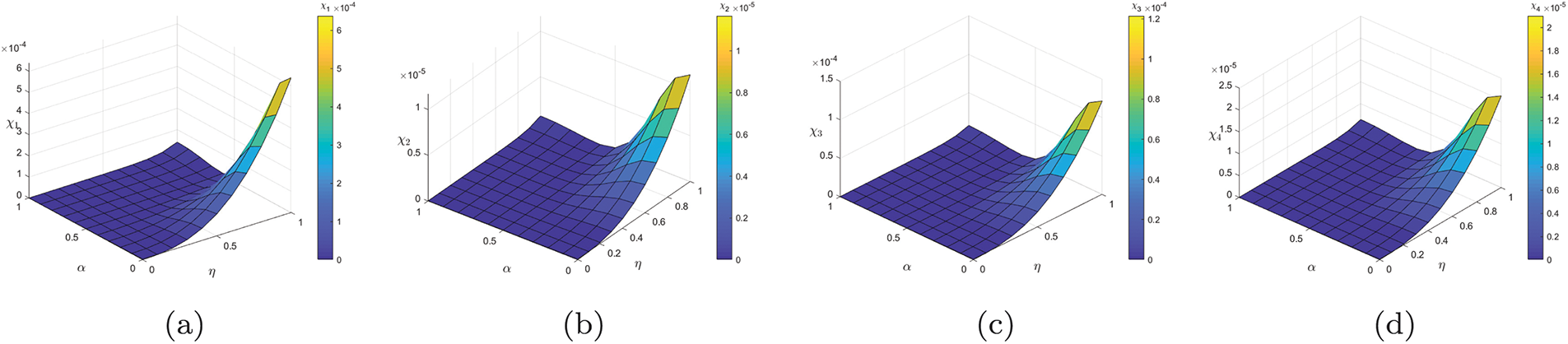
Figure 10: Shows the values
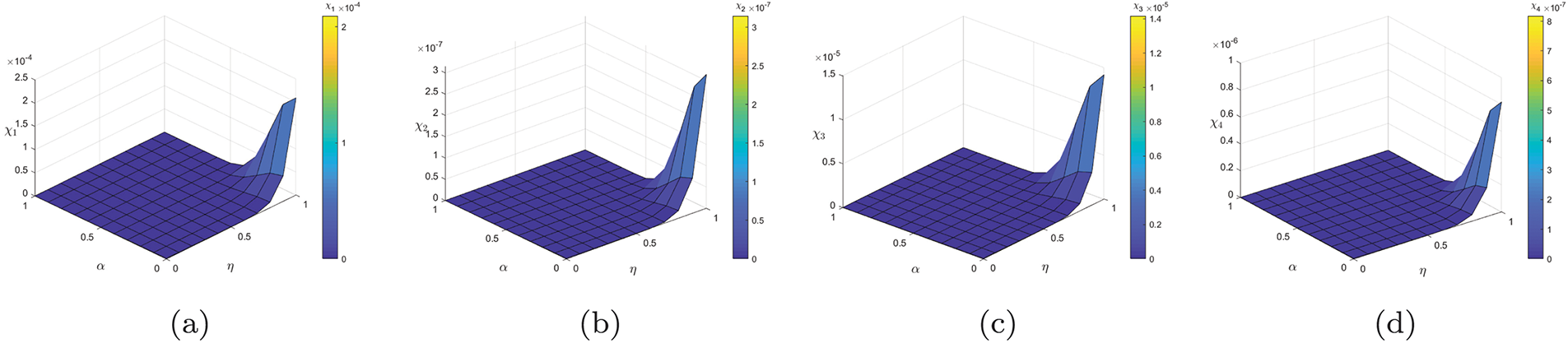
Figure 11: To clarify the stability in the sense of


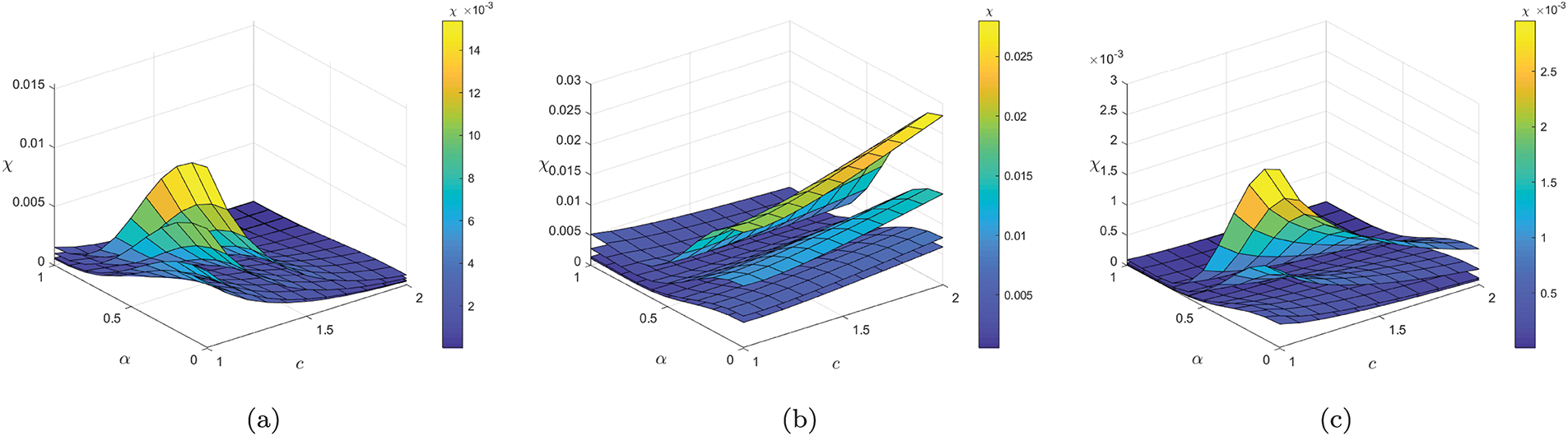
Figure 12: The graphical representation demonstrates that
Public health interventions that focus on improving sanitation, access to clean water, and health education are crucial in reducing the burden of ascariasis in this region. A total of 400 people participated, including 270 with asthma and 130 controls, who visited general hospitals in Duhok City, Iraq. The results indicate that the presence of ascariasis reduced lung function and was associated with a higher prevalence of asthma among the participants. In addition, the findings emphasize the need to investigate the effects of helminth infections on long-term lung health worldwide. Additionally, mathematical analysis of the solution for the fractal-fractional mathematical model for the four stages of the life cycle of Ascaris lumbricoides has been conducted in the sense of the Caputo-Fabrizio derivative. The uniqueness theorem is proved using Banach’s contraction mapping with the Hölder inequality, and the Krasnosel’skii fixed-point theorem is used in proving the existence of the solution. To understand the behavior of the solution, the (Ulam-Hyers, Ulam-Hyers-Rassias) stability is also discussed in
There are some limitations in this study. Firstly, it is confined to Duhok City, Iraq, which limits the generalizability of the findings to other regions or populations. Secondly, it was difficult to follow up with the patients to fully understand the exact mechanism of the pathogenicity of Ascaris lumbricoides in causing asthma. Thirdly, it was unable to find patients under the age of 15.
Acknowledgement: D. K. Almutairi extends sincere appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research. Thabet Abdeljawad and Aziz Khan would like to thank Prince Sultan University for covering the article processing charges (APC) and for the support provided through the TAS Research Lab.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Manal Adil Murad: Conceptualization, Methodology, Data curation, Interpretation, Formal analysis, Investigation, Validation, Writing—original draft, Writing—review and editing, Supervision. Shayma Adil Murad: Conceptualization, Methodology, Formal analysis, Investigation, Validation, Writing—original draft, Writing—review and editing, Supervision. Thabet Abdeljawad: Conceptualization, Investigation, Methodology, Writing—review and editing, Supervision. Aziz Khan & D. K. Almutairi: Validation, Methodology, Visualization, Resources. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: The ethical approval was obtained from the Research Ethics Committee of the General Health Directorate, Duhok, Iraq. No. 05022025-2-5.
Informed Consent: Informed written consent was obtained from all participants, and data collection was primarily conducted by administering a questionnaire to gather the necessary information.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Wu Y, Adeniyi IG, Adkins TM, Seasock M, Suarez RC, Fujiwara R, et al. Host gastric corpus microenvironment facilitates Ascaris suum larval hatching and infection in a murine model. PLoS Negl Trop Dis. 2024;18(2):e0011930. doi:10.1371/journal.pntd.0011930. [Google Scholar] [PubMed] [CrossRef]
2. Agrawal R, Pattnaik S, Kshatri JS, Kanungo S, Mandal N, Palo SK, et al. Prevalence and correlates of soil-transmitted helminths in schoolchildren aged 5 to 18 years in low-and middle-income countries: a systematic review and meta-analysis. Front Public Health. 2024;12:1283054. doi:10.3389/fpubh.2024.1283054. [Google Scholar] [PubMed] [CrossRef]
3. Walelign S, Tesfaye M, Tasew G, Desta K, Tsegaye A, Taye B. Association between helminth infection and allergic disorders among children in Batu, Ethiopia. Immun Inflamm Dis. 2024;12(3):e1222. doi:10.1002/iid3.1222. [Google Scholar] [PubMed] [CrossRef]
4. Ahumada V, Zakzuk J, Aglas L, Coronado S, Briza P, Regino R, et al. Comparison of antibody responses against two molecules from Ascaris lumbricoides: the allergen Asc I 5 and the immunomodulatory protein Al-CPI. Biology. 2023;12(10):1340. doi:10.3390/biology12101340. [Google Scholar] [PubMed] [CrossRef]
5. Vacca F, Le Gros G. Tissue-specific immunity in helminth infections. Mucosal Immunol. 2022;15(6):1212–23. doi:10.1038/s41385-022-00531-w. [Google Scholar] [PubMed] [CrossRef]
6. Sapartini G, Wong GW, Indrati AR, Kartasasmita CB, Setiabudiawan B. The association between vitamin D, interleukin-4, and interleukin-10 levels and CD23+ Expression with bronchial asthma in stunted children. Biomedicines. 2023;11(9):2542. doi:10.3390/biomedicines11092542. [Google Scholar] [PubMed] [CrossRef]
7. Senaratna CV, Perera PK, Arulkumaran S, Abeysekara N, Piyumanthi P, Hamilton GS, et al. Association of helminth infestation with childhood asthma: a nested case-control study. Int J Infect Dis. 2023;128:272–7. doi:10.1016/j.ijid.2023.01.004. [Google Scholar] [PubMed] [CrossRef]
8. Murad MA, Al-Saeed AT, Mustafa AA. Prevalence of intestinal parasites among patients attended azadi teaching hospital in duhok city-kurdistan region/Iraq. J Duhok Univ. 2019;21(2):68–74. doi:10.26682/sjuod.2018.21.2.7. [Google Scholar] [CrossRef]
9. Mohammed SH, Jabbr AS, Ibrahim NK. Impact of parasitic infection with Ascaris lumbricoides on pulmonary function tests in asthmatic and non-asthmatic children. Respir Med Case Rep. 2021;34(3):101552. doi:10.1016/j.rmcr.2021.101552. [Google Scholar] [PubMed] [CrossRef]
10. Taher HM, Mohamed AH, Yaseen SS. Prevalence of intestinal Parasitic infections among children in Kirkuk City, Iraq. Bionatura. 2022;7(2):1–4. doi:10.21931/RB/2022.07.02.4. [Google Scholar] [CrossRef]
11. Bragagnoli G, Silva MT. Ascaris lumbricoides infection and parasite load are associated with asthma in children. J Infect Develop Countries. 2014;8(7):891–7. doi:10.3855/jidc.3585. [Google Scholar] [PubMed] [CrossRef]
12. Penaranda GD. Effects of Ascaris lumbricoides in eosinophils, regulatory B cells and asthma severity in asthmatic patients from a helminth endemic population [doctoral dissertation]. Bolivar, Colombia: University of Cartagena; 2019. doi:10.57799/11227/1341. [Google Scholar] [CrossRef]
13. Jõgi NO, Kitaba N, Storaas T, Schlünssen V, Triebner K, Holloway JW, et al. Ascaris exposure and its association with lung function, asthma, and DNA methylation in Northern Europe. J Allergy Clin Immunol. 2022;149(6):1960–9. doi:10.1016/j.jaci.2021.11.013. [Google Scholar] [PubMed] [CrossRef]
14. Jan R, Khan MA, Kumam P, Thounthong P. Modeling the transmission of dengue infection through fractional derivatives. Chaos Solit Fract. 2019;127(20):189–216. doi:10.1016/j.chaos.2019.07.002. [Google Scholar] [CrossRef]
15. Mohammadpoor H, Eghbali N, Sajedi L, Nosrati Sahlan M. Stability analysis of fractional order breast cancer model in chemotherapy patients with cardiotoxicity by applying LADM. Adv Contin Disc Models. 2024;2024(1):6. doi:10.1186/s13662-024-03800-z. [Google Scholar] [CrossRef]
16. Khan MA, DarAssi MH, Ahmad I, Seyam NM, Alzahrani E. The transmission dynamics of an infectious disease model in fractional derivative with vaccination under real data. Comput Biol Med. 2024;181(4):109069. doi:10.1016/j.compbiomed.2024.109069. [Google Scholar] [PubMed] [CrossRef]
17. Sooppy Nisar K, Sivashankar M, Sabarinathan S, Ravichandran C, Sivaramakrishnan V. Evaluating the stability and efficacy of fractal-fractional models in reproductive cancer apoptosis with ABT-737. J Inequal Appl. 2025;2025(1):10. doi:10.1186/s13660-024-03249-4. [Google Scholar] [CrossRef]
18. Joshi H, Yavuz M, Taylan O, Alkabaa A. Dynamic analysis of fractal-fractional cancer model under chemotherapy drug with generalized Mittag-Leffler kernel. Comput Methods Programs Biomed. 2025;260(6859):108565. doi:10.1016/j.cmpb.2024.108565. [Google Scholar] [PubMed] [CrossRef]
19. Davis EL, Danon L, Prada JM, Gunawardena SA, Truscott JE, Vlaminck J, et al. Seasonally timed treatment programs for Ascaris lumbricoides to increase impact—an investigation using mathematical models. PLoS Negl Trop Dis. 2018;12(1):e0006195. doi:10.1371/journal.pntd.0006195. [Google Scholar] [PubMed] [CrossRef]
20. Singh R, Akgül A, Mishra J, Gupta VK. Mathematical evaluation and dynamic transmissions of a cervical cancer model using a fractional operator. Contempor Mathem. 2024;5(3):2646–67. doi:10.37256/cm.5320244539. [Google Scholar] [CrossRef]
21. Murad SA, Ameen ZA. Existence and Ulam stability for fractional differential equations of mixed Caputo-Riemann derivatives. AIMS Math. 2022;7(4):6404–19. doi:10.3934/math.2022357. [Google Scholar] [CrossRef]
22. Cui Z, Zhou Z. Existence of solutions for Caputo fractional delay differential equations with nonlocal and integral boundary conditions. Fixed Point Theo Algori Sci Eng. 2023;2023(1):1. doi:10.1186/s13663-022-00738-3. [Google Scholar] [CrossRef]
23. Li C. Uniqueness and existence for a fractional differential equation with functional boundary condition. IFAC-PapersOnLine. 2024;58(12):296–301. doi:10.1016/j.ifacol.2024.08.206. [Google Scholar] [CrossRef]
24. Abulahad J, Murad S. Existence, uniqueness and stability theorems for certain functional fractional initial value problem. AL-Rafidain J Comput Sci Mathem. 2011;8(1):59–70. doi:10.33899/csmj.2011.163608. [Google Scholar] [CrossRef]
25. Muniyappan P, Rajan S. Hyers-Ulam-Rassias stability of fractional differential equation. Int J Pure Appl Mathem. 2015;102(4):631–42. doi:10.12732/ijpam.v102i4.4. [Google Scholar] [CrossRef]
26. Dai Q, Gao R, Li Z, Wang C. Stability of Ulam-Hyers and Ulam-Hyers-Rassias for a class of fractional differential equations. Adv Diff Equat. 2020;2020(1):1–5. doi:10.1186/s13662-020-02558-4. [Google Scholar] [CrossRef]
27. Murad SA. Certain analysis of solution for the nonlinear two-point boundary value problem with caputo fractional derivative. J Funct Spaces. 2022;2022(1):1385355. doi:10.1155/2022/1385355. [Google Scholar] [CrossRef]
28. Agarwal RP, Hristova S. Ulam-type stability for a boundary-value problem for multi-term delay fractional differential equations of Caputo type. Axioms. 2022;11(12):742. doi:10.3390/axioms11120742. [Google Scholar] [CrossRef]
29. Abdulahad JG, Murad SA. Local existence theorem of fractional differential equations in Lp Space. AL-Rafidain J Comput Sci Mathem. 2012;9(2):71–8. doi:10.33899/CSMJ.2012.163702. [Google Scholar] [CrossRef]
30. Souid MS, Refice A, Sitthithakerngkiet K. Stability of p(.)-integrable solutions for fractional boundary value problem via piecewise constant functions. Fract Fracti. 2023;7(2):198. doi:10.3390/fractalfract7020198. [Google Scholar] [CrossRef]
31. Murad SA, Rafeeq AS, Abdeljawad T. Caputo-Hadamard fractional boundary-value problems in
32. Agarwal RP, Asma A, Lupulescu V, O'Regan D. Lp-solutions for a class of fractional integral equations. J Integral Equat Applicat. 2017;29(2):251–70. doi:10.1216/JIE-2017-29-2-251. [Google Scholar] [CrossRef]
33. Burton TA, Zhang B. Lp-solutions of fractional differential equations. Nonlinear Stud. 2012;19(2):161–77. [Google Scholar]
34. Murad MA, Eissa SH. Effects of latent toxoplasmosis on autoimmune thyroid diseases in pregnant women-Duhok City-Kurdistan Region-Iraq. Duhok Medical J. 2023;17(1):101–13. doi:10.31386/dmj.2023.17.1.8. [Google Scholar] [CrossRef]
35. Murad MA, Eassa SH. Detection of toxoplasmosis in association with autoimmune thyroid disease during pregnancy in Duhok, Iraq. J Pure Appl Microbiol. 2023;17(2):799–810. doi:10.22207/JPAM.17.2.05. [Google Scholar] [CrossRef]
36. Solomon Y, Woldu B, Mesfin N, Enawgaw B. Selected hematological abnormalities and their associated factors among asthmatic patients in Northwest Ethiopia: a cross-sectional study. BMC Pulm Med. 2022;22(1):228–48. doi:10.14202/IJOH.2023.43-48. [Google Scholar] [CrossRef]
37. Abdeljawad T. Fractional operators with exponential kernels and a Lyapunov type inequality. Adv Differ Equat. 2017;2017(1):1–11. doi:10.1186/s13662-017-1285-0. [Google Scholar] [CrossRef]
38. Dlamini A, Goufo EF, Khumalo M. On the Caputo-Fabrizio fractal fractional representation for the Lorenz chaotic system. AIMS Math. 2021;6(11):12395–421. doi:10.3934/math.2021717. [Google Scholar] [CrossRef]
39. Atangana A. Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solit Fract. 2017;102(5):396–406. doi:10.1016/j.chaos.2017.04.027. [Google Scholar] [CrossRef]
40. Granas A, Dugundji J. Fixed point theory. New York, NY, USA: Springer; 2003. [Google Scholar]
41. Krasnosel’skii MA. Two remarks on the method of successive approximations. Uspekhi Matematicheskikh Nauk. 1955;10(1):123–7. [Google Scholar]
42. Hajare ST, Mulu T, Upadhye VJ, Chauhan NM, Eriso F. Prevalence of Ascaris lumbricoides infections among elementary school children and associated risk factors from Southern Ethiopia. J Parasitic Dis. 2022;46(3):643–52. doi:10.1007/s12639-022-01475-5. [Google Scholar] [PubMed] [CrossRef]
43. Bria M, Yudhaswara NA, Susilawati NM. Prevalence and intensity of Ascaris lumbricoides infection in children of Oemasi village, Kupang District, East Nusa Tenggara Province, Indonesia. Sci Midwifery. 2022;10(4):3011–6. doi:10.35335/midwifery.v10i4.749. [Google Scholar] [CrossRef]
44. Hamad AA, Mauti GO. Determination of the prevalence of Ascaris lumbricoides in children under the age of five years attending at Kongowe health centre, Kibaha District, Pwani region. J Parasitol Res. 2024;2024(1):1932633. doi:10.1155/2024/1932633. [Google Scholar] [PubMed] [CrossRef]
45. Sufyan M, Kareem F, Riaz FB, Fairy AA, Akhtar N, Farhaj R, et al. Epidemiology of Ascaris lumbricoides in District Karak, Khyber-Pakhtunkhwa Pakistan: prevalence of Ascaris lumbricoides in District Karak. J Health Rehabilit Res. 2024;4(3):1–4. doi:10.61919/jhrr.v4i2.1140. [Google Scholar] [CrossRef]
46. Phiri K, Whitty CJ, Graham SM, Ssembatya-Lule G. Urban/rural differences in prevalence and risk factors for intestinal helminth infection in southern Malawi. Ann Trop Med Parasitol. 2000;94(4):381–7. doi:10.1080/00034983.2000.11813553. [Google Scholar] [PubMed] [CrossRef]
47. Hawlader MD, Ma E, Noguchi E, Itoh M, Arifeen SE, Persson LÅ, et al. Ascaris lumbricoids infection as a risk factor for asthma and atopy in rural Bangladeshi children. Trop Med Health. 2014;42(2):77–85. doi:10.2149/tmh.2013-19. [Google Scholar] [PubMed] [CrossRef]
48. AL-Salami EH, Sarhan NH, Al-Roubaey DA. Effect of Ascaris lumbricoides on some hematological parameters and the concentrationl levels of interleukin-10 and interleukin-22. Med Sci J Adv Res. 2023;4(2):147–54. doi:10.46966/msjar.v4i2.131. [Google Scholar] [CrossRef]
49. Weatherhead JE, Gazzinelli-Guimaraes P, Knight JM, Fujiwara R, Hotez PJ, Bottazzi ME, et al. Host immunity and inflammation to pulmonary helminth infections. Front Immunol. 2020;11:594520. doi:10.3389/fimmu.2020.594520. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools