Quantum-Driven Spherical Fuzzy Model for Best Gate Security Systems

1  Introduction

Global security threats have become a major concern in recent years, according to researchers. To make an organization invulnerable, it is essential to have a reliable security entrance system. Schools and universities must provide staff and students with a secure environment where they can perform their duties. Traditional security methods, such as pins and passwords, are easily falsified, and keys are commonly lost [1]. Biometric authentication is proving to be an effective way of combating these security threats. This type of application has gained popularity because of biometric identification, which verifies a person’s identity and behavioral patterns [2]. A variety of biometric techniques are used in various professions, such as the face [3], fingerprints [4], infrared recognition and identification system (IRIS) [5], voice [6]. By providing precise and efficient recognition systems, biometric systems play a crucial role in improving security. The choice of the right security system, particularly in complex scenarios, requires careful consideration. Data-driven insights will help us choose the right security framework by considering accuracy, cost, and reliability. A decision-making process minimizes the gap between current security options and the optimal solution, ensuring that the system not only meets technical constraints but also aligns with strategic objectives. Thus, integrating biometrics into a security system must take into account current and future security needs. To meet the demands of the modern world, maximize outcomes, and solve our problems, we must make efficient decisions. Decision making is highly beneficial when confronted with selecting the best option based on a single criterion. We use a combination of criteria when rating possibilities to come up with a more flexible answer, rather than relying solely on one criterion. As part of multi-criteria decision-making (MCDM), alternatives are selected whose rankings are being examined, as well as criteria that summarize their crucial attributes. It is crucial that these criteria be carefully weighed because they influence how a ranking system for alternatives is devised based on the weighting of these criteria. Following the assessment information, we gather several approaches to create a precise potential resolution based on a matrix format. Engineers, doctors, economists, and social scientists all rely on MCDM in their daily lives. A significant proportion of the research field has been examined by MCDM in recent decades [7–10].

The integration of biometrics into security systems raises the question of which biometric method is the most effective in specific scenarios. For example, facial recognition may be more suitable for public spaces, while fingerprints may be better for controlled environments like offices. Decision-making in such scenarios requires tools that can handle uncertainty and complexity. To address this, advanced mathematical frameworks like fuzzy sets (FS) [11], intuitionistic fuzzy sets (IFS) [12], Pythagorean fuzzy sets (PFS) [13], and their extensions (e.g., q-rung orthopair fuzzy sets (q-ROFS) [14], p, q-quasirung orthopair fuzzy sets (p, q-QOFS) [15]) have been developed. These frameworks allow for more nuanced decision-making by incorporating degrees of membership (MB) and non-membership (NMB). Neutrosophic sets (NS) [16] and spherical fuzzy sets (SFS) [17], which extend the capabilities of fuzzy logic by incorporating additional parameters like indeterminacy degree (ID), have also gained attention. These advancements have been applied to fields like decision support systems, pattern recognition, and medical diagnosis, demonstrating their versatility and potential for addressing real-world problems [18–20]. Furthermore, the integration of quantum mechanics into decision-making frameworks, such as quantum spherical fuzzy sets (QSFS), has opened new avenues for modeling complex, uncertain, and dynamic systems [21]. QSFS are implemented to address carbon emissions and foster sustainable business investments [21].

This research is motivated by the following reasons. A variety of fields have implemented spherical fuzzy sets and aggregation operators to deal with uncertainty and ambiguity. Although modern decision-making processes are complex, achieving accurate solutions can be challenging. This makes it essential to develop a new multi-layer, comprehensive decision-making model. A gate security system (GSS) operates in a high-stakes environment in which uncertainty and ambiguity play an important role in decision-making. The growing challenges in security infrastructure necessitate the selection of the best GSS. Today, these challenges pose a significant threat to society. To ensure robust protection, organizations must implement effective security systems. An effective decision-making framework must be capable of dynamically addressing such uncertainties. The proposed model integrates spherical fuzzy sets (SFS) with quantum logic to incorporate probabilities in a variety of scenarios. A limited amount of literature integrates spherical fuzzy numbers with quantum theory, hindering the exploration of decision-making to date. It also uses the golden ratio to calculate degrees, which makes it easier to enhance performance. In the final stage, the proposed model ranks the options with the help of TOPSIS model.

This paper contributes to the field by introducing a novel framework that integrates QSFS with the technique for order preference by similarity to ideal solution (TOPSIS) method. This combination enhances the ability to handle uncertainty and ambiguity in decision-making processes, particularly in the context of gate security systems. The paper also addresses key limitations in existing methods, such as inadequate integration of quantum mechanics, limited granularity, and challenges in real-time adaptability. The framework provides a multi-layered, comprehensive decision-making model that dynamically addresses uncertainties, making it ideal for high-stakes environments like gate security systems.

The theoretical understanding of QSFS and its practical utility has been advanced. In decision-making under uncertainty, they provide a solid foundation for future research and applications. The study structure is as follows: Section 1 provides an introduction, followed by a comprehensive literature review in Section 2. The preliminary definitions required in this study are discussed in Section 3. Section 4 introduces the proposed work. Section 5 examines the application of the proposed MCDM method. Section 6 presents performance evaluation metrics. An overview of the detailed discussion is presented in Section 7. Section 8 concludes the study and future avenues.

2  Literature Review

Making the right decisions is an art and a science that is crucial to navigating today’s complex challenges. Science fields such as engineering, economics, agriculture, and manufacturing face uncertain data problems. Several researchers have tackled this dilemma in their research [22–25]. Classical mathematical structures cannot be used to model problems involving uncertain data. In 1965, Zadeh introduced the fuzzy set concept (FS) that represents ambiguous, vague, and uncertain elements [11]. FS did not account for NMB and ID. After that, many extensions of FS are presented, like: IFS and PFS, etc. Al-Shamiri et al. [17] have developed spherical fuzzy sets (SFS). In essence, the purpose of SFS is to give decision-makers the ability to generalize fuzzy set extensions in other ways through the definition of membership functions on a spherical surface. A large domain can be mapped to the parameters of that membership function independently. The sum of squares of MB, ID, and NMB must not exceed 1. In this way, SFS offers a clearer and more accurate reflection of membership within a set as it incorporates the MB, NMB, and ID levels. SFS has demonstrated considerable potential in decision-making, as highlighted by recent studies. Qianwen conducted research [26] to improve the efficiency and effectiveness of the metaverse system by utilizing spherical fuzzy linguistics. Almulhim’s study [27] employs interval-valued spherical numbers to improve decision-making for early-stage investments in start-up businesses. Nhieu [28] introduced the SFS Einstein operation matrix energy decision-making approach to evaluate offshore wind energy storage technologies in Vietnam, tackling complex factor interactions. Nhieu and Dang [29] extended this framework by incorporating SFS into a group decision-making model for assessing concrete 3D printing robots in Vietnam, integrating perspectives from multiple stakeholders. These contributions underscore the adaptability of SFS to managing uncertainty, capturing nuanced preferences, and improving decision quality in diverse fields such as energy, construction, and technology. Although these advancements have been achieved, the extent of optimal MB in SFS remains to be precisely defined in decision-making processes [30].

In recent years, quantum mechanics has brought an alternative viewpoint to decision-making techniques employing the principles of quantum theory, such as amplitude and phase angle [21]. Through quantum models of mass functions, it was possible to analyze the probability of several conditions, enabling a more precise understanding of spherical theory in complex information sets. Hence, QSFS are formed. It is highly accurate, enables enhanced analysis of uncertainty, is broad in application, integrates multiple parameters, and has a solid mathematical basis [31]. A more accurate elaboration of complex decision-making problems can be achieved by using QSFS with the golden cut. Using this approach, decision makers can concurrently evaluate multiple parameters of uncertain information, allowing them to make intelligent decisions. Quantum mechanics, fuzzy sets, and the golden cut [21] are used in the methodology. This methodology gains credibility and reliability from existing academic frameworks by integrating them, enhancing their robustness and rigor. The present study proposes a comprehensive MCDM approach that combine the TOPSIS method with QSF numbers. Through the integration of the QSF, this study examines the relationships and weights of the criteria. It determines the weights of the criteria through the SFS and ranks alternatives using the QSF-TOPSIS. The purpose of this integrated approach is to determine the optimal gate security system for an organization. An overview of the research conducted using TOPSIS is given in Table 1.

Biometric security systems have been a central focus in cybersecurity, with researchers examining their vulnerabilities and proposing solutions. Faundez [42] highlighted that these systems are susceptible to various attacks and suggested solutions that could improve their security. Subsequent studies have continued to explore these vulnerabilities. Abdullahi et al. [1] emphasize the need to address biometric template attacks and their impact on sensitive personal data, while also reviewing recent protective measures and their effectiveness. Biometric systems, including fingerprints, IRIS, and face recognition, are susceptible to diverse security threats. Grunenberg [43] observed that these systems are vulnerable to attacks that compromise their security and functionality. Kaiwartya et al. [44] investigated the challenges and metrics of biometric recognition across various network communications, identifying it as a critical e-security solution with both strengths and limitations. Despite their vulnerabilities, biometric authentication offers substantial cybersecurity advantages. Khan et al. [45] conducted a systematic analysis demonstrating that biometric authentication enhances cybersecurity in conventional and Islamic banking by verifying physical and behavioral traits, thereby providing robust safety and security. Benarous et al. [46] argue that biometric authentication effectively mitigates cybersecurity threats by leveraging users’ unique physical and behavioral characteristics. To mitigate vulnerabilities in biometric systems, several strategies have been proposed. Sett et al. [47] suggested integrating fingerprint recognition with traditional password-based authentication to enhance data security and protect sensitive information. Shuford [48] explores the potential of behavioral biometrics in detecting and combating cyber threats, offering continuous authentication and reducing dependence on static credentials, though challenges such as data privacy and system integration remain. Mohammed [49] presents a feature-level-based multi-biometric identification system aimed at enhancing secure and reliable communication systems in smart cities by leveraging an in-depth analysis of multiple biometric features, including fingerprints, facial recognition, and IRIS scanning. Sasikala [50] proposes a multi-modal secure biometric framework, which incorporates attention mechanisms and hash compression to efficiently process and analyze combined biometric modalities for applications such as security surveillance and identity verification. Kansal et al. [51] developed a deep learning-based privacy-preserving multimodal biometric recognition system for cross-silo datasets, facilitating seamless integration and analysis of data from diverse sources in smart cities.

Many studies collectively explore various applications of fuzzy-based decision-making and machine learning techniques in different security domains. Ogundoyin and Kamil [52] proposed an integrated model for gateway selection in the fog-bolstered Internet of Things, highlighting the role of fuzzy methods in handling uncertainty in network decision-making. Alamleh et al. [53] focused on federated learning for Internet of Things (IoT) applications, presenting a framework for intrusion detection systems, while Qahtan et al. [54] developed a multi-security and privacy benchmarking framework for blockchain-driven IoT healthcare systems, emphasizing security in IoT applications. Tanaji and Roychowdhury [55] used an integrated method with neutrosophic fuzzy sets for cybersecurity risk assessment of connected and autonomous vehicles, addressing the risk evaluation problem in the context of emerging vehicle technologies. Albahri et al. [56] introduced a rough Fermatean fuzzy decision-based approach to modeling Intrusion Detection System classifiers in the federated learning of IoT applications, further advancing fuzzy logic in intrusion detection. Almotiri [57] presented an integrated fuzzy-based computational mechanism for selecting effective malicious traffic detection approaches, contributing to the field of network security. Deb and Roy [58] conducted a software-defined network information security risk assessment using Pythagorean fuzzy sets, and Lin et al. [59] developed an MCDM model for site selection of car-sharing stations in a picture fuzzy environment, demonstrating the versatility of fuzzy methods in different decision-making scenarios. Erdogan et al. [60] proposed a fuzzy-based MCDM methodology for risk evaluation of cyber-security technologies, providing a comprehensive framework for assessing security risks. In general, these studies showcase the wide-ranging applications of fuzzy techniques in addressing complex decision-making and security problems across multiple domains. While existing fuzzy-based models have demonstrated impressive adaptability across various security domains, they still face several critical limitations when applied to specialized real-time systems like gate security. Current approaches often suffer from insufficient adaptability, struggling to handle dynamic data streams characteristic of modern gate systems. For instance, while neutrosophic fuzzy frameworks [55] and rough Fermatean fuzzy methods [56] improve uncertainty handling, they fail to integrate advanced quantum-inspired techniques, which could significantly enhance optimization and parallel processing capabilities for multi-criteria evaluations. Additionally, the lack of domain-specific customization for gate security where real-time threat assessment, sensor fusion, and multi-criteria are essential leaves these frameworks ill-suited to this application.

The proposed QSF-TOPSIS model addresses these gaps by combining SFS geometric precision with quantum principles computational power. SFS inherently captures MB and NMB, and ID values, providing a more nuanced representation of ambiguities in gate security scenarios. By incorporating quantum techniques, the model achieves parallel processing capabilities for real-time assessment. Moreover, QSF-TOPSIS extends classical TOPSIS by leveraging spherical geometry to evaluate criteria in decision space, enabling more intuitive integration of diverse metrics in high-stakes environments. This model is specifically tailored to gate security, supporting biometrics, and dynamic security prioritization. This makes it an ideal solution for edge-deployed, resource-constrained systems.

3  Preliminaries

This research incorporates the MCDM technique and quantum spherical fuzzy numbers to investigate the optimal choice of gate security systems. To accomplish our goal, we employ the TOPSIS method as an MCDM methodology. Fig. 1 summarizes the research procedure. The research is divided into two phases. The literature review process is used to identify and validate the criteria factors. Experts’ assessments of these criteria are weighted according to their education and experience. Our second step was to implement the QSF-TOPSIS method to rank the alternatives and select the most appropriate gate security system. There is also done a comparison between the results of the study and the results of previous studies. A notable feature of expert assessments is that they are collected in linguistic form. They are then transformed into QSF numbers based on the scale presented in Tables 2 and 3.

Figure 1: Flowchart of QSFS-TOPSIS method

3.1 Spherical Fuzzy Sets

Let it be assumed that the SFS [17] A~s of the universe of discourse ‘U’ is given by

A~s={⟨μA~s(u),νA~s(u),πA~s(u)⟩|u∈U}(1)

where μAs∼(u):U→[0,1], νAs∼(u):U→[0,1], and πAs∼(u):U→[0,1]

0≤μA~s2(u)+νA~s2(u)+πA~s2(u)≤1∀u∈U(2)

The weight of criteria can be calculated using the Eq. (3).

criteria weight=cwr=Wr∑r=1eWr(3)

where cwr∈[0,1] and ∑cwr=1.

Wr=1−E(4)

E=1n∑r=1e[1−45(|μrs2−νrs2|+|πrs2−0.25|)](5)

An overview of the SFS evaluation scale is provided in Table 2.

3.2 Quantum Spherical Fuzzy Set

The behavior of very small particles can be explained by quantum theory with golden cuts. It offers certain indications about their behavior. These issues are examined by considering particle properties in different situations. A key advantage of quantum theory is its ability to make precise measurements. Even when uncertainty is high, particle analyses can be performed comprehensively and sensitively. As a result of this advantage, it might be beneficial to use quantum theory in fuzzy MCDM. A major problem in decision-making analysis is the high level of uncertainty involved in the process. It may reduce the accuracy of the results. To maximize the accuracy and reliability of decision-making, some new applications are suggested [63]. This study integrates quantum theory with fuzzy MCDM. As a result, uncertainty is minimized more effectively. Eqs. (6)–(8) explain quantum theory.

K(|f⟩)=ϖejΘ(6)

|Ω⟩=|f1⟩,|f2⟩,...,|fn⟩(7)

∑|f⟩⊆|Ω⟩|K(|f⟩)|=1(8)

Spherical fuzzy numbers belong to the fuzzy number family. Three-dimensional spaces define spherical fuzzy numbers [64]. This makes them different from other fuzzy numbers. Spherical fuzzy numbers are flexible and can deal with a wide range of data, including linguistic, numerical, and interval data for more accurate results [65]. A description of these sets and their conditions can be found in Eqs. (9) and (10). During this process, ℶE, ℸE, and ℷE are used to represent MB, NMB and ID.

E={⟨f,(ℶE(f),ℸE(f),ℷE(f)|f∈F)⟩}(9)

0≤ℶE2(f),ℸE2(f),ℷE2(f)≤1,∀f∈F(10)

A new model is proposed by integrating quantum theory with spherical fuzzy sets. A detailed explanation can be found in Eqs. (11)–(13) where ΩℶE, ΩℸE, and ΩℷE define MB, NMB and ID, respectively. An overview of the respondent evaluation scale is provided in Table 3.

|ΩE⟩={⟨f,(ΩℶE(f),ΩℸE(f),ΩℷE(f)|f∈2|ΩE⟩)⟩}(11)

Accordingly, quantum spherical fuzzy numbers Ω are formulated as below, with their amplitudes and phase angles:

Ω=[Ωℶ.ei2π.J,Ωℸ.ei2π.K,Ωℷ.ei2π.L](12)

ϖ2=|Ωℶ(|fi⟩)|(13)

The amplitudes Ωℶ, Ωℸ, and Ωℷ correspond to quantum membership, non-membership, and hesitancy degrees, respectively. The phase angles J, K, and L correspond to the sets of Θ phase angles. ϖ2 indicates the amplitude of the MB function Ωℶ of QFS. The accuracy of evaluations depends on the efficient calculation of degrees. To achieve this, the golden ratio (GR) is used [66]. A detailed explanation of the calculations can be found in Eqs. (14) and (15). Along the straight line, a and b represent large and small quantities, respectively. It is difficult for SFSs to agree on membership and other scales. A golden ratio is used in the proposed model to address this issue. To calculate this ratio, extreme and mean ratios along a straight line are used to create coefficients. Thus, this classification is considered more meaningful, which increases the originality and accuracy of the proposed model [67,68].

G=ab(14)

G=1+52=1.618…(15)

The amplitude of NMB and ID are computed as in Eqs. (16) and (17).

Ωℸ=ΩℶG(16)

Ωℷ=1−Ωℶ−Ωℸ(17)

Similarly, the phase angle of MB is calculated as in Eq. (18).

J=|Ωℶ(|fi⟩)|(18)

The phase angles of NMB and ID are computed in Eqs. (19) and (20).

L=JG(19)

K=1−J−L(20)

The basic operations of QSF number are presented in Eqs. (21)–(26). Consider ΩR and ΩS be two QSF numbers.

ΩR=[ΩRℶ.ei2π.JR,ΩRℸ.ei2π.KR,ΩRℷ.ei2π.LR] and

ΩS=[ΩSℶ.ei2π.J,ΩSℸ.ei2π.K,ΩSℷ.ei2π.L], then

Ξ∗ΩR=((1−(1−ΩRℶ2)Ξ)1/2ei2π(1−(1−JR2π)1/2(ΩRℸ)Ξei2π(KR2π)Ξ((1−ΩRℷ2)Ξ−(1−ΩRℶ2−ΩRℷ2)Ξ)1/2ei2π((1−(LR2π)2)Ξ−(1−(JR2π)2−(LR2π)2)Ξ)1/2)(21)

ΩRΞ=((ΩRℶ)Ξei2π(JR2π)Ξ(1−(1−ΩRℸ2)Ξ)1/2ei2π(1−(1−KR2π))1/2((1−ΩRℷ2)Ξ−(1−ΩRℶ2−ΩRℷ2)Ξ)1/2ei2π((1−(LR2π)2)Ξ−(1−(JR2π)2−(LR2π)2)Ξ)1/2)(22)

ΩR⊕ΩS=((ΩRℶ2+ΩSℶ2−ΩRℶ2ΩSℶ2)1/2ei2π((JR2π)2+(JS2π2)−(JR2π)2(JS2π)2)1/2ΩRℸΩSℸei2π((KR2π)(KS2π))((1−ΩRℶ2)ΩSℷ2+(1−ΩSℶ2)ΩRℷ2−ΩRℷ2ΩSℷ2)1/2ei2π((1−(LR2π)2)(JS2π)2+(1−(LS2π)2)(JR2π)2−(LR2π)2)(LS2π)2))1/2)(23)

ΩR⊗ΩS=(ΩRℸΩSℸei2π((KR2π)(KS2π))(ΩRℶ2+ΩSℶ2−ΩRℶ2ΩSℶ2)1/2ei2π((JR2π)2+(JS2π2)−(JR2π)2(JS2π)2)1/2((1−ΩRℶ2)ΩSℷ2+(1−ΩSℶ2)ΩRℷ2−ΩRℷ2ΩSℷ2)1/2ei2π((1−(LR2π)2)(JS2π)2+(1−(LS2π)2)(JR2π)2−(LR2π)2)(LS2π)2))1/2)(24)

Ω~=([1−∏i=1k(1−Ωℶ2)1/k]1/2e2π[1−∏i=1k(1−(J2π)2)1/k]1/2∏i=1k(Ωℸ)1/ke2π∏i=1k(K2π)1/k[∏i=1k(1−Ωℷ2)1/k−∏i=1k(1−Ωℶ2−Ωℷ2)1/k]1/2e2π[∏i=1k(1−(L2π)2)1/k−∏i=1k(1−(J2π)2−(L2π)2)1/k]1/2)(25)

def(Ω~)=Ωℶ+Ωℷ(ΩℶΩℶ+Ωℸ)+(J2π)+(K2π)(J2πJ2π+L2π)(26)

4  Quantum Spherical Fuzzy TOPSIS Model

An extension of TOPSIS with QSF is described in this section. The process involves the following steps:

Step 1. Spherical fuzzy decision matrix

The spherical fuzzy numbers (SFNs) are used in a decision-making process involving m decision makers to assess e alternatives based on f criteria. According to the yth expert, the spherical fuzzy decision matrix (SF-DM) is constructed as follows:

Qy=[Q11yQ12y⋯Q1fyQ21yQ22y⋯Q2fy⋮⋮⋱⋮Qe1yQe2y⋯Qefy](27)

where Qrsy=(μrs(u),νrs(u),πrs(u)), 1≤r≤e and 1≤s≤f and Qrsy represents assessment value of rth criteria in relation to sth criteria.

Step 2. Integrated spherical fuzzy decision matrix

Next, combine the expert decision matrices of each decision maker and create an integrated SF-DM as outlined below:

I=[I11I12⋯I1fI21I22⋯I2f⋮⋮⋱⋮Ie1Ie2⋯Ief](28)

where Irs={Qrs1,Qrs2,Qrs3,…,Qrsm} is the collection of expert assessments for a single alternative in relation to a specific criteria.

Step 3. Calculate criteria weight

The weight of criteria can be calculated using the Eq. (29).

criteria weight=cwr=Wr∑r=1eWr(29)

where cwr∈[0,1] and ∑cwr=1.

Wr=1−E(30)

E=1n∑r=1e[1−45(|μrs2−νrs2|+|πrs2−0.25|)](31)

Step 4. Formation of QSF decision matrix

The next step is to convert each cluster (outlined above) of integrated SF-DM to QSF numbers by employing Eqs. (9)–(13) or with the help of Table 3. The new formulated QSF numbers based DM is as follows:

G=[0G12⋯G1fG210⋯G2f⋮⋮⋱⋮Ge1Ge2⋯0](32)

In matrix G, Grs=[ℶGrs.ei2π.J,ℸGrs.ei2π.K,ℷGrs.ei2π.L], where 1≤r≤e and 1≤s≤f.

Step 5. Aggregated decision matrix

An aggregated decision matrix was formulated applying Eq. (25) to matrix G.

Gagg=[0G12agg⋯G1faggG21agg0⋯G2fagg⋮⋮⋱⋮Ge1aggGe2agg⋯0](33)

In matrix Gagg, Grsagg=[ℶGrs,ℸGrs,ℷGrs], where 1≤r≤e and 1≤s≤f.

Step 6. Normalization of the QSF decision matrix

Normalize the decision matrix Gagg to create a normalized decision matrix Nrs using Eq. (34), where 1≤r≤e and 1≤s≤f.

Nrs=Grsagg∑r=1e(Grsagg)2(34)

Step 7. Formation of weighted normalized decision matrix

Using the criterion weights, construct the weighted normalized decision matrix described in Eq. (35).

Gn=cwr×Nrs=[0G12n⋯G1fnG21n0⋯G2fn⋮⋮⋱⋮Ge1nGe2n⋯0](35)

Step 8. Calculate positive and negative ideal solutions

Formulate matrices for the positive ideal solution (I+) and the negative ideal solution (I−) using Eqs. (36) and (37).

I+={(max(ℶrs)|s∈B),(min(ℸrs)|s∈C),(min(ℷrs)|s∈C)}=(p1s+,p2s+,p3s+,…,pns+)(36)

I−={(min(ℶrs)|s∈B),(max(ℸrs)|s∈C),(max(ℷrs)|s∈C)}=(p1s−,p2s−,p3s−,…,pns−)(37)

where B is benefit criteria and C is cost criteria.

Step 9: Calculate the distance to ideal solutions

Compute the distance of each alternative from the positive ideal solution I+ using Eq. (38), where i=1,2,…,m.

Dr+=∑r=1e(prs−Ir+)2(38)

Similarly, calculate the distance from the negative ideal solution I− using Eq. (39).

Dr−=∑r=1e(prs−Ir−)2(39)

Step 10: Calculate the score values for each alternative

Calculate the value of preference Vr for each alternative using Eq. (40), where 1≤r≤e.

Vr=Dr−Dr++Dr−(40)

Step 11: Rank the alternatives

Arrange the alternatives according to the score values Vr and select the most suitable one.

A flowchart of the QSF-TOPSIS method can be found in Fig. 1.

5  Decision Making Application

In this section, we aim to demonstrate the decision-making process for selecting the most suitable security system for an organization, incorporating various expert perspectives and security system features. To address global security threats, an organization must make an informed decision that balances cost, reliability, accuracy, and other crucial factors. A multi-criteria decision-making model is used to determine the best security system, considering both the technical and operational needs.

5.1 Problem Background and Solution

The rapid evolution of technology, increasing urbanization, and growing concerns regarding security threats are driving a significant need for reliable and efficient gate security systems across various sectors globally. Traditional security methods such as PIN codes, passwords, and physical keys have shown limitations in terms of reliability, ease of use, and vulnerability to security breaches [69]. This has led to the need for more advanced, secure, and automated solutions to safeguard entrances to critical facilities such as businesses, schools, universities, and government buildings. In line with the rising demand for enhanced security and technological advancement, organizations are increasingly shifting towards biometric-based or IoT-enabled security systems that are not only secure but also user-friendly and scalable [70]. Gate security systems must address several challenges, including the prevention unauthorized access, ease of installation and operation, and compatibility with existing infrastructure. They must also balance cost-effectiveness with high reliability, accuracy, and minimal maintenance requirements. The effectiveness of a security system also depends on how well it integrates with the overall safety protocols of an organization while considering factors such as environmental conditions, user convenience, and scalability.

The growing complexity of security systems demands a structured approach to evaluating potential solutions. To optimize the selection of the most suitable gate security system, multiple factors need to be considered, including cost, security level, user experience, operational feasibility, system scalability, and environmental compatibility [53,54,60]. Given the vast number of security technologies available, selecting the best gate security system requires a holistic and MCDM approach to identify a solution that not only meets the technical and security needs of the organization but also ensures compliance with broader operational and organizational goals. Given the complexity of the decision-making process, a hybrid model has been developed, which incorporates QSF numbers and TOPSIS model. The model helps prioritize systems that align with the organization’s security objectives. Here we focus on a case study presented in a research by Akram et al. [20]. Through this comprehensive approach, organizations can confidently choose a security solution that ensures both the safety and convenience of users while meeting operational requirements. Four decision experts have been selected to help make this decision [20].

•   T1: Financial security expert: Expert in finance who evaluates security systems taking into account the cost of establishing security systems.

•   T2: System engineer: To manage the functionality, scalability, and compatibility of the security system with the existing infrastructure of the organization.

•   T3: IoT security expert: He will work on the IoT security aspects of the system. He will assure that all interacting devices and systems within the network are well protected against vulnerabilities and cyber threats.

•   T4: IT operations manager: Assuring a user-friendly operating environment, operational feasibility, and ease of operation will enable users to adopt the system more readily.

The security system mechanisms such as ID cards, and biometric devices use cutting-edge technology to facilitate access. Below are five state-of-the-art security systems under consideration:

•   S1: IRIS recognition system: IRIS scanning is an optical biometric technique that identifies an individual’s IRIS by analyzing patterns in their IRIS using a computational algorithm. All of us have our own unique, complex pattern that remains stable throughout our lifetimes. It is impossible to have the same pattern as two different people. Infrared light detects the eye’s pattern, which is then converted into a code (transformed into a square design similar to a bar code or Quick Response system) and verified. Fast-processing devices are more efficient.

•   S2: Card scanner system: Card scanning systems mount keycard readers on doors as part of the system. Upon swiping or inserting the cards into the smart card scanner, the encoded information on the cards is read and the doors are unlocked. Student cards, Bank cards, and ID cards are just a few of the most common cards.

•   S3: Facial recognition system: Face recognition systems are generally considered to be most reliable when using convolutional neural networks. Algorithms, computations, and AI are all used in facial recognition systems. Using 3D imaging, the technologies can recognize and convert the attributes of an individual’s face into electronic data. A “face print” is a digitized representation of this information. The data needed to operate these systems requires a tremendous amount of space.

•   S4: Voice recognition system: This type of biometric validation or identification involves recording the voice of the individual, converting it into a particular format using specialized software, and then using computational processing to confirm that individual’s identity. Through the use of pitch, intensity, and amplitude, the system is able to distinguish between different types of voices.

•   S5: Fingerprint scanner system: The reading and storing of fingerprint scans is enabled by optical sensor technology, which uses light as a source of illumination. Then a comparison is made between the fingerprint scans and the source information in the system. In addition, the system incorporates thermographic and ultrasonic sensors.

Further information regarding these five security systems is available on the following websites:

•   https://www.istockphoto.com/stock-photos/artificial-intelligence (accessed on 25 March 2025)

•   https://www.spottersecurity.com/blog/gate-security-access-control/ (accessed on 25 March 2025)

•   https://www.myq.com/commercial/industries/education (accessed on 25 March 2025)

•   https://swiftlane.com/solutions-enterprise/ (accessed on 25 March 2025)

•   https://smartrent.com/news/best-gate-entry-systems/ (accessed on 25 March 2025)

Analysis of these security systems’ key characteristics are used to evaluate their effectiveness. A comparison of security systems revealed seven characteristics that should be considered when evaluating them. Following are some of the categories described in more detail below:

•   V1: Cost: The relative expenditure on establishing a security system is determined by this criterion.

•   V2: Reliability: An important component of a system is its reliability. This guarantees the optimal performance of an application component, despite when the system is down.

•   V3: Accuracy: A system has accuracy level evaluation, which measures how precisely a system performs and record information in its information system in relation to how efficiently it works.

•   V4: IP rating: The IP rating indicates that the system is water-resistant. In addition, it determines whether the system stops functioning when water or dust enters.

•   V5: Compatibility with existing infrastructure: A security system cannot function in every environment. There is a special architecture required for installing them. For them to work efficiently, they must be compatible with their surroundings.

The selection of the optimal security system is executed through the implementation of a novel QSF-TOPSIS model. Fig. 2 illustrates a flow chart of the numerical application.

Figure 2: Flowchart of numerical application

5.2 Evaluation of Alternatives Ranking by QSF-Based TOPSIS Model

The ranking of all alternatives is calculated using the TOPSIS technique based on QSFNs. The technique is outlined in the following way:

Step 1. Surveys are conducted to gather objective opinions from decision makers regarding the relative importance of different security technologies. The linguistic variables used for alternative assessment are listed in Table 2. Table 4 presents the individual judgements of experts T1, T2, T3, and T4 for the alternatives.

Step 2. Next, combine the expert decision matrices of each decision maker and create an integrated SF-DM as outlined in Table 5.

Step 3. The weights of criterion are calculated using the Eq. (29). The weights of criterion corresponding to V1, V2, V3, V4 and V5 are 0.2030, 0.1994, 0.1855, 0.2231, and 0.1890, respectively.

Step 4. The next step is to formulate the QSF decision matrix using experts’ values. The linguistic variables used for assessment are listed in Table 3 and a combined QSF-DM is given in Table 6.

Step 5. An aggregated decision matrix was formulated by applying Eq. (25) to Table 6 and aggregated values are shown in Table 7.

Step 6. Normalize the aggregated decision values to create a normalized decision matrix using Eq. (34) and normalized values are shown in Table 8.

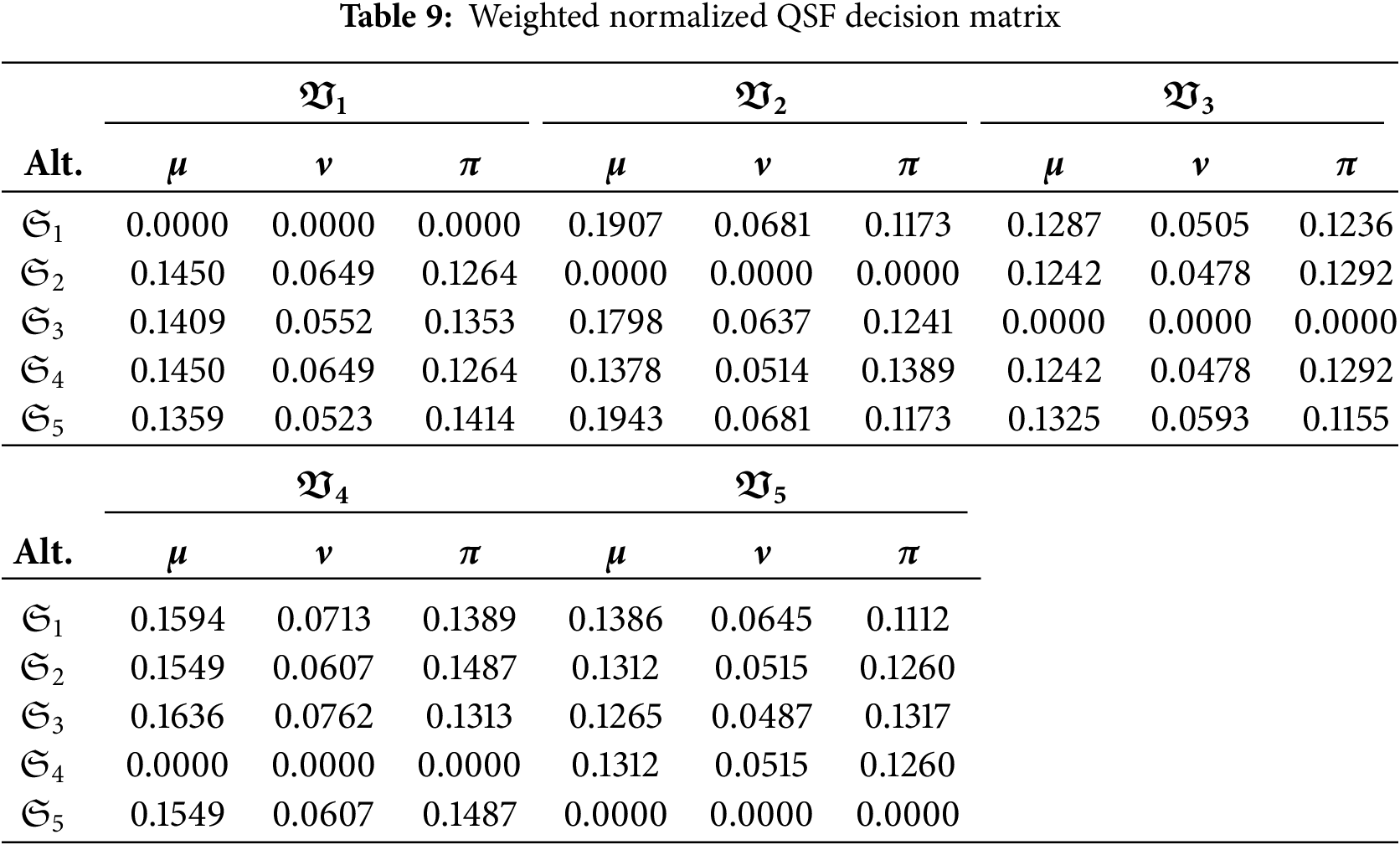
Step 7. Using the criterion weights, construct the weighted normalized decision matrix described in Table 9.

Step 8. Calculate the positive ideal solution (I+) and the negative ideal solution (I−) using Eqs. (36) and (37) and ideal solutions are given below:

I+={(0.1450,0,0),(0.1943,0,0),(0.1325,0,0),(0.1636,0,0),(0.1386,0,0)}I−={(0,0.0649,0.1414),(0,0.0681,0.1389),(0,0.0593,0.1292),(0,0.0762,0.1487),(0,0.0645,0.1317)}

Step 9. Compute the distance of each alternative from the positive ideal solution I+ using Eq. (38). Compute the distance of each alternative from the negative ideal solution I− using Eq. (39) and final values are outlined in Table 10.

Step 10. Calculate the preference value for each alternative using Eq. (40) and results are shown in Table 11.

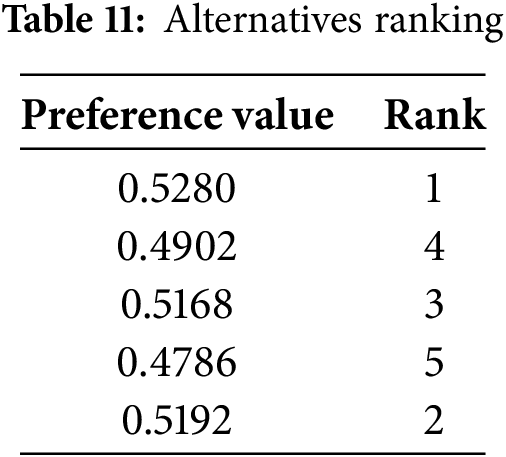
Step 11. Arrange the alternatives in descending order and IRIS is the most suitable option for the best gate security system.

6  Comparison of the Developed Approach with Existing Methods

In the following section, we evaluate the proposed method against three well-established existing techniques. To verify the validity and productivity of our proposed method, we applied the Spherical fuzzy TOPSIS (SF-TOPSIS) [71], Spherical fuzzy VlseKriterijumska Optimizacija I Kompromisno Resenje (SF-VIKOR) [72], and Spherical fuzzy Weighted aggregated sum product assessment (SF-WASPAS) [73] methods.

6.1 Spherical Fuzzy Number-Based TOPSIS Approach

SFN-based TOPSIS method [71] is now used to select the best gate security system which is summarized as:

Step 1. The spherical fuzzy decision matrices T1, T2, T3 and T4, presented in Table 4, provide complete information on expert evaluation.

Step 2. Next, combine the expert decision matrices of each decision maker and create an integrated SF-DM as outlined in Table 5.

Step 3. The weights of criterion are calculated using the Eq. (29). The weights of criterion corresponding to V1, V2, V3, V4 and V5 are 0.2030, 0.1994, 0.1855, 0.2231, and 0.1890, respectively.

Step 4. Normalize the integrated decision matrixI to create a normalized decision matrix using Eq. (41) and normalized values are shown in Table 12.

Nrs=Irs∑r=1e(Irs)2(41)

Step 5. Using the criterion weights, construct the weighted normalized decision matrix described in Table 13.

Step 6. Calculate the positive ideal solution (I+) and the negative ideal solution (I−) using Eqs. (36) and (37) and ideal solutions are given below:

I+={(0.1955,0.0489,0.0244),(0.1943,0.0412,0.0177),(0.1673,0.0717,0.0358),(0.2194,0.0387,0.0129),(0.1842,0.0391,0.0167)

I−={(0.1663,0.0998,0.0660),(0.1378,0.1247,0.0722),(0.1600,0.0800,0.0541),(0.1629,0.1333,0.0741),(0.1307,0.1182,0.0684)}

Step 7. Compute the distance of each alternative from the positive ideal solution I+ using Eq. (42). Compute the distance of each alternative from the negative ideal solution I− using Eq. (43) and final values are outlined in Table 14.

Dr+=∑r=1e(prs−Ir+)2(42)

Dr−=∑r=1e(prs−Ir−)2(43)

Step 8. Calculate the preference value for each alternative using Eq. (44) and results are shown in Table 15.

Vr=Dr−Dr++Dr−(44)

Step 9. Arrange the alternatives in descending order and IRIS is the most suitable option for the best gate security system.

6.2 Spherical Fuzzy Number-Based VIKOR Approach

SFN-based VIKOR method [72] is now used to select the best gate security system which is summarized as:

Step 1. The spherical fuzzy decision matrices T1, T2, T3 and T4, presented in Table 4, provide complete information on expert evaluation.

Step 2. Next, combine the expert decision matrices of each decision maker and create an integrated SF-DM as outlined in Table 5.

Step 3. The weights of criterion are calculated using the Eq. (29). The weights of criterion corresponding to V1, V2, V3, V4 and V5 are 0.2030, 0.1994, 0.1855, 0.2231, and 0.1890, respectively.

Step 4. In the following step, we formulate the vectors closest to the positive ideal solution v+ and the farthest from the negative ideal solution v−. The required values are shown in Eqs. (45) and (46).

v+={(0.9631,0.2408,0.1204),(0.9744,0.2067,0.0886),(0.9018,0.3865,0.1932),(0.9831,0.1735,0.0578),(0.9744,0.2067,0.0886)(45)

v−={(0.8193,0.4916,0.3253),(0.6912,0.6254,0.3621),(0.8624,0.4312,0.2914),(0.7301,0.5974,0.3319),(0.6912,0.6254,0.3621)(46)

Step 5. This step involves the computation of utility and regret measures for each alternative, leveraging criterion weights and Euclidean distances as described in Eqs. (47) and (48). The required values are shown in Table 16.

U=∑r=1ecwrd(vr+,Irs)d(vr+,vr−)(47)

R=maxr(cwrd(vr+,Irs)d(vr+,vr−))(48)

Step 6. Calculate the VIKOR score V for the alternatives using Eq. (49) and calculated VIKOR scores are shown in Table 17.

V=δ(Ur−Ur−Ur+−Ur−)+(1−δ)(Rr−Rr−Rr+−Rr−)(49)

Step 7. Arrange the alternatives in ascending order and IRIS is the most suitable option for the best gate security system.

6.3 Spherical Fuzzy Number-Based WASPAS Approach

SFN-based WASPAS method [73] is now used to select the best gate security system which is summarized as:

Step 1. The spherical fuzzy decision matrices T1, T2, T3 and T4, presented in Table 4, provide complete information on expert evaluation.

Step 2. A Spherical Weighted Arithmetic Mean operator (Eq. (50)) is used to aggregate evaluations of DMs. The aggregated decision matrix is shown in Table 18. A moderator can assign DMs directly or use any method proposed in the literature to determine their expertise level ξr.

agg=(1−∏r=1e(1−μr2)ξr,∏r=1eνrξr, ∏r=1e(1−μr2)ξr−∏r=1e(1−μr2−πr2)ξr)(50)

Step 3. The weights of criterion are calculated using the Eq. (29). The weights of criterion corresponding to V1, V2, V3, V4 and V5 are 0.2039, 0.2001, 0.1927, 0.2129 and 0.1903, respectively.

Step 4. The Simple Additive Weighting (SAW) approach is applied to Table 18 by incorporating the weights of the criterion to determine the SAW^ scores of all alternatives using Eq. (51). A subsequent addition operation is performed to sum up the weighted evaluations per attribute using Eq. (52). The results of the SAW addition operator are presented in Table 19.

SAW^=∑r=1ewr(μr,νr,πr)(51)

(μr1,νr1,πr1)⊕(μr2,νr2,πr2)={(μr1)2+(μr2)2−(μr1)2(μr2)2,νr1νr2,(1−μr12)πr22+(1−μr22)πr12−πr12πr22}(52)

Step 5. The Weighted Product Model (WPM) approach is applied to Table 18 by incorporating the weights of the criterion to determine the WPM^ scores of all alternatives using Eq. (53). A subsequent product operation is performed to take the product of the weighted evaluations per attribute using Eq. (54). The results of the WPM product operator are presented in Table 20.

WPM^=∏r=1ewr(μr,νr,πr)(53)

(μr1,νr1,πr1)⊗(μr2,νr2,πr2)={μr1μr2,(νr1)2+(νr2)2−(νr1)2(νr2)2,(1−νr12)πr22+(1−νr22)πr12−πr12πr22}(54)

Step 6. To integrate spherical fuzzy values of SAW and WPM, a threshold number δ is applied to them. The aggregated value for each alternative is derived using Eq. (55) and is displayed in Table 21.

Z^=δWPM^+(1−δ)WPM^(55)

Step 7. Arrange the alternatives in descending order and IRIS is the most suitable option for the best gate security system.

6.4 Sensitivity Analysis

To further demonstrate the robustness and reliability of the proposed model, we performed a Spearman correlation, Kendall correlation, and sensitivity analysis of the criteria weights.

To assess the stability and validity of the proposed QSF-TOPSIS approach, a sensitivity analysis of criteria weights was performed by altering the criteria weights for five different variations. The original weight set used in the model was:

Original Weights: {0.2030, 0.1994, 0.1855, 0.2231, 0.1890}

The five alternative weight sets used for sensitivity analysis were:

Set 1:{0.203, 0.198, 0.186, 0.224, 0.189}Set 2:{0.204, 0.198, 0.184, 0.223, 0.191}Set 3:{0.202, 0.200, 0.185, 0.222, 0.191}Set 4:{0.205, 0.197, 0.186, 0.221, 0.191}Set 5:{0.203, 0.199, 0.183, 0.224, 0.191}

This analysis examined how changes in the relative importance of criteria affect the final outcome of decision-making. For each of these weight variations, the closeness coefficients of the alternatives were recalculated to evaluate the influence of weight variation. As shown in Table 22, the values of the closeness coefficient for the alternatives showed minor numerical fluctuations; however, the overall rankings remained completely consistent with those produced by the original weight distribution.

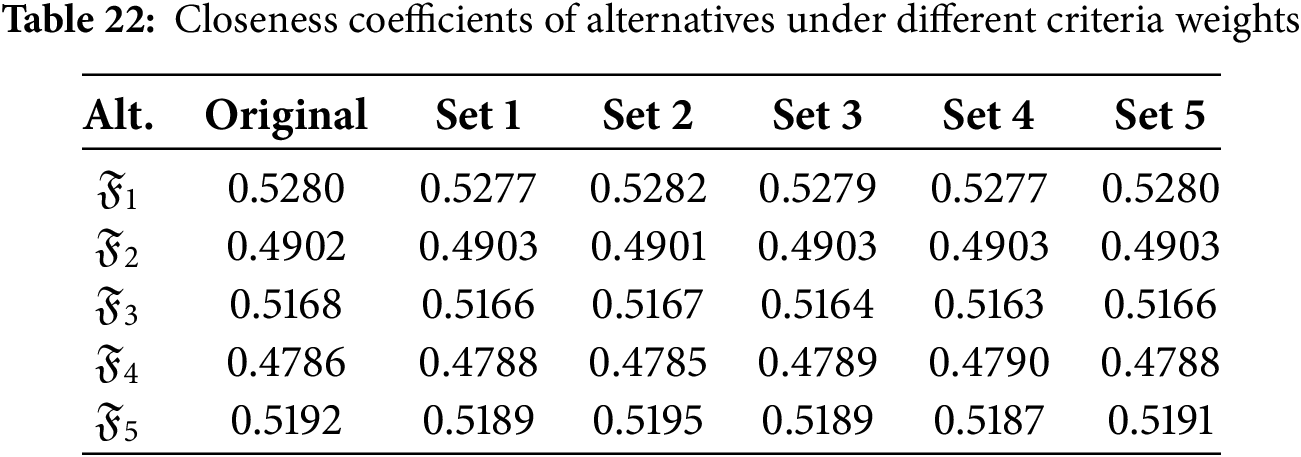
This consistency across all tested weight sets demonstrates the robustness and reliability of the proposed QSF-TOPSIS model. The model maintained its ranking results despite a moderate weight-change distribution. This is particularly critical in real-world decision-making contexts, where subjective expert judgments and changing priorities often lead to variations in assigned weights. Furthermore, Fig. 3 presents a graphical representation of closeness coefficient values across all scenarios. Therefore, the results of the sensitivity analysis confirm the effectiveness and validity of the QSF-TOPSIS method under varying decision conditions.

Figure 3: Visualization of different closeness coefficients

Spearman rank correlation coefficient is a nonparametric assessment of statistical relationships between two variables. Using a monotonic function, it evaluates whether two variables have a good relationship. Spearman coefficients [74] can be calculated using the following formula:

Sρ=1−6∑t=1ndt2(n2−1)n(56)

where dt=(Mt−Et), the difference between the ranks of the t-th observation in two variables is given by d. Here, Mt represents the rank of the t-th observation in the first variable. Et represents the rank of the t-th observation in the second variable and n is the number of observations (sample size).

Spearman rank correlation is applied to assess consistency between rankings generated by the proposed model and those produced by selected benchmark models. The correlation coefficients obtained between the proposed model and the benchmark models are (1, 0.9, 1), reflecting a very strong positive monotonic association. These high values indicate that the proposed model produces rankings that are highly consistent with benchmark techniques. Fig. 4 presents a detailed visualization of Spearman correlation values across all evaluated methods, illustrating the strength of associations between the models.

Figure 4: Spearman correlation

Kendall’s tau (τ) is a nonparametric measure that evaluates the strength and direction of association between two ordinal variables [75]. It relies on the likelihood that a randomly selected pair of observations is ranked in the same order (concordant) or in opposite order (discordant). This coefficient is particularly useful when dealing with ranking or ordinal data, as it does not assume any specific distribution. This makes it a distribution-free alternative to conventional correlation metrics. In studies involving bivariate normal distributions, researchers have also examined how Kendall’s tau relates to other rank-based correlation measures [75].

Kendall’s tau is well-suited to ordinal data, offering a reliable way to gauge associations without relying on parametric assumptions. For a data set with k total observations, where CN denotes the number of concordant pairs and S the number of discordant pairs, Kendall’s tau is defined as:

τ=CN−Sk(k−1)/2=2(CN−S)k(k−1)(57)

The coefficient ranges from −1 (indicating complete disagreement in rankings) to +1 (indicating complete agreement).

To evaluate the ordinary relation between the proposed model and the selected benchmark models, Kendall’s tau correlation is employed. The resulting correlation matrix, as shown in Fig. 5, demonstrates the degree of consistency in the rankings produced by each method. QSF-TOPSIS model shows perfect agreement with SF-TOPSIS (τ = 1) and SF-WASPAS (τ = 1), and a strong association (τ = 0.8) with SF-VIKOR. Similarly, SF-TOPSIS and SF-WASPAS also exhibit perfect concordance with each other and with the proposed model. The high Kendall’s tau values confirm a strong ordinal correlation among the methods. This reinforces the reliability and robustness of the proposed model’s ranking behavior when compared to established alternatives.

Figure 5: Kendall’s tau correlation

7  Discussion

According to the comparison, the discussion consists of the following points:

1. A comparison between the proposed technique for MCDM and other existing MCDM methods, namely SF-TOPSIS, SF-VIKOR, and SF-WASPAS, is performed to confirm its validity and efficiency. An overview of the results can be found in Table 23. According to the comparison, alternative S1 is the best method based on all the approaches considered, thus supporting the proposed method. A graph showing the results of the comparison can also be found in Fig. 6.

Figure 6: Comparison analysis

2. One of the methods available for ranking alternatives in the MCDM is SF-TOPSIS, which performs the ranking of alternatives by taking the distances in addition to finding the closeness index for each alternative. As a result, the chosen alternative is most optimal and farthest from the worst-case scenario. Although it uses sophisticated uncertainty modeling, SF-TOPSIS is highly computationally efficient and robust.

3. The SF-VIKOR ranking method minimizes the distance from the ideal solution while balancing conflicting criteria. This method ranks alternatives based on utility and regret measures. Due to its ability to balance conflicting criteria, SF-VIKOR is a perfect solution for our chosen problem. Incorporating different levels of confidence allows decision-makers to adjust the weight of criteria according to their validity.

4. The SF-WASPAS method is a flexible approach that provides a more precise way of determining the relative importance of alternatives in an MCDM process by integrating the SAW and WPM decision-making models. This method is a hybrid method that balances additive and multiplicative aggregation. In addition, spherical fuzzy numbers are used to manage uncertain data. The alternative ranking becomes more accurate and precise as a result.

Limitations

QSF numbers (QSFNs) integrated with TOPSIS leads to an escalation in computational complexity. Quantum mechanics introduces additional intricacies to both mathematical and computational calculations, necessitating specialized expertise. The combination of spherical fuzzy sets with quantum operations often results in resource-intensive processes, particularly in the context of large-scale problems. The QSF-TOPSIS model assumes criterion independence that is not always true in practice. TOPSIS may become complicated in situations where there are many alternatives and requirements. As a result of some complicated calculations, understanding the logic behind the results can be challenging. Real-world scenarios might not always align with assumptions associated with quantum states. Similarly to other TOPSIS-based approaches, QSF-TOPSIS assigns weights to the criteria, which can have a substantial impact on the final rankings. Although QSFN are capable of handling uncertainty, inaccurately determined weights might cause results to be unreliable.

8  Conclusion

In this study, QSFNs were studied, which are extensions of SFNs. Their wider structure makes them more accommodating of uncertainty than SFNs. We evaluated and selected the most optimal gate security system using the QSF-TOPSIS method. The analysis revealed IRIS recognition as the most optimal alternative due to its superior performance across multiple criteria. In addition, the analysis was substantiated via comparisons using TOPSIS, VIKOR, and WASPAS methods for SF numbers. QSF-TOPSIS rankings were consistently aligned across all applied methods, indicating their robustness and reliability. The IRIS recognition system gained the highest ranking across all applied methodologies. For modern security needs, IRIS recognition provides superior effectiveness, reliability, and performance in gate security applications. Quantum mechanics principles are incorporated into QSF-TOPSIS, which enhances the method’s ability to deal with uncertainty and vagueness. It improves preference computation efficiency and enables a better understanding of decision space. This is especially important in scenarios with high levels of ambiguity and incomplete information.

Future research will address emerging challenges by applying quantum mechanics to decision-making, integrating real-world data, and constructing hybrid models. We aim to integrate QSF-TOPSIS with other MCDM methods like WASPAS, VIKOR, and Grey Relational Analysis. By using these approaches, we could gain a deeper understanding of the relationship between criteria and alternatives. A QSF-TOPSIS method can be automated through the integration of artificial intelligence and decision support systems.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R716), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank Prof. Dragan Pamucar for his valuable guidance and support during the development of this manuscript.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R716), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: Conceptualization, Muhammad Amad Sarwar and Yuezheng Gong; methodology, Muhammad Amad Sarwar; software, Sarah A. Alzakari and Amel Ali Alhussan; validation, Muhammad Amad Sarwar and Amel Ali Alhussan; formal analysis, Muhammad Amad Sarwar and Sarah A. Alzakari; investigation, Yuezheng Gong; data curation, Amel Ali Alhussan; writing—original draft preparation, Muhammad Amad Sarwar; writing—review and editing, Yuezheng Gong, Sarah A. Alzakari, and Amel Ali Alhussan; visualization, Muhammad Amad Sarwar; supervision, Yuezheng Gong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data inquiries should be directed to the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Abdullahi SM, Sun S, Wang B, Wei N, Wang H. Biometric template attacks and recent protection mechanisms: a survey. Inf Fusion. 2024;103:102144. doi:10.1016/j.inffus.2023.102144. [Google Scholar] [CrossRef]

2. Gawande U, Golhar Y, Hajari K. Biometric-based security system: issues and challenges. In: Intelligent techniques in signal processing for multimedia security. Cham, Switzerland: Springer; 2017. p. 151–76. [Google Scholar]

3. Hammouche R, Attia A, Akhrouf S, Akhtar Z. Gabor filter bank with deep autoencoder based face recognition system. Expert Syst Appl. 2022;197:116743. doi:10.1016/j.eswa.2022.116743. [Google Scholar] [CrossRef]

4. Mu H, Guo J, Liu X, Han C, Gong L. Personalized multimodal federated learning for fingerprint and finger vein recognition. In: International Conference on Intelligent Computing. Singapore: Springer Nature Singapore; 2024. p. 365–76. [Google Scholar]

5. Ashwini K, Keshava Murthy GN, Raviraja S, Srinidhi GA. A novel multimodal biometric person authentication system based on ECG and Iris data. Biomed Res Int. 2024;2024(1):8112209. doi:10.1155/2024/8112209. [Google Scholar] [CrossRef]

6. Kheddar H, Hemis M, Himeur Y. Automatic speech recognition using advanced deep learning approaches: a survey. Inf Fusion. 2024;109:102422. doi:10.1016/j.inffus.2024.102422. [Google Scholar] [CrossRef]

7. Hwang CL, Yoon K, Hwang CL, Yoon K. Methods for multiple attribute decision making. In: Multiple attribute decision making: methods and applications a state-of-the-art survey. Berlin/Heidelberg, Germany: Springer; 1981. p. 58–191. [Google Scholar]

8. Opricovic S. Multicriteria optimization of civil engineering systems. Facu Civil Eng, Belgrade. 1998;2(1):5–21. [Google Scholar]

9. Saaty TL. The analytic hierarchy process (AHP). J Operat Res Soc. 1980;41(11):1073–6. [Google Scholar]

10. Brans JP, Vincke P. Note—a preference ranking organisation method: (The PROMETHEE Method for Multiple Criteria Decision-Making). Manage Sci. 1985;31(6):647–56. doi:10.1287/mnsc.31.6.647. [Google Scholar] [CrossRef]

11. Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53. doi:10.1016/s0019-9958(65)90241-x. [Google Scholar] [CrossRef]

12. Krassimir TA, Parvathi R. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi:10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

13. Yager RR. Pythagorean fuzzy subsets. In: 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS); 2013 Jun 24–28; Edmonton, AB, Canada. p. 57–61. [Google Scholar]

14. Yager RR. Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst. 2016;25(5):1222–30. doi:10.1109/tfuzz.2016.2604005. [Google Scholar] [CrossRef]

15. Seikh MR, Mandal U. Multiple attribute group decision making based on quasirung orthopair fuzzy sets: application to electric vehicle charging station site selection problem. Eng Appl Artif Intell. 2022;115(4):105299. doi:10.1016/j.engappai.2022.105299. [Google Scholar] [CrossRef]

16. Smarandache F. A unifying field in logics: neutrosophic logic. In: Philosophy. Champaign, IL, USA: American Research Press; 1999. p. 1–141. [Google Scholar]

17. Al-Shamiri MMA, Ali G, Abidin MZU, Adeel A. Multi-attribute group decision-making method under spherical fuzzy bipolar soft expert framework with its application. Comput Model Eng Sci. 2023;137(2):1891–936. doi:10.32604/cmes.2023.027844. [Google Scholar] [CrossRef]

18. Garg H. Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput Indust Eng. 2016;101(4):53–69. doi:10.21203/rs.3.rs-2377299/v1. [Google Scholar] [CrossRef]

19. Garg H. Novel intuitionistic fuzzy decision making method based on an improved operation laws and its application. Eng Appl Artif Intell. 2017;60(8):164–74. doi:10.1016/j.engappai.2017.02.008. [Google Scholar] [CrossRef]

20. Akram M, Azam S, Al-Shamiri MMA, Pamucar D. An outranking method for selecting the best gate security system using spherical fuzzy rough numbers. Eng Appl Artif Intell. 2024;138(2):109411. doi:10.1016/j.engappai.2024.109411. [Google Scholar] [CrossRef]

21. Kou G, Yüksel S, Dinçer H. A facial expression and expert recommendation fuzzy decision-making approach for sustainable business investments within the metaverse world. Appl Soft Comput. 2023;148(4):110849. doi:10.1016/j.asoc.2023.110849. [Google Scholar] [CrossRef]

22. Lo HW. A novel interval neutrosophic-based group decision-making approach for sustainable development assessment in the computer manufacturing industry. Eng Appl Artif Intell. 2024;132(2):107984. doi:10.1016/j.engappai.2024.107984. [Google Scholar] [CrossRef]

23. Aydin N, Seker S, Deveci M, Zaidan BB. Post earthquake debris waste management with interpretive-structural-modeling and decision-making-trial, and evaluation-laboratory under neutrosophic fuzzy sets. Eng Appl Artif Intell. 2024;138(3):109251. doi:10.1016/j.engappai.2024.109251. [Google Scholar] [CrossRef]

24. Zhang C, Yang G, Wang C, Huo Z. Linking agricultural water-food-environment nexus with crop area planning: a fuzzy credibility-based multi-objective linear fractional programming approach. Agric Water Manag. 2023;277(3):108135. doi:10.1016/j.agwat.2022.108135. [Google Scholar] [CrossRef]

25. Kara K, Yalcin GC, Gurol P, Simic V, Pamucar D. Enhancing decision support system for finished vehicle logistics service provider selection through a single-valued neutrosophic Dombi Bonferroni-based model. Eng Appl Artif Intell. 2024;138(3):109441. doi:10.1016/j.engappai.2024.109441. [Google Scholar] [CrossRef]

26. Fu Q, Liu Q, Lu X, Hu T, Wang Y, Pan J. Interval-valued spherical fuzzy quality function deployment methodology: metaverse collaborative system design application. Eng Appl Artif Intell. 2024;133(10):108644. doi:10.1016/j.engappai.2024.108644. [Google Scholar] [CrossRef]

27. Almulhim T. Interval-valued spherical fuzzy extension of DEMATEL and its application in early-stage investment. IEEE Access. 2024;12:89275–90. doi:10.1109/access.2024.3418988. [Google Scholar] [CrossRef]

28. Nhieu NL. The T-spherical fuzzy einstein interaction operation matrix energy decision-making approach: the context of vietnam offshore wind energy storage technologies assessment. Mathematics. 2024;12(16):2498. doi:10.3390/math12162498. [Google Scholar] [CrossRef]

29. Nhieu NL, Dang TD. An integrated T-spherical fuzzy einstein interaction aggregator group decision-making approach: a case study of concrete 3d printing robot application in Vietnam. Mathematics. 2024;12(13):2086. doi:10.3390/math12132086. [Google Scholar] [CrossRef]

30. Hacioglu U, Dincer H, Yilmaz MK, Yüksel S, Sonko M, Delen D. Optimizing sustainable industry investment selection: a golden cut-enhanced quantum spherical fuzzy decision-making approach. Appl Soft Comput. 2023;148(3):110853. doi:10.1016/j.asoc.2023.110853. [Google Scholar] [CrossRef]

31. Dincer H, Yüksel SERHAT, Hacioglu U, Erdebilli B. Multidimensional analysis of investment priorities for circular economy with quantum spherical fuzzy hybrid modeling. Int J Inf Technol Decis Mak. 2025;24(1):61–87. doi:10.1142/S021962202350075X. [Google Scholar] [CrossRef]

32. Wang YM, Elhag TM. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst Appl. 2006;31(2):309–19. doi:10.1016/j.eswa.2005.09.040. [Google Scholar] [CrossRef]

33. Boran FE, Genç S, Kurt M, Akay D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst Appl. 2009;36(8):11363–8. doi:10.1016/j.eswa.2009.03.039. [Google Scholar] [CrossRef]

34. Zhang X, Xu Z. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst. 2014;29(12):1061–78. doi:10.1002/int.21676. [Google Scholar] [CrossRef]

35. Tho Thong N, Lan LTH, Chou SY, Son LH, Dong DD, Ngan TT. An extended TOPSIS method with unknown weight information in dynamic neutrosophic environment. Mathematics. 2020;8(3):401. doi:10.3390/math8030401. [Google Scholar] [CrossRef]

36. Saeidi P, Mardani A, Mishra AR, Cajas VEC, Carvajal MG. Evaluate sustainable human resource management in the manufacturing companies using an extended Pythagorean fuzzy SWARA-TOPSIS method. J Clean Prod. 2022;370:133380. doi:10.1016/j.jclepro.2022.133380. [Google Scholar] [CrossRef]

37. Karamoozian A, Wu D. A hybrid approach for the supply chain risk assessment of the construction industry during the COVID-19 pandemic. IEEE Trans Eng Manag. 2022;71:4035–50. doi:10.1109/TEM.2022.3210083. [Google Scholar] [CrossRef]

38. Asante D, Ampah JD, Afrane S, Adjei-Darko P, Asante B, Fosu E, et al. Prioritizing strategies to eliminate barriers to renewable energy adoption and development in Ghana: a CRITIC-fuzzy TOPSIS approach. Renew Energy. 2022;195(9):47–65. doi:10.1016/j.renene.2022.06.040. [Google Scholar] [CrossRef]

39. Karamoozian A, Luo C, Wu D. Risk assessment of occupational safety in construction projects using uncertain information. Hum Ecol Risk Assess. 2023;29(7–8):1134–51. doi:10.1080/10807039.2023.2248266. [Google Scholar] [CrossRef]

40. Cui Z, Taiwo OL, Aaron PM. An application of AHP and fuzzy entropy-TOPSIS methods to optimize upstream petroleum investment in representative African basins. Sci Rep. 2024;14(1):6956. doi:10.1038/s41598-024-57445-9. [Google Scholar] [CrossRef]

41. Gaeta A, Loia V, Orciuoli F. An explainable prediction method based on Fuzzy Rough Sets, TOPSIS and hexagons of opposition: applications to the analysis of Information Disorder. Inf Sci. 2024;659(1–2):120050. doi:10.1016/j.ins.2023.120050. [Google Scholar] [CrossRef]

42. Faundez-Zanuy M. On the vulnerability of biometric security systems. IEEE Aerosp Electron Syst Mag. 2004;19(6):3–8. doi:10.1109/maes.2006.1662038. [Google Scholar] [CrossRef]

43. Grunenberg K. Wearing someone else’s face: biometric technologies, anti-spoofing and the Fear of the Unknown. Ethnos. 2022;87(2):223–40. doi:10.1080/00141844.2019.1705869. [Google Scholar] [CrossRef]

44. Kaiwartya O, Prasad M, Prakash S, Samadhiya D, Abdullah AH, Abd Rahman SO. An investigation on biometric internet security. Int J Netw Secur. 2017;19(2):167–76. doi:10.6633/IJNS.201703.19(2).01. [Google Scholar] [CrossRef]

45. Khan HU, Malik MZ, Nazir S, Khan F. Utilizing bio metric system for enhancing cyber security in banking sector: a systematic analysis. IEEE Access. 2023;11:80181–98. doi:10.1109/ACCESS.2023.3298824. [Google Scholar] [CrossRef]

46. Benarous L, Kadri B, Bouridane A. A survey on cyber security evolution and threats: biometric authentication solutions. In: Biometric security and privacy: opportunities & challenges in the big data era. Cham, Switzerland: Springer; 2017. p. 371–411. [Google Scholar]

47. Sett S, Gupta H. A biometric security model for the enhancement of data security. In: 2024 11th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO); 2024 Mar 14–15; Noida, India. p. 1–5. [Google Scholar]

48. Shuford J. Exploring the efficacy of behavioral biometrics in cybersecurity. J Artif Intell Gen Sci (JAIGS). 2024;6(1):577–93. doi:10.60087/jaigs.v6i1.285. [Google Scholar] [CrossRef]

49. Mohammed BO. A new feature level-based multi-biometric identification system to enable secure and reliable communication systems for next-generation smart cities. Secur Priv. 2025;8(1):e501. doi:10.1002/spy2.501. [Google Scholar] [CrossRef]

50. Sasikala TS. Multimodal secure biometrics using attention efficient-net hash compression framework. Digit Signal Process. 2025;160(12):105018. doi:10.1016/j.dsp.2025.105018. [Google Scholar] [CrossRef]

51. Kansal I, Khuallar V, Gupta G, Gupta D, Juneja S, Nauman A, et al. Deep learning-based privacy preserving multimodal biometrics recognition for cross-silo datasets. Expert Syst. 2025;42(6):e70053. doi:10.1111/exsy.70053. [Google Scholar] [CrossRef]

52. Ogundoyin SO, Kamil IA. An integrated Fuzzy-BWM, Fuzzy-LBWA and V-Fuzzy-CoCoSo-LD model for gateway selection in fog-bolstered Internet of Things. Appl Soft Comput. 2023;143(5):110393. doi:10.1016/j.asoc.2023.110393. [Google Scholar] [CrossRef]

53. Alamleh A, Albahri OS, Zaidan AA, Albahri AS, Alamoodi AH, Zaidan B, et al. Federated learning for IoMT applications: a standardization and benchmarking framework of intrusion detection systems. IEEE J Biomed Health Inform. 2022;27(2):878–87. doi:10.1109/JBHI.2022.3167256. [Google Scholar] [CrossRef]

54. Qahtan S, Sharif KY, Zaidan AA, AlSattar HA, Albahri OS, Zaidan B, et al. Novel multi security and privacy benchmarking framework for blockchain-based IoT healthcare Industry 4.0 systems. IEEE Trans Ind Inform. 2022;18(9):6415–23. doi:10.1109/TII.2022.3143619. [Google Scholar] [CrossRef]

55. Tanaji BA, Roychowdhury S. BWM Integrated VIKOR method using Neutrosophic fuzzy sets for cybersecurity risk assessment of connected and autonomous vehicles. Appl Soft Comput. 2024;159(3):111628. doi:10.1016/j.asoc.2024.111628. [Google Scholar] [CrossRef]

56. Albahri OS, Al-Samarraay MS, AlSattar HA, Alamoodi AH, Zaidan AA, Albahri A, et al. Rough Fermatean fuzzy decision-based approach for modelling IDS classifiers in the federated learning of IoMT applications. Neural Comput Appl. 2023;35(30):22531–49. doi:10.1007/s00521-023-08933-y. [Google Scholar] [CrossRef]

57. Almotiri SH. Integrated fuzzy based computational mechanism for the selection of effective malicious traffic detection approach. IEEE Access. 2021;9:10751–64. doi:10.1109/access.2021.3050420. [Google Scholar] [CrossRef]

58. Deb R, Roy S. A Software Defined Network information security risk assessment based on Pythagorean fuzzy sets. Expert Syst Appl. 2021;183:115383. doi:10.1016/j.eswa.2021.115383. [Google Scholar] [CrossRef]

59. Lin M, Huang C, Xu Z. MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain Cities Soc. 2020;53(2):101873. doi:10.1016/j.scs.2019.101873. [Google Scholar] [CrossRef]

60. Erdogan M, Karasan A, Kaya I, Budak A, Colak M. A fuzzy based MCDM methodology for risk evaluation of cyber security technologies. In: Intelligent and Fuzzy Techniques in Big Data Analytics and Decision Making: Proceedings of the INFUS 2019 Conference; 2019 Jul 23-25; Istanbul, Turkey. Cham, Switzerland: Springer International Publishing. p. 1042–9. [Google Scholar]

61. Moslem S. A novel parsimonious spherical fuzzy analytic hierarchy process for sustainable urban transport solutions. Eng Appl Artif Intell. 2024;128(1):107447. doi:10.1016/j.engappai.2023.107447. [Google Scholar] [CrossRef]

62. Shishavan SAS, Gündogdu FK, Farrokhizadeh E, Donyatalab Y, Kahraman C. Novel similarity measures in spherical fuzzy environment and their applications. Eng Appl Artif Intell. 2020;94:103837. doi:10.1016/j.engappai.2020.103837. [Google Scholar] [CrossRef]

63. Nguyen PH, Pham TV, Nguyen LAT, Narayanamoorthy S, Nguyen THT, Vu TG. Analysis of quantum computing’s applicability in data analysis: utilizing a hybrid MCDM approach with quantum spherical fuzzy sets. IEEE Access. 2024;12(1):110526–49. doi:10.1109/access.2024.3439629. [Google Scholar] [CrossRef]

64. Akram M, Zahid K, Kahraman C. Integrated outranking techniques based on spherical fuzzy information for the digitalization of transportation system. Appl Soft Comput. 2023;134(2):109992. doi:10.1016/j.asoc.2023.109992. [Google Scholar] [CrossRef]

65. Zahid K, Akram M, Kahraman C. A new ELECTRE-based method for group decision-making with complex spherical fuzzy information. Knowl Based Syst. 2022;243(7):108525. doi:10.1016/j.knosys.2022.108525. [Google Scholar] [CrossRef]

66. Xu X, Yüksel S, Dinçer H. An integrated decision-making approach with golden cut and bipolar q-ROFSs to renewable energy storage investments. Int J Fuzzy Syst. 2023;25(1):168–81. doi:10.1007/s40815-022-01372-2. [Google Scholar] [CrossRef]

67. Al-Binali T, Aysan AF, Dinçer H, Unal IM, Yüksel S. New horizons in bank mergers: a quantum spherical fuzzy decision-making framework for analyzing Islamic and conventional bank mergers and enhancing resilience. Sustainability. 2023;15(10):7822. doi:10.3390/su15107822. [Google Scholar] [CrossRef]

68. Yüksel S, Dinçer H. Sustainability analysis of digital transformation and circular industrialization with quantum spherical fuzzy modeling and golden cuts. Appl Soft Comput. 2023;138(4):110192. doi:10.1016/j.asoc.2023.110192. [Google Scholar] [CrossRef]

69. Shah SU, Riphah F, Minhas AA. New factor of authentication: something you process. In: 2009 International Conference on Future Computer and Communication; 2009 Apr 3–5; Kuala Lumpar, Malaysia. p. 102–6. [Google Scholar]

70. De Keyser A, Bart Y, Gu X, Liu SQ, Robinson SG, Kannan PK. Opportunities and challenges of using biometrics for business: developing a research agenda. J Bus Res. 2021;136:52–62. doi:10.1016/j.jbusres.2021.07.028. [Google Scholar] [CrossRef]

71. Toker K, Görener A. Evaluation of circular economy business models for SMEs using spherical fuzzy TOPSIS: an application from a developing countries’ perspective. Environ, Develop Sustain. 2023;25(2):1700–41. doi:10.1007/s10668-022-02119-7. [Google Scholar] [CrossRef]

72. Kumar S, Younis J, Hussain A. A novel spherical fuzzy VIKOR approach based on TODIM for evaluating and ranking the opinion polls with shannon entropy and jensen-shannon divergence measure. IEEE Access. 2023;11:103242–53. doi:10.1109/access.2023.3314673. [Google Scholar] [CrossRef]

73. Nguyen PH, Dang TT, Nguyen KA, Pham HA. Spherical fuzzy WASPAS-based entropy objective weighting for international payment method selection. Comput Mater Contin. 2022;72(1):2055–75. doi:10.32604/cmc.2022.025532. [Google Scholar] [CrossRef]

74. Ullah I, Akram M, Allahviranloo T. An outranking method with Dombi aggregation operators based on multi-polar fuzzy Z-numbers for selection of best rehabilitation center. J Ind Inf Integr. 2025;44(79):100781. doi:10.1016/j.jii.2025.100781. [Google Scholar] [CrossRef]

75. Essam F, El H, Ali SRH. A comparison of the pearson, spearman rank and kendall tau correlation coefficients using quantitative variables. Asian J Probab Stat. 2022;20(3):36–48. doi:10.9734/ajpas/2022/v20i3425. [Google Scholar] [CrossRef]