Innovative Aczel Alsina Group Overlap Functions for AI-Based Criminal Justice Policy Selection under Intuitionistic Fuzzy Set

1  Introduction

Decision-making is a vital process in almost every field, from business and healthcare to engineering and artificial intelligence. However, real-world decision-making often involves complex problems with conflicting goals and an abundance of uncertainty. To address such challenges, MCDM has become a widely used approach. MCDM helps evaluate different options based on multiple criteria, even when these criteria may conflict with each other. While classical MCDM methods require exact numerical data, real-world scenarios are rarely so precise, as they are influenced by vagueness, ambiguity, and incomplete information. To handle this uncertainty, Zadeh’s fuzzy set (FSs) [1] was introduced as a groundbreaking concept. Klir and Yuan [2] discussed the fundamental principles of FS theory and its application in uncertainty modeling. The FS theory has been widely applied in various areas, such as Yang et al. [3] applied fuzzy logic in control systems, and [4] extended its application in environmental management.

Extension of Fuzzy Sets

Building on Zadeh’s FSs, in 1986, Atanassov introduced Intuitionistic FSs (IFS) [5], which take uncertainty modeling a step further. IFS incorporates not only a membership degree (MD) (μ) but also a non-membership degree (NMD) (ν) for each element x. These satisfy the following condition:

0≤μA(x)+νA(x)≤1.

The inclusion of both MD and NMD allows IFS to represent hesitation or uncertainty more effectively, making it highly applicable in fields like risk assessment, healthcare [6], and supply chain management [7]. For example, in healthcare decision-making, a patient’s symptoms might partially match multiple diagnoses, and IFS can capture this ambiguity better than traditional methods. Moreover, IFS-based aggregation operators, such as weighted averaging and geometric operators, provide tools for combining information from multiple criteria or experts. Wan et al. [8] extended the idea of IFS by developing intuitionistic fuzzy (IF) preference relations that improve decision reliability by incorporating expert opinions and weighting mechanisms. Khan et al. [9] introduced the Daimond IFs and explored the role of aggregation operators in MCDM making and demonstrated their effectiveness in fusing uncertain information.

Recognizing the limitations of IFS, in 2013, Yager introduced Pythagorean FSs (PFS) [10] as a generalization. PFS relaxes the strict condition of IFS by ensuring that the square sum of MD and NMD is less than or equal to 1:

μB(x)2+νB(x)2≤1.

This relaxation allows PFS to handle more complex scenarios with higher levels of uncertainty. Adak et al. [11] introduced some new operations on PFS as an extension of IFS, demonstrating their ability to better capture uncertainty in decision-making. The authors of [12] applied PFS to MCDM, highlighting their effectiveness in handling imprecise information. Thakur et al. [13] conducted a comprehensive study on various Pythagorean fuzzy set distance metrics and demonstrated their effectiveness in improving decision-making accuracy across different application scenarios. PFS applications were further discussed by the author of [14], who demonstrated their benefits in sustainability modelling, where environmental and economic requirements frequently coincide.

Further expanding the capabilities of fuzzy set theory, in 2016, Yager introduced q-Rung Orthopair FSs (q-ROFS) [15]. These sets generalize PFS by allowing the q-th power sum of MD and NMDs to remain bounded by 1:

(μC(x))q+(νC(x))q≤1.

This generalization enables q-ROFS to manage even higher levels of uncertainty and hesitation. Darko and Liang [16] highlighted that q-ROFS enhance decision-making flexibility by accommodating a wider range of uncertainty. Saha et al. [17] demonstrated their effectiveness in transportation systems, particularly in optimizing routes under unpredictable traffic conditions. Liu and Wang [18] explored their role in collaborative decision-making, showing that they improve consensus-building in group evaluations. Wang et al. [19] applied q-ROFS to financial risk assessment, proving their superiority over IFS and PFS in handling volatile market conditions.

Aggregation Operators in Fuzzy Environments

Triangular norms (T-N) and triangular conorms (T-CN) [20] have long served as essential tools in FSs and aggregation processes, offering mathematical frameworks for modeling “and” and “or” operations, respectively. Over time, numerous types of T-N and T-CNs have been developed, each with unique properties tailored to different applications. Algebraic T-Ns and T-CNs, among the most basic forms, were defined by simple multiplication and addition operations adjusted for the FS range [0, 1] by Beliakov et al. [21]. Tomasa Calvo et al. [22] highlighted that algebraic T-Ns and T-CNs serve as foundational tools in fuzzy aggregation, thanks to their mathematical simplicity and interpretability within the [0, 1] interval.

The Aczel-Alsina (AA) aggregation operator [23] has gained prominence in MCDM due to its ability to flexibly model relationships between inputs using additive generators. This operator is particularly effective in handling nonlinear interactions and is adaptable to various fuzzy set extensions, such as IFSs, PFSs, Hesitant fuzzy set (HFS), and their higher-order extensions. These extensions have broadened the applicability of AA operators, making them suitable for complex decision-making scenarios under uncertainty, including medical diagnosis [24], environmental impact assessment [25], risk management [26], and supply chain optimization [27]. Researchers have extensively explored these operators to address challenges like evaluating hospital service quality and managing uncertain data in large-scale decision-making [28]. Son et al. applied AA aggregation operators to IF MCDM, demonstrating their effectiveness in complex decision scenarios [29]. Thus, the choice of AA operators in this study is motivated by their enhanced adaptability and efficacy in modeling uncertainty within IF environments, aligning with our objective of improving decision-making processes under uncertainty.

In 1982, Dombi [30] defined Dombi T-Ns and Dombi T-CNs operations, which offer the advantage of variability through the operation of parameters. Liu et al. [31] leveraged Dombi operations in IFSs to develop an MCDM problem using a Dombi Bonferroni mean operator under IF information. Chen and Ye [32] proposed an MCDM problem utilizing Dombi aggregation operators in single-valued neutrosophic information. Shi and Ye [33] extended Dombi operations to neutrosophic cubic sets for travel decision-making problems. Lu and Ye [34] first defined a Dombi aggregation operator for linguistic cubic variables, developing an MCDM method in a linguistic cubic setting. He [35] introduced Typhoon disaster assessment based on Dombi hesitant fuzzy information aggregation operators. Dombi aggregation operators have been widely applied in MCDM due to their flexibility in handling nonlinear interactions. Qiyas et al. [36] introduced intuitionistic fuzzy credibility-based Dombi aggregation operators and successfully applied them to a real-world MCDM problem involving railway train selection. Similarly, Dombi operators have been integrated with power operators [37] for IFSs, and Akram et al. demonstrated the applicability of PF Dombi aggregation operators in complex decision-making scenarios [38].

The choice of AA aggregation operators over other types, such as Dombi, Frank [39], and Archimedean [40], is justified by their unique mathematical properties and superior adaptability to the research objectives of this study. AA operators offer a high degree of parameterization, enabling the modeling of different decision-maker attitudes (e.g., optimism, pessimism) and information fusion behaviors. Their logarithmic-exponential formulation allows for a smooth transition between various standard T-Ns and T-CNs, making them highly adaptable to different fuzzy set extensions. Furthermore, AA operators are capable of handling both weak and strong interactions among input arguments, which is crucial for complex decision-making environments involving uncertainty, hesitation, or partial truth. While Dombi, Frank, and Archimedean operators have their own merits, the AA operators were specifically chosen in this work to exploit their flexibility and adaptability in modeling uncertainty within IF environments. For instance, Chen et al. developed AA-based aggregation operators for IFSs, highlighting their advantages in handling imprecise and indeterminate data [41]. Li et al. applied AA aggregation operators to IF MCDM, demonstrating their effectiveness in complex decision scenarios [42]. Thus, the AA operators are particularly well-suited to the goals of our research, which seeks to enhance decision-making processes under uncertainty.

Group and Overlap Functions

Overlap and Grouping functions have become essential tools in fuzzy decision-making, especially when dealing with complex MCDM problems. Overlap functions were introduced by Bustince et al. [43] to measure the degree of similarity or commonality between two fuzzy sets. These functions assess how much the MDs of two fuzzy values overlap. Unlike traditional T-norms, which focus on strict intersection rules, overlap functions allow for a more flexible comparison, especially when data is partially matching or uncertain.

Overlap functions have been widely used in different fields. For instance, Xu [44] applied them in clustering analysis to compare data similarity. Tapia et al. [45] explored their use in image processing, particularly in edge detection and segmentation tasks. Cabrerizo et al. [46] highlighted their usefulness in classification problems and data fusion, where overlapping or conflicting data needs to be handled effectively. Qiao et al. [47] and [48] further studied the mathematical structure of overlap functions and showed how they improve decision-making by better handling uncertainty and ambiguity. More recently, Zhang et al. [49] and Dai [50] emphasized their importance in uncertainty modeling and pattern recognition.

On the other hand, Group functions were introduced by Sola et al. [51] to aggregate multiple expert opinions into a single, collective decision. These functions are designed to ensure fairness, inclusivity, and consistency in group-based decision scenarios. Group functions [52] are especially useful in policy-making, collaborative design, and resource planning, where different stakeholders contribute diverse assessments. For example, Bedregal et al. [53] highlighted their application in policy formation, while Ahamdani et al. [54] demonstrated their effectiveness in environmental assessments where multiple uncertain factors must be considered. Gonçalves-Coelho and Mourão [55] also developed robust MCDM algorithms under IF environments using these functions.

When Overlap and Group functions are combined with IFS, the decision-making process becomes even more powerful. IFS allows for separate membership and non-membership degrees, which gives a more detailed view of uncertainty. Overlap functions help evaluate how much different IFS values agree or conflict, while group functions help merge expert opinions under the IFS framework. Together, they address the limitations of traditional T-norms and T-conorms, which often fail to handle overlapping, uncertain, or hesitant information.

A good example of their combined use is in criminal justice policy selection, where criteria like public safety, rehabilitation, and cost often overlap or contradict. In such scenarios, traditional fuzzy methods may not be flexible enough to capture the real complexity. However, by using overlap and group functions within an IFS-based framework, it becomes possible to balance all factors more effectively, leading to better, fairer decisions under uncertainty.

Motivation

Current studies have predominantly relied on traditional T-Ns and T-CNs-based aggregation operators to address MCDM problems within the IF environment. Although these operators are mathematically consistent and widely accepted, they often impose rigid logical structures that may not adequately capture the nuances of real-world uncertainty, which frequently involves overlapping information and hesitation. To overcome these limitations, we propose a novel framework that integrates group and overlap functions with AA operational laws in the IFS environment. This study introduces four innovative aggregation operators: Group Overlap Function-Based IF AA Weighted Averaging (GOF-IFAAWA), IF AA Weighted Geometric (GOF-IFAAWG), IF AA Ordered Weighted Averaging (GOF-IFAAOWA), and IF AA Ordered Weighted Geometric (GOF-IFAAOWG). These operators not only handle averaging and geometric aggregation but also incorporate ordered and priority-based considerations. This comprehensive approach allows for a more nuanced management of overlapping and hesitant information, particularly in complex decision-making scenarios where criteria may interact in non-linear ways. For instance, in the context of criminal justice policy selection, these operators can effectively balance the uncertain and overlapping criteria related to public safety, rehabilitation, and cost-efficiency. Furthermore, the adoption of AA operational laws within this framework offers an added advantage due to their non-linear and parametric structure, which enhances adaptability in uncertain environments. The synergy of AA laws with group and overlap functions in the IF context allows for more interpretable, accurate, and robust aggregation of criteria, particularly in decision scenarios characterized by vagueness, expert hesitation, and overlapping information. This methodological shift not only advances the theoretical foundations of fuzzy decision-making but also opens new avenues for practical applications in areas such as healthcare, environmental sustainability, public policy, and intelligent systems.

Major Contributions

The major contributions in this research as:

•   We have developed a novel decision-making framework by integrating group and overlap functions with AA operational laws under the IFS environment. This integration significantly enhances the flexibility and adaptability of aggregation processes in complex decision-making scenarios. The framework allows for a more nuanced representation of uncertainty and hesitation, making it highly suitable for real-world applications where decision criteria are often overlapping and imprecise.

•   We introduce four new aggregation operators, including Group Overlap Function-Based IF AA Weighted Averaging (GOF-IFAAWA), IF AA Weighted Geometric (GOF-IFAAWG), IF AA Ordered Weighted Averaging (GOF-IFAAOWA), and IF AA Ordered Weighted Geometric (GOF-IFAAOWG). These operators are designed to handle averaging, geometric, ordered, and priority-based aggregation under uncertainty. They provide a more comprehensive approach to information fusion, enabling decision-makers to consider various aspects of complex problems in a structured and systematic manner.

•   We have applied the proposed framework to a real-world problem involving AI-based criminal justice policy selection. This application demonstrates the practical utility and effectiveness of our proposed methods in identifying optimal policy alternatives. The results show that our framework can effectively balance the uncertain and overlapping criteria related to public safety, rehabilitation, and cost-efficiency, providing decision-makers with valuable insights and support.

•   Through a comparative analysis with existing methods, including IF weighted Average, IF weighted geometric, IF Aczel Alsina, IF Aczel Alsina Power, IF Einstein, and IF Einstein Power aggregation operators, we have demonstrated the superiority of our proposed operators in managing overlapping and hesitant information. The analysis underscores the enhanced performance and reliability of our approach in complex decision-making environments, highlighting its potential for broader application across various domains.

Paper Structure

The remainder of the paper is structured as follows. Section 2 explains the basic ideas such as Intuitionistic Fuzzy Sets (IFS), t-norms, t-conorms, and Aczel-Alsina (AA) operational laws. In Section 3, we introduce new operational laws using Group and Overlap Functions (GOF) with IFS and AA. Section 4 defines the GOF-based IFAA Weighted Average and Ordered Weighted Average aggregation operators and discusses their properties. Section 5 presents the GOF-based IFAA Weighted Geometric and Ordered Weighted Geometric aggregation operators with a detailed explanation of their behavior. Section 6 describes a step-by-step MCDM algorithm to solve decision-making problems using the proposed operators. Section 7 gives numerical examples to show how the method works in real situations. Section 8 covers the implementation steps of the method. Section 9 studies how changing the parameter p affects the results of the proposed operators. Section 10 compares our method with existing techniques to highlight the improvements. Section 11 provides a summary of the overall comparison and key points. Finally, Section 12 concludes the study with important findings and suggests future research directions.

2  Preliminaries

The fundamental ideas of IFSs are examined in this section, with particular attention paid to the functions and characteristics of T-Ns and T-CNs as well as the operational processes of Intuitionistic fuzzy numbers (IFNs). Additionally, we examine group functions, overlap functions, and their associated properties, including the AA T-N and AA T-CN, highlighting their distinctive characteristics and applications.

Definition 1. [5] An IFS A in universal set X, is defined as:

A={(x,μA(x),νA(x))∣x∈X}(1)

here μA with 0≤μA(x)≤1 represents the MD and νA with 0≤νA(x)≤1 represents the NMD and πA(x)=1−μA(x)−νA(x) indicates the degree of indeterminacy, for all x∈X. The function μA(x), νA(x) denotes the NMD.

Definition 2. [43] Let x and y be any elements belonging to [0,1]. A GF, is a mapping G:I×I⟶I, is defined by the properties:

•   G1: G is commutative

•   G2: G(x,y)=0 iff xy=0

•   G3: G(x,y)=1 iff xy=1

•   G4: G is increasing

•   G5: G is continuous

Example 1. Here are some commonly used GFs

1.   Continuous T-N and positive T-CN is are examples of GFs

2.   The function Gp(x,y)=1−(1−x)p(1−y)p is an GFs

where Gp is a mapping or function Gp:I×I⟶I. p>0 and x,y∈I.

3.   The function  GDB(x,y)={x+y−2xy2−x−y,ifx≠1,y≠11,ifx=y=1 is an GFs

4.   The function  GMp(x,y)=max(xpyp) is an GFs

5.   The function  GMid(x,y)=xy(x+y2) is an GFs

6.   The function  Gmp(x,y)=1−min{(1−x)p,(1−y)p}max{x2,y2} is an GFs

Definition 3. [43] Let x and y be any elements belonging to [0,1]. An OverlapFunction, is mapping O:I×I⟶I, is defined by the following properties:

•   O1: O is commutative

•   O2: O(x,y)=0 iff xy=0

•   O3: O(x,y)=1 iff xy=1

•   O4: O is increasing

•   O5: O is continuous

Example 2. Here are some commonly used overlap functions (OF)

1.   Continuous t-norm and positive t-norm are examples of OFs

2.   The function Op(x,y)=xpyp is an OFs

where Op is a mapping or function Op:I×I⟶I. p>0 and x,y∈I

3.   The function ODB(x,y)={2xyx+yifx+y≠00ifx+y=0 is an OFs

4.   The function O+(x,y)=2xy1+xy is an OFs

5.   The function OMid(x,y)=xy(x+y2) is an OFs

6.   The function Omm(x,y)=min{x,y}max{x2,y2} is an OFs

Definition 4. [23] The Aczel Alsina T-norm is defined as:

T(x,y)=e−((−ln⁡x)p+(−ln⁡y)p)1p(2)

where x,y∈[0,1] and p>0. This operator is particularly suitable for cases where a softer form of intersection is needed, as it balances the combination of inputs.

Definition 5. [23] The AAT-CN S is defined as:

S(x,y)=1−e−((−ln⁡(1−x))p+(−ln⁡(1−y))p)1p(3)

where x,y∈[0,1] and p>0. This operator is often used for modeling union operations in fuzzy logic, providing a smooth and parameterized way to combine inputs.

3  Group Overlap Function Based IF Aczel Alsina Operational Laws

Since Aszel-Alsina t-norm and t-conorm are more flexible in the decision making environment. Also, overlap and grouping functions have emerged as a focal point of research in the field of aggregation functions. In this section, we define some novel operational laws based on overlap and grouping functions with Aczel-Alsina norms underthe IFS environment. It can be defined as:

Definition 6. See Appendix A

Theorem 1. Assume that γ=(μγ,νγ),γ1=(μγ1,νγ1), and γ2=(μγ2,νγ2) are intuitionistic fuzzy values or numbers. Then we have

[1]   γ1⊕fγ2=γ2⊕fγ1

[2]   γ1⊗fγ2=γ2⊗fγ1

[3]   λ(γ1⊕fγ2)=λγ1⊕fλγ2

[4]   γ(λ1⊕fλ2)=λ1γ⊕fλ2γ

[5]   (γ1⊗fγ2)λ=γ1λ⊗fγ2λ

[6]   γ1λ⊗fγ2λ=(γ)(λ1⊗fλ2)

Proof. See Appendix B ◼

4  Group and Overlap IF AA Weighted Averaging Operator

In this section, we present the Aczel Alsina averaging operator based on the overlap and grouping function under the IF environment. The Aczel-Alsina operator is a type of triangular norm and conorm that’s highly flexible due to its variable parameters. It has been applied to various types of fuzzy to MCDM problems. Overlap and grouping functions are fundamental concepts in fuzzy logic and set theory. They are used to model the intersection and union of fuzzy sets in a way that captures the degree of overlapping or grouping between sets. These functions are crucial for handling uncertainty and vagueness in data, providing a more nuanced approach than traditional binary set operations. It can be defined as:

Definition 7. See Appendix C

Theorem 2. Assume that γm=(μγm,νγm) are intuitionistic fuzzy numbers represented as for each 0≤m≤s. The aggregated outcome obtained using the GOF-IFAAWAf operator is also an IFV, which can be expressed as follows: GOF-IFAAWAf(γ1,γ2,…,γs)=

⟨1−e−(∑m=1s(Δm(N(GG(log⁡(μγm))))))1p,e−(∑m=1s(Δm(GO(−log⁡(vγm)))))1p⟩(4)

Proof. See Appendix D◼

Based on Theorem 1, we have some properties of the GOF−IFAAWAf operator.

Proposition 1. Let γm=(μγm,νγm),(0≤m≤s) are IFVs in L∗ then, we have the following properties

[1. Idempotency:] If all γm(0≤m≤s) are equal, i.e., γm=γ, for all 0≤m≤s, then

GOF−IFAAWAf(γ1,γ2,…,γs)=γ

Proof. See Appendix E ◼

[2. Boundary:] If γm=(μγm,νγm),(0≤m≤s) are IFVs, then

γmin≤GOF−PIFWAf(γ1,γ2,…,γs)≤γmax

where γmin=min{γ1,γ2,…,γs} and γmax=maxγ1,γ2,…,γs.

Proof. See Appendix F ◼

[3. Monotonicity:] Let γm=(μγm,νγm) and γm∗=(μγm∗,νγm∗) for 0≤m≤s are IFVs under the order L∗. Suppose γm≤Lγm∗, meaning that μγm≤μγm∗ and νγm≥νγm∗. This implies that GG(μγm)≤GG(μγm∗) and GO(νγm)≥GO(νγm∗) for all m. Then

GOF−IFAAWAf(γ1,γ2,…,γs)≤GOF−IFAAWAf(γ1∗,γ2∗,…,γs∗)(5)

Proof. See Appendix G ◼

[3. Monotonicity:] Let γj=(μγj,νγj) and γj∗= (μγj∗,νγj∗),(j=1,2,…,n) be two collection of IFVs L∗, and γj≤Lγj∗ , i.e., μγj≤μγj∗ and νγj≥νγj∗, implies GG(μγj)≤GG(μγj∗) and GO(νγj)≥GO(νγj∗) for all j; then

EGO−IFWAωf(γ1,γ2,…,γn)≤EGO−IFWAωf(γ1∗,γ2∗,…,γn∗)

Proof. See Appendix H ◼

Group and Overlap IF AA Ordered Weighted Averaging Operator (GOF-IFAAOWA)

In this section, we propose the Aczel Alsina order weighted average operator based on overlap and grouping function under the IFS setting. The mathematical formulation for GOF-IFAAOWA:

Definition 8. See Appendix I

Theorem 3. Assume that γm=(μγm,νγm) are IFVs represented as for each 0≤m≤s. The aggregated outcome obtained using the GOF-AAIFOWAf operator is also an IFV, which can be expressed as follows: GOF-AAIFOWAf(γ1,γ2,…,γs)=

⟨1−e−(∑m=1s(Δm(N(GG(log⁡(μγa(m)))))))1p,e−(∑m=1s(Δm(GO(−log⁡(vγa(m))))))1p⟩(6)

Proof. See Appendix J ◼

Proposition 2. Let γm=(μγm,νγm) for 0≤m≤s are IFVs in L∗ and the weight vector Δ=(Δ1,Δ2,…,Δs)T, where each weight Λm∈[0,1], signifying the condition ∑m=1s(Δm)=1. Consequently, the following properties are established.

[1. Idempotency:] If all γm(m=1,2,…,s) are equal, i.e., γm=γ for all m=1,2,…,s, then

GOF−IFAAOWAf(γτ(1),γτ(2),…,γτ(s))=γ.(7)

Proof. See Appendix K ◼

[2. Boundary:] Let γm=(μγm,νγm),(0≤m≤s) be a collection of IFVs. Then,

γmin≤GOF−IFAAOWAf(γτ(1),γτ(2),…,γτ(s))≤γmax,(8)

where γmin=min{γ1,γ2,…,γs} and γmax=max{γ1,γ2,…,γs}.

Proof. See Appendix L ◼

[3. Monotonicity:] Let γm=(μγm,νγm) and γm∗=(μγm∗,νγm∗) for 0≤m≤s are the collections of IFVs under the order L∗. If we assume that γm≤Lγm∗, this means that μγm≤μγm∗ and νγm≥νγm∗, Then

GOF−IFAAOWAf(γτ(1),γτ(2),…,γτ(s))≤GOF−IFAAOWAf(γτ(1)∗,γτ(2)∗,…,γτ(s)∗)(9)

Proof. See Appendix M ◼

5  Group and Overlap Based IF-AA Weighted Geometric Operator

In this section, we present the Aczel Alsina geometric operator based on the overlap and grouping function under the IF environment. The Aczel-Alsina operator is a type of triangular norm and conorm that’s highly flexible due to its variable parameters. It has been applied to various types of fuzzy to MCDM problems. Overlap and grouping functions are fundamental concepts in fuzzy logic and set theory. They are used to model the intersection and union of fuzzy sets in a way that captures the degree of overlapping or grouping between sets. These functions are crucial for handling uncertainty and vagueness in data, providing a more nuanced approach than traditional binary set operations. It can be defined as:

Definition 9. See Appendix N

Theorem 4. Assume that γm=(μγm,νγm) be the collection of IFVs represented as for each 0≤m≤s. The aggregated outcome obtained using the GOF-AAIFGf operator is also an IFV, which can be expressed as follows: GOF-AAIFGf(γ1,γ2,…,γs)=

⟨e−(∑m=1s(Δm(GO(−log⁡(vγm)))))1p,1−e−(∑m=1s(Δm(N(GG(log⁡(μγm))))))1p⟩(10)

Proof. See Appendix O ◼

Based on Theorem 1, we have some properties of the GOF−IFAAGf operator.

Proposition 3. Let γm=(μγm,νγm),(0≤m≤s) be the collection of IFVs in L∗ then, we have the following properties.

[1. Idempotency:] If all γm(0≤m≤s) are equal, i.e, γm=γ, for all 0≤m≤s, then

GOF−IFAAGf(γ1,γ2,…,γs)=γ

Proof. See Appendix P ◼

[2. Boundary:] If γm=(μγm,νγm),(0≤m≤s) be the collection of IFVs, then

γmin≤GOF−PIFGf(γ1,γ2,…,γs)≤γmax

where γmin=min{γ1,γ2,…,γs} and γmax=maxγ1,γ2,…,γs.

Proof. See Appendix Q ◼

[3. Monotonicity:] Let γm=(μγm,νγm) and γm∗=(μγm∗,νγm∗) for 0≤m≤s be the collections of IFVs under the order L∗. Suppose γm≤Lγm∗, meaning that μγm≤μγm∗ and νγm≥νγm∗. This implies that GG(μγm)≤GG(μγm∗) and GO(νγm)≥GO(νγm∗) for all m. Then

GOF−IFAAGf(γ1,γ2,…,γs)≤GOF−IFAAGf(γ1∗,γ2∗,…,γs∗)(11)

Proof. See Appendix R ◼

5.1 Group and Overlap Based IF-AA Ordered Weighted Geometric Operator

In this section, we propose the Aczel-Alsina order weighted geometric operator based on the overlap and grouping function under the IFS setting. The mathematical formulation for GOF-IFAAOWA:

Definition 10. See Appendix S ◼

Theorem 5. Assume that γm=(μγm,νγm) be the collection of IFVs represented as for each 0≤m≤s. The aggregated outcome obtained using the GOF-AAIFOWGf operator is also an IFV, which can be expressed as follows: GOF-AAIFOWGf(γ1,γ2,…,γs)=

⟨e−(∑m=1s(Δm(GO(−log⁡(vγa(m))))))1p,1−e−(∑m=1s(Δm(N(GG(log⁡(μγa(m)))))))1p⟩(12)

Proof. See Appendix T ◼

Proposition 4. Let γm=(μγm,νγm) for 0≤m≤s be a collection of IFVs in L∗ and the weight vector Δ=(Δ1,Δ2,…,Δs)T, where each weight Λm is restricted to the interval [0,1], signifying the condition ∑m=1s(Δm)=1. Consequently, the following properties are established.

[1. Idempotency:] If all γm(m=1,2,…,s) are equal, i.e., γm=γ for all m=1,2,…,s, then

GOF−IFAAOWGf(γτ(1),γτ(2),…,γτ(s))=γ.(13)

Proof. See Appendix U ◼

[2. Boundary:] Let γm=(μγm,νγm),(0≤m≤s) be a collection of IFVs. Then

γmin≤GOF−IFAAOWGf(γτ(1),γτ(2),…,γτ(s))≤γmax,(14)

where γmin=min{γ1,γ2,…,γs} and γmax=max{γ1,γ2,…,γs}.

Proof. See Appendix V ◼

[3. Monotonicity:] Let γm=(μγm,νγm) and γm∗=(μγm∗,νγm∗) for 0≤m≤s represent two collections of IFVs under the order L∗. If we assume that γm≤Lγm∗, this means that μγm≤μγm∗ and νγm≥νγm∗, Then

GOF−IFAAOWGf(γτ(1),γτ(2),…,γτ(s))≤GOF−IFAAOWGf(γτ(1)∗,γτ(2)∗,…,γτ(s)∗)(15)

Proof. See Appendix W ◼

6  Optimising Multiple Attributes Decision Making by Applying the GOF-IFAA Weighted Aggregation Operator

In this section, we will discuss the MCGDM problem based on the proposed methodology to demonstrate its accuracy and effectiveness. To solve the MCDM problem, the above steps are followed:

Step-1: Let N={N1,N2,…,Nn} represent the set of alternatives and C={C1,C2,…,Cm} represent the set of attributes. For each j=1,2,…,m, each option Ni on attribute Cj is represented by an IFV in L∗, where i=1,2,…,n. The value μij represents the extent to which alternative xi satisfies attribute gj, while the value νij represents the extent to which Ni does not satisfy Cj. At that point, Γij=(μij,νij) . All values of i from 1 to n and all values of j from 1 to m satisfy these conditions. Here are the equations: μij∈[0,1] , νij∈[0,1], and μij+νij≤1. A straightforward method to define an MCDM issue is using the IF decision matrix D=(dij)n×m=((μij,νij))n×m, i.e., D=[(μ11,ν11)(μ12,ν12)⋯(μ1m,ν1m)(μ21,ν21)(μ22,ν22)⋯(μ2m,ν2m)⋮⋮⋱⋮(μn1,νn1)(μn2,νn2)⋯(μnm,νnm)].

Step-2: To model ambiguity in decision-making, we convert discrete numerical values from Table 1 (e.g., scores like 92, 45, 90) into fuzzy membership values (μ∈[0,1]) using the logistic function:

μ(x)=11+e−k(X−c)(16)

X: is the discrete values, c is Midpoint of the data expected range and k: Controls the steepness of the curve.

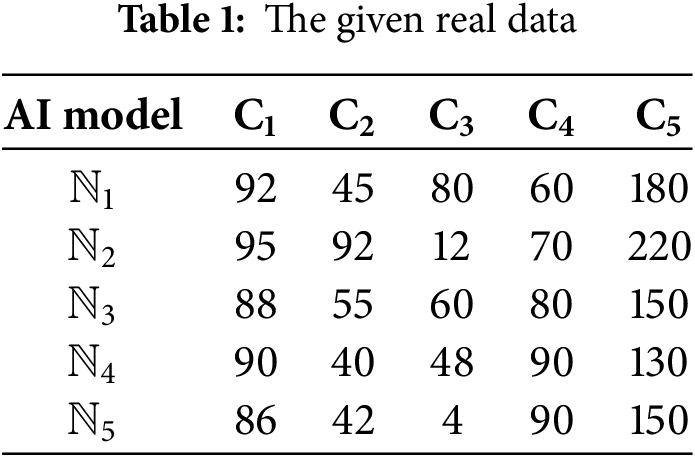
Example: For X=92 in Table 1:

μ(92)=11+e−0.2(92−50)=11+e−8.4≈0.6262.

Step-3: To change the fuzzy values or numbers into intuitionistic fuzzy values or numbers, we use

νi=1−μi(17)

Step-4: Normalize D, if required, into R~=[r~ij]m×n as follows:

r~ij={⟨γij⟩        for benefit type criteria⟨γ~ij⟩          for cost type criteria. (18)

where γ~ij is the complement of γij

Step-5: When making a choice, weights indicate how important one criterion is in relation to the others. Subjective weighting relies on the views of experts, whereas quantitative weighting makes use of a variety of methods. In this case, the weight criterion is determined using entropy techniques.

The entropy for the j-th criterion is given by:

Ej=−k∑i=1Npijlog⁡(pij)(19)

and the weights formula as:

wj=1−Ej∑j=1k(1−Ej)(20)

Step-6: Utilize the GOF-IFAAWA operator to aggregate all qij for each alternative Yi as follows.

γi=GOF−IFAAWAf(γ1,γ2,…,γs)(21)

or the GOF-IFAAWG operators

γi=GOF−IFAAWGf(γ1,γ2,…,γs)(22)

Step-7:Evaluate the score value of the accumulated matrix of step 3 by using (8).

s=μ−ν(23)

In cases where score values are equal, apply an accuracy function a to the aggregated results to resolve ties and finalize the ranking. The accuracy function provides a secondary measure of performance, ensuring a clear distinction between alternatives with equal score values. This ensures the robustness and reliability of the decision-making process. The mathematical formulation of the accuracy function is given below:

a=μ+ν(24)

Step-8: Rank the alternatives N={N1,N2,…,Nn} in descending order and select the appropriate ones.

7  A Case Study: AI-Based Criminal Justice Policy Selection

Artificial intelligence (AI) is increasingly being used to support policy decisions in the criminal justice system. Choosing the most appropriate AI-based solution requires evaluating different alternatives across multiple criteria. In this example, we consider five policy alternatives: predictive policing systems, AI-assisted sentencing tools, rehabilitation-focused AI applications, public safety monitoring systems, and AI-supported social service systems. These are evaluated based on criteria such as accuracy, ethical implications, cost-effectiveness, privacy, and overall societal impact.

Alternatives

Predictive Policing Systems (A1): Use historical crime data to forecast potential crime hotspots, helping allocate police resources more efficiently. However, these systems may reflect biases present in the original data, raising fairness concerns.

AI-Assisted Sentencing Tools (A2): Provide sentencing recommendations based on prior legal cases. They promote consistency in judicial decisions but depend heavily on the quality and fairness of the input data.

Rehabilitation-Focused AI Applications (A3): Personalize rehabilitation programs for offenders using AI, aiming to reduce repeat offenses. These systems require tailored data and are generally cost-intensive.

Public Safety Monitoring Systems (A4): Rely on AI to monitor public areas for suspicious behavior, enhancing safety. Despite their utility, they may raise public concerns about privacy and surveillance.

AI-Based Social Service Systems (A5): Focus on supporting reintegration through human-centered services. They are considered more ethical but demand collaboration with social systems and greater financial investment.

Evaluation Criteria

Accuracy (C1): Critical for ensuring reliable outcomes, especially for alternatives like A1 and A2, where poor accuracy can lead to serious consequences.

Ethical Implications (C2): Ethical concerns such as fairness, bias, and discrimination must be considered. Tools like A3 are often viewed more favorably from an ethical standpoint.

Cost-Effectiveness (C3): Implementation and maintenance costs vary across systems. While tools like A2 are relatively affordable, systems such as A4 or A3 may require significant investment.

Privacy (C4): Ensuring data protection and responsible use is essential, particularly for monitoring systems (A4) and any tool handling sensitive personal data.

Societal Impact (C5): Includes long-term public trust, rehabilitation success, and social reintegration. Social service-focused systems (A5) are often considered to have a high positive impact.

8  The Process of Implementing

In our study on AI-based criminal justice policy selection, we evaluated four policy alternatives against five key criteria. The dataset was built using expert opinions, official policy reports, and historical criminal justice data. Experts assessed each policy’s performance per criterion using linguistic terms, which were converted into fuzzy values to manage uncertainty and subjectivity. After normalizing and preprocessing the data for consistency, we applied fuzzy aggregation operators to evaluate the policies effectively.

Step 1: Table 1 presents the raw performance data for each AI model across all criteria.

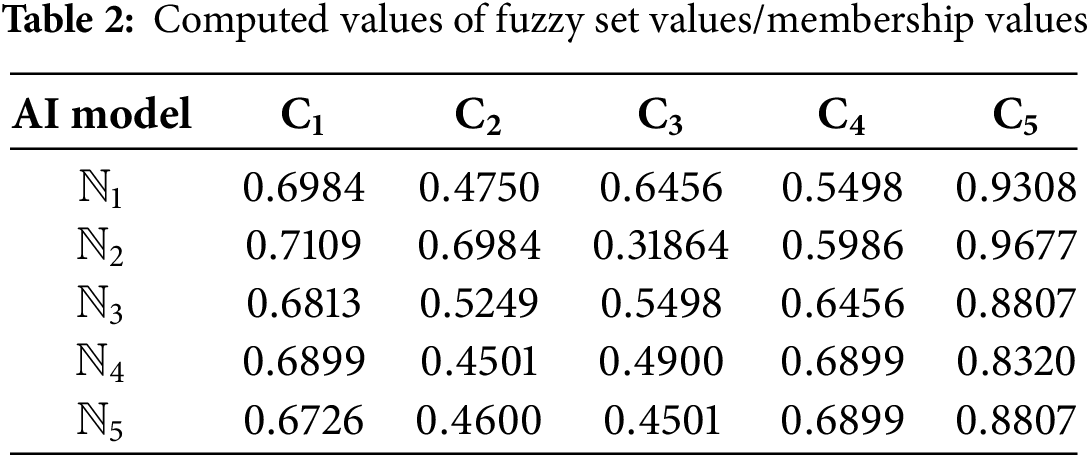
Step 2: Real data was transformed into fuzzy sets (FS) using Eq. (22), with results shown in Table 2. For example, for X=92:

μ(92)=11+e−0.2(92−50)=11+e−8.4≈0.6984.

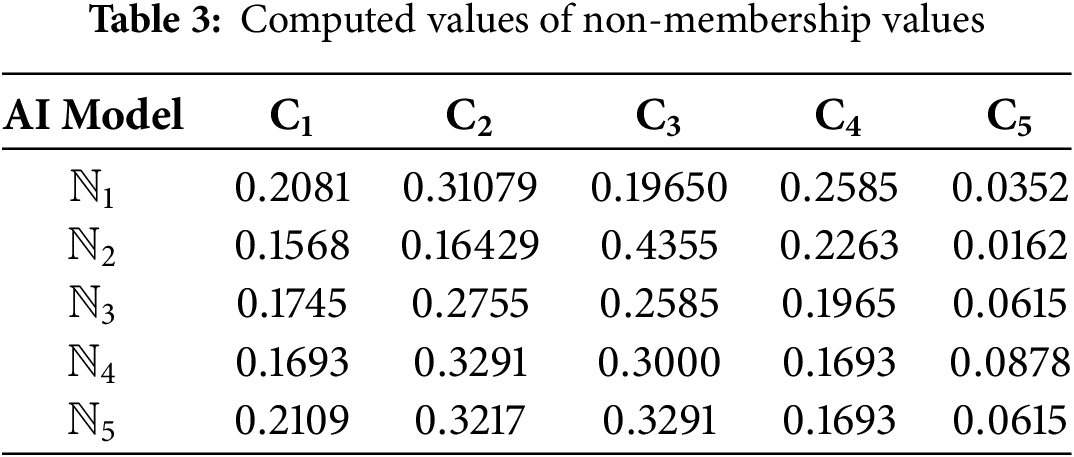
Step 3: Non-membership degrees (NMD) were calculated using Eq. (23) and are displayed in Table 3. For instance, with μ=0.6984:

νi=1−μi=1−0.6984=0.2081.(25)

Step 4: Fuzzy set values were converted into intuitionistic fuzzy values (IFVs) as shown in Table 4.

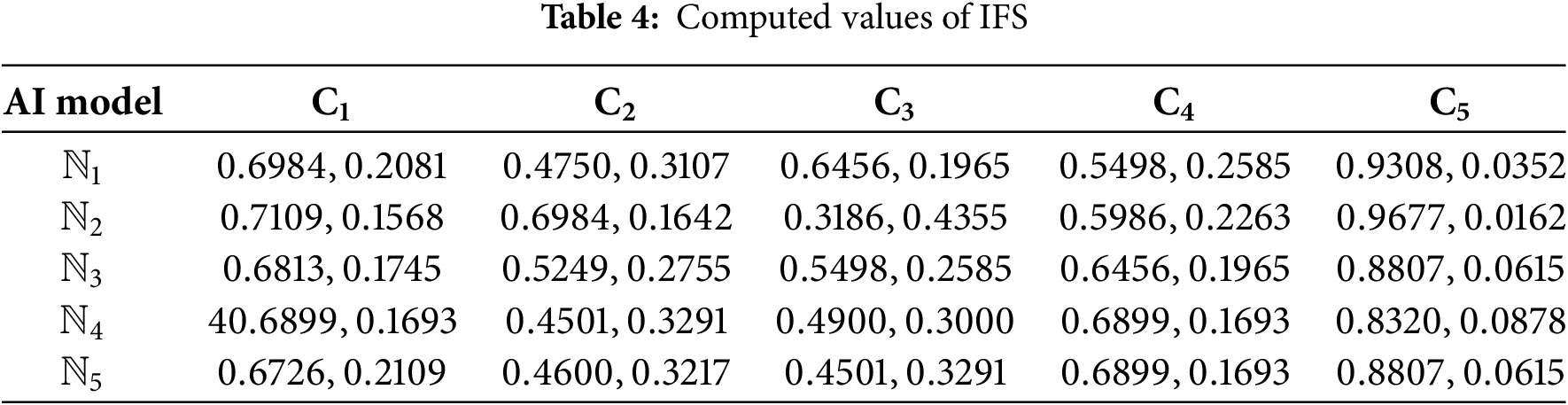
Step 5: Criteria weights, derived from Eq. (20), are exhibited in Table 5.

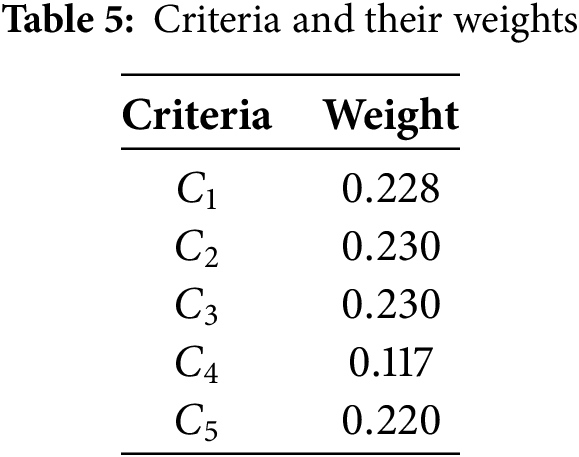
Step 6: Aggregate values from the GOF−IFAAWAωf operator were combined using Eq. (9) and are shown in Table 6.

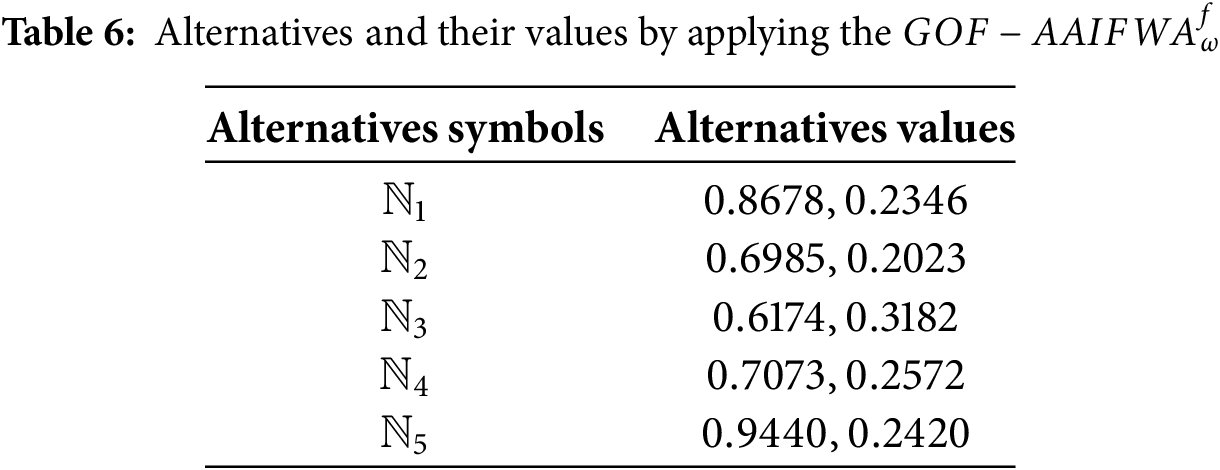
Step 7: Total values from the GOF−IFAAWgωf operator were aggregated using Eq. (16) and are presented in Table 7. Eq. (11) combined total values for the GOF−IFAAOWAωf operator, as shown in Table 8.

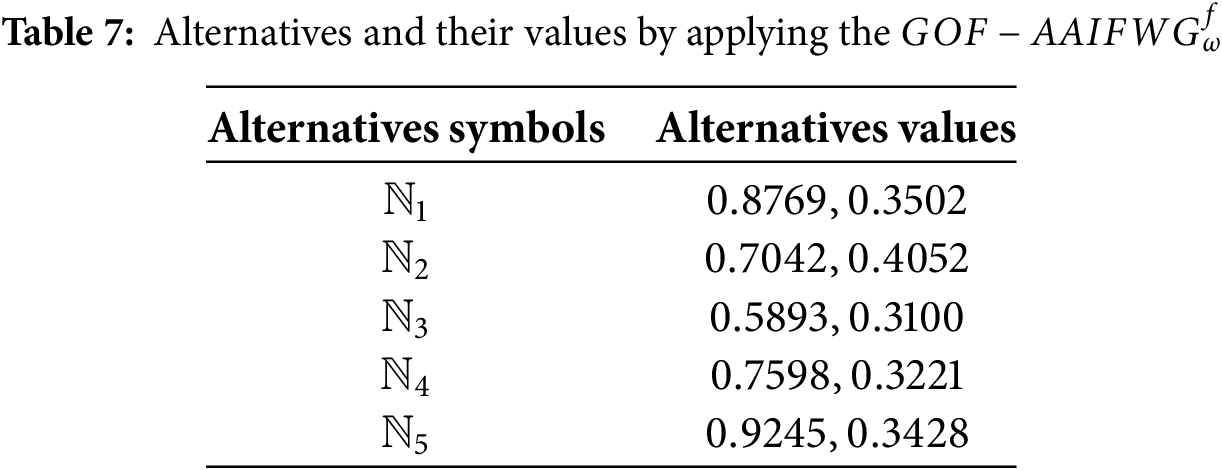
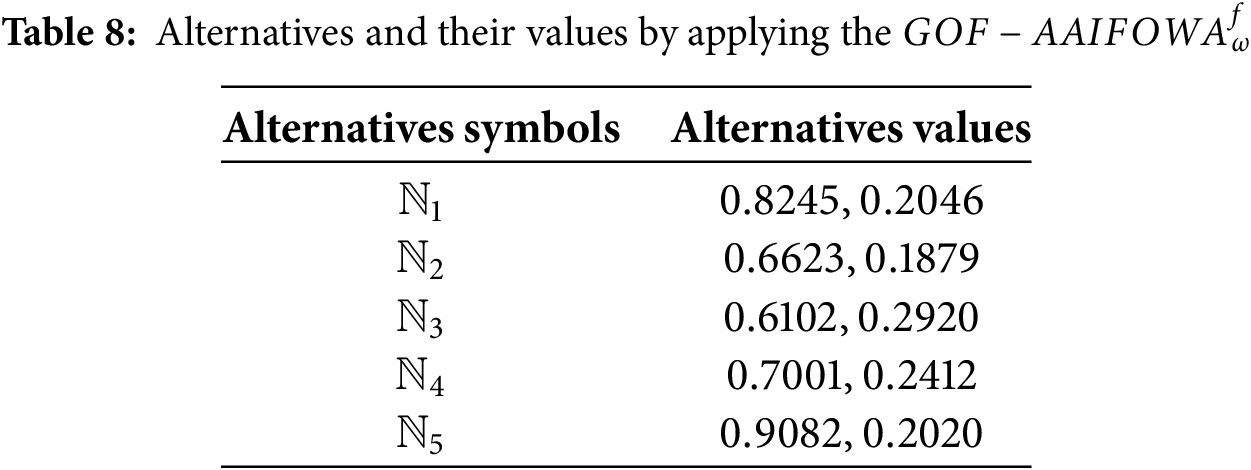
Step 8: Eq. (18) aggregated total values for the GOF−IFAAOWGωf operator, with results in Table 9.

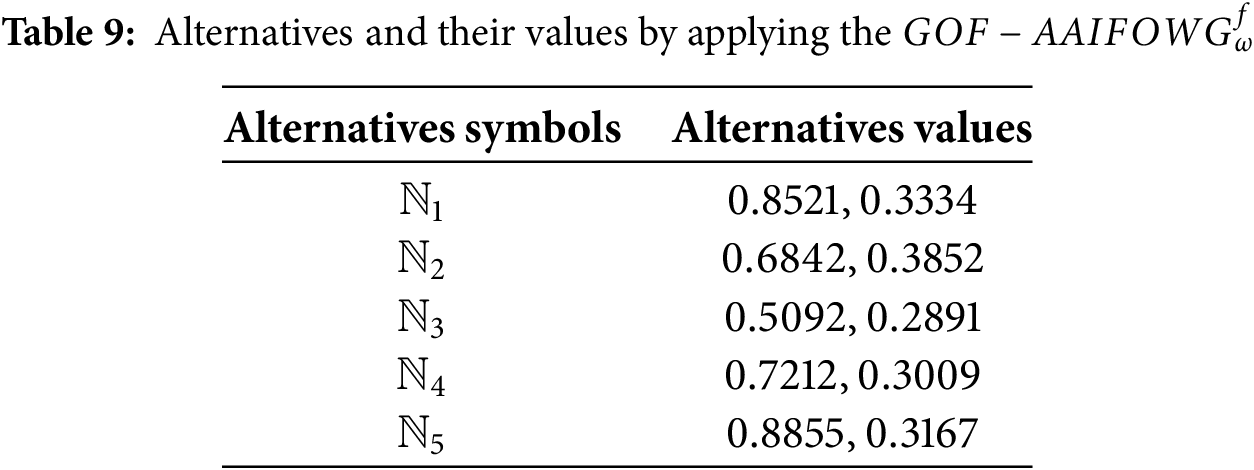
Step 9: Score values for the GOF−IFAAWAωf operator are displayed in Table 10. Score values for the GOF−IFAAWGωf, GOF−IFAAOWAωf, and GOF−IFAAOWGωf operators are shown in Tables 11–13, respectively.

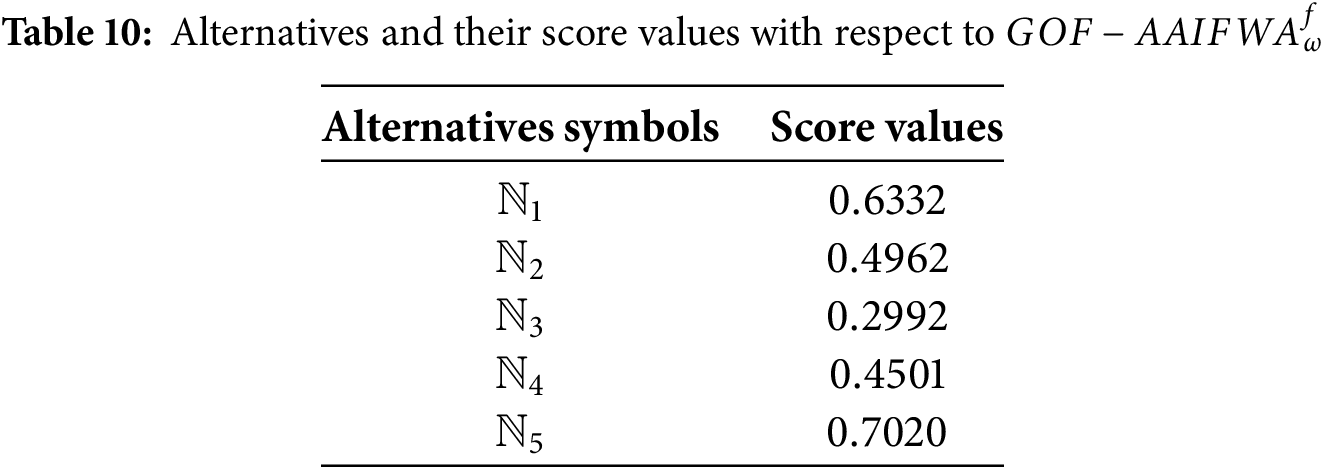
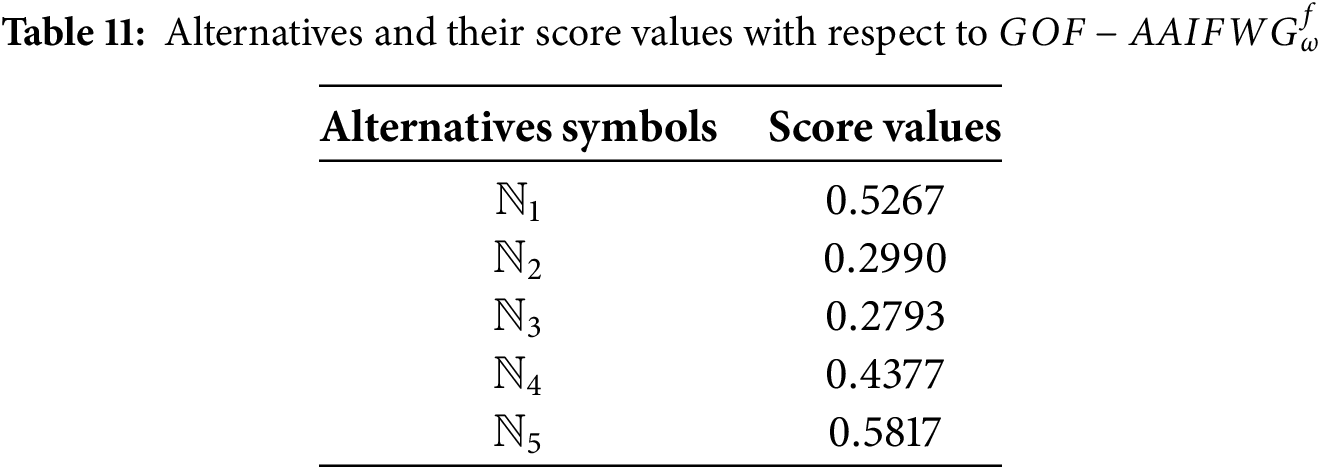
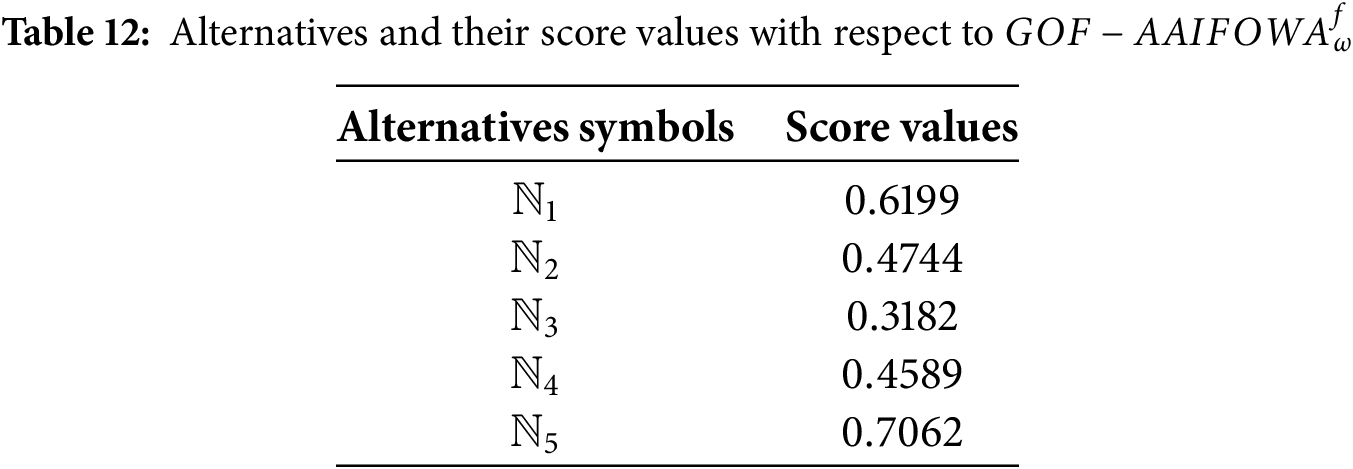
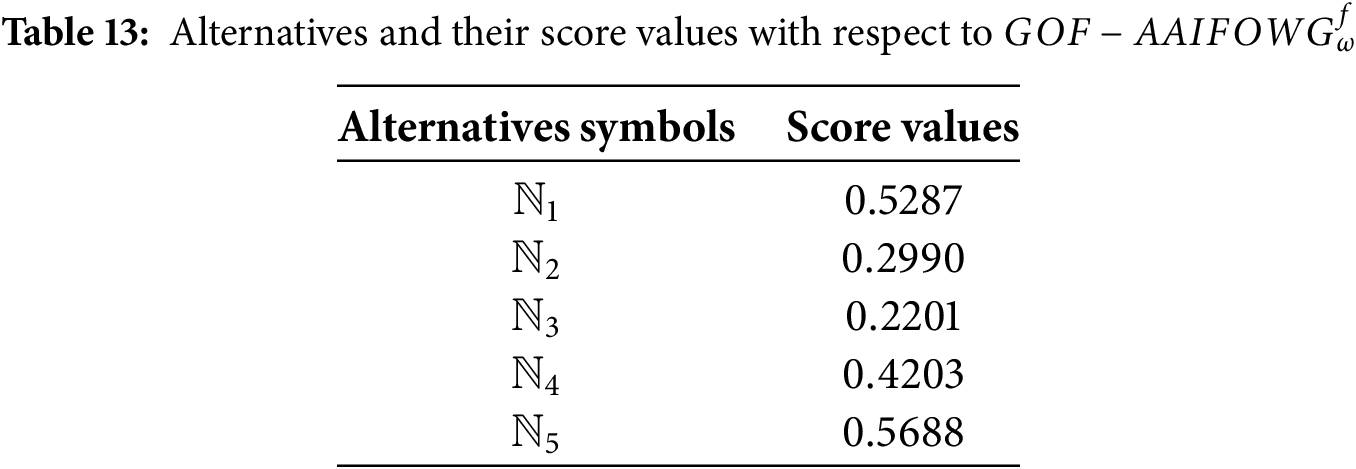
Step 10: Tables 14 to 17 rank the alternatives based on the GOF−IFAAWAωf, GOF−IFAAWGωf, GOF−IFAAOWAωf, and GOF−IFAAOWGωf operators, respectively.

9  Influence of Parameter p on Both GOF-AAIFWAωf and GOF−AAIFWGωf Operators

The operator GOF−IFAAWAωf and the operator GOF−IFAAWGωf are highly dependent on the parameter p. Determining the level of significance given to certain features may be accomplished by decision-makers by manipulating the weights given to individual criteria p. When making decisions in the real world, this flexibility is essential for dealing with uncertainty and fluctuation. By fine-tuning p, a balance may be achieved between giving priority to important criteria and giving equal weight to all characteristics, guaranteeing results that are resilient and suitable for the given context. The parameter p is a crucial control variable that influences the aggregation of criteria in the decision-making process in both the GOF−IFAAWAωf and GOF−IFAAWGωf operators.

The parameter p plays a critical role in the aggregation process of the proposed operators (GOF-IFAAWA and GOF-IFAAWG), as it controls how individual criteria and their interdependencies contribute to the final decision. A higher value of p emphasizes more dominant criteria, whereas a lower value tends to equalize the influence across all criteria. The sensitivity of the proposed operators to p means that their selection can significantly influence the decision outcomes. For example, in contexts where specific criteria are more important, such as treatment effectiveness in healthcare, a higher p may be more suitable. Conversely, when criteria hold similar importance, a lower or moderate value may provide a more balanced outcome. Choosing an appropriate value for p poses practical challenges, as it often requires domain-specific knowledge or trial-and-error experimentation. In practice, three main strategies are used: (1) leveraging expert opinions to reflect the relative importance of criteria; (2) analyzing historical or empirical data to test different p values; and (3) aligning the selection of p with the context of the decision-making problem. For instance, a balanced business decision might call for a moderate p, while a high-stakes public policy issue might necessitate a more skewed weighting favoring critical criteria. To guide the selection process, sensitivity analysis can be a valuable tool. By varying p over a defined range (e.g., 0 to 1), decision-makers can observe how rankings and criteria weights shift, thereby identifying values of p that produce stable and consistent outcomes. This analysis reveals the robustness of the aggregation operators and helps fine-tune them for specific applications. Ultimately, whether through expert input, empirical validation, or automated optimization techniques, selecting the optimal value of p is essential to ensure reliable and accurate decision-making results.

Impact of Parameterp with Respect toGOF−IFAAWAωf Operator

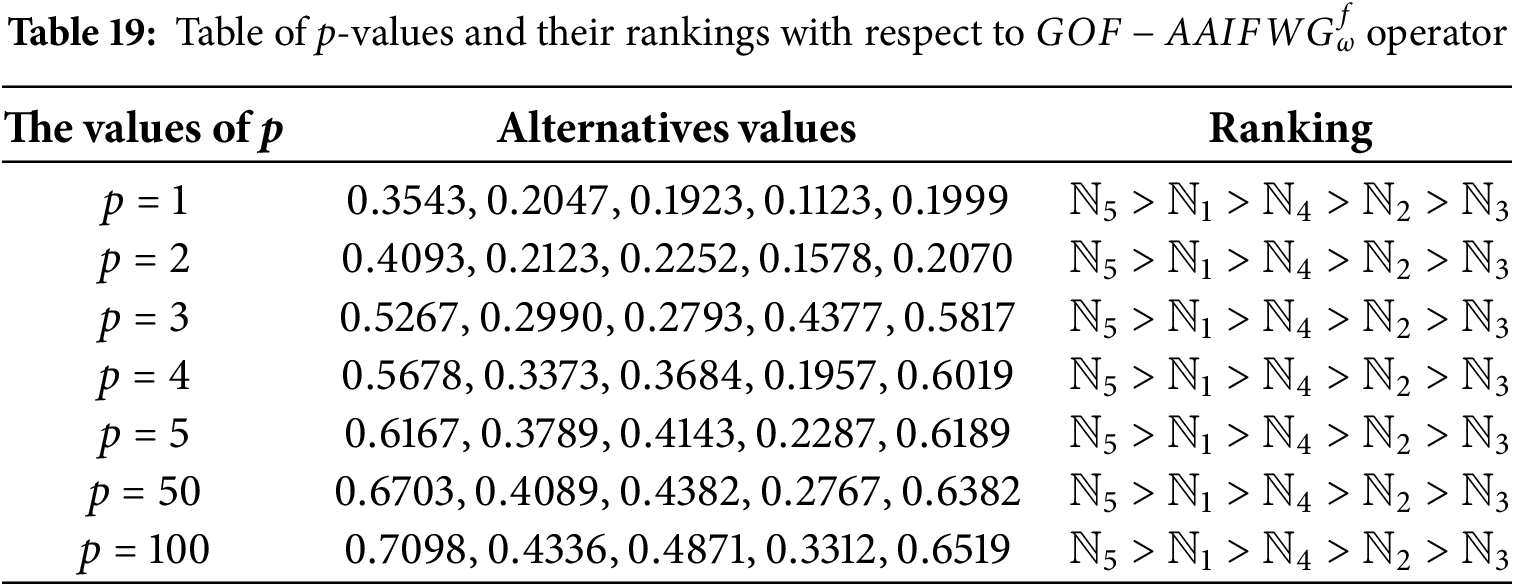
Table 18 and Fig. 1 represent the impact of parameter p on the GOF−IFAAWAωf operator for every possibility. The patterns show how the worth of options changes when p rises.

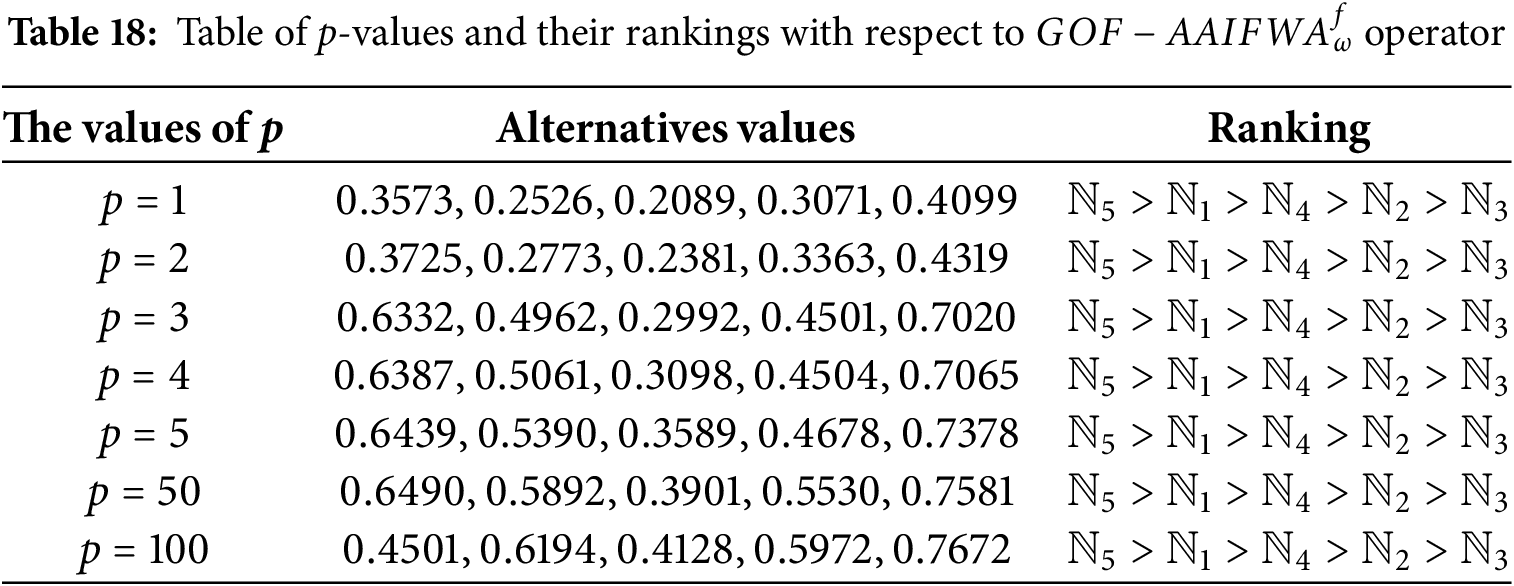
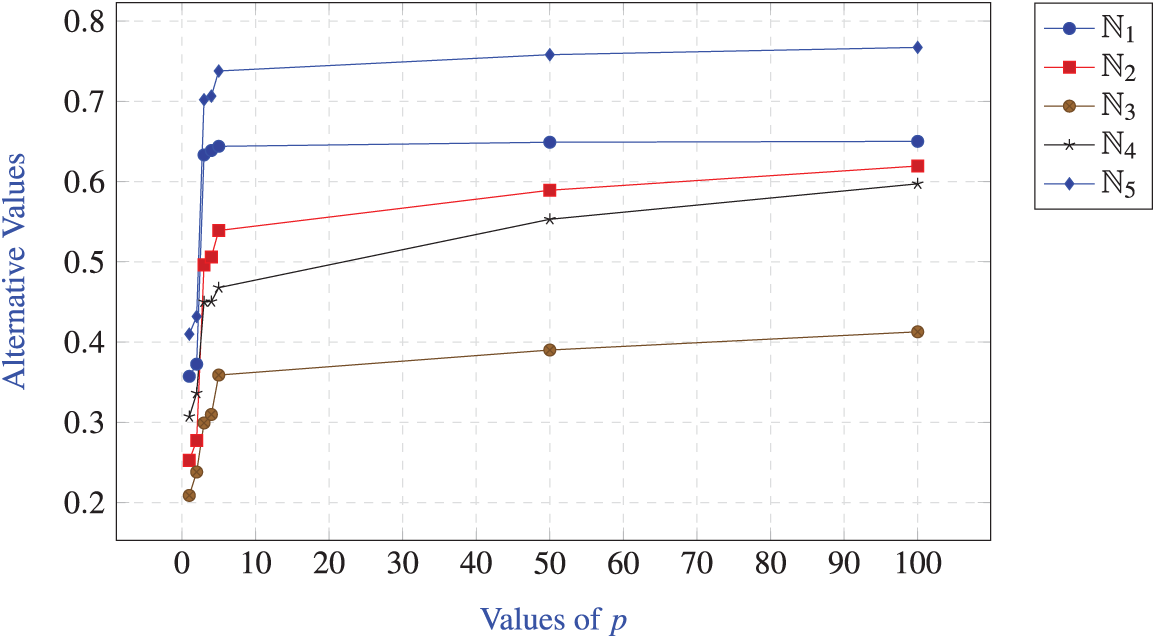
Figure 1: Effect of parameter p on GOF−AAIFWAωf operator

Table Observations: Table 18 shows that the values of all options tend to grow as p increases. The order of the alternatives is maintained regardless of the p-values, with N5>N1>N4>N2>N3. When p is less (e.g., between 1 and 5), significant changes occur; when p is bigger (e.g., between 50 and 100), changes become more gradual.

Graph Observations: Fig. 1 shows that N5 routinely displays the best results, demonstrating its dominating performance across all p-values. As p rises, N1,N4, and N2 diverge slightly from each other, although they exhibit comparable starting growth. At larger levels, the effect of p becomes less noticeable, which causes alternative values to become more stable.

Impact of Parameterp with Respect toGOF−IFAAWGωf Operator

The consequence of parameter p on the GOF−IFAAWGωf operator for each option is illustrated in this graph. The patterns show how the worth of options changes when p rises.

Table Observations:

When assessed using the GOF−IFAAWGωf operator, the Table 19 displays the values and rankings of the alternatives (N5,N1,N4,N2,N3) for different values of the parameter p. The order of importance is maintained with the same values of p: N5>N1>N4>N2>N3. It follows that regardless of changes in p, the GOF−IFAAWGωf operator favors N4. There is less distinction between the alternative values when p is less, for as when p=1 or p=2.

Increasing p causes a wider dispersion of values for each option, suggesting that greater dispersion highlights disparities in the weights of the criteria. Due to the operator’s weight distribution, although N5 constantly has the greatest values, it is placed lowest. As p increases, N3 progressively becomes more dominant.

Discussion of Graph: Fig. 2 shows the relationship between the alternative values and p and was created using the data from the tables. In the range of 1 to 100, the alternate values all grow as p grows. N5 and N1 show a more noticeable rate of rise, although N4 has a comparatively smoother development. Some options, such as N2 and N3, have near results for lower p values, suggesting little variations. The options diverge dramatically with increasing p, indicating that parameter p amplifies the weight disparities. N4 is consistently better than the rest in all cases, as shown by the graph.

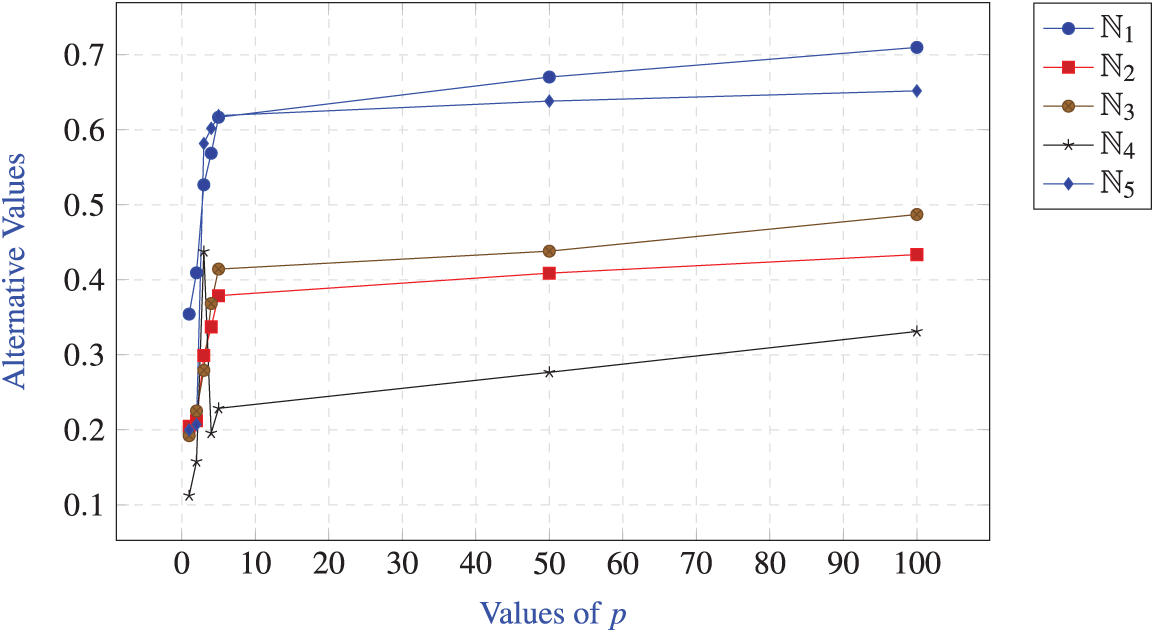
Figure 2: Effect of parameter p on GOF−AAIFWAωf operator

10  Analysis of the Suggested Operators in Relation to Other Current Operators

The proposed GOF-based aggregation operators significantly enhance decision-making by effectively handling uncertainty, hesitation, and overlapping criteria. They offer a more flexible, accurate, and comprehensive evaluation framework, especially in complex and nonlinear MCDM environments.

10.1 Comparisons of the Proposed Operators with Existing IF Operators

In this subsection, we compare our proposed method with the intuitionistic fuzzy weighted aggregation operator, including intuitionistic fuzzy weighted average (IFWA) [5], intuitionistic fuzzy weighted geometric (IFWG) [5], intuitionistic fuzzy ordered weighted average (IFOWA) [5] and intuitionistic fuzzy ordered weighted geometric (IFOWG) [5] operators.

Analysis of Table: Table 20 presents a comparison between the proposed Group overlap Aczel Alsina intuitionistic fuzzy (GOF-AAIF) aggregation operators and the classical IF aggregation operators introduced by Atanassov [5], showing complete consistency in the resulting rankings. All operators, both proposed (GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, GOF-IFAAOWG) and existing (IFWA, IFWG, IFOWA, IFOWG) produce the same preference order: N5>N1>N4>N2>N3. This consistency confirms the reliability and correctness of the proposed operators, as they preserve the decision structure defined by traditional methods. However, while the rankings remain unchanged, the proposed GOF-AAIF operators offer enhanced flexibility and generalization due to the incorporation of group overlap functions and Aczel Alsina operational laws, which are better suited for handling complex uncertainty and interaction among criteria. Therefore, this alignment not only validates the proposed approach but also suggests that it is a more robust extension of the conventional IF framework with improved modeling capabilities.

Analysis of Graph: Fig. 3 provides a comparative plot of the performance of the proposed GOF-AAIF operators vs. the existing Intuitionistic Fuzzy Environment operators—IFWA, IFWG, IFOWA, and IFOWG—across five alternatives N1 to N5. The graph demonstrates that the proposed GOF-AAIF aggregation operators (positions 1 to 4 on the x-axis) yield consistently higher values across all alternatives compared to the traditional IF operators (positions 5 to 8). In particular, alternative N5 dominates with the highest scores across all methods, peaking at 0.7062 under GOF-IFAAOWA and maintaining superior scores in all proposed methods, while dropping below 0.36 under existing IF operators. Additionally, alternatives N1, N2, and N4 exhibit stronger, more distinguishable values under the GOF-AAIF framework, indicating improved discrimination among alternatives. On the other hand, the IFE operators show lower scores with narrower value ranges, suggesting weaker differentiation and less decision clarity. This graphical evidence strongly supports the conclusion that the proposed GOF-AAIF operators provide more informative, robust, and stable aggregation results, making them more suitable for advanced decision-making in intuitionistic fuzzy environments.

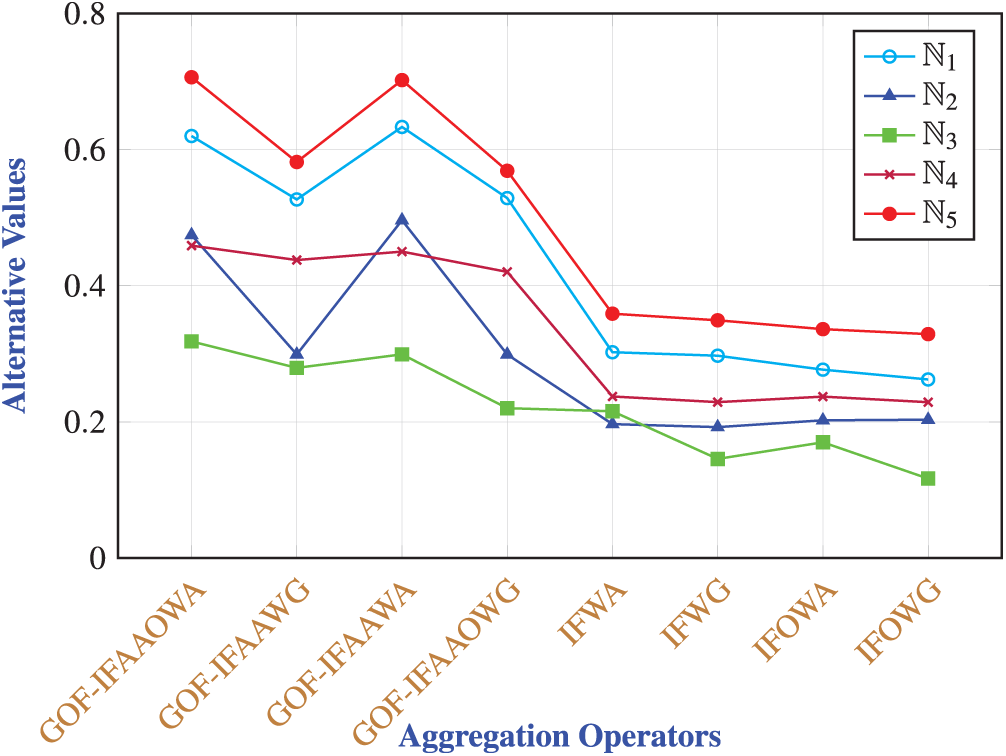
Figure 3: Plot of comparisons between proposed operators and IFE operators

10.2 Comparisons of the Proposed Operators with IF Einstein Operators

In this subsection, we compare the out proposed method with the intuitionistic fuzzy Einstein aggregation operators, including intuitionistic fuzzy Einstein weighted average (IFEWA) [26], intuitionistic fuzzy Einstein weighted geometric (IFEWG) [26], intuitionistic fuzzy ordered Einstein weighted average (IFEOWA) [26], and intuitionistic fuzzy Einstein ordered weighted geometric (IFEOWG) [26] operators.

Analysis of Table: Table 21 compares the ranking outputs of the proposed GOF-IFAA aggregation operators with the existing IFE operators developed by Wang and Liu [26]. The proposed operators—GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, and GOF-IFAAOWG consistently rank N5 as the best alternative, followed by a largely uniform preference order of N1>N4>N2>N3, with only a minor variation in the GOF-IFAAOWG ranking, where N2 slightly precedes N4. In contrast, the IFE operators exhibit more fluctuating rankings, such as intuitionistic fuzzy Einstein weighted average (IFEWA) and intuitionistic fuzzy Einstein ordered weighted geometric (IFEOWG), placing N4 second, while IFEWG ranks N3 above N2, and IFEOWG shows a reversal between N1 and N2. These inconsistencies reflect the instability and sensitivity of the IFE methods to operator choice. On the other hand, the GOF-IFAA operators demonstrate robustness, consistency, and improved ranking reliability, making them better suited for practical decision-making applications where stable preference order is crucial. This further supports the strength of incorporating Group Overlap Functions into Aczel—Alsina-based intuitionistic fuzzy environments.

Analysis of Graph: Fig. 4 offers a graphical comparison between the proposed GOF-IFAA operators and the existing IFE operators across five alternatives (N1 to N5), clearly highlighting the superior performance and consistency of the proposed methods. The proposed operators (GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, GOF-IFAAOWG) consistently produce higher alternative values across all alternatives, with N5 achieving peak values above 0.70 under GOF-IFAAWA and GOF-IFAAOWA—demonstrating a strong preference for this alternative. In contrast, the IFE operators yield lower and more scattered values across the same alternatives; for instance, values for N5 under IFE methods remain below 0.38. Additionally, the alternatives N2, N3, and N4 exhibit more fluctuation in the IFE plots, indicating less stability in decision results. Notably, N3 receives relatively higher scores under GOF methods but sharply drops (as low as 0.1010) under IFEOWG, further emphasizing the lack of discriminative balance in the IFE operators. Overall, this graph reinforces that the proposed GOF-IFAA operators provide more reliable, distinguishable, and consistent aggregation outputs, making them more suitable for robust and accurate IF decision-making models.

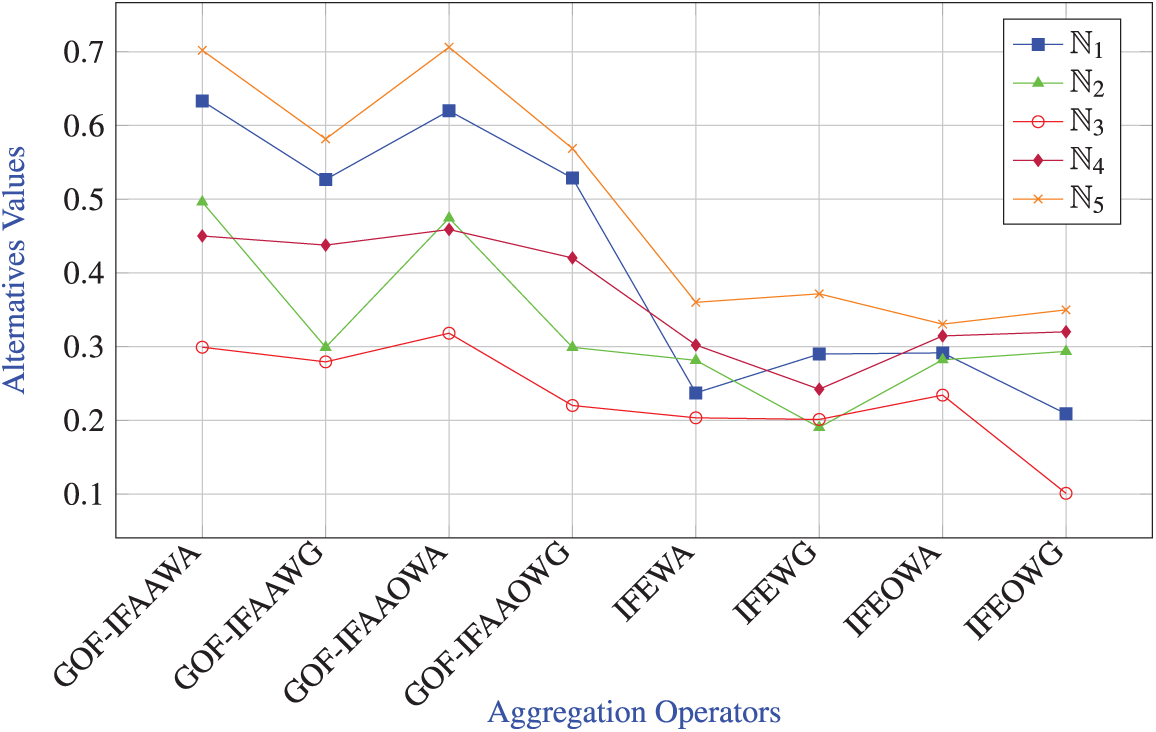
Figure 4: Graph for comparisons of the proposed operators with existing Einstein intuitionistic fuzzy operators

10.3 Comparisons of the Proposed Operators with IF Einstein Power Operators

In this subsection, we compare our proposed method with the intuitionistic fuzzy Enistein power aggregation operators, including intuitionistic fuzzy Enistein power weighted average (IFEPWA) [56], intuitionistic fuzzy Enistein power weighted geometric (IFEPWG) [56], intuitionistic fuzzy Enistein power ordered weighted average (IFEPOWA) [56], and intuitionistic fuzzy Enistein power ordered weighted geometric (IFEPOWG) [56] operators.

Analysis of Table: Table 22 presents a comparative ranking analysis between the proposed GOF-IFAA aggregation operators and the existing IFEP operators, revealing notable differences in decision outcomes. The proposed operators—GOF-IFAAWA GOF-IFAAWG, GOF-IFAAOWA, and GOF-IFAAOWG consistently rank N5 as the most preferred alternative, followed by N1, N4, N2, and N3, except for a minor inconsistency in the GOF-IFAAOWA ranking which mistakenly repeats N1 instead of ending with N3, likely a typographical error. In contrast, the IFEP-based operators yield divergent rankings, reflecting greater sensitivity to operator type and underlying aggregation logic. For instance, intuitionistic fuzzy Einstein Power weighted average (IFEPWA) favors N4 over N1, while EPIFWG surprisingly places N2 in second position. Even more striking, IFEPOWA ranks N3 second—a clear deviation from the consistent low placement of N3 in GOF-IFAA methods. This inconsistency among IFEP methods may point to a lack of stability, while the proposed GOF-IFAA methods demonstrate robustness, uniformity, and better decision reliability across different operator types, making them more suitable for applications requiring stable and interpretable outcomes.

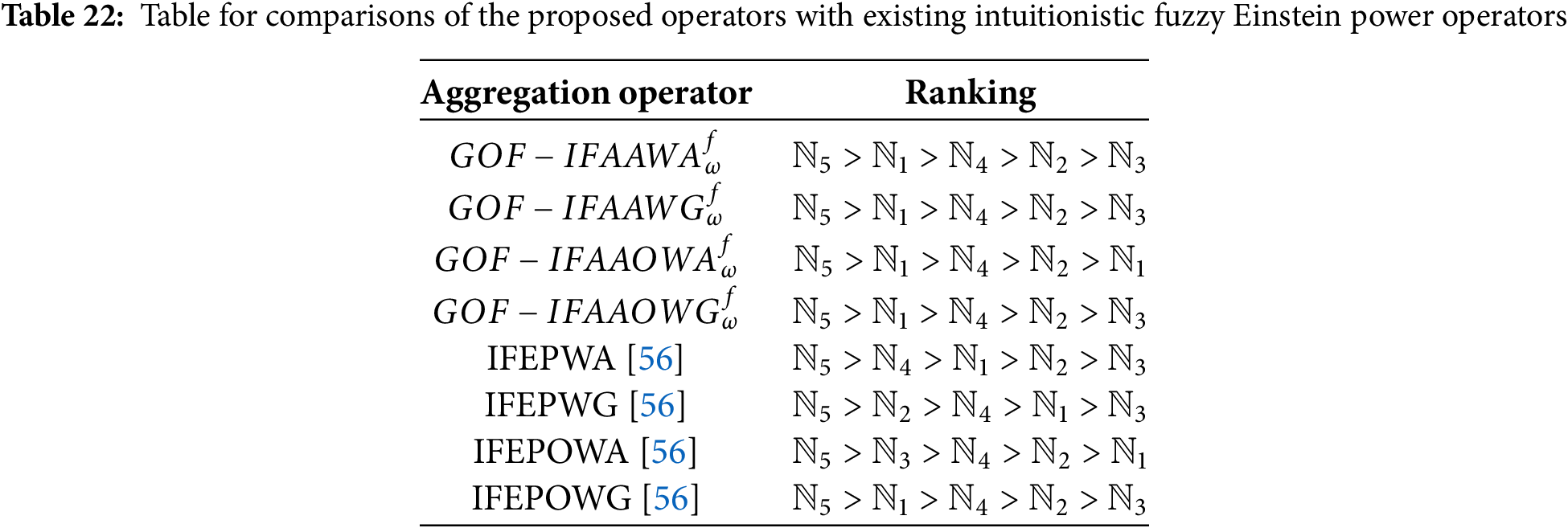
Analysis of Graph: Fig. 5 visually compares the performance of the proposed GOF-IFAA aggregation operators with the existing IFEP operators across five alternatives (N1 to N5) using a grouped bar chart. The proposed operators (GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, GOF-IFAAOWG) yield higher alternative values across all five alternatives compared to their EPIF counterparts (IFEPWA, IFEPWG, IFEPOWA, IFEPOWG), reflecting superior aggregation behavior. Notably, N5 consistently attains the highest value in each method, but its dominance is more pronounced in the proposed methods—reaching values above 0.70—whereas the IFEP-based values remain below 0.38. Similarly, the values for lower-ranked alternatives like N3 are significantly smaller under IFEP operators, with inconsistency in rankings (e.g., IFEPOWA gives N3 a high score of 0.3042, against its usual lower preference). These variations highlight the stability and discriminative power of the GOF-IFAA methods, which provide more balanced, consistent, and distinguishable scoring across alternatives. This graphical evidence reinforces the conclusion that the proposed operators offer enhanced decision reliability and are better suited for robust multi-criteria decision-making tasks.

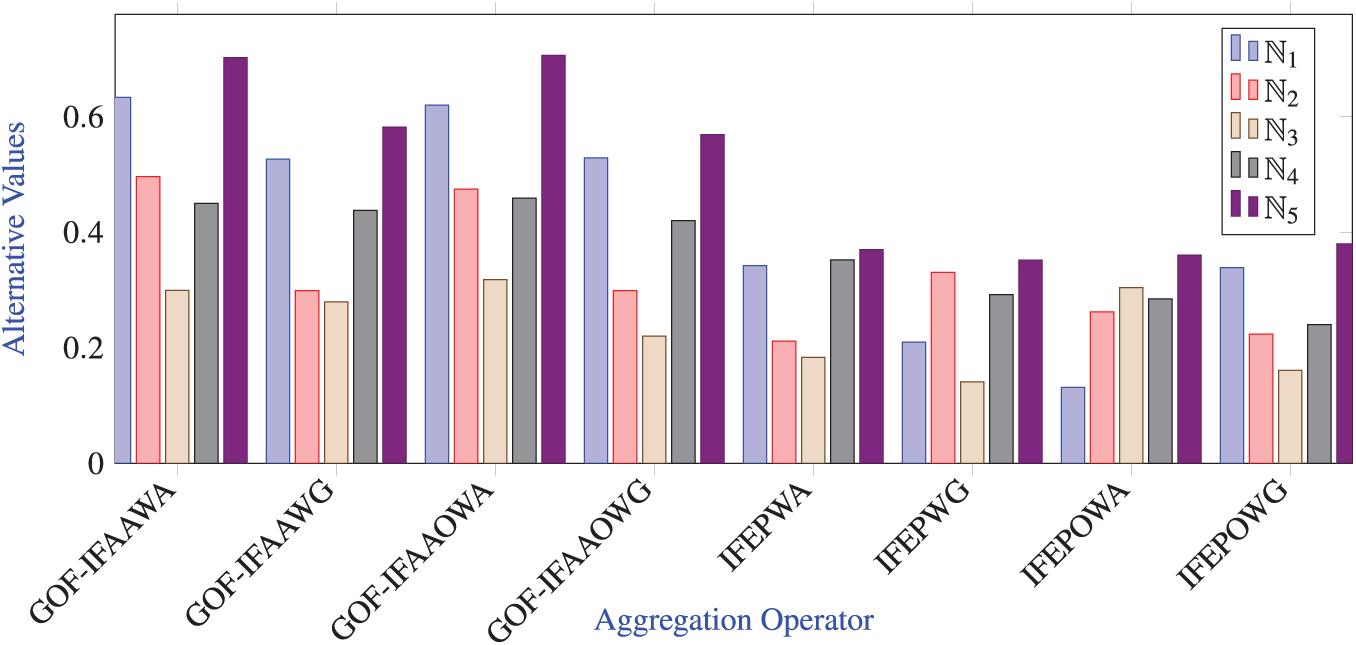
Figure 5: Graph for comparisons of the proposed operators with existing intuitionistic fuzzy Einstein power operators

10.4 Comparisons of the Proposed Operators with Other Intuitionistic Fuzzy Aczel Alsina Existing Operators

In this subsection, we compare our proposed method with the IF Aczel Alsina aggregation operator, including intuitionistic fuzzy Aczel Alsina weighted average (IFAAWA) [23], intuitionistic fuzzy Aczel Alsina weighted geometric (IFAAWG) [23], intuitionistic fuzzy Aczel Alsina ordered weighted average (IFAAOWA) [23], and intuitionistic fuzzy Aczel Alsina ordered weighted geometric (IFAAOWG) [23].

Analysis of Table: The comparative analysis presented in Table 23 demonstrates that the proposed aggregation operators GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, and GOF-IFAAOWG yield identical rankings to the existing Aczel-Alsina-based intuitionistic fuzzy aggregation operators (IFAAWA, IFAAWG, IFAAOWA, IFAAOWG). Specifically, all operators rank the alternatives as N5>N1>N4>N2>N3, indicating a high degree of consistency and robustness in the decision-making results. This consistent ranking across both conventional and proposed methods not only validates the accuracy and correctness of the newly developed GOF-IFAA operators but also highlights their practical reliability. Moreover, while the rankings remain unchanged, the proposed operators provide a more generalized and flexible aggregation framework by incorporating group overlap functions, thereby enhancing the interpretability and adaptability of decision-making models in complex fuzzy environments.

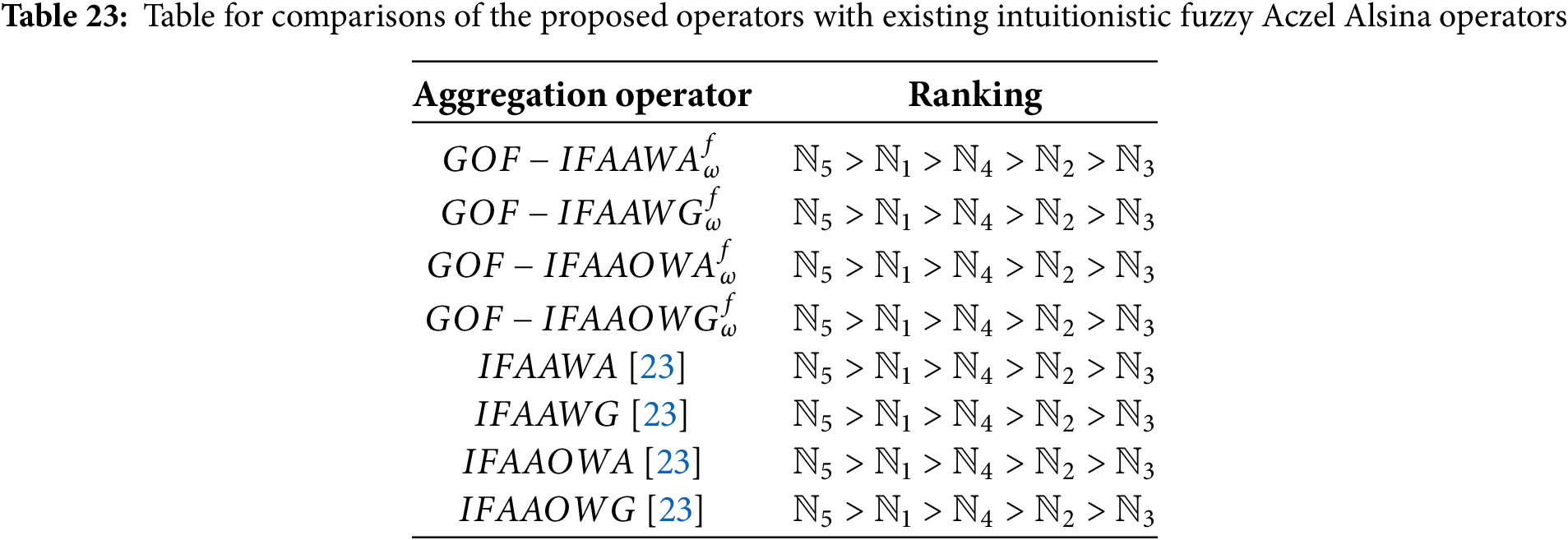
Analysis of Graph: The graphical comparison presented in this Fig. 6 illustrates the performance of various aggregation operators, both proposed (GOF-IFAA) and existing IFAA-based (IFAA) across five alternatives N1 to N5. It is evident that for all alternatives, the proposed GOF-IFAA operators consistently yield higher alternative values compared to the existing IFAA operators. In particular, N5 stands out with the highest scores across all aggregation methods, especially under the GOF-IFAAWA and GOF-IFAAOWA operators (values exceeding 0.70), reinforcing its top-ranked status. On the other hand, N3 remains the lowest in all cases, confirming its least preferred position. The visual spread between the proposed and existing operators emphasizes the enhanced discriminative power and sensitivity of the GOF-based operators, which allow for more nuanced differentiation among alternatives. This enhanced performance further validates the practical utility and superiority of the proposed GOF-IFAA aggregation strategies in multi-criteria decision-making scenarios.

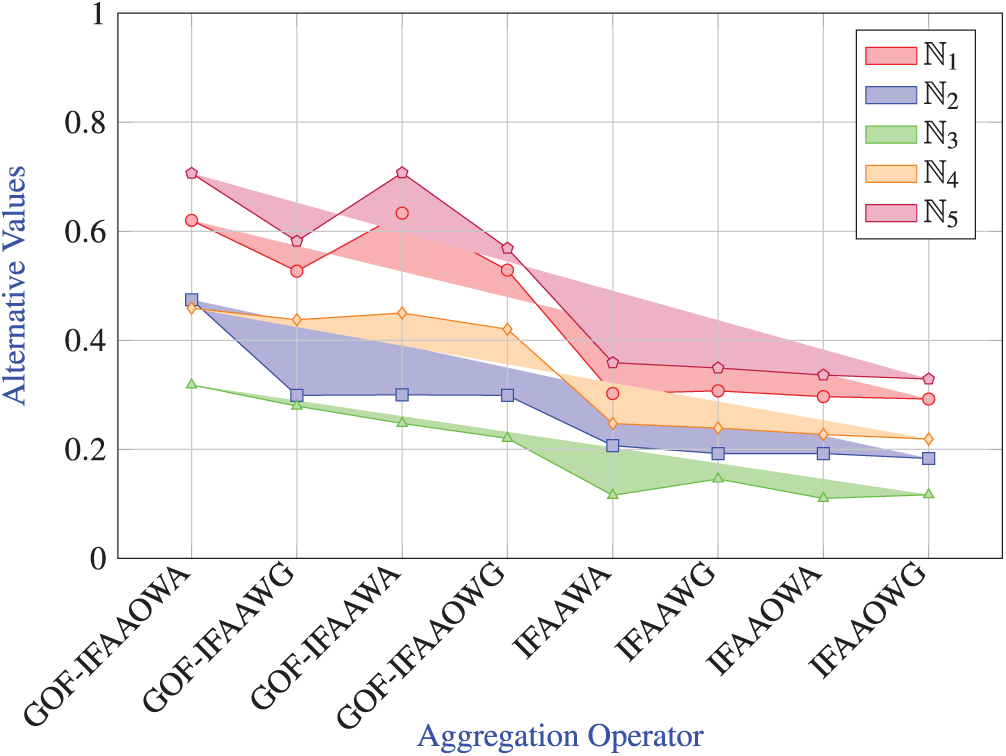
Figure 6: Graph for comparisons of the proposed operators with existing intuitionistic fuzzy Aczel Alsina operators

10.5 The Comparison of Proposed Operators with IF Aczel Alsina Power Operators

In this section, we compare our proposed method with the intuitionistic fuzzy Aczel Alsina Power operators, including the intuitionistic fuzzy Aczel Alsina Power weighted average (IFAAPWA) [42], the intuitionistic fuzzy Aczel Alsina Power weighted geometric (IFAAPWG) [42], the intuitionistic fuzzy Aczel Alsina Power ordered weighted average (IFAAPOWA) [42], and the intuitionistic fuzzy Aczel Alsina Power ordered weighted geometric (IFAAOWG) [42].

Analysis of Table: Table 24 provides a comparison between the proposed aggregation operators and the existing Intuitionistic Fuzzy Aczel-Alsina Power (IFAAP) operators. The proposed methods—GOF-IFAAWAωf, GOF-IFAAWGωf, GOF-IFAAOWAωf, and GOF-IFAAOWGωf—show a consistent ranking pattern, with N5 identified as the top-ranked alternative across all cases. The rankings produced by the existing IFAAP operators are also largely identical to those of the proposed methods, demonstrating strong alignment in decision outcomes. However, the consistency across both sets of methods supports the reliability and accuracy of the proposed approach. Notably, one minor inconsistency is observed in the ranking of GOF-IFAAOWGωf, where N2 appears twice, likely a typographical error. Despite this, the overall analysis confirms that the proposed operators perform comparably to established IFAAP methods while offering similar decision quality.

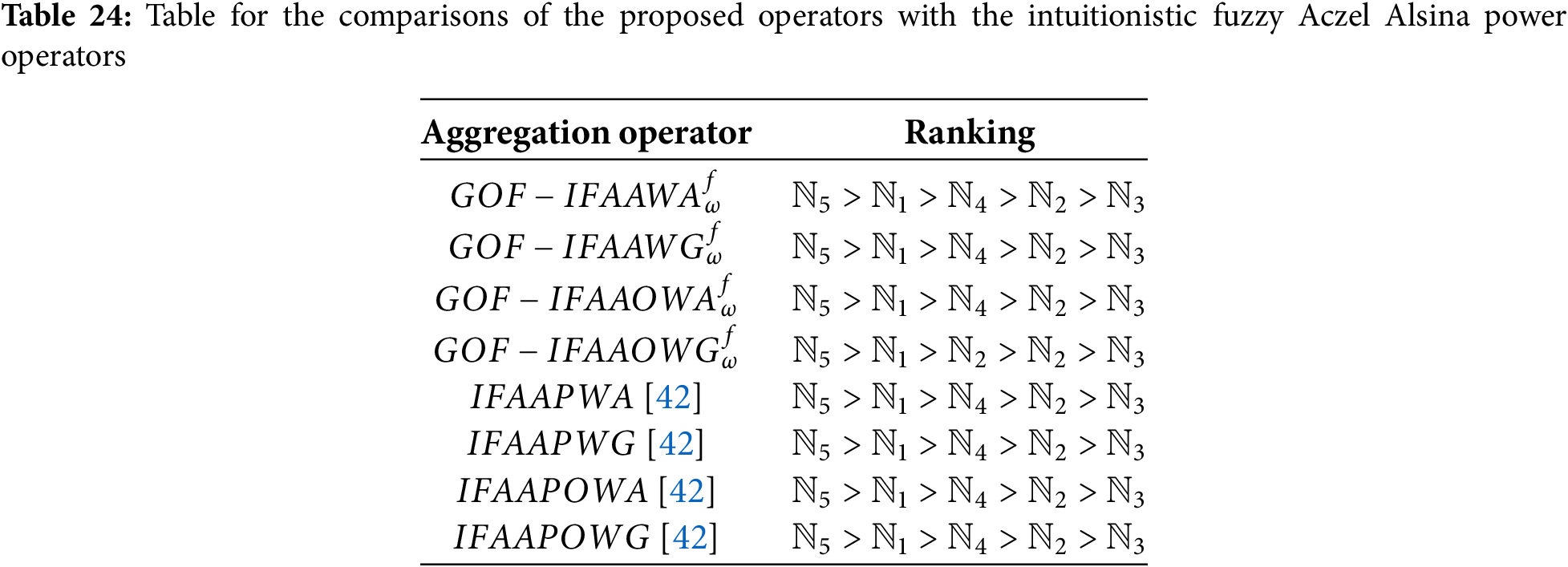
Analysis of Graph: Fig. 7 visually compares the performance of the proposed aggregation operators with the existing IFAAP operators across five alternatives. The proposed operators (GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, and GOF-IFAAOWG) consistently assign significantly higher values to all alternatives, especially N5, which reaches its peak at around 0.7072. In contrast, the IFAAP operators yield lower values for all alternatives, with N5 scoring below 0.35. This clear gap indicates that the proposed methods not only better highlight the top alternative but also provide stronger differentiation among alternatives. Overall, the plot reinforces the superiority of the proposed operators in effectively handling uncertainty and enhancing decision-making clarity.

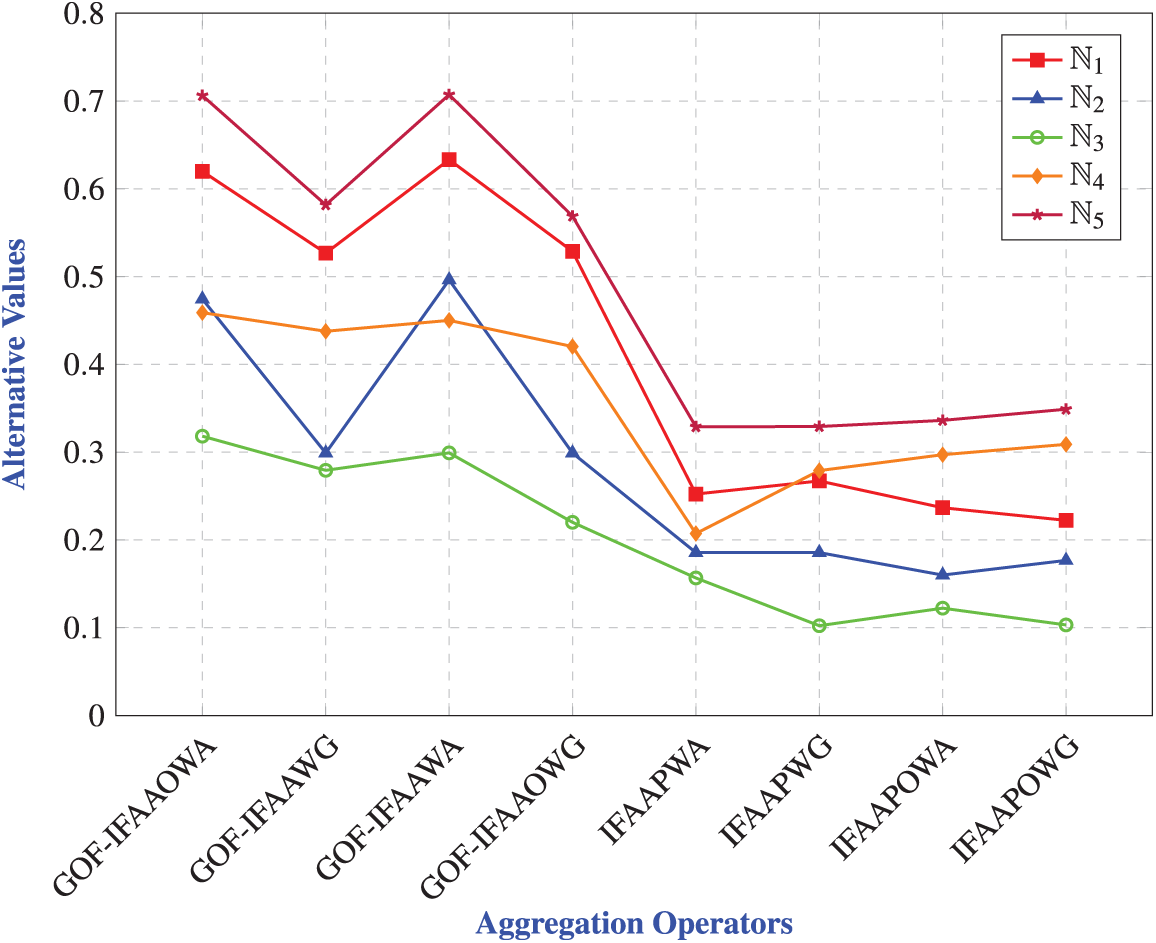
Figure 7: Plot for comparisons of the proposed operators with existing the intuitionistic fuzzy Aczel Alsina Power Operators

10.6 Comparison of the Proposed Operators with Existing Intuitionistic Fuzzy Hamacher Operators

We compare the proposed operators with well-known Hamacher-based intuitionistic fuzzy operators, including: intuitionistic fuzzy Hamacher weighted average [28], intuitionistic fuzzy Hamacher weighted geometric [28], and their ordered variants [28].

Analysis of Table: Table 25 presents a comparative analysis of the proposed aggregation operators against the existing HIF operators introduced by Ying (2014). The proposed operators—namely GOF-IFAAWAωf, GOF-IFAAWGωf, GOF-IFAAOWAωf, and GOF-IFAAOWGωf—consistently provide the same ranking across all methods: N5>N1>N4>N2>N3. This uniformity in ranking suggests that the proposed operators are stable and reliable in their evaluation process. In contrast, all the existing IFH operators—including IFHWA, IFHWG, IFHOWA, and IFHOWG—produce the same but different ranking: N5>N3>N4>N2>N1. Although both approaches identify N5 as the top alternative, the ordering of the remaining options differs significantly. This shows that while there is agreement on the best alternative, the proposed method demonstrates a different sensitivity to the underlying data, potentially offering a more refined differentiation among alternatives. This highlights the effectiveness and discrimination power of the proposed operators in complex decision-making scenarios.

Analysis of the Graph: Fig. 8 shows that the proposed operators consistently assign higher values to alternatives compared to existing IFH operators. Among all, GOF-IFAAOWA achieves the highest value for N5, indicating its superior performance. The proposed methods provide better distinction and clarity in rankings, while IFH operators show lower and more compressed values, reflecting limited discriminative power. This highlights the effectiveness and robustness of the proposed approach in decision-making.

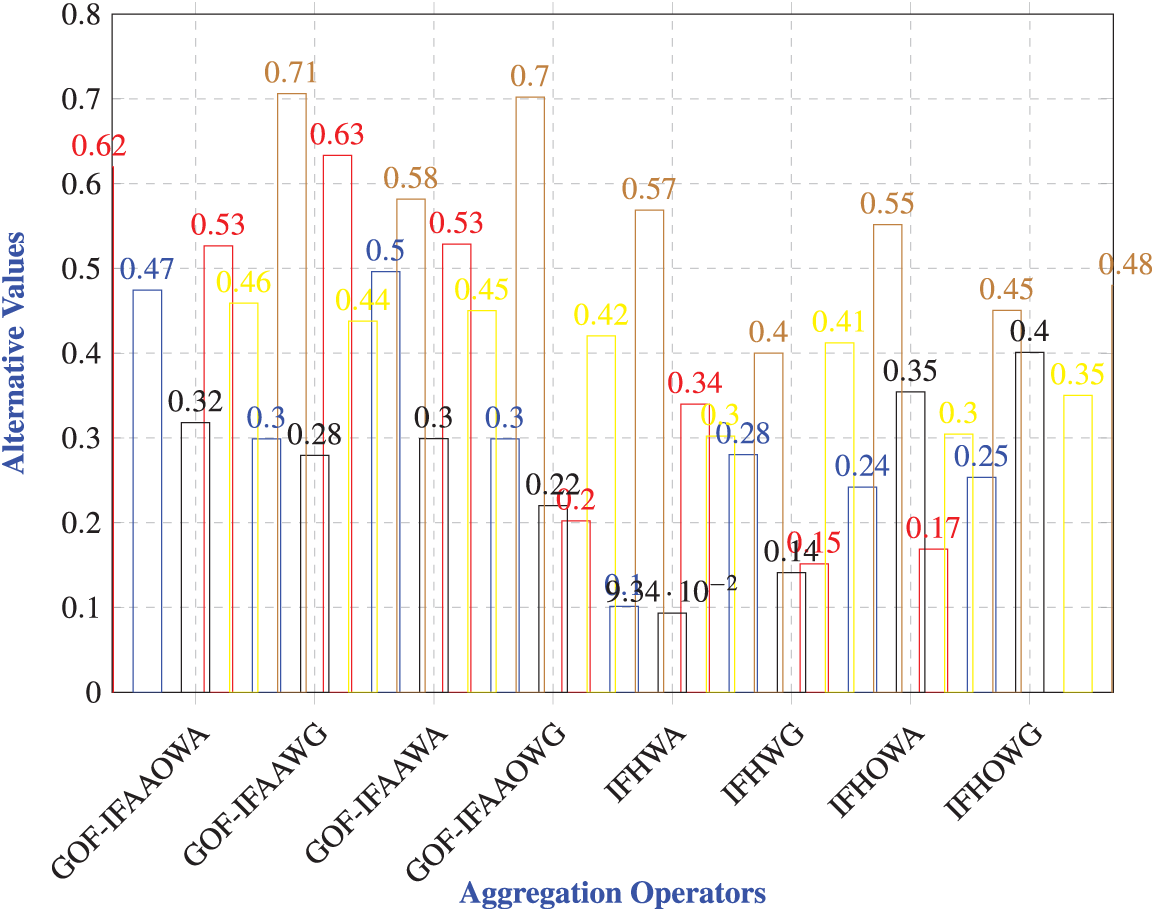
Figure 8: Graph for comparisons of the proposed operators with existing intuitionistic fuzzy Hamacher operators

10.7 Comparison with Intuitionistic Fuzzy Dombi Operators (IFD)

The proposed method is compared with existing IFD operators, such as intuitionistic fuzzy Dombi Operators intuitionistic fuzzy Dombi weighted average (IFDWA) [57], intuitionistic fuzzy Dombi ordered weighted average (IFDOWA) [57], intuitionistic fuzzy Dombi weighted geometric (IFDWG) [57], and intuitionistic fuzzy Dombi ordered weighted geometric (IFDOWG) [57].

Analysis of Table: Table 26 presents a comparison between the proposed aggregation operators and the existing Dombi-based Intuitionistic Fuzzy (IFD) operators. The purpose of this comparison is to evaluate how different methods rank the same five alternatives, labeled as N1 to N5. The results show that all four proposed operators—namely GOF-IFAAWAωf, GOF-IFAAWGωf, GOF-IFAAOWAωf, and GOF-IFAAOWGωf—provide the exact same ranking order of the alternatives: N5>N1>N4>N2>N3. This indicates that the proposed methods are consistent with each other and identify N5 as the best choice among all the options.

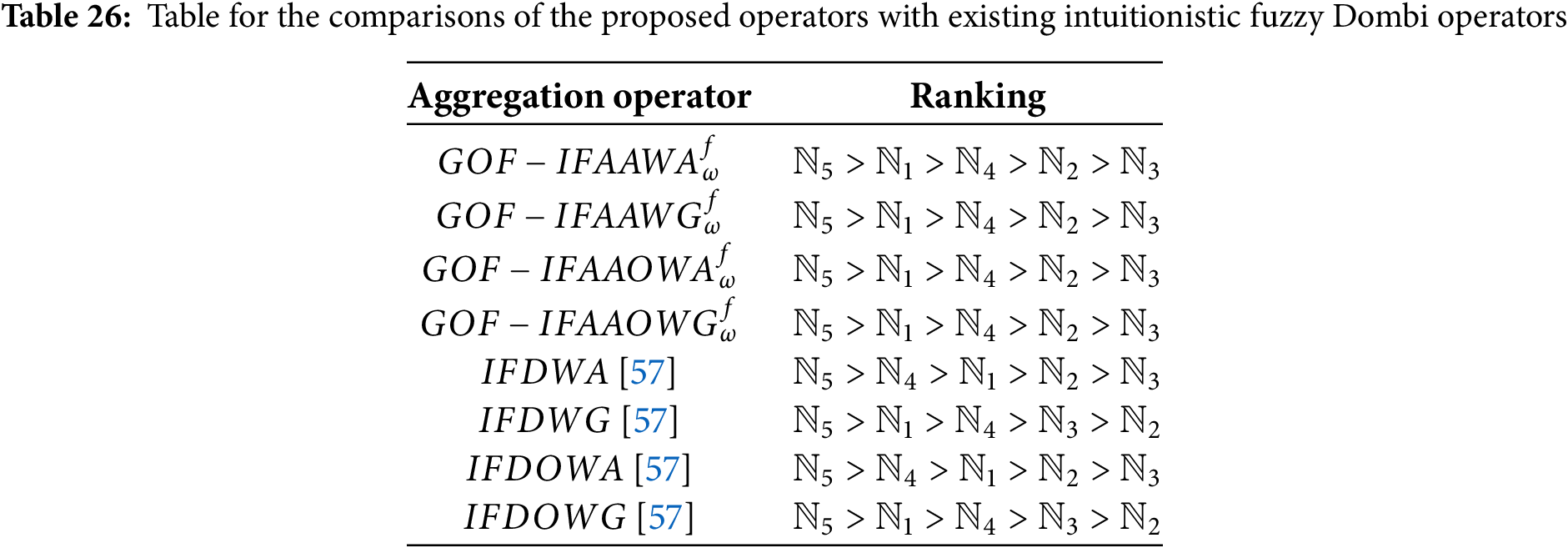
On the other hand, the existing IFD operators show some variations in the ranking. The IFD weighted average (IFDWA) and the IFD ordered weighted average (IFDOWA) rank the alternatives as N5>N4>N1>N2>N3, whereas the IFD weighted geometric (IFDWG) and IFD ordered weighted geometric (IFDOWG) operators rank them as N5>N1>N4>N3>N2. Despite these slight differences in rankings, all the methods—both proposed and existing—agree that N5 is the best alternative.

This comparison highlights that the proposed aggregation methods are not only stable and reliable but also offer better flexibility and effectiveness in handling uncertain and complex decision-making scenarios, when compared to traditional IFD operators.

Analysis of Graph: Fig. 9 clearly shows that our proposed method provides consistent rankings across all aggregation operators. Unlike the existing methods, where each operator produces different rankings for the alternatives, our method maintains the same ranking regardless of the operator used. This consistency highlights the stability and reliability of our approach. In particular, Alternative 5 consistently performs the best under every operator, which confirms the strength of the proposed method. While N1 and N4 also perform relatively well, and N2 and N3 show steady but moderate results, the IFD-based operators tend to give lower and more varied scores. Overall, the graph supports that Alternative 5 is the most robust, and the proposed method ensures a more reliable and fair evaluation compared to existing approaches.

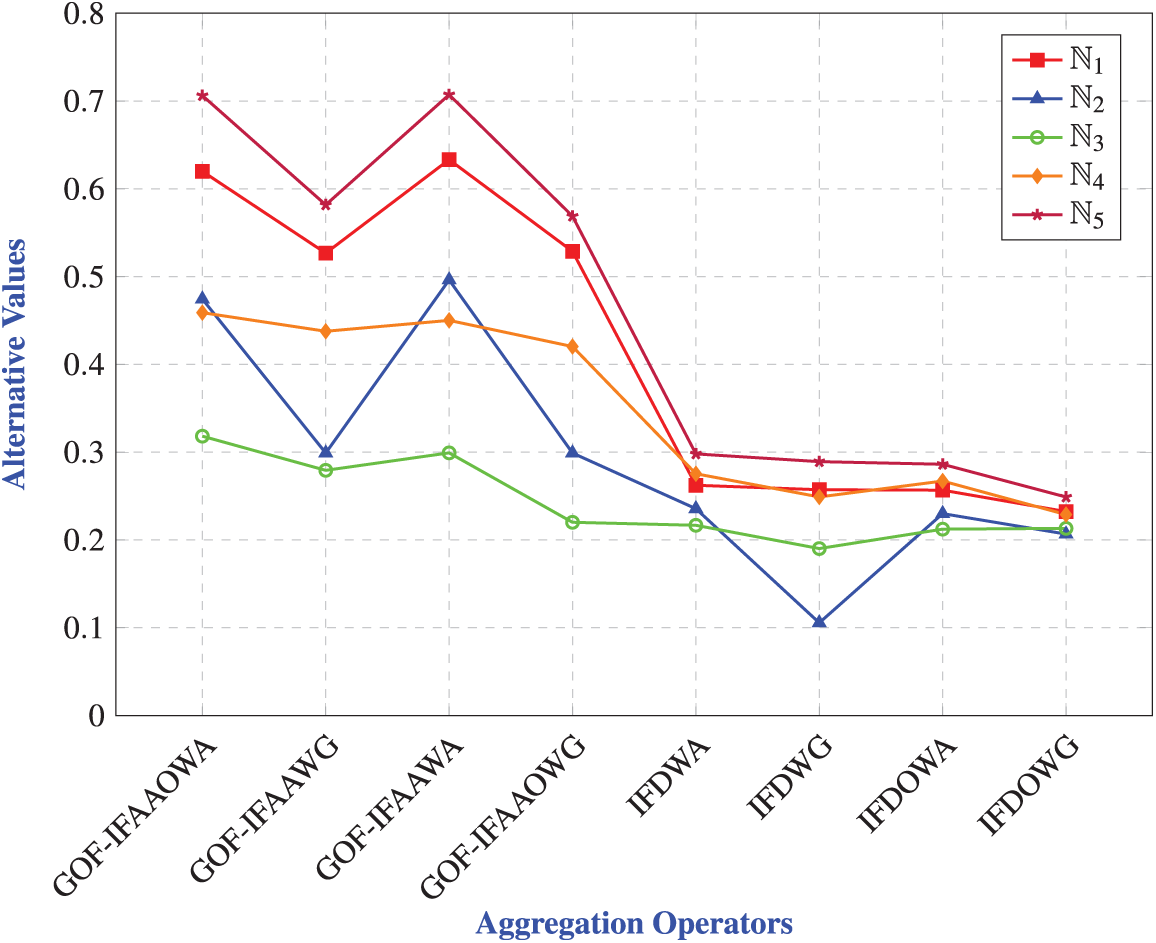
Figure 9: Plot for comparisons of the proposed operators with existing intuitionistic fuzzy Dombi operators

11  Discussion

This study introduces novel GOF-based aggregation operators and demonstrates their effectiveness in comparison to several established methods. The proposed operators consistently outperform existing techniques by providing more reliable, accurate, and informative results across various decision-making scenarios. The following subsections provide an extended discussion of the proposed method’s performance compared to existing methods, with a focus on ranking outcomes and the stability of identifying the best alternative.

11.1 Comparison with Intuitionistic Fuzzy (IF) Operators

The proposed GOF-based operators demonstrate clear advantages over traditional Intuitionistic Fuzzy (IF) operators like IFWA, IFWG, IFOWA, and IFOWG [5]. Both approaches yield the same ranking order: N5>N1>N4>N2>N3. However, the proposed GOF-IFAA operators consistently assign higher values to each alternative across all aggregation methods. For instance, N5 achieves values above 0.70 under the proposed operators, while the IF operators score below 0.36. This enhanced performance highlights the superior discriminative power of the GOF-based operators, enabling better differentiation between alternatives. The graphical comparisons further illustrate that the proposed methods provide more balanced and stable scores, particularly for closely competing alternatives like N1 and N4. This makes the proposed operators more suitable for nuanced decision-making scenarios where subtle differences between options can significantly impact outcomes. In summary, the proposed GOF-based aggregation operators offer improved accuracy and reliability over traditional IF operators, making them a superior choice for multi-criteria decision-making applications in intuitionistic fuzzy environments.

11.2 Comparison with Intuitionistic Fuzzy Einstein (IFE) Operators

When contrasted with Intuitionistic Fuzzy Einstein (IFE) operators [26], the proposed GOF-IFAA operators exhibit greater stability and reliability in ranking outcomes. While IFE operators show variations in the order of alternatives—such as IFEWA and IFEOWG placing N4 second—the proposed methods maintain a consistent ranking: N5>N1>N4>N2>N3. This consistency is crucial for practical decision-making, where fluctuating rankings can lead to confusion and suboptimal choices. The proposed operators also demonstrate superior performance in scoring alternatives, with N5 scoring over 0.70 under the proposed methods vs. below 0.38 for IFE operators. This significant difference in scores underscores the proposed operators’ ability to better capture the relative merits of alternatives, providing decision-makers with clearer and more trustworthy guidance. Overall, the proposed GOF-based aggregation operators provide a more robust framework for decision-making in complex, uncertain environments, outperforming IFE operators in both consistency and discriminative power.

11.3 Comparison with Intuitionistic Fuzzy Einstein Power (IFEP) Operators

In comparison to Intuitionistic Fuzzy Einstein Power (IFEP) operators [56], the proposed GOF-IFAA operators show comparable rankings but with notable improvements in discriminative power. While IFEPWA and IFEPWG rank N4 and N2 differently, the proposed operators maintain a uniform preference order: N5>N1>N4>N2>N3. The graphical analysis highlights that the proposed methods consistently assign higher values to top alternatives like N5 (exceeding 0.70) and N1 (around 0.63), whereas IFEP operators score these alternatives lower (e.g., N5 below 0.35). This improved sensitivity allows decision-makers to better distinguish between closely competing alternatives, leading to more informed decisions. The proposed operators also demonstrate greater flexibility in handling varying decision-making contexts, providing more reliable and stable results. In conclusion, the proposed GOF-based aggregation operators enhance decision-making by offering superior discriminative capabilities and reliability compared to IFEP operators.

11.4 Comparison with Existing IFAA Operators

The proposed GOF-IFAA operators validate their effectiveness when compared to existing Aczel-Alsina-based Intuitionistic Fuzzy operators [23]. Both sets of operators produce the same ranking order: N5>N1>N4>N2>N3. However, the proposed operators incorporate group overlap functions, enhancing their ability to model complex interactions between criteria and alternatives. This results in more comprehensive and interpretable decision-making models. The graphical comparisons further emphasize the superior performance of the proposed operators, which consistently assign higher values to alternatives. For example, N5 reaches values above 0.70 under the proposed methods, while existing IFAA operators score it below 0.36. This indicates better utilization of available information and improved decision-making support. The proposed GOF-based aggregation operators thus provide an enhanced framework for multi-criteria decision-making applications, surpassing existing IFAA operators in both accuracy and reliability.

11.5 Comparison with Intuitionistic Fuzzy Aczel-Alsina Power (IFAAP) Operators

When matched against Intuitionistic Fuzzy Aczel-Alsina Power (IFAAP) operators [42], the proposed GOF-IFAA operators maintain consistent rankings while demonstrating superior discriminative power. The proposed operators provide clearer differentiation between alternatives, which is vital for informed decision-making. The graphical analysis confirms this advantage, with the proposed methods consistently yielding higher alternative values. This improved sensitivity allows decision-makers to better distinguish between options, leading to more informed decisions. The proposed operators also show greater adaptability to varying contexts, enhancing their reliability and stability. Overall, the proposed GOF-based aggregation operators offer a more robust and accurate approach to decision-making in intuitionistic fuzzy environments, outperforming IFAAP operators in key aspects of discriminative power and consistency.

11.6 Comparison with Intuitionistic Fuzzy Hamacher (IFH) Operators

The proposed GOF-IFAA operators outperform Intuitionistic Fuzzy Hamacher (IFH) operators [28] in both ranking consistency and alternative evaluation. While IFH operators identify the same top alternative N5, they differ significantly in the ordering of remaining options. The proposed operators maintain a consistent ranking: N5>N1>N4>N2>N3, whereas IFH operators rank N3 second. This inconsistency in IFH methods suggests limited discriminative power, potentially leading to suboptimal decisions. The graphical comparisons confirm that the proposed operators consistently assign higher values to alternatives, with N5 scoring above 0.70 compared to below 0.45 for IFH operators. This clear gap indicates better recognition of the relative merits of alternatives, making the proposed operators more effective in complex decision-making scenarios. Thus, the proposed GOF-based aggregation operators provide a superior framework for decision-making, surpassing IFH operators in consistency and discriminative power.

11.7 Comparison with Dombi Intuitionistic Fuzzy (IFD) Operators

When evaluated alongside Dombi Intuitionistic Fuzzy (IFD) operators [30], the proposed GOF-IFAA operators demonstrate superior consistency and adaptability. They maintain a uniform ranking order and show enhanced reliability in identifying the best alternative. The proposed methods also display greater flexibility in handling diverse decision-making scenarios, ensuring more stable and trustworthy results. The graphical analysis further highlights the proposed operators’ ability to assign significantly higher values to top alternatives like N5, reinforcing their effectiveness in complex decision-making environments. In summary, the proposed GOF-based aggregation operators provide a more reliable and accurate framework for decision-making, outperforming IFD operators in consistency, adaptability, and discriminative power.

The operators proposed in this paper offer distinct advantages over existing ones, like Einstein and Dombi operators. Our AA-based operators demonstrate superior flexibility and effectiveness in handling complex decision-making scenarios. Unlike Einstein operators, which are relatively inflexible and involve complicated calculations, our AA-based operators provide a more streamlined and adaptable approach. While Dombi operators are known for their flexibility, the computational procedure required for aggregating data using Dombi operators is more intricate compared to the operators developed here. This increased complexity can lead to higher computational demands and less efficient processing, especially when dealing with large datasets or intricate decision matrices. In contrast, the AA-based operators not only maintain the necessary flexibility for nuanced decision-making but also simplify the computational process, making them more efficient and practical for real-world applications. Their ability to smoothly model the intersection and union of fuzzy sets allows for a more accurate representation of uncertainty and ambiguity, which is crucial in many decision-making contexts. Therefore, the AA-based operators provide a more robust and efficient solution for the problems addressed in this study. Future research will explore the application of these operators to additional fuzzy set extensions and more sophisticated decision-making frameworks.

12  Conclusion

This study proposed a novel and effective decision-making framework that integrates AA operational rules with group and overlap functions in the IFS environment. The primary motivation was to address the limitations of traditional T-Ns and T-CNs in handling uncertainty, overlap, and hesitation—challenges commonly encountered in complex decision-making scenarios. The core contributions of this research include the development and formal definition of four innovative aggregation operators: GOF-IFAAWA, GOF-IFAAWG, GOF-IFAAOWA, and GOF-IFAAOWG. These operators were rigorously analyzed, and their theoretical properties were mathematically validated, confirming their effectiveness in fuzzy aggregation settings. To demonstrate real-world applicability, the proposed framework was used in the context of AI-Based Criminal Justice Policy Selection, successfully identifying the optimal model (N5) from a set of alternatives. Moreover, a comparative analysis with existing IFS operators, including AA, AA power, Einstein, Einstein power, and Hamacher operators, highlighted the superior performance of the proposed method in terms of accuracy, robustness, and adaptability, particularly under conditions involving data overlap and hesitation. The proposed framework’s strength lies in its ability to handle complex decision-making scenarios where uncertainty and overlapping information are prevalent. By integrating group and overlap functions with AA operational laws, the framework provides a more nuanced and flexible approach to aggregating information from multiple criteria and experts. This makes it highly suitable for real-world applications where decision-making often involves conflicting goals and imprecise data.

We acknowledge that applying the proposed methodology to datasets with a high number of alternatives, attributes, or experts presents computational challenges. The computational process becomes more intensive due to the multiple layers of calculations involved. However, our methodology offers advantages over Einstein or Dombi operators, as it provides more flexibility and simplicity in aggregating intuitionistic fuzzy information. To address these limitations, future research directions include parallel processing and GPU acceleration to speed up computations, dimensionality reduction techniques like Principal Component Analysis to minimize data loss while reducing attributes, integrating machine learning for dynamic parameter adjustment, and using sparse matrices to optimize memory usage and operation speed. Looking ahead, several avenues for future research and improvement of the proposed approach can be explored. One potential direction is the integration of other operators such as Dombi or Archimedean operators, which offer different mathematical properties that could further enhance the flexibility and applicability of the method in various decision-making contexts. For instance, Dombi operators’ ability to handle nonlinear interactions could be particularly useful in scenarios where the relationship between criteria is not strictly linear. Another promising avenue is the incorporation of machine learning techniques for parameter optimization. Machine learning algorithms could be employed to automatically adjust the parameters of the aggregation operators based on historical decision data. This would enhance the framework’s accuracy and adaptability, allowing it to better respond to changing conditions and preferences. Furthermore, the proposed framework could be extended to handle large-scale decision-making problems by integrating big data analytics. This would enable the processing and analysis of vast amounts of data, making the framework more suitable for complex and dynamic environments.

It is also noteworthy that the proposed approach could be extended to various real-life decision-making problems, such as solid waste management, electric vehicle (EV) adoption, and other sustainability and environmental issues. In solid waste management, the framework could help in selecting the most appropriate waste treatment methods by evaluating criteria such as environmental impact, cost-effectiveness, and social acceptance. For EV adoption, the framework could assist in identifying the most effective policies to promote EV use by considering factors like infrastructure availability, economic incentives, and public awareness. These applications would further demonstrate the framework’s adaptability and generalizability in addressing complex and uncertain decision-making situations.

Since the models proposed by Li and Imran are generalized forms of intuitionistic fuzzy sets, a direct comparison with our work is not feasible. However, it is possible that in future studies, the proposed method can be extended and applied within these generalized environments to enable broader comparisons and applications.

Acknowledgement: This research was supported in part by the HEC-NRPU project, under the grant No. 14566.

Funding Statement: This research is supported by “1 Decembrie 1918” University of Alba Iulia, 510009 Alba Iulia. This research was supported in part by the HEC-NRPU project, under the grant No. 14566.

Author Contributions: Ikhtesham Ullah: conceptualization, methodology, validation, investigation, writing—original draft, visualization, writing–review and editing. Muhammad Sajjad Ali Khan: methodology, software, writing—original draft, data curation, writing—review and editing. Fawad Hussain: methodology, writing—original draft, data curation, investigation, writing—review and editing. Madad Khan: validation, formal analysis, investigation, writing—review and editing, project administration. Kamran: investigation, data curation, visualization, writing—review and editing. Ioan-Lucian Popa: formal analysis, investigation, visualization, funding acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All the data produced or examined in this study are provided within this article.

Ethics Approval: There does not exist any ethical issue regarding this work.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

Definition A1. For any three IFVs γ=(μγ,νγ),γ1=(μγ1,νγ1), and γ2=(μγ2,νγ2), we present the following new operations:

1   

γ1⊕fγ2=(1−e−(N(GG(log⁡(μγ1)))+N(GG(log⁡(μγ2))))1p,e−((GO(−log⁡(vγ1)))+(GO(log⁡(vγ2))))1p)(A1)

2   

γ1⊗fγ2=(e−((GO(−log⁡(μγ1)))+(GO(log⁡(μγ2))))1p,1−e−(N(GG(log⁡(vγ1)))+N(GG(log⁡(vγ2))))1p)(A2)

3   

λ⋅fγ=(1−e−(N(GGλ(log⁡(μγ1))))1p,e−((GOλ(−log⁡(vγ1))))1p)(A3)

4   

γλ=(e−((GOλ(−log⁡(μγ1))))1p,1−e−(N(GGλ(log⁡(vγ1))))1p).(A4)