Beyond Classical Elasticity: A Review of Strain Gradient Theories, Emphasizing Computer Modeling, Physical Interpretations, and Multifunctional Applications

1  Introduction

Low-dimensional structures, from atomically thin sheets to one-dimensional nanowires, have emerged as a cornerstone of modern science and technology, offering unprecedented opportunities to explore fundamental physics and engineer novel devices with tailored functionalities. Moreover, advances in manufacturing are enabling the production of such small-scale structures. A wide application of these small-scale structures requires the efficacy of design and simulation. Examples include micro-beams utilized in MEMS (Micro-Electro-Mechanical Systems) as actuators [1] and sensors [2], where the beam thickness is usually of the order of microns. Further, many of these applications employ thin films for specific performance needs [3,4].

Classical continuum mechanics is based on the assumption that material behavior can be described using only the first gradient of displacement. Although effective at larger scales, this framework is inadequate for micro- and nanoscales, where size effects on elastic response become prominent. Experimental investigations using high-precision instruments, such as nanoindenters, have confirmed that classical theories cannot accurately capture the elastic response at these small scales [5,6]. Lam et al. [6] reported increased bending rigidity in experiments on epoxy micro-beams, while McFarland and Colton [7] observed similar stiffening behavior in micro-plates. At low dimensions, the structural response shows significant deviations from the predictions of classical elasticity theory. A key limitation of classical continuum theories is their inability to incorporate a material length scale that reflects the influence of microstructure. This omission makes them inadequate for problems in which the microstructure significantly affects the mechanical behavior. Both experimental and theoretical studies have shown that incorporating such length scales is essential to accurately capture the influence of microstructure on material behavior [8–12]. Further, classical continuum mechanics cannot eliminate singularities that arise from point loads, crack tips, dislocation lines, or interface discontinuities, making such problems mathematically ill-posed [13]. To address these limitations, Eringen [14,15] introduced microcontinuum field theories as an extension of classical models, tailored for materials characterized by microscale dimensions and dynamic behavior over short time scales.

In these microcontinuum theories, materials are modeled not as a collection of point-like particles, as in classical mechanics, but as assemblies of deformable entities with inherent orientation. A conceptual example often used to illustrate this framework is the crystal lattice of cesium chloride (CsCl), as shown in Fig. 1. Unlike classical elasticity, where a material point is rigid and has only translational degrees of freedom, this approach allows the material point to have three deformable directional vectors (directors). These directors add nine new degrees of freedom collectively referred to as micro-deformations to the three translational degrees of freedom (macro-deformations) of classical theories.

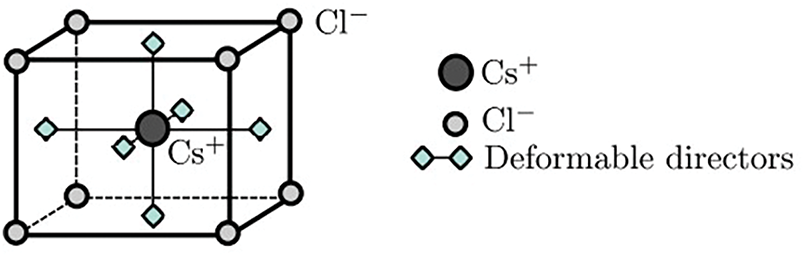
Figure 1: Schematic of the Cesium Chloride lattice indicating the deformable directors associated with the microstructure [16]

This approach to modeling structural response is relevant for materials and systems with internal microstructures, such as liquid crystals with dipolar molecules, polymers, solids with defects such as microcracks or dislocations, biological fluids with deformable particles (e.g., blood platelets) and composite materials [15,17–19]. Further, various types of microcontinuum theories have evolved depending on the nature of internal constraints applied to these deformable elements. The most general form, the micromorphic theory [14,20], includes all nine degrees of freedom of the microstructure. Simplified variants include the microstretch theory, which disallows shear deformations between directors, and the micropolar theory, which treats the directors as rigid. Together, these micromorphic, microstretch, and micropolar formulations are known as 3M microcontinuum theories [15]. Note that the 3M continuum theories introduce additional degrees of freedom to capture microstructural effects, resulting in a more complex extension of classical continuum mechanics. Alternatively, modeling of micro-deformations can also be explored by employing the gradients of macro-deformation variables to reduce the number of degrees of freedom [21]. In detail, Mindlin [21] addressed the effects of size by formulating higher-grade continuum models, where the mechanical behavior of solids is described using higher order gradients of existing displacement field variables. Thus, in gradient elasticity, the strain energy function involves both the strain terms and their gradients, resulting in stresses that depend on higher-order derivatives of the displacement field. For detailed historical insights, the reader may refer to Mindlin [22].

The origins of this strain gradient elasticity approach can be traced back to Cauchy and Augustin [23], who proposed an infinite series representation of constitutive relations for isotropic materials with periodic crystal structure, and Voigt [24] further analyzed the kinematic constitutive equations of discrete lattice models, incorporating molecular displacements and rotations. In the early twentieth century, the Cosserat brothers [25] advanced a generalized continuum theory, introducing enriched kinematics in which material particles possess both translational and rotational degrees of freedom. However, these developments largely went unnoticed until the 1960s, when interest in gradient continuum theories was significantly revived. Key contributions during this period include foundational works by Toupin [26], Kröner [27], Mindlin [21,28,29], and Green and Rivlin [30]. Building upon the seminal work by Mindlin [21] in connecting micro-deformations to macro-deformation gradients, Mindlin and Tiersten [28] simplified the couple stress theory by expressing it in terms of rotation gradient tensors derived from macroscopic displacement vectors. This approach can be viewed as a reduced form of the broader framework developed by Mindlin et al. [21,31], which considers all components of the higher-order displacement gradients. Variants of this general theory have been proposed depending on the specific macro-deformation tensors used to evaluate these gradients [31]. The initial work by Mindlin included only first-order strain gradients [31], but was later expanded to include second-order gradients [29]. This allowed for the introduction of the significant effects of surface elasticity at low dimensions. In the early 1970s, Germain [32,33] developed the equilibrium relations for the first-strain gradient elasticity theory, including the effect of microstructure via additional degrees of freedom, using the method of virtual power. A second resurgence in gradient continuum theories occurred in the 1980s, driven by Eringen [9]. This formulation proposes a gradient elasticity framework via reformulation of earlier work on the integral approach to nonlocal elasticity, replacing integral-type constitutive equations with differential equations, offering a more tractable framework for these theories. However, these are fundamentally different from the Strain gradient elasticity (SGE) framework proposed by Mindlin [31].

The seminal studies reported above by Mindlin et al. [21,29,31] paved the way for numerous simplified SGE frameworks. A substantial body of literature explores analytical and numerical techniques for the solution of governing differential equations (GDEs) for a simplified SGE framework. The challenge lies in these partial differential equations (PDEs) being of higher order compared to classical elasticity. The higher-order governing differential equations arising from these strain gradient formulations have been extensively solved through exact and analytical solutions [34–37], without imposing prior assumptions on the displacement field beyond the necessary continuity conditions in the structural domain. Further, given the higher-order partial differential equations for SGE, interpolation schemes with enhanced continuity are sought in numerical formulations [38,39]. To address this, various numerical methods have been developed, including mixed formulations [40], C1 continuous elements [41], and isogeometric analysis (IGA) [42].

Strain gradient theory offers significant advantages, particularly in modeling micro- and nano-scale structures where classical elasticity falls short. Firstly, the model incorporates length scale parameters to account for the deformation of the material microstructure. This enables an accurate description of the structural response at low dimensions, where the effects of microstructure are significant. Furthermore, unlike alternate higher-order theories (3M), SGE does not introduce additional degrees of freedom [31]. Finally, the constitutive framework of the SGE remains consistent with the classical elasticity even when the material length scale tends to zero, ensuring broad applicability. Its versatility extends to static, dynamic, and stability problems, making it a powerful tool in the design and analysis of advanced materials and structures.

In particular, the presence of strain gradients was theorized to present a novel multiphysics coupling that can be leveraged to develop interesting applications at low dimensions [43]. This opens exciting avenues for micro- and nano-architected smart structures [44,45]. Among these, the coupling between the electric field and the strain gradients was first studied theoretically in crystals nearly fifty years ago [46]. Much later to these theoretical advancements, Cross and colleagues conducted experimental investigations in various dielectric materials to experimentally demonstrate this behavior [47,48]. It has been observed that non-uniform strains in a general dielectric material can induce a non-zero electric field, a phenomenon known as the flexoelectric effect. These experiments often focused on deformation of structures in bending (flexure), which generates significant strain gradients; thereby drawing the name ‘flexoelectricity’. Of significant interest is the fact that a coupling involving strain gradients is observed to be universal, without restriction to limited (non-centrosymmetric for piezoelectric) crystal structures [43]. Subsequently, extensive research has been conducted to explore the flexoelectric effect in solids, leading to advances in the design of actuators, sensors, and energy harvesting devices based on this phenomenon. Analogously to the electro-mechanical coupling above considering strain gradients, its coupling with other field variables such as the magnetic [49] and thermal field [50] variables are also noted in the literature.

A detailed time history and a quantitative assessment of the literature produced in the general area of strain gradient theory are provided in Fig. 2. An exponential increase in the literature on SGE in the last 20 years indicates a growing interest in fundamental and applied research on strain gradients. In particular, research on strain gradients has been carried out predominantly in the domain of plasticity. Conventional plasticity theory lacks an intrinsic length scale in its constitutive laws and therefore cannot capture size-dependent effects. However, numerous plasticity phenomena exhibit clear size effects, where smaller structures show a stronger mechanical response [51–53]. For example, indentation hardness in metals and ceramics increases with decreasing indenter size, due to smaller reinforcing particles leading to higher rates of strengthening and work hardening in metals for the same volume fraction [54,55]. Although these effects may arise from different mechanisms, all require a length scale for proper interpretation. A common approach to capture such size effects is to make the yield stress a function of both the strain and the strain gradient [56–60]. In this article, we review the literature on strain gradients, highlighting their role on the elastic and multi-physics coupled response of low-dimensional structures, areas that have received less attention.

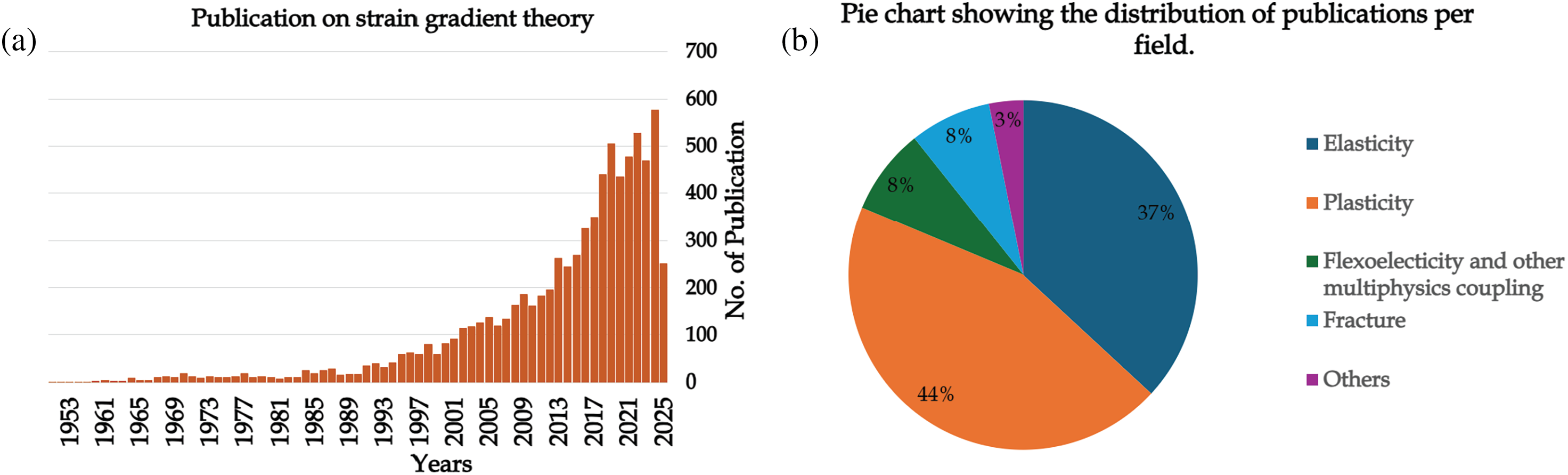
Figure 2: (a) Histogram chart showing the historical evolution of scientific publications of strain gradient theories per year starting from 1941. (b) Pie chart showing the distribution of publications per field. The data used in this figure were collected from Scopus

We begin this review article with a description of the constitutive models for SGE in Section 2. This includes a detailed derivation of the constitutive relations for strain gradient theory, including an overview of the simplified SGE models and the approaches used in the literature to estimate the corresponding material constants. This is followed by a discussion of the various analytical and numerical approaches (finite element (FE) and non-FE based) used to solve the governing differential equations for SGE in Section 3. Before proceeding to a discussion of the literature on applications of SGE and related multi-physics coupling, Section 4 discusses the physical significance of SGE. Subsequently, Sections 5 and 6 highlight the foundational and applied research on multiscale elastic and multiphysics coupling (flexo- electric, magnetic, and caloric effects) within the framework of strain gradient theories. Finally, Section 7 presents a review of alternate integral and integro-differential approaches to capture nonlocal effects beyond strain gradient elasticity. We conclude with some probable directions for future research on strain gradient elasticity.

2  Constitutive Models for SGE

The deformation energy density of an elastic continuum considering microstructural effects can be expressed as [15,21]:

𝒲(ε,η)=𝒲CT(ε)+𝒲SGE(η),(1)

where 𝒲CT(ε) is the classical (strain) deformation energy density which is a function of the first gradients of displacement (strain, ε) [61]. 𝒲SGE(η), expressed in terms of a higher-order deformation metric η, is an additional deformation energy metric that introduces size effects. The classical theories of elasticity can be recovered by ignoring the contribution of the latter term towards the complete deformation energy.

Above, we introduce the additional contribution in 𝒲SGE(η) by carefully choosing the higher-order deformation metric, η. To begin with, Eringen proposed “3M” microcontinuum theories to account for the energy associated with higher-order deformation metrics 𝒲SGE. This was achieved by introducing additional deformation variables, such as micro-rotations of the directors in a microstructure by Cosserat [25]. A schematic illustration of the deformable directors is provided in Fig. 1 with the example of a crystalline cesium chloride (CsCl) lattice structure. This was further extended by Mindlin in his seminal work [21] to develop a framework for incorporating the effects of microstructure via micro-rotations on mechanical behavior of the macro structure. Later, these studies were extended to include additional deformation variables such as micro-stretch by Eringen [14,15]. However, considering the complexity of introducing additional degrees of freedom, alternative simpler frameworks were developed. In these frameworks, η is expressed as higher-order gradients of conventional deformation measures. Examples include the couple stress theory [26,28] in which the micro-rotation variable is replaced by a rotation gradient tensor defined in terms of the second-order strain tensor.

Another example of a higher-order deformation metric is the first gradient of the second-order strain tensor proposed by Mindlin [31]. This approach incorporates the effects of the micro-structure within the constitutive relations via gradients of the classical (second-order) strain tensor. Thereby, no additional degrees of freedom are introduced within the constitutive model following the strain gradient approach to capture microstructure effects. It is worth noting that the set of higher-order metrics can be expanded further to include contributions from the second gradient of the strain tensor, enriching the total deformation energy density described in Eq. (1).

We present here the details of a constitutive model for the first strain gradient theory. More specifically, the constitutive relations for SGE considering the first derivative of strain gradients are detailed. Later, a discussion on the alternate forms for the first strain gradient theories (either as second gradients of displacements or first gradients of the strain tensor or their components) is provided. Subsequent to this, simplified forms of the SGE proposed in literature, following from the generalized form, are introduced, and details on their relevance to different studied are provided. We follow this with brief discussions of the characterization of the additional material constants introduced via SGE.

Before proceeding further, we note that an experimental observation of a non-zero polarization in centrosymmetric crystals [47,62] that cannot be explained by piezoelectric coupling. Moreover, when a strain gradient is applied across the symmetric crystal domain, the symmetry of the centrosymmetric crystal can be disrupted, resulting in net polarization upon deformation. This phenomenon is illustrated in Fig. 3. As shown, prior to deformation, the positive ion aligns with the centroid of the negative charges in the lattice, leading to zero net polarization. When a strain gradient is applied, the centroid of the negative charges shifts relative to the positive ion, and a net polarization is induced in the centrosymmetric crystal. This electro-mechanical coupling follows from the strain gradient referred to as the flexoelectric effect. This will be discussed in detail later in Section 6.

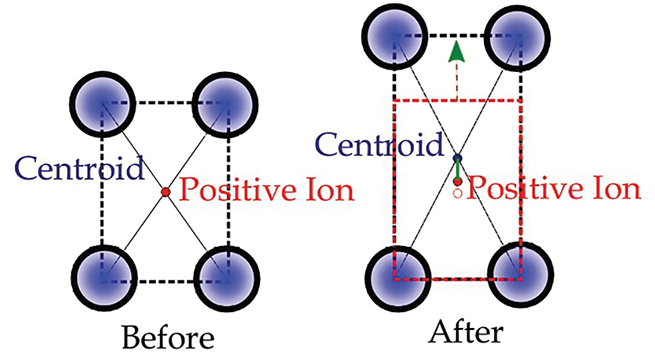
Figure 3: Net polarization induced in a centrosymmetric crystalline structure due to strain gradients [16]

2.1 First Strain Gradient Theory of Elasticity

Following Eq. (1), the deformation energy density of a homogeneous, centro-symmetric elastic continuum considering the strain gradients is given by [21,31]:

𝒲CT(ε)=12 ε : C : ε,   and   𝒲SGE(η)=12η :˙ G :˙ η.(2)

Here, the definitions of second-order tensor, ε, and third-order strain gradient tensor, η, are given as:

ε =12(∇⊗u+u⊗∇),   and   η= ε⊗∇.(3)

In this expression, u represents the displacement vector, ∇ is the gradient vector, and ⊗ is the dyadic product.

Alternatively, the third-order strain gradient tensor (η) can be expressed as either a second gradient of the displacement vector or in terms of gradients of the decomposed strain tensor. In particular, the above formulation is commonly referred to as Form II of the SGE proposed by Mindlin [31]. Additionally, Mindlin proposed that strain gradients be expressed in terms of the second gradients of the displacement vector (Form I of SGE) as follows:

η^ijk=uk,ij(4)

Further to this, Mindlin also proposed an alternative equivalent form (Form III) of strain gradients in terms of the dilatational gradient vector γi, deviatoric stretch gradient tensor η^ijk, and rotation gradient (curvature) tensor χij. The latter formulation follows from an orthogonal decomposition of the strain gradient tensor η into symmetric and antisymmetric components and hydrostatic/deviatoric components similar to the decomposition of the strain tensor to dilation and deviatoric components [21,63]. They are given as follows:

γi=ηikk=εkk,i ,   χij=eipqηpqj ,   η^ijk=ηijks−15(δijηmmks+δjkηmmis+δikηmmjs),(5)

where, ηijks=13(ηijk+ηjki+ηkij) and eijk is the third-order permutation tensor [61]. Further, the rotation gradient χ can be further decomposed into symmetric and anti-symmetric components as follows [64,65]:

χijs=12[χij+χji],     χija=12[χij−χji](6)

The material constitutive relations can be expressed directly in terms of the first gradient of strain defined in Eq. (3), or alternate forms given in Eqs. (4) and (5).

The constitutive relations for the work conjugates of the second-order strain and third-order strain gradient tensors are defined following thermodynamic considerations [66,67]. In particular, the constitutive relations for the second-order (Cauchy) stress tensor, σ, and the third-order (hyper) stress tensor, τ, are given by:

σ=∂𝒲∂ε=C: ε,  and   τ=∂𝒲∂η=g :˙ η.(7)

In the above relations, C and g are the material constant tensors. Recall that C is the fourth-order material constant tensor from classical elasticity theories [61]. Additionally, g is the sixth-order strain gradient elasticity tensor connecting the strain gradient tensor introduced in Eq. (3) and the hyper-stress tensor. In particular, the Cauchy (second-order) stress is expressed as a work-conjugate of the second-order strain tensor, and the higher-order stress is a work-conjugate of the strain-gradient tensor. The additional field variables (η and τ) account for size effects, such as increased stiffness or strength, in micro- and nanostructures. These variables play a key role in capturing localized deformations near defects, interfaces, or cracks, and for depicting nonlocal interactions where stress depends on strain over a finite region (instead of a point-wise correlation noted via classical elasticity). By introducing effects of the microstructure within the constitutive relations, higher-order strain gradient theories provide a more realistic representation of material behavior in scenarios dominated by small-scale phenomena.

The fourth-order material constant tensor C for an isotropic material is given by [61]:

C=λ 1⊗1+2μI,(8)

where λ and μ are the Lamé parameters, and 1 and I are the second- and fourth-order identity tensors, respectively [61]. Although two material constants (the Lamé parameters) suffice to completely define the material constant tensor for isotropic material symmetry, additional constants will be required for other material symmetries.

The sixth-order material constant tensor g corresponding to SGE involves at least five independent material constants for an isotropic material [31]. Considering the difficulty in characterization of these five independent constants, simpler formulations are proposed in the literature necessitating a lower number of material constants. Furthermore, the material constant tensor g for a lower material symmetry requires a greater number of constants (atleast 171 for anisotropic material symmetry [68]). Estimation of the additional constants is extremely difficult, and limited studies have explored this direction [69]. Therefore, the definition of g tensor corresponding to isotropic solids is extended to other material symmetries in an ad hoc manner [68]. In this section, we restrict the discussion to isotropic materials, when the deviation of g is precise. A short summary of the approaches for the estimation of material constants through experiments and MD simulations is provided in Section 2.5.

Imposing the appropriate conditions for directional symmetries inherent in isotropic materials over g tensor, Mindlin provided [31]:

gijklmn=a14((δijδkl+δikδjl)δmn+(δimδln+δinδlm)δjk)+a24(δij(δkmδln+δknδlm)+δik(δjmδln+δjnδlm)+δil(δjmδkn+δjnδkm))+a3δilδjkδmn+a42δil(δjmδkn+δjnδkm)+a54(δim(δjlδkn+δjnδkl)+δin(δjlδkm+δjmδkl)),(9)

where a◻, ◻=1,2,...,5 are five material constants. This complete expression of the sixth-order tensor may be considered as the generalized form of the sixth-order tensor. In particular, the expression above based on five independent constants is devoid of ad hoc assumptions or simplifications for the definition of the g tensor. Recall that three different frameworks (forms) of the strain gradient tensor are proposed in the literature (see Eqs. (3)–(5)). We note here that five independent material constants are required by all the equivalent frameworks proposed in [31].

Considering the challenges involved in the characterization of five constants associated with the g tensor, simplified models of SGE, employing fewer material constants, are proposed in the literature. These models follow from ad hoc assumptions that neglect the contributions of specific deformation modes to 𝒲SGE(η). These assumptions facilitate a reduction in the number of material constants required for the sixth-order tensor.

As mentioned above, Mindlin [21] developed a comprehensive SGE theory to capture the effects of microstructure. The proposed model introduced 16 additional constitutive parameters (length scales) for isotropic materials in addition to the classical Lamé constants. Due to the complexity involved in determining these constants, the practical use of this framework is limited. To address this, Mindlin and Eshel [31] further proposed three simplified versions of the theory (given in Eq. (9)), each requiring only five internal length scale parameters/additional material constants. Despite this reduction, an experimental determination of the five parameters remains challenging. Later works by Yang et al. [65], Lam et al. [6], and others [63] proposed simplified models that further reduced the number of independent parameters, thereby enhancing the feasibility for engineering applications. A detailed discussion of the different simplified strain gradient theories available in the literature is provided in Section 2.2.

2.2 Simplified Models of SGE

We list here a few seminal works proposing simplified models for SGE. However, we note that the below is intended to be a summary of alternate SGE constitutive models, and not an account of all the micromorphic theories and higher-order formulations in literature.

•   Zhou’s Three Constant Model: Zhou et al. [63] revised the sixth-order tensor through two independent orthogonal decompositions of the strain gradient tensor, indicating that only three independent constants are necessary to evaluate the g tensor. As a result, the five coefficients in Eq. (9) are reduced to three independent coefficients as follows:

a1=−23(a2+a5),   a3=23a2+16a5.(10)

Further, these material constants can be recast in terms of three independent material length scales l0,l1,and l2 given by:

a2=215(27μl02−4μl12−15μl22),   a4=23(μl12+6μl22),   a5=43(μl12−3μl22).(11)

l0 represents the characteristic material length scale for dilatational gradients, l1 corresponds to deviatoric stretch gradients, and l2 relates to the symmetric curvature tensor. To provide a better context of these length scales, and their physical relevance, the above constitutive relations can be recast in the Form III framework proposed by Mindlin [31] to be:

p=2μl02γ,   τ^=2μl12η^,   m=4μl22χs+365μl02χa(12)

where μ is the shear modulus defined in Eq. (8); p, τ^ and m are the work conjugates of the deformation metrics γ, η^ and χ, respectively, introduced in Eq. (5). This constitutive model does not consider prior assumptions regarding deformation metrics, such as incompressibility (γi=0, [57]) or a symmetric curvature tensor (χija=0, [6,65]). The simplified models discussed in the following may be obtained by ignoring one or more of these deformation modes or the associated length scales. Therefore, this framework is also referred to as the Generalized First Strain Gradient Elasticity Theory (GFSGET) [70].

•   Lam’s Strain Gradient Theory of Elasticity: Lam et al. [6] proposed to ignore the contribution of anti-symmetric component of the rotation gradient tensor. In particular, this constitutive model can be expressed as a simplification of the GFSGET, introduced above, by considering χija=0. This was proposed to satisfy the balance of angular momentum via a symmetric definition of the couple stress mij [65]. Thus, the constitutive relations for the couple stress given in Eq. (12) reduce to:

m=4μl22χs(13)

We note here that the other two components of the constitutive relations in Eq. (7) remain unchanged. This theory is also referred to as Modified Strain Gradient Theory (MSGT). In addition to proposing this, Lam et al. have conducted experimental studies on epoxy polymeric beams to confirm the MSGT constitutive relations and provide a route for characterization of the length scales l0, l1, and l2.

•   Modified Couple Stress Theory (MCST): Yang et al. [65] proposed a simplified version of Mindlin’s constitutive model considering only the contribution of couple stresses toward the deformation energy. In particular, the constitutive model for SGE proposed by Yang et al. can be realized as a simplified version of MSGT where the stretch gradient tensors (deviatoric and dilatational) do not contribute to the deformation energy density. Simply put, l0 and l1 are considered trivially zero, reducing the higher-order constitutive relations to Eq. (13), with p and τ^ being zero. The study assumes that the deformation energy density 𝒲 depends solely on the strain tensor and the symmetric curvature tensor, without explicit dependence on the rotation (antisymmetric part of the deformation gradient) or the antisymmetric part of the curvature tensor. This finding greatly simplifies experimental characterization, reducing the number of independent material length scales to one (from five in [31]). Finally, we note that this constitutive model has been popular among researchers owing to only one additional constant for the strain gradient deformation energy and the ease of implementation in analytical and numerical solvers. However, researchers have highlighted fundamental limitations of the symmetric assumption over couple stress (discussed in the following) [64] and the ad hoc assumptions to ignore stretch gradients [6].

•   Consistent Couple Stress Theory: Hadjesfandiari and Dargush [64] noted the mathematical and physical inconsistencies caused by a symmetric assumption for couple stress. For instance, inconsistent constitutive relations are realized from an indeterminacy of the spherical component of the couple-stress tensor and the emergence of the body couple for the force-stress tensor. To address these, they proposed an alternate framework for SGE involving a couple stress conjugate to the anti-symmetric curvature tensor χa, while the contribution of the symmetric rotation gradient tensor χs towards the deformation energy density is ignored. This framework is termed a consistent couple stress theory, and can be expressed as:

m∝μl2χa.(14)

The above relation may also be obtained from the GFSGET proposed above (see Eq. (12)) by ignoring the contributions of γ, χs and η^ towards deformation energy. By adopting the continuum approach to kinematic displacement and rotation, the couple stress tensor is established to be skew-symmetric only for a skew-symmetric component of the rotation gradient tensor. However, several authors [71,72] have noted physical and mathematical limitations of a skew-symmetric definition for couple stresses. This primarily follows from an asymmetric definition for couple-stresses that does not satisfy the invariance requirement under coordinate system rotation [73]. Therefore, extremely limited studies are available in the literature employing these constitutive relations strain gradient elasticity.

•   Indeterminate Couple Stress Model [28,74]: This theory proposes a couple stress model considering the complete curvature tensor as follows:

m=μl0′2χs+μl1′2χa.(15)

In this framework, the complete energy corresponding to rotation gradient tensors are considered. However, the energy contributions by the (dilatation and deviatoric) stretch gradients are ignored. In agreement with Eq. (12), it may be noted that two distinct material length constants (l0′, l1′) are assumed here that correspond to the symmetric and skew-symmetric components of the curvature tensor. Further, the MCST and the consistent couple stress theory discussed above may be obtained as suitable reductions from this model.

•   Simplified Strain Gradient Elasticity Theory (SSGET) [75,76]: This theory follows from ad hoc assumptions over the sixth-order elasticity tensor corresponding to Form II given in Eq. (7). In particular, recall that five independent constants are proposed to be necessary for the sixth-order g tensor defined in Eq. (9). These are in addition to the two Lamé parameters employed for the definition of the fourth-order classical material constant tensor C. However, owing to the difficulties in characterization of these five constants, Aifantis [75] proposed the following single parameter-based definition for the higher-order material constant tensor:

gijklmn=l2Cjkmnδil,(16)

where l is a characteristic material length scale, and C is the fourth-order material constant tensor defined in Eq. (8). Gao et al. [76] refered to this constitutive model as the Simplified Strain Gradient Elasticity Theory (SSGET) owing to the ease in formulation and its implementation. Exadaktylos and Vardoulakis [77] further simplified the above model for the sixth-order tensor to be:

gijklmn=μl22δil(δjmδkn+δjnδkm).(17)

This may also be obtained from the general form of this tensor given in Eq. (9) by assuming a1=a2=a3=a5=0 and a4=μl2. This framework is popular among researchers for qualitative studies of SGE owing to the ease of developing analytical and numerical solutions.

A brief comparison of the assumptions, advantages, and limitations of the simplified gradient theories is provided in tabular form in Table A1 of Appendix A.

2.3 Second Strain Gradient Theory of Elasticity

Mindlin [29] demonstrated that the incorporation of the third gradient of displacements into the strain energy density function can lead to the emergence of surface tension in isotropic, centro-symmetric, linearly elastic solids. This arises because of the presence of initial, homogeneous, self-equilibrating triple stresses within the constitutive relations. Around the same time, Toupin and Gazis [78] reported that within the first strain gradient theory, such effects occur only in non-centrosymmetric materials. More recently, Cordero et al. [79] revisited the role of the third gradient of the displacement vector in isotropic solids. In this study, contributions to surface tension (by the second gradient of strains) are highlighted. Further to this, the coupling between the strain tensor and their second gradients in the strain energy density is identified to present free surface effects.

In the context of Mindlin’s second strain gradient theory of elasticity, the potential energy density 𝒲 for centro-symmetric and isotropic material is defined as a function of the strain tensor and its first and second gradients as follows:

𝒲=12Cijklεijεkl⏟Classical+12gijklmnηijkηlmn⏟First SGE+12bijklmnopεijklεmnop⏟Second SGE+bijklmnεijεklmn⏟Free surface+b0εiijj⏟Surface tension(18)

where

ηij,k=∂ijuk,   εijkl=∂ijkul.(19)

Recall that εij is the second-order strain tensor and ηijk and εijkl, respectively, denote the first and second-gradients of the strain tensors. Cijkl,gijklmn and bijklmnop are the material constants corresponding to the strain, the first gradient, and the second gradient of the strain tensor. In the above constitutive relations, of specific interest is the coefficient b0 introduced in Eq. (18). This constant, referred to as the modulus of cohesion, introduces surface energy within the constitutive relations and is responsible for the surface effects on the bulk response along with the coupling coefficient bijklmn. This observation was further explored in detail by Cordero et al. [79]. Thus, unlike the first strain gradient theories studied by [78], surface tension can be accounted within centro-symmetric materials.

The additional material constants introduced in the second strain gradient theory of elasticity have been proposed to be determined from first-principles calculations and have shown good agreement with analytical solutions for simple geometries [80,81]. Using this framework, the mechanical response of the cantilever beams was investigated using Euler-Bernoulli beam displacement theory [80]. Karparvarfard et al. [82] extended these frameworks to derive the geometrically nonlinear governing differential equation of motion and associated boundary conditions for small-scale Euler–Bernoulli beams based on the SSG theory.

Theory of surface elasticity: Gurtin and Murdoch, in their seminal paper [83], introduced the concept of surface elasticity by modeling the surface as a thin elastic membrane, characterized by surface elastic constants distinct from those of the bulk material, and incorporating an intrinsic residual strain. This residual strain arises because surface atoms typically have shorter bond lengths compared to atoms within the bulk. Although at the macroscale such surface effects can often be ignored allowing bulk properties to represent the overall behavior, this is not the case for nanoscale structures. In low-dimensional nanostructures, the surface-to-volume ratio is significantly high, making the energy contribution of surface atoms non-negligible. This leads to significant surface-induced residual stresses and altered elastic properties compared to bulk material [84]. This framework rigorously incorporates surface stress and surface elastic constants, enabling the analysis of size-dependent mechanical behavior at the nanoscale. Moreover, the second strain gradient elasticity, defined in Eq. (18), can also be conceptually viewed as comprising two interacting subsystems: a bulk region that behaves as a classical Cauchy continuum and a surface that acts as a membrane-like boundary layer, both at equilibrium at local and global scales [85]. However, except for a few investigations of fluid films and rigid interfaces, such treatments are relatively rare. Instead, the Gurtin-Murdoch treatment of surface effects has been extensively employed in the literature. The effects of surface elasticity are also realized on the coupled multiphysics response, such as the electromechanical response of MEMS and NEMS [86–89].

2.4 Governing Differential Equations of Motion

In this section, we derive and discuss the governing differential equations of motion for a solid employing strain gradients to capture the effects of microstructure and micro-inertia. More specifically, the governing differential equations (GDEs) and the associated boundary conditions (BCs) for a strain gradient elastic solid are derived here following variational principles [90–92]. We provide here only the salient steps in the derivation and the physical insights drawn from the expressions encountered here. For a complete derivation, interested readers may refer to [93]. For a solid body of volume Ω, bounded by a surface ∂Ω, the total deformation energy 𝒰 of the body is given by:

𝒰=∫Ω𝒲   dV,(20)

where 𝒲 is the deformation energy density of the solid defined in Eq. (1). Using the constitutive relations given in Eq. (7), the variation of the total deformation energy can be expressed as:

δ𝒰=∫Ω(σ:δ ε+τ ⋮ δη)   dV.(21)

By the definition of strain and strain gradients given in Eq. (3), the first variation of the potential energy can be rewritten as:

δ𝒰=∫Ω(σ:(δu⊗∇)+τ ⋮ (δε⊗∇))   dV.(22)

The variations δu and δε are not independent of each other. Thus, the δε is split into surface and normal components as:

δu⊗∇=R⋅(δu⊗∇)+(n⊗n)⋅(δu⊗∇),(23)

where n is normal vector to surface ∂Ω and the surface projector tensor R is defined as R=1−n⊗n. In case of sharp edges Γ in the solid, the following result is employed [76]:

∫∂Ωn⋅(∇∧(n∧((n⋅τ)⋅δu)))dA=∮Γ[[s⋅(n⋅τ)]]⋅δu   dL,(24)

where ∧ denotes conventional vector-cross product, and s is the co-normal vector given as s=e∧n; e is a unit vector tangent to the edge Γ, and [[⋅]] denotes difference across the edge Γ. This result is of interest as it allows for the capture of jump in the displacement variable across the edges/discontinuities. This has physical relevance to modeling and alleviating discontinuities and singularities (such as those encountered in fracture mechanics) using the SGE framework [94,95].

Finally, the first variation of the external work done 𝒱 and the kinetic energy 𝒯 are assumed to be given by [96]:

δ𝒱=∫Ωb¯⋅δu   dV+∫∂Ω(t¯⋅δu+q¯⋅n⋅(δu⊗∇))   dA+∮Γr¯⋅δu   dL,(25a)

and

δ𝒯=12∫Ωρ (u˙⋅u˙) dV+16∫Ωρ d2 (ε˙ : ε˙) dV,(25b)

where b¯, t¯, q¯, and r¯ are the prescribed values of body force per unit volume, surface traction per unit area, double stress traction vector, and line load along a sharp edge, respectively. Therefore, it is clear that external work corresponding to all independent deformation modes and captured here. Further, the second term in the kinetic energy corresponds to the micro-inertia corresponding to additional deformation modes of the microstructure [96,97], and d being the associated characteristic material length scale. The role of micro-interia within the elastodynamic behavior is discussed in detail in [98]. Finally, ρ is the density of the solid.

Now applying the variational principle (Hamilton’s stationary principle: δℐ=0, where ℐ=∫0t(Π−𝒯) dt and Π is the potential energy Π=𝒰−𝒱), the following GDEs are obtained:

∇⋅(σ−∇⋅τ)+b¯=ρ(u¨−d23∇⋅(∇⊗u¨)),   in Ω.(26a)

The variational principle also yields following boundary conditions associated with the above GDEs:

n⋅(σ−∇⋅τ)−[R:(n⋅τ)⊗∇]+[R:(∇⊗n)][(n⊗n):τ]+ρd23n⋅(∇⊗u¨)=t¯,   or   u=u¯   on ∂Ω,(n⊗n):τ=q¯,   or   n⋅(δu⊗∇)=n⋅(δu¯⊗∇)   on ∂Ω,[[s⋅(n⋅τ)]]=r¯,   or   u=u¯   on Γ,(26b)

where u¯ is the prescribed value for the displacement.

The above set of GDEs (or an equivalent form) is established to be well-posed with unique solutions [99]. Although this result is trivial considering the positive definiteness of the strain energy density, this observation is in contrast to the alternate (integral) theories explored for size effects in structures [100]. Thus, the solution to the above GDEs is not expected to demonstrate any paradoxical observations noted from the integral theories [101,102].

A solution of the above governing equations (including associated boundary conditions) includes the effect of the micro-structure over the elastic response of the solid. Note that the above set of governing equations is relevant to homogeneous solids such as monolithic beams, and non-homogeneous solids such as laminates or functionally graded composites [70]. In other words, the above set of governing equations employ the general form of constitutive relations for SGE given in Eq. (7). Thereby, the boundary conditions over surface and jump conditions at the edges/discontinuities are devoid of ad hoc assumptions. Furthermore, this framework can be extended to study multiphysics behavior such as the flexoelectric response of solids, allowing for electro-mechanical coupling analysis. We will discuss this aspect more in Section 6.

2.5 Estimation of Material Constants

In this section, we present some directions used in the literature for the characterization of additional material constants corresponding to the sixth-order g tensor. We note here that different formulations for this tensor are available in the literature; some of which have been discussed in Section 2.2. Therefore, the material constants reported by various studies may not be consistent. However, a majority of the studies on characterization for the g tensor focus on the estimation of length scales (such as l0, l1 and l2 in Eq. (11)) characteristic to the microstructure. These length scales are identified through empirical or experimental approaches, in a manner to accurately capture size-effects over the mechanical behavior, or relate them to intrinsic material properties like the lattice constant or polymer chain lengths.

Experiments: The significance of microstructure-dependent material length scales in determining the size-dependent behavior of structures has led to numerous experimental investigations aimed at evaluating these parameters. Lakes et al. pioneered experimental investigations into the bending response of fibrous and granular materials for the estimation of the characteristic length scale corresponding to the couple stress and micro-polar theories [11,12]. These studies aimed at estimation of the material length scales for the human compact bone also present experimental evidence of microstructure effects on the structural response (either via torsion, bending or wave dispersion) as illustrated in Fig. 4. Typical values of length scales for human bone have been reported to be below 1 mm.

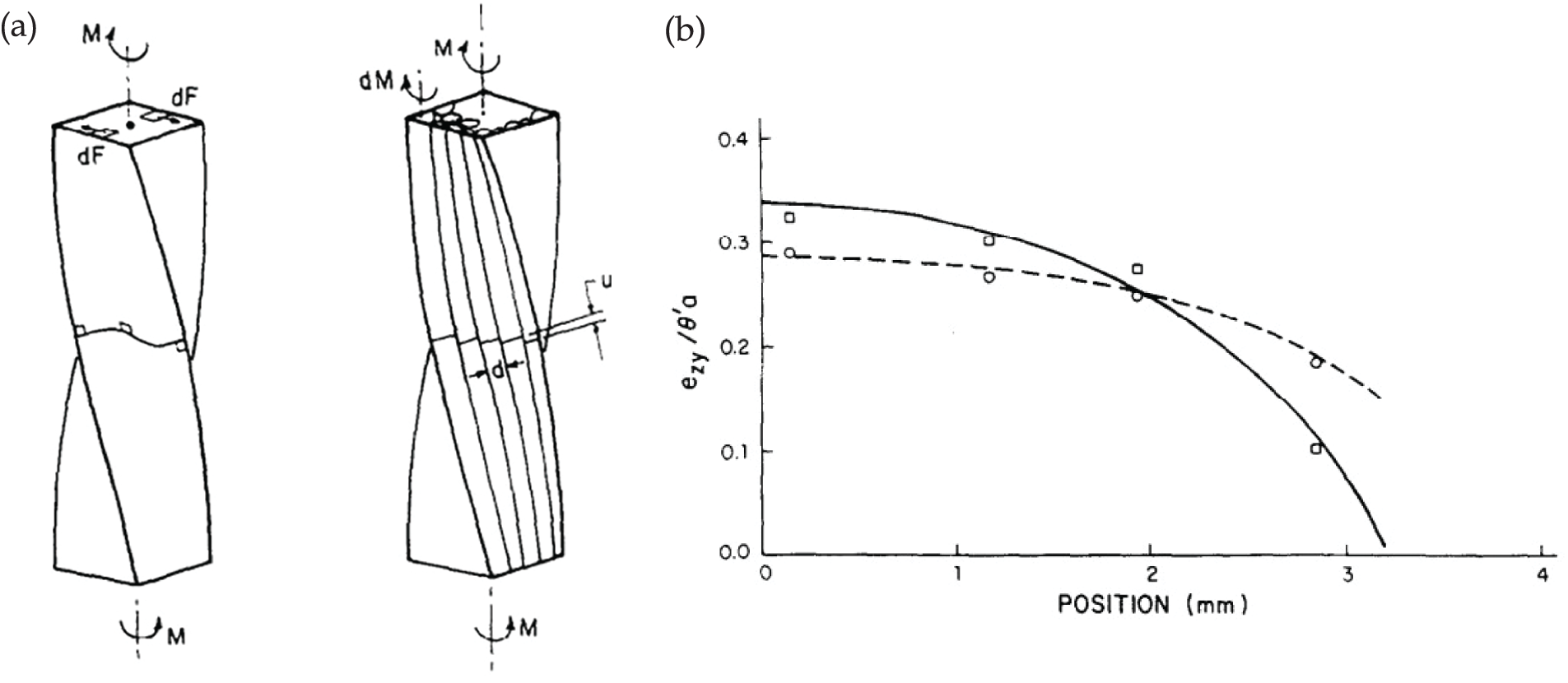
Figure 4: (a) Comparison of warp and strain patterns produced by torsion in a homogeneous prism modeled with classical elasticity and a fibrous human bone prism, based on the work of Park and Lakes [11]. (b) Strain distribution observed along the boundary of human bone: the solid curve corresponds to predictions from classical elasticity theory, the dashed curve represents results from Cosserat elasticity theory; Experimental data points are shown as circles for wet bone and squares for dry bone, adapted from Park and Lakes [11]

Similar effects of microstructure are reported to reduce the stress concentration around small holes [103]. Furthermore, Lakes [104] summarized observations from experimental studies on a variety of classes of materials. Metals, amorphous polymers, and particulate compounds have been reported to generally exhibit classical mechanical behavior. However, for certain cellular and fibrous materials, the characteristic lengths align with the size of the largest structural elements. Moreover, considering the example of fiber-reinforced composites, it is reported that these length scales can exceed cell size.

Later, Lam et al. [6] conducted experimental studies on bending responses of polymeric micro-beams of 10–100 µm dimensions to realize the effects of strain gradients on elastic behavior. In addition, these experimental results are used to quantitatively estimate the additional material constants corresponding to MSGT provided in Eq. (13).

Finally, a series of experimental studies on perovskites confirmed the influence of strain gradients on the elastic response of low-dimensional structures [47,105], further extending to observations and material characterization for electro-mechanical coupling through flexoelectricity.

Ab-initio calculations: Marangati and Sharma [106] explored an alternate method based on molecular dynamics (MD) simulations to determine the additional constants. Using statistical mechanics techniques, they derived equations that link the strain gradient material constants to displacement within a Molecular Dynamics (MD) computational ensemble. They also compiled characteristics length scale for SGE for a range of material systems, including metals (Cu, Al), single-component semiconductors (Si, Ge, C), multi-component semiconductors (GaAs, GaP), amorphous silica, and a polymeric system (polythene). A comparison of the length scale parameters between material classes is provided in Fig. 5.

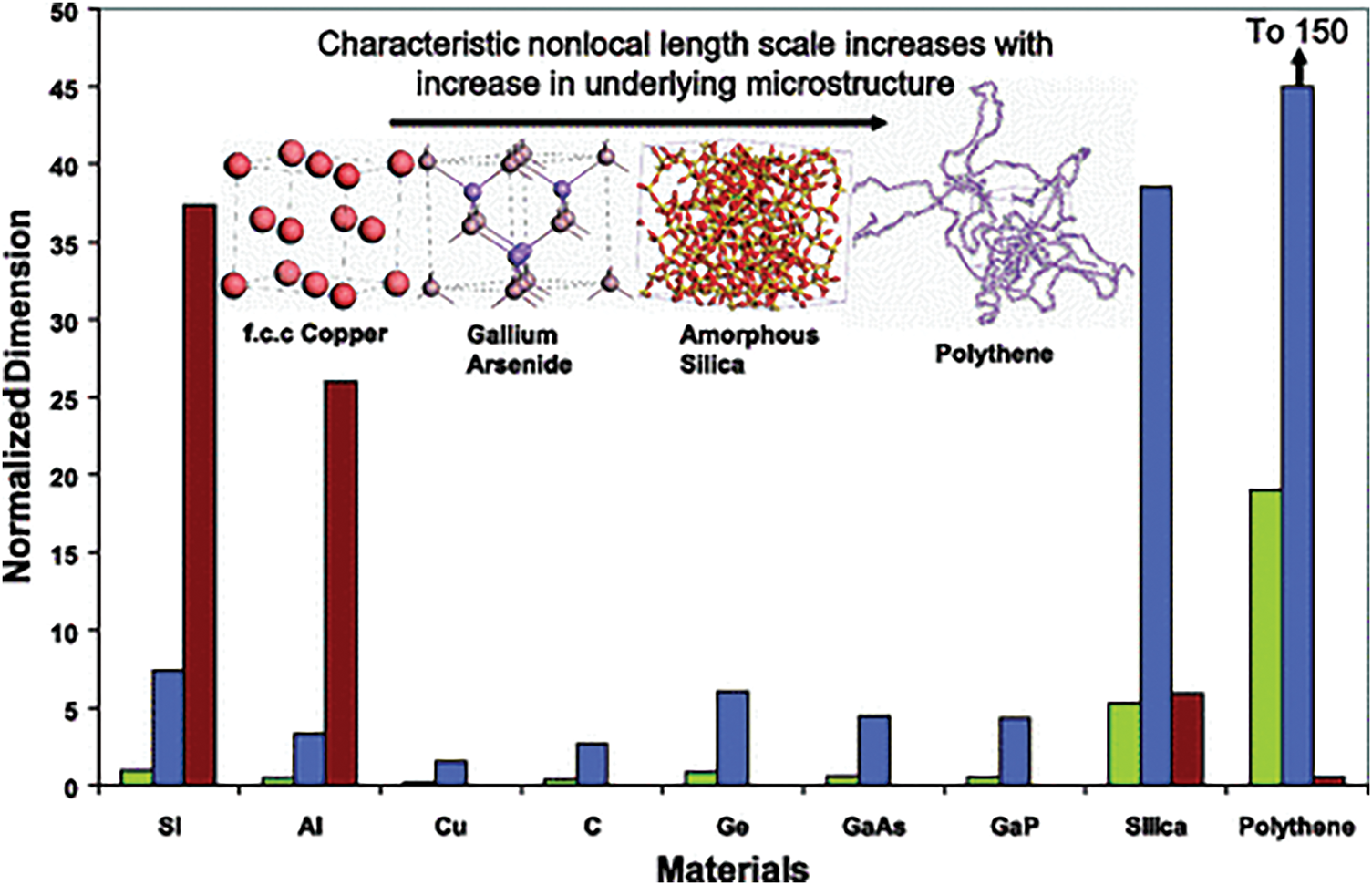
Figure 5: Length scale parameters determined from the molecular dynamics and lattice dynamics studies compared for different materials [107]

This result from [107] highlights the growing significance of microstructural effects in materials, such as polymers, compared to crystalline materials. Shodja et al. [108] determined the length scales for use in SGE constitutive relations of the body-centered cubic (BCC) and face-centered cubic (FCC) metal crystals using ab initio calculations. Another route for material length characterization is via guided elastic waves that exhibit multiple modes and dispersion properties. For instance, Liu et al. [109] conducted MD simulations to investigate multi-mode guided elastic wave propagation in a 2D aluminum plate. The results of these simulations are used to calibrate the size parameters in nonlocal strain gradient theory.

Homogenization: A common approach to determine the response of heterogeneous materials involves homogenizing the behavior of a Representative Volume Element (RVE) [110].

In particular, leveraging the recent advancements in scale-transition methods, particularly second-order homogenization, gradient theories are used at the macroscopic level to capture the response of heterogeneous materials [113–116]. These theories incorporate a length scale parameter l, determined from the RVE size and characteristics, allowing them to capture the heterogeneous material response as shown in Fig. 6a. Notably, Gitman et al. [117] and Kouznetsova et al. [115] independently developed the first and second order homogenization for linear-elasticity and hardening processes, respectively; this framework leads to the dynamic consistent gradient elasticity theory. Here, the material constants corresponding to the strain and acceleration gradients can be obtained from the homogenization of static and dynamic RVE sizes, respectively [117,118]. Peerlings and Fleck [119] developed a three-dimensional linear elasticity model and introduced a computational framework based on asymptotic homogenization theory to analyze length scales in matrix-inclusion composites. This approach enhances homogenization methods by integrating static and dynamic effects across multiple scales. For instance, an example of the lattice core structure studied using micropolar theories is illustrated in Fig. 6b. A SGE approach to model such a lattice core structure was proposed by [120,121].

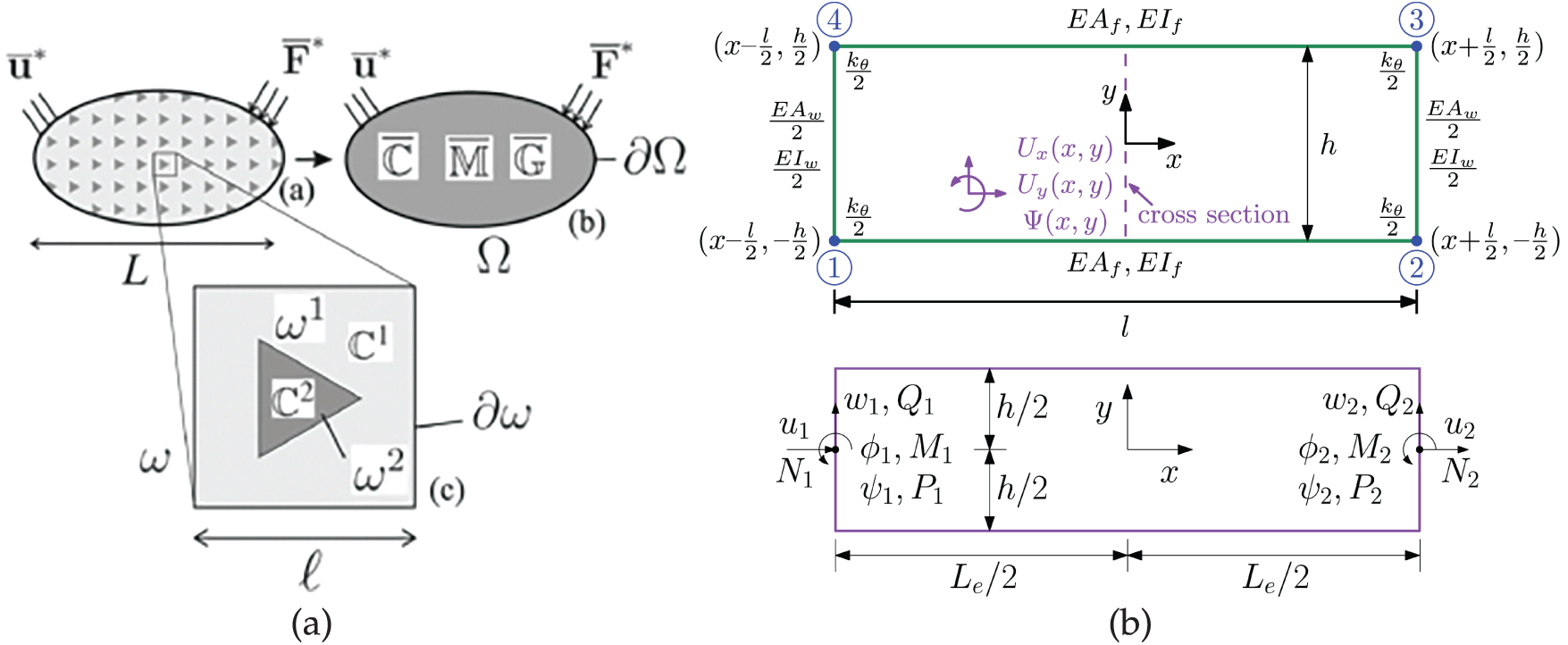
Figure 6: (a) Heterogeneous structure equivalent to strain-gradient homogeneous structure [111], (b) Arbitrary cross-section of the micropolar beam possessing microstructure [112]

Recently, Hu et al. [122] investigated the mechanical properties and deformation behavior of bio-inspired sandwich structures fabricated using selective laser melting. They examined various gradient lattice structures to analyze their response under compressive loading, as illustrated in Fig. 7a. Liu et al. [123] established that the nonlinear beam-like truss structure illustrated in Fig. 7b is equivalent to a nonlinear homogeneous Timoshenko beam. In particular, the nonlinear dynamics of a microscale beam is analyzed using the SGE theory and the MCST discussed in Section 2.2. Thereby, they developed and implemented an equivalent nonlinear beam model (ENBM) based on SGE for the forced vibration analysis of the nonlinear beam-like truss. Most recently, Sarhil et al. [124] scaled the curvature measurements, which are isotropic in 2D, to incorporate the size of the beam, followed by a fitting procedure to determine the characteristic length and the shear modulus associated with the micro-distortion field. The relaxed micromorphic model successfully captures the size effects consistently across both loading cases.

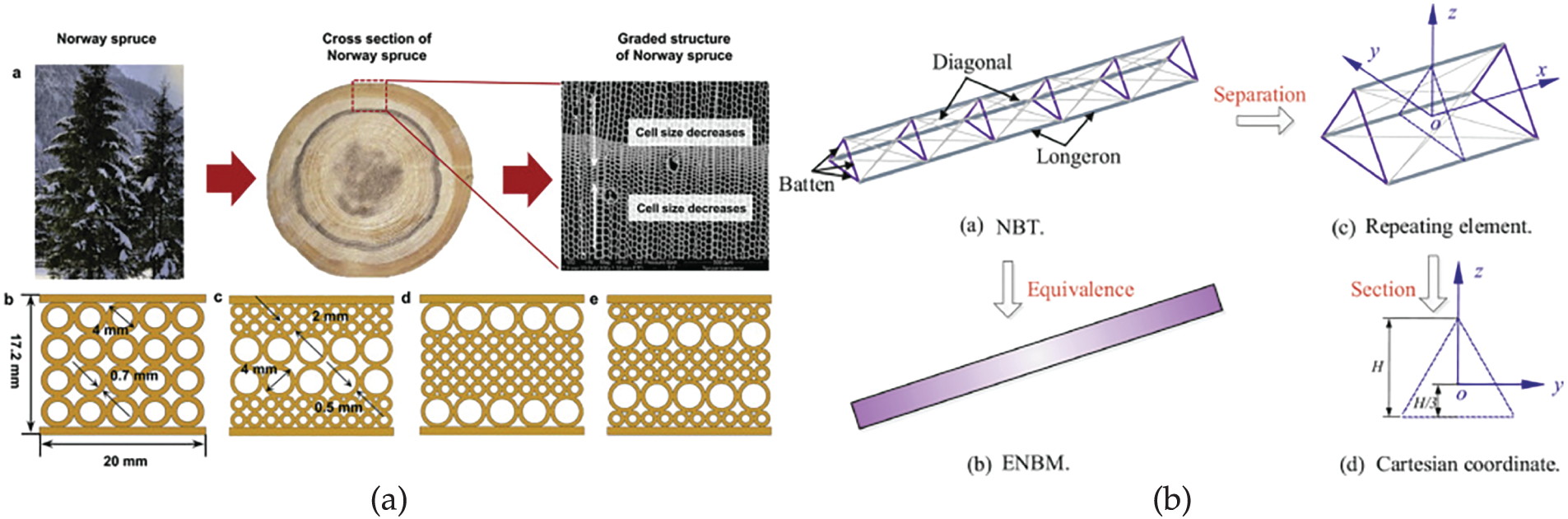
Figure 7: (a) Bio-inspired sandwich gradient structures [122], (b) Schematic view of nonlinear beamlike truss composed of 36 spatial repeating elements [123]

Data-driven approaches: In recent years, data-driven approaches have emerged as a powerful alternative to traditional methods for material characterization [125]. These methods have facilitated the development of machine learning (ML) techniques that enable rapid predictions based solely on existing data, eliminating the need for direct experiments or simulations [126]. For instance, Stainier et al. [127] proposed a data-driven approach to mechanics that operates without predefined models, allowing the identification of material properties and the solving of mechanical problems directly from data. Following a similar approach, Karapiperis et al. [128] introduced a data-driven framework for the mechanical analysis of generalized continua, incorporating the nonlocal effects arising from the microstructure of the material. In their study, they specifically focus on the micropolar continuum as a representative example of generalized continua. This framework is entirely parameter-free, eliminating the need to define constitutive relations or internal length scales, as these are implicitly determined from the material dataset. Additionally, it effectively captures nonlocal history-dependent behavior while explicitly ensuring thermodynamic consistency. Similar to this, Lal et al. [129] proposed a framework based on supervised ML to predict the length scale parameter for a given material. Most recently, Ulloa et al. [130] introduced generalized data-driven mechanics for micromorphic continua, motivated by the challenges of softening materials with strain localization. It has been observed that material length scale parameters vary depending on the complexity of the microstructure. Although the primary computational expense lies in generating training data from MD simulations, once trained, these models offer computationally efficient predictions of material behavior. Recently, ML has been extensively applied to predict material properties using known parameters such as microstructure or chemical composition [131]. ML models trained on output from MD simulations are increasingly being used for this purpose [132–135].

3  Solution of GDEs

This section presents a concise overview of approaches for solving boundary value problems, including strain gradient terms within the constitutive relations (example is Eq. (26a)). We present a detailed account of the analytical and numerical methods explored in the literature for solving these equations. Before we begin, we note that Hosseini and Niiranen [136] established uniqueness of a solution for these higher-order GDEs, including SGE terms, assuming continuity and coercivity of the bilinear form (available thanks to the energy framework introduced in Eq. (1)). Although their proof is available for a 3D boundary-value problem (BVP) considering the SGE framework, these equations are similar to those developed previously in Eq. (26a)), and hence the observations can be extended. This result is significant because it provides a foundation for analytical and numerical methods, including the FE, meshfree, and IGA methods.

3.1 Analytical Solutions

We discuss below some approaches employed by researches for an analytical solution of higher-order GDEs developed for SGE.

Stress Functions: The stress function approach, analogous to Airy stress functions for classical elasticity, presents significant ease for a solution of GDEs. This includes the reduction of a set of governing differential equations via the introduction of a single-scalar function. Further, in most cases, the GDEs are trivially satisfied (or reduced to biharmonic equations). Weitsman et al. [34–36] pioneered the stress function approach for solving GDEs based on a deformation energy that includes strain and strain gradient terms. More specifically, a stress function that satisfies the governing differential equation, including the SGE term, over the domain was assumed, and the boundary conditions were enforced. Following this approach, they explored the stress concentrations for spherical and cylindrical inclusions and cavities, including Form III of Mindlin’s SGE given in Eq. (5). The stress function approach employed by Eshel and Rosenfeld [137] to analytically solve the stress state around a cylindrical hole gained prominence, particularly due to their improved explanation of the extra material constants arising from SGE. Their solution to the plane stress problem of a circular cylindrical hole under uniaxial tension involved the use of modified Bessel functions of the second kind. They investigated stress concentration away from the hole, comparing their findings with predictions from couple-stress theory and classical elasticity. Further, Eshel and Rosenfeld [138] extended their methodology to solve axisymmetric exterior problems with uniform pressure applied to a circular internal boundary. This approach has also been used for analytical solutions of GDEs that involve multiphysics coupling with strain gradients to provide the stress state in flexoelectric solids [139]. Moreover, the above approach using stress functions was also extended to simplified theories of SGE, such as the SSGET provided in Eq. (16) [140].

Assumed solution forms: Recall that Mindlin introduced the foundational framework for strain gradient theory in his seminal study [21]. In addition to this, this work demonstrated the solution of the GDEs for SGE employing a simple harmonic function. Later, Savin et al. [37,141] developed an analytical model to study wave dispersion in low-dimensional structures using SGE. Their approach utilizes expressions derived using a simple harmonic function of the static and dynamic displacements for the velocities of longitudinal and transverse elastic waves in a nonlinear infinite Cosserat continuum with constrained rotation. A similar approach was adopted by Sidhardh and Ray [97] for dispersion curves of Rayleigh–Lamb waves in a micro-plate considering strain gradient elasticity. Gao et al. [142] used a method based on the harmonic traveling wave solution to solve for band gaps in periodic composite beam structures. This approach allowed them to include the effects of surface energy, transverse shear, and rotational inertia on the band gaps in the periodic structure.

In the early 2000s, Lam et al. [6] employed a power series expansion for the displacement field variable to solve the GDEs corresponding to MSGT. This analysis specifically addresses the cases of hydrostatic and uniaxial compression and dilation. More commonly, elastic field variables in the 3D structures are reduced to 1D or 2D by assuming displacement fields. We note a plethora of studies exploring analytical solutions for the SGE assuming a prescribed displacement field: Euler-Bernoulli beam displacement theory for 1D [143–145], and Kirchhoff plate displacement theory for 2D structures [146–148]. Please refer to the review article by Roudbari et al. highlighting several such studies [149].

Green’s function approach derives analytical solutions for point loads, and has significance in extending to a solution of the GDEs in case of general loads. Zhang and Sharma [150] pioneered this approach for Eshelby’s tensor of an inclusion/inhomogeneity embedded in higher-order continua. More specifically, considering the couple stresses within the constitutive relations, Green’s functions were proposed in terms of appropriate potentials for the solution of higher-order GDEs. Alternately, Gao and Ma [151] developed Green’s function for the GDEs following the SSGET provided in Eq. (16). Thereby, they provided an analytical method for solving Eshelby’s tensor in an infinite homogeneous isotropic elastic medium containing inclusions of arbitrary shapes. Sidhardh and Ray developed a similar framework for an inclusion of any arbitrary shape, under uniform eigenfields following the GFSGET in Eq. (10) [152,153]. Gourgiotis et al. [154] developed a theoretical framework by deriving Green’s functions for a concentrated force and couple in an infinite relaxed micromorphic medium. Using Fourier transform analysis and generalized functions, they obtained closed-form solutions and demonstrated that several classical continuum solutions emerge as singular limiting cases of the relaxed micromorphic model.

Fourier and Laplace transforms: The Fourier approach serves as a powerful tool for solving higher-order GDEs by transforming differential equations into algebraic equations in the frequency domain. Day et al. [155] were the first to develop an analytical solution by this approach, based on Mindlin’s strain gradient elasticity theory, to investigate bonding stresses at the interface in composite microlayers under higher-order contact conditions. Similarly, Baren and McCoy et al. [156] developed an analytical solution for a point force in an infinite medium considering the first strain gradient theory of elasticity (modified Kelvin problem). Rogula [157] developed benchmark analytical solutions for several standard problems (in 1D, 2D, and 3D, and dislocation line) employing the Fourier transform approach. Zhou et al. [158] investigated the influence of surface energy on the band structures of flexural waves in a periodic nanobeam considering Fourier series expansion according to the Bloch theory. A similar approach was used by Qian [159], considering surface energy effects, to study wave propagation in a thermo-magneto-mechanical nanobeam. Recently, Rizzi et al. [160] derived closed-form solutions for the simple shear problem across various isotropic linear-elastic micromorphic models, with a focus on the relaxed micromorphic continuum. The Cosserat model, the classical micromorphic model (except when it approaches the second gradient limit), and the microstrain model exhibit similar size effects under simple shear but show notable differences under bending [161,162]. Importantly, the relaxed micromorphic model remains well-posed and bounded, except in the limit μmicro→∞ and h/Lc→0, where it degenerates into the Cosserat model, which subsequently collapses into the indeterminate couple stress model.

The transform approach is also commonly employed for the solution of Eshelby’s tensor, a fundamental problem for studies on micromechanics, dislocations, and fracture. For instance, alternative to the Fourier approach, instead employing the Laplace transform approach to convert differential equations to algebraic equations, Karlis et al. [163] developed analytical solutions for higher-order GDEs corresponding to Mindlin’s strain gradient theory of elasticity for a static response of elastic 2D and 3D strain gradient solids.

Exact solutions

An exact solution satisfies the governing differential equations and all the (natural and essential) boundary conditions of a problem precisely. This is in contrast to the analytical solutions of the GDEs, following assumptions either on the primary variables or approximations over the derived quantities. For instance, exact solutions of the GDEs provided in Eq. (26a) for the displacement vector are devoid of any assumptions, except for continuity requirements across the domain. In a continuum where these conditions are trivially satisfied, it is possible to obtain exact solutions for specific loading and boundary conditions. Instead, considering the displacement field to be Euler-Bernoulli beam displacement theory significantly simplifies the 3D GDEs to be 1D equations. However, a solution of these equations is limited by assumptions on the Euler-Bernoulli beam displacement theory. Here, we discuss the limited studies on exact solutions of GDEs corresponding to SGE. These results may serve a crucial role in providing benchmark results for the validation of analytical, numerical, and experimental studies on SGE.

In the early 1970s, Kiusalaas et al. [164] formulated an exact solution for strain gradient elasticity in pre-strained laminated materials composed of thin, rigid reinforcing sheets interspersed with thick, compliant matrix layers. However, there was a significant gap in researchers exploring exact solutions of GDEs for SGE, maybe owing to the improvements in computational models and resources. Recently, Sidhardh and Ray [93] developed the exact solution for the elastic response in micro- and nanobeams, considering the GFSGET (see Eq. (10)) for a simply-supported beam subject to sinusoidally distributed transverse load. This follows from considering a characteristic solution that satisfies the boundary conditions (both essential and natural) in a trivial manner. Later, this was extended to develop exact solutions for size-dependent elastic response in low-dimensional heterogeneous structures: laminated beams [70] and functionally graded beams [153]; with relevance to smart structures. Finally, these exact solutions were extended to multiphysics studies involving electro-mechanical coupling via flexoelectricity. In particular, exact solutions for the electrical and mechanical field variables were developed assuming independent characteristic solutions for the flexoelectric response of the nanobeams subject to combined electro-mechanical loads [92].

3.2 Numerical Solutions

Clearly, limited studies are available in the literature for an analytical solution of higher-order BVPs and I-BVPs following the inclusion of strain gradients in the constitutive framework. This is owing to higher-order gradients encountered within the GDEs, increasing the difficulty in obtaining analytical solutions when compared with GDEs for classical elasticity. In the following, we present a summary of numerical approaches considered for a solution of these GDEs.

Owing to higher-order partial differential equations for SGE when compared to classical elasticity, the interpolation schemes are modified for an approximation of the primary field variables. Thereafter, numerical approaches based on mesh-based and alternate methods can be employed for a solution of these equations. A brief discussion on numerical approaches is provided below.

3.2.1 Mesh-Based Numerical Methods

First, we discuss the numerical solutions of the GDEs for SGE employing the Finite Element Method (FEM). This is in view of the popularity of FEM as a tool for the numerical solution of partial differential equation. Although the sequence of steps for developing an FE numerical solver for SGE does not differ from that of classical elasticity, there are certain fundamental differences. Firstly, considering the higher order of the GDEs, it is essential to enforce C1 continuity across the elements. This requires the nodal values of the displacement gradients to be specified in addition to the nodal displacements. Further, the displacement (primary variable) requires to be approximated by atleast cubic interpolation functions due to the continuity requirements of the gradient term. For instance, consider a typical finite element e that is temporarily isolated from the rest. Let ui(x,t) represent the displacement field variable at a point within the element. This is then approximated over the element using functions of the following form [38]:

ui=ψN(x)uNi+φNj(x)uNi,j.(27)

where i,j=1,2,3 and the repeated indices N are summed from 1 to Ne, Ne being the total number of nodal points in element e. In this equation, uNi are the displacement components of the node N of the element, and uNi,j are the displacement gradients at the node N of the element. In the above expression, ψN(x) and φNj(x) are interpolation functions. This is unlike classical elasticity, where interpolation of the field variable at a point in the domain can be expressed only in terms of the corresponding nodal values.

Following this approach, Oden et al. [38] developed a numerical solution for 1D, 2D, and 3D problems on linear first strain gradient elasticity. Felippa used similar approximations for plane stress problems using SGE [165]. These FE solutions are established to agree well with benchmark solutions for all the cases considered. However, the higher-order requirements for interpolation increase the complexity of the FE model. For instance, the 3D FE model that employs C1 elements requires 60 (for 3D) independent boundary conditions to determine the nodal values [38,166]. This renders the approach to develop FE-based numerical models cumbersome and prohibitive. However, it has been extensively used in studies involving strain gradients in elasticity and plasticity. Pamin and de Borst [39] extended finite element analysis to gradient-dependent plasticity. Their study employed C1 continuous interpolation functions for a numerical approximation of the plastic strain and captured the dependence of the yield function on the Laplacian of the plastic strain measure. Several researchers explored FE solutions of standard structural elements (bar, beam, plates, etc.) employing SGE by considering appropriate displacement field theories. A summary of these studies is available in the review by Askes and Aifantis [110]. In addition, this approach has been extended to develop numerical solvers for general studies. Recently, Yang et al. [167] extended this approach for the second strain gradient theory (see Section 2.3) and proposed a numerical method specializing in studies of dynamic analysis. Constructing the problem within the spectral domain and discretizing the domain to one-dimensional unit-cell structures, a Wave Finite Element Method (WFEM) has been proposed for numerical studies on the dynamic behavior of micro-sized structures. This reduction of the domain to a unit cell greatly reduces the computational time of the numerical solver.

Alternatively, Shu et al. [168] introduced mixed-type finite elements for a numerical approximation of strain gradients. In particular, this approach employs two separate C0-continuous shape functions for the interpolation of displacement and its derivatives. Thereby, additional nodal degrees of freedom are introduced corresponding to the primary variable and its derivatives. Thereafter, kinematic constraints between displacement and strain are enforced via Lagrange multipliers. An example of the above constraint between strain and displacement gradients, following from kinematic relations, is given as [168]:

∫v(ψjk−uk,j)δτijk,idV=0.(28)

In the above expression, ψij is the relaxed displacement gradient, which is different from the true displacement gradient uk,j, and τijk,i are the Lagrange multipliers. In the above expression, the variation of the third-order hyperstress δτijk serves as a Lagrange multiplier for enforcing the kinematic constraint connecting the independent approximations for the strain and strain-gradients. Thereby, this approach achieves the continuous approximations of the field variables while simplifying implementation and reducing the computational cost. Amanatidou and Aravas [169] employed a similar approach to develop a mixed finite element formulation for Mindlin’s Type I and Type III formulation. Although this approach has been developed and explored in several studies, it has some limitations. For instance, this approach following linear shape functions presents constant strain across the elements. This makes it difficult to estimate the strain gradients within the element, which is necessary here within the SGE formulation. Han et al. [170] developed projection algorithms to address this issue and estimate strain gradients within the element.

Askes et al. [171] devised a different approach referred to as staggered gradient elasticity, where it is demonstrated that C0-continuous interpolations are sufficient for discretization in gradient elasticity. This is achieved by decomposing the original fourth-order equations into two sets of second-order equations that are independently solved (staggered). The first set corresponds to the GDEs for classical elasticity, while the second set corresponds to the Helmholtz equations corresponding to gradient elasticity. The staggered approach, which leads to a Helmholtz-type equation acting on the strain or stress tensor (rather than on the displacement vector or strain invariants), can be formally derived from the displacement-based formulation. Reiher et al. [172] reformulated the weak form with additional kinematic fields corresponding to higher-order gradients and implemented the FE model with lower continuity requirements in commercial finite element analysis (FEA) software. This implementation was studied numerically for various polyhedra geometries subject to different types of loading and boundary conditions, focusing on a material with constitutive behavior characterized by the second and third gradients of displacement. Recently, the use of open-source packages such as Firedrake and FEniCS for comparative analysis of FEM formulations in SGE is gaining traction. Explicit finite element programs, developed using object-oriented programming paradigms (e.g., C++), are being released under open-source licenses [173,174].

Previously, the FEA for SGE was built on elements and shape functions built for local elastic constitutive framework. Therefore, their extension to the gradient elasticity framework presented significant computational challenges. In the literature, researchers explored the development of new element types and the corresponding shape functions for structures modeled following the SGE framework. For instance, the Stress-Driven Finite Element Method (SD-FEM), formulated in a differential framework, develops nonlocal shape functions based on the Constitutive Boundary Conditions (CBC) and Constitutive Continuity Conditions (CCC). Thereafter, a systematic method to derive both the nonlocal stiffness matrix and the corresponding equivalent nodal forces for a nanobeam is presented. A key advantage of this approach is its ability to deliver the exact stress-driven solution using even a single two-noded element [175–177]. Similar approaches are also explored for the SGE framework [178].

While strain gradient plasticity problems are frequently solved analytically and verified experimentally [57], extending these solutions to general problems requires numerical methods such as FEM [179]. The difficulties listed above in using FE, the need for C1-continuous elements, as well as handling higher-order tensors and natural boundary conditions, also hold here. Notably, Niordson and Hutchinson [57,180] introduced plane quadrilateral elements with plastic strain degrees of freedom, while Wei [181] created a three-noded triangular elasto-plastic element aligned with the Fleck and Hutchinson’s theory. Similarly, numerous finite element models have also been developed for plasticity [170,182,183]. Further, numerical methods have been extended for approximate solutions of multiphysics coupled boundary-value problems, such as flexoelectricity. Abdollahi et al. [184] introduced the FEM for flexoelectricity in solids employing C1 continuous basis functions. Their work expanded to studies of finite elements in sensors, actuators [185], and pyramid compression tests, which are commonly used for experimental determination of flexoelectric coefficients [186]. Yvonnet et al. [187] employed the staggered framework for a numerical solution of nonlinear dielectrics under finite strain, incorporating the coupling effects of Maxwell stress and flexoelectricity. Although a staggered approach was also employed for studies on elastic response following SGE theory, they are demonstrated to be particularly useful for numerical solutions of large deformations (finite strains). Further, Deng et al. [188] developed a mixed finite element method (FEM) that incorporates strain gradient elasticity and flexoelectricity. Their approach begins with the formulation of a modified energy functional based on the total electrical enthalpy of the system. To ensure consistency between the displacement field and its spatial gradient, they enforce a kinematic constraint using the Lagrange multiplier method (similar to that in Eq. (28)).

3.2.2 Alternate Numerical Methods

The finite element method in its current formulation requires at least C1-continuity in the elements. Developing C1-continuous shape functions for elements with more than two nodes poses challenges. Further, mixed finite element formulations, which use separate interpolations for displacement and strain fields, tend to be complex. Alternate numerical methods, such as meshfree numerical solvers using arbitrary node distributions, are suited for studies on strain gradients. Unlike finite element (FE) solvers, meshfree methods approximate field variables based on nodes that are distributed arbitrarily and lack connections, meaning the field variable approximation is not tied to any element created through domain discretization by mesh. Further, meshfree approaches offer improved flexibility in increasing the order of interpolation. Among them, the element-free Galerkin (EFG) method, using moving least-squares interpolation, allows for a straightforward increase in the continuity of the approximation (interpolation) functions. The EFG numerical solver, built upon Moving Least Squares (MLS) approximants, handles the continuity demands of higher-order gradient terms with relative ease [189]. Askes et al. [190] and Pamin et al. [191] developed EFG solvers capable of approximating the strain gradient terms and used them in numerical studies on strain localization due to damage and plasticity. Subsequently, Pan and Yuan extended EFG solvers to model nonlocal damage in the context of finite strains [192]. More recently, Sidhardh and Ray [193] demonstrated the relevance of the EFG numerical solver for studies of SGE. Similarly to the MLS approximants for the EFG method, meshfree solvers built upon reproducing kernel shape functions were successfully explored for a numerical solution of SGE response in [189].

In addition to the meshfree methods mentioned above, there exist alternate approaches for numerical approximation of strain gradients. Das and Chaudari first introduced a 2D boundary element formulation for micropolar elasticity using the reciprocal theorem [194], but it was limited to smooth surfaces. Although its use is primarily restricted to relatively small-scale problems, the Boundary Element Method (BEM) offers notable advantages over the FEM. Key benefits include precise calculation of strains and stresses, reduction of the dimensionality of 3D/2D structure (by one), and the ability to compute elastic fields for both compressible and incompressible materials. BEM has also been applied to solve two-dimensional strain gradient elastostatic problems in the context of the micropolar framework [195].

Ke et al. [196] solved the GDEs for SGE using the differential quadrature (DQ) method for an investigation of the dynamic stability based on MCST (see Section 2.2). The approximation of the n-th gradient of the displacement field variable at i-th grid point (u(xi)) following differential quadrature method (DQM) is given by [197,198]:

dnu(xi)dxn≈∑j=1Nwij(n)u(xj)

where wij(n) are the weighting coefficients at point i with respect to j-th point in the domain. Choosing a suitable weighting function provides the flexibility to increase the interpolation order of the displacement field, simplifying the evaluation of higher-order gradients in the GDE. This has been demonstrated in a series of studies using DQM for studies on the static and dynamic response of nonlocal structures modeled using different constitutive models for SGE [199,200].

4  Physical Relevance of Strain Gradient Theory

As discussed in Section 1, the origins of SGE go back to enriched kinematics for material particles possessing a microstructure. In particular, unlike classical elasticity theories that treat particles as rigid, the Cosserat brothers [25] introduced enriched kinematics in which material particles possess both translational and rotational degrees of freedom. These additional degrees of freedom correspond to the deformation of the microstructure of the particle; a schematic example of the same for CsCl is shown in Fig. 3. Subsequently, a continualization of the microstructure effects introduces higher-order gradients within the constitutive relations. More specifically, a variety of higher-order continuum theories have been introduced in Section 2, each incorporating different choice of higher-order gradients into the continuum framework to capture the specific effects of the microstructure. In particular, gradient elasticity formulations have initially been proposed to better approximate the effect of discrete lattice behavior in wave propagation studies [97,201]. The effect of lattice deformations over high-frequency (low-wavelength) wave propagation is studied using micro-deformations of the directors within the lattice (see Fig. 3) [21]. Among higher-order continuum theories, the strain gradient elasticity theory successfully models size-dependent behavior in small-scale structures. It introduces three material length scale parameters, each associated with dilatation, deviatoric stretch, and symmetric rotation gradients. This theory has been used to study the static and dynamic responses of microscale Bernoulli–Euler beams [144,202,203] and Timoshenko beams [204–206]. By setting two length scale parameters corresponding to the dilatation and deviatoric terms to zero, it simplifies to the modified couple stress theory by Yang et al. [65]. This highlights the specific applicability of the strain gradient elasticity theories to capture diverse deformation mechanisms of the microstructure. In all these cases, gradients are used to enhance the representation of the complex microstructure over the structural response. This approach allows gradient to be used to regularize the solution by reducing singularities or discontinuities and smoothen the heterogeneity of the material [56,57,120,207]. In other cases, gradients are used to introduce heterogeneity, enhancing the representation of the complex microstructure over the structural response.

Higher-order continuum models in the literature differ in several aspects, particularly in the manner of incorporating the strain gradient terms. Some examples of the same are discussed in Section 2.2 above. Some models introduce these gradients directly, either through the energy functional or the constitutive equations, following ad hoc approaches. Other models derive higher-order terms from discrete lattice structures using homogenization techniques. This approach preserves a connection with the microstructure of the material, allowing additional material parameters to be interpreted in terms of microscale properties. In this section, we propose to demonstrate the physical significance of the SGE following both of these approaches. More specifically, we derive the SGE terms within the deformation energy following from a 1D chain of spring mass representation for an axial bar. Thereby, we demonstrate the higher-order terms corresponding to long-range interactions, beyond immediate neighbors, within this discrete structure way the foundation for strain gradient elasticity. We conclude this derivation via a continualization of the discrete structure and illustrate the higher-order terms reducing to strain gradients. Thereafter, the higher-order gradients are also connected to the specific deformation modes in a complex microstrfollows.

An infinite one-dimensional lattice of identical particles, each with mass M, is considered, arranged in a collinear manner along the x-axis with a spatial period of le, as illustrated in Fig. 8. The particles are restricted to longitudinal motion. The position and displacement of the i-th particle (i∈R) at time t are denoted by xi(t) and ui(t), respectively. Interactions between particles are modeled using lumped springs with stiffness ki,j, where i and j represent the indices of interacting particles with i≠j. Here, the comma in the subscript indicates particle indices, not differentiation. Assuming all springs are initially unstressed at t=0, the potential energy stored in the i-th cell of the lattice corresponding to its interaction with j-th particle is given by:

𝒰i,j=12ki,j|ui−uj|2.(29)

Figure 8: Schematic of a 1D chain of discrete spring mass system. The chain is considered to infinity to avoid boundary effects

Assuming small displacement gradients (O(ε)), a Taylor series expansion about the point xi yields:

ui−uj=(xi−xj)Dxj1uj+12(xi−xj)2Dxj2uj+H.O.T.(30)

The first term in the above expression caters to the interaction of point i with the immediate neighbors. The second-order terms introduced above expands the interaction to points beyond the immediate neighbors, resulting in a weakly nonlocal interactions being captured here. It is well established that cohesive forces between particles weaken with increasing interatomic distance. At the continuum level, particularly in strain gradient formulations, this behavior is typically represented through convolution terms involving power-law kernels of order one in the stress–strain constitutive relations. In lattice models, the stiffness of springs connecting distant particles serves a similar role to these kernels given as follow:

ki,j=k0[c1|xij|+c2|xij|2].(31)

Here, |xij|=|xi−xj| denotes the distance between the i-th and j-th particles. It is important to note that the above equation is valid only for i≠j, as i=j would imply a particle is connected to itself, which is not physically meaningful. The coefficients c1 and c2 are defined as functions chosen to ensure both dimensional consistency and frame invariance of the formulation. Furthermore, the constant k0, which has the units of classical stiffness [MT−2], will be further interpreted when deriving the continuum limit of the lattice model. Substituting Eqs. (30) and (31) in Eq. (29).

𝒰i,j=k02[c1(Dxj1uj)2⏟strain+14c2(Dxj2uj)2⏟strain gradients].(32)

By assuming a small le and applying a continualization process, the discrete variables representing the particle positions and displacements can be replaced with their continuum counterparts (xi→x). In the continuum limit, the constant k0 can be defined as:

k0=EAle.(33)

Here, E and A represent the Young’s modulus and the cross-sectional area of the equivalent one-dimensional continuum, respectively. Thus, the constant k0 can be interpreted as the equivalent spring stiffness for an axial element characterizing the nearest-neighbor interaction forces in the lattice, which models the microstructure without considering size-effects. Furthermore, the constants c1 and c2 in Eq. (31) are defined as:

c1=le2,  c2=le4.(34)

The above choice follows from scaling the contributions of strain and strain gradient terms towards the total deformation energy, and to maintain the dimensional consistency. Under these assumptions, the continuum limit of the discrete sum in Eq. (32) ∀ i,j can be expressed as the following strain gradient representation:

𝒰(x)=EA2l∗[le2(Dx1u)2+le44(Dxj2uj)2].(35)

The deformation energy density at a point x in the continuum can be expressed as:

Π(x)=𝒰(x)Ale=E2[(Dx1u)2⏟strain+le24(Dxj2uj)2⏟strain~gradient].(36)

The second term in the above integral represents the deformation energy density corresponding to strain gradient elasticity. The preceding discussion highlights that incorporating strain gradients into the continuum model enables it to be weakly nonlocal across the domain. Further, the above derivation is limited to axial deformations, but can be extended to more general deformation modes as well.

We proceed to interpret the strain gradient terms as (additional) micro-deformation variables [21,208]. This allows us to capture the deformation of the director vectors within the microstructure. In this discussion, the second-order tensor e describes the state of strain of the microstructure (similar to ε employed earlier). Furthermore, the third-order micro-displacement/deformation tensor, denoted by ϕ and having dimensions of length, is analogous to the hyperstress tensor defined in Eq. (7), and therefore physically related to the strain-gradient tensor (η). The physical/kinematic interpretation of these tensors in the context of strain gradient theory is schematically illustrated in Fig. 9. The micro-displacements ϕpij can be interpreted as the displacements of the free ends of a triplet of fibers of length ℓ emerging from a generic point x and aligned with the coordinate axes. These fibers are typically chosen along the deformable directors illustrated in Fig. 3. In particular, the micro-displacement components, defined as ϕpij=ℓ2eij,p (i,j,p=1,2,3), are similar to the hypertresses available following SSGET defined in Eq. (16). These components represent the configuration change of a triplet of orthogonal fibers of length ℓ aligned with the reference coordinate axes along the direction xp of the gradient. Therefore, for each p∈1,2,3, the component ϕpij describes the displacement of the free ends of the fibers in the (i,j) plane when i≠j, and the displacement of the fiber i along its own axis when i=j. These components collectively capture the local microstructural deformation using strain gradients.

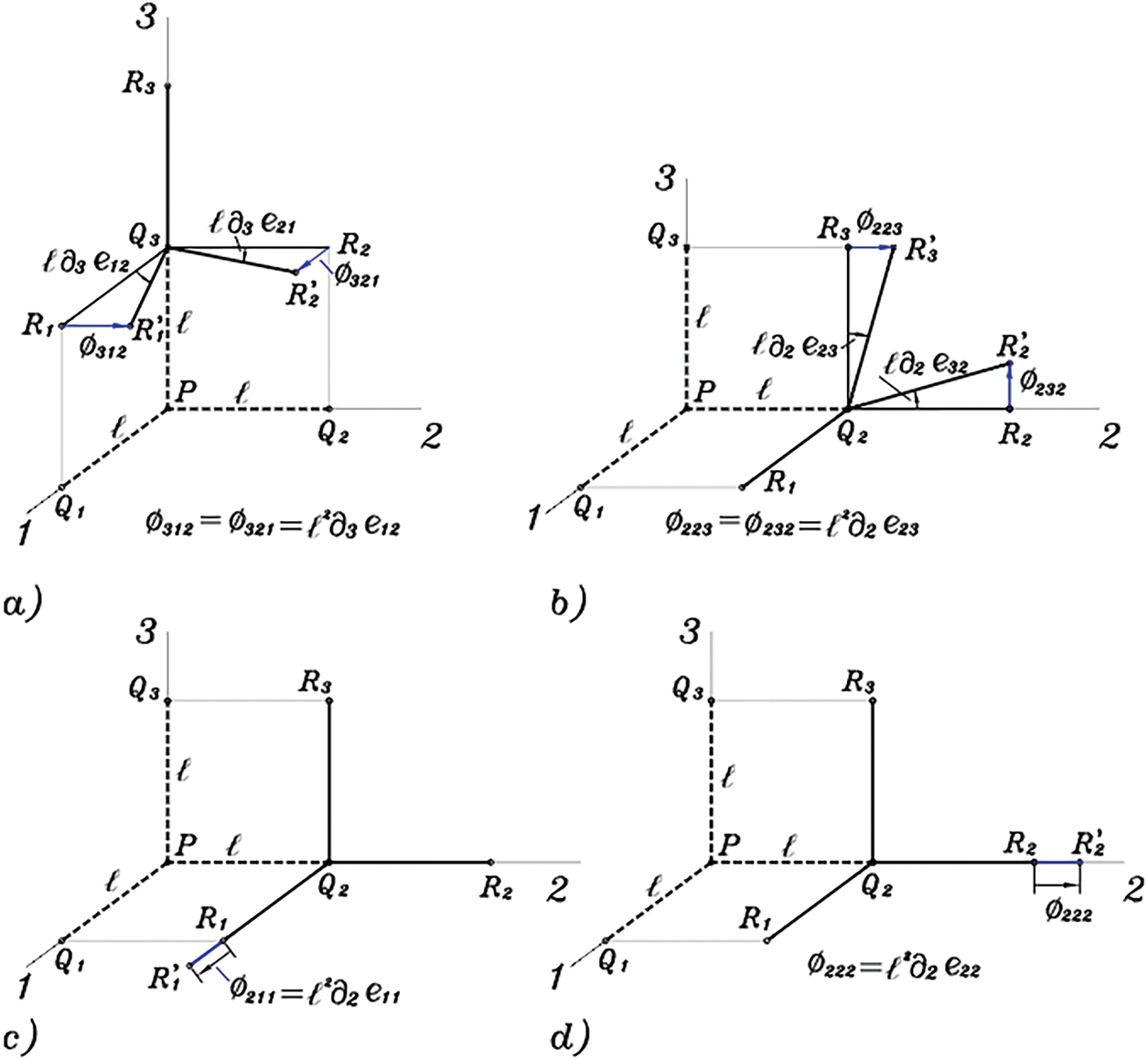
Figure 9: A schematic illustration of the interpretation of higher-order continuum theories in terms of deformation of the microstructure. For instance, the strain gradient corresponding to: a) e12 varying along the x3 direction; b) e23 varying along the x2 direction; c) e11 varying along the x2 direction; d) e22 varying along the x2 direction; are depicted here [208]

5  Application for Elastic Behavior

Classical continuum theory is widely used to predict the elastic response in structural analysis and design. However, it fails to accurately predict structural behavior at the micro- and nanoscales. For instance, experimental studies on quasistatic bending of the human compact bone demonstrated a stiffening of up to a factor of two with reducing dimension, which cannot be accounted for following classical elasticity [12]. This is demonstrated to be better captured following the micropolar and couple stress (see Section 2.2) theories of elasticity. Similarly to this, Yang and Lakes repeated the tests on torsion response of the human compact bone specimen [11,12], and experimentally demonstrated the size-effects on torsional stiffness. More specifically, as the dimensions of structure decrease, the classical continuum theory tends to underestimate the structural stiffness [12,209]. To address these limitations of classical elasticity theory, higher-order elasticity theories that incorporate length scale parameters corresponding to the material microstructure have been proposed. These include Cosserat theory [25], couple stress theory [28], micromorphic theory [14], micropolar theory [210], and a family of strain gradient elasticity theories [26,29,31]. Among these, we focus here on the application of strain gradient theories for modeling the size-dependent elastic response.

Structural response: Several studies have explored gradient-based (higher-order) theories to improve the predictions of structural behavior at the micro- and nanoscales. Lam et al. [6] conducted early research in this area, observing an increase in the bending stiffness (compared to classical elasticity predictions) of epoxy microbeams as their thickness was reduced from 115 to 20 µm. Most recently, similar observations were observed from studies on the bending response of epoxy microbeams (thickness, h≈8−170µm) by Liebold and Müller [211], Fu et al. [212], and Choi et al. [213]. An illustration of the increase in bending stiffness with decreasing thickness is depicted in Fig. 10a. This observation is different from the constant (normalized) bending stiffness for different dimensions predicted by the classical continuum theory. The additional deformation modes corresponding to the strain gradients are proposed to capture the effect of microstructure on the elastic response of the low-dimensional structures. For instance, the size-dependent response of micro-cantilever beams noted earlier in [6] is captured via MSGT given in Eq. (13). Moreover, the effect of the microstructure, and thereby the additional deformation modes introduced by the higher-order gradients, is negligible for structures with dimensions atleast a couple of orders greater than the characteristic length scale corresponding to the microstructure. This is also reflected in Fig. 10, where the results of higher-order and classical theories agree with increasing thickness. Therefore, the efficacy of SGE theories is demonstrated to capture the effects of microstructure over structural behavior at low dimensions.

Figure 10: (a) Demonstration of size-dependent bending stiffness in an epoxy cantilever microbeam, adapted from [212]. (b) Normalized transverse deflection of a simply supported beam under a point load (aspect ratio L/h=20, thickness h=50 µm), comparing predictions from classical theory (CT), modified couple stress theory (MCST), and modified strain gradient theory (MSGT)

Recall the detailed comparison of the different higher-order strain gradient elasticity theories provided in 2.2. The simplified constitutive models differ according to the specific deformation modes they account for. For instance, the MCST proposed by [65] accounts for only the rotation gradients of the deformable directors (see Fig. 3). In contrast to this, the MSGT provided in Eq. (13) also considers the gradients of the stretch and deviatoric deformation modes of these directors within the microstructure. Finally, the GFSGET considers all the probable modes of deformation of the directors within the microstructure. This specific choice of the constitutive framework depends on the microstructure and the mechanics of its deformation. A comparison of the relative size effects realized following the GFSGET (see Eq. (11)), MSGT (Eq. (13)) and MCST over the bending response of an elastic beam is provided in Fig. 10b. Therefore, appropriate choice of the SGE theory must be chosen for modeling the structural response of low-dimensional structures composed of different material types.

Elastodynamics: The study of the propagation of elastic waves in solids is of immense theoretical and practical significance, offering valuable insights into the elastic behavior of materials and structures. Given the growing importance of micro- and nano-structures, extensive research has been conducted to analyze wave propagation in low-dimensional structures [214–218]. The effect of increasing stiffness with reducing dimensions is reflected in different forms in elastic behavior; for instance, with reference to the current context, an increase in natural frequencies with reducing microstructure dimensions [37,219]. In addition, a dispersion of elastic waves is another example of the effect of microstructure on the behavior of the material. Recall that the governing differential equation for strain gradient elasticity given in Eq. (26a). These GDEs can be further simplified using Navier’s solution. The resulting Navier’s governing equations for the first strain gradient theory of elasticity, assuming the body forces to be absent, may be expressed as [97]:

(λ+2μ)(1+lλ2∇2)∇(∇.u)−μ(1+lμ2∇2)∇×∇×u=ρu¨−ρld2∇2u¨,(37)

where the term ρld2 corresponds to micro-inertia, with ld2=d23 and the characteristics lengths lλ and lμ correspond to the effect of the strain gradients on the longitudinal and transverse waves, respectively. These length scales are given by:

lλ=a1+a2+a3+a4+a5λ+2μ,  lμ=a2+2a4+a54μ.(38)

Furthermore, if the SGE effects are neglected (ai=0, i=1,...,5), both lλ and lμ reduce to zero, effectively simplifying the formulation to that of classical elasticity. More importantly, the phase velocity of the longitudinal and transverse waves following GFSGET are given by:

Vpl=λ+2μρ1+lλ2ξ21+ld2ξ2,Vpt=μρ1+lμ2ξ21+ld2ξ2(39)

where ξ is the wavenumber. The dependence of the phase velocities on the wavenumber confirms the dispersive behavior on account of microstructure. These observations are unlike the predictions of classical elasticity, where the wave propagation through the solid is predicted to be non-dispersive. However, this agrees with a prediction of dispersive wave propagation by Gazis et al. [220], as early as 1960, following an investigation of surface elastic waves in cubic crystals. Their study used both continuum mechanics and discrete particle models to analyze wave displacements, velocities, and attenuation constants for different elastic parameters.

To better illustrate the effect of SGE over wave propagation, we note that in the long-wavelength limit (wavelength>>characteristic length scale of microstructure) the phase velocities are given as:

Vpl|ξ→0=λ+2μρ,Vpt|ξ→0=μρ(40a)

thereby reducing to the velocities evaluated from classical elasticity. Alternatively, in the short-wavelength limit, the phase velocities of the longitudinal and transverse waves reduce as:

Vpl|ξ→∞=lλldλ+2μρ,Vpt|ξ→∞=lμldμρ(40b)

In the short-wavelength limit, the influence of the microstructure, captured by the SGE, is clearly significant for the elastodynamic behavior. This observation agrees with the seminal work of Mindlin [21] on elastic wave propagation, which also incorporates microstructural effects through SGE.

Building upon this, Savin et al. [37,141] explored wave dispersion in low-dimensional structures incorporating SGE. Moreover, employing the results of these studies, Savin experimentally determined the elastic constants of polycrystalline metals using ultrasonic techniques. Later, Mühlhaus et al. [201] proposed a one-dimensional Cosserat model for longitudinal wave propagation in granular media, introducing additional rotational degrees of freedom to capture grain rotations. Vardoulakis et al. [221] extended Mindlin’s theory to develop a linear gradient-elastic model with surface energy (see Section 2.3), effectively predicting Shear horizontal surface wave motions in a homogeneous half-space. Georgiadis et al. [222] further demonstrated that the couple-stress elasticity theory with microstructure enhances the accuracy of Rayleigh wave modeling, bridging classical continuum mechanics and atomistic lattice models. Incorporating SGE allowed for improved agreement with both experimental data and high-frequency predictions of discrete particle theories. Askes et al. [223] introduced four simplified versions of SGE theory, focusing on their dispersive properties, causality in accordance with Einstein’s principles, and behavior in basic boundary and initial value problems. Further, Vavva et al. [224] employed the simplified Mindlin Form-II (dipolar gradient elasticity theory) to investigate symmetric and antisymmetric wave modes in 2D stress-free gradient plates. Their study showed that variations in elastic constants highlight the influence of microstructure, which significantly affects the propagation of bulk longitudinal and shear waves by introducing both material and geometrical dispersion.

Papargyri et al. [96] highlighted that incorporating shear and rotary inertia corrections in beams and plates mimics the inclusion of micro-elastic and micro-inertia terms, contributing to wave dispersion in structural elements. Extending this perspective, Sidhardh and Ray [97] investigated the dispersion of Rayleigh–Lamb waves in micro-plates using the generalized first strain gradient elasticity theory (GFSGET). More recently, Gao et al. [142] proposed a model for elastic wave band gap analysis in periodic composite beams, accounting for surface energy, shear deformation, and rotational inertia using harmonic wave solutions—further enriching the modeling of wave propagation in gradient elastic media.

Composite homogenization: More than half a century ago, Boutin [225] studied the effects of microstructure on periodic elastic composites. In this study, higher-order terms in the form of higher-order gradients of macroscopic strain are included to introduce nonlocal effects due to the microstructure. Similar homogenization techniques have attracted renewed interest from researchers, particularly due to recent advances in manufacturing that enable the fabrication of complex microstructures. Although studies based on classical elasticity establish the influence of geometry and volume fraction of the inclusion phase on the effective properties of composites [226], several researchers [227–230] observed that the elastic properties of composites vary with the dimensions of the inclusion phase. In particular, size effects due to nonlocal interactions of low-dimensional inclusions are realized over the homogenized properties of the composite.

To address this, Eshelby’s inhomogeneity problem has been reworked within the framework of gradient elasticity theory. Recently, Sidhardh and Ray developed the modified Eshelby’s tensor for spherical, cylindrical, and elliptical inclusions considering the generalized first strain gradient elasticity theory (GFSGET in Eq. (11)) [152,153]. As expected, the Eshelby’s tensor in the SGE framework depends on the length scale of the microstructure controlling the nonlocal interactions, and varies for different simplified forms of the SGE discussed in Section 2.2. This is unlike a constant value for the Eshelby’s tensor, within the inclusion, following classical elasticity; see Fig. 11. This study and the observations therein follow from similar works by Zhang and Sharma [150] and Gao and Ma et al. [151] for Eshelby’s tensor of spherical and cylindrical inclusions within the couple stress and SSGET frameworks (discussed in Eq. (16)), respectively.

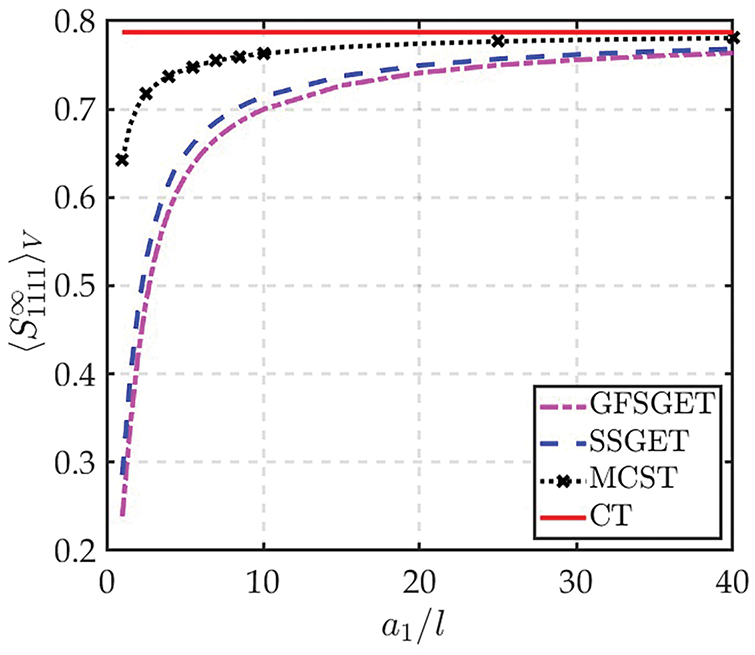
Figure 11: Volume-averaged component of the Eshelby’s tensor for different dimensions of the ellipsoidal inclusion (a1 is major radius; l is characteristic length scale) compared for classical theory (CT) with different strain gradient theories [16]

Using this approach and an extension of Eshelby’s integral representation to SGE, an exact solution was derived for the problem of a spherical inhomogeneity with interphase [231]. This solution was later applied to study the scale effects on the effective material properties at low dimensions. Furthermore, within the same extended Eshelby integral framework, the problem of coated spherical inhomogeneity with surface cohesive phenomena was analyzed [232] for predicting the effective properties of the composite material. Ameen et al. [233] applied the classical and higher order method to a two-phase microstructure and compared with a rigorous full-scale numerical solution. The accuracy of classical and higher-order homogenized solutions depends only mildly on the degree of stiffness contrast. For the particle-reinforced system considered here, the error increases with increasing stiffness contrast but eventually stabilizes in the rigid-particle limit. It is noted that, higher-order periodic homogenization can effectively refine the classical solution with sufficient accuracy at low scale ratios.

Reduced-order modeling: Modeling complex 3D structures and time-dependent problems presents high computational demands due to a large number of system of equations being involved. Among the several reduced-order models explored for improvement in the computational burden, modeling via nonlocal theories, and more specifically SGE, has attracted the research community. The nonlocal interactions presented by SGE (see Section 4) enable to capture the complex interactions within the microstructure. More specifically, the SGE allows a development of accurate reduced-order models for complex macrostructures by modeling complex interactions via nonlocal effects. For instance, modeling a beamlike lattice structure by 1D micropolar beam was carried out in [234]. Recently, Tran et al. [143] demonstrated the effectiveness of SGE theory in analyzing 2D triangular lattice structures, from the linear regime to von Kármán–type geometric nonlinearity. In addition to this, substantial computational savings were demonstrated following this approach, thanks to reduced numbers of the degrees of freedom, while still maintaining high accuracy compared to conventional 2D finite element simulations. Furthermore, Karttunen et al. [112,235] proposed a localization method to extract the response of periodic classical beam from micropolar formulations. This 1D beam model was later applied to linear bending and vibration analyses of 2D web-core sandwich panels with flexible joints, demonstrating excellent agreement with both experimental results and two-dimensional finite element beam frame simulations. Further, Nampally et al. [120] extended the formulation to a nonlinear analysis of micropolar Timoshenko beams by employing a two-scale energy method. This approach was used to derive the micropolar constitutive equations for various core topologies, including web, hexagonal, Y-frame, and corrugated cores, enabling a more comprehensive representation of their mechanical behavior. This emerging direction holds considerable promise for employing SGE in modeling complex engineering structures. For instance, an example of the lattice core structure studied using micropolar theories is illustrated in Fig. 6b.

MEMS and NEMS: MEMS technology has emerged as a significant high-tech industry, following the rise of microelectronics. However, as MEMS devices scale down in size, their surface area to volume ratio increases significantly. This leads to pronounced size effects, where mechanical behavior deviates from that of macro-scale systems, and surface effects become increasingly dominant [236–238]. Therefore, various studies have explored size-effects over the dynamic behavior of MEMS and NEMS [239].

An example of the size-effects on performance of MEMS is the effect of nonlocal elastic interactions over pull-in instability; in addition to its effect on the elastic behavior. One critical challenge in designing MEMS is avoiding pull-in instability, which can cause the microbeam to collapse and lead to device failure. For instance, Xue et al. [240] investigated the size-effects in MEMS devices using a mechanism-based strain gradient approach, and noted a significant increase in mechanical strain energy (when compared to classical theory) in the digital micromirror device. Further, Hamid [241] studied the influence of vibrational amplitude on pull-in instability and natural frequency of actuated microbeams using a second-order frequency–amplitude model. Incorporating electrostatic and fringing field effects within strain gradient elasticity, the analysis showed that this theory predicts a higher pull-in voltage compared to classical and modified couple stress theories. Kahrobaiyan et al. [242] developed a FE model for Timoshenko beams based on strain gradient theory, capable of reproducing various classical and non-classical beam formulations (strain gradient Euler–Bernoulli beam element, modified couple stress Timoshenko and Euler–Bernoulli beam elements, and also classical Timoshenko and Euler–Bernoulli beam elements). This model was used to compute the static pull-in voltage of an electrostatically actuated microswitch, showing strong agreement with experimental results and outperforming classical FEM predictions. Soroush et al. [243] investigated the impact of Van der Waals forces on the stability of NEMS, considering gradient effects in nanobeams under electrostatic loading. Their findings show that stronger intermolecular forces lead to reduced pull-in deflection and voltage of the actuators. These studies underscore the necessity of advanced mathematical and computational methods for analyzing and designing MEMS and NEMS, considering the limitations of classical theories and the importance of long-range interactions at this scale.

Carbon nano-structures: Since their discovery in the early 1990s [244], carbon nanotubes (CNTs) have attracted attention because of their exceptional electrical, thermal, and chemical properties [245]. However, experimental findings on elastic behavior of CNTs often vary significantly from predictions by classical theories, reflecting discrepancies due to differing test environments and methodologies [246–249]. This can be partly owed to the size-effects realized at these length scales. Therefore, several studies have focused on the elastic response of CNTs including size-effects via SGE constitutive theories, when subject to a myriad of load types and corresponding deformation modes (axial/bending, structural stability, static/dynamic) [250–254]. The improvement in predictions of the elastic response after including SGE is demonstrated via comparison with atomistic simulations. The work of Sun and Liew [255] provides a clear example of this agreement, showing that higher-order gradient theories accurately predict Single Walled NanoTubes (SWNTs) buckling as determined by atomistic simulations. In most studies, it is reported that the introduction of strain gradients within the potential energy given in Eq. (1) presents a greater stiffness of the structure with reducing dimensions (below µm). Further, SGE theories have been employed to explore the elastic response of 2D nanostructures like graphene. Specifically, experimental and atomistic simulation studies have revealed a pronounced size-effect in mechanical properties of graphene sheets [52,256–258]. To address the limitation to classical elasticity in capturing this effect, several studies employed SGE constitutive theories for the elastic response of graphene sheets [259–262]. For example, Lu et al. [263] proposed a nonlocal strain gradient third-order beam model to analyze the nonlinear bending response of functionally graded porous micro/nano-beams reinforced with graphene platelets. Notably, upon including SGE within the constitutive framework for graphene, some exciting observations were realized. In their study, Kundalwal et al. [264] observed that, strain gradients in non-piezoelectric graphene sheets affect both ionic positions and the asymmetric redistribution of electron density. This induces a strong polarization to obtain an apparent piezoelectric behavior from a graphene sheet containing non-centrosymmetric trapezoidal shaped pore, such as shown in Fig. 12. More details on exploitation of the strain gradients in nanostructures for multiphysics coupling will be discussed in the next section.

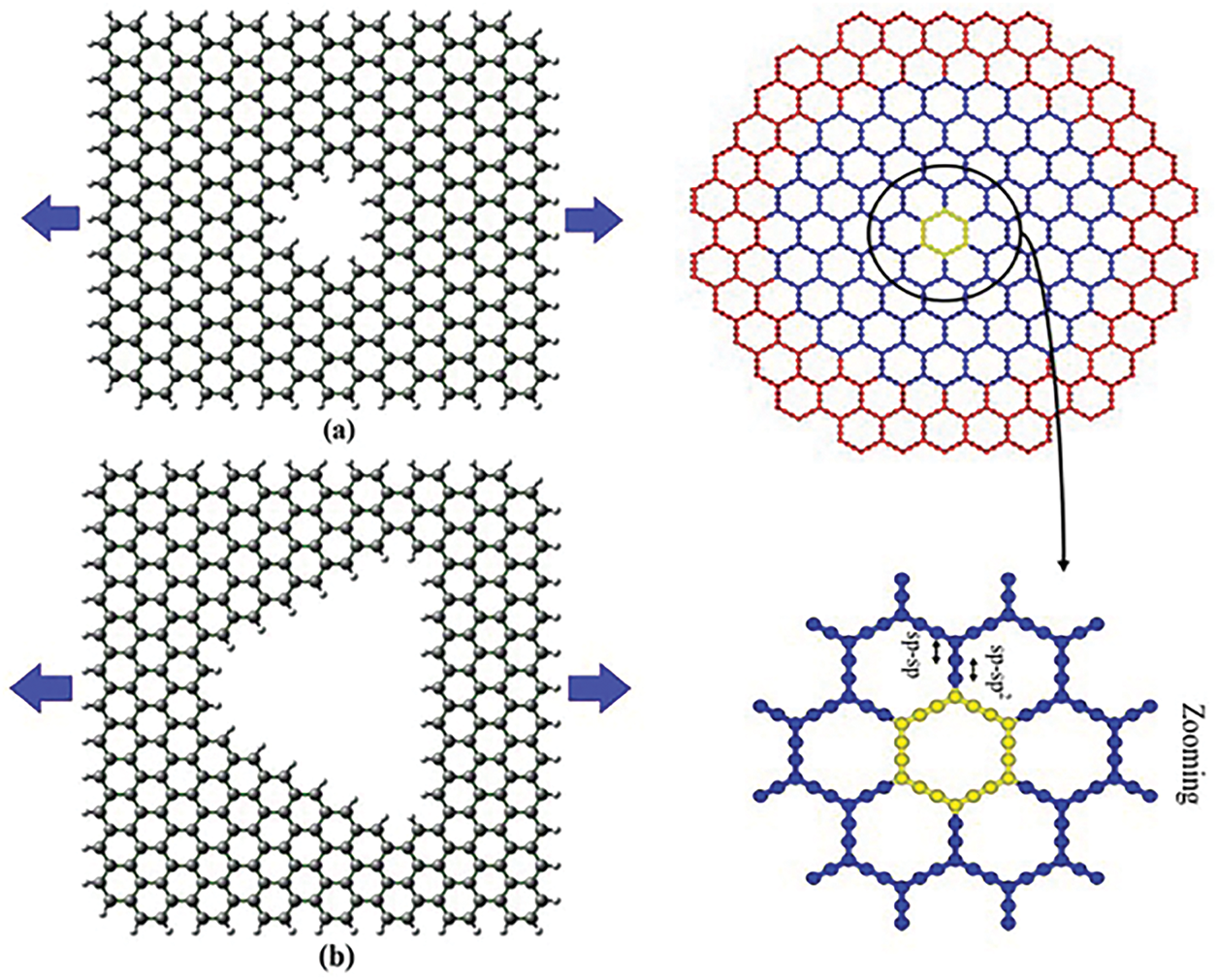
Figure 12: Schematic of passivated armchair graphene sheet with trapezoidal pore subjected to an axial stress [264]

6  Application for Multiphysics Coupling

Ferroelectric materials are widely used in actuators, sensors, memory devices, electro-optics, and MEMS because of their multifunctional properties driven by interactions between internal polarization and external factors like temperature, pressure, and electric fields. Among these, piezoelectric effect, presenting a non-zero electrical polarization to applied mechanical pressure (or vice versa), is well established. This coupling of the electro-mechanical field variables is limited to the non-centrosymmetric crystalline (and semi-crystalline) materials. Surprisingly, experiments detected a non-zero polarization in ferroelectrics even in their centrosymmetric crystalline phase. More specifically, Ma and Cross [47,48,62] note a non-zero polarization upon bending of ferroelectric crystals in their centrosymmetric phase at very low dimensions. This is attributed to a loss in symmetry and a resultant polarization in the materials as a result of the strain gradients across the structure. The loss in centrosymmetry and the resulting net polarization across the crystals due to the presence of a strain gradient is called the phenomenon of flexo-electricity. The suffix flexo- follows from initial observations of non-zero polarization in centrosymmetric crystals when subject to bending (flexure). This observation is significant because it reveals that electro-mechanical coupling in smart materials is a universal property, extending beyond the limitations of non-centrosymmetric structures. Similar observations of multiphysics coupling involving strain gradients are realized over magneto-elastic and thermo-elastic field variables, and discussed briefly in the section below.

Electro-mechanical coupling: The flexoelectric effect, coupling strain-gradients and electrical polarization, was theorized long before any experimental evidence. It may be interpreted as an electro-mechanical phenomenon in which a material exhibits a non-zero electric polarization in response to a strain gradient (non-uniform mechanical deformation) as demonstrated in Fig. 3b. As seen in this figure, strain gradients (following from a non-uniform strain across the thickness due to a bending load) present an asymmetric redistribution of electrons. Thereby, a net polarization is realized in centrosymmetric material. Understanding these interactions is key for advancing nanoscale electro-mechanical coupling with relevance for energy harvesting and actuation technologies.

The constitutive relations for the flexoelectric solid can be derived from the following expression for the internal energy density in centrosymmetric solids [265]:

𝒲=12aijPiPj+12bijklPi,kPj,l⏟Electrical+12Cijklεijεkl+12gijklmnηijkηlmn⏟Mechanical; See \hyperlink{ref-1}{Eq. (1)}−12flijk(Plηijk−εijPl,k)⏟Flexoelectric(41)

where Pi and Pi,j are the polarization field and its first gradient. The above expression for energy can be decomposed into three distinct parts: electrical, mechanical, and electro-mechanical coupling. The terms corresponding to elastic deformation energy are already introduced in Eq. (1). Additional terms for electrical and coupled energy are introduced above to model flexoelectric solids. a and b are second-order dielectric susceptibility and fourth-order polarization gradient tensors, respectively, and f is the (effective) flexocoupling tensor. The complete definition of this coupling material constant depends on the material symmetry; analogous to the definition for g corresponding to SGE. Mindlin [43] presented the definition of this material constant for isotropic solids. The coupling term in the above expression presents a non-zero electric polarization induced for a non-uniform strain across the domain, referred to as the direct flexoelectric effect. Additionally, converse flexoelectric field presents a non-uniform strain across the domain in response to applied electric polarization. The internal energy density corresponding to the piezoelectric effect is omitted above, owing to the assumption of centrosymmetry (the third-order material coefficient tensor is identically zero). From the above expression for internal energy, the constitutive relations for mechanical stresses (σ and τ; see Eq. (7)) and electrical field can be derived [266].

In the late 1950s, Mashkevich [267] experimentally observed the presence of the flexoelectric effect in crystals. Further, Kogan [46] and Harris [268] presented additional insights into the flexoelectric effect and improved understanding of its underlying mechanisms. Following the seminal work on SGE by Mindlin [31], the coupling of strain gradients with electrical polarization was explored in [43,269,270]. In particular, in this work, Mindlin extended the classical piezoelectric theory and developed a framework for electro-mechanical coupling involving strain gradients (the term ‘flexoelectricity’ was not coined yet). This phenomenon may also be interpreted as the size effect involving multi-physics coupling realized as a consequence of the strain gradients in low-dimensional structures. Therefore, the effect of the coupling decreases with increasing dimensions of the structure/crystal, confirmed in later numerical studies [271].

In the later experiments by Indenbom [272], the flexoelectric coefficients coupling polarization and strain gradient were observed to be four orders of magnitude higher than the initial theoretical estimates. Despite the important role of the flexoelectric effect, experimental measurements of flexoelectric coefficients have been limited to a few ferroelectric materials [62,273], biological structures [274–276], and polymeric materials [277–279]. For instance, Lu et al. [280] experimentally determined the flexoelectric coefficients of macroscopic polyvinylidene fluoride (PVDF) polymers, revealing notable differences between their bulk and thin film forms. Given the several number of material constants involved, a series of experiments is necessary for the characterization of the flexoelectric coupling tensor. A schematic illustration of the experimental setup used for the direct measurement of flexoelectric constants is presented in Fig. 13 [281]. Further, Sharma et al. [282,283] theoretically estimated the flexoelectric coefficients using molecular dynamics simulations. However, significant discrepancies between theoretical predictions and experimental findings have highlighted a promising area of research in material modeling. This growing interest was further reflected in the comprehensive review by Yudin and Tagantsev [284].

Figure 13: Schematic illustrations of experimental setups for direct measurements of flexoelectric constants: (a) Cantilever bending, (b) cylinder twisting, (c) four-point bending, (d) three-point bending, (e) pyramid compression. Further, illustration of experimental setup for characterization of converse flexoelectric constants: (f) normal-electrode pyramid and (g) side-electrode pyramid [281]

Building on the initial modeling framework developed by Mindlin [43], Hu and Shen [266,285] developed a variational approach to analyze the flexoelectric behavior of structures. This was possible by incorporating extended linear theory for dielectrics including surface effects. These frameworks make it possible to conduct analytical and numerical studies on flexoelectric solids for various structural configurations. For instance, the implications of flexoelectricity at the nanoscale were explored by Majdoub et al. [286,287], using Bernoulli-Euler beam theory to model lead zirconate titanate (PZT) and Barium titanate (BT) nanowires. Their results highlighted enhanced electromechanical coupling because of the combined influence of piezoelectricity and flexoelectricity, suggesting promising applications in energy harvesting. The analysis is further extended to thick beams where shear effects become more prominent [204,288]. The shear deformation effects on the flexoelectric coupling were explored.

Following from a coupling involving the strain gradients, the flexoelectric effect is expected to demonstrate size-dependent behavior. This underscores the critical role of flexoelectricity in the electro-mechanical behavior of nanoscale piezoelectric structure. For instance, Yan and Jiang [289] investigated the impact of flexoelectric coupling on the static bending behavior of piezoelectric nanobeams within the framework of the Euler–Bernoulli beam model. Their study revealed that the flexoelectric effect significantly enhances the electroelastic response as the beam thickness decreases, these indicating a strong size dependence. Further, Liang et al. [290] investigated the combined influence of surface piezoelectricity (also gains relevance with reducing dimensions) and bulk flexoelectricity on the bending response of piezoelectric nanobeams. Their findings revealed a substantial enhancement in the effective electromechanical coupling coefficient when both surface and bulk effects were considered. The inclusion of bulk flexoelectricity contributed to a stiffening of the structure, resulting in reduced deflections compared to predictions made by conventional piezoelectric models.

Although flexoelectricity follows from a non-zero strain gradient, realized in low-dimensional structures, most studies have ignored the simultaneous effect of strain gradients over the elastic behavior. In particular, several studies on flexoelectricity proceeded with ignoring the effect of SGE (follows from ignoring the deformation energy due to strain gradients in Eq. (41) while retaining the strain gradients in flexoelectric coupled energy). Since both flexoelectricity and strain gradients can significantly alter the electromechanical behavior of these structures, a unified analysis is essential. In this direction, Sidhardh and Ray [92] explored the combined effect of GFSGET and flexoelectricity on the electro-mechanical response of flexoelectric solids as an actuator and energy harvester. The enhanced stiffness resulting from SGE produced a significant reduction in the deformations induced by the flexoelectric coupling. These observations are drawn from an exact solution developed in their study, which is devoid of assumptions such as displacement or electrical field variable distributions across the domain. Static analyses offer limited insight into piezoelectric and flexoelectric energy harvesting, typically following from dynamic behaviors such as harmonic vibrations. Therefore, based on theoretical and numerical frameworks to investigate the flexoelectric response for static loading conditions, several studies [53,291] explored the dynamic response of flexoelectric solids. Further, Liang et al. [271] developed analytical expressions for the maximum electric potential generated through the combined piezoelectric and flexoelectric effect in various dielectric materials. Wang and Wang [292] explored the distribution of electric potential in piezoelectric nanowires by incorporating combined flexoelectric and surface effects. It is observed that the surface effect significantly influences the electro-mechanical response (displacements and electric potential). Unlike the studies above on the monolithic dielectric structure that demonstrates a flexoelectric effect, Qi et al. [51] explored the flexoelectric layers attached to the surface of a substrate beam for actuation.

Leveraging the large flexoelectric coefficients in ferroelectric materials and the high strain gradients present in small-scale dielectrics, various applications have been developed. Among these, the most interesting is the universal nature of flexoelectricity being exploited to develop apparent piezoelectric solids. An example of the same is depicted in Fig. 12. In this example, under external load, a non-zero strain gradient is realized in the vicinity of an asymmetric cutout in the 2D graphene sheet [264]. This presents an electrical response to the mechanical load that follows from the flexoelectric coupling. A similar observation was noted earlier in molybdenum oxide (MoO2) by Sharma et al. [293], and it was proposed to enhance the (otherwise low) electro-mechanical coupling coefficients by introducing asymmetric cutouts in the domain. Further to this, as an electromechanical coupling phenomenon, the flexoelectric effect has potential for use in sensors, actuators, transducers, and energy harvesting devices [291,294]. To complement these theoretical insights, Fig. 14a presents an example of flexoelectricity in soft elastomers for application in a robotic appendage [295]. Ferroelectric behavior has also been observed in a specific class of soft materials, particularly biological membranes; see Fig. 14b. These membranes, composed of key biopolymers within the extracellular matrix of various soft tissues, show notable ferroelectric characteristics [296,297]. Within biological systems, membrane flexoelectricity has been postulated to contribute critically to fundamental processes, including mechanotransduction and auditory function [298,299]. Recently, Zelisko et al. [300] developed an analytical model based on statistical mechanics, supported by molecular dynamics simulations, to propose a plausible mechanism underlying biological ferroelectricity in tropoelastin. Their study predicted piezoelectric constants that surpass those of any known polymer. These studies offer compelling evidence highlighting the significance of flexoelectricity in soft lipid bilayers [297].

Figure 14: (a) Schematic of a soft robotic appendage, deforming in order to grab an object due to electrical stimuli [295]. (b) Lipid bilayer inside an electrolyte bath [297]

Magneto-elastic coupling: Just as flexoelectricity couples strain gradients with electrical polarization, a similar coupling occurs for magneto-elastic field variables, involving strain gradients. As noted previously, most existing research on strain gradients is centered on strain gradient elasticity or the flexoelectric effect. In contrast, the magneto-elastic coupling in crystals arising from an interaction between strain gradients and induced magnetic fields has received relatively little attention [301]. For instance, even in studies on magneto-elastic coupling in low-dimensional structures, the coupling of the strain gradient and magnetic field variables is not considered [302]. This interaction, known as the flexomagnetic effect, leads to the generation of a non-zero magnetic field under inhomogeneous strain. A schematic illustration for the same is depicted in Fig. 15b, where perovskite ABO3 lattice undergoes a deformation from symmetric cross-section (square) to asymmetric cross-section (rectangular and inclined parallelogram), thereby causing a spontaneous flexoeffect in nanowires. It is considered a specific case of the broader flexomagnetoelectric effect, a concept introduced by Bobylev and Pikin [49] to explore the combined magneto-electric and elastic behavior in liquid crystals. Flexo-electromagnetism fundamentally arises from the coupling between mechanical strain gradients and electromagnetic fields. A time-varying strain gradient induces a dynamic electric field. In response, the electromechanical interaction generates a magnetic field. This coupled mechanism results in the excitation of electromagnetic waves [303], as schematically illustrated in Fig. 15a.

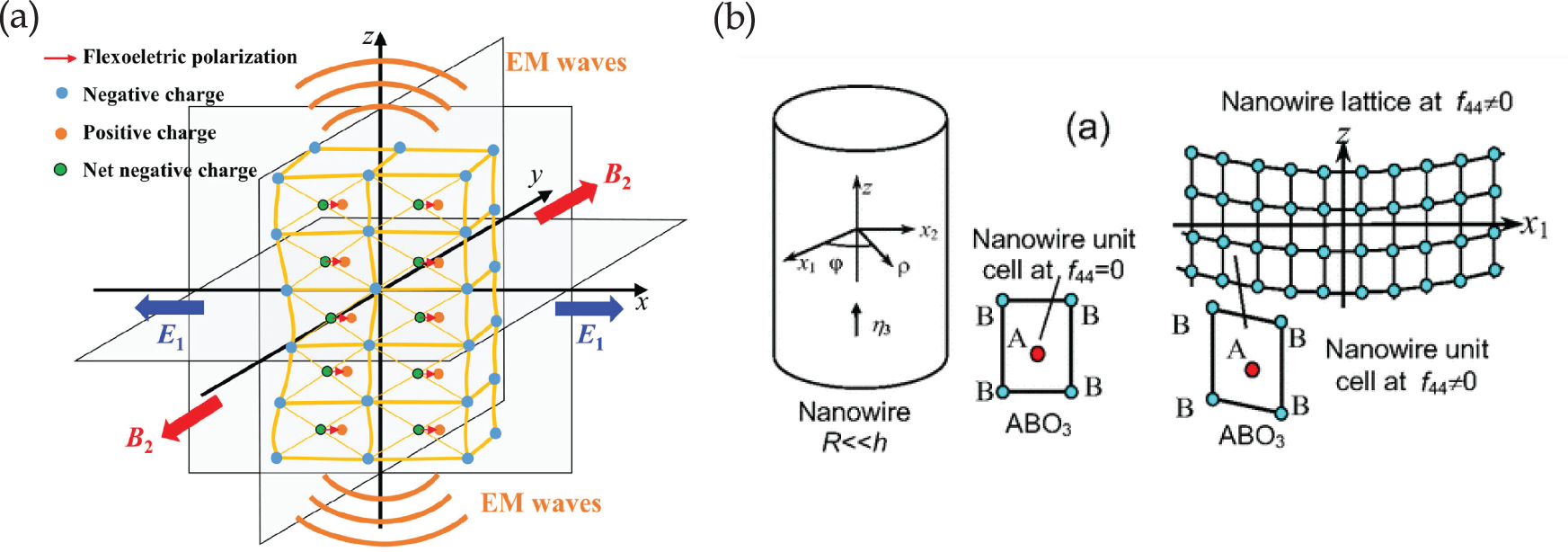
Figure 15: (a) Electro-magnetic wave propagation in a flexoelectric plate [303], (b) Schematics of the perovskite ABO3 lattice radial deformation from square to rectangular/inclined parallelogram-shaped cross-section caused by spontaneous flexoeffect in nanowires [304]

Restricting the above coupling to magnetic and elastic field variables, a flexomagnetic effect is proposed in the literature. Anaologus to Eq. (41), the free energy density of a centrosymmetric ferromagnetic solid is given as [145,304,305]:

𝒲=−12aijmHiHj⏟Magnetic+12Cijklεijεkl+12gijklmnηijkηlmn⏟Elastic; See \hyperlink{ref-1}{Eq. (1)}−fijklmHiηjkl⏟Flexomagnetic.(42)

where Hi is the magnetic field vector. The above expression for energy can be decomposed into three distinct parts: magnetic, elastic, and magneto-elastic coupling. The terms corresponding to elastic deformation energy are already introduced in Eq. (1). Additional terms for magnetic and magneto-elastic energy are introduced above for modeling flexomagnetic solids. In the above expression, am is the second-order magnetic permeability tensor, and the fourth-order tensor fm, coupling strain gradient and magnetic field is, the flexomagnetic tensor. The superscripts in am and fm are introduced here to differentiate from the constants introduced previously in Eq. (41) for flexoelectricity. The complete form of the flexomagnetic material constant for different magnetic classes is provided by Eliseev et al. [305]. The constitutive relations for mechanical stresses and magnetic induction can be derived from the above expression using thermodynamic balance laws [145]. Following from the coupling energy term above, we see a non-uniform strain inducing a magnetic field across the domain, referred to as the direct flexomagnetic effect. Furthermore, a converse flexomagnetic effect presenting non-uniform strain (strain gradient) across the domain in response to an applied magnetic field.

Eliseev et al. [304–306] conducted extensive theoretical analyses using symmetry theory to determine the form of the flexocoupling tensor in various magnetic classes. Their findings suggest that all 90 magnetic classes exhibit a non-zero flexomagnetic effect, at least near the surface. This is a significant observation, as this renders the flexomagnetic effect to be global and not restricted to a limited (mostly non-centrosymmetric in case of piezomagnetism) class of materials. Furthermore, Lukashev et al. [307,308] performed first-principles studies on Mn-based antiperovskites to compute the coupling tensor coefficients. These results imply the potential for the development of piezomagnetic-like structures that exploit flexomagnetic coupling without relying on traditional piezomagnetic materials.

Pyatakov and Zvezdin [309] investigated the combined electro-magneto-elastic coupling via third-order flexomagnetoelectric coupling tensors in antiferromagnetics, demonstrating its influence on inhomogeneous magnetoelectric coupling in various multiferroic systems. Expanding on the idea of inhomogeneous magnetoelectric coupling, the flexomagnetoelectric effect is characterized by a nonlinear interaction that is linearly dependent on polarization and quadratically on magnetization. This phenomenon was explored in detail by [310,311].

This phenomena can be visualized via the mechanism demonstrated in Fig. 16 above. The strain gradient defines a polar axis within the crystal, enabling the development of electric polarization due to symmetry considerations. This coupling between mechanical bending and electrical polarization is known as the flexoelectric effect, observed in solids (Fig. 16a) and in liquid crystals (Fig. 16b) [312]. A related phenomenon, spin flexoelectricity, refers to the polarization induced by spatial variations in magnetization. A notable example is the fan-like spin cycloid structure depicted in Fig. 16c, which emerges in magnetic atom monolayers [312,313] and is attributed to interfacial electric fields, demonstrating the effects of spin flexoelectric interactions [314].

Figure 16: The symmetry analogy: (a) flexoelectric effect in nonmagnetic solids, (b) molecular structures in liquid crystals and (c) spin cycloid structure in magnets [312]

Recently, Sidhardh and Ray [145] developed a constitutive model of the flexomagnetic effect and employed it to evaluate the magnetoelastic response of a beam, providing a deeper understanding of the interplay between strain gradients and magnetic field generation in multiferroic systems. This formulation simplified a detailed analysis of the flexomagnetic effect in solids. Malikan et al. [315,316] extended this constitutive framework for a magnetoelastic response analysis of cobalt-ferrite magnetic nanostructures (CFMNs), focusing on bifurcation buckling and post-buckling phenomena. This was achieved using the Euler-Bernoulli beam theory, nonlinear Lagrangian-von Kármán strains, and the nonlocal strain gradient elasticity (NSGT) approach. Further, Borkar et al. [317] developed a framework to study the effect of macroscopic inhomogeneous strain gradients on magnetic moments in multiferroic composites. Their results show that strong magneto-mechanical coupling under inhomogeneous strain can significantly enhance magnetic susceptibility at lower magnetic fields compared to relaxed Pb[(Zr0.52Ti0.48)0.60(Fe0.67W0.33)0.40]O3]0.80−[CoFe2O4]0.20 (PZTFW-CFO) composites. The application of inhomogeneous strain also led to increased zero-field-cooled (ZFC) and field-cooled (FC) magnetizations by reducing surface spin disorder.

Thermo-elastic coupling: In recent years, the pursuit of more efficient and eco-friendly cooling technologies has gained momentum, driven by the need to reduce harmful greenhouse emissions. Among various emerging approaches, flexocaloric cooling has shown significant promise. In general, caloric effects refer to reversible temperature changes in solid materials triggered by external fields, such as magnetic, electrical, or mechanical. The effect may arise from variations in magnetic spin states, electric-dipole alignments, or structural configurations. The thermodynamic cooling mechanisms include both vapor compression and ferroic-based cycles. Significant thermal responses are generally observed in materials that exhibit spontaneous phase transitions near the target operating temperature [318]. Specifically, the flexocaloric effect involves temperature changes resulting from the application of mechanical stress [319,320].

Existing studies indicate that the flexocaloric effect induced by a strain gradient is generally realized through an asymmetric electron distribution within the material commonly observed in structures such as truncated pyramids [321] or the bending of thin films made of non-centrosymmetric materials [322]. The flexoelectric coupling significantly alters the misfit strain–temperature phase diagram by promoting out-of-plane polarization phases due to a built-in field. Considering both flexoelectric and work function-induced fields leads to a notable enhancement in electrocaloric performance. For instance, Bai et al. [323] investigated the size-dependent behavior of paraelectric Ba0.67Sr0.33TiO3 (BST) truncated pyramids using a phenomenological thermodynamic framework. Their findings revealed that the flexoelectricity-induced entropy and adiabatic temperature changes are size dependent (which is obvious from previous studies involving strain gradients) and vary with applied stress and working temperature. Specifically, as the thickness of the pyramid decreases and the external stress increases, the resulting strain gradient is enhanced. Consequently, a greater flexocaloric effect is realized, leading to greater entropy and temperature changes. Further, Patel et al. [321,324] examined the caloric effect induced by flexoelectricity in truncated pyramids of BST ceramics of varying heights. The results suggest that ferroelectric materials can effectively generate cooling even beyond their Curie temperature, which was previously thought to be a limiting factor. Qiu et al. [325] employed an extended nonlinear thermodynamic framework to model the flexocaloric effect in BaTiO3 thin films. Furthermore, BaTiO3 and BST thin films have been extensively studied for their high caloric effects, which complement the electrocaloric effect and have potential for solid-state cooling applications [326].

Recently, an alternative approach has emerged that involves the induction of strain gradients in uniform structures through the varying material composition; for instance using functionally graded materials (FGM) [327]. Sharma et al. [322] developed a numerical framework to study the flexocaloric effect in FGMs. The flexocaloric effect is realized by virtue of the flexoelectric polarization generated in the FGM due to the inhomogeneous material composition.

These findings highlight the exciting possibilities for achieving novel approaches for multi-physics coupling involving a strain gradient coupling with electrical, magnetic, and thermal field variables. In particular, we also note the rather global nature of such couplings, which extend beyond a limited choice of materials typically used for multiphysics coupling.

7  Integral Models and Hybrid Model for Nonlocal Elasticity

The fundamental idea behind nonlocal theories is that all particles within a defined region, usually referred to as the horizon of nonlocality, interact with one another through long-range cohesive forces. This interaction can be modeled using either gradient or integral relations in the constitutive equations, leading to “weak” gradient methods or “strong” integral methods, respectively. A schematic illustration of the nonlocal interactions across the domain is provided in Fig. 8. We note that, unlike the local elastic constitutive relations, the mechanical response in a nonlocal solid depends on the relevant field variables at all points within the domain of nonlocal influence. We have provided a detailed account of the gradient models for nonlocal elasticity in this review article. We conclude with a brief overview of some integral theories for nonlocal interactions proposed in the literature.

We begin by presenting some limitations of the gradient-based theories documented in the literature. To begin with, we revisit the governing equations and corresponding boundary conditions for the gradient elasticity developed in Eq. (26b). The physical motivation behind the additional boundary conditions (essential and natural) for SGE is unclear, leading to ambiguity in enforcing them and problems with their application in practical problems [10]. This is in addition to the difficulties in arriving at analytical or numerical solutions for the GDEs in Eq. (26a) on account of the higher-order derivatives. This aspect has been discussed in detail in Section 3.2. Finally, gradient elastic models have a limited range for the nonlocal horizon [328]. For instance, recall from Section 5 that microstructure effects were realized only in structures not much larger (at most one order of magnitude) than the nonlocal length scale. Owing to this limitation, these models are not suitable for capturing the nonlocal interactions over a larger geometric span.

Integral models for nonlocal elasticity, also referred to as the strong form of nonlocal elasticity, are mathematically better suited to account for the long-range interactions across the domain. In addition, these constitutive models can be divided into three different approaches: (i) the strain-driven approach, (ii) the stress-driven approach, and (iii) the displacement-driven approach. A brief overview of these models is provided below.

7.1 Strain Driven Approach

Eringen and Edelen [329] proposed an integral stress-strain material constitutive relations, wherein the stress at a point in the solid is expressed in terms of the strains at all points within its horizon of influence. Mathematically, this is given by:

σ(x)=∫Ωϕλ(x−ξ) E(ξ) εel(ξ)dΩξ,(43)

where the stress is evaluated at the point x within the solid, and the contributions of all points ξ in its domain of influence are accounted for via the convolution integral. Moreover, the scalar kernel ϕλ(x−ξ) is a monotonically decreasing function of the distance between the points x and ξ, and denotes the weight associated with their interaction. This kernel function is identically equal to zero for points outside the domain of influence of x. In the above expression,

ε=εth+εel,(44)

where the total strain field is comprising both non-elastic components (e.g., thermal strains) and elastic strain, and must satisfy kinematic compatibility. The model described in Eq. (43) is known as the strain-driven integral constitutive relation, as it is driven by the elastic strain εel as the source field.

This nonlocal constitutive model follows from a long-range cohesive force-based elasticity theory proposed by Kröner [27]. For six decades, researchers have widely utilized this framework due to its straightforward implementation and, critically, its ability to intuitively model nonlocal interactions. However, this framework suffers from mathematical inconsistencies, including ill-posed governing equations, limiting its extension beyond simple case studies. For instance, Batra [330] demonstrated that the constitutive relation given above cannot be extended to heterogeneous material systems. This model has been widely used to study size effects in nanoscale beams, often using a differential form assumed to be equivalent to the original integral formulation [9]. Furthermore, Gurtin-Murdoch surface elasticity theory has been coupled with nonlocal strain-driven models to improve the accuracy of mechanical predictions at the nanoscale [87,88].

Two-phase strain-driven elasticity mode: The constitutive relation in Eq. (43) is a Fredholm integral equation of the first kind, and suffers from fundamental drawbacks including non-unique and ill-posed solutions [331,332]. Therefore, this nonlocal constitutive relation is relaxed to be expressed as a two-phase local/nonlocal strain-driven elasticity model (Fredholm integral equation of the second kind) [333]. Following this approach, the total stress at a point is influenced not only by the local strain but also by the strain at the surrounding points. For a one-dimensional, isotropic and homogeneous structure, this relationship can be expressed as [334]:

τ(x)=E(ζ2ε(x)+(1−ζ2)∫0Lφ(x,x¯,k2)ε(x¯)dx¯)(45)

Here, ζ2 is the local phase fraction associated with the strain-driven two-phase elasticity model. The function φ(x,x¯,k2) denotes the nonlocal convolution kernel, which depends on the internal length scale k1, and is related to the specific properties of the material. In this formulation, ε(x) and σ(x) correspond to the partial (local) strain and the total stress at the point x, respectively. Thus, the constitutive relation above captures the softening effect of nonlocal interactions.

Nonlocal strain gradient model: A key limitation of the integral model introduced above and the SGE formulations lies in their ability to capture only a softening or stiffening effect on the mechanical behavior, but not both simultaneously. However, there exists experimental evidence pointing to size effects that present softening and stiffening responses, depending on the loading and boundary conditions [335]. The nonlocal gradient elasticity framework proposed in [336] has demonstrated the ability to model both stiffening and softening responses. This framework combines Eringen’s strain-driven integral nonlocal model with strain gradient elasticity, resulting in a higher-order nonlocal formulation. In this model, stress is expressed as the sum of the contributions from two integral components: (i) classical convolution of strain with a smoothing kernel (Eringen’s nonlocal model) and (ii) strain gradients via a convolution with an independent smoothing kernel. Thus, the corresponding deformation energy density is redefined as [336]:

W=12Cijkl εij∫Vα0(|x−x′|,e0a)εkldV+l22Cijklεij,m∫Vα1(|x−x′|,e1a)εkl,m′dV,(46)

where εij is the strain tensor and Cijkl is the classical elastic stiffness tensor. The parameters e0 and e1 are nonlocal scaling constants associated with the internal characteristic length a. The attenuation kernels α0(|x−x′|,e0a) and α1(|x−x′|,e1a) capture the nonlocal effects, on a point x due to a point x′, corresponding to the classical strain field and the first-order strain gradient field, respectively. A material length scale l is also introduced to characterize the influence of higher-order strain gradients. The above framework captures both softening and stiffening effects due to nonlocal interactions.

7.2 Stress Driven Approach

Noting the mathematical and physical drawbacks of the strain-driven approach discussed above, Romano and Baretta [337,338] proposed an alternative in the stress-driven integral constitutive model for nonlocal elasticity. The inherent issues associated with strain-driven integral convolution models are fundamentally eliminated following this approach. The key feature of this new theory lies in treating the stress field as the input for the integral constitutive relation, with the nonlocal elastic strain as the resulting output. Mathematically, this is expressed as follows [338].

εel(x)=∫0Lϕ(x−ξ)E−1σ(ξ)dξ,(47)

where the elastic strains εel are derived from stresses σ through a convolution weighted by the kernel ϕ(x,ξ). As in case of strain-driven approach, this kernel is a function of the distance between the points interacting within the nonlocal horizon, and is a monotonically reducing positive semidefinite function (equal to zero outside the horizon of nonlocal influence). Although the stress-driven approach resolves the previous mathematical problems, it introduces new physical inconsistencies. For instance, the deformation energy density of a solid following the stress-driven approach is not positive definite. This result is essential for a consistent structural stiffness matrix, when developed following numerical methods like FEM. Further to this, the stress-driven approach is not immediately physically intuitive. In contrast to the action-at-a-distance approach realized following a strain-driven approach, the stress-driven approach is found to be lacking for the physical interpretation of the nonlocal interactions. This is further realized by ad hoc boundary conditions introduced within this framework for a solution of the governing differential equations [337]. This integral model was further simplified to give an equivalent stress gradient-based differential constitutive framework. This extended model offers a significant advantage over the original formulation by enabling numerical studies on stiffening behavior at nanoscales [339]. Further, similar to the nonlocal gradient elasticity model defined over the strain-driven approach in Eq. (46), stress-driven [340] nonlocal gradient approaches have also been proposed in the literature. These alternate frameworks specifically address the limitations of Eringen’s strain-driven nonlocal approach by exploring stress-driven integral models for a combination with gradient theories.

The above given stress-driven nonlocal model has been combined with the surface elasticity theory proposed by Gurtin and Murdoch [83], to present a Surface Stress-Driven Model (SSDM), which effectively incorporates both long-range interatomic forces and surface energy. This model accounts for the size-effects within the bulk and the surfaces in a simultaneous manner, and has been used to investigate the static response [89], free vibration [341], buckling behavior [342], and electromechanical coupling effects [343] in low-dimensional structures.

Two-phase stress-driven elasticity model: Similarly to the two-phase strain-driven approach for elasticity, a two-phase stress-driven elasticity model is defined. Following this approach, the total strain at a point is influenced not only by the local stress but also by the stresses at the surrounding points. For a one-dimensional, isotropic and homogeneous structure, this relationship can be expressed as [333]:

ε(x)=1E(ζ1σ(x)+(1−ζ1)∫0Lφ(x,x¯,k1)σ(x¯)dx¯)(48)

Here, ζ1 is the local phase fraction associated with the stress-driven two-phase elasticity model. The function φ(x,x¯,k1) denotes the nonlocal convolution kernel, which depends on the internal length scale k1, and is related to the specific properties of the material. In this formulation, ε(x) and σ(x) correspond to the total strain and the partial (local) stress at the point x, respectively. The constitutive relation described above captures the stiffening effect of nonlocal interactions.

Among recent developments, two- and three-parameter models, derived from simultaneously considering strain- and stress-driven approaches, have been widely used for studies on the static and dynamic behavior of low-dimensional structures [333]. By simultaneously considering two-phase strain/stress-driven nonlocal constitutive relations, it becomes possible to capture both softening and stiffening behaviors, provided that the material constants k1 and k2 are appropriately chosen in Eqs. (45) and (48).

7.3 Displacement Driven Approach

In recent years, the displacement-driven approach has emerged as a powerful mathematical framework for modeling various nonlocal and multiscale phenomena [328,344–347].

From the above expressions in Eqs. (43) and (47), it is evident that in both the strain- and stress-driven approaches, the strain energy density generally cannot be reduced to a quadratic form and, therefore, is not necessarily positive definite [348,349]. Although a positive total strain energy can still be achieved, this requires specific conditions on the kernel that it must be positive and symmetric in nature [337,350]. A viable approach to ensure a convex and positive definite deformation energy density is to preserve the quadratic form of the strain energy density, similar to that in classical local elastic continuum mechanics. To ensure this, nonlocality is introduced via redefined strain-displacement relations, while keeping the stress–strain constitutive relation in its classical local form. In particular, the nonlocal kinematic relations, for infinitesimal deformations, are given by [348]:

ε=12(∇¯u(x)+(∇¯u(x))T),(49)

where u(x) is the displacement field. ∇¯ is the nonlocal gradient operator defined as:

∇¯ju(x)=∫x−jx+jcj∗ 𝒦(x)   Dx′j1u(x)   dxj′.(50)

Here, cj∗ is a scaler multiplier for the differ-integral operator in the xj direction, which will be used to enforce frame invariance and dimensional consistency for the modified strain-displacement (kinematic) constitutive relations. 𝒦(x,x′) denotes the nonlocal kernel for the displacement-driven approach, analogous to previous definitions for stress- and strain-driven nonlocal elasticity. Further, Dx′j1 is the classical first-order derivative. The length of the horizon of nonlocality on the either side of the point x in the xj direction denoted as l−j=xj−x−j and l+j=x+j−xj. Finally, the stress within the solid is given by the work-conjugate definition with respect to the nonlocal strain defined above, similar to classical elasticity. This approach is termed the “displacement-driven approach to nonlocal elasticity,” as nonlocality is introduced through strain-displacement kinematic constitutive relations. The above definition is reported to alleviate the physical, mathematical and thermodynamic inconsistencies realized by the stress- and strain-driven approaches to the integral nonlocal elasticity discussed above [349].

Among the different choices for the kernel in Eq. (50), the particular choice of a power-law function transforms this expression into a Reisz-Caputo (RC) fractional-order derivative. In particular, the nonlocal strain-displacement relations in Eq. (49) reduce to a fractional-order RC derivative of the displacement field for this specific and admissible choice of the kernel function. These constitutive relations have been explored in detail in the literature, due to evidence of nonlocal interactions following a power-law distribution away from the point of interest [350]. The fractional-order constitutive model for nonlocal elasticity has been employed for several multiscale and multiphysics studies [344,349]. Finally, similar to the nonlocal gradient elasticity model over the strain-driven approach in Eq. (46) and the stress-driven approach, a displacement-driven approach for nonlocal gradient elasticity have also been proposed in the literature. To elaborate, the fractional-order constitutive models defined above are extended to fractional gradients of higher order in [344], thus generating a unified approach to modeling the softening and stiffening effects in material response.

8  Conclusion and Future Direction

This review provides a comprehensive overview of strain gradient elasticity, highlighting its importance in addressing the limitations of classical elasticity at small length scales. In addition, various constitutive models for SGE are explored here, from generalized higher-order gradient theories to simplified versions tailored for specific applications, including second-order SGE introducing surface effects. The physical relevance of SGE, particularly its ability to capture size effects and (weakly) nonlocal interactions, has been discussed. Furthermore, the review has covered the analytical and numerical techniques developed to solve the higher-order governing differential equations presented by the SGE framework. We present detailed applications of SGE in multiscale elasticity and multiphysics coupling scenarios, highlighting its ability to bridge the limitations of classical continuum mechanics. Finally, a discussion of alternative integral and integro-differential theories provides a broader perspective on non-classical continuum mechanics.

Potential Areas for Future Research

Despite significant progress in the field of strain gradient elasticity, several avenues remain open for future research and development. Moreover, since most of the literature has concentrated on simplified theories of SGE, the entire potential of the gradient effects on the solids has not yet been realized. Some potential areas for future research are:

•   Fundamental gaps: As mentioned earlier, the physical relevance of the additional boundary conditions derived from the variational principles within the SGE framework remains unclear. This ambiguity is compounded by mathematical inconsistencies in higher-order gradient terms within the SGE constitutive laws. For instance, the consistency of the symmetric and asymmetric parts of rotational gradients in higher-order elasticity, proposed almost half a century ago, is still being debated. Consequently, a fundamental investigation into the physical and mathematical significance and consistency of different deformation mechanisms captured via higher-order continuum theories requires to be explored. Future research in SGE should also explore bridging the gap between the theoretical framework and its physical interpretation, as well as improving experimental validation to increase its practical utility.

•   Finite strain theory and broader generalizations: Extending SGE into the realm of finite-strain theory, also known as large-deformation theory, is necessary to account for cases where the strains and/or rotations are significant. Note that, under these conditions, the assumptions of infinitesimal strain theory and linear SGE in the literature are invalidated. This expansion is essential for SGE to expand beyond idealized academic problems to practical engineering challenges. Further, a generalization of the SGE constitutive framework to lower material symmetries (orthotropic and anisotropic) can be explored. Finally, the unification of SGE with other generalized continua (e.g. micromorphic or higher-order Cosserat models) and exploration of their individual appropriateness can be investigated.

•   Homogenization of heterogeneous materials: While the scope of nonlocal theories is typically associated with low dimensions, recently, these are being explored for homogenization of macrostructures. In particular, by incorporating the influence of microstructural features, say lattice design, through strain gradients, SGE-based homogenization techniques can provide more accurate effective properties for composite materials, porous media, and other complex microstructures, when compared to classical methods. For instance, in woven composites, SGE-based constitutive laws are established to capture complex bending deformation properties, particularly to address spurious wrinkles that may occur in 3D bending simulations due to low plane shear stiffness. This allows for improved predictions of the overall elastic behavior without explicitly modeling every microstructural detail at the macroscale.

•   Development of experimentally validated material parameters: A key challenge in SGE is the difficulty in experimentally measuring strain gradients and characterization of all independent material constants. We currently lack direct experimental methods for imposing higher-order tractions or their conjugate displacement gradients, making it difficult to determine elastic constants. However, promising techniques such as Digital Image Correlation (DIC), X-ray Diffraction (XRD), and nanoindentation are crucial for estimating characteristic lengths and validating theoretical predictions.

•   Development of efficient numerical methods: Higher-order governing equations in SGE require advanced numerical techniques, such as higher-order FEM or IGA. Future research should focus on developing more efficient and robust numerical methods to handle the increased computational cost associated with SGE, particularly for large-scale simulations. For instance, further development of higher-continuity discretizations (e.g., subdivision IGA, virtual element methods) will simplify the implementation of SGE. Stabilization techniques for dynamic SGE and error estimation algorithms will improve reliability. Furthermore, a shift towards mixed formulations and enriched elements can be explored to accurately capture highly localized phenomena while making SGE models more practical and accessible within existing commercial software environments. Finally, an implementation of strain gradient models in commercial FEM software like ABAQUS can be achieved through user subroutines (UEL, UMAT), enabling the analysis of complex problems.

•   Integration with atomistic and molecular dynamics simulations: SGE can serve as a crucial link in hierarchical modeling approaches, where information is passed between different scales. Multiscale modeling, coupling constitutive frameworks at different scales (from quantum mechanics to classical MD and continuum mechanics), is emerging as a dominant research methodology. This approach aims to increase the size of the system under study without compromising the accuracy of the calculations. Moreover, multiscale approaches can also present with atomistic representations of higher-order elastic tensors (e.g., double stress and strain gradient elastic moduli). In other words, parameter estimation can be shifted from empirical fitting to predictive science, providing a deeper understanding of the microstructural origins of gradient effects. Finally, hybrid multiscale approaches can seamlessly integrate these different scales could provide valuable insights.

•   Application to novel materials and structures: The unique capabilities of SGE can be used to design and analyze novel materials and microarchitectured structures with tailored mechanical properties. Future research should explore the application of SGE in the design of metamaterials, nanocomposites, and other advanced materials with enhanced performance characteristics. More interesting potential for SGE lies in understanding the mechanics of biological tissues, which are complex, heterogeneous, and often exhibit size-dependent behavior. Flexoelectricity has been observed in biological materials like cells, cell membranes, and bone, playing a role in vital biological processes such as auditory sensing and mechanotransduction. Understanding these effects through SGE can significantly improve the applications of regenerative medicine and drug delivery.

By addressing these potential research areas, the field of strain gradient elasticity can continue to evolve and provide increasingly accurate and insightful tools for understanding and designing materials and structures at small (and also higher) length scales, paving the way for advancements in various technological domains.

Acknowledgement: None.

Funding Statement: Shubham Desai and Sai Sidhardh acknowledge the financial support from the Anusandhan National Research Foundation (ANRF), erstwhile Science and Engineering Research Board (SERB), India, under the startup research grant program (SRG/2022/000566).

Author Contributions: The authors confirm contribution to the paper as follows: Formal analysis: Shubham Desai and Sai Sidhardh, investigation: Shubham Desai and Sai Sidhardh, data curation: Shubham Desai and Sai Sidhardh, writing—original draft preparation: Shubham Desai, writing—review and editing: Sai Sidhardh, visualization: Shubham Desai, supervision: Sai Sidhardh, project administration: Sai Sidhardh, funding acquisition: Sai Sidhardh. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflict of interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A: A brief comparison of their assumptions, advantages, and limitations is presented in the table below:

References

1. de Boer MP, Luck DL, Ashurst WR, Maboudian R, Corwin AD, Walraven JA, et al. High-performance surface-micromachined inchworm actuator. J Microelectromech Syst. 2004;13(1):63–74. doi:10.1109/jmems.2003.823236. [Google Scholar] [CrossRef]

2. Moser Y, Gijs MA. Miniaturized flexible temperature sensor. J Microelectromech Syst. 2007;16:1349–54. doi:10.1109/JMEMS.2007.908437. [Google Scholar] [CrossRef]

3. Qu H, Xie H. Process development for cmos-mems sensors with robust electrically isolated bulk silicon microstructures. J Microelectromech Syst. 2007;16(5):1152–61. doi:10.1109/jmems.2007.906079. [Google Scholar] [CrossRef]

4. Mouaziz S, Boero G, Popovic RS, Brugger J. Polymer-based cantilevers with integrated electrodes. J Microelectromech Syst. 2006;15:890–5. doi:10.1109/JMEMS.2006.879376. [Google Scholar] [CrossRef]

5. Chong AC, Lam DC. Strain gradient plasticity effect in indentation hardness of polymers. J Mater Res. 1999;14:4103–10. doi:10.1557/JMR.1999.0554. [Google Scholar] [CrossRef]

6. Lam DC, Yang F, Chong A, Wang J, Tong P. Experiments and theory in strain gradient elasticity. J Mech Phys Solids. 2003;51:1477–508. doi:10.1016/S0022-5096(03)00053-X. [Google Scholar] [CrossRef]

7. McFarland AW, Colton JS. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J Micromech Microeng. 2005;15:1060. [Google Scholar]

8. Eringen AC, Suhubi E. Nonlinear theory of simple micro-elastic solids—i. Int J Eng Sci. 1964;2:189–203. [Google Scholar]

9. Eringen AC. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys. 1983;54(9):4703–10. doi:10.1063/1.332803. [Google Scholar] [CrossRef]

10. Aifantis EC. Update on a class of gradient theories. Mech Mater. 2003;35(3-6):259–80. doi:10.1016/s0167-6636(02)00278-8. [Google Scholar] [CrossRef]

11. Park H, Lakes R. Cosserat micromechanics of human bone: strain redistribution by a hydration sensitive constituent. J Biomech. 1986;19(5):385–97. doi:10.1016/0021-9290(86)90015-1. [Google Scholar] [PubMed] [CrossRef]

12. Yang J, Lakes RS. Experimental study of micropolar and couple stress elasticity in compact bone in bending. J Biomech. 1982;15:91–8. doi:10.1016/0021-9290(82)90040-9. [Google Scholar] [PubMed] [CrossRef]

13. Javili A, Dell’Isola F, Steinmann P. Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J Mech Phys Solids. 2013;61:2381–401. doi:10.1016/j.jmps.2013.06.005. [Google Scholar] [CrossRef]

14. Eringen AC. Balance laws of micromorphic mechanics. Int J Eng Sci. 1970;8(10):819–28. doi:10.1016/0020-7225(70)90084-4. [Google Scholar] [CrossRef]

15. Eringen AC. Microcontinuum field theories: I. Foundations and solids. Berlin/Heidelberg, Germany: Springer Science & Business Media; 2012. [Google Scholar]

16. Sidhardh S. Analysis of elastic and coupled flexo-physics problems using generalized strain gradient theories. [Ph.D. thesis]. Kharagpur, India: IIT Kharagpur; 2019. [Google Scholar]

17. Grot RA. Thermodynamics of a continuum with microstructure. Int J Eng Sci. 1969;7(8):801–14. doi:10.1016/0020-7225(69)90062-7. [Google Scholar] [CrossRef]

18. Říha P. On the theory of heat-conducting micropolar fluids with microtemperatures. Acta Mech. 1975;23(1–2):1–8. doi:10.1007/bf01177664. [Google Scholar] [CrossRef]

19. Říha P. On the microcontinuum model of heat conduction in materials with inner structure. Int J Eng Sci. 1976;14(6):529–35. doi:10.1016/0020-7225(76)90017-3. [Google Scholar] [CrossRef]

20. Eringen AC. Mechanics of micromorphic continua. In: Mechanics of Generalized Continua: Proceedings of the IUTAM-Symposium on the Generalized Cosserat Continuum and the Continuum Theory of Dislocations with Applications, Freudenstadt and Stuttgart (Germany). Cham, Switzerland: Springer; 1968. p. 18–35. [Google Scholar]

21. Mindlin RD. Micro-structure in linear elasticity. Arch Ration Mech Anal. 1964;16(1):51–78. doi:10.1007/bf00248490. [Google Scholar] [CrossRef]

22. Mindlin R. Elasticity, piezoelectricity and crystal lattice dynamics. J Elast. 1972;2(4):217–82. doi:10.1007/bf00045712. [Google Scholar] [CrossRef]

23. Cauchy A-L. Note sur l’equilibre et les mouvements vibratoires des corps solides. CR Acad Sci Paris. 1851;32:323–6. [Google Scholar]

24. Voigt W. Theoretische studien über die elasticitätsverhältnisse der krystalle. Gottingen, Germany: Dieterich; 1887. [Google Scholar]

25. Cosserat EMP, Cosserat F. Théorie des corps déformables. Nature. 1909;81:67. doi:10.1038/081067a0. [Google Scholar] [CrossRef]

26. Toupin R. Elastic materials with couple-stresses. Arch Ration Mech Anal. 1962;11(1):385–414. doi:10.1007/bf00253945. [Google Scholar] [CrossRef]

27. Kröner E. Elasticity theory of materials with long range cohesive forces. Int J Solids Struct. 1967;3(5):731–42. doi:10.1016/0020-7683(67)90049-2. [Google Scholar] [CrossRef]

28. Mindlin RD, Tiersten H. Effects of couple-stresses in linear elasticity. Arch Ration Mech Anal. 1962;11:415–48. doi:10.1007/BF00253946. [Google Scholar] [CrossRef]

29. Mindlin RD. Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct. 1965;1(4):417–38. doi:10.1016/0020-7683(65)90006-5. [Google Scholar] [CrossRef]

30. Green AE, Rivlin RS. Simple force and stress multipoles. In: Collected papers of RS rivlin: volume I and II. Cham, Switzerland: Springer; 1964. p. 1725–53. [Google Scholar]

31. Mindlin RD, Eshel N. On first strain-gradient theories in linear elasticity. Int J Solids Struct. 1968;4:109–24. doi:10.1016/0020-7683(68)90036-X. [Google Scholar] [CrossRef]

32. Germain P. La méthode des puissances virtuelles en mécanique des milieux continus, premiere partie: théorie du second gradient. J De Mécanique. 1973;12:235–74. [Google Scholar]

33. Germain P. The method of virtual power in continuum mechanics, part 2: microstructure. SIAM J Appl Math. 1973;25(3):556–75. doi:10.1137/0125053. [Google Scholar] [CrossRef]

34. Weitsman Y. Strain-gradient effects around cylindrical inclusions and cavities in a field of cylindrically symmetric tension. ASME J Appl Mech. 1966 Mar;33(1):57–67. doi:10.1115/1.3625026. [Google Scholar] [CrossRef]

35. Cook TS, Weitsman Y. Strain-gradient effects around spherical inclusions and cavities. Int J Solids Struct. 1966;2:393–406. doi:10.1016/0020-7683(66)90029-1. [Google Scholar] [CrossRef]

36. Hazen GA, Weitsman Y. Stress concentration in strain-gradient bodies. J Eng Mech Div. 1968;94:773–95. doi:10.1061/JMCEA3.0000986. [Google Scholar] [CrossRef]

37. Savin G, Lukashev A, Lysko E, Veremeenko S, Agas’ ev G. Elastic wave propagation in a cosserat continuum with constrained particle rotation. Sov Appl Mech. 1970;6:599–602. doi:10.1007/BF00888458. [Google Scholar] [CrossRef]

38. Oden J, Rigsby D, Cornett D. On the numerical solution of a class of problems in a linear first strain-gradient theory of elasticity. Int J Numer Methods Eng. 1970;2:159–74. doi:10.1002/nme.1620020203. [Google Scholar] [CrossRef]

39. Pamin J, de Borst R. Numerical simulation of localization phenomena using gradient plasticity and finite elements. Heron. 1995;40:71–92. [Google Scholar]

40. Phunpeng V, Baiz P. Mixed finite element formulations for strain-gradient elasticity problems using the fenics environment. Finite Elem Anal Des. 2015;96(4):23–40. doi:10.1016/j.finel.2014.11.002. [Google Scholar] [CrossRef]

41. Papanicolopulos S-A, Zervos A, Vardoulakis I. A three-dimensional c1 finite element for gradient elasticity. Int J Numer Methods Eng. 2009;77:1396–415. doi:10.1002/nme.2449. [Google Scholar] [CrossRef]

42. Rudraraju S, Van der Ven A, Garikipati K. Three-dimensional isogeometric solutions to general boundary value problems of toupin’s gradient elasticity theory at finite strains. Comput Methods Appl Mech Eng. 2014;278:705–28. doi:10.1016/j.cma.2014.06.015. [Google Scholar] [CrossRef]

43. Mindlin RD. Polarization gradient in elastic dielectrics. Int J Solids Struct. 1968;4(6):637–42. doi:10.1016/0020-7683(68)90079-6. [Google Scholar] [CrossRef]

44. Li Y, Feng W. Microstructure-dependent piezoelectric beam based on modified strain gradient theory. Smart Mat Struct. 2014;23:095004. doi:10.1088/0964-1726/23/9/095004. [Google Scholar] [CrossRef]

45. Sadeghi B, Cavaliere P, Pruncu CI, Balog M, Marques de Castro M, Chahal R. Architectural design of advanced aluminum matrix composites: a review of recent developments. Crit Rev Solid State Mat Sci. 2024;49(1):1–71. doi:10.1080/10408436.2022.2078277. [Google Scholar] [CrossRef]

46. Kogan SM. Piezoelectric effect during inhomogeneous deformation and acoustic scattering of carriers in crystals. Sov Phys Solid State. 1964;5:2069–70. [Google Scholar]

47. Ma W, Cross LE. Large flexoelectric polarization in ceramic lead magnesium niobate. Appl Phys Lett. 2001;79:4420–2. doi:10.1063/1.1426690. [Google Scholar] [CrossRef]

48. Ma W, Cross LE. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl Phys Lett. 2003;82(19):3293–5. doi:10.1063/1.1570517. [Google Scholar] [CrossRef]

49. Bobylev YP, Pikin S. Pis’ ma zh. tekh. fiz. Sov Tech Phys Lett. 1979;5:1032. [Google Scholar]

50. Sharar DJ, Radice J, Warzoha R, Hanrahan B, Smith A. Low-force elastocaloric refrigeration via bending. Appl Phys Lett. 2021;118:184103. doi:10.1063/5.0041500. [Google Scholar] [CrossRef]

51. Qi L, Zhou S, Li A. Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos Struct. 2016;135(13):167–75. doi:10.1016/j.compstruct.2015.09.020. [Google Scholar] [CrossRef]

52. Qiu Z, Zhang Z, Xiong Y, Luo X, Li Z, Zheng K, et al. Size effects of graphene sheets on the strengthening mechanism of al-graphene composites: a molecular dynamics study. Appl Surf Sci. 2022;596(5934):153546. doi:10.1016/j.apsusc.2022.153546. [Google Scholar] [CrossRef]

53. Yan Z, Jiang L. Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J Phy D Appl Phy. 2013;46(35):355502. doi:10.1088/0022-3727/46/35/355502. [Google Scholar] [CrossRef]

54. Asumadu TK, Mensah-Darkwa K, Gikunoo E, Klenam DEP, Vandadi M, Rahbar N, et al. Strain gradient plasticity phenomenon in surface treated plain carbon steel. Mat Sci Eng A. 2023;871:144806. doi:10.1016/j.msea.2023.144806. [Google Scholar] [CrossRef]

55. Schiavi A, Origlia C, Germak A, Prato A, Genta G. Indentation modulus, indentation work and creep of metals and alloys at the macro-scale level: experimental insights into the use of a primary vickers hardness standard machine. Materials. 2021;14(11):2912. doi:10.3390/ma14112912. [Google Scholar] [PubMed] [CrossRef]

56. Fleck N, Muller G, Ashby MF, Hutchinson JW. Strain gradient plasticity: theory and experiment. Acta Metallurgica Mater. 1994;42:475–87. doi:10.1016/0956-7151(94)90502-9. [Google Scholar] [CrossRef]

57. Fleck N, Hutchinson JW. Strain gradient plasticity. Adv Appl Mech. 1997;33:295–361. [Google Scholar]

58. Fleck N, Hutchinson J. A reformulation of strain gradient plasticity. J Mech Phys Solids. 2001;49:2245–71. doi:10.1016/S0022-5096(01)00049-7. [Google Scholar] [CrossRef]

59. Gao H, Huang Y, Nix WD, Hutchinson J. Mechanism-based strain gradient plasticity—i. Theory. J Mech Phys Solids. 1999;47:1239–63. doi:10.1016/S0022-5096(98)00103-3. [Google Scholar] [CrossRef]

60. Huang Y, Gao H, Nix WD, Hutchinson J. Mechanism-based strain gradient plasticity—ii. Analysis. J Mech Phys Solids. 2000;48:99–128. doi:10.1016/S0022-5096(99)00022-8. [Google Scholar] [CrossRef]

61. Jog CS. Continuum mechanics. Vol. 1. Cambridge, UK: Cambridge University Press; 2015. [Google Scholar]

62. Ma W, Cross LE. Flexoelectric polarization of barium strontium titanate in the paraelectric state. Appl Phys Lett. 2002;81(18):3440–2. doi:10.1063/1.1518559. [Google Scholar] [CrossRef]

63. Zhou S, Li A, Wang B. A reformulation of constitutive relations in the strain gradient elasticity theory for isotropic materials. Int J Solids Struct. 2016;80:28–37. doi:10.1016/j.ijsolstr.2015.10.018. [Google Scholar] [CrossRef]

64. Hadjesfandiari AR, Dargush GF. Couple stress theory for solids. Int J Solids Struct. 2011;48:2496–510. doi:10.1016/j.ijsolstr.2011.05.002. [Google Scholar] [CrossRef]

65. Yang F, Chong A, Lam DCC, Tong P. Couple stress based strain gradient theory for elasticity. Int J Solids Struct. 2002;39:2731–43. doi:10.1016/S0020-7683(02)00152-X. [Google Scholar] [CrossRef]

66. Polizzotto C, Borino G. A thermodynamics-based formulation of gradient-dependent plasticity. European J Mech-A/Solids. 1998;17:741–61. doi:10.1016/S0997-7538(98)80003-X. [Google Scholar] [CrossRef]

67. Forest S, Sievert R, Aifantis EC. Strain gradient crystal plasticity: thermomechanical formulations and applications. J Mech Behav Mater. 2002;13:219–32. doi:10.1515/JMBM.2002.13.3-4.219. [Google Scholar] [CrossRef]

68. Polizzotto C. Anisotropy in strain gradient elasticity: simplified models with different forms of internal length and moduli tensors. European J Mech-A/Solids. 2018;71(6):51–63. doi:10.1016/j.euromechsol.2018.03.006. [Google Scholar] [CrossRef]

69. d’Agostino MV, Martin RJ, Lewintan P, Bernardini D, Danescu A, Neff P. On the representation of fourth-and higher-order anisotropic elasticity tensors in generalized continuum models. Math Mech Solids. 2024;30(8):1789–849. doi:10.1177/10812865241288797. [Google Scholar] [CrossRef]

70. Sidhardh S, Ray M. Exact solution for size-dependent elastic response in laminated beams considering generalized first strain gradient elasticity. Compos Struct. 2018;204(5):31–42. doi:10.1016/j.compstruct.2018.07.030. [Google Scholar] [CrossRef]

71. Shaat M. Physical and mathematical representations of couple stress effects on micro/nanosolids. Int J Appl Mech. 2015;7(01):1550012. doi:10.1142/s1758825115400128. [Google Scholar] [CrossRef]

72. Neff P, Münch I, Ghiba I-D, Madeo A. On some fundamental misunderstandings in the indeterminate couple stress model. a comment on recent papers of ar hadjesfandiari and gf dargush. Int J Solids Struct. 2016;81(12):233–43. doi:10.1016/j.ijsolstr.2015.11.028. [Google Scholar] [CrossRef]

73. Münch I, Neff P. Rotational invariance conditions in elasticity, gradient elasticity and its connection to isotropy. Math Mech Solids. 2018;23(1):3–42. doi:10.1177/1081286516666134. [Google Scholar] [CrossRef]

74. Koiter W. Couple-stresses in the theory of elasticity, i & ii. Amsterdam, The Netherlands: Koninklijke Nederlandse Akademie van Wetenschappen; 1969. [Google Scholar]

75. Aifantis EC. Strain gradient interpretation of size effects. Fracture Scaling. 1999;95(1986):299–314. doi:10.1007/978-94-011-4659-3_16. [Google Scholar] [CrossRef]

76. Gao X-L, Park S. Variational formulation of a simplified strain gradient elasticity theory and its application to a pressurized thick-walled cylinder problem. Int J Solids Struct. 2007;44(22–23):7486–99. doi:10.1016/j.ijsolstr.2007.04.022. [Google Scholar] [CrossRef]

77. Exadaktylos G, Vardoulakis I. Surface instability in gradient elasticity with surface energy. Int J Solids Struct. 1998;35:2251–81. doi:10.1016/S0020-7683(97)89945-3. [Google Scholar] [CrossRef]

78. Toupin R, Gazis D. Surface effects and initial stress in continuum and lattice models of elastic crystals. In: Lattice dynamics. Amsterdam, The Netherlands: Elsevier; 1965. p. 597–605. [Google Scholar]

79. Cordero NM, Forest S, Busso EP. Second strain gradient elasticity of nano-objects. J Mech Phys Solids. 2016;97:92–124. doi:10.1016/j.jmps.2015.07.012. [Google Scholar] [CrossRef]

80. Shodja HM, Ahmadpoor F, Tehranchi A. Calculation of the additional constants for fcc materials in second strain gradient elasticity: behavior of a nano-size bernoulli-euler beam with surface effects. J Appl Mech Mar. 2012;79(2):021008. doi:10.1115/1.4005535. [Google Scholar] [CrossRef]

81. Ojaghnezhad F, Shodja HM. A combined first principles and analytical determination of the modulus of cohesion, surface energy, and the additional constants in the second strain gradient elasticity. Int J Solids Struct. 2013;50(24):3967–74. doi:10.1016/j.ijsolstr.2013.08.004. [Google Scholar] [CrossRef]

82. Karparvarfard S, Asghari M, Vatankhah R. A geometrically nonlinear beam model based on the second strain gradient theory. Int J Eng Sci. 2015;91:63–75. doi:10.1016/j.ijengsci.2015.01.004. [Google Scholar] [CrossRef]

83. Gurtin ME, Ian Murdoch A. A continuum theory of elastic material surfaces. Arch Ration Mech Anal. 1975;57:291–323. doi:10.1007/BF00261375. [Google Scholar] [CrossRef]

84. Wang J, Duan H, Huang Z, Karihaloo BL. A scaling law for properties of nano-structured materials. Proc Royal Soc A Mathem Phys Eng Sci. 2006;462:1355–63. doi:10.1098/rspa.2005.1637. [Google Scholar] [CrossRef]

85. Polizzotto C. A second strain gradient elasticity theory with second velocity gradient inertia-part i: constitutive equations and quasi-static behavior. Int J Solids Struct. 2013;50(24):3749–65. doi:10.1016/j.ijsolstr.2013.06.024. [Google Scholar] [CrossRef]

86. Ebrahimi F, Barati MR. Dynamic modeling of embedded nanoplate systems incorporating flexoelectricity and surface effects. Microsyst Technol. 2019;25(1):175–87. doi:10.1007/s00542-018-3946-7. [Google Scholar] [CrossRef]

87. Mahmoud F, Eltaher M, Alshorbagy A, Meletis E. Static analysis of nanobeams including surface effects by nonlocal finite element. J Mech Sci Technol. 2012;26:3555–63. doi:10.1007/s12206-012-0871-z. [Google Scholar] [CrossRef]

88. Khorshidi K, Bahrami M, Eshaghi M, Ghasemi M. A comprehensive nonlocal surface-piezoelectricity model for thermal and vibration analyses of piezoelectric nanoplates. Compos Struct. 2021;263(3):113654. doi:10.1016/j.compstruct.2021.113654. [Google Scholar] [CrossRef]

89. Lovisi G. Application of the surface stress-driven nonlocal theory of elasticity for the study of the bending response of fg cracked nanobeams. Compos Struct. 2023;324(1):117549. doi:10.1016/j.compstruct.2023.117549. [Google Scholar] [CrossRef]

90. Polizzotto C. A unifying variational framework for stress gradient and strain gradient elasticity theories. European J Mech-A/Solids. 2015;49(1):430–40. doi:10.1016/j.euromechsol.2014.08.013. [Google Scholar] [CrossRef]

91. Mühlhaus H-B, Alfantis E. A variational principle for gradient plasticity. Int J Solids Struct. 1991;28:845–57. doi:10.1016/0020-7683(91)90004-Y. [Google Scholar] [CrossRef]

92. Sidhardh S, Ray M. Exact solutions for flexoelectric response in elastic dielectric nanobeams considering generalized constitutive gradient theories. Int J Mech Mater Des. 2019;15(3):427–46. doi:10.1007/s10999-018-9409-6. [Google Scholar] [CrossRef]

93. Sidhardh S, Ray MC. Exact solutions for elastic response in micro-and nano-beams considering strain gradient elasticity. Math Mech Solids. 2019;24(4):895–918. doi:10.1177/1081286518761182. [Google Scholar] [CrossRef]

94. Aifantis K, Askes H. Gradient elasticity with interfaces as surfaces of discontinuity for the strain gradient. J Mech Behav Mater. 2007;18:283–306. doi:10.1515/JMBM.2007.18.4.283. [Google Scholar] [CrossRef]

95. Polizzotto C. Gradient elasticity and nonstandard boundary conditions. Int J Solids Struct. 2003;40(26):7399–423. doi:10.1016/j.ijsolstr.2003.06.001. [Google Scholar] [CrossRef]

96. Papargyri-Beskou S, Polyzos D, Beskos D. Wave dispersion in gradient elastic solids and structures: a unified treatment. Int J Solids Struct. 2009;46:3751–9. doi:10.1016/j.ijsolstr.2009.05.002. [Google Scholar] [CrossRef]

97. Sidhardh S, Ray M. Dispersion curves for rayleigh-lamb waves in a micro-plate considering strain gradient elasticity. Wave Motion. 2019;86(5):91–109. doi:10.1016/j.wavemoti.2019.01.002. [Google Scholar] [CrossRef]

98. Madeo A, Neff P, Aifantis EC, Barbagallo G, d’Agostino MV. On the role of micro-inertia in enriched continuum mechanics. Proce Royal Soc A Mathem Phys Eng Sci. 2017;473:20160722. doi:10.1098/rspa.2016.0722. [Google Scholar] [PubMed] [CrossRef]

99. Eremeyev VA, Lurie SA, Solyaev YO, dell’Isola F. On the well posedness of static boundary value problem within the linear dilatational strain gradient elasticity. Zeitschrift Für Angewandte Mathematik Und Physik. 2020;71(6):1–16. doi:10.1007/s00033-020-01395-5. [Google Scholar] [CrossRef]

100. Challamel N, Zhang Z, Wang CM, Reddy JN, Wang Q, Michelitsch T, et al. On nonconservativeness of eringen’s nonlocal elasticity in beam mechanics: correction from a discrete-based approach. Arch Appl Mech. 2014;84(9–11):1275–92. doi:10.1007/s00419-014-0862-x. [Google Scholar] [CrossRef]

101. Fernandez-Saez J, Zaera R, Loya J, Reddy J. Bending of euler-bernoulli beams using eringen’s integral formulation: a paradox resolved. Int J Eng Sci. 2016;99(8):107–16. doi:10.1016/j.ijengsci.2015.10.013. [Google Scholar] [CrossRef]

102. Ceballes S, Larkin K, Rojas E, Ghaffari S, Abdelkefi A. Nonlocal elasticity and boundary condition paradoxes: a review. J Nanopart Res. 2021;23:1–27. doi:10.1007/s11051-020-05107-y. [Google Scholar] [CrossRef]

103. Yang X, Tan L, Sui T, Shi D, Fan Y. Low cycle fatigue behaviour of a single crystal Ni-based superalloy with a central hole: effect of inhomogeneous rafting microstructure. Int J Fatig. 2021;153(9):106467. doi:10.1016/j.ijfatigue.2021.106467. [Google Scholar] [CrossRef]

104. Lakes R. Experimental methods for study of cosserat elastic solids and other generalized elastic continua. Contin Mod Mat Microstruct. 1995;70:1–25. [Google Scholar]

105. Harbola V, Crossley S, Hong SS, Lu D, Birkhölzer YA, Hikita Y, et al. Strain gradient elasticity in srtio3 membranes: bending versus stretching. Nano Lett. 2021;21(6):2470–5. doi:10.1021/acs.nanolett.0c04787. [Google Scholar] [PubMed] [CrossRef]

106. Maranganti R, Sharma P. A novel atomistic approach to determine strain-gradient elasticity constants: tabulation and comparison for various metals, semiconductors, silica, polymers and the (ir) relevance for nanotechnologies. J Mech Phys Solids. 2007;55(9):1823–52. doi:10.1016/j.jmps.2007.02.011. [Google Scholar] [CrossRef]

107. Maranganti R, Sharma P. Length scales at which classical elasticity breaks down for various materials. Phy Rev Lett. 2007;98(19):195504. doi:10.1103/physrevlett.98.195504. [Google Scholar] [PubMed] [CrossRef]

108. Shodja H, Zaheri A, Tehranchi A. Ab initio calculations of characteristic lengths of crystalline materials in first strain gradient elasticity. Mech Mater. 2013;61(2):73–8. doi:10.1016/j.mechmat.2013.03.006. [Google Scholar] [CrossRef]

109. Liu C, Yu J, Zhang B, Zhang C. Size parameter calibration of nonlocal strain gradient theory based on molecular dynamics simulation of guided wave propagation in aluminum plates. Thin-Walled Struct. 2024;198(4):111659. doi:10.1016/j.tws.2024.111659. [Google Scholar] [CrossRef]

110. Askes H, Aifantis EC. Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct. 2011;48(13):1962–90. doi:10.1016/j.ijsolstr.2011.03.006. [Google Scholar] [CrossRef]

111. Yvonnet J, Auffray N, Monchiet V. Computational second-order homogenization of materials with effective anisotropic strain-gradient behavior. Int J Solids Struct. 2020;191:434–48. doi:10.1016/j.ijsolstr.2020.01.006. [Google Scholar] [CrossRef]

112. Karttunen AT, Reddy J, Romanoff J. Two-scale constitutive modeling of a lattice core sandwich beam. Compos Part B Eng. 2019;160:66–75. doi:10.1016/j.compositesb.2018.09.098. [Google Scholar] [CrossRef]

113. Kouznetsova V, Geers MG, Brekelmans WM. Multi-scale constitutive modelling of heterogeneous materials with a gradient-enhanced computational homogenization scheme. Int J Numer Methods Eng. 2002;54:1235–60. doi:10.1002/nme.541. [Google Scholar] [CrossRef]

114. Kouznetsova V, Geers MG, Brekelmans W. Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Comput Methods Appl Mech Eng. 2004;193(48–51):5525–50. doi:10.1016/j.cma.2003.12.073. [Google Scholar] [CrossRef]

115. Kouznetsova VG, Geers MG, Brekelmans W. Size of a representative volume element in a second-order computational homogenization framework. Int J Multiscale Comput Eng. 2004;2(4):575–98. doi:10.1615/IntJMultCompEng.v2.i4.50. [Google Scholar] [CrossRef]

116. Gitman I, Askes H, Sluys L. Representative volume size as a macroscopic length scale parameter. In: 5th International Conference on Fracture Mechanics of Concrete and Concrete Structures; 2004. Vol. 1, p. 483–91. [Google Scholar]

117. Gitman IM, Askes H, Aifantis EC. The representative volume size in static and dynamic micro-macro transitions. Int J Fract. 2005;135:L3–9. doi:10.1007/s10704-005-4389-6. [Google Scholar] [CrossRef]

118. Gitman IM. Gradient elasticity with internal length and internal inertia based on the homogenisation of a representative volume element. J Mech Behav Mater. 2007;18(1):1–16. doi:10.1515/jmbm.2007.18.1.1. [Google Scholar] [CrossRef]

119. Peerlings R, Fleck N. Computational evaluation of strain gradient elasticity constants. Int J Multiscale Comput Eng. 2004;2(4):599–619. doi:10.1615/IntJMultCompEng.v2.i4.60. [Google Scholar] [CrossRef]

120. Nampally P, Karttunen AT. Nonlinear finite element analysis of lattice core sandwich beams. European J Mech-A/Solids. 2019;74:431–9. doi:10.1016/j.euromechsol.2018.12.006. [Google Scholar] [CrossRef]

121. Yang H, Timofeev D, Giorgio I, Müller WH. Effective strain gradient continuum model of metamaterials and size effects analysis. Continuum Mech Thermodyn. 2023;35:775–97. doi:10.1007/s00161-020-00910-3. [Google Scholar] [CrossRef]

122. Hu K, Lin K, Gu D, Yang J, Wang H, Yuan L. Mechanical properties and deformation behavior under compressive loading of selective laser melting processed bio-inspired sandwich structures. Mat Sci Eng A. 2019;762:138089. doi:10.1016/j.msea.2019.138089. [Google Scholar] [CrossRef]

123. Liu M, Cao D, Zhang X, Wei J, Zhu D. Nonlinear dynamic responses of beamlike truss based on the equivalent nonlinear beam model. Int J Mech Sci. 2021;194(5):106197. doi:10.1016/j.ijmecsci.2020.106197. [Google Scholar] [CrossRef]

124. Sarhil M, Scheunemann L, Schröder J, Neff P. Size-effects of metamaterial beams subjected to pure bending: on boundary conditions and parameter identification in the relaxed micromorphic model. Comput Mech. 2023;72(5):1091–113. doi:10.1007/s00466-023-02332-9. [Google Scholar] [CrossRef]

125. Ramprasad R, Batra R, Pilania G, Mannodi-Kanakkithodi A, Kim C. Machine learning in materials informatics: recent applications and prospects. npj Computat Mat. 2017;3:54. doi:10.1038/s41524-017-0056-5. [Google Scholar] [CrossRef]

126. Schleder GR, Padilha AC, Acosta CM, Costa M, Fazzio A. From dft to machine learning: recent approaches to materials science—a review. J Phys Mater. 2019;2:032001. doi:10.1088/2515-7639/ab084b. [Google Scholar] [CrossRef]

127. Stainier L, Leygue A, Ortiz M. Model-free data-driven methods in mechanics: material data identification and solvers. Comput Mech. 2019;64:381–93. doi:10.1007/s00466-019-01731-1. [Google Scholar] [CrossRef]

128. Karapiperis K, Ortiz M, Andrade JE. Data-driven nonlocal mechanics: discovering the internal length scales of materials. Comput Meth Appl Mech Eng. 2021;386:114039. doi:10.1016/j.cma.2021.114039. [Google Scholar] [CrossRef]

129. Lal HP, Abhiram B, Ghosh D. Prediction of nonlocal elasticity parameters using high-throughput molecular dynamics simulations and machine learning. European J Mech-A/Solids. 2024;103:105175. doi:10.1016/j.euromechsol.2023.105175. [Google Scholar] [CrossRef]

130. Ulloa J, Stainier L, Ortiz M, Andrade JE. Data-driven micromorphic mechanics for materials with strain localization. Comput Meth Appl Mech Eng. 2024;429:117180. doi:10.1016/j.cma.2024.117180. [Google Scholar] [CrossRef]

131. Fish J, Wagner GJ, Keten S. Mesoscopic and multiscale modelling in materials. Nat Mater. 2021;20:774–86. doi:10.1038/s41563-020-00913-0. [Google Scholar] [PubMed] [CrossRef]

132. Rahman A, Deshpande P, Radue MS, Odegard GM, Gowtham S, Ghosh S, et al. A machine learning framework for predicting the shear strength of carbon nanotube-polymer interfaces based on molecular dynamics simulation data. Compos Sci Technol. 2021;207(37):108627. doi:10.1016/j.compscitech.2020.108627. [Google Scholar] [CrossRef]

133. Liu J, Zhang Y, Zhang Y, Kitipornchai S, Yang J. Machine learning assisted prediction of mechanical properties of graphene/aluminium nanocomposite based on molecular dynamics simulation. Mater Design. 2022;213:110334. doi:10.1016/j.matdes.2021.110334. [Google Scholar] [CrossRef]

134. Čanadjija M. Deep learning framework for carbon nanotubes: mechanical properties and modeling strategies. Carbon. 2021;184(14):891–901. doi:10.1016/j.carbon.2021.08.091. [Google Scholar] [CrossRef]

135. Xu Y, Shi Q, Zhou Z, Xu K, Lin Y, Li Y, et al. Machine learning assisted insights into the mechanical strength of nanocrystalline graphene oxide. 2D Mater. 2022;9(3):035002. doi:10.1088/2053-1583/ac635d. [Google Scholar] [CrossRef]

136. Hosseini S, Niiranen J. 3D strain gradient elasticity: variational formulations, isogeometric analysis and model peculiarities. Comput Meth Appl Mech Eng. 2022;389(12):114324. doi:10.1016/j.cma.2021.114324. [Google Scholar] [CrossRef]

137. Eshel N, Rosenfeld G. Effects of strain-gradient on the stress-concentration at a cylindrical hole in a field of uniaxial tension. J Eng Math. 1970;4:97–111. doi:10.1007/BF01535082. [Google Scholar] [CrossRef]

138. Eshel N, Rosenfeld G. Some two-dimensional exterior problems in a linear elastic solid of grade two. ZAMM-J Appl Mathem Mech/Zeitschrift Für Angewandte Mathematik Und Mechanik. 1973;53:761–72. doi:10.1002/zamm.19730531105. [Google Scholar] [CrossRef]

139. Xie J, Linder C. Analysis of flexoelectric solids with a cylindrical cavity. J Appl Mech. 2024;91:011007. doi:10.1115/1.4063145. [Google Scholar] [CrossRef]

140. Wang S, Chen H, Qi C. Analysis on spherical cavity expansion in gradient elastic media. Mech Res Communicat. 2020;104:103486. doi:10.1016/j.mechrescom.2020.103486. [Google Scholar] [CrossRef]

141. Savin G, Lukashev A, Lysko E. Elastic wave propagation in a solid with microstructure. Sov Appl Mech. 1970;6:725–8. doi:10.1007/BF00892125. [Google Scholar] [CrossRef]

142. Gao R, Zhang G, Ioppolo T, Gao X-L. Elastic wave propagation in a periodic composite beam structure: a new model for band gaps incorporating surface energy, transverse shear and rotational inertia effects. J Micromech Mol Phy. 2018;3:1840005. doi:10.1115/imece2018-87236. [Google Scholar] [CrossRef]

143. Tran LV, Niiranen J. A geometrically nonlinear euler-bernoulli beam model within strain gradient elasticity with isogeometric analysis and lattice structure applications. Math Mech Complex Syst. 2020;8(4):345–71. doi:10.2140/memocs.2020.8.345. [Google Scholar] [CrossRef]

144. Kong S, Zhou S, Nie Z, Wang K. Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int J Eng Sci. 2009;47:487–98. doi:10.1016/j.ijengsci.2008.08.008. [Google Scholar] [CrossRef]

145. Sidhardh S, Ray M. Flexomagnetic response of nanostructures. J Appl Phys. 2018;124:244101. doi:10.1063/1.5060672. [Google Scholar] [CrossRef]

146. Movassagh AA, Mahmoodi M. A micro-scale modeling of kirchhoff plate based on modified strain-gradient elasticity theory. European J Mech-A/Solids. 2013;40(14):50–9. doi:10.1016/j.euromechsol.2012.12.008. [Google Scholar] [CrossRef]

147. Cornacchia F, Fantuzzi N, Luciano R, Penna R. Solution for cross-and angle-ply laminated kirchhoff nano plates in bending using strain gradient theory. Compos Part B Eng. 2019;173:107006. doi:10.1016/j.compositesb.2019.107006. [Google Scholar] [CrossRef]

148. Bacciocchi M, Fantuzzi N, Ferreira A. Conforming and nonconforming laminated finite element kirchhoff nanoplates in bending using strain gradient theory. Comput Struct. 2020;239:106322. doi:10.1016/j.compstruc.2020.106322. [Google Scholar] [CrossRef]

149. Roudbari MA, Jorshari TD, Lv C, Ansari R, Kouzani AZ, Amabili M. A review of size-dependent continuum mechanics models for micro-and nano-structures. Thin-Walled Struct. 2022;170(4):108562. doi:10.1016/j.tws.2021.108562. [Google Scholar] [CrossRef]

150. Zhang X, Sharma P. Inclusions and inhomogeneities in strain gradient elasticity with couple stresses and related problems. Int J Solids Struct. 2005;42(13):3833–51. doi:10.1016/j.ijsolstr.2004.12.005. [Google Scholar] [CrossRef]

151. Gao X-L, Ma H. Green’s function and eshelby’s tensor based on a simplified strain gradient elasticity theory. Acta Mech. 2009;207(3–4):163–81. doi:10.1007/s00707-008-0109-4. [Google Scholar] [CrossRef]

152. Sidhardh S, Ray M. Inclusion problem for a generalized strain gradient elastic continuum. Acta Mech. 2018;229:3813–31. doi:10.1007/s00707-018-2199-y. [Google Scholar] [CrossRef]

153. Sidhardh S, Ray M. Size-dependent eshelby’s ellipsoidal inclusion problem based on generalized first strain gradient elasticity theory. Math Mech Solids. 2019;24(7):2251–73. doi:10.1177/1081286518820901. [Google Scholar] [CrossRef]

154. Gourgiotis P, Rizzi G, Lewintan P, Bernardini D, Sky A, Madeo A, et al. Green’s functions for the isotropic planar relaxed micromorphic model—concentrated force and concentrated couple. Int J Solid Struct. 2024;292(2187):112700. doi:10.1016/j.ijsolstr.2024.112700. [Google Scholar] [CrossRef]

155. Day FD, Weitsman Y. Strain-gradient effects in microlayers. J Eng Mech Divi. 1966;92:67–86. doi:10.1061/JMCEA3.0000788. [Google Scholar] [CrossRef]

156. Beran M, McCoy J. The use of strain gradient theory for analysis of random media. Int J Solids Struct. 1970;6:1267–75. doi:10.1016/0020-7683(70)90102-2. [Google Scholar] [CrossRef]

157. Rogula D. Some basic solutions in strain gradient elasticity theory of an arbitrary order. Archiwum Mechaniki Stosowanej. 1973;25:43–68. [Google Scholar]

158. Zhou W, Chen W, Muhammad, Lim CW. Surface effect on the propagation of flexural waves in periodic nano-beam and the size-dependent topological properties. Compos Struct. 2019;216(5485):427–35. doi:10.1016/j.compstruct.2019.03.016. [Google Scholar] [CrossRef]

159. Qian D. Wave propagation in a thermo-magneto-mechanical phononic crystal nanobeam with surface effects. J Mater Sci. 2019;54(6):4766–79. doi:10.1007/s10853-018-03208-7. [Google Scholar] [CrossRef]

160. Rizzi G, Hütter G, Madeo A, Neff P. Analytical solutions of the simple shear problem for micromorphic models and other generalized continua. Arch Appl Mech. 2021;91(5):2237–54. doi:10.1007/s00419-021-01881-w. [Google Scholar] [CrossRef]

161. Hütter G. Application of a microstrain continuum to size effects in bending and torsion of foams. Int J Eng Sci. 2016;101(4):81–91. doi:10.1016/j.ijengsci.2015.12.006. [Google Scholar] [CrossRef]

162. Rizzi G, Hütter G, Madeo A, Neff P. Analytical solutions of the cylindrical bending problem for the relaxed micromorphic continuum and other generalized continua. Continuum Mech Thermodyn. 2021;33(4):1505–39. doi:10.1007/s00161-021-00984-7. [Google Scholar] [CrossRef]

163. Karlis G, Charalambopoulos A, Polyzos D. An advanced boundary element method for solving 2D and 3D static problems in mindlin’s strain-gradient theory of elasticity. Int J Numer Methods Eng. 2010;83(11):1407–27. doi:10.1002/nme.2862. [Google Scholar] [CrossRef]

164. Kiusalaas J, Jaunzemis W, Conway J. A strain-gradient theory for prestrained laminates. Int J Solids Struct. 1973;9:1317–30. doi:10.1016/0020-7683(73)90041-3. [Google Scholar] [CrossRef]

165. Felippa C. Refined finite element analysis of linear and nonlinear two-dimensional structures. Berkeley, CA, USA: University of California; 1966. [Google Scholar]

166. Chen S-X, Sahmani S, Safaei B. Size-dependent nonlinear bending behavior of porous FGM quasi-3D microplates with a central cutout based on nonlocal strain gradient isogeometric finite element modelling. Eng Comput. 2021;37(2):1657–78. doi:10.1007/s00366-021-01303-z. [Google Scholar] [CrossRef]

167. Yang B, Droz C, Zine A, Ichchou M. Dynamic analysis of second strain gradient elasticity through a wave finite element approach. Compos Struct. 2021;263:113425. doi:10.1016/j.compstruct.2020.113425. [Google Scholar] [CrossRef]

168. Shu JY, King WE, Fleck NA. Finite elements for materials with strain gradient effects. Int J Numer Methods Eng. 1999;44:373–91. doi:10.1002/(SICI)1097-0207(19990130)44:3<373::AID-NME508>3.0.CO;2-7. [Google Scholar] [CrossRef]

169. Amanatidou E, Aravas N. Mixed finite element formulations of strain-gradient elasticity problems. Comput Methods Appl Mech Eng. 2002;191:1723–51. doi:10.1016/S0045-7825(01)00353-X. [Google Scholar] [CrossRef]

170. Han C-S, Ma A, Roters F, Raabe D. A finite element approach with patch projection for strain gradient plasticity formulations. Int J Plast. 2007;23:690–710. doi:10.1016/j.ijplas.2006.08.003. [Google Scholar] [CrossRef]

171. Askes H, Morata I, Aifantis EC. Finite element analysis with staggered gradient elasticity. Comput Struct. 2008;86:1266–79. doi:10.1016/j.compstruc.2007.11.002. [Google Scholar] [CrossRef]

172. Reiher JC, Giorgio I, Bertram A. Finite-element analysis of polyhedra under point and line forces in second-strain gradient elasticity. J Eng Mech. 2017;143(2):04016112. doi:10.1061/(asce)em.1943-7889.0001184. [Google Scholar] [CrossRef]

173. Sarar BC, Yildizdag ME, Fabbrocino F, Abali BE. A comparative analysis for different finite element types in strain-gradient elasticity simulations performed on firedrake and fenics. arXiv:2411.12043. 2024. [Google Scholar]

174. Shekarchizadeh N, Abali BE, Bersani AM. A benchmark strain gradient elasticity solution in two-dimensions for verifying computational approaches by means of the finite element method. Math Mech Solids. 2022;27(10):2218–38. doi:10.1177/10812865221114336. [Google Scholar] [CrossRef]

175. Pinnola FP, Vaccaro MS, Barretta R, de Sciarra FM. Finite element method for stress-driven nonlocal beams. Eng Anal Bound Elem. 2022;134:22–34. doi:10.1016/j.enganabound.2021.09.009. [Google Scholar] [CrossRef]

176. Bian P-L, Qing H, Yu T. A new finite element method framework for axially functionally-graded nanobeam with stress-driven two-phase nonlocal integral model. Compos Struct. 2022;295(17):115769. doi:10.1016/j.compstruct.2022.115769. [Google Scholar] [CrossRef]

177. Iranmanesh F, Nazari MA. Finite element modeling of avascular tumor growth using a stress-driven model. J Biomech Eng. 2017;139:081009. doi:10.1115/1.4037038. [Google Scholar] [PubMed] [CrossRef]

178. Kahrobaiyan M, Asghari M, Ahmadian M. Strain gradient beam element. Finite Elem Anal Des. 2013;68:63–75. doi:10.1016/j.finel.2012.12.006. [Google Scholar] [CrossRef]

179. De Borst R, Mühlhaus H-B. Gradient-dependent plasticity: formulation and algorithmic aspects. Int J Numer Methods Eng. 1992;35:521–39. doi:10.1002/nme.1620350307. [Google Scholar] [CrossRef]

180. Niordson CF, Hutchinson JW. On lower order strain gradient plasticity theories. European J Mech-A/Solids. 2003;22:771–8. doi:10.1016/S0997-7538(03)00069-X. [Google Scholar] [CrossRef]

181. Wei Y. A new finite element method for strain gradient theories and applications to fracture analyses. European J Mech-A/Solids. 2006;25(6):897–913. doi:10.1016/j.euromechsol.2006.03.001. [Google Scholar] [CrossRef]

182. Martínez-Pañeda E, Natarajan S, Bordas S. Gradient plasticity crack tip characterization by means of the extended finite element method. Comput Mech. 2017;59(5):831–42. doi:10.1007/s00466-017-1375-6. [Google Scholar] [CrossRef]

183. Xia ZC, Hutchinson JW. Crack tip fields in strain gradient plasticity. J Mech Phys Solids. 1996;44:1621–48. doi:10.1016/0022-5096(96)00035-X. [Google Scholar] [CrossRef]

184. Abdollahi A, Peco C, Millan D, Arroyo M, Arias I. Computational evaluation of the flexoelectric effect in dielectric solids. J Appl Phys. 2014;116:093502. doi:10.1063/1.4893974. [Google Scholar] [CrossRef]

185. Abdollahi A, Arias I. Constructive and destructive interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. J Appl Mech. 2015;82(12):121003. doi:10.1115/1.4031333. [Google Scholar] [CrossRef]

186. Abdollahi A, Millán D, Peco C, Arroyo M, Arias I. Revisiting pyramid compression to quantify flexoelectricity: a three-dimensional simulation study. Phys Rev B. 2015;91:104103. doi:10.1103/PhysRevB.91.104103. [Google Scholar] [CrossRef]

187. Yvonnet J, Liu L. A numerical framework for modeling flexoelectricity and maxwell stress in soft dielectrics at finite strains. Comput Methods Appl Mech Eng. 2017;313:450–82. doi:10.1016/j.cma.2016.09.007. [Google Scholar] [CrossRef]

188. Deng F, Deng Q, Yu W, Shen S. Mixed finite elements for flexoelectric solids. J Appl Mech. 2017;84:081004. doi:10.1115/1.4036939. [Google Scholar] [CrossRef]

189. Du H, Wu J, Wang D, Chen J. A unified reproducing kernel gradient smoothing galerkin meshfree approach to strain gradient elasticity. Comput Mech. 2022;70:73–100. doi:10.1007/s00466-022-02156-z. [Google Scholar] [CrossRef]

190. Askes H, Pamin J, de Borst R. Dispersion analysis and element-free galerkin solutions of second-and fourth-order gradient-enhanced damage models. Int J Numer Methods Eng. 2000;49:811–32. doi:10.1002/1097-0207(20001030)49:6<811::aid-nme985>3.3.co;2-0. [Google Scholar] [CrossRef]

191. Pamin J, Askes H, de Borst R. Two gradient plasticity theories discretized with the element-free galerkin method. Comput Methods Appl Mech Eng. 2003;192:2377–403. doi:10.1016/S0045-7825(03)00263-9. [Google Scholar] [CrossRef]

192. Pan X, Yuan H. Nonlocal damage modelling using the element-free galerkin method in the frame of finite strains. Comput Mater Sci. 2009;46:660–6. doi:10.1016/j.commatsci.2009.03.044. [Google Scholar] [CrossRef]

193. Sidhardh S, Ray M. Element-free galerkin model of nano-beams considering strain gradient elasticity. Acta Mech. 2018;229(7):2765–86. doi:10.1007/s00707-018-2139-x. [Google Scholar] [CrossRef]

194. Das A, Chaudhuri P. A note on boundary elements for micropolar elasticity. Int J Eng Sci. 1992;30:397–400. doi:10.1016/0020-7225(92)90085-U. [Google Scholar] [CrossRef]

195. Huang F-Y, Lian K-Z. Boundary element analysis of stress concentration in micropolar elastic plate. Int J Numer Methods Eng. 1997;40:1611–22. doi:10.1002/(SICI)1097-0207(19970515)40:9<1611::AID-NME130>3.3.CO;2-W. [Google Scholar] [CrossRef]

196. Ke L-L, Wang Y-S. Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos Struct. 2011;93(2):342–50. doi:10.1016/j.compstruct.2010.09.008. [Google Scholar] [CrossRef]

197. Civan F, Sliepcevich C. Differential quadrature for multi-dimensional problems. J Math Anal Appl. 1984;101:423–43. doi:10.1016/0022-247X(84)90111-2. [Google Scholar] [CrossRef]

198. Torabi J, Niiranen J, Ansari R. Multi-patch variational differential quadrature method for shear-deformable strain gradient plates. Int J Numer Methods Eng. 2022;123(10):2309–37. doi:10.1002/nme.6939. [Google Scholar] [CrossRef]

199. Zhang B, Li H, Kong L, Wang J, Shen H. Strain gradient differential quadrature beam finite elements. Comput Struct. 2019;218:170–89. doi:10.1016/j.compstruc.2019.01.008. [Google Scholar] [CrossRef]

200. Singh SS, Nair DK, Rajagopal A, Pal P, Pandey AK. Dynamic analysis of microbeams based on modified strain gradient theory using differential quadrature method. European J Computat Mech. 2018;27:187–203. doi:10.1080/17797179.2018.1485338. [Google Scholar] [CrossRef]

201. Mühlhaus H, Oka F. Dispersion and wave propagation in discrete and continuous models for granular materials. Int J Solids Struct. 1996;33:2841–58. doi:10.1016/0020-7683(95)00178-6. [Google Scholar] [CrossRef]

202. Ishaquddin M, Gopalakrishnan S. Static, stability and dynamic analyses of second strain gradient elastic euler-bernoulli beams. Acta Mech. 2021;232(4):1425–44. doi:10.1007/s00707-020-02902-5. [Google Scholar] [CrossRef]

203. Yin S, Xiao Z, Zhang G, Bui TQ, Wang X, Liu J. Size-dependent postbuckling for microbeams: analytical solutions using a reformulated strain gradient elasticity theory. Acta Mech. 2022;233(12):5045–60. doi:10.1007/s00707-022-03360-x. [Google Scholar] [CrossRef]

204. Wang B, Zhao J, Zhou S. A micro scale timoshenko beam model based on strain gradient elasticity theory. Eur J Mech-A/Solids. 2010;29:591–9. doi:10.1016/j.euromechsol.2009.12.005. [Google Scholar] [CrossRef]

205. Banerjee JR, Papkov SO, Vo TP, Elishakoff I. Dynamic stiffness formulation for a micro beam using timoshenko-ehrenfest and modified couple stress theories with applications. J Vib Control. 2023;29(1–2):428–39. doi:10.1177/10775463211048272. [Google Scholar] [CrossRef]

206. Li C, Qing H. Theoretical thermal damping vibration analysis of functionally graded viscoelastic timoshenko microbeam with integral nonlocal strain gradient model. Mech Based Des Struct Mach. 2024;52(7):4337–60. doi:10.1080/15397734.2023.2227702. [Google Scholar] [CrossRef]

207. Chen J, Huang Y, Ortiz M. Fracture analysis of cellular materials: a strain gradient model. J Mech Phys Solids. 1998;46:789–828. doi:10.1016/S0022-5096(98)00006-4. [Google Scholar] [CrossRef]

208. Polizzotto C. A micromorphic approach to stress gradient elasticity theory with an assessment of the boundary conditions and size effects. Z Angew Math Mech. 2018;98(9):1528–53. doi:10.1002/zamm.201700364. [Google Scholar] [CrossRef]

209. Yang J, Lakes R. Transient study of couple stress effects in compact bone: torsion. J Biomech Eng. 1981;103(4):275–9. doi:10.1115/1.3138292. [Google Scholar] [PubMed] [CrossRef]

210. Eringen AC. Mechanics of micropolar continua. In: Contributions to mechanics. Amsterdam, The Netherlands: Elsevier; 1969. p. 23–40. [Google Scholar]

211. Liebold C, Müller WH. Comparison of gradient elasticity models for the bending of micromaterials. Comput Mater Sci. 2016;116:52–61. doi:10.1016/j.commatsci.2015.10.031. [Google Scholar] [CrossRef]

212. Fu G, Zhou S, Qi L. On the strain gradient elasticity theory for isotropic materials. Int J Eng Sci. 2020;154:103348. doi:10.1016/j.ijengsci.2020.103348. [Google Scholar] [CrossRef]

213. Choi JH, Kim H, Kim J, Hyeok K, Chai B, Sim GD. Micro-cantilever bending tests for understanding size effect in gradient elasticity. Mat Des. 2022;214:110398. doi:10.1016/j.matdes.2022.110398. [Google Scholar] [CrossRef]

214. Wang L, Hu H. Flexural wave propagation in single-walled carbon nanotubes. Phys Rev B. 2005;71:195412. doi:10.1103/PhysRevB.71.195412. [Google Scholar] [CrossRef]

215. Narendar S, Gopalakrishnan S. Nonlocal scale effects on wave propagation in multi-walled carbon nanotubes. Comput Mater Sci. 2009;47:526–38. doi:10.1016/j.commatsci.2009.09.021. [Google Scholar] [CrossRef]

216. Mitra M, Gopalakrishnan S. Wave propagation in multi-walled carbon nanotube. Comput Mater Sci. 2009;45:411–8. doi:10.1016/j.commatsci.2008.10.022. [Google Scholar] [CrossRef]

217. Wang X, Liu J, Hu B, Zhang B, Shen H. Wave propagation responses of porous bi-directional functionally graded magneto-electro-elastic nanoshells via nonlocal strain gradient theory. Appl Math Mech. 2023;44(10):1821–40. doi:10.1007/s10483-023-3043-7. [Google Scholar] [CrossRef]

218. Xuan Tung D. A nonlocal strain gradient theory for wave propagation analysis in transversely isotropic elastic medium. J Micromech Mol Phys. 2023;8(4):163–70. doi:10.1142/s2424913023500029. [Google Scholar] [CrossRef]

219. Georgiadis H, Vardoulakis I, Velgaki E. Dispersive rayleigh-wave propagation in microstructured solids characterized by dipolar gradient elasticity. J Elast. 2004;74(1):17–45. doi:10.1023/b:elas.0000026094.95688.c5. [Google Scholar] [CrossRef]

220. Gazis DC, Herman R, Wallis RF. Surface elastic waves in cubic crystals. Phys Rev. 1960;119:533. doi:10.1103/PhysRev.119.533. [Google Scholar] [CrossRef]

221. Vardoulakis I, Georgiadis H. Sh surface waves in a homogeneous gradient-elastic half-space with surface energy. J Elast. 1997;47(2):147–65. doi:10.1023/a:1007433510623. [Google Scholar] [CrossRef]

222. Georgiadis H, Velgaki E. High-frequency rayleigh waves in materials with micro-structure and couple-stress effects. Int J Solids Struct. 2003;40:2501–20. doi:10.1016/S0020-7683(03)00054-4. [Google Scholar] [CrossRef]

223. Askes H, Metrikine AV, Pichugin AV, Bennett T. Four simplified gradient elasticity models for the simulation of dispersive wave propagation. Philos Mag. 2008;88:3415–43. doi:10.1080/14786430802524108. [Google Scholar] [CrossRef]

224. Vavva MG, Protopappas VC, Gergidis LN, Charalambopoulos A, Fotiadis DI, Polyzos D. Velocity dispersion of guided waves propagating in a free gradient elastic plate: application to cortical bone. J Acoust Soc Am. 2009;125(5):3414–27. doi:10.1121/1.3110203. [Google Scholar] [PubMed] [CrossRef]

225. Boutin C. Microstructural effects in elastic composites. Int J Solids Struct. 1996;33(7):1023–51. doi:10.1016/0020-7683(95)00089-5. [Google Scholar] [CrossRef]

226. Mura T. Micromechanics of defects in solids. Berlin/Heidelberg, Germany: Springer Science & Business Media; 2013. [Google Scholar]

227. Weng G. Some elastic properties of reinforced solids, with special reference to isotropic ones containing spherical inclusions. Int J Eng Sci. 1984;22(7):845–56. doi:10.1016/0020-7225(84)90033-8. [Google Scholar] [CrossRef]

228. Vollenberg P, Heikens D. Particle size dependence of the young’s modulus of filled polymers: 1. Preliminary experiments. Polymer. 1989;30:1656–62. doi:10.1016/0032-3861(89)90326-1. [Google Scholar] [CrossRef]

229. Kouzeli M, Mortensen A. Size dependent strengthening in particle reinforced aluminium. Acta Mater. 2002;50:39–51. doi:10.1016/S1359-6454(01)00327-5. [Google Scholar] [CrossRef]

230. Cho J, Joshi M, Sun C. Effect of inclusion size on mechanical properties of polymeric composites with micro and nano particles. Compos Sci Technol. 2006;66:1941–52. doi:10.1016/j.compscitech.2005.12.028. [Google Scholar] [CrossRef]

231. Lurie S, Volkov-Bogorodskii D, Tuchkova N. Exact solution of eshelby-christensen problem in gradient elasticity for composites with spherical inclusions. Acta Mech. 2016;227(1):127–38. doi:10.1007/s00707-015-1422-3. [Google Scholar] [CrossRef]

232. Bonfoh N, Sabar H. Exact solution of eshelby’s inhomogeneity problem in strain gradient theory of elasticity and its applications in composite materials. Appl Math Model. 2023;117(2004):1–26. doi:10.1016/j.apm.2022.11.040. [Google Scholar] [CrossRef]

233. Ameen MM, Peerlings RH, Geers MG. A quantitative assessment of the scale separation limits of classical and higher-order asymptotic homogenization. European J Mech-A/Solids. 2018;71:89–100. doi:10.1016/j.euromechsol.2018.02.011. [Google Scholar] [CrossRef]

234. Noor AK, Nemeth MP. Micropolar beam models for lattice grids with rigid joints. Comput Methods Appl Mech Eng. 1980;21:249–63. doi:10.1016/0045-7825(80)90034-1. [Google Scholar] [CrossRef]

235. Karttunen AT, Reddy J, Romanoff J. Micropolar modeling approach for periodic sandwich beams. Compos Struct. 2018;185:656–64. doi:10.1016/j.compstruct.2017.11.064. [Google Scholar] [CrossRef]

236. Tambe NS, Bhushan B. Scale dependence of micro/nano-friction and adhesion of mems/nems materials, coatingsand lubricants. Nanotechnology. 2004;15(11):1561. doi:10.1088/0957-4484/15/11/033. [Google Scholar] [CrossRef]

237. Williams J. Friction and wear of rotating pivots in mems and other small scale devices. Wear. 2001;251(1–12):965–72. doi:10.1016/s0043-1648(01)00720-7. [Google Scholar] [CrossRef]

238. Bhushan B. Tribology on the macroscale to nanoscale of microelectromechanical system materials: a review. Proc Institut Mech Eng Part J J Eng Tribol. 2001;215(1):1–18. doi:10.1243/1350650011541657. [Google Scholar] [CrossRef]

239. Abdi J, Koochi A, Kazemi A, Abadyan M. Modeling the effects of size dependence and dispersion forces on the pull-in instability ofelectrostatic cantilever nems using modified couple stress theory. Smart Mat Struct. 2011;20:055011. doi:10.1088/0964-1726/20/5/055011. [Google Scholar] [CrossRef]

240. Xue Z, Saif MTA, Huang Y. The strain gradient effect in microelectromechanical systems (mems). J Microelectromech Syst. 2002;11:27–35. doi:10.1109/84.982860. [Google Scholar] [CrossRef]

241. Sedighi HM. Size-dependent dynamic pull-in instability of vibrating electrically actuated microbeams based on the strain gradient elasticity theory. Acta Astronaut. 2014;95(2):111–23. doi:10.1016/j.actaastro.2013.10.020. [Google Scholar] [CrossRef]

242. Kahrobaiyan M, Asghari M, Ahmadian M. A strain gradient timoshenko beam element: application to mems. Acta Mech. 2015;226:505–25. doi:10.1007/s00707-014-1188-z. [Google Scholar] [CrossRef]

243. Soroush R, Koochi A, Kazemi AS, Abadyan M. Modeling the effect of van der waals attraction on the instability of electrostatic cantilever and doubly-supported nano-beams using modified adomian method. Int J Struct Stabi Dynam. 2012;12(5):1250036. doi:10.1142/s0219455412500368. [Google Scholar] [CrossRef]

244. Iijima S. Helical microtubules of graphitic carbon. Nature. 1991;354(6348):56–8. doi:10.1038/354056a0. [Google Scholar] [CrossRef]

245. Wong EW, Sheehan PE, Lieber CM. Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes. science. 1997;277:1971–5. doi:10.1126/science.277.5334.1971. [Google Scholar] [CrossRef]

246. Rafiee R, Moghadam RM. On the modeling of carbon nanotubes: a critical review. Compos Part B Eng. 2014;56:435–49. doi:10.1016/j.compositesb.2013.08.037. [Google Scholar] [CrossRef]

247. Pal G, Kumar S. Modeling of carbon nanotubes and carbon nanotube-polymer composites. Prog Aerosp Sci. 2016;80:33–58. doi:10.1016/j.paerosci.2015.12.001. [Google Scholar] [CrossRef]

248. Yan Y, Li J-X, Ma X-F, Wang W-Q. Application and dynamical behavior of cnts as fluidic nanosensors based on the nonlocal strain gradient theory. Sens Actuat A Phys. 2021;330(9):112836. doi:10.1016/j.sna.2021.112836. [Google Scholar] [CrossRef]

249. Antar K, Derbal R, Amara K. A study of thermal effects and strain gradient elasticity in wave propagation through matrix-embedded wall carbon nanotubes. J Vibrat Eng Technol. 2024;12(7):8285–93. doi:10.1007/s42417-024-01359-3. [Google Scholar] [CrossRef]

250. Liew KM, Wang Q. Analysis of wave propagation in carbon nanotubes via elastic shell theories. Int J Eng Sci. 2007;45:227–41. doi:10.1016/j.ijengsci.2007.04.001. [Google Scholar] [CrossRef]

251. Shen H-S, Zhang C-L. Postbuckling prediction of axially loaded double-walled carbon nanotubes with temperature dependent properties and initial defects. Phys Rev B. 2006;74(3):035410. doi:10.1103/physrevb.74.035410. [Google Scholar] [CrossRef]

252. Shen H-S, Zhang C-L. Postbuckling of double-walled carbon nanotubes with temperature dependent properties and initial defects under combined axial and radial mechanical loads. Int J Solids Struct. 2007;44(5):1461–87. doi:10.1016/j.ijsolstr.2006.06.027. [Google Scholar] [CrossRef]

253. Shen H-S, Zhang C-L. Torsional buckling and postbuckling of double-walled carbon nanotubes by nonlocal shear deformable shell model. Compos Struct. 2010;92(5):1073–84. doi:10.1016/j.compstruct.2009.10.002. [Google Scholar] [CrossRef]

254. Shen H-S, Zhang C-L. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Mat Design. 2010;31(7):3403–11. doi:10.1016/j.matdes.2010.01.048. [Google Scholar] [CrossRef]

255. Sun Y, Liew K. The buckling of single-walled carbon nanotubes upon bending: the higher order gradient continuum and mesh-free method. Comput Methods Appl Mech Eng. 2008;197(33–40):3001–13. doi:10.1016/j.cma.2008.02.003. [Google Scholar] [CrossRef]

256. Cao G. Atomistic studies of mechanical properties of graphene. Polymers. 2014;6(9):2404–32. doi:10.3390/polym6092404. [Google Scholar] [CrossRef]

257. Zhu F, Leng J, Guo Z, Chang T. Size-dependent mechanical properties of twin graphene. Proc Inst Mech Eng Part N J Nanomat Nanoeng Nanosyst. 2021;235:4–11. doi:10.1177/2397791420972553. [Google Scholar] [CrossRef]

258. Nie F, Jian W, Lau D. An atomistic study on the thermomechanical properties of graphene and functionalized graphene sheets modified asphalt. Carbon. 2021;182(12–13):615–27. doi:10.1016/j.carbon.2021.06.055. [Google Scholar] [CrossRef]

259. Scarpa F, Adhikari S, Phani AS. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology. 2009;20:065709. doi:10.1088/0957-4484/20/6/065709. [Google Scholar] [PubMed] [CrossRef]

260. Korobeynikov S, Alyokhin V, Annin B, Babichev A. Quasi-static buckling simulation of single-layer graphene sheets by the molecular mechanics method. Math Mech Solids. 2015;20(7):836–70. doi:10.1177/1081286514554353. [Google Scholar] [CrossRef]

261. Ebrahimi F, Barati MR. Vibration analysis of nonlocal strain gradient embedded single-layer graphene sheets under nonuniform in-plane loads. J Vib Control. 2018;24(20):4751–63. doi:10.1177/1077546317734083. [Google Scholar] [CrossRef]

262. Sha’bani F, Rash-Ahmadi S. A novel upgraded molecular mechanics framework with considering the length scale parameter and its advantages in analyzing the behavior of nanostructures. Proc Inst Mech Eng Part C J Mech Eng Sci. 2024;238(4):984–98. doi:10.1177/09544062231179058. [Google Scholar] [CrossRef]

263. Lu L, Guo X, Zhao J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl Math Model. 2019;68:583–602. doi:10.1016/j.apm.2018.11.023. [Google Scholar] [CrossRef]

264. Kundalwal S, Meguid S, Weng G. Strain gradient polarization in graphene. Carbon. 2017;117:462–72. doi:10.1016/j.carbon.2017.03.013. [Google Scholar] [CrossRef]

265. Codony D. Mathematical and computational modeling of flexoelectricity at mesoscopic and atomistic scales [Ph.D. thesis]. Barcelona, Spain: Universitat Politècnica de Catalunya; 2021. [Google Scholar]

266. Hu S, Shen S. Electric field gradient theory with surface effect for nano-dielectrics. Comput Mater Contin. 2009;13(1):63–88. doi:10.3970/cmc.2009.013.063. [Google Scholar] [CrossRef]

267. Mashkevich V. Electrical, optical, and elastic properties of diamond-type crystals ii. Lattice vibrations with calculation of atomic dipole moments. Sov Phys JETP. 1957;5:707–13. [Google Scholar]

268. Harris P. Mechanism for the shock polarization of dielectrics. J Appl Phys. 1965;36(3):739–41. doi:10.1063/1.1714210. [Google Scholar] [CrossRef]

269. Zabalo A, Stengel M. Switching a polar metal via strain gradients. Phy Rev Lett. 2021;126:127601. doi:10.1103/PhysRevLett.126.127601. [Google Scholar] [PubMed] [CrossRef]

270. Nicolenco A, de h Óra M, Yun C, MacManus-Driscoll J, Sort J. Strain-gradient effects in nanoscale-engineered magnetoelectric materials. APL Mater. 2021;9:020903. doi:10.1063/5.0037421. [Google Scholar] [CrossRef]

271. Liang X, Hu S, Shen S. Nanoscale mechanical energy harvesting using piezoelectricity and flexoelectricity. Smart Mat Struct. 2017;26:035050. doi:10.1088/1361-665X/26/3/035050. [Google Scholar] [CrossRef]

272. Indenbom V, Loginov E, Osipov M. Flexoelectric effect and crystal-structure. Kristallografiya. 1981;26:1157–62. [Google Scholar]

273. Cross LE. Flexoelectric effects: charge separation in insulating solids subjected to elastic strain gradients. J Mater Sci. 2006;41(6):53–63. doi:10.1007/978-0-387-38039-1_5. [Google Scholar] [CrossRef]

274. Vasquez-Sancho F, Abdollahi A, Damjanovic D, Catalan G. Flexoelectricity in bones. Adv Mater. 2018;30:1705316. doi:10.1002/adma.201801413. [Google Scholar] [PubMed] [CrossRef]

275. Mohammadkhah M, Slavkovic V, Klinge S. Flexoelectricity in biological materials and its potential applications in biomedical research. Bioengineering. 2025;12(6):579. doi:10.3390/bioengineering12060579. [Google Scholar] [PubMed] [CrossRef]

276. Venkateshwarlu A, Akshayveer, Singh S, Melnik R. Piezoelectricity and flexoelectricity in biological cells: the role of cell structure and organelles. Biomech Model Mechanobiol. 2025;24:47–76. doi:10.1007/s10237-024-01895-7. [Google Scholar] [PubMed] [CrossRef]

277. Baskaran S, He X, Chen Q, Fu JY. Experimental studies on the direct flexoelectric effect in α-phase polyvinylidene fluoride films. Appl Phys Lett. 2011;98:242901. doi:10.1063/1.3599520. [Google Scholar] [CrossRef]

278. Hafner TA, Örnek M, Costello C, Nunes CT, Son SF. The flexoelectric properties of various polymers and energetic composites. Appl Phys Lett. 2024;124:092903. doi:10.1063/5.0187151. [Google Scholar] [CrossRef]

279. Trellu H, Le Scornec J, Leray N, Moreau C, Villares A, Cathala B, et al. Flexoelectric and piezoelectric effects in micro-and nanocellulose films. Carbohyd Polym. 2023;321(9):121305. doi:10.1016/j.carbpol.2023.121305. [Google Scholar] [PubMed] [CrossRef]

280. Lu J, Lv J, Liang X, Xu M, Shen S. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J Appl Phys. 2016;119:094104. doi:10.1063/1.4943069. [Google Scholar] [CrossRef]

281. Wang B, Gu Y, Zhang S, Chen L-Q. Flexoelectricity in solids: progress, challenges, and perspectives. Progress Mat Sci. 2019;106:100570. doi:10.1016/j.pmatsci.2019.05.003. [Google Scholar] [CrossRef]

282. Sharma ND, Maranganti R, Sharma P. On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J Mech Phys Solids. 2007;55:2328–50. doi:10.1016/j.jmps.2007.03.016. [Google Scholar] [CrossRef]

283. Sharma N, Landis C, Sharma P. Piezoelectric thin-film superlattices without using piezoelectric materials. J Appl Phys. 2010;108:024304. doi:10.1063/1.3443404. [Google Scholar] [CrossRef]

284. Yudin PV, Tagantsev AK. Fundamentals of flexoelectricity in solids. Nanotechnology. 2013;24:432001. doi:10.1088/0957-4484/24/43/432001. [Google Scholar] [PubMed] [CrossRef]

285. Hu S, Shen S. Variational principles and governing equations in nano-dielectrics with the flexoelectric effect. Sci China Phy Mech Astr. 2010;53:1497–504. doi:10.1007/s11433-010-4039-5. [Google Scholar] [CrossRef]

286. Majdoub M, Sharma P, Cagin T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phy Rev B. 2008;77(12):125424. doi:10.1103/physrevb.77.125424. [Google Scholar] [CrossRef]

287. Majdoub M, Sharma P, Çağin T. Dramatic enhancement in energy harvesting for a narrow range of dimensions in piezoelectric nanostructures. Phy Rev B. 2008;78(12):121407. doi:10.1103/physrevb.78.121407. [Google Scholar] [CrossRef]

288. Zhang R, Liang X, Shen S. A timoshenko dielectric beam model with flexoelectric effect. Meccanica. 2016;51:1181–8. doi:10.1007/s11012-015-0290-1. [Google Scholar] [CrossRef]

289. Yan Z, Jiang L. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J Appl Phys. 2013;113(19):194102. doi:10.1063/1.4804949. [Google Scholar] [CrossRef]

290. Liang X, Hu S, Shen S. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mat Struct. 2014;23:035020. doi:10.1088/0964-1726/23/3/035020. [Google Scholar] [CrossRef]

291. Deng Q, Kammoun M, Erturk A, Sharma P. Nanoscale flexoelectric energy harvesting. Int J Solids Struct. 2014;51:3218–25. doi:10.1016/j.ijsolstr.2014.05.018. [Google Scholar] [CrossRef]

292. Wang K, Wang B. Electrostatic potential in a bent piezoelectric nanowire with consideration of size-dependent piezoelectricity and semiconducting characterization. Nanotechnology. 2018;29(25):255405. doi:10.1088/1361-6528/aab970. [Google Scholar] [PubMed] [CrossRef]

293. Apte A, Mozaffari K, Samghabadi FS, Hachtel JA, Chang L, Susarla S, et al. 2D electrets of ultrathin moo2 with apparent piezoelectricity. Adv Mater Weinheim. 2020;32(24):2000006. doi:10.1002/adma.202000006. [Google Scholar] [PubMed] [CrossRef]

294. Tripathy A, Saravanakumar B, Mohanty S, Nayak SK, Ramadoss A. Comprehensive review on flexoelectric energy harvesting technology: mechanisms, device configurations, and potential applications. ACS Appl Electr Mat. 2021;3:2898–924. doi:10.1021/acsaelm.1c00267. [Google Scholar] [CrossRef]

295. Grasinger M, Mozaffari K, Sharma P. Flexoelectricity in soft elastomers and the molecular mechanisms underpinning the design and emergence of giant flexoelectricity. Proc Nat Acad Sci. 2021;118:e2102477118. doi:10.1073/pnas.2102477118. [Google Scholar] [PubMed] [CrossRef]

296. Deng Q, Liu L, Sharma P. Flexoelectricity in soft materials and biological membranes. J Mech Phys Solids. 2014;62:209–27. doi:10.1016/j.jmps.2013.09.021. [Google Scholar] [CrossRef]

297. Ahmadpoor F, Deng Q, Liu L, Sharma P. Apparent flexoelectricity in lipid bilayer membranes due to external charge and dipolar distributions. Phys Rev E. 2013;88(5):050701. doi:10.1103/physreve.88.050701. [Google Scholar] [PubMed] [CrossRef]

298. Mohammadi P, Liu L, Sharma P. A theory of flexoelectric membranes and effective properties of heterogeneous membranes. J Appl Mech. 2014;81:011007. doi:10.1115/1.4023978. [Google Scholar] [CrossRef]

299. Deng Q, Ahmadpoor F, Brownell WE, Sharma P. The collusion of flexoelectricity and hopf bifurcation in the hearing mechanism. J Mech Phys Solids. 2019;130:245–61. doi:10.1016/j.jmps.2019.05.018. [Google Scholar] [CrossRef]

300. Zelisko M, Li J, Sharma P. What is the mechanism behind biological ferroelectricity? Extreme Mech Lett. 2015;4:162–74. doi:10.1016/j.eml.2015.07.001. [Google Scholar] [CrossRef]

301. Cremer P, Löwen H, Menzel AM. Superelastic stress-strain behavior in ferrogels with different types of magneto-elastic coupling. Phys Chem Chem Phys. 2016;18(38):26670–90. doi:10.1039/c6cp05079d. [Google Scholar] [PubMed] [CrossRef]

302. Jamalpoor A, Ahmadi-Savadkoohi A, Hosseini-Hashemi S. Free vibration and biaxial buckling analysis of magneto-electro-elastic microplate resting on visco-pasternak substrate via modified strain gradient theory. Smart Mat Struct. 2016;25(10):105035. doi:10.1088/0964-1726/25/10/105035. [Google Scholar] [CrossRef]

303. Duan B, Zhu F, Zhao Z, Pan E, Qu Y. A variational principle in flexo-electromagnetism with an application to electromagnetic wave generation from flexoelectric plates. Math Mech Solids. 2025;30(8):1647–64. doi:10.1177/10812865241307312. [Google Scholar] [CrossRef]

304. Eliseev EA, Morozovska AN, Glinchuk MD, Blinc R. Spontaneous flexoelectric/flexomagnetic effect in nanoferroics. Phy Rev B. 2009;79:165433. doi:10.1103/PhysRevB.79.165433. [Google Scholar] [CrossRef]

305. Eliseev EA. Complete symmetry analyses of the surface-induced piezomagnetic, piezoelectric and linear magnetoelectric effects. Ferroelectrics. 2011;417(1):100–9. doi:10.1080/00150193.2011.578503. [Google Scholar] [CrossRef]

306. Eliseev EA, Glinchuk MD, Khist V, Skorokhod VV, Blinc R, Morozovska AN. Linear magnetoelectric coupling and ferroelectricity induced by the flexomagnetic effect in ferroics. Phys Rev B. 2011;84(17):174112. doi:10.1103/physrevb.84.174112. [Google Scholar] [CrossRef]

307. Lukashev P, Sabirianov RF. Flexomagnetic effect in frustrated triangular magnetic structures. Phy Rev B. 2010;82:094417. doi:10.1103/PhysRevB.82.094417. [Google Scholar] [CrossRef]

308. Lukashev P, Sabirianov RF. Spin density in frustrated magnets under mechanical stress: Mn-based antiperovskites. J Appl Phys. 2010;107(9):09E115. doi:10.1063/1.3365136. [Google Scholar] [CrossRef]

309. Pyatakov A, Zvezdin A. Flexomagnetoelectric interaction in multiferroics. Eur Phys J B. 2009;71:419–27. doi:10.1140/epjb/e2009-00281-5. [Google Scholar] [CrossRef]

310. Bar’Yakhtar V, L’vov V, Yablonskii D. Inhomogeneous magnetoelectric effect. ZhETF Pisma Redaktsiiu. 1983;37(12):565–7. [Google Scholar]

311. Tanygin BM. Symmetry theory of the flexomagnetoelectric effect in the magnetic domain walls. J Magn Magn Mater. 2011;323(5):616–9. doi:10.1016/j.jmmm.2010.10.028. [Google Scholar] [CrossRef]

312. Pyatakov A, Sergeev A, Mikailzade F, Zvezdin A. Spin flexoelectricity and chiral spin structures in magnetic films. J Magn Magn Mater. 2015;383:255–8. doi:10.1016/j.jmmm.2014.11.035. [Google Scholar] [CrossRef]

313. Bode M, Heide M, von Bergmann K, Ferriani P, Heinze S, Bihlmayer G, et al. Chiral magnetic order at surfaces driven by inversion asymmetry. nature. 2007;447(7141):190–3. doi:10.1038/nature05802. [Google Scholar] [PubMed] [CrossRef]

314. Pyatakov A, Meshkov G, Zvezdin A. Electric polarization of magnetic textures: new horizons of micromagnetism. J Magn Magn Mater. 2012;324:3551–4. doi:10.1016/j.jmmm.2012.02.087. [Google Scholar] [CrossRef]

315. Malikan M, Uglov NS, Eremeyev VA. On instabilities and post-buckling of piezomagnetic and flexomagnetic nanostructures. Int J Eng Sci. 2020;157:103395. doi:10.1016/j.ijengsci.2020.103395. [Google Scholar] [CrossRef]

316. Malikan M, Eremeyev VA. On nonlinear bending study of a piezo-flexomagnetic nanobeam based on an analytical-numerical solution. Nanomaterials. 2020;10(9):1762. doi:10.3390/nano10091762. [Google Scholar] [PubMed] [CrossRef]

317. Borkar H, Gaikwad VM, Choudhary RJ, Tomar M, Gupta V, Kumar A. Flexomagnetic effects on inhomogeneously strained multiferroics composites. J Magnet Mag Mat. 2022;553(3):169274. doi:10.1016/j.jmmm.2022.169274. [Google Scholar] [CrossRef]

318. Takeuchi I, Sandeman K. Solid-state cooling with caloric materials. Phys Today. 2015;68:48–54. doi:10.1063/PT.3.3022. [Google Scholar] [CrossRef]

319. Mañosa L, Planes A. Solid-state cooling by stress: a perspective. Appl Phys Lett. 2020;116:050501. doi:10.1063/1.5140555. [Google Scholar] [CrossRef]

320. Moya X, Mathur N. Caloric materials for cooling and heating. Science. 2020;370:797–803. doi:10.1126/science.abb0973. [Google Scholar] [PubMed] [CrossRef]

321. Patel S, Chauhan A, Madhar NA, Ilahi B, Vaish R. Flexoelectric induced caloric effect in truncated pyramid shaped ba 0.67 sr 0.33 tio 3 ferroelectric material. J Electron Mater. 2017;46(7):4166–71. doi:10.1007/s11664-017-5362-7. [Google Scholar] [CrossRef]

322. Sharma S, Vaish R, Kumar R. An isogeometric analysis-based investigation of the flexocaloric effect in functionally graded dielectrics. Acta Mech. 2021;232(11):4261–71. doi:10.1007/s00707-021-03051-z. [Google Scholar] [CrossRef]

323. Bai G, Qin K, Xie Q, Yan X, Gao C, Liu Z. Size dependent flexocaloric effect of paraelectric ba0. 67sr0. 33tio3 nanostructures. Mater Lett. 2017;186:146–50. doi:10.1016/j.matlet.2016.10.001. [Google Scholar] [CrossRef]

324. Patel S, Chauhan A, Vaish R. Flexo/electro-caloric performance of bati0. 87sn0. 13o3 ceramics. Appl Phys Lett. 2020;117(9):092904. doi:10.1063/5.0017687. [Google Scholar] [CrossRef]

325. Qiu Y, Wu H, Wang J, Lou J, Zhang Z, Liu A, et al. Giant electrocaloric effect in ferroelectric ultrathin films at room temperature mediated by flexoelectric effect and work function. J Appl Phys. 2017;122(2):024103. doi:10.1063/1.4992811. [Google Scholar] [CrossRef]

326. Starkov A, Starkov I. Flexocaloric effect in thin plates of barium titanate and strontium titanate. Phys Solid State. 2019;61(12):2542–6. doi:10.1134/s1063783419120539. [Google Scholar] [CrossRef]

327. Kumar A, Kiran R, Kumar R, Chandra Jain S, Vaish R. Flexoelectric effect in functionally graded materials: a numerical study. Eur Phys J Plus. 2018;133:1–9. doi:10.1140/epjp/i2018-11976-1. [Google Scholar] [CrossRef]

328. Patnaik S, Sidhardh S, Semperlotti F. A ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. Int J Solids Struct. 2020;202(3):398–417. doi:10.1016/j.ijsolstr.2020.05.034. [Google Scholar] [CrossRef]

329. Eringen AC, Edelen D. On nonlocal elasticity. Int J Eng Sci. 1972;10:233–48. doi:10.1016/0020-7225(72)90039-0. [Google Scholar] [CrossRef]

330. Batra RC. Misuse of eringen’s nonlocal elasticity theory for functionally graded materials. Compos Struct. 2010;92(9):2520–4. doi:10.1016/j.ijengsci.2020.103425. [Google Scholar] [CrossRef]

331. Zaera R, Serrano Ó, Fernández-Sáez J. On the consistency of the nonlocal strain gradient elasticity. Int J Eng Sci. 2019;138:65–81. doi:10.1016/j.ijengsci.2019.02.004. [Google Scholar] [CrossRef]

332. Zaera R, Serrano Ó, Fernández-Sáez J. Non-standard and constitutive boundary conditions in nonlocal strain gradient elasticity. Meccanica. 2020;55:469–79. doi:10.1007/s11012-019-01122-z. [Google Scholar] [CrossRef]

333. Behdad S, Arefi M. A mixed two-phase stress/strain driven elasticity: in applications on static bending, vibration analysis and wave propagation. European J Mech-A/Solids. 2022;94(3):104558. doi:10.1016/j.euromechsol.2022.104558. [Google Scholar] [CrossRef]

334. Fernández-Sáez J, Zaera R. Vibrations of bernoulli-euler beams using the two-phase nonlocal elasticity theory. Int J Eng Sci. 2017;119:232–48. doi:10.1016/j.ijengsci.2017.06.021. [Google Scholar] [CrossRef]

335. Karim TB, McKenna GB. Comparison of surface mechanical properties among linear and star polystyrenes: surface softening and stiffening at different temperatures. Polymer. 2013;54(21):5928–35. doi:10.1016/j.polymer.2013.07.067. [Google Scholar] [CrossRef]

336. Lim C, Zhang G, Reddy J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids. 2015;78:298–313. doi:10.1016/j.jmps.2015.02.001. [Google Scholar] [CrossRef]

337. Romano G, Barretta R. Nonlocal elasticity in nanobeams: the stress-driven integral model. Int J Eng Sci. 2017;115:14–27. doi:10.1016/j.ijengsci.2017.03.002. [Google Scholar] [CrossRef]

338. Romano G, Barretta R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos Part B: Eng. 2017;114(3–5):184–8. doi:10.1016/j.compositesb.2017.01.008. [Google Scholar] [CrossRef]

339. Darban H, Luciano R, Caporale A, Basista M. Modeling of buckling of nanobeams embedded in elastic medium by local-nonlocal stress-driven gradient elasticity theory. Compos Struct. 2022;297(5496):115907. doi:10.1016/j.compstruct.2022.115907. [Google Scholar] [CrossRef]

340. Barretta R, de Sciarra FM. Variational nonlocal gradient elasticity for nano-beams. Int J Eng Sci. 2019;143:73–91. doi:10.1016/j.ijengsci.2019.06.016. [Google Scholar] [CrossRef]

341. Lovisi G, Feo L, Lambiase A, Penna R. Application of surface stress-driven model for higher vibration modes of functionally graded nanobeams. Nanomaterials. 2024;14(4):350. doi:10.3390/nano14040350. [Google Scholar] [PubMed] [CrossRef]

342. Penna R, Lovisi G, Feo L. Buckling analysis of functionally graded nanobeams via surface stress-driven model. Int J Eng Sci. 2024;205:104148. doi:10.1016/j.ijengsci.2024.104148. [Google Scholar] [CrossRef]

343. Penna R, Lovisi G. Surface and nonlocal effects in piezoelectric nanobeams. European J Mech-A/Solids. 2025;113:105715. doi:10.1016/j.euromechsol.2025.105715. [Google Scholar] [CrossRef]

344. Patnaik S, Sidhardh S, Semperlotti F. Towards a unified approach to nonlocal elasticity via fractional-order mechanics. Int J Mech Sci. 2021;189:105992. doi:10.1016/j.ijmecsci.2020.105992. [Google Scholar] [CrossRef]

345. Desai S, Sidhardh S. A fractional-order constitutive model for nonlocal piezoelectricity. Acta Mech. 2025;236:4387–415. doi:10.1007/s00707-025-04387-6. [Google Scholar] [CrossRef]

346. Sumelka W. Thermoelasticity in the framework of the fractional continuum mechanics. J Therm Stresses. 2014;37(6):678–706. doi:10.1080/01495739.2014.885332. [Google Scholar] [CrossRef]

347. Rajan A, Desai S, Sidhardh S. Element-free galerkin method for a fractional-order boundary value problem. Int J Num Meth Eng. 2024;125:e7429. doi:10.1002/nme.7429. [Google Scholar] [CrossRef]

348. Patnaik S, Sidhardh S, Semperlotti F. Displacement-driven approach to nonlocal elasticity. European J Mech-A/Solids. 2022;92:104434. doi:10.1016/j.euromechsol.2021.104434. [Google Scholar] [CrossRef]

349. Sidhardh S, Patnaik S, Semperlotti F. Thermodynamics of fractional-order nonlocal continua and its application to the thermoelastic response of beams. European J Mech-A/Solids. 2021;88(3–6):104238. doi:10.1016/j.euromechsol.2021.104238. [Google Scholar] [CrossRef]

350. Polizzotto C. Nonlocal elasticity and related variational principles. Int J Solids Struct. 2001;38(42–43):7359–80. doi:10.1016/s0020-7683(01)00039-7. [Google Scholar] [CrossRef]