Fuzzy Logic-Based Robust Global Consensus in Leader-Follower Robotic Systems under Sensor and Actuator Attacks Using Hybrid Control Strategy

1  Introduction

Technological advancements have increasingly driven the integration of automation into various fields, revolutionizing efficiency and functionality across industries [1]. Robotics has become an important technology among these innovations, by providing imaginative options that allow for ongoing assistance with human jobs. Recent works have proposed event-triggered optimal impedance control for exoskeletons using critic neural networks [2], robust constraint-based controllers for uncertain nonlinear manipulators [3], and hierarchical adaptive coordination strategies for large-scale traffic networks [4]. High-precision simultaneous localization and mapping (SLAM)-based positioning in GPS-denied environments [5] and output feedback stabilization for aperiodic sampled-data systems via looped functionals [6] further contribute to advanced control design. To enhance contour tracking, reference [7] proposed a time-varying internal model principle-based control method and a hybrid-excited vernier reluctance linear machine with Halbach Permanent Magnet (PM) arrays. Mobility on rough terrains was improved through a creeping gait strategy using fuzzy logic in wheeled robots [8], while reference [9] introduced a prescribed performance adaptive robust control for uncertain manipulators with Lyapunov-based guarantees. A prestretch-free dielectric elastomer actuator for soft robotics was developed ([10,11]) to address Lurie system stabilization using a cone complementary linearization algorithm. Robotic tracking under uncertainty was handled via a second-order sliding mode adaptive controller in [12], and Connected and Automated Vehicles were coordinated under actuation constraints using a bi-level distributed framework in [13]. Optimal consensus for delayed multiagent systems (MASs) was achieved through a delay-free deterministic policy gradient method [14], and encoder accuracy in robotic arms was improved using a hybrid deep learning-based error compensation model [15]. When coordinating a swarm, each robot must respond not only to external environmental changes but also to the movements of neighboring robots to preserve the overall formation and direction toward the target ([16,17]). The challenge, therefore, lies in developing robust control algorithms that allow swarm robots to navigate, adapt, and maintain formation cohesively while responding to unpredictable elements or situations in real-time applications [18]. With increasing indoor occupancy, occupant thermal comfort monitoring using mobile robots has emerged to overcome the inefficiencies of fixed sensors in non-uniform environments [19]. Joint LiDAR-based scene flow estimation and moving object segmentation improve autonomous driving tasks by exploiting shared geometric constraints [20]. Flexible actuators like DEA and IPMCs enable biomimetic control via FLS and barrier Lyapunov function (BLF)-based adaptive pseudo inverse schemes for constrained hysteretic systems [21]. For heavy trucks, an adaptive memory event-triggered output feedback ensures finite-time lane-keeping with roll prevention under nonlinear dynamics [22]. Microwave-based deicing struggles with Z-shaped contact wires on moving trains [23], while binocular stereo vision-based GOAL enhances robotic grasping under occlusion [24]. A sweeping-spinning gait and Bayesian optimization improve planetary rover escape from soft terrain [25]. SPL offers nano-fabrication capabilities, though limited by atomic force microscope (AFM) scanner stroke [26], and a single-step fused filament fabrication (FFF)-based method improves the rapid design and fabrication of soft pneumatic actuators [27]. Leader-follower approach, by contrast, is simpler to adopt, with a single robot designated as the leader and other robots following in a framework ([28–30]). One of the major advantages of this policy is for maintaining stability in challenging and rapidly changing critical situations [31]. To avoid complex back-stepping and coupled observer-controller designs, a neural network prescribed-time observer-based output-feedback control method is proposed for uncertain pure-feedback nonlinear systems, enabling fast and accurate estimation of states and disturbances [32]. For autonomous driving, an integrated decision-making and motion planning framework is introduced to eliminate oscillations and enhance safety in dynamic environments ([33,34]). Addressing actuator faults in heavy-lift launch vehicles, a predefined-time observer facilitates quantized attitude control with precise temporal guarantees [35]. In robotic milling, a multi-channel chatter detection method is developed to identify structural and tool-mode chatter under low-frequency vibration interferences [36]. For machining large components, mobile robot base position and cabin angle are jointly optimized using a homogeneous stiffness domain index, improving structural rigidity and machining precision [37]. Leader-follower frameworks have been recommended by a number of studies in recent years for swarm robotics formation stability [38]. In several investigations, scholars looked into the leader-follower approach in plain settings. Although these controlled situations offer valuable insights into fundamental swarm formation, they are very different from real-world situations where robots have to move around a variety of obstacles. In control systems for swarm robotics divided into two main categories: conventional control and intelligent control methods [39]. The semi-global stabilization of parabolic partial differential equations (PDEs)–ordinary differential equation (ODE) systems with input saturation is achieved via low-gain controllers under complex boundary conditions [40], while a PDE-based observer with predictor control enables output-feedback stabilization for systems with infinite delays [41]. For uncertain systems, a Padé-approximation-based optimal preview repetitive control with equivalent-input-disturbance (EID) enhances robustness [42]. Magnetic millirobots with switchable adhesion enable versatile manipulation in constrained environments [43], and force feedback bilateral teleoperation advances remote control in hazardous and medical applications [44]. A one-step FFF process simplifies soft actuator fabrication for adaptive bio-inspired robots [45]. A graph-based leader–follower strategy ensures precise tracking [46], while ship synchronization uses a stochastic observer under unknown leader velocity [47]. CB-MTE improves bot detection via multi-source fusion [48], and adaptive impedance control reduces docking collisions in unmanned vehicles [49].

Motivated by our previous discussion, we outlined contributions in a way that

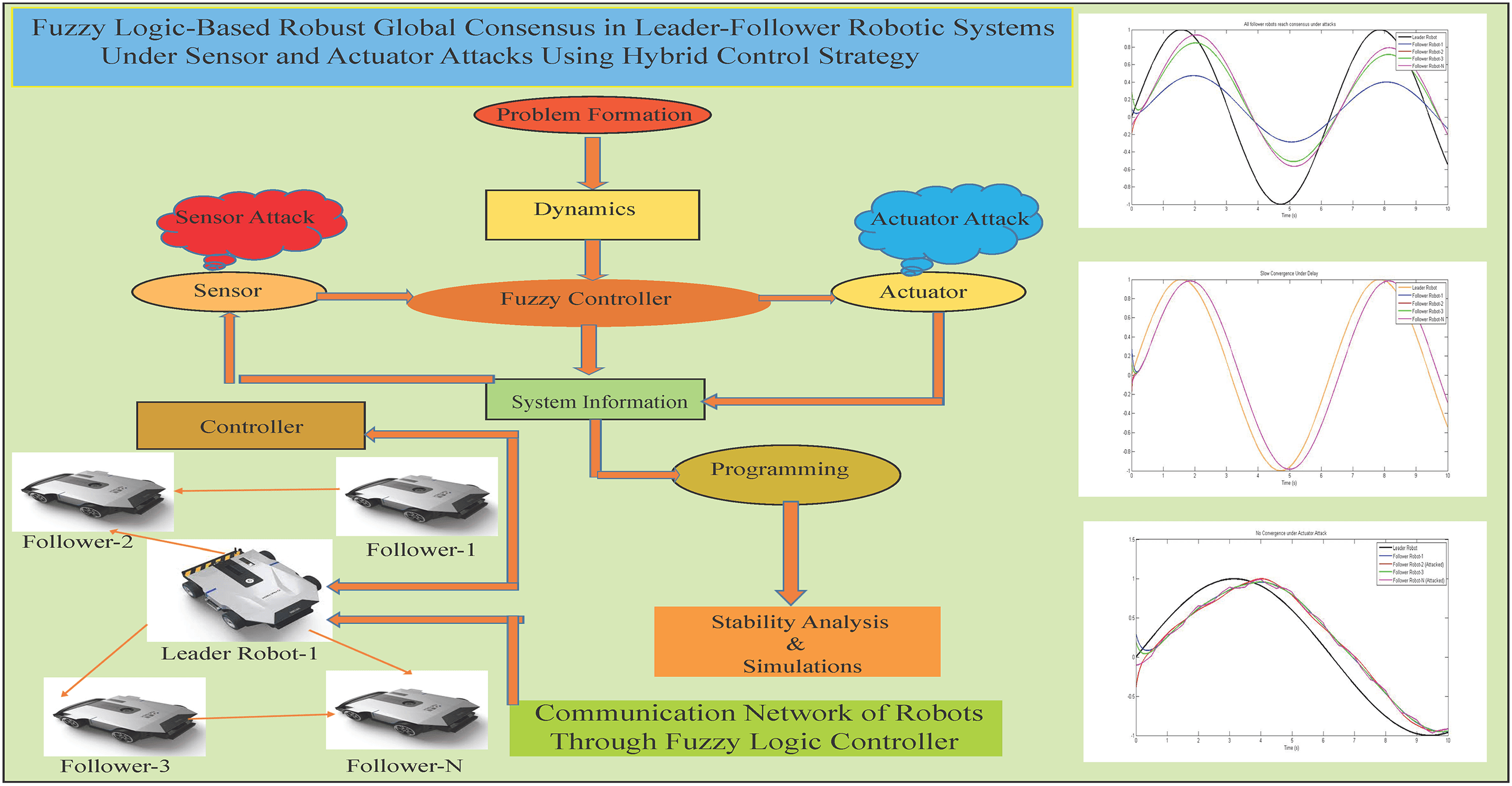
In this paper, we contribute a robust hybrid distributed adaptive control strategy for leader-follower robotic systems with both first-order and second-order dynamics, addressing simultaneous sensor and actuator faults. A specialized controller is designed to mitigate the combined effects of these attacks while ensuring system resilience. The leader robot, modeled with second-order dynamics, communicates its state information to follower robots, which approximate unknown nonlinear dynamics using fuzzy logic systems. A Lyapunov-based stability analysis is conducted to ensure the system’s asymptotic consensus. The proposed strategy is validated through simulations on two directed communication topologies, demonstrating its effectiveness and adaptability in achieving stable and robust global consensus. A comprehensive graphical representation of the proposed approach is presented in Fig. 1. The content of this article is organized as follows:

1.   In Section 1, we discussed the fuzzy logic system of robots under the effect of sensor attacks and actuator attacks.

2.   In Section 2, we present the graph theory for the communication of the robot system graph.

3.   In Section 3, we provided a problem formation for N robots and also gave the position, velocity, and acceleration dynamics of robots, including the signal attacks.

4.   Section 4 presents the influence of sensor attack and actuator attack, assumptions, and fuzzy control design framework and theorem.

5.   In Section 5, we present two examples with different communication topologies under the sensor attack and actuator attack.

6.   In Section 6, at the end of this paper, we wind up this paper with conclusions.

Figure 1: Graphical representation of abstract

The framework of the paper is described in Fig. 2.

Figure 2: Framework of the paper

2  Preliminaries

Graph Theory

Consider a network of robotic systems represented by a directed weighted graph 𝒢=(𝒩,ℰ), where 𝒩={r1,r2,…,rN} denotes the set of robots, and ℰ⊆𝒩×𝒩 specifies the directed communication links between them. Each robot is indexed by the set N={1,2,3,…,N}. The communication structure of the network is captured by the adjacency matrix ℬ=[bij]∈RN×N, defined as,

bij={>0,if robot ri sends information to robot rj,0,otherwise.

A directed edge (ri,rj)∈ℰ implies that robot ri communicates with robot rj, i.e., it sends information to rj. Thus, a positive entry bij>0 indicates a direct communication link from ri to rj. It is assumed that bii=0 for all i∈N, meaning that a robot does not communicate with itself. The set of neighbors that receive information from robot ri is defined as, Ni={j∈𝒩:(ri,rj)∈ℰ or equivalently bij>0}, i.e., robots that receive data directly from ri.

To describe the network dynamics, we define a diagonalmatrix 𝒟 = diag(d¯1,…,d¯N), where each diagonal entry is given by d¯i=∑j≠ibij, representing the total outgoing communication weight from robot ri. The Laplacian matrix of the network is then constructed as, ℒ=𝒟−ℬ. By construction, the Laplacian matrix satisfies the property ℒ⋅1N=0N, where 1N and 0N are column vectors of size N×1 with all entries equal to one and zero, respectively. This fundamental property reflects the conservation of information flow within the network and ensures that the sum of each row in ℒ is zero, which is essential for collective consensus or formation behavior in multi-robotic systems.

3  Problem Formation

We consider a heterogeneous group of nonlinear robots consisting of first-order, second-order, and third-order follower robots, indexed by i=1,2,…,N, each subject to external signal attacks. The system includes different dynamic orders to reflect practical diversity in robot capabilities. Below, we define the dynamics for each class. The third-order follower robots are those that track the leader’s position, velocity, and acceleration.

{y˙ip(k)=yiv(k),y˙iv(k)=yia(k),y˙ia(k)=hi(k,y¯i(k))+χi(k)ωi(k)+ϕ(k)+gi(k),wherey¯i(k)=[yip(k),yiv(k),yia(k)]T,(1)

where yip(k)∈R is the position state of the i-th follower robot at discrete time step k, yiv(k)∈R is the velocity state, and yia(k)∈R is the acceleration state. The full state vector is denoted by y¯i(k). The term hi(k,y¯i(k)) is an unknown nonlinear function representing the internal dynamics of the system. The variable χi(k) represents a time-varying control gain (replacing ρi(t) from the original description), which satisfies |χi(k)|∈[χmin,χmax] with χmax>χmin>0.

The control input protocol is denoted by ωi(k), and ϕ(k) corresponds to the external bounded input interference, satisfying |ϕ(k)|≤ci, where ci>0 is a known constant. Furthermore, gi(k) is the signal attack acting on the i-th robot’s input. In this context, the control gain χi(k) is partially unknown. That is, among N followers, r0 followers (with 0<r0≤N) have unknown identical control directions, while the remaining N−r0 followers have known positive control gains. For modeling simplicity and to facilitate controller design, those known gains χi(k) are assumed to be positive, as a known negative gain can easily be transformed into a positive one using χ^i(k)=−χi(k) if the sign is known.

The first-order follower robots are those that track the leader’s robot.

y˙ia(k)=hi(k,y¯i(k))+χi(k)ωi(k)+ϕ(k)+gi(k),where y¯i(k)=[00yia(k)]T(2)

where yia(k)∈R acceleration state of the i-th robot, y¯i(k) state vector including only the acceleration term, all other parameters hi(k,⋅), χi(k), ωi(k), ϕ(k), and gi(k) have the same definitions as in Eq. (1).

Similarly, we define the leader dynamics of robots as follows,

{y˙0p=y0v,y˙0v=y0a,y˙0a=h(k,y¯0(k)),wherey¯0(k)=[y0p(k),y0v(k),y0a(k)]T(3)

where consisting of its position y0p(k), velocity y0v(k), and acceleration y0a(k). The function h(k,y¯0(k)) represents an unknown nonlinear dynamic behavior of the leader.

Now, we define the leader-follower robots tracking error for position, velocity, and acceleration such that

{εip(k)=yip(k)−y0p(k)εiv(k)=yiv(k)−y0v(k)εia(k)=yia(k)−y0a(k)(4)

And we define the consensus error for position, velocity and acceleration robots.

{ℰip=∑i∈Nbij(yip−yip)+fi(y0p−yip)ℰiv=∑i∈Nbij(yiv−yiv)+fi(y0v−yiv)ℰia=∑i∈Nbij(yia−yia)+fi(y0a−yia)(5)

Now we rewrite the consensus errors position, velocity, and acceleration for all follower robots in a compact matrix form. For all followers of robots, we get the vector of consensus errors. We need to express y0p, y0v, and y0a more concerning all robots. To do this, we introduce a vector of ones 1𝒩 which is of dimension 𝒩 (the total number of robots). This vector is used to replicate the leader’s position, velocity, and acceleration across all robots.

Thus, we can rewrite the term y0p as, y0p1𝒩=[y1p,y1p,y1p,…,ymp]T, y0v as, y0v1𝒩=[y1v,y1v,y1v,…,ymv]T and y0a as, y0a1𝒩=[y1a,y1a,y1a,…,yma]T. We define the Sp=ℒp+Fp, Sv=ℒv+Fv and Sa=ℒa+Fa represents the combination of the follower-to-follower interactions and the follower-to-leader interactions. Now substituting tracking error Eqs. (4) into (5). We get the result,

ℰip=−(ℒp+Fp)εip=−Sp(yip(k)−y0p(k))=−Spεip(6)

ℰiv=−(ℒv+Fv)εiv=−Sv(yiv(k)−y0v(k))=−Svεiv(7)

ℰia=−(ℒa+Fa)εia=−Sa(yia(k)−y0a(k))=−Saεia(8)

where Fp=diag{f1,f2,f3,…,fm}, Fv=diag{f1,f2,f3,…,fm} and Fa=diag{f1,f2,f3,…,fm}.

Now we define the local consensus error for the follower robots. To extend the local consensus filter error ξi. ξi={ℰiv+αℰip+βℰia,i∈N1∪N2ℰiv+βℰia,i∈N3. Where α>0 and β>0 are weighting factors for the position and acceleration terms, respectively. Here ℰip represents the position error, ℰiv represents the velocity error, and ℰia represents the acceleration error.

We can write it in this form,

ξ=ξ1n+ξ2n+ξ3n(9)

where ξ1n=ℰN2v captures the velocity error for followers in N2, ξ2n=ℰN1v+αℰp captures both the position and velocity errors for followers in N1, ξ3n=βℰa captures the acceleration error for all followers with a weight β>0.

Now using (1), (2), (3), (6), (7), (8) and (9), we get result,

ξi˙=−2Sa(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0)))+αSp(yiv(k)−y0v(k))+βSa(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0)))(10)

where h(y¯)=[hi(y1¯),…,hn(yn¯)]T is a nonlinear function, and gi(k) is a signal attack, including sensor attack and actuator attack which we defined below.

4  Influence of Actuator and Sensor Attacks on Robot Dynamics

Actuator faults in robotic systems are modeled as,

ωic~(k)=∑j∈𝒩iωj(k)+⊮{i}ωib(k),(11)

where ωi(k) represents the nominal actuator state, ωic~(k) is the modified control input received by the robot, and ωib(k) denotes the injected actuator attack signal. The term ⊮{i} is an indicator function that becomes active under specific conditions, allowing the actuator attack to occur.

Similarly, the behavior of the system under sensor anomalies is described by,

yic(k)=∑i∈Niyi(k)+ℐ{i}yib(k),(12)

where yi(k) is the nominal sensor state, yic(k) is the corrupted measurement, and yib(k) is the attack signal injected into the sensor data. The indicator function ℐ{i} determines whether a sensor fault is active for a specific robot. The combined effect of actuator and sensor attacks Eqs. (11) and (12) on the robot’s dynamics can be formulated as,

gi(k)=∑j∈𝒩i(⊮{i}ωib(k)+bijsk(ℐ{j}yjb(k)−ℐ{i}yib(k))),(13)

where ωib(k) and yib(k) represent the actuator and sensor attack signals, respectively. The term yjb(k) denotes the sensor attack signals originating from neighboring robots j in the vicinity of robot i, represented by 𝒩i. The parameter sk acts as a scalar gain, while (bij) represents the adjacency matrix, indicating the communication structure between robots i and j.

This formulation captures the joint influence of actuator and sensor attacks on robotic systems, providing a foundation for analyzing and mitigating their effects through robust control strategies.

Assumption 1. Assume that each follower robot i has dynamics which is governed by a nonlinear function hi(yi) satisfying the Lipschitz continuity condition,

‖hi(yi)−hi(y0)‖≤μi‖yi−y0‖,

where σi>0 is a constant.

Assumption 2. The leader’s state of robot y0 evolves according to a nonlinear function h0(y0) and is constrained by,

‖f0(x0)‖≤FMh0.

Assumption 3. The leader’s state of y0 remains in a compact set F⊂R2, meaning that,

x0∈F.

This formulation allows for tracking errors in position, velocity, and acceleration, providing a more comprehensive approach to handling consensus errors in each state component. Fig. 3 shows the N robots model under the sensor attack and actuator attacks controlled by fuzzy logic.

Figure 3: Network communication topology with directed connected graph agents under the sensor attack and actuator attack

4.1 Robust Control Framework

We design a fuzzy logic robust control protocol that addresses nonlinearities and provides robustness against sensor and actuator attacks, using adaptive techniques for optimal performance. The protocol employs fuzzy logic-based estimation, dynamic gain adjustments, and nonlinear function handling, enabling the system to adapt to disturbances while ensuring stability. To address the heterogeneity among agents with first-order, second-order, and third-order dynamics, we propose a fuzzy logic-based robust control framework that incorporates adaptive design and nonlinear estimation mechanisms. The set of follower robots is partitioned into three disjoint subsets, such that N1: robots that track the leader’s position (first-order dynamics), N2: robots that track the leader’s velocity (second-order dynamics) and N3: robots that track the leader’s acceleration (third-order dynamics).

This partitioning enables us to customize the control input ωi(k) for each class of robots, ensuring that the heterogeneity is explicitly addressed in both control design and stability analysis. To achieve robustness and resilience against nonlinearities and signal attacks, we propose a fuzzy logic-based adaptive control framework. The proposed method integrates a Fuzzy Logic System (FLS) to approximate the unknown nonlinear functions hi(⋅), accompanied by adaptive parameter tuning. The follower robots are partitioned into disjoint sets, N1: robots tracking the leader’s position, N2: robots tracking the leader’s velocity, and N3: robots tracking the leader’s acceleration.

This partitioning enables us to design customized control laws for different dynamics. The control protocol for robot i is defined as,

ωi(k)=Θi(k)+∑j∈𝒩i(⊮{i}ωib(k)+bijsk(ℐ{j}yjb(k)−ℐ{i}yib(k)))(14)

Here, the second term estimates the attack signal, while Θi(k) is the adaptive control core designed as,

Θi={−di(k)ξi+Giδi(y¯0)−FMitanh⁡(FMi⋅ξiΦ(k)),i∈N1∩z1,−di(k)ξi+Giδi(y¯0v)−FMitanh⁡(FMi⋅ξiΦ(k)),i∈N2∩z2,−di(k)ξi+Giδi(y¯0a)−FMitanh⁡(FMi⋅ξiΦ(k)),i∈N3∩z3,−di(k)ξi−Gitanh⁡(Gi⋅ξiΦ(k))−FMitanh⁡(FMi⋅ξiΦ(k)),i∈z3.(15)

Here, Gi is the fuzzy gain function, di(k) is the time-varying parameter, and δi(⋅) represents the fuzzy basis function. The variables y¯0=[0,0,y0a]T, y¯0v and y¯0a are the input vectors for the fuzzy system.

4.2 Fuzzy Logic System Design

Each unknown nonlinear function hi(⋅) is approximated by a fuzzy logic estimator δi(⋅), constructed as follows. The FLS uses the leader’s state vector y¯0 (or its variants y¯0v, y¯0a) as input,

δi(y¯0)=WiTΛi(y¯0)

where Wi∈Rr is the adaptive parameter vector, and Λi(y¯0)∈Rr is the fuzzy basis function vector with r rules. Each basis function Λiℓ is generated by product inference over Gaussian membership function ([49]),

Λiℓ(y¯0)=∏j=1qexp⁡(−(y0j−cℓj)22σℓj2),ℓ=1,2,…,r

where q is the number of input variables, cℓj and σℓj are centers and spreads of the Gaussian membership functions (MFs). The fuzzy rule base consists of r rules of the form, if y0p is Aℓ1 and y0v is Aℓ2 and y0a is Aℓ3 then δi=Wiℓ with Aℓj representing linguistic fuzzy sets (e.g., “Low”, “Medium”, “High”). Parameters below are defined as,

{Gi=ς1iξiδi(y¯0)−δ(k)αG1iGi,FMi=ς3i|ξi|−δ(k)αFMiFMi,di(k)=ς4iξi2−δ(k)βcici(k),σi=−ξiΘi(k)ξi(16)

This architecture guarantees the approximation of nonlinear dynamics with bounded error. Clear mapping from robot class to control behavior. Reproducibility of the fuzzy estimator δi(⋅) due to explicit membership functions, rule base, and update mechanism. This formulation ensures that each follower class receives a distinct and dynamically tuned control input based on its order of dynamics. Fuzzy estimators and damping terms are state- and class-dependent, ensuring robustness and adaptivity. The system maintains resilience against sensor and actuator attacks via distributed estimation terms in (14). The block diagram of the proposed structure is presented in Fig. 4.

Figure 4: Block diagram of the fuzzy logic-based robust control framework under sensor and actuator attacks

Lemma 1. [9]. 𝒱(k) is a positive definite function on [0,kp). Then, one has that,

∑i=1n∫0kμi(χi(τ)N¯(σi(τ))+1)σ˙i(τ)dτ,

where σi(k)(i∈N) and 𝒱(k) are bounded on [0,kp) if

𝒱(k)≤∑i=1n∫0kμi(χi(τ)N¯(ϑi(τ))+1)σ˙i(τ)dτ+ϕ¯0,

where,

N¯(σi)={−h¯eσi22(σi2+2)sin⁡(σi),if χi(k) is known,−σieϑi22,if χi(k) is unknown.

where σi(0) is bounded, and ζ, μi, and ϕ¯0 are positive constants.

Theorem 1. Take the leader-following robots system defined by Eqs. (1) and (3) and by using the Assumptions (1), (2) and (3). Let 𝒢a, 𝒢v and 𝒢a represent the communication graphs associated with the follower robots and the leader which are linked to the position, velocity and acceleration with Eqs. (1) and (3). Specifically, 𝒢p and 𝒢v and 𝒢a are network graph linking the followers, i∈Ni.

Using the consensus protocol outlined in Eqs. (14), (15) and the defined parameters Eq. (16), the system achieves the following outcomes,

{1. Convergence of Consensus Errors:εip,εiv,εia→0ask→∞,2. Boundedness of Control Parameters:Control inputs and learning parametersremain finite and bounded.

This implies that each follower robot in the network can asymptotically synchronize its state with that of the leader, achieving precise tracking over time and ensuring stability within the system.

Proof. To analyze the stability of the error system defined in Eq. (10), we construct the following Lyapunov candidate function,

𝒱1=12(ξiTSa−1ξi+qξvTξv+rξpTξp),q,r>0,(17)

where ξi=yia−y0a, ξv=yiv−y0v, and ξp=yip−y0p are the acceleration, velocity, and position tracking errors, Sa∈Rn×n is a symmetric positive-definite matrix and q,r∈R>0 are positive scalar weights.

Taking the time derivative of (17), we get,

𝒱˙1=12(ξ˙iTSa−1ξi+ξiTSa−1ξ˙i+qξ˙vTξv+qξvTξ˙v+rξ˙pTξp+rξpTξ˙p).(18)

By using the Eq. (10) and simplifying the expression, we get,

𝒱˙1=ξiTSa−1ξ˙i+qξvTξ˙v+rξpTξ˙p.(19)

Substituting ξ˙i into the expression for 𝒱˙1, we have,

𝒱˙1={ξiTSa−1[−2Sa(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0)))]+ξiTSa−1[qSp(yiv(k)−y0v(k))]+ξiTSa−1[rSa(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0)))](20)

We distribute these terms such that,

𝒱˙1(1)=−2ξiT(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0))),𝒱˙1(2)=qξiTSa−1Sp(yiv(k)−y0v(k)),𝒱˙1(3)=rξiT(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0))).

Finally, combining all the terms, we obtain,

+qξiTSa−1Sp(yiv(k)−y0v(k))+rξiT(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0))).

Now we take the term,

𝒱˙1(1)=−2ξiT(h(k,y¯(ki))+χi(k)ωi(k)+ϕ(k)+gi(k)−h(k,y¯(k0))).

𝒱˙1(1)=−∑i∈N[1+χi(k)Ni](ξiΘi+gi(k))+∑i∈N(ξiΘi+gi(k))−[∑i∈Nξihi(y0¯)−∑i∈Nξi(hi(yi¯)−hi(y0¯))−∑i∈Nξi(hi(yi¯)−hi(y0a¯))−∑i∈N1ξihi(y0a¯)−∑i∈N(ϕi(k)−h0(k,y0¯))ξi].(21)

Now using the [38–40] and use the unknown function like hi(y¯0) and hi(y¯0a)ζ are estimated by fuzzy logic systems GiTδ(yo¯) and GiTδ(yoa¯), respectively. Now we define the fuzzy logic systems estimated error such that,

ζi(k)=hi(k)−GiTδi(k),(22)

where ‖δi(k)‖≤δi¯ and where δi¯ is an constant. Now using Eqs. (21) and (22), and applying the Lipschitz continuity of hi(⋅) from Assumption (1), the boundedness of the leader’s dynamics from Assumption (2), and the compactness of the leader’s state from Assumption (3), we obtain,

𝒱˙1(1)≤−∑i∈N[1+χi(k)Ni](ξiΘi+gi(k))+∑i∈N(ξiΘi+gi(k))−∑i∈NiGiδi(y0¯)−∑i∈NiGiδi(y0a¯)+∑i∈Ni|ξi|(FMh0+ci)+∑i∈Niμi‖ξi‖(‖ℰip‖+‖ℰiv‖+‖ℰia‖),

𝒱˙1(1)≤−∑i∈Ni[1+χi(k)Ni](ξiΘi+gi(k))+∑i∈N(ξiΘi+gi(k))−∑i∈Niξi[(Giδi(y¯0p)+ζi(y¯0p)+Giδi(y¯0v)+ζi(y¯0v)+Giδi(y¯0a)+ζi(y¯0a))]+∑i∈Ni|ξi|[(FMh0+ci)]+μmaxξT𝒦ξℰaℰa+μmaxξT𝒦ξℰvℰv+μmaxξT𝒦ξℰpℰp.

𝒱˙1≤−∑i∈𝒩di(k)‖ξi‖2−∑i∈𝒩ξiTGiδi(y¯0)−∑i∈𝒩ξiTFMitanh⁡(FMi⋅ξiΦ(k))+∑i∈𝒩|ξi|Gi+∑i∈𝒩|ξi|FMi+∑i∈𝒩ξiTSa−1(ϕ(k)+gi(k))+qξvTξ˙v+rξpTξ˙p.(23)

Now using the Eqs. (6)–(8), we obtain the result,

𝒱˙1≤−∑i∈𝒩di(k)‖ξi‖2−∑i∈𝒩ξiTGiδi(y¯0)−∑i∈𝒩ξiTFMitanh⁡(FMi⋅ξiΦ(k))+∑i∈𝒩|ξi|Gi+∑i∈𝒩|ξi|FMi+∑i∈𝒩ξiTSa−1(ϕ(k)+gi(k))+qξvTξ˙v+rξpTξ˙p.(24)

Now, we take the term second 𝒱˙1(2) and we can write it as,

𝒱˙1(2)=αξTSa−1SvSp[ℐm000(n−m)×(n−m)]Sa−1ξ+βξTSa−1SvSp[ℐm000(n−m)×(n−m)]Sa−1ξ−α22ξTSa−1SvSp[ℐm000(n−m)×(n−m)]Sa−1εv−β22ξTSa−1SvSp[ℐm000(n−m)×(n−m)]Sa−1εp≤α‖ξ‖2ΥSa−12ΥSvΥSp+β‖ξ‖2ΥSa−12ΥSvΥSp+α22ΥSa−14ΥSv2ΥSp2ξTξ+β22ΥSa−14ΥSv2ΥSp2ξTξ+α22(εv)Tεv+β22(εp)Tεp,(25)

where ΥSa−1, ΥSv and ΥSp are eigenvalues of matrices Sa−1, Sv and Sp. Now we take the last third term 𝒱˙1(3) and solve it as,

𝒱˙1(3)=q(εv)TSv[ℐm000(n−m)×(n−m)]Sa−1ξ−qα(εv)TSv[ℐm000(n−m)×(n−m)]Sa−1εv+r(εp)TSp[ℐm000(n−m)×(n−m)]Sa−1ξ−rβ(εp)TSp[ℐm000(n−m)×(n−m)]Sa−1εp.

𝒱˙1(3)=q(εv)TSv[ℐm000(n−m)×(n−m)]Sa−1ξ−qα(εv)TSv𝒫1𝒫2+r(εp)TSp[ℐm000(n−m)×(n−m)]Sa−1ξ−rβ(εp)TSp𝒫3𝒫4

where 𝒫1=[Sv00ν1], 𝒫2=[𝒦1100ν2], and 𝒫3=[Sp00ν3], 𝒫4=[𝒦2200ν4], and where 𝒫=𝒫1𝒫2+𝒫2𝒫1+𝒫3𝒫4+𝒫4𝒫3, with ν1=diag⁡(Γ11,…,Γ1(n−m)), ν2=diag⁡(Γ21,…,Γ2(n−m)) ν3=diag⁡(Γ22,…,Γ2(n−m)) and ν4=diag⁡(Γ31,…,Γ3(n−m)). Where 𝒫1, 𝒫2, 𝒫3, and 𝒫4 are positive definite matrices. Take Γ11,…,Γ1(n−m),Γ21,…,Γ2(n−m) and Γ22,…,Γ2(n−m),Γ31,…,Γ3(n−m) such that,

𝒦𝒫1+1𝒦𝒫1<2+4𝒦𝒫2,

and

𝒦𝒫3+1𝒦𝒫3<2+4𝒦𝒫4.𝒦𝒫1=Υmax(𝒫1)Υmin(𝒫1),𝒦𝒫2=Υmax(𝒫2)Υmin(𝒫2),

where Υmax(𝒫1), Υmax(𝒫2), Υmin(𝒫1), and Υmin(𝒫2) denote the eigenvalues of 𝒫1 and 𝒫2 and,

𝒦𝒫3=Υmax(𝒫3)Υmin(𝒫3),𝒦𝒫4=Υmax(𝒫4)Υmin(𝒫4),

where Υmax(𝒫3), Υmax(𝒫4), Υmin(𝒫3), and Υmin(𝒫4) denote the eigenvalues of 𝒫3 and 𝒫4.

By using the theorem 2 from [41], we can conclude that 𝒫 is a positive matrix. Therefore,

𝒱˙1(3)≤Γmax2(Sv)2(εv)Tεv+q22Γmax2(Sv−1)ξTξ−q2Γ𝒫(εv)Tεv+Γmax2(Sp)2(εp)Tεp+r22Γmax2(Sp−1)ξTξ−r2Γ𝒫(εp)Tεp.(26)

Now combining the Eqs. (14), (15), (24), (25) and (26), and using in (20), we conclude that,

𝒱˙1≤∑i∈N1Λi(χi(k)Ni+1)gi(k)σ˙i−∑i∈Nξidi2(k)−∑i∈NiξiGiTδi(y¯0)−∑i∈NiξiGiTδi(y¯v0)−∑i∈NiξiGiTδi(y¯a0)−∑i∈NiξiFMitanh⁡(ξiFMiΦ(k))−∑i∈Niξitanh⁡(GiξΦ(k))+∑i∈z2|ξi|Gi+∑i∈N|ξi|FMi+12μmaxξT𝒦2ξδvξ+12μmaxξTεv−1ξ2+μmaxαξT𝒦ξδvεv−1ℰ−μmaxξT𝒦ξδpεp−1ℰ+αξTξΥ2εv−1Υεp−1+12α2Υ4εv−1Υ2εp−1+12α2(sp)Tsp+Υ2εp−12(sp)Tsp+(2Υ2εv−1ξTξ−αΥ𝒫(sp)Tsp)(27)