 Open Access
Open Access
ARTICLE
An Improved Interval-Valued Picture Fuzzy TOPSIS Approach Based on New Divergence Measures for Risk Assessment
1 Department of Applied Mathematics and Statistics, Johns Hopkins University, Baltimore, MD 21218, USA
2 Cw Chu College, Jiangsu Normal University, Xuzhou, 221116, China
3 Department of Computer Science, College of Computer Science, King Khalid University, Abha, 62521, Saudi Arabia
4 Symbiosis Institute of Technology, Hyderabad Campus, Symbiosis International (Deemed University), Pune, 412115, India
5 Jadara Research Center, Jadara University, Irbid, 21110, Jordan
6 College of Mathematics and Computer, Xinyu University, Xinyu, 338004, China
7 School of Computer Sciences, Universiti Sains Malaysia, Penang, 11800, Malaysia
* Corresponding Authors: Prasanalakshmi Balaji. Email: ; Zhe Liu. Email:
(This article belongs to the Special Issue: Algorithms, Models, and Applications of Fuzzy Optimization and Decision Making)
Computer Modeling in Engineering & Sciences 2025, 144(2), 2099-2121. https://doi.org/10.32604/cmes.2025.068734
Received 05 June 2025; Accepted 18 July 2025; Issue published 31 August 2025
Abstract
While interval-valued picture fuzzy sets (IvPFSs) provide a powerful tool for modeling uncertainty and ambiguity in various fields, existing divergence measures for IvPFSs remain limited and often produce counterintuitive results. To address these shortcomings, this paper introduces two novel divergence measures for IvPFSs, inspired by the Jensen-Shannon divergence. The fundamental properties of the proposed measures—non-degeneracy, symmetry, triangular inequality, and boundedness—are rigorously proven. Comparative analyses with existing measures are conducted through specific cases and numerical examples, clearly demonstrating the advantages of our approach. Furthermore, we apply the new divergence measures to develop an enhanced interval-valued picture fuzzy TOPSIS method for risk assessment in construction projects, showing the practical applicability and effectiveness of our contributions.Keywords
Uncertainty and imprecision are standard daily, especially during decision-making processes [1,2]. There has been a growing interest in recent years in how to deal with uncertainty and imprecision across multiple applications [3–5]. Over time, a wide range of classical theories has been extensively studied, for example, fuzzy set theory [6–8], Z-numbers [9], rough set theory [10], and R-numbers [11]. One significant contribution is Zadeh’s [12] introduction of fuzzy sets (FSs), which have since gained widespread attention in addressing ambiguous and imprecise information. Later, researchers applied fuzzy set theory in numerous domains, including decision-making, image processing, and control systems [13–15]. Based on this, Atanassov [16] proposed intuitionistic fuzzy sets (IFSs), which integrate membership, non-membership, and hesitation degrees to handle uncertainty precisely. This approach provides a flexible framework for representing ambiguous data and has been effectively employed in areas like multi-criteria decision-making (MCDM) [17–20]. For example, to enhance ranking stability and better reflect user preferences in e-commerce decision-making, Kizielewicz et al. [21] proposed the FN-MABAC method integrates fuzzy normalization to mitigate ranking reversals and improve alignment with reference rankings. Later, Atanassov [22] introduced interval-valued intuitionistic fuzzy sets (IvIFSs). IvIFSs use interval values for membership and non-membership, defined by their respective lower and upper bounds. This enables a flexible representation of uncertainty, making IvIFS helpful in solving various problems [23,24]. Then, Cuong and Kreinovich [25] introduced picture fuzzy sets (PFSs) to extend classical fuzzy set theory by incorporating a neutral membership degree alongside positive and negative memberships, thereby enabling a better representation of uncertainty or indecision. PFSs, with their four degrees-positive, negative, neutral, and refusal-are particularly useful in decision-making scenarios that involve ambiguity, such as medical diagnostics and personnel evaluations [26–29].
Although PFSs improve the ability to manage uncertainty, they still depend on exact membership values. This can be a limitation in complex situations where uncertainty changes or the information is unclear. Therefore, Cuong and Kreinovich [30] introduced interval-valued picture fuzzy sets (IvPFSs), a significant development of PFSs. IvPFSs address the limitations of fixed membership degrees in the original PFS framework. It represents positive, negative, neutral, and refusal membership degrees as intervals instead of single values, offering a more flexible and comprehensive approach. This adjustment considers the natural variability and uncertainty in real-world decisions. The interval values in IvPFSs make it easier to model uncertainty more accurately, especially in applications like risk assessment, medical diagnosis, and construction decision-making, where data are often not exact and range within specific ranges [31,32]. Researchers [33–36] have developed various measures to enhance the applicability of IvPFSs. Khalil et al. [37] introduced novel operations and addressed related decision-making challenges. Ma et al. [38] combined IvPFS with an MCDM process to effectively evaluate design concepts under uncertainty, using an integrated approach with entropy weighting and an extended TOPSIS method.
The exploration of divergence measures has played a crucial role in developing fuzzy sets and has drawn extensive interest [39,40]. Many researchers have developed measures for IFSs and PFSs. For instance, Hatzimichilidis et al. [41] introduced matrix norms and fuzzy implications for IFSs. Jiang et al. [42] proposed an IFS distance method and validated its effectiveness through clustering. Wu et al. [43] proposed an important intuitionistic fuzzy distance measure based on Jensen-Shannon (JS) divergence, enhancing the ability to distinguish and rank IFSs. Singh et al. [44] developed a range of distance measures on PFSs with adjustable parameters, including the normalized Hamming, Euclidean, and Hausdorff distances. Yuan et al. [45] introduced a JS divergence-based distance measure for PFSs with a maximum deviation approach for alternative ranking. Zhu et al. [46] introduced two distance measures on PFSs based on JS divergence. However, these works did not extend the fuzzy numbers to interval values. Thus, several distance or divergence measures have been specifically created for IvIFSs and IvPFSs. Xu and Chen [47] provided enhanced IvIFSs with weighted and geometric distance models. Gohain et al. [48] proposed an optimistic distance measure for IvIFSs with cross-time information and applied it to clustering tasks in engineering problems. Mishra et al. [49] introduced a novel divergence measure for IvIFSs and proposed a vehicle insurance solution. Zhu and Liu [50] developed novel distance metrics for PFSs and IvPFSs using Hellinger distance and showed superior performance. Khan et al. [51] combined IvPFSs and hypergraphs to evaluate their role in enhancing processes. While these methods have demonstrated differing degrees of effectiveness, some limitations remain:
• There is a significant gap in divergence measures for IvPFSs, with limited research and scarce literature available on this topic.
• Several existing distance measures for IvPFSs fail to satisfy the basic axioms.
• Certain established measures produce inconsistent or unforeseen outcomes when evaluating the differences between diverse IvPFSs.
The work presents two novel measures for IvPFSs, intending to resolve the limitations of existing methods and the significant gap for IvPFSs. The key contributions can be summarized in four aspects:
• We propose two new JS divergence measures for IvPFSs.
• We prove that the introduced measures satisfy the fundamental principles that define divergence measures.
• We introduce divergence measures that can efficiently solve and correct the counterintuitive results observed in some instances with existing measures.
• We propose an improved interval-valued picture fuzzy TOPSIS approach based on new divergence measures for risk assessment in construction projects.
The structure of this manuscript is illustrated in Fig. 1. Section 2 gives the fundamental concepts. In Section 3, two novel distance measures based on Jensen-Shannon divergence for IvPFSs are introduced with comprehensive proofs and derivations. Section 4 conducts various numerical analyses to assess proposed measures in comparison to existing ones, using diverse case studies. Section 5 implements the TOPSIS method within the context of a construction risk assessment challenge, culminating in significant findings and recommendations for future research in risk evaluation. Finally, Section 6 provides the conclusions and prospective future work.
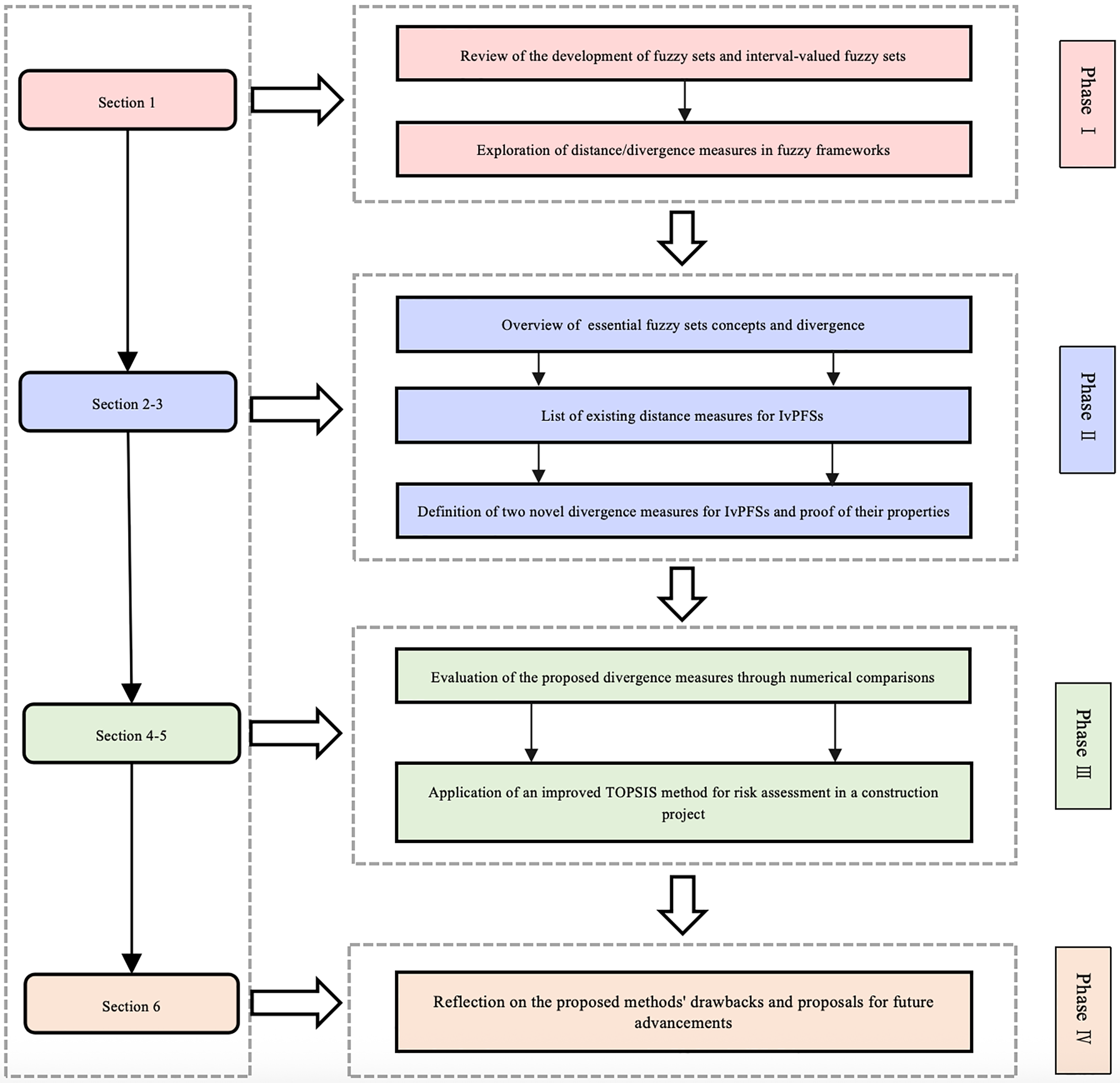
Figure 1: The flow chart of the whole work
This section will present some essential concepts and review several existing distance measures.
2.1 Basic Concepts of Fuzzy Sets
Definition 1 ([12]). Consider a universe of discourse (UOD)
where
Definition 2 ([16]). An intuitionistic fuzzy set (IFS) in
where
Definition 3 ([22]). An interval-valued intuitionistic fuzzy set (IvIFS) in X is defined as follows:
where
Definition 4 ([25]). A picture fuzzy set (PFS) in X is defined as follows:
where
Definition 5 ([30]). An interval-valued picture fuzzy set (IvPFS) in X is defined as follows:
where
2.2 The Existing Distance Measures for IvPFSs
To showcase the advantages of the distance measure proposed in this paper, this subsection will first present current distance measures in Table 1 and compare them with the proposed measure, highlighting their limitations in Section 4.
The Jensen-Shannon (JS) divergence finds extensive applications in areas such as machine learning and information theory for comparing different probability distributions.
Definition 6. Let
where the entropy
3 New Divergence Measure for IvPFSs
This section presents two new divergence measures for IvPFSs from the Jensen-Shannon divergence.
Definition 7. Let
Definition 8. Assume
Definition 9. The normalized distance based on the Jensen-Shannon divergence between IvPFSs
Specifically, we define that when
Remark: The divergence values from our proposed Jensen-Shannon-based measures for IvPFSs possess interpretable informational significance. Specifically, the JS divergence quantifies the dissimilarity between two IvPFSs by evaluating the average information gain when one distribution is used to approximate another. For IvPFSs, this means that the divergence score reflects the cumulative uncertainty difference across all interval-valued membership components (i.e., positive, negative, neutral, and refusal).
A divergence value close to 0 indicates that the two IvPFSs exhibit highly similar uncertainty structures. In contrast, values closer to 1 imply substantial differences in their interval-based representations of membership and hesitation. Geometrically, these measures correspond to the “distance” between interval-valued vectors in a normalized probabilistic space, accounting for both the position and spread of the intervals.
Property 1. Let
1.
2.
3.
4.
We illustrate the validity of the above axiom by taking
Proof: Given
Then, we can obtain
Likewise, if
Hence, it can be deduced that
Therefore, we can prove that
Proof: We know that
As a result, we can obtain
Proof: Four assumptions are proposed:
• Assumption 1:
• Assumption 2:
• Assumption 3:
• Assumption 4:
From Assumption 1, we can prove that
Given this Assumption 2, the proof is structured as follows:
The proof under Assumption 3 is as follows:
Obviously, it is known that
The proof based on Assumption 4 is given below:
Likewise, it can be shown that
In conclusion, under these four assumptions, we have proven that
By the same reasoning, it follows that
Hence, it can be seen that
Proof: Suppose that
For each
When n = 1, it is defined as
where
Therefore, it is proven that
This section shows four numerical examples to demonstrate the introduced divergence measures.
Example 1. Consider three IvPFSs
We can compute the divergence measures between these IvPFSs as follows:
These results demonstrate that both divergence measures,
Example 2. Consider three interval-valued Picture fuzzy sets (IvPFSs)
The computed divergence measures between these IvPFSs are as follows:
These results satisfy the triangular inequality property:
demonstrating that both divergence measures,
Example 3. For each


The findings shown in Table 3 and illustrated in Fig. 2 indicate that the two proposed divergence measures for IvPFSs are particularly effective at distinguishing between different scenarios. However, in scenarios with highly similar instances, such as between

Figure 2: The comparison between existing measures and proposed measures in example 3
Example 4. Consider three known patterns

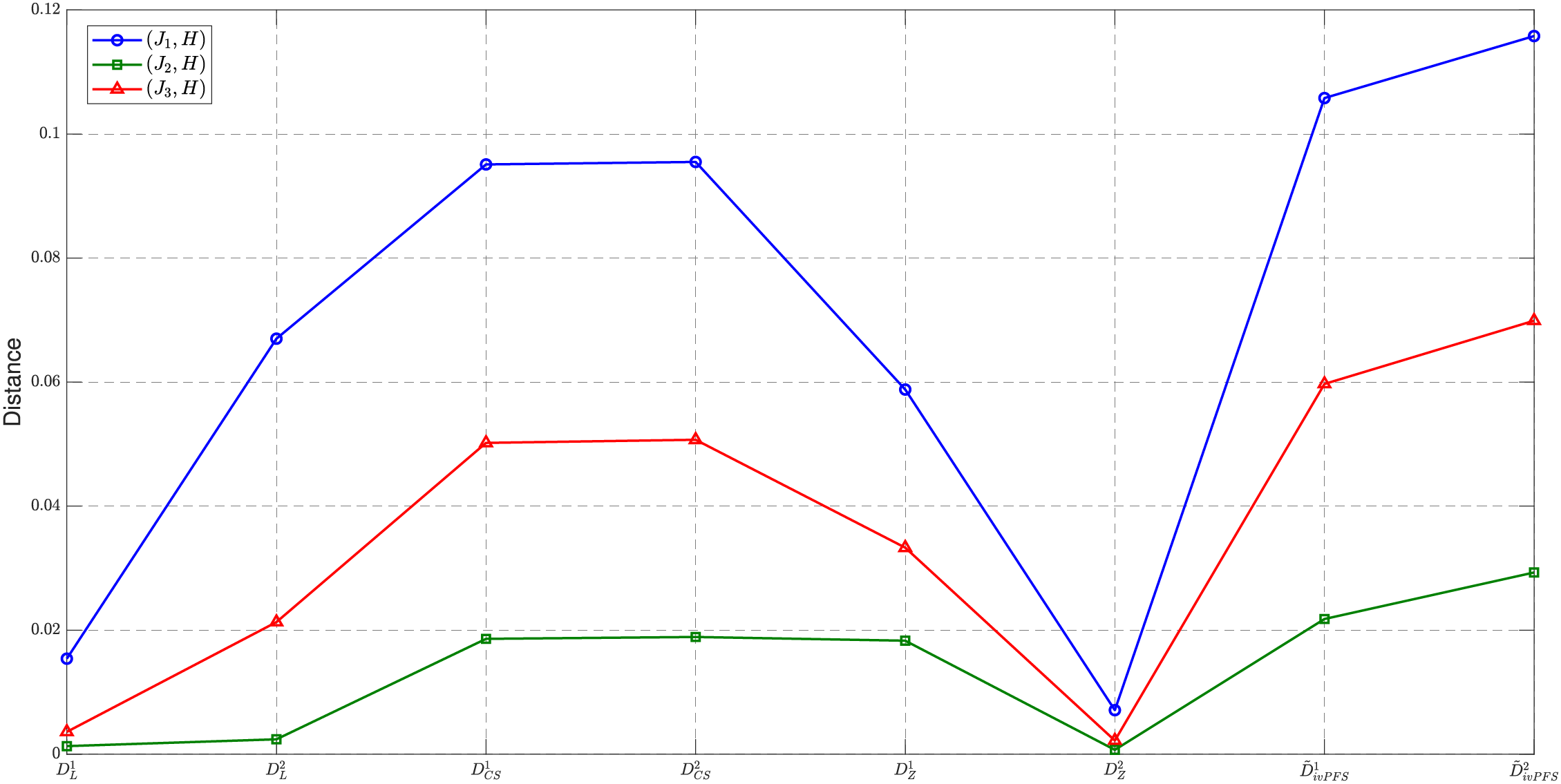
Figure 3: The comparison between existing measures and proposed measures in example 4
Based on the results presented in Table 4, the following conclusion can be drawn: across all measures (
The divergence scores reflect the degree of dissimilarity between
It is important to note their practical application. For instance, the IvPFSs in Example 3 and Example 4 can be viewed as abstract representations of expert evaluations in real-world scenarios, such as engineering risk levels, patient symptoms, or environmental assessments. Each component of the IvPFS corresponds to the interval-valued judgment on positive, negative, or neutral aspects of an alternative. Consequently, smaller divergence values indicate higher consistency in expert opinions or higher similarity in attributes.
In this section, we will introduce an improved TOPSIS for a risk assessment in a construction project.
5.1 The Improved TOPSIS Approach
TOPSIS is a method used in MCDM to determine the optimal solution from multiple options. Its basic principle is to evaluate each option by comparing it with a positive ideal solution (PIS) and a negative ideal solution (NIS). Our improved TOPSIS method for IvPFSs is as follows:
• Step 1: Define the performance of each alternative
• Step 2: Based on the nature of each criterion, determine the PIS and NIS by selecting the maximum and minimum spherical fuzzy values for each criterion:
Generally,
• Step 3: Calculate the separation of each alternative from the PIS and NIS, then generate the separation measures
• Step 4: For each alternative
• Step 5: Determine the weight of each criterion
• Step 6: Rank the alternatives based on their relative closeness and select the one with the highest closeness as the optimal alternative.
5.2 Risk Assessment in Construction Project
A construction company managing multiple projects wants to assess risks to ensure safety, profitability, and smooth operations. Because each project presents unique challenges, it is critical to systematically identify, evaluate, and prioritize risks. Proper risk assessment helps the company allocate resources efficiently and take preventive measures to mitigate potential threats.
The process accounts for uncertainty and incorporates objective and subjective judgments from stakeholders, including project managers, safety inspectors, financial analysts, and environmental experts.
The company evaluates four major ongoing projects:
•
•
•
•
The risk evaluation considers the following essential criteria:
•
•
•
•
•
5.2.2 Modeling Assumptions and Data Preparation
In construction risk assessment, uncertainty frequently arises from fluctuating environmental, financial, and operational factors. To effectively capture this uncertainty, expert judgments on key risk indicators—such as cost overrun, schedule delay, and safety violations—are collected using linguistic terms.
Each alternative (i.e., construction project plan) is evaluated across five criteria within this IvPFS framework. To ensure logical consistency and model validity, a fuzzy consistency check is performed, and all fuzzy evaluations are normalized to satisfy the IvPFS constraint as mentioned in Section 2.
The improved TOPSIS method proposed in this study incorporates the new divergence measures to provide a robust means of ranking alternatives by their proximity to the optimal risk profile under uncertain conditions. By integrating expert knowledge with fuzzy modeling of uncertainty, the proposed approach supports comprehensive, reliable decision-making and helps stakeholders prioritize risk mitigation strategies effectively.
5.2.3 Detailed Calculation Example
Let us consider our proposed divergence measure
• Step 1: To construct the decision matrix
• Step 2: These criteria of credit risk evaluation
• Step 3: Compute the separation measures by using Eqs. (13) and (14). Using our proposed measures, we calculate the distance for risk assessment in a construction project.
• Step 4: Form the composite spherical fuzzy distance matrix
• Step 5: Compute the weighted IvSFS divergence measures for each alternative according to Eq. (16). The weights assigned to each criterion are given by
• Step 6: The alternatives are ranked according to their relative closeness to PIS. Based on the weighted IvSFS divergence measures of each alternative, denoted as
The results, shown in Table 5 and Fig. 4, reveal the ranking of alternatives to the ideal solution as follows:
– First:
– Second:
– Third:
– Fourth:


Figure 4: The most sustainable transport system selection result
Based on the analysis, commercial office construction is identified as the best option for a low-risk, sustainable, and profitable construction project. It offers an ideal balance of critical criteria, making it the most suitable choice to achieve the project’s safety goals, cost-effectiveness, regulatory compliance, environmental friendliness, and technical feasibility.
This paper presents two divergence measures for IvPFSs by the Jensen-Shannon divergence, to overcome the limitations of existing measures. These proposed measures have completed comprehensive validation and meet all required axioms, which ensure a robust and consistent approach to measuring distance in an interval-valued fuzzy environment. The proposed divergence measures enhance accuracy and reliability in construction project risk assessment by capturing subtleties overlooked by previous methods. Its application in ranking project risks has shown promising results, supporting better decision-making for safety and efficiency in real-world scenarios. In future work, we intend to extend the proposed divergence measure to complex interval-valued picture fuzzy sets (CIvPFSs) to improve the flexibility of fuzzy sets in evaluating risks in construction projects. This extension aims to broaden its applicability, providing a more comprehensive framework for addressing uncertainties and capturing complex risk factors in construction and other critical decision-making environments. Additionally, we aim to explore the development of an improved interval-valued picture fuzzy FN-MABAC model that incorporates the proposed divergence measures. Given FN-MABAC’s strong resistance to rank reversal and its ability to reflect decision-maker preferences, integrating it with our divergence framework may further improve ranking accuracy and robustness.
Acknowledgement: The authors would like to express their gratitude to King Khalid University, Saudi Arabia, for providing administrative and technical support.
Funding Statement: The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Small Research Project under grant number RGP1/141/46.
Author Contributions: Conceptualization, Zhe Liu; methodology, Zhe Liu; software, Sijia Zhu; validation, Sijia Zhu, Yuhan Li and Akila Thiyagarajan; formal analysis, Yuhan Li, Akila Thiyagarajan and Rajanikanth Aluvalu; investigation, Sijia Zhu and Prasanalakshmi Balaji; resources, Prasanalakshmi Balaji and Zhe Liu; writing—original draft preparation, Sijia Zhu and Yuhan Li; writing—review and editing, Prasanalakshmi Balaji, Akila Thiyagarajan, Rajanikanth Aluvalu and Zhe Liu; visualization, Sijia Zhu, Yuhan Li and Rajanikanth Aluvalu; supervision, Zhe Liu; project administration, Prasanalakshmi Balaji and Akila Thiyagarajan; funding acquisition, Prasanalakshmi Balaji. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data information is included in this paper.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Liu Z, Letchmunan S. Enhanced fuzzy clustering for incomplete instance with evidence combination. ACM Trans Knowl Discov Data. 2024;18(3):1–20. doi:10.1145/3638061. [Google Scholar] [CrossRef]
2. Liu Z. A new sine similarity measure based on evidence theory for conflict management. Commun Stat Theory Methods. 2025;54(11):3350–66. doi:10.1080/03610926.2024.2391415. [Google Scholar] [CrossRef]
3. Barandas M, Famiglini L, Campagner A, Folgado D, Simão R, Cabitza F, et al. Evaluation of uncertainty quantification methods in multi-label classification: a case study with automatic diagnosis of electrocardiogram. Inf Fusion. 2024;101(3):101978. doi:10.1016/j.inffus.2023.101978. [Google Scholar] [CrossRef]
4. Liu Z, Qiu H, Letchmunan S, Deveci M, Abualigah L. Multi-view evidential c-means clustering with view-weight and feature-weight learning. Fuzzy Sets Syst. 2025;498(12):109135. doi:10.1016/j.fss.2024.109135. [Google Scholar] [CrossRef]
5. Alreshidi NA, Shah Z, Khan MJ. Similarity and entropy measures for circular intuitionistic fuzzy sets. Eng Appl Artif Intell. 2024;131(10):107786. doi:10.1016/j.engappai.2023.107786. [Google Scholar] [CrossRef]
6. Fahmi A, Hassan MAS, Khan A, Abdeljawad T, Almutairi DK. A bipolar Fermatean fuzzy Hamacher approach to group decision-making for electric waste. Eur J Pure Appl Math. 2025;18(1):5691–1. doi:10.29020/nybg.ejpam.v18i1.5691. [Google Scholar] [CrossRef]
7. Fahmi A, Khan A, Maqbool Z, Abdeljawad T. Circular intuitionistic fuzzy Hamacher aggregation operators for multi-attribute decision-making. Sci Rep. 2025;15(1):5618. doi:10.1038/s41598-025-88845-0. [Google Scholar] [PubMed] [CrossRef]
8. Fahmi A, Khan A, Abdeljawad T, Hassan MAS, Almutairid DK. Einstein aggregation operators with cubic Fermatean fuzzy sets. Eur J Pure Appl Math. 2025;18(2):5891. doi:10.29020/nybg.ejpam.v18i2.5891. [Google Scholar] [CrossRef]
9. Chu J, Xiao X. Benefits evaluation of the Northeast Passage based on grey relational degree of discrete Z-numbers. Inf Sci. 2023;626(4):607–25. doi:10.1016/j.ins.2023.02.085. [Google Scholar] [CrossRef]
10. Song Y, Lin H, Li Z. Outlier detection in a multiset-valued information system based on rough set theory and granular computing. Inf Sci. 2024;657(1):119950. doi:10.1016/j.ins.2023.119950. [Google Scholar] [CrossRef]
11. Cheng R, Fan J, Wu M, Seiti H. A dual-level multi-attribute group decision-making model considering interaction factors based on CCSD and MARCOS methods with R-numbers. Expert Syst Appl. 2024;243(20):122839. doi:10.1016/j.eswa.2023.122839. [Google Scholar] [CrossRef]
12. Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53. doi:10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
13. Jebadass JR, Balasubramaniam P. Color image enhancement technique based on interval-valued intuitionistic fuzzy set. Inf Sci. 2024;653:119811. doi:10.1016/j.ins.2023.119811. [Google Scholar] [CrossRef]
14. Ferreira MA, Ribeiro LC, Schuffner HS, Libório MP, Ekel PI. Fuzzy-set-based multi-attribute decision-making, its computing implementation, and applications. Axioms. 2024;13(3):142. doi:10.3390/axioms13030142. [Google Scholar] [CrossRef]
15. Kizielewicz B, Sałabun W. Benchmark study of re-identification methods based on stochastic fuzzy normalization and their application to decision-making problems in engineering. Facta Univ Ser Mech Eng. 2025;23(1):145–60. doi:10.22190/FUME240123008K. [Google Scholar] [CrossRef]
16. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi:10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
17. Dutta D, Dutta P, Gohain B. Similarity measure on intuitionistic fuzzy sets based on Benchmark Line and its diverse applications. Eng Appl Artif Intell. 2024;133(2):108522. doi:10.1016/j.engappai.2024.108522. [Google Scholar] [CrossRef]
18. Ejegwa PA, Onyeke IC, Kausar N, Kattel P. A new partial correlation coefficient technique based on intuitionistic fuzzy information and its pattern recognition application. Int J Intell Syst. 2023;38(1):5540085. doi:10.1155/2023/5540085. [Google Scholar] [CrossRef]
19. Wang T, Wu X, Garg H, Liu Q. Novel strict intuitionistic fuzzy similarity measures based on fuzzy negation and their applications. Expert Syst Appl. 2024;252(1):124192. doi:10.1016/j.eswa.2024.124192. [Google Scholar] [CrossRef]
20. Mahmood T, Ahmmad J, Ali Z, Yang M-S. Confidence level aggregation operators based on intuitionistic fuzzy rough sets with application in medical diagnosis. IEEE Access. 2023;11(12):8674–88. doi:10.3390/sym14122537. [Google Scholar] [CrossRef]
21. Kizielewicz B, Wiȩckowski J, Sałabun W. Fuzzy normalization-based multi-attributive border approximation area comparison. Eng Appl Artif Intell. 2025;141(1):109736. doi:10.1016/j.engappai.2024.109736. [Google Scholar] [CrossRef]
22. Atanassov KT. Operators over interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994;64(2):159–74. doi:10.1016/0165-0114(94)90331-x. [Google Scholar] [CrossRef]
23. Malik M, Gupta SK. On basic arithmetic operations for interval-valued intuitionistic fuzzy sets using the Hamming distance with their application in decision making. Expert Syst Appl. 2024;239(3):122429. doi:10.1016/j.eswa.2023.122429. [Google Scholar] [CrossRef]
24. Kalsoom U, Ullah K, Akram M, Pamucar D, Senapati T, Naeem M, et al. Schweizer-Sklar power aggregation operators based on complex interval-valued intuitionistic fuzzy information for multi-attribute decision-making. Int J Comput Intell Syst. 2023;16(1):170. doi:10.1007/s44196-023-00343-1. [Google Scholar] [CrossRef]
25. Cuong BC, Kreinovich V. Picture fuzzy sets—a new concept for computational intelligence problems. In: 2013 Third World Congress on Information and Communication Technologies (WICT 2013); 2013 Dec 15–18; Hanoi, Vietnam. p. 1–6. doi:10.1109/wict.2013.7113099. [Google Scholar] [CrossRef]
26. Luo M, Zhang G. Divergence-based distance for picture fuzzy sets and its application to multi-attribute decision-making. Soft Comput. 2024;28(1):253–69. doi:10.1007/s00500-023-09205-6. [Google Scholar] [CrossRef]
27. Kahraman C. Proportional picture fuzzy sets and their AHP extension: application to waste disposal site selection. Expert Syst Appl. 2024;238(3):122354. doi:10.1016/j.eswa.2023.122354. [Google Scholar] [CrossRef]
28. Singh A, Kumar S. Picture fuzzy set and quality function deployment approach based novel framework for multi-criteria group decision making method. Eng Appl Artif Intell. 2021;104(6):104395. doi:10.1016/j.engappai.2021.104395. [Google Scholar] [CrossRef]
29. Devi NSK, Narayanamoorthy S, Nallasivan Parthasarathy T, Thilagasree CS, Pamucar D, Simic V, et al. An integrated bipolar picture fuzzy decision-driven system to scrutinize food waste treatment technology through assorted factor analysis. Comput Model Eng Sci. 2024;140(3):2665–87. doi:10.32604/cmes.2024.029374. [Google Scholar] [CrossRef]
30. Cuong BC, Kreinovich V. Picture fuzzy sets. J Comput Sci Cybern. 2014;30(4):409–20. doi:10.15625/1813-9663/30/4/5032. [Google Scholar] [CrossRef]
31. Kishorekumar M, Karpagadevi M, Krishnaprakash S, Mariappan R, Ramesh R. Interval-valued picture fuzzy topological spaces and application of interval-valued picture fuzzy sets in multi-criteria decision-making. In: AIP Conference Proceedings. Melville, NY, USA: AIP Publishing; 2024. Vol. 3122. p. 1–6. doi:10.1063/5.0216036. [Google Scholar] [CrossRef]
32. Zhu S, Liu Z, Ulutagay G, Deveci M, Pamučar D. Novel α-divergence measures on picture fuzzy sets and interval-valued picture fuzzy sets with diverse applications. Eng Appl Artif Intell. 2024;136(12):109041. doi:10.1016/j.engappai.2024.109041. [Google Scholar] [CrossRef]
33. Amanathulla S, Khatun J. Multiple attribute decision making problem using interval-valued picture fuzzy graphs. J Fuzzy Ext Appl. 2025;6(2):284–99. doi:10.22105/jfea.2025.397502.1298. [Google Scholar] [CrossRef]
34. Khan WA, Zahid A, Rashmanlou H. Novel concepts of strong paired domination in interval-valued picture fuzzy graphs and their applications towards selection criteria. J Appl Math Comput, 2024:1–29. doi:10.1007/s12190-024-02101-9. [Google Scholar] [CrossRef]
35. Shanthi SA, Gayathri M. Efficiency of eco-friendly construction materials in interval-valued picture fuzzy soft environment. In: Recent developments in algebra and analysis. Cham, Switzerland: Birkhäuser; 2024. p. 245–54. doi:10.1007/978-3-031-37538-5_24. [Google Scholar] [CrossRef]
36. Gul R, Sarfraz M. Enhancing artificial intelligence models with interval-valued picture fuzzy sets and Sugeno-Weber triangular norms. Spectrum Eng Manag Sci. 2025;3(1):126–46. doi:10.1234/sem.2025.0301126. [Google Scholar] [CrossRef]
37. Khalil AM, Li S-G, Garg H, Li H, Ma S. New operations on interval-valued picture fuzzy set, interval-valued picture fuzzy soft set and their applications. IEEE Access. 2019;7:51236–53. doi:10.1109/access.2019.2910844. [Google Scholar] [CrossRef]
38. Ma Q, Sun H, Chen Z, Tan Y. A novel MCDM approach for design concept evaluation based on interval-valued picture fuzzy sets. PLoS One. 2023;18(11):e0294596. doi:10.1371/journal.pone.0294596. [Google Scholar] [PubMed] [CrossRef]
39. Ejegwa PA, Anum MT, Kausar N, Nwokoro CO, Aydin N, Yu H. New Fermatean fuzzy distance metric and its utilization in the assessment of security crises using the MCDM technique. Math. 2024;12(20):3214. doi:10.3390/math12203214. [Google Scholar] [CrossRef]
40. Mishra AR, Chen S-M, Rani P. Multi-attribute decision-making based on picture fuzzy distance measure-based relative closeness coefficients and modified combined compromise solution method. Inf Sci. 2024;664(6):120325. doi:10.1016/j.ins.2024.120325. [Google Scholar] [CrossRef]
41. Hatzimichailidis AG, Papakostas GA, Kaburlasos VG. A novel distance measure of intuitionistic fuzzy sets and its application to pattern recognition problems. Int J Intell Syst. 2012;27(4):396–409. doi:10.1002/int.21529. [Google Scholar] [CrossRef]
42. Jiang Q, Jin X, Lee S-J, Yao S. A new similarity/distance measure between intuitionistic fuzzy sets based on the transformed isosceles triangles and its applications to pattern recognition. Expert Syst Appl. 2019;116(1):439–53. doi:10.1016/j.eswa.2018.08.046. [Google Scholar] [CrossRef]
43. Wu X, Zhu Z, Chen S-M. Strict intuitionistic fuzzy distance/similarity measures based on Jensen-Shannon divergence. Inf Sci. 2024;661(6):120144. doi:10.1016/j.ins.2024.120144. [Google Scholar] [CrossRef]
44. Singh P, Mishra NK, Kumar M, Saxena S, Singh V. Risk analysis of flood disaster based on similarity measures in picture fuzzy environment. Afr Mat. 2018;29(7–8):1019–38. doi:10.1007/s13370-018-0597-x. [Google Scholar] [CrossRef]
45. Yuan J, Chen Z, Wu M. A novel distance measure and CRADIS method in picture fuzzy environment. Int J Comput Intell Syst. 2023;16(1):186. doi:10.1007/s44196-023-00354-y. [Google Scholar] [CrossRef]
46. Zhu S, Liu Z, Ur Rahman A. Novel distance measures of picture fuzzy sets and their applications. Arab J Sci Eng. 2024;49(9):12975–88. doi:10.1007/s13369-024-08925-7. [Google Scholar] [CrossRef]
47. Xu ZS, Chen J. An overview of distance and similarity measures of intuitionistic fuzzy sets. Int J Uncertain Fuzziness Knowl Based Syst. 2008;16(4):529–55. doi:10.1142/s0218488508005406. [Google Scholar] [CrossRef]
48. Gohain B, Chutia R, Dutta P. A distance measure for optimistic viewpoint of the information in interval-valued intuitionistic fuzzy sets and its applications. Eng Appl Artif Intell. 2023;119(1):105747. doi:10.1016/j.engappai.2022.105747. [Google Scholar] [CrossRef]
49. Mishra AR, Rani P, Pardasani KR, Mardani A, Stevi’c Ž, Pamučar D. A novel entropy and divergence measures with multi-criteria service quality assessment using interval-valued intuitionistic fuzzy TODIM method. Soft Comput. 2020;24(15):11641–11661. doi:10.1007/s00500-019-04627-7. [Google Scholar] [CrossRef]
50. Zhu S, Liu Z. Distance measures of picture fuzzy sets and interval-valued picture fuzzy sets with their applications. AIMS Math. 2023;8(12):29817–48. doi:10.3934/math.20231525. [Google Scholar] [CrossRef]
51. Khan WA, Arif W, Rashmanlou H, Kosari S. Interval-valued picture fuzzy hypergraphs with application towards decision making. J Appl Math Comput. 2024;70(2):1103–25. doi:10.1007/s12190-024-01996-7. [Google Scholar] [CrossRef]
52. Liu P, Munir M, Mahmood T, Ullah K. Some similarity measures for interval-valued picture fuzzy sets and their applications in decision making. Information. 2019;10(12):369. doi:10.3390/info10120369. [Google Scholar] [CrossRef]
53. Cao G, Shen L. A novel parameter similarity measure between interval-valued picture fuzzy sets with its application in pattern recognition. J Intell Fuzzy Syst. 2023;44(6):10213–39. doi:10.3233/JIFS-224314. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools