Auto-Weighted Neutrosophic Fuzzy Clustering for Multi-View Data

1  Introduction

As data continues to grow across diverse domains, it is often gathered from numerous heterogeneous sources or perspectives, each contributing unique and complementary information about the underlying structure. Multi-view datasets are ubiquitous, found in areas such as multimedia applications (e.g., image-text data), the Internet of Things (e.g., sensor readings), and healthcare (e.g., clinical records). These datasets consist of data from different sources, modalities, or feature sets that describe the same set of entities. Each view brings unique strengths and weaknesses and often differs in completeness, consistency, and relevance. Although widely applied in practice, algorithms such as k-means [1], fuzzy clustering [2], spectral [3], and hierarchical [4] tend to perform poorly when confronted with multi-view data [5].

To tackle the challenges posed by such heterogeneous data, multi-view clustering is now regarded as a powerful approach that jointly utilizes information from all available views so as to achieve better clustering results. In contrast to using a single view, multi-view clustering integrates complementary information across views, thereby improving data understanding and clustering accuracy. Among various strategies, partition-based hard clustering methods are widely adopted for their simplicity and computational efficiency. For example, Ref. [6] introduced a robust variant using the ℓ2,1 norm to improve noise resistance. A low-rank tensor regularized graph fuzzy learning (LRTGFL) algorithm was introduced in Ref. [7] to handle multi-view data. Subsequently, Ref. [8] proposed a two-level weighted k-means (TW-k-means) framework with feature weighting, and Ref. [9] further advanced this line of work through TW-Co-k-means, enabling joint optimization across different views. Ref. [10] enhanced k-means by incorporating multiple discriminative subspaces, especially for high-dimensional data. Ref. [11] applied nonnegative matrix factorization to discover latent views, and Ref. [12] introduced mixture correntropy to mitigate noise effects. In more recent studies, Ref. [13] presented the multi-view alternative hard c-means(MVAHCM) framework, which incorporates both global (MVAHCM-GW) and local (MVAHCM-LW) weighting schemes to characterize view importance. Subsequently, Ref. [14] made further progress by developing robust variants of multi-view clustering methods, improving stability and accounting for intra-view contributions in noisy environments. In addition, extensive research has been conducted on multi-view graph clustering [15–18], subspace clustering [19–22], and spectral clustering [23–26]. However, these hard clustering approaches assign each instance to a single cluster, lacking the flexibility to model uncertainty or overlapping area, an inherent limitation in many real-world scenarios.

In contrast, fuzzy clustering methods offer a more adaptive framework by allowing samples to be associated with several clusters at different membership levels, which is particularly suitable for ambiguous or overlapping area in multi-view contexts. Among them, fuzzy c-means (FCM) [27] is a foundational method. Various multi-view extensions of FCM [28,29] have been developed. WV-Co-FCM [30] introduced view-level weighting to overcome the limitation of treating all views equally. Co-FW-MVFCM [31] further incorporated both view and feature weighting to reduce redundancy. Then in [32], a novel multi-view picture fuzzy clustering is proposed that combines picture fuzzy sets and a dual-anchor graph method. Ref. [33] proposed MVASM, employing sparse fuzzy partitioning to effectively model inter-view consensus. Additionally, Ref. [34] extended fuzzy multi-view clustering into a federated setting for privacy-preserving distributed data analysis, and Ref. [35] improved robustness within multi-view fuzzy clustering, where exponential distance transformation is combined with adaptive weighting of views. Beyond FCM-based frameworks, other soft-based multi-view clustering methods [36,37] have also shown promise in addressing overlapping clusters and inter-view inconsistencies. Although these methods have significantly advanced the field, many still rely solely on either hard or fuzzy partition schemes, limiting their capability to capture the uncertainty and inconsistency often present in multi-view data.

To address such limitations, neutrosophic set theory (NST) has been increasingly applied to clustering. Ref. [38] first introduced the neutrosophic c-means (NCM) algorithm, which uses three membership degrees to better represent each sample’s affiliation. Subsequent advancements include kernelized NCM for nonlinear data [39], picture-neutrosophic trusted safe semi-supervised fuzzy clustering [40] and interval-valued NCM for robust clustering under uncertainty [41]. Nevertheless, traditional NCM algorithms are limited to single-view scenarios and thus cannot leverage complementary information from multiple views. To overcome this, we previously proposed two multi-view neutrosophic c-means (MVNCM) algorithms (sum-to-1 constraint and product-to-1 constraint), which incorporate view-level weighting into the NCM framework, allowing adaptive evaluation of view importance and better modeling of uncertainty in multi-view environments [42]. Furthermore, one advantage of the product-to-1 constraint is that there is no need to add additional parameter. Therefore, this paper will adopt the product-to-1 constraint.

We introduce a more granular and effective algorithm: auto-weighted multi-view neutrosophic fuzzy clustering (AW-MVNFC). The proposed algorithm not only adaptively learns view-level weights but also integrates feature-level weighting within each view, enabling a more refined representation of intra-view structure. AW-MVNFC is formulated as a unified optimization problem, simultaneously learning cluster prototypes, neutrosophic memberships, view weights, and feature weights. The main contributions are summarized as follows:

•   We propose a novel AW-MVNFC clustering algorithm that jointly models uncertainty and imprecision across multiple views.

•   A new auto-weighted strategy is introduced, incorporating feature-level importance learning within each view in addition to view-level weighting, thereby achieving finer-grained modeling of intra-view contributions.

•   Comprehensive experiments on both simulated and real-world datasets demonstrate that the proposed method consistently outperforms existing multi-view clustering techniques.

The structure of the study is outlined below. Section 2 gives an overview of NCM and MVNCM, Section 3 introduces the AW-MVNFC framework, Section 4 discusses the experimental findings, and Section 5 closes with the conclusions.

2  Related Work

In this section, we will take a brief review of NCM [38] and MVNCM [42].

2.1 Neutrosophic c-Means Clustering

Consider a multi-view dataset 𝒳={x1,x2,…,xN}, where each sample xi∈R𝒫. The dataset is clustered into c groups according to the discernment set Ω={ω1,…,ωc}. The NCM algorithm achieves this by minimizing the following objective function:

JNCM(T,I,F,V)=∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi−vj‖2+∑i=1N{ϖ2ℐi}β‖xi−vimax‖2+δ2∑i=1N{ϖ3ℱi}β∑j=1c𝒯ij+ℐi+ℱi=1,  0<𝒯ij,ℐi,ℱi<1(1)

with

vimax=vpi+vqi2(2)

pi=arg⁡maxj=1,⋯,c⁡(𝒯ij),  qi=arg⁡maxj≠pi∩j=1,⋯,c⁡(𝒯ij)(3)

where the terms 𝒯ij, ℐi, and ℱi represent the membership degrees of sample xi to the precise, boundary, and noise clusters, respectively. Cluster centers are indicated by vj, while vimax corresponds to the center of the boundary cluster linked to xi. The indices pi and qi denote the clusters with the highest and second-highest values of 𝒯. The parameter δ serves as a threshold for identifying outliers. Here, N and c indicate the total number of samples and clusters, respectively. The weighting factors are expressed as ϖ1, ϖ2, and ϖ3, and the exponent β holds the same definition as in the FCM method. The resulting cluster assignments are obtained according to the following equations:

•   Update neutrosophic partition matrix:

𝒯ij=1ϖ1𝒟(‖xi−vj‖2)−1β−1(4)

ℐi=1ϖ2𝒟(‖xi−vimax‖2)−1β−1(5)

ℱi=1ϖ3𝒟(δs)−2β−1(6)

where

𝒟=1ϖ1(∑j=1c‖xi−vj‖2)−1β−1+1ϖ2‖xi,s−vimax,s‖−2β−1+1ϖ3(δs)−2β−1(7)

•   Update view cluster centers matrix

vj=∑i=1N(ϖ1𝒯ij)βxi∑i=1N(ϖ1𝒯ij)β(8)

2.2 Multi-View Neutrosophic c-Means Clustering

Consider a multi-view dataset 𝒳={X1,X2,⋯,XS} to be segmented into c clusters within the framework Ω={ω1,…,ωc}. The s-th view of the dataset is represented as Xs={x1,s,x2,s,⋯,xN,s}, where xi,s∈R𝒫s. The MVNCM algorithm aims to minimize the following objective function:

JMVNCM(T,I,F,V,r)=∑s=1𝒮rs(∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,s−vj,s‖2+∑i=1N{ϖ2ℐi}β‖xi,s−vimax,s‖2+δs2∑i=1N{ϖ3ℱi}β)s.t.∑j=1c𝒯ij+ℐi+ℱi=1,  0<𝒯ij,ℐi,ℱi<1,  ∏s=1Srs=1(9)

with

vimax,s=vpi,s+vqi,s2(10)

pi=arg⁡maxj=1,⋯,c⁡(𝒯ij),  qi=arg⁡maxj≠pi∩j=1,⋯,c⁡(𝒯ij)(11)

where rs indicates the weight assigned to the s-th view. The membership degrees of sample xi to the precise, boundary (imprecise), and noise clusters are denoted by 𝒯ij, ℐi, and ℱi, respectively. The center of the j-th cluster in view s is vj,s, and the center of the corresponding imprecise cluster for xi is vimax,s. The variables pi and qi identify the clusters with the maximum and second-maximum values of 𝒯. δ serves as a parameter for detecting outliers. 𝒮 means the number of views. The parameters ϖ1, ϖ2, ϖ3, and other terms follow the same definitions as in NCM. The clustering results are obtained through the following equations:

•   Update neutrosophic partition matrix:

𝒯ij=1ϖ1ℰij(∑s=1Srs‖xi,s−vj,s‖2)−1β−1(12)

ℐi=1ϖ2ℰij(∑s=1Srs‖xi,s−vimax,s‖2)−1β−1(13)

ℱi=1ϖ3ℰij(∑s=1Srsδs2)−1β−1(14)

where

ℰij=1ϖ1∑j=1c(∑s=1Srs‖xi,s−vj,s‖2)−1β−1+1ϖ2(∑s=1Srs‖xi,s−vimax,s‖2)−1β−1+1ϖ3(∑s=1Srsδs2)−1β−1(15)

•   Update cluster centers matrix

vj,s=∑i=1N(ϖ1𝒯ij)βxi,s∑i=1N(ϖ1𝒯ij)β(16)

•   Update view weights:

rs=(∏l=1S𝒢l)1S𝒢s(17)

where

𝒢s=∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,s−vj,s‖2+∑i=1N{ϖ2ℐi}β‖xi,s−vimax,s‖2+δs2∑i=1N{ϖ3ℱi}β(18)

3  A Novel Multi-View Clustering Algorithm

Although the previous work, MVNCM, adaptively learns view-level weights and achieves promising results, it is fundamentally limited by its inability to account for heterogeneity at the feature level. Real-world multi-view data often contains noisy, redundant, or irrelevant features within each view, which can significantly degrade clustering performance. To solve this critical limitation, we propose an improved algorithm, AW-MVNFC, which introduces a hierarchical dual-weighting strategy. For the first time, this algorithm integrates feature-level weighting into the neutrosophic clustering framework, enabling the algorithm to not only assess the importance of each view but also the relevance of individual features within that view. This finer-grained control allows for a more robust and effective clustering solution, especially in complex environments.

3.1 Objective Function

Given a multi-view dataset denoted by 𝒳={X1,X2,⋯,XS}, the goal is to partition it into c distinct clusters represented by Ω={ω1,…,ωc}. Each view s provides a representation Xs={x1,s,x2,s,⋯,xN,s}, where each sample xi,s lies in the feature space R𝒫s. The objective function of AW-MVNFC algorithm is shown as follows:

JAW−MVNFC(T,I,F,V,r,w)=∑s=1𝒮rs(∑i=1N∑j=1c∑o=1Os{ϖ1𝒯ij}βwo,s‖xi,o,s−vj,o,s‖2+∑i=1N∑o=1Os{ϖ2ℐi}βwo,s‖xi,o,s−vimax,o,s‖2+δs2∑i=1N∑o=1Os{ϖ3ℱi}β)s.t.∑j=1c𝒯ij+ℐi+ℱi=1,  0<𝒯ij,ℐi,ℱi<1,  ∏s=1Srs=1 ∏o=1Oswo,s=1(19)

with

vimax,o,s=vpi,o,s+vqi,o,s2(20)

pi=arg⁡maxj=1,⋯,c⁡(𝒯ij),  qi=arg⁡maxj≠pi∩j=1,⋯,c⁡(𝒯ij)(21)

Let rs denote the weight of the s-th view and wo,s the weight of the o-th feature in that view. For each sample xi, 𝒯ij, ℐi, and ℱi indicate membership to the precise, boundary (imprecise), and noise clusters, respectively. The cluster center corresponding to the j-th cluster, feature o, and view s is vj,o,s, while vimax,o,s denotes the center of the imprecise cluster for xi. The indices pi and qi identify the clusters with the largest and second-largest membership values. The parameter δ serves as a threshold for outlier detection. 𝒮 is the number of views and 𝒪s is the number of features in the s-th view. All constants, including ϖ1, ϖ2, ϖ3, β, follow the definitions in the original NCM framework.

3.2 Optimization

We follow the Lagrange multiplier method used in NCM [38] to optimize neutrosophic partition matrix, cluster centers, view weights matrix, and feature weights in turn. The following is the derivation process:

(1) Updating T, I, and F with fixed V, r, and w

Since the derivation process of this step is highly similar to the method in NCM, the proof process is omitted. We give the final optimization formula as follows:

𝒯ij=1ϖ1ℰij(∑s=1S∑o=1Osrswo,s‖xi,o,s−vj,o,s‖2)−1β−1(22)

ℐi=1ϖ2ℰij(∑s=1S∑o=1Osrswo,s‖xi,o,s−vimax,o,s‖2)−1β−1(23)

ℱi=1ϖ3ℰij(∑s=1Srsδs2)−1β−1(24)

where the normalizing term ℰij is defined as:

ℰij=1ϖ1∑j=1c(∑s=1S∑o=1Osrswo,s‖xi,o,s−vj,o,s‖2)−1β−1+1ϖ2(∑s=1S∑o=1Osrswo,s‖xi,o,s−vimax,o,s‖2)−1β−1+1ϖ3(∑s=1Srsδs2)−1β−1(25)

(2) Updating V with fixed T, I, F, r, and w

To minimize 𝒥AW−MVNFC with respect to vj,o,s, we take the partial derivative and set it to zero:

∂𝒥∂vj,o,s=−2∑i=1Nrs{ϖ1𝒯ij}βwo,s(xi,o,s−vj,o,s)=0(26)

Then we obtain:

vj,o,s=∑i=1N(ϖ1𝒯ij)βxi,o,s∑i=1N(ϖ1𝒯ij)β(27)

(3) Updating r while fixing T, I, F, V, and w

Lagrange multipliers μ are introduced to enforce the constraint ∑s=1Srs=1. The associated Lagrangian is defined as:

𝒥(r,μ)=𝒥AW−MVNFC(T,I,F,V,r,w)−μ(∏s=1Srs−1)(28)

To derive the necessary conditions, we set the partial derivatives of the Lagrangian function 𝒥 with respect to rs and the Lagrange multiplier μ to zero:

∂𝒥∂rs=∑i=1N∑j=1c∑o=1Os{ϖ1𝒯ij}βwo,s‖xi,o,s−vj,o,s‖2+∑i=1N∑o=1Os{ϖ2ℐi}βwo,s‖xi,o,s−vimax,o,s‖2+δs2∑i=1N{ϖ3ℱi}β−μrs=0(29)

∂𝒥∂μ=∏s=1Srs−1=0(30)

Thus, we obtain from (29):

rs=μ(∑i=1N∑j=1c∑o=1Os{ϖ1𝒯ij}βwo,s‖xi,o,s−vj,o,s‖2+∑i=1N∑o=1Os{ϖ2ℐi}βwo,s‖xi,o,s−vimax,o,s‖2+δs2∑i=1N{ϖ3ℱi}β)−1(31)

Using (30) and (31):

μ=[∏s=1S(∑i=1N∑j=1c∑o=1Os{ϖ1𝒯ij}βwo,s‖xi,o,s−vj,o,s‖2+∑i=1N∑o=1Os{ϖ2ℐi}βwo,s‖xi,o,s−vimax,o,s‖2+δs2∑i=1N{ϖ3ℱi}β)]1S(32)

Returning in (31), we have:

rs=(∏l=1S𝒢l)1S𝒢s(33)

where

𝒢s=∑i=1N∑j=1c∑o=1Os{ϖ1𝒯ij}βwo,s‖xi,o,s−vj,o,s‖2+∑i=1N∑o=1Os{ϖ2ℐi}βwo,s‖xi,o,s−vimax,o,s‖2+δs2∑i=1N{ϖ3ℱi}β(34)

(4) Updating w while fixing T, I, F, V, and r

The minimization of 𝒥AW-MVNFC with respect to wo,s constitutes an unconstrained optimization problem. To incorporate the normalization constraint on feature weights, we introduce the Lagrange multiplier σs and define the corresponding Lagrangian function as:

𝒥(w,σs)=𝒥AW−MVNFC(T,I,F,V,r,w)−σs(∏o=1Oswo,s−1)(35)

Then we set the derivatives of the Lagrangian function with respect to wo,s and σs to zero:

∂𝒥∂wo,s=rs(∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,o,s−vj,o,s‖2+∑i=1N{ϖ2ℐi}β‖xi,o,s−vimax,o,s‖2)−σswo,s=0(36)

∂𝒥∂σs=∏o=1Oswo,s−1=0(37)

Thus, we obtain:

wo,s=σsrs(∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,o,s−vj,o,s‖2+∑i=1N{ϖ2ℐi}β‖xi,o,s−vimax,o,s‖2)−1(38)

Using (37) and (38):

σs=rs[∏o=1Os(∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,o,s−vj,o,s‖2+∑i=1N{ϖ2ℐi}β‖xi,o,s−vimax,o,s‖2)]1Os(39)

Returning in (39), we have:

wo,s=(∏o=1Osℋo,s)1Osℋo,s(40)

where

ℋo,s=∑i=1N∑j=1c{ϖ1𝒯ij}β‖xi,o,s−vj,o,s‖2+∑i=1N{ϖ2ℐi}β‖xi,o,s−vimax,o,s‖2(41)

Fig. 1 and Algorithm 1 summarize AW-MVNFC algorithm in detail.

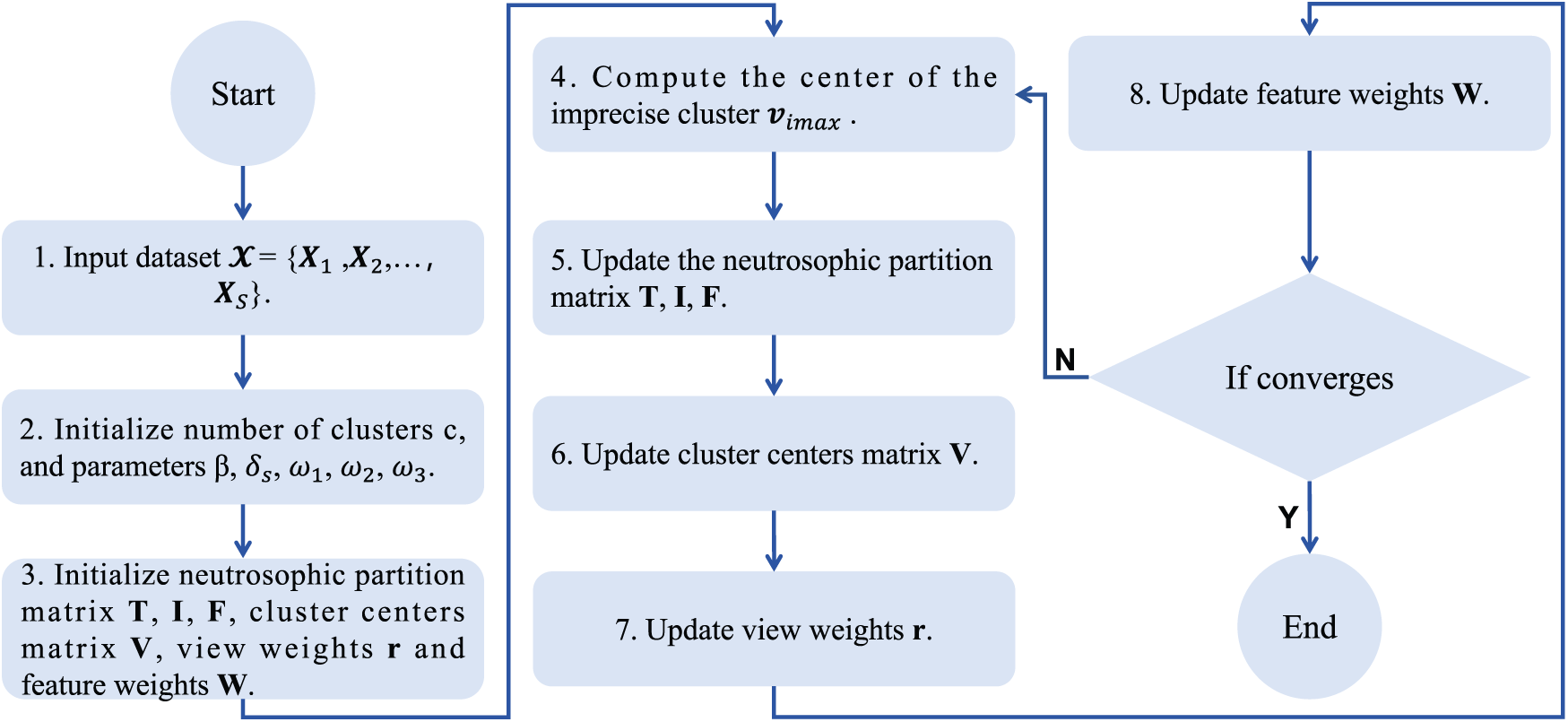
Figure 1: Flow diagram of AW-MVNFC

3.3 Computational Complexity Analysis

In this section, we provide a time complexity analysis for the AW-MVNFC algorithm, summarized in Algorithm 1. The computational bottleneck is associated with updating the neutrosophic partition matrix, which operates in 𝒪(𝒮⋅Os⋅N⋅(c+2)) time, where N, c, 𝒮, and Os denote the number of samples, clusters, views, and features, respectively. For t iterations, the overall complexity is 𝒪(t⋅𝒮⋅Os⋅N⋅(c+2)).

4  Experiment

4.1 Experimental Setting

For evaluation, the AW-MVNFC algorithm is benchmarked against nine contemporary multi-view clustering techniques: Co-FCM [30], WV-Co-FCM [30], TW-Co-k-means [9], Co-FW-MVFCM [31], MVASM [33], FedMVFCM [34], MVAHCM-GW [13], MVAHCM-LW [13], and MVNCM [42]. Specifically, TW-Co-k-means, MVAHCM-GW, and MVAHCM-LW represent hard-partition approaches, while Co-FCM, WV-Co-FCM, Co-FW-MVFCM, MVASM, and FedMVFCM correspond to soft-partition methods. MVNCM stands for neutrosophic clustering method and also represents a degenerate version of AW-MVNFC without considering feature weights.

The optimal parameters are determined via a grid-search procedure, based on achieving the maximum clustering performance. For the comparative algorithms mentioned above, the parameter search ranges and default configurations are set in accordance with the recommendations provided in their respective original papers. More precisely, the weighting exponent β is varied within the range of 1.1 to 2.0, incremented by 0.1, as part of the default parameter configuration. The weight factors ϖ1, ϖ2, and ϖ3 are fine-tuned within the discrete set {0.01, 0.02, …, 0.97, 0.98} to achieve optimal performance. The value of δs, which influences the assignment of samples to the noise cluster, is selected from the set {10−2,10−1,100,101,102}.

For a comprehensive assessment of AW-MVNFC and the comparative algorithms on multi-view data, we utilize six standard evaluation metrics: Accuracy (ACC), Normalized Mutual Information (NMI), Rand Index (RI), F1 score (F1), Fowlkes-Mallows Index (FMI), and Jaccard Index (JI). In general, larger values of these metrics correspond to better clustering performance.

4.2 Experimental Results on Synthetic Multi-View Datasets

To rigorously evaluate the effectiveness of AW-MVNFC, we construct a synthetic dataset (SD) and conduct a comparative analysis against eight representative multi-view clustering algorithms, comprising Co-FCM, WV-Co-FCM, TW-Co-k-means, MVASM, MVAHCM-GW, MVHACM-LW, and MVNCM. The assessment focuses on both hard and soft partitioning capabilities derived from the neutrosophic framework. Performance is quantitatively measured using the indices Re and Ri, with detailed results presented in the captions of each corresponding subfigure.

As illustrated in Fig. 2, we construct a synthetic dataset consisting of two distinct views, each comprising three clusters of unequal sizes, denoted as θ1, θ2, and θ3. Specifically, θ1 contains 2000 samples, θ2 includes 1500 samples, and θ3 comprises 1000 samples, where each sample is represented by two-dimensional features.

Figure 2: Synthetic dataset from two views

View 1: The clusters are assumed to follow Gaussian distributions, each with distinct mean vectors μi and covariance matrices Σi for i=1,2,3:

μ1=(0,1)⊤,Σ1=[0.20000.20],μ2=(1.7,1)⊤,Σ2=[0.10000.10],μ3=(3,1)⊤,Σ3=[0.05000.05].

Additionally, three outliers are added at coordinates (−2,0.875), (−2,1.125), and (−1.75,1.125) to simulate noise.

View 2: In a similar manner, each cluster is modeled as a Gaussian distribution characterized with the following parameters:

μ1=(0,3)⊤,Σ1=[0.200.200.200.40],μ2=(1.7,5.5)⊤,Σ2=[0.100.100.100.20],μ3=(3,7.5)⊤,Σ3=[0.050.050.050.10].

Three additional outliers are placed at positions (−2,8), (−2,8.25), and (−1.75,8.25).

Figs. 3 and 4 provide a visual representation of the clustering results obtained by the eight algorithms under evaluation, enabling a comparative analysis of their performance on the constructed dataset.

Figure 3: Clustering results of nine clustering algorithms in view 1

Figure 4: Clustering results of nine clustering algorithms in view 2

As illustrated in Figs. 3a and 4a, Co-FCM exhibits a clear performance deficiency due to its equal treatment of all views, failing to leverage view-specific information. The results presented in Figs. 3c,f,g and 4c,f,g indicate that clustering methods based on hard partitions tend to misclassify samples near cluster boundaries. In contrast, soft partition-based methods, shown in Figs. 3b,d,e and 4b,d,e, offer improved interpretability by accommodating uncertainty during assignment. However, despite this advantage, they still encounter difficulties in resolving overlapping clusters and often misallocate outliers.

Within the framework of neutrosophic partition, Figs. 3h,i and 4h,i demonstrate that the MVNCM and AW-MVNFC algorithms exhibit superior capability in managing both the imprecision and uncertainty arising from overlapping clusters. These algorithms proficiently assign ambiguous samples to an imprecise cluster-visualized by yellow plus markers, while simultaneously identifying and labeling the three outliers using magenta pentagram symbols. Notably, this ability to effectively detect outliers is a distinct advantage of the proposed neutrosophic clustering and is not observed in the compared algorithms. Compared to MVNCM, the proposed AW-MVNFC incorporates not only view-specific weights but also adaptive feature weighting. This enhancement leads to a notable reduction in mis-assignments relative to MVNCM and other competing algorithms.

4.3 Experimental Results on Real-World Multi-View Datasets

An extensive experimental study was performed to assess the performance of the newly proposed AW-MVNFC algorithm in comparison with thirteen state-of-the-art multi-view clustering algorithms. The experiment is carried out using five diverse real-world datasets: IS [43], Forest Type [13], Prokaryotic Phyla [36], MSRCv1 [31], Seeds1 and Caltech101-7 [31], with the basic details provided in Table 1. We normalize all raw data to make the values between 0 and 1.

Clustering performance is evaluated using six distinct metrics: ACC, NMI, RI, F1, FMI and JI. Tables 2–7 summarize the experimental outcomes, with the highest-ranking algorithms highlighted in bold and the second-highest in underline. A detailed analysis of these outcomes leads to several key observations.

First, the proposed AW-MVNFC achieves superior performance compared to most baseline methods with respect to ACC, NMI, RI, F1, FMI and JI across five multi-view datasets. The observed clustering performance indicates that adaptively learning view and feature weights enables precise quantification of the roles played by each view and feature in the clustering process. The key advantage of AW-MVNFC is that it integrates neutral partitioning, which enables the model to explicitly represent uncertainty and imprecision in the clustering process. This capability greatly reduces the risk of cluster assignment errors, making AW-MVNFC particularly suitable for applications requiring high-stakes or critical decisions.

Second, compared with MVNCM, the proposed AW-MVNFC algorithm not only retains the original view-level weighting mechanism but also introduces a novel feature-level weighting strategy. This enhancement enables AW-MVNFC to assess the contribution of each individual feature with finer granularity. By capturing the differential importance of features within and across views, the method demonstrates heightened sensitivity to feature relevance, leading to more accurate clustering outcomes. Consequently, AW-MVNFC exhibits improved efficiency and effectiveness in handling complex multi-view data where both inter-view and intra-view information play critical roles.

To validate the effectiveness of the proposed auto-weighted mechanism, AW-MVNFC is evaluated on datasets including MSRCv1, Seeds and Caltech101-7, with its ability to jointly assign view weights and feature weights. As depicted in Figs. 5–8, the model allocates varying weights to different views based on their global discriminative relevance, while simultaneously learning fine-grained feature weights that capture the local importance of individual attributes. This hierarchical weighting strategy enables more nuanced representation learning and contributes to improved clustering accuracy.

Figure 5: The view weights generated by AW-MVNFC on real-world datasets

Figure 6: The feature weights generated by AW-MVNFC on MSRCv1

Figure 7: The feature weights generated by AW-MVNFC on Seeds

Figure 8: The feature weights generated by AW-MVNFC on Caltech101-7

4.4 Parameter Analysis

In this section, we investigate the impact of variations in the parameter β on the clustering results. Specifically, we analyze how adjustments to β influence the quality of the resulting clusters, and examine the resulting changes in key clustering metrics.

To assess the impact of the parameter β on clustering performance, we fix the weights ϖ1, ϖ2, and ϖ3 to their optimal values and systematically vary β within the range 1.1 to 2.0 with an interval of 0.1. The corresponding results for ACC, NMI, RI, F1, FMI and JI on ProP, MSRCv1 and Caltech101-7 datasets are illustrated in Fig. 9 for the proposed AW-MVNFC. The experimental findings indicate that β exerts a considerable influence on clustering outcomes, as it governs the sparsity level within the neutrosophic partition. Appropriately tuning β can lead to marked improvements in the clustering quality of the algorithm across different datasets.

Figure 9: Clustering results of different β on the ProP, MSRCv1 and Caltech101-7 datasets

4.5 Statistical Analysis

In order to determine the statistical significance of performance differences between the proposed AW-MVNFC algorithm and competing approaches, we employ the Friedman–Nemenyi test following the procedure in [43]. The average ranks (AR) of the ten algorithms across all multi-view datasets, evaluated by Across all multi-view datasets, the ten algorithms were evaluated and their average ranks (AR) determined by ACC, NMI, RI, F1, FMI, and JI, are reported in Table 8.

To begin, the value of τ for the Friedman test is computed using the following formula:

τχ2=12NFKF(KF+1)(∑i=1KFARi2−KF(KF+1)24)(42)

τF=(NF−1)τχ2NF(KF−1)−τχ2(43)

In this context, KF refers to the total number of algorithms considered, while NF corresponds to the number of datasets involved. Specifically, our evaluation includes ten algorithms applied to six datasets, giving KF = 10 and NF = 6. The test statistic τF is computed with reference to the chi-square distribution, considering the degrees of freedom (KF−1) and (KF−1) (NF−1). At the 95% confidence level, the corresponding critical value is obtained as F0.05((10 − 1), (10 − 1) ⋅ (6 − 1)) = 2.0960. Notably, the computed critical value is considerably lower than the observed τF statistic, which are τF = 5.5544 w.r.t ACC, τF = 3.0292 w.r.t NMI, τF = 7.1971 w.r.t RI, τF = 7.9525 w.r.t F1, τF = 7.5158 w.r.t FMI and τF = 7.5475 w.r.t JI. This indicates that the differences among the ten evaluated algorithms are statistically significant at the 5% significance level.

Subsequently, a Nemenyi post-hoc test is conducted following the Friedman test. The outcomes are illustrated in Fig. 10, where each horizontal line represents a clustering algorithm: the midpoint indicates its average rank, while the line length corresponds to the critical difference (CD). The CD is computed as follows:

CD=qαKF(KF+1)6NF(44)

Figure 10: Friedman test graph in terms of ACC, NMI, RI, F1, FMI and JI

The critical value qα, linked to KF, is calculated as 3.1640 for KF=10 and a significance level of α=0.05. From this, the corresponding critical difference (CD) is obtained as 5.5307. This result highlights that the proposed AW-MVNFC significantly outperform the other algorithms under comparison.

5  Conclusion

In this study, we present AW-MVNFC, a new auto-weighted multi-view neutrosophic fuzzy clustering algorithm designed with adaptive learning of view and feature weights. Building upon the MVNCM algorithm, the proposed clustering algorithm incorporate feature-level weights, effectively learning the varying contributions of views and features. This fine-grained weighting enhances the algorithm’s ability to handle imprecision and uncertainty in cluster assignments. We formulate the objective functions for the proposed methods and introduce an iterative optimization strategy to obtain their solutions efficiently. Experiments conducted on synthetic and real-world datasets confirm the performance of the proposed methods, along with a sensitivity analysis of key parameters, which provide strong evidence of the efficiency and stability of our proposed methods. However, to avoid excessive computational burden, we only consider the imprecise clusters between two different singleton clusters, but not the imprecise clusters that may occur between multiple clusters. In future work, we aim to propose an adaptive multi-view clustering that includes different imprecise clusters, and explore its performance in real-world application scenarios.

Acknowledgement: The authors Dania Sanatina and Nabil Mlaiki would like to thank Prince Sultan University for paying the APC and for the support through the TAS research lab.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Zhe Liu; methodology, Zhe Liu; validation, Dania Santina, Yulong Huang and Nabil Mlaiki; formal analysis, Jiahao Shi and Yulong Huang; investigation, Zhe Liu, Dania Santina and Nabil Mlaiki; visualization, Jiahao Shi; software: Jiahao Shi; writing—original draft preparation, Zhe Liu, Dania Santina and Jiahao Shi; writing—review and editing, Zhe Liu, Yulong Huang and Nabil Mlaiki; supervision, Nabil Mlaiki. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data information is included in this paper.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1https://archive.ics.uci.edu/ml/datasets/seeds (accessed on 02 September 2025).

References

1. Naz H, Saba T, Alamri FS, Almasoud AS, Rehman A. An improved robust fuzzy local information k-means clustering algorithm for diabetic retinopathy detection. IEEE Access. 2024;12:78611–23. doi:10.1109/access.2024.3392032. [Google Scholar] [CrossRef]

2. Naz H, Nijhawan R, Ahuja NJ, Saba T, Alamri FS, Rehman A. Micro-segmentation of retinal image lesions in diabetic retinopathy using energy-based fuzzy C-Means clustering (EFM-FCM). Microsc Res Techn. 2024;87(1):78–94. doi:10.1002/jemt.24413. [Google Scholar] [PubMed] [CrossRef]

3. Jia H, Ding S, Xu X, Nie R. The latest research progress on spectral clustering. Neural Comput Appl. 2014;24(7):1477–86. doi:10.1007/s00521-013-1439-2. [Google Scholar] [CrossRef]

4. Liu Z, Letchmunan S. Representing uncertainty and imprecision in machine learning: a survey on belief functions. J King Saud Univ-Comput Inf Sci. 2024;36(1):101904. doi:10.1016/j.jksuci.2023.101904. [Google Scholar] [CrossRef]

5. Mahmood T, Saba T, Alamri FS, Tahir A, Ayesha N. MVLA-Net: a multi-view lesion attention network for advanced diagnosis and grading of diabetic retinopathy. Comput Mater Contin. 2025;83(1):1173–93. doi:10.32604/cmc.2025.061150. [Google Scholar] [CrossRef]

6. Cai X, Nie F, Huang H. Multi-view k-means clustering on big data. In: Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence; 2013 Aug 3–9; Beijing, China. p. 2598–604. [Google Scholar]

7. Pan B, Li C, Che H, Leung MF, Yu K. Low-rank tensor regularized graph fuzzy learning for multi-view data processing. IEEE Transact Cons Electr. 2024;70(1):2925–38. doi:10.1109/tce.2023.3301067. [Google Scholar] [CrossRef]

8. Chen X, Xu X, Huang JZ, Ye Y. TW-(k)-means: automated two-level variable weighting clustering algorithm for multiview data. IEEE Trans Knowl Data Eng. 2013;25(4):932–44. doi:10.1109/tkde.2011.262. [Google Scholar] [CrossRef]

9. Zhang GY, Wang CD, Huang D, Zheng WS, Zhou YR. TW-Co-k-means: two-level weighted collaborative k-means for multi-view clustering. Knowl-Based Syst. 2018;150(12):127–38. doi:10.1016/j.knosys.2018.03.009. [Google Scholar] [CrossRef]

10. Pedrycz W. Collaborative fuzzy clustering. Pattern Recognit Lett. 2002;23(14):1675–86. doi:10.1016/s0167-8655(02)00130-7. [Google Scholar] [CrossRef]

11. Deng Z, Liu R, Xu P, Choi KS, Zhang W, Tian X, et al. Multi-view clustering with the cooperation of visible and hidden views. IEEE Transact Knowl Data Eng. 2022;34(2):803–15. [Google Scholar]

12. Xing L, Zhao H, Lin Z, Chen B. Mixture correntropy based robust multi-view K-means clustering. Knowl Based Syst. 2023;262(1):110231. doi:10.1016/j.knosys.2022.110231. [Google Scholar] [CrossRef]

13. Liu Z, Zhu S, Lyu S, Letchmunan S. Multi-view alternative hard c-means clustering. Int J Data Sci Anal. 2024;110(2):104743. doi:10.1007/s41060-024-00685-9. [Google Scholar] [CrossRef]

14. Liu Z, Aljohani S, Zhu S, Senapati T, Ulutagay G, Haque S, et al. Robust vector-weighted and matrix-weighted multi-view hard c-means clustering. Intell Syst Appl. 2025;25(3):200470. doi:10.1016/j.iswa.2024.200470. [Google Scholar] [CrossRef]

15. Yang B, Wu J, Zhang X, Zheng X, Nie F, Chen B. Discrete correntropy-based multi-view anchor-graph clustering. Inf Fusion. 2024;103(8):102097. doi:10.1016/j.inffus.2023.102097. [Google Scholar] [CrossRef]

16. Wang R, Li L, Tao X, Wang P, Liu P. Contrastive and attentive graph learning for multi-view clustering. Inform Process Manag. 2022;59(4):102967. doi:10.1016/j.ipm.2022.102967. [Google Scholar] [CrossRef]

17. Chen Z, Li L, Zhang X, Wang H. Deep graph clustering via aligning representation learning. Neural Netw. 2025;183(6):106927. doi:10.1016/j.neunet.2024.106927. [Google Scholar] [PubMed] [CrossRef]

18. Chen J, Ling Y, Xu J, Ren Y, Huang S, Pu X, et al. Variational graph generator for multiview graph clustering. IEEE Trans Neural Netw Learn Syst. 2025;36(6):11078–91. doi:10.1109/tnnls.2024.3524205. [Google Scholar] [PubMed] [CrossRef]

19. Zhang C, Fu H, Hu Q, Cao X, Xie Y, Tao D, et al. Generalized latent multi-view subspace clustering. IEEE Transact Pattern Anal Mach Intell. 2020;42(1):86–99. doi:10.1109/tpami.2018.2877660. [Google Scholar] [PubMed] [CrossRef]

20. Dong A, Wu Z, Zhang H. Multi-view subspace clustering based on adaptive search. Knowl Based Syst. 2024;289(1):111553. doi:10.1016/j.knosys.2024.111553. [Google Scholar] [CrossRef]

21. Wang J, Wu B, Ren Z, Zhang H, Zhou Y. Multi-scale deep multi-view subspace clustering with self-weighting fusion and structure preserving. Expert Syst Appl. 2023;213(6):119031. doi:10.1016/j.eswa.2022.119031. [Google Scholar] [CrossRef]

22. Wang Q, Zhang Z, Feng W, Tao Z, Gao Q. Contrastive multi-view subspace clustering via tensor transformers autoencoder. In: Proceedings of the 39th AAAI Conference on Artificial Intelligence; 2025 Feb 25–Mar 4; Philadelphia, PA, USA. p. 21207–15. [Google Scholar]

23. Houthuys L, Langone R, Suykens JAK. Multi-view kernel spectral clustering. Inform Fusion. 2018;44(5):46–56. doi:10.1016/j.inffus.2017.12.002. [Google Scholar] [CrossRef]

24. Khan A, Maji P. Multi-manifold optimization for multi-view subspace clustering. IEEE Transact Neural Netw Learn Syst. 2022;33(8):3895–907. doi:10.1109/tnnls.2021.3054789. [Google Scholar] [PubMed] [CrossRef]

25. Yan X, Zhong G, Jin Y, Ke X, Xie F, Huang G. Binary spectral clustering for multi-view data. Inf Sci. 2024;677(2):120899. doi:10.1016/j.ins.2024.120899. [Google Scholar] [CrossRef]

26. Wu Y, Lan S, Cai Z, Fu M, Li J, Wang S. SCHG: spectral clustering-guided hypergraph neural networks for multi-view semi-supervised learning. Expert Syst Appl. 2025;277(1):127242. doi:10.1016/j.eswa.2025.127242. [Google Scholar] [CrossRef]

27. Ruspini EH, Bezdek JC, Keller JM. Fuzzy clustering: a historical perspective. IEEE Comput Intell Mag. 2019;14(1):45–55. doi:10.1109/mci.2018.2881643. [Google Scholar] [CrossRef]

28. Cleuziou G, Exbrayat M, Martin L, Sublemontier JH. CoFKM: a centralized method for multiple-view clustering. In: 2009 Ninth IEEE International Conference on Data Mining; 2009 Dec 6–9; Miami, FL, USA. p. 752–7. [Google Scholar]

29. Zhang W, Deng Z, Zhang T, Choi KS, Wang S. One-step multiview fuzzy clustering with collaborative learning between common and specific hidden space information. IEEE Transact Neural Netw Learn Syst. 2024;35(10):14031–44. doi:10.1109/tnnls.2023.3274289. [Google Scholar] [PubMed] [CrossRef]

30. Jiang Y, Chung FL, Wang S, Deng Z, Wang J, Qian P. Collaborative fuzzy clustering from multiple weighted views. IEEE Trans Cybern. 2015;45(4):688–701. doi:10.1109/tcyb.2014.2334595. [Google Scholar] [PubMed] [CrossRef]

31. Yang MS, Sinaga KP. Collaborative feature-weighted multi-view fuzzy c-means clustering. Pattern Recognit. 2021;119:108064. doi:10.1016/j.patcog.2021.108064. [Google Scholar] [CrossRef]

32. Thong PH, Canh HT, Lan LTH, Huy NT, Giang NL. Multi-view picture fuzzy clustering: a novel method for partitioning multi-view relational data. Comput Mater Contin. 2025;83(3):5461–85. doi:10.32604/cmc.2025.065127. [Google Scholar] [CrossRef]

33. Han J, Xu J, Nie F, Li X. Multi-view K-means clustering with adaptive sparse memberships and weight allocation. IEEE Transact Knowl Data Eng. 2022;34(2):816–27. doi:10.1109/tkde.2020.2986201. [Google Scholar] [CrossRef]

34. Hu X, Qin J, Shen Y, Pedrycz W, Liu X, Liu J. An efficient federated multiview fuzzy c-means clustering method. IEEE Transact Fuzzy Syst. 2024;32(4):1886–99. doi:10.1109/tfuzz.2023.3335361. [Google Scholar] [CrossRef]

35. Liu Z, Qiu H, Deveci M, Letchmunan S, Martinez L. Robust multi-view fuzzy clustering with exponential transformation and automatic view weighting. Knowl Based Syst. 2025;315(7):113314. doi:10.1016/j.knosys.2025.113314. [Google Scholar] [CrossRef]

36. Benjamin JBM, Yang MS. Weighted multiview possibilistic c-means clustering with L2 regularization. IEEE Transact Fuzzy Syst. 2021;30(5):1357–70. doi:10.1109/tfuzz.2021.3058572. [Google Scholar] [CrossRef]

37. Liu Z, Qiu H, Letchmunan S, Deveci M, Abualigah L. Multi-view evidential c-means clustering with view-weight and feature-weight learning. Fuzzy Sets Syst. 2025;498(12):109135. doi:10.1016/j.fss.2024.109135. [Google Scholar] [CrossRef]

38. Guo Y, Sengur A. NCM: neutrosophic c-means clustering algorithm. Pattern Recogni. 2015;48(8):2710–24. doi:10.1016/j.patcog.2015.02.018. [Google Scholar] [CrossRef]

39. Akbulut Y, Sengür A, Guo Y, Polat K. KNCM: kernel neutrosophic c-means clustering. Appl Soft Comput. 2017;52(2):714–24. doi:10.1016/j.asoc.2016.10.001. [Google Scholar] [CrossRef]

40. Thong PH, Smarandache F, Huan PT, Tuan TM, Ngan TT, Thai VD, et al. Picture-neutrosophic trusted safe semi-supervised fuzzy clustering for noisy data. Comput Syst Sci Eng. 2023;46(2):1981–97. doi:10.32604/csse.2023.035692. [Google Scholar] [CrossRef]

41. Qiu H, Liu Z, Letchmunan S. INCM: neutrosophic c-means clustering algorithm for interval-valued data. Granul Comput. 2024;9(2):34. doi:10.1007/s41066-024-00452-y. [Google Scholar] [CrossRef]

42. Liu Z, Qiu H, Deveci M, Pedrycz W, Siarry P. Multi-view neutrosophic c-means clustering algorithms. Expert Syst Appl. 2025;260:125454. doi:10.1016/j.eswa.2024.125454. [Google Scholar] [CrossRef]

43. Deng Z, Liang L, Yang H, Zhang W, Lou Q, Choi KS, et al. Enhanced multiview fuzzy clustering using double visible-hidden view cooperation and network LASSO constraint. IEEE Transact Fuzzy Syst. 2022;30(11):4965–79. doi:10.1109/tfuzz.2022.3164796. [Google Scholar] [CrossRef]