Non-Newtonian Electroosmotic Flow Effects on a Self-Propelled Undulating Sheet in a Wavy Channel

1  Introduction

Motility refers to the intrinsic ability of an organism or cell to move autonomously, which is vital for numerous biological processes, including reproduction, nutrient acquisition, immune responses, and tissue repair. In microorganisms such as bacteria and spermatozoa, motility is achieved through mechanisms like flagella, cilia, or shape modulation, which convert chemical or mechanical energy into directed motion. Understanding these mechanisms is essential not only in biology but also in engineering applications, as the swimming strategies of microorganisms have inspired the design of micro- and nano-robots capable of navigating complex environments within the human body for tasks such as drug delivery, medical imaging, and microsurgery [1,2]. Since the seminal work of Taylor [3,4], who modeled a microorganism as an infinitely long sheet propagating transverse waves in a viscous fluid, the study of microorganism motility has been a central topic in fluid mechanics. Taylor’s analytical framework enabled the computation of swimming velocity and power dissipation using lubrication approximations and perturbation techniques. Subsequent extensions considered cylindrical filaments, finite-length sheets, and more complex fluid environments. Lauga [5] revisited Taylor’s approach in viscoelastic fluids, demonstrating that fluid elasticity affects swimming kinematics and energy expenditure, often reducing speed relative to Newtonian conditions. Teran et al. [6] further highlighted the role of elastic stress relaxation in enhancing propulsion efficiency, while Dasgupta et al. [7] quantified how shear-thinning and constant-viscosity viscoelastic fluids modify swimming speed. A comprehensive review by Li et al. [8] outlines developments in microswimming models, emphasizing cilia, flagella, and helical propulsion in complex fluids.

The interaction between microorganisms and boundaries also plays a crucial role in motility. Studies have shown that fluid elasticity, near-wall confinement,viscosity gradients, and Brinkmann layer can significantly alter swimming speed and direction. For instance, Ives and Morozov [9] showed enhanced swimming velocity of a Taylor sheet near a rigid wall in a viscoelastic fluid, whereas Jha et al. [10] highlighted the impact of soft boundaries on energy dissipation and swimming efficiency. Harsh Soni [11] investigated swimming in smectic-A liquid crystals, revealing faster locomotion due to the elastic layered structure. More recently, Ali and Sajid [12], Asghar et al. [13], and Shah et al. [14] have explored inertial effects, bounded flows, and complex rheological responses, further demonstrating the intricate interplay between fluid mechanics and microorganism motility. The research [15] investigates how cilia motion in the cervical canal influences electroosmotic flow to aid sperm transport. The study uses mathematical modeling to analyze this biomechanical process within human reproductive fluid dynamics. Further, transient and unsteady swimming phenomena have also been studied extensively. Pak and Lauga [16] examined the startup behavior of a waving sheet, revealing time-dependent effects on propulsion and net flow. Ali and Ardekani [17] extended this to non-Newtonian fluids, showing significant influence of viscoelasticity on transient swimming. Gaojin Li [18] investigated the role of fluid and swimmer inertia, identifying velocity overshoots and enhanced burst performance under strong inertial conditions. Alternative models, such as squirmers, have been used to study nutrient uptake, hydrodynamic interactions, and wall effects in Newtonian and non-Newtonian fluids [19–26]. These studies collectively underscore the sensitivity of swimming dynamics to fluid rheology, swimmer type, and environmental confinement. Beyond purely mechanical effects, external fields (magnetic and electric fields) offer unique opportunities to control and enhance microswimmer propulsion. Magnetic microswimmers have been extensively studied, demonstrating precise steering and speed modulation [27–30]. In contrast, electrokinetic effects, particularly electroosmosis, present a distinct approach for manipulating microscale flows. Electroosmosis arises when an applied electric field drives the motion of ions in an electrolyte solution, creating a net fluid movement.

The classical electroosmotic flow (EOF) in microchannels was first analyzed by Burgreen and Nakache [31] and Rice and Whitehead [32], who derived velocity profiles under the Debye-Hückel approximation. Later studies extended this analysis to two-dimensional rectangular microchannels [33–36] and thermal flow conditions [37]. This phenomenon has been widely exploited in microfluidic systems, including lab-on-a-chip devices, chromatography, and drug delivery applications. In recent years, the focus has shifted to non-Newtonian electroosmotic flows. Analytical and numerical studies have considered power-law [38–41], two-fluid stratified [42], and viscoelastic Phan-Thien-Tanner (PTT) fluids [43–45] under combined pressure-driven and electrokinetic forces. These works demonstrated that non-Newtonian rheology, wall zeta potential, and memory effects significantly influence flow profiles, pressure distribution, and pumping efficiency. For example, Akhtar et al. [46] showed that fractional Maxwell fluids exhibit slower flow due to strong memory effects, while Sangeetha et al. [47] highlighted the benefits of variable viscosity and electroosmotic forcing on mechanical efficiency and reduced trapping in peristaltic flows.

Theoretical modeling of physiological and bio-inspired systems, such as seminal fluid transport via metachronal waves, is explored in studies like [48], microfluidic pumping with surface roughness [49], and electroosmotic flow in wavy channels [50–56]. These studies collectively indicate that electrokinetic forces, combined with non-Newtonian fluid properties, enable precise control over micro-scale transport and swimmer propulsion. The integration of electroosmosis with motile surfaces provides a powerful framework to study electrically modulated swimming. Electric fields can enhance or suppress locomotion depending on fluid properties, boundary conditions, and channel geometry. For instance, electroosmotic-peristaltic flows have been shown to improve pressure rise, reduce trapping, and optimize energy efficiency in biorheological fluids [57–59]. Such insights are relevant for biomedical applications, including micro-robotics, drug delivery, and artificial cilia-based pumps. These studies analyze how the undulating or peristaltic motion of a channel’s walls influences the swimming mechanics and speed of self-propelling spermatozoa and microorganisms. They focus on hydrodynamic interactions, wall effects, and the impact of mechanical peristalsis on propulsion. References [60–63] explore how viscoelasticity (the property of fluids like biological gels that are both viscous and elastic) impacts micro-swimmer locomotion. They find that fluid elasticity can enhance propulsion speed for small-amplitude and flexible swimmers, challenging the notion that complex fluids always hinder movement. Shah et al. [64] analyzed shear-thinning slime layers beneath active bacterial surfaces, showing that local viscosity variations significantly affect swimming velocity and energy dissipation. Similarly, Asghar et al. [65] studied microswimmers in viscoelastic biofluids within complex cervical geometries, demonstrating that fluid elasticity and confinement strongly influence propulsion efficiency. Building on these findings, the present study examines an electrically actuated undulating sheet in a shear-thinning non-Newtonian electrolyte within a wavy channel. Unlike [64] and [65], which focused on passive or purely mechanical interactions, our work incorporates electroosmotic forcing, allowing exploration of how electric fields combined with complex fluid rheology impact propulsion, energy dynamics, and microscale transport in confined environments.

Motivated by these observations, the present study focuses on the swimming dynamics of an electrically controlled undulating sheet in a non-Newtonian electrolyte solution confined within a wavy channel. The electrolyte solution is modeled using the Carreau–Yasuda rheology, capturing shear-thinning behavior under creeping flow and long-wavelength approximations. We derive the governing equations, nondimensionalize them, and analyze the resulting system to investigate propulsion and energy characteristics. The novelty of this work lies in combining (i) electroosmotic forcing, (ii) complex non-Newtonian rheology, and (iii) confinement effects in a wavy geometry. By doing so, we aim to bridge biological relevance (e.g., cilia-driven transport in reproductive or respiratory tracts) with engineering applications (e.g., electrokinetically actuated microfluidics and soft robotics). Our findings are expected to provide theoretical insights into fluid–structure–field interactions at the microscale, with implications for both natural and artificial swimmers.

2  Basic Equations and Model Description

A diagram illustrating the physical model is presented in Fig. 1. It shows the swimming of a self-propelling undulating sheet in a non-Newtonian incompressible electrolyte solution flowing through a planar channel with flexible walls. Peristaltic waves of finite amplitude are imposed along the flexible walls of the channel.

Figure 1: Self-propelled undulating sheet centered in a wavy microchannel with Carreau–Yasuda flow under an external electric field

The deformations of upper and lower walls are represented by functions W1 and W2, respectively. The sheet is assumed to swim with velocity US in the negative longitudinal direction by sending down lateral waves of finite amplitude with speed C¯ and wavelength λ along its length. Additionally, it is assumed that the waves moving along the channel walls are in sync with those traveling along the sheet.

The wave profiles at the upper (Y=W1) and lower walls (Y=W2) and the sheet (Y=WS) are mathematically defined by the following equations [60,64,65].

Upperwall:W1=h0+bWCoskW(X−C¯t+USt),(1)

Lowerwall:W2=−h0−bWCoskW(X−C¯t+USt),(2)

Undulatingsheetsurface:WS=bSSinkS(X−C¯t+USt).(3)

It’s important to note that the net speed of the sheet relative to the inertial frame is C¯−US. In the above equations, kW and kS are the wave numbers on the wavy channel and the undulating sheet, h0 symbolizing the mean distance of the undulating sheet to either of the wavy walls (lower or upper), bS and bW refer to the wave amplitudes in the undulating and wavy walls, respectively.

We consider that the flow is driven by the combined action of the self-propelling undulating sheet, peristaltic walls, and the electroosmotic body force. The non-Newtonian fluid within the channel, modeled by the Carreau-Yasuda equation, is considered an electrolyte solution that reacts to an externally imposed electric potential across the channel’s length. When the negatively charged channel walls interact with the electrolyte solution, an electrical double layer is formed inside the flow field. Typically, the electrical double layer (EDL) comprises two sub-layers. The first zone, known as the “Stern layer,” contains ions that are closely attached to the charged surface. The second zone, called the “diffuse layer,” has ions that are more spread out and move freely in the surrounding area. When an external electric field is applied tangentially to the electric double layer, the counter-ions migrate and drag the surrounding solvent molecules by viscous interactions. This phenomenon gives rise to an electroosmotic flow. This flow can interact with the undulating sheet, altering its propulsion dynamics. Depending on the direction and magnitude of the electric field, electroosmosis can either enhance or hinder the sheet’s movement. The electroosmotic flow can act in synergy with the self-propulsion mechanism of the sheet, increasing its speed and providing additional control over its trajectory. Alternatively, if the electric field opposes the direction of the sheet’s motion, it can resist its movement and potentially impede its propulsion. Thus, the interplay between electroosmosis and the undulation of the swimming sheet in a wavy microchannel introduces complex and intriguing dynamics that warrant further exploration for applications in microfluidics and bioengineering.

In the inertial frame, the kinematic boundary conditions at the boundary walls are specified as follows:

U⌢1+=0,U⌢2+=0atY=W1,(4)

U⌢1−=0,U⌢2−=0atY=W2,(5)

U⌢1±=−USU⌢2±=dWSdt}atY=WS,(6)

here U⌢1± is the horizontal velocity component, and U⌢2± is the vertical velocity component in the inertial frame.

The self-propelled massless sheet is force-free [60]:

∫(FC++FC−)ds=0.(7)

In the above Eq. (7), FC+ and FC− are the fluid forces acting on the sheet from both sides, s represents the sheet’s surface area. We refer to Eq. (7) as the dynamic equilibrium condition.

The fundamental equations that govern the flow are:

Continuity equation:

∇.U⌢±=0.(8)

Navier-Stokes equation:

∇p±+ρdU⌢±dt−∇.T±−Fe=0,(9)

where ρ is the density of the fluids, T± signifies the stress field, p± indicates the hydrostatic pressure, Fe refers to external forces acting on the fluid, t denotes the time, and d is the total derivative. The constitutive equation for the Carreau-Yasuda fluid model is given by:

T±=(η∞+(η0−η∞)[1+Γa(γ˙±)a]n−1a)γ˙±.(10)

In the above equation, η∞,η0,Γ,n and a represent the high shear viscosity, low shear viscosity, characteristic time scale, power-law index, and transition parameter. Moreover, the rate of deformation tensor γ˙± and its magnitude (γ˙±) are expressed as follows:

γ˙±=(∇U⌢±)+(∇U⌢±)T,

γ˙±=(12trace((γ˙±)2))12(11)

Let’s define the Galilean coordinate transformations:

x=X−(C¯−US)t,y=Y,ω1±=U⌢1±−(C¯−US),ω2±=U⌢2±,P±=p±,(12)

where ω1± and ω2± denote the velocity components within the moving frame.

3  Problem Formulation

The velocity field associated with the flow resulting from the combined action of an undulating sheet, active channel walls, and electroosmotic body force is characterized as U⌢±=[ω1±,ω2±,0]. Eqs. (8) and (9) after the applications of the Galilean transformation defined in Eq. (12) become:

∂ω1±∂x+∂ω2±∂y=0,(13)

(∂∂t+ω1±∂∂x+ω2±∂∂y)ω1±+1ρ∂p±∂x=1ρ(∂Txy±∂x+∂Tyy±∂y)+Fe,(14)

(∂∂t+ω1±∂∂x+ω2±∂∂y)ω2±+1ρ∂p±∂y=1ρ(∂Txy±∂x+∂Tyy±∂y),(15)

where:

Txx±=2(η∞+(η0−η∞)[1+Γa(γ˙±)a]n−1a)(∂ω1±∂x),(16)

Txy±=(η∞+(η0−η∞)[1+Γa(γ˙±)a]n−1a)(∂ω1±∂y+∂ω2±∂x),(17)

Tyy±=2(η∞+(η0−η∞)[1+Γa(γ˙±)a]n−1a)(∂ω2±∂y),(18)

where:

γ˙±=[(∂ω1±∂x)2+(∂ω2±∂y)2]+12(∂ω1±∂y+∂ω2±∂x)2.(19)

Several studies have examined the axial force distribution in electroosmotic flows. For instance, reference [40] analyzed velocity and wall shear stress in microchannels, while reference [46] highlighted the influence of non-Newtonian rheology. The effects of pulsatile forcing were reported in [47], and memory-dependent viscoelastic behavior was described in [48]. More recently, reference [49] addressed the role of surface roughness, and reference [50] investigated two-phase systems. Based on these contributions, the force distributed along the axial direction can be described as:

Fe=ρeExk.(20)

In the equation above, k denotes the unit vector along the axial direction, ρe represents the surface charge density at any point in the fluid, and Ex stands for the axial electric field.

The Poisson equation is denoted as [46–49,53,56]:

∇2φ±+ρeε=0,(21)

where ε is the dielectric constant.

The expression of ρe is defined as [46–49,53,56]:

ρe=ez(n+−n−),(22)

where n+ and n− symbolize the number density of cations and anions, respectively, e is the elementary charge, and z is the valence of ions. To determine the potential distribution, our initial step involves calculating the charge density. The distribution of ionic numbers for individual species is determined using the Nernst–Planck (NP) equation for each specific species [46–49,53,56]:

∂n±∂t+ω1±∂n±∂x+ω2±∂n±∂y=D0(∂2n±∂x2+∂2n±∂y2)±D0ezkBT(∂∂x(n±∂φ±∂x)+∂∂y(n±∂φ±∂y)),(23)

where kB and D0 refers to the Boltzmann constant and diffusivity of the ionic species, respectively, and T is the absolute temperature.

The following dimensionless quantities are defined to render the previous equations in normalized form:

W1,2,S∗=W1,2,Sh0,bW,S∗=bW,Sh0,(ω1±)∗=ω1±C¯,x∗=kWx,(ω2±)∗=ω2±δC¯,y∗=yh0,(γ˙±)∗=h0C¯γ˙±,δ=kWh0,Re=ρC¯h0η0,p∗=kWh02η0C¯p,US∗=USC¯,De=ΓC¯h0,α=η∞η0,n∗=nn0,(φ±)∗=ezφ±kBT,(Tij±)∗=ηC¯h0Tij±,Sc=ηρD0,Pe=ReSc,Ue=−Exεξη0C¯,(ω1±)∗=∂ψ±∂y∗,(ω2±)∗=−∂ψ±∂x∗,β=kSkW,(24)

where Re,De,δ,Pe,Sc,n symbolize the Reynolds number, Deborah number, wave number, ionic Peclet number, Schmidt number, the density of the Carreau-Yasuda electrolyte, and β is the dimensionless parameter that represents the ratio of the wave number of the sheet to the wave number on the wall.

Since the Reynolds number in such analysis is of O(10−3), it is assumed that the motion is primarily driven by viscous forces, and inertial forces are neglected. Moreover, the mean width of the channel is larger than the wavelength of waves propagating along the walls. This situation usually gives rise to the condition δ<<1. Thus, the theory of long-wavelength approximation is applicable here. The non-linear terms in the momentum equation are O(Reδ2), while in the Nernst–Planck equation, they are found to be of O(Peδ2). By utilizing the non-dimensional quantities (24) and the approximation that Pe,Re,δ<<1, we get from Eq. (21) (dropping asterisk) the following equation [46–49,53,56]:

2∂2φ±∂y2+k2(n+−n−)=0.(25)

Similarly, the Nernst–Planck equation reduces to:

∂2n±∂y2±∂∂y(n±∂φ±∂y)=0,(26)

where k=h0ez2n0εkbT=h0λd, is the electroosmotic parameter and λd∝1k is the Debye length. Here λd is the electric double layer thickness, and n0 is the electrolyte ion density.

For Eq. (26), the bulk conditions are [46–49,53,56]:

n±|φ±=0=1 and

∂n±∂y|dφ±dy=0=0.(27)

The solution of Eq. (26) using condition (27) yields:

n±=e∓φ±.(28)

Solving Eqs. (25) and (28), we obtained the following equation:

∂2φ±∂y2−k2sinh⁡φ±=0.(29)

By invoking the linearization approximation [46–49,53,56], Eq. (29) reduces to:

∂2φ±∂y2−k2φ±=0.(30)

Solving Eq. (30) using the conditions ∂φ±∂y|y=WS=bssin⁡βx=0 and φ−(−W2)=1. The potential function at the lower region is obtained as:

φ−=cosh⁡(k(WS−y))cosh⁡(k(W2+WS)).(31)

By symmetry, the potential for the upper region is:

φ+=cosh⁡(k(WS−y))cosh⁡(k(W2−WS)).(32)

By using dimensionless quantities and parameters defined in Eq. (24), Eq. (13) is found to hold true, while Eqs. (14)–(19) become (neglecting the asterisk):

δRe[(∂ψ±∂y∂∂x−∂ψ±∂x∂∂y)(∂ψ±∂y)]=−∂p±∂x+δ∂∂xTxx±+∂∂yTxy±+k2Ueφ±,(33)

−δ3Re[(∂ψ±∂y∂∂x−∂ψ±∂x∂∂y)(∂ψ±∂x)]=−∂p±∂y+δ2∂∂xTxy±+δ∂∂yTyy±,(34)

Txx±=2δ(α+(1−α)[1+(Deγ˙±)a]n−1a)(∂2ψ±∂x∂y),(35)

Txy±=(α+(1−α)[1+(Deγ˙±)a]n−1a)(∂2ψ±∂y2−δ2∂2ψ±∂x2),(36)

Tyy±=−2δ2(α+(1−α)[1+(Deγ˙±)a]n−1a)(∂2ψ±∂x∂y),(37)

(γ˙±)2=2(δ∂2ψ±∂x∂y)2+12(∂2ψ±∂y2−δ2∂2ψ±∂x2)2.(38)

After applying the Stokes flow approximations, i.e., Re<<1 and δ<<1, Eqs. (35)–(38) reduced to:

Txx±=Tyy±=0,Txy±=(α+(1−α)[1+(Deγ˙±)a]n−1a)∂2ψ±∂y2,(γ˙±)2=12(∂2ψ±∂y2)2.(39)

These results, when integrated with simplified Eq. (33), yield:

∂p±∂x=∂∂y[(α+(1−α)(1+(De∂2ψ±∂y2)a)n−1a)(∂2ψ±∂y2)]+k2Uecosh⁡(k(WS−y))cosh⁡(k(W2∓WS)).(40)

By eliminating the axial pressure gradient from simplified Eqs. (33) and (34), we get the following result:

∂2∂y2[(α+(1−α)(1+(De∂2ψ±∂y2)a)n−1a)(∂2ψ±∂y2)]−k3Uesin⁡h(k(WS−y))cosh⁡(k(W2∓WS))=0.(41)

The dimensionless boundary conditions in the wave frame are listed as:

ψ+=0,∂ψ+∂y=−1+USaty=W1=1+bWcos⁡x,ψ−=0,∂ψ−∂y=−1+USaty=W2=−1−bWcos⁡x,ψ±=±Q,∂ψ±∂y=−1aty=WS=bSsin⁡βx.(42)

The rate of flow is:

Q=∫y=W2y=WS∂ψ∂y−dy=∫y=WSy=W1∂ψ+∂ydy.(43)

After employing the long-wavelength approximation, the force equilibrium condition results in [60,64,65].

∫−ππ[(Txy+−Txy−)+dWSdx(p+−p−)]dx=0.(44)

Performing integration of the second term, we get

∫−ππ[(Txy+−Txy−)−WS(dp+dx−dp−dx)]dx=0.(45)

For the free channel case:

ΔPλ=∫−ππdp±dxdx=p±(π)−p±(−π)=0.(46)

The energy loss by the undulating sheet against viscous forces per unit depth is:

EL=∫−ππζj[Tji]ωids,(47)

where ζj denotes the components of the unit normal vector that is perpendicular to the surface of the sheet and ωi the velocities of particles on the sheet. After utilizing the long wavelength assumption and keeping only the term of O(δ0) the above equation reduces to:

EL=∫−ππdWSdx(p+−p−)dx.(48)

Using Eqs. (44) and (45), the above formula reduces to:

EL=∫−ππWS(dp+dx−dp−dx)dx.(49)

4  Methodology

4.1 Newtonian Case: Closed-Form Solution

To begin the analysis, we consider a special case where the fluid behaves as Newtonian. This is achieved by taking De=0 or n=1, removing the non-Newtonian effects from the governing equations (Eqs. (41) and (42)). Under these simplifications, the equations become analytically tractable, allowing for the derivation of closed-form expressions for the key flow parameters. One can find the closed form expressions of ψ±,dp±dx and Txy± as follows:

Stream function in the upper region and lower regions:

ψ+=1kA13[−kB1(QB1(W1−3Ws+2y)−A1C1(W1−(−1+Ue+US)Ws+(−2+Ue+US)y))+...Ue(3W1−Ws−2y)C12tanh(kA1)](50)

ψ−=1kA23[kB2(QB2(W2−3Ws+2y)+A2C1(W2+Ws−USWs+(−2+US)y))+...−C12(3W2+Ws+2y)sinh(kA2)+A23sinh(kC1))]](51)

Pressure gradient in upper and lower regions:

dp+dx=1kA13[6k(−2Q+(−2+US)A1)+12Uecosh(D1)sech(kA1)(kA1cosh(D1)+2sinh(D1))](52)

dp−dx=1kA23[6k(2Q+(−2+US)A2)+12Uecosh(D2)sech(kA2)(kA2cosh(D2)+2sinh(D2))](53)

Stress component in upper and lower regions:

Txy+=1kA13[6kQA1−2kA1((−3+Ue+Us)W1+3WS−(Ue+Us)Ws)−2kUe(2W1−2WS)A1sech(kA1)+6UeA1tanh(kA1)](54)

Txy−=1kA23[6k(2Q+(−2+US)A2)Ws−2k(3QE2+A2((−3+US)W2+…−2kA22cosh(kA2)+6A2sinh(kA2))],(55)

where:

A1=(W1−WS),A2=(W2−WS),B1=(W1−y),B2=(W2−y),C1=(Ws−y),D1=−12kA1,

D2=1/2kA2 and E2=W2+Ws.

For a Newtonian fluid, the equilibrium conditions used to calculate the unknowns US and Q are:

∫−ππWS(dp+dx−dp−dx)dx=0(56)

∫−ππ(d2ψ+dx2−d2ψ−dx2)y=Ws−WS(dp+dx−dp−dx)dx=0(57)

Substituting Eqs. (50)–(55) into Eqs. (56) and (57), it becomes evident that analytical integration is not feasible due to the nonlinear nature of the resulting algebraic equations. Therefore, a numerical root-finding method is necessary to compute the unknowns Q and Us. A suitable choice for this is the modified Newton–Raphson method.

However, in the absence of an electric field (Ue=0) and with flat (non-wavy) walls (bw=0), the system simplifies significantly. In this case, one can derive much simpler expressions for the stream function and pressure gradient, making the integration in Eqs. (56) and (57) are straightforward.

Finally, the solution reduces to a system of two algebraic equations with two unknowns, yielding closed-form expressions for Q and Us in the Newtonian limit. Put (bs=b).

Us=3b21+2b2andQ=−1+b21+2b2(58)

These expressions perfectly match the results previously reported by Shack and Lardner [60], confirming that our formulation is consistent and in agreement with well-established published studies.

4.2 Numerical Technique: Modified Newton-Raphson Technique

In this section, we describe the procedure to calculate US and Q solve the boundary value problem (41), (42) with the equilibrium conditions (45) and (46). To do this, we employ a combination of MATLAB bvp5c routine and a modified Newton-Raphson scheme. The computations are initiated by assigning suitable initial values to US and Q. All the remaining parameters are fixed at some suitable values. Hence, for some initial values of US and Q, Eqs. (41) and (42) are solved via a bvp5c routine. The obtained solution of boundary value problems (41) and (42) is then tested in Eqs. (45) and (46) (dynamic equilibrium conditions). If the dynamic equilibrium conditions are satisfied, the numerical procedure is terminated. Otherwise, we refine the values of US and Q via the modified Newton-Raphson method so that it satisfies the dynamic equilibrium conditions.

5  Results and Discussion

The governing differential Eq. (41) with the corresponding boundary conditions (specified in Eq. (42)) has six dimensionless parameters, i.e., De,α,n,a,Ue and k. The selected parameter values are representative and lie within the typical ranges used in theoretical and numerical studies of microfluidic and electroosmotic systems. This section aims to investigate how these physical parameters impact the undulating sheet’s speed and the associated energy loss by the undulating sheet.

5.1 Undulating Sheet Speed and Energy Loss

In Fig. 2, we present the relationship between the speed of the undulating sheet (US), and the Deborah number (De) for three distinct values of Helmholtz-Smoluchowski velocity (Ue). This comparison emphasizes how shear-thinning and shear-thickening fluids influence the velocity of the sheet. Fig. 2a reveals a distinct non-monotonic relationship between the undulating sheet’s speed and the Deborah number for a shear-thinning fluid (n=0.5). Initially, the sheet’s speed increases with Deborah number, attains a maximum, around De≈0.8, beyond which a gradual decline is observed. This behavior highlights that at lower De, elasticity increases the response of the fluid to the sheet’s undulations, improving propulsion. However, after an optimal point, rising elastic resistance impedes the deformation propagation, causing a decrease in the speed of the undulating sheet. This trend demonstrates that shear-thinning fluids significantly impact the speed of the undulating sheet, where an optimal Deborah number maximizes the speed before it starts to decline. In contrast, Fig. 2b shows a distinct kind of non-monotonic behavior for a shear-thickening fluid. Here, the speed of the undulating sheet initially experiences a minor fall for small values of De, suggesting a local minimum, before progressively rising across the remaining range. This implies that in a shear-thickening scenario, weak elasticity can initially resist the motion slightly, but as De increases, the memory of the fluid and thickening properties begin to aid propulsion. Physically, higher elasticity in such fluids contributes to stronger elastic recoil and better momentum transmission along the undulating sheet, thereby continuously boosting its speed. Furthermore, our observations reveal that the sheet moves faster in a shear-thinning Carreau-Yasuda fluid with a lower value of Deborah or in a shear-thickening Carreau-Yasuda fluid with a higher value of Deborah. It can also be seen in both scenarios that as the Deborah number increases, the speed of the undulating sheet tends to approach an asymptotic value. This suggests that at sufficiently high De, the elastic effects saturate, and the fluid’s ability to respond to further increases in deformation rate diminishes. These figures further predicted that for Ue<0, the speed of the undulating sheet would be enhanced. The definition of (Ue) suggests that it is directly proportional to the intensity of the axial electric field. For Ue<0, the electric field acts in the negative x-direction. As a result, it decelerates the axial flow. However, for Ue>0, the axial electric field is oriented in the positive x-direction. In this context, it is intriguing to note that when considering negative Helmholtz-Smoluchowski velocities, the sheet’s speed is increasing. Specifically, we observe that the sheet’s speed is enhanced by decreasing the Helmholtz-Smoluchowski velocity in the range Ue<0. Conversely, the sheet’s speed reduces by increasing the Helmholtz-Smoluchowski velocity in the range Ue>0.. This notable phenomenon suggests that a negative Helmholtz-Smoluchowski velocity might be viewed as an assisting factor in enhancing effective swimming. Therefore, in the present study, we have only plotted the results for negative values of Helmholtz-Smoluchowski velocities (Ue). These insights highlight the important role of the axial electric field’s direction in affecting the speed of the undulating sheet. Understanding this relationship helps optimize conditions for achieving higher swimming speeds in different fluid environments. The increase in speed with negative Helmholtz-Smoluchowski velocities suggests a way to improve the efficiency of microswimmers and other applications where controlled movement in a fluid is important. It is important to note that our results agree well with those reported in references [61,62]. In these studies, the authors predicted a similar trend for microswimmer speed, as shown in Fig. 2. Specifically, they showed that the speed of the microswimmer reaches a maximum or minimum and then gradually changes to an asymptotic value as the parameters characterizing the fluid’s non-Newtonian response increase. Additionally, it should be noted that the electroosmotic parameter and Helmholtz-Smoluchowski velocity appear in the momentum equation as pre-factors of the electroosmotic body force term. Therefore, it is anticipated that the impact of the electroosmotic parameter would be like that of the Helmholtz-Smoluchowski velocity. This similarity helps to explain the trends observed in our results and underscores the interconnected effects of these parameters on the speed of the undulating sheet.

Figure 2: Effect of Deborah number (De) on the undulating sheet speed (Us) across various Helmholtz-Smoluchowski velocity (Ue) in a Carreau-Yasuda fluid. (a) represents results for a power law index n=0.5, while (b) shows results for n=1.4. the parameters used are transition parameter a=4, viscosity ratio α=0.6, electroosmotic parameter k=0.3, occlusion parameter bs=0.3, and wall parameter bw=0.2

Fig. 3a,b shows the behavior of undulating sheet speed against the power law index (n) for three distinct values of Helmholtz-Smoluchowski velocities (Ue) at two Deborah numbers, De=0.8 and De=2, respectively. These figures highlight how the fluid’s shear-dependent viscosity influences propulsion in various elastic regimes. Fig. 3a shows that when De=0.8 the speed of the undulating sheet Us decreases monotonically as n increases. This behavior corresponds directly to the fluid’s rheological regime, i.e., for n<1 (shear-thinning), the fluid’s viscosity reduces with strain rate, decreasing flow resistance and enabling the sheet to attain higher speeds, at n=1 (Newtonian fluid), the viscosity remains constant, resulting in moderate speeds and for n>1 (shear-thickening), the fluid’s viscosity raises with strain rate, imposing greater resistance and thereby decreasing propulsion efficiency. On the other hand, Fig. 3b shows a distinct pattern for De=2, where the sheet’s speed increases as n rises. In this higher elasticity regime, shear-thickening behavior becomes significant. At lower n (shear-thinning), the sheet moves slower, but as n increases, the thickening response enhances the fluid’s ability to support elastic recoil, which helps in transferring momentum along the sheet. This leads to improved propulsion. These results highlight a rheological crossover, for lower Deborah numbers, shear-thinning fluids are better for faster motion, whereas for higher Deborah numbers, shear-thickening fluids excel by effectively using elasticity to enhance propulsion.

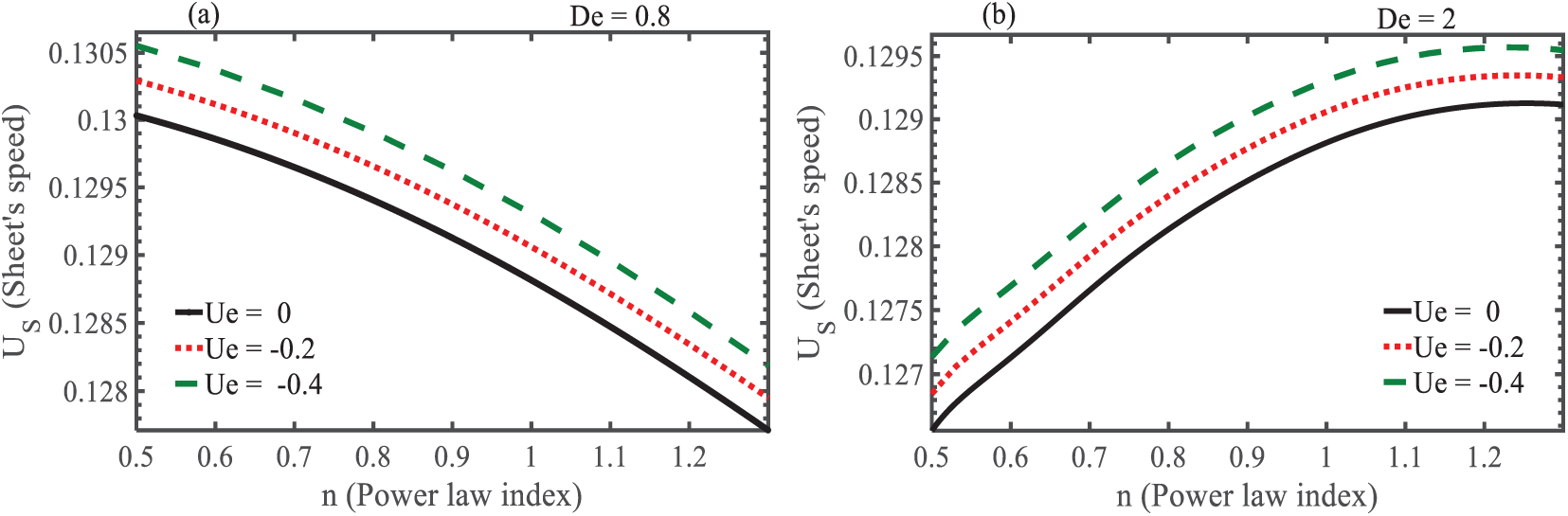
Figure 3: Effect of power law index (n) on the undulating sheet speed (Us) across various Helmholtz-Smoluchowski velocity (Ue) at two different Deborah numbers (De). (a) represents results for De=0.8, while (b) shows results for De=2. The parameters used are transition parameter a=4, viscosity ratio α=0.7, electroosmotic parameter k=0.3 and wall parameter bw=0.2

Fig. 4 shows combined profiles of the speed against (De) for shear-thinning, shear-thickening, and Newtonian conditions. This graph reveals intriguing insights into the relationship between the fluid rheological behavior and the speed of the sheet. Remarkably, the graph reveals distinct points where the sheet’s speed is identical across the different rheological scenarios. The Newtonian straight line cuts the profile for the shear-thinning case at two distinct values of the Deborah number (De). Similarly, it also intersects the profile for the shear-thickening case at two specific Deborah numbers (De). The profiles associated with shear-thinning and shear-thickening cases also intersect twice at two distinct Deborah numbers (De) . This indicates that there exist specific values of Deborah number (De) at which the speed of the sheet becomes identical for two distinct power-law indices.

Figure 4: Combined profiles of the undulating sheet speed (Us) against the Deborah number (De) for different fluid types: shear-thinning, shear-thickening, and Newtonian fluids. The parameters used are transition parameter a=4, viscosity ratio α=0.5, Helmholtz-Smoluchowski velocity Ue=−0.1, electroosmotic parameter k=0.3, occlusion parameter bs=0.3 and wall parameter bw=0.2

Fig. 5 illustrates the impact of the occlusion parameter (bs) on the speed of the undulating sheet (Us) for various values of Helmholtz-Smoluchowski velocity (Us). As shown, the sheet speed (Us) increases with the occlusion parameter (bs), meaning that higher occlusion leads to faster movement of the sheet. This increase is more pronounced at negative values of Helmholtz-Smoluchowski velocity (Ue=−0.4), which aligns with the observation that negative Ue assists in enhancing the effective speed of the sheet. The different behaviors in both figures (a) and (b), with varying power-law indices (n=0.5andn=1.3), further illustrate that the sheet speed depends on both the fluid’s rheological properties and the occlusion parameter.

Figure 5: Effect of occlusion parameter (bs) on the undulating sheet speed (Us) across various Helmholtz-Smoluchowski velocity (Ue) at a fixed Deborah number De=2. (a) represents results for a power law index n=0.5, while (b) shows results for n=1.3. The parameters used are transition parameter a=4, viscosity ratio α=0.5, electroosmotic parameter k=0.3 and wall parameter bw=0.2

Fig. 6 explores how energy loss (EL)varies with the occlusion parameter (bs) for different types of fluids, namely shear-thinning, Newtonian, and shear-thickening. As seen, energy loss increases with (bs) for all fluid types, but the rate of increase is higher for shear-thickening fluids. This suggests that the rheological nature of the fluid plays a significant role in energy dissipation. Shear-thinning fluids, which reduce resistance at higher strain rates, experience less energy loss than shear-thickening fluids, which increase resistance. Overall, these figures reinforce the idea that both the occlusion and the properties of the fluid (whether shear-thinning or thickening) have a direct impact on the dynamics of the undulating sheet. Specifically, they highlight that lower Helmholtz-Smoluchowski velocities and higher occlusion parameters enhance the sheet’s speed while increasing energy loss, particularly in shear-thickening fluids. Additionally, it is also observed that the energy loss (EL) by the undulating sheet in a wavy channel exhibits a linear relationship with both the occlusion parameter (bs) and the Helmholtz-Smoluchowski velocity. As the occlusion parameter (bs) increases, the energy loss rises correspondingly, indicating that a larger undulation in the sheet leads to greater energy dissipation. Similarly, more negative values of Ue result in a proportional increase in energy loss.

Figure 6: Variation of energy loss (EL) with the occlusion parameter (bs) for different types of fluids: shear-thinning, shear-thickening, and Newtonian fluids. The parameters used are transition parameter a=4, viscosity ratio α=0.5, Helmholtz-Smoluchowski velocity Ue=−0.4, electroosmotic parameter k=0.3, Deborah number De=2 and wall parameter bw=0.2

Mathematically, this behavior can be expressed as:

EL∝bs.Ue

This relationship underscores the significant influence of both the channel occlusion and the Helmholtz-Smoluchowski velocity on the energy dissipation by the undulating sheet. Specifically, higher values of bs or more negative values of Ue, cause increased energy loss, as the sheet encounters greater resistance in the flow.

The findings elucidated herein underscore the importance of fluid rheology in controlling the speed of an undulating sheet, which may be associated with biological propulsion mechanisms. In biological systems, like sperm motility, the viscosity of the fluid around it and the elasticity of the environment affect how well it moves. For shear-thinning fluids, whose viscosity goes down with strain rate, movement is enhanced, simulating how spermatozoa pass through cervical mucus, where the fluid becomes less resistive under strain. In contrast, shear-thickening fluids, whose viscosity rises with strain rate, resemble environments where higher elasticity assists in propulsion, similar to the enhanced elastic recoil found in cilia-driven motion in reproductive or respiratory systems. Our results reveal that, like biological swimmers, the speed of artificial microswimmers can be optimized by adjusting fluid properties such as viscosity and elasticity, especially under controlled electroosmotic forces. Additionally, the finding indicates that occlusion parameter similar to physical confinement in biological channel may have a considerable impact on swimming speed, with increasing occlusion resulting to faster propulsion, particularly when combined with negative Helmholtz-Smoluchowski velocities. These findings are consistent with biological mechanisms in which confinement in narrow channels, such as the fallopian tubes, or fluid interactions in small regions may influence swimmer efficiency. This study therefore fills a gap between theoretical fluid dynamics and biological applications by providing a framework for enhancing microswimmer efficiency in biomedical technologies such as targeted drug delivery and micro-robotic surgery.

The streamlines of the Carreau-Yasuda fluid, depicting the flow behavior under various parameter settings, are illustrated in Figs. 7 and 8. Fig. 7 specifically compares the streamline patterns in both rigid and wavy channels, considering three distinct values of the occlusion parameter (bs). This comparison provides insight into how the occlusion parameter influences the flow dynamics in channels with different geometrical configurations. By keeping k=0.5,Ue=−0.5,α=0.5,De=2 and n=0.5 (constant across both rigid and wavy channels), figures (a), (c), and (e) display the streamlines plots for rigid channels (bw=0), while figures (b), (d) and (f) depict the streamlines for wavy channels (bw=0.2). It can be observed that varying values of bs lead to different pairs of Us and Q. In these figures, a red-white curved line represents a self-propelled sheet exhibiting an undulating motion from right to left in the channel’s center. Generally, Fig. 7 shows that streamlines near the undulating sheet mimic its shape in both scenarios. One can also witness from plots 7(a) and (b) that no recirculating zones are present in the lower part of the channel. However, as the occlusion parameter increases, distinct recirculating zones emerge in the upper and lower regions of the channel. These zones, absent at lower occlusion parameter values, suggest a transition from a uniform flow to one with localized recirculation zones. This transition, likely due to the increasing impact of the occlusion on the flow, has implications for mixing and transport processes.

Figure 7: Streamlines of flow in both rigid (bw=0) and wavy (bw=0.2) channels for various combinations of sheet speed (Us) and flow rate (Q) under different occlusion parameter (bs). The parameters used are transition parameter a=4, viscosity ratio α=0.5, power law index n=0.5, Helmholtz-Smoluchowski velocity Ue=−0.4, electroosmotic parameter k=0.3 and Deborah number De=2

Figure 8: Streamlines of flow in wavy (bw=0.2) channel for various combinations of sheet speed (Us) and flow rate (Q) under different Helmholtz-Smoluchowski velocity (Ue). The parameters used are transition parameter a=4, viscosity ratio α=0.7, occlusion parameter bs=0.3, power law index n=1.5, electroosmotic parameter k=0.5 and Deborah number De=5

The analysis of streamline patterns depicting the flow of Carreau-Yasuda fluid surrounding an undulating sheet in the context of active channels with varying Helmholtz-Smoluchowski velocities is illustrated in Fig. 8a–c. A detailed examination of these figures reveals that as the values of Helmholtz-Smoluchowski velocity (Ue) increase, there is a corresponding increase in the strength and size of the recirculating zones observed in both the upper and lower parts of the channels. This behavior suggests that the Helmholtz-Smoluchowski velocity (Ue) has a similar impact on the flow characteristics as the occlusion parameter (bs), influencing the formation and intensity of these recirculating zones.

These findings have significant implications for biological flow systems where peristaltic pumping occurs. The occlusion parameter (bs) can be directly correlated to pathological conditions such as the constriction of airways in asthma or the narrowing of blood vessels by atherosclerotic plaques. Our demonstration that increased occlusion leads to flow separation and recirculation zones provides a mechanistic explanation for reduced transport efficiency in these diseases, where mucus or blood may become trapped, exacerbating the condition. Furthermore, the similarity in effect between occlusion and Helmholtz-Smoluchowski velocity (Ue) suggests that electrokinetic phenomena, which are prevalent in physiological environments like the gut lining or charged mucosal layers, can actively modulate flow patterns. This insight could be harnessed in biomedical applications, such as the design of advanced drug delivery systems that use external electric fields to enhance mixing and retention of therapeutic agents in targeted locations.

5.2 Energy Loss for the Undulating Sheet

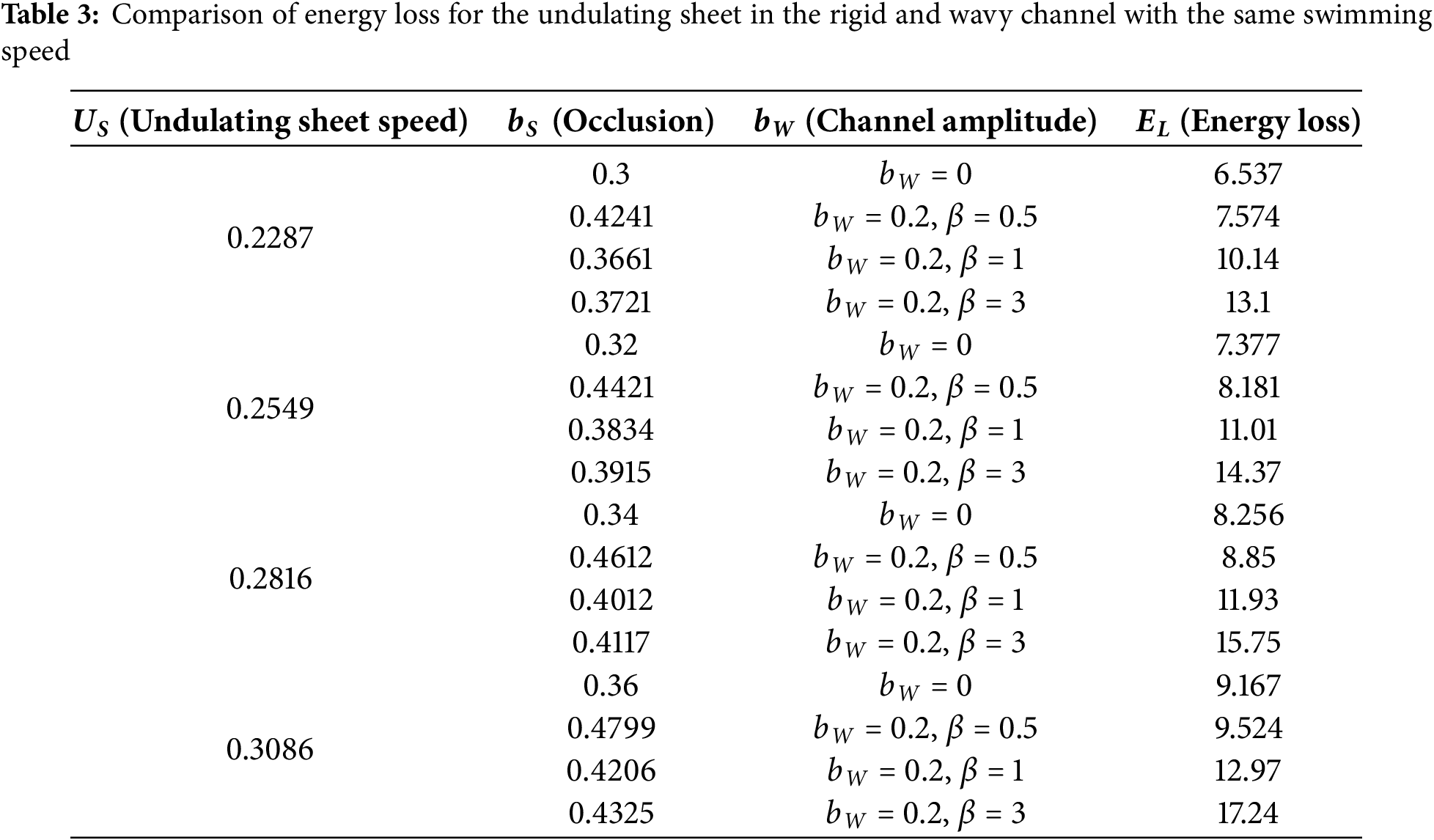
The optimal scenario for an undulating sheet is to sustain a maximum speed while minimizing energy consumption. Therefore, it is more suitable to compare energy loss by the undulating sheet in different scenarios while swimming at the same velocity. Therefore, we have examined four different options for energy comparison:

i. Swimming of an undulating sheet in the absence (Ue=0) and presence (Ue≠0) of the Helmholtz-Smoluchowski velocity.

ii. Swimming of an undulating sheet in Newtonian (n=1) and non-Newtonian (n∈(0,1) and n>1) scenarios.

Swimming of an undulating sheet in rigid (bW=0) and wavy channels (bW=0.2).

Swimming of an undulating sheet for varying Deborah number (De) in shear-thinning and shear-thickening fluids.

The first case is shown in Table 1. It is observed that energy loss by the undulating sheet is smaller in the presence of the Helmholtz-Smoluchowski velocity. Table 2 reveals that altering the rheology of the surrounding liquid is another way to reduce energy losses. In this context, the shear-thinning characteristics are especially suitable to attain the desired result. In shear-thinning fluids, viscosity decreases with increasing shear rate, allowing the sheet to move more easily and consume less energy. In contrast, shear-thickening fluids have increasing viscosity with the shear rate, requiring more energy for movement. Newtonian fluids have a constant viscosity regardless of shear rate. This difference in viscosity behavior explains the varying energy consumption despite the same sheet speed.

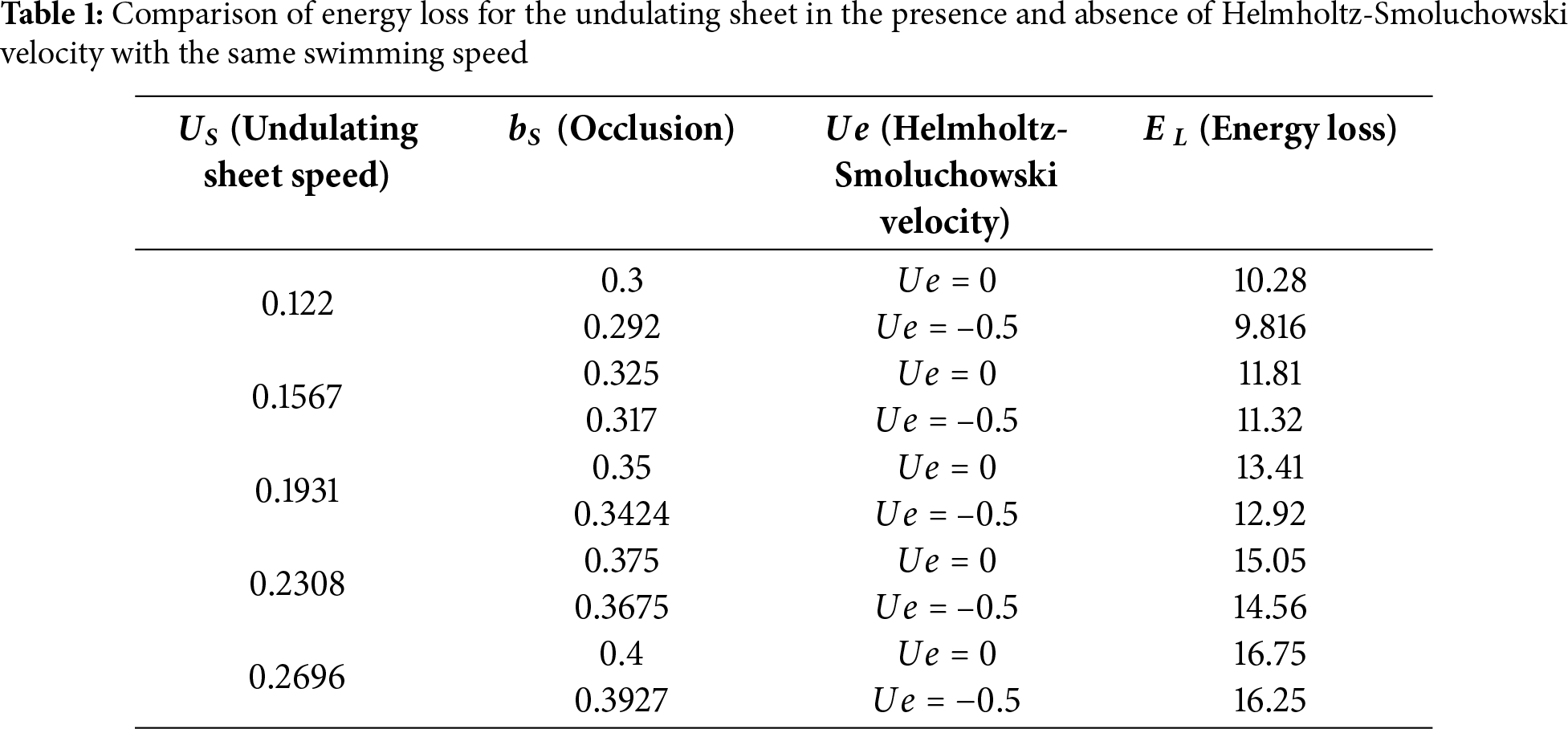
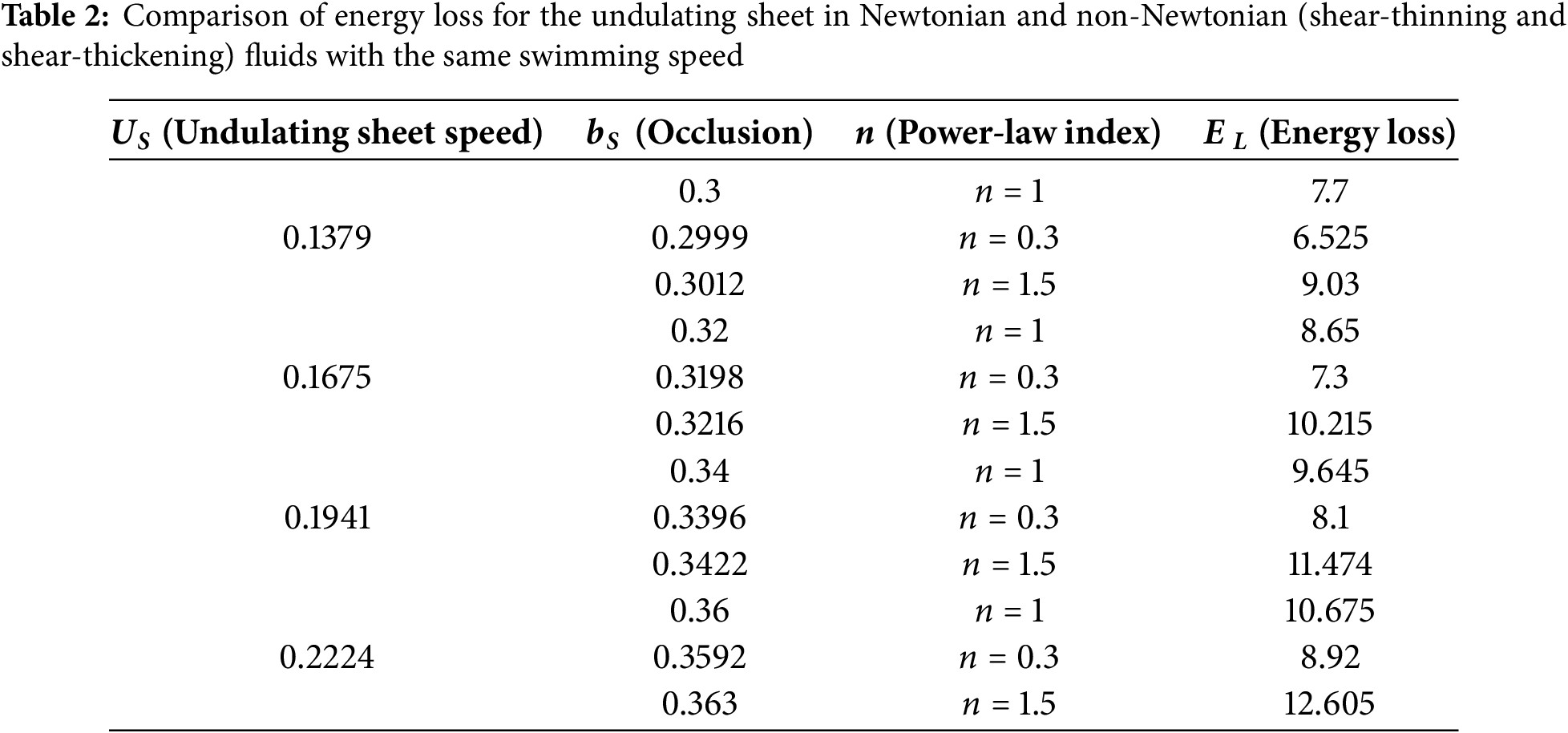
Table 3 highlights that the nature of the channel is also another way to reduce energy consumption. The data demonstrates that the undulating sheet undergoes greater energy dissipation in a wavy channel than in a rigid channel. Here, we have discussed three conditions in connection with β, namely β<1, β=1 and β>1. The scenario β<1 indicates that the wave number on the sheet is less than the wave number on the channel, whereas the case β>1 indicates that the wave number on the sheet is greater than the wave number on the channel. Moreover, the case β=1 corresponds to equal wave numbers between the sheet and channel. Here, it is observed that for β=0.5, the difference in energy loss between rigid and wavy channels is minimal. With a further increase in the wave number on the sheet from 0.5 to 1 and then 3, this energy difference between the rigid and complex wavy channels becomes large. The difference in energy consumption between the undulating sheet in the rigid and the wavy channels could be due to various factors. One key factor could be the interaction between the sheet and the channel walls. In the wavy channel, the irregular shape of the walls might lead to increased friction and mixing, causing the sheet to expend more energy to maintain its speed. On the other hand, in the rigid channel, the smoother walls might result in less friction and mixing, requiring less energy from the sheet to move at the same speed. Other factors, such as the flow and pressure gradients in the two channels, could also contribute to this energy difference. Table 4 reveals that varying Wi in shear-thinning and shear-thickening scenarios is another way to control the energy loss for the undulating sheet. It has been observed that the difference in energy loss is minimal between shear-thinning and shear-thickening scenarios for small values of (De). However, this difference of energy loss by the undulating sheet increases with (De). It also reveals that shear-thinning fluid can lead to more efficient swimming.

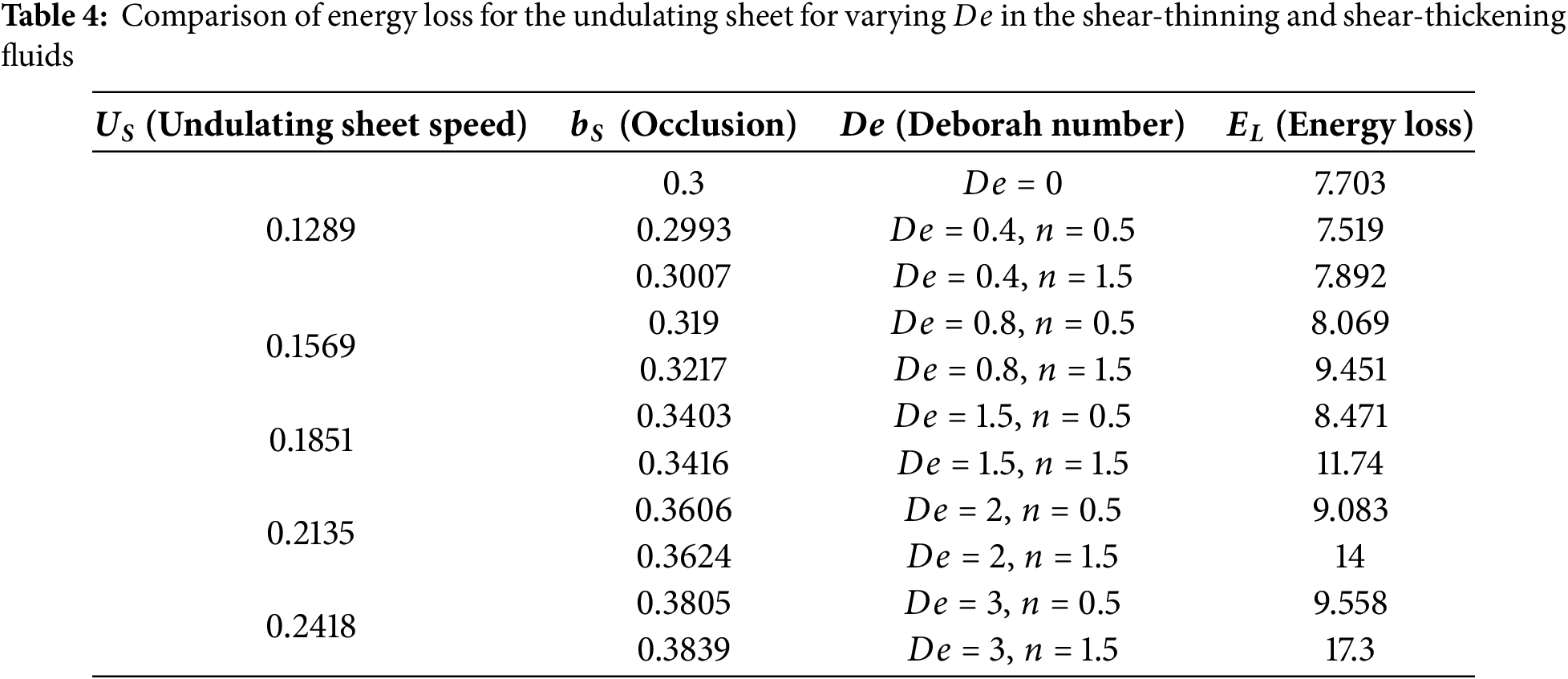
Our energy-loss analysis directly relvant to biological system, as sperm attempt to move quickly while losing as lower energy as possible. When comparing equal-speed scenerios, we find that an applied electric field and shear-thinning medium (like healthy mucus) allow the swimmer to attain the same speed with minimum energy loss, but shear-thickening media increases loss. Flat, straight channels also reduce loss compared with wavy confinement, and a larger mismatch between wall undulations and beat wavelength increases loss. Finally, choosing a Deborah number that matches beat timing to fluid relaxation lowers energy loss and can improve speed. These links show how our results translate to sperm-driven transport and to guided microrobots that target fast motion with minimal energy loss.

6  Conclusions and Future Directions

An attempt is made to investigate the influence of electroosmotic forces on the swimming dynamics of an undulating sheet in a wavy channel. The speed of the undulating sheet and energy loss by it are evaluated by solving the hydrodynamical equations for the fluid motion based on the Carreau-Yasuda constitutive equation. The derivation of the aforesaid equations is carried out under the assumptions of long wavelengths, low Reynolds numbers, and the linearization approximation of the Debye–Hückel theory, with numerical solutions obtained via MATLAB’s bvp5c routine using a modified Newton-Raphson method. A detailed parametric study is performed to estimate the impacts of the Carreau–Yasuda fluid’s rheological properties, electroosmotic forces, and the amplitude ratio on both the propulsion speed and energy loss of the undulating sheet.

The primary findings of this study highlight the pivotal role of electroosmotic effects and fluid rheology in governing the propulsion of the undulating sheet. Electroosmotic forces, when applied in the negative axial direction, assist the sheet’s propulsion, enhancing its speed while simultaneously reducing energy loss. The results underscore a rheological crossover: in shear-thinning fluids, lower Deborah numbers promote faster swimming speeds, while in shear-thickening fluids, higher Deborah numbers lead to better performance. This shift is tied to the fluid’s elastic response and its ability to support momentum transfer, especially in the high-elasticity regime where shear-thickening fluids outpace Newtonian counterparts. The study also reveals that the amplitude of undulation plays a significant role in enhancing the sheet’s speed, with larger amplitudes resulting in faster propulsion. Additionally, it was observed that the undulating sheet consumes less energy in a rigid channel compared to a wavy channel, emphasizing the importance of channel geometry in optimizing energy efficiency. Similarly, the presence of the Helmholtz–Smoluchowski velocity reduces energy loss, indicating the significance of electrokinetic effects in minimizing energy dissipation. Altogether, the findings indicate that the undulating sheet’s motion can be effectively enhanced in three primary ways: by adjusting the amplitude of surface waves, by tuning the rheological properties of the surrounding non-Newtonian fluid, and by utilizing electroosmotic effects to minimize resistance and energy expenditure.

This study is motivated by a deep intellectual curiosity and a desire to better understand the physics of self-propelling undulating sheets in complex fluids. The results demonstrate that electroosmosis can significantly influence sheet propulsion, offering new insights for controlling microscale transport and locomotion. These findings carry important implications for the design and optimization of artificial microswimmers across various fields, including medicine, biotechnology, and environmental monitoring. Moreover, the outcomes of this research are potentially valuable in the development of biomimetic mechanical crawlers and soft robotic devices, where fluid–structure interaction plays a pivotal role in achieving effective and energy-efficient movement.

The current model is based on a two-dimensional undulating sheet in a generalized Newtonian fluid, which captures shear-thinning and thickening behavior but does not account for fluid elasticity. Incorporating viscoelastic models in future work would allow for a more complete understanding of stress memory and elastic effects. The formulation also assumes a simplified geometry. Extending the analysis to three-dimensional filaments or sheets would help represent more realistic configurations. Additionally, replacing wavy walls with rough or actively controlled surfaces could uncover new flow behaviors relevant to microchannel transport.

This work also omits magnetohydrodynamic (MHD) effects, porous media, thermal effects, nature of walls, and the time dependency of sheet movement, which are important in many engineering systems. Including these factors could enhance the model’s applicability to smart microfluidics and thermal-electrokinetic transport.

Acknowledgement: Zeeshan Asghar would like to thank Prince Sultan University for their support through the TAS research lab. Rehman Ali Shah gratefully acknowledges the support of the Higher Education Commission (HEC) of Pakistan through the International Research Support Initiative Program (IRSIP) for enabling a six-month research exchange at Purdue University, USA.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: conceptualization and formulation of research goals: Zeeshan Asghar, Arezoo Ardekani; methodology and model development: Zeeshan Asghar, Arezoo Ardekani, Rehman Ali Shah; software implementation and data analysis: Rehman Ali Shah, Chenji Li; validation and formal analysis: Zeeshan Asghar, Rehman Ali Shah; investigation and data collection: Rehman Ali Shah, Chenji Li; visualization and draft manuscript preparation: Rehman Ali Shah, Zeeshan Asghar; writing—review and editing: Zeeshan Asghar, Arezoo Ardekani, Nasir Ali; supervision, project administration, and funding acquisition: Zeeshan Asghar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Liu J, Fu Y, Liu X, Ruan H. Theoretical perspectives on natural and artificial micro-swimmers. Acta Mech Solida Sin. 2021;34(6):781–782. doi:10.1007/s10338-021-00260-w. [Google Scholar] [CrossRef]

2. Teng X, Qiao Z, Yu S, Liu Y, Lou X, Yang W. Recent advances in microrobots powered by multi-physics field for biomedical and environmental applications. Micromachines. 2024;15(4):492. [Google Scholar] [PubMed]

3. Taylor GI. Analysis of the swimming of microscopic organisms. Proc R Soc Lond A. 1951;209(1099):447–61. doi:10.1098/rspa.1951.0218. [Google Scholar] [CrossRef]

4. Taylor GI. The action of waving cylindrical tails in propelling microscopic organisms. Proc R Soc Lond A. 1952;211(1105):225–39. doi:10.1098/rspa.1952.0035. [Google Scholar] [CrossRef]

5. Lauga E. Propulsion in a viscoelastic fluid. Phys Fluids. 2007;19:083104. [Google Scholar]

6. Teran J, Fauci L, Shelley M. Viscoelastic fluid response can increase the speed and efficiency of a free swimmer. Phys Rev Lett. 2010;104(3):38101. [Google Scholar]

7. Dasgupta M, Liu B, Fu HC, Berhanu M, Breuer KS, Powers TR, et al. Speed of a swimming sheet in Newtonian and viscoelastic fluids. Phys Revi E—Stat Nonlin Soft Matter Phys. 2013;87(1):13015. [Google Scholar]

8. Li G, Lauga E, Ardekani AM. Microswimming in viscoelastic fluids. J Non-Newton Fluid Mech. 2021;297:104655. [Google Scholar]

9. Ives TR, Morozov A. The mechanism of propulsion of a model microswimmer in a viscoelastic fluid next to a solid boundary. Phys Fluids. 2017;29(12):121612. doi:10.1063/1.4996839. [Google Scholar] [CrossRef]

10. Jha A, Amarouchene Y, Salez T. Taylor’s swimming sheet near a soft boundary. Soft Matter. 2025;21(5):826–34. [Google Scholar] [PubMed]

11. Soni H. Taylor’s swimming sheet in a smectic-A liquid crystal. Physical Review E. 2023;107(5):055104. [Google Scholar] [PubMed]

12. Ali N, Sajid M. Inertial swimming in an Oldroyd-B fluid. Eur Phys J E. 2025;48(4):1–14. [Google Scholar]

13. Asghar Z, Khan MWS, Ali N, Waqas M. On IFDM simulation of Oldroyd 8-constant fluid flowing due to motile microorganisms. Chin J Phys. 2025;93(3):158–71. doi:10.1016/j.cjph.2024.11.033. [Google Scholar] [CrossRef]

14. Shah RA, Asghar Z, Ali N. Mathematical modeling related to bacterial gliding mechanism at low Reynolds number with Ellis Slime. Eur Phys J Plus. 2022;137(5):1–12. [Google Scholar]

15. Abdelsalam SI, Zaher AZ. On behavioral response of ciliated cervical canal on the development of electroosmotic forces in spermatic fluid. Math Model Nat Phenom. 2022;17:27. doi:10.1051/mmnp/2022030. [Google Scholar] [CrossRef]

16. Pak OS, Lauga E. The transient swimming of a waving sheet. Proc Royal Soc A Math Phys Eng Sci. 2010;466(2113):107–26. [Google Scholar]

17. Ali N, Ardekani AM. Transient swimming of an undulating sheet in a second-order fluid. J Non-Newton Fluid Mech. 2025;105435. doi:10.1016/j.jnnfm.2025.105435. [Google Scholar] [CrossRef]

18. Li G. Transient motion of a swimming sheet in the inertial regime. J Fluid Mech. 2025;1011:A2. doi:10.1017/jfm.2025.382. [Google Scholar] [CrossRef]

19. Lambert RA, Picano F, Breugem WP, Brandt L. Active suspensions in thin films: nutrient uptake and swimmer motion. J Fluid Mech. 2013;733:528–57. [Google Scholar]

20. Magar V, Pedley TJ. Average nutrient uptake by a self-propelled unsteady squirmer. J Fluid Mech. 2005;539:93–112. [Google Scholar]

21. Lin Z, Thiffeault JL, Childress S. Stirring by squirmers. J Fluid Mech. 2011;669:167–77. [Google Scholar]

22. Wang S, Ardekani AM. Inertial squirmer. Phys Fluids. 2012;24(10):101902. doi:10.1063/1.4758304. [Google Scholar] [CrossRef]

23. Doostmohammadi A, Stocker R, Ardekani AM. Low-Reynolds-number swimming at pycnoclines. Proc Nat Acad Sci. 2012;109(10):3856–61. [Google Scholar] [PubMed]

24. Li G, Ardekani AM. Hydrodynamic interaction of microswimmers near a wall. Phys Rev E. 2014;90(1):013010. [Google Scholar]

25. Papavassiliou D, Alexander GP. The many-body reciprocal theorem and swimmer hydrodynamics. Europhys Lett. 2015;110(4):44001. [Google Scholar]

26. Lintuvuori JS, Brown AT, Stratford K, Marenduzzo D. Hydrodynamic oscillations and variable swimming speed in squirmers close to repulsive walls. Soft Matter. 2016;12(38):7959–68. doi:10.1039/c6sm01353h. [Google Scholar] [PubMed] [CrossRef]

27. Gutman E, Or Y. Simple model of a planar undulating magnetic microswimmer. Phys Rev E. 2014;90(1):13012. [Google Scholar]

28. Asghar Z, Ali N, Sajid M, Bég OA. Magnetic microswimmers propelling through biorheological liquid bounded within an active channel. J Magn Magn Mater. 2019;486(475):165283. doi:10.1016/j.jmmm.2019.165283. [Google Scholar] [CrossRef]

29. Temel FZ, Yesilyurt S. Confined swimming of bio-inspired magnetic microswimmers in rectangular channels. Presented at the 67th Annual Meeting of the APS Division of Fluid Dynamics; 2014; San Francisco, CA, USA. [Google Scholar]

30. Yamanaka T, Arai F. Electroosmotic self-propelled microswimmer with magnetic steering. IEEE Robot Autom Lett. 2023;9(1):747–54. [Google Scholar]

31. Burgreen D, Nakache FR. Electrokinetic flow in ultrafine capillary slits. J Phys Chem. 1964;68(5):1084–91. [Google Scholar]

32. Rice CL, Whitehead R. Electrokinetic flow in a narrow cylindrical capillary. J Phys Chem. 1965;69(11):4017–24. [Google Scholar]

33. Dutta P, Beskok A. Analytical solution of combined electroosmotic/pressure driven flows in two-dimensional straight channels: finite Debye layer effects. Anal Chem. 2001;73(9):1979–86. doi:10.1021/ac001182i. [Google Scholar] [PubMed] [CrossRef]

34. Arulanandam S, Li D. Liquid transport in rectangular microchannels by electroosmotic pumping. Coll Surf A Physicochem Eng Aspects. 2000;161(1):89–102. [Google Scholar]

35. Wang C, Wong TN, Yang C, Ooi KT. Characterization of electroosmotic flow in rectangular microchannels. Int J Heat Mass Transf. 2007;50(15–16):3115–21. [Google Scholar]

36. Wang X, Chen B, Wu J. A semianalytical solution of periodical electro-osmosis in a rectangular microchannel. Phys Fluids. 2007;19(12):127101. doi:10.1063/1.2784532. [Google Scholar] [CrossRef]

37. Zade AQ, Manzari MT, Hannani SK. An analytical solution for thermally fully developed combined pressure-electroosmotically driven flow in microchannels. Int J Heat Mass Transf. 2007;50(5–6):1087–96. doi:10.1016/j.ijheatmasstransfer.2006.07.037. [Google Scholar] [CrossRef]

38. Das S, Chakraborty S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal Chim Acta. 2006;559(1):15–24. doi:10.1016/j.aca.2005.11.046. [Google Scholar] [CrossRef]

39. Chakraborty S. Electroosmotically driven capillary transport of typical non-Newtonian biofluids in rectangular microchannels. Anal Chim Acta. 2007;605(2):175–84. doi:10.1016/j.aca.2007.10.049. [Google Scholar] [PubMed] [CrossRef]

40. Srinivas B. Electroosmotic flow of a power law fluid in an elliptic microchannel. Coll Surf A Physicochem Eng Aspects. 2016;492(1):144–51. doi:10.1016/j.colsurfa.2015.12.034. [Google Scholar] [CrossRef]

41. Afonso AM, Alves MA, Pinho FT. Electro-osmotic flow of viscoelastic fluids in microchannels under asymmetric zeta potentials. J Eng Math. 2011;71(1):15–30. doi:10.1007/s10665-010-9421-9. [Google Scholar] [CrossRef]

42. Dhinakaran S, Afonso AM, Alves MA, Pinho FT. Steady viscoelastic fluid flow between parallel plates under electro-osmotic forces: phan-Thien-Tanner model. J Colloid Interface Sci. 2010;344(2):513–20. doi:10.1016/j.jcis.2010.01.025. [Google Scholar] [PubMed] [CrossRef]

43. Afonso AM, Alves MA, Pinho FT. Analytical solution of mixed electro-osmotic/pressure driven flows of viscoelastic fluids in microchannels. J Non-Newton Fluid Mech. 2009;159(1–3):50–63. doi:10.1016/j.jnnfm.2009.01.006. [Google Scholar] [CrossRef]

44. Park HM, Lee WM. Helmholtz-Smoluchowski velocity for viscoelastic electroosmotic flows. J Colloid Interface Sci. 2008;317(2):631–6. [Google Scholar] [PubMed]

45. Qi C, Ng CO. Electroosmotic flow of a FENE-P fluid in a slit microchannel with gradually varying channel height and wall potential. Eur J Mech-B/Fluids. 2015;52:160–8. doi:10.1016/j.euromechflu.2015.03.005. [Google Scholar] [CrossRef]

46. Akhtar S, Jamil S, Shah NA, Chung JD, Tufail R. Effect of zeta potential in fractional pulsatile electroosmotic flow of Maxwell fluid. Chin J Phys. 2022;76:59–67. [Google Scholar]

47. Sangeetha J, Ponalagusamy R, Selvi RT, R. T. Electroosmotic peristaltic flow of thixotropic-Newtonian fluids in a circular tube: effect of variable viscosity co-efficient of core fluid. Chin J Phys. 2024;92(2):470–93. doi:10.1016/j.cjph.2024.06.002. [Google Scholar] [CrossRef]

48. Khan MWS, Asghar Z, Shatanawi W, Gondal MA. Cilia-assisted flow for the Johnson-Segalman fluid inside a convergent complex wavy passage with the magnetic field, hall effect, and porous medium. Kuwait J Sci. 2025;53(1):100480. doi:10.1016/j.kjs.2025.100480. [Google Scholar] [CrossRef]

49. Vaidya H, Prasad KV, Choudhari RV, Tripathi D, Naganur M. Surface roughness impact on bioinspired rhythmic contractile microfluidic membrane pumping mechanism: a computational analysis. Phys Fluids. 2025;37(6):061901. doi:10.1063/5.0261414. [Google Scholar] [CrossRef]

50. Arcos J, Bautista O, Méndez F, Peralta M. Analysis of an electroosmotic flow in wavy wall microchannels using the lubrication approximation. Revista Mexicana de Física. 2020;66(6):761–70. [Google Scholar]

51. Tripathi D, Prakash J, Gnaneswara Reddy M, Kumar R. Numerical study of electroosmosis-induced alterations in peristaltic pumping of couple stress hybrid nanofluids through microchannel. Indian J Phys. 2021;95(11):2411–21. doi:10.1007/s12648-020-01906-0. [Google Scholar] [CrossRef]

52. Asghar Z, Saeed Khan MW, Gondal MA, Ghaffari A. Channel flow of non-Newtonian fluid due to peristalsis under external electric and magnetic field. Proc Instit Mech Eng Part E J Process Mech Eng. 2022;236(6):2670–8. [Google Scholar]

53. Kumar A, Tripathi D, Tiwari AK, Seshaiyer P. Magnetic field modulation of electroosmotic-peristaltic flow in tumor microenvironment. Phys Fluids. 2025;37(4):043109. doi:10.1063/5.0261414. [Google Scholar] [CrossRef]

54. Ponalagusamy R, Murugan D. Transport of a reactive solute in electroosmotic pulsatile flow of non-Newtonian fluid through a circular conduit. Chin J Phys. 2023;81:243–69. doi:10.1016/j.cjph.2022.11.002. [Google Scholar] [CrossRef]

55. Ali N, Hussain S, Ullah K. Theoretical analysis of two-layered electro-osmotic peristaltic flow of FENE-P fluid in an axisymmetric tube. Phys Fluids. 2020;32(2):023105. doi:10.1063/1.5132863. [Google Scholar] [CrossRef]

56. Hussain S, Ali N, Ullah K. Peristaltic flow of Phan-Thien-Tanner fluid: effects of peripheral layer and electro-osmotic force. Rheologica Acta. 2019;58(9):603–18. doi:10.1007/s00397-019-01158-8. [Google Scholar] [CrossRef]

57. Shukla JB, Chandra P, Sharma R, Radhakrishnamacharya G. Effects of peristaltic and longitudinal wave motion of the channel wall on movement of micro-organisms: application to spermatozoa transport. J Biomech. 1988;21(11):947–54. doi:10.1016/0021-9290(88)90133-9. [Google Scholar] [PubMed] [CrossRef]

58. Philip D, Chandra P. Self-propulsion of spermatozoa in microcontinua: effect of transverse wave motion of channel walls. Arch Appl Mech. 1995;66(1-2):90–9. doi:10.1007/bf00786692. [Google Scholar] [CrossRef]

59. Radhakrishnamacharya G, Sharma R. Motion of a self-propelling micro-organism in a channel under peristalsis: effects of viscosity variation. Nonlin Anal Model Control. 2007;12(3):409–18. doi:10.15388/na.2007.12.3.14703. [Google Scholar] [CrossRef]

60. Shack WJ, Lardner TJ. A long wavelength solution for a microorganism swimming in a channel. Bull Math Biol. 1974;36(4):435–44. [Google Scholar] [PubMed]

61. Riley EE, Lauga E. Small-amplitude swimmers can self-propel faster in viscoelastic fluids. J Theor Biol. 2015;382:345–55. doi:10.1016/j.jtbi.2015.06.045. [Google Scholar] [PubMed] [CrossRef]

62. Espinosa-Garcia J, Lauga E, Zenit R. Fluid elasticity increases the locomotion of flexible swimmers. Phys Fluids. 2013;25(3):031701.doi:10.1063/1.4795166. [Google Scholar] [CrossRef]

63. Salazar D, Roma AM, Ceniceros HD. Numerical study of an inextensible, finite swimmer in Stokesian viscoelastic flow. Phys Fluids. 2016;28(6):063101. doi:10.1063/1.4953376. [Google Scholar] [CrossRef]

64. Shah RA, Asghar Z, Waqas M, Gondal MA. Mathematical analysis of the Shear-thinning slime layer flowing beneath an active bacterial surface. Multi Multidis Model Exp Des. 2025;8(2):154. doi:10.1007/s41939-025-00746-x. [Google Scholar] [CrossRef]

65. Asghar Z, Rehman KU, Shatanawi W, Khan MWS. Efficiency optimization of micro-swimmers in viscoelastic bio-fluids within complex cervical environments. Chin J Phys. 2025;96(1099):664–77. doi:10.1016/j.cjph.2025.06.003. [Google Scholar] [CrossRef]